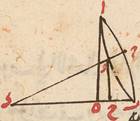⟨I⟩

أحمد الله مبدأ كلّ مبدأ وغاية كلّ غاية ومفيض كلّ خير ووليّ كلّ هداية وأرجو حسن توفيقه في كلّ بداية ونهاية وأصلّي على عباده المخصوصين بالعناية والدراية سيّما †محمّد† وآله الموسومين بالنبوّة والولاية المنقذين من كلّ عماية وغواية وبعذ must be corrected to وبعد فقد كنت برهةً من الزمان عازمًا على أن أحرّر لنفسي ولسائر طلبة العلم من الإخوان كتاب المجسطي المنسوب إلى بطلميوس القلوذي الذي هو الدستور العظيم لأصحاب صناعة الهيئة والتنجيم †تحريرًا† لا يفوته مقاضد must be corrected to مقاصد ذلك الكتاب النظريّة ومناهجه العمليّة حتّى ترتيب الفصول وأبواب الحساب ورسوم الجداول وأوضاع الأشكال ولا يشوبه شيء خارج منه غير ما يحتاج إلى تقديمه في تيسير عسير أو حلّ إشكال وأشير إلى بعض ما استنبطه المحدّثون أو ذهب إليه المتأخّرون ممّا زادت النظريّات به حسنًا وبهاءً أو نقصت العمليّات منه كدًا وعناء بشرط إيثار الإيجاز والاختصار والاحتراز عن الإسهاب والتكرار وذلك لأنّي لم أكن أظفر في اختصارات هذا الكتاب على كثرتها بمستجمع لهذه الشروط بجملتها وكانت العوائق شاغلة إيّاي دونه حائلة بيني وبينه إلى أن استسعدت بلقاء الجناب الرفيع والأخ العزيز أفضل العصر وأوحد الدهر حسام الدين وسيف المناظرين الحسن بن محمّد السيواسيّ أدام الله فضله وكثّر في الأفاضل مثله فزادني رغبته في ذلك رغبة وجدّد جدّة لي همّة فعملت ذلك مع قلّة البضاعة وقصور الباع something crossed out in N, like هي. في الصناعة بحسب ما أعان عليه الوقت وساعد التوفيق والبخت ونبهّت صريحًا على ما هو خارج من أصل الكتاب ممّا أضفت إليه ليحصل الوقوف بأيسر السعي عليه وخالفت بين أشكال المتن وغيرها ممّا أوردته بلون الخطوط والأرقام ليتميّزا في باذئ must be corrected to بادئ. النظر من غير احتياج إلى زيادة اهتمام وإنّما تكلّفت ذلك لكون الكتاب علمًا بين أهل العلم ينصّون عليه في محاوراتهم ويشيرون إلى مواضع مسائله من الفصول والأشكال في حوالاتهم ثمّ إنّي وسمته بتحرير المجسطي حين أتممته فإن زللت في بعض المواضع لسؤفهم المعاني المقصودة †...† عنّي عند قصد العبارة عنها بالألفاظ المطابقة فأرجو أن يصلحه من ينظر فيه من أهل الخير ويعثر عليه والله يوفّقهم وإيّاي أنّه المستعان وعليه التكلان وها أنا أخوض في المقصود وأقول الكتاب مشتمل على ثلاث عشرة مقالة ومائة واحد وأربعين فصلًا ومائة وستّة وتسعين شكلًا على ما في النسخة التي نقلها إسحق بن حنين وأصلحها ثابت بن قرّة كما سيجيء مفصّلًا

⟨I.1⟩

المقالة الأولى أربعة عشر فصلًا وستّة عشر شكلًا

ا صدر الكتاب

استحسن فيه بطلميوس من الفلاسفة أفراد الفلسفة النظريّة عن العمليّة مع كون العمليّة قبل العمل أيضًا نظريّة لا بسبب إمكان حصول بعض الأخلاق الفاضلة وامتناع حصول العلوم النظريّة من غير تعلّم فقط بل وبسبب أنّ طريق الوصول إلى أحد ممّا كثرة العمل وإلى الآخر كثرة النظر ثمّ حثّ على إصلاح العمل بالبحث عن جليله ودقيقه على وجه يقتضي جماله ونظامه وعلى صرف أكثر العمر في طلب العلوم النظريّة لكثرتها وفرط بهائها لا سيّما في النوع الموسوم بالتعليميّ واستحسن قسمة أرسطوطاليس الفلسفة النظريّة أوّلًا إلى أجناس ثلاثة طبيعيّ وتعليميّ والإهيّ إذ كان قوام الأشياء من عنصر وصورة وحركة لا يوجد واحد منها وحده وإن كان يعقل وحده ثمّ قال فإذا عقلنا الحركة وحدها ورأينا و add sl أنّ علّة الحركة الأولى المنسوبة إلى الكلّ آلة غير محسوس وغير متحرّك متعال بالذات والفعل عن المحسوسات فسمّينا البحث عنه إلهيًّا add mg وكذلك سمّينا البحث عن الكيفيّات العنصريّة المتعاقبة على الأكثر دائمًا في الجوهر الكائن الفاسد الذي تحت فلك القمر طبيعيًّا والبحث عن الشكل والعدد والعظم والمكان والزمان وما أشبهها من حال الصورة وحركات النقلة تعليميًّا فموضوع هذه الأمور متوسّط بين الأوّلين لا لكونه مدركًا بالعقل والحسّ جميعًا فقط بل ولاشتراك ما يفسد وما لا يفسد فيه فإنّ هذه الأمور تتعاقب فيما يفسد على الصورة التي لا تزول عن المادّة وتلزمها فيما لا يفسد قال ولمّا رأينا إدراك الإلهيّ والطبيعيّ من جهة ما هو أشبه وأخرى لا باليقين أمّا الإلهيّ فلاستعلائه عن الحسّ وعن أن يحاط به وأمّا الطبيعيّ فلعدم ثبات العنصر وخفاء حاله ولذلك لم يرج اتّفاق الحكماء فيهما ورأينا التعليميّ يقينيًّا ثابتًا ببراهين عدديّة أو هندسيّة لا شكّ فيها صار †...† به أكثر لا سيّما بعلم الأجرام السماويّة لأنّ موضوعاتها ثابتة منتظمة والعلم الثابت هو الحقيقيّ لا غير قال وقد يعين هذا العلم على غيره أمّا على الإلهيّ فلاختصاصه بالإعانة على تصوّر الفعل المجرّد عن الحركة وسائر الأمور المادّيّة لكونه متعلّقًا بجواهر تحرّك وتتحرّك دائمًا على نظام من غير تغيّر وأمّا على الطبيعيّ فلدلالة هي om DLP حركة النقلة بكونها من الوسط أو إلى الوسط أو على الوسط على أحوال الأجسام من قبول الفساد ولا قبوله وسائر الأفعال والانفعالات وأمّا على الخلقيّ فلأنّ إدراك ثبات الحال وحسن الترتيب والاعتدال والخلوّ عمّا لا احتياج إليه من تلك الأجرام تقتضي أيثار هذه الأمور ومحبّتها ويصير ذلك مبدأ عادّة أو خلق وبالجملة حالة للنفس شبيهة بها ثمّ قال فنحن نروم ازدياد محبّة هذه الحالة بتعلّم ما أدركه المتقدّمون المحقّقون من هذا العلم وبإضافة ما أدركناه بحسب تأخّر زماننا عنهم إليه ونجمعهما في كتاب على الترتيب الواجب بأيجاز غير †...† وإجمال فيما ذكره الأوائل وبسط فيما لم يدركوه أو أدركوه لا على ما يجب

⟨I.2⟩

ب في مراتب أنواع هذا العلم

ينبغي أن نبدأ بالنظر في حال السماء والأرض ليتبيّن أنّ السماء كريّة وحركاتها مستديرة والأرض بجلّ أجزائها كريّة وهي كالمركز للسماء وكالنقطة عند كرة الثوابت وغير منتقلة عن الوسط ثمّ في وضع الفلك المتحرّك بالحركة المائلة والمواضع المسكونة من الأرض ولخلاف اختلاف DLP أحوالها بحسب العرض ثمّ في حركة الشمس والقمر وما يتّبعهما ثمّ في الكواكب الثابتة ونختم بالمتحيّرة فإنّ هذا الترتيب نافع في البعض وواجب في البعض على ما سيأتي ونطلب أصول ذلك من المبادئ المعلومة إمّا بالإحساس أو بالإرصاد المعتمدة المنقولة عن القدماء والتي تولّيناها نحن وفروعها من البراهين الهندسيّة

⟨I.3⟩

ج‍‍ في أنّ السماء كريّة وحركاتها مستديرة

القدماء لمّا رأوا الأجرام النيّرة طالعة من مشارق الأرض مرتفعة بالتدريج إلى حدّ ما هابطة منه كذلك إلى أن تغيب في المغارب ماكثة في غيبتها زمانًا ما عائدة بعد ذلك إلى المشارق متكافئة في أزمنة الظهور والخفاء وفي المشارق والمغارب في جلّ الأمر كأنها على دوائر متوازيّة مترتّبة حكموا بكرية السماء واستدارة الحركات وقد أكدّ ذلك مشاهدة استدارة الكواكب الأبديّة الظهور حول نقطة تصلح لأن تكون قطبًا للكلّ في دوائر متوازيّة مختلفة الصغر والكبر على الترتيب بحسب البعد من تلك النقطة إلى أن تنتهي إلى ما يطلع ويغيب وتزداد أزمنة الخفاء وتنقص أزمنة الظهور بحسب ازدياد البعد إلى أن تتساويا ثمّ تختلفا على عكس الأوّل بنسبة واحدة فهذه وأمثالها قد أوقعت التصديق بذلك أوّلًا والتكذيب بما يخالفه من الآراء بعده وذلك كما يطنّ أنّها تتحرّك بالاستقامة إلى غير نهاية فإنّه يقتضي امتناع العود إلى الطلوع من غير رجوع والرجوع من غير مشاهدة ويوجب انتقاص النور والعظم بحسب ازدياد البعد عن الناظرين إلى أن يغيب من غاية الصغر بخلاف ما عليه الوجود فإنّ الأجرام النيّرة توجد متساوية الأحوال في الأكثر وقد تعظم عند الطلوع add mg N om DLP الغروب وتستتر حالة الغروب شيئًا بعد شتي وكما قال قوم إنّها تشتعل من الأرض فتطلع وتنطفئ فتغيب فإنّ ذلك ينافي النظام المتعلّق بهذه الأجرام وأحوالها الذي سيتبيّن وجوده في هذا العلم ومع ذلك يقتضي كون جانب من الارض مشتعلًا وجانب مطفئًا بل الجزء الواحد مشتعلًا لقوم ومنطفئًا لقوم وكون كوكب بعينه في زمان بعينه مشتعلًا لقوم ومنطفئًا لقوم وهذه ضحكة وسخريّة ومع ذلك فليت شعري ما يقولون في كواكب تظهر دائمًا لقوم وتطلع وتغيب لقوم إذ لا وجه لاجتماع الحالتين لكوكب بعينه في زمان بعينه على رأيهم المذكور وبالجملة تعدم استدارة حركات الأجرام حول الناظرين يقتضي اختلاف أبعادها المستلزم لاختلاف أقدارها عند أبصارهم في الدورة الواحدة لكنّ الأقدار متساوية فالحركات مستديرة وكون البعض أعظم عند الأفق لا ينافي ذلك لأنّ الأبخرة المائيّة تقتضي ذلك لذلك يرى الشيء في الماء أعظم منه في الهواء والأكثر رسوبًا أعظم من الأقلّ وممّا يدلّ على استدارة الشكل وجوب استدارة آلات القياس بيطابق المعلوم بها الموجود وأيضًا فأسهل الأشكال حركة الدائرة من السطوح والكرة من الأجسام وممّا أوسع من كلّ شكل يساويهما في المحيط والحركات السماويّة أسهل الحركات وجرم السماء المحيط بغيره من الأجسام ينبغي أن يكون أوسع ممّا †...† لكنّه ليس بسطح فهو كرة مستديرة الحركة ويدلّ على ذلك أيضًا أمور طبيعيّة منها بساطة الفلك في طبعه وتشابه أجزاء جرمه فإنّ ذلك يقتضي استدارة الشكل لأنّ ما يقتضيه الطبيعة البسيطة لشيء غير مختلف لا يمكن أن يختلف وأيضًا المركّبات الكائنة الفاسدة إنّما خرجت من الاستدارة لاختلاف طبائعها وغاياتها والنيّرات العلويّة مستديرة متشابهة وإلّا فلم ترَ من نواحي الأرض في وقت بعينه متساوية كما لا ترى القضعة أو الجسم المسطوح من الجوانب متساوي الشكل والجرم المحيط بها ينبغي أن يشابهها في الطبع فهو كريّ ولتشابه أجزائه تكون حركته مستديرة أقول وبعض هذه الحجج إقناعيّة

⟨I.4⟩

د في أنّ الأرض كريّة في الحسّ بالقياس إلى الكلّ

يدلّ على ذلك طلوع الأجرام النيّرة وغروبها في البقاع الشرقيّة قبل طلوعها وغروبها في الغربيّة بقدر ما يقتضيه أبعاد تلك البقاع في الجهتين على ما يتّضح من أرصاد كسوفات بعينها لا سيّما القمريّة في بقاع مختلفة فإنّ ما أثبته القدماء منها ليس في ساعات متساوية البعد من نصف النهار بل على الوجه المذكور وكون الاختلاف متقدّرًا بقدر الأبعاد دالّ على الاستدارة المتشابهة الساترة †...† للمواضع التي يتلو بعضها بعضًا على قياس واحد وأيضًا عدم الاستدارة يستلزم أمورًا غير موجودة مثلًا لو كانت مقعّرة لكان الطلوع أوّلًا على الغربيّين ولو كانت مسطّحة لكان على الجميع معًا ولو كانت كثيرة القواعد لكان على ساكني كلّ سطح منها معًا ولو كانت اسطوانيّة قاعدتاها نحو القطبين كما ظنّ قوم لم يكن لساكني الاستدارة كوكب أبديّ الظهور بل إمّا الجميع طالعة غاربة أو كانت كواكب تكون من كلّ واحد من القطبين على بعد تستره القاعدتان أبديّة الخفاء والباقية طالعة غاربة وليس كذلك أيضًا فالسائر إلى الشمال قد تغيب عنه دائمًا كواكب كانت تظهر له وتظهر له دائمًا كواكب كانت تغيب عنه بقدر إمعانه في السير وذلك يدلّ على استدارتها في هاتين الجهتين أيضًا وأيضًا فطلوع رؤوس الجبال الشائخة على السائرين في البحر أوّلًا ثمّ ما يلي رؤوسها شيئًا بعد شيء في جميع الجهات يدلّ على استدارة سطح الماء

⟨I.5⟩

ه في أنّ الأرض في وسط السماء كالمركز في الكرة

و لم يكن كذلك لكانت إمّا خارجة عن محور الحركة اليوميّة متساوية البعد عن قطبيها وإمّا على المحور غير متساوية البعد عنهما وإمّا خارجة منه غير متساوية البعد عنهما والأوّل باطل لأنّ خروجها إن كان إلى فوق أو إلى أسفل †للزم† أن لا يتساوي نهار وليل حيث الكرة منتصبة البتّة لأنّ الأفق حينئذ يفصل جميع مدارات الحركة إلى ظاهر وخفي غير متساويتين ولا حيث الكرة مائلة وقت كون الشمس على منطقة الحركة بل أمّا أن لا يتساوي هناك نهار وليل ويتساويان في وقت آخر وذلك لأنّ الأفق لا ينصف المنطقة بل ينصف أحد المدارات عن أحد الجانبين فقط لكنّ مساواة ازدياد النهار على الليل من المنقلب الذي نهاره في غاية القصر إلى الذي نهاره في غاية الطول لانتقاصه عنه فيما نقابله التي تلزمها مساواة النهار والليل في الوسط مرّتين ظاهرة في جميع الآفاق المائلة وذلك يقتضي انفصال كلّ واحد من المدارات الموازية للمنطقة إلى مختلفين يساوي الظاهر منها الخفي من نظيرتها المساويّة لها عن الجانب الآخر وانتصاف المنطقة فقط وإن كان خروجها إلى الشرق أو المغرب للزم عدم تساوي أقدار الكواكب عند البصر من الجانبين في الدورة الواحدة وعدم تساوي زماني الارتفاع والانخطاط في القسم الظاهر من الدورة الواحدة والوجود بخلافه والثاني أيضًا باطل لأنّ الأفق حينئذ لا ينصف السماء بظاهر وخفي إلّا حيث الكرة منتصبة فقط وإنّما يفصّلها حيث الكرة مائلة بمختلفين أصغر ممّا في كلّ موضع يظهر فيه القطب الأقرب دائمًا القسم الظاهر ويزداد صغره بازدياد ارتفاع القطب وتكون المنطقة والمدارات اليوميّة جميعًا مختلفة الأقسام والمدارات كما تكون مختلفة الأقسام في أنفسها فإنّها أيضًا تكون مختلفة بالقياس إلى نظائرها والأفق أيضًا لا ينصف منطقة البروج والوجود بخلاف ذلك لما مرّ من أحوال المدارات ولكون الظاهر من البروج دائمًا مساويًّا للخفي وبالجملة لو كانت الأرض مائلة عن معدّل النهار إلى أحد قطبيه لم يكن ظلّ add mg مقياسي طلوع الشمس وغروبها في يوم الاستواء على خطّ مستقيم واحد في موضع من الأرض وهو هكذا في جميعها والثالث أيضًا باطل لاستلزامة النوعين المذكورين من الفساد معًا بحسب تركب السببين فيه وبالجملة فخروج الأرض من الوسط مستلزم لعدم الترتيب الموجود في النهار والليل بل بحسب الزيادة والنقصان والامتناع وقوع الخسوفات في المقاطرة الخفيفيّة للنيّرين إذ لا يصير القمر حينئذ مستورًا بالأرض بل لعلّها تستره في غير تلك الحال

⟨I.6⟩

و في أنّ الأرض كالنقطة عند فلك البروج

من أعظم ما يدلّ عليه أنّه كلّما نرصد أقدار الأجرام النيّرة أو أبعاد ما بينها في إقليم واحد في أوقات مختلفة أو في أقاليم مختلفة من الأرض في وقت واحد بحيث تكون تارةً أو عند قوم قريبًا من سمت الرأس وتارةً أو عند آخرين قريبًا من الأفق فإنّها توجد غير مختلفة لشيء أقول الطريق إلى ذلك تولّي الأرصاد أو مواطأة الثقة فيها وأوّل الوجهين هو الأصل إلّا أنّ ظاهر الكتاب يقتضي الثاني ثمّ أنّ كون الأرض ذات قدر محسوس عند السماء يوجب عظم ما يقرب من سمت الرأس وصغر ما يقرب من الأفق لاختلاف البعدين فإذن الأرض لا قدر لها عند السماء وممّا يدلّ على ذلك أيضًا أنّ أحكام مقاييس الظلّ المنصوبة على سطح الأرض في جميع نواحيها كأحكامها لو نصبت على مركز الأرض من السطح المارّ به وأحكام مراكز ذوات الحلق وغيرها كأحكام مركز الأرض يعرف ذلك بتطابق ما يدرك بهما على ظاهر الأرض وما تقتضيه الأصول الموضوعة على أنّها عند مركزها ومن ذلك أنّ سطوح الآفاق المارّة بالإبصار تفصل الكرة أبدًا بنصفين كما يفصلها المارّ بالمركز وكون الأرض ذات قدر عند السماء يقتضي الأجناس بالتفاوت بين المدرك بالرصد والمعلوم من من الأصول المذكورة وكون الظاهر من الكرة أصغر من الخفي

⟨I.7⟩

ز في أنّ الأرض ليس لها حركة الانتقال

لو تحرّكت عن الوسط لعرضت الأعراض المذكورة التي كانت تعرض لو لم تكن في الوسط ¹¹ولمّا تبيّن أنّها في الوسط ^-11 add mg وأنّ الثقال بطبعها تميل إلى الوسط فالبحث بعد ذلك عن سبب الحركة إلى الوسط فضل والثقال إنّما تميل إلى الوسط وتتحرّك إليه على سمت مستقيم يقوم عمودًا على السطح الذي يماسّ كرة الأرض على مسقط ذلك العمود فهي تنتهي إلى المركز لو لا ممانعة الأرض إيّاها لأنّ الخطّ المستقيم الخارج من نقطة تماسّ الكرة والسطح إلى المركز يكون عمودًا على السطح أيضًا والتعجّب من كون الأرض مع فرط ثقلها وكونها غير محمولة على شيء ساكنة ليس بوارد لأنّه يحدث بسبب قياس الأرض على أجزائها المنحدرة من العلو إلى السفل أيّ من جانب الرأس إلى جانب القدم لكنّ العالم في نفسه لا علو له ولا سفل إنّما العلو والسفل لما فيه من الأجرام فالسفل جهة المركز والعلو ما يقابلها والخفيف يميل إلى العلو والثقيل إلى السفل فالأرض بجملتها في موضع المركز وبأجزائها متدافعة من جميع الجوانب إليه ساكنة فيه والأجزاء المباينة لها تهوي إليها وهي تقبلها من جميع نواحيها لثباتها بالسبب المذكور وتكون تلك الأجزاء في غاية الصغر بالقياس إليها ولو كانت الأرض هاويّةً في السفل دائمًا لم يمكن أن يلحقها هاوٍ غيرها لأنّ الأثقل أشدّ هويًّا فكان ما عليها الحيوانات وغيرها متخلّفًا عنها في الهواء ولوصلت بسرعة إلى السماء المحيطة بها وجازتها وهذا التوهّم وما يشبهه يستحقّ لأن نضحك منه وقد ظنّ قوم أنّ الأرض متحرّكة بالاستدارة حول محور الحركة اليوميّة من المغرب إلى المشرق ونسبوا الحركة اليوميّة إليها وحدّها على تقدير كون السماء sl غير متحرّكة على هذا المحور أو إليهما معًا على تقدير كونها أيضًا متحرّكة عليه وذلك ممكن بالنظر إلى السماويّات وليس ممكن بالنظر إلى الهواء والأشخاص الأرضيّة لأنّ صاحب هذا القول مع التزامه لأمور مخالفة للطبيعة وهي نفي الحركة المستديرة عن الجرم اللطيف المتشابه الأجزاء وإثباتها للكثيف المختلف الأجزاء وقد نشاهد حركة ما يشبه الأوّل ممّا هو أقلّ لطفًا منه كالهواء أسهل وأسرع وحركة ما هو على طبيعة الثاني كالأجسام الأرضيّة أعسر وأبطأ والقول يتشاركهما فيها مع تضادّ طبيعتهما مقرّ بأنّ الأرض أسرع حركة ممّا عداها قيلزم أن لا يدرك للأشخاص السفليّة كالسحب والطيور والسهام حركة إلى المشرق إذ الأرض تسبقها إليه بل ترى متحرّكة إلى المغرب أبدًا فإن قيل إنّ الهواء أيضًا يتحرّك تلك الحركة معها لزم أن تشاهد الأجرام التي فيها متأخرة عنهما وأن جعلت لاصقة بمواضها كالملتحمة لزم أن لا ينتقل عن مواضعها ولا يتبدّل في أوضاعها أقول وبعض هذه الحجج أيضًا إقناعيّة

⟨I.8⟩

ح في أنّ أصناف الحركات الأوّل للسماء إثنان

الحركة اليوميّة التي من المشرق إلى المغرب حركة مستوية حول قطبها يتحرّك بها الكلّ على مدارات متوازيّة وتسمّى منطقتها المقاطعة للأفق على التناصف في جميع المواضع بمعدّل النهار لتعادل النهار والليل في الحسّ عند كون الشمس عليها في جميع الأرض وإنّما يدلّ على وجود هذه الحركة مشاهدة طلوع الأجرام النيّرة وغروبها وتوسّطها السماء في اليوم الواحد وبالجملة حركتها على مدارات متوازيّة وموازية لمعدّل النهار حركة متشابهة في ظاهر الأمر وهاهنا حركة أخرى إلى خلاف جهة الحركة الأولى على قطبين غير قطبيها تظهر في أكثر أكر DLP الكواكب السيّارة يدلّ عليها في بادئ النظر قياسها بغيرها من الكواكب التي لا يختلف must be corrected to تختلف. أوضاعها البتة فإنّ جميعها توجد متحرّكة إلى المشرق وإن كانت مختلفة مقادير الحركات وليست حركاتها على موازاة معدّل النهار وإلّا لكان الاقتصار على الحركة الأولى كافيًّا لإمكان أسناد اختلافاتها إلى تأخّرها عن تلك الحركة بل جميعها تميل مع حركاتها إلى المشرق تارةً نحو الشمال وتارةً نحو الجنوب فتبعد في الجهتين عن معدّل النهار مقادير لها متساوية أو مختلفة لها ترتيب على وجه يقتضي اشتراك الجميع في منطقة واحدة مقاطعة لمعدّل النهار في موضعين تسمّى دائرة البروج وقطبين بعينهما والشمس تتحرّك على تلك المنطقة دائمًا ولتساوي بتساوي DLP قدر ميلها عن معدّل النهار في الجهتين تعرف أنّها أيضًا من العظام والقمر والخمسة تجوز عليها وتبعد منها في الجهتين ولكن لا تجاوز أبعادها المحدودة وإذا توهّمنا دائرة عظيمة تمرّ بالأقطاب الأربعة وبنصف كلّ واحد من المنطقين must be corrected to المنطقتين. على زوايا قوائم حدثت على دائرة البروج أربع نقط اعتدالان ربيعيّ وخريفيّ وانقلابان صيفيّ وشتويّ فالحركة الأولى المحرّكة للكلّ محيطة بالثانية محرّكة لمنطقتها وقطبيها وللدائرة المارّة بالأقطاب الأربعة على قطبيها اللذين تلزمهما نقطتان بعينهما من المارّة وقياس المارّة إلى معدّل النهار كقياس الدائرة المنصّفة لكلّ واحد من القسمين الظاهر الخفي من كلّ مدار في كلّ أفق الموسمة بنصف النهار أيضًا إليه إلّا أنّ نصف النهار لا يمرّ بقطبي البروج إلّا وقت انطباق المارّة عليها والمارّة لا تقطع الأفق على زوايا قوائم إلّا عند انطباقها على نصف النهار والحركة الثانية محيطة جميع أكر الكواكب محرّكة إيّاها على قطبيها المتحرّكين بالحركة الأولى الثابتين بالقياس إلى هذه الحركة اللازمين لنقطتين بعينهما من المارّة

⟨I.9⟩

ط في العلوم الجزئيّة

وإذ تقدّم ما ينبغي أن نبدأ به من الأصول وأردنا أن نشرع في الجزئيات التي أوّلها معرفة قدر ما بين قطبي الحركتين وكان البرهان عليها مأخوذًا من الخطوط المستقيمة وجب تقديم القول في معرفة مقادير أوتار القسيّ وقسيّ الأوتار بالبرهان ووضعها في الجداول لتكون معدّة في جميع الأحوال فرأينا تجزئة الدائرة بثلاثمائة وستّين والقطر بمائة وعشرين وتجزئة أجزائها المتربّتة أجزائهما المرتبة P أجزائهما المتربّتة L أجزائها المرتبة D بعضها تحت بعض أعني الدقائق والثواني بستّين ستّين فإنّ ذلك أسهل وجعلنا تفاضل القسيّ الموضوعة في الجداول نصف جزء نصف جزء توخّينا في استخراجها بالضرب والقسمة والجذر تقريبًا لا يغادر الحسّ

⟨I.10⟩

ى في مقادير الأوتار

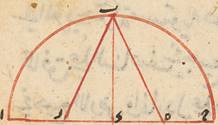
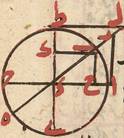
ونبدأ بضلع المعشّر المخمّس فليكن ا ب ج‍‍ نصف دائرة على قطر ا د ج‍‍ ومركز د وب د عمودًا على القطر وننصّف ج‍ د على ه ونصل ب ه ونجعل ه ز مساويًّا لب ه ونصل ب ز فنقول دز ضلع المعشّر وب ز ضلع المخمّس وذلك لأنّ ج‍ د نصف على ه وزيد فيه د ز فسطح ج‍ ز في ز ذ must be corrected to ز د. مع مربّع د ه يساوي مربّع ه ز mg ه ب ق أعني مربّع ه ب أعني مربّعي ه د د ب ويلقي مربّع ه د المشترك يبقي سطح ج‍ ز في ز د مساويًّا لمربّع د ب أعني مربّع ج‍ د فخطّ ج‍ ز على نقطة د مقسوم بنسبة ذات وسط وطرفين add mg †...† وج‍ د الأطول وتر المسدّس فد ز وتر المعشّر add mg †...† وب ز القوي عليهما وتر المخمّس add mg بج‍ بج‍

ولمّا كان القطر ١٢٥ فه د ٣٥ ومربّعه ٩٥٥ وب د ٦٥ ومربّعه ٩٥٥ ٣ فمربّع ب ه ٤٥٥ ٤ فخطّ ب ه ٦٧ د نه ويبقي خطّ د ز ٣٧ د نه وهو ضلع المعشّر الموتّر لقوس ٣٦ ومربّع ضلع المعشّر ١٣٧٥ د نه فمربّع ضلع المخمّس ٩٧٥ ٤ د نه وضلع المخمّس ٧٥ لب ج‍ وهو وتر قوس ٧٢ ومعلوم أنّ كلّ واحد من قوس المسدّس ووتره بأجزائها ٦٥ وأيضًا ضعف مربّع نصف القطر أعني مربّع ضلع المربّع ٧٢٥٥ جذره ٨٤ نا ي وهو وتر قوس ٩٠ وأيضًا ثلثه أمثال مربّع نصف القطر أعني مربّع ضلع المثلّث ١٥٨٠٠ جذره ١٥٣ نه كج‍ وهو وتر قوس ١٢٥ فهذه أوتار يسهل must be corrected to تسهل معرفتها وقد تسمّى بالأمّهات ومعلوم أنّ القطر یقوی على كلّ وتر وعلى وتر تمام قوسه من نصف الدائرة فإذا ألقينا مربّع ضلع المعشّر من مربّع القطر الذي هو ١٤٤٥٥ یبقی مربّع وتر أربعة أعشار الدائرة ٥٢٤ ١٣ نه مه جذره ١١٤ ز لو وهو وتر قوس ١٤٤ وعلى هذا المثال في سائرها

مقدّمة نافعة فيما بعد

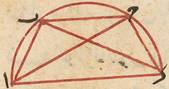
وهي أنّ كلّ ذي أربعة أضلاع في دائرة فإنّ مجموع سطحي كلّ ضلع في مقابلة يساوي سطح أحد قطر به في الآخر فليكن ذو أربعة أضلاع ا ب ج‍ د في دائرته فأقول مجموع سطحي ب ج‍ في أ د وب ا في دج‍ يساوي سطح ب د في ج‍ ا فلنجعل زاوية ا ب ه مساويّة لزاوية ج‍ ب د ونجعل زاوية ه ب د مشتركة فيكون في مثلّثي ج‍ ب ه ا ب د زاويتا ج‍ ب ه ا ب د متساويتان وكذلك زاويتا ا ج‍ ب ب د ا الواقعتان على قوس ب ا فهما متشابهان ونسبة ب ج‍ إلى ج‍ ه كنسبة ب د إلى د ا فسطح ب ج‍ في د ا كسطح ب د في ج‍ ه وأيضًا في مثلّثي ا ب ه ب ج‍ د زاويتا ا ب ه ج‍ ب د متساويتان وكذلك زاويتا ب ا ه ب د ج‍ الواقعتان على قوس ب ج‍ فهما متشابهان ونسبة ب ا إلى ا ه كنسبة ب د إلى د ج‍ فسطح ب ا في د ج‍ كسطح ب د في ا ه فإذًا سطحا ب ج‍ في ا د وب ا في د ج‍ كسطحي ب د في ج‍ ه وب ج‍ في ا ه أعني ب د في ج‍ ا وذلك ما أردناه

في معرفة وتر الفصل بين قوسين معلومتي الوترين

ليكن ا ب ج‍ د نصف دائرة على قطر ا د وا ب ا ج‍ قوسين منها مختلفتين ووتراهما وهما خطّا ا ب ا ج‍ معلومان ونصل ب ج‍ وتر الفضل ونقول إنّه أيضًا معلوم فنصل د ب د ج‍ وترى تمام القوسين وهما معلومان كما مرّ فسطح ا ج‍ في ب د القطرين معلوم وإذا ألقينا منه سطح ا ب في ج‍ د المعلوم بقي سطح ا د القطر في ب ج‍ المطلوب معلومًا فإذا قسمناه على ا د خرج ب ج‍ فهو إذا معلوم وذلك ما أردناه وبهذا الوجه يمكن أن يعرف وتر قوس إثني عشر جزءًا التي هي الفضل بين وترى الخمس والسدس وغيره من الأوتار

في معرفة وتر نصف قوس معلوم الوتر

ليكن نصف دائرة ابج‍ على قطر ا ج‍ ووتر ب ج‍ معلوم وقد قسم قوسه على د بنصفين فنقول إّنّ وتر ج‍ د أيضًا معلوم فنصل خطوط ا ب ا د ب د د ج‍ وخرج عمود د ز على ا ج‍ فيكون ج‍ ز نصف فضل ا ج‍ القطر على ا ب وتر تمام القوس المعلومة الوتر ونجعل ا ه مثل ا ب ووصلنا د ه يكون ضلعا ه ا ا د كضلعي ب ا ا د وزاويتا ه ا د ب ا د متساويتين فيكون ه د مساويًّا لب د أعني د ج‍ ولكنّ د ج‍ د ه المتساويان يقويان على د ز المشترك وج‍ د ز ه فهما متساويان ومجموعهما هو فضل ا ج‍ على ا ب وفي مثلّث ا د ج‍ القائم الزاوية قد خرج عمود د ز من القائمة على وترها فنسبة ا ج‍ إلى ج‍ د كنسبة ج‍ د إلى ج‍ ز وسطح ا ج‍ القطر في ج‍ ز المعلوم تساوي مربّع د ج‍ فهو معلوم وذلك ما أردناه وبهذا الوجه يمكن أن يعرف من وتر أعني عشر وتر ستّة ثمّ وتر ثلاثة ثمّ وتر واحد ونصف وهو †...† ثمّ وتر نصف وربع وهو †...† وغير ذلك من الأوتار

في معرفة وتر مجموع قوسين معلومتي الوترين

ليكن must be corrected to لتكن. دائرة ا ب ج‍ د على قطر ا د ومركز ز والقوسان المعلومتا الوترين قوسي ا ب ب ج‍ ونصل ا ج‍ ونقول إنّه أيضًا معلوم فخرج قطر ب ز ه ونصل خطوط ا د add mg ب د ج‍ د ج‍ ه د ه فيكون د ه مساويًّا لاب إذ كلّ واحد منهما وتر لتمام قوس ب د فيكون في ذي أربعة أضلاع ب ج‍ د ه قطرا ب د ج‍ ه add mg وهما وترا تمامي القوسين معلومين وضلعا ب ج‍ د ه وهما الوتران المعلومان بعينهما أيضًا معلومين فإذا ألقينا مضروب أحد الضلعين في الآخر من مضروب أحد القطرين في الآخر وقسمنا الباقي على ب ه القطر خرج ج‍ د وتر تمام قوس ا ج‍ ويصير منه وتر ا ج‍ معلومًا وفي وفي N نسخة ثابت لخرج قطر ب د فقط ونصل ا د ج‍ د قسّم ذو أربعة أضلاع ا ب ج‍ د ويصير ا ج‍ بمثل ما مرّ معلومًا وهكذا يكون الشكل وذلك ما أردناه

وبهذا وبهذا N الوجه يمكن أن نعرف أوتار القسيّ التي تحدث من ضعف قوس جزء ونصف وأضعافه إلى نصف الدور وهي بالجملة كلّ قوس يكون لضعفها ثلاث ويبقي بين كلّ قوسين منها من القسيّ المتفاضلة بنصف جزء نصف جزء قوسان مجهولتا الوتر يتوقّف العلم بأوتارها على العلم بوتر نصف جزء بل لو كان هذا الوتر معلومًا أو لا لكان جميع الأوتار المذكورة أيضًا معلومة لكن ليس إلى تحصيله سبيل إذ ليس إلى معرفة وتر ثلاث القوس المعلومة الوتر من جهة الخطوط طريق بوجه فلمّا كان الأمر كذلك احتلنا في وجود وتر جزء واحد بتقريب دقيق لا يخالف المقادير المحتلّة المحصلة P فإنّ به يتمّ المقصود وذلك على ما نصف

مقدّمة نافعة فيما نقصده

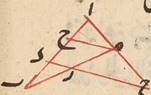
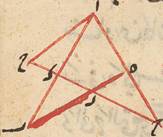
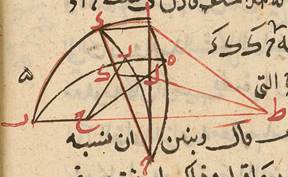
وهي أنّ نسبة وتر الأطول إلى الأقصر أصغر من نسبة قوسيهما فليكن في دائرة ا ب ج‍ د وتر ب ج‍ أطول من وتر ب ا ونقول نسبة ³²ب ج‍ إلى ^-30 add mg ب ا أصغر من نسبة قوسيهما فلتتصّف زاوية ا ب ج‍ بخطّ ب د ونصل د ج‍ ا د ا ج‍ فيكون ج‍ د ا د متساويين لتساويّ زاويتي ج‍ ب د ا ب د ويكون ج‍ ه أطول من ه ا لأنّهما على نسبة ج‍ ب ب ا ونخرج عمود د ز على ج‍ ا فيقع بين ج‍ ه لأنّه بنصف ج‍ ا ويكون د ا أطول من ه د وهو أطول من ز د فإذا أدرنا على مركز د وبعد د ه دائرة قطعت د ا على ح وجاوزت د ز وليخرجه إليها على ط فيكون قطاع د ه ط أعظم من مثلّث د ه ز وقطاع د ه ح أصغر من مثلّث د ه ا فإذن نسبة المثلّث إلى المثلّث أعني نسبة ز ه إلى ه ا أصغر من نسبة القطاع إلى القطاع أعني نسبة زاوية ط د ه إلى زاوية ه د ح وبالتركيب نسبة ز ا إلى ه ا أصغر من نسبة زاوية ز د ا إلى زاوية ه د ا وبعد تضعيف المقدّمين نسبة ج‍ ا إلى ه ا أصغر من نسبة زاوية ج‍ د ا إلى زاوية ه د ا وبالتفصيل نسبة ج‍ ه إلى ه ا أعني نسبة ج‍ ب إلى ب ا أصغر من نسبة زاوية ج‍ د ب إلى زاوية ب د ا أعني نسبة قوس ب ج‍ إلى قوس ب ا وذلك ما أردناه

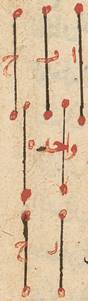
فلنفرض في دائرة ا ب ج‍ أوّلًا خطّ ا ب وتر نصف وربع جزء وخطّ ا ج‍ وتر جزء ولأنّ نسبة ج‍ ا إلى ب ا أصغر من نسبة قوسيهما أعني من نسبة الواحد والثلث إلى الواحد فإذًا ج‍ ا أقلّ من مثل وثلث ب ا الذي هو ا مز ح على ما مرّ فهو أقلّ من ا ب ق ولنفرض ثانيًا خطّ ا ب وتر جزء وخطّ ا ج‍ ا ج N وتر جزء ونصف ويبيّن أنّ ج‍ ا أقلّ من مثل ونصف ب ا وج‍ ا هو ا لد یه على ما مرّ فإذًا ا ب أكثر من ثلاثة وهو ا ب ه ولمّا كان وتر جزء واحد أقلّ وأكثر من مقدار بعينه ظهر أنّه ليس لذينك التفاوتين قدر نعتدّ به وأنّ المقدار المذكور هو الذي قصدناه وبعد ذلك يتمّ بالطرق المذكورة تحصيل سائر الأوتار ثمّ إنّ بطلميوس وضعها في ا جداول قسمها في الطول DLP إلى خمسة وأربعين سطرًا ليكون معتدلًاو في العرض إلى ثلاثة صفوف يشتمل أحدها على القسيّ المتفاضلة بنصف جزء وثانها على مقادير أوتارها وثالثها على الجزء من ثلاثين من تفاضل ما بين كلّ سطرين من الأوتار وهو حصّة دقيقة واحدة بالتقريب الذي لا مخالف الحقيقة بشيء معتدّ به ليسهل وجود حصيص الكسور به فإن وقع الشكّ في سطر بسبب انتقال الناسخ أمكن إصلاحه إمّا من جهة وتر ضعف قوسه أو تمامها من نصف الدور أو من جهة التفاوت بين قوسه وبين فوس أخرى معلومها الوتر وهذا رسم الجداول

أقول لمّا كانت طريقة المتأخّرين في هذا الباب وهو إقامة الجيوب في الأعمال مقام الأوتار أقرب تناولًا كما سيتّضح أردت أن أشير إليها أيضًا فأقول جيب القوس هو نصف وتر ضعفها وهو لا تجاوز نصف القطر كما لا تجاوز الوتر القطر بل حاله من نصف القطر حال الوتر من القطر وكلّ عمود يخرج من أحد طرفي قوس من دائرة ويقوم على قطر تمرّ بالطرف الآخر فهو جيب لها ويكون الواقع بين موقع العمود ومركز الدائرة جيبًا لتمام الوتر من ربع الدور فليكن ا ب من دائرة ا ب ج‍ التي مركزها د قوسًا ما وب ج‍ تمامها من الربع وا د نصف قطر يمرّ بطرف ا وب ه عمودًا عليه من الطرف الآخر فهو جيب قوس ب ا وكذلك ب ز الواقع على ج‍ د جيب تمامها وهو مساو له د الواقع بين نقطة ه موقع العمود ود المركز وكلّ واحد من جيب القوس وجيب تمامها معلوم من صاحبه لكون نصف القطر بخطّ ب د قويًّا عليهما وإذا تقدّم ذلك فأقول ليس لنصف الدور جيب كما ليس للكلّ وتر وجيب الثلث والسدس واحد وهو جذر ثلاثة أرباع مربّع نصف القطر وجيب الربع نصف القطر وجيب الثمن جذر نصف مربّع القطر وجيب العشر نصف وتر الخمس وجيب نصف السدس ربع القطر وجيب نصف العشر نصف وتر العشر وجميع ذلك معلوم ممّا تقدّم في الأوتار

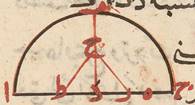
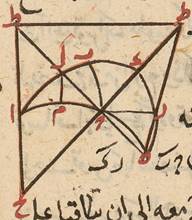
وإن أردنا أعدّنا لمعرفة جيب العشر ونصفه نصف دائرة ا ب ج‍ على مركز د وب د عمود على ا ج‍ وننصّف ج‍ د على ه وه د على ز وب د على ح ونصل ز ح ونجعل زط مثله ونصل ح ط ونبيّن مثل ما مرّ أنّ ه ط على د مقسوم بنسبة ذات وسط وطرفين والأطول ه د نصف وتر السدس فد ط نصف وتر العشر أعني جيب نصف العشر وح ط القوي عليهما نصف وتر الخمس أعني جيب العشر

وإذا كان قوسان مختلفان معلومتا الجيبين وأردنا جيب فضل أحديهما على الأخرى أو جيب مجموعهما فينبغي أن نمهّد المقدّمة الثانية ثمّ أقول ليكن ا ب ا ج‍ القوسين المفروضتين من دائرة مركزها د ونخرج د ب د ج‍ نصفي قطرين وا ه ا ز عمودين عليهما وهما جيباهما المعلومان ونصل ه ز فأقول إنّه جيب لقوس ب ج‍ وهو أيضًا معلوم أمّا الأوّل فلأنّا إذا أخرجنا عمودي ا ه ا ز إلى نقطتي ح ط ووصلنا وتر ح ط كان هو ضعفًا له ز وقوسه أعني قوس ح ط ضعفًا لقوس ب ج‍ فه ز هو جيب ب ج‍ وأمّا الثاني فلأنّا إذا وصلنا ا د وجعلناه قطر دائرة فإنّها تمرّ بنقطتي ه ز لكون زاويتي ا ه د ا ز د قائمتين وحينئذ يحيط بذي أربعة أضلاع ا ه د ز ويصير سطح ه ز في ا د نصف القطر من سطحي ا ه في ز د وا ز في ه د المعلومي معلومًا وا د معلوم فه ز يصير معلومًا وهو المطلوب

وبهذا الطريق نعرف جيب فضل العشر على نصف السدس وهو ستّة ثمّ إذا أردنا أن نعرف جيب نصف قوس معلومة الجيب نفرض ا ب تلك القوس وا ه الواقع على نصف قطر ب د جيبه المعلوم وج‍ ب نصف قوس ا ب وب ا وترها وننصّفه بنصف قطر د ج‍ الواقع عليه عمودًا على ز فب ز جيب ج‍ ب وأقول إنّه معلوم لأنّا إذا أخرجنا من ز عمود ز ح على ب د كان ب ح نصف ب ه لأنّ ب ز نصف ب ا وهما على نسبة واحدة ولكنّ ه د معلوم لأنّه جيب تمام ب ا فب ه معلوم وب ح نصفه معلوم وسطح ب ح في ب د المساويّ لمربّع ب ز معلوم فب ز معلوم وذلك ما أردناه

وبهذا الوجه نعرف جيب ثلاثة من جيب ستّة ثمّ جيب جزء نصف ثمّ جيب ثلاثة أرباع جزء ونبيّن أنّ نسبة الجيب الأطول إلى الجيب الأقصر أصغر من نسبة قوسيهما هكذا ليكن ا ب ا ج‍ قوسين مختلفين من دائرة مركزها د ونصف قطرها د ا وب ه ج‍ ز جيبيهما ونخرج وتر ج‍ ب حتّى يلقي ا د على ح ونصل د ب د ج‍ ونقول نسبة ج‍ ز إلى ب ه أصغر من نسبة قوس ا ج‍ إلى قوس ا ب لأنّ نسبة قوس ب ج‍ إلى قوس ا ب كنسبة قطاع ب د ج‍ إلى قطاع ا د ب ونسبة مثلّث د ج‍ ب إلى مثلّث د ب ح أعني ج‍ ب إلى ب ح أصغر من نسبة قطاع ب د ج‍ إلى قطاع ا د ب أعني قوس ب ج‍ إلى قوس ب ا فبالتركيب نسبة ج‍ ح إلى ب ح أعني نسبة ج‍ ز إلى ب ه أصغر من نسبة قوس ا ج‍ إلى قوس ا ب ثمّ نستخرج جيب جزء واحد ونصفه بمثل ما مرّ في الأوتار ومنه سائر الجيوب وبوضع الجداول

وإن أردنا أخذنا الجيوب من القسيّ أو القسيّ من الجيوب من جداول بطلميوس فإنّ أنصاف الأوتار الموضوعة فيها جيوب الأنصاف قسيّها المنفاضلة مربّع جزء ربع جزء والعمل به أن ننصّف وتر ضعف القوس المطلوب جيبه أو قوس ضعف الجيب المطلوب قوسه وهذا جدول الجيب

⟨I.11⟩

يا في القوس التي بين الانقلابين

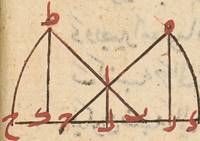
هي ضعف القوس الواقعة بين منطقتي معدّل النهار وفلك البروج أو بين قطبيهما من الدائرة المارّة بالأقطاب الأربعة وتسمّى غاية الميل وتوجد بالرصد هكذا لتتّخذ دائرة من نحاس تحيط بها سطوح أربعة متوازية ويقام مقام نصف النهار ويقسم بالأجزاء الثلاثمائة والستّين وكسوراتها ما أمكن ونجعل دائرة أصغر منها شبيهة بها في جوفها بحيث متماسّان بتمام سطحيهما ويكون وجهاهما من الجانبين في سطح واحد وتدور الداخلة في جوف الخارجة إلى الشمال والجنوب من غير أن يخرج عن سطحها ونجعل في جزئين متقاطرين على أحد جزئي وجزئي DLP الداخلة شظيتين متساويتين كشظيتي الأسطرلاب بعينهما وتوضّع في وسط عرضهما مقياسين دقيقين يلقيان موضع القسمة من وجه الخارجة لنعرف مقدار حركة الداخلة في جوف الخارجة من تلك الأجزاء ولننصب هذه الآلة عند الرصد على عمود في موضع مكشوف بحيث يكون سطح الدائرتين قائمًا على سطح الأفق على زوايا قائمة نعرف ذلك بشاقول يعلّق من النقطة المحاذية لسمت الرأس فتلقي النقطة المقاطرة إيّاها باستواء ومطبق سطحهما على سطح نصف النهار بأن يخرج خطّ نصف النهار على سطح الموضع الذي نصب العمود عليه وذلك سهل ثمّ نجعل بطحهما موازيًا لذلك الخطّ وتحكم الآلة بحيث لا تزول عن هذه المواضع ثمّ ليرصد تباعد الشمس في الشمال والجنوب بإدارة الداخلة في جوف الخارجة عند إنصاف النهار حتّى تستظلّ الشظية السفلى كلّها بالعليا وحينئذ يستدلّ نظر في المقياسين على مقدار بعد مركز جرم الشمس عن النقطة المحاذيّة لسمت الرأس في دائرة نصف النهار ولنا وجه أسهل فهو أن نتّخذ لبنة من حجر أو خشب مربّعة مستوية الوجه صالحة العرض والثخن ونجعل إحدى الزوايا التي على وجهها مركزًا ويدار عليه ربع دائرة ونخرج من المركز خطّان خطّين DLP محيطان بقائمة عند المركز بوترهما بوترها DLP الربع وتقسم Perhaps preferable is نقسم الربع بالأجزاء التسعين وكسورها ونوتّد على المركز وعلى الطرف الآخر من أحد الخطّين المذكورين وتدين أسطوانتين متساويتين صغير من قائمين على وجه اللبنة على زوايا قائمة ثمّ ننصب اللبنة بحيث يلي الوتدان ناحية ناحيت N الجنوب ونجعل المركزي محاذيًّا للسماء والآخر تحته ونجعل الخطّ المارّ بهما قائمًا على سطح الأفق بشاقول تعلّق من الوتد الأعلى فيلقي الأسفل على استواء ونجعل وجه اللبنة في سطح نصف النهار موازيًا بخطّ نصف النهار المخرج على سطح الأفق ونرصد موقع الظلّ الحادث من الوتد المركزيّ على محيط الربع وتوضّع شيء عند المحيط لستّين موقع الظلّ فنعلم على وسط الظلّ ونؤخذ ذلك الجزء فيستدلّ به على ممرّ الشمس في نصف النهار نحو الشمال والجنوب فبهذا الرصد سيّما ما add DLP امتحناه منه في حقيقة الانقلابين بدوائر كثيرة بعدان جعلنا أكثر الاستدلالات من النقطة المحاذيّة لسمت الرأس وجدنا القوس الواقعة بين أبعد بعدي الشمس في الشمال والجنوب يعني ضعف غاية الميل سبعة وأربعين جزءًا وأكثر من ثلثي جزء وأقلّ من نصف وربع جزء فيكاد أن يوافق ذلك قول أرطوشتانس DLP have أرسطالس, but give in the margin as variant the text from N (among other variants). The reading of N, however, is the correct one; al-Ṭūsī cites Almagest I.12, ed. Heiberg, p. 68:3-6, where Ptolemy refers to this value that stems from Eratosthenes. الذي وافقه أبرخس عليه وهو أنّ هذا القوس أحد عشر جزءًا بالتقريب من الأجزاء التي بها دائرة نصف النهار ثلاثة وثمانون جزءًا أقول ومقداره من الأجزاء الثلاثمائة والستّين في مز مب لط ب وشيء قال وقد يسهل بهذا الرصد أيضًا معرفة عرض البقعة التي يقع الرصد فيها بأن يوجد ما بين سمت الرأس والنقطة المتوسّطة بين هذين الطرفين وهي الكائنة على معدّل النهار فيكون ذلك مساويًّا لبعد القطبين عن الأفق

⟨I.12⟩

يب فيما يقدر جزء توطية للبراهين على المعاني الكريّة

وإذ تحقّق غاية الميل فيجب أن نمهّد لمعرفة الميول الجزئيّة أصولًا يتفرّع منها براهين الأمور الكريّة وابتدأ بطلميوس بالشكل الموسوم بالقطاع السطحيّ وهو مبنيّ على تأليف النسب فرأيت أن أورد هاهنا ما يجب أن يعرف منه على وجه الإجاز فأقول تأليف النسب على ما حدّه أقليدس في صدر المقالة السادسة من كتاب الأصول هو تضعيف بعض أقدارها ببعض لتحدث منها المؤلّفة وتجزئتها قسمة أقدارها على أقدار نسب مغروضة لتحدث أقدار نسبها قاعدة كما أن تقدير الكمّية المنفصلة يتمّ إلّا بعروض بعض لوازم الكمّية المنفصلة لها مثل فرض تجزئتها إلى غير ... كذلك لا يتأتي تقدير الكمّية المتّصلة إلّا بعروض لوازم الكمّية المنفصلة لها وهو وتركيبها من ... مفروضة تقدر بما تلك المقادير add mg N وقد يعبّر عليها بإلقاء المغروضة من المتجزّئة لتبقي الحادثة وكلّ ثلاثة مقادير متجانسة فإذا جعل أحدها وسطًا بين الأخرين كانت نسبة الطرفين مؤلّفة من نسبة أحدهما إلى الوسط ونسبة الوسط إلى الآخر مثاله ا ب ج‍ مقادير متجانسة جعل ب وسطًا بين أ ج‍ فنسبة ا إلى ج‍ مؤلّفة من نسبة ا إلى ب ومن نسبة ب إلى ج‍ ونسبة ا إلى ب مؤلّفة من نسبة ا إلى ج‍ ومن نسبة ج‍ إلى ب ونسبة ج‍ إلى ب مؤلّفة من نسبة ج‍ إلى ا ومن نسبة ا إلى ب add mg N ولنضع لبيانة الواحد الذي به يرام تقدير هذا الجنس من المقادير وليكن must be corrected to ولتكن. نسبته إلى ه نسبة ا إلى ب وإلى ز نسبة ب إلى ج‍ وإلى ح نسبة ا إلى ج‍ فيكون ه ز ح أقدار هذه النسب ولمّا كانت نسبة ه إلى الواحد بالخلاف كنسبة ب إلى ا ونسبة الواحد إلى ح كنسبة ا إلى ج‍ فبالمساواة فبالمسواة N نسبة ه إلى ح كنسبة ب إلى ج‍ وكانت نسبة ب إلى ج‍ كنسبة الواحد إلى ز eras N فنسبة الواحد إلى ز كنسبة ه إلى ح فيضعف فتضعيف DP ح بالواحد الذي هو ح د نسبة ح نفسه DLP أعني قدر نسبة ا إلى ج‍ يساوي تضعيف ه بز أعني قدر add DLP نسبة ا إلى ب بقدر نسبة ب إلى ج‍ فإذًا نسبة ا إلى ج‍ مؤلّفة منهاوكذلك كلّ نسبة تساويهما وأيضًا هي وكلّ نسبة يساويها must be corrected to تساويها مؤلّفة من كلّ نسبتين تساويان المذكورتين لأنّ أقدار النسب المتساوية لا تختلف وذلك ما أردناه

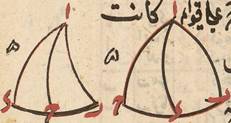
فإن كانت النسبتان واحدة كانت نسبة الطرفين كنسبة أحدهما إلى الوسط مثنّاة وإن كان مقداران من الثلاثة متساويتين كانت المؤلّفة مؤلّفة من نسبة مثلها ومن نسبة الميل وإذا تبيّن هذا في ثلاثة مقادير فهو فيما يتجاوزها ظاهر وهذه النسب الثلاثة إذا تباينت أركانها كانت الأركان ستّة إثنان للمؤلّفة وأربعة للبسيطين وتسمّى مقدّم المؤلّفة مع تالي البسيطتين جزءًا أوّلًا والثلاثة الباقيين must be corrected to الباقية جزءًا ثانيًا ويحصل من ضرب أقدار كلّ حيّز بعضها في بعض مجسّمًا فأقول مجسّما الحيّزين متساويان مثاله نسبة ا إلى ب مؤلّفة من نسبة ج‍ إلى د ومن نسبة ه إلى و فالمجسّم الحاصل من أقدار ا د والحيّز الأوّل يساوي المجسّم الحاصل من أقدار ب ج‍ ه الحيّز الثاني فليضرب ج‍ في ه وليكن ز ود في ه وليكن ح ود في و فليكن ط فج‍ د ضربًا في ه وحصل ز ح فنسبة ح إلى د كنسبة ز إلى ح ود ضرب في ه ز وحصل ح ط فنسبة ه إلى ز كنسبة ح إلى ط فنسبة ز إلى ط مؤلّفة من نسبة ز إلى ح أعني ج‍ إلى د ومن نسبة ح إلى ط أعني ه إلى د فإذًا هي كنسبة ا إلى ب فا في ط أعني في د في ز فب في ز أعني نسبة ج‍ في ه وذلك ما أردناه

ثمّ أقول ونسبة كلّ واحد من أقدار أحد الحيّزين eras N إلى كلّ واحد من أقدار الحيّز الآخر مؤلّفة من نسبتين تقع بين الأقدار الأربعة الباقية بشرط أن يكون مقدّماهما بين من DLP الحيّز الذي يكون تالي المؤلّفة منه وتالياهما من الحيّز الذي يكون مقدّم المؤلّفة منه على التكافي بمثاله نسبة د إلى ج‍ مؤلّفة من نسبة ب إلى ا ومن نسبة ه إلى و وذلك لأنّا إذا جعلنا د في مجسّم د ا وأعني مجسّم الحيّز الأوّل ارتفاعه وج‍ في المجسّم الآخر ارتفاعه بقي مسطّح ا في و قاعدة المجسّم الأوّل ومسطّح ب في ه قاعدة المجسّم الثاني ولمّا كان المجسّمان متساويين كانت نسبة الاتفاعين كنسبة القاعدتين على التكافي لمّا ثبت في كتاب الأصول ولكنّ نسبة مسطّح ب في ه إلى مسطّح ا في و مؤلّفة من نسبة أضلاعهما أعني من نسبة ب إلى ا ومن نسبة ه إلى و فإذًا نسبة د إلى ج‍ التي هي كنسبة القاعدتين أيصًا مؤلّفة منهما وذلك ما أردناه وأيضًا نسبة المسطّحين كما كانت مؤلّفة من نسبة ب إلى ا ومن نسبة ه إلى و فهي مؤلّفة أيضًا من نسبة ب إلى و ومن نسبة ا إلى ه على تبادل المقدّمين أو التاليين وكذلك نسبة د إلى ج‍ فإذًا كلّ نسبة مؤلّفة من نسبتين فهي مؤلّفة من نسبتين أخرتين محدثان بين أركانها إذا تبادلت المقدّمان أو التاليان ولمّا كانت أقدار كلّ حيّز ثلاثة والثلاثة في الثلاثة تسعة فهاهنا تسع نسب مقدّماتها من أحد الحيّزين وتواليها من الحيّز الآخر كلّ واحدة منها مؤلّفة نوعين من التأليف فهي بالحقيقة ثماني عشرة نسبة مؤلّفة وتسع نسب مثلها مقدّماتها من الحيّز الثاني وتواليها من الأوّل والجميع ستّ وثلاثون كلّها متلازمة تثبت بثبوت واحدة منها فإن تساوي مقداران من حيّزين تناسبت الأربعة الباقية من غير تأليف لأنّ نسب †المجسّمات† المتساوية الارتفاعات نسب قواعدها فإذا جعل المقداران المتساويان ارتفاعين كانا مجسّمين متساويتين must be corrected to متساويين متساوي الارتفاعين وكانت قواعدهما متساوية وأضلاع السطوح القائمة الزوايا المتساوية متناسبة على التكافي فإذن التناسب بين الأضلاع الأربعة حاصل مثاله إن يساوي قدرا ا ب من حيّزي ا د و ب ج‍ ه كان سطح د في ز مساويًا لمسطّح ج‍ في ه وكانت نسبة د إلى ج‍ كنسبة ه إلى و أو نسبة د إلى ه كنسبة ج‍ إلى و وأقول كما إذا كان أحد أربعة مقادير متناسبة مجهولًا فقط أمكن معرفته من الثلاثة الباقية بقسمة مضروب واحد منها في الذي لا يقع معه في نسبة على الثالث بتخرّج المجهول فإذا كان أحد هذه الستّة مجهولًا فقط أمكن معرفته من الخمسة الباقية بوجهين أحدهما أن يقسّم مجسّم الحيّز المعلوم الأقدار على مسطّح القدرين المعلومين من الحيّز الذي وقع المجهول فيه لتخرّج المجهول والثاني أن يوضّع الأقدار في ثلاثة سطور متوازية على وجه يبقي فرجه بين ركني النسبة المؤلّفة وبعد ركني إحدى الباقيين وقبل ركني الأخيرة هكذا فإن كان المجهول مثلًا ا طلبنا إمّا وسطًا بين ا ب يكون must be corrected to تكون نسبته إلى ب نسبة ه إلى و وليكن ز فيكون must be corrected to فتكون نسبة ا إلى ز كنسبة ج‍ إلى د ويصير ا معلومًا وإمّا لاحقًا بج‍ د يكون must be corrected to تكون نسبة د إليه نسبة ه إلى و وليكن ح فيكون must be corrected to فتكون نسبة ا إلى ب كنسبة ج‍ إلى ح ويصير ا معلومًا وإمّا سابقًا على ه يكون نسبته إلى ه كنسبة ج‍ إلى و ليكن ط ويكون نسبة ا إلى ب كنسبة ط إلى و ويصير ا معلومًا ويصير هكذا وعلى هذا القياس في سائر الأركان فهذا ما أردت تقديمه من أحكام النسب المؤلّفة ونعود إلى الكتاب

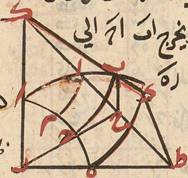
وهو القطاع السطحي add DLP خطّا ب ه ج‍ د خرجا من طرفي في خطّي ا ب ا ج‍ المحيطين بزاوية ا وتقاطعا بينهما على ز وانتهيا إليهما على ه د فنسبة ج‍ ا إلى ا ه بالتركيب مؤلّفة من نسبة ج‍ د د ز الأولى ونسبة زب ب ه الثانية لأنّا إذا أخرجنا ه ح موازيًا لج‍ د وجعلنا د ز وسطًا بين ج‍ د ه ح اللذين نسبتهما نسبة ج‍ ا ا ه بسبب تشابه مثلّثي ا د ج‍ ا ح ه صارت تلك النسبة مؤلّفة من نسبة ج‍ د د ز الأولى بعينها ونسبة د ز ه ح المساوية لنسبة ز ب ب ه الثانية بسبب تشابه مثلّثي ب د ز ب ح ه وكذلك نسبة ج‍ ه ه ا على التفصيل مؤلّفة من نسبة ج‍ ز ز د الأولى نسبة د ب ب الثانية لأنّا إذا أخرجنا ح موازيًا له ب وج‍ د إليه ثمّ جعلنا ز د وسطًا بين ج‍ ز ز ح صارت نسبة ج‍ ز ز ح المساوية لنسبة ج‍ ه ه ا بسبب تشابه مثلّثي ج‍ ز ه ج‍ ح ا مؤلّفة من نسبة ج‍ ز ز د الأولى بعينها ونسبة ز د ز ح المساوية †لنسبة† د ب ب ب ا DLP الثانية بسبب تشابه مثلّثي د ز ب د ا ح

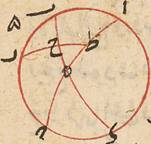
أقول وإذا †اعتبر مثلها† بين النسبتين في الجانب الآخر من الشكل أعني نسبة ب ا ا د بالتركيب وب د د ا بالتفصيل واعتبر مع كلّ واحدة من هذه النسب خمسة must be corrected to خمس وثلاثون نسبة يلازمها must be corrected to تلازمها وتقع †في أركانها† حصلت أنواع كثيرة من تأليف النسب في هذا الشكل دائرة ا ب ج‍ †على مركز د وعلى محيط دائرة نقط† mg N, على مركز محيكها نقط DLP ا ب ج‍ كيف ما وقعت محيط بقوسي ا ب ب ج‍ بشرط أن يكون كلّ واحدة أصغر من نصف الدائرة وكذلك كلّ قوس نذكره فيما بعد ونصل نصف قطر ب د ووتر ا ج‍ متقاطعين على ه ونقول نسبة جيب ا ب إلى جيب ب ج‍ كنسبة ا ه إلى و ج‍

وبطلميوس يبيّن النسب في أوتار أضعاف القسيّ في كلّ موضع لكن لمّا كانت النسب في الأضعاف والأنصاف واحدة استعمل المحدثون الجيوب تخفيفًا فلنخرج لبيان ما أدعيناه عمودي ا ز ج‍ ح على ب د ومحدث مثلّثا ا ز ه ج‍ ح ه المتشابهين لتساوي متقابلتي ه وقائمتي ز ح فتكون النسبة على ما دمرناه وأيضًا إذا كانت قوس ا ج‍ ز نسبة جيب ا ب إلى جيب ب ح معلومتين كانت كلّ واحدة من قوسي ا ب ب ج‍ معلومة وا با must be corrected to وأمّا أقدم قبل بيان ذلك أحكام المثلّثات المستقيمة الخطوط فإنّها كثيرة الغناء في هذا الكتاب فأقول مقدار الزاوية المستقيمة الخطّين هو مقدار القوس التي بوترها عند وقوعها على محيط دائرة أو مركزها فإذا أحاطت دائرة بمثلّث كان المحيط موزّعًا على زواياه وإذا أعرفت مقادير القسيّ صارت مقادير الزوايا ونسب بعضها إلى بعض معلومة وصارت نسب الأضلاع بعضها إلى بعض نسب أوتار القسيّ أيضًا معلومة وكان مقدار الزاوية القائمة نصف الدور أمّا إذا وقعت الزوايا على المركز صارت مقاديرها أنصاف ما كانت على المحيط لأنّ الزوايا تتناسب تناسب القسيّ فكما كانت المركزيّة ضعف المحيطيّة عند تساوي قوسيهما يكون must be corrected to تكون قوس المحيطيّة ضعف قوس المركزيّة عند تساويهما والأضلاع الموتّرة لها تتناسب تناسب جيوبها أعني في مثلّث ا ب ج‍ مثال نسبة ا ب إلى ا ج‍ كنسبة جيب زاوية ج‍ إلى جيب زاوية ب برهانه نخرج الأضلاع المحيطة بزاويتي ج‍ ب ونجعل ج‍ د ج‍ ه ب ح ب ط متساوية وندير على مركزي ج‍ ب بهذه الأبعاد قوسي د ه ح ط ونخرج عمودي ه ز ط ك على د ح فيهما جيبا زاويتي ج‍ ب ونخرج عمود ا ل على ب ج‍ فليشابه مثلّثي ا ل ج‍ ه ز ج‍ نسبة ه ز إلى ا ل كنسبة ه ح إلى ا ج‍ وليشابه مثلّثي ا ل ب ط ك ب نسبة ا ل إلى ط ك كنسبة ا ب إلى ط ب أعني ه ج‍ فبالمساواة المضطرّيّة نسبة ه ز إلى ط ك الجيبين كنسبة ا ب إلى ا ج‍ الضلعين وإذا يتبيّن ذلك فالمعلوم في المثلّث القائم الزاوية إن كان ضلعين أو ضلعا وزاوية غير القائمة كان باقي الأضلاع والزوايا معلومة لأنّ القائمة معلومة والباقية هي تمام المعلومة من الربع والأضلاع على نسب جيوب الزوايا إمّا إن كان زاوية فقط كانت الزوايا ونسب الأضلاع معلومة دون مقاديرها وإن كان ضلعًا فقط لم نعد شيئًا وفي غير القائم الزاوية إن كان المعلوم جميع الأضلاع أو ضلعين وزاوية كانت الباقية معلومة بإخراج عمود يجعل المثلّث مثلّثين قائمي زاويتين وإن كان ضلعين وزاويتين كانت الباقية معلومة من غير إخراج العمود لأنّ الزاوية الباقية هي تمام المعلومتين إلى نصف الدور والأضلاع على نسبها وإن كان جميع الزوايا فلا يعلم بها إلّا نسب الأضلاع وإن كان أقلّ من ذلك فلا يفيد شيئًا ونعود إلى الكتاب

ونعيد الشكل العاشر ونصل نصف قطر ا د ونخرج عمود د ز إلى ا ج‍ ونقول †لمّا† كانت †قوس† ا ج‍ معلومة كان ا ز †جيب نصفها ود ز† جيب تمام نصفها وزاوية ز د ا معلومة فمثلّث ا د ز القائم الزاوية معلوم بأيسره ولمّا كان ا ج‍ معلومًا †ونسبة† ا ه إلى ه ج‍ معلومة كان كلّ واحد من ا ه ه ج‍ بالانفراد معلومًا فإذًا مثلّث †ه† د ز من ضلعي ه ز ز د المعلومين معلوم بأيسره فزاوية ا د ب وهي مقدار قوس ا ب معلومة وقوس ب ج‍ الباقية أيضًا معلومة

وأيضًا فأن كانت إحدى القوسين اللتين محيط بهما النقط الثلاث منطبقة على الأخرى كقوسي ا ب ا ج‍ في هذه الصورة أخرجنا د ا ج‍ ب حتّى تتلاقيا على ه في إحدى الجهتين ونخرج عمودي ب ز ج‍ ح على القطر فيكون لتشابه مثلّثي ه ز ب ع ح ج‍ نسبة ب ز جيب ا ب إلى ج‍ ح جيب ا م كنسبة ب ه إلى ه ج‍ وأيضًا فإذا كانت قوس ج‍ ب ونسبة جيب ا ج‍ إلى ا ب معلومتين فقوس ا ب معلومة ولنصل د ب ]د ب[ ونخرج عمودي ونقول لمّا كانت زاوية ز د ب وضلعا ب ز ز د معلومة من قوس ب ج‍ فمثلّث ب د ز معلوم بأيسره ولأنّ نسبة ج‍ ه إلى ه ب معلومة وج‍ ب معلوم فه ب معلوم وجميع ز ه معلوم وز د معلوم فمثلّث ز د ه معلوم وزاوية ز د ه معلومة فزاوية ب د ا أعني قوس ا ب معلومة وكذلك قوس ا ج‍ ا ج‍ اN أقول وإن توازي خطّا د ا ج‍ ب يساوي جيبًا قوسي ا ب ا ج‍ وكان ا ب تمام نصف ج‍ ب من الربع وذلك ظاهر

وزاد ثابت في نسخته شكلًا لكونهما متلاقتين في جهة ج‍ وهو القطاع الكبرى قوسا ا ب ا ج‍ على سطح كرة وقعت عليهما ب ه ج‍ د المتقاطعتان على ز وكلّها من العظام بنسبة جيب قوس ج‍ ه إلى جيب قوس ه ا بالتفصيل مؤلّفة من نسبة جيب قوس ج‍ ز إلى جيب قوس ز د ومن نسبة جيب قوس د ب إلى جيب قوس ب ا

وليكن مركز الكرة ح ونخرج منه خطوط ح ب ح ز ح ه ونصل ا د ونخرجه إلى أن يلقى ح ب على ط ونصل د ج‍ ا ج‍ فيقطعان ح ز ح ه على ك ل فنقط ط ك ل الكائنة في سطح مثلّثي ا ج‍ د ودائرة ب ز ه معًا يكون على فصلهما المشترك وهو خطّ ط ك ل فمحدث قطاع ج‍ ا ط ك السطحي فتكون فيه نسبة ج‍ ل إلى ل ا ل ا N بالتفصيل مؤلّفة من نسبتي ج‍ ك ك د ود ط ط ا لكنّ نسبة ج‍ ل ل ا كنسبة جيبي ج‍ ه ه ا ونسبة ج‍ ك ك د كنسبة جيبي ج‍ ز ز د ونسبة د ط ط ا كنسبة جيبي د ب ب ا فإذًا نسبة جيبي ج‍ ه ه ا مؤلّفة من نسبتي ج‍ ز ز د ونسبة جيبي د ب ب ا

أقول وإن كان يلاقي ا د ح ب في جهة ج‍ أخرجنا قوسي ب ه ب ا إلى أن يتلاقيا لتمام نصف الدائرتين على ج‍ وتمّمنا الشكل كما في هذه الصورة وكان القطاع السطح الحادث هو ط د ج‍ ل وفيه نسبة ج‍ ل ل ا التي هي كنسبة جيبي ج‍ ه ه ا مؤلّفة من نسبة ج‍ ك ك د التي هي كنسبة جيبي ج‍ ز ز د ومن نسبة د ط ط ا التي هي كنسبة جيبي د م م ا أعني جيبي د ب ب ا لأنّ جيب د م هو جيب د ب لكونهما معًا نصف دائرة وكذلك جيب ا م هو جيب ا ب

وإن كانا أعني د ا ح ب موازيتين كان أيضًا ك ل موازيًا لح ب وإلّا فليلقه على ط وحينئذ تكون نقط د ا ط في سطحي مثلّث ا ج‍ د ودائرة ب د ا فيكون على خطّ مستقيم ويكون د ا ملاقيًا لب ح وقد فرض موازيًا له هذا خلف فإذن في مثلّث ج‍ ا د الذي وقع ك ل الموازي لقاعدته على ساقيه نسبة ج‍ ل لب ا التي هي كنسبة جيبي ج‍ ه ه ا كنسبة ج‍ ك ك د أعني نسبة جيبي ج‍ ز ز د فنسبة جيبي ج‍ ه ه ا مؤلّفة من نسبة جيبي ج‍ ز ز د التي هي مثل نسبتهما ومن نسبة جيبي د ب ب ا التي هي نسبة المثل ونعود إلى الكتاب

قال ونبيّن أنّ نسبة جيبي ج‍ ا ا ه بالتركيب أيضًا مؤلّفة من نسبة جيبي ج‍ د د ز ونسبة جيبي ز ب ب ه أقول وذلك بأن يتمّم نصفي دائرتي ج‍ ا ح ج‍ د ح فيقول في قطاع ح ه ب د نسبة جيب ح ا أعني جيب ج‍ ا إلى جيب ا ه بالتفصيل مؤلّفة من نسبة جيب ح د أعني جيب ج‍ د إلى جيب د ز ومن نسبة جيب ز ب إلى جيب ب ه وفي نسخة ثابت أيضًا قد زيّدت نظائر هذه الأشكال الثلاثة التي أوردناها

واعلم أنّه إذا اعتبرت النسب التي تلازم هاتين النسبتين واقعة في أركانها والنسب التي تلازم ما يشبههما من سائر النسب حصلت أنواع كثيرة من تأليف النسب في هذا الشكل كما كانت في القطاع السطحي وهاهنا تمّت المقدّمات الموضوعة في الكتاب وقد اخترع المتأخرون شكلين يقومان مقام القطاع ويغنيان عنه وعن النسب المؤلّفة الواقعة فيه يعرف أحدهما بالمعنى والآخر بالظلّي وأقاموا على مطالبهما براهين كثيرة وإنّا أوردهما هاهنا وأبيّنهما ممّا يناسب القطاع فأقول في بيان المعنى ليكن مثلّث ا ب ج‍ على سطح الكرة من العظام وليس في أضلاعه ما يجاوز الربع وزاوية ب منه قائمة فأقول نسبة جيب إحدى زاويتيه الباقيتين ولكنّ ا إلى جيب الضلع الذي بوترها وهو ب ج‍ كنسبة جيب زاوية ب القائمة أعني نصف القطر إلى جيب الضلع الذي بوترها وهو ا ج‍ ولنخرج ا ب ا ج‍ لتمام الربع إلى د ه ويدار على قطب ا قوس د ه من العظام فهي قدر زاوية ا ويفصل من د ز بقدر ب ج‍ ونوصّل ج‍ ز بخطّ مستقيم فيكون موازيًا لسطح دائرة ا د لتساوي ز د ج‍ ب القائمين عليه على زوايا قائمة ولكنّ مركز الكرة ح ونصل وتر ه ز ونخرج ح د معه إلى أن يتلاقيا على ط ضرورة لكون ه د أقلّ من الربع ونصل أيضًا وتر ه ج‍ ونصف قطر ح ا ونخرجهما إلى أن يتلاقيا على ك ونصل ط ك فيكون لكونه في سطح دائرة ا د وفي سطح مثلّث ه ز ج‍ موازيًا لز ج‍ ويكون في مثلّث ه ط ك البه الذي DLP وقع ج‍ ز الموازي لقاعدته على ساقيه نسبة ه ط إلى ط ل أعني نسبة جيب ه د إلى د ز بل نسبة جيب زاوية ا إلى جيب ب ج‍ وترها لنسبة ه ك إلى ك ج‍ أعني جيب ه ا الربع إلى جيب ج‍ ا بل جيب زاوية ب القائمة إلى وترها وهو المطلوب

وأيضًا بالإبدال نسبة جيب زاوية ا إلى جيب زاوية ب القائمة كنسبة جيب ضلع ب ج‍ إلى جيب ضلع ا ج‍ فإن كانت لزاوية ا أو لزاوية أخرى من العظام تساويها وتر آخر من العظام قائم على أحد ضلعيها كوتر ل م القائم على ا د كانت نسبة جيب ا م إلى جيب م ل كنسبة جيب ا ج‍ إلى جيب ج‍ ب لكونهما جميعًا كنسبة جيب القائمة إلى جيب زاوية ا وقد تسمّى قوسا ج‍ ب م ل وأمثالها بالقياس إلى قوسي ا ج‍ ا م ميولًا و أوله mg Nبالقياس إلى فوسي اب ال عروضًا وميولًا ثانية فإذًا جيوب القسيّ تتناسب نتاسب جيوب ميولها وفي المثلّثات غير القائم الزاوية من العظام كا ز ج‍ يكون must be corrected to تكون نسبة جيب زاوية ب إلى جيب زاوية ج‍ ب كنسبة جيبي وتريهما لأنّه إذا قامت قوس ا د على ب قوائم كانت في مثلّث ا ب د فنسبة جيب زاوية ب إلى جيب ا د كنسبة جيب القائمة إلى جيب ا ب وفي مثلّث ا د ج‍ نسبة جيب ا د إلى جيب زاوية ج‍ كنسبة جيب ا ج‍ إلى جيب القائمة فبالمساواة المضطرّيّة نسبة جيب زاوية ب إلى جيب زاوية ج‍ كنسبة جيب ا ج‍ إلى جيب ا ب

وأمّا الظلّي فتحتاج إلى تقديم تعريف الظلّ وأحواله وتعني بظلّ القوس هاهنا ما يقع بين قطرين يمرّان بطرفي القوس من عمود يقوم على طرف أحدهما كما إذا فرضنا في دائرة ا ب ج‍ حول مركز د قوس ا ب وقطري ا ج‍ ب ه مارّين بطرفهما بطرفها DLP وأقمنا على نقطة ا من قطر ا ج‍ عمودًا عليه وأخرجناه مع قطر ب ه حتّى يتلاقيا على ز فا ز ظلّ قوس ا ب وهو مواز لعمود ب ح الذي هو جيبها ونسبة ا ز ظلّ القوس إلى ا د نصف القطر كنسبة ب ح جيبها إلى ح د جيب تمامها وإذا أقمنا قطر ط ي على ا ج‍ ومن نقطة ط عمود ط ل كان ط ل ظلّي تمام ا ب وهو مواز بجيب تمامه وكان نصف القطر وسطًا في النسبة بين ظلّ القوس وظلّ تمامها لأنّ نسبة ز ا إلى ا د أعني د ط كنسبة د ط إلى ط ل وكان ضرب الشيء في أحدهما كقسمته على الآخر لأنّا إذا جعلنا نصف القطر واحدًا بقدر منه هذه المقادير وضربنا مثلًا م mg N في ظلّ ا ز فيحصل ن ه كأنّ نسبة الواحد إلى ظلّ ا ز كنسبة م إلى ن ه ثمّ قسمنا م أيضًا على ظلّ ط ل فيحصل س ه كأنّ نسبة الواحد إلى ظلّ ط ل كنسبة س ه إلى م وبالخلاف نسبة ط ل إلى الواحد كنسبة م إلى س ه ولكنّ نسبة ط ل إلى الواحد كنسبة الواحد إلى ا ز أعني نسبة م إلى ن ه فنسبة م إلى س ه كنسبة إلى ن ه فإذًا ن ه وس ه الحاصل من الضرب والقسمة شيء واحد وذلك عند ما نجعل أجزاء القطر دقائق وللأظلال خواصّ أخر بطول الكتاب بشرحها وهذان الظلّان أعني ظلّ القوس وظلّ تمامها يعرفان الأوّل والثاني إذًا نسبتا إلى قوس واحدة كقوس ا ب في المثال المذكور وسيأتي ذكر الظلّ الثاني في المقالة الثانية وإنّا وضعت الأظلال الأوفي للقسيّ المتفاضلة بنصف جزء إلى ثمن الدائرة مقداره بأجزاء القطر وكسورها في جدول ما تمّمت الربع لفرط تزايد التفضلات التفاضلات DLP في الثمن الثاني وقيام هذا الثمن بالقوّة مقامة في أكثر المواضع كما مرّ في الجدول

ونعود إلى بيان الظلّي فنعيد مثلّث ا ب ج‍ على ما وضعناه ونقول نسبة ظلّ زاوية غير القائمة مثلًا ا إلى ظلّ وترها وهو ب ج‍ كنسبة جيب زاوية ب القائمة إلى جيب الضلع الواقعة بين الزاويتين وهو ا ب ويخرج ا ب ا ج‍ إلى د ه تمام †الربع† ويدير د ه من العظام ويخرج من مركز الكرة وهو ز خطوط ز ا ز ج‍ ز ه ويخرج عمودي ب ح د ط على سطح دائرة ا د إلى أن يلقيا ز ح ز ه على ح ط فهما أعني ب ح د ط طلّا قوسي ب ج‍ د ه ونصل و ز د ب ونخرجه إلى أن يلقى ز ا على ك فتكون نقط ط ح ك على خطّ مستقيم لكونهما في سطحي عمودي ب ح د ط المتوازيين وفي سطح دائرة ا ه ونصل ط ح ك ثمّ نقول في مثلّث د ط ك الذي وقع ب ح الموازي لقاعدته على ساقيه نسبة د ط ظلّ زاوية ا إلى ب ح ظلّ وترها كنسبة د ك إلى ك ب أعني كنسبة جيب د ا الربع وهو جيب القائمة إلى جيب ا ب وهو المطلوب وأيضًا بالإبدال نسبة ظلّ زاوية ا إلى جيب القائمة كنسبة ظلّ ب ج‍ إلى جيب ب ا فإن كان لزاوية ا أو زاوية أخرى تساويها وتر آخر من العظام قائم على أحد ضلعها ضلعيها DLP كوتر ل م القائم على ا د كانت نسبة ظلّ ل م إلى جيب ل ا كنسبة ظلّ ب ج‍ إلى جيب ب ا لكونهما معًا كنسبة ظلّ زاوية ا إلى جيب القائمة فإذًا جيوب القسيّ تتناسب تناسب أظلال عروضها وتتفرّع على كلّ واحد من هذين الأصلين أعني المعنى والظلّ فرعان

فلنعد لبيانها في قسي DLP الشكل المتقدّم ويخرج د ه ب ج‍ حتّى يتلاقيا على ز قطب دائرة ا د ويتمّ القطاع ونقول أمّا الفرع الأوّل للمعنى فهو أنّ نسبة جيب تمام ب ج‍ وتر زاوية ا إلى جيب تمام ا ج‍ وتر القائمة كنسبة جيب القائمة إلى جيب تمام ا ب لضلع الباقي في ذلك لأنّ في مثلّث ج‍ ه ز زاوية ه ايضًا قائمة لأنّ ا قطب د ز فنسبة جيب ز ج‍ الذي هو تمام ب ج‍ إلى جيب ج‍ ه الذي هو تمام ا ج‍ كنسبة جيب القائمة إلى جيب زاوية زا وية N ز أعني جيب د ب الذي هو تمام ا ب وأمّا الفرع الثاني فهو أنّ نسبة جيب تمام زاوية ا إلى جيب تمام ب ج‍ وتررها كنسبة جيب زاوية ج‍ إلى جيب القائمة وذلك لأنّ نسبة جيب ه ز في مثلّث ج‍ ه ز الذي هو تمام زاوية ا إلى جيب ج‍ ز الذي هو تمام ضلع ب ج‍ كنسبة جيب زاوية ج‍ إلى جيب القائمة وأمّا الفرع الأوّل الظلّي فهو أنّ نسبة جيب تمام زاوية ا إلى جيب القائمة كنسبة ظلّ تمام ا ج‍ إلى ظلّ تمام ا ب وذلك لأنّ add DLP في مثلّث ه ز ج‍ نسبة جيب ز ه الذي هو تمام زاوية ا إلى جيب ز د الذي هو جيب القائمة كنسبة ظلّ ه ج‍ الذي هو تمام ز ج‍ إلى ظلّ زاوية ز أعني د ب الذي هو تمام ا ب وأمّا الفرع الثاني فهو أنّ نسبة جيب تمام ا ج‍ إلى جيب القائمة كنسبة ظلّ ه ز الذي هو تمام زاوية ا إلى ظلّ زاوية ج‍ فهذا ما أردناه ولنعد في الكتاب

⟨I.13⟩

يج‍ في معرفة الميول الجزئية

لأجزاء منطقة البروج عن معدّل النهار وهي قسيّ تقع بينهما من دائرة عظيمة تمرّ بقطبي معدّل النهار وبجزء مفروض من منطقة البروج وتسمّى هذه الدائرة الميل وهي كدائرة نصف النهار لو لا وجوب مرور نصف النهار بقطبي الأفق فليكن ا ب ج‍ د المارّة بالأقطاب الأربعة وا ه ج‍ نصف معدّل النهار وب ه د نصف فلك البروج وه الاعتدال الربيعيّ وب الانقلاب الشتويّ ود الانقلاب الصيفيّ وز قطب معدّل النهار وه ح ثلاثين جزءًا من فلك البروج وليمرّ must be corrected to ولتمرّ قوس ز ط بنقطتي ز ح من العظام فح ط ميل قوس ه ح المطلوب معرفته فلأنّ في قطاع ه ا ز ح نسبة نسبت N جيب ز ا الربع إلى جيب ا ب غاية الميل مؤلّفة من نسبة نسبت N جيب ز ط الربع إلى جيب ط ح المطلوب ونسبة جيب ه ح ثلاثين جزءًا إلى جيب ه ب الربع

وكان من الجيوب الستّة خمسة معلومة ثلاثة منها نصف القطر وواحد جيب غاية الميل وهو كد يه نز ل على أنّ غاية الميل هو ما اتّفقنا عليه من نسبة أحد عشر إلى ثلاثة وثمانين ومقداره كج‍‍ نا ك والخامس جيب ه ح وهو أيضًا ثلاثون فإذا ألقينا النسبة الثانية عن المؤلّفة بقيت النسبة الأولى نصف القطر إلى يب ز نط وهو جيب الميل فالميل يا م بالتقريب أقول لمّا كان الأوّل من المقادير الستّة في هذه النسبة مساويًا للثالث وهما من حيّزين كانت نسبة الثاني في جيب غاية الميل إلى الرابع جيب ط ح كنسبة السادس الجيب كلّه إلى الخامس جيب الثلاثين وبالمعنى نسبة جيب ه ح إلى جيب ط ح كنسبة الجيب كلّه إلى زاوية ه وبالظلّي نسبة جيب تمام زاوية ه إلى الجيب كلّه كنسبة ظلّ ط ح إلى ظلّ زاوية ه فط ح معلوم وأعود إلى الكتاب قال ولنضع قوس ه ح ستّين فيكون جيبه نا نز ما ويكون جيب الميل كا ه ند والميل ك ل ط وعلى هذا المثال حسبنا لجزء جزء من الربع add mg ووضعنا الجميع في الجدول وميول أجزاء سائر الأرباع وهذا هو الجدول

⟨I.14⟩

يد في مطالع الكرة المنتصبة

وهي ما يقع من معدّل النهار بين نقطة التقاطع وبين دوائر الميول المارّة بأجزاء مفروضة من فلك البروج وبها يعرف مقادير الأزمان التي تمرّ فيها أجزاء فلك البروج على نصف النهار في جميع الآفاق والأفق حيث الكرة منتصبة هي إحدى تلك الدوائر فلذلك عرف بها لنعدّ الشكل المتقدّم بعينه والمطلوب هاهنا معرفة قوس ه ط من قوس ه ح ففي القطاع المذكور نسبة جيب ز ب إلى جيب ب ا مؤلّفة من نسبة جيب ز ح إلى جيب ح ط ومن نسبة جيب ط ه إلى جيب ه ا وقوس ز ب سو ح م جيبه ند نب كو ل وقوس ب ا وجيبه ما مرّ ما مرّ N وقوس ز ح عح ك ج‍‍ ل وجيبه لح مه لز ل وقوس ح ط وجيبه ما مرّ ما مرّ N وه ا الربع فإذا ألقينا النسبة الأولى من النسبة المؤلّفة بقيت النسبة الثانية نسبة كز كو لج‍‍ إلى فح مه لز ل وهي نسبة كح ه نز مب ل جيب المطالع إلى نصف القطر فإذًا قوس ه ط كز فه أقول وبالمعنى نسبة جيب تمام ح ط إلى جيب تمام ه ح كنسبة الجيب كلّه إلى جيب تمام ه ط للفرع الأوّل وأمّا بالظلّي فكما مرّ قال ولنضع ه ح ستّين فيصير ز ح سط كط نا جيب om. DLP جيبه نو نا نح وح ط وجيبه ما مرّ ما مرّ N والباقية بحالها وتبقی نسبة جيب ط ه إلى ه ا نسبة مز لا ك ل إلى نو نا نح فيكون جيب ط ه فه مد ي قوسه نز مد وظهر أنّ زمان طلوع البرج الأوّل add DLP كز فه وزمان طلوع البرج الثاني نط ند فیبقی زمان طلوع البرج الثالث إلى تمام الربع لب نو ونحن حسبنا بهذا الوجه لعشرة عشرة من الأجزاء إذ لا يتفاوت فيما دون ذلك بسبب التفاضل شيء يعتدّ به فوجدناها هكذا وسائر الأنواع كهذا الربع تمّت المقالة الأولى