⟨Prefatio translatoris⟩

Quemadmodum Ptolomeus et ante eum nonnulli veteris auctoritatis viri antiquas seculi scribunt historias, que cunctis disciplinalibus scientiis finis est, ipsa earundem omnium principium existit nature comitata seriem, cuius omnis fere terminus in originis meta concluditur. Quod quoniam presentis est negocii, locus exigit ab integro exponi, quo plane constet, quonam presentis instituti spectet auspicium, ac ne longa fiat digressio, nichil prohibere videtur, quin ad imitationem alterius translationis nostre hic quoque breviter commemoremus, ne, si diutius insequamur, scribendis moram faciamus. Narratur quippe, transacto primo et universali diluvio, qua primum undis ad priores alveos reversis arida patuit, senem cum filiis superstitem, cum ex Armenia temperatiores auras sequens inter Tigrim et Eufratem descenderet, in quarto climate, qua postea Babilonia surrexit, constitisse. Hic ex nepotibus eius quidam, ut ferunt, filius primogeniti, plane quidem antequam nepotum successio aut trans Kascarum aut citra Kufam haut longe a Mesopotamie terminis diffunderetur, seu avita memoria commonitus seu divino fortasse nutu commotus primus sidereos cursus sequens effectus mirari cepit, a quo paulatim sequentis etatis studium in orbem derivatum in tantum usque accrevit, quoad plane demum deprehenderet, omnem superioris mundi scientiam principe loco in geminas dividi species, in motus celestes et motuum effectus, tanto quidem intervallo discretas, quanta est inter disciplinale studium et naturalem speculationem distantia. Quarum eius, que motum sequitur, omnis vis et ratio in numero, mensura et proportione constat, ut omnis matheseos discipline et primordialis et finalis extiterit causa. Est enim stellarum motus omnino bipartitus, in eundem et diversum, quorum alter accidentalis omnibus idem, alter proprius omnifariam diversus atque eidem contrarius, uterque circularis, ut necesse fuerit ad concepti artificii constitutionem et dimensioni circulorum et habitudini ad invicem ipsorumque motuum momentis singula proponi studia; quorum quoniam primi traduntur autores Indi, Perse et Egyptii inventionem secuti sunt, que disciplina primis ordinavit gradibus. Idem ergo motus quoniam equabilis est circuli super centrum et axem inmobilem omnia continentis spere, seorsum hunc scribendum duxit Ptolomeus quippe primum in ipso tanquam vestibulo astronomie quasi thema quoddam totius studii proponens, prout idem diversi principium et equalitatem inequalitatis cardinem intellexit nec, opinor, sine imitatione Abracaz, quem in omni celesti motu auctorem habet, quemadmodum Sicheum in motus effectu. Ex quibus et duo Ionica lingua collegit volumina, in primam Sintasim, in secundam Tetrastim, Arabice dicta Almagesti et Alarba; quorum Almagesti quidem Albeteni commodissime restringit, Tetrastim vero Albumasar non minus commode exampliat. In utroque et ipse et sequaces eius eas dividendas ordinant, ut, quoniam altera submota alteram relinqui inpossibile est, nec convertitur illa naturaliter, ut finis est disciplinalis studii, naturalis quoque speculationis existat origo; cuius prior pars superioris mundi, ut sequens inferioris, naturam contemplatur, id autem est materiales rerum causas, quemadmodum illa formales, omnis videlicet geniture principia post primam ipsam causam utrumque moventem, ut in eo, quod de essentiis instituimus, plenius patebit. Cum itaque motus quidem sit huiusmodi, effectus vero motum consequens, omne hoc studium ab eodem motu rectissime inchoat. Quod igitur omnium humanitatis studiorum summa radix et principium est, cui potius destinarem quam tibi, quem primam summamque hoc tempore philosophie sedem atque inmobiliter fixam varia tempestate fluitantium studiorum anchoram plane quidem, ut novi, et fateor; nec enim diis placeat, me, sicut iners vulgus solet, invidia teneat, ut sponte quidem aut mendatio locum prestem aut veritatem dissimulem; tibi, inquam, diligentissime preceptor Theodorice, quem haut equidem ambigam Platonis animam celitus iterum mortalibus accomodatam. Quo factum est principaliter, ut non aliter, quam aureis culmis Cererem, maturo palmite Bachum, unum te Latini studii patrem astronomie primitiis donandum iudicarim, quippe cum nec ego, quid offerrem, melius haberem nec tibi sapientie dono quicquam acceptius cognoscerem, secundo vero, ut id, quod solertiam tuam minime latere potest, aliis quoque per te innotescat interim, quanta presumptione astronomie nomen usurpant, qui necdum principium eius viderint, que sine tribus premissis ita recte possibilis est, ut Ycarus volare potuit, nisi forte his, qui novo freti ingenio conversis discipline gradibus a fine incipiunt, qui tamquam neglecto naturali gressu retrocedentes postpositis nimirum luminibus cecum carpant iter necesse est. Tertio vero, ut, quoniam tanti viri primarium hoc opus celestisque scientie quasi clavem quandam labor noster nunc tandem Latio confert, antequam in profanas insidiantium manus incideret, tua sanctissima constaret auctoritate. Quantam enim putas hominum partem hoc tempore superstitem, que propria contenta sorte non alieni cupiditate boni ferveat aut potius odio contabescat, que passio maxime Latinitatis inopiam hucusque fovit necdum, licet, pereunte materia quiescens; quin me quoque, qui longe inter alios latere putabam, usque adeo saepius inpellat, ut tanquam cedens invidie voto remisso tanto labore potius ad commune quodlibet vivendi negotium confugiam, cum presertim cunctis iam animi divitiis postpositis nichil preter fortuitas opum sarcinas in pretio videam, nisi unum te virtutis exemplar haberem, quem nec labor vincit nec delicie temperant nec denique potentissima pervertit ambitio, ut tu quoque ceteris diffugientibus deserte et tamquam mediis exposite fluctibus philosophie naufragium patiaris. Tuam itaque virtutem quasi propositum intuentes speculum ego et unicus atque illustris socius Robertus Ketenensis nequitie dispicere, licet plurimum possit, perpetuum habemus propositum, cum, ut Tullius meminit, misera sit fortuna, cui nemo invideat. His habitis, ne diu differamus, ab ipsis eius verbis tractatus initium statuamus non alia transferendi lege, quam qua id ipsum Maslem in Arabicam transtulit.

⟨Textus⟩

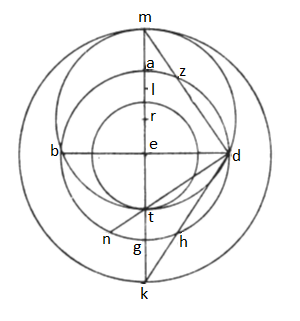1. Cum sit possibile, Iesure, et plerumque necessarium, ut in plano represententur circuli in speram corpoream incidentes, tamquam plana esset, consultum visum est in veritate scientie, ut, qui scire velit hec, describat demonstrantem rationem, qua assignari conveniat circulum declivem ac circulos equidistantes circulo equinoctiali pariter et circulos notos per circulum meridianum, et quicquid intenditur adaptum ei, quod apparet in spera corporea. Cogit igitur huiusmodi intentio loco meridiani circuli rectis uti lineis, inter circulos vero equidistantes recto circulo, ut fiat primum circulus magnus declivem assignans hinc inde attingens equidistantes recto pari utrimque distantia, quem medium secet, in hunc modum. Describimus circulum equinoctialem notis A, B, G, D circa centrum E, cuius diametra ortogonaliter se invicem secantia sint AG et BD. Intelligemus igitur alterum diametrum meridianum circulum, punctum vero E polum septemtrionalem; nec enim alterum apponi convenit in planitie spectante ad hunc, quemadmodum in sequentibus constabit; quorum cum septemtrionalis in parte nostra perpetuo appareat, is potius accomodus est in planitie, cuius nostra est assignatio. Oportet igitur circulorum equidistantium recto septemtrionalem intrinsecus describi, australem vero extrinsecus. Quod ut recte fiat, producimus lineam AG utramque in partem sicque de circulo ABGD utraque ex parte G duos arcus equales resecamus, desuper GH, infra GN, continuamusque rectis lineis D cum utrisque notis, ita quidem, ut DH usque in lineam AG perveniat, locumque K signabit, DN vero ubi lineam AG tetigerit, T notabitur. Quo facto fixo in E centro ad mensuram EK fiet circulus super diametro KM, sicque non moto consequenter et alter fiet ad mensuram ET lineae super diametrum TL. Divisa deinde TM linea per medium circa divisionis punctum R describetur circulus ad mensuram medietatis. Dico igitur illos duos circulos equidistantes equinoctiali pari utrimque distantia, tertium vero super R centrum declivem, quem TM linea per equalia secat, quousque utrumque illorum attingat, alterum ad notam M alterum ad punctum T, equinoctialem per medium secare, quem ad opposita duo puncta B et D intercipit. Quod ut ratione constet, continuabit linea recta D cum M ad punctum Z equinoctialem circulum transiens. Quoniam igitur arcus AZ equalis est arcui GH, qui equalis datus est arcui GN, arcum ZDN totius circuli dimidium esse necesse est; unde angulum MDT rectum esse consequens est. Quoniam itaque circulus super lineam TM descriptus triangulum rectangulum MDT circumscribens super punctum D transit, et super punctum B transire necesse habet; consequenter ergo circulum equinoctialem per equalia secat. Hinc itaque constat inter circulos equidistantes recto, cum duplicamus ex utraque parte puncti G arcus equales, quantitatem eorum metiri arcum totius declinationis; quorum fines ubi continuamus rectis lineis cum puncto D, ponimus, quas resecant lineas rectas de linea EK, distantias circulorum, quos circa centrum E descripsimus, artificio dati exempli, ut sit intrinsecus quidem tropicus Cancri, extrinsecus vero tropicus Capricorni attingentis hos zodiaci ysemerinum per equalia secantis, ut descriptum est. Metitur igitur deprehensio nostra utrumque arcuum NG et GH partibus XXIII punctis fere LI ex eis, que CCCLX totum ABGD circulum metiuntur, que par est distantia utriusque tropicorum A circulo equinoctiali. Est igitur hinc inde equidistantium circulorum TL quidem tropicus estivus, KM tropicus hyemalis; ex quo constans est circulum MBTD medium attingentem circulos tropicos, apud T quidem solstitium estivum, apud M vero solstitium hyemale, equinoctialem per equalia secantem, ac si principio a puncto B sumpto per A transiens in D perducatur; propter quod declinantis circuli partes non convenit ut sint equalium arcuum, sed quemadmodum in sequenti exemplo adaptabitur. Id autem dico, ut sumamus principia signorum a punctis, ubi secat circulos equidistantes equinoctiali designatos ratione, qua docuimus, ad distantiam uniuscuiusque signi a circulo recto, prout est in spera corporea circuli signorum. Hac itaque ratione erit omnis recta linea, que per polum transierit, loco meridiani circuli deducta per zodiacum in partes denotantes eas, que per diametrum opponuntur in spera corporea.

2. Designabitur deinde omnis orizon, quemadmodum circulum declivem designavimus, non quia equinoctialem per equalia secat, quin etiam zodiacum potentia per medium secet; id autem dico, quoniam designari habet per partes potentia respicientes eas, que per diametrum opponuntur in spera corporea. Describatur enim circulus equinoctialis ut ante notis A, B, G, D circa centrum E, declivis vero circulus notis Z, B, H, D medium equinoctialem secans ad puncta B et D. Deducemus deinde per polum C loco circuli meridiani lineam rectam utcunque atque, si placet, per Z, A, E, H, G. Dico itaque, puncta Z, H respicientia ea, que per diametrum opponuntur in spera; id autem dico, ut circuli equidistantes recto ad hec puncta designati resecent arcus equales ex utraque parte circuli equinoctialis, quo modo exposuimus, ac si esset in ipsa spera. Quod ut ratum fiat, consurget a puncto 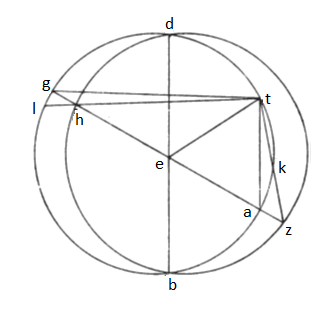E linea recta perpendicularis super AG usque ad circumferentiam in punctum T; perducentur deinde linee recte TKZ et TA sicque THL et TG. Quoniam igitur in semicirculo est angulus ATG, rectum esse constans est. At vero, quoniam, quanta est ZE in ED, tanta ED in se ipsam ducta, erit etiam tanta ET in se ipsam; unde necesse est, ut, que fuerit proportio ZE ad ET, ea sit ET ad EH; rectus est ergo et angulus ZTH. Constitit autem rectus et ATG; sublato igitur communi medio anguli ATK et GTL necessario equales relinquuntur; unde et arcus AK et LG equos esse consequens est. Ex his igitur, quoniam linee TK et TL applicant ad arcus, quorum eadem distantia a puncto de circulo equinoctiali, que educte a puncto T equidistante oppositis punctis A et G per quadrantes feriunt in linea ZG puncta Z et H, per que designari habent circuli duo equidistantes recto pari utrimque distantia, necesse est, lineam ZEH continuare puncta potentia diametrum circuli declivis terminantia.

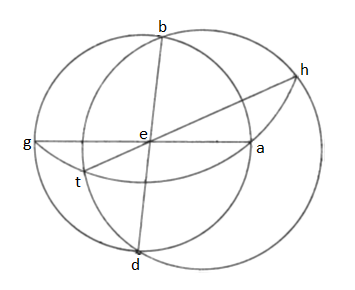3. Designamus deinde circulum alium declivem a circulo equinoctiali loco orizontis, quousque secet solum equinoctialem per medium; unde puncta duo, ubi hic et zodiacus se invicem interceperint, potentialiter per diametrum esse opposita necesse sit; id autem dico, ut linea continuans ea puncta per centrum equinoctialis transeat. Sit enim, ut consuevimus, circulus equinoctialis ABGD circa centrum E, zodiacus vero HBTD, quorum sectionis puncta continuans diametros BED, orizon autem HATG equinoctialem per equalia secans super diametrum AEG, cuius et zodiaci communis sectio ad puncta H et T. Dico igitur, quod si applicuerit punctum H cum centro E linea recta loco circuli meridian producaturque in directum, necessario per punctum T transibit. Applicet igitur HE linea recta eatque in directum, quousque orizontem feriat atque interim in puncto T. Dico itaque punctum T commune quoque circulo zodiaci. Quoniam enim in circulo HATG linee due se invicem secant AG et HT, erit, quanta AE in EG, tanta HE in ET; igitur et quanta BE in ED; unde et BD atque HT in eodem esse circulo necesse est. Quapropter et super zodiacum T signatum esse consequens est. Fuit autem T signatum super orizontem, qui est circulus HATG; quorum communem sectionem continuat linea TH, quam per centrum equinoctialis transire constans est. Unde manifestum est, et zodiacum nichilominus ab orizonte secari ad puncta per diametrum opposita.

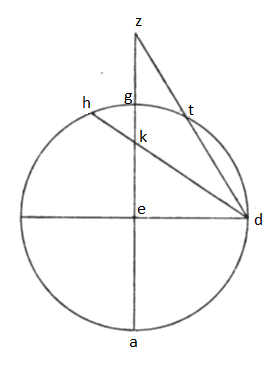4. His ita constitutis nunc intuenda est proportio semidiametrorum equidistantium circulorum, qui designati sunt supra signa circuli declivis, ad semidiametrum circuli recti, quousque deprehendamus ortum eorum certoque metiamur numero, prout apparet in spera corporea applanes et declivi. Describatur itaque circulus equinoctialis ABGD circa centrum E, cuius diametra ortogonaliter se invicem secantia AG et DB, et protrahemus AG secundum rectitudinem usque ad punctum Z, deinde circa G resecabimus duos arcus equales GT et GH, producenturque pariter linee DKH et DTZ ea quidem ratione, qua constituimus, equidistantium circulorum septemtrionalem quidem fieri circa centrum E ad mensuram EK, australem vero circa idem centrum ad mensuram EZ. Dico igitur, quod, que fuerit proportio EZ ad ED, eadem sit ED ad EK. Siquidem arcus GH et GT equales, arcus BT et BH semicirculum equant; unde angulos BDT et BDK recto equales esse consequens est. Sunt autem et anguli EDK atque EKD recto equales; sunt ergo similes rectanguli duo trianguli EDK et EDZ; unde necesse est, ut, que fuerit proportio EZ ad ED, eadem sit ED ad EK. Deinde et arcuum eorumque cordarum proportiones assumimus. Manifestum est enim, que proportio est anguli BDT ad angulum EZD, eam esse arcus BT ad arcum TD, cum equalis sit BH; que nimirum et arcus EZ ad arcum ED, de circulo videlicet designato super triangulum EDZ. Unde consequens est, ut, que fuerit linearum EZ et ED atque ED et EK, eadem sit corde BT ad cordam TD proportio. His habitis metiemur in primis utrumque arcuum GH et GT partibus XXIII punctis LI secundis XX ex eis, que CCCLX circulum rectum metiuntur; que par est, ut prediximus, utriusque tropicorum ab equinoctiali distantia in spera corporea. Erit igitur secundum hanc distantie quantitatem arcus BT gradus CXIII puncta LI secunde XX ex numero eo, qui totum circulum metitur absolutis videlicet CCCLX gradibus, arcus autem BH residuus de semicirculo gradus LXVI puncta VIII secunde XL, linea vero recta, corda videlicet arcus BT, partes C puncta XXXIII secunde XXVIII ex eis partibus, que CXX totam circuli diametrum metiuntur, quemadmodum in Almagesti constitutum est, corda vero BH partes LXV puncta. XXIX secunde Ō est. Ergo que proportio partium C cum punctis XXXIII secundis XXVIII ad partes LXV cum punctis XXIX secundis Ō, ea est linee EZ ad lineam ED atque ED ad lineam EK. Quoniam igitur ED semidiametros circuli recti absolute LX partium est, metiuntur quidem ex eis partibus XCII puncta VIII secunde XV lineam EZ semidiametrum hyemalis tropici, semidiametrum autem estivi partes XXXIX puncta IIII secunde XVIIII. Ex his consequens est, quoniam hec semidiametra. Simul iuncta totam zodiaci diametrum faciunt, simul autem accepta sunt partes CXXXI puncta XII secunde XXXIIII, semidiametrum zodiaci constare ex partibus LXV punctis XXXVI secundis XVII, centrumque eius ab equinoctiali centro distare partibus XXVI punctis XXXI secundis LVIII.

5. Ponemus deinde utrumque arcuum GH et GT partes XX puncta XXX secundas IX, quanta est distantia inter equinoctialem et equidistantes infra puncta tropica trigenis gradibus zodiaci, eritque arcus BT gradus CX puncta XXX secunde IX, cuius arcus corda partes XCVIII puncta XXXV secunde LIX, arcus vero BK gradus LXIX puncta XXIX secunde LI, cuius corda partes LXVIII puncta XXIII secunde LI. Hic ergo, que fuerit proportio partium XCVIII cum punctis XXXV secundis LVIIII ad partes LXVIII puncta XXIII secundas LI, eam esse necesse est linee EZ ad lineam ED atque ED ad lineam EK; unde ex partibus, que LX lineam ED metiuntur, numerari necesse est in linea EZ partes LXXXVI puncta XXIX secundas XLII, in linea vero EK partes XLI puncta XXXVIIII secundas XV.

6. Nec aliter, si ponamus utrumque arcuum GH et GT partes XI puncta XXXVIIII secundas LIX, quanta est distantia inter equinoctialem et equidistantes infra tropica puncta sexagenis gradibus, erit totus arcus BT gradus CI puncta XXXIX secunde LIX, corda eius partes XCIII puncta II secunde XIIII, arcus vero BH gradus LXXVIII puncta XX secunda I, corda eius partes LXXV puncta XLVII secunde XXIII. Quoniam igitur, que proportio est partium XCIII cum punctis II secundis XIIII ad partes LXXV cum punctis XLVII secundis XXIII, eadem linee EZ ad lineam ED atque ED ad lineam EK, necesse est ex eis partibus, que LX lineam ED conplent, lineam EZ metiri partes LXXIII puncta XXXIX secundas VII, lineam vero EK partes XLVIII puncta LII secundas XLII.

7. Quodsi et utrumque arcuum GH et GT ponamus partes LIIII, quanta est distantia ab equinoctiali equidistantium, quos tangit orizon in climate Rhodos, quod clima exempli gratia assumimus in spera corporea, erit itidem arcus BT gradus CXLIIII, corda eius partes CXIIII puncta Vll secunde XXXVII, arcus vero BH gradus XXXVI, cuius corda partes XXXVII puncta IIII secunde LV. Sic ergo, quoniam, que proportio est partium CXIIII cum punctis VII secundis XXXVII ad partes XXXVII cum punctis IIII secundis LV, eadem linee EZ ad lineam ED atque ED ad lineam EK, de partibus, que LX lineam ED faciunt, habebit linea EZ partes CLXXXIIII puncta XXXIX secundas XLVIII, linea vero EK partes XIX puncta XXIX secundas XLII. Ex his constans est, siquidem hee due linee simul iuncte diametron orizontis faciunt, cuius modo mentionem fecimus, quemadmodum diametrum zodiaci tropicorum semidiametra, eam diametrum metiri partes CCIIII puncta IX secundas XXX ex eis, que CXX diametrum equinoctialis metiuntur. Unde semidiametrum orizontis esse necesse est partes Cll puncta IIII secundas XLV centrique eius ab equinoctiali centro distantiam partes LXXXII puncta XXXV secundas III.

8. 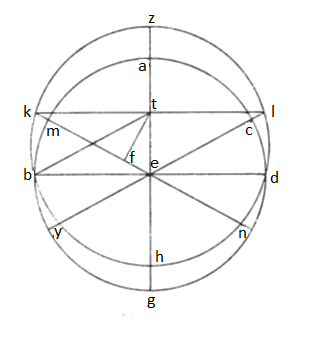His habitis deinceps metiri convenit quantitatem ortus signorum, prout accidit in spera corporea. Esto enim, ut solet, circulus equinoctialis ABGD circa centrum E, zodiacus vero ZBHD circa centrum T, diametrorum ortogonaliter super E deductorum loco meridiani circuli alterum puncta sectionum continuans B et D, que et equinoctialia, alterum per utrumque centrum GH et AZ, quorum puncta tropica H et Z. Quoniam igitur intentio nostra demonstrandi, quantum in spera recta oriatur de circulo equinoctiali cum quotlibet partibus zodiaci, orizontis autem in spera recta positio qualis circuli meridiani potentia quidem linearum rectarum per polum equinoctialis circuli, punctum videlicet E, transeuntium, que est positio circuli meridiani, constat igitur, quoniam arcus ZB et HD quadrantes sunt circuli declivis, eos oriri cum arcubus AB et GD quadrantibus equinoctialis circuli cum eisque celum mediare pariter et cum eisdem occumbere; lineam siquidem BD in circulo ABGD cum per medium secet semidiametros TH et ortogonaliter ad punctum E, equales duos arcus de zodiaco resecari necesse est, BK videlicet et DL. Perducentur itaque linee KMEN et LCEY. Quo facto, quoniam per puncta K, L et Y, N transeunt circuli equidistantes, quorum par utrimque ab equinoctiali circulo distantia, quousque punctum K potentia oppositum sit puncto N sicque punctum L puncto Y, si ponamus arcum BK signum Piscium, erit LD signum Libre, eodem modo BY loco Arietis sicque DN loco Virginis. Perducta itaque linea KTL, quoniam triangulus KTE equalium est et laterum et angulorum triangulo LTE, erit et angulus KET equalis angulo LET sicque reliqui anguli KEB et LED sicque his oppositi. Qui quoniam apud centrum equinoctialis circuli, arcus etiam eiusdem circuli sub his angulis, qui cum singulis his signis oriuntur, equos esse necesse est, ex quibus unius ad cuiusque ortum metiendum quantitatem indagari sufficiat atque, si placeat, BM. Producimus igitur super lineam KE perpendicularem TF. Quo facto, quoniam de eis, que LX semidiametron equinoctialis circuli continent, lineam quidem TK semidiametron zodiaci metiuntur partes LXV puncta XXXVI secunde XVII, lineam vero ET inter circulorum centra partes quidem XXVI puncta XXXI secunde LVIII, lineam autem EK semidiametron equidistantis circuli designati ad caput Piscium et caput Scorpionis, puncta videlicet K et L, partes quidem LXXIII puncta XXXVIIII secunde VII, notus est triangulus TKE. Si ergo comparemus ad lineam KE tetragonum TK, subtracto ei tetragono TE determinabitur augmentum linee KF super lineam EF. Quotiens enim duorum se invicem secantium circulorum maior minorem per medium secat, de maioris semidiametro in se ducto si tetragonus distantie centrorum subtrahatur, relinquitur tetragonus semidiametri minoris circuli. Hic igitur, quoniam in hunc modum declivis equinoctialem medium secat, semidiametros maioris TK in se ducta maior est tetragono TE centrorum distantie, quantum semidiametros minoris EB ex se ipsa producit, cum rectus quidem sit angulus BET et linea TB equalis linee TK. Lineam autem EB semidiametron equinoctialis circuli quoniam partes LX metiuntur, ex eisdem tetragonum eius continere necesse est ĪĪĪDC, de quibus inter supradicta lineam EK metiuntur partes quidem LXXIII puncta XXXVIIII secunde VII; ad quam si differentiam illam, tetragonum videlicet EB, comparemus, procedet augmentum linee KF super lineam FE, que sunt partes quidem XLVIII puncta LII secunde XLII. Quod cum subtractum fuerit de linea KE, relinquuntur partes XXIIII puncta XLVI secunde XXV, cuius dimidium metietur lineam FE, que sunt partes Xll puncta XIII secunde Xll, ex eis scilicet, quarum XXVI cum punctis XXXI secundis LVIII lineam et metiuntur. Ex eis itaque partibus, que fuerint in linea ET CXX, opposita scilicet recto angulo EFT, necesse est numerari in linea FE partes LV eum punctis fere LIX, arcum vero corde FE metiri gradus LV cum punctis XL ex CCCLX totius circuli rectangulum triangulum FET continentis. Ex gradibus igitur, qui fuerint in IIII rectis angulis CCCLX, continebit angulus FTE XXVII cum punctis L. Hic autem cum angulo FET angulo recto equatur, qui ipse cum angulo BEK nichilominus angulum rectum complet; subtracto igitur communi medio relinquitur angulus BEK equalis angulo FTE; metiuntur itaque angulum BEK gradus XXVII puncta L. Qui quoniam apud centrum equinoctialis circuli, et subiectum ei arcum BM metiri necesse est gradus XXVII puncta L ex CCCLX totius circuli equinoctialis. Hii sunt itaque gradus et puncta, prout in spera corporea positum est, ex gradibus equinoctialis circuli, quibus IIII signa circumposita punctis equinoctialibus in spere aplanes situ oriuntur. Possumus autem et leviori modo ad hoc pervenire. Quanta est enim KE in EN, tanta BE in ED. Est autem BE in ED partes ĪĪĪDC; quod cum divisum fuerit per lineam EK, colligetur linea EN; itaque notam esse constans est. Quam quoniam KE superat duplo linee FE, pariter et FE notam esse consequens est. Est autem et ET nota; que quoniam recto angulo apud F opponitur, erit et angulus FTE notus, angulo vidilicet KEB equalis, quem arcus BM notitia consequitur.

9. Simili exemplo metiri licet et sequentium ortum, ut si ponamus arcum declivis circuli BK arcum duorum signorum, quousque punctum K notet principium Aquarii punctumque L caput Sagittarii, quorum opposita per diametron N quidem caput Leonis, Y vero principium Geminorum. Ceteris itaque simili modo perductis remanebunt quidem KT et TE eiusdem quantitatis, linea vero KE accrescet, prout demonstratum est, semidiametron equidistantis circuli designati ad principium Aquarii et Sagittarii metiri partes quidem LXXXVI puncta XXIX secundas XLII. Si ergo differentia supra dicta, id est ĪĪĪDC, per eam lineam dividatur, colligitur augmentum linee KF super lineam FE, que sunt partes XLI puncta XXXVIII secunde XVIII. Quod ubi subtractum fuerit de linea KE, remanebunt partes XLIIII puncta LI secunde XXIIII, cuius dimidium, id est partes XXII puncta XXV secundas XLII, lineam FE terminare consequens est, ex eis videlicet partibus, quarum XXVI cum punctis XXXI secundis LVIII lineam et numerant. Ex eis itaque partibus, que CXX lineam ET recto angulo oppositam constituant, erit linea FE partium CI cum punctis XXVIII, arcus corde FE gradus CXV puncta XXVIII ex CCCLX totius circuli rectangulum triangulum FET continentis. Ex eis itaque gradibus, qui fuerint in IIII rectis angulis CCCLX, habebit angulus FTE gradus LVII puncta XLIIII. Cui equalis est angulus BEK; qui quoniam apud centrum equinoctialis circuli, et arcum BM eius quantitatis esse necesse est. Unde portione Piscium sublata portio Aquarii relinquitur partium XXIX cum punctis LIIII. Quam eandem esse et reliquorum trium eadem ab equinoctialibus punctis quantitate distantium, id est Tauri, Leonis et Scorpionis, supra data necessitate consequitur. Unde reliquum de quadrante, id est gradibus XC, reliquorum IIII, Geminorum videlicet et Cancri, Sagittarii, Capricorni, ortus quantitatem metiri consequens est.

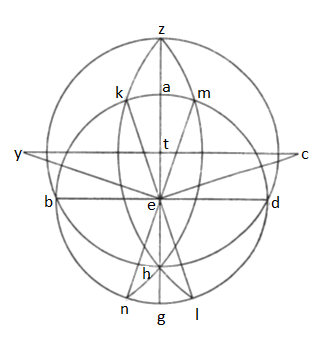10. His ita firmatis intuendum est deinceps, idemne sit ortus signorum in ipsa spera declivi, an alium exigat ratio, quam qui in spera recta constitutus est. Sequemur itaque modum exempli dati in libro Almagesti de circulo transeunte per Rhodos insulam, cuius orizonti polus septemtrionalis XXXVI gradibus ascendit, cuius semidiametron, ut inter supradicta constitutum est, metiuntur partes Cll puncta IIII secunde XLV, centrique eius ab equinoctiali centro distantia partes LXXXII puncta XXXV secunde III. Esto itaque, ut mos est, circulus equinoctialis ABGD circa centrum E, zodiacus vero ZBHD circa centrum T; quo facto intelligemus motum spere tamquam in puncto E fixo septemtrionali polo a puncto D per puncta G et B in punctum A. Intelligemus itaque primum de his orizontum circulis duos arcus transeuntes pariter per utrumque tropicum punctum, que sunt Z et H, quorum alter ZKHL, alter ZMHN. Constat igitur, cum fuerit orizontis positio, ut situs est arcus ZKHL, necessario simul oriri punctum Z et punctum K oppositaque his puncta H et L eodem momento occumbere, cum vero, ut situs est arcus ZMHN, converso, id est puncta N et H simul oriri eademque hora M et Z occumbere, dum motus spere intelligatur, qualem assignavimus, fixo videlicet in nota E polo septemtrionali. His constitutis, quoniam, ut supra dictum est, non solus zodiacus equinoctialem medium secat, verum etiam orizon omnis tam hunc quam illum, cum eos in hunc modum signaverimus, necesse est, ut linee recte puncta sectionum continuantes KL et MN transeant per centrum E; ex quo constans est, arcum GL equalem esse arcui KA sicque arcum AM equalem arcui GN; superest, ut arcus AM etiam arcui AK equalis constituatur. Figemus itaque secundum hos arcus orizontis duo centra in puncto C et puncto Y perducemusque lineas CT et TY sicque CE et YE. Quoniam igitur, quotiens duo circuli se invicem secant, si lineam puncta sectionum continuantem centra continuans linea producta secet, necesse est per equalia et ortogonaliter secare, unam et rectam esse lineam CTY consequens est lineam ZH medio et ortogonaliter secantem. Nec aliter CE perpendicularis KL sicque YE perpendicularis MN. Sunt igitur utrique trianguli circa ET inter C et Y tam lateribus quam angulis, prout sese respiciunt, equales, angulus vidilicet CET angulo yet. Sunt autem et anguli YEM atque CEK ut qui recti equales; unde residuos quoque angulos, videlicet AEM atque AEK equos esse consequens est, sicque et arcus AM atque AK equales esse manifestum est sicque LG atque GN ipsique utrique utrisque. Quoniam igitur arcus HB oritur cum arcu NB sicque arcus BZ cum arcu BK, qui equalis BN, rursumque arcus ZD cum arcu KD atque arcus DH cum arcu DN, qui equalis DK, ex his constat, arcus declivis circuli, ut equaliter utrimque ab equinoctialibus punctis distant, equali oriri quantitate. Amplius, quoniam arcus BZ decrescit ab ortu suo recte spere quantitate arcus KA, oppositus vero arcus DH tanto acrescit, quantus est arcus GN, equalis videlicet KA, estivusque tropicus punctus H, constans est, signa circa vernale equinoctium tanto quidem ab ortu suo recte spere decrescere, quanto opposita his ortum suum spere superant. Unde consequens est minimum eius climatis diem tanto equinoctiali die minorem, quantum conficiunt utrique arcus AK et GN, maximumque tanto maiorem.

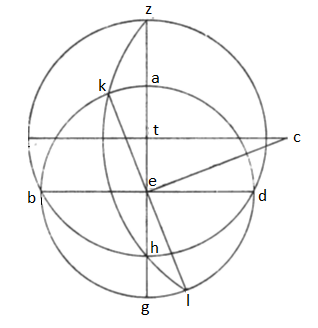11. His quoque cognitis videndum in primis in hoc climate, utrumne dierum eius differentia, quam exposuimus, concordet ei, que in spera corporea accidit. Describemus igitur huiusmodi figuram in eaque ut ante orizontem per puncta Z, K, H, L singulariter. Ut ergo, quod intendimus, deprehendamus, quantitatem videlicet arcus AK, figemus ut ante centrum orizontis in puncto C perducemusque lineas CT et CE perpendiculares lineis ZH et KL. Quoniam igitur, ut constitutum est, lineam CE distantiam scilicet centrorum equinoctialis circuli atque orizontis eius climatis metiuntur partes LXXXII puncta XXXV secunde III ex partibus videlicet, quarum lineam ET, distantiam scilicet centrorum equinoctialis et zodiaci, continent XXVI puncta XXXI secunde LVIII, ex partibus, quarum in linea EC recto angulo opposita numeramus CXX, erunt partes XXXVIII puncta XXXIII; cuius corde arcus graduum XXXVII cum punctis XXX ex CCCLX gradibus totius circuli triangulum ECT continentis. Ex gradibus itaque CCCLX, quos in IIII rectis angulis numeramus, continebit angulus ECT gradus XVIII puncta XLV, angulus vero CET rectum cum hoc perficiens gradus LXXI cum punctis XV. Necesse est igitur et angulum AEK constare ex gradibus XVIII punctis XLV, unde et arcum AK eiusdem esse quantitatis consequens est. Metiuntur igitur ortum utriusque quadrantis a vernali equinoctio gradus LXXI puncta XV, ab autumnali vero gradus CVIII puncta XLV; unde dierum longissimi et brevissimi ab equinoctiali die differentia graduum XXXVII cum punctis XXX, que sunt equales horæ II et semis, prout in spera corporea constitutum est.

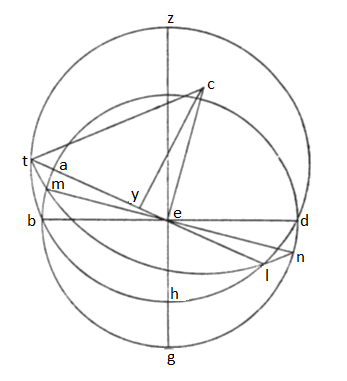12. Deinceps igitur ad metiendum signorum ortum in hoc climate constituemus item equinoctialem circulum ABGD circa centrum E, zodiacum vero HDZB. Quo facto de zodiaco resecabimus arcum BT, primumque ad mensuram unius signi, quod Pisces esse constans est, continuabimus[que] TEL lineam rectam pariterque circinabimus circulum orizontis latitudine graduum XXXVI ut ante per puncta T et L transeuntem atque equinoctialem ad puncta M et N secantem perducemusque et lineam NEM sicque et a centro orizontis ut ante locato C lineas rectas CE et CT, postremo et perpendicularem linee TL, lineam videlicet CY. Est igitur, ut supra dictum est, arcus AM ea differentia, qua Aries et Pisces utrumque in hoc climate decrescit ab ortu suo recte spere, eademque, qua oppositorum his utrumque super ortum suum spere applanes accrescit. Constat autem et lineam ET semidiametron equidistantis circuli designati ad caput Piscium partium quidem LXXIII cum punctis XXXIX secundis VII ex eis scilicet, quarum lineam EC, centrorum videlicet distantiam, continent partes LXXXII puncta XXXV secunde Ill. Quoniam igitur augmentum tetragoni TC super tetragonum EC in partibus ĪĪĪDC, is numerus si per lineam ET dividatur prosequamurque sequentia per ordinem quemadmodum in spera recta, colligemus lineam EY ut ante partium XII cum punctis XXII secundis XII. Ex partibus vero, quarum in linea EC recto angulo opposita numeremus CXX, habebit linea EY partes XVIII et fere punctum; cuius corde arcus graduum XVII cum punctis XVI ex CCCLX totius circuli triangulum ECY continentis. Ex gradibus igitur, quos in IIII rectis angulis numeremus CCCLX, habebit angulus ECY gradus VIII puncta XXXVIII; qui quoniam equalis angulo TEM, metiuntur et arcum AM gradus VIII puncta XXXVIII ex CCCLX totius circuli equinoctialis. Quoniam igitur, ut supra dictum est, unumquodque de IIII signis circa puncta equinoctialia in spera aplanes oritur cum gradibus XXVII punctis L, cum de hac summa hos gradus VIII cum punctis XXXVIII subtraxerimus, relinquetur numerus ortus Arietis ortusque Piscium in hoc climate, gradus scilicet XVIIII puncta XII; si vero eosdem gradus VIII cum suis punctis supra posite summe adiciamus, accrescet numerus ortus Virginis ortusque Libre, gradus videlicet XXXVI puncta XXVIII.

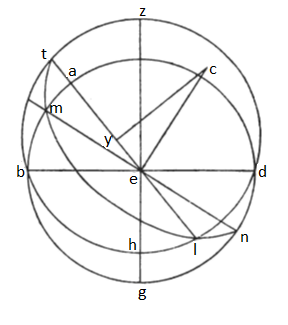13. Simili exemplo metiri licet et sequentium ortum, ut si resecemus arcum BT ad quantitatem duorum signorum, Piscium scilicet et Aquarii, quousque et cetera superiori modo perficiantur. Unde lineam et utpote semidiametron equidistantis circuli designati ad caput Aquarii accrescere necesse est, quousque partes quidem LXXXVI puncta XXIX secundas XLII contineat; per quam ubi diviserimus supra dictam differentiam ĪĪĪDC sequentiaque per ordinem supradicto modo expleverimus, colligemus ut ante lineam EY partium XXII cum punctis XXV secundis XLII. Ex partibus igitur, quas in linea EC recto angulo opposita numeremus CXX, continebit linea EY partes XXXII puncta XXXVI; cuius corde arcus gradus XXXI puncta XXXII ex CCCLX totius circuli triangulum rectangulum ECY continentis; ex gradibus igitur, quos CCCLX in IIII rectis angulis numeremus, habebit angulus ECY gradus XV puncta XLVI qui quoniam equalis angulo TEM, metientur et arcum AM gradus XV puncta XLVI, augmentum videlicet ortus horum duorum signarum super ortum eorum in spera aplanes, quem, ut supra dictum est, metiuntur gradus LVII puncta XLIIII. De qua summa ubi gradus XV puncta XLVI subtraxerimus, relinquitur ortus Piscium simul et Aquarii graduum XLI cum punctis LVlll; unde portione Piscium dempta relinquitur ortus Aquarii in gradibus XXII punctis XLVI. Quodsi predicte summe eos gradus XV cum suis punctis adiciamus, accrescet ortus Leonis simul et Virginis graduum LXXIII cum punctis XXX. Unde portione Virginis dempta relinquitur ortus Leonis graduum XXXVII cum punctis II. Constat autem, Taurum equaliter oriri Aquario sicque Scorpionem Leoni; nam Geminos et Capricornum in residuis temporis spatiis sui utrumque quadrantis, quoniam et Cancer atque Sagittarius in sui utrumque quadrantis temporis spatiis residuis oriuntur, que sunt Geminorum quidem et Capricorni gradus XXIX puncta XVII, Cancri vero et Sagittarii gradus XXXV puncta XV ex CCCLX equabilis circuli gradibus in IIII videlicet climate Rhodos insule, quod medium habitabilium climatum exempli causa in spera corporea assumimus ceteris imitatione eius ad eundem modum constituendis.

14. Superior tractatus particula de circulis equidistantibus recto usque ad signorum ortum continet; huius series habet equidistantes zodiaco, quousque assignent loca stellarum fixarum, qua ratione ea contineat id, quod in horoscopio instrumento aranea vocatur. Assumimus igitur ex descriptis circulis eum, qui extrinsecus ambiens omnes alios infra se continet, eumque describimus notis A, B, G, D circa centrum E loco circulorum meridianorum; cuius diametra ortogonaliter se invicem secantia AG et BD. Quo facto resecamus a puncto D arcum DZ, cuius quantitas ad mensuram distantie a circulo equinoctiali circuli equidistantis ei descripti ex parte poli australis in spera corporea; 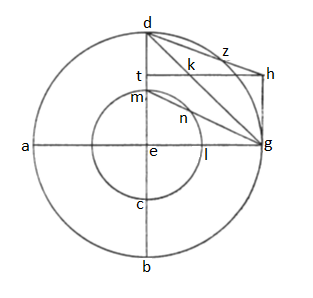producimus deinde lineam a puncto G equidistantem linee ED terminatam notis G, H, descendetque pariter ex puncto H supra lineam ED perpendicularis HT; applicabit etiam G cum D lineam HT transiens ad punctum K. Dico igitur, quod, si de linea EG recidamus equum TK idque ad punctum L, describamusque circa E centrum ad mensuram EL circulum CLM, erit distantia ABDG a circulo CLM designata ad quantitatem arcus similis arcui DZ. Quod ut plane constet, applicabit G cum M secans circulum CLM ad punctum N, eritque arcus MN similis arcui DZ, sicque arcus GZ reliquus de quadrante sui circuli est similis arcui LN remanenti de quarta circuli; quod ita plane sumi potest. Est enim, quanta DE ad lineam EG, tanta DT ad lineam TK. Est autem DE equalis EG; est igitur et DT equalis TK. At vero TK equalis EM; ergo EM equalis TD. Accepta igitur TM in commune medium erit et equalis MD. Extitit autem et equalis et equidistans GH; sic igitur et MD equidistans et equalis est eidem GH; unde et HD atque GM et equales et equidistantes esse necesse est. Est igitur angulus GME equalis angulo ZDE; unde arcum CLN arcui BGZ similem esse consequitur, sicque et residuum residuo de semicirculis, id est MN ei qui est ZD, similem esse consequens est. Si ergo circulus CLM statuatur equinoctialis, erit circulus ABGD designatus ab eo ad distantiam arcus LN arcui GZ similis.

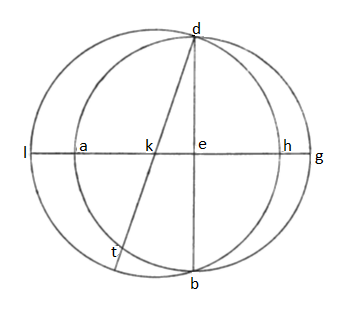15. Deinceps convenit propositum insequi, designandi videlicet circulos, quorum habitudo ad zodiacum, qualis eorum, qui descripti sunt, ad equinoctialem, quousque pateat nobis positio stellarum habitudine earum ad hunc circulum preter eam que ad equinoctialem. Esto enim primo loco circulus equinoctialis de circulis planisperii descriptus notis A, B, G, D circa centrum E, zodiacus vero LBHD circa centrum K, linea recta per utrumque centrum transiens LAHG, sectiones vero circulorum continuans linea BED. Resecamus itaque arcum BT ad quantitatem arcus distantie inter polum equinoctialis circuli et polum zodiaci; transibit et linea per DKT, punctum vero K potentia erit polus zodiaci. Constat igitur, quod, si hec distantia statuto terminetur compoto, circulus ab hoc puncto per gemina zodiaci puncta per diametron opposita transiena secet etiam equinoctialem circulum per medium; constat enim, omnem circulum, qui alterutrum horum per diametron secuerit, et alterum necessario per diametron secare; eritque circulus hic magnus ille ambiens utrumque ortogonaliter intercipiens.

16. Nunc equidistantium zodiaco in planisperio descriptio notanda. Describimus itaque circulum meridianum per utrumque polum transeuntem ABGD circa centrum E, axem intelligibilem lineam DEB, punctum D polum australem intelligentes, diametron equinoctialis circuli AEG, diametron circuli equidistantis zodiaco ZHT, quem in planisperio describere propositum sit. Deducimus itaque per punctum H lineam equidistantem linee AG notis K, L terminatam, lineas DMZ et DCL atque DNT continuantes. Dico igitur, circulum, cuius diametros ZT, designari posse circa diametron MN. Probatio eius. Continget enim hinc inde circulos duos equidistantes equinoctiali, quorum ab eo distantia in quantitate arcuum AZ et GT; et idcirco describemus istos duos circulos cum duabus longitudinibus EM, EN; et ipse secabit etiam circulum equidistantem equinoctiali, cuius diametros LK, per medium apud circulum meridianum, cuius diametros BD, quem ad quantitatem CE describimus inter n 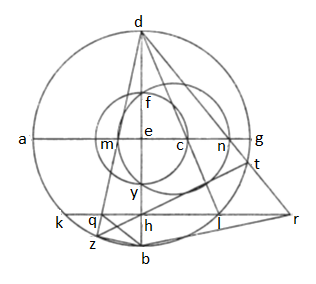otas C, Y, F, quem per medium secabit circulus circa MN descriptus per puncta Y, F transiens et dividet circulum CY in duas medietates, sicut contingit in spera corporea. Applicabunt igitur linee recte B cum Z et B cum Q procedent et KL atque DT in directum, quousque concurrant ad punctum R, quod postremo cum B applicabit. Quoniam igitur anguli duo BZD et BHQ recti sunt, consequens est puncta B, H, Z, Q super circumferentiam circuli locata; unde angulum BQH equalem esse necesse est angulo BZH, qui equalis est angulo BDT, quorum eedem bases; sic igitur angulus BQR equalis est angulo BDR, unde puncta B, D, R, Q super circumferentiam circuli locata constans est. Est igitur, quantum BH in HD, tantum RH in HQ ducta. Quantum vero BH in HD, tantum est, quod HL ex se ipsa producit; est ergo, quantum HL in se ipsam ducta, tantum RH in HQ. Est autem RQ equidistans linee NM; est igitur, quanta EM in EN, tanta EC in se ipsam ducta. Que quoniam equalis est linee EY et EF, puncta N, Y, M, F super circumferentiam circuli locata esse consequens est.

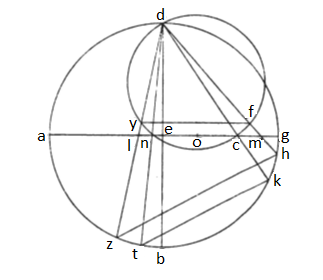17. Circulorum equidistantium zodiaco in hunc modum designatorum diversa semper esse centra necesse est. Sit enim ut ante circulus meridianus ABGD circa centrum E, axis linea BED, diametros circuli equinoctialis linea AG, diametra circulorum equidistantium zodiaco linee ZH et TK; producentur et linee DLZ, DMH, DNT, DCK. Designamus deinde circa triangulum DNC circulum DYF perductaque linea YF dividemus lineam LM per medium apud punctum O. Cum igitur constans sit, circulum, cuius diametros ZH, describi posse circa diametron LM sicque circulum, cuius diametros TK, circa diametron NC, dico, hos duos circulos nequaquam eiusdem esse centri, id est punctum O minime in diametro NC medium esse. Quoniam enim arcus ZT equalis est arcui KH, erit et arcus YN equalis arcui CF; unde linee LM et FY equidistantes. Igitur, que proportio linee DL ad lineam LY, eadem linee DM ad MF. At vero, que proportio linee DL ad LY, eadem linee DL in se ducte ad DL in LY ductam, eademque linee DM in se ducte ad DM in MF ductam, que DM ad MF lineam proportio. Quoniam itaque loco circuli DL in LY equalis est LC in LN sicque DM in MF equalis NM in CM, erit, que proportio DL in se ducte ad CL in LN, eadem linee DM in se ipsam ad MN in CM; permutatim igitur, que proportio tetragoni DL ad tetragonum DM, eadem superficiei ex CL et LN producte ad superficiem ex NM et CM constitutam. Est autem tetragonus DM maior tetragono DL, prout DM longior quam DL; sic ergo NM in CM maior quam NL in LN. Cum igitur commune medium NC maius sit cum CM in MC quam cum NL in LN, maiorem esse CM quam NL constans est. Data vero est MO equalis LO; minorem igitur esse OC quam ON consequens est. Nec ergo punctum O in diametro NC medium esse possibile est; quod cum medium datum sit in diametro ML, circulorum equidistantium zodiaco idem esse centrum impossibile est.

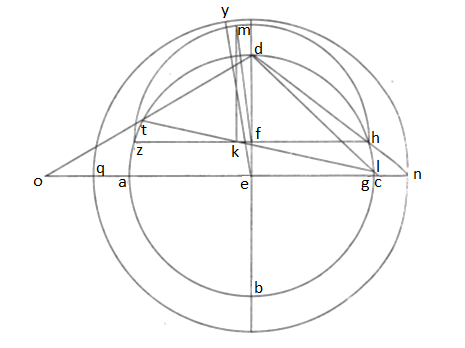18. Deinceps, quoniam circulus equidistans zodiaco nec in planisperio descriptus nec in spera designatus, cuius portio in parte non apparente secat equidistantes circulo recto circulos non apparentes penes polum australem, quorum distantia a zodiaco aut a capite Cancri minus altitudine eius in loco definito aut a capite Capricorni minus eius altitudine in loco determinato, ponemus circulum meridianum ABGD circa centrum E. Intelligemus itaque punctum D polum australem, axem vero DB, diametron circuli equinoctialis AG, diametron circuli equidistantis ei numquam apparentis lineam ZH, diametron circuli hunc secantis de equidistantibus zodiaco lineam TKL. Quibus ita positis designamus supra lineam ZH semicirculum ZMH erigimusque lineam a puncto K in M equidistantem linee DE. Ex quo itaque, si produxerimus lineas AGN et DHN atque DLC, erit circulus, qui describatur ad quantitatem EN inter notas N, Y, Q, de circulis planisperio perpetuo negatis. Circulus vero, qui describatur vice circuli, qui super lineam TKL, transire necesse habet per punctum C circulum NYQ secans in arcus similes arcubus HM et MZ, cum sit linea KM commune medium superficiebus eorum. Applicet igitur F cum M, fiatque ad punctum E super lineam EA angulus equalis angulo MFK, qui sit angulus AEY; unde linea producta in punctum Y perveniens arcum YQ similem arcui MZ demonstret. Est itaque circulus designatus vice circuli, qui super lineam TKL equidistans zodiaco, cuius distantia ab equinoctiali in quantitate arcus GL, perpetuo latentes circulos recto equidistantes huiusmodi similitudine secans. Hoc circulo tamquam in descriptione figure apposito intelligendum est, ut per C et Y transiens in opposito punctum O deprehendat, qua DT et EA in directum producte concurrunt ea ratione, qua DH et EG ad punctum N conducit.

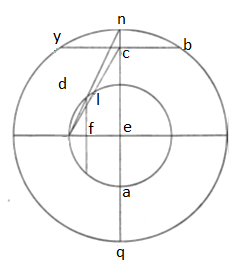19. Similis descriptionis exemplo nichilominus concipi potest et circulus equidistans zodiaco, qui supra diametron DL, ut DL producamus ad latitudinem, quam diximus. Usque ad punctum C educimus, deinde a puncto C lineam CB perpendicularem linee AEN, que linea in planisperio locum optinet circuli, cuius diametros DL, cum omnes linee recte a puncto D educte vice horum circulorum in eadem sint planicie, que planicies est circuli; cuius planiciei atque planiciei circuli equinoctialis commune medium linea BCY. Planicies quoque circuli meridiani, que super lineam FD, eadem et super utramque illarum planicierum ortogonaliter.

20. Hac itaque ratione convenit in planisperio fieri constitutionem eorum que in spera corporea circulorum, videlicet quorum inventio causa circuli equinoctialis, qui eorum equidistantes ei, qui etiam circuli meridiani, circulorum quoque, quorum inventio causa zodiaci, et qui eorum equidistantes ei, qui etiam orizontis; tum quidem in huiusmodi constitutione polus equinoctialis circuli centri locum optinet et ipsi circulo recto et cunctis recto equidistantibus. Que ratio cogit septemtrionales semper esse minores, australes semper maiores, illos quidem decrescendo ut in spera, hos vero crescendo conversa vice atque in spera, partier et meridianos omnes in rectum extendens. Polus autem zodiaci neque ipsi centrum est neque ulli equidistantium ei; quibus id evenit, quod unus eorum sine centro est, id est linea fit recta. In circulis vero magnis per hunc polum transeuntibus aliter; transeuntes enim per utrumque polum recte fiunt linee, in quibus centra equidistantium zodiaco locantur minime equalium. Unde in assignatione stellarum utrumlibet fiat positio habitudine ad circulum equinoctialem sive habitudine ad zodiacum, in utraque et equinoctialem et zodiacum dividimus; sed si fuerit habitudine ad equinoctialem, dividemus cum ipso pariter et equidistantes ei, si vero habitudine ad zodiacum, cum ipso etiam equidistantes ei. Utrumlibet itaque fiat, positionem stellarum assignat; certissimum autem inter hec, ut utroque modo adequetur, quod fit in spera corporea; determinatis videlicet eis, quorum inventio propter circulum equinoctialem, hii, qui propter zodiacum adhibentur, ad exemplum fiant, quantum fieri potest, propinquum Egipto. Nec est necesse omnia in planisperio exsequi, observatis tantum circulis transeuntibus gradus binos vel ternos aut etiam senos in positione scilicet mediocri; qui numeri comunes, trigenis videlicet signorum gradibus atque XXIIII fere distantie gradibus, que inter equinoctialem et utrumque punctum tropicum, quousque incidant cum ipsis circulis tropicis et cum circulis meridianis signa distinguentibus.