بسم ﷲ الرحمن الرحيم وصلّى ﷲ على محمّد

كتاب بطلميوس من اهل قلاوذية

في تسطيح بسيط الكرة

قال

[١]

إنّه لما كان من الممكن، يا سورا، وممّا ينتفع به في ابواب كثيرة أن يوجد في بسيط مسطح الدواير التي تقع في الكرة المجسمة كأنّها مبسوطة، رايت أنّ ممّا يجب في حق العالم أن اكتب لمن اراد معرفة ذلك كتابًا بايجاز ابيّن فيه على ايّ وجه يمكن أن ترسم دايرة الفلك المايل، والدواير الموازية لدايرة معدل النهار، والدواير المعروفة بدواير نصف النهار، على ما يصير به جميع ما يعرض في ذلك موافقًا لما يظهر في الكرة المجسمة.

وقد يتهيّأ لنا هذا الغرض الذي قصدنا له متى استعملنا مكان دواير نصف النهار خطوطًا مستقيمة، ورتّبنا الدواير الموازية لدايرة معدل النهار ترتيبًا يتهيّأ به اولا أن تكون الدواير العظيمة المرسومة من الدواير المايلة المماسة للدواير الموازية لدايرة معدل النهار، التي بعدها عن جنبتيها بعد سوا، تقطع ابدًا دايرة معدل النهار بنصفين. ويلتأم لنا ذلك على هذه الصفة.

نضع دايرة معدل النهار دايرة ا ب ج‍ د، وأنّها حول مركز ه. ونخط فيها قطرين، يتقاطعان على زوايا قايمة، وهما خط ا ج‍ وخط ب د. ونتوهّم هذين الخطين مكان دواير نصف النهار. وأنّ نقطة ه القطب الشمالي، لأنّ القطب الاخر لا يمكن وضعه في بسيط مسطح، اذ كان بسيطه يمتدّ الى ما لا نهاية له، كما سنبيّن ذلك فيما بعد. واذا كان القطب الشمالي هو الظاهر في بلداننا دايمًا، فالأولا أن نستعمله خاصّة فيما نريد رسمه.

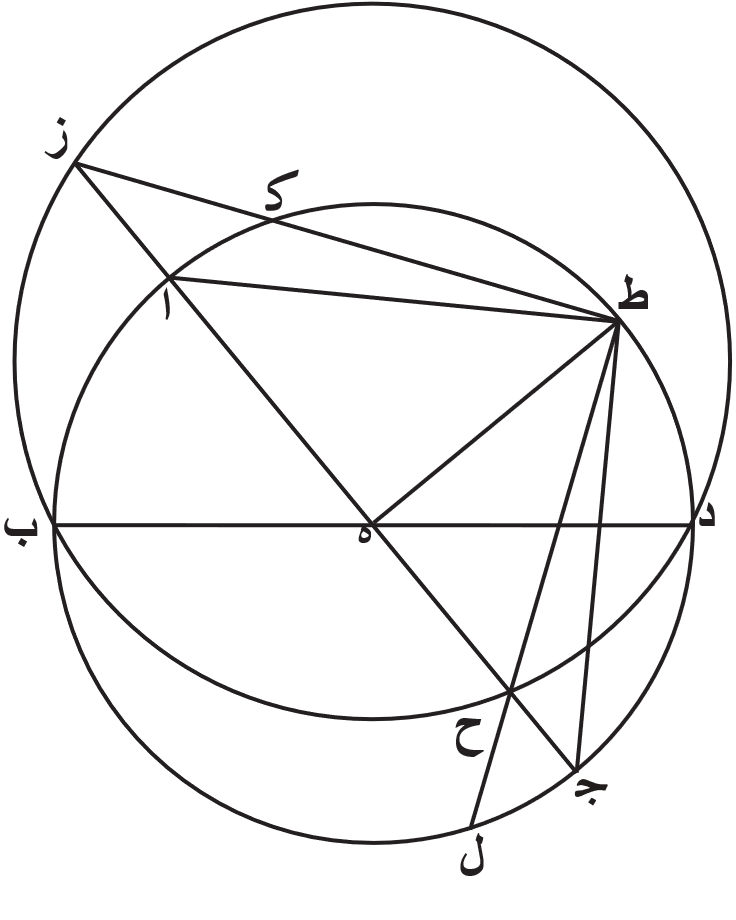
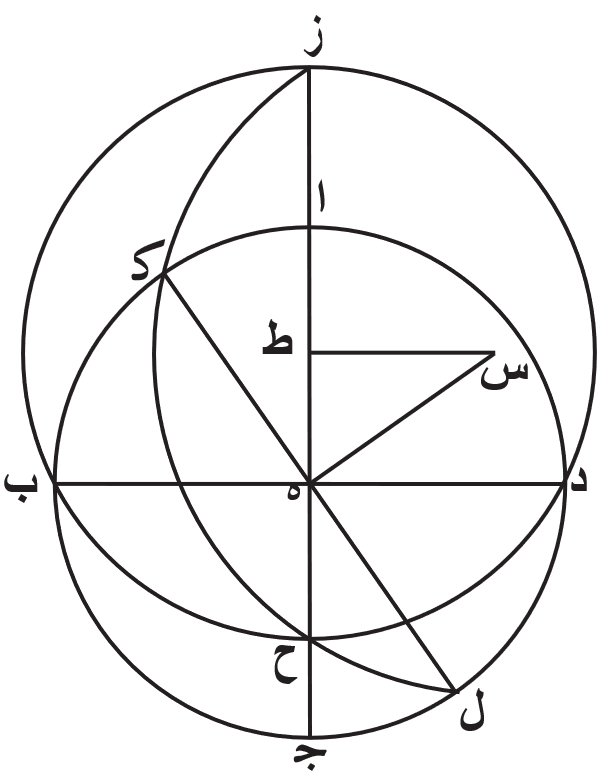
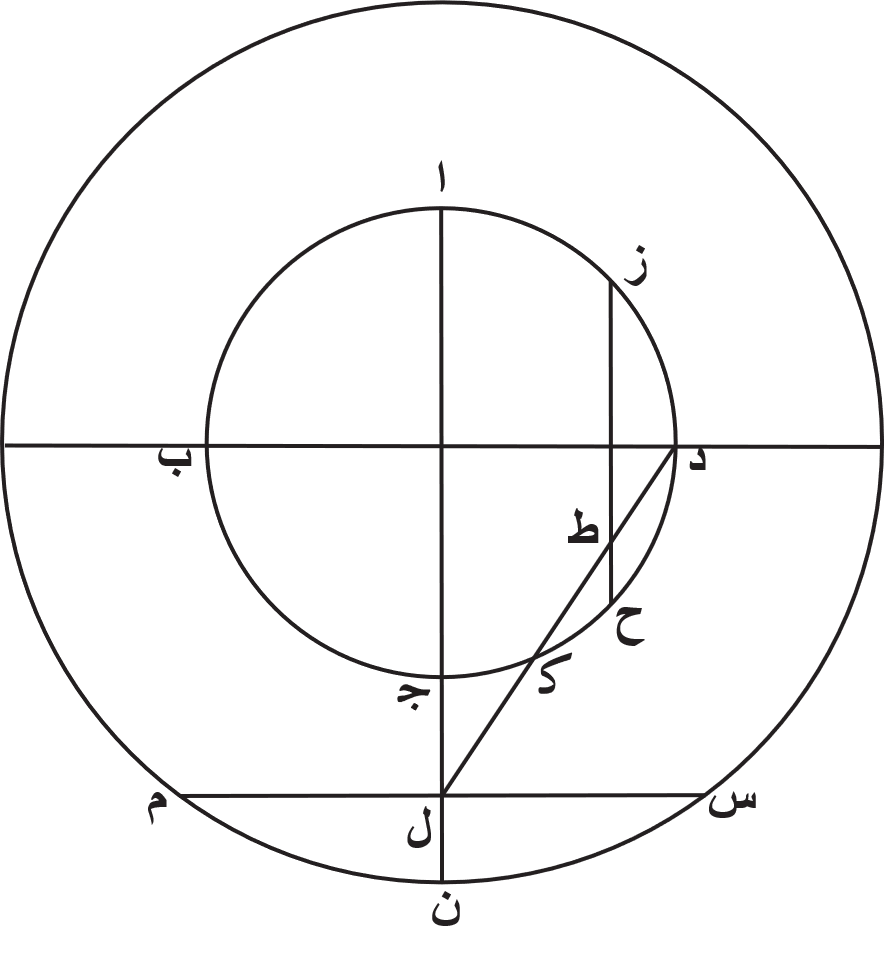
ومن البيّن أنّ الدواير الموازية لمعدل النهار، التي هي اميل الى الشمال من دايرة معدل النهار، ينبغي أن ترسم داخل دايرة ا ب ج‍ د، والدواير الموازية، التى هي اميل الى الجنوب، يجب أن ترسم خارجًا عنها. فنخرج خطي ا ج‍ ب د، ونفصل من الدايرة عن جنبتي نقطة ج‍ قوسين متساويتين، وهما ج‍ ز ج‍ ح. ونصل خط د ط ز وخط د ح ك. ونجعل نقطة ه مركزًا، ونرسم ببعد خط ه ط وببعد خط ه ك دايرة ط ل ودايرة ك م.

فاقول إنّ هاتين الدايرتين هما نظيرتا الدايرتين من الدوير التي في الكرة المجسمة عن جنبتي دايرة معدل النهار، بعدهما منها بعد سوا، وأنّ دايرة الفلك المايل، التي ترسم على مركز يقطع خط ط م بنصفين حتى تماس هاتين الدايرتين على نقطة ط وعلى نقطة م، تقسم دايرة ا ب ج‍ د بنصفين، اعني أنّها تمر بنقطة ب ونقطة د. برهان ذلك أن نصل خط د ن م، فلأنّ قوس ا ن مساوية لقوس ج‍ ح، التي هي مساوية لقوس ج‍ ز، تكون قوس ن د ز نصف دايرة. فزاوية م د ط اذًا قايمة، والدايرة التي ترسم على قطر ط م من مثلث م د ط القايم الزاوية تمر بنقطة د. فهي اذًا تقسم دايرة معدل النهار بنصفين.

فقد تبيّن من ذلك أنّا في جميع الدواير الموازية لمعدل النهار اذا فصلنا عن جنبتي نقطة ج‍ قسيًا يكون مقدارها بحسب بعد كل واحد من هذه الدواير من دايرة معدل النهار، ووصلنا اطراف القسي بنقطة د بخطوط مستقيمة، وجعلنا ما تفصله الخطوط المستقيمة من خط ه ك ابعادًا، وجعلنا نقطة ه مركزًا، وادرنا دواير، كان القياس في ذلك على هذا المثال الذي وضعناه.

ومن البيّن أنّا وإن وضعنا كل واحدة من قوسي ز ج‍ ج‍ ح ثلثًا وعشرين درجة واحدى وخمسين دقيقة بالتقريب، بالدرج التي بها دايرة معدل النهار وهو دايرة ا ب ج‍ د ثلثماية وستين درجة، وهي البعد فيما بين دايرة معدل النهار وبين كل واحدة من دايرتي المنقلبين في الدايرة المرسومة على قطبي دايرة معدل النهار، كانت دايرة ط ل، من الدايرتين المرسومتين على نقطة ط وعلى نقطة م، دايرة المنقلب الصيفي ودايرة ك م دايرة المنقلب الشتوي. وعلى هذا المثال تكون الدايرة المرسومة على نقطة م ونقطة ب ونقطة ط ونقطة د، وهي الدايرة التي تمر في وسط البروج، تماس دايرتي المنقلبين على نقطة ط، وهي المنقلب الصيفي، وعلى نقطة م، وهي المنقلب الشتوي، وتقسم دايرة معدل النهار بنصفين على نقطّي ب د. فتكون نقطة ب نقطة الربيع، ونقطة د نقطة الخريف، لأنّ حركة الكل إنّما هي كأنّها من نقطة ب نحو نقطة ا ثم الى نقطة د.

الّا أنّ قسمة دايرة الفلك المايل الى البروج لا يمكن أن تقع على قسي متساوية ولا قسمته الى اربعة اجزا ايضًا تقع على قسي متساوية كلها. لكن إنّما قسمته على ما ينبغي على هذا المثال فقط، اعني أن تجعل أوايل البروج على النقط التي عليها تقسم الدواير الموازية لمعدل النهار، التي ترسم بالطريق الذي قد أوضحنا على البعد الموافق لبعد كل واحد من البروج من دايرة معدل النهار في الكرة المجسمة، دايرة فلك البروج. فأنّ بهذه الدرجة وحده تكون جميع الخطوط المستقيمة التى تجاز على قطب ه مكان دواير نصف النهار تمر من دايرة الفلك المايل على الاجزا التى هي نظاير الاجزا المتقابلة على القطر في الكرة المجسمة.

[٢]

وتكون جميع دواير الافق، التى ترسم على مثل ما رسمت دايرة الفلك المايل، ليس إنّما تقسم دايرة معدل النهار فقط بنصفين، لكنّها تقسم ايضًا دايرة فلك البروج بنصفين بالقوة، اعني أنّها ايضًا ترسم على الاجزا التي هي بالقوة نظاير الاجزا المتقابلة على القطر في الكرة المجسمة.

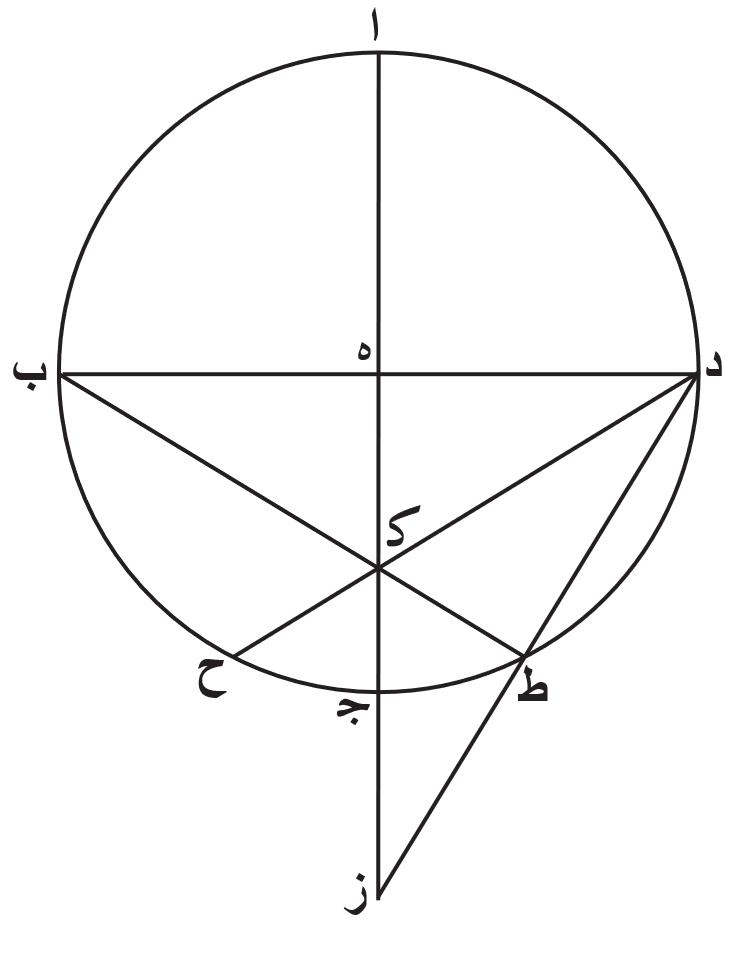
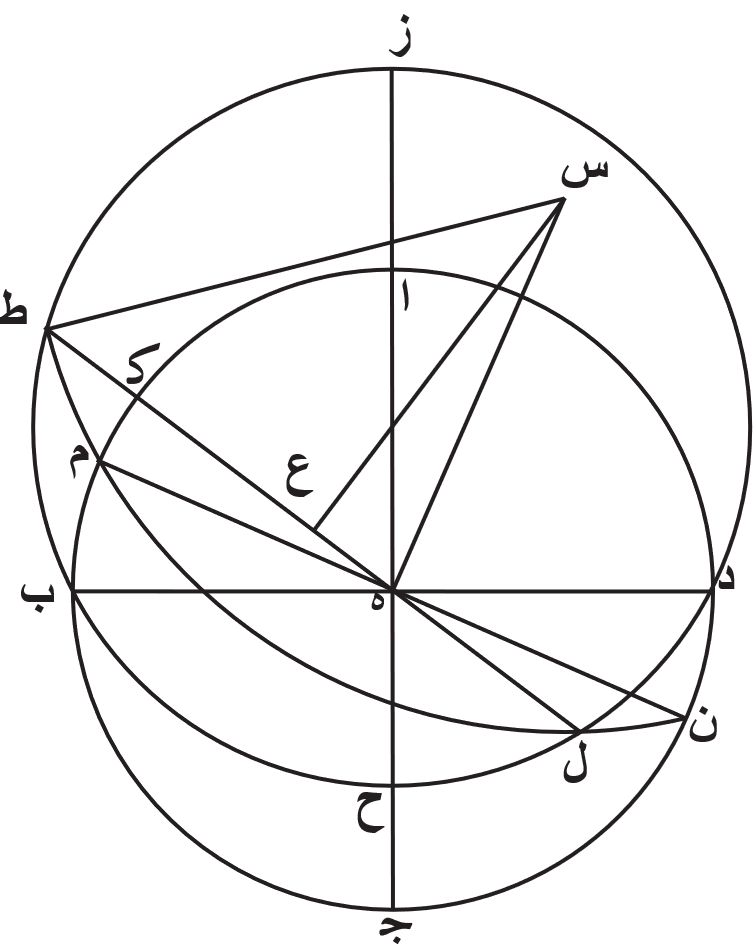
فلتكن دايرة معدل النهار دايرة ا ب ج‍ د حول مركز ه. والدايرة التي تمر في وسط البروج دايرة ز ب ح د، وتقطع دايرة معدل النهار بنصفين على نقطة ب ونقطة د. ونجيز على قطب ه مكان دايرة نصف النهار خطًا مستقيمًا، كيف ما وقع. وليكن خط ز ا ه ح ج‍.

فاقول إنّ نقطّي ز ح نظيرتان للنقطّين اللتين هما متقابلتان على القطر في الكرة المجسمة، اعني أنّ الدواير الموازية لدايرة معدل النهار التي ترسم على هاتين النقطّين تفصل قوسين متساويتين عن جنبتي دايرة معدل النهار على المثال الذي وصفناه، كما أنّ ذلك شي يعرض في الكرة المجسمة ايضًا.

برهان ذلك أن نخرج من نقطة ه خطًا مستقيمًا على زوايا قايمة على خط ا ج‍، وهو خط ه ط. ونصل خط ا ط وخط ج‍ ط وخط ز ك ط وخط ط ح ل. فمن البيّن أنّ زاوية ا ط ج‍ قايمة، وذلك أنّ قوس ا ط ج‍ نصف دايرة. ولأنّ ضرب خط ز ه في خط ه ح مثل ه د في مثله، اعني أنّه مثل ه ط في مثله، تكون نسبة خط ز ه الى خط ه ط كنسبة خط ه ط الى خط ه ح. [ف‍]يكون مثلث ز ط ح ايضًا قايم الزاوية، وزاوية ز ط ح هي القايمة. فزاوية ز ط ل اذًا مساوية لزاوية ا ط ج‍. فاذا سقطنا زاوية ا ط ح مشتركة، صارت زاوية ك ط  الباقية مساوية لزاوية ح ط ج‍ الباقية. فقوس ك ا ايضًا مساوية لقوس ج‍ ل. فقد بيّنّا أنّ خطي ط ك ز ط ل لما وصلا بطرفي القوسين اللتين بعدهما من دايرة معدل النهار بعد سوا، وكان مخرجهما من النقطة التي بعدها من نقطة ا ونقطة ج‍ الربع، وهي نقطة ط، اخذنا في خط ز ج‍ نقطة ز ونقطة ح، وهي النقط التي عليها ترسم الدايرتين الموازيتين لدايرة معدل النهار اللتين بعدهما عنها بعد سوا. ولذلك، يكون خط ز ه ح قد مرّ بالنقط التي هي بالقوة على قطر دايرة الفلك المايل.

[٣]

واقول إنّا وإن رسمنا دايرة اخرى مايلة عن دايرة معدل النهار مكان دايرة الافق حتى تكون هذه الدايرة تقسم دايرة معدل النهار وحدها بنصفين، كان موضعا تقاطع هذه الدايرة والدايرة التي تمر في وسط البروج متقابلتين على القطر بالقوة، اعني أنّ الخط الذي يصل بينهما يمر بمركز دايرة معدل النهار.

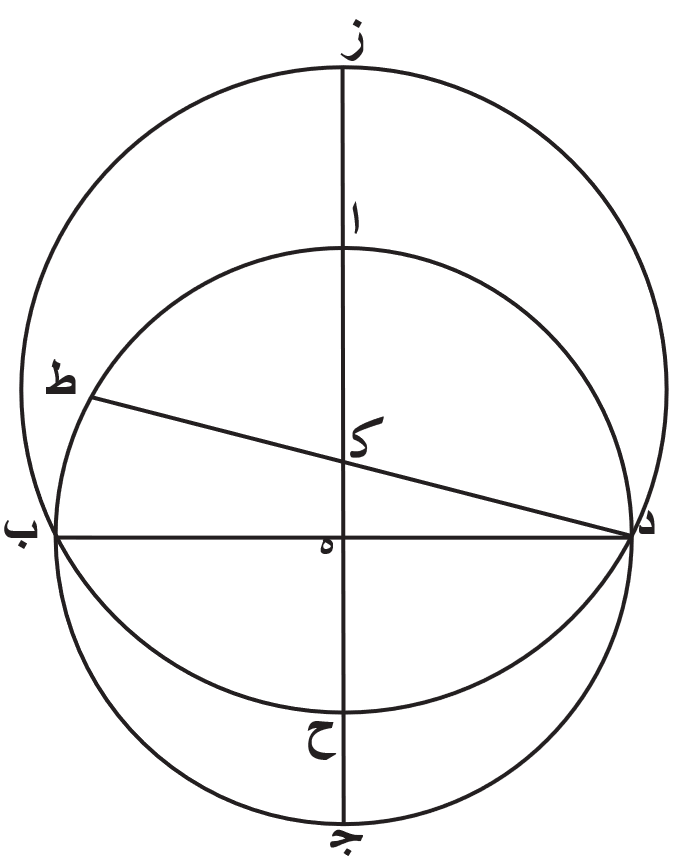
فلتكن ايضًا دايرة معدل النهار دايرة ا ب ج‍ د حول مركز ه، ودايرة فلك البروج دايرة ح ب ط د، ولتقسم دايرة معدل النهار بنصفين على قطر ب ه د. ودايرة الافق دايرة ح ا ط ج‍، وتقسم هذه الدايرة ايضًا دايرة معدل النهار بنصفين على قطر ا ه ج‍. وليكن التقاطع المشترك لدايرة فلك البروج ودايرة الافق نقطة ح ونقطة ط. فاقول إنّا إن وصلنا نقطة ح بمركز ه بخط مستقيم مكان دايرة نصف النهار، وأخرجنا ذلك الخط على الاستقامة، صار الى نقطة ط. برهان ذلك أنّا نصل خط ح ه، ونخرجه على الاستقامة حتى يقطع دايرة الافق، وهي دايرة ح ا ج‍، على نقطة ط. فاقول أنّ نقطة ط مشتركة لدايرة فلك البروج ايضًا، وهي دايرة ح ب ط د. فلأنّه قد اخرج في دايرة ح ا ط ج‍ خطا ح ط ا ج‍ متقاطعان على نقطة ه، يكون خط ح ه في خط ه ط مثل خط ا ه في خط ه ج‍، وكذلك خط ا ه في خط ه ج‍ مثل خط ب ه في خط ه د. فخط ب ه اذًا في خط ه د مثل خط ح ه في خط ه ط. فخطا ب د ط ح اذًا في دايرة واحدة. فيجب من ذلك أن تكون نقطة ط على دايرة فلك البروج، وهي دايرة ح ب ط د، وقد كنّا وصفنا أنّها على دايرة الافق، وهي دايرة ح ا ط ج‍. فالخط الذي يصل بين موضعي تقاطع دايرة فلك البروج ودايرة الافق هو خط قد يمر بمركز دايرة معدل النهار، وهو نقطة ه. فقد تبيّن من ذلك أنّ دايرة الافق ودايرة فلك البروج يتقاطعان على نقطّين متقابلتين على القطر بالقوة. وذلك ما اردنا أن نبيّن.

[٤]

فاذ قد تقدّمنا فبيّنّا ذلك، فلننظر الآن الى ما نسبة انصاف اقطار الدواير المتوازية، التي ترسم على بروج دايرة الفلك المايل، الى نصف قطر دايرة معدل النهار، التي تقدّمنا فوضعناها حتى نعلم أن مطالعها توجد بالعدد ايضًا موافقة لما يظهر في الكرة المجسمة.

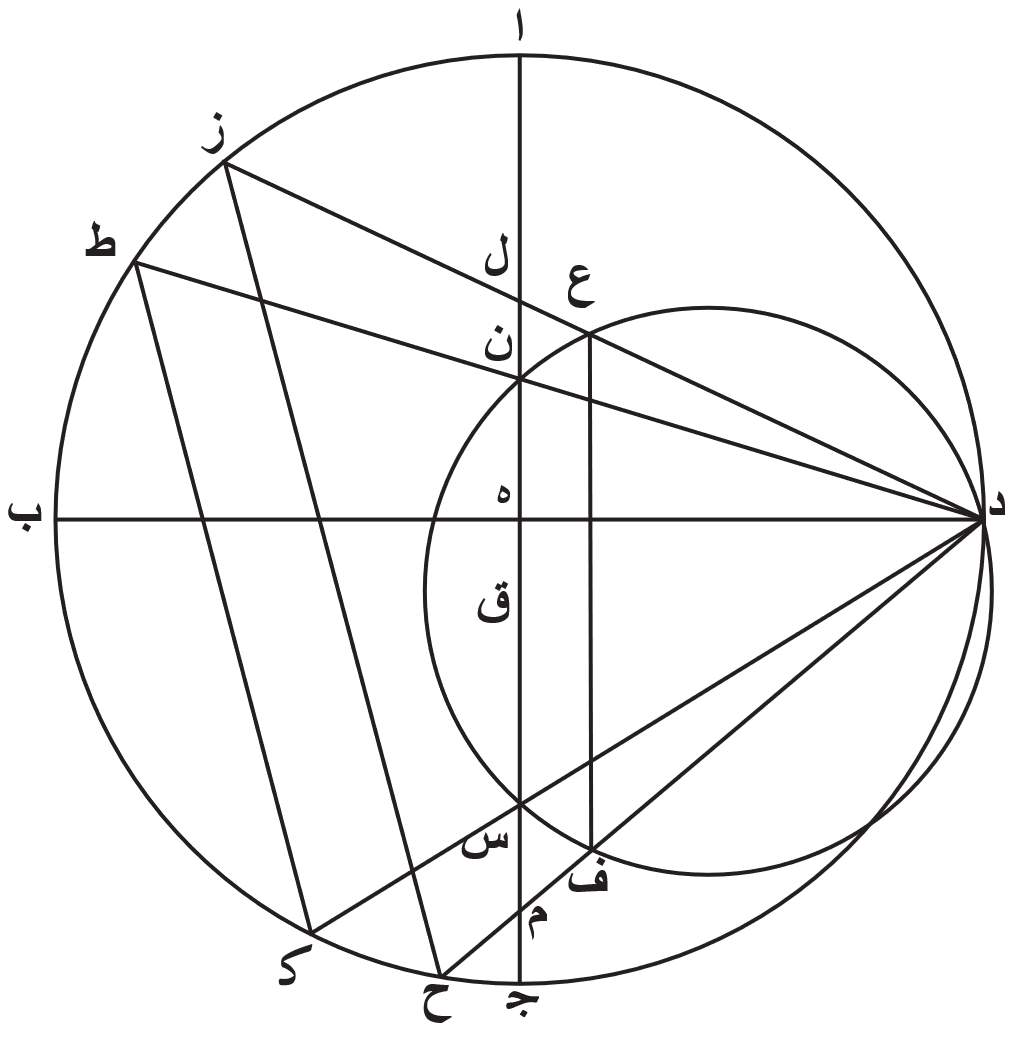
فلتكن ايضًا دايرة معدل النهار دايرة ا ب ج‍ د حول مركز ه. ونخرج منها قطرين يتقاطعان على زوايا قايمة، وهما ا ج‍ ب د. ونخرج خط ا ج‍ على الاستقامة الى نقطة ز. ونفصل عن جنبتي نقطة ج‍ قوسين متساويتين، وهما ج‍ ح ج‍ ط. ونصل خط د ك ح وخط د ط ز. وقد تقدّمنا فأوضحنا أنّ الدواير الموازية لدايرة معدل النهار، التي بعدها عنها بعد سوا، ما كان منها اميل الى الشمال فإنّما رسم على مركز ه وببعد ه ك، وما كان منها اميل الى الجنوب فعلى مركز ه وببعد ه ز.

ويتبيّن لنا أنّ نسبة خط ه ز الى خط ه ك على هذا المثال. لأنّ قوس ج‍ ح مساوية لقوس ج‍ ط فقوس ب ح، وقوس ب ج‍ ط، مجموعين هما نصف دايرة. فالزوايا المقابلة لها، اعني زاوية ه د ك وزاوية ه د ز، مجموعين مساويتين لزاوية قايمة. وزاوية ه د ك مع زاوية ه ك د ايضًا قايمة، فزاوية ه د ز مساوية لزاوية ه ك د. فمثلث ز ه د اذًا القايم الزاوية شبيهة بمثلث د ه ك القايم الزاوية، فنسبة خط ز ه الى خط ه د كنسبة خط د ه الى خط ه ك. لكن نسبة قوس ب ط الى ما بقي من نصف الدايرة، اعني القوس المساوية لقوس ب ح، كنسبة زاوية ه د ز الى زاوية ه ز د، وكنسبة القوس التي على خط ه ز من الدايرة المرسومة على مثلث د ه ز القايم الزاوية الى القوس التي على خط ه د من هذه الدايرة بعينها. فنسبة الخط المستقيم الذي يوتر قوس ب ط الى الخط الذي يوتر ما بقي من نصف الدايرة، اعني قوس ب ح، كنسبة خط ز ه الى خط ه د وكنسبة خط د ه الى خط ه ك.

فاذ قد تقدّمنا فحصّلنا ذلك، فنضع اولا في مثل هذه الصورة كل واحد من قوسي ج‍ ح ج‍ ط ثلثًا وعشرين درجة واحدى وخمسين دقيقة وعشرين ثانية، بالدرج التي بها دايرة ا ب ج‍ د ثلثماية وستين درجة، وهي الدرج التي وضعنا أنّها البعد فيما بين دايرة معدل النهار وبين كل واحدة من دايرتي المنقلبين في كلامنا في الكرة المجسمة ايضًا. فتكون قوس ب ط ماية وثلثة عشر درجة واحدى وخمسين دقيقة وعشرين ثانية، بالدرج التي بها هذه الدايرة ثلثماية وستين درجة، وقوس ب ح ما بقي من نصف الدايرة وهو ست وستون درجة وثمان دقايق واربعون ثانية. والخط المستقيم الذي يوتر قوس ب ط ماية جز وثلث وثلثون دقيقة وثماني وعشرون ثانية، بالاجزا التي بها القطر ماية وعشرون جزًا فقد وضعنا ذلك في كتاب المجسطي، والخط الذي يوتر ب ح خمسة وستون جزًا من هذه الاجزا وتسع وعشرون دقيقة. نسبة خط ز ه اذًا الى خط ه د ونسبة خط ه د الى خط ه ك هي نسبة ماية جز وثلث وثلثين دقيقة وثمان وعشرين ثانية الى خمسة وستين جزًا وتسع وعشرين دقيقة. ولذلك خط ه د، الذي هو نصف قطر دايرة معدل النهار، بالاجزا التي هو بها ستين جزًا بتلك الاجزا يكون نصف قطر دايرة المنقلب الشتوي، وهو خط ه ز، اثنان وتسعون جزًا وثمان دقايق وخمس عشرة ثانية، ونصف قطر دايرة المنقلب الصيفي تسعة وثلثين جزًا واربع دقايق وتسع عشرة ثانية.

وقد وضح من ذلك أنّ قطر دايرة فلك البروج، اذا كانت تماس هاتين الدايرتين بطرفي قطرها، هو نصف قطريهما جميعًا، وهو ماية واحدى وثلثون جزًا واثنتا عشر دقيقة واربع وثلثون ثانية، بالاجزا التي يكون بها نصف قطر دايرة معدل النهار ستين جزًا، وأنّ نصف قطر دايرة فلك البروج خمسة وستون جزًا وست وثلثون دقيقة وسبع عشرة ثانية. والخط الذي بين مركزه ومركز دايرة معدل النهار يكون ستة وعشرون جزًا من هذه الاجزا واحدى وثلثين دقيقة وثمانيا وخمسين ثانية.

[٥]

ونضع ايضًا كل واحدة من قوسي ح ج‍ ج‍ ط عشرين درجة وثلثين دقيقة وتسع ثواني، وهو البعد فيما بين دايرة معدل النهار وبين الدايرتين الموازيتين لمعدل النهار اللتين تفصلان من الدايرة التي تمر بوسط البروج عن جنبتي نقطّي المنقلبين ثلثين درجة، حتى يكون قوس ب ط ماية وعشر درجات وثلثين دقيقة وتسع ثواني، والخط المستقيم الذي يوترها ثمانية وتسعين جزًا وخمسًا وثلثين دقيقة وسبعًا وخمسين ثانية، وقوس ب ح تسعًا وستين درجة وتسعًا وعشرين دقيقة واحدى وخمسين ثانية، والخط المستقيم الذي يوترها ثمانية وستين جزًا وثلث وعشرين دقيقة واحدى وخمسين ثانية. فنسبة خط ز ه اذًا الى خط ه د ونسبة خط ه د ايضًا الى خط ه ك، هي نسبة ثمانية وتسعين جزًا وخمس وثلثين دقيقة وسبع وخمسين ثانية الى ثمانية وستين جزًا وثلث وعشرين دقيقة واحدى وخمسين ثانية. فالاجزا التي بها يكون خط ه د ستين جزًا، يكون بها خط ه ز ستة وثمانين جزًا وتسعًا وعشرين دقيقة واثنين واربعين ثانية، وخط ه ك يكون واحدًا واربعين جزًا من هذه الاجزا وسبعًا وثلثين دقيقة وخمس عشرة ثانية.

[٦]

وعلى هذا المثال، نضع كل واحدة من قوسي ح ج‍ وج ط احدى عشرة درجة وتسعًا وثلثين دقيقة وتسعًا وخمسين ثانية، وهي البعد في الدايرة العظمى التي ترسم على قطبي دايرة معدل النهار فيما بين دايرة معدل النهار وبين الدايرتين الموازيتين لها اللتين يفصلان ستين درجة من الدايرة التي تمر بوسط البروج عن جنبتي نقطّي المنقلبين. فتكون جملة قوس ب ط ماية درجة ودرجة وتسعًا وثلثين دقيقة وتسعًا وخمسين ثانية، والخط المستقيم الذي يوترها ثلثة تسعين جزًا ودقيقتين واربع عشرة ثانية، وتكون قوس ب ح ثمانيًا وسبعين درجة وعشرين دقيقة، والخط المستقيم الذي يوترها خمسة وسبعين جزًا وسبعًا واربعين دقيقة وثلثًا وعشرين ثانية. فنسبة خط ز ه الى خط ه د ونسبة خط د ه الى خط ه ك هي نسبة ثلثة وتسعين جزًا ودقيقتين واربع عشرة ثانية الى خمس وسبعين جزًا وسبع واربعين دقيقة وثلث وعشرين ثانية، والاجزا التي يكون بها خط ه د ستين جزًا، بها يكون خط ه ز ثلثة وسبعين جزًا وتسعًا وثلثين دقيقة وسبع ثواني، وخط ه ك ثمانية واربعين جزًا من هذه الاجزا واثنين وخمسين دقيقة.

[٧]

وكذلك إن جعلنا كل واحدة من قوسي ح ج‍ وج ط اربعًا وخمسين درجة، وهي بعد الدايرتين الموازيتين لمعدل النهار اللتين يماسها الافق الذي في إقليم رودس، وهو الافق الذي مثّلنا به في الكرة المجسمة، عن جنبتي دايرة معدل النهار، كان في هذا ايضًا قوس ب ط ماية واربعًا واربعين درجة، والخط الذي يوترها ماية واربعة عشر جزًا وسبع دقايق وسبعًا وثلثين ثانية، وقوس ب ح ستًا وثلثين درجة، والخط الذي يوترها سبعة وثلثين جزًا واربع دقايق وخمسًا وخمسين ثانية. ونسبة خط ز ه الى خط ه د وخط د ه الى خط ه ك هي نسبة ماية واربعة عشر جزًا وسبع دقايق وسبع وثلثين ثانية الى سبعة وثلثين جزًا واربع دقايق وخمس وخمسين ثانية. فالاجزا التي بها يكون خط ه د ستين جزًا، بها يجتمع خط ه ز ايضًا ماية واربعة وثمانين جزًا وتسعًا وثلثين دقيقة وثمانيًا واربعين ثانية، ويكون خط ه ك تسعة عشر جزًا من هذه الاجزا وتسعًا وعشرين دقيقة واثنين واربعين ثانية. ومن البيّن أنّه لما كان هذين الخطين اذا جمعا كانا قطر الافق الذي تقدّمنا فوضعناه، كما يكون من قطري دايرتي المنقلبين قطر دايرة فلك البروج، صار هذا القطر مايتين واربعة اجزا وتسع دقايق وثلثين ثانية، بالاجزا التي بها يكون قطر دايرة معدل النهار ماية وعشرين جزًا. ويجب من ذلك أن يكون نصف قطر دايرة الافق ماية جز وجزين واربع دقايق وخمس واربعين ثانية، ويكون الخط الذي بين مركز هذه الدايرة ودايرة معدل النهار اثنين وثمانين جزًا من هذه الاجزا وخمسًا ثلثين دقيقة وثلث ثواني. وذلك ما اردنا أن نبيّن.

[٨]

واذ قد وضعنا ذلك فلنبيّن أن في مثل هذه الصورة ايضًا يرى مقادير المطالع وجميع ما يعرض فيها على مثال ما بيّنّا في الكرة المجسمة.

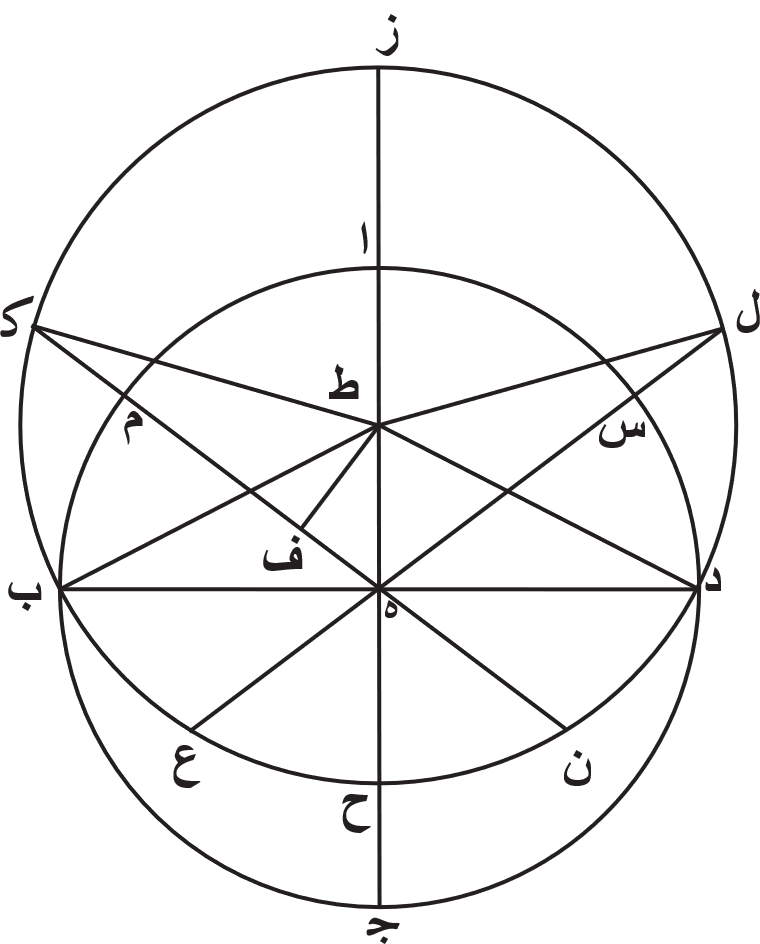
فلتكن دايرة معدل النهار دايرة ا ب ج‍ د حول مركز ه، والدايرة التي تمر بوسط البروج دايرة ز ب ح د حول نقطة ط. ونخرج قطرين يمران بنقطة ه التي هي مركز دايرة معدل النهار ومكان دايرة نصف النهار. احدهما يمر بالتقاطع الذي على نقطّي ب ود، وهما نقطّي الاستوا، وهو خط ب ه د. والاخر يمر بمركز دايرة البروج، وهو خط ز ط ه ح، فيحدث نقطّي المنقلبين، وهما ز وح. وليكن قصدنا اولا أن نبيّن ما يطلع في الكرة المستقيمة من دايرة معدل النهار مع اجزا الدايرة التي تمر في وسط البروج. فلأنّ الافق في الكرة المستقيمة وضعه وضع دايرة نصف النهار، والخطوط المستقيمة في هذه الصورة التي تجاز على قطب دايرة معدل النهار، وهي نقطة ه، هي نظاير دواير نصف النهار، فمن البيّن أنّ كل واحدة من قوسي ز ب ح د، وهما ربعا دايرة الفلك المايل، يطلع مع كل واحدة من قوسي ا ب ج‍ د، وهما ربعا دايرة معدل النهار، ويتوسّطان السما معها ويغربان معها، لأنّ خط ب د في دايرة ز ب ح د يقسمه نصف القطر، وهو خط ط ح، بنصفين وعلى زوايا قايمة على نقطة ه. فنفصل من الدايرة التى تمر بوسط البروج قوسين متساويتين، وهما قوس ب ك وقوس د ل، ونجيز خط ك م ه ن وخط ل س ه ع. فاذ كنّا قد بيّنّا أن نقطّي ك ل ونقطّي ع ن تمر بها الدواير المتوازية، التي بعدها عن جنبتي دايرة معدل النهار بعد سوا، حتى أنّ نقطة ك هي مقابلة لنقطة ن بالقوة، ونقطة ل مقابلة لنقطة ع. إن نحن وضعنا اولا أنّ قوس ب ك برج الحوت، فمن البيّن أنّ قوس ل د تكون برج الميزان، وعلى هذا المثال قوس ب ع تحتوى على برج الحمل وقوس ن د تحتوى على برج السنبلة. لكنّا إن وصلنا خطوط ك ط ل ط، كان مثلث ك ه ط مساوي الاضلاع والزوايا لمثلث ل ه ط، فزاوية ك ه ط مساوية لزاوية ل ه ط، والزوايا الباقية، اعني زاوية ك ه ب وزاوية ل ه د، مساوية بعضها لبعض وللزوايا المقابلة لها. فاذ كانت هذه الزاوية عند مركز دايرة معدل النهار، فأنّ القسي ايضًا التي تطلع من دايرة معدل النهار مع كل واحد من البروج التي وضعناها مساوية بعضها لبعض. فإن نحن وجدنا مقدار واحدة من هذه القسي، كأنّا وجدنا مقدار قوس م ب، فقد حصّلنا مع ذلك ما كنّا في طلبه من المطالع.

فنخرج من نقطة ط عمودًا على خط ك ه، وليكن خطط ف. فاذ قد بيّنّا أنّ الاجزا التي بها نصف قطر دايرة معدل النهار ستين جزًا يكون خط ط ك، وهو نصف قطر الدايرة التي تمر في وسط البروج، خمسة وستين جزًا وست وثلثين دقيقة وسبع عشرة ثانية، وخط ه ط، وهو الخط الذي بين مركز هذه الدايرة ومركز دايرة معدل النهار، ستة وعشرين جزًا واحدى وثلثين دقيقة وثمان وخمسين ثانية، وخط ه ك، وهو نصف قطر الدايرة الموازية لدايرة معدل النهار التي ترسم على راس الحوت وراس العقرب، اعني التي تمر بنقطّي ك ل، يكون من هذه الاجزا ثلثة وسبعين جزًا وتسع وثلثين دقيقة وسبع ثواني، فمثلث ه ط ك معلوم.

فإن اضفنا الى خط ك ه مربع ك ط في مثله منقوص منه مربع ط ه في مثله حدث فضل خط ك ف على خط ف ه. الّا أنّ كل دايرتين يتقاطعان، وتقسم الدايرة العظمى منهما الدايرة الصغرى بنصفين، كم كان مقدار الدايرتين، فأنّ مربع نصف قطر الدايرة العظمى في مثله منقوص منه [مربع] الخط الذي بين مركزيهما [في مثله] يحدث عنه مربع نصف قطر الدايرة الصغرى في مثله. وذلك أنّا على مثال ما فعلنا في هذه الدواير إن وصلنا خط ب د، كان الخط الذي يوصل بين موضعي التقاطع يمر بمركز ه في الدايرة الصغرى. فاذ كانت زاوية د ه ط قايمة، فأنّ خط ط د في مثله، وهو الخط الذي يوتر الزاوية، مساوٍ لما يجتمع من خطي ط ه وه د كل واحد في مثله. فيجب من ذلك أن يكون فضل [مربع] نصف قطر الدايرة التي تقسم دايرة معدل النهار بنصفين [في مثله]، كم كان مقدارها، عند [مربع] الخط الذي بين مركزيهما [في مثله] ثلثة الف وستماية جز من الاجزا التي بها يكون نصف قطر دايرة معدل النهار ستين جزًا.

ومن قبل أنّ خط ه ك ايضًا يحسب ما تقدّمنا فوضعناه، هو ثلثة وسبعون جزًا من هذه الاجزا وتسع وثلثون دقيقة وسبع ثواني، إن اضفنا الى ذلك الفضل، وهو ثلثة الف وستماية جز، حصل لنا فضل خط ك ف عند خط ف ه، وهو ثمانية واربعون جزًا من هذه الاجزا واثنتان وخمسون دقيقة واثنتان واربعون ثانية. فاذ انقصنا ذلك من ثلثة وسبعين جزًا وتسع وثلثين دقيقة وسبع ثواني واخذنا نصف ما بقي، وهو اربعة وعشرون جزًا وست واربعون دقيقة وخمس وعشرون ثاينة، كان خط ه ف اثنا عشر جزًا وثلث وعشرون دقيقة واثنا عشرة ثانية، بالاجزا التي وضعنا أنّ خط ه ط بها ستة وعشرون جزًا واحدى وثلثون دقيقة وثماني وخمسون ثانية. فالاجزا التي بها خط ه ط، وهو الخط الذي يوتر زاوية ه ف ط القايمة، ماية وعشرين جزًا بها يكون خط ه ف ايضًا خمسة وعشرين جزًا وثلثين دقيقة بالتقريب، والقوس التي يوترها خمسًا وخمسين درجة واربعين دقيقة، بالدرج التي بها تكون الدايرة التي حول مثلث ه ط ف القايم الزاوية ثلثماية وستين درجة. فزاوية ه ط ف، التي هي مثل زاوية ف ه ب، اذ كانت زاوية ط ه ب ايضًا قايمة، بالدرج التي بها تكون زاويتين قايمتين ثلثماية وستين درجة، بها تكون خمسًا وخمسين درجة واربعين دقيقة، وبالدرج التي بها يكون اربع زوايا قايمة ثلثماية وستين درجة، بها تكون هذه الزاوية سبعًا وعشرين درجة وخمسين دقيقة. ولما كانت هذه الزاوية عند مركز دايرة معدل النهار، صارت قوس ب م ايضًا سبعًا وعشرين درجة [وخمسين دقيقة]، بالدرج التي بها دايرة معدل النهار ثلثماية وستين درجة.

فقد تبيّن لنا من ذلك على مثل ما بيّنّا في الكرة المجسمة أنّ كل واحد من البروج التي عند نقطة الاستوا، اعني الحوت والحمل والسنبلة والميزان، في وضع الكرة المستقيمة يطلع مع هذه السبع وعشرين درجة وخمسين دقيقة من دايرة معدل النهار.

وقد كان يمكننا أن نبيّن ذلك بقول اسهل من هذا على هذا المثال، خط ك ه في ه ن مساوٍ لخط ب ه في ه د وخط ب ه في ه د ثلثة الف وستماية جز. فاذا نحن قسمنا ذلك على خط ك ه، كان خط ه ن معلومًا. لكنّ خط ك ه يفضل على خط ه ن بمثل خط ه ف مرتين، فخط ه ف ايضًا معلوم. وخط ط ه معلوم، والزاوية القايمة التي عند نقطة ف معلومة، فزاوية ه ط ف اذًا معلومة.

[٩]

فنضع ايضًا في مثل هذه الصورة قوس ب ك من دايرة فلك البروج قوسي برجين حتى تكون نقطة ك راس الدلو ونقطة ل راس القوس، وقبالة هذه النقط على القطر تكون نقطة ن راس الاسد ونقطة ع راس الجوزا. فمن البيّن أنّا إن بيّنّا كم مقدار قوس ب م من دايرة معدل النهار، فأنّا قد عرفنا الازمان التي فيها يطلع في الكرة المستقيمة كل واحد من البروج التي تقدّمنا فوضعناها.

ومن البيّن ايضًا أنّ خطي ك ط ط ه يبقي مقدارهما على ما كان، وخط ك ه يزداد مقداره. من قبل أنّا قد بيّنّا أنّ نصف قطر الدايرة الموازية لدايرة معدل النهار، التي ترسم على راس القوس وراس الدلو، هو [ستة] وثمانون جزًا وتسع وعشرون دقيقة واثنتان واربعون ثانية، بالاجزا التي بها يكون نصف قطر دايرة معدل النهار ستين جزًا، فإن قسمنا اجزا الفضل، وهي ثلثة الف ستماية جز، على خط ك ه، اعني إن قسمناها على ستة وثمانين جزًا وتسع وعشرين دقيقة واثنين واربعين ثانية، خرج لنا فضل خط ك ف على خط ف ه واحدًا واربعين جزًا من هذه الاجزا وسبعًا وثلثين دقيقة وخمس عشرة ثانية. واذا نقصنا ذلك من ستة وثمانين جزًا وتسع وعشرين دقيقة واثنين واربعين ثانية، واخذنا نصف ما يبقي، وهو اربعة واربعون جزًا واثنتان وخمسون دقيقة وسبع وعشون ثانية، خرج لنا خط ف ه اثنين وعشرين جزًا وست وعشرين دقيقة وثلثة عشر ثانية بالتقريب، بالاجزا التي كان بها خط ط ه ستة وعشرين جزًا واحدى وثلثين دقيقة وثمان وخمسين ثابية. فالاجزا التي يكون بها خط ط ه الذي يوتر الزاوية القايمة ماية وعشرين جزًا، بها يكون خط ه ف ماية جز وجز وثمان وعشرين دقيقة، والقوس التي يوترها ماية وخمسة عشر درجة وثمان وعشرين دقيقة، بالدرج التي تكون بها الدايرة التي حول مثلث ه ط ف القايم الزاوية ثلثماية وستين درجة. فتكون زاوية ه ط ف، التي هي مثل زاوية ف ه ب، ماية وخمسة عشر درجة وثمان وعشرين دقيقة، بالدرج التي بها تكون زاويتين قايمتين ثلثماية وستين درجة. فامّا الدرج التي يكون بها اربع زوايا قايمة ثلثماية وستين درجة، فتكون سبع وخمسين درجة واربع واربعين دقيقة. ولما كانت هذه الزاوية عند مركز دايرة معدل النهار، صارت قوس ب م ايضًا سبعًا وخمسين درجة واربع واربعين دقيقة.

فإن نقصنا من ذلك مطالع البروج التي عند نقطّي الاستوا، التي بيّنّا أنّها سبع وعشرين درجة وخمسين دقيقة، خرج لنا الازمان الباقية، تسع وعشرين زمانًا واربع وخمسين دقيقة، وهي التي [فيها] يطلع في الكرة المستقيمة كل واحد من هذه البروج، اعني الدلو والثور والاسد والعقرب. ومن البيّن أنّ كل واحد من هذه الاربعة البروج الباقية، اعني القوس والجدي والجوزا والسرطان، يطلع في الازمان التي تبقي من قوس ربع واحد، وهو تسعون زمانًا، وهي اثنان وثلثون زمانًا وستة عشر دقيقة. وذلك موافق لما بيّنّاه في الكرة المجسمة.

[١٠]

ويتبع ذلك أن ننظر هل يتهيّأ في الكرة المايلة ايضًا تلك المطالع باعيانها التي تقدّمنا فذكرناها من مطالع البروج على ما في هذه الصورة.

ونستعمل ايضًا على طريق المثال الدايرة الموازية لمعدل النهار التي استعملناها في كتاب المجسطي، اعني الدايرة التي تمر بجزيرة رودس. وارتفاع القطب الشمالي في هذه الدايرة عن الافق ست وثلثون درجة. وامّا الافق الذي يرسم بالدواير الموازية لمعدل النهار، التي بعدها البعد الذي تقدّمنا فبيّنّاه، فأنّ نصف قطره ماية جز وجزان واربع دقايق وخمس واربعون ثانية، بالاجزا التي بها يكون نصف قطر دايرة معدل النهار ستين جز، ويكون الخط الذي بين مركز دايرة هذا الافق ودايرة معدل النهار اثنين وثمانين جزًا بهذه الاجزا وخمسًا وثلثين دقيقة وثلث ثواني.

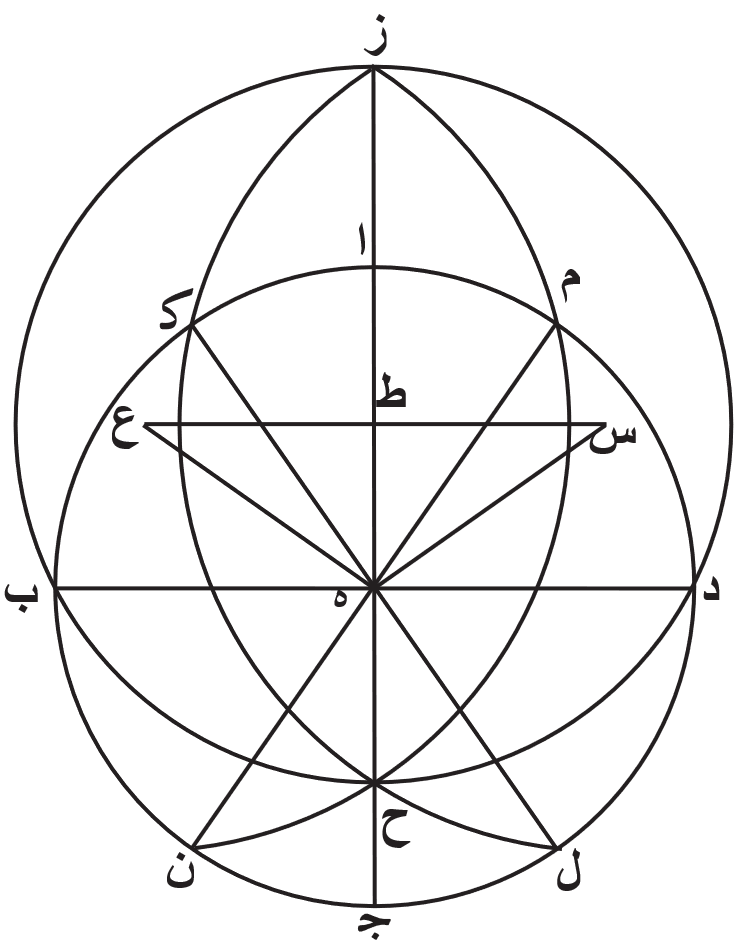
فنجعل دايرة معدل النهار ا ب ج‍ د حول مركز ه، ودايرة البروج ز ب ح د حول مركز ط. ونتوهّم حركة الكرة، اذ كانت نقطة ه قد وضعت القطب الشمالي، كأنّها من نقطة د نحو نقطة ج‍ ثم الى نقطة ب ثم الى نقطة ا. ونرسم اولا من هذه الدايرة من دواير الافق قوسين تمران بنقطّي المنقلبين، وهما نقطّي ز وح. ولتكونا قوسي ز ك ح ل ز م ح ن. فمن البيّن أنّه متى كان الافق وضعه وضع قوس ز ك ح ل، كان ما على نقطة ز وعلى نقطة ك طالعًا وما على نقطة ح وعلى نقطة ل غاربًا، ومتى كان وضعه وضع قوس ز م ح ن، كان الامر بخلاف ذلك، اعني أنّ ما كان على نقطّي ن وح فهو طالع وما كان على نقطّي م وز فهو غارب، اذ كانت حركة الكرة إنّما هي كأنّها من نقطة د نحو نقطة ج‍، وكان قطب ه قد وضع انّه ظاهر ابدًا.

فاذ كنّا قد بيّنّا أنّ الدايرة التي تمر بوسط البروج ليس هي وحدها تقسم دايرة معدل النهار بنصفين لكن تقسمه معًا بنصفين دواير الافق التي ترسم على هذا المثال، فيجب من ذلك أن يكون الخطان المستقيمان اللذان فصلا فيما بين مواضع التقاطع، اعني خط ك ل وخط م ن، يمران بمركز ه. فمن البيّن أنّ قوس ك  ايضًا من دايرة معدل النهار مساوية لقوس ج‍ ل، وقوس ا م مساوية لقوس ج‍ ن.

ولكن قوس م  ايضًا مساوية لقوس ك . وذلك أنّا إن جعلنا مركزي دايرة الافق على هذين الوضعين، نقطة س ونقطة ع، ووصلنا خطوط س ه ع ه س ط ع، فكان خط س ط ع مستقيمًا وعلى زوايا قايمة على خط ز ح، وكان خط س ه على زوايا قايمة على خط ك ل، وخط ع ه على زوايا قايمة على خط م ن، وكانت الخطوط التي تخرج اليها اعمدة من المراكز تقسّمها الاعمدة بنصفين، صارت اضلاع كل واحد من مثلثي ه ط ع ه ط س مساوية لاضلاع الاخر، وصارا قايمتين الزاويتين، وزاوية ط ه ع من مثلث ه ط ع هي المساوية لزاوية ط ه س من مثلث ه ط س. ولكن زاوية م ه ع مساوية لزاوية ك ه س، وذلك أنّ كل واحدة منهما قايمة. فزاوية م ه  اذًا الباقية مساوية لزاوية ك ه  الباقية. ولذلك صارت قوس م  مساوية لقوس ك .

فالقوي اذًا التي تبتدىء من نقط ك م ل ن وتنتهي الى نقطّي ا ج‍ متساوية. والقسي ايضًا التي تبتدىء من حيث ذكرنا وتنتهي الى نقطّي ب د متساوية.

ولما كانت قوس ب ح تطلع مع قوس ب ن وقوس ز ب مع قوس ك ب، وهذه القوس مساوية لقوس ب ن، ولذلك قوس د ز ايضًا تطلع مع قوس د ك وقوس ح د مع قوس د ن، وهذه القوس مساوية لقوس د ك، فقد تبيّن من ذلك ايضًا أنّ قسي الدايرة التي تمر في وسط البروج التي بعدها من نقطة واحدة بعينها من نقطّي الاعتدال بعد سوا تطلع في ازمان متساوية.

وايضًا لما كانت قوس ز ب ناقصة عن مطالع الكرة المستقيمة بقوس ك ، وقوس ح د، وهي القوس المقابلة لهذه القوس على القطر، تفضل على مطالع الكرة المستقيمة بقوس ج‍ ن، وهذه القوس مساوية لقوس ك ، وكانت نقطة ح نقطة المنقلب الصيفي، فمن البيّن أنّ في هذه الصورة ايضًا يكون مقدار نقصان قسي دايرة البروج التي عند نقطة الربيع عن المطالع التي في الكرة المستقيمة بمقدار زيادة القسي المساوية لها المقابلة لها على القطر على هذه المطالع باعيانها. وممّا يسهّل معرفته مع بيان ذلك أنّ اقصر ما يكون [من] النهار ينقص عن نهار الاستوا بقوسي ك  ون ج‍، واطول ما يكون من النهار يزيد على نهار الاستوا بهاتين القوسين.

[١١]

فاذ قد عرفنا ذلك فلننظر في هذا الإقليم الذي وضعناه هل يوجد ولا فضل ما بين اطول ما يكون من النهار او اقصر ما يكون منه وبين نهار الاستوا موافقًا لما يعرض في الكرة المجسمة.

فنضع صورة مثل هذه الصورة فيها الافق الذي يمر بنقط ز ك ح ل وحده. وليكن غرضنا أن نجد مقدار قوس ك . فنجعل ايضًا مركز دايرة الافق الذي هذه حاله نقطة س. ونصل خطي س ط س ه، فيكونان عمودين على خطي ز ح ك ل لما تقدّمنا فبيّنّاه. فمن اجل أنّا قد بيّنّا أنّ خط ه س، وهو الخط الذي بين مركز دايرة معدل النهار وبين مركز دايرة افق هذا الإقليم الذي وضعناه، هو اثنان وثمانون جزًا وخمس وثلثون دقيقة وثلث ثواني، بالاجزا التي وضع أنّ خط ه ط، وهو الخط الذي بين مركز هذه الدايرة وبين مركز دايرة فلك البروج، بها ستة وعشرين جزًا واحدى وثلثون دقيقة وثمان وخمسون ثانية، فالاجزا اذًا التي يكون بها خط ه س، وهو الخط الذي يوتر الزاوية القايمة، ماية وعشرين جزًا، بها يكون خط ه ط ايضًا ثمانية وثلثين جزًا وثلثًا وثلثين دقيقة بالتقريب، والقوس التي عليه سبعًا وثلثين درجة [وثلثين دقيقة]، بالدرج التي بها تكون الدايرة التي حول مثلث ه س ط القايم الزاوية ثلثماية وستين درجة. فزاوية ط س ه اذًا، التي هي مثل زاوية ا ه ك، تكون سبعًا وثلثين درجة وثلثين دقيقة، بالدرج التي بها تكون زاويتين قايمتين ثلثماية وستين درجة، وتكون ثمان عشرة درجة وخمسًا واربعين دقيقة، بالدرج التي بها يكون اربع زوايا قايمة ثلثماية وستين درجة. ولما كانت هذه الزاوية عند مركز دايرة معدل النهار، صارت قوس ا ك ايضًا ثمان عشرة درجة وخمسًا واربعين دقيقة.

فكل واحد اذًا من الربعين اللذين عند نقطة الربيع يكون واحدًا وسبعين زمانًا وخمس عشرة دقيقة، وكل واحد من الربعين اللذين عند نقطة الخريف يكون ماية وثمانية ازمان وخمسًا واربعين دقيقة. ولذلك يكون فضل ما بين اطول ما يكون من النهار واقصر ما يكون منه وبين نهار الاستوا سبعة وثلثين زمانًا وثلثين دقيقة، ويكون من ساعات الاستوا ساعتين ونصف على مثل ما بيّنّا في الكرة المجسمة.

[١٢]

ولكن نجد مطالع البروج ايضًا في هذا الإقليم الذي وضعناه. نضع على هذا المثال دايرة معدل النهار والدايرة التي تمر في وسط البروج حول قطري ب د وز ح، ونفصل من الدايرة التي تمر في وسط البروج قوس ب ط. ولتكن قوس برج واحد اولا، ومن البيّن أنّه برج الحوت. ونصل خط ط ه ل، وندير دايرة الافق الذي تقدّمنا فوضعناه مارة بنقطّي ط ل. ولتقطع دايرة معدل النهار علي نقطّي م ن. ونصل خط م ه ن، ونخرج ايضًا من نقطة س، وهي مركز دايرة الافق، خطين مستقيمين، وهما س ه وس ط، ونخرج منها عمودًا على خط ط ل، وهو خط س ع.

وقد بيّنّا قبيل أنّ قوس ك م هي التي بها ينقص برج الحوت وبرج الحمل من الجانبين عن مطالعهما في الكرة المستقيمة، ويفضل بها برج السنبلة وبرج الميزان على مطالعهما في الكرة المستقيمة.

وقد بيّنّا أنّ خط ه ط، وهو نصف قطر الدواير الموازية لدايرة معدل النهار التي ترسم على راس الحوت، هو ثلثة وسبعون جزًا تسع وثلثون دقيقة وسبع ثواني، بالاجزا التي وضع بها خط ه س، وهو الخط الذي بين مركز دايرة معدل النهار ومركز دايرة الافق، اثنين وثمانين جزًا وخمسًا وثلثين دقيقة وثلث ثواني، وأنّ فضل مربع خط ط س في مثله على مربع خط ه س في مثله ثلثة الف وستماية جز من هذه الاجزا. واذا قسمنا ذلك على مثال ما فعلنا قبل على ثلثة وسبعين جزًا وتسع وثلثين دقيقة وسبع ثواني، وفعلنا ما يتلوا ذلك كما فعلنا في الكرة المستقيمة، خرج لنا خط ه ع اثني عشر جزًا وثلثًا وعشرين دقيقة واثنتي عشرة ثانية، بالاجزا التي بها يكون خط ه س اثنين وثمانين جزًا وخمس وثلثين دقيقة وثلث ثواني. فالاجزا التي يكون بها خط ه س، وهو الذي يوتر الزاوية القايمة، ماية وعشرين جزًا، بها يكون خط ه ع ثمانية عشر جزًا ودقيقة بالتقريب، والقوس التي عليه سبع عشرة درجة وست عشرة دقيقة، بالاجزا التي بها تكون الدايرة التي حول مثلث ه س ع ثلثماية وستين درجة. فزاوية ه س ع ايضًا، التي هي مثل زاوية ك ه م، تكون سبعة عشر درجة وست عشر دقيقة، بالدرج التي بها تكون زاويتين قايمتين ثلثماية وستين درجة، وتكون ثمان درج وثمان وثلثين دقيقة، بالدرج التي بها يكون اربع زوايا قايمة ثلثماية وستين درجة. فقوس ك م ايضًا هي ثمان درج وثمان وثلثين دقيقة، بالدرج التي بها تكون دايرة معدل النهار ثلثماية وستين درجة.

وقد كانت مطالع كل واحد من الاربعة البروج التي وضعناها في الكرة المستقيمة سبعة وعشرين زمانًا وخمسين دقيقة. فاذا نقصنا منها هذه الثمانية الازمان والثمان والثلثين الدقيقة، خرج لنا مطالع كل واحد من برجي الحوت والحمل تسعة عشر زمانًا واثنتي عشرة دقيقة. فاذا زدنا على هذا ذلك بعينه، خرج لنا مطالع كل واحد من برجي السنبلة والميزان ستة وثلثين زمانًا وثمان وعشرين دقيقة.

[١٣]

فنضع ايضًا في مثل هذه الصورة قوس ب ط قوس برجين، اعني الحوت والدلو، حتى يقرّ ساير ما ذكرناه على حاله. فيكون ه ط، وهو نصف قطر الدايرة الموازية لدايرة معدل النهار التي ترسم على راس الدلو، ستة وثمانين جزًا من هذه الاجزا وتسعًا وعشرين دقيقة واثنين واربعين ثانية. واذا قسم ذلك على ثلثة الف وستماية جز على مثال ما ذكرنا فيما تقدّم، خرج لنا خط ه ع اثنين وعشرين جزًا وستًا وعشرين دقيقة وثلث عشرة ثانية، بالاجزا التي بها يكون خط ه س اثنين وثمانين جزًا وخمسًا وثلثين دقيقة وثلث ثواني. والاجزا ايضًا التي بها يكون خط ه س، وهو الخط الذي يوتر الزاوية القايمة، ماية وعشرين جزًا، بها يكون خط ه ع اثنين وثلثين جزًا وستًا وثلثين دقيقة بالتقريب، والقوس التي عليه احدى وثلثين درجة واثنين وثلثين دقيقة، بالدرج التي بها تكون الدايرة التي ترسم حول مثلث ه س ع القايم الزاوية ثلثماية وستين درجة. فزاوية ه س ع اذًا، التي هي مثل زاوية ك ه م، هي احدى وثلثون درجة واثنتان وثلثون دقيقة، بالدرج التي بها تكون زاويتان قايمتان ثلثماية وستين درجة، وهو خمس عشرة درجة وستة واربعون دقيقة، بالدرج التي بها يكون اربع زوايا قايمة ثلثماية وستين درجة. فقوس ك م اذًا، وهي الفضل المشترك بين مطالع البرجين اللذين وضعناهما وبين المطالع في الكرة المستقيمة، تكون خمس عشرة درجة وستًا واربعين دقيقة، بالدرج التي بها تكون دايرة معدل النهار ثلثماية وستين درجة.

وقد كانت مطالعها في الكرة المستقيمة سبعًا وخمسين زمانًا واربع واربعين دقيقة، فإن نقصنا هذه الخمس عشرة درجة والست والاربعين دقيقة من سبع وخمسين درجة واربع واربعين دقيقة، خرج لنا مطالع الحوت ومطالع الدلو مجموعين واحدًا واربعين زمانًا وثمان وخمسين دقيقة. وامّا مطالع الدلو وحده، فيكون اثنين وعشرين زمانًا وستًا واربعين دقيقة، من قبل أنّ الخوت كان يطلع في تسعة عشر زمانًا واثنتي عشرة دقيقة. وإن زدنا الخمس عشرة الدرجة والست والاربعين الدقيقة على سبع وخمسين درجة واربع واربعين دقيقة، خرج لنا مطالع الاسد ومطالع السنبلة، ويكون مطالعهما اذا جمعت ثلثة وسبعين زمانًا وثلثين دقيقة. فامّا مطالع الاسد وحده، فتكون سبعة وثلثين زمانًا ودقيقتين، من قبل أنّ السنبلة ايضًا كانت تطلع في ستة وثلثين زمانًا وثمان وعشرين دقيقة. ومن البيّن أنّ الثور ايضًا يطلع في ازمان مساوية لازمان طلوع الدلو، وهي اثنان وعشرون زمانًا وست واربعون دقيقة، والعقرب يطلع في ازمان مساوية لازمان طلوع الاسد، وهي سبع وثلثون درجة ودقيقان، وأنّ طلوع كل واحد من الجدي والجوزا يكون في الازمان الباقية في هذا الربع، وهي تسعة وعشرون زمانًا وسبع عشرة دقيقة، وأنّ طلوع كل واحد من السرطان والقوس يكون في الازمان الباقية من هذا الربع ايضًا، وهي خمسة وثلثون زمانًا وخمس عشرة دقيقة، على ما يليق بغرضنا المتقدّم.

[١٤]

فقد بيّنّا أنّ في هذه الصورة ايضًا التي في بسيط مسطح يكون الامر في مطالع بروج الدايرة التي تمر في وسط البروج وجميع ما يتبع ذلك موافقًا لما بيّنّاه في الكرة المجسمة.

ولكن نجعل الصورة على حسب مقدار الموضع المعلوم الذي نريد أن نرسم فيه ما ذكرناه، وحتى يتهيّأ لنا فيه أن نرسم وضع الكواكب الثابتة، إن اردنا ذلك. وإن اردنا أن نضع فيه الشي الذي يسمّي خاصّة في آلات الساعات العنكبوت، فأنّا نضع الدايرة التي تكون خارج الدواير كلها واعظمها دايرة ا ب ج‍ د حول مركز ه. ونخط بدل دواير نصف النهار قطرين يتقاطعان على زوايا قايمة. وليكونا خطي ا ج‍ ب د. ونفصل من عند نقطة د قوس د ز. وليكن مقدارها بمقدار بعد الدايرة الموازية لدايرة معدل النهار التي وضعناها عن القطب الجنوبي في الكرة المجسمة. ونخرج من نقطة ج‍ خطًا موازيًا لخط ه د، وليكن خط ج‍ ح. ونصل خط د ز ح، ونخرج من نقطة ح عمودًا على خط ه د، وهو خط ح ط.

فاقول إنّا إن فعلنا مثل ما فعلنا فيما تقدّم حتى نفصل من عند نقطة ج‍ قوسًا، هي بعد كل واحدة من الدواير الباقية الموازية لدايرة معدل النهار الى جانب الموافق، ووصلنا خطوطًا مستقيمة من نقطة د وبين اطراف القسي التي نفصل مثل خط د ك ج‍ مثلًا إن كان غرضنا أن نرسم دايرة معدل النهار، وجعلنا خط ه ل مساويًا لخط ط ك، وجعلنا نقطة ه مركزًا، وادرنا ببعد مساوٍ لبعد ه ل دايرة ل م س، كان وضع هذه الدايرة وضع دايرة معدل النهار.

وكل واحدة من الدواير الباقية على هذا المثال، وذلك أنّا إن فعلنا عكس ذلك على ما بيّنّا فيما تقدّم حتى نضع دايرة معدل النهار دايرة ل م س ونرسم في سطحّا الدايرة الموازية لها التي بعدها عنها الى الجنوب بقدر قوس شبيهة بقوس ج‍ ز، كانت دايرة ا ب ج‍ د هي الدايرة التي نرسم. فنصل خط م ج‍ وليقطع دايرة ل م، وهي دايرة معدل النهار، على نقطة ن حتى تكون دايرة ا ب ج‍ د مرسومة على مركز ه وببعد ه ج‍، كما فعلنا اخيرًا.

فاقول إنّ قوس م ن شبيهة بقوس د ز. برهان ذلك أنّ نسبة خط د ه الى خط ه ج‍ كنسبة خط د ط الى خط ط ك، وخط د ه مساوٍ لخط ه ج‍، فخط د ط ايضًا مساوٍ لخط ط ك. ولكن خط ط ك مساوٍ لخط ه م، فخط د ط ايضًا مساوٍ لخط ه م. وخط ط ح ايضًا مساوٍ لخط ه ج‍ وموازٍ له، فخط د ز اذًا موازٍ لخط م ن. فزاوية ه م ن مساوية لزاوية ه د ز، فقوس س ل ن اذًا شبيهة بقوس ب ج‍ ز، فقوس م ن الباقية شبيهة بقوس د ز الباقية.

[١٥]

وينبغي ايضًا أن نتمم غرضنا بأن نبيّن كيف نرسم الدواير التي حالها عند الدايرة التي تمر في وسط البروج كحال الدواير التي تقدّم ذكرها عند معدل النهار، حتى يمكنا أن نضع الكواكب التي رصدت وعرفت مواضعها بقياسها الى هذا الفلك من غير أن نستعمل اولا الاضلاع التي لها بقياسها الى دايرة معدل النهار.

فلتكن اولا دايرة معدل النهار من الدواير التي توضع في الصفيحة دايرة ا ب ج‍ د حول مركز ه، ودايرة البروج دايرة ز ب د، والخط المستقيم الذي يمر بالقطبين جميعًا خط ز ا ه ح ج‍، وخط الذي يمر بموضع التقاطع من دايرة معدل النهار خط ب ه د. فإن نحن فصلنا قوس ب ط وجعلناها مساوية للقوس التي بين قطبي دايرة معدل النهار والدايرة التي تمر في وسط البروج، ووصلنا خط د ك ط، كانت نقطة ك نظيرة قطب الدايرة التي تمر في وسط البروج بالقوة. ومن البيّن أنّ ذلك يكون بحسب ما اوضحنا.

وكانت الدواير التي تمر بهذه النقطة وبالنقط التي هي متقابلة على القطر في الدايرة التي تمر في وسط البروج قاسمة لدايرة معدل النهار ايضًا بنصفين. وتكون هذه الدواير المرسومة هي التي تقوم مقام الدواير العظام القايمة على دايرة البروج على زوايا قايمة، لأنّا قد بيّنّا أنّ جميع الدواير بالجملة التي تقطع احدى هاتين الدايرتين اللتين وضعناهما على القطر، فأنّها تقطع الدايرة الاخرى الباقية على القطر ايضًا.

[١٦]

وقد يمكننا أن نضع في الصفيحة الدواير الموازية لدايرة البروج ايضًا على هذا المثال.

[ف‍]نجعل دايرة نصف النهار التي تمر بالقطبين دايرة ا ب ج‍ د حول مركز ه. وليكن المحور ب ه د، ونتوهّم نقطة د القطب الخفي، وقطر دايرة معدل النهار ا ه ج‍، وقطر احدى الدواير الموازية لدايرة البروج خط ز ح ط. وليكن غرضنا أن نضع الدايرة التي هذا الخط قطر لها في الصفيحة. فنجيز على نقطة ح خطًا موازيًا لخط ا ه ج‍، وليكن خط ل ح ك، ونصل خطوط د م ز د ن ط د س ل.

فمن البيّن أنّ الدايرة التي قطرها خط ز ط ترسم حول قطر م ن. وذلك أنّها تماس الدايرتين الموازيتين لدايرة معدل النهار اللتين بعدهما عنها بقدر قوسين ا ز ج‍ ط، ولذلك ترسم هاتان الدايرتان ببعدين ه م ه ن.

ولكن لما كانت الدايرة الموازية لدايرة معدل النهار التي قطرها ل ك تقسمها الدايرة الموازية لدايرة البروج التي قطرها خط ز ط بنصفين على دايرة نصف النهار التي قطرها خط ب د، وهذه الدايرة ايضًا ترسم ببعد ه س مثل دايرة س ع ف، فيجب أن نبيّن أنّ الدايرة التي ترسم حول قطر م ن تمر بنقطّي ع ف.

ونصل خطي ب ز ب ق، ونخرج خطي ك ل د ط حتى يلتقيا على نقطة ر. فمن قبل أنّ زاويتي ب ز ق ب ح ق قايمتان، تكون نقط ب ح ق ز على خط محيط بدايرة واحدة. فزاوية ب ق ر مساوية لزاوية ب ز ط التي هي مساوية لزاوية ب د ر، فنقط ب ر د ق ايضًا على خط محيط بدايرة واحدة. والذي يكون من ضرب خط ق ح في خط ح ر مساوٍ للذي يكون من ضرب خط ب ح في خط ح د. واذا كان كذلك فهو مساوٍ لمربع خط ح ل في مثله. فخط م ه ايضًا في خط ه ن مساوٍ لخط ه س في مثله الذي هو مساوٍ لخط ف ه في خط ه ع، فنقط م ع ن ف اذًا ايضًا على خط محيط بدايرة واحدة.

[١٧]

وينبغي أن نبيّن أنّ مراكز الدواير الموازية لدايرة البروج ايضًا التي ترسم على هذا المثال تكون مختلفة ابدًا.

فلتكن دايرة نصف النهار التي تمر بالقطبين دايرة ا ب ج‍ د حول مركز ه، والمحور خط ب ه د، وقطر دايرة معدل النهار خط ا ج‍، وقطري دايرتين موازيتين لدايرة البروج خطي ز ح ط ك. ونصل خطوط د ل ز د م ح د ن ط د س ك، ونرسم حول مثلث د ن س دايرة ع س ف. ونصل خط ع ف، ونقسم خط ل م بنصفين على نقطة ق. فمن البيّن أنّ الدايرة التي على قطرها ز ح الموازية لدايرة البروج ترسم على قطر ل م، وأنّ الدايرة التي قطرها ط ك الموازية لدايرة البروج ترسم حول قطر ن س.

واقول إنّ هاتين الدايرتين ليس مركزهما واحدًا بعينه، اعني أنّ نقطة ق لا تقسم خط ن س ايضًا بنصفين. برهان ذلك أنّ قوس ز ط مساوية لقوس ك ح، ولذلك تكون زاوية ز د ط مساوية لزاوية ح د ك، وقوس ن ع مساوية لقوس س ف، فخطا ل م ع ف متوازيان. فنسبة خط د ل الى خط ل ع كنسبة خط د م الى خط م ف، ولكن نسبة خط د ل الى خط ل ع كنسبة خط د ل في مثله الى خط د ل في خط ل ع، ونسبة خط د م الى خط م ف كنسبة خط د م في مثله الى خط د م في خط م ف. فنسبة خط د ل في مثله اذًا الى خط د ل في خط ل ع كنسبة خط د م في مثله الى خط د م في خط م ف. ولكون الدايرة، يكون خط د ل في خط ل ع مساويًا لخط س ل في خط ل ن، ويكون خط د م في خط م ف مساويًا لخط ن م في خط م س. فنسبة خط د ل في مثله الى خط س ل في خط ل ن كنسبة خط د م في مثله الى خط ن م في خط م س، واذا بدّلنا، كانت نسبة خط د ل في مثله الى خط د م في مثله كنسبة خط س ل في خط ل ن الى خط ن م في خط م س. ولكن خط د م في مثله اعظم من خط د ل في مثله، اذ كان خط د م اطول من خط د ل، فخط ن م في خط م س اعظم من خط س ل في خط ل ن. وخط ن س مشترك مع خط ل ن ومع خط م س، فخط م س اذًا اطول من خط ل ن. ولكن خط ل ق مساوٍ لخط م ق، فخط ن ق اذًا اطول من خط ق س. نقطة ق مركز الدايرة التي يكون خط ن س قطرًا لها.

[١٨]

ويجب الآن، لمكان الدواير الموازية لدايرة البروج التي ليس هي محصورة في الصفيحة لكن يقع بعضها في القطعة التي لا تظهر وهي غير مرسومة من الكرة، اعني الدواير التي تقطع الدايرة الخفية ابدًا، أن نضع ايضًا الدايرة التي تمر بالقطبين دايرة ا ب ج‍ د حول مركز ه. وليكن المحور خط ب د، ونتوهّم نقطة د القطب الخفي، وقطر دايرة معدل النهار خط ا ج‍، وقطر الدايرة الموازية لها الخفية دايمًا خط ز ح، وقطر الدايرة التي يقاطع هذه الدايرة، الموازية لدايرة البروج خط ط ك ل.

ونرسم على خط ز ح نصف دايرة، ولتكن ز م ح. ونخرج خطًا موازيًا لخط ه د، وليكن خط ك م. فمن قبل أنّا أن اخرجنا خط ا ج‍ ن وخطي د ح ن د ل س، كانت الدايرة التي ترسم ببعد ه ن، كأنّها دايرة ع ن، هي الدايرة الخفية دايمًا في الصفيحة، وكانت الدايرة التي ترسم بدل الدايرة التي على خط ط ك ل تمر هي ايضًا بنقطة س، وتقسم الدايرة الخفية دايمًا بقسي شبيهة بقوس ح م، اذ كان خط ك م هو فصل مشترك لسطحيهما. وذلك أنّا أن رسمنا حول مركز ه دايرة مساوية لدايرة ز م ح، كأنّا رسمنا دايرة ق ر ش، واخرجنا خط م ك ر ق، واخرجنا خطي ه ق ع ه ر ف، جعلنا قوسي ن ع ن ف شبيهتين بقوسي ش ق ش ر. فتكونان شبيهتين بقوس ح م. وتكون الدايرة الموازية لدايرة البروج التي ترسم على خط ط ل تمر في الصفيحة بنقط ع س ف.

[١٩]

ومن البيّن أنّا وإن توهّمنا في مثل هذه الصورة الدايرة الموازية لدايرة البروج التي ترسم على نقطة د، كأنّا جعلناها الدايرة التي ترسم على خط د ك، واخرجنا خط د ك للعرض الذي ذكرناه، واجزنا على نقطة ل خط م ل س على زوايا قايمة على خط ا ج‍ ن، كان هذا الخط في الصفيحة مكان الدايرة التي قطرها خط د ط ك. وذلك أنّ جميع الخطوط المستقيمة التي تخرج من نقطة د مارة بهذه الدايرة هي في سطح واحد، وهو سطح الدايرة، والفصل المشترك لهذا السطح ولسطح دايرة معدل النهار، هو خط م ل س، وذلك أنّ سطح دايرة نصف النهار ايضًا التي على خط ا ج‍ هي على زوايا قايمة على كل واحد من هذين السطحين اللذين ذكرناهما.

[٢٠]

فعلى هذا المثال الذي بيّنّا يجب أن يرسم في الصفيحة قياس لما في الكرة المجسمة الدواير التي توجد بسمت دايرة معدل النهار، ما كان منها من دواير نصف النهار وما كان منها موازيًا لمعدل النهار، والدواير التي توجد بسبب الدايرة التي تمر في وسط البروج.

ومن قبل أنّ قطب دايرة معدل النهار يكون ايضًا مركزًا لهذه الدايرة ولجميع الدواير الموازية لها، فأنّ جميع دواير نصف النهار تكون مع ذلك خطوطًا مستقيمة. وأنّ قطب الدايرة التي تمر في وسط البروج لا يكون مركزًا لهذه الدايرة ولا لواحدة من الدواير الاخر التي هي نظاير الدواير الموازية لها. وأنّ واحدة من هذه الدواير تكون بلا مركز، اعني تكون خطًا مستقيمًا. وأنّ الدواير العظيمة التي ترسم وتمر بهذا القطب تكون خلاف ذلك، وذلك أنّ الدايرة التي هي مكان الدايرة التي تمر بالقطبين تكون خطًا مستقيمًا، تقع على مراكز الدواير الموازية لدايرة البروج، وتكون الدواير الباقية دواير غير أنّها تكون غير متساوية.

وجب من ذلك أن يكون ممكنّا في الاوضاع التي توجد بقياس الى دايرة معدل النهار أن نرسم الكواكب من غير أن نرسم جميع الدواير بمسطرة تقسم على نسب الدواير الموازية لدايرة معدل النهار وبقسمة دايرة معدل النهار وحدها. وامّا في الاوضاع التي توجد بقياس الى الدايرة التي تمر في وسط البروج فليس يمكن ذلك. لكن يجب أن نرسم جميع الدواير او اكثرها لكي نستدلّ بها على المواضع التي يجب أن توضع فيها الكواكب.

ومن اصلح الامور في أن يستوفي في كل واحد من هذين الرسمين ما يستعمل في الكرة المجسمة أن نضع الدواير التي [توجد] بسبب دايرة معدل النهار، ما كان منها من دواير نصف النهار وما كان من الدواير الموازية لدايرة معدل النهار، والدواير التي توجد بسبب الدايرة التي تمر في وسط البروج على مثال ما عليه الاكر المضروبة. فإن كان لا يمكن رسم جميع ذلك في الصفيحة، فينبغي أن نرسم فيها الدواير التي تمر بدرجتين او بثلث درج او بست درج، اذ كان ذلك رسمَ متوسّطٍ، من قبل أنّ هذه الثلثة الاعداد هي عدد مشترك لثلثين درجة التي هي درج كل واحد من البروج، ولاربع وعشرين درجة، وهي البعد فيما بين دايرة معدل النهار وبين كل واحدة من دايرتي المنقلبين بالتقريب، حتى يقع معما يرسم من الدواير دايرتا المنقلبين ودواير نصف النهار التي تمر بالبروج، ولا يكون في الابعاد التي توجد على غير هذا المثال اختلاف.

تم كتاب بطلميوس من اهل

قلاوذية في تسطيح بسيط الكرة

والحمد للّه وصلواته على محمد نبيه آله صحبه وسلم