Claudii Ptolemei Liber de analemmate incipit

⟨1⟩

Consideranti mihi, o Syre, angulorum acceptorum in locum gnomonicum quod rationale et quod non, habitum quidem virorum illorum in lineis accidit admirari etiam in hiis et valde acceptare, non coattendere autem ubique, et eam que secundum naturam in metodis consequentiam ipsarum rerum non solum clamantium, quod et naturali theorie opus est aliqua coassumptione magis mathematica et mathematice magis naturali, nullatenus exprobravimus. Non enim licitum est quod tale viro amanti addiscere pure, sed observare, ut non propter dictam cogitationem unumquemque tractatuum aliqualiter imperfectiorem accidat fieri. Que itaque certitudinaliter deprehensa sunt michi michi] seq. del. misi tibi V secundum expositum locum, misi tibi consideraturo summatim, si quid tibi videmur ad intellectum coauxisse et ad rationabilitatem suppositionum et ad promptitudinem usus eius qui per ⟨…⟩. ⟨…⟩] ἀναλήμματος i. m. V

⟨2⟩

Quoniam igitur eas que secundum unamquamque molem ⟨…⟩ dimensiones consequens est determinatas esse et positione et multitudine sicut et magnitudine, declinationum autem que ad rectos angulos sole hunc habent modum, omnes enim alie et indeterminate secundum speciem et infinite secundum numerum, consequtum est tres solas esse tales secundum unamquamque molem dimensiones, quoniam et solas tres rectas ad rectos angulos invicem constitui possibile est, plures autem hiis est impossibile. Propter quod quidem et in spera sole tres diametri constituuntur constituuntur] construuntur H ad rectos angulos invicem, et maximi circuli soli tres in recto angulo faciunt declinationes ad invicem acceptorum in spera mundi, et uno quidem ipsorum intellecto secundum distinguentem quod sub terra emisperium ab eo quod super terram, vocatum autem orizontem, secundo autem penes distinguentem orientale emisperium ab occidentali, vocatum autem meridianum, reliquus et tertius erit penes separantem boreale emisperium ab eo quod ad meridiem, vocatum autem secundum verticem. Et dictarum autem diametrorum communis quidem orizontis et meridiani vocatur meridiana, communis autem sectio meridiani et eius qui secundum verticem vocatur gnomon, communis autem sectio eius qui secundum verticem et orizontis vocetur equinoctialis, quoniam et ipsius equinoctialis ad ipsos fit communis sectio. Simul translatis itaque cum Sole hiis circulis circa manentes communes sectiones ut circa axes duas quidem possibile est intelligere lationes, orizontis quidem circa equinoctialem diametrum ut ad id quod super terram et sub terra et circa meridionalem ut ad orientem et occasum, meridiani autem circa meridionalem diametrum ut ad ortus et occasus et circa diametrum gnomonis ut ad aquilonem et meridiem, eius autem qui secundum verticem circa diametrum gnomonis ut ad aquilonem et meridiem, et circa equinoctialem ut ad id quod super terram et sub terra. Sed quoniam non est possibile eundem simul duabus ferri lationibus, convenientiorem et priorem duarum dictarum assignandum unicuique, hoc est orizonti quidem eam que circa equinoctialem diametrum, ut rursum determinet positionem ad id quod sub terra et super terram, meridiano autem eam que circa meridianum, ut notet distinctionem que ad ortum et occasum, ei autem qui secundum verticem eam que circa gnomonem, ut insinuet transitum ad aquilonem et meridiem. Facit autem orizontis quidem latio circulum, quem vocamus ektimoron, id est sex partium, quia altitudinem usque ad sextam horam manifestat, latio autem meridiani circulum, quem vocamus horarium, quia longitudini que secundum unamquamque horam comprogreditur, latio autem eius qui secundum verticem circulum, quem vocamus katavaticum, id est descensivum, quia notificat descensionem ab altissimo ad humillimum. Rursum unusquisque dictorum circulorum in coexaltatione cum solari radio super terram facit duas declinationes, quibus datis et positio radii determinatur, quoniam una ad tale non sufficit, harum autem alteram quidem a rectis contentam, scilicet a delata et manente, hoc est a radio et a diametro, circa quam fertur, alteram autem ab ipsis planis similiter similiter] sil’r sil’r V a moto et a manente, ita ut duorum circulorum utriusque una sola declinationum data determinetur et positio radii. Et eorum quidem qui ab ab] seq. del. ex V ektimoro circulo fiunt angulorum consistentem quidem apud radium et apud diamatrum equinoctialem non videmus ab antiquis acceptum in locum gnomonicum, eum autem, qui ab ipsius declinatione ad orizontem fit, vocant ektimoron. Factorum autem a circulo horario duorum angulorum eum quidem, qui apud radium et apud diametrum equinoctialem consistit, vocant horarium, eum autem qui ab ipsius declinatione ad meridianum in plano eius qui secundum verticem. Factorum autem a circulo descensivo duorum angulorum hic quidem apud radium et apud gnomonem consistit iterum, hic autem ab ipsius declinatione ad eum qui secundum verticem; utuntur autem non hiis, sed pro angulo quidem, qui a gnomone et a radio continetur, utuntur deficiente ad unum rectum et vocant ipsum descensivum, pro angulo autem, qui ab ipsius declinatione ad eum qui secundum verticem continetur, utuntur eo, qui constituitur a declinatione ipsius ad meridianum, vocant autem et hunc antiskion, id est contraumbralem. Sextum autem angulum inserunt pro relicto eum, qui fit ab equinoctiali diametro et a communi sectione circuli horarii et equinoctialis, quem vocant, in equinoctialis plano, et quidem equinoctiali non in omni climate eandem servante positionem, aliter aliter] uncertain reading (aliter H) passus est et orizon et meridianus et qui secundum verticem.

⟨3⟩

Ut autem sub visu nobis magis cadat consequentia angulorum et quod supponitur, sit meridianus quidem circulus qui ABGD, recti autem super ipsum et orientales semicirculi orizontis quidem qui AEB, eius autem qui secundum verticem qui GED, et supposita positione radii alicuius penes Z describantur per ipsum trium circulorum orientales semicirculi 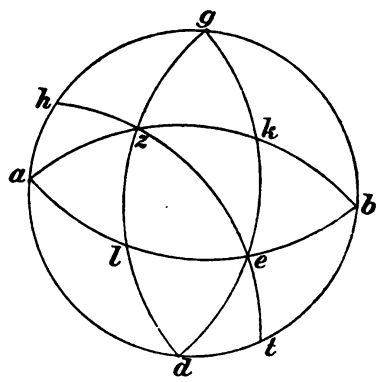circumdelati cum radio circa proprias diametros, ipsius quidem orizontis AEB facti ektimori semicirculus HZET circa diametrum que per per] apud H E et per oppositum sibi diametraliter, ipsius autem meridiani AGB facti horarii semicirculus AZKB circa diametrum que per A et B, ipsius autem GED qui secundum verticem facti descensivi semicirculus GZD circa diamatrum que per G et D. Et accipiantur differentie angulorum in periferiis propriorum circulorum subtensis unicuique propter simpliciorem ostensionem. Angulis quidem itaque, quos dicebamus constitui a radio et ab axe, periferie subtenduntur que ZE ektimori periferia et que ZA horarii et que ZG descensivi, angulis autem, qui fiunt a declinationibus planorum manentis circuli et transcidentis ipsum, subtenduntur que AH meridiani periferia continens declinationem orizontis et ektimori et que GK eius qui secundum verticem periferia continens declinationem meridiani et horarii et que EL orizontis periferia continens declinationem eius qui secundum verticem et descensivi.

⟨4⟩

Huius itaque consequentie subicientis angulosque et periferias convenientes nature circulorum unam secundum unumquemque manentium et motorum antiqui ipsam quidem EZ ektimori praetermiserunt, ut diximus, ponentes pro ipsa, quem vocant in equinoctialis plano, ipsam autem AZ servant et vocant proprie horariam, pro ipsa autem ZL assumpserunt autem ZL assumpserunt] autem ZG assumpserunt ZL conjectured H nominantes ipsam descensivam et rursum ipsam quidem AH servant et vocant ektimoron, similiter autem et ipsam GK vocantes ipsam in plano eius qui secundum verticem, pro ipsa autem EL assumunt ipsam AL vocantes ipsam antiskion id est contraumbralem. Differentia quidem igitur rationabilitatis penes id, quod supponitur, ad eos qui ante nos manifesta.

⟨5⟩

Quoniam autem omnis angulus facit aliquas magnitudines ex utraque parte declinationis et quandoque quidem equales, ut in positione recta, quandoque autem inequales, ut in reliquis, necessarium utique erit et in angulis expositis aut periferiis condeterminari principium secundum unamquamque speciem, a quo acceptio et contrarietates declinationum earum que ad ortus vel occasus et earum que ad aquilonem vel meridiem. Proposito igitur nobis existente acceptiones et expositiones et appellationes periferiarum facere secundum ordinem a ratione productum consequens erit et suppositionibus determinatio propria secundum unamquamque speciem. Nominationes enim facimus ab ipsis circulis, quorum sunt periferie, et vocamus eas quidem que in motis ektimoriales et horarias et descensivas, eas autem que in manentibus similiter meridionales et secundum verticem et orizontes. Et in magnitudinibus semper eligimus acutum angulum consistentium ex utraque parte, si non sint recti, et principia acceptionum facimus earum quidem que in circulis motis ab altero polorum circulationis, ad quam declinatio, hoc est in his quidem que ipsius ektimori a termino diametri equinoctialis ante mediationem quidem celi ab orientali, post mediationem autem ab occidentali, in hiis autem que horarii a termino diametri meridiani, quando quidem positio radii fuerit borealior circulo qui secundum verticem, ab arctico, quando autem australior, a meridiano, quod etiam etiam] et H ipsum oportet observare, quoniam non eandem habet determinationem; in hiis vero que descensivi solum a termino gnomonis qui super terram. Earum autem que in circulis manentibus ab altero termino tamquam communi sectione uniuscuiusque et suppositi plani, ad quem faciens angulum declinatio, hoc est in hiis quidem que meridiani a a] corr. ex ab V termino recte meridiane, radio quidem existente borealiori quam circulus qui secundum verticem ab arctico, australiori autem a meridiano; et hoc enim rursum oportebit determinare; in hiis que eius qui secundum verticem a termino qui super terram gnomonis solum, in hiis autem que orizontis a termino diametri equinoctialis ante mediationem quidem celi ab orientali, post mediationem autem celi ab occidentali, vel borealiori quidem existente radio quam circulus qui secundum verticem ut ad aquilonem, australiori autem ut ad meridiem; quod et ipsum oportebit oportebit] oport and ebit sup. lin. V; oportebat H observare, et quia universaliter eas que ex utraque parte positiones earum, que in ortibus vel occasibus determinantur, dico autem earum que horarii et earum que descensivi et earum que eius qui secundum verticem, mediatio celi simpliciter designat, earum autem que versus aquilonem aut meridiem, dico autem earum que descensivi rursum et earum que ektimori et earum que meridiani et earum que orizontis, positio radii ex utraque parte circuli qui secundum verticem, et has ipsas non habentes unum et eundem terminum.

⟨6⟩

Premissis itaque hiis exponemus instrumentales acceptiones secundum unamquamque speciem subiacentium nobis angulorum, exempli gratia, ut promptam habeamus methodum, que erit in ⟨…⟩ ⟨…⟩] ἀναλήμματος(ε del.) i. m. V prius autem secundum se superveniemus super anguli anguli] followed by one erased letter V praetermissi ab antiquis, quem nos vocamus ektimorum, acceptionem instrumentalem, quoniam et demonstrationem huius necessarium utique erit coniungere hiis, que ab illis aliter tractata tractata] corr. ex trastata V sunt. Quod quidem igitur in equinoctiis anguli inquisiti semper iidem fiant hiis qui in plano equinoctialis, palam ex se. Congruit enim ipsi quod per totam circulationem et circulus ektimorus facienti equales invicem periferias que secundum unamquamque equinoctialem horam ex 15 gradibus consistentes et angulos ipsi consequentes continentes ektimoria, id est sextas partes unius recti.

Gratia autem reliquorum mensilium esto meridianus circulus qui ABGD, in quo orizontis quidem diameter diameter] diametrus H qui AB, ad angulos autem rectos ipsi et secundum gnomonem que GD, et centrum quidem solaris spere E, unius autem parallelorum mensilium magis borealium quam equinoctialis diameter diameter] diametrus H sit que ZHT, super quam orientalis semicirculus in eodem plano intelligatur qui ZKT, et ducatur ad rectos angulos ipsi ZT que KH, ita ut ZK portio parallelli 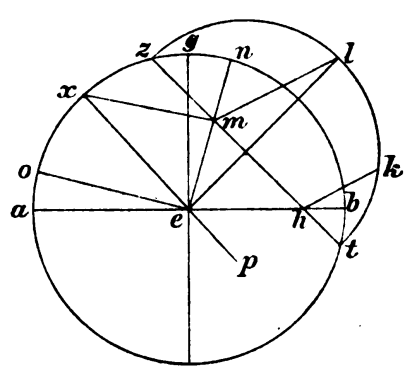sit super terram, et absumpta periferia KL ducatur perpendicularis ab L super ZT que LM, et centro quidem M, distantia autem que ML, accipiatur signum in meridiano, quod sit X, et copulentur que EL, EMN et EX EX] EZ i. m. V et MX, ducatur autem ipsi EN ad rectos angulos que EO. Dico, quod angulus qui sub XEO est equalis quesito. Intelligatur enim semicirculus ZLT conversus ad propriam positionem, hoc est rectam ad planum meridiani, et producatur ab E recta ad idem planum pro equinoctiali diametro que EP. Quod quidem igitur et ipsa LM existente recta ad meridianum que EN et ML et EP recte sunt in uno plano recto ad ABGD, palam. Similiter autem, quod quod] sup. lin. V et que quidem EN est communis sectio circuli circuli] seq. del. EX V ektimori et meridiani, que autem EL in recta ad solarem radium, quesitus autem angulus, contentus autem a radio et a diametro equinoctiali, qui sub LEP. Demonstrandum igitur, quod angulus qui sub XEO est equalis ei qui sub LEP. Quoniam enim equalis est est] corr. ex enim V que quidem EL ipsi EX, que autem ML ipsi MX, communis autem que EM, et angulus ergo qui sub MEL est equalis ei qui sub MEX. Rectus autem qui sub MEP et qui sub MEO, quoniam et qui sub EML, et reliquus reliquus] corr. ex reliqus V ergo qui sub LEP reliquo ei qui sub MEX, hoc est ei qui sub XEO, equalis est. Quod quidem oportebat demonstrare.

⟨7⟩

Consequenter autem et communes ipsorum acceptiones exponemus, que fiunt seorsum super equinoctialem et rursum super aliquem borealiorum borealiorum] boraliorem H aut australiorum australiorum] australiorem H ipso parallelorum mensilium. Sit igitur meridianus circulus qui ABGD, in quo orizontis quidem diameter que que] qui H AB, ad rectos autem ipsi et secundum gnomonem que GD, et centrum quidem solaris spere E, climatis autem periferia que GZ, et producatur prius equinoctialis diameter que ZEH, super quam semicirculus ZTH iaceat quidem in plano meridiani, intelligatur autem 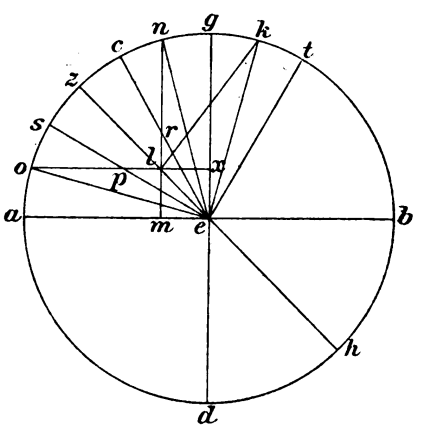in emisperio ad orientem, describaturque Sol ad sensum in una circumvolutione horum et aliorum mensilium parallelorum, parallelorum] έκας` i. m. V et producta que ET perpendiculari ad ZH, ita ut quod ZT tetartimorion, id est quarta pars, sit supra terram, absumatur que TK periferia datarum horarum, et intendatur angulos qui in hac positione accipere. Ducantur itaque perpendiculares a K quidem super ZH que EK, ab L autem super EH que MLN, super EG autem que XLO, et ipsi LK equales iaceant que XP et que RM, et copulentur que EK et EN et EO et adhuc que EPS et ERC.

Quod quidem igitur australior est radius circulo qui secundum verticem per totam circulationem supra terram in equinoctiali et in parallelis borealioribus borealioribus] australioribus in Greco i. m. V ipso, quia inclinatio spere spere] corr. ex specie V in habitata secundum nos versa est ad meridiem, et oportet adnuitiones consequentes positioni ipsius determinare, manifestum. Continet autem angulus qui sub EKL, hoc est qui sub TEK, angulum angulum] seq. del. qui V circuli ektimori, qui sit idem, ut diximus, hic ei qui in plano equinoctialis, angulus autem qui sub AEN eum qui horarii, qui autem sub GEO eum qui descensivi, et rursum qui quidem sub AEZ eum qui meridiani, qui autem sub GEC eum qui orizontis.

⟨8⟩

Exponatur itaque rursum qui ABGD meridianus cum diametris AB et GD, et protrahantur in ipso diametri parallelorum mensilium borealiorum equinoctiali que que om. H ZHTK, super quam similiter describatur semicirculus orientalis qui ZLK, et ad rectos angulos ipsi ZK ducatur que TL, ita ut ZL portio paralleli sit super terram. Absumpta autem LM periferia datarum horarum ducatur ab M perpendicularis super ZT que MN ipso N faciente videlicet positionem radii borealiorem quidem circulo qui secundum verticem, quando fuerit super HT, australiorem autem, quando fuerit super ZH. Protrahatur etiam rursum que ENX, et recta ad ipsam erigatur que EO. Accipiantur igitur in meridiano signa tria, centro quidem N, distantia autem MN quod P, centro autem T, distantia vero TM quod R, centro etiam H, distantia autem HM quod ⟨…⟩. ⟨…⟩] (e del.)ψ i. m. V Deinde productis RNC et SNY, ipse enim sunt per N accepte perpendiculares ad EB et EG, absumantur in ipsis similiter equales ipsi MN que YNF et CNQ, et copulentur que EP et ER et ES et MT et adhuc que EFΨ et que EQΩ. Continet itaque et hic angulus quidem qui sub PEO angulum circuli ektimori, qui autem sub BER eum qui horarii, qui vero sub GEO eum qui descensivi, et rursum qui quidem sub BEX eum qui meridiani, qui autem sub GEΨ eum qui eius qui secundum verticem, qui vero sub GEΩ eum qui orizontis, angulo qui sub TMN faciente eum qui in plano equinoctialis.

⟨9⟩

Instrumentales quidem igitur acceptiones hunc continent modum assumpta simili consequentia in omnibus positionibus; in expositione autem quantitatum consistentium secundum unumquodque clima et signum et gradum, sufficiet sufficiet] sufficient H quidem in ipsis solis periferiis subtendentibus angulos facere mensurationes, ut promptas ipsas habeamus in numeris et non descriptiones determinatas. Neque Neque] scilicet H secundum semel cogimur negotiari per ⟨…⟩ ⟨…⟩] ἀναλήμματος i. m. V inquisitos angulos rectarum fere ubique confusarum, sed in unaquaque oportunitatum una quadam quadam] corr. ex qualia (?) V quarta parte circuli divisa in unius recti portiones 90 equale inscribentes et circumscribentes concentricum cum dato ad ⟨…⟩ ⟨…⟩] κατασκευήν i. m. corr. ex κατασκεωμ V et accipientes a diviso distantias continentes numerum convenientium graduum transferimus ad equalem sibi quartam partem et per deprehensos terminos et per commune centrum circulorum producentes rectas inveniamus angulos et periferias in datis circulis maioribus vel minoribus. Talis autem acceptio exstabit quidem utique et per lineas ad certissimum volentibus, fiet autem utique facilius acquisibilis et per ipsum ⟨…⟩, ⟨…⟩] ἀναλήμματος i. m. V et si non sit eque invitiabilis invitiabilis] ἀπαράλλακτος i. m. V ei que per lineares demonstrationes, tamen usque ad examinationem que ad sensum, ad quam reducitur finis usualis suppositi negotii. Quo autem modo uterque processuum ad promptissimum nobis accipietur, ostendemus in parte summatim premissa consideratione que per numeros ita se habente.

Exponatur meridianus qui ABGD circa centrum E, in quo diametri ad rectos angulos invicem, communis quidem sectionis ipsius et orizontis que AB, gnomonis autem que GD, sitque data elevatio poli et contineatur a periferia AZ, et protrahatur axis quidem qui ZEH, equinoctialis autem prius diameter que TEK, et absumatur data periferia que ZL, et ab L ducantur perpendiculares super EZ quidem que LM, super EK autem que LN, similiter autem 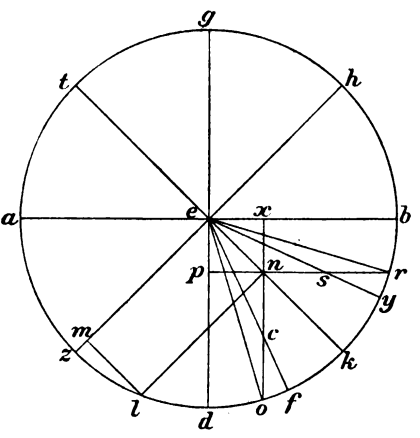et ab N super EB quidem que XNO, super ED autem que PNR. Quoniam igitur data est periferia AZ, hoc est que DK, datus datus] corr. ex data V erit et angulus qui sub PEN. Rectus autem qui apud P, data est ergo et ipsius EN subtense proportio ad utramque earum que circa rectum, hoc est ad ipsas EP et PN, et ad equales ipsis, scilicet NX et EX. Rursum, quoniam data est que LZ periferia, quarte autem partis est que KZ, quare et reliqua que KL data est, subtenditur autem duple ipsius LZ periferie dupla ipsius LM recte, duple autem ipsius LK periferie dupla ipsius LN LN] LM H recte, data erit et proportio utraqua ipsarum LM et LN ad diamatrum meridiani. Quare et proportio ipsius EN, que est equalis ipsi LM, et proportio ipsarum EP, NX laterum tetragoni. Sumantur itaque ipsi LN equales que PS et que XC, et protrahantur que OE et ER et ESY et ECF. Que quidem igitur ZL periferia existens equalis ei que circuli ektimori et adhuc ei que in plano equinoctialis ex se data est. Quoniam et ipsius EXO rectanguli trigoni data est que EX et que XO, et que EO subtendens dabitur et angulus qui sub EOX et reliquus qui sub OEX. Quare et que BO periferia continens eum qui circuli horarii. Similiter autem, quoniam et ipsius EPR rectanguli data est que EP et que PR, et que ER subtendens dabitur et angulus qui sub ERP ERP] corr. ex EPRP V et reliquus qui sub PER, simul cum ipso et que DR periferia existens equalis ei que circuli descensivi. Rursum que quidem HK periferia faciens eum qui meridiani ex se data est. Quoniam et ipsius EPS rectanguli que EP et que PS, dabitur et que ES subtensa et angulus qui sub PSE PSE] PSE et reliquus PES conjectured H ipseque et que DY periferia existens equalis ei que circuli qui secundum verticem. Similiter autem, quoniam et ipsius EXC rectanguli data est que EX et que XC, dabitur et subtensa que EC et angulus qui sub CEX, CEX] ECX conjectured H hoc est qui sub DEC ipseque et que DF periferia existens equalis ei que orizontis.

⟨10⟩

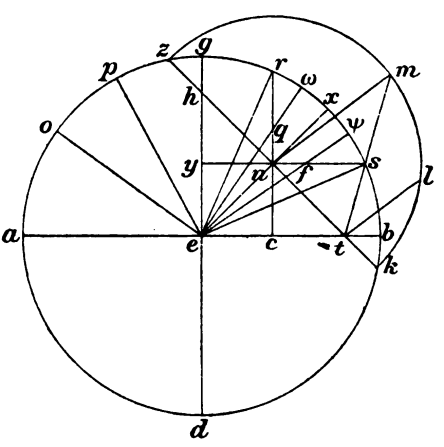
Et aliorum autem mensilium gratia exponatur qui ABGD meridianus cum diametris ad rectos invicem et cum axe EZ, et producatur unius rursum australiorum equinoctiali mensilium parallelorum diameter que HTK, super quam ad orientem intellectus 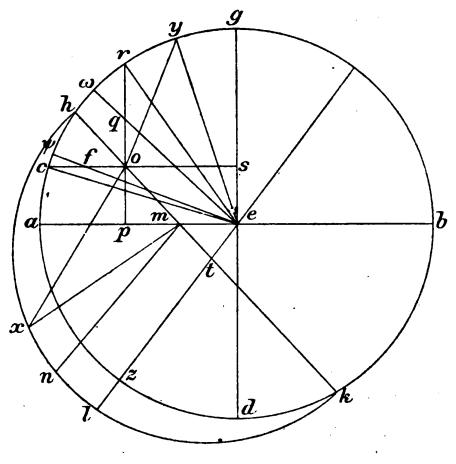semicirculus describatur qui HLK, et usque ad ipsum educatur axis EZL in duo equa videlicet secans ipsam HTK diametrum penes T et semicirculum HK penes L. Producatur autem et que MN recta super HT determinans HN HN] seq. del. S V portionem semicirculi super terram ab ea que sub terra, et accepta ipsa NX periferia datarum horarum ducatur ab X perpendicularis super HM que XO, et per O producantur perpendiculares super AE quidem que POR, super GE autem que SOC. Quoniam igitur data est ZL ZL] HZK conjectured H meridiani periferia, residue autem in semicirculum subtenditur dupla ipsius ET recte, data erit proportio ipsius HTK et proportio ipsius ET ad diametrum meridiani. Similiter, quoniam data est que AZ periferia elevationis, datus erit et ipsius MET trigoni rectanguli angulus qui sub MET. Quare data erit proportio ipsius ET ad utramque ipsarum EM et MT et adhuc proportio ipsius EK EK] HK conjectured H diametri ad unamquamque ipsarum. Sed ipsius MT recte dupla subtenditur duple ipsius LN periferie. Quare et que LN periferia data erit et residua in quartam partem que NXH. Data est autem et que NX, data ergo erit et que LX et que XH. Subtenditur autem duple quidem ipsius NX NX] HX conjectured H periferie dupla ipsius XO recte, duple autem ipsius XA XA] XL conjectured H periferie dupla ipsius HT HT] OT conjectured H recte, quare data erit ipsarum XO et OT proportio ad diametrum HK, propter hoc autem et ad eam que meridiani. Quoniam autem et ipsius TM data est proportio, data erit et proportio ipsius MO, et est, ut que EM ad MO, ita que TM ad MP et que ET ad OP; equiangula enim sunt trigona EMT et OPM. Data ergo erit et ipsarum MP et OP proportio ad diamatrum meridiani, propter hoc autem et proportio ipsius ES et proportio ipsius EMP totius, hoc est ipsius OS. Hiis igitur demonstratis sumatur centro O et distantia OX signum in meridiano scilicet G, G] Y conjectured H et absumantur rursum ipsi OX equales que PQ et que que] seq. del. S V SF, et copulentur que EY et ER et EC et XM et adhuc que EO et EFΨ et EQΩ. Quoniam igitur in precedentibus angulus qui sub EOY demonstratus est esse rectus, data est autem et que EY subtensa existens ex centro meridiani et que OY existens equalis ipsi OX, data erit et angulus qui sub EYO continens eum qui circuli ektimori. Similiter autem, quoniam et rectanguli XMO data est que XO et que OM, data erit et que MX subtensa et angulus qui sub MXO faciens eum qui in plano equinoctialis. Rursum, quoniam ipsius EPR rectanguli date sunt que EP et PR, data erit et que ER subtensa et angulus qui sub PER et que GR GR] AR conjectured H periferia. Rursum, quoniam ipsius ESC rectanguli date sunt que ES et que EC subtensa, data erit et angulus qui sub CES et que CG CG] GS in Greco i. m. V periferia descensivi. Consequenter autem, quoniam et ipsius EOP rectanguli date sunt que OP et que EP, data erit et que EO subtensa et angulus qui sub OEP faciens meridiani periferiam. Rursum, quoniam ipsius SFE rectanguli date sunt que ES et que SF, data erit et que EF subtensa et adhuc angulus qui sub SEF et que GΨ periferia eius qui secundum verticem. Restat autem, quoniam et ipsius EPQ rectanguli date sunt que EP et que PQ, data erit et que EQ subtensa et et] seq. del. ah V adhuc angulus qui sub EPQ, EPQ] EQP conjectured H hoc est qui sub QEG et et] seq. del. perif V que GΩ periferia orizontis.

⟨11⟩

Que quidem igitur per lineas acceptiones angulorum et subtensarum ipsis periferiarum sic utique nobis ad manum fient. In hiis autem que negotiantur ex ipso ⟨…⟩, ⟨…⟩] ἀναλήμμ ... i. m. V maxime utique facile acquisibilis fiet expositionum unaqueque hoc modo. Predemonstratur quidem igitur quoniam eorum que inscribuntur in ⟨…⟩ ⟨…⟩] ἀναλήμμ ... i. m. V hec quidem in omni climate servantur eadem, alia autem variantur. In hiis quidem igitur, que servantur, contenti erimus meridiano circulo et diametro equinoctialis et alteris solis mensilium parallelorum cum circumscriptis ipsorum semicirculis, ipsam tamen tropicorum et eam que mensilis post equinoctialem ordinantes ut ad eundem polum, eam autem que eius qui post tropicum tropicum] corr. ex tropicos and cum tropicis i. m. V ut ad oppositum polum, ne existens existens] seq. del. post V tropicum prope confundat eas que in ipsis ea … ipsis] i. m. V notas semicirculorum ipsis circumscriptorum. Propter quod et utemur tympanoydali plano suscepturo descriptionem, ad hoc quod verso tympano dicte mensilium diametri cum semicirculis possint adaptari et positionibus eorum que ex opposito vel secundum diametrum. In hiis autem, que secundum unumquodque clima ordinantur, rursum contenti erimus solis duabus diametris, ea videlicet que secundum communem sectionem meridiani et orizontis et ea que secundum gnomonem, utemur autem et quodam lato subtili valde et examinate rectangulo non habente eas que circa rectum latus minores quam ea que ex centro meridiani gratia sumendi alia signa et perpendiculares per ipsum de facili, facili] corr. ex facile V altera quidem earum que circa rectum latus adaptata recte ad quam perpendicularis, altera autem adducta ad signum per quod perpendicularis. Et totaliter autem faciemus acceptiones earum que in meridiano periferiarum per solum Cancrum et per latum illud rectangulum nusquam conscribentes conscribentes] προσπαραγράφοντ ... i. m. V alteram rectam predictarum, sed nudam servantes descriptionem ad facilitatem acceptionis eorum que deinceps primis ⟨…⟩ ⟨…⟩] ὑποκείρα i. m. V secundum modum, quem diximus in expositione, translatis. Exponantur enim ipsius ostensionis gratia planum tympanoydale circa diametrum AB et centrum G, et ipsius AG tertia parte proxime versus A accepta ut penes D centro G, distantia autem GD describatur describatur] seq. del. circulum equalis meridiano quarta pars V qui de ⟨…⟩ ⟨…⟩] ἀναλήμματ … i. m. V meridianus circulus ipsa DGE diametro secundum eam que equinoctialis intellecta. Deinde et ipsius GD tertia parte proxime versus G accepta ut penes Z centro Z distantia autem GD describatur circuli equalis meridiano quarta pars secta in duo equa ab AG que HTK et dividatur in 90 portiones equales diligenter.

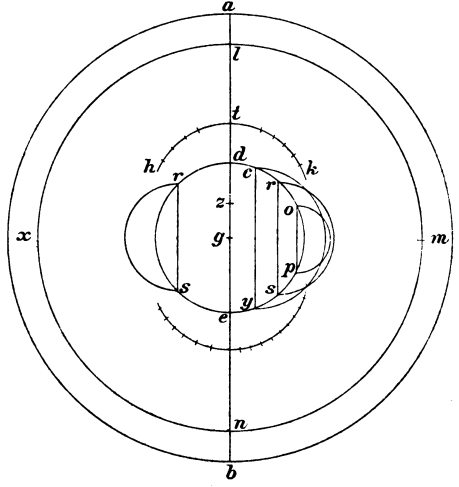
In Greco hic erat iste semicirculus et non non] sup. lin. V ex alia parte. In Greco… parte] note in the diagram referring to the semicircle RS

Nichil autem prohibet et super alias partes diametri idem facere gratia conversionis tympani. Similiter autem et centro G distantia autem ea que a G ad sectionem in duo proxime ipsius AT circulum describimus ut eum qui per quartas L M N X, quarum unam dividentes similiter in 90 portiones et excipientes in ipsa eas que secundum unumquodque clima distantias partium elevationis asscribemus equales et in reliquis tribus quartis incipientes quidem a sectionibus L M N X, educentes autem ut ad dextram eorum qui ad orientem semicirculorum, qui qui] seq. del. sub V supponuntur semper descripti esse ad nos. Continet autem elevatio poli, ubi quidem maxima dies et nox est horarum 13, partes proxime 16 tertiam et duodecimam. Ubi autem est horarum 13 et ½, partes 23 dimidiam et tertiam. Ubi autem horarum 14, partes 36. Ubi vero est horarum 14 et dimidie, partes 43 et quartam. At ubi est horarum 15, partes ⟨…⟩. Ubi autem est horarum 15 et dimidie, partes 45. Ubi vero est horarum 16, partes 48 et dimidiam et decimam. Copulabimus autem et diametros dictorum mensilium accipientes proprias ipsorum distantias ab equinoctiali in ipsa meridiani periferia uniuscuiusque divisionis equalis ipsorum quarte. Distat enim et que quidem tropici et secundum OP ab equinoctiali partes proxime 23 dimidiam et tertiam, que autem continui tropico mensilis et secundum RS partes 20 et dimidiam, que autem continui et secundum CY partes 13 et tertiam. Circumscribimus itaque et semicirculum qui in unaquaque harum et hos quidem cum propriis diametris sinemus secundum se, meridiani autem eorum qui circa equinoctialem equinoctialem] seq. del. circulum V diametrum semicirculorum utrumque dividentes in equales horarias distantias 12 signabimus sectiones. Similiter autem et eas, que super DGE fiunt a per perpendicularibus ad ipsam ab unaquaque divisionum horariarum, horariarum] corr. ex horariumarum V quoniam quidem hec servantur secundum omnes declinationes. Tympano quidem igitur existente ereo vel ⟨…⟩ ⟨…⟩] ψηφινω i. m. V nulla iam opus erit deletione caracterum caracterum] ἀποχαράξει i. m. V hiis quidem existentibus in superlinitionibus eorum, que secundum clima ordinantur, ut duabus diametris et horariis divisionibus; ligneo autem existente superliniendum ⟨…⟩ ⟨…⟩] ἀποχαράξεις i. m. V nigro quidem colore alias omnes, rubeo autem meridianum et diametrum equinoctialis cum signis, et super totum tympanum cera consimiliter speris, ut non simul cum variandis superliniantur, que debent remanere.

⟨12⟩

Hiis autem suppositis facile in promptu nobis erit acceptionum unaqueque, si prius quidem ordine assequentes radici supposite elevationis diametros copulaverimus orizontisque et gnomonis, deinde tropici semicirculi sectionem distinguentem quod supra terram ab eo quod sub terra et utrarumque harum portionum in sex equalia divisiones acceperimus et in propria ipsius diametro factas a divisionibus super ipsam perpendiculares. Hiis enim solis contenti procedemus secundum modum ostendendum. Primas quidem quidem] seq. del. igitur V rursum eas que ektimori circuli secundum quamlibet horam periferias, has quidem ex portione super terram consistentes proprii signi ea que mensilis positione, has autem ex ea que sub terra eius quod ex opposito sibi. Deinde eas que horarii omnium horarum, postea eas que descensivi et rursum convenienter eas que meridiani seorsum. Deinde eas que eius qui secundum verticem, post quas eas que orizontis, et ultimas, si voluerimus, eas que in plano equinoctiali. Post hoc autem acceptas quidem designationes liniemus. liniemus] corr. ex abliniemus et τελει. ψομ^υ i. m. V Similia autem faciemus in reliquis duobus mensilibus utroque in parte et similiter in equinoctiali. Deinde et priores diametros simul ablinientes copulabimus eas que consequentis climatis et eodem ordine utentes pertransibimus omnes suppositas differentias. Ceterum autem gratia modi acceptionis periferiarum subtensarum angulis exponatur meridianus qui in ⟨…⟩ ⟨…⟩] ἀναλήμματος i. m. V et sit ABGD circa centrum E, et copulentur per regulam examinate rectam que quidem AB diameter secundum communem sectionem ipsius et orizontis, que autem GD secundum gnomonem. Subiaceatque prius que ZEH diameter equinoctialis, et sit que quidem in duo equa sectio semicirculi ZTH penes T, que autem super terram quarta ZT, horariarum autem que in ipso sectionum una quidem que penes K, et et] seq. del. signum V quod a perpendiculari per ipsum ipsum] scilicet K sup. lin. V ad ZE fit in ipsa signum, sit L; hec enim ⟨…⟩ ⟨…⟩] εχ`εν (H suggests ἔχομεν) i. m. V a principio accepta. Eam quidem igitur que ektimori periferiam ex se ostendit que TK, super quam statuentes Cancrum et postponentes super divisam quartam exponemus gradus contentos a distantia. Continet autem semper tot, quot multitudo subpositarum ab ortu horarum, tempora equinoctialia, eadem existens ei que in plano equinoctialis. Eam autem que horarii accipiemus adducentes lati illius rectanguli alterum laterum ad signum L, ita ut reliquum adaptetur diametro orizontis AB, et secetur secetur] seq. del. qui a V meridianus ab eo quod quod] corr. ex qui V apud L latere penes M; que enim AM periferia faciet dictam. Similiter autem, si unum laterum adduxerimus ad L, ita ut alterum adaptetur diametro gnomonis GD, et secetur meridianus ab eo quod apud L latere penes N, que GN periferia faciet eam que descensivi. Rursum autem que quidem AZ ex se facit eam que meridiani. Si autem statuerimus Cancrum super signa K et L et unum lati illius laterum apposuerimus ad L 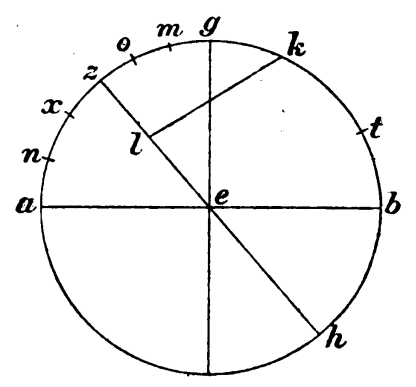altero adaptato ipsi GE, deinde alterum quidem terminum Cancri apposuerimus ei que que] seq. del. a V secus rectum angulum portioni ipsius GE, alterum autem apposuerimus lateri quod apud L, et manente ipso converterimus idem latus counitum similiter ipsi apud centrum E, ita ut secetur meridianus ab ipso ipso] latere scilicet i. m. V ut penes X, que GX periferia faciet eam que eius qui secundum verticem. Similiter autem, si unum laterum apposuerimus ad L altero adaptato ipsi AE et Cancri Cancri] corr. ex cancro V; Cancri i. m. V eandem ipsi KL distensionem habentis habentis] corr. ex habentes V; tis i. m. V alterum quidem terminum apposuerimus ei que secus rectum angulum portioni ipsius AE, alterum autem applicuerimus ei quod apud L lateri, deinde hoc manente converterimus rursum idem latus servata coniunctione super centrum E, ita ut secet meridianum ut penes O, que GO periferia faciet eam que orizontis. Et in hiis quidem periferiis et in omnibus simpliciter simpliciter] semper H intelligendum, ut non idem repetamus, quod distensiones ipsarum ipsarum] seq. del. cum V simul cum acceptione per Cancrum transferentes super divisam quartam deprehense deprehense] deprehensos conjectured H ab ipsis gradus debemus exponere.

⟨13⟩

Rursum supponatur alicuius aliorum mensilium parallelorum diameter et sit que ZHTK, super quam orientalis semicirculus qui ZLK, et centro quidem T distantia autem TA accipiatur signum in semicirculo ZLK quod L, in quo distinguitur quod quidem ZL super terram semicirculi et quod LK sub terra. Accipitur autem signum L per platinam rectangulam, platinam rectangulam] πλατυσμάτος i. m. V si angulus adductus fuerit ad H, ita ut alterum laterum adaptetur ipsi ZK. Secundum quod enim reliquum reliquum] vo. ca. scilicet latus i. m. V secat semicirculum, erit determinatum signum, quoniam 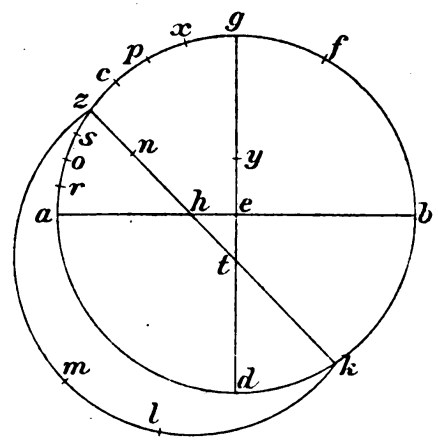quidem que ab H H] vel N i. m. V ipsi HK perpendicularis producta fit sectio planorum orizontis et circuli mensilis. Dividatur itaque portionum utraque in 6 equalia, et signatis ipsis accipiantur per appositionem appositionem] seq. del. p V platine rectangule et signa super ZK facta a perpendicularibus ad ipsam ab acceptis divisionibus in semicirculo. Sit autem una earum que super terram que penes M et quod eiusdem ordinis cum ipso signum eorum que super ZH quod N. Centro quidem itaque ipso N et distantia NM accepto secundum meridianum signo X et latere ⟨…⟩ ⟨…⟩] πλατυσμάτος i. m. V adducto ad signa E et H, ita ut secet meridianum penes O, que quidem ZO periferia faciet residuam in quarta periferie ektimori, que autem ab X super sectionem alterius alterius] scilicet lateris s. l. V ipsius ⟨…⟩ ⟨…⟩] πλατυσμάτος i. m. V et meridiani ipsam que ektimori, consequenter autem centro H et distantia HM accepto secundum meridianum signo P que AP periferia faciet eam que horarii. Similiter autem centro T et distantia TM accepto secundum meridianum signo R que GR periferia faciet eam que descensivi. Rursum que quidem AO periferia faciet eam que meridiani. Si autem unum laterum ⟨…⟩ ⟨…⟩] πλατύς i. m. V apposuerimus ipsi N reliquo adaptato ipsi GE, et Cancri Cancri] corr. ex Cancro V distensionem habentis habentis] corr. ex habentes V equalem ipsi NM alterum quidem terminum apposuerimus apposuerimus] seq. del. portioni V ei ei] sup. lin. V que penes angulum rectum portioni ipsius GE, alterum autem apposuerimus ei quod apud N lateri, deinde hoc manente converterimus latus quod ad ipsum servata ipsorum coniunctione ad centrum E, ita ut secet meridianum penes S, que GS periferia faciet faciet] corr. V eam que eius qui secundum verticem. Similiter autem rursum, si unum laterum apposuerimus ipsi N altero adaptato ipsi AE et Cancri distensionem habentis eandem ipsi NM alterum quidem apposuerimus ei que secus rectum angulum portioni ipsius AE, alterum autem applicuerimus ei quod apud N lateri, deinde hoc manente converterimus id quod apud N rursum servata ipsorum coniunctione ad centrum E, ita ut secet meridianum penes C, que CG periferia faciet eam que orizontis. Ceterum autem, si ipsam MN ponentes equalem ipsi EY apposuerimus ipsi Y rectum angulum uno uno] corr. ex uni V laterum adaptato ipsi EY et Cancri distensionem habentis eandem ipsi NM alterum quidem terminum apposuerimus penes Y, alterum autem applicuerimus recto angulo ad latus EG et manente hoc rursum converterimus latus quod apud id ipsum servata ipsorum coniunctione ad centrum E, ita ut secet meridianum secundum F, que GF periferia faciet eam que in plano equinoctialis.

Nunc autem, si diameter ZK ad sinistras nostri partes positionem habens sit unius parallelorum mensilium australiorum equinoctiali, transverso tympano ad positionem ex opposito et que ZK et qui super ipsam semicirculus secus dextras nostri partes erunt in situ eodem cum mensili parallelo descripto per opposita signa, borealiora autem equinoctiali, et que quidem KL portio erit super terram, que autem ZL sub terra. Quare Quare] vel ut i. m. V nos facientes eadem ostensis in divisionibus portionis KL inveniamus et eas que in oppositis signis consistentes periferias. Nam secundum quidem eam que in hyemali diametrum accepta ipsa ZK quod quidem ZG faciet eas que a principio Capricorni fiunt super terram angulorum periferias, quod autem DK DK] LKC in Greco i. m. V; LK conjectured H eas que a principio Cancri. Secundum eam autem que mensilis consequentis hyemali tropico diametrum supposita ipsa ZK semicirculus quidem ZL faciet eas que a principio Sagittarii et Aquarii consistentes super terram periferias, qui autem LK eas que in principio Geminorum et Leonis. Secundum eam autem que mensilis contigui equinoctiali diametrum accepta ipsa ZK qui quidem ZL semicirculus faciet eas que in principio Scorpionis et Piscium factas super terram periferias, qui autem LK eas que in principio Tauri et Virginis. Eas enim que in principio Arietis et Libre existentes easdem in una quacumque quartarum equinoctialis demonstratas esse accidit.

⟨14⟩

Et angulos vero ab antiquis determinatos, quoscunque non eodem modo nobiscum exposuerunt, ab hiis in promptu licebit transumere. Eum quidem enim qui circuli ektimori secundum nos, ut diximus, non assumpserunt, aliorum autem qui quidem horarius et qui in plano circuli qui secundum verticem et qui in plano equinoctialis iidem sunt hiis qui apud nos, qui autem ab ipsis vocatur ektimorus, est isdem cum apud nos meridiano, reliquorum autem descensivum quidem facit residuus residuus] deficiens i. m. V ad unum rectum eius qui apud nos descensivi, eum autem qui antiskius, id est contraumbralis, rursum residuus residuus] vel deficiens i. m. V ad unum rectum eius qui apud nos orizontis. Quod autem distracto distracto] seq. del. p V quidem plano equinoctialis accipitur, et per tale palam fit. Ostendit quidem enim et hoc eam que circuli horarii positionem. Hanc autem continet proprie que eius qui secundum verticem per polos horarii descriptorum descriptorum] ti i. m. V et uno existente eorum qui a principio necessarie suppositorum trium circulorum servantium ubique ad invicem positionem ad rectos angulos, propter quod et ektimori quidem periferia, pro qua eam que equinoctialis assumpserunt, non solum cum ea que horarii ostendit positionem radii, set et cum ea que meridiani, que autem equinoctialis cum sola ea que horarii et non adhuc neque cum ea que meridiani neque cum aliqua alia reliquarum. Hoc autem quia neque secundum proprietatem ferentium radium comprehendit semper utique aut solum equinoctiis neque secundum proprietatem manentium eandem ubique servat positionem ad reliquos non delatorum. Exposuimus autem et non consistentes quantitates secundum illum, quem ostendimus, modum consequentium rationabilitati periferiarum, in subiectis subiectis] seq. del. autem V septem parallelis et secundum unumquodque principium signorum et horarum in canonibus continentibus pertractatum a nobis ordinem in omnibus adiectionibus adiectionibus] ἐπiβολ ... i. m. V ad promptitudinem earum que in declinationibus acceptionum. Adhuc autem quoniam periferias quidem in meridiano circulo determinatas prompte faciunt manifestas orientaliores ipso et occidentaliores positiones horarum, horarum] των ρων i. m. V eas autem que in circulo qui secundum verticem borealiores ipso et australiores casus radiorum, in quibus quibus] seq. del. quod V consequentiam diximus oportere coexquirere, asscripsimus singulis horarum signa, per que eam que ad borealia circuli qui secundum verticem et rursum ad australia radii positionem licebit considerare aliqualiter a convenientibus hiis, que predeterminata sunt principium facientes ⟨…⟩ ⟨…⟩] faciamus i. m. V adiacentium quantitatum expressiones. expressiones] ἐκβολ^υ i. m. V Promptum autem adhuc et coniugationes, a quibus positio radii datur, datur] uncertain reading V sex numero esse accidit, tres quidem ab hiis que ad invicem invicem] seq. del. fer n V delatorum trium circulorum ektimorique ad horarium et ektimori ad descensivum, tres autem eas que ab unoquoque delatorum cum eo, qui inclinationem ipsius continet, manentium, ektimori quidem ad meridianum, horarii autem ad eum qui secundum verticem, descensivi autem ad orizontem. Habent autem et canones ita:

Cancri principii horarum 13 Table: in five places, the scribe left a sign, here denoted by the asterisk (*), referring to the symbol Γ̥ (=⅔) copied under the table