Tractatus sinuum et chordarum Georgii Peurbachii

Sinuum cordarum et arcuum notitia ad celestium motuum cognitionem pervalde necessaria existit. Ideo de eorum doctrina restat in presenti perquirendum. Unde videndum quid sit sinus, quid sinus rectus, quid versus, quid corda, quid arcus, quid kardaga.

Magistri geometrie non potuerunt perfecta ratione comprehendere quanta esset dyameter circuli respectu sue circumferentie eo quod recti ad curvum non est proportio. Practici tamen posuerunt circumferentiam triplam sesquiseptimam dyametro. Arsinides Arsinides] Archimedes N autem probat circumferentiam continere ter dyametrum et minus quam 10 70^as et plus quam 10 71^as. Sed Ptholomeus in Almagesti probat quod decima circumferentie habet cordam 27 graduum et 4 minutorum fere. Et ergo ergo] ideo N dicit: si ponimus dyametrum 150 graduum erit circumferentia fere 377 graduum, qui nunc ad numerum graduum dyametri nullam proportionem habent notam. Indi vero dicunt: si quis sciret radices numerorum recta radice carentium invenire ille faciliter inveniret quanta esset dyameter respectu circumferentie. Et secundum eos: si dyameter fuerit unitas erit circumferentia radix de 10. Si 2 erit radix de 40. Si 3 erit radix de 90 et sic de aliis. Et est differentia inter Indos et practicos geometrie 1 minutum et plus quam septima pars unius minuti, unde patet dyametrum ex circumferentia et circumferentiam ex dyametro diversimode posse reperiri. Dicunt etiam nonnulli quod proportio dyametri ad circumferentiam sit sicut 20000 ad 62832 et ex hoc iterum uno noto alterum reperitur. Sed his modis diversis non semper reperitur eadem quantitas, sed diversa secundum quod auctores diversimode ymaginati sunt de proportione eorum. Primus tamen modus communior est aliis. Item licet inter sinum et portionem non sit proportio propie loquendo eo quod rectum et curvum non sunt eiusdem speciei, est tamen inter eos mutua relatio. Nam sinus est portionis sinus et portio est sinus portio. Quamquam igitur non sit nobis notitia certa de proportione dyametri ad circumferentiam, possumus tamen ad placitum ponere dyametrum quotquot partium voluerimus et secundum eas quantitates cordarum aliarum et sinuum reperire.

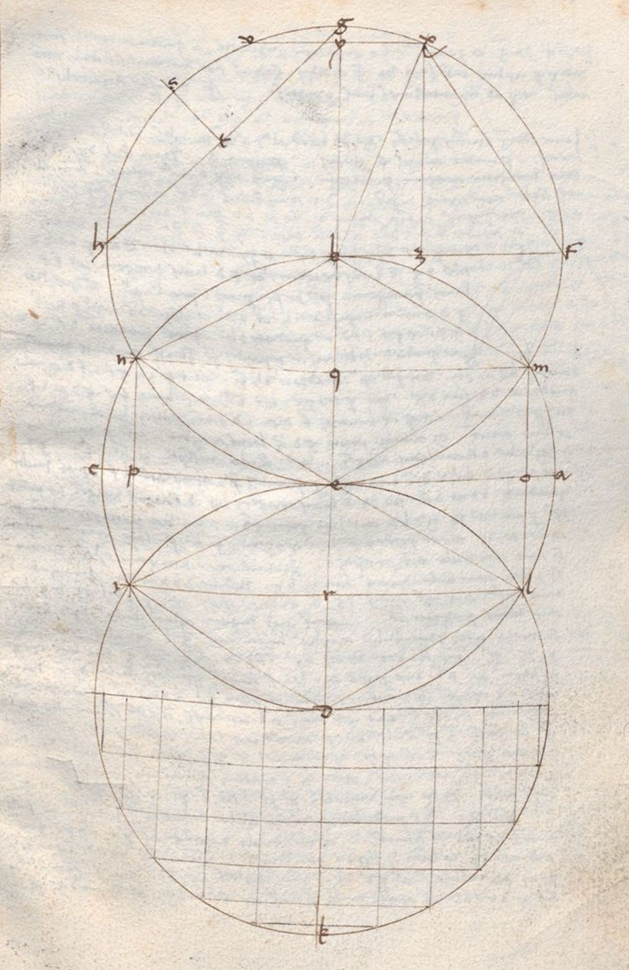
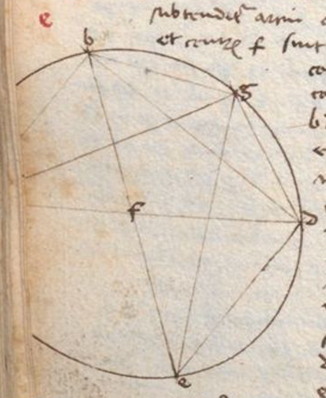
Ad demonstrandum igitur quantitatem sinus cuiuslibet portionis et primo 6 kardagarum circuli. Sit circulus ABCD, centrum eius E, quadratus duabus dyametris orthogonaliter se sectantibus AC, BD. Sit etiam circulus FGH equalis priori supra centrum B cuius circumferentia contingit lineam AC supra centrum E. Item circulus IKL supra centrum D equalis priori contingens similiter lineam AC in E. Et primus secet secundum in punctis M et N et primus primus] secundus N tertium in punctis I et L. Circulo ABCD inscribatur exagonus equilaterus per penultimam quarti qui sit BNIDLM, ex qua etiam patet quod latus exagoni talis est equale semidyametro circuli. Ducaturque linea MN secans BE in Q, similiter IL secans ED in E. Quia igitur linea MN eadem de circulis equalibus abscindit duos arcus, scilicet MBN et NEM, ipsi erunt equales per 27 tertii. Eadem ratione arcus arcus] corr. ex portio V MB equalis erit arcui ME eruntque 4 arcus MB, BN, NC, CM sibi invicem equales. Item per 8 primi vel 4 vel 4] add. sup. lin. V et 26^am primi patet quod linea BE dividitur in duo equa in Q, similiter NM NM] corr. ex NB V dividitur per equa in Q. Eadem ratione linea IL dividit lineam CD per equa et econtra. Et ita patet quatuor lineas BQ, QE, ER, RD sibi esse equales et lineam QR esse equalem semidiametro et per 27 tertii patet circulum esse divisum in 6 arcus equales. Item per quartam secundam partem 28^e et 34^tam primi NP et QE esse equales et NQ et PE similiter equales et ita NP erit quarta pars dyametri circuli sive medietas semidyametri. Unde sinus 12^e partis circuli sive 30 graduum erit quarta pars dyametri. Et ita notus est sinus duarum kardagarum simul. Linea autem NQ est sinus rectus quatuor kardagarum sive sexte partis circuli et ipsa nota erit per penultimam primi eo quod EQ est nota, similiter EN. Postea in circulo FGH protrahe dyametrum FH orthogonaliter secantem GE in centro B et, ducta linea GH, quam per 11 primi divide per equa in T, similiter arcum GH per 29 tertii per equa in S. Tunc arcus GS erit octava circuli sive 45 gradus que sunt tres kardage et cuius sinus GT notus erit per penultimam primi. Quadratum GH duplum est ad quadratum semidyametri, unde sinus totus est quadrandus et postea dupli eius radix quadrata erit linea GH cuius medietas est GT sinus trium kardagarum sive 45 graduum. Patet AM esse 30 graduum et eius corda erit nota subtrahendo EO que est equalis NQ sinui 60 graduum ab EA sinu toto et manebit OA cuius quadratum iungatur cum quadrato MO, scilicet sinus 30 graduum. Et producti radix erit corda quesita cuius medietas est sinus prime kardage sive 15 graduum. Deinde in circulo FGH accipiatur portio 30 graduum que sit VGX ita quod VG sit 15 graduum, similiter GX 15 graduum et erit arcus XF 75 graduum. Duc ergo per 31 primi lineam XZ equidistantem linee GB que erit sinus portionis XF 75 graduum. Ductaque linea BX a quadrato semidyametri, scilicet BX, auffer quadratum sinus portionis 15 graduum, scilicet linee YX, et manebit quadratum linee YB que est equalis linee XZ. Erit ergo sinus portionis 75 graduum notus et est sinus 5 kardagarum. Sinus autem totus sive semidyameter est sinus 6 kardagarum.

Habitis igitur sinibus sex kardagarum minue sinum arcus 15 graduum de sinu arcus 30 graduum et residuum erit sinus kardage secunde. Deinde subtrahe sinum duarum kardagarum, hoc est arcus 30 graduum, a sinu arcus trium kardagarum et remanebit sinus tertie kardage et ita de ceteris. Ex hys igitur manifesta est quantitas tam sinus recti quam versi cuiuslibet kardage et quarumlibet simul sumptarum. Nam sinus rectus prime kardage est sinus versus sexte et sinus rectus secunde est sinus versus quinte etc. Item sinus rectus duarum kardagarum primarum, scilicet prime et secunde, est sinus versus duarum ultimarum, scilicet quinte et sexte. Et sinus versus primarum duarum est sinus rectus duarum ultimarum. Hec siquidem sunt sex kardage gratia quarum introducta est hec demonstratio.

Ad inveniendum autem sinus minorum circuli portionum, sinum sexte kardage multiplica per sinum arcus 30 graduum et producti radix erit sinus arcus 7 graduum et dimidii. Quem in se multiplicatum auffer a quadrato totius sinus et remanentis radix erit sinus 82 et dimidii gradus. Hunc minue a toto sinu et residuum multiplica per sinum 30 graduum et provenientis radix erit sinus arcus 3 graduum et trium quartarum. Et quadratum huius auffer de quadrato totius sinus et residui radix erit sinus 86 graduum et unius quarte. Post subtrahe sinum 45 graduum de toto sinu. Residuum multiplica per sinum arcus 30 graduum et collecti radix erit sinus arcus 22 graduum et dimidii. Cuius quadratum minue de quadrato totius sinus et radix remanentis erit sinus arcus 67 graduum et dimidii. Quem auffer de sinu toto et remanens multiplica per sinum 30 graduum et excrescentis radix erit sinus arcus 11 graduum et 15 15] corr. ex 45 V minutorum. Cuius quadratum minue a quadrato totius sinus et radix residui erit sinus portionis 78 graduum et 45 45] corr. ex 15 (?) V minutorum. Post hec deme sinum 15 graduum de sinu toto et residuum multiplica per sinum 30 graduum et numeri producti radix erit sinus

portionis 37 graduum et 30 minutorum. Cuius quadratum subtrahe a quadrato totius sinus radixque residui erit sinus 52 graduum et dimidii. Eodem modo fit universis circuli portionibus usque ad minutissimas eius portiones. Hec de mente Arzachelis.

Nunc secundum sententiam Ptholomei in prima dictione Almagesti 9^o et 10 capitulis videndum est de inventione cordarum. Premittit autem primo 6 propositiones.

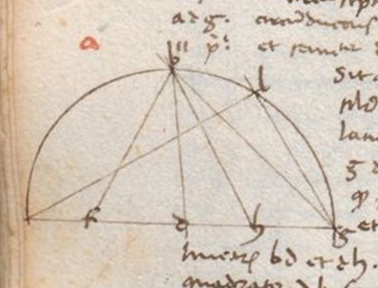
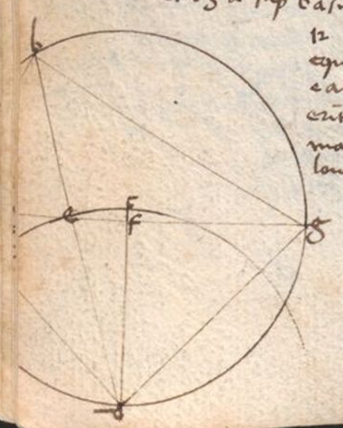
Prima est: data circuli dyametro latera decagoni, exagoni, pentagoni, tetragoni atque trianguli equilateri, omnium ab eodem circulo circumscriptorum reperire. Sit semicirculus ABG erectus supra dyametrum ADG circumductus super centrum D et sit DB perpendicularis a centro super AG per 11 primi et semidyameter DG in duo media divisa in H per 10 primi et ducta linea BH sitque HF equalis HB per 3 primi et protrahatur linea BF. Dico quod linea BD, similiter DG est latus exagoni et FD latus decagoni et FB latus pentagoni. Primum Primum] followed by a word that was crossed out: sic V patet per corollarium penultime quarti. Secundum sic: nam GD dividitur in equalia in H et additur ei in longum DF, igitur per 6 secundi quod fit ex GF in FD cum quadrato DH equatur quadrato HF, igitur et quadrato HB, unde etiam per penultimam primi quadratis quadratum duarum linearum BD et DH. Dempto igitur quadrato DH communi erit quod ex GF in FD equale quadrato BD sive DG. Igitur per secundam partem 16^e sexti tres linee FG, GD et DF continue proportionales erunt. Estque etiam linea GF divisa in D secundum proportionem habentem medium et duo extrema cuius maior portio GD est latus exagoni. Igitur per conversam 9 13ⁱ linea DF erit latus decagoni equilateri circulo inscripti et hoc est secundum. Tertium vero sic: nam angulus D est rectus, igitur per penultimam primi quadratum BF equatur duobus quadratis BD et DF, sed BD est latus exagoni et DF latus decagoni ut patuit. Igitur per conversam 10 13ⁱ BF erit latus pentagoni, nam latus pentagoni equilateri per eandem 10 13ⁱ tanto potentius est latere exagoni quantum potentius latus decagoni equilateri si sint eidem circulo omnes inscripti. Latus vero tetragoni equilateri invenitur si in priori semicirculo ducatur linea BG. Nam linea DB dividit semicirculum in duo media, erit igitur arcus BG quarta circumferentie circuli, unde per quartam sexti BG linea erit latus quadrati etc. Latus autem trigoni equilateri circulo inscripti habebitur si intra eundem semicirculum coaptetur linea recta GL equalis semidyametro GD per primam quarti que tangat dyametrum AG in termino eius, scilicet G. Ipsaque erit latus exagoni et ducatur linea AL, dico quod ipsa erit latus trigoni equilateri circulo inscripti. Nam latus GL exagoni abscindit de semicirculo arcum GL qui erit sexta pars circumferentie totius circuli, scilicet 60 gradus, erit igitur arcus AL residuus complementum semicirculi, scilicet 120 gradus, et ipsum est tertia pars circuli. Eius igitur corda erit latus trigoni per 28 tertii. Et ita patet tota propositio. Corollarium ex hoc: unde manifestum est quod si nota fuerit circuli dyameter et prenominata latera nota erunt, corde quoque que residuis semicirculi arcubus subtenduntur erunt note, patet ex ipsa demonstratione prima pars, sed secunda patet ex 30^a tertii et 46 primi. Cuiuscumque arcus sinus versus se habet ad sinum rectum medietatis arcus sicut idem sinus rectus se habet ad sinum arcus 30 graduum. Hoc est dicere: cuiuslibet arcus in quarta circuli sinus rectus est medio loco proportionalis inter sinum versum arcus dupli et sinum rectum arcus 30 graduum add. VN. This gloss, edited at this place in smaller characters in N, is found at the bottom of fol. 124v in V, as an addition apparently by the scribe (Regiomontanus), but in different ink. It is unclear where this gloss belongs.

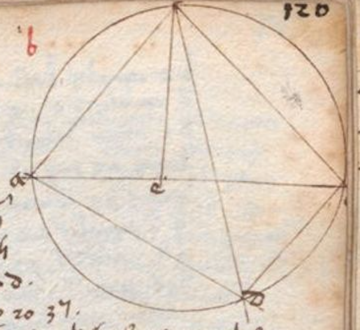
Secunda propositio est: si quadrilaterum infra circulum describatur, rectangulum quod sub duabus eius dyametris continetur est equale duobus rectangulis pariter acceptis que sub utrisque eius lateribus oppositis continentur. Sit circulus ABGD in quo describam quadrilaterum ABGD et eius duas dyametros AG, BD. Dico quod rectangulum quod fit ex AG in BD est equale duobus que fiunt ex AD in BG et AB in DG simul acceptis. Faciam enim per 23 primi angulum ABE equalem angulo GBD adiectoque utrique eorum angulo EBD erit angulus ABD equalis angulo GBE. Sed per 20 tertii angulus BGE equatur angulo BDA. Igitur per secundam partem 32^e primi residuus angulus BEG erit equalis residuo angulo BAD, sunt igitur trianguli equianguli, igitur per 4 sexti latera equos angulos respicientia proportionalia erunt, unde AD ad EG AD] AD est N sicut BD ad BG, ergo per 15 sexti quod fit ex AD in BG equatur ei quod fit ex EG in BD. Item angulus ABE per hypothesim equatur angulo DBG, sed per 20 tertii angulus BAE equatur angulo BDG. Igitur per secundam partem 32 primi tertius angulus tertio est equalis, unde triangulus ABE est equiangulus triangulo DBG, igitur per quartam sexti latera erunt proportionalia. Erit igitur AB ad BD sicut AE ad DG et permutatim AB ad AE sicut BD ad DG, ergo per 15 sexti quod fit ex AB in DG est equale ei quod fit ex AE in BD. Iam autem demonstratum est quod fit ex AD in BG est equale ei quod fit ex EG in BD, igitur per primam secundi totum rectangulum quod fit ex ductu AG in BD equatur duobus rectangulis quorum unum fit ex AD in BG et aliud ex AB in DG. Nam quod fit ex AG in BD equatur duobus rectangulis per primam secundi, scilicet uni quod fit ex BD in EG et alii quod fit ex BD in AE simul sumptis. Sed primum rectangulum equatur ei quod fit ex AD in BG et aliud ei quod fit ex AB in DG. Unde quod fit ex AG in BD est equale duobus rectangulis, scilicet ei quod fit ex AD in BG et illi quod fit ex AB in DG simul sumptis, quod est propositum.

Tertia est: si in semicirculo corde arcuum inequalium note fuerint corda quoque arcus quo maior minorem superat erit nota. Sint in semicirculo ABGD supra dyametro AD descripto due corde AB et AG note, dico quod corda arcus BG nota erit. Ductis enim duabus cordis BD et GD que, cum due AB et AG sint note, erunt manifeste erunt manifeste] erit manifestum N per corollarium prime huius eo quod quelibet earum est corda residui semicirculi. Est igitur quadrilaterum ABGD infra circulum cuius due dyametri AG et BD sunt note, tunc per premissam duo recta simul que fiunt ex AB in GD et ex BG in AD nota erunt. Rectangulum autem quod fit ex AB in GD est notum eo quod ambe linee ipsum rectangulum continentes sint note. Quo ablato de totali rectangulo quod fit ex AG in BD manebit rectangulum quod fit ex BG in AD et quia una eius linearum ipsum continentium est nota, quia AD dyameter circuli erit per divisionem reliqua linea, scilicet BG, nota, quod est propositum.

Propositio quarta est hec: si in semicirculo alicuius arcus corda nota fuerit corda quoque que eius medietati subtenditur nota erit. Sit sit] si N in semicirculo ABG descripto supra dyametro AG arcus BG cordam notam habens, diviso arcu BG per equa per 29 tertii et ductis cordis AB, BD, AD et DG ducatur perpendicularis DF supra dyametrum per 12 primi. Dico quod linea FG est medietas superflui linee AG super lineam AB. Pono enim lineam DE equalem linee AB per tertiam primi et produco DE. Et quia AB est equalis AE posita AD communi erunt due linee AB et AD trianguli ABD equales duabus lineis AE et AD trianguli AED, quelibet videlicet sue relative, et arcus BD equalis arcui DG, et arcus BD equalis arcui DG] add. i. m. V et per 26 tertii angulus BAD equalis angulo EAD, igitur per quartam primi basis BD equalis basi ED. Et quia linea BD per 28 tertii est equalis linee DG, igitur DG est equalis DE, igitur per quintam primi trianguli DEG anguli supra basim sunt equales. Quare DF linea demissa per 26 primi dividit EG in equalia. Tota autem EG est superfluum linee AG super AB et FG est medietas superflui et ita patet quod dictum est. Et quia corda arcus BG est nota ex hypothesi, erit corda residui semicirculi que est linea AB nota que est equalis AE. Erit igitur EG nota et per consequens eius medietas FG. Quia ergo per 30 tertii angulus ADG in semicirculo consistens est rectus et ab eo super basim egreditur DF perpendicularis, erit DG per 8 sexti per 8 sexti] add. sup. lin. V medium proportionale inter AG et GF. Sed cum AG et GF sint nota una ducta in aliam erit quadratum linee DG notum et per consequens ipsa linea.

Quinta: Quinta] i. m. V si due corde duorum arcuum in semicirculo fuerint note corda quoque que toti subtenditur arcui ex illis duobus arcubus composito erit nota. Circuli, cuius dyameter AD et centrum F, sint duo arcus noti AB et BG notas cordas habentes et sit una corda alteri copulata in B et protracta corda AG, dico quod ipsa corda AG nota erit. Protraho enim dyametrum BFE et lineas BD, DG, DE et GE. Tunc enim ex notitia linee BG nota erit linea GE et ex notitia AB nota erit BD et ex notitia BD scietur DE. Est ergo quadrilaterum BGDE circulo inscriptum, cuius sunt due due] duo N dyametri BD et GE, per secundam huius rectangulum quod fit ex eis erit equale duobus rectangulis quorum unum fit ex BE in GD et aliud aliud] AD N ex BG in DE. Quia igitur dyametri sunt noti, erunt illa duo rectangula nota. Sed unum eorum rectangulorum notum est eo quod BG et DE sunt note, erit aliud rectangulum notum, scilicet quod fit ex BE in GD, et quia unum eius latus est notum, scilicet dyameter BE, erit per divisionem ipsius rectanguli per dyametrum linea GD nota, qua nota per corollarium prime huius erit GA nota, nam ipsa est residui arcus de semicirculo corda. Vel aliter et facilius: quia corde EG et ED sunt note, erit per tertiam huius corda GD nota unde et AG similiter nota erit. erit] erunt N Et nota quod corda ED est equalis corde AB, quia utraque earum earum] eorum N est corda residui de semicirculo ultra arcum BD.

Propositio sexta est hec: si protrahantur in circulo due due] duo N linee inequales proportio corde longioris ad cordam breviorem erit minor proportione arcus arcus] followed by a word that was crossed out: breviorem V longioris ad arcum breviorem. Sint in circulo ABGD protracte due corde, minor AB et longior BG, dico quod proportio corde BG ad cordam AB est minor proportione arcus BG ad arcum AB. Dividam enim angulum ABG per equalia secundum 9 primi per lineam BD eritque per 25 tertii arcus ABGD equalis arcui DABG super quos ipsi anguli equales cadunt. Dempto igitur arcu vel vel] unclear reading V; om. N ABG communi utrique manebit arcus AD equalis arcui DG eritque per 28 tertii linea DA equalis linee DG et per 5 primi anguli DAG et DGA supra basim equales. Et a puncto D duco super AG perpendicularem DF per 12 primi eruntque per 26 primi AF et FG equales et angulus ADF equalis angulo GDF et per consequens linea GE erit maior linea EA. Et quia angulus EFD rectus est, igitur maior angulorum eiusdem trianguli erit per 18 primi DE maior DF. Angulus autem AED extrinsecus per 32 primi maior est angulo recto, igitur per 18 primi AD longior CD. Est ergo AD longior ED et ED longior DF. Circulus descriptus super D secundum quantitatem linee DC procul dubio lineam AD secabit, sed lineam DF DF] F N non attinget. Circumducto igitur super D circulo HEC secante DA in H et ducta DF usque ad C, sector EDC erit maior triangulo EDF et triangulus ADE est maior sectore HDE. Igitur per primam partem octave quinti Euclidis proportio trianguli EDF ad sectorem HDE est minor proportione sectoris EDC ad sectorem HDE. Et per secundam partem eiusdem proportio trianguli EDF ad triangulum ADE est minor proportione eiusdem trianguli ad sectorem HDE. Quare per communem animi conceptionem quidquid est minus minore est etiam minus maiore, erit proportio trianguli EDF ad triangulum ADE minor proportione sectoris EDC ad sectorem HDE. Proportio autem trianguli EDF ad triangulum ADE per primam sexti est sicut proportio linee EF ad lineam EA. Proportio vero sectoris EDC ad sectorem HDE est sicut arcus EC ad arcum EH que est sicut anguli FDE FDE] corr. ex FDD V ad angulum ADE per ultimam sexti. Igitur proportio linee FE ad lineam EA est minor proportione anguli FDE ad angulum EDA. Igitur coniunctim proportio linee FA ad lineam EA est minor proportione anguli FDA ad angulum ADE. Quare proportio linee duple predicte linee AF que est linee AG ad lineam AE minor erit proportione anguli EDA EDA] EDA qui est duplus ADF N. The situation is unclear in V. The scribe wrote GDA and corrected G into something that cannot be read and above A he put a sign referring to a gloss in the margin: qui est A. ad angulum ADE. Ergo disiunctim proportio linee GE ad lineam AE minor erit proportione anguli GDE ad angulum EDA. Et quia in triangulo ABG linea BE ducta ab angulo ABG ad basim AG dividit eundem angulum per equa, erunt per tertiam sexti due partes ipsius basis, scilicet GE et EA, reliquis eiusdem trianguli lateribus, scilicet lineis BG et BA, proportionales. Igitur proportio linee GE ad EA est sicut proportio corde GB ad cordam BA et proportio anguli GDB ad angulum BDA per ultimam sexti est sicut arcus GB ad arcum BA. Quare proportio corde BG ad cordam BA est minor proportione arcus BG ad arcum BA, quod erat demonstrandum.

Ex premissis propositionibus cuiuslibet arcus noti quantitas corde reperitur. Ex prima enim propositione nota est corda sexte partis circuli eo quod ipsa est equalis semidyametro. Nota est etiam corda decime partis circuli, scilicet arcus 36 graduum, nam ipsa est latus decagoni. Nota est similiter corda quinte partis circuli eo quod ipsa est latus pentagoni et ipsa est corda arcus 72 graduum. Similiter corda arcus 90 graduum, ipsa enim est latus quadrati. Item corda 120 graduum, quia latus trigoni.

Amplius ex sequentibus propositionibus constat ex certorum arcuum differentiis cordas multas posse inveniri. Per secundam enim propositionem et tertiam possunt inveniri plures corde superflui superflui] superflue N arcuum secundum seipsas cordas notas habentium. Et hoc taliter: propositis namque cordis duabus arcuum inequalium notis, si vis invenire cordam arcus quo maior excedit minorem, primo scias cordas arcuum residuorum semicirculi respectu utriusque corde proposite subtrahendo quadratum corde proposite a quadrato dyametri. Et manebit quadratum corde residui arcus semicirculi ultra arcum corde proposite per corollarium prime huius, cuius radix ostendit quantitatem talis corde. Illud autem quod fit ex ductu corde arcus maioris in cordam residui arcus minoris est equale illis duobus que fiunt ex ductu corde arcus minoris in cordam residui arcus maioris et ex ductu dyametri in cordam arcus quo maior excedit minorem ut patet patet] potest N deduci ex tertia propositione. Subtracto igitur eo quod fit ex ductu corde arcus minoris in cordam arcus residui maioris remanet quod fit ex ductu dyametri in cordam arcus quo maior minorem excedit. Quod si dividitur per dyametrum exibit ipsa corda arcus quo maior excedit minorem. Ita per cordam arcus 60 graduum et cordam arcus 72 graduum invenies cordam arcus 12 graduum. Item per cordam arcus 36 graduum graduum] repeated V et per cordam arcus 60 graduum reperies cordam arcus 24 graduum. Item per cordam arcus 60 graduum et cordam arcus 90 graduum invenies cordam arcus 30 graduum. Sicque de ceteris similibus debes operari et cordas multorum arcuum habebis. Consequenter ex quarta habetur qualiter habita corda alicuius arcus inveniri queat corda medietatis eiusdem arcus, ut ex corda arcus 12 graduum potest reperiri corda arcus 6 graduum. Deinde arcus trium, post arcus unius gradus cum dimidio, deinde arcus dimidii gradus et quarte. quarte] 4 N Primo debet queri corda residui talis arcus per corollarium primi huius. Qua ablata a dyametro residui medietas ducatur in dyametrum et producti radix est corda quesita, nam ipsa est corda medietatis arcus propositi. Et ita potes ex corda 60 graduum reperire cordam arcus 30 graduum dupliciter per precedentem et illam. Et ex corda arcus 30 graduum cordam arcus 15 graduum, deinde cordam arcus 7 graduum et dimidii et ex corda arcus 36 graduum cordam arcus 18 graduum, deinde 9, deinde 4 graduum cum dimidio. Et sic de aliis consimilibus eodem modo est procedendum.

Deinde ex quinta habebitur qualiter per arcum unius gradus et dimidii et eius cordam multorum arcuum corde possunt inveniri, ut si corda arcus unius gradus et dimidii componatur cum quacumque cordarum notarum, aut si arcus illarum cordarum duplantur vel triplantur et sic deinceps, aut si ad arcum habentem cordam notam addatur arcus sibi equalis, aut arcus maior aut minor eo cordam etiam habens notam quomodo corda totius arcus ex eisdem compositi debeat inveniri. Illud autem generaliter debet inveniri hoc modo: primo quere cordam residui arcus semicirculi ad arcum corde primo proposite per corollarium prime huius. Deinde quere etiam cordam residui arcus semicirculi super arcum secunde corde prime superaddite per eundem modum. Post cordam residui primi arcus duc in cordam residui secundi arcus et productum serva. Post hec cordam primo propositam duc in cordam secundam prime superadditam et quod exit subtrahe a producto iam servato et quod remanet divide per dyametrum et exit quantitas corde superflui arcus semicirculi ultra arcum totalem compositum ex illis duobus arcubus. Quadratum igitur ipsius subtrahe a quadrato dyametri et residui radix erit corda totius arcus compositi. Ita ex corda arcus trium graduum et corda arcus unius gradus cum dimidio reperies cordam 4 graduum et dimidii et etiam cordam arcus 175 graduum et dimidii. Et similiter in aliis. Si alicui arcui habenti notam cordam addatur arcus maior aut minor minor] followed by two words that were crossed out: aut equalis V similiter cordam habens notam invenies cordam totius arcus ex hiis compositi. Si vero alicuius arcus notam cordam habentem dupli arcus cordam reperire volueris, primo est est] followed by several words that were crossed out: talis arcus residui de semicirculo per corollarium prime s… (?) corda V quadranda corda arcus propositi et ipsum quadratum dematur de quadrato dyametri. Et a residuo dematur quadratum corde arcus propositi et residuum per dyametrum dividatur et exibit corda residui de semicirculo ultra arcum compositum ex duplo arcus propositi, cuius quadratum de quadrato dyametri aufferatur, et residui radix erit corda arcus dupli ad arcum propositum. Ita ex corda arcus 4 graduum et dimidii poteris invenire cordam arcus 9 graduum. Consimiliter cuiuscumque alterius dupli arcus ad aliquem arcum cordam habentem notam poteris cordam invenire.

Postremo ex sexta propositione potest haberi qualiter per cordam arcus unius gradus et dimidii et per cordam arcus medietatis et quarte unius gradus inveniri debeat corda unius gradus. Si enim haberetur corda arcus 30 minutorum qui est tertia pars arcus unius gradus et dimidii omnes corde arcuum aliorum veraciter essent note. Nam in tabula Ptholomei ponuntur arcus secundum augmentum dimidii gradus. Unde si reperiretur corda arcus medietatis gradus invenirentur cum ea per precedens precedens] precendentem N capitulum quantitates cordarum reliquorum arcuum que sunt inter cordas notas. Quas nominamus secundum veritatem numerationis linearum et per hoc compleremus omnes cordas semicirculi secundum superfluum dimidii gradus. Hoc autem secundum veritatem non reperitur, quoniam etsi corda arcus unius gradus et medii sit nota corda, tamen eius tertie, tertie] tertia N scilicet arcus 30 minutorum, sub numeri compoto et secundum veritatem numerationis non est reperta. Eiusdem tamen rei notitia presenti intentioni est necessaria. Summo igitur studio et industria, quamvis non contineat vere quantitatem omnium cordarum, possibile tamen est ut per ipsum inveniatur quantitas cordarum parvorum arcuum, ita, ut secundum veritatem nichil quod sensibilis sit quantitatis deficiat, inventus est modus quo corda arcus arcus] followed by several words that were crossed out: unius gradus et medii V medietatis gradus per cordam arcus unius gradus et dimidii et per cordam arcus medietatis et quarte gradus reperta est. Et est talis:

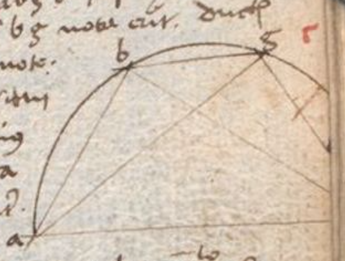
Sit circulus ABDG in quo sint tres corde, una AB subtendatur arcui medietatis et quarte gradus, alia AD subtendatur uni gradui, tertia AG subtendatur arcui gradus et dimidii. Quia ergo per sextam huius proportio corde AD ad cordam AB minor est proportione arcus AD ad arcum AB, arcus autem AD ad arcum AB est sesquitertius, ostensum est autem ex dictis quod corda AB est 0 gradus, 47 minuta et 7 secunda. Si eius tertia que est 15 minuta, 42 secunda et 20 tertia sibi superadditur proveniet 1 gradus, 2 minuta, 49 secunda et 20 tertia, et hoc est sesquitertium ad cordam AB. Sed corda AD minor est ad AB quam sesquitertia, ideo corda AD minor erit quod 1 gradus, 2 minuta, 49 secunda et 20 tertia. Rursum quia proportio corde AG ad cordam AD minor est quam proportio arcus AG ad arcum AD per sextam, arcus autem AG sesquialterus est ad arcum AD, ex dictis autem patet quod corda AG est 1 gradus, 34 minuta, 14 secunda. Et si ab ea subtrahitur eius tertia pars que est 31 minuta, 24 secunda et 40 tertia residuum erit unus gradus, 2 minuta, 49 secunda et 20 tertia et ad illud corda AG est sesquialtera. Igitur corda AD respectu corde AG est maior quam 1 gradus, 2 minuta, 49 secunda et 20 tertia. Est ergo corda corda] followed by a word that was crossed out: unius V arcus unius gradus respectu corde unius medietatis et quarte gradus minor quam 1 gradus, 2 minuta, 49 secunda et 20 tertia et respectu corde unius gradus et medietatis maior est quam 1 gradus, 2 minuta, 49 secunda et 20 tertia. Manifestum est quod conveniens est ut pro corda unius gradus circuli accipiamus 1 gradus, 2 minuta et 49 secunda de gradibus de quibus semidyameter est 60. 60] corr. ex 120 V Sic enim minus quam in duabus tertiis unius tertii erit error, quare multo minus quam in uno secundo, sed in inquisitione cordarum quod minus quam secundum fuerit postponitur. Et ex hoc patet que sit quantitas corde arcus dimidii gradus. Ipsa enim erit 0 gradus, 31 minuta, 25 secunda fere. Et per illius quantitatem complebitur residuum reliquarum cordarum que binatim cadunt inter duas cordas notas. Cordam namque arcus duorum graduum sciemus per compositionem arcus unius gradus et dimidii cum arcu unius medietatis gradus, sed cordam arcus 2 graduum et dimidii sciemus per superfluum arcus trium graduum supra arcum medietatis gradus. Et similiter sciemus quantitates reliquarum cordarum. Facilis ergo est secundum premissorum tenorem cordarum ad suos arcus cognitio.

Finis