بسم الله الرحمن الرحيم

⟨I⟩ تعاليق لمسلمة بن أحمد الأندلسي على كتاب بطلميوس في تسطيح بسيط الكرة

قال في الشكل الأوّل عند قول بطلميوس أعني أن تُجعل أوائل البروج على النقط التي عليها تُقسم الدوائر الموازية لمعدّل النهار التي تُرسم بالطريق الذي أوضحنا Must be corrected to أوضحناه على البعد الموافق لبعد كلّ واحد من البروج من دائرة معدّل النهار في الكرة المجسّمة دائرة فلك البروج.

قال Crossed out by the scribe, kept in KL. أراد بطلميوس بقوله هذا أنّه يعمل تعمل KL دوائر موازية لدائرة معدّل النهار التي هي دائرة ابج‍د ببعد ميل برج برج فيما بينها ودائرة طل التي هي المنقلب الصيفي وفيما بينها وبين دائرة كم التي هي المنقلب الشتوي فحيث ما قاطعت هذه الدوائر الموازية لمعدّل النهار التي داخلها وخارجها دائرة فلك البروج فتلك النقط تكون أوائل البروج وكذلك لو عملت دوائر موازية لبعد ميل درجة درجة من فلك البروج لقسمت دائرة فلك البروج على جزء جزء ولكنّك إذا أردت أن تخرج هذه الصناعة إلى الفعل حدث لك في ذلك تقريب كبير إذ الدوائر المتماسّة لا تتماسّ بالعقل إلّا على نقطة وبالفعل على خطّ.

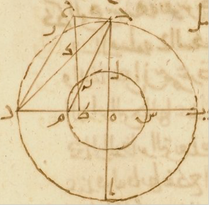
قال مسلمة بعد تمام الشكل الثالث لو قصد بطلميوس إلى البرهان بالخلف لكان أقرب إلى الفهم وذلك أنّه حيث قال إنّا أنا KL نصل خطّ هح ونخرجه على استقامة حتّى يقطع دائرة الأفق على نقطة ط لو قال فإن لم يمرّ بنقطة ط فليمرّ بنقطة أخرى إمّا دونها وإمّا فوقها فليمرّ أوّلًا بنقطة م وننفذه إلى دائرة فلك البروج حتّى يقاطعها على نقطة ز فيكون ضرب حه في هم كضرب اه في هج‍ وضرب اه في هج‍ كضرب به في هد فضرب به في هد إذًا كضرب حه في هم وضرب به في هد كضرب حه في هز فيجب إذًا أن يكون ضرب حه في هم كضرب حه في هز فهو إذًا مساو لهز هذا خلف لا يمكن وكذلك لا يمكن أن يخرج على استقامة فوق نقطة ط.

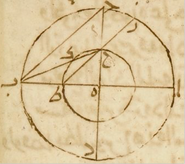
قال مسلمة بعد فراغ جميع الكلام في الشكل الرابع ولمّا استبان أنّ الدوائر الموازية لمعدّل النهار بأي بعد كانت يحدّها خطّ در ودكح وأنّ نصف قطر الدائرة الموازية لمعدّل النهار من ناحية الجنوب يكون من نقطة ه إلى النقطة التي عليها يتقاطع خطّ هز دط KL مع خطّ هج‍ وفرضنا قوس ج‍ط تسعة وثمنين جزءًا وجب أن يقع التقاطع على نصف قطر دائرة بعدها من دائرة معدّل النهار إلى ناحية الجنوب تسعة وثمنين ثمنون KL جزءًا وقد علمنا أنّ بعد القطب الجنوبي من دائرة معدّل النهار تسعون جزءًا وهو ميل كلّ قوس دج‍ فإنّما يجب أن يُحدّ القطب الجنوبي في هذا السطح تقاطع خطّ هج‍ مع خطّ مواز له يخرج من نقطة د والمتوازيان لا يتقاطعان فالقطب الجنوبي إذًا لا يمكن وضعه في هذا السطح كذلك لو وضعنا نقطة ه القطب الجنوبي لكان القطب الشمالي لا يمكن وضعه معه في السطح وأيضًا قد أثبت عندنا بطلميوس أنّ الخطوط المستقيمة المارّة على مركز ه هي بدل الدوائر المعروفة بدوائر نصف النهار المارّة على القطبَين وأنّ تلك الدوائر تتقاطع في موضعين فالموضع الواحد القطب الشمالي والآخر الجنوبي وهذه الخطوط المستقيمة لا تتقاطع إلّا في موضع واحد فإذا فرضنا ذلك الموضع القطب الواحد لم يكن لك إلى KL حيث تفرض نفرض KL الثاني إذ الخطوط المستيمة لا تتقاطع في موضعين وهذا استبان ما قاله بطلميوس في صدر هذا الكتاب.

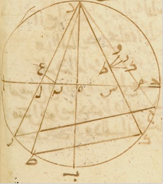
قال مسلمة في الشكل الخامس وهو الذي يقول بطلميوس في أوّله فإذ قد وصفنا ذلك فنبيّن في مثل هذه الصورة أنّه تُرى مقادير المطالع وجميع ما يعرض فيها على ما بيّنّا في الكرة المجسّمة. بعد قوله فزاوية هطف إذّا معلومة وذلك ما أردنا أن نبيّن Corrupted at the end of the line وكان له أيضًا طريق أسهل من ذلك وذلك أنّه قد ذكر قطر كلّ واحدة من الدائرتين الموازيتين لمعدّل النهار ببعد واحد إلى الجنوب وإلى الشمال فإذا كان خطّ هك نصف قطر الدائرة الجنوبية من معدّل النهار فخطّ هن نصف قطر الدائرة الشمالية التي هي بذلك البعد وقد تقدّم له ذكر كمّية قطرها في المسئلة التي قبل هذه والبرهان على ذلك في المسئلة الثانية من كتابه.

قال مسلمة في الشكل ⟨...⟩ Lacuna وهو الذي في أوّله ولكن نجعل الصورة على حسب مقدار الموضع المعلوم الذي نريد أنّ نرسم فيه ما ذكرنا وحتّى يتهيّأ لنا أن نرسم مواضع الكواكب الثابتة إن أردنا ذلك. بعد قوله شبيهة بقوس ج‍ز وذلك ما أردنا أن نبيّن. ولو قصد بطلميوس في هذه المسئلة إلى ما أذكره لكان أقرب مأخذًا إن شاء الله وذلك أنّه إذا وصل د بنقطة ز لو أخرج من نقطة ج‍ خطًّا موازيًا لخطّ دز وهو ج‍م ثمّ عمل الدائرة التي تكون مدار الحَمَل ببعد هم لكانت دائرة الحمل وذلك أنّ زاوية نمه مساوية لزاوية زده فقوس بج‍ز شبيهة بقوس سلن فتبقي قوس نل شبيهة بقوس ج‍ز.

وله وجه آخر قريب أيضًا وذلك أنّا نجعل أعظم الدوائر الواقعة في الآلة دائرة ابج‍د حول مركز ه ونخرج قطرَي الدائرة يتقاطعان على زوايا قائمة ونريد أن نرسم داخلها ⟨دائرة⟩ Add. KL يكون بُعد هذه الدائرة من المرسومة داخلها ببعد قوس شبيهة بقوس ج‍ز فنصل بز وليقاطع خطّ هج‍ على نقطة ح ونجعل ه مركزًا ونرسم دائرة ببعد هح وهي دائرة حكط فأقول إنّ قوس كط شبيهة بقوس زج‍ برهان ذلك أنّا نصل ج‍ب حط فحط مواز لج‍ب فزاوية كحط مساوية لزاوية ج‍بز وكلّ واحدة منهما على محيط الدائرة فقوس كط شبيهة بقوس ج‍ز فإذا كانت دائرة حطط Must be corrected to حكط, as in KL معدّل النهار كانت دائرة ابج‍د مرسومة عنها ببعد كط التي هي شبيهة بقوس ج‍ز وذلك ما أردنا بيانه.

قال مسلمة في الشكل ⟨...⟩ Lacuna وهو الذي أوّله وأيضًا ينبغي أن نتمّم عرضنا بأن نبيّن كيف تُرسم الدوائر التي حالها عند الدائرة التي تمرّ توسط Must be corrected to بوسط, as in KL البروج كحال الدوائر التي تقدّم ذكرها عند معدّل النهار. عند قوله فإنّها تقطع الدائرة الأجزاء Must be corrected to الأخرى, as in KL الباقية على القطر أيضًا. وهذه الدوائر إذا رُسمت في البسيط المسطّح ومرّت بدرجة كوكب من الكواكب الثابتة فإنها تمرّ بالكوكب بعنه وكذلك إن Corrupted at the end of the line, add. KL مرّت بالكوكب بعنه فإنّها تمرّ بدرجته والخطوط المستقيمة التي Corrupted at the end of the line, add. KL تمرّ بمركز دائرة معدّل النهار في السطح إذا مرّت بالكوكب بعينه فإنّها تمرّ بالدرجة التي معها يتوسّط الكوكب السماء وإن مرّت الخطوط بالدرجة التي معها يتوسّط الكوكب السماء فإنها تمرّ بالكوكب بعينها فإعلم.

قال مسلمة في الشكل الذي أوّله وقد يمكننا أن نضع في الصفيحة الدوائر الموازية لدائرة فلك البروج أيضًا على هذا المثال. وفي آخره فنقط ن ع م ف على محيط دائرة. فإذا عملتَ دائرة موازيةّ لدائرة فلك البروج يكون ميلها عن فلك البروج بمقدار عرض كوكب من الكواكب الثابتة ثمّ طرحت قوسًا تمرّ بقطب فلك البروج الذي هو نقطة ك في المسئلة التي قبل هذه وبدرجة الكوكب في فلك البروج وتقطع فلك البروج بنصفين فإنّها ستقطع فلك معدّل النهار أيضًا بنصفين فحيث ما تقاطعت هذه القوس مع الدائرة الموازية لفلك البروج فتلك النقطة موضع الكوكب في الصفيحة ومن هذه الصورة تعمل الدوائر الموازية لدائرة الأفق وهي المقنطرات ويقوم عليها البرهان منها.

قال مسلمة في الشكل الذي أوّله وينبغي أن نبيّن أنّ مراكز الدوائر الموازية لدائرة البروج التي ترسم على هذا المثال تكون مختلفة أبدًا. وفي آخره فليس نقطة و لمركز الدائرة بنقتَي ن س وذلك ما أردنا أن نبيّن لم يبيّن أنّ المراكز ليست على نقطة واحدة إلّا بعد أن بيّن أنّ خطّ مس أطول من خطّ نل وقد نبيّن ذلك بأقرب من هذا وذلك أن نعيد الشكل وذلك أن نخرج من نقطة ن خطًّا يكون عمودًا على خطّ دم دل KL وهو نع ونبيّن أنّ دن أقصر من دس ودل أقصر من دم فلنقطع في خطّ دس خطًّا مساويًا لخطّ دن وهو دط ومن خطّ دم خطًّا مساويّا لدل وهو دز فيصير مثلّث دطز مساويًا لمثلّث ]لمثلّث[ دنم دنل KL ويقع عمود نع كوقوع عمود طو وتكون زاوية دنل مساوية لزاوية دطز ولأنّ خطّ دس أطول من خطّ ند تكون زاوية دنس أعظم من زاوية دسن فزاوية دسم الباقية أعظم من زاوية دنل الباقية التي هي مثل زاوية دطز فإذا أخرجنا من نقطة ط خطًّا موازيًا لخطّ مس سيقع طرفه الآخر تحت نقطة ز وهو خطّ طك فنسبة سد إلى طد كنسبة مس إلى طك فهو أطول من Om. KL طك وطك أطول من طز فمس أطول من طز الذي هو مثل نل. وأيضًا فإنّا نبيّن ذلك دون أن نخرج العمود بأن نقول إنّ زاوية دزط التي هي مثل زاوية دلن حادّة فخطّ كط أطول من خط زط. ومن هذا الشكل يتبيّن أنّ الأقسام التي تقسمها الخطوط المستقيمة المخرجة من نقطة د في خطّ ج‍ا على قُسي متساوية تكون في خطّ ج‍ا غير متساوية وأنّ كلّ ما قرب من المركز كان أقصر ممّا بعد عنه.

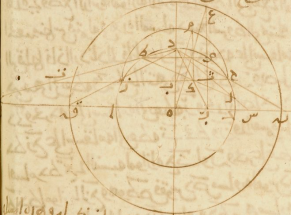
قال مسلمة في الشكل الذي أوّله ويجب الآن لمكان الدائرة الموازية لدائرة فلك البروج التي ليست محصورة في الصفيحة لكن يقع بعضها في القطعة التي لا تظهر وهي غير مرسومة في الكرة. وفي آخره وقسمت دائرة نعق على نقطة ع بقوسَين مشابهين Must be corrected to مشابهتين, as in KL لقوسَي ج‍م حم KL مز. ومن تمام هذه المسئلة هق على استقامة ودط على استقامة حتّى يلتقيا على نقطة و يبهرن ]أيضًا[ Crossed out by the scribe, see KL أنّ الدائرة التي تمرّ بنقطة س ونقطة ع تمرّ بنقطة و أيضًا على ما برهن في المسئلة التي قبل هذه في وضع الدائرة الموازية لدائرة فلك البروج التي لا يقع في الدائرة الخفية منها شيء فتتمّ له في هذه المسئلة جميع الشروط التي تمّت له في التي قبلها فإذا أردنا ذلك فإنّا نصل دز ونخرجه على استقامة حتّى ينتهي إلى نقطة ق على ما انتهى دح إلى نقطة ن ونصل دك ونخرجه على استقامة إلى Crossed out by the scribe, kept in KL نقطة ر وكذلك أيضًا نخرج خطّ زح على استقامة إلى نقطة ت فخطّ ون قد انقسم بمثل أقسام خطّ تح في النسبة لموازاة حت لون ونجيز على نقطة ط خطًّا موازيًا لزح وهو طص فقوس دص مساوية لقوس دط فزاوية دطص مساوية لزاوية دلط وزاوية دطص هي مساوية لزاوية دتح للموازاة فزاوية دلط مساوية لزاوية دتح فنقط ل ث ط ت على محيط دائرة فصرت Must be corrected to فضرب, as in KL تك في كث كضرب كط في كل وقد كان ضرب طك في كل مساو مساويا KL لكز في كح ف كز في كح مساو لكت في كث فضرب إذن قر في رن كضرب رو في رس ونصل رع فمثلّث رهع شبيه بمثلّث كفم لأنّ Add. i.m. زاوية ب ف KL مثل زاوية ه والخطّان المحيطان بها متناسبة لأنّ نسبة ره إلى بك فك KL كنسبة هق إلى بز فز KL للموازاة فزاوية عره إذًّ قائمة فضرب قر في رن مثل رع في مثله وقد كان قر في رن كضرب رو في رس فضرب رو في رس مثل ضرب رع في مثله ورع عمود فنقط س ع و على محيط دائرة وذلك ما أردنا أن نبيّن.

قال مسلمة أيضًا ولكي نكمل ما يجب أن نكمله في هذه المسئلة Corrupted at the end of the line, see KL وذلك أن نبيّن أنّ هذه الدائرة الموازية لدائرة فلك البروج ستقطع أيضًا بنصفين الدائرة الموازية لدائرة معدّل النهار التي تقطعها في الكرة المجسّمة بنصفين. برهان ذلك أنّا نجعل دائرة نصف النهار دائرة ابج‍د حول مركز ه والقطب الخفي نقطة د وقطر الدائرة الموازية لدائرة فلك البروج طكل ونصل دل ونخرجه إلى س ودط ونخرجه إلى و ثمّ نجيز على نقطة ك خطًّا موازيًا لقطر دائرة معدّل النهار الذي هو اج‍ وهو خطّ نحكز ونصل دح ونخرجه على اسلقامة إلى ق فممّا قد تقدّم أنّ الدائرة التي ترسم ببعد هق هي الدائرة الموازية لدائرة معدّل النهار التي بُعدها منها قوس اح وهي الدائرة التي تقسمها الدائرة الموازية لدائرة فلك البروج في الكرة بنصفين على خطّ نصف النهار ثمّ نخرج هب إلى ف وليكن هف مثل هق فنبيّن أنّ الدائرة التي تمرّ بنقط س و ع ستمرّ بنقطة ف فنجيز على نقطة ط خطًّا موازيًا لخطّ كح وهو طم فزاوية دطم مساوية لزاوية دلط لأنّهما على قوسين متساويتين وزاوية دطم مساوية لزاوية دنك للموازاة فزاوية دنك مساوية لزاوية دلط فنقط ل ز ط ن على محيط دائرة فضرب كن في كز مساو لكط في كل وكط في كل مساو لكح في مثله فكن في كز مثل كح في مثله وقد انقسم خطّ وس بمثل انقسام خطّ نز في النسبة فيجب أن يكون ضرب وه في هس كضرب قه في مثله و قه مثل هف فضرب وه في هس كضرب ]كضرب[ هف في مثله فالدائرة التي تمرّ بنقط س ع و تمرّ أيضًا بنقطة ف وذلك ما أردنا بيانه.

وعلى مثل هذه الرتبة نخرج الدائرة الموازية لدائرة الأفق الواقعة تحتها ]لافق[ لا فرق بينهما فتكون المقنطرات الواقعة في الصفيحة على الأسطرلاب الجنوبي خطّ دلس مستقيم وخطّ طل مستقيم.

قال مسلمة في الشكل الذي أوّله ومن البيّن أنّا إن توهّمنا في مثل هذه الصورة الدائرة الموازية لدائرة فلك البروج التي على قطرها دل. وفي آخره وذلك أنّ سطح دائرة نصف النهار أيضًا التي على خطّ بد هو على زوايا قائمة على كلّ واحد من السطحين الذين ذكرناهما. وأريد أنّ هذا الخطّ المستقيم يقطع الدائرة الخفية بقسي شبيهة بالقسي التي تقسمها في الكرة المجسّمة في شكل وذلك أن نعيد الصورة وليكن قطر الدائرة الموازية لمعدّل النهار الخفية خطّ زكح فالدائرة المرسومة ببعد هن خفية أبدًا ونقيم على خطّ زح نصف دائرة ونخرج من نقطة ك خطًّا موازيًا لهد وهو كم فالدائرة الموازية لدائرة فلك البروج المرسومة على قطر دل تقطع في الكرة الدائرة الخفية على نقطة م فتقسمها بقوسين وهما حم ومز وكذلك يقسم خطّ بع دائرة نعق بقوسين شبيهتين بقوسَي حم مز ]وكذلك يقسم خطّ[ Crossed out by the scribe, see KL وهما نع عق. برهان ذلك أنّا نصل هع فم فمن أجل أنّ خطّ زح موازٍ لنه تكون نسبة نه إلى سه كنسبة حف إلى فك ونه مثل هع وحف مثل فم فنسبة عه إلى هس كنسبة مف إلى فك وزاوية عسه قائمة وهي مساوية لزاوية مكف يكون مثلّث مفك شبيهًا بمثلّث عهس وتكون زاوية عهس مساوية لزاوية مفك فقوس نع شبيهة بقوس حم وكذلك الباقية من نصف الدائرة وهي Corrected by the scribe from وهو قوس عق تكون شبيهة بالباقية من نصف الدائرة وهي قوس مز فقد قسم خطّ بع دائرة ]دائرة[ نعق بقوسين شبيهتين بالقوسين اللتين تقسم الدائرة الموازية لفلك البروج ⟨من⟩ Add. KL الدائرة الخفية في الكرة المجسّمة وأيضًا فإنّ هذه الدائرة تمرّ في الكرة بالقطب الخفي ولن يقع في هذا السطح القطب الخفي مع القطب المرئي إذ سطح هذا القطب يمتدّ إلى ما لا نهاية ولا يبلغ إلى القطب الجنوبي وكذلك خطّ بع إن أخرج إلى ما لا نهاية لم يلتق مع خطّ ج‍د وذلك ما أردنا بيانه.

تمّ تعاليق مسلمة بن أحمد على كتاب بطلميوس في تسطيح بسيط الكرة والحمد لله وحده وفرغ من تعليقه بظاهر أسداباذ بالمعسر المنصور †...† KL suggest either العناني or العتابي في د يا ح ثمد وصلى الله على سيدنا محمّد