⟨I⟩ Fragmentum versionis M. Bergii ex libello manuscripto et incorrecto, cuius titulus erat Κλαυδίου Πτολεμαίου περὶ ὑποθέσεων τῶν πλανωμένων Fragmentum … πλανωμένων] Κλαυδίου Πτολεμαίου περὶ ὑποθέσεων τῶν πλανωμένων Mi; ex versione Io. Praetorii add. i. m. Mi; Κλαυδίου Πτολεμαίου περὶ ὑποθέσεων τῶν πλανωμένων O

⟨I.1⟩

Hypotheses, o Syre, coelestium motuum in iis quidem, quas de mathematicis scripsimus commentariis, oratione explicare conati sumus, indicata sigillatim illorum cum concinnitate concinnitate] concincitate Mu tum praeclarissima praeclarissima] certa sup. lin. add. et del. Mu in universum concordia concordia] ex corr. Mu in arguenda coelestium motuum certa constanteque ratione, quam esse conveniebat in iis naturis, naturis] ex corr. O quae perennem constantemque motum haberent, haberent] ac add. i. m. Mi nullaque nullaque] nulla MiO ratione id quod est magis ac ac] et MiO minus recipere possent. Hoc vero in scripto in scripto] corr. ex inscripto Mi in eam modo partem nos dedimus, ut summatim tantum illa exponeremus ita ut intelligi possent, cum a vobis ipsis, tum ab iis quoque quibus fabricam harum rerum adornare est propositum, sive adeo seorsim manuario opere motus uniuscuiusque uniuscuiusque] corr. ex unumcuiusque Mu; corr. ex uniuscunque Mi ratione ad suam epocham accommodata id efficiunt, sive etiam mechanico artificio coniungunt cum inter sese orbes, tum omnes ceteros ad primi orbis sphaeram. Neque tamen hoc faciunt eo quo solent sphaerae construi modo – eiusmodi namque fabrica praeterquam quod aberrant aberrant] corr. ex aberant Mu eius hypotheses etiam nil nisi phaenomena exhibent exhibent] corr. in exhibet Mi subiecto ipso neglecto, neglecto] corr. ex neglegto Mu quocirca artificii est in his documentum, non hypothesium astronomicarum specimen –, verum eo modo ut ordo simul et differentia motuum una cum ea quae in circularibus conversionibus etsi aequalibus aspectantibus, tamen nobis prae oculis versatur inaequalitate. Neque vero omnes orbium motus ad eum, qui propositus est, modum convertere convertere] corr. in connectere Mi possumus, sed illud fieri potest, ut seorsim uniuscuiusque rationem rationem] corr. ex ratione Mi; ratione O huiusmodi esse ostendamus.

⟨I.2⟩

Eum vero tenebimus in hac doctrina modum, ut in iis quidem quae universalia sunt, talia assumamus quae consentiant consentiant] corr. ex confetiunt Mi iis, quae in Sintaxi de his disseruimus, disseruimus] corr. in desseruimus Mi in particularibus autem, ut omnia accommodent ad emendationes nostras, quas de assiduis observationibus observationibus] ex corr. Mu confecimus, aut in ipsarum hypothesium ratione aut in particularibus considerationibus aut in periodicis revolutionibus ipsis. Ad haec ut cohereat expositio ista cum ipsa hypothesium doctrina, hoc est ut quod quidem ad aequales motus attinet, attinet] ex corr. Mi dividamus, ubi est opus, est opus] inv. MiO et et] corr. ex eo Mi rursus convertamus convertamus] corr. in connectamus Mi altera illa ratione proposita, hunc in modum – nimirum quod ad partes zodiaci etiam ipsa ipsarum definitionum initia referantur idque propter supputationis commoditatem –, quo scilicet demonstretur isto pacto, quod sit cuiusque circumvolutionis proprium, etiam cum ad eadem puncta absolvuntur.

Quod vero attinet ad eorum circulorum positionem atque rationem, qui inaequalitatem efficiunt motuum, ut simplicioribus illis abutamur ad commodam commodam] commodum Mi effectionem machinae machinae] seq. del. null O utut parva aliqua diversitas etiam coincidat. Denique ut etiam ipsis circulis in praesentia accommodemus motus, tamquam seorsim sumptis, extra eas a quibus continentur sphaeris, dirigendo eos veluti ad nudas et in aperto positas ipsarum hypothesium lationes.

Incipiemus vero ab ipso universi motu quando quidem is et is et] inv. MiO particeps est omnium reliquorum motuum et omnes alios continet, et et] seq. del. denique quod Mu; et quod MiO idem veluti specimen est ad cognoscendum pleraque alia naturae admirabilis opera, quae consimilia quaedam consimilis naturae rebus attribuit, quemadmodum quemadmodum] quemdam MiO de illis ipsis quae hic ostendentur perspicuum fiet.

⟨I.3⟩

Cogitetur circulus maximus circa centrum sphaerae mundanae semper manens, voceturque aequinoctialis, ac dividatur huius circumferentia in segmenta aequalia 360, vocenturque haec segmenta propria appellatione tempora. Postea alius circulus ipsi concentricus circumducatur in eodem plano et circa idem centrum aequabili motu ab ortu in occasum, voceturque circulus deferens. Vehat autem autem] seq. del. hic Mu; unum MiO alium magnum circulum sibi inclinatum super eodem centro fixa inclinatione, qui circulus appelletur zodiacus, ac declinatio horum planorum contineat angulum partium 23° 51′ 20′′, qualium unus rectus habet 90. Divisa porro etiam ipsa zodiaci circumferentia in aequalia segmenta 360, vocentur haec segmenta segmenta om. MiO proprio vocabulo partes, et puncta quidem in quibus sese sese] se MiO mutuo mutuo] mutu Mi dispescunt dispescunt] secant MiO deferens et zodiacus dicantur aequinoctialia, at quae utrinque per quadrantem circuli distant a singulis tropica, per quadrante … tropica] circuli quadrante removentur a singulis tropica dicant MiO et horum horum] corr. ex in his Mu illud quidem punctum quod ad septentriones declinat, aestivus sive borealis limes dicatur, alterum vero illi oppositum, limes hybernus sive australis. Similiter et aequinoctialium aequinoctialium] aequinoctiorum MiO punctorum illud quod aestivum tropicum, secundum eum quem posuimus motum, praecedit, vernum appelletur, quod vero hybernum antecedit, autumnale.

⟨I.4⟩

Mundi vero conversio una conversio una] inv. MiO efficitur, cum aliquod deferentis punctum moveri coeptum ab aliquo item certo puncto immobilis illius aequinoctialis circuli, ad idem punctum prius punctum prius] prius corr. ex primum Mu; inv. MiO revertitur, ac perspicuum est huiusmodi revolutionem complecti tempora 360. Verum quia mundi conversionum conversionum] corr. ex conversiones Mu restitutiones restitutiones] corr. ex integros Mu non adaequantur manifeste, adaequantur manifeste] inv. MiO ut scilicet scilicet] sup. lin. Mu sensui appareant, sed dies potius dies potius] inv. MiO a Sole pendentes, ideo per hosce alios motus metimur.

Est autem diurnum tempus in quo Sol illum immobilem aequinoctialem ipso mundi circumactu absolvit una revolutione. una revolutione] corr. ex unam revolutionem Mu Ac manifestum est, si Sol in zodiaco non moveretur, eandem futuram cum ipsius mundi conversione diei diei] corr. ex diem Mu revolutionem. Verum, quia ponitur ille moveri etiam altero illo motu, ut ut] quo MiO scilicet interim in ortum procedat, procedat] progreditur MiO fit ut longius sit spacium diurnae revolutionis, quem quem] (aequalis diei definitio, non apparentis) add. i. m. Mu; diem aequalem intellige, non apparentem illi enim metiuntur motus add. i. m. MiO est conversionis mundi. Et continetur in se una diei revolutio unam mundi conversionem, hoc est tempora 360, insuperque insuperque] et insuper MiO tantam aequinoctialis partem, partem] seq. del. Sol Mu quantam Sol in zodiaco confecit secundum aequalem motum.

⟨I.5⟩

His positis iam deinceps etiam ad errantium hypotheses nos convertemus nos convertemus] sup. lin. MuO primo loco exponendo simplices et separatos eorum circuitus, e quibus particulares et compositi compositi] expositi Mi illi motus existunt, quos quidem nos sumimus, proxime accedentes ad rationes revolutionum e nostris correctionibus collecturum. collecturum] sumptarum MiO

In annis ergo Aegyptiis 300 et diebus 74 Sol ponatur conficere revolutiones – eas quae ad tropica et aequinoctialia zodiaci aequinoctialia zodiaci] solstitialia MiO puncta sumuntur – 300. 300] Ergo una [1.] revolutio habet dies 365 ¼ minus ⅓₀₀ diei ut Ptol. alias add. i. m. Mu

Inerrantium vero sphaera et insuper apogaea quinque planetarum ponantur quinque planetarum ponantur] in planetam 5 ponant Mi conficere in una tali Solis revolutione 36′′, hoc est in dicto annorum spacio partes 3, qualium circulus habet 360. Quare etiam etiam] etiam aliam(sup. lin.) Mi in annis solaribus 36,000, qui sunt anni Aegyptii 36,024, dies 120, unam tantum revolutionem perficit perficit] corr. ex perficere Mu inerrantium sphaera. sphaera] corr. ex sphaeram Mu

Solares vero circuitus in hac conversione comprehensi erunt 35,999. 35,999] dies ergo: 13148880. Solaris revolutio 35999. Ergo mundi(corr. ex diurnas) conversiones in annis 36000 fuerunt 13184829 add. i. m. Mu Mundi denique conversiones tot, tot om. MiO quot sunt in dicto tempore dies, et insuper quot sunt solares conversiones.

⟨I.6⟩

Luna vero in annis annis] seq. del. solibus Mu solaribus – quales ad aequinoctialia et tropica puncta spectantur – 8,523, qui sunt anni Aegyptii 8,528, dies 277 28′ 4′′ consecutiones solares – id est menses integros seu synodicos – absolvat 109,416. Rursumque in mensibus integris 3,204, anomaliae revolutiones 3,512. Mensibus vero integris 5,058, latitudinis restitutiones 5,923.

⟨I.7⟩

Similem in modum Mercurii stella in annis solaribus, qui ad apogaea et inerrantium sphaeram sumuntur 993, qui sunt Aegyptii anni 993 et dies 255 0′ 54′′ 56′′′ 51′′′′ fere, anomaliae revolutiones efficiat 3,150. 3,150] corr. ex 5203 Mu

Veneris Veneris] corr. ex Iovis Mu vero vero om. O stella in annis solaribus similibus in annis solaribus similibus] in similibus annis solaribus MiO 1,010, qui sunt Aegyptii 1,010 et et om. MiO dies 259 22′ 50′′ 56′′′ 16′′′′ 27^v 50^vi, propemodum anomaliae revolutiones efficiat 5,703.

At Iovis stella in annis solaribus similibus stella … similibus] in similibus annis solaribus MiO 771, qui sunt Aegyptiaci 771 cum diebus 198 0′ 9′′ 18′′′ 0′′′′ 26^v 57^vi, propemodum propemodum] fere Mi anomaliae revolutiones faciet 703. 703] in hisce anni solaris quantitas ponitur dierum in 365 ⁷⁷/₃₀₀ et paulo plus add. i. m. Mu

Saturnus Saturnus] omissus est motus Martis add. i. m. Mi in similibus annis solaribus 324, qui sunt Aegyptiaci 324, dies 83 12′ 26′′ 19′′′ 14′′′′ 14′′′′] corr. ex 16 Mu; i. m. Mi 25^v 48^vi fere, anomaliae revolutiones absolvit 313. 313] 203 O

⟨I.8⟩

Iam quidem pro Solis sphaera cogitetur in plano zodiaci circulis eccentricus, ut ea quae ex centro ipsius ad eam quae inter centra – ipsius et zodiaci ­– rationem habeat tamquam 60 ad 2 30′. Quae vero recta proiicitur per utraque centra per per] et O apogaeum eccentrici, ea ab aequinoctii verni puncto in consequentia in consequentia] i. m. Mu sibi sibi om. MiO vendicet absumat absumat] add. sup. lin. Mu; nam locum apogaeum fixum faciet in 5 30 add. i. m. Mu semper partes 65 30′.

Solis vero centrum moveatur in iam dicto eccentrico circulo ab occasu in ortum super suo centro aequaliter, ut diebus 37 supra annos Aegyptios 150 revolutiones absolvat 150, quales ab apogaeo eccentrici spectant. Porro inerrantium stellarum sphaera sphaera] seq. del. seq Mu circa zodiaci centrum ac super eiusdem polis moveatur moveatur] momento Mi versus ortum aequali motu in iam dicto tempore parte parte] corr. ex partibus MuO 1° 30′, qualibus qualibus] corr. ex qualium Mu; scilicet add. MiO zodiacus constat 360.

Anno itaque itaque] autem MiO primo ab obitu Alexandri Magni secundum Aegyptios primo die mensis Thoth in in] sup. lin. Mu Alexandrino meridiano Alexandrino meridiano] corr. ex Alexandria in meridie Mu; inv. MiO Sol quidem ad apogaeo eccentrici in consequentia mundi abfuit partibus 160 10′. 10′] 50 Mi Stella autem quae est in corde Leonis a verno aequinoctio similiter in consequentia mundi numerando, partibus zodiaci 117 54′. 54′] hic desinit Bergii versio et antecedentia quidem intelligi et conciliari possunt, mediocriter, sed quae sequuntur videntur esse admodum corrupta add. i. m. Mu

⟨I.9⟩

At vero pro lunari sphaera cogitetur iterum circulus zodiaco concentricus mobilis in eiusdem zodiaci plano et circa eius centrum aequabili motu ab ortu in occasum, occasum] seq. del. eo scilicet, motu, quo supra aequalium Solis et Lunae motum, ipsa Luna eodem tempore extra zodiacum in latitudinis excurrit Mu eo scilicet excessu, quo motus latitudinis superat utriusque Solis et Lunae eiusdem eiusdem] corr. ex temporis Mu temporis motum, eo … motum] seq. del. eo scilicet motu quo supra aequalem Solis et Lunae motum, ipsa Luna eodem tempre extra zodiacum in latitudinis excurrit Mu; eo scilicet excessu quo latitudinis motus ad zodiacum relatus (ad … relatus i. m. MiO) superat utriusque Solis et Lunae eiusdem temporis motum MiO ita ut in diebus integris 88 supra annos Aegyptios 37 revolutiones in zodiaco faciat 2 fere, assumit enim ad accuratum calculum unius partis sexagesimae 1.

Vehat autem hic circulus alium sibi inclinatum super eodem centro non variata inclinatione, angulum comprehendens talium partium 5, qualium unus rectus est 90.

In plano vero huius obliqui circuli ponatur circulus eccentricus, ut ea quae ex centro ipsius ad eccentricitatem rationem habeat velut 60 ad 12 30′. Et hoc eccentrici centrum centrum] moveatur add. MiO circa centrum zodiaci moveatur moveatur] praem. MiO aequaliter ab ortu in occasum occasum] seq. del. a boreo limite Mu et a limite limite] limen Mu medii motus Solis At vero … Solis] Mu preserves on f. 15r an alternative translation tantum discedens, quantus est excessus mediorum motuum Solis et Lunae, et a … Lunae] a boreo limite eo excessu(excesu Mi) quo medius motus Solis superat duplum eiusdem temporis latitudinis motus ad zodiacum relati(ad … relati i. m.) MiO sic ut diebus 348 supra annos Aegyptios 17 restitutiones in obliquo circulo faciat 200 fere, deficiunt enim in accurato calculo unius partis sexagesimae 2. 2] hoc loco a sextu discessi (est u del.) videri enim et admodum corruptus i. m. Mu

Centrum autem epicycli ab occasu in ortum ab apogaeo eccentricitatis duplo velocius movetur, quem centrum centrum] sup. lin. Mu illud a medio moto Solis recedebat recedebat] seq. del. ut in Mu aequaliter circa centrum zodiaci, ut in Centrum … in] Centrum autem epicycli ab occasu in ortum ab apogaeo eccentrici semper eccentrici positum respiciens mediam illam epocham duplicat hoc est utrumque dictum motum conficiens ita in intgris supra nominatis MiO diebus 300 supra annos Aegyptios 19 ad ipsum eccentricum revolutiones perficiat 400 proxime, proxime] fere MiO assumit enim ad accuratam supputationem unius partis sexagesimae 4.

Tandem circa dictum centrum epicycli epicycli] seq. del. quod est in Mu existentis in plano obliqui circuli, circuli] aeque sem add. i. m. et del. Mu ad cuius semidiametrum eccentrici semidiameter rationem habet quam 60 ad 6 3′ ad cuius … 3′] i. m. Mu et ab ea recta quae quae] seq. del. est (corr. ex ex) diametro censui eccentrici Mu a puncto diametraliter opposito centro eccentrici in circello, quem idem centrum eccentrici describit, per centrum epicycli ducta, secans ambitum epicycli in duobus punctis quae vocamus apogaeum et perigaeum, ponatur centrum Lunae moveri aequaliter in apogaea epicycli parte versus occasum secundum secundum] iuxta MiO medium anomaliae motum, ut in diebus 99 supra annos Aegyptios 26 ad epicyclum restitutiones absolvat 348 fere, deficit enim ad accuratum calculum sexagesimae 1.

In In om. MiO primo autem anno ab obitu Alexandri secundum Aegyptios primi diei diei] corr. ex mense Mu Thoth in meridiano Alexandrino, boreus limes circuli obliqui circuli obliqui] inv. Mi abfuit ab aequinoctio verno in antecedentia mundi partibus 230 sexagesimis 13. Centrum vero epicycli ab apogaeo eccentrici in consequentia mundi partibus 261 22′. Centrum Lunae ab apogaeo epicycli in antecedentia mundi partibus 85 36′.

⟨I.10⟩

In In] Pro MiO Mercurii sphaera Mercurii sphaera] inv. MiO imaginatione concipiatur circulus zodiaco concentricus, qui moveatur in ipsius plano et super eius centro, ab occasu in ortum, quantum et inerrantium sphaera.

Vehat autem hic circulus alium sibi inclinatum circulum super eodem centro, immutabili inclinatione planorum angulum comprehendens comprehendens] includens Mi partis unius, partis unius] inv. MiO qualium qualium] scilicet add. MiO unus rectus est 90.

In hoc quidem obliquo circulo circulo] seq. del. pon Mu ducatur diameter per boreum et australem limitem, et in ipsa diametro diametro] sup. lin. Mu inter centrum zodiaci et et] seq. del. borei Mu australem limitem sumantur sumantur] sumunt Mi duo puncta, prope prope] corr. ex iuxta Mu centrum zodiaci et super remotissimo eorum moveatur aequaliter centrum eccentrici circuli in antecedentia mundi ab apogaeo eccentricitatis, eo excessu quo medius motus Solis excedit eodem eodem] corr. ex in eiusdem Mu; eiusdem temporis add. i. m. Mu tempore inerrantium motum, adeo ut in diebus 37 supra annos Aegyptios 144 revolutiones perficiat 144 proxime. Nam assumit adhuc in accuratiore calculo unius partis sexagesimae 2. 2] ξ ξ β add. i. m. Mu

Circa proximum vero punctum moveatur semper centrum epicicli in consequentia mundi ab apogaeo eccentrici eadem velocitate qua centrum eccentrici, adeo ut in diebus 37 supra annos Aegyptios 144 restitutiones faciat ad ipsum eccentricum ipsum eccentricum] ipsam eccentricitatem sup. lin. Mu; ipsam eccentricitatem MiO 144 proxime, assumit enim ad accuratum calculum partis unius sexagesimae 2.

Sit autem qualium semidiameter eccentrici 60 talium ea quae inter centrum zodiaci et proximum proximum] seq. del. punctum Mu duorum punctorum 3. Quae vero inter centrum zodiaci et remotissimum remotissimum] corr. ex remotissimorum Mu; illud add. MiO duorum punctorum 5 30′ et quae inter remotissimum punctum remotissimum punctum] inv. MiO et centrum circelli circelli] corr. ex eccentrici Mu; eccentrici MiO 2 30′. Rursus imaginatione concipiatur circellus circa centrum sphaerae sphaerae] sup. lin. Mu epicycli in plano obliqui circulo, circulo] circuli MiO et sumatur recta linea per utraque centra, ipsius scilicet (epicycli) epicycli om. MiO et proximum punctorum, ad quod moventur semper aequaliter semper aequaliter] sup. lin. Mu; semper et qualiter Mi puncta puncta] illa add. Mi; illa i. m. O circelli, quae vocamus circelli … vocamus] corr. ex quae utrumque circellum secans quae vocamus Mu apogaeum et perigaeum, et alius circellus ipsi concentricus mobilis in eodem plano, et circa idem centrum aeque velociter, velociter] seq. del. qui Mu qui secundum distantiam ab apogaeo in eandem partem mundi conversionis mundi conversionis] inv. MiO absolvat eodem tempore eodem tempore] sup. lin. Mu medium illum motum motum] eccentrici add. et del. Mu centri eccentrici vel epicycli. Et hic circellus alium vehat circellum inclinatum sibi circellus … sibi] seq. del. circa ad Mu; alium vehat circellum sibi inclinatum MiO super eodem centro, immutabili inclinatione angulum comprehendens partium 5 30′, qualium unus rectus est 90.

Quae autem ex centro eccentrici ad eam quae ex centro circelli, rationem habeat veluti 60 ad 22 4′, et in hoc circello cogitetur stella circa centrum ipsius aequaliter, aequaliter] seq. del. tamquam ab apogaeo Mu ab apogaeo scilicet, scilicet] seq. del. et Mu contra motum mundi motum mundi] inv. MiO circumverti, perficiens aequalem motum utriusque, centri scilicet eccentrici vel epicycli, et anomaliae stellae, ut in diebus 174 supra annos Aegyptios 208 revolutiones perficiat in obliquo epicyclo 865 proxime, assumit enim ad accuratum calculum unius partis sexagesimae 4.

Primo vero vero] autem MiO anno ab obitu Alexandri secundum Aegyptios prima die Thoth in meridiano meridiano] meridiae MiO Alexandriae apogaeum eccentrici ab aequinoctio verno in consequentia mundi abfuit partibus 185 sexagesimis 24. Centrum vero eccentrici ab apogaeo eccentricitatis in antecedentia mundi partibus 52 sexagesimis 16.

Centrum epicycli ab apogaeo eccentrici in consequentia mundi, partibus similiter 54 sexagesimis sexagesimis om. MiO 16 et et] seq. del. tandem O rursus boreus limes obliqui circelli ab apogaeo epicycli in antecedentia mundi partibus 132 sexagesimis sexagesimis om. MiO 16′. Stella tandem tandem] seq. del. ab Mu a boreo limite obliqui circelli in consequentia mundi, partibus 346 sexagesimis sexagesimis om. MiO 41′.

⟨I.11⟩

Pro Veneris stella animo animo] animus et Iupiter animo add. i. m. Mi; animus O concipiatur circulus zodiaco concentricus in ipsius plano mobilis, et circa ipsius centrum aequaliter ab occasu in ortum quantum et inerrantium sphaera.

Vehat autem hic hic] sup. lin. O alium circulum sibi inclinatum in eodem centro, immutabili inclinatione planorum, angulum comprehendente partis unius, qualium unus rectus est 90.

In huius obliqui circuli plano describatur diameter per boreum et australem australem] seq. del. punctum Mu limitem, et in ea inter centrum zodiaci et boreum limitem sumantur duo puncta puncta] seq. del. aequalem limen facientes Mu a centro zodiaci aequalibus intervallis distantia, et circa circa] seq. del. remotissum Mu proximum signum signum] punctum MiO circulus eccentricus et immutabilis, ut quae ex eius centro, ad eam quae inter centra, suum scilicet, et zodiaci rationem habeat, quam habet 60 ad 15. Circa remotissimum remotissimum] remotissum Mu vero punctum moveatur aequaliter epicycli centrum, quod semper maneat in peripheria eccentrici circuli in consequentia mundi, et circa dictam dictam] dictum MiO diametrum, eo excessu, quo Solis motus medius excedit (aequalis aequalis] eiusdem MiO temporis) motum inerrantium.

Iterum cogitetur in sphaerula epicycli circellus circa ipsius centrum in obliqui circuli plano, sumpta recta linea per utraque centra, ipsius scilicet (epicycli) et remotissimi duorum punctorum, ad quod quod] seq. del. nam Mu ipsa epicycli puncta semper moveantur aequaliter, quae vocamus apogaeum et perigaeum, et alius circellus ipsi concentricus qui moveatur moveatur] corr. ex mobilis Mu in ipsius plano et circa circa] seq. del. aeq Mu idem centrum aequaliter et et] corr. ex que Mu ab apogaeo in in] seq. del. consequentia Mu eandem partem conversionis mundi mundi] mundi add. Mi perficiat aequalem illum, quem diximus centri epicycli motum. Hic autem circellum alium circellum alium] inv. MiO sibi inclinatum vehat vehat] seq. del. in su Mu super eodem centro centro] seq. del. immuta Mu fixa fixa] manente add. MiO inclinatione angulum angulum] seq. del. fai Mu comprehendens partium 3 30′, qualium unus rectus est 90. Ea Ea] corr. ex eaque Mu vero quae ex centro eccentrici ad eam quae ex centro circelli rationem habeat veluti 60 ad 53 6′ 53 6′] Ptol. 43 10′ add. i. m. Mu et in hoc circello stella moveatur circa centrum ipsius aequaliter aequaliter] seq. del. ab Mu a mobili illo apogaeo in adversam partem conversionis mundi, motum aequalem conficiens utrique, epicycli scilicet et stellae, adeo ut in diebus 33 supra annos Aegyptios 35 35] seq. del. res Mu revolutiones faciat 17 fere, ad accuratiorem enim calculum accedit accedit] corr. ex accedunt Mu sexagesimae 1.

Primo autem anno ab obitu Alexandri secundum Aegyptios prima mense Thoth Alexandriae in meridie, eccentrici apogaeum abfuit ab aequinoctio verno, in consequentia mundi partibus 50 sexagesimis 24 et tantundem boreus limites. Centrum vero epicycli ab apogaeo eccentrici in consequentia mundi partibus 50 … partibus om. MiO177 sexagesimis 12′.

Boreus vero limes obliqui circelli ab apogaeo epicycli in antecedentia mundi, partibus 27 sexagesimis sexagesimis om. MiO 16′. Stella tandem tandem] seq. del. ab Mu a boreo limite obliqui circelli in consequentia mundi partibus 168 sexagesimis 35.

⟨I.12⟩

Pro Pro] In MiO Martis sphaera cogitetur similiter circulus concentricus zodiaco mobilis in ipsius plano et circa eius centrum aequaliter ab occasu in ortum, quantum inerrantium sphaera.

Deferat autem hic circulus circulus om. MiO alium circulum ad ipsum ad ipsum] sibi MiO inclinatum super eodem centro fixa fixa] manente add. MiO inclinatione planorum, comprehendente angulum partis 1 30′ 3′′, qualium est est om. MiO unus rectus 90.

In plano autem obliqui circuli exponatur exponatur] ducatur MiO diameter per boreum et australem limitem, in qua inter centrum zodiaci et boreum limitem duo puncta sumantur aequali intervallo a centro zodiaci distantia, et circa proximum punctum circulus eccentricus et immobilis, ut quae ex centro eius eius] ipsius MiO ad eam quae inter inter] seq. del. centrum zod Mu utraque centra, sui sui] ipsius Mi; ipsius corr. ex sui O scilicet et zodiaci, rationem habent veluti 60 ad 6. Circa remotius remotius] corr. ex remotissimum Mu autem aequaliter moveatur epicycli centrum, semper situm habens in eccentrici ambitu in consequentia mundi circa dictam dictam] dictum Mi diametrum, eo ipso excessu, quo Solis medius motus superat utriusque eiusdem eiusdem] ex. corr. Mu temporis motum, inerrantium videlicet videlicet] scilicet MiO et ipsius stellae, ut in diebus 361 supra annos Aegyptios 95 revolutiones faciat 51 proxime, deficiunt enim ad ad] corr. ex ab O accuratam supputationem sexagesimae 3.

Deinde cogitetur in sphaerula epicycli circellus circa ipsius centrum in obliqui circuli plano, recta sumpta recta sumpta] corr. ex recta ente et sumpta add. i. m. Mu; inv. MiO linea per utraque centra, epicycli scilicet et remotissimum illorum duorum illorum duorum] inv. MiO punctorum, circa quod moveantur moveantur] corr. ex moventur Mu semper semper] sup. lin. Mu aequaliter illa illa] corr. ex et e Mu puncta circelli, quae vocamus apogaeum et perigaeum, et perigaeum] i. m. Mi et alius circellus ipsi concentricus mobilis in eodem plano, et circa idem centrum aequaliter aequaliter] seq. del. tamquam Mu secundum distantiam ab apogaeo apogaeo] seq. del. contra Mu contra motum motum] seq. del. mundi Mu conversionis mundi, perficiens motum aequalem ei, qui dicebatur esse centri epicycli. Deferat autem hic circellus alium sibi inclinatum circa idem centrum, immota inclinatione angulum comprehendente similiter partium 1 30′ 3′′, qualium unus rectus est 90. Quae vero ex centro eccentrici ad eam quae ex centro circelli rationem habeat velut 60 ad 39 30′, et in hoc circello moveatur stella circa centrum ipsius aequaliter ab apogaeo in antecedentia antecedentia] contra add. sup. lin. Mu conversionis mundi, perficiens motum aequalem utrique, utrique] corr. ex utriusque Mu; motui epicylli(del.) add. Mi; motui add. O epicycli scilicet et stellae, hoc est excessum illum illum] eum MiO quo excedit Solis motus eiusdem temporis inerrantium motum.

Primo autem anno ab obitu Alexandri secundum Aegyptios prima die mensis Thoth in meridiano meridiano] meridiae MiO Alexandrino Alexandrino] seq. del. maxime boreum punctum Mu; Alexandriae MiO apogaeum eccentrici abfuit ab aequinoctio verno in consequentia mundi partibus 110 44′, tantum etiam boreus limes. Centrum vero epicycli ab apogaeo eccentrici in consequentia mundi partibus 356 sexagesimis 20′. Item boreus limes obliqui circelli ab apogaeo epicycli in antecedentia mundi partibus 176 sexagesimis 10′. Et stella a boreo limite obliqui circelli, in consequentia mundi partibus 96 sexagesimis 46′.

⟨I.13⟩

Pro Iovis sphaera cogitetur circulus zodiaco concentricus mobilis in ipsius ipsius] illius MiO plano aequaliter ob occasu in ortum quantum et inerrantium sphaera.

Vehat Vehat] sup. lin. Mi autem hic circulus circulus om. MiO alium sibi inclinatum circulum ad ad] corr. ex circa Mu idem centrum centrum] fixa add. MiO manente manente] fixa add. sup. lin. Mu planorum planorum] sup. lin. Mu inclinatione angulum comprehendente partium partium om. MiO 1 30′, qualium unus rectus est 90.

In plano autem obliqui circuli imaginatione ducta recta linea a centro zodiaci ad punctum quod boreum limitem antecedit partibus 20, sumantur in ipsa duo signa signa] puncta Mi intercipientia aequalem rectamque rectamque] rectam lineam ei quae MiO inter zodiaci centrum zodiaci centrum] seq. del. et Mu; inv. MiO ei ei] et MiO quae inter duo illa puncta, quae … puncta] proximum punctorum MiO et circa proximum (zodiaci centro) (zodiaci centro) om. MiO punctum, circulus circulus] corr. ex circellus O eccentricus et immobilis, aeque quae ex centro ad eam quae inter centra ipsius, ipsius] scilicet add. MiO et zodiaci rationem habeat velut 60 ad 2 34′, circa remotissimum vero punctum aequaliter moveatur epicycli centrum, quod semper situm sit in dicto eccentrico in consequentia mundi, et circa dictam diametrum eo excessu, quo Solis motus superat utrumque (aequalis temporis) motum, inerrantium videlicet videlicet] scilicet MiO et stellae, ut in diebus integris 240 supra annos Aegytios 213 revolutiones faciat 18 fere, nam assumit ad accuratum calculum unius partis sexagesimae 1.

Item in epicycli sphaerula cogitetur circellus circa ipsius centrum in obliqui circuli plano, ducta linea recta per utraque centra ipsius, videlicet epicycli, et per remotissimum illud duorum punctorum, circa quod semper aequaliter moventur eadem puncta circelli, quae vocamus apogaeum et perigaeum, et alius circellus ei concentricus mobilis mobilis] mobili Mi in eodem plano et circa idem centrum aequaliter tamquam ab apogaeo mobili in eandem partem conversionis mundi perficiens aequalem motum ei, quem centrum epicycli habere diximus. Vehat autem hic circellus alium sibi inclinatum super eodem centro fixa inclinatione, angulum comprehendente partium 1 30′, partium 1 30′] inv. MiO qualium unus rectus 90. Quae vero ex centro eccentrici ad eam, quae ex centro circelli, rationem habeat tanquam 60 ad 11 30′, et in hoc circello stella moveatur circa eius centrum aequaliter tamquam tamquam om. MiO ab apogaeo in adversam partem conversionis mundi, conficiens motum aequalem utrique, aequalem utrique] inv. MiO epicycli scilicet et stellae, hoc est est] seq. del. ep Mu excessum iterum quo Solis motus medius excedit eiusdem temporis inerrantium motum.

In primo autem anno a morte Alexandri secundum Aegyptios prima die Thoth Alexandriae in meridie apogaeum eccentrici abfuit ab aequinoctio verno in consequentia mundi partibus 292 292] 222 add. sup. lin. Mu; 222 add. i. m. O 43′. Item boreus limes obliqui circuli ab apogaeo in consequentia mundi partibus 22 22] corr. ex 92 Mu 43′. Stella vero a boreo limite obliqui circelli in consequentia mundi partibus 31/319 31/319] 31 del. et 319 i. m. MiO sexagesimis 31.

⟨I.14⟩

Pro Saturni sphaera cogitetur circulus zodiaco concentricus mobilis in ipsius plano et circa idem centrum aequaliter ab occasu versus ortum quantum et inerrantium sphaera.

Vehat autem hic circulus alium sibi inclinatum circulum et et] seq. del. super eodem O circa idem centrum invariabili planorum inclinatione comprehendente angulum partium 2 30′, qualium unus rectus 90.

In obliqui autem circuli plano cogitetur recta linea a centro zodiaci zodiaci] seq. del. in alium retro Mu per punctum in consequentia per … consequentia] sup. lin. et seq. del. mundi Mu; ad … consequentia MiO distans a boreo limite partibus 50, 50] 40 del. et 50 i. m. MuMiO in qua sumantur duo puncta puncta] seq. del. quae facit Mu aequalem rectam intercipientes inter centrum zodiaci zodiaci] seq. del. et alterum punctorum MiO et circa proximum duorum punctorum circulus eccentricus eccentricus] seq. del. et immobilis MuMiO aeque, quae ex centro ad eam quae inter centra, suum scilicet et zodiaci, rationem habeat tamquam 60 ad 3 3′, circa remotius remotius] remotissimum MiO vero moveatur aequaliter centrum epicycli semper locum habens locum habens] situm add. sup. lin. Mi; corr. in situm O in eccentrici ambitu in consequentia mundi, et circa dictam diametrum eo excessu, quo motus medius Solis excedit utrumque (aequalis aequalis] eiusdem add. sup. lin. Mu temporis) motum, inerrantium scilicet et stellae, adeo ut in diebus 330 supra annos Aegyptios 117 revolutiones perficiat 4 fere, fere] seq. del. accuratum Mu assumitur enim ad accuratum calculum unius partis sexagesimae 1.

Item in epicycli sphaera cogitetur circellus circa ipsius centrum in obliqui circuli plano obliqui circuli plano] plano obliqui circuli MiO ducta linea per utraque centra, epicycli scilicet et remotioris puncti, circa quod semper ea ipsa puncta puncta] apogaeum et perigaeum add. sup. lin. Mu aequaliter moventur, quae vocamus apogaeum et perigaeum, et alius circellus ipsi concentricus qui moveatur in ipsius plano et circa idem centrum aequaliter, ab apogaeo nimirum in eandem partem cum mundi conversione absolutum absolutum] absolvens Mi motum motum] qui aequalis sit motui centri epicycli add. sup. lin. Mu aequalem centri epicycli. Vehat autem hic circellus alium sibi inclinatum ad ad] corr. ex circa Mu idem centrum immutabili inclinatione, quae angulum includat similiter partium 2 30′, qualium unus rectus est 90. Quae vero ex centro eccentrici ad eam quae ex centro circelli rationem habeat velut 60 ad 6 30′, et in hoc circello moveatur stella circa ipsius centrum aequaliter, ab apogaeo nimirum in adversam partem conversionis mundi perficiens motum aequalem utrique, aequalem utrique] inv. MiO epicycli scilicet et ipsius stellae, stellae] Solis sub. lin. Mu hoc est excessum excessum] quo add. MiO iterum quo motus motus] motus sup. lin. Mu Solis motus Solis] inv. MiO superat inerrantium motum et stellae. et stellae] sup. lin. Mu; om. MiO

Primo autem anno ab obitu Alexandri Alexandri] Magni add. MiO in meridie primi diei mensis Thoth Alexandriae apogaeum quidem eccentrici abfuit ab aequinoctio verno in consequentia mundi partibus. partibus] seq. del. et boreus limes obliqui circelli Mu

Centrum vero epicycli ab apogaeo eccentrici in consequentia mundi.

Item boreus limes limes] G. add. sub. lin. Mu obliqui circelli ab apogaeo in consequentia mundi.

Stella tandem a boreo limite obliqui circelli in consequentia mundi partibus. Finis.

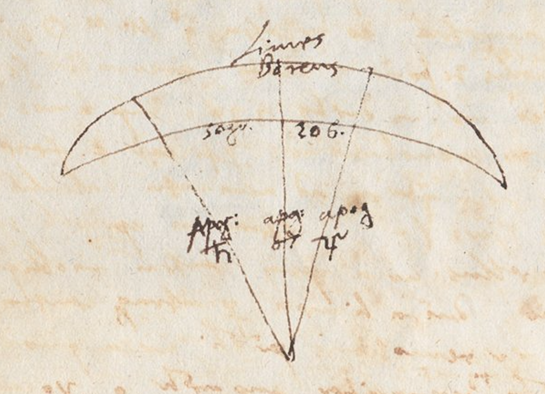
⟨I.9ᵇⁱˢ⟩

Pro lunari sphaera cogitetur iterum circulus zodiaco concentricus mobilis in ipsius plano et circa eius centrum aequaliter ab ortu in occasum, eo excessu quo latitudinis motus aequalis aequalis] eiusdem add. sup. lin. Mu temporis excedit Solis et Lunae motum, adeo ut in diebus 88 supra annos Aegyptios 37 revolutiones ad zodiacum faciat 2 proxime, assumit enim ad accuratum calculum unius partis sexagesimae 1.

Vehat autem hic circulus alium sibi inclinatum circulum circa idem centrum immutabili inclinatione angulum comprehendente partium 5, qualium unus rectus est 90.

In plano autem huius obliqui circuli ponatur circulus eccentricus, adeo ut quae ex ipsius centro ad ea quae inter centra, ipsius scilicet et zodiaci, rationem habeat velut 60 ad 12 ½, et moveatur centrum illud eccentrici circa centrum zodiaci aequaliter ab ortu in occasum a boreo limite, et excessu quo excedit medius motus Solis.