Ptolemaeus Arabus et Latinus

〈II〉 Erasmi Osvaldi Schrekhenfuchsii, in Magnae compositionis Claudii Ptolemaei Pelusiensis Alexandrini, libri II annotationes

〈II.1〉 Caput I

In superiori libro brevissime atque luculentissime dedit propositiones, seu principia ipsa quibus tota ars inititur, quod scilicet terra sit rotunda et in medio totius posita, ac habeat respectu firmamenti puncti vicem, et sit prorsus immobilis. Porro quod coeli figura sit circularis et circulariter volvatur. Post haec docet conficere tabulas chordarum et tabulas obliquationis Solis. Postremo, quomodo tabulae quae requiruntur ad rectarum ascensionum rationem. In hoc vero libro secundo, cuius argumentum est primum caput pergit, et docet omnia quae accidunt sphaerae obliquae, scilicet quomodo ex data maximae diei longitudine longitudine] logitudine B ortiva et occidua latitudo sit inquirenda, et quomodo, his datis, elevatio poli; aut, data elevatione poli, longitudo diei et latitudo occidua ac ortiva sit investiganda. Ad haec docet in hoc libro proportionem umbrarum in meridie ad gnomones, coortum atque occasum seu ascensiones obliquas aequinoctiales, una cum ratione magnitudinis angulorum, et cetera.

〈II.2〉 Caput II

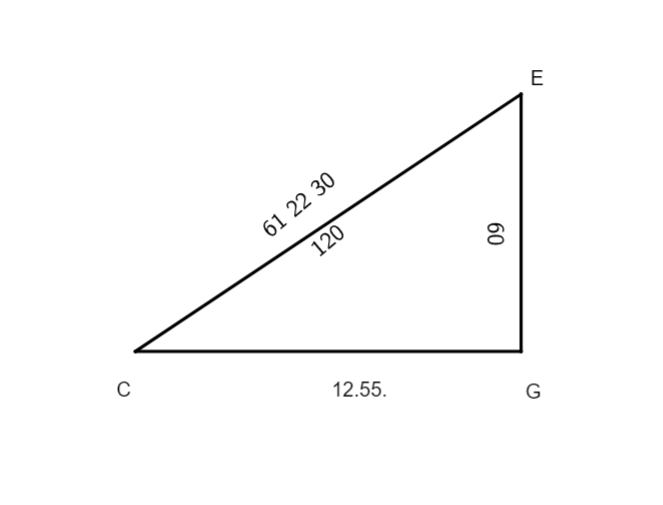
Quod in recta sphaera appellatur Solis declinatio, illud appellatur in obliqua sphaera ortiva aut occidua latitudo, et est nihil aliud quam arcus qui ab aequinoctiali et obliquo circulo in horizonte intercipitur, huius usus est duplex: alter spectat ad eclypsium lunarium inclinationem et aliarum stellarum aspectus, de quo infra; alter vero ad inventionem poli altitudinis. Nam data magnitudine maximae diei, et ortiva latitudine tui climatis seu paralleli, quicunque ille fuerit, poteris illius climatis seu paralleli invenire polarem altitudinem. Et ut haec facilius adiequi queas, visum est nobis tibi rem exemplis, iuxta doctrinam divini Ptolemaei, illustriorem reddere. Quapropter, cum volueris invenire ortivam latitudinem paralleli tui, subtrahe duodecim horas, quantitatem scilicet diei rectae sphaerae, a maxima die tuae regionis, et quod superest divide in duas partes aequales, quarum alteram resolvito per quindecim in tempora aequinoctialia, productum dupla, et quod nascitur subduc a 180 gradibus, residuumque erit arcus IA. Deinde subtrahe maximam Solis declinationem a 90 gradibus, aut dupla eam et productum subtrahe a 180 gradibus, et habebis arcum FI, BE, TF, AE: hi tres arcus sunt quartae circuli. Exempli gratia. Volumus quaerere latitudinem ortivam cum Sol fuerit in maxima sua obliquatione sub parallelo decimoquarto, qui scribitur per Massiliam, ubi dies maximus est 15 horarum 15 minutorum, differentia diei huius paralleli et aequinoctialis est 3 horarum 15 minutorum, cuius dimidium erit 1 horae 27 minutorum et 30 secundarum, quibus resolutis per 15 in tempora venerunt 24 gradus 22 minuta 30 secundae, arcus scilicet TE, haec duplicavimus, et produximus a 180°. Quod relictum est fuerunt 131 gradus 15 minuta pro arcu TA; quo facto, subduximus duplum maximae Solis declinationis a 180 gradibus, hoc est arcum IT ab arcu FT, productum fuerunt 132 gradus 17 minuta et 20 secundae pro arcu FI, reliqui arcus, ut diximus diximus] dixmus B, sunt quartae circuli. Postquam horum arcuum omnium eduximus chordas, ordinavimus eos ita ut sequitur:

Subtensa arcus IB est nobis inventa 99 graduum 57 minutorum et 58 secundarum. Arcus eius duplus est 112 graduum 49 minutorum, hunc subduximus ab arcu EB, hoc est a 180 gradibus, quod reliquum mansit post subtractionem fuerunt 67 gradus 10 minuta, arcus scilicet EI, cuius medietas, scilicet 33 gradus 35 minuta et 30 secundae, est ortiva latitudo quae quaerebatur.

〈II.3〉 Caput III

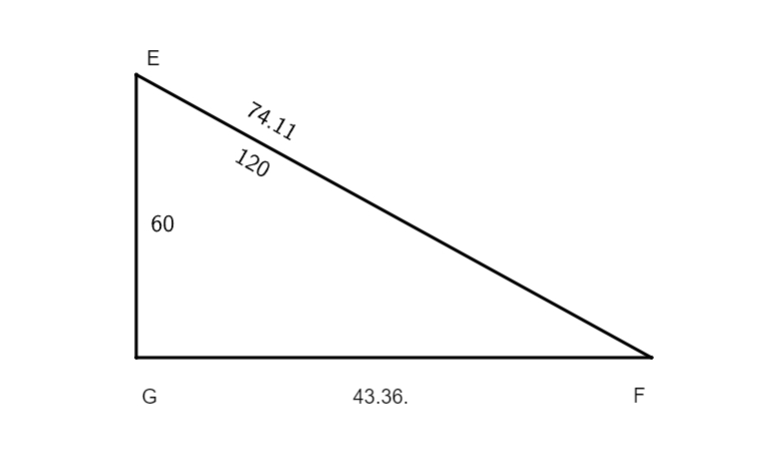
Hoc igitur］ Postquam demonstravit rationem inveniendi ortivam latitudinem, nunc pergit et tradit modum qui invenienda sit elevatio poli, ad hoc requiruntur duo praecipue, scilicet medietas differentiae maximae diei ad diem aequinoctialem et latitudo ortiva, quam capite superiori docuit invenire. Arcus qui necessarii sunt ad operationem hanc ita quaeras, scilicet subtrahe tempora medietatis differentiae maximae diei paralleli suppositi a 90 gradibus, residuum dupla una cum media differentia, et habebis arcum TA, complementum quartae EA, et arcum ET, postea subtrahe latitudinem ortivam. Producta erunt arcus EI et IB, FA est quarta circuli, horum arcuum quaeras deinde subtensas, et opereris ratione quae sequitur. Pro exemplo iterum accepimus parallelum decimumquartum, ubi dies maximus est 15 horarum 15 minutorum et tempora medietatis differentiae sunt 24 gradus 112 minuta et 40 secundae.

Sed in eadem rursus］ Porro data poli altitudine et Solis obliquatione ad tempus quo cupis scire diei quantitatem, poteris facile per regulam sex quantitatum aut per rationum subtractionem eiusmodi diei quantitatem invenire, et pro omnibus diebus anni tabulam quantitas dierum, tuo ipsius marte, ad tuam elevationem polarem condere. Exempli gratia. Volumus scire diei quantitatem cum Sol ingreditur primum punctum Cancri ubi polus elevatur supra horizontem 46 gradus 51 minuta. Esto arcus BF altitudo poli data, BA complementum altitudinis polaris, FI complementum obliquationis solis datae, IT ipsa obliquatio Solis, EA quarta circuli; arcus TE quaeritur, qui est media pars differentiae inter diem aequinoctialem et diem paralleli nostri, ad quem decrevimus quaerere quantitatem diei. Facta solita duplatione et subtractione arcuum, et extractione chordarum, ordinavimus arcus et chordas iuxta formam quae sequitur. Et absolvimus opus nostrum.

〈II.4〉 Caput IIII

Facile autem］ Triplex est ratio habitationis terrae terrae] ferrae B. Nam sut quaedam loca terrae quibus Sol bis in anno transit per caput, ut sunt loca quae continentur inter ambos tropicos; quando vero Sol fiat illis verticalis, id facile est cognitu ex tabula obliquationis Solis hoc modo: nam cum Sol tantum obliquatur ab aequatore quantum polus elevatur supra horizontem, tunc erit verticalis. Alia sunt loca terrae quibus Sol tantum semel in anno est verticalis, et sunt loca, quae directe reperiuntur sita sub ipsis tropicis, quorum altitudo poli est aequalis maximae Solis obliquationi, scilicet 23 gradibus 51 minutis et 20 secundis. Illis erit Sol verticalis cum fuerit in punctis tropicis. Postremo, sunt loca ad quorum verticem nunquam Sol pervenire potest, et sunt ea quae sunt extra tropicos circulos, hoc est quorum poli altitudo excedit maximam Solis obliquationem, tum versus austrum ab aequinoctiali circulo tum versus aquilonem, et cetera.

〈II.5〉 Caput V

Quod autem arcum］ In superioribus capitibus docuit quomodo data magnitudine diei latitudo ortiva, et rursus data magnitudine diei ac latitudine ortiva elevatio poli, et ex elevatione poli data magnitudo diei invenienda sit. Insuper quibus fiat Sol verticalis et quoties, et quibus non. Nunc porro pergit ac demonstrat qua ratione ex demonstratis proportio gnomonum aequinoctialis et tropicae umbrae in ipsis meridiebus in singulis parallelis invenienda sit. Verum, ut operatio fiat facilior visum est, hoc exemplum quod Ptolemaeus, vir divini ingenii, adduxit prolixiori calculo illustrare. Cum itaque volueris in hoc et in aliis exemplis consimilibus operari, subtrahe maximam Soli obliquationem ab elevatione poli data, productum erit arcus GT, et si addideris poli elevationi maximam Solis obliquationem emerget arcus GM, arcus vero GD est arcus elevationis poli supra horizontem. Esto pro exemplo altitudo poli 36 graduum, a quibus si subduxeris 23 gradus 51 minuta et 20 secundas relinquentur 12 gradus 51 minuta 40 secundae pro arcu GT. Si eos gradus minuta et secundas addideris 36 gradus, venient pro arcu GM 59 gradus 51 minuta 20 secundae. Quantitas angulorum est aequalis quantitati arcuum qui illis praetenduntur. Duplicatis his arcubus, erit quantitas anguli CEG 24 graduum 17 minutorum 20 secundarum, et anguli FEG 12 graduum, anguli vero NEG 119 graduum 42 minutorum et 40 secundarum. Nunc restat ut subtrahas hos arcus a semicirculo, hoc est a 180 gradibus; quo facto, habebis residuum GE in semicirculum 115 graduum 24 minutorum 40 secundarum, et residuum ipsorum 72 graduum in semicirculum erit 108 graduum. Postremo vero residuum de gradibus, hoc est 119 gradibus 42 minutis 80 secundis, erit 60 graduum 17 minutorum et 20 secundarum. Habitis itaque arcubus, quaerantur eorum chordae, quae ita se habent: chorda dupli arcus GT, scilicet GC, est 25 graduum 14 minutorum 43 secundarum, chorda residui huius arcus, scilicet GE, est 117 graduum 18 minutorum 51 secundarum. Ipsius GD, scilicet chorda GT, est 70 graduum 32 minutorum 4 secundarum, et residui, scilicet GE, 97 graduum 4 minutorum 56 secundarum. Et chorda arcus GM, scilicet GN, 103 graduum 46 minutorum 16 secundarum, et residuum, scilicet GE, 60 graduum 15 minutorum et 42 secundarum. Ad inveniendum proportionem umbrarum ad gnomonas, ordinato numeros in regulam de tribus, secundum modum qui sequitur.

Si hos numeros quemlibet sorsim Sorsim] read sorsum tractaveris, prius reductis illis ut solet in minimam denominationem, habebis producta umbrarum ita ut sunt illis in fine annexa: sic operandum est in omnibus aliis exemplis.

Hinc per se patet］ Quemadmodum supra docuit ex data poli elevatione et maxima Solis obliquatione proportionem umbrarum ad gnomonas invenire, ita docet hic, datis duabus proportionibus de tribus, poli altitudinem invenire, cuius rei operatio per penultimam primi et doctrinam triangulorum planorum absolvitur. In triangulo rectangulo EGC duo latera nota sunt, scilicet EG et GC; ex his duabus lateribus, cognoscetur

per penultimam primi latus EC. Nam si multiplicaveris latus CG in se, et latus EG in se, et addideris haec producta, et ex producto estraxeris radicem quadratam, emergent tibi pro latere EC 61 gradus 22 minuta et 30 secundae.

Cum itaque in hoc triangulo duo latera, scilicet EC et GC, sint data, dabitur etiam angulus GEC, hoc modo si duxeris latus GC, hoc est 12 gradus 55 minuta, in 120 gradibus, et productum diviseris per lineam EC, scilicet per 61 gradus 22 minuta, prodibunt 25 gradus 15 minuta 16 secundae, quarum arcus est 24 graduum 17 minutorum 20 secundarum, cuius dimidium sunt 12 gradus 8 minuta 40 secundae; tantus est angulus GEC. Et similiter operatur in inventione lineae EF et anguli GEF. Nam cum linea GF et linea GE ducentur 〈i〉n se more solito, et ambo producta addentur et ex eiusmodi producto extrahetur radix quadrata, prodibit ipsa linea EF; habitis duabus lineis, scilicet GF et EF, facilis erit angulus GEF inventu, ordinatis numeris

iuxta rationem supra dictam, hoc est si multiplicaveris 43 gradus 36 minuta per 120 gradus et productum diviseris per 74 gradus 11 minuta, nascentur tibi 70 gradus 32 minuta, quorum arcus est 72 graduum proxime, cuius dimidium erit 36°, angulus nimirum GEF; sed arcus GD, qui huic angulo praetenditur, erit quantitas elevationis poli huius paralleli. Et si auferes ab hoc angulo, scilicet a 36 gradibus, angulum GEC quem supra invenisti, hoc est 12 gradus 8 minuta 40 secundas, relinquetur angulus CEF, 23 graduum 51 minutorum 20 secundarum. Tanta, inquam, est maxima Solis obliquatio. Ad hunc modum cures etiam angulum GEN inventum. Porro si subtraxeris angulum GEC, hoc est 12 gradus 8 minuta 40 secundas, ab angulo recto, scilicet a 90 gradibus, relinquentur 77 gradus 51 minuta et 20 secundae pro angulo ECG, similiter fiat in investigatione anguli EFG et ENG. Non aliter etiam in aliis parallelis operandum est.

〈II.6〉 Caput VI

Secundus parallelus］ Cum Sol in hoc parallelo ingredietur 10 gradus 30 minuta Arietis, tunc erit habitatoribus eius verticalis et ante meridiem proiiciet umbram ad occasum, post meridiem ad ortum, in ipso meridie vero carebunt erecta perpendiculariter ad horizontem umbra, ab hinc autem usque ad gradus 19 minuta 20 Virginis proiicientur umbrae ad austrum, sed in ipso 19 gradibus 20 minutis erit iterum Sol verticalis, et deinde usque ad integrum circulum vergent umbrae in plagam borealem: si vis in hoc et in aliis parallelis qui sunt inter duos tropicos scire quando Sol fiat verticalis, accipias altitudinem poli tui paralleli, illamque immittas in secundam lineam tabulae obliquationis Solis, et numerus qui huic correspondet in prima linea erit distantia in zodiaco ab Ariete seu sectione vernali, et cum Sol fuerit in tali puncto, erit in illo parallelo verticalis, sicut supra etiam meminimus. Exempli gratia. Volumus scire quando Sol fiat verticalis in tertio parallelo, ubi polus extollitur supra horizontem graduum 8 minutorum 25. His gradibus immissis in lineam secundam obliquationis tabulae, statim offerent se 21 gradus in prima linea, hinc dicimus, cum Sol destiterit a sectione vernali quod sit verticalis in hoc parallelo, qui cum ab hoc removebitur puncto umbrae gnomonum tendent in austrum usque ad 9 gradus Virginis, et arcus inter haec duo puncta inventus est 138 graduum, transito hoc arcu erit iterum verticalis, ut antea, et hinc usque ad finem proiicientur umbrae ad septentrionem, et sic in reliquis.

〈II.7〉 Caput VII

Primum autem］ In hoc capite, non tam ingeniose quam breviter et clare, docet omnium climatum fabricare obliquarum ascensionum tabulas, et ut commodius hoc fiat, proposuit duos modos quibus intentum suum absolvi potest, quorum posteriorem maxime sequi censet, propterea quod sit brevior et commodior priore. Et priusquam aggreditur opus ratiocinationis, demonstrat in utroque modo quod zodiaci arcus aequaliter distantes ab aequinoctialibus punctis habeant aequales ascensiones obliquas, hoc est aequales differentias ascensionales.

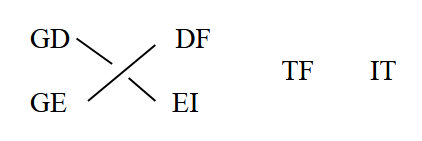
Quoniam ergo］ Ad operandum secundum primum modum oportet tria esse cognita, scilicet altitudinem poli, Solis obliquationem et arcum zodiaci, cuius adminiculo elicitur Solis obliquatio; his cognitis facile scientur sex arcus quibus opus habetur ad hanc operationem, ut arcus duplus CD est elevatio poli dupla, DG eius complementum ad semicirculum, CL est complementum dupli arcus LM, hoc est duplae obliquationis Solis, EG est duplum quartae circuli, EM est differentia qua differt ascensio rectae sphaerae dati arcus TL in recta sphaera ab ascensione obliqua dati arcus TL in praesupposito parallelo. Numeri ordinentur secundum arcuum horum positionem, ut: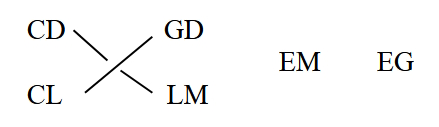

Duc GD in CL secundum dieresim, productum statue primum numerum, postea duc CD in LM, productum erit numerus secundus, et EG tertius; ordinatis numeris ad hunc modum, multiplicato secundum cum tertio, productum dividito cum primo et prodibit quartus, scilicet EM, differentia quaesita, quam si subtraxeris ab arcu TM, qui ascendit cum arcu zodiaci TL in recta sphaera, residuabitur tibi arcus ET, qui ascendit in obliqua sphaera cum arcu TL. Quae sit vero ratio in addendo hanc differentiam, tum in signis borealibus tum australibus, clarius in explicatione secundi modi perspicietur.

Verum quoniam］ Si resolveris 14 horae 30 minuta, item 9 horae 30 minuta, per 15 gradus in tempora, habebis arcum a principio Cancri usque ad Sagittarium 217 graduum 30 minutorum, et a Capricorno usque ad Geminos 142 graduum 30 minutorum, quae nascunt ex resolutione 9 horarum 30 minutorum per 15 gradus. Et si diviseris 217 gradus 30 minuta in duas partes aequales, habebit in quot temporibus Libra, Scorpio et Sagittarius ascendant, nempe in 108 gradus et 45ʹ, et similiter si 142 gradus 30 minuta mediaveris mediaveris] medaveris B, producentur 71 gradus 15 minuta: in tot etiam temporibus ascendent Aries, Taurus et Gemini.

Si ergo］ Primo intuitu apparet iste modus investigandi differentias ascensionales, esse difficilis scitu, qui tamen non est, quoniam non solum brevis est, imo habet etiam adiunctam quandam facilitatem calculandi differentias ascensionales, ut postea videbitur. Quemadmodum superior modus tria requirebat, ita quoque iste. Sed in hoc differunt, quod iste modus unum tantum arcum habet mutabilem, nempe ET, qui per singula climata mutationi est subiectus, reliqui vero, scilicet TI, IF, LC, CF, sunt immutabiles, quod in praecedente non aeque fit, ut visum est: proinde si semel quesieris quesieris] read quaesieris subtensas duplorum arcuum TI et IF sufficiet TI per omnia climata, propterea quod maxima Solis obliquatio non variatur ratione climatum neque reliquae obliquationes solares, unde sequitur etiam subtensas duplorum arcuum LC et CF non mutari: in arcu LC fecit Ptolemaeus saltum per denarium, nihil obstat quin possis ad singulos gradus calculum tuum instituere. Arcus autem TE variatur secundum diei variationem in omnibus parallelis et climatibus, proportio chordae dupli arcus TE ad chordam dupli arcus EL invenitur in omnibus declinationibus eadem proportione 60°.

Ut diximus gradibus abest］ Cum tibi placuerit scire numeros seu proportiones has, pone pro arcu TE 60° et operare ut fieri solet in subtractione proportionum iuxta rationem diereseos. Sed, ut haec clarus videantur, proponam exemplum in quo docebo arcum EL dupliciter invenire: primo oportet invenire proportionem arcus TE ad arcum EL, quod fiet hoc modo. Duc arcum TI in arcum FC, productum fac primum numerum, deinde duc IF in CL quod nasctur sit tibi numerus

secundus, pro tertia accipias semper 60°. Ordinatis numeris, multiplica tertium in secundum, productum divide cum primo et obtinebis quaesitum, hoc est pro primo denario habebis 9 gradus 33 minuta, pro secundo 18 gradus 56 minuta, et sic deinceps. Ad inveniendum differentiam primi denarii ubi maximus dies est 14 horarum 30 minutorum, operati sumus hac via, scilicet posuimus primum numerum 60°, secundum 9° 33ʹ et tertium 38° 34ʹ subtensam, scilicet dupli arcus TE qui est 37° 30ʹ (et cum hunc arcum volueris quaerere, accipe dimidiam differentiam maximi diei tui paralleli ad diem aequinoctialem, illa resolvito in tempora, et productum duplato, ut solet fieri, eius quod nascitur elicias e tabula chordarum subtensam) et si multiplicaveris 9° 33ʹ in 38° 34ʹ et productum diviseris per 60°, prosilient 6 gradus 8 minuta, chorda scilicet dupli arcus arcus] araus B EL; arcus vero duplus EL invenitur esse 5 graduum 42 minuta, horum dimidium sunt 2 gradus 56 minuta, tanta, inquam, est differentia primi decadi sub hoc parallelo, qua subtracta a recta ascensione relinquetur ascensio obliqua. Si vero libet uti secunda inventione, ponito differentiam minimi aut maximi diei, quam paulo ante docuimus invenire, pro 60°, hoc est arcum TE, et operare ut es edoctus, et immediate nascetur arcus EL. Hoc etiam non praetereundum est, nempe quod differentia ascensionalis in borealibus signis subtrahitur a recta ascensione et in australibus additur, reliquia facilia sunt, ubi recte animadverteris praecendencium documentum.

〈II.9〉 Caput VIIII

Nam primum］ Cum libuerit tibi quaerere diei artificialis propositi longitudinem, cape gradum in quo Sol tempore tuo erit e tabula tui paralleli, quem subtrahas, ut docet Ptolemaeus, a gradu consimili signi oppositi, productum iterum subtrahas a 360 gradibus et habebis gradus qui nocti debentur in tali parallelo: divisis his gradibus per 15 gradus, prodibit quantitas diei artificialis atque noctis. Huius rei cape tale exemplum. En placet scire quantitatem diei artificialis et noctis Sole gradiente in 10 gradus Leonis, ubi polus septentrionalis extollitur supra horizontem 48 graduum 32 minutorum, sub hac elevatione ascendunt cum 10 gradu Leonis de aequatore 110 gradus 14 minuta, et cum signo opposito, scilicet 10 gradu Aquarii, ascendunt 334 gradus 9 minuta. Subtracto minori a maiori prodierunt 223 gradus 14 minuta, quo producto ablato a 360 remanserunt pro gradibus nocturnae longitudo 136 gradus 46 minutis. Redactis his gradibus, tum diei tum noctis, per 15 in horas aequales, nascentur pro die 14 horae 51 minuta 56 secundae, pro nocte vero 9 horae 7 minuta 4 secundae, et sic de aliis. Porro si diviseris 223 gradus 14 minuta gradus diei per 12, et similiter 136 gradus 46 minuta gradus noctis, habebis partes horae temporalis diurnae 18 graduum 36 minutorum 10 secundarum, et nocturnae 11 graduum 23 minutorum 50 secundarum.

Sed facilius］ Si subtracta fuerint tempora aggregata tui loci Solis in tuo parallelo a recta ascensione, et productum divisum fuerit per 6°, ac addentur producto in signis borealibus 15 gradus, aut productum illud auferetur a 15 gradibus in signis australibus, prodibunt partes quae debentur uni horae temporali; ut in praesupposito exemplo, subtraxerimus 110 gradus 55 minuta qui ascendunt cum 10 gradu Leonis in obliqua sphaera a 132 gradibus 32 minutis qui ascendunt cum hoc gradu in sphaera recta, et reliqui fuerunt 21 gradus 37 minuta, quibus divisis, ut dictum est, per 6°, provenerunt 3 gradus 36 minuta 10 secundas; hoc productum, cum Sol in signo boreali sit, addidimus ipsis 15 gradibus et nati sunt 18 gradus 36 minuta 10 secundae, ut supra pro nocte eadem ratione operandum est.

Datas etiam］ Porro cum volueris tum in hoc tum aliis exemplis datas horas aequales ad inaequales reducere, age iuxta canonem praescriptum a Ptolemaeo, exempli gratia in hoc proposito paradigmate. Cupio scire, quando 3 horae aequales transierunt ab ortu, quot illae constituant horas inaequales, duxi 3° in 15° et divisi productum per 18 gradus 36 minuta et prodierunt 2 horae 31 minuta proxime. Si vero volueris scire, datis inaequalibus horis, quot facient aequales, tunc resolvas datas horas per partes horae inaequalis, productum dividas per 15, et cetera.

Si vero］ De ratione quae pendet ab horis temporalibus alibi dicetur, hic adducam exemplum quomodo ad datas horas aequales gradus medii coeli sit inveniendus, deinde ad horizontis gradus, et contra. Oblati temporis horas resolvas per 15 gradus in tempora aequinoctialis, si tempus tuum transiit meridianum: si vero fuerit in ipso meridiani puncto, tunc quaere locum Solis temporis tui in recta sphaera, et habebis quaesitum, si autem, ut dixi, transiit meridianum, resolve illas horas modo praedicto et productum immitte in tabulam rectae sphaerae in tertiam lineam, et si numerum graduum tuorum praecise habebis in temporibus aggregatis, erit gradus in prima linea ille qui est in medio coeli, sin minus, subtrahe numerum proxime minorem tuo numero a proxime maiore: productum constitue primum numerum, quo facto, subtrahe illum numerum qui proxime minor est a numero tuo, quod relinquitur erit secundus, pro tertio accipias 10. Qui distendit tabulas has per denos gradus: ordinatis numeris ad hunc modum, multiplica tertium cum secundo, productum divide in primum, quod nascitur adiicias numero quem seorsum ex prima linea scripsisti, quodlibet suae speciei, scilicet gradus gradibus, minuta minutis, et cetera. At hoc etiam sciendum est, nempe quod gradibus qui nati sunt ex resolutione horarum adiiciendi sunt gradus qui sunt ab Ariete in recta sphaera, usque ad gradum Solis propositi temporis, et hoc est quod Ptolemaeus appellat dirigere, et si productum excesserit integrum circulum, tunc abiiciantur ab eo 360 gradus, cum reliquo operetur, ut dictum est. Esto pro exemplo tempus propositum in quo Sol movetur in 20 gradu Geminorum, qui distat a meridie versus ortum 4 horas, ad hoc tempus volumus quaerere gradum qui mediat coelum, primum resolvimus 20 horas quae lapsae sunt a meridie per 15°, et prodierunt 300 gradus, his adiecimus 79 gradus 5 minuta quibus distat 20 gradus Geminorum, in quo Sol est, secundum rectam ascensionem ab Ariete, et cum productum sit maius integro circulo abiecimus 360 gradus et remanserunt 19 gradus 5 minuta. Cum his ingressi sumus in tertiam lineam tabulae rectae sphaerae, et cum eos praecise non invenerimus, accepimus, iuxta doctrinam paulo ante traditam, proxime minorem numerum, scilicet 18 gradus 25´, e quorum regione in prima linea scripsimus seorsum 20 gradus Arietis, deinde subtraximus hunc numerum a proxime maiore, scilicet a 27 gradibus 50 minutis, relicti sunt 9 gradus 25 minuta pro primo numero: et postquam subtractus est a 19 gradibus 5 minutis exivit numerus secundus, pro tertio accepimus 10 gradus, excessum scilicet numerorum primae lineae; facta, ut solet, multiplicatione et divisione, prodierunt 42 minuta proxime, quibus adiectis producto supra seorsim scripto, invenimus 20 gradus 42 minuta Arietis tempore praesupposito ad medium coeli venisse. Et cum instituimus hoc exemplum calculare ad septimum clima, ubi polus tollitur supra horizontem 48 graduum 32 minutorum, nunc porro exemplum ostendemus quomodo gradus oriens sit inveniendus. Canon quem author praescripsit docet rectae ascensioni medii coeli addere 90 gradus, et productum quaerere in tabula obliquae ascensionis quae debetur climati seu parallelo presupposito. Ideo adiecimus 19 gradus 5 minuta quae ascendunt in recta sphaera cum 20 gradibus 42 minutis Arietis 90 gradus, et prosilierunt nobis 109 gradus 5 minuta, quibus quaesitis in tertia linea tabulae septimi climatis, et proportionatis iuxta regula supra propositam, invenimus 8 gradus 39 minuta 30 secundas Leonis devenire in ortum, cum 20 gradus 42 minuta inveniuntur in medio coeli, et sic de aliis quae sequuntur perfacilia sunt, his rectis intellectis.

〈II.10〉 Caput X

Sit enim aequinoctialis］ Angulum CBI esse aequalem angulo TBL, et angulum CIB angulo BTL, et cetera, hoc probat Regiomontanus libro tertio, propositione 35 de triangulis, quod vero latus IB sit aequale lateri BT, et latus CB lateri BL, hoc facile constat ex aequalibus declinationibus. Nam latus IC est aequale lateri LT propter aequales declinationes. Unde aequales declinationes requirunt aequales ascensiones tum rectas tum obliquas, ergo latus BC est aequale lateri BL, et sic etiam de aliis, hoc est de angulis qui aequaliter distant a tropicis.

His iam inspectis］ Postquam demonstravit angulos qui aequaliter hinc inde distant tum a tropicis tum ab aequinoctialibus punctis esse invicem aequales, nunc calculo rem aggreditur, ac docet quomodo quantitas eiusmodi angolorum sit perscrutanda per rationem figurae sectoris, cuius rei operatio valde facilis est, superioribus recte intellectis. Arcus BA est arcus declinationis puncti

suppositi, AI complementum huius arcus, BF est arcus datus, FT complementum huius arcus, TE est arcus qui quaeritur, EI est quarta circuli. Cum volueris itaque operari, duc AI secundum dieresim in BF, productum sit numerus primus; deinde duc BA in FT, et quod prodierit statue numerum secundum, et EI tertium, quo facto, fac secundum documentum regulae de tribus, et veniet TE, cuius dimidium arcum, ut fieri solet, adiice quartae CE et habebis totum CT et hinc angulum CBT orientalem. Ratio subtractionis huius anguli a recto manifesta est per demonstrationem praemissam. Quare autem eiusmodi angulos appellaverit infra in tabula angulorum: orientales cum fiant ut proposuit in meridiano, hoc per se clarum est: nam anguli qui fiunt in sectione meridiani et zodiaci non alii sunt quam anguli horizontis in recta sphaera.

〈II.11〉 Caput XI

Verum ut etiam］ Tria maxime necessaria sunt ad inventionem reliquorum angulorum horizontis, scilicet poli altitudo supra horizontem, Solis declinatio, quae debetur gradui medii coeli sub terra, et signum quod est in oriente ad tempus suppositum. Ex gradu qui obtinet horizontem, ut supra capite nono docuit, venit in noticiam gradus medii coeli supra terram, cuius gradus oppositus est gradus qui est in medio coeli sub terra, quem hoc pacto inventum curabis: accipe a numero collecto gradus horizontis qui debetur gradui dato tui climatis, 90 gradus si poteris, sin minus, addice illi numero collecto 360 gradus et perge operando; quod relinquetur post subtractionem immitte in tertiam lineam tabulae rectae ascensionis, facta prius proportionatione, si usus postulaverit, quod invenitur in prima linea erit gradus medii coeli supra terram, et oppositus, et cetera. Ut, cupio scire quis gradus veniat ad medium coeli sub elevatione poli 36 graduum cum principium Tauri est praecise in ipso horizonte: principio Tauri respondent, sub dicta elevatione, de temporibus aggregatis in tertia linea 19 gradus 12 minuta, ex quo non potest fieri subtractio 90 graduum, adicio illis 360 gradus et subtraho, relinquuntur post subtractionem 289 gradus 12ʹ, quibus immissis in tertiam lineam tabulae rectae sphaerae reperiuntur, facta proportionatione, ex prima linea 17 gradus 14 minuta Capricorni, quod signum ad medium coeli sub hoc situ venire dicimus, unde 17 gradus 41 minuta Arietis sunt in medio coeli sub terra, et sic de aliis.

Rursus quoniam］ Exempla haec sunt facilia calculatu ubi quis recte intellexerit rationem subtrahendi proportionem a proportione secundum modum diereticum. Sed priusquam nobis calculus instituatur, ostendemus quomodo quinque arcus per quos sexto innotescet sint eliciendi. Cum itaque habueris per documentum praemissum punctum zodiaci qui mediat coelum sub terra, quaeras illius puncti declinationem ab aequatore, quam adiicias poli elevationi, et emerget arcus FG, qui constat ex poli elevatione et declinatione puncti praesuppositi. Ut in hoc exemplo, si addideris 22 gradus 40 minuta ad 36 gradus emergent 58 gradus 40 minuta, arcus scilicet FG; sublato hoc producto a 90 gradibus, remanebunt 31 gradus 20 minuta, quae representant arcum primum, scilicet GD, DF est quarta circuli et arcus secundus. Ad habendum arcum tertium GE, numeres secundum ordinem signorum a puncto horizontali usque ad punctum medii coeli sub terra, ut in hoc exemplo a principio Tauri usque ad 17 gradus 41 minuta Cancri et prodibunt tibi 77 gradus 41 minuta, arcus simplex GE. Quartus arcus EI erit iterum quarta circuli, quemadmodum arcus quintus TF est quarta, duplicatis his arcubus erit arcus GD 62° 40ʹ, DF 180°, GE 155° 22ʹ, EI 180° et TF 180°, horum arcuum chordas quaeras iuxta regulam supra de inventione chordarum traditam.

Operatio. Duc EG in DF, productum fac primum numerum, quo facto, duc iterum EI in GD, quod prodibit esto numerus secundus, tertius erit TF, si igitur moltiplicaveris tertium in secundum et productum divideris per primum, proveniet arcus IT qui quaerebatur; reliqua sunt facilia intellectu.

〈II.12〉 Caput XII

Quantum usum angulorum qui causantur a circulo verticali et zodiaco cognitio praestat in eclypsium calculatione, maxime solarium, nemo facile dicere potest: nam nisi solertia artificum inventionem horum angulorum excogitasset, impossibile foret rationem eclypsium solarium esse certam. Quid? Non solum, inquam, ratio certa eclypsium pendet ab hoc capite, imo etiam inventio umbrarum tum rectarum tum versarum, quae sciri non possunt si non prius constiterit de elevatione Solis qualibet hora praesuppositi climatis, haec, dico, Solis elevatio seu altitudo non difficulter cognoscitur per arcus secundae lineae, sicut suo loco ostendere decrevimus. Sed ne quid vocetur in dubium, prius, more suo, demonstrat singula de quibus possit dubitari, postea addit exempla duo dieretica, in quorum altero docet invenire arcus qui sunt in circulo verticali a puncto verticis usque ad punctum in zodiaco datum, in altero vero quomodo anguli tum orientales tum occidentales qui causantur a circulo verticali et zodiaco sint inveniendi.

Cum igitur haec］ Hoc primum exemplum per dieresim calculandum est, ad quod quatuor requiruntur, scilicet altitudo poli, punctus medii coeli, et punctus horizontalis ac Solis declinatio, quae debetur puncto medii coeli: sed ratio, qua isti puncti in noticiam veniunt, supra exposita est. In hoc exemplo quaestio est de arcu EI, ad cuius investigationem opus habemus quinque arcubus notis, FB, BA, FT, TI et EA, duo horum arcuum sunt quartae circuli, scilicet EA et BA, et si subtraxeris declinationem Solis, quae requiritur pro 16° 12ʹ Geminorum, hoc est 23 gradus 7 minuta ab elevatione poli, scilicet 36 gradibus, relinquentur 12 gradus 53ʹ, quibus subtractis a 90 gradibus residuabuntur 77 gradus et 7 minuta pro arcu BF; duplicatis illis, provenient 154° 14ʹ. Porro a 16° 12ʹ Geminorum usque ad 17° 37ʹ Virginis reperiuntur 91 gradus 25 minuta, duplicatis illis nascentur 182° 50ʹ pro duplo arcu FT, item a principio Cancri usque ad 17° 37ʹ Virginis sunt 77 gradus 37 minuta, quibus duplicatis, emergent pro duplo arcu IT 155° 14ʹ, horum arcuum chordas quaeras iuxta canonem in primo libro traditum. Deinde redigas eas in minimam denominationem, quo facto, duc FT in BA, quod emerget esto numerus primus, et productum arcus FB in arcum TI sit numerus secundus, EA erit tertius numerus. Et si multiplicaveris secundum in tertium, et quod prodibit diviseris per primum, productum dabit chordam IE, cuius arcus medietas subtracta a 90 gradibus relinquetur AI qui quaerebatur, sed EI erit semper altitudo Solis ab horizonte horae datae.

Deinde angulum］ Inventio anguli TIA non difficilis est cognitu his prius gustatis, qui etiam per subtractionem proportionum secundum dieresim manifectus manifectus] read manifestus fit. Chorda dupli arcus EI ex superioribus nota est, et si subtraxeris duplum arcum EI a 180 gradibus relinquetur duplus arcus EC, IT antea notus est, quem si subtraxeris a 180 gradibus habebis duplum arcum TL, CM est quarta circuli, per hos quinque arcus in noticiam veniet arcus LM, qui quaeritur, quo sublato a 90 reliquum erit arcus CL, qui praetenditur angulo occidentali CIL, et cum hunc angulum subtraxeris a duobus rectis, quia angulus TIA est maior uno recto, quod relinquitur erit ipse angulus TIA, qui quaerebatur. Hactenus de angulorum inventionem. Sed quomodo angulus accipiatur cum horis adhaerebunt minutiae et signa non erunt integra, hoc infra, cum agetur de eclypsibus, regulis demonstrabimus.