Ptolemaeus Arabus et Latinus

〈III〉 Erasmi Osvaldi Schrekhenfuchsii, in Magnae compositionis Claudii Ptolemaei Pelusiensis Alexandrini, libri III annotationes

〈III.0〉 Argumentum

In hoc libro docet author invenire verum locum Solis in zodiaco et, cum impossibile sit quocunque tempore dato, talem locum invenire absque medio motu, qui semper regularis est in corporibus coelestibus, tum, inquam, cum a centra suorum excentricorum consideratur, coactus est author primum omnium quantitatem huiusmodi motus in Sole invenire. Qui aequalis et regularis dicitur, quia in aequalibus temporibus aequales arcos conficit, non in zodiaco sed in excentrico, in quo aequalis et regularis est motus Solis. Et cum infinitum per finitum, et irregulare ac inaequale per regulare et aequale cognoscitur, non immerito tantopere sudatum est ut invenieretur verum annuum tempus, quo cognito, facile scitur diurnus Solis motus aequalis, sine quo, ut dictum est, fieri non potest ut inaequalis reperiatur motus, qui propterea inaequalis dicitur quod Sol, aut alius quivis planetarum in zodiaco propter excentricitatem, inaequales arcus in temporibus aequalibus describat ut audietur suo loco. In prioribus duobus capitibus, tradit rationem inveniendi aequalem Solis motum, qui non nisi ex vera annui temporis quantitate habetur, in tertio ostendit causam inaequalitatis Solis, a qua pendet etiam aliarum apparentiarum coelestium inaequalitas. In quarto docet indagare proportionem semidiametri excentrici ad distantiam centri excentrici a centro mundi seu zodiaci, et locum remotissimum Solis a centro terrae, qui dicitur longitudo longior, apud iuniores autem astronomos aux in prima significatione. Ad haec, quanta sit in maxima Solis diversitas inter aequalem et inaequalem motum, secundum utramque positionem, tam excentrici quam concentrici et epicycli. In quinto proponit rationem quae particulares inaequalitatis anguli, dato angulo motus aequalis, sint enodandi, iuxta utramque positionem, scilicet excentrici et epicycli, et contra dato angulo inaequali, et cetera. Sextum et septimum capita habent compositionem tabularum inaequalitatis solaris. Octavum et nonum complectuntur inventionem radicis per observationem, ad cuiuscumque temporis principium: et investigationem medii motus Solis ad quodcunque tempus oblatum. In decimo vero ac ultimo tradit rationem inaequalitatis diei naturalis, et satis prolixe ac ingeniose.

〈III.1〉 Caput I

Nam apparentiae］ Duae sunt causae potissimae quae assignari possunt quare a Solis theorica exorditus sit et non a quodam aliorum planetarum, neque a superiori, ut Saturno, neque ab inferiori, ut Lunae. Altera est, licet non precipua, quod theorica Solis paucioribus orbibus conflatur, et facilior est imaginatu, eo quod Sol non evagatur ab eclyptica quemadmodum reliqui planetae omnes, qui non solum multas habent sphaeras, quibus eorum cursus absolvitur ac in noticiam provenit, imo saepe exorbitant ab eclyptica modo in austrum modo in aquilonem, qui modo sunt retrogradi, modo stationarii, et modo feruntur in rectum, quae accidentia non possunt precipi imaginando, nisi prius probe constiterit de ratione motus Solis. Ideo Ptolemaeus, vir singulari prudentia et artifex mirus, a facilioribus atque notioribus, ut decet tantum philosophum, incepit. Altera vero causa est, et potior, nempe quod omnes reliqui planetae a motu Solis regulantur, quemadmodum ipsemet in hoc capite testis est, quod sic intelligi debet, videlicet, quod nullius planetae verus motus indagari potest ignorato medio motu Solis, adeo communicat Sol cum omnibus planetis. Cum Luna communicat scilicet quod centrum, seu media distantia, quae duplata centrum Lunae nascitur, ex medio motu Solis indagatur. In tribus superoribus et Venere ac Mercurio venatur argumentum medium, hoc est medius motus diversitatis, mediante motu aequali Solis. Venus et Mercurius plus communicant cum Sole reliquis, quia habita tempore nostro quo aux Solis mobilis inventa est, auge in secunda significatione, et similiter medio motu Solis, habebitur etiam aux et medius motus Veneris ac Mercurii, hinc recte dixit author: ʻNam apparentiae, quae caeteris stellisʼ, et cetera.

〈III.2〉 Caput II

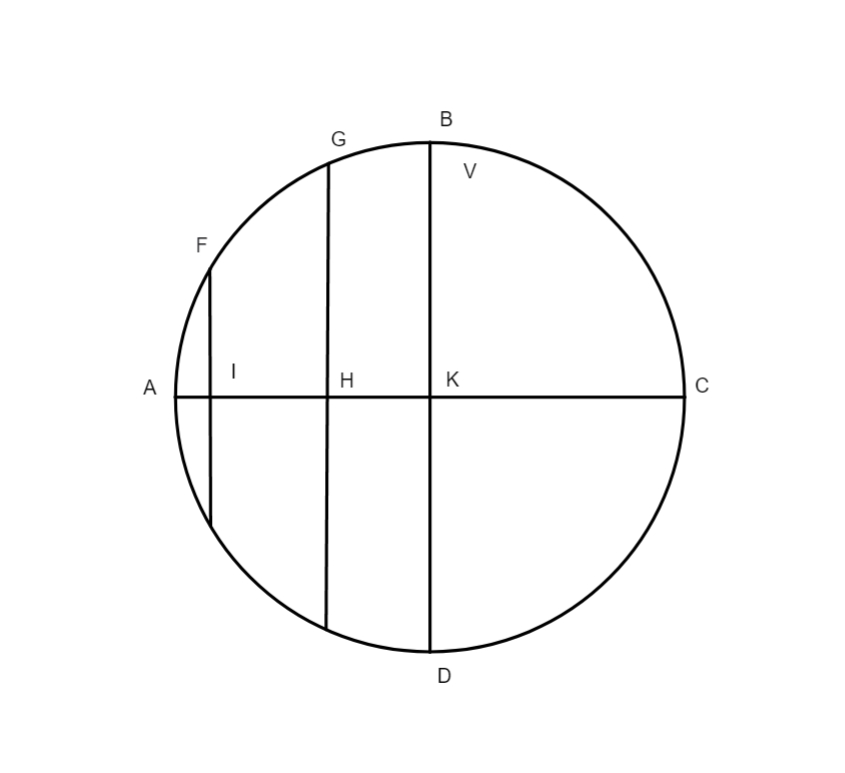
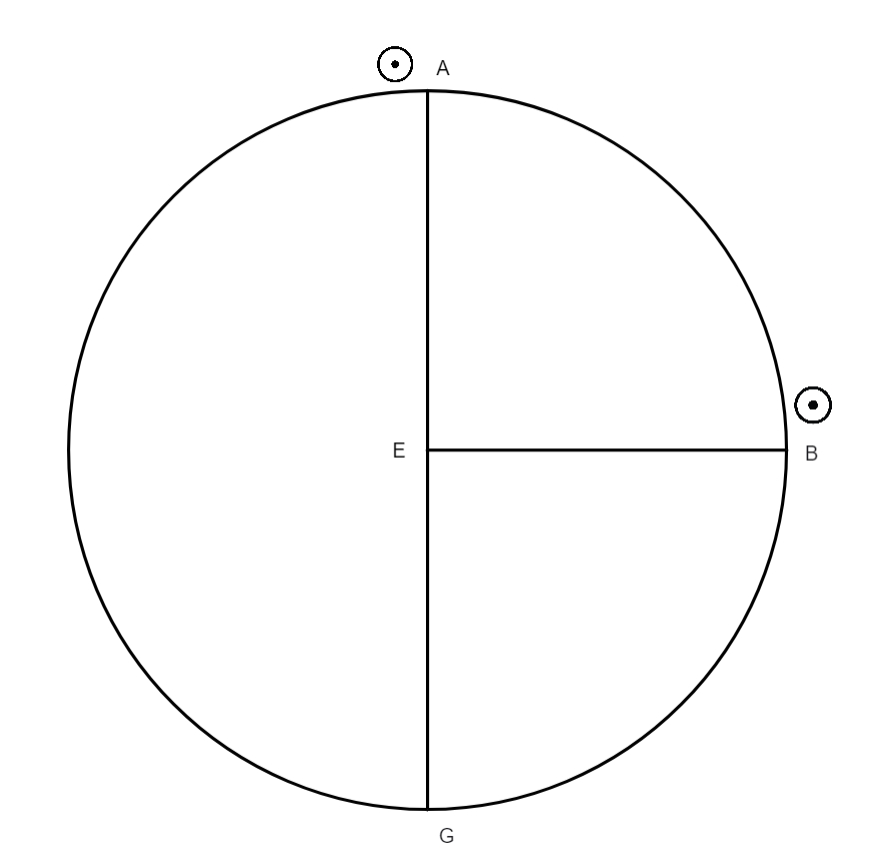
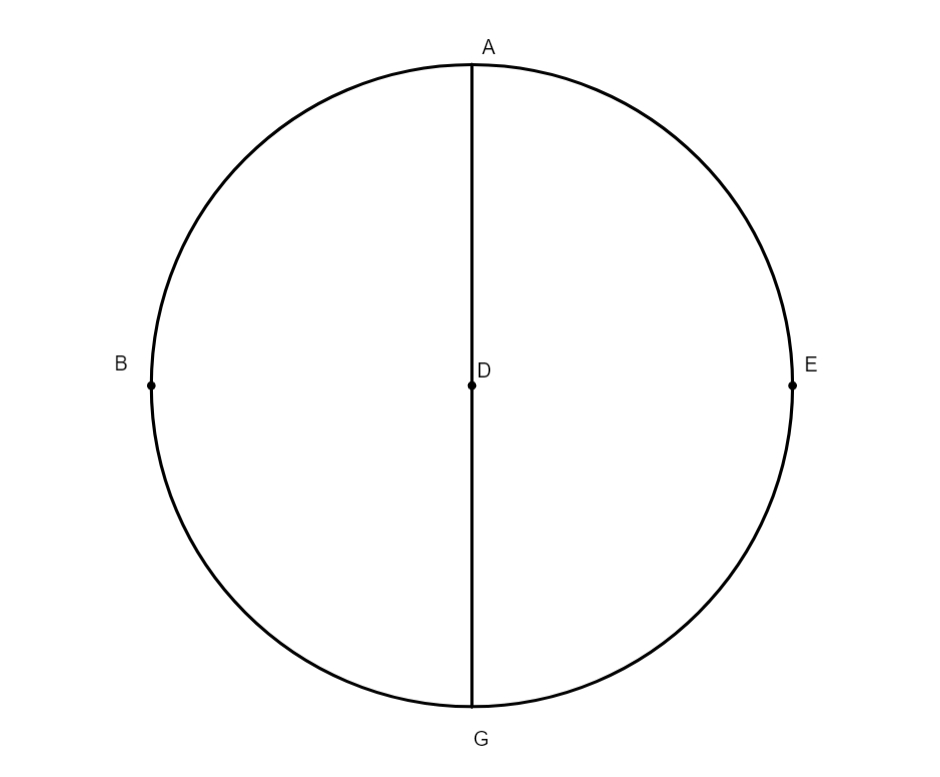
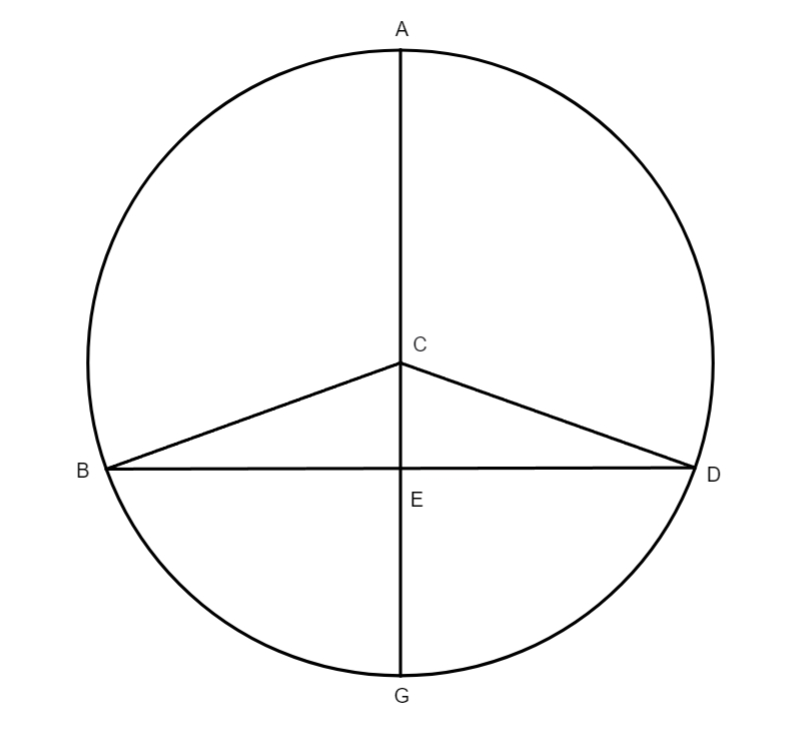
Cum igitur caeterorum］ Priusque incipiat docere quomodo tabulae motus aequalis sint conficiendae, definit annui temporis spacium, quod nihil aliud est quam redicio solaris corporis, secundum ordinem signorum, ad punctum illud fixum in zodiaco a quo antea digredi coeperat, hoc est a puncto aequinoctii, iterum ad illud punctum; huius spacii quantitatem, quod annus solaris dicitur, veteres triplici modo observarunt. Vetustissimi observarunt ad stellas fixas. Et dixerunt annum solarem esse redicionem Solis ad aliquam stellam fixam, huius observationem exercuerunt tempore deliquii lunaris. Et cum Hypparchus videbat annum tempus per talem observationem excedere 365 dies et quartam unius, propter motum stellarum fixarum in consequentia, deservit eam tanquam inconvenientem, qui etiam a Ptolemaeo explodendus iudicatur. Alii, ut fuit Menton ac Euctemon, sumpserunt suas observationes a punctis solstitialibus, sed cum Sol in illis punctis per aliquot dies non sentitur progredi, censuit Hypparchus adeoque Ptolemaeus ab his punctis non certo posse accepi annuum tempus Solis, hoc est annum solarem. His duobus modis iudicatis infirmioribus quam ut pro annui temporis spacio discernendo sumantur, elegerunt tertium, nempe aequinoctialia puncta, in quibus meridiana Solis elevatio aut declinatio Solis in uno die per 24 minuta variatur. Quod vero maior sit variatio declinationis Solis existente eo circa puncta aequinoctialia quam circa solstitialia puncta, hoc facilimum est diiudicatu, sumptis aequalibus arcubus in zodiacus aequaliter ab his punctis distantibus, ut videre est in hac figura, in qua ABCD sit zodiacus, AC horizon rectus, BD aequinoctialis, GB

arcus aequalis arcui AF, et quando Sol graditur a puncto B ad punctum H arcus HK causatur in horizonte recto aut in circulo meridiano in sphaera obliqua, qui longe maior est arcu AI, qui causatur dum Sol movetur per arcum AF, qui aequalis est arcui GB, et multo magis sentitur in eo variatio meridianae altitudinis quam in arcu AF, licet sint aequales: hinc non frustra est quod Ptolemaeus et Hypparchus statuerunt haec puncta, scilicet aequinoctialia, pro suis annui temporis observationibus, licet etiam ipsi observarint per solstitialia puncta, tamen illis plus fisi sunt quam his, ut testantur observationes, quarum hic fit mentio. Quod autem tempus annuum, cum observatur ad stellas fixas, sit maius 365 dies et 6 horae, sic patuit veteribus. Nam observarunt eclypsim lunarem, in cuius medio tempore Sol diametrialiter Lunae centro opponitur, talem, inquam, quae contingeret in nodo aequinoctiali: quo facto, observarunt per astrolabium armillarum alicuius stellae fixae distantiam a centro corporis lunaris. Deinde post aliquod tempus, cum in eodem nodo seu loco contingeret eclypsis alia, iterum observarunt distantiam lunaris corporis ab eadem stella, invenerunt arcum seu distantiam illam crevisse, ut exempli gratia in hac praescripta figura in qua ABG sit zodiacus, centrum eius E et diameter BEG, et B sit aequinoctium autumnale, G vero vernale. Tempore observationis erat Luna in B, et stella fixa ei propinqua in puncto F, et Sol super puncto G; per astrolabium armillarum

acceperunt quantitate arcus BF. Postea observarunt aliam eclypsim lunarem, et iterum mensurarunt arcum BF, quem invenerunt maiorem, scilicet FA, et cum erat Luna in puncto A opponebatur ei Sol diametraliter in puncto D et non in puncto G, ut antea: hic indicaverunt Solem in aequinoctialibus non semper esse in eodem signo, imo conficere tanto maiorem peripheriam toto circulo quanto est arcus GD, ex his certe concluserunt annum maiorem esse 365 diebus et quarta unius.

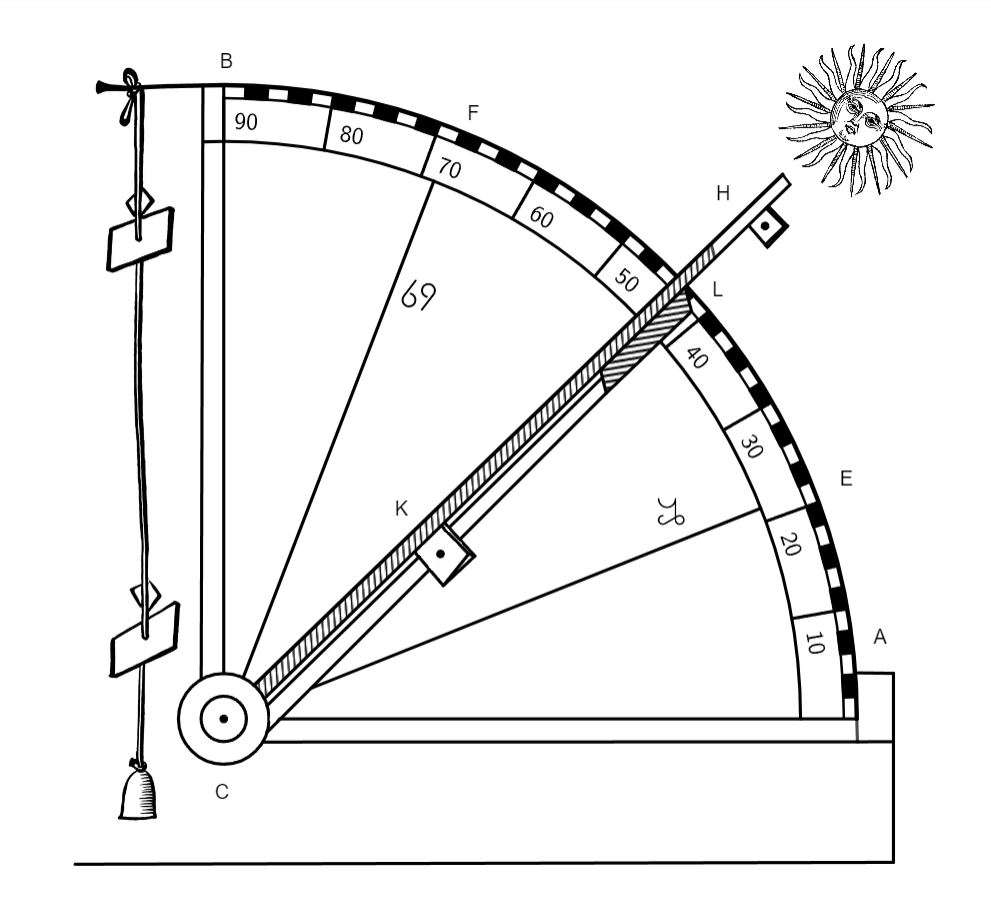
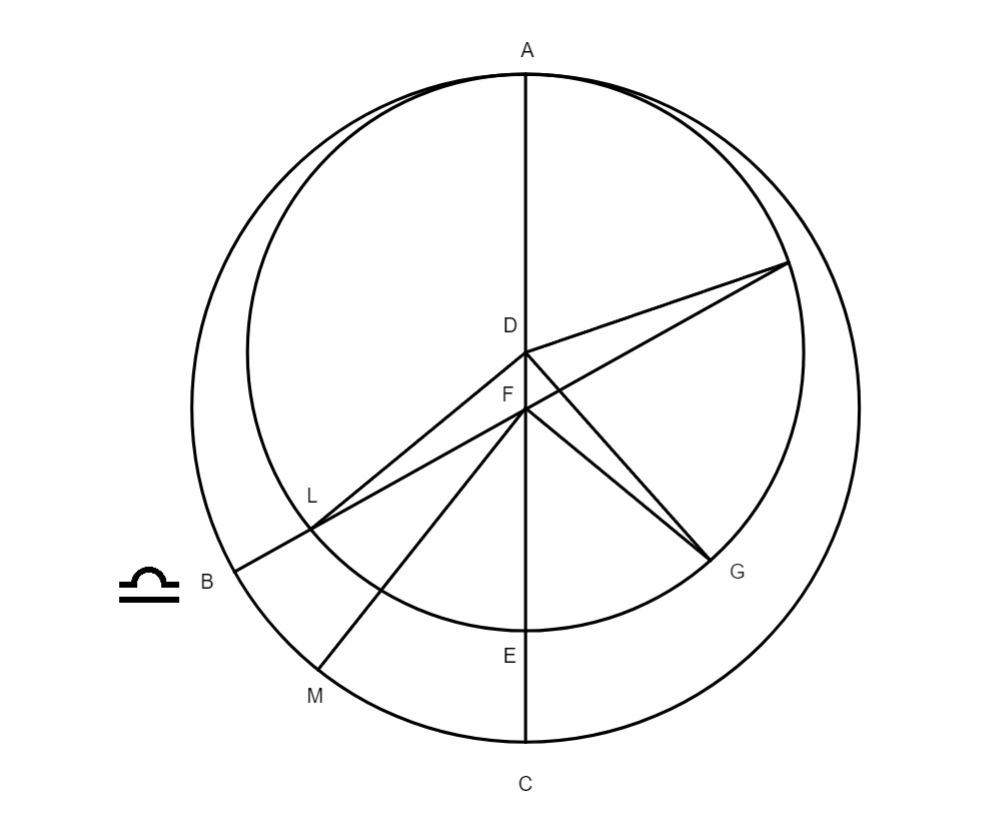
Usi autem sumus］ Duo sunt instrumenta quibus aequinoctia a veteribus observata sunt, alterius facta est mentio in primo libro, cum tradebat modum observandi maximam Solis obliquationem. Alterius autem hactenus nullibi mentio facta est, tamen nequid desit, huic etiam ascribemus eorum structuram, quae ut sunt simplicissima, ita sunt maxime certa si modo recte preparabuntur. Structura primi est haec: fabricetur quadrans in superfice meridiana, quemadmodum supra libro primo factum est, quod sit ABC, cuius linea CD sit linea meridiana, KL regula visoria, hoc est per cuius pinnacidiorum foramina KL radii solares incidant tempore observationis cum volueris per hoc instrumentum observare, erigas illud ad planum meridiani, prope tempus aequinoctii, quod ex altitudinibus meridianis quotidie habere potes, nam quo proprior erit altitudo complemento polaris altitudinis tuae regionis eo propius erit centrum Solis aequinoctio. Sed oportet te haec tria prius explorata habere, scilicet altitudinem poli tui loci, maximam Solis declinationem et reliquas declinationes singulorum punctorum zodiaci, et si altitudo Solis fuerit in meridie ad unguem aequalis complemento poli, scias tunc aequinoctium esse in meridie siquidem, cum Sol pervenit in punctum aequinoctii, complementum et altitudo meridiana idem fiunt, ut exempli gratia, volo observare aequinoctium, sit quodcunque, in loco in quo polus elevatur supra horizontem 49 gradus, huius elevationis complementum sunt 41 gradus. Simpliciter, posito instrumento super lineam ED meridianam, dirigo pinnacidia pinnacidia] pinnicidia B KL ad corpus Solis, et cum linea CH transiens per corpus Solis in ipso meridie cadet super 41 gradus a puncto A versus H, dico eo die esse aequinoctium in meridie. Non dissimili ratione poteris solstitium prope verum per hoc instrumentum venari, quamvis cognitio eius ad hoc negotium, ut dictum est, non sit satis firma, in quo hoc modo procedas, scilicet addito maximam Solis declinationem, si quaeris solstitium aestivuum, complemento polaris altitudinis, in quaerendo autem solstitio hyemali fiat contra, quo facto, observa in meridie, et si altitudo Solis meridiana fuerit aequalis producto tuo, hoc est lineae CF a puncto A versus F aut lineae CE ab eodem puncto, dic solstitium eo die esse in meridie. Si autem altitudo Solis meridiana fuerit maior aut minor complemento polaris altitudinis, tunc alia via procedendum est, nempe hac: si fuerit Sol iuxta aequinoctium vernale, accipias pro quolibet minuto differentiae minoris meridianae altitudinis et poli complementi unam horam, et similiter si fuerit iuxta autumnale aequinoctium accipias unam horam pro quolibet minuto differentiae maioris altitudinis meridianae et complementi poli, horisque numeratis a meridie praecedente aequinoctium, fit talis ingressus in punctum aequinoctii. Verum, ne cui non bene versato in his rebus hoc mirum videatur, visum est adiicere figuram ex qua facile deduci potest quare in hoc loco quodlibet minutum differentiae maioris aut minoris meridianae altitudinis et poli complementi pro hora accipiatur. In qua sit ABD meridianus, BED semicirculus zodiaci, AEG semicirculus aequinoctialis, FCH arcus magnus transiens per polum borealem et punctum datum eclypticae. Et cum EC arcus proponitur esse unius gradus, erit CH arcus Solis declinationis, iuxta Ptolemaeum, 24 minutorum et 16 secundarum, sed cum diurnus motus Solis sit 59 minutorum et 8 secundarum fere, qui perficitur in 24 horis, sequitur quodlibet minutum arcus CH, quorum sunt 24 fere, valere unam horam, hoc est arcum CH qualibet hora crescere aut decrescere per unum minutum, sicut ex tabula maximae Solis declinationis manifestum est: hactenus de structura et usu huius quadrantis.

Nunc sequitur alterum instrumentum, quo veteres mathematici usi sunt in indagandis aequinoctiis a quibus pendet annui temporis cognitio, nec non in indagandis solstitiis. Cuius structura sic se habet: praeparentur primum duo circuli aequales et mediocres magnitudine, quorum superficies diligentissime sint praeparatae, hoc est ad normam politae, alter sit pro meridiano et dividatur in 360 partes aequales, sicut est circulus ABDG in hac figura, alter vero referat planum aequatoris, et sit circulus AQP. Et cum aliquando hoc sequenti instrumento observetur ingressus Solis in puncta solstitialia, possunt etiam duo tropici adiungi, quemadmodum sunt minores duo circuli BNO, tropicus aestivalis, et HRS, tropicus brumalis, qui aeque sunt diligenter poliendi ac superiores duo: hii quatuor circuli adaptentur meridiano ad angulos rectos, non secus ac in sphaera materiali coluris, quo facto, fabricetur sedes instrumenti ad formam FTGYH, cuius pars FTG sit excavata, ut queat in ea volvi, hoc est elevari et deprimi, postremo adiungatur perpendiculum IRK in puncto vertitis vertitis] read verticis I ut sit volubile. Et cum volueris eo uti, ponito super planum LM, super lineam meridianam LV, quod planum sit perpendiculare ad horizontale planum: sic situato instrumento directe ad planum meridiani, elevetur circulus meridionalis a puncto T verus verus] read versus G secundum quantitatem complementi polaris altitudinis loci tui, aut numera a puncto A versus C polarem altitudinem et demitte perpendiculum a verticali puncto; quo facto, observes circa aequinoctium, et cum tota superficies aequatoris superior APQ illuminabitur, ac concavitas eius fuerit tota obumbrata circa aequinoctium vernale, dicas eo tempore Solem esse in ipso aequinoctio, et sic agendum est etiam in reliquo puncto aequinoctiali. De solstitiis non est alia ratio

nisi quod talis observatio fit in circulis tropicis, scilicet tempore aestivo, in circulo BNDO, et tempore hyemali in circulo HRFS, in quibus semper superior superficies in hora solstitiali illuminabitur et concavitas obumbratur, horum duorum instrumentorum structuram praemittere visum est eo quod alterius hoc loci fit mentio. De astrolabio armillarum, quo etiam in hoc negotio aliquando uti solebant, libro quinto dicetur. Cum Ptolemaeus viderat Hipparchum perturbari ex eo quod aliquando invenerat annum solarem minorem 365 diebus et quarta unius, sed quanto minor esset invenire non poterat, decrevit hoc explorare, ad quod sumpsit observationem Hipparchi, qua diligentissime observavit aequinoctium autumnale anno 178 post mortem Alexandri, quod factum est die tertia intercalarium in media nocte Alexandriae. Sciendum est quod Aegyptii longe aliam rationem habuerunt in numerandi diebus mensium, teste Macrobio, quam latini, qui singulis mensibus assignarunt 30 dies et superfluos quinque dies apposuerunt ultimo mensi, scilicet Mesori, qui respondet nostro Iulio; hos, inquam, quinque dies appellant superadditos superadditos] supperadditos B seu epactas aut intercalares.

Deinde sumpsit suam observationem aequinoctii autumnalis quam habuit post excessum Alexandri anno 463 Aegyptio, quae facta est 9 die mensis Athyr, qui respondet nostro Octobri et est tertius mensium Aegyptiorum, post ortum Solis per unam fere horam; intervallum harum duarum observationum fuit 285 annorum Aegyptiorum, 70 dierum, 7 horarum et quintae unius horae. Nam si subtraxeris 178 annos a 463 annis et numerabis a tertio die intercalarium ab hora mediae noctis, cuius crastinus fuit dies quartus, usque ad 8 diem et 19 horas ac 20 minuta mensis tertii Aegyptiorum Athyr, prosilient tibi 70 dies, 7 horae et quinta unius horae. Si annus constaret ex 365 diebus et 6 horis, debebat intervallum esse 285 anni Aegyptii, 71 dies et 6 horae. Siquidem cum multiplicaveris 285 annos per sex horas quae sunt ultra dies 365 annui temporis, seu anni solaris, et quod provenit diviseris per 14 horas aequales, nascentur tibi 71 dies et sex horae, a quibus si subduxeris 70 dies 7 horas et 12 minuta, residuabuntur 0 dies, 22 horae et 48 minuta, deficiunt igitur in 285 annis Aegyptiis 0 dies 22 horae et 48 minuta, ex his manifestum est si tempus inter duas observaciones fuerit 300 annorum quod integer dies deficiet. Idem iudicium est de observationibus quas consideravit ad vernum aequinoctium, porro si diviseris 0 dies 22 horas et 48 minuta per 285 annos Aegyptiacos, provenient in producto 12 secundae, quemadmodum ex divisione unius diei qui deficit in 300 per 300 annos.

Quae cum ita se habeant］ Si subtraxeris has 12 secundas quae natae sunt ex divisione 0 dierum 22 et 48 minutorum per 285 annos, aut unius diei per 300 annos a 365 diebus et 6 horis, hoc est a 365 diebus et 15 minutis, progredietur quantitas anni solaris, 365 dies 14 minuta et 48 secundae. Hic sciendum est quod Ptolemaeus in hoc loco pro die naturali ponit 60 minuta, unde quarta pars horum minutorum est 15 minuta, quae valent horas 6 quartae partis de 24 horis. Nunc habito anno solari, erit structura tabularum aequalis motus Solis perfacilis. Nam si hanc Solis restitutionem resolveris in secundas et cum illis parcieris integrum zodiacum, qui more solito partitur in 360 partes aequales, quae modo partes, modo gradus appellantur apud Ptolemaeum, proveniet tibi motus diurnus Solis, harum vigesima quarta pars erit motus horarius, et si hunc diurnum motum multiplicaveris per 30 dies, in tot enim dies deducitur quilibet mensis Aegyptius, habebis motum mensis medium et sic de reliquis, has tabulas poteris extendere at quotquot annos volueris. Quomodo vero medius motus ad quodvis tempus propositum querendus sit, infra docebitur.

〈III.3〉 Caput III

Omnes lineae］ Supra docuit indagare annuam Solis restitutionem, et hoc per observationes tum a se tum ab Hypparcho Hypparcho] Hyparcho B consideratas, qua habita ostendit regulas quibus tabulae medii motus, qui est canon quasi in omnibus stellarum motibus ad inquirendum verum, inaequalem seu apparentem motum, sint conficiendae. Et cum tantum retulerit novisse medium motum, praemittendum non duxi quid sit medius motus. Qui, ut author innuit, nihil aliud est quam motus ille qui in temporibus aequalibus aequales arcus, quorum anguli sunt aequales in centro excentrici, describit. Describatur circulus ABG super centro E et imaginetur Sol seu alia quaevis stella moveri ab A versus B seu ad B, et AB ad G. Et cum arcus

AB sit aequalis arcui BG, erit angulus AEB aequalis angulo GEB per ultimam sexti, et in quanto tempore Sol perficit arcum AB in tanto perficiet etiam arcum GB motu aequali, seu medio iuxta definitionem medii motus. Eadem est ratio in suppositione concentrici et epicycli, si centrum epicycli imaginabitur moveri a puncto A ad punctum B, et deinde a puncto B ad G punctum quod etiam fiet in tempore aequali, cum hi duo arcus, ut dictum est, sint aequales.

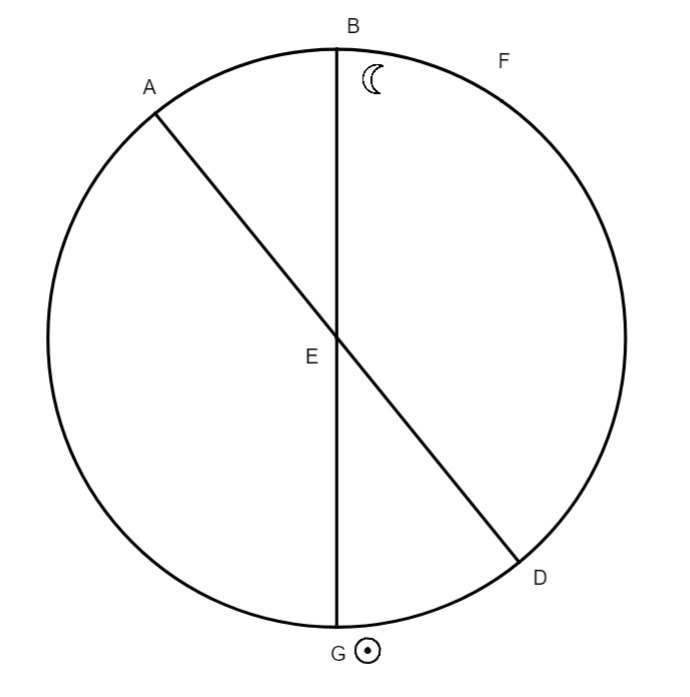
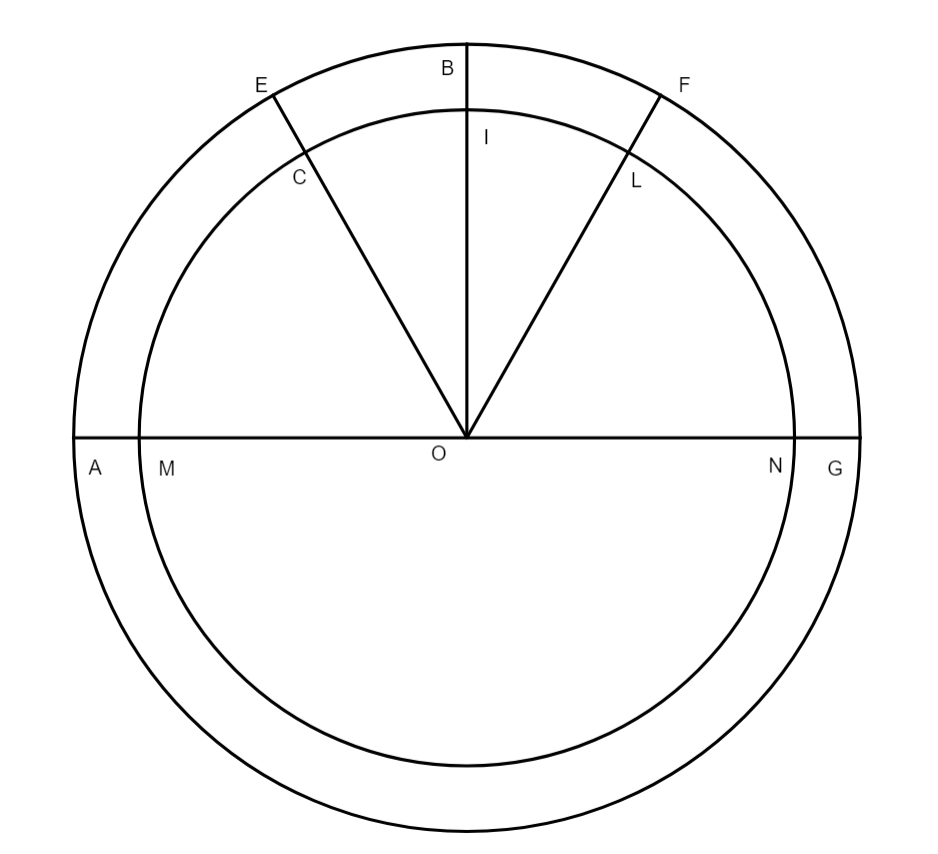
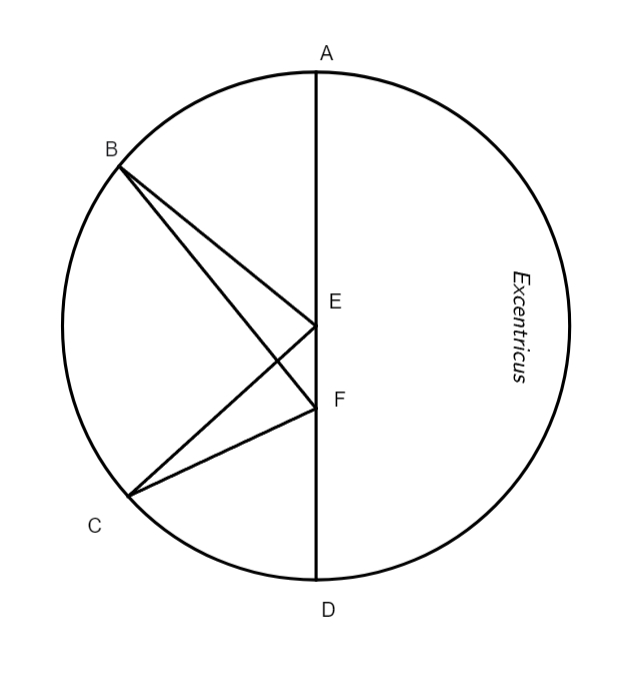
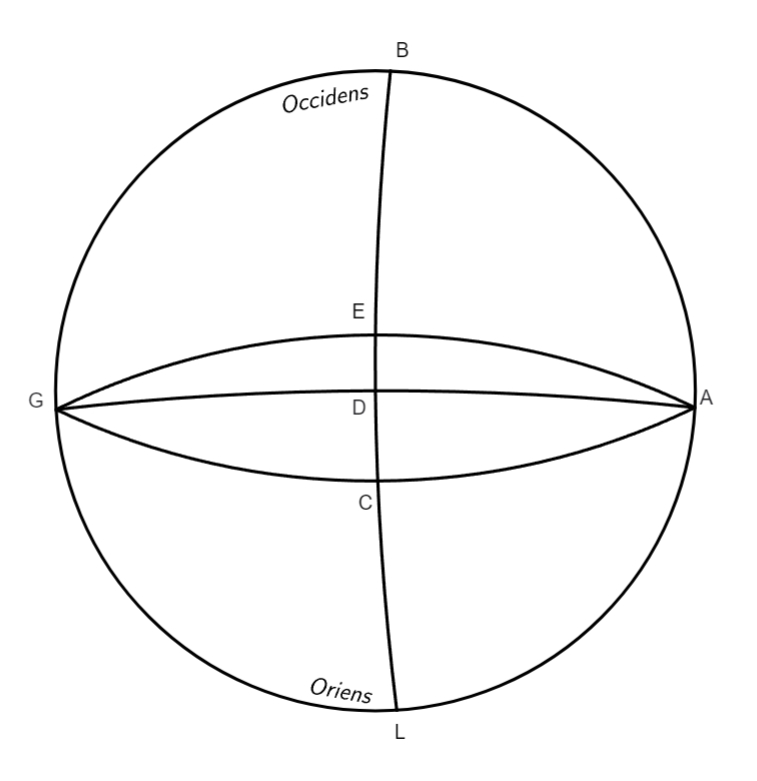
Causa vero］ Duplici ratione contingere potest quod Sol inaequaliter moveri videatur, altera est excentrici suppositio, altera autem suppositio concentrici cum epicyclo. Impossibile est Solem super circulo vehi qui sit zodiaco concentricus, nam si hoc concederetur, appareret nobis Solis motus in zodiaco aequalis, sicut apparet ex hac figura, in qua ABG sit zodiacus, MIN concentricus seu deferens corpus Solis, AOG diameter, O centrum utriusque, sumantur nunc duo arcus, CI et IL, aequales in circulo MIG, et excurrant ex centro O duae lineae, OLF et OCE, nunc imaginetur Sol in tanto tempore moveri per arcum BF in quanto movetur per arcum IL, et in quanto pertransit CI in tanto pertransiet EB, sed pertransit arcum totum CIL in tempore aequali, ergo etiam arcum zodiaci EBF pertransiet in tempore aequali, quod est contra observationes sicut videbitur in capite consequente. At cum in hoc capite et in aliis toties fiat puncti remotissimi a terra et similiter puncti terrae proximi et loci aequalis ac inaequalis Solis et aliarum stellarum, ac similium, mentio non inaepte fieri arbitror si huc adscribantur

eiusmodi vocum definitiones. Locus aequalis planetae dicitur locus in quo est in excentrico suo. Locus vero inaequalis planetae in zodiacus consideratus est punctus in zodiaco quem ostendit linea quae trahitur ad zodiacum a centro mundi, et est parallela lineae quae excurrit ex centro circuli excentrici ad corpus planetae: ut haec omnia faciliora fiant, describatur figura in qua AKB sit zodiacus seu zodiaco concentricus, LIH excentricus descriptus super centro G, H est locus medii motus stellae in excentrico, qui consideratur ex centro mundi seu stantis in superficie terrae, et cum terra comparata ad zodiacum sit instar puncti erit centrum terrae et locus intuentis stellas, idem linea FB, qua ostenditur medii motus locus in zodiaco, est parallela linea GH. Verus locus, qui etiam apparens et inaequalis dicitur, est locus Solis, seu alterius cuiusvis stellae in zodiaco, quae ostendit linea excurrens e centro mundi per centrum stellae usque ad zodiacum, quemadmodum est linea FHC, cuius extremitas C est verus locus stellae. Apogium est punctus excentrici remotissimus a centro mundi, sicut est punctus L. Perigium est F punctus excentrici centro terrae proximus, veluti est punctus I, hi duo puncti ostenduntur per lineam quae transit

per utraque centra, sicut est linea AFK. Verus motus, seu inaequalis, ipsius Solis est arcus zodiaci ab apogio aut perigio usque ad locum veri motus in zodiaco, sicut est arcus AC. Apud Ptolemaeum est alia ratio incohandi arcus motuum quam apud nostri seculi astronomos, qui soliti sunt inchoare motus ab Ariete. Medius motus Sol seu stellae est arcus zodiaci ab apogio seu perigio usque ad locum sive lineam medii motus, ut est arcus AB; his cognitis facile erit scitu quid sit angulus medii motus et angulus veri sive inaequalis motus, ac angulus aequationis. In hac figura est angulus AFB angulus medii motus, et AFC angulus veri motus, et CFB angulus aequationis, arcus vero BC aequatio medii ac veri motus. Media distantia seu media longitudo est puncto qui in zodiaco a maximam longitudine distat per quartam, hoc est, cum angulus AFB fuerit rectus: hinc fit media longitudo, in qua maxima reperitur aequatio inter aequalem et inaequalem Solis motum, ab aliis definitur, quod tamen idem est, esse puncta quae ostenduntur per lineam orthogonaliter ad lineam augis et oppositi, transeuntem per centrum mundi: locum huius longitudinis representat punctus B in praemissio schemate. Sicut se habet ratio horum vocabulorum in suppositione excentrici, ita se habet quoque in concentrici cum epicyclo suppositione. Esto ABG concentricus, FMF zodiacus. Imaginetur centrum epicycli moveri ab A ad B, stella vero in epicyclo a puncto F ad punctum L, locus motus aequalis epicycli erit in concentrico super puncto B, stellae in epicyclo super puncto L, linea EBF sit linea ostendens locum medii motus in zodiaco, qui sit punctus F, punctus M erit locus veri motus in

zodiaco, quem ostendet linea ELM tracta ex centro concentrici ad zodiacum usque. In concentrico concentrico] cencentrico B autem erit N locus verus, F est apogium et T perigium, reliqua sunt ex superioribus per se manifesta.

Utraque enim istarum］ Explicatis hactenus terminis et vocabulis quorum usus est apud Ptolemaeum, deinde quid aequalis seu medius modus sit. Nunc porro pergit et dicit duas esse suppositiones propter quas motus aequalis possit apparere nobis inaequalis, quarum altera est excentrici suppositio, altera autem concentrici cum epicyclo suppositio. Et cum prior sit aptior huic simplici Solis inaequalitati, eam more suo geometrice astruit. Accipiantur in excentrico duo arcus aequales, quos Sol inaequali tempore pertranseat. Angulum AEB esse aequalem angulo CED constat per ultimam sexti, quae docet eandem esse proportionem arcuum datorum in circulis aequalibus, quae est triangulorum eorum arcuum. Vigesima prima primi confirmat angulum AEB maiorem esse angulo AFB, quia linea BE, tracta ex puncto terminali B, cadit intra triangulum et est brevior linea BF, unde angulus AEB est maior angulo AFB, ex eadem propositione probatur angulus CED minor esse angulo CFD. Nunc per communem sententiam quicquid est maius maiore, et cetera, erit angulus CFD maior angulo AFB, nam cum anguli AEB et CED per ultimam sexti sint aequales, et angulus AEB est maior angulo AFB, et angulus CED demonstratus est minor esse angulo CFD, erit necessario ex communi sententia CFD maior AFB. Igitur, cum Sol in aequali tempore perficit hos angulos, propterea quod arcus

AB sit aequalis arcui CD, erit motus aequalis respectu centri E inaequalis seu diversus ad centrum F, idem contingit per epicycli suppositionem. Hactenus.

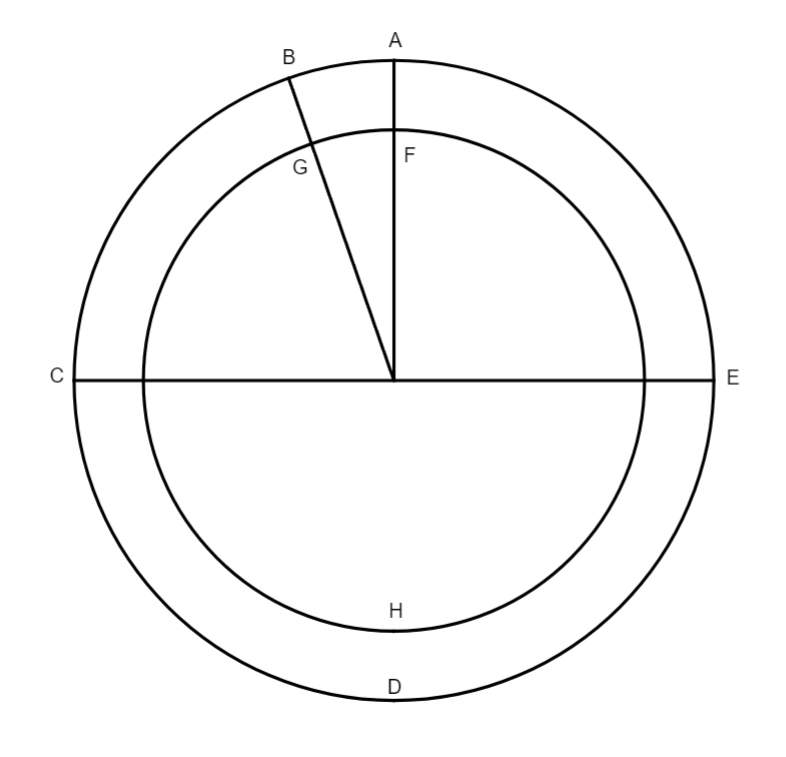
Sed in suppositione quidem］ Ex iam dictis facile est intellectu quare verus seu apparens motus sit apud apogion minor quam apud perigion. Sed ut adhuc clarius fiat, describatur excentricus circulus ABCD, et concentricus zodiaco GHIK super centro mundi F, sit A maxima longitudo, C minima, accipiantur in excentrico, in quo Solis motus est semper aequalis, duo arcus similes, AB et CD.

Imaginetur Sol corpus esse super puncto B aut super puncto D, ex excurrat linea recta a puncto D usque ad punctum B, quo facto, trahantur a centro mundi per centrum Solis usque ad zodiacum lineae FH et FK. Nunc dico angulum veri motus GFH apud apogion esse minorem angulo veri motus IFH apud perigion. Nam angulus IFD est maior per 16 primi aut 21 angulo IED, qui est aequalis angulo AEB, ut dictum est, ex quo sequitur angulum IFD etiam esse maiorem angulo AEB, qui est maior ex supra dictis angulo veri motus GFH, unde per communem sententiam, quidquid est maius maiore, et cetera, erit angulus IFK veri motus apud perigion longe maior angulo GFH apud apogion. Et cum Sol arcum AB, qui aequatur arcui CD, aequali motu in aequalibus temporibus perambulet, sequitur apparentem motum diurnum esse maiorem KI quam in arcu GH, propter dissimilem eorum magnitudinem, ex his erit epicycli ratio per se manifesta.

Dico igitur primum］ postquam declaravit causa inaequalitatis Solis, nunc pergit et demonstrat ubi talis inaequalitas sit maxima. In praecedentibus, inter alia, habita est definitio punctorum mediae longitudinis, quae ostenduntur in circulo quo per medium signorum est, per lineam quae hinc inde excurrit per centrum mundi ad circunferentiam dicti circuli, et facit cum linea augis angulos rectos sicut est in sequenti figura linea BD utrinque ad zodiacum usque protracta, cum Sol in suo excentrico fuerit super puncto B, erit AEB angulus motus aequalis, AFB autem angulus motus apparentis, angulum B esse maiorem angulis T et C et omnibus reliquis angulis,

qui sunt citra ultraque punctum B aut D, sic demonstravit. Maius latus per 19 primi maiori angulo subtenditur, igitur in triangulo FTD latus FT maius est per 7 tertii latere FD, sequitur angulum FDT esse maiorem angulo FTD. Porro in triangulo ETD angulus ETD per 19 primi aequalis est angulo EDT, eo quod latera ET et ED sunt aequalia, unde per communem sententiam, si ab inaequalibus aequalia auferuntur, residua erunt inaequalia, sequitur reliquum angulum EDF esse maiorem residuo angulo ETF. Verum angulus EDF est aequalis angulo EBF per quintam primi, igitur angulus EBF est maior angulo ETF, haec eadem ratione probabitur EBF aut EDF esse maior angulo C. Ex his manifestum est maximam inaequalitatem inter medium et verum motum contingere in nullo alio puncto quam in B aut D. Non alio modo est agendum etiam in suppositione epicycli.

Quod autem etiam］ In his quae praemittuntur in hoc capite demonstravit causas inaequalis motus, locaque in quibus solet evenire velox motus diurnus et in quibus tardus, et ubi fiat secundum utramque suppositionem maxima diversitas inter motum aequalem et inaequalem. Sed in his quae sequuntur demonstrabit, sive imaginetur excentricus aequalis excentrico, sive minor, sive maior eo, eadem omnia in particularibus motibus secundum utranque suppositionem fieri in aequalibus temporibus: lineam BF esse aequalem linea DT, et angulos CBF, BDA, FTE, et similiter angulos BDF et DFT esse invicem aequales, hoc totum pendet ab his notatis propositionibus, scilicet 33, 29, 4, 27 primi Elementorum Euclidis, quae etiam secundae figurae deserviunt.

〈III.4〉 Caput IIII

His ita expositis］ Quae supra geometrice ordine quodam pulcherrimo perstrinxit, ea nunc per exempla numerorum in hoc capite persequitur, in quo primum generaliter docet invenire quantitatem lineae quae est inter utraque centra excentrici, scilicet et circuli qui est cum circulo per medium signorum concentricus et locum maximae et minimae longitudinis in zodiaco. Deinde quanta sit maxima secundum utrunque modum, inter medium et apparentem motum differentia seu diversitas. Verum, cum tota huius negocii operatio pendeat a triangulorum cognitione, adducam eorum triangulorum operationem qui ad hoc negotium requiruntur. Cum itaque volueris scire omnes angulos trianguli rectanguli ex duobus lateribus notis, operare ad hunc qui sequitur modum. Constituas numerum lateris quod praetenditur angulo recto pro primo numero, sinum totum pro secundo, et latus quod opponitur angulo qui quaeritur pro tertio; quo facto, operare secundum regulam proportionum, quod veniet in producto erit sinus qui subtenditur arcui anguli quaesiti, huic sinui elicias e tabulis sinuum arcum et habebis angulum, quo subtracto a 90 gradibus, productum erit et alius angulus acutus, aut operare modo dicto et idem eveniet.

Porro, cum tibi libuerit, per unum ex duobus angulis acutis notum similiter per unum latus eius cognitum, alia latera metiri. Elicias sinum anguli cogniti cum sinu illius complementi; hoc facto, constituas sinus totum primum numerum, quemvis numerum novae dationis seorsim pro secundo, et numerum lateris dati pro tertio, et operare iuxta tenorem regulae proportionum: quod proveniet post operationem erunt latera quae quaerebantur, horum usum melius percipies ubi infra tractaverimus rem per exempla. Post quam Ptolemaeus per observationes didicit Solem plus temporis facere a minimo motu usque ad medium,quam a medio usque ad maximum, hoc est diutius morari in medietate zodiaci, quae est a verno aequinoctio per signa borealia usque ad autumnale aequinoctium, quam in reliquia medietate, huic conclusit maxima Solis longitudinem esse in hac medietate et non in alia.

Quomodo solstitiorum fiat observatio, et quibus instrumentis, supra expositum est, ubi duorum instrumentorum structuram explicavimus.

In diebus］ Pro 30 minutis pone 12 horas. Nam, ut supra meminimus, Ptolemaeus solet diem aliquando solvere in 60 minuta, quo facto, ingredere in tabulam medii motus, quem supra componere docuit, primum cum 90 diebus in tabula mensium, quod e regione scribitur, notato seorsim, deinde ingredere cum 4 diebus in tabulam dierum, et quod ibi invenies subscripto producto ante servato partes sub partibus, minuta sub minutis, et cetera. Postremo, ingrediaris cum 12 horis in tabulam horarum et quicquid inibi invenctum fuerit subscribatur, quemadmodum dictum est; postea, singulas denominationes addas singulis denominationibus, si productum transcenderit sexagenarium numerum adiicias praecedenti denominationi unitatem pro quolibet sexagenario numero, et habebis 93 gradus et 9 minuta proxime, et sic agito cum reliquis.

Et chorda］ Regula quaerendi chordas supra in fine libri primi tradita est.

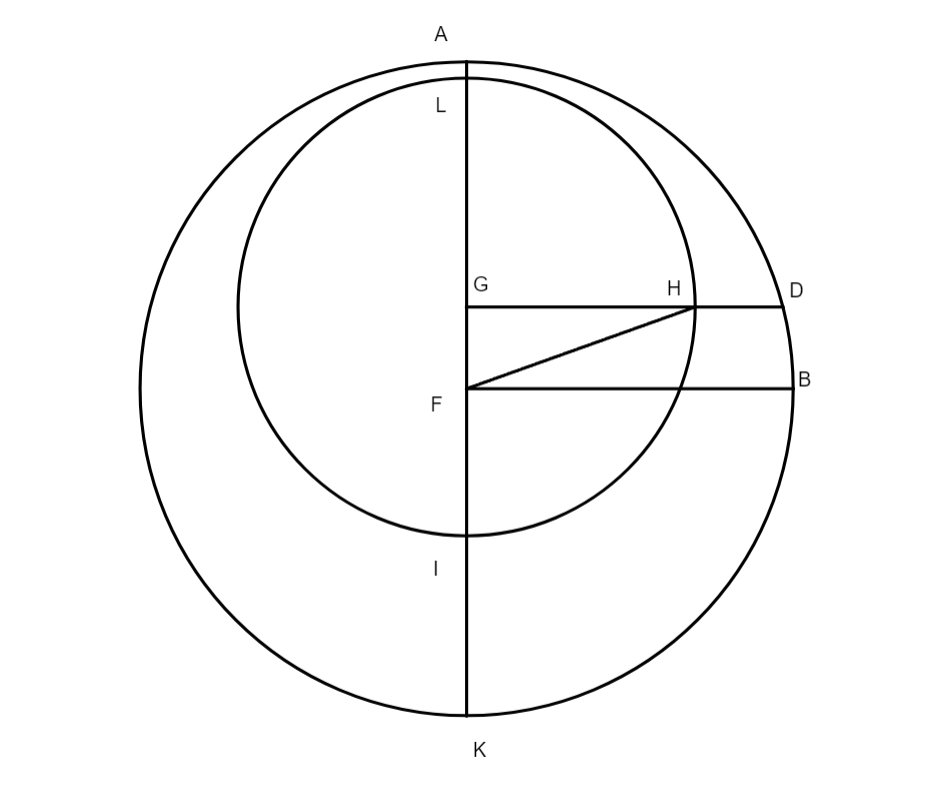
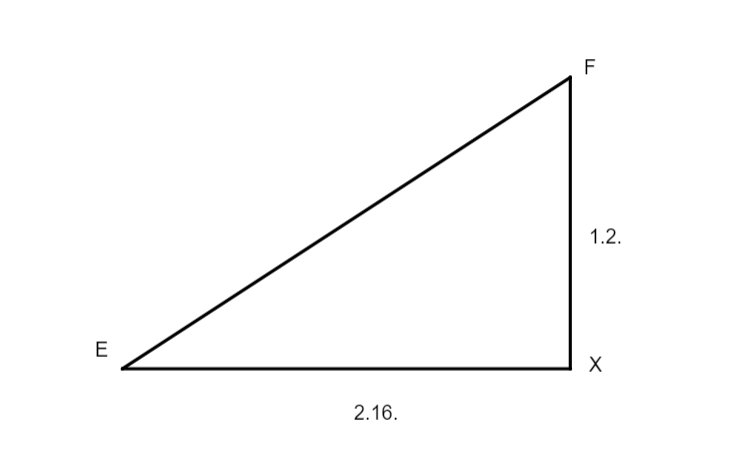
Et quoniam］ Per penultimam primi habetur quod quadrata linearum FX et EX tantum faciant quantum quadratum lineae EF, quae praetenditur angulo recto EXF. Ex multiplicatione lineae EX in se prodierunt 5 gradus 8 minuta 16 secundae, deinde ex multiplicatione alterius lineae, scilicet FX, provenerunt 1 gradus 4 minuta et 4 secundae. His duobus productis in unum collectis, et inde extracta radice quadrata, habuimus 2 gradus et 29 minuta proxime, tanta est linea EF, excentricitatis nimirum seu linea inter duo centra, quorum diameter

excentrici TCL est 60 graduum.

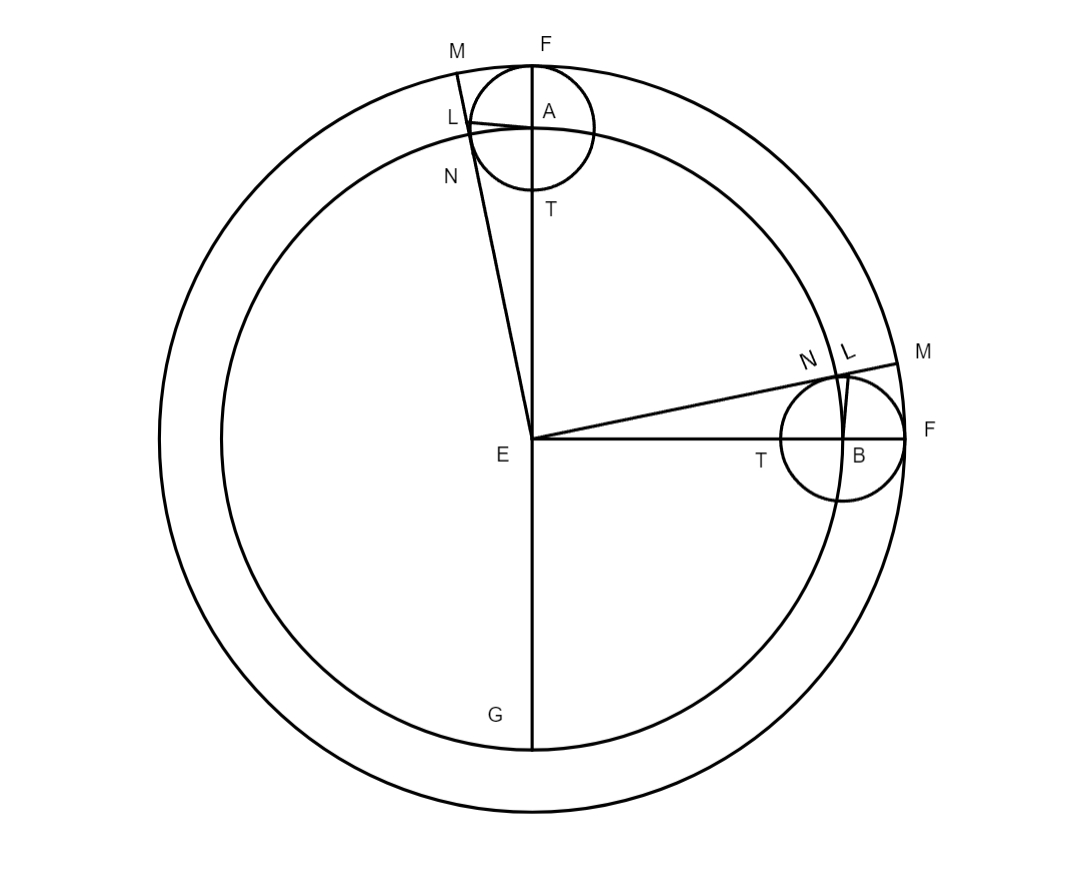
Rursus quoniam］ Habita excentricitate, nunc restat quaerere quantitatem anguli FEX. In triangulo rectangulo EFX sunt tria latera nota, itaque, si volueris scire quantus sit angulus FEX, tunc confugias ad regulam quam

paulo ante tradidimus de inventione angulorum laterum cognitorum, hoc est ordina ordina] ordna B numeros ad hunc qui sequitur modum: 2° 29ʹ | 120° | 1° 2ʹ. Quo facto, resolve primum et secundum in minimas denominationes, postea, iuxta doctrinam supra traditam duc tertium in secundum et productum divide per primum, producti dimidium arcus erit arcus ille qui praetenditur angulo FEX, et cum angulus FEX sit in centro zodiaci, erit arcus BY in figura Ptolemaei idem qui YC excentrici, punctus Y est maxima longitudo seu punctus remotissimus a terra. Et si subtraxeris 24 gradus et 30 minuta quibus distat maximas longitudo a puncto solstitiali aestivo, residuabuntur 65 gradus 30 minuta. Tantus est arcus AY, ex his manifestum est punctum maximae longitudinis tempore Ptolemaei fuisse in 5 gradibus 30 minutis Geminorum.

Verum quoniam］ Aufer arcum OL, id est 2 gradus 10 minuta, a 90 gradibus; prodibunt 86 gradus 50 minuta Sic in the witness. However, subtracting 2° 10' from 90° yields 87° 50'. The final result of 86° 51' is correct; therefore, the intermediate value must be a scribal mistake., a quibus si iterum auferes arcum MS, scilicet 0 gradus 59 minuta, erit arcus LM 86 graduum 51 minutorum. Porro si iterum arcus OL, scilicet 2 gradus 10 minuta, subtrahentur ab arcu NM, id est a 90 gradibus 59 minutis, erit arcus MT 88 graduum 49 minutorum. Ad habendum dies partesque dierum horum graduum et minutorum, dic 0 gradus 59 minuta et 8 secundae dant unum diem, quot dies dabunt 88 gradus 49 minuta? Reliqua perclara sunt.

Per has igitur quantitates］ Nunc porro, habita excentricitate, hoc est proportione lineae quae est inter duo centra ad semidiametrum excentrici, docet per numeros invenire maximum angulum seu differentiam motus inaequalitatis ad motum aequalem, quod per doctrinam triangulorum absolvitur. Ex superioribus linea DE inventa est 2 graduum 30 minutorum et linea DB

60 graduum eorundem, sinus totus vero est 120 graduum. Pone lineam BD, id est 60 gradus, numerum primum, iuxta doctrinam supra de ratione triangulorum planorum tradita, et sinum totum, scilicet 120 gradus numerum secundum, ac lineam DE, hoc est 2 gradus et 30 minuta, numerum tertium: his ita positis, duc more solito tertium in secundum et divide productum per primum, et habebis in producto 5 gradus, chorda scilicet quae praetenditur angulo acuto EBD. Et cum elicueris e tabula sinuum huius chordae arcum, habebis 4 gradus 46 minuta, quorum dimidium sunt 2 gradus 23 minuta. Tantus est angulus maximae differentiae inter aequalem et inaequalem motum, scilicet angulus DBE. Ad hunc modum agitur etiam cum angulo ADF in epicycli suppositione, in quo fit angulus maximae aequationis cum stella in epicyclo pervenerit ad punctum contactus. Hactenus de his.

〈III.5〉 Caput V

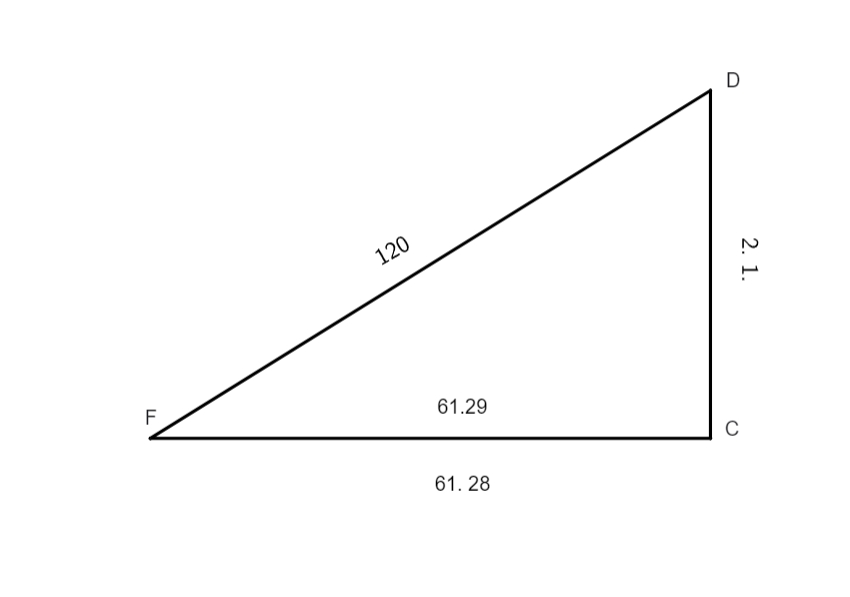
Verum ut particulares］ Cum suppositio epicycli non aliam requirat angulorum investigationem quam excentrici suppositio, eam dimittere visum est, et tantum exempla excentrici tractabimus, et quemadmodum Ptolemaeus duo proposuit exempla, alterum existente epicyclo supra lineam media longitudinis, alterum autem existente eo infra dictam lineam, sic et nos duo alia non sine causa adiiciemus, et ex quorum operatione etiam autoris exempla recte intelligentur: sed ut rudioribus huius artis via indagandi angulos inaequalitatis et ratio conficiendi eiusmodi tabulas aperiatur, nos integram tractationem horum exemplorum ascribemus, ex quibus facile quisque pervidebit unde pendeat hoc negotium, quod ut est laboriosissimum, ita est tractatu iucundissimum, quid nam est iucundius, quidve animo gratius? Quam posse, dato quocunque motu medio, angulum inaequalis motus invenire, et contra ex dato motu apparente aut angulo inaequalitatis, quicunque ille sit, posse in lucem producere motum medium seu aequalem, harum, inquam, rerum operatio in hoc capite, licet brevissime, demonstratur. In tractatione primi exempli nostri hoc modo processimus, sicut videbitur in sequentibus, scilicet duplavimus propositum arcum EF medii motus, productum subtraximus a 180 gradibus, hoc est semicirculo, quo facto, elicuimus e tabula chordarum dictorum duorum arcuum chordas, scilicet chordam DC et TC, nam angulus ETF per decimamquintam primi

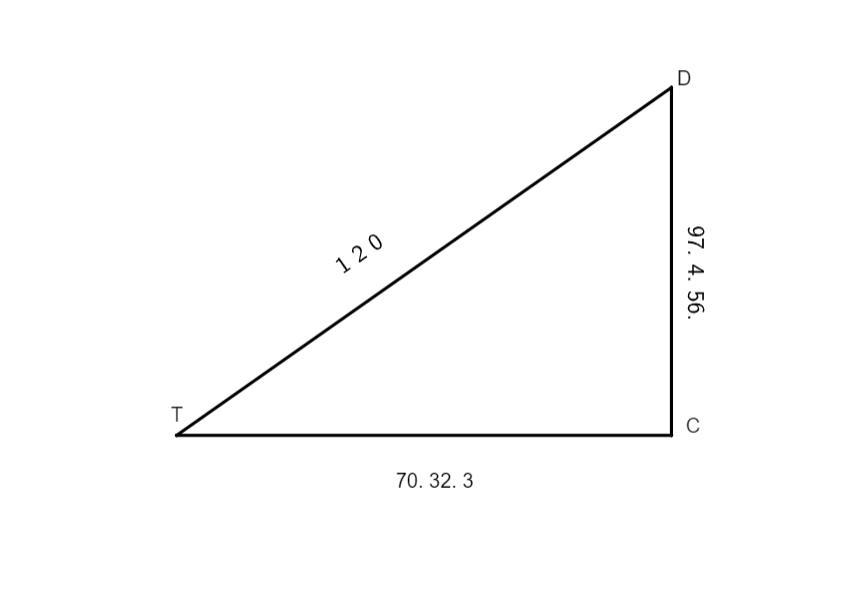
est aequalis angulo DTC, quia sunt anguli contrapositi, TC linea est complementum. Et cum in triangulo rectangulo DTC unum latus, nempe DT, cum uno angulo acuto DTC sit notum, quaesivimus per doctrinam supra traditam reliqua latera, scilicet DC et TC, quibus habitis, addidimus productum lineae TC semidiametro excentrici FT, tunc lineam FC multiplicavimus in seipsam et similiter lineam DC, haec duo producta addidimus alterum altero, e producto estraximus radicem quadratam pro linea FD. Et sic habuimus in triangulo rectangulo DFC tria latera cognita; ad habendum angulum DFC, ordinavimus numeros iuxta doctrina quem supra tradidimus et duximus tertium numerum in secundum, productum divisum est per primum, producti quaesitus est arcus e tabula chordarum, cuius medietatem diximus esse angulum inaequalitatis DFC. Sic arcus EF motus aequalis datus 54 graduum, cuius duplum sunt 108 gradus; subtractis illis a 180 gradibus, remanent 72 gradus, horum arcuum chordae sunt 97 gradus 4 minuta 56 secundae pro linea DC et 70 gradus 52 minuta 3 secundae pro linea TC.

Ordinatio numerorum post resolutionem:

Si productum lateris TC adieceris semidiametro excentrici TF, creabuntur 61 gradus, 28 minuta tota linea, scilicet FC.

Quod vero］ Nunc porro docet, ex dato vero motu, inquirere medium motum. Sciendum est quod, cum angulus medii motus minor fuerit 180 gradibus, fieri subtractionem anguli differentiae medii et veri motus, si vero maior fit contra, quia in huiusmodi situ medius motus maior est vero et linea medii motus praecedit lineam veri motus. Haec res ex praecedenti exemplo satis perspicua est. Itaque cum volueris per verum seu apparentem motum cognoscere medium sive aequalem motum, tunc debes elicere angulum inaequalitatis, quo habito, adiicias eum motui apparenti, et procreabitur medius motus, tunc, ut dictum est, hoc fiat cum datus motus aequalis fuerit minor 180 gradibus, seu sex signis, haec in exemplo hoc clariora fient. In quo, iuxta Ptolemaei doctrinam, hac processimus via: duplicavimus propositum

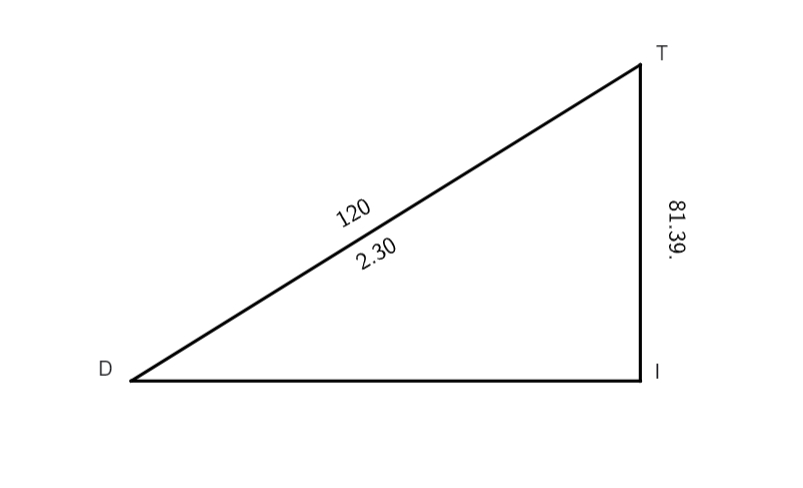
angulum motus inaequalis, scilicet angulum TDI, qui fuit in hoc exemplo simplus 81 graduum 39 minutorum, duplus vero 163 graduum 18 minutorum, deinde de prompsimus e tabula chordarum duplam chordam arcus 163 graduum 18 minutorum, quae fuit 118 graduum 43 minutorum 40 secundarum. Hic habitis, disposuimus numeros secundum viam invenendi latera quaeque ex uno latere et uno angulo noto, et inventa est linea TI habere 2 gradus 28 minuta. Verum, cum ex supra dictis proportio lineae DT ad lineam TF sit data in triangulo TFI, quaesivimus angulum TFI hoc modo,

scilicet duximus 2 gradus 28 minuta in sinum totum, hoc est 120 gradus, quod provenit divisum est nobis per 60°, prius omnibus, more solito, resolutis atque aequatis quod prosiliit post divisionem, fuerunt 4 gradus 56 minuta. Tanta est dupla chorda TI, quae praetendetur angulo TFI, huius producti arcus desumptus est e tabula chordarum, qui fuit 4 graduum 43 minutorum, dimidium vero eius fuerunt 2 gradus 21 minuta proxime, angulus scilicet quaesitus TFI, hoc productum postquam addidimus motui inaequali 81 gradus 39 minuta prodierunt 84 gradus, motus scilicet aequalis: hinc videre est quando motus aequalis proponitur 84 gradus quod differentia inaequalitatis Inaequalitatis] inaequalitis B sit 2 graduum 21 minutorum et motus verus, ut supra, 81 graduum 39 minutorum. His recte intellectis facile erit, dato angulo diversitatis, indagare per illum motum medium.

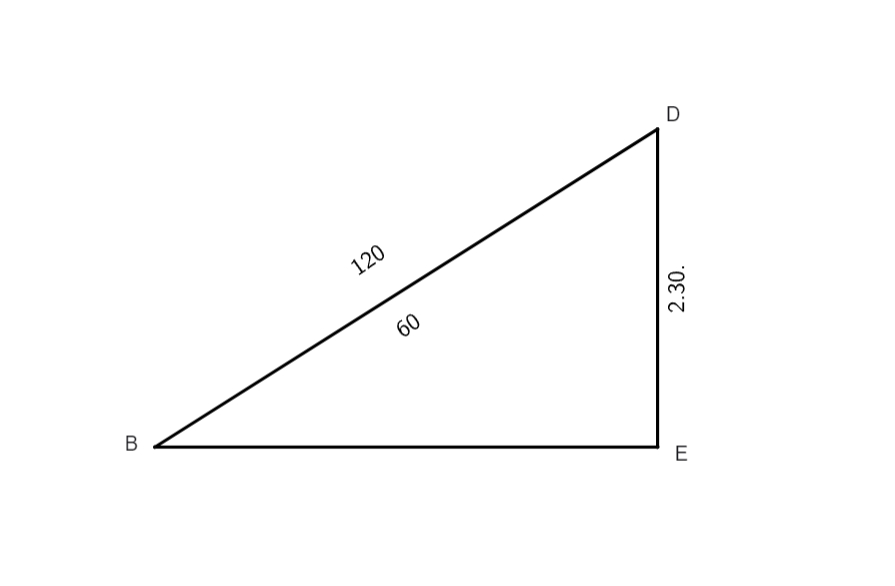
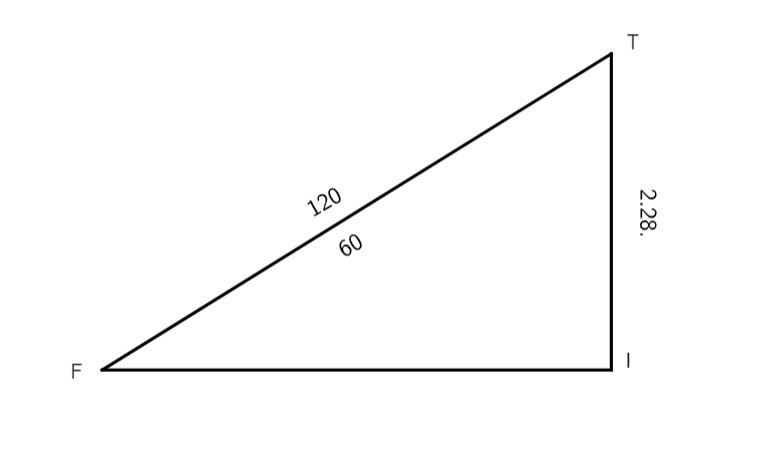
Rursum in praeposita］ Hactenus tractata sunt ea quae requiruntur ad indagationem angulorum diversitatis, cum centrum corporis solaris fuerit supra medietatem concentrici, hoc est supra locum in quo fit maxima aequatio, et similiter quo modo huiuscemodi anguli investigentur. Nunc properabimus ad exemplum secundum, in quo paulo alia via procedendum est, sicut in hoc exemplo videre est. Esto arcus medii motus EF 144 graduum, quem subtraximus a 180 gradibus et remanserunt 36 gradus, angulus nimirum ITF; hoc arco duplato pervenerunt 71 gradus, arcus scilicet qui subtenditur rectangulo DTC, quem si subtraxeris a 180 gradibus remanebit

angulus CDT, horum duorum arcuum chordae sunt, scilicet, 70 gradus 32 minuta 3 secundae pro CD et 97 gradus 4 minuta 56 secundae pro CT. His habitis, ordinavimus numeros pro habendis lateribus DC et CT ad hunc modum:

et operati sumus secundum documentum de quo in praecedentibus dictum est, et venerunt in producto pro latere CD 1 gradus 28 minuta et pro latere CT 2 gradus et 1 minutum. Ad habendum angulum inaequalitatis CFD ad hunc situm: subtraximus lineam CT, hoc est 2 gradus et 1 minutum, a semidiametro excentrici, scilicet 60 gradibus, et residuati sunt 57 gradus 59 secundae pro linea CF, qua ducta in seipsam, et similiter CD, et duobus quadratis additis ac radice quadrata inde extracta, venerunt in producto pro linea FD 58 gradus 0 minuta. Cum nunc duo latera trianguli CFD sint nota, nempe latus CD et latus FD, non difficile erit indagatu quantus sit angulus CFD, quem hac via indagavimus, scilicet posuimus numerum lateris FD primum, sinum totum secundum ac numerum lateris CD tertium, et operati sumus iuxta rationem regulae aureae, et prodierunt post investigationem arcus 2 gradus 54 minuta, quibus dimidiatis habuimus in producto 1 gradus 27 minuta. Tantus, inquam, est angulus diversitatis CFD, et sic de reliquis. Iuxta documentum horum duorum exemplorum tabula inaequalitatis solaris calculata est. Porro, sextum et septimum caput per se clara sunt, id eo consulto ea praeterivimus.

〈III.8〉 Caput VIII

Hactenus Ptolemaeus, miro quodam artificio, tradidit omnia quae pertinent ad fabricam tum tabularum medii motus tum tabulae angulorum inaequalitatis, ad haec datis veris motibus, quomodo inde cognosci debent medii motus, aut ex datis angulis uterque motus tam medius quam verus, et hoc secundum utranque suppositionem, suppositionem] supposiionem B scilicet excentrici et concentrici cum epicyclo. Nunc pergit et tradit quo pacto per observationem radix motus solaris sit constituenda ad quodcunque principium temporis, ad quod haec in primis requiruntur, scilicet cognitio tabularum medii motus et cognitio proportionis lineae quae est inter duo centra ad semidiametrum, et quo modo ex vero motu cognito sit investigandus angulus differentiae inter verum et medium motum, unde habebitur, per subtractionem aut additionem, secundum quod locus Solis in excentrico expostulat, medius motus. Sed cum author hoc loci paulo aliter per verum motum angulum differentiae venari doceat quam supra a nobis traditum sit, non inutile esse videtur ut uterque modus paucis hic clarior reddatur.

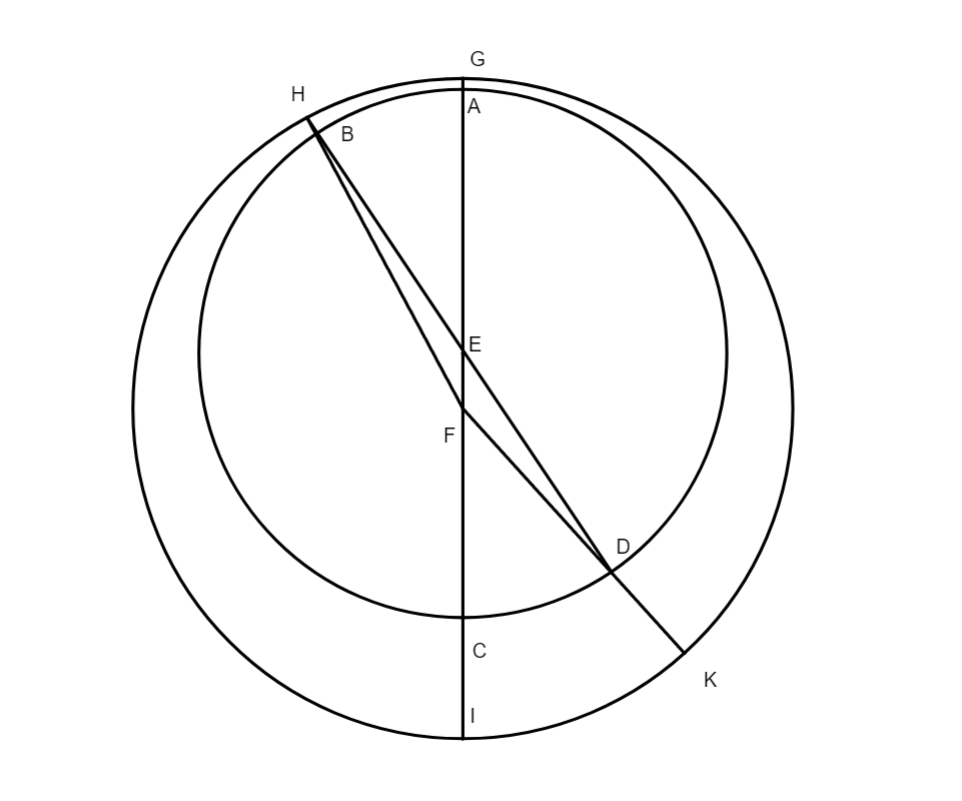
Sit igitur］ Ex doctrina quarti capitis manifestum est augem temporibus Ptolemaei fuisse in 5 gradibus 30 minutis Geminorum, unde oppositum eius est in 5 gradibus 30 minutis Sagittarii, et si numeraveris secundum ordinem signorum a principio Librae, in quo est punctum autumnale, usque ad 5 gradus 30 minuta Sagittarii, erit angulus BDG, ut habetur in textu, veri motus 65 gradus 30 minuta. Tantus est etiam angulus TDC per decimam quintam primi, quia est angulus contrapositus. Ad eliciendam lineam TC, quae praetenditur angulo TFC, duplavit Ptolemaeus brevitatis gratia 2 graduum 30 minutorum excentricitatem, quos statuit secundum numerum, primus fuit sinus totus, deinde duplavit 65 gradus 30 minuta et producti accepit lineam rectam, quae fuit 109 graduum 12 minutorum, et duxit more solito tertium in secundum, productum per primum divisit, et nati sunt 4 gradus 33 minuta, horum arcus duplus fuerunt 4 gradus 20 minuta et medietas eius 2 gradus 10 minuta, angulus nimirum diversitatis TFC, qui quaerebatur, et cum angulus veri motus ad hunc situm sit maior angulo medii motus, subtractus est iste angulus, ad habendum medium motum, a 65 gradibus 30 minutis, et quod relinquebatur erant 63 gradus 20 minuta. Tantus fuit angulus FTI medii motus, de hac subtractione superius mentio facta est. Ad secundum modum proportionum in praecedenti capite traditum aliter operatur, nempe sic: in triangulo TDC, ut dictum est, unus angulus acutus, scilicet TDC, notus est cum uno latere, TD, quod ex quarto capite notum est, sed ut habeatur latus TC ordinati sunt nobis numeri sic: gradus 120, gradus 2 minuta 30, gradus 109 minuta 12. Redactis singulis numeris in minimam denominationem, operati sumus, ut solet, in regula de tribus et provenerunt 2 gradus 16 minuta 30 secundae. Hoc facto, statuimus latus TF trianguli TFC, hoc est,60 gradus, primum numerum, sinum totum secundum, et 2 gradus 16 minuta 30 secundae tertium numerum, et post operationem idem prodiit quod supra. Hinc evidens est quod Sol secundum medium motum quando fuit in puncto aequinoctii autumnali abfuit ab opposito augis contra ordinem signorum 63 gradibus 20 minutis, et a maxima longitudine secundum ordinem signorum seu auge 116 gradibus 40 minutis. Hii gradus nascuntur cum 63 gradus 20 minuta subtraxeris a 180 gradibus. His datis, nunc restat scire quantum Sol distet a maxima longitudine seu auge, si medius motus Solis calculabitur a primo anno et primo mense thot Nabonassari usque ad tempus instans quo facta est observatio, hanc quantitatem reperit Ptolemaeus esse 265 graduum 15 minutorum, hoc modo scilicet quaesivit medium motum Solis 879 annorum 66 dierum, et duarum horarum aequalium, quem reperit (reiectis integris circulis, ut solet, ubi numerus collectus excedit 260 gradus) 211 gradus 25 minuta, quos subtraxit a 116 gradibus 40 minutis, sed cum numerus subtrahendus sit maior quam numerus a quo debet fieri subtractio adiecit integrum circulum, scilicet 360 gradus, et postea subtraxit ac invenit Solem primo die thot in meridie, primo anno Nabonassari, distitisse a maxima longitudine 265 gradus 15 minuta. Sed ut talis subtractio manifestior fiat, esto ABGE circulus excentricus Solis, cuius centrum sit D et diameter ADG, ponamus quod Sol tempore observationis, scilicet 17 anno Adriani, et cetera, fuerit super puncto B,

hoc est autumnali aequinoctio, et primo meridie mensis thot primo anno Nabonassari super puncto E, ex superioribus est arcus BA notus, qui inventus est esse 116 graduum 40 minutorum, et similiter arcus EAB, qui est 211 graduum 25 minutorum. Et cum arcus BA sit minor arcu BAE, non potest ab eo fieri subtractio. Ideo adiiciatur integer circulus ABGE, hoc est 360 gradus, ad 116 gradus et 40 minuta, a quibus, si subtrahitur arcus EAB, relinquetur arcus BGE. At cum arcus EAB auferatur ab arcu AB, et integro circulo, necesse est relinqui arcum BGE una cum arcu AB, additis his duobus arcubus fit arcus ABGE, hoc est distantia Solis a maxima longitudine, quae inventa est 265 graduum et 15 minutorum. Si itaque numeraveris a puncto A, qui augem repraesentat, hoc est a 5 gradibus 30 minutis Geminorum, usque ad finem 265 gradus 15 minuta, id est punctum E in quo fuit Sol in meridie primo die thot, provenies ad 0 gradus 45ʹ Piscium.

〈III.9〉 Caput IX

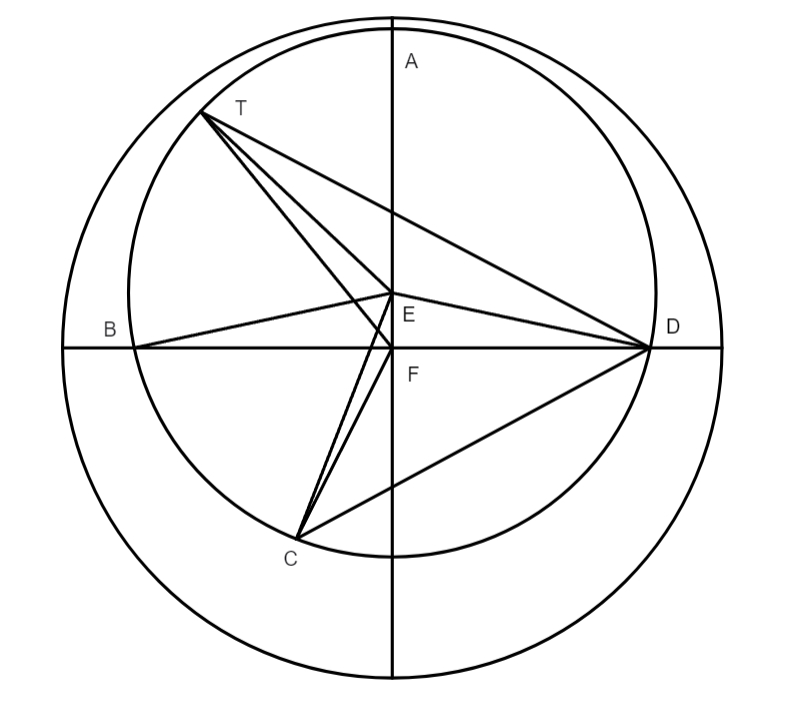
Quando igitur］ Hoc capite brevissimis traditurus est quomodo tam medius quam verus motus Solis sit inveniendus, et hoc ad quodlibet tempus propositum, sed tempus propositum est id quod est a principio regni Nabonassari usque ad tempus illud in quo motus quaerendus est. Verum, ut res clarior fiat, visum est eam exemplo quodam illustrare. En volo quaerere medium ac verum motum Solis ad annum 882 et 72 dies 5 horas 50 minuta post principium regni Nabonassari, hoc tempus fuit vigesimus annus Adriani, 13 diem mensis Athyr secundum Aegyptios, 5 horas 50 minuta. Cum non inveniam 882 annos praecise in tabula medii motus, accepi proxime minorem, scilicet 810 annos, quibus adhaerent in dextra 163 gradus 4 minuta 12 secundae 15 tertiae. Subtractis 810 annis a 882, remanserunt 72 anni, hos quaesivi in linea annorum collectorum, in quorum latere dextro inventi sunt 342 gradus 29 minuta 42 secundae 25 tertiae. Hoc productum subscriptum est superiori, gradus scilicet gradibus, minuta minutis, et cetera. Porro cum 72 dies non inventi sint praecise in tabula mensium, accepi numerum proxime minorem, nempe 60 dies, qui secum habebant 59 gradus 8 minuta 17 secundas et 13 tertias, quos subscripsi superioribus, quo facto, intravi cum reliquis 12 diebus in tabulam dierum, et inveni 11 gradus 49 minuta 39 secundas 26 tertias, qui etiam subscripti sunt: postea immissae sunt 5 horae in tabulam horarum, quod circa eas inventum est fuerunt 0 gradus 12 minuta 19 secundae 13 tertiae, in quibus egi secundum modum dictum. Postremo, ingressus sum in tabulam horarum cum 50 minutis, bis cum 24 minutis et semel cum 2 minutis, et pro minutis in tabula inventis posui secundas, et sic de reliquis appellationibus, et subscripsi bis 59 secundas et 8 tertias, et pro 2 minutis 14 secundis producto ante habito: his ita stantibus, addidi singulas appellationes singulis appellationibus, reiectis integris circulis, productum fuerunt 216 gradus 46 minuta, quibus additi sunt 265 gradus 15 minuta quibus distitit Sol a maxima longitudine, in primo anno Nabonassari thot secundum Aegyptios Aegyptios] Aegytios B die primo in meridie, tota summa excrevit, reiectis integris circulis, ad 122 gradus 1 minutum. Et cum numeravi hos gradus a maxima longitudine, id est 5 gradibus et 30 minutis Geminorum, perveni ad 7 gradus 31 minuta Librae secundum medium motum. In aequando hoc motu ita processi, scilicet iterum ingressus sum cum 122 gradibus 1 minutis in tabulam inaequalitatis, et cum iste numerus non reperiatur precise accipi, ut solet, proxime minorem 120 graduum cuius differentiam ad immediate sequentem seorsim scripsi, scilicet 3 gradus, et quod scribitur in tertia et quarta linea notavi extra, et fuerunt 2 gradus 6 minuta. Quo facto, subtraxi 120 gradus a 122 gradibus 1 minuto et remanserunt 2 gradus et 1 minutum. Differentia 2 graduum 6 minutorum, anguli diversitatis ad proxime sequentem, fuerunt 4 minuta, has tres differentias ordinavi ad hunc modum: 3 gradus, 2 gradus 1 minutum, 0 gradus 4 minuta, et operatus sum secundum exigentiam regulae de tribus, et procreata sunt ex eiusmodi operatione 3 minuta quae, cum sequens angulus diversitatis sit minor, subtracta sunt a 2 gradus 6 minuta, et residuati sunt 2 gradus 3 minuta pro angulo equationis, quem, iuxta doctrina huius capitis, cum medius motus, qui numeratur sicut supra dictum est a maxima longitudine, sit minor 180 gradus, subtraximus a 122 gradibus 1 minuto, quod supererat fuerunt 119 gradus 58 minuta pro vero motu Solis, quibus numeratis a maxima longitudine pervenimus ad 5 gradus et 28 minuta Librae, et ita conclusimus ad tempus propositum Solem secundum verum motum fuisse in 5 gradibus 28 minutis Librae, et secundum medium seu aequalem motum in 7 gradibus 31 minutis eiusdem signi, et sic de reliquis. Sed ut haec magis manifesta fiant, proponatur talis figura, in qua singula demonstrabuntur, ut dici solet, ad oculum: circulus ABG esto

zodiacus, ALHG excentricus circulus, E locus Solis in principio regni Nabonassari, locus vero medii motus, qui quaeritur, sit punctus L, verus locus in zodiaco punctus B, et protrahatur linea veri motus BLFE per centrum mundi F, et lineae DL, DE et DG ad loca Solis in excentrico. Ex tempore dato, scilicet 882 annorum 72 dierum et 5 horarum 50ʹ, elicuimus e tabula medii motus arcum EAL, qui inventus est 216 graduum 46 minutorum, et per doctrinam praecedentis capitis notus fuit arcus ALE, qui complectitur 265 gradus 15 minuta. His duobus productis additis, natus est maius productum integro circulo, ideo abiecimus a producto 360 gradus. Quod reliquum fuit fuerunt 122 gradus 1 minutum, angulus scilicet ADL medii motus, et cum linea medii motus FM praecedat lineam veri motus FB, angulus medii motus ADL maior est angulo veri motus AFB, ideo subtractus est angulus inaequalitatis DLF, qui aequalis est per 29 propositionem primi angulo BFM, hoc est, subtraximus 2 gradus 3 minuta a 122 gradibus 1 minuto, nempe arcum BM ab arcu ABM, et relicti sunt 119 gradus 28ʹ pro arcu AB, et sic de reliquis punctis.

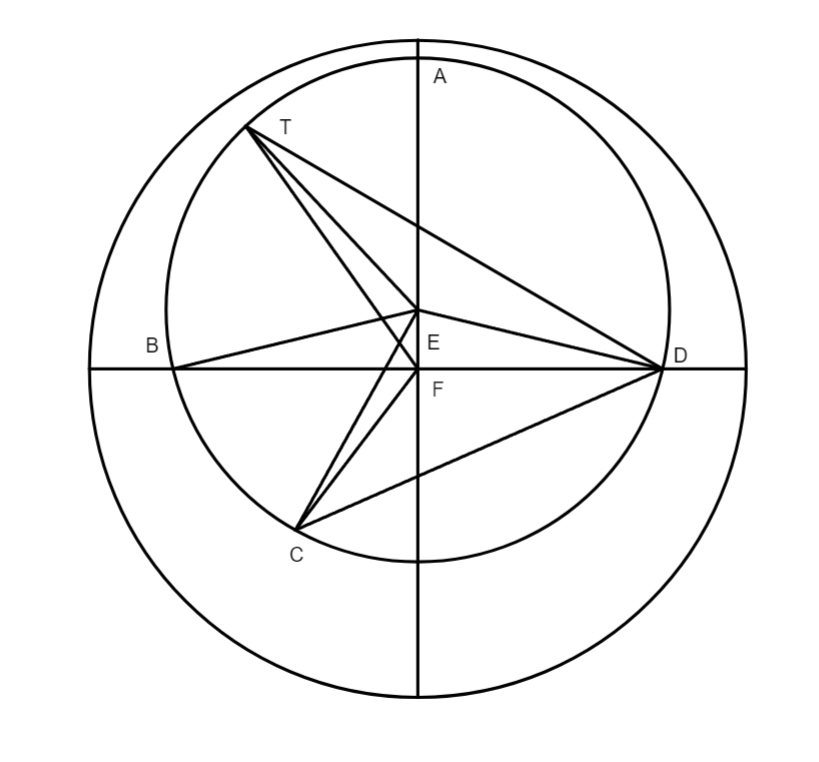
Ad Alexandriae meridiani］ Cum quaedam civitates sint orientaliores quam Alexandria, quaedam vero occidentaliores, oportebit calculum vel temporis, vel motuum planetarum et maxime Lunae, quae velocioris cursus est reliquis, ad meridianum Alexandriae reducere. Quae reductio ad hunc fiat modum, scilicet: perpende an locus seu civitas in qua eiusmodi calculus factus est minus distet a meridiano fixo qui transit per Insulas Fortunatas quam Alexandria, hoc est an longitudo talis civitatis vel loci sit minor longitudine Alexandriae, si sic, aufer longitudinem illius civitatis a longitudine Alexandriae. Si vero illius longitudo fuerit maior longitudine alexandrina, subtrahas longitudinem alexandrinam et differentiam redigas per 15 in horas, et horarum minuta, hoc infra in exemplo clarius intelliges. Ut res manifestior sit, adducemus schema in quo ABGL sit meridianus fixus, ductus per Insulas Fortunatas, BDL aequinoctialis, circulus ADG meridianus alexandrinus, ACG meridianus babilonicus, AEG meridianus transiens per Romam. Si BE longitudinem romanam romanam] romamam B, quae minor est longitudine alexandrina, subduxeris ab excu excu] read arcu BD, qui repraesentat longitudinem alexandrinam, tunc residuabitur arcus DE, differentia horum meridianorum, scilicet Alexandriae et Romae. Porro, si longitudo alexandrina et longitudo babilonica fuerint datae, et cupis scire earum differentiam in meridianis,

tunc subtrahito BD ab arcu BC, et residuabitur differentia DC; proponatur, exempli gratia, longitudo alexandrina esse 60 graduum 30 minutorum, quae sit arcus BD, et longitudo babylonica 73 graduum, et sit arcus BC, subtracta maiore a minore relinquetur arcus DC 12 graduum 30 minutorum, quibus divisis per 15, ut supra dictum est, provenient 50 sexagesimae, unius horae aequalis. Hoc paucis etiam animadvertendum est, quod productum talis differentiae post resolutionem in tempora aequinoctialia debet addi in tempore pro civitate orientaliori, et subtrahi pro civitate orientaliori: sed in motu fit contrarium, nempe medii motus dictae differentiae, hoc est temporis, sunt addendi pro occidentaliori civitate et subtrahendi pro orientaliori: quomodo medii motus sint eliciendi ex tempore differentiae meridianorum alio loco dicetur, quod omnino nihil difficultatis habet ubi medius motus planetae in die fuerit notus. Exempli gratia. In superioribus habitum est quod differentia meridianorum Alexandriae et Babyloniae fuerit in tempore 50 minutis unius horae. Si itaque medium alicuius eclypsis fuerit Alexandriae, ad cuius meridiem in his libris fit operatio, horis 8, 40 minutis post meridiem, et vis reducere illud ad meridianum babylonicum babylonicum] babilonicum B, tunc, cum Babilonia sit orientalior Alexandria, 50 sexagesimas seu minuta unius horae aequalis addas 8 horas 40 minuta et provenient 9 horae 30 minuta medii eclypsis pro meridiano babylonico, hoc fit eam ob rem quod Babyloniae propter tumorem terrae citius meridies est quam Alexandriae, de hac re fusius tractatum est in annotationibus primi libri, ubi res convenienti figura illustrata est.

〈III.10〉 Caput X

In hoc capite author primum definit diem naturalem, deinde paucis ob oculos ponit commodius esse ut principium diei naturalis sumatur a puncto meridiano diurno aut nocturno quam ab horizonte; tertio, ostendit quanta sit maxima differentia dierum naturalium, et in quibus syderibus minime negligenda sit eiusmodi differentia. Postremo tradit regulam quomodo dies naturales sint reducendi ad aequalitatem.

Quare aequalis dies］ Motum Solis contrarium esse motui primi mobilis, hoc est Solem moveri ab occasu ad ortum, ex primo libro manifestum est. Unde dies naturalis mediocris seu aequalis est integra reductio corporis solaris a puncto meridiano iterum ad illud punctum

quae complectitur unam aequatoris revolutionem, una cum tanta aequatoris portiuncula quanta respondet diurno medio motui Solis, scilicet 0 gradibus 59 minutis 8 secundis. Ex hoc liquet diem inaequalem comprehendere 360° tempora aequinoctialis aequinoctialis] aequinoctiais B

et praeterea id quod, cum Solis motu vero, de aequatore ascendit in recta sphaera. Esto ABCDE circulus aequatoris, FGH Solis excentricus, punctus A referat intersectionem meridiani cum aequatore et CE sit horizon, et Sol ponatur esse in suo circulo in puncto F sub puncto meridionali A, et imaginetur rapi cum primo mobili ad punctum occidentalem E, et ex E ad D ac C, et redire ad punctum meridionalem A, et priusque rediit ad punctum A, motus est medio motu in suo circulo ab F ad G, qui arcus est 59 minutorum 8 secundarum, cui respondet in aequatore arcus BA, recta nimirum ascensio, quae est 54 minutorum. Continet ergo dies naturalis integram revolutionem circuli aequinoctialis, scilicet circulum AEDCBA, et insuper arcum BA, hoc est 360 gradus una cum 54 minutis, sic etiam de intelligendum est de die inaequali. Duae assignantur causae, quibus hoc additamentum variatur. Altera quod Sol in temporibus aequalibus, ut dictum est, motu suo inaequales in zodiaco abscindit arcus, altera vero quod aequales arcus circuli per medium signorum habent inaequales ascensiones tum rectas tum obliquas, ut exempli gratia: in recta sphaera ascendunt cum prima decade Arietis 9 tempora et 10 minutis, cum secunda autem 18 tempora et 25 minutis, quae differunt 15 minutis. Sed quomodo Sol motu suo medio inaequalibus temporibus abscindat de circulo per medium signorum inaequales arcus supra satis superque auditum est.

Penes igitur］ Maximam differentiam ait fieri ex distantiis ab uno medio motu ad alterum medium motum, quod non aliter intelligendum est quam causam inaequalitatis dierum provenientem ex diversitate motus Solis, incipere ab altera mediarum longitudinum et finire ad alteram: sed quod maluit hic incipere quam ab ullo aliorum punctorum excentrici causa est haec, nempe quod motus Solis aequalis seu apparens ibi medio motui fit conformis ac aequalis. Verum, ut haec melius intelligantur, describatur excentricus ABGD super centro C, cuius diameter sit ACG, in quo capiatur centrum zodiaci E, et excurrat ad circumferentiam linea BED, quae sit orthogonalis ad diametrum ACG, et trahantur ex puncto C, ad puncta B, D, lineae CB et CD; anguli CBE, CDE continent maximam Solis inaequalitatem, sicut ex supra dictis manifestum est. Dierum naturalium maxima diversitas fit ratione excentrici Sole existente in distantiis BAD, BGD, quae sunt ab uno medio motu, hoc est media longitudine B, ad alterum medium motum, scilicet G. Manifestum est ex superioribus quod procedendo per superiorem medietatem circuli per medium signorum, ubi punctus maximae distantiae Solis a terra est, medium motum maiorem esse apparente in duplo maximae aequationis, nam anguli excentrici ACB, ACD maiores sunt quam anguli zodiaci

BEG, DEG, angulis inaequalitatis CBE, CDE, quorum uterque inventus est esse 2 graduum 23ʹ, quibus additis fit tota diversitas inter medium apparentem motum, in superiori medietate zodiaci, 4 graduum 46 minutorum. Sed procedendo per inferiorem medietatem zodiaci, in qua reperitur minima longitudo, medius motus est minor quam verus seu apparens tantum quanti sunt duo anguli CBE, CDE, qui, ut dictum est, sunt 4 graduum 46 minutorum. Siquidem anguli excentrici seu medii motus BCG, DCG sunt minores angulis veri motus BEG, DEG secundum quantitatem angulorum maximae diversitatis CBE, CDE. Hinc fit, quod quantum diversus seu verus motus minuit per superiorem medietatem a medio motu tantum augeat per inferiorem, productum quod nascitur de additione et diminutione in ambabus medietatibus fit 9 graduum 32 minutorum fere; tanta, inquam, est diversitas dierum naturalium per excentricitatem Solis causata.

Penes autem］ Quemadmodum inaequalitas dierum quae causatur per excentricitatem Solis, initianda est, in eo loco ubi medius motus diurnus adaequatur vero motui diurno, nempe in mediis longitudinibus, sic etiam causa inaequalitatis dierum propter rectarum ascensionum inaequalitatem proveniens initianda est ubi unus gradus aequinoctialis ascendit in recta sphaera cum uno gradu zodiaci, nempe a 16 gradu Tauri et 14° Leonis, ac a punctis, qui sunt his oppositi, ut est 16 gradus Scorpii, et 14 gradus Aquarii.

Nam si numeraveris a 16 gradu Tauri in zodiaco usque ad 14 gradus Leonis, invenies distantiam horum duorum punctorum 88 graduum, quibus respondent in aequatore 93 gradus, quos hac via elicias, scilicet accipias rectam ascensionem 16 gradus Tauri, quae est 43 graduum 31 minutorum proxime, quos subtrahas ab ascensione recta 14 gradus Leonis, hoc est a 136 gradibus 29 minutis, et relinquentur 92 gradus 58 minuta, qui excedunt 88 gradus per 5 gradus. Idem continget in signis seu punctis oppositis hoc modo, si numeraveris a 14 gradu Leonis usque ad 16° Scorpii, habebis de zodiaco 92 gradus et de ascensione recta Scorpii 223 gradus 31 minuta, a quibus sublatis 136 gradibus 29 minutis, residuabuntur 87 gradus fere, quos cum auferes a 92 gradibus erit id quod reliquum est 5 gradus, differentia scilicet dierum naturalium; additis his duobus productis, prodibunt 10 gradus quibus dies naturales ob hanc causam differunt, et sic de reliquis punctis deferuentibus huic negotio iudicandum est.

Hac de causa］ Facile est intellectu quare Ptolemaeus indicaverit commodius esse dies naturales numerari a meridiano quam ab horizonte, siquidem cum manifestum sit horizontes non esse fixos per omnes regiones, imo variari, oportuit, ne nasceretur tertia causa inaequalitatis dierum naturalium, ordine dies a quodam puncto seu circulo sphaerae qui, in quolibet loco, suppleret vices horizontis recti, ad quod nullus circulorum sphaerae commodior est quam meridianus, quia, si ab eo exorditur dies naturalis, permanet inaequalitas dierum quae provenit ex rectarum ascensione diversitate, per omnem regionem eadem.

Penes solarem quidem］ Priusquam ostendat modum convertendi dies inaequales ad dies aequales, operae precium esse arbitratus est docere quo loco principium additionis dierum inaequalium super aequales sit, et quantum sit differentia ex utrique causis collecta, quae in hunc modum elicitur: primum investigetur ea quae fit ratione solaris inaequalitatis, deinde altera, quae fit penes meridiani transitum: prima ita quaeritur, scilicet numera a medio Aquarii secundum ordinem signorum usque ad principium Scorpii, hoc est a puncto D in subiecta figura ad punctum B, et habebis in producto 255 gradus zodiaci, ad habendum quantitatem arcus excentrici EIF, vide quot graduum sit arcus zodiaci DA, id est a medio Aquarii usque ad maximam

longitudinem, 5 gradus 30 minuta Geminorum; si rite numeraveris nascentur tibi 110 gradus 30 minuta, quorum angulus aequationis EHG inventus est 2 graduum 16 minutorum proxime, quo facto, numera iterum a puncto A, qui est punctus maximae longitudinis, ad punctum B, principium scilicet Scorpionis; quod ascendet de numeratione erit 144 gradus 30 minuta, horum, inquam, graduum aequationis angulus FHG est 1 graduum 22 minutorum. Si haec duo producta in unum compones, prosilient 3 gradus 38 minuta, solaris scilicet inaequalitas qua deficit arcus zodiaci DAB ab arcu excentrici EIF; additis illis 255 gradibus, fiet medius motus arcus EIF 258 graduum 38 minutorum proxime. Nunc ad investigationem inaequalitatis quae contingit penes meridiani transitum, quae sic manifestabitur, scilicet: quaeratur recta ascensio 15 gradus Aquarii, quae est 317 graduum 31 minutorum, et recta ascensio principii Scorpionis, quam invenimus esse 207 graduum 50 minutorum, a qua si subtracta fuerit, adiecto integro circulo, ascensio Aquarii residuabuntur 250 gradus 19 minuta. Cum hoc productum subtraxerimus a 255 gradibus zodiaci, relinquentur 4 gradus 41 minuta pro inaequalitate contingente in meridiano, hae duae inaequalitates simul faciunt octo gradus et 19 minuta, differentiam scilicet ex utrisque causis collectam. Hactenus.

Ut ergo］ In aequatione dierum hoc maxime venit observandum, nempe quod sit alia ratio aequandi tempus quod incipit a quadam radice praescripta, item alia ubi tempus datum non pendet a certa radice, sicut perspicue videbitur in exemplis quae hic adducemus. Cum tempus propositum non erit adligatum certae radici, veluti cum datur tempus interiacens duarum eclypsium, aut aliud consimile, et vis illud aequare, tunc quaere verum et medium motum dati temporis, quibus inventis, immitte verum motum in tabulam rectarum ascensionum, et extrahe inde rectam ascensionem, quae ad hanc operationem incipit ab Arietis principio, hanc rectam ascensionem subtrahas a medio motu si fuerit minor eo, aut subtrahas medium motum ab hac recta ascensione nuper inventa tum, inquam, cum medius totus fuerit minor; differentia inde proveniens erit dati temporis aequatio, quam per quatuor tempora aequinoctialia redigas in minuta, ut solet, multiplicando hanc aequationem adde diebus inaequalibus si ascensio recta fuerit maior medio motu, sin minus eam subtrahas, et exibunt dies aequati.

Porro, si libuerit dies aequatos reducere ad dies inaequales, similiter habeas modo dicto medium et verum motum, et motui vero accipe rectam ascensionem; sicut meminimus, eius differentia ad medium motum erit aequatio, cuius tempus addito aequali motui si medius motus superaverit sua quantitate ascensionem, vel minue si e contra, et prodibunt dies inaequales: ut res fit clarior, habeas eiusmodi exemplum. Proponuntur mihi 354 dies, et horae aequinoctiales simpliciter 2 ac 30 minuta, hoc tempus volo reducere ad horas aequales, quod factum est hoc modo. Scilicet, desumpsi e tabula medii motus huius temporis motum aequalem, qui fuit 349 gradus 2 minuta, quo aequato iuxta praecepta praemissa, provenerunt in producto pro vero motu 349 gradus et 15 minuta, cum quibus intravi in tabulam rectae ascensionis et reperi ascensionem rectam ab Ariete 350 graduum ac 9 minutorum fere, et cum hoc productum fit maius medio motu, subduxi ab eo medium motum, quod reliquum fuit erat 1 gradus et 7 minuta, quibus ductis in quatuor prodierit 4 minuta 28 secundae pro aequatione temporis, sed cum tempora aequinoctialia superent medium motum, addidi ea tempori seu diebus inaequalibus, et prodiit tempus exactum 354 dierum 2 horarum et 34 minutorum, et sic de reliquis. In secundo modo aliter proceditur, nempe sic: cum tempus inaequale proponitur quod sit reducendum ad tempus aequale, tunc quaeratur ad utrumque terminum, scilicet ad principium et finem propositi temporis, medius et verus motus Solis, sicut ipsemet author admonet, quod breviter ita intelligendum est: habeatur locus Solis verus et medius in zodiaco ad principium radicis, sicut in hoc capite Sol in primo anno Nabonassari secundum Aegyptios thot, in prima meridie, aequaliter obtinebat 0 gradus 45 minuta Piscium, inaequaliter vero 3 gradus 8 minuta eiusdem signi.

Cum quaevis res melius percipiatur exemplis propositis quam prolixa verborum serie, proponatur tale exemplum: en volumus hoc tempus inaequale, scilicet 620 annos, 219 dies et horas aequales simpliciter 18 et 20 minuta a primo Nabonassari anno secundum Aegyptios thot in prima meridie, ad tempus seu dies aequales convertere; primum quaesivimus, secundum praecepta noni capitis, medium motum huius temporis oblati, quem invenimus 65 graduum 52 minutorum, integris circulis reiectis, cui adiecti sunt 265 gradus 15 minuta et nati sunt 331 gradus 7 minuta, quibus aequatis, prodierunt pro aequali motu 332 gradus 7 minuta, hos enumeravimus secundum ordinem signorum a 5 gradibus 30 minutis Geminorum, et pervenimus secundum medium motum ad 6 gradus 37 minuta Tauri, et secundum verum motum ad 7 gradus 37 minuta eiusdem signi; quo facto, numeravimus a 0 gradibus 45 minutis Piscium, ubi Sol medio motu in meridie erat primo anno Nabonassari secundum Aegyptios thot, usque ad 6 gradus 37 minuta Tauri, et ascenderunt 65 gradus 56 minuta. Sed verum motum radicis numeravimus a 3 gradibus 8 minutis Piscium, usque ad 7 gradus 37 minuta Tauri, quod ex hoc productum est fuerunt 4 gradus 29ʹ, cum quibus a 3 gradibus 8 minutis Piscium ad 7 gradus 37 minuta Tauri ascenderunt, in rectarum ascensionum tabula, 60 gradus 12 minuta, quibus subductis a medio motu, scilicet 65 gradibus 56 minutis, relicti sunt 5 gradus 44 minuta, postquam multiplicavimus eos per 4, inventa est aequatio 22 minutorum fere, quae, iuxta rationem constitutionis radicis, subducta sunt a tempore proposito, et relictum est tempus aequale 620 annorum, 219 dierum, 17 horarum et 58 minutorum.

Hactenus de hoc capite.

Erasmi Osvaldi Schreckhenfuchsii, in Almagesti priores tres libros annotationum finis.

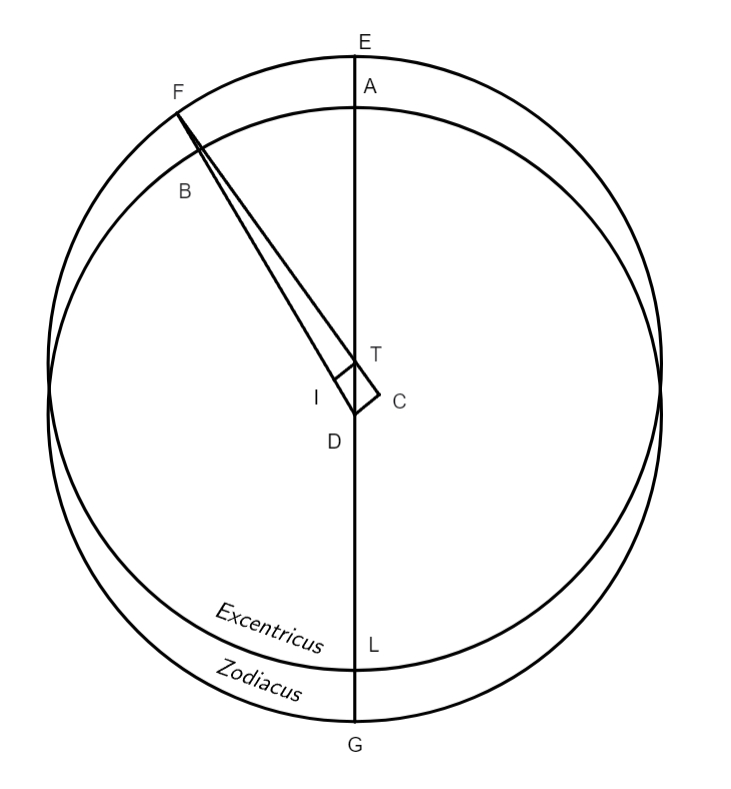
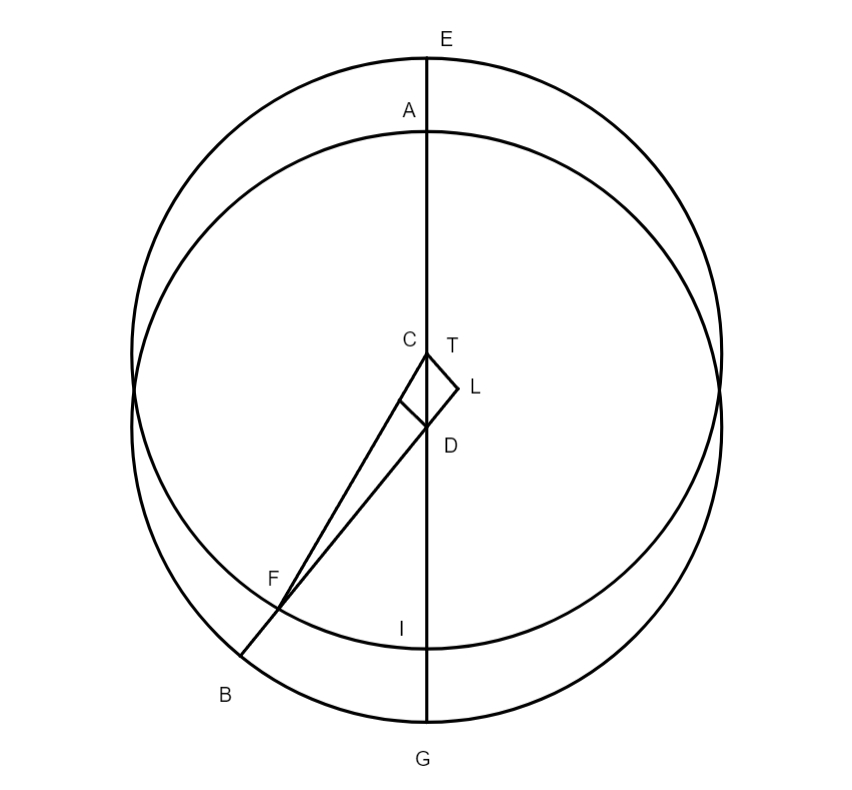
Haec figura pro ea ponatur quae habetur folio 64 columna prima, libro 3 capite 3.

In ultimum caput libri quinti annotatio

Empedocles duplam esse a terra ad Lunam distantiam asseruit.

Quidam vero mathematici, diligentius perscrutantes, decies octies. Eratosthenes Solem distare a terra 308 stadiorum myriadas, 3,080,000 stadiorum, 385,000 miliariorum. Lunam vero a terra 78 myriadas stadiorum, 780,000 stadiorum, 97,500 miliariorum.

Haec figura debet ad primum caput libri quinti poni, pro ea quae habetur folio 101.