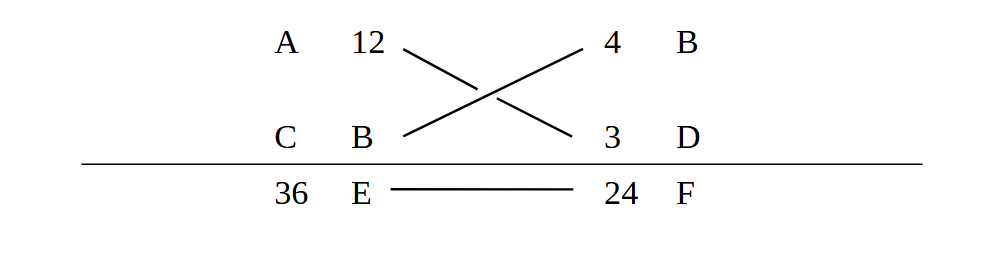Erasmi Osvaldi Schrekhenfuchsii ad lectorem praefatio. Qua Claudii Ptolemaei in Almagesto difficiliora explicantur

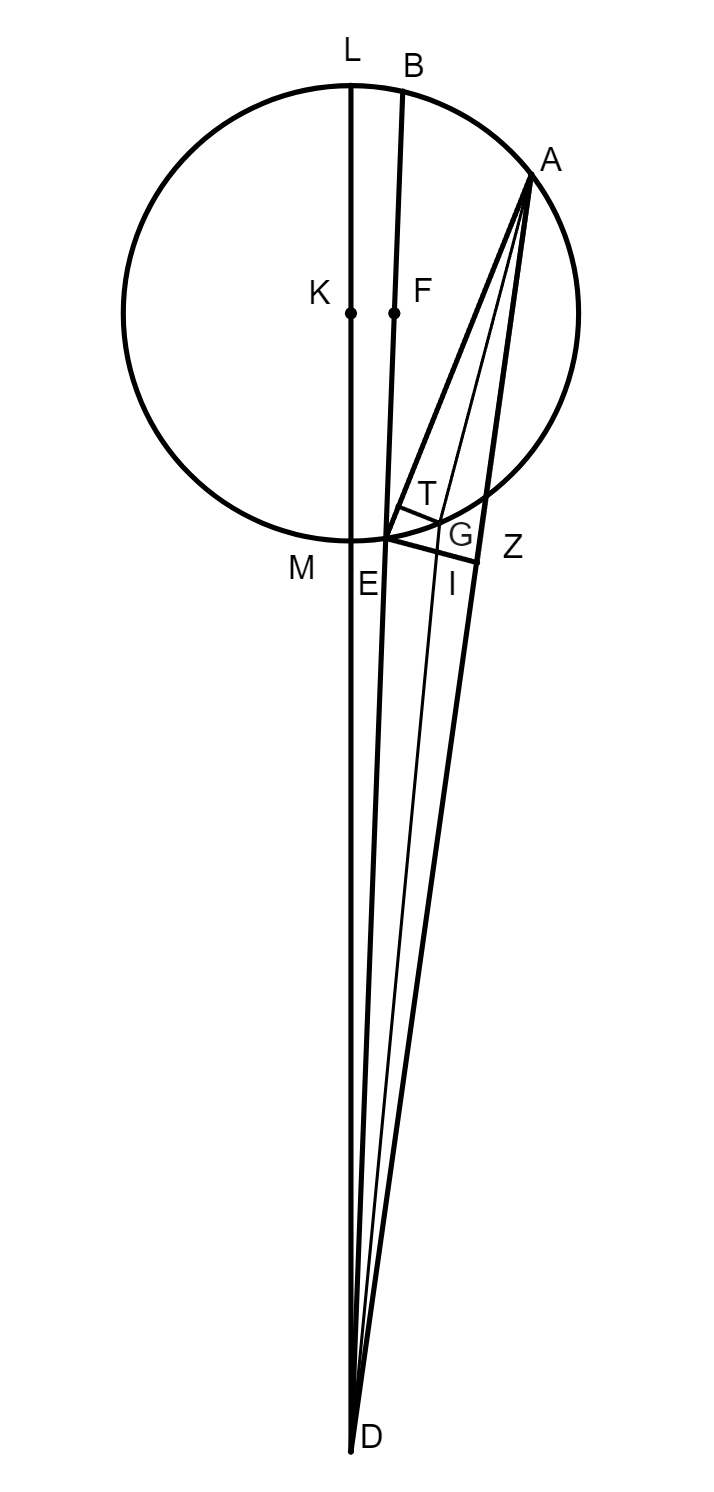
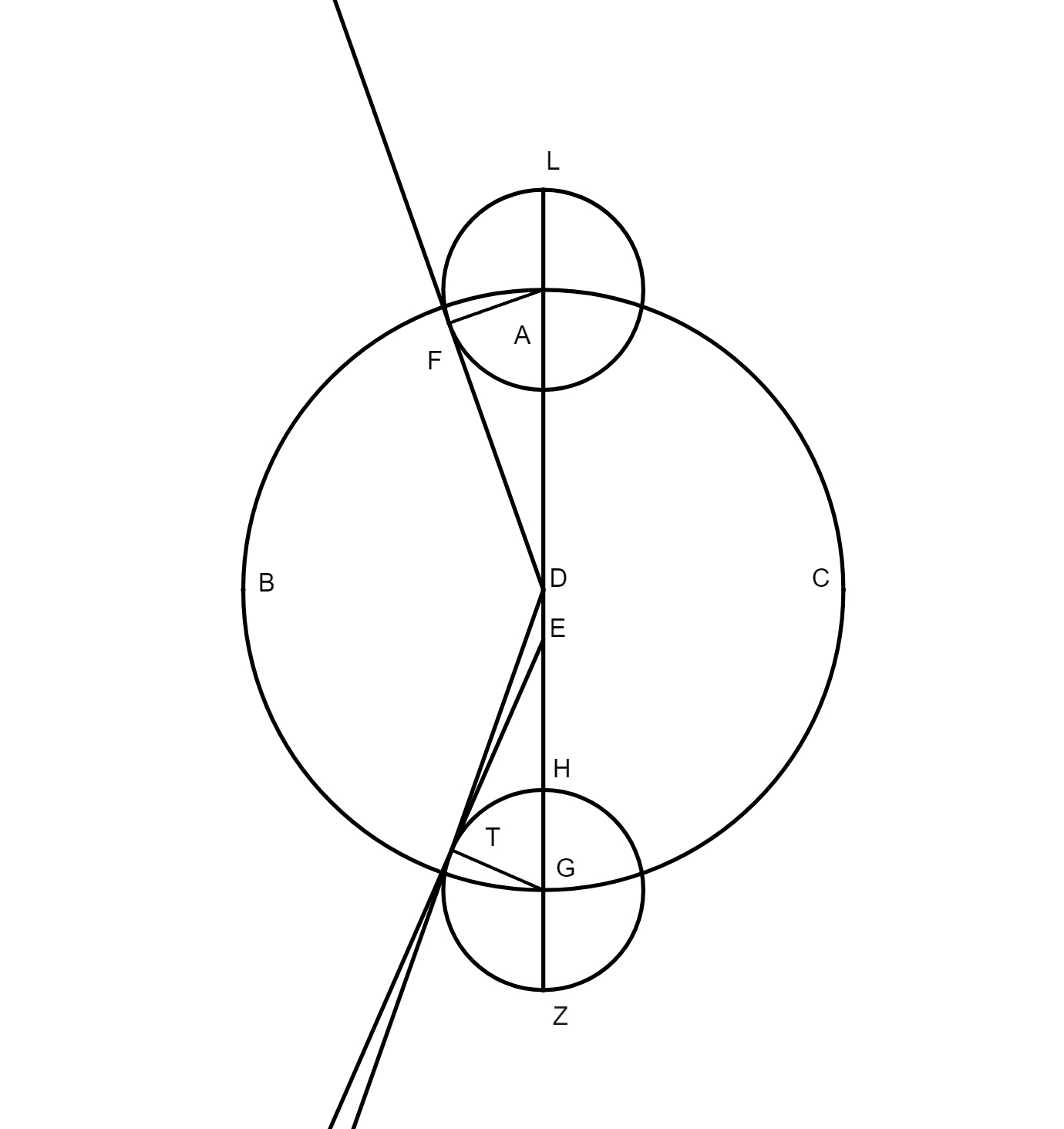
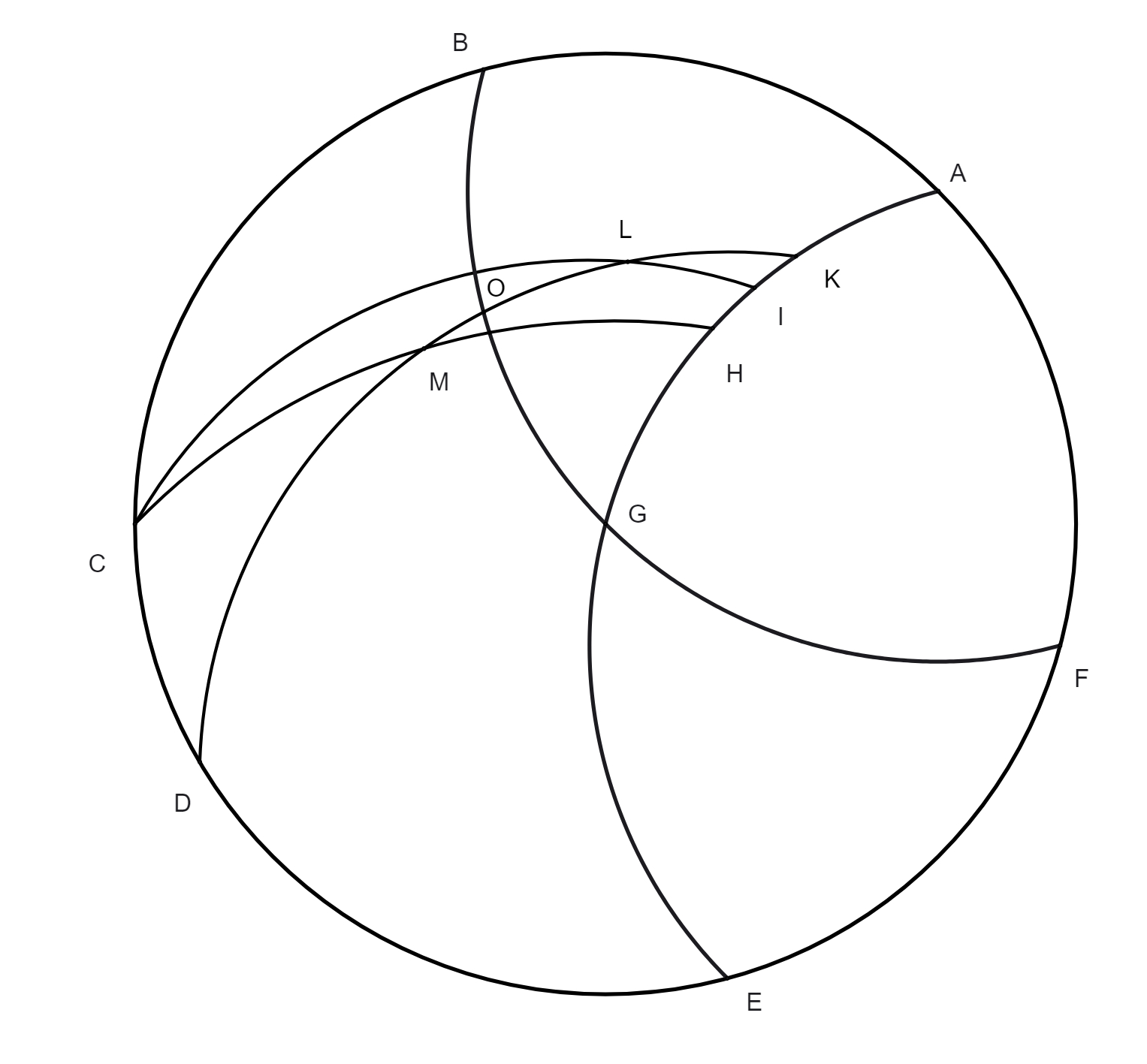
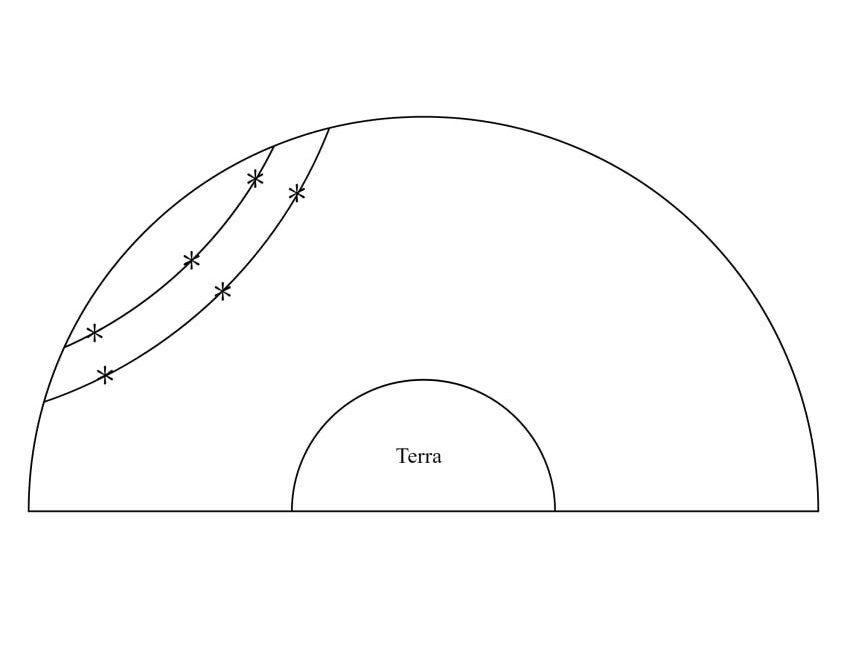
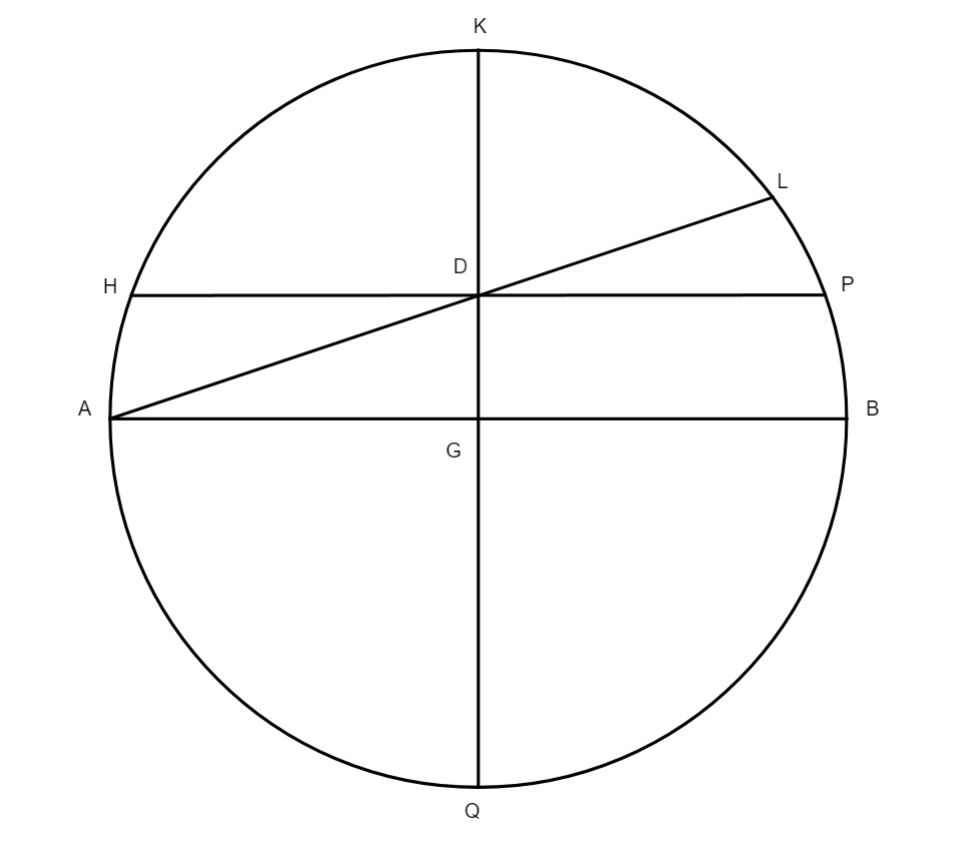
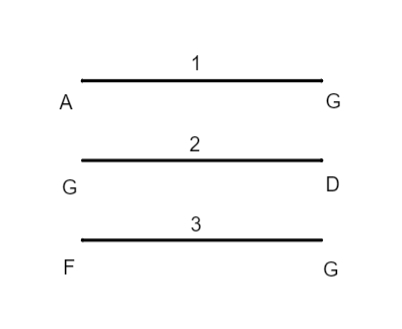
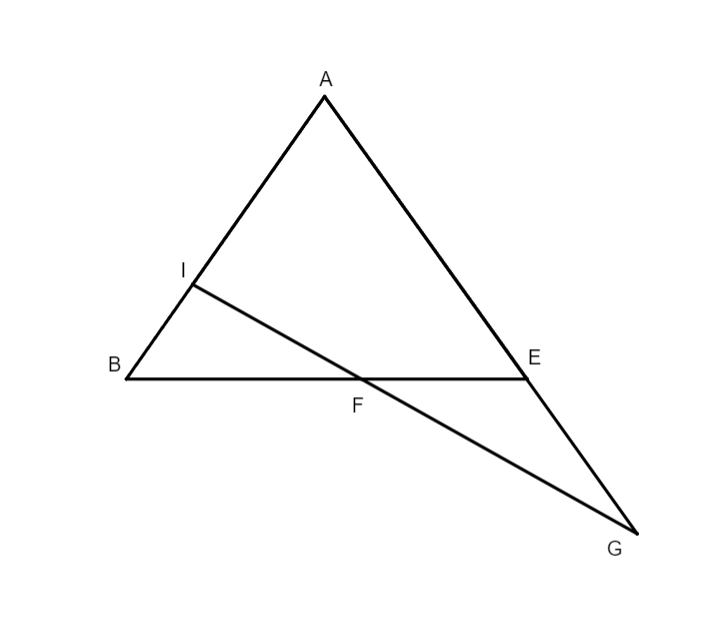
In primis duobus libris, optime lector, breviusculis annotationibus, quomodo tabulae chordarum, tabulae obliquationis Solis et rectarum ascensionum, ac tabulae obliquarum ascensionum, nec non tabulae angulorum tum orientalium tum occidentalium sint conficiendae et hoc ad omnia climata, licet Ptolemaeus haec omnia copiose tradiderit, tamen cum regula sex quantitatum, aut doctrina triangularum sphaeralium una cum subtractione proportionum, vel secundum synthesim vel secundum dieresim sit paulo difficilior quam ut possit a quovis, etiam in libris sphaericis bene versato, intelligi, operae precium nos facturos arbitrati sumus, si rem per exempla illustriorem redderemus. Non dubitamus quin candidatus huius pulcherrimae artis facile assequetur rationem componendi tabulas obliquarum ascensionum vel ad singulas polorum elevationes, quid tabulas obliquarum ascensionum? Imo etiam tabulas ortivarum et occiduarum latitudinum, quae maximae requiruntur ad cognitionem inclinationis eclypsium lunarium, et ad multa alia de quibus non est locus dicendi, et tabulas omnis generis angulorum ad singula climata, quae non solum deserviunt negotio deliquiorum solarium, imo multis aliis speculationibus iucundissimis, de quibus suo loco abunde satis dicemus. In tertio libro adiecimus quoque annotationes et exempla, quae ita tractavimus quod speramus, studiosum suo marte, si habuerit theoricarum solidam cognitionem, intellecturum quo modo tabulae angulorum inaequalitatis sint componendae, quae, ut videre est, fluunt ex cognitione triangulorum planorum, et quo modo ex dato motu aequali Solis inaequalis eliciatur, et contra, dato motu inaequali, aut angulo inaequalitatis motus aequalis investigandus. Maluimus rem per exempla illustrare quam prolixis demonstrationibus geometricis, maxime cum Ptolemaeus ipsemet adduxerit demonstrationes, ubi res postulaverat. Qui in hoc tertio libro et in reliquis consequentibus hoc ordine processit, scilicet primum observavit, suasque observationes contulit cum priscorum mathematicorum observationibus, quo facto, composuit mediorum motuum planetarum tabulas, deinde demonstravit quibus circulorum suppositionibus planetarum motus salvari possunt. His habitis, aggressus est inventionem excentricitatis, sine qua fieri non potest ut sciantur anguli inaequalitatis, inventa scilicet excentricitate contulit se ad investigationem angolorum inaequalitatis et eorundem tabularum compositionem. Sed hoc sciendum esse duximus, nempe quod in Sole tantum sufficiat ad angulorum dictorum inventionem excentricitatis cognitio, in reliquis vero opus habetur etiam quantitate semidiametri epicycli. Quibus autem modis excentricitatem Solis, et punctum longitudinis longioris invenerit hoc satis explicatum est in annotationibus tertii libri. In Luna et in tribus superioribus, non pendet eiusmodi excentricitatis et quantitatis semidiametri epicycli inventio a tempore ingressus Solis in primum punctum aequinoctii vernalis usque ad solstitium aestivale, et a tempore solstitii aestivalis usque ad aequinoctium autumnale, quemadmodum in Sole, imo ab aliis rebus, hoc est ab eclypsibus lunaribus et oppositionibus. Nam cum Ptolemaeus volebat venari semidiametrum epicycli Lunae, coepit tres eclypses Lunae, per quas operatio certior est, quam per instrumenta, vel respectu stellarum fixarum aut eclypses solares, easque examinavit ut mox videbitur, et quod deprehendit in Luna per eclypses, hoc in tribus superioribus, cum nunquam depriventur lumine suo per interpositionem terrae, coactus est per tres oppositiones deprehendere. In Venere vero et Mercurio, qui non tantum recedunt a Sole ut fierent ei oppositi, excentricitatis et loca maximarum longitudinum, ac quantitatem semidiametrorum epicyclorum etiam alia via investigavit, nempe per observationes maximarum eorum recessionum a Sole tum matutinarum, tum vespertinarum. Verum cum inventio semidiametri epicycli Lunae non parum lucis addat inventioni excentricitatis trium superiorum, nam utuntur fere iisdem propositionibus Euclidis, ut videbitur, visum est calculo paulo illustrius reddere examen investigationis semidiametri epicycli Lunae per tres antiquissimas eclypses lunares. Fiat igitur figurae descriptio in hunc, qui sequitur modum, in qua D sit centrum zodiaci

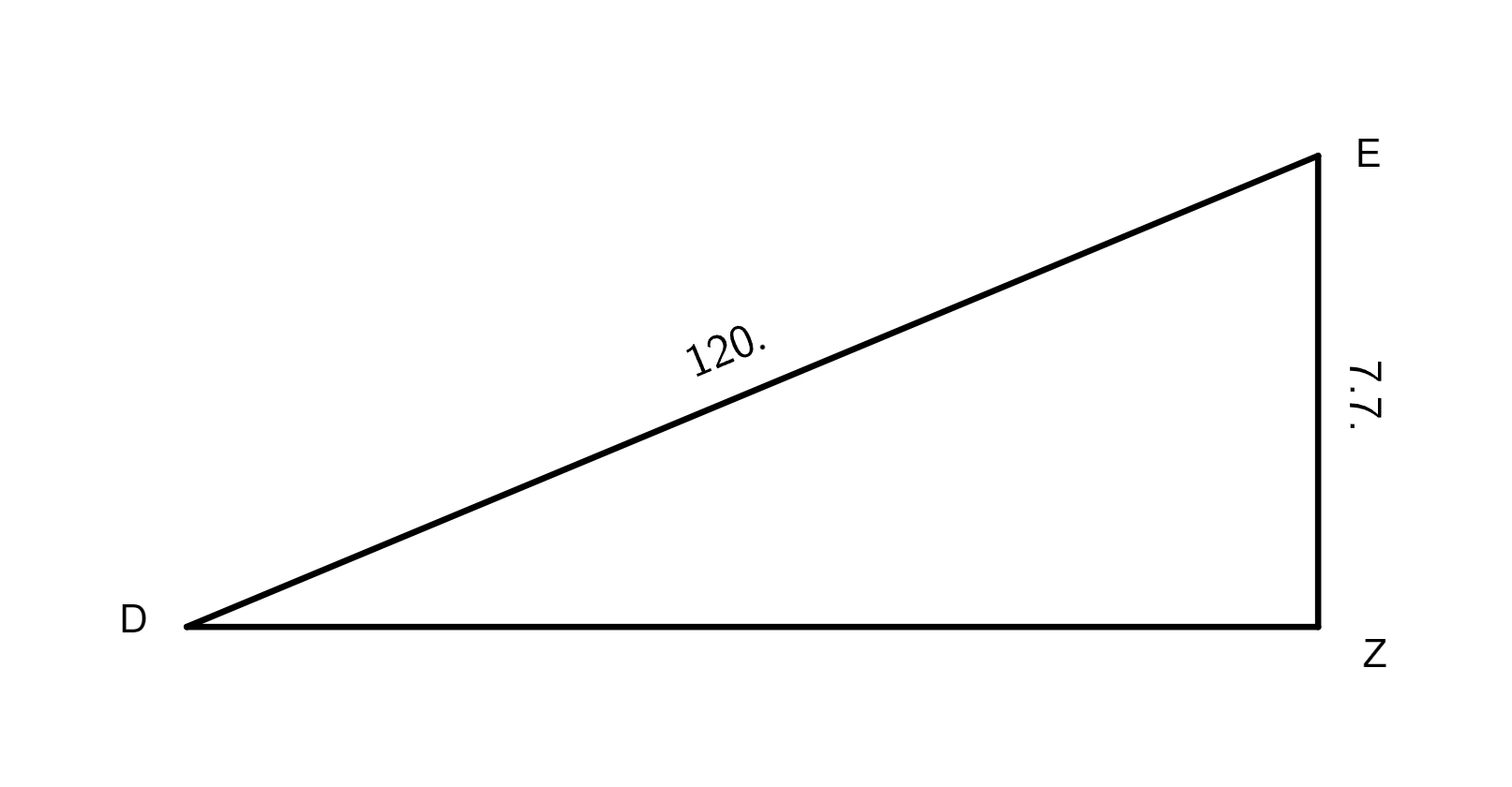
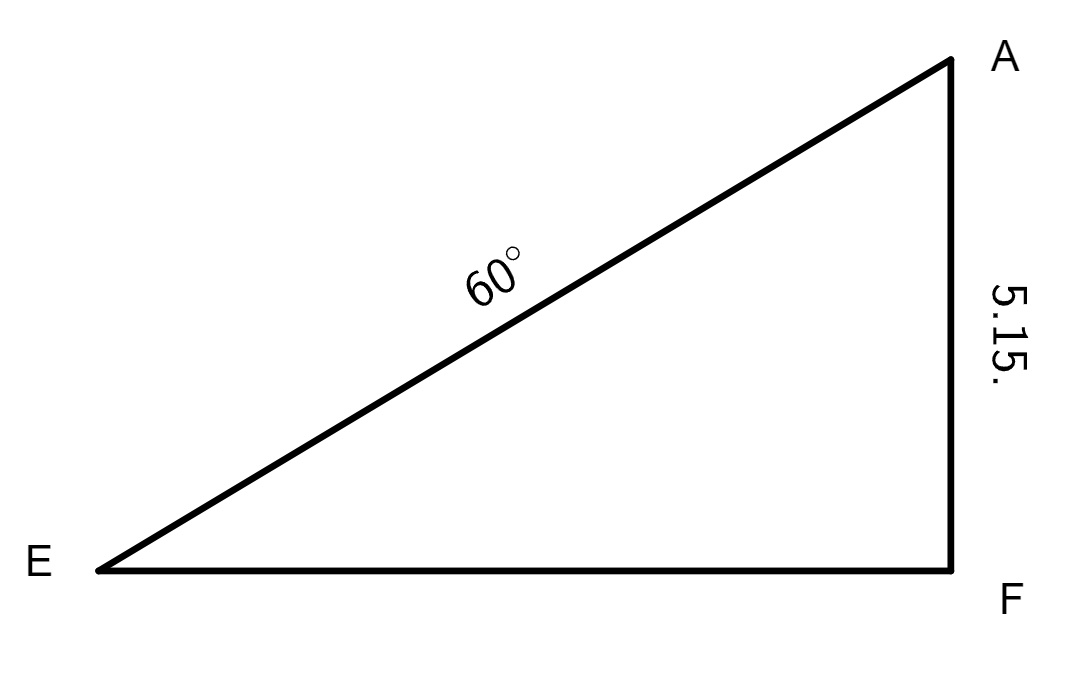
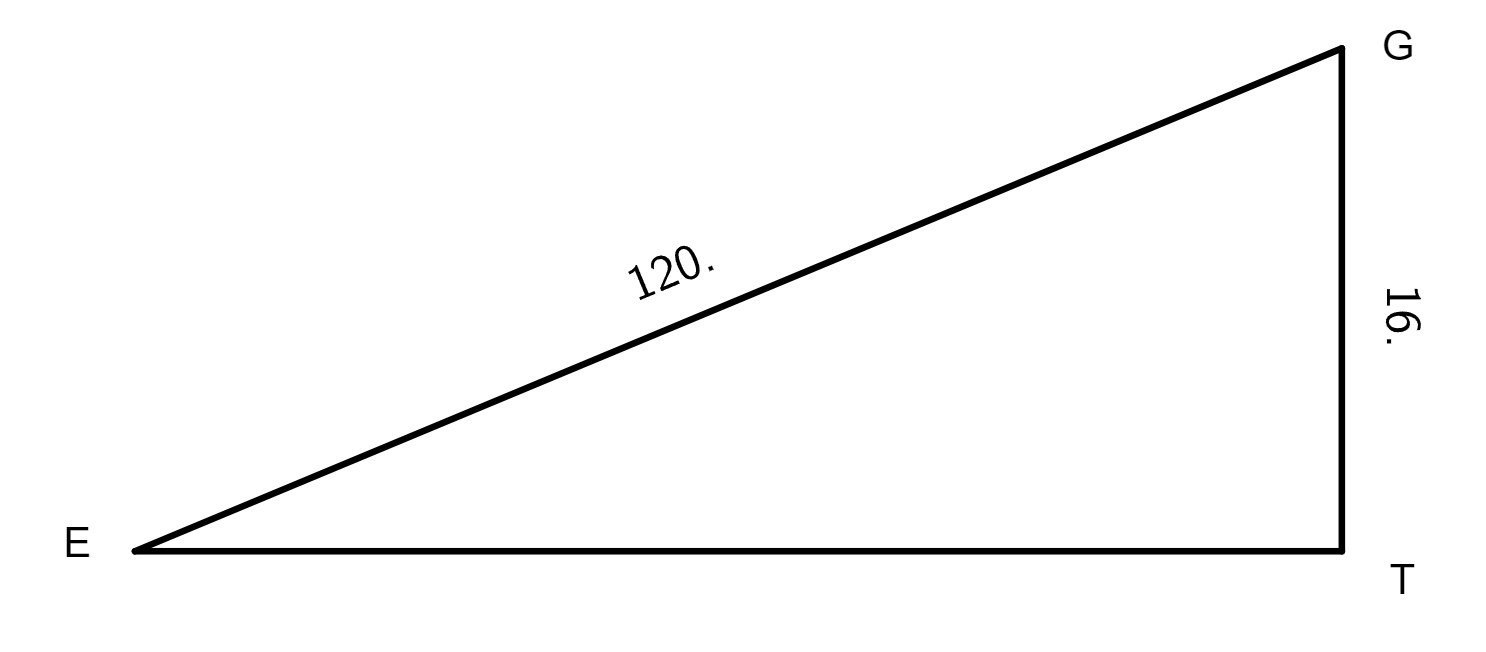
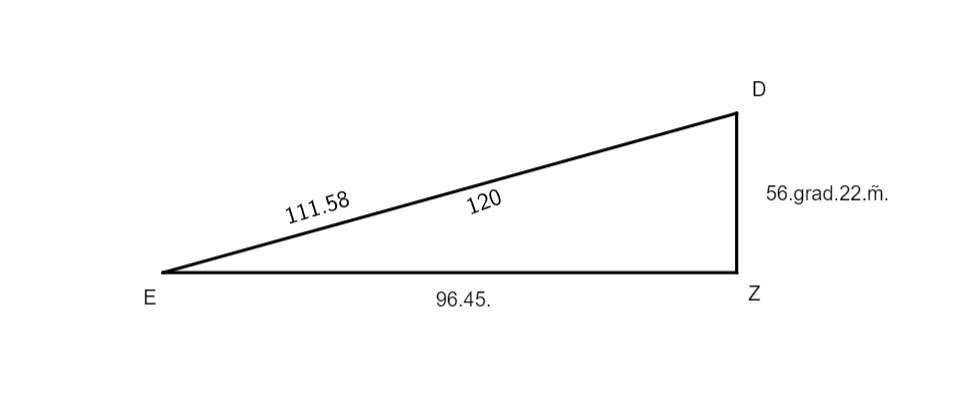
seu mundi, LAGM epicyclus qui describitur circa centrum eius K, linea DKL transeat per maximam et minimam longitudinem epicycli, punctus L sit maxima longitudo, M minima, A sit locus Lunae tempore medio primae eclypsis, per quae transeat DZA linea, B sit locus in quo erat linea tempore medio secundae eclypsis, per hunc excurrat e centro mundi D linea DEB, punctus autem G sit locus tertiae eclypsis in tempore medio. Ex puncto E trahatur linea EA ad quam cadat perpendicularis GT, ad lineas DZA et AG cadant perpendiculares EZ et EI. Nunc propositum erit invenire proportionem lineae LK ad lineam KD, qua habita facile postea noscetur excentricitas Lunae et punctus ad quem inclinat epicyclus, hoc est punctus longitudinis mediae epicycli, siquidem his habitis non difficile erit, modo ea quae in tertio libro exempla tradita sunt de triangulis planis recte intellecta sint, elicere angulos utriusque inaequalitatis Lunae, sicut videbitur infra. Et priusquam accedamus ad operationem, visum est paucis praefari qua ratione ea requiri debent quibus opus est ad huiusmodi rei tractationem. Primum oportet scire medium tempus eclypsis praesuppositae ad cuius temporis horam inveniatur medius motus Solis, quo habito, eliciatur verus motus eius. Exempli gratia, si volueris scire verum motum Solis primae antiquissimarum eclypsium, et sic de reliquis, habeas medium motum Solis, quem scire impossibile est nisi prius habeatur tempus, quod ad medium huius primae eclypsis fuit 26 annorum, 28 dierum, 8 horarum, ac 40 minutorum. Nam certum est ex consequentibus quod initium regni Mardocempadi fuerit anno vicesimo sexto a morte Nabonassari, et si 3 horas, 20 minuta (quibus medium tempus eclypsis praecedit mediam noctem vigesimae nonae diei thot, primi mensis Aegyptiorum) subtraxeris a 12 horis, residuabuntur 8 horae et 40 minuta, quaesito igitur medio motu Solis ad hoc tempus propositum eoque aequato iuxta doctrinam supra libro tertio de hac re traditam, reperietur Sol esse in 24 gradibus 30 minutis Piscium. Non secus agendum est in reliquis duabus eclypsibus, in quibus tempus facile est investigatu hoc prius delibato. Et cum constiterit tibi de veris motibus Solis, consequens est ut quaeras quantum Sol et Luna, reiectis integris circulis, a medio tempore primae eclypsis usque ad medium secundae, et similiter a tempore medio secundae usque ad medium tempus tertiae eclypsis, motu vero moti sint. Nam cum numeraveris a 24 gradibus 30 minutis Piscium (ubi fuit Sol secundum verum motum in medio tempore primae eclypsis), iuxta ordinem signorum, usque ad 13 gradus 45 minuta eorundem Piscium, in quo loco inventus est Sol vero motu in tempore medio secundae eclypsis, invenies eos fuisse motos 349 graduum 15 minutorum, ad eundem modum cum numeraveris a 13 gradibus 45 minutis Piscium secundae antiquissimarum eclypsium ab 3 gradibus 15 minutis Virginis tertiae eclypsis, et hoc secundum ordinem signorum, exibunt tibi in producto 169 gradus 30 minuta, motus scilicet verus quo Sol et Luna interea temporis moti sunt. His habitis, deinde quaerenda sunt tempora interiacentia, hoc est intervallum quod est inter primam et secundam, et similiter inter secunda et tertia eclypsim, quo habito, quaerendi sunt medii motus Lunae tam secundum longitudinem quam secundum inaequalitatem, prius aequatis illis temporibus per documentum in fine tertii libri a nobis traditum. Inventio horum temporum interiacentium hoc modo tibi absolvetur. Scilicet numera a medio tempore primae eclypsis usque ad medium tempus secundae eclypsis, et similiter a medio tempore secundae ad tempus medium tertiae eclypsis, et productum tum annorum, tum dierum et horarum ac partium horarum seorsim nota quod erit tempus tuum quaesitum, ut exempli gratia. Si cupis scire tempus interiacens inter primam et secundam antiquissimarum eclypsium, quarum prima fuit secundum medium tempus apud Babylonios primo anno Mardocempadi, vigesima nona die thot, mensis primi Aegyptorum, quam sequebatur trigesima, hora 2, 39 minuta ante mediam noctem; et cum dies inchoantur a meridie constat de die trigesima nona transiisse 9 horas 30 minuta, et adhuc restare ad meridiem immediate consequentem 14 horas et 30 minuta, quae extra scribas una cum uno die qui reliquus est de mense thot, nam quilibet mensis Aegyptorum constat triginta diebus, numeres itaque ab hoc tempore usque dum pervenias ad medium tempus secundae eclypsis, quod scribitur fuisse 18 die eiusdem mensis thot in ipsa media nocte, secundo anno Mardocempadi, sed ea conditione ut 5 dies, quas epactas appellant, adnumerentur ultimo mensi, scilicet mesori, et producentur tibi 352 dies, 12 horae, quae lapsae sunt de 18 die mensis thot, quibus additis producto seorsim scripto 1 die 14 horae provenient 354 dies, 2 horae 30 minuta, tempus scilicet interiacens inter medium primae et secundae eclypsis, et sic agas etiam in investigando tempus interiacens secundae et tertiae eclypsis, et nascentur tibi pro interiacenti tempore non aequato 176 dies et 20 horae 30 minuta, quibus temporibus aequatis, illorumque illorumque] illotumque B mediis motibus e tabulis mediorum motuum extractis, tum ad longitudinem tum ad inaequalitatem, habebis pro tempore interiacente primae et secundae eclypsis 306 gradus 25 minuta, scilicet inaequalitatis, et 345 gradus 51 minuta longitudinis. Et pro tempore quod est inter secundam et tertia eclypsim, longitudinis 170 gradus 7 minuta, inaequalitatis vero 150 gradus et 26 minuta. Et cum subtraxeris medium motum longitudinis temporis interiacentis primae et secundae eclypsis, scilicet 345 gradus 51 minuta a 349 gradibus 15 minutis quibus Sol et Luna a medio tempore primae eclypsis usque ad medium secundae moti sunt, residuabuntur tibi 3 gradus 24 minuta, quos 306 gradus 25 minuta inaequalitatis in prima distantia addiderunt medio motui Lunae, eodem modo, si subduxeris a 170 gradibus 7 minutis motus medii longitudinis temporis quod reperitur inter secundam et tertiam eclypsim, 169 gradus 30 minuta quibus, ut dictum est, Sol et Luna a medio tempore secundae eclypsis usque ad medium tertiae eclypsis moti sunt, relinquentur 0 gradus 37 minuta quos subtrahunt. Porro ad sciendum an arcus AB et arcus BG sint adiectivi aut ablativi sic perreximus, scilicet subtraximus 306 gradus 25 minuta a toto circulo, et reliqui fuerunt 53 gradus 35 minuta pro arcu AB, quibus sublatis a 150 gradibus 26 minutis remansit arcus AG 96 graduum 51 minutorum. Postquam habuimus quantitatem horum duorum arcuum, iterum subtraximus 306 gradus 25 minuta a 345 gradibus 51 minutis, quod reliquum fuit fuerunt 39 gradus 26 minuta, his numeratis a 24 gradibus 40 minutis Virginis, ubi fuit Luna in medio tempore F primae eclypsis, pervenimus ad 3 gradus 56 minuta Scorpii. Deinde numeravimus a 13 gradibus 45 minutis Virginis, ubi fuit Luna tempore medio secundae eclypsis, usque ad finem 3 graduum 56 minutorum, habuimus in zodiaco 50 gradus 11 minuta, qui subtrahunt 3 gradibus 24 minutis a medio motu, et sic est arcus AB subtractivus. Eodem modo incessimus pro cognitione arcus AG, scilicet subtracti sunt nobis 150 gradus 26 minuta a 170 gradibus 7 minutis, et reliqui fuerunt 19 gradus 41 minuta, quos numeravimus a 13 gradibus 45 minutis Virginis, et pervenimus ad 3 gradus 26 minuta Librae, a quo loco reperiuntur usque 3 gradus 15ʹ Piscium, ubi erat Luna medio tempore tertiae eclypsis, 149 gradus 49 minuta in zodiaco, a quibus postquam subtraximus 50 gradus 11 minuta, prioris distantiae residuati sunt nobis 99 gradus 38 minuta qui addunt medio motui F, scilicet 96 gradus 51 minuta, quantitati arcui AG 2 graduum 47 minutorum, hinc apparet arcum AG esse adiectivum. Nunc redeatur ad operationem institutam, ex iam dictis angulus zodiaci ZDE notus est, qui inventus est 3 graduum 24 minutorum, ideo nota est

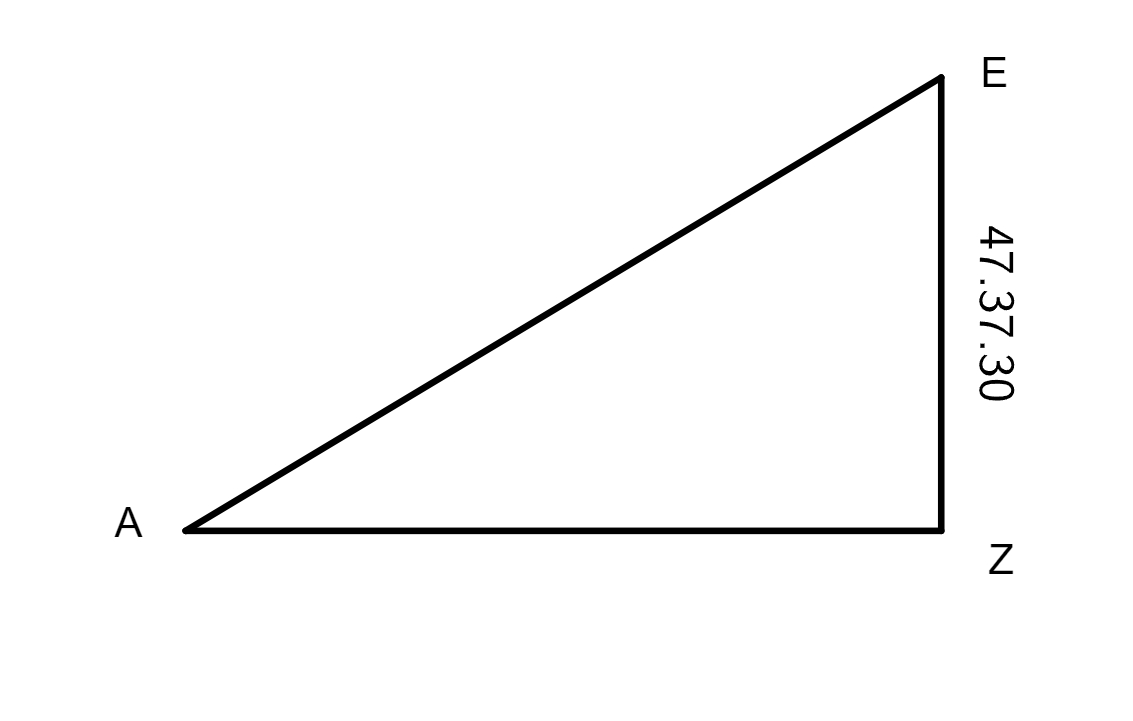
proportio DE ad EZ, et angulus GEA epicycli notus est, qui est 53 graduum 35 minutorum. Erat autem angulus zodiaci EDZ 3 graduum 24 minutorum, in quo duplato fient 6 gradus 48 minuta, et si hoc productum ablatum fuerit a 53 gradibus 35 minutis relinquentur 46 gradus 47 minuta, angulus intrinsecus EAD, ideo proportio linea AE ad EZ erit nota, chordae EZ et EZ sunt 7 graduum 7 minutorum et 47 graduum 38 minutorum 30 secundarum. His habitis, intentum est nostrum

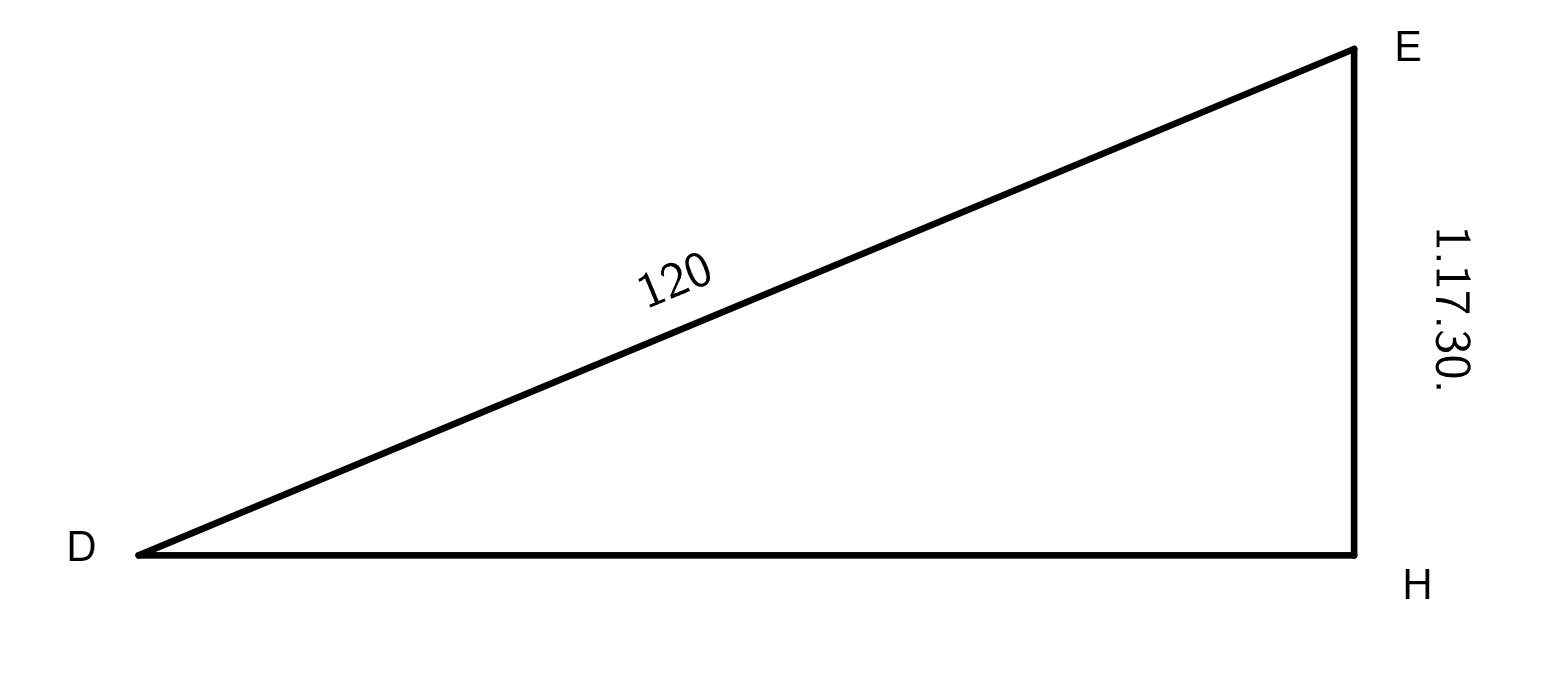
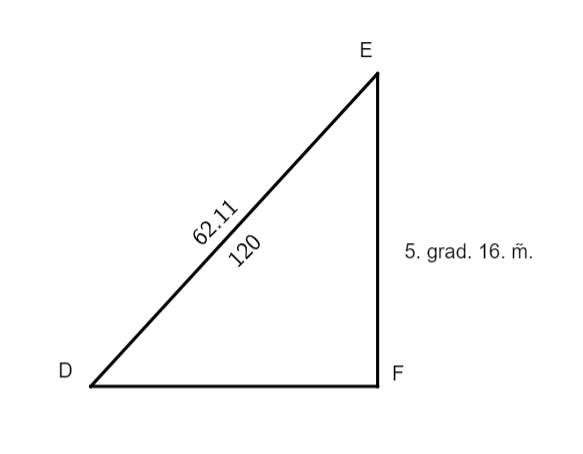
invenire proportionem lineae ED ad lineam AE, quod absolvetur per quartam sexti, scilicet quae est proportio EZ ad ED, ea est proportio EZ ad EA, hoc est, quae est proportio 47 gradus 38 minuta 30 secundae lineae EZ ad 120 gradus lineae ED, ea erit proportio 7 gradus 7 minuta lineae EZ ad 17 gradus 55 minuta 32 secundas lineae EA, quod prodiit ex multiplicatione 7 gradus 7 minuta in 120 gradibus et divisione per 47 gradus 38 minuta et 30 secundas. Ad haec, quia angulus GDE zodiaci inventus est 0 graduum 37 minutorum, erit proportio DE ad EH nota. Porro cum arcus epicycli epicycli] epycycli B BAG sit 150 graduum 25 minutorum, erit

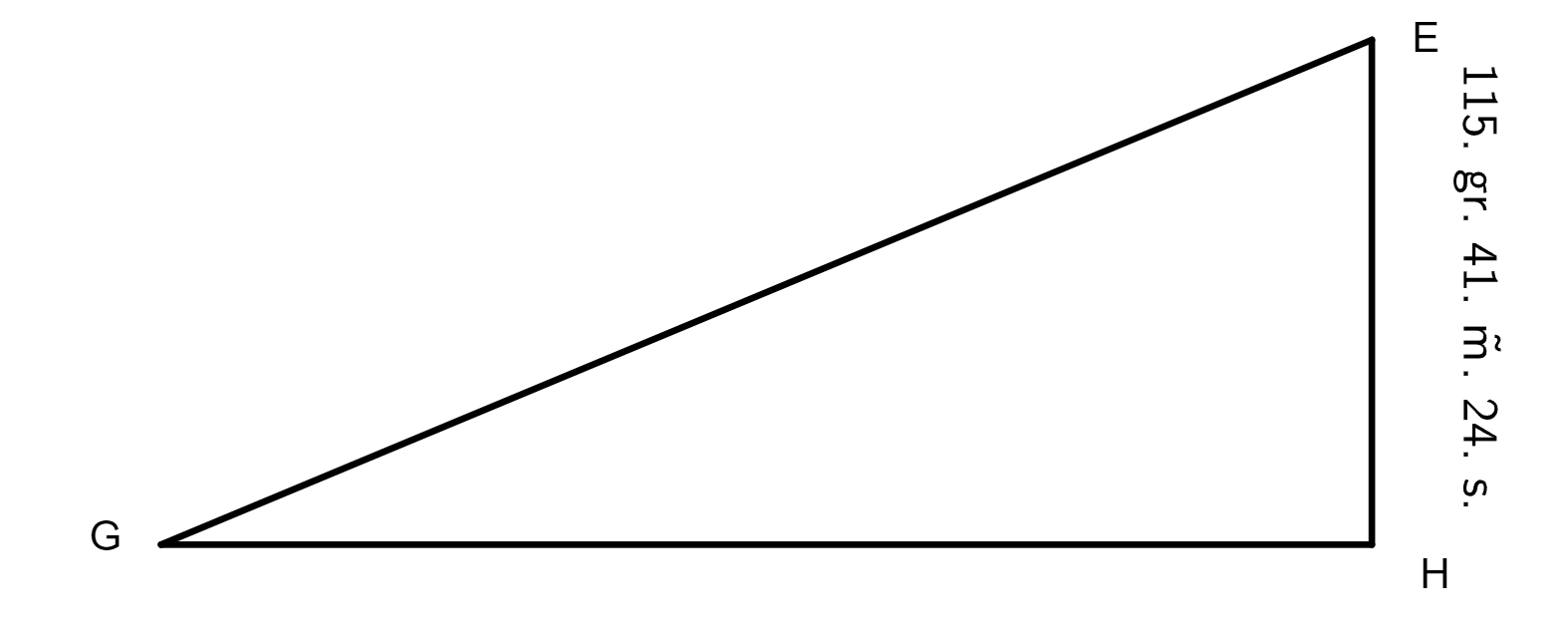
etiam angulus BEG cum sit in circumferentia epicycli talium 150° 26ʹ qualium duo recti sunt, nunc duplatis 0° 37 minutis, angulo scilicet DE, prodibunt 1 gradus 14 minuta, quibus subtractis ab angulo BEG, scilicet 150 gradibus 26 minutis, residuabuntur 149 gradus 12 minuta pro angulo EGD. Hinc nota est proportio lineae HE ad EG, ex tabula chordarum eliciuntur lineae EH et EH, 1 gradus 17 minuta 30 secundae et 115 gradus 41 minuta 24 secundae, his habitis facile est per quartam sexti et

regulam proportionum invenire lineam EG. Nam cum ordinabuntur numeri ad hunc qui sequitur modum, scilicet 115° 41ʹ 24ʹʹ | 120° | 1° 17ʹ 30ʹʹ |, et multiplicabitur tertius in secundum, et productum dividetur per primum numerum, prosilient 1 gradus 20 minuta 23 secundae pro linea GE. Cum vero angulus AEG sit notus propter arcum AG notum, qui est 96 graduum 51 minutorum, nota fiet proportio lineae EG ad utramque GT et TE, et hoc per doctrinam triangulorum planorum, ubi docetur si alter duorum angulorum acutorum fuerit notus cum uno eius latere, quod reliqui anguli cum reliquis lateribus metientur.

In hoc triangulo GET, latus EG notum est ex praemissis, quod est 1 gradus 20 minutorum 23 secundarum, et similiter angulus GET, qui est 96 graduum 51 minutorum, quem si subtraxeris a duobus rectis, relinquentur pro angulo TGE 83 gradus 9 minuta. Chordae arcuum horum angulorum sunt 89 gradus 46 minuta 14 secundas et 79 gradus 37 minuta 55 secundas. Nunc ordinatis his numeris in regulam ut sequitur:

et multiplicato tertio in quemlibet secundorum, ac productis divisis per primum, prodibunt pro latere TG 1° 0ʹ 8ʹʹ et pro latere ET 0° 53ʹ 21ʹʹ. Ad habendum lineam AG primae figurae sic perreximus, scilicet subtraximus lineam ET, hoc est 0° 53ʹ 21ʹʹ, a linea AE, quae est inventa 17 gradus 55 minuta 32 secundae, et quod relictum est fuerunt 17 gradus, 2 minuta 11 secundae, linea scilicet TA, quo facto multiplicata est nobis linea AT in se, et similiter linea TG, et producta sunt addita invicem per penultima primi Euclidis, et ex producto quaesita est radix quadrata, quam invenimus esse 17° 3ʹ 57ʹʹ, pro longitudine lineae AG. Ex his suppositis non difficile est ad elicendum quot graduum sint lineae GE, DE eorundem nimirum, quorum AG est 89 graduum 46 minutorum 14ʹʹ, et ut hoc facilius habet, ordinentur numeri in regulam DE DE] read de tribus:

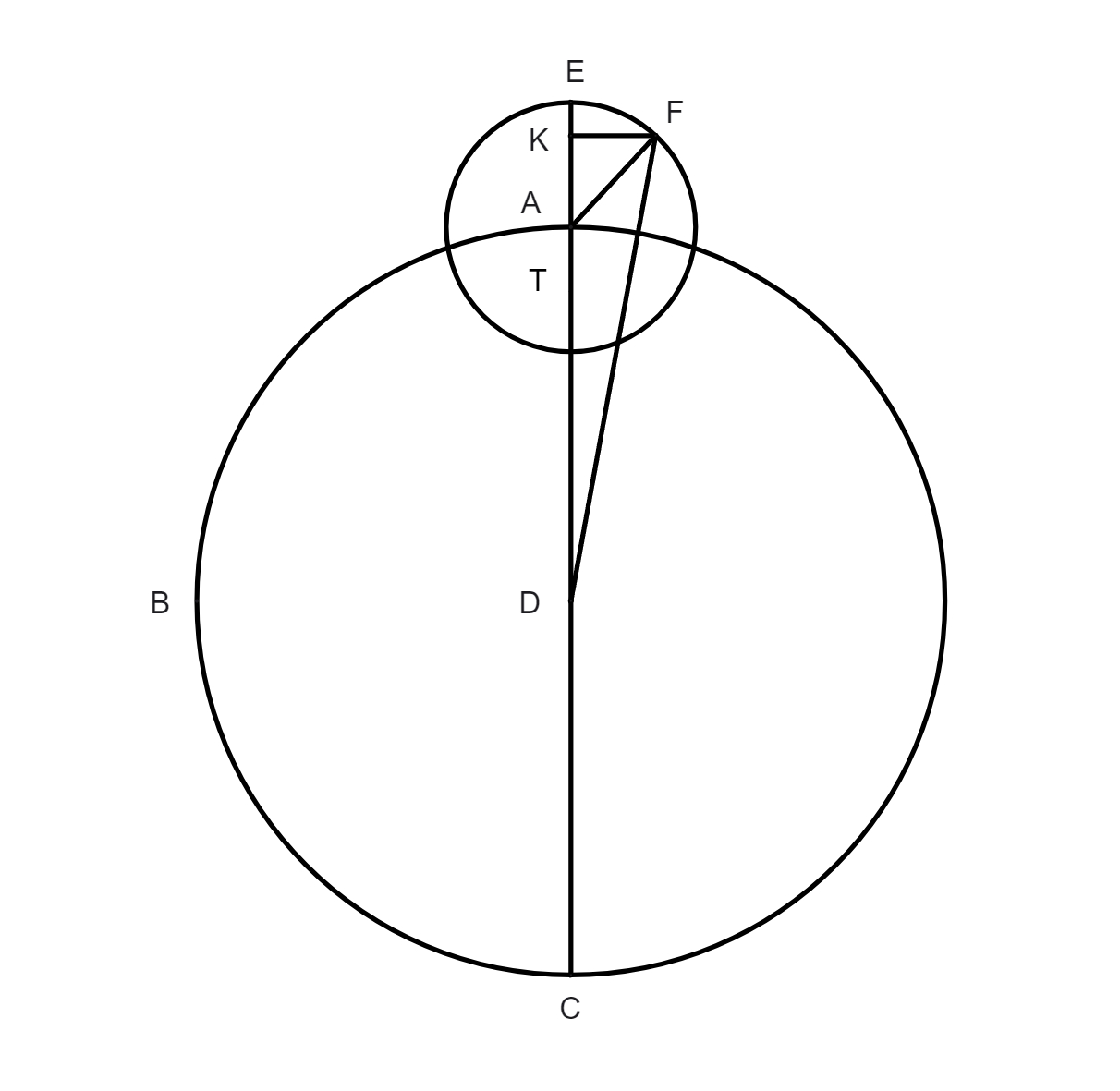
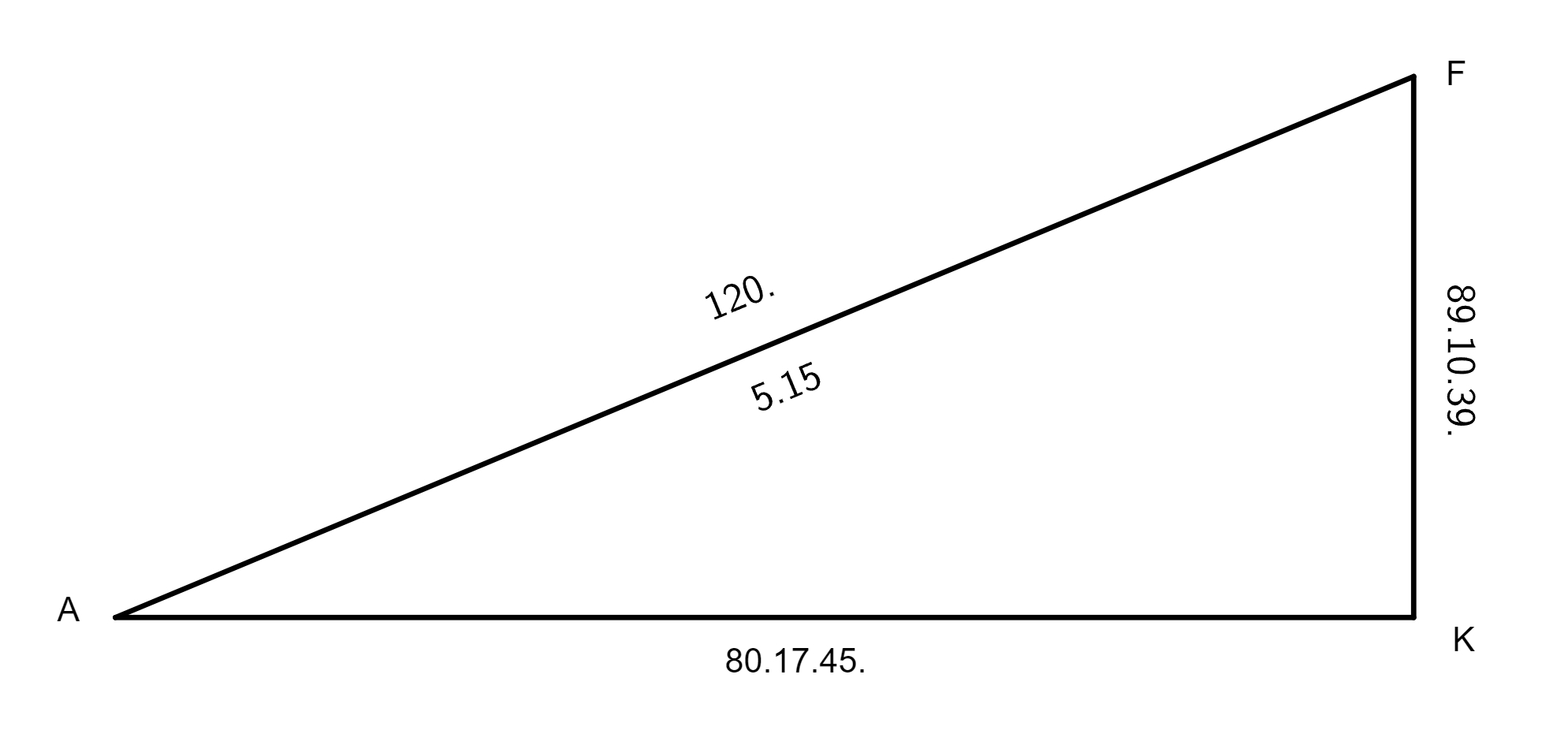
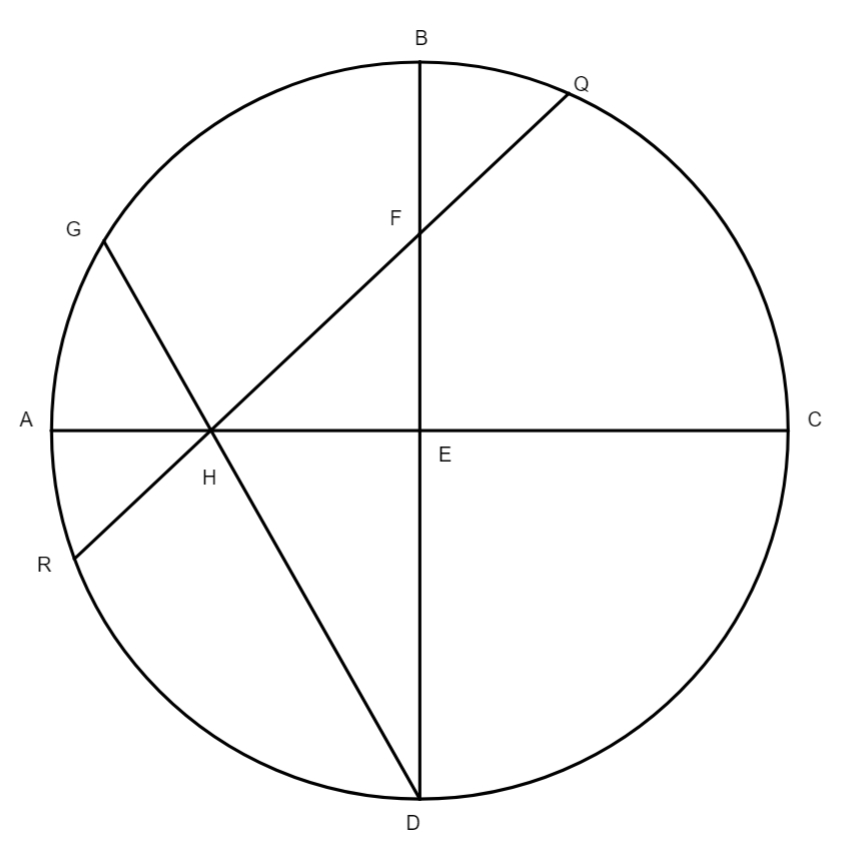
et procedatur more solito, et provenient pro DE 631° 13ʹ 48ʹʹ et pro GE 7° 2ʹ 50ʹʹ. Deinde eruatur arcus chordae GE, qui est 6° 44ʹ 30ʹʹ. Ex superioribus arcus BAG notus est, qui est arcus inter secundam et tertiam eclypsim comprehensus, et continet 150° 26ʹ. Cum addideris ei 6 gradus 44 minuta 30 secundas, quantitatem scilicet arcus GE, prodibunt tibi pro toto arcu BGE 157 gradus 11 minuta, cuius chorda BE est 11° 37ʹ 32ʹʹ, minor scilicet diametro epicycli qui est 120 gradus. Certum est, per 30 theorema tertii Euclidis, quod rectangulum comprehensum sub LA et DM sit aequale rectangulo quod est sub BD et DE. Cum itaque diameter epicycli dividatur in duo aequalia in puncto K, et addatur ei in directum linea DM, erit per sextum secundi Euclidis rectangulum quod continetur sub LD, DM, in una cum quadrato KM, aequale quadrato DK. Cum addidimus quantitatem lineae ED quantitati lineae BE, hoc est 631° 13ʹ 48ʹʹ ad 117° 37ʹ 32ʹʹ, provenit tota linea BD 748° 51ʹ 20ʹʹ. Hoc productum resolvimus in secundas ac duximus in lineam DE, id est in 631° 13ʹ 48ʹʹ, prius reductis illis in minimam denominationem, et prodierunt 472.700 gradus 5 minuta 32 secundae pro rectangulo BD et DE, hoc est pro DL in DM, huic producto adiecimus quadratum KM, scilicet 3600°. Productum fuerunt 476.300° 5ʹ 32ʹʹ pro quadrato lineae DK, cuius radix fuerunt 690 gradus 8 minuta 42 secundae. Nunc restat restat] testat B invenire proportionem LK ad KD, quae hoc pacto eruebatur nobis, scilicet ordinavimus numeros in regulam de tribus, ut sequitur 690° 8ʹ 42ʹʹ | 60° | 60° |, et resolvimus singulos numeros in secundas, et duximus tertium in secundum, et productum divisimus per primum et prosilierunt 5 gradus 13 minuta, quantitas scilicet semidiametri epicycli, ex his manifestum est quae sit proportio semidiametri epicycli ad semidiametrum deferentis epicyclum. Hic vides, optime lector, quantum olim divinissima ingenia astronomorum sudaverint in venandis motibus coelestibus. Cum nostrum institutum sit in hac praefatione tantum ostendere quomodo sedulus auctoris lector suo marte, prius bene cognitis theoricis planetarum, possit se extricare e locis difficilioribus, hic, priusquam accedamus ad inventionem excentricitatis excentrici Lunae, placuit adiicere quomodo tabula primae ac simplicis inaequalitatis Lunae sit fabricanda, quae apud nos appellatur tabula aequationis argumenti Lunae: sit ABC circulus concentricus zodiaco, EFT epicyclus, E longitudo longior epicycli, T oppositum eius, F sit locus Lunae in epicyclo et ducantur lineae KF, AF et DF. Nunc sit nostrum propositum invenire quantus sit angulus aequationis simplicis Lunae inaequalitatis, cum Luna destiterit a puncto E apogei epicycli per 48 gradus, nempe angulus in hac figura EDF, quem invenimus hac ratione, scilicet: habuimus ex supositione angulum EAF datum 48 graduum, duplicis illis et producto sublato a semicirculo, prosilierunt nobis pro angulo KFA 84 gradus et pro angulo EAF 98 gradus, horum arcuum chordae elicitae sunt e tabula chordarum, scilicet 89° 10ʹ 39ʹʹ et 80° 17ʹ 45ʹʹ, hos numeros ordinavimus ut sequitur:

et operati sumus iuxta regulam supra de triangulis datam, in quibus unus ex angulis acutis est notus cum

uno latere, et invenimus latus KF, 3° 54ʹ 5ʹʹ, et latus KA, 3° 30ʹ 46ʹʹ, quo facto, adiecimus productum lateris KA

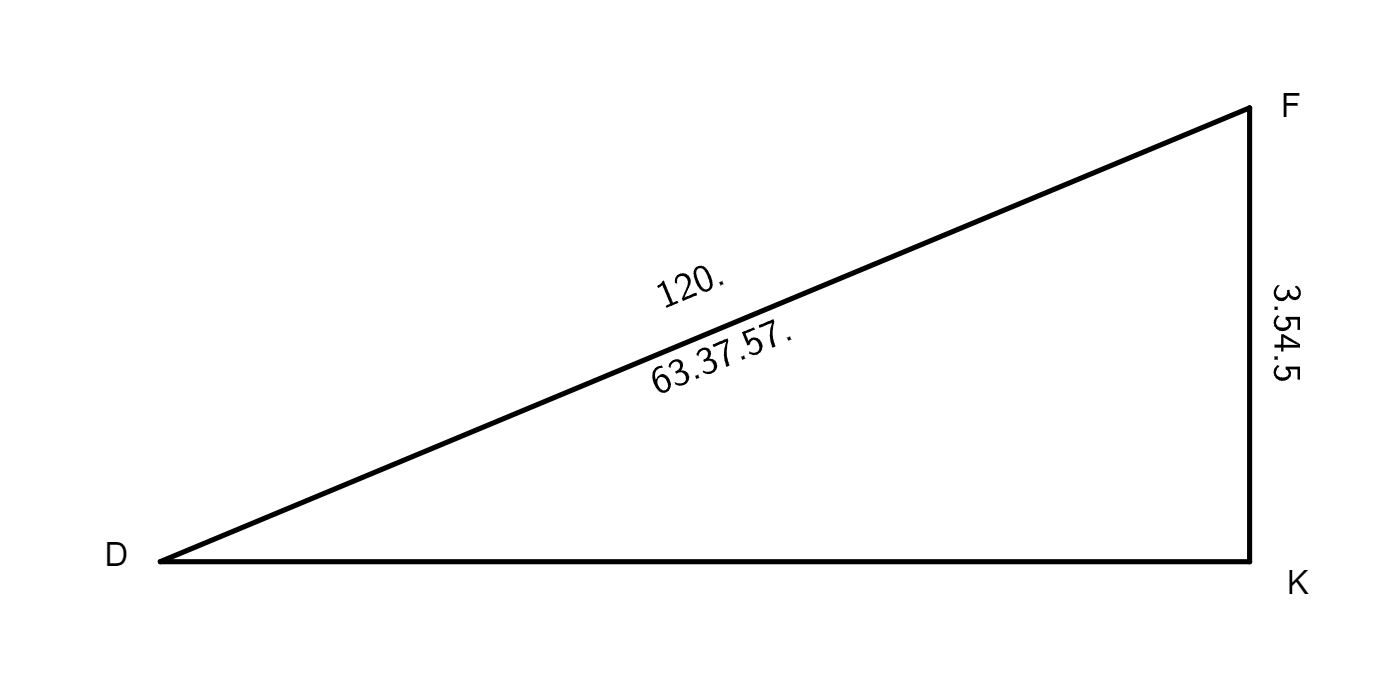
semidiametro excentrici, scilicet AD, hoc est 60 gradus, et fuit tota linea KD 63 gradus 30 minuta 46 secundae. Hanc lineam multiplicavimus in se et productum notavimus seorsim, quo facto, multiplicavimus etiam lineam KF in se, haec duo producta composita sunt per penultimam primi, et prodiit quadratum lineae DF, cuius radix fuerunt 63° 37ʹ 57ʹʹ. His habitis, perreximus ad inventionem FDK anguli, in quo duo latera sunt cognita, ordinavimus igitur numeros ad regulam secundum doctrinam triangulorum planorum ad hunc modum: 63° 37ʹ 57ʹʹ | 120° | 3° 54ʹ 5ʹʹ, et absoluta operatione provenerunt pro latere KF 7 gradus 21 minuta 26 secundae, quorum arcus fuit 7 graduum 6 minutorum fere,

quibus dimidiatis habuimus angulum EDF 3 graduum 33 minutorum. Tantus est angulus simplici inaequalitatis, qui debetur 48 gradus, et sic de reliquis. Cum Ptolemaeus per instrumentum armillarum subinde rectificaverat locum Lunae, deprehendit eum modo aequalem numerationi supra traditae, modo maiorem ea; quo vero Lunae corpus quadraturis mediis propinquis erat eo reperit talem variationem esse maiorem, unde conclusit epicyclum ferri in excentrico circulo et non concentrico, et reperiri in Luna secundam diversitatem quandam, quam invenit contingere in quadraturis mediis, et cum corpus Lunae destiterit ab auge seu longitudine maxima epicycli per quartam partem, quae, ut ipsemet testatur, cum fuerit maxima est 7 graduum 40 minutorum, maior, inquam, simplici diversitate 2 graduum et 39 minutorum. Quid multis? Per hanc diversitatem elicitur distantia centri excentrici a

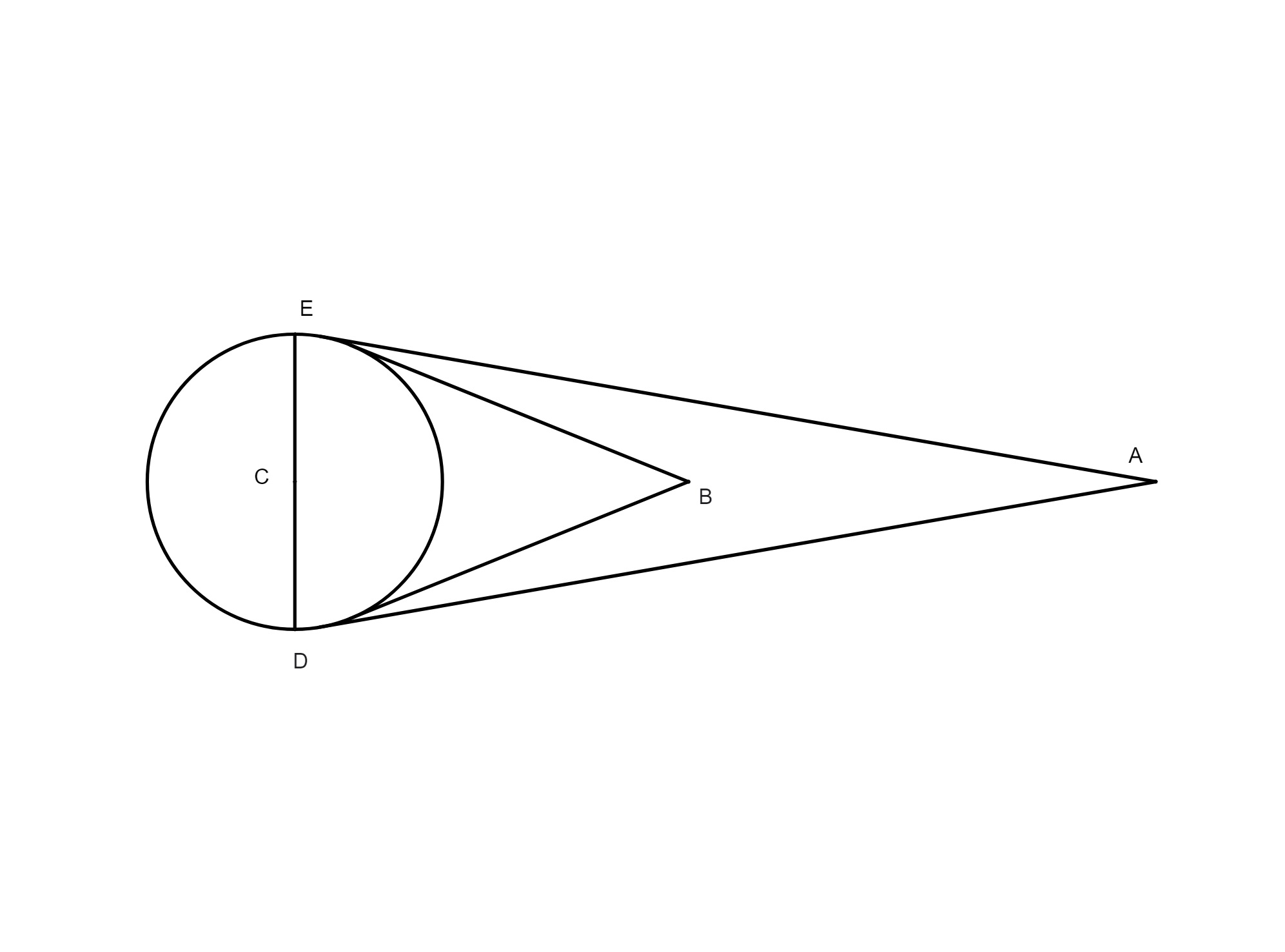
centro mundi hoc modo. Esto ABGC deferens excentricus epicycli, E centrum mundi, D centrum excentrici, ET contingens epicyclum propiorem centro mundi et EF contingens epicyclo remotiorem a centro mundi. Ductis lineis TG et AF, nunc quaerimus quantitatem lineae DE. Cum angulus TEG sit notus, erit proportio TG ad GE nota. Sed ex supradictis nota est proportio lineae AF ad EA, hinc GE ad EA nota erit, et hoc per quartam sexti, sed chorda arcus TG est 16° proxime, quae est igitur proportio TG ad FA ea est proportio

GE ad AE. Nam si duxeris 5° 25ʹ in 120° et diviseris productum per 16°, nascentur 39 gradus 22 minuta pro linea GE; si adieceris ei lineam EA, hoc est 60°,

habebis 99° 22ʹ totam lineam AG, cuius dimidium scilicet AD est 49° 41ʹ, subtractis illis a 60°, relinquentur 10 gradus 19ʹ. Tanta est linea ED, hoc est Lunae excentricitas. De puncto inclinationis epicycli nunc nihil dicemus, similiter de ratione motus Lunae in latitudinem, sed adducemus adhuc exemplum unum aut alterum, quae ubi recte fuerint intellecta, reliquia erunt per se non solum in Luna, verumetiam in reliquis planetis facilia intellectu, quo facto dirigetur noster sermo ad illustrandas aliquot propositiones octavi libri, ut videat candidatus huius pulcherrimae artis unde Regiomontanus, vir divini ingenii, desumpserit suas tabulas directionum.

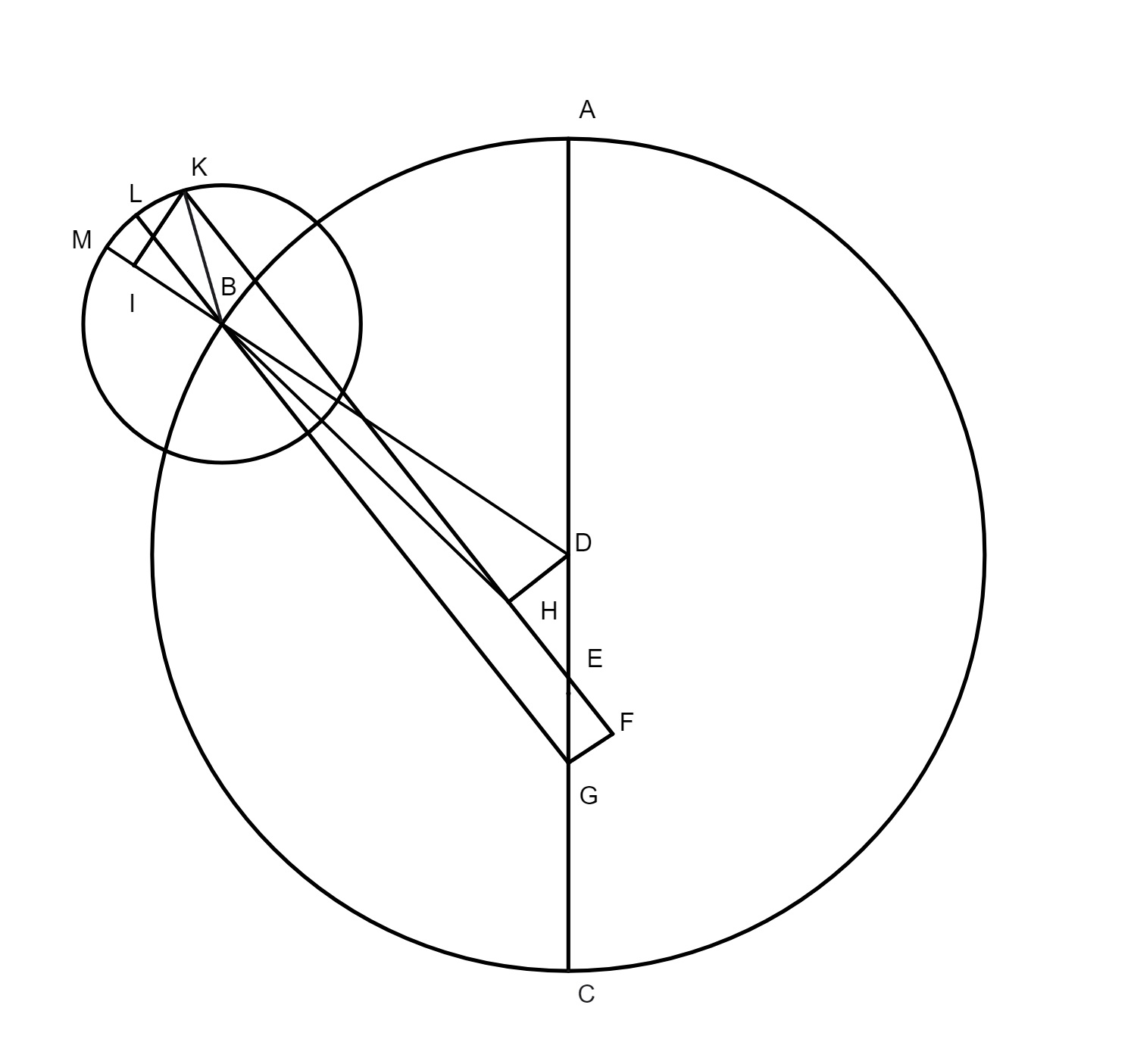
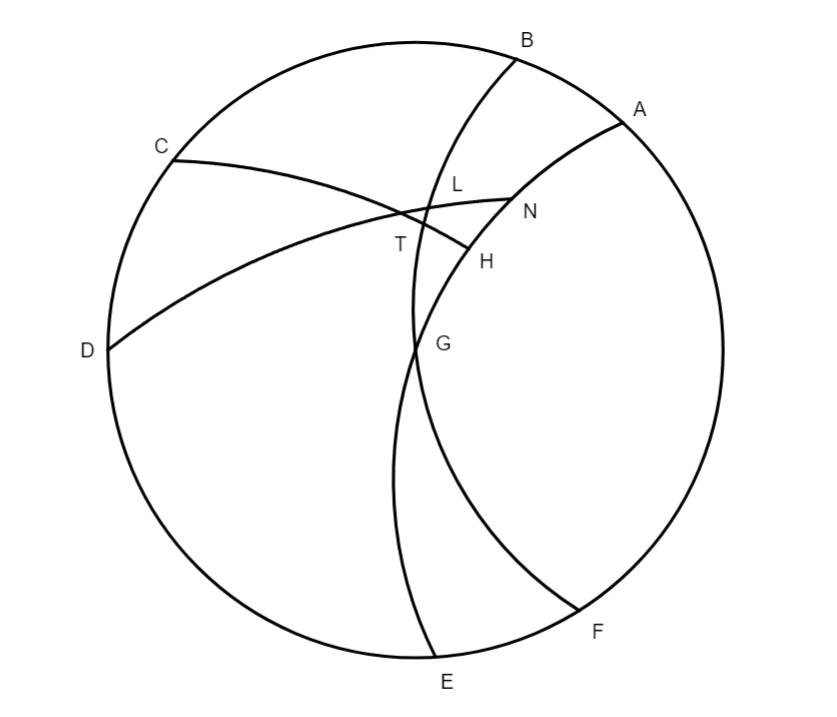
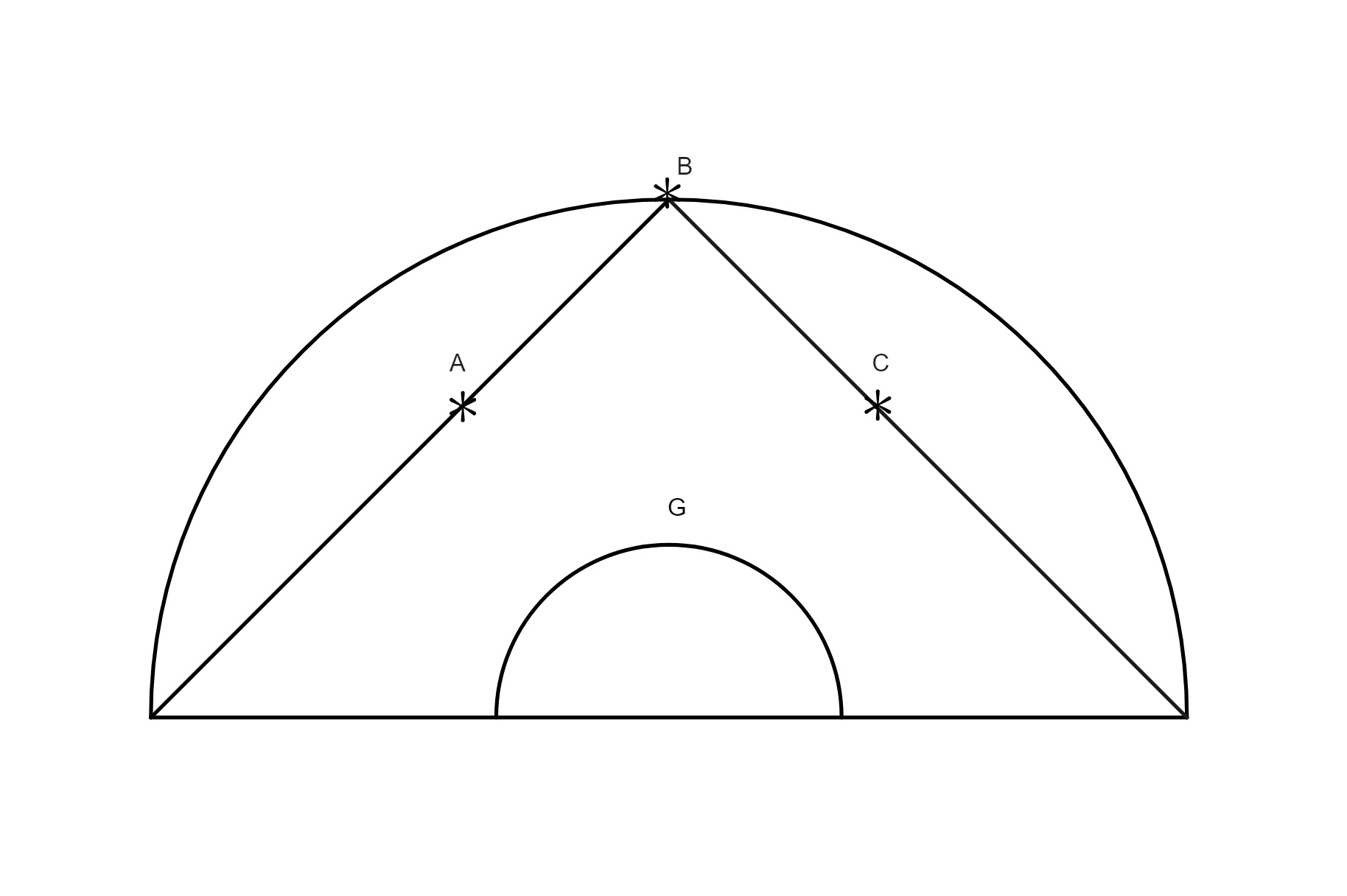
Esto ABC excentricus Lunae, descriptus super centro D, E centrum mundi, G centrum ad quod inclinat epicyclus, B centrum

epicycli, MLK epicyclus qui defertur a puncto A versus punctum B secundum ordinem signorum, GL sit linea medii longitudinis epicycli, centrum Lunae moveatur a puncto M versus punctum K contra ordinem signorum, K sit locus Lunae, LK mediae longitudinis arcus, seu argumentum medium, ut nostri loquuntur, MLK arcus veri argumenti, angulus MBL sit angulus aequationis centri seu duplicis distantiae, punctus A sit maxima longitudo in excentrico, AB duplex distantia, quae praesupponitur in hoc exemplo esse 48 graduum. Ad inquirendum angulum MBL, cui aequalis est GBF per decimamquintam primi, hac via processimus, scilicet cum arcus AB sit datus dabitur etiam angulus AEB, qui est 48 graduum in triangulo, DEH est unus ex angulis acutis datus, cum uno latere scilicet DE, duplicatis 48 gradibus prodierunt 96°. Subtractis illis a semicirculo habuimus pro angulo HDE 84 gradus, horum angulorum arcuum subtensae fuerunt, scilicet, DH 89° 10ʹ 39ʹʹ, HE 80° 17ʹ 45ʹʹ. His numeris ordinatis modo supra dicto, et facta operatione, prodierunt pro latere DH 7° 40ʹ et pro latere HE 6° 54ʹ, quorum DE est 10 graduum 19 minutorum, et ut habeamus lineam BF duximus semidiametrum excentrici BD, qui est supra inventus 49° 41ʹ, in se, et lineam DH in se, et quadratum DH sublatum est a quadrato BD, et radix eius quod relinquebatur erant per penultimam primi 49° 5ʹ. Tanta fuit linea BH, cui adiecta est linea HE, scilicet 6° 54ʹ, et exiit linea BE 55° 59ʹ; et cum EF sit aequalis lineae HE, iterum addidimus 6° 54ʹ ipsis 55° 59ʹ et habuimus totam lineam BF 62° 53ʹ. Haec linea ducta est in se, et similiter linea GF, cui aequalis est HD, cum HE et EF sint aequales, harum linearum quadrata composita faciunt per penultimam primi quadratum lineae BG, cuius radix nobis inventa est 63 gradus 21 minuta proxime. In triangulo GBF sunt duo latera nota, per doctrinam triangulorum dabitur angulus GBF quem, redactis numeris in ordinem suum et operatione solita absoluta, invenimus esse 6 graduum 58 minutorum fere, hic cum duplex distantia sit minor sex signis seu semicirculo, addendus venit arcui LK in epicyclo, quem praesupponimus 36 graduum, et fuit totus arcus MLK 42 graduum 58 minutorum. Nunc porro restat inveniendus MEK. In triangulo acuto IBK est unus angulus notus, scilicet angulus B, cum uno latere BK, quod est 5° 15ʹ; ad habenda latera BI, IK non aliter pergantur quam in inventione laterum DH, HE. Subtensa dupli arcus in K est 81° 47ʹ 19ʹʹ et subtensa arcus trianguli IKB est 87° 47ʹ 16ʹʹ. Post operationem, ut fieri solet, provenerunt pro latere IK 3° 34ʹ 41ʹʹ et pro IB 3° 50ʹ 20ʹʹ, et postquam addidimus 3° 50ʹ 20ʹʹ ipsis 55° 59ʹ, hoc est lineam IB lineae EB, nata est tota linea IE 59° 49ʹ 20ʹʹ, qua ducta in se, et similiter linea IK, et compositis duobus quadratis ac inde elicita radice, fuit linea KE inventa esse 59° 55ʹ 40ʹʹ. His habitis, restabat inveniendus angulus IEK, quem omnibus rite absolutis in operatione de inveniendo aliquo angulo duobus lateribus in triangulo supposito notis, invenimus 3 gradus 25ʹ. Tantus, inquam, est angulus aequationis in EK, hoc est argumenti, cum argumentum fuerit 42 graduum 58 minutorum. Cum vero Ptolemaeus ipsemet adduxerit exemplum, quando duplex distantia sit maior una quarta excentrici, hic de hac re cessandum censuimus, in qua licet multa adhuc requirantur, tamen ne prolixiores simus quam aequum est, reservabimus ea donec prodeant a nobis alia in hunc autorem. Haec arbitramur non inutilia futura incipientibus in hoc autore, etiam ad ea quae sequuntur de reliquis planetis. Nunc ad reliqua de quibus paucula dicere statuimus, nempe de quibusdam propositionibus octavi libri: nam manifestum est quod ratio declinationum sit in triplicis forma, scilicet aut latitudo est septentrionalis et similiter declinatio, aut latitudo est meridionalis et declinatio septentrionalis, aut latitudo et declinatio sunt simul meridionales; ut res evidentior et clarior sit adducemus tria exempla, in quibus ad oculum ponemus quomodo hae tres rationes inter se distent. Haec exempla duplici via calculari possunt aut per doctrinam triangulorum sphaericorum, aut per regulam sex quantitatum.

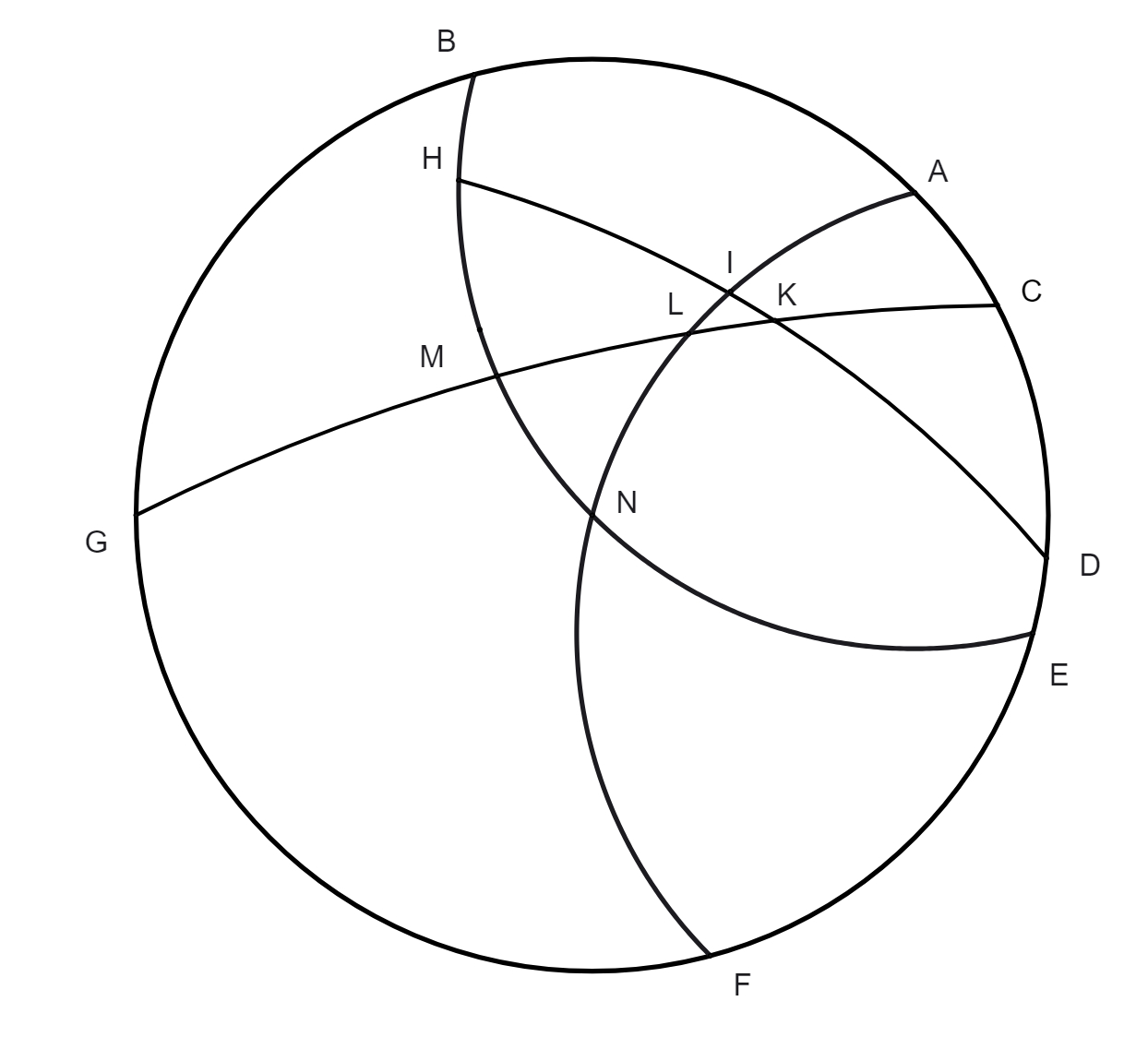
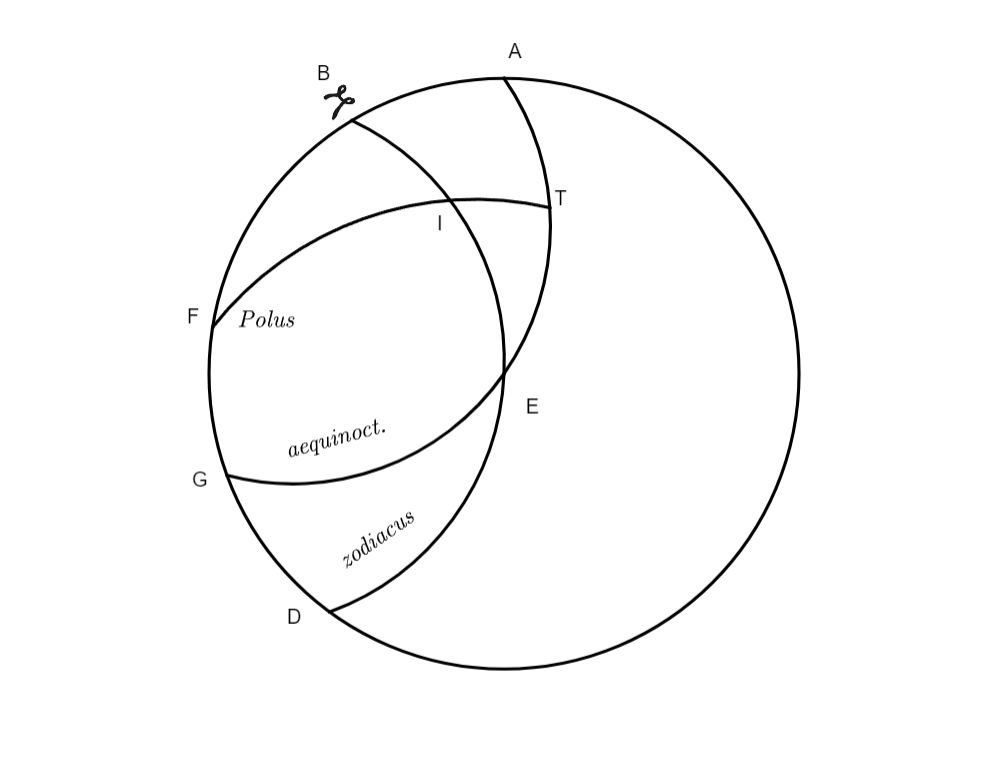
Sit ABCF colurus solstitiorum, BGF medietas circuli qui est per medium signorum, AGE medietas aequinoctialis, C

sit polus aequinoctialis, D polus zodiaci septentrionalis, G initium Arietis, M locus stellae quando latitudo eius septentrionalis, arcus OM sit arcus latitudinis, OLK sit declinatio arcus OG in zodiaco dati, MH arcus declinationis, qui quaeritur. Nunc propositum nostrum est quaerere quantum sit declinatio alicuius stellae quae distat ab Arietis initio 86 gradus, et latitudo eius septentrionalis est 6 graduum. In hoc exemplo est arcus OG ex hypotesi notus, qui est 86, tanquam ascensio recta, quibus respondent in eclyptica 86° 20ʹ 36ʹʹ, quemadmodum est arcus GK, huius arcus dupli est chorda 119 graduum 45 minutorum 39 secundarum. In triangulo BGA est angulus G notus ratione maximae Solis declinationis, quae supponitur esse 23° 30ʹ, cuius duplum sunt 47 gradus. Ad habendum arcum OK declinationem, scilicet quae debetur arcui GK, multiplicavimus per doctrinam triangulorum sphaericorum angulum BGA, hoc est 47° 51ʹ, in 119° 45ʹ 39ʹʹ, chordae dupli arcus GK, productum divisimus per 120° et prodierunt 47° 45ʹ 17ʹʹ, chorda nimirum dupli arcus OK qui est 46° 54ʹ, cuius dimidium sunt 23° 27ʹ. Tanta est declinatio quaesita. Postquam ei adiecti sunt 6 gradus, fuit arcus MK 29° 27ʹ, quo duplato nati sunt 58 gradus 54 minuta, horum chorda fuit 58° 47ʹ 11ʹʹ. Cum a puncto A descendant duo arcus, scilicet arcus AD et arcus AH, a quorum terminis reflectuntur duo alii arcus DK et HC, erit proportio sinus dupli arcus DA ad sinum dupli arcus AC composita ex duabus proportione, scilicet sinus dupli arcus DK ad sinum dupli arcus KM et proportione sinus dupli arcus MH ad sinum dupli arcus HC, et ut habeatur arcus MH ordinentur numeri ut sequitur:

quo facto ducetur primus in quartum, ut fieri solet in regula sex quantitatum quando quintus desideratur numerus, et productum dividatur per tertium, quod inde nascitur iterum in sextum ducatur et productum dividatur per secundum, quod prosiliit fuerunt 58° 45ʹ 53ʹʹ, quorum arcus invenimus 58° 39ʹ. Hunc arcum per medium disposimus et habuimus pro arcu in H, qui quaerebatur, 39° 20ʹ. Tanta est declinatio septentrionalis 86 gradus a principio Arietis cum latitudo fuerit septentrionalis 6 gradus, et sic agendum est in reliquis. Nunc ad exemplum quando latitudo fuerit meridionalis et minor declinatione puncti dati. Sit arcus GO notus, qui est 46 graduum, ascensio scilicet recta, cui respondent, ut manifestum est ex tabula rectarum ascensionum, 48° 29ʹ eclyptica, quorum duplum sunt 98° 58ʹ. Huius dupli sinus inventus est nobis e tabula chordarum, 89° 51ʹ 3ʹʹ, hunc sinum duximus in angulum BGA, scilicet in 47° 51ʹ, chordam dupli arcus BA, et provenerunt 35° 49ʹ 41ʹʹ, sinus dupli arcus OK, cuius sinus arcus est 34° 48ʹ, horum medietas sunt 17° 24ʹ. Tantus est arcus declinationis OK, quae declinatio debetur 48° 29ʹ arcui scilicet GK. Ab hac declinatione subtraximus arcum OL, nempe latitudinem arcus dati, quae supponitur esse meridionalis 3 gradus ab arcu OK, et reliquum fuit 14° 24ʹ arcus LK. His habitis, ordinati sunt numeri, ut sequitur:

In hoc exemplo non aliter operati sumus quam in superiori, nempe resolutis numeris more solito, ductus est sinus dupli arcus AD in sinum dupli arcus KL, productum divisum est per sinum dupli arcus DK, quod ex eiusmodi divisione nascebatur iterum ductum est in sinum dupli arcus CH, quod hinc provenit divisum est per sinum dupli arcus AC, et prosilierunt nobis 28° 40ʹ 49ʹʹ, sinus scilicet dupli arcus LI, huius sinus arcus inventus est 27° 39ʹ, cuius dimidium sunt 13° 49ʹ, arcus scilicet LI. Tanta est declinatio quaesita, quae etiam septentrionalis est, cum arcus OL sit minor arcui OLK. Si vero arcus OL fuerit maior arcu OLK, tunc alia est via quaerendi declinationem, cuius rei etiam propriam figuram cum exemplo adducere visum est. Esto circulus ABF colurus solstitiorum, BNE semicirculus zodiaci, ANF medietas aequinoctialis, polus zodiaci sit punctus C, aequinoctialis autem D punctus, et transeat maximi circuli pars per polum zodiaci, quae sit CLMG, et similiter transeat pars maximi circuli per polum aequinoctialis D, et stellam, aut alium punctum coeli scilicet, per punctum K, qui in hoc loco supponitur quae sit DKIH. Quia autem a puncto A descendunt duo arcus AL et AD, a quorum extremitatibus

reflectuntur duo arcus LKC et DKI, qui secant se in puncto K, erit igitur proportio sinus duplis arcus DA ad sinum dupli arcus AC composita ex proportione sinus dupli arcus DI ad sinum dupli arcus IK, et ex proportione sinus dupli arcus KL ad sinum dupli arcus LC. Nunc propositum est nostrum invenire quanta sit declinatio meridionalis nempe arcus IK, cum proponitur distantia puncti M a puncto N 5 gradus et latitudo meridionalis MLK 8 gradus, hanc declinationem ad hunc qui sequitur modum venati sumus, scilicet primum elicuimus e tabula ascensionum rectarum arcum eclyptici NL, qui respondet rectae ascensioni NM, quem invenimus 5 gradus 13 minuta, hunc duplicavimus, et duplati quaesivimus sinum, qui fuit 11° 15ʹ 29ʹʹ. Hunc sinum duximus in angulum BNA, hoc est in 47° 51ʹ, producti quaesivimus arcum, qui inventus est esse 2° 9ʹ. Tantus est arcus ML declinatio, scilicet quae respondet 5° 23ʹ. Haec sublata est a 8 gradibus, hoc est arcus ML ad arcum MLK, et residuatus est arcus LK 5° 51ʹ, duplum eius fuerunt 11° 42ʹ et sinus eorum 12° 13ʹ 51ʹʹ, arcus DA et DI fuerunt quartae, quae se habent ut saepe dictum est. Arcus AC est 133° 0ʹ, eius sinus est 110° 2ʹ 50ʹʹ, sicut supra. Arcum LT sic formavimus, scilicet 5° 51ʹ, subtraximus a 90°, residuum duplavimus et prodierunt 168° 18ʹ, horum chorda est 119° 22ʹ 29ʹʹ. Inventis his arcubus, et chordis eorum posuimus producta eorum in regulam sex quantitatum, ut sequitur:

Sic dispositis numeris, ductus est numerus arcus AC in numerum arcus DI, et productum divisum est per numerum arcus DA, ut fieri consuetum est ubi quartus numerus desideratur in regula sex quantitatum, productum iterum ductum est in numerum arcus KL, et quotiens inde numerus divisus per sextum, scilicet numerum arcus LC, resultaverunt 11° 16ʹ 30ʹʹ, sinus dupli arcus IK, huius sinus arcus est 10° 47ʹ, quorum medietas est 5 graduum 23 minutorum proxime, tanta est distantia puncti K a puncto I, declinatio scilicet meridionalis, et sic de reliquis, his rationibus conficendae sunt tabulae declinationum stellarum, aut aliorum punctorum coeli quaecunque sit latitudo. Et cum negotium componendae tabulae mediationum coeli sit coniunctum huic negotio, paucis illud et unico tantum exemplo, quod sufficere arbitramur pro utrisque latitudinibus, illustrabimus. Esto

ABE colurus solstitiorum, sicut supra. Nunc animus est quaerere punctum H, cum quo stella ad medium coeli venit, seu arcum GH. Cum arcus GL fuerit 47°, latitudo TL 6°, GN 49° 28ʹ, TH 22° 42ʹ, proportio CD ad DA componitur ex duabus proportionibus CT ad TH et HN ad NA. Sed quinque horum nota sunt, scilicet duplus arcus DC, qui est 47°, et eius chorda 47° 51ʹ et duplus arcus DA 113° cum sua chorda, quae est 110° 2ʹ 50ʹʹ. Porro duplus arcus declinationis stellae TH notus est, cum suo complemento, scilicet CT, complementum est 134° 36ʹ et chorda sua 110° 42ʹ 9ʹʹ, et declinatonis arcus TH ex superioribus notus est, qui est duplus 45° 24ʹ, et chorda sua est 45° 55ʹ 42ʹʹ, et arcus NA est notus, qui est complementum arcus GN, quem supponimus duplum 81° 4ʹ, et eius chordam 77° 59ʹ 12ʹʹ. Horum arcuum numeros sic ordinavimus:

Postquam resolvimus hos numeros, ut solet, ductus est primus in quartum, quod resultavit divisum est per tertium et quotiens numerus iterum ductus est in sextum numerum, et id quod prodiit divisum est per secundum, et natus est sinus dupli arcus HN 14° 4ʹ 2ʹʹ qui erat ignotus, huius sinus arcus inventus est 13° 28ʹ cuius dimidium sunt 6° 44ʹ. Hoc productum sublatum est ab arcu GN, qui prosupponebatur 49° 28ʹ et reliqui fuerunt 42 gradus 44 proxime, tantus est arcus GH qui quaerebatur. Hactenus de his. Quomodo autem tabulae differentiarum componendae sint et tabulae positionum generales, facile ex secundo libro diligens huius divini autoris lector percipere potest. Hactenus visum est, optime lector, de his rebus verba facere, quae ubi recte fuerint a candidato huius pulcherrimae artis intellecta habebit magnum aditum ad reliquia; vale.

Praefationis Erasmi Osvaldi Schrekhenfuchsii ad lectorem finis.

〈I〉 Erasmi Osvaldi Schrekhenfuchsii, in Magnae compositionis Claudii Ptolemaei Pelusiensis Alexandrini, libri I annotationes

〈I.2〉 Caput II

Propositi autem.］ In hoc capite proponitur totius Almagesti series ac ordo, quod est tanquam argumentum omnium horum librorum. Et quae aguntur in primis octo capitibus sunt principia prima totius artis.

Primum est.］ Ab octavo capite ad finem usque primi libri tractantur omnia quae requiruntur ad solidum intellectum sphaerae rectae, et primum omnium docet paucis propositionibus quomodo chordae rectae sint investigandae, quae singulis arcubus subtenduntur. Secundus vero complectitur accidentia singula, quae accidunt penes singulas inclinationes horizontum: nisi haec omnia recte intelligantur, reliqua quae sequuntur intelligi non possunt.

Alterum.］ Haec aguntur in tertio, quarto, quinto ac sexto libro, in quibus tum medii tum veri motus Solis ac Lunae, una cum reliquis accidentibus eorum, per demonstrationes quae sequuntur ex solertissimis observationibus demonstrantur.

Quae quidem.］ In septimo et octavo enarrat quae sunt de stellis fixis, quae, quamvis non destituantur motu ab occidente ad orientem super polis zodiaci, tamen ob nimiam tarditatem huius motus dicuntur fixae.

Sequentur autem.］ In reliquis libris usque ad calcem operis, omnia quae requiruntur ad perfectam et absolutam intellectionem reliquarum stellarum erraticarum, quae sunt Saturnus, Mars, Iupiter, Venus et Mercurius.

〈I.3〉 Caput III

Prima igitur.］ Hoc capite tribus argumentis probat coeli rotunditatem, nempe ratione experimentali, quae ducitur a stellarum ortu et occasu. Confutatione, qua interimitur ac exploditur adversariorum opinio, qui conati sunt probare stellas ferri ad infinitum, aut in occasu extingui in terram et in ortu iterum incendi, cuius opinionis fuit Heraclitus. Et ratione ipsa per quam convincimur perfecto corpori perfectam convenire figuram, scilicet sphaericam, quae omnibus reliquis figuris probatur esse perfectior et capacior.

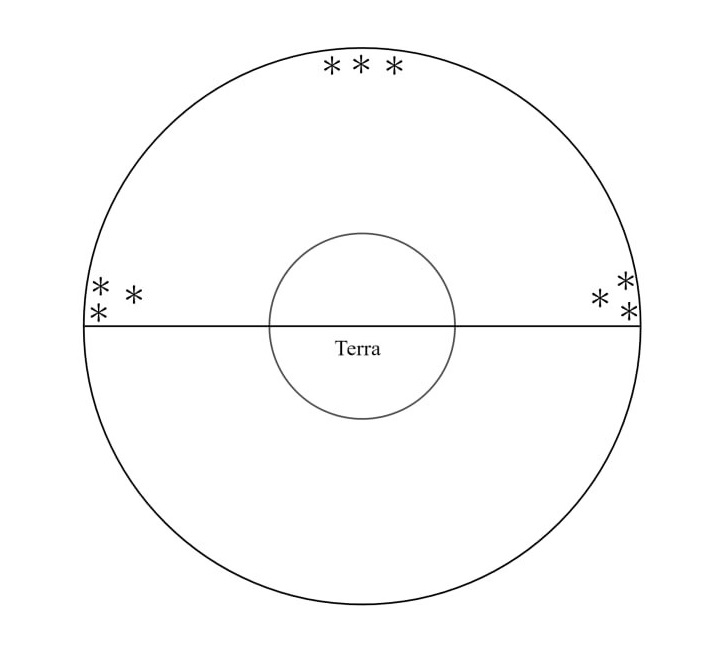
Primum argumentum sumitur a stellis occidentibus et orientibus, cuius est sequens figura:

Sed stellarum］ Quod coelum sit sphaericum et volvatur globi modo confirmatur etiam per stellas semper apparentes circa polum arcticum, sicut est videre in hoc schemate:

Quarum etiam propinquores］ Alia est ratio, quae sumpta est a distantia stellarum a polis mundi. Nam dicit stellas orientales, quae polis sunt propinquores, minores describere circulos motu diurno et citius oriri quam sunt circuli stellarum quae remotiores sunt a polis mundi, hoc, inquam, facile pervidere poteris, sumptis duabus stellis fixis, quarum distantia est inaequalis a polis universi et ascensio earum fere eadem. Sint in exemplum duae stellae secundae magnitudinis in Pegaso, eiusdem fere ascensioni rectae. Altera est secundum longitudinem suam in 22 gradibus et 14 minutis Piscium et est in humero dextro, ac in ipsa pedis radice, quae distat a polo arctico 65 gradus, et oritur hoc nostro tempore cum Sole, ubi est altitudo poli 58 gradus cum 11 gradibus Cancri. Altera autem est quoque de secunda magnitudine, quae est secundum longitudinem in 16 gradibus 49 minutis Cancri, et est ea quae est in occipicio et humero alae, cuius distantia est a polo arctico 78 gradus fere, quae oritur in eadem poli altitudine cum 30 gradibus Cancri. Hinc manifestum est remotiorem stellam maiorem describere circulum motu primi mobilis quam propinquiorem, et differre ortum suum spacio 19 graduum fore.

Nam si quis stellam motum.］ Impossibile est stellas ad infinitum ferri, quod probatur per optimam suppositionem, videlicet quae sub minori perspiciuntur angulo minora apparent, quae sub maiori, maiora. Nam corpus seu stella C maius apparet oculo B quam

oculo A, propterea quod angulus EBD, maior est angulo EAD, ex sententia 21 propositionis primi Euclidis. Unde si corpus seu stella C ad infinitum discederet a puncto A, evanesceret angulus EAD et fieret corpus C insensibile, quod in stellis non videmus fieri, imo contrarium.

Incendi autem ipsas.］ Heraclitus fuit huius opinionis: stellas in occasu extingui in terram et in ortu iterum incendi, hanc opinionem Ptolemaeus confutat. Primo quod servant semper certas distantias et loca certa, ac oriuntur et occidunt certis temporibus, quod minime fieret si extinguerentur in terram in occasu et iterum in ortu a terra incenderentur. Secundo, confutat hanc opinionem ab impossibili, nempe quod fieri non queat unam et eandem terram habere virtutem incendendi et exstinguendi. Nam manifestum est quod noster ortus sit antipodibus occasus, et illorum occasus noster ortus, unde sequi necessum est quod illorum ortus et noster occasus idem sit, et habere vim extinguendi et incendendi quod est contra naturam, sicut apparet ex stellis nobis semper apparentibus quae illis qui habitant sub recta sphaera occidunt.

Necesse erit.］ Si coelum foret triangulare, oporteret nobis stellas aliis temporibus maiores aliis minores apparere, quod fieret propter vicinitatem laterum trianguli et angulorum, sicut ostenditur in figura sequenti, in qua stella et C sunt puncto G in superficie terrae propinquores quam stella quae est in angulo B.

Nam quod.］ Quod stellae in oriente vel occasu aliquando maiores apparent quam in medio coeli, non alia est causa nisi vaporum exhalatio, qua visus nostri radii disgregantur, quo minus videant stellas eadem magnitudine qua re ipsa sunt, quod Ptolemaeus probat, similitudine sumpta a rebus in aquam proiectis, quae quo magis profondiora perierint eo maiores apparebunt, non quod maiores sint in aqua quam extra aquam, imo quod radii visus nostri disgregantur in aqua. Haec clarius videbis in figura sequenti.

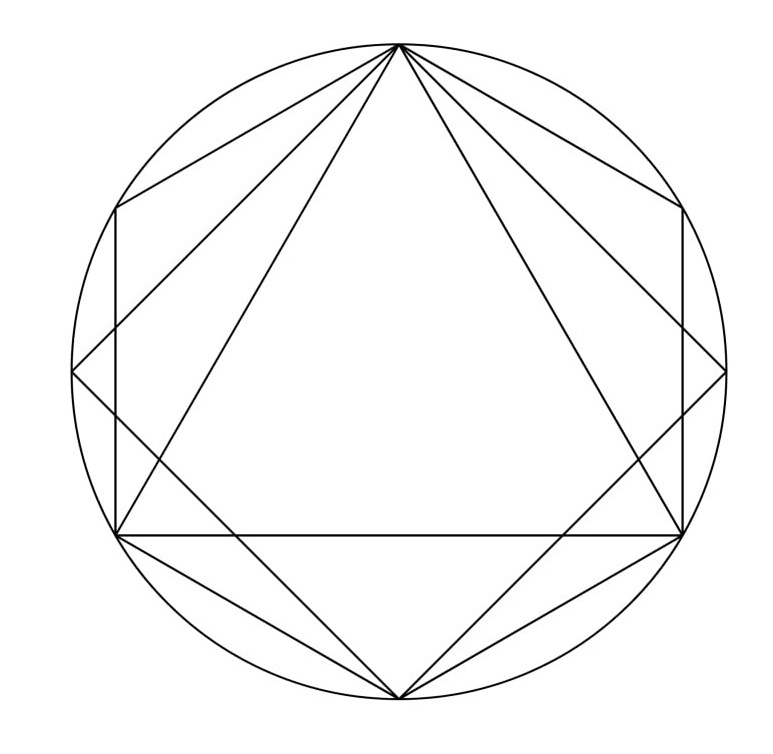
Figurarum quoque.］ In superficiebus planis circularem figuram, et in solidis sphaericam, esse omnium reliquarum figurarum capacissimam per se primo intuitu clarum est ex hoc schemate, in quo videmus figuras plurium angulorum circuli inscriptas capaciores esse figuris paucorum angulorum, attamen non tam capaces quam est sphaerica figura.

〈I.4〉 Caput IIII

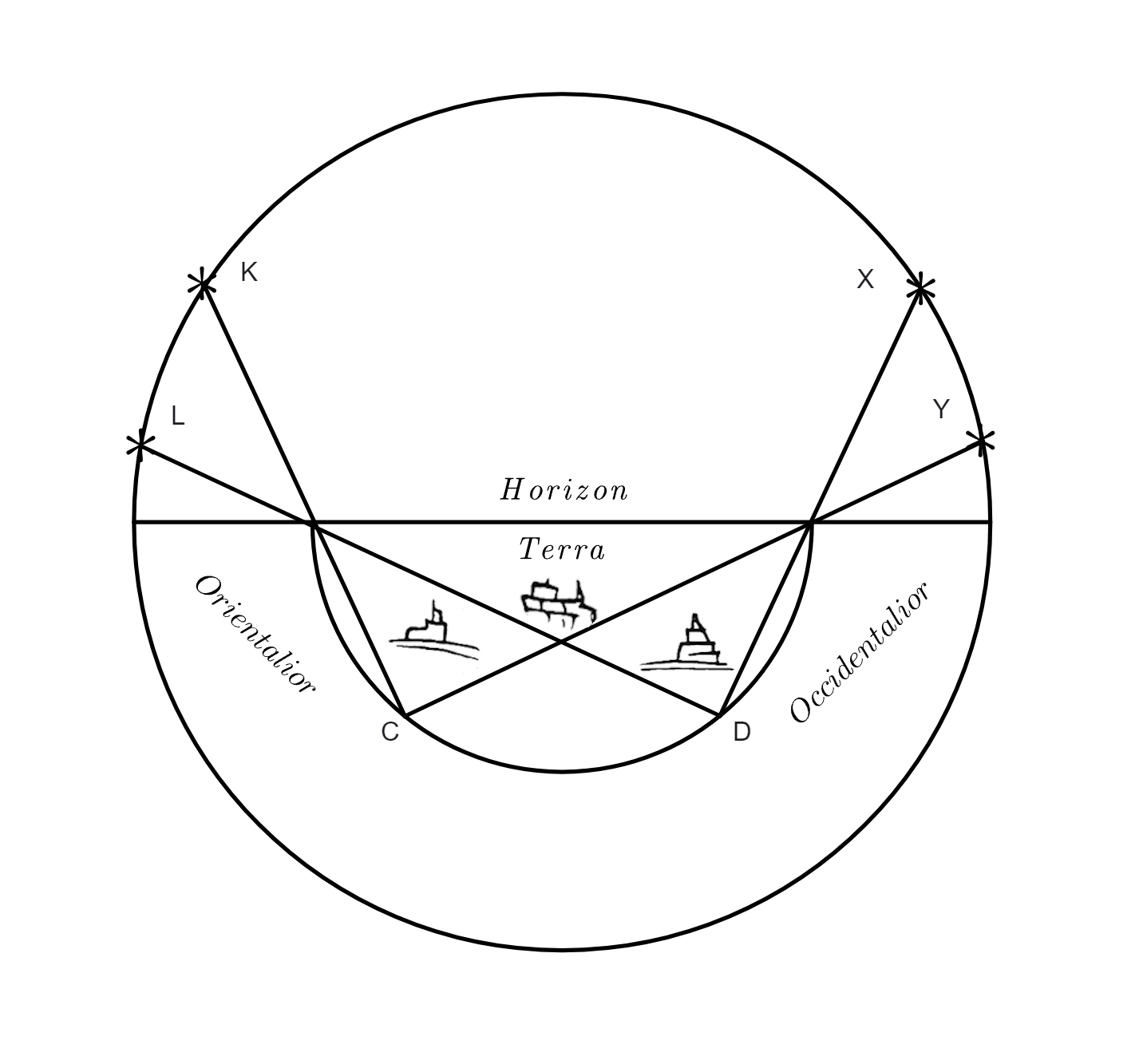
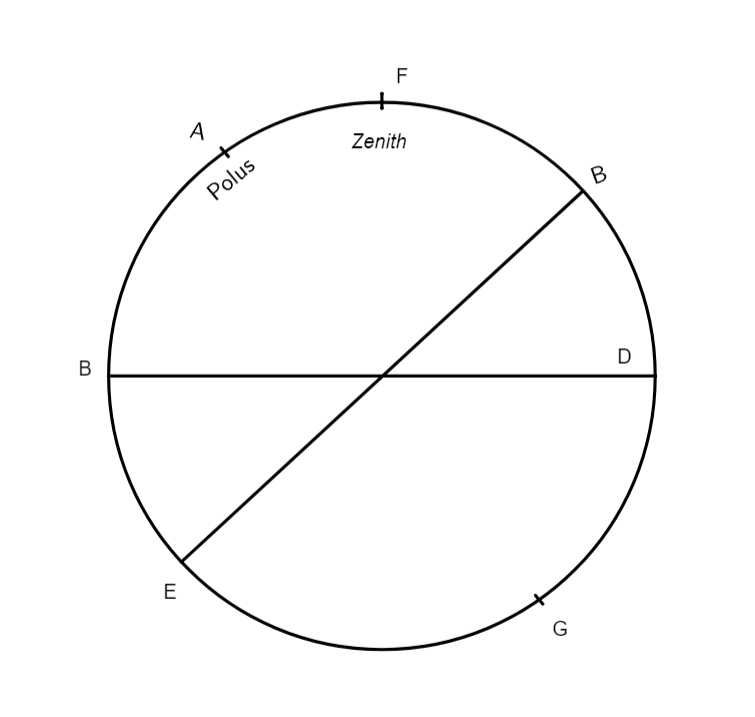
Nam etiam.］ In superiori capite probavit coelum esse sphaericum et sphaerice moveri, in hoc vero probat terrae rotunditatem ad universas partes, quod fit duabus rationibus praecipuis, quarum altera sumpta est ab eclypsibus, altera autem ab elevatione poli. Ratio quae ducitur a defectibus lunaribus pertinet ad confirmationem eam qua probatur terrae rotunditas ab ortu ad occasum et contra. Nam si non esset rotunda ab ortu ad occasum, apparet sine dubio eclypsis Lunae omnibus simul, sed nos videmus diversum fieri. Quia tempus orientalium semper maius esse reperitur quam occidentalium, non re ipsa. In exemplum sit haec figura in qua ostenditur quod eclypsis quae orientalibus, qui habitant in superficie terrae super puncto B, fit hora tertia noctu, illa fuit occidentalioribus,

scilicet qui habitant super puncto F, hora prima. Talis nimirum eclypsium varietas non posset fieri si terra non foret rotunda seu sphaerica ab ortu ad occasum: hoc argumento excluduntur omnes reliquae superficies seu figurae terrae, cava scilicet plana et triangularis, quae si esset cava, sequeretur necessario occidentalioribus stellas citius oriri quam orientalioribus et contra, sicut cernitur ex hac figura in qua habitanti super D, qui est occidentalior, stella L citius apparet quam orientaliori, cuius radius oculorum CK non proiicitur in punctum seu stellam L quae occidentaliori apparet, imo ad punctum K, quod tamen per eclypsium rationem aliter se habere inventum est, quemadmodum diximus. Plana quoque non potest esse,

quia non videmus stellas uno eodemque tempore oriri et occidere, sicut supra de coelo dictum est.

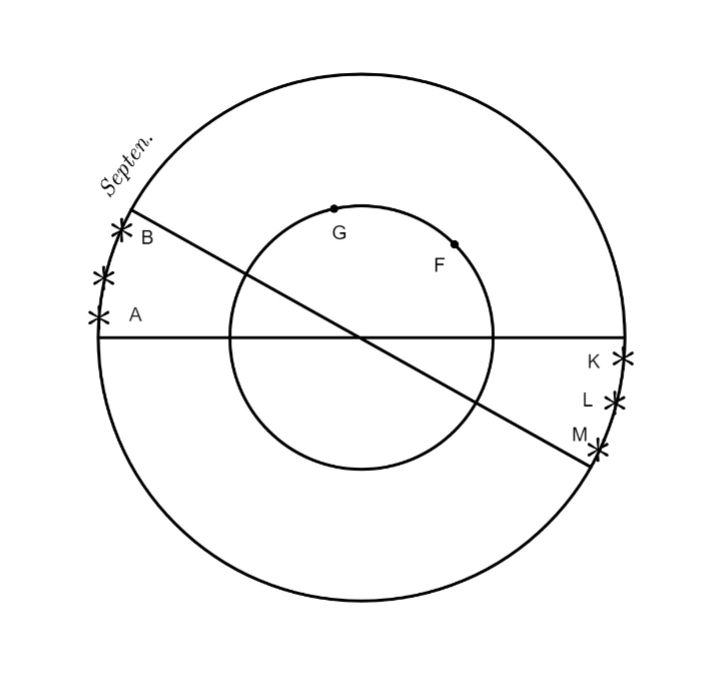
Quod autem.］ Secunda ratio qua probatur terrae rotunditas ab aquilone ad meridiem ducitur ab elevatione poli, qua cylindrica seu columnaris figura plane excluditur. Siquidem cernimus, euntibus nobis versus aquilonem, aliquot stellas de meridionalibus paulatim occultari, quod nullo modo fieret si terrae forma ab aquilone versus meridiem foret cylindrica. Ad haec, est etiam argumento quod sit sphaerica, quod videmus quantitatem dierum variari quando tendimus versus aquilonem ab aequatore. En tibi figura. Qui habitat versus septentrionem in puncto G, cui elevatur polus, illi videntur stellae ABC et stellae MKL occultantur ei, sed habitanti in F fit contrarium.

Ad haec si omnibus.］ Aquam esse rotundam non difficile est probatu. Nam argumentum quo utitur Ptolemaeus ad probandum aquae rotunditatem sumptum est a navigatione, quod per se omnino planum est et minime abstrusum. Siquidem videmus navigantibus nobis in mari, quod montes seu turres, quo magis eis accedimus, eo altiores incipiant apparere, quasi emergant ex aquis, quod prorsus non fieri possit si aqua esset plana et non sphaerica.

〈I.5〉 Caput V

Nam si sic.］ Proponit triplicem terrae situm posse imaginari, si quis contenderit eam non in medio tanquam centrum esse locatam. Aut quod sit extra axem et aequaliter distans ab utroque polorum, aut quod sit in ipso axe et sit proprior alteri polorum, aut quod sit extra axem et distet aequaliter a polis. Terram esse in medio totius probat tribus argumentis. Quorum primum similiter ab aequinoctiis, quo confutatur opinio eorum qui imaginantur terram sursum aut deorsum extra axem positam, nam si sic dividentur per horizontem, vel quae sub terra, vel quae supra terram sunt duo inaequalia, et nunquam continget iis qui sub aequinoctiali habitant aequinoctium, neque iis quibus sunt extra aequinoctialem, hoc est sub sphaeram obliquam, quod est contra experimentum. Siquidem videmus quod horizon tam rectus quam obliquus dividat aequatorem in duo aequalia, quod causa est aequinoctii, hoc planius percipietur ex figura consequenti. Esto AHKB meridianus circulus, KQ aequinoctialis, AB axis mundi. Et si

terra fuerit extra medium universi, aequaliter remota a polis mundi, iuxta primam positionem, necesse est eam esse in puncto D; quo concesso, erit HP horizon sphaerae rectae, non transiens per centrum universi, unde accidit aequatorem per eum secari in duas portiones inaequales et nunquam habitantibus sub aequatorem fieri aequinoctium, quod est contra sensum. Porro si imaginaberis AL esse horizontem obliquam idem continget, nempe quod nunquam continget aequinoctium cum Sol fuerit in punctis aequinoctialibus, scilicet capite Arietis et Librae, quia aequator KQ dispescitur in duo inaequalia, scilicet KD et DQ, sed contrarium contingit, ergo terra non est extra centrum universi. Quae si esset propius accederet aut ad ortum aut ad occasum, et oriens tempus usque ad meridiem esse longius quam tempus a meridie seu zenith usque ad occasum, et contra, sicut linea AD longior est linea DL, et stellae modo maiores modo minores apparerent, et umbrae essent inter se diversae quantitatis, quod non fit: igitur terra non est extra centrum universi. Alterum argumentum sumptum est a divisione sphaerae et gnomonum umbra, quae directe ad occasum cadit cum Sol oritur cum punctis aequinoctialibus, hoc argumento interimitur opinio seu positio secunda, terrae scilicet quod sit in axe mundi, sed inaequaliter remota a polis universi.

Esto terra super puncto H, in axe axe] axi B

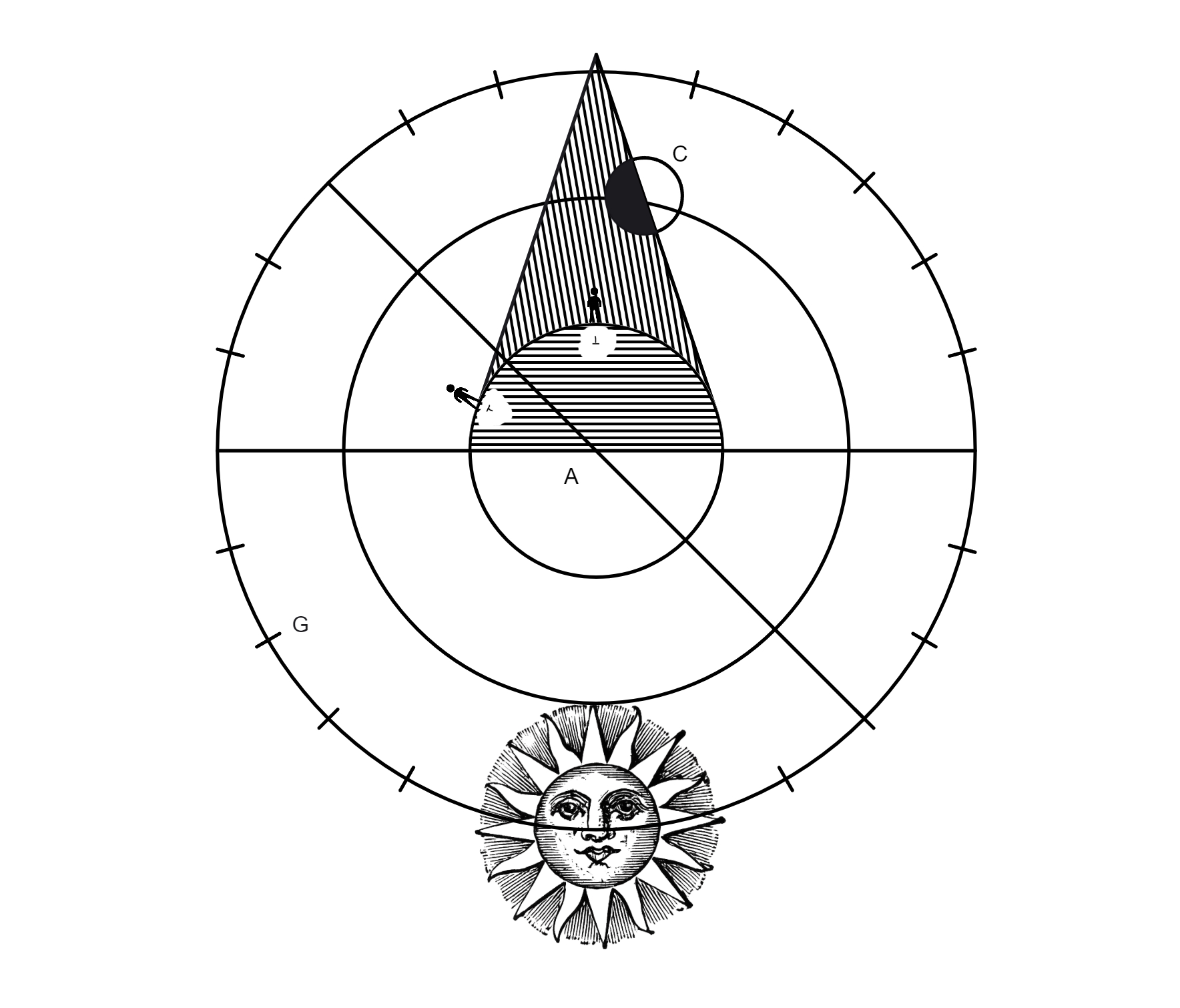
universi, inaequaliter distant distant] read distans a polis REQ, sit horizon obliquus dividens universum in partes inaequales una cum omnibus circulis suis, scilicet aequatore et zodiaco, unde non potest fieri, ut iuxta hanc imaginationem, sint semper sex signa supra horizontem et sex intra horizontem, quae tamen esse comprobata sunt, neque secundum hunc positum terrae aequinoctium fieri potest cum Sol fuerit in signis seu punctis illis in quibus solet aequinoctium contingere, quia horizon obliquus HF non dirimit aequatorem DB in duo aequalia, sequitur etiam hinc quod stellae quae sunt in sectione RABQ sint terrae propinquiores et appareant maiores quam quae sunt in reliqua sectione, quod nequaquam ita se habere manifestum est ex praecedentibus. Postremo si concedatur terram esse in axe, sed extra centrum axis, tunc concedendum est umbram, cum Sol fuerit in puncto aequinoctiorum, scilicet D, directe cadere oriente Sole ad occasum, quod non fit, imo cadit a D in G et non in B, quod nobis certis experimentis constat cadere. Ideo neque haec terrae positio constare potest. Tertium argumentum sumptum est ab eclypsibus lunaribus, quas crebrae observationes et longa consuetudo docuerunt, non nisi oppositione luminarium fieri, quod falsum esset si terra esset extra centrum universi, imo fieret extra opposita puncta luminarium. Sicut deduci potest ex hac figu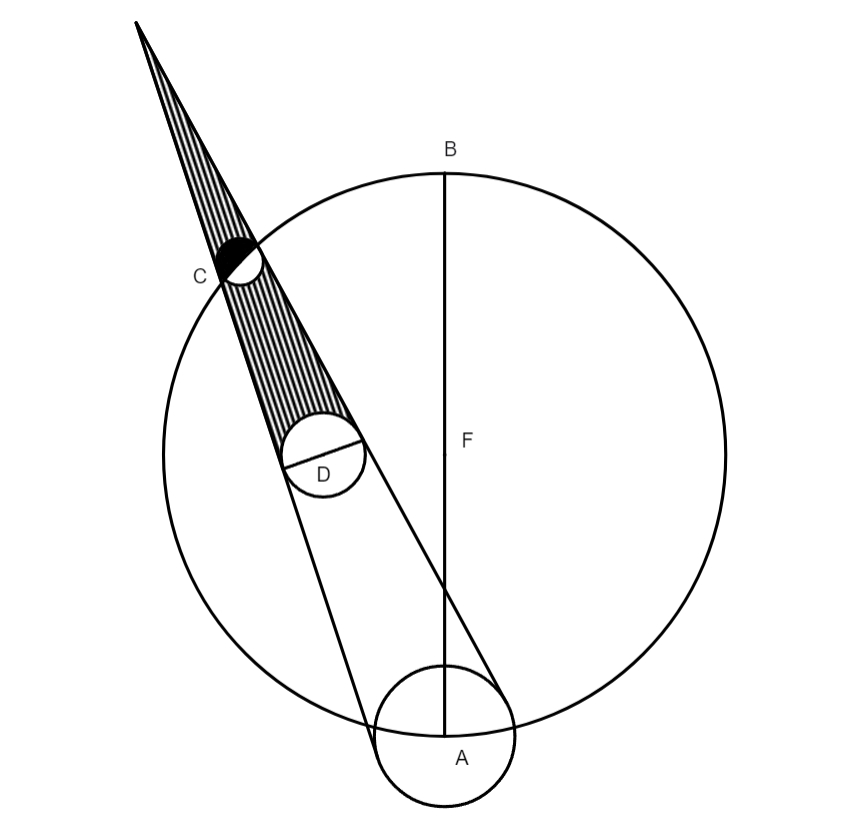
ra, in qua ABC refert sphaeram coeli, F centrum universi a quo distat

terra in puncto D, et cum Solis centrum fuerit in puncto A, tunc cadit conus umbrae in punctum E, et cum Luna tempore quod possibile est fieri eclypsim in eam incidet, fiet sine dubio eclypsis. Hinc ad oculum apparet, si terra est extra centrum totius, eclypsim posse fieri extra oppositionem luminarium, talis hactenus nunquam visa est, igitur certum est terram esse in centro totius. Etiam hinc manifestum est tertiam opinionem, quae ponit terram extra centrum universi ita ut sit inaequaliter remota a polis mundi, non habere locum, quae iisdem argumentis refutari potest quibus reliquiae duae.

〈I.6〉 Caput VI

Quod vero puncti.］ Hoc capite Ptolemaeus tribus rationibus probat terram quasi punctum ad coelestia comparatam. Prima ratio deducitur a stellarum magnitudine, quae ubique terrarum manet eadem. Nam si terra comparata ad coelum stellarum, haberet haberet] habetet B aliquam rationem magnitudinis, et non esset instar puncti, sine dubio stellae observatae in diversis climatibus forent diversae quantitatis, quod prorsus non est: hinc concluditur eam, cum comparabitur ad stellarum fixarum magnitudinem, esse instar puncti. Nam certum est quamlibet stellam fixam multis vicibus maiorem esse terra, ex hac ratione quisquam facile persuaderi poterit terram nullius magnitudinis esse ubi comparata fuerit ad tantam distantiam.

Accidit quod gnomones.］ Altera ratio sumitur a gnomonibus ac reliquis instrumentis mathematicis, ut sunt astrolabia, armillae, torqueta et reliquia huius generis. Quae in quacumque parte terrae ponuntur, ita servant ad amussim circonductiones umbrarum ac si ponerentur in centrum terrae, haec, inquam, ratio per se clarissima est.

Haec ita se habere.］ Tertia ratio ex superioribus clara est, quae ducitur a superficiebus horizontalibus quibus superius hemisphaerium dirimitur aequaliter ab interiori, ita quod semper sex signa supra et sex sub terra sint, hoc minime fieret si magnitudo terrae esset sensibilis ad stellarum fixarum sphaeram comparata. Hactenus.

〈I.7〉 Caput VII

Per eadem.］ Si terra, et non coelum ipsum, moveretur, accideret ei motus rectus aut motus circularis. Sed in superioribus tribus firmissimis argumentis monstravit impossibile esse ut terra sit extra centrum totius, nam si moveretur in rectum cogeretur relinquere centrum in infinitum moveri motu violenti, quod prorsus motui gravium contrarium est. Nam cum gravia corpora naturaliter moveantur deorsum, et terra sit gravissima, erit motus eius tantum ad centrum universi, ad quod naturaliter tendit, et non secus ac ferrum ad magnetem, ideo non credendum est eam moveri recto motu. In qua etiam circularis motus, sicut Ptolemaeus hoc capite abunde probat, ecluditur, quae si moveretur circa axem mundi ab occidente ad orientem, fieret hoc propter immensam gravitatem suam motu velocissimo, et omnia quae in aere moventur, ut sunt nubes, volucres et reliquae huius generis, viderentur semper moveri ad occasum, sed nos experimur contrarium. Est etiam hoc satis vehemens argumentum quod terra omnino non admittit localem motum, nempe quod videmus non tantum in Sole ac Luna verumetiam in aliis syderibus subinde fieri coniunctiones, quod nequaquam fieri posset si terra foret localiter mobilis. Haec omnia Ptolemaeus hoc capite copiose tractat, ad diluenda argumenta pythagoricorum, qui statuebant terram et non coelum mobilem.

〈I.8〉 Caput VIII

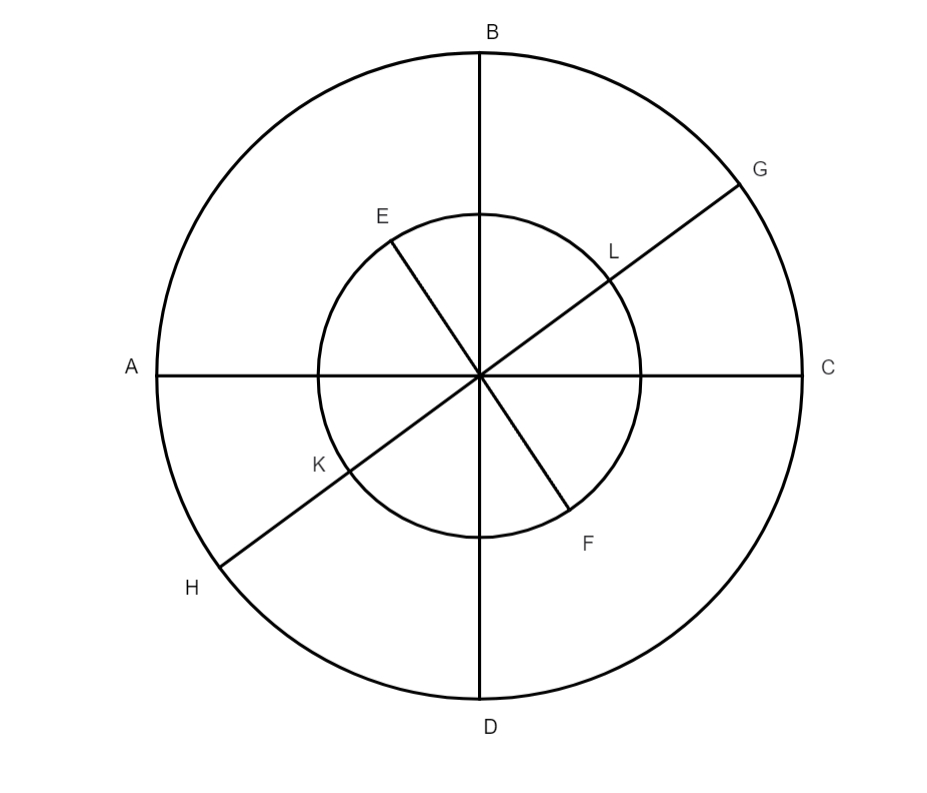
In hoc capite Ptolemaeus agit de differentia duorum motuum, quorum alter est ab ortu ad occasum, alter autem ab occasu ad ortum, contrarium priori. Deinde paucis ob oculos ponit quibus rationibus hii duo motus qui ab hominibus prisci seculi inventi sint, et qui sint precipui circuli in coelo. Primus motus est circularis et regularis super duobus polis mundi, qui omnibus coelestibus est communis, a quo rapiuntur ab ortu ad occasum, et hoc in vigintiquatuor horis aequalibus: hinc consequitur quod singula puncta aequaliter distantia a polis mundi describant circulos aequidistantes, quorum omnium maximus appellatur aequinoctialis, eo quod cum Sol sub eo graditur fiat aequinoctium per universam terram. Est et alius motus superiori contrarius, et est motus secundorum mobilium, qui fit ab occasu ad ortum. Hi duo motus differunt inter se, scilicet secundum priorem describunt puncta quae quae] que B sunt extra aequinoctialem circulos aequidistantes aequinoctiali, secundum vero posteriorem hoc non fit, quia perficitur super aliis polis quam polis primi mobilis. Hoc duos motus, scribit Ptolemaeus in hoc capite, a priscis syderum observationibus hac ratione esse deprehensos, nempe cum viderent Solem ac alia sydera oriri, et paulatim ascendere ad meridiem, et deinde iterum meridiem relinquere, et occidere, ac aliquandiu sub terra moram facere, et in ortu rursus apparere, statim concluserunt hoc fieri super polis mundi. At cum notaverant locum ortus Solis in orientali horizonte, et viderant post aliquot dies locum eius variari, concluserunt eum in alio circulo vehi qui contramitteretur primo mobili, per quem posset deferri ad punctum verticis nostrae, et iterum ab eo discedere motu eiusmodi circuli cuius poli essent alii quam poli motus ab ortu ad occasum, et eandem rationem deprehenderunt etiam in aliis secundis mobilibus, haec omnia luculentissime a Ptolemaeo hoc capite tractantur. Ut hoc melius perspiciatur visum est, duo schemata adponere. Alterum de duobus motibus, alterum vero de circulis quorum hoc capite fit mentio.

Prima figura

Circulus ABCD refert globum primi mobilis, quod movetur super polis mundi

AC a B puncto in D, et a D in B, hoc est ab ortu ad occasum. Circulus autem EKFL referat globum, seu sphaeram Solis seu alterius cuiusdam de stellis erraticis, cuius motus super polis GH distantibus a polis mundi, fiat ab E versus F motu contrario, hoc est ab occidente in orientem.

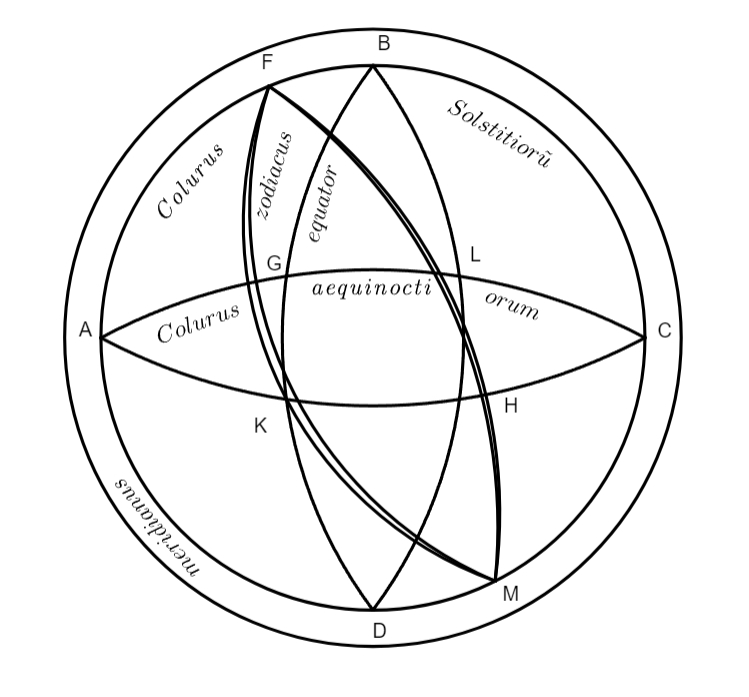
Altera figura

In hac figura est ABCD colurus solstitiorum. Exterior circulus est meridianus, FGHM zodiacus, BKDL refert aequatorem. Et AGLHK est colurus aequinoctiorum. Hactenus de prima principiis astronomiae, sine quibus apparentiae salvari non possunt.

〈I.9〉 Caput IX

Quinque Ptolemaeus propositiones in hoc capite proponit, quibus docet tabulam rectarum linearum, quae singulis arcubus in semicirculo subtenduntur, conficere. Prima docet, data circuli diametro, latera decagoni, hexagoni, pentagoni, tetragoni et trianguli rectorum laterum invenire.

Secunda docet quomodo, data alicuius arcus chorda per primam inventa, innotescet chorda arcus residui de semicirculo. Tertia manifestat inventionem chordae qua differunt duo arcus inaequales, quorum chordae seu subtensae sunt datae. In quarta traditur doctrina de invenienda medietate chordae datae in semicirculo. Quinta tradit rationem quomodo, datis subtensis duorum arcuum in semicirculo, subtensa arcus ex his compositis investigetur. Ex his paucis propositionibus docuit Ptolemaeus ingeniosissime componere tabulam subtensarum.

Utemur.］ Gradus unus dividitur in sexaginta minuta, et minutum iterum in sexaginta partes quae secundae appellantur, et secundae per sexagenarium numerum in tertias, et sic deinceps.

Nam quoniam.］ Hac demonstratur propositione sexta secundi Euclidis. GD est linea tota cui additur DF, si multiplicabitur GF in FD et producto additur quadratum DE, prosiliet quantitas quadrati lineae FE, quae est dimidium lineae datae, et lineae adiectae. Sed cum DF sit ignota ac linea FE aequalis BE, erit EB quaerenda, quod fit pro penultimam primi, ubi docetur duo quadrata ED et DB tantum valere quantum quadratum BE; extracta radice, habebimus lineam FE, a qua subtracta DE, relinquetur FD latus decagoni. In extrahendis radicibus, quo plures adieceris cyphras, eo exactius prodibit quaesitum.

Linea ergo.］ Ratio dividendi aliquam lineam secundum proportionem habentem medium et duo extrema docet propositio 16 sexti et nona tredecimi.

Erit profecto.］ Hoc confirmatur per conversam decimae tredecimi.

Similiter quoniam.］ Ratio huius sententiae demonstratur ab Euclidis propositione octava, libri tredecimi.

Nam quoniam.］ Quod angulus ABG sit rectus habetur ex trigesima propositione libri tertii Elementorum, in qua affirmatur quod rectilineus angulus constitutus super semicirculum fit rectus, operatio absolvitur per penultimam primi. Duc AB in seipsum, et similiter AG, et subtrahe quadratum ipsius a quadrato AG, ex residuo quaere radicem quadratam, productum dabit tibi lineam BG, per hanc propositionem multae lineae subtensae investigantur, sive linea data sit maior sive minor semicirculo.

Prout forte.］ Priusquam perveniat ad contendendum quomodo differentia duarum subtensarum quae datae sunt investiganda sit, praemittit theorema in quo demonstrat quod quadrangulum quod fit ex duobus diametris diametris] diamemetris B quadrilatae figurae tantum valeat quantum duo quadrangula quae fiunt ex lateribus oppositis. Et cum angulus ABD sit aequalis angulo EBG, nam angulus EBD est communis, erit per sextam sexti proportio BG ad GE sicut BD ad DA, quare per 17 sexti quadrangulum AG in AD aequale est quadrangulo BG in EG. Ut,

Porro, cum triangulus ABE aequalium est angulorum cum triangulo BGD, erit proportio per eandem ipsius AB ad AE, sicut proportio BD ad GD, et quadrangulum quod fit ex AB in BG, per 17 sexti, quemadmodum quadrangulum quod fit ex BD in AE.

Nunc si duxeris numerum lineae BD in numerum lineae AG duorum diametrorum, erit productum aequale producto quod provenit ex multiplicatione laterum oppositorum, hoc est lateris BG in AD et lateris AB in GD.

Hoc ita opposito.］ Sed priusquam tradatur exemplum quo docebitur qua ratione differentia duarum subtensarum quarum quantitas nota est quaerenda sit, ut exempli gratia chorda arcus BG per duas datas, scilicet AB et AG, investigentur per penultimam primi duo diametri quadrilaterae figurae ABGD, scilicet per AB ipsa BD, et per AG, GD; quibus habitis, duc lineam AG in lineam BD, productum serva seorsim, deinde duc AB in GD, illud quadrangulum subtrahe a quadrangulo servato, et quod reliquum est divide per lineam AD, hoc est diametrum, productum erit ipsa differentia, scilicet linea BG.

Exemplum

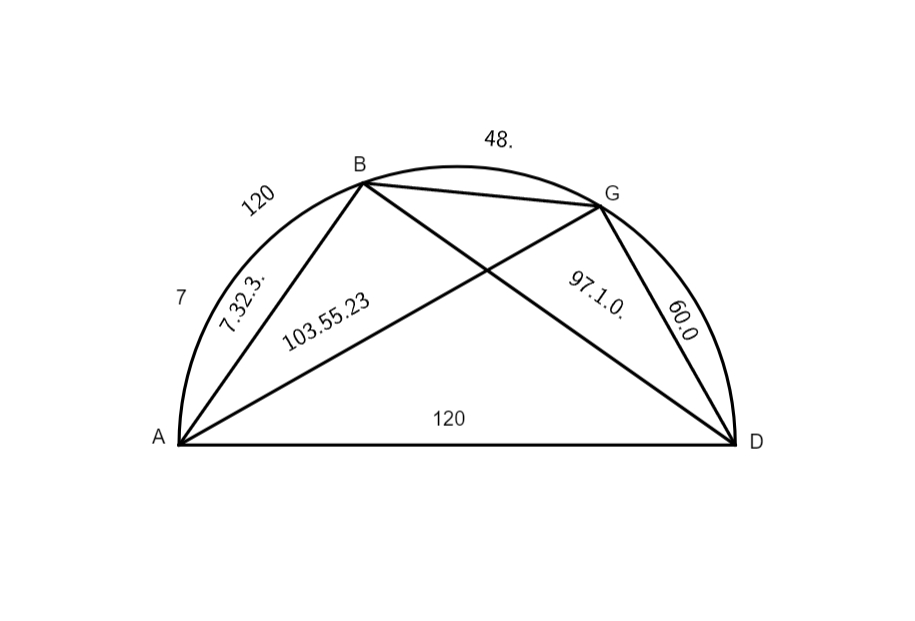
Sit chorda arcus AB data per primam huius, quae est chorda pentagoni, scilicet 70 gradus 32

minuta 3 secundae. Et similiter chorda arcus AG, quae mota mota] read nota est ex superioribus, et est 103 graduum 55 minutorum ac 23 secundarum per chordam AB, et penultimam primi inveni chordam BD, quae est 97 graduum 5 minutorum et 8 secundarum proxime. Eodem modo investigavi etiam chordam GD, quam reperi esse 60 graduum. Quo facto, duxi chordam AG in chordam BD, productum servavi, deinde duxi opposita latera quadrilaterae figurae ABGD unum in alterum, productum subtraxi a quadranguli servati producto, residuum mihi divisum est per 120 gradus diametri qui opponitur lateri BG, quod quaeritur, et prodierunt 48 gradus 48 minuta et 35 secundae feret feret] read fere; tanta est chordae quae arcui BG subtenditur, per hanc propositionem multae subtensae quaeruntur, et non solum subtensae arcuum differentiarum, imo etiam arcuum residuorum de semicirculo, sicut videre est in hac figura, ubi per subtensam arcus AB datam nobis innotuit chorda arcus BD, residui de semicirculo, et similter chorda arcus GD.

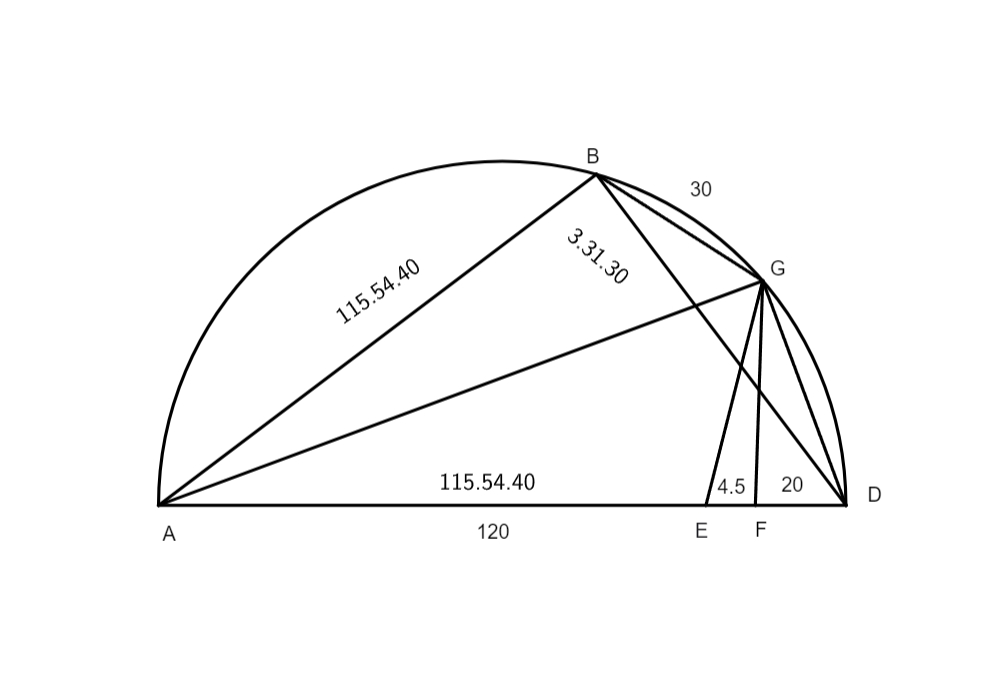
Sit rursus.］ In praecedenti docuit invenire lineam, quae subtenditur arcui, quo differunt duo arcus inaequales in semicirculo, in hac vero medietatem chordae quae medietati arcus chordae datae subtenditur invenire docet. In operatione huius propositionis duae requiruntur propositiones, scilicet decimasexta sexti et ultima primi, qua investigatur, per chordam arcus BG datam et diametrum AG, linea AB, cuius productum subducatur a diametri

quantitate, et residuum erit linea ED, excessus minorum lineae AD supra lineam AB, cuius medietas erit linea FD, quo proacto, quaeras GD lineam, quae subtenditur dimidio arcui lineae BD, quod efficies per decimamsextam sexti, ut dictum est, in qua docetur scilicet, datis tribus lineis proportionalibus, quod quadrangulum primae et tertiae sit aequale quadrato lineae mediae.

Esto in hac figura AG prima, GD secunda, FG autem tertia, et si duxeris numerum lineae AG in numerum lineae GF exibit quadratum ipsius GD, si inde quaesieris radicem quadratam, aut proxime quadratam, habebis lineam GD quam quaerebas.

Exemplum.

Esto arcus BG 30 graduum, subtensa eius est 31 graduum 3 minutorum 30 secundarum, quam resolvimus per sexagenarium numerum in secundas, et venerunt in producto 111,810 secundae, secundae] seeundae B quibus multiplicatis in se provenerunt 12,502,476,100 quartae, hoc productum ablatum est a producto diametri, scilicet a 186,624,000,000 quartis, et remanserunt 174,122,523,900 quadratum, scilicet lineae AB; ex hoc numero eduximus radicem quadratam, cuius productum fuerunt 417,280 secundae, divisis illis bis per sexaginta exierunt 115 gradus 54 minuta 40 secundae. Tanta, inquam, est linea quae subtenditur arcui AB, qui est residuus de semicirculo, hoc est 150°. Productum hoc subtraximus a diametro et reliqui fuerunt 4 gradus 5 minuta 20 secundae, quarum dimidium sunt 2 gradus 2 minuta 40 secundae, medietas scilicet excessus lineae AG supra lineam AB; hoc peracto habuimus duas lineas, nempe primam et tertiam de tribus lineis proportionalibus in hoc semicirculo notas, per quas documentum decimaesextae sexti invenimus mediam seu secundum eius quadratum, quod prosiliit ex multiplicatione prima in tertiam fuerunt 3,179,520,000

quartae. Huius numeri radix quadrata sunt 56,387 secundae, quas postquam per sexaginta dividimus more solito, habuimus 15 gradus 39 minuta et 47 secundas, subtensam scilicet, quae medietati arcus dati AB subtenditur, hoc est 15 gradus. Per hanc propositionem, ut inquit Ptolemaeus, possunt multae subtensae inveniri. Hactenus de hac propositione.

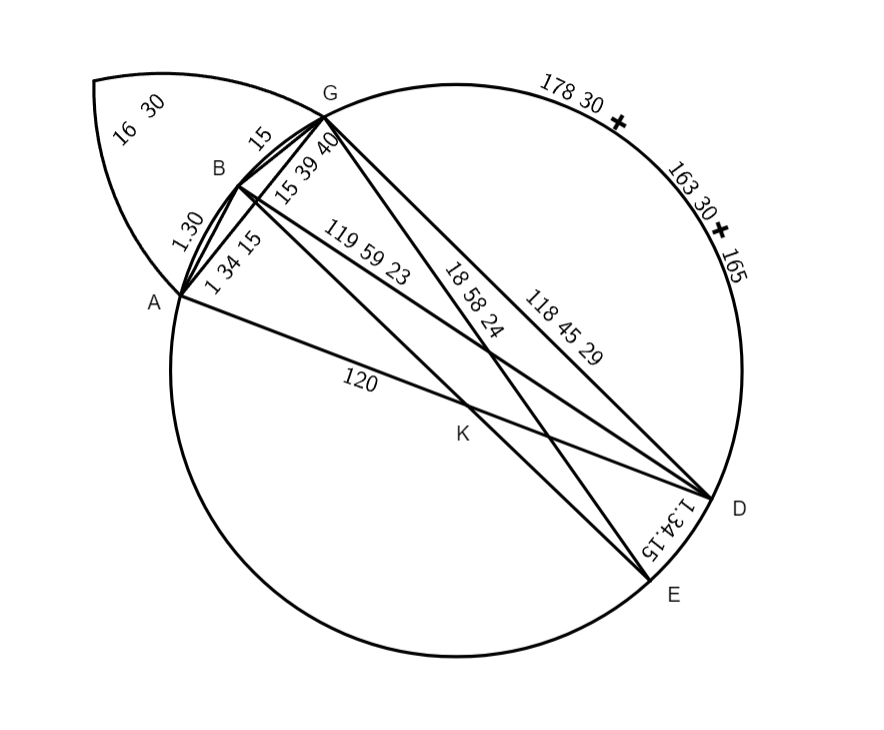
Sit rursum.］ Per hanc propositionem quatuor arcuum subtensae, sicut parebit, investigari possunt, nempe subtensa arcus compositi ex duobus arcubus datis, subtensa arcus residui de semicirculo BGD, subtensa arcus GDE et subtensa arcus residui ad semicirculum GD. Tota operatio huius propositionis perficitur adminiculo duarum propositionum, quarum altera est penultima primi, altera vero decimaseptima sexti. Itaque cum lubet quaerere quanta sit chorda quae subtenditur arcui 16 graduum et 30 minutorum, qui componitur ex 15 gradibus et 1 gradu ac 30 minutis, quemadmodum est arcus AG in hac figura, huius, inquam, arcus subtensam hoc modo quaesivimus, scilicet primo per AG lineam notam, quae est 1 gradus et 34 minutorum ac 15 secundarum, et per AD lineam, opitulante penultima primi, investigata est nobis chorda BD, quam invenimus esse 119 graduum 59 minutorum et 23 secundarum. Tanta est chorda arcus BGD, residui de semicirculo, qui est 178 graduum et 30 minutorum. Ad eundem modum invenimus per penultimam primi et chordam notam BG, quae in hoc exemplo est 15 graduum 39 minutorum et 40 secudarum, chordam GE, nam multiplicavimus BG in se, et diametrum, scilicet lineam AD, in se, et subtraximus quadratum ipsius BG a quadrato AD; residui radix educta est, quae erat 118 graduum 58 minutorum et 24 secundarum. Tanta est subtensa arcus residui de semicirculo, hoc est ipsius GDE, qui est 165 graduum quorum tota circumferentia circuli est 360. Ut supra meminit Ptolemaeus, harum duarum subtensarum producta iuxta sententiam decimaeseptimam sexti multiplicata sunt unum cum altero, et provenerunt 185,011,480,752 quartae, ab his subtraximus productum lineae BG ductae in lineam DE, quae sunt opposita latera, scilicet 318,868,485, et remanserunt 184,692,612,267. Hunc numerum dividimus per lineam AD, scilicet 120 gradus, et prodierunt 427,529 secundae. Has redegimus per 60 in minuta, et minuta in gradus, et habuimus 118 gradus 45 minuta ac 29 secundas pro linea GD, sine qua impossibile est inveniri subtensam arcus compositi, scilicet AG, sic habetur etiam chorda arcus GD residui ad semicirculum, nempe 163 graduum et 30 minutorum. Nunc porro multiplicavimus 118 gradus 45 minuta et 29 secundas in se, productum servabatur nobis seorsim, deinde multiplicavimus diametrum in se, a cuius producto subtraximus id quod servatum est seorsim, radix residui fuerunt 61,989 secundae, quibus divisis per 60 venerunt 1,033 minuta et remanserunt 9 secundae, his iterum divisis per 60 prosilierunt 17 gradus et reliqua fuerunt 13 minuta productum, scilicet lineae arcus compositi AG est 17 graduum 13 minutorum 9 secundarum.

Perspicuum autem est.］ Hoc animadvertere decet, quod cum volueris alicuius arcus compositi rectam lineam invenire, semper altera linearum cognitarum, ex quibus arcus compositus, cuius subtensa quaeritur, constat, debet esse linea illa, quae uni gradui, et triginta minutis subtenditur, sicut in hoc exemplo est linea AB, quae est 1 gradus 34 minutorum 15 secundarum; huius lineae arcui adde seu appone arcum alterius lineae notae qui sit minor quam quarta semicirculi, ut exempli gratia: volo quaerere per compositionem lineam quae subtenditur arcui 37 graduum et 30 minutorum, qui arcus constat ex 1 gradu 30 minutis et ex 36 gradibus, horum 36 graduum subtensa est 37 graduum 4 minutorum et 55 secundarum, altera scilicet linea nota, et per subtractionem habebis etiam 142 gradus 30 minuta residuum, scilicet de semicirculo: nam per hanc propositionem possunt quatuor arcuum subtensae investigari, sicut superius dixi, hoc solum animadvertas quod ratio arcus AB et ratio arcus BGD, residuum de semicirculo respectu arcus AB, semper manet invariabilis in operatione huius propositionis.

Dico igitur.］ Priusquam Ptolemaeus doceat quomodo linea quae uni gradui de circumferentia subtenditur venari queat, affirmat geometricis demonstrationibus quod datis duobus arcubus inaequalibus maioris arcus proportio ad minorem sit maior, et proportio subtensae maioris arcus sit minor ad subtensam arcus minoris.

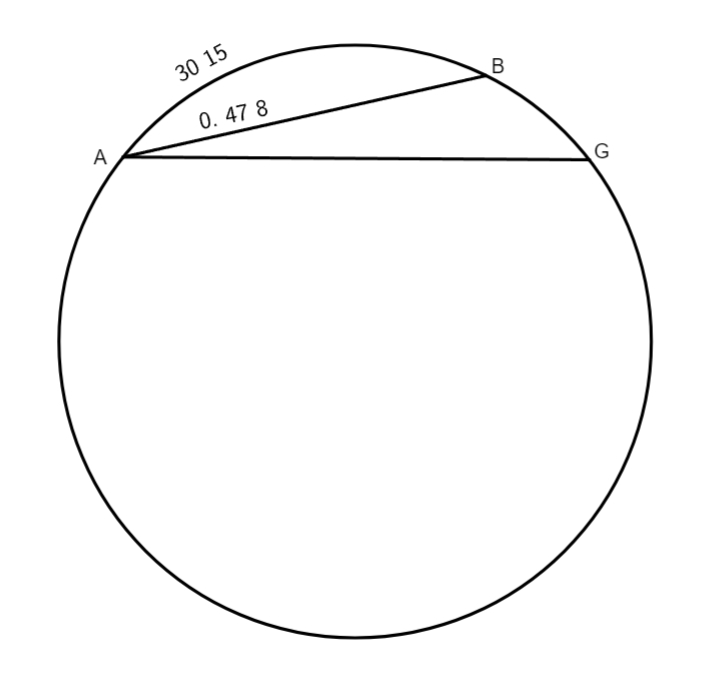
Hoc ita proposito.］ Quod supra ingeniose demonstravit, nunc exemplis ob oculos ponit. Sit arcus AB 30 minutorum et 15 secundarum et arcus ABG gradus unius, huius chorda quaeritur, quae hac ratione nobis nota fiet, nam ex quo proportio arcus ABG ad arcum AB sit sesquitertia, hoc est arcus ABG complectatur arcum AB semel et unam tertiam eius, erit linea AG minor quam linea AB sesquitertia, sed ut hoc clarius videas, accipe tertiam partem lineae AB, quae

est 15 minutorum 42 secundarum et 40 tertiarum. Hunc numerum adde ipsis 47 minutis et 8 secundis, habebis in producto 1 gradus 2 minuta 50 secundas et 〈40〉 The number is omitted in the witness, 〈40〉 has been supplied based on preceding numerical context. tertias. Erit igitur linea AG minor quam unus gradus 2 minuta 50 secundas et 40 tertias. Porro sit arcus ABG 1 gradus 30 minutorum et arcus AB unius gradus, linea AG ex superioribus inventa est 1 gradus 34 minutorum et 15 secundarum. Per hunc numerum investigaturi sumus lineam AB, quod ita fit. Nam cum arcus ABG continet arcum AB semel et eius medietatem, erit linea AG minor linea AB sesquialtera, quae nobis in hunc modum innotescet: accipiatur tertia pars lineae AG, quae est 31 minutorum 25 secundarum, hunc numerum subtrahe subtrahe] subttahe B a 34 minutis et 15 secundis, et relinquentur 1 gradus 2 minuta et 50 secundae, quantitas scilicet lineae AB, quae maior est quam unus gradus 2 minuta et 50 secundas. Hinc manifestum est si chorda arcus unius gradus, ponetur 1 gradus 2 minutorum et 50 secundarum, nullum errorem sensibilem nasci in calculo astronomico; per quartam aut quintam Ptolemaeus invenit chordam dimidii gradus esse 31 minutorum 25 secundarum. His quinque propositionibus seu theorematibus absolvit Ptolemaeus suam tabulam chordarum, quae non minus satis facit negotio chordarum quam illae quae ex multis foliis constant.

Tertiae trigesimam.］ Paucis tangit usum trigesimarum, qui non alius est nisi quod per eas tabula chordarum corrigitur et quaeruntur subtensae eorum arcuum quibus pauciora quoque 30 minuta adhaerent, ut, exempli gratia, offertur nobis arcus 42 graduum et 25 minutorum et 30 secundarum. Huius arcus subtensam hac via quaesimus, nempe accepimus subtensam arcus proxime minoris, quae est 43 graduum 0 minutorum et 15 secundarum, quam servavimus seorsim, deinde accepimus in linea trigesimarum 58 secundas et 36 tertias, cum illis multiplicavimus 25 minuta et 30 secundas, productum redegimus per 60 in denominationem grossiorem, hoc est in secundas et minuta, et prodierunt in producto 24 minuta 54 secundae. Ea addidimus producto servato, quod inde ascendit fuerunt 45 gradus 25 minuta 9 secundae. Tanta, inquam, est subtensa quae arcui 42 graduum 25 minutorum et 30 secundarum subtenditur. De secundo usu harum trigesimarum infra dicam. Sed ut queas tutius operari in hac tabula, praescribam tibi duos canones, quorum altero quaeres subtensam arcus oblati, altero vero arcum ipsum qui debetur subtensae oblatae. Itaque cum tibi offeretur arcus cui nulla minuta adhaerent, hoc est integrorum graduum, ingredere directe in tabulam chordarum, et numerus qui tibi obviaverit erit id quod quaeritur. Si autem in minuta aut secundae adhaerebunt gradibus arcus dati, ingredere cum numero proxime minore quod tibi occurret in tabula subtensarum, scribe seorsim, quo facto, sume differentiam inter numerum seorsim scriptum et proxime maiorem: illa erit pro secundo numero, primus erit semper incrementum illud quo gradus gradum superat. Deinde sume etiam arcum proxime minorem ab arcu oblato, id est arcu tuo, quod relinquitur erit tertius numerus, resolve singula in minimam denominationem, et operare iuxta tenorem regulae de tribus, quod inde veniet adde numero servato scilicet gradus gradibus, minuta minutis, et sic deinceps: ut cupio scire secundum hunc canonem quanta sit chorda quae subtenditur arcui 42 graduum 25 minutorum et 30 secundarum. Hunc arcus non invenimus in linea arcuum, ideo accepimus proxime minorem, hoc est arcum 42 graduum, et e regione eius in linea chordarum invenimus 43 gradus 0 minuta 15 secundas, quae seorsim scripsimus, et cum ea abstraximus a numero immediate consequente, scilicet proxime maiore, reliquum fuit 29 minutorum et 18 secundarum, quibus resolutis per 60 in secundas prodierunt 1,758 secundae pro medio numero, primus fuit 30 minuta. Hoc absoluto, subtraximus arcum 42 graduum ab arcu oblato, scilicet 42 gradibus 25 minutis 30 secundis, et relicta sunt 25 minuta 30 secundae. Redactis illis per 60 in minimam denominationem habuimus pro tertio numero 1530 secundas. Hinc operati sumus iuxta documentum prescriptum, et venerunt in producto 24 minuta et 54 secundae, quibus adiectis, servato habuimus 43 gradus 25 minuta et 9 secundas. Tanta est linea recta quae arcui oblato subtenditur, ut supra. Porro cum volueris scire ex chorda data arcum, tunc ingredere in tabulam chordarum cum chorda tua, si eam praecise inveneris, arcus eius erit iam inventus, sin minus subtrahe chordam proxime minorem a proxime maiore, quod reliquum est statue primum numerum, et incrementum, hoc est 30 minuta, alterum, postea subtrahe proxime maiorem a numero tuo, quod residuabitur erit tertius numerus. Deinde duc tertium in secundum et productum divide per primum, quod inde prosiliet addito numero graduum et minutorum, qui scribitur in linea arcuum in latere numeri proxime minoris, et habebis quaesitum. Exemplum. Si cupis scire quantus sit arcus subtensae 37 graduum 55 minutorum et 16 secundarum, et cum ista subtensa praecise in tabula chordarum non inveniatur, cape proxime minorem scilicet 37 secundas, gradus 34 et minuta 47, et arcum eius scribe seorsim et serva, quo facto, minue eam a proxime maiore, scilicet a 38 gradibus 4 minutis 36 secundis. Residuabuntur tibi 29 minuta 49 secundas, primus numerus, secundus erunt 30 minuta ut diximus. Postea minue proxime minorem, scilicet 37 gradus 34 minuta 47 secundas, a 37 gradibus 55 minutis et 16 secundis, et reliquum erit 20 minuta 29 secundae pro tertio numero, nunc multiplica et divide sicut dictum est, et prodibunt prodibunt] prodibut B 20 minuta, quae adiicias 36 gradibus et 30 minutis, quae scripta sunt in latere numeri minoris, et habebis quaesitum tuum, 36 gradus et 50 minuta, et sic operare etiam in reliquis; hic manifestum est quod Ptolemaeus tam satis faciet tibi sua brevitate, si modo scis operari per arcus duplices, quam alii sua prolixitate.

Hic etiam.］ Quae hic breviter ad corrigendas tabulas chordarum proponuntur ex superioribus satis nota sunt. Sed ne offendaris ex eo quod dicit, vel ab excessu aliarum, tradam tibi paucis regulam, qua poteris facile cognoscere an in aliqua chorda sit error, ex quo etiam pervidebis secundum usum tabulae trigesimarum. Ideo cum volueris scire alicuius chordae errorem, resolve eius trigesimam per 60 in tertias, ut fieri solet, productum duc in 30 minuta. Si post reductionem per 60 in grossiorem denominationem productum conveniet cum differentia quae est inter hanc et proxime sequentem chordam, nihil erroris erit in illa chorda. Et per contrarium emendabuntur etiam trigesimae, sed semper prius proposita chorda examinetur per propositiones quarum Ptolemaeus hic breviter meminit. Exempli gratia: volumus scire an ne sit error in chorda quae subtenditur 41 gradus, quae est 42 graduum 1 minuti 30 secundarum et 48 tertiarum. Hunc numerum redegimus per 60 in minimam denominationem, scilicet in tertias, et fuerunt 1,229 tertiae. Eas duximus in 30 minutas, productum divisimus per 60 et venerunt 1,764 secundae, quas iterum more solito divisimus et venerunt 29 minutae, et remanserunt post divisionem 29 secundae. Porro subtraximus 42 gradus 1 minutum 30 secundas a chorda proxime maiore, scilicet a 42 gradibus 30 minutis et 54 secundis, et differentia fuit 29 minutorum 24 secundarum, quae conveniunt cum superiori producto, igitur concludimus nihil erroris esse in hac chorda, et sic facito in reliquis. Etiam hic sciendum est quod trigesimae quae subtensas sequuntur nihil aliud sunt quam unius minuti in tali situ semicirculi, hoc est nihil aliud sunt quam trigesima pars distantiae quae est inter duas chordas; huius rei cape exemplum hoc. Differentia chordae arcus 44 graduum 30 minutorum et chordae arcus 45° est 29 minutorum et 3 secundarum, quarum trigesima pars est 58 secundarum et 6 tertiarum, hinc haud difficile est scitu an error sit in trigesimis.

〈I.10〉 Caput X

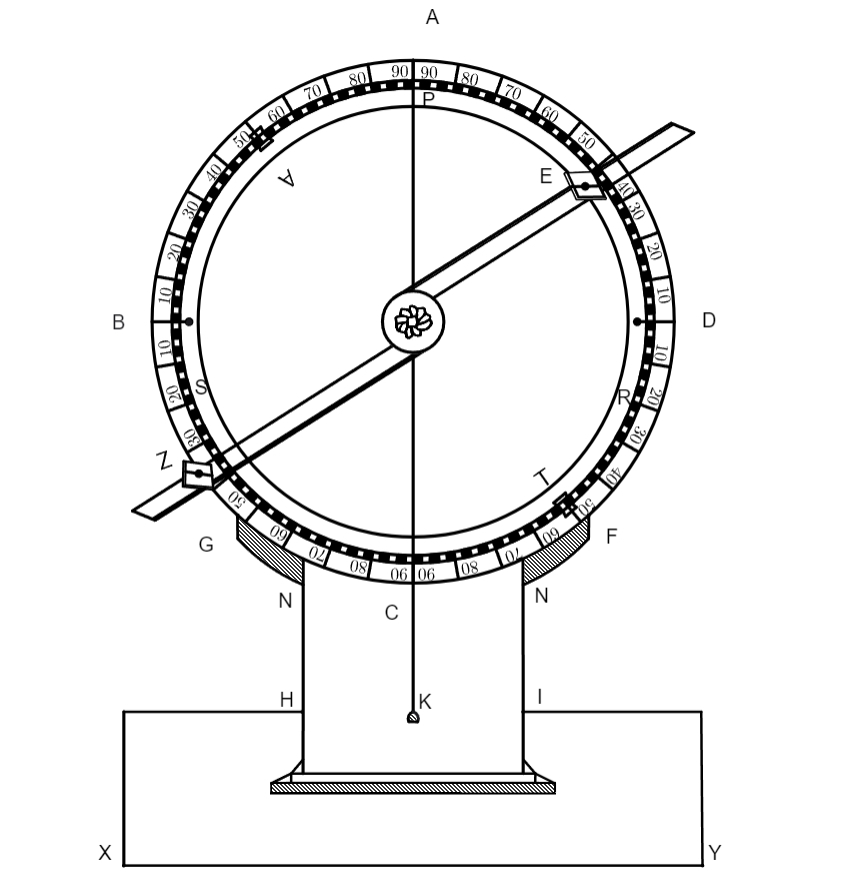
Sic igitur.］ Cum maxima Solis declinatio sit propemodum totius astronomiae fundamentum, non immerito Ptolemaeus, huius artis monarcha, hoc capite tam diligenter docet conferre instrumenta quibus talis declinatio, hoc est arcus qui inter tropicos est, venari possit, quam, inquam, declinationem artifices diversis temporibus diversam invenerunt, et hoc propter sphaerae octavae trepidationem, quae Ptolemaeo et aliis, propter observationum brevitatem, fuit penitus incognita; quid multis? Duo sunt, ut Ptolemaeus hoc capite docet, instrumenta per quae eiusmodi declinatio observari potest. Quorum alterum constat ex duobus circulis et basi, alterum vero ex quadrante, cuius preparatio et fabrica, ut ipse inquit, difficilior, et observatione commodior est: fabricam instrumenti horum circulorum, Proclus in libro 1 Hypotyposis astronomicarum positionum copiose describit, in qua nulla difficultas est: primo preparetur circulus ex metallo aut ligno purissimo mediocris magnitudine, summa diligentia tornatus, cuius superficies sit quadrata, qui sit circulus ABGD, et referat meridianum divisus in 360 partes. Huic aptetur alius circulus, qui sit PSR, ita ut

convexa superficies minoris

tangat superficiem concavam superioris, et sub ea semper maneat ac circumvolubilis sit absque impedimento, nunc ad septentrionem nunc ad meridiem pro usu instrumenti. Et in eo sint diametraliter parvae regulae, in quarum medio, hoc est linea fiduciae, fabricentur duae lingulae foraminatae, sicut sunt in hac figura ZE, quae inclinentur tum ad seipsas tum ad centrum circulorum. Hi duo circuli, cum prius fuerint ingeniose coaptati, ponantur super substentaculum, scilicet HIXY, perpendiculariter erectum in superficie horizontali directe ad lineam meridianam, ut est linea XY, hoc fiet tum ratione superficiei horizontalis tum ratione superficiei circuli meridiani per perpendiculum AK. Reliqua per se clara sunt: at cum haec certius et commodius habeantur per quadratum, sit ABC quadratus habens in latere BC, cuius adiutorio erigatur super linea meridiana CA, perpendiculariter super horizontalem superficiem paratam ad libellam. Et cum volueris observare maximam Solis obliquationem, adverte quo die Sol ingrediatur in puncta solstitialia, si in primum gradum Cancri et Capricorni. Exempli gratia, si vis scire quantum Sol declinet ab aequinoctiali cum fuerit in primo gradu Cancri, tunc eleva et deprime, eo existente in ipso meridie, regulam CD, donec Solis radius transeat per duo foramina pinnacidiorum, et signa punctum in AB arcu, quem tum tangit linea fiduciae CD; hoc toties facias donec tibi oblata fuerit maxima Solis altitudo, tempore aestivo pro exemplo sit punctus F. Et hac eadem ratione opereris etiam cum Sol fuerit in primo gradu Capricorni, scilicet eleves et deprimas regulam CD in meridie donec Sol transeat duo foramina pinnacidiorum, quo facto, signa punctum in arcu AB, ubi linea fiduciae scindet ipsum AB, ille erit minima Solis altitudo tempore hyemali. Itaque, si diviseris arcum EF, in exemplum cape punctum E quem circumscribunt haec duo puncta, per medium habebis quantum Sol tempore tuo declinet ab aequatore.

Nam circumferentia］ Eratosthenes Eratosthenes] Enatostenes B divisit totum circulum in 83 tantum partes. Sed Ptolemaeus hanc rationem dividendi circulum mutavit, eumque commoditatis causa divisit in 360 partes, unde quae est proportio 11 ad 83 ea est 43 gradus 42 minuta et 40 secundas ad 360 gradus.

Ab hac］ Quod altitudo poli sit aequalis distantiae puncti verticalis ab aequatore sic manifestum fit. Sit ABCD circulus meridianus, BD horizon obliquus, CE aequator, F punctus verticalis, A polus

mundi supra horizontem elevatus, G vero polus anctarticus, qui tantum deprimitur sub horizontem quantum alter elevatur. Nam A, polus mundi, distat ab aequatore CE per quartam meridiani cui aequidistat punctus F verticalis ab horizonte BD, unde quadrans AE est aequalis quadranti BF, nam omnes quartae unius circuli sunt invicem aequales, his duabus quartis est arcus AF communis, quo communi arco sublato ab utrisque aequalibus, AF et AE, quae relinquuntur sunt aequalia per communem sententiam, unde concluditur quod AB sit aequale ipsi FE. Nunc si vis scire altitudinem poli per Solis maximam declinationem, aut alias quascumque declinationes, accipe hanc regulam. Quae re per hoc quadratum Solis altitudinem supra horizontem in ipso meridie, et si Sol fuerit in signis borealibus, subtrahe ab altitudine meridiana inventa maximam Solis declinationem, aut eam quam Sol habet eo die quo observasti, quod relinquitur erit distantia aequatoris ab horizonte, hoc productum aufer a quadrante, quod residuabitur erit distantia puncti zenith ab aequatore, quae est equalis elevationi poli. In signis vero australibus per contrarium agendum est. Exempli gratia, fuimus in Europa in quodam loco ignotae altitudinis poli, hanc quaerere nobis animus est. Itaque observavimus per quadratum Solis altitudinem in meridie, quam reperimus cum Sol foret in primo puncto Cancri, 65 graduum et 19 minutorum. Ab hac altitudine subtraximus maximam Solis declinationem, quae est, iuxta Ptolemaeum, 23 graduum et 51 minutorum; quod residuabatur erant 41 gradus 28 minuta, elevatio scilicet aequatoris ab horizonte, et hoc ablato a 90 gradibus meridiani productum fuerunt 48 gradus 32 minuta, tantum est arcus inter zenith et aequatorem, cui similis est elevatio poli, ut dictum est. Ad hunc modum etiam in aliis tibi operandum est.

〈I.12〉 Caput XII

Nunc cum sequatur］ Postquam Ptolemaeus per observationes maximam Solis seu zodiaci obliquationem reperit, statim illi cogitandum fuit quomodo arcus particulares qui inter zodiacum et equinoctialem sunt possent commode inveniri, quod fecit per regulam sex quantitatum, quam ipsemet primum ingeniosissime excogitavit, atque in hoc capite demonstratam reliquit. Quoniam vix alia est regula commodior ad investigandum rationem coelestium motuum quam regula sex quantitatum. Et cum ubique brevitate studeat in opere suo numquam satis laudato, demonstravit hoc loci tantum duas rationum compositiones, quibus omnia quae ad coelestium motuum cognitionem requiruntur absolvit. Sed ut queas facilius assequi modum componendi tabulas quae necessariae sunt obliquationi Solis, ascensionibus rectis et obliquis angulorum inventioni ac latitudinum ortus et occasus, visum est tibi brevibus adscribere regulas, quibus numerus quilibet sex quantitatum oblatarum inveniendus sit. Esto GA secundum synthesim proportionum prima quantitas, AE secunda, GD tertia, DF quarta, FB quinta, BE sexta. Aut secundum disiunctionem proportionum. Esto GE prima quantitas, EA secunda, GF tertia, FD quarta, DB quinta, BA sexta.

Itaque si prima quantitas, hoc est GA, te fugerit, duc secundum in tertium, productum divide in quartum, quod exibit duc iterum in quintum, quod inde venit divide per sextum, dabitur tibi quantitas prima. Pro habenda secunda. Ducenda erit prima in quartam, productum dividendum per tertiam quantitatem, et quod natum est ducito in sextum, id quod provenerit dividito per quintum, et habebis secundam. Nunc porro si tertia desiderabitur, ducatur primus in quartum et quod natum est dividatur cum secunda, et numerus ex hac partitione natus multiplicetur in sextum et provenientis fiat particio per quintam. Nunc ad quartae quantitatis inventionem, cum igitur quartus ignorabitur numerus ducendus erit secundus numerus in tertium et productum dividendum per primum, et quotiens numerus per quintum multiplicandus, quod provenit iterum dividendum erit per sextum, resultans numerus erit numerus quaesitus. Si vero libuerit quintam quantitatem investigare. Dicito Dicito] read Ducito primum numerum in quartum, quod inde prosilierit dividito per tertiura, et hoc productum iterum multiplices in sextum numerum, quod pocreabitur cum secundo divides et obtinebis numerum qui querebatur tibi. Adhuc restat investigatio sexti numeri seu quantitatis,

quam hoc modo venari poteris, scilicet fiat multiplicatio secundae quantitatis in tertium, quod ex eiusmodi multiplicatione procreabitur dividatur per primum numerum quocientem, qui nascitur ex hac divisione ducito iterum in quintum, productum dividas per quartum, quod nascitur erit id quod desiderabas. Verum cum Ptolemaeus in calculo suo frequenter usus sit subtractione rationum, ut infra patebit, nos operaeprecium facturos putamus si hunc scribemus modus subtrahendi proportiones. Igitur, cum volueris subtrahere proportionem seu rationem a proportione seu ratione.

Ducito terminum secundum auferendae in terminum primum alterius, exempli gratia D in A, et fiet E, quo facto, ducito terminum primum auferendae in terminum secundum superioris, hoc est C in B, et fiet F. Porro sciendum est quod ea quae per regulam sex quantitatum investigantur bona ext parte per propositionem decimam quintam sexti Euclidis venari possunt, quemadmodum suo loco exemplis declarabimus.

Hinc sequitur］ Superioribus duobus theorematibus docuit invenire sextam quantitatem ex quinque notis, tum secundum synthesim tum secundum dieresim. Sed hoc theoremate sequente docebit: si arcus cognitus in semicirculo divisus fuerit in duos, et proportio chordae dupli unius ad chordam dupli alterius fuerit data, quomodo uterque eorum quos dividit cognitus erit. Investigaturus igitur hos arcus, dividas arcum cognitum per medium si proportio fuerit proportio aequalitatis. Sin minus, adde duos terminos proportionis datae, productum constitue primum numerum, chordam arcus cogniti secundum et terminum minorem tertium, quo facto, operare iuxta regulam de tribus, quod nascitur erit quantitas lineae EG; hoc productum subtrahe a dimidietate chordae arcus dati, residuum erit linea FE. Porro dimidia chorda arcus dati erit quantitas anguli ADF, quem si subduxeris ab angulo recto AFD, hoc est a 90 gradibus, remanebit angulus DAF, cui praetenditur chorda DF, nam angulus FDA et angulus DAF valent unum rectum. Et cum multiplicaverit lineam FE in se, et addideris haec duo quadrata secundum penultimam primi, habebis quadratum, ipsus DE; extracta radice quadrata, cognita erit linea DE. Nunc restat quaerere angulum FDE, qui est differentia duorum arcuum ignotorum, hunc, inquam, ita quaeras iuxta doctrinam triangulorum planorum, scilicet: duc numerum lineae FE in sinum totum, productum divide per numerum DE, producti quaeras arcum quem, si subtraxeris a media chorda arcus cogniti, nascetur tibi arcus quaesitus BG, si vero eum arcum addideris medietati chordae dicti arcus, habebis arcum AB, huius rei capias tale exemplum. Esto arcus AG cognitus 46 graduum, cuius chorda inventa est 46 graduum 53 minutorum, proportio duplae chordae arcus AB ad chordam duplam arcus BG est sicut 11 ad 7. Additis his duobus terminis, nascuntur 18° pro primo numero, chorda arcus cogniti sit numerus secundus, et terminis minor sit numerus tertius, quo multiplicato cum secundo, productoque diviso per primum, producentur 18 gradus 10 minuta, linea scilicet EG. Et si subtraxeris hoc productum a dimidia chorda arcus cogniti, hoc est a 23 gradibus et 26 minutis, habebis in producto 5 gradus 16 minuta, lineam nimirum FE. Et cum dimidius arcus sit cognitus erit etiam angulus FDA notus, qui est 23 graduum, quo ablato a 90 gradibus residuabuntur 67 gradus pro angulo DAF, cuius chorda subtendens, scilicet linea FD, inventa est 66 graduum et 14 minutorum, qua duplicata in seipsa provenerunt 15,792,676. Huic quadrato adiectum est quadratum lineae FE, 99,856 scilicet, prodierunt 15,892,532. Huius

numeri radix quadrata fuerunt 62 gradus et 11 minuta, tanta est linea DE. Nunc ad investigationem anguli EDF. In hoc rectangulo, EFD, sunt duo latera nota, scilicet ED, quod est 62 graduum et 11 minutorum, et latus EF quod est 5 graduum ac 16 minutorum. Si itaque, iuxta doctrinam triangulorum planorum, multiplicabis latus EF in 120 gradus et productum divides per latus DE, nascentur 10 gradus 9 minuta 48 secundae, huius producti arcus sunt 9 gradus et 30 minuta fere, quo dimidiato prodibunt tibi 4 gradus et 45 minuta angulus, scilicet EDF; hoc productum si ablatum fuerit a dimidio arcu cognito, hoc est a 23 gradibus, quod relinquitur erit 18 graduum et 15 minutorum arcus, nempe GB. Si vero dimidio arcui cognito adiectum fuerit, prosilient 27 gradus 45 minuta, tantus est arcus AB, et cetera.

Hinc etiam］ Huius teorematis operatio pendet tota a penultima primi, quarta sexti et triangulorum planorum cogntione. Si proportio sinuum fuerit aequalitatis, tunc subtrahendus erit arcus datus a semicirculo, et residuum per medium dividendum, productum erit arcus AB, huic adiecto arcu dato conflabitur arcus ABG. Si vero proportio sinuum fuerit proportio inaequalitatis, quaerendus erit angulus EDZ, quem hoc modo inventum curabis. Multiplica dimidiam chordam arcus dati, qui est arcus differentialis, hoc est lineam BZ, quae pretenditur angulo BDZ in se, hoc quadratum aufer a quadrato quadrato] quadratro B lineae BD, id est a quadrato semidiametri, ex residuo quaeras radicem quadratam, iuxta documentum penultimae primi, ea erit quantitas lineae DZ. Linea ZE hac via venabitur. Statue differentiam proportionum datarum numerum primum, arcum cognitum secundum, et terminum minoris proportionis numerum tertium, quo facto, operare secundum modum regulae de tribus, productum inde erit linea EB, cui si addideris medietatem chordae arcus dati nota erit linea EZ, hanc ducito in se, et lineam DZ in se: harum linearum quadrata tantum faciunt, ex doctrina penultimae primi, quantum quadratum lineae ED, cuius radix erit ipsa linea ED. Cognitis tribus lateribus anguli EDZ, restat hic angulus EDZ quaerendus, quem sic invenies. Duc lineam EZ in 120°, productum divide per lineam ED, quod hinc nascitur erit angulus EDZ, cuius arcus est ABI. Itaque, cum ab hoc arcu auferes medietatem arcus cogniti, residuum erit arcus AB, si vero ei adieceris, habebis arcum ABIG. In exemplo haec omnia clariora fient. Esto arcus datus 40 graduum, et subtensa eius 41 graduum 3 minutorum, huius medietas sunt 20 gradus 31 minuta, linea scilicet quae praetenditur angulo BDZ. Et proportio sinuum est sicut sunt 20 ad 13, quarum differentia sunt 7. Nunc si multiplicaveris hanc lineam in se, et productum subtraxeris a quadrato lineae BD, remanebit quadratum lineae DZ, cuius radix quadrata est 56 graduum 22 minutorum, linea DZ.

Porro, pro habenda linea EZ, duc 13 in 41 gradus et 3 minuta, productum divide in 7, quod nascitur redige per 60 in gradus: quod inde proveniet erunt 96 gradus 45 minuta; tanta est linea EZ huius trianguli rectanguli. Deinde duc lineam DZ in se, et lineam EZ in se, et adde ambo quadrata, quo facto, estrahe radicem quamque invenies esse 111 gradus 58 minuta quae mensurabit lineam ED. Nunc habes triangulum rectangulum trium laterum cognitorum. Cum itaque volueris certior fieri quantus sit angulus EDZ, qui quaeritur, duc 120 gradus iuxta doctrinam triangulorum planorum in latus ED, hoc est in 96° 45ʹ, et productum divide per 111 gradus 58 minuta. Habebis in producto 103 gradus 3 minuta et 59ʹʹ, eorum arcus erit 118 graduum 23 minutorum, cuius medietas sunt 59 gradus 11 minuta, tantus est angulus EDZ. Si auferes ab eo 20 gradus, remanebunt pro arcu AB 39 gradus 11 minuta, si vero addideris 20° ipsis 59 gradibus 11 minutis, nascetur tibi arcus AG 79 graduum et 11 minutorum. Ad hunc modum etiam in aliis absolvas tuam operationem.

Et sicut.］ Haec figura facilis erit imaginatu, ubi semel recte impresseris memoriae circulorum rationem qui in sphaera materiali proponuntur. Arcus AG esto quarta meridiani, AB arcus quartae aequinoctialis, punctus B sectio communis aequatoris et circuli qui est per medium signorum arcus, qui a puncto B reflectitur ad punctum E esto quarta illius circuli qui est per medium signorum, et arcus GD sit arcus qui reflectitur ab extremitate quartae circuli meridiani usque ad [ad] quartam aequinoctialis circuli, FD esto arcus qui quaeritur pro obliquatione particulari ipsius zodiaci. Arcus BD deputabitur ascensionibus rectis et obliquis. Arcus EA esto maxima Solis obliquatio, punctus A esto locus ubi meridianus circulus secat ad angulos rectos aequatorem. Lineae, quae his arcubus subtenduntur nihil aliud sunt nisi figura primi theorematis.

〈I.13〉 Caput XIII

Quoniam ergo］ Supra meminimus triplicem esse rationem qua arcus seu quantitas ignota de sex quantitatibus venari queat. De his singulis exempla proponere decrevimus. Itaque si volueris scire quanta sit Solis obliquatio, hoc est arcus IT, cum Sol distiterit a sectione vernali 26 gradus. Ordina arcus una cum suis numeris, ita ut supra edoctus, et ut videbis in hoc exemplo a nobis calculato, postea operare secundum doctrinam quam in superioribus tradidimus ad inveniendum quartum numerum regulae sex quantitatum, et obtinebis quaesitum.

Primae rationis exemplum per regulam sex quantitatum.

Exemplum secundae rationis secundum subtractionem proportionum

Cum volueris operari, duc terminum secundum auferendae proportionis in terminum primum proportionis a qua debet fieri subtractio; productum constitue numerum primum. Deinde duc terminum primum auferendae in terminum secundum alterius, quod nascitur sit secundus numerus, pro tertio numero constituas illum qui proportionatur ad numerum quaesitum: huius rei cape tale exemplum. Si cupio scire quanta sit Solis obliquatio cum abest a sectione vernali 39 gradus.

Exemplum tertiae rationis

Quod subtensa duplicis AE sit ad subtensam duplicis AB sicut subtensa duplicis EI ad subtensam duplicis IT. Regiomontanus pulchre demonstrat propositione 18 Epitomes suae. Unde subtensa arcus IT facilis erit venatu mediante propositione 15 sexti, in qua docetur, si quatuor lineae fuerint proportionales, quod rectangulum comprehensum sub prima et ultima sit aequale rectangulo quod comprehenditur sub reliquis duabus. Si igitur multiplicaveris lineam AB in lineam EI, et quod nascitur diviseris per lineam AE, productum erit linea IT, cuius arcus erit id quod quaeritur. Porro, si linea EI fuerit ignota, duc lineam IT in AE, productum divide per lineam AB et prodibit linea EI, contra, si linea AB fuerit ignota, duc lineam IT iterum in AE et obtinebis quaesitum. Postremo, si AE fuerit linea quae quaeritur, multiplica lineam EI in AB et divide productum per IT, et prodibit linea AE, cuius arcus erit id quod quaeritur. Exemplo hac clariora erunt: ut. Volo quaerere quantus sit arcus Solis declinationis, cum abfuerit a sectione vernali 49 gradus. Tunc ordino numeros arcuum propositorum ad hunc modum:

Hoc modo in particularibus］ Cum itaque volueris hac tabula uti, tunc ingredere lateraliter in hanc tabulam cum numero tuo, si non excesserit 90 gradus statim offeret se in secunda linea numerus qui debetur declinationi quam quaeris. Exempli gratia. Si volueris scire declinationem Solis cum abfuerit a sectione vernali 40 gradus, id est cum gradietur in 10 gradus Tauri, tunc quaere 40 gradus in prima linea, et offerent se 16 gradus 4 minuta 4 secundae in secunda linea. Et si numerus tuus excesserit 90 gradus, tunc tunc] tuuc B aufer eum a 180 gradibus, reliquum quaere modo dicto, ut. Volo scire quanta sit declinatio Solis si destiterit a sectione vernali 165 gradus, hoc est cum fuerit in 15 gradibus Virginis, hos gradus subtraho a 180 gradibus et relinquuntur 15 gradus, e quorum regione reperiuntur in secunda linea 6 gradus 0 minuta 30 secundae. Postremo, si numerus tuus maior erit 180 graduum, subtrahito eum a 360 gradibus, cum reliquo operare quemadmodum instructus est: hactenus de usu huius tabulae.

〈I.14〉 Caput XIIII

Sequitur ut una］ Calculaturus exempla dieresis per modum subtractionis, paulo aliter tibi operandum erit quam supra instructus es in calculatione exemplorum syntheseos: de hoc habeas tale documentum, scilicet: duc primum terminum rationis auferendae in secundum alterius, productum statue primum numerum.

Postea, duc terminum secundum in terminum primum superioris rationis, quod nascitur sit tibi numerus secundus, numerus ad quem quaesitum proportionatur sit numerus tertius, quo facto, operare ut supra. Si vero libuerit operari per praxim sex quantitatum, operare iuxta sensum regulae quae docet quintam quantitatem invenire. Ad inveniendum arcus ita procedas. Subtrahe arcum maximae declinationis a 90 gradibus, productum dupla, et habebis arcum FB et arcum duplum BA, scilicet arcum maximae declinationis Solis. Deinde accipe declinationem dati arcus EI, eam dupla et productum subtrahe a 180 gradibus et relinquetur arcus FI pro sexto arcu, ad quem proportionatur arcus ET qui quaeritur; accipias arcum EA, cuius duplum est 180 graduum. Reliqua per exemplum praecedens manifesta sunt. In quo arcus FB et arcus AB manent invariabiles. Sed priusquam accedas ad operationem, quaeras omnium arcuum chordas e tabula chordarum, deinde ordines omnia ita ut vides in hoc praecedenti exemplo, in quo proposuimus 88 gradus zodiaci, quorum ascensionem rectam quaerere decrevimus.