〈IV〉
Claudii Ptolemei Pheludiensis dictio quarta libri Almagesti undecem capitulis rite fabricata succedit.
Capitulum primum: Ex quibus considerationibus oporteat esse investigationem Lune
Capitulum secundum: De scientia temporum revolutionum Lune
Capitulum tertium: De scientia dividendi motus Lune medios
Capitulum quartum: De positione tabularum in quibus sunt motus lunares medii
Capitulum quintum: De duobus modis, scilicet modo centri egredientis et modo orbis revolutionis, in motibus Lune significantibus rem unam
Capitulum sextum: De demonstratione diversitatis motus lunaris prime singularis
Capitulum septimum: De equatione medii cursus Lune in longitudine et diversitate
Capitulum octavum: De scientia loci motuum Lune mediorum in longitudine et diversitate
Capitulum nonum: De equatione cursus Lune medii in latitudine et principio sui
Capitulum decimum: De positione computationis et tabularum diversitatis Lune singularis
Capitulum undecimum: Quod quantitas diversitatis Lune non est propter diversitatem duorum modorum, sed propter diversitatem computationis et fallacie estimationis in sermone Abrachis
〈IV.1〉 Capitulum primum: Ex quibus considerationibus oportuit esse investigationes Lune
Iam narravimus et demonstravimus in dictione que est ante hanc totum quod contingit in motu Solis. Et postquam voluimus incipere post illud secundum quod sequitur loqui de motu Lune, vidimus quod primum per quod oportet nos inquirere illud ex considerationibus est ut non sit illud secundum tentationem, sed quidem in comprehensione illius totius oportet ut assumamus demonstrationes que non sunt ex longitudine temporum tantum, sed sunt ex ea et ex horis in quibus etiam fuerunt eclypses lunares. Per has namque tantum reperiuntur loca Lune secundum veritatem. In toto enim quod videtur ex aliis considerationibus, scilicet que sunt aut ex loco Lune a stellis fixis in cursu suo aut propter instrumenta aut propter eclypses Solis, possibile est ut sit error magnus propter diversitatem aspectuum lunarium. In comprehensione autem partium illius et divisionum eius per illas considerationes et per considerationes alias comprehenditur illud. Longitudo enim que est inter spheram Lune et inter centrum terre non est equalis longitudini orbis signorum, ita ut sit quantitas magnitudinis terre apud ipsum sicut punctum. Necessarium est ergo ut non sit linea que producitur a centro terre, quod centrum est orbis signorum, et transit supra centrum Lune usque ad partes orbis signorum, ad quem considerantur vere transitus omnium stellarum secundum sensum in omni hora, equalis linee que producitur a loco faciei terre, scilicet linee aspectus oculorum, que producitur usque ad centrum Lune, supra quam videtur Lune transitus visibilis. Cum ergo fuerit Luna supra summitatem capitis consideratoris, tunc tantum erunt due linee una, scilicet que protrahitur a centro terre et ab aspectu consideratoris usque ad centrum Lune et usque ad orbem signorum. Sed cum fuerit Luna inclinata quolibet modo a summitate capitis consideratoris, diversificabunt se due linee et secabunt se secundum quantitatem declinationis Lune. Quapropter non erit cursus Lune visibilis equalis vero. Quoniam visus movetur et deprimitur ad locum post locum diversum a locis orbis signorum, quos separant linee que transeunt per centrum terre super quem cadunt visus secundum quantitatem angulorum qui sunt ex declinatione earum linearum et sectione earum. Ex hoc igitur accidit in eclypsibus Solis, que sunt propter transitum Lune et tegumentum Solis ab oculis cum ceciderit in umbra pineali que est inter oculos et inter Solem, ut fiant tenebre diverse a principio sui usque ad finem eius neque sint secundum habitudinem unam in omni loco, neque in magnitudine neque in temporibus, propter causas quas prediximus, quod Luna per eas cooperit Solem et erunt que ex eo cooperiuntur loca diversa corporis eius. In eclypsibus autem lunaribus nihil eorum accidit que contingunt propter diversitatem aspectuum lunarium. Aspectus enim oculorum non est causa eorum que accidunt Lune ex eclypsi. Luna autem non illuminatur nisi a lumine Solis. Sol ergo semper illuminat supra totam medietatem sphere eius oppositam Soli, et in quibusdam temporibus videtur tota Luna plena lumine, quoniam medietas sphere eius illuminata est tunc tota inclinata nobis facie eius ad nos versa. Cum autem fuerit oppositio Lune et Solis, in qua erit casus eius in umbra terre pineali, cuius revolutio semper est contraria revolutioni Solis, tunc tenebrabitur et minuetur ex lumine eius secundum quantitatem qua cadit in umbram ex ea et tegit terra ex lumine Solis ab ea. Quapropter videtur eclypsis Lune in omnibus finibus terre secundum habitudinem unam in quantitate eius quod eclypsatur ex ea et in quantitatibus temporum eclypsis. Et propter hoc oportet in omnibus que investigamus ex rebus Lune ut premittamus inquisitionem locorum Lune verorum, et non locorum eius apparentium secundum visum. Eorum namque que sunt equalia et similia et secundum mensurationem unam convenit et oportet nos premittere narrationem ante positionem eius quod est diverse mensurationis. Et dico quod non convenit in inquisitione locorum Lune verorum operatio considerationum eclypsium solarium, quoniam loca comprehenduntur per visus considerantium, et neque convenit nisi operatio considerationum eclypsium lunarium tantummodo. Non enim per visum iuvatur in ea ad comprehendendum loca Lune. Quoniam pars orbis signorum in qua erit Sol tempore medie eclypsis est ea in qua est centrum Lune in oppositione Solis in longitudine secundum veritatem. Manifestum est igitur quod centrum Lune erit in parte opposita Soli secundum veritatem in tempore medie eclypsis.
〈IV.2〉 Capitulum secundum: De scientia temporum revolutionum Lune
Considerationes quibus convenit nos investigare scientiam summe eorum que contingunt in Luna sunt quas premisimus et posuimus exemplum. Modum autem quo operati sunt antiqui et ex quo sumpserunt demonstrationes et quo voluimus discernere inter illud quod iam convenit de duobus modis et inter illud quod videtur secundum id quo planius et manifestius fit operatio laborabimus declarare. Et quia Luna videtur moveri secundum diversitatem in longitudine et latitudine, non secans orbem signorum in omni hora in temporibus equalibus neque in transitu eius in latitudine usque ad ipsius reversionem in temporibus equalibus, et necessarium est ut non sit possibile invenire revolutiones alias absque inventione temporum reversionis diversitatis Lune, Luna vero iam videtur in omni parte orbis signorum secundum species considerationum moveri motu maiore et motu minore et motu medio et videtur moveri inclinata ad duas partes linee orbis signorum, scilicet ad longitudinem eius longiorem in septentrione et meridie et in medio linee orbis signorum, convenienter ergo antiqui doctrinales perscrutati sunt tempus in cuius equali moveretur Luna semper in longitudine motu equali. Per hoc namque tantum possibile est equari diversitatem Lune. Et posuerunt considerationes eclypsium lunarium propter causas quas prediximus et cogitaverunt que longitudo temporis et multitudo mensium sit equalis multis temporibus equalibus continens revolutiones equales in longitudine, sive revolutiones integras sive cum quibus sint arcus equales. Qui autem his antiquis sunt antiquiores dixerunt sermonem communiorem et convenientiorem, scilicet quod hoc tempus est sex milia et quingenti et octuagintaquinque dies et tertia diei. Ipsi enim viderunt ex hoc numero dierum compleri ducentos et vigintitres menses fere, et ex reversionibus diversitatis ducentas et trigintanovem reversiones, et ex reversionibus latitudinis ducentas et quadragintaduas reversiones, et ex revolutionibus cursus in longitudine revolutiones ducentas et quadragintaunam, et etiam decem partes et duas tertias partis, que sunt partes quas superfluit Sol in decem et octo revolutionibus huius temporis quod prediximus, et quod he reversiones non videntur nisi ex loco suo a stellis fixis, et nominaverunt hoc tempus continens, quoniam ipsum est tempus primum quod reducit diversitates motuum ad reversionem unam fere. Et ut ipsi equarent hoc tempus et facerent dies eius integros, multiplicaverunt numerum dierum eius in tres, et facti sunt decem et novem milia et septingenti et quinquagintasex dies, et vocaverunt illud cursum. Et similiter multiplicaverunt numerum mensium et revolutionum et reversionum omnium in tres, et facti sunt menses sexcenti et sexagintanovem et reversiones diversitatis septingente et decem et septem et reversiones latitudinis septingente et vigintisex et revolutiones cursus in longitudine septingente et vigintitres et etiam partes trigintadue, que superfluit Sol in quinquagintaquatuor revolutionibus in hoc tempore. Abrachis autem iam etiam declaravit, cum intellexit ex considerationibus suis et considerationibus Chaldeorum, quod hoc tempus et menses et revolutiones et reditiones non sunt secundum veritatem. Ipse enim demonstravit per ea que posuit ex revolutionibus quod numerus primus qui est dierum in quibus tempus eclypsis semper est in mensibus equalibus et motibus equalibus circularibus est centum milia et vigintisex milia et septem dies et una hora equalis (et illud est quo reperit compleri ex mensibus menses quatuor milia et ducentos et sexagintaseptem, et ex reversionibus diversitatis quatuor milia quingentas et septuagintatres reversiones, et ex revolutionibus orbis signorum quatuor milia et sexcentas et duodecem revolutiones, exceptis septem partibus et medietate partis fere, que sunt partes quas minuit Sol in trecentis et quadragintaquinque revolutionibus huius temporis) et quod he reditiones non videntur etiam nisi ex loco eius a stellis fixis. Et ex hoc invenit Abrachis tempus medium mensurnum lunare, ubi divisit numerum horum dierum per quatuor milia ducentos et sexagintaseptem menses. Provenit enim numerus dierum mensis lunaris 29 dies et 31 minuta et 50 secunda et 8 tertia et 9 quarta et 20 quinta fere. In longitudine autem temporis huius non declaravit nisi quod due longitudines alternate que sunt ab eclypsi lunari usque ad eclypsim lunarem sunt equales. Et per hoc declarabitur diversitas. Quoniam per longitudinem huius temporis erunt menses semper equales et revolutiones in longitudine equales, scilicet quatuor milia sexcente et undecem, cum quibus erunt partes equales trecente et quinquagintadue et medietas partis secundum quod sequitur ex coniunctione Lune cum Sole. Per coniunctionem scilicet intelligimus coniunctionem et oppositionem. Quod si aliquis dixerit: ‘Non inquiro numerum mensium ab eclypsi lunari ad eclypsim lunarem, sed inquiro quod est a coniunctione usque ad coniunctionem sibi equalem aut ab oppositione usque ad oppositionem sibi similem’, reperiet numerum reditionum diversitatis et numerum mensium minorum cum acceperit numerum unum communem tantum his duabus longitudinibus numerantem eas, qui est una decem et septem partium cuiusque earum que aggregatur, ex numero mensium scilicet ducentorum et quinquagintaunius, et ex numero reversionum diversitatis scilicet ducentarum et sexagintanovem. In hoc autem tempore non complentur reversiones latitudinis. Alternatio namque eclypsium non demonstratur servare equalitatem nisi secundum quantitatem longitudinis temporis et revolutionum que sunt in longitudine, et non secundum quantitatem magnitudinis neque secundum quantitatem similium tenebrarum, quibus comprehenditur latitudo.
Post ea autem que iam premissa sunt de comprehensione scientie temporis reversionum diversitatis posuit Abrachis longitudines mensium in quibus fuerunt eclypses similes in omni modo, scilicet in magnitudine Probably et is missing here, which would correspond to the Greek text (see Toomer, loc. cit., p. 176, line 15 from the bottom). In Paris, BnF, lat. 14738 (57r, line 14 from the bottom) et is missing too. in temporibus tenebrarum, in quibus non fuit aliquid diversitatis propter diversitatem Lune. Propter hoc declarabitur reversio Lune in latitudine. Et manifestum est quod hec revolutio completur cum quinque milibus et quadringentis et quinquagintaocto mensibus et revolutionibus in latitudine quinque milibus nongentis et vigintitribus. Modus autem quo operati sunt antiqui qui fuerunt ante nos in comprehensione huius et similis ei est quem iam narravimus. Iam vero declarabitur nobis quod illud non est planum neque inventum vel inventioni propinquum, immo inquisitione indiget vehementique studio et scientia que non est parva. Et illius ostensio est ut ponamus quod tempus harum duarum longitudinum inventum est secundum veritatem, scilicet quod ipsum est equale. Dico ergo primum quod in eo non est utilitas nisi si Sol fuerit aut non habens diversitatem aut fuerit eius diversitas una in unaquaque duarum longitudinum. Si enim non fuerit ita et fuerit propter Solem diversitas, quemadmodum prediximus, tunc ex revolutionibus Solis revolutiones equales non erunt etiam in temporibus equalibus. Et manifestum est quod neque revolutiones equales que sunt ex revolutionibus Lune erunt etiam in temporibus equalibus. Cum enim fuerint verbi gratia tempora annorum integrorum equalia quorum principia sunt ab unaquaque duarum longitudinum mediarum, et cum eis fuerit tempus medietatis anni superfluens, et in hac medietate non fuerit principium motus Solis, sed fuerit aut a longitudine prima que est transitus medius, scilicet a Piscibus, aut a longitudine secunda que est transitus medius, scilicet a Virgine, tunc Sol minuet de medietate circuli sui in suo transitu a longitudine longiore quatuor partes et medietatem et quartam partis fere et in transitu suo a longitudine secunda addet illas partes, que sunt quatuor et medietas et quarta. Quapropter erit cursus Lune in temporibus equalibus post revolutiones integras a longitudine prima centum et septuagintaquinque partes et quarta partis et a longitudine secunda centum et octuagintaquatuor partes et medietas et quarta partis. Dico ergo primo quod primum quod accidit in latitudinibus propter Solem oportet ut aut sit Sol continens revolutiones integras, aut ut superfluat in una duarum longitudinum medietate circuli, que est a longitudine longiore, aut ut superfluat in longitudine altera medietate circuli, que est a longitudine propinquiore, aut ut sit principium motus eius in unaquaque duarum longitudinum a loco uno, aut ut sit eius longitudo a longiore longitudine et a longitudine propinquiore equalis in eclypsi prima in longitudine prima et in eclypsi secunda in longitudine altera. Sic ergo aut non erit diversitas aut erit diversitas una propter diversitatem Solis in unaquaque duarum longitudinum. Quapropter erunt arcus qui superfluunt equales, scilicet aut equales ad invicem aut equales et equales medio. Et dico secundo quod nos oportet loqui in cursu Lune que similia sunt eis que prediximus de scientia in cursu Solis. Si enim illud remanserit non comprehensum, possibile etiam erit ut Luna videatur secare multotiens in temporibus equalibus arcus equales in longitudine absque reversione que sit diversitatis Lune omnino. Et erit illud cum fuerit principium cursus Lune in unaquaque duarum longitudinum ab uno loco ubi erit cursus eius augmentatus aut cursus eius diminutus neque revertetur ad ipsum, et hoc cum fuerit principium cursus eius in una duarum longitudinum a loco cursus maioris et finis eius ad locum cursus minoris, et in longitudine altera cum fuerit principium cursus eius a loco cursus minoris et finis eius ad locum cursus maioris, et cum fuerit principium cursus primi, qui est in una duarum longitudinum, et principium cursus alterius, qui est in longitudine altera, equalis longitudinis ab unoquoque duorum locorum, scilicet a loco cursus minoris et a loco cursus maioris. Cum ergo fuerit unumquodque eorum que prediximus quemadmodum narravimus, fiet ut aut non sit Lune diversitas aut ut sit diversitas una. Quapropter erunt arcus superfluentes qui sunt in longitudine equales. Reversio vero diversitatis non erit omnino. Non ergo oportet ut accidat in his temporibus acceptis aliquod horum accidentium si oportuerit ut sint continentia tempus reversionis diversitatis Lune. Sed oportet nos eligere tempus significans multas reversiones diversitatis, cum non fuerit continens omnes reversiones diversitatis. Per quod scilicet intelligi volumus: cum fuerint eorum principia non a motibus diversis tantum, sed a motibus multis diversis, aut in magnitudine aut in potentia. In magnitudine vero sicut si fuerit principium cursus eius in una duarum longitudinum a loco cursus minoris et non pervenerit ad locum cursus maioris, aut in longitudine altera, ubi fuerit principium cursus eius a loco cursus maioris et non pervenerit ad locum cursus minoris. Superfluitas enim in longitudine tunc erit multa, quoniam ex revolutionibus diversitatis Lune non complentur revolutiones integre. Quoniam cum fuerit superfluitas que est diversitatis unius quarta una aut tres quarte, tunc erunt due longitudines duarum diversarum quantitatum cum diversitatibus duabus. In potentia vero, cum fuerit principium cursus eius in unaquaque duarum longitudinum a loco cursus medii, et non ab uno mediorum duorum tantum, sed cum fuerit in una duarum longitudinum et fuerit eius principium ab eo in quo est augmentum, et cum fuerit in longitudine altera et fuerit eius principium ab eo in quo est diminutio, tunc erit maior diversitas que est inter duas longitudines in longitudine, scilicet ex superfluitate que est unius earum super alteram. Et etiam cum fuerit superfluitas que est diversitatis unius quarta una aut tres quarte, tunc diversitas erit due diversitates. Et cum fuerit superfluitas que est diversitatis unius medietas circuli, tunc diversitas que est inter duas longitudines erit quattuor diversitates. Quapropter vidimus quod Abrachis operatus est in inquisitione harum longitudinum et temporum assumptorum cum electione eius ad ea consideratione subtilissima secundum plurimum, et estimavit mittendam Lunam in suo opere in illo cum fuerit in una duarum longitudinum, quando incipit a cursu suo maiore et non pervenit ad cursum suum minorem et cum incipit a longitudine sua altera a cursu suo minore et non pervenit ad cursum suum maiorem, et equavit diversitatem que est propter diversitatem Solis, quamvis sit parva, propter hoc quod diminutio reversionis Solis a revolutione integra non est nisi quarta unius duodecim signorum fere, et non est ita signi unius ut non sit alterius, sed est quarta signi quod est in unaquaque duarum longitudinum cuius diversitas est equalis diversitati alterius. Et nos non dicimus ea que prediximus ut per ea vituperemus ea quibus comprehenduntur reversiones harum revolutionum, sed ut declaremus quod cum fuerit inquisitio cum eo quod convenit ex scientia et secundum quod sequitur in sententia, erit possibile equare illud et verificare. Si enim pretermiserimus parvum aliquod horum accidentium que prediximus, mentietur nobis inventio, cuius inquiritur comprehensio, omnino. Et si tentare voluerimus similes istis considerationibus et complere totum quod oportet esse in eis secundum certitudinem, aggravabitur eius inventio apud subtiles in eius inquisitionibus. Eorum vero que posuit Abrachis de reversionibus revolubilibus quas reperit suis cogitationibus, scilicet que posuit de mensibus, quemadmodum prediximus, in pluribus que conveniunt et sunt vera, non apparet quod sint contraria veritati secundum aliquod sensibile. Reversionum vero diversitatis et latitudinis error apparens est et manifestus. Et propter hoc fit apud nos aggregatum inventum per capitula que sumuntur ad cognoscendum hoc et eius simile planiori intellectu et modo, que declarabuntur nunc cum declaratione nostra que erit de quantitate diversitatis Lune. Et premittam primum ad explanandum quod sequitur particularitates motuum mediorum qui sunt in longitudine et latitudine et diversitate secundum ea que consequuntur hec tempora que sunt reversionum motuum revolutionum et que aggregantur ex eis que declarabuntur ex equationibus eorum.
〈IV.3〉 Capitulum tertium: De particularibus motibus mediis
Cum nos multiplicaverimus quod iam ostensum est ex motu Solis medio unius diei, qui est 59 minuta et 8 secunda et 17 tertia et 13 quarta et 12 quinta et 31 sexta, in numerum dierum mensis unius, qui est 29 dies et 31 minuta et 50 secunda et 8 tertia et 9 quarta et 20 quinta, deinde addiderimus supra illud quod aggregatur numerum partium revolutionis unius, scilicet 360 partes, erit illud partes quas percurrit Luna per motum suum medium in longitudine in mense, que sunt 389 partes et 6 minuta et 23 secunda et tertium unum et 24 quarta et duo quinta et 30 sexta et 50 septima fere. Cum ergo diviserimus illud per numerum dierum mensis lunaris positi, erit portio medii cursus Lune diei in longitudine 13 partes et 10 minuta et 34 secunda et 58 tertia et 33 quarta et 30 quinta et 30 sexta fere. Et cum multiplicaverimus 269 revolutiones que sunt diversitatis Lune in 360 que sunt revolutionis unius, erit illud nonagintasex milia et octingenta et quadraginta. Et cum diviserimus illud per numerum dierum mensium 251, qui sunt 7412 dies et 10 minuta et 44 secunda et 51 tertia et 40 quarta, erit illud portio cursus diversitatis Lune medii unius diei, que est 13 partes et 3 minuta et 53 secunda et 56 tertia et 17 quarta et 51 quinta et 59 sexta. Et similiter cum multiplicaverimus quinque milia et nongenta et vigintitria, que sunt reversiones latitudinis in 360 que sunt revolutio una, proveniet illud duo mille milia et centum milia et trigintaduo milia et ducenta et octuaginta. Cum ergo diviserimus illud per numerum dierum mensium quinque milium et quadringentorum et quinquagintaocto, qui sunt 164177 dies et 58 minuta et 58 secunda et 3 tertia et 20 quarta, proveniet nobis portio medii cursus Lune in latitudine unius diei, que est 13 partes et 13 minuta et 45 secunda et 39 tertia et 48 quarta et 56 quinta et 37 sexta. Et etiam cum nos minuerimus ex medio cursu Lune diei medium cursum Solis diei, erit residuum longitudo media que est inter Solem et Lunam per motum medium diei, que est 12 partes et 11 minuta et 26 secunda et 41 tertia et 20 quarta et 17 quinta et 59 sexta. Et quemadmodum iam prediximus per capitula que assumemus in eis que sequentur similia huius inquisitionis, inveniemus motum Lune diei in longitudine. Nos namque reperiemus hoc non diversum a loco quem posuit Abrachis. Et manifestum est quod longitudo media similiter erit. Diversitatem vero inveniemus minui ab hoc loco 11 quartis et 46 quintis et 39 sextis, donec fiet portio medii cursus diversitatis Lune diei 13 partes et 3 minuta et 53 secunda et 56 tertia et 17 quarta et 51 quinta et 59 sexta. Sed et latitudinem inveniemus iam augmentari super locum positum 8 quartis et 39 quintis et 18 sextis, donec fiat portio medii cursus Lune in latitudine diei 13 partes et 13 minuta et 45 secunda et 39 tertia et 48 quarta et 56 quinta et 37 sexta. Et similiter cum acceperimus ex motu diei cuiusque horum que prediximus partem vigesimamquartam, erit motus medius hore unius, sed in longitudine 32 minuta et 56 secunda et 27 tertia et 26 quarta et 23 quinta et 46 sexta et 15 septima, motus vero diversitatis hore 32 minuta et 39 secunda et 44 tertia et 50 quarta et 44 quinta et 39 sexta et 57 septima et 30 octava, motus vero latitudinis hore 33 minuta et 4 secunda et 24 tertia et 9 quarta et 32 quinta et 21 sexta et 32 septima et 30 octava, sed residuum longitudinis que est inter Solem et Lunam cursuum eorum mediorum 30 minuta et 28 secunda et 36 tertia et 43 quarta et 20 quinta et 44 sexta et 57 septima et 30 octava. Et cum multiplicaverimus cursum cuiusque eorum que prediximus diei in 30 et minuerimus ex eo quod aggregatur revolutiones integras, fiet residuum cursus medius mensis unius, sed in longitudine quidem 35 partes et 17 minuta et 29 secunda et 16 tertia et 45 quarta et 15 quinta, cursus vero diversitatis mensis unius 31 partes et 56 minuta et 58 secunda et 8 tertia et 55 quarta et 59 quinta et 30 sexta, sed medius cursus latitudinis mensis 36 partes et 52 minuta et 49 secunda et 54 tertia et 28 quarta et 18 quinta et 30 sexta, residuum vero longitudinis que est inter Solem et Lunam cursuum eorum mediorum mensis quinque partes et 43 minuta et 20 secunda et 40 tertia et 8 quarta et 59 quinta et 30 sexta. Et etiam cum multiplicaverimus cursum diei uniuscuiusque eorum que prediximus in numerum dierum anni Egyptii, qui sunt 365 dies, et minuerimus ex eo quod aggregabitur ex unoquoque eorum revolutiones integras, fiet residuum medius cursus anni, sed in longitudine quidem 129 partes et 22 minuta et 46 secunda et 13 tertia et 50 quarta et 32 quinta et 30 sexta, cursus vero diversitatis anni 88 partes et 43 minuta et 7 secunda et 28 tertia et 41 quarta et 13 quinta et 55 sexta, residuum vero cursus latitudinis anni 148 partes et 42 minuta et 47 secunda et 12 tertia et 44 quarta et 25 quinta et 5 sexta, longitudo autem que est inter Solem et Lunam cursuum eorum mediorum 129 partes et 37 minuta et 21 secunda et 28 tertia et 29 quarta et 23 quinta et 55 sexta. Deinde post hoc multiplicabimus residuum cuiusque eorum que prediximus anni in 18, scilicet numerum annorum coniunctorum, ad hoc ut sit preparatum in tabulis, et proiiciemus ex eo quod aggregatur ex unoquoque revolutiones integras, et fiet residuum cursus medius 18 annorum, sed in longitudine 168 partes et 49 minuta et 52 secunda et 9 tertia et 9 quarta et 45 quinta, residuum vero cursus diversitatis 18 annorum 156 partes et 56 minuta et 14 secunda et 36 tertia et 22 quarta et 10 quinta et 30 sexta, residuum autem cursus latitudinis 18 annorum 156 partes et 50 minuta et 9 secunda et 49 tertia et 19 quarta et 31 quinta et 30 sexta, residuum vero longitudinis que est inter Solem et Lunam cursuum eorum mediorum 18 annorum 173 partes et 12 minuta et 26 secunda et 32 tertia et 49 quarta et 10 quinta et 30 sexta.
〈IV.4〉 Capitulum quartum: De artificio tabularum motuum Lune mediorum
Describam autem motuum Lune horum quatuor modorum tabulas in duodecem partibus quorum cuiusque motus sint tres partes quinque temporum, quemadmodum in Sole descripsimus, et dividam unamquamque partem in septem tabulas in longitudine et quadragintaquinque areas in latitudine, scilicet partium et minutorum et secundorum et tertiorum et quartorum et quintorum et sextorum etcetera. Et signabo in tabulis prime partis ex partibus motus longitudinis numerum annorum coniunctorum et motus Lune in longitudine in eis, et in tabulis partis secunde numerum annorum separatorum et motus Lune in longitudine in eis, et sub eis numerum horarum et motus Lune in longitudine in eis, et in tabulis partis tertie numerum mensium et motus Lune in longitudine in eis, et sub eis numerum dierum mensis et motus Lune in longitudine in eis. Et similiter faciemus in partibus motus diversitatis et in tabulis eius, et in partibus motus latitudinis et in tabulis eius, et in partibus motus longitudinis que est inter Solem et Lunam ex cursibus eorum mediis et in tabulis eorum. Et hec est tabularum descriptio:
Fuit radix Lune in principio regni Nabuchodonosor per motum eius medium in longitudine 11 gradus et 22 minuta Tauri, et radix eius in diversitate, scilicet longitudinis eius a longitudine longiore in orbe revolutionis suo, 268 gradus et 49 minuta, et radix eius in latitudine plaga septentrionali in orbe eius declivi 354 gradus et 45 minuta, et longitudo eius a Sole 70 gradus et 37 minuta.
☽
Differentia sive descriptio tabularum motuum mediorum Lune in tribus partibus primi prefatorum quattuor modorum ·☽·
Motus Lune medius in longitudine in annis coniunctis |
Motus Lune medius in longitudine in annis expansis |
Motus Lune medius in longitudine in mensibus |
|||||||||||||||||||||||
Anni coniuncti secundum 18 |
Superfluum graduum 11 minutorum 22 ♉ |
Anni expansi |
☽ |
Menses |
☽ |
||||||||||||||||||||
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||
18
36
54 |
168
337
146 |
49
39
29 |
52
44
36 |
9
18
27 |
9
19
29 |
45
30
15 |
1
2
3 |
129
258
28 |
22
45
8 |
46
32
18 |
13
27
41 |
50
41
31 |
32
5
37 |
30
0
30 |
1
2
3 |
35
70
105 |
17
34
52 |
29
58
27 |
16
33
50 |
45
30
15 |
15
30
45 |
0
0
0 |
|||
72
90
108 |
315
124
292 |
19
9
59 |
28
20
12 |
36
45
54 |
39
48
58 |
0
45
30 |
4
5
6 |
157
286
56 |
31
53
16 |
4
51
37 |
55
19
23 |
22
12
3 |
10
42
15 |
0
30
0 |
4
5
6 |
141
176
211 |
9
27
44 |
57
26
55 |
7
23
40 |
1
46
31 |
0
15
30 |
0
0
0 |
|||
126
144
162 |
101
270
79 |
49
38
28 |
5
57
49 |
4
13
22 |
8
18
27 |
15
0
45 |
7
8
9 |
185
315
84 |
39
2
24 |
23
9
56 |
36
50
4 |
53
44
34 |
47
20
52 |
30
0
30 |
7
8
9 |
247
282
317 |
2
19
37 |
24
54
23 |
57
14
30 |
16
2
47 |
45
0
15 |
0
0
0 |
|||
180
198
216 |
248
57
225 |
18
8
58 |
41
33
25 |
31
40
49 |
37
47
57 |
30
15
0 |
10
11
12 |
213
343
112 |
47
10
33 |
42
28
14 |
18
32
46 |
25
15
6 |
25
57
30 |
0
30
0 |
10
11
12 |
352
28
63 |
54
12
29 |
52
22
51 |
47
4
21 |
32
17
3 |
30
45
0 |
0
0
0 |
|||
234
252
270 |
34
203
12 |
48
38
28 |
17
10
2 |
59
8
17 |
6
16
26 |
45
30
15 |
13
14
15 |
241
11
140 |
56
18
41 |
0
47
33 |
59
13
27 |
57
47
38 |
2
35
7 |
30
0
30 |
Motus Lune medius in longitudine in diebus |
||||||||||
Dies |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||||||||||||||
288
306
324 |
181
350
158 |
17
7
57 |
54
46
38 |
26
35
44 |
36
45
55 |
0
45
30 |
16
17
18 |
270
39
168 |
4
27
49 |
19
5
52 |
41
55
9 |
28
19
9 |
40
12
45 |
0
30
0 |
1
2
3 |
13
26
39 |
10
21
31 |
34
9
44 |
58
57
55 |
33
7
40 |
30
1
31 |
30
0
30 |
|||
342
360
378 |
327
136
305 |
47
37
27 |
30
23
15 |
54
3
12 |
5
15
24 |
15
0
45 |
Motus Lune medius in longitudine in horis |
4
5
6 |
52
65
79 |
42
52
3 |
19
54
29 |
54
52
51 |
14
47
21 |
2
32
3 |
0
30
0 |
||||||||||
Hore |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
|||||||||||||||||
396
414
432 |
114
283
91 |
17
6
56 |
7
59
51 |
21
30
39 |
34
44
54 |
30
15
0 |
1
2
3 |
0
1
1 |
32
5
38 |
56
52
49 |
27
54
22 |
26
52
19 |
23
47
11 |
46
32
18 |
15
30
45 |
7
8
9 |
92
105
118 |
14
24
35 |
4
39
14 |
49
48
47 |
54
28
1 |
33
4
34 |
30
0
30 |
||
450
468
486 |
260
79
248 |
46
36
26 |
43
35
28 |
49
58
7 |
3
13
23 |
45
30
15 |
4
5
6 |
2
2
3 |
11
44
17 |
45
42
38 |
49
17
44 |
45
11
38 |
35
58
22 |
5
51
37 |
0
15
30 |
10
11
12 |
131
144
158 |
45
56
6 |
49
24
59 |
45
44
42 |
35
8
42 |
5
35
6 |
0
30
0 |
||
504
522
540 |
57
216
24 |
16
6
56 |
20
12
4 |
16
25
34 |
33
42
52 |
0
45
30 |
7
8
9 |
4
5
5 |
50
23
56 |
35
31
28 |
12
39
6 |
4
31
57 |
46
10
33 |
23
10
56 |
45
0
15 |
13
14
15 |
171
184
197 |
17
28
38 |
34
9
44 |
41
39
38 |
15
49
22 |
36
7
37 |
30
0
30 |
||
558
576
594 |
193
262
71 |
45
35
25 |
56
48
41 |
44
53
2 |
2
12
21 |
15
0
45 |
10
11
12 |
6
7
7 |
29
2
35 |
24
21
17 |
34
1
29 |
23
50
16 |
57
21
45 |
42
28
15 |
30
45
0 |
16
17
18 |
210
223
237 |
49
59
10 |
19
54
29 |
36
35
34 |
56
29
3 |
8
38
9 |
0
30
0 |
||
612
630
648 |
240
149
317 |
15
5
55 |
33
25
17 |
11
20
29 |
31
41
51 |
30
15
0 |
13
14
15 |
8
8
8 |
8
41
14 |
13
10
6 |
56
24
51 |
43
9
35 |
9
32
56 |
1
47
33 |
15
30
45 |
19
20
21 |
250
263
276 |
21
31
42 |
4
39
14 |
32
31
29 |
36
10
43 |
39
10
40 |
30
0
30 |
||
666
684
702 |
126
295
104 |
45
35
24 |
9
1
53 |
39
48
57 |
0
10
20 |
45
30
15 |
16
17
18 |
8
9
9 |
47
19
52 |
3
59
56 |
19
46
13 |
2
28
55 |
20
44
7 |
20
6
52 |
0
15
30 |
22
23
24 |
289
303
316 |
52
3
13 |
49
24
59 |
28
26
25 |
17
50
24 |
11
41
12 |
0
30
0 |
||
720
738
756 |
273
82
250 |
14
4
54 |
46
38
30 |
6
15
24 |
30
39
49 |
0
45
30 |
19
20
21 |
10
10
11 |
25
58
31 |
52
49
45 |
41
8
36 |
21
47
14 |
31
55
19 |
38
25
11 |
45
0
15 |
25
26
27 |
329
342
355 |
24
35
45 |
34
9
44 |
23
22
21 |
57
31
4 |
42
13
43 |
30
0
30 |
||
774
792
810 |
59
228
37 |
44
34
24 |
22
14
6 |
33
43
52 |
59
9
18 |
15
0
45 |
22
23
24 |
12
12
13 |
4
37
10 |
42
38
34 |
3
31
58 |
40
7
33 |
42
6
30 |
57
43
30 |
30
45
0 |
28
29
30 |
8
22
35 |
56
6
17 |
19
54
29 |
19
18
16 |
38
11
45 |
14
44
15 |
0
30
0 |
||
Differentia sive descriptio tabularum motuum mediorum Lune in tribus partibus secundi prefatorum quattuor modorum ·☽·
☽
Motus Lune medius in diversitate in annis coniunctis |
Motus Lune medius in diversitate in annis expansis |
Motus Lune medius in diversitate in mensibus |
|||||||||||||||||||||||||
Anni coniuncti secundum 18 |
Superfluum graduum 268 minutorum 49 |
Anni expansi |
☽ |
Menses |
☽ |
||||||||||||||||||||||
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||||||
18
36
54 |
156
313
110 |
56
52
48 |
14
29
43 |
36
12
49 |
22
44
6 |
10
21
31 |
30
0
30 |
1
2
3 |
88
177
266 |
43
26
9 |
7
14
22 |
28
57
26 |
41
22
3 |
13
27
41 |
55
50
45 |
1
2
3 |
31
63
95 |
56
53
50 |
58
56
54 |
8
17
26 |
55
51
47 |
59
59
58 |
30
0
30 |
||||
72
90
108 |
267
64
221 |
44
41
37 |
58
13
27 |
25
1
38 |
28
50
13 |
42
52
3 |
0
30
0 |
4
5
6 |
354
83
172 |
52
35
18 |
29
37
44 |
54
23
52 |
44
26
7 |
55
9
23 |
40
35
30 |
4
5
6 |
127
159
191 |
47
44
41 |
52
50
48 |
35
44
53 |
43
39
35 |
58
57
57 |
0
30
0 |
||||
126
144
162 |
18
175
332 |
33
29
26 |
42
56
11 |
14
50
27 |
35
57
19 |
13
24
34 |
30
0
30 |
7
8
9 |
261
349
78 |
1
44
28 |
52
59
7 |
20
49
18 |
48
29
11 |
37
51
5 |
25
20
15 |
7
8
9 |
223
255
287 |
38
35
32 |
47
45
43 |
2
11
20 |
31
27
23 |
56
56
55 |
30
0
30 |
||||
180
198
216 |
129
286
83 |
22
18
14 |
26
40
55 |
3
40
16 |
41
3
26 |
45
55
6 |
0
30
0 |
10
11
12 |
167
255
344 |
11
54
37 |
14
22
29 |
46
15
44 |
52
33
14 |
19
33
47 |
10
5
0 |
10
11
12 |
319
351
23 |
29
26
23 |
41
39
37 |
29
38
47 |
19
15
11 |
55
54
54 |
0
30
0 |
||||
234
252
270 |
240
37
194 |
11
7
3 |
9
24
39 |
52
29
5 |
48
10
32 |
16
27
37 |
30
0
30 |
13
14
15 |
73
162
250 |
20
3
46 |
37
44
52 |
12
41
10 |
56
37
18 |
0
14
28 |
55
50
45 |
Motus Lune medius in diversitate in diebus |
|||||||||||
Dies |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||||||||||||||||
288
306
324 |
350
147
304 |
59
56
52 |
53
8
22 |
41
18
54 |
54
16
39 |
48
58
9 |
0
30
0 |
16
17
18 |
339
68
156 |
29
13
56 |
59
7
14 |
38
7
36 |
59
40
22 |
42
56
10 |
40
35
30 |
1
2
3 |
13
26
39 |
3
7
11 |
53
47
41 |
56
52
48 |
17
35
53 |
51
43
35 |
59
58
57 |
||||
342
360
378 |
101
258
55 |
48
44
41 |
37
52
6 |
31
7
43 |
1
23
45 |
19
30
40 |
30
0
30 |
Motus Lune medius in diversitate in horis |
4
5
6 |
52
65
78 |
15
19
23 |
35
29
23 |
45
41
37 |
11
29
47 |
27
19
11 |
56
55
54 |
|||||||||||
Hore |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
||||||||||||||||||
396
414
432 |
212
9
166 |
37
33
29 |
21
35
50 |
20
56
32 |
7
30
52 |
51
1
12 |
0
30
0 |
1
2
3 |
0
1
1 |
32
5
37 |
39
19
59 |
44
29
14 |
50
41
32 |
44
29
13 |
39
19
59 |
57
55
52 |
30
0
30 |
7
8
9 |
91
104
117 |
27
31
35 |
17
11
5 |
34
30
26 |
5
22
40 |
3
55
47 |
53
52
51 |
||
450
468
486 |
323
120
277 |
26
22
18 |
5
19
34 |
9
45
21 |
14
36
58 |
22
33
43 |
30
0
30 |
4
5
6 |
2
2
3 |
10
43
15 |
38
18
58 |
59
44
29 |
22
13
4 |
58
43
27 |
39
19
59 |
50
47
45 |
0
30
0 |
10
11
12 |
130
143
156 |
38
42
46 |
59
53
47 |
22
19
15 |
58
16
34 |
39
31
23 |
50
49
48 |
||
504
522
540 |
74
231
28 |
14
11
7 |
48
3
18 |
58
34
11 |
20
43
5 |
54
4
15 |
0
30
0 |
7
8
9 |
3
4
4 |
48
21
53 |
38
17
57 |
13
58
43 |
55
45
36 |
12
57
41 |
39
19
59 |
42
40
37 |
30
0
30 |
13
14
15 |
169
182
195 |
50
54
58 |
41
35
29 |
11
8
4 |
52
10
27 |
15
7
59 |
47
46
45 |
||
558
576
594 |
185
341
138 |
3
59
56 |
32
47
2 |
47
23
0 |
27
49
11 |
25
36
46 |
30
0
30 |
10
11
12 |
5
5
6 |
26
59
31 |
37
17
56 |
28
13
58 |
27
18
8 |
26
11
55 |
39
19
59 |
35
32
30 |
0
30
0 |
16
17
18 |
209
222
235 |
2
6
10 |
23
16
10 |
0
57
53 |
45
3
21 |
51
43
35 |
44
43
42 |
||
612
630
648 |
295
92
249 |
52
48
44 |
16
31
45 |
36
12
49 |
33
56
18 |
57
7
18 |
0
30
0 |
13
14
15 |
7
7
8 |
4
37
9 |
36
16
56 |
42
27
12 |
59
50
41 |
40
25
9 |
39
19
59 |
27
25
22 |
30
0
30 |
19
20
21 |
248
261
274 |
14
17
21 |
4
58
52 |
49
45
42 |
39
57
15 |
27
19
11 |
41
40
39 |
||
666
684
702 |
46
203
0 |
40
37
33 |
0
15
29 |
25
2
38 |
40
2
24 |
28
39
49 |
30
0
30 |
16
17
18 |
8
9
9 |
42
15
47 |
35
15
55 |
57
42
27 |
31
22
13 |
54
39
23 |
39
19
59 |
20
17
15 |
0
30
0 |
22
23
24 |
287
300
313 |
25
29
33 |
46
40
34 |
38
34
31 |
33
50
8 |
3
55
47 |
38
37
36 |
||
720
738
756 |
157
314
111 |
29
25
22 |
44
58
13 |
14
51
27 |
47
9
31 |
0
10
21 |
0
30
0 |
19
20
21 |
10
10
11 |
20
53
25 |
35
14
54 |
12
56
41 |
4
54
45 |
8
53
37 |
39
19
59 |
12
10
7 |
30
0
30 |
25
26
|
326
339
352 |
37
41
45 |
28
22
16 |
27
23
20 |
26
44
2 |
39
31
23 |
35
34
33 |
||
774
792
810 |
268
65
222 |
18
14
10 |
28
42
57 |
3
40
16 |
53
15
37 |
31
42
52 |
30
0
30 |
22
23
24 |
11
12
13 |
58
31
3 |
34
14
53 |
26
11
56 |
36
27
17 |
22
7
51 |
39
19
59 |
5
2
0 |
0
30
0 |
28
29
30 |
5
18
31 |
49
53
56 |
10
4
58 |
16
12
8 |
20
38
55 |
15
7
59 |
32
31
30 |
||
Differentia sive descriptio tabularum motuum mediorum Lune in tribus partibus tertii prefatorum quattuor modorum ·☽·
☽
Motus Lune medius in latitudine in annis coniunctis |
Motus Lune medius in latitudine in annis expansis |
Motus Lune medius in latitudine in mensibus |
|||||||||||||||||||||||||
Anni coniuncti secundum 18 |
Superfluum graduum 354 minutorum 15 |
Anni expansi |
☽ |
Menses |
☽ |
||||||||||||||||||||||
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||||||
18
36
54 |
156
313
110 |
50
40
30 |
9
19
29 |
49
38
27 |
19
39
58 |
31
3
34 |
30
0
30 |
1
2
3 |
148
297
86 |
42
25
8 |
47
34
21 |
12
25
38 |
44
28
13 |
25
50
15 |
5
10
15 |
30
60
90 |
36
73
110 |
52
45
38 |
49
39
29 |
54
48
43 |
28
56
24 |
18
37
55 |
30
0
30 |
||||
72
90
108 |
267
64
221 |
20
10
0 |
39
49
58 |
17
6
55 |
18
37
57 |
6
37
9 |
0
30
0 |
4
5
6 |
234
23
172 |
51
33
16 |
8
56
43 |
50
3
16 |
57
42
26 |
40
5
30 |
20
25
30 |
120
150
180 |
147
184
221 |
31
24
16 |
19
9
59 |
37
32
26 |
53
21
49 |
14
32
51 |
0
30
0 |
||||
126
144
162 |
17
174
331 |
51
41
31 |
8
18
28 |
45
34
23 |
16
36
55 |
40
12
43 |
30
0
30 |
7
8
9 |
320
109
258 |
59
42
25 |
30
17
4 |
29
41
54 |
10
55
39 |
55
20
45 |
35
40
45 |
210
240
270 |
258
295
331 |
9
2
55 |
49
39
29 |
21
15
10 |
18
46
14 |
9
28
46 |
30
0
30 |
||||
180
198
216 |
128
285
82 |
21
11
1 |
38
48
57 |
13
2
51 |
15
34
54 |
15
46
18 |
0
30
0 |
10
11
12 |
47
195
344 |
7
50
33 |
52
39
26 |
7
20
32 |
24
8
53 |
10
35
1 |
50
55
0 |
300
330
360 |
8
45
82 |
48
41
33 |
19
8
58 |
4
59
53 |
43
11
39 |
5
23
42 |
0
30
0 |
||||
234
252
270 |
238
35
192 |
52
42
32 |
7
17
27 |
41
30
19 |
13
33
52 |
49
21
52 |
30
0
30 |
13
14
15 |
133
281
70 |
16
59
41 |
13
0
48 |
45
58
11 |
37
21
6 |
26
51
16 |
5
10
15 |
Motus Lune medius in latitudine in diebus |
|||||||||||
Dies |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||||||||||||||||
288
306
324 |
349
146
303 |
22
12
2 |
37
46
56 |
9
58
47 |
12
31
51 |
24
55
27 |
0
30
0 |
16
17
18 |
219
8
156 |
24
7
50 |
35
22
9 |
23
36
49 |
50
35
19 |
41
6
31 |
20
25
30 |
1
2
3 |
13
26
39 |
13
27
41 |
45
31
16 |
39
19
59 |
48
37
26 |
56
53
49 |
37
14
51 |
||||
342
360
378 |
99
256
53 |
53
43
33 |
6
16
26 |
37
26
15 |
10
30
50 |
58
30
1 |
30
0
30 |
Motus Lune medius in latitudine in horis |
4
5
6 |
52
66
79 |
55
8
22 |
2
48
33 |
39
19
58 |
15
4
53 |
46
43
39 |
28
5
42 |
|||||||||||
Hore |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
||||||||||||||||||
396
414
432 |
210
7
164 |
23
13
3 |
36
45
55 |
5
54
43 |
9
29
48 |
33
4
36 |
0
30
0 |
1
2
3 |
0
1
1 |
33
6
39 |
4
8
13 |
24
48
12 |
9
19
28 |
32
4
37 |
21
43
4 |
32
5
37 |
30
0
30 |
7
8
9 |
92
105
119 |
36
50
3 |
19
5
50 |
38
18
58 |
42
31
20 |
36
32
29 |
19
56
33 |
||
450
468
486 |
320
117
274 |
54
44
34 |
5
15
25 |
33
22
11 |
8
27
47 |
7
39
10 |
30
0
30 |
4
5
6 |
2
2
3 |
12
45
18 |
17
22
26 |
36
0
24 |
38
47
57 |
9
41
14 |
26
47
9 |
10
42
15 |
0
30
0 |
10
11
12 |
132
145
158 |
17
31
45 |
36
22
7 |
38
17
57 |
9
58
47 |
26
22
19 |
10
47
24 |
||
504
522
540 |
71
228
25 |
24
14
4 |
35
44
54 |
1
50
39 |
6
26
45 |
42
13
45 |
0
30
0 |
7
8
9 |
3
4
4 |
51
24
57 |
30
35
39 |
49
13
37 |
6
16
25 |
46
18
51 |
30
52
13 |
47
20
52 |
30
0
30 |
13
14
15 |
171
185
198 |
58
12
26 |
53
39
24 |
37
17
57 |
36
25
14 |
16
12
9 |
1
38
15 |
||
558
576
594 |
181
338
135 |
55
45
35 |
4
14
24 |
29
18
7 |
5
24
44 |
16
48
19 |
30
0
30 |
10
11
12 |
5
6
6 |
30
3
36 |
44
48
52 |
1
25
49 |
35
44
54 |
23
55
28 |
35
56
18 |
25
57
30 |
0
30
0 |
16
17
18 |
211
224
238 |
40
53
7 |
10
56
41 |
37
16
56 |
3
52
40 |
5
2
59 |
52
29
6 |
||
612
630
648 |
292
89
246 |
25
15
5 |
33
43
53 |
57
46
35 |
3
23
42 |
51
22
54 |
0
30
0 |
13
14
15 |
7
7
8 |
9
43
16 |
57
1
6 |
14
38
2 |
4
13
23 |
0
33
5 |
40
1
23 |
2
35
7 |
30
0
30 |
19
20
21 |
251
264
277 |
21
35
48 |
27
13
58 |
36
16
56 |
29
18
7 |
55
52
48 |
43
20
57 |
||
666
684
702 |
42
199
356 |
56
46
36 |
3
13
23 |
25
14
3 |
2
21
41 |
25
57
28 |
30
0
30 |
16
17
18 |
8
9
9 |
49
22
55 |
10
14
19 |
26
50
14 |
32
42
51 |
37
10
42 |
44
6
27 |
40
12
45 |
0
30
0 |
22
23
24 |
291
304
317 |
2
16
30 |
44
30
15 |
35
15
55 |
56
45
34 |
45
42
38 |
34
11
48 |
||
720
738
756 |
153
310
107 |
26
16
6 |
32
42
52 |
53
42
31 |
1
20
40 |
0
31
3 |
0
30
0 |
19
20
21 |
10
11
11 |
28
1
34 |
23
28
32 |
39
3
27 |
1
10
20 |
14
47
19 |
49
10
32 |
17
50
22 |
30
0
30 |
25
26
27 |
330
343
357 |
44
57
11 |
1
47
32 |
35
15
55 |
23
12
1 |
35
32
28 |
25
2
39 |
||
774
792
810 |
263
60
217 |
57
47
37 |
2
12
21 |
20
10
59 |
59
19
38 |
34
6
37 |
30
0
30 |
22
23
24 |
12
12
13 |
7
40
13 |
36
41
45 |
51
15
39 |
29
39
48 |
51
24
56 |
53
15
37 |
55
27
0 |
0
30
0 |
28
29
30 |
10
23
36 |
25
39
52 |
18
4
49 |
34
14
54 |
50
39
28 |
25
21
18 |
16
53
30 |
||
Differentia sive descriptio tabularum motuum mediorum Lune in tribus partibus quarti prefatorum quattuor modorum ·☽·
☽ ───────── a ───────── ☉
〈IV.5〉 Capitulum quintum: De hoc quod duo modi, scilicet modus orbis centri egredientis et orbis revolutionis, in motibus Lune significant rem unam
Que autem iam narravimus sequitur ut declaremus modum quo scietur diversitas Lune et quantitas eius. In presenti vero sufficit nobis dicere in hoc quod diversitas Lune est una. Et nos similiter vidimus antiquos qui fuerunt ante nos dixisse et secundum hoc operatos fuisse. Per quod videlicet intelligi volumus diversitatem que completur cum tempore reversionis. Deinde post illud demonstrabimus quod Luna habet diversitatem secundam propter sui elongationem a Sole, et quod diversitas tunc erit maior cum fuerit in ambabus quadraturis que sunt a duabus partibus impletionis, et erit reversio Lune ad eam in tempore mensurno duabus vicibus, scilicet in coniunctionibus et impletionibus. Et secundum hunc ordinem ostendemus demonstrationem, propter hoc quod diversitas secunda pendet semper ex diversitate prima et neque est possibile invenire ipsam absque inventione prime. Prima vero possibile est invenire absque secunda, quoniam eius assumptio non est nisi ex eclypsibus lunaribus, in quibus non est diversitas sensibilis propter Solem. In demonstratione vero diversitatis precedentis operabimur per capitula quibus vidimus Abrachim operatum fuisse. Assumemus tres eclypses lunares et demonstrabimus quantum erit augmentum motus diversitatis maioris super motum medium et super locum longitudinis longioris, et quod hec diversitas non videtur nisi per seipsam et secundum modum orbis revolutionis. Et totum quod videtur secundum modum orbis revolutionis videtur secundum modum orbis centri egredientis simile et equale. Et dignius cui referenda est diversitas que est ex commixtione duarum diversitatum est diversitas secunda, que est propter Solem. Et declarabitur etiam nobis per unumquemque duorum modorum quod totum quod videtur in unoquoque eorum est equale, quamvis tempora reversionum non sint equalia, sicut fuerunt in eis que declaravimus in Sole, scilicet reversionis diversitatis et reversionis orbis signorum. Sed si fuerint, sicut sunt in Luna, diversa et fuerint proportiones tantum une, ita sciemus cum operati fuerimus inquisitionem nostram de diversitate una singulari posita. Et quia reversio Lune in orbe signorum est velocior hac diversitate posita in temporibus equalibus, tunc manifestum est quod secundum modum orbis revolutionis arcus quem secat centrum orbis revolutionis orbis cuius centrum est centrum orbis signorum erit semper maior in proportione arcu quem secat Luna orbis revolutionis. Et secundum modum orbis centri egredientis Luna secat arcum orbis centri egredientis similem arcui quem secat in orbe revolutionis. Quantitas vero arcus quem secat orbis centri egredientis ad partem Lune et super centrum orbis signorum est secundum quantitatem qua erit augmentum cursus Lune in longitudine supra cursum eius in diversitate. Per quod intelligi volumus augmentum arcus qui est orbis cuius centrum est centrum orbis signorum supra arcum qui est orbis revolutionis. Per hoc enim conservabitur similitudo in modis ambobus, non similitudo proportionum tantum, verum similitudo etiam temporum cuiusque duorum motuum. Et postquam iam affirmatum est hoc necessario et factum est sequens que sunt ante ipsam, sequitur demonstratio.
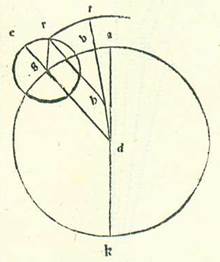 Describam ad illius exemplum circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et sit diameter eius ADK, et orbem revolutionis, supra quem sint E, R, supra centrum G, et ponam ut quando fuerit centrum orbis revolutionis in puncto loci A, sit Luna in longitudine longiore orbis revolutionis, et in tempore uno centrum orbis revolutionis secet per cursum suum arcum AG, et Luna secet ex orbe revolutionis arcum ER, et protraham lineam EGD et lineam GR. Et quia arcus AG est maior in proportione arcu ER, assumam arcum BG similem arcui ER et protraham lineam BD. Manifestum est igitur quod in tempore uno erit motus orbis centri egredientis ipse angulus ADB, qui est superfluum quod est inter duos motus, et sit centrum eius et longitudo eius longior supra lineam BD. Postquam igitur hoc ita est, sit linea GR equalis linee HD. Supra centrum ergo H et secundum longitudinem HR describam arcum circuli orbis egredientis, supra quem sint R, T, et producam lineam DB secundum rectitudinem usque ad punctum T. Dico igitur quod proportio RH ad HD est sicut proportio DG ad GR. Et secundum hunc modum erit Luna supra punctum R, scilicet in similitudine, et arcus RT similatur arcui ER. Et quia angulus BDG est equalis angulo RGE, erit linea DH equidistans linee GR. Ergo linea RH est equalis et equidistans equistans M. linee DG, et proportio GR ad GD sicut proportio DH ad HR. Et etiam quia DG equidistat linee HR, erit angulus GDB equalis angulo THR. Propter hoc ergo erit arcus RT similis arcui ER. Erit ergo Luna in tempore uno et secundum ambos modos in loco puncti R, quoniam duo motus, qui sunt ER orbis revolutionis et RT orbis centri egredientis, sunt similes, quemadmodum iam declaratum est nobis, et motus centri orbis revolutionis est AG, et motus centri orbis egredientis centri est AB, qui est superfluitas AG super ER. Et illud est quod nos oportuit declarare.
Describam ad illius exemplum circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et sit diameter eius ADK, et orbem revolutionis, supra quem sint E, R, supra centrum G, et ponam ut quando fuerit centrum orbis revolutionis in puncto loci A, sit Luna in longitudine longiore orbis revolutionis, et in tempore uno centrum orbis revolutionis secet per cursum suum arcum AG, et Luna secet ex orbe revolutionis arcum ER, et protraham lineam EGD et lineam GR. Et quia arcus AG est maior in proportione arcu ER, assumam arcum BG similem arcui ER et protraham lineam BD. Manifestum est igitur quod in tempore uno erit motus orbis centri egredientis ipse angulus ADB, qui est superfluum quod est inter duos motus, et sit centrum eius et longitudo eius longior supra lineam BD. Postquam igitur hoc ita est, sit linea GR equalis linee HD. Supra centrum ergo H et secundum longitudinem HR describam arcum circuli orbis egredientis, supra quem sint R, T, et producam lineam DB secundum rectitudinem usque ad punctum T. Dico igitur quod proportio RH ad HD est sicut proportio DG ad GR. Et secundum hunc modum erit Luna supra punctum R, scilicet in similitudine, et arcus RT similatur arcui ER. Et quia angulus BDG est equalis angulo RGE, erit linea DH equidistans linee GR. Ergo linea RH est equalis et equidistans equistans M. linee DG, et proportio GR ad GD sicut proportio DH ad HR. Et etiam quia DG equidistat linee HR, erit angulus GDB equalis angulo THR. Propter hoc ergo erit arcus RT similis arcui ER. Erit ergo Luna in tempore uno et secundum ambos modos in loco puncti R, quoniam duo motus, qui sunt ER orbis revolutionis et RT orbis centri egredientis, sunt similes, quemadmodum iam declaratum est nobis, et motus centri orbis revolutionis est AG, et motus centri orbis egredientis centri est AB, qui est superfluitas AG super ER. Et illud est quod nos oportuit declarare.
Veruntamen si fuerint proportiones tantum similes, et non fuerint quantitates eorum equales, sed neque quantitas orbis centri egredientis et orbis cuius centrum est centrum orbis signorum equales, continget etiam totum quod prediximus et similiter declarabitur nobis. 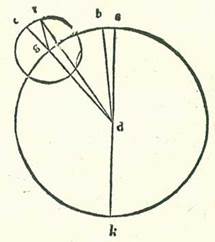 Describam enim unicuique duorum modorum circulum sigillatim, scilicet circulum cuius centrum est centrum orbis signorum, supra quem sint A, B, G, supra centrum D et diametrum AK, et orbem revolutionis, supra quem sint E, R, supra centrum G, et etiam circulum orbis centri egredientis, supra quem sint H, T, K, supra centrum L et diametrum TD, et sit supra ipsam centrum orbis signorum, quod sit punctum M, et sit Luna super punctum K, et protraham in forma prima lineas DGE et GR et DR et in forma secunda lineas HM et KM et KL, et ponam ut proportio GD ad GE sit sicut proportio TL ad LM, et in tempore uno sit motus centri orbis revolutionis angulus ADG, et motus Lune angulus EGR, et motus centri orbis egredientis angulus HMT, et motus Lune etiam angulus TLK. Propter has ergo proportiones positas que sunt motuum erit angulus EGR equalis angulo TLK et angulus ADG equalis ambobus angulis TLK et HMT simul. Et postquam hoc ita est, dico etiam quod in unoquoque duorum modorum in tempore eodem seu equali videtur Luna secare duos arcus equales, scilicet quod angulus ADR est equalis angulo HMK. Quoniam in principio longitudinis fuit Luna in longitudine longiore et fuit visa super duas lineas DA et MH, et in fine longitudinis fuit Luna super duas notas R et K et fuit visa super duas lineas DR et MK.
Describam enim unicuique duorum modorum circulum sigillatim, scilicet circulum cuius centrum est centrum orbis signorum, supra quem sint A, B, G, supra centrum D et diametrum AK, et orbem revolutionis, supra quem sint E, R, supra centrum G, et etiam circulum orbis centri egredientis, supra quem sint H, T, K, supra centrum L et diametrum TD, et sit supra ipsam centrum orbis signorum, quod sit punctum M, et sit Luna super punctum K, et protraham in forma prima lineas DGE et GR et DR et in forma secunda lineas HM et KM et KL, et ponam ut proportio GD ad GE sit sicut proportio TL ad LM, et in tempore uno sit motus centri orbis revolutionis angulus ADG, et motus Lune angulus EGR, et motus centri orbis egredientis angulus HMT, et motus Lune etiam angulus TLK. Propter has ergo proportiones positas que sunt motuum erit angulus EGR equalis angulo TLK et angulus ADG equalis ambobus angulis TLK et HMT simul. Et postquam hoc ita est, dico etiam quod in unoquoque duorum modorum in tempore eodem seu equali videtur Luna secare duos arcus equales, scilicet quod angulus ADR est equalis angulo HMK. Quoniam in principio longitudinis fuit Luna in longitudine longiore et fuit visa super duas lineas DA et MH, et in fine longitudinis fuit Luna super duas notas R et K et fuit visa super duas lineas DR et MK. 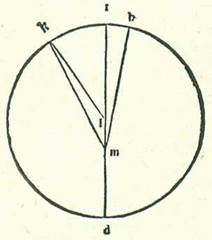 Et sit etiam arcus BG similis cuique duorum arcuum TK et ER, et protraham lineam BD. Et quia proportio DG ad GR est sicut proportio KL ad LM et duo anguli L et G sunt equales, qui continentur ab his lateribus proportionalibus, erit triangulus GDR equalium angulorum cum triangulo LKM et erunt anguli quibus subtenduntur latera proportionalia equales. Erit ergo angulus GRD equalis angulo LMK. Sed angulus BDR equatur angulo GRD, propter hoc quod GR et BD sunt equidistantes quoniam duo anguli RGE et BDG sunt equales. Erit ergo angulus BDR equalis angulo LMK, et erit angulus ADB, qui est superfluitas unius duorum motuum super alterum, equalis angulo HMT, qui est angulus motus Lune in orbe centri egredientis. Totus ergo angulus ADR est equalis toti angulo HMK. Et hoc est quod demonstrare voluimus.
Et sit etiam arcus BG similis cuique duorum arcuum TK et ER, et protraham lineam BD. Et quia proportio DG ad GR est sicut proportio KL ad LM et duo anguli L et G sunt equales, qui continentur ab his lateribus proportionalibus, erit triangulus GDR equalium angulorum cum triangulo LKM et erunt anguli quibus subtenduntur latera proportionalia equales. Erit ergo angulus GRD equalis angulo LMK. Sed angulus BDR equatur angulo GRD, propter hoc quod GR et BD sunt equidistantes quoniam duo anguli RGE et BDG sunt equales. Erit ergo angulus BDR equalis angulo LMK, et erit angulus ADB, qui est superfluitas unius duorum motuum super alterum, equalis angulo HMT, qui est angulus motus Lune in orbe centri egredientis. Totus ergo angulus ADR est equalis toti angulo HMK. Et hoc est quod demonstrare voluimus.
〈IV.6〉 Capitulum sextum: De demonstratione diversitatis Lune prime simplicis
Hoc est illud ad quod pervenit nostra consideratio. Ponam autem demonstrationem diversitatis Lune posite secundum modum orbis revolutionis propter causam quam prediximus. Primum vero accipiemus ex eclypsibus precedentibus que sunt in nostris manibus tres eclypses ex scriptis et memorie commendatis in quibus non fuit dubitatio. Deinde assumemus post hoc etiam tres eclypses ex eclypsibus nostri temporis quas accepimus secundum veritatem nostrarum considerationum. Et ita declarabitur nobis secundum inquisitionem et secundum plurimum quod possibile fuit ex longitudine temporis quod quantitas diversitatis Lune in ambabus demonstrationibus est una fere, et quod superfluitas que superfluit a motibus mediis erit conveniens ei quod aggregatur ex temporibus revolutionum positarum cum equationibus ipsarum. Et in declaratione eius quod videtur per se de diversitate prima assumemus de modo orbis revolutionis secundum quod diximus, et imaginabimur in sphera Lune circulum cuius centrum sit centrum orbis signorum et sit in eius superficie, et imaginabimur circulum alium declinatum ab hoc circulo secundum quantitatem transitus Lune in latitudine et in longitudine eius, et sit eius centrum etiam centrum orbis signorum, supra quod revolvatur equaliter contra continuitatem signorum secundum quantitatem superfluitatis motus Lune in latitudine supra motum eius in longitudine, et imaginabimur orbem (qui nominatur orbis revolvens) moveri supra circulum declinatum per motum equalem etiam secundum continuitatem signorum et secundum illud quod sequitur reversionem latitudinis, que demonstratur quod ipsa facit Lunam in motu suo in longitudine videri supra summitatem orbis signorum, et sit motus Lune in orbe revolvente in arcu longitudinis longioris contra continuitatem signorum secundum illud quod sequitur reversionem diversitatis. Hoc autem quod iam declaravimus non est causa prohibens quin sit sicut narravimus. Quoniam quantitas huius declinationis que est lunaris circuli et eius premissio que est propter latitudinem non faciunt contingere in cursu Lune in longitudine diversitatem cuius sit magna quantitas. Incipiemus autem de eclypsibus tribus premissis quas accepimus ex considerationibus que fuerunt in Babylonia. Prima autem eclypsis ex eis fuit secundum ea que invenimus scripta in primo anno Mardochei vigintinovem diebus transactis mensis Thot, qui est ex mensibus Egyptiis, cuius mane fuit tricesimus dies. In qua incepit Luna eclypsari post ortum suum longiore spacio quam hore integre et eclypsata est tota. Et quia Sol fuit in fine Piscis et fuit longitudo noctis duodecem hore equales fere, tunc manifestum est nobis quod principium eclypsis fuit ante mediam noctem quatuor horis equalibus et medietate, et fuit tempus eclypsis medium ante mediam noctem duabus horis et medietate, quoniam eclypsis fuit integra, et fuit tempus eclypsis medium secundum medium diem Alexandrie in hac eclypsi ante mediam noctem tribus horis et tertia hore. Nos enim non equavimus loca stellarum nisi secundum horas medii diei Alexandrie. Orbis vero medii diei Alexandrie precedit orbem medii diei Babylonie medietate et tertia hore fere. Et fuit tunc Sol secundum horas quas posuimus secundum computationem nostram in vigesimaquarta parte et medietate partis Piscis fere. Secunda autem eclypsis fuit secundum ea que invenimus scripta in secundo anno Mardochei transactis decem et octo diebus mensis Thot, qui est ex mensibus Egyptiorum, in media nocte cuius mane fuit decimusnonus dies. In qua eclypsati fuerunt ex Luna a parte meridiei tres digiti. Et quia tempus medium fuit visum in Babylonia in media nocte, ergo in Alexandria etiam oportuit ut esset ante mediam noctem medietate et tertia hore equalis. Et fuit Sol tunc secundum veritatem in tredecima parte et medietate et quarta partis Piscis fere. Tertia autem eclypsis fuit in illo anno secundo qui fuit ex annis Mardochei transactis quindecem diebus mensis Phamenoth, qui est unus mensium Egyptiorum, in nocte cuius mane fuit sextusdecimus dies. In qua incepit Luna eclypsari post ortum suum et eclypsatum est ex ea a parte septentrionis plus medietate sua. Et quia Sol fuit in principio Virginis, fuit longitudo noctis in Babylonia undecem hore equales fere et fuit medietas noctis quinque hore et medietas hore. Et fuit principium eclypsis ante mediam noctem quinque horis equalibus, quoniam principium eius fuit post ortum suum. Et fuit tempus medium ante mediam noctem tribus horis et medietate hore, quoniam totum tempus quod est magnitudinis huius obscuritatis oportuit ut essent tres hore fere. Ergo in Alexandria etiam fuit tempus medium huius eclypsis ante mediam noctem quatuor horis equalibus et tertia hore. Et fuit Sol tunc secundum veritatem in tertia parte et quarta partis Virginis fere. Manifestum est igitur quod Sol pertransivit a tempore medio eclypsis prime usque ad tempus medium eclypsis secunde, et Luna quidem post revolutiones integras 349 partes et 15 minuta et a tempore medio eclypsis secunde usque ad tempus medium eclypsis tertie 169 partes et 30 minuta. Longitudo autem temporis quod fuit inter medium eclypsis prime et secunde fuit 354 dies. Ex horis vero equalibus secundum sermonem absolutum fuerunt due hore et medietas hore. Cum autem equate fuerint secundum equationem diversitatis que est inter dies cum noctibus suis, erunt due hore et medietas et pars quintadecima hore unius. Et a tempore medio eclypsis secunde usque ad tempus medium eclypsis tertie 170 dies, et ex horis equalibus secundum sermonem absolutum 20 hore et medietas hore. Cum autem equabuntur per equationem diversitatis que est inter dies cum noctibus suis 20 hore et quinta hore secundum veritatem. Motus autem Lune in illo fuit equalis. Non enim in simili huius quantitatis temporis erit motus eius diversitas sensibilis. Quod si aliquis voluerit sequi propinquitatem veritatis motus Lune, inveniet scilicet in trecentis et quinquagintaquatuor diebus et duabus horis et medietate et parte quintadecima partes diversitatis post revolutiones integras 306 partes et 25 minuta et partes longitudinis 345 partes et 51 minuta, et in 170 diebus et 20 horis et quinta hore scilicet partes diversitatis 150 partes et 26 minuta et partes longitudinis 170 partes et 7 minuta fere. Manifestum est igitur quod partes longitudinis prime orbis revolutionis, scilicet 306 partes et 25 minuta, addunt in motu Lune medio 3 partes et 24 minuta, et quod partes longitudinis secunde, 150 partes et 26 minuta, minuunt ex motu Lune medio 37 minuta.
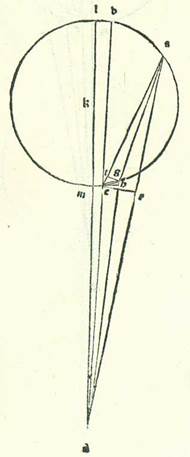 Et ad illius exemplum describam circulum orbis revolutionis Lune, supra quem sint A, B, G, et locus in quo fuit Luna in tempore medio eclypsis prime sit punctum A, et locus in quo fuit Luna in tempore medio eclypsis secunde sit punctum B, et locus in quo fuit Luna in tempore medio eclypsis tertie sit punctum G, et imaginemur localem motum Lune in orbe revolvente a puncto B ad punctum A et a puncto A ad punctum G. Erit ergo arcus AGB, quem secat Luna ab eclypsi prima usque ad eclypsim secundam, qui est 306 partes et 25 minuta, addens supra cursum medium tres partes et 24 minuta, et erit arcus BAG, quem secat Luna ab eclypsi secunda usque ad eclypsim tertiam, qui est 150 partes et 26 minuta, minuens a cursu medio 37 minuta. Propter hoc ergo erit transitus quem pertransit Luna a puncto B ad punctum A, qui est 53 partes et 35 minuta, minuens ex motu medio 3 partes et 24 minuta, et transitus quem pertransit Luna a puncto A ad punctum G, qui est 96 partes et 51 minuta, erit addens supra cursum medium duas partes et 47 minuta. Et manifestum est quod non potest esse ut sit longitudo propinquior que est orbis revolventis in arcu BAG. Quoniam ipse est imminutus et minor medietate circuli, et motus maior non erit nisi in loco longitudinis propinquioris.
Et ad illius exemplum describam circulum orbis revolutionis Lune, supra quem sint A, B, G, et locus in quo fuit Luna in tempore medio eclypsis prime sit punctum A, et locus in quo fuit Luna in tempore medio eclypsis secunde sit punctum B, et locus in quo fuit Luna in tempore medio eclypsis tertie sit punctum G, et imaginemur localem motum Lune in orbe revolvente a puncto B ad punctum A et a puncto A ad punctum G. Erit ergo arcus AGB, quem secat Luna ab eclypsi prima usque ad eclypsim secundam, qui est 306 partes et 25 minuta, addens supra cursum medium tres partes et 24 minuta, et erit arcus BAG, quem secat Luna ab eclypsi secunda usque ad eclypsim tertiam, qui est 150 partes et 26 minuta, minuens a cursu medio 37 minuta. Propter hoc ergo erit transitus quem pertransit Luna a puncto B ad punctum A, qui est 53 partes et 35 minuta, minuens ex motu medio 3 partes et 24 minuta, et transitus quem pertransit Luna a puncto A ad punctum G, qui est 96 partes et 51 minuta, erit addens supra cursum medium duas partes et 47 minuta. Et manifestum est quod non potest esse ut sit longitudo propinquior que est orbis revolventis in arcu BAG. Quoniam ipse est imminutus et minor medietate circuli, et motus maior non erit nisi in loco longitudinis propinquioris. 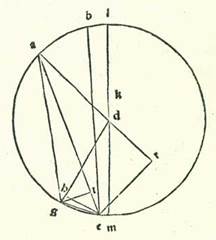 Et quia longitudo propinquior est necessario super arcum GEB, tunc sumatur centrum orbis signorum et centrum orbis qui revolvit centrum orbis revolutionis punctum D, et protraham ab eo tres lineas ad puncta eclypsium trium, supra quas sint DA et DEB et DG. Et dico sermonem communem, ut cum voluerimus convertere demonstrationes similes in hoc capitulo, sit illud nobis levius si voluerimus declarare illud quod demonstrare volumus secundum modum orbis revolventis, quemadmodum volumus nunc.
Et quia longitudo propinquior est necessario super arcum GEB, tunc sumatur centrum orbis signorum et centrum orbis qui revolvit centrum orbis revolutionis punctum D, et protraham ab eo tres lineas ad puncta eclypsium trium, supra quas sint DA et DEB et DG. Et dico sermonem communem, ut cum voluerimus convertere demonstrationes similes in hoc capitulo, sit illud nobis levius si voluerimus declarare illud quod demonstrare volumus secundum modum orbis revolventis, quemadmodum volumus nunc. 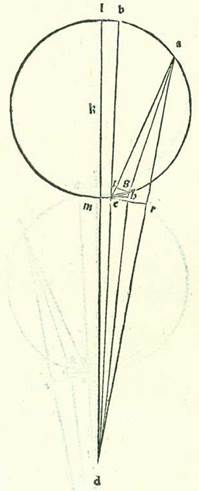 Et si voluerimus declarare illud secundum modum orbis centri egredientis, erit centrum tunc punctum D, et erit deintus, et protraham unam linearum trium usque ad arcum qui ei opponitur, sicut protraximus lineam DEB ad punctum E, deinde ad punctum B, quod est eclypsis secunde, et ab uno duorum punctorum reliquorum, que sunt duarum eclypsium aliarum, ad aliud protraham lineam, sicut protrahimus hic lineam AG, et producam a loco sectionis, qui est punctum E, duas lineas ad puncta duo reliqua, scilicet quemadmodum protrahimus hic duas lineas EA et EG, et protraham etiam ab eodem ad duas lineas que producuntur a duobus punctis reliquis ad centrum signorum duas perpendiculares, sicut protraximus hic ad lineam AD perpendicularem ER et ad lineam DG perpendicularem EH, et etiam protraham ab uno duorum punctorum que prediximus perpendicularem ad lineam AE, sicut produximus hic lineam GT. Nos ergo, quia accepimus proportiones in eis que posuimus in hac forma, inveniemus proportiones cum numeris huius demonstrationis unas, et remansit eligere planiores tantum quibus operemur. Et quia iam declaratum est nobis quod arcus AB pertransit ex orbe signorum tres partes et 24 minuta, erit angulus BDA, qui est apud centrum orbis signorum, tres partes et 24 minuta fere secundum quantitatem qua erunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit angulus BDA sex partes et 48 minuta. Quapropter erit arcus qui est supra chordam ER sex partes et 48 minuta secundum quantitatem qua erit circulus continens triangulum DER ortogonium 360 partes, et erit chorda ER septem partes et 7 minuta secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus BA est 53 partes et 35 minuta, erit angulus BEA, qui est apud arcum, 53 partes et 35 minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Et cum hoc fuit angulus BDA sex partes et 48 minuta. Angulus ergo EAD reliquus erit 46 partes et 47 minuta. Quapropter erit arcus qui est super chordam ER 46 partes et 47 minuta secundum quantitatem qua erit circulus continens triangulum AER ortogonium 360 partes, et chorda ER erit 47 partes et 38 minuta et 30 secunda secundum quantitatem qua erit diameter EA 120 partes. Ergo secundum quantitatem qua erit chorda ER septem partes et 7 minuta, et iam ostensum est quod DE est 120 partes, erit chorda AE 17 partes et 55 minuta et 32 secunda. Et etiam quia arcus BAG pertransit ex orbe signorum 37 minuta, erit angulus BDG, qui est apud centrum orbis signorum, 37 minuta secundum quantitatem qua erunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes, erit angulus BDG pars et 14 minuta. Quapropter erit arcus qui est super lineam EH pars et 14 minuta, et linea EH pars et 17 minuta et 30 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus BAG est 150 partes et 26 minuta, erit angulus BEG, qui est apud arcum, 150 partes et 26 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum illam quantitatem erit angulus BDG pars et 14 minuta. Remanet ergo angulus EGD secundum illam quantitatem 149 partes et 12 minuta. Quapropter erit arcus qui est supra lineam EH 149 partes et 12 minuta secundum quantitatem qua erit circulus continens triangulum GEH ortogonium 360 partes, et erit chorda EH 115 partes et 41 minuta et 24 secunda secundum quantitatem qua erit diameter GE 120 partes. Ergo secundum quantitatem qua erit linea EH pars et 17 minuta et 30 secunda, et iam ostensum est quod est diameter DE 120 partes, erit linea GE pars et 20 minuta et 23 secunda. Et secundum illam quantitatem declaratur quod linea EA est 17 partes et 55 minuta et 32 secunda. Et etiam quia iam ostensum est quod arcus AG est 96 partes et 51 minuta, erit angulus AEG, qui est apud arcum, secundum illam quantitatem 96 partes et 51 minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Quapropter erit arcus qui est supra chordam GT 96 partes et 51 minuta secundum quantitatem qua erit circulus continens triangulum GET ortogonium 360 partes, et arcus qui est supra chordam ET residuus ad complendum semicirculum erit 83 partes et 9 minuta. Erunt ergo linee que subtenduntur arcubus, scilicet GT 89 partes et 46 minuta et 14 secunda secundum quantitatem qua erit diameter GE 120 partes, et ET secundum illam quantitatem erit 79 partes et 37 minuta et 55 secunda. Secundum quantitatem ergo qua erit linea EG pars et 20 minuta et 23 secunda erit linea GT pars una et octo secunda, et linea ET erit 53 minuta et 21 secunda. Sed secundum illam quantitatem fuit tota linea EA 17 partes et 55 minuta et 32 secunda. Remanet ergo linea TA 17 partes et duo minuta et 11 secunda secundum quantitatem qua ostensum est quod linea GT est pars et octo secunda. Et erit quadratum quod est ex multiplicatione AT linee in se 290 partes et 14 minuta et 19 secunda. Et quadratum quod est ex multiplicatione GT in se est pars et 17 secunda. Cum ergo aggregabuntur ipsa, erunt equalia quadrato AG, scilicet 291 partibus et 14 minutis et 36 secundis. Longitudo ergo linee AG erit 17 partes et 3 minuta et 51 secunda secundum quantitatem qua erit diameter DE 120 partes, et linea GE fuit secundum illam quantitatem pars et 20 minuta et 23 secunda. Et secundum quantitatem qua est diameter orbis revolventis 120 partes erit linea AG 89 partes et 46 minuta et 14 secunda, quoniam ipsa est chorda arcus AG, qui est 96 partes et 51 minuta. Secundum quantitatem ergo qua est linea AG 89 partes et 46 minuta et 14 secunda et diameter orbis revolventis 120 partes erit linea DE 631 partes et 13 minuta et 48 secunda, et linea GE erit septem partes et duo minuta et octo secunda, et arcus qui est super illam, qui est GE, erit sex partes et 44 minuta et 30 secunda secundum quantitatem qua est orbis revolvens 360 partes. Et secundum illam quantitatem est arcus BAG 150 partes et 26 minuta. Totus ergo arcus BGE erit 157 partes et 11 minuta fere, et eius chorda, que est BE, erit 117 partes et 37 minuta et 32 secunda secundum quantitatem qua est diameter orbis revolventis 120 partes. Si ergo reperiremus lineam BE equalem diametro orbis revolventis, manifestum est quod eius centrum esset supra eam. Et propter hoc demonstraretur proportio duarum diametrorum. Et quia BE est brevior diametro et arcus BGE est minor semicirculo, tunc manifestum est quod centrum orbis revolventis cadit extra portionem BGE. Ponam ergo punctum K centrum orbis revolventis, et protraham AD, quod est centrum orbis signorum, lineam transeuntem super K, supra quam sint D, M, K, L, sitque punctum L longitudo longior orbis revolventis et punctum M longitudo propinquior. Et quia ductus linee BD in DE est equalis ductui LD in DM, et iam declaravimus quod secundum quantitatem qua est diameter orbis revolventis, que est linea LKM, 120 partes, erit linea BE 117 partes et 37 minuta et 32 secunda et linea ED secundum illam quantitatem 631 partes et 13 minuta et 48 secunda. Et manifestum est quod tota linea BD est 748 partes et 51 minuta et 20 secunda. Ergo erit ductus linee BD in DE, qui est equalis ductui linee LD in DM, secundum illam quantitatem 472700 partes et quinque minuta et 32 secunda. Et etiam quia quadratum duarum linearum LD in DM cum quadrato KM in se est equale quadrato KD in se, et linea KM, que est medietas diametri orbis revolventis, est secundum illam quantitatem 60 partes. Et cum nos addiderimus quadratum eius quod est 3600 supra 472700 partes et 5 minuta et 32 secunda, erit illud equale quadrato linee DK in se, scilicet 476300 partibus et 5 minutis et 32 secundis. Ergo erit longitudo linee DK, que est medietas diametri orbis revolventis orbem revolutionis, cuius centrum est centrum orbis signorum, secundum illam quantitatem 690 partes et 8 minuta et 42 secunda, secundum quantitatem qua erit linea KM, que est medietas diametri orbis revolutionis, 60 partes. Quapropter erit medietas diametri orbis revolutionis secundum quantitatem qua est medietas diametri orbis revolventis centrum orbis revolutionis, cuius centrum est aspectus oculorum, 60 partes quinque partes et 13 minuta fere.
Et si voluerimus declarare illud secundum modum orbis centri egredientis, erit centrum tunc punctum D, et erit deintus, et protraham unam linearum trium usque ad arcum qui ei opponitur, sicut protraximus lineam DEB ad punctum E, deinde ad punctum B, quod est eclypsis secunde, et ab uno duorum punctorum reliquorum, que sunt duarum eclypsium aliarum, ad aliud protraham lineam, sicut protrahimus hic lineam AG, et producam a loco sectionis, qui est punctum E, duas lineas ad puncta duo reliqua, scilicet quemadmodum protrahimus hic duas lineas EA et EG, et protraham etiam ab eodem ad duas lineas que producuntur a duobus punctis reliquis ad centrum signorum duas perpendiculares, sicut protraximus hic ad lineam AD perpendicularem ER et ad lineam DG perpendicularem EH, et etiam protraham ab uno duorum punctorum que prediximus perpendicularem ad lineam AE, sicut produximus hic lineam GT. Nos ergo, quia accepimus proportiones in eis que posuimus in hac forma, inveniemus proportiones cum numeris huius demonstrationis unas, et remansit eligere planiores tantum quibus operemur. Et quia iam declaratum est nobis quod arcus AB pertransit ex orbe signorum tres partes et 24 minuta, erit angulus BDA, qui est apud centrum orbis signorum, tres partes et 24 minuta fere secundum quantitatem qua erunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit angulus BDA sex partes et 48 minuta. Quapropter erit arcus qui est supra chordam ER sex partes et 48 minuta secundum quantitatem qua erit circulus continens triangulum DER ortogonium 360 partes, et erit chorda ER septem partes et 7 minuta secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus BA est 53 partes et 35 minuta, erit angulus BEA, qui est apud arcum, 53 partes et 35 minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Et cum hoc fuit angulus BDA sex partes et 48 minuta. Angulus ergo EAD reliquus erit 46 partes et 47 minuta. Quapropter erit arcus qui est super chordam ER 46 partes et 47 minuta secundum quantitatem qua erit circulus continens triangulum AER ortogonium 360 partes, et chorda ER erit 47 partes et 38 minuta et 30 secunda secundum quantitatem qua erit diameter EA 120 partes. Ergo secundum quantitatem qua erit chorda ER septem partes et 7 minuta, et iam ostensum est quod DE est 120 partes, erit chorda AE 17 partes et 55 minuta et 32 secunda. Et etiam quia arcus BAG pertransit ex orbe signorum 37 minuta, erit angulus BDG, qui est apud centrum orbis signorum, 37 minuta secundum quantitatem qua erunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes, erit angulus BDG pars et 14 minuta. Quapropter erit arcus qui est super lineam EH pars et 14 minuta, et linea EH pars et 17 minuta et 30 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus BAG est 150 partes et 26 minuta, erit angulus BEG, qui est apud arcum, 150 partes et 26 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum illam quantitatem erit angulus BDG pars et 14 minuta. Remanet ergo angulus EGD secundum illam quantitatem 149 partes et 12 minuta. Quapropter erit arcus qui est supra lineam EH 149 partes et 12 minuta secundum quantitatem qua erit circulus continens triangulum GEH ortogonium 360 partes, et erit chorda EH 115 partes et 41 minuta et 24 secunda secundum quantitatem qua erit diameter GE 120 partes. Ergo secundum quantitatem qua erit linea EH pars et 17 minuta et 30 secunda, et iam ostensum est quod est diameter DE 120 partes, erit linea GE pars et 20 minuta et 23 secunda. Et secundum illam quantitatem declaratur quod linea EA est 17 partes et 55 minuta et 32 secunda. Et etiam quia iam ostensum est quod arcus AG est 96 partes et 51 minuta, erit angulus AEG, qui est apud arcum, secundum illam quantitatem 96 partes et 51 minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Quapropter erit arcus qui est supra chordam GT 96 partes et 51 minuta secundum quantitatem qua erit circulus continens triangulum GET ortogonium 360 partes, et arcus qui est supra chordam ET residuus ad complendum semicirculum erit 83 partes et 9 minuta. Erunt ergo linee que subtenduntur arcubus, scilicet GT 89 partes et 46 minuta et 14 secunda secundum quantitatem qua erit diameter GE 120 partes, et ET secundum illam quantitatem erit 79 partes et 37 minuta et 55 secunda. Secundum quantitatem ergo qua erit linea EG pars et 20 minuta et 23 secunda erit linea GT pars una et octo secunda, et linea ET erit 53 minuta et 21 secunda. Sed secundum illam quantitatem fuit tota linea EA 17 partes et 55 minuta et 32 secunda. Remanet ergo linea TA 17 partes et duo minuta et 11 secunda secundum quantitatem qua ostensum est quod linea GT est pars et octo secunda. Et erit quadratum quod est ex multiplicatione AT linee in se 290 partes et 14 minuta et 19 secunda. Et quadratum quod est ex multiplicatione GT in se est pars et 17 secunda. Cum ergo aggregabuntur ipsa, erunt equalia quadrato AG, scilicet 291 partibus et 14 minutis et 36 secundis. Longitudo ergo linee AG erit 17 partes et 3 minuta et 51 secunda secundum quantitatem qua erit diameter DE 120 partes, et linea GE fuit secundum illam quantitatem pars et 20 minuta et 23 secunda. Et secundum quantitatem qua est diameter orbis revolventis 120 partes erit linea AG 89 partes et 46 minuta et 14 secunda, quoniam ipsa est chorda arcus AG, qui est 96 partes et 51 minuta. Secundum quantitatem ergo qua est linea AG 89 partes et 46 minuta et 14 secunda et diameter orbis revolventis 120 partes erit linea DE 631 partes et 13 minuta et 48 secunda, et linea GE erit septem partes et duo minuta et octo secunda, et arcus qui est super illam, qui est GE, erit sex partes et 44 minuta et 30 secunda secundum quantitatem qua est orbis revolvens 360 partes. Et secundum illam quantitatem est arcus BAG 150 partes et 26 minuta. Totus ergo arcus BGE erit 157 partes et 11 minuta fere, et eius chorda, que est BE, erit 117 partes et 37 minuta et 32 secunda secundum quantitatem qua est diameter orbis revolventis 120 partes. Si ergo reperiremus lineam BE equalem diametro orbis revolventis, manifestum est quod eius centrum esset supra eam. Et propter hoc demonstraretur proportio duarum diametrorum. Et quia BE est brevior diametro et arcus BGE est minor semicirculo, tunc manifestum est quod centrum orbis revolventis cadit extra portionem BGE. Ponam ergo punctum K centrum orbis revolventis, et protraham AD, quod est centrum orbis signorum, lineam transeuntem super K, supra quam sint D, M, K, L, sitque punctum L longitudo longior orbis revolventis et punctum M longitudo propinquior. Et quia ductus linee BD in DE est equalis ductui LD in DM, et iam declaravimus quod secundum quantitatem qua est diameter orbis revolventis, que est linea LKM, 120 partes, erit linea BE 117 partes et 37 minuta et 32 secunda et linea ED secundum illam quantitatem 631 partes et 13 minuta et 48 secunda. Et manifestum est quod tota linea BD est 748 partes et 51 minuta et 20 secunda. Ergo erit ductus linee BD in DE, qui est equalis ductui linee LD in DM, secundum illam quantitatem 472700 partes et quinque minuta et 32 secunda. Et etiam quia quadratum duarum linearum LD in DM cum quadrato KM in se est equale quadrato KD in se, et linea KM, que est medietas diametri orbis revolventis, est secundum illam quantitatem 60 partes. Et cum nos addiderimus quadratum eius quod est 3600 supra 472700 partes et 5 minuta et 32 secunda, erit illud equale quadrato linee DK in se, scilicet 476300 partibus et 5 minutis et 32 secundis. Ergo erit longitudo linee DK, que est medietas diametri orbis revolventis orbem revolutionis, cuius centrum est centrum orbis signorum, secundum illam quantitatem 690 partes et 8 minuta et 42 secunda, secundum quantitatem qua erit linea KM, que est medietas diametri orbis revolutionis, 60 partes. Quapropter erit medietas diametri orbis revolutionis secundum quantitatem qua est medietas diametri orbis revolventis centrum orbis revolutionis, cuius centrum est aspectus oculorum, 60 partes quinque partes et 13 minuta fere.
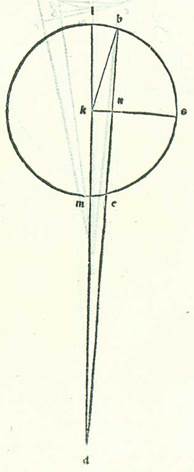 Protraham autem perpendicularem in forma huic simili a centro K cadentem supra lineam BE, supra quam sint K, N, S, et producam lineam BK. Et quia secundum quantitatem eam qua iam ostensum est quod linea DK est 690 partes et octo minuta et 42 secunda, est linea DE 631 partes et 13 minuta et 48 secunda, et linea EN, que est medietas BE, secundum illam quantitatem est 58 partes et 48 minuta et 46 secunda. Ergo propter hoc erit tota linea DEN secundum illam quantitatem 690 partes et duo minuta et 34 secunda. Ergo secundum quantitatem qua erit diameter DK 120 partes erit linea DN 119 partes et 58 minuta et 57 secunda, et arcus qui est super eam erit 178 partes et duo minuta fere secundum quantitatem qua erit circulus continens triangulum DKN ortogonium 360 partes. Propter hoc ergo erit angulus DKN 178 partes et duo minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Et secundum quantitatem qua sunt quatuor anguli recti 360 partes erit angulus DKN 89 partes et minutum unum. Ergo et arcus SM, qui est orbis revolutionis, erit 89 partes et unum minutum et arcus LBS residuus ex complemento semicirculi erit 90 partes et 59 minuta. Et secundum illam quantitatem erit arcus SB, qui est medietas arcus BSE, 78 partes et 35 minuta et 30 secunda. Iam enim ostensum fuit quod totus arcus BE est 157 partes et 11 minuta fere. Ergo arcus LB reliquus orbis revolventis, qui est longitudo loci Lune a longitudine longiore in tempore medio eclypsis secunde, erit 12 partes et 24 minuta fere. Et illud est quod oportuit nos declarare.
Protraham autem perpendicularem in forma huic simili a centro K cadentem supra lineam BE, supra quam sint K, N, S, et producam lineam BK. Et quia secundum quantitatem eam qua iam ostensum est quod linea DK est 690 partes et octo minuta et 42 secunda, est linea DE 631 partes et 13 minuta et 48 secunda, et linea EN, que est medietas BE, secundum illam quantitatem est 58 partes et 48 minuta et 46 secunda. Ergo propter hoc erit tota linea DEN secundum illam quantitatem 690 partes et duo minuta et 34 secunda. Ergo secundum quantitatem qua erit diameter DK 120 partes erit linea DN 119 partes et 58 minuta et 57 secunda, et arcus qui est super eam erit 178 partes et duo minuta fere secundum quantitatem qua erit circulus continens triangulum DKN ortogonium 360 partes. Propter hoc ergo erit angulus DKN 178 partes et duo minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Et secundum quantitatem qua sunt quatuor anguli recti 360 partes erit angulus DKN 89 partes et minutum unum. Ergo et arcus SM, qui est orbis revolutionis, erit 89 partes et unum minutum et arcus LBS residuus ex complemento semicirculi erit 90 partes et 59 minuta. Et secundum illam quantitatem erit arcus SB, qui est medietas arcus BSE, 78 partes et 35 minuta et 30 secunda. Iam enim ostensum fuit quod totus arcus BE est 157 partes et 11 minuta fere. Ergo arcus LB reliquus orbis revolventis, qui est longitudo loci Lune a longitudine longiore in tempore medio eclypsis secunde, erit 12 partes et 24 minuta fere. Et illud est quod oportuit nos declarare.
Et similiter quia iam ostensum est quod angulus DKN est 89 partes et minutum unum secundum quantitatem qua erunt quattuor anguli recti 360 partes, ostenditur quod angulus reliquus KDN secundum residuum complementi anguli unius recti est 59 minuta, et ipse est angulus cui subtenditur arcus diminutus a cursu medio in longitudine quem secat arcus LB orbis revolventis, qui est diversitas Lune. Fuit ergo locus Lune per cursum suum medium in tempore medio eclypsis secunde in 14 parte Virginis et 44 minuto, quoniam fuit locus eius secundum veritatem in 13 parte et in 45 minuto. Et fuit locus Solis in Piscibus in partibus similibus illis partibus. Fuit etiam prima trium eclypsium quas consideravimus in Alexandria secundum quod subtilius possibile fuit in decimoseptimo annorum Adriani 20 diebus mensis Tegni transactis, qui est unus mensium Egyptiorum, nocte cuius mane fuit dies vicesimusprimus. Consideravimus autem secundum veritatem et invenimus quod tempus medium fuit ante medietatem noctis medietate et quarta hore equalis, et eclypsata fuit Luna tota, et fuit locus Solis in illa hora tertiadecima pars et quarta partis Tauri fere. Secunda vero eclypsis fuit in anno decimonono annorum Adriani duobus diebus mensis Signach transactis nocte cuius mane fuit dies tertius. Et consideravimus et invenimus quod tempus medium fuit ante mediam noctem una hora equali, et eclypsata est ex Luna a parte septentrionis medietas et tertia diametri ipsius, et fuit Sol in illa hora secundum veritatem in 25 parte et 10 minuto Libre fere. Tertia autem eclypsis fuit in anno qui fuit vicesimus annorum Adriani transacto decimonono die mensis Formiche, qui est unus mensium Egyptiorum, nocte cuius mane fuit dies vicesimus. Et consideravimus et invenimus quod tempus medium fuit post medietatem noctis quattuor horis equalibus, et fuit eclypsata medietas diametri Lune a parte septentrionis, fuitque Sol in illa hora in 14 parte et 5 minuto Piscis fere. Iam ergo demonstratum est hic quod Luna peragravit post revolutiones integras a tempore medio quod fuit eclypsis prime ad tempus medium eclypsis secunde quantum perambulavit Sol, scilicet 161 partes et 55 minuta, et perambulavit a medio eclypsis secunde usque ad medium eclypsis tertie 138 partes et 55 minuta. Et fuit tempus quod fuit inter eclypsim primam et eclypsim secundam annus Egyptius et 166 dies et 23 hore et medietas et quarta hore equalis, secundum veritatem vero 23 hore et medietas et octava hore. Et fuit tempus quod fuit inter medium eclypsis secunde et inter medium eclypsis tertie annus unus etiam et 137 dies et 5 hore equales secundum semonem absolutum, sed secundum veritatem erant quinque hore et medietas hore. Et erat cursus Lune medius etiam post revolutiones integras, scilicet in anno uno et 166 diebus et 23 horis et medietate et octava hore, cursus videlicet diversitatis 110 partes et 21 minuta, et cursus eius in longitudine 169 partes et 37 minuta fere. Et erat cursus eius in anno uno et 137 diebus et 5 horis et medietate hore equalis, videlicet cursus diversitatis 81 partes et 36 minuta, sed in longitudine 137 partes et 34 minuta fere. Manifestum est ergo quod 110 partes et 21 minuta que sunt longitudinis prime orbis revolventis minuunt ex cursu Lune medio in longitudine septem partes et 42 minuta, et partes longitudinis secunde, scilicet 81 partes et 36 minuta orbis revolventis, addunt etiam supra cursum Lune medium in longitudine partem unam et 21 minuta. Postquam ergo hoc est secundum quod declaravi, tunc describam etiam orbem revolutionis Lune, supra quem sint A, B, G, sitque locus in quo fuit Luna in tempore medio eclypsis prime punctum A, et locus eius in tempore medio eclypsis secunde punctum B, et locus eius in tempore medio eclypsis tertie punctum G. Et similiter imaginemur motum Lune a puncto A ad punctum B, et postea a puncto B ad punctum G, et sit arcus AB, qui est 110 partes et 21 minuta, minuens, quemadmodum diximus, ex cursu medio in longitudine septem partes et 42 minuta, et sit arcus BG, qui est 81 partes et 36 minuta, addens supra cursum medium in longitudine partem unam et 21 minuta, et sit arcus GA residuus, qui est 168 partes et 3 minuta, addens supra cursum medium in longitudine partes residuas, scilicet 6 partes et 21 minuta. Et manifestum est quod oportet ut sit longitudo longior in arcu AB, quoniam non est possibile ut sit in arcu BG neque in arcu GA, eo quod unusquisque eorum est addens et minor semicirculo. 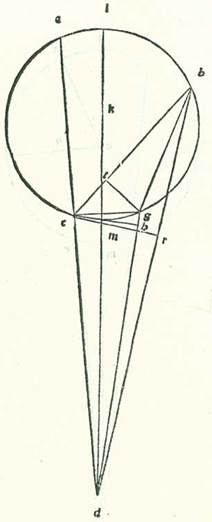 Et secundum hoc ponam centrum orbis signorum et centrum orbis supra quem currit centrum orbis revolventis punctum D, et protraham ab eo lineas ad puncta locorum eclypsium trium, que sint DEA et DB et DG, et producam lineam BG, et protraham a puncto E lineas, scilicet ad punctum B et ad punctum G duas lineas EB et EG et ad duas lineas BD et DG duas perpendiculares ER et EH, et etiam producam a puncto G ad lineam BE perpendicularem GT. Et quia arcus AB comprehendit ex orbe signorum septem partes et 42 minuta, erit angulus ADB qui est apud centrum orbis signorum septem partes et 42 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 15 partes et 24 minuta. Et similiter erit arcus qui est supra lineam ER 15 partes et 24 minuta secundum quantitatem qua erit circulus continens triangulum DER ortogonium 360 partes, et chorda ER erit 16 partes et 4 minuta et 42 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus AB est 110 partes et 21 minuta, erit angulus AEB, qui est apud circulum, 110 partes et 21 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum illam quantitatem fuit angulus ADB 15 partes et 24 minuta. Ergo angulus EBD reliquus secundum illam quantitatem erit 94 partes et 57 minuta. Quapropter erit arcus qui est supra lineam ER 94 partes et 57 minuta secundum quantitatem qua erit circulus continens triangulum EBR ortogonium 360 partes, et chorda ER erit 88 partes et 26 minuta et 17 secunda secundum quantitatem qua erit diameter BE 120 partes. Secundum quantitatem ergo qua erit linea ER 16 partes et 4 minuta et 42 secunda, et quia iam ostensum est quod linea DE est 120 partes, erit linea BE 21 partes et 48 minuta et 59 secunda. Et etiam quia iam ostensum est quod arcus GEA comprehendit ex orbe signorum sex partes et 21 minuta, erit angulus ADG, qui est apud centrum orbis signorum, sex partes et 21 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 12 partes et 42 minuta. Quapropter erit arcus qui est supra lineam EH 12 partes et 42 minuta secundum quantitatem qua erit circulus continens triangulum DHE ortogonium 360 partes, et erit chorda EH 13 partes et 16 minuta et 19 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia totus arcus ABG est 191 partes et 57 minuta, erit angulus AEG, qui est apud circulum, similiter 191 partes et 57 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum illam quantitatem fuit angulus ADG 12 partes et 42 minuta. Ergo angulus EDG reliquus secundum illam quantitatem erit 179 partes et 15 minuta. Et propter hoc erit arcus qui est super lineam EH 179 partes et 15 minuta secundum illam quantitatem qua erit circulus continens triangulum GEH orthogonium 360 partes, et chorda EH erit 119 partes et 59 minuta et 50 secunda secundum quantitatem qua erit diameter EG 120 partes. Secundum quantitatem ergo qua erit linea EH 13 partes et 16 minuta et 19 secunda et linea DE, quemadmodum iam ostensum est, 120 partes erit linea GE 13 partes et 16 minuta et 20 secunda. Et secundum illam quantitatem ostensum est quod linea BE est 21 partes et 48 minuta et 49 secunda. Et etiam quia arcus BG est 81 partes et 36 minuta, erit angulus BEG, qui est apud circulum, 81 partes et 36 minuta secundum illam quantitatem qua erunt duo anguli recti 360 partes. Quapropter erit arcus qui est supra lineam GT 81 partes et 36 minuta secundum quantitatem qua erit circulus continens triangulum GET orthogonium 360 partes, et arcus qui est supra lineam ET residuus ad complendum semicirculum 98 partes et 24 minuta. Ergo linee que subtenduntur eis, scilicet linea GT erit 78 partes et 24 minuta et 37 secunda secundum quantitatem qua erit diameter EG 120 partes, et secundum eam erit chorda ET 90 partes et 50 minuta et 22 secunda. Ergo secundum quantitatem qua erit linea GE 13 partes et 16 minuta et 20 secunda erit linea GT 8 partes et 40 minuta et 20 secunda, et linea ET similiter erit 10 partes et duo minuta et 49 secunda. Et secundum illam quantitatem est tota linea EB 21 partes et 48 minuta et 49 secunda. Oportet ergo ut sit linea TB secundum illam quantitatem 11 partes et 46 minuta et 10 secunda secundum quantitatem qua fuit linea GT octo partes et 40 minuta et 20 secunda. Erit ergo quadratum TB in se 138 partes et 31 minuta et 11 secunda, et quadratum GT secundum illam quantitatem erit 75 partes et 12 minuta et 27 secunda. Cum ergo aggregaverimus ea, erit ex eis quadratum BG in se scilicet 213 partes et 46 minuta et 38 secunda. Erit ergo longitudo linee BG 14 partes et 37 minuta et 10 secunda secundum quantitatem qua erit diameter DE 120 partes, et linea GE 13 partes et 16 minuta et 20 secunda. Sed secundum quantitatem qua erit diameter orbis revolventis 120 partes erit linea BG 78 partes et 24 minuta et 37 secunda. Et ipsa subtenditur arcui BG, qui est 81 partes et 36 minuta. Ergo secundum quantitatem qua est linea BG 78 partes et 24 minuta et 37 secunda et diameter orbis revolventis 120 partes erit linea DE 643 partes et 36 minuta et 39 secunda, et linea GE secundum illam quantitatem erit 71 partes et 11 minuta et 4 secunda, et arcus qui est super eam erit 72 partes et 46 minuta et 10 secunda secundum quantitatem qua erit orbis revolvens 360 partes. Et secundum eam erit arcus GEA 168 partes et tria minuta. Ergo arcus EA residuus erit 95 partes et 16 minuta et 50 secunda, et eius chorda AE erit 88 partes et 40 minuta et 17 secunda secundum quantitatem qua erit diameter orbis revolventis 120 partes, et linea ED 643 partes et 36 minuta et 39 secunda. Et illud est quod oportuit nos declarare.
Et secundum hoc ponam centrum orbis signorum et centrum orbis supra quem currit centrum orbis revolventis punctum D, et protraham ab eo lineas ad puncta locorum eclypsium trium, que sint DEA et DB et DG, et producam lineam BG, et protraham a puncto E lineas, scilicet ad punctum B et ad punctum G duas lineas EB et EG et ad duas lineas BD et DG duas perpendiculares ER et EH, et etiam producam a puncto G ad lineam BE perpendicularem GT. Et quia arcus AB comprehendit ex orbe signorum septem partes et 42 minuta, erit angulus ADB qui est apud centrum orbis signorum septem partes et 42 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 15 partes et 24 minuta. Et similiter erit arcus qui est supra lineam ER 15 partes et 24 minuta secundum quantitatem qua erit circulus continens triangulum DER ortogonium 360 partes, et chorda ER erit 16 partes et 4 minuta et 42 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia arcus AB est 110 partes et 21 minuta, erit angulus AEB, qui est apud circulum, 110 partes et 21 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum illam quantitatem fuit angulus ADB 15 partes et 24 minuta. Ergo angulus EBD reliquus secundum illam quantitatem erit 94 partes et 57 minuta. Quapropter erit arcus qui est supra lineam ER 94 partes et 57 minuta secundum quantitatem qua erit circulus continens triangulum EBR ortogonium 360 partes, et chorda ER erit 88 partes et 26 minuta et 17 secunda secundum quantitatem qua erit diameter BE 120 partes. Secundum quantitatem ergo qua erit linea ER 16 partes et 4 minuta et 42 secunda, et quia iam ostensum est quod linea DE est 120 partes, erit linea BE 21 partes et 48 minuta et 59 secunda. Et etiam quia iam ostensum est quod arcus GEA comprehendit ex orbe signorum sex partes et 21 minuta, erit angulus ADG, qui est apud centrum orbis signorum, sex partes et 21 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 12 partes et 42 minuta. Quapropter erit arcus qui est supra lineam EH 12 partes et 42 minuta secundum quantitatem qua erit circulus continens triangulum DHE ortogonium 360 partes, et erit chorda EH 13 partes et 16 minuta et 19 secunda secundum quantitatem qua erit diameter DE 120 partes. Et similiter quia totus arcus ABG est 191 partes et 57 minuta, erit angulus AEG, qui est apud circulum, similiter 191 partes et 57 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum illam quantitatem fuit angulus ADG 12 partes et 42 minuta. Ergo angulus EDG reliquus secundum illam quantitatem erit 179 partes et 15 minuta. Et propter hoc erit arcus qui est super lineam EH 179 partes et 15 minuta secundum illam quantitatem qua erit circulus continens triangulum GEH orthogonium 360 partes, et chorda EH erit 119 partes et 59 minuta et 50 secunda secundum quantitatem qua erit diameter EG 120 partes. Secundum quantitatem ergo qua erit linea EH 13 partes et 16 minuta et 19 secunda et linea DE, quemadmodum iam ostensum est, 120 partes erit linea GE 13 partes et 16 minuta et 20 secunda. Et secundum illam quantitatem ostensum est quod linea BE est 21 partes et 48 minuta et 49 secunda. Et etiam quia arcus BG est 81 partes et 36 minuta, erit angulus BEG, qui est apud circulum, 81 partes et 36 minuta secundum illam quantitatem qua erunt duo anguli recti 360 partes. Quapropter erit arcus qui est supra lineam GT 81 partes et 36 minuta secundum quantitatem qua erit circulus continens triangulum GET orthogonium 360 partes, et arcus qui est supra lineam ET residuus ad complendum semicirculum 98 partes et 24 minuta. Ergo linee que subtenduntur eis, scilicet linea GT erit 78 partes et 24 minuta et 37 secunda secundum quantitatem qua erit diameter EG 120 partes, et secundum eam erit chorda ET 90 partes et 50 minuta et 22 secunda. Ergo secundum quantitatem qua erit linea GE 13 partes et 16 minuta et 20 secunda erit linea GT 8 partes et 40 minuta et 20 secunda, et linea ET similiter erit 10 partes et duo minuta et 49 secunda. Et secundum illam quantitatem est tota linea EB 21 partes et 48 minuta et 49 secunda. Oportet ergo ut sit linea TB secundum illam quantitatem 11 partes et 46 minuta et 10 secunda secundum quantitatem qua fuit linea GT octo partes et 40 minuta et 20 secunda. Erit ergo quadratum TB in se 138 partes et 31 minuta et 11 secunda, et quadratum GT secundum illam quantitatem erit 75 partes et 12 minuta et 27 secunda. Cum ergo aggregaverimus ea, erit ex eis quadratum BG in se scilicet 213 partes et 46 minuta et 38 secunda. Erit ergo longitudo linee BG 14 partes et 37 minuta et 10 secunda secundum quantitatem qua erit diameter DE 120 partes, et linea GE 13 partes et 16 minuta et 20 secunda. Sed secundum quantitatem qua erit diameter orbis revolventis 120 partes erit linea BG 78 partes et 24 minuta et 37 secunda. Et ipsa subtenditur arcui BG, qui est 81 partes et 36 minuta. Ergo secundum quantitatem qua est linea BG 78 partes et 24 minuta et 37 secunda et diameter orbis revolventis 120 partes erit linea DE 643 partes et 36 minuta et 39 secunda, et linea GE secundum illam quantitatem erit 71 partes et 11 minuta et 4 secunda, et arcus qui est super eam erit 72 partes et 46 minuta et 10 secunda secundum quantitatem qua erit orbis revolvens 360 partes. Et secundum eam erit arcus GEA 168 partes et tria minuta. Ergo arcus EA residuus erit 95 partes et 16 minuta et 50 secunda, et eius chorda AE erit 88 partes et 40 minuta et 17 secunda secundum quantitatem qua erit diameter orbis revolventis 120 partes, et linea ED 643 partes et 36 minuta et 39 secunda. Et illud est quod oportuit nos declarare.
Et etiam quia iam ostensum est quod arcus EA est minor semicirculo, ergo manifestum est quod centrum orbis revolventis cadit extra portionem EA. Ponam itaque punctum K centrum orbis revolventis et protraham lineam DMKL donec sit etiam punctum L ipsa longitudo longior et punctum M ipsa longitudo propinquior. Et quia ductus linee AD in DE est equalis ductui LD in DM, et iam ostendimus quod secundum quantitatem qua erit diameter orbis revolventis, que est linea LKM, 120 partes erit linea AE 88 partes et 40 minuta et 17 secunda, et linea ED secundum illam quantitatem 643 partes et 36 minuta et 39 secunda, ergo manifestum est quod tota linea AD est 732 partes et 16 minuta et 56 secunda. Erit ergo ductus AD in DE, qui est equalis ductui linee LD in DM, 471304 partes et 46 minuta et 17 secunda. Et etiam quia ductus linee LD in DM cum quadrato linee KM in se est equalis quadrato DK in se, et linea KM, que est medietas diametri orbis revolventis, est secundum illam quantitatem 60 partes, tunc cum nos addiderimus eius quadratum, quod est 3600 super 471304 partes et 46 minuta et 17 secunda, erit ex eis quadratum linee DK in se secundum illam quantitatem 474904 partes et 46 minuta et 17 secunda. Erit ergo longitudo linee DK, que est medietas diametri orbis supra quem currit centrum orbis revolventis et cuius centrum est centrum orbis signorum, 689 partes et 8 minuta fere secundum illud, et secundum quantitatem qua est longitudo que est inter duo centra, scilicet centrum orbis signorum et centrum orbis revolventis 60 partes erit medietas diametri orbis revolventis quinque partes et 14 minuta fere. Et hoc est illi proportioni propinquius que fuit eclypsium precedentium quas declaravimus ante has parum. Et illud est quod oportuit nos declarare.
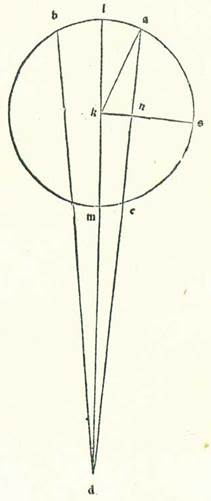 Protraham etiam in consimili huius forme a puncto K, quod est centrum orbis revolventis, perpendicularem supra lineam DEA, supra quam sint K, N, S, et producam lineam AK. Et quia iam ostensum est quod secundum quantitatem qua erit linea DK 689 partes et octo minuta fuit linea DE 643 partes et 36 minuta et 39 secunda, et linea NE, que est medietas linee AE, erit secundum illam quantitatem 44 partes et 20 minuta et octo secunda, ergo linea DEN erit secundum illam quantitatem 687 partes et 56 minuta et 47 secunda. Secundum quantitatem ergo qua erit diameter DK 120 partes erit linea DN 119 partes et 47 minuta et 36 secunda, et arcus qui est supra eam erit 173 partes et 17 minuta fere secundum quantitatem qua erit circulus continens triangulum DKN orthogonium 360 partes. Et similiter erit angulus DKN 173 partes et 17 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Secundum quantitatem vero qua sunt quatuor anguli recti 360 partes erit 86 partes et 38 minuta et 30 secunda. Ergo arcus MES circuli orbis revolventis erit 86 partes et 38 minuta et 30 secunda, et arcus LAS, qui est residuum complementi semicirculi, erit 93 partes et 21 minuta et 30 secunda. Et erit arcus AS secundum illam quantitatem, qui est medietas arcus AE, 47 partes et 38 minuta et 30 secunda fere. Arcus igitur AL residuus erit 45 partes et 43 minuta. Iam autem fuit totus arcus AB secundum illam quantitatem 110 partes et 21 minuta. Quapropter erit arcus LB residuus, qui fuit longitudo Lune a puncto longitudinis longioris in tempore medio eclypsis secunde posite, 64 partes et 38 minuta. Et illud est quod oportuit nos ostendere.
Protraham etiam in consimili huius forme a puncto K, quod est centrum orbis revolventis, perpendicularem supra lineam DEA, supra quam sint K, N, S, et producam lineam AK. Et quia iam ostensum est quod secundum quantitatem qua erit linea DK 689 partes et octo minuta fuit linea DE 643 partes et 36 minuta et 39 secunda, et linea NE, que est medietas linee AE, erit secundum illam quantitatem 44 partes et 20 minuta et octo secunda, ergo linea DEN erit secundum illam quantitatem 687 partes et 56 minuta et 47 secunda. Secundum quantitatem ergo qua erit diameter DK 120 partes erit linea DN 119 partes et 47 minuta et 36 secunda, et arcus qui est supra eam erit 173 partes et 17 minuta fere secundum quantitatem qua erit circulus continens triangulum DKN orthogonium 360 partes. Et similiter erit angulus DKN 173 partes et 17 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Secundum quantitatem vero qua sunt quatuor anguli recti 360 partes erit 86 partes et 38 minuta et 30 secunda. Ergo arcus MES circuli orbis revolventis erit 86 partes et 38 minuta et 30 secunda, et arcus LAS, qui est residuum complementi semicirculi, erit 93 partes et 21 minuta et 30 secunda. Et erit arcus AS secundum illam quantitatem, qui est medietas arcus AE, 47 partes et 38 minuta et 30 secunda fere. Arcus igitur AL residuus erit 45 partes et 43 minuta. Iam autem fuit totus arcus AB secundum illam quantitatem 110 partes et 21 minuta. Quapropter erit arcus LB residuus, qui fuit longitudo Lune a puncto longitudinis longioris in tempore medio eclypsis secunde posite, 64 partes et 38 minuta. Et illud est quod oportuit nos ostendere.
Et quia iam ostensum est quod angulus DKN est 86 partes et 38 minuta fere secundum quantitatem qua sunt quattuor anguli recti 360 partes, erit angulus KDN residuus ex complemento anguli unius recti 3 partes et 22 minuta. Iam autem fuit totus angulus ADB secundum illam quantitatem septem partes et 42 minuta. Angulus ergo LDB reliquus erit quattuor partes et 20 minuta. Et ipse est cui subtenditur arcus orbis signorum qui minuitur ex cursu medio in longitudine diversitatis que est arcus AB orbis revolventis. Fuit ergo locus Lune per cursum medium in longitudine in tempore medio eclypsis secunde vigesimanona pars et trigesimum minutum Arietis, quoniam locus eius secundum veritatem fuit vigesimaquinta pars et decimum minutum. Et ipse sunt partes in quarum similibus Libre fuit Sol.
〈IV.7〉 Capitulum septimum: De equatione medii cursus Lune in longitudine et medii cursus eius in diversitate
Et quia iam ostendimus quod Luna fuit in tempore medio eclypsis que fuit secunda trium eclypsium antiquarum per cursum suum medium in longitudine in quartadecima parte et quadragesimoquarto minuto Virginis et per cursum diversitatis in duodecima parte et vigesimoquarto minuto a longitudine longiore orbis revolventis, et fuit locus eius in tempore medio eclypsis que fuit secunda trium eclypsium nostri temporis novarum per cursum suum medium, sicut ostendimus, in longitudine in vigesimanona parte et trigesimo minuto Arietis et per cursum diversitatis in sexagesimaquarta parte et trigesimooctavo minuto a longitudine longiore, tunc manifestum est quod in hoc tempore quod est inter duas eclypses secuit Luna per cursum suum medium post revolutiones integras in longitudine 224 partes et 46 minuta et per cursum diversitatis 52 partes et 14 minuta. Et tempus quod fuit inter annum secundum annorum Mardochei transacto decimooctavo die mensis Thot, qui est unus mensis Egyptiorum, cuius mane fuit dies decimusnonus, ante mediam noctem secundum medietatem et tertiam hore equalis et inter annum decimumnonum annorum Adriani transacto secundo die mensis Sangnach, qui est unus mensium Egyptiorum, cuius mane fuit dies tertia, ante medietatem noctis per unam horam equalem continet 854 annos et 73 dies et 23 horas et medietatem et tertiam hore equalis secundum sermonem absolutum. Et fuerunt secundum veritatem per equationem diversitatis dierum cum noctibus ctibus M. suis 23 hore et tertia hore. Et fuit numerus summe dierum eius 311783 dies et 23 hore et tertia hore. Et invenimus hoc tempus ex eis quorum premisimus narrationem de motibus Lune in diebus superfluere post revolutiones integras per motum medium ante equationem secundum cursum longitudinis 224 partibus et 46 minutis et secundum cursum diversitatis 52 partibus et 31 minutis. Superfluitatem vero cursus longitudinis invenimus, quemadmodum diximus, non diversificari ab eo quod aggregatur ex superfluitate que est propter considerationes nostras positas. Superfluitatem autem cursus diversitatis invenimus augeri decem et septem minutis. Quapropter quia posituri sumus tabulas et ea que volumus de equatione motuum dierum, divisimus hec decem et septem minuta per numerum horum dierum positorum, et dedimus diei uni portionem suam 11 quarta et 46 quinta et 39 sexta, et minuimus illud ex motu diei unius medii cursus diversitatis comprehenso ante equationem, et invenimus residuum equatum 13 partes et 3 minuta et 53 secunda et 56 tertia et 17 quarta et 51 quinta et 59 sexta. Et postea duplavimus illud et posuimus in tabulis.
〈IV.8〉 Capitulum octavum: De scientia loci Lune ex motu eius medio in longitudine et diversitate
Ad hoc ut equemus loca eius in primo annorum Nabuchodonosor in primo die mensis Thot in media die, qui est unus mensium Egyptiorum, accipiemus tempus quod est inter hanc horam et inter horam temporis medii eclypsis secunde trium eclypsium primarum que sunt propinquiores huic hore, que fuit, quemadmodum diximus, in secundo annorum Mardochei decem et octo diebus mensis Thot transactis, cuius mane fuit decimusnonus dies, ante medietatem noctis per medietatem et tertiam hore equalis, et inveniemus illud 27 annos Egyptios et 17 dies et 11 horas et sextam hore equalis secundum sermonem absolutum et secundum veritatem fere, et inveniemus illud quod opponitur huic tempori in tabulis post revolutiones integras ex superfluitate in longitudine quidem 123 partes et 22 minuta et in diversitate 103 partes et 35 minuta. Cum ergo minuerimus illud ex loco Lune in tempore medio eclypsis secunde, scilicet unumquodque ex suo relativo ei proprio, erit quod remanebit locus Lune medius in primo annorum Nabuchodonosor in prima die mensis Thot in media die in longitudine quidem in 11 parte et 22 minutis Tauri et in cursu diversitatis a longitudine longiore orbis revolventis in 268 partibus et 49 minutis. Et manifestum est quod longitudo que est inter Solem et Lunam est 70 partes et 37 minuta. Iam enim ostensum est quod locus Solis fuit in eo tempore quadragesimumquintum minutum Piscis.
〈IV.9〉 Capitulum nonum: De scientia equandi revolutiones Lune medias in latitudine et loca eius
Revolutiones quidem motuum Lune in longitudine et diversitate et loca eius sunt sicut iam equavimus ea per hec capitula. In latitudine autem dico primum quod erravimus cum nos operati fuimus sicut operatus est Abrachis et putavimus quod Luna numerat orbem sui sexcentis et sexaginta vicibus fere et numerat circulum umbre bis et semis secundum quantitatem longitudinis medie in applicatione Lune et Solis in coniunctione et oppositione. Cum enim fuerit illud positum ita et fuerit quantitas declinationis orbis Lune declivis nota, erunt termini divisionum eclypsium noti. Nos namque cum acceperimus longitudines eclypticas, inveniemus ex magnitudine tenebrarum Lune in tempore medio eclypsis veritatem revolutionum amborum nodorum in latitudine in orbe a motibus declivi. Per quantitatem enim qua iam ostensum est nobis ex diversitate et cognovimus motus revolutionum quidem verarum. Similiter inveniemus loca revolutionum in latitudine in temporibus mediis eclypsium et superfluitatem qua superfluit Luna in tempore quod est inter duas eclypses post revolutiones integras. Nunc autem iam accepimus capitula pulchra inventa absque illis capitulis que nobis sufficiunt et non indigemus aliquo eorum quorum premisimus narrationem in comprehensione quesiti. Quibus quidem ostendimus quod illud quod nos comprehendimus ex cursu latitudinis propter magnitudinem tenebrarum et longitudines et illos modos falsum est et erroneum et equavimus ipsum per hoc. Et similiter fecimus in modis Saturni et Iovis, ubi inquisivimus et novimus quasdam res que non fuerunt assumpte secundum veritatem suam, quoniam invenimus in fine nostrarum considerationum non esse dubitationem. Iam vero opus est investigatoribus huius scientie cum inquisitione veritatis secundum veritatem et valde caute in ea cum perscrutatione et studio ne removeant equationem modorum precedentium tantum quos posuerunt antiqui per illud quod invenerunt ex considerationibus veris, in quibus non est dubitatio, verum removeant et equent errorem si fuerit in aliquo eorum que ipsi posuerunt, et neque abhorreant illud neque verecundentur ex eo. Quoniam res cui refertur hec scientia est ex rebus celestibus altis, scilicet ex rebus Dei altissimi et gloriosi, et ex virtutibus eius, quamvis non sint eorum equationes ipsorum tantum, sed sint ex equationibus aliorum, que sint veratiores et certiores. Modos vero quibus declarabitur unumquodque eorum que narravimus dicam post hunc locum libri Almagesti in propriis locis eorum. Nunc autem, ut illud sit secundum ordines suos, reiterabo sermonem in declaratione cursus Lune in latitudine, cuius capitulum est quemadmodum narrabo.
Primum quidem inquirimus in equatione cursus Lune medii, qui est orbis revolventis in orbe declivi, duas eclypses lunares ex eclypsibus scriptis apud nos in quibus non sit dubitatio inter quas fuit ex longitudine temporis propter quam fuit quantitas magnitudinis tenebrarum Lune in eis equalis, et fuerunt etiam ambe in uno duorum nodorum, et fuit egressus Lune in utraque earum terra aut a parte septentrionis aut a parte meridiei, et fuit longitudo Lune etiam a longitudine sua longiore in unaquaque earum una. Cum enim illud ita fuerit, erit longitudo centri Lune necessario in unaquaque duarum eclypsium in parte una a nodo uno equalis. Quapropter erit cursus Lune verus, qui est in tempore quod est inter duas considerationes, continens revolutiones integras in latitudine. Et fuit prima duarum eclypsium quas accepimus, cuius consideratio fuit in Babilonia in anno trigesimoprimo annorum Darii primi tertio die transacto mensis Coe, qui est unus mensium Egyptiorum, cuius mane fuit dies quartus, in medio hore sexte. Et manifestum est quod in illa hora eclypsata fuit ex Luna a parte meridiei quantitas duorum digitorum. Secunde autem eclypsis consideratio fuit in Alexandria, que fuit in nono annorum Adriani decimoseptimo die transacto mensis Machur, qui est unus mensium Egyptiorum, cuius mane fuit dies decimusoctavus, ante medietatem noctis tribus horis et tertia et quinta hore equalis. Et eclypsata fuit de Luna in illa hora sexta diametri eius a parte meridiei. Et fuit transitus Lune in latitudine in nodo caude in unaquaque duarum eclypsium. Si ergo illud ita fuerit, comprehenditur causa eius ab omnibus modis. Sed eius longitudo est propinqua equalitati in utraque eclypsi aut est inferior medio parum ad longitudinem propinquiorem. Et illud declaratur nobis ex eo cuius iam precessit ostensio in diversitate. Et quia cum Luna fuerit eclypsata a parte meridiei, erit centrum Lune ad partem septentrionis orbis signorum, tunc manifestum est quod in unaquaque duarum eclypsium fuit antecessio centri Lune a nodo caude equalis. Sed in eclypsi quidem prima fuit elongatio Lune a longitudine longiore orbis revolventis centum partes et decem et novem minuta. Fuit ergo tempus medium in Babilonia quidem ante medietatem noctis per medietatem hore equalis et in Alexandria ante medietatem noctis per unam horam et tertiam hore equalis. Et fuit quod aggregatum est ex tempore ex loco Lune in principio temporis Nabuchodonosor usque ad hanc horam 256 anni et 122 dies et 10 hore et due tertie hore equalis, et secundum veritatem, cum equatum fuerit quod est inter dies cum noctibus suis, decem hore et quarta hore. Quapropter fuit cursus verus minuens ex cursu medio quinque partes. Et fuit longitudo Lune in eclypsi secunda a longitudine longiore in orbe revolvente 251 partes et 53 minuta. Quoniam illud quod aggregatur ex tempore loci Lune in principio temporis Nabuchodonosor usque ad tempus medium huius eclypsis secunde est 871 anni et 256 dies et octo hore et due quinte hore equalis, sed secundum veritatem octo hore et medietas sexte hore unius. Quapropter fuit cursus verus addens supra cursum medium quattuor partes et 53 minuta. In tempore ergo quod fuit inter duas eclypses aggregabuntur 615 anni Egyptii et 133 dies et 21 hora et medietas et tertia hore. Et erit cursus Lune verus in latitudine revolutionis integre. Et erit cursus eius medius minuens a revolutionibus integris partes que aggregantur ex ambabus diversitatibus, scilicet novem partes et 53 minuta. Et minuuntur ex eo cuius precessit narratio secundum modum quem posuit Abrachis de cursu medio in hoc tempore a revolutionibus integris decem partes et duo minuta fere. Cursus ergo Lune medius in latitudine fit maior novem minutis. Cum ergo divisimus hanc quantitatem per dies qui aggregantur ex hoc tempore, scilicet 224609 dies fere, fuit portio unius diei ex eo octo quarta et 39 quinta et 18 sexta. Cum ergo addidimus illud supra medium cursum Lune in latitudine, cuius declaratio iam precessit, invenimus equationem medii cursus Lune in latitudine diei unius 13 partes et 13 minuta, 45 secunda et 39 tertia et 48 quarta et 56 quinta et 37 sexta. Postea duplavimus illud et posuimus in tabulis. Et postquam declaravimus hoc modo cursum Lune medium in latitudine, quesivimus etiam in equatione loci eius longitudinem temporis quod fuit inter duas eclypses lunares verificatas in quibus non est dubitatio in quibus fuerit totum quod fuit in illis que fuerunt ante eas de longitudinibus Lune equalibus et tenebris et partibus in quibus fuerunt due eclypses, scilicet aut in septentrione aut in meridie, sed non sint in illo nodo, sed in opposito ei. Prima autem harum duarum eclypsium est eclypsis per quam operati fuimus in declaratione diversitatis, que est ea que fuit in anno secundo annorum Mardochei 18 diebus transactis mensis Thot, qui est unus mensium Egyptiorum, cuius mane fuit dies decimusnonus, in Babilonia quidem in medietate noctis, sed in Alexandria ante medietatem noctis per medietatem et tertiam hore equalis. Et eclypsati sunt de Luna in illa hora tres digiti a parte meridiei. Et eclypsis secunda est per quam operatus fuit Abrachis, que fuit in anno vigesimo annorum Darii, qui fuit post Philippum, vigesimooctavo die transacto mensis Ambaki, qui est unus mensium Egyptiorum, cuius mane fuit dies vigesimusnonus, postquam preterierunt de nocte sex hore et tertia hore equalis. Et similiter eclypsata fuit de Luna in illa hora quarta diametri eius a parte meridiei. Et fuit tempus medium in Babilonia quidem ante medietatem noctis per duas quintas hore unius equalis, quoniam medietas noctis fuit tunc sex hore et medietas et quarta hore fere, in Alexandria autem ante medietatem noctis per unam horam equalem et quartam hore. Et fuit unaqueque harum duarum eclypsium ubi fuit Luna in longitudine longiore. Fuitque eclypsis prima apud nodum capitis et eclypsis secunda apud nodum caude. Et fuit centrum Lune etiam hic in ambabus eclypsibus in parte septentrionis equaliter ab orbe signorum remotum.
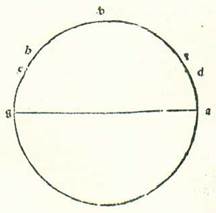 Describam autem circulum orbis Lune declivis, supra quem sint A, B, G, super diametrum AG, et sit punctum A nodus capitis, et punctum G nodus caude, et punctum B sit longitudo longior septentrionis, et assumam duos arcus equales a duobus punctis A et G, que sunt duo nodi, ad punctum B, quod est longitudo longior septentrionis, qui sint duo arcus AD et GE, et sit centrum quidem Lune in eclypsi prima supra punctum D et in eclypsi secunda supra punctum E. Sed tempus quod fuit a loco Lune in radice ad medium eclypsis prime fuit 27 anni et 17 dies et 11 hore et sexta hore equalis et vere. Quapropter fuit elongatio Lune a longitudine longiore orbis revolventis 12 partes et 24 minuta, et fuit cursus revolutionis Lune medius maior vero 59 minutis, et fuit tempus quod est a loco Lune in radice ad medium eclypsis secunde 245 anni et 327 dies et 10 hore et medietas et quarta hore equalis absolute, et secundum veritatem 10 hore et quarta hore. Quapropter fuit elongatio Lune a longitudine longiore in orbe revolvente due partes et 44 minuta, et fuit cursus revolutionis Lune medius maior vero 13 minutis. Et tempus quod fuit inter duas considerationes est 218 anni et 309 dies et 23 hore equales et pars duodecima hore. Et aggregatur superfluitas secundum quod iam declaravimus ex cursu medio in latitudine, scilicet 160 partes et 4 minuta. Et est cursus centri Lune medius propter hoc quod diximus in eclypsi quidem prima super punctum R et in eclypsi secunda super punctum H. Et quia arcus RH est 160 partes et 4 minuta et arcus DR est 59 minuta et arcus EH est 13 minuta, erit arcus DE 160 partes et 50 minuta. Ergo duo arcus AD et EG simul minuunt a complemento semicirculi 19 partes et 10 minuta, et unusquisque eorum, quoniam ipsi sunt equales, erit secundum illam quantitatem novem partes et 35 minuta. Et ipse sunt partes secundum quantitatem quarum cursus Lune verus in eclypsi quidem prima fuit diminutus a loco nodi capitis. Et in eclypsi secunda fuit augmentatus secundum quantitatem illarum partium supra locum nodi caude. Totus ergo arcus AR erit 10 partes et 34 minuta, et arcus HG residuus erit 9 partes et 22 minuta. Propter hoc ergo erit cursus revolutionis Lune medius in eclypsi quidem prima diminutus a loco nodi capitis 10 partibus et 34 minutis. Et fuit elongatio eius a longitudine longiore septentrionis 280 partes et 34 minuta. Et in eclypsi secunda fuit addens supra nodum caude novem partes et 22 minuta. Et fuit elongatio eius a longitudine longiore septentrionis 80 partes et 38 minuta. Et illud est quod oportuit nos demonstrare.
Describam autem circulum orbis Lune declivis, supra quem sint A, B, G, super diametrum AG, et sit punctum A nodus capitis, et punctum G nodus caude, et punctum B sit longitudo longior septentrionis, et assumam duos arcus equales a duobus punctis A et G, que sunt duo nodi, ad punctum B, quod est longitudo longior septentrionis, qui sint duo arcus AD et GE, et sit centrum quidem Lune in eclypsi prima supra punctum D et in eclypsi secunda supra punctum E. Sed tempus quod fuit a loco Lune in radice ad medium eclypsis prime fuit 27 anni et 17 dies et 11 hore et sexta hore equalis et vere. Quapropter fuit elongatio Lune a longitudine longiore orbis revolventis 12 partes et 24 minuta, et fuit cursus revolutionis Lune medius maior vero 59 minutis, et fuit tempus quod est a loco Lune in radice ad medium eclypsis secunde 245 anni et 327 dies et 10 hore et medietas et quarta hore equalis absolute, et secundum veritatem 10 hore et quarta hore. Quapropter fuit elongatio Lune a longitudine longiore in orbe revolvente due partes et 44 minuta, et fuit cursus revolutionis Lune medius maior vero 13 minutis. Et tempus quod fuit inter duas considerationes est 218 anni et 309 dies et 23 hore equales et pars duodecima hore. Et aggregatur superfluitas secundum quod iam declaravimus ex cursu medio in latitudine, scilicet 160 partes et 4 minuta. Et est cursus centri Lune medius propter hoc quod diximus in eclypsi quidem prima super punctum R et in eclypsi secunda super punctum H. Et quia arcus RH est 160 partes et 4 minuta et arcus DR est 59 minuta et arcus EH est 13 minuta, erit arcus DE 160 partes et 50 minuta. Ergo duo arcus AD et EG simul minuunt a complemento semicirculi 19 partes et 10 minuta, et unusquisque eorum, quoniam ipsi sunt equales, erit secundum illam quantitatem novem partes et 35 minuta. Et ipse sunt partes secundum quantitatem quarum cursus Lune verus in eclypsi quidem prima fuit diminutus a loco nodi capitis. Et in eclypsi secunda fuit augmentatus secundum quantitatem illarum partium supra locum nodi caude. Totus ergo arcus AR erit 10 partes et 34 minuta, et arcus HG residuus erit 9 partes et 22 minuta. Propter hoc ergo erit cursus revolutionis Lune medius in eclypsi quidem prima diminutus a loco nodi capitis 10 partibus et 34 minutis. Et fuit elongatio eius a longitudine longiore septentrionis 280 partes et 34 minuta. Et in eclypsi secunda fuit addens supra nodum caude novem partes et 22 minuta. Et fuit elongatio eius a longitudine longiore septentrionis 80 partes et 38 minuta. Et illud est quod oportuit nos demonstrare.
Et quia superfluitas in latitudine que fuit a tempore quod fuit inter locum Lune in radice usque ad tempus medium eclypsis prime est 286 partes et 19 minuta, tunc si nos minuerimus has partes ex 280 partibus et 34 minutis que sunt loci Lune in eclypsi prima postquam addiderimus super eas revolutionem unam, erit quod residuum fuerit locus revolutionis latitudinis a longitudine longiore septentrionis in primo anno annorum Nabuchodonosor in prima die mensis Thot, qui est unus mensium Egyptiorum, in media die, scilicet 354 partes et 15 minuta. Et in comprehensione eorum que erunt ex computatione coniunctionis Lune et impletionis in hoc cursu non indigemus diversitate secunda quam nominavimus, neque est nobis necessaria in hoc loco. Et ponam tabulas secundum divisionem partium per lineas etiam sicut descripsimus tabulas Solis. Et assumemus in eo proportionem 60 ad 5 partes et ad quartam partis. Et dividam quemadmodum divisimus in Sole, scilicet duas quartas que sunt a duabus partibus longitudinis longioris secundum sex partes et sex partes, et duas quartas que sunt a duabus partibus longitudinis propinquioris secundum tres partes et tres partes, donec sint divisiones tabularum similes eis que sunt in tabulis Solis, scilicet quadragintaquinque aree in latitudine in tribus partibus trium tabularum. Sed in duabus primis tabulis erit numerus partium diversitatis. In tertia vero tabula erunt portiones que contingunt portioni cuiusque numerorum ex augmento et diminutione. Et erit diminutio in numeratione longitudinis et latitudinis cum fuerit numerus qui aggregatur ex diversitate loci longitudinis longioris in orbe revolvente usque ad 180 partes, et erit additio cum fuerit numerus plus 180 partibus. Et hec est tabularum descriptio:
☾
〈IV.10〉 Capitulum decimum: De descriptione tabularum diversitatis Lune prime simplicis
☽ |
|||||
Tabula diversitatis Lune prime simplicis |
|||||
Numeri communes |
Additiones et divisiones |
||||
Prima |
Secunda |
Tertia |
|||
Partes |
Partes |
Partes |
Minuta |
||
6
12
18 |
354
348
342 |
0
0
1 |
29
57
25 |
||
24
30
36 |
336
330
324 |
1
2
2 |
53
19
44 |
||
42
48
54 |
318
312
306 |
3
3
3 |
8
31
51 |
||
60
66
72 |
300
294
288 |
4
4
4 |
8
24
38 |
||
78
84
90 |
282
276
270 |
4
4
4 |
49
56
59 |
||
93
96
99 |
267
264
261 |
5
5
5 |
0
1
0 |
||
102
105
108 |
258
255
252 |
4
4
4 |
59
57
53 |
||
111
114
117 |
249
246
243 |
4
4
4 |
49
44
37 |
||
120
123
126 |
240
237
234 |
4
4
4 |
32
25
17 |
||
129
132
135 |
231
228
225 |
4
3
3 |
7
57
46 |
||
138
141
144 |
222
219
216 |
3
3
3 |
35
23
10 |
||
147
150
153 |
213
210
207 |
2
2
2 |
57
43
28 |
||
156
159
162 |
204
201
198 |
2
1
1 |
13
57
41 |
||
165
168
171 |
195
192
189 |
1
1
0 |
25
9
52 |
||
174
177
180 |
186
183
180 |
0
0
0 |
35
18
0 |
||
〈IV.11〉 Capitulum undecimum: Quod quantitas diversitatis Lune non est propter diversitatem horum duorum modorum, sed propter diversitatem numerationis et erroris in sermone Abrachis
Quantitas diversitatis Lune in sententia Abrachis non est propter diversitatem modorum, sed propter diversitatem revolutionum. Et postquam hoc est secundum quod iam ostensum est, tunc secundum veritatem inquirimus qua de causa in eclypsibus lunaribus quas posuit Abrachis in investigatione harum diversitatum non est proportio similis proportioni quam declaravimus et non convenit proportio prima, que iam affirmata est per modum orbis centri egedientis, proportioni secunde, que est per modum orbis revolventis. Verum in ostensione prime ipse aggregat proportionem medietatis diametri orbis centri egredientis ad lineam que est inter duo centra, scilicet centrum ipsius et centrum orbis signorum, que est proportio trium milium et centum et quadragintaquattuor partium ad trecentas et vigintiseptem partes et duas tertias partis fere, et ipsa est proportio 60 ad 6 partes et 15 minuta. Et in declaratione secunde ipse adunat proportionem linee que progreditur a centro orbis signorum ad centrum orbis revolventis ad medietatem diametri orbis revolventis, que est proportio 3122 ad 247 et medietatem, et ipsa est proportio 60 ad 4 partes et 46 minuta fere. Plurimum vero diversitatis quod faciunt proportiones, scilicet proportio 60 ad 6 partes et quartam partis, est quinque partes et 49 minuta. Et proportio 60 ad 4 partes et 46 minuta est quattuor partes et 34 minuta. Sed secundum illud quod nos narravimus proportio 60 ad quinque partes et quartam partis non facit hanc diversitatem positam nisi quinque partes propinque. Et iam declaratum est nobis ex sermone qui est parum ante hoc quod hic error qui accidit non fuit propter diversitatem duorum modorum, quemadmodum estimant quidam hominum. Quoniam totum quod videtur in unoquoque eorum videtur in altero ei equale, non diversum. Et si nos voluerimus cum declaratione illius secundum sermonem facere ostensionem eius per mensuram et numerationem, inveniemus proportionem unam in ambobus modis cum nos consideraverimus rem unam ex eis que contingunt in eis, et non aspexerimus res diversas, quemadmodum fecit Abrachis. Et iam possibile est ut cum fuerint eclypses diverse, sit error aut propter considerationes ipsas aut propter numerationem longitudinis temporis. Nos enim invenimus in illis eclypsibus, scilicet oppositionum, veras considerationes et convenientes eis que declaravimus de eclypsibus oppositionum secundum duos modos, per motum medium et motum diversitatis. Numerationem vero longitudinis temporis qua demonstrabuntur proportiones invenimus non investigatam fuisse studiose. Et ostendam unumquodque horum duorum. Et incipiam a tribus eclypsibus primis. Abrachis namque dixit quod he tres eclypses sunt ex eis que ad ipsum pervenerunt ex eclypsibus que fuerunt in Babilonia considerate et quod prima eclypsis earum fuit cum fuit Chaisteratis dominus Athenarum, scilicet civitatis philosophorum, in mense Iesdusen. Et dixit quod tunc circuli Lune pars parva minuta fuit a parte orientis estivalis in medietate hore remanentis ex nocte. Et dixit etiam quod eclypsata est et postea occultata est. Et fuit hoc tempus in anno trecentesimo et sexagesimosexto annorum Nabuchodonosor et, sicut ipse dixit, fuit etiam in vigesimosexto die mensis Thot transacto, cuius mane fuit dies vigesimusseptimus, post mediam noctem per quinque horas et medietatem hore temporales. Quoniam non fuit residuum noctis nisi medietas hore. Et quia Sol fuit tunc in fine Sagittarii, in Babilonia fuerunt tempora hore nocturne decem et octo tempora et fuit nox quatuordecem hore equales et due quinte hore. Quinque ergo hore et medietas hore temporalis fiunt sex hore et tres quinte hore equales. Fuit ergo principium eclypsis post medietatem diei Iomin vigesimisexti decem et octo horis et tribus quintis hore equalibus. Quia ergo illud quod eclypsatum est de Luna fuit pars parva, oportuit ut sit totum eclypsis tempus hora et medietas hore fere. Et manifestum est quod tempus medium fuit post decem et novem horas et tertiam hore equales. Fuit ergo tempus medium eclypsis etiam in Alexandria post medietatem diei Iomin vigesimisexti decem et octo horis et medietate hore equalibus. Et fuit tempus quod fuit a loco Lune in primo annorum Nabuchodonosor usque ad hoc tempus 365 anni Egyptii et 25 dies et 18 hore et medietas hore absolute, sed secundum veritatem 18 hore et quarta hore. Et invenimus locum Solis in hoc tempore cum numeravimus per unumquemque duorum modorum quos posuimus vigesimamoctavam partem et decimumoctavum minutum Sagittarii secundum veritatem. Et invenimus locum Lune per motum medium 24 partes et 20 minuta Geminorum et secundum veritatem 28 partes et 17 minuta. Quoniam eius elongatio fuit in diversitate a longitudine longiore in orbe revolvente 227 partes et 43 minuta. Et rememoratus est etiam eclypsis que fuit post illam secundum tempus Chaisteratis in civitate Athenarum, scilicet civitate philosophorum, vigesimoquarto die transacto mensis Phamenoth, qui est unus mensium Egyptiorum, cuius mane fuit dies vigesimusquintus, in qua eclypsata fuit Luna a parte orientis estivalis in fine hore prime noctis. Et illud fuit in anno trecentesimo sexagesimosexto annorum Nabuchodonosor vigesimoquarto die transacto mensis Phamenoth, cuius mane fuit dies vigesimusquintus, ante medietatem noctis quinque horis et medietate hore temporalibus. Et quia Sol fuit in fine Geminorum, fuit hora nocturna in Babilonia 12 tempora. Quinque ergo hore et medietas hore erunt quattuor hore et due quinte hore equales. Ergo prima hora eclypsis fuit post medietatem diei Iomin vigesimiquarti 7 horis et tribus quintis hore equalibus. Et quia totum tempus eclypsis fuit tres hore secundum quod scriptum est, tunc manifestum est quod tempus medium fuit post novem horas et decimam hore equales. Oportuit ergo ut esset in Alexandria post medietatem diei Iomin vigesimiquarti octo horis et quarta hore fere. Et etiam erit tempus quod est a loco Solis et Lune ac si esset in radice usque ad hanc horam trecenti et sexagintaquinque anni et ducenti et tres dies et octo hore et quarta hore equales absolute, et secundum veritatem septem hore et medietas et tertia hore. Et in hoc tempore reperitur locus Solis verus vigesimaprima pars et quadragesimumsextum minutum Geminorum. Et reperitur locus Lune per cursum medium vigesimatertia pars et quinquagesimumoctavum minutum Sagittarii, et secundum veritatem vigesimaprima pars et quadragesimumoctavum minutum, quoniam eius longitudo fuit in diversitate a longitudine longiore in orbe revolvente 27 partes et 37 minuta. Et erit quod aggregatur ex longitudine temporis quod fuit inter eclypsim primam et eclypsim secundam 177 dies et 13 hore et 3 quinte unius hore equales, et partes quas perambulavit Sol in his diebus 173 partes et 28 minuta. Sed secundum hoc quod operatus est Abrachis fuit longitudo huius temporis quod fuit inter has duas eclypses 177 dies et 13 hore et medietas et quarta hore equales, et cursus Solis in eo 173 partes excepta octava partis. Et dixit quod eclypsis tertia etiam fuit in tempore Andree regis Athenarum, scilicet civitatis philosophorum, sextodecimo die mensis Thot transacto, cuius mane fuit dies decimusseptimus. Et dixit quod Luna eclypsata fuit tota a parte orientis estivalis post quattuor horas transactas a principio noctis. Et fuit hoc in anno trecentesimo et sexagesimoseptimo annorum Nabuchodonosor decimosexto die transacto mensis Thot, cuius mane fuit dies decimusseptimus, ante medietatem noctis duabus horis et medietate hore temporalis. Et quia Sol fuit in secunda parte Sagittarii, erit hora una nocturna in Babilonia circiter decem et octo tempora. Due ergo hore et medietas hore temporales erunt tres hore equales. Propter hoc ergo fuit principium eclypsis post medium diem Iomin decimisexti novem horis. Et quia Luna tota fuit eclypsata, fuit totum tempus quattuor hore equales. Et manifestum est quod tempus medium fuit post medium diem Iomin sextidecimi undecem horis. Oportuit ergo ut esset tempus medium eclypsis in Alexandria post decem horas et sextam hore equales transactas post medium diem iomin decimisexti. Et tempus quod fuit loci Solis et Lune ac si esset in radice a principio regni Nabuchodonosor usque ad hanc horam trecenti sexaginta et sex anni Egyptii et 15 dies et decem hore et sexta hore equales absolute, secundum verificationem vero novem hore et medietas ac tertia hore. Et invenimus in illo tempore locum Solis verum decimamseptimam partem et trigesimum minutum Sagittarii et locum Lune per cursum suum medium decimamseptimam partem et vigesimum minutum Geminorum, sed secundum veritatem decimamseptimam partem et vigesimumoctavum minutum, quoniam elongatio eius in diversitate fuit a longitudine longiore in orbe revolvente 181 partes et 12 minuta. Et aggregata longitudo temporis que fuit inter eclypsim secundam et eclypsim tertiam erit 177 dies et due hore equales. Et erit cursus Solis in eo 175 partes et 44 minuta. Abrachis vero iam posuit longitudinem huius temporis etiam 177 dies et horam et duas tertias hore et partes Solis 175 partes et octavam partis. In numeratione autem prima sua huius temporis iam videtur error in diebus quidem tertia hore equalis et in partibus circiter tres quinte partis. Et quod adducit hunc errorem diversitatis in quantitates proportionum non est parvum. Et moveamus nos ad eclypses tres postremas quas ipse posuit et rememoratus est. Et dixit quod earum considerationes fuerunt in Alexandria. Et dixit quod eclypsis prima earum fuit in anno vigesimoquarto revolutionis Philippi secunde sextodecimo die transacto mensis Mesure. Et incepit Luna in illa hora eclypsarii Probably corrupt for eclypsari, which is also the reading of Paris, BnF, lat. 14738 (74r, line 4 from the bottom) (spelt eclipsari here) and would correspond to the Greek text (see Toomer, loc. cit., p. 214, line 6). ante ortum suum medietate hore, et postea postremum sue eclypsis fuit in medio hore secunde, fuitque tempus medium in principio hore secunde et ante medietatem noctis quinque horis temporalibus et equalibus, eo quod Sol fuit in fine Virginis. Propter hoc ergo fuit tempus medium eclypsis in Alexandria post medium diem Iomin sextidecimi septem horis equalibus. Et fuit tempus a loco Solis et Lune ac si essent in radice in primo annorum Nabuchodonosor usque ad hanc horam quingenti et quadragintasex anni Egyptii et trecenti quadragintaquinque dies et septem hore absolute equales, sed secundum verificationem sex hore et medietas hore. Et invenimus etiam locum Solis in illa hora secundum verificationem vigesimamsextam partem et sextum minutum Virginis, et locum Lune per cursum suum medium vigesimamsecundam partem Piscis, et secundum verificationem vigesimamsextam partem et septimum minutum, quoniam eius elongatio fuit in diversitate a longitudine longiore in orbe revolvente 13 partes et 13 minuta. Et dixit quod eclypsis secunda fuit in anno quinquagesimoquinto illius revolutionis nono die mensis Mesir transacto, qui est ex mensibus Egyptiorum. Et fuit eius initium post quinque horas et tertiam hore transactas de nocte. Et eclypsata fuit Luna tota. Et fuit initium eclypsis post medium diem Iomin noni undecim horis et tertia hore equalibus, quoniam Sol etiam fuit in fine Piscis. Et fuit tempus medium post tredecem horas et tertiam hore equales, ideo quod Luna fuit eclypsata tota. Et tempus quod fuit a loco Solis et Lune ac si essent in radice usque ad hanc horam 547 anni et 158 dies et 13 hore et tertia hore equales et vere fere. Et similiter invenimus locum Solis in illa hora 26 partem et 17 minutum Piscis, et invenimus locum Lune per cursum suum medium partem unam et 7 minuta libre, secundum verificationem vero 26 partem et 17 minuta Virginis, quoniam eius elongatio fuit in diversitate a longiore longitudine in orbe revolvente 109 partes et 28 minuta. Et est tempus quod fuit inter duas eclypses, scilicet primam et secundam, 178 dies et 6 hore et medietas et tertia hore equales. Et partes Solis 180 partes et 11 minuta. Et fuit in eis que declaravit Abrachis usque ad hoc tempus 178 dies et sex hore equales. Et partes Solis 180 et 20 minuta. Et dixit quod eclypsis tertia fuit etiam in anno 55 revolutionis secunde quinto die transacto mensis Mesure, qui est ex mensibus Egyptiorum. Fuitque initium eclypsis post sex horas et duas tertias hore transactas de nocte. Et eclypsata fuit Luna tota. Et dixit quod tempus medium eclypsis fuit post octo horas et tertiam hore preteritas de nocte. Et fuit illud post medietatem noctis duabus horis et tertia hore temporalibus. Et quia Sol fuit in medietate Virginis, fuit hora temporalis in Alexandria quattuordecem tempora et due quinte temporis. Due ergo hore et tertia hore temporales erunt due hore equales et quarta hore circiter. Quapropter fuit tempus medium eclypsis post medium diem Iomin quinti quattuordecem hore et quarta hore equales. Et fuit tempus etiam quod fuit a loco Solis et Lune ac si essent in radice usque ad hanc horam 547 anni et 334 dies et 14 hore et quarta hore absolute equales, sed secundum veritatem 13 hore et medietas et quarta hore. Et invenimus locum Solis secundum veritatem in illo tempore decimamquintam partem et duodecimum minutum Virginis, et locum Lune per cursum suum medium 10 partes et 24 minuta Piscis, et secundum veritatem decimamquintam partem et tertiumdecimum minutum Piscis, quoniam elongatio eius fuit in diversitate a longitudine longiore orbis revolventis 249 partes et 9 minuta. Et fuit tempus quod fuit inter duas eclypses, scilicet secundam et tertiam, 176 dies et due quinte hore equalis. Et partes Solis 168 partes et 55 minuta. Et longitudo huius temporis secundum quod posuit Abrachis etiam dies quidem 176 et hora et tertia hore equalis. Partes vero Solis 168 partes et 33 minuta. Iam ergo demonstratum est hic etiam quod in hoc tempore est error in partibus quidem quinta et sexta circiter et in diebus medietas et tertia et decima hore fere. Hic autem error quem prediximus possibile est ut mittat diversitatem plurimam manifestam in proportione in modo. Iam ergo ostensa est causa visibiliter huius diversitatis. Et nos firmiter utamur illo cuius premisimus declarationem de numeratione diversitatis que est in oppositionibus Solis et Lune. Nos enim iam invenimus has eclypses convenientes modo quem narravimus.
Expleta est dictio quarta libri Almagesti Ptolomei Pheludiensis.