〈XIII〉
Claudii Ptolemei Pheludiensis dictio tertiadecima et novissima libri Almagesti undecem capitulis seriatim coornata fauste succedit.
Capitulum primum: In radicibus secundum quas agitur in cursibus stellarum quinque erraticarum in latitudine
Capitulum secundum: In modo secundum quem currit res in motu harum declinationum et reflexionum secundum has radices que posite sunt
Capitulum tertium: In quantitate declinationis et declinationis et reflexionis et reflexionis
Capitulum quartum: In modo faciendi tabulas cursuum particularium in latitudine
Capitulum quintum: In tabulis factis ad sciendam latitudinem
Capitulum sextum: In numeratione motus stellarum quinque erraticarum in latitudine
Capitulum septimum: In apparitionibus stellarum quinque erraticarum et occultationibus earum
Capitulum octavum: In hoc quod illud quod invenitur ex proprietatibus in apparitionibus Veneris et Mercurii et occultationibus eorum est conveniens radicibus que posite sunt eis
Capitulum nonum: In radice qua reperiuntur longitudines particulares a Sole in apparitionibus harum stellarum et occultationibus earum
Capitulum decimum: In tabula facta apparitionum stellarum quinque erraticarum et occultationum earum
Capitulum undecimum: In complemento libri
〈XIII.1〉 Capitulum primum: In radicibus secundum quas agitur in cursibus stellarum quinque erraticarum in latitudine
Et quia iam remanserunt apud nos adhuc in scientia stellarum quinque erraticarum due res, quarum una est scientia eius quod provenit ex cursibus in latitudine per cursum suum in orbe signorum et altera consideratio in longitudinibus apparitionum earum et occultationum in orbe signorum per comparationem ad Solem, et oportet etiam hic ut scientia longitudinum in latitudine cuiusque earum premittatur, quoniam iam contingit propter hanc intentionem etiam in apparitionibus et occultationibus earum diversitas quantitatem habens, tunc nos premittemus primo narrationem rerum universalium communium eis secundum quas agitur in declinationibus orbium earum, propterea quod iam invenimus unamquamque harum stellarum facientem duas diversitates in latitudine etiam, quemadmodum faciunt in longitudine duos modos diversitatis, unus quorum est secundum partes orbis signorum propter orbem egredientis centri declivem a superficie orbis signorum et alter secundum Solem propter orbem revolutionis earum. Nos ponemus hac de causa in his stellis omnibus orbem egredientis centri declivem a superficie orbis signorum et orbem revolutionis declivem a superficie orbis egredientis centri, quoniam non accidit propter illud, quemadmodum diximus in dictione nona, aliquid alterationis de qua sit curandum, neque in cursu longitudinis neque in cursu diversitatis, in eo cuius hec est summa declinationis secundum quod demonstrabimus in sequentibus. Et propterea quod iam invenimus per considerationes particulares in unaquaque earum quod quando fuerit numerus longitudinis equate et numerus diversitatis equate cuiusque earum quarta circuli, numerus quidem longitudinis equate a parte septentrionis aut a parte meridiei orbis egredientis centri et numerus quidem diversitatis a longitudine longiore que est ei propria, tunc hec stella videtur in ipsa superficie orbis signorum, nos ponemus propter hanc causam declinationes orbium earum egredientium centrorum super centrum orbis signorum, quemadmodum fecimus in Luna, et super diametros earum que transeunt per partes septentrionales et meridionales, et ponemus orbes revolutionis earum super diametros earum oppositas centro orbis signorum, et sunt diametri super quas reperitur longitudo longior et longitudo propinquior que videtur cuiusque earum. Et consideravimus etiam in his tribus stellis erraticis, et sunt Saturnus, Iuppiter et Mars, quod quando fuerit cursus earum in longitudine in sectione longiore altera orbis egredientis centri, semper videntur longiores ad septentrionem, sed earum longitudo in septentrione, cum fuerit earum cursus in longitudine propinquiore orbium revolutionis earum, erit maior longitudine earum cum fuerit cursus earum in longitudine longiore earum, et illud est finis longitudinis earum, et quando fuerit cursus earum in longitudine in sectione orbis egredientis centri propinquiore terre, videntur, quia res est econtrario illius, declinate ad meridiem magis ab orbe signorum, et quod partes septentrionales orbium earum egredientium centrorum in stella quidem Saturni et stella Iovis sunt in principio signi Libre et stelle quidem Martis sunt in postremo signi Cancri. Et fortasse erunt in ipsa longitudine longiore donec aggregetur ex illo quod quecunque plagarum orbium egredientium centrorum ipsorum fuerint super partes quas diximus orbis signorum sunt declinate quasi ad septentrionem et quecunque plagarum eorum fuerint super partes condiametrales eis sunt declinate quasi ad meridiem cum simili illius quantitatis declinationis, orbium autem revolutionis longitudo propinquior est semper in parte ad quam declinant orbes egredientium centrorum, et eorum diametri que sunt ortogonaliter super diametros eorum que videntur per longitudinem longiorem eorum sunt semper equidistantes superficiei orbis signorum.
Et invenimus in stella Veneris et stella Mercurii quod quando fuerit cursus earum in longitudine in parte longitudinis longioris aut longitudinis propinquioris orbis egredientis centri, tunc erit motus quidem earum in longitudine propinquiore orbium revolutionis earum absque alteratione aliqua latitudinis cum motibus earum in longitudine longiore duorum orbium revolutionis earum, sed ipse erunt secundum habitudinem unam, aut declinate ad septentrionem ab orbe signorum aut declinate ad meridiem. Venus vero erit declivior ad septentrionem semper, et Mercurius erit declivior ad meridiem semper. Cursus autem earum in maiore longitudinum earum habitudines diversificantur abinvicem in ultimo diversitatis, scilicet habitudo matutinalis ab habitudine vespertina. Et diversificantur etiam habitudines duorum orbium revolutionis earum cum fuerint in longitudine longiore aut longitudine propinquiore, scilicet propter diversitatem habitudinum earum a diversitate que est ex declinatione orbis egredientis centri ad contrariam partem equaliter. Ergo erit longitudo sequens vespertina que est longitudo maior, longitudo in stella quidem Veneris in longitudine longiore orbis egredientis centri declivior ad septentrionem et in longitudine propinquiore declivior ad meridiem, et in stella Mercurii econtrario illius in longitudine quidem longiore erit declivior ad meridiem et in longitudine propinquiore declivior ad septentrionem. Et quando fuerit cursus earum equatus in longitudine in duobus nodis, tunc erunt longitudines quarum summa a longitudine longiore et a longitudine propinquiore a duabus partibus duorum orbium revolutionis earum est quarta circuli simul in superficie orbis signorum, et erit cursus earum in longitudine propinquiore secundum ultimum diversitatis a cursu earum in longitudine longiore, et erit declinatio in stella Veneris tunc quidem cum fuerit in nodo qui est in medietate circuli que est diminutionis, ad meridiem, et quando fuerit in nodo condiametrali ei, ad septentrionem, in stella autem Mercurii econtrario illius in nodo qui est in medietate circuli que est diminutionis ad septentrionem et in nodo quidem condiametrali ei ad meridiem, ita ut aggregentur ex istis rebus etiam quod declinationes orbium eorum egredientium centrorum sint mobiles et redeant in motu earum cum reversione revolutionum duorum orbium revolutionis earum, ita ut cum he due fuerint in duobus nodis, fiant cum eis in superficie una et eadem, et est superficies orbis signorum. In longitudine autem longiore et in longitudine propinquiore in stella quidem Veneris ponimus orbem revolutionis sue in ultimo longitudinis in septentrione, et in stella Mercurii ponimus orbem revolutionis sue in ultimo longitudinis in meridie. Due vero orbes revolutionis earum faciunt duas species diversitatis: Et faciunt declinare duas diametros que transeunt per duas longitudines longiores que subtenduntur ultimitati declinationis earum quando fuerint in duobus nodis duorum orbium egredientium centrorum, et reflecti faciunt duas diametros erectas ortogonaliter super has duas diametros in ultimo reflexionis sue cum fuerint in longitudine longiore aut in longitudine propinquiore duorum orbium egredientium centrorum. Et faciunt contrarium illius, scilicet ipsi ponunt duas illas diametros in superficie duorum orbium egredientium centrorum cum fuerint in longitudine longiore aut longitudine propinquiore eorum et ponunt has duas diametros in superficie orbis signorum cum fuerint in duobus nodis quorum precessit relatio. Nos namque per hoc nomen divisimus inter hanc declinationem et inter illam declinationem.
〈XIII.2〉 Capitulum secundum: In modo secundum quem currit res in motu harum declinationum et reflexionum secundum has radices que posite sunt
Quod vero colligitur omnino ex istis radicibus est secundum hunc modum quia orbes egredientium centrorum stellarum quinque erraticarum sunt declinati a superficie orbis signorum super centrum orbis signorum, sed eorum declinatio in his tribus stellis, scilicet Saturno, Iove et Marte, est fixa secundum habitudinem unam, quia duo cursus condiametrales orbium revolutionis earum moventur in latitudine ad duas partes oppositas, in Venere autem et Mercurio moventur motu duorum orbium revolutionis earum ad partem unam et eandem in latitudine, in Venere quidem ad septentrionem semper, et in Mercurio ad meridiem semper; et quod orbium revolutionum diametri que transeunt per longitudines longiores eorum que videntur, cum fuerit in superficie orbis egredientis centri, incipiunt a loco illo moveri super circulos parvos apud extremitatem eorum que est longitudo propinquior – et hi circuli sunt summe recessionis in latitudine et sunt ortogonaliter super superficies orbium egredientium centrorum, et centra eorum sunt posita in eis, et moventur secundum equalitatem cum cursibus et secundum consequentiam cursuum in longitudine ab uno duorum principiorum que sunt super sectionem harum superficierum et superficierum orbium revolutionis versus septentrionem secundum radicem secundum quam agitur cum eis in superficiebus orbium revolutionis, sed in revolutionibus eorum in quarta quidem prima ad partem septentrionalem, et illud manifestum est, et in quarta secunda ad superficiem orbis egredientis centri a capite, in quarta vero tertia ad finem meridianam, in reversione autem reliqua ad superficiem in qua fuit principium initii rei; et quod principium huius separationis et reversionis in Saturno quidem et Iove et Marte erit a sectione que est in nodo ascendente, in Venere autem erit a longitudine propinquiore orbis egredientis centri, sed in Mercurio erit a longitudine longiore orbis egredientis centri – diametri vero orbium revolutionis erecte ortogonaliter super diametros quarum precessit relatio in stellis quidem tribus faciunt, quemadmodum diximus, semper equidistantiam superficiei orbis signorum, et quamvis reflectantur ab ea, earum tamen reflexio non habet quantitatem de qua sit curandum, Venus autem et Mercurius, quando fuerint in superficie orbis signorum, incipiunt sic ab illo loco quod moventur super circulos parvos ac si ipsi essent positi apud extremitates eorum sequentes, et hi circuli sunt equales etiam summe recessionis in latitudine et sunt ortogonaliter super superficiem orbis signorum, et centra eorum sunt posita super diametros equidistantes superficiei orbis signorum, et ipsi moventur motu equali in velocitate illis diametris aliis ab uno duorum principiorum que sunt super sectionem horum circulorum parvorum et superficierum orbium revolutionis versus septentrionem etiam secundum radicem secundum quam agitur, et differunt secum extremitates harum diametrorum positarum que sunt vespertine secundum similitudinem illius ordinis eiusdem cuius precessit relatio, et illud manifestum est; et quod per istas diametros etiam sunt principia separationis et reversionis opposita, in stella quidem Veneris ex nodo qui est super medietatem circuli que est additionis, et in stella quidem Mercurii ex nodo qui est super medietatem circuli que est diminutionis. Iam vero oportet ut sciatur ex re horum circulorum parvorum super quos est motus orbium revolutionis quod ipsi etiam dividuntur in duas medietates et duas medietates super superficies in quibus dico quod circa eas est motus declinationum et quod hoc modo tantum preparatur ut sit cursus earum in latitudine in equalibus partibus duabus semper. Eorum autem revolutio secundum motum equalem non est circa centrum quod est eis proprium, sed super centrum aliud, et est illud quod facit per considerationem suam ad circulum parvum egressionem a centro similem illi quam facit stella in longitudine per considerationem suam ad orbem signorum. Et illud est quia cum ponitur tempus reversionum equale in orbe signorum et in circulo parvo et ponuntur etiam cursus in quartis in unoquoque eorum oppositi adinvicem secundum quod videtur, tunc revolutio circuli parvi si fuerit super centrum quod est ei proprium, non preparatur quod diximus omnino, propterea quod cursuum per circulum parvum in unaquaque quartarum sunt tempora equalia, et sunt cursus orbis revolutionis in orbe signorum, et sunt cursus qui videntur non equalium temporum propter orbem egredientis centri positum in unaquaque earum. Quod si fuerit super centrum cuius situs est sicut situs centri orbis egredientis centri et in quartis oppositis orbis signorum et circuli parvi, tunc reversiones declinationum complentur in temporibus equalibus. Neque estimet aliquis quod harum radicum et eis similium sit difficilis casus, ad hoc ut ponat speculationem suam ad ea que exemplificavimus sicut eius speculatio est ad id quod est ex rebus que accipiuntur ingenio et subtilitate artis et quarum est etiam difficilis casus. Et illud est quia non oportet ut considerentur res divine per res humanas neque ut elevetur ad certificandum cuius nobilitatis et valitudinis hec est summa cum acceptione exemplorum eius a rebus que sunt in ultimo longitudinis ab eius similitudine neque ad res que currunt secundum exemplum unum ex rebus que non sunt ita, neque in una horarum. Neque est maior dissimilitudo quam rerum quibus accidunt impedimenta ab omni parte a rebus quibus non accidit impedimentum, neque ab aliis neque a seipsis. Sed non oportet nisi ut inquirat in ultimo, quo possibile est, ut conveniat motibus qui sunt in celo simplicibus quod est ex radicibus secundum quas currit res eorum. Quod si non preparatur illud, inquirat ex radicibus quod est possibile ut sit eis conveniens et aptum. Si autem invenerimus aliquo modorum unamquamque rerum que videtur in eo comitantem illas radices que ponuntur neque ab eis diversas, non erit ad negandum quin similis huic compositioni et permixtioni iam accidat celestibus motibus locus. Non est enim in eis natura prohibens neque impediens omnino. Immo eorum natura est conveniens ut obediat et aptetur et offerat se unicuique motuum naturalium, quamvis sint contrarii, donec ipsa quasi sit potens ut penetret sive compleat species naturales omnes absolute, ex quibus est eorum essentia aut status, et appareat eorum operatio in eis, et ut levitas incessus non sit in circulis particularibus tantum, immo in spheris ipsis etiam. Et ipse pertranseunt revolutiones suas (est enim permixtio harum etiam in motibus diversis), et supponuntur alie aliis donec conveniant. In exemplis vero que nos accepimus invenimus difficilem et gravem operationem cum in eis inquiritur ut sit motus absque prohibitione. In celo autem invenimus motum quem non prohibet nec impedit hec permixtio absolute aliquo modorum omnino. Verum de intentione simplicis ipsius in corporibus celestibus non oportet iudicari ex corporibus que sunt ante ea apud nos de quibus estimatur quod sint secundum hunc modum. Nos enim invenimus simplex in nobis ipsis non ipsum simplex in omni re secundum exemplum unum. Cum igitur nos processerimus hac via speculationis, non videbimus quod sit aliqua rerum que sunt in celo simplex, neque habitudo ipsa que est motus primi, qui non alteratur, nedum que sunt preter ipsam. Propter hanc intentionem ipsam, scilicet ut sit res in omni tempore secundum exemplum unum, non solum est in nobis difficilis et gravis, verum etiam est impossibilis omnino. Nature vero que sunt in celo ipso et in motibus eius qui non alterantur non sunt cum difficultate neque gravitate. Videmus igitur quod hoc modo declaratur nobis quod omne simplex et quod est dignum eo ex rebus que sunt apud nos de quibus estimatur quod sint hoc modo quod non est possibile ut imaginetur quod accidat eis in revolutione sua modus lassitudinis neque tristitie neque impedimento aliquo modorum. Videmus ... modorum: Corrupt sentence. Cf. Toomer, loc. cit., p. 601, lines 17-19. Paris, BnF, lat. 14738 (199r, lines 12-14 from the bottom) does not offer any better text.
〈XIII.3〉 Capitulum tertium: In quantitate declinationis et declinationis et reflexionis et reflexionis
Summam autem rei in situ declinationis circulorum et in ordine eius ex istis rebus est possibile homini extrahere donec sciat eam. Quantitatum autem particularium in unaquaque harum stellarum arcuum quos separant declinationes circulorum qui describuntur transeuntes per duos polos circuli declinati super superficiem orbis signorum super eam erecti ortogonaliter, et est circulus secundum quem videntur cursus in latitudine, iam alleviatur numeratio in Venere et Mercurio propter cursus qui videntur in latitudine in sitibus notis. Et illud est quia quando fuerint motus earum in longitudine longiore aut longitudine propinquiore duorum orbium earum egredientium centrorum, tunc si fuerit cursus duarum stellarum in longitudine longiore aut longitudine propinquiore duorum orbium revolutionis earum, res erit in eis quemadmodum diximus. Et illud est quoniam quando scivimus illud considerando eas et ipse propinque his duobus locis, videbuntur decliviores ad septentrionem aut ad meridiem ab orbe signorum equaliter, sed stella Veneris ad septentrionem semper quasi sexta partis unius ut multum et Mercurii ad meridiem semper medietate et quarta partis unius, ita ut appareat ex eo quod declinationis cuiusque duorum orbium egredientium centrorum sit hec quantitas. Si autem fuerit cursus earum in longitudinibus earum maioribus a Sole, tunc ipse ambe videbuntur declinate ad septentrionem et meridiem a duabus longitudinibus maioribus secundum contrarietatem earum quasi quinque partibus secundum rem mediam in consideratione, propterea quod stella Veneris videtur facere hanc contrarietatem quam diximus in latitudine minorem quinque partibus in longitudine longiore orbis egredientis centri et maiorem quinque partibus in longitudine propinquiore eius secundum id de quo non est curandum et stella Mercurii videtur esse diversa in hac medietate partis ut multum, ita ut reflexiones orbis revolutionis in una duarum partium duarum superficierum in quibus sunt duo orbes egredientium centrorum subtendantur secundum rem mediam in consideratione plus duabus partibus et medietati partis circuli ortogonaliter erecti super orbem signorum. Propter has autem reflexiones inveniuntur quantitates angulorum qui proveniunt a reflexionibus duorum orbium revolutionis a duobus orbibus egredientium centrorum, quemadmodum apparebit in eis que demonstrabimus in sequentibus de re eorum ut non interrumpatur subito applicatio sermonis quem loquor in declinationibus stellarum quinque erraticarum. Et quando fuerint motus earum in longitudine equati in duobus modis et in eo quod est circa longitudines medias, stella quidem Veneris tunc, quando fuerit cursus eius in longitudine longiore orbis revolutionis eius, videbitur declinata ad meridiem aut ad septentrionem ab orbe signorum parte una, et quando fuerit cursus eius in longitudine propinquiore eius, videbitur declinata ad meridiem aut ad septentrionem sex partibus et tertia partis fere, ita ut declinatio orbis revolutionis eius comprehendat ex circulo qui describitur super duos polos orbis revolutionis eius secundum modum quem diximus duas partes et medietatem partis. Nos namque invenimus propter diversitatem in orbe revolutionis eius in longitudinibus mediis quod hec quantitas partium in longitudine longiore orbis revolutionis subtenditur angulo apud visum cuius summa est pars una et duo minuta et in longitudine propinquiore subtenditur angulo cuius summa est sex partes et 22 minuta. Stelle autem Mercurii tunc, quando fuerit cursus eius in longitudine longiore orbis revolutionis, eius declinatio ad meridiem aut ad septentrionem ab orbe signorum erit pars una et medietas et quarta partis secundum quod scitur ex eo secundum numerationem acceptam propter apparitionem eius propinquam huic loca Probably corrupt for loco, which is also the reading of Paris, BnF, lat. 14738 (199v, line 17 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 602, line 18)., et quando fuerit eius cursus in longitudine propinquiore, tunc eius declinatio erit quatuor partes fere, ita ut declinatio orbis revolutionis sit sex partes et quarta partis. Nos namque invenimus etiam propter diversitatem in orbe revolutionis eius in longitudinibus que sunt declinationum maiorum, scilicet cum fuerit longitudinis equate elongatio a longitudine longiore quarta circuli, quod hec quantitas partium subtenditur angulo apud visum in longitudine longiore quidem orbis revolutionis eius quem posuimus partem unam et 46 minuta et in longitudine quidem propinquiore eius quem posuimus quatuor partes et quinque minuta.
In reliquis vero tribus stellis, et sunt Saturnus et Iuppiter et Mars, non potest homo scire leviter hac semita quantitates declinationum, quoniam ambe species in eis semper sunt permixte, scilicet que earum est propter orbem egredientis centri et que earum est propter orbem revolutionis. Nos vero dividemus unamquamque duarum specierum declinationum ab altera propter considerationes et iam et iam: Probably corrupt for etiam, which is the reading of Paris, BnF, lat. 14738 (199v, line 8 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 602, line 11 from the bottom). cursuum in latitudine qui sunt earum in longitudine propinquiore et in longitudine longiore orbium egredientium centrorum et orbium revolutionis hoc modo quem narrabo: 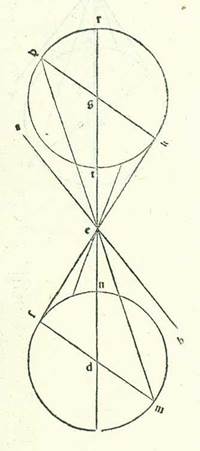 Sit itaque in superficie erecta ortogonaliter super superficiem orbis signorum differentia communis inter ipsam et inter superficiem orbis signorum linea AB et differentia communis inter ipsam et inter superficiem orbis egredientis centri linea GD, et punctum E sit centrum orbis signorum in differentia communi inter superficies, et describatur circa punctum G, et est longitudo longior orbis egredientis centri, et circa punctum D, et est longitudo propinquior eius in superficie posita, duos circulos HTK et MNS equales sicut sunt duo circuli qui transeunt per polos orbium revolutionis, et applicabo super eos duas superficies orbium revolutionis, linea HGK et linea MDS, secundum quantitatem duorum angulorum qui sunt apud duo puncta G et D, et manifestum est quod ipsi sunt equales, et coniungantur inter punctum E, quod est centrum orbis signorum et super quod est visus, et inter duas longitudines longiores et inter duas longitudines propinquiores duorum orbium revolutionis, inter ipsum quidem et inter duas longiores longitudines duabus lineis EH et EM et inter ipsum et inter duas longitudines propinquiores duabus lineis EK et ES, et manifestum est quod duo puncta K et S comprehendunt duos cursus comparatos ad extremitatem noctis et duo puncta H et M comprehendunt duos cursus coiniunctionales. In stella vero Martis accepimus cursus qui sunt ei in latitudine in habitudinibus extremitatis noctis que sunt in longitudine longiore orbis egredientis centri, scilicet que sunt super punctum K orbis revolutionis, et in habitudinibus extremitatis noctis que sunt ei in longitudine propinquiore orbis egredientis centri, scilicet que sunt super punctum S orbis revolutionis, quoniam superfluitas in istis cursibus valde manifesta est sensui. Invenimus itaque eam elongatam ab orbe signorum in habitudinibus quidem extremitatis noctis que sunt in longitudine longiore quatuor partibus et tertia partis in septentrione et in habitudinibus extremitatis noctis que sunt in longitudine propinquiore septem partibus in meridie fere, ita ut angulus AEK sit etiam quatuor partes et tertia partis secundum partes quibus quatuor anguli recti sunt 360 partes et sit angulus BES secundum istas partes septem partes. Postquam igitur explanavimus has res, inveniemus angulum quem continet declinatio orbis egredientis centri, scilicet angulum AEG, et angulum quem continet declinatio orbis revolutionis, scilicet angulum GEK, hoc modo: Propterea quod est ex eis quorum facilis est intellectus propter diversitates quas declaravimus Martis, scilicet quod quicunque Probably corrupt for quibusque, which is the reading of Paris, BnF, lat. 14738 (200r, line 17). The Greek text is somewhat different here (see Toomer, loc. cit., p. 603, lines 4-6). angulorum fuerit cursus ex eis qui sunt apud visum sub quibus tenduntur apud longitudinem propinquiorem orbis revolutionis arcus equales, erit proportio cursuum qui sunt per eos super arcus qui sunt apud longitudinem longiorem orbis egredientis centri ad cursus qui sunt per eos super arcus qui sunt apud longitudinem propinquiorem eius sicut proportio quinque partium fere ad novem partes. Duo vero arcus TK et NS sunt equales. Ergo proportio anguli GEK ad angulum DES erit sicut proportio quinque partium ad novem partes. Quapropter propterea quod duo anguli AEK et BES sunt noti et quod proportio anguli GEK ad angulum DES est nota et quod angulus AEG est equalis angulo BED, si nos consideraverimus quota pars sit superfluitas inter duas summas duarum quantitatum superfluitatis inter duos numeros proportionis et acceperimus similem illi parti ex unoquoque duorum numerorum proportionis, proveniet nobis summa cuiusque duarum quantitatum inter quas proprie cecidit proportio. Et illud manifestum est per unum parvum capitulorum numeralium. Una enim duarum quantitatum est quatuor partes et tertia partis, et altera septem partes, et superfluitas que est inter eas est due partes et due tertie partis, et proportio est proportio quinque partium ad novem partes, et superfluitas inter hos duos numeros est quatuor partes, et due partes et due tertie partis quatuor partium sunt due tertie. Ergo si nos acceperimus ex quinque partibus et ex novem partibus similem huic parti, proveniet nobis angulus GEK tres partes et tertia partis, et proveniet angulus NES Probably corrupt for DES, which would correspond to the Greek text (see Toomer, loc. cit., p. 604, line 15). Paris, BnF, lat. 14738 (200r, line 9 from the bottom) reads NES too. per istas partes sex partes, et unusquisque duorum angulorum AEG et BED reliquorum, et sunt duo anguli declinationis orbis egredientis centri, secundum quod sequitur est pars una, et provenit ex eo arcus TK, et est arcus declinationis orbis revolutionis, due partes et quarta partis, quoniam hec est summa quam comprehendit partium fere in tabula diversitatis he sunt quantitates quas scivimus angulorum GEK et DES hec est summa ... GEK et DES: Corrupt passage. The same text is found in Paris, BnF, lat. 14738 (200r, lines 5-6 from the bottom). But cf. Toomer, loc. cit., 604, lines 18-20.. In Saturno autem et Iove, propterea quod nos invenimus cursus eorum qui sunt in arcubus longitudinis propinquioris duorum orbium eorum egredientium centrorum non diversificari in sensu a cursibus eorum qui sunt in arcubus longitudinis propinquioris ipsorum condiametralibus, etiam in illis cursibus numeravimus quod intendimus de re eorum secundum unumquemque duorum modorum propter comparationem inter duos cursus eorum in longitudine longiore duorum orbium revolutionis eorum et inter duos cursus eorum in longitudine propinquiore eorum. Et fuit summa longitudinis secundum quod scivimus ipsam ex considerationibus particularibus eorum in cursibus quidem qui sunt in apparitione et in occultatione plurimum quod est ad septentrionem et ad meridiem in Saturno quidem due partes fere et in Iove pars una, et in cursibus qui sunt in habitudinibus extremitatis noctis in Saturno quidem usque ad tres partes et in Iove usque ad duas partes. Propterea igitur quod iam apparuit propter diversitatem que est eorum in cursibus etiam quod angulorum quibus apud visum subtenduntur in longitudine longiore et in longitudine propinquiore orbis revolutionis equales arcus quicunque proveniunt a cursibus in longitudine longiore, proportio ad angulos qui proveniunt a cursibus in longitudine propinquiore in Saturni quidem stella est proportio decem et octo partium ad vigintitres partes, et in stella Iovis est proportio vigintinovem partium ad vigintitres partes, et sunt duo arcus RH et TK orbis revolutionis equales, tunc proportio anguli REH etiam ad angulum REK erit in stella quidem Saturni proportio decem et octo partium ad vigintitres partes et in stella Iovis proportio vigintinovem partium ad quadragintatres partes. Angulus vero HEK, quia est superfluitas que est inter duos cursus in latitudine ambarum stellarum, provenit pars una. Cum ergo diviserimus hanc partem unam per duas proportiones dictas, proveniet nobis angulus REH in stella quidem Saturni 26 minuta et in stella Iovis 24 minuta, et proveniet angulus REK in Saturno quidem 34 minuta et in Iove 36 minuta. Proveniet ergo angulus AEG reliquus, et est angulus declinationis orbis egredientis centri, in Saturno due partes et 26 minuta et in Iove pars una et 24 minuta. Nos vero restauravimus et exercuimus loco horum duorum numerorum Here probably numerum is missing, which is contained in Paris, BnF, lat. 14738 (200v, line 16) and would correspond to the Greek text (see Toomer, loc. cit., p. 605, line 11). duarum partium et semis et numerum partis et semis querendo facilitatem in operatione. Et propter illud aggregatur arcus TK etiam, et est arcus declinationis duorum orbium revolutionis, in Saturno quidem quatuor partes et medietas partis et in Iove due partes et medietas partis. Et illud est quoniam hec quantitas partium in unaquaque earum in tabula diversitatis continet etiam fere duas quantitates quas scivimus duorum angulorum REH et REK. Et iste sunt res quarum intendimus inventionem.
Sit itaque in superficie erecta ortogonaliter super superficiem orbis signorum differentia communis inter ipsam et inter superficiem orbis signorum linea AB et differentia communis inter ipsam et inter superficiem orbis egredientis centri linea GD, et punctum E sit centrum orbis signorum in differentia communi inter superficies, et describatur circa punctum G, et est longitudo longior orbis egredientis centri, et circa punctum D, et est longitudo propinquior eius in superficie posita, duos circulos HTK et MNS equales sicut sunt duo circuli qui transeunt per polos orbium revolutionis, et applicabo super eos duas superficies orbium revolutionis, linea HGK et linea MDS, secundum quantitatem duorum angulorum qui sunt apud duo puncta G et D, et manifestum est quod ipsi sunt equales, et coniungantur inter punctum E, quod est centrum orbis signorum et super quod est visus, et inter duas longitudines longiores et inter duas longitudines propinquiores duorum orbium revolutionis, inter ipsum quidem et inter duas longiores longitudines duabus lineis EH et EM et inter ipsum et inter duas longitudines propinquiores duabus lineis EK et ES, et manifestum est quod duo puncta K et S comprehendunt duos cursus comparatos ad extremitatem noctis et duo puncta H et M comprehendunt duos cursus coiniunctionales. In stella vero Martis accepimus cursus qui sunt ei in latitudine in habitudinibus extremitatis noctis que sunt in longitudine longiore orbis egredientis centri, scilicet que sunt super punctum K orbis revolutionis, et in habitudinibus extremitatis noctis que sunt ei in longitudine propinquiore orbis egredientis centri, scilicet que sunt super punctum S orbis revolutionis, quoniam superfluitas in istis cursibus valde manifesta est sensui. Invenimus itaque eam elongatam ab orbe signorum in habitudinibus quidem extremitatis noctis que sunt in longitudine longiore quatuor partibus et tertia partis in septentrione et in habitudinibus extremitatis noctis que sunt in longitudine propinquiore septem partibus in meridie fere, ita ut angulus AEK sit etiam quatuor partes et tertia partis secundum partes quibus quatuor anguli recti sunt 360 partes et sit angulus BES secundum istas partes septem partes. Postquam igitur explanavimus has res, inveniemus angulum quem continet declinatio orbis egredientis centri, scilicet angulum AEG, et angulum quem continet declinatio orbis revolutionis, scilicet angulum GEK, hoc modo: Propterea quod est ex eis quorum facilis est intellectus propter diversitates quas declaravimus Martis, scilicet quod quicunque Probably corrupt for quibusque, which is the reading of Paris, BnF, lat. 14738 (200r, line 17). The Greek text is somewhat different here (see Toomer, loc. cit., p. 603, lines 4-6). angulorum fuerit cursus ex eis qui sunt apud visum sub quibus tenduntur apud longitudinem propinquiorem orbis revolutionis arcus equales, erit proportio cursuum qui sunt per eos super arcus qui sunt apud longitudinem longiorem orbis egredientis centri ad cursus qui sunt per eos super arcus qui sunt apud longitudinem propinquiorem eius sicut proportio quinque partium fere ad novem partes. Duo vero arcus TK et NS sunt equales. Ergo proportio anguli GEK ad angulum DES erit sicut proportio quinque partium ad novem partes. Quapropter propterea quod duo anguli AEK et BES sunt noti et quod proportio anguli GEK ad angulum DES est nota et quod angulus AEG est equalis angulo BED, si nos consideraverimus quota pars sit superfluitas inter duas summas duarum quantitatum superfluitatis inter duos numeros proportionis et acceperimus similem illi parti ex unoquoque duorum numerorum proportionis, proveniet nobis summa cuiusque duarum quantitatum inter quas proprie cecidit proportio. Et illud manifestum est per unum parvum capitulorum numeralium. Una enim duarum quantitatum est quatuor partes et tertia partis, et altera septem partes, et superfluitas que est inter eas est due partes et due tertie partis, et proportio est proportio quinque partium ad novem partes, et superfluitas inter hos duos numeros est quatuor partes, et due partes et due tertie partis quatuor partium sunt due tertie. Ergo si nos acceperimus ex quinque partibus et ex novem partibus similem huic parti, proveniet nobis angulus GEK tres partes et tertia partis, et proveniet angulus NES Probably corrupt for DES, which would correspond to the Greek text (see Toomer, loc. cit., p. 604, line 15). Paris, BnF, lat. 14738 (200r, line 9 from the bottom) reads NES too. per istas partes sex partes, et unusquisque duorum angulorum AEG et BED reliquorum, et sunt duo anguli declinationis orbis egredientis centri, secundum quod sequitur est pars una, et provenit ex eo arcus TK, et est arcus declinationis orbis revolutionis, due partes et quarta partis, quoniam hec est summa quam comprehendit partium fere in tabula diversitatis he sunt quantitates quas scivimus angulorum GEK et DES hec est summa ... GEK et DES: Corrupt passage. The same text is found in Paris, BnF, lat. 14738 (200r, lines 5-6 from the bottom). But cf. Toomer, loc. cit., 604, lines 18-20.. In Saturno autem et Iove, propterea quod nos invenimus cursus eorum qui sunt in arcubus longitudinis propinquioris duorum orbium eorum egredientium centrorum non diversificari in sensu a cursibus eorum qui sunt in arcubus longitudinis propinquioris ipsorum condiametralibus, etiam in illis cursibus numeravimus quod intendimus de re eorum secundum unumquemque duorum modorum propter comparationem inter duos cursus eorum in longitudine longiore duorum orbium revolutionis eorum et inter duos cursus eorum in longitudine propinquiore eorum. Et fuit summa longitudinis secundum quod scivimus ipsam ex considerationibus particularibus eorum in cursibus quidem qui sunt in apparitione et in occultatione plurimum quod est ad septentrionem et ad meridiem in Saturno quidem due partes fere et in Iove pars una, et in cursibus qui sunt in habitudinibus extremitatis noctis in Saturno quidem usque ad tres partes et in Iove usque ad duas partes. Propterea igitur quod iam apparuit propter diversitatem que est eorum in cursibus etiam quod angulorum quibus apud visum subtenduntur in longitudine longiore et in longitudine propinquiore orbis revolutionis equales arcus quicunque proveniunt a cursibus in longitudine longiore, proportio ad angulos qui proveniunt a cursibus in longitudine propinquiore in Saturni quidem stella est proportio decem et octo partium ad vigintitres partes, et in stella Iovis est proportio vigintinovem partium ad vigintitres partes, et sunt duo arcus RH et TK orbis revolutionis equales, tunc proportio anguli REH etiam ad angulum REK erit in stella quidem Saturni proportio decem et octo partium ad vigintitres partes et in stella Iovis proportio vigintinovem partium ad quadragintatres partes. Angulus vero HEK, quia est superfluitas que est inter duos cursus in latitudine ambarum stellarum, provenit pars una. Cum ergo diviserimus hanc partem unam per duas proportiones dictas, proveniet nobis angulus REH in stella quidem Saturni 26 minuta et in stella Iovis 24 minuta, et proveniet angulus REK in Saturno quidem 34 minuta et in Iove 36 minuta. Proveniet ergo angulus AEG reliquus, et est angulus declinationis orbis egredientis centri, in Saturno due partes et 26 minuta et in Iove pars una et 24 minuta. Nos vero restauravimus et exercuimus loco horum duorum numerorum Here probably numerum is missing, which is contained in Paris, BnF, lat. 14738 (200v, line 16) and would correspond to the Greek text (see Toomer, loc. cit., p. 605, line 11). duarum partium et semis et numerum partis et semis querendo facilitatem in operatione. Et propter illud aggregatur arcus TK etiam, et est arcus declinationis duorum orbium revolutionis, in Saturno quidem quatuor partes et medietas partis et in Iove due partes et medietas partis. Et illud est quoniam hec quantitas partium in unaquaque earum in tabula diversitatis continet etiam fere duas quantitates quas scivimus duorum angulorum REH et REK. Et iste sunt res quarum intendimus inventionem.
〈XIII.4〉 Capitulum quartum: In modo faciendi tabulas cursuum particularium in latitudine
Ex his itaque rebus proveniunt nobis quantitates universales declinationum maiorum orbium egredientium centrorum et orbium revolutionis. Ut autem possimus invenire leviter omni hora cursus in latitudine in longitudinibus particularibus etiam, assumpsimus tabulas stellis quinque erraticis et in omni tabula earum simile ei ex areis quod est in unaquaque tabularum diversitatum, et eius aree sunt quinque. In duabus igitur primis harum arearum sunt numeri sicut in illis areis.
In areis vero tertiis sunt longitudines in latitudine ab orbe signorum que pertinent sectionibus orbium revolutionis particularibus in declinationibus maioribus ipsis, in stella quidem Veneris et in stella Mercurii in duobus nodis orbium egredientium centrorum et in stellis tribus reliquis in partibus septentrionalibus orbium egredientium centrorum, et in areis quartis etiam in his tribus stellis quod pertinet divisionibus longitudinum oppositis illis versus partes meridionales orbium egredientium centrorum adiuncto ad illud in his tribus stellis plurimo quod est etiam elongationis orbium eorum egredientium centrorum in septentrione et meridie. 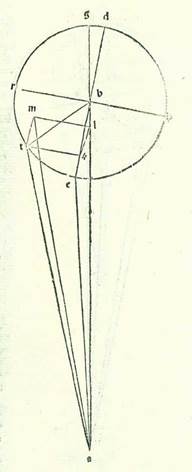 Nostra autem numeratio harum sectionum in stella quidem Veneris et in stella Mercurii fuit uno capitulo secundum hunc modum ut sit in superficie ortogonaliter erecta super superficiem orbis signorum linea quidem ABG differentia communis inter ipsam et inter superficiem orbis signorum et linea quidem DBE differentia communis inter ipsam et inter superficiem orbis revolutionis, et sit centrum orbis signorum punctum A et centrum orbis revolutionis punctum B, et sit linea AB elongatio duorum orbium revolutionis harum duarum stellarum in declinationibus earum maioribus. Et signabo circa punctum B orbem revolutionis DERH, et producam diametrum RBH ortogonaliter erectam super lineam DE, et ponam ut superficies orbis revolutionis etiam sit ortogonaliter erecta supra superficiem narratam positam, ita ut sint omnes linee ortogonaliter protracte super lineam DE in superficie orbis revolutionis equidistantes superficiei orbis signorum, excepta linea RH sola. Ipsa namque est in superficie orbis signorum. Et sit nostra intentio, quando dederimus proportionem linee AB ad lineam BE et quantitatem declinationis, scilicet angulum ABE, ut inveniamus cursus harum duarum stellarum in latitudine quando fuerit verbi gratia longitudo earum a puncto E, et est longitudo propinquior orbis revolutionis, quadragintaquinque partes secundum partes quibus orbis revolutionis est 360 partes. Et illud est quia nos eligimus ut declaremus superfluitates que sunt in cursibus in longitudine propter illud cuius hec est summa declinationis. Oportet vero ut he superfluitates in locis cursuum qui sunt in eo quod est inter punctum E, et est longitudo propinquior, et inter punctum R et punctum H diversificentur in ultimo quod est diversitatis earum, propterea quod cursus qui sunt in his punctis que nominavimus sunt convenientes cursibus qui sunt vacui a declinatione. Separabo igitur arcum quantitatis harum partium quas diximus, et sunt quadragintaquinque partes, sitque arcus ET, et protraham super lineam EB perpendicularem TK et supra superficiem orbis signorum duas perpendiculares KL et TM, et coniungam lineas TB et LM et AM et AT. Manifestum est igitur ex propinquo quod quadrilaterum super quod sunt L, K, T, M est equidistantium laterum et rectorum angulorum, propterea quod linea KT est equidistans superficiei orbis signorum. Et manifestum est etiam quod augmentum et diminutionem in longitudine comprehendit angulus LAM et cursus in latitudine comprehendit angulus TAM, quoniam duo anguli ALM et AMT sunt etiam recti, propterea quod linea AM etiam cadit in superficie orbis signorum. Quantitates autem cursuum quesitorum in unaquaque duarum stellarum quarum precessit relatio quantum comprehendant iam oportet nunc ut ostendamus, et incipiemus a stella Veneris. Dico igitur quod arcus ET quia est quadragintaquinque partes secundum partes quibus orbis revolutionis est 360 partes, tunc angulus EBT, quia est apud centrum orbis revolutionis, erit secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes, et secundum partes quibus duo anguli recti sunt 360 partes erit 90 partes. Quapropter erit unusquisque duorum arcuum etiam qui sunt super duas lineas BK et KT 90 partes secundum partes quibus circulus qui describitur circa triangulum BKT ortogonium est 360 partes, et unaqueque duarum linearum que subtenduntur eis erit 84 partes et 52 minuta minnta M. secundum partes quibus chorda BT est 120 partes. Quapropter erit etiam secundum partes quibus chorda BT, et est a centro orbis revolutionis, est 43 partes et 10 minuta et linea AB, et est linea longitudinis medie, est 60 partes, quoniam in hac longitudine proprie est declinatio orbis revolutionis maior, unaquaque duarum linearum BK et KT 30 partes et 32 minuta. Et etiam quia angulus ABE, et est angulus declinationis positus, est secundum partes quibus quatuor anguli recti sunt 360 partes due partes et medietas partis et secundum partes quibus duo anguli recti sunt 360 partes quinque partes, erit etiam arcus qui est super lineam LK quinque partes secundum partes quibus circulus qui describitur circa triangulum BLK ortogonium est 360 partes, et erit arcus qui est super lineam BL partes relique ad complendum semicirculum, et sunt 175 partes. Duarum igitur linearum que subtenduntur eis linea quidem LK erit 5 partes et 14 minuta secundum partes quibus chorda BK est 120 partes, et linea BL earum erit secundum istas partes 119 partes et 53 minuta. Quapropter oportet etiam ut secundum partes quibus chorda BK est 30 partes et 32 minuta et linea AB 60 partes sit linea KL pars una et 20 minuta et linea BL 30 partes et 30 minuta, et erit linea AL partes relique, et sunt 19 partes et 30 minuta. Et secundum istas partes linea BK, quia est equalis linee KT, est 30 partes et 32 minuta. Oportet ergo propter illud ut aggregetur chorda AM secundum istas partes 42 partes et 27 minuta. Ergo secundum partes quibus chorda AM est 120 partes erit linea LM 86 partes et 19 minuta, et angulus LAM, et est angulus diminutionis et augmenti in longitudine, tunc erit secundum partes quibus duo anguli recti sunt 360 partes 92 partes et secundum partes quibus quatuor anguli recti sunt 360 partes 46 partes. Et secundum hoc exemplum, quia secundum partes quibus linea AM est 42 partes et 27 minuta est linea TM, quia est equalis linee KL, pars una et 20 minuta, et quia cum aggregabitur quod est ex quadratis earum, erit ex eo quadratum quod est ex eo quadrato linee eo quadrato linee: Corrupt passage. Sense requires linea instead, and this would also correspond to the Greek text (see Toomer, loc. cit., p. 608, line 13). Paris, BnF, lat. 14738 (201v, line 5) is equally corrupt. It reads quod est ex quadrato linee instead of quadratum quod est ex eo quadrato linee. AT, erit linea AT etiam in longitudine secundum istas partes 42 partes et 29 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea TM tres partes et 46 minuta, et erit angulus TAM, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes tres partes et 36 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit pars una et 48 minuta. Firmabimus ergo illud in tabula tertia tabularum Veneris in area in qua est numerus 135 partium.
Nostra autem numeratio harum sectionum in stella quidem Veneris et in stella Mercurii fuit uno capitulo secundum hunc modum ut sit in superficie ortogonaliter erecta super superficiem orbis signorum linea quidem ABG differentia communis inter ipsam et inter superficiem orbis signorum et linea quidem DBE differentia communis inter ipsam et inter superficiem orbis revolutionis, et sit centrum orbis signorum punctum A et centrum orbis revolutionis punctum B, et sit linea AB elongatio duorum orbium revolutionis harum duarum stellarum in declinationibus earum maioribus. Et signabo circa punctum B orbem revolutionis DERH, et producam diametrum RBH ortogonaliter erectam super lineam DE, et ponam ut superficies orbis revolutionis etiam sit ortogonaliter erecta supra superficiem narratam positam, ita ut sint omnes linee ortogonaliter protracte super lineam DE in superficie orbis revolutionis equidistantes superficiei orbis signorum, excepta linea RH sola. Ipsa namque est in superficie orbis signorum. Et sit nostra intentio, quando dederimus proportionem linee AB ad lineam BE et quantitatem declinationis, scilicet angulum ABE, ut inveniamus cursus harum duarum stellarum in latitudine quando fuerit verbi gratia longitudo earum a puncto E, et est longitudo propinquior orbis revolutionis, quadragintaquinque partes secundum partes quibus orbis revolutionis est 360 partes. Et illud est quia nos eligimus ut declaremus superfluitates que sunt in cursibus in longitudine propter illud cuius hec est summa declinationis. Oportet vero ut he superfluitates in locis cursuum qui sunt in eo quod est inter punctum E, et est longitudo propinquior, et inter punctum R et punctum H diversificentur in ultimo quod est diversitatis earum, propterea quod cursus qui sunt in his punctis que nominavimus sunt convenientes cursibus qui sunt vacui a declinatione. Separabo igitur arcum quantitatis harum partium quas diximus, et sunt quadragintaquinque partes, sitque arcus ET, et protraham super lineam EB perpendicularem TK et supra superficiem orbis signorum duas perpendiculares KL et TM, et coniungam lineas TB et LM et AM et AT. Manifestum est igitur ex propinquo quod quadrilaterum super quod sunt L, K, T, M est equidistantium laterum et rectorum angulorum, propterea quod linea KT est equidistans superficiei orbis signorum. Et manifestum est etiam quod augmentum et diminutionem in longitudine comprehendit angulus LAM et cursus in latitudine comprehendit angulus TAM, quoniam duo anguli ALM et AMT sunt etiam recti, propterea quod linea AM etiam cadit in superficie orbis signorum. Quantitates autem cursuum quesitorum in unaquaque duarum stellarum quarum precessit relatio quantum comprehendant iam oportet nunc ut ostendamus, et incipiemus a stella Veneris. Dico igitur quod arcus ET quia est quadragintaquinque partes secundum partes quibus orbis revolutionis est 360 partes, tunc angulus EBT, quia est apud centrum orbis revolutionis, erit secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes, et secundum partes quibus duo anguli recti sunt 360 partes erit 90 partes. Quapropter erit unusquisque duorum arcuum etiam qui sunt super duas lineas BK et KT 90 partes secundum partes quibus circulus qui describitur circa triangulum BKT ortogonium est 360 partes, et unaqueque duarum linearum que subtenduntur eis erit 84 partes et 52 minuta minnta M. secundum partes quibus chorda BT est 120 partes. Quapropter erit etiam secundum partes quibus chorda BT, et est a centro orbis revolutionis, est 43 partes et 10 minuta et linea AB, et est linea longitudinis medie, est 60 partes, quoniam in hac longitudine proprie est declinatio orbis revolutionis maior, unaquaque duarum linearum BK et KT 30 partes et 32 minuta. Et etiam quia angulus ABE, et est angulus declinationis positus, est secundum partes quibus quatuor anguli recti sunt 360 partes due partes et medietas partis et secundum partes quibus duo anguli recti sunt 360 partes quinque partes, erit etiam arcus qui est super lineam LK quinque partes secundum partes quibus circulus qui describitur circa triangulum BLK ortogonium est 360 partes, et erit arcus qui est super lineam BL partes relique ad complendum semicirculum, et sunt 175 partes. Duarum igitur linearum que subtenduntur eis linea quidem LK erit 5 partes et 14 minuta secundum partes quibus chorda BK est 120 partes, et linea BL earum erit secundum istas partes 119 partes et 53 minuta. Quapropter oportet etiam ut secundum partes quibus chorda BK est 30 partes et 32 minuta et linea AB 60 partes sit linea KL pars una et 20 minuta et linea BL 30 partes et 30 minuta, et erit linea AL partes relique, et sunt 19 partes et 30 minuta. Et secundum istas partes linea BK, quia est equalis linee KT, est 30 partes et 32 minuta. Oportet ergo propter illud ut aggregetur chorda AM secundum istas partes 42 partes et 27 minuta. Ergo secundum partes quibus chorda AM est 120 partes erit linea LM 86 partes et 19 minuta, et angulus LAM, et est angulus diminutionis et augmenti in longitudine, tunc erit secundum partes quibus duo anguli recti sunt 360 partes 92 partes et secundum partes quibus quatuor anguli recti sunt 360 partes 46 partes. Et secundum hoc exemplum, quia secundum partes quibus linea AM est 42 partes et 27 minuta est linea TM, quia est equalis linee KL, pars una et 20 minuta, et quia cum aggregabitur quod est ex quadratis earum, erit ex eo quadratum quod est ex eo quadrato linee eo quadrato linee: Corrupt passage. Sense requires linea instead, and this would also correspond to the Greek text (see Toomer, loc. cit., p. 608, line 13). Paris, BnF, lat. 14738 (201v, line 5) is equally corrupt. It reads quod est ex quadrato linee instead of quadratum quod est ex eo quadrato linee. AT, erit linea AT etiam in longitudine secundum istas partes 42 partes et 29 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea TM tres partes et 46 minuta, et erit angulus TAM, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes tres partes et 36 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit pars una et 48 minuta. Firmabimus ergo illud in tabula tertia tabularum Veneris in area in qua est numerus 135 partium.
Et ut experiamur quod cadit ex superfluitate propter augmentum et diminutionem in longitudine, describam formam similem huic, ita ut orbis revolutionis sit in ea non declivis. Et quia iam ostendimus quod unaqueque linearum duarum BK, KT est 30 partes et 32 minuta secundum partes quibus linea AB est 60 partes, ita ut linea AK sit partes relique, et sunt 29 partes et 29 minuta, et ex eo quod est ex quadrato huius linee et ex quadrato linee TK quando aggregantur est quadratum quod est ex linea AT, erit linea AT etiam in longitudine secundum istas partes 42 partes et 26 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea KT 86 partes et 21 minutum, et angulus TAK, et est angulus augmenti diminutionis in longitudine, erit secundum partes quibus duo anguli recti sunt 360 partes 92 partes et tria minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 46 partes et duo minuta fere. Iam vero fuit ostensum in declinatione quod eius summa secundum istas partes quantitatum est 46 partes. Iam ergo minuitur numerus additionis et diminutionis in longitudine propter declinationem orbis revolutionis duobus minutis. Et illud est quod intendimus invenire. Et describam etiam ad declarandos cursus in latitudine stelle Mercurii similem illi forme que est ante istam, ita ut arcus ET ponantur partes ille eedem, et sunt 45 partes, ita ut unaqueque duarum linearum BK et KT aggregetur etiam 84 partes et 52 minuta secundum partes quibus chorda BT est 120 partes. Secundum partes igitur quibus linea BT, et est a centro orbis revolutionis, est 22 partes et 30 minuta et linea AB, et est longitudinis linea in declinatione eius maiore, est 56 partes et 40 minuta (nos enim iam demonstravimus has res omnes etiam) erit unaqueque duarum linearum BK et KT 15 partes et 55 minuta. Et etiam quia angulus ABE, et est angulus declinationis orbis revolutionis, secundum partes quibus quatuor anguli recti sunt 360 partes est positus sex partes et 15 minuta et secundum partes quibus duo anguli recti sunt 360 partes 12 partes et 30 minuta, erit etiam arcus qui est super lineam LK 12 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum BKT ortogonium est 360 partes, et erit arcus qui est super lineam BL partes relique complementi semicirculi, et illud est 168 partes et 30 minuta. Linea igitur KL, una duarum linearum que subtenduntur eis, erit 13 partes et 4 minuta secundum partes quibus chorda BK est 120 partes, et linea BL secundum illas partes erit 119 partes et 17 minuta. Oportet ergo ex eo ut secundum partes quibus ostensum est quod linea BK est 15 partes et 55 minuta et posita est linea AB 56 partes et 40 minuta sit linea quidem KL pars una et 44 minuta, et linea quidem BL secundum illud exemplum 15 partes et 49 minuta, et sit linea AL reliqua secundum istas partes 40 partes et 51 minutum. Linea autem LM etiam, quia est equalis linee KT, est secundum istas partes 15 partes et 55 minuta. Ergo quia ex quadrato quod est ex linea AL cum quadrato quod est ex linea LM est quadratum quod est ex linea AM, tunc hec linea etiam proveniet nobis in longitudine 43 partes et 50 minuta secundum partes quibus linea LM est 15 partes et 55 minuta. Ergo secundum partes quibus chorda AM est 120 partes est linea LM 43 partes et 34 minuta, et angulus LAM, et est angulus augmenti et diminutionis in longitudine, erit secundum partes quibus duo anguli recti sunt 360 partes 42 partes et 34 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 21 pars et 17 minuta. Et secundum illud exemplum, quia secundum partes quibus linea AM est 43 partes et 55 minuta fit linea TM, quia est equalis linee KL, pars una et 44 minuta et ex duobus quadratis que sunt ex eis quando aggregantur est quadratum quod est ex linea AT, tunc hec linea proveniet nobis in longitudine secundum istas partes 43 partes et 52 minuta. Ergo secundum partes quibus linea AT est 120 partes erit linea TM quatuor partes et 44 minuta, et angulus TAM, et est angulus elongationis in latitudine, erit secundum partes quibus duo anguli recti sunt 360 partes 4 partes et 32 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 16 minuta. Firmabimus ergo illud in tabula tertia tabule stelle Mercurii in illa area eadem in qua est numerus 135 partium. Et illud est cuius intendimus inventionem.
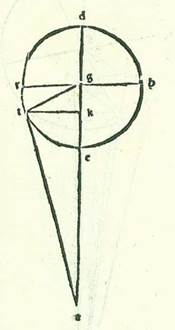 Et describam etiam causa experiendi numerum additionis et diminutionis in illa forma in qua non est declinatio. Et quia iam ostensum est quod secundum partes quibus linea AB est 56 partes et 40 minuta est unaqueque duarum linearum TK et KB 15 partes et 55 minuta, et manifestum est quod linea AL remanet secundum istas partes 40 partes et 45 minuta, et ex quadrato quod est ex ea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine 43 partes et 45 minuta secundum partes quibus linea TK est 15 partes et 55 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea quidem TK 43 partes et 39 minuta, et angulus quidem KAT, et est angulus augmenti et diminutionis, erit secundum partes quidem quibus duo anguli recti sunt 360 partes 42 partes et 40 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 21 partes et 20 minuta. Iam vero manifestum est nobis in declinatione quod eius summa secundum istas partes est 21 partes et 17 minuta. Iam ergo minuitur hic etiam numerus additionis et diminutionis in longitudine propter declinationem orbis revolutionis tribus minutis. Et iste sunt res quarum intendimus inventionem.
Et describam etiam causa experiendi numerum additionis et diminutionis in illa forma in qua non est declinatio. Et quia iam ostensum est quod secundum partes quibus linea AB est 56 partes et 40 minuta est unaqueque duarum linearum TK et KB 15 partes et 55 minuta, et manifestum est quod linea AL remanet secundum istas partes 40 partes et 45 minuta, et ex quadrato quod est ex ea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine 43 partes et 45 minuta secundum partes quibus linea TK est 15 partes et 55 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea quidem TK 43 partes et 39 minuta, et angulus quidem KAT, et est angulus augmenti et diminutionis, erit secundum partes quidem quibus duo anguli recti sunt 360 partes 42 partes et 40 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 21 partes et 20 minuta. Iam vero manifestum est nobis in declinatione quod eius summa secundum istas partes est 21 partes et 17 minuta. Iam ergo minuitur hic etiam numerus additionis et diminutionis in longitudine propter declinationem orbis revolutionis tribus minutis. Et iste sunt res quarum intendimus inventionem.
In cursibus autem harum duarum stellarum in latitudine in declinationibus maioribus hoc modo quem narravimus egimus quod in eis fecimus propterea quod hi cursus sunt in orbe egredientis centri in ipsa superficie orbis signorum. Quod vero in cursibus stellarum trium fecimus fecimus intentione forme preter hanc formam propterea quod cum declinationibus maioribus orbium earum egredientium centrorum conveniunt declinationes maiores orbium revolutionis eorum. Et sequitur ex illo ut sint cursus earum in latitudine qui aggregantur ex duabus declinationibus sensibiles simul. 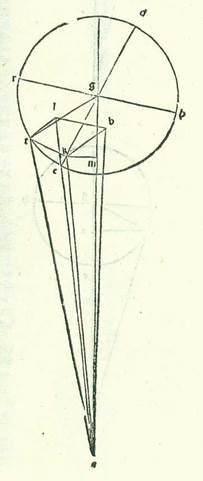 Sit itaque etiam in superficie que ortogonaliter est super superficiem orbis signorum differentia communis inter ipsam et inter superficiem orbis signorum linea AB, et differentia communis inter ipsam et inter orbem egredientis centri linea AG, et differentia communis inter ipsam et inter orbem revolutionis linea DG, et ponam ut centrum orbis signorum sit punctum A et centrum orbis revolutionis sit punctum G, et signabo circa punctum G orbem revolutionis DREH ita ut sit diametrus RGH ex lineis que ortogonaliter protrahuntur super lineam DE in superficie orbis egredientis centri et fiat equidistans superficiei orbis signorum. Ille autem relique linee sint equidistantes duabus superficiebus quas diximus simul. Et abscindam arcum ET secundum illud exemplum ad hoc ut ipse sit 45 partes, et protraham a puncto T, et est locus stelle, perpendicularem TK super lineam EG et a duobus punctis T et K etiam super superficiem orbis signorum duas perpendiculares KB et TL, et applicabo lineas BL, AL, AT, et sit nostra intentio ut inveniamus numerum additionis et diminutionis in longitudine, et est quem comprehendit angulus BAL, et cursum in latitudine, et est angulus quem comprehendit angulus LAT, et producam super lineam AG etiam a puncto K perpendicularem KM, et applicabo duas lineas GT et AK, et ponatur etiam propter illud cuius declaratio precessit unaqueque duarum linearum GK et KT 84 partes et 52 minuta secundum partes quibus chorda GT est 120 partes. Et quia iam ostensum est in stella Saturni prius quod linea que est a centro orbis revolutionis est sex partes et 30 minuta secundum partes quibus longitudo media est 60 partes, et est etiam unaqueque duarum linearum GK et KT secundum istas partes 4 partes et 36 minuta secundum partes quibus chorda GT est 6 partes et 36 minuta, et quia angulus AGE, et est angulus declinationis orbis revolutionis positus, est secundum partes quidem quibus quatuor anguli recti sunt 360 partes 4 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 9 partes tes M., erit etiam arcus qui est super lineam KM 9 partes secundum partes quibus circulus qui describitur circa triangulum GKM ortogonium est 360 partes, et arcus qui est super lineam GM est residuum complementi semicirculi, et est 171 partes. Linea igitur KM, una duarum linearum que subtenduntur eis, erit 9 partes et 25 minuta secundum partes quibus chorda GK est 120 partes, et linea GM secundum istas partes erit 119 partes et 38 minuta. Igitur secundum partes quibus linea GK est 4 partes et 36 minuta erit linea quidem KM 22 minuta, et linea GM secundum illud exemplum 4 partes et 35 minuta. Linea autem AG in declinatione maiore in medietate circuli remotiore, et est linea longitudinis in principio Libre, aggregatur propter intentionem quam premisimus et declaravimus in diversitatibus secundum istas partes 62 partes et 10 minuta. Remanet igitur linea AM reliqua eius 57 partes et 35 minuta secundum partes quibus linea GK est 22 minuta. Et propter illud erit linea AK 57 partes et 35 minuta. Igitur secundum partes quibus chorda AK est 120 partes erit linea KM 46 minuta, et angulus KAM 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero positus fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes 2 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes 5 partes. Ergo angulus BAK totus est 5 partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Erit igitur arcus etiam qui est super lineam BK 5 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB residuum complementi medietatis circuli, et est 174 partes et 16 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit sex partes et 2 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, una earum, secundum istas partes erit 119 partes et 51 minuta. Quapropter secundum partes quibus linea AK est 57 partes et 35 minuta erit linea BK due partes et 53 minuta, et linea AB secundum illud exemplum 57 partes et 31 minuta, et secundum istas partes fit linea BL et, quia est equalis linee KT, 4 partes et 36 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, provenit nobis linea hec etiam in longitudine secundum istas partes 57 partes et 42 minuta. Et secundum illud exemplum, quia linea LT, quoniam fuit equalis linee BK, fit secundum istas partes due partes et 53 minuta et ex quadrato quod est ex linea AL cum quadrato quod ex linea LT est quadratum quod est ex linea AT, tunc hec linea provenit nobis in longitudine secundum istas partes 57 partes et 46 minuta. Quapropter secundum partes quibus chorda AT est 120 partes erit linea TL 5 partes et 59 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes est 5 partes et 44 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 2 partes et 52 minuta. Affirmabimus ergo illud in tabula tertia tabule Saturni coram numero 135 partium in area eius. In declinatione autem eius maiore que est in medietate circuli propinquiore, quia linea AG, et est linea longitudinis propinquioris in principio Arietis, aggregatur 57 partes et 40 minuta secundum partes quibus ostensum est quod linea KM et est 22 minuta, tunc linea GM secundum illud exemplum est 4 partes et 35 minuta. Et propter illud fit linea AM reliqua 53 partes et 5 minuta. Et secundum istas partes erit chorda AK etiam, quia de summa qua est ipsa maior linea AM non est curandum, 53 partes et 5 minuta. Igitur secundum partes quibus chorda AK est 120 partes erit linea KM 50 minuta, et angulus KAM 48 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et secundum istas vero partes positus est angulus BAG etiam 5 partes. Ergo angulus BAK totus est 5 partes et 48 minuta secundum partes quibus duo anguli recti sunt 360 partes. Propter illud ergo erit arcus qui est super lineam BK 5 partes et 48 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 174 partes et 12 minuta. Ergo linea BK, una duarum linearum que subtenduntur eis, fit 6 partes et 4 minuta secundum partes quibus chorda AL est 120 partes, et linea AB, altera earum, est 119 partes et 51 minuta. Ergo secundum partes quibus chorda AK est 53 partes et 5 minuta erit linea BK due partes et 41 minuta, et linea AL secundum hoc exemplum 53 partes et minutum unum. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL et secundum istas partes est ostensum quod linea BL est 4 partes et 36 minuta, proveniet nobis linea AL etiam in longitudine secundum istas partes 53 partes et 13 minuta. Ergo secundum partes quibus chorda AL est 120 partes erit linea BL 10 partes et 23 minuta, et angulus BAL, et est angulus augmenti et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes 9 partes et 56 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 4 partes et 58 minuta. Et etiam quia secundum partes quibus linea AL est 53 partes et 13 minuta fit linea TL etiam, quia est equalis linee KB, due partes et 41 minuta et ex duobus quadratis que sunt ex eis quando aggregantur est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 53 partes et 17 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea TL 6 partes et tria minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 5 partes et 46 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 53 minuta. Ergo firmabimus illud in tabula quarta tabule Saturni coram numero 135 partium in area eius.
Sit itaque etiam in superficie que ortogonaliter est super superficiem orbis signorum differentia communis inter ipsam et inter superficiem orbis signorum linea AB, et differentia communis inter ipsam et inter orbem egredientis centri linea AG, et differentia communis inter ipsam et inter orbem revolutionis linea DG, et ponam ut centrum orbis signorum sit punctum A et centrum orbis revolutionis sit punctum G, et signabo circa punctum G orbem revolutionis DREH ita ut sit diametrus RGH ex lineis que ortogonaliter protrahuntur super lineam DE in superficie orbis egredientis centri et fiat equidistans superficiei orbis signorum. Ille autem relique linee sint equidistantes duabus superficiebus quas diximus simul. Et abscindam arcum ET secundum illud exemplum ad hoc ut ipse sit 45 partes, et protraham a puncto T, et est locus stelle, perpendicularem TK super lineam EG et a duobus punctis T et K etiam super superficiem orbis signorum duas perpendiculares KB et TL, et applicabo lineas BL, AL, AT, et sit nostra intentio ut inveniamus numerum additionis et diminutionis in longitudine, et est quem comprehendit angulus BAL, et cursum in latitudine, et est angulus quem comprehendit angulus LAT, et producam super lineam AG etiam a puncto K perpendicularem KM, et applicabo duas lineas GT et AK, et ponatur etiam propter illud cuius declaratio precessit unaqueque duarum linearum GK et KT 84 partes et 52 minuta secundum partes quibus chorda GT est 120 partes. Et quia iam ostensum est in stella Saturni prius quod linea que est a centro orbis revolutionis est sex partes et 30 minuta secundum partes quibus longitudo media est 60 partes, et est etiam unaqueque duarum linearum GK et KT secundum istas partes 4 partes et 36 minuta secundum partes quibus chorda GT est 6 partes et 36 minuta, et quia angulus AGE, et est angulus declinationis orbis revolutionis positus, est secundum partes quidem quibus quatuor anguli recti sunt 360 partes 4 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 9 partes tes M., erit etiam arcus qui est super lineam KM 9 partes secundum partes quibus circulus qui describitur circa triangulum GKM ortogonium est 360 partes, et arcus qui est super lineam GM est residuum complementi semicirculi, et est 171 partes. Linea igitur KM, una duarum linearum que subtenduntur eis, erit 9 partes et 25 minuta secundum partes quibus chorda GK est 120 partes, et linea GM secundum istas partes erit 119 partes et 38 minuta. Igitur secundum partes quibus linea GK est 4 partes et 36 minuta erit linea quidem KM 22 minuta, et linea GM secundum illud exemplum 4 partes et 35 minuta. Linea autem AG in declinatione maiore in medietate circuli remotiore, et est linea longitudinis in principio Libre, aggregatur propter intentionem quam premisimus et declaravimus in diversitatibus secundum istas partes 62 partes et 10 minuta. Remanet igitur linea AM reliqua eius 57 partes et 35 minuta secundum partes quibus linea GK est 22 minuta. Et propter illud erit linea AK 57 partes et 35 minuta. Igitur secundum partes quibus chorda AK est 120 partes erit linea KM 46 minuta, et angulus KAM 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero positus fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes 2 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes 5 partes. Ergo angulus BAK totus est 5 partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Erit igitur arcus etiam qui est super lineam BK 5 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB residuum complementi medietatis circuli, et est 174 partes et 16 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit sex partes et 2 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, una earum, secundum istas partes erit 119 partes et 51 minuta. Quapropter secundum partes quibus linea AK est 57 partes et 35 minuta erit linea BK due partes et 53 minuta, et linea AB secundum illud exemplum 57 partes et 31 minuta, et secundum istas partes fit linea BL et, quia est equalis linee KT, 4 partes et 36 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, provenit nobis linea hec etiam in longitudine secundum istas partes 57 partes et 42 minuta. Et secundum illud exemplum, quia linea LT, quoniam fuit equalis linee BK, fit secundum istas partes due partes et 53 minuta et ex quadrato quod est ex linea AL cum quadrato quod ex linea LT est quadratum quod est ex linea AT, tunc hec linea provenit nobis in longitudine secundum istas partes 57 partes et 46 minuta. Quapropter secundum partes quibus chorda AT est 120 partes erit linea TL 5 partes et 59 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes est 5 partes et 44 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 2 partes et 52 minuta. Affirmabimus ergo illud in tabula tertia tabule Saturni coram numero 135 partium in area eius. In declinatione autem eius maiore que est in medietate circuli propinquiore, quia linea AG, et est linea longitudinis propinquioris in principio Arietis, aggregatur 57 partes et 40 minuta secundum partes quibus ostensum est quod linea KM et est 22 minuta, tunc linea GM secundum illud exemplum est 4 partes et 35 minuta. Et propter illud fit linea AM reliqua 53 partes et 5 minuta. Et secundum istas partes erit chorda AK etiam, quia de summa qua est ipsa maior linea AM non est curandum, 53 partes et 5 minuta. Igitur secundum partes quibus chorda AK est 120 partes erit linea KM 50 minuta, et angulus KAM 48 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et secundum istas vero partes positus est angulus BAG etiam 5 partes. Ergo angulus BAK totus est 5 partes et 48 minuta secundum partes quibus duo anguli recti sunt 360 partes. Propter illud ergo erit arcus qui est super lineam BK 5 partes et 48 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 174 partes et 12 minuta. Ergo linea BK, una duarum linearum que subtenduntur eis, fit 6 partes et 4 minuta secundum partes quibus chorda AL est 120 partes, et linea AB, altera earum, est 119 partes et 51 minuta. Ergo secundum partes quibus chorda AK est 53 partes et 5 minuta erit linea BK due partes et 41 minuta, et linea AL secundum hoc exemplum 53 partes et minutum unum. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL et secundum istas partes est ostensum quod linea BL est 4 partes et 36 minuta, proveniet nobis linea AL etiam in longitudine secundum istas partes 53 partes et 13 minuta. Ergo secundum partes quibus chorda AL est 120 partes erit linea BL 10 partes et 23 minuta, et angulus BAL, et est angulus augmenti et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes 9 partes et 56 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 4 partes et 58 minuta. Et etiam quia secundum partes quibus linea AL est 53 partes et 13 minuta fit linea TL etiam, quia est equalis linee KB, due partes et 41 minuta et ex duobus quadratis que sunt ex eis quando aggregantur est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 53 partes et 17 minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea TL 6 partes et tria minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 5 partes et 46 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 53 minuta. Ergo firmabimus illud in tabula quarta tabule Saturni coram numero 135 partium in area eius.
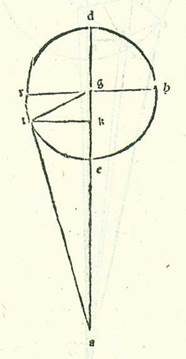 Et ut faciamus considerationem etiam numerorum additionis et diminutionis, describemus etiam figuram in qua non sit aliquid duarum declinationum. Et quia secundum partes quibus linea AG, et est longitudinis linea, tunc est 57 partes et 40 minuta iam posita est unaqueque duarum linearum GK, KT 4 partes et 36 minuta, et est linea AK reliqua secundum istas partes 53 partes et 4 minuta, et ex quadrato quod est ex ea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, provenit nobis linea AT etiam in longitudine 53 partes et 16 minuta. Quapropter erit etiam secundum partes quibus chorda AT est 120 partes linea KT 10 partes et 22 minuta, et angulus TAK, et est angulus augmenti et diminutionis in longitudine, erit secundum partes quibus duo anguli recti sunt 360 partes 9 partes et 54 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 4 partes et 57 minuta. Iam vero ostensum fuit quod eius summa etiam in duabus declinationibus secundum istas partes est 4 partes et 58 minuta. Iam ergo augetur numerus additionis et diminutionis propter duas declinationes simul minuto uno.
Et ut faciamus considerationem etiam numerorum additionis et diminutionis, describemus etiam figuram in qua non sit aliquid duarum declinationum. Et quia secundum partes quibus linea AG, et est longitudinis linea, tunc est 57 partes et 40 minuta iam posita est unaqueque duarum linearum GK, KT 4 partes et 36 minuta, et est linea AK reliqua secundum istas partes 53 partes et 4 minuta, et ex quadrato quod est ex ea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, provenit nobis linea AT etiam in longitudine 53 partes et 16 minuta. Quapropter erit etiam secundum partes quibus chorda AT est 120 partes linea KT 10 partes et 22 minuta, et angulus TAK, et est angulus augmenti et diminutionis in longitudine, erit secundum partes quibus duo anguli recti sunt 360 partes 9 partes et 54 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 4 partes et 57 minuta. Iam vero ostensum fuit quod eius summa etiam in duabus declinationibus secundum istas partes est 4 partes et 58 minuta. Iam ergo augetur numerus additionis et diminutionis propter duas declinationes simul minuto uno.
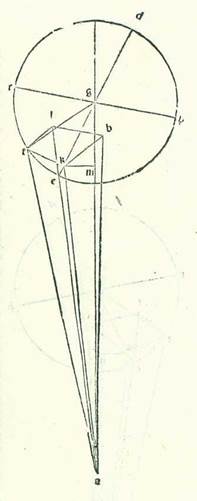 Deinceps vero scribemus primum formam in qua sunt due declinationes que sunt ante istam comprehendentem proportiones que demonstrate sunt in Iove, ita ut secundum partes quibus linea GT, que est a centro orbis revolutionis, est 11 partes et 30 minuta sit unaqueque duarum linearum GK et KT octo partes et octo minuta. Et quia angulus AGE, et est angulus declinationis orbis revolutionis, secundum partes quibus quatuor anguli recti sunt 360 partes est positus due partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes est quinque partes, erit etiam arcus qui est super lineam KM quinque partes secundum partes quibus circulus qui describitur circa triangulum MGK ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique complementi semicirculi, et sunt 175 partes. Linea igitur KM, una duarum linearum que subtenduntur eis, erit 5 partes et 14 minuta secundum partes quibus chorda GK est 120 partes, et linea GM secundum istas partes est 119 partes et 53 minuta. Erit ergo secundum illas partes quibus linea GK est octo partes et octo minuta et linea AG, et est linea longitudinis in principio Libre, est 62 partes et 30 minuta linea KM 21 minuta, et linea GM secundum illud exemplum octo partes et octo minuta, et linea MA reliqua 54 partes et 22 minuta. Chorda igitur AL, quia non est maior linea AB nisi secundum illud de quo non est curandum, est etiam secundum istas partes 54 partes et 22 minuta. Ergo secundum partes quibus linea AL est 120 partes erit linea KM 46 minuta fere, et angulus KAM 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes pars una et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes tres partes. Angulus igitur BAK totus est tres partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Quapropter erit arcus qui est super lineam BK tres partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 176 partes et 16 minuta. Linea igitur KB, una duarum linearum que subtenduntur eis, erit tres partes et 55 minuta fere secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, secundum istas partes erit 119 partes et 56 minuta. Quapropter secundum partes quibus linea AL est 54 partes et 22 minuta erit linea KB pars una et 46 minuta, et linea AB secundum illud exemplum 54 partes et 20 minuta, et secundum istas partes propter illud cuius precessit declaratio est linea BL octo partes et octo minuta. Et quia ex duobus quadratis que sunt ex his duabus lineis cum aggregantur est quadratum quod est ex linea AL, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 54 partes et 56 minuta. Et secundum illud exemplum, quia linea LT secundum istas partes est pars una et 46 minuta et ex duobus quadratis que sunt ex istis duabus lineis quando aggregantur est quadratum quod est ex linea AT, tunc linea AT etiam proveniet nobis in longitudine 54 partes et 58 minuta. Erit ergo propter illud secundum partes quibus chorda AT est 120 partes linea LT tres partes et 52 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes erit tres partes et 42 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes pars una et 51 minuta. Firmabimus ergo illud in area tertia tabule stelle Iovis coram numero 135 partium. Et similiter etiam propterea quod linea AG, et est linea longitudinis in principio Arietis, provenit 57 partes et 30 minuta secundum partes quibus ostensum est quod linea KM est 21 minuta, et quoniam linea GM secundum istud exemplum est octo partes et octo minuta donec sit linea AM reliqua, scilicet linea AK, quia non est curandum de eo quo augetur super ipsam, secundum istas partes 49 partes et 22 minuta, et propter illud secundum partes quibus chorda AK est 120 partes linea KM fit 51 minuta, et fit angulus KAM 49 minuta secundum partes quibus duo anguli recti sunt 360 partes, tunc angulus BAK totus provenit secundum istas partes tres partes et 49 minuta. Quapropter erit arcus etiam qui est super lineam KB tres partes et 49 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 176 partes et 11 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit tres partes et 59 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, erit secundum istas partes 119 partes et 56 minuta. Quapropter secundum partes quibus linea AK est 49 partes et 22 minuta erit linea KB pars una et 39 minuta, et erit linea AB secundum illud exemplum 49 partes et 20 minuta. Et propter illud, propterea quod linea BL secundum istas partes est octo partes et octo minuta, et quia ex duobus quadratis earum cum coniunguntur erit quadratum quod est ex linea AL, tunc linea AL etiam proveniet nobis in longitudine 59 partes. Quapropter secundum partes quibus chorda AL est 120 partes erit linea BK 19 partes et 31 minuta, et angulus BAL, et est angulus additionis et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 18 partes et 44 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 9 partes et 22 minuta. Et etiam quia secundum partes quibus linea AL est 50 partes linea TL fit pars una et 39 minuta et cum aggregantur duo quadrata que sunt ex eis, est ex eis quadratum quod est ex linea AT, tunc linea AT etiam proveniet nobis in longitudine secundum istas partes 50 partes et duo minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea LT tres partes et 57 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes tres partes et 46 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes est pars una et 53 minuta. Firmabimus ergo illud etiam in tabula quarta tabule eius coram numero 135 partium.
Deinceps vero scribemus primum formam in qua sunt due declinationes que sunt ante istam comprehendentem proportiones que demonstrate sunt in Iove, ita ut secundum partes quibus linea GT, que est a centro orbis revolutionis, est 11 partes et 30 minuta sit unaqueque duarum linearum GK et KT octo partes et octo minuta. Et quia angulus AGE, et est angulus declinationis orbis revolutionis, secundum partes quibus quatuor anguli recti sunt 360 partes est positus due partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes est quinque partes, erit etiam arcus qui est super lineam KM quinque partes secundum partes quibus circulus qui describitur circa triangulum MGK ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique complementi semicirculi, et sunt 175 partes. Linea igitur KM, una duarum linearum que subtenduntur eis, erit 5 partes et 14 minuta secundum partes quibus chorda GK est 120 partes, et linea GM secundum istas partes est 119 partes et 53 minuta. Erit ergo secundum illas partes quibus linea GK est octo partes et octo minuta et linea AG, et est linea longitudinis in principio Libre, est 62 partes et 30 minuta linea KM 21 minuta, et linea GM secundum illud exemplum octo partes et octo minuta, et linea MA reliqua 54 partes et 22 minuta. Chorda igitur AL, quia non est maior linea AB nisi secundum illud de quo non est curandum, est etiam secundum istas partes 54 partes et 22 minuta. Ergo secundum partes quibus linea AL est 120 partes erit linea KM 46 minuta fere, et angulus KAM 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes pars una et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes tres partes. Angulus igitur BAK totus est tres partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Quapropter erit arcus qui est super lineam BK tres partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 176 partes et 16 minuta. Linea igitur KB, una duarum linearum que subtenduntur eis, erit tres partes et 55 minuta fere secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, secundum istas partes erit 119 partes et 56 minuta. Quapropter secundum partes quibus linea AL est 54 partes et 22 minuta erit linea KB pars una et 46 minuta, et linea AB secundum illud exemplum 54 partes et 20 minuta, et secundum istas partes propter illud cuius precessit declaratio est linea BL octo partes et octo minuta. Et quia ex duobus quadratis que sunt ex his duabus lineis cum aggregantur est quadratum quod est ex linea AL, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 54 partes et 56 minuta. Et secundum illud exemplum, quia linea LT secundum istas partes est pars una et 46 minuta et ex duobus quadratis que sunt ex istis duabus lineis quando aggregantur est quadratum quod est ex linea AT, tunc linea AT etiam proveniet nobis in longitudine 54 partes et 58 minuta. Erit ergo propter illud secundum partes quibus chorda AT est 120 partes linea LT tres partes et 52 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes erit tres partes et 42 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes pars una et 51 minuta. Firmabimus ergo illud in area tertia tabule stelle Iovis coram numero 135 partium. Et similiter etiam propterea quod linea AG, et est linea longitudinis in principio Arietis, provenit 57 partes et 30 minuta secundum partes quibus ostensum est quod linea KM est 21 minuta, et quoniam linea GM secundum istud exemplum est octo partes et octo minuta donec sit linea AM reliqua, scilicet linea AK, quia non est curandum de eo quo augetur super ipsam, secundum istas partes 49 partes et 22 minuta, et propter illud secundum partes quibus chorda AK est 120 partes linea KM fit 51 minuta, et fit angulus KAM 49 minuta secundum partes quibus duo anguli recti sunt 360 partes, tunc angulus BAK totus provenit secundum istas partes tres partes et 49 minuta. Quapropter erit arcus etiam qui est super lineam KB tres partes et 49 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et erit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 176 partes et 11 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit tres partes et 59 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, erit secundum istas partes 119 partes et 56 minuta. Quapropter secundum partes quibus linea AK est 49 partes et 22 minuta erit linea KB pars una et 39 minuta, et erit linea AB secundum illud exemplum 49 partes et 20 minuta. Et propter illud, propterea quod linea BL secundum istas partes est octo partes et octo minuta, et quia ex duobus quadratis earum cum coniunguntur erit quadratum quod est ex linea AL, tunc linea AL etiam proveniet nobis in longitudine 59 partes. Quapropter secundum partes quibus chorda AL est 120 partes erit linea BK 19 partes et 31 minuta, et angulus BAL, et est angulus additionis et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 18 partes et 44 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 9 partes et 22 minuta. Et etiam quia secundum partes quibus linea AL est 50 partes linea TL fit pars una et 39 minuta et cum aggregantur duo quadrata que sunt ex eis, est ex eis quadratum quod est ex linea AT, tunc linea AT etiam proveniet nobis in longitudine secundum istas partes 50 partes et duo minuta. Ergo secundum partes quibus chorda AT est 120 partes erit linea LT tres partes et 57 minuta, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes tres partes et 46 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes est pars una et 53 minuta. Firmabimus ergo illud etiam in tabula quarta tabule eius coram numero 135 partium.
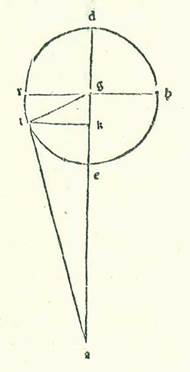 Et describemus causa experiendi numerum augmenti et diminutionis in longitudine formam vacuam a declinatione. Et quia in hac longitudine nota secundum partes quibus unaqueque duarum linearum TK et KG est octo partes et octo minuta est linea AG tota 57 partes et 30 minuta, et linea AK reliqua secundum istas partes est 49 partes et 22 minuta, et ex quadrato quod est ex hac linea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 50 partes et duo minuta. Erit ergo propter illud secundum partes quibus chorda AT est 120 partes linea TK 19 partes et 30 minuta, et angulus TAK, et est angulus augmenti et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes est 18 partes et 42 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes est 9 partes et 21 minuta. Iam vero fuit ostensum quod eius summa in declinatione secundum istas partes est 9 partes et 22 minuta. Iam ergo addit numerus additionis et diminutionis in longitudine propter duas declinationes coniunctas minutum unum tantum. Et iste sunt res quarum nos intendimus inventionem.
Et describemus causa experiendi numerum augmenti et diminutionis in longitudine formam vacuam a declinatione. Et quia in hac longitudine nota secundum partes quibus unaqueque duarum linearum TK et KG est octo partes et octo minuta est linea AG tota 57 partes et 30 minuta, et linea AK reliqua secundum istas partes est 49 partes et 22 minuta, et ex quadrato quod est ex hac linea cum quadrato quod est ex linea KT est quadratum quod est ex linea AT, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 50 partes et duo minuta. Erit ergo propter illud secundum partes quibus chorda AT est 120 partes linea TK 19 partes et 30 minuta, et angulus TAK, et est angulus augmenti et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes est 18 partes et 42 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes est 9 partes et 21 minuta. Iam vero fuit ostensum quod eius summa in declinatione secundum istas partes est 9 partes et 22 minuta. Iam ergo addit numerus additionis et diminutionis in longitudine propter duas declinationes coniunctas minutum unum tantum. Et iste sunt res quarum nos intendimus inventionem.
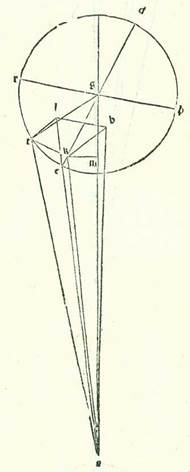 Deinde post illud describemus ad hanc intentionem declarandam in stella Martis formam in qua sunt due declinationes. Sit itaque unaqueque duarum linearum GK et KT 27 partes et 56 minuta secundum partes quibus linea GT, et est ea que est a centro orbis revolutionis, est 39 partes et 30 minuta. Et quia angulus AGE, et est angulus declinationis orbis revolutionis, iam fuit nobis secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 15 minuta et secundum partes quibus duo anguli recti sunt 360 partes 4 partes et 30 minuta, erit etiam arcus qui est super lineam KM 4 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum GMK ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique ad complendum semicirculum, et sunt 175 partes et 30 minuta. Linea ergo KM, una duarum linearum que subtenduntur eis, erit 4 partes et 43 minuta secundum partes quibus chorda GK est 120 partes, et linea GM, altera earum, secundum istas partes erit 119 partes et 54 minuta. Oportet ergo propter illud ut secundum partes etiam quibus linea GK est 27 partes et 56 minuta et linea AG, et est linea maioris longitudinis, est 66 partes sit linea MK pars una et sex minuta, et linea GM secundum illud exemplum 27 partes et 54 minuta, et linea AM partes relique, et sunt 38 partes et sex minuta. Quapropter erit chorda AK etiam secundum istas partes 38 partes et septem minuta. Ergo secundum partes quibus chorda AK est 120 partes erit linea KM tres partes et 28 minuta, et erit angulus KAM reliquus tres partes et 19 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes pars una et secundum partes quibus duo anguli recti sunt 360 partes due partes. Angulus igitur BAK totus proveniet secundum istas partes 5 partes et 19 minuta. Oportet ergo propter illud ut sit etiam arcus qui est super lineam KB 5 partes et 19 minuta secundum partes quibus circulus qui describitur circa triangulum BAK ortogonium est 360 partes, et sit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 174 partes et 41 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, est 5 partes et 34 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, secundum istas partes est 119 partes et 52 minuta. Oportet ergo propter illud etiam ut secundum partes quibus linea AL est 38 partes et septem minuta sit linea KB pars una et 48 minuta, et linea AB secundum istud exemplum 38 partes et 5 minuta, et secundum istas partes linea BL etiam est 27 partes et 56 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, tunc hec linea etiam provenit nobis in longitudine 47 partes et 14 minuta. Et secundum illud exemplum, quia linea TK secundum istas partes est pars una et 46 minuta et ex quadrato quod est ex linea AL cum quadrato quod est ex linea LT est quadratum quod est ex linea AT, tunc hec linea proveniet nobis in longitudine secundum istas partes 47 partes et 16 minuta. Oportet ergo propter illud ut sit secundum partes quibus chorda AT est 120 partes linea TL 4 partes et 30 minuta fere, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes est 4 partes et 18 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et novem minuta. Firmabimus ergo illud etiam in area tertia tabule Martis coram numero 135 partium. Et similiter etiam in duabus declinationibus que sunt in minore longitudine, propterea quod linea AG est 54 partes secundum partes quibus ostensum est quod linea KM est pars una et sex minuta et quod linea GM secundum istud exemplum est 27 partes et 54 minuta, ita ut linea AM remaneat partes relique, et sunt 26 partes et 6 minuta, et provenit chorda AK secundum istas partes 26 partes et 7 minuta. Ergo secundum partes quibus chorda AK est 120 partes erit linea KM quinque partes et tria minuta, et angulus KAM erit 4 partes et 59 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et propter illud etiam erit angulus BAL totus secundum istas partes sex partes et 49 minuta. Oportet ergo propter illud ut fit arcus qui est super lineam KB sex partes et 49 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et sit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 173 partes et 11 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit septem partes et 10 minuta secundum partes quibus chorda AL est 120 partes, et linea AB, altera earum, secundum istas partes 119 partes et 47 minuta. Oportet ergo propter illud ut secundum partes quibus linea AK est 26 partes et septem minuta fit linea BK pars una et 33 minuta, et linea AB secundum istud exemplum 26 partes et 4 minuta. Et secundum istas partes etiam fuit linea BL 27 partes et 56 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, tunc hec linea provenit nobis in longitudine 38 partes et 12 minuta. Ergo secundum partes quibus chorda AL est 120 partes erit linea BL 87 partes et 45 minuta, et angulus BAL, et est angulus additionis et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 94 partes et secundum partes quibus quatuor anguli recti sunt 360 partes 47 partes. Et secundum istud exemplum, quia secundum partes quibus linea AL est 38 partes et 12 minuta fit linea LT etiam pars una et 33 minuta et quando aggregantur duo quadrata que sunt ex istis duabus lineis est ex eis quadratum quod est ex linea TA, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 38 partes et 14 minuta. Oportet ergo propter illud ut secundum partes quibus chorda TA est 120 partes sit linea LT 4 partes et 52 minuta et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes 4 partes et 40 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 20 minuta. Firmabimus ergo illud etiam in area quarta tabule coram illo numero eodem qui est 135 partium.
Deinde post illud describemus ad hanc intentionem declarandam in stella Martis formam in qua sunt due declinationes. Sit itaque unaqueque duarum linearum GK et KT 27 partes et 56 minuta secundum partes quibus linea GT, et est ea que est a centro orbis revolutionis, est 39 partes et 30 minuta. Et quia angulus AGE, et est angulus declinationis orbis revolutionis, iam fuit nobis secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 15 minuta et secundum partes quibus duo anguli recti sunt 360 partes 4 partes et 30 minuta, erit etiam arcus qui est super lineam KM 4 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum GMK ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique ad complendum semicirculum, et sunt 175 partes et 30 minuta. Linea ergo KM, una duarum linearum que subtenduntur eis, erit 4 partes et 43 minuta secundum partes quibus chorda GK est 120 partes, et linea GM, altera earum, secundum istas partes erit 119 partes et 54 minuta. Oportet ergo propter illud ut secundum partes etiam quibus linea GK est 27 partes et 56 minuta et linea AG, et est linea maioris longitudinis, est 66 partes sit linea MK pars una et sex minuta, et linea GM secundum illud exemplum 27 partes et 54 minuta, et linea AM partes relique, et sunt 38 partes et sex minuta. Quapropter erit chorda AK etiam secundum istas partes 38 partes et septem minuta. Ergo secundum partes quibus chorda AK est 120 partes erit linea KM tres partes et 28 minuta, et erit angulus KAM reliquus tres partes et 19 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero fuit angulus BAG, et est angulus declinationis orbis egredientis centri, secundum partes quibus quatuor anguli recti sunt 360 partes pars una et secundum partes quibus duo anguli recti sunt 360 partes due partes. Angulus igitur BAK totus proveniet secundum istas partes 5 partes et 19 minuta. Oportet ergo propter illud ut sit etiam arcus qui est super lineam KB 5 partes et 19 minuta secundum partes quibus circulus qui describitur circa triangulum BAK ortogonium est 360 partes, et sit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 174 partes et 41 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, est 5 partes et 34 minuta secundum partes quibus chorda AK est 120 partes, et linea AB, altera earum, secundum istas partes est 119 partes et 52 minuta. Oportet ergo propter illud etiam ut secundum partes quibus linea AL est 38 partes et septem minuta sit linea KB pars una et 48 minuta, et linea AB secundum istud exemplum 38 partes et 5 minuta, et secundum istas partes linea BL etiam est 27 partes et 56 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, tunc hec linea etiam provenit nobis in longitudine 47 partes et 14 minuta. Et secundum illud exemplum, quia linea TK secundum istas partes est pars una et 46 minuta et ex quadrato quod est ex linea AL cum quadrato quod est ex linea LT est quadratum quod est ex linea AT, tunc hec linea proveniet nobis in longitudine secundum istas partes 47 partes et 16 minuta. Oportet ergo propter illud ut sit secundum partes quibus chorda AT est 120 partes linea TL 4 partes et 30 minuta fere, et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes est 4 partes et 18 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et novem minuta. Firmabimus ergo illud etiam in area tertia tabule Martis coram numero 135 partium. Et similiter etiam in duabus declinationibus que sunt in minore longitudine, propterea quod linea AG est 54 partes secundum partes quibus ostensum est quod linea KM est pars una et sex minuta et quod linea GM secundum istud exemplum est 27 partes et 54 minuta, ita ut linea AM remaneat partes relique, et sunt 26 partes et 6 minuta, et provenit chorda AK secundum istas partes 26 partes et 7 minuta. Ergo secundum partes quibus chorda AK est 120 partes erit linea KM quinque partes et tria minuta, et angulus KAM erit 4 partes et 59 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et propter illud etiam erit angulus BAL totus secundum istas partes sex partes et 49 minuta. Oportet ergo propter illud ut fit arcus qui est super lineam KB sex partes et 49 minuta secundum partes quibus circulus qui describitur circa triangulum ABK ortogonium est 360 partes, et sit arcus qui est super lineam AB partes relique ad complendum semicirculum, et sunt 173 partes et 11 minuta. Linea igitur BK, una duarum linearum que subtenduntur eis, erit septem partes et 10 minuta secundum partes quibus chorda AL est 120 partes, et linea AB, altera earum, secundum istas partes 119 partes et 47 minuta. Oportet ergo propter illud ut secundum partes quibus linea AK est 26 partes et septem minuta fit linea BK pars una et 33 minuta, et linea AB secundum istud exemplum 26 partes et 4 minuta. Et secundum istas partes etiam fuit linea BL 27 partes et 56 minuta. Et quia ex quadrato quod est ex linea AB cum quadrato quod est ex linea BL est quadratum quod est ex linea AL, tunc hec linea provenit nobis in longitudine 38 partes et 12 minuta. Ergo secundum partes quibus chorda AL est 120 partes erit linea BL 87 partes et 45 minuta, et angulus BAL, et est angulus additionis et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes erit 94 partes et secundum partes quibus quatuor anguli recti sunt 360 partes 47 partes. Et secundum istud exemplum, quia secundum partes quibus linea AL est 38 partes et 12 minuta fit linea LT etiam pars una et 33 minuta et quando aggregantur duo quadrata que sunt ex istis duabus lineis est ex eis quadratum quod est ex linea TA, tunc hec linea etiam proveniet nobis in longitudine secundum istas partes 38 partes et 14 minuta. Oportet ergo propter illud ut secundum partes quibus chorda TA est 120 partes sit linea LT 4 partes et 52 minuta et angulus TAL, et est angulus elongationis in latitudine, secundum partes quibus duo anguli recti sunt 360 partes 4 partes et 40 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 20 minuta. Firmabimus ergo illud etiam in area quarta tabule coram illo numero eodem qui est 135 partium.
Quod si causa experiendi numerum additionis et diminutionis in longitudine descripserimus formam expoliatam a duabus declinationibus, fiet in minore longitudine, et est locus in quo proprie convenit necessario ut sit superfluitas sensibilis, proportio linee AG ad unamquamque duarum linearum GK et KT proportio 54 partium ad 27 partes et 56 minuta donec propter illud linea AK remaneat partes relique, et sunt 26 partes et 4 minuta, et proveniet chorda AT secundum istas partes 38 partes et 12 minuta. Propter illud ergo secundum partes etiam quibus chorda AT est 120 partes linea TK fit 87 partes et 45 minuta, et est angulus TAL, qui est angulus additionis et diminutionis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes 94 partes et secundum partes quibus quatuor anguli recti sunt 360 partes 47 partes. Et quia hec est quantitas que fuit ostensa propter numerationem in duabus declinationibus summe earum, non ergo diversificatur propter declinationes duas duorum orbium numerus additionis et diminutionis in stella Martis secundum aliquod omnino. Et illud est cuius intendimus inventionem.
In duabus vero remanentibus quartis areis duarum tabularum stelle Veneris et stelle Mercurii sunt cursus in latitudine quos comprehendunt reflexiones maiores duorum orbium revolutionis earum. He autem reflexiones non reperiuntur nisi in longitudine longiore et in longitudine propinquiore duorum orbium earum egredientium centrorum. Ipse tamen sole secundum suam habitudinem vacue sunt a superfluitate que est propter declinationem duorum orbium earum egredientium centrorum, propterea quod si nos permisceremus eas cum ea, indigeremus in illo tabulis pluribus eis quas posuimus et esset earum numeratio difficilior, propterea quod cursuum vespertinorum et cursuum matutinalium nature est ut non sint equales et ut non sint penitus in parte una eadem orbis signorum. Et cum illo, quoniam declinatio duorum orbium earum egredientium centrorum propterea quod quoniam ... propterea quod: Two rivalling conjunctions. Both appear also in Paris, BnF, lat. 14738 (lines 15-16 from the bottom). non remanent Probably corrupt for remanet, which is the reading of Paris, BnF, lat. 14738 (line 15 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 622, line 6 from the bottom). secundum habitudinem unam, superfluitates diminutionis a declinationibus maioribus diversificant superfluitates diminutionis a reflexionibus maioribus. Propterea igitur quod separavimus superfluitatem cum inquisitione cuiusque earum, alleviatur nobis quemadmodum fit comprehensio cuiusque earum levior, quemadmodum declarabitur ex ipso quod sequitur hunc sermonem. 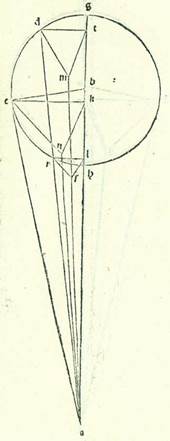 Fit itaque linea ABG differentia superficiei communis orbis signorum et orbis revolutionis, et ponam ut punctum A sit centrum orbis signorum et punctum B centrum orbis revolutionis, et describam super ipsum orbem revolutionis GDER reflexum a superficie orbis signorum ita ut sint linee que protrahuntur in ipso ortogonaliter erecte super differentiam eis communem, et est linea GH, et ponam angulos omnes qui sunt super lineam GH equales, et protraham lineam AE contingentem orbem revolutionis et lineam ARD secantem ipsum quocunque modo contingat, et producam a punctis D et E et R super lineam HG perpendiculares DT et EK et RL et super superficiem orbis signorum perpendiculares DM et EN et RS, et applicabo lineas TM et KN et LS et etiam lineam NA et lineam ASM. Linea igitur ASM est recta, propterea quod tria puncta A et S et M sunt in duabus superficiebus et sunt super sectionem duarum superficierum, scilicet superficiei orbis signorum et superficiei que transit per lineam ARD ortogonaliter erectam super superficiem orbis signorum. Manifestum igitur est quod in hac declinatione narrata illud quod comprehendit additiones et diminutiones in longitudine harum duarum stellarum et Nonsensical conjunction, which probably entered by mistake. Cf. Toomer, loc. cit., p. 623, line 4 from the bottom. There is no et in Paris, BnF, lat. 14738 (205r, lines 1-2 from the bottom). est angulus TAM et angulus KAN, et in latitudine quidem angulus DAM et angulus EAN. Oportet ergo iam ut ostendam primum quod angulus EAN, et est angulus cursus in latitudine qui est apud contactum, est maior angulis omnibus. Et similiter additionis et diminutionis in longitudine est angulus KAE maior his angulis omnibus. Proportio igitur linee KE ad lineam AE est maior proportione cuiusque duarum linearum DT et LR ad unamquamque duarum linearum RA et DA. Sed proportio linee KE ad lineam EN est sicut proportio linee DT ad lineam DM et sicut proportio linee LR ad lineam RS. Et illud est quia isti trianguli qui sunt hoc modo omnes sunt similes seu equalium angulorum, quemadmodum diximus, et anguli qui sunt apud punctum M et N et S sunt recti. Ergo proportio linee NE ad lineam EA est maior proportione cuiusque duarum linearum MD et SR ad unamquamque duarum linearum DA et RA. Anguli vero DMA et ENA et RSA etiam sunt recti. Ergo angulus EAN est maior angulo DAM. Et est manifestum quod ipse est maior angulis omnibus qui sunt secundum hunc modum. Et manifestum est etiam evicino quod superfluitatibus que sunt additionum et diminutionum in longitudine propter reflexiones maior est superfluitas que cadit apud cursus maiores qui sunt apud punctum E. Et illud est quoniam ipsos comprehendunt anguli qui subtenduntur superfluitati inter lineas TD et KE et LR et inter lineas TM et KN et LS. Et propterea quod fuit proportio cuiusque harum linearum ad illud quo superfluit proportio ipsa una et eadem, tunc iam sequitur ex eo ut sit proportio superfluitatis inter duas lineas EK et KN ad lineam EA maior proportione superfluitatis inter omnes duas lineas reliquarum linearum oppositarum istis duabus ad lineas oppositas sive relatas linee AD. Et manifestum est ex illo etiam quod proportio maioris que est additionis et diminutionis in longitudine ad maiorem que est cursuum in latitudine est proportio que est in sectionibus orbis revolutionis omnibus additionum et diminutionum in longitudine, scilicet in unaquaque sectione earum ad cursus in latitudine, propterea quod proportio linee KE ad lineam EN est sicut proportio linearum oppositarum duabus lineis LR et DT omnium ad lineas oppositas duabus lineis RS et DM. Et iste sunt res quas voluimus ostendere.
Fit itaque linea ABG differentia superficiei communis orbis signorum et orbis revolutionis, et ponam ut punctum A sit centrum orbis signorum et punctum B centrum orbis revolutionis, et describam super ipsum orbem revolutionis GDER reflexum a superficie orbis signorum ita ut sint linee que protrahuntur in ipso ortogonaliter erecte super differentiam eis communem, et est linea GH, et ponam angulos omnes qui sunt super lineam GH equales, et protraham lineam AE contingentem orbem revolutionis et lineam ARD secantem ipsum quocunque modo contingat, et producam a punctis D et E et R super lineam HG perpendiculares DT et EK et RL et super superficiem orbis signorum perpendiculares DM et EN et RS, et applicabo lineas TM et KN et LS et etiam lineam NA et lineam ASM. Linea igitur ASM est recta, propterea quod tria puncta A et S et M sunt in duabus superficiebus et sunt super sectionem duarum superficierum, scilicet superficiei orbis signorum et superficiei que transit per lineam ARD ortogonaliter erectam super superficiem orbis signorum. Manifestum igitur est quod in hac declinatione narrata illud quod comprehendit additiones et diminutiones in longitudine harum duarum stellarum et Nonsensical conjunction, which probably entered by mistake. Cf. Toomer, loc. cit., p. 623, line 4 from the bottom. There is no et in Paris, BnF, lat. 14738 (205r, lines 1-2 from the bottom). est angulus TAM et angulus KAN, et in latitudine quidem angulus DAM et angulus EAN. Oportet ergo iam ut ostendam primum quod angulus EAN, et est angulus cursus in latitudine qui est apud contactum, est maior angulis omnibus. Et similiter additionis et diminutionis in longitudine est angulus KAE maior his angulis omnibus. Proportio igitur linee KE ad lineam AE est maior proportione cuiusque duarum linearum DT et LR ad unamquamque duarum linearum RA et DA. Sed proportio linee KE ad lineam EN est sicut proportio linee DT ad lineam DM et sicut proportio linee LR ad lineam RS. Et illud est quia isti trianguli qui sunt hoc modo omnes sunt similes seu equalium angulorum, quemadmodum diximus, et anguli qui sunt apud punctum M et N et S sunt recti. Ergo proportio linee NE ad lineam EA est maior proportione cuiusque duarum linearum MD et SR ad unamquamque duarum linearum DA et RA. Anguli vero DMA et ENA et RSA etiam sunt recti. Ergo angulus EAN est maior angulo DAM. Et est manifestum quod ipse est maior angulis omnibus qui sunt secundum hunc modum. Et manifestum est etiam evicino quod superfluitatibus que sunt additionum et diminutionum in longitudine propter reflexiones maior est superfluitas que cadit apud cursus maiores qui sunt apud punctum E. Et illud est quoniam ipsos comprehendunt anguli qui subtenduntur superfluitati inter lineas TD et KE et LR et inter lineas TM et KN et LS. Et propterea quod fuit proportio cuiusque harum linearum ad illud quo superfluit proportio ipsa una et eadem, tunc iam sequitur ex eo ut sit proportio superfluitatis inter duas lineas EK et KN ad lineam EA maior proportione superfluitatis inter omnes duas lineas reliquarum linearum oppositarum istis duabus ad lineas oppositas sive relatas linee AD. Et manifestum est ex illo etiam quod proportio maioris que est additionis et diminutionis in longitudine ad maiorem que est cursuum in latitudine est proportio que est in sectionibus orbis revolutionis omnibus additionum et diminutionum in longitudine, scilicet in unaquaque sectione earum ad cursus in latitudine, propterea quod proportio linee KE ad lineam EN est sicut proportio linearum oppositarum duabus lineis LR et DT omnium ad lineas oppositas duabus lineis RS et DM. Et iste sunt res quas voluimus ostendere.
Et quia iam precessit simplex ostensio harum rerum, consideremus igitur primum quante quantitatis sit angulus in unaquaque duarum stellarum quem facit reflexio orbis revolutionis postquam fecerimus secundum quod premisimus et perduxerimus ipsum in principio ut unaqueque earum in longitudine sua, plurimum quod declinat in septentrionem aut meridiem secundum duos cursus oppositos eis in orbe revolutionis sue sit longitudo media inter maiorem que est longitudinum et inter minorem que est longitudinum eius, et est quinque partes, propterea quod stella Veneris videtur separari in longitudine longiore et propinquiore longitudine orbis egredientis centri plus et minus quinque partibus secundum id de quo non est curandum et in stella Mercurii plus et minus quinque partibus quasi medietate partis. 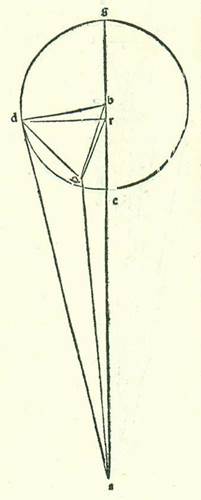 Itaque sit etiam differentia communis orbis signorum et orbis revolutionis linea ABG, et describam circa punctum B orbem revolutionis GDE reflexum a superficie orbis signorum secundum modum quem narravimus, et producatur a puncto A, et est centrum orbis signorum, linea contingens orbem revolutionis, et sit linea AD, et protraham a puncto D super lineam GE perpendicularem DR et super superficiem orbis signorum perpendicularem DH, et applicentur linee BD et RH et AH, et ponam ut angulus DAH comprehendat medietatem elongationis narrate in latitudine in unaquaque duarum stellarum, et est due partes et medietas partis secundum partes quibus quatuor anguli recti sunt 360 partes, sitque nostra intentio ut inveniamus quantitatem reflexionis cuiusque duorum orbium revolutionis, scilicet quantitatem anguli DRH. In stella igitur Veneris, quoniam secundum partes quibus linea que est a centro orbis revolutionis est 43 partes et 10 minuta longitudo maior est 61 partes et 15 minuta et longitudo minor est 58 partes et 45 minuta et quod est inter has duas etiam fit 60 partes, tunc proportio linee AB ad lineam BD est sicut proportio 60 partium ad 43 partes et 10 minuta. Et quia quadratum quod est ex linea BD, cum minuitur ex quadrato quod est ex linea AB, provenit quadratum quod est ex linea AD, tunc hec linea provenit nobis in longitudine secundum istas partes 41 partes et 40 minuta. Et secundum hoc exemplum, quia proportio linee BA ad lineam AD est sicut proportio linee BD ad lineam DR, tunc linea DR etiam provenit nobis secundum has partes 29 partes et 58 minuta. Et etiam quia angulus DAH positus est secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes quinque partes, erit etiam arcus qui est super lineam DH quinque partes secundum partes quibus circulus qui describitur circa triangulum DAH ortogonium est 360 partes, et erit eius chorda, que est linea DH, quinque partes et 14 minuta secundum partes quibus chorda AD est 120 partes. Igitur secundum partes quibus linea AD est 41 partes et 40 minuta erit linea DH etiam pars una et 50 minuta. Sed secundum istas partes est ostensum quod linea DR est 29 partes et 58 minuta. Quapropter secundum partes quibus chorda DR est 120 partes erit linea DH 7 partes et 20 minuta, et angulus DRH, et est angulus reflexionis, secundum partes quibus duo anguli recti sunt 360 partes 7 partes et secundum partes quidem quibus quatuor anguli recti sunt 360 partes tres partes et medietas partis, sitque augmentum anguli DAR super angulum HAR comprehendens superfluitatem que est additionis et diminutionis in longitudine. Iam ergo oportet ut numeremus hanc superfluitatem etiam leviter propter illud quod progreditur ex quantitatibus eius. Et illud est quoniam propterea quod iam ostensum est quod secundum partes quibus linea DH est pars una et 50 minuta et chorda AD 41 partes et 40 minuta, et linea RD secundum illud exemplum est 29 partes et 58 minuta, et cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex unaquaque duarum linearum AD et DR, est quadratum quod est ex unaquaque duarum linearum AH et HR, tunc linea AH etiam proveniet nobis in longitudine secundum istas partes 41 partes et 37 minuta, et linea RH secundum illud exemplum 29 partes et 55 minuta. Quapropter secundum partes quibus chorda AH est 120 partes erit linea RH 36 partes et 16 minuta et angulus RAH secundum partes quibus duo anguli recti sunt 360 partes 91 partes et 56 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes et 58 minuta. Et secundum istud exemplum, quia secundum partes quibus chorda AD est 120 partes fit linea DR 86 partes et 16 minuta, tunc angulus DAR etiam provenit nobis secundum partes quidem quibus duo anguli recti sunt 360 partes 91 partes et 58 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes et 59 minuta. Iam ergo minuitur numerus additionis et diminutionis in longitudine propter reflexionem minuto uno.
Itaque sit etiam differentia communis orbis signorum et orbis revolutionis linea ABG, et describam circa punctum B orbem revolutionis GDE reflexum a superficie orbis signorum secundum modum quem narravimus, et producatur a puncto A, et est centrum orbis signorum, linea contingens orbem revolutionis, et sit linea AD, et protraham a puncto D super lineam GE perpendicularem DR et super superficiem orbis signorum perpendicularem DH, et applicentur linee BD et RH et AH, et ponam ut angulus DAH comprehendat medietatem elongationis narrate in latitudine in unaquaque duarum stellarum, et est due partes et medietas partis secundum partes quibus quatuor anguli recti sunt 360 partes, sitque nostra intentio ut inveniamus quantitatem reflexionis cuiusque duorum orbium revolutionis, scilicet quantitatem anguli DRH. In stella igitur Veneris, quoniam secundum partes quibus linea que est a centro orbis revolutionis est 43 partes et 10 minuta longitudo maior est 61 partes et 15 minuta et longitudo minor est 58 partes et 45 minuta et quod est inter has duas etiam fit 60 partes, tunc proportio linee AB ad lineam BD est sicut proportio 60 partium ad 43 partes et 10 minuta. Et quia quadratum quod est ex linea BD, cum minuitur ex quadrato quod est ex linea AB, provenit quadratum quod est ex linea AD, tunc hec linea provenit nobis in longitudine secundum istas partes 41 partes et 40 minuta. Et secundum hoc exemplum, quia proportio linee BA ad lineam AD est sicut proportio linee BD ad lineam DR, tunc linea DR etiam provenit nobis secundum has partes 29 partes et 58 minuta. Et etiam quia angulus DAH positus est secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes quinque partes, erit etiam arcus qui est super lineam DH quinque partes secundum partes quibus circulus qui describitur circa triangulum DAH ortogonium est 360 partes, et erit eius chorda, que est linea DH, quinque partes et 14 minuta secundum partes quibus chorda AD est 120 partes. Igitur secundum partes quibus linea AD est 41 partes et 40 minuta erit linea DH etiam pars una et 50 minuta. Sed secundum istas partes est ostensum quod linea DR est 29 partes et 58 minuta. Quapropter secundum partes quibus chorda DR est 120 partes erit linea DH 7 partes et 20 minuta, et angulus DRH, et est angulus reflexionis, secundum partes quibus duo anguli recti sunt 360 partes 7 partes et secundum partes quidem quibus quatuor anguli recti sunt 360 partes tres partes et medietas partis, sitque augmentum anguli DAR super angulum HAR comprehendens superfluitatem que est additionis et diminutionis in longitudine. Iam ergo oportet ut numeremus hanc superfluitatem etiam leviter propter illud quod progreditur ex quantitatibus eius. Et illud est quoniam propterea quod iam ostensum est quod secundum partes quibus linea DH est pars una et 50 minuta et chorda AD 41 partes et 40 minuta, et linea RD secundum illud exemplum est 29 partes et 58 minuta, et cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex unaquaque duarum linearum AD et DR, est quadratum quod est ex unaquaque duarum linearum AH et HR, tunc linea AH etiam proveniet nobis in longitudine secundum istas partes 41 partes et 37 minuta, et linea RH secundum illud exemplum 29 partes et 55 minuta. Quapropter secundum partes quibus chorda AH est 120 partes erit linea RH 36 partes et 16 minuta et angulus RAH secundum partes quibus duo anguli recti sunt 360 partes 91 partes et 56 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes et 58 minuta. Et secundum istud exemplum, quia secundum partes quibus chorda AD est 120 partes fit linea DR 86 partes et 16 minuta, tunc angulus DAR etiam provenit nobis secundum partes quidem quibus duo anguli recti sunt 360 partes 91 partes et 58 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes et 59 minuta. Iam ergo minuitur numerus additionis et diminutionis in longitudine propter reflexionem minuto uno.
In stella autem Mercurii etiam, quia secundum partes quibus linea que est a centro orbis revolutionis est 22 partes et 30 minuta iam ostensum est quod maior longitudo est 69 partes et quod longitudo condiametralis ei est 57 partes, tunc longitudo media inter has duas longitudines proveniet nobis secundum istas partes 63 partes et est proportio linee AB ad lineam BD proportio 63 partium ad 22 partes et 30 minuta. Et quia cum quadratum quod est ex linea DB minuitur ex quadrato quod est ex linea AB, est quadratum quod est ex linea AD, tunc hec linea etiam provenit nobis in longitudine secundum istas partes 58 partes et 51 minuta. Et secundum illud exemplum, quia proportio linee AB ad lineam AD est sicut proportio linee BD ad lineam DR, tunc linea DR etiam erit secundum istas partes 21 partes et minutum unum. Et etiam quia angulus DAH iam positus est quinque partes secundum partes quibus duo anguli recti sunt 360 partes, tunc arcus qui est super lineam DH sit quinque partes secundum partes quibus circulus qui describitur circa triangulum ADH ortogonium est 360 partes, et erit chorda eius, et est linea DH, quinque partes et 14 minuta secundum partes quibus chorda AD est 120 partes. Igitur secundum partes quibus linea AD est 58 partes et 51 minuta erit linea DH due partes et 34 minuta. Secundum istas vero partes ostensum est quod linea DR est 21 partes et minutum unum. Quapropter secundum partes quibus chorda DR est 120 partes erit linea DH 14 partes et 40 minuta, et angulus DRH, et est angulus reflexionis, secundum partes quibus duo anguli recti sunt 360 partes erit 14 partes et secundum partes quibus quatuor anguli recti sunt 360 partes erit septem partes. Et secundum istud exemplum etiam causa experiendi additionem et diminutionem, quia secundum partes etiam quibus linea DH est due partes et 34 minuta est iam ostensum quod linea AD subtendens est 58 partes et 51 minutum et linea DR secundum istud exemplum est 21 partes et minutum unum, et cum quadratum quod est ex linea DH minuitur ex duobus quadratis que sunt ex unaquaque duarum linearum AD et DR, erunt propter illud duo quadrata que sunt ex unaquaque duarum linearum AH et HR, tunc proveniet nobis linea AH in longitudine 58 partes et 49 minuta et linea RH secundum istas partes 20 partes et 53 minuta. Oportet ergo propter illud ut secundum partes quibus chorda AH est 120 partes sit linea RH 42 partes et 38 minuta, et angulus RAH secundum partes quibus duo anguli recti sunt 360 partes 41 partes et 38 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 20 partes et 49 minuta. Et similiter etiam quia secundum partes quibus chorda AD est 120 partes proveniet nobis linea DR 42 partes et 50 minuta, tunc angulus DAR etiam provenit nobis secundum partes quibus duo anguli recti sunt 360 partes 41 partes et 50 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 20 partes et 55 minuta. Iam ergo minuitur in hac etiam propter reflexionem numerus additionis et diminutionis in longitudine sex minutis. Et iste sunt res quarum intendimus inventionem.
Consideremus ergo nunc post illud annos Corrupt for utrum? Cf. Toomer, loc. cit., 628, line 9. Paris, BnF, lat. 14738 (206v, line 13) reads annos too., quando posuerimus quod hec sit summa quantitatum reflexionis, inveniamus maiorem cursum in latitudine in maiore longitudine et minore earum convenientem ei quod invenimus ex eis per considerationem. Ponamus itaque in forma simili huic precedenti in pagina eadem longitudinem maiorem primo stelle Veneris, scilicet ut proportio linee AB ad lineam BD sit proportio 61 partium et 15 minutorum ad 43 partes et 10 minuta. Propter illud igitur, quia cum quadratum quod est ex linea DB minuitur ex quadrato quod est ex linea AB, est ex illo quadratum quod est ex linea AD, tunc hec linea etiam provenit nobis secundum istas partes 43 partes et 27 minuta. Proportio autem linee AB ad lineam AD est sicut proportio linee BD ad lineam DR. Ergo linea DR erit secundum istas partes 30 partes et 37 minuta. Et etiam quia angulus DRH, et est angulus reflexionis, iam positus est septem partes secundum partes quibus duo anguli recti sunt 360 partes et linea DH posita est septem partes et 20 minuta secundum partes quibus chorda DR est 120 partes, tunc secundum partes quibus linea DR est 30 partes et 37 minuta et linea AD secundum illud exemplum 43 partes et 27 minuta erit linea DB etiam pars una et 52 minuta. Oportet ergo propter illud ut secundum partes quibus chorda AD est 120 partes sit linea DH quinque partes et novem minuta, et angulus DAH, et est angulus recessionis maioris in latitudine, secundum partes quibus duo anguli recti sunt 360 partes sit 4 partes et 54 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 27 minuta. In longitudine autem minore, quia secundum partes quibus linea BD, que est a centro orbis revolutionis, est 43 partes et 10 minuta linea AB iam posita est 58 partes et 45 minuta et quadratum quod est ex linea DB, cum minuitur ex quadrato quod est ex linea AB, est ex eo quadratum quod est ex linea AD, tunc hec linea proveniet nobis in longitudine secundum istas partes 39 partes et 51 minuta. Et secundum illud exemplum, quia proportio linee AB ad lineam AD est sicut proportio linee DB ad lineam RD, tunc linea DR erit etiam secundum istas partes 29 partes et 17 minuta. Sed proportio linee DR ad lineam DH iam posita est sicut proportio 120 partium ad 7 partes et 20 minuta. Ergo secundum partes quibus linea DR est 29 partes et 17 minuta et linea AD secundum istud exemplum est 39 partes et 51 minuta fit linea DH pars una et 47 minuta. Quapropter secundum partes quibus chorda AD est 120 partes erit linea DH 5 partes et 22 minuta, et angulus DAH, et est angulus recessionis maioris in latitudine, secundum partes quibus duo anguli recti sunt 360 partes erit quinque partes et octo minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 34 minuta. Quia igitur iam posita fuit recessio in latitudine secundum proportionem mediam due partes et medietas partis, tunc quod est ex ea in longitudine longiore reperitur minus illo secundum id quod non facit diversitatem apud sensum. Et similiter quod est in longitudine propinquiore invenitur maius secundum id quod non sentitur. Et illud est quoniam recessio in longitudine maiore non est nisi tria minuta tantum et recessio in longitudine propinquiore non addit nisi quatuor minuta. Hec igitur quantitas non est ex eis que possibile est consequi et sciri etiam per considerationem.
Deinceps ponam longitudinem maiorem stelle Mercurii, scilicet ut proportio linee AB ad lineam BD sit proportio 69 partium ad 22 partes et 30 minuta donec proveniat propter illas res easdem quas paulo ante narravimus linea quidem AD secundum istas partes 65 partes et 14 minuta et linea DR secundum istud exemplum 21 partes et 16 minuta. Sed hic etiam angulus DRH, et est angulus reflexionis, positus est 14 partes et 40 minuta secundum partes quibus duo anguli recti sunt 360 partes, et linea DH est 14 partes et 40 minuta secundum partes quibus chorda DR est 120 partes. Ergo secundum partes quibus linea DR est 21 partes et 16 minuta et linea AD secundum illud exemplum 65 partes et 14 minuta erit linea RH etiam due partes et 36 minuta. Et propter illud erit etiam secundum partes quibus chorda AD est 120 partes linea DH 4 partes et 47 minuta. Ergo angulus DAH, et est angulus recessionis maioris in latitudine, secundum partes quibus duo anguli recti sunt 360 partes est 4 partes et 34 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 17 minuta. In longitudine autem minore, quia proportio linee AB ad lineam BD posita est proportio 57 partium ad 22 partes et 30 minuta et propter illas res easdem etiam est linea AD secundum istas partes 52 partes et 22 minuta, et est linea DR secundum istud exemplum 20 partes et 40 minuta, quoniam linee DR propter hanc reflexionem eandem posita est proportio ad lineam DH proportio 120 partium ad 14 partes et 40 minuta. Ergo secundum partes quibus linea DR est 20 partes et 40 minuta et linea AD secundum illud exemplum est 52 partes et 22 minuta erit linea DH due partes et 32 minuta. Quapropter secundum partes etiam quibus chorda AD est 120 partes erit linea DH 5 partes et 48 minuta, et angulus DAH secundum partes quibus duo anguli recti sunt 360 partes erit 5 partes et 32 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 46 minuta. Iam ergo diversificatur recessio maior in latitudine secundum quantitatem mediam, que iam posita est etiam hic due partes et medietas partis, recessio quidem in longitudine longiore tredecem minutis ad diminutionem et recessio in longitudine propinquiore sexdecem minutis ad additionem. Nos igitur exercuimus loco illius in verificatione numerationis propter proportionem mediam quartam partis unius secundum quod invenimus in consideratione, quoniam propter illud non contingit superfluitas sensibilis. Et quia firmate sunt iste res etiam et ostensum est quod proportio numeri additionum et diminutionum maiorum in longitudine ad cursus maiores in latitudine est sicut proportio numeri additionum et diminutionum particularium in longitudine in reliquis sectionibus orbis revolutionis ad cursus particulares in latitudine, levior fit nobis propter illud affirmatio eius quod firmavimus in duabus areis quartis quas posuimus in duabus tabulis Veneris et Mercurii ex cursibus in latitudine acceptis propter reflexionem. Isti autem cursus quos firmavimus non sunt nisi cursus qui sunt propter reflexionem duorum orbium revolutionis eorum solum aggregati, quemadmodum diximus, ex parte media. Superfluitatem vero que est propter declinationem duorum orbium earum egredientium centrorum et etiam propter longitudinem longiorem et longitudinem propinquiorem stelle Mercurii verificabimus leviori acceptione in illo secundum numerationem quam nos narraturi sumus post hec, et est quoniam propterea quod iam ostensum est quod in his cursibus mediis notis cursus quidem maior in latitudine ambarum stellarum qui est ex declinatione a duabus partibus orbis signorum est due partes et 30 minuta, et maior quidem additio et diminutio in longitudine in stella quidem Veneris est 46 partes et in stella Mercurii est 22 partes fere, et fuerunt nobis posite in tabula diversitatis earum portiones additionis et diminutionis que pertinent sectionibus particularibus duorum orbium revolutionis earum, nos considerabimus quantum he portiones sint ex summa additionis et diminutionis, et accipiemus partem illi parti similem cuiusque duarum stellarum ex duabus partibus et 30 minutis, et quod fuerit firmabimus in duabus areis quartis duarum tabularum latitudinis coram illis numeris eisdem. Quintas autem areas posuimus equationi que est recessionis in latitudine in reliquis cursibus in orbibus egredientium centrorum cum numeris firmatis in eis coram unoquoque eorum. Et illud est quoniam propterea quod, sicut diximus, illud quod faciunt declinationes orbium revolutionis et eorum reflexiones ex numero additionis et diminutionis ad locum illorum circulorum parvorum qui sunt propinquiores illis est secundum considerationem reversionis ad orbem egredientis centri, et inter quantitates harum declinationum et reflexionum omnium et inter declinationem in orbe Lune declivi non est differentia magna, et remotiones particulares quarum declinationum summa hec est sunt propinque ut sint secundum proportionem illam etiam, et sunt ille remotiones in Luna preparate vel scripte nobis per semitam linearum, tunc nos accepimus unumquemque illorum numerorum servatorum vel firmatorum ibi et multiplicavimus illum per duodecem vices, quoniam proportio maior ibi est quasi quinque partes, et hic posuimus eam sexaginta partes, et quod provenit nobis firmavimus coram numero qui est eius in unaquaque tabularum quinque. Ita faciemus tabulas secundum quod precessit eius narratio in principio capituli quarti.
〈XIII.5〉 Capitulum quintum: In tabulis factis ad sciendum latitudines per eas in omni hora
Prima |
Secunda |
Longitudo ♄ |
Longitudo ♃ |
Longitudo ♂ |
Longitudo ☿ |
Quinta |
||||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Tertia |
Quarta |
Tertia |
Quarta |
Tertia |
Quarta |
Tertia |
Quarta |
Quinta |
||||||||||||
Numeri communes |
Efegion |
Efregion |
Efegion |
Efregion |
Efegion |
Efregion |
Declinatio |
Reflexio |
Declinatio |
Reflexio |
Portio stellarum 5 |
|||||||||||||
Septentrio |
Meridies |
Septentrio |
Meridies |
Septentrio |
Meridies |
|||||||||||||||||||
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Minuta |
Secunda |
|||
6
12 |
354
348 |
2
2 |
3
4 |
2
2 |
2
3 |
1
1 |
7
8 |
1
1 |
5
6 |
0
0 |
7
9 |
0
0 |
4
4 |
1
1 |
2
1 |
0
0 |
8
16 |
1
1 |
45
44 |
0
0 |
11
22 |
59
58 |
36
7 |
Longitudo longior septentrionis |
18
24 |
342
336 |
2
2 |
6
7 |
2
2 |
4
4 |
1
1 |
8
9 |
1
1 |
6
7 |
0
0 |
11
13 |
0
0 |
5
6 |
1
0 |
0
59 |
0
0 |
24
33 |
1
1 |
43
40 |
0
0 |
33
44 |
57
54 |
0
36 |
|
30
36 |
330
324 |
2
2 |
8
10 |
2
2 |
5
7 |
1
1 |
10
11 |
1
1 |
8
9 |
0
0 |
14
16 |
0
0 |
7
9 |
0
0 |
57
55 |
0
0 |
41
49 |
1
1 |
36
30 |
0
1 |
55
6 |
52
48 |
0
24 |
|
42
48 |
318
312 |
2
2 |
11
12 |
2
2 |
8
10 |
1
1 |
12
13 |
1
1 |
10
11 |
0
0 |
18
21 |
0
0 |
12
15 |
0
0 |
51
46 |
0
1 |
57
5 |
1
1 |
23
16 |
1
1 |
17
26 |
44
40 |
25
0 |
|
54
60 |
306
300 |
2
2 |
14
16 |
2
2 |
12
15 |
1
1 |
14
16 |
1
1 |
13
16 |
0
0 |
24
28 |
0
0 |
18
22 |
0
0 |
41
36 |
1
1 |
13
20 |
1
0 |
8
59 |
1
1 |
35
44 |
35
30 |
12
0 |
|
66
72 |
294
288 |
2
2 |
18
21 |
2
2 |
18
21 |
1
1 |
18
21 |
1
1 |
18
21 |
0
0 |
32
36 |
0
0 |
26
30 |
0
0 |
29
23 |
1
1 |
28
35 |
0
0 |
49
38 |
1
2 |
52
0 |
24
18 |
24
24 |
|
78
84 |
282
276 |
2
2 |
24
27 |
2
2 |
24
28 |
1
1 |
24
26 |
1
1 |
24
27 |
0
0 |
41
46 |
0
0 |
36
43 |
0
0 |
16
8 |
1
1 |
43
50 |
0
0 |
26
16 |
2
2 |
10
14 |
12
6 |
24
24 |
|
90
96 |
270
264 |
2
2 |
30
33 |
2
2 |
30
34 |
1
1 |
30
33 |
1
1 |
30
33 |
0
0 |
52
59 |
0
0 |
49
56 |
0
0 |
0
10 |
1
2 |
57
3 |
0
0 |
0
15 |
2
2 |
20
25 |
0
6 |
0
24 |
|
102
108 |
258
252 |
2
2 |
36
39 |
2
2 |
37
39 |
1
1 |
36
39 |
1
1 |
36
39 |
1
1 |
6
14 |
1
1 |
4
13 |
0
0 |
20
32 |
2
2 |
9
15 |
0
0 |
31
48 |
2
2 |
28
29 |
12
18 |
24
24 |
|
114
120 |
246
240 |
2
2 |
42
45 |
2
2 |
42
45 |
1
1 |
42
45 |
1
1 |
42
45 |
1
1 |
23
34 |
1
1 |
24
37 |
0
0 |
45
59 |
2
2 |
20
25 |
1
1 |
6
25 |
2
2 |
30
39 |
24
30 |
24
0 |
|
126
132 |
234
228 |
2
2 |
47
50 |
2
2 |
48
51 |
1
1 |
47
50 |
1
1 |
48
51 |
1
2 |
48
1 |
1
2 |
51
10 |
1
1 |
13
33 |
2
2 |
28
30 |
1
2 |
45
6 |
2
2 |
26
20 |
35
40 |
12
0 |
|
138
144 |
222
216 |
2
2 |
53
55 |
2
2 |
54
56 |
1
1 |
52
55 |
1
1 |
54
57 |
2
2 |
16
32 |
2
2 |
33
56 |
1
2 |
59
23 |
2
2 |
30
28 |
2
2 |
26
47 |
2
2 |
11
0 |
44
48 |
24
24 |
|
150
156 |
210
204 |
2
2 |
57
59 |
2
3 |
58
0 |
1
2 |
58
0 |
2
2 |
0
3 |
2
3 |
55
16 |
3
4 |
29
9 |
3
3 |
3
44 |
2
2 |
22
12 |
3
3 |
7
26 |
1
1 |
45
29 |
52
54 |
0
36 |
|
162
168 |
198
192 |
3
3 |
0
1 |
3
3 |
2
3 |
2
2 |
2
3 |
2
2 |
5
6 |
3
4 |
38
0 |
4
5 |
55
53 |
4
5 |
26
13 |
1
1 |
55
27 |
3
3 |
42
54 |
1
0 |
10
48 |
57
58 |
0
36 |
|
174
180 |
186
180 |
3
3 |
2
4 |
3
3 |
4
5 |
2
2 |
4
5 |
2
2 |
7
8 |
4
4 |
14
21 |
6
7 |
36
7 |
6
7 |
12
22 |
0
0 |
48
0 |
4
4 |
2
5 |
0
0 |
24
0 |
59
60 |
36
0 |
Longitudo longior meridiei |
Numeri communes |
Addit ♄ 50. |
Minuit ♃ 20. |
Non addit ♂ nec minuit. |
♀ |
☿ |
Portio stellarum 5 |
||||||||||||||||||
〈XIII.6〉 Capitulum sextum: In numeratione motuum stellarum quinque erraticarum in latitudine
Et quia sunt iste res secundum quod narravimus, tunc illud quo procedemus in numeratione harum stellarum quinque in latitudine est secundum quod ego narrabo. In stellis quidem tribus, scilicet Saturno et Iove et Marte, mittemus longitudinem equatam ad numeros tabule stelle que est eius propria, stelle quidem Martis illum numerum equatum eundem, et stelle Iovis postquam minuerimus ex eo viginti partes, et stelle Saturni postquam addiderimus ei 50 partes. Deinde considerabimus quod est coram ipso ex minutis in tabula quinta latitudinis et firmabimus ipsum. Et secundum hoc exemplum mittemus numerum equatum diversitatis ad illos numeros eosdem, et quod fuerit coram ipso ex superfluitate in latitudine, si fuerit longitudo equata in areis quindecem primis, quod fuerit ex illo in tabula tertia, et si fuerit in areis aliis, que sunt post eas, quod fuerit ex illo in tabula quarta, multiplicabimus in minuta que firmavimus, et quod provenerit nobis est summa elongationis stelle ab orbe signorum. Tunc si fuerit quod acceptum est ex superfluitate latitudinis non assumptum nisi ex tabula tertia, in septentrione, et si non fuerit acceptum nisi ex tabula quarta, in meridie. Veneris vero et Mercurii mittemus prius numerum diversitatis equate ad numeros qui sunt in tabula propria stelle earum. Deinde considerabimus quod fuerit coram ipso in tabula tertia et in tabula quarta ex latitudine et firmabimus quod fuerit ex ea in tabula tertia et in tabula quarta, unumquodque per se et secundum suum modum, excepto eo quod est in tabula quarta stelle Mercurii, nam et nos considerabimus. Si enim fuerit longitudo equata in areis quindecem primis, minuemus ex eo decimam eius, deinde firmabimus ipsum, et si fuerit in areis que sunt sub eis, addemus ei illam partem eandem, postea firmabimus ipsum. Deinde post illud addemus super longitudinem equatam semper in stella quidem Veneris nonaginta partes et in stella Mercurii ducentas et septuaginta partes. Deinde reiciemus revolutionem unam si fuerit nobis aggregatum illud, et quod provenerit mittemus ad illos numeros eosdem, et secundum quantitatem eius quod fuerit coram illo numero ex minutis in tabula quinta accipiemus ex partibus firmatis in tabula tertia, et quod fuerit firmabimus ipsum latitudini. Quod si fuerit longitudo cum augmento narrato in areis quindecim primis et si fuerit numerus diversitatis equate in areis quindecim primis, in meridie, et si fuerit in areis que sunt post eas, in septentrione. Quod si ceciderit numerus longitudinis quem diximus in eo quod est sub areis quindecim primis ex areis et fuerit numerus diversitatis quem diximus in areis quindecim primis, in septentrione, et si ceciderit in eo quod est post eas ex areis, in meridie. Deinde post illud etiam tendemus ad longitudinem equatam, ad illam quidem que est Veneris eandem absolute, Mercurii vero postquam addiderimus ei centum et octuaginta, et mittemus eam ad illos numeros eosdem, et secundum quantitatem eius quod fuerit coram illo numero etiam ex minutis in tabula quinta accipiemus ex eo quod firmavimus in tabula quarta, et quod provenerit firmabimus in latitudine. Quod si fuerit, quemadmodum diximus, longitudo que missa fuit cadens in areis quindecim primis, tunc si fuerit longitudo equata diversitatis in eo quod est infra centum et octuaginta partes, in septentrione, et si fuerit plus centum et octuaginta partibus, in meridie. Quod si fuerit numerus longitudinis quem diximus cadens in areis que sunt sub quindecim areis et fuerit numerus diversitatis in eo quod est infra centum et octuaginta partes, in meridie, et si fuerit plus centum et octuaginta partibus, in septentrione. Deinde post illud tendemus ad hec minuta eadem etiam que invenimus mittendo longitudinem secundo, et accipimus ex eis secundum quantitatem partis qua ipsa sunt ex sexaginta partibus, et eius quod provenerit in Venere accipiemus semper sextam et firmabimus in septentrione, et in Mercurio semper accipiemus medietatem et quartam et firmabimus in meridie. Hoc igitur opere sciemus comprehensionem nostram horum numerorum trium quos firmavimus secundum cursum suum qui videtur per considerationem ad orbem signorum. Et ita est operatio in latitudine.
〈XIII.7〉 Capitulum septimum: In apparitionibus stellarum quinque erraticarum et occultationibus earum
Et quia iam precessit scientia accipiendi recessionem stellarum quinque in latitudine, tunc iam remansit complementum eius quod est necessarium etiam ad scientiam rei apparitionum stellarum et occultationum earum que sunt secundum loca earum a Sole. Iam enim cadit in eis, quemadmodum ostendimus etiam in scientia scentia M. rei stellarum fixarum, ut earum longitudines a Sole in orbe signorum sint inequales secundum modos diversos in apparitionibus earum et occultationibus earum propter causas plures. Quarum prima est quoniam magnitudines earum sunt inequales, et secunda quoniam declinationes orbis signorum sunt super orbes dissimiles, et tertia propter cursus earum in latitudine. 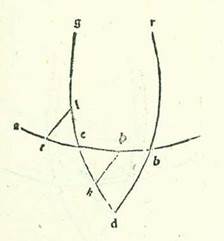 Ergo propterea imaginati fuimus etiam duas portiones duorum circulorum ex maioribus circulis, quarum una est horizontis, et est portio AB, et altera orbis signorum, et est portio GD, et posuimus punctum E differentiam communem eis orientalem aut occidentalem etiam et duo puncta H et T declinata versus meridiem et septentrionem et punctum D centrum Solis, et scripsimus portionem DBR maioris circuli transeuntem per centrum Solis et polum horizontis, et posuimus stellam oriri et occidere super horizonta AB, tunc quidem cum est in orbe signorum, super punctum E, et illud manifestum est, et tunc quidem cum est declivior ad septentrionem ab orbe signorum, super punctum H, et tunc quidem cum est declivior ad meridiem, super punctum T, et produximus ad orbem signorum a duobus punctis H et T duas perpendiculares HK et TL, et provenit nobis arcus BD etiam arcus cui, quando arcus longitudinis Solis sub terra est equalis, tunc illa hora est semper prima horarum in quibus videtur stella aut occultatur. Et illud est quoniam illud quod proiicit Sol ex radiis super stellam eandem ex longitudinibus equalibus sub terra non est nisi unum et idem secundum circulum maiorem qui describitur secundum illum modum. Quia igitur sequitur in primis ut iste arcus sit inequalis in stellis que non sunt equales, tunc oportet necessario, quamvis sint relique res omnes secundum habitudinem unam, ut sint etiam arcus orbis signorum qui subtenduntur angulo recto, scilicet longitudinis opposite longitudini ED, diversi. Et qui est stelle maioris est minor, et illud est manifestum, et qui eorum est stelle minoris est maior. Et secundum hoc exemplum etiam, quamvis sit arcus BD unus et idem in stella una et eadem, sed angulus BED, et est angulus declinationis orbis signorum, diversificatur aut propter diversitatem signorum aut propter diversitatem locorum habitabilium, arcus longitudinis ED diversificatur et augetur quanto plus minuatur angulus narratus et minoratur et abreviatur quanto magis augetur angulus. Et similiter etiam, si additur super rem primam quod declinatio etiam est una et eadem, sed stella non est super orbem signorum ipsum, sed est aut super punctum H, quod est longitudo in septentrione, aut super punctum T, quod est longitudo in meridie, principium apparitionis eius et occultationis non est cum est eius longitudo a Sole arcus ED, immo non est principium apparitionis et occultationis eius nisi aut quando est declivior ad septentrionem ab orbe signorum, cum est eius longitudo arcus DK, qui est minor illo, aut cum est declivior ad meridiem, tunc cum est eius longitudo arcus DEL, et est illo maior. Indigemus igitur necessario in scientia particularium huius intentionis ut ponamus primo quantitates arcuum BD universales in unaquaque stellarum quinque erraticarum propter apparitiones que sunt considerate consideratione in qua non cadit neque cum qua est dubitatio. He autem considerationes non equantur nisi in estate et in signo Cancri, propterea quod aer in hac hora horarum anni est subtilis purus et propterea quod declinationes orbis signorum super horizontas sunt in eo mediantes. Iam enim invenimus per considerationes orientales quarum vestigia videntur secundum hanc semitam inquisitionis quod in principia Cancri secundum rem plurimam Saturnus quidem elevatur et eius longitudo a loco Solis verificato est quatuordecem partes, et stella Iovis oritur et eius longitudo secundum illud exemplum est duodecem partes et medietas et quarta partis, et stella Martis oritur et eius longitudo est quatuordecem partes et medietas, et stella Veneris oritur vespere et eius longitudo est quinque partes et due tertie partis, et stella Mercurii oritur vespere et eius longitudo secundum hoc exemplum est undecem partes et due tertie partis.
Ergo propterea imaginati fuimus etiam duas portiones duorum circulorum ex maioribus circulis, quarum una est horizontis, et est portio AB, et altera orbis signorum, et est portio GD, et posuimus punctum E differentiam communem eis orientalem aut occidentalem etiam et duo puncta H et T declinata versus meridiem et septentrionem et punctum D centrum Solis, et scripsimus portionem DBR maioris circuli transeuntem per centrum Solis et polum horizontis, et posuimus stellam oriri et occidere super horizonta AB, tunc quidem cum est in orbe signorum, super punctum E, et illud manifestum est, et tunc quidem cum est declivior ad septentrionem ab orbe signorum, super punctum H, et tunc quidem cum est declivior ad meridiem, super punctum T, et produximus ad orbem signorum a duobus punctis H et T duas perpendiculares HK et TL, et provenit nobis arcus BD etiam arcus cui, quando arcus longitudinis Solis sub terra est equalis, tunc illa hora est semper prima horarum in quibus videtur stella aut occultatur. Et illud est quoniam illud quod proiicit Sol ex radiis super stellam eandem ex longitudinibus equalibus sub terra non est nisi unum et idem secundum circulum maiorem qui describitur secundum illum modum. Quia igitur sequitur in primis ut iste arcus sit inequalis in stellis que non sunt equales, tunc oportet necessario, quamvis sint relique res omnes secundum habitudinem unam, ut sint etiam arcus orbis signorum qui subtenduntur angulo recto, scilicet longitudinis opposite longitudini ED, diversi. Et qui est stelle maioris est minor, et illud est manifestum, et qui eorum est stelle minoris est maior. Et secundum hoc exemplum etiam, quamvis sit arcus BD unus et idem in stella una et eadem, sed angulus BED, et est angulus declinationis orbis signorum, diversificatur aut propter diversitatem signorum aut propter diversitatem locorum habitabilium, arcus longitudinis ED diversificatur et augetur quanto plus minuatur angulus narratus et minoratur et abreviatur quanto magis augetur angulus. Et similiter etiam, si additur super rem primam quod declinatio etiam est una et eadem, sed stella non est super orbem signorum ipsum, sed est aut super punctum H, quod est longitudo in septentrione, aut super punctum T, quod est longitudo in meridie, principium apparitionis eius et occultationis non est cum est eius longitudo a Sole arcus ED, immo non est principium apparitionis et occultationis eius nisi aut quando est declivior ad septentrionem ab orbe signorum, cum est eius longitudo arcus DK, qui est minor illo, aut cum est declivior ad meridiem, tunc cum est eius longitudo arcus DEL, et est illo maior. Indigemus igitur necessario in scientia particularium huius intentionis ut ponamus primo quantitates arcuum BD universales in unaquaque stellarum quinque erraticarum propter apparitiones que sunt considerate consideratione in qua non cadit neque cum qua est dubitatio. He autem considerationes non equantur nisi in estate et in signo Cancri, propterea quod aer in hac hora horarum anni est subtilis purus et propterea quod declinationes orbis signorum super horizontas sunt in eo mediantes. Iam enim invenimus per considerationes orientales quarum vestigia videntur secundum hanc semitam inquisitionis quod in principia Cancri secundum rem plurimam Saturnus quidem elevatur et eius longitudo a loco Solis verificato est quatuordecem partes, et stella Iovis oritur et eius longitudo secundum illud exemplum est duodecem partes et medietas et quarta partis, et stella Martis oritur et eius longitudo est quatuordecem partes et medietas, et stella Veneris oritur vespere et eius longitudo est quinque partes et due tertie partis, et stella Mercurii oritur vespere et eius longitudo secundum hoc exemplum est undecem partes et due tertie partis.
Quia igitur iam explanate sunt iste res secundum hunc modum, signabimus figuram forme quam exemplificavimus, et neque impedit in arcubus quorum quantitatum hec est summa si nos ponimus proportiones in chordis eorum querendo levitatem in operatione earum, quia non est inter eos et inter chordas eorum differentia in sensu. Sit itaque punctum E ipsa differentia communis orbis signorum et horizontis punctum quod oritur in his apparitionibus quas intendimus super principium Cancri trium stellarum in matutinis, scilicet Saturni, Iovis et Martis, et occidit in apparitionibus Veneris et Mercurii in vesperis veperis M., et illud manifestum est. Et ponamus quod clima est clima quod transit ab Ascena per terras Choniche. Et dies qui est longior hic est quatuordecem horarum et quarte hore equalitatis. Et neque eligimus hoc clima nisi quia in hoc circulo hic equidistante proprie et in eo quod sequitur ipsum ceciderunt plures considerationes. Est igitur conveniens ut sint considerationes Chaldeorum. Quod vero cecidit in eo quod sequitur ipsum ex considerationibus est in terris Elleym sive Ellenorum et in terris Egypti. In hoc enim climate quod narravimus, quando oritur Cancer, invenimus angulum BED propter illud cuius declaratio precessit ex scientia angulorum esse centum et tres partes secundum partes quibus duo anguli recti sunt 360 partes, et invenimus propter illud proportionem que est inter duas lineas continentes angulum rectum proportionem nonagintaquatuor partium ad septuagintaquinque partes fere, et secundum istas partes erunt linee subtendentes centum et viginti partes. Et ex modo scientie latitudinis, quando tres stelle preter alias aut sine aliis oriuntur in principio Cancri, scilicet quando cursus earum est in eo quod sequitur longitudinem longiorem in orbibus revolutionis earum, quantacunque fuerit eorum longitudo a longitudine longiore preter quod non pertransierint signum unum, invenimus quod stella Saturni et stella Iovis forsitan erunt super ipsum orbem signorum preter quod accidit illi diversitas apud sensum, et invenimus stellam Martis decliviorem ad septentrionem ab orbe signorum quinta partis unius ut multum. Arcus enim DE erit arcus quo a Sole in orbe signorum elongantur stella Saturni et stella Iovis, et erit arcus DK arcus quo elongatur a Sole stella Martis, quoniam magis elongatur in septentrione secundum quantitatem arcus KH, et est duodecem minuta. Et quia proportio arcus KH ad arcum KE est proportio nonagintaquatuor partium ad septuagintaquinque partes, tunc arcus KE erit etiam secundum istas partes decem minuta fere. Iam autem positus fuit arcus DK in Marte quatuordecem partes et medietas partis. Est ergo arcus DE totus aggregatus quatuordecem partes et 40 minuta, et est in stella Saturni quatuordecem partes et in stella Iovis duodecem partes et medietas et quarta. Oportet ergo, propterea quod proportio arcus ED etiam ad arcum DB est proportio centum et viginti partium ad nonagintaquatuor partes, et arcus DB etiam, quoniam est arcus circuli maioris qui describitur transiens per duos polos horizontis, proveniat nobis in stella Saturni undecem partes, et in stella Iovis decem partes, et in stella Martis undecem partes et medietas fere. Et similiter etiam in Venere et Mercurio, propterea quod quando occidit principium Cancri, facit cum horizonte similem huic angulum quem narravimus in declinatione huic simili, et iam posuimus quod stella Veneris oritur vespere et huius partis orbis signorum longitudo a loco Solis vero est quinque partes et due tertie partis et quod stella Mercurii oritur in vespere et eius longitudo est undecem partes et medietas partis, ergo declinatio Solis in elevatione eius secundum veritatem quidem in stella Veneris erit super vigintiquatuor partes et tertiam partis Geminorum et in stella Mercurii super decem et octo partes et medietatem partis, secundum medium vero motum in stella quidem Veneris super vigintiquinque partes et in stella Mercurii super decem et novem partes fere. Hec est ergo comprehensio motus medii in longitudine harum duarum stellarum. Cum autem fuerit longitudo secundum hunc modum et videbimus eas in principio Cancri, erit stelle Veneris tunc longitudo a longitudine longiore orbis revolutionis quasi quatuordecem partium et stelle Mercurii quasi duodecem partium. Illud namque manifestum est per intentiones quarum precessit narratio in diversitatibus earum. Et sequitur inde ut in istis cursibus stella Veneris reperiatur declivior ad septentrionem ab orbe signorum parte una et in stella Mercurii parte una et duobus tertiis partis fere, quoniam illa est summa arcus KH. Et illud manifestum est propterea quod proportio eius ad arcum KE est proportio nonagintaquatuor partium ad septuagintaquinque partes et hec proportio etiam est proportio unius ad medietatem et quartam partis et proportio partis unius ad unum et tertiam partis unius fere. Provenit ergo nobis arcus EK etiam in Venere medietas et quarta partis et in Mercurio pars una et tertia partis. Sed secundum istas partes positus est etiam arcus DK, et est arcus qui videtur esse cuiusque eorum longitudo a Sole, in Venere quidem quinque partes et due tertie partis et in Mercurio undecem partes et medietas partis. Provenit ergo arcus DKE totus in Venere sex partes et due quinte partis et in Mercurio duodecem partes et medietas et tertia partis fere. Ergo etiam, propterea quod proportio arcus ED ad arcum BD est proportio centum et viginti partium ad nonagintaquatuor partes et iam convenit hec proportio proportioni sex partium et duarum quintarum partis ad quinque partes fere et proportioni duodecem partium et duarum tertiarum partis ad decem partes fere, provenit nobis arcus DB, et est quantitas longitudinis totius, in Venere quidem quinque partes et in Mercurio decem partes. Et illud est cuius intendimus inventionem.
〈XIII.8〉 Capitulum octavum: In hoc quod illud quod reperitur de proprietatibus in apparitionibus Veneris et Mercurii et occultationibus eorum est conveniens radicibus que posite sunt eis
Quod autem res faciles que in apparitionibus Veneris et Mercurii et occultationibus eorum reperiuntur sint comitantes et convenientes radicibus quas posuimus eis, scilicet quod in stella Veneris tempus quod est ab occasu eius vespertino ad ortum eius matutinum tunc quando stella est in principio Piscis est quasi duo dies ut multum et tunc quidem quando est in principio Virginis est sexdecem dies, et in stella Mercurii tunc quando est conveniens ut videatur in principio Scorpionis tunc eius apparitio vespertina destruitur et deletur et quando est conveniens ut videatur in principio Tauri tunc eius apparitio matutina destruitur et deletur, hoc isto modo scitur. 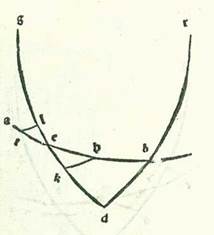 Et incipiamus primo a stella Veneris et ponamus similem illius descriptionis quam descripsimus in apparitionibus. Ponamus igitur in primis quod punctum E orbis signorum sit punctum supra quod est principium Piscis. Et hic locus, quando convenit ut sit in eo stella Veneris in longitudine longiore orbis revolutionis, sit declinatus ab orbe signorum in septentrionem sex partibus et tertia partis fere. Et ponamus ut figura sit figura occasus vespertini. Et in hoc occasu proveniet angulus BED in hoc climate quod posuimus 154 partes secundum partes quibus duo anguli recti sunt 360 partes. Et propter illud erit secundum partes quibus chorda subtendens est 120 partes maior duarum linearum continentium angulum rectum 117 partes et minor earum 27 partes fere. Quapropter secundum partes etiam quibus linea BD, et est longitudo universalis, est quinque partes linea DE fit quinque partes et octo minuta. Sed quia fuit stella longius elongata in septentrione ab orbe signorum sex partibus et tertia partis, et quia hec est summa arcus KH et fuit proportio decem et septem partium ad vigintiseptem partes ipsa proportio sex partium et tertie partis ad partem et medietatem partis fere, tunc arcus KE erit pars una et medietas partis, et erit arcus KD reliquus, et est arcus longitudinis stelle in occasu vespertino a Sole ad illud quod est retro ipsum, tres partes et 38 minuta. Et hec etiam est forma illius.
Et incipiamus primo a stella Veneris et ponamus similem illius descriptionis quam descripsimus in apparitionibus. Ponamus igitur in primis quod punctum E orbis signorum sit punctum supra quod est principium Piscis. Et hic locus, quando convenit ut sit in eo stella Veneris in longitudine longiore orbis revolutionis, sit declinatus ab orbe signorum in septentrionem sex partibus et tertia partis fere. Et ponamus ut figura sit figura occasus vespertini. Et in hoc occasu proveniet angulus BED in hoc climate quod posuimus 154 partes secundum partes quibus duo anguli recti sunt 360 partes. Et propter illud erit secundum partes quibus chorda subtendens est 120 partes maior duarum linearum continentium angulum rectum 117 partes et minor earum 27 partes fere. Quapropter secundum partes etiam quibus linea BD, et est longitudo universalis, est quinque partes linea DE fit quinque partes et octo minuta. Sed quia fuit stella longius elongata in septentrione ab orbe signorum sex partibus et tertia partis, et quia hec est summa arcus KH et fuit proportio decem et septem partium ad vigintiseptem partes ipsa proportio sex partium et tertie partis ad partem et medietatem partis fere, tunc arcus KE erit pars una et medietas partis, et erit arcus KD reliquus, et est arcus longitudinis stelle in occasu vespertino a Sole ad illud quod est retro ipsum, tres partes et 38 minuta. Et hec etiam est forma illius.
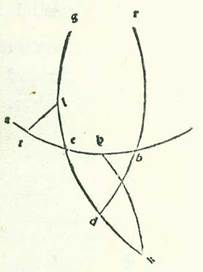 Et etiam in forma huic simili, propterea quod angulus BED fit in ortu matutino 69 partes secundum partes quibus duo anguli recti sunt 360 partes, et propter illud erit secundum partes quibus chorda subtendens est 120 partes linea minor duarum linearum continentium angulum rectum 68 partes et maior earum 99 partes, et est proportio 68 partium ad 120 partes ipsa proportio quinque partium ad octo partes et 49 minuta et proportio 68 partium ad 99 partes ipsa proportio sex partium et tertie partis ad novem partes et 13 minuta, et tunc arcus DE provenit secundum istas partes octo partes et 49 minuta, et proveniet arcus KE, et est arcus superfluitatis que est propter latitudinem, 9 partes et 13 minuta, et erit arcus DK reliquus, et manifestum est quod ipse est arcus longitudinis stelle a Sole retrorsum, 24 minuta, et iam fuit eius elongatio secundum istud exemplum ad posteriora in occasu vespertino etiam tres partes et 38 minuta, tunc motus stelle in tempore quod est in eo quod est inter occasum vespertinum et inter ortum matutinum fuit minor motu Solis in hoc tempore, scilicet minor cursu eius in proprietate suiipsius in longitudine fere propter antecessionem que est propter orbem revolutionis eius tribus partibus et 14 minutis. Et quia stella equat hanc quantitatem partium anterius secundum quod scitur de ipsa ex tabula diversitatis quando movetur, et est in longitudine propinquiore orbis revolutionis sue parte una et quarta partis, et stella secat illud secundum medium in propinquo duorum dierum, tunc apparet quod hec est summa temporis huius longitudinis quam diximus. Et illud est conveniens ei quod videmus.
Et etiam in forma huic simili, propterea quod angulus BED fit in ortu matutino 69 partes secundum partes quibus duo anguli recti sunt 360 partes, et propter illud erit secundum partes quibus chorda subtendens est 120 partes linea minor duarum linearum continentium angulum rectum 68 partes et maior earum 99 partes, et est proportio 68 partium ad 120 partes ipsa proportio quinque partium ad octo partes et 49 minuta et proportio 68 partium ad 99 partes ipsa proportio sex partium et tertie partis ad novem partes et 13 minuta, et tunc arcus DE provenit secundum istas partes octo partes et 49 minuta, et proveniet arcus KE, et est arcus superfluitatis que est propter latitudinem, 9 partes et 13 minuta, et erit arcus DK reliquus, et manifestum est quod ipse est arcus longitudinis stelle a Sole retrorsum, 24 minuta, et iam fuit eius elongatio secundum istud exemplum ad posteriora in occasu vespertino etiam tres partes et 38 minuta, tunc motus stelle in tempore quod est in eo quod est inter occasum vespertinum et inter ortum matutinum fuit minor motu Solis in hoc tempore, scilicet minor cursu eius in proprietate suiipsius in longitudine fere propter antecessionem que est propter orbem revolutionis eius tribus partibus et 14 minutis. Et quia stella equat hanc quantitatem partium anterius secundum quod scitur de ipsa ex tabula diversitatis quando movetur, et est in longitudine propinquiore orbis revolutionis sue parte una et quarta partis, et stella secat illud secundum medium in propinquo duorum dierum, tunc apparet quod hec est summa temporis huius longitudinis quam diximus. Et illud est conveniens ei quod videmus.
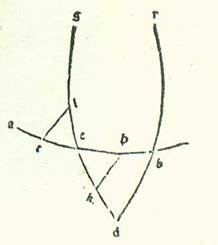 Et in simili huic forme etiam ponam ut punctum E sit super principium Virginis, et est locus quando contingit ut si stella Veneris fuerit in eo in longitudine propinquiore orbis revolutionis sue, videatur declivior ad meridiem ab orbe signorum evicino illarum partium, et sunt sex partes et tertia partis. Et ponamus primum occultationem eius vespertinam. Et tunc erit angulus BED 69 partes secundum partes quibus duo anguli recti sunt 360 partes. Igitur secundum partes quibus chorda subtendens est 120 partes erit minor duarum linearum continentium angulum rectum 68 partes et maior earum 99 partes fere. Et quia proportiones que sunt hic sunt ille proportiones eedem que fuerunt in apparitione matutinali in Pisce et est longitudo in latitudine hic talis qualis ibi, tunc arcus EK provenit nobis secundum istas partes 9 partes et 49 minuta, et provenit arcus EL, et est arcus superfluitatis que est propter latitudinem, 9 partes et 13 minuta, et est arcus DL totus, et est arcus longitudinis stelle a Sole retrorsum, 18 partes et duo minuta. Quod ergo pertinet huic quantitati ex partibus, et sunt partes antecessionis a loco motus medii Solis et stelle, est septem partes et medietas partis fere a longitudine propinquiore orbis revolutionis secundum quod est in tabula diversitatis, sicut diximus. Et similiter etiam in ortu matutino qui est huius stelle in principio Virginis, quando erit angulus BED 154 partes secundum partes quibus duo anguli recti sunt 360 partes, erit tunc secundum partes quibus chorda subtendens est 120 partes maior duarum linearum continentium rectum angulum 117 partes et minor earum 27 partes, et erunt proportiones ille etiam proportiones eedem que posite sunt in occultatione vespertina in Pisce, et proveniet nobis secundum istas partes arcus DE quinque partes et octo minuta, et arcus EL, et est arcus superfluitatis que est propter latitudinem, pars una et 30 minuta, et arcus DL totus, et est longitudo stelle a Sole ad anteriora, sex partes et 38 minuta. Et est quod pertinet istis partibus secundum illum modum a longitudine propinquiore orbis revolutionis due partes et medietas partis fere. Stella igitur Veneris movetur ab occultatione sua vespertina ad ortum matutinum istis partibus omnibus orbis revolutionis, et sunt decem partes, et ipsa non secat hanc quantitatem partium nisi in propinquo dierum quos diximus, et sunt sexdecem dies. Et illud est conveniens ei quod videtur.
Et in simili huic forme etiam ponam ut punctum E sit super principium Virginis, et est locus quando contingit ut si stella Veneris fuerit in eo in longitudine propinquiore orbis revolutionis sue, videatur declivior ad meridiem ab orbe signorum evicino illarum partium, et sunt sex partes et tertia partis. Et ponamus primum occultationem eius vespertinam. Et tunc erit angulus BED 69 partes secundum partes quibus duo anguli recti sunt 360 partes. Igitur secundum partes quibus chorda subtendens est 120 partes erit minor duarum linearum continentium angulum rectum 68 partes et maior earum 99 partes fere. Et quia proportiones que sunt hic sunt ille proportiones eedem que fuerunt in apparitione matutinali in Pisce et est longitudo in latitudine hic talis qualis ibi, tunc arcus EK provenit nobis secundum istas partes 9 partes et 49 minuta, et provenit arcus EL, et est arcus superfluitatis que est propter latitudinem, 9 partes et 13 minuta, et est arcus DL totus, et est arcus longitudinis stelle a Sole retrorsum, 18 partes et duo minuta. Quod ergo pertinet huic quantitati ex partibus, et sunt partes antecessionis a loco motus medii Solis et stelle, est septem partes et medietas partis fere a longitudine propinquiore orbis revolutionis secundum quod est in tabula diversitatis, sicut diximus. Et similiter etiam in ortu matutino qui est huius stelle in principio Virginis, quando erit angulus BED 154 partes secundum partes quibus duo anguli recti sunt 360 partes, erit tunc secundum partes quibus chorda subtendens est 120 partes maior duarum linearum continentium rectum angulum 117 partes et minor earum 27 partes, et erunt proportiones ille etiam proportiones eedem que posite sunt in occultatione vespertina in Pisce, et proveniet nobis secundum istas partes arcus DE quinque partes et octo minuta, et arcus EL, et est arcus superfluitatis que est propter latitudinem, pars una et 30 minuta, et arcus DL totus, et est longitudo stelle a Sole ad anteriora, sex partes et 38 minuta. Et est quod pertinet istis partibus secundum illum modum a longitudine propinquiore orbis revolutionis due partes et medietas partis fere. Stella igitur Veneris movetur ab occultatione sua vespertina ad ortum matutinum istis partibus omnibus orbis revolutionis, et sunt decem partes, et ipsa non secat hanc quantitatem partium nisi in propinquo dierum quos diximus, et sunt sexdecem dies. Et illud est conveniens ei quod videtur.
Postquam igitur iam firmate sunt he res, tunc iam oportet ut reducamus considerationem nostram ad illud quod sequitur in apparitionibus stelle Mercurii que destruuntur et delentur. Et incipiamus primo ut ostendamus quod, quando est in principio Scorpionis, est eius elongatio a Sole ad posteriora, et si esset ultima longitudo que est inter ipsum et ipsam in eo, non tamen esset possibile ut videretur vespere. 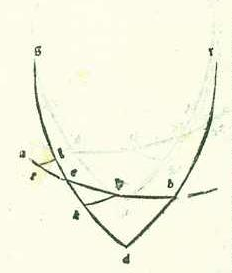 Ponamus itaque formam quam posuimus in apparitionibus, et ponamus ut punctum E orbis signorum sit in principio Scorpionis, et hic locus sit in quo in occasu angulus BED sit 69 partes secundum partes quibus duo anguli recti sunt 360 partes. Ergo erit minor duarum linearum continentium angulum rectum 68 partes secundum partes quibus subtendens est 120 partes, et maior duarum linearum continentium ipsum erit 99 partes. Ergo secundum partes quibus arcus BD, et est arcus longitudinis universalis, est decem partes erit arcus DE 17 partes et 39 minuta. Sed cum huius stelle locus fuerit locus quem narravimus, erit declivior ad meridiem ab orbe signorum tribus partibus fere. Quapropter, propterea quod in istis proportionibus narratis secundum partes etiam quibus arcus LT, et est arcus longitudinis, est tres partes est arcus LE 4 partes et 22 minuta, et est arcus DL totus secundum istas partes 22 partes fere. Et tunc iam oportet ut sit hec quantitas partium longitudinis stelle a loco Solis vero ut sit possibile ut videatur prima visio. Sed propterea quod plurimum quod est longitudinis eius a loco Solis verificato, quando est in principio Scorpionis, non est nisi 20 partes et 58 minuta, quia nos iam premisimus et declaravimus illud per capitula que simpliciter demonstravimus ei in scientia longitudinum maiorum, ergo apparet quod illud quod sic est in apparitionibus necessarium est ut destruetur et deleatur. Nos namque, si posuerimus similem illi forme que est apparitionum et posuerimus ut punctum E sit principium Tauri in ortu vespertino, tunc cum erit stella secundum cursus narratos declinata ad meridiem ab orbe signorum tribus partibus et sex minutis fere et fuerint proportiones accepte in triangulis ortogoniis ille proportiones narrate eedem, proveniet nobis arcus DE 17 partes et 39 minuta secundum istas partes, et arcus LE 4 partes et 37 minuta secundum partes quibus arcus TL, et est arcus latitudinis, est tres partes et decem minuta, et arcus DEL totus 22 partes et 16 minuta. Quapropter necessarium est hic etiam ut sit longitudo stelle a loco Solis verificato ut videatur prima visio eius hec quantitas partium. Sed propterea quod non fuit elongata maior eius elongatio super partes quas declaravimus, et sunt 22 partes et 13 minuta, tunc necessario fit ut he apparitiones destruantur et deleantur. Manifestum est igitur quod illud quod iam intendimus est conveniens ei quod videtur et radicibus que posite sunt.
Ponamus itaque formam quam posuimus in apparitionibus, et ponamus ut punctum E orbis signorum sit in principio Scorpionis, et hic locus sit in quo in occasu angulus BED sit 69 partes secundum partes quibus duo anguli recti sunt 360 partes. Ergo erit minor duarum linearum continentium angulum rectum 68 partes secundum partes quibus subtendens est 120 partes, et maior duarum linearum continentium ipsum erit 99 partes. Ergo secundum partes quibus arcus BD, et est arcus longitudinis universalis, est decem partes erit arcus DE 17 partes et 39 minuta. Sed cum huius stelle locus fuerit locus quem narravimus, erit declivior ad meridiem ab orbe signorum tribus partibus fere. Quapropter, propterea quod in istis proportionibus narratis secundum partes etiam quibus arcus LT, et est arcus longitudinis, est tres partes est arcus LE 4 partes et 22 minuta, et est arcus DL totus secundum istas partes 22 partes fere. Et tunc iam oportet ut sit hec quantitas partium longitudinis stelle a loco Solis vero ut sit possibile ut videatur prima visio. Sed propterea quod plurimum quod est longitudinis eius a loco Solis verificato, quando est in principio Scorpionis, non est nisi 20 partes et 58 minuta, quia nos iam premisimus et declaravimus illud per capitula que simpliciter demonstravimus ei in scientia longitudinum maiorum, ergo apparet quod illud quod sic est in apparitionibus necessarium est ut destruetur et deleatur. Nos namque, si posuerimus similem illi forme que est apparitionum et posuerimus ut punctum E sit principium Tauri in ortu vespertino, tunc cum erit stella secundum cursus narratos declinata ad meridiem ab orbe signorum tribus partibus et sex minutis fere et fuerint proportiones accepte in triangulis ortogoniis ille proportiones narrate eedem, proveniet nobis arcus DE 17 partes et 39 minuta secundum istas partes, et arcus LE 4 partes et 37 minuta secundum partes quibus arcus TL, et est arcus latitudinis, est tres partes et decem minuta, et arcus DEL totus 22 partes et 16 minuta. Quapropter necessarium est hic etiam ut sit longitudo stelle a loco Solis verificato ut videatur prima visio eius hec quantitas partium. Sed propterea quod non fuit elongata maior eius elongatio super partes quas declaravimus, et sunt 22 partes et 13 minuta, tunc necessario fit ut he apparitiones destruantur et deleantur. Manifestum est igitur quod illud quod iam intendimus est conveniens ei quod videtur et radicibus que posite sunt.
〈XIII.9〉 Capitulum nonum: In radice qua reperiuntur longitudines particulares a Sole in apparitionibus harum stellarum et occultationibus earum
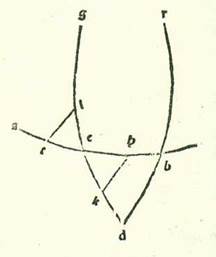 Iam autem apparet ex illo quod omnino quando fuerint arcus BD noti in unaquaque stellarum et fuerint principia signorum que sunt super sectionem E data, et propter illud erit angulus BED datus. Tunc arcus DE erit datus, et erit cursus in latitudine que est stellarum in longitudine hac, scilicet arcus KH aut arcus TL, datus. Et propter illud erit etiam arcus KE aut arcus EL datus, et erit longitudo etiam que videtur data, scilicet arcus KD aut arcus LD. Numeravimus igitur hoc modo, ut non prolongetur liber, in hoc climate medio quod diximus solo, quoniam in eo est sufficientia in signis omnibus uniuscuiusque stellarum quinque, longitudines a loco Solis verificato que videntur in elevationibus et occultationibus ita ut stelle omnes sint posite in principiis signorum et firmavimus eas propter facilitatem operandi per eas in quinque tabulis stellarum quinque, in unaquaque tabula quarum sunt duodecem linee. Tabule igitur prime tres harum stellarum quinque sunt Saturni, Iovis et Martis. Et firmavimus in omni tabula earum tres areas, et firmavimus in area prima earum principia signorum, et in areis secundis longitudines ortuum matutinorum, et in areis tertiis occasuum vespertinorum longitudines. Duas vero reliquas tabulas Veneris ac stelle Mercurii firmavimus in quinque areis, et firmavimus in duabus areis primis secundum illud exemplum principia signorum, et in duabus areis secundis longitudines ortuum vespertinorum, et in duabus areis tertiis longitudines occasuum vespertinorum, et firmavimus etiam in duabus areis quartis longitudines ortuum matutinorum, et in duabus areis quintis longitudines occasuum matutinorum. Et ita est artificium tabularum secundum quod declaravimus ipsum.
Iam autem apparet ex illo quod omnino quando fuerint arcus BD noti in unaquaque stellarum et fuerint principia signorum que sunt super sectionem E data, et propter illud erit angulus BED datus. Tunc arcus DE erit datus, et erit cursus in latitudine que est stellarum in longitudine hac, scilicet arcus KH aut arcus TL, datus. Et propter illud erit etiam arcus KE aut arcus EL datus, et erit longitudo etiam que videtur data, scilicet arcus KD aut arcus LD. Numeravimus igitur hoc modo, ut non prolongetur liber, in hoc climate medio quod diximus solo, quoniam in eo est sufficientia in signis omnibus uniuscuiusque stellarum quinque, longitudines a loco Solis verificato que videntur in elevationibus et occultationibus ita ut stelle omnes sint posite in principiis signorum et firmavimus eas propter facilitatem operandi per eas in quinque tabulis stellarum quinque, in unaquaque tabula quarum sunt duodecem linee. Tabule igitur prime tres harum stellarum quinque sunt Saturni, Iovis et Martis. Et firmavimus in omni tabula earum tres areas, et firmavimus in area prima earum principia signorum, et in areis secundis longitudines ortuum matutinorum, et in areis tertiis occasuum vespertinorum longitudines. Duas vero reliquas tabulas Veneris ac stelle Mercurii firmavimus in quinque areis, et firmavimus in duabus areis primis secundum illud exemplum principia signorum, et in duabus areis secundis longitudines ortuum vespertinorum, et in duabus areis tertiis longitudines occasuum vespertinorum, et firmavimus etiam in duabus areis quartis longitudines ortuum matutinorum, et in duabus areis quintis longitudines occasuum matutinorum. Et ita est artificium tabularum secundum quod declaravimus ipsum.
〈XIII.10〉 Capitulum decimum: De tabulis factis apparitionibus stellarum quinque erraticarum et occultationibus earum
Capita signorum |
Ortus ♄ matutinalis |
Ortus ♃ matutinalis |
Ortus ♂ matutinalis |
Ortus ♀ matutinalis |
Ortus ♀ vespertinalis |
Ortus ☿matutinalis |
Ortus ☿vespertinalis |
|||||||||||||||||
12 |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
||||||||||
1 Aries
2 Taurus |
♈
♉ |
29
27 |
28
26 |
19
18 |
33
21 |
29
27 |
0
12 |
3
4 |
36
9 |
15
13 |
31
48 |
22
24 |
43
23 |
24
21 |
10
15 |
|||||||||
3 Gemini
4 Cancer |
♊
♋ |
22
17 |
10
18 |
14
11 |
14
44 |
22
18 |
14
15 |
5
10 |
4
12 |
10
8 |
39
38 |
22
18 |
28
48 |
17
14 |
10
9 |
|||||||||
5 Leo
6 Virgo |
♌
♍ |
14
13 |
8
8 |
9
9 |
44
7 |
16
15 |
7
8 |
17
23 |
45
40 |
7
6 |
5
53 |
15
13 |
8
15 |
12
12 |
53
8 |
|||||||||
7 Libra
8 Scorpio |
♎
♏ |
12
13 |
15
1 |
9
9 |
0
7 |
14
15 |
12
8 |
22
15 |
27
14 |
6
7 |
57
51 |
12
12 |
29
10 |
12
12 |
10
41 |
|||||||||
9 Sagittarius
10 Capricornus |
♐
♑ |
13
16 |
47
36 |
9
11 |
44
44 |
16
18 |
7
15 |
7
2 |
1
18 |
7
9 |
56
58 |
11
12 |
16
16 |
14
16 |
3
19 |
|||||||||
11 Aquarius
12 Pisces |
♒
♓ |
21
26 |
16
46 |
14
18 |
14
21 |
22
27 |
14
11 |
1
2 |
36
43 |
12
15 |
47
28 |
14
18 |
25
22 |
20
24 |
15
18 |
|||||||||
♄ |
♃ |
♂ |
A 180 ad 223 |
Ab uno ad 137 |
A 180 ad 248 |
Ab uno ad 112 |
||||||||||||||||||
Capita signorum |
Occasus ♄ vespertinalis |
Occasus ♃ vespertinalis |
Occasus ♂ vespertinalis |
Occasus ♀ matutinalis |
Occasus ♀ vespertinalis |
Occasus ☿matutinalis |
Occasus ☿vespertinalis |
|||||||||||||||||
12 |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
||||||||||
1 Aries
2 Taurus |
♈
♉ |
13
14 |
46
7 |
9
9 |
28
38 |
14
16 |
12
8 |
7
7 |
25
29 |
2
3 |
27
30 |
12
12 |
20
18 |
12
12 |
9
12 |
|||||||||
3 Gemini
4 Cancer |
♊
♋ |
15
17 |
8
9 |
10
11 |
16
44 |
17
18 |
7
15 |
7
8 |
38
18 |
8
10 |
47
44 |
12
14 |
37
9 |
14
19 |
44
48 |
|||||||||
5 Leo
6 Virgo |
♌
♍ |
19
22 |
48
0 |
13
15 |
32
23 |
22
27 |
14
11 |
9
10 |
19
46 |
11
7 |
30
43 |
16
20 |
39
23 |
23
26 |
29
56 |
|||||||||
7 Libra
8 Scorpio |
♎
♏ |
22
21 |
32
20 |
16
15 |
7
23 |
29
27 |
0
11 |
11
11 |
9
26 |
6
6 |
40
17 |
23
23 |
50
49 |
25
20 |
38
35 |
|||||||||
9 Sagittarius
10 Capricornus |
♐
♑ |
18
16 |
54
36 |
13
11 |
32
44 |
22
18 |
14
15 |
12
9 |
27
18 |
5
2 |
12
18 |
20
16 |
44
19 |
17
12 |
41
30 |
|||||||||
11 Aquarius
12 Pisces |
♒
♓ |
14
14 |
40
0 |
10
9 |
16
38 |
16
15 |
7
8 |
8
7 |
29
43 |
3
6 |
24
31 |
14
12 |
7
14 |
11
11 |
32
47 |
|||||||||
♄ |
♃ |
♂ |
A 224 ad 360 |
A 138 ad 180 |
A 249 ad 360 |
A 153 ad 180 |
||||||||||||||||||
〈XIII.11〉 Capitulum undecimum: In consumatione libri
Quia igitur iam consumavimus has intentiones et perfecimus omnia eis necessaria ostendendo scientiam earum in hoc libro secundum quantitatem possibilitatis nostre scientie et summe nostri consilii propter difficilia earum secundum quantitatem eius quo adiuvit nos tempus quod pervenit ad nos ad inveniendum id cuius est inventio necessaria ex illo et pretermittendum id cuius est necessaria pretermissio et verificatio eius ex eo et secundum quod sit quod scripsimus inde conferens in hac scientia preter quod inquiramus per ipsum prolongationum vel abbreviationum arrogantiam et collaudationem, tunc iam sequitur et honestum est ut imponamus hic finem libro.
Expleta est dictio tertiadecima et ultima libri Almagesti Ptolemei Pheludiensis Alexandrini. Et ita ingens ac nobile opus totius Almagesti seu Magne constructionis absolutum est ingenio, labore et sumptibus Petri Liechtenstein Coloniensis anno Virginei partus 1515 die 10 ianuarii Venetiis.