⟨III⟩
Claudii Ptolemei Pheludiensis dictio tertia libri Almagesti decem capitulis aptissime contexta fauste enitet.
Capitulum primum: De scientia quantitatis longitudinis anni et numero dierum eius
Capitulum secundum: De positione tabularum motus Solis medii
Capitulum tertium: De scientia partis motus circularis convenientis
Capitulum quartum: De scientia eorum que apparent ex diversitate motus Solis in aspectu et visione
Capitulum quintum: De inquisitionibus particularibus ex diversitate
Capitulum sextum: De artificio divisionum tabularum portionum particularium que sunt diversitatis
Capitulum septimum: De positione tabularum diversitatis motus Solis
Capitulum octavum: De scientia loci Solis ex cursu eius medio
Capitulum nonum: De computatione, idest equatione, Solis et scientia veritatis loci eius
Capitulum decimum: De scientia diversitatis allegenu, que est inter diem Iomin et noctem eius et diem Iomin alterius et noctem eius (Iomin autem est tempus constans ex 24 horis quod simul continet diem et noctem)
⟨III.1⟩ Capitulum primum: De scientia quantitatis longitudinis anni et numero eiemeye, idest dierum eius
Postquam declaravimus in his que precesserunt hanc dictionem summam eorum que premittenda erant de scientia celi et terre, et etiam de declinatione orbis Solis, qui est medium cinguli signorum, et de divisione eorum que contingunt in sphera recta et sphera declivi in omni loco habitabili, vidimus quod oportunum est ut sequatur illud dictio de Sole et Luna et illis que accidunt in motibus eorum. Non est enim possibile scire aliquid eorum que videntur in stellis antequam precedat scientia eorum omnino. Vidimus autem ut a Sole ante Lunam incipiamus. Non est enim possibile scire aliquid eorum que contingunt in Luna ante scientiam Solis et eorum que in ipso contingunt. Primum autem omnium que oportet nos demonstrare de causa Solis est inventio scientie quantitatis longitudinis anni et numeri dierum eius. Ea vero in quibus dubitaverunt et diversificati sunt antiqui sciemus ex eis que ipsi narraverunt, et precipue Abrachis, vir bone scientie et amator scientie et veritatis. Plurimum autem eorum que perduxerunt eum ad hanc dubitationem fuit quod ipse videbat ex revolutionibus Solis et principiis eius et reditionibus ipsius a duobus punctis equalitatis et duobus punctis tropicis numerum dierum anni fieri 365 dies et minus quarta diei, et videbat ex coniunctione Solis cum aliqua stellarum fixarum et revolutionibus eius et ex reversionibus eius ad eam fieri 365 dies et plus quarta diei. Ex hoc igitur, ut apparet, estimavit spheram stellarum fixarum habere motum localem tardum longi temporis, et hic quidem motus ad partem motus stellarum retrogradarum secundum continuitatem signorum, qui est secundus a motu primo, cum orbe descripto supra duos polos duorum orbium simul, orbis equationis diei et orbis declivis ab eo. Nos autem ostendemus in nostro libro de stellis fixis quod hoc ita est et narrabimus modum per quem scietur et quod non est possibile scire aliquid eorum ante scientiam Solis et Lune. In scientia vero quantitatis longitudinis anni et numeri dierum eius non oportet ut sit nostra intentio et nostrum studium nisi motus Solis per seipsum et revolutiones eius et principia ipsius et reversiones eius in orbe declivi. Diffiniam autem dies anni quod est tempus motus Solis ab aliquo punctorum fixo immobili huius orbis secundum continuitatem signorum donec redeat ad idem punctum. Videmus vero ut primum punctorum eius et proprietatum principiorum eius a quo incipiamus sint duo puncta equalitatis et duo puncta tropica. Non enim reperiemus revolutiones et principium et reversionem in illa figura in loco et tempore digniore his punctis, sive apud horizontas sive apud orbem meridiei sive a longitudine diei Iomin et noctis eius ad eius equalem, neque sunt principia orbis signorum preter ea. Si enim aliquis consideraverit secundum modum naturalem, non reperiet principium neque reversionem convenientiorem principiis complexionis temporis usque ad eius similem, sicut principium motus Solis a tropico donec redeat ad eius similem aut a differentia ad eius similem, neque principia alia nisi principia per que separatur unumquodque quattuor temporum ab alio. Et cum hoc quoniam revolutiones quarum principia et reversiones sunt a coniunctione Solis cum aliqua stellarum fixarum non in veritate sua sunt ut iste, neque videmus non esse confidendum in eis absque causa. Et plurimum huius est quoniam orbis earum movetur in celo motu locali secundum continuitatem signorum cum mensuratione. Postquam igitur hoc ita est, non est quod prohibeat aliquem quin etiam dicat quod longitudo temporis anni Solis verbi gratia est tempus in quo consequitur Sol Saturnum aut unam stellarum retrogradarum donec redeat ad ipsam. Erunt ergo tempora Solis multa diversa. Quapropter videmus oportere ut dicatur quod tempus anni Solis inventum secundum considerationes est ab aliqua differentiarum quattuor temporum ad eius similem in multis revolutionibus et longitudine temporum. Et quoniam estimant quod dubitatio reperta est in his per que investigatur longitudo temporis anni Solis secundum hec principia que nominavimus cum consideratione in considerationibus mutaguetireti, qua dubitavit Abrachis, elaborabimus ostendere breviter quod hoc non est dubitare faciens. Illud autem quo certificati sumus et quod apud nos firmavit quod hec tempora non sunt diversa est quod vidimus per considerationes mutaguetireti cum instrumentis a differentiis quattuor temporum. Non enim invenimus in eis multam diversitatem, que sit inter ipsum et quartam diei superfluam. Sed iam possibile est quod forsitan fuit error parvus propter artificium instrumenti aut propter ipsius positionem. Et cum consideraverimus ea que dixit Abrachis et aspexerimus in eis, erit error diversitatis propter considerationem. Abrachis namque iam firmavit in his que posuit de motu duorum punctorum equalitatis et duorum punctorum conversionis, que consideravit ex tropicis estivali et hiemali mutaguetireti secundum subtilissimam acceptionem veritatis eorum, quod diversitas que est inter ea non habet quantitatem impedientem in longitudine temporis annorum Solis. Et in libro suo dixit quemadmodum narrabo. Inquit enim: ‘Ostendam propter has considerationes quod diversitas que est inter tempora annorum Solis minima, scilicet in annis quorum principia sunt a punctis differentiarum quattuor temporum, non est mirum si preterit apud me et apud Arsamidem in consideratione et estimatione quantitatem quarte diei. Iam vero possumus scire veritatem diversitatis revolutionum temporum anni Solis ex considerationibus cum armilla erea posita in riuguat quadrato Alexandrie, que significat diem equalem in hora qua completur egressus luminis Solis ab interiori armille ab una duarum partium et incipit ingressus luminis Solis ab interiori armille a parte altera.’ Deinde post hoc dicit primum tempora equalitatis autumnalis, que consideravit secundum veritatem sue verificationis. Consideratio vero que fuit in anno 17 revolutionis tertie annorum Philippi in uno mensium Egyptiorum Mesur in tricesima die ipsius fuit apud occasum Solis. Deinde post tres annos in anno 20 fuit in principio primi quinque dierum restauratorum. Oportuit vero ut esset in meridie ad hoc ut diversitas fuisset cum quarta diei. Et post annum in anno 21 fuit in hora diei sexta, que convenientius debuit sequi considerationem que fuit ante hanc. Et post 11 annos in anno 32 in die tertio dierum quinque restauratorum fuit in medio noctis cuius mane fuit diei quarti. Sed oportuit ut fuisset in mane ad hoc ut diversitas etiam esset cum quarta diei. Et post annum in anno 33 in quarto quinque dierum restauratorum fuit in principio diei. Et hec fuit convenientior ad sequendum considerationem que fuit ante ipsam. Et post tres annos in anno 36 in quarto quinque dierum restauratorum fuit apud occasum Solis. Oportuit vero ut fuisset in media nocte ad hoc ut diversitas esset cum quarta diei tantum. Et post hoc posuit Abrachis considerationes vernales secundum veritatem verificationis earum, scilicet in anno 32 revolutionis tertie annorum Felis. Dixit ergo quod equalitas vernalis fuit in 27 die mensis Mesir in principio diei. Iam enim tunc adhesit lumen duabus superficiebus armille enee in Alexandria utrinque equaliter in hora quinta a circulo ad circulum rubeum antequam diceret considerationes positas. Vidit ergo, quando considerationes erant in una duarum equalitatum ad suam similem in considerationibus mutaguetireti, diversificari quod erat inter duas considerationes fere per quinque horas. Et que post hoc sunt considerationes, quemadmodum dixit, usque ad annum 37 conveniunt secundum augmentum quarte die. Sed post undecim annos in anno 43 in 29 die mensis Mesir post mediam noctem cuius mane fuit dies tricesimus fuit equalitas vernalis. Et hec fuit que debuit sequi considerationem que fuit in anno 32, et fuit hoc etiam conveniens in considerationibus que fuerunt post eam usque ad annos 50. Si ergo fuit in principio mensis Menub apud occasum Solis post diem et fere medietatem diei et quartam diei a consideratione que fuit in anno 43, quod est portio septem annorum inter 43 et 50 qui sunt inter duas considerationes, tunc non fuit in hac consideratione multa diversitas. Et tamen est possibile ut huic accidat aliquid erroris non in considerationibus tropicis tantum, verumetiam in considerationibus duorum punctorum equalitatis, et ut sit quantitas illius quarta diei. Si enim fuerit error qui est propter positionem instrumenti et divisionem partium eius secundum veritatem una trium milium et sexcentarum partium tantum ex partibus orbis descripti supra duos polos orbis equationis diei, tunc illud est longum in latitudine. Et quando Sol movetur per quartam partis in longitudine in orbe declivi ubi ipsum secat orbis equationis diei, pervenit error ille in diversitate fere ad quartam diei. Error vero qui fit propter positionem instrumenti erit maior si non fuerit positio eius in tempore secundum certificationem veritatis considerationis, eo quod eius preparator ipsum inclinat et movet et adiungit illud alicui rei ad hoc ut ipsum firmet. Firmabitur ergo longo tempore secundum habitudinem unam. Error ergo qui ipsi accidit in eo est quod removetur a sensu, sicut iam contingit in armillis eneis positis in locis in quibus congregantur consideratores in terris nostris, quarum superficies et superficies equationis diei estimatur esse una. Iam enim declarata est nobis per considerationem alteratio locorum earum, et illud magis in illis que sunt ex eis grosse et magis antique, et forsitan vidimus lumen in interioribus earum in tempore unius duarum equalitatum. Hec autem et horum similia sunt que vidit Abrachis non significare veritatem eorum que estimavit de diversitate temporum annorum. Et de quibusdam significationibus considerationum eius inquisitionis eclypsium lunarium dixit quia iam reperit quod illud quod est inter tempora annorum diversorum et inter tempora eorum media non est maius medietate et quarta unius diei. Quod si hec oratio esset vera, esset scientia receptibilis. Sed non est vera, quod quidem declaratur nobis ex eis que dixit et narravit. Dixit enim et narravit in quibusdam in quibus excogitavit et subtiliter aspexit ubi reperit quasdam stellas fixas propinquas eclypsibus lunaribus quas iam consideravit quantum precessit stella fixa que nominatur Spica punctum autumnale in omni eclypsi. Reperit enim secundum quod estimavit quod plurimum quo precessit ipsum fuit septem partes et medietas partis secundum proprietatem temporis et minus quam quinque partes et quarta partis. Necesse est ergo ex hac oratione, postquam non est possibile ut motus huius stelle sit in quantitate huius temporis parvi, quantumcunque dixit, quod secundum veritatem non sint Solis, per quem investigatur scientia locorum stellarum fixarum, equales anni et revolutiones. Et defuit ei quod ea in quibus excogitavit et subtiliter aspexit non est possibile compleri omnino nisi per scientiam loci Solis in eclypsi. Et ex hoc quod accepit considerationes veraciter in illis annis a duobus punctis equalitatis et conversionis significatur quod superfluum quod est inter duas considerationes non est maius quarta diei in omni anno. Et ponam ad hoc exemplum unum, quod sit consideratio que fuit in anno 32 revolutionis tertie annorum Felis. Reperit enim secundum quod estimavit quod stella Spica precessit punctum autumnale septem partibus et medietate partis. In consideratione vero que fuit in anno 43 illius revolutionis reperit stellam Spicam precessisse punctum autumnale quinque partibus et quarta partis. Et similiter posuit secundum illam estimationem et subtilem inspectionem considerationes veraciter in illis annis que sunt a punctis vernalibus, ad hoc ut per eas acciperet loca Solis que sunt in medio temporis eclypsis, et ex illis locis acciperet loca Lune, et ex locis Lune acciperet loca stellarum fixarum. Et dixit quod consideratio que fuit in anno 32 fuit in 27 die mensis Mesir et in principio diei et consideratio que fuit in anno 43 in 29 die in nocte cuius mane fuit dies 30 post mediam noctem post duos dies et medietatem et quartam diei a consideratione in qua fuit eclypsis anni tricesimisecundi. Quod quidem fuit quarta diei tantum super 365 dies in uno quoque undecim annorum. Si ergo fuerint non in tempore maiore neque in tempore minore revolutiones Solis et reversiones ad dua puncta equalitatis secundum superfluum maius quarta diei, sed stellam Spicam non est possibile moveri in his annis paucis parte una et quarta partis, tunc quomodo non est indecens accipere hanc sententiam in scientia acquisita ex istis principiis instrumentum ad delendum et destruendum ea per que certificatur et affirmatur, aut quomodo non comparant causam propter quam non est possibile ut sit omnis hic motus stelle Spice, et non hunc errorem ad duo puncta equalitatis tantum, per que fuit consideratio secundum veritatem aut non secundum veritatem. Illius autem propter quod hunc errorem esse est possibile cause multe sunt. Ex quibus est elongatio Lune in eclypsi a stellis que sunt ei propinque, aut propter diversitatem aspectus et considerationis ad Lunam et locum eis aut propter motum Solis a duobus punctis equalitatis ad medium temporum eclypsis aut propter ea que considerantur et assumuntur absque subtilitate et absque veritate. Estimo autem quod Abrachis scivit quod nihil eorum que prediximus cogit aut firmat apud nos quod Sol habeat equationem secundam. Ipse vero propter vehementem amorem veritatis horruit relinquere ad dicendum aliquid eorum que hominibus dubietatem afferunt. Ipsemet enim fecit in equatione diversitatis cursus Solis et Lune et posuit Solis equatione unam que equat complementum revolutionis anni solaris a punctis differentiarum temporum. Et non videmus propterea quod posuit revolutiones Solis istas equalium temporum ut que videntur in eclypsibus diversificent hec accidentia posita secundum rem magnam. Et illud est quod oportuit esse sensibile manifeste, postquam non acceperunt equationem diversitatis temporis anni. Et si sit illud pars una tantum, est tamen fere in eclypsi duarum horarum. Ex omnibus ergo que diximus et consideravimus de revolutionibus Solis invenimus longitudinem temporis anni non diversificari cum inceptio et reversio fuerit ab uno punctorum differentiarum temporum et ad ipsum, et non quandoque a punctis equalitatis et tropicis et quandoque a coniunctione stellarum fixarum. Et neque est reversio alia propior ea que est a puncto conversionis aut a puncto equationis diei aut ab alio punctorum orbis signorum a quo incipit Sol et ad quod revertitur. Videmus autem quod oportet nos demonstrare ea que videmus et declarare quam brevissime est possibile et ut diversitas que est inter considerationem et ea que dicere voluimus non sit magne quantitatis. Ex eis vero que declaravit Abrachis iam demonstratum est nobis quod quantitas temporis anni qui incipit a punctis equalitatis et conversionis donec ad ea redeat minor est quarta addita supra 365 dies. Neque est possibile invenire quantitatem illius parvitatis secundum veritatem, eo quod augmenta annorum plurium cum quarta fere deficiunt secundum sensum propter diversitatis parvitatem. Et propter hoc in considerationibus eorum que sunt longi temporis iam possibile est, cum diviserint dies inventos qui superfluunt et aggregantur ex quartis per annos multos aut per annos paucos qui sunt inter duas considerationes, ut sit portio una que provenit ex divisione anni unius. Acceptio vero huius inceptionis et reversionis secundum propinquitatem veritatis est secundum quantitatem plurium revolutionum et longitudinem temporis quod est inter duas considerationes et duas inspectiones. Quantum enim tempus magis elongatur, tantum erit propinquior veritati. Neque est in his revolutionibus et inceptione et reversione tantum, verum etiam in omnibus revolutionibus et reversionibus. Error enim qui est propter debilitatem considerationum, quamvis subtilissime accipiatur et quamvis error sit parvus aut equalitati vicinus secundum sensum in eis que videntur in tempore longo et tempore brevi, tamen cum dividetur per annos paucos, error anni erit maior et quod etiam aggregabitur ex eo in longitudine annorum plurium accrescet, et cum dividetur per annos plures, erit error minor. Quapropter videmus conveniens esse ut sufficiat secundum quod possibile est nobis addere longitudinem temporis quod est inter considerationes nostras et considerationes antiquorum subtilium in revolutionibus propinqui temporis. Et secundum huius similitudinem laborabimus addere in hac scientia et non relinquemus ex eis que conveniunt de inquisitionibus scienter. Inquisitio vero temporis totius aut eius cuius tempus elongatum est a longitudine temporum considerationum per tempus longum duplum dicimus quod non est ex amore scientie neque ex amore veritatis. Eorum vero quorum tempus antiquatum est ex considerationibus quas comparavimus nostris considerationibus et quibus experiemur et cum nostris oportet ut iam accipiamus considerationes quas consideravit Midan et Attamin a tropicis estivalibus, et post eos Aristocos. Sed propter summam eorum que scivimus de difficultate considerationum tropicorum et cum difficultate earum, quoniam ipsi posuerunt ipsas aggregatas et ignotas, quemadmodum illud iam declaratum fuit ab Abrachi, abhorremus confidere in eis et vidimus ut acciperemus considerationes que fuerunt in equalitate diei et ex eis acciperemus, quoniam voluimus, subtiles considerationes Abrachis, quoniam ipse accepit eas quam subtilius, et considerationes nostras, quas invenimus absque hesitatione cum instrumento quod ad hoc et eius simile in principio libri huius nostri Almagesti declaravimus. Quapropter invenimus principium motus Solis a punctis differentiarum temporum eius et reversionum eius ad ea in fere trecentis annis antecedere per diem unum secundum augmentum quarte diei integre in omni anno supra 365 dies. Abrachis namque iam vehementer consideravit equalitatem autumnalem quam subtilissime consideravit in anno 32 revolutionis tertie annorum Felis et dixit quod fuit in die tertio quinque dierum adiunctorum in media nocte cuius mane fuit quarta dies. Fuitque annus ille post mortem Alexandri annus 178. Deinde post 285 annos ab anno tertio annorum Attamenis, quod quidem fuit post mortem Alexandri in 463 anno, consideravimus nos etiam equalitatem autumnalem secundum quod subtilius possibile fuit, et fuit illud in die nono mensis Athus post ortum Solis fere per unam horam. Fuit ergo totum quod aggregatum est ex quartis dierum 285 annorum Egyptiacorum 70 dies et quarta diei et una 20 partium diei loco dierum qui aggregantur ex quartis perfectis adiunctis supra 365 dies, quos oportuit esse 71 dies et quartam diei horum annorum. Iam ergo antecessit reversio Solis ea que aggregantur ex superfluitatibus quartarum si essent integre per diem unum absque una 20 partium diei unius. Similiter quoque dixit Abrachis in consideratione vernali que fuit in anno 32 revolutionis tertie annorum Felis subtili acceptione quod fuit in 27 die mensis Mesir in principio diei, et fuit annus 178 post mortem Alexandri. Nos quoque iam invenimus equalitatem vernalem in anno 473 post mortem Alexandri in die septimo mensis Mathur. Deinde post 285 annos, quod fuit post mortem Alexandri in 463 anno, consideravimus equalitatem vernalem in die septimo mensis Mathur post medietatem diei fere per horam et invenimus que contingunt istis revolutionibus ex superfluitatibus dierum aggregatorum ex quartis in istis annis 70 dies et quartam diei excepta fere una 20 partium loco 71 dierum et quarte diei qui sunt augmentum quarte integre cuiusque horum annorum. Iam ergo hic etiam antecessit reversio Solis vernalis superfluitatem quarte integre per diem unam excepta una 20 partium. Proportio igitur 300 annorum ad 285 annos est sicut proportio diei unius ad diem cui deest una 20 partium diei unius. Fit ergo ut antecedat reversio Solis ad punctum equalitatis dies qui aggregantur ex quartis integris per diem in trecentis annis. Quod si nos propter multam antecessionem annorum comparaverimus considerationes nostras, in quibus non dubitamus, ad considerationes Midan et Attamin que fuerunt a tropico estivali, similiter reperiemus eas. Illa enim consideratio fuit in tempore Assuris regis civitatis sapientum et in vigesimoprimo die mensis Phemenut, qui est unus mensium Egyptiorum, in principio diei. Et nos invenimus secundum veritatem considerationis cum subtilitate que fuit in anno 463 post mortem Alexandri in 11 die mensis Memire post mediam noctem cuius mane fuit dies duodecimus fere post duas horas. Et erat quod fuit inter considerationem tropici estivalis que fuit in tempore Assuris et considerationem que fuit in tempore Arsatochis in anno 50 revolutionis prime accomodate Feli, quemadmodum dixit Abrachis, 152 anni. Et quod fuit inter annum 50 hunc, qui fuit in anno 44 a morte Alexandri, et inter annum 463, in quo fuit consideratio nostra, est 419 anni. Si ergo in his 571 annis fuit consideratio estivalis quam consideravit Attamin in vigesimoprimo die mensis Phemenut, fiet aggregatum ex augmento dierum super annos Egyptiacos fere 140 dies et medietas et tertia diei loco 142 dierum et medietatis et quarte diei qui fierent in 571 annis si quarte fuissent integre superfluentes super annos Egyptiacos. Iam ergo antecessit hec reversio in his annis dies superfluentium quartarum si fuissent integre per duos dies excepta medietate sexte partis diei. Iam ergo declaratum est quod ipsa precessit in 600 annis fere per duos dies integros in hac postrema consideratione. Et similiter invenimus nos in considerationibus multis aliis postremis. Et similiter vidimus Abrachim concessisse hoc. Ipse enim dicit in libro suo De quantitate longitudinis anni quod comparavit considerationem tropici estivalis que fuit in postremo anni quinquagesimi revolutionis Felis prime ad eam quam etiam consideravit vere et subtiliter, que fuit in postremo anni 43 revolutionis Felis tertie, ubi dixit quod ostendit quod in 145 annis festinat tropicus ante superfluitatem quarte per medietatem diei et noctis. Ipse quoque in libro suo De mensibus et diebus, postquam premisit sermonem, dixit: ‘Secundum vero quod dixerunt Midan et Attamin est longitudo temporis anni 365 dies et quarta et una pars 76 partium et medietas diei unius. Sed secundum quod dixit Felis est 365 dies et quarta tantum.’ Post hoc quoque dixit, quemadmodum narrabo verbum ex verbo: ‘Nos autem iam invenimus menses integros contineri a 19 annis, quemadmodum invenerunt illi. Longitudinem vero anni invenimus iam minorem quarta per unam 300 partium diei unius. Et in trecentis annis desunt sermoni Midan quinque dies et sermoni Felis deest unus dies.’ Ubi autem aggregantur eius sententie in libro suo dixit, quemadmodum narrabo: ‘Iam scripsi unum librum de longitudine temporis anni, in quo declaravi quod annus Solis est tempus in quo incipit motus Solis a tropico ad tropicum sui similem aut ab equalitate ad equalitatem sui similem quod continet ex diebus 365 dies et minus quarta diei fere per unam 300 partium diei unius cum nocte sua. Neque est, sicut estimant disciplinales, ut sit augmentum supra 365 dies quarta diei integra. Estimo autem iam declaratum esse quod quantum apparuit in longitudine temporis anni usque ad hec nostra tempora ex reversione Solis a punctis tropici et equalitatis conveniens est huic quantitati quam nominavimus secundum quod convenit ex considerationibus antiquis et novis.’ Postquam ergo est hoc sicut diximus, fiet ut cum diviserimus diem unum per 300 annos, sit portio unius anni ex eo 12 secunda unius diei. Cum ergo minuerimus ea ex 365 diebus et 15 minutis, que sunt quarta diei, remanebit tempus anni quem scire voluimus 365 dies et 14 minuta et 48 secunda. Hic est ergo numerus dierum repertorum ex eis que diximus secundum quod magis est possibile brevius esse. Et quia volunt investigationem Solis et stellarum aliarum et cursus earum in partibus orbis signorum, cuius inventio est facilis et quam demonstrant partes que sunt in tabulis, tunc iam convenit erudito in disciplinalibus ut sit eius intentio et desiderium ostendere omnia que videntur in celo de motibus earum mediis qui sunt super circulos orbium earum et ut faciat tabulas convenientes intentioni sue, dividendo inter motus earum medios cursus earum in partibus orbis signorum et inter motus qui sunt propter circulos orbium earum propter quos est diversitas estimata, deinde etiam tabulas coniunctionis duorum motuum simul significantes visionem cursuum earum. Et ad hoc ut ea que diximus sint faciliora et vicinioris acceptionis cum eorum fuerit necessitas, ponam tabulas motus Solis medii in partibus orbis revolutionis eius secundum hunc modum quem dicam. Postquam igitur iam ostensum est quod reversio temporis Solis est in 365 diebus et 14 minutis et 48 secundis, fit ut cum diviserimus per illud 360, scilicet numerum partium orbis signorum, sit motus Solis medius in die una 59 minuta et 8 secunda et 17 tertia et 13 quarta et 12 quinta et 31 sexta fere. Ut autem in divisione hec minuta usque ad sexta perveniant sufficit. Nos quoque, cum iam acceperimus ex motu diei partem 24am, inveniemus motum Solis in una hora duo minuta et 27 secunda et 50 tertia et 43 quarta et tria quinta et sextam unam propinque. Et similiter cum multiplicaverimus motum diei unius in 30 dies, scilicet mensis unius, erit motus Solis medius in mense 29 partes et 34 minuta et 8 secunda et 36 tertia et 36 quarta etiam et 15 quinta et 30 sexta. Et cum multiplicaverimus motum diei unius in numerum dierum anni Egyptii, scilicet 365 dies, inveniemus illud motum Solis medium in anno 359 partes et 45 minuta et 24 secunda et 45 tertia et 21 quarta et 8 quinta et 35 sexta. Et etiam cum multiplicaverimus motum Solis in anno in 18 annos, propter hoc quod demonstratur ex bonitate mensurationis tabularum, et proiecerimus ex eis que aggregantur revolutiones integras, scilicet queque revolutio 360, superfluent ex motu Solis medio in 18 annis 355 partes et 37 minuta et 25 secunda et 36 tertia et 20 quarta et 34 quinta et 30 sexta.
⟨III.2⟩ Capitulum secundum: De positione tabularum motus Solis medii
Describam autem motus Solis medii tabulas in tribus partibus quinque temporum. Et dividam partem in septem tabulas in longitudine et 45 areas in latitudine. Et signabo in tabulis partis prime numerum annorum coniunctorum et motum Solis in eis, et in tabulis partis secunde numerum annorum disgregatorum et motum Solis in eis, et sub eis numerum horarum et motum Solis in eis, et in tabulis partis tertie numerum dierum mensium et motum Solis in eis, et sub eis numerum dierum mensis unius et motum Solis in eis. Et hec est tabularum descriptio:
Fuit radix Solis in principio regni Nabuchodonosor, scilicet elongatio eius a longitudine longiore in orbe ecentrico qui est eius orbis proprius, 265 gradus et 15 minuta. Et fuit tunc locus eius in orbe signorum per motum eius medium in 45 minutis Piscis, et per motum eius diversum qui videtur in eo tres gradus et 8 minuta Piscis fere, et eius elongatio a Luna 70 gradus et trigintaseptem minuta.
Fuit primus dies Iumedi primi anni 359 secundum regulam dies Veneris. Et primus dies Veneris qui fuit octavus ab eo fuit annus Persarum 337 et 12 menses. Et fuit dies sabbati primus quinque dierum adiunctorum.
Radix autem posita in capite harum tabularum est annorum Persarum in media die qui fuit ante diem primum per diem unum.
Riguat est locus quadratus in quo conveniunt homines coopertus quasi turris.
Motus Solis medius in annis coniunctis |
Motus Solis medius in annis disgregatis |
Motus Solis medius in mensibus |
|||||||||||||||||||||||
Anni
coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Anni
disgregati |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||
18
36
54 |
355
351
346 |
37
14
52 |
25
51
16 |
36
12
49 |
20
41
1 |
34
9
43 |
30
0
30 |
1
2
3 |
359
359
359 |
45
30
16 |
24
49
14 |
45
30
16 |
21
42
3 |
8
17
25 |
35
10
45 |
30
60
90 |
29
59
88 |
34
8
42 |
8
17
25 |
36
13
49 |
36
12
48 |
15
31
46 |
30
0
30 |
||
72
90
108 |
342
338
333 |
29
7
44 |
42
8
33 |
25
1
38 |
22
42
3 |
18
52
27 |
0
30
0 |
4
5
6 |
359
358
358 |
1
47
32 |
39
3
28 |
1
46
32 |
24
45
6 |
34
42
51 |
20
55
30 |
120
150
180 |
118
147
177 |
16
50
24 |
34
43
51 |
26
3
39 |
25
1
37 |
2
17
33 |
0
30
0 |
||
126
144
162 |
329
324
320 |
21
59
36 |
59
24
50 |
14
50
27 |
24
44
5 |
1
36
10 |
30
0
30 |
7
8
9 |
358
358
357 |
17
3
48 |
53
18
42 |
17
2
48 |
28
49
10 |
0
8
17 |
5
40
15 |
210
240
270 |
206
236
266 |
59
33
7 |
0
8
17 |
16
52
29 |
13
50
26 |
48
4
19 |
30
0
30 |
||
180
198
216 |
316
311
307 |
14
51
29 |
16
41
7 |
3
39
16 |
25
46
6 |
45
19
54 |
0
30
0 |
10
11
12 |
357
357
357 |
34
19
4 |
7
32
57 |
33
18
4 |
31
52
13 |
25
34
43 |
50
25
0 |
300
330
360 |
295
325
354 |
41
15
49 |
26
34
43 |
6
42
19 |
2
38
15 |
35
50
6 |
0
30
0 |
||
234
252
270 |
303
298
294 |
6
43
21 |
32
58
24 |
52
28
5 |
27
48
8 |
28
3
37 |
30
0
30 |
13
14
15 |
356
356
356 |
50
35
21 |
21
46
11 |
49
34
20 |
34
56
17 |
51
0
8 |
35
10
45 |
Motus Solis medius in diebus |
|||||||||
Dies |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||||||||||||||
288
306
324 |
289
285
281 |
58
36
13 |
49
15
40 |
41
17
54 |
29
49
10 |
12
46
21 |
0
30
0 |
16
17
18 |
356
356
355 |
6
52
37 |
36
0
25 |
5
50
36 |
38
59
20 |
17
25
34 |
20
55
30 |
1
2
3 |
0
1
2 |
59
58
57 |
8
16
24 |
17
34
51 |
13
26
39 |
12
25
37 |
31
2
33 |
||
342
360
378 |
276
272
268 |
51
28
5 |
6
32
57 |
30
6
43 |
30
51
12 |
55
30
4 |
30
0
30 |
Motus Solis medius in horis |
4
5
6 |
3
4
5 |
56
55
54 |
33
41
49 |
8
26
43 |
52
6
19 |
50
2
15 |
4
35
6 |
|||||||||
Hore |
Partes |
Minuta |
Quarta |
Quinta |
Sexta |
||||||||||||||||||||
396
414
432 |
263
259
254 |
43
20
58 |
23
48
14 |
19
55
32 |
32
53
13 |
39
13
48 |
0
30
0 |
1
2
3 |
0
0
0 |
2
4
7 |
27
55
23 |
50
41
32 |
43
26
9 |
3
6
9 |
1
2
3 |
7
8
9 |
6
7
8 |
53
53
52 |
58
6
14 |
0
17
34 |
32
45
58 |
27
40
52 |
37
8
39 |
||
450
468
486 |
250
246
241 |
35
13
50 |
40
5
31 |
8
44
21 |
34
54
15 |
22
57
31 |
30
0
30 |
4
5
6 |
0
0
0 |
9
12
14 |
51
19
47 |
22
13
4 |
52
35
18 |
12
15
18 |
5
6
7 |
10
11
12 |
9
10
11 |
51
50
49 |
22
31
39 |
52
9
26 |
12
25
38 |
5
17
30 |
10
41
12 |
||
504
522
540 |
237
233
228 |
27
5
42 |
56
22
48 |
57
33
10 |
36
56
17 |
6
40
15 |
0
30
0 |
7
8
9 |
0
0
0 |
17
19
22 |
14
42
10 |
55
45
36 |
1
44
27 |
21
24
27 |
9
10
11 |
13
14
15 |
12
13
14 |
48
47
47 |
47
56
4 |
43
1
18 |
51
4
18 |
42
55
7 |
43
14
45 |
||
558
576
594 |
224
219
215 |
20
57
35 |
13
39
4 |
46
22
59 |
37
58
18 |
49
24
58 |
30
0
30 |
10
11
12 |
0
0
0 |
24
27
29 |
38
6
34 |
27
17
8 |
10
53
36 |
30
33
36 |
12
14
15 |
16
17
18 |
15
16
17 |
46
45
44 |
12
20
29 |
35
52
9 |
31
44
57 |
20
32
45 |
16
47
18 |
||
612
630
648 |
211
206
202 |
12
49
27 |
30
56
21 |
35
12
48 |
39
0
20 |
33
7
42 |
0
30
0 |
13
14
15 |
0
0
0 |
32
34
36 |
1
29
57 |
59
50
40 |
19
2
45 |
39
42
45 |
16
18
19 |
19
20
21 |
18
19
20 |
43
42
41 |
37
45
54 |
27
44
1 |
10
24
37 |
57
10
22 |
49
20
51 |
||
666
684
702 |
198
193
189 |
4
42
19 |
47
13
38 |
24
1
37 |
41
1
22 |
16
51
25 |
30
0
30 |
16
17
18 |
0
0
0 |
39
41
44 |
25
53
21 |
31
22
12 |
28
11
54 |
48
51
54 |
20
21
23 |
22
23
24 |
21
22
23 |
41
40
39 |
2
10
18 |
18
36
53 |
50
3
17 |
35
47
0 |
22
53
24 |
||
720
738
756 |
184
180
176 |
57
34
11 |
4
29
55 |
13
50
26 |
43
3
24 |
0
34
9 |
0
30
0 |
19
20
21 |
0
0
0 |
46
49
51 |
49
16
44 |
3
54
45 |
37
21
4 |
57
0
3 |
24
25
27 |
25
26
27 |
24
25
26 |
38
37
36 |
27
35
43 |
10
27
44 |
30
43
56 |
12
25
37 |
55
26
57 |
||
774
792
810 |
171
167
163 |
49
26
4 |
21
47
13 |
2
39
15 |
44
5
25 |
43
18
52 |
30
0
30 |
22
23
24 |
0
0
0 |
54
56
59 |
12
40
8 |
35
26
17 |
47
30
13 |
6
9
12 |
28
29
31 |
28
29
30 |
27
28
29 |
35
35
34 |
52
0
8 |
2
19
36 |
9
23
36 |
50
2
15 |
28
59
30 |
||
⟨III.3⟩ Capitulum tertium: De scientia modorum motus revolubilis convenientis
Quia autem ea que iam narravimus consequitur ut demonstremus ea que videntur et apparent de diversitate motus Solis, vidimus ut premittamus sermonem universalem. Dicam ergo quod motus Solis et motus stellarum retrogradarum in celo, qui sunt secundum continuitatem signorum, et motus localis totius, qui est econtrario illorum, omnes sunt secundum revolutionem et equalitatem et convenientes secundum naturam, scilicet quod linee recte que sunt elongationes stellarum a centris orbium ipsarum quas imaginamur movere stellas aut movere orbes ipsarum in temporibus equalibus faciunt angulos qui sunt apud centrum cuiuscunque circulorum earum equales, et quod diversitas que apparet in eis non est nisi secundum loca et ordines circulorum qui sunt in sphera cuiusque earum supra quos sunt earum motus. Et neque aliquid eorum que imaginamur, scilicet quod sit contrarium permanentie eternitatis motuum earum sicut diversitas estimata, accidit in eis vere et neque accidit nisi secundum imaginationem. Causam vero estimationis huius diversitatis possibile est esse secundum duos modos primos absolutos. Quod si motus stellarum qui videtur esset in orbe cuius centrum estimatur esse centrum mundi quod est in superficie orbis signorum et neque esset aspectus oculorum nostrorum nisi a centro, non videretur in motu earum diversitas. Quapropter estimamus quod motus earum sint secundum unum duorum modorum, aut supra orbes quorum centra non sunt centrum mundi, sed sunt egredientia ab ipso, et sunt motus earum medii, aut sunt super orbes quorum centra sunt centrum mundi, sed non sunt supra ipsos secundum sermonem absolute, sed sunt supra orbes alios, qui sunt supra hos orbes revolventes eas qui nominantur orbes revolventes stellas. Declarabitur namque quod possibile est ut videantur secundum unumquemque horum duorum modorum in temporibus equalibus transire super arcus diversos orbis signorum cuius centrum est centrum mundi. Describam autem cuiusque horum duorum modorum exemplum, et primum ponam circulum orbis ecentrici.
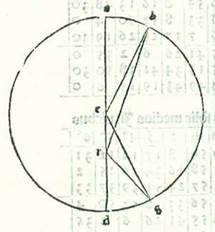 Describam itaque circulum orbis ecentrici, supra quem sint A, B, G, D, supra quem est motus stelle equalis cuius centrum sit E et eius diameter AED, sitque supra ipsam nota RA, qua est aspectus oculorum nostrorum, et ponam ut punctum A sit locus longitudinis longioris a terra et punctum D sit locus longitudinis propinquioris terre, et secabo ex eo duos arcus equales, arcum AB et arcum GD, et protraham lineas BE et BR et GE et GR. Declarabitur ergo nobis quod cum movetur stella in temporibus equalibus super arcum AB et arcum GD, estimatur quod transitus stelle fuit supra duos arcus diversos orbis revoluti supra centrum R, ideo quod angulus BEA est equalis angulo GED. Estimamus ergo quod angulus BRA est minor unoquoque eorum et quod angulus GRD est maior unoquoque eorum.
Describam itaque circulum orbis ecentrici, supra quem sint A, B, G, D, supra quem est motus stelle equalis cuius centrum sit E et eius diameter AED, sitque supra ipsam nota RA, qua est aspectus oculorum nostrorum, et ponam ut punctum A sit locus longitudinis longioris a terra et punctum D sit locus longitudinis propinquioris terre, et secabo ex eo duos arcus equales, arcum AB et arcum GD, et protraham lineas BE et BR et GE et GR. Declarabitur ergo nobis quod cum movetur stella in temporibus equalibus super arcum AB et arcum GD, estimatur quod transitus stelle fuit supra duos arcus diversos orbis revoluti supra centrum R, ideo quod angulus BEA est equalis angulo GED. Estimamus ergo quod angulus BRA est minor unoquoque eorum et quod angulus GRD est maior unoquoque eorum. 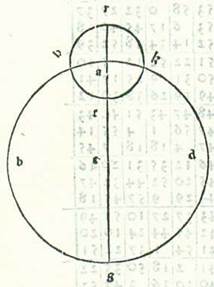 Quod si nos imaginati fuerimus motum stelle secundum modum orbis revolutionis et descripserimus orbem cuius centrum sit centrum circuli signorum, supra quem sint A, B, G, D et cuius centrum sit E et eius diameter sit AEG, et descripserimus super ipsum orbem revolutionis supra quem revolvatur stella, supra quem sint R, H, T, K supra centrum A, et sit revolutio centri orbis revolutionis supra orbem cuius centrum est centrum orbis signorum, supra quem sunt A, B, G, D, similiter declarabitur nobis quod cum fuerit motus medius orbis revolutionis supra orbem ABGD a puncto A, verbi gratia ad punctum B, et fuerit motus stelle etiam secundum hoc exemplum in orbe revolutionis, tunc cum fuerit stella supra duo puncta R et T, non videbitur diversitas in puncto A, quod est centrum orbis revolutionis. Et cum fuerit alibi inter duo puncta, non erit ita, sed estimabitur verbi gratia ut cum videatur supra punctum H, sit motus eius maior medio secundum arcum AH, et cum fuerit supra punctum K, estimabitur quod motus eius sit minor medio secundum arcum AK. Secundum modum vero orbis ecentrici erit minor duorum motuum semper in longitudine longiore et maior eorum erit in longitudine propinquiore, eo quod angulus ARB sit minor angulo DRG semper. Sed secundum modum orbis revolutionis possibile est ut sint ambo motus simul in longitudine longiore, verbi gratia quod centrum orbis revolutionis non moveatur nisi ab occidente ad orientem, quod est ab A ad B. Cum ergo motus stelle fuerit in orbe revolutionis a longitudine longiore ab occidente ad orientem etiam, quod est ab R ad H, tunc motus stelle maior erit in longitudine longiore, propter hoc quod duo motus simul sunt in partem unam. Sed cum motus stelle fuerit a longitudine longiore in orbe revolutionis ab oriente ad occidentem, quod est ab R ad K, tunc econtrario illius erit motus minor in longitudine longiore, quoniam motus stelle est contra motum orbis revolutionis. Postquam ergo hec ita sunt, premittam post hec et dicam quod quecunque stellarum habuerit duas diversitates possibile est hos duos modos componi in ea, quemadmodum demonstrabimus illud in libro nostro de ea cum pervenerimus ad locum eius. Sed quecunque earum fuerit non habens nisi diversitatem unam tantum, unus duorum modorum sufficiet iam nobis in ea. Omne enim quod apparet in unoquoque duorum modorum reperitur non eis contrarium que sunt in altero quando proportiones in utrisque modis simul sunt une, scilicet cum fuerit secundum modum centri egredientis proportio spacii quod est inter duo centra, quod est spacium aspectus oculorum a centro egrediente ad longitudinem centri egredientis ab orbe suo, equalis proportioni longitudinis centri orbis revolutionis ab orbe suo ad longitudinem centri orbis supra quem revolvitur orbis revolutionis ab orbe suo, et etiam tempus in quo erit motus stelle in orbe ecentrico ab occidente ad orientem orbe ecentrico fixo et immobili fuerit equale tempori in quo erit motus centri orbis revolutionis in orbe cuius centrum est aspectus oculorum ab occidente ad orientem, et equale etiam tempori in quo erit motus stelle in orbe revolutionis, sed eius motus localis erit a longitudine longiore ab oriente ad occidentem. Et postquam hoc ita est, demonstrabo breviter et quam paucissimis verbis quod totum quod apparet est in utrisque modis equale. Deinde post illud ostendam per numeros computationis diversitatem motus Solis. Et dico primum quod in unoquoque duorum modorum erit diversitas maior que est inter motum equalem et motum qui apparet diversus apud transitum stelle medium intellectum cum numerabitur eius cursus a principio motus sui a longitudine longiore usquequo secet quartam orbis signorum, et quod tempus quod est a longitudine longiore usque ad hunc transitum medium quem nominavimus est longius tempore quod est a transitu medio usque ad longitudinem propinquiorem. Quapropter secundum modum orbis centri egredientis similiter erit semper. Sed secundum modum orbis revolutionis, cum fuerit motus localis stelle a longitudine longiore in orbe revolutionis ab oriente ad occidentem, erit tempus quod est a motu minore ad motum medium longius tempore quod est a motu medio ad motum maiorem, eo quod secundum unumquemque duorum modorum erit motus minor in longitudine longiore. Et cum fuerit motus localis stelle in orbe revolutionis a longitudine longiore ab occidente ad orientem, erit motus stelle a longitudine longiore econtrario illius, scilicet erit tempus quod est a motu maiore ad medium longius tempore quod est a motu medio ad minorem, quoniam motus maior erit in longitudine longiore.
Quod si nos imaginati fuerimus motum stelle secundum modum orbis revolutionis et descripserimus orbem cuius centrum sit centrum circuli signorum, supra quem sint A, B, G, D et cuius centrum sit E et eius diameter sit AEG, et descripserimus super ipsum orbem revolutionis supra quem revolvatur stella, supra quem sint R, H, T, K supra centrum A, et sit revolutio centri orbis revolutionis supra orbem cuius centrum est centrum orbis signorum, supra quem sunt A, B, G, D, similiter declarabitur nobis quod cum fuerit motus medius orbis revolutionis supra orbem ABGD a puncto A, verbi gratia ad punctum B, et fuerit motus stelle etiam secundum hoc exemplum in orbe revolutionis, tunc cum fuerit stella supra duo puncta R et T, non videbitur diversitas in puncto A, quod est centrum orbis revolutionis. Et cum fuerit alibi inter duo puncta, non erit ita, sed estimabitur verbi gratia ut cum videatur supra punctum H, sit motus eius maior medio secundum arcum AH, et cum fuerit supra punctum K, estimabitur quod motus eius sit minor medio secundum arcum AK. Secundum modum vero orbis ecentrici erit minor duorum motuum semper in longitudine longiore et maior eorum erit in longitudine propinquiore, eo quod angulus ARB sit minor angulo DRG semper. Sed secundum modum orbis revolutionis possibile est ut sint ambo motus simul in longitudine longiore, verbi gratia quod centrum orbis revolutionis non moveatur nisi ab occidente ad orientem, quod est ab A ad B. Cum ergo motus stelle fuerit in orbe revolutionis a longitudine longiore ab occidente ad orientem etiam, quod est ab R ad H, tunc motus stelle maior erit in longitudine longiore, propter hoc quod duo motus simul sunt in partem unam. Sed cum motus stelle fuerit a longitudine longiore in orbe revolutionis ab oriente ad occidentem, quod est ab R ad K, tunc econtrario illius erit motus minor in longitudine longiore, quoniam motus stelle est contra motum orbis revolutionis. Postquam ergo hec ita sunt, premittam post hec et dicam quod quecunque stellarum habuerit duas diversitates possibile est hos duos modos componi in ea, quemadmodum demonstrabimus illud in libro nostro de ea cum pervenerimus ad locum eius. Sed quecunque earum fuerit non habens nisi diversitatem unam tantum, unus duorum modorum sufficiet iam nobis in ea. Omne enim quod apparet in unoquoque duorum modorum reperitur non eis contrarium que sunt in altero quando proportiones in utrisque modis simul sunt une, scilicet cum fuerit secundum modum centri egredientis proportio spacii quod est inter duo centra, quod est spacium aspectus oculorum a centro egrediente ad longitudinem centri egredientis ab orbe suo, equalis proportioni longitudinis centri orbis revolutionis ab orbe suo ad longitudinem centri orbis supra quem revolvitur orbis revolutionis ab orbe suo, et etiam tempus in quo erit motus stelle in orbe ecentrico ab occidente ad orientem orbe ecentrico fixo et immobili fuerit equale tempori in quo erit motus centri orbis revolutionis in orbe cuius centrum est aspectus oculorum ab occidente ad orientem, et equale etiam tempori in quo erit motus stelle in orbe revolutionis, sed eius motus localis erit a longitudine longiore ab oriente ad occidentem. Et postquam hoc ita est, demonstrabo breviter et quam paucissimis verbis quod totum quod apparet est in utrisque modis equale. Deinde post illud ostendam per numeros computationis diversitatem motus Solis. Et dico primum quod in unoquoque duorum modorum erit diversitas maior que est inter motum equalem et motum qui apparet diversus apud transitum stelle medium intellectum cum numerabitur eius cursus a principio motus sui a longitudine longiore usquequo secet quartam orbis signorum, et quod tempus quod est a longitudine longiore usque ad hunc transitum medium quem nominavimus est longius tempore quod est a transitu medio usque ad longitudinem propinquiorem. Quapropter secundum modum orbis centri egredientis similiter erit semper. Sed secundum modum orbis revolutionis, cum fuerit motus localis stelle a longitudine longiore in orbe revolutionis ab oriente ad occidentem, erit tempus quod est a motu minore ad motum medium longius tempore quod est a motu medio ad motum maiorem, eo quod secundum unumquemque duorum modorum erit motus minor in longitudine longiore. Et cum fuerit motus localis stelle in orbe revolutionis a longitudine longiore ab occidente ad orientem, erit motus stelle a longitudine longiore econtrario illius, scilicet erit tempus quod est a motu maiore ad medium longius tempore quod est a motu medio ad minorem, quoniam motus maior erit in longitudine longiore.
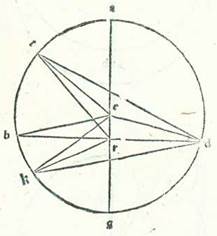 Describam itaque stelle primum orbem ecentricum, supra quem sint A, B, G, D, supra centrum E et diametrum AEG, et ponam in diametro centrum orbis signorum, quod est aspectus oculorum, supra quod sit nota R, et faciam transire per R lineam ortogonaliter super diametrum AEG, supra quam sint B, R, D, sitque stella super duas notas B et D ad hoc ut sit spacium earum quod videtur a duobus finibus usque ad punctum A quod est longitudo longior quarta circuli. Demonstrabitur enim tunc quod diversitas maior que est inter motum medium et motum diversum erit apud duas notas B et D. Protraham ergo duas lineas EB et ED. Ex hoc enim declarabitur quod proportio anguli EBR ad quattuor angulos rectos est sicut proportio arcus diversitatis ad totum circulum, quoniam angulus AEB est sub arcu motus medii, et angulus ARB est sub arcu eius quod apparet ex diversitate, et superfluum quod est inter eos est angulus EBR. Et dico quod non erigitur alius angulus, qui sit maior unoquoque horum duorum angulorum, in circulo ABGD super lineam ER. Erigantur ergo duo anguli apud punctum T et punctum K, qui sint angulus ETR et angulus EKR, et protraham duas lineas TD et KD. Et quia in omni triangulo linea longior subtenditur angulo maiori et linea TR est longior linea RD, erit angulus TDR maior angulo DTR. Sed angulus EDT est equalis angulo ETD, quoniam linea ED est equalis linee ET. Ergo angulus EDR, qui est equalis angulo EBR, erit maior angulo ETR. Et quia etiam linea DR est longior linea KR, erit angulus RKD maior angulo RDK. Totus autem angulus EKD est equalis toti angulo EDK, quoniam linea EK etiam est equalis linee ED. Ergo angulus EDR residuus, qui est equalis angulo EBR, est maior angulo EKR. Non est ergo possibile ut erigantur anguli alii maiores his duobus angulis secundum modum quem prediximus apud duo puncta B et D. Iam vero demonstratum est cum hoc quod arcus AB, qui est tempus quod est a motu minore ad motum medium, est longior arcu BG, qui est apud tempus quod est a motu medio ad motum maiorem, per duos arcus qui videntur ex diversitate, quoniam angulus AEB est maior angulo ERB per angulum EBR et angulus BEG est minor eo per ipsum.
Describam itaque stelle primum orbem ecentricum, supra quem sint A, B, G, D, supra centrum E et diametrum AEG, et ponam in diametro centrum orbis signorum, quod est aspectus oculorum, supra quod sit nota R, et faciam transire per R lineam ortogonaliter super diametrum AEG, supra quam sint B, R, D, sitque stella super duas notas B et D ad hoc ut sit spacium earum quod videtur a duobus finibus usque ad punctum A quod est longitudo longior quarta circuli. Demonstrabitur enim tunc quod diversitas maior que est inter motum medium et motum diversum erit apud duas notas B et D. Protraham ergo duas lineas EB et ED. Ex hoc enim declarabitur quod proportio anguli EBR ad quattuor angulos rectos est sicut proportio arcus diversitatis ad totum circulum, quoniam angulus AEB est sub arcu motus medii, et angulus ARB est sub arcu eius quod apparet ex diversitate, et superfluum quod est inter eos est angulus EBR. Et dico quod non erigitur alius angulus, qui sit maior unoquoque horum duorum angulorum, in circulo ABGD super lineam ER. Erigantur ergo duo anguli apud punctum T et punctum K, qui sint angulus ETR et angulus EKR, et protraham duas lineas TD et KD. Et quia in omni triangulo linea longior subtenditur angulo maiori et linea TR est longior linea RD, erit angulus TDR maior angulo DTR. Sed angulus EDT est equalis angulo ETD, quoniam linea ED est equalis linee ET. Ergo angulus EDR, qui est equalis angulo EBR, erit maior angulo ETR. Et quia etiam linea DR est longior linea KR, erit angulus RKD maior angulo RDK. Totus autem angulus EKD est equalis toti angulo EDK, quoniam linea EK etiam est equalis linee ED. Ergo angulus EDR residuus, qui est equalis angulo EBR, est maior angulo EKR. Non est ergo possibile ut erigantur anguli alii maiores his duobus angulis secundum modum quem prediximus apud duo puncta B et D. Iam vero demonstratum est cum hoc quod arcus AB, qui est tempus quod est a motu minore ad motum medium, est longior arcu BG, qui est apud tempus quod est a motu medio ad motum maiorem, per duos arcus qui videntur ex diversitate, quoniam angulus AEB est maior angulo ERB per angulum EBR et angulus BEG est minor eo per ipsum.
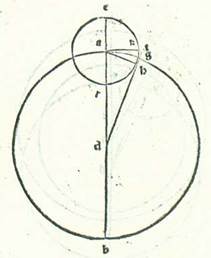 Ad hoc vero ut declaretur etiam secundum modum alium quod ea que accidunt similiter reperiuntur in eo, describam circulum cuius centrum sit centrum mundi, supra quem sint A, B, G, supra centrum D et diametrum ADB, et revolutionis orbem qui revolvitur super ipsum et in eius superficie, supra quem sint E, R, H, supra centrum A, sitque stella supra punctum H cum videtur eius longitudo a puncto longitudinis longioris quarta circuli. Protraham autem duas lineas AH et DHG. Dico ergo quod DHG contingit orbem revolutionis in puncto H et quod apud illum erit diversitas maior que est inter motum medium et diversum. Et quia motus medius qui est a longitudine longiore continetur ab angulo EAH propter hoc quod motus stelle in orbe revolutionis et motus centri orbis revolutionis in orbe ABG sunt equalis velocitatis, sed diversitas que est inter motum medium et motum qui videtur continetur ab angulo ADH, ergo manifestum est quod superfluum quod est inter duos angulos EAH et ADH, qui est angulus AHD, continet spacium quod videtur inter stellam et longitudinem longiorem. Et quia hoc spacium est quarta circuli, erit angulus AHD rectus. Quapropter erit linea DHG contingens orbem revolutionis, supra quem sunt E, R, H. Arcus ergo AG est diversitas maior que est inter motum medium et motum diversum. Quapropter arcus EH, qui est tempus quod est a motu minore ad motum medium, secundum quod declaratum est hic ex motu locali stelle in orbe revolutionis erit maior HR, qui est tempus quod est a medio motu ad maiorem per duplum arcus AG. Si enim protraxerimus lineam DHT et lineaverimus AKT ortogonaliter super lineam ER, erit angulus KAH equalis angulo ADG et arcus KH similis arcui AG. Et cum hoc arcu erit arcus EKH maior quarta una et arcus RH minor quarta una cum eo. Et hoc est quod oportuit nos demonstrare.
Ad hoc vero ut declaretur etiam secundum modum alium quod ea que accidunt similiter reperiuntur in eo, describam circulum cuius centrum sit centrum mundi, supra quem sint A, B, G, supra centrum D et diametrum ADB, et revolutionis orbem qui revolvitur super ipsum et in eius superficie, supra quem sint E, R, H, supra centrum A, sitque stella supra punctum H cum videtur eius longitudo a puncto longitudinis longioris quarta circuli. Protraham autem duas lineas AH et DHG. Dico ergo quod DHG contingit orbem revolutionis in puncto H et quod apud illum erit diversitas maior que est inter motum medium et diversum. Et quia motus medius qui est a longitudine longiore continetur ab angulo EAH propter hoc quod motus stelle in orbe revolutionis et motus centri orbis revolutionis in orbe ABG sunt equalis velocitatis, sed diversitas que est inter motum medium et motum qui videtur continetur ab angulo ADH, ergo manifestum est quod superfluum quod est inter duos angulos EAH et ADH, qui est angulus AHD, continet spacium quod videtur inter stellam et longitudinem longiorem. Et quia hoc spacium est quarta circuli, erit angulus AHD rectus. Quapropter erit linea DHG contingens orbem revolutionis, supra quem sunt E, R, H. Arcus ergo AG est diversitas maior que est inter motum medium et motum diversum. Quapropter arcus EH, qui est tempus quod est a motu minore ad motum medium, secundum quod declaratum est hic ex motu locali stelle in orbe revolutionis erit maior HR, qui est tempus quod est a medio motu ad maiorem per duplum arcus AG. Si enim protraxerimus lineam DHT et lineaverimus AKT ortogonaliter super lineam ER, erit angulus KAH equalis angulo ADG et arcus KH similis arcui AG. Et cum hoc arcu erit arcus EKH maior quarta una et arcus RH minor quarta una cum eo. Et hoc est quod oportuit nos demonstrare.
Demonstrabimus autem per illud quod narrabimus cuique volenti comprehendere scientiam quod totum quod est in motuum speciebus, scilicet motuum mediorum et motuum qui videntur, et quod est inter eos ex superfluo, quod est diversitas, in temporibus equalibus est equale semper secundum unumquemque duorum modorum. 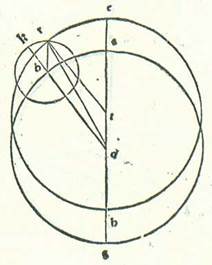 Et describam ad hoc circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et circulum alium ei equalem, cuius centrum egrediatur a centro eius, supra quem sint E, R, H, super centrum T super diametrum unam ambobus communem quam faciam transire supra duo centra usque ad punctum E, quod est longitudo longior, supra quam sint E, A, T, D, et dividam ex circulo ABG arcum secundum quam quantitatem voluerimus, supra quem sint A, B, et describam orbem revolutionis supra centrum B et secundum longitudinem DT, supra quem sint K, R, et protraham lineam DBK. Dico ergo quod stella in unoquoque duorum motuum in uno tempore vadit ad locum sectionis orbis ecentrici et orbis revolutionis sine dubio, qui est punctum R, et erunt arcus tres similes, arcus scilicet ER orbis ecentrici et arcus AB orbis signorum et arcus KR orbis revolutionis, et diversitas que est inter motum medium et inter diversum et motum stelle qui videtur cum hoc toto est secundum duos modos cum re una et similitudine una equaliter. Protraham ergo lineas RT et BR et DR. Fit igitur figura quadrilatera, supra quam sunt B, D, T, R, et fiunt omnia duo latera eius opposita equalia, scilicet TR equale BD et BR equale DT. Erit ergo quadrilaterum equidistantium laterum, scilicet BD equidistat RT et BR equidistat DT. Erunt ergo tres anguli equales, scilicet angulus ETR et angulus ADB et angulus RBK. Et quia ipsi sunt apud centrum, tunc arcus qui subtenduntur eis sunt similes, scilicet arcus ER circuli ecentrici et arcus AB circuli orbis signorum et arcus KR orbis revolutionis. Secundum ergo ambos motus in tempore uno vadit stella ad punctum R et ad arcum orbis signorum quem iam videtur stella secuisse a longitudine longiore. Hoc vero sequitur ut sit quantitas diversitatis etiam in unoquoque duorum modorum una. Nos enim iam demonstravimus quod hec diversitas secundum modum orbis ecentrici continetur ab angulo DRT et secundum modum orbis revolutionis continetur ab angulo BDR. Hi autem duo anguli sunt equales coalterni, propter hoc quod iam ostendimus quod RT equidistat BD. Et manifestum est quod illud in omnibus longitudinibus erit similiter. Quadrilaterum namque supra quod sunt B, D, R, T est semper equidistantium laterum, et motus stelle localis in orbe revolutionis est qui signat orbem ecentricum cum fuerint proportiones in unoquoque duorum modorum similes et equales.
Et describam ad hoc circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et circulum alium ei equalem, cuius centrum egrediatur a centro eius, supra quem sint E, R, H, super centrum T super diametrum unam ambobus communem quam faciam transire supra duo centra usque ad punctum E, quod est longitudo longior, supra quam sint E, A, T, D, et dividam ex circulo ABG arcum secundum quam quantitatem voluerimus, supra quem sint A, B, et describam orbem revolutionis supra centrum B et secundum longitudinem DT, supra quem sint K, R, et protraham lineam DBK. Dico ergo quod stella in unoquoque duorum motuum in uno tempore vadit ad locum sectionis orbis ecentrici et orbis revolutionis sine dubio, qui est punctum R, et erunt arcus tres similes, arcus scilicet ER orbis ecentrici et arcus AB orbis signorum et arcus KR orbis revolutionis, et diversitas que est inter motum medium et inter diversum et motum stelle qui videtur cum hoc toto est secundum duos modos cum re una et similitudine una equaliter. Protraham ergo lineas RT et BR et DR. Fit igitur figura quadrilatera, supra quam sunt B, D, T, R, et fiunt omnia duo latera eius opposita equalia, scilicet TR equale BD et BR equale DT. Erit ergo quadrilaterum equidistantium laterum, scilicet BD equidistat RT et BR equidistat DT. Erunt ergo tres anguli equales, scilicet angulus ETR et angulus ADB et angulus RBK. Et quia ipsi sunt apud centrum, tunc arcus qui subtenduntur eis sunt similes, scilicet arcus ER circuli ecentrici et arcus AB circuli orbis signorum et arcus KR orbis revolutionis. Secundum ergo ambos motus in tempore uno vadit stella ad punctum R et ad arcum orbis signorum quem iam videtur stella secuisse a longitudine longiore. Hoc vero sequitur ut sit quantitas diversitatis etiam in unoquoque duorum modorum una. Nos enim iam demonstravimus quod hec diversitas secundum modum orbis ecentrici continetur ab angulo DRT et secundum modum orbis revolutionis continetur ab angulo BDR. Hi autem duo anguli sunt equales coalterni, propter hoc quod iam ostendimus quod RT equidistat BD. Et manifestum est quod illud in omnibus longitudinibus erit similiter. Quadrilaterum namque supra quod sunt B, D, R, T est semper equidistantium laterum, et motus stelle localis in orbe revolutionis est qui signat orbem ecentricum cum fuerint proportiones in unoquoque duorum modorum similes et equales.
Demonstrabo autem quod quantitates arcuum similium, etsi sint diversarum quantitatum, tamen quod videtur ex eis que accidunt in eis equale est ei quod videtur in illis que sunt equalium quantitatum. 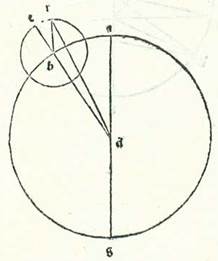 Et ad huiusmodi exemplum circumducam circulum cuius centrum sit centrum mundi, supra quem sint A, B, G supra centrum D, sitque diameter eius, supra quam currit stella in longiore et propinquiore longitudine, supra quam sint A, D, G, et circulus revolutionis revolutus supra centrum, scilicet punctum B, cuius remotio a longitudine longiore est arcus AB, secundum quam quantitatem voluerimus, supra quem sint E, R. Moveatur vero stella in orbe revolutionis secundum quantitatem arcus ER, qui monstratur esse similis arcui AB, propter hoc quod reversiones orbium sunt in temporibus equalibus. Protraham autem lineas DBE et BR et DR. Et propter hoc declarabitur quod duo anguli ADE et RBE sunt equales semper et quod stella secundum hunc modum videtur supra lineam DR.
Et ad huiusmodi exemplum circumducam circulum cuius centrum sit centrum mundi, supra quem sint A, B, G supra centrum D, sitque diameter eius, supra quam currit stella in longiore et propinquiore longitudine, supra quam sint A, D, G, et circulus revolutionis revolutus supra centrum, scilicet punctum B, cuius remotio a longitudine longiore est arcus AB, secundum quam quantitatem voluerimus, supra quem sint E, R. Moveatur vero stella in orbe revolutionis secundum quantitatem arcus ER, qui monstratur esse similis arcui AB, propter hoc quod reversiones orbium sunt in temporibus equalibus. Protraham autem lineas DBE et BR et DR. Et propter hoc declarabitur quod duo anguli ADE et RBE sunt equales semper et quod stella secundum hunc modum videtur supra lineam DR.
Et dico quod cum secundum modum orbis centri egredientis sit ecentricus maior orbe ABG, cuius centrum est centrum mundi, aut sit minor eo, cum fuerint proportiones similes tantum et reversiones in temporibus equalibus, super lineam DR etiam videbitur stella. 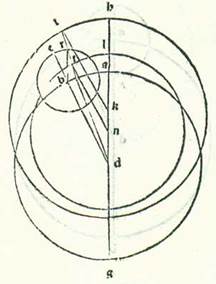 Describam autem orbem ecentricum quem ponam maiorem, sicut diximus, supra quem sint H, T, et sit eius centrum K, supra diametrum AG, et ponam ipsum etiam minorem, supra quem sint L, I, supra centrum N, et producam duas lineas DIR et DAL secundum rectitudinem usque ad T et ad H, et protraham lineas duas TK et IN, et sit proportio DB ad BR sicut proportio TK ad KD et sicut proportio IN ad ND, sed angulus BRD est equalis angulo IDH, quoniam DH et BR sunt equidistantes. Quapropter erunt anguli quibus latera proportionalia subtenduntur quisque minor recto, quoniam sunt anguli diversitatis et equales, scilicet angulus BDR et angulus DTK et angulus DIN. Linee ergo BD et TK et IN sunt equidistantes. Quapropter erunt anguli ADB et AKT et ANI equales. Et quia omnes sunt super centra orbium, erunt arcus qui subtenduntur eis similes, scilicet arcus AB et arcus HT et arcus LI. Non ergo in tempore uno secat orbis revolutionis tantum arcum AB. Stella autem secat arcum ER. Sed stella etiam secat ex orbe ecentrico arcum HT et arcum LI. Quapropter videbitur semper super lineam DIRT, sed in orbe revolutionis cum fuerit supra punctum R, et in orbe ecentrico maiore cum fuerit supra punctum T, et in orbe ecentrico minore cum fuerit supra punctum I. Et similiter videbitur in locis omnibus secundum omnium situs. Et illud est quod oportuit nos demonstrare.
Describam autem orbem ecentricum quem ponam maiorem, sicut diximus, supra quem sint H, T, et sit eius centrum K, supra diametrum AG, et ponam ipsum etiam minorem, supra quem sint L, I, supra centrum N, et producam duas lineas DIR et DAL secundum rectitudinem usque ad T et ad H, et protraham lineas duas TK et IN, et sit proportio DB ad BR sicut proportio TK ad KD et sicut proportio IN ad ND, sed angulus BRD est equalis angulo IDH, quoniam DH et BR sunt equidistantes. Quapropter erunt anguli quibus latera proportionalia subtenduntur quisque minor recto, quoniam sunt anguli diversitatis et equales, scilicet angulus BDR et angulus DTK et angulus DIN. Linee ergo BD et TK et IN sunt equidistantes. Quapropter erunt anguli ADB et AKT et ANI equales. Et quia omnes sunt super centra orbium, erunt arcus qui subtenduntur eis similes, scilicet arcus AB et arcus HT et arcus LI. Non ergo in tempore uno secat orbis revolutionis tantum arcum AB. Stella autem secat arcum ER. Sed stella etiam secat ex orbe ecentrico arcum HT et arcum LI. Quapropter videbitur semper super lineam DIRT, sed in orbe revolutionis cum fuerit supra punctum R, et in orbe ecentrico maiore cum fuerit supra punctum T, et in orbe ecentrico minore cum fuerit supra punctum I. Et similiter videbitur in locis omnibus secundum omnium situs. Et illud est quod oportuit nos demonstrare.
Accidit autem in hoc ut cum stella fuerit visa secuisse duos arcus equalis longitudinis a longitudine longiore et a longitudine propinquiore, tunc diversitas sit in unoquoque ipsorum duorum locorum una. 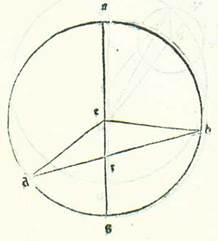 Si enim lineaverimus circulum secundum modum orbis ecentrici super centrum E, super quem sint A, B, G, D, et diameter eius sit AEG, et posuerimus aspectum oculorum super diametrum a puncto R transeuntem super ipsam usque ad punctum A, quod est longior longitudo, et protraxerimus supra punctum R lineam sicut voluerimus, supra quam sint B, R, D, et protraxerimus duas lineas EB et ED, tunc duo arcus supra quos visa est stella pertransisse erunt oppositi et equales. Per quod scilicet intelligi volumus quod anguli ARB, qui est longitudinis longioris, et anguli GRD, qui est longitudinis propinquioris, erit diversitas una, quoniam BE est equalis ED et angulus EBR est equalis angulo EDR. Diversitas ergo, que est quantitatis arcus qui videtur, est una, scilicet arcus qui subtenditur unicuique duorum angulorum ARB et GRD. Secundum quantitatem ergo illius arcus erit arcus motus stelle a puncto A, quod est longitudo longior, maior motu medio, et secundum quantitatem illius arcus etiam erit arcus motus stelle qui est a puncto G, quod est longitudo propinquior, minor, propter hoc quod angulus AEB est maior angulo ARB et angulus GED est minor angulo GRD equaliter. Et illud est quod oportuit nos demonstrare.
Si enim lineaverimus circulum secundum modum orbis ecentrici super centrum E, super quem sint A, B, G, D, et diameter eius sit AEG, et posuerimus aspectum oculorum super diametrum a puncto R transeuntem super ipsam usque ad punctum A, quod est longior longitudo, et protraxerimus supra punctum R lineam sicut voluerimus, supra quam sint B, R, D, et protraxerimus duas lineas EB et ED, tunc duo arcus supra quos visa est stella pertransisse erunt oppositi et equales. Per quod scilicet intelligi volumus quod anguli ARB, qui est longitudinis longioris, et anguli GRD, qui est longitudinis propinquioris, erit diversitas una, quoniam BE est equalis ED et angulus EBR est equalis angulo EDR. Diversitas ergo, que est quantitatis arcus qui videtur, est una, scilicet arcus qui subtenditur unicuique duorum angulorum ARB et GRD. Secundum quantitatem ergo illius arcus erit arcus motus stelle a puncto A, quod est longitudo longior, maior motu medio, et secundum quantitatem illius arcus etiam erit arcus motus stelle qui est a puncto G, quod est longitudo propinquior, minor, propter hoc quod angulus AEB est maior angulo ARB et angulus GED est minor angulo GRD equaliter. Et illud est quod oportuit nos demonstrare.
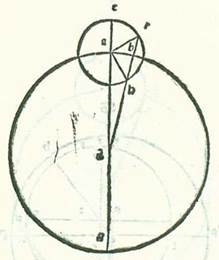 Quod si lineaverimus circulum secundum modum orbis revolutionis cuius centrum sit centrum mundi, supra quem sint A, B, G super centrum D, sitque diameter eius ADG, et supra orbem revolutionis sint E, R, H, et sit super centrum A, et protraxerimus a puncto D lineam rectam, supra quam sint D, H, R quocunque modo voluerimus, et protraxerimus lineas duas AR et AH, fiet ut arcus AB sit etiam arcus diversitatis, sive fuerit stella supra punctum R sive supra punctum H, et videatur eius longitudo a longitudine longiore in orbe signorum cum fuerit supra punctum R et longitudo eius a longitudine propinquiore cum fuerit supra punctum H una, quoniam arcus qui videtur a longitudine longiore subtenditur angulo DRA. Iam enim ostensum est quod ipse est diversitas que est inter motum medium et motum visionis. Et arcus visionis qui subtenditur angulo RHA ipse est etiam equalis motui medio qui est a longitudine propinquiore et diversitati visionis. Sed angulus DRA est equalis angulo RHA, quoniam linea AR est equalis linee AH. Ex his igitur colligitur etiam ut secundum diversitatem unam, que est angulus ADB, sit motus medius qui est apud longitudinem longiorem maior eo qui videtur (per quod scilicet intelligi volumus quod angulus EAR est maior angulo ARD) et motus medius qui est apud longitudinem propinquiorem sit minor eo qui videtur, qui est ipse idem. Per quod scilicet intelligi volumus quod angulus HAD est minor angulo AHR. Et illud est quod oportuit nos demonstrare.
Quod si lineaverimus circulum secundum modum orbis revolutionis cuius centrum sit centrum mundi, supra quem sint A, B, G super centrum D, sitque diameter eius ADG, et supra orbem revolutionis sint E, R, H, et sit super centrum A, et protraxerimus a puncto D lineam rectam, supra quam sint D, H, R quocunque modo voluerimus, et protraxerimus lineas duas AR et AH, fiet ut arcus AB sit etiam arcus diversitatis, sive fuerit stella supra punctum R sive supra punctum H, et videatur eius longitudo a longitudine longiore in orbe signorum cum fuerit supra punctum R et longitudo eius a longitudine propinquiore cum fuerit supra punctum H una, quoniam arcus qui videtur a longitudine longiore subtenditur angulo DRA. Iam enim ostensum est quod ipse est diversitas que est inter motum medium et motum visionis. Et arcus visionis qui subtenditur angulo RHA ipse est etiam equalis motui medio qui est a longitudine propinquiore et diversitati visionis. Sed angulus DRA est equalis angulo RHA, quoniam linea AR est equalis linee AH. Ex his igitur colligitur etiam ut secundum diversitatem unam, que est angulus ADB, sit motus medius qui est apud longitudinem longiorem maior eo qui videtur (per quod scilicet intelligi volumus quod angulus EAR est maior angulo ARD) et motus medius qui est apud longitudinem propinquiorem sit minor eo qui videtur, qui est ipse idem. Per quod scilicet intelligi volumus quod angulus HAD est minor angulo AHR. Et illud est quod oportuit nos demonstrare.
⟨III.4⟩ Capitulum quartum: De scientia eorum que apparent ex diversitate motus Solis in aspectu et visione
Et postquam premisimus ea que premittenda erant de ea, premittemus nunc sermonem de eis que videntur de diversitate motus Solis, propter hoc quod ipsa est una. Et ponam tempus quod est a motu minore usque ad motum medium longius tempore quod est a motu medio usque ad motum maiorem. Nos namque iam invenimus illud conveniens ei quod videtur et apparet. Iam ergo possibile est ut sit hoc secundum unumquemque horum duorum modorum. Sed cum ipsum fuerit acceptum secundum modum orbis revolutionis, non erit nisi cum fuerit motus localis Solis in arcu longitudinis longioris ab oriente ad occidentem. Et convenientior duorum modorum quo investigatur scientia diversitatis motus Solis est modus orbis ecentrici, eo quod ipse est manifestior et velocior et facilior et quod ipse est ex uno motu, et non est ex duobus. Et postquam oportet ut premittamus in hoc inquisitionem inventionis proportionis orbis ecentrici solaris, per quod intelligi volumus proportionem linee que est inter duo centra, scilicet centrum orbis ecentrici et centrum aspectus oculorum, quod est centrum orbis signorum ad lineam que egreditur a centro orbis ecentrici usque ad orbem ipsius, et etiam supra quam partem orbis signorum cadat punctum longitudinis longioris orbis ecentrici, tunc declarabimus illud. Iam enim manifestum fuit hoc Abrachis vehementi studio. Et posuit tempus quod est ab equalitate vernali usque ad tropicum estivalem nonagintaquattuor dies et medietatem diei, et tempus quod est a tropico estivali usque ad equalitatem autumnalem nonagintaduos dies et medietatem diei. Per ea ergo que declaravit nobis ex hoc tantum demonstrabitur quantitas longitudinis que est inter duo centra, quam diximus esse unam vigintiquattuor partium linee que progreditur a centro egrediente usque ad orbem suum. Et eius longitudo longior precedit tropicum estivum vigintiquattuor partibus et medietate partis secundum quantitatem qua est orbis signorum 360 partes. Nos quoque similiter invenimus duo tempora harum duarum quartarum et has proportiones. Et ex hoc declarabitur nobis quod orbis ecentricus fixus est in loco suo semper a duobus punctis equalitatis et conversionis. Et ut non pretermittamus dicere hunc locum, sed eius demonstremus scientiam nostra computatione, ponemus eius declarationem per orbem ecentricum et assumemus in declaratione illius has causas apparentes et manifestas, que sunt, sicut premisimus, quod tempus quod est ab equalitate vernali usque ad tropicum estivalem est 94 dies et medietas diei et tempus quod est a tropico estivali usque ad equalitatem autumnalem est 92 dies et medietas diei. Nos quoque similiter reperimus numerum dierum horum duorum spaciorum certificatione nostrarum considerationum de temporibus equalitatis et conversionis estive quas consideravimus in anno 463 post mortem Alexandri convenientem. Quoniam, sicut diximus, fuit equalitas autumnalis in nono die mensis Athus post ortum Solis, et equalitas vernalis fuit septimo die mensis Mathur post medium diem. Aggregantur ergo inter duas considerationes ex numero dierum 178 dies et quarta diei. Et fuit conversio estiva undecimo die mensis Mesur post mediam noctem cuius mane fuit duodecimus dies mensis Mesur. Aggregatio igitur numeri dierum qui fuerunt ab equalitate vernali usque ad conversionem estivam fuit 94 dies et medietas diei. Et remanserunt ex numero dierum qui sunt a tropico estivali usque ad equalitatem autumnalem que est post ipsum 92 dies et medietas diei.
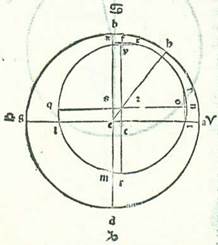 Describam autem circulum orbis signorum, supra quem sint A, B, G, D, supra centrum E, et describam duas eius diametros sese ortogonaliter secantes et euntes supra duo puncta conversionum et duarum equalitatum, supra quas sint A, B, G, D, sitque punctum A equalitas vernalis et punctum B conversio estivalis, et que sunt post hec apposita sint secundum quod oportet. Manifestum est igitur quod centrum orbis egredientis centri cadit inter duas lineas EA et EB, eo quod medietas circuli, supra quam sunt A, B, G, est longius tempus medietate anni. Quapropter secat et comprehendit arcum orbis centri egredientis maiorem medietate circuli. Et quarta supra quam sunt A, B longius tempus est quarta BG et secat ex orbe egredientis centri et comprehendit arcum maiorem eo quem comprehendit BG. Et quoniam quidem hoc ita est, ponam punctum R centrum orbis egredientis centri, et protraham semidiametrum super duo centra et supra longitudinem longiorem, supra quam sint E, R, H, et describam circulum orbis egredientis centri, qui est Solis, super centrum R et secundum longitudinem quam voluerimus, supra quem sint T, K, L, M, et faciam transire duas lineas supra centrum R equidistantes duabus lineis AG et BD, supra quarum unam sint NSQ equidistantem AG et supra alteram FCR equidistantem BD. A puncto quoque T ad lineam NSQ protraham perpendicularem, supra quam sint T, O, P, et a puncto K ad lineam FCR perpendicularem, supra quam sint K, V, X. Et quia Sol transeundo super orbem TKLM per motum suum medium secat arcum TK in 94 diebus et medietate diei et secat arcum KL in nonagintaduobus diebus et medietate diei et est motus eius medius in 94 diebus et medietate diei 93 partes et fere 9 minuta secundum quantitatem qua circulus est 360 partes et in 92 diebus et medietate diei 91 partes et 11 minuta, erit ergo portio TKL 184 partes et 20 minuta et erunt duo arcus TN et LQ, qui sunt residui post medietatem circuli, quattuor partes et 20 minuta. Unusquisque ergo eorum erit due partes et decem minuta. Duplum autem arcus TN est TP. Ergo est quattuor partes et 20 minuta, et erit eius chorda quattuor partes et 32 minuta fere secundum quantitatem qua erit diameter orbis centri egredientis 120 partes, et eius medietas, que est TO et est equalis ES, erit due partes et 16 minuta. Et etiam quia tota portio TNFK est 93 partes et 9 minuta et TN due partes et decem minuta et quarta supra quam sunt N, F 90 partes, remanet arcus FK cifre et 59 minuta, et duplum eius, quod est KFX, pars una et 58 minuta, et eius chorda, que est KVX, erit due partes et quattuor minuta secundum quantitatem qua diameter orbis egredientis centri est 120 partes, et eius medietas, que est KV et est equalis RS, est pars una et duo minuta. Iam vero ostensum fuit quod linea ES est due partes et 16 minuta. Et quia cum coniunxerimus quod aggregatur ex multiplicatione cuiusque earum in se, erit equale multiplicationi ER in se, ergo erit longitudo linee ER due partes et 29 minuta et medium fere secundum quantitatem qua erit linea que est a centro egrediente usque ad ipsius orbem 60 partes. Linea ergo que egreditur a centro egrediente ad ipsius orbem est equalis longitudini que est inter duo centra 24 vicibus fere. Et etiam quia iam est ostensum quod linea ER est due partes et 29 minuta et medium et fuit linea RS pars una et duo minuta, ergo secundum quantitatem qua erit chorda ER 120 partes erit linea RS secundum eam 49 partes et 46 minuta fere, et arcus qui erit super ipsam orbis descripti supra triangulum ERS ortogonium erit 49 partes secundum quantitatem qua erit circulus 360 partes. Angulus ergo RES erit secundum quantitatem qua erunt duo anguli recti 360 partes 49 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit 24 partes et 30 minuta. Et quia angulus est apud centrum orbis signorum, erit arcus BH, qui est inter longitudinem longiorem et inter tropicum estivum, 24 partes et 30 minuta et remanebit unaqueque duarum quartarum supra quas sunt Q, R et R, N 90 partes. Unusquisque autem arcuum QL et TN est due partes et decem minuta, et MR est cifre et 59 minuta. Ergo arcus LM erit 86 partes et 51 minuta, et arcus MT erit 88 partes et 49 minuta. Sol vero secat has 86 partes et 51 minuta per motum suum medium in 88 diebus et octava diei fere et secat 88 partes et 49 minuta in 90 diebus et octava diei fere. Propter hoc ergo videbitur Sol secare arcum GD, qui est ab equalitate autumnali ad conversionem hiemalem, in 88 diebus et octava diei, et arcum DA, qui est a tropico hiemali ad equalitatem vernalem, in 90 diebus et octava diei fere. Iam ergo invenimus ex hoc quod diximus convenire dicto Abrachis.
Describam autem circulum orbis signorum, supra quem sint A, B, G, D, supra centrum E, et describam duas eius diametros sese ortogonaliter secantes et euntes supra duo puncta conversionum et duarum equalitatum, supra quas sint A, B, G, D, sitque punctum A equalitas vernalis et punctum B conversio estivalis, et que sunt post hec apposita sint secundum quod oportet. Manifestum est igitur quod centrum orbis egredientis centri cadit inter duas lineas EA et EB, eo quod medietas circuli, supra quam sunt A, B, G, est longius tempus medietate anni. Quapropter secat et comprehendit arcum orbis centri egredientis maiorem medietate circuli. Et quarta supra quam sunt A, B longius tempus est quarta BG et secat ex orbe egredientis centri et comprehendit arcum maiorem eo quem comprehendit BG. Et quoniam quidem hoc ita est, ponam punctum R centrum orbis egredientis centri, et protraham semidiametrum super duo centra et supra longitudinem longiorem, supra quam sint E, R, H, et describam circulum orbis egredientis centri, qui est Solis, super centrum R et secundum longitudinem quam voluerimus, supra quem sint T, K, L, M, et faciam transire duas lineas supra centrum R equidistantes duabus lineis AG et BD, supra quarum unam sint NSQ equidistantem AG et supra alteram FCR equidistantem BD. A puncto quoque T ad lineam NSQ protraham perpendicularem, supra quam sint T, O, P, et a puncto K ad lineam FCR perpendicularem, supra quam sint K, V, X. Et quia Sol transeundo super orbem TKLM per motum suum medium secat arcum TK in 94 diebus et medietate diei et secat arcum KL in nonagintaduobus diebus et medietate diei et est motus eius medius in 94 diebus et medietate diei 93 partes et fere 9 minuta secundum quantitatem qua circulus est 360 partes et in 92 diebus et medietate diei 91 partes et 11 minuta, erit ergo portio TKL 184 partes et 20 minuta et erunt duo arcus TN et LQ, qui sunt residui post medietatem circuli, quattuor partes et 20 minuta. Unusquisque ergo eorum erit due partes et decem minuta. Duplum autem arcus TN est TP. Ergo est quattuor partes et 20 minuta, et erit eius chorda quattuor partes et 32 minuta fere secundum quantitatem qua erit diameter orbis centri egredientis 120 partes, et eius medietas, que est TO et est equalis ES, erit due partes et 16 minuta. Et etiam quia tota portio TNFK est 93 partes et 9 minuta et TN due partes et decem minuta et quarta supra quam sunt N, F 90 partes, remanet arcus FK cifre et 59 minuta, et duplum eius, quod est KFX, pars una et 58 minuta, et eius chorda, que est KVX, erit due partes et quattuor minuta secundum quantitatem qua diameter orbis egredientis centri est 120 partes, et eius medietas, que est KV et est equalis RS, est pars una et duo minuta. Iam vero ostensum fuit quod linea ES est due partes et 16 minuta. Et quia cum coniunxerimus quod aggregatur ex multiplicatione cuiusque earum in se, erit equale multiplicationi ER in se, ergo erit longitudo linee ER due partes et 29 minuta et medium fere secundum quantitatem qua erit linea que est a centro egrediente usque ad ipsius orbem 60 partes. Linea ergo que egreditur a centro egrediente ad ipsius orbem est equalis longitudini que est inter duo centra 24 vicibus fere. Et etiam quia iam est ostensum quod linea ER est due partes et 29 minuta et medium et fuit linea RS pars una et duo minuta, ergo secundum quantitatem qua erit chorda ER 120 partes erit linea RS secundum eam 49 partes et 46 minuta fere, et arcus qui erit super ipsam orbis descripti supra triangulum ERS ortogonium erit 49 partes secundum quantitatem qua erit circulus 360 partes. Angulus ergo RES erit secundum quantitatem qua erunt duo anguli recti 360 partes 49 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit 24 partes et 30 minuta. Et quia angulus est apud centrum orbis signorum, erit arcus BH, qui est inter longitudinem longiorem et inter tropicum estivum, 24 partes et 30 minuta et remanebit unaqueque duarum quartarum supra quas sunt Q, R et R, N 90 partes. Unusquisque autem arcuum QL et TN est due partes et decem minuta, et MR est cifre et 59 minuta. Ergo arcus LM erit 86 partes et 51 minuta, et arcus MT erit 88 partes et 49 minuta. Sol vero secat has 86 partes et 51 minuta per motum suum medium in 88 diebus et octava diei fere et secat 88 partes et 49 minuta in 90 diebus et octava diei fere. Propter hoc ergo videbitur Sol secare arcum GD, qui est ab equalitate autumnali ad conversionem hiemalem, in 88 diebus et octava diei, et arcum DA, qui est a tropico hiemali ad equalitatem vernalem, in 90 diebus et octava diei fere. Iam ergo invenimus ex hoc quod diximus convenire dicto Abrachis.
Secundum similitudinem vero harum quantitatum inquiram primo quanta sit maior diversitas que est inter motum medium et motum qui videtur et apud que puncta sit hec. 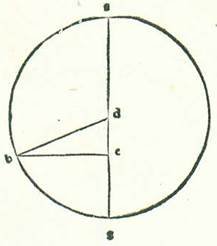 Describam itaque circulum orbis egredientis centri, supra quem sint A, B, G, supra centrum D et diametrum transeuntem a puncto A, quod est longitudo longior, supra quam sint A, D, G, et sit supra ipsam centrum orbis signorum supra punctum E, et protraham a puncto E lineam ortogonaliter supra lineam AG, que sit EB, et protraham lineam DB. Et quia secundum quantitatem qua erit linea BD, que est a centro ad circulum, 60 partes, erit DE, que est inter duo centra, due partes et 30 minuta fere, ergo proportio BD ad DE est vigiesquater tantum. Secundum quantitatem ergo qua chorda BD erit 120 partes erit linea DE quinque partes, et arcus qui erit supra ipsam circuli continentis triangulum BDE ortogonaliter erit quattuor partes et 46 minuta fere secundum quantitatem qua erit circulus 360 partes. Quapropter angulus DBE secundum illas quantitates erit quattuor partes et 46 minuta, qui est angulus continens diversitatem maiorem, et erit hoc secundum quantitatem qua erunt duo anguli recti 360 partes quattuor partes et 46 minuta, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit due partes et 23 minuta. Et secundum illas quantitates erit angulus BED rectus 90 partes, et angulus equalis duobus angulis, qui est angulus BDA, manifestum est quod est 92 partes et 23 minuta. Et quia ipsi sunt apud duo centra, scilicet angulus BDA apud centrum egrediens et angulus BED apud centrum orbis signorum, erit diversitas maior que est inter motum medium et inter motum visionis due partes et 23 minuta, et erunt duo arcus apud quos erit illud, scilicet arcus orbis centri egredientis, qui est motus equalis vel medius, 92 partes et 23 minuta a longitudine longiore, et arcus orbis signorum, qui est motus visionis diverse, erit quarta, scilicet 90 partes, sicut iam ostendimus. Ex his autem que demonstravimus declarabitur quod diversitas maior erit in medietate orbis opposita huic medietati, et motus qui videtur medius erit super 270 partes a longitudine longiore, et motus equalis, qui est super orbem centri egredientis, erit a longitudine longiore etiam super 267 partes et 37 minuta. Et illud est quod oportuit nos demonstrare.
Describam itaque circulum orbis egredientis centri, supra quem sint A, B, G, supra centrum D et diametrum transeuntem a puncto A, quod est longitudo longior, supra quam sint A, D, G, et sit supra ipsam centrum orbis signorum supra punctum E, et protraham a puncto E lineam ortogonaliter supra lineam AG, que sit EB, et protraham lineam DB. Et quia secundum quantitatem qua erit linea BD, que est a centro ad circulum, 60 partes, erit DE, que est inter duo centra, due partes et 30 minuta fere, ergo proportio BD ad DE est vigiesquater tantum. Secundum quantitatem ergo qua chorda BD erit 120 partes erit linea DE quinque partes, et arcus qui erit supra ipsam circuli continentis triangulum BDE ortogonaliter erit quattuor partes et 46 minuta fere secundum quantitatem qua erit circulus 360 partes. Quapropter angulus DBE secundum illas quantitates erit quattuor partes et 46 minuta, qui est angulus continens diversitatem maiorem, et erit hoc secundum quantitatem qua erunt duo anguli recti 360 partes quattuor partes et 46 minuta, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit due partes et 23 minuta. Et secundum illas quantitates erit angulus BED rectus 90 partes, et angulus equalis duobus angulis, qui est angulus BDA, manifestum est quod est 92 partes et 23 minuta. Et quia ipsi sunt apud duo centra, scilicet angulus BDA apud centrum egrediens et angulus BED apud centrum orbis signorum, erit diversitas maior que est inter motum medium et inter motum visionis due partes et 23 minuta, et erunt duo arcus apud quos erit illud, scilicet arcus orbis centri egredientis, qui est motus equalis vel medius, 92 partes et 23 minuta a longitudine longiore, et arcus orbis signorum, qui est motus visionis diverse, erit quarta, scilicet 90 partes, sicut iam ostendimus. Ex his autem que demonstravimus declarabitur quod diversitas maior erit in medietate orbis opposita huic medietati, et motus qui videtur medius erit super 270 partes a longitudine longiore, et motus equalis, qui est super orbem centri egredientis, erit a longitudine longiore etiam super 267 partes et 37 minuta. Et illud est quod oportuit nos demonstrare.
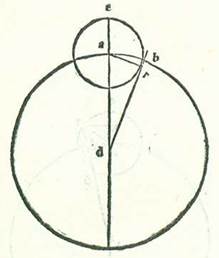 Ad hoc autem ut demonstremus etiam secundum modum orbis revolutionis per numeros quod quantitates ille sunt une cum proportiones fuerint secundum quod diximus, describam circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, super centrum D et diametrum ADG, et orbem revolutionis, supra quem sint E, R, B, supra centrum A, et protraham AD lineam contingentem orbem revolutionis, supra quam sint D, R, B, et protraham lineam AR. Erit ergo in triangulo ADR ortogonio linea AD vigesiesquater tantum quantum linea AR. Et secundum quantitatem qua erit diameter AD 120 partes erit linea AR quinque partes, et arcus qui erit supra ipsam orbis descripti super triangulum ARD ortogonium erit quatuor partes et 46 minuta secundum quantitatem qua erit orbis 360 partes. Angulus ergo ADR tunc secundum partes quibus duo anguli recti sunt 360 partes erit 4 partes et 46 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit due partes et 23 minuta. Diversitatem ergo maiorem, que est arcus AB, iam invenimus quod convenit esse partes duas et 23 minuta. Sed arcus motus diversi, quia subtenditur angulo ARD ortogonio, erit 90 partes, et arcus motus medii qui subtenditur angulo EAR erit 92 partes et 23 minuta. Et ex hoc etiam erit arcus motus centri orbis revolutionis 92 partes et 23 minuta. Et illud est quod oportuit nos declarare.
Ad hoc autem ut demonstremus etiam secundum modum orbis revolutionis per numeros quod quantitates ille sunt une cum proportiones fuerint secundum quod diximus, describam circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, super centrum D et diametrum ADG, et orbem revolutionis, supra quem sint E, R, B, supra centrum A, et protraham AD lineam contingentem orbem revolutionis, supra quam sint D, R, B, et protraham lineam AR. Erit ergo in triangulo ADR ortogonio linea AD vigesiesquater tantum quantum linea AR. Et secundum quantitatem qua erit diameter AD 120 partes erit linea AR quinque partes, et arcus qui erit supra ipsam orbis descripti super triangulum ARD ortogonium erit quatuor partes et 46 minuta secundum quantitatem qua erit orbis 360 partes. Angulus ergo ADR tunc secundum partes quibus duo anguli recti sunt 360 partes erit 4 partes et 46 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit due partes et 23 minuta. Diversitatem ergo maiorem, que est arcus AB, iam invenimus quod convenit esse partes duas et 23 minuta. Sed arcus motus diversi, quia subtenditur angulo ARD ortogonio, erit 90 partes, et arcus motus medii qui subtenditur angulo EAR erit 92 partes et 23 minuta. Et ex hoc etiam erit arcus motus centri orbis revolutionis 92 partes et 23 minuta. Et illud est quod oportuit nos declarare.
⟨III.5⟩ Capitulum quintum: De inquisitionibus particularibus ex diversitate
Et ut possimus habere cognitionem partium diversitatis motuum in omni hora, demonstrabo etiam secundum unumquemque duorum modorum, cum scitus fuerit aliquis horum arcuum positorum, 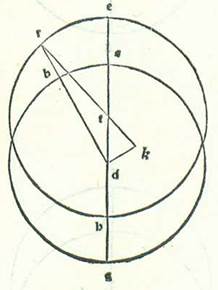 qualiter sciantur arcus reliqui. Describam ergo primum circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et orbem centri egredientis, supra quem sint E, R, H, supra centrum T, et diametrum transeuntem supra centra eorum et supra punctum E, quod est longitudo longior, supra quam sint E, A, T, D, et separabo arcum ER, quem ponam primum, verbi gratia 30 partes, et protraham duas lineas RD et RT, et producam lineam RT usque ad K, et protraham AD perpendicularem supra lineam RTK, que sit DK. Et quia arcus ER iam positus est 30 partes, erit angulus ETR, qui est equalis angulo DTK, 30 partes secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 60 partes. Arcus ergo qui est super DK erit 60 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et arcus qui est supra KT, qui est residuus ad complendam medietatem circuli, est 120 partes, et erunt eorum chorde, scilicet chorda DK, 60 partes secundum quantitatem qua erit DT chorda 120 partes, et erit chorda KT secundum illam quantitatem 103 partes et 55 minuta. Quapropter secundum quantitatem qua erit linea DT due partes et 30 minuta et linea RT, que est a centro, 60 partes erit KD pars et 15 minuta et KT secundum eandem due partes et 10 minuta et tota linea KTR 62 partes et 10 minuta. Et quia cum coniunxerimus multiplicationem cuiusque earum in se, erit equalis multiplicationi RD in se, erit chorda RD 62 partes et 11 minuta fere secundum quantitatem qua fuit DK pars et 15 minuta. Secundum quantitatem ergo qua erit linea RD 120 partes erit linea DK due partes et 25 minuta, et arcus qui est super ipsam due partes et 18 minuta secundum quantitatem qua circulus continens triangulum DRK ortogonium erit 360 partes. Quapropter erit angulus DRK due partes et 18 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit pars et 9 minuta. Illud ergo est diversitas que erit tunc. Et secundum illam quantitatem erit angulus ETR 30 partes. Angulus ergo ADB reliquus, cui subtenditur arcus AB orbis signorum, erit 28 partes et 51 minuta.
qualiter sciantur arcus reliqui. Describam ergo primum circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et orbem centri egredientis, supra quem sint E, R, H, supra centrum T, et diametrum transeuntem supra centra eorum et supra punctum E, quod est longitudo longior, supra quam sint E, A, T, D, et separabo arcum ER, quem ponam primum, verbi gratia 30 partes, et protraham duas lineas RD et RT, et producam lineam RT usque ad K, et protraham AD perpendicularem supra lineam RTK, que sit DK. Et quia arcus ER iam positus est 30 partes, erit angulus ETR, qui est equalis angulo DTK, 30 partes secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 60 partes. Arcus ergo qui est super DK erit 60 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et arcus qui est supra KT, qui est residuus ad complendam medietatem circuli, est 120 partes, et erunt eorum chorde, scilicet chorda DK, 60 partes secundum quantitatem qua erit DT chorda 120 partes, et erit chorda KT secundum illam quantitatem 103 partes et 55 minuta. Quapropter secundum quantitatem qua erit linea DT due partes et 30 minuta et linea RT, que est a centro, 60 partes erit KD pars et 15 minuta et KT secundum eandem due partes et 10 minuta et tota linea KTR 62 partes et 10 minuta. Et quia cum coniunxerimus multiplicationem cuiusque earum in se, erit equalis multiplicationi RD in se, erit chorda RD 62 partes et 11 minuta fere secundum quantitatem qua fuit DK pars et 15 minuta. Secundum quantitatem ergo qua erit linea RD 120 partes erit linea DK due partes et 25 minuta, et arcus qui est super ipsam due partes et 18 minuta secundum quantitatem qua circulus continens triangulum DRK ortogonium erit 360 partes. Quapropter erit angulus DRK due partes et 18 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit pars et 9 minuta. Illud ergo est diversitas que erit tunc. Et secundum illam quantitatem erit angulus ETR 30 partes. Angulus ergo ADB reliquus, cui subtenditur arcus AB orbis signorum, erit 28 partes et 51 minuta.
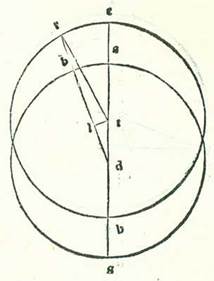 Iam vero declarabitur quod cum scitus fuerit angulus alius preter hunc angulum, scientur anguli reliqui cum nos lineaverimus in simili huius figure perpendicularem a puncto T ad lineam RD, supra quam sint T, L. Si enim fecerimus arcum AB orbis signorum notum, qui subtenditur angulo visionis BDA, erit propter hoc proportio linee DT ad lineam TL nota. Sed proportio DT ad TR est nota. Ergo proportio TR ad TL est nota. Quapropter erit angulus TRD, qui est diversitas, notus, et angulus ETR, cui subtenditur arcus ER orbis centri egredientis, notus. Quod si nos fecerimus diversitatem notam que est angulus TRD, erit similiter econtrario. Et propter hoc erit proportio RT ad TL nota. Et iam scivisti prius proportionem RT ad TD. Quapropter erit proportio TD ad TL nota. Et scies ex eo angulum TDL, cui subtenditur arcus AB orbis signorum, et erit angulus ETR, cui subtenditur arcus ER orbis centri egredientis, notus secundum illam proportionem.
Iam vero declarabitur quod cum scitus fuerit angulus alius preter hunc angulum, scientur anguli reliqui cum nos lineaverimus in simili huius figure perpendicularem a puncto T ad lineam RD, supra quam sint T, L. Si enim fecerimus arcum AB orbis signorum notum, qui subtenditur angulo visionis BDA, erit propter hoc proportio linee DT ad lineam TL nota. Sed proportio DT ad TR est nota. Ergo proportio TR ad TL est nota. Quapropter erit angulus TRD, qui est diversitas, notus, et angulus ETR, cui subtenditur arcus ER orbis centri egredientis, notus. Quod si nos fecerimus diversitatem notam que est angulus TRD, erit similiter econtrario. Et propter hoc erit proportio RT ad TL nota. Et iam scivisti prius proportionem RT ad TD. Quapropter erit proportio TD ad TL nota. Et scies ex eo angulum TDL, cui subtenditur arcus AB orbis signorum, et erit angulus ETR, cui subtenditur arcus ER orbis centri egredientis, notus secundum illam proportionem.
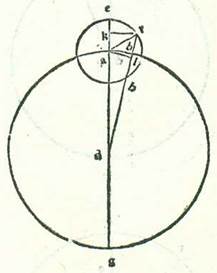 Describam etiam circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, super centrum D et diametrum ADG, et orbem revolutionis secundum similitudinem sive proportionem illius, supra quem sint E, R, H, T, super centrum A, et separabo arcum ER, quem etiam ponam 30 partes, et protraham duas lineas RHD et RA, et producam ab R perpendicularem super lineam AE, que sit RK. Et quia arcus ER est 30 partes, erit angulus EAR secundum quantitatem qua sunt quatuor anguli recti 360 partes 30 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est supra RK erit 60 partes secundum quantitatem qua erit circulus continens triangulum ARK ortogonium 360 partes, et arcus qui est supra AK, qui est reliquus ad complendam medietatem circuli, erit 120 partes, et erunt eorum chorde, scilicet chorda RK 60 partes secundum quantitatem qua diameter RA est 120 partes, et chorda KA secundum illam quantitatem 103 partes et 55 minuta. Quapropter secundum quantitatem qua erit linea AR due partes et 30 minuta et AD que est a centro ad orbem signorum 60 partes erit linea RK pars et 15 minuta et linea KA secundum illam quantitatem due partes et 10 minuta et tota KAD 62 partes et 10 minuta. Et quia aggregatum ex ductu duarum linearum RK et KD in se est equale ductui DR in se, erit DR in longitudine 62 partes et 11 minuta secundum quantitatem qua fuit linea RK pars et 15 minuta. Secundum quantitatem ergo qua erit chorda DR 120 partes erit linea RK due partes et 25 minuta, et arcus qui est supra RK due partes et 18 minuta secundum quantitatem qua erit circulus continens triangulum DRK ortogonium 360 partes. Quapropter angulus RDK erit due partes et 18 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit pars et 9 minuta. Ergo illud est diversitas arcus AB. Et secundum illam quantitatem etiam est angulus EAR 30 partes. Remanet ergo angulus ARD, cui subtenditur arcus visionis, qui est orbis signorum 28 partes et 51 minuta. Et illud est quod iam convenit ei quod iam ostensum est secundum modum orbis centri egredientis.
Describam etiam circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, super centrum D et diametrum ADG, et orbem revolutionis secundum similitudinem sive proportionem illius, supra quem sint E, R, H, T, super centrum A, et separabo arcum ER, quem etiam ponam 30 partes, et protraham duas lineas RHD et RA, et producam ab R perpendicularem super lineam AE, que sit RK. Et quia arcus ER est 30 partes, erit angulus EAR secundum quantitatem qua sunt quatuor anguli recti 360 partes 30 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est supra RK erit 60 partes secundum quantitatem qua erit circulus continens triangulum ARK ortogonium 360 partes, et arcus qui est supra AK, qui est reliquus ad complendam medietatem circuli, erit 120 partes, et erunt eorum chorde, scilicet chorda RK 60 partes secundum quantitatem qua diameter RA est 120 partes, et chorda KA secundum illam quantitatem 103 partes et 55 minuta. Quapropter secundum quantitatem qua erit linea AR due partes et 30 minuta et AD que est a centro ad orbem signorum 60 partes erit linea RK pars et 15 minuta et linea KA secundum illam quantitatem due partes et 10 minuta et tota KAD 62 partes et 10 minuta. Et quia aggregatum ex ductu duarum linearum RK et KD in se est equale ductui DR in se, erit DR in longitudine 62 partes et 11 minuta secundum quantitatem qua fuit linea RK pars et 15 minuta. Secundum quantitatem ergo qua erit chorda DR 120 partes erit linea RK due partes et 25 minuta, et arcus qui est supra RK due partes et 18 minuta secundum quantitatem qua erit circulus continens triangulum DRK ortogonium 360 partes. Quapropter angulus RDK erit due partes et 18 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit pars et 9 minuta. Ergo illud est diversitas arcus AB. Et secundum illam quantitatem etiam est angulus EAR 30 partes. Remanet ergo angulus ARD, cui subtenditur arcus visionis, qui est orbis signorum 28 partes et 51 minuta. Et illud est quod iam convenit ei quod iam ostensum est secundum modum orbis centri egredientis.
Et similiter cum fuerit angulus alius notus, erunt reliqui anguli noti. Cum protraxerimus in eadem vel in simili huius forme perpendicularem a puncto A ad lineam DR, supra quam sint A, L, et si postea posuerimus arcum visionis orbis signorum notum, qui est angulus ARD, erit propter hoc proportio RA ad AL nota. Et postquam iam prius facta fuit proportio RA ad AD nota, erit proportio DA ad AL nota. Quapropter erit angulus ADL, qui est arcus AB, notus, et illud est diversitas, et angulus EAR, qui est arcus ER orbis revolutionis, erit notus. Quod si nos fecerimus diversitatem notam, scilicet angulum ADB, econtrario erit propter hoc proportio AD ad AL nota. Et quia iam scivisti prius proportionem DA ad AR, erit proportio RA ad AL nota. Quapropter erit angulus ARD notus, qui est arcus visionis orbis signorum, et angulus EAR, qui est arcus ER orbis revolutionis, erit notus.
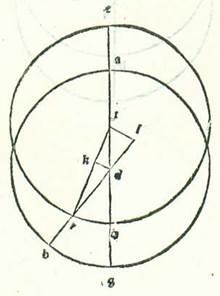 Et etiam in forma orbis centri egredientis hac separemus arcum HR a puncto H, quod est longitudo propinquior orbis centri egredientis, et ponamus ipsum notum, scilicet 30 partes secundum illas quantitates, et protrahamus lineas DRB et TR, et protrahamus perpendicularem a puncto D super lineam TR, supra quam sint D, K. Et quia arcus RH est 30 partes, angulus RTH secundum quantitatem qua sunt quatuor anguli recti 360 partes erit 30 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est super lineam DK erit 60 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et arcus qui est super KT, qui est residuum medietatis circuli, est 120 partes. Linee ergo que subtenduntur eis, scilicet DK est 60 partes secundum quantitatem qua erit diameter DT 120 partes, et chorda KT secundum quantitatem eandem erit 103 partes et 55 minuta. Secundum quantitatem ergo qua erit chorda DT due partes et 30 minuta et chorda TR, que est a centro ad circulum, 60 partes erit linea DK pars et 15 minuta, et similiter TK erit due partes et 10 minuta, et residuum erit 57 partes et 50 minuta. Et quia aggregatum ex multiplicatione cuiusque duarum linearum DK et KR in se est equale multiplicationi DR in se, erit longitudo DR 57 partes et 51 minuta fere secundum quantitatem qua est DK pars et 15 minuta. Ergo secundum quantitatem qua erit chorda DR 120 partes erit linea DK due partes et 34 minuta, et arcus qui est super ipsam erit due partes et 27 minuta secundum quantitatem qua erit circulus continens triangulum DRK ortogonium 360 partes. Quapropter erit angulus DRK due partes et 27 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, sed secundum quantitatem qua sunt quatuor anguli recti 360 partes erit pars et 14 minuta fere. Illud ergo est diversitas. Et quia secundum illas quantitates fit angulus RTH 30 partes, erit totus angulus BDG, qui est arcus GB orbis signorum, 31 partes et 14 minuta.
Et etiam in forma orbis centri egredientis hac separemus arcum HR a puncto H, quod est longitudo propinquior orbis centri egredientis, et ponamus ipsum notum, scilicet 30 partes secundum illas quantitates, et protrahamus lineas DRB et TR, et protrahamus perpendicularem a puncto D super lineam TR, supra quam sint D, K. Et quia arcus RH est 30 partes, angulus RTH secundum quantitatem qua sunt quatuor anguli recti 360 partes erit 30 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est super lineam DK erit 60 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et arcus qui est super KT, qui est residuum medietatis circuli, est 120 partes. Linee ergo que subtenduntur eis, scilicet DK est 60 partes secundum quantitatem qua erit diameter DT 120 partes, et chorda KT secundum quantitatem eandem erit 103 partes et 55 minuta. Secundum quantitatem ergo qua erit chorda DT due partes et 30 minuta et chorda TR, que est a centro ad circulum, 60 partes erit linea DK pars et 15 minuta, et similiter TK erit due partes et 10 minuta, et residuum erit 57 partes et 50 minuta. Et quia aggregatum ex multiplicatione cuiusque duarum linearum DK et KR in se est equale multiplicationi DR in se, erit longitudo DR 57 partes et 51 minuta fere secundum quantitatem qua est DK pars et 15 minuta. Ergo secundum quantitatem qua erit chorda DR 120 partes erit linea DK due partes et 34 minuta, et arcus qui est super ipsam erit due partes et 27 minuta secundum quantitatem qua erit circulus continens triangulum DRK ortogonium 360 partes. Quapropter erit angulus DRK due partes et 27 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, sed secundum quantitatem qua sunt quatuor anguli recti 360 partes erit pars et 14 minuta fere. Illud ergo est diversitas. Et quia secundum illas quantitates fit angulus RTH 30 partes, erit totus angulus BDG, qui est arcus GB orbis signorum, 31 partes et 14 minuta.
Et in eadem vel simili illius Probably forme is missing here. Cf. the expression in eadem vel in simili huius forme on 32v, line 37. Paris, BnF, lat. 14738 (52r, line 4 from the bottom) reads secundum similitudinem instead of in eadem vel simili. protraham lineam BD et producam super eam perpendicularem a puncto T, que sit TL. Si ergo nos posuerimus arcum BG orbis signorum, qui est anguli TDL, notum, erit proportio linee DT ad TL nota. Et postquam iam scivisti prius proportionem linee DT ad TR, erit proportio RT ad TL nota. Quapropter sciemus angulum TRD, qui est diversitas, et sciemus angulum RTD, qui est arcus HR orbis centri egredientis. Quod si nos posuerimus diversitatem notam, per quod scilicet intelligi volumus angulum TRD, sciemus propter hoc econtrario proportionem RT ad TL. Et quia iam scivisti prius proportionem RT ad TD, erit proportio DT ad TL nota. Quapropter erit angulus TDL notus, qui est arcus GB orbis signorum, et erit etiam angulus RTH, qui est arcus HR orbis centri egredientis, notus.
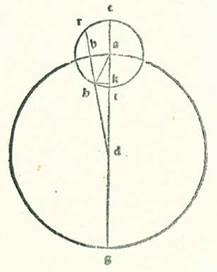 Et similiter in forma precedente circuli cuius centrum est centrum orbis signorum et circuli orbis revolutionis separabo arcum a puncto T, quod sit longitudo propinquior, supra quem sint T, H, et sit quemadmodum posuimus 30 partes, et protraham duas lineas AH et DHBR, et producam perpendicularem a puncto H super lineam AG, que sit HK. Et quia etiam arcus TH est 30 partes, erit angulus TAH 30 partes secundum quantitatem qua quatuor anguli recti sunt 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est super lineam HK circuli continentis triangulum HKA ortogonium erit 60 partes secundum quantitatem qua est circulus 360 partes, et arcus qui est super lineam AK residuus medietatis circuli erit 120 partes, et erunt chorde eorum, scilicet chorda HK 60 partes secundum quantitatem qua erit diameter AH 120 partes, et chorda AK secundum illas quantitates erit 103 partes et 55 minuta. Secundum quantitatem ergo qua linea AH erit due partes et 30 minuta et linea DA, que est a centro ad circulum, 60 partes erit linea HK pars et 15 minuta, et similiter linea AK due partes et 10 minuta, et linea KD residua 57 partes et 50 minuta. Et quia aggregatum ex ductu cuiusque earum in se est equale ductui DH in se, erit longitudo DH 57 partes et 51 minuta fere secundum quantitatem qua fuit linea KH pars et 15 minuta. Secundum quantitatem ergo qua erit chorda DH 120 partes erit chorda HK due partes et 34 minuta, et arcus qui erit super ipsam due partes et 27 minuta secundum quantitatem qua erit circulus continens triangulum DHK ortogonium 360 partes. Quapropter angulus HDK erit due partes et 27 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum quantitatem qua sunt quatuor anguli recti 360 partes erit pars una et 14 minuta fere. Illud ergo est quantitas diversitatis. Et quia secundum quantitatem hanc angulus HAK est 30 partes, erit totus angulus BHA, qui est arcus visionis orbis signorum, 31 partes et 14 minuta, quod conveniens est quantitati quam invenimus in orbe centri egredientis.
Et similiter in forma precedente circuli cuius centrum est centrum orbis signorum et circuli orbis revolutionis separabo arcum a puncto T, quod sit longitudo propinquior, supra quem sint T, H, et sit quemadmodum posuimus 30 partes, et protraham duas lineas AH et DHBR, et producam perpendicularem a puncto H super lineam AG, que sit HK. Et quia etiam arcus TH est 30 partes, erit angulus TAH 30 partes secundum quantitatem qua quatuor anguli recti sunt 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 60 partes. Quapropter arcus qui est super lineam HK circuli continentis triangulum HKA ortogonium erit 60 partes secundum quantitatem qua est circulus 360 partes, et arcus qui est super lineam AK residuus medietatis circuli erit 120 partes, et erunt chorde eorum, scilicet chorda HK 60 partes secundum quantitatem qua erit diameter AH 120 partes, et chorda AK secundum illas quantitates erit 103 partes et 55 minuta. Secundum quantitatem ergo qua linea AH erit due partes et 30 minuta et linea DA, que est a centro ad circulum, 60 partes erit linea HK pars et 15 minuta, et similiter linea AK due partes et 10 minuta, et linea KD residua 57 partes et 50 minuta. Et quia aggregatum ex ductu cuiusque earum in se est equale ductui DH in se, erit longitudo DH 57 partes et 51 minuta fere secundum quantitatem qua fuit linea KH pars et 15 minuta. Secundum quantitatem ergo qua erit chorda DH 120 partes erit chorda HK due partes et 34 minuta, et arcus qui erit super ipsam due partes et 27 minuta secundum quantitatem qua erit circulus continens triangulum DHK ortogonium 360 partes. Quapropter angulus HDK erit due partes et 27 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum quantitatem qua sunt quatuor anguli recti 360 partes erit pars una et 14 minuta fere. Illud ergo est quantitas diversitatis. Et quia secundum quantitatem hanc angulus HAK est 30 partes, erit totus angulus BHA, qui est arcus visionis orbis signorum, 31 partes et 14 minuta, quod conveniens est quantitati quam invenimus in orbe centri egredientis.
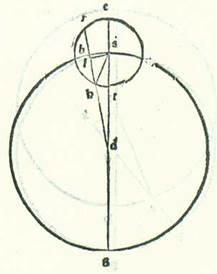 Et similiter, cum protrahetur perpendicularis AL supra lineam HB et fecerimus arcum orbis signorum notum, qui est anguli AHL, erit propter hoc proportio AH ad AL nota. Et postquam iam prius scivisti proportionem HA ad AD, erit proportio DA ad AL nota. Quapropter erit angulus ADB, qui est arcus AB, notus, qui est quantitas diversitatis, et angulus HAT, qui est arcus TH orbis revolutionis, erit etiam notus. Quod si nos etiam fecerimus arcum AB, qui est quantitas diversitatis, notum, qui est angulus ADB, similiter econtrario sciemus proportionem DA ad AL. Et quia iam prius scivisti proportionem DH ad HA, scies proportionem HA ad AL. Quapropter erit angulus AHL, qui est arcus visionis circuli orbis signorum, notus, et angulus TAH, qui est arcus TH orbis revolutionis, notus. Iam ergo claruit illud.
Et similiter, cum protrahetur perpendicularis AL supra lineam HB et fecerimus arcum orbis signorum notum, qui est anguli AHL, erit propter hoc proportio AH ad AL nota. Et postquam iam prius scivisti proportionem HA ad AD, erit proportio DA ad AL nota. Quapropter erit angulus ADB, qui est arcus AB, notus, qui est quantitas diversitatis, et angulus HAT, qui est arcus TH orbis revolutionis, erit etiam notus. Quod si nos etiam fecerimus arcum AB, qui est quantitas diversitatis, notum, qui est angulus ADB, similiter econtrario sciemus proportionem DA ad AL. Et quia iam prius scivisti proportionem DH ad HA, scies proportionem HA ad AL. Quapropter erit angulus AHL, qui est arcus visionis circuli orbis signorum, notus, et angulus TAH, qui est arcus TH orbis revolutionis, notus. Iam ergo claruit illud.
⟨III.6⟩ Capitulum sextum: De divisione tabularum portionum particularium diversitatis
Postquam sit possibile per hec capitula ponere multas tabulas diversas partium quarum portiones diversitatis motuum investigantur et cognoscere eas et dividere ad ea que volumus de inventione quantitatum equationis diversitatis et divisione eius quam brevissimo opere, vidimus nobis sufficere ex hoc ponere tabulas in quibus sint quantitates diversitatis opposite arcubus motus medii equalis, propter facilitatem et levitatem illius in numeratione cum earum incubuerit necessitas. Et propter hoc elegimus ut operaremur in divisione et separatione per prima capitula que narravimus numerorum et computationis secundum quod eorum precessit declaratio cum lineis mensuratis, et ut poneremus portiones arcuum motus medii, scilicet cuiusque arcus portionem diversitatis. Dico autem sermonem communem quod duarum quartarum que sunt a duabus partibus longitudinis longioris Solis et stellarum aliarum quamque divisimus in 15 portiones equales, et fuit queque portio sex partes, et quamque duarum quartarum que sunt a duabus partibus longitudinis propinquioris divisimus in 30 portiones equales, et fuit queque portio earum tres partes. Quoniam quantitates superflui diversitatis que est arcuum qui sunt duarum quartarum que sunt a duabus partibus longitudinis propinquioris sunt maiores quantitatibus superflui diversitatis que est arcuum equalium eis qui sunt duarum quartarum que sunt a duabus partibus longitudinis longioris.
⟨III.7⟩ Capitulum septimum: De positione tabularum motus Solis diversi
Describam autem tabularum diversitatis motus Solis etiam 45 areas in tribus partibus. In duabus autem primis partibus erit numerus partium 360 motus medii. Et ponam ut quindecem aree prime sint duarum quartarum que sunt a duabus partibus longitudinis longioris. Et ponam ut triginta aree relique sint duarum quartarum que sunt a duabus partibus longitudinis propinquioris. In tertia vero parte erunt portiones diversitatis secundum augmentum et diminutionem cuiusque numerorum motus medii. Et ista est tabularum descriptio:
Tabula diversitatis motus Solis
☉ |
||||
Partes motus medii |
Diversitas motus Solis | |||
Partes |
Partes |
Partes |
Minuta |
|
6
12
18 |
354
348
342 |
0
0
0 |
14
28
42 |
|
24
30
36 |
336
330
324 |
0
1
1 |
56
9
21 |
|
42
48
54 |
318
312
306 |
1
1
1 |
33
43
53 |
|
60
66
72 |
300
294
288 |
2
2
2 |
2
8
13 |
|
78
84
90 |
282
276
270 |
2
2
2 |
19
21
22 |
|
93
96
99 |
267
264
261 |
2
2
2 |
23
23
22 |
|
102
105
108 |
258
255
252 |
2
2
2 |
21
19
18 |
|
111
114
117 |
249
246
243 |
2
2
2 |
16
13
10 |
|
120
123
126 |
240
237
234 |
2
2
1 |
7
3
59 |
|
129
132
135 |
231
228
225 |
1
1
1 |
54
49
44 |
|
138
141
144 |
222
219
216 |
1
1
1 |
39
33
27 |
|
147
150
153 |
213
210
207 |
1
1
1 |
21
15
7 |
|
156
159
162 |
204
201
198 |
1
0
0 |
0
54
46 |
|
165
168
171 |
195
192
189 |
0
0
0 |
39
31
23 |
|
174
177
180 |
186
183
180 |
0
0
0 |
16
8
0 |
|
⟨III.8⟩ Capitulum octavum: De scientia loci Solis in quo est per motum eius medium
Postquam iam remansit scientia equandi locum Solis per motum eius medium cum inquisitione divisionis motuum eius in omni hora, demonstrabo illud et operabor in omnibus eis etiam, scilicet in Sole et in stellis aliis, per considerationes nostras subtiles et veraces in motibus earum. Et incipiam in hoc a principio regni Nabuchodonosor cum motibus mediis quos iam demonstravimus. Plurimum namque quod ad nos pervenit ex considerationibus memorie commendatis antiquis non est nisi ab hoc tempore. 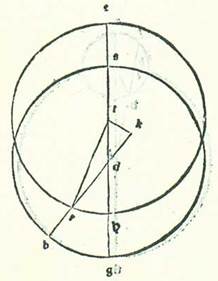 Et describam ad exemplum huius circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et circulum orbis centri egredientis, qui est Solis, supra quem sint E, R, H, supra centrum T, et diametrum que transit super duo centra et super punctum E, quod est longitudo longior, supra quem sint E, A, H, G, et sit punctum B orbis signorum punctum autumnale, et protraham duas lineas BRD et RT, et producam lineam RD, et protraham super ipsam perpendicularem a puncto T, que sit TK. Et quia punctum B est principium Libre et punctum G est longitudo propinquior et est supra quinque partes et medietatem partis Sagittarii, erit arcus BG 65 partes et 30 minuta, et angulus BDG, qui est equalis angulo TDK, erit 65 partes et 30 minuta secundum quantitatem qua quatuor anguli recti sunt 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 131 partes. Quapropter erit arcus qui est supra lineam TK 131 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et eius chorda, que est TK, 109 partes et 12 minuta secundum quantitatem qua erit chorda DT ut diameter 120 partes. Secundum quantitatem ergo qua erit linea DT quinque partes et chorda RT 120 partes erit linea TK quatuor partes et 33 minuta, et arcus qui est supra ipsam quatuor partes et 20 minuta secundum quantitatem qua erit circulus continens triangulum ortogonium RTK 360 partes. Quapropter erit angulus TRD quatuor partes et 20 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit due partes et 10 minuta. Et secundum eam erit angulus RDG 65 partes et 30 minuta. Angulus ergo HTR reliquus, qui est arcus RH orbis centri egredientis, erit 63 partes et 20 minuta. Cum ergo Sol fuerit in equalitate autumnali, tunc ipse precedet longitudinem propinquiorem, que est in quinque partibus et medietate partis Sagittarii, per motum suum medium 63 partibus et 20 minutis, et elongatur a longitudine longiore, que est in quinque partibus et medietate partis Geminorum, per motum suum medium secundum continuitatem signorum centum et sexdecem partibus et quadraginta minutis.
Et describam ad exemplum huius circulum cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, supra centrum D, et circulum orbis centri egredientis, qui est Solis, supra quem sint E, R, H, supra centrum T, et diametrum que transit super duo centra et super punctum E, quod est longitudo longior, supra quem sint E, A, H, G, et sit punctum B orbis signorum punctum autumnale, et protraham duas lineas BRD et RT, et producam lineam RD, et protraham super ipsam perpendicularem a puncto T, que sit TK. Et quia punctum B est principium Libre et punctum G est longitudo propinquior et est supra quinque partes et medietatem partis Sagittarii, erit arcus BG 65 partes et 30 minuta, et angulus BDG, qui est equalis angulo TDK, erit 65 partes et 30 minuta secundum quantitatem qua quatuor anguli recti sunt 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 131 partes. Quapropter erit arcus qui est supra lineam TK 131 partes secundum quantitatem qua erit circulus continens triangulum DTK ortogonium 360 partes, et eius chorda, que est TK, 109 partes et 12 minuta secundum quantitatem qua erit chorda DT ut diameter 120 partes. Secundum quantitatem ergo qua erit linea DT quinque partes et chorda RT 120 partes erit linea TK quatuor partes et 33 minuta, et arcus qui est supra ipsam quatuor partes et 20 minuta secundum quantitatem qua erit circulus continens triangulum ortogonium RTK 360 partes. Quapropter erit angulus TRD quatuor partes et 20 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit due partes et 10 minuta. Et secundum eam erit angulus RDG 65 partes et 30 minuta. Angulus ergo HTR reliquus, qui est arcus RH orbis centri egredientis, erit 63 partes et 20 minuta. Cum ergo Sol fuerit in equalitate autumnali, tunc ipse precedet longitudinem propinquiorem, que est in quinque partibus et medietate partis Sagittarii, per motum suum medium 63 partibus et 20 minutis, et elongatur a longitudine longiore, que est in quinque partibus et medietate partis Geminorum, per motum suum medium secundum continuitatem signorum centum et sexdecem partibus et quadraginta minutis.
Et post declarationem horum, quia una ex primis considerationibus equalitatis subtilissima et veracissima fuit consideratio equalitatis autumnalis in decimoseptimo annorum Adriani in die septimo mensis Athus, qui est unus mensium Egyptiorum, post medium diem per duas horas fere equales, tunc manifestum est quod Solis in ea hora per motum suum medium fuit elongatio a longitudine longiore in orbe centri egredientis secundum continuitatem signorum 116 partes et 40 minuta. Et aggregantur ex annis qui fuerunt a principio regni Nabuchodonosor usque ad mortem Alexandri quadringenti et vigintiquatuor anni Egyptii, et a morte Alexandri usque ad principium regni Augusti 294 anni, et a principio anni primi annorum regni Augusti Egyptiorum, quod fuit in primo die mensis Thut et in media die, eo quod equatio stellarum incipit a media die, usque ad decimumseptimum annorum Adriani et ad diem septimum mensis Athus, qui est unus mensium Egyptiorum, post mediam diem per duas horas equales aquales M. sunt 161 anni et 66 dies et due hore equales. Ergo a principio primi annorum Nabuchodonosor Egyptiorum, quod fuit in principio mensis Thut in media die, usque ad horam in qua fuit hec equalitas autumnalis aggregantur anni Egyptii octingenti et septuagintanovem et sexagintasex dies et due hore equales. Et erit motus Solis medius in tempore huic equali post proiectionem revolutionum integrarum 211 partes et 25 minuta fere. Cum ergo nos addiderimus supra partes longitudinis Solis a longitudine longiore orbis ecentrici, que, ut supra diximus, fuit in consideratione hac quam diximus, scilicet equalitatis autumnalis 116 partes et 40 minuta 360 partes, que sunt partes revolutionis unius, et proiecerimus ex eo quod aggregatur ex eis 211 partes et 25 minuta, que sunt superfluum quod est inter duo tempora, remanebit loci motus Solis medii in principio primi annorum Nabuchodonosor et primo die mensis Thut, qui est unus mensium Egyptiorum, et in media die longitudo a longitudine longiore secundum continuitatem signorum per motum suum medium 265 partes et 15 minuta. Et illud erit in quadragesimoquinto minuto prime partis Piscis.
⟨III.9⟩ Capitulum nonum: De computatione Solis et scientia certitudinis loci eius
Quotiens voluerimus scire locum Solis in unoquoque tempore quesito, assumemus quod aggregatur ex tempore loci Solis usque ad tempus quesitum per horas Alexandrie et mittemus illum numerum in tabulas motus Solis medii et accipiemus partes que opponuntur portioni cuiusque numerorum et aggregabimus eas cum partibus loci Solis que pro radice ponuntur 265 partibus et 15 minutis et proiiciemus ex eo quod inde aggregatur revolutiones integras. Quod ergo remanebit ex partibus proiiciemus ex loco quinque partium et medietatis partis Geminorum, qui est longitudo longior, secundum continuitatem signorum. Et quo pervenerit nobis numerus, ibi dicemus Solis locum per motum eius medium. Deinde post hoc assumemus numerum illum qui est temporis quod est a longitudine longiore usque ad locum Solis per motum eius medium et immittemus ipsum in tabulas diversitatis Solis et assumemus partes que opponuntur illi numero in area tertia. Cum ergo ceciderit numerus in area prima, quod erit cum fuerit ab uno usque ad 180 partes, proiiciemus eas ex loco Solis per motum eius medium. Et cum ceciderit numerus in area secunda, quod erit cum transierit 180, addemus illud supra locum Solis per motum eius medium. Et ita reperiemus locum Solis secundum certitudinem et visionem.
⟨III.10⟩ Capitulum decimum: De cognitione differentie, scilicet que est inter diem Iomin unum et noctem eius et diem Iomin alterum et noctem suam
Quod autem videtur in Sole solummodo plurimum eius est quod iam narravimus. Et sequitur illud ut addamus supra ipsum quam paucissimis verbis quod convenit nos premittere de diversitate dierum cum noctibus suis, scilicet de diversitate que est inter diem Iomin unum cum nocte sua et diem Iomin alterum cum nocte sua, propter hoc quod quicquid narravimus de motu medio non fuit relatum nisi secundum superfluitatem equalem, ac si dies cum noctibus suis essent equales aut equalium temporum. Non autem videtur ita. Iam vero innotuit nobis quod revolutio totius non est nisi secundum equalitatem supra duos polos equationis diei cuius principia sunt a puncto et reversiones eius ad ipsum, aut orbis horizontis aut orbis meridiei. Manifestum est igitur quod revolutio totius una est cuius principium est ab aliquo punctorum equationis diei quod sit in linea orbis horizontis aut in linea orbis meridiei donec redeat illud punctum ad ipsum. Et Iomin unus, scilicet dies et nox eius, secundum sermonem absolutum est tempus cuius principium est ab inceptione Solis a puncto orbis horizontis aut orbis meridiei usque ad reversionem Solis ad illud punctum. Quapropter erit dies unus medius cum nocte sua tempus in quo elevantur ab orbe horizontis aut ab orbe meridiei tempora equationis diei 360 omnia que sunt revolutionis unius et augmentum eius quod elevatur ex eo cum 59 minutis, que sunt de minutis unius temporis orbis centri egredientis quod est cursus Solis medius in die una. Dies vero diversus unus cum nocte sua est tempus in quo elevantur ab orbe horizontis aut ab orbe meridiei tempora equationis diei 360 omnia que sunt revolutionis unius et augmentum quod elevatur de temporibus cum cursu Solis diverso in die una cum nocte sua. Hec ergo portio equationis diei addita supra 360 tempora necessario erit diversa, non equalis, propter duas causas. Quarum una est quod videtur de diversitate motus Solis, et altera quod portiones orbis signorum equales non elevantur ab horizonte neque transeunt orbem meridiei cum temporibus equalibus. Diversitas autem que est inter diem unum medium et diem unum diversum que est propter has duas causas erit in die una cum nocte sua non sensibilis. Cum vero aggregatur in diebus pluribus cum noctibus suis est sensibilis et manifesta.
Plurimum autem diversitatis dierum que est propter diversitatem motus Solis medii non erit nisi in unaquaque duarum medietatum orbis que est inter duas longitudines medias in quibus est motus Solis medius. Quod est quoniam illud quod est inter id quod aggregatur de temporibus dierum diversorum cum noctibus suis et inter id quod aggregatur de temporibus dierum mediorum cum noctibus suis erit quatuor tempora et medietas et quarta temporis fere, aut addita super ea aut diminuta ab eis. Tempora autem que sunt inter augmentum super medium et diminutionem ab eo sunt duplum illius, quod est novem tempora et dimidium temporis, propter hoc quoniam quod videtur de transitu Solis diverso cum fuerit in medietate in qua est longitudo longior, erit diminutio eius quatuor tempora et medietas et quarta temporis, et cum fuerit in medietate orbis in qua est longitudo propinquior, erit augmentum eius quatuor tempora et medietas et quarta temporis. Plurimum vero diversitatis dierum, que est propter diversitatem eorum que elevantur et occidunt, non erit nisi in duabus medietatibus circuli que inveniuntur esse duo puncta conversionum in unaquaque duarum medietatum orbis signorum. Diversitas namque que est inter tempora equationis diei, que elevantur cum unaquaque harum duarum medietatum, et inter id quod videtur de temporibus 180 equalibus est diversitas que est inter diem longiorem aut diem breviorem et diem equalem. Et erit quod est inter tempora que elevantur cum unaquaque harum duarum medietatum diversitas que est inter diem et noctem longiorem et inter diem et noctem breviorem. Plurimum autem diversitatis que erit propter diversitatem elevationum in medio celi erit in duabus longitudinibus continentibus duo signa que ambo sunt aut a duabus partibus cuiusque punctorum duorum tropicorum aut a duabus partibus cuiusque duorum punctorum duarum equalitatum. Diversitas autem que erit inter unumquodque eorum que sunt apud ambos tropicos et inter tempus equale erit quatuor tempora et dimidium temporis fere. Sed diversitas que erit inter unumquodque eorum que sunt apud ambas equalitates et inter unumquodque eorum que sunt apud duos tropicos et inter tempus equale erit novem tempora. Unum namque eorum minuit ex tempore equali, et aliud addit supra ipsum quantum est quod minuit primum. Quapropter posuimus initium dierum et noctium in equatione computationis locorum stellarum a medio celo, et non ab elevationibus Solis neque ab occasibus ipsius. Diversitas namque que videtur apud horizontas possibile est ut sit in horis pluribus, et non sit illud ita in omni loco. Diversificatur namque illud cum diversitate augmenti diei et diminutione eius in unaquaque declinationum sphere. Diversitas vero que est in medio celi est una in omni loco. Neque augetur eius diversitas super id quod aggregatur de temporibus que aggregantur ex diversitate Solis et elevationibus medii celi. Et plurimum diversitatis que erit ex aggregatione horum duorum modorum simul, quorum diversitas est que est propter Solem et ea que est propter medium celum, erit in duabus longitudinibus in quibus est diversitas que est horum duorum modorum, aut cum augmento simul aut cum diminutione simul. Locus autem diminutionis est a medietate Aquarii usque ad finem Libre, et locus augmenti est a principio Scorpii usque ad medietatem Aquarii, propter hoc quod plurimum quod addit unaqueque harum duarum portionum aut minuit propter diversitatem Solis est tria tempora et due tertie temporis et propter medium celum quatuor tempora et due tertie temporis fere, donec sit plurimum quod aggregatur ex diversitate dierum cum noctibus suis aggregatum ex duobus modis simul in unaquaque duarum portionum. Quod autem est inter ipsam et inter medium est octo tempora et tertia temporis, que sunt medietas unius hore equalis et una decem et octo partium hore. Quod autem est inter dies cum noctibus suis augmentatos et diminutos est duplum illius, scilicet 16 tempora et due tertie temporis, quod est una hora equalis et nona pars hore. Hec vero quantitas, cum dimissa fuerit in Sole et stellis aliis, non eveniet propter eius dimissionem quantitas sensibilis in inquisitione eorum in aliquo eorum que videntur. In Luna autem propter velocitatem sui cursus erit diversitas manifesta sensibilis, scilicet erit quasi tres quinte unius partis.
Ad hoc autem ut possimus dies convertere cum noctibus suis temporales diversos datos qui sunt in qualibet duarum medietatum duarum longitudinum, scilicet qui sunt a medietate diei aut a medietate noctis usque ad medietatem diei aut usque ad medietatem noctis, et facere eos dies medios equales, considerabimus quanta sit longitudo dierum cum suis noctibus que est inter locum primum notum, in quo fuit Sol, et inter locum eius secundum, ad quem pervenit in illis diebus cum noctibus suis, et in quo loco partium orbis signorum fuit, et ad quem pervenit per cursum medium et per cursum diversum. Deinde post hoc assumemus quod ex partibus erit inter duo loca per motum Solis diversum qui videtur et mittemus illud in tabulas elevationum sphere recte et considerabimus quot tempora equationis diei quibus celum mediatur sint coram ipsis. Deinde assumemus superfluum quod erit inter illa tempora inventa et inter partes motus medii et videbimus quantitatem illius superflui, quota scilicet pars sit unius hore equalis, et servabimus ipsam. Cum ergo fuerit numerus temporum maior longitudine partium motus medii, addemus illud numero dierum cum noctibus suis positorum. Et cum ille fuerit minor, minuemus ipsum ex numero dierum. Quod ergo provenit post augmentum vel diminutionem est quod comprehensum est et conversum ex diebus diversis in dies equales cum noctibus suis. Per hos ergo dies comprehensos equabis computationem Lune per motum suum medium, qui est in tabulis Lune. Et ex hoc manifestum est nobis quod cum voluerimus convertere dies medios equales cum noctibus suis in dies temporales diversos cum noctibus suis, assumemus augmentum illorum temporum aut diminutionem ipsorum et operabimur per ipsum secundum conversionem eorum que narravimus. Fuit autem locus in quo fuit Sol secundum computationem nostram in principio annorum Nabuchodonosor in prima die mensis Thut, qui est ex mensibus Egyptiorum, in media die per motum eius medium, sicut iam ostendimus ante hec parum, in quadragesimoquinto minuto prime partis Piscis et per motum suum diversum in tertia parte et octavo minuto Piscis fere.
Expleta est dictio tertia Almagesti Ptolemei Pheludiensis.
Cum addideris super annos Iazdaiart One could equally read Iamdaiart. Paris, BnF, lat. 14738 (55v, line 5) reads Iazdaiart too. The Greek text does not contain the annex to chapter 3. et menses et dies eius 955 annos et tres menses, erunt qui proveniunt anni Alexandri, per quos intravi in canonem Theonis Alexandrini. Et cum addideris annis Iazdaiart One could equally read Iamdaiart. Paris, BnF, lat. 14738 (55v, line 7) reads Iazdaiart too. The Greek text does not contain the annex to chapter 3. et mensibus eius et diebus 1379 annos et tres menses, erunt qui provenerint anni Nabuchodonosor, qui sunt anni per quos intrabis in hunc librum.
Ferie annorum |
Feria |
Primus dies annorum Alexandri |
2 |
Primus dies annorum Philippi |
1 |
Primus dies annorum Nabuchodonosor |
4 |
Primus dies annorum diluvii |
5 |
Primus dies annorum Arabum |
5 |
3 |
|
Primus dies annorum Diocletiani |
5 |
Reductio erarum |
Anni |
Menses |
Dies |
Quod addunt anni Alexandri super annos Christi |
311 |
3 |
2 |
955 |
3 |
0 |
|
Quod est inter annos Philippi et annos Arabum |
945 |
3 |
26 |
3735 |
10 |
23 |
|
1379 |
3 |
0 |
|
Quod est inter annos Alexandri et annos Arabum |
932 |
9 |
17 |
Quod est inter annos Christi et annos Arabum |
621 |
6 |
15 |