⟨II⟩
Claudii Ptolemei Pheludiensis dictio secunda libri Almagesti tredecem capitulis constans auspicato prodit.
Capitulum primum: De scientia locorum habitabilium terre
Capitulum secundum: Qualiter sciantur quantitates arcuum circuli horizontis qui sunt inter orbem equationis diei et orbem declivem propter quantitatem diei longioris dati
Capitulum tertium: Qualiter sciatur altitudo poli per hos arcus, cum ponuntur, et propter quantitatem diei longioris, cum fuerit datus, et econverso
Capitulum quartum: Qualiter sciatur quas terras inhabitent illi supra summitatem capitum quorum Sol transit, et quando et quotiens sit illud
Capitulum quintum: Qualiter sciantur proportiones instrumentorum ad umbras suas in orbis signorum equalitate diei et in tropicis duobus in medietatibus diei per quedam que prediximus, cum fuerint data
Capitulum sextum: De modo proprietatum linearum orbium equidistantium orbi equationis diei
Capitulum septimum: De scientia partium orbis equationis diei que elevantur cum partibus orbis signorum in sphera declivi
Capitulum octavum: De modo positionis tabularum eius quod elevatur de orbe equationis diei cum omnibus decem partibus orbis signorum in locis orbium equidistantium
Capitulum nonum: De divisione eorum que sequuntur scientiam elevationum et specificatione eorum
Capitulum decimum: De scientia angulorum provenientium inter orbem signorum et orbem meridiei
Capitulum undecimum: De scientia angulorum provenientium inter orbem signorum et lineam circuli horizontis
Capitulum duodecimum: De scientia angulorum provenientium inter orbem declivem et orbem descriptum super duos polos horizontis
Capitulum tredecimum: De positione tabularum arcuum et angulorum quos narrabimus in orbibus equidistantibus
⟨II.1⟩ Capitulum primum: De scientia habitabilium terre
Et post ea que narravimus in dictione prima Almagesti de forma totius et communitate eorum que sunt in ea sicut principia et antecedentia, et que necessitas sit eius, et que estimavimus utilia in hac scientia ex eis que accidunt in orbe recto, studebimus ut ostendamus etiam in sequentibus plurimum eorum que accidunt in orbe declivi prout levius possibile est. Et hic quoque summa eius quod premittendum est est quod terra dividitur in quattuor quartas, quas separant orbis equationis diei et unus orbium descriptorum supra polos eius, et quod una quartarum duarum septentrionalium continet fere totam terram habitabilem quam scimus. Illud autem duobus modis declaratur. Quorum unus est propter latitudinem, que est spacium quod est a meridie ad septentrionem, quoniam umbre instrumentorum quibus fit consideratio in equalitate noctis et diei in medietatibus diei in omni loco declinatio erit ad septentrionem neque unquam declinabit ad meridiem. Alter vero propter longitudinem, que est spacium quod est ab oriente ad occidentem, quia eclypses, et precipue lunares, que sunt in hora una, vident illi qui habitant in extremitate orientis terre habitabilis quam scimus et in extremitate occidentis eius non antecedentes neque subsequentes plus duodecim horis equalibus. Totum vero spacium quarte in longitudine est duodecim horarum, quoniam una duarum medietatum orbis equationis diei comprehendit ipsum. Divisiones autem quas oportet nos scire et quod estimamus conveniens ei quod est necessarium in hoc libro sunt scientia eius quod accidit in locis habitabilibus que sunt sub unoquoque orbium equidistantium et equidistantium orbi equationis diei. Et hoc est quanta sit longitudo duorum polorum sphere prime ab horizonte, aut quanta sit longitudo puncti quod est supra summitatem capitum in orbe meridiei ab orbe equationis diei, et in quibus locis currat Sol supra summitatem capitum, et quando et quotiens sit illud, et que sit proportio instrumentorum ad umbras suas per que consideratur in equalitate diei et in duobus tropicis in medietatibus diei, et quantum addat dies longior et minuat dies brevior de die equali. Et preter hoc que sint augmenta et diminutiones que accidunt nocti et diei, et que sint diversitates eius cum quo elevatur equator diei et orbis declivis et cum quo occultantur ambo, et que sint proprietates angulorum provenientium ex sectione orbium maiorum et magnitudines eorum et omnia que ex eis contingunt et que in eis accidunt.
⟨II.2⟩ Capitulum secundum: Qualiter sciantur quantitates arcuum circuli horizontis qui sunt inter orbem equationis diei et orbem declivem propter quantitatem diei longioris cum fuerit datus et econverso
Huius itaque exemplum ponam lineam que est supra Rhodum equidistantem orbi equationis diei, ubi est altitudo poli 36 partes et in quo dies longior 14 horas et medietatem hore ex horis equalibus habet. 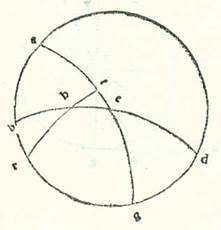 Et describam propter hoc meridiei orbem, supra quem sint A, B, G, D, et describam in eo medietatem circuli horizontis orientalis, supra quam sint B, E, D, et medietatem orbis equationis diei, supra quam sint A, E, G, et signabo supra polum meridianum R et supra ortum tropici hiemalis orbis signorum H, et describam supra duo puncta R et H arcum RHT, et ponam longitudinem diei longioris, et inquiram quantitatem arcus EH circuli horizontis. Et quia revolutio sphere non est nisi super duos polos equationis diei, tunc manifestum est quod duo puncta H et T cadunt simul in tempore uno super arcum AB orbis meridiei propter motum sphere. Tempus autem puncti H quod est ab oriente ad medium celi quod supra terram est est quantitas arcus TA. Tempus vero a medio celi sub terra ad oriens est quantitas arcus GT. Et sequitur hoc ut sit tempus diei quantitas dupli arcus TA et tempus noctis existat quantitas dupli arcus GT. Sectiones enim orbium equidistantium orbi equationis diei separate sunt supra terram et sub terra, eo quod orbis meridiei secat eos omnes in duo media et duo media. Quapropter erit arcus ET, qui est medietas superflui quod est inter longiorem diem vel breviorem et inter equalitatem, hora et quarta hore in loco huius linee, et illud est 18 tempora et 45 minuta. Arcus autem residuus ad complendam quartam, qui est TA, erit 71 tempora et 15 minuta. Secundum ergo quod iam precessit ex declaratione, iam secant se inter duos arcus orbium maiorum, qui sunt AE et AR, duo arcus EHB et RHT supra H. Ergo proportio chorde dupli arcus EA ad chordam dupli arcus AT aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus TR ad chordam dupli arcus RH et ex proportione chorde dupli arcus HB ad chordam dupli arcus BE. Duplum autem arcus TA est 142 partes et 30 minuta, et eius chorda est 113 partes et 37 minuta et 54 secunda, et duplum arcus AE est 180 partes, et eius chorda 120. Duplum quoque arcus TR est 180 partes, et eius chorda 120 partes. Et duplum arcus RH est 132 partes et 17 minuta et 20 secunda, et eius chorda 109 partes et 44 minuta et 53 secunda. Cum ergo proiecerimus ex proportione 113 partium et 37 minutorum et 54 secundorum ad 120 proportionem 120 ad 109 partes et 44 minuta et 53 secunda, remanebit proportio chorde dupli arcus HB ad chordam dupli arcus BE, que est proportio 103 partium et 55 minutorum et 23 secundorum ad 120. Chorda vero dupli arcus BE, quoniam ipse est quarta circuli, est 120. Ergo chorda dupli arcus HB fere secundum illas partes est 103 partes et 55 minuta et 23 secunda. Quapropter erit duplum arcus HB 120 partes et arcus HB solum secundum illas partes 60 partes. Remanet ergo arcus EH secundum illas partes 30 partes secundum quantitatem qua circulus horizon est 360 partes. Et hoc est quod oportuit nos demonstrare.
Et describam propter hoc meridiei orbem, supra quem sint A, B, G, D, et describam in eo medietatem circuli horizontis orientalis, supra quam sint B, E, D, et medietatem orbis equationis diei, supra quam sint A, E, G, et signabo supra polum meridianum R et supra ortum tropici hiemalis orbis signorum H, et describam supra duo puncta R et H arcum RHT, et ponam longitudinem diei longioris, et inquiram quantitatem arcus EH circuli horizontis. Et quia revolutio sphere non est nisi super duos polos equationis diei, tunc manifestum est quod duo puncta H et T cadunt simul in tempore uno super arcum AB orbis meridiei propter motum sphere. Tempus autem puncti H quod est ab oriente ad medium celi quod supra terram est est quantitas arcus TA. Tempus vero a medio celi sub terra ad oriens est quantitas arcus GT. Et sequitur hoc ut sit tempus diei quantitas dupli arcus TA et tempus noctis existat quantitas dupli arcus GT. Sectiones enim orbium equidistantium orbi equationis diei separate sunt supra terram et sub terra, eo quod orbis meridiei secat eos omnes in duo media et duo media. Quapropter erit arcus ET, qui est medietas superflui quod est inter longiorem diem vel breviorem et inter equalitatem, hora et quarta hore in loco huius linee, et illud est 18 tempora et 45 minuta. Arcus autem residuus ad complendam quartam, qui est TA, erit 71 tempora et 15 minuta. Secundum ergo quod iam precessit ex declaratione, iam secant se inter duos arcus orbium maiorum, qui sunt AE et AR, duo arcus EHB et RHT supra H. Ergo proportio chorde dupli arcus EA ad chordam dupli arcus AT aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus TR ad chordam dupli arcus RH et ex proportione chorde dupli arcus HB ad chordam dupli arcus BE. Duplum autem arcus TA est 142 partes et 30 minuta, et eius chorda est 113 partes et 37 minuta et 54 secunda, et duplum arcus AE est 180 partes, et eius chorda 120. Duplum quoque arcus TR est 180 partes, et eius chorda 120 partes. Et duplum arcus RH est 132 partes et 17 minuta et 20 secunda, et eius chorda 109 partes et 44 minuta et 53 secunda. Cum ergo proiecerimus ex proportione 113 partium et 37 minutorum et 54 secundorum ad 120 proportionem 120 ad 109 partes et 44 minuta et 53 secunda, remanebit proportio chorde dupli arcus HB ad chordam dupli arcus BE, que est proportio 103 partium et 55 minutorum et 23 secundorum ad 120. Chorda vero dupli arcus BE, quoniam ipse est quarta circuli, est 120. Ergo chorda dupli arcus HB fere secundum illas partes est 103 partes et 55 minuta et 23 secunda. Quapropter erit duplum arcus HB 120 partes et arcus HB solum secundum illas partes 60 partes. Remanet ergo arcus EH secundum illas partes 30 partes secundum quantitatem qua circulus horizon est 360 partes. Et hoc est quod oportuit nos demonstrare.
⟨II.3⟩ Capitulum tertium: Qualiter sciatur altitudo poli propter hos arcus, cum ponuntur, et propter quantitatem diei longioris, cum fuerit datus, et econverso
Sit ergo illud datum, et investigemus inventionem altitudinis poli, que sit arcus BR orbis meridiei. Erit ergo in hac forma proportio chorde dupli arcus ET ad chordam dupli arcus TA aggregata ex duabus proportionibus, ex proportione chorde dupli arcus EH ad chordam dupli arcus HB et ex proportione chorde dupli arcus BR ad chordam dupli arcus RA. Duplum vero arcus ET est 37 partes et 30 minuta, et eius chorda est 38 partes et trigintaquattuor minuta et 22 secunda, et duplum arcus TA est 142 partes et 30 minuta, et chorda eius 113 partes et 37 minuta et 54 secunda. Duplum quoque arcus EH est 60 partes, et chorda eius 60 partes, et duplum arcus HB est 120 partes, et eius chorda 103 partes et 55 minuta et 23 secunda. Cum ergo proiecerimus ex proportione 38 partium et 34 minutorum et 22 secundorum ad 113 partes et 37 minuta et 54 secunda proportionem 60 partium ad 103 partes et 55 minuta et 23 secunda, remanebit proportio chorde dupli arcus BR ad chordam dupli arcus RA que est proportio 70 partium et 33 minutorum ad 120 partes vicinius. Chorda quoque dupli arcus RA est 120 partes. Ergo chorda dupli arcus BR secundum illam quantitatem est 70 partes et 33 minuta. Quapropter erit duplum arcus BR 72 partes et unum minutum et arcus BR solum secundum illam quantitatem 36 partes vicinius.
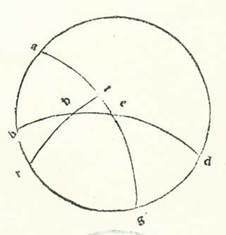 Secundum huius quoque conversionem in hac forma ponam arcum BR, qui est altitudo poli data, trigintasex partes et inquiram inventionem superflui quod est inter quantitatem diei longioris et brevioris et inter equalitatem, et illud est duplum arcus ET. Quapropter erit proportio chorde dupli arcus BR ad chordam dupli arcus BA aggregata ex duabus proportionibus, ex proportione chorde dupli arcus RH ad chordam dupli arcus HT et ex proportione chorde dupli arcus TE ad chordam dupli arcus EA. Duplum autem arcus RB est 72 partes, et chorda eius 70 partes et 32 minuta et 3 secunda, et duplum arcus BA est 108 partes, et eius chorda est 97 partes et 4 minuta et 55 secunda. Duplum quoque arcus RH est 132 partes et 17 minuta et 20 secunda, et chorda eius est 109 partes et 44 minuta et 53 secunda, et duplum arcus HT est 47 partes et 42 minuta et 40 secunda, et eius chorda est 48 partes et 31 minuta et 55 secunda. Cum ergo proiecerimus ex proportione 70 partium et 32 minutorum et trium secundorum ad 97 partes et 4 minuta et 55 secunda proportionem 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, que est proportio 31 partium et 11 minutorum et 33 secundorum ad 97 partes et 4 minuta et 55 secunda. Hoc namque propinquius est proportioni 38 partium et 34 minutorum ad 120. Chorda autem dupli arcus EA est 120. Fit ergo chorda dupli arcus ET secundum illam quantitatem 38 partes et 34 minuta. Quapropter duplum arcus ET erit 37 partes et 30 minuta vicinius, et ipse sunt due hore et dimidia ex horis equalibus. Et illud est quod oportuit nos demonstrare.
Secundum huius quoque conversionem in hac forma ponam arcum BR, qui est altitudo poli data, trigintasex partes et inquiram inventionem superflui quod est inter quantitatem diei longioris et brevioris et inter equalitatem, et illud est duplum arcus ET. Quapropter erit proportio chorde dupli arcus BR ad chordam dupli arcus BA aggregata ex duabus proportionibus, ex proportione chorde dupli arcus RH ad chordam dupli arcus HT et ex proportione chorde dupli arcus TE ad chordam dupli arcus EA. Duplum autem arcus RB est 72 partes, et chorda eius 70 partes et 32 minuta et 3 secunda, et duplum arcus BA est 108 partes, et eius chorda est 97 partes et 4 minuta et 55 secunda. Duplum quoque arcus RH est 132 partes et 17 minuta et 20 secunda, et chorda eius est 109 partes et 44 minuta et 53 secunda, et duplum arcus HT est 47 partes et 42 minuta et 40 secunda, et eius chorda est 48 partes et 31 minuta et 55 secunda. Cum ergo proiecerimus ex proportione 70 partium et 32 minutorum et trium secundorum ad 97 partes et 4 minuta et 55 secunda proportionem 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, que est proportio 31 partium et 11 minutorum et 33 secundorum ad 97 partes et 4 minuta et 55 secunda. Hoc namque propinquius est proportioni 38 partium et 34 minutorum ad 120. Chorda autem dupli arcus EA est 120. Fit ergo chorda dupli arcus ET secundum illam quantitatem 38 partes et 34 minuta. Quapropter duplum arcus ET erit 37 partes et 30 minuta vicinius, et ipse sunt due hore et dimidia ex horis equalibus. Et illud est quod oportuit nos demonstrare.
Similiter quoque sciemus arcum HE horizontis, eo quod proportio chorde dupli arcus RA ad chordam dupli arcus AB datam aggregatur ex duabus proportionibus, scilicet ex proportione chorde dupli arcus RT ad chordam dupli arcus TH, que est data, et ex proportione chorde dupli arcus EH ad chordam dupli arcus EB. Arcus vero EB est datus. Remanet itaque quantitas arcus EH data. Manifestum est igitur quod licet illud cuius inquiritur scientia non sit punctum tropici hiemalis, quod est H, sed sit illud quod est de partibus circuli signorum, ut est E, similiter etiam scientur duo arcus ET et EH, eo quod nos iam premisimus tabulam declinationis cuiusque partium orbis signorum ab orbe equationis diei in orbe meridiei et illud est oppositum HT ex arcubus.
Sequitur autem illud ut orbes equidistantes orbi equationis diei qui secant partes orbis signorum equalis longitudinis a puncto cuiuslibet duorum tropicorum secent etiam ex horizonte utrinque arcus equales, in quibuscunque duarum partium fuerint orbis equationis diei, et fiant quantitates noctis et diei equales, omnis scilicet quantitas sue opposite. Et declaratur cum hoc etiam ut orbes equidistantes orbi equationis diei equalis longitudinis a quolibet duorum punctorum equantium diem similiter secent ex horizonte arcus equales ab utrisque lateribus orbis equationis diei et sint quantitates noctis et diei in illis alternate. 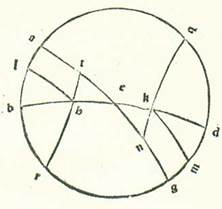 Et hoc est quod si nos signaverimus in hac forma punctum K, supra quod secet orbis equidistans orbi equationis diei equalis descripto supra H medietatem circuli horizontis, supra quam sint B, E, D, et compleverimus duos arcus HL et KM, qui sint due sectiones duorum orbium equidistantium econtrario, quos manifestum est esse equales, et descripserimus supra K et supra polum septentrionalem, qui sit punctum Q, quartam orbis, supra quam sint K, N, erunt duo arcus AT et NG equales, ideo quod ipsi sunt similes arcubus duobus LH et MK, quisque videlicet suo relativo, et remanebit arcus ET equalis arcui EN residuo, et erunt duorum triangulorum EHT et EKN duo latera unius duobus lateribus alterius equalia, videlicet ET equale EN et HT equale KN, et angulus T equalis angulo N. Quapropter erit basis EH equalis basi KE. Et illud est quod oportuit nos demonstrare.
Et hoc est quod si nos signaverimus in hac forma punctum K, supra quod secet orbis equidistans orbi equationis diei equalis descripto supra H medietatem circuli horizontis, supra quam sint B, E, D, et compleverimus duos arcus HL et KM, qui sint due sectiones duorum orbium equidistantium econtrario, quos manifestum est esse equales, et descripserimus supra K et supra polum septentrionalem, qui sit punctum Q, quartam orbis, supra quam sint K, N, erunt duo arcus AT et NG equales, ideo quod ipsi sunt similes arcubus duobus LH et MK, quisque videlicet suo relativo, et remanebit arcus ET equalis arcui EN residuo, et erunt duorum triangulorum EHT et EKN duo latera unius duobus lateribus alterius equalia, videlicet ET equale EN et HT equale KN, et angulus T equalis angulo N. Quapropter erit basis EH equalis basi KE. Et illud est quod oportuit nos demonstrare.
⟨II.4⟩ Capitulum quartum: Quo sciuntur provincie in quibus Sol transit supra summitatem capitum illas inhabitantium, et quando et quotiens sit illud
Manifestum est igitur quod nunquam Sol currit supra summitatem capitum habitantium in locis que sunt sub lineis equidistantibus orbi equationis diei que plus elongantur ab orbe equationis diei quam sit longitudo puncti tropici estivalis, que est 23 partes 51 minuta et 20 secunda. Supra summitatem vero capitum inhabitantium loca que sunt sub linea equidistanti orbi equationis diei cuius longitudo ab equatione diei est partes iste currit Sol semel in anno, cum est in puncto tropici estivalis. Sed supra summitatem capitum inhabitantium loca que sunt sub lineis equidistantibus equationi diei quorum longitudo ab ea minor est his partibus Sol bis in anno currit. Quando vero illud erit quo levius invenitur a nobis, est ut intremus numerum partium longitudinis linee ab equatione diei equidistantis ei in linea secunda tabule declinationis et consideremus quod est coram ea consequenter in linea prima ex numero partium quarte. Cum enim Solis longitudo ab unoquoque duorum punctorum equantium diem ad partem tropici estivalis fuerit equalis illis partibus in longitudine, tunc Sol curret supra summitatem capitum eorum qui sunt sub illa linea.
⟨II.5⟩ Capitulum quintum: Qualiter sciantur proportiones instrumentorum ad umbras suas in equalitate diei et in duobus tropicis in medietatibus dierum per quedam predicta, cum fuerint data
Facilius quoque quo sciuntur proportiones umbre ad instrumenta, postquam iam scivimus quantitatem arcus qui est inter duos tropicos et arcus qui est inter horizontem et inter duos polos, est quemadmodum narrabo. 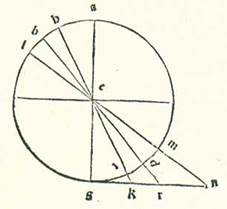 Describam orbem meridiei, supra quem sint A, B, G, D, supra centrum E, et ponam punctum quod est supra summitatem capitum A, et protraham diametrum AEG, et producam AG in superficie orbis meridiei lineam ortogonaliter, supra quam sint G, K, R, N. Manifestum est igitur quod hec linea equidistat linee que transit supra duo puncta supra que se secant orbis meridiei et circulus horizon. Et quoniam quantitas totius terre apud quantitatem orbis Solis est sicut punctum et centrum secundum sensum, ponam centrum E caput instrumenti, et imaginabor instrumentum lineam GE, sitque linea GKRN supra quam cadit extremitas umbre in medietatibus dierum, et sit radius Solis in die breviori et in die longiore et in die equali transiens supra punctum E, et sit radius Solis in die equali linea BEDR, et radius eius in die longiore linea HETK, et radius eius in die breviori linea LEMN, sitque linea GK umbra diei longioris, et linea GR umbra diei equalis, et linea GN umbra diei brevioris. Et quia arcus GD equatur altitudini poli septentrionalis ab horizonte in hoc climate, que est 36 partes secundum quantitatem qua circulus est 360 partes, et unusquisque duorum arcuum TD et DM est secundum illam quantitatem 23 partes et 51 minuta et 20 secunda, ergo manifestum est quod arcus GT residuus est 12 partes et 8 minuta et 40 secunda. Sed totus arcus GM secundum illam quantitatem est 59 partes et 51 minuta et 20 secunda. Quapropter erunt anguli qui sunt sub eis secundum quantitatem qua quattuor anguli recti sunt 360 partes. Ita scilicet erit angulus KEG 12 partes et 8 minuta et 40 secunda, et angulus REG 36 partes, et angulus NEG 59 partes et 51 minuta et 20 secunda. Secundum quantitatem vero qua duo anguli recti sunt 360 partes erit angulus KEG 24 partes et 17 minuta et 20 secunda, et angulus REG secundum illam quantitatem 72 partes, et angulus NEG 119 partes et 42 minuta et 40 secunda. Arcus ergo qui sunt portiones circuli descripti supra tres angulos supra quos sunt KEG et REG et NEG ortogonios erunt sic: videlicet erit arcus qui est supra lineam GK 24 partes et 17 minuta et 20 secunda, et ille qui est supra lineam EG, qui est id quod minuitur ex semicirculo, erit secundum quantitatem illam 155 partes et 42 minuta et 40 secunda, et ille qui est supra lineam GR erit 72 partes, et ille qui est supra lineam GE erit secundum illam quantitatem 108 partes, et ille qui est supra lineam GN erit 119 partes et 42 minuta et 40 secunda, et ille qui est supra GE, qui est id quod minus est etiam ex semicirculo, 60 partes et 17 minuta et 20 secunda. Secundum quantitatem ergo qua GK erit 25 partes et 14 minuta et 43 secunda erit GE 117 partes et 18 minuta et 51 secunda. Et secundum quantitatem qua etiam GR erit 70 partes et 32 minuta et 3 secunda erit GE 97 partes et 4 minuta et 55 secunda. Et secundum illam quantitatem qua est GN 103 partes et 46 minuta et 16 secunda erit GE 60 partes et 15 minuta et 42 secunda. Secundum illam ergo quantitatem qua instrumentum GE erit 60 partes erit umbra GK estivalis 12 partes et 55 minuta. Et erit umbra GR, que est diei equalis, 43 partes et 36 minuta fere. Et erit umbra GN hiemalis 103 partes et 20 minuta propinquius. Quapropter secundum conversionem declarabitur nobis quod cum due trium proportionum instrumenti GE ad umbras suas fuerint scite, quecunque due fuerint, scientur per illud altitudo poli et quod est inter duos tropicos. Quoniam cum sciti fuerint duo trium angulorum, quicunque duo fuerint, scietur reliquus angulus, propter hoc quod duo arcus TD et DM sunt equales. Verum acceptio inventionis vere secundum considerationem ad sciendum duos arcus, in qua non est dubitatio, est secundum modum quem premisimus. Scire autem illud propter proportiones instrumentorum ad umbras suas non est ita certum, eo quod tempus umbre equalitatis in se non est discretum et extremitates capitum umbrarum hiemalium in ea difficulter comprehenduntur.
Describam orbem meridiei, supra quem sint A, B, G, D, supra centrum E, et ponam punctum quod est supra summitatem capitum A, et protraham diametrum AEG, et producam AG in superficie orbis meridiei lineam ortogonaliter, supra quam sint G, K, R, N. Manifestum est igitur quod hec linea equidistat linee que transit supra duo puncta supra que se secant orbis meridiei et circulus horizon. Et quoniam quantitas totius terre apud quantitatem orbis Solis est sicut punctum et centrum secundum sensum, ponam centrum E caput instrumenti, et imaginabor instrumentum lineam GE, sitque linea GKRN supra quam cadit extremitas umbre in medietatibus dierum, et sit radius Solis in die breviori et in die longiore et in die equali transiens supra punctum E, et sit radius Solis in die equali linea BEDR, et radius eius in die longiore linea HETK, et radius eius in die breviori linea LEMN, sitque linea GK umbra diei longioris, et linea GR umbra diei equalis, et linea GN umbra diei brevioris. Et quia arcus GD equatur altitudini poli septentrionalis ab horizonte in hoc climate, que est 36 partes secundum quantitatem qua circulus est 360 partes, et unusquisque duorum arcuum TD et DM est secundum illam quantitatem 23 partes et 51 minuta et 20 secunda, ergo manifestum est quod arcus GT residuus est 12 partes et 8 minuta et 40 secunda. Sed totus arcus GM secundum illam quantitatem est 59 partes et 51 minuta et 20 secunda. Quapropter erunt anguli qui sunt sub eis secundum quantitatem qua quattuor anguli recti sunt 360 partes. Ita scilicet erit angulus KEG 12 partes et 8 minuta et 40 secunda, et angulus REG 36 partes, et angulus NEG 59 partes et 51 minuta et 20 secunda. Secundum quantitatem vero qua duo anguli recti sunt 360 partes erit angulus KEG 24 partes et 17 minuta et 20 secunda, et angulus REG secundum illam quantitatem 72 partes, et angulus NEG 119 partes et 42 minuta et 40 secunda. Arcus ergo qui sunt portiones circuli descripti supra tres angulos supra quos sunt KEG et REG et NEG ortogonios erunt sic: videlicet erit arcus qui est supra lineam GK 24 partes et 17 minuta et 20 secunda, et ille qui est supra lineam EG, qui est id quod minuitur ex semicirculo, erit secundum quantitatem illam 155 partes et 42 minuta et 40 secunda, et ille qui est supra lineam GR erit 72 partes, et ille qui est supra lineam GE erit secundum illam quantitatem 108 partes, et ille qui est supra lineam GN erit 119 partes et 42 minuta et 40 secunda, et ille qui est supra GE, qui est id quod minus est etiam ex semicirculo, 60 partes et 17 minuta et 20 secunda. Secundum quantitatem ergo qua GK erit 25 partes et 14 minuta et 43 secunda erit GE 117 partes et 18 minuta et 51 secunda. Et secundum quantitatem qua etiam GR erit 70 partes et 32 minuta et 3 secunda erit GE 97 partes et 4 minuta et 55 secunda. Et secundum illam quantitatem qua est GN 103 partes et 46 minuta et 16 secunda erit GE 60 partes et 15 minuta et 42 secunda. Secundum illam ergo quantitatem qua instrumentum GE erit 60 partes erit umbra GK estivalis 12 partes et 55 minuta. Et erit umbra GR, que est diei equalis, 43 partes et 36 minuta fere. Et erit umbra GN hiemalis 103 partes et 20 minuta propinquius. Quapropter secundum conversionem declarabitur nobis quod cum due trium proportionum instrumenti GE ad umbras suas fuerint scite, quecunque due fuerint, scientur per illud altitudo poli et quod est inter duos tropicos. Quoniam cum sciti fuerint duo trium angulorum, quicunque duo fuerint, scietur reliquus angulus, propter hoc quod duo arcus TD et DM sunt equales. Verum acceptio inventionis vere secundum considerationem ad sciendum duos arcus, in qua non est dubitatio, est secundum modum quem premisimus. Scire autem illud propter proportiones instrumentorum ad umbras suas non est ita certum, eo quod tempus umbre equalitatis in se non est discretum et extremitates capitum umbrarum hiemalium in ea difficulter comprehenduntur.
⟨II.6⟩ Capitulum sextum: De modo proprietatum linearum orbium equidistantium orbi equationis diei
Ad huius autem similitudinem in reliquis lineis equidistantibus equationi diei accipiam summam proprietatum earum et ponam superfluum declinationis aliarum ab aliis quartam hore que sit horarum equalium. In hoc namque existit sufficientia. Et narrabo summam eorum que in eis contingunt. Et ante divisionem huius et partitionem etiam incipiam loqui de equidistanti que est sub equatione diei, quam invenimus finem meridiei a tota quarta terre habitabilis. Hec autem sola tantum facit diem et noctem in omnibus diebus anni equales semper, quoniam in ea tantum secat circulus horizon omnes orbes equidistantes equationi diei in duo media et duo media. Et sunt omnes portiones eorum que sunt super terram similes et equales portionibus eorum que sunt sub terra, quod equidem est quod non contingit in aliquo eorum orbium maiorum declinatorum ab equatione diei. Orbem vero equationis diei, qui est ex magnis orbibus, circulus horizon solum secat in duo media in omni loco terre, et equantur dies et nox in eo et sunt equales secundum sensum ubique terrarum, quoniam circulus horizon est etiam ex magnis circulis. Unumquemque autem orbium ei equidistantium ab eo declinatorum qui sunt preter ipsum in parte habitabili et in parte meridiei horizon secat in duas portiones diversas. Et erunt portiones que sunt supra terram eorum qui sunt in parte meridiei ab eo minores eis que sunt sub terra, et erunt dies brevioris temporis noctibus. Sed quecunque portiones sunt ex eis qui sunt ex parte septentrionis ab eo erunt secundum conversionem eius. Erunt scilicet portiones que sunt supra terram maiores eis que sunt sub terra. Et erunt dies longioris temporis noctibus. Et umbra huius linee equidistantis in sphera terre equationi diei declinat ad ambas partes, quoniam transitus Solis erit supra summitatem capitum eorum qui sunt sub ea duabus vicibus, scilicet in duobus locis sectionum circuli equationis diei et circuli declivis. Et tunc tantum erunt instrumenta in medietatibus dierum non habentia umbram. Quando vero fuerit cursus Solis in medietate orbis signorum septentrionali, erit declinatio umbre instrumentorum ad partem meridiei. Et cum fuerit cursus Solis in medietate orbis signorum meridiana, erit declinatio umbre instrumentorum ad partem septentrionis. Et erit quantitas umbre estivalis et hiemalis in hoc loco secundum quantitatem qua erit longitudo instrumentorum 60 partes 26 partes et medietas partis propinquius. Totum autem quod narrabimus in omni sermone nostro de quantitate umbre non erit nisi de umbra meridiei. Et nos non accipere possumus veritatem meridiei, neque in duobus punctis equalitatis neque in duobus punctis duorum tropicorum. Sed tamen cum nos acceperimus umbram in his temporibus apud horam meridiei, erit propinquum veritati neque variabitur in aliquo cuius quantitas sit sensibilis. Et erit cursus stellarum que sunt super hanc lineam supra summitatem capitum eorum qui habitant sub ea. Et clare manifestum est quod stelle celi eis oriuntur omnes et occidunt. Quoniam duo poli sphere in veritate circuli horizontis non describunt orbem equidistantem equationi diei semper apparentem neque semper occultum secantem orbem meridiei. Quidam autem dicunt quod possibile est ut illud quod est sub hac linea equidistante ex terra sit habitabile, ideo quod eius complexio est valde bona, eo quod Sol non prolonget obumbrationem suam supra puncta summitatis capitum propter velocitatem sue declinationis in latitudine ab equatione diei. Et propter hoc sunt estas et hiems bone complexionis propter brevitatem longitudinis Solis a summitate capitum quando est in utrisque tropicis. Hoc autem quod dicimus est secundum estimationem et putatur. Utrum vero illud quod est sub hac linea habitetur, nos huius scientiam non comprehendimus, quoniam aliquis non pervenit ad eam qui sunt in nostris regionibus habitabilibus usque ad diem hunc nostrum. Proprietates autem que sunt sub hac linea equidistante circulo equationis diei absolute dico quod sunt he quas narravimus. Reliquarum vero equidistantium equationi diei, in quibus possibile est scire que sint regiones et loca que sub eis habitantur, narrabo summam proprietatis cuiusque, ne reiteremus sermonem in hora omni. Stelle que sunt supra summitates capitum in unaquaque linea earum sunt que secant de orbe descripto supra duos polos equationis diei arcus inter stellas et orbem equationis diei equales spacio quod est inter lineam et orbem equationis diei. Et quia circulus semper apparens est cuius centrum est polus equationis diei septentrionalis descriptus secundum longitudinem altitudinis poli ab horizonte, erunt stelle quas iste continet circulus semper apparentes. Stelle autem semper occulte sunt que sunt in circulo cuius centrum est polus equationis diei meridianus descripto secundum longitudinem depressionis poli ab horizonte.
De secunda
Linea vero equidistans secunda est cuius longioris diei longitudo est 12 hore et quarta hore, que sunt de horis equalibus. Et eius spacium ab equatione diei est quattuor partes et quarta partis fere, descripta supra insulam Berbenis, que est ex lineis in quibus declinant umbre meridiei ad duo latera, quoniam Sol obumbrat supra summitatem capitum eorum qui sunt sub ea bis in anno. Instrumenta vero seu gnomones non habebunt umbram in medietatibus diei cum fuerit spacium Solis a tropico estivali ad quamlibet duarum partium 79 partes et medietas partis. Cum ergo fuerit transitus Solis et ipse in his 159 partibus, erit declinatio umbre gnomonum ad partem meridiei in medietatibus dierum. Et cum fuerit transitus Solis et ipse in 201 partibus residuis, erit declinatio umbre gnomonum ad partem septentrionis in medietatibus dierum. Et erit in hoc loco umbra equalitatis quattuor partes et tertia partis et tertia quarte partis vicinius secundum quantitatem qua erunt gnomones 60 partes. Et erit umbra estivalis 21 partes et tertia partis vicinius, et umbra hiemalis 32 partes vicinius.
De tertia
Linea autem equidistans tertia est in qua longitudo diei longioris est 12 hore et medietas hore. Et elongatio eius ab equatione diei est 8 partes et 25 minuta, descripta supra Chaalingir Filisolitus. Ipsa quoque est ex lineis in quibus declinat umbra meridiei ad duo latera. Et obumbrat Sol supra summitatem capitum eorum bis in anno. Et neque gnomones habebunt umbram in medietatibus dierum cum fuerit spacium Solis a tropico estivali ad utrasque partes 69 partes fere. Quapropter cum fuerit transitus Solis et ipse in his 138 partibus, erit declinatio umbre gnomonum ad partem meridianam in medietatibus diei. Et cum fuerit transitus eius et ipse in 222 partibus residuis, erit declinatio umbre ad partem septentrionis. Et erit in hoc loco umbra equalitatis 8 partes et medietas et tertia partis, et umbra estatis 16 partes et medietas et tertia quarte partis fere, et umbra hiemis 37 partes et medietas et tertia et tertia quinte partis fere.
De quarta
Linea equidistans quarta est in qua longitudo diei longioris est 12 hore et medietas et quarta hore. Et eius elongatio ab equatione diei est 12 partes et medietas partis, descripta supra Chaalingir Filisolitus. Et ipsa etiam est ex lineis in quibus declinat umbra meridiei ad utraque latera. Et obumbrat Sol supra summitatem capitum eorum qui sunt sub ea bis in anno. Et neque gnomones in medietatibus diei habebunt umbram cum fuerit elongatio Solis a tropico estivali ad utrasque partes 57 partes et due tertie partis. Quapropter cum fuerit transitus Solis et ipse in his 115 partibus et tertia partis, erit declinatio umbre gnomonum ad partem meridiei. Et cum fuerit transitus Solis et ipse in 244 partibus et duabus tertiis partis residuis, erit declinatio umbre gnomonum ad partem septentrionis. Et erit umbra equalitatis 13 partes et tertia partis fere, et umbra estatis 12 partes et tertia quinte partis fere, et umbra hiemalis 44 partes et sexta partis fere.
De quinta
Linea equidistans quinta est in qua longitudo diei longioris est 13 hore. Et eius elongatio ab equatione diei sedecim partes et 27 minuta, descripta supra insulam Maros. Que etiam est ex lineis in quibus umbra meridiei ad utraque latera declinat. Et obumbrat Sol supra summitatem capitum eorum qui sunt sub ea bis in anno. Et neque gnomones in medietatibus diei habent umbram cum fuerit elongatio Solis a tropico estivo ad duas partes 45 partes. Quapropter cum fuerit transitus Solis et ipse in his 90 partibus, erit declinatio umbre gnomonum ad partem meridiei. Et cum fuerit transitus Solis et ipse in 270 partibus residuis, erit declinatio umbre ad partem septentrionis. Et erit umbra equalitatis 17 partes et medietas et quarta partis, et umbra estiva septem partes et medietas et quarta partis, et umbra hiemalis 51 partes.
De sexta
Linea vero equidistans sexta est in qua longitudo diei longioris est 13 hore et quarta hore. Et eius elongatio ab equatione diei est 20 partes et 14 minuta, descripta supra Thebatin. Que etiam est ex lineis in quibus umbra meridiei declinat ad utraque latera. Et obumbrat Sol supra summitatem capitum eorum qui sunt sub ea bis in anno. Et neque gnomones in medietatibus diei habebunt umbram cum fuerit elongatio Solis a tropico estivali ad utraque latera 31 partes. Quapropter cum fuerit transitus Solis et ipse in his 62 partibus, erit declinatio umbre gnomonum ad partem meridiei. Et cum fuerit transitus Solis et ipse in 298 partibus residuis, erit declinatio umbre gnomonum ad partem septentrionis. Et erit umbra equalitatis 22 partes et 8 minuta, et umbra estiva 3 partes et medietas partis et quarta partis, et umbra hiemalis 58 partes et sexta partis.
De septima
Linea equidistans septima est in qua longitudo diei longioris est 13 hore et medietas hore. Et eius elongatio ab equatione diei est 23 partes et 51 minuta et 20 secunda, descripta supra Sannis. Et ipsa est prima linea equidistantium in quibus umbra meridiei declinat ad partem unam. Neque unquam erit declinatio umbre gnomonum eis qui sunt sub ea ad partem meridiei. Veruntamen Sol obumbrat supra summitatem eorum capitum in tropico estivo tantum. Et non habebunt tunc gnomones in medietatibus diei umbram, eo quod spacium huius linee ab equatione diei est sicut tropici estivalis ab eo. In reliquis vero lineis erit declinatio umbre gnomonum in medietatibus diei semper ad partem septentrionis. Eritque umbra equalitatis sub hac linea 26 partes et medietas partis et umbra hiemalis 66 partes fere. Estas vero non habebit umbram. Et in omnibus lineis equidistantibus que sunt ad septentrionem ab hac linea usque ad lineam que terminat regiones habitabiles declinabit umbra gnomonum in medietatibus dierum ad partem septentrionis. Et neque gnomones in eis unquam erunt in medietatibus dierum absque umbra, neque umbra unquam declinat ad partem meridiei, sed est eius declinatio semper ad partem septentrionis, quoniam Sol nunquam obumbrat supra summitatem capitum ipsorum.
De octava
Linea vero equidistans octava est in qua longitudo diei longioris est 13 hore et medietas et quarta hore. Et eius elongatio ab equatione diei est 27 partes et 40 minuta, descripta supra Arnues. Et umbra estatis est quattuor partes, et umbra equalitatis est 31 partes et tertia et medietas quinte partis vicinius, et umbra hiemis est 75 partes et medietas partis.
De nona
Linea equidistans nona est in qua longioris diei longitudo est 14 hore. Et eius elongatio ab equatione diei 30 partes et 22 minuta, descripta supra infimum terre Egypti. Et umbra estatis sex partes et medietas et tertia partis, et umbra equalitatis 35 partes et sexta partis fere, et umbra hiemis 83 partes et quarta partis.
De decima
Linea equidistans decima est in qua longitudo diei longioris est 14 hore et quarta hore. Et eius elongatio ab equatione diei 33 partes et 18 minuta, descripta supra medium Sein. Et umbra estiva est 10 partes, et umbra equalitatis 39 partes et tertia et medietas sexte partis fere, et umbra hiemalis est 93 partes vicinius.
De undecima
Linea equidistans undecima est in qua longitudo diei longioris est 14 hore et medietas. Et eius elongatio ab equatione diei est 36 partes, descripta supra insulam Rhodum. Et umbra estiva est 12 partes et medietas et tertia et medietas sexte partis, et umbra equalitatis 43 partes et medietas et quarta partis, et umbra hiemalis est 103 partes et tertia partis.
De duodecima
Linea equidistans duodecima est in qua longitudo diei longioris est 14 hore et tres quarte. Et eius elongatio ab equatione diei est 38 partes et 35 minuta, descripta supra Sembret. Et umbra estiva est 15 partes et medietas et quarta partis vicinius, et umbra equalitatis est 47 partes et medietas et tertia partis vicinius, et umbra hiemalis est 114 partes et medietas et tertia et medietas quinte partis.
De tredecima
Linea equidistans tredecima est in qua longitudo diei longioris est 15 hore. Et eius elongatio ab equatione diei est 40 partes et 56 minuta fere, descripta supra Scinnitas. Et umbra estiva est 18 partes et tertia et medietas quinte partis fere, et umbra equalitatis 52 partes vicinius, et umbra hiemalis 127 partes et tertia et medietas quinte partis.
De decimaquarta
Linea equidistans decimaquarta est in qua longitudo diei longioris est 15 hore et quarta hore. Et eius elongatio ab equatione diei 43 partes et duodecima partis, descripta supra Nulis. Et umbra estiva est 20 partes et medietas et tertia et medietas quinte partis fere, et umbra equalitatis est 55 partes et medietas quinte, et umbra hiemalis 141 partes fere.
De decimaquinta
Linea equidistans decimaquinta est in qua longitudo diei longioris est 15 hore et medietas hore. Et eius elongatio ab equatione diei est 45 partes et unum minutum, descripta supra medium Malisnitas. Et umbra estiva est 23 partes et quarta partis fere, et umbra equalitatis est 60 partes, et umbra hiemalis est 155 partes et quarta partis.
De decimasexta
Linea equidistans decimasexta est in qua longitudo diei longioris est 15 hore et tres quarte. Et eius elongatio ab equatione diei 46 partes et 51 minuta, descripta supra fontes fluminis Astos. Et umbra estiva est 25 partes et medietas partis fere, et umbra equalitatis 64 partes vicinius, et umbra hiemalis est 171 partes et tertia et medietas sexte partis fere.
De decimaseptima
Linea equidistans decimaseptima est in qua longitudo diei longioris est 16 hore. Et eius elongatio ab equatione diei est 48 partes et 32 minuta, descripta supra egressiones Bauristenis. Et umbra estiva est 27 partes et medietas partis et medietas quinte partis fere, et umbra equalitatis est 67 partes et medietas et tertia partis vicinius, et umbra hiemalis est 189 partes fere.
De decimaoctava
Linea equidistans decimaoctava est in qua longitudo diei longioris est 16 hore et quarta hore. Et elongatio eius ab equatione diei est 50 partes et quarta partis, descripta supra medium paludis Meotide. Et estiva umbra est 29 partes et medietas et quarta partis vicinius, et umbra equalitatis est 72 partes et sexta partis fere, et umbra hiemalis est 210 partes et due tertie partis vicinius.
De decimanona
Linea equidistans decimanona est in qua longitudo diei longioris est 16 hore et medietas. Et eius elongatio ab equatione diei est 51 partes et medietas partis, descripta super ultimam partem meridiei Britannie. Et umbra estiva est 31 partes et tertia et medietas sexte partis, et umbra equalitatis 75 partes et tertia et medietas sexte partis vicinius, et umbra hiemalis 229 partes et due tertie partis fere.
De vigesima
Linea equidistans vigesima est in qua longitudo diei longioris est 16 hore et tres quarte. Et eius elongatio ab equatione diei est 52 partes et 50 minuta, descripta supra egressiones Ribes. Et umbra estiva est 33 partes et quarta partis fere, et umbra equalitatis 79 partes et sexta partis fere, et umbra hiemalis 253 partes et medietas et medietas sexte partis secundum supradictam quantitatem.
De vigesimaprima
Linea equidistans vigesimaprima est in qua longioris diei longitudo est 17 hore. Et elongatio eius ab equatione diei est 54 partes et unum minutum, descripta super egressiones Tanais. Et umbra estiva est trigintaquattuor partes et medietas et tertia partis vicinius, et umbra equalitatis 82 partes et due tertie partis fere, et umbra hiemalis 279 partes et sexta partis fere.
De vigesimasecunda
Linea equidistans vigesimasecunda est in qua longitudo diei longioris est 17 hore et quarta hore. Et eius elongatio ab equatione diei est 55 partes, descripta super Bericanas Britannie maioris. Et umbra estiva est 36 partes et quarta partis vicinius, et umbra equalitatis octuagintaquinque partes et due tertie partis, et umbra hiemalis est 304 partes et medietas partis.
De vigesimatertia
Linea equidistans vigesimatertia est in qua longitudo diei longioris est 17 hore et medietas hore. Et eius elongatio ab equatione diei est 56 partes, descripta supra medium Britannie maioris. Et umbra estiva est 37 partes et due tertie partis vicinius, et umbra equalitatis 88 partes et medietas et tertia et medietas sexte partis vicinius, et umbra hiemalis est 335 partes et tertia partis.
De vigesimaquarta
Linea equidistans vigesimaquarta est in qua longitudo diei longioris est 17 hore et tres quarte hore. Et eius elongatio ab equatione diei 57 partes, descripta super Catononiz One could equally read Catononim. Paris, BnF, lat. 14738 (22v, line 4) reads Catononiz too. The Greek text reads ‘Caturactonium’ (see Toomer, loc. cit., p. 88, line 10). Britannie. Et umbra estiva est 39 partes et sexta partis, et umbra equalitatis 92 partes et tertia et medietas sexte partis fere, et umbra hiemalis 372 partes et medietas et tertia partis fere.
De vigesimaquinta
Linea equidistans vigesimaquinta est cuius longitudo longioris diei est 18 hore. Et eius elongatio ab equatione diei est 58 partes, descripta super meridiem Britannie minoris. Et umbra estiva 40 partes et due tertie partis vicinius, et umbra equalitatis 96 partes vicinius, et umbra hiemalis 119 partes et quarta partis secundum supradictam quantitatem.
De vigesimasexta
Linea equidistans vigesimasexta est in qua longitudo diei longioris est 18 hore et medietas hore. Et eius elongatio ab equatione diei 59 partes et medietas partis, descripta supra Britanniam minorem.
Nos autem non posuimus hic superfluum horarum cum augmento quarte et quarte unius hore propter coangustationem que est inter lineas et propinquitatem aliarum ad alias. Ex superfluo enim altitudinis poli supra altitudinem poli non completur pars una. Et non oportet ut sit operatio nostra in his quorum elongatio accrescit ad septentrionem sicut est in illis quorum elongatio minoratur. Quapropter videtur nobis quod labor positionis proportionum umbrarum ad gnomones suos, quemadmodum fecimus in locis determinatis, superfluus est nobis.
De vigesimaseptima
Et ubi est longitudo diei longioris decem et novem hore, elongatio illius linee equidistantis ab equatione diei est 61 partes. Et ipsa est descripta supra septentrionem Britannie minoris.
De vigesimaoctava
Et ubi est longitudo diei longioris 19 hore et medietas hore, elongatio illius linee ab equatione diei est 62 partes, descripta supra insulas Boroen.
De vigesimanona
Et ubi est longitudo diei longioris 20 hore, longitudo illius linee equidistantis ab equatione diei est 63 partes. Et est descripta supra insulam Tyle.
De trigesima
Et ubi est longitudo diei longioris 21 hore, elongatio illius linee equidistantis ab equatione diei est sexagintaquattuor partes et medietas partis. Et est descripta supra Sachaliba.
De trigesimaprima
Et ubi est longitudo diei longioris 22 hore, elongatio illius linee equidistantis ab equatione diei est 65 partes et medietas partis.
De trigesimasecunda
Et ubi est longitudo diei longioris 23 hore, elongatio illius linee equidistantis ab equatione diei est 66 partes.
De trigesimatertia
Et ubi est longitudo diei longioris 24 hore, elongatio illius linee equidistantis ab equatione diei est 66 partes et sexta partis fere. Et ipsa est prima linearum in quibus revolvuntur umbre circa gnomones. Et Sol tunc cum fuerit in puncto tropici estivalis tantum, non occidet unquam. Et declinabit umbra gnomonum ad omnes partes horizontis. Et erit linea equidistans equationi diei descripta supra punctum tropici estivalis semper apparens et linea equidistans etiam equationi diei descripta supra punctum tropici hiemalis semper occulta, eo quod ipse utreque semper contingunt horizonta secundum coalternationem. Et erit orbis signorum ipse horizon cum ab eo orietur punctum equalitatis vernale.
Quod si quis voluerit perscrutari scientiam eorum quorum elongationes augmentantur ad septentrionem ex declinatione et summam eorum que accidunt in eis, inveniet ubi est altitudo poli septentrionalis 67 partes 15 fere partes orbis signorum a duabus partibus puncti tropici estivi non occidere unquam. Quapropter erit longitudo diei longioris et revolutio umbre gnomonum ad omnes partes horizontis fere mensis unius.
Bene autem erit cum scietur illud ex tabulis declinationis. Partes namque quas tu reperies in tabulis sunt longitudo linee equidistantis equationi diei ab ea quas ipsa secat ex orbe signorum ab utrisque partibus puncti cuiusque duorum tropicorum, sicuti si diceremus 15 partes cuiuscunque partis, erit illa linea ibi cum partibus quas ipsa secat aut semper apparentes aut semper occulte. Et quantum minuuntur he partes que sunt in tabula, que sunt longitudo linee equidistantis, ex quarta, que est 90, tantum est altitudo poli septentrionalis.
Ubi vero altitudo poli est 69 partes et medietas partis, ibi nunquam occidet Sol cum fuerit eius elongatio a puncto tropici estivalis ad utrasque partes 30 partes. Quapropter erit longitudo diei longioris fere duorum mensium et revolvetur umbra gnomonum in circuitu eorum ad omnes partes horizontis.
Et ubi est altitudo poli 73 partes et tertia partis, non occultabitur Sol cum fuerit eius elongatio a puncto tropici estivalis ad utrasque partes 45 partes. Quapropter erit longitudo diei longioris et revolutio umbre gnomonum ad omnes partes horizontis trium mensium.
Et ubi est altitudo poli 78 partes et tertia partis, ibi non occultabitur Sol cum fuerit eius longitudo a puncto tropici estivi ad ambas partes 60 partes. Quapropter erit longitudo diei longioris et revolutio umbre gnomonum quattuor mensium.
Et ubi est altitudo poli 84 partes, ibi non occultabitur Sol cum fuerit eius longitudo a puncto tropici estivi ad utrasque partes 75 partes. Et erit longitudo diei longioris et revolutio umbre gnomonum quinque mensium.
Et ubi est altitudo poli ab horizonte complementum quarte, scilicet 90 partes, ibi tota medietas orbis signorum septentrionalis non occultabitur unquam sub terra neque tota medietas orbis signorum meridiana apparebit unquam super terram. Quapropter erit annus totus dies unus, cuius medietas erit dies et medietas nox, quorum cuiusque longitudo erit sex mensium. Et umbra gnomonum volvetur semper circa eos ad omnes partes horizontis. Ex proprietatibus vero huius declinationis est ut sit polus septentrionis supra summitatem capitum captum M., et sit orbis equationis diei in loco semper apparentis et in termino semper occulti et sit etiam in loco horizontis, et fiat medietas orbis signorum septentrionalis semper apparens supra terram et medietas meridiana occulta sub terra semper.
⟨II.7⟩ Capitulum septimum: De scientia partium orbis equationis diei que elevantur cum partibus orbis signorum in sphera declivi
Postquam retulimus omnes proprietates linearum equidistantium que sunt in circulis declivibus et summam eorum que eveniunt in eis et apparent, demonstrabimus qualiter sciantur numeri temporum equationis diei que elevantur cum elevationibus arcuum orbis signorum, per quorum scientiam sciemus divisiones eorum que sunt preter hec et partes. Et nominabimus partes orbis signorum declivis 12, et ponemus earum principia a duobus punctis tropicis et duobus punctis equalitatis, et nominabimus primam duodecimam, que est a puncto equalitatis vernalis ad ea que sequuntur et elevantur motu totius, Arietem, et secundam Taurum, et que sunt post illas secundum ordines suos, quibus nominaverunt eas antiqui. Et ostendemus prius quod arcus orbis signorum equalis elongationis a quolibet duorum punctorum equalitatis elevantur semper cum arcubus equalibus orbis equationis diei. 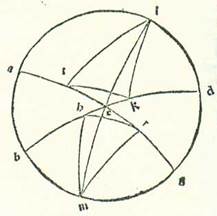 Quapropter describam circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint, B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et duas portiones orbis signorum, supra quas sint R, H et T, K, et sit unumquodque duorum punctorum R et T equalitatis vernalis, et duo arcus equales elevati a duabus partibus, supra quos sint R, H et T, K, transeant super duo puncta K et H. Dico ergo quod unusquisque eorum elevatur cum duobus arcubus equalibus orbis equationis diei supra quos sunt R, E et T, E. Sint itaque loca duorum polorum equationis diei due note L et M. Et describam portiones orbium magnorum, supra quas sint M, R et L, T et M, E, L et K, L et M, H. Et quia RH equatur TK, ergo due linee equidistantes descripte supra K et H sunt equalis longitudinis ab equatione diei a duabus partibus, et erit LK equalis MH, et EK equalis EH, et erunt latera trianguli LKT equalia lateribus trianguli MHR, et latera trianguli LEK equalia lateribus trianguli MEH. Angulus vero KLE equatur angulo HME, et totus angulus KLT equatur toti angulo HMR. Quapropter est angulus ELT reliquus equalis angulo EMR reliquo. Ergo basis ET equatur basi ER. Et illud voluimus demonstrare.
Quapropter describam circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint, B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et duas portiones orbis signorum, supra quas sint R, H et T, K, et sit unumquodque duorum punctorum R et T equalitatis vernalis, et duo arcus equales elevati a duabus partibus, supra quos sint R, H et T, K, transeant super duo puncta K et H. Dico ergo quod unusquisque eorum elevatur cum duobus arcubus equalibus orbis equationis diei supra quos sunt R, E et T, E. Sint itaque loca duorum polorum equationis diei due note L et M. Et describam portiones orbium magnorum, supra quas sint M, R et L, T et M, E, L et K, L et M, H. Et quia RH equatur TK, ergo due linee equidistantes descripte supra K et H sunt equalis longitudinis ab equatione diei a duabus partibus, et erit LK equalis MH, et EK equalis EH, et erunt latera trianguli LKT equalia lateribus trianguli MHR, et latera trianguli LEK equalia lateribus trianguli MEH. Angulus vero KLE equatur angulo HME, et totus angulus KLT equatur toti angulo HMR. Quapropter est angulus ELT reliquus equalis angulo EMR reliquo. Ergo basis ET equatur basi ER. Et illud voluimus demonstrare.
Ostendemus etiam quod duo arcus orbis equationis diei qui elevantur cum duobus arcubus orbis signorum equalibus et equalis longitudinis a quolibet punctorum duorum tropicorum erunt equalium elevationum elevationibus in orbe recto cum his duobus arcubus coniunctis. 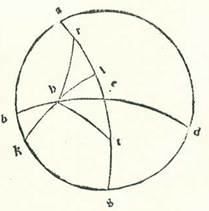 Describam ergo propter hoc circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et describam duos arcus orbis signorum equales et equalium elongationum a puncto tropici hiemalis, qui sint RH et TH, sitque R punctum autumnale, et T punctum vernale, et sit punctum H commune elevationibus eorum et horizonti, propter hoc quod duos arcus RH et TH continet unus orbis equidistans equationi diei. Et manifestum est quod TE elevatur cum TH et ER elevatur cum RH. Et ex hoc manifestum est quod TER totus equatur elevationi RH et TH in orbe recto. Si enim posuerimus ut nota K sit polus meridianus et descripserimus supra KH quartam orbis magni equalem in potentia quarte horizontis in orbe recto, supra quam sint K, H, L, et erit arcus TL ipse qui elevatur cum arcu TH in orbe recto, et erit LR ipse qui elevatur cum RH. Quapropter erunt duo arcus TL et LR equalium elevationum cum duobus arcubus TE et ER, quos unus arcus coniungit, qui est RLET. Et illud est quod oportuit nos declarare.
Describam ergo propter hoc circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et describam duos arcus orbis signorum equales et equalium elongationum a puncto tropici hiemalis, qui sint RH et TH, sitque R punctum autumnale, et T punctum vernale, et sit punctum H commune elevationibus eorum et horizonti, propter hoc quod duos arcus RH et TH continet unus orbis equidistans equationi diei. Et manifestum est quod TE elevatur cum TH et ER elevatur cum RH. Et ex hoc manifestum est quod TER totus equatur elevationi RH et TH in orbe recto. Si enim posuerimus ut nota K sit polus meridianus et descripserimus supra KH quartam orbis magni equalem in potentia quarte horizontis in orbe recto, supra quam sint K, H, L, et erit arcus TL ipse qui elevatur cum arcu TH in orbe recto, et erit LR ipse qui elevatur cum RH. Quapropter erunt duo arcus TL et LR equalium elevationum cum duobus arcubus TE et ER, quos unus arcus coniungit, qui est RLET. Et illud est quod oportuit nos declarare.
Iam ergo nobis declaratum est ex eis que prediximus quod cum sciverimus dividere elevationes in quarta una in omni declinatione, sciemus dividere tres quartas residuas. Et ponam etiam huius exemplum lineam equidistantem descriptam super Rhodum, ubi est longitudo diei longioris 14 hore et medietas et altitudo poli septentrionalis ab horizonte 36 partes. 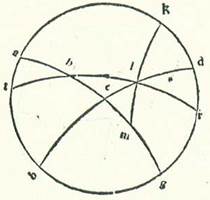 Describam itaque circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem orbis signorum, supra quam sint R, L, H, T, et sit locus sectionis, supra quem est H, ipsum punctum vernale, et faciam transire supra polum equationis diei septentrionalem, qui sit K, et supra L, ubi se secant orbis signorum et orbis horizontis, quartam orbis magni, supra quam sint K, L, M, et sit arcus HL notus, et inquiramus inventionem arcus orbis equationis diei qui cum eo elevatur, qui est EH, et sit HL ipse Aries prius. Et quia etiam inter duos arcus orbium maiorum, scilicet arcus EG et GK, duo arcus ED et KM sese secant supra L, erit proportio chorde dupli arcus KD ad chordam dupli arcus DG aggregata ex duabus proportionibus, ex proportione chorde dupli arcus KL ad chordam dupli arcus LM et ex proportione chorde dupli arcus ME ad chordam dupli arcus EG. Duplum vero arcus KD est 72 partes, et est eius chorda 70 partes et 32 minuta et tria secunda, et duplum arcus GD est 108 partes, et eius chorda 97 partes et 4 minuta et 55 secunda, et duplum arcus KL est 156 partes et 40 minuta, et eius chorda est 117 partes et 31 minuta et 15 secunda, et duplum arcus LM est 23 partes et 19 minuta et 59 secunda, et eius chorda 24 partes et 15 minuta et 57 secunda. Cum ergo proiecerimus ex proportione 70 partium et 32 minutorum et trium secundorum ad 97 partes et quatuor minuta et 55 secunda proportionem 117 partium et 31 minutorum et 15 secundorum ad 24 partes et 15 minuta et 57 secunda, remanebit proportio chorde dupli arcus ME ad chordam dupli arcus EG, et illud est proportio 18 partium et cifre et quinque secundorum ad 120 partes. Chorda autem dupli arcus EG est 120 partes. Quapropter chorda dupli arcus ME secundum illas partes est 18 partes et cifre et quinque secunda. Et propter hoc erit duplum arcus ME 17 partes et 16 minuta propinquius, et ME secundum illas partes erit 8 partes et 38 minuta. Sed totus arcus MH, quia elevatur in orbe recto cum HL quemadmodum eius declaratio precessit, est 27 partes et 50 minuta. Ergo EH residua erit 19 partes et 12 minuta.
Describam itaque circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem orbis signorum, supra quam sint R, L, H, T, et sit locus sectionis, supra quem est H, ipsum punctum vernale, et faciam transire supra polum equationis diei septentrionalem, qui sit K, et supra L, ubi se secant orbis signorum et orbis horizontis, quartam orbis magni, supra quam sint K, L, M, et sit arcus HL notus, et inquiramus inventionem arcus orbis equationis diei qui cum eo elevatur, qui est EH, et sit HL ipse Aries prius. Et quia etiam inter duos arcus orbium maiorum, scilicet arcus EG et GK, duo arcus ED et KM sese secant supra L, erit proportio chorde dupli arcus KD ad chordam dupli arcus DG aggregata ex duabus proportionibus, ex proportione chorde dupli arcus KL ad chordam dupli arcus LM et ex proportione chorde dupli arcus ME ad chordam dupli arcus EG. Duplum vero arcus KD est 72 partes, et est eius chorda 70 partes et 32 minuta et tria secunda, et duplum arcus GD est 108 partes, et eius chorda 97 partes et 4 minuta et 55 secunda, et duplum arcus KL est 156 partes et 40 minuta, et eius chorda est 117 partes et 31 minuta et 15 secunda, et duplum arcus LM est 23 partes et 19 minuta et 59 secunda, et eius chorda 24 partes et 15 minuta et 57 secunda. Cum ergo proiecerimus ex proportione 70 partium et 32 minutorum et trium secundorum ad 97 partes et quatuor minuta et 55 secunda proportionem 117 partium et 31 minutorum et 15 secundorum ad 24 partes et 15 minuta et 57 secunda, remanebit proportio chorde dupli arcus ME ad chordam dupli arcus EG, et illud est proportio 18 partium et cifre et quinque secundorum ad 120 partes. Chorda autem dupli arcus EG est 120 partes. Quapropter chorda dupli arcus ME secundum illas partes est 18 partes et cifre et quinque secunda. Et propter hoc erit duplum arcus ME 17 partes et 16 minuta propinquius, et ME secundum illas partes erit 8 partes et 38 minuta. Sed totus arcus MH, quia elevatur in orbe recto cum HL quemadmodum eius declaratio precessit, est 27 partes et 50 minuta. Ergo EH residua erit 19 partes et 12 minuta.
Iam autem ostensum est cum hoc quod Piscis elevatur secundum equalitatem illorum temporum, et unumquodque duorum signorum, scilicet Virgo et Libra, cum eis quibus diminuuntur hec tempora ex duplo temporum quibus Aries elevatur in orbe recto, quod est tempora 36 et 28 minuta. Sit etiam arcus HL duo signa, scilicet Aries et Taurus simul, videlicet 60 partes. Que vero preter hec sunt in forma sint secundum habitudinem suam. Quapropter erit duplum arcus KL 138 partes et 59 minuta et 42 secunda, et eius chorda est 112 partes et 23 minuta et 56 secunda, et duplum arcus LM erit 41 partes et cifre et 18 secunda, et chorda eius 42 partes et unum minutum et 48 secunda. Cum ergo minuerimus ex proportione 70 partium et 32 minutorum et trium secundorum ad 97 partes et quatuor minuta et 55 secunda proportionem 112 partium et 23 minutorum et 56 secundorum ad 42 partes et unum minutum et 48 secunda, remanebit proportio chorde dupli arcus ME ad chordam dupli arcus EG, que est proportio 32 partium et 36 minutorum et quatuor secundorum ad 120. Chorda autem dupli arcus EG est 120 partes. Ergo chorda dupli arcus ME est 32 partes et 36 minuta et quattuor secunda. Ergo et duplum arcus ME est 31 partes et 32 minuta fere. Quapropter erit arcus ME secundum illas partes 15 partes et 46 minuta. Sed totus arcus MH secundum quod eius declaratio precessit est 57 partes et 44 minuta. Ergo totus HE est 41 partes et 58 minuta. Ergo Aries et Taurus elevantur ambo cum 41 temporibus et 58 minutis. Sed ex hoc quod iam ostensum est quod Aries elevatur cum 19 temporibus et 12 minutis remanent ea cum quibus elevatur Taurus 22 tempora et 46 minuta. Et propter hoc etiam erunt tempora quibus elevatur Aquarius equalia temporibus quibus elevatur Taurus, scilicet 22 tempora et 46 minuta. Et unumquodque duorum, scilicet Leo et Scorpio, elevatur cum eis quibus iste partes minuuntur ex duplo temporum quibus elevatur Taurus in orbe recto, quod est 37 tempora et duo minuta. Et quia longitudo diei longioris est 14 hore et medietas hore equalis et longitudo diei brevioris est 9 hore et medietas, ergo manifestum est quod medietas orbis que est a Cancro usque ad finem Sagittarii elevatur cum 217 temporibus et medio equationis diei et quod medietas orbis que est a Capricorno usque ad finem Geminorum elevatur cum 142 temporibus et medio equationis diei. Quapropter unaqueque duarum quartarum que sunt a duabus partibus puncti vernalis elevatur cum 71 temporibus et quarta temporis, et unaqueque duarum quartarum que sunt a duabus partibus puncti autumnalis elevatur cum 108 temporibus et medietate et quarta temporis ex temporibus equationis diei. Et propter hoc etiam unumquodque signorum duorum, idest Capricornus et Gemini, elevatur cum 29 temporibus et 17 minutis, que desunt ad complendam unamquamque duarum quartarum. Et remanet ut unumquodque duorum signorum, scilicet Cancer et Sagittarius, elevetur cum eis que desunt ad complendam quartam que est 108 tempora et medietas et quarta temporis, que sunt 35 tempora et quarta temporis. Et manifestum est quod hoc modo sciemus equationis diei tempora que elevantur cum partibus orbis signorum paucioribus his partibus.
Has quoque elevationes sciemus compendiosius et facilius et opere sapientiore eo quod prediximus, quemadmodum narrabo. 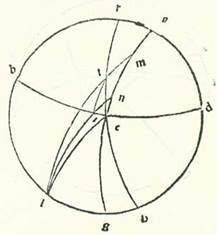 Describam primum orbem meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem orbis signorum, supra quam sint R, E, H, sitque punctum E, quod est locus sectionis, punctum vernale, ponamque arcum ET quantum voluero, et ponam portionem equidistantis equationi diei supra T, que sit TI, et ponam polum equationis diei meridionalem L, et describam supra ipsum quartas orbium maiorum, supra quas sint L, T, M et L, I, N et L, E. Ergo ex hoc manifestum est quod portio ET orbis signorum elevatur in sphera recta cum arcu orbis equationis diei EM et elevatur in sphera declivi cum arcu MN, eo quod arcus IT equidistantis, cum qua elevatur portio ET, est similis arcui NM equationis diei. Arcus vero similes orbium equidistantium elevantur in temporibus equalibus in omni loco. Elevationes ergo portionis ET in sphera declivi sunt minus elevationibus eius in sphera recta quantum est arcus EN. Ergo secundum hoc declaratur quod cum protrahentur arcus harum quartarum orbium maiorum, erit arcus LIN determinans portionem EN, quod est superfluum quod est inter elevationes ET in sphera declivi et inter elevationes eius in sphera recta partium orbis signorum quod determinat punctum E et equidistans descripta super T.
Describam primum orbem meridiei, supra quem sint A, B, G, D, et medietatem circuli horizontis, supra quam sint B, E, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem orbis signorum, supra quam sint R, E, H, sitque punctum E, quod est locus sectionis, punctum vernale, ponamque arcum ET quantum voluero, et ponam portionem equidistantis equationi diei supra T, que sit TI, et ponam polum equationis diei meridionalem L, et describam supra ipsum quartas orbium maiorum, supra quas sint L, T, M et L, I, N et L, E. Ergo ex hoc manifestum est quod portio ET orbis signorum elevatur in sphera recta cum arcu orbis equationis diei EM et elevatur in sphera declivi cum arcu MN, eo quod arcus IT equidistantis, cum qua elevatur portio ET, est similis arcui NM equationis diei. Arcus vero similes orbium equidistantium elevantur in temporibus equalibus in omni loco. Elevationes ergo portionis ET in sphera declivi sunt minus elevationibus eius in sphera recta quantum est arcus EN. Ergo secundum hoc declaratur quod cum protrahentur arcus harum quartarum orbium maiorum, erit arcus LIN determinans portionem EN, quod est superfluum quod est inter elevationes ET in sphera declivi et inter elevationes eius in sphera recta partium orbis signorum quod determinat punctum E et equidistans descripta super T.
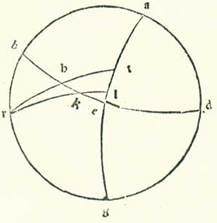 Postquam premisimus ista, affirmabimus formam orbis meridiei et medietatem orbis horizontis et medietatem orbis equationis diei et polum equationis diei meridianum, qui sit punctum R, et describam duas quartas orbium magnorum, que sint RHT et RKL, et ponam punctum H, scilicet ubi communicant linea equidistans et punctum tropici hiemalis, et ponam punctum K, ubi communicant verbi gratia principium Piscis aut alia partium quarte date et linea equidistans. Ergo inter duos arcus etiam duorum orbium magnorum RT et ET sunt duo arcus duorum magnorum orbium RKL et EKH sese secantes supra K. Ergo proportio chorde dupli arcus TH ad chordam dupli arcus RH aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus TE ad chordam dupli arcus EL et ex proportione chorde dupli arcus KL ad chordam dupli arcus KR. In omnibus autem locis declinationis quantitas dupli arcus TH est una, quoniam ipse arcus est qui est inter duos tropicos. Quapropter duplum arcus HR residui note quantitatis erit. Et similiter in reliquis portionibus orbis signorum in omnibus locis declinationis erit duplum arcus LK unius quantitatis, et scietur ex tabulis declinationum. Et propter hoc etiam scietur duplum arcus KR residui. Et propter hoc etiam remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EL nota in omnibus locis declinationis et in omnibus partibus quarte.
Postquam premisimus ista, affirmabimus formam orbis meridiei et medietatem orbis horizontis et medietatem orbis equationis diei et polum equationis diei meridianum, qui sit punctum R, et describam duas quartas orbium magnorum, que sint RHT et RKL, et ponam punctum H, scilicet ubi communicant linea equidistans et punctum tropici hiemalis, et ponam punctum K, ubi communicant verbi gratia principium Piscis aut alia partium quarte date et linea equidistans. Ergo inter duos arcus etiam duorum orbium magnorum RT et ET sunt duo arcus duorum magnorum orbium RKL et EKH sese secantes supra K. Ergo proportio chorde dupli arcus TH ad chordam dupli arcus RH aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus TE ad chordam dupli arcus EL et ex proportione chorde dupli arcus KL ad chordam dupli arcus KR. In omnibus autem locis declinationis quantitas dupli arcus TH est una, quoniam ipse arcus est qui est inter duos tropicos. Quapropter duplum arcus HR residui note quantitatis erit. Et similiter in reliquis portionibus orbis signorum in omnibus locis declinationis erit duplum arcus LK unius quantitatis, et scietur ex tabulis declinationum. Et propter hoc etiam scietur duplum arcus KR residui. Et propter hoc etiam remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EL nota in omnibus locis declinationis et in omnibus partibus quarte.
Postquam ergo hec sunt quemadmodum narravimus, si nos descripserimus Probably super is missing here, which follows in Paris, BnF, lat. 14738 (25r, line 11). The Greek text is somewhat different here (see Toomer, loc. cit., p. 96, lines 6-7). superflua augmentorum que adduntur in tota quarta orbis signorum super omnes decem partes a puncto vernali ad punctum hiemale arcum LK, propter bonitatem mensure divisionis huius et quia in eo est sufficientia, erit duplum arcus TH semper 47 partes et 42 minuta et 40 secunda, et chorda eius 48 partes et 31 minuta et 55 secunda, et duplum arcus HR residui 132 partes et 17 minuta et 20 secunda, et chorda eius 109 partes et 44 minuta et 53 secunda. Similiter quoque in arcu quidem cuius elongatio a puncto vernali est 10 partes versus punctum hiemale erit duplum arcus KL 8 partes et tria minuta et 16 secunda, et eius chorda 8 partes et 25 minuta et 40 secunda, et duplum arcus KR 171 partes et 56 minuta et 44 secunda, et eius chorda 119 partes et 42 minuta et 14 secunda. Sed in arcu cuius elongatio est 20 partes erit duplum arcus LK 15 partes et 54 minuta et 6 secunda, et eius chorda 16 partes et 35 minuta et 56 secunda, et duplum arcus KR 164 partes et 5 minuta et 54 secunda, et eius chorda 118 partes et 50 minuta et 47 secunda. In arcu vero cuius elongatio est 30 partes erit duplum arcus LK 23 partes et 19 minuta et 58 secunda, et eius chorda 24 partes et 15 minuta et 56 secunda, et duplum arcus KR 156 partes et 40 minuta et 2 secunda, et chorda eius 117 partes et 31 minuta et 15 secunda. Verum in arcu cuius elongatio est 40 partes erit duplum arcus LK 30 partes et 8 minuta et 10 secunda, et eius chorda 31 partes et 11 minuta et 45 secunda, et duplum arcus KR 149 partes et 51 minuta et 50 secunda, et eius chorda 115 partes et 52 minuta et 27 secunda. Sed in arcu cuius elongatio est 50 partes erit duplum arcus LK 36 partes et quinque minuta et 46 secunda, et eius chorda 37 partes et 10 minuta et 39 secunda, et duplum arcus KR 143 partes et 54 minuta et 14 secunda, et eius chorda 114 partes et quinque minuta et 44 secunda. In arcu vero cuius elongatio est 60 partes erit duplum arcus LK 41 partes et cifre et 18 secunda, et eius chorda 42 partes et unum minutum et 48 secunda, et duplum arcus KR est 138 partes et 59 minuta et 42 secunda, et eius chorda 112 partes et 23 minuta et 57 secunda fere. Sed in arcu cuius elongatio est 70 partes erit duplum arcus LK 44 partes et 40 minuta et 22 secunda, et eius chorda 45 partes et 36 minuta et 18 secunda, et duplum arcus KR 135 partes et 19 minuta et 38 secunda, et eius chorda 110 partes et 59 minuta et 47 secunda fere. Verum in arcu cuius elongatio est 80 partes erit duplum arcus LK 46 partes et 56 minuta et 32 secunda, et eius chorda 47 partes et 47 minuta et 40 secunda, et duplum arcus KR 133 partes et 3 minuta et vigintiocto secunda, et eius chorda 110 partes et quattuor minuta et sedecim secunda. Quapropter cum nos proiecerimus ex proportione chorde dupli arcus TH ad chordam dupli arcus HR, que est proportio quadragintaocto partium et 31 minutorum et 55 secundorum ad 109 partes et 44 minuta et 53 secunda, proportionem chorde dupli declinationis cuiusque arcuum superfluentium 10 et 10 partibus, que est proportio chorde dupli arcus LK ad chordam dupli arcus KR, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EL in omni loco declinationis que est proportio 60 partium, scilicet in eo cuius elongatio est decem partes ad novem partes et 33 minuta, et in arcu cuius elongatio est 20 partes ad 18 partes et 57 minuta, et in eo cuius elongatio est 30 partes ad 28 partes et minutum unum, et in eo cuius elongatio est 40 partes ad 36 partes et 32 minuta, et in eo cuius elongatio est 50 partes ad 44 partes et 12 minuta, et in eo cuius elongatio est 60 partes ad 50 partes et 44 minuta, et in eo cuius elongatio est 70 partes ad 55 partes et 45 minuta, et in eo cuius elongatio est 80 partes ad 58 partes et 55 minuta. Ergo ex hoc manifestum est nobis quod cum nos sciverimus quantitatem dupli arcus TE in omni declinatione, quoniam ipse est superfluum quo augetur dies equalis supra breviorem, et sciverimus chordam eius, et sciverimus proportionem eius ad chordam dupli arcus EL, tunc sciemus elevationes arcus TE dati et sciemus duplum arcus EL, cuius cum proiecerimus medietatem, que est EL, de elevationibus arcus inquisiti orbis signorum in sphera recta, erunt que remanebunt ascensiones illius arcus orbis signorum in loco declinato quem voluerimus. Et propter hoc ponam exemplum lineam equidistantem super Rhodum, ubi est duplum arcus TE 37 partes et 30 minuta, et eius chorda 38 partes et 34 minuta vicinius. Et quia proportio 60 ad 38 partes et 34 minuta est sicut proportio aut 9 partium et 33 minutorum ad sex partes et octo secunda, aut 18 partium et 57 minutorum ad 12 partes et 11 minuta, aut 28 partium et minuti unius ad 18 partes et unum minutum, aut 36 partium et 33 minutorum ad 23 partes et 29 minuta, aut 44 partium et 12 minutorum ad 28 partes et 25 minuta, aut 50 partium et 44 minutorum ad 32 partes et 37 minuta, aut 55 partium et 45 minutorum ad 35 partes et 52 minuta, aut 58 partium et 55 minutorum ad 37 partes et 52 minuta, et erit chorda dupli arcus EL, qui est superfluum in omnibus decem partibus, et eius medietas, que est EL, scilicet in decena prima erunt due partes et 56 minuta, et in decena secunda 5 partes et 4 minuta, et in decena tertia 8 partes et 38 minuta, et in decena quarta 11 partes et 17 minuta, et in decena quinta 13 partes et 42 minuta, et in decena sexta 15 partes et 46 minuta, et in decena septima 17 partes et 24 minuta, et in decena octava 18 partes et 24 minuta. Et manifestum est quod in decena nona erunt 18 partes et 45 minuta. Et quemadmodum iam precessit in elevationibus sphere recte arcus quidem decene prime elevatur cum 9 temporibus et 10 minutis equationis diei, et in decena secunda cum 18 temporibus et 25 minutis, et in decena tertia cum 27 temporibus et 50 minutis, et in decena quarta cum 37 temporibus et 30 minutis, et in decena quinta cum 47 temporibus et 28 minutis, et in decena sexta cum 57 temporibus et 44 minutis, et in decena septima cum 68 temporibus et 18 minutis, et in decena octava cum 79 temporibus et 5 minutis, et in decena nona cum temporibus quarte totius, que sunt 90 tempora. Manifestum est ergo quod si nos minuerimus de elevationibus cuiusque harum decenarum (quas nominavimus in sphera recta) portionem eius que est quantitas arcus EL, que remanebunt erunt elevationes cuiusque decenarum in hoc loco declinationis quam volumus. Elevabitur ergo arcus qui est a puncto vernali usque ad postremum decene prime cum temporibus residuis que sunt 6 tempora et 14 minuta, et qui est usque ad finem decene secunde cum duodecim temporibus et 35 minutis, et qui est usque ad finem decene tertie cum 19 temporibus et duodecim minutis, et qui est usque ad finem decene quarte cum vigintisex temporibus et tredecim minutis, et qui est usque ad finem decene quinte cum 33 temporibus et 46 minutis, et qui est ad finem decene sexte cum 41 temporibus et 58 minutis, et qui est ad finem decene septime cum 50 temporibus et 54 minutis, et qui est ad finem decene octave cum 60 temporibus et 41 minutis, et qui est ad finem decene none, qui est quarta tota, cum medietate temporum longitudinis diei brevioris, que sunt 71 tempora et 15 minuta. Elevationes igitur cuiuscunque decenarum he sunt: scilicet prima elevatur cum sex temporibus et 14 minutis, secunda cum sex temporibus et 21 minutis, et tertia cum sex temporibus et 37 minutis, et quarta cum 7 temporibus et uno minuto, et quinta cum septem temporibus et 33 minutis, et sexta cum 8 temporibus et 12 minutis, et septima cum 8 temporibus et 56 minutis, et octava cum 9 temporibus et 47 minutis, et nona cum 10 temporibus et 34 minutis.
⟨II.8⟩ Capitulum octavum: De modo positionis tabularum eius quod elevatur de orbe equationis diei cum omnibus decem partibus orbis signorum in locis orbium equidistantium
Ex his quorum iam declaratio precessit de elevationibus quarte unius sciemus que sequuntur de elevationibus trium quartarum reliquarum. Et similiter sciemus elevationes decenarum cuiuscunque voluerimus in unaquaque linearum equidistantium. Et faciemus ad hoc tabulas undecem preparatas ad illud inveniendum ex quocunque possibile est, ut sciamus, cum necesse est, que sunt preter ipsum. Et ponemus principia nostra in tabulis a linea equidistante que est sub equatione diei et perveniemus ad lineam equidistantem in qua est longitudo diei longioris 17 hore. Et ponam superfluum linearum medietatem hore propterea quod id quod est inter superfluum vere, quod est minus medietate unius hore, et superfluum equalitatis non est quantitas sensibilis. Et premittemus in tabulis cuiusque linearum equidistantium tabulam orbis signorum et describam in ea nomina signorum. Et scribam in tabula secunda partes signorum 360 secundum superfluum 10 graduum, scilicet consequenter post unumquodque signum ex latere partes suas. Et in tabula tertia scribam consequenter ex latere tempora equationis diei que elevantur cum omnibus decem partibus et minuta temporum. Et describam in tabula quarta summas temporum et minutorum eorum. Et hec est tabularum descriptio:
Tabule elevationum signorum septem climatum suis singule linearum ab equatione diei equidistantium horizontibus seriatim attribute
Prima |
Secunda |
Tertia
Clima primum |
Quarta
Clima secundum |
||||||||||||||||||
Signa |
Decene |
Elevationes signorum in sphera recta, ubi longior dies duodecem horas et nox totidem semper habent absque latitudine |
Elevationes signorum in horizonte declivi linee equidistantis |
Elevationes signorum in horizonte declivi linee equidistantis |
Elevationes signorum in horizonte declivi linee equidistantis |
||||||||||||||||
cuius longior dies est horarum 12, minutorum 30, |
cuius longior dies est horarum 13, minutorum 0, |
cuius longior dies est horarum 13, minutorum 30, |
|||||||||||||||||||
et eius latitudo graduum 8, minutorum 25 |
et eius latitudo graduum 16, minutorum 27 |
et eius latitudo graduum 23, minutorum 51 |
|||||||||||||||||||
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
||||||
Aries
♈ |
10
20
30 |
9
9
9 |
10
15
25 |
9
18
27 |
10
25
50 |
8
8
8 |
35
39
52 |
8
17
26 |
35
14
6 |
7
8
8 |
58
5
17 |
7
16
24 |
58
3
20 |
7
7
7 |
24
30
43 |
7
14
22 |
24
54
37 |
||||
Taurus
♉ |
40
50
60 |
9
9
10 |
40
58
16 |
37
47
57 |
30
28
44 |
9
9
9 |
8
29
51 |
35
44
54 |
14
43
34 |
8
9
9 |
36
1
27 |
32
41
51 |
56
57
24 |
8
8
9 |
4
31
3 |
30
39
48 |
41
12
15 |
||||
Gemini
♊ |
70
80
90 |
10
10
10 |
34
47
55 |
68
79
90 |
18
5
0 |
10
10
10 |
15
35
51 |
64
75
86 |
49
24
15 |
9
10
10 |
56
23
47 |
61
71
82 |
20
43
30 |
9
10
10 |
36
11
43 |
57
68
78 |
51
2
45 |
||||
Cancer
♋ |
100
110
120 |
10
10
10 |
55
47
34 |
100
111
122 |
55
42
16 |
10
10
10 |
59
59
53 |
97
108
119 |
14
13
6 |
11
11
11 |
3
11
12 |
93
104
115 |
33
44
56 |
11
11
11 |
7
23
32 |
89
101
112 |
52
15
47 |
||||
Leo
♌ |
130
140
150 |
10
9
9 |
16
58
40 |
132
142
152 |
32
30
10 |
10
10
10 |
41
27
12 |
129
140
150 |
47
14
26 |
11
10
10 |
5
55
44 |
127
137
148 |
1
56
40 |
11
11
11 |
29
25
16 |
124
135
146 |
16
41
57 |
||||
Virgo
♍ |
160
170
180 |
9
9
9 |
25
15
10 |
161
170
180 |
35
50
0 |
9
9
9 |
58
51
45 |
160
170
180 |
24
15
0 |
10
10
10 |
33
25
22 |
159
169
180 |
13
38
0 |
11
11
10 |
7
0
56 |
158
169
180 |
4
4
0 |
||||
Libra
♎ |
190
200
210 |
9
9
9 |
10
15
25 |
189
198
207 |
10
25
50 |
9
9
9 |
45
51
58 |
189
199
209 |
45
36
34 |
10
10
10 |
22
25
33 |
190
200
211 |
22
47
20 |
10
11
11 |
56
0
7 |
190
201
213 |
56
56
3 |
||||
Scorpio
♏ |
220
230
240 |
9
9
10 |
40
58
16 |
217
227
237 |
30
28
44 |
10
10
10 |
12
27
41 |
219
230
240 |
46
13
54 |
10
10
11 |
44
55
5 |
222
232
244 |
4
59
4 |
11
11
11 |
16
25
29 |
224
235
247 |
19
44
13 |
||||
Sagittarius
♐ |
250
260
270 |
10
10
10 |
34
47
55 |
248
259
270 |
18
5
0 |
10
10
10 |
53
59
59 |
251
262
273 |
47
46
45 |
11
11
11 |
12
11
3 |
255
266
277 |
16
27
30 |
11
11
11 |
32
23
7 |
258
270
281 |
45
8
15 |
||||
Capricornus
♑ |
280
290
300 |
10
10
10 |
55
47
34 |
280
291
302 |
55
42
16 |
10
10
10 |
51
35
15 |
284
295
305 |
36
11
26 |
10
10
9 |
47
23
56 |
288
298
308 |
17
40
36 |
10
10
9 |
43
11
36 |
291
302
311 |
58
9
45 |
||||
Aquarius
♒ |
310
320
330 |
10
9
9 |
16
58
40 |
312
322
332 |
32
30
10 |
9
9
9 |
51
29
8 |
315
324
333 |
17
46
54 |
9
9
8 |
27
1
36 |
318
327
335 |
3
4
40 |
9
8
8 |
3
31
4 |
320
329
337 |
48
19
23 |
||||
Pisces
♓ |
340
350
360 |
9
9
9 |
25
15
10 |
341
350
360 |
35
50
0 |
8
8
8 |
52
39
35 |
342
351
360 |
46
25
0 |
8
8
7 |
17
5
58 |
343
352
360 |
57
2
0 |
7
7
7 |
43
30
24 |
345
352
360 |
6
36
0 |
||||
Tabule elevationum signorum septem climatum suis singule linearum ab equatione diei equidistantium horizontibus seriatim attribute
Quinta
Clima tertium |
Sexta
Clima quartum |
Septima
Clima quintum |
Octava
Clima sextum |
||||||||||||||||||
Elevationes signorum in horizonte declivi linee equidistantis |
Elevationes signorum in horizonte declivi linee equidistantis |
Elevationes signorum in horizonte declivi linee equidistantis |
Elevationes signorum in horizonte declivi linee equidistantis |
||||||||||||||||||
cuius longior dies est horarum 14, minutorum 0, |
cuius longior dies est horarum 14, minutorum 30, |
cuius longior dies est horarum 15, minutorum 0, |
cuius longior dies est horarum 15, minutorum 30, |
||||||||||||||||||
Signa |
Decene |
et eius latitudo graduum 30, minutorum 22 |
et eius latitudo graduum 36, minutorum 0 |
et eius latitudo graduum 40, minutorum 56 |
et eius latitudo graduum 45, minuti 1 |
||||||||||||||||
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
Elevationes |
Aggregationes |
||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
||||||
Aries
♈ |
10
20
30 |
6
6
7 |
48
55
10 |
6
13
20 |
48
43
53 |
6
6
6 |
14
21
37 |
6
12
19 |
14
35
12 |
5
5
6 |
40
47
5 |
5
11
17 |
40
27
32 |
5
5
5 |
8
15
32 |
5
10
15 |
8
23
55 |
||||
Taurus
♉ |
40
50
60 |
7
8
8 |
33
2
37 |
28
36
45 |
26
28
5 |
7
7
8 |
1
33
12 |
26
33
41 |
13
46
58 |
6
7
7 |
29
4
46 |
24
31
38 |
1
5
51 |
5
6
7 |
58
34
20 |
21
28
35 |
53
27
47 |
||||
Gemini
♊ |
70
80
90 |
9
10
10 |
18
0
37 |
54
64
75 |
23
23
0 |
8
9
10 |
56
47
34 |
50
60
71 |
54
41
15 |
8
9
10 |
37
33
29 |
47
57
67 |
28
1
30 |
8
9
10 |
15
19
24 |
44
53
63 |
2
21
45 |
||||
Cancer
♋ |
100
110
120 |
11
11
11 |
13
34
50 |
86
97
109 |
13
47
37 |
11
11
12 |
16
47
12 |
82
94
106 |
31
18
30 |
11
12
12 |
21
1
31 |
78
90
103 |
51
52
23 |
11
12
12 |
26
15
53 |
75
87
100 |
11
26
19 |
||||
Leo
♌ |
130
140
150 |
11
11
11 |
55
54
47 |
121
133
145 |
32
26
13 |
12
12
12 |
20
23
19 |
118
131
143 |
50
13
32 |
12
12
12 |
46
52
51 |
116
129
141 |
9
1
52 |
13
13
13 |
12
22
22 |
113
126
140 |
31
53
15 |
||||
Virgo
♍ |
160
170
180 |
11
11
11 |
40
35
32 |
156
168
180 |
53
28
0 |
12
12
12 |
13
9
6 |
155
167
180 |
45
54
0 |
12
12
12 |
45
43
40 |
154
167
180 |
37
20
0 |
13
13
13 |
18
15
12 |
153
166
180 |
33
48
0 |
||||
Libra
♎ |
190
200
210 |
11
11
11 |
32
35
40 |
191
203
214 |
32
7
47 |
12
12
12 |
6
9
13 |
192
204
216 |
6
15
28 |
12
12
12 |
40
43
45 |
192
205
218 |
40
23
8 |
13
13
13 |
12
15
18 |
193
206
219 |
12
27
45 |
||||
Scorpio
♏ |
220
230
240 |
11
11
11 |
47
54
55 |
226
238
250 |
34
28
23 |
12
12
12 |
19
23
20 |
228
241
253 |
47
10
30 |
12
12
12 |
51
52
46 |
230
243
256 |
59
51
37 |
13
13
13 |
22
22
12 |
233
246
259 |
7
29
41 |
||||
Sagittarius
♐ |
250
260
270 |
11
11
11 |
50
34
13 |
262
273
285 |
13
47
0 |
12
11
11 |
12
47
16 |
265
277
288 |
42
29
45 |
12
12
11 |
31
1
21 |
269
281
292 |
8
9
30 |
12
12
11 |
53
15
26 |
272
284
296 |
34
49
15 |
||||
Capricornus
♑ |
280
290
300 |
10
10
9 |
37
0
18 |
295
305
314 |
37
37
55 |
10
9
8 |
34
47
56 |
299
309
318 |
19
6
2 |
10
9
8 |
29
33
37 |
302
312
321 |
59
32
9 |
10
9
8 |
24
19
15 |
306
315
324 |
39
58
13 |
||||
Aquarius
♒ |
310
320
330 |
8
8
7 |
37
2
33 |
323
331
339 |
32
34
7 |
8
7
7 |
12
33
1 |
326
333
340 |
14
47
48 |
7
7
6 |
46
4
29 |
328
335
342 |
55
59
28 |
7
6
5 |
20
34
58 |
331
338
344 |
33
7
5 |
||||
Pisces
♓ |
340
350
360 |
7
6
6 |
10
55
48 |
346
353
360 |
17
12
0 |
6
6
6 |
37
21
14 |
347
353
360 |
25
46
0 |
6
5
5 |
5
47
40 |
348
354
360 |
33
20
0 |
5
5
5 |
32
15
8 |
349
354
360 |
37
52
0 |
||||
Tabule elevationum signorum septem climatum suis singule linearum ab equatione diei equidistantium horizontibus seriatim attribute
⟨II.9⟩ Capitulum nonum: De divisione eorum que sequuntur scientiam elevationum et preparatione eorum
Postquam narravimus elevationes temporum secundum hunc modum, tunc reliqua omnia que in hoc modo sunt necessaria fient leviora non indigentibus nobis lineis mensurationis geometricis in aliquo eorum neque tabulis pluribus eis quas posuimus. Illud namque declarabitur nobis ex capitulis que posuimus. Eorum autem primum est ut scientiam accipiamus elevationum longitudinis diei aut noctis date, postquam comprehenderimus numerum temporum elevationum illius climatis, sed Probably corrupt for scilicet, which would correspond to the Greek text (see Toomer, loc. cit., p. 99, line 16 from the bottom). Paris, BnF, lat. 14738 (28v, line 8) reads sed too. in die a parte Solis usque ad partem que ei opponitur, et est eius relativa secundum continuationem signorum, in nocte vero a relativo partis Solis quod ei opponitur usque ad partem Solis. Ergo postquam acceperimus temporum que nobis aggregata fuerint partem decimamquintam, erit illud numerus horarum equalium illius longitudinis. Et cum acceperimus illorum temporum que nobis aggregata sunt partem duodecimam, illud erit numerus temporum hore temporalis illius longitudinis. Accipiemus etiam quantitatem hore temporalis facilius et propinquiore acceptione illa cum nos acceperimus ex tabula elevationum superfluum quod est inter summam que est diei consequentem partem Solis et illam que est noctis consequentem partem, que opponitur parti Solis in linea equidistante que est sub equatione diei et in linea equidistante equationi diei climatis quesiti. Cum enim acceperimus ex illo sextam medietatis superflui quod est inter eas et cum pars cum qua intramus tabulas est medietas orbis septentrionalis, addimus ipsam super tempora que sunt 15, et cum est in medietate meridiana, minuimus eam ex 15 temporibus. Tunc ita sciemus numerum temporum hore temporalis. Deinde post hoc, cum voluerimus ut fiant hore temporales date hore equales, multiplicabimus numerum horarum, scilicet diurnarum in numerum temporum hore temporalis diurne illius diei in illo climate, nocturnarum vero in numerum temporum hore temporalis nocturne noctis illius in illo climate. Pars namque quintadecima summe que aggregabitur nobis erit numerus horarum equalium. Et in conversione illius fient hore equales date temporales cum nos multiplicaverimus numerum earum in 15 et diviserimus quod aggregabitur nobis per numerum temporum hore temporalis diurne, si fuerint ex horis diei, aut nocturne, si fuerint ex horis noctis in illo climate quesito. Et postquam equaverimus tempora cuiuscunque hore temporalis, aut noctis aut diei, et voluerimus invenire partem orientem orbis signorum in illa hora, multiplicabimus numerum horarum, si fuerint diurne, ab ortu Solis, et si sunt nocturne, ab occasu Solis, in numerum temporum hore diurne aut nocturne, qualis illa fuerit, et quod aggregatur proiiciemus ex parte Solis, si fuerit diei, aut ex opposito partis Solis, si fuerit noctis, secundum continuitatem signorum quidem per elevationes climatis. Et dicemus quod pars oriens orbis signorum est pars ad quam pervenit numerus illius signi. Quod si nos voluerimus invenire partem medii celi supra terram, accipiemus semper numerum horarum que sunt a medietate diei preterite usque ad horam datam et multiplicabimus ipsum in numerum temporum hore temporalis, scilicet diei diurne et noctis nocturne, et quod aggregabitur nobis proiiciemus ex parte Solis secundum continuationem signorum per elevationes sphere directe. Et dicemus quod pars medii celi super terram in hora illa est pars ad quam pervenit numerus illius signi. Et similiter sciemus partem medii celi supra terram propter partem orientem si acceperimus numerum qui sequitur partem orientem in tabula elevationum, que est aggregationum in illo climate, et proiecerimus ex eo semper tempora quarte, que sunt 90. Pars enim que consequitur numerum residuum in tabula sphere recte est pars medii celi. Et econverso etiam, cum voluerimus invenire partem orientem propter partem medii celi, accipiemus numerum qui sequitur medium celi in tabula aggregationum, que sit ex tabulis sphere recte, et addemus supra ipsum semper numerum temporum quarte, que sunt 90, et quod aggregabitur nobis considerabimus in tabula aggregationum, que sit ex tabulis illius climatis ubi inveniemus equale illius numeri. Dicemus namque quod pars que sequitur numerum illum est pars oriens. Manifestum est autem quod eis qui sunt sub uno orbium meridiei longitudo Solis a linea meridiei supra terram aut a linea meridiei sub terra est secundum horas equales que sunt ex horis equalitatis, et eis qui non sunt sub uno orbium meridiei erit diversitatis meridiei secundum tempora que sunt ex temporibus equalitatis numerus equalis numero partium que sunt inter duos orbes.
⟨II.10⟩ Capitulum decimum: De scientia angulorum provenientium inter orbem signorum declivem et orbem meridiei
Postquam remansit iam de complemento eorum que narrabimus de hac scientia in hac dictione scientia angulorum provenientium in linea orbis signorum, premittam iam propositum. Nos nominamus angulum quem continent due portiones duorum orbium maiorum rectum cum est punctus sectionis eorum communis eis polus et describitur super ipsum circulus secundum, quodcunque spacium fuerit, et est arcus eius quem comprehendunt due portiones continentes angulum quarta circuli descripti. Et universaliter dico quod proportio huius arcus ad circulum suum ex quo ipse est secundum modum quem prediximus est sicut proportio anguli quem continet declinatio duarum superficierum duorum orbium ad quattuor angulos rectos. Et quia posuimus circulum 360 partes, erit quantitas partium arcus ad circulum suum sicut quantitas anguli cui ipse subtenditur ad quattuor angulos rectos secundum quantitatem qua est angulus rectus 90 partes. Angulorum autem qui proveniunt propter sectionem orbis declivis maior eorum necessitas et maior utilitas in hac scientia est scientia angulorum qui fiunt ex sectione orbis declivis et orbis meridiei et sectione orbis declivis et orbis horizontis in omni loco, et similiter qui sunt ex sectione orbis declivis et orbis maioris descripti super duos polos horizontis. Et cum scientia horum angulorum iam sciemus orbis huius arcus quos terminat locus sectionis et polus horizontis, qui est supra summitatem capitum. Cum enim declarata fuerit scientia cuiusque horum que prediximus, erit locus eius in hac scientia magnus. Et in eo in quo est eius necessitas ad sciendum diversitatem que est inter locum Lune secundum considerationem et visum et locum eius verum est necessitas horum angulorum et eorum scientia magna. Scire tamen ea non est possibile ante premissionem scientie angulorum. Et quia anguli qui fiunt ex sectione duorum orbium, orbis signorum et unius eorum qui ipsum secant, sunt quattuor et volumus ut sit sermo super unum, tunc ostendam quod nolumus nisi unum angulorum duorum qui sequuntur arcum orbis signorum apud locum sectionis, scilicet septentrionalem sequentem ex eis, ut sit quantitas quam declarare volumus huius et quod accidit in eo manifesta. Et quoniam declaratio angulorum provenientium ex sectione orbis declivis et orbis meridiei est levior et ad sumendum vicinior, tunc ab ea incipiemus. Et ostendemus prius quod puncta orbis signorum que sunt equalis intervalli ab orbe equationis diei faciunt hos angulos ad invicem equales. Et huius exemplum ponemus:  Describam arcum orbis equationis diei, supra quem sint A, B, G, et arcum orbis signorum, supra quem sint D, B, E, et polum equationis diei punctum R, et sint duo arcus equales supra quos sint B, H et B, T a duabus partibus puncti B equationis diei, et describam duos arcus orbis meridiei supra polum R et supra duo puncta H et T, supra quos sint R, K, H et R, T, L. Dico ergo quod angulus KHB equalis est angulo RTE, quoniam enim triangulus BHK est equalium angulorum cum triangulo BTL eo quod latera eorum sunt equalia, unumquodque latus et eius relativum, HB equale BT, et HK equale TL, et BK equale BL. Et iam declaratum est hoc totum in his que precesserunt. Ergo angulus KHB equatur angulo BTL, qui est equalis angulo RTE. Et illud est quod oportuit nos demonstrare.
Describam arcum orbis equationis diei, supra quem sint A, B, G, et arcum orbis signorum, supra quem sint D, B, E, et polum equationis diei punctum R, et sint duo arcus equales supra quos sint B, H et B, T a duabus partibus puncti B equationis diei, et describam duos arcus orbis meridiei supra polum R et supra duo puncta H et T, supra quos sint R, K, H et R, T, L. Dico ergo quod angulus KHB equalis est angulo RTE, quoniam enim triangulus BHK est equalium angulorum cum triangulo BTL eo quod latera eorum sunt equalia, unumquodque latus et eius relativum, HB equale BT, et HK equale TL, et BK equale BL. Et iam declaratum est hoc totum in his que precesserunt. Ergo angulus KHB equatur angulo BTL, qui est equalis angulo RTE. Et illud est quod oportuit nos demonstrare.
Ostendam etiam quod cum fuerint duo puncta orbis signorum equalis longitudinis a puncto tropici, duo anguli qui sunt apud orbem meridiei ambo equantur duobus angulis rectis.  Et ob hoc describam arcum orbis signorum, supra quem sint A, B, G, et sit punctum B punctum tropici, et describam duos arcus elongationis equalis a puncto tropici, supra quos sint B, D et B, E, et describam super duo puncta D et E et super R, quod est polus equationis diei, duos arcus orbis meridiei, supra quos sint R, D et R, E. Dico ergo quod angulus RDB et angulus REG simul equantur duobus angulis rectis. Huius autem ostensio est quoniam duo puncta D et E sunt equalis elongationis a puncto tropici. Propter hoc erit arcus DR equalis arcui RE. Ergo angulus RDB equalis est angulo REB. Angulus autem REB et angulus REG equantur duobus angulis rectis. Ergo angulus RDB cum angulo REG equantur duobus angulis rectis. Et illud est quod oportuit nos declarare.
Et ob hoc describam arcum orbis signorum, supra quem sint A, B, G, et sit punctum B punctum tropici, et describam duos arcus elongationis equalis a puncto tropici, supra quos sint B, D et B, E, et describam super duo puncta D et E et super R, quod est polus equationis diei, duos arcus orbis meridiei, supra quos sint R, D et R, E. Dico ergo quod angulus RDB et angulus REG simul equantur duobus angulis rectis. Huius autem ostensio est quoniam duo puncta D et E sunt equalis elongationis a puncto tropici. Propter hoc erit arcus DR equalis arcui RE. Ergo angulus RDB equalis est angulo REB. Angulus autem REB et angulus REG equantur duobus angulis rectis. Ergo angulus RDB cum angulo REG equantur duobus angulis rectis. Et illud est quod oportuit nos declarare.
 Et post scientiam eorum que premisimus describam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli orbis signorum, supra quam sint A, E, G, et sit punctum ipsum A tropicum hiemale, et describam supra polum A secundum spacium lateris quadrati medietatem circuli, supra quam sint B, E, D. Et quia orbis meridiei, qui est ABGD, est descriptus supra duos polos AEG et BED, erit arcus ED quarta circuli. Angulus ergo DAE erit rectus. Et propter hoc etiam cuius iam precessit declaratio erit etiam angulus qui est apud tropicum estivum rectus. Et illud est quod oportuit nos declarare.
Et post scientiam eorum que premisimus describam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli orbis signorum, supra quam sint A, E, G, et sit punctum ipsum A tropicum hiemale, et describam supra polum A secundum spacium lateris quadrati medietatem circuli, supra quam sint B, E, D. Et quia orbis meridiei, qui est ABGD, est descriptus supra duos polos AEG et BED, erit arcus ED quarta circuli. Angulus ergo DAE erit rectus. Et propter hoc etiam cuius iam precessit declaratio erit etiam angulus qui est apud tropicum estivum rectus. Et illud est quod oportuit nos declarare.
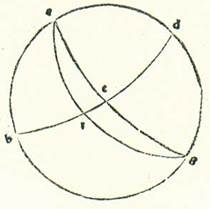 Describam etiam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et describam medietatem circuli orbis signorum, supra quam sint A, R, G, et sit punctum A ipsum punctum equationis diei autumnale, et describam supra polum A secundum spacium lateris quadrati semicirculum BRED. Propter hoc ergo quod circulus ABGD est descriptus supra duos polos AEG et BED erit unusquisque horum AR et ED quarta circuli. Et propter hoc quod R est ipsum punctum tropicum hiemale et arcus RE est partes de quibus iam ostensum est quod ipse sunt 23 partes et 51 minuta erit totus arcus RED 113 partes et 51 minuta secundum quantitatem qua erit angulus rectus 90 partes. Et propter ea quorum iam precessit declaratio erit angulus puncti equalitatis vernalis ipsum complementum eorum que remanserunt ex duobus angulis rectis, quod est 66 partes et 9 minuta.
Describam etiam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et describam medietatem circuli orbis signorum, supra quam sint A, R, G, et sit punctum A ipsum punctum equationis diei autumnale, et describam supra polum A secundum spacium lateris quadrati semicirculum BRED. Propter hoc ergo quod circulus ABGD est descriptus supra duos polos AEG et BED erit unusquisque horum AR et ED quarta circuli. Et propter hoc quod R est ipsum punctum tropicum hiemale et arcus RE est partes de quibus iam ostensum est quod ipse sunt 23 partes et 51 minuta erit totus arcus RED 113 partes et 51 minuta secundum quantitatem qua erit angulus rectus 90 partes. Et propter ea quorum iam precessit declaratio erit angulus puncti equalitatis vernalis ipsum complementum eorum que remanserunt ex duobus angulis rectis, quod est 66 partes et 9 minuta.
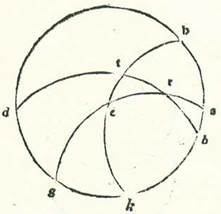 Et describam etiam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem circuli orbis signorum, supra quam sint B, R, D, sitque R ipsum punctum autumnale, et sit arcus BR primo signum unum, quod sit Virgo. Manifestum est autem quod punctum B erit principium Virginis. Et describam etiam supra polum B secundum longitudinem lateris quadrati semicirculum, supra quem sint H, T, E, K, et inquiram inventionem anguli KBT. Et quia circulus orbis meridiei, qui est ABGD, est descriptus supra duos polos AEG et supra duos polos HEK, erit unusquisque arcuum BH et BT et EH quarta circuli. Et propter hanc formam erit proportio chorde dupli arcus BA ad chordam dupli arcus AH aggregata ex duabus proportionibus, ex proportione chorde dupli arcus BR ad chordam dupli arcus RT et ex proportione chorde dupli arcus TE ad chordam dupli arcus EH. Duplum vero arcus BA propter ea quorum iam precessit declaratio est 23 partes et 20 minuta fere, et eius chorda 24 partes et 16 minuta, et duplum arcus AH est 156 partes et 40 minuta, et eius chorda 117 partes et 31 minuta. Duplum quoque arcus BR est 60 partes, et eius chorda 60 partes, et duplum arcus RT est 120 partes, et eius chorda 103 partes et 55 minuta et 23 secunda. Ergo cum nos proiecerimus ex proportione 24 partium et 16 minutorum ad 117 partes et 31 minuta proportionem partium 60 ad 103 partes et 55 minuta et 23 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EH, que est proportio 42 partium et 58 minutorum fere ad 120 partes. Sed chorda dupli arcus EH est 120 partes. Igitur chorda dupli arcus TE erit secundum illam quantitatem 42 partes et 58 minuta. Quapropter erit duplum arcus TE propinquum 42 partibus. Ergo TE secundum illam quantitatem est 21 partes. Ergo unusquisque duorum, scilicet arcus TEK et angulus KBT, erit propter ea quorum precessit declaratio 111 partes, et angulus qui est apud caput Scorpii similiter etiam erit 111 partes, et unusquisque duorum angulorum qui sunt apud caput Tauri et apud caput Piscis est ad complendum ea que remanent ex duobus angulis rectis, que sunt 69 partes. Et illud est quod oportuit nos demonstrare.
Et describam etiam circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli equationis diei, supra quam sint A, E, G, et medietatem circuli orbis signorum, supra quam sint B, R, D, sitque R ipsum punctum autumnale, et sit arcus BR primo signum unum, quod sit Virgo. Manifestum est autem quod punctum B erit principium Virginis. Et describam etiam supra polum B secundum longitudinem lateris quadrati semicirculum, supra quem sint H, T, E, K, et inquiram inventionem anguli KBT. Et quia circulus orbis meridiei, qui est ABGD, est descriptus supra duos polos AEG et supra duos polos HEK, erit unusquisque arcuum BH et BT et EH quarta circuli. Et propter hanc formam erit proportio chorde dupli arcus BA ad chordam dupli arcus AH aggregata ex duabus proportionibus, ex proportione chorde dupli arcus BR ad chordam dupli arcus RT et ex proportione chorde dupli arcus TE ad chordam dupli arcus EH. Duplum vero arcus BA propter ea quorum iam precessit declaratio est 23 partes et 20 minuta fere, et eius chorda 24 partes et 16 minuta, et duplum arcus AH est 156 partes et 40 minuta, et eius chorda 117 partes et 31 minuta. Duplum quoque arcus BR est 60 partes, et eius chorda 60 partes, et duplum arcus RT est 120 partes, et eius chorda 103 partes et 55 minuta et 23 secunda. Ergo cum nos proiecerimus ex proportione 24 partium et 16 minutorum ad 117 partes et 31 minuta proportionem partium 60 ad 103 partes et 55 minuta et 23 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EH, que est proportio 42 partium et 58 minutorum fere ad 120 partes. Sed chorda dupli arcus EH est 120 partes. Igitur chorda dupli arcus TE erit secundum illam quantitatem 42 partes et 58 minuta. Quapropter erit duplum arcus TE propinquum 42 partibus. Ergo TE secundum illam quantitatem est 21 partes. Ergo unusquisque duorum, scilicet arcus TEK et angulus KBT, erit propter ea quorum precessit declaratio 111 partes, et angulus qui est apud caput Scorpii similiter etiam erit 111 partes, et unusquisque duorum angulorum qui sunt apud caput Tauri et apud caput Piscis est ad complendum ea que remanent ex duobus angulis rectis, que sunt 69 partes. Et illud est quod oportuit nos demonstrare.
In hac quoque forma ponam arcum RB duo signa et ponam punctum B principium Leonis. Sint autem linee secundum habitudinem suam. Erit ergo duplum arcus BA 41 partes, et eius chorda 42 partes et unum minutum et 30 secunda. Duplum vero arcus AH est 139 partes, et eius chorda 112 partes et 24 minuta. Duplum quoque arcus RB est 120 partes, et eius chorda 103 partes et 55 minuta et 23 secunda. Et duplum arcus RT est 60 partes, et eius chorda 60 partes. Ergo cum nos proiecerimus ex proportione 42 partium et fere duorum minutorum ad 112 partes et 24 minuta proportionem 103 partium et 55 minutorum et 23 secundorum ad 60 partes, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EH, que est proportio 25 partium et 53 minutorum ad 120 partes. Ergo erit chorda dupli arcus TE secundum illam quantitatem 25 partes et 53 minuta. Quapropter erit duplum arcus TE 25 partes fere, et arcus TE prope 12 partes et medietas partis. Ergo ambo, scilicet arcus TEK et angulus KBT, sunt 102 partes et medietas partis, et angulus qui est apud caput Sagittarii similiter erit etiam 102 partes et medietas partis, et unusquisque duorum angulorum qui sunt apud caput Geminorum et apud caput Aquarii residuorum ex complemento duorum angulorum rectorum est 77 partes et medietas partis. Iam vero manifestum est ex eis que narravimus quod acceptio partium orbis signorum in eis que sunt minores et parviores his est una. Sed in opere signi unius et signi unius ad ea que necessaria sunt in hoc libro est sufficientia.
⟨II.11⟩ Capitulum undecimum: De scientia angulorum provenientium ex concursu orbis declivis cum orbe horizontis
Post ista demonstrabo qualiter oporteat ut sit inventio angulorum provenientium in climate dato ex concursu orbis declivis et orbis horizontis. Horum namque inventio facilis etiam est acceptionis. Manifestum est autem quod anguli qui fiunt ex concursu orbis signorum et orbis meridiei sunt anguli qui fiunt ex concursu orbis signorum et orbis horizontis in sphera recta. Ut autem sciamus invenire angulos in sphera declivi, demonstrabimus etiam. Et dicemus primum quod puncta orbis signorum que sunt equalis longitudinis a puncto equationis diei faciunt angulos qui sunt apud horizontem unum equales. 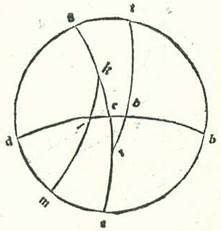 Et describam propter hoc meridiei orbem, supra quem sint A, B, G, D, et medietatem orbis equationis diei, supra quam sint A, E, G, et medietatem orbis horizontis, supra quam sint B, E, D, et describam duas portiones orbis declivis, supra quas sint R, H, T et K, L, M, sitque unumquodque duorum R et K punctum autumnale, et sit arcus RH equalis arcui KL. Dico ergo quod angulus EHT equatur angulo DLK (latera namque trianguli EHR sunt equalia lateribus trianguli EKL propter ea quorum precessit declaratio) quodque latus suo relativo, scilicet RH equale KL, et EH horizontis equale EL, et ER orbis equationis diei equale EK. Ergo angulus EHR equatur angulo ELK, et angulus EHT residuus equatur angulo DLK residuo. Et illud est quod oportuit nos demonstrare.
Et describam propter hoc meridiei orbem, supra quem sint A, B, G, D, et medietatem orbis equationis diei, supra quam sint A, E, G, et medietatem orbis horizontis, supra quam sint B, E, D, et describam duas portiones orbis declivis, supra quas sint R, H, T et K, L, M, sitque unumquodque duorum R et K punctum autumnale, et sit arcus RH equalis arcui KL. Dico ergo quod angulus EHT equatur angulo DLK (latera namque trianguli EHR sunt equalia lateribus trianguli EKL propter ea quorum precessit declaratio) quodque latus suo relativo, scilicet RH equale KL, et EH horizontis equale EL, et ER orbis equationis diei equale EK. Ergo angulus EHR equatur angulo ELK, et angulus EHT residuus equatur angulo DLK residuo. Et illud est quod oportuit nos demonstrare.
Et dico quod duo anguli qui sunt apud duo puncta opposita, orientale cum occidentali, equantur duobus angulis rectis.  Nos namque, si descripserimus duos circulos, quorum unus sit orbis horizontis, supra quem sint A, B, G, D, et alter circulus orbis signorum, supra quem sint A, E, G, R, se supra duo puncta A et G secantes, tunc duo anguli qui sunt ex RAD et DAE erunt equales duobus angulis rectis. Angulus vero RAD est equalis angulo RGD. Quapropter ambo qui sunt ex RGD et ex DAE equantur duobus angulis rectis.
Nos namque, si descripserimus duos circulos, quorum unus sit orbis horizontis, supra quem sint A, B, G, D, et alter circulus orbis signorum, supra quem sint A, E, G, R, se supra duo puncta A et G secantes, tunc duo anguli qui sunt ex RAD et DAE erunt equales duobus angulis rectis. Angulus vero RAD est equalis angulo RGD. Quapropter ambo qui sunt ex RGD et ex DAE equantur duobus angulis rectis.
Et quia iam ostensum est quod anguli equalis longitudinis a puncto equationis diei qui sunt in uno horizonte sunt equales, tunc iam sequitur illud ut sint etiam anguli equalis longitudinis a puncto tropico, orientalis eorum cum occidentali, equales duobus angulis rectis. Quapropter cum nos sciverimus angulos orientales qui sunt ab Ariete usque ad Libram, sciemus etiam iam cum scientia nostra eorum angulos orientales qui sunt in medietate altera orbis et sciemus etiam angulos occidentales qui sunt in medietatibus ambabus. Et faciam propter modum inveniendi illud secundum brevitatem sermonis exemplum in linea equidistanti cuius altitudo poli septentrionalis ab horizonte est 36 partes. Anguli vero qui proveniunt ex duobus punctis equalitatis orbis signorum apud horizonta possibile est ut inveniantur faciliori acceptione. 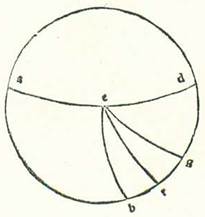 Et describam propter hoc circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli huius horizontis orientalis, supra quam sint A, E, D, et quartam equationis diei, supra quam sint E, R, et duas quartas orbis signorum, supra quas sint E, B et E, G, et sit punctum E, scilicet quod est quarte EB, punctum autumnale, et quod est quarte EG punctum vernale, et sit punctum B tropicum hiemale, et punctum G tropicum estivum. Colligitur ergo ex hoc ut sit arcus DR 54 partes, et unusquisque duorum arcuum BR et RG 23 partes et 51 minuta vicinius, et arcus GD vicinius 30 partes et 9 minuta, et arcus BD secundum illam quantitatem 77 partes et 51 minuta. Et quia punctum E est polus orbis meridiei, supra quem sunt A, B, G, D, erit angulus DEG, qui est sub capite Arietis, 30 partes et 9 minuta secundum quantitatem qua angulus rectus est 90 partes, et angulus qui est ex DEB sub capite Libre erit secundum illam quantitatem 77 partes et 51 minuta.
Et describam propter hoc circulum orbis meridiei, supra quem sint A, B, G, D, et medietatem circuli huius horizontis orientalis, supra quam sint A, E, D, et quartam equationis diei, supra quam sint E, R, et duas quartas orbis signorum, supra quas sint E, B et E, G, et sit punctum E, scilicet quod est quarte EB, punctum autumnale, et quod est quarte EG punctum vernale, et sit punctum B tropicum hiemale, et punctum G tropicum estivum. Colligitur ergo ex hoc ut sit arcus DR 54 partes, et unusquisque duorum arcuum BR et RG 23 partes et 51 minuta vicinius, et arcus GD vicinius 30 partes et 9 minuta, et arcus BD secundum illam quantitatem 77 partes et 51 minuta. Et quia punctum E est polus orbis meridiei, supra quem sunt A, B, G, D, erit angulus DEG, qui est sub capite Arietis, 30 partes et 9 minuta secundum quantitatem qua angulus rectus est 90 partes, et angulus qui est ex DEB sub capite Libre erit secundum illam quantitatem 77 partes et 51 minuta.
Sed ut sit acceptio nostra in angulis manifesta, assumemus etiam ad illud exemplum et inquiremus inventionem scientie anguli orientalis qui est inter caput Tauri et horizontem. 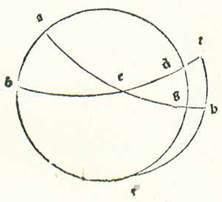 Et describemus propter hoc circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli huius horizontis orientalem, supra quam sint B, E, D, et medietatem circuli orbis signorum, supra quam sint A, E, G, et sit punctum E caput Tauri. Et quia in hoc climate, quando elevatur caput Tauri, erunt in medio celi sub terra 17 partes et 41 minuta Cancri et iam declaravimus quomodo hec facilius assumantur per ea que narravimus ex elevationibus, erit ergo arcus EG minor quarta circuli. Describam autem supra polum E secundum longitudinem lateris quadrati portionem orbis maioris, supra quam sint T, H, R, et complebo duas quartas EGH et EDT, et erit unusquisque duorum arcuum RGD et RHT quarta circuli, eo quod horizon BET est descriptus supra polum RGD orbis meridiei et supra polum RHT, que est orbis magni, et etiam quia partium Cancri 17 et 41 minutorum longitudo ab equatione diei ad partem septentrionalem in orbe magno descripto supra duos polos equationis diei est 22 partes et 40 minuta fere (hoc namque ex eis est que iam affirmavimus etiam) et longitudo equationis diei a polo horizontis, qui est punctum R, in illo arcu, qui est RGD, est 36 partes. Colligitur ergo ut sit arcus RG 58 partes et 40 minuta. Et postquam iam scivisti hec, erit propter hanc formam proportio chorde dupli arcus GD ad chordam dupli arcus DR aggregata ex duabus proportionibus, ex proportione chorde dupli arcus GE ad chordam dupli arcus EH et ex proportione chorde dupli arcus HT ad chordam dupli arcus TR. Et propter hunc modum positum erit duplum arcus GD 62 partes et 40 minuta, et chorda eius 62 partes et 24 minuta, et duplum arcus DR 180 partes, et eius chorda 120 partes, et etiam duplum arcus GE 155 partes et 22 minuta, et chorda eius 117 partes et 14 minuta, et duplum arcus EH 180 partes, et chorda eius 120 partes. Cum ergo nos proiecerimus ex proportione 62 partium et 24 minutorum ad 120 partes proportionem 117 partium et 14 minutorum ad 120 partes, remanebit proportio chorde dupli arcus TH ad chordam dupli arcus TR, que est proportio 63 partium et 52 minutorum ad 120 partes. Chorda autem dupli arcus TR est 120 partes. Ergo chorda dupli arcus HT secundum illam quantitatem erit 63 partes et 52 minuta. Quapropter erit duplum arcus HT 64 partes et 20 minuta, et erit unusquisque duorum, scilicet arcus HT et angulus HET, secundum illam quantitatem 32 partes et 10 minuta. Et illud est quod demonstrare intendimus. Ut autem non iteretur sermo et prolongetur dictio in hoc libro, secundum similitudinem huiusmodi inquiratur inventio scientie in signis 12 etiam in reliquis climatibus.
Et describemus propter hoc circulum meridiei, supra quem sint A, B, G, D, et medietatem circuli huius horizontis orientalem, supra quam sint B, E, D, et medietatem circuli orbis signorum, supra quam sint A, E, G, et sit punctum E caput Tauri. Et quia in hoc climate, quando elevatur caput Tauri, erunt in medio celi sub terra 17 partes et 41 minuta Cancri et iam declaravimus quomodo hec facilius assumantur per ea que narravimus ex elevationibus, erit ergo arcus EG minor quarta circuli. Describam autem supra polum E secundum longitudinem lateris quadrati portionem orbis maioris, supra quam sint T, H, R, et complebo duas quartas EGH et EDT, et erit unusquisque duorum arcuum RGD et RHT quarta circuli, eo quod horizon BET est descriptus supra polum RGD orbis meridiei et supra polum RHT, que est orbis magni, et etiam quia partium Cancri 17 et 41 minutorum longitudo ab equatione diei ad partem septentrionalem in orbe magno descripto supra duos polos equationis diei est 22 partes et 40 minuta fere (hoc namque ex eis est que iam affirmavimus etiam) et longitudo equationis diei a polo horizontis, qui est punctum R, in illo arcu, qui est RGD, est 36 partes. Colligitur ergo ut sit arcus RG 58 partes et 40 minuta. Et postquam iam scivisti hec, erit propter hanc formam proportio chorde dupli arcus GD ad chordam dupli arcus DR aggregata ex duabus proportionibus, ex proportione chorde dupli arcus GE ad chordam dupli arcus EH et ex proportione chorde dupli arcus HT ad chordam dupli arcus TR. Et propter hunc modum positum erit duplum arcus GD 62 partes et 40 minuta, et chorda eius 62 partes et 24 minuta, et duplum arcus DR 180 partes, et eius chorda 120 partes, et etiam duplum arcus GE 155 partes et 22 minuta, et chorda eius 117 partes et 14 minuta, et duplum arcus EH 180 partes, et chorda eius 120 partes. Cum ergo nos proiecerimus ex proportione 62 partium et 24 minutorum ad 120 partes proportionem 117 partium et 14 minutorum ad 120 partes, remanebit proportio chorde dupli arcus TH ad chordam dupli arcus TR, que est proportio 63 partium et 52 minutorum ad 120 partes. Chorda autem dupli arcus TR est 120 partes. Ergo chorda dupli arcus HT secundum illam quantitatem erit 63 partes et 52 minuta. Quapropter erit duplum arcus HT 64 partes et 20 minuta, et erit unusquisque duorum, scilicet arcus HT et angulus HET, secundum illam quantitatem 32 partes et 10 minuta. Et illud est quod demonstrare intendimus. Ut autem non iteretur sermo et prolongetur dictio in hoc libro, secundum similitudinem huiusmodi inquiratur inventio scientie in signis 12 etiam in reliquis climatibus.
⟨II.12⟩ Capitulum duodecimum: De scientia angulorum provenientium inter orbem signorum et orbem descriptum supra duos polos horizontis
Postquam iam restat ut sciamus qualiter oporteat esse acceptionem inventionis scientie angulorum qui sunt ex orbe signorum et orbe descripto supra duos polos horizontis in omni declinatione et in omni loco, ex quorum scientia sciemus in hora omni, quemadmodum prediximus, quantitatem arcus qui est orbis descripti supra duos polos horizontis inter punctum quod est supra summitatem capitum et punctum quod est sectionis que est orbis signorum et orbis descripti supra duos polos horizontis, tunc ponam etiam que ponenda sunt in hac parte huius scientie. Et demonstrabo prius quod puncta orbis signorum que sunt equalis longitudinis a puncto tropico quorum temporum elevationes sunt equales ab utrisque lateribus orbis meridiei, quorum unum est ad orientem et alterum ad occidentem, faciunt etiam arcus qui sunt a puncto summitatis capitum ad illa puncta orbium magnorum equales adinvicem. Angulorum quoque qui sunt apud ea erunt omnes duo equales duobus angulis rectis secundum modum quem prediximus. 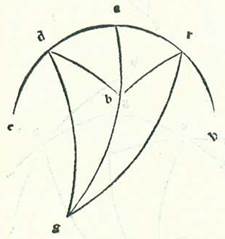 Describam itaque portionem orbis meridiei, supra quam sint A, B, G, sitque punctum eius B supra summitatem capitum, et punctum eius G sit polus equationis diei, et describam duas portiones orbis signorum, supra quas sint A, D, E et A, R, H, et sint punctum D et punctum R equalis longitudinis a duobus punctis tropici, et sint duo arcus qui secantur ex linea equidistanti ab utroque latere orbis meridiei equales, et describam etiam duos arcus orbium magnorum super unumquodque duorum punctorum D et R, scilicet a puncto G, quod est polus equationis diei, duos arcus GD et GR, et a puncto B, quod est punctum summitatis capitum, duos arcus BD et BR. Dico ergo quod arcus BD equatur arcui BR et angulus BDE cum angulo BRA equantur duobus angulis rectis. Et quia duorum punctorum D et R elongatio ab orbe meridiei, supra quem sunt A, B, G, est secundum duos arcus equales equidistantis supra ipsam descripte, erit angulus BGD equalis angulo BGR. Cuiusque ergo duorum triangulorum BGD et BGR duo latera unius sunt equalia duobus lateribus alterius, quodque latus suo relativo, scilicet GD equale GR, et latus BG est eis commune, et duo anguli qui continentur a duobus lateribus equalibus sunt equales, scilicet angulus BGD equalis angulo BGR. Ergo basis BD est equalis basi BR, et angulus BRG equalis angulo BDG. Et quia iam ostensum fuit in his que precesserunt parumper quod duo anguli qui sunt apud orbem descriptum supra duos polos orbis equationis diei elongationis equalis a puncto tropici equantur duobus angulis rectis, tunc duo anguli simul qui sunt ex GDE et GRA equantur duobus angulis rectis. Iam vero ostensum fuit quod angulus BDG equatur angulo BRG. Igitur summa duorum angulorum BDE et BRA equantur duobus angulis rectis. Et hoc est quod oportuit nos declarare.
Describam itaque portionem orbis meridiei, supra quam sint A, B, G, sitque punctum eius B supra summitatem capitum, et punctum eius G sit polus equationis diei, et describam duas portiones orbis signorum, supra quas sint A, D, E et A, R, H, et sint punctum D et punctum R equalis longitudinis a duobus punctis tropici, et sint duo arcus qui secantur ex linea equidistanti ab utroque latere orbis meridiei equales, et describam etiam duos arcus orbium magnorum super unumquodque duorum punctorum D et R, scilicet a puncto G, quod est polus equationis diei, duos arcus GD et GR, et a puncto B, quod est punctum summitatis capitum, duos arcus BD et BR. Dico ergo quod arcus BD equatur arcui BR et angulus BDE cum angulo BRA equantur duobus angulis rectis. Et quia duorum punctorum D et R elongatio ab orbe meridiei, supra quem sunt A, B, G, est secundum duos arcus equales equidistantis supra ipsam descripte, erit angulus BGD equalis angulo BGR. Cuiusque ergo duorum triangulorum BGD et BGR duo latera unius sunt equalia duobus lateribus alterius, quodque latus suo relativo, scilicet GD equale GR, et latus BG est eis commune, et duo anguli qui continentur a duobus lateribus equalibus sunt equales, scilicet angulus BGD equalis angulo BGR. Ergo basis BD est equalis basi BR, et angulus BRG equalis angulo BDG. Et quia iam ostensum fuit in his que precesserunt parumper quod duo anguli qui sunt apud orbem descriptum supra duos polos orbis equationis diei elongationis equalis a puncto tropici equantur duobus angulis rectis, tunc duo anguli simul qui sunt ex GDE et GRA equantur duobus angulis rectis. Iam vero ostensum fuit quod angulus BDG equatur angulo BRG. Igitur summa duorum angulorum BDE et BRA equantur duobus angulis rectis. Et hoc est quod oportuit nos declarare.
Ostendam quoque quod cum elongatio unius puncti orbis signorum ab orbe meridiei ab utrisque lateribus eius fuerit secundum tempora equalia, tunc arcus orbium magnorum qui producuntur a puncto summitatis capitum ad illud punctum erunt equales, et erunt duo anguli simul qui erunt apud duo puncta ad orientem et occidentem equales duplo anguli qui est apud punctum unum orbis meridie cum fuerit unumquodque duorum punctorum mediantium celum orbis signorum aut ad partem meridianam a puncto summitatis capitum aut ad partem septentrionalem ab eo. Sit ergo prius ad partem meridianam. Describam autem portionem orbis meridiei, supra quam sint A, B, G, D, summitasque capitum eius sit punctum G, et polus equationis diei sit punctum D, et describam duas portiones orbis signorum, supra quas sint A, E, R et B, H, T, et sit longitudo puncti E et puncti H ab orbis meridiei utrisque partibus secundum duos arcus equales linee equidistantis equationi diei. 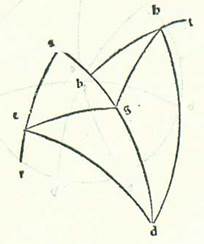 Describam etiam super hec duo puncta portiones orbium magnorum, scilicet super G GE et GH et super D DE et DH. Propter ea ergo que iam declarata sunt, quoniam super duo puncta E et H est descripta linea equidistans una, erunt duo arcus eius a duobus lateribus orbis meridiei equales, et erunt duo trianguli equalium laterum et angulorum equalium, scilicet triangulus GDE et triangulus GDH, et erit GE equale GH. Et dico quod duo anguli simul qui sunt ex GER et GHB equantur duplo anguli DER. Angulus namque DER est equalis angulo DHB. Sed angulus GED equatur angulo DHG. Ergo ambo illi qui sunt ex GED et GHB sunt equales angulo DER. Quapropter ambo illi qui sunt ex GER toto et qui sunt ex GHB equantur duplo anguli DER. Et illud est quod proposuimus probare.
Describam etiam super hec duo puncta portiones orbium magnorum, scilicet super G GE et GH et super D DE et DH. Propter ea ergo que iam declarata sunt, quoniam super duo puncta E et H est descripta linea equidistans una, erunt duo arcus eius a duobus lateribus orbis meridiei equales, et erunt duo trianguli equalium laterum et angulorum equalium, scilicet triangulus GDE et triangulus GDH, et erit GE equale GH. Et dico quod duo anguli simul qui sunt ex GER et GHB equantur duplo anguli DER. Angulus namque DER est equalis angulo DHB. Sed angulus GED equatur angulo DHG. Ergo ambo illi qui sunt ex GED et GHB sunt equales angulo DER. Quapropter ambo illi qui sunt ex GER toto et qui sunt ex GHB equantur duplo anguli DER. Et illud est quod proposuimus probare.
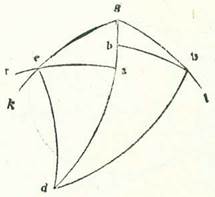 Describam quoque illas portiones que sunt orbium positorum in forma, et sint duo puncta A et B ex eis que sequentur septentrionem a puncto G. Dico ergo quod illud similiter accidit, scilicet quod duo anguli simul qui sunt ex KER et LHB equantur duplo anguli DER. Angulus enim DER est equalis angulo DHB. Sed angulus DEK equatur angulo DHL. Ergo totus angulus LHB equatur duobus angulis simul qui sunt ex DER et ex DEK. Quapropter erunt duo anguli qui sunt ex LHB et ex KER equales duplo anguli qui est ex DER.
Describam quoque illas portiones que sunt orbium positorum in forma, et sint duo puncta A et B ex eis que sequentur septentrionem a puncto G. Dico ergo quod illud similiter accidit, scilicet quod duo anguli simul qui sunt ex KER et LHB equantur duplo anguli DER. Angulus enim DER est equalis angulo DHB. Sed angulus DEK equatur angulo DHL. Ergo totus angulus LHB equatur duobus angulis simul qui sunt ex DER et ex DEK. Quapropter erunt duo anguli qui sunt ex LHB et ex KER equales duplo anguli qui est ex DER.
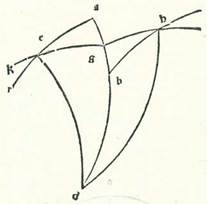 Describam quoque similem huius forme, et sit punctum A portionis orientalis in medio celi in parte meridiana a puncto G supra summitatem capitum, et sit punctum B portionis occidentalis que est in medio celi a parte septentrionali puncti G. Dico ergo quod ambo anguli qui sunt ex GER et LHB sunt maiores duplo anguli DER secundum duos angulos rectos. Angulus namque DHG equatur angulo DEG. Duo vero anguli DHG et DHL equantur duobus angulis rectis. Ergo duo anguli DEG et DHL simul equantur duobus rectis. Angulus autem DER est equalis angulo DHB. Quapropter erunt duo anguli GER et LHB maiores duobus angulis DER et DHB, scilicet maiores duplo anguli DER secundum duos angulos DEG et DHL, qui sunt equales duobus angulis rectis. Et illud est quod oportuit nos demonstrare.
Describam quoque similem huius forme, et sit punctum A portionis orientalis in medio celi in parte meridiana a puncto G supra summitatem capitum, et sit punctum B portionis occidentalis que est in medio celi a parte septentrionali puncti G. Dico ergo quod ambo anguli qui sunt ex GER et LHB sunt maiores duplo anguli DER secundum duos angulos rectos. Angulus namque DHG equatur angulo DEG. Duo vero anguli DHG et DHL equantur duobus angulis rectis. Ergo duo anguli DEG et DHL simul equantur duobus rectis. Angulus autem DER est equalis angulo DHB. Quapropter erunt duo anguli GER et LHB maiores duobus angulis DER et DHB, scilicet maiores duplo anguli DER secundum duos angulos DEG et DHL, qui sunt equales duobus angulis rectis. Et illud est quod oportuit nos demonstrare.
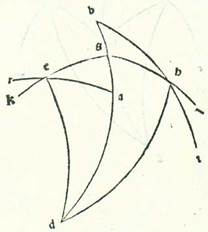 Describam quoque forme huius similem ad id quod residuum est ex hoc capitulo, sitque punctum A portionis orientalis in linea medii celi in parte septentrionali a puncto G, et sit punctum B portionis occidentalis in linea medii celi in parte meridiana a puncto G. Dico ergo quod duo anguli qui sunt ex KER et GHB simul sunt minores duplo anguli DER secundum duos angulos rectos, ideo etiam quoniam duo anguli KER et GHB simul sunt minores duobus angulis DER et DHB, scilicet minores duplo anguli DER secundum duos angulos simul qui sunt ex DEK et DHG. Sed hi duo anguli equantur duobus angulis rectis eo quod ambo anguli qui sunt ex DEK et DEG equantur duobus angulis rectis et ille qui est ex DEG est equalis ei qui est ex DHG. Et illud est quod oportuit nos declarare.
Describam quoque forme huius similem ad id quod residuum est ex hoc capitulo, sitque punctum A portionis orientalis in linea medii celi in parte septentrionali a puncto G, et sit punctum B portionis occidentalis in linea medii celi in parte meridiana a puncto G. Dico ergo quod duo anguli qui sunt ex KER et GHB simul sunt minores duplo anguli DER secundum duos angulos rectos, ideo etiam quoniam duo anguli KER et GHB simul sunt minores duobus angulis DER et DHB, scilicet minores duplo anguli DER secundum duos angulos simul qui sunt ex DEK et DHG. Sed hi duo anguli equantur duobus angulis rectis eo quod ambo anguli qui sunt ex DEK et DEG equantur duobus angulis rectis et ille qui est ex DEG est equalis ei qui est ex DHG. Et illud est quod oportuit nos declarare.
Ex hoc declarabitur nobis quod iam possibile est levius assumere inventionem angulorum provenientium in orbe meridiei et orbe horizontis, scilicet angulorum et arcuum qui sunt ex orbe declivi et orbe magno descripto supra punctum summitatis capitum secundum modum quem prediximus. 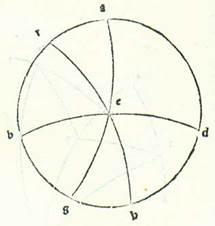 Nos enim cum descripserimus orbem meridiei, supra quem sint A, B, G, D, et medietatem orbis horizontis, supra quam sint B, E, D, et medietatem orbis signorum, supra quam sint R, E, H, quocunque modo sint, tunc si imaginati fuerimus orbem magnum descriptum supra punctum A, quod est summitas capitum, transeuntem per medium celi supra punctum R, erit tunc ipse orbis meridiei, et erit angulus DRE per ea que predicta sunt notus, eo quod punctum R est notum et angulus qui provenit apud orbem meridiei est notus, et erit arcus AR notus, ideo quod scivimus quot partium sit longitudo puncti R in orbe meridiei ab equatione diei et quot partium sit longitudo equationis diei a puncto A, quod est summitas capitum. Et cum imaginati fuerimus orbem magnum descriptum supra punctum A transeuntem per punctum E, quod est punctum orientis, et descripserimus supra eum AEG, tunc etiam manifestum erit quod arcus AE erit semper quarta orbis, eo quod punctum A sit polus circuli horizontis BED. Et propter has causas erit angulus AED rectus semper, et erit angulus DEH, qui est ex orbe declivi et orbe horizontis, notus, et erit etiam totus angulus AEH notus. Et illud est quod oportuit nos demonstrare.
Nos enim cum descripserimus orbem meridiei, supra quem sint A, B, G, D, et medietatem orbis horizontis, supra quam sint B, E, D, et medietatem orbis signorum, supra quam sint R, E, H, quocunque modo sint, tunc si imaginati fuerimus orbem magnum descriptum supra punctum A, quod est summitas capitum, transeuntem per medium celi supra punctum R, erit tunc ipse orbis meridiei, et erit angulus DRE per ea que predicta sunt notus, eo quod punctum R est notum et angulus qui provenit apud orbem meridiei est notus, et erit arcus AR notus, ideo quod scivimus quot partium sit longitudo puncti R in orbe meridiei ab equatione diei et quot partium sit longitudo equationis diei a puncto A, quod est summitas capitum. Et cum imaginati fuerimus orbem magnum descriptum supra punctum A transeuntem per punctum E, quod est punctum orientis, et descripserimus supra eum AEG, tunc etiam manifestum erit quod arcus AE erit semper quarta orbis, eo quod punctum A sit polus circuli horizontis BED. Et propter has causas erit angulus AED rectus semper, et erit angulus DEH, qui est ex orbe declivi et orbe horizontis, notus, et erit etiam totus angulus AEH notus. Et illud est quod oportuit nos demonstrare.
Manifestum est autem, postquam hec sunt secundum quod prediximus, quod cum nos sciverimus illos angulos et arcus tantum qui sunt orbis signorum solum a principio Cancri usque ad principium Capricorni in omni declinatione que est ante orbem meridiei, sciemus iam cum hoc angulos et arcus qui sunt horum signorum post orbem meridiei, et etiam cum illo angulos et arcus reliquorum signorum, qui sunt ante orbem meridiei et post ipsum. Et ut hoc capitulum sit nobis manifestum in omni loco, assumemus ad illud exemplum etiam et ponemus demonstrationem universalem, que est in omni loco, in capitulo uno et declinatione una et ubi est altitudo poli septentrionalis ab horizonte 36 partes et faciemus illius exemplum ut sit longitudo puncti principii Cancri ab orbe meridiei ad orientem hora una equalis. Et in loco illo supra quem est hec linea equidistans sint in illa hora in medio celi 16 partes et 12 minuta Geminorum et ascendant 17 partes et 37 minuta Virginis. 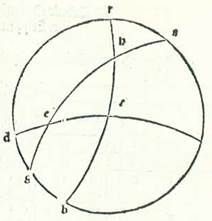 Describam vero orbem meridiei, supra quem sint A, B, G, D, et medietatem orbis horizontis, supra quam sint B, E, D, et medietatem orbis signorum, supra quam sint R, H, T, sitque punctum H caput Cancri, et punctum R sit loco sextedecime partis et duodecimi minuti Geminorum in medio celi, et sit punctum T loco decimeseptime partis et 37i minuti Virginis, et supra punctum summitatis capitum A et supra punctum capitis Cancri H faciam transire portionem orbis magni, supra quam sint A, H, E, G. Et perscrutabor prius inventionem arcus AH. Manifestum est ergo quod arcus RT est 91 partes et 25 minuta et arcus HT est 77 partes et 37 minuta. Et similiter, quia partes Geminorum sunt 16 partes et 12 minuta et est earum elongatio ab equatione diei in orbe meridiei ad septentrionem 23 partes et 7 minuta et elongatio equationis diei a puncto summitatis capitum A 36 partes, erit arcus AR 12 partes et 53 minuta et erit arcus RB propter complementum quarte 77 partes et 7 minuta. Postquam autem iam scivisti hec, ita erit etiam in hac forma proportio chorde dupli arcus RB ad chordam dupli arcus BA aggregata ex duabus proportionibus, ex proportione chorde dupli arcus RT ad chordam dupli arcus TH et ex proportione chorde dupli arcus HE ad chordam dupli arcus EA. Duplum vero arcus RB est 154 partes et 14 minuta, et eius chorda 116 partes et 59 minuta fere, et duplum arcus BA 180 partes, et eius chorda 120 partes, duplum quoque arcus RT est 182 partes et 50 minuta, et eius chorda 119 partes et 58 minuta, et duplum arcus TH 155 partes et 14 minuta, et eius chorda 117 partes et 12 minuta. Cum ergo nos proiecerimus ex proportione 116 partium et 59 minutorum ad 120 partes proportionem 119 partium et 58 minutorum ad 117 partes et 12 minuta, remanebit proportio chorde dupli arcus HE ad chordam dupli arcus EA, que est proportio 114 partium et 16 minutorum vicinius ad 120 partes. Chorda vero dupli arcus EA est 120 partes. Ergo chorda dupli arcus HE secundum illam quantitatem est 114 partes et 16 minuta vicinius. Quapropter erit duplum arcus HE 144 partes et 26 minuta fere, et erit arcus EH secundum illam quantitatem 72 partes et 13 minuta. Ergo arcus AH residuum complementi quarte erit 17 partes et 47 minuta. Et illud est quod fuit declarandum.
Describam vero orbem meridiei, supra quem sint A, B, G, D, et medietatem orbis horizontis, supra quam sint B, E, D, et medietatem orbis signorum, supra quam sint R, H, T, sitque punctum H caput Cancri, et punctum R sit loco sextedecime partis et duodecimi minuti Geminorum in medio celi, et sit punctum T loco decimeseptime partis et 37i minuti Virginis, et supra punctum summitatis capitum A et supra punctum capitis Cancri H faciam transire portionem orbis magni, supra quam sint A, H, E, G. Et perscrutabor prius inventionem arcus AH. Manifestum est ergo quod arcus RT est 91 partes et 25 minuta et arcus HT est 77 partes et 37 minuta. Et similiter, quia partes Geminorum sunt 16 partes et 12 minuta et est earum elongatio ab equatione diei in orbe meridiei ad septentrionem 23 partes et 7 minuta et elongatio equationis diei a puncto summitatis capitum A 36 partes, erit arcus AR 12 partes et 53 minuta et erit arcus RB propter complementum quarte 77 partes et 7 minuta. Postquam autem iam scivisti hec, ita erit etiam in hac forma proportio chorde dupli arcus RB ad chordam dupli arcus BA aggregata ex duabus proportionibus, ex proportione chorde dupli arcus RT ad chordam dupli arcus TH et ex proportione chorde dupli arcus HE ad chordam dupli arcus EA. Duplum vero arcus RB est 154 partes et 14 minuta, et eius chorda 116 partes et 59 minuta fere, et duplum arcus BA 180 partes, et eius chorda 120 partes, duplum quoque arcus RT est 182 partes et 50 minuta, et eius chorda 119 partes et 58 minuta, et duplum arcus TH 155 partes et 14 minuta, et eius chorda 117 partes et 12 minuta. Cum ergo nos proiecerimus ex proportione 116 partium et 59 minutorum ad 120 partes proportionem 119 partium et 58 minutorum ad 117 partes et 12 minuta, remanebit proportio chorde dupli arcus HE ad chordam dupli arcus EA, que est proportio 114 partium et 16 minutorum vicinius ad 120 partes. Chorda vero dupli arcus EA est 120 partes. Ergo chorda dupli arcus HE secundum illam quantitatem est 114 partes et 16 minuta vicinius. Quapropter erit duplum arcus HE 144 partes et 26 minuta fere, et erit arcus EH secundum illam quantitatem 72 partes et 13 minuta. Ergo arcus AH residuum complementi quarte erit 17 partes et 47 minuta. Et illud est quod fuit declarandum.
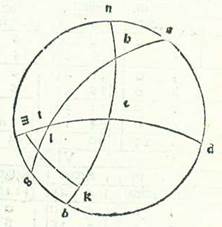 Post illud vero erit inventio anguli AHT ut reiteremus hanc figuram secundum habitudinem suam et describemus supra polum puncti H secundum longitudinem lateris quadrati portionem orbis magni, supra quam sint K, L, M. Et quia orbis AHE est descriptus super duos polos ETM et KLM, erit quilibet duorum arcuum EM et KM quarta circuli. Propter hanc quoque formam erit proportio chorde dupli arcus HE ad chordam dupli arcus EK aggregata ex duabus proportionibus, ex proportione chorde dupli arcus HT ad chordam dupli arcus TL et ex proportione chorde dupli arcus LM ad chordam dupli arcus MK. Duplum vero arcus HE est 144 partes et 26 minuta, et eius chorda 114 partes et 16 minuta, et duplum arcus EK est 35 partes et 34 minuta, et chorda eius 36 partes et 38 minuta, duplum quoque arcus TH est 155 partes et 14 minuta, et eius chorda 117 partes et 12 minuta, et duplum arcus TL est 24 partes et 46 minuta, et eius chorda 25 partes et 34 minuta. Cum ergo nos proiecerimus ex proportione 114 partium et 16 minutorum ad 36 partes et 38 minuta proportionem 117 partium et 12 minutorum ad 25 partes et 44 minuta, remanebit proportio chorde dupli arcus LM ad chordam dupli arcus MK, que est proportio 82 partium et 11 minutorum propinquius ad 120 partes. Sed chorda dupli arcus MK est 120 partes. Ergo chorda dupli arcus LM erit 82 partes et 11 minuta. Quapropter erit duplum arcus LM 86 partes et 28 minuta, et arcus LM secundam illam quantitatem erit 43 partes et 14 minuta. Ergo arcus LK residuus et angulus LHK erunt 46 partes et 46 minuta. Quapropter angulus AHT complementum eorum que remanent ex duobus angulis rectis erit 133 partes et 14 minuta. Et hoc est quod voluimus ostendere.
Post illud vero erit inventio anguli AHT ut reiteremus hanc figuram secundum habitudinem suam et describemus supra polum puncti H secundum longitudinem lateris quadrati portionem orbis magni, supra quam sint K, L, M. Et quia orbis AHE est descriptus super duos polos ETM et KLM, erit quilibet duorum arcuum EM et KM quarta circuli. Propter hanc quoque formam erit proportio chorde dupli arcus HE ad chordam dupli arcus EK aggregata ex duabus proportionibus, ex proportione chorde dupli arcus HT ad chordam dupli arcus TL et ex proportione chorde dupli arcus LM ad chordam dupli arcus MK. Duplum vero arcus HE est 144 partes et 26 minuta, et eius chorda 114 partes et 16 minuta, et duplum arcus EK est 35 partes et 34 minuta, et chorda eius 36 partes et 38 minuta, duplum quoque arcus TH est 155 partes et 14 minuta, et eius chorda 117 partes et 12 minuta, et duplum arcus TL est 24 partes et 46 minuta, et eius chorda 25 partes et 34 minuta. Cum ergo nos proiecerimus ex proportione 114 partium et 16 minutorum ad 36 partes et 38 minuta proportionem 117 partium et 12 minutorum ad 25 partes et 44 minuta, remanebit proportio chorde dupli arcus LM ad chordam dupli arcus MK, que est proportio 82 partium et 11 minutorum propinquius ad 120 partes. Sed chorda dupli arcus MK est 120 partes. Ergo chorda dupli arcus LM erit 82 partes et 11 minuta. Quapropter erit duplum arcus LM 86 partes et 28 minuta, et arcus LM secundam illam quantitatem erit 43 partes et 14 minuta. Ergo arcus LK residuus et angulus LHK erunt 46 partes et 46 minuta. Quapropter angulus AHT complementum eorum que remanent ex duobus angulis rectis erit 133 partes et 14 minuta. Et hoc est quod voluimus ostendere.
⟨II.13⟩ Capitulum tredecimum: De positione tabularum arcuum et angulorum quos narravimus in orbibus equidistantibus
Inventio autem eorum que remanent de arcubus et angulis est secundum hunc modum quem iam declaravimus. Ut autem sciamus levius invenire ea cum necessaria fuerint, accipiemus eis tabulas. Et incipiemus prius a climate et linea equidistante cuius longioris diei longitudo est 13 hore equales et perveniemus ad clima et lineam equidistantem cuius longioris diei longitudo est 16 hore equales. Et faciemus superfluum quod est inter climata et lineas equidistantes medietatem hore et medietatem hore etiam secundum quod fecimus ipsum in elevationibus, et superfluum partium orbis signorum secundum signum et signum unum, et superfluum locorum que sunt a duobus lateribus orbis meridiei ad orientem et occidentem secundum unam horam equalem. Et faciam propter hoc tabulas omnis climatis et omnis signi. Et describam scilicet in lineis primis numerum horarum equalium que sunt longitudo orbis meridiei ad orientem et ad occidentem, in lineis vero secundis quantitatem arcuum qui sunt a summitate capitum usque ad caput signi dati, quemadmodum prediximus, in lineis autem tertia et quarta quantitatem angulorum provenientium ex locis sectionis secundum modum quem prediximus. Tertie vero linee sunt angulorum provenientium in locis eis que sequuntur orientem ab orbe meridiei. Quarte autem linee erunt angulorum provenientium in locis eis que sequuntur occidentem ab orbe meridiei, quemadmodum iam determinavimus. Recordemur autem eius quod diximus, scilicet quod duorum angulorum qui sunt ex portionibus orbis signorum secundum continuitatem nunquam accipimus nisi septentrionalem sepentrionalem M., et ostendemus cuiusque horum quantitatem secundum quantitatem qua angulus rectus est nonaginta partes. Et hec quidem est tabularum descriptio:
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima primum, sub linea equidistante cuius hore in longiore die sunt 13. Et eius latitudo est partium 16, minutorum 27.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||||||||||||||||||||
Meridies |
7 |
24 |
90 |
sep. | 0 |
0 |
sep. | 0 |
Meridies |
16 |
27 |
113 |
me. | 51 |
0 |
mer. | 0 |
|||||||||||||||||||||||
1 |
0 |
15 |
55 |
25 |
16 |
154 |
44 |
1 |
0 |
22 |
8 |
154 |
53 |
72 |
49 |
|||||||||||||||||||||||||
2 |
0 |
29 |
3 |
9 |
15 |
170 |
45 |
2 |
0 |
33 |
7 |
183 |
17 |
54 |
25 |
|||||||||||||||||||||||||
3 |
0 |
42 |
42 |
1 |
58 |
178 |
2 |
3 |
0 |
47 |
20 |
1 |
se. | 23 |
46 |
19 |
||||||||||||||||||||||||
4 |
0 |
56 |
25 |
175 |
mer. | 7 |
4 |
53 |
4 |
0 |
61 |
32 |
5 |
8 |
42 |
34 |
||||||||||||||||||||||||
5 |
0 |
70 |
2 |
170 |
18 |
9 |
me. | 42 |
5 |
0 |
75 |
39 |
7 |
9 |
40 |
23 |
||||||||||||||||||||||||
6 |
0 |
83 |
27 |
164 |
41 |
15 |
19 |
6 |
0 |
90 |
0 |
7 |
24 |
40 |
18 |
|||||||||||||||||||||||||
6 |
30 |
90 |
0 |
161 |
57 |
18 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||||||||||||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||
Meridies |
4 |
3 |
102 |
se. | 30 |
0 |
0 |
Meridies |
28 |
7 |
111 |
sep. | 0 |
0 |
mer. | 0 |
||||||||||||||||||||||||
1 |
0 |
14 |
20 |
26 |
3 |
178 |
57 |
1 |
0 |
31 |
46 |
139 |
0 |
83 |
0 |
|||||||||||||||||||||||||
2 |
0 |
28 |
42 |
15 |
28 |
9 |
me. | 32 |
2 |
0 |
40 |
52 |
157 |
59 |
64 |
1 |
||||||||||||||||||||||||
3 |
0 |
42 |
43 |
10 |
5 |
14 |
55 |
3 |
0 |
52 |
30 |
169 |
23 |
52 |
37 |
|||||||||||||||||||||||||
4 |
0 |
56 |
49 |
6 |
19 |
18 |
41 |
4 |
0 |
65 |
40 |
176 |
41 |
45 |
19 |
|||||||||||||||||||||||||
5 |
0 |
70 |
38 |
2 |
33 |
22 |
27 |
5 |
0 |
79 |
18 |
1 |
me. | 41 |
40 |
19 |
||||||||||||||||||||||||
6 |
0 |
84 |
17 |
177 |
mer. | 0 |
28 |
0 |
5 |
46 |
90 |
0 |
4 |
9 |
37 |
51 |
||||||||||||||||||||||||
6 |
25 |
90 |
0 |
174 |
51 |
30 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||||||||||||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||
Meridies |
4 |
47 |
111 |
sep. | 0 |
0 |
mer. | 0 |
Meridies |
36 |
57 |
102 |
me. | 30 |
0 |
mer. | 0 |
|||||||||||||||||||||||
1 |
0 |
15 |
20 |
0 |
0 |
42 |
0 |
1 |
0 |
39 |
46 |
125 |
12 |
79 |
48 |
|||||||||||||||||||||||||
2 |
0 |
29 |
28 |
8 |
0 |
34 |
0 |
2 |
0 |
47 |
15 |
143 |
5 |
61 |
55 |
|||||||||||||||||||||||||
3 |
0 |
43 |
40 |
9 |
15 |
32 |
45 |
3 |
0 |
57 |
33 |
156 |
3 |
48 |
57 |
|||||||||||||||||||||||||
4 |
0 |
58 |
18 |
8 |
39 |
33 |
21 |
4 |
0 |
69 |
30 |
164 |
48 |
40 |
12 |
|||||||||||||||||||||||||
5 |
0 |
72 |
36 |
6 |
53 |
35 |
7 |
5 |
0 |
82 |
18 |
171 |
43 |
33 |
17 |
|||||||||||||||||||||||||
6 |
0 |
86 |
41 |
5 |
37 |
36 |
23 |
5 |
35 |
90 |
0 |
174 |
51 |
30 |
9 |
|||||||||||||||||||||||||
6 |
14 |
90 |
0 |
4 |
9 |
37 |
51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||||||||||||||||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||
Meridies |
40 |
18 |
90 |
mer. | 0 |
0 |
mer. | 0 |
Meridies |
16 |
27 |
66 |
mer. | 9 |
0 |
mer. | 0 |
|||||||||||||||||||||||
1 |
0 |
42 |
54 |
111 |
24 |
68 |
36 |
1 |
0 |
22 |
8 |
107 |
11 |
25 |
7 |
|||||||||||||||||||||||||
2 |
0 |
49 |
58 |
128 |
51 |
51 |
9 |
2 |
0 |
33 |
7 |
125 |
35 |
6 |
se. | 43 |
||||||||||||||||||||||||
3 |
0 |
59 |
35 |
141 |
49 |
38 |
11 |
3 |
0 |
47 |
20 |
133 |
41 |
178 |
37 |
|||||||||||||||||||||||||
4 |
0 |
71 |
4 |
151 |
25 |
28 |
35 |
4 |
0 |
61 |
32 |
137 |
26 |
174 |
52 |
|||||||||||||||||||||||||
5 |
0 |
83 |
31 |
158 |
48 |
21 |
12 |
5 |
0 |
75 |
39 |
139 |
27 |
172 |
51 |
|||||||||||||||||||||||||
5 |
30 |
90 |
0 |
161 |
57 |
18 |
3 |
6 |
0 |
90 |
0 |
139 |
42 |
172 |
36 |
|||||||||||||||||||||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||
Meridies |
36 |
57 |
77 |
me. | 30 |
0 |
mer. | 0 |
Meridies |
4 |
47 |
69 |
mer. | 0 |
0 |
sep. | 0 |
|||||||||||||||||||||||
1 |
0 |
39 |
46 |
100 |
12 |
54 |
48 |
1 |
0 |
15 |
20 |
138 |
0 |
180 |
0 |
|||||||||||||||||||||||||
2 |
0 |
47 |
15 |
118 |
5 |
36 |
55 |
2 |
0 |
29 |
28 |
146 |
0 |
172 |
0 |
|||||||||||||||||||||||||
3 |
0 |
57 |
33 |
131 |
3 |
23 |
57 |
3 |
0 |
43 |
40 |
147 |
15 |
170 |
45 |
|||||||||||||||||||||||||
4 |
0 |
69 |
30 |
139 |
48 |
15 |
12 |
4 |
0 |
58 |
18 |
146 |
39 |
171 |
21 |
|||||||||||||||||||||||||
5 |
0 |
82 |
18 |
146 |
43 |
8 |
17 |
5 |
0 |
72 |
36 |
144 |
53 |
173 |
7 |
|||||||||||||||||||||||||
5 |
35 |
90 |
0 |
149 |
51 |
5 |
9 |
6 |
0 |
86 |
41 |
143 |
37 |
174 |
23 |
|||||||||||||||||||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
14 |
90 |
0 |
142 |
9 |
175 |
51 |
|||||||||||||||||||||||||
PISCES ♓ |
GEMINI ♊ | |||||||||||||||||||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||||||||||||||||
Meridies |
28 |
7 |
69 |
mer. | 0 |
0 |
mer. | 0 |
Meridies |
4 |
3 |
77 |
se. | 30 |
0 |
sep. | 0 |
|||||||||||||||||||||||
1 |
0 |
31 |
46 |
97 |
0 |
41 |
0 |
1 |
0 |
14 |
20 |
71 |
3 |
153 |
57 |
|||||||||||||||||||||||||
2 |
0 |
40 |
52 |
115 |
59 |
22 |
1 |
2 |
0 |
28 |
42 |
170 |
28 |
164 |
32 |
|||||||||||||||||||||||||
3 |
0 |
52 |
30 |
127 |
23 |
10 |
37 |
3 |
0 |
42 |
43 |
165 |
5 |
169 |
55 |
|||||||||||||||||||||||||
4 |
0 |
65 |
40 |
134 |
41 |
3 |
se. | 19 |
4 |
0 |
56 |
49 |
161 |
me. | 19 |
173 |
me. | 41 |
||||||||||||||||||||||
5 |
0 |
79 |
18 |
139 |
se. | 41 |
18 |
19 |
5 |
0 |
70 |
38 |
157 |
33 |
177 |
27 |
||||||||||||||||||||||||
5 |
46 |
90 |
0 |
142 |
9 |
175 |
51 |
6 |
25 |
84 |
17 |
152 |
0 |
3 |
0 |
|||||||||||||||||||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
90 |
0 |
149 |
51 |
5 |
9 |
|||||||||||||||||||||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima secundum, sub linea equidistante cuius hore in longiore die sunt 13 et medietas. Et eius latitudo est partium 23, minutorum 51.
CANCER ♋ |
LIBRA ♎ |
||||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
||||||||
Meridies |
0 |
0 |
90 |
0 |
0 |
0 |
Meridies |
23 |
51 |
113 |
51 |
0 |
0 |
||||||||||
1 |
0 |
13 |
43 |
176 |
15 |
3 |
45 |
1 |
0 |
27 |
56 |
144 |
10 |
83 |
32 |
||||||||
2 |
0 |
27 |
23 |
173 |
51 |
6 |
9 |
2 |
0 |
37 |
36 |
162 |
13 |
65 |
29 |
||||||||
3 |
0 |
41 |
20 |
168 |
15 |
11 |
45 |
3 |
0 |
49 |
42 |
171 |
45 |
55 |
57 |
||||||||
4 |
0 |
54 |
27 |
166 |
51 |
13 |
9 |
4 |
0 |
62 |
47 |
176 |
59 |
50 |
43 |
||||||||
5 |
0 |
67 |
42 |
162 |
42 |
17 |
18 |
5 |
0 |
76 |
20 |
179 |
3 |
48 |
39 |
||||||||
6 |
0 |
80 |
36 |
157 |
59 |
22 |
1 |
6 |
0 |
90 |
0 |
180 |
0 |
47 |
42 |
||||||||
6 |
45 |
90 |
0 |
153 |
46 |
26 |
14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
LEO ♌ |
SCORPIO ♏ |
||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||
Meridies |
3 |
21 |
102 |
30 |
0 |
0 |
Meridies |
35 |
31 |
111 |
0 |
0 |
0 |
||||||||||
1 |
0 |
14 |
18 |
176 |
4 |
28 |
56 |
1 |
0 |
38 |
25 |
133 |
15 |
88 |
45 |
||||||||
2 |
0 |
27 |
56 |
180 |
0 |
25 |
0 |
2 |
0 |
46 |
2 |
150 |
18 |
71 |
42 |
||||||||
3 |
0 |
41 |
44 |
179 |
3 |
25 |
57 |
3 |
0 |
56 |
30 |
161 |
41 |
60 |
19 |
||||||||
4 |
0 |
55 |
54 |
177 |
18 |
27 |
42 |
4 |
0 |
68 |
31 |
169 |
5 |
52 |
55 |
||||||||
5 |
0 |
68 |
43 |
173 |
40 |
31 |
20 |
5 |
0 |
81 |
22 |
174 |
30 |
47 |
30 |
||||||||
6 |
0 |
81 |
52 |
168 |
56 |
36 |
4 |
5 |
39 |
90 |
0 |
176 |
41 |
45 |
19 |
||||||||
6 |
38 |
90 |
0 |
166 |
53 |
38 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||
Meridies |
12 |
11 |
111 |
0 |
0 |
0 |
Meridies |
44 |
21 |
102 |
30 |
0 |
0 |
||||||||||
1 |
0 |
18 |
42 |
158 |
40 |
63 |
20 |
1 |
0 |
46 |
40 |
121 |
30 |
83 |
30 |
||||||||
2 |
0 |
30 |
57 |
173 |
44 |
48 |
16 |
2 |
0 |
53 |
4 |
137 |
16 |
67 |
44 |
||||||||
3 |
0 |
44 |
22 |
178 |
3 |
43 |
57 |
3 |
0 |
62 |
18 |
149 |
29 |
55 |
35 |
||||||||
4 |
0 |
58 |
1 |
180 |
0 |
42 |
0 |
4 |
0 |
73 |
20 |
157 |
58 |
47 |
2 |
||||||||
5 |
0 |
71 |
43 |
179 |
15 |
42 |
45 |
5 |
0 |
85 |
23 |
164 |
46 |
40 |
14 |
||||||||
6 |
0 |
85 |
20 |
177 |
39 |
44 |
21 |
5 |
22 |
90 |
0 |
166 |
53 |
38 |
7 |
||||||||
6 |
21 |
90 |
0 |
176 |
41 |
45 |
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
CAPRICORNUS ♑ |
ARIES ♈ |
||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||
Meridies |
47 |
42 |
90 |
0 |
0 |
0 |
Meridies |
23 |
51 |
66 |
9 |
0 |
0 |
||||||||||
1 |
0 |
49 |
52 |
108 |
3 |
71 |
57 |
1 |
0 |
27 |
56 |
96 |
28 |
35 |
50 |
||||||||
2 |
0 |
55 |
52 |
123 |
31 |
56 |
29 |
2 |
0 |
37 |
36 |
114 |
31 |
17 |
47 |
||||||||
3 |
0 |
64 |
37 |
135 |
37 |
44 |
23 |
3 |
0 |
49 |
42 |
124 |
3 |
8 |
15 |
||||||||
4 |
0 |
75 |
12 |
144 |
57 |
35 |
3 |
4 |
0 |
62 |
47 |
129 |
17 |
3 |
1 |
||||||||
5 |
0 |
86 |
54 |
152 |
0 |
28 |
0 |
5 |
0 |
76 |
20 |
131 |
21 |
0 |
57 |
||||||||
5 |
15 |
90 |
0 |
153 |
46 |
26 |
14 |
6 |
0 |
90 |
0 |
132 |
18 |
0 |
0 |
||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||
AQUARIUS ♒ |
TAURUS ♉ |
||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||
Meridies |
44 |
21 |
77 |
30 |
0 |
0 |
Meridies |
12 |
11 |
69 |
0 |
0 |
0 |
||||||||||
1 |
0 |
46 |
40 |
96 |
30 |
58 |
30 |
1 |
0 |
18 |
42 |
116 |
40 |
21 |
20 |
||||||||
2 |
0 |
53 |
4 |
112 |
16 |
42 |
44 |
2 |
0 |
30 |
57 |
131 |
44 |
6 |
16 |
||||||||
3 |
0 |
62 |
18 |
124 |
25 |
30 |
35 |
3 |
0 |
44 |
22 |
136 |
3 |
1 |
57 |
||||||||
4 |
0 |
73 |
20 |
132 |
58 |
22 |
2 |
4 |
0 |
58 |
1 |
138 |
0 |
0 |
0 |
||||||||
5 |
0 |
85 |
23 |
139 |
46 |
15 |
14 |
5 |
0 |
71 |
43 |
137 |
15 |
0 |
45 |
||||||||
5 |
22 |
90 |
0 |
141 |
53 |
13 |
7 |
6 |
0 |
85 |
20 |
135 |
39 |
2 |
21 |
||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
21 |
90 |
0 |
134 |
41 |
3 |
19 |
||||||||
PISCES ♓ |
GEMINI ♊ |
||||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
||||||||||||||
Meridies |
35 |
31 |
69 |
0 |
0 |
0 |
Meridies |
3 |
21 |
77 |
30 |
0 |
0 |
||||||||||
1 |
0 |
38 |
25 |
91 |
15 |
46 |
45 |
1 |
0 |
14 |
18 |
151 |
4 |
3 |
56 |
||||||||
2 |
0 |
46 |
2 |
108 |
18 |
29 |
42 |
2 |
0 |
27 |
56 |
155 |
0 |
0 |
0 |
||||||||
3 |
0 |
56 |
30 |
119 |
41 |
18 |
19 |
3 |
0 |
41 |
44 |
154 |
3 |
0 |
57 |
||||||||
4 |
0 |
68 |
31 |
127 |
5 |
10 |
55 |
4 |
0 |
55 |
54 |
152 |
18 |
2 |
42 |
||||||||
5 |
0 |
81 |
22 |
132 |
30 |
5 |
30 |
5 |
0 |
68 |
43 |
148 |
40 |
6 |
20 |
||||||||
5 |
39 |
90 |
0 |
134 |
41 |
3 |
19 |
6 |
0 |
81 |
52 |
143 |
56 |
11 |
4 |
||||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
38 |
90 |
0 |
141 |
53 |
13 |
7 |
||||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima tertium, sub linea equidistante cuius hore in longiore die sunt 14. Et eius latitudo est partium 30, minutorum 22.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||
Meridies |
6 |
31 |
90 |
0 |
0 |
0 |
Meridies |
30 |
22 |
113 |
51 |
0 |
0 |
|||||||||
1 |
0 |
14 |
56 |
150 |
0 |
30 |
0 |
1 |
0 |
33 |
35 |
137 |
32 |
90 |
10 |
|||||||
2 |
0 |
27 |
23 |
159 |
38 |
20 |
22 |
2 |
0 |
41 |
39 |
154 |
19 |
73 |
23 |
|||||||
3 |
0 |
40 |
19 |
160 |
30 |
19 |
30 |
3 |
0 |
52 |
25 |
164 |
10 |
63 |
32 |
|||||||
4 |
0 |
53 |
14 |
158 |
51 |
21 |
9 |
4 |
0 |
64 |
28 |
169 |
47 |
57 |
55 |
|||||||
5 |
0 |
65 |
15 |
156 |
0 |
24 |
0 |
5 |
0 |
77 |
6 |
172 |
21 |
55 |
21 |
|||||||
6 |
0 |
78 |
15 |
151 |
49 |
28 |
11 |
6 |
0 |
90 |
0 |
173 |
29 |
54 |
13 |
|||||||
7 |
0 |
90 |
0 |
146 |
28 |
33 |
32 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
9 |
12 |
102 |
30 |
0 |
0 |
Meridies |
42 |
2 |
111 |
0 |
0 |
0 |
|||||||||
1 |
0 |
16 |
45 |
153 |
13 |
51 |
47 |
1 |
0 |
44 |
26 |
129 |
32 |
92 |
28 |
|||||||
2 |
0 |
28 |
44 |
166 |
22 |
38 |
38 |
2 |
0 |
50 |
58 |
144 |
38 |
77 |
22 |
|||||||
3 |
0 |
41 |
31 |
169 |
26 |
35 |
34 |
3 |
0 |
60 |
19 |
155 |
33 |
66 |
27 |
|||||||
4 |
0 |
54 |
27 |
169 |
8 |
35 |
52 |
4 |
0 |
71 |
20 |
162 |
56 |
59 |
4 |
|||||||
5 |
0 |
67 |
17 |
167 |
1 |
37 |
59 |
5 |
0 |
83 |
19 |
167 |
54 |
54 |
6 |
|||||||
6 |
0 |
79 |
48 |
163 |
46 |
41 |
14 |
5 |
32 |
90 |
0 |
169 |
55 |
52 |
5 |
|||||||
6 |
51 |
90 |
0 |
159 |
49 |
45 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
18 |
42 |
111 |
0 |
0 |
0 |
Meridies |
50 |
52 |
102 |
30 |
0 |
0 |
|||||||||
1 |
0 |
23 |
18 |
145 |
18 |
76 |
42 |
1 |
0 |
52 |
53 |
118 |
39 |
86 |
21 |
|||||||
2 |
0 |
33 |
30 |
162 |
25 |
59 |
35 |
2 |
0 |
58 |
27 |
132 |
51 |
72 |
9 |
|||||||
3 |
0 |
45 |
36 |
169 |
34 |
52 |
26 |
3 |
0 |
66 |
44 |
144 |
1 |
60 |
59 |
|||||||
4 |
0 |
58 |
21 |
172 |
10 |
49 |
50 |
4 |
0 |
76 |
51 |
152 |
37 |
52 |
23 |
|||||||
5 |
0 |
71 |
15 |
172 |
28 |
49 |
32 |
5 |
0 |
88 |
9 |
158 |
43 |
46 |
17 |
|||||||
6 |
0 |
84 |
7 |
171 |
5 |
50 |
55 |
5 |
9 |
90 |
0 |
159 |
49 |
45 |
11 |
|||||||
6 |
28 |
90 |
0 |
169 |
55 |
52 |
5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
54 |
18 |
90 |
0 |
0 |
0 |
Meridies |
30 |
22 |
66 |
9 |
0 |
0 |
|||||||||
1 |
0 |
56 |
6 |
105 |
34 |
74 |
26 |
1 |
0 |
33 |
35 |
89 |
50 |
42 |
28 |
|||||||
2 |
0 |
61 |
22 |
119 |
23 |
60 |
37 |
2 |
0 |
41 |
39 |
106 |
37 |
25 |
41 |
|||||||
3 |
0 |
69 |
17 |
130 |
46 |
49 |
14 |
3 |
0 |
52 |
25 |
116 |
28 |
15 |
50 |
|||||||
4 |
0 |
78 |
59 |
139 |
30 |
40 |
30 |
4 |
0 |
64 |
28 |
122 |
5 |
10 |
13 |
|||||||
5 |
0 |
90 |
0 |
146 |
28 |
33 |
32 |
5 |
0 |
77 |
6 |
124 |
39 |
7 |
39 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
90 |
0 |
125 |
47 |
6 |
31 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
50 |
52 |
73 |
30 |
0 |
0 |
Meridies |
18 |
42 |
69 |
0 |
0 |
0 |
|||||||||
1 |
0 |
52 |
53 |
93 |
39 |
61 |
21 |
1 |
0 |
23 |
18 |
103 |
18 |
34 |
42 |
|||||||
2 |
0 |
58 |
27 |
107 |
51 |
47 |
9 |
2 |
0 |
33 |
30 |
120 |
25 |
17 |
35 |
|||||||
3 |
0 |
66 |
44 |
119 |
1 |
35 |
59 |
3 |
0 |
45 |
36 |
127 |
34 |
10 |
26 |
|||||||
4 |
0 |
76 |
51 |
127 |
37 |
27 |
23 |
4 |
0 |
58 |
21 |
130 |
10 |
7 |
50 |
|||||||
5 |
0 |
88 |
9 |
133 |
43 |
21 |
17 |
5 |
0 |
71 |
15 |
130 |
28 |
7 |
32 |
|||||||
5 |
9 |
90 |
0 |
134 |
49 |
20 |
11 |
6 |
0 |
84 |
7 |
129 |
5 |
8 |
55 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
28 |
90 |
0 |
127 |
55 |
10 |
5 |
|||||||
PISCES ♓ |
GEMINI ♊ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
42 |
2 |
69 |
0 |
0 |
0 |
Meridies |
9 |
12 |
77 |
30 |
0 |
0 |
|||||||||
1 |
0 |
44 |
26 |
87 |
32 |
50 |
28 |
1 |
0 |
16 |
45 |
128 |
13 |
26 |
47 |
|||||||
2 |
0 |
50 |
58 |
102 |
38 |
35 |
22 |
2 |
0 |
28 |
44 |
141 |
22 |
13 |
38 |
|||||||
3 |
0 |
60 |
19 |
113 |
33 |
24 |
27 |
3 |
0 |
41 |
31 |
144 |
26 |
10 |
34 |
|||||||
4 |
0 |
71 |
20 |
120 |
56 |
17 |
4 |
4 |
0 |
54 |
27 |
144 |
8 |
10 |
52 |
|||||||
5 |
0 |
83 |
19 |
125 |
54 |
12 |
6 |
5 |
0 |
67 |
17 |
142 |
1 |
12 |
59 |
|||||||
5 |
32 |
90 |
0 |
127 |
55 |
10 |
5 |
6 |
0 |
79 |
48 |
138 |
46 |
16 |
14 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
51 |
90 |
0 |
134 |
49 |
20 |
11 |
|||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima quartum, sub linea equidistante cuius hore in longiore die sunt 14 et medietas. Et eius latitudo est partium 36, minutorum 0.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||
Meridies |
12 |
9 |
90 |
0 |
0 |
0 |
Meridies |
36 |
0 |
113 |
51 |
0 |
0 |
|||||||||
1 |
0 |
17 |
47 |
133 |
14 |
46 |
46 |
1 |
0 |
38 |
37 |
133 |
23 |
94 |
19 |
|||||||
2 |
0 |
28 |
22 |
147 |
45 |
32 |
15 |
2 |
0 |
45 |
31 |
148 |
23 |
79 |
19 |
|||||||
3 |
0 |
40 |
27 |
151 |
46 |
28 |
14 |
3 |
0 |
55 |
6 |
158 |
9 |
69 |
33 |
|||||||
4 |
0 |
52 |
36 |
151 |
52 |
28 |
8 |
4 |
0 |
66 |
9 |
163 |
58 |
63 |
44 |
|||||||
5 |
0 |
64 |
36 |
149 |
54 |
30 |
6 |
5 |
0 |
77 |
56 |
166 |
36 |
61 |
6 |
|||||||
6 |
0 |
76 |
16 |
146 |
25 |
33 |
35 |
6 |
0 |
90 |
0 |
167 |
51 |
59 |
51 |
|||||||
7 |
0 |
87 |
23 |
141 |
30 |
38 |
30 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
15 |
90 |
0 |
140 |
1 |
39 |
59 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
15 |
30 |
102 |
30 |
0 |
0 |
Meridies |
47 |
40 |
111 |
0 |
0 |
0 |
|||||||||
1 |
0 |
20 |
20 |
139 |
32 |
65 |
28 |
1 |
0 |
49 |
42 |
126 |
50 |
95 |
10 |
|||||||
2 |
0 |
30 |
28 |
155 |
19 |
49 |
41 |
2 |
0 |
55 |
26 |
140 |
20 |
81 |
40 |
|||||||
3 |
0 |
42 |
6 |
160 |
37 |
44 |
23 |
3 |
0 |
63 |
48 |
150 |
34 |
71 |
26 |
|||||||
4 |
0 |
54 |
12 |
162 |
11 |
42 |
49 |
4 |
0 |
73 |
55 |
157 |
51 |
64 |
9 |
|||||||
5 |
0 |
66 |
17 |
161 |
5 |
43 |
55 |
5 |
0 |
85 |
5 |
162 |
28 |
59 |
32 |
|||||||
6 |
0 |
78 |
7 |
158 |
10 |
46 |
50 |
5 |
25 |
90 |
0 |
164 |
7 |
57 |
53 |
|||||||
7 |
0 |
89 |
27 |
153 |
39 |
51 |
21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
3 |
90 |
0 |
153 |
36 |
51 |
24 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
24 |
20 |
111 |
0 |
0 |
0 |
Meridies |
56 |
30 |
102 |
30 |
0 |
0 |
|||||||||
1 |
0 |
27 |
51 |
137 |
38 |
84 |
22 |
1 |
0 |
58 |
14 |
116 |
39 |
88 |
21 |
|||||||
2 |
0 |
36 |
24 |
153 |
59 |
68 |
1 |
2 |
0 |
63 |
13 |
129 |
23 |
75 |
37 |
|||||||
3 |
0 |
47 |
14 |
162 |
10 |
59 |
50 |
3 |
9 |
70 |
41 |
139 |
47 |
65 |
13 |
|||||||
4 |
0 |
59 |
0 |
165 |
40 |
56 |
20 |
4 |
0 |
80 |
2 |
147 |
47 |
57 |
13 |
|||||||
5 |
0 |
71 |
5 |
166 |
34 |
55 |
26 |
4 |
57 |
90 |
0 |
153 |
36 |
51 |
24 |
|||||||
6 |
0 |
83 |
9 |
165 |
30 |
56 |
30 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
6 |
35 |
90 |
0 |
164 |
7 |
57 |
53 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
59 |
51 |
90 |
0 |
0 |
0 |
Meridies |
36 |
0 |
66 |
9 |
0 |
0 |
|||||||||
1 |
0 |
61 |
30 |
103 |
45 |
76 |
15 |
1 |
0 |
38 |
37 |
85 |
41 |
46 |
37 |
|||||||
2 |
0 |
66 |
12 |
116 |
10 |
63 |
50 |
2 |
0 |
45 |
31 |
100 |
41 |
31 |
37 |
|||||||
3 |
0 |
78 |
22 |
126 |
36 |
53 |
24 |
3 |
0 |
55 |
6 |
110 |
27 |
21 |
51 |
|||||||
4 |
0 |
82 |
24 |
134 |
56 |
45 |
4 |
4 |
0 |
66 |
9 |
116 |
16 |
16 |
2 |
|||||||
4 |
45 |
90 |
0 |
140 |
1 |
39 |
59 |
5 |
0 |
77 |
56 |
118 |
54 |
13 |
24 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
90 |
0 |
120 |
9 |
12 |
9 |
|||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
56 |
30 |
77 |
30 |
0 |
0 |
Meridies |
24 |
20 |
69 |
0 |
0 |
0 |
|||||||||
1 |
0 |
58 |
14 |
91 |
39 |
63 |
21 |
1 |
0 |
27 |
51 |
95 |
38 |
42 |
22 |
|||||||
2 |
0 |
63 |
13 |
104 |
23 |
50 |
37 |
2 |
0 |
36 |
24 |
111 |
59 |
26 |
1 |
|||||||
3 |
0 |
70 |
41 |
114 |
47 |
40 |
13 |
3 |
0 |
47 |
14 |
120 |
10 |
17 |
50 |
|||||||
4 |
0 |
80 |
2 |
122 |
47 |
32 |
13 |
4 |
0 |
59 |
0 |
123 |
40 |
14 |
20 |
|||||||
4 |
57 |
90 |
0 |
128 |
36 |
26 |
24 |
5 |
0 |
71 |
5 |
124 |
34 |
13 |
26 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
83 |
9 |
123 |
30 |
14 |
30 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
35 |
90 |
0 |
122 |
7 |
15 |
53 |
|||||||
PISCES ♓ |
GEMINI ♊ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
47 |
40 |
69 |
0 |
0 |
0 |
Meridies |
15 |
30 |
77 |
30 |
0 |
0 |
|||||||||
1 |
0 |
49 |
42 |
84 |
50 |
53 |
10 |
1 |
0 |
20 |
20 |
114 |
32 |
40 |
28 |
|||||||
2 |
0 |
55 |
26 |
98 |
20 |
39 |
40 |
2 |
0 |
30 |
28 |
130 |
19 |
24 |
41 |
|||||||
3 |
0 |
63 |
48 |
108 |
34 |
29 |
26 |
3 |
0 |
42 |
6 |
135 |
37 |
19 |
23 |
|||||||
4 |
0 |
73 |
55 |
115 |
51 |
22 |
9 |
4 |
0 |
54 |
12 |
137 |
11 |
17 |
49 |
|||||||
5 |
0 |
85 |
5 |
120 |
28 |
17 |
32 |
5 |
0 |
66 |
17 |
136 |
5 |
18 |
55 |
|||||||
5 |
25 |
90 |
0 |
122 |
7 |
15 |
53 |
6 |
0 |
78 |
7 |
133 |
10 |
21 |
50 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
89 |
27 |
128 |
39 |
26 |
21 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
3 |
90 |
0 |
138 |
36 |
26 |
24 |
|||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima quintum, sub linea equidistante cuius hore in longiore die sunt 15. Et eius latitudo est partium 40, minutorum 56.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||
Meridies |
17 |
5 |
90 |
0 |
0 |
0 |
Meridies |
40 |
56 |
113 |
51 |
0 |
0 |
|||||||||
1 |
0 |
21 |
18 |
122 |
32 |
57 |
38 |
1 |
0 |
43 |
8 |
129 |
57 |
97 |
45 |
|||||||
2 |
0 |
30 |
17 |
138 |
29 |
41 |
31 |
2 |
0 |
49 |
7 |
143 |
38 |
84 |
4 |
|||||||
3 |
0 |
41 |
37 |
144 |
18 |
35 |
42 |
3 |
0 |
57 |
42 |
153 |
8 |
74 |
34 |
|||||||
4 |
0 |
52 |
25 |
145 |
38 |
34 |
22 |
4 |
0 |
67 |
50 |
158 |
47 |
68 |
55 |
|||||||
5 |
0 |
63 |
47 |
144 |
28 |
35 |
32 |
5 |
0 |
78 |
45 |
161 |
59 |
65 |
43 |
|||||||
6 |
0 |
74 |
48 |
141 |
30 |
38 |
30 |
6 |
0 |
90 |
0 |
162 |
55 |
64 |
47 |
|||||||
7 |
0 |
85 |
9 |
137 |
5 |
42 |
55 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
30 |
90 |
0 |
134 |
16 |
45 |
44 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
20 |
26 |
102 |
30 |
0 |
0 |
Meridies |
52 |
36 |
111 |
0 |
0 |
0 |
|||||||||
1 |
0 |
24 |
5 |
131 |
6 |
73 |
54 |
1 |
0 |
54 |
23 |
124 |
46 |
97 |
14 |
|||||||
2 |
0 |
32 |
37 |
147 |
0 |
58 |
0 |
2 |
0 |
59 |
25 |
136 |
55 |
85 |
5 |
|||||||
3 |
0 |
43 |
8 |
153 |
50 |
51 |
10 |
3 |
0 |
66 |
38 |
146 |
24 |
75 |
36 |
|||||||
4 |
0 |
54 |
19 |
156 |
5 |
48 |
55 |
4 |
0 |
76 |
15 |
153 |
10 |
68 |
50 |
|||||||
5 |
0 |
65 |
36 |
155 |
8 |
49 |
52 |
5 |
0 |
86 |
38 |
157 |
45 |
64 |
15 |
|||||||
6 |
0 |
76 |
46 |
153 |
24 |
51 |
36 |
5 |
19 |
90 |
0 |
158 |
59 |
63 |
1 |
|||||||
7 |
0 |
87 |
24 |
149 |
6 |
55 |
54 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
16 |
90 |
0 |
148 |
6 |
56 |
54 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
29 |
16 |
111 |
0 |
0 |
0 |
Meridies |
61 |
26 |
102 |
30 |
0 |
0 |
|||||||||
1 |
0 |
32 |
5 |
132 |
30 |
89 |
30 |
1 |
0 |
63 |
0 |
115 |
5 |
89 |
55 |
|||||||
2 |
0 |
39 |
22 |
147 |
30 |
74 |
30 |
2 |
0 |
67 |
24 |
126 |
29 |
78 |
31 |
|||||||
3 |
0 |
49 |
3 |
156 |
0 |
66 |
0 |
3 |
0 |
74 |
13 |
136 |
10 |
68 |
50 |
|||||||
4 |
0 |
59 |
50 |
160 |
7 |
61 |
53 |
4 |
0 |
82 |
48 |
143 |
45 |
61 |
15 |
|||||||
5 |
0 |
71 |
5 |
161 |
24 |
60 |
36 |
4 |
44 |
90 |
0 |
148 |
6 |
56 |
54 |
|||||||
6 |
0 |
82 |
22 |
160 |
40 |
61 |
20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
6 |
41 |
90 |
0 |
158 |
59 |
63 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
64 |
47 |
90 |
0 |
0 |
0 |
Meridies |
40 |
56 |
66 |
9 |
0 |
0 |
|||||||||
1 |
0 |
66 |
15 |
102 |
27 |
77 |
33 |
1 |
0 |
43 |
8 |
82 |
15 |
50 |
3 |
|||||||
2 |
0 |
70 |
30 |
113 |
35 |
66 |
25 |
2 |
0 |
49 |
7 |
95 |
56 |
36 |
22 |
|||||||
3 |
0 |
77 |
4 |
122 |
55 |
57 |
5 |
3 |
0 |
57 |
42 |
105 |
26 |
26 |
52 |
|||||||
4 |
0 |
85 |
18 |
130 |
58 |
49 |
2 |
4 |
0 |
67 |
50 |
111 |
5 |
21 |
13 |
|||||||
4 |
30 |
90 |
0 |
134 |
16 |
45 |
44 |
5 |
0 |
78 |
45 |
114 |
17 |
18 |
1 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
90 |
0 |
115 |
13 |
17 |
5 |
|||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
61 |
26 |
77 |
30 |
0 |
0 |
Meridies |
29 |
16 |
69 |
0 |
0 |
0 |
|||||||||
1 |
0 |
63 |
0 |
90 |
5 |
64 |
55 |
1 |
0 |
32 |
5 |
90 |
30 |
47 |
30 |
|||||||
2 |
0 |
67 |
24 |
101 |
29 |
53 |
31 |
2 |
0 |
39 |
22 |
105 |
30 |
32 |
30 |
|||||||
3 |
0 |
74 |
13 |
111 |
10 |
43 |
50 |
3 |
0 |
49 |
3 |
114 |
0 |
24 |
0 |
|||||||
4 |
0 |
82 |
48 |
118 |
45 |
36 |
15 |
4 |
0 |
59 |
50 |
118 |
7 |
19 |
53 |
|||||||
4 |
44 |
90 |
0 |
23 |
6 |
31 |
54 |
5 |
0 |
71 |
5 |
119 |
24 |
18 |
36 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
82 |
22 |
118 |
40 |
19 |
20 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
41 |
90 |
0 |
116 |
59 |
21 |
1 |
|||||||
PISCES ♓ |
GEMINI ♊ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
52 |
36 |
69 |
0 |
0 |
0 |
Meridies |
20 |
26 |
77 |
30 |
0 |
0 |
|||||||||
1 |
0 |
54 |
23 |
82 |
46 |
55 |
14 |
1 |
0 |
24 |
5 |
106 |
6 |
48 |
54 |
|||||||
2 |
0 |
59 |
25 |
94 |
55 |
43 |
5 |
2 |
0 |
32 |
37 |
122 |
0 |
33 |
0 |
|||||||
3 |
0 |
66 |
38 |
104 |
24 |
33 |
36 |
3 |
0 |
43 |
8 |
128 |
50 |
26 |
10 |
|||||||
4 |
0 |
76 |
15 |
111 |
10 |
26 |
50 |
4 |
0 |
54 |
19 |
131 |
5 |
23 |
55 |
|||||||
5 |
0 |
86 |
38 |
115 |
45 |
22 |
15 |
5 |
0 |
65 |
36 |
130 |
8 |
24 |
52 |
|||||||
5 |
19 |
90 |
0 |
116 |
59 |
21 |
1 |
6 |
0 |
76 |
46 |
128 |
24 |
26 |
36 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
87 |
24 |
124 |
6 |
30 |
54 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
16 |
90 |
0 |
123 |
6 |
31 |
54 |
|||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima sextum, sub linea equidistante cuius hore in longiore die sunt 15 et media. Et eius latitudo est partium 45, minuti 1.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||
Meridies |
21 |
10 |
90 |
0 |
0 |
0 |
Meridies |
45 |
1 |
113 |
51 |
0 |
0 |
|||||||||
1 |
0 |
24 |
32 |
116 |
5 |
63 |
55 |
1 |
0 |
46 |
55 |
128 |
19 |
99 |
23 |
|||||||
2 |
0 |
32 |
52 |
131 |
30 |
48 |
30 |
2 |
0 |
52 |
17 |
140 |
26 |
87 |
16 |
|||||||
3 |
0 |
42 |
1 |
138 |
17 |
41 |
43 |
3 |
0 |
60 |
1 |
149 |
4 |
78 |
38 |
|||||||
4 |
0 |
52 |
29 |
140 |
31 |
39 |
29 |
4 |
0 |
69 |
19 |
154 |
48 |
72 |
54 |
|||||||
5 |
0 |
63 |
30 |
140 |
2 |
39 |
58 |
5 |
0 |
79 |
28 |
157 |
55 |
69 |
47 |
|||||||
6 |
0 |
73 |
24 |
137 |
32 |
42 |
28 |
6 |
0 |
90 |
0 |
158 |
50 |
68 |
52 |
|||||||
7 |
0 |
83 |
16 |
133 |
26 |
46 |
34 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
45 |
90 |
0 |
129 |
21 |
50 |
39 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
24 |
31 |
102 |
30 |
0 |
0 |
Meridies |
56 |
41 |
111 |
0 |
0 |
0 |
|||||||||
1 |
0 |
27 |
29 |
124 |
49 |
80 |
11 |
1 |
0 |
58 |
19 |
123 |
31 |
98 |
29 |
|||||||
2 |
0 |
34 |
48 |
140 |
47 |
64 |
13 |
2 |
0 |
62 |
19 |
134 |
16 |
87 |
44 |
|||||||
3 |
0 |
44 |
20 |
148 |
5 |
56 |
55 |
3 |
0 |
69 |
42 |
143 |
12 |
78 |
48 |
|||||||
4 |
0 |
54 |
37 |
151 |
5 |
53 |
55 |
4 |
0 |
78 |
16 |
149 |
31 |
72 |
29 |
|||||||
5 |
0 |
65 |
16 |
151 |
7 |
53 |
53 |
5 |
0 |
87 |
16 |
154 |
6 |
67 |
54 |
|||||||
6 |
0 |
75 |
39 |
149 |
20 |
55 |
40 |
5 |
12 |
90 |
0 |
154 |
43 |
67 |
17 |
|||||||
7 |
0 |
85 |
39 |
145 |
39 |
59 |
21 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
28 |
90 |
0 |
143 |
25 |
61 |
35 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
33 |
21 |
111 |
0 |
0 |
0 |
Meridies |
65 |
31 |
102 |
30 |
0 |
0 |
|||||||||
1 |
0 |
35 |
43 |
129 |
15 |
92 |
45 |
1 |
0 |
66 |
55 |
113 |
50 |
91 |
10 |
|||||||
2 |
0 |
42 |
26 |
142 |
50 |
79 |
10 |
2 |
0 |
70 |
58 |
124 |
21 |
80 |
39 |
|||||||
3 |
0 |
50 |
46 |
151 |
9 |
70 |
51 |
3 |
0 |
77 |
14 |
133 |
19 |
71 |
41 |
|||||||
4 |
0 |
60 |
44 |
155 |
31 |
66 |
29 |
4 |
0 |
85 |
10 |
140 |
20 |
64 |
40 |
|||||||
5 |
0 |
71 |
52 |
157 |
3 |
64 |
57 |
4 |
32 |
90 |
0 |
143 |
25 |
61 |
35 |
|||||||
6 |
0 |
81 |
46 |
156 |
31 |
65 |
29 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
6 |
48 |
90 |
0 |
154 |
43 |
67 |
17 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
68 |
52 |
90 |
0 |
0 |
0 |
Meridies |
45 |
1 |
66 |
9 |
0 |
0 |
|||||||||
1 |
0 |
70 |
14 |
101 |
11 |
78 |
49 |
1 |
0 |
46 |
55 |
80 |
37 |
51 |
41 |
|||||||
2 |
0 |
74 |
5 |
111 |
30 |
68 |
30 |
2 |
0 |
52 |
17 |
92 |
44 |
39 |
34 |
|||||||
3 |
0 |
80 |
6 |
120 |
29 |
59 |
31 |
3 |
0 |
60 |
1 |
101 |
22 |
30 |
56 |
|||||||
4 |
0 |
87 |
42 |
128 |
13 |
51 |
47 |
4 |
0 |
69 |
19 |
107 |
6 |
25 |
12 |
|||||||
4 |
15 |
90 |
0 |
129 |
21 |
50 |
39 |
5 |
0 |
79 |
28 |
110 |
13 |
22 |
5 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
90 |
0 |
111 |
8 |
21 |
10 |
|||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
65 |
31 |
77 |
30 |
0 |
0 |
Meridies |
33 |
21 |
69 |
0 |
0 |
0 |
|||||||||
1 |
0 |
66 |
55 |
88 |
50 |
66 |
10 |
1 |
0 |
35 |
43 |
87 |
15 |
50 |
45 |
|||||||
2 |
0 |
70 |
58 |
99 |
21 |
55 |
39 |
2 |
0 |
42 |
26 |
100 |
50 |
37 |
10 |
|||||||
3 |
0 |
77 |
14 |
108 |
19 |
46 |
41 |
3 |
0 |
50 |
46 |
109 |
9 |
28 |
51 |
|||||||
4 |
0 |
85 |
10 |
115 |
20 |
39 |
40 |
4 |
0 |
60 |
44 |
113 |
31 |
24 |
29 |
|||||||
4 |
32 |
90 |
0 |
118 |
25 |
36 |
35 |
5 |
0 |
71 |
52 |
115 |
3 |
22 |
57 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
81 |
46 |
114 |
31 |
23 |
29 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
48 |
90 |
0 |
112 |
43 |
25 |
17 |
|||||||
PISCES ♓ |
GEMINI ♊ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
56 |
41 |
69 |
0 |
0 |
0 |
Meridies |
24 |
31 |
77 |
30 |
0 |
0 |
|||||||||
1 |
0 |
58 |
19 |
81 |
31 |
56 |
29 |
1 |
0 |
27 |
29 |
99 |
49 |
55 |
11 |
|||||||
2 |
0 |
62 |
19 |
92 |
16 |
45 |
44 |
2 |
0 |
34 |
48 |
115 |
47 |
39 |
13 |
|||||||
3 |
0 |
69 |
42 |
101 |
12 |
36 |
48 |
3 |
0 |
44 |
20 |
123 |
5 |
31 |
55 |
|||||||
4 |
0 |
78 |
16 |
107 |
31 |
30 |
29 |
4 |
0 |
54 |
37 |
126 |
5 |
28 |
55 |
|||||||
5 |
0 |
87 |
16 |
112 |
6 |
25 |
54 |
5 |
0 |
65 |
16 |
126 |
7 |
28 |
53 |
|||||||
5 |
12 |
90 |
0 |
112 |
43 |
25 |
17 |
6 |
0 |
75 |
39 |
124 |
20 |
30 |
40 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
85 |
39 |
120 |
39 |
34 |
21 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
28 |
90 |
0 |
118 |
25 |
36 |
35 |
|||||||
Tabule quantitatum arcuum et angulorum ex coincidentia circulorum altitudinis et eclyptice in cuiusvis septem climatum paralello scaturientium
Clima septimum, sub linea equidistante cuius hore in longiore die sunt 16. Et eius latitudo est partium 48, minutorum 32.
CANCER ♋ |
LIBRA ♎ |
|||||||||||||||||||||
Arcus |
Anguli orientales |
Anguli occidentales |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||||||
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Hore |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||||
Meridies |
24 |
41 |
90 |
0 |
0 |
0 |
Meridies |
48 |
32 |
113 |
51 |
0 |
0 |
|||||||||
1 |
0 |
27 |
30 |
111 |
44 |
68 |
16 |
1 |
0 |
50 |
21 |
126 |
30 |
101 |
12 |
|||||||
2 |
0 |
34 |
9 |
126 |
7 |
53 |
53 |
2 |
0 |
54 |
59 |
137 |
40 |
90 |
2 |
|||||||
3 |
0 |
43 |
2 |
133 |
18 |
46 |
42 |
3 |
0 |
62 |
5 |
145 |
46 |
81 |
56 |
|||||||
4 |
0 |
52 |
44 |
136 |
6 |
43 |
54 |
4 |
0 |
70 |
41 |
151 |
18 |
76 |
24 |
|||||||
5 |
0 |
62 |
40 |
136 |
4 |
43 |
56 |
5 |
0 |
80 |
8 |
154 |
23 |
73 |
19 |
|||||||
6 |
0 |
72 |
24 |
134 |
0 |
46 |
0 |
6 |
0 |
90 |
0 |
155 |
19 |
72 |
23 |
|||||||
7 |
0 |
81 |
38 |
130 |
16 |
49 |
44 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
8 |
0 |
90 |
0 |
124 |
58 |
55 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
LEO ♌ |
SCORPIO ♏ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
28 |
2 |
102 |
30 |
0 |
0 |
Meridies |
60 |
12 |
111 |
0 |
0 |
0 |
|||||||||
1 |
0 |
30 |
32 |
122 |
9 |
82 |
51 |
1 |
0 |
61 |
38 |
122 |
5 |
99 |
55 |
|||||||
2 |
0 |
36 |
55 |
135 |
54 |
69 |
6 |
2 |
0 |
65 |
36 |
132 |
16 |
89 |
44 |
|||||||
3 |
0 |
45 |
32 |
143 |
28 |
61 |
32 |
3 |
0 |
72 |
5 |
140 |
26 |
81 |
34 |
|||||||
4 |
0 |
55 |
3 |
146 |
50 |
58 |
10 |
4 |
0 |
80 |
3 |
146 |
28 |
75 |
32 |
|||||||
5 |
0 |
64 |
59 |
147 |
19 |
57 |
41 |
5 |
0 |
89 |
3 |
151 |
2 |
70 |
58 |
|||||||
6 |
0 |
74 |
47 |
145 |
46 |
59 |
14 |
5 |
6 |
90 |
0 |
151 |
22 |
70 |
38 |
|||||||
7 |
0 |
84 |
10 |
142 |
37 |
62 |
23 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
7 |
40 |
90 |
0 |
139 |
20 |
65 |
40 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
VIRGO ♍ |
SAGITTARIUS ♐ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
36 |
52 |
111 |
0 |
0 |
0 |
Meridies |
69 |
2 |
102 |
30 |
0 |
0 |
|||||||||
1 |
0 |
38 |
56 |
126 |
45 |
95 |
15 |
1 |
0 |
70 |
20 |
112 |
49 |
92 |
11 |
|||||||
2 |
0 |
44 |
31 |
139 |
7 |
82 |
53 |
2 |
0 |
74 |
2 |
122 |
31 |
82 |
29 |
|||||||
3 |
0 |
52 |
25 |
147 |
9 |
74 |
51 |
3 |
0 |
79 |
48 |
130 |
49 |
74 |
11 |
|||||||
4 |
0 |
61 |
35 |
151 |
36 |
70 |
24 |
4 |
0 |
87 |
14 |
137 |
25 |
67 |
35 |
|||||||
5 |
0 |
71 |
22 |
153 |
23 |
68 |
37 |
4 |
20 |
90 |
0 |
139 |
20 |
65 |
40 |
|||||||
6 |
0 |
81 |
17 |
152 |
58 |
69 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
6 |
54 |
90 |
0 |
151 |
22 |
70 |
38 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|||||||
CAPRICORNUS ♑ |
ARIES ♈ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
72 |
23 |
90 |
0 |
0 |
0 |
Meridies |
48 |
32 |
66 |
9 |
0 |
0 |
|||||||||
1 |
0 |
73 |
38 |
100 |
15 |
79 |
45 |
1 |
0 |
50 |
21 |
78 |
48 |
53 |
30 |
|||||||
2 |
0 |
77 |
10 |
109 |
47 |
70 |
13 |
2 |
0 |
54 |
59 |
89 |
58 |
42 |
20 |
|||||||
3 |
0 |
82 |
44 |
118 |
3 |
61 |
57 |
3 |
0 |
62 |
5 |
98 |
4 |
34 |
14 |
|||||||
4 |
0 |
90 |
0 |
124 |
58 |
55 |
2 |
4 |
0 |
70 |
41 |
103 |
36 |
28 |
42 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
5 |
0 |
80 |
8 |
106 |
41 |
25 |
37 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
90 |
0 |
107 |
37 |
24 |
41 |
|||||||
AQUARIUS ♒ |
TAURUS ♉ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
69 |
2 |
77 |
30 |
0 |
0 |
Meridies |
36 |
52 |
69 |
0 |
0 |
0 |
|||||||||
1 |
0 |
70 |
20 |
88 |
49 |
67 |
11 |
1 |
0 |
38 |
56 |
84 |
45 |
53 |
15 |
|||||||
2 |
0 |
74 |
2 |
97 |
31 |
57 |
29 |
2 |
0 |
44 |
31 |
97 |
7 |
40 |
53 |
|||||||
3 |
0 |
79 |
48 |
105 |
49 |
49 |
11 |
3 |
0 |
52 |
25 |
105 |
9 |
32 |
51 |
|||||||
4 |
0 |
87 |
14 |
112 |
25 |
42 |
35 |
4 |
0 |
61 |
35 |
109 |
36 |
28 |
24 |
|||||||
4 |
20 |
90 |
0 |
114 |
20 |
40 |
40 |
5 |
0 |
71 |
22 |
111 |
23 |
26 |
37 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
81 |
17 |
110 |
58 |
27 |
2 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
6 |
54 |
90 |
0 |
109 |
22 |
28 |
38 |
|||||||
PISCES ♓ |
GEMINI ♊ |
|||||||||||||||||||||
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
Hore |
Minuta |
Arcus |
Anguli orientales |
Anguli occidentales |
|||||||||||||
Meridies |
60 |
12 |
69 |
0 |
0 |
0 |
Meridies |
28 |
2 |
77 |
30 |
0 |
0 |
|||||||||
1 |
0 |
61 |
38 |
80 |
5 |
57 |
55 |
1 |
0 |
30 |
32 |
97 |
9 |
57 |
51 |
|||||||
2 |
0 |
65 |
36 |
90 |
16 |
47 |
44 |
2 |
0 |
36 |
55 |
110 |
54 |
44 |
6 |
|||||||
3 |
0 |
72 |
5 |
98 |
26 |
39 |
34 |
3 |
0 |
45 |
32 |
118 |
28 |
36 |
32 |
|||||||
4 |
0 |
80 |
3 |
104 |
28 |
33 |
32 |
4 |
0 |
55 |
3 |
121 |
50 |
33 |
10 |
|||||||
5 |
0 |
89 |
3 |
109 |
2 |
28 |
58 |
5 |
0 |
64 |
59 |
122 |
19 |
32 |
41 |
|||||||
5 |
6 |
90 |
0 |
109 |
22 |
28 |
38 |
6 |
0 |
74 |
47 |
120 |
46 |
34 |
14 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
84 |
10 |
117 |
37 |
37 |
23 |
|||||||
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
40 |
90 |
0 |
114 |
20 |
40 |
40 |
|||||||
Et postquam executi sumus scientiam angulorum, restat iam inquisitio scientie locorum que sunt in celo coram unaquaque sphera obumbrante supra civitates notas in longitudine et latitudine secundum considerationem eorum que apparent et accidunt in eis. Ad hoc autem faciam librum proprium huius et singularem ab hoc libro, in quo ostendam divisiones terre et loca civitatum, in quo sequar vestigia antiquorum qui habuerunt studium et scientiam huius speciei scientie et narrabo quot partium erit longitudo cuiusque linee equidistantis supra civitatem et civitatem ab equatione diei in orbe meridiei descripto supra quamque civitatem, et quot partium erit longitudo cuiusque orbium meridiei ab orbe meridiei descripto supra quamque civitatem, et quot partium erit longitudo cuiusque orbium meridiei ab orbe meridiei descripto supra civitatem Alexandriam in orbe equationis diei ad orientem et occidentem, eo quod ad ipsum comparabimus tempora locorum que sunt preter ipsum. In hoc autem nostro libro erimus quasi narrantes loca iam nota. Quotiens ergo voluerimus scire hora nobis definita in aliquo locorum que hora sit in loco alio ab illo cum orbis meridiei cuiusque duorum locorum propositorum fuerit alius ab altero, oportebit ut sciamus quot partium erit longitudo que erit inter eos in orbe equationis diei, et quis eorum orientalis, et quis occidentalis. Addemus enim secundum quantitatem illarum partium temporum supra illam horam aut minuemus eas ex ea donec invenerimus horam quesitam in illo loco quesito in illa hora. Augmentum autem erit cum fuerit locus ille quesitus ex eis que sequuntur orientem a loco altero, diminutio vero cum fuerit locus quesitus ex eis que sequuntur occidentem a loco altero.
Finita est dictio secunda libri Almagesti Ptolemei.