Ptolemaeus Arabus et Latinus

⟨X⟩

Claudii Ptolemei Pheludiensis dictio decima libri Almagesti decem capitulis pulcerrime decorata succedit.

Capitulum primum: In declaratione longitudinis longioris stelle Veneris

Capitulum secundum: In quantitate orbis revolutionis stelle Veneris

Capitulum tertium: In proportionibus egressionis orbis egredientis centri que est stelle Veneris a centro

Capitulum quartum: In verificatione revolutionum motuum stelle Veneris

Capitulum quintum: De loco revolutionum motuum stelle Veneris

Capitulum sextum: In eo quod necessario est premittendum et sciendum in demonstrationibus aliarum stellarum

Capitulum septimum: In declaratione summe egressionis stelle Martis a centro et longitudinis eius longioris

Capitulum octavum: In declaratione quantitatis orbis revolutionis Martis

Capitulum nonum: In certificatione revolutionum motuum Martis

Capitulum decimum: In radice sive in loco revolutionum motuum Martis

⟨X.1⟩ Capitulum primum: In declaratione longitudinis longioris stelle Veneris

Radices vero secundum quas agitur in stella Mercurii et quantitates diversitatum et preter illud etiam summam motuum et revolutionum eius et locorum ipsius secundum hunc modum invenimus. In stella autem Veneris primum etiam inquirimus super quas partes orbis signorum est locus longitudinis longioris et longitudinis propinquioris orbis centri egredientis propter longitudines suas que sunt in ultimo longitudinis vespertine que est in parte una et eadem. Et non invenimus in eo considerationem antiquorum propinquam veritati. Sed nos invenimus quod intendimus de eo per considerationes que fuerunt secundum tempus nostrum. Et nos invenimus in considerationibus que pervenerunt ad nos ex considerationibus Taionis doctrinalis considerationem que fuit in anno sextodecimo annorum Adriani in mense apud Egyptios nominato Sumugui in die vigesimoprimo eius in nocte quam sequitur dies vigesimussecundus. Scripsit namque quod stella Veneris fuit in hac consideratione in prima hora noctis secundum plurimum longitudinis eius a Sole. Ipsa namque precedebat stellam que est in medio Pleiadum secundum longitudinem Pleiadum et fuit visa quasi esset in cursu suo meridionalis ab ea parumper. Et quia stelle medie Pleiadum fuit locus in illa hora secundum numerationem principiorum nostrorum super tres partes et mediam partis Tauri et longitudo Pleiadum est pars et medietas partis fere, tunc manifestum est quod locus Veneris fuit super partem et medietatem partis Tauri. Et quia Solis per motum medium suum fuit locus in illa hora super quatuordecem partes et quartam Piscis, tunc plurimum quod fuit longitudinis eius vespertine a cursu medio fuit 47 partes et quarta partis. Et consideravimus nos in anno quarto annorum Antonii in mense Thut apud Egyptios in die eius undecimo in nocte quam sequitur dies duodecimus stellam Veneris in mane, et ipsa iam fuit in plurimo quod est longitudinis eius a Sole, et invenimus longitudinem eius a medio genu Geminorum in septentrione et in oriente medietatem octave unius. Et fuit locus huius stelle que est una stellarum fixarum apud nos in illa hora super decem et octo partes et quarta partis Geminorum. Et fuit stella Veneris super decem et octo partes et medietatem fere eorum. Et fuit locus Solis per motum suum medium super quinque partes et medietatem et quartam partis Leonis. Fuit ergo plurimum quod est longitudinis matutinalis 47 partes et quarta partis secundum istas partes. Et quia cursus medii fuit locus in consideratione prima super quatuordecem partes et quartam Piscis, et in consideratione secunda super quinque partes et medietatem et quartam Leonis, et punctum medium quod est inter eos orbis signorum cadit super vigintiquinque partes Tauri et Scorpionis, manifestum erit quod diametrus que transit per longitudinem longiorem et longitudinem propinquiorem non cadet nisi super hec duo puncta. Et similiter etiam invenimus in considerationibus Taionis considerationem que fuit in anno secundo annorum Adriani in mense apud Egyptios nominato Anun in nocte quam sequitur dies vigesimussecundus eius. Et fuit stella Veneris in mane super plurimum quod est longitudinis eius a Sole inventa posterior stella que est in extremitate ale meridionalis Virginis secundum quantitatem longitudinis Pleiadum aut minus illa parum secundum quantitatem stelle ipsius, et fuit visus cursus eius ac si esset ipse declinatus in meridie secundum quantitatem diametri lunaris unius. Et quia huius stelle fixe apud nos fuit locus in illa hora super 28 partes et medietatem et tertiam partis duodecime Leonis, ita quod fuit stelle Veneris locus super tertiam partis unius Virginis et fuit locus Solis per cursum suum medium super 17 partes et medietatem et tertiam partis et tricesimam partis unius Libre, ergo fuit plurimum quod est longitudinis eius matutinalis a cursu medio 47 partes et medietas et pars tricesima partis. Et consideravimus nos in anno vigesimoprimo annorum Adriani in mense nominato apud Egyptios Machur in die nono eius in prima hora noctis quam sequitur dies decimus stellam Veneris, et fuit in plurimo quod est longitudinis eius a Sole, et invenimus eam precedentem stellam septentrionalem stellarum quatuor que sunt quasi in quadrilatero post stellam sequentem que est super rectitudinem altioris partis Aquarii duabus partibus fere Lune quintedecime, et fuit stella visa ac si ipsa scintillaret. Et quia huius stelle fixe fuit locus in illa hora secundum numerationem nostram super viginti partes Aquarii, et propter illud fuit stella Veneris super decem et novem partes et tres quintas partis eius, et fuit locus Solis per cursum suum medium super duas partes et partem quintamdecimam unius partis Capricorni, tunc fuit in hac consideratione etiam longitudo que est longitudinis eius vespertine 47 partes et medietas et trigesima pars partis unius. Et duo puncta orbis signorum que sunt in medio inter decem et septem partes et medietatem et tertiam partis et partem trigesimam partis unius Libre, que fuerunt locus Solis in consideratione prima, et inter duas partes et partem quintamdecimam partis unius Capricorni, que fuerunt locus Solis in consideratione secunda, cadunt etiam quasi super partem vigesimamquintam Scorpionis et Tauri.

⟨X.2⟩ Capitulum secundum: In quantitate orbis revolutionis stelle Veneris

Per istas res invenimus quod longitudo longior et longitudo propinquior orbis eius egredientis centri in nostro tempore est super vigintiquinque gradus Tauri et Scorpionis. Postea secuti sumus illud secundum quod oportet inquirendo longiorem longitudinem que fuit eius a Sole cum fuit per motum suum medium in vigintiquinque partibus Tauri et in vigintiquinque partibus Scorpionis. Et invenimus in considerationibus que pervenerunt ad nos de considerationibus Taionis considerationem que fuit in anno tertiodecimo annorum Adriani in mense Athica apud Egyptios in matutino diei tertii in qua invenit stellam Veneris in plurimo quod est longitudinis eius a Sole. Et precedebat lineam rectam que transit per stellam antecedentem trium stellarum que sunt in capite Arietis et per stellam que est super pedem eius postremum parte una et duabus quintis partis. Et fuit longitudo eius a stella antecedente stellarum que sunt in capite Arietis propinqua duo longitudinis eius a stella que est super pedem eius. Et fuit locus stelle stellarum trium que sunt in capite Arietis in illa hora secundum numerationem nostram super sex partes et tres quintas partis Arietis, et eius longitudo ab orbe signorum in septentrione fuit septem partes et tertia partis. Et fuit locus stelle que est in pede postremo super quatuordecem partes et medietatem et quartam partis Arietis, et eius longitudo in meridie ab orbe signorum quinque partes et quarta partis. Fuit ergo locus stelle Veneris super decem partes et tres quintas partis Arietis, et fuit meridionalis ab orbe signorum secundum partem et medietatem. Et quia Solis per motum suum medium fuit locus in illa hora vigintiquinque partes et due quinte partis Tauri, fuit longitudo que est in ultima longitudine a cursu medio quadragintaquatuor partes et quatuor quinte partis unius. Nos consideravimus in anno vigesimoprimo annorum Adriani in mense nominato apud Egyptios Tobe in die secundo eius in prima hora noctis quam sequitur dies tertius stellam Veneris, et ipsam in plurimo quod est longitudinis eius a Sole. Et consideravimus ipsam cum duabus stellis que sunt in duobus cornibus Capricorni. Et vidimus locum eius super duodecem partes et medietatem et tertiam partis Capricorni. Et fuit locus Solis per motum suum medium super vigintiquinque partes et medietatem partis Scorpionis. Fuit ergo plurimum quod est longitudinis eius a motu medio in hac consideratione 47 partes et tertia partis. Et declaratum est quod longitudo longior est in vigintiquinque partibus Tauri et longitudo propinquior in vigintiquinque partibus Scorpionis. Et apparuit etiam quod orbis egrediens revolvens orbem revolutionis Veneris est fixus, propterea quod nos non invenimus in loco orbis signorum duas longitudines maiores que sunt super duo latera cursus medii coniunctas, neque minores duabus longitudinibus que sunt in Tauro coniunctis neque maiores duabus longitudinibus que sunt in Scorpione coniunctis. 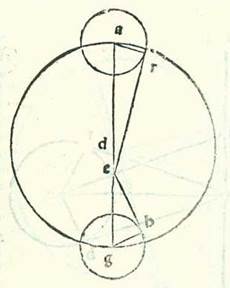Et postquam iam explanavimus has res, sit orbis centri egredientis super quem movetur semper orbis revolutionis Veneris circulus ABG circa diametrum AG, et ponam super ipsam centrum orbis egredientis centri punctum D, et centrum orbis signorum punctum E, et punctum A punctum quod est sub vigintiquinque partibus Tauri, et punctum G punctum quod est sub vigintiquinque partibus Scorpionis, et signabo circa duo puncta A et G duos orbes revolutionis equales, super quos sint R et H, et protraham lineas ER et EH contingentes eos, et continuabo lineas duas AR et GH. Et quia angulus AER, cum fuerit apud centrum orbis signorum, subtenditur plurimo quod est longitudinis huius stelle in longitudine sua longiore, et summa illius secundum quod narravimus est 44 partes et quatuor quinte partis, et est iste angulus secundum partes quidem quibus quatuor anguli recti sunt 360 partes 44 partes et 48 minuta, et secundum partes quibus duo anguli recti sunt 360 partes est 89 partes et 36 minuta, ergo erit arcus qui est super lineam AR 89 partes et 36 minuta secundum partes quibus circulus qui describitur circa triangulum AER ortogonium est 360 partes, et chorda eius, que est linea AR, 84 partes et 33 minuta fere secundum partes quibus AE subtendens est 120 partes. Et secundum hoc exemplum, quia fuit angulus HEG longitudo que est plurimum quod est longitudinis in longitudine propinquiore et iam posita est etiam 47 partes et tertia partis, erit hic angulus etiam secundum partes quibus quatuor recti anguli sunt 360 partes 47 partes et 20 minuta, et secundum partes quibus duo anguli recti sunt 360 partes est 94 partes et 40 minuta. Erit ergo arcus qui est super lineam HG 94 partes et 40 minuta secundum partes quibus circulus qui describitur circa triangulum GEH ortogonium est 360 partes, et eius chorda, que est linea GH, erit 88 partes et 13 minuta fere secundum partes quibus linea EG subtendens est 120 partes. Ergo secundum partes quibus linea GH, scilicet equalis linea AR, que est a centro orbis revolutionis, est 84 partes et 33 minuta et linea AE est 120 partes erit linea EG 115 partes et minutum unum. Et manifestum est quod linea AG tota erit secundum illud 235 partes et minutum unum et linea AD, que est medietas eius, est 117 partes et 30 minuta fere. Et remanet linea DE, que est inter duo centra, due partes et 30 minuta. Erit ergo secundum illas partes quibus linea AD, que est a centro orbis egredientis centri, est 60 partes linea DE, que est inter duo centra, pars una et quarta partis fere et linea AR, que est a centro orbis revolutionis, 43 partes et sexta partis. Et illud volebamus ostendere.

⟨X.3⟩ Capitulum tertium: In scientia proportionum egressionis orbis egredientis centri que est stelle Veneris a centro

Et quia non fuit manifestum utrum motus orbis revolutionis huius stelle sit circa punctum D, accepimus hic etiam duas longitudines in ultimo magnitudinis in duabus partibus oppositis in unaquaque quarum fuit cursus Solis medii longitudo a longitudine longiore quarta circuli. Fuit itaque nostra consideratio unius earum in anno decimooctavo annorum Adriani in mense Pharmoti apud Egyptios in die secundo eius in nocte quam sequitur dies tertius. Et fuit stella Veneris in matutino huius noctis in plurimo quod est longitudinis eius a Sole. Et consideravimus ipsam cum corde Scorpionis. Et fuit locus eius super undecem partes et medietatem et tertiam et partem duodecimam partis unius Capricorni. Et fuit locus Solis in illa hora per cursum suum medium super vigintiquinque partes et medietatem partis Aquarii. Fuit ergo plurimum quod est longitudinis matutinalis a cursu medio quadragintatres partes et medietas et pars duodecima partis unius. Et fuit consideratio nostra altera in anno tertio annorum Antonii in mense Pharmoti apud Egyptios in die quarto eius in vespere noctis quam sequitur dies quintus. Fuitque in hoc vespere stella Veneris super plurimum quod est longitudinis eius a Sole. Et consideravimus ipsam cum Aldebaran. Et invenimus locum eius super tredecem partes et medietatem et tertiam partis Arietis. Et fuit locus Solis per cursum suum medium super vigintiquinque partes et medietatem Aquarii. Fuit ergo longitudo maior vespertina a cursu medio 48 partes et tertia. 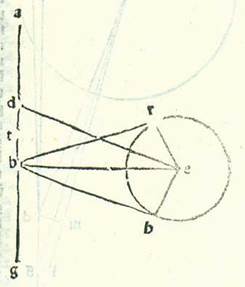Et quia iam planas feci has res, sit diametrus que transit per longitudinem longiorem orbis centri egredientis linea ABG, et ponam ut punctum A sit punctum quod est sub vigintiquinque partibus Tauri, et punctum B centrum orbis signorum, sitque nostra intentio ut inveniamus centrum circa quod dicimus esse motum orbis revolutionis equalem, sitque illud punctum D, et producam ab ipso lineam DE secundum angulos rectos super lineam AG ad hoc ut sit longitudo cursus medii orbis revolutionis a longitudine longiore quarta circuli, sicut fuit in duabus considerationibus, et inveniatur super lineam DE centrum orbis revolutionis in duabus considerationibus quas diximus, et sit punctum E, et signemus circa ipsum orbem revolutionis RH, et protraham a puncto B duas lineas contingentes ipsum, sintque linee BR et BH, et coniungam lineas BE et ER et HE. Et quia in cursu medio quem narravimus posita est maior longitudo matutinalis a cursu medio quadragintatres partes et medietas partis et pars duodecima partis unius et longitudo maior vespertina 48 partes et tertia partis, ergo angulus RBH totus est 91 partes et 55 minuta secundum partes quibus quatuor anguli recti sunt 360 partes, et erit eius medietas, que est angulus RBE, 91 partes et 55 minuta secundum partes quibus duo anguli recti sunt 360 partes. Quapropter erit arcus qui est super lineam ER 91 partes et 55 minuta secundum partes quibus circulus qui describitur circa triangulum BER ortogonium est 360 partes, et linea ER ipsa est 86 partes et 16 minuta secundum partes quibus linea BE subtendens est 120 partes. Ergo secundum partes quibus linea ER, que est a centro orbis revolutionis, est 43 partes et 10 minuta erit linea BE 60 partes et tria minuta. Et etiam quia superfluitas que est inter has duas longitudines maiores est 4 partes et 45 minuta, et illud comprehendit superfluitatem que fuit in illa hora propter diversitatem additam orbi signorum duplicem et continet illud angulus BED, ergo angulus BED erit secundum partes quibus quatuor anguli recti sunt 360 partes due partes et 22 minuta et medietas minutis, et secundum partes quibus duo anguli recti sunt 360 partes erit 4 partes et 45 minuta. Erit ergo propter illud arcus que est super lineam BD etiam 4 partes et 45 minuta secundum partes quibus circulus qui describitur circa triangulum BDE ortogonium est 360 partes, et erit linea BD ipsa 4 partes et 59 minuta fere secundum partes quibus linea BE est 120 partes. Ergo secundum partes quibus linea BE est 60 partes et tria minuta et linea que est a centro orbis revolutionis est 43 partes et 10 minuta erit linea BD due partes et medietas fere. Iam vero fuit ostensum quod illud quod est inter punctum B, quod est centrum orbis signorum, et inter centrum orbis egredientis centri supra quem est semper centrum orbis revolutionis secundum istas partes est pars una et quarta partis. Erit ergo propter illud medietas linee BD. Nos enim si diviserimus lineam BD in duo media super punctum T, erit manifestum quod secundum partes quibus linea TA, que est a centro orbis revolventis orbem revolutionis, est 60 partes erit unaqueque duarum linearum BT, TD, que sunt inter centra, pars una et quarta partis et linea ER, que est a centro orbis revolutionis, 43 partes et 10 minuta. Et iste sunt res quas intendimus demonstrare.

⟨X.4⟩ Capitulum quartum: In verificatione revolutionum motuum Veneris

Modum autem radicis secundum quam agitur in hac stella et proportiones diversitatum eius invenimus in hac semita. Postea accepimus proportiones revolutionum motuum eius et locorum ipsius per duas considerationes in quibus non fuit dubitatio. Quarum una fuit ex nostris considerationibus, et altera ex considerationibus antiquis. Nos namque consideravimus stellam Veneris in anno secundo annorum Antonii in mense Tobi apud Egyptios in die vigesimonono eius in nocte quam sequitur dies tricesimus cum instrumento considerationis. Et ipsa iam pertransierat plurimum quod est longitudinis sue matutinalis. Et consideravimus ipsam cum Ascimech Inermi. Et vidimus locum eius super sex partes et medietatem partis Scorpionis. Et fuit in illa hora inter stellam que est longior stellarum que sunt in fronte Scorpionis in septentrione et inter centrum Lune quod videtur. Et fuit secundum rectitudinem cum eis. Et precedebat centrum Lune tantum quantum erat posterior stella que est longior stellarum que sunt in fronte Scorpionis in septentrione vice una et medietate vicis. Huius autem stelle fixe que est in fronte Scorpionis fuit locus in illa hora secundum numerationem principiorum nostrorum supra sex partes et 20 minuta Scorpionis. Et ipsa est septentrionalis ab orbis signorum secundum partem unam et viginti minuta. Et fuit illa hora post medietatem noctis quatuor horis et medietate et quarta hore equalis, quoniam fuit Sol super vigintitres partes Sagittarii. Fuit ergo medium celi per instrumentum considerationis due partes Virginis. Et in illa hora fuit Sol per cursum suum medium super vigintiduas partes et novem minuta Sagittarii, et fuit locus Lune medius super 15 partes et 24 minuta Scorpionis, et diversitatis super 87 partes et 30 minuta a longitudine longiore, et latitudinis super 12 partes et 22 minuta a fine septentrionali. Et propter illud fuit locus centri Lune secundum veritatem super 5 partes et 45 minuta Scorpionis et fuit declinatum in septentrionem ab orbe signorum quinque partibus. Et vidimus in Alexandria locum eius in longitudine super octo partes et 45 minuta Scorpionis et eius declinationem ab orbe signorum in septentrionem 4 partes et 40 minuta. Fuit ergo locus stelle Veneris propter has res etiam super sex partes et 30 minuta Scorpionis et fuit septentrionalis ab orbe signorum secundum duas partes et 40 minuta. 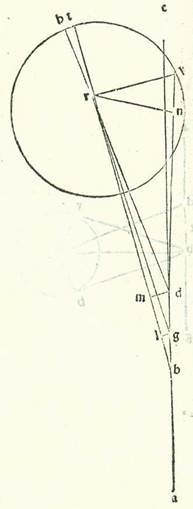Et quia iam explanavimus has res, tunc sit diametrus que transit per longitudinem longiorem orbis et longitudinem propinquiorem, supra quam sint A, B, G, D, E, et ponam ut punctum A sit super partem vigesimamquintam Tauri, et punctum E super vigesimamquintam partem Scorpionis, et punctum B punctum circa quod movetur orbis revolutionis equaliter, et punctum G centrum orbis egredientis centri super quem revolvitur centrum orbis revolutionis, et punctum D centrum orbis signorum. Et quia Solis per motum suum medium fuit locus in consideratione super 27 partes et 9 minuta Sagittarii, tunc fuit propter illud cursus medii orbis revolutionis locus super 27 partes et 9 minuta a longitudine propinquiore, super quam videtur punctum E. Ponam igitur ut centrum orbis revolutionis sit super punctum R, et signabo circa ipsum orbem revolutionis, supra quem sint H, T, K, et producam lineas DRH et BRT et GR, et producam a duobus punctis D et G super lineam BRT duas perpendiculares GL et DM, et ponam stellam super punctum K, et protraham lineas duas DK et RK, et producam perpendicularem RN. Et sit intentio nostra ut inveniamus arcum TK, qui est longitudo stelle a puncto T, quod est longitudo longior orbis revolutionis. Et quia angulus EBR secundum partes quibus quatuor anguli recti sunt 360 partes est 27 partes et 9 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 54 partes et 18 minuta, erit propter hoc arcus qui est super lineam GL 54 partes et 18 minuta secundum partes quibus circulus qui describitur circa triangulum BGL ortogonium est 360 partes, et arcus qui est super lineam BL erit quod remanet ad complendum semicirculum, et est 125 partes et 42 minuta. Linea igitur GL, que est una duarum linearum que subtenduntur eis, erit 54 partes et 46 minuta secundum partes quibus linea BG subtendens est 120 partes, et erit linea BL secundum istas easdem partes 106 partes et 47 minuta. Propter illud ergo secundum partes quibus linea BG est pars una et 15 minuta et linea GR que est a centro orbis egredientis centri est 60 partes erit linea GL 34 minuta et linea BL secundum illud exemplum pars una et septem minuta. Et quia quod est ex linea GR diminuto ex eo quod est ex linea GL erit ex eo quod est ex linea RL, tunc linea RL erit secundum istas partes 60 partes fere. Linea autem ML est equalis linee LB, et linea DM est duplum linee GL, propterea quod linea BG etiam est equalis linee GD. Erit ergo propter illud linea RM partes relique, et sunt 58 partes et 54 minuta fere. Et erit linea DM secundum istas partes pars una et octo minuta. Et similiter linea RD subtendens erit 58 partes et 54 minuta fere. Sed secundum partes quibus linea RD subtendens est 120 partes erit linea DM due partes et 16 minuta, et arcus qui est super eam erit due partes et duodecem minuta secundum partes quibus circulus qui describitur circa triangulum RDM ortogonium est 360 partes. Erit ergo propter illud angulus BRD due partes et 12 minuta secundum partes quibus duo anguli recti sunt 360 partes, et totus angulus EDR extrinsecus erit 56 partes et 30 minuta secundum istas partes. Et angulus KDE secundum partes quibus quatuor anguli recti sunt 360 partes erit 18 partes et 30 minuta, propterea quod illud est summa partium quibus stella in consideratione precedebat longitudinem propinquiorem, que est super punctum E, scilicet vigintiquinque partes Scorpionis, et secundum partes quibus duo anguli recti sunt 360 partes erit 37 partes. Angulus ergo KDR totus erit 93 partes et 30 minuta secundum partes quibus duo anguli recti sunt 360 partes, et arcus qui est super lineam RN erit 93 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum DRN ortogonium est 360 partes. Linea igitur que subtenditur ei, et est linea RN, erit secundum partes quibus linea RD est 120 partes 87 partes et 25 minuta et secundum partes quibus hec linea est 58 partes et 54 minuta, scilicet secundum partes quibus linea RK, que est a centro orbis revolutionis, est 43 partes et 10 minuta erit 42 partes et 55 minuta. Erit ergo secundum partes quibus linea RK subtendens est 120 partes linea RN 119 partes et 18 minuta, et arcus qui est super eam erit 167 partes et 38 minuta secundum partes quibus circulus qui describitur circa triangulum RKN ortogonium est 360 partes. Angulus igitur RKD erit 167 partes et 38 minuta, et angulus totus KDH est 93 partes et 30 minuta. Ergo angulus totus KRH extrinsecus erit 261 pars et octo minuta. Iam vero fuit ostensum quod angulus BRD, scilicet angulus HRT, secundum istas partes est due partes et duodecem minuta. Angulus igitur TRK reliquus secundum partes quibus duo anguli recti sunt 360 partes erit 258 partes et 56 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit 129 partes et 28 minuta. Fuit ergo longitudo stelle Veneris in hora nota a puncto T, quod est longitudo longior orbis revolutionis, anterius quidem partes quas diximus, et sunt 129 partes et 28 minuta, et posterius secundum quod convenerit in radice secundum quam agitur in hac stella quod remanet ad complendum circulum unum, et sunt 230 partes et 32 minuta. Et illud est quod fuit necesse nos invenire.

Quod autem accepimus de considerationibus antiquis est consideratio quam firmavit Thimocharides secundum hunc modum: In anno tertiodecimo annorum Pheledicos in mense nominato apud Egyptios Mesure in die decimoseptimo eius in hora duodecima noctis quam sequitur dies decimusoctavus vidit stellam Veneris iam comprehendisse secundum veritatem super stellam fixam oppositam stelle que nominatur Berthoamites, cuius nominis intentio est apud nos precedens calcatorem uvarum, et hec stella apud nos est ea que est post stellam que est super extremitatem ale Virginis meridionalis. Et fuit locus huius stelle in anno primo annorum Antonii super octo partes et quartam partis Virginis. Et quia annus in quo fuit hec consideratio fuit annus quadringentesimus et septuagesimussextus annorum Nabuchodonosor, et annus primus annorum Antonii est annus octingentesimus et octuagesimusquartus a tempore Nabuchodonosor, erit ergo quod debetur quadringentis et octo annis qui sunt inter duo tempora de motu stellarum fixarum et longitudinis longioris quatuor partes et pars duodecima fere. Et manifestum est quod stelle Veneris locus fuit in illa hora super quatuor partes et sextam partis Virginis et fuit longitudo propinquior orbis egredientis centri super viginti partes et medietatem et tertiam et partem duodecimam partis Scorpionis. Et stella Veneris in hac consideratione etiam iam pertransierat plurimum quod est longitudinis sue matutinalis. Et illud est quia post quatuor dies ab hac consideratione in die vigesimaprima mensis Mesure in nocte quam sequitur dies vigesimussecundus factus est locus eius secundum quod dixit Thimocharides secundum principia nostra quasi super octo partes et medietatem et tertiam partis Virginis. Et fuit locus cursus Solis medii in consideratione quidem prima, scilicet quam dixit prius (et ipse consideravit eam quam diximus nunc, et est consideratio antiqua) super decem et septem partes et tertiam partis Libre, in consideratione autem que est post eam super viginti partes et 59 minuta Libre. Erit ergo quod aggregatur ex longitudine in consideratione prima 43 partes et 10 minuta et illud quod aggregatur in illa que est post eam 42 partes et 9 minuta. 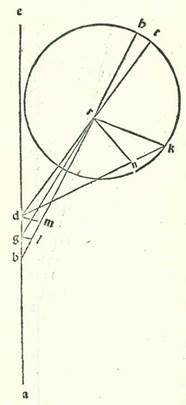Et postquam res iste posite sunt, ponam etiam formam qualis illa est, excepto quod non ponam in ea orbem revolutionis nisi ab eo quod sequitur punctum E, quod est longitudo propinquior, propterea quod cursus orbis revolutionis medii locus est super decem et septem partes et tertiam partis Libre et longitudo longior super viginti partes et 55 minuta Scorpionis. Et quia propter illud erit angulus EBR secundum partes quibus quatuor anguli recti sunt 360 partes 33 partes et 52 minuta et secundum partes quibus duo anguli recti sunt 360 partes erit 67 partes et 44 minuta, ergo arcus qui est super lineam GL erit 67 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum BGL ortogonium est 360 partes, et arcus qui est super lineam BL est quod remanet ad complendum semicirculum, et est 112 partes et 16 minuta. Ergo linea GL, una duarum linearum que subtenduntur eis, erit 66 partes et 52 minuta secundum partes quibus linea BG subtendens est 120 partes. Sed linea BL secundum istas partes erit 99 partes et 38 minuta. Quapropter secundum partes quibus linea BG est pars una et 15 minuta et linea GR, que est a centro orbis egredientis centri, 60 partes erit linea GL 42 minuta et linea BL secundum illam similitudinem pars una et duo minuta. Et quia ex quadrato quod est ex linea GR diminuto ex eo quadrato quod est ex linea GL erit quadratum quod est ex linea RL, ergo linea RL etiam in longitudine secundum istas partes erit 60 partes fere. Et propter illud idem erit linea BL equalis linee LM et linea DM dupla linee GL. Erit ergo linea RM reliqua 58 partes et 58 minuta et linea DM secundum istas partes pars una et 24 minuta. Et propter illud idem erit linea DR subtendens 58 partes et 59 minuta fere. Ergo secundum partes quibus linea DR est 120 partes erit linea DM due partes et 51 minutum, et arcus qui est super eam erit due partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum DRM ortogonium est 360 partes. Quapropter angulus BRD etiam erit due partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Ergo angulus EDR totus erit secundum istas partes 70 partes et 28 minuta. Et angulus EDK, et est longitudo stelle ad anterius a longitudine propinquiore, secundum partes quibus quatuor anguli recti sunt 360 partes erit 76 partes et 45 minuta. Et secundum partes quibus duo anguli recti sunt 360 partes erit 153 partes et medietas partis. Erit ergo angulus RDK secundum istas partes 83 partes et duo minuta, et arcus qui est super lineam RN erit 83 partes et duo minuta secundum partes quibus circulus qui describitur circa triangulum DRN ortogonium est 360 partes. Chorda igitur eius, que est linea RN, secundum partes quibus linea RD subtendens est 120 partes erit 79 partes et 33 minuta et secundum partes quibus linea DR est 58 partes et 59 minuta, scilicet secundum partes quibus linea RK, que est a centro orbis revolutionis, est 43 partes et 10 minuta erit 39 partes et 7 minuta. Ergo secundum partes quibus linea RK est 120 partes erit linea RN 108 partes et 45 minuta, et arcus qui est super eam erit 130 partes fere secundum partes quibus circulus qui describitur circa triangulum RKN ortogonium est 360 partes. Angulus igitur RKN est 130 partes secundum partes quibus fuit angulus RDK 83 partes et duo minuta. Ergo angulus TRK totus secundum istas partes est 213 partes et duo minuta. Iam vero ostensum fuit quod angulus BRD, scilicet angulus HRT, secundum istas partes est due partes et 44 minuta. Ergo angulus HRK totus secundum partes quibus duo anguli recti sunt 360 partes est 215 partes et 46 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes est 107 partes et 53 minuta. Fuit ergo in illa hora stelle Veneris longitudo a puncto H, quod est longitudo longior orbis revolutionis, comprehendens quod remansit ad complendum circulum unum, et est 252 partes et 7 minuta. Et illud est quod necesse fuit nobis declarare.

Et quia eius longitudo in hora considerationis nostre secundum illud exemplum a longitudine longiore orbis revolutionis fuit 230 partes et 32 minuta, et temporis quod est inter duas considerationes summa annorum Egyptiorum est 409 anni et 167 dies fere, et reversionum diversitatis integrarum 255 reditiones, propterea quod in omnibus octo annis Egyptiis sunt quasi quinque revolutiones, tunc aggregantur in quadringentis et octo annis ducente et quinquagintaquinque reditiones, et ex anno uno residuo cum eo quod superfluit super ipsum ex diebus non completur tempus reditionis unius. Iam ergo apparet nobis quod in 409 annis Egyptiis et 167 diebus superfluit stella Veneris post ducentas et quinquagintaquinque revolutiones integras diversitatis in orbe revolutionis trecentis et trigintaocto partibus et vigintiquinque minutis. Et illud est summa quam addidit locus eius in tempore nostro super locum eius in consideratione antecedente. Et fortasse contingit ut hec sit summa que evenit nobis de partibus superfluitatis in tabulis etiam quas premisimus et posuimus motuum mediorum, propterea quod earum verificatio non completur nisi propter superfluitatem que reperitur post revolutiones, ut totum tempus fiat dies et reversiones revolutionum cum superfluitate partes. Cum enim diviserimus numerum harum partium per numerum horum dierum verificabitur motus medius diversitatis in die uno quam premisimus et posuimus in tabula stelle Veneris.

⟨X.5⟩ Capitulum quintum: De loco revolutionum motuum stelle Veneris

Et quia iam remansit nobis equatio locorum revolutionum motuum huius stelle etiam in anno primo annorum Nabuchodonosor in mense Thut ex mensibus Egyptiorum in die primo eius in medietate diei, tunc nos accepimus etiam tempus quod fuit in eo quod fuit inter illam horam et inter horam antiquioris duarum considerationum, et fuit eius summa quadringenti et septuagintaquinque anni ex annis Egyptiis et trecenti et quadragintasex dies et medietas et quarta diei fere. Et opponitur hoc tempus in areis diversitatis superfluitatis secundum motum medium 181 parti fere. Cum ergo nos minuerimus illud de partibus que provenerunt in illa consideratione, et sunt 252 partes et 7 minuta, proveniet nobis locus diversitatis in anno primo annorum Nabuchodonosor in mense Thut apud Egyptios in die primo eius in medietate diei super 71 partem et 7 minuta a longitudine longiore orbis revolutionis secundum quod motus medii in longitudine locus eius sit locus Solis ipsius, et est super 45 minuta Piscis. Et manifestum est quod longitudo longior quando fuerit in consideratione super viginti partes et 55 minuta Tauri et fuerit illud quod pertinet quadringentis et septuagintasex annis fere illud quod est in eo quod est inter duas horas quatuor partes et medietas et quarta partis, tunc longitudo longior erit in illa hora que posita est loco super 16 partes et 10 minuta Tauri.

⟨X.6⟩ Capitulum sextum: In eo quod necessarium est ut premittatur et sciatur in demonstrationibus que sunt in aliis stellis

In his autem duabus stellis, scilicet stella Mercurii et stella Veneris, per hec capitula produximus radices secundum quas agitur in eis et declaravimus diversitates earum. Sed stellarum trium reliquarum, scilicet stelle Martis et stelle Iovis et stelle Saturni, invenimus radicem secundum quam agitur in motibus earum unam similem radici que producta est in stella Veneris, scilicet radicis in qua sit ut orbis egredientis centri super quem revolvitur semper centrum orbis revolutionis non describatur nisi super centrum existens punctum quod dividit in duo media lineam que est inter centrum orbis signorum et inter centrum orbis qui facit revolutionem orbis revolutionis equalem. In unaquaque enim harum stellarum pervenit secundum apparitionem considerationis quod invenitur de egressione a centro secundum plurimum quod est superfluitatis propter diversitatem comparatam ad orbem signorum propinquum duplo egressionis a centro cuius equatio est propter quantitates longitudinis in maiore eius latitudinum et minore que fuerint orbis revolutionis. Nos autem in productione demonstrationum quibus inveniuntur quantitates cuiusque duarum diversitatum et longitudinis longioris in unaquaque earum non invenimus semitam qua procedamus in his tribus stellis sicut invenimus viam qua processimus in illis duabus stellis, propterea quod he stelle iam elongantur a Sole longitudine tota et non apparet ex considerationibus sicut apparuit in maiore longitudine in stella Mercurii et stella Veneris quando stella sit super locum super quem contingit linea egrediens a visibus nostris orbem revolutionis. Ergo quia non invenimus ad illud viam, fecimus considerationes in quibus reperiuntur ad sciendum stelle opposite cursui Solis medio per diametrum et fabricavimus et ostendimus eas prius propter causam egressionis a centro et longitudinis longioris in unaquaque earum. Et nos neque usi fuimus his considerationibus nisi quia in eo cuius est hic modus tantum cursus stellarum invenimus diversitatem comparatam ad orbem signorum solitariam secundum seipsam. Non enim cadit ex eo tunc aliquid superfluitatis propter diversitatem que est per considerationem ad Solem. 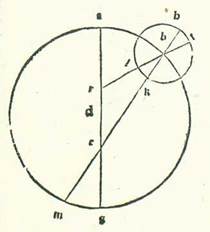Sit ergo stelle orbis centri egredientis super quem revolvitur centrum orbis revolutionis ABG circa centrum D, et sit diametrus que transit per longitudinem longiorem ADG, et punctum E super quod est centrum orbis signorum, et punctum R centri orbis egredientis centri super quem videtur cursus orbis revolutionis medius in longitudine, et describam circa punctum B orbem revolutionis, supra quem sint H, T, K, L, et producam lineam RLBT et lineam HBKEM. Dico igitur primum quod quando stella videbitur super lineam EBH, que transit per punctum B et est centrum orbis revolutionis, tunc cursus Solis medius erit semper super illam eandem lineam, et quod stella, cum sit super punctum H, erit concurrens Soli per cursum suum medium et videbitur per cursum suum medium apud punctum B, et cum sit super punctum K, erit cum eo secundum diametrum per cursum suum medium et videbitur apud punctum M. Quod sic probatur: Quia propterea quod ex longitudine que est inter unamquamque harum stellarum inter longitudinem longiorem in longitudine et inter ipsam et inter longitudinem longiorem in diversitate, cum aggregatur, est cursus Solis medius ab illo eodem principio, et superfluitas que est inter angulum qui est apud punctum R, et est ille qui comprehendit motum stelle equalem in longitudine, et inter angulum qui est apud punctum E, et est qui comprehendit motum qui videtur, existens semper angulus qui est apud punctum B, et hic angulus comprehendit cursum eius equalem in orbe revolutionis sue, tunc manifestum est quod cum stella fuerit apud punctum H, erit diminuta ex reversione ad punctum T, quod est longitudo longior secundum angulum HBT. Cum ergo comparatur illud ad angulum ARB, scilicet cum aufertur hic angulus ex angulo ARB, provenit angulus quo continetur cursus Solis medius qui est angulus AEH. Et ipse idem est angulus visionis stelle. Et cum stella fuerit super punctum K, erit etiam iam mota in orbe revolutionis sue secundum angulum TBK. Ergo cum comparabitur seu adiungitur iste angulus ad angulum AEK, erit ex eo cursus Solis medius a puncto A, quod est longitudo longior comprehendens medietatem circuli et cum ea angulum AEK diminuto ex eo angulo ABK, scilicet angulum GEM, et erit tunc Sol per cursum suum medium super diametrum cursus stelle que videtur. Quapropter erit secundum illud quod currit hoc cursu figurarum linea que protrahitur a puncto B, scilicet a centro orbis revolutionis ad stellam, et lineam Probably corrupt for linea, which is also the reading of Paris, BnF, lat. 14738 (161v, line 7 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 483, line 4). que progreditur a puncto E, et est super visus nostros ad Solem per cursum suum medium, coniuncte simul secundum rectitudinem. In reliquis autem longitudinibus omnibus locus earum diversificatur. Sed tamen ipse semper erunt equidistantes. Et illud est quoniam si nos protraxerimus in forma simili huic in quocunque volueris loco a puncto B lineam rectam ad stellam, sicut linea BN, et a puncto E ad Solem per cursum suum medium lineam rectam, sicut linea ES, tunc angulus AES erit per id quod precessit equalis angulo ART et angulo TBN coniunctis, et angulus ART equalis angulo AEH et angulo HBT coniunctis. Quapropter erit angulus AES equalis angulo AEH et angulo HBN toti coniunctis, scilicet in oppositionibus. Cum ergo minuetur angulus AEB communis, erit angulus HES reliquus equalis angulo HBN reliquo. Linea igitur ES erit equidistans linee BN. Et quia in his speciebus figurarum que dicuntur coniunctionales, quarum sunt ille que nominantur extremitas noctis, que videntur per comparationem ad cursum Solis medium, invenimus stellam videri secundum lineam rectam que transit per centrum orbis revolutionis sicut videretur si non esset motus eius super orbem revolutionis omnino, sed esset ipsa eadem posita super circulum ABG et linea RB revolveret eam equaliter sicut revolvit centrum orbis revolutionis, tunc manifestum est quod iam preparata est per hos cursus declaratio proportionum diversitatis comparate ad orbem signorum que est propter egressionem a centro. Et postquam figure coniunctionales sunt non ordinate, tunc iam oportet ut laboremus in semita demonstrationum habitudinum que nominantur extremitas noctis.

⟨X.7⟩ Capitulum septimum: In ostensione summe egressionis stelle Martis a centro et longitudinis eius longioris

Quemadmodum autem nos in Luna accepimus loca trium eclypsium ex eclypsibus eius et tempora earum et declaravimus per semitas linearum proportionem diversitatis eius et locum longitudinis eius longioris, similiter etiam hic consideravimus tres habitudinum que nominantur extremitas noctis oppositas Soli, idest condiametrales Soli per cursum suum medium in unaquaque harum trium stellarum, et verificavimus loca earum in ultimo subtilis inquisitionis, prout potuimus, cum instrumento considerationis, et verificavimus etiam tempus condiametrationis et locum eius ad augmentandam subtilitatem in eis propter cursus Solis medios in considerationibus, et declaravimus per illud quantitatem egressionis a centro et longitudinis longioris in eis. Accepimus itaque primum in stella Martis tres habitudinum que nominantur extremitas noctis. Quarum primam consideravimus in anno quintodecimo annorum Adriani in mense Tobi apud Egyptios in die vigesimosexto eius in nocte quam sequitur dies vigesimusseptimus post unam horarum equalium a medietate noctis. Et fuit stella in vigesimaprima parte Geminorum. Et fuit consideratio secunda in anno decimonono annorum Adriani in mense Pharmoti apud Egyptios in die sexto eius in nocte quam sequitur dies septimus ante medietatem noctis tribus horis. Et fuit in 28 partibus et 50 minutis Leonis. Et consideratio tertia fuit in anno secundo annorum Antonii in mense Athica apud Egyptios in die duodecimo in nocte quam sequitur dies tertiusdecimus ante medietatem noctis duabus horis equalibus. Et fuit in duabus partibus et 33 minutis Sagittarii. Duorum vero temporum duarum longitudinum summa eius, scilicet quod est ab habitudine prima ad habitudinem secundam, fuit quatuor anni Egyptii et sexagintanovem dies et 20 hore equales. Et eius quidem quod fuit ab habitudine secunda ad habitudinem tertiam fuerunt quatuor anni etiam Egyptii et nonagintasex dies et hora una equalis. Provenerunt ergo ex tempore longitudinis prime post revolutiones integras longitudinis ex motu medio stelle Martis 81 pars et 44 minuta. Et provenerunt ex tempore longitudinis secunde propter motum medium in longitudine etiam 95 partes et 28 minuta. Quamvis enim ponamus numerationem nostram motuum mediorum in eo tempore cuius quantitas est cum reversionibus revolutionum que ponuntur secundum crossitudinem numerationis, non tamen propter illud continget diversitas de qua sit curandum. Et manifestum est quod in longitudine prima fuit stella iam mota secundum visum post revolutiones integras 67 partibus et 50 minutis, et in longitudine secunda 93 partibus et 44 minutis. 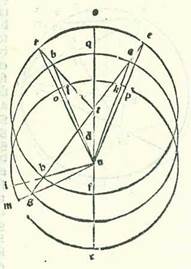Signabo itaque in superficie orbis signorum tres circulos equales, sitque orbis unus eorum orbis qui revolvit centrum orbis revolutionis Martis, et sit ABG circa punctum D, et alius orbis egredientis centri qui est equalis motus, et ipse est ERH circa punctum T, et tertius orbis cuius centrum est centrum orbis signorum, et est KLM circa centrum N, et sit diametrus que transit per centra omnia SQFC, et ponam ut punctum A sit punctum super quod fuit centrum orbis revolutionis in habitudine prima que nominatur extremitas noctis, et punctum B punctum super quod fuit in habitudine secunda, et punctum G super quod fuit in habitudine tertia, et applicentur linee TAE et TBR et THG et NKA et NLB et NGM. Erit ergo arcus ER orbis centri egredientis etiam partes longitudinis revolutionis prime, et sunt 81 pars et 44 minuta, et arcus RH partes longitudinis revolutionis secunde, et sunt 95 partes et 28 minuta, et arcus KL etiam orbis signorum partes longitudinis prime que videtur, et sunt 67 partes et 50 minuta, et arcus LM partes longitudinis secunde, et sunt 93 partes et 44 minuta. Si enim duobus arcubus ER et RH orbis egredientis centri subtenderentur duo arcus KL et LM orbis signorum, non indigeremus demonstratione cause egressionis a centro aliqua re maiore illo. Sed quia hi duo arcus orbis signorum non subtenduntur nisi duobus arcubus AB et BG orbis egredientis centri medii, et ipsi sunt non dati, et cum nos coniunxerimus lineas NRE et NOR et NHI, non erunt duo arcus qui subtenduntur duobus arcubus ER et RH orbis egredientis centri nisi duo arcus PO et OI orbis signorum, et hi duo arcus etiam non sunt dati, tunc manifestum est quod necessarium est primum ut sint sectiones superfluitatis, et sunt arcus KP et LO et MI, date ut declaratur veritas quantitatis egressionis a centro ex eo quod est inter duos arcus ER et RH separatos et inter duos arcus PO et OI.

Sed quia etiam non est possibile ut sciantur hi duo arcus secundum veritatem ita ut nisi sciatur ante illud quantitas egressionis a centro et longitudinis longioris, et iam est possibile ut sciantur secundum propinquitatem, quamvis non precedat eos scientia illius, propterea quod non cadit in eis ex diversitate aliquid magnum, tunc nos ostendemus prius causam in nostra numeratione eorum secundum hoc quod non cadit inter duos arcus KL et LM et inter duos arcus PO et OI diversitas cui sit quantitas de qua sit curandum. 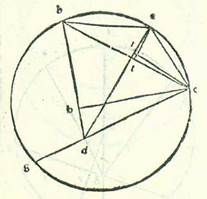Sit itaque orbis centri egredientis qui est cursus Martis medii, super quem sint A, B, G, et sit punctum A punctum habitudinis prime que nominatur extremitas noctis, et punctum B punctum habitudinis secunde, et punctum G punctum habitudinis tertie, et assumatur intra ipsum centrum orbis signorum, et est illud super quod sunt visus nostri, et sit punctum D, et applicabo semper lineas rectas a punctis tribus qui sunt habitudinum nominatarum extremitas noctis et a puncto visus, sicut coniungitur hic linea AD et linea BD et linea GD, et protraham omnino unam trium linearum que iam posite sunt secundum rectitudinem ad arcum oppositum arcui a quo protrahitur, sicut protrahitur hic linea GDE, et copulabo inter duo puncta reliqua punctorum habitudinum trium, sicut coniungit hic linea AB, et coniungantur inter sectionem que provenit in orbe egredientis centri super lineam que protrahitur secundum rectitudinem, sicut punctum E hic, et inter duo puncta reliqua linee punctorum habitudinum trium, sicut coniungit hic linea EA et linea EB, et protraham ab E super duas lineas que coniungunt inter illa dua puncta et inter centrum orbis signorum duas perpendiculares, sicut protrahuntur hic super lineam AD perpendicularis ER et super lineam BD perpendicularis EH, et protraham etiam ab uno illorum duorum punctorum perpendicularem super lineam que contingit inter punctum aliud eorum et inter punctum additum quod provenit in orbe egredientis centri, sicut hic a puncto A super lineam BE perpendicularis AT. Cum ergo servaverimus has res semper secundum habitudinem suam in forma simili huic secundum quemcunque modum voluerimus, inveniemus proportiones que provenerunt nobis secundum numeros proportiones easdem. Residuum autem demonstrationis estimatur arcuum quos posuimus in Marte secundum hunc modum: Quoniam arcus BG orbis centri egredientis iam positus est subtendi orbi signorum 93 partibus et 44 minutis, et quia angulus BDG, cum fuerit apud centrum orbis signorum, erit secundum partes quibus quatuor anguli recti sunt 360 partes 93 partes et 44 minuta et secundum partes quibus duo anguli recti sunt 360 partes erit 187 partes et 28 minuta, erit angulus qui sequitur eum, et ipse est angulus EDH, secundum istas partes 172 partes et 32 minuta. Ergo arcus qui est super lineam EH erit propter illud 172 partes et 32 minuta secundum partes quibus circulus qui describitur circa triangulum DEH ortogonium est 360 partes, et linea EH erit 119 partes et 45 minuta secundum partes quibus ED subtendens est 120 partes. Et similiter etiam propterea quod arcus BG est 95 partes et 28 minuta, erit angulus BEG, cum fuerit apud arcum, 95 partes et 28 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et secundum istas partes fuit angulus BDE 172 partes et 32 minuta. Erit ergo angulus EBH, qui est reliquus, secundum istas partes 92 partes. Quapropter erit arcus qui est super lineam EH 92 partes secundum partes quibus est circulus qui describitur circa triangulum BHE ortogonium 360 partes, et linea EH erit 86 partes et 19 minuta secundum partes quibus linea BE subtendens est 120 partes. Ergo secundum partes quibus declaratur quod linea EH est 119 partes et 45 minuta, et linea ED secundum illud exemplum est 120 partes, erit linea BE 166 partes et 29 minuta. Et etiam quia arcus ABG totus orbis centri egredientis iam positus est subtendi orbis signorum partibus aggregatis ex duabus longitudinibus simul, et sunt 161 partes et 34 minuta, erit angulus ADG 161 pars et 34 minuta secundum partes quibus quatuor anguli recti sunt 360 partes. Et angulus ADE reliquus secundum istas partes erit 18 partes et 26 minuta. Sed secundum partes quibus duo anguli recti sunt 360 partes erit 36 partes et 52 minuta. Quapropter erit arcus etiam qui est super lineam ER 36 partes et 52 minuta secundum partes quibus circulus qui describitur circa triangulum EDR ortogonium est 360 partes, et erit linea ER 37 partes et 57 minuta secundum partes quibus linea DE subtendens est 120 partes. Et similiter etiam quia arcus ABG orbis centri egredientis comprehendit 177 partes et 12 minuta, erit etiam angulus AEG 177 partes et 12 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes fuit angulus ADE 36 partes et 52 minuta. Ergo angulus DAE reliquus secundum istas partes erit 145 partes et 56 minuta. Quapropter erit arcus qui est super lineam ER 145 partes et 56 minuta secundum partes quibus circulus qui describitur circa triangulum AER ortogonium est 360 partes, et erit linea ER 114 partes et 44 minuta secundum partes quibus linea AE subtendens est 120 partes. Ergo secundum partes quibus demonstratum est quod linea ER secundum eas est 37 partes et 57 minuta et linea ED est 120 partes erit linea AE 39 partes et 42 minuta. Et etiam quia arcus AB orbis egredientis centri est 81 partes et 44 minuta, erit etiam angulus AEB 81 partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Erit ergo propter illud arcus qui est super lineam AT 81 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes. Et arcus qui est super lineam ET est quod remanet ad complendum semicirculum, et est 98 partes et 16 minuta. Ergo linea AT, una duarum linearum que subtenduntur eis, erit 78 partes et 31 minuta secundum partes quibus linea DE subtendens est 120 partes, et erit linea ET secundum istas partes 90 partes et 45 minuta. Quapropter secundum partes quibus ostensum est quod linea AE est 39 partes et 42 minuta et quibus linea DE posita est 120 partes erit linea AT 25 partes et 58 minuta, et linea ET secundum illud exemplum 30 partes et duo minuta. Et secundum istas partes fuit ostensum quod linea EB tota est 166 partes et 29 minuta. Ergo linea BT reliqua est 136 partes et 27 minuta secundum partes quibus fuit linea AT 25 partes et 58 minuta, et quadratum quod est ex linea TB est 18618 partes et 36 minuta, et quadratum quod est ex linea TA secundum hoc exemplum erit 674 partes et 16 minuta. Et cum hec aggregantur, est ex eis quadratum quod est ex linea AB, et est 19292 partes et 52 minuta. Linea ergo AB in longitudine est 138 partes et 53 minuta secundum partes quibus fuit linea ED 120 partes et linea AE 39 partes et 42 minuta. Et secundum partes quibus diametrus orbis egredientis centri est 120 partes erit linea AB 78 partes et 31 minutum. Et illud est quod subtenditur arcui existenti 81 partes et 44 minuta. Ergo secundum partes quibus linea AB est 78 partes et 31 minutum et diametrus orbis centri egredientis 120 partes erit linea ED 67 partes et 50 minuta, et linea AE erit secundum eas 22 partes et 27 minuta. Erit ergo arcus qui est super eam orbis egredientis centri 21 pars et 41 minutum. Arcus ergo EABG totus est 198 partes et 53 minuta. Ergo arcus GE reliquus est 161 pars et septem minuta. Et erit linea que subtenditur ei, et est linea GDE, 118 partes et 22 minuta secundum partes quibus diametrus orbis egredientis centri est 120 partes. Tunc si linea GE esset iam inventa equalis diametro orbis centri egredientis, manifestum esset quod super eam caderet centrum circuli ABG, quod est centrum egrediens, et appareret evicino egressus eius a centro. Sed quia non cecidit ei equalis, immo posita est portio EABG maior semicirculo, tunc facile apparet quod centrum orbis egredientis centri cadit intra hanc portionem. 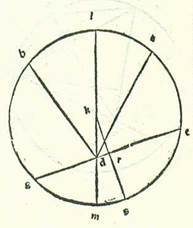Ponam ergo ut sit punctum K, et protraham super ipsum et super punctum D diametrum que transit per centrum, sitque linea LKDM, et producam a puncto K super lineam GE perpendicularem KRS. Et quia iam ostensum est quod linea GE est 118 partes et 22 minuta secundum partes quibus diametrus LM est 120 partes, et secundum has partes fuit linea DE 67 partes et 50 minuta, tunc linea GD reliqua erit secundum illas partes 50 partes et 32 minuta. Quapropter erit propterea quod superficies ortogonia que continetur ab his duabus lineis ED et DG est equalis ei que continetur ab his duabus lineis LD et DM, sed superficies ortogonia que continetur ab his duabus lineis ED et GD est 3427 partes et 51 minuta, ergo superficies que continetur ab his duabus lineis LD et DM est 3427 partes et 51 minuta. Superficies vero ortogonia que continetur ab his duabus lineis LD et DM cum quadrato quod est ex linea DK est equalis quadrato quod est ex medietate linee totius, scilicet quadrato quod est ex linea KM. Si nos ergo minuerimus ex quadrato medietatis linee, quod est 3600 partes, superficiem que continetur ab his duabus lineis LD et DM, et est 3427 partes et 51 minuta, remanebit nobis quadratum quod est ex linea DK secundum istas partes 172 partes et 9 minuta. Evenit ergo nobis linea DK, et est ea que est inter duo centra in longitudine 13 partes et 7 minuta fere secundum partes quibus linea KL, que est a centro orbis egredientis centri, est 60 partes. Et etiam quia medietas linee GE, scilicet linea GR, et est 59 partes et 11 minuta secundum partes quibus diametrus LM est 120 partes, et secundum istas partes est ostensum quod linea GD est 50 partes et 32 minuta, tunc linea DR reliqua est octo partes et 39 minuta. Ergo secundum partes quibus linea DK subtendens est 120 partes erit linea DR 79 partes et octo minuta, et arcus qui est super eam erit 82 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum DKR ortogonium est 360 partes. Ergo angulus DKR secundum partes quibus duo anguli recti sunt 360 partes est 82 partes et 30 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit 41 pars et 15 minuta. Et quia ipse est apud centrum orbis egredientis centri, tunc arcus MS provenit nobis 41 pars et 15 minuta. Sed arcus GMS totus, quia est medietas arcus GSE, erit secundum istas partes 80 partes et 34 minuta. Ergo arcus GM reliquus, et est ille qui est ab habitudine tertia ad longitudinem propinquiorem, est 39 partes et 19 minuta, et arcus LG est quod remansit de medietate circuli, et est 140 partes et 41 minuta. Et apparet quod arcus BG cum fuerit positus 95 partes et 28 minuta, tunc arcus LB reliquus, et est ille qui est a longitudine longiore ad habitudinem secundam, erit 45 partes et 13 minuta. Et quia fuit iam positus arcus AB 81 pars et 44 minuta, tunc arcus AL reliquus, et est ille qui est ab habitudine prima ad longitudinem longiorem, est 36 partes et 31 minutum.

Et quia iam explanate sunt iste res, tunc inquiramus summam superfluitatum ex quibus comprehenduntur arcus quesiti in unaquaque habitudinum que nominatur extremitas noctis orbis signorum secundum hunc modum: 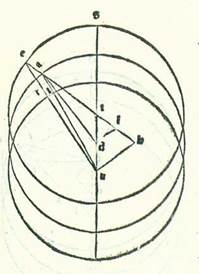Ponam igitur figure quam premisimus et signavimus habitudinum trium descriptionem habitudinis prime solummodo, et applicabo in ea lineam AD, et protraham a duobus punctis D et N duas perpendiculares DL et NH super lineam AT cum producetur. Et quia arcus SE est 36 partes et 31 minuta, erit angulus ETS secundum partes quibus quatuor anguli recti sunt 360 partes 36 partes et 31 minuta. Et secundum partes quibus duo anguli recti sunt 360 partes erit ipse angulus qui est super caput eius, et est angulus DTL, 73 partes et duo minuta. Quapropter erit arcus qui est super lineam DL 73 partes et duo minuta secundum partes quibus circulus qui describitur circa triangulum DTL ortogonium est 360 partes. Et erit arcus qui est super lineam LT illud quod remanet ad complendum semicirculum, et est 106 partes et 58 minuta. Ergo linea DL, una duarum linearum que subtenduntur eis, erit 71 partes et 23 minuta secundum partes quibus linea DT subtendens est 120 partes, et linea LT secundum istas partes 96 partes et 27 minuta. Ergo secundum partes quibus linea DT est 6 partes et 33 minuta et medietas et linea DA, que est a centro orbis egredientis centri, est 60 partes, erit linea quidem DL 3 partes et 54 minuta et linea LT similiter 5 partes et 16 minuta. Et quia cum quadratum quod est ex linea LD minuitur ex quadrato quod est ex linea DA, est ex eo quadratum quod est ex linea LA, erit linea LA etiam in longitudine 59 partes et 52 minuta, et erit linea HA tota, propterea quod linea LH est equalis linee LT, 65 partes et octo minuta secundum partes quibus linea NH, quia est dupla linee DL, comprehendit 7 partes et 48 minuta. Quapropter erit linea NA subtendens secundum istas partes 65 partes et 36 minuta. Ergo secundum partes quibus linea NA subtendens est 120 partes erit linea NH 14 partes et 16 minuta, et arcus qui est super eam 13 partes et 40 minuta secundum partes quibus circulus qui describitur circa triangulum ANH ortogonium est 360 partes. Quapropter erit angulus NAH 13 partes et 40 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et etiam quia secundum partes quibus linea TE, que est a centro orbis egredientis centri, est 60 partes, et iam ostensum est quod linea NH est septem partes et 48 minuta, et linea HT secundum hoc exemplum est 10 partes et 32 minuta, erit linea HTE tota secundum hoc exemplum per has partes 70 partes et 32 minuta. Et propter illud erit EN subtendens 71 pars fere. Et secundum partes quibus linea NE est 120 partes erit linea NH 13 partes et 10 minuta, et arcus qui est super eam 12 partes et 36 minuta secundum partes quibus circulus qui describitur circa triangulum ENH ortogonium est 360 partes. Quapropter erit angulus NEH etiam 12 partes et 36 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes fuit angulus NA 913 partes et 40 minuta. Ergo angulus ANE reliquus secundum partes quibus duo anguli recti sunt 360 partes erit pars una et quatuor minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit 32 minuta. Hec igitur est summa arcus IR orbis signorum partium.

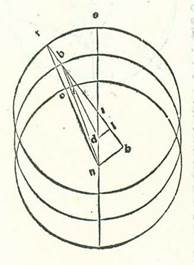Ponam itaque huius figure similem et ponam ipsam formam habitudinis secunde. Et quia arcus RS iam positus fuit 45 partes et 13 minuta, erit angulus STR etiam secundum partes quibus quatuor anguli recti sunt 360 partes 45 partes et 13 minuta. Et secundum partes quibus duo anguli recti sunt 360 partes erit ipse et angulus qui est super caput eius, qui est angulus DTL, 90 partes et 26 minuta. Erit ergo propter illud arcus etiam qui est super lineam DL 90 partes et 26 minuta secundum partes quibus circulus qui describitur circa triangulum DTL ortogonium est 360 partes. Et arcus qui est super lineam LT est quod remanet ad complendum semicirculum, et est 89 partes et 34 minuta. Linea igitur DL, una duarum linearum que subtenduntur eis, est 85 partes et 10 minuta secundum partes quibus linea DT subtendens est 120 partes. Et linea LT secundum istas partes est 84 partes et 32 minuta. Quapropter secundum partes quibus linea DT est sex partes et 33 minuta et medietas, et linea RT, que est a centro orbis egredientis centri, est 60 partes, erit linea DL quatuor partes et 39 minuta, et linea LT secundum hoc exemplum pars una et 38 minuta. Et quia ex quadrato quod est ex linea DL diminuto ex quadrato quod est ex linea DB erit quadratum quod est ex linea LB, tunc linea LB in longitudine est 59 partes et 49 minuta. Et erit linea HB tota, propterea quod linea HL est equalis linee LT, 64 partes et 27 minuta secundum partes quibus linea HN, quia est dupla linee DL, comprehendit 9 partes et 18 minuta. Et propter illud linea BN subtendens est secundum illas partes 65 partes et sex minuta. Ergo secundum partes quibus linea BN est 120 partes erit linea NH 17 partes et 9 minuta. Et erit arcus qui est super eam 16 partes et 26 minuta secundum partes quibus circulus qui describitur circa triangulum BNH ortogonium est 360 partes. Quapropter erit angulus NBH etiam 16 partes et 26 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et etiam quia secundum partes quibus linea TR, que est a centro orbis centri egredientis, est 60 partes, et iam ostensum est quod linea NB est novem partes et 18 minuta, et linea HT secundum illud exemplum est novem partes et 16 minuta, erit linea HTR tota secundum istas partes 69 partes et 14 minuta. Et propter illud erit linea NR subtendens 69 partes et 51 minuta. Ergo secundum partes quibus linea NR subtendens est 120 partes erit linea NH 16 partes fere. Et erit arcus qui est super eam 15 partes et 20 minuta secundum partes quibus circulus qui describitur circa triangulum NRH ortogonium est 360 partes. Erit ergo propter illud angulus NRH etiam 15 partes et 20 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit angulus BNR reliquus secundum istas quidem partes pars una et sex minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit ipse 33 minuta. Hec igitur est summa arcus IO orbis signorum partium. Et quia invenimus in habitudine prima arcum IR 33 minuta, tunc manifestum est quod longitudo prima, que est secundum orbem centri egredientis, est maior longitudine que videtur secundum partes amborum arcuum, et est pars una et quinque minuta, et quod eius summa est 68 partes et 55 minuta.

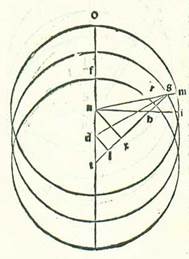Ponam autem formam habitudinis tertie etiam. Et quia arcus FH positus est 39 partes et 19 minuta, erit angulus FTH etiam secundum partes quibus quatuor anguli recti sunt 360 partes 39 partes et 19 minuta et secundum partes quibus duo anguli recti sunt 360 partes 78 partes et 38 minuta. Erit ergo propter illud arcus qui est super lineam DL 78 partes et 38 minuta secundum partes quibus circulus qui describitur circa triangulum DTL ortogonium est 360 partes. Et erit arcus qui est super lineam TL illud quod remanet ad complendum semicirculum, et est 101 partes et 22 minuta. Linea igitur DL, una duarum linearum que subtenduntur eis, est 76 partes et duo minuta secundum partes quibus linea DT subtendens subtendns M. est 120 partes, et linea TL secundum istas partes est 92 partes et 50 minuta. Erit ergo propter illud secundum partes quibus linea DT, et est ea linea que est inter duo centra, est sex partes et 33 minuta et medietas et linea DG, que est a centro orbis egredientis centri, est 60 partes linea DL 4 partes et 20 minuta, et linea TL secundum illud exemplum quinque partes et quatuor minuta. Et quia cum quadratum quod est ex linea DL minuitur ex quadrato quod est ex linea DG, provenit quadratum quod est ex linea GL, erit linea GL 59 partes et 51 minuta. Et erit linea GX reliqua, propterea quod linea TL est equalis linee LX, 54 partes et 47 minuta secundum partes quibus linea NX, quia est dupla linee DL, comprehendit octo partes et 18 minuta. Et propter illud sit linea GN secundum istas partes 55 partes et 25 minuta. Ergo secundum partes quibus linea NG est 120 partes erit linea NX 17 partes et 59 minuta, et erit arcus qui est super eam 17 partes et 14 minuta secundum partes quibus circulus qui describitur circa triangulum GXN ortogonium est 360 partes. Quapropter erit angulus NGX etiam 17 partes et 14 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et etiam quia secundum partes quibus linea TH, que est a centro orbis egredientis centri, est 60 partes tunc, quia iam ostensum est quod linea NX est 8 partes et 18 minuta et linea TX secundum illud exemplum est 10 partes et 8 minuta, erit linea HX reliqua 49 partes et 52 minuta et propter illud erit linea NH subtendens 50 partes et 33 minuta, ergo secundum partes quibus linea NH est 120 partes erit linea NX 19 partes et 42 minuta, et erit arcus qui est super eam 18 partes et 54 minuta secundum partes quibus circulus qui describitur circa triangulum NHX ortogonium est 360 partes. Quapropter erit angulus NHX 18 partes et 54 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes ostensum est quod angulus NGX est 17 partes et 14 minuta. Ergo angulus GNH reliquus secundum istas partes erit pars una et 40 minuta. Sed secundum quantitatem qua sunt quatuor anguli recti 360 partes erit 50 minuta. Hec igitur est summa arcus MI orbis signorum partium. Et quia invenimus in habitudine secunda arcum IO 33 minuta, tunc manifestum est quod longitudo secunda que reperitur in orbe egredientis centri est minor longitudine que videtur secundum partes duorum arcuum coniunctorum, et est pars una et 23 minuta, et quod summa eius est 92 partes et 21 minutum.

Quod si nos processimus in eo quod est inter duos arcus orbis signorum qui provenerunt duabus longitudinibus et in arcubus etiam quos posuimus secundum naturam in orbe egredientis centri via qua processimus in intentione cuius precessit declaratio ante hec, qua declaravimus longitudinem longiorem et quantitatem egressionis a centro, ut hic non prolongetur sermo cum iteratione earundem rerum, inveniemus lineam que est inter duo centra, et est linea TN, 11 partes et 50 minuta secundum partes quibus linea que est a centro orbis egredientis centri est 60 partes, et arcus FH orbis egredientis centri, et est ille qui est ab habitudine tertia ad longitudinem propinquiorem etiam 45 partes et 33 minuta. Et erit etiam arcus IB huius circuli 38 partes et 59 minuta. Et arcus AL secundum hoc exemplum erit 42 partes et 45 minuta. Si ergo nos imitati fuerimus illud et comitati in declaratione unius et unius habitudinum extremitatis noctis, inveniemus tunc quantitates cuiusque horum arcuum secundum veritatem. Inveniemus enim arcum IR 28 minuta, et arcum IO equalem illi fere 28 minuta, et arcum MI 40 minuta. Cum ergo aggregaverimus minuta habitudinis prime ad minuta habitudinis secunde et quod provenerit, et est 56 minuta, addiderimus super partes longitudinis prime orbis signorum, et sunt 67 partes et 50 minuta, proveniet nobis longitudo que reperitur in orbe egredientis centri secundum veritatem 68 partes et 46 minuta. Et cum nos aggregaverimus minuta habitudinis secunde et minuta habitudinis tertie et minuerimus quod provenerit, et est pars una et octo minuta ex partibus que videntur orbis signorum in longitudine secunda, et sunt 93 partes et 44 minuta, inveniemus etiam longitudinem longiorem repertam secundum veritatem in orbe egredientis centri 92 partes et 36 minuta. Et ex istis rebus, propterea quod fecimus illam eandem viam demonstrationis, verificavimus quantitatem egressionis a centro et locum longitudinis longioris et invenimus lineam que est inter duo centra, et est linea DK, 12 partes fere secundum partes quibus linea KL, et est ea que est a centro orbis egredientis centri, est 60 partes. Et arcus GM orbis egredientis centri est 44 partes et 21 minutum. Erit ergo in hoc orbe etiam arcus LS 40 partes et 11 minuta, et arcus AL secundum illud exemplum 41 pars et 33 minuta. Et iam nunc possibile est ut demonstremus quod longitudines que invente sunt per considerationes secundum visum in habitudinibus tribus sint convenientes istis quantitatibus propter illas res easdem.

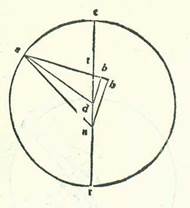Ponam itaque formam habitudinis prime et in ea orbem egredientis centri tantum super quem revolvitur semper centrum orbis revolutionis, sitque ER. Et quia angulus ATE secundum partes quibus quatuor anguli recti sunt 360 partes est 41 partes et 33 minuta, et secundum partes quibus duo anguli recti sunt 360 partes est ipse et ille qui est super caput eius, et est angulus DTB, 83 partes et 6 minuta, erit arcus qui est super lineam BD 83 partes et 6 minuta secundum partes quibus circulus qui describitur circa triangulum DTB ortogonium est 360 partes, et erit arcus qui est super lineam BD 83 partes et 6 minuta, et erit arcus qui est super lineam BT quod remanet ad complendum semicirculum, et est 46 partes et 54 minuta. Linea igitur DB, una duarum linearum que subtenduntur eis, erit 79 partes et 35 minuta secundum partes quibus linea DT subtendens est 120 partes, et linea BT secundum istas partes erit 89 partes et 48 minuta. Quapropter secundum partes quibus linea DT est sex partes et linea DA subtendens est 60 partes erit linea DB 3 partes et 58 minuta et medietas, et linea BT secundum hoc exemplum erit quatuor partes et 30 minuta. Et quia cum quadratum quod est ex linea DB minuitur ex quadrato quod est ex linea DA, est ex eo quadratum quod est ex linea BA, erit hec linea etiam in longitudine secundum istas partes 59 partes et 52 minuta. Et etiam quia linea TB est equalis linee BH et linea BD est medietas linee HN, proveniet nobis linea AH tota 64 partes et 22 minuta secundum partes quibus linea NH est 7 partes et 57 minuta. Et propter illud erit linea NA subtendens secundum istas partes 64 partes et 52 minuta. Propter illud ergo secundum partes quibus etiam linea NA est 120 partes erit linea NH 14 partes et 44 minuta, et arcus qui est super eam erit 14 partes et sex minuta secundum partes quibus circulus qui describitur circa triangulum ANH ortogonium est 360 partes. Angulus igitur NAH secundum partes quibus duo anguli recti sunt 360 partes est 14 partes et sex minuta et secundum partes quibus quatuor anguli recti sunt 360 partes est 7 partes et tria minuta. Sed secundum istas partes fuit angulus ATE 41 partes et 33 minuta. Ergo angulus ANE reliquus, et est angulus cursus qui videtur, est 34 partes et 30 minuta, et sunt partes quibus fuit stella in habitudine prima precedens longitudinem longiorem.

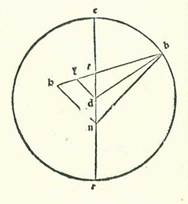Et ponam etiam formam similem huic habitudini secunde. Et quia angulus BTE, et est angulus cursus medii orbis revolutionis, secundum partes quibus quatuor anguli recti sunt 360 partes est 40 partes et 11 minuta, et secundum partes quibus duo anguli recti sunt 360 partes est ipse et ille qui est super caput eius, et est angulus DTY, 80 partes et 22 minuta, erit arcus qui est super lineam DY secundum istas partes 80 partes et 22 minuta secundum partes quibus circulus qui describitur circa triangulum DTY ortogonium est 360 partes, et erit arcus qui est super lineam YT partes relique ad complendum semicirculum, et sunt 99 partes et 38 minuta. Ergo linea DY, una duarum linearum que subtenduntur eis, est 77 partes et 26 minuta secundum partes quibus linea DT subtendens est 120 partes, et linea YT secundum istas partes est 91 partes et 41 minuta. Ergo secundum partes quibus linea DT est sex partes et linea DB subtendens est 60 partes erit linea DY tres partes et 52 minuta, et linea TY secundum hoc exemplum 4 partes et 35 minuta. Et quia cum quadratum quod est ex linea DY minuitur ex quadrato quod est ex linea DB, est ex eo quadratum quod est ex linea YB, tunc hec linea erit in longitudine secundum istas partes 59 partes et 52 minuta. Et similiter etiam quia linea TY est equalis linee YH et linea NH est dupla linee DY, erit linea BH tota 64 partes et 27 minuta secundum partes quibus linea NH est septem partes et 44 minuta. Et ex eo erit linea BN subtendens secundum istas partes 64 partes et 54 minuta. Ergo secundum partes quibus linea BN subtendens est 120 partes erit linea NH 14 partes et 19 minuta, et arcus qui est super eam erit 13 partes et 42 minuta secundum partes quibus circulus qui describitur circa triangulum BNH ortogonium est 360 partes. Quapropter erit angulus NBH etiam secundum partes quibus duo anguli recti sunt 360 partes 13 partes et 42 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes sex partes et 51 minutum. Verum secundum istas partes fuit angulus BTE 40 partes et 11 minuta. Ergo angulus ENB reliquus, et est angulus cursus qui videtur, secundum istas partes est 33 partes et 20 minuta. Secundum ergo istas partes fuit stella visa posterior longitudine longiore in habitudine secunda. Iam vero fuit ostensum quod in longitudine prima fuit visa precedere longitudinem longiorem 34 partibus et 30 minutis. Provenit ergo longitudo tota ab habitudine prima ad habitudinem secundam 67 partes et 50 minuta. Et illud est conveniens ei cuius summam invenimus per duas considerationes.

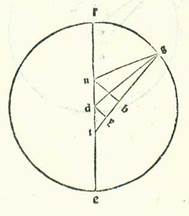Et ponam etiam secundum hanc similitudinem formam habitudinis tertie. Et quia angulus GTR hec etiam, et est angulus cursus equalis orbis revolutionis, secundum partes quibus quatuor anguli recti sunt 360 partes est 44 partes et 21 minutum et secundum partes quibus duo anguli recti sunt 360 partes est 88 partes et 42 minuta, erit arcus qui est super lineam DY 88 partes et 42 minuta secundum partes quibus circulus qui describitur circa triangulum DTY ortogonium est 360 partes, et arcus qui est super lineam YT est partes relique ad complendum semicirculum, et sunt 91 partes et 18 minuta. Ergo linea DY, una duarum linearum que subtenduntur eis, est 83 partes et 53 minuta secundum partes quibus linea DT subtendens est 120 partes, et linea YT secundum istas partes est 85 partes et 49 minuta. Erit ergo propter illud secundum partes quidem quibus linea DT est sex partes et linea DG, que est a centro orbis egredientis centri, 60 partes linea DY 4 partes et 11 minuta et medietas, et linea YT secundum hanc similitudinem erit 4 partes et 17 minuta. Et quia quadrato quod est ex linea DY diminuto ex quadrato quod est ex linea DG, erit ex eo quadratum quod est ex linea GY, proveniet nobis hec linea etiam in longitudine secundum istas partes 59 partes et 51 minutum. Et etiam quia linea YT est equalis linee YH et linea NH est dupla linee DY, tunc linea GH reliqua provenit nobis 55 partes et 34 minuta secundum partes quibus linea NH est octo partes et 23 minuta. Et propter illud proveniet nobis etiam linea GN subtendens secundum istas partes 56 partes et 12 minuta. Ergo secundum partes quibus linea GN subtendens est 120 partes erit linea NH 17 partes et 55 minuta, et erit arcus qui est super eam 17 partes et 10 minuta secundum partes quibus circulus qui describitur circa triangulum GNH ortogonium est 360 partes. Erit ergo propter illud angulus TGN etiam secundum partes quibus duo anguli recti sunt 360 partes 17 partes et 10 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes octo partes et 35 minuta. Verum secundum istas partes fuit angulus GTR etiam 44 partes et 21 minutum. Ergo angulus GNR totus secundum istas partes est 52 partes et 56 minuta. Hec igitur summa partium quibus fuit visa stella in habitudine tertia precedere longitudinem propinquiorem. Iam autem fuit ostensum quod fuit visa in habitudine tertia posterior a longitudine longiore trigintatribus partibus et viginti minutis. Ergo partes que provenerunt residue ab habitudine secunda ad habitudinem tertiam, et sunt 93 partes et 44 minuta, iam reperte sunt convenientes ei quod invenimus per considerationem in longitudine secunda. Et manifestum est quod propterea quod visa fuit stella super lineam GN in habitudine tertia, et fuit locus eius secundum quod invenimus per considerationem super duas partes et 34 minuta Sagittarii, et ostensum fuit quod angulus GNR, et est apud centrum orbis signorum, est 52 partes et 56 minuta secundum partes quibus quatuor anguli recti sunt 360 partes, fuit ergo locus longitudinis propinquioris in orbe egredientis centri, que est super punctum R, super 25 partes et 30 minuta Capricorni, et locus longitudinis longioris super partem condiametralem ei, et est vigesimaquinta pars et trigesimumquartum minutum Cancri. 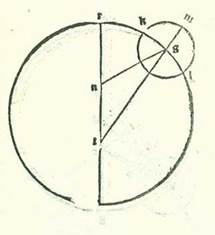Si enim descripserimus circa centrum G orbem revolutionis Martis, supra quem sint M, K, L, et protraxerimus lineam TGM, proveniet nobis in tempore habitudinis tertie cursus medius orbis revolutionis a longitudine longiore in orbe egredientis centri 135 partes et 39 minuta, propterea quod angulus GTR iam ostensum est quod est partes residue ad complendum semicirculum, et sunt 44 partes et 21 minutum, et provenit cursus medius stelle a puncto M, quod est longitudo longior in orbe revolutionis, scilicet arcus MK, 171 partes et 25 minuta. Et propterea quod angulus TGN iam fuit ostensum quod est octo partes et 35 minuta secundum partes quibus quatuor anguli recti sunt 360 partes, et fuit hic angulus apud centrum orbis revolutionis, tunc arcus KL, et est ille qui est a stella ad longitudinem propinquiorem, et est punctum L, erit secundum istas partes octo partes et 35 minuta. Erit ergo arcus qui est a puncto M, et est longitudo longior, ad stellam super quam est punctum K illud quod remanet ad complendum semicirculum, sicut narravimus, et est 171 partes et 25 minuta. Iam ergo demonstratum est nobis cum ceteris que declarata sunt quod in tempore habitudinis tertie, scilicet in anno secundo annorum Antonii in mense Athica apud Egyptios in die duodecimo eius in nocte quam sequitur dies tertiusdecimus ante medietatem noctis duabus horis equalibus fuit stella Martis in intentione que nominatur longitudo elongatio eius per motum suum medium a longitudine longiore in orbe egredientis centri 135 partes et 39 minuta, et fuit eius longitudo in diversitate a longitudine longiore in orbe revolutionis 171 partes et 25 minuta. Et iste sunt res quas intendimus invenire.

⟨X.8⟩ Capitulum octavum: In declaratione quantitatis orbis revolutionis Martis

Et quia iam sequitur illud ut demonstrem proportionem orbis revolutionis, tunc inveniam propter illud considerationem in qua consideravimus hanc stellam quasi post tres dies ab habitudine tertia, scilicet in anno secundo annorum Antonii in mense Athica apud Egyptios in die quintodecimo eius in nocte quam sequitur dies decimussextus ante medietatem noctis tribus horis equalibus, propterea quod medians celum secundum considerationem fuit vicesima pars Libre. Et erat Solis per medium cursum suum locus tunc super quinque partes et 27 minuta Geminorum. Ergo consideravimus Ascimech Alahazel et invenimus eam in loco qui pertinet ei. Et vidimus locum stelle Martis super partem unam et tres quintas partis Sagittarii. Et in illa hora eadem vidimus longitudinem eius etiam a centro Lune posterius partem unam etiam et tres quintas partis. Et fuit in illa hora cursus Lune medius in quatuor partibus et viginti minutis Sagittarii, et eius cursus verificatus fuit in 29 partibus et 30 minutis Scorpionis, propterea quod fuit eius longitudo a longitudine longiore in orbe revolutionis 92 partes, et eius cursus qui videtur fuit in principio Sagittarii. Fuit ergo ex hoc modo etiam locus stelle Martis conveniens ei qui repertus fuit tunc per considerationem super partem unam et 36 minuta Sagittarii. Et manifestum est quod fuit eius longitudo a longitudine longiore precedens 53 partibus et 54 minutis. Et illud quod comprehendit tempus quod fuit inter habitudinem tertiam et inter hanc considerationem ex partibus longitudinis in longitudine quidem est una pars et 32 minuta et in diversitate quidem pars una et 21 minutum fere. Si ergo nos addiderimus illud super locos duos quos declaravimus in hac habitudine tertia, inveniemus longitudinem stelle Martis fuisse in hora huius considerationis in longitudine quidem super 137 partes et 11 minuta a longitudine longiore in orbe egredientis centri et in diversitate super 172 partes et 46 minuta a longitudine longiore in orbe revolutionis. 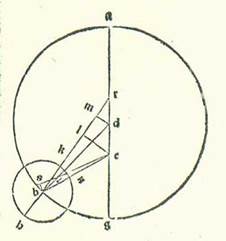Postquam igitur explanate sunt he res, tunc sit orbis egredientis centri qui revolvit centrum orbis revolutionis supra quem sint A, B, G circa centrum D, et diametrus eius sit ADG, et ponam super ipsam centrum orbis signorum, punctum E, et centrum orbis egredientis centri maioris exitus, punctum R, et describam circa punctum B orbem revolutionis, supra quem sint B, N, K, et protraham lineas RKBH et ENB, et protraham a duobus punctis D et E super lineam RB duas perpendiculares EL et DM, et ponam ut stella sit supra punctum T orbis revolutionis, et producam lineas duas ET et BD, et protraham super lineam ET, cum producetur secundum rectitudinem a puncto B, perpendicularem BS. Et quia stelle fuit longitudo a longitudine longiore in orbe centri egredientis 137 partes et 11 minuta, tunc angulus BRG etiam secundum partes quidem quibus quatuor anguli recti sunt 360 partes est 42 partes et 49 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 85 partes et 38 minuta, et arcus qui est super lineam DM est 85 partes et 38 minuta secundum partes quibus circulus qui describitur circa triangulum DRM ortogonium est 360 partes, et arcus qui est super lineam RM est quod remanet ad complendum semicirculum, et est 94 partes et 22 minuta. Linea igitur DM una duarum linearum que subtenduntur eis erit 81 pars et 34 minuta secundum partes quibus linea DR subtendens est 120 partes, et linea RM secundum istas partes est 88 partes et minutum unum. Erit ergo propter illud secundum partes quibus linea DR, que est inter duo centra, est sex partes et linea DB, que est a centro orbis egredientis centri, est 60 partes linea DM quatuor partes et quinque minuta, et linea RM secundum illud exemplum quatuor partes et 24 minuta. Et quia quadrato quod est ex linea DM diminuto ex quadrato quod est ex linea DB erit ex eo quadratum quod est ex linea BM, erit linea BM secundum istas partes 59 partes et 52 minuta. Et secundum hanc similitudinem etiam, quia fuit linea RM equalis linee ML et linea EL dupla linee DM, tunc linea BL reliqua erit 55 partes et 28 minuta, et linea EL secundum istas partes erit octo partes et 10 minuta. Et propter illud erit linea EB subtendens 56 partes et quatuor minuta. Ergo secundum partes quibus linea EB est 120 partes erit linea EL 17 partes et 28 minuta, et arcus qui est super eam erit 16 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum BEL ortogonium est 360 partes. Quapropter erit angulus EBL etiam 16 partes et 44 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et etiam quia angulus GES, et est ille quo videtur stella Martis precedere punctum G, et est longitudo propinquior secundum partes quibus quatuor anguli recti sunt 360 partes, est positus 53 partes et 54 minuta, et secundum partes quibus duo anguli recti sunt 360 partes est 107 partes et 48 minuta, et secundum istas partes etiam angulus GEB est 102 partes et 22 minuta, propterea quod ipse est equalis duobus angulis coniunctis, scilicet angulo RBE, et iam ostensum est quod ipse est secundum istas partes 16 partes et 44 minuta, et angulo GRB iam posito secundum istas partes 85 partibus et 38 minutis, tunc manifestum est quod angulus BES reliquus secundum istas partes erit 5 partes et 26 minuta. Et erit arcus que est super lineam BS 5 partes et 26 minuta secundum partes quibus circulus qui describitur circa triangulum BES ortogonium est 360 partes. Et propter illud etiam erit linea BS 5 partes et 41 minutis secundum partes quibus linea EB subtendens est 120 partes. Ergo secundum partes quibus demonstratur quod linea EB est 56 partes et 4 minuta et linea que est a centro orbis egredientis centri est 60 partes erit linea BS due partes et 39 minuta. Et secundum hanc similitudinem, quia puncti T longitudo a puncto H, et est longitudo longior in orbe revolutionis, est 172 partes et 46 minuta et eius longitudo a puncto K, et est longitudo propinquior, est 7 partes et 14 minuta, erit angulus KBT etiam secundum partes quibus quatuor anguli recti sunt 360 partes 7 partes et 14 minuta et secundum partes quibus duo anguli recti sunt 360 partes 14 partes et 28 minuta. Verum secundum istas partes fuit angulus KBN 16 partes et 44 minuta. Erit ergo angulus TBN reliquus due partes et 16 minuta, et angulus STB totus secundum istas partes erit 7 partes et 42 minuta. Quapropter erit arcus qui est super lineam BS etiam 7 partes et 42 minuta secundum partes quibus circulus qui describitur circa triangulum BTS ortogonium est 360 partes, et erit linea BS eadem octo partes et tria minuta secundum partes quibus linea BT subtendens est 120 partes. Ergo secundum partes quibus linea BS est due partes et 39 minuta et linea que est a centro orbis egredientis centri est 60 partes erit linea BT, que est a centro orbis revolutionis, 39 partes et 30 minuta fere. Ergo proportio linee que est a centro orbis egredientis centri ad lineam que est a centro orbis revolutionis est proportio 60 partium ad 39 partes et 30 minuta. Et illud est cuius investigavimus inventionem.

⟨X.9⟩ Capitulum nonum: In verificatione revolutionum motuum Martis

Accepimus etiam propter causam verificationis revolutionum motuum Martis mediorum unam considerationum antiquarum in qua dicitur etiam quod in anno tredecimo annorum Dionysii in mense nominato Haor stella Martis estimabatur iam cooperuisse stellam que est in latere septentrionali frontis Scorpionis. Et tempus huius considerationis fuit in anno quinquagesimosecundo a morte Alexandri. Et illud fuit in anno quadringentesimo et septuagesimosexto a tempore Nabuchodonosor in mense nominato apud Egyptios Athus in die vigesimo eius in diluculo vigesimiprimi. Et in hac hora invenimus Solis locum fuisse per cursum suum medium mediuum M. super 23 partes et 54 minuta Capricorni, et stelle que est in latere septentrionali frontis Scorpionis invenimus locum per considerationem super sex partes et tertiam partis Scorpionis. Quapropter, quia quod fuit etiam inter hanc considerationem et inter regnum Antonii ex annis est quadringenti et novem anni, in quibus movetur stella fixa que fuit in hora considerationis quam narravimus 4 partibus et 42 minutis fere tunc ipsa fuit in hora considerationis super duas partes et quatuor minuta Scorpionis, et manifestum est quod ille etiam fuit locus stelle Martis. Et secundum hanc similitudinem etiam, quia fuit in nostro tempore, scilicet in principio regni Antonii, locus longitudinis longioris Martis in 25 partibus et 30 minutis Cancri, tunc invenitur quod eius locus fuit in hora considerationis super 21 partes et 25 minuta Cancri. Et manifestum est quod stelle secundum visum fuit longitudo a longitudine longiore in hora illa 100 partes et 50 minuta, et fuit longitudo Solis per motum suum medium ab illa eadem longitudine longiore 182 partes et 29 minuta, et fuit eius longitudo a longitudine propinquiore due partes et 29 minuta. Et illud est manifestum. 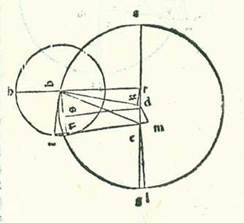Postquam igitur iam explanavimus has res, sit orbis egredientis centri revolvens centrum orbis revolutionis, supra quem sint A, B, G circa centrum D, et sit eius diametrus ADG, et ponam super ipsam centrum orbis signorum punctum E, et centrum orbis egredientis centri maioris egressus punctum R, et signabo circa centrum B orbem revolutionis, supra quem sint HT, et protraham duas lineas RBH et BD, et producam a puncto R super lineam DB perpendicularem RK, et ponam ut stella sit super punctum T orbis revolutionis, et coniungam lineam BT, et protraham a puncto E lineam EL equidistantem ei, et est super quam videtur cursus Solis medius propter illud cuius iam processit declaratio, et applicabo lineam ET, et producam a duobus punctis D et B duas perpendiculares DM et BN, et protraham etiam a puncto D super lineam BN perpendicularem DS, ita ut sit figura DMNS equidistantium laterum et rectorum angulorum. Et quia angulus AET, et est angulus cursus qui videtur stelle a longitudine longiore, est 100 partes et 50 minuta secundum partes quibus quatuor anguli recti sunt 360 partes, et angulus GEL, et est angulus cursus Solis medii, secundum istas partes est due partes et 29 minuta, erit angulus TEL, qui est etiam angulus equalis angulo BTE, secundum partes quibus quatuor anguli recti sunt 360 partes 81 partes et 39 minuta, et secundum partes quibus duo anguli recti sunt 360 partes erit 163 partes et 18 minuta. Quapropter erit arcus qui est super lineam BN etiam 163 partes et 18 minuta secundum partes quibus circulus qui describitur circa triangulum BTN ortogonium est 360 partes, et erit linea BN eadem 118 partes et 43 minuta secundum partes quibus linea BT subtendens est 120 partes. Ergo secundum partes quibus linea BT, que est a centro orbis revolutionis, est 39 partes et 30 minuta, et linea ED, que est inter duo centra, est sex partes erit linea BN 39 partes et tria minuta. Et etiam quia angulus AET etiam secundum partes quibus quatuor anguli recti sunt 360 partes est 100 partes et 50 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 201 pars et 40 minuta et propter illud est angulus qui sequitur eum, et est angulus DEM, secundum istas partes 158 partes et 20 minuta, erit arcus qui est super lineam DM etiam 158 partes et 20 minuta secundum partes quibus circulus qui describitur circa triangulum DEM ortogonium est 360 partes, et erit linea DM eadem 117 partes et 52 minuta secundum partes quibus linea DE, cum sit subtendens, est 120 partes. Igitur secundum partes quibus linea DE est sex partes et linea BT secundum quod declaratum est est 39 partes et medietas partis et linea BN 39 partes et 3 minuta, quod declaratum est, erit linea DM, scilicet que est equalis linee NS, 5 partes et 54 minuta, et erit linea SB reliqua 33 partes et novem minuta secundum partes quibus linea BD, que est a centro orbis egredientis centri, est 60 partes. Igitur secundum partes quibus linea BD, cum sit subtendens, est 120 partes erit linea BS 66 partes et 18 minuta, et arcus qui est super eam erit 67 partes et 4 minuta fere secundum partes quibus circulus qui describitur circa triangulum BDS ortogonium est 360 partes. Quapropter erit angulus BDS etiam 67 partes et 4 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit angulus BDM totus 247 partes et 4 minuta. Et secundum istas partes erit angulus EDM 21 partes et 40 minuta, quoniam iam ostensum est quod angulus DEM est 158 partes et 20 minuta. Ergo angulus BDE reliquus provenit 225 partes et 24 minuta, et angulus qui sequitur eum, et est angulus BDA, secundum illam similitudinem est 134 partes et 36 minuta. Quapropter erit arcus qui est super lineam RK 134 partes et 36 minuta secundum partes quibus circulus qui describitur circa triangulum DRK ortogonium est 360 partes, et erit arcus qui est super lineam KD partes relique ad complendum semicirculum, et sunt 45 partes et 24 minuta. Linea igitur RK, una duarum linearum que subtenduntur eis, erit 110 partes et 42 minuta secundum partes quibus linea RD, cum sit subtendens, est 120 partes, et erit linea DK secundum istas partes 46 partes et 18 minuta. Ergo secundum partes quibus linea DR est sex partes et linea DB, et est ea que est a centro orbis egredientis centri, est 60 partes erit linea RK 5 partes et 32 minuta, et linea DK secundum illud exemplum due partes et 19 minuta. Ergo linea KB reliqua est 57 partes et 57 minuta fere. Et propterea erit linea BR, cum sit subtendens, secundum istas partes 57 partes et 57 minuta fere. Ergo secundum partes quibus linea BR est 120 partes erit linea RK 11 partes et 28 minuta, et erit arcus qui est super eam 10 partes et 58 minuta secundum partes quibus circulus qui describitur circa triangulum BRK ortogonium est 360 partes. Ergo angulus RBD est 10 partes et 58 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes fuit angulus BDA 134 partes et 36 minuta. Ergo angulus BRA totus secundum istas quidem partes erit 145 partes et 34 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes est ipse 72 partes et 47 minuta. Fuit ergo longitudo cursus stelle medii in longitudine in hora considerationis quam narravimus, scilicet puncti B, et est centrum orbis revolutionis a longitudine longiore, 72 partes et 47 minuta. Et propter illud fuit eius locus super 4 partes et 12 minuta Libre. Et quia angulus GEL positus est secundum istas partes due partes et 29 minuta, et hic angulus cum duobus angulis semicirculi ABG, et sunt equales duobus rectis, est equalis aggregationi anguli ARB, et est angulus cursus medii in longitudine, et angulus Probably corrupt for anguli, which would correspond to the Greek text (see Toomer, loc. cit., p. 504, lines 16-17 from the bottom). Paris, BnF, lat. 14738 (167v, line 8 from the bottom) reads angulus too. HBT, et est angulus diversitatis, scilicet angulus motus stelle in orbe revolutionis, erit propterea angulus HBT reliquus eveniens nobis secundum istas partes 109 partes et 42 minuta. Fuit ergo longitudo stelle in hora illius considerationis a longitudine longiore in orbe revolutionis partes quas diximus diversitatis, et sunt 109 partes et 42 minuta. Et hoc est cuius quesivimus inventionem. Nos autem iam demonstravimus quod longitudo eius fuit in hora habitudinis tertie in diversitate a longitudine longiore in orbe revolutionis 171 partes et 25 minuta. Iam ergo superfluunt ei in tempore quod est inter duas considerationes, cuius summa annorum Egyptiorum est quadringenti et decem anni et ducenti et trigintaunus dies et tertia diei fere post revolutiones integras, et sunt ducente et nonagintadue revolutiones 61 partes et 43 minuta. Et illud est propinquum superfluitati que invenitur evenire nobis per tabulas quas fecimus motui eius medio, propterea quod non equavimus motum eius in die nisi ex hoc ut divideremus partes que eveniunt ex numero superfluitatis revolutionum per dies qui proveniunt ex tempore quod est inter duas considerationes. Et illud est quod oportuit nos demonstrare.

⟨X.10⟩ Capitulum decimum: In radice sive in loco motuum stelle Martis revolubilium

Et etiam quia tempus quod est ab anno primo annorum Nabuchodonosor a mense Thut apud Egyptios a die primo eius a medietate diei ad horam huius considerationis dicte est ex annis Egyptiis quadringenti et septuagintaquinque anni et octuaginta dies et medietas diei et quarta fere, et in hoc tempore proveniunt ex superfluitate in longitudine 180 partes et 40 minuta et in diversitate quidem 142 partes et 29 minuta, tunc si nos minuerimus hec duo, scilicet unumquodque ex suo relativo ex duobus locis quos narravimus in consideratione, scilicet ex partibus loci in longitudine, et sunt 4 partes et 22 minuta Libre, et ex partibus loci in diversitate, et sunt 109 partes et 42 minuta, provenient nobis in anno primo annorum Nabuchodonosor in mense eius Thut apud Egyptios in die primo eius in medietate diei duo loca duorum motuum Martis revolubilium, ille quidem qui est in longitudine super tres partes et 32 minuta Arietis et ille qui est in diversitate super 327 partes et 13 minuta a longitudine longiore in orbe revolutionis. Et propter illud idem, quia fuit motus localis longitudinis longioris in 475 annis comprehendens 4 partes et medietatem et quartam partis et fuit longitudo longior Martis in consideratione illa in 21 parte et 25 minutis Cancri, tunc manifestum est quod locus eius erit in tempore posito locorum super 16 partes et 40 minuta Cancri. Et illud est quod voluimus ostendere.

Expleta est dictio decima libri Almagesti Ptolemei Pheludiensis.