⟨XII⟩
Claudii Ptolemei Pheludiensis dictio duodecima libri Almagesti novem capitulis constans fauste prodit.
Capitulum primum: In eo quod necessario est premittendi ad sciendam precessionem stellarum
Capitulum secundum: In declaratione precessionis Saturni
Capitulum tertium: In declaratione precessionis Iovis
Capitulum quartum: In ostensione precessionis Martis
Capitulum quintum: In declaratione precessionis Veneris
Capitulum sextum: In declaratione precessionis Mercurii
Capitulum septimum: In demonstratione faciendi tabulas stationum
Capitulum octavum: In positione tabularum stationum
Capitulum nonum: In declaratione longitudinum maiorum a Sole Veneris et Mercurii
⟨XII.1⟩ Capitulum primum: In eo quod necessario premittendum est ad sciendam antecessionem sive precessionem stellarum quinque erraticarum
Postquam demonstrate sunt iste res, tunc iam sequitur eas etiam consideratio in eo quod est cuiusque stellarum quinque erraticarum ex premissione minore eius et maiore et elevatione probationis secundum quod quantitates illius cum radicibus quas narravi sint convenientes secundum ultimum quod est possibile ex illo ei quod reperitur ex eo per considerationes. Et iam premiserunt et declaraverunt in hac parte doctrine plures scientium disciplinalium et Appollonius, qui fuit ex habitatoribus Fargamis, quod diversitas est una, et est ea que est propter Solem. Quoniam si illud est cum radice in qua agitur secundum orbem revolutionis, ita ut orbis revolutionis sit cursus in longitudine ad successionem signorum super circulum cuius centrum est conveniens centro orbis signorum et stelle cursus sit in diversitate cum est in arcu longitudinis longioris secundum succesionem signorum super orbem revolutionis eius circa centrum eius, tunc cum transierit linea aliqua recta a visibus nostris secans orbem revolutionis ita ut sit proportio medietatis sectionis que separatur ex ea in orbe revolutionis ad lineam que est inter visus nostros et inter lineam orbis revolutionis que est super portionem in qua est longitudo propinquior sicut proportio velocitatis orbis revolutionis ad velocitatem stelle, erit punctum quod provenit a stella que est secundum hunc modum in arcu longitudinis propinquioris in orbe revolutionis determinans quod est inter id quod est stelle ex posterioritate et inter id quod est eius ex precessione, ita ut stellam, cum sit super illud punctum, videamus stantem. Et si fuerit diversitas que est propter Solem necessaria etiam propter radicem in qua agitur secundum orbem egredientis centri, et illud non est possibile ut sit nisi in stellis tribus tantum que elongantur a Sole longitudine tota, ut centrum orbis egredientis centri moveatur circa centrum orbis signorum ad successionem signorum motu equali in velocitate motui Solis, et stella moveatur secundum orbem egredientis centri super centrum suum ad conversionem signorum velocitate equali transitui eius in diversitate, etiam progrediatur linea in orbe egredientis centri transiens super centrum orbis signorum, scilicet super visum, donec sit proportio medietatis linee totius ad minorem duarum sectionum eius que sunt super visum sicut proportio velocitatis orbis egredientis centri ad velocitatem stelle, tunc stella, cum sit super illud punctum super quod dividit linea recta arcum longitudinis propinquioris orbis egredientis centri, videbimus eam stantem. Et nos etiam sumus demonstrantes hanc intentionem non minus quam illi demonstraverunt breviori via et faciliori acceptione et ponentes declarationem communem permixtam in duabus radicibus simul, ut significemus per illud earum convenientiam et earum similitudinem in istis propositionibus etiam.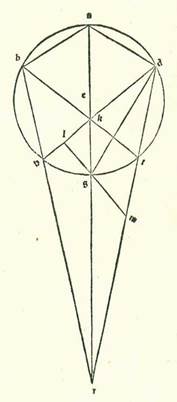 
Sit itaque orbis revolutionis, super quem sint A, B, G, D circa centrum E, et sit eius diametrus AEG, et producatur usque ad punctum R, et est centrum orbis signorum, scilicet visus, et secentur a duobus lateribus puncti G, et est longitudo propinquior, duo arcus equales, sintque GH et GT, et protrahantur a puncto R ad duo puncta H et T due linee RHB et RTD, et applicentur due linee DH et BT sese secantes super punctum K, et manifestum est quod hoc punctum cadit super lineam AG. Dico igitur primum quod proportio linee AR ad lineam RG est sicut proportio linee AK ad lineam KG. Et coniungam lineam AD et lineam DG, et protraham super punctum G lineam LM equidistantem linee AD, et manifestum est quod ipsa est ortogonaliter super lineam DG, propterea quod angulus ADG etiam est rectus. Et quia angulus GDH est equalis angulo GDT, erit linea GL equalis linee GM. Ergo proportio linee AD ad unamquamque earum erit una. Proportio autem linee AD ad lineam GM est sicut proportio linee AR ad lineam RG, et proportio linee AD ad lineam GL est sicut proportio linee AK ad lineam KG. Ergo proportio linee AR ad lineam RG est sicut proportio linee AK ad lineam KG. Si nos ergo imaginemur orbem revolutionis, supra quem sint A, B, G, D, in radice in qua agitur secundum orbem egredientis centri ipsum, sit punctum K centrum orbis signorum et dividitur diametrus AG secundum hanc eandem proportionem que reperitur in radice in qua agitur secundum orbem revolutionis. Quoniam iam ostendimus quod proportio linee AR in orbe revolutionis, et est longius quod est longitudinis, ad lineam RG, et est propinquius quod est longitudinis, est sicut proportio linee AK in orbe egredientis centri, et est longius quod est longitudinis, ad lineam KG, et est propinquius quod est longitudinis. Et dico etiam quod proportio linee DR ad lineam RT est sicut proportio linee BK ad lineam KT. 
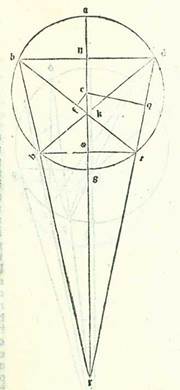Producatur enim in forma huic simili linea BD, et manifestum est quod ipsa est ortogonaliter super diametrum AG, et protrahatur a puncto T linea ST equidistans ei. Et quia linea BN est equalis linee ND, tunc proportio cuiusque earum ad lineam ST est proportio una. Sed proportio linee ND ad lineam ST est sicut proportio linee DR ad lineam RT, et proportio linee BN ad lineam ST est sicut proportio linee BK ad lineam KT. Ergo proportio linee DR ad lineam RT est sicut proportio linee BK ad lineam KT. Ergo secundum compositionem erit proportio duarum linearum DR et RT ad lineam RT sicut proportio linee BT ad lineam TK. Et secundum divisionem, cum producentur due perpendiculares EF et EQ, erit proportio linee QR ad lineam RT sicut proportio linee FT ad lineam TK. Et secundum divisionem erit proportio linee QT ad lineam RT sicut proportio linee FK ad lineam KT. Si ergo fuerit in radice in qua agitur secundum orbem revolutionis linee RD iam protractione producta cum qua sit proportio linee QT ad lineam RT sicut proportio velocitatis orbis revolutionis ad velocitatem stelle, tunc in radice in qua agitur secundum orbem egredientis centri erit proportio linee FK ad lineam KT illa proportio eadem. Causa autem quare non sit hic etiam in statione stellarum hec proportio divisa, scilicet proportio linee FK ad lineam KT, immo non sit nisi proportio non divisa, scilicet proportio linee FT ad lineam KT, est quod proportio velocitatis orbis revolutionis ad velocitatem stelle est proportio cursus in longitudine solum ad cursum diversitatis. Proportio autem velocitatis orbis egredientis centri ad stelle velocitatem est sicut proportio cursus Solis medii, scilicet cursus stelle in longitudine et cursus eius in diversitate, cum aggregantur simul, ad cursum diversitatis. Et propter illud in stella Martis verbi gratia proportio quidem velocitatis orbis revolutionis ad velocitatem stelle est proportio quadragintaduarum partium fere ad trigintaseptem partes. Proportionis namque cursus in longitudine ad proportionem diversitatis iam ostendimus quod hec est summa fere. Et propter hoc erit proportio linee QT ad lineam RT hec proportio. Sed proportio velocitatis orbis egredientis centri ad velocitatem stelle est proportio 77 partium aggregatarum ad 37 partes, scilicet per compositionem fere proportio linee ST ad lineam TK. Quoniam proportio que est secundum divisionem, et est proportio linee FK ad lineam KT, est sicut proportio linee QT ad lineam TR, scilicet sicut proportio quadragintaduarum partium ad trigintaseptem partes. Sit itaque hec summa que precessit et quam scivimus ex istis rebus.
Iam vero remansit apud nos ut declaremus quod he due linee recte que se secant secundum hanc proportionem, cum protrahuntur in unaquaque duarum radicum, erunt duo puncta H et T terminantia duo loca que nos faciunt imaginari stationem in eis. Et oportet necessario ut sit arcus HGT arcus antecessionis et arcus alius reliquus arcus posterioritatis et tarditatis. Apollonius namque premisit ad hoc antecedens ei preparatum secundum hunc modum, et est quia si separetur in triangulo ABG, et latus BG iam positum sit longius latere AG, et linea GD non minor linea AG, erit proportio linee GD ad lineam DB maior proportione anguli ABG ad angulum AGB. Et demonstravit illud secundum hunc modum: Inquit: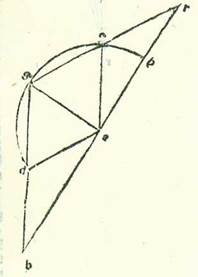 
Compleatur superficies ADGE equidistantium laterum, et producantur due linee AB et GE secundum rectitudinem, et concurrant super punctum R. Et quia linea AE non est minor linea AG, tunc circulus qui describitur supra centrum A et cum longitudine AE aut est ut transeat per dua puncta G et E aut ut transeat ultra punctum G. Signetur igitur transiens per punctum G, sitque circulus GEH. Et quia triangulus AER est maior sectore AEH et triangulus AEG est minor sectore AEG, tunc proportio trianguli AER ad triangulum AEG est maior proportione sectoris AEH ad sectorem AEG. Sed proportio sectoris AEH ad sectorem AEG est sicut proportio anguli EAR ad angulum EAG, et proportio trianguli AER ad triangulum AEG est sicut proportio basis RE ad basim EG. Ergo proportio linee RE ad lineam EG est maior proportione anguli RAE ad angulum EAG. Sed proportio linee RE ad lineam EG est sicut proportio linee GD ad lineam DB, et angulus EAH est equalis angulo ABG, et angulus EAG est equalis angulo BGA. Ergo proportio linee GD ad lineam DB est maior proportione anguli ABG ad angulum AGB. Et manifestum est quod proportio altera est maior quando non ponitur linea GD, scilicet linea AE, equalis linee AG, sed ponitur maior ea. 
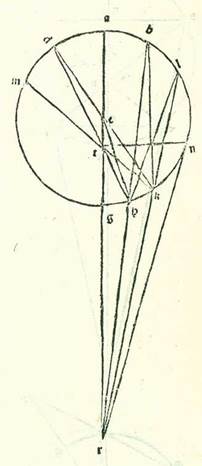Et postquam scitur illud, sit circulus ABGD orbis revolutionis circa centrum E, sitque eius diametrus AEG, et producatur secundum rectitudinem usque ad punctum R, et est visus, protractione cum qua sit proportio linee EG ad lineam GR maior proportione velocitatis orbis revolutionis ad velocitatem stelle. Iam igitur possibile est, si sunt due linee RG et EG sicut diximus, ut producatur linea RHB donec sit proportio medietatis linee BH ad lineam RH sicut proportio velocitatis orbis revolutionis ad velocitatem stelle. Et si nos propter illud cuius precessit ostensio separaverimus arcum AD equalem arcui AB, et produxerimus lineam DTH, et imaginati fuerimus punctum T in radice in qua agitur secundum orbem egredientis centri punctum visus, et fuerit proportio medietatis linee DH ad lineam TH sicut proportio velocitatis orbis egredientis centri ad velocitatem stelle, dico igitur nunc quod quando stella fuerit super punctum H, in ambabus radicibus imaginabitur nobis stans, et quod arcus qui separatur a duabus partibus puncti H, secundum quamcunque quantitatem fuerit, si fuerit ab ea parte que sequitur longitudinem longiorem, invenietur arcus posterioritatis, et si fuerit ab eo quod sequitur longitudinem propinquiorem, invenietur arcus antecessionis. Dividatur igitur ab ea parte que sequitur longitudinem longiorem prius arcus, quocunque modo contingat, sitque arcus KH, et protraham duas lineas RKL et KTM, et applicetur linea BK et linea DK et etiam linea EK et linea EH. Et quia in triangulo BKR linea BH est maior linea BK, tunc proportio linee BH ad lineam HR est maior proportione anguli HRK ad angulum HBK. Quapropter erit proportio medietatis linee BH ad lineam HR maior proportione anguli HRK ad duplum anguli KBH, scilicet angulum KEH. Sed proportio medietatis linee BH ad lineam HR est sicut proportio velocitatis orbis revolutionis ad velocitatem stelle. Ergo proportio anguli HRL ad angulum KEH est minor proportione velocitatis orbis revolutionis ad velocitatem stelle. Angulus ergo cuius proportio ad angulum KEH est sicut proportio velocitatis orbis revolutionis ad velocitatem stelle est maior angulo HRK, sit igitur angulus HRN. Et quia tempori in quo percurrit stella arcum KH orbis revolutionis in tempore simili iam movetur centrum orbis revolutionis ad contrarium illius partis cursu equali longitudini que est inter lineam RH et inter lineam RN, tunc manifestum est quod in tempore simili illi tempori arcus KH orbis revolutionis iam movit stellam anterius in angulo apud visum nostrum, et est angulus HRK, minore angulo in quo movit ipsam orbis revolutionis ipse ad contrarium, scilicet angulo HRN, ita ut sit stella iam posteriorata secundum angulum KRN. Et secundum hoc exemplum convenit nobis ut consideremus in radice in qua agitur secundum orbem centri egredientis. Dico ergo quia proportio linee BH ad lineam RH est maior proportione anguli HRL ad angulum HBK, tunc secundum compositionem erit proportio linee BR ad lineam RH maior proportione anguli BKL extrinseci a triangulo ad triangulum HBK. Proportio autem linee BR ad lineam RH est sicut proportio linee DT ad lineam HT, et angulus BKL est equalis angulo DKM, et angulus HBK est equalis angulo HDK. Ergo proportio linee DT ad lineam TH est maior proportione anguli DKM ad angulum HDK. Quapropter secundum compositionem erit proportio linee DH ad lineam HT maior proportione anguli HTK extrinseci a triangulo DTK ad angulum HDK. Secundum divisionem igitur erit proportio medietatis linee DH ad lineam HT maior proportione anguli HTK ad duplum anguli HDK, scilicet angulum HEK. Proportio vero medietatis linee DH ad lineam HT est sicut proportio velocitatis orbis egredientis centri ad velocitatem stelle. Ergo proportio anguli HTK ad angulum HEK est minor proportione velocitatis orbis egredientis centri ad velocitatem stelle. Angulus igitur cuius proportio ad angulum HEK est sicut proportio velocitatis orbis egredientis centri ad velocitatem stelle est maior angulo HTK. Sit igitur etiam angulus HTN. Et quia in tempore equali percurrit stella ipsa arcum KH, et movetur anterius angulo KTH, et movet eam orbis egredientis centri per motum suum in seipso ad successionem signorum angulo HTN, et est maior angulo KTH, tunc manifestum est quod hoc modo etiam videtur stella posteriorata angulo KTN. Ex his autem que cum hic Probably corrupt for hoc, which is also the reading of Paris, BnF, lat. 14738 (186r, line 13). The Greek text is somewhat different here (see Toomer, loc. cit., p. 561, line 18). facilius faciunt scire illud est quod iste res eedem demonstrabunt contrarium illius si nos posuerimus in forma simili huic proportionem medietatis linee LK ad lineam KR sicut proportionem velocitatis orbis revolutionis ad velocitatem stelle donec sit etiam proportio medietatis linee KM ad lineam KT sicut proportio velocitatis orbis egredientis centri ad velocitatem orbis revolutionis et imaginati fuerimus arcum KH iam separatum ab ea parte que sequitur longitudinem propinquiorem a linea LR. Cum ergo producta fuerit linea LH et provenerit triangulus LRH et fuerit posita in eo linea KR longior linea HR, fiet proportio linee LK ad lineam KR minor proportione anguli HRL ad angulum HLK. Quapropter erit etiam proportio medietatis linee LK ad lineam KR minor proportione anguli HRK ad duplum anguli HLK, scilicet angulum KEH. Et econverso eius quod declaravimus etiam proveniet secundum illas res easdem contrarium illius, et est ut anguli KEH proportio ad angulum HRK sit minor proportione velocitatis stelle ad velocitatem orbis revolutionis et proportio quidem eius ad angulum HEK sit minor proportione velocitatis stelle ad velocitatem orbis egredientis centri donec sit angulus cuius proportio ad hunc angulum est equalis huic proportioni maior angulo KEH et ut sit etiam motus antecessionis maior motu posterioritatis. Et manifestum est quod in longitudinibus in quibus est proportio linee EG ad lineam GR non maior proportione velocitatis orbis revolutionis ad velocitatem stelle non est possibile, si fuerit linea AGR recta in proportione huic simili, ut videatur stella stans neque precedens. Et illud est quia propterea quod iam fuit posita in triangulo EKR linea EG non minor linea EK, tunc proportio anguli GRK ad angulum GEK erit minor proportione linee EG ad lineam GR. Sed proportio linee EG ad lineam GR non est maior proportione velocitatis orbis revolutionis ad velocitatem stelle. Ergo proportio anguli GRK ad angulum GEK est minor proportione velocitatis orbis revolutionis ad velocitatem stelle. Quapropter quia nos iam ostendimus quod ubicunque convenerit illud quod stella videtur posterior, tunc nos vero invenimus orbis revolutionis neque orbis egredientis centri arcum omnino in quo videatur antecedens.
⟨XII.2⟩ Capitulum secundum: In declaratione antecessionis Saturni
Et quia illud est ita, tunc nos modo narrabimus numerationem antecessionis in una et in una stellarum secundum quod sequitur ex radicibus que firmate sunt. Et incipiemus in hoc a Saturno secundum hunc modum: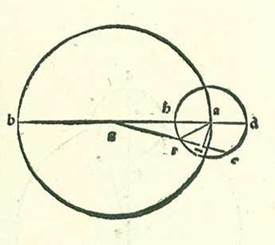 
Sit itaque circulus qui revolvit centrum orbis revolutionis, supra quem sint A, B, circa diametrum AGB, et ponam supra ipsam centrum orbis signorum, scilicet visum, super punctum G, et signabo circa centrum A orbem revolutionis, supra quem sint D, E, R, H, et producam lineam GRE protractione cum qua sit, cum protraheretur super ipsam perpendicularis AT, proportio medietatis linee ER, et est linea RT, ad lineam GR sicut proportio velocitatis orbis revolutionis ad velocitatem stelle. Et ponam primum ut orbis revolutionis sit positus in longitudine media donec sint duo motus eius ipsimet, quos volo motum in loco et quod est propinquum ei, ita ut inter visionem eorum et inter illud quod est secundum orbem signorum non sit plurima diversitas. Quoniam motus eius hic in cursibus eius mediis duobus revolubilibus in longitudine et diversitate sunt ipsimet secundum propinquitatem duo motus eius qui videntur secundum centrum orbis signorum. Et quia in stella Saturni secundum partes quibus linea GA, et est linea longitudinis medie, est 60 partes iam ostensum est quod linea AD, et est ea que est a centro orbis revolutionis, est 6 partes et medietas partis donec sit linea GD tota 66 partes et 30 minuta, et est linea GH reliqua secundum istas partes 53 partes et 30 minuta, et est superficies ortogonia quam continent 3557 partes et 45 minuta, sed superficies ortogonia quam continent due linee DG et GH est equalis ei quam continent due linee EG et GR, tunc proveniet nobis etiam superficies quam continent due linee EG et GR 3557 partes et 45 minuta. Et etiam propterea quod secundum quod sequitur cursus medios secundum partes quibus velocitas orbis revolutionis est unum, scilicet linea RT, est velocitas stelle, scilicet linea RG, 28 partes et 25 minuta et 46 secunda fere donec proveniat linea EG tota 30 partes et 25 minuta et 46 secunda et superficies ortogonia quam continent due linee EG et GR secundum istas partes est 865 partes et 5 minuta et 32 secunda, tunc si nos diviserimus per numerum 865 partium et 5 minutorum et 32 secundorum tria milia et quingentas et quinquagintaseptem partes et 45 minuta, et eius quod provenerit ex divisione, et est quatuor partes et sex minuta et 45 secunda, acceperimus latus, et est due partes et unum minutum, 240 secunda, et multiplicaverimus ipsum in numerum linee TR, et est unum secundum seipsum, et in numerum linee RG, et est 28 partes et 25 minuta et 46 secunda, proveniet nobis linea TR etiam due partes et minutum unum et 40 secunda secundum partes quibus linea AR est sex partes et 30 minuta et linea AG est 60 partes, et proveniet linea GR secundum istas partes 57 partes et 38 minuta et 55 secunda. Et quia cum protrahitur linea AR, tunc secundum partes quibus linea AR est sex partes et 30 minuta est linea RT due partes et minutum unum et 40 secunda et secundum partes quibus linea AR est 120 partes est linea TR 37 partes et 26 minuta et 9 secunda, erit etiam arcus qui est super lineam TR 36 partes et 21 minutum et 15 secunda secundum partes quibus circulus qui describitur circa triangulum ART ortogonium est 360 partes, et erit angulus RAT secundum partes quibus duo anguli recti sunt 360 partes 36 partes et 21 minutum et 15 secunda et secundum partes quibus quatuor anguli recti sunt 360 partes 18 partes et 10 minuta et 38 secunda fere. Et etiam quia secundum partes quibus chorda GA est 60 partes linea GRT tota provenit 59 partes et 40 minuta et 35 secunda et secundum partes quibus chorda GA est 120 partes est linea GRT 119 partes et 21 minutum et 10 secunda, erit arcus etiam qui est super lineam GT 168 partes et 5 minuta et 39 secunda secundum partes quibus circulus qui describitur circa triangulum AGT ortogonium est 360 partes, et erit angulus HAT secundum partes quibus duo anguli recti sunt 360 partes 168 partes et 5 minuta et 39 secunda et secundum partes quibus quatuor anguli recti sunt 360 partes parpartes M. 84 partes et duo minuta et 50 secunda fere. Et propter illud proveniet nobis angulus AGT partes relique ad complendum angulum rectum, et sunt quinque partes et 57 minuta et 10 secunda, et angulus RAH partes relique post angulum RAT, et sunt 65 partes et 52 minuta et 12 secunda. Si ergo stella in statione prima fuit visa super lineam RG et visa in habitudine que nominatur extremitas noctis super lineam GH, tunc manifestum est quod si centrum orbis revolutionis non moveretur secundum aliquid ad successionem signorum, partes arcus RH eius, et sunt 65 partes et 52 minuta et 12 secunda, comprehenderent ex antecessione partes anguli AGR, et sunt quinque partes et 57 minuta et 10 secunda. Sed propterea quod in hac proportione posita, que est velocitas orbis revolutionis ad velocitatem stelle, iam comprehenderunt etiam partes que posite sunt diversitati, et sunt 65 partes et 52 minuta et 12 secunda, partes longitudinis, et sunt due partes et 19 minuta fere, proveniet nobis antecessio quidem que est ab una duarum horarum ad habitudinem que nominatur extremitas noctis partes relique, et sunt tres partes et 38 minuta et 10 secunda et ex diebus 69 dies, et sunt dies in quibus fere movetur hec stella duabus partibus et 19 minutis revolutionis in longitudine, et antecessio quidem tota erit septem partes et 16 minuta et 20 secunda et ex diebus 138 dies.
Deinde post hoc sumus considerantes in his quantitatibus in maiore longitudine cum his rebus eisdem, scilicet cum fuerit habitudo que nominatur extremitas noctis media inter illas duas horas in quibus est centrum orbis revolutionis super ipsum punctum quod est in longitudine longiore in orbe egredientis centri et fuerit unaqueque duarum horarum et res in eo manifesta super elongationem in longitudine equali propinqua partibus que firmate sunt secundum proportionem mediam, et sunt due partes et 19 minuta, ab habitudine que nominatur extremitas noctis, scilicet a longitudine longiore.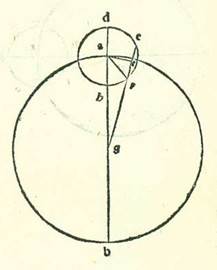 
Et ex hoc loco etiam linea AG, et est linea longitudinis in illa hora, reperitur cum intentionibus quas premisimus et abreviavimus non diversa a maiori longitudine. Quod autem provenit parti uni longitudinis ex additione et diminutione reperitur propinquum sex minutis et 30 secundis donec sit proportio longitudinis equate ad diversitatem equatam, scilicet velocitatis que videtur in illa hora orbis revolutionis ad velocitatem que videtur stelle, sicut proportio 53 minutorum et 30 secundorum ad 28 partes et 32 minuta et 16 secunda. In hac igitur forma eadem, propterea quod secundum partes quibus linea DA, et est ea que est a centro orbis revolutionis, est sex partes et 30 minuta est linea GA, quia fuit non diversa a maiori quod est ex longitudine, 63 partes et 25 minuta et propter illud provenit linea DG tota 69 partes et 55 minuta et provenit linea GH 56 partes et 55 minuta, erit superficies ortogonia quam continent, scilicet que continetur ab his duabus lineis EG et GR, 3979 partes et 25 minuta et 25 secunda, et secundum partes quibus posita est linea RT 53 minuta et 30 secunda, et sunt ea que sunt velocitatis orbis revolutionis, et linea GR 28 partes et 32 minuta et 16 secunda, et sunt partes que sunt velocitatis stelle, et linea EG tota est 30 partes et 19 minuta et 16 secunda, erit superficies ortogonia que continetur ab his duabus lineis GR et GE 865 partes et 17 minuta et 50 secunda. Cum nos igitur diviserimus 3979 partes et 25 minuta et 25 secunda per 865 partes et 17 minuta et 50 secunda, et iverimus scienter ad illud quod provenit ex divisione, et est 4 partes et 35 minuta et 56 secunda, et acceperimus latus eius, et est due partes et octo minuta et 40 secunda, et multiplicaverimus ipsum per partes linee TR secundum seipsas, et sunt 53 minuta et 30 secunda, et per partes linee RG secundum illud exemplum, et sunt 28 partes et 32 minuta et 16 secunda, proveniet nobis linea TR pars una et 54 minuta et 44 secunda secundum partes quibus linea AR est sex partes et 30 minuta et linea AG secundum illud exemplum 63 partes et 25 minuta, et linea GR proveniet secundum istas partes 61 partes et 11 minuta et 52 secunda. Ergo linea GT tota erit 63 partes et sex minuta et 36 secunda. Ergo secundum partes quibus chorda AR est 120 partes erit linea TR 35 partes et 18 minuta et 9 secunda, et secundum partes quibus chorda GA etiam est 120 partes erit linea GT 119 partes et 25 minuta et 11 secunda. Et propter illud erit arcus qui est super lineam RT 34 partes et 13 minuta et 4 secunda secundum partes quibus circulus qui describitur circa triangulum ART ortogonium est 360 partes, et erit arcus qui est super lineam TG 168 partes et 43 minuta et 38 secunda secundum partes quibus circulus qui describitur circa triangulum ATG ortogonium est 360 partes. Ergo secundum partes quibus duo anguli recti sunt 360 partes erit angulus RAT 34 partes et 13 minuta et 4 secunda, et erit angulus GAT secundum illud exemplum 168 partes et 43 minuta et 38 secunda. Sed secundum partes quibus quatuor anguli recti sunt 360 partes erit angulus RAT 17 partes et 6 minuta et 32 secunda, et erit angulus GAT secundum illud exemplum 84 partes et 21 minuta et 49 secunda, et angulus AGT reliquus, et est ille qui est ab una duarum horarum ad habitudinem que nominatur extremitas noctis, si non fuerit orbis revolutionis diminutus ab aliquo, proveniet nobis 5 partes et 38 minuta et 11 secunda, et proveniet angulus RAH reliquus etiam, et est angulus cursus qui videtur in orbe revolutionis, in hac longitudine eadem 67 partes et 15 minuta et 17 secunda. Et cum istarum partium fuerit proportio longitudinis equate secundum proportionem duarum velocitatum acceptarum in longitudine longiore due partes et sex minuta et sex secunda, tunc medietas antecessionis totius proveniet nobis partes relique, et sunt tres partes et 32 minuta et 5 secunda et ex diebus 70 dies et tertia diei, et sunt dies in quibus fere movetur hec stella duabus partibus et 21 minutis et 25 secundis, et sunt partes revolubiles que debentur partibus que posite sunt longitudinis equate, et sunt due partes et sex minuta et sex secunda, et provenit antecessio tota septem partes et quatuor minuta et decem secunda et ex diebus 140 dies et due tertie diei. Et nos considerabimus etiam ad similitudinem illarum rerum in quantitatibus in minori longitudine in illa forma eadem cum fuerit habitudo que nominatur extremitas noctis media inter duas horas in ipsa longitudine propinquiore orbis egredientis centri et fuerit unaqueque duarum horarum in elongatione nota in longitudine ab habitudine que nominatur extremitas noctis, scilicet a longitudine propinquiore. Et in hoc loco reperietur linea AG, et est linea elongationis in illa habitudine, non diversa secundum illud exemplum linee minoris longitudinis. Et illud quod pertinebit parti uni in longitudine ex additione et diminutione erit propinquum septem minutis et 20 secundis donec sit in hoc loco etiam proportio velocitatis orbis revolutionis que videtur ad velocitatem stelle que videtur ipsa proportio partis unius et septem minutorum et 20 secundorum ad 28 partes et 18 minuta et 26 secunda. Quapropter secundum partes quibus linea TR est pars una et septem minuta et 20 secunda erit linea GR 28 partes et 18 minuta et 26 secunda, et linea EG tota 30 partes et 33 minuta et 6 secunda, et superficies ortogonia que continetur ab his duabus lineis EG et GR erit 864 partes et 49 minuta et 58 secunda. Et secundum partes etiam quibus linea DA, que est a centro orbis revolutionis, est sex partes et 30 minuta erit linea AG, quia non differt inter ipsam et inter minorem longitudinem, 56 partes et 35 minuta. Et propter illud erit linea DG tota secundum istas partes 63 partes et 5 minuta, et erit linea GH reliqua 50 partes et 5 minuta, et superficies ortogonia que continetur ab his duabus lineis EG et GR erit 3159 partes et 25 minuta et 25 secunda. Ergo cum nos diviserimus secundum illud exemplum 3159 partes et 25 minuta et 25 secunda per 864 partes et 49 minuta et 58 secunda, et eius quod provenerit ex divisione, et est 3 partes et 39 minuta et 12 secunda, acceperimus latus, et est pars una et 54 minuta et 41 secunda, et multiplicaverimus ipsum in partes linee RT secundum seipsas, et sunt pars una et 17 minuta et 20 secunda, et in partes linee RG secundum illud exemplum, et sunt 28 partes et 18 minuta et 26 secunda, proveniet nobis linea TR due partes et octo minuta et 43 secunda secundum partes quibus linea AR, que est a centro orbis revolutionis, est sex partes et 30 minuta et linea AG, et est linea longitudinis in illa habitudine, est 56 partes et 35 minuta, et linea quidem GR secundum istas partes erit 54 partes et 6 minuta et 22 secunda, et linea quidem GT tota secundum illud exemplum erit 56 partes et 15 minuta et 5 secunda. Ergo secundum partes quibus chorda AR est 120 partes erit linea TR 39 partes et 36 minuta et 18 secunda, et secundum partes quibus chorda AG est 120 partes erit linea GT secundum illud exemplum 119 partes et 17 minuta et 46 secunda. Quapropter erit arcus qui est super lineam RT 38 partes et 32 minuta et 34 secunda secundum partes quibus circulus qui describitur circa triangulum ART ortogonium est 360 partes, et erit arcus qui est super lineam GT 167 partes et 34 minuta et 54 secunda secundum partes quibus circulus qui describitur circa triangulum AGT ortogonium est 360 partes. Quapropter secundum partes quibus duo anguli recti sunt 360 partes erit angulus RAT 38 partes et 32 minuta et 34 secunda, et angulus HAT secundum illud exemplum erit 167 partes et 34 minuta et 54 secunda. Et secundum partes quibus quatuor anguli recti sunt 360 partes erit angulus RAT 19 partes et 16 minuta et 17 secunda, et erit angulus HAT secundum illud exemplum 83 partes et 47 minuta et 27 secunda. Proveniet ergo nobis angulus AGT reliquus, et est angulus antecessionis que est propter velocitatem stelle ab una duarum horarum ad habitudinem que nominatur extremitas noctis, sex partes et 12 minuta et 33 secunda, et proveniet nobis angulus RAH reliquus, et est angulus cursus qui videtur in orbe revolutionis in hac longitudine eadem, 64 partes et 31 minuta et 10 secunda. Et cum secundum istas partes provenerunt ex longitudine equata secundum proportionem inter duas velocitates acceptas a longitudine propinquiore duas partes et 33 minuta et 28 secunda, tunc medietas antecessionis totius proveniet nobis 3 partes et 39 minuta et 5 secunda et ex diebus 68 dies, et sunt dies in quibus fere movetur stella per motum suum medium duabus partibus et 16 minutis et 45 secundis, et sunt partes revolubiles que pertinent partibus quas diximus longitudinis equate, et sunt due partes et 33 minuta et 28 secunda, et erit longitudo tota septem partes et 18 minuta et 10 secunda et ex diebus 136 dies.
⟨XII.3⟩ Capitulum tertium: In declaratione antecessionis Iovis
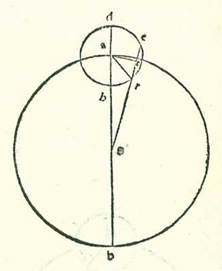In stella autem Iovis proportio linee TR ad lineam GR aggregatur et provenit secundum numerationem in longitudine media proportio partis unius ad 10 partes et 51 minuta et 29 secunda, et provenit proportio linee EG ad lineam GR proportio 12 partium et 51 minutorum et 29 secundorum ad 10 partes et 51 minuta et 29 secunda, et superficies ortogonia quam ipse continent erit 139 partes et 36 minuta et 48 secunda, et erit etiam proportio linee GA ad lineam AH proportio 60 partium ad 11 partes et 32 minuta et 30 secunda. Ergo proportio linee DG ad lineam GH est proportio 61 partium et 30 minutorum ad 48 partes et 30 minuta, et superficies ortogonia quam ipse continent est 3467 partes et 45 minuta. Et partium que proveniunt ex divisione, et sunt 24 partes et 59 minuta et 17 secunda, et cum acceperimus latus, et est 4 partes et 59 minuta et unum secundum, et multiplicaverimus ipsum in proportionem dictam narratam (per multiplicationem in proportionem volo in hoc loco multiplicationem in duas quantitates inter quas est proportio duarum linearum RG et RT), proveniet linea TR secundum quantitatem duarum linearum GA et AR que posite sunt 4 partes et 59 minuta et unum secundum, et proveniet linea GR secundum istas partes 54 partes et sex minuta et 44 secunda, et erit linea GT tota 59 partes et 5 minuta et 45 secunda. Et propter illud erit secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG linea RT 52 partes et 10 secunda, et linea GT secundum illud exemplum 118 partes et 11 minuta et 30 secunda, et erit arcus qui est super lineam RT duorum arcuum qui sunt super eas 51 partes et 21 minuta et 41 secunda, et arcus qui est super lineam GT 160 partes et 4 minuta et 55 secunda. Et sequitur ex hoc ut proveniat angulus RAT 25 partes et 40 minuta et 50 secunda fere secundum partes quibus quatuor anguli recti sunt 360 partes et angulus HAT secundum istas partes 82 partes et 2 minuta et 28 secunda. Duorum vero angulorum reliquorum angulus quidem RGA, et est angulus antecessionis qui est propter velocitatem stelle, erit 9 partes et 57 minuta et 32 secunda, et angulus RAH erit partes diversitatis que videntur, et sunt 54 partes et 21 minuta et 38 secunda. Et quia illud quod pertinet istis partibus cursus in longitudine secundum hanc proportionem narratam est quinque partes et unum minutum et 24 secunda, tunc medietas antecessionis erit 4 partes et 56 minuta et octo secunda et ex diebus 60 dies et medietas diei fere. Et erit antecessio tota 9 partes et 52 minuta et 16 secunda et ex diebus 121 dies. Et longitudo cuius summa a longitudine longiore et a longitudine propinquiore non est nisi quinque partes est minor maiore longitudine et est maior minore longitudine secundum id in quo non est diversitas. Secundum numerationem vero apud maiorem longitudinem invenitur additio et diminutio equationis quinque minuta et decem secunda. Et propter illud erit proportio linee TR ad lineam GR proportio 54 minutorum et 50 secundorum ad 10 partes et 56 minuta et 39 secunda, et erit proportio linee EG ad lineam GR proportio 12 partium et 46 minutorum et 19 secundorum ad 10 partes et 56 minuta et 39 secunda, et erit superficies ortogonia quam ipse continent 139 partes et 46 minuta et 42 secunda, et erit etiam proportio linee GA ad lineam AH sicut proportio 62 partium et 45 minutorum ad 11 partes et 30 minuta, et proportio linee DG ad lineam GH est proportio 74 partium et 15 minutorum ad 51 partes et 15 minuta, et erit superficies ortogonia quam ipse continent 3805 partes et 18 minuta et 45 secunda, et erunt partes que proveniunt ex divisione 27 partes et 13 minuta et 26 secunda. Et cum acceperimus latus earum, et est 5 partes et 13 minuta et 4 secunda, et multiplicaverimus in proportionem que est duarum linearum TR et RG narratam, proveniet linea RT secundum duas quantitates duarum linearum AG et AR narratas 4 partes et 46 minuta et 6 secunda, et proveniet linea GR secundum istas partes 57 partes et sex minuta et 19 secunda, et erit linea GT tota 61 pars et 52 minuta et 25 secunda. Quapropter erit secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG linea quidem RT 49 partes et 45 minuta et 23 secunda, et linea GT secundum illud exemplum 118 partes et 19 minuta et 27 secunda, et duorum arcuum qui sunt super eas arcus quidem qui est super lineam RT erit 48 partes et 59 minuta et 34 secunda, et arcus qui est super lineam GT erit 160 partes et 49 minuta et 36 secunda. Et sequitur ex hoc ut sit angulus RAT etiam 24 partes et 29 minuta et 47 secunda secundum partes quibus quatuor anguli recti sunt 360 partes et sit angulus HAT secundum istas partes 80 partes et 24 minuta et 48 secunda. Duorum autem angulorum reliquorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 9 partes et 35 minuta et 12 secunda, et angulus RAH erit partes diversitatis que videtur, et sunt 55 partes et 55 minuta et unum secundum. Et quia istis partibus pertinet secundum proportionem acceptam a longitudine longiore in longitudine equata 4 partes et 40 minuta et 35 secunda et longitudinis revolubilis 5 partes et 6 minuta et 35 secunda, tunc medietas antecessionis erit 4 partes et 54 minuta et 37 secunda et ex diebus 61 dies et medietas diei fere. Et erit antecessio tota 9 partes et 49 minuta et 14 secunda et ex diebus 123 dies. Secundum numerationem vero apud minorem longitudinem additio et diminutio equationis invenitur quinque minuta et due tertie minuti. Quapropter erit proportio linee TR ad lineam RG proportio partis unius et 5 minutorum et 40 secundorum ad 10 partes et 45 minuta et 49 secunda, et erit proportio linee EG ad lineam GR proportio 12 partium et 57 minutorum et 9 secundorum ad 10 partes et 45 minuta et 49 secunda, et erit superficies ortogonia quam ipse continent 139 partes et 24 minuta et 56 secunda, et erit etiam proportio linee GA ad lineam AH proportio 57 partium et 15 minutorum ad 11 partes et 30 minuta, et erit proportio linee DG ad lineam GH proportio 68 partium et 45 minutorum ad 45 partes et 45 minuta, et erit superficies ortogonia que continetur ab eis 3145 partes et 18 minuta et 45 secunda. Cum ergo partium que provenerunt ex divisione, et sunt 22 partes et 33 minuta et 39 secunda, accipietur latus, et est 4 partes et 45 minuta, et multiplicabitur in proportionem que est duarum linearum TR et RG narratam, proveniet secundum duas quantitates GA et AR narratas linea quidem TR 5 partes et 11 minuta et 55 secunda, et linea GR secundum istas partes 51 partes et 7 minuta et 38 secunda, et erit linea GT tota 56 partes et 19 minuta et 33 secunda. Quapropter secundum proportionem 120 partium ad unamquamque duarum chordarum RA et AG erit linea RT 54 partes et 14 minuta et 47 secunda, et erit linea TG secundum illud exemplum 118 partes et tria minuta et 46 secunda. Arcuum vero duorum qui sunt super eas arcus quidem qui est super lineam RT erit 53 partes et 45 minuta et 4 secunda, et arcus qui est super lineam GT erit 159 partes et 22 minuta et 40 secunda. Et sequitur ex hoc ut sit angulus RAT etiam 26 partes et 52 minuta et 32 secunda secundum partes quibus quatuor anguli recti sunt 360, et erit angulus GAT secundum istas partes 79 partes et 41 minuta et 20 secunda.
Duorum vero angulorum reliquorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 10 partes et 18 minuta et 40 secunda, et angulus RAH erit partes diversitatis que videtur, et sunt 52 partes et 48 minuta et 48 secunda. Et cum pertinuerint istis partibus secundum proportionem narratam in longitudine propinquiore ex longitudine quidem equata 5 partes et 21 minuta et 20 secunda et ex longitudine revolubili 4 partes et 54 minuta et 20 secunda, tunc medietas antecessionis provenit 4 partes et 56 minuta et 20 secunda et ex diebus 59 dies fere. Et erit antecessio tota 9 partes et 54 minuta et 40 secunda et ex diebus 118 dies.
⟨XII.4⟩ Capitulum quartum: In demonstratione antecessionis Martis
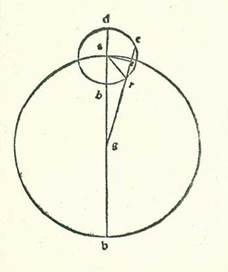Et in antecessione Martis etiam quod aggregatur per numerationem proportionis linee TR ad lineam GR in longitudine media est proportio partis unius ad 52 minuta et 51 secunda et proportionis inter duas lineas EG et GR proportio duarum partium et 52 minutorum et 51 secundorum ad 52 minuta et 51 secunda, et erit superficies ortogonia quam ipse continent due partes et 32 minuta et 15 secunda, et erit etiam proportio linee GA ad lineam AH proportio 60 partium ad 39 partes et 30 minuta, et proportio linee GD ad lineam HG proportio 99 partium et 30 minutorum ad 20 partes et 30 minuta, et erit superficies ortogonia que continetur ab eis 2039 partes et 45 minuta. Et cum partium que proveniunt ex divisione, et sunt 803 partes et 50 minuta et 32 secunda, acceptum fuerit latus, et est 28 partes et 21 minuta et 8 secunda, et multiplicatum fuerit in proportionem narratam duarum linearum RT et RG, provenient secundum quantitates duas duarum linearum AG et AR dictas linea RT 28 partes et 21 minutum et octo secunda, et linea GR secundum istas partes 24 partes et 58 minuta et 25 secunda, et fit linea GT tota 53 partes et 19 minuta et 33 secunda. Quapropter erit linea RT secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG 86 partes et octo minuta, et erit linea GT secundum illud exemplum 106 partes et 39 minuta et sex secunda. Duorum igitur arcuum arcus quidem qui est super lineam RT erit 91 partes et 44 minuta et 35 secunda, et erit arcus qui est super lineam GT 125 partes et 26 minuta et 10 secunda. Et iam sequitur ex hoc ut sit angulus RAT 45 partes et 52 minuta et 17 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus GAT secundum istas partes 62 partes et 43 minuta et 5 secunda. Duorum vero angulorum reliquorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 27 partes et 16 minuta et 55 secunda, et erit angulus RAH partes diversitatis, et sunt 16 partes et 50 minuta et 48 secunda. Et quia est quod pertinet istis partibus ex cursu in longitudine in hac proportione narrata 19 partes et 7 minuta et 33 secunda, tunc medietas antecessionis fit 8 partes et 9 minuta et 22 secunda et ex diebus 36 dies et medietas diei fere, et fit antecessio tota 16 partes et 18 minuta et 44 secunda et ex diebus 73 dies. Et longitudo stationis inter quam colligitur spacium et inter longitudinem longiorem et stationis inter quam et inter longitudinem propinquiorem sunt 16 partes et 7 minuta et 33 secunda. Illa quidem est minor maiore longitudine, et hec quidem est maior minore longitudine viginti minutis fere secundum longitudinem mediam. Apud longitudinem autem maiorem invenitur secundum numerationem additionis et diminutionis equationis secundum portionem partis unius decem minuta et tertia minuti. Et propter illud erit proportio linee TR ad lineam RG proportio 49 minutorum et 40 secundorum ad partem unam et tria minuta et 11 secunda, et erit proportio linee EG ad lineam GR proportio duarum partium et 42 minutorum et 31 secundorum ad partem unam et tria minuta et 11 secunda, et erit superficies ortogonia quam ipse continent due partes et 51 minuta et octo secunda, et erit etiam proportio linee GA ad lineam AH proportio 65 partium et 40 minutorum ad 39 partes et 30 minuta et octo secunda. Proportio linee DG ad lineam GH est proportio 105 partium et 10 minutorum ad 26 partes et 10 minuta. Et erit superficies ortogonia quam ipse continent 2751 partes et 51 minuta et 40 secunda. Et partium que proveniunt ex divisione, et sunt 964 partes et 48 minuta et 47 secunda, cum acceptum fuerit latus, et est 31 partes et tria minuta et 41 secunda, et multiplicabitur in proportionem narratam duarum linearum TR et GR, proveniet secundum duas quantitates duarum linearum GA et AR narratas linea TR 25 partes et 42 minuta et 43 secunda, et linea GR secundum istas partes 32 partes et 42 minuta et 34 secunda, et est linea GT tota 58 partes et 25 minuta et 17 secunda. Quapropter secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG fit linea TR 78 partes et 6 minuta et 44 secunda, et fit linea GT secundum illud exemplum 106 partes et 45 minuta et 36 secunda. Duorum vero arcuum arcus qui est super lineam RT erit 81 partes et 13 minuta et octo secunda, et erit arcus qui est super lineam GT 125 partes et 39 minuta et 46 secunda. Et iam sequitur ex hoc ut angulus RAT sit etiam 40 partes et 36 minuta et 34 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus HAT secundum istas partes 62 partes et 49 minuta et 53 secunda. Duorum vero angulorum reliquorum angulus RGA, et est angulus longitudinis que est propter velocitatem stelle, erit 27 partes et 10 minuta et 7 secunda, et angulus RAH erit partes diversitatis que videtur, et sunt 22 partes et 13 minuta et 19 secunda. Et quia illud quod pertinet istis partibus secundum proportionem acceptam in longitudine longiore ex longitudine quidem equata est 17 partes et 13 minuta et 21 secunda et ex longitudine revolubili 20 partes et 58 minuta et 21 secunda, tunc medietas antecessionis proveniet 9 partes et 56 minuta et 46 secunda et ex diebus 40 dies fere. Ergo erit antecessio tota 19 partes et 53 minuta et 32 secunda et ex diebus 80 dies. Apud vero minorem longitudinem invenitur secundum numerationem additionis et diminutionis equationis 12 minuta et 40 secunda. Quapropter erit proportio linee TR ad lineam RG proportio partis unius et 12 minutorum et 40 secundorum ad 40 minuta et 11 secunda, et erit proportio linee EG ad lineam GR proportio trium partium et 5 minutorum et 31 secundorum ad 40 partes et 11 minuta, et erit superficies ortogonia quam ipse continent due partes et 4 minuta et 14 secunda, et erit etiam proportio linee GA ad lineam AH proportio 54 partium et 20 minutorum ad 39 partes et 30 minuta, et erit proportio linee DG ad lineam GH proportio 93 partium et 50 minutorum ad 14 partes et 50 minuta, et erit superficies ortogonia quam ipse continent 1391 partes et 51 minuta et 40 secunda. Et partium que proveniunt ex divisione, et sunt 672 partes et 13 minuta, cum acceptum fuerit latus, et est 25 partes et 55 minuta et 38 secunda, et multiplicabitur in proportionem narratam duarum linearum TR et RG, proveniet per illud secundum duas quantitates duarum linearum GA et AR narratas linea quidem TR 31 partes et 24 minuta et 3 secunda, et linea GR secundum istas partes 17 partes et 21 minutum et 51 secundum, et est linea GT tota 48 partes et 45 minuta et 54 secunda. Et propter illud fit linea RT secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG 95 partes et 23 minuta et 42 secunda, et fit linea GT secundum illud exemplum 107 partes et 42 minuta et 7 secunda. Duorum autem arcuum arcus qui est super lineam RT erit 105 partes et 18 minuta et 10 secunda, et erit arcus qui est super lineam GT 127 partes et 40 minuta et 42 secunda. Et sequitur ex hoc ut sit etiam angulus RAT 52 partes et 39 minuta et 5 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus GAT secundum istas partes 63 partes et 50 minuta et 11 secunda. Duorum igitur reliquorum angulorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 26 partes et 9 minuta et 49 secunda, et erit angulus RAH partes diversitatis que videtur, et sunt 11 partes et 11 minuta et 6 secunda. Et quia illud quod pertinet istis partibus secundum proportiones acceptas in longitudine propinquiore ex longitudine quidem equata est 20 partes et 33 minuta et 42 secunda et ex longitudine revolubili 16 partes et 52 minuta et 52 secunda, tunc medietas antecessionis proveniet 5 partes et 36 minuta et 7 secunda et ex diebus 32 dies et quarta diei fere, et erit antecessio tota 11 partes et 12 minuta et 14 secunda et ex diebus 64 dies et medietas diei.
⟨XII.5⟩ Capitulum quintum: In declaratione antecessionis stelle Veneris
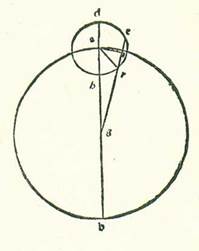Etiam in antecessione stelle Veneris secundum numerationem in longitudine media proportio linee TR ad lineam RG aggregatur ex proportione partis unius ad 37 minuta et 31 secunda, et proportio linee EG ad lineam GR est proportio duarum partium et 37 minutorum et 31 secundorum ad 37 minuta et 31 secunda. Et superficies ortogonia quam ipse continent erit pars una et 38 minuta et 30 secunda. Et etiam erit proportio linee GA ad lineam AH proportio 60 partium ad 43 partes et 10 minuta, et proportio linee DH ad lineam GH erit proportio 103 partium et 10 minutorum ad 16 partes et 50 minuta. Et erit superficies ortogonia quam ipse continent 1736 partes et 38 minuta et 20 secunda. Et partium que proveniunt ex divisione, et sunt pars una et 57 minuta et 50 secunda et 56 tertia, cum acceptum fuerit latus, et est 32 partes et 32 minuta et 29 secunda, et multiplicabitur in proportionem narratam duarum linearum TR et RG, proveniet secundum duas quantitates duarum linearum GA et AR narratas linea TR 32 partes et 31 minutum et 29 secunda, et linea GR secundum istas partes easdem 20 partes et 20 minuta et 13 secunda, et est linea GT tota 52 partes et 51 minuta et 42 secunda. Et propter illud secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG erit linea RT 90 partes et 24 minuta et 58 secunda, et erit linea GT secundum illud exemplum 105 partes et 43 minuta et 24 secunda. Duorum autem arcuum arcus qui est super lineam RT erit 97 partes et 47 minuta, et erit arcus qui est super lineam GT 123 partes et 31 minuta et 49 secunda. Et iam sequitur ex hoc ut sit angulus RAT 48 partes et 53 minuta et 30 secunda secundum partes quibus quatuor anguli recti sunt 360, et erit angulus HAT secundum istas partes 61 partes et 45 minuta et 54 secunda fere. Duorum vero reliquorum angulorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 28 partes et 14 minuta et 6 secunda, et erit angulus RAH partes diversitatis, et sunt 12 partes et 52 minuta et 24 secunda. Et quia illud quod pertinet istis partibus in proportione narrata, et est media ex cursu in longitudine, est 20 partes et 35 minuta et 17 secunda, tunc medietas antecessionis aggregatur septem partes et 38 minuta et 49 secunda et ex diebus 20 dies et medietas et tertia diei fere, et erit antecessio tota 15 partes et 17 minuta et 34 secunda et ex diebus 41 dies et due tertie diei. Et longitudo cuius hec est summa a longitudine longiore et longitudine propinquiore stationis non minuitur a maiore longitudine. Et neque addit super longitudinem minorem nisi 5 minuta secundum longitudinem mediam fere. Numeratio autem apud maiorem longitudinem additionis et diminutionis equationis reperitur duo minuta et tertia minuti. Quapropter erit proportio linee TR ad lineam RG proportio 57 minutorum et 40 secundorum ad 39 minuta et 51 secunda, et erit proportio linee GE ad lineam GR proportio duarum partium et 35 minutorum et 11 secundorum ad 39 minuta et 51 secunda, et erit superficies ortogonia quam ipse continent pars una et 43 minuta et 4 secunda, et erit etiam proportio linee GA ad lineam AH proportio 61 partium et 10 minutorum ad 43 partes et 10 minuta, et proportio linee DG ad lineam GH proportio 104 partium et 20 minutorum ad 18 partes, et erit superficies ortogonia quam ipse continent 1878 partes. Et partium provenientium ex divisione, et sunt 1093 partes et 16 minuta et 23 secunda, cum acceptum fuerit latus, et est 33 partes et 3 minuta et 53 secunda, et multiplicabitur in proportionem narratam inter duas lineas TR et GR, proveniet secundum duas quantitates duarum linearum GA et AR narratas linea quidem TR 31 partes et 45 minuta et 53 secunda, et linea GR secundum istas partes 21 partes et 57 minuta et 2 secunda, et est linea GT tota 53 partes et 42 minuta et 55 secunda. Quapropter secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG fit linea RT 88 partes et 18 minuta et 12 secunda, et linea GT fit secundum illud exemplum 105 partes et 22 minuta et 53 secunda. Duorum vero arcuum arcus qui est super lineam RT erit 94 partes et 48 minuta et 54 secunda, et erit arcus qui est super lineam GT 122 partes et 56 minuta et 27 secunda. Et iam sequitur ex hoc ut sit angulus RAT etiam 47 partes et 24 minuta et 27 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus HAT secundum istas partes 61 partes et 28 minuta et 24 secunda. Duorum vero angulorum reliquorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 28 partes et 31 minuta et 46 secunda, et erit angulus RAH partes diversitatis que videtur, et sunt 14 partes et tria minuta et 47 secunda. Et quia quod pertinet istis partibus secundum proportionem acceptam in longitudine longiore ex longitudine quidem equata est 20 partes et 19 minuta et tertia minuti et ex longitudine quidem revolubili 21 partes et 9 minuta et tria secunda, tunc medietas antecessionis aggregatur octo partes et 12 minuta et 43 secunda et ex diebus vigintiunus dies et medietas diei fere, et erit antecessio tota 16 partes et 25 minuta et 26 secunda et ex diebus quadragintatres dies. Verum secundum numerationem apud minorem longitudinem additio et diminutio equationis invenitur secundum istas partes duo minuta et tertia minuti. Quapropter erit proportio linee TR ad lineam RG proportio partis unius et duorum minutorum et 20 secundorum ad 35 minuta et 11 secunda, et erit proportio linee EG ad lineam GR proportio duarum partium et 39 minutorum et 51 secundorum ad 35 minuta et 11 secunda, et erit superficies ortogonia quam ipse continent pars una et 33 minuta et 44 secunda, et erit proportio linee GA ad lineam AH proportio 58 partium et 50 minutorum ad 43 partes et 10 minuta, et proportio linee DH ad lineam HG est proportio centum et duarum partium ad 15 partes et 40 minuta, et erit superficies ortogonia quam ipse continent 1598 partes. Et partium que proveniunt ex divisione, et sunt 1022 partes et 54 minuta et 7 secunda, cum acceptum fuerit latus, et est 31 partes et 58 minuta et 58 secunda, et multiplicatum fuerit in proportionem narratam duarum linearum TR et RG, proveniet secundum duas quantitates duarum linearum GA et AR narratas linea TR 33 partes et 13 minuta et 36 secunda, et linea GR secundum istas partes 18 partes et 45 minuta et 16 secunda, et proveniet linea GT tota 51 partes et 58 minuta et 52 secunda. Quapropter secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG fit linea TR 92 partes et 22 minuta et tria secunda, et fit linea GT secundum illud exemplum 106 partes et unum minutum et 26 secunda. Duorum vero arcuum arcus qui est super lineam RT erit 100 pars et 39 minuta et 34 secunda, et arcus qui est super lineam GT erit 124 partes et 8 minuta et 22 secunda. Et sequitur ex eo ut sit angulus RAT 50 partes et 19 minuta et 47 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus GAT secundum istas partes 62 partes et 4 minuta et 11 secunda. Duorum vero reliquorum angulorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 27 partes et 55 minuta et 49 secunda, et erit angulus RAG partes diversitatis que videtur, et sunt 11 partes et 44 minuta et 24 secunda. Et quia quod pertinet istis partibus secundum proportionem acceptam a longitudine propinquiore ex longitudine quidem equata est 20 partes et 53 minuta et 30 secunda et ex longitudine quidem revolubili 20 partes et 4 minuta et 30 secunda, tunc medietas antecessionis aggregatur secundum quod sequitur 7 partes et duo minuta et 19 secunda et ex diebus 20 dies et tertia diei fere, et erit antecessio tota 14 partes et 4 minuta et 38 secunda et ex diebus 40 dies et due tertie diei.
⟨XII.6⟩ Capitulum sextum: In declaratione antecessionis Mercurii
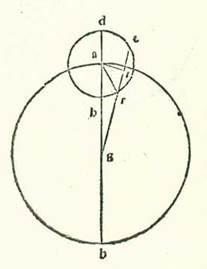Et in stella Mercurii etiam in longitudine media proportio linee TR ad lineam RG aggregatur secundum numerationem proportionis unius partis ad tres partes et novem minuta et octo secunda, et proportio linee EG ad lineam GR est proportio quinque partium et novem minutorum et octo secundorum ad tres partes et novem minuta et octo secunda. Et erit superficies ortogonia quam ipse continent 16 partes et 14 minuta et 27 secunda. Et erit etiam proportio linee GA ad lineam GH proportio 60 partium ad 22 partes et medietatem partis, et proportio linee GD ad lineam GH proportio 82 partium et 30 minutorum ad 37 partes et 33 minuta. Et erit superficies ortogonia quam ipse continent 3093 partes et 45 minuta. Et partium provenientium ex divisione, et sunt 190 partes et 29 minuta et 31 secunda, cum accipietur latus, et est 13 partes, 48 minuta et 7 secunda, et multiplicabitur in proportionem que est duarum linearum TR et RG narratam, proveniet secundum proportionem duarum quantitatum duarum linearum GA et AR narratas linea TR secundum partes istas 13 partes et 48 minuta et 7 secunda, et linea RG secundum illud exemplum 43 partes et 30 minuta et 24 secunda, et erit linea GT tota 57 partes et 18 minuta et 31 secunda. Et propter illud secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG fit linea RT 93 partes et 36 minuta et 37 secunda, et fit linea GT secundum illud exemplum 114 partes et 37 minuta et duo secunda. Duorum igitur arcuum arcus qui est super lineam RT erit 75 partes et 40 minuta et 28 secunda, et arcus qui est super lineam GT erit 145 partes et 32 minuta et 52 secunda. Et sequitur ex hoc ut sit angulus RAT etiam 37 partes et 50 minuta et 14 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus TAG secundum istas partes 72 partes et 46 minuta et 26 secunda. Duorum vero reliquorum angulorum angulus EGA, et est angulus antecessionis que est propter velocitatem stelle, erit 17 partes et 13 minuta et 34 secunda, et angulus RAG erit partes diversitatis, et sunt 34 partes et 56 minuta et 12 secunda. Et quia quod pertinet istis partibus in hac proportione narrata ex cursu in longitudine est 11 partes et 4 minuta et 59 secunda, tunc medietas antecessionis remanet sex partes et octo minuta et 35 secunda et ex diebus undecem dies et quarta diei fere, et aggregatur antecessio tota 12 partes et 17 minuta et 10 secunda et ex diebus 22 dies et medietas diei. Numeratio autem apud maiorem elongationem, scilicet cum est longitudinis equate elongatio a longitudine longiore 11 partium aut quasi, ipse et quod partibus istis pertinet ex partibus equalibus est undecem partes et medietas fere. Tunc additio aut diminutio equationis oportet ut sit secundum portionem partis unius duo minuta et tertia minuti fere. Et propter illud erit proportio linee TR ad lineam GR proportio 57 minutorum et 40 secundorum ad 3 partes et 11 minuta et 28 secunda, et proportio linee EG ad lineam GR proportio 5 partium et 6 minutorum et 48 secundorum ad 3 partes et 11 minuta et 28 secunda, et erit superficies ortogonia quam ipse continent 16 partes et 19 minuta et duo secunda, et erit etiam proportio linee GA ad lineam AH proportio 68 partium et 36 minutorum ad 22 partes et 30 minuta, et proportio linee DG ad lineam HG proportio 91 partium et 6 minutorum ad 46 partes et 6 minuta, et erit superficies ortogonia quam ipse continent 4199 partes et 42 minuta et 36 secunda. Et partium que proveniunt ex divisione, et sunt 257 partes et 22 minuta et 44 secunda, cum acceptum fuerit latus, et est 16 partes et duo minuta et 35 secunda, et multiplicabitur in proportionem positam duarum linearum TR et RG, proveniet secundum quantitates duarum linearum GA et AR positas linea TR 15 partes et 25 minuta et 9 secunda, et linea RG secundum istas partes 51 partes et 11 minuta et 43 secunda, et est linea GT tota 66 partes et 36 minuta et 52 secunda. Et propter illud secundum proportionem 120 partium ad unamquamque duarum chordarum RA et AG fit linea RT 82 partes et 14 minuta et 8 secunda, et fit linea GT secundum illud exemplum 116 partes et 31 minuta et 36 secunda. Duorum autem arcuum arcus qui est super lineam RT erit 86 partes et 31 minuta et 4 secunda, et erit arcus qui est super lineam GT secundum illud exemplum 152 partes et 27 minuta et 56 secunda. Et sequitur ex hoc ut sit angulus RAT etiam 43 partes et 15 minuta et 32 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus TAH secundum istas partes 76 partes et 13 minuta et 58 secunda. Duorum autem angulorum reliquorum angulus RGA, et est angulus antecessionis que est propter velocitatem stelle, erit 13 partes et 46 minuta et duo secunda, et angulus RAH erit partes diversitatis que videtur, et sunt 32 partes et 52 minuta et 26 secunda. Et quia illud quod pertinet istis partibus secundum proportionem acceptam a longitudine longiore ex longitudine quidem equata est 9 partes et 48 minuta et 51 secunda et ex longitudine revolubili 10 partes et 16 minuta et 51 secunda, tunc medietas antecessionis remanet 3 partes et 56 minuta et 11 secunda, et ex diebus erunt decem dies et medietas diei fere, et erit antecessio tota septem partes et 54 minuta et 22 secunda et ex diebus vigintiunus dies. Cum numeratione autem apud longitudines minores, et he longitudines erunt cum fuerit spacium super 120 partes revolubiles a longitudine longiore, invenietur per eas additio et diminutio equationis cum aggregabitur illud propter proportionem in undecem partibus ab utraque parte longitudinis propinquioris, que est propinqua minuto uno et medietati minuti. Et propter illud erit proportio linee TR ad lineam RG proportio partis unius et minuti unius et 30 secundorum ad 3 partes et 7 minuta et 38 secunda, et erit proportio linee EG ad lineam GR proportio 5 partium et 10 minutorum et 38 secundorum ad 3 partes et 7 minuta et 38 secunda, et erit superficies quam ipse continent 16 partes et 11 minuta et 25 secunda, et erit etiam proportio linee GA ad lineam AH proportio 55 partium et 42 minutorum fere ad 22 partes et 30 minuta, et erit proportio linee DG ad lineam GH proportio 78 partium et 12 minutorum ad 33 partes et 12 minuta, et erit superficies quam continent ipse 2596 partes et 14 minuta et 24 secunda. Et partium provenientium ex divisione, et sunt 160 partes et 21 minuta et 27 secunda, cum accipietur latus, et est 12 partes et 39 minuta et 48 secunda, et multiplicabitur unumquodque secundum se in proportionem positam duarum linearum TR et RG secundum duas quantitates duarum linearum GA et AR positas, erit linea TR 12 partes et 58 minuta et 47 secunda, et linea RG secundum istas partes 39 partes et 36 minuta et 4 secunda, et est linea GT tota 52 partes et 34 minuta et 51 secunda. Quapropter secundum proportionem 120 partium ad unamquamque duarum chordarum AR et AG fit linea TR 69 partes et 13 minuta et 30 secunda, et fit linea GT secundum illud exemplum 113 partes et 16 minuta et 48 secunda. Duorum autem arcuum arcus qui est super lineam TR erit 70 partes et 27 minuta et 44 secunda, et arcus qui est super lineam TG erit 141 pars et 28 minuta et 14 secunda. Et sequitur ex eo ut sit angulus TAR 35 partes et 13 minuta et 52 secunda secundum partes quibus quatuor anguli recti sunt 360 partes, et erit angulus TAH secundum istas partes 70 partes et 44 minuta et 7 secunda. Duorum vero reliquorum angulorum angulus RGA, et est angulus antecessionis qui est propter velocitatem stelle, erit 19 partes et 15 minuta et 53 secunda, et angulus RAH erit partes diversitatis que videtur, et sunt 35 partes et 30 minuta et 15 secunda. Et quia illud quod pertinet istis partibus secundum proportionem notam ex longitudine quidem equata est 11 partes et 37 minuta et 30 secunda et ex longitudine revolubilium 11 pars et 22 minuta, tunc medietas antecessionis est septem partes et 30 minuta et 23 secunda et ex diebus undecem dies et medietas diei fere, et erit antecessio tota 15 partes et 12 minuta et 46 secunda et ex diebus vigintitres dies.
In his autem quantitatibus, que demonstrate sunt convenientes fere ei quod reperitur propter illud quod videtur in una et una harum stellarum, et in illis per quas accepimus portiones cursus in longitudine in longitudinibus maioribus et in longitudinibus minoribus processimus hac via: Propterea quod iam demonstravimus in Marte verbi gratia quod cum fuerit in maiore longitudine sua, erit arcus qui est ab una duarum horarum ad habitudinem que nominatur extremitas noctis, que reperitur propter orbem revolutionis, scilicet qui reperitur secundum centrum orbis signorum, 22 partes et 13 minuta et 19 secunda, et erit eius quod pertinet istis partibus ex longitudine revolubili secundum proportionem partis unius ad partem unam et 3 minuta et 11 secunda, et est 21 partes et 10 minuta fere. Et hec non est summa eius secundum certificationem, propterea quod proportio velocitatis posita in duabus horis non comitatur rem unam non alterantem eam in antecessione etiam tota omnino. Verum ipsa non alterat rem certam et veram alteratione cum qua quod pertinet ei ex additione et diminutione, et est 3 partes et 45 minuta, diversificetur in aliquo de quo sit curandum. Nos namque si minuerimus has partes ex 22 partibus et 13 minutis et 19 secundis orbis revolutionis propterea quod apud longitudines maiores sunt cursus qui videntur in orbe revolutionis maiores cursibus revolubilibus, inveniemus quod pertinet eis ex cursu revolubili diversitatis ab una duarum horarum ad habitudinem que nominatur extremitas noctis 18 partes et 28 minuta et 19 secunda. Et quia quod pertinet istis partibus est secundum proportionem motuum mediorum ex revolubilitate est est ... est: Two rivalling verbs. Paris, BnF, lat. 14738 (192r, line 8) contains only the latter. 20 partes et 58 minuta et 21 secunda, tunc nos exercuimus has partes secundum quod ipse certe sunt loco 21 partium et 10 minutorum. Et propterea quod partes additionis et diminutionis, et sunt tres partes et 45 minuta, remanent ipsemet fere etiam hic, tunc si nos minuerimus eas ex illo, propterea quod apud longitudines maiores erunt cursus qui videntur in longitudine minores cursibus revolubilibus, et inveniemus etiam cursum qui videtur in longitudine in hac elongatione narrata 17 partes et 13 minuta et 21 secunda.
⟨XII.7⟩ Capitulum septimum: In demonstratione faciendi tabulas stationum
Ut autem possimus etiam in longitudinibus que sunt in eo quod est inter longitudinem mediam et maiorem longitudinem et minorem earum scire facile quod quando in aliqua differentiarum orbis revolutionis fit unaqueque harum stellarum, videatur nobis stans, accepimus ad illud tabulam in qua sunt triginta aree et duodecem tabule. In duabus autem tabulis primis earum numeri longitudinis revolubilis firmantur in additione secundum senas et senas partes secundum quod firmatur in ceteris tabulis. In tabulis vero decem que sunt post eas sunt numeri in unaquaque stellarum quinque diversitatis equate a longitudine longiore que videtur orbium revolutionis. In prima itaque tabula in unaquaque harum stellarum decem tabularum sunt longitudines stationis prime, et in tabula secunda in unaquaque earum sunt longitudines stationis secunde. Harum quidem longitudinum quantitates accepimus etiam ex rebus quas premisimus in primis et declaravimus in longitudinibus mediis et maioribus et minoribus. Hanc autem superfluitatem in longitudinibus que sunt in eo quod est inter istas iam premisimus et abbreviavimus et exposuimus ponendo minuta que sunt in tabula octava in tabulam diversitatis illarum tabularum. Et illud est quia iam ostense sunt in omni cursu longitudinis revolubilis cum declaratione quantitatis plurime superfluitatis que est propter diversitatem longitudines orbium revolutionis etiam. Et secundum has longitudines proprie reperitur diversitas in stationibus etiam. Et primum a quo incepimus est quod nos, perperea Probably corrupt for propterea, which is also the reading of Paris, BnF, lat. 14738 (192r, line 11 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 583, line 15 from the bottom). quod invenimus duas longitudines quas firmavimus apud longitudinem longiorem et longitudinem propinquiorem non comprehendere quod provenit ex statione cum fuerint centra orbium revolutionis in ipsa longitudine longiore et longitudine propinquiore, immo non comprehendere illud nisi quando sunt inter eas et inter illud quod provenit in unaquaque stellarum, accepimus ex istis longitudinibus quantitates que pertinent longitudini longiori ipsi et longitudini propinquiori secundum hanc semitam. Et in stella quidem Saturni et stella Iovis, propterea quod longitudines duorum orbium revolutionum earum in longitudine longiore ipsa et in longitudine propinquiore non alterant longitudines in spaciis notis per quod sit curandum, ivimus ad numeros diversitatis qui sunt inventi in his duabus stellis, et sunt numeri longitudinis earum a longitudine longiore que videtur duorum orbium revolutionum earum, et firmavimus eos in duabus areis que sunt eorum, omnem numerum in area sua, scilicet nos firmavimus numerum longitudinis longioris in area in qua est numerus 360 et firmavimus numerum longitudinis propinquioris in area in qua est numerus 180. Iam autem ostensum est in stella Saturni quod longitudo eius in longitudine longiore orbis centri egredientis a longitudine longiore orbis revolutionis sue est 67 partes et 15 minuta fere et longitudo eius in longitudine propinquiore est 64 partes et 31 minuta. Et ostensum est in stella Iovis quod eius longitudo in longitudine longiore est 55 partes et 55 minuta et eius longitudo in longitudine propinquiore est 52 partes et 49 minuta. Ivimus ergo ad numeros qui pertinent istis partibus ex longitudine longiore duorum orbium revolutionis, propterea quod illud est facilioris acceptionis, et firmavimus eos in tabulis quatuor que sequuntur istas, que sunt longitudinis, scilicet omnem numerum cum area in qua est numerus 360 longitudinis longioris, in tabula quidem tertia earum 112 partes et 45 minuta stationis prime Saturni et in tabula quarta 247 partes et 15 minuta stationis secunde eius, et secundum istud exemplum in tabula quinta 124 partes et 5 minuta stationis prime Iovis et in tabula sexta 235 partes et 55 minuta stationis secunde eius, et firmavimus in area in qua est numerus 180 longitudinis propinquioris secundum illum ordinem et dispositionem 115 partes et 29 minuta, deinde 244 partes et 31 minuta, et secundum illud exemplum 127 partes et 11 minuta, postea 232 partes et 49 minuta. In stella autem Martis, quia iam premisimus quod cum centri orbis revolutionis longitudo a longitudine longiore orbis egredientis centri est 20 partes et 50 minuta revolubiles, erit huius stelle statio et eius elongatio a longitudine propinquiore que videtur orbis revolutionis eius 22 partes et 13 minuta, et cum fuerit eius cursus in longitudine media, erit statio et summa longitudinis stelle 16 partes et 51 minuta donec sit superfluitas in illo 5 partes et 22 minuta, et secundum partes quibus longitudo media est 60 partes (est enim maior longitudo 66 partes) et eius augmentum super hanc longitudinem mediam eius est sex partes erit longitudo in hoc spacio noto a longitudine longiore 65 partes et 40 minuta et eius augmentum super longitudinem mediam est 5 partes et 40 minuta, nos ergo multiplicavimus sex partes in 5 partes et 22 minuta et divisimus quod provenit nobis per 5 partes et 40 minuta, et provenit nobis per illud augmentum apud longitudinem longiorem ipsam super longitudinem mediam 5 partes et 41 minutum fere donec partes que sunt a longitudine propinquiore que videtur orbis revolutionis aggregentur 22 partes et 32 minuta et partes que sunt a longitudine longiore stationis prime 157 partes et 28 minuta. Firmavimus igitur istas in tabula septima in area 360 partium. Et stationis quidem secunde 202 partes et 32 minuta, et firmavimus istas in tabula octava illius aree eiusdem. Et similiter etiam propterea quod quando est centrum orbis revolubilis elongatum a longitudine propinquiore 16 partibus et 53 minutis revolubilibus, est huius stelle statio et eius elongatio a longitudine propinquiore que videtur orbis revolutionis 11 partes et 11 minuta donec sit augmentum in illo secundum longitudinem mediam 5 partes et 40 minuta, et est minor longitudo secundum istas partes 54 partes secundum 6 partes additas apud longitudinem mediam, et longitudo in hoc spacio noto a longitudine propinquiore orbis egredientis centri secundum eas est 54 partes et 20 minuta, et augmentum in illo apud longitudinem mediam est 5 partes et 40 minuta, tunc superfluitas provenit nobis apud longitudinem propinquiorem ipsam sex partes. Et propter illud erit cursus a longitudine propinquiore que videtur orbis revolutionis 10 partes et 51 minuta, et erit cursus a longitudine longiore stationis prime 169 partes et 9 minuta et stationis secunde 190 partes et 51 minuta. Firmavimus ita quod ita quod: Probably corrupt for itaque, which is also the reading of Paris, BnF, lat. 14738 (192v, line 6 from the bottom). The Greek text is somewhat different here (see Toomer, loc. cit., p. 584, lines 9-10 from the bottom). etiam coram area 180 omnem numerum in tabula sua. In stella autem Veneris, quia nos premisimus quod centrum orbis revolutionis, quando est elongatum in longitudine a longitudine longiore in orbe egredientis centri 21 partibus et 9 minutis revolubilibus, tunc est huius stelle statio et eius elongatio a longitudine longiore que videtur orbis revolutionis est 14 partes et 4 minuta, et quando est cursus eius in longitudine media, est eius statio et summa longitudinis stelle est 12 partes et 52 minuta donec sit augmentum in illo pars una et 12 minuta secundum partes quibus longitudo media est 60 partes (est enim maior longitudo 61 partes et 15 minuta, et est eius augmentum super longitudinem mediam pars una et 15 minuta), erit longitudo in hoc spacio noto a longitudine longiore 61 partes et 10 minuta, et superfluitas illius super longitudinem mediam est pars una et 10 minuta. Tunc quando nos multiplicaverimus partem unam et 15 minuta in partem unam et 12 minuta et diviserimus quod exierit per partem unam et 10 minuta, proveniet nobis per illud augmentum apud longitudinem longiorem ipsam super longitudinem mediam pars una et 17 minuta. Partes igitur que sunt a longitudine propinquiore orbis revolutionis aggregabuntur 14 partes et 9 minuta. Et partes que sunt longitudinis stationis quidem prime sunt 165 partes et 51 minuta. Firmavimus igitur istas in tabula nona in area in qua est numerus 360 partium. Stationis autem secunde 194 partes et 9 minuta, firmavimus itaque illas etiam in tabula decima in illa area eadem. Et secundum hoc exemplum, cum orbis revolutionis fuerit longitudo a longitudine propinquiore orbis egredientis centri 20 partes fere per cursum equalem in longitudine, tunc huius stelle erit statio et eius longitudo a longitudine propinquiore que videtur orbis revolutionis erit 11 partes et 44 minuta donec sit superfluitas in illo secundum longitudinem mediam pars una et 8 minuta. Et fuerit minor longitudo 58 partes et 45 minuta secundum partes quibus longitudo media est 60 partes. Et superfluitas in illo est pars una et 15 minuta. Et fuerit longitudo in spacio noto a longitudine propinquiore secundum istas partes 58 partes et 50 minuta. Et superfluitas in illo apud longitudinem mediam est pars una et 10 minuta. Ergo cum nos multiplicaverimus etiam partem unam et 15 minuta in partem unam et octo minuta et diviserimus quod provenerit ex eo per partem unam et 10 minuta, proveniet nobis per illud superfluitas etiam apud longitudinem propinquiorem ipsam super longitudinem mediam ipsam pars una et 13 minuta. Et propter illud erit cursus a longitudine propinquiore que videtur orbis revolutionis 11 partes et 39 minuta, et erit cursus a longitudine longiore stationis prime 168 partes et 21 minuta et stationis secunde 191 partes et 39 minuta. Affirmavimus itaque istas etiam in illis tabulis eisdem in area 180 partium. In stella autem Mercurii, quia nos declaravimus quando est orbis revolutionis eius elongatus a longitudine longiore orbis egredientis centri 10 partibus et 17 minutis revolubilibus in longitudine, tunc huius stelle est statio et eius elongatio a longitudine propinquiore que videtur in orbe revolutionis eius etiam est 32 partes et 52 minuta, et quando est cursus in longitudine media, est statio et summa longitudinis stelle est 34 partes et 56 minuta donec sit superfluitas due partes et 4 minuta, et est secundum partes quibus longitudo media est 60 partes (maior enim longitudo est 69 partes et augmentum in eo 9 partes) et longitudo in spacio noto a longitudine longiore 68 partes et 36 minuta et augmentum super illam longitudinem mediam 8 partes et 36 minuta, tunc si nos fecerimus quemadmodum fecimus in eo quod precessit, et multiplicaverimus novem partes in duas partes et quatuor minuta, et diviserimus quod provenerit per octo partes et 36 minuta, proveniet nobis per illud superfluitas apud longitudinem longiorem ipsam super longitudinem mediam due partes et 10 minuta fere donec partes que sunt a longitudine propinquiore que videtur orbis revolutionis aggregate sint 32 partes et 46 minuta et sint partes que sunt a longitudine longiore stationis prime 147 partes et 14 minuta. Itaque firmavimus etiam istas in tabula undecima aree in qua sunt 360 partes. Et stationis secunde 212 partes et 46 minuta, et firmavimus etiam has in tabula duodecima illius aree eiusdem. Et similiter etiam propterea quod quando est longitudo orbis revolutionis a longitudine propinquiore 11 partes et 22 minuta revolubilia, tunc huius stelle est statio, et eius longitudo a longitudine propinquiore que videtur orbis revolutionis est 35 partes et 30 minuta donec augmentum super longitudinem mediam sit 34 minuta, et est minor longitudinum 55 partes et 34 minuta secundum partes quibus longitudo media est 60 partes, et augmentum in ea est 4 partes et 26 minuta, et elongatio in spacio noto a longitudine propinquiore secundum istas partes est 55 partes et 42 minuta fere, et superfluitas in illo apud longitudinem mediam est 4 partes et 18 minuta, tunc quando nos multiplicaverimus 4 partes et 26 minuta in 34 minuta et diviserimus quod provenerit per 4 partes et 18 minuta, inveniemus per illud etiam augmentum apud longitudinem propinquiorem ipsam super longitudinem mediam 35 minuta. Et propter illud erit cursus stationis a longitudine propinquiore que videtur orbis revolutionis 35 partes et 31 minuta, et erit eius cursus a longitudine longiore stationis quidem prime 144 partes et 29 minuta et stationis secunde 215 partes et 31 minuta. Firmabimus itaque istas etiam in illis tabulis eisdem. Non tamen firmabimus eas coram numero 180 partium que sunt longitudinis, sed coram numero 120 et 240 partium, propterea quod in istis duobus numeris demonstratur quod cadit propinquior propinquitas orbis egredientis centri qui est stelle Mercurii. Postquam igitur iam explanate sunt he res, tunc iam possibile est alicui imitanti hanc viam ut comprehendat per hec capitula eadem superfluitates in cursibus qui sunt in eo quod est inter eas. Ponam itaque secundum viam exempli quod nos intendimus ut inveniamus portiones diversitatis que videtur in statione prima cum est cursus medii longitudo in longitudine a longitudine longiore 30 partes. Et in hoc loco provenit longitudo orbis revolutionis secundum partes quibus longitudo media earum omnium est 60 partes in stella quidem Saturni per capitula quorum precessit scientia vie, sicut diximus, 63 partes et duo minuta, et in stella Iovis 62 partes et 26 minuta, et in stella Martis 65 partes et 24 minuta, et in Veneris stella 61 partes et 6 minuta, et in stella Mercurii 66 partes et 35 minuta donec sint additiones in unaquaque earum super longitudinem mediam secundum ordinem quo processimus, ut non prolungetur sermo, tres partes et duo minuta, et due partes et 26 minuta, et 5 partes et 24 minuta, et pars una et sex minuta, et 6 partes et 35 minuta. Additiones autem apud longitudinem longiorem ipsam super longitudines medias, quia sunt numeri noti longitudinis maioris in omnibus eis a media longitudine, sunt secundum istas partes 3 partes et 25 minuta, et due partes et 45 minuta, et sex partes et pars una, et 15 minuta et novem partes. Et quia ex quantitatibus superfluitatis partium diversitatis que videtur omnium que sunt longitudinis longioris per considerationem ad longitudines medias aggregatur secundum illum eundem ordinem pars una et 23 minuta, et pars una et 33 minuta, et 5 partes et 41 minutum, et pars una et 17 minuta, et due partes et decem minuta, tunc quando nos multiplicaverimus unamquamque harum quantitatum superfluitatis in unaquaque stellarum secundum augmentum suum in augmentum longitudinis in illa hora super longitudinem mediam ac si multiplicaverimus verbi gratia partem unam et 23 minuta in tres partes et duo minuta, et diviserimus diviserimns M. quod provenerit ex eo per augmentum totum longitudinis maioris ac si divideremus ipsum per tres partes et 25 minuta, proveniet nobis superfluitas in unaquaque stellarum in cursu noto in longitudine qui est partium diversitatis per comparationem partium longitudinis medie pars una et 14 minuta, et pars una et 22 minuta, et 5 partes et 7 minuta, et pars una et octo minuta, et pars una et 35 minuta. Partes autem que sunt in longitudinibus mediis a longitudine longiore que videtur orbis revolutionis sunt 114 partes et octo minuta, et 125 partes et 38 minuta, et 163 partes et 9 minuta, et 167 partes et 8 minuta, et 145 partes et 4 minuta. Partes vero que sunt in longitudinibus maioribus in reliquis stellis sunt pautiores istis partibus quas narravimus, sed in stella Mercurii sunt plures eis. Has ergo quantitates superfluitatis quas invenimus in hac longitudine nota in reliquis quidem stellis minuemus ex partibus que sunt in longitudinibus mediis et in stella quidem Mercurii addemus super eas. Provenient ergo nobis partes que sunt coram triginta partibus longitudinis revolubilis in tabulis stationis prime diversitatis que videtur a longitudine longiore orbis revolutionis in stella quidem Saturni 112 partes et 54 minuta, et in stella Iovis 124 partes et 16 minuta, et in stella Martis 158 partes et duo minuta, et in stella Veneris 166 partes, et in stella Mercurii 146 partes et 39 minuta. Et reiterabimus etiam propter illud et narrabimus tabulas stationis secunde ut consideremus quod remansit ad complementum trecentarum et sexaginta partium in unaquaque arearum post numeros stationis prime, et firmabimus coram ipsis in illis areis eisdem in tabulis stationis secunde, et verbi gratia in hac longitudine nota firmabimus in tabulis stationis secunde 247 partes et sex minuta, et 235 partes et 44 minuta, et 201 partes et 58 minuta, et 194 partes, et 213 partes et 21 minuta. Ex eo autem quo levior fit intellectus huius est quod nos noluimus ut firmentur partes diversitatis que reperiuntur secundum longitudinem longiorem que videtur orbis revolutionis, sed contenti sumus querendo facilitatem partibus que sunt secundum cursum revolubilem qui est non equatus. Iam enim possibile est ut faciamus illud etiam faciliori studio: ut tendamus ad omnem numerum additionis et diminutionis posite coram aliquo numerorum longitudinis revolubilis in tabulis diversitatis, et minuamus ipsum ex partibus quas inveniemus diversitatis revolubilis quando fuerit elongatio a longitudine longiore orbis egredientis centri minor 180, et addemus ipsum super eas quando fuerit longitudo maior 180.
⟨XII.8⟩ Capitulum octavum: In positione tabularum stationum quinque stellarum
Prima
Prima |
Secunda
Secunda |
Tertia
Tertia |
Quarta
Quarta |
Quinta
Quinta |
Sexta
Sexta |
Septima
Septima |
Octava
Octava |
Nona
Nona |
Decima
Decima |
Undecima
Undecima |
Duodecima
Duodecima |
||||||||||||
Numeri communes |
Statio prima Saturni |
Statio secunda Saturni |
Statio prima Iovis |
Statio secunda Iovis |
Statio prima Martis |
Statio secunda Martis |
Statio prima Veneris |
Statio secunda Veneris |
Statio prima Mercurii |
Statio secunda Mercurii |
|||||||||||||
* |
Prima ♄ |
Secunda ♄ |
Prima ♃ |
Secunda ♃ |
Prima ♂ |
Secunda ♂ |
Prima ♀ |
Secunda ♀ |
Prima ☿ |
Secunda ☿ |
* |
||||||||||||
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
Gradus |
Minuta |
||||
6
12 |
354
348 |
112
112 |
45
47 |
247
247 |
15
13 |
124
124 |
5
7 |
235
235 |
55
53 |
157
157 |
33
37 |
202
202 |
27
23 |
165
165 |
52
54 |
294
294 |
8
6 |
147
147 |
12
8 |
212
212 |
48
52 |
||
18
24 |
342
336 |
112
112 |
49
52 |
247
247 |
11
8 |
124
124 |
8
11 |
235
235 |
52
49 |
157
157 |
47
59 |
202
202 |
13
1 |
165
165 |
57
59 |
294
294 |
3
1 |
147
146 |
0
49 |
213
213 |
0
11 |
||
30
36 |
330
324 |
112
113 |
56
2 |
247
246 |
4
58 |
124
124 |
17
23 |
235
235 |
43
37 |
158
158 |
15
33 |
201
201 |
45
27 |
166
166 |
1
6 |
293
293 |
59
54 |
146
146 |
37
21 |
213
213 |
24
39 |
||
42
48 |
318
312 |
113
113 |
8
14 |
246
246 |
52
46 |
124
124 |
29
35 |
235
235 |
31
25 |
158
159 |
57
20 |
201
200 |
3
40 |
166
166 |
12
18 |
293
293 |
48
42 |
146
145 |
6
50 |
213
214 |
54
10 |
||
54
60 |
306
300 |
113
113 |
20
27 |
246
246 |
40
33 |
124
124 |
44
53 |
235
235 |
16
7 |
159
160 |
51
21 |
200
199 |
9
39 |
166
166 |
24
30 |
293
293 |
36
30 |
145
145 |
34
19 |
214
214 |
26
41 |
||
66
72 |
294
288 |
113
113 |
36
44 |
246
246 |
24
16 |
125
125 |
1
12 |
234
234 |
59
48 |
160
161 |
56
31 |
199
198 |
4
29 |
166
166 |
36
43 |
293
293 |
24
17 |
145
144 |
5
55 |
214
215 |
55
5 |
||
78
84 |
282
276 |
113
114 |
55
4 |
246
245 |
5
56 |
125
125 |
22
32 |
234
234 |
38
28 |
162
162 |
9
47 |
197
197 |
51
13 |
166
167 |
53
2 |
293
293 |
7
58 |
144
144 |
49
43 |
215
215 |
11
17 |
||
90
96 |
270
264 |
114
114 |
11
19 |
245
245 |
49
41 |
125
125 |
42
50 |
234
234 |
18
10 |
163
163 |
25
57 |
196
196 |
35
3 |
167
167 |
11
17 |
292
292 |
49
43 |
144
144 |
37
34 |
215
215 |
23
26 |
||
102
108 |
258
252 |
114
114 |
27
35 |
245
245 |
33
25 |
125
126 |
58
6 |
234
233 |
2
54 |
164
165 |
31
5 |
195
194 |
29
55 |
167
167 |
23
29 |
292
292 |
37
26 |
144
144 |
32
30 |
215
215 |
28
30 |
||
114
120 |
246
240 |
114
114 |
43
50 |
245
245 |
17
10 |
126
126 |
14
24 |
233
233 |
46
36 |
165
166 |
39
11 |
194
193 |
21
49 |
167
167 |
37
45 |
292
292 |
23
15 |
144
144 |
30
29 |
215
215 |
30
31 |
||
126
132 |
234
228 |
114
115 |
57
3 |
245
244 |
3
57 |
126
126 |
32
42 |
233
233 |
28
18 |
166
167 |
41
11 |
193
192 |
19
49 |
167
167 |
52
56 |
292
292 |
8
4 |
144
144 |
29
30 |
215
215 |
31
30 |
||
138
144 |
222
216 |
115
115 |
9
15 |
244
244 |
51
45 |
126
126 |
48
54 |
233
233 |
12
6 |
167
168 |
37
1 |
192
191 |
23
59 |
168
168 |
2
6 |
291
291 |
58
54 |
144
144 |
32
34 |
215
215 |
28
26 |
||
150
156 |
210
204 |
115
115 |
19
22 |
244
244 |
41
38 |
127
127 |
0
4 |
233
232 |
0
56 |
168
168 |
21
41 |
191
191 |
39
19 |
168
168 |
10
14 |
291
291 |
50
46 |
144
144 |
36
38 |
215
215 |
24
22 |
||
162
168 |
198
192 |
115
115 |
25
27 |
244
244 |
35
32 |
127
127 |
7
10 |
232
232 |
53
50 |
168
169 |
53
5 |
191
190 |
7
55 |
168
168 |
17
19 |
291
291 |
43
41 |
144
144 |
39
40 |
215
215 |
21
20 |
||
174
180 |
186
180 |
115
115 |
29
30 |
244
244 |
31
30 |
127
127 |
11
11 |
232
232 |
49
49 |
169
169 |
11
15 |
190
190 |
49
45 |
168
168 |
20
21 |
291
291 |
40
39 |
144
144 |
41
42 |
215
215 |
19
18 |
||
* |
Prima ♄ |
Secunda ♄ |
Prima ♃ |
Secunda ♃ |
Prima ♂ |
Secunda ♂ |
Prima ♀ |
Secunda ♀ |
Prima ☿ |
Secunda ☿ |
* |
||||||||||||
⟨XII.9⟩ Capitulum nonum: In declaratione longitudinum maiorum a Sole Veneris et Mercurii
Et quia iam ostendimus absque argumentatione capitula quibus scitur quod invenitur de re antecessionis, tunc iam oportet ut sequamur istud ostendendo summam longitudinum maiorum a Sole que sunt stelle Veneris et stelle Mercurii in unoquoque signorum, quarum inventio necessaria est propter radices positas eis secundum quas agitur. Nos vero iam posuimus quod narrabimus ex illo secundum cursum Solis qui videtur et secundum hoc ut he due stelle ipsemet sint in principio signorum secundum hoc quod loca longitudinis longioris cuiusque earum sint posita in nostro tempore secundum duo puncta duorum tropicorum et duo puncta duarum equalitatum, scilicet ut sit stelle Veneris super vigintiquinque partes Tauri et stelle Mercurii super decem partes Libre, quoniam alterationem que accidit longitudinibus maioribus propter motum longitudinis longioris iam possibile est aliquem venientem post nos emendare et certificare per hec capitula eadem, et cum illo etiam quia in eo quod posuimus de hoc non cadit aliquid alterationis in qua sit superfluitas de qua sit curandum usque ad tempus longum. Et ut nos abbreviemus intellectum vie qua processimus in his capitulis, tunc iam oportet ut demonstremus secundum viam exempli in stella Veneris longitudines maiores que sunt eius, sicut diximus, matutinales et vespertinas cum hec stella est in equalitate vernali in principio initii Arietis.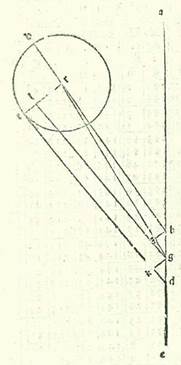 
Sit itaque linea que transit per longitudinem longiorem in orbe egredientis centri, et est punctum A, linea ABGDE, et ponam super centrum motus equalis punctum B et centrum orbis egredientis centri qui revolvit centrum orbis revolutionis punctum G et centrum orbis signorum punctum D, et protraham a centro orbis egredientis centri lineam BRH, et describam super punctum R orbem revolutionis HT, et protraham a puncto D lineam contingentem partem matutinalem antecedentem eius, sitque linea DT, et applicetur linea BRH et linea RT, et producam perpendiculares GK et MB et RT et GL. Et quia linea DA est super vigintiquinque partes Tauri et linea DT est in initio Arietis, erit angulus ADT secundum partes quibus quatuor anguli recti sunt 360 partes 55 partes, et secundum partes quibus duo anguli recti sunt 360 partes erit ipse 110 partes, et erit angulus GDK partes residue ad complendum angulum unum rectum, et sunt 70 partes. Quapropter erit arcus qui est super lineam GK 110 partes secundum partes quibus circulus qui describitur circa triangulum GDK ortogonium est 360 partes, et erit linea GK 98 partes et 18 minuta secundum partes quibus chorda DG est 120 partes. Ergo secundum partes quibus linea DG est pars una et 15 minuta et linea RT, et est a centro orbis revolutionis, est 43 partes et 10 minuta erit linea GK, scilicet linea LT, pars una et minutum unum et linea RL reliqua 42 partes et 9 minuta secundum partes quibus linea GR, que est a centro orbis egredientis centri, est posita 60 partes. Ergo secundum partes quibus chorda GR est 120 partes erit linea RL 84 partes et 18 minuta et arcus qui est super eam 89 partes et 16 minuta secundum partes quibus circulus qui describitur circa triangulum GRL ortogonium est 360 partes. Quapropter erit angulus RGL etiam 89 partes et 16 minuta secundum partes quibus duo anguli recti sunt 360 partes. Angulus vero DGK secundum istas partes est 70 partes, et angulus LGK est rectus. Ergo angulus RGD aggregatur 339 partes et 16 minuta, et erit angulus AGR reliquus secundum istas partes 20 partes et 44 minuta. Quapropter erit arcus qui est super lineam BM 20 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum BGM ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique ad complendum semicirculum, et sunt 159 partes et 16 minuta. Duarum ergo linearum que subtenduntur eis linea quidem BM erit 21 partes et 35 minuta secundum partes quibus chorda BG est 120 partes, et linea GM erit secundum istas partes 118 partes et duo minuta. Quapropter secundum partes quibus linea BG est pars una et 15 minuta et linea GR, et est a centro orbis egredientis centri, est 60 partes est linea BM 13 minuta, et linea GM secundum illud exemplum est pars una et 14 minuta, et linea MR reliqua 58 partes et 46 minuta. Et propter illud erit chorda BR secundum istas partes 58 partes et 46 minuta. Ergo secundum partes quibus linea BR est 120 partes erit linea BM 27 minuta et arcus qui est super eam 26 minuta secundum partes quibus circulus qui describitur circa triangulum BRM ortogonium est 360 partes. Quapropter erit angulus BRM etiam 26 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam vero ostensum fuit quod angulus AGR secundum istas partes est 20 partes et 44 minuta. Ergo angulus ABR, et est angulus cursus equalis in longitudine, secundum partes quibus duo anguli recti sunt 360 partes est 21 partes et 10 minuta, sed secundum partes quibus quatuor anguli recti sunt 360 partes est 10 partes et 35 minuta. Longitudo igitur Solis per cursum medium a longitudine longiore que est super punctum A antecedit 10 partibus et 35 minutis. Et manifestum est quod ipse est secundum cursum medium super 14 partes et 25 minuta Tauri. Et est eius cursus secundum veritatem super 15 partes et 14 minuta eius. Quapropter erit plurimum quo elongatur hec stella in matutino, cum est in principio Arietis, a Sole per cursum suum verificatum 45 partes et 14 minuta.
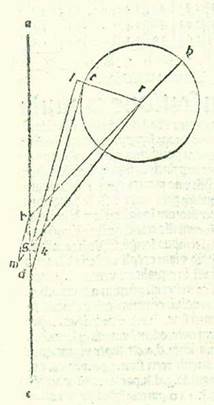Deinde ponam formam que sequitur hanc, ita ut hec linea contingens iam protracta sit ad partem orbis revolutionis vespertinam sequentem secundum quod stella posita sit secundum illud exemplum in principio Arietis. Propter illud igitur cuius precessit declaratio remanet angulus ADT secundum habitudinem suam, et est angulus DGK 70 partes secundum partes quibus duo anguli recti sunt 360 partes, et erit linea GK, scilicet linea LT, pars una et minutum unum secundum partes quibus linea GR, et est ea que est a centro orbis egredientis centri, est 60 partes, et erit linea RT, et est ea que est a centro orbis revolutionis, 43 partes et 10 minuta. Propter illud igitur aggregatur linea RL tota secundum istas partes 44 partes et 11 minuta. Et manifestum est quod secundum partes quibus linea GR subtendens est 120 partes erit linea RL 88 partes et 22 minuta et arcus qui est super eam 94 partes et 51 minuta secundum partes quibus circulus qui describitur circa triangulum GRL ortogonium est 360 partes. Quapropter erit angulus RGL 94 partes et 51 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit angulus RGK partes relique ad complendum angulum rectum, et sunt 85 partes et 9 minuta. Ergo erit angulus totus RGD, scilicet angulus BGM, secundum istas partes 155 partes et 9 minuta. Et propter illud erit etiam arcus qui est super lineam BM 155 partes et 9 minuta secundum partes quibus circulus qui describitur circa triangulum BGM ortogonium est 360 partes, et erit arcus qui est super lineam GM partes relique semicirculi, et sunt 24 partes et 51 minuta. Duarum igitur linearum que subtenduntur eis linea quidem BM est 117 partes et 11 minuta secundum partes quibus chorda BG est 120 partes et linea GM secundum istas partes 25 partes et 49 minuta. Quapropter erit secundum partes etiam quibus linea GB est pars una et 15 minuta linea BM pars una et 13 minuta et linea GM secundum illud exemplum 16 minuta. Ergo linea MR tota est 60 partes et 16 minuta. Et propter illud erit chorda BR secundum istas partes 60 partes et 16 minuta. Ergo secundum partes quibus linea BR est 120 partes erit linea quidem BM due partes et 25 minuta, et arcus quidem qui est super eam erit 2 partes et 19 minuta secundum partes quibus circulus qui describitur circa triangulum BRM ortogonium est 360 partes, et erit propter illud angulus BRM etiam due partes et 19 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed angulus BGR secundum istas partes est 204 partes et 51 minutum, propterea quod angulus DGR iam ostensum est quod est secundum istas partes 155 partes et 9 minuta. Ergo angulus ABR totus, et est angulus cursus equalis in longitudine, secundum partes quidem quibus duo anguli recti sunt 360 partes aggregatur 207 partes et 10 minuta et secundum partes quidem quibus quatuor anguli recti sunt 360 partes 103 partes et 35 minuta. Cursus igitur Solis medii locus est super 11 partes et 25 minuta Aquarii, secundum veritatem vero super 13 partes et 38 minuta eius. Plurimum igitur quod elongatur hec stella in vesperis veperis M., cum fuerit secundum illud exemplum in principio Arietis, a loco Solis secundum verificationem est 46 partes et 22 minuta.
In stella autem Mercurii ponam causa alleviationis que contingit in demonstrationibus quas afferemus in sequentibus in apparitionibus eius que faciunt imaginari nos intendisse ut sciamus quantum est maius quo elongatur hec stella a Sole per cursum suum verificatum in vesperis cum fuerit in principio Scorpionis et in matutino cum fuerit in principio Tauri. Dico ergo quod propterea quod fuit secundum radicem secundum quam agitur in Mercurio non, quando ponitur cursus huius stelle qui videtur, erit cursus medius in longitudine comprehensus et scitus, propterea quod linea GA non semper est una et eadem nec equalis linee que progreditur a centro orbis egredientis centri secundum exemplum secundum quod currit res in radice secundum quam agitur in ceteris stellis, sed ex cursu equali in longitudine cum ponitur apparet cursus qui videtur etiam, firmavimus duo loca in longitudine in unoquoque signorum quibus possibile est ut fiat hec stella in principio signi de quo intenditur, in uno eorum anterior et in altero posterior, et secundum plurimum quod est longitudinis eius in cursibus quos scivimus invenimus per illud plurimum quod provenit ex longitudine eius in ipso principio illius signi, quemadmodum apparebit et intelligetur per has res quarum intendimus inventionem, et primum illius in plurimo quod est longitudinis in vesperis in principio Scorpionis.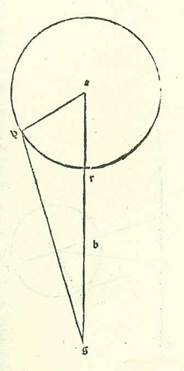 
Sit itaque diametrus que transit per longitudinem longiorem, et est punctum A, linea ABG, et ponam super ipsam centrum orbis signorum, punctum G, et centrum motus equalis orbis revolutionis, punctum B, et imaginabor prius ut centrum orbis revolutionis sit super longitudinem longiorem ipsam donec sit cursus Solis medii in longitudine locus super decem partes Libre et cursus verificati super octo partes eius, et describam circa punctum A orbem revolutionis RH, et protraham a puncto G lineam GH contingentem ipsum orbem revolutionis a parte vespertina, et producam perpendicularem AH. Quia igitur iam ostensum est per capitula que premisimus et posuimus quod secundum partes quibus linea GA, et est linea maioris longitudinis, est 69 partes est linea AH, et est a centro orbis revolutionis, 22 partes et medietas partis et secundum partes etiam quibus chorda AG est 120 partes est linea AH 39 partes et 8 minuta, tunc propter illud erit arcus qui est super lineam AH 38 partes et 4 minuta secundum partes quibus circulus qui describitur circa triangulum AGH ortogonium est 360 partes, et erit angulus AGH secundum partes quidem quibus duo anguli recti sunt 360 partes 38 partes et 4 minuta, et secundum partes quidem quibus quatuor anguli recti sunt 360 partes erit 19 partes et duo minuta. Sed linea GA est super decem partes Libre. Ergo stelle locus est super 29 partes et duo minuta Libre, et eius longitudo que est maior longitudo eius a Sole secundum veritatem est 21 partes et duo minuta. Et ponam etiam ut longitudinis medie elongatio a longitudine longiore sit tres partes. Erit ergo Solis per cursum suum medium locus super tredecem partes Libre et cursus eius verificati super undecem partes et 4 minuta. 
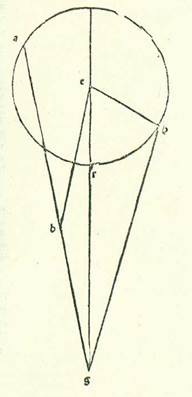Et protraham lineam BE, et describam circa centrum E orbem revolutionis RH, et protraham lineam GH contingentem secundum illud exemplum, et producam duas lineas EH et EG. Et quia in hoc loco narrato, scilicet quia angulus ABE est positus tres partes secundum partes quibus quatuor anguli recti sunt 360 partes et ostensum est secundum viam quam premisimus et qua perreximus quod angulus AGE, et est angulus acceptus ex superfluitate que est propter egressionem a centro, secundum istas partes est partes due et 52 minuta, tunc linea EG, et est linea longitudinis orbis revolutionis in hac habitudine, est 68 partes et 58 minuta fere secundum partes quibus linea EH, et est a centro orbis revolutionis, est 22 partes et 30 minuta, et est linea EH etiam 39 partes et 9 minuta secundum partes quibus linea EG subtendens est 120 partes, quapropter erit arcus qui est super lineam EH 38 partes et 5 minuta secundum partes quibus circulus qui describitur circa triangulum GEH ortogonium est 360 partes, et erit angulus EGH secundum partes quibus duo anguli recti sunt 360 partes 38 partes et 5 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes 19 partes et tria minuta fere. Quapropter erit angulus AGH totus secundum istas partes 21 partes et 55 minuta. Ergo cum fuerit locus huius stelle super partem unam et 55 minuta Scorpionis, plurimum quod erit longitudinis eius a Sole per cursum suum verificatum erit 20 partes et 51 minutum. Iam vero fuit ostensum quod quando fuerit eius locus super 29 partes et duo minuta Libre, tunc plurimum quod elongatur a Sole per cursum suum verificatum est 21 partes et duo minuta. Et quia superfluitas in eo quod est inter duo loca est due partes et 53 minuta et superfluitas inter duas longitudines maiores est 11 minuta donec sit quod pertinet 58 minutis que sunt a loco primo ad principium Scorpionis 4 minuta fere, tunc quando nos minuerimus hec quatuor minuta ex 21 partibus et duobus minutis, proveniet nobis maius quod est longitudinis eius vespertine a Sole per cursum verificatum in principio Scorpionis ipso 20 partes et 58 minuta. Deinde post illud ponam causa plurimi quod est elongationis eius matutinalis in principio Tauri primo quidem cursus medii elongationem secundum successionem signorum a longitudine propinquiore trigintanovem partes donec sit Solis per cursum suum medium locus super decem et novem partes Tauri et per cursum suum verificatum super 19 partes et 38 minuta. 
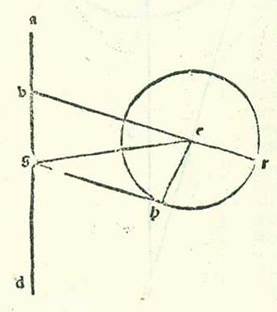Et describam similem huic forme, ita ut orbis revolutionis sit locatus in figura secundum successionem signorum a longitudine propinquiore et secundum hoc quod linea contingens protrahatur ad partem matutinalem orbis revolutionis. Et quia in hoc cursu narrato, scilicet quia angulus DBR positus est 39 partes secundum partes quibus quatuor anguli recti sunt 360 partes, et ostensum est per capitula que premisimus et secundum que processimus quod angulus DGE secundum istas partes est 40 partes et 57 minuta, et quia linea GE, et est linea longitudinis, tunc est 55 partes et 59 minuta secundum partes quibus linea EH, et est ea que est a centro orbis revolutionis, est 22 partes et 30 minuta, et secundum partes quibus chorda GE est 120 partes est linea EH 48 partes et 14 minuta, et arcus qui est super eam est 47 partes et 24 minuta secundum partes quibus circulus qui describitur circa triangulum GEH ortogonium est 360 partes, tunc propter proter M. illud erit angulus EGH etiam secundum partes quibus duo anguli recti sunt 360 partes 47 partes et 24 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 23 partes et 42 minuta. Erit ergo angulus HGD reliquus secundum istas partes 17 partes et 15 minuta. Stelle igitur Mercurii cum fuerit locus super 27 partes et 15 minuta Arietis, plurimum quo elongabitur in matutino a Sole per cursum suum verificatum erit 22 partes et 23 minuta. Postea ponam etiam ut longitudinis elongatio in illa parte eadem a longitudine propinquiore sit quadragintadue partes donec sit locus Solis secundum medium quidem cursum suum super vigintiduas partes Tauri et secundum verificationem quidem super 22 partes et 31 minuta. Et quia in hoc cursu etiam, scilicet quia angulus DBR positus est quadragintadue partes secundum partes quibus quatuor anguli recti sunt 360 partes, ostensum est quod angulus DGE secundum istas partes est quadragintaquatuor partes et quod linea GE, et est linea longitudinis, tunc est 55 partes et 50 minuta secundum partes quibus linea EH, et est a centro orbis revolutionis, est 22 partes et 30 minuta, erit secundum partes etiam quibus chorda EG est 120 partes linea EH 48 partes et 19 minuta, et arcus qui est super eam erit 47 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum EGH ortogonium est 360 partes. Propter illud ergo erit angulus EGH etiam secundum partes quibus duo anguli recti sunt 360 partes 47 partes et 30 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 23 partes et 45 minuta, et erit angulus HGD reliquus secundum istas partes 20 partes et 19 minuta. Cum ergo fuerit stelle Mercurii locus super decem et novem minuta partis prime Tauri, plurimum quod elongabitur in matutinis a Sole per cursum suum verificatum erit 20 partes et 12 minuta. Iam autem ostensum fuit quod cum eius locus fuerit super 27 partes et 15 minuta Arietis, erit eius longitudo erit erit ... erit: Two rivalling verbs. Paris, BnF, lat. 14738 (196v, line 11 from the bottom) contains only the former. secundum illud exemplum 22 partes et 23 minuta. Ergo quia superfluitas etiam in eo quod est inter hec duo loca est octo partes et quatuor minuta et superfluitas inter has duas longitudines maiores est undecem minuta donec sit quod pertinet duabus partibus et 45 minutis que sunt a loco primo ad principium Tauri decem minuta fere, tunc cum nos minuerimus hec decem minuta ex vigintiduabus partibus et vigintitribus minutis, proveniet nobis plurimum quod est longitudinis eius matutinalis in ipso principio Tauri a Sole per cursum suum verificatum 22 partes et 13 minuta. Et illud est quod intendimus invenire. Et hoc eodem modo numeravimus longitudines maiores matutinales et vespertinas que proveniunt in reliquis signis ambarum stellarum, et scripsimus eas in tabula quam posuimus in duodecem areis in qua sunt quinque tabule, et firmavimus in tabula prima earum prius principia cuiusque duodecem signorum, et incepimus in illo ab Ariete, et firmavimus coram ipsis in tabulis quatuor que sunt post eam longitudines maiores a Sole per cursum suum verificatum qui provenit nobis per numerationem, in secunda quidem longitudines matutinales stelle Veneris, et in tertia longitudines eius vespertinales, et in quarta longitudines matutinales stelle Mercurii, et in quinta longitudines eius vespertinales. Et hec est forma tabule:
Tabula longitudinum maiorum a Sole Veneris et Mercurii
Signa 12 |
Longitudines matutinales |
Longitudines vespertinales |
Longitudines matutinales |
Longitudines vespertinales |
||||||||
♀ |
♀ |
☿ |
☿ |
|||||||||
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
|||||
Aries |
♈ |
45 |
34 |
47 |
27 |
24 |
14 |
19 |
30 |
|||
Taurus |
♉ |
45 |
37 |
45 |
31 |
24 |
13 |
21 |
50 |
|||
Gemini |
♊ |
45 |
34 |
44 |
49 |
20 |
18 |
23 |
41 |
|||
Cancer |
♋ |
45 |
36 |
44 |
25 |
18 |
17 |
26 |
56 |
|||
Leo |
♌ |
46 |
20 |
44 |
31 |
16 |
35 |
26 |
37 |
|||
Virgo |
♍ |
46 |
38 |
44 |
55 |
16 |
8 |
26 |
57 |
|||
Libra |
♎ |
46 |
45 |
45 |
41 |
17 |
46 |
23 |
31 |
|||
Scorpio |
♏ |
46 |
47 |
46 |
30 |
21 |
32 |
20 |
38 |
|||
Sagittarius |
♐ |
46 |
30 |
47 |
33 |
26 |
9 |
19 |
28 |
|||
Capricornus |
♑ |
46 |
7 |
47 |
35 |
28 |
37 |
19 |
14 |
|||
Aquarius |
♒ |
45 |
41 |
47 |
34 |
28 |
17 |
18 |
11 |
|||
Pisces |
♓ |
45 |
20 |
47 |
50 |
26 |
24 |
18 |
0 |
|||
♀ |
♀ |
☿ |
☿ |
|||||||||
Expleta est dictio duodecima libri Almagesti Ptolemei Pheludiensis.