PAL: Print/1/70/Text/6

`_`	(the underscore) is the placeholder for exactly one character.
`%`	(the percent sign) is the placeholder for no, one or more than one character.
`%%`	(two percent signs) is the placeholder for no, one or more than one character, but not for blank space (so that a search ends at word boundaries).

⟨VI⟩

Claudii Ptolemei Pheludiensis dictio sexta libri Almagesti tresdecem capitulis seriatim coornata huic loco congruit.

Capitulum primum: De coniunctionibus et impletionibus lunaribus mediis

Capitulum secundum: De aptatione differentiarum tabularum applicationum mediarum

Capitulum tertium: De positione differentiarum tabularum

Capitulum quartum: Quomodo oportet ut sit perscrutatio applicationum verarum et habentium revolutiones

Capitulum quintum: De terminis eclypsium que sunt Solis et Lune

Capitulum sextum: De longitudine que est inter menses eclypticos

Capitulum septimum: De artificio lineationis tabularum eclypsium

Capitulum octavum: De positione tabularum eclypsium Solis et Lune

Capitulum nonum: De cognitione eclypsium lunarium

Capitulum decimum: De cognitione eclypsium solarium

Capitulum undecimum: De inclinationibus et declinatione que erunt in eclypsibus

Capitulum duodecimum: De positione lineationis que est apud declinationem et inclinationes

Capitulum tredecimum: De cognitione declinationis et inclinationum

⟨VI.1⟩ Capitulum primum: De coniunctionibus et impletionibus lunaribus mediis

Postquam sequitur quod iam precessit positio libri in applicationibus eclypsium que sunt Solis et Lune et precedit hunc librum etiam inquisitio eorum que videntur ex veritate coniunctionum et oppositionum Solis et Lune, vidimus nobis sufficere in comprehensione primum horum et similium ea quorum iam precessit declaratio ex motibus qui sunt cuiusque duorum luminarium revolutionum et diversitatis. Et propter hoc possibile est aliquem non pigrum ab hac inquisitione scientie locorum eorum in omni hora, cum considerat quod est inter unum eorum et alterum, scire tempora et loca applicationum localium que reperiuntur ex motibus mediis et cum diversitatibus verificatis. Et cum hoc, ut sit nobis planius illud, premittemus breviter positionem temporum et locorum revolutionum coniunctionum et oppositionum et eorum que sunt locorum Lune per tempora media et per diversitatem et latitudinem, quibus erit equatio que est applicationum verificatarum. Ex eis vero que prediximus erit equatio que est applicationum eclypticarum. Et iam lineabimus inquisitionis huius tabulas secundum hunc modum:

⟨VI.2⟩ Capitulum secundum: De aptatione differentiarum tabularum applicationum mediarum

Dico primum ut equemus etiam loca mensium, sicut fuit nostra equatio aliorum locorum, a primo anno annorum Nabuchodonosor. Accipiemus superfluitatem longitudinis que fuit inter Solem et Lunam in primo annorum Nabuchodonosor in primo die mensis Thot, qui est ex mensibus Egyptiorum, in meridie, que est 70 partes et 37 minuta, et dividemus eam per motum medium, qui est longitudinis diei unius, et provenient nobis quinque dies et 47 minuta et 33 secunda diei unius. Fuit ergo coniunctio media preterita, que fuit ante medium diem diei principii mensis Thot, per hos quinque dies et minuta eorum. Et fuit coniunctio secunda media post illum medium diem 23 diebus et 44 minutis et 17 secundis diei unius fere, scilicet post medium diem Iomin vigesimiquarti 44 minuta et 17 secunda diei unius. Et erit motus Solis medius in his 23 diebus et 44 minutis et 17 secundis 23 partes et 23 minuta et 50 secunda, et motus Lune in diversitate 310 partes et 8 minuta et 15 secunda, et motus eius in latitudine 314 partes et 2 minuta et 21 secunda. Et fuit locus Solis per motum suum medium in media die primi mensis in quadragesimoquinto minuto Piscis. Et fuit eius longitudo a longitudine sua longiore in orbe suo proprio 265 partes et 15 minuta. Et fuit longitudo Lune a longitudine sua longiore in orbe revolutionis per motum diversitatis 268 partes et 49 minuta. Et fuit eius longitudo in latitudine ab ultima longitudine septentrionis in orbe suo declivi 354 partes et 15 minuta. Fuit ergo in hoc tempore longitudo Solis et Lune, scilicet amborum media, post medium diem principii mensis in coniunctione media, Solis quidem longitudo a longitudine sua longiore, scilicet a quinque partibus et 30 minutis Geminorum, 288 partes et 38 minuta et 50 secunda, et fuit longitudo Lune a longitudine longiore in diversitate quidem 218 partes et 57 minuta et 15 secunda, et in latitudine quidem fuit eius longitudo ab ultima longitudine septentrionis 308 partes et 17 minuta et 21 secunda.

⟨VI.3⟩ Capitulum tertium: De positione differentiarum tabularum

Describam autem tabulas et describam primum in prima differentiarum earum, que est coniunctionum, 45 areas etiam in quinque tabulis. Et ponam in tabula prima in prima area primum annorum Nabuchodonosor, et in tabula secunda numerum dierum mensis Thot, qui est 24 dies et 44 minuta et 17 secunda, quoniam minuta que sequuntur non sunt nisi medietatis diei que est Iomin vigesimiquarti, et in tabula tertia partes que sunt longitudo Solis media a longitudine longiore, que sunt 288 partes et 38 minuta et 50 secunda, et in tabula quarta partes diversitatis Lune longitudinis longioris, que sunt 218 partes et 57 minuta et 15 secunda, et in tabula quinta partes latitudinis Lune ultime longitudinis septentrionis, que sunt 308 partes et 17 minuta et 21 secunda. Et quia medietas temporis medii mensis continet ex diebus 14 dies et 45 minuta et 55 secunda fere, et ex partibus longitudinis illas quidem que sunt longitudo Solis 14 partes et 33 minuta et 12 secunda, et ex diversitate quidem Lune 192 partes et 54 minuta et 30 secunda, et ex latitudine quidem 195 partes et 20 minuta et 6 secunda, ergo minuam hos numeros ex numeris coniunctionis posite, et premittam quod remanebit, et ponam ipsum in area prima differentie secunde, que est oppositionis, secundum similitudinem illius quod posuimus in differentia prima, que est equalis huic secunde. Erit ergo quod remanebit ex diebus novem dies et 58 minuta et 22 secunda, et quod remanet ex partibus longitudinis quidem Solis longioris 274 partes et 5 minuta et 38 secunda, et quod remanet ex diversitate longitudinis longioris que est Lune 26 partes et 2 minuta et 45 secunda, et quod remanet ex latitudine que est longitudo ab ultima longitudine septentrionis 112 partes et 57 minuta et 15 secunda. Et quia in omnibus 25 annis Egyptiis diminutis ex die uno duobus minutis et 47 secundis et 5 tertiis complentur menses integri fere, et superfluunt post revolutiones integras per motum medium, Sol quidem 353 partibus et 52 minutis et 34 secundis et 13 tertiis, et Luna superfluit cum cursu quidem diversitatis 57 partibus et 21 minutis et 44 secundis et uno tertio, et in latitudine 117 partibus et 12 minutis et 49 secundis et 54 tertiis, ponam ergo additiones duarum tabularum primarum ex ambabus superfluitatibus per 25 annos, et ponam diminutiones duarum tabularum secundarum ex ambabus superfluitatibus duo minuta et 47 secunda et 5 tertia, et reliquarum tabularum ponam quidem additiones duarum quidem tabularum tertiarum ex ambabus superfluitatibus 353 partes et 52 minuta et 34 secunda et 13 tertia, et duarum quidem tabularum quartarum ponam additiones ambarum superfluitatum 57 partes et 21 minuta et 44 secunda et unum tertium, et duarum tabularum quintarum ambarum superfluitatum ponam additiones 117 partes et 12 minuta et 49 secunda et 54 tertia. Et post has duas superfluitates describam quinque tabulas in differentia ultima annorum expansorum in vigintiquattuor areis. Et describam sub eis quinque tabulas alias in duodecem areis mensium. Et ponam in principio arearum que sunt mensium in tabula quidem prima mensem unum, et in tabula secunda numerum dierum mensis, qui sunt 29 dies et 31 minuta et 50 secunda et 8 tertia et 20 quarta, et in tabula tertia partes Solis que aggregantur in hoc tempore, que sunt 29 partes et 6 minuta et 23 secunda et tertium unum, et in tabula quarta partes diversitatis Lune, que sunt 25 partes et 49 minuta et cifre et octo tertia, et in tabula quinta partes latitudinis, que sunt 30 partes et 40 minuta et 14 secunda et 9 tertia. Et ponam additiones harum arearum et tabularum per numeros qui sunt in area prima quinque tabularum. Et ponam in principio arearum tabularum annorum expansorum in tabula quidem prima annum primum, et in tabula secunda numerum dierum qui superfluunt in 13 mensibus, qui sunt 18 dies et 53 minuta et 51 secunda et 48 tertia, et in tabula tertia partes que in hoc tempore superfluunt ex cursu Solis, que sunt 18 partes et 22 minuta et 59 secunda et 18 tertia, et in tabula quarta partes diversitatis Lune, que sunt 335 partes et 37 minuta et unum secundum et 51 tertia, et in tabula quinta partes latitudinis, que sunt 38 partes et 43 minuta et tria secunda et 51 tertia. Et ponam additiones harum tabularum quandoque secundum id quod superfluit in 13 mensibus et quandoque secundum id quod superfluit in 12 mensibus, in quibus aggregatur quidem ex diebus 354 dies et 22 minuta et secundum unum et 40 tertia, sed ex partibus quidem partes longitudinis Solis a longitudine sua longiore 349 partes et 16 minuta et 36 secunda et 12 tertia, et partes quidem diversitatis Lune 309 partes et 48 minuta et secundum unum et 36 tertia, partes vero latitudinis octo partes et duo minuta et 49 secunda et 48 tertia. Et posuimus ea que narravimus secundum quantitatem qua sufficiat nobis in applicatione una post annos Egyptios integros ad minuta et ad secunda. Firmata fuit hec tabula post hec.

Termini eclypsium luminarium

	☉		☽
☉ et ☽	Partes	Minuta	Partes	Minuta
Ex hoc Ad	69 101	19 22	74 105	48 12
Ex hoc Ad	258 290	38 41	254 285	48 12

Tabularum differentia prima, que est coniunctionum luminarium

		☉						☾
Prima		Secunda			Tertia			Quarta			Quinta
Anni collecti secundum 25		Dies mensis Thot			Longitudo Solis media a longitudine longiore ☉			Partes diversitatis Lune ☾			Partes latitudinis
Anni collecti secundum 25	Dies		Minuta	Secunda	Partes	Minuta	Secunda	Partes	Minuta	Secunda	Partes	Minuta	Secunda
1 26 51		24 24 24	44 41 38	17 30 43	288 282 276	38 31 23	50 24 58	218 276 333	57 18 40	15 59 43	308 65 182	17 30 43	21 11 1
76 101 126		24 24 24	35 33 30	56 9 22	270 264 258	16 9 1	33 7 41	31 88 145	2 24 45	27 11 55	299 57 174	55 8 21	51 41 31
151 176 201		24 24 24	27 24 22	35 47 0	251 245 239	54 46 39	15 50 24	203 260 317	7 29 51	39 23 7	291 48 166	34 47 0	20 10 0
226 251 276		24 24 24	19 16 13	13 26 39	233 227 221	31 24 17	58 32 6	15 72 129	12 34 56	51 35 19	283 40 157	12 25 38	50 40 30
301 326 351		24 24 24	10 8 5	52 5 18	215 209 202	9 2 54	41 15 49	187 244 302	18 39 1	3 47 31	274 32 149	51 4 17	20 10 0
376 401 426		24 23 23	2 59 56	31 44 57	196 190 184	47 39 32	23 57 32	359 56 114	23 44 6	15 59 43	266 23 140	29 42 55	50 39 29
451 476 501		23 23 23	54 51 48	10 22 35	178 172 166	25 17 10	6 40 14	171 228 286	28 50 11	27 11 55	258 15 132	8 21 33	19 9 59
526 551 576		23 23 23	45 43 40	48 1 14	160 153 147	2 55 47	49 23 57	343 40 98	33 55 17	29 23 7	249 6 124	46 59 12	49 39 29
601 626 651		23 23 23	37 34 31	27 40 53	141 135 129	40 33 25	31 5 40	155 213 270	38 0 22	51 35 19	241 358 115	25 38 50	19 9 59
676 701 726		23 23 23	29 26 23	6 19 32	123 117 111	18 10 3	14 48 22	327 25 82	44 5 27	3 47 31	233 350 107	3 16 29	48 38 28
751 776 801		23 23 23	20 17 15	45 57 12	104 98 92	55 48 41	57 31 5	139 197 254	49 11 32	16 0 44	224 341 99	42 55 7	18 8 58
826 851 876		23 23 23	12 9 6	13 36 49	86 80 74	33 26 18	39 13 48	311 9 66	54 16 37	28 12 56	216 333 90	20 33 46	48 38 28
901 926 951		23 23 23	4 1 58	2 15 28	68 62 55	11 3 56	22 56 30	123 181 238	59 21 43	40 24 8	207 325 82	59 12 25	17 7 57
976 1001 1026		22 22 22	55 52 50	41 54 7	49 43 37	49 41 34	4 39 13	296 353 50	4 26 48	52 36 20	199 316 74	37 50 3	47 37 27
1051 1076 1101		22 22 22	47 44 41	19 32 45	31 25 19	26 19 11	47 21 56	108 165 222	10 31 53	4 48 32	191 308 65	16 29 41	16 6 56

Tabularum differentia secunda, que est impletionum luminarium

					☉							☾

Prima		Secunda				Tertia			Quarta				Quinta
Anni expansi		Dies mensis Thot				Longitudo Solis media a longitudine longiore ☉			Partes diversitatis Lune ☾				Partes latitudinis
secundum 25	Dies		Minuta	Secunda		Partes	Minuta	Secunda	Partes	Minuta	Secunda		Partes	Minuta	Secunda
1 26 51		9 9 9	58 55 52	22 35 48		274 267 261	5 58 50	38 12 46	26 83 140	2 24 46	45 29 13		112 230 347	57 10 22	15 6 55
76 101 126		9 9 9	50 47 44	1 14 27		255 249 243	43 35 28	21 55 29	198 255 312	7 29 51	57 41 25		104 221 339	35 48 1	45 34 24
151 176 201		9 9 9	41 38 36	40 53 5		237 231 225	21 13 6	3 38 12	10 67 124	13 34 56	9 53 37		96 213 330	14 27 39	14 4 54
226 251 276		9 9 9	33 30 27	18 31 44		218 212 206	58 51 43	46 20 54	182 239 297	18 40 1	21 5 49		87 205 322	52 5 18	44 34 24
301 326 351		9 9 9	24 22 19	57 10 23		200 194 188	36 29 21	28 3 37	354 51 109	23 45 7	33 17 1		79 196 313	31 44 56	14 4 54
376 401 426		9 9 9	16 13 11	36 49 2		182 176 169	14 6 59	11 45 19	166 223 281	28 50 12	45 29 13		79 188 305	9 22 35	44 33 23
451 476 501		9 9 9	8 5 2	15 27 40		163 157 151	51 44 37	54 28 2	338 35 93	33 55 17	57 41 25		62 180 297	48 1 13	13 3 53
526 551 576		8 8 8	59 57 54	53 6 19		145 139 133	29 22 14	37 11 45	150 208 265	39 0 22	9 53 37		54 171 288	26 39 52	43 33 23
601 626 651		8 8 8	51 48 45	32 45 58		127 120 114	7 59 52	19 53 28	322 20 77	44 6 27	21 5 49		46 163 280	5 18 30	13 3 52
676 701 726		8 8 8	43 40 37	11 24 37		108 102 96	45 37 30	2 36 10	134 192 249	49 11 33	33 17 1		37 154 272	43 56 9	42 32 22
751 776 801		8 8 8	34 32 29	51 2 15		90 84 74	22 15 7	44 19 53	306 4 61	54 16 38	46 30 14		29 146 263	22 35 47	12 2 52
826 851 876		8 8 8	26 23 20	38 41 54		78 65 59	7 53 45	27 1 36	118 176 233	59 21 43	58 42 26		21 138 255	0 13 26	42 32 22
901 926 951		8 8 8	18 19 12	7 20 23		53 47 41	38 30 23	10 44 18	291 348 45	5 26 48	10 54 38		12 129 247	39 52 4	11 1 51
976 1001 1026		8 8 8	9 6 4	46 59 12		35 29 23	15 8 1	52 26 1	103 160 217	10 32 53	22 6 50		4 121 238	16 29 43	41 31 21
1051 1076 1101		8 7 7	1 58 55	15 37 50		16 10 4	53 46 38	35 9 44	275 332 29	15 37 59	33 18 2		355 113 230	56 9 21	11 1 51

Tabularum differentia tertia communis annis expansis et mensibus coniunctionibus et impletionibus simul. Et in ea sunt superfluitates comparate que sunt coniunctionum et impletionum.

					☉							☾
Prima		Secunda				Tertia			Quarta				Quinta
Anni expansi		Dies mensis Thot				Longitudo Solis media a longitudine longiore ☉			Partes diversitatis Lune ☾				Partes latitudinis
secundum 25	Dies		Minuta	Secunda		Partes	Minuta	Secunda	Partes	Minuta	Secunda		Partes	Minuta	Secunda
1 2 3		18 8 27	53 15 9	52 54 45		18 7 26	22 39 2	59 36 35	335 285 261	37 25 2	2 4 5		38 46 85	43 45 28	4 54 57
4 5 6		16 5 24	31 53 47	47 49 40		15 4 22	19 35 58	11 47 46	210 160 136	50 38 15	7 9 11		93 101 140	31 34 17	47 37 41
7 8 9		14 3 22	9 31 25	42 44 36		12 1 19	15 31 54	23 59 59	86 35 11	3 51 28	12 14 16		148 156 195	20 23 6	30 20 24
10 11 12		11 1 20	47 9 3	37 39 32		9 358 16	11 28 51	35 11 10	321 271 246	16 4 41	18 19 21		203 211 249	9 12 55	14 3 7
13 14 15		9 28 17	25 19 41	33 24 26		6 24 13	7 30 47	47 46 22	196 172 121	29 6 54	23 25 26		257 296 304	57 41 43	57 1 50
16 17 18		7 25 15	3 57 19	28 20 22		3 21 10	3 26 43	59 58 34	71 47 357	42 19 7	28 30 32		312 351 359	46 29 32	40 44 34
19 20 21		4 23 12	41 35 57	23 15 17		0 18 7	0 23 39	10 10 46	306 282 232	55 32 20	33 35 37		7 46 54	35 18 21	23 27 17
22 23 24		2 21 10	19 13 35	19 11 13		356 15 4	56 19 35	22 22 58	182 157 107	8 45 33	39 41 43		62 101 109	24 7 10	7 10 0

Tabularum differentia quarta coniunctionum et impletionum in mensibus

Prima	Secunda			Tertia			Quarta			Quinta
Menses	Dies	Minuta	Secunda	Partes	Minuta	Secunda	Partes	Minuta	Secunda	Partes	Minuta	Secunda
1 2 3	29 59 88	31 3 35	50 40 30	29 58 87	6 12 19	23 46 9	25 51 77	49 38 27	0 0 0	30 61 92	40 20 0	14 28 42
4 5 6	118 147 177	7 39 11	21 11 1	116 145 174	25 31 38	32 55 18	103 129 154	16 5 54	1 1 1	122 153 184	40 21 1	7 1 The 1 and the 7 above are preceded by a 5 which could belong to either number as it is placed right in the middle of them. The Greek text has a 57 above an 11 above a 25 in this field (see Toomer, loc. cit. p. 280). 15
7 8 9	206 236 265	42 14 46	51 41 31	232 203 261	44 51 57	41 4 27	180 206 232	43 32 21	1 1 1	214 245 276	41 21 2	39 53 7
10 11 12	295 324 354	18 50 22	21 12 2	291 320 349	3 10 16	50 13 36	258 283 309	10 59 48	1 2 2	306 337 8	42 22 2	21 36 50

Termini eclypsium luminarium

		Partes	Minuta		Partes	Minuta		Partes	Minuta		Partes	Minuta
☉	Ex	69	19	Ad	101	22	Et ex	258	38	Ad	290	41
☽	Ex	74	48	Ad	105	12	Et ex	254	48	Ad	285	12

⟨VI.4⟩ Capitulum quartum: Qualiter oporteat ut sit perscrutatio applicationum verarum et habentium revolutiones

Cum voluerimus scire applicationes medias que videntur in quocunque annorum quesitorum, fuerit illud: Considerabimus quantum sit inter primum annorum Nabuchodonosor et inter illum annum, et mittemus illum numerum in tabulam primam, cuiuscunque duarum differentiarum primarum voluerimus, et videbimus in qua area annorum vigintiquinque collectorum reperiamus numerum illum et in qua area etiam prime tabule differentie tertie, que est annorum expansorum, et quod opponetur illis duobus numeris in illis duabus areis in eis que sunt post eas ex tabula aggregabimus, scilicet quod in unaquaque tabula fuerit per se ex eo quod proprium est cuiusque duorum numerorum. Et postea accipiemus in applicationibus quidem coniunctionis quod fuerit in differentia prima et quod fuerit in differentia tertia. Et in impletionibus quidem oppositionum accipiemus quod fuerit in differentia secunda et in differentia tertia et aggregabimus ea. Fiet ergo aggregatum ex eo quod est in tabula secunda tempus applicationis que est a principio illius anni, sicut coniunctio 24 dierum et 44 minutorum que sunt post medietatem diei Iomin vigesimiquarti mensis Thot. Quod si essent dies 34 et 44 minuta, esset illud post medium diem Iomin quarti mensis Phemenut secundum minuta equalia illis minutis. Per illud vero quod aggregatur ex eis que sunt in tabula tertia sciemus partes longitudinis Solis a longitudine longiore. Et per id quod aggregatur ex eis que sunt in tabula quarta sciemus partes diversitatis Lune a longiore longitudine. Et per id quod aggregatur ex eis que sunt in tabula quinta sciemus partes ultime longitudinis septentrionis, que est latitudinis. Et post illud, quemadmodum sequitur, si voluerimus assumere omnibus tabulis aut quibusdam earum ex eo quod aggregatur ex eo quod est in differentia quarta, que est mensium, scilicet proprietati cuiusque earum, alleviabitur illud nobis cum nos breviter converterimus unum dierum vel minuta diei, si que fuerint, ad horas equales. Erit enim superfluitas eius quod aggregatur ex horis secundum hoc quod omnes dies cum noctibus suis sunt equales. Et non accipiantur temporales secundum veritatem in omni hora, verum accipiantur dies cum noctibus suis diversi. Diversitas vero que est inter dies cum noctibus suis diverse acceptos equetur per id cuius premisimus narrationem. Et eius declaratio est quod cum fuerit superfluitas temporum maior longitudine diversa, minuemus eam ex eo quod aggregatur ex longitudine equali, et cum fuerit superfluitas temporum minor ea, addemus eam super longitudinem equalem. Et post nostram acceptionem secundum hunc modum temporis oppositionis aut coniunctionis que videntur secundum cursum medium et quod in eo est ex diversitatibus que sunt in unoquoque duorum luminarium, alleviabitur acceptio temporis et loci in quibus erit applicatio vera et etiam acceptio transitus Lune in latitudine cum comparaverimus unam duarum diversitatum alteri. Cum enim profunde perscrutati fuerimus in unaquaque earum et inquisiverimus transitum verum qui est Solis et Lune et latitudinis per id quod invenerimus ex augmento et diminutione in tempore duarum revolutionum, si invenerimus eos in parte una aut in duabus partibus oppositis, tunc illud est tempus applicationis vere. Et si non invenerimus eos ita, accipiemus partes longitudinis que est inter eos, et addemus super eas partem duodecimam earum, que est motus Solis in illis partibus fere, et considerabimus in quot horis equalibus secet Luna cum diversitate sua illas partes. Deinde accipiemus illas horas. Tunc si fuerit verificatio Lune minor verificatione Solis, addemus illud super tempus duarum revolutionum, et si fuerit maior, minuemus illud ex eo. Et similiter accipiemus longitudinem que est inter eos ex partibus cum parte duodecima earum. Tunc si fuerit verificatio Lune in tempore duarum revolutionum minor verificatione Solis, addemus illud super verificationem Lune in tempore revolutionis, et si fuerit maior ea, minuemus illud ex ea. Inveniemus ergo per illud locum verificationis applicationis et transitum Lune verum in orbe declivi in longitudine et in latitudine fere. Et invenitur etiam motus Lune diversus hore unius in hora applicationis secundum hunc modum quem narrabo: Mittam numerum partium diversitatis Lune in hora quesita in tabulam superfluitatis diversitatis Lune, et accipiam ex superfluitatibus que ei opponuntur additionis et diminutionis portionem diversitatis unius superfluitatum diversitatis, et multiplicabimus eam in motum diversitatis medium hore unius, qui est 32 minuta et 56 secunda, et quod provenerit considerabimus. Tunc si ceciderit numerus diversitatis in superioribus areis, que sunt maioris additionis et diminutionis, minuemus illud ex motu medio in longitudine hore unius, que est 32 minuta et 56 secunda, et si ceciderit numerus diversitatis in inferioribus areis, addemus illud. Quod ergo comprehenditur est motus Lune in diversitate in illa hora hore unius equalis. Temporum autem que sunt in Alexandria applicationum verarum ita est inventio. Non enim inventionis locorum omnium assumitur temporum horarum equatio nisi secundum orbem meridiei merid ei M. Alexandrie. Et iam alleviatur inventio temporum applicationis, in quocunque climate erit illud, ex temporibus Alexandrie cum fuerit numerus horarum Alexandrie equalium et eius elongatio ab orbe meridiei notus. Ex diversitate namque que est inter loca scietur quota pars sit diversitas que est inter orbem meridiei loci quesiti et inter orbem meridiei Alexandrie. Si ergo fuerit orbis meridiei loci quesiti ab orbe meridiei Alexandrie orientalis, secundum quantitatem illorum temporum tardabitur quod videtur ex consideratione applicationis, et si fuerit occidentalis, precedet secundum quantitatem illorum temporum. Et manifestum est etiam quod ex omnibus quindecim temporibus erit hora equalis.

⟨VI.5⟩ Capitulum quintum decimumquintum M.: De terminis eclypsium que sunt Solis et Lune

Iam consequitur quod diximus ut addamus quo indigemus in terminis eclypsium ex eis que percurrit Sol et Luna, ut, etsi non reiteremus considerationem in omnibus applicationibus habentibus revolutiones, sed in applicationibus in quibus possibile est accidere eclypses tantum, sit cognitio nobis illius facilior per ea que opponuntur unicuique applicationum habentium revolutiones ex transitu Lune in cursu suo medio in latitudine. In dictione autem que est ante istam iam declaravimus quod diameter Lune subtenditur arcui orbis magni descripti super Lune longitudinem magnam et super centrum orbis signorum qui est partis unius et 31 minutorum et 20 secundorum. Quod quidem scivimus per duas eclypses que fuerunt. Et fuit Luna super longitudinem longiorem orbis revolutionis sue. Nunc vero, quia volumus inventionem magnorum terminorum eclypticorum, et hi quidem termini non erunt nisi cum Luna fuerit in longitudine propinquiore orbis revolutionis sue, illud igitur demonstrabo etiam per duas eclypses quarum fuit consideratio cum fuit Luna in longitudine propinquiore orbis revolutionis sue. Quoniam decentius, planius et firmius quo demonstratur istud et eius simile est quod videtur et apparet. Et demonstrabo hic quantitatem arcus cui subtenditur diameter Lune. Fuit namque eclypsis Lune in anno septimo annorum Philometoris, qui est annus quingentesimus et septuagesimusquartus annorum Nabuchodonosor, transactis vigintiseptem diebus mensis Phemenut, qui est ex mensibus Egyptiorum, in nocte cuius mane fuit dies vigesimusoctavus a principio hore octave usque ad finem hore decime. Et fuit plurimum eclypsis Lune in Alexandria a parte septentrionis septem digiti. Et quia tempus medium fuit post medietatem noctis duabus horis et medietate hore temporalibus, que equate erunt due hore et tertia hore, quoniam locus Solis verus fuit in septima parte Tauri, fuitque tempus quod fuit a primo annorum Nabuchodonosor usque ad locum Solis in tempore medio huius eclypsis 573 anni Egyptii et ducenti et sex dies et 14 hore et tertia hore absolute equalis, que erunt secundum equationem dierum cum noctibus suis 14 hore tantum, et fuit in illa hora locus centri Lune medius septem partes et 49 minuta Scorpionis, verus autem sex partes et 16 minuta, et fuit eius elongatio a longitudine longiore in orbe revolutionis 160 partes et 40 minuta, et fuit elongatio eius ab ultima longitudine septentrionis in orbe suo declivi 98 partes et 20 minuta, manifestum est igitur quod cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe declivi octo partes et 20 minuta, et fuerit etiam in longitudine sua propinquiore, et fuerit centrum umbre in orbe magno descripto super ipsum super angulos rectos orbis declivis, et illud est transitus in quo erunt magne tenebre, cadet ex diametro in umbram medietas et pars duodecima. Et etiam in anno 37 revolutionis tertie revolutionum Philippi, qui est annus sexcentesimus et septimus annorum Nabuchodonosor duobus diebus transactis mensis Tobi, qui est ex mensibus Egyptiorum, in nocte cuius mane fuit dies tertius in principio quinte hore ipsius in Rhodo incepit Luna eclypsari. Et fuit plurimum umbre eius a parte meridiei tres digiti. Et quia etiam hic fuit principium eclypsis ante medietatem noctis duabus horis temporalibus, que fuerunt in Rhodo et Alexandria due hore equales et tertia hore, quoniam locus Solis secundum veritatem fuit in quinque partibus et octava partis Aquarii, et fuit tempus medium, in quo fuit plurimum tenebre eius, ante medietatem noctis hora una equali et medietate et tertia hore fere, et aggregantur ex tempore loci Solis in primo annorum Nabuchodonosor usque ad hoc tempus medium eclypsis 606 anni Egyptii et 121 dies et decem hore et sex minuta hore equalis absolute et secundum equationem dierum cum noctibus suis, et fuit locus centri Lune per cursum medium in illa hora in quinque partibus et 16 minutis Leonis, secundum verificationem vero in quinque partibus et octo minutis, et fuit eius longitudo a longitudine longiore orbis revolutionis 178 partes et 46 minuta, et fuit eius elongatio ab ultima longitudine septentrionis in orbe declivi 80 partes et 36 minuta, ergo manifestum est hic quod cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe suo declivi et in longitudine sua propinquiore decem partes et 36 minuta, et fuerit centrum umbre in loco sectionis orbis signorum et orbis magni descripti super centrum Lune super rectos angulos orbis Lune declivis, erit quod cadet in umbra ex diametro Lune quarta eius. Sed cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe suo declivi octo partes et tertia partis, erit eius longitudo ab orbe signorum in orbe magno descripto super duos polos eius 43 minuta et tria secunda partis unius. Et cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe suo declivi decem partes et tres quinte partis, erit longitudo eius ab orbe signorum in orbe magno descripto super duos polos eius 54 minuta et medietas et tertia minuti unius partis. Et quia superfluitas que est inter duas eclypses continet tertiam diametri Lune, et superfluitas que est inter duas longitudines centri Lune in orbe illo magno ab illo puncto orbis signorum, scilicet centro umbre, est undecim minuta et 47 secunda, tunc manifestum est quod tota diameter Lune subtenditur orbis magni descripti super minorem longitudinem Lune et super centrum orbis signorum arcui qui erit 35 minuta et tertia minuti partis unius fere. Et quia longitudo centri Lune fuit in eclypsi secunda, in qua eclypsata fuit quarta diametri eius, a centro quidem umbre 54 minuta et medietas et tertia minuti et a puncto quidem super quod secant se arcus umbre et linea que aggregat duo centra quarta diametri Lune, que est octo minuta et medietas et tertia minuti, ex hoc ergo demonstratur quod oportet quod sit medietas diametri umbre in longitudine Lune minore 46 minuta. Et illud est quod non diversificatur quin sit duplum medietatis diametri Lune et tres quinte eius equalis, que est 17 minuta et due tertie minuti. Medietas autem diametri Solis similiter subtenditur arcui orbis magni descripti super ipsum et super centrum orbis signorum qui erit 15 minuta et 40 secunda. Iam igitur ostensum est quod cum Sol et Luna fuerint in applicationibus in longitudine magna, quisque eorum numerabit proprie orbem suum duobus numeris equalibus. Cum ergo fuerit centri Lune quod videtur longitudo a centro Solis in duabus partibus orbis signorum 33 minuta et 20 secunda, tunc possibile erit ut sit primum locus Lune qui videtur in contactu Solis. 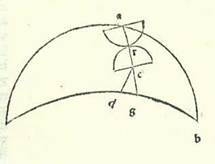Sicut si imaginemur arcum linee medii cinguli signorum, supra quem sint A, B, et arcum orbis Lune declivis, supra quem sint D, G, et imaginemur eos equidistantes in sensu, et describam arcum, supra quem sint A, E, G, orbis magni descripti super duos polos orbis Lune declivis ad locum revolutionum Lune in temporibus eclypticis, et imaginemur quidem supra punctum A medietatem circuli Solis et super punctum E medietatem circuli Lune qui videtur, donec sit principium contactus eorum super punctum R, et iam possibile est ut sit tempus in quo erit arcus AE, qui est longitudo que est inter centrum Lune quod videtur super punctum E et inter centrum Solis quod videtur super punctum A, hic 33 minuta et 20 secunda posita. In locis autem que sunt a climate primo, ubi erit dies longior qui est in eis tredecem horarum equalium, usque ad clima septimum, scilicet in locis in quibus erit dies longior sexdecim horarum equalium, erit maior diversitas aspectus Lune in latitudine, cum fuerit in longitudine sua minore, in hora applicationum ad partem septentrionis cum diversitate aspectus Solis octo minuta fere. Et similiter erit maior diversitas aspectus eius ex parte meridiei 58 minuta. Maior autem diversitas aspectus eius in longitudine, cum quidem fuerit illa octo minuta ad partem septentrionis, non erit illud in Leone et in Geminis nisi 30 minuta fere. Et cum fuerit diversitas aspectus eius ad partem meridiei 58 minuta, non erit illud in Scorpione et in Piscibus nisi quidecem minuta fere. Cum ergo nos posuerimus centrum Lune verum super punctum D et produxerimus lineam DE, que est totius diversitatis aspectus, erit linea quidem DG diversitas aspectus in longitudine fere et linea quidem GE diversitas aspectus in latitudine. Quapropter cum fuerit Luna ex parte septentrionis a Sole et fuerit in maiore diversitate aspectus sui ad partem meridiei, erit linea DG 15 minuta et erit linea EG pars una et 31 minuta et 20 secunda fere. Et quia proportio arcus qui est inter nodum et inter punctum G ad arcum GA in longitudine que est inter duos terminos eclypticos est sicut proportio undecim et medii ad unum (alleviatur scientia nobis illius ex eis quorum precessit declaratio in tali qualis est orbis Lune), erit ergo hic arcus qui est a nodo ad punctum G 17 partes et 26 minuta, et erit etiam cum DG secundum illam quantitatem 17 partes et 41 minuta. Et cum fuerit Luna ex parte meridiei a Sole et fuerit in maiore diversitate aspectus sui ad partem septentrionis, erit arcus DG 30 minuta et totus arcus AEG 41 minuta. Et propter hoc erit arcus quidem qui est inter nodum ad punctum G septem partes et 52 minuta, et erit totus cum arcu GD secundum illam quantitatem octo partes et 22 minuta. Cum ergo fuerit longitudo centri Lune verificati a quolibet duorum nodorum in orbe declivi ad partem septentrionis 17 partes et 41 minuta et ad partem meridiei octo partes et 22 minuta, tunc possibile erit in locis habitabilibus ut sit principium eius quod videtur locus Lune quo contingit Solem. Et illud est quod oportuit nos demonstrare.

Et etiam quoniam iam fuit ostensum quod maior diversitas Solis est due partes et 23 minuta et maior diversitas Lune in applicationibus est quinque partes et unum minutum, possibile est ut sit longitudo Lune a Sole in quibusdam temporibus in horis applicationum habentium revolutiones secundum veritatem septem partes et 24 minuta. In tempore vero in quo pertransit Luna has partes precedit Sol partem tertiamdecimam earum fere, scilicet 34 minuta fere. Et in tempore etiam in quo pertransit Luna hec 34 minuta precedit etiam Sol tertiamdecimam partem earum, que est tria minuta fere, quorum tertiedecime partis non est quantitas magna. Ergo si nos aggregaverimus illud donec sint 37 minuta, que sunt septem partium et 24 minutorum primorum pars duodecima, et postea addiderimus illud super partes diversitatis Solis, que sunt due partes et 23 minuta, fiet summa illius tres partes. Et est plurimum quod erit ex diversitate que est inter revolutiones applicationum mediarum in longitudine et latitudine et inter verificatas fere. Cum ergo fuerit etiam longitudo que est inter centrum Lune ab uno duorum nodorum per cursum suum medium in orbe suo declivi ad partem quidem septentrionis 20 partes et 41 minuta et ad partem meridiei undecim partes et 22 minuta, tunc possibile erit in locis habitabilibus ut sit primus locus Lune quo videtur contingere Solem. Et propter hoc cum fuerit numerus qui est ab ultima longitudine septentrionis orbis Lune declivis oppositus partibus applicationum revolutionum, scilicet partibus que sunt a 69 partibus et 19 minutis ad 101 partes et 22 minuta, aut oppositus partibus que sunt a 258 partibus et 38 minutis ad 290 partes et 41 minuta, tunc tantum erit possibile ut contingant in istis locis quos prediximus ea que narravimus ex contactu Lune et Solis. Et etiam propter terminos eclypticos lunares, quoniam iam ostensum est quod medietas diametri Lune in longitudine sua minore subtenditur 17 minutis et 40 secundis et quod medietas diametri umbre in magnitudine est duplum et tres quinte medietatis diametri Lune fere, et est 45 minuta et 56 secunda, tunc manifestum est quod cum fuerit longitudo centri Lune vera a centro umbre in orbe quidem magno descripto super ipsum et super duos polos orbis eius declivis a duabus partibus orbis signorum pars una et tria minuta et 36 secunda et in orbe quidem declivi, in quocunque duorum nodorum fuerit, secundum proportionem unius ad undecim et medium illud erit 12 partes et 12 minuta fere, erit tunc possibile primum ut contingat Luna umbram. Et propter hoc per id quod iam ostensum est ex diversitatibus, cum fuerit longitudo centri Lune que accipitur per cursum suum medium a duobus nodis in orbe suo declivi 15 partes et 12 minuta, tunc similiter cadit Luna etiam in numeris qui sunt ab ultima longitudine septentrionis in eis que sunt inter 74 partes et 48 minuta ad 105 partes et 12 minuta et in eis que sunt inter 254 partes et 48 minuta ad 285 partes et duodecim minuta, tunc erit possibile ut sit principium contactus Lune et umbre. Affirmavimus igitur in his tabulis que sunt applicationum numeros partium terminorum solarium et lunarium qui accidunt Lune, ut ponamus cognitionem eius quod possibile est cadere in eclypsim preparatam.

⟨VI.6⟩ Capitulum sextum: De longitudine que est inter menses eclypticos

O quam bonum est et utile ut addamus eis que iam prediximus in quot mensibus secundum maius sit possibile ut sint applicationes eclyptice, quatinus cum nos assumpserimus locum unum applicationis eclyptice, non accipiamus etiam omnes applicationes que se adivicem sequuntur, sed accipiamus applicationes in quibus possibile est esse eclypsim in tot aut tot mensibus et accipiamus illud ad inquisitionem terminorum. Quod autem possibile sit ut eclypsentur Sol et Luna in omnibus sex mensibus ex hoc declaratur. Aggregatur namque ut cursus Lune quidem medius in latitudine sit in sex mensibus 184 partes et minutum unum et 25 secunda. Arcus vero qui erunt in his que sunt inter terminos eclypticos in Sole et Luna, illi quidem qui erunt in portionibus minoribus semicirculo non continebunt partes nisi pauciores suis partibus, et arcus quidem qui erunt in portionibus maioribus semicirculo continent partes suis partibus plures. Termini enim Solis secant, in quocunque duorum nodorum fuerint, orbis Lune declivis a parte quidem septentrionis partes que iam affirmate sunt esse 20 partes et 41 minuta et a parte quidem meridiei 11 partes et 22 minuta. Arcus autem qui est a parte septentrionis in quo non erit eclypsis est 138 partes et 38 minuta, et arcus qui est a parte meridiei in quo non erit eclypsis 157 partes et 16 minuta. Arcus vero lunares secant in ambabus partibus orbis signorum in illo orbe ab uno duorum nodorum 15 partes et 12 minuta. Et colligitur ut sit quisque duorum arcuum in quibus non erit eclypsis 149 partes et 36 minuta.

Et ex istis modis possibile erit ut sit eclypsis lunaris in maiore quinque mensibus, scilicet cum fuerit Sol in cursu suo maiore et Luna in suo cursu minore. Et ita declarabitur nobis illud: In quinque enim mensibus mediis invenimus cursum quidem cuiusque duorum luminarium in longitudine superfluere in cursu medio Solis 145 partes et 32 minuta et in Luna quidem in diversitate sua in orbe revolutionis 129 partes et quinque minuta. Sed 145 partes et 32 minuta que sunt Solis non erunt nisi in cursu eius magno, qui erit a duabus partibus longitudinis propinquioris, que addunt super medium 4 partes et 38 minuta. Et erunt partes orbis revolutionis Lune 129 partes et quinque minuta in cursu Lune minore ab utraque parte longitudinis longioris, que minuunt ex cursu medio octo partes et 40 minuta. In tempore ergo medio, quod est quinque mensium, cum fuerit Sol quidem in maiore cursu suo et Luna in minore cursu suo, Luna erit precedens Solem partibus aggregatis ex ambabus diversitatibus, scilicet 13 partibus et 18 minutis. Et illud est quod cum ex eo acceperimus partem duodecimam propter illud cuius iam precessit declaratio, erit pars una et sex minuta fere. Et illud est quod cucurrit Sol ad hoc ut consequeretur eum Luna. Et quia Sol superfluit quattuor partibus et 38 minutis ex proprietate diversitatis sue et ex consecutione sua ad applicationem veram superfluit parte una et sex minutis, erit hora quinque mensium magnorum addens super medium in longitudine quinque partes et 44 minuta. Et similiter superfluit Luna fere per cursum suum in latitudine in orbe suo declivi super illud quod aggregatur ex portionibus latitudinalibus que sunt quinque mensium mediorum, que sunt 153 partes et 21 minuta fere. Erit ergo quod aggregatur ex cursu vero qui videtur in latitudine in quinque mensibus magnis 159 partes et 5 minuta. Termini vero eclyptici qui sunt ab utraque parte orbis signorum in longitudine Lune media continent ex partibus in orbe quidem magno descripto super duos polos orbis Lune declivis partem unam fere, quoniam partes que sunt longitudinis minoris erunt pars una et tria minuta et 36 secunda, et que sunt longitudinis maioris erunt 56 minuta et 24 secunda, in orbe vero declivi a duobus nodis undecim partes et 30 minuta. Quapropter aggregatur ut sit arcus qui est inter eos qui non eclypsantur 157 partes tantum, que sunt minores eis quas secant quinque menses maiores ex orbe declivi, scilicet 159 partibus et quinque minutis secundum duas partes et 5 minuta. Manifestum est igitur ex eis que prediximus quod possibile est ut eclypsetur Luna in quinque mensibus magnis in oppositione prima et separatione sua, a quocunque duorum nodorum fuerit, et eclypsetur in oppositione postrema etiam in cursu suo ad nodum oppositum illi nodo, et ut sint tenebre in ambabus eclypsibus ab eisdem partibus orbis signorum, et ut nunquam sint econtrario illius. Et ita declarabitur nobis quod possibile est ut sint in quinque mensibus magnis due eclypses lunares.

Secundum similitudinem vero iam narrati declarabitur nobis quod non est possibile ut sit illud in septem mensibus, quamvis ponamus eos septem menses minores, in quibus erit Sol in cursu suo minore et Luna in cursu suo maiore. Quoniam etiam in septem mensibus mediis erit cursus medius in longitudine (qui est cuiusque duorum luminarium) secans 203 partes et 45 minuta et cursus Lune in orbe revolutionis 180 partes et 43 minuta. Harum vero partium 203 partes et 45 minuta cum fuerit Sol in cursu suo minore ab utraque parte longitudinis longioris minuent ex motu medio quattuor partes et 42 minuta, et 180 partes et 43 quidem minuta que sunt orbis revolutionis Lune cum fuerit Luna in cursu suo maiore ab utraque parte longitudinis propinquioris addent super cursum medium novem partes et 58 minuta. In tempore ergo septem mensium minorum, cum fuerit Sol in cursu suo minore et Luna in cursu suo maiore, erit Luna iam pertransiens Solem secundum id quod aggregatur ex partibus ambarum diversitatum, quod est 14 partes et 40 minuta. Quapropter cum acceperimus partem duodecimam earum et addiderimus ipsam super quattuor partes et 42 minuta, que est quidem diversitas Solis, erit quod aggregabitur ex eo quinque partes et 55 minuta fere. Et illud est quod minuit cursus in longitudine in septem mensibus minoribus a medio. Et est etiam quod minuit cursus in latitudine ab eo quod aggregatur ex partibus septem mensium mediorum, que sunt 214 partes et 42 minuta. In septem ergo mensibus minoribus erit illud quod superfluit Luna in latitudine in orbe suo declivi 208 partes et 47 minuta. Erit ergo totus arcus magnus qui est inter terminos eclypticos in longitudine Lune media orbis declivis que est apud unum duorum nodorum, scilicet illum ad quem vadit et illum nodum a quo recedit opposito illi, 203 partes tantum. Iam ergo manifestum est quod non erit possibile quod cum eclypsabitur Luna in septem mensibus minoribus in oppositione prima, quocunque modo fuerit, ut eclypsetur in oppositione postrema.

Ostendam igitur etiam quod iam possibile est apud illud quod est illius simile quod diximus ut eclypsetur Sol duabus vicibus in quinque mensibus magnis in omnibus plagis habitabilibus. Nos enim iam ostendimus quod in quinque mensibus magnis erit cursus Lune in latitudine 159 partes et 5 minuta. Et erit arcus qui est super Solem, in quo non erit eclypsis in longitudine Lune media, secundum illam quantitatem 167 partes et 36 minuta, quoniam elongatio terminorum eclypticorum ab orbe signorum in orbe descripto super duos polos eius erit 32 minuta et 20 secunda et in orbe quidem Lune declivi sex partes et 12 minuta. Manifestum igitur est quod cum non fuerit Lune diversitas aspectus, non erit possibile ut sit illud, propter hoc quod arcus in quo non erit eclypsis erit maioris longitudinis arcu cursus Lune in quinque mensibus magnis, in orbe quidem Lune declivi cum octo partibus et 31 minutis et in orbe quidem qui est super rectum angulum orbis signorum 45 minutis fere. Ubi vero erit possibile ut sit diversitas aspectus in una duarum coniunctionum extremarum aut in ambabus simul addens in latitudine super 45 minuta, tunc ergo erit possibile ut sint ambe coniunctiones extreme eclyptice. Manifestum igitur iam est quod in tempore medio quinque mensium, cum fuerit Luna in cursu suo minore et Sol in cursu suo maiore a duabus tertiis Virginis ad duas tertias Aquarii, Luna precedet Solem etiam partibus ambarum diversitatum, que sunt 13 partes et 18 minuta. Has vero partes et partem duodecimam earum percurrit Luna per cursum suum medium in die et duabus horis et quarta hore. Manifestum est igitur quod quia fuit tempus medium quinque mensium 147 dies et 15 hore et medietas et quarta hore fere, erit tempus maius quinque mensium 148 dies et 18 hore. Et propter hoc cum fuerit coniunctio prima in duabus tertiis Virginis, erit coniunctio postrema in duabus tertiis Aquarii ante omnes hos dies sex horis. Inquirimus ergo ubi et quando erit possibile ut sit diversitas aspectus Lune in uno horum duorum signorum aut in ambobus super stationem loci Aquarii et ante locum Virginis sex horis et 45 minutis. Non enim, quemadmodum diximus, reperitur diversitas aspectus Lune a parte septentrionis in aliquo locorum habitabilium maior his 45 minutis. Et ex hoc non est possibile ut eclypsetur elypsetur M. Sol bis in quinque mensibus magnis in cursu Lune a parte meridiei orbis signorum, scilicet cum fuerit Luna elongata in coniunctione prima a nodo caude et appropinquaverit in coniunctione postrema nodo capitis. Iam autem possibile est ut eclypsetur Sol ad partem meridiei apud eos qui habitant post orbem equationis diei ad septentrionem secundum hanc quantitatem in ambobus his signis et ante hunc locum sex horis cum fuerint due tertie Virginis in coniunctione prima in descensione occasus et due tertie Aquarii in coniunctione secunda in orbe meridiei. Nos enim iam invenimus Lune in his locis in longitudine media diversificari aspectum ad partem meridiei. Et erit diversitas aspectus Solis et Lune sub orbe quidem equationis diei in loco Virginis 22 minuta fere et in loco Aquarii 14 minuta, et ubi erit longitudo diei longioris 12 hore et medietas hore in loco Virginis 27 minuta et in loco Aquarii 22 minuta, donec sit superfluitas duarum diversitatum aspectus super hec 45 minuta 4 minuta. Et cum fuerit diversitas aspectus in locis septentrionalibus maior semper diversitate aspectus in locis meridianis, erit plus firmum semper. Manifestum est igitur quod est possibile ut videant eclypsim Solis in illis locis habitantes duabus vicibus in quinque mensibus magnis. Illud vero non erit nisi in cursu Lune in parte septentrionis ab orbe signorum tantum, scilicet cum fuerit in eclypsi prima recedens a nodo capitis et in eclypsi secunda accedens ad nodum caude.

Et dico etiam quod iam possibile est ut eclypsetur Sol duabus vicibus apud illos in septem mensibus parvis. Quoniam iam declaravimus quod in septem mensibus parvis erit cursus Lune in latitudine 208 partes et 47 minuta. Et erit arcus quem pertransivit Luna qui est inter terminos eclypticos orbis declivis maior arcu qui est a loco qui appropinquat uni duorum nodorum ad locum qui opponitur ei et a quo recedit et accedit ad nodum alterum. Et colligitur ut sit hec longitudo in Sole in longitudine Lune media 192 partes et 24 minuta. Igitur manifestum est etiam quod cum non erit Lune diversitas aspectus, non erit possibile ut sit quod diximus. Quoniam arcus orbis declivis qui est septem mensium parvorum erit maior arcu magno quem pertransivit Luna ex terminis Solis eclypticis in orbe quidem declivi 16 partibus et 23 minutis et in orbe descripto super duos polos orbis signorum parte una et 25 minutis. Ubi vero est possibile aspectum diversificari donec diversitates aspectuum que sunt cuiuscunque coniunctionum verarum aut ambarum simul sint diversitates aspectuum addentes super partem unam et 25 minuta, tunc ergo erit possibile ut sint due coniunctiones extreme eclyptice. Et quia iam declaravimus quod in tempore septem mensium mediorum, cum fuerit Luna in cursu suo maiore et fuerit Sol in cursu suo minore a postremis Aquarii ad medium Virginis, erit Luna preteriens iam Solem 14 partibus et 40 minutis, et has partes et partem earum duodecimam percurrit Luna per cursum suum medium in die una et in quinque horis, tunc manifestum est, quia tempus septem mensium mediorum continet 206 dies et 17 horas fere, quod tempus septem mensium parvorum erit 205 dies et 12 hore. Quapropter erit tempus coniunctionis postreme, que est in medio Virginis, post duodecem horas temporis coniunctionis prime, que est in postremo Aquarii. Inquirimus ergo ubi et quando erit possibile ut sit diversitas aspectus Lune maior parte una et 25 minutis aut in uno horum duorum signorum aut in ambobus secundum prolongationem duodecem horarum a duobus locis, scilicet cum fuerit unum eorum occidens et alterum eorum oriens, propter hoc quod non aliter est possibile ut sint ambe eclypses super terram a parte quidem septentrionis. Non enim reperitur Lune diversitas aspectus secundum hanc quantitatem in aliquo locorum habitabilium, et neque habitantibus sub orbe equationis diei erit diversitas aspectus Lune in parte latitudinis in longitudine sua media maior vigintitribus minutis. Ex hoc ergo non est possibile ut eclypsetur Sol duabus vicibus in septem mensibus parvis per cursum Lune in parte meridiei ab orbe signorum, scilicet cum fuerit in coniunctione quidem prima appropinquans nodo capitis et in coniunctione postrema recedens a nodo caude. Iam autem invenimus quod diversitas aspectus huius erit ad partem meridiei a linea equidistante descripta super Rhodum cum fuerit postremum Aquarii oriens et medium Virginis occidens. Lune namque aspectus diversificatur in Rhodo et in locis que sunt sub linea equidistante descripta super Rhodum in unoquoque horum duorum locorum in longitudine media diversitatis aspectus solaris secundum diminutionem 46 minuta fere a parte meridiei, donec erunt diversitates aspectuum que sunt duarum coniunctionum simul maius parte una et 25 minutis et erit diversitas aspectus que est ad partem meridiei maior in locis qui magis intrant in septentrionem a linea Rhodi. Manifestum est igitur quod possibile est ut videant qui sunt in his locis habitabilibus in septem mensibus parvis eclypsim Solis duabus vicibus. Veruntamen illud etiam non erit nisi cum fuerit cursus Lune in parte septentrionis ab orbe signorum tantum, scilicet cum fuerit in eclypsi quidem prima appropinquans nodo caude et in eclypsi secunda recedens a nodo capitis.

Restat autem ut ostendamus etiam quod in uno mense non est possibile ut Sol eclypsetur bis in locis habitabilibus, neque in climate uno neque in climatibus diversis. Si enim aliquis aggregaverit causas eclypsium omnes simul, quarum est impossibilis coniunctio et convenientia, sed est forte possibile ut secundum voluntatem suam imaginetur eas si ipse posuerit has causas possibiles, non erit possibile illud. Per quod volo intelligi quod ipse posuerit Lunam quidem in longitudine sua minore, ut sit diversitas aspectus eius maior, et posuerit mensem minorem, ut sit secundum quantitatem qua possibile est ut sit mensis minor erit sit ... erit: Two rivalling verbs. Both are also contained in Paris, BnF, lat. 14738 (101r, line 10). cursus Lune in latitudine mensis maior cursu Solis quem continent termini Solis eclyptici, quamvis imaginemur eam non alteratam in horis neque in signis in quibus videntur maiores diversitates aspectuum Lune. Et quia in mense medio superfluit quodque duorum luminarium per cursum suum medium in longitudine 29 partes et 6 minuta, et cursus Lune in orbe revolutionis superfluit 25 partes et 49 minuta, sed 29 quidem partes et 6 minuta que sunt Solis in cursu eius minore a duabus partibus longitudinis longioris minuunt ex cursu eius medio partem unam et octo minuta, et 25 quidem partes et 49 minuta que sunt orbis revolutionis Lune in cursu eius maiore a duabus partibus longitudinis propinquioris addunt super cursum eius medium duas partes et 28 minuta, tunc si nos consequenter secundum illud cuius precessit declaratio aggregaverimus additiones et diminutiones que sunt duarum diversitatum simul, que sunt tres partes et 36 minuta, et postea acceperimus partem earum duodecimam, que est 18 minuta, et addiderimus eam super illud quod provenit ex diminutione Solis, fiet illud pars una et 26 minuta. Et secundum illud erit cursus mensis minoris minor cursu mensis medii in longitudine et latitudine. Et quia cursus Lune in mense medio in latitudine erit 30 partes et 40 minuta, erit cursus eius medius in mense minore 29 partes et 14 minuta, que faciunt latitudinem in orbe magno qui est in orbe signorum super rectum angulum duas partes et 33 minuta fere. Aggregatur vero ut sit totus transitus terminorum Solis eclypticorum, cum fuerit Luna in longitudine sua minore, pars una et sex minuta, donec sit cursus mensis minoris maior parte una et 27 minutis. Oportet ergo penitus, si Sol eclypsatus fuerit in mense uno duabus vicibus, ut aut non sit Lune diversitas aspectus in una duarum coniunctionum et sit diversitas aspectus eius in coniunctione postrema maior parte una et 27 minutis, aut sit in unaquaque duarum coniunctionum diversitas aspectus Lune ad partem unam et sit superfluitas diversitatum aspectuum maior parte una et 27 minutis, aut ut sit diversitas duorum aspectuum simul maior hac quantitate, ita ut sit diversitas que est unius duarum coniunctionum ad partem septentrionis et sit alia ad partem meridiei. Sed neque alicubi terrarum in applicationibus neque in longitudine minore diversificatur aspectus Lune in latitudine plus diversitate aspectus Solis, que est pars una. Non est ergo possibile in mense minore ut eclypsetur Sol bis cum fuerit Luna aut in una duarum coniunctionum, ita ut non sit ei diversitas, aut sit diversitas eius in coniunctionibus duabus ad partem unam et non sit eius superfluitas plus parte una. Oportet ergo ut dicamus partem unam et 27 minuta. Non enim est possibile ut sit illud nisi cum fuerit queque duarum diversitatum duorum aspectuum in oppositione alterius et fuerit quod aggregatur ex unaquaque duarum diversitatum maius parte una et 27 minutis tantum. Et neque est possibile ut sit illud nisi in duobus locis habitabilibus diversis oppositis, propter hoc quod possibile est ut sit diversitas aspectus Lune apud illos quidem qui sunt in parte septentrionis ab orbe equationis diei a loco habitabili qui sequitur nos ad partem meridiei et apud illos qui sunt in parte meridiei ab equatione diei ab eis qui nominantur ‘oppositi nostre terre’ erit diversitas aspectus Lune sit diversitas aspectus Lune ... erit diversitas aspectus Lune: Two rivalling passages. Both are also contained in Paris, BnF, lat. 14738 (101v, lines 3-5). ad partem septentrionis post diversitatem aspectus Solis a 25 minutis usque ad partem unam. In loco autem uno habitabili non erit illud semper, quoniam Lune augetur diversitas aspectus. Et similiter apud illos qui sunt sub equatione diei erit diversitas aspectus Lune ad septentrionem et ad meridiem cum eo quod non est maius 25 minutis. Sed apud illos qui declinant ab eis ad septentrionem et ad meridiem erit diversitas aspectus Lune qui sunt econtrario illorum absque maiore hac una parte donec erit quod aggregatur ex duabus diversitatibus aspectus Lune simul minus parte et 27 minutis. Et erit minus illo minore valde apud illos qui sunt inter equationem diei et inter unam duarum extremitatum longitudinis ultime, que erit semper cuiusque duarum diversitatum aspectus duorum contrariorum. Et erit prohibitio possibilitatis apud eos etiam maior. Non est ergo possibile apud illos in uno loco ut eclypsetur Sol in mense uno duabus vicibus, neque in aliquo locorum terre. Apud illos vero in duobus locis oppositis diversis iam est possibile illud. Sed tamen non est possibile ut sint terre unius habitabilis. Et illud est quod oportuit nos demonstrare.

⟨VI.7⟩ Capitulum septimum: De artificio lineationis tabularum eclypticarum

Quas vero longitudinum applicationum conveniat nobis assumere in inquisitione eclypsium iam est declaratum per illud quod diximus. Sed qualiter iam cognita fiant tempora media que sunt applicationum et acceptus fuerit cursus Lune in eis in applicationibus quidem coniunctionalibus que videntur et in applicationibus oppositis verificatis cum scientia loci Lune in latitudine, et qualiter possimus inquirere de eo breviter et de applicationibus eclypticis que procul dubio erunt, et qualiter sciantur earum magnitudines et tempora tenebrarum earum, iam posuimus ad cognoscendum illud tabulas, eclypsium quidem solarium tabulas duas et eclypsium lunarium tabulas duas. Et posuimus illud cum fuerit Luna in longitudine sua maiore et in longitudine sua minore. Et posuimus superfluitatem additionum tenebrarum secundum partem et partem duodecimam diametri que obscuratur cuiusque duorum luminarium. Primam vero tabulam, que est eclypsium solarium continentem terminos eclypticos qui erunt cum fuerit Luna in longitudine sua maiore, describam secundum vigintiquinque areas et secundum quattuor tabulas. Et erunt due prime tabule harum quattuor continentes cursum Lune qui videtur in latitudine in orbe declivi in unaquaque tenebrarum. Et quia diameter quidem Solis est 31 minuta et 20 secunda et de diametro quidem Lune iam ostensum est quod cum fuerit in longitudine sua maiore, erit secundum illam quantitatem 31 minuta et 20 secunda, propter hoc cum fuerit longitudo centri Lune que videtur a centro quidem Solis in orbe magno descripto super duo centra 31 minuta et 20 secunda et a nodo quidem in orbe suo declivi secundum proportionem cuius iam premisimus narrationem sex partes, erit tunc primum quod continget Luna Solem. In areis vero primis duarum tabularum ponam in prima quidem 84 partes et in secunda 276 partes, sed in postremis areis in tabula quidem prima etiam 96 partes et in secunda etiam 264 partes. Et quia portio unius partis duodecime diametri Solis orbis declivis est 30 minuta partis unius fere, posuimus hic 30 minuta ipsam superfluitatem que additur et minuitur in his duabus tabulis. Et incipiam in eis ab extremis areis usque ad medium earum. Et firmabo in medio earum 90 partes et 270 partes. Et ponam in tabula tertia magnitudinem quantitatum tenebrarum. In areis quidem que sunt in extremitatibus ponam contactum cifre et cifre, et in eis quidem areis que sequuntur post eas digitum unum in loco unius partis duodecime diametri, et similiter in areis que residue sunt. Et ponam additiones earum secundum digitum unum donec perveniatur ad aream mediam que est ad quam pervenit numerus 12 digitorum. Et ponam in tabula quarta transitus centri Lune qui erunt in totis tenebris, ita quod non computabuntur cum eis que accidunt illi ex motibus Solis aut que accidunt ex diversitatibus aspectus Lune. Et ponam in differentia secunda, que est eclypsium solarium continente terminos eclypticos qui erunt in longitudine Lune minore, sicut quod est in differentia prima, sed illud in vigintiseptem areis et quattuor tabulis. Et quia iam ostensum est quod medietas diametri Lune in longitudine sua minore est 17 minuta et 40 secunda secundum quantitatem qua erit medietas diametri Solis 15 minuta et 40 secunda, tunc cum Luna primum contigerit Solem, erit longitudo centri Lune que videtur a centro quidem Solis 33 minuta et 20 secunda partis unius et ab uno duorum nodorum in orbe declivi sex partes et 24 minuta. Erunt ergo numeri latitudinis que videtur in areis que sunt in extremitatibus qui sunt 83 partes et 36 minuta et 276 partes et 24 minuta, et etiam 96 partes et 24 minuta et 263 partes et 36 minuta. Numerus autem qui est in medio digitorum propter superfluitatem additionum similem est 12 digiti et quattuor quinte digiti unius. Et tunc erit transitus more. Ponam autem unamquamque duarum differentiarum eclypsium lunarium in quadragintaquinque areis et in quinque tabulis. Et ponam in differentia prima numeros latitudinis cum fuerit Luna in longitudine sua maiore. Et quia iam ostensum est quod medietas diametri Lune, cum fuerit in longitudine sua maiore, erit 15 minuta et 40 secunda et medietas diametri umbre secundum illam quantitatem 40 minuta et 44 secunda, ergo cum primum tanget Luna umbram, erit longitudo centri eius a centro umbre in orbe magno descripto super duo centra 56 minuta et 24 secunda et a duobus quidem nodis in orbe declivi decem partes et 48 minuta. Firmabimus igitur super areas primas numerum 79 partium et 12 minutorum et numerum 280 partium et 48 minutorum, et super areas quidem postremas numerum 100 partium et 48 minutorum et numerum 259 partium et 12 minutorum. Et propter hoc fit superfluitas additionum earum et diminutionum in principio secundum portionem que debetur uni parti duodecime diametri Lune, que erit tunc 30 minuta. Et ponam in differentia secunda numeros latitudinis cum fuerit Luna in longitudine sua minore. De qua iam ostensum est quod medietas diametri Lune, cum fuerit in longitudine sua minore, erit 17 minuta et 40 secunda, et medietas diametri umbre erit secundum illam quantitatem 45 minuta munita M. et 56 secunda. Quapropter cum primum Luna contingerit umbram, erit tunc longitudo centri eius a centro quidem umbre pars una et tria minuta et 36 secunda, et a nodo quidem in orbe declivi 12 partes et 12 minuta. Quapropter firmabimus super primas areas numerum 77 partium et 48 minutorum et numerum 282 partium et 12 minutorum, et super postremas areas numerum 102 partium et 12 minutorum et 257 partium et 48 minutorum. Et ponam superfluitatem additionum earum et diminutionum secundum portionem que convenit uni parti duodecime diametri Lune, que tunc est 34 minuta. Et ponam tabulas tres (que sunt digitorum) secundum similitudinem modi solaris, et similiter tabulas que sequuntur illud continentes transitus Lune in unaquaque tenebrarum et transitus cuiusque principiorum casus et complementi eius et etiam medietatem more.

Et imaginabimur in unaquaque tenebrarum transitus Lune positos secundum lineas mensurabiles. Et accipiemus demonstrationes in hoc secundum quod sint in superficie una et linee recte. Arcuum enim quorum magnitudo quantitatum non est nisi ad similitudinem quantitatis huius non diversificant quantitates quantitatem chordarum eorum secundum quantitatem sensibilem, neque etiam diversificat transitus Lune in orbe declivi transitum ipsius qui videtur in orbe signorum diversitate cui sit quantitas. Non ergo estiment aliqui quod nos ignoremus illud. Et penitus dico quod iam erit diversitas in transitu Lune in longitudine, propter hoc quod accepimus arcus orbis declivis loco arcuum orbis signorum et quia non est possibile ut sint tempora applicationum similia temporibus mediis eclypsium secundum equalitatem non diversa. 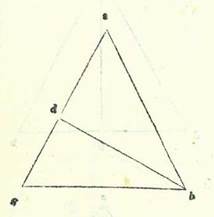Si nos enim acceperimus a nodo A duos arcus equales horum duorum orbium, scilicet arcum AB et arcum AG, et protraxerimus arcum BG, et produxerimus a puncto B perpendicularem ad lineam AG, que sit BD, tunc ex hoc declarabitur quod cum fuerit Luna super punctum B et acceperimus arcum AG orbis signorum loco arcus AD, propter hoc quod transitus Lune qui videntur apud orbem signorum non videntur nisi in orbibus descriptis super duos polos eius, erit diversitas declinationis orbis lunaris secundum arcum GD. Et cum nos etiam imaginati fuerimus Solem aut centrum umbre super punctum B, erit tempus quidem applicationis absque diversitate orbium cum fuerit Luna super punctum G, et inter tempus quidem medie eclypsis cum fuerit super punctum D, propter hoc quod tempora media que sunt tenebrarum etiam non videntur nisi in orbibus descriptis super duos polos orbis lunaris. Erit diversitas inter hoc tempus et inter tempus applicationis, scilicet secundum arcum GD. Et illud est quod oportuit nos demonstrare.

Causa autem que prohibet nos cogitare in istis arcubus in partitionibus libri nostri est quod ipsi sunt parvi et eorum diversitas non est sensibilis. Ignorare vero aliquid istorum vel horum similium est turpe. Dimissio tamen illius propter vilitatem eius ex industria est propter difficultatem ipsius in divisione capitulorum numerationis. Secundum quantitatem vero qua possibile est videre in modis et considerationibus in utilitate quidem que pervenit ex scientia eius est magnum in sensu. In errore vero eorum que videntur aut nunquam erit error aut, si fuerit, erit perexiguus. Dico autem penitus quod arcum similem arcui GD non invenimus plus quinque minutis partis unius. Et illud declaratur per capitulum quo scivimus diversitatem que est inter In M there follows diversitatem que est inter. arcus equationis diei et inter arcus orbis signorum, sicut quod est in orbibus descriptis super duos polos equationis diei. In eclypsibus autem non invenimus ipsum plus duobus minutis. Quoniam secundum quantitatem qua erit unusquisque duorum arcuum AB et AG duodecem partes (transituum enim Lune qui erunt in eclypsibus fines non sunt nisi ut perveniant ad hanc fere quantitatem), erit linea BD pars una fere. Quapropter erit AD secundum illam quantitatem undecem partes et 58 minuta. Et restat ut sit DG residua duo minuta. Et illud est quod non erit pars sextadecima hore unius equalis. Perscrutari autem subtilitatem in quantitate huic simili non est nisi extollentia et vana gloria et neque est dilectio veritatis. Et propter hoc posuimus quod scripsimus ex transitibus Lune in his tenebris ac si inter orbes non esset diversitas sensibilis.

Pervenimus vero ad hanc cogitationem etiam in exemplo uno aut in duobus que continentur in eo quod narrabo. 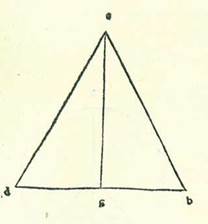Sit itaque centrum Solis aut centrum umbre punctum A et linea que erit loco arcus orbis lunaris BGD, Et sit punctum B centrum Lune cum primum contingit Solem aut umbram, et sit punctum D separatum, et coniungam duas lineas AB et AD, et producam perpendicularem ab A super lineam BD, supra quam sint A, G. Manifestum est igitur quod cum fuerit centrum Lune super punctum G, tunc erit tempus medium quod est eclypsis et tenebre maioris, propter hoc quod linea AB est equalis linee AD, et propter hoc erit transitus BG equalis GD, et propter hoc quod linea AG est brevior omnibus lineis que protrahuntur ad lineam BD et aggregat Probably corrupt for aggregant, which would correspond to the Greek text (see Toomer, loc. cit., p. 298, line 11 from the bottom). Paris, BnF, lat. 14738 (102v, line 7 from the bottom) reads aggregat too. duo centra. Et manifestum est quod unaqueque duarum linearum AB et AD continet medietates diametrorum Lune quidem et Solis, et Lune quidem et umbre, et linea AG est brevior unaquaque earum secundum partem diametri eclypsati quam continet tenebra diametri in qua est eclypsis. Et quia hoc est ut diximus, faciemus ad hoc exemplum et ponemus tenebram tres digitos, et sit punctum A imprimis centrum Solis. Cum ergo fuerit Luna in longitudine maiore, erit linea AB 31 minuta et 20 secunda et quadratum eius 981 secunda et 47 tertia fere. Et linea AG erit secundum illam quantitatem 23 minuta et 30 secunda. Ipsa enim est bevior AB secundum tres duodecimas partes diametri Solis, scilicet secundum septem minuta et 50 secunda. Et quadratum AG est 552 secunda et 15 tertia. Quapropter erit quadratum BG secundum illam quantitatem 429 secunda et 32 tertia, et erit longitudo BG 20 minuta et 43 secunda fere. Et illud est quod ponam in prima differentiarum solarium oppositum tribus digitis in quarta tabula. Cum autem fuerit Luna in longitudine minore, erit etiam linea AB 33 minuta et 20 secunda et quadratum eius mille et centum et undecem secunda et septem tertia. Et erit linea AG secundum illam quantitatem 25 minuta et 30 secunda et quadratum eius 650 secunda et 15 tertia. Et quadratum BG residue erit quadringenta et sexaginta secunda et 52 tertia. Longitudo igitur linee BG erit secundum illam quantitatem 21 minuta et 28 secunda. Et illud est quod firmavimus in differentia que est secunda differentiarum solarium oppositum tribus digitis in tabula quarta. Sit etiam centrum umbre punctum A et locus tenebre in diametro Lune. Erit ergo linea AB in longitudine Lune maiore 56 minuta et 24 secunda et quadratum eius 3180 secunda et 58 tertia. Et linea AG erit secundum illam quantitatem 48 minuta et 34 secunda. Est namque brevior AB secundum quartam diametri Lune, scilicet secundum minuta que sunt in illa longitudine, scilicet que sunt septem minuta et 50 secunda. Et erit quadratum linee AG 2358 secunda et 43 tertia. Et restat ut sit quadratum BG 822 secunda et 15 tertia. Et erit longitudo linee BG secundum illam quantitatem 28 minuta et 41 secunda. Et illud est quod firmavimus in prima differentiarum lunarium oppositum tribus digitis in tabula quarta. Et est continens transitum Lune in casu suo in tenebram, que est in sensu complementum tenebre. In longitudine autem Lune minore erit linea AB 63 minuta et 36 secunda, et quadratum eius erit 4044 secunda et 58 tertia. Et linea AG erit secundum illam quantitatem 54 minuta et 46 secunda. Superfluitas igitur que est inter eas est octo minuta et 50 secunda, que sunt etiam quarta diametri Lune que est in longitudine minore. Et erit quadratum linee AG 2999 secunda et 23 tertia. Et remanet ut sit quadratum linee BG 1045 secunda et 35 tertia. Longitudo ergo BG secundum illam quantitatem erit 32 minuta et 20 secunda. Et illud est quod firmavimus oppositum tribus digitis in tabula quarta differentie, que est secunda differentiarum lunarium. Et illud est quod nos oportuit demonstrare.

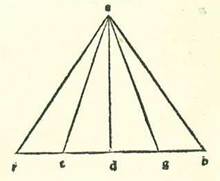Et etiam propter tenebram lunarem que habet tempus more ponam punctum A centrum umbre et lineam rectam que est loco arcus orbis Lune declivis lineam BGDER, et ponam punctum B centrum Lune cum primum contingit umbram exterius, et punctum G super quod sit centrum Lune in principio quo eclypsatur tota et contingit interius circulum umbre, et punctum E super quod sit etiam centrum Lune cum prius separatur interius et tangit circulum umbre, et sit punctum R cum fuerit centrum Lune super ipsum in fine eius egressus et contactus umbre exterius, et producam etiam a puncto A perpendicularem AD super lineam BR. Cum igitur firmabitur hic illud cuius precessit declaratio, demonstrabimus quod unaqueque duarum linearum AG et AE continet superfluitatem qua superfluit medietas diametri umbre super medietatem diametri Lune donec sit transitus DG equalis DE. Et erit unaqueque earum continens moram. Et remanet ut sit linea BG residua, que est casus, equalis linee ER, que est complementi. Ponam autem eclypsim in qua erunt 15 digiti Lune, scilicet eclypsim in qua erit centrum D interius ab ultima extremitate que est in terminis eclypticis secundum diametrum unam lunarem et quartam diametri, scilicet cum fuerit linea AD brevior unaquaque harum AB et AR secundum hanc diametrum lunarem et quartam eius et unaquaque duarum linearum AG et AE secundum quartam diametri lunaris. Cum igitur fuerit Luna in longitudine maiore, erit linea hec AB 56 minuta et 24 secunda que prediximus, et erit quadratum eius 3180 secunda et 58 tertia, et erit linea AG secundum illam quantitatem 25 minuta et 4 secunda. Diameter enim Lune in longitudine maiore erit 31 minuta et 20 secunda, et erit eius quadratum 628 secunda et 20 tertia. Et propter hoc erit linea AD 17 minuta et 14 secunda, et erit quadratum eius 296 secunda et 59 tertia. Quapropter remanet ut sit quadratum linee BD 2883 secunda et 59 tertia. Et erit longitudo linee BD secundum illam quantitatem 53 minuta et 42 secunda. Et superest ut sit quadratum linee GD 331 secunda et 21 tertia. Eritque longitudo eius secundum illam quantitatem 18 minuta et 12 secunda, et erit linea BG residua secundum illam quantitatem 35 minuta et 30 secunda. Firmabimus ergo opposita numero 15 digitorum qui sunt in prima differentiarum eclypsium lunarium in tabula quidem quarta minuta casus Lune in eclypsim, scilicet 35 minuta et 30 secunda equalia minutis complementi, et in tabula quidem quinta minuta medii temporis more, scilicet 18 minuta et 12 secunda. Cum autem fuerit Luna in longitudine minore, erit linea quidem AB hic 63 minuta et 36 secunda et quadratum eius 4044 secunda et 58 tertia, et linea AG erit 28 minuta et 16 secunda secundum illam quantitatem, et erit quadratum eius 799 secunda et cifre. Iam enim ostensum est quod diameter Lune in longitudine minore erit 35 minuta et 20 secunda. Quapropter erit linea AD 19 minuta et 26 secunda, et erit quadratum eius 377 secunda et 39 tertia. Et remanet ut sit quadratum linee BD 3667 secunda et 19 tertia, et ut sit longitudo BD 60 minuta et 34 secunda secundum illam quantitatem, et quadratum linee GD 421 secunda et 21 tertia. Et erit longitudo GD 20 minuta et 32 secunda secundum illam quantitatem. Et remanet ut sit linea BG 40 minuta et duo secunda. Firmabimus ergo in secunda differentiarum eclypsium lunarium opposita 15 digitis in tabula quidem quarta minuta casus Lune in eclypsim, scilicet 40 minuta et duo secunda, que sunt etiam equalia minutis complementi, et in tabula quinta minuta medii temporis more, scilicet 20 minuta et 32 secunda. Et illud est quod voluimus demonstrare.

Ut autem inveniamus breviter in transitibus Lune in orbe revolutionis in eo quod est inter longitudinem maiorem et longitudinem minorem portionem cuiusque superfluitatis additionum diversitatis totius per numerationem capitulorum minutorum, posuimus sub istis differentiis differentiam aliam parvam continentem numeros transitus Lune in orbe revolutionis, et illud est quod pertinet ex portione minutorum cuiusque eorum que videbuntur ex differentiis in differentiis primis et differentiis secundis que sunt eclypsium. Nos autem firmavimus quantitatem minutorum in differentia lunari que est diversitatis aspectus in tabula septima ac si orbis revolutionis esset in longitudine longiore orbis centri egredientis propter applicationes. Et quia plures eorum qui considerant principia eclypsium non numerant quantitates magnitudinis tenebrarum secundum diametros orbium, sed plures eorum numerant eas secundum totas superficies orbium que videntur per contactum aspectus absoluti qui addit totum quod videtur ad illud quod non videtur, addidimus super has differentias differentiam parvam in qua erunt duodecem aree et tres tabule. Et posuimus in tabula prima 12 digitos, ac si omnis digitus contineret partem duodecimam diametri cuiusque duorum luminarium, quemadmodum posuimus in differentiis eclypticis. Et firmavimus in duabus tabulis reliquis portiones omnis digiti superficiei, et illud est pars duodecima etiam omnis superficiei, in tabula quidem secunda portionem solarem et in tabula tertia portionem lunarem. Et subtiliter indagavimus has portiones ex quantitatibus tenebrarum tantum cum fuerit Luna in longitudine media. Proportio enim erit una fere in quantitate simili his additionibus et diminutionibus que sunt diametrorum. Est autem proportio circulorum ad diametros sicut proportio trium partium et 8 minutorum et 30 secundorum ad partem unam. Hec enim proportio est que est inter triplum et septimam eius et inter triplum et decem septuagesimasprimas partium ipsius fere, et illud est opus Arsamidis secundum opus absolutum. 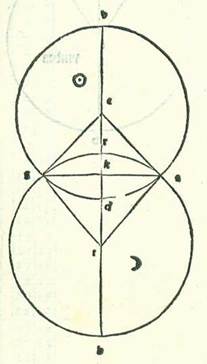Describam autem primo causa eclypsium solarium circulum quidem Solis, scilicet circulum ABGD super centrum E, et circulum Lune in longitudine media circulum AHGR super centrum T secantem circulum Solis super duo puncta G et A. Et cum nos produxerimus duas lineas BE et TH et posuerimus ut sit eclypsis Solis quarta diametri Solis donec sit RD quidem tres partes secundum quantitatem qua erit diameter BD duodecem partes, et sit RH diameter Lune 12 partes et 20 minuta fere secundum illam quantitatem, scilicet sicut proportio 15 partium et 40 minutorum ad 16 partes et 40 minuta, et propter illud aggregatur ut sit linea ET novem partes et decem minuta, erit proportio duorum circulorum secundum proportionem unius ad tria et octo minuta et 30 secunda. Circulus vero solaris est 37 partes et 42 minuta, et circulus Lune est 38 partes et 46 minuta secundum illam quantitatem. Et similiter est proportio aree intra unumquemque duorum circulorum. Quoniam cum multiplicaverimus medietatem diametri in totum circulum, proveniet inde duplum aree circuli. Et erit area intra circulum solarem 113 partes et sex minuta, et area intra circulum lunarem 119 partes et 32 minuta secundum illam quantitatem. Et postquam illud est quemadmodum diximus, oportet ut sciamus qualiter inveniamus quantitatem aree quam continent A, D, G, R secundum quantitatem qua erit tota superficies circuli solaris 12 partes. 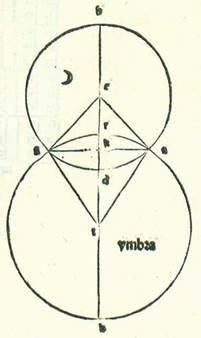Protraham igitur duas lineas AE et AT et duas lineas GE et GT et producam etiam perpendicularem AKG. Et quia secundum quantitatem qua erit linea ET novem partes et decem minuta erit unaqueque duarum linearum AE et EG sex partes, et unaqueque duarum linearum AT et TG sex partes et decem minuta secundum illam quantitatem, et angulus qui est apud K est rectus, si nos comparaverimus additionem qua superfluit quadratum linee TA super quadratum linee AE, scilicet duas partes et duo minuta ad lineam ET, scilicet diviserimus differentiam illam quadratorum per hanc, erit quod inveniemus superfluum quod est inter EK et KT 13 minuta et 18 secunda, et quod est inter duo quadrata earum duas partes et duo minuta. Et aggregatur ut sit linea EK 4 partes et 28 minuta et linea KT 4 partes et 42 minuta secundum illam quantitatem. Et propter hoc erit unaqueque duarum linearum AK et KG, quoniam ipse sunt equales, quatuor partes fere. Et sequitur illud ut sit area superficiei quidem trianguli AEG 17 partes et 52 minuta et area superficiei trianguli ATG 18 partes et 48 minuta secundum illam quantitatem. Et etiam quia secundum quantitatem qua erit diameter BD duodecem partes et diameter RH 12 partes et 20 minuta colligitur ut sit linea AG octo partes, et secundum quantitatem qua erit diameter DB 120 partes erit linea AG 80 partes, et secundum quantitatem qua erit diameter RH 120 partes erit linea AG 77 partes et 50 minuta, tunc duo arcus qui sunt super eam, arcus quidem ADG erit 83 partes et 37 minuta secundum quantitatem qua erit circulus ABGD 360 partes, et arcus ARG erit 80 partes et 52 minuta secundum quantitatem qua erit circulus ARGH 360 partes. Et quia proportio orbium ad arcus est equalis proportioni superficierum earum ad superficies sectorum qui subtenduntur arcubus, erit area inter sectorem AEG 26 partes et 16 minuta secundum quantitatem qua demonstratum est quod superficies orbis ABGD est 113 partes et sex minuta, et area quidem inter sectorem ATG 26 partes et 51 minuta secundum illam quantitatem qua area superficiei orbis ARGH fuit secundum illam quantitatem 119 partes et 32 minuta. Iam vero fuit ostensum quod area superficiei inter triangulum AEG est 17 partes et 52 minuta secundum illam quantitatem, et area superficiei intra triangulum ATG similiter 18 partes et 48 minuta. Superest ergo ut sit area intra portionem ADGK octo partes et 24 minuta, et area intra portionem ARGK octo partes et tria minuta secundum illam quantitatem. Area ergo totius superficiei que continetur ab ARGD est 16 partes et 27 minuta secundum quantitatem qua fuit area superficiei circuli ABGD 113 partes et sex minuta. Ergo secundum quantitatem qua fuit area superficiei intra circulum solarem duodecem partes erit illud quod comprehendit eclypsim pars una et medietas et quarta partis fere. Et illud est quod firmavimus in differentia quam diximus in area trium digitorum in tabula secunda. Et hoc est quod oportuit ostendi.

Et propter eclypses lunares etiam sit in hac forma circulus quidem Lune ABGD et circulus umbre secundum longitudinem mediam circulus ARGH, et sit quod eclypsatur ex diametro lunari quarta eius, donec sit RD, que est eclypsis, tres partes secundum quantitatem qua erit diameter BD duodecem partes, et sit RH diameter umbre secundum quantitatem proportionis unius ad duo et 36 minuta 31 partes et 12 minuta secundum illam quantitatem. Et propter illud colligitur ut sit linea EKT 18 partes et 36 minuta. Duorum ergo circulorum circumferentie etiam erunt, circumferentia quidem circuli Lune 37 partes et 42 minuta, et circumferentia circuli umbre 98 partes et unum minutum munitum M. secundum illam quantitatem. Et aree eorum intra ipsos, area quidem circuli lunaris erit 113 partes et sex minuta, et area circuli umbre 764 partes et 32 minuta. Et quia hic etiam secundum quantitatem qua erit linea TE 18 partes et 36 minuta erit unaqueque duarum linearum AE et EG sex partes, et unaqueque duarum linearum AT et TG 15 partes et 36 minuta secundum illam quantitatem, tunc si nos comparaverimus similiter augmentum quadrati TA super quadratum AE ad lineam ET, inveniemus superfluum quod est inter TK et KE undecim partes et octo minuta, donec colligatur ut sit linea quidem EK tres partes et 44 minuta et linea KT 14 partes et 52 minuta. Quapropter erit unaqueque duarum linearum AK et KG quatuor partes et 42 minuta secundum illam quantitatem. Sequitur vero quod diximus, ut sit area intra triangulum AEG 17 partes et 33 minuta et area intra triangulum ATG 69 partes et 52 minuta. Et etiam quia secundum quantitatem qua erit diameter BD duodecem partes et diameter RH 31 partes et 12 minuta colligitur ut sit linea AG 9 partes et 24 minuta, et secundum quantitatem qua erit diameter BD 120 partes aggregatur ut sit linea AG 94 partes, et secundum quantitatem qua erit diameter RH 120 partes erit AG 36 partes et 9 minuta, et ex duobus arcubus qui sunt super ipsam erit arcus quidem ADG 103 partes et 8 minuta secundum quantitatem qua erit circulus ABGD 360 partes, et arcus quidem ARG 35 partes et 4 minuta secundum quantitatem qua erit circulus ARGH 360 partes, ergo propter sermones qui iam premissi sunt erit area intra sectorem AEGD 32 partes et 24 minuta secundum quantitatem qua iam ostensum est quod area intra circulum ABGD secundum eam est 113 partes et sex minuta, et area intra sectorem ATGR 74 partes et 28 minuta secundum illam quantitatem qua area intra circulum ARGH fuit 764 partes et 32 minuta. Iam vero fuit ostensum quod area quidem intra triangulum AEG est 17 partes et 33 minuta secundum illam quantitatem, et area quidem intra triangulum ATG 69 partes et 52 minuta. Remanet ergo ut sit area quidem intra portionem ADGK 14 partes et 51 minuta et area quidem intra portionem ARGK quatuor partes et 36 minuta secundum illam quantitatem. Tota igitur superficies interior quam continent A, R, G, D erit 19 partes et 27 minuta secundum quantitatem qua erit area circuli ABGD 113 partes et sex minuta. Et propter illud secundum quantitatem qua erit area intra circulum lunarem duodecem partes erit area que continet portionem eclypsis Lune due partes et quintadecima partis unius fere. Et illud est quod firmavimus in illa differentia in area trium digitorum in tabula tertia lunari. Et illud est quod nos decuit demonstrare.

⟨VI.8⟩ Capitulum octavum: De lineatione tabularum eclypticarum Solis et Lune

☉
Tabule eclypsium solarium longitudinum
Maioris									Minoris
Latitudinis						Partium casus				Latitudinis						Partium casus
Partes	Minuta	Partes	Minuta	Digiti			Minuta	Secunda		Partes	Minuta	Partes	Minuta	Digiti			Minuta	Secunda
84 84 85	0 30 0	276 275 275	0 30 0		0 1 2		0 12 17	0 32 19		83 84 84	36 6 36	276 275 275	24 54 24		0 1 2		0 12 17	0 57 54
85 86 86	30 0 30	274 274 273	30 0 30		3 4 5		20 23 25	43 27 38		85 85 86	6 36 6	274 274 273	54 24 54		3 4 5		21 24 26	28 14 27
87 87 88	0 30 0	273 272 272	0 30 0		6 7 8		27 28 29	8 29 32		86 87 87	36 6 36	273 272 272	24 54 24		6 7 8		28 29 30	16 45 55
88 89 89	30 0 30	271 271 270	30 0 30		9 10 11		30 30 31	20 54 13		88 88 89	6 36 6	271 271 270	54 24 54		9 10 11		31 32 33	51 33 11
90 90 91	0 30 0	270 269 269	0 30 0		12 11 10		31 31 30	20 13 54		89 90 90	36 0 24	270 270 269	24 0 36		12 12 12		33 33 33	16 29 16
91 92 92	30 0 30	268 268 267	30 0 30		9 8 7		30 29 28	22 32 29		90 91 91	54 24 54	269 268 268	6 36 6		11 10 9		33 32 31	11 33 51
93 93 94	0 30 0	267 266 266	0 30 0		6 5 4		27 25 23	8 38 27		92 92 93	24 54 24	267 267 266	36 6 36		8 7 6		30 29 28	55 45 16
94 95 95	30 0 30	265 265 264	30 0 30		3 2 1		20 17 12	43 19 32		93 94 94	54 24 54	266 265 265	6 36 6		5 4 3		26 24 21	27 14 28
96	0	264	0		0		0	0		95	24	264	36		2		17	54
										95 96	54 24	264 263	6 36		1 0		12 0	57 0

Tabule eclypsium lunarium utrarumque longitudinum

Tabule eclypsium lunarium longitudinis maioris										Tabule eclypsium lunarium longitudinis minoris
Latitudinis					Partium casus			Mora		Latitudinis					Partium casus			Mora
Partes	Minuta	Partes	Minuta	Digiti		Minuta	Secunda	Minuta	Secunda	Partes	Minuta	Partes	Minuta	Digiti		Minuta	Secunda	Minuta	Secunda
79 79 80	12 42 12	280 280 279	48 18 48		0 1 2	0 16 23	0 59 43	0 0 0	0 0 0	77 78 78	48 22 56	282 281 281	12 38 4		0 1 2	0 19 26	0 9 45	0 0 0	0 0 0
80 81 81	42 12 42	279 278 278	18 48 18		3 4 5	28 32 36	41 42 6	0 0 0	0 0 0	79 80 80	30 4 38	280 279 279	30 56 22		3 4 5	32 36 40	20 53 42	0 0 0	0 0 0
82 82 83	12 42 12	277 277 276	48 18 48		6 7 8	39 41 43	1 34 50	0 0 0	0 0 0	81 81 82	12 46 20	278 278 277	48 14 40		6 7 8	43 46 49	59 53 25	0 0 0	0 0 0
83 84 84	42 12 42	276 275 275	18 48 18		9 10 11	45 47 49	48 35 9	0 0 0	0 0 0	82 83 84	54 28 2	277 276 275	6 32 58		9 10 11	51 53 55	40 39 25	0 0 0	0 0 0
85 85 86	12 42 12	274 274 273	48 18 48		12 13 14	50 40 37	31 35 28	0 11 15	0 9 20	84 85 85	36 10 44	275 274 274	24 50 16		12 13 14	56 45 42	19 47 55	0 12 17	0 34 17
86 87 87	42 12 42	273 272 272	18 48 18		15 16 17	35 34 33	30 6 7	18 20 22	12 22 0	86 86 87	18 52 26	273 273 272	42 8 34		15 16 17	40 38 37	2 28 24	20 22 24	32 58 49
88 88 89	12 42 12	271 271 270	48 18 48		18 19 20	32 31 31	23 51 32	23 24 24	14 8 43	88 88 89	0 34 8	272 271 270	0 26 52		18 19 20	36 35 35	37 15 34	26 27 27	1 13 12
89 90 90	42 0 18	270 270 269	18 0 42		21	31 31 31	22 20 22	25 25 25	1 3 1	89 90 90	42 0 18	270 270 269	18 0 42		21	35 35 35	22 20 22	28 28 28	12 16 12
				complementum										complementum
					21										21
90 91 91	48 18 48	269 268 268	12 42 12		20 19 18	31 31 32	32 51 23	24 24 23	43 8 14	90 91 92	52 26 0	269 268 268	8 34 0		20 19 18	35 35 36	34 15 37	27 27 26	12 13 1
92 92 93	18 48 18	267 267 266	42 12 42		17 16 15	33 34 35	7 6 30	22 20 18	0 22 12	92 93 93	34 8 42	267 266 266	26 52 18		17 16 15	37 38 40	24 28 2	24 22 20	49 58 32
93 94 94	48 18 48	266 265 265	12 42 12		14 13 12	37 40 50	28 35 31	15 11 0	20 9 0	94 94 95	16 50 24	265 265 264	44 10 36		14 13 12	42 45 56	55 47 19	17 12 0	17 34 0
95 95 96	18 48 18	264 264 263	42 12 42		11 10 9	49 47 45	9 35 48	0 0 0	0 0	95 96 97	58 32 6	264 263 262	2 28 54		11 10 9	55 53 51	25 39 40	0 0 0	0 0 0
96 97 97	48 18 48	263 262 262	12 42 12		8 7 6	43 41 39	50 31 1	0 0 0	0 0 0	97 98 98	40 14 48	262 261 261	20 46 12		8 7 6	49 46 43	25 53 59	0 0 0	0 0 0
98 98 99	18 48 18	261 261 260	42 12 42		5 4 3	36 32 28	6 42 41	0 0 0	0 9 0	99 99 100	22 56 30	260 260 259	38 4 30		5 4 3	40 36 32	42 53 20	0 0 0	0 0 0
99 100 100	48 18 48	260 259 259	12 42 12		2 1 0	23 16 0	43 59 0	0 0 0	0 0 0	101 101 102	4 38 22	258 258 257	56 22 48		2 1 0	26 19 0	45 9 0	0 0 0	0 0 0

Tabula equationis digitorum per minuta superfluitatum Solis et Lune et partium casus et more secundum proportionem horum minutorum ex gradibus

Partium diversitatis aree communes		Superfluitatum
Partes		Minuta	Secunda
6 12 18	354 348 342	0 0 1	21 42 42
24 30 36	336 330 324	2 4 5	42 1 21
42 48 54	318 312 306	7 9 11	18 15 38
60 66 72	300 294 288	14 16 19	0 48 36
78 84 90	282 276 270	22 25 28	36 36 42
96 102 108	264 258 252	31 34 38	48 54 0
114 120 126	246 240 234	41 44 46	0 0 45
132 138 144	228 222 216	49 51 53	30 39 48
150 156 162	210 204 198	55 57 58	32 15 18
168 174 180	192 186 180	59 59 60	21 41 0

Tabula digitorum equatorum Solis et Lune

Partes duodecime digitorum
	Solis			et	Lune
	☉				☽
Digiti	Digiti		Minuta		Digiti		Minuta
1 2 3		0 1 1	30 0 45			0 1 2	30 10 4
4 5 6		2 3 4	40 40 40			3 4 5	10 20 30
7 8 9		5 7 8	50 0 20			6 8 9	45 0 10
10 11 12		9 11 12	40 50 0			10 11 12	20 20 0

⟨VI.9⟩ Capitulum nonum: De cognitione eclypsium lunarium ☽

Postquam premisimus ea que prediximus, inquisitio quidem eclypsium lunarium est secundum modum quem narrabimus. Firmabo quod aggregabitur ex numero partium oppositionis quesite, et horam temporis medii quod est applicationis in Alexandria, et numerum partium que sunt longitudinis longioris orbis revolutionis, que nominantur partes diversitatis, et numerum partium que sunt ab ultima longitudine septentrionis, que sunt latitudo, post cognitionem additionis et diminutionis, et mittam numerum latitudinis primum in tabulam eclypsium lunarium. Si ergo invenerimus illum numerum in numeris qui sunt in duabus tabulis primis, accipiemus quod opponitur numero latitudinis ex eis que sunt in unaquaque duarum differentiarum in tabulis transituum et in tabulis digitorum et firmabimus unumquemque eorum per se. Deinde post illud accipiemus numerum diversitatis, et mittemus ipsum in differentiam equationis equatitionis M., et accipiemus quod opponitur ei ex minutis que sunt superfluitas que est inter digitos et minuta scripta in unaquaque duarum differentiarum, et addemus ea super numeros quos invenimus in differentia prima. Si ergo acciderit ut cadat numerus latitudinis in differentia secunda tantum, firmabimus minuta reperta que sunt digitorum et partium que opponuntur 0, idest cifre, solummodo. Et totum quod invenerimus provenire nobis ex digitis ex hac equatione, dicemus quod secundum numerum illorum digitorum erit numerus partium ex duodecem partibus quas comprehendit tenebra ex diametro Lune in tempore medio eclypsium. Postea addemus semper super minuta que erunt ex illa equatione partem duodecimam eorum, et illud est cursus Solis in illis partibus. Deinde dividemus illud per cursum Lune diversum in una hora in illo tempore. Et quod provenerit ex numero vicium est numerus horarum equalium que sunt totius temporis temporum revolutionum eclypsis. Que vero aggregantur earum ex eis que sunt in tabula quarta sunt hore temporis casus et complementi, et que earum aggregantur ex eis que sunt in tabula quinta sunt medietas temporis more. Et ex hoc monstrantur loca horarum principii introitus et finis eius ex eis que sunt inter tempus more, scilicet que sunt impletionis verificate fere ex additione et diminutione que sunt cuiusque portionum repertarum ex divisione. Et ex hoc cum miserimus partes duodecime diametri in differentiam parvam, inveniemus partes duodecimas aree interiorum omnium superficierum per ea que opponuntur que sunt in tabula tertia. Et similiter reperiemus partes duodecimas aree interiorum superficierum solarium per ea que opponuntur que sunt in tabula secunda. Consideratio vero significat quod non in omni hora erit tempus eclypsis a principio sui usque ad medium ipsius equale tempori quod est a medio eius usque ad finem ipsius propter diversitatem transituum equalium qui sunt Solis et Lune, quoniam simile huic erit in temporibus non equalibus. Per sensum vero non fiunt hec tempora non equalia. Errori namque illius secundum quod videtur non inest magna quantitas. Et neque si fuerit in transitu medio, ubi erunt additiones superfluitatis maiores Corrected into maioris? According to the Greek text (see Toomer, loc. cit., p. 309, lines 9-10) it should be maiores. In Paris, BnF, lat. 14738 (107r, line 10 from the bottom) the sentence is missing due to a homoioteleuton., erit errori illius magna quantitas. Transitus autem qui erit ad quantitatem numeri harum horarum sic repertarum, que sunt tempus totius eclypsis, nunquam erit diversitati additionis supra motum quantitas sensibilis. Nos tamen invenimus in consideratione Abrachis (quam fecit in transitu latitudinis Lune) errorem. Superfluitas namque que firmatur in eo quod est inter eclypsim secundum modum quidem quem posuit est parva, secundum comprehensionem vero nostram est magna. Ipse enim assumpsit ad declarationem eius quod voluit duas eclypses lunares inter quas fuerunt 7160 menses in quarum unaquaque fuit eclypsata quarta diametri Lune secundum transitum unum a nodo capitis. Prime eclypsis earum consideratio fuit in anno qui fuit secundus annorum Mardochei. Et fuit secunde eclypsis consideratio in anno 37 revolutionis Philippi tertie. Et quia operatus est in illo secundum hoc quod transitus Lune in latitudine in unaquaque duarum eclypsium continet equalitas apud declarationem reversionis, propter hoc quod eclypsis prima fuit cum fuit Luna in longitudine longiore orbis revolutionis sue, et fuit eclypsis secunda cum fuit Luna in longitudine propinquiore orbis revolutionis sue, propter hoc estimavit quod non contingeret diversitas Lune. Erravit igitur eius estimatio in hoc primum quidem quoniam iam erit propter diversitatem Lune diversitas manifesta, propter hoc quod additio cursus medii super cursum verificatum non reperitur equalis in ambabus eclypsibus, sed in eclypsi quidem prima reperitur pars una fere et in eclypsi secunda reperitur pars eius octava fere, hoc est unius partis (secundum hoc ergo erit diminutio revolutionis Lune in latitudine in reversionibus integris secundum medietatem et quartam et octavam partis unius secundum quantitatem qua erit orbis Lune declivis 360 partes), deinde etiam quia non reputavit diversitatem que contingit in quantitatibus magnitudinis tenebrarum propter longitudines Lune in his duabus eclypsibus, propter hoc quod eclypsis prima fuit Luna existente in longitudine sua maiore et fuit eclypsis secunda Luna in longitudine sua minore existente. Oportuit namque ut esset necessario tenebra illius quarta diametri Lune, in eclypsi quidem prima a longitudine minore a nodo capitis et in eclypsi secunda a longitudine maiore. Et illud est quod iam demonstravimus, quod diversitas que est inter eas est pars una et quinta partis. Quapropter erit superfluitas revolutionis latitudinis ibi post reditiones integras hec quantitas. Quod autem est propter tarditatem Lune, erit quod aggregatur ex errore reditionis revolutionis latitudinis due partes fere, que essent ex ambobus erroribus si fecissent diversitatem. Ad longitudinem vero maiorem a nodo, quia una duarum eclypsium fecit reversionem diminutam et altera fecit eam augmentatam secundum unum modorum quibus vidit Abrachis quod equatio additionis et diminutionis per complementum reversionis est diminuta et neque erit ex superfluitate que est inter duos errores tantum nisi tertia partis unius, declaratur quod superfluitas addit super reditionem.

⟨VI.10⟩ Capitulum decimum: De cognitione eclypsium solarium

Inquisitio quidem eclypsium lunarium istis modis quos narravimus considerationum verarum verificatur tantum. Post illud autem ostendam cognitionem eclypsium solarium, que sunt difficiliores propter diversitates aspectuum Lune, secundum hunc modum: Considerabimus tempus coniunctionis vere que est in Alexandria secundum quotam horam equalem fuerit ante meridiem aut post meridiem. Deinde post illud considerabimus civitatem in qua numerabitur eclypsis. Si ergo non fuerit sub linea orbis meridiei Alexandrie, accipiemus superfluitatem que erit inter orbem meridiei sue et inter orbem meridiei Alexandrie in longitudine horarum equalium, et addemus eam aut minuemus ipsam donec sciamus ante quotam horam meridiei aut post quotam horam meridiei horarum equalium erit tempus coniunctionis verum in illa civitate. Postea cognoscemus primo tempus coniunctionis que videtur in climate quesito, quod est equale tempori eclypsis medie fere, per additionem eorum que narravimus in his que precesserunt de diversitate aspectus, et accipiemus ex differentia tabularum in quibus sunt anguli et ex differentia tabularum diversitatum aspectuum secundum proprietatem climatis et proprietatem longitudinis earum horarum que sunt inter duos orbes meridiei et etiam proprietatem partis signorum in qua erit coniunctio et cum hoc proprietatem longitudinis Lune a terra et accipiemus et accipiemus ... et accipiemus: Two rivalling passages. Both appear also in Paris, BnF, lat. 14738 (107v, lines 7-10 from the bottom). primo diversitatem aspectus Lune que erit in orbe magno descripto super punctum summitatis capitum et super centrum Lune, et proiciemus ex ea semper diversitatem aspectus Solis que opponitur ei in illa area, et cognoscemus de residuo per angulum quem inveniemus apud sectionem orbis signorum et orbis magni descripti super punctum summitatis capitum quod aggregatur ex diversitate aspectus apud transitum in longitudine tantum, et addemus super ipsam semper portionem que fit ex diversitate temporum equalium que continet diversitas aspectus (per quod intelligi volo quod inveniemus ex superfluitate que est inter duas diversitates aspectus que opponuntur in illa differentia longitudini prime a puncto summitatis capitum et longitudini que est ex augmento temporum equalium et addemus etiam portionem diversitatis aspectus in longitudine tantum cum parte, si fuerit illa ei sensibilis, aut secundum quantitatem qua erit illa pars diversitatis aspectus primi), et addemus etiam super partes que aggregantur ex tota diversitate aspectus in longitudine partem duodecimam earum loco motus Solis, et quod aggregatur ex divisione cursus horarum diversarum que sunt apud coniunctionem dividemus per horas equales. Tunc si fuerit diversitas aspectus que est in longitudine secundum continuitatem signorum, tunc iam declaravimus in his que precesserunt qualiter inveniamus coniunctionem illius. Partes vero quas divisimus per horas equales minuemus ex partibus Lune comprehensis que sunt in tempore coniunctionis vere et ponemus unumquodque quod erit ex longitudine et latitudine et cursu diversitatis per se. Quod vero remanebit erit ipsi transitus Lune veri in tempore coniunctionis que videtur et erunt ille hore quas inveniemus hore quibus precedit coniunctio que videtur coniunctionem veram. Quod si fuerit diversitas aspectus in longitudine inventa precedens signa, faciemus conversionem illius, scilicet tunc addemus illas partes super cursus quos equavimus prius ad tempus verum coniunctionis cuiusque, scilicet longitudinis et latitudinis et diversitatis, et erunt nobis ille hore quibus posterioratur coniunctio que videtur a coniunctione vera. Postea considerabimus de re longitudinis que est inter coniunctionem que videtur et inter medietatem diei horarum equalium per illa capitula eadem, scilicet quantum prius erit diversitas aspectus Lune in circulo maiore qui describitur transiens per punctum quod est super summitatem capitum, et minuemus ex eo quod inveniemus ex illo diversitatem aspectus Solis que est coram illo numero eodem, et equabimus quod remanebit secundum illud exemplum per angulum qui reperitur in illa hora apud sectionem duorum circulorum, scilicet diversitatem aspectus que erit in latitudine, scilicet in primo circulo qui est ortogonaliter super orbem signorum, et quod aggregabitur de partibus convertemus ad divisiones que pertinent eis in circulo declivi, scilicet multiplicabimus eas undecies et semis, et quod proveniet ex partibus si fuerit diversitas aspectus in latitudine in eo quod sequitur septentrionem ab orbe signorum considerabimus. Tunc si fuerit Luna versus nodum capitis, addemus ipsum super cursum in latitudine quem nos prius equavimus ad tempus coniunctionis que videtur. Quod si Luna fuerit versus nodum caude, minuemus ipsum ex eo secundum illud exemplum. Si vero fuerit diversitas aspectus in latitudine ab eo quod sequitur meridiem ab orbe signorum, faciemus econtrario illius, scilicet minuemus partes diversitatis aspectus de partibus latitudinis quas equavimus ad tempus coniunctionis que videtur si fuerit Luna versus nodum capitis, et addemus eas super ipsas si fuerit Luna versus nodum caude. Proveniet ergo nobis tunc latitudo que videtur in tempore coniunctionis que videtur. Mittemus igitur illum numerum in tabulas eclypsium Solis. Tunc si convenerit ut cadat in numeris duarum arearum primarum, pronunciabimus eclypsim Solis proventuram medium temporis cuius fere terminat coniunctio que videtur. Scribemus igitur quantitatem eius quod est coram numero latitudinis que videtur ex digitis et ex partibus que sunt casus et clarificationis unumquodque per se cuiusque duarum tabularum. Postea mittemus etiam numerum diversitatis Lune que est a longitudine longiore in coniunctione que videtur in tabulam equationis et considerabimus quod est coram ipso de minutis. Accipiemus igitur secundum illam quantitatem de superfluitate cuiusque illarum rerum que scripte fuerunt et addemus ipsum semper super partes que assumuntur ex tabula prima. Quod ergo proveniet per hanc equationem de digitis est summa 12 partium diametri Solis super quibus continentur digiti in medio temporis eclypsis fere. Postea addemus etiam super partes cuiusque duorum cursuum partem duodecimam earum loco eius quod Sol addit per motum suum. Quod ergo provenerit ponemus horas equales secundum motum Lune diversum. Et erit illud ipsa summa temporis cuiusque temporis casus et reversionis impletionis. Hoc autem sit secundum quod non contingat in hoc tempore superfluitas propter diversitatem aspectus. Sed postquam iam acciderit in eo diversitas aliqua sensibilis propter diversitatem aspectus Lune, non propter diversitatem aspectus duorum luminarium, erit propter id unumquodque duorum temporum per se longius semper duobus temporibus que nos premisimus. Et posuimus secundum plurimum equale unum eorum alteri. Et nos etiam non dimittemus quin faciamus te scire illud, quamvis sit parvum. Dico ergo quod hoc accidens contingit propterea quod est semper in cursu Lune qui videtur causa diversitatis aspectus cum dubia tollerantia antecessionis, quia fecit nos percipere quod non ei motus est proprius secundum successionem signorum. Et illud est quoniam si fuerit cursus eius ante medietatem diei, tunc videtur quod quanto plus elevatur paulatim et paulatim, erit quod est ei de diversitate aspectus ab eo quod sequitur orientem maius semper eo quod pertransivit ex eo existente quod videtur de motu eius locali secundum successionem signorum tardiore. Quod si fuerit cursus eius post medietatem diei, tunc videtur etiam quod quanto plus deprimitur paulatim et paulatim, erit quod est ei de diversitate aspectus ab eo quod sequitur occidentem minus semper eo quod pertransivit ex eo existente secundum illud exemplum quod videtur de motu eius locali secundum successionem signorum tardiore. Ex hac ergo causa erunt duo tempora quorum narratio precessit longiora semper duobus temporibus que reperiuntur ita absolute. Et quia fuit semper superfluitas additionis inter duas diversitates aspectus maior in cursibus qui sunt propinquiores medietati diei, oportet necessario ut sit tarditas temporis eclypsis que cadit apud medietatem diei proprie. Et propter hanc eandem causam, quando cadet medium temporis eclypsis in ipsa hora meridiei, tunc tantum erit tempus casus equale fere tempori reversionis impletionis aut fuit maius, quia quod imaginatur propter diversitates aspectus ex antecessione cadet tunc in unoquoque duorum temporum equaliter fere. Et quando cadet ante medietatem diei, tunc erit tempus reversionis impletionis, quia fuit propinquior medietati diei, maius. Et quando ceciderit post medietatem diei, tunc erit tempus casus, quia est propinquior medietati diei, maius. Et ut nos verificaremus hec tempora hoc modo verificationis etiam protraximus per modum quem innuimus tempus cuiusque duorum cursuum narratorum quod provenit ante hanc verificationem et cuius longitudo a puncto quod est supra summitatem capitum est in medio tempore eclypsis. Sitque causa exempli unumquodque duorum temporum hora una equalis et longitudo a puncto quod est supra summitatem capitum 75 partes. Considerabimus igitur in tabula diversitatis aspectus minuta que sunt coram numero 75 partium, scilicet diversitatem aspectus secundum quod Luna sit in longitudine longiore, que fuerit longitudo eius verbi gratia. Et secundum hanc longitudinem sit quod invenitur ex minutis in area tertia. Et quod invenerimus pertineat 75 partibus de minutis, scilicet 52. Et quia unumquodque duorum temporum casus et reversionis impletionis iam posuimus acceptione nostra secundum medium horarum quidem equalium horam unam et temporum quidem 15 tempora, tunc cum nos minuerimus hec tempora de partibus 75 que sunt longitudo, inveniemus coram reliquis, que sunt 60 partes, de minutis diversitatis aspectus que sunt in illa eadem area 47 que erunt ex minutis diversitatis aspectus in illa tabula 47 minuta. Et aggregatur ut sit quod precessit in transitu medio qui est apud orbem meridiei ex diversitate aspectus quinque minuta. Cum vero addiderimus illa tempora 15 super 75 partes, inveniemus quod aggregatur ex partibus, scilicet 90 partibus, 53 minuta et medietatem minuti que sunt totius diversitatis aspectus, donec aggregatur et hic ut sit quod precessit ex transitu qui est apud horizonta minutum et medietas minuti. Accipiemus ergo ex istis duabus diversitatibus repertis quod opponitur longitudini. Postea accipiemus ex eo quod provenerit ex unoquoque etiam motu Lune diverso diviso per partes horarum equalium, sicut est manifestum. Postea quod aggregatur ex unoquoque addemus super portionem cuiusque duorum temporum que accepimus per medium absolutum ex casu et complemento. Et maius quidem addemus super transitum propinquiorem orbis meridiei, et minus addemus super transitum propinquiorem orbis horizontis. Et manifestum est quod additio horum duorum temporum secundum minuta quidem est tria minuta et medietas minuti et ex hora quidem equali nona hora fere in qua erit motus Lune medius hec minuta. Oportet vero ut dividamus horas equales subtili brevitate cum addiderimus in unaquaque longitudine super partes horarum temporalium secundum modum cuius precessit declaratio.

⟨VI.11⟩ Capitulum undecimum: De declinatione et inclinationibus que sunt in eclypsibus

Et quia post hec necessaria est inquisitio inclinationum tenebrarum, cuius comprehensio erit ex declinatione tenebrarum apud orbem medii signorum et ex declinatione orbis medii signorum apud orbem horizontis, et unaqueque harum duarum in omni tempore temporum ecypticorum fit opposita permutans et alterans loca propter locales motus valde et neque comprehenditur, etiam si aliquis voluerit subtiliter perscrutari pro scientia inclinationum futurarum que erunt in tempore toto, in quo premittere sermonem non est aliquid quod sit magne utilitatis et quod sit necessarium, et hoc quoniam communitas orbis signorum et orbis horizontis videtur ex puncto orbis signorum quod oritur et occidit in locis orbis horizontis, tunc necessarium est ut in tempore eclypsium, cum fuerit quod oritur et occidit ex partibus orbis signorum diversum in omni hora, sint loca illarum sectionum in orbe horizontis diversa in omni hora. Et videtur similiter declinatio inclinationum tenebrarum apud orbem medii signorum in orbe magno descripto super duo centra Lune et umbre et super duo centra Lune et Solis. Igitur necessarium est etiam propter transitum centri Lune in tempore eclypsis ut alteretur locus orbis magni descripti super duo centra et fiat locus eius locus alteratus semper in orbe signorum et ut sint anguli quos continent sectiones eorum in omni hora non equales. Ea vero que de hac inquisitione diximus sufficiunt nobis in eis que futura sunt si acceperimus ea in illis tenebris notis tantum que habent principia et que videntur super omnes arcus qui sunt apud horizonta. Et ex hoc possibile est illis qui omnia ad unguem diligentissime inquirunt que accidunt ex eo ut considerent per illud quod videtur in omni duarum declinationum magnitudinem inclinationum. Et in hoc quidem et in eius simili, quemadmodum diximus, sufficit nobis inquisitio universalis.

Et cum eo ut non pretermittamus hunc locum, studebimus ut ponamus in hoc capitulo modos planiores et ad assumendum propinquiores secundum quod possibile est. Assumpsimus quidem ex principiis tenebrarum verificatarum merentium principium initii eclypsis, quod est in initio totius temporis eclypsis, et principium finis eclypsis, quod est in initio totius temporis more, et principium initii complementi, quod est in fine temporis more, et principium finis complementi, quod erit in fine totius temporis eclypsis. Et accepimus etiam ex inclinationibus que ad assumendum fuerunt digniores et manifestiores quas comprehendit orbis meridiei orientales et occidentales que sunt orbis medii signorum, equalitatis diei et estivales et hyemales. Ceterorum autem principia plurima que sunt apud plures hominum estimantur secundum diversitatem. Iam vero possibile est ut si aliquis voluerit, declaret illud per angulos qui sunt apud horizonta et ex sectione orbis meridiei et orbis horizontis. Sectionem vero septentrionalem vocavi Benetuaas, idest Filias Feretri, et Pisces sinistrationes. Et sectionem quidem meridianam vocavi Sueel One could equally read Sneel. Paris, BnF, lat. 14738 (109r, lines 12-13 from the bottom) reads Sueel too. The name does not appear in the Greek text (see Toomer, loc. cit., p. 315, line 7)., idest Canopus, et Geminos dexterationes. Sectiones autem orientales et occidentales que fuerint ex sectione orbis horizontis et capite Arietis et capite Libre, quorum longitudines ab orbe meridiei sunt semper quarte equales, vocabimus orientalem equalitatem et occidentalem equalitatem, et que fuerint ex sectione orbis horizontis et capite Cancri orientalem estivalem et occidentalem estivalem, et que fuerint ex sectione horizontis et capite Capricorni orientalem hyemalem et occidentalem hyemalem. Elongationes vero earum in omni climate diversificantur. Nos tamen contenti erimus relatione inclinationum cum fuerit visum illud aut super unum horum terminorum aut in eis que sunt inter quosdam et inter quosdam. Et propter communitatem orbis signorum et orbis horizontis in omni hora numeravimus longitudines que erunt in orbe horizontis in orientalibus et occidentalibus a capite cuiusque duodecem signorum secundum modum quem iam declaravimus in principio libri Almagesti ad omnem duarum partium orbis equationis diei, et erit in eis sectio in unoquoque climatum que sunt inter clima primum et inter clima septimum. Super que lineavimus et firmavimus angulos qui sunt secundum pulchrius quod videtur loco differentie tabularum in octo circulis super centrum unum quos imaginati sumus in superficie orbis horizontis, et continent longitudines septem climatum cum nominibus suis. Post illud lineavimus duas lineas super omnes circulos quarum unaqueque est super rectum angulum alterius. Et una quidem earum transversa est communis sectionis duarum superficierum duorum orbium, scilicet orbis horizontis et equationis diei, et altera quidem erecta est communis sectionis duarum superficierum, scilicet orbis horizontis et orbis meridiei. Et posuimus super duas extremitates duarum linearum, que sunt apud circulum interiorem, scilicet apud duas extremitates linee transverse orientalem equalitatem et occidentalem equalitatem et apud duas extremitates linee erecte septentrionem et meridiem dexterationem et sinistrationem. Et similiter descripsimus ab ambabus partibus linee equalitatis duas lineas secundum duas longitudines equales super omnes circulos etiam, et scripsimus super has, in eis quidem que sunt inter longitudines climatum septem longitudines (quas diximus cuiusque climatis) inter duo puncta duorum tropicorum et inter orbem equationis diei in orbe horizontis, ac si tota quarta esset 90 partes, et in extremitatibus quidem que sunt apud circulum interiorem apud extremitatem quidem que est apud dexterationem orientalem hyemalem et occidentalem hyemalem, et apud extremitatem quidem que est apud Pisces sinistrationem orientalem estivalem et occidentalem estivalem. Et propter hoc quod demonstratum est illud ex signis firmavimus in eis que sunt inter unamquamque longitudinum quattuor duas lineas alias, et firmavimus super eas longitudines portionis cuiusque signorum ab orbe equationis diei in orbe horizontis, et firmavimus nomen cuiusque signorum scriptum super circulum exteriorem, et signavimus super lineam que est inter sinistrationem et dextrationem nomina linearum equidistantium que sunt climatum et magnitudinem horarum et altitudines polorum in unaquaque earum, et posuimus scripturam super longitudines longiores ad septentrionem super circulum maiorem continentem circulos.

Et ut sint inclinationes tenebrarum que sunt apud orbem medii signorum firmate posite nobis, per quod intelligi volumus angulos qui erunt apud unumquodque horum principiorum que diximus sectiones orbis signorum et orbis magni descripti super ambo centra que narravimus, numeravimus eas in omni transituum Lune in quo erit diversitas que est inter tenebras digiti unius, et illud est ut sint que erunt in illis transitibus qui sunt in longitudine media tantum, et sint in eis arcus medii signorum et orbis Lune declivis in tenebris quasi equidistantes in sensu. 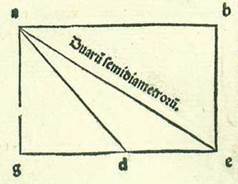Et describam ad illud etiam exemplum. Linea quidem que est loco arcus qui est orbis medii signorum sit linea AB, et sit in ea centrum Solis aut centrum umbre super punctum A, et linea quidem que est loco orbis Lune declivis sit linea GDE, et sit punctum G locus centri Lune qui erit in tempore medio eclypsis, et sit punctum D locus etiam in quo erit centrum Lune cum eclypsabitur tota et cum fuerit principium initii clarificationis eius, scilicet cum fuerit contactus orbis umbre deintus, et sit punctum E locus in quo erit centrum Lune cum fuerit principium inceptionis eclypsis eius aut finis complementi clarificationis aut Solis aut Lune, scilicet cum fuerint orbes eorum sese exterius contingentes, et protraham lineas AG et AD et AE. Et postquam duo anguli BAG et AGE continent medium tempus eclypsium, erunt recti in sensu, et erit angulus BAE continens principium eclypsis et finem complementi, et angulus BAD continet finem eclypsis et principium complementi. Et illud manifestum est. Et ex hoc declarabitur etiam quod linea AE continet duas lineas protractas ab ambobus centris duorum circulorum et linea AD continet superfluitatem que est inter eas. Et ponam exemplum eclypsim solarem in cuius tempore medio obscurata est medietas diametri Solis. Et sit punctum A centrum Solis, et erit linea AE semper 32 partes et 20 minuta, propter hoc quod illud est in longitudine Lune media, et sit linea AG minor ea secundum medietatem diametri Solis. Ergo erit secundum illam quantitatem 16 partes et 40 minuta. Et quia secundum quantitatem qua erit chorda AE 32 partes et 20 minuta colligitur ut sit linea AG secundum illam quantitatem secundum magnitudinem tenebre posite 16 partes et 40 minuta, igitur secundum illam quantitatem qua erit chorda AE 120 partes erit linea AG 61 partes et 51 minuta, et erit arcus qui est super eam 62 partes et duo minuta secundum quantitatem qua erit circulus continens triangulum AGE ortogonium 360 partes. Quapropter erit angulus AEG equalis angulo BAE secundum quantitatem quidem qua erunt duo anguli recti 360 partes 62 partes et duo minuta, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit 31 partes et minutum unum. Et etiam in eclypsibus lunaribus ponam punctum A centrum umbre. Et similiter quia Luna est in longitudine sua media, colligitur ut sit linea AE semper secundum illam quantitatem 60 partes. Quapropter linea AD erit 26 partes et 40 minuta. Et sit eclypsis Lune secundum transitum 18 digiti donec sit AG minor AD secundum medietatem diametri Lune. Et remaneat secundum illam quantitatem 10 partes et cifre. Et quia secundum quantitatem qua erit chorda EA 120 partes erit linea quidem AG 20 partes et cifre et arcus qui est super eam 19 partes et 12 minuta secundum quantitatem qua erit circulus continens triangulum AGE ortogonium 360 partes, erit ergo angulus AEG equalis angulo BAE 19 partes et 12 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit novem partes et 36 minuta. Et similiter quia secundum quantitatem qua erit chorda AD 120 partes erit linea quidem AG 45 partes et arcus quidem qui est super eam 44 partes et duo minuta secundum quantitatem qua erit circulus continens triangulum AGD ortogonium 360 partes, tunc erit angulus ADG equalis angulo BAD 44 partes et duo minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quatuor anguli recti 360 partes erit vigintidue partes et unum minutum. Et hoc oportuit demonstrari.

Et secundum similitudinem huiusmodi faciam in reliquis digitis, scilicet accipiam quantitates angulorum qui sunt minores angulo recto secundum hoc quod angulus unus rectus sit 90 partes secundum quantitatem quarte orbis horizontis, et describam differentiam tabularum secundum vigintiduas areas in quatuor tabulis, et ponam in tabula que est prima quatuor numeros digitorum inventorum qui obscurantur de diametro in tempore medio eclypsis, et in tabula quidem secunda angulos qui erunt in eclypsibus solaribus in tempore principii eclypsis et tempore finis complementi, et in tabula tertia angulos qui erunt in eclypsibus lunaribus in tempore principii eclypsis et in tempore finis complementi, et in tabula quarta angulos etiam qui erunt in eclypsibus lunaribus in fine temporis eclypsis et in principio temporis complementi. Et sit descriptio tabularum differentie et circulorum secundum hunc modum.

Et hic est modus descriptionis tabularum:

⟨VI.12⟩ Capitulum duodecimum: De descriptione tabularum que sunt declinationis et inclinationum

	Principium eclypsis							Finis eclypsis Lune
	Solis				Lune			Finis eclypsis Lune
Digiti	et finis impletionis eius							et principium impletionis eius
	☉			☽				et principium impletionis eius
		Gradus	Minuta			Gradus	Minuta	Gradus	Minuta
0 1		90 66	0 50			90 72	0 30	0 0	0 0
2 3		57 49	19 16			65 59	10 27	0 0	0 0
4 5		42 36	36 15			54 50	27 14	0 0	0 0
6 7		31 25	1 46			46 42	15 31	0 0	0 0
8 9		20 15	44 51			39 35	2 42	0 0	0 0
10 11		11 6	6 25			32 29	29 23	0 0	0 0
12 13		1 0	42 0			26 23	23 28	90 63	0 57
14 15		0 0	0 0			20 16	38 48	52 43	21 26
16 17		0 0	0 0			15 12	1 18	35 28	41 38
18 19		0 0	0 0			9 6	36 55	22 15	1 43
20 21		0 0	0 0			4 2	15 0	9 3	36 35

⟨VI.13⟩ Capitulum tertiumdecimum: De cognitione declinationis et inclinationum

Et quia iam facte sunt nobis temporum omnium que sunt horum principiorum positorum secundum modum cuius premisimus declarationem cognitiones et equationes, tunc manifestum est quod propter tempora sciemus partes orbis medii signorum que elevantur in eis et occidunt, et sciemus ex eis que sunt in tabulis loca earum in orbe horizontis. Cum autem fuerit centrum Lune quod videtur secundum veritatem orbis medii signorum sicut illud quod est in eclypsibus solaribus aut centrum eius verum sicut quod est in eclypsibus lunaribus, inclinationes quidem que erunt in principio eclypsis Solis et etiam eas que erunt in fine eclypsis Lune et complementi eius sciemus propter locum qui occidit in illa hora orbis signorum in orbe horizontis. Et inclinationes quidem que erunt in fine complementi eclypsis Solis et etiam inclinationes que erunt in principio eclypsis Lune et complementi eius sciemus propter locum qui elevatur in illa hora ex orbe signorum in orbe horizontis. Cum autem non fuerit centrum Lune secundum veritatem in orbe medii signorum, accipiemus ex differentia tabularum propria numeros angulorum qui opponuntur quantitati digitorum et protrahemus eos ex communitate sectionis orbis horizontis et orbis medii signorum. Tunc si fuerit centrum Lune ad partem septentrionis ab eo, in principio quidem eclypsis Solis et in fine eclypsis Lune, erit locus portionis occasus ad partem septentrionis. Et cum fuerit in fine complementi eclypsis Solis et in principio complementi eclypsis Lune, erit locus portionis elevationis ad partem septentrionis. Et etiam in principio quidem eclypsis Lune erit locus portionis elevationis ad partem meridiei, et in fine complementi casus Lune erit locus portionis occasus ad meridiem. Et cum fuerit centrum Lune ad partem meridiei orbis medii signorum in principio eclypsis Solis et in fine eclypsis Lune, erit locus portionis occasus ad partem meridiei. Et in fine quidem complementi eclypsis Solis et principio complementi eclypsis Lune erit locus portionis elevationis ad partem meridiei. Et etiam in principio casus Lune erit locus portionis elevationis ad partem septentrionis, et in fine quidem complementi eclypsis Lune erit locus portionis occasus ad partem septentrionis. Pars autem orbis horizontis quam cognoscimus ex hac equatione erit ipsa pars ad quam erunt omnes inclinationes partium duorum luminarium recipientium principia et fines initiorum eclypsis et complementorum.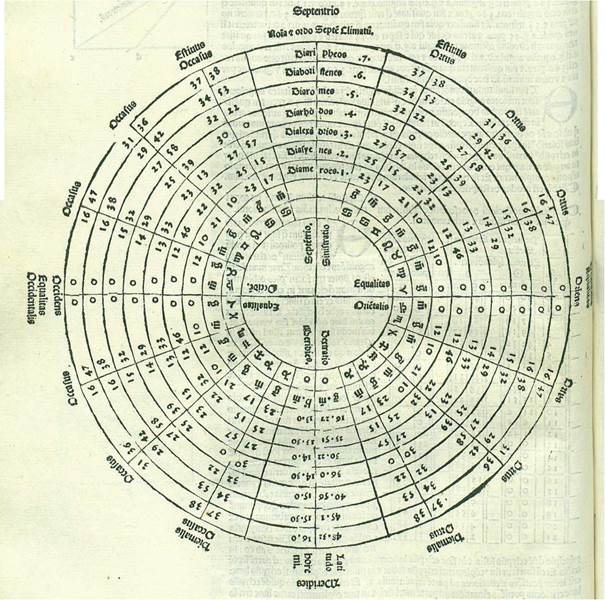

Nota quod loco nominum signorum iuxta tenorem textus in exteriori circulo situandorum characteres cuiusque eorundemque graduum infimo commoditatis gratia e regione impinximus.