⟨XI⟩
Claudii Ptolemei Pheludiensis dictio undecima libri Almagesti duodecem capitulis illustrata feliciter adest.
Capitulum primum: In declaratione egressionis a centro Iovis et longitudinis eius longioris
Capitulum secundum: In declaratione quantitatis orbis revolutionis stelle Iovis
Capitulum tertium: In verificatione motuum stelle Iovis revolubilium
Capitulum quartum: In diversitate revolutionum stelle Iovis
Capitulum quintum: In declaratione egressionis a centro stelle Saturni et longitudinis longioris eius
Capitulum sextum: In ostensione quantitatis orbis revolutionis stelle Saturni
Capitulum septimum: In verificatione motuum stelle Saturni circularium
Capitulum octavum: In radicibus motuum stelle Saturni revolubilium
Capitulum nonum: Qualiter proveniant cursus veri propter motus revolubiles secundum semitam linearum
Capitulum decimum: In modo tabularum diversitatis
Capitulum undecimum: In opere tabularum equationis stellarum quinque in longitudine
Capitulum duodecimum: In numeratione motus localis stellarum quinque erraticarum in longitudine
⟨XI.1⟩ Capitulum primum: In declaratione egressionis a centro Iovis et longitudinis eius longioris
Et quia iam declaravimus revolutiones motuum in stella Martis et radices eius, tunc nos modo sequamur illud narrando has res etiam in stella Iovis secundum illum eundem modum. Accepimus itaque etiam primum ad declarandam longitudinem eius longiorem et summam egressionis orbis eius a centro tres habitudinum que nominantur extremitates noctis oppositas cursui Solis medio. Quarum unam consideravimus per instrumenta considerationum in anno decimoseptimo annorum Adriani in mense Athica apud Egyptios in die primo eius in nocte quam sequitur dies secundus ante medietatem noctis hora una. Et fuit stella in vigintitribus partibus et undecem minutis Scorpionis. Et habitudinem secundam consideravimus in vigesimoprimo annorum Adriani in mense Phaophi et in die tredecimo eius in nocte quam sequitur dies quartusdecimus ante medietatem noctis duabus horis. Et fuit stella in septem partibus et 54 minutis Piscis. Et habitudinem tertiam consideravimus in anno primo annorum Antonii in mense Athus in die vigesimo eius in nocte quam sequitur dies vigesimusprimus post quinque horas a medietate noctis. Et fuit stella in 14 partibus et 23 minutis Arietis. Longitudinis igitur ab habitudine prima ad habitudinem secundam fuit tempus ex annis Egyptiis tres et ex diebus centum et sex dies et ex horis vigintitres hore et ex partibus cursus stelle qui videtur 104 partes et 43 minuta. Et longitudinis ab habitudine secunda ad habitudinem tertiam fuit tempus ex annis annus unus Egyptius et trigintaseptem dies et septem hore et ex partibus que sunt secundum illud exemplum 36 partes et 29 minuta. Et quod provenit ex cursu medio in longitudine temporis quidem longitudinis prime 99 partes et 55 minuta et temporis quod est longitudinis secunde 33 partes et 26 minuta. Ex his igitur duabus longitudinibus secundum semitam quam narravimus in Marte posuimus primum declarationem rerum quas intendimus scire secundum quod orbis egredientis centri sit unus etiam secundum hunc modum quem narravimus.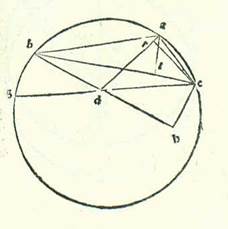 
Sit orbis egredientis centri supra quem sint A, B, G, et ponam ut punctum A sit punctum super quod fuit centrum orbis revolutionis in habitudine prima habitudinum extremitatis noctis, et punctum B sit punctum habitudinis secunde habitudinum extremitatis noctis, et punctum G sit punctum habitudinis tertie habitudinum extremitatis noctis, et accipiam intra orbem ABG egredientis centri punctum D centrum orbis signorum, et applicabo lineas AD et BD et GD, et faciam pertransire linea GDE, et applicabo lineas EA et AB, et protraham a puncto E super duas lineas DA et BD duas perpendiculares ER et EH et a puncto A super lineam EB perpendicularem AT. Et quia arcus BG orbis egredientis centri iam positus fuit subtendi orbis signorum 36 partibus et 29 minutis, erit angulus BDG etiam, scilicet angulus EDH, quia est apud centrum orbis signorum, secundum partes quibus quatuor anguli recti sunt 360 partes 36 partes et 29 minuta et secundum partes quibus duo anguli recti sunt 360 partes 72 partes et 58 minuta. Erit ergo propter illud arcus etiam qui est super lineam EN 72 partes et 58 minuta secundum partes quibus circulus qui describitur circa triangulum DEH ortogonium est 360 partes, et erit linea EH 71 partes et 21 minuta secundum partes quibus linea DE subtendens est 120 partes. Et secundum hanc similitudinem, quia arcus BG est 33 partes et 26 minuta, erit angulus BEG, qui est apud circumferentiam, 33 partes et 26 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed angulus DEH iam ostensum est quod est 107 partes et duo minuta, et angulus BEH totus est 140 partes et 28 minuta. Erit ergo angulus EBH residuus secundum istas partes 39 partes et 32 minuta. Erit ergo propter illud arcus etiam qui est super lineam EH 39 partes et 32 minuta secundum partes quibus circulus qui describitur circa triangulum BEH ortogonium est 360, et erit linea EH 40 partes et 35 minuta secundum partes quibus linea BE subtendens est 120 partes. Secundum partes igitur quibus demonstratur quod linea EH est 71 partes et 21 minuta et linea ED 120 partes erit linea BE 210 partes et 58 minuta. Et etiam quia arcus ABG totus orbis egredientis centri iam positus est subtendi partibus orbis signorum que proveniunt ex duabus longitudinibus coniunctis, et sunt 141 pars et 12 minuta, erit angulus ADG etiam, qui est apud centrum orbis signorum, secundum partes quibus quatuor anguli recti sunt 360 partes 141 partes et 12 minuta et secundum partes quibus duo anguli recti sunt 360 partes 282 partes et 24 minuta, et erit angulus qui sequitur eum, et est angulus ADE, secundum istas partes 77 partes et 36 minuta. Quapropter erit arcus etiam qui est super lineam ER 77 partes et 36 minuta secundum partes quibus circulus qui describitur circa triangulum DER ortogonium est 360 partes, et erit linea ER 75 partes et 12 minuta secundum partes quibus linea DE subtendens est 120 partes. Et secundum hanc similitudinem, quia arcus ABG orbis egredientis centri comprehendit 133 partes et 21 minutum, erit angulus AEG etiam, quia est apud circumferentiam, 133 partes et 21 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes fuit angulus ADE 77 partes et 36 minuta. Ergo angulus EAR, reliquus angulus, erit secundum istas partes 149 partes et 3 minuta. Erit ergo propter illud etiam arcus qui est super lineam ER 149 partes et 3 minuta secundum partes quibus circulus qui describitur circa triangulum AER ortogonium est 360 partes, et erit linea ER 115 partes et 39 minuta miminuta M. secundum partes quibus linea EA subtendens est 120 partes. Ergo secundum partes quibus demonstratum est quod linea ER est 75 partes et 12 minuta et linea ED posita est secundum eas 120 partes erit linea EA 78 partes et 2 minuta. Et etiam quia arcus AB orbis egredientis centri est 99 partes et 55 minuta, erit angulus AEB etiam, quia est apud circumferentiam, 99 partes et 55 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit propter illud etiam arcus qui est super lineam AT 99 partes et 55 minuta secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes, et erit arcus qui est super lineam ET partes relique ad complendum semicirculum, et sunt 80 partes et 5 minuta. Linea igitur AT, una duarum linearum que subtenduntur eis, erit 91 pars et 52 minuta secundum partes quibus linea AE subtendens est 120 partes, et linea ET secundum istas partes erit 77 partes et 12 minuta. Erit ergo propter illud secundum partes quibus demonstratum est quod linea AE est 78 partes et duo minuta et linea DE secundum eas 120 partes et linea AT 59 partes et 44 minuta et linea ET secundum illud exemplum 50 partes et duodecem minuta. Sed secundum istas partes iam fuit ostensum quod linea EB tota est 210 partes et 58 minuta. Ergo linea TB reliqua est 160 partes et 46 minuta secundum partes quibus linea AT est 59 partes et 44 minuta, et quadratum quod est ex linea TB est 25845 partes et 55 minuta, et quadratum quod est ex linea TA secundum illud exemplum est 3568 partes et 4 minuta. Cum ergo aggregatur illud, est ex eo quadratum quod est ex linea AB 29413 partes et 59 minuta. Erit ergo linea AB in longitudine 177 partes et 30 minuta secundum partes quibus fuit linea ED 120 partes et linea EA secundum illud exemplum 78 partes et duo minuta. Sed secundum partes quibus diametrus orbis egredientis centri est 120 partes erit linea AB 91 partes et 52 minuta. Et illud est quia subtenditur arcui cuius summa est 99 partes et 55 minuta. Ergo secundum partes quibus linea AB est 91 pars et 52 minuta et diametrus orbis egredientis centri 120 partes erit linea ED 64 partes et 17 minuta et linea EA 41 partes et 47 minuta. Oportet ergo ex eo ut sit arcus qui est super lineam EA orbis egredientis centri 40 partes et 45 minuta, et erit arcus EABG totus 174 partes et sex minuta. Propter illud ergo erit linea EDG 119 partes et 50 minuta fere secundum partes quibus diametrus orbis egredientis centri est 120 partes. 
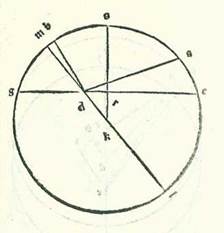Et quia portio EABG est minor semicirculo et propter illud cadit centrum orbis egredientis centri extra ipsam, tunc ponam ut punctum K sit centrum orbis egredientis centri, et protraham super ipsam et super punctum D diametrum, et est que transit per duo centra, sitque diametrus LKDM, et protraham a puncto K super lineam GE perpendicularem KR, et producam usque ad punctum S. Et quia secundum partes quibus diametrus LM est 120 partes est ostensum quod linea GE tota est 119 partes et 50 minuta et linea ED 64 partes et 17 minuta, erit linea GD reliqua secundum istas partes 55 partes et 33 minuta. Quapropter propterea quod superficies ortogonia que continetur ab his duabus lineis ED et DG est equalis ei que continetur ab his duabus lineis LD et DM, erit ea que continetur etiam ab his duabus lineis LD et DM 3570 partes et 56 minuta secundum partes quibus diametrus LM est 120 partes. Ex superficie vero que continetur ab his duabus lineis LD et DM cum quadrato quod est ex linea DK erit quadratum quod est ex medietate diametri, scilicet linea LK. Cum igitur nos minuerimus ex quadrato quod est ex medietate diametri, scilicet 3600 partibus, superficiem que continetur ab his duabus lineis LD et DM, scilicet 3570 partes et 56 minuta, remanebit nobis quadratum quod est ex linea KD secundum istas partes 29 partes et 4 minuta. Proveniet ergo nobis linea DK in longitudine, et est ea que est inter duo centra, secundum has partes 5 partes et 23 minuta fere secundum partes quibus linea KL, que est a centro orbis egredientis centri, est 60 partes. Et etiam quia medietas linee GE, scilicet linea GR, est 59 partes et 55 minuta secundum partes quibus diametrus LM est 120 partes et secundum istas partes ostensum est quod linea GD est 55 partes et 33 minuta, erit linea DR reliqua 4 partes et 22 minuta secundum partes quibus linea DK est quinque partes et 23 minuta, et erit propter illud secundum partes quibus linea DK subtendens est 120 partes linea DR 97 partes et 20 minuta, et arcus qui est super eam erit 108 partes et 24 minuta secundum partes quibus circulus qui describitur circa triangulum DKR ortogonium est 360 partes. Angulus igitur RKD secundum partes quidem quibus duo anguli recti sunt 360 partes est 108 partes et 24 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes est ipse 54 partes et 12 minuta. Et quia ipse est apud centrum orbis egredientis centri, erit arcus MS etiam 54 partes et 12 minuta secundum partes quibus orbis egredientis centri est 360 partes. Arcus vero GMS totus, quia est medietas arcus GSE, est 87 partes et 3 minuta. Ergo arcus MG reliquus, qui est a longitudine propinquiore ad habitudinem tertiam habitudinum extremitatis noctis, erit 32 partes et 51 minutum. Et apparet quod longitudo BG quia fuit iam posita 33 partes et 26 minuta, erit arcus BM reliquus, et est ille qui est ab habitudine secunda ad longitudinem propinquiorem, proveniet erit ... proveniet: Two rivalling verbs. Paris, BnF, lat. 14738 (169v, line 19 from the bottom) contains only the latter. nobis 35 minuta, et longitudo AB quia fuit iam posita 99 partes et 55 minuta, tunc arcus reliquus, et est ille qui est a longitudine longiore ad habitudinem primam, proveniet nobis 79 partes et 30 minuta. Si ergo centrum orbis revolutionis non revolveretur nisi super hunc orbem egredientis centri, essemus iam contenti agere secundum istas quantitates, quia non alterarentur. Sed quia secundum quod sequitur in radice qua agitur non revolvitur nisi super circulum alium, et est ille qui describitur cum centro dividente lineam DK in duo media et cum longitudine KL, tunc iam necesse est etiam, quemadmodum oportuit in stella Martis, ut numerentur prius superfluitates que sunt longitudinum que videntur et ut demonstretur quante sunt quantitates earum, quia sunt quantitates egressionis a centro fere. 
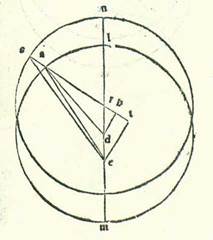Quod si centrum orbis revolutionis non revolvitur super orbem egredientis centri alium, sed super orbem primum, qui sit super diversitatem que est propter orbem signorum, scilicet orbem qui describitur circa centrum K, tunc sit nunc orbis egredientis centri deferens centrum orbis revolutionis orbis LM circa centrum D, et orbem Probably corrupt for orbis, which is also the reading of Paris, BnF, lat. 14738 (149v, line 10 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 511, line 12). qui est motus equalis sit orbis NS circa centrum R equalis orbi LM. Et applicetur diametri que transit per duo centra, et sit linea LM, et assumatur super ipsam centrum orbis signorum etiam punctum E, et ponam primum in habitudine prima habitudinum extremitatis noctis centrum orbis revolutionis super punctum A, et applicabo lineas DA et EA et RAS et ES, et producam a duobus punctis D et E ad lineam AR, cum producetur secundum rectitudinem, duas perpendiculares DH et ET. Et quia angulus NRS, et est angulus cursus equalis in longitudine, iam ostensum est quod est 79 partes et 30 minuta secundum partes quibus quatuor anguli recti sunt 360 partes et etiam angulus qui est super caput eius, et est angulus DRH, secundum partes quibus quatuor anguli recti sunt 360 partes est 79 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes 159 partes, erit propter illud arcus qui est super lineam DH 159 partes secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et arcus qui est super lineam RH est partes relique ad complendum semicirculum, et sunt 21 partes. Linea ergo DH, una duarum linearum que subtenduntur eis, erit 117 partes et 59 minuta secundum partes quibus chorda DR est 120 partes, et linea RH erit secundum istas partes 21 partes et duo minuta. Ergo secundum partes quibus linea DR, quia est medietas ER, est due partes et 42 minuta fere et linea quidem DA, et est EA, que est a centro orbis egredientis centri, est 60 partes erit linea DH due partes et 39 minuta et linea RH secundum hoc exemplum 30 minuta. Et quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DA, est ex eo quadratum quod est ex linea AH, proveniet nobis linea AH secundum istas partes 59 partes et 56 minuta. Et secundum hoc exemplum, quia linea RH est equalis linee HT et linea ET est dupla linee DH, erit linea AT tota 60 partes et 26 minuta secundum partes quibus linea ET est 5 partes et 18 minuta. Quapropter erit chorda AE secundum istas partes 60 partes et 40 minuta. Ergo secundum partes quibus linea AE est 120 partes erit linea ET 10 partes et 29 minuta et arcus qui est super eam 10 partes et 1 minutum fere secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes. Erit ergo propter illud angulus TAE 10 partes et unum minutum secundum partes quibus duo anguli recti sunt 360 partes. Et quia secundum partes quibus linea ET est 5 partes et 18 minuta est linea RS, quia est a centro orbis egredientis centri, est 60 partes et linea RT pars una et manifestum est quod linea ST tota est 61 partes, proveniet nobis linea SE subtendens etiam secundum istas partes 61 partes et 14 minuta. Quapropter secundum partes quibus linea SE est 120 partes erit linea ET 10 partes et 23 minuta, et arcus qui est super eam erit 9 partes et 55 minuta secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Angulus igitur EST est 9 partes et 55 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes est ostensum quod angulus EAT est 10 partes et 1 minutum. Ergo angulus AES reliquus, et est angulus superfluitatis quesite, secundum partes quibus duo anguli recti sunt 360 partes erit sex minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit tria minuta. Huius autem stelle solum quia locus in habitudine prima habitudinum extremitatum noctis fuit visus super lineam EA super 23 partes et 11 minuta Scorpionis, tunc apparet quod si centrum orbis revolutionis non moveretur super orbem egredientis centri, sed super orbem NS, esset iam centrum orbis revolutionis super punctum S huius orbis, et stella fuisset visa super lineam ES. Et fuit summa superfluitatis in eo quod est inter duo loca tria minuta. Est igitur eius locus super 23 partes et 14 minuta Scorpionis.
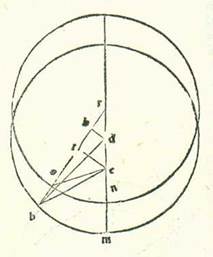Et etiam in figura huic simili ponam formam exempli habitudinis secunde habitudinum extremitatis noctis ita ut ipsa sit in figura precedens parum longitudinem propinquiorem. Et quia arcus SN orbis egredientis centri iam ostensum est quod est 35 minuta, erit angulus NRS secundum partes quibus quatuor anguli recti sunt 360 partes 35 minuta et secundum partes quibus duo anguli recti sunt 360 partes pars una et 10 minuta. Erit ergo propter illud arcus qui est super lineam DH pars una et 10 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et arcus qui est super lineam RH erit illud quod remanet ad complendum semicirculum, et est 178 partes et 50 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, erit pars una et 13 minuta secundum partes quibus linea DR subtendens est 120 partes, et linea RH erit secundum istas partes fere 120 partes. Ergo secundum partes quibus linea DR est due partes et 42 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea quidem DH duo minuta et linea RH secundum illud exemplum due partes et 42 minuta, et similiter linea HB, quia non est inter lineam DB subtendentem et inter ipsam differentia, secundum istas partes erit 60 partes. Et etiam quia linea TH est equalis linee HR et linea ET est dupla linee DH, proveniet nobis linea TB reliqua 57 partes et 18 minuta secundum partes quibus linea ET est 4 minuta. Et propter illud erit chorda EB secundum istas partes 57 partes et 18 minuta. Quapropter secundum partes quibus linea EB est 120 partes erit linea ET octo minuta fere, et arcus qui est super eam erit octo minuta etiam secundum partes quibus circulus qui describitur circa triangulum EBT ortogonium est 360 partes. Angulus igitur EBT est octo minuta secundum partes quibus duo anguli recti sunt 360 partes. Et similiter etiam quia secundum partes quibus linea RS, que est a centro orbis egredientis centri, est 60 partes est iam ostensum quod linea RT tota est 5 partes et 24 minuta, proveniet nobis linea TS reliqua 54 partes et 36 minuta secundum partes quibus fuit linea ET quatuor minuta. Et propter illud erit chorda ES secundum istas partes 54 partes et 36 minuta. Ergo secundum partes quibus est linea ES 120 partes erit linea ET decem minuta fere et arcus qui est super eam decem minuta fere secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Quapropter erit angulus EST etiam decem minuta secundum partes quibus duo anguli recti sunt 360 partes. Ergo angulus BES reliquus secundum istas partes erit duo minuta, sed secundum partes quibus quatuor anguli recti sunt 360 partes 1 minutum. Apparet ergo etiam hic quia fuit stella in habitudine secunda et fuit visa super lineam EB et fuit eius locus super 7 partes et 54 minuta Piscis. Quoniam si non esset visa etiam nisi super lineam ES, esset eius locus super 7 partes et 53 minuta Piscis.
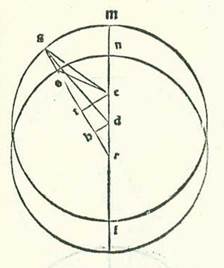Ponam itaque etiam formam habitudinis tertie ita quod ipsa sit posterior in figura a longitudine propinquiore. Et quia arcus NS orbis egredientis centri iam positus est 32 partes et 51 minutum, erit angulus NRS etiam secundum partes quibus quatuor anguli recti sunt 360 partes 32 partes et 51 minutum et secundum partes quibus duo anguli recti sunt 360 partes 65 partes et 42 minuta. Erit ergo propter illud arcus qui est super lineam DH 65 partes et 42 minuta secundum partes quibus circulus qui describitur circa triangulum DHR ortogonium est 360 partes, et erit arcus qui est super lineam RH quod remanet ad complendum semicirculum, et sunt 114 partes et 18 minuta. Linea igitur DH una duarum linearum que subtenduntur eis erit 65 partes et sex minuta secundum partes quibus chorda DR est 120 partes, et erit linea RH secundum istas partes 100 partes et 49 minuta. Quapropter secundum partes quibus linea DR est due partes et 42 minuta et linea DG, que est a centro orbis egredientis centri, est 60 partes, erit linea DH pars una et 28 minuta et linea RH secundum illud exemplum due partes et 16 minuta. Et quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea GD, est ex eo quadratum quod est ex linea GH, proveniet nobis hec linea etiam secundum istas partes 59 partes et 59 minuta fere. Et secundum illud exemplum, quia linea TH est equalis linee HR et linea ET est dupla linee DH, proveniet nobis linea GT reliqua 57 partes et 43 minuta secundum partes quibus linea ET est due partes et 56 minuta. Et propter illud erit chorda EG secundum istas partes 57 partes et 47 minuta. Ergo secundum partes quibus linea EG est 120 partes erit linea ET sex partes et 5 minuta et arcus qui est super eam quinque partes et 48 minuta fere secundum partes quibus circulus qui describitur circa triangulum GET ortogonium est 360 partes. Quapropter erit angulus EGT 5 partes et 48 minuta fere secundum partes quibus duo anguli recti sunt 360 partes. Et similiter propterea quod secundum partes quibus linea RS, que est a centro orbis egredientis centri, est 60 partes est linea RT tota aggregata quatuor partes et 32 minuta, proveniet nobis linea ST reliqua 55 partes et 28 minuta secundum partes quibus fuit linea ET due partes et 56 minuta. Et propter illud erit chorda ES secundum istas partes 55 partes et 33 minuta. Quapropter secundum partes quibus linea ES subtendens est 120 partes erit linea ET sex partes et 20 minuta, et arcus qui est super eam erit sex partes et duo minuta secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Ergo angulus EST est sex partes et duo minuta secundum partes quibus duo anguli recti sunt 360 partes, et angulus GES reliquus secundum istas partes erit quatuordecem minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit septem minuta. Quapropter quia stella in habitudine tertia quando fuit visa super lineam EG fuit locus super 14 partes et 23 minuta Arietis, tunc manifestum est quod si fuisset etiam super lineam ES, fuisset eius locus super 14 partes et 30 minuta Arietis. Iam vero ostensum est quod in habitudine prima fuit eius locus super 23 partes et 14 minuta Scorpionis et in habitudine secunda super septem partes et 53 minuta Piscis. Provenient igitur due longitudines que videntur huius stelle, si non aspiciatur in eis secundum orbem egredientis centri deferentem centrum orbis revolutionis, sed secundum orbem egredientis centri quo agitur super motum equalem, longitudo quidem inter habitudinem primam et inter habitudinem secundam 104 partes et 39 minuta et longitudo inter habitudinem secundam et inter habitudinem tertiam 36 partes et 37 minuta. Cum nos ergo sequemur intentionem cuius declaratio precessit, inveniemus lineam que est in eo quod est inter centrum orbis signorum et inter centrum orbis egredientis centri quo agitur super motum orbis revolutionis equalem 5 partes et 30 minuta fere secundum partes quibus diametrus orbis egredientis centri est 120 partes, et inveniemus arcum orbis egredientis centri qui est inter longitudinem longiorem et inter habitudinem primam habitudinum extremitatis noctis 77 partes et 15 minuta et arcum qui est inter habitudinem secundam et inter longitudinem propinquiorem duas partes et 50 minuta et arcum qui est inter longitudinem propinquiorem et inter habitudinem tertiam 30 partes et 36 minuta. Iam vero apparet ex hoc loco qualiter producantur secundum veritatem quantitates dicte cum superfluitas inter longitudines ex istis quantitatibus etiam provenerit conveniens fere superfluitati cuius relatio precessit longitudinem stellarum que videntur accepta per istas proportiones que inveniuntur convenientes ei quod reperitur ex eis per considerationes. Et illud est manifestum ex eo quod nos narramus.
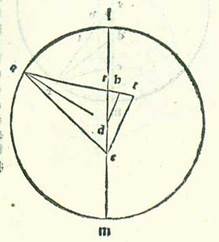Ponamus etiam formam habitudinis prime habitudinum extremitatis noctis, et sit in ea orbis egredientis centri deferens centrum orbis revolutionis tantum. Et quia angulus LRA secundum partes quibus quatuor anguli recti sunt 360 partes iam ostensum est quod est 77 partes et 15 minuta et secundum partes quibus duo anguli recti sunt 360 partes est ipse et angulus qui est super caput eius, et est angulus DRH, 154 partes et 30 minuta, erit arcus qui est super lineam DH 154 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH quod remansit ad complendum semicirculum, et sunt 25 partes et 30 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, est 117 partes et duo minuta secundum partes quibus diameter DR est 120 partes, et linea RH secundum istas partes est 26 partes et 29 minuta. Ergo secundum partes quidem quibus linea RD est due partes et 45 minuta et linea DA, que est a centro orbis egredientis centri, est 60 partes erit linea quidem DH due partes et 41 minuta et linea RH secundum hoc exemplum 36 minuta. Et propter illud idem quod precessit ex eius declaratione erit linea AH secundum istas partes 59 partes et 56 minuta, et erit linea AT tota 60 partes et 32 minuta secundum partes quibus linea ET, quia est dupla linee DH, est quinque partes et 22 minuta. Quapropter aggregatur chorda AE secundum istas partes 60 partes et 46 minuta. Ergo secundum partes quibus linea AE est 120 partes erit linea ET 10 partes et 36 minuta, et erit arcus qui est super eam 10 partes et 8 minuta secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes. Angulus igitur EAT est 10 partes et 8 minuta secundum partes quibus duo anguli recti sunt 360 partes, et angulus LEA reliquus secundum istas partes erit 144 partes et 22 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 72 partes et 11 minuta. Hec igitur fuit summa partium longitudinis stelle in habitudine prima a longitudine longiore in orbe signorum que est super punctum L.
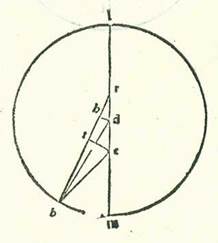Et ponam etiam formam habitudinis secunde. Et quia angulus BRM secundum partes quibus quatuor anguli recti sunt 360 partes iam ostensum quod est 5 partes et 40 minuta, erit arcus qui est super lineam DH 5 partes et 40 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH reliquum ad complendum semicirculum, et est 174 partes et 20 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, erit 5 partes et 56 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes erit 119 partes et 51 minuta. Ergo secundum partes quibus linea DR est due partes et 45 minuta et linea RB, que est a centro orbis egredientis centri, est 60 partes erit linea DH octo minuta et linea RH secundum hoc exemplum due partes et 45 minuta fere. Et propter illud idem erit linea BHR secundum istas partes 60 partes fere, et erit linea BTH secundum istas partes 60 partes fere, et erit linea BT reliqua 57 partes et 15 minuta. Ergo secundum partes quibus linea ET est 16 minuta oportet ex inde ut sit chorda EB aggregata secundum istas partes 57 partes et 15 minuta. Ergo secundum partes quibus linea EB est 120 partes erit linea ET 33 minuta, et erit arcus qui est super eam 32 minuta secundum partes quibus circulus qui describitur circa triangulum EBT ortogonium est 360 partes. Quapropter erit angulus EBT 32 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit angulus BEM totus secundum istas partes sex partes et 12 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit tres partes et sex minuta. Fuit ergo longitudo stelle in habitudine secunda precedens longitudinem propinquiorem tribus partibus et sex minutis. Et iam ostensum fuit quod eius longitudo fuit in habitudine prima posterior a longitudine longiore 72 partibus et 11 minutis. Provenit ergo longitudo ab habitudine prima ad habitudinem secundam que videtur ex eo quod remanet ad complendum semicirculum, et est 104 partes et 43 minuta. Et illud est conveniens longitudini que per considerationes producitur.
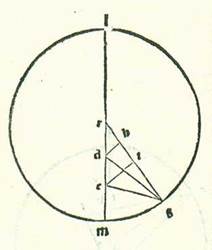Ponam igitur etiam tertie habitudinis formam. Et quia angulus MRG secundum partes quibus quatuor anguli recti sunt 360 partes est iam ostensum quod est 30 partes et 36 minuta et secundum partes quibus duo anguli recti sunt 360 est 61 partes et 12 minuta, erit arcus qui est super lineam DH etiam 61 partes et 12 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH quod remanet ad complendum semicirculum, et est 118 partes et 48 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, erit 61 pars et sex minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum partes istas erit 103 partes et 17 minuta. Quapropter secundum partes quibus linea DR est due partes et 45 minuta et linea GD, que est a centro orbis egredientis centri, est 60 partes erit linea DH pars una et 24 minuta et linea quidem RH secundum illud exemplum due partes et 22 minuta. Et propter illud idem erit linea GH secundum istas partes 59 partes et 59 minuta, et erit linea GT reliqua 57 partes et 37 minuta secundum partes quibus aggregata linea ET est due partes et 48 minuta. Erit ergo propter illud chorda EG 57 partes et 41 minutum. Ergo secundum partes quibus linea EG est 120 partes erit linea ET 5 partes et 50 minuta et arcus qui est super eam 5 partes et 34 minuta secundum partes quibus circulus qui describitur circa triangulum ETG ortogonium est 360 partes. Erit ergo propter illud angulus EGT 5 partes et 34 minuta secundum partes quibus duo anguli recti sunt 360 partes, et erit angulus MEG totus secundum istas partes 66 partes et 46 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit ipse 33 partes et 23 minuta. Hec igitur fuit summa longitudinis stelle in habitudine tertia a longitudine longiore posterioris ab ea. Iam autem fuit ostensum quod eius longitudo fuit in habitudine secunda ab hac eadem longitudine propinquiore precedens ipsam tres partes et sex minuta. Aggregatur ergo longitudo que videtur ab habitudine secunda ad habitudinem tertiam cum colligitur 36 partes et 29 minuta. Et illud est conveniens etiam ei quod consideratum fuit.
Et iam manifestum est ex eo quod quando fuit stella in habitudine tertia, fuit locus eius secundum quod invenimus per considerationem super 14 partes et 23 minuta minunuta M. Arietis, et fuit eius longitudo a longitudine propinquiore posterior ab ea secundum quod ostensum est 33 partes et 23 minuta. Nam longitudinis propinquioris orbis eius egredientis centri fuit locus in illa hora super undecem partes Piscis et longitudinis longioris super partem condiametralem illi parti, et est pars undecima Virginis.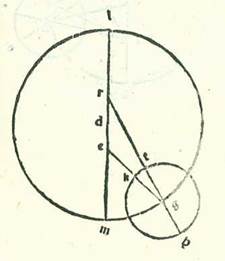 
Si ergo descripserimus circa centrum G orbem revolutionis, supra quem sint H, T, K, erit manifestum quod cursus medius in longitudine a longitudine longiore orbis egredientis centri super punctum L proveniet 210 partes et 36 minuta. Et propterea quod angulus MRH iam fuit ostensum quod est 30 partes et 36 minuta secundum partes quibus quatuor anguli recti sunt 360 partes et quod arcus TK orbis revolutionis, qui est inter punctum T, et est longitudo propinquior, et inter punctum K, super quod fuit stella, est due partes et 47 minuta et propterea quod angulus EGR iam fuit ostensum quod est 5 partes et 34 minuta secundum partes quibus duo anguli recti sunt 360 partes et secundum partes quibus quatuor anguli recti sunt 360 partes est due partes et 47 minuta, ergo in hora habitudinis tertie habitudinum extremitatis noctis, scilicet in anno primo annorum Antonii in mense apud Egyptios nominato Athus in die vigesimo eius in nocte quam sequitur dies vigesimusprimus post quinque horas a medietate noctis fuit stelle Iovis, cum conspicitur in re eius cursus medii, longitudo in longitudine a longitudine longiore orbis egredientis centri 210 partes et 36 minuta, scilicet quod locus eius fuit super 11 partes et 36 minuta Arietis, et fuit eius locus in diversitate super 182 partes et 47 minuta a puncto H, quod est longitudo longior orbis revolutionis.
⟨XI.2⟩ Capitulum secundum: In ostensione quantitatis orbis revolutionis stelle Iovis
Deinde post illud accepimus ad ostensionem quantitatis orbis revolutionis Iovis considerationem eius in qua iam cecidit nobis experientia in anno secundo annorum Antonii in mense nominato apud Egyptios Mesure in die vigesimosexto eius in nocte quam sequitur dies vigesimusseptimus ante elevationem Solis, scilicet post quinque horas equales fere a medietate noctis, quoniam Solis cursus medii fuit locus super 26 partes et 11 minuta Cancri et fuit medians celum in instrumento considerationis pars secunda Arietis. Consideravimus itaque stellam Iovis in illa hora cum stella nominata Aldebaran et invenimus locum eius per visionem super quindecem partes et medietatem et quartam partis Geminorum. Et fuit visa equalis in loco suo centro Lune, et tamen Luna fuit tunc declivior ad meridiem. In illis autem horis invenimus Lune secundum numerationem cuius precessit declaratio locum per motum suum medium in novem partibus Geminorum et per diversitatem super 272 partes et 5 minuta a longitudine longiore orbis revolutionis. Et propter illud fuit locus eius verus in 14 partibus et 50 minutis Geminorum, et est eius locus qui videtur in Alexandria in 15 partibus et 45 minutis Geminorum. Ergo fuit locus Iovis ex hoc modo super 15 partes et medietatem et quartam partis Geminorum. Et etiam quia temporis quod fuit inter habitudinem tertiam habitudinum extremitatis noctis et inter horam huius considerationis quam narravimus summa fuit annus unus Egyptius et 276 dies et in eo quod comprehendit hoc tempus non cadit diversitas sensibilis, quamvis numerentur secundum crossitudinem numerationis, et est in longitudine 53 partes et 17 minuta et in diversitate 218 partes et 31 minutum, tunc cum nos addidimus illud super superfluitates quas demonstravimus in habitudine tertia, erit in hora huius considerationis radix in longitudine super 263 partes et 53 minuta fere a longitudine longiore orbis egredientis centri et radix diversitatis super 41 partes et 18 minuta a longitudine longiore orbis revolutionis.
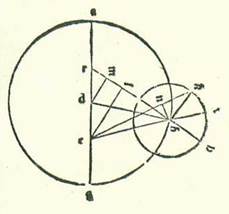Postquam igitur iam explanate sunt he res secundum hunc modum, tunc ponam etiam formam similem forme quam declaravimus secundum hanc intentionem in stella Martis, sitque in ea locus orbis revolutionis posterior a longitudine propinquiore orbis egredientis centri, et sit locus stelle eiusdem a longitudine longiore orbis revolutionis secundum quod convenit ei quod narravimus hic de duobus cursibus mediis in longitudine et in diversitate. Et quia cursus medius in longitudine a longitudine longiore orbis egredientis centri est 263 partes et 53 minuta, erit angulus BRG etiam secundum partes quidem quibus quatuor anguli recti sunt 360 partes 83 partes et 53 minuta et secundum partes quibus duo anguli recti sunt 360 partes 167 partes et 46 minuta. Quapropter arcus qui est super lineam DM erit 167 partes et 46 minuta secundum partes quibus circulus qui describitur circa triangulum DRM ortogonium est 360 partes, et arcus qui est super lineam RM erit quod remanet ad complendum semicirculum, et est 12 partes et 14 minuta. Linea igitur DM, una duarum linearum que subtenduntur eis, erit 119 partes et 19 minuta secundum partes quibus chorda DR est 120 partes, et linea RM secundum partes istas erit 12 partes et 47 minuta. Ergo secundum partes quibus linea DR est due partes et 45 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea DM due partes et 44 minuta fere et linea RM secundum illud exemplum 18 minuta. Et quia cum quadratum quod est ex linea DM minuitur ex quadrato quod est ex linea DB est ex eo quadratum quod est ex linea BM, erit linea BM secundum istas partes 59 partes et 56 minuta et secundum illud exemplum, quia linea RM est equalis linee ML, reliqua 59 partes et 38 minuta secundum partes quibus provenit linea EL 5 partes et 28 minuta. Et propter illud erit linea EB subtendens secundum istas partes 59 partes et 44 minuta. Ergo secundum partes quibus linea EB est 120 partes erit linea EL 10 partes et 58 minuta fere et arcus qui est super eam 10 partes et 30 minuta secundum partes quibus circulus qui describitur circa triangulum BEL ortogonium est 360 partes. Quapropter erit angulus EBR 10 partes et 30 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum vero istas partes fuit angulus BRG 167 partes et 46 minuta. Erit ergo angulus BEG totus secundum istas partes 178 partes et 16 minuta. Et etiam quia puncti G, et est longitudo propinquior, fuit locus super 11 partes Piscis fere et fuit stella visa super lineam EK et eius locus super 15 partes et 45 minuta Geminorum, erit angulus KEG secundum partes quidem quibus quatuor anguli recti sunt 360 partes 94 partes et 45 minuta et secundum partes quibus duo anguli recti sunt 360 partes 189 partes et 30 minuta. Ergo angulus BEK reliquus secundum istas partes erit 11 partes et 14 minuta. Erit ergo propter illud arcus qui est super lineam BN 11 partes et 14 minuta secundum partes quibus circulus qui describitur circa triangulum BEN ortogonium est 360 partes, et erit linea BN 11 partes et 44 minuta secundum partes quibus chorda EB est 120 partes. Ergo secundum partes quibus linea EB et linea EL est dupla linee DM erit linea LB et linea EL est dupla linee DM erit linea LB: This passage, which does not fit into the text, is neither contained in Paris, BnF, lat. 14738 (172v, lines 9-11 from the bottom) nor in the Greek text (see Toomer, loc. cit., p. 522, lines 1-2) and has probably entered due to a corruption. est 59 partes et 44 minuta et linea que est a centro orbis egredientis centri 60 partes erit linea BN 5 partes et 50 minuta. Et secundum istud exemplum, quia arcus HK est 41 partes et 18 minuta, erit angulus HBK etiam secundum partes quibus quatuor anguli recti sunt 360 partes 41 pars et 18 minuta et secundum partes quibus duo anguli recti sunt 360 partes 82 partes et 36 minuta. Sed secundum istas partes fuit angulus EBR, scilicet angulus HBT, 10 partes et 30 minuta. Erit ergo angulus TBK reliquus 72 partes et sex minuta. Et iam fuit ostensum quod angulus KET secundum istas partes est 11 partes et 14 minuta. Ergo angulus BKN reliquus secundum istas partes est 60 partes et 52 minuta. Quapropter erit arcus qui est super lineam BN 60 partes et 52 minuta secundum partes quibus circulus qui describitur circa triangulum BKN ortogonium est 360 partes. Sed linea BN secundum partes quibus diameter BK est 120 partes est 60 partes et 47 minuta. Ergo secundum partes quibus linea BN est 5 partes et 50 minuta et linea quidem que est a centro orbis egredientis centri est 60 partes erit linea BK, que est a centro orbis revolutionis, 11 partes et 30 minuta fere. Et illud est cuius indiguimus inventione.
⟨XI.3⟩ Capitulum tertium: In verificatione motuum revolubilium stelle Iovis
Deinde post illud accepimus revolutionem motuum stelle Iovis revolutionem motuum stelle Iovis: Corrupt passage, which likewise appears in Paris, BnF, lat. 14738 (173r, line 3). In the Greek text the sentence reads: ‘Next, to [determine] the periodic motions, we again took one of the precisely recorded ancient observations’ (see Toomer, loc. cit., 522, line 17). etiam considerationem unam considerationum antiquarum que multa inquisitione firmate sunt in qua non est dubitatio in qua etiam dixerunt quod in anno quadragesimoquinto secundum tempus Dionysii in die decimo mensis nominati Berbeunis aut Iunenun cooperuerat stella Iovis in mane stellam nominatam Alhahamar, idest Asinum meridianum. Et hec hora fuit in anno octuagesimotertio a morte Alexandri in mense mensium Egyptiorum nominato Athica in die decimoseptimo eius in nocte quam sequitur dies decimusoctavus eius in matutino. Et invenimus Solis in hora illa locum per cursum eius medium super 9 partes et 56 minuta Virginis. Sed stelle nominate Asinus meridianus, et est ex stellis que sunt circa Volutabrum in Cancro, fuit locus in hora considerationis nostre super undecem partes et tertiam partis Cancri, et manifestum est quod eius locus fuit in hora illius considerationis quam narravimus super septem partes et 33 minuta eius, propterea quod illud quod pertinet tempori quod est inter duas considerationes, et est trecenti et septuagintaocto anni, est tres partes et 47 minuta. Stelle ergo Iovis etiam fuit in illa hora locus, propterea quod cooperuerat illam stellam super septem partes et 33 minuta Cancri. Et similiter etiam propterea quod fuit longitudo longior in tempore nostro in 11 partibus Virginis, oportet ut sit eius locus in illa hora super septem partes et 13 minuta eius. Et manifestum est quod huius stelle per visum fuit longitudo a longitudine sua longiore orbis egredientis centri in illa hora 300 partes et 20 minuta et fuit longitudo Solis per motum suum medium ab illa longitudine longiore due partes et 43 minuta.
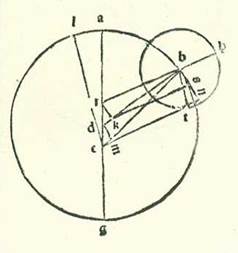Postquam igitur iam explanate sunt iste res, tunc ponatur etiam forma similis ei que declarata fuit hec intentio hec intentio: Corrupt passage which likewise appears in Paris, lat. 14738 (173r, line 19), but not in the Greek text (see Toomer, loc. cit., 522, line 4 from the bottom). de re Martis excepto quod ponamus eam hic convenientem cursibus qui ponuntur in consideratione, ita ut in ea sit positus orbis revolutionis qui est circa punctum B ante punctum A, quod est longitudo longior, et locus Solis per motum suum medium sit super punctum L post illam longitudinem longiorem parumper, et propter illud sit etiam situs stelle super punctum T post punctum H, quod est longitudo longior orbis revolutionis. Et applicentur secundum illud exemplum linee RBH et BT et EB et TE, et producatur super lineam DB perpendicularis RK et super lineam ET perpendicularis DM et perpendicularis BN et super lineam BN, cum addetur in eius productione in hoc loco, perpendicularis DS, ita ut proveniat ex perpendicularibus superficies equidistantium laterum et rectorum angulorum, et est superficies DMNS. Et quia angulus AET, quem continet quod remanet ad complendum circulum unum, et est circulus orbis signorum, scilicet post 300 partes et 20 minuta, est 59 partes et 40 minuta secundum partes quibus quatuor anguli recti sunt 360 partes et angulus AEL secundum istas partes est due partes et 43 minuta, erit angulus LET totus, scilicet angulus BTE, secundum partes quibus quatuor anguli recti sunt 360 partes 62 partes et 23 minuta et secundum partes quibus duo anguli recti sunt 360 partes 124 partes et 46 minuta. Ergo arcus qui est super lineam BN est 124 partes et 46 minuta secundum partes quibus circulus qui describitur circa triangulum BTN ortogonium est 360 partes, et erit linea BN 106 partes et 20 minuta secundum partes quibus chorda BT est 120 partes. Igitur secundum partes quibus linea BT, que est a centro orbis revolutionis, est 11 partes et 30 minuta erit linea BN 10 partes et 12 minuta. Et etiam quia angulus DEM secundum partes quibus quatuor anguli recti sunt 360 partes iam positus fuit 59 partes et 40 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 119 partes et 20 minuta et angulus MDE reliquus secundum istas partes est 60 partes et 40 minuta, erit arcus qui est super lineam DM 119 partes et 20 minuta secundum partes quibus circulus qui describitur circa triangulum DEM ortogonium est 360 partes, et erit linea DM 103 partes et 34 minuta secundum partes quibus diameter DE est 120 partes. Ergo secundum partes quibus linea DE est due partes et 45 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea DM due partes et 23 minuta et linea BSN tota 12 partes et 35 minuta secundum istas partes. Quapropter secundum partes quibus chorda BD est 120 partes erit linea BS 25 partes et 10 minuta et arcus qui est super eam 24 partes et 14 minuta secundum partes quibus circulus qui describitur circa triangulum BSD ortogonium est 360 partes. Angulus ergo BDS erit 24 partes et 14 minuta secundum partes quibus duo anguli recti sunt 360. Ergo angulus DBS reliquus secundum istas partes erit 155 partes et 46 minuta, et angulus BDE totus secundum illud exemplum erit 216 partes et 26 minuta, et angulus BDR reliquus secundum istas partes etiam erit 143 partes et 34 minuta. Quapropter arcus qui est super lineam RK erit 143 partes et 34 minuta secundum partes quibus circulus qui describitur circa triangulum DRK ortogonium est 360 partes, et arcus qui est super lineam DK erit quod remanet ad complendum semicirculum, et est 36 partes et 26 minuta. Et propter illud erit linea RK una duarum linearum que subtenduntur eis 113 partes et 59 minuta secundum partes quibus diameter RD est 120 partes, et erit linea DK secundum istas partes 37 partes et 31 minuta. Ergo secundum partes quibus linea DR est due partes et 45 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea RK due partes et 37 minuta et linea DK secundum istud exemplum 52 minuta, et erit linea KB reliqua secundum istas partes 59 partes et octo minuta. Et propter illud erit chorda RB secundum istas partes 59 partes et 12 minuta. Quapropter secundum partes quibus linea RB est 120 partes erit linea RK 5 partes et 18 minuta et arcus qui est super eam quinque partes et quatuor minuta secundum partes quibus circulus qui describitur circa triangulum BRK ortogonium est 360 partes. Angulus igitur RBD erit quinque partes et quatuor minuta secundum partes quibus duo anguli recti sunt 360 partes, et angulus ARB totus, et est ille qui comprehendit motum equalem in longitudine, erit secundum istas partes 148 partes et 38 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 74 partes et 19 minuta. Et quia angulus HBT cum angulo BRA, quando aggregatur, est equalis duobus angulis semicirculi cum angulo AEL, et cum minuitur ex eis in hoc loco angulus ARB, provenit angulus HBT, et est ille qui comprehendit cursum stelle a longitudine longiore in orbe revolutionis, erit ipse secundum istas partes 77 partes et duo minuta. Iam ergo manifestum est nobis quod in hora illius considerationis quam narravimus fuit longitudo stelle Iovis, cum aspexerint in ea per cursum suum medium, in longitudine 285 partes et 41 minuta a longitudine longiore et fuit in illa hora in orbe egredientis centri, scilicet eius locus fuit per motum eius medium super 22 partes et 54 minuta Geminorum, et fuit locus eius in diversitate super 77 partes et duo minuta a longitudine longiore in orbe revolutionis. Nos autem iam ostendimus quod eius longitudo fuit in hora habitudinis tertie a longitudine longiore in orbe revolutionis 182 partes et 47 minuta. Iam igitur superfluunt ei in tempore quod est inter duas considerationes, cuius summa annorum Egyptiorum est 377 anni et 128 dies diminuta quasi una hora post revolutiones integras diversitatis, et sunt 345 revolutiones, 105 partes et 45 minuta. Et illud etiam est propinquum superfluitati diversitatis que invenitur provenisse nobis per motus medios quos fecimus ante. Nos enim ex his eisdem equavimus motum eius in die, quia divisimus partes que proveniunt ex numero superfluitatis revolutionum per numerum dierum qui proveniunt ex tempore quod fuit inter duas considerationes.
⟨XI.4⟩ Capitulum quartum: In descriptione radicis motuum eiusdem stelle Iovis revolubilium
Et in hoc etiam quia tempus quod fuit inter annum primum annorum Nabuchodonosor a mense Thut apud Egyptios a die primo eius a medietate diei et inter considerationem antiquam dictam est ex annis Egyptiis quingenti et sex anni et trecenti et sexdecem dies et medietas et quarta diei fere. Et quod provenit in hoc tempore ex superfluitate in longitudine est 258 partes et 13 minuta et in diversitate quidem 290 partes et 58 minuta. Tunc si nos minuerimus hec duo unumquodque ex suo relativo ex duobus locis que narravimus in consideratione, erit nobis radix stelle Iovis etiam per motum suum medium in illa hora eadem posita cum locis reliquarum stellarum in longitudine quidem super quatuor partes et 41 minuta Libre et in diversitate super 146 partes et 4 minuta a longitudine longiore in orbe revolutionis. Et propter illud idem erit etiam radix longitudinis longioris orbis centri egredientis super duas partes et 9 minuta Virginis.
⟨XI.5⟩ Capitulum quintum: In declaratione egressionis a centro stelle Saturni et longitudinis eius longioris
Et quia iam remansit nobis in hoc loco ut declaremus diversitatem et radices sive applicationes que videntur in stella Saturni etiam, tunc accepimus primum causa speculandi in longitudine longiore et summa egressionis orbis egredientis centri a centro, sicut fecimus in reliquis stellis, tria loca huius stelle in habitudinibus que nominantur extremitas noctis in quibus fuit stella condiametralis Soli per cursum suum medium. Et prima harum habitudinum in quibus consideravimus cum instrumentis considerationis fuit in anno undecimo annorum Adriani in mense apud Egyptios Machur in die septimo eius in hora prima noctis quam sequitur dies octavus. Et invenimus eam in parte una et in 13 minutis Libre. Et in habitudine quidem secunda consideravimus eam in anno decimoseptimo annorum Adriani in mense apud Egyptios Athica in die decimooctavo. Horam autem condiametrationis vere et loci stelle in ea numeravimus cum comparatione inter ea et inter illud quod scivimus ex eis per considerationes que provenerunt nobis apud condiametrationem. Provenit ergo nobis hora post quatuor horas a medietate diei Iomin decimioctavi, et provenit nobis locus stelle in 9 partibus et 40 minutis Sagittarii. In habitudine autem tertia consideravimus eam in anno vigesimo annorum Adriani etiam in mense Mesure apud Egyptios in die vigesimoquarto eius. Et numeravimus horam condiametrationis vere secundum illud exemplum et invenimus eam fuisse in ipsa medietate diei Iomin vigesimiquarti et numeravimus locum eius et invenimus ipsum in quartadecima parte et quartodecimo minuto Capricorni. Harum ergo duarum longitudinum longitudinis quidem inter habitudinem primam et inter habitudinem secundam summa est sex anni Egyptii et septuaginta dies et vigintidue hore et partium cursus stelle qui videtur est 68 partes et 27 minuta. Et longitudinis quidem inter habitudinem secundam et inter habitudinem tertiam summa est tres anni Egyptii et trigintaquinque dies et viginti hore et partium secundum illud exemplum est 34 partes et 34 minuta. Et quod provenit ex partibus cursus medii in longitudine etiam secundum crossitudinem numerationis temporis quidem longitudinis prime est 75 partes et 43 minuta et temporis longitudinis secunde est 37 partes et 52 minuta. Et quia iam explanate sunt iste due longitudines, tunc nos affirmabimus etiam quod intendimus per illam eadem intentionem secundum quod primum videtur res secundum quod sit et quod primum videtur secundum quod orbis egredientis centri sit unus secundum hunc modum.
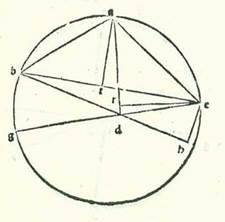Ponam igitur formam similem huic forme quam fecimus in hac intentione ex demonstratione ut sit res una. Et quia arcus BG orbis egredientis centri iam positus est subtendi orbis signorum 34 partibus et 34 minutis, erit angulus BDG etiam, scilicet angulus EDH, quia est apud centrum orbis signorum, secundum partes quibus quatuor anguli recti sunt 360 partes 34 partes et 34 minuta et secundum partes quibus duo anguli recti sunt 360 partes 69 partes et octo minuta. Oportet ergo propter illud ut sit arcus qui est super lineam EH 69 partes et octo minuta secundum partes quibus circulus qui describitur circa triangulum DEH ortogonium est 360 partes, et erit linea EH, una duarum etiam continentium angulum rectum, 68 partes et 5 minuta secundum partes quibus chorda DE est 120 partes. Et secundum hoc exemplum, quia arcus BG orbis egredientis centri est 37 partes et 52 minuta, erit angulus BED etiam, quia est apud lineam circumductam, 37 partes et 52 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed angulus DEH iam ostensum est quod est 110 partes et 52 minuta. Ergo angulus BEH totus erit 148 partes et 44 minuta, et erit angulus EBH reliquus secundum istas partes 31 pars et 18 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam EH 31 partes et 18 minuta secundum partes quibus circulus qui describitur circa triangulum BEH ortogonium est 360 partes, et erit linea EH 31 partes et 22 minuta secundum partes quibus chorda BE est 120 partes. Ergo secundum partes quibus linea EH est 60 partes et 5 minuta et linea ED est 120 partes erit linea BE 252 partes et 41 minutum. Et etiam quia arcus ABG totus subtenditur orbis signorum partibus aggregatis ambarum longitudinum, et sunt centum et tres partes et unum minutum, erit angulus ADG etiam, quia est apud centrum orbis signorum, centum et tres partes et minutum unum secundum partes quibus quatuor anguli recti sunt 360 partes. Et propter illud erit angulus qui sequitur eum, et est angulus ADE, secundum istas partes 76 partes et 59 minuta, et secundum partes quibus duo anguli recti sunt 360 erit 153 partes et 58 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam ER 153 partes et 58 minuta secundum partes quibus circulus qui describitur circa triangulum DER ortogonium est 360 partes, et erit linea ER 116 partes et 55 minuta secundum partes quibus chorda DE est 120 partes. Et secundum hoc exemplum, quia arcus ABG orbis egredientis centri summa est 113 partes et 35 minuta, erit angulus AEG etiam, quia est apud circumferentiam, 113 partes et 35 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes fuit angulus ADE 153 partes et 58 minuta. Ergo angulus EAR reliquus erit secundum istas partes 92 partes et 27 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam ER 92 partes et 27 minuta secundum partes quibus circulus qui describitur circa triangulum AER ortogonium est 360 partes, et erit linea ER 86 partes et 39 minuta secundum partes quibus chorda AE est 120 partes. Ergo secundum partes quibus linea ER secundum quod ostensum est est 116 partes et 55 minuta et linea ED est 120 partes erit linea EA 161 pars et 55 minuta. Et etiam quia arcus AB orbis egredientis centri est 75 partes et 43 minuta, erit angulus AEB, quia est apud circumferentiam, 75 partes et 43 minuta secundum partes quibus duo anguli recti sunt 360 partes. Oportet ergo propter illud ut sit arcus etiam qui est super lineam AT 75 partes et 43 minuta secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes, et erit arcus qui est super lineam ET partes relique ad complendum semicirculum, et sunt 104 partes et 17 minuta. Linea igitur AT, una duarum linearum que subtenduntur eis, erit 73 partes et 39 minuta secundum partes quibus chorda EA est 120 partes, et erit linea ET secundum istas partes 94 partes et 45 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea AE secundum quod ostensum est est 161 partes et 55 minuta et linea DE est 120 partes linea AT 99 partes et 23 minuta et linea ET secundum illud exemplum 127 partes et 51 minuta. Sed secundum istas partes fuit ostensum quod linea EB tota est 252 partes et 41 minuta. Ergo linea TB reliqua est 124 partes et 50 minuta secundum partes quibus linea AT est 99 partes et 23 minuta, et erit quadratum quod est ex linea TB 15583 partes et 22 minuta, et quadratum quod est ex linea AT secundum illud exemplum est 9877 partes et tria minuta. Et quando aggregabuntur, erit ex eo quadratum quod est ex linea AB, et est 25460 partes et 25 minuta. Erit ergo linea AB in longitudine 159 partes et 34 minuta secundum partes quibus fuit linea ED 120 partes et linea EA secundum illud exemplum 161 partes et 55 minuta. Sed secundum partes quibus diametrus orbis egredientis centri est 120 partes erit linea AB 73 partes et 39 minuta. Et illud est quia subtenditur arcui cuius summa est 75 partes et 43 minuta. Ergo secundum partes quibus linea AB est 73 partes et 39 minuta et diametrus orbis egredientis centri est 120 partes erit linea ED 55 partes et 23 minuta et linea EA 74 partes et 43 minuta. Oportet ergo propter illud ut sit arcus AE etiam orbis egredientis centri 77 partes et minutum unum et sit arcus EABG totus 190 partes et 36 minuta. Et manifestum est quod arcus GE reliquus est 169 partes et 24 minuta. Et propter illud erit linea GE 119 partes et 28 minuta fere secundum partes quibus diametrus orbis egredientis centri est 120 partes.
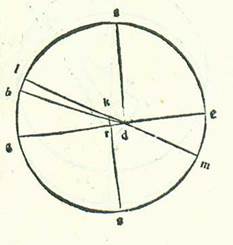Assumatur itaque centrum orbis egredientis centri intra portionem EABG, quia fuit maior semicirculo, et sit punctum K, et protrahatur super ipsum et super punctum D diameter orbis egredientis centri que transeat per ambo centra, sitque linea LKDM, et producatur a puncto K super lineam GE perpendicularis KR, et protrahatur usque ad punctum S. Et quia secundum partes quibus diametrus LM est 120 partes et 23 minuta linea EG tota, ut iam ostensum est, est 119 partes et 28 minuta et linea ED 55 partes et 23 minuta, tunc linea GD reliqua proveniet nobis secundum istas partes 64 partes et 5 minuta. Quare oportet, propterea quod superficies ortogonia que continetur ab his duabus lineis ED et DG est equalis superficiei ortogonie que continetur ab his duabus lineis LD et DM, ut sit nobis superficies ortogonia que continetur ab his duabus lineis LD et DM 3549 partes et 9 minuta. Sed ex superficie ortogonia que continetur ab his duabus lineis LD et DM cum quadrato quod est ex linea DK est quadratum quod est ex medietate diametri, scilicet linea LK, et illud est 3600 partes. Cum ergo nos minuerimus ex quadrato quod est ex medietate diametri quod est 3600 partes 3549 partes et 9 minuta, remanebit nobis quadratum quod est ex linea DK secundum istas partes 50 partes et 51 minuta. Proveniet igitur nobis DK linea in longitudine, et est linea que est inter duo centra septem partes et octo minuta fere secundum partes quibus diametrus orbis egredientis centri est 120. Et etiam quia medietas linee GE, scilicet linea ER, est 59 partes et 44 minuta secundum partes quibus diametrus LM est 120 partes et iam ostensum est quod linea ED secundum istas partes est 55 partes et 23 minuta, tunc linea DR reliqua proveniet nobis 4 partes et 21 minuta secundum partes quibus linea DK fuit septem partes et octo minuta. Oportet ergo propter illud ut secundum partes quibus subtendens chorda DK est 120 partes sit linea DR 73 partes et 11 minuta et arcus qui est super eam 75 partes et 10 minuta secundum partes quibus circulus qui describitur circa triangulum DKR ortogonium est 360 partes. Angulus igitur DKR secundum partes quibus duo anguli recti sunt 360 partes erit 75 partes et 10 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 37 partes et 35 minuta. Et quia ipse est apud centrum orbis egredientis centri, proveniet nobis arcus SM 37 partes et 35 minuta. Arcus autem GS, quia est medietas arcus GSE, est 84 partes et 42 minuta. Ergo arcus GL reliquus, qui est a longitudine longiore ad habitudinem tertiam, erit 57 partes et 43 minuta. Secundum istas vero partes positus fuit arcus GB 37 partes et 52 minuta. Ergo arcus LB reliquus, et est ille qui est a longitudine longiore qui est ad habitudinem secundam, erit 19 partes et 51 minuta. Et secundum hoc exemplum, quia arcus AB est positus 75 partes et 43 minuta, tunc arcus AL reliquus, et est ab habitudine prima ad longitudinem longiorem, erit 55 partes et 52 minuta.
Et quia centrum orbis revolutionis non revolvitur super hunc orbem egredientis centri, sed super orbem qui signatur super centrum medium inter duo puncta D et K et cum longitudine KL, numeravimus secundum quod provenit ex eo, sicut fecimus in reliquis stellis, superfluitates que sunt inter has longitudines et inter longitudines que videntur in orbe signorum, ad hoc ut sint iste proportiones fere si moverimus cursum orbis revolutionis ad orbem egredientis centri quem narravimus, per quem est diversitas que sequitur propter orbem signorum.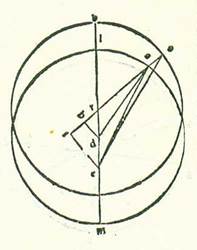 
Et illud est ut ponamus formam in tali qualis est hic intentio ex demonstratione in habitudine prima secundum quod stella sit posita in figura elongata a puncto L, et est longitudo longior. Et quia angulus BRS, et est angulus cursus equalis in longitudine, scilicet angulus DRH, secundum partes quibus quatuor anguli recti sunt 360 partes iam ostensum est quod est 55 partes et 52 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 111 partes et 44 minuta, erit arcus qui est super lineam DH 111 partes et 44 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH quod remanet ad complendum semicirculum, et est 68 partes et 16 minuta. Ergo linea DH, una duarum linearum que subtenduntur eis, erit 99 partes et 20 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes erit 67 partes et 20 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea DR, que est inter duo centra, est tres partes et 34 minuta et linea DA, et est ea que est a centro orbis egredientis centri, est 60 partes linea DH due partes et 57 minuta et linea RH secundum illud exemplum due partes. Et quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DA, est ex eo quadratum quod est ex linea AH, proveniet nobis linea AH secundum istas partes 59 partes et 56 minuta. Et secundum illud exemplum, quia linea RH est equalis linee TH et linea TE est dupla linee HD, erit linea AT tota 61 partes et 56 minuta secundum partes quibus linea ET est 5 partes et 54 minuta. Et propter illud erit chorda AE secundum istas partes 62 partes et 13 minuta. Oportet ergo propter illud ut sit secundum partes quibus chorda AE est 120 partes linea ET 11 partes et 21 minuta et arcus qui est super eam 10 partes et 51 minuta fere secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes. Angulus igitur EAT est 10 partes et 51 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et etiam quia secundum partes quibus linea ET est 5 partes et 54 minuta est linea RS, et est ea que est a centro orbis egredientis centri, 60 partes et linea RT quatuor partes et manifestum est quod linea TS tota est 64 partes et proveniet nobis chorda ES secundum istas partes 64 partes et 16 minuta, tunc secundum partes quibus chorda ES est 120 partes erit linea ET undecem partes et duo minuta, et erit arcus qui est super eam 10 partes et 33 minuta secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EST etiam 10 partes et 33 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes est ostensum quod angulus EAT est 10 partes et 51 minuta. Ergo angulus EAS reliquus, et est angulus superfluitatis quesite, secundum partes quibus duo anguli recti sunt 360 partes est decem et octo minuta et secundum partes quibus quatuor anguli recti sunt 360 partes est novem minuta. Sed hec stella fuit visa in habitudine prima super lineam AE, et eius locus fuit super partem unam et 13 minuta Libre. Manifestum est igitur quod si centrum orbis revolutionis non revolveretur super circulum AL, sed super circulum BS, esset huius circuli super punctum S, et videretur stella super lineam ES precedere locum suum super punctum A novem minutis, et esset eius locus super partem unam et quatuor minuta Libre. Et hec est forma illius.
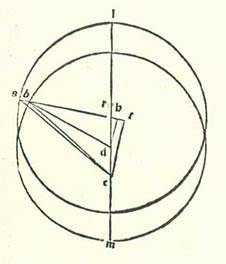Deinde ponam etiam formam habitudinis secunde in intentione huic simili ex declaratione quod stella sit posterior a longitudine longiore. Et quia arcus LS orbis egredientis centri iam ostensum est quod est 19 partes et 51 minuta, erit angulus LRS et angulus etiam qui est super caput eius, et est angulus DRH, secundum partes quibus quatuor anguli recti sunt 360 partes 19 partes et 51 minuta et secundum partes quibus duo anguli recti sunt 360 partes 39 partes et 42 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam DH 39 partes et 42 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH partes relique ad complendum semicirculum, et sunt 140 partes et 18 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, erit 40 partes et 45 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes erit 112 partes et 52 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea DR est tres partes et 34 minuta et linea RB, que est a centro orbis egredientis centri, est 60 partes linea RH pars una et 13 minuta et linea DH secundum illud exemplum tres partes et 21 minuta. Et quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DB, est ex eo quadratum quod est ex linea BH, erit linea BH secundum istas partes 59 partes et 59 minuta fere. Et secundum illud exemplum, quia linea RH est equalis linee BT et linea ET est dupla linee DH, proveniet nobis linea BT tota 63 partes et 20 minuta secundum partes quibus linea ET est due partes et 26 minuta. Quapropter erit chorda EB secundum istas partes 63 partes et 23 minuta. Ergo secundum partes quibus linea BE est 120 partes erit linea ET quatuor partes et 36 minuta, et erit arcus qui est super eam quatuor partes et 24 minuta secundum partes quibus circulus qui describitur circa triangulum BET ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EBT etiam quatuor partes et 24 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et similiter etiam, quia secundum partes quibus linea RS, que est a centro orbis egredientis centri, est 60 partes provenit linea RT sex partes et 42 minuta, erit nobis linea ST tota 66 partes et 42 minuta secundum partes quibus posita est linea TE due partes et 26 minuta. Et propter illud erit chorda ES secundum istas partes 66 partes et 45 minuta. Oportet ergo propter illud ut sit secundum partes quibus chorda ES est 120 partes linea ET quatuor partes et 23 minuta et arcus qui est super eam quatuor partes et 12 minuta secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Angulus ergo EST est etiam quatuor partes et 12 minuta secundum partes quibus duo anguli recti sunt 360 partes. Iam autem ostensum fuit quod angulus EBT secundum istas partes est 4 partes et 24 minuta. Ergo angulus BES reliquus erit secundum istas partes 12 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes sex minuta. Manifestum est igitur hic quod stella, quia in habitudine secunda, quando fuit visa super lineam EB, locus eius fuit super novem partes et 46 minuta Sagittarii, tunc si fuisset visa etiam super lineam ES, esset eius locus super novem partes et 46 minuta Sagittarii. Iam vero fuit ostensum quod eius locus fuit in habitudine prima secundum hoc exemplum super partem unam et quatuor minuta Libre. Manifestum est igitur quod longitudo que est inter habitudinem primam et inter habitudinem secundam proveniret si fuisset stella visa in orbe LS egredientis centri 68 partes et 42 minuta orbis signorum. Et hec est forma illius.
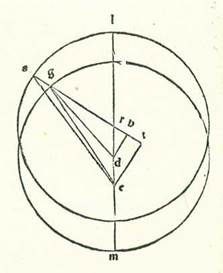Et similiter etiam ponam descriptionem habitudinis tertie secundum similitudinem forme que posita est in habitudine secunda. Et quia arcus LS iam ostensum est quod est 57 partes et 43 minuta, erit angulus LRS, scilicet angulus DRH, secundum partes quibus quatuor anguli recti sunt 360 partes 57 partes et 43 minuta et secundum partes quibus duo anguli recti sunt 360 partes 115 partes et 26 minuta. Oportet ergo propter illud ut sit arcus qui est super linea DH 115 partes et 26 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH partes relique ad complendum semicirculum, et sunt 64 partes et 34 minuta. Ergo linea DH, una duarum linearum que subtenduntur eis, est 101 partes et 27 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes est 64 partes et 6 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea DR est 3 partes et 34 minuta et linea RG, que est a centro orbis egredientis centri, 60 partes linea DH tres partes et minutum unum et linea RH secundum illud exemplum pars una et 54 minuta. Et etiam quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DG, est ex eo quadratum quod est ex linea HG, tunc linea HG provenit nobis secundum istas partes 59 partes et 56 minuta. Et secundum istud exemplum, quia linea RH est equalis linee HT et linea ET est dupla linee DH, proveniet nobis linea GT tota 61 partes et 50 minuta secundum partes quibus est linea ET sex partes et duo minuta. Quapropter erit chorda EG secundum istas partes 62 partes et octo minuta. Ergo secundum partes quibus chorda GE est 120 partes erit linea ET 11 partes et 39 minuta, et erit arcus qui est super eam 11 partes et 9 minuta fere secundum partes quibus circulus qui describitur circa triangulum GET ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus TGE etiam 11 partes et 9 minuta secundum partes quibus duo anguli recti sunt 360 partes. Et similiter quia secundum partes quibus linea RS, que est a centro orbis egredientis centri, est 60 partes linea RT provenit 3 partes et 48 minuta, tunc linea ST tota proveniet nobis 63 partes et 48 minuta secundum partes quibus fuit linea ET sex partes et duo minuta. Et propter illud erit chorda ES secundum istas partes 64 partes et 5 minuta. Ergo secundum partes quibus chorda ES est 120 partes erit linea ET 11 partes et 18 minuta. Erit ergo arcus qui est super eam 10 partes et 49 minuta secundum partes quibus circulus qui describitur circa triangulum ETS ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EST etiam 10 partes et 49 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes est ostensum quod angulus EGT est 11 partes et 9 minuta. Ergo angulus GES reliquus erit secundum istas partes 20 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes et 10 minuta. Quare oportet, propterea quod stella est in habitudine tertia, ut quando fuerit visa super lineam EG, sit eius locus super 14 partes et 14 minuta Capricorni. Et manifestum est quod si conveniret ut esset super lineam ES, esset eius locus super 14 partes et 24 minuta Capricorni, et esset etiam longitudo que videtur inter habitudinem secundam et habitudinem tertiam, que invenitur in orbe LS egredientis centri, 34 partes et 38 minuta. Postquam igitur contenti sumus eo quod he due longitudines significant in hac eadem intentione, inveniemus longitudinem in eo quod est inter centrum orbis signorum et inter centrum orbis egredientis centri qui comprehendit motum orbis revolutionis equalem, scilicet lineam equalem linee ER, sex partes et 50 minuta fere secundum partes quibus diametrus orbis egredientis centri est 120 partes, et inveniemus arcus huius orbis egredientis centri, arcum quidem qui est ab habitudine prima ad longitudinem longiorem 57 partes et 5 minuta et arcum qui est a longitudine longiore ad habitudinem secundam 18 partes et 38 minuta et arcum qui est a longitudine longiore ad habitudinem tertiam 56 partes et 30 minuta. Et he quantitates posite iam accepte fuerunt hic etiam secundum veritatem, propterea quod superfluitates arcuum orbis signorum proveniunt cum istis etiam similes illis que precesserunt secundum propinquitatem et quod longitudines stelle que videntur inveniuntur convenientes longitudinibus que reperiuntur per considerationes secundum quod declarabitur nobis per operationem.
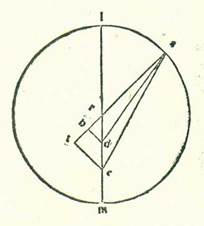Ponam itaque figuram habitudinis prime in orbe egredientis centri tantum, scilicet deferentem centrum orbis revolutionis. Et quia angulus ARL, quia supponitur orbis egredientis centri 57 partibus et 5 minutis, est secundum partes quibus quatuor anguli recti sunt 360 partes 57 partes et 5 minuta et secundum partes quibus duo anguli recti sunt 360 partes est ipse et angulus qui est super caput eius, scilicet angulus DRH, 114 partes et 10 minuta, erit arcus qui est super lineam DH 114 partes et 10 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH quod remanet ad complendum semicirculum, et est 65 partes et 50 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, est 100 partes et 44 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes est 65 partes et 13 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea DR, et est chorda que est inter duo centra, est tres partes et 25 minuta et linea DA, que est a centro orbis egredientis centri, est 60 partes linea DH due partes et 52 minuta et linea RH secundum illud exemplum pars una et 51 minuta. Et etiam quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea AD, est ex eo quadratum quod est ex linea AH, tunc linea AH etiam provenit nobis secundum istas partes 59 partes et 56 minuta. Et secundum illud exemplum, quia linea RH est equalis linee HT et linea ET est dupla linee DH, tunc linea AT tota proveniet nobis 61 partes et 47 minuta secundum partes quibus provenit linea ET 5 partes et 44 minuta. Et propter illud erit chorda EA 62 partes et 33 minuta. Ergo erit secundum partes quibus chorda AE est 120 partes linea ET undecem partes et quinque minuta, et erit arcus qui est super eam 10 partes et 36 minuta secundum partes quibus circulus qui describitur circa triangulum AET ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EAR 10 partes et 36 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes fuit positus angulus ARL 114 partes et 10 minuta. Ergo angulus AEL reliquus erit secundum istas partes 103 partes et 34 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes erit 51 partes et 47 minuta. Secundum istas ergo partes fuit stella in habitudine prima precedens longitudinem longiorem.
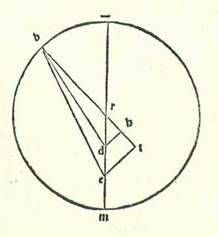Et ponam etiam in forma huic simili descriptionem habitudinis secunde. Et quia angulus BRL secundum partes quibus quatuor anguli recti sunt 360 partes iam ostensum est quod est 18 partes et 38 minuta et secundum partes quibus duo anguli recti sunt 360 partes est ipse et angulus qui est super caput eius, et est angulus DRH, 37 partes et 16 minuta, erit arcus qui est super lineam DH 37 partes et 16 minuta secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus qui est super lineam RH partes relique ad complendum semicirculum, et sunt 142 partes et 44 minuta. Linea igitur DH, una duarum linearum que subtenduntur eis, erit 38 partes et 20 minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes erit 113 partes et 43 minuta. Oportet ergo propter illud ut sit secundum partes quibus linea DR est tres partes et 25 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes linea DH pars una et quinque minuta et linea RH secundum illud exemplum tres partes et 14 minuta. Et quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DB, est ex eo quadratum quod est ex linea BH, provenit nobis linea BH secundum istas partes 59 partes et 59 minuta. Et secundum illud exemplum, quia linea RH est equalis linee HT et linea ET est dupla linee DH, proveniet nobis linea BT tota 63 partes et 13 minuta secundum partes quibus linea ET est due partes et 10 minuta. Et propter illud erit chorda EB secundum istas partes 63 partes et 15 minuta. Ergo secundum partes quibus chorda EB est 120 partes erit linea ET quatuor partes et septem minuta, et erit arcus qui est super eam tres partes et 56 minuta secundum partes quibus circulus qui describitur circa triangulum BET ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EBR 3 partes et 56 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes fuit positus angulus BRL 37 partes et 16 minuta. Ergo angulus BEL reliquus erit secundum istas partes 33 partes et 20 minuta, et erit secundum partes quibus quatuor anguli recti sunt 360 partes 16 partes et 40 minuta. Ergo in habitudine secunda fuit stella secundum visum posterior longitudine longiore 16 partibus et 40 minutis. Iam vero ostensum fuit quod ipsa in habitudine prima fuit precedens hanc longitudinem longiorem 51 partibus et 47 minutis. Aggregatur ergo longitudo que videtur inter habitudinem primam et habitudinem secundam ex partibus ex parte una 68 partes et 27 minuta. Et illud est conveniens ei quod productum est ex eo per considerationes.
Et ponam etiam descriptionem habitudinis tertie. Et quia angulus GRL secundum partes quibus quatuor anguli recti sunt 360 partes iam ostensum est quod est 56 partes et 30 minuta et secundum partes quibus duo anguli recti sunt 360 partes est ipse et angulus qui est super caput eius, et est angulus DRH, 113 partes et erit arcus etiam qui est super lineam DH 113 partes secundum partes quibus circulus qui describitur circa triangulum DRH ortogonium est 360 partes, et erit arcus etiam qui est super lineam RH reliquus ad complendum semicirculum 67 partes. Ergo linea DH, una duarum linearum que subtenduntur eis, erit centum partes et quatuor minuta secundum partes quibus chorda DR est 120 partes, et linea RH secundum istas partes erit 66 partes et 14 minuta. Oportet ergo propter illud ut secundum partes quibus linea DR est 3 partes et 35 minuta et linea DG, que est a centro orbis egredientis centri, est 60 partes sit linea DH due partes et 51 minuta et linea RH secundum illud exemplum pars una et 53 minuta. Et etiam quia cum quadratum quod est ex linea DH minuitur ex quadrato quod est ex linea DG, est ex eo quadratum quod est ex linea GH, proveniet nobis linea GH secundum istas partes 59 partes et 56 minuta. Et secundum istud exemplum, quia linea RH est equalis linee HT et linea ET est dupla linee DH, tunc linea GT tota proveniet nobis 61 partes et 49 minuta secundum partes quibus provenit linea ET 5 partes et 42 minuta. Et propter illud erit chorda EG secundum istas partes 62 partes et 5 minuta. Ergo secundum partes quibus chorda GE est 120 partes erit linea ET undecem partes et minutum unum, et erit arcus qui est super eam 10 partes et 32 minuta secundum partes quibus circulus qui describitur circa triangulum GET ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EGT etiam 10 partes et 32 minuta secundum partes quibus duo anguli recti sunt 360 partes. Sed secundum istas partes positus fuit angulus GRL 113 partes. Ergo angulus GEL reliquus erit secundum istas partes 102 partes et 28 minuta, et secundum partes quibus quatuor anguli recti sunt 360 partes erit 51 partes et 14 minuta. Hec ergo est summa partium quibus stella in habitudine tertia fuit visa diversa a longitudine longiore. Iam autem fuit ostensum quod in habitudine secunda fuit diversa ab hac longitudine longiore 16 partibus et 40 minutis. Oportet ergo propter illud ut sit quod provenit ex longitudine que videtur inter habitudinem secundam et habitudinem tertiam ipsa superfluitas inter duas longitudines, et illud est 34 partes et 34 minuta. Et illud est conveniens etiam ei quod provenit ex eis per considerationes.
Et manifestum est ex eo quod quia huius stelle locus fuit in habitudine tertia super 14 partes et 14 minuta Capricorni et fuit diversa a longitudine longiore secundum quod ostensum est 51 partibus et 14 minutis, tunc longitudinis longioris in orbe centri egredientis fuit locus super 23 partes Scorpionis et longitudinis propinquioris super partem oppositam huic parti, et est vigesimatertia pars Tauri.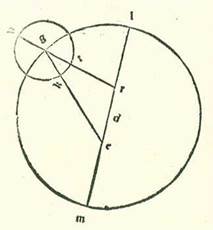 
Et similiter etiam, si descripserimus circa centrum G orbem revolutionis, super quem sint HTK, et posuerimus in illo cursum medium in longitudine orbis revolutionis a longitudine longiore in orbe egredientis centri partes quarum summa demonstrata est ex eo, et sunt 56 partes et 30 minuta, proveniet arcus TK orbis revolutionis 5 partes et 16 minuta, propterea quod angulus EGR iam ostensum est quod est 10 partes et 32 minuta secundum partes quibus duo anguli recti sunt 360 partes. Oportet ergo ut arcus HT reliquus, et est ille qui est a longitudine longiore in orbe revolutionis ad stellam, proveniat 174 partes et 44 minuta. Ergo in hora habitudinis tertie, scilicet in anno vigesimo annorum Adriani in mense Mesure apud Egyptios in die vigesimoquarto eius in medietate diei fuit stelle Saturni, cum aspexerunt in re eius secundum cursum medium, elongatio in longitudine a longitudine longiore in orbe egredientis centri 56 partes et 30 minuta, scilicet quia eius locus fuit super 19 partes et 30 minuta Capricorni, et fuit eius longitudo in diversitate a longitudine longiore in orbe revolutionis 174 partes et 44 minuta. Et iste sunt res quarum intendimus inventionem.
⟨XI.6⟩ Capitulum sextum: In declaratione quantitatis orbis revolutionis stelle Saturni
Deinde post illud accepimus ad declarandam quantitatem orbis revolutionis stelle Saturni considerationem quam consideravimus in anno secundo annorum Antonii in mense Mathir apud Egyptios in die sexto eius in nocte quam sequitur dies septimus ante medietatem noctis quatuor horis equalibus. Et illud est quia fuit medians celum in instrumento considerationis pars postrema Arietis, quia fuit pars loci Solis super 28 partes et 41 minuta Sagittarii. Et fuit tunc stelle Saturni, propterea quod consideravimus eam cum Aldebaran, visus locus super novem partes et partem quintamdecimam partis Aquarii, et fuit diversa a centro Lune in medietate partis fere, et illud quia fuit hec quantitas longitudinis eius a cornu eius septentrionali. Locus autem Lune fuit in illa hora per cursum suum medium super octo partes et 55 minuta Aquarii, et fuit eius locus in diversitate super 174 partes et 15 minuta a longitudine longiore in orbe revolutionis. Et propter illud oportuit ut cursus eius veri fuisset locus super novem partes et 40 minuta Aquarii et cursus eius qui visus est in Alexandria super octo partes et 34 minuta eius. Ex hoc itaque modo etiam oportuit in stella Saturni, quia fuit diversa a centro Lune medietate partis fere, ut fuisset eius locus super novem partes et partem quintamdecimam partis Aquarii et ut fuisset eius longitudo a longitudine longiore in orbe suo egredientis centri, quia non evenit ei ex motu locali in hac quantitate partis temporis de quo sit curandum 76 partes et 4 minuta. Quia igitur tempus quod fuit ab habitudine tertia usque ad habitudinem huius considerationis est duo anni Egyptii et centum et sexagintaseptem dies et octo hore et fuit etiam stella Saturni mota secundum crossitudinem numerationis in hac quantitate temporis in longitudine quidem parte una et octo minutis et in diversitate 134 partibus et 24 minutis, tunc cum nos addiderimus super has duas radices quas narravimus in habitudine tertia, proveniet nobis in hora huius considerationis cuius premisimus nominationem radix stelle Saturni in longitudine quidem super 86 partes et 33 minuta a longitudine longiore in orbe egredientis centri et in diversitate super 309 partes et 8 minuta a longitudine longiore in orbe revolutionis.
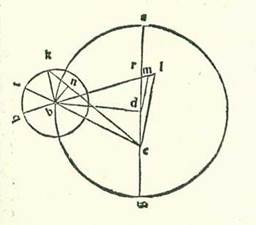Postquam igitur iam explanate sunt he due intentiones, ponam etiam descriptionem que posita est opposito huius intentionis cursu ad hoc ut ponatur orbis revolutionis in ea sequens longitudinem longiorem in orbe egredientis centri et ponatur stella in eadem antecedens longitudinem longiorem in orbe revolutionis secundum quod convenit ei quod positum est de duobus cursibus. Et quia angulus ARB, scilicet angulus DRM, secundum partes quibus quatuor anguli recti sunt 360 partes iam positus est 86 partes et 33 minuta et secundum partes quibus duo anguli recti sunt 360 partes est 173 partes et sex minuta, erit etiam arcus qui est super lineam DM 173 partes et sex minuta secundum partes quibus circulus qui describitur circa triangulum DRM ortogonium est 360 partes, et erit arcus qui est super lineam RM partes relique ad complendum semicirculum, et sunt sex partes et 54 minuta. Linea igitur DM, una duarum linearum que subtenduntur eis, erit 119 partes et 47 minuta secundum partes quibus chorda DR est 120 partes, et erit linea RM secundum istas partes 7 partes et 13 minuta. Oportet ergo propter illud ut secundum partes quibus linea DR, et est ea que est inter duo centra, est tres partes et 25 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes sit linea DM tres partes et 25 minuta fere et linea RM secundum illud exemplum duodecem minuta. Et quia cum quadratum quod est ex linea DM minuitur ex quadrato quod est ex linea DB, est ex eo quadratum quod est ex linea BM, proveniet nobis linea BM etiam secundum istas partes 59 partes et 54 minuta. Et secundum illud exemplum, quia linea RM est equalis linee ML et linea EL est dupla linee DM, proveniet nobis linea BL tota 60 partes et sex minuta secundum partes quibus colligitur ut linea EL sit 6 partes et 50 minuta. Et propter illud erit chorda EB secundum istas partes 60 partes et 29 minuta. Ergo secundum partes quibus chorda EB est 120 partes erit linea EL 13 partes et 33 minuta, et erit arcus qui est super eam 12 partes et 58 minuta secundum partes quibus circulus qui describitur circa triangulum BEL ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus EBL etiam 12 partes et 58 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum istas vero partes positus fuit angulus ARB 173 partes et sex minuta. Ergo angulus AEB reliquus secundum istas partes erit 160 partes et 8 minuta. Sed angulus AEK, quia comprehendit longitudinem que videtur inter stellam et inter longitudinem longiorem, ergo ipse est positus secundum partes quibus quatuor anguli recti sunt 360 partes 76 partes et quatuor minuta, et secundum partes quibus duo anguli recti sunt 360 partes est 152 partes et octo minuta. Ergo angulus KEB reliquus proveniet nobis secundum istas partes octo partes. Oportet ergo propter illud ut sit arcus etiam qui est super lineam BN octo partes secundum partes quibus circulus qui describitur circa triangulum BEN ortogonium est 360 partes, et erit linea BN octo partes et 22 minuta secundum partes quibus chorda EB est 120 partes. Ergo secundum partes quibus linea EB est 60 partes et 29 minuta et linea que est a centro orbis egredientis centri est 60 partes erit linea BN 4 partes et 13 minuta. Et etiam quia longitudo stelle a puncto H, et est longitudo longior in orbe revolutionis, est 309 partes et 8 minuta, erit etiam arcus HTK reliquus 50 partes et 52 minuta. Ergo angulus HBK est secundum partes quibus quatuor anguli recti sunt 360 partes 50 partes et 52 minuta et secundum partes quibus duo anguli recti sunt 360 partes 101 partes et 44 minuta. Sed secundum istas partes fuit angulus EBR, scilicet angulus HBT, 12 partes et 58 minuta. Ergo angulus TBK reliquus erit 88 partes et 46 minuta secundum partes quibus ostensum est quod angulus KEB est octo partes. Erit ergo angulus EKB reliquus secundum istas partes 80 partes et 46 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam BN 80 partes et 46 minuta secundum partes quibus circulus qui describitur circa triangulum BKN ortogonium est 360 partes, et erit linea BN 77 partes et 45 minuta secundum partes quibus chorda BK est 120 partes. Ergo secundum partes quibus ostensum est quod linea BN est 4 partes et 13 minuta et linea que est a centro orbis ergedientis centri est 60 partes, et erit linea BK, que est a centro orbis revolutionis, proveniet erit ... proveniet: Two rivalling verbs. Paris, BnF, lat. 14738 (178v, line 14) contains only the former. sex partes et medietas partis fere. Iam igitur provenit nobis quidem quod longitudinis longioris stelle Saturni fuit locus in principio regni Antonii super 23 partes Scorpionis et quod secundum partes quibus linea que est a centro orbis deferentis orbem revolutionis est 60 partes est linea que est in eo quod est inter duo centra, scilicet in eo quod est inter centrum orbis signorum et inter centrum orbis egredientis centri qui facit motum equalem, provenit est ... provenit: Two rivalling verbs. Paris, BnF, lat. 14738 (178v, lines 17-18) contains only the latter. sex partes et 58 minuta et quod linea que est a centro orbis revolutionis secundum istas partes est sex partes et 30 minuta. Et iste sunt res quarum intendimus inventionem.
⟨XI.7⟩ Capitulum septimum: In verificatione motuum stelle Saturni revolubilium
Et quia iam remansit nobis ut declaremus qualiter verificantur motus eius revolubiles, accepimus propter illud etiam unam considerationum antiquarum que firmata fuit secundum verificationem et in qua non est dubitatio in qua dixerunt etiam quod in anno 802 annorum Chaldeorum in uno mensium eorum nominato Chescendesin One could equally read Chescemdesin. Paris, BnF, lat. 14738 (178v, line 15 from the bottom) reads Chestende{f/s}in. The Greek text reads ‘Xanthikos’ (see Toomer, loc. cit., p. 541, line 5). in die quinto eius in prima parte noctis fuit stella Saturni sub humero meridiano Virginis duobus digitis. Et hec hora fuit in anno quingentesimo et decimonono a tempore Nabuchodonosor in mense Tobi in die 14 eius apud Egyptios in vespere. Et in hac hora invenimus locum Solis per cursum suum medium super sex partes et decem minuta Piscium. Verum stelle fixe que est in humero meridiano Virginis fuit locus in hora quidem nostre considerationis super tredecem partes et sextam partis Virginis. Et in hora quidem huius considerationis quam narravimus, propterea quod pertinet trecentis et sexagintasex annis qui sunt in eo quod est inter duas considerationes ex motu stellarum fixarum tres partes et due tertie partis fere, tunc manifestum est quod eius locus fuit super novem partes et medietatem aut tertiam partis Virginis. Et ille fuit locus Saturni etiam quia declivior fuit ad meridiem illa stella fixa duobus digitis. Et similiter etiam, quia eius longitudo longior iam ostensum est quod fuit in tempore nostro super 23 partes Scorpionis, tunc oportet quod fuerit eius locus in illa consideratione dicta super decem et novem partes et tertiam partis Scorpionis. Ex eo igitur colligitur quod in illa hora dicta fuit stelle per visum longitudo a longitudine longiore in orbe signorum 290 partes et 10 minuta et fuit cursus medii Solis longitudo ab illa longitudine longiore 106 partes et 50 minuta.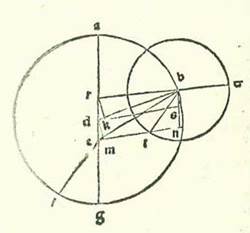 
Et postquam he due intentiones explanate sunt, ponatur etiam descriptio que est in tali qualis est hec intentio in declaratione, ita ut ponatur orbis revolutionis in ea antecedens longitudinem longiorem et ponatur medius cursus Solis precedens longitudinem propinquiorem, quia linea que est a centro orbis revolutionis ad stellam equidistat linee que est a centro orbis signorum ad Solem. Et quia stella Saturni visa est precedere longitudinem longiorem secundum partes reliquas ad complendum circulum unum, et sunt 69 partes et 50 minuta, erit angulus AET, quia est apud centrum orbis signorum, secundum partes quibus quatuor anguli recti sunt 360 partes 69 partes et 50 minuta, et secundum partes quibus duo anguli recti sunt 360 partes erit 139 partes et 40 minuta. Iam autem positus fuit angulus AEL, et est angulus longitudinis Solis a longitudine longiore, secundum partes quibus quatuor anguli recti sunt 360 partes 106 partes et 50 minuta et secundum partes quibus duo anguli recti sunt 360 partes 213 partes et 40 minuta. Ergo angulus TEL totus, scilicet angulus BTE, quia sunt due linee BT et EL equidistantes, erit 353 partes et 20 minuta secundum partes quibus duo anguli recti sunt 360 partes, et angulus BTN reliquus secundum istas partes erit 6 partes et 40 minuta. Oportet ergo propter illud ut sit etiam arcus qui est super lineam BN 6 partes et 40 minuta secundum partes quibus circulus qui describitur circa triangulum BTN ortogonium est 360 partes, et erit linea BN sex partes et 58 minuta secundum partes quibus chorda BT est 120 partes. Ergo secundum partes quibus linea BT, que est a centro orbis revolutionis, est 6 partes et 30 minuta erit linea BN vigintitria minuta. Et secundum illud exemplum, quia angulus AET est 139 partes et 40 minuta secundum partes quibus duo anguli recti sunt 360 partes et angulus EDM secundum istas partes est 40 partes et 20 minuta, erit etiam arcus qui est super lineam DM 139 partes et 40 minuta secundum partes quibus circulus qui describitur circa triangulum DEM ortogonium est 360 partes, et erit linea DM ipsa etiam 112 partes et 39 minuta secundum partes quibus chorda ED est 120 partes. Ergo secundum partes quibus linea ED, que est in eo quod est inter duo centra, est 3 partes et 25 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea DM, scilicet linea NS, 3 partes et 12 minuta et erit linea BSN tota 3 partes et 35 minuta secundum partes quibus chorda DB est 60 partes. Ergo secundum partes quibus linea DB est 120 partes erit linea BS septem partes et 10 minuta, et erit arcus qui est super eam sex partes et 52 minuta secundum partes quibus circulus qui describitur circa triangulum BDS ortogonium est 360 partes. Oportet ergo propter illud ut sit angulus BDS sex partes et 52 minuta secundum partes quibus duo anguli recti sunt 360, et erit angulus DBS reliquus secundum istas partes 173 partes et octo minuta, et erit angulus DBE totus secundum illud exemplum 213 partes et 28 minuta, et erit angulus BDA reliquus secundum istas partes 146 partes et 32 minuta. Oportet ergo propter illud ut sit arcus qui est super lineam RK 146 partes et 32 minuta secundum partes quibus circulus qui describitur circa triangulum DRK ortogonium est 360 partes, et erit arcus qui est super lineam DK partes relique ad complendum semicirculum, et sunt 33 partes et 28 minuta. Linea igitur RK, una duarum linearum que subtenduntur eis, erit 114 partes et 55 minuta secundum partes quibus chorda DR est 120 partes, et erit linea DK secundum istas partes 34 partes et 33 minuta. Ergo secundum partes quibus linea DR, que est inter duo centra, est 3 partes et 25 minuta et linea DB, que est a centro orbis egredientis centri, est 60 partes erit linea DK secundum illud exemplum 59 partes et unum minutum secundum partes quibus fuit linea RK 3 partes et 17 minuta. Et propter illud erit chorda RB secundum istas partes 59 partes et 6 minuta. Oportet ergo propter illud ut secundum partes quibus chorda RB est 120 partes sit linea RK sex partes et 40 minuta et arcus qui est super eam sex partes et 22 minuta secundum partes quibus circulus qui describitur circa triangulum BRK ortogonium est 360. Ergo angulus RBK erit 6 partes et 22 minuta secundum partes quibus duo anguli recti sunt 360 partes. Secundum vero istas partes fuit angulus ADB 146 partes et 32 minuta. Ergo angulus ARB totus, et est ille qui comprehendit cursum equalem in longitudine, provenit nobis secundum istas partes 152 partes et 54 minuta et secundum partes quibus quatuor anguli recti sunt 360 partes 76 partes et 27 minuta. Fuit ergo longitudo stelle Saturni in hora illius considerationis dicte a longitudine longiore per cursum suum medium in longitudine 283 partes et 33 minuta, scilicet quia locus eius fuit super duas partes et 53 minuta Virginis. Et quia cursus Solis medius iam fuit positus 106 partes et 50 minuta, tunc si nos addiderimus super illud partes circuli unius, et sunt 360 partes, et minuerimus ex eo quod aggregatur, et est 466 partes et 50 minuta, partes longitudinis, et sunt 283 partes et 33 minuta, proveniet nobis eius longitudo in illa hora eadem in diversitate etiam a longitudine longiore in orbe revolutionis 183 partes et 17 minuta. Et quia in hora huius considerationis quam intendimus, et fuit in anno quingentesimo et decimonono perfecto a tempore Nabuchodonosor in mense Tobi in die quartodecimo eius in prima hora noctis, demonstratum est quod eius longitudo fuit a longitudine longiore in orbe revolutionis 183 partes et 17 minuta in hora habitudinis tertie, et fuit in anno octingentesimo et octuagesimotertio a tempore Nabuchodonosor in mense Mesure in die vigesimoquarto eius in medietate diei, et fuit eius longitudo ab ea 174 partes et 44 minuta, tunc manifestum est quod in tempore quod est inter duas considerationes, et comprehendit trecentos et sexagintaquatuor annos et ducentos et decem et novem dies et medietatem et quartam diei, mota fuit stella Saturni post revolutiones integras in diversitate 351 partibus et 27 minutis. Et fortasse erit hec summa etiam que aggregatur ei ex partibus superfluitatis in tabulis quas premisimus et narravimus cursus motuum mediorum, quoniam fuit etiam cursus medius in die Ionum One could equally read Ionun. Paris, BnF, lat. 14738 (179v, line 14) reads Ioini(m/n) or Iomi(m/n) or Ionu(m/n). This name does not appear in the Greek text (see Toomer, loc. cit., p. 543, line 9 from the bottom). per has easdem rectificatus, quia divisimus partes que aggregantur ex numero revolutionum et ex superfluitate per numerum dierum qui aggregantur in eo quod est inter duas considerationes.
⟨XI.8⟩ Capitulum octavum: In descriptione radicis motuum stelle Saturni revolubilium
Et quia tempus quod est a primo annorum Nabuchodonosor a die prima mensis Thuth a medietate diei ad horam considerationis antique dicte est quingenti et decem et octo anni Egyptii et centum et trigintatres dies et quarta diei et in hoc tempore superfluunt ex partibus in longitudine 216 partes et 10 minuta et in diversitate 147 partes et 15 minuta, tunc si nos minuerimus has duas superfluitates ex duabus radicibus dictis in consideratione, proveniet etiam nobis in illa hora nota in comprehensionibus sive in radicibus radix stelle Saturni per motum suum medium in longitudine super 26 partes et 43 minuta Capricorni et in diversitate super 33 partes et 5 minuta a longitudine longiore in orbe revolutionis eius. Et propter illud idem erit longitudo longior in orbe egredientis centri in 14 partibus et 10 minutis Scorpionis. Et iste sunt res quarum intendimus inventionem.
⟨XI.9⟩ Capitulum nonum: Qualiter proveniant cursus veri propter motus revolubiles secundum semitas linearum
Et secundum istas res easdem declaratur nobis quod cum convertentur res et fuerint duo arcus duarum revolutionum, scilicet arcus qui est orbis egredientis centri quem comprehendit motus equalis et arcus qui est orbis revolutionis dati, tunc iam preparata erit protractio cursuum stellarum secundum visum facili studio per semitam linearum.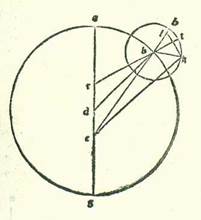 
Et illud quia si nos descripserimus formam superficialem in qua sint orbis egredientis centri et orbis revolutionis et produxerimus in ea duas lineas RBT et EBH, tunc quando fuerit cursus medius in longitudine datus, scilicet angulus ARB, erit angulus AEB datus, et erit angulus EBR, scilicet angulus HBT, datus in duabus radicibus simul secundum quas operamur propter res quarum premisimus narrationem et declarationem. Et propter illud etiam erit proportio linee BE ad lineam que est a centro orbis revolutionis data. Et cum posita fuerit stella verbi gratia super punctum K orbis revolutionis et coniuncte fuerint linee EK et BK et fuerit arcus TK datus, producemus super lineam EBH a stella K perpendicularem KL, producemus a puncto quod est super stellam, et est punctum K, perpendicularem super lineam EBH, sicut produximus hic perpendicularem KL. Ergo angulus HBK totus erit datus. Et propter illud erit proportio linee KL ad lineam LB et ad lineam BK et ad lineam EB data. Et illud est manifestum. Et sequitur ex eo ut sit proportio linee EL totius ad lineam LK data. Oportet ergo propter illud, cum fuerit angulus LEK datus, ut proveniat nobis angulus AEK totus etiam datus. Et ipse comprehendit longitudinem que videtur a longitudine longiore stelle.
⟨XI.10⟩ Capitulum decimum: In modo faciendi tabulas diversitatis stellarum
Ut autem non sit nobis necesse in hora omni numerare cursus qui videntur per semitas linearum mensurabilium, quamvis hoc modo tantum verificetur quesitum ex eo (sed secundum ipsum operari est difficile et prolixe acceptionis cum necesse fuerit agere illud quod est ex eo numeratum et preparatum ex eo cuius cursus est mensurabilis), studuimus facere tabulas cuiusque quinque stellarum erraticarum quam facilioris acceptionis potuimus et propinquioris, preter hoc perscrutationis vehementis et subtilis, comprehendentes diversitates earum particulares equatas, ut cum positi fuerint nobis motus earum revolubiles a longitudine longiore, scilicet unius et unius earum, possimus numerare ex eo facilius cursus earum qui videntur in omni hora. Iam vero firmavimus unamquamque harum tabularum in quadragintaquinque areis querendo pulcritudinem mensurationis et in tabulis octo. Due itaque prime harum tabularum comprehendunt numeros cursuum mediorum in longitudine, sicut factum est in Sole et in Luna. Sed prima earum ordinata est 180 partibus, quarum principium est ab altitudine circuli ad inferiora eius descendendo, et secunda earum est ordinata 180 partibus reliquis medietatis circuli ab inferiori ascendendo, ita ut numerus 180 sit positus in duabus tabulis simul in area postrema. Et posuimus superfluitatem inter eas in quindecem quidem areis que sunt a superiori earum senas partes et senas partes et in triginta areis reliquis que sunt sub eis ternas partes et ternas partes, propterea quod augmenta divisionum diversitatum eius quod sequitur longitudinem longiorem parum diversificantur ab invicem. Eius vero quod sequitur longitudinem propinquiorem, alteratio earum augetur velociter. Tabularum octo duarum que sequuntur has duas tertia earum comprehendit augmenta et diminutiones que sunt super numeros qui sunt in areis cuiusque stellarum medii cursus in longitudine propter orbem egredientis centri maioris egressionis a centro. Eius tamen acceptio est secundum rem simplicem et sicut si centrum orbis revolutionis moveretur super orbem ipsum egredientis centri. Et tabula quarta est ea que comprehendit superfluitatem que aggregatur ex additionibus et diminutionibus, propterea quod centrum orbis revolutionis non super hunc orbem cuius precessit narratio revolvitur, sed super orbem alium. Modus autem quo invenitur unaquaque harum duarum rerum simul et singulariter secundum viam linearum iam leviter scitur per figuras plures quas premisimus et posuimus in loco alio ab isto. Et quia intendimus firmare has duas intentiones in libro, tunc melius igitur nobis est ut sciamus hanc equationem diversitatis comparate ad orbem signorum visibiliter. Et ideo posuimus eam in duabus tabulis. Sed tamen cum necesse esset per ipsam operari et agere, contenti essemus tabula una, et est ea que comprehendit augmentum et diminutionem inventam in his duabus tabulis. Trium autem tabularum que sequuntur has duas queque comprehendit augmenta et diminutiones que sunt propter orbem revolutionis. Et iste etiam sunt accepte secundum rem simplicem et secundum quod in longitudine longiore et longitudine propinquiore in unaquaque earum non operamur nisi secundum duas longitudines a visibus nostris et secundum quod modus illius in declaratione eius etiam iam facilius scitur per figuras quas nos prius posuimus. Et tabula media harum trium tabularum, et est tabula sexta a prima tabula, comprehendit augmenta et diminutiones que aggregantur secundum longitudines medias. Quinta vero comprehendit summam superfluitatis que est in divisionibus similibus illis eisdem inter augmenta et diminutiones in maiori longitudine et inter ea in longitudine media. Tabula vero septima comprehendit summam superfluitatis que est inter augmenta et diminutiones in minori longitudine et inter ea in longitudine media. Nos enim iam demonstravimus quod secundum partes quibus linea que est a centro orbis revolutionis stelle Saturni quidem (est namque melius nunc ut incipiamus a superiori) est sex partes et 30 minuta, et stelle Iovis 11 partes et 30 minuta, et stelle Martis 39 partes et 30 minuta, et stelle Veneris 43 partes et 10 minuta, et stelle Mercurii 22 partes et 30 minuta est longitudo omnium earum media 60 partes, scilicet longitudo que reperitur per comparationem ad lineam egredientem a centro orbis egredientis centri deferentem orbem revolutionis, et quod maior longitudo earum secundum centrum orbis signorum in stella quidem Saturni est 63 partes et 25 minuta, et in stella Iovis est 62 partes et 45 minuta, et in stella Martis 66 partes, et in stella Veneris 61 partes et 15 minuta, et in stella Mercurii 69 partes, et quod minor longitudo earum secundum illud exemplum in stella Saturni est 56 partes et 35 minuta, et in stella Iovis 57 partes et 15 minuta, et in stella Martis 54 partes, et in stella Veneris 58 partes et 45 minuta, et in stella Mercurii 55 partes et 34 minuta. Tabulam autem sequentem eas, et est tabula octava, ordinavimus quoniam ex ea sumuntur partes que pertinent superfluitatibus quas narravimus cum non fuerunt orbes revolutionis stellarum in antiqua longitudine media a maiore aut minore, sed contingerit ut sint in cursibus qui sunt in eo quod est inter eas. Quod autem numeravimus ex hac verificatione et firmavimus in tabulis non firmavimus ex eo nisi quod est maius tantum ex additionibus et diminutionibus in unaquaque longitudinum que sunt in eo quod est inter ea quod provenit per lineas rectas que producuntur a visibus nostris in eo quod est inter orbem revolutionis. Non enim inter illud quod pertinet istis superfluitatibus secundum divisiones particulares orbis revolutionis et inter id quod pertinet eis in plurimo quod est ex additionibus et diminutionibus est diversitas que habeat quantitatem de qua sit curandum.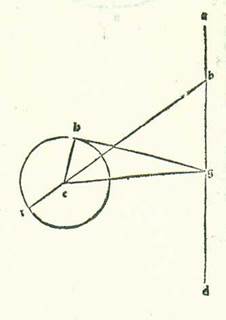 
Et ut augeatur in eo quod narravimus manifestatio et sciatur capitulum ipsum in inventione harum portionum, ponam lineam transeuntem per centrum orbis signorum et per centrum orbis qui comprehendit motum orbis revolutionis equalem, sitque linea ABGD, et ponam ut centrum orbis signorum sit punctum G et centrum motus equalis orbis revolutionis punctum B, et protraham lineam BE, et signabo circa punctum E orbem revolutionis, super quem sint R, H, et producam a puncto G lineam GH contingentem ipsum, et protraham lineam GE et perpendicularem EH, et ponam secundum viam exempli in unaquaque quinque stellarum ut centri orbis revolutionis longitudo secundum equalitatem a longitudine longiore in orbe egredientis centri sit 30 partes. Dico ergo (ut non reiteremus probationem et prolongetur eius relatione numeratio et propterea quod iam fuit ostensum per figuras plures in eo quod precessit in radice secundum quam agitur in stella Mercurii et in radice secundum quam agitur in reliquis stellis) quod angulus ABE, cum fuerit datus, erit proportio linee GE ad lineam que est a centro orbis revolutionis, scilicet linea EH data. Et hec proportio proveniet secundum numerationem in unaquaque stellarum quinque cum positus fuerit angulus ABE triginta partes secundum partes quibus quatuor anguli recti sunt 360 partes in stella quidem Saturni proportio sexagintatrium partium et duorum minutorum ad sex partes et triginta minuta, et in stella quidem Iovis proportio sexagintaduarum partium et vigintisex minutorum ad undecem partes et triginta minuta, et in stella quidem Martis proportio sexagintaquinque partium et vigintiquatuor minutorum ad trigintanovem partes et triginta minuta, et in stella Veneris proportio 61 partium et sex minutorum ad quadragintatres partes et decem minuta, et in stella Mercurii proportio sexagintasex partium et trigintaquinque minutorum ad vigintiduas partes et triginta minuta. Angulus EGH, et est ille qui comprehendit tunc maius quod est ex augmento et diminutione propter orbem revolutionis, proveniet nobis secundum partes quibus quatuor anguli recti sunt 360 partes in stella quidem Saturni quinque partes et 55 minuta et medietas minuti, et in stella Iovis decem partes et 36 minuta et medietas minuti, et in stella Martis 37 partes et 9 minuta, et in stella Veneris 44 partes et 56 minuta et medietas minuti, et in stella Mercurii 19 partes et 45 minuta. Illud autem quod ex maiori quod est ex additionibus et diminutionibus provenit secundum proportiones quas posuimus ante in longitudinibus mediis secundum ordinem quo cucurrimus in stellis ut sit preparatum est sex partes et 13 minuta et 11 partes et tria minuta et 41 partes et 10 minuta et 46 partes et 22 partes et duo minuta, et in maioribus que sunt ex longitudinibus 5 partes et 53 minuta et 10 partes et 34 minuta et 36 partes et 45 minuta et 44 partes et 48 minuta et 19 partes et duo minuta, et in minoribus que sunt ex longitudinibus sex partes et 36 minuta et 11 partes et 35 minuta et 47 partes et unum minutum et 47 partes et 17 minuta et 23 partes et 43 minuta. Est ergo diversitas inter additiones et diminutiones in longitudinibus mediis quia Probably corrupt for et, which would correspond to the Greek text (see Toomer, loc. cit., p. 548, line 5). Paris, BnF, lat. 14738 (181r, line 8) offers an et ligature, which can easily be misread for quia. inter eas in longitudinibus maioribus 20 partes et 29 minuta et 4 partes et 25 minuta et pars una et 12 minuta et tres partes, et est diversitas inter eas in longitudinibus mediis et inter eas in longitudinibus minoribus 23 partes et 32 minuta et 5 partes et 51 minuta et pars una et 17 minuta et pars una et 51 minuta. Et quia additionum et diminutionum que sunt longitudinum quesitarum minores sunt in longitudinibus mediis et diversitas inter eas et inter eas est decem et septem minuta et medietas et vigintisex minuta et medietas et quatuor partes et minutum unum et pars una et tria minuta et medietas et due partes et decem et septem minuta, et hec sunt ex summis superfluitatis totius quam narravimus inter longitudines medias et inter longitudines maiores in stella quidem Saturni 52 minuta et 30 secunda, et in stella Iovis 54 minuta et 50 secunda, et in stella Martis 54 minuta et 34 secunda, et in stella Veneris 52 minuta et 55 secunda, et in stella Mercurii 45 minuta et 40 secunda, et simile huic est inter longitudines medias et minores ex superfluitate, tunc nos firmavimus hec minuta in tabula octava in unaquaque tabula opposita aree in qua est numerus triginta partium revolutionis in longitudine. Sed in quibus longitudinibus sunt additiones et diminutiones plures additionibus et diminutionibus in longitudinibus mediis, addidimus etiam secundum illud exemplum superfluitatem que est inter eas, scilicet partes ex 60, sed nos non fecimus illud nisi quia accepimus summas superfluitatis inter additiones et diminutiones in eis et inter additiones et diminutiones in longitudinibus minoribus, non in longitudinibus maioribus, sicut fecimus ante. Et secundum hunc modum in reliquis comprehensionibus sive radicibus numeravimus minuta que sunt ex summis superfluitatis sex partium et sex partium a longitudine media et posuimus ea opposita numeris quorum sunt et demonstravimus rem secundum hoc, ita ut quod acciderit ex diversitate sit conveniens ei in sensu, sicut diximus, quamvis non sint cursus stellarum in ipso maiore quod est ex additionibus et diminutionibus orbis revolutionis, sed sint in reliquis partibus. Et hec est descriptio tabularum que sequitur.
⟨XI.11⟩ Capitulum undecimum: In descriptione tabularum equationis quinque stellarum erraticarum in longitudine
Tabula equationis stellarum quinque in longitudine
Equatio Saturni in longitudine
♄ |
♄ |
|||||||||||||||||||||
Numeri communes |
Additiones et diminutiones in longitudine |
Superfluitas additionum aut diminutionum |
Superfluitas additionum aut diminutionum in longitudine maiore |
Additiones aut diminutiones in duabus longitudinibus mediis |
Superfluitas additionis aut diminutionis in longitudine minore |
Minuta superfluitatis additionum aut diminutionum |
||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
|||||||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Secunda |
|||||||||
6
12
18 |
354
348
342 |
0
1
1 |
37
18
49 |
0
0
0 |
2
4
6 |
0
0
0 |
2
4
5 |
0
1
1 |
36
11
45 |
0
0
0 |
2
4
7 |
60
58
57 |
0
30
0 |
|||||||||
24
30
36 |
336
330
324 |
2
2
3 |
23
19
29 |
0
0
0 |
8
9
10 |
0
0
0 |
3
8
10 |
2
2
3 |
18
50
20 |
0
0
0 |
9
11
13 |
55
52
49 |
30
30
30 |
|||||||||
42
48
54 |
318
312
306 |
3
4
4 |
59
28
55 |
0
0
0 |
11
11
10 |
0
0
0 |
11
12
14 |
3
4
4 |
49
47
42 |
0
0
0 |
15
17
19 |
46
43
39 |
30
30
0 |
|||||||||
60
66
72 |
300
294
288 |
5
5
6 |
20
42
0 |
0
0
0 |
9
8
7 |
0
0
0 |
15
17
18 |
5
5
5 |
4
25
42 |
0
0
0 |
20
20
21 |
34
30
24 |
0
0
0 |
|||||||||
78
84
90 |
282
276
270 |
6
6
6 |
14
24
30 |
0
0
0 |
5
3
1 |
0
0
0 |
18
19
19 |
5
6
6 |
15
5
12 |
0
0
0 |
21
22
22 |
18
12
4 |
0
0
30 |
|||||||||
93
96
99 |
267
264
261 |
6
6
6 |
31
32
31 |
0
0
0 |
0
2
3 |
0
0
0 |
20
20
20 |
6
6
6 |
12
13
12 |
0
0
0 |
23
23
24 |
0
2
5 |
45
32
11 |
|||||||||
102
105
108 |
258
255
252 |
6
6
6 |
30
27
23 |
0
0
0 |
4
5
6 |
0
0
0 |
21
21
21 |
6
6
6 |
12
9
5 |
0
0
0 |
24
24
25 |
9
11
14 |
8
45
21 |
|||||||||
111
114
117 |
249
246
243 |
6
6
6 |
19
14
7 |
0
0
0 |
7
8
9 |
0
0
0 |
20
20
19 |
6
5
5 |
0
15
48 |
0
0
0 |
25
24
24 |
16
19
22 |
28
31
11 |
|||||||||
120
123
126 |
240
237
234 |
5
5
5 |
19
30
39 |
0
0
0 |
10
10
11 |
0
0
0 |
19
19
18 |
5
5
5 |
40
31
21 |
0
0
0 |
23
23
22 |
24
27
30 |
47
25
0 |
|||||||||
129
132
135 |
231
228
225 |
5
5
5 |
27
14
0 |
0
0
0 |
11
12
12 |
0
0
0 |
18
17
17 |
5
4
4 |
10
18
45 |
0
0
0 |
22
21
20 |
32
35
37 |
37
13
50 |
|||||||||
138
141
144 |
222
219
216 |
4
4
4 |
45
29
12 |
0
0
0 |
12
12
11 |
0
0
0 |
16
15
14 |
4
4
4 |
31
16
0 |
0
0
0 |
19
18
17 |
40
43
45 |
26
3
39 |
|||||||||
147
150
153 |
213
210
207 |
3
3
3 |
14
35
16 |
0
0
0 |
12
12
11 |
0
0
0 |
14
12
11 |
3
3
3 |
43
25
7 |
0
0
0 |
15
14
13 |
47
49
51 |
37
34
32 |
|||||||||
156
159
162 |
204
201
198 |
2
2
2 |
16
35
15 |
0
0
0 |
10
9
8 |
0
0
0 |
10
9
7 |
2
2
2 |
48
29
9 |
0
0
0 |
12
11
10 |
53
54
56 |
29
48
6 |
|||||||||
165
168
171 |
195
192
189 |
1
1
1 |
13
31
9 |
0
0
0 |
7
6
5 |
0
0
0 |
6
5
5 |
1
1
1 |
48
27
6 |
0
0
0 |
8
7
5 |
57
58
59 |
24
22
21 |
|||||||||
174
177
180 |
186
183
180 |
0
0
0 |
47
24
0 |
0
0
0 |
3
2
0 |
0
0
0 |
4
2
0 |
0
0
0 |
45
28
0 |
0
0
0 |
4
2
0 |
60
60
60 |
0
0
0 |
|||||||||
Tabula equationis stellarum quinque in longitudine
Equatio Iovis in longitudine
♃ |
♃ |
|||||||||||||||||||||
Numeri communes |
Additiones et diminutiones in longitudine |
Superfluitas additionis aut diminutionis. Addatur |
Superfluitas additionis aut diminutionis in longitudine maiore |
Additio aut diminutio in duabus longitudinibus mediis |
Superfluitas additionis aut diminutionis in longitudine minore |
Minuta superfluitatis additionis aut diminutionis. Minuatur |
||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
|||||||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Secunda |
|||||||||
6
12
18 |
354
348
342 |
0
1
1 |
30
0
30 |
0
0
0 |
1
2
3 |
0
0
0 |
2
5
7 |
0
1
2 |
18
16
12 |
0
0
0 |
2
5
7 |
60
58
56 |
0
18
16 |
|||||||||
24
30
36 |
336
330
324 |
1
2
2 |
18
26
32 |
0
0
0 |
4
5
6 |
0
0
0 |
9
11
13 |
3
4
5 |
48
42
34 |
0
0
0 |
9
11
13 |
56
54
51 |
14
50
43 |
|||||||||
42
48
54 |
318
312
306 |
3
3
4 |
16
40
1 |
0
0
0 |
7
7
7 |
0
0
0 |
15
17
19 |
6
7
7 |
25
12
17 |
0
0
0 |
15
18
20 |
47
43
39 |
35
27
19 |
|||||||||
60
66
72 |
300
294
288 |
4
4
4 |
20
37
11 |
0
0
0 |
7
5
4 |
0
0
0 |
21
23
24 |
8
9
9 |
17
14
46 |
0
0
0 |
22
24
26 |
32
28
22 |
8
48
45 |
|||||||||
78
84
90 |
282
276
270 |
5
5
5 |
2
9
14 |
0
0
0 |
3
2
1 |
0
0
0 |
25
26
26 |
10
10
10 |
13
35
11 |
0
0
0 |
28
30
31 |
17
11
4 |
35
23
40 |
|||||||||
93
96
99 |
267
264
261 |
5
5
5 |
15
16
15 |
0
0
0 |
0
1
1 |
0
0
0 |
27
27
27 |
10
11
11 |
17
0
2 |
0
0
0 |
31
32
32 |
1
1
5 |
8
12
9 |
|||||||||
102
105
108 |
258
255
252 |
5
5
5 |
14
12
9 |
0
0
0 |
2
2
3 |
0
0
0 |
28
28
29 |
11
11
10 |
3
1
19 |
0
0
0 |
32
33
33 |
8
11
15 |
26
43
0 |
|||||||||
111
114
117 |
249
246
243 |
5
5
4 |
5
0
14 |
0
0
0 |
4
5
5 |
0
0
0 |
29
30
30 |
10
10
10 |
13
45
35 |
0
0
0 |
33
34
34 |
17
20
23 |
49
37
27 |
|||||||||
120
123
126 |
240
237
234 |
4
4
4 |
47
39
30 |
0
0
0 |
6
6
7 |
0
0
0 |
30
29
29 |
10
10
9 |
24
10
14 |
0
0
0 |
34
33
33 |
26
29
31 |
15
30
12 |
|||||||||
129
132
135 |
231
228
225 |
4
4
3 |
20
9
18 |
0
0
0 |
7
8
8 |
0
0
0 |
28
28
27 |
9
9
8 |
36
14
14 |
0
0
0 |
32
32
31 |
34
37
40 |
41
30
19 |
|||||||||
138
141
144 |
222
219
216 |
3
3
3 |
46
33
20 |
0
0
0 |
8
8
7 |
0
0
0 |
26
25
23 |
8
8
7 |
30
6
36 |
0
0
0 |
30
28
26 |
43
45
47 |
7
28
49 |
|||||||||
147
150
153 |
213
210
207 |
3
2
2 |
6
11
36 |
0
0
0 |
7
6
6 |
0
0
0 |
23
21
19 |
7
6
6 |
6
34
0 |
0
0
0 |
25
23
21 |
49
51
52 |
42
34
18 |
|||||||||
156
159
162 |
204
201
198 |
2
2
1 |
20
4
47 |
0
0
0 |
5
5
4 |
0
0
0 |
17
15
13 |
5
4
4 |
24
47
9 |
0
0
0 |
19
17
15 |
54
55
57 |
22
47
11 |
|||||||||
165
168
171 |
195
192
189 |
1
1
0 |
30
13
15 |
0
0
0 |
3
2
2 |
0
0
0 |
11
9
7 |
3
2
2 |
29
49
7 |
0
0
0 |
13
10
8 |
57
58
58 |
40
8
30 |
|||||||||
174
177
180 |
186
183
180 |
0
0
0 |
37
18
0 |
0
0
0 |
1
1
0 |
0
0
0 |
5
3
0 |
1
0
0 |
25
43
0 |
0
0
0 |
5
3
0 |
59
59
60 |
4
32
0 |
|||||||||
Tabula equationis stellarum quinque in longitudine
Equatio Martis in longitudine
♂ |
♂ |
|||||||||||||||||||||
Numeri communes |
Additio aut diminutio in longitudine |
Superfluitas additionis aut diminutionis. Addatur |
Superfluitas additionis aut diminutionis in longitudine maiore |
Additio aut diminutio in duabus longitudinibus mediis |
Superfluitas additionis aut diminutionis in longitudine minore |
Minuta superfluitatis additionis aut diminutionis. Minuatur |
||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
|||||||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Secunda |
|||||||||
6
12
18 |
354
348
342 |
1
2
2 |
5
0
18 |
0
0
0 |
0
10
15 |
0
0
0 |
8
16
24 |
2
4
7 |
21
46
8 |
0
0
0 |
9
18
28 |
59
58
57 |
23
15
11 |
|||||||||
24
30
36 |
336
330
324 |
3
4
5 |
16
12
16 |
0
0
0 |
20
24
27 |
0
0
0 |
32
45
51 |
9
11
14 |
30
11
11 |
0
0
0 |
37
46
16 |
56
54
52 |
36
34
11 |
|||||||||
42
48
54 |
318
312
306 |
6
7
8 |
39
28
15 |
0
0
0 |
28
29
28 |
1
1
1 |
0
5
18 |
16
18
21 |
29
46
0 |
1
1
1 |
6
16
28 |
49
46
42 |
28
17
18 |
|||||||||
60
66
72 |
300
294
288 |
8
9
10 |
17
36
9 |
0
0
0 |
27
24
20 |
1
1
1 |
27
37
46 |
23
25
27 |
13
22
29 |
1
1
2 |
40
53
6 |
38
33
28 |
8
26
20 |
|||||||||
78
84
90 |
282
276
270 |
10
11
11 |
38
2
15 |
0
0
0 |
15
14
4 |
2
2
2 |
1
14
28 |
29
31
33 |
32
30
22 |
2
2
2 |
19
33
15 |
22
16
10 |
46
33
5 |
|||||||||
93
96
99 |
267
264
261 |
11
11
11 |
24
29
32 |
0
0
0 |
0
4
8 |
2
2
2 |
35
42
29 |
34
35
35 |
15
6
16 |
2
3
3 |
17
6
15 |
6
3
0 |
34
3
5 |
|||||||||
102
105
108 |
258
255
252 |
11
11
11 |
32
31
28 |
0
0
0 |
12
16
19 |
2
3
3 |
15
4
13 |
36
37
38 |
43
27
9 |
3
3
3 |
25
36
47 |
3
6
8 |
13
11
49 |
|||||||||
111
114
117 |
249
246
243 |
11
11
11 |
22
14
5 |
0
0
0 |
22
25
28 |
3
3
3 |
22
32
48 |
38
39
39 |
48
21
16 |
3
4
4 |
18
9
21 |
11
14
17 |
44
37
33 |
|||||||||
120
123
126 |
240
237
234 |
10
10
10 |
13
39
23 |
0
0
0 |
31
33
35 |
3
4
4 |
54
5
14 |
40
40
40 |
43
44
9 |
4
4
5 |
35
50
5 |
20
23
26 |
27
35
42 |
|||||||||
129
132
135 |
231
228
225 |
10
9
9 |
4
47
21 |
0
0
0 |
37
39
40 |
4
4
4 |
24
35
45 |
41
41
41 |
50
2
9 |
5
5
5 |
21
36
15 |
29
32
35 |
31
20
9 |
|||||||||
138
141
144 |
222
219
216 |
8
8
7 |
15
27
19 |
0
0
0 |
41
41
41 |
4
5
5 |
16
7
18 |
40
40
39 |
45
16
37 |
6
6
6 |
17
30
13 |
37
40
43 |
28
35
12 |
|||||||||
147
150
153 |
213
210
207 |
7
6
6 |
27
14
19 |
0
0
0 |
40
38
36 |
5
5
5 |
28
34
18 |
38
37
35 |
40
25
12 |
7
7
7 |
12
30
45 |
45
47
49 |
25
39
50 |
|||||||||
156
159
162 |
204
201
198 |
5
5
4 |
41
3
22 |
0
0
0 |
33
37
27 |
5
5
5 |
18
34
18 |
33
31
28 |
23
50
35 |
7
8
7 |
18
3
18 |
52
53
55 |
30
47
32 |
|||||||||
165
168
171 |
195
192
189 |
3
2
2 |
41
13
14 |
0
0
0 |
23
19
15 |
4
4
3 |
12
12
1 |
25
21
16 |
3
0
26 |
7
7
5 |
47
6
49 |
56
57
58 |
44
15
49 |
|||||||||
174
177
180 |
186
183
180 |
1
0
0 |
30
45
0 |
0
0
0 |
10
5
0 |
2
1
0 |
27
16
0 |
11
5
0 |
15
45
0 |
4
2
0 |
26
20
0 |
59
59
60 |
43
12
0 |
|||||||||
Tabula equationis stellarum quinque in longitudine
Equatio Veneris in longitudine
♀ |
♀ |
|||||||||||||||||||||
Numeri communes |
Additio aut diminutio in longitudine |
Superfluitas additionis aut diminutionis. Addatur |
Superfluitas additionis aut diminutionis in longitudine maiore |
Additio aut diminutio in duabus longitudinibus mediis |
Superfluitas additionis aut diminutionis in longitudine minore |
|||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
|||||||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Secunda |
|||||||||
6
12
18 |
354
348
342 |
0
0
0 |
14
28
42 |
0
0
0 |
1
1
1 |
0
0
0 |
1
3
5 |
2
5
7 |
31
1
31 |
0
0
0 |
2
4
6 |
59
57
56 |
10
15
40 |
|||||||||
24
30
36 |
336
330
324 |
0
1
1 |
56
9
21 |
0
0
0 |
2
2
2 |
0
0
0 |
7
9
11 |
10
12
14 |
30
30
18 |
0
0
0 |
8
10
12 |
55
52
49 |
0
55
35 |
|||||||||
42
48
54 |
318
312
306 |
1
1
1 |
32
43
53 |
0
0
0 |
3
3
3 |
0
0
0 |
13
15
18 |
17
19
22 |
25
21
15 |
0
0
0 |
14
16
18 |
45
42
37 |
50
5
5 |
|||||||||
60
66
72 |
300
294
288 |
2
2
2 |
1
8
54 |
0
0
0 |
2
2
2 |
0
0
0 |
20
22
24 |
24
26
29 |
38
37
14 |
0
0
0 |
20
23
25 |
31
26
20 |
40
55
25 |
|||||||||
78
84
90 |
282
276
270 |
2
2
2 |
58
21
23 |
0
0
0 |
1
1
1 |
0
0
0 |
27
29
31 |
31
33
35 |
27
38
44 |
0
0
0 |
28
30
33 |
17
8
4 |
35
20
40 |
|||||||||
93
96
99 |
267
264
261 |
2
2
2 |
23
23
2 |
0
0
0 |
0
1
1 |
0
0
0 |
33
35
38 |
36
37
38 |
40
43
40 |
0
0
0 |
36
38
40 |
1
4
7 |
31
42
39 |
|||||||||
102
105
108 |
258
255
252 |
2
2
2 |
21
20
45 |
0
0
0 |
1
1
1 |
0
0
0 |
40
42
45 |
39
40
41 |
35
29
20 |
0
0
0 |
43
45
47 |
10
13
16 |
35
32
28 |
|||||||||
111
114
117 |
249
246
243 |
2
2
2 |
16
13
10 |
0
0
0 |
1
2
2 |
0
0
0 |
47
49
52 |
42
43
44 |
9
14
35 |
0
0
0 |
50
52
55 |
19
22
25 |
25
21
18 |
|||||||||
120
123
126 |
240
237
234 |
2
2
1 |
6
2
58 |
0
0
0 |
2
2
2 |
0
0
1 |
54
57
0 |
44
44
45 |
12
15
14 |
0
1
1 |
58
1
4 |
28
0
33 |
15
0
44 |
|||||||||
129
132
135 |
231
228
225 |
1
1
1 |
54
49
44 |
0
0
0 |
2
3
3 |
1
1
1 |
3
6
10 |
45
45
45 |
36
11
19 |
1
1
1 |
8
11
14 |
36
38
41 |
18
50
51 |
|||||||||
138
141
144 |
222
219
216 |
1
1
1 |
39
33
27 |
0
0
0 |
3
3
2 |
1
1
1 |
14
19
24 |
45
45
45 |
17
45
20 |
1
1
1 |
18
22
27 |
43
45
47 |
32
44
12 |
|||||||||
147
150
153 |
213
210
207 |
1
1
1 |
21
14
7 |
0
0
0 |
2
2
2 |
1
1
1 |
29
33
37 |
44
43
42 |
40
39
18 |
1
1
1 |
32
38
43 |
49
51
52 |
37
23
46 |
|||||||||
156
159
162 |
204
201
198 |
1
0
0 |
0
53
46 |
0
0
0 |
2
2
1 |
1
1
1 |
39
41
42 |
40
38
35 |
28
50
7 |
1
1
1 |
48
51
52 |
54
55
56 |
8
18
26 |
|||||||||
165
168
171 |
195
192
189 |
0
0
0 |
39
32
24 |
0
0
0 |
1
1
1 |
1
1
1 |
38
31
19 |
31
26
21 |
24
46
55 |
1
1
1 |
50
43
27 |
57
58
59 |
28
26
31 |
|||||||||
174
177
180 |
186
183
180 |
0
0
0 |
16
8
0 |
0
0
0 |
1
1
0 |
0
0
0 |
38
31
0 |
14
7
0 |
41
33
0 |
1
0
0 |
5
35
0 |
59
59
60 |
36
48
0 |
|||||||||
Tabula equationis stellarum quinque in longitudine
Equatio Mercurii in longitudine
☿ |
☿ |
|||||||||||||||||||||
Numeri communes |
Additio aut diminutio in longitudine |
Superfluitas additionis aut diminutionis. Addatur |
Superfluitas additionis aut diminutionis in longitudine maiore |
Additio aut diminutio in duabus longitudinibus mediis |
Superfluitas additionis aut diminutionis in longitudine minore |
Minuta superfluitatis additionis aut diminutionis. Minuatur |
||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
|||||||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Secunda |
|||||||||
6
12
18 |
354
348
342 |
0
0
0 |
58
34
11 |
0
0
0 |
1
2
4 |
0
0
0 |
9
19
29 |
1
3
4 |
38
16
53 |
0
0
0 |
5
11
17 |
59
57
54 |
20
20
40 |
|||||||||
24
30
36 |
336
330
324 |
1
1
1 |
4
22
37 |
0
0
0 |
5
5
4 |
0
0
0 |
39
49
59 |
6
8
9 |
29
4
36 |
0
0
0 |
23
28
34 |
50
45
39 |
40
40
40 |
|||||||||
42
48
54 |
318
312
306 |
1
2
2 |
11
4
15 |
0
0
0 |
4
3
1 |
1
1
1 |
8
18
28 |
11
12
13 |
6
33
58 |
0
0
0 |
40
45
50 |
33
25
18 |
0
40
0 |
|||||||||
60
66
72 |
300
294
288 |
2
2
2 |
25
34
41 |
0
0
0 |
0
2
4 |
1
1
1 |
39
49
59 |
15
16
17 |
58
33
43 |
0
1
1 |
56
4
11 |
10
2
9 |
20
20
54 |
|||||||||
78
84
90 |
282
276
270 |
2
2
2 |
46
50
12 |
0
0
0 |
6
7
9 |
2
2
2 |
9
19
25 |
18
19
20 |
47
54
33 |
1
1
1 |
17
23
29 |
20
29
39 |
0
44
23 |
|||||||||
93
96
99 |
267
264
261 |
2
2
2 |
12
12
11 |
0
0
0 |
10
10
11 |
2
2
2 |
34
39
44 |
20
21
21 |
54
58
29 |
1
1
1 |
32
34
38 |
43
47
50 |
31
34
0 |
|||||||||
102
105
108 |
258
255
252 |
2
2
2 |
50
48
46 |
0
0
0 |
10
10
10 |
2
2
2 |
48
13
18 |
21
21
21 |
42
52
19 |
1
1
1 |
41
44
47 |
52
54
57 |
26
52
58 |
|||||||||
111
114
117 |
249
246
243 |
2
2
2 |
44
41
37 |
0
0
0 |
9
9
9 |
3
3
3 |
2
4
6 |
22
22
21 |
2
1
56 |
1
1
1 |
49
52
55 |
58
59
59 |
23
28
44 |
|||||||||
120
123
126 |
240
237
234 |
2
2
2 |
33
28
23 |
0
0
0 |
8
7
7 |
3
3
3 |
8
9
10 |
21
21
21 |
47
33
15 |
1
1
2 |
57
59
0 |
60
59
59 |
0
44
28 |
|||||||||
129
132
135 |
231
228
225 |
2
2
2 |
18
12
6 |
0
0
0 |
6
6
5 |
3
3
3 |
12
12
9 |
20
20
19 |
13
25
50 |
2
2
2 |
0
1
1 |
58
57
56 |
39
50
46 |
|||||||||
138
141
144 |
222
219
216 |
2
1
1 |
0
53
46 |
0
0
0 |
4
4
3 |
3
3
2 |
6
2
17 |
19
18
17 |
10
24
32 |
2
2
1 |
0
0
58 |
55
54
52 |
41
3
26 |
|||||||||
147
150
153 |
213
210
207 |
1
1
1 |
38
30
22 |
0
0
0 |
3
2
2 |
2
2
2 |
11
42
32 |
16
15
14 |
35
31
20 |
1
1
1 |
53
47
41 |
50
49
47 |
48
11
34 |
|||||||||
156
159
162 |
204
201
198 |
1
1
0 |
53
5
56 |
0
0
0 |
2
1
1 |
2
2
1 |
21
9
35 |
13
11
10 |
3
41
53 |
1
1
1 |
34
26
17 |
45
44
43 |
57
36
58 |
|||||||||
165
168
171 |
195
192
189 |
0
0
0 |
47
38
28 |
0
0
0 |
1
0
0 |
1
1
1 |
38
59
1 |
8
7
5 |
40
1
59 |
1
0
0 |
7
16
43 |
42
41
40 |
26
37
48 |
|||||||||
174
177
180 |
186
183
180 |
0
0
0 |
59
9
0 |
0
0
0 |
0
0
0 |
0
0
0 |
42
21
0 |
3
1
0 |
35
43
0 |
0
0
0 |
24
14
0 |
40
39
39 |
0
44
28 |
|||||||||
⟨XI.12⟩ Capitulum duodecimum: In numeratione motus localis stellarum quinque erraticarum in longitudine
Cum ergo voluerimus scire per has tabulas quas fecimus propter motus revolubiles in longitudine et in diversitate cursus qui sunt unius et unius stellarum harum, ponemus numerationem nostram motus localis earum, et est una et eadem in stellis quinque, hoc modo quam narrabo. Aggregabimus ex tabulis motus medii comprehensiones equales que sunt in hora quesita in qua est illud post revolutiones integras in longitudine et in diversitate. Deinde scienter ibimus ad partes que sunt inter longitudinem longiorem in illa hora in orbe egredientis centri et inter cursum medium in longitudine prius et mittemus eas in tabulas diversitatis que est illius stelle que intenditur et quod fuerit coram illo numero in tabula tertia ex equatione in longitudine cum additione et diminutione minutorum que comprehenduntur in tabula quarta considerabimus. Tunc si fuerit longitudo quam posuimus diversitatis in tabula prima, minuemus illud ex partibus longitudinis et addemus ipsum super partes diversitatis. Quod si fuerit in tabula secunda, addemus illud super partes longitudinis et minuemus ipsum ex partibus diversitatis, ut proveniant nobis duo cursus equati. Postea tendemus scienter ad numerum equatum ex longitudine longiore diversitatis et mittemus etiam ipsum in duas tabulas primas et quod fuerit coram ipso ex additione aut diminutione in tabula sexta, que est longitudinis medie, firmabimus. Et similiter etiam tendemus ad numerum longitudinis equalis quem premisimus, cum quo intravimus in principio, et mittemus ipsum in has duas tabulas easdem. Quod si nos invenerimus ipsum in areis primis, que sunt magis elongate a longitudine media, et illud manifestum est ex minutis que sunt in tabula octava, considerabimus quod erit coram ipso extremitatis in eadem tabula octava. Quotcumque enim fuerint, accipiemus secundum quantitatem numerationis eorum ex superfluitate que est coram in area in qua est additio aut diminutio media que accepta fuit et firmata in tabula quinta, que est longitudinis maioris. Quod ergo provenerit minuemus ex eo quod accepimus et firmavimus. Quod si invenerimus numerum longitudinis quem diximus in areis inferioribus, que sunt propinquiores longitudini medie, considerabimus quid erit coram ipso secundum illud exemplum ex minutis in tabula octava, et quod fuerit accipiemus secundum quantitatem numerationis eorum ex superfluitate que est coram additione et diminutione media que accipitur et firmatur in tabula septima, que est minoris longitudinis, et quod provenerit, addemus ipsum super illud quod accepimus et firmavimus, et quod aggregatur ex partibus additionis aut diminutionis equatis considerabimus. Tunc si nos invenerimus numerum diversitatis equate in tabula prima, addemus illud super partes longitudinis equate. Quod si invenerimus ipsum in tabula secunda, minuemus ipsum ex eis. Quod ergo aggregabitur ex numero partium proiciemus et incipiemus a longitudine longiore stelle in illa hora. Perveniemus enim ad locum eius super quem videtur orbis signorum.
Expleta est dictio undecima libri Almagesti Ptolemei Pheludiensis.