〈IX〉
Claudii Ptolemei Pheludiensis dictio nona libri Almagesti undecem continens capitula fauste succedit.
Capitulum primum: De ordinibus spherarum Solis et Lune et stellarum quinque retrogradarum
Capitulum secundum: In equatione de premissione modorum diversitatum stellarum quinque retrogradarum
Capitulum tertium: De reditionibus revolutionum que sunt quinque stellarum retrogradarum
Capitulum quartum: In positione tabularum motuum mediorum que sunt stellarum quinque erraticarum in longitudine et diversitate
Capitulum quintum: In eo cuius necessaria est premissio in modis stellarum quinque retrogradarum
Capitulum sextum: In declaranda diversitate secundum duos modos
Capitulum septimum: De probatione longitudinis longioris que est stelle Mercurii secundum motum suum localem
Capitulum octavum: De hoc quod stella Mercurii est in longitudine propinquiore propinquore M. in revolutione una bis
Capitulum nonum: In scientia diversitatis cursus Mercurii
Capitulum decimum: De equatione motuum Mercurii qui sunt revolutionum eius
Capitulum undecimum: In loco motuum qui sunt revolutionis eius
〈IX.1〉 Capitulum primum: De ordinibus spherarum Solis et Lune et quinque stellarum retrogradarum
Quantum vero fuit possibile aliquem loqui de stellis fixis et speciebus scientie habitudinum earum secundum quantitatem quam fecit nos adipisci quod vidimus in tempore usque ad tempus nostrum hoc augmenti et de comprehensione eius quod inquiritur de scientia earum est quod diximus. Et quia iam remansit de complemento nostri libri huius declaratio habitudinum stellarum quinque erraticarum, reducam sermonem in eo et non reiterabo sermonem in omnibus et aggregabo illud in capitulis secundum quantitatem qua possibile est nobis in unaquaque earum. Et in principio illius narrabo de ordinibus spherarum earum, quarum revolutio locorum est etiam super duos polos orbis declivis qui transit per medium signorum. Sed quod omnes sphere iste sint sub inferiore longitudine sphere stellarum fixarum a terra et super longiorem sphere Lune a terra et quod sphere tres, quarum maior est Saturni et secunda que est sub longitudine eius inferiore a terra est Iovis et illa que est sub ea est Martis, sint in longitudine longiore spherarum reliquarum et sphere Solis, illud est in quo vidimus antiquos doctrinales convenisse. De sphera autem stelle Veneris et sphera stelle Mercurii dixerunt antiqui quod ipse sint sub sphera Solis. Quidam vero eorum qui fuerunt post eos viderunt quod he due sphere etiam sunt supra spheram Solis, propterea quia non tegunt Solem unquam. Nos autem videmus quod hec consideratio non est vera, propterea quod iam possibile est ut sit aliqua earum sub Sole et non sit in linea una que est inter Solem et inter oculos nostros necessario. Et propter hoc non videtur tegere Solem sicut Luna apud coniunctionem. Plerumque namque non tegit Solem. Non autem est possibile ut sit quod dixerunt hi neque secundum modum alium, propterea quod neque una stellarum harum est que habeat diversitatem aspectus sensibilem cuius longitudines assumantur cum videtur. Et ex hoc declaratur nobis quod ordines antiquorum veri sunt et certi. Ipsi namque secundum aptitudinem nature diviserunt inter unamquamque longitudinum earum que elongantur a Sole per Solem medium et inter eas que non elongantur ab eo, sed revolvuntur semper circa eum secundum quantitatem qua non sit longitudini earum que est longitudinis earum inferioris a terra aliquid cuius diversitas aspectus sit magna quantitas.
〈IX.2〉 Capitulum secundum: In equatione de premissione modorum diversitatis stellarum quinque retrogradarum
Ordo vero harum spherarum est secundum quod diximus. Et quia voluimus ut declaremus quod videmus de omnibus diversitatibus motuum stellarum quinque erraticarum que Probably corrupt for quod, which would correspond to the Greek text (see Toomer, loc. cit., p. 420, line 7). Paris, BnF, lat. 14738 (141r, line 17) reads que too. sunt secundum motus similes in revolutionibus absque diversitate, sicut demonstravimus in Sole et Luna (isti namque motus non sunt nisi proprietates nature spiritalis aliene ab omni cuius motus est non secundum similitudinem et absque ordine), tunc oportet ut estimemus quod sapiens rectificatio illius et eius equatio est magna et quod secundum veritatem est complementum doctrine sapientie doctrinalium et quod est difficilis secundum veritatem propter multas causas et quod non pervenit ad rectitudinem omnis equationis eius aliquis eorum qui precesserunt. In inquisitione enim motuum revolutionum cuiusque stellarum, quia possibile est ut attenuetur a visibus subtile quod volunt apud obviationem considerationum et comparatione aliorum ad alias, tunc velociter fiat diversitas sensibilis in eo quod pervenit ex tempore cum fuerit inquisitio eius in tempore brevi, sed cum fuerit in tempore longo, tarde fiet sensibilis. Et illud tempus ex quo perveniunt ad nos considerationes scripte que sunt stellarum quinque retrogradarum, quia est breve apud magnitudinem eius cuius volunt comprehensionem in tempore longo, quod est duplum dupli eius, facit sermonem qui precessit in eo quod est factum non verum. In inquisitione vero diversitatum ingreditur ex dubitatione sententie non parum, propterea quod videntur cuiusque stellarum due diversitates que non sunt equales neque in magnitudine neque in temporibus reditionum. Quarum una videtur propter Solem et altera propter partes orbis signorum. Et cum coniunxerimus eas ambas, erit semper proprietas cuiusque earum propter illud difficilis cognitionis. Et propterea quod plures considerationes antiquorum sunt scripte et aggregate non sapienter, tunc propinque earum continent stationes stellarum et ortus earum. Sed comprehensio proprietatum cuiusque harum duarum non est absque dubitatione in se. Stationes quidem non est possibile ut declaretur tempus verum. Quoniam earum localis motus ad loca in diebus pluribus non est sensibilis ante stationem et post stationem, sed ortus, non quia ipsi delent loca subito cum eo quod apparet primum et postremum tantum, sed quia possibile est ut sit in eis error in tempore propter diversitatem aeris in locis et visuum eorum qui considerant. Et universaliter dico quod considerationes que sunt in tempore longo quarundam stellarum erraticarum cum una stellarum fixarum, si considerator non aspexerit doctrinaliter et sapienter secundum omnes causas, erit quantitas mensurationis eius cuius vult comprehensionem impossibilis et difficilis considerationis et erit illud estimatio et meditatio, non propter lineas que sunt inter stellas visas tantum que faciunt angulos diversos apud orbem signorum qui non sunt anguli recti secundum habitudinem (ex hoc enim secundum veritatem erit in eis error plurimus propter multitudinem modorum declinationis orbis signorum apud cognitionem locorum earum in longitudine et latitudine), sed propterea quod earum longitudines, cum fuerint apud horizontes, videbuntur secundum visus maiores, et cum fuerint in medio celi, videbuntur minores. Et manifestum est quod propter illud est possibile ut sint quandoque ad maiorem et quandoque ad minorem quantitatem longitudinis vere. Et propter illud estimavit Abrachis amore veritatis propter omnia que diximus et precipue quoniam non pervenerunt ad eum cause multe considerationum verarum eorum qui fuerunt ante eum, quamvis multe sunt considerationes quas ipse ad nos transmisit et quas nos adipisci fecit (modos quidem Solis et Lune fecit nos adipisci secundum quod convenit nobis eorum inquisitio et declaratio secundum demonstrationem omni ingenio qui sunt per motus in revolutionibus absque diversitate, sed stellas quinque erraticas non dixit in aliquo qui ad nos pervenerunt suorum librorum, neque dixit nisi considerationes earum tantum quibus conficeretur et quibus demonstretur quod cause que videntur in eis non sunt similes causis modorum antiquorum doctrinalium qui fuerunt tunc, quoniam ipse non fuit contentus narratione eius quod convenit tantum), quod unaqueque stellarum habet duas diversitates et quod rectitudo cuiusque earum non est equalis et quod postremi doctrinales posuerunt demonstrationes que sunt cum lineis mensurabilibus secundum diversitatem unam et rectitudinem unam. Et ipse non fuit contentus etiam quod he due diversitates sint aut super orbes egredientium centrorum aut super orbes quorum centra sunt centrum orbis signorum et sunt revoluti et revolvunt orbes revolutionis aut contingit ut sint ambe diversitates et sit diversitas que est propter orbem signorum quantitatis talis et diversitas que est propter Solem quantitatis talis. Sermo enim hic est eorum qui nominantur positores tabularum septentrionalium. Ipsi namque voluerunt affirmare quod motus est in revolutione et quod ipse est absque diversitate, et illud cum falsitate et absque probatione recepta. Sunt namque quidam hominum qui non sequuntur hunc sermonem, et eorum sunt quidam qui sequuntur ipsum, sed ipsi sunt numerationis parve. Abrachis vero vidit quod illi qui pervenerunt in omnibus doctrinalibus ad finem subtilitatis et amorem veritatis non sunt contenti stare apud hoc, sicut contenti sunt alii, qui estimant quod eorum sermo non est cum contrarietate veritatis, sed necessario oportet illum qui vult sedare seipsum et sedare aspicientes cum veritate ut declaret quantitatem cuiusque duarum diversitatum per probationes earum que videntur et in quibus conveniunt et ut demonstret eas ambas et demonstret orbes in quibus he due diversitates sunt secundum ordines suos et loca earum et modos motuum earum donec assumantur et inveniantur secundum quod videtur conveniens proprietati quam posuit de modo orbium. Iam autem estimo quod illud quod dixi fuit ei difficile. Non tamen hoc dico quod dixi ut extollar per ipsum, sed ut This conjunction lacks a predicate complement. In the Greek text there follows: ‘we may [be allowed to] accede [to this compulsion]’ (see Toomer, loc. cit., p. 422, lines 5-6 from the bottom). In Paris, BnF, lat. 14738 (141v, line 17 from the bottom) there is no predicate complement either., si coegerit nos res eadem, ubicunque fuerit opus operari, tractare de quibusdam stellis secundum plurimum et magis quam hic, sicut verbi gratia ponemus demonstrationes per orbes extractos solum quos lineant motus earum in spheris suis, et sunt earum superficies, in quibus ipse sunt, ipsa superficies orbis medii signorum propter decorem qui sequitur illud, et ponemus quasdam stellas principia, et non sit earum comprehensio ex principio viso, sed sit cum consequentia experimenti, et earum convenientia primum facit opportere ut ponatur modus motuum omnium earum aut modus declinationis orbium modus unus, ita ut non alteretur scientie nostre. Non enim impeditur opus nostrum in eo aliquo modo ex hoc aut eius simili, neque quod ponitur absque probatione, quod non affert diversitatem que habeat quantitatem. Et postquam fuerit illud quod comprehenditur ex eo conveniens ei quod videtur, quamvis sit eius inventio absque via scientie et quamvis sit modus comprehensionis eius difficilis sensus (penitus enim dico quod principiorum primorum causa secundum naturam aut non est aliquid aut est cum quo non ratiocinamur et quod diversitas manerierum partium orbium ubicunque cuius comprehensio videtur in stellis omnibus non est equalis), non ergo convenit alicui ut estimet illud miraculum. Que fuerunt stelle cum eo quod servat earum summa de motibus earum simplicibus absque diversitate, demonstrabo totum quod videtur magis integre et aggregate quod fuerit de modorum simili earum, et faciemus in demonstrationibus cuiusque earum considerationes in quibus non dubitatur, scilicet in quibus erunt stelle et Luna connexe aut secundum proprietatem multam, et precipue considerationes que inveniuntur per instrumenta, sicut quando fuerit visus precedens in duobus foraminibus oppositis que sunt in orbibus armillarum secundum longitudines equales ab omnibus partibus et fuerit visus aspiciens ex arcubus similibus transitus cuiusque stellarum ad orbem medii signorum in longitudine et latitudine secundum quod subtilius et verius est possibile cum revolutione armille orbis signorum que est in instrumento et revolutione duorum foraminum oppositorum que sunt in orbibus descriptis super duos polos orbis medii signorum ad illud quod consideravimus de stellis.
〈IX.3〉 Capitulum tertium: De reditionibus revolubilibus que sunt stellarum quinque retrogradarum
Et postquam premisi earum acceptionem sicut diximus, ponam primum quod elegit Abrachis de reditionibus revolubilibus parvis que sunt simul cuiusque stellarum quinque erraticarum fere, quas equavimus ex eo quod declaratum est nobis ex propinquitate locorum earum post probationes diversitatum, quemadmodum declaravimus in locis suis. Et nos non premiserimus eas nisi ut sit quod comparavimus ad considerationes diversitatum positum preparatum ex divisione motuum mediorum qui sunt cuiusque earum in longitudine et diversitate. Et hic non est plurima diversitas, quamvis aliquis faciat transitus medios centri eorum. Communiter autem quod necessario longitudo quidem est motus centri orbis revolutionis in orbe centri egredientis, et diversitas quidam Probably corrupt for quidem, which is also the reading of Paris, BnF, lat. 14738 (142r, line 8) and would correspond to the Greek text (see Toomer, loc. cit., p. 424, line 2). est motus stelle in orbe revolutionis. Diversitatis vero stelle Saturni iam invenimus 57 revolutiones compleri in annis solaribus nostrorum annorum, scilicet qui sunt ab uno duorum tropicorum aut ab una duarum equalitatum usque ad eius simile, 59 annis et die uno et medietate et quarta diei fere. Et manifestum est quod revolutiones stelle sunt due revolutiones et pars una et due tertie partis et medietas decime partis. In stellis enim tribus quas consequitur Sol semper est numerus revolutionum quas revolvit Sol in tempore reditionis que est cuiusque earum sicut numerus revolutionum stellarum in longitudine et diversitate coniunctis. Et invenimus 65 revolutiones que sunt diversitatis Iovis compleri similiter in 71 anno solari exceptis quatuor diebus et medietate et tertia diei et parte quintadecima diei fere et cum sex revolutionibus revolutionum stelle que sunt a tropico usque ad sui simile diminutis inde quatuor partibus et medietate et tertia partis. Et invenimus 37 revolutiones que sunt diversitatis Martis compleri in 79 annis solaribus nostrorum annorum et tribus diebus et sexta diei et parte vicesima diei fere et cum revolutionibus revolutionum stelle que sunt a tropico usque quo redeat ad ipsum 42 partibus et 3 partibus et sexta partis. Et invenimus quinque revolutiones que sunt diversitatis Veneris compleri in octo annis solaribus nostrorum annorum demptis duobus diebus et quarta diei et parte vigesima diei fere et cum revolutionibus equalis numeri numero revolutionum Solis octo revolutiones demptis inde duabus partibus et quarta partis. Et reperimus 145 revolutiones que sunt diversitatis stelle Mercurii compleri in 46 annis solaribus et die uno et parte trigesima diei fere et cum revolutionibus numeri equalis numero revolutionum Solis etiam 46 revolutiones et partem unam. Si nos ergo diviserimus in unaquaque stellarum tempus reditionis per dies secundum quod declaravimus de diebus anni et numerum revolutionum quidem diversitatis per partes cuiusque revolutionum, scilicet 360 partes, erit tempus in Saturno quidem dies 21551 dies et quinta et decima diei et erunt partes diversitatis 2520 partes, et in Iove quidem 25927 dies et quarta et quinta et sexta diei et erunt partes diversitatis 23400 partes, et in stella quidem Martis erunt dies 28857 dies et medietas et tertia et medietas decime diei et erunt partes diversitatis 13320 partes, et in stella quidem Veneris erunt dies 2919 dies et medietas et quinta diei et erunt partes diversitatis 1800 partes, et in stella Mercurii erunt dies 16802 dies et due quinte diei et erunt partes diversitatis 52200 partes. Cum ergo nos diviserimus summam numeri partium proprietatis que est cuiusque stelle ex diversitate per summam numeri dierum eius, inveniemus portionem diei unius diversitatis que est motus medii Saturni quidem cifre et 57 minuta et 7 secunda et 43 tertia et 41 quartum et 43 quinta et 40 sexta fere, et Iovis quidem cifre et 54 minuta et 9 secunda et 2 tertia et 46 quarta et 26 quinta, et Martis quidem cifre et 27 minuta et 41 secunda et 40 tertia et 19 quarta et 20 quinta et 58 sexta, et Veneris quidem cifre et 36 minuta et 59 secunda et 25 tertia et 53 quarta et 11 quinta et 28 sexta, et Mercurii quidem tres partes et 6 minuta et 24 secunda et 6 tertia et 59 quarta et 35 quinta et 50 sexta. Cum ergo acceperimus ex unaquaque harum partium partem vicesimamquartam earum, erit illud portio diversitatis medie cuiusque stellarum hore unius Saturni quidem 0 et 2 minuta et 22 secunda et 49 tertia et 19 quarta et 14 quinta et 19 sexta et 10 septima, et Iovis 0 et 2 minuta et 15 secunda et 22 tertia et 36 quarta et 56 quinta et 5 sexta, et Martis 0 et unum minutum et 9 secunda et 14 tertia et 10 quarta et 48 quinta et 22 sexta et 25 septima, et Veneris quidem 0 et unum minutum et 32 secunda et 28 tertia et 34 quarta et 42 quinta et 58 sexta et 40 septima, et Mercurii 0 et 7 minuta et 46 secunda et 0 tertia et 17 quarta et 18 quinta et 49 sexta et 35 septima. Et etiam cum nos multiplicaverimus portionem unius diei unius cuiusque stelle in 30, erit motus diversitatis medie mensis unius Saturni quidem 28 partes et 33 minuta et 51 secunda et 50 tertia et 51 quartum et 50 quinta, et Iovis 27 partes et 4 minuta et 31 secunda et 23 tertia et 13 quarta, et Martis 13 partes et 50 minuta et 50 secunda et 9 tertia et 40 quarta et 29 quinta, et Veneris 18 partes et 29 minuta et 42 secunda et 56 tertia et 35 quarta et 44 quinta, et Mercurii 93 partes et 12 minuta et 3 secundo et 29 tertia et 47 quarta et 55 quinta. Et similiter cum nos multiplicaverimus portionem omnis stelle diei unius in numerum dierum anni unius Egyptii, scilicet 365, erit motus diversitatis medie anni unius Saturni quidem 347 partes et 32 minuta et 0 secunda et 48 tertia et 50 quarta et 38 quinta et 20 sexta, et Iovis 329 partes et 25 minuta et 1 secundum et 52 tertia et 28 quarta et 10 quinta et 0, et Martis 168 partes et 28 minuta et 30 secunda et 17 tertia et 42 quarta et 32 quinta et 50 sexta, et Veneris 225 partes et 1 minutum et 32 secunda et 28 tertia et 34 quarta et 39 quinta et 15 sexta, et Mercurii superfluitas post proiectionem revolutionum 53 partes et 56 minuta et 42 secunda et 32 tertia et 32 quarta et 59 quinta et 10 sexta. Et similiter cum nos multiplicaverimus portionem cuiusque stelle anni unius Egyptii in 18, quemadmodum fecimus in tabulis Solis et Lune, erit quod remanebit ex superfluitate post revolutiones integras 18 annorum Egyptiorum quod est motus diversitatis medie Saturni quidem 135 partes et 36 minuta et 14 secunda et 39 tertia et 11 quarta et 30 quinta, et Iovis quidem 169 partes et 30 minuta minunuta M. et 33 secunda et 44 tertia et 27 quarta, et Martis 152 partes et 33 minuta et 5 secunda et 18 tertia et 45 quarta et 51 quintum, et Veneris 90 partes et 27 minuta et 44 secunda et 34 tertia et 23 quarta et 46 quinta et 30 sexta, et Mercurii 251 pars et 0 et 45 secunda et 45 tertia etiam et 53 quarta et 45 quinta et 0. Et secundum hoc exemplum pertractabimus motus medios in longitudine. Sed tamen non est nobis necesse ut dividamus summam numeri partium revolutionum per dies temporis positi cuiusque stelle. Quoniam quod est Veneris et quod est Mercurii ex motu est ille idem cuius iam premisimus narrationem Solis. Quod vero relique stelle tres habent ex motibus est quod deest motui cuiusque earum in diversitate ex motu Solis in longitudine et cum quo erit complementum eius in numeris prorietatis cuiusque stelle earum. Quapropter erit motus diei unius medius in longitudine Saturni quidem 0 et 2 minuta et 0 et 33 tertia et 31 quartum et 28 quinta et 51 sextum, et Iovis 0 et 4 minuta et 59 secunda et 14 tertia et 26 quarta et 46 quinta et 31 sextum, et Martis 0 et 31 minutum et 26 secunda et 36 tertia et 53 quarta et 51 quintum et 33 sexta. Et erit motus unius hore in longitudine Saturni quidem 0 et 0 etiam et 5 secunda et 1 tertium et 23 quarta et 48 quinta et 42 sexta et 31 septimum et 1 octavum, et Iovis 0 et 0 etiam et 12 secunda et 28 tertia et 6 quarta et 6 quinta et 56 sexta et 17 septima et 20 octava, et Martis 0 et 1 minutum et 18 secunda et 36 tertia et 32 quarta et 14 quinta et 38 sexta et 52 septima et 30 octava. Et erit motus mensis unius in longitudine Saturni quidem pars una et 0 et 16 secunda et 45 tertia et 44 quarta et 25 quinta et 30 sexta, et Iovis quidem 2 partes et 29 minuta et 37 secunda et 13 tertia et 23 quarta et 15 quinta et 30 sexta, et Martis 15 partes et 43 minuta et 18 secunda et 26 tertia et 55 quarta et 46 quinta et 30 sexta. Et erit motus anni unius Egyptii in longitudine Saturni quidem 12 partes et 13 minuta et 23 secunda et 56 tertia et 30 quarta et 30 quinta et 15 sexta, et Iovis quidem 30 partes et 20 minuta et 22 secunda et 52 tertia et 52 quarta etiam et 38 quinta et 35 sexta, et Martis 191 partes et 16 minuta et 54 secunda et 27 tertia et 38 quarta et 35 quinta et 45 sexta. Et erit motus in longitudine 18 annorum Egyptiorum Saturni quidem 220 partes et 1 minutum et 10 secunda et 57 tertia et 9 quarta et 4 quinta et 30 sexta, et Iovis quidem superfluitas revolutionum 186 partes et 6 minuta et 51 secundum et 51 tertium etiam et 53 quarta et 34 quinta et 30 sexta, et superfluitas revolutionum Martis 203 partes et 4 minuta et 20 secunda et 17 tertia et 34 quarta et 43 quinta et 30 sexta. Et ordinabo etiam causa alleviationis differentias tabularum secundum ordinem cuiusque stellarum ad componendum motus medios positos in fine huius capituli post hoc in 45 areis secundum similitudinem eius quod fecimus in his que precesserunt. Et in prima trium differentiarum erit compositio annorum coniunctorum 18, et in secunda earum compositio annorum expansorum et horarum, et in tertia earum compositio mensium et dierum.
〈IX.4〉 Capitulum quartum: In positione differentiarum tabularum motuum mediorum que sunt quinque stellarum erraticarum in longitudine et diversitate
Et hec est lineatio tabularum:
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Saturni in annis coniunctis longitudinis et diversitatis
♄
|
♄ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
18
36
54 |
220
80
300 |
1
2
3 |
10
21
32 |
57
54
51 |
9
18
27 |
4
9
13 |
30
0
30 |
135
271
46 |
36
12
48 |
14
29
43 |
39
18
57 |
11
23
34 |
30
0
30 |
0
0
0 |
|
72
90
108 |
160
20
240 |
4
5
7 |
43
54
5 |
48
45
42 |
36
45
54 |
18
22
27 |
0
30
0 |
182
318
93 |
24
1
37 |
58
13
27 |
36
15
54 |
46
57
9 |
0
30
0 |
0
0
0 |
|
126
144
162 |
100
320
180 |
8
9
10 |
16
27
38 |
40
37
34 |
3
12
21 |
31
36
40 |
30
0
30 |
229
4
140 |
13
49
26 |
42
57
11 |
34
13
52 |
20
32
43 |
30
0
30 |
0
0
0 |
|
180
198
216 |
40
260
120 |
11
13
14 |
49
0
11 |
31
28
25 |
30
39
48 |
45
49
54 |
0
30
0 |
276
51
186 |
2
38
14 |
26
41
55 |
31
11
50 |
55
6
18 |
0
30
0 |
0
0
0 |
|
234
252
270 |
340
200
60 |
15
16
17 |
22
33
44 |
22
20
17 |
57
7
16 |
58
3
7 |
30
0
30 |
322
98
234 |
51
27
3 |
10
25
39 |
29
8
47 |
29
41
52 |
30
0
30 |
0
0
0 |
|
288
306
324 |
280
140
0 |
18
20
21 |
55
6
17 |
14
11
8 |
25
34
43 |
12
16
21 |
0
30
0 |
9
145
280 |
39
16
52 |
54
9
23 |
27
6
45 |
4
15
27 |
0
30
0 |
0
0
0 |
|
342
360
378 |
220
80
300 |
22
23
24 |
28
39
50 |
5
3
0 |
52
1
10 |
25
30
34 |
30
0
30 |
56
192
327 |
28
4
41 |
38
53
7 |
24
3
43 |
38
50
1 |
30
0
30 |
0
0
0 |
|
396
414
432 |
160
20
240 |
26
27
28 |
0
11
22 |
57
54
51 |
19
28
37 |
39
43
48 |
0
30
0 |
103
238
14 |
17
53
29 |
22
37
51 |
22
1
40 |
13
24
36 |
0
30
0 |
0
0
0 |
|
450
468
486 |
100
320
180 |
29
30
31 |
33
44
55 |
48
45
43 |
46
55
5 |
52
57
1 |
30
0
30 |
150
285
61 |
6
42
18 |
6
20
35 |
19
58
38 |
47
59
10 |
30
0
30 |
0
0
0 |
|
504
522
540 |
40
260
120 |
33
34
35 |
6
17
28 |
40
37
34 |
14
23
32 |
6
10
15 |
0
30
0 |
196
332
108 |
54
31
7 |
50
4
19 |
17
56
35 |
22
33
45 |
0
30
0 |
0
0
0 |
|
558
576
594 |
340
300
60 |
36
37
39 |
39
50
1 |
31
28
25 |
41
50
59 |
19
24
28 |
30
0
30 |
243
19
154 |
43
19
56 |
34
48
3 |
14
54
33 |
56
8
19 |
30
0
30 |
0
0
0 |
|
612
630
648 |
280
140
0 |
40
41
42 |
12
23
34 |
23
20
17 |
8
17
26 |
33
37
42 |
0
30
0 |
290
66
201 |
32
8
44 |
18
32
47 |
12
51
30 |
31
42
54 |
0
30
0 |
0
0
0 |
|
666
684
702 |
220
80
300 |
43
44
46 |
45
56
7 |
14
11
8 |
35
44
53 |
46
51
55 |
30
0
30 |
337
112
248 |
21
57
33 |
2
16
31 |
10
49
28 |
5
16
28 |
30
0
30 |
0
0
0 |
|
720
738
756 |
160
20
240 |
47
48
49 |
18
29
40 |
6
3
0 |
3
12
21 |
0
4
9 |
0
30
0 |
24
159
295 |
9
46
22 |
46
15 |
7
46
26 |
40
51
3 |
0
30
0 |
0
0
0 |
|
774
792
810 |
100
320
180 |
50
52
53 |
50
1
12 |
57
54
51 |
30
39
48 |
13
18
22 |
30
0
30 |
70
206
342 |
58
34
10 |
30
44
59 |
5
44
23 |
14
26
37 |
30
0
30 |
0
0
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Saturni in annis expansis et horis longitudinis et latitudinis
♄
|
♄ |
||||||||||||||||||||||||||
Longitudo |
Diversitas |
||||||||||||||||||||||||||
Anni expansi |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||||||||||||
1
2
3 |
12
24
36 |
13
26
40 |
23
47
11 |
56
53
49 |
30
1
31 |
30
0
30 |
15
30
45 |
347
335
322 |
32
4
36 |
0
1
2 |
48
37
26 |
50
41
31 |
38
16
55 |
20
40
0 |
|||||||||||||
4
5
6 |
48
61
73 |
53
6
20 |
35
59
23 |
46
42
39 |
2
32
3 |
1
31
1 |
0
15
30 |
310
297
285 |
8
40
12 |
3
4
4 |
15
4
53 |
22
13
3 |
33
11
50 |
20
40
0 |
|||||||||||||
7
8
9 |
85
97
110 |
33
47
0 |
47
11
35 |
35
32
28 |
33
4
34 |
31
2
32 |
45
0
15 |
272
260
247 |
44
16
48 |
5
6
7 |
41
30
19 |
54
45
35 |
28
6
45 |
20
40
0 |
|||||||||||||
10
11
12 |
122
134
146 |
13
27
40 |
59
23
47 |
25
21
18 |
5
35
6 |
2
32
3 |
30
45
0 |
235
222
210 |
20
52
24 |
8
8
9 |
8
57
46 |
26
17
7 |
23
1
40 |
20
40
0 |
|||||||||||||
13
14
15 |
158
171
183 |
54
7
20 |
11
35
59 |
14
11
7 |
36
7
37 |
33
3
33 |
15
30
45 |
197
185
173 |
56
28
0 |
10
11
12 |
34
23
12 |
58
48
39 |
18
56
35 |
20
40
0 |
|||||||||||||
16
17
18 |
195
207
220 |
34
47
1 |
23
47
10 |
4
0
57 |
8
38
9 |
4
34
4 |
0
15
30 |
160
148
135 |
32
4
36 |
13
13
14 |
1
50
39 |
30
20
11 |
13
51
30 |
20
40
0 |
|||||||||||||
Hore |
Longitudo |
Diversitas |
|||||||||||||||||||||||||
1
2
3 |
0
0
0 |
0
0
0 |
5
10
15 |
1
2
4 |
23
47
11 |
48
37
26 |
42
24
6 |
0
0
0 |
2
4
7 |
22
45
8 |
49
38
27 |
19
38
37 |
14
28
42 |
19
38
57 |
|||||||||||||
4
5
6 |
0
0
0 |
0
0
0 |
20
25
30 |
5
6
8 |
35
59
22 |
14
3
52 |
48
30
13 |
0
0
0 |
9
11
14 |
31
54
16 |
17
6
55 |
16
36
55 |
57
11
25 |
16
35
54 |
|||||||||||||
7
8
9 |
0
0
0 |
0
0
0 |
35
40
45 |
9
11
12 |
46
10
34 |
40
29
18 |
55
36
19 |
0
0
0 |
16
19
21 |
39
2
25 |
45
34
23 |
14
33
53 |
40
54
8 |
14
33
52 |
|||||||||||||
10
11
12 |
0
0
0 |
0
0
1 |
50
55
0 |
13
15
16 |
58
21
45 |
7
55
44 |
1
43
25 |
0
0
0 |
23
26
28 |
48
11
33 |
13
2
51 |
12
31
50 |
23
37
51 |
11
30
49 |
|||||||||||||
13
14
15 |
0
0
0 |
1
1
1 |
5
10
15 |
18
19
20 |
9
33
57 |
33
21
10 |
7
49
31 |
0
0
0 |
30
33
35 |
56
19
42 |
41
30
19 |
10
29
48 |
6
20
34 |
9
28
47 |
|||||||||||||
16
17
18 |
0
0
0 |
1
1
1 |
20
25
30 |
22
23
25 |
20
44
8 |
59
47
36 |
13
55
38 |
0
0
0 |
38
40
42 |
5
27
50 |
9
58
47 |
7
27
46 |
49
3
17 |
6
26
45 |
|||||||||||||
19
20
21 |
0
0
0 |
1
1
1 |
35
40
45 |
26
27
29 |
32
56
20 |
25
14
2 |
20
2
44 |
0
0
0 |
45
47
49 |
13
36
59 |
37
26
15 |
5
24
43 |
32
46
0 |
4
33
42 |
|||||||||||||
22
23
24 |
0
0
0 |
1
1
2 |
50
55
0 |
30
32
33 |
43
7
31 |
51
40
28 |
26
8
51 |
0
0
0 |
52
54
57 |
22
44
7 |
5
54
43 |
3
22
41 |
15
29
43 |
1
20
40 |
|||||||||||||
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Saturni in mensibus et diebus longitudinis et diversitatis
♄
|
♄ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
1
2
3 |
0
0
0 |
16
33
50 |
45
31
17 |
44
28
13 |
25
51
16 |
30
0
30 |
28
57
85 |
33
7
41 |
51
43
35 |
50
41
32 |
51
43
35 |
50
40
30 |
0
0
0 |
|
4
5
6 |
4
5
6 |
1
1
1 |
7
23
40 |
2
48
34 |
57
42
26 |
42
7
33 |
0
30
0 |
114
142
171 |
15
49
23 |
27
19
11 |
23
14
5 |
27
19
11 |
20
10
0 |
0
0
0 |
|
7
8
9 |
7
8
9 |
1
2
2 |
57
4
30 |
20
5
51 |
10
55
39 |
58
24
49 |
30
0
30 |
199
228
257 |
57
30
4 |
2
54
46 |
56
46
37 |
2
54
46 |
50
40
30 |
0
0
0 |
|
10
11
12 |
10
11
12 |
2
3
3 |
47
4
21 |
37
23
8 |
24
8
53 |
15
40
6 |
0
30
0 |
285
314
342 |
38
12
46 |
38
30
22 |
28
19
10 |
38
30
22 |
20
10
0 |
0
0
0 |
|
Dies |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
0
0 |
2
4
6 |
0
1
1 |
33
7
40 |
31
2
34 |
28
57
26 |
51
42
33 |
0
1
2 |
57
54
51 |
7
15
23 |
43
27
11 |
41
23
5 |
43
27
11 |
40
20
0 |
|
4
5
6 |
0
0
0 |
8
10
12 |
2
2
3 |
14
47
21 |
5
37
8 |
55
24
53 |
24
15
6 |
3
4
5 |
48
45
42 |
30
38
46 |
54
38
22 |
46
28
10 |
54
38
22 |
40
20
0 |
|
7
8
9 |
0
0
0 |
14
16
18 |
3
4
5 |
54
28
1 |
40
11
43 |
21
50
19 |
57
48
39 |
6
7
8 |
39
37
34 |
54
1
9 |
5
49
33 |
52
33
15 |
5
49
33 |
40
20
0 |
|
10
11
12 |
0
0
0 |
20
22
24 |
5
6
6 |
35
8
42 |
14
46
17 |
48
17
46 |
30
21
12 |
9
10
11 |
31
28
25 |
17
25
32 |
16
0
44 |
57
39
20 |
16
0
44 |
40
20
0 |
|
13
14
15 |
0
0
0 |
26
28
30 |
7
7
8 |
15
49
22 |
49
20
52 |
15
43
12 |
3
54
45 |
12
13
14 |
22
19
16 |
40
48
55 |
27
11
55 |
2
44
25 |
27
11
55 |
40
20
0 |
|
16
17
18 |
0
0
0 |
32
34
36 |
8
9
10 |
56
29
3 |
23
55
26 |
41
10
39 |
36
27
18 |
15
16
17 |
14
11
8 |
3
11
19 |
39
22
6 |
7
49
31 |
38
22
6 |
40
20
0 |
|
19
20
21 |
0
0
0 |
38
40
42 |
10
11
11 |
36
10
44 |
58
29
1 |
8
37
5 |
9
0
51 |
18
19
19 |
5
2
59 |
26
34
42 |
50
33
17 |
12
54
36 |
49
33
17 |
40
20
0 |
|
22
23
24 |
0
0
0 |
44
46
48 |
12
12
13 |
17
51
24 |
32
4
35 |
34
3
32 |
42
33
24 |
20
21
22 |
56
53
51 |
50
57
5 |
1
44
28 |
18
59
41 |
0
44
28 |
40
20
0 |
|
25
26
27 |
0
0
0 |
50
52
54 |
13
14
15 |
58
31
5 |
7
38
9 |
1
30
58 |
15
6
57 |
23
24
25 |
48
45
42 |
13
21
28 |
12
55
39 |
23
4
46 |
11
55
39 |
40
20
0 |
|
28
29
30 |
0
0
1 |
56
58
0 |
15
16
16 |
38
12
45 |
41
12
44 |
27
56
25 |
48
39
30 |
26
27
28 |
39
36
33 |
36
44
51 |
23
7
50 |
28
10
51 |
22
6
50 |
40
20
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Iovis in annis coniunctis longitudinis et diversitatis
♃
|
♃ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
18
36
54 |
186
12
198 |
6
13
20 |
51
43
35 |
51
43
35 |
53
47
40 |
34
9
43 |
30
0
30 |
169
339
148 |
30
1
31 |
33
7
41 |
44
28
13 |
27
54
21 |
0
0
0 |
0
0
0 |
|
72
90
108 |
24
210
36 |
27
34
41 |
27
19
11 |
27
19
11 |
34
27
21 |
18
52
27 |
0
30
0 |
318
127
297 |
2
32
3 |
14
48
22 |
57
42
26 |
48
15
42 |
0
0
0 |
0
0
0 |
|
126
144
162 |
222
48
235 |
48
54
1 |
3
55
47 |
3
55
47 |
15
8
2 |
1
36
10 |
30
0
30 |
106
276
85 |
33
4
35 |
56
29
3 |
11
55
40 |
9
36
3 |
0
0
0 |
0
0
0 |
|
180
198
216 |
61
247
73 |
8
15
22 |
38
30
22 |
38
30
22 |
55
49
42 |
45
19
53 |
0
30
0 |
255
64
234 |
5
36
6 |
37
11
44 |
24
8
53 |
30
57
24 |
0
0
0 |
0
0
0 |
|
234
252
270 |
259
85
271 |
29
36
42 |
14
6
57 |
14
6
58 |
36
30
23 |
28
3
37 |
30
0
30 |
43
213
22 |
37
7
38 |
18
52
26 |
37
22
6 |
51
18
45 |
0
0
0 |
0
0
0 |
|
288
306
324 |
97
283
110 |
49
56
3 |
49
41
33 |
49
42
34 |
17
10
4 |
12
46
21 |
0
30
0 |
192
1
171 |
8
39
10 |
59
33
7 |
51
35
20 |
12
39
6 |
0
0
0 |
0
0
0 |
|
342
360
378 |
296
122
308 |
10
17
24 |
25
17
9 |
25
17
9 |
57
51
45 |
55
30
4 |
30
0
30 |
340
150
319 |
40
11
41 |
41
14
48 |
4
49
33 |
33
0
27 |
0
0
0 |
0
0
0 |
|
396
414
432 |
134
320
146 |
31
37
44 |
1
52
44 |
1
53
45 |
38
32
25 |
39
13
48 |
0
30
0 |
129
298
108 |
12
42
13 |
22
56
29 |
17
2
46 |
54
21
48 |
0
0
0 |
0
0
0 |
|
450
468
486 |
332
158
345 |
51
58
5 |
36
28
20 |
37
29
21 |
19
12
6 |
22
57
31 |
30
0
30 |
277
87
256 |
44
14
45 |
3
37
11 |
31
15
0 |
15
42
9 |
0
0
0 |
0
0
0 |
|
504
522
540 |
171
357
183 |
12
19
25 |
12
4
55 |
13
4
56 |
0
53
47 |
6
40
15 |
0
30
0 |
66
235
45 |
15
46
16 |
44
18
52 |
44
29
13 |
36
3
30 |
0
0
0 |
0
0
0 |
|
558
576
594 |
9
195
21 |
32
39
46 |
47
39
31 |
48
40
32 |
40
34
27 |
49
24
58 |
30
0
30 |
214
24
193 |
47
17
48 |
25
59
33 |
57
42
26 |
57
24
51 |
0
0
0 |
0
0
0 |
|
612
630
648 |
107
34
220 |
53
0
7 |
23
15
7 |
24
16
8 |
21
15
8 |
32
7
42 |
0
30
0 |
3
172
342 |
19
49
20 |
7
40
14 |
11
55
40 |
18
45
12 |
0
0
0 |
0
0
0 |
|
666
684
702 |
46
232
58 |
13
20
27 |
59
50
42 |
0
51
43 |
2
55
49 |
17
51
25 |
30
0
30 |
151
321
130 |
50
21
51 |
48
22
55 |
24
9
53 |
39
7
33 |
0
0
0 |
0
0
0 |
|
720
738
756 |
244
70
256 |
34
41
48 |
34
26
18 |
35
27
19 |
43
36
30 |
0
34
9 |
0
30
0 |
300
109
279 |
22
53
23 |
29
3
36 |
38
22
6 |
0
27
55 |
0
0
0 |
0
0
0 |
|
774
792
810 |
82
269
95 |
55
2
8 |
10
2
53 |
11
3
55 |
23
17
10 |
43
18
53 |
30
0
30 |
88
258
67 |
54
24
55 |
10
44
18 |
51
35
20 |
22
48
15 |
0
0
0 |
0
0
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Iovis in annis expansis et horis longitudinis et diversitatis
♃
|
♃ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni expansi |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
30
60
91 |
20
40
1 |
22
45
8 |
52
45
38 |
52
45
38 |
38
17
55 |
35
10
45 |
329
298
268 |
25
50
15 |
1
3
5 |
52
44
37 |
28
56
24 |
10
20
30 |
0
0
0 |
|
4
5
6 |
121
151
182 |
21
41
2 |
31
54
17 |
31
24
17 |
31
24
17 |
34
12
51 |
20
55
30 |
237
207
176 |
40
5
30 |
7
9
11 |
29
22
14 |
52
20
49 |
40
50
0 |
0
0
0 |
|
7
8
9 |
212
242
273 |
22
43
3 |
40
3
25 |
10
3
56 |
10
3
56 |
30
8
47 |
5
40
15 |
145
115
84 |
55
20
45 |
13
14
16 |
7
59
52 |
17
45
13 |
10
20
30 |
0
0
0 |
|
10
11
12 |
303
333
4 |
23
44
4 |
48
11
34 |
48
41
34 |
49
42
35 |
25
4
43 |
50
25
0 |
54
23
353 |
10
35
0 |
18
20
22 |
44
37
29 |
41
9
38 |
40
50
0 |
0
0
0 |
|
13
14
15 |
34
64
95 |
24
45
5 |
57
20
43 |
27
20
13 |
28
21
14 |
21
59
38 |
35
10
45 |
322
291
261 |
25
50
15 |
24
26
28 |
22
14
7 |
6
34
2 |
10
20
30 |
0
0
0 |
|
16
17
18 |
125
155
186 |
26
46
6 |
6
28
51 |
6
59
51 |
7
0
53 |
17
55
34 |
20
55
30 |
230
200
169 |
40
5
30 |
29
31
33 |
59
51
44 |
30
58
27 |
40
50
0 |
0
0
0 |
|
Hore |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
0
0 |
0
0
0 |
12
24
37 |
28
56
24 |
6
12
18 |
6
13
20 |
56
52
48 |
0
0
0 |
2
4
6 |
15
30
46 |
22
45
7 |
36
13
50 |
56
52
48 |
5
10
15 |
|
4
5
6 |
0
0
0 |
0
1
1 |
49
2
14 |
52
20
48 |
24
30
36 |
27
34
41 |
45
41
37 |
0
0
0 |
9
11
13 |
1
16
32 |
30
53
15 |
27
4
41 |
44
40
36 |
20
25
30 |
|
7
8
9 |
0
0
0 |
1
1
1 |
27
39
52 |
16
44
12 |
42
48
55 |
48
55
2 |
33
30
36 |
0
0
0 |
15
18
20 |
47
3
18 |
38
0
23 |
18
55
32 |
32
28
24 |
35
40
45 |
|
10
11
12 |
0
0
0 |
2
2
2 |
4
17
29 |
41
9
37 |
1
7
13 |
9
16
23 |
22
19
15 |
0
0
0 |
22
24
27 |
33
49
4 |
46
8
31 |
9
46
23 |
20
16
13 |
50
55
0 |
|
13
14
15 |
0
0
0 |
2
2
3 |
42
54
7 |
5
33
1 |
19
25
31 |
30
37
44 |
11
7
4 |
0
0
0 |
29
31
33 |
19
35
50 |
54
16
39 |
0
37
14 |
9
5
1 |
5
10
15 |
|
16
17
18 |
0
0
0 |
3
3
3 |
19
31
44 |
29
57
25 |
37
43
50 |
51
57
4 |
0
56
53 |
0
0
0 |
36
38
40 |
6
21
36 |
1
24
47 |
50
27
4 |
57
53
49 |
20
25
30 |
|
19
20
21 |
0
0
0 |
3
4
4 |
56
9
21 |
53
22
50 |
56
2
8 |
11
18
25 |
49
45
41 |
0
0
0 |
42
45
47 |
52
7
22 |
9
32
54 |
41
18
55 |
45
41
37 |
35
40
45 |
|
22
23
24 |
0
0
0 |
4
4
4 |
34
46
59 |
18
46
14 |
14
20
26 |
32
39
46 |
37
34
31 |
0
0
0 |
49
51
54 |
38
53
9 |
17
40
2 |
32
9
46 |
33
29
26 |
50
55
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Iovis in mensibus et diebus longitudinis et diversitatis
♃
|
♃ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
2
4
7 |
29
59
28 |
37
14
51 |
13
26
40 |
23
46
9 |
15
31
46 |
30
0
30 |
27
54
81 |
4
8
13 |
31
2
34 |
23
46
9 |
13
26
39 |
0
0
0 |
0
0
0 |
|
4
5
6 |
9
12
14 |
58
28
57 |
28
6
43 |
53
6
20 |
33
56
19 |
2
17
33 |
0
30
0 |
108
135
162 |
18
22
27 |
5
36
8 |
32
56
19 |
52
5
18 |
0
0
0 |
0
0
0 |
|
7
8
9 |
17
19
22 |
27
56
26 |
20
57
35 |
33
47
0 |
42
6
29 |
48
4
19 |
30
0
30 |
189
216
243 |
31
36
40 |
39
11
42 |
42
5
28 |
31
44
57 |
0
0
0 |
0
0
0 |
|
10
11
12 |
24
27
29 |
56
25
55 |
12
49
26 |
13
27
40 |
52
15
39 |
35
50
6 |
0
30
0 |
270
297
324 |
45
49
54 |
13
45
16 |
52
15
38 |
10
23
36 |
0
0
0 |
0
0
0 |
|
Dies |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
0
0 |
4
9
14 |
59
58
57 |
14
28
43 |
26
53
20 |
46
33
19 |
31
2
33 |
0
1
2 |
54
48
42 |
9
18
27 |
2
5
8 |
46
32
19 |
26
52
18 |
0
0
0 |
|
4
5
6 |
0
0
0 |
19
24
29 |
56
56
55 |
57
12
26 |
47
13
40 |
6
52
39 |
4
35
6 |
3
4
5 |
36
30
24 |
36
45
54 |
11
13
16 |
5
52
38 |
44
10
36 |
0
0
0 |
|
7
8
9 |
0
0
0 |
34
39
44 |
54
53
53 |
41
55
10 |
7
34
0 |
25
12
58 |
37
8
39 |
6
7
8 |
19
13
7 |
3
12
21 |
19
22
24 |
25
11
57 |
2
28
54 |
0
0
0 |
|
10
11
12 |
0
0
0 |
49
54
49 |
52
51
50 |
24
38
53 |
27
54
21 |
45
31
18 |
10
41
12 |
9
9
10 |
1
55
49 |
30
39
48 |
27
30
33 |
44
30
17 |
20
46
12 |
0
0
0 |
|
13
14
15 |
1
1
1 |
4
9
14 |
50
49
48 |
7
22
36 |
48
14
41 |
4
51
37 |
42
14
45 |
11
12
13 |
43
38
32 |
57
6
15 |
36
38
41 |
3
50
36 |
38
4
30 |
0
0
0 |
|
16
17
18 |
1
1
1 |
19
24
29 |
47
47
46 |
51
5
20 |
8
35
1 |
24
10
57 |
16
47
18 |
14
15
16 |
26
20
14 |
24
33
42 |
44
47
49 |
22
9
55 |
56
22
48 |
0
0
0 |
|
19
20
21 |
1
1
1 |
34
39
44 |
45
44
44 |
34
48
3 |
28
55
22 |
43
30
16 |
49
20
51 |
17
18
18 |
8
3
57 |
51
0
9 |
52
55
58 |
42
28
15 |
14
40
6 |
0
0
0 |
|
22
23
24 |
1
1
1 |
49
54
59 |
43
42
41 |
17
32
46 |
49
15
42 |
3
49
36 |
22
53
24 |
19
20
21 |
51
45
39 |
19
28
37 |
1
3
6 |
1
47
34 |
32
58
24 |
0
0
0 |
|
25
26
27 |
2
2
2 |
4
9
14 |
41
40
39 |
1
15
30 |
9
36
2 |
22
9
55 |
55
26
57 |
22
23
24 |
33
27
22 |
46
55
4 |
9
12
14 |
20
7
53 |
50
16
42 |
0
0
0 |
|
28
29
30 |
2
2
2 |
19
24
29 |
38
37
37 |
44
58
13 |
29
56
23 |
42
28
15 |
28
59
30 |
25
26
27 |
16
10
4 |
13
22
31 |
17
20
23 |
40
26
13 |
8
34
0 |
0
0
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Martis in annis coniunctis longitudinis et diversitatis
♂
|
♂ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
18
36
54 |
203
46
249 |
4
8
13 |
20
40
0 |
17
35
52 |
34
9
44 |
43
27
10 |
30
0
30 |
152
305
97 |
33
6
39 |
5
10
15 |
18
37
56 |
45
31
17 |
51
42
33 |
0
0
0 |
|
72
90
108 |
92
295
138 |
17
21
26 |
21
41
1 |
10
27
45 |
18
53
28 |
54
37
21 |
0
30
0 |
250
42
195 |
12
45
18 |
21
26
31 |
15
33
52 |
3
49
35 |
24
15
6 |
0
0
0 |
|
126
144
162 |
341
184
27 |
30
34
39 |
22
42
2 |
3
20
38 |
3
37
12 |
4
48
31 |
30
0
30 |
347
140
292 |
51
24
57 |
37
42
47 |
11
30
48 |
20
6
52 |
57
48
39 |
0
0
0 |
|
170
198
216 |
280
73
276 |
43
47
52 |
22
43
3 |
55
13
30 |
27
21
56 |
15
58
42 |
0
30
0 |
85
238
30 |
30
3
37 |
53
58
3 |
7
26
45 |
38
24
10 |
30
21
12 |
0
0
0 |
|
234
252
270 |
119
323
166 |
56
0
5 |
23
43
4 |
48
6
23 |
31
6
40 |
25
19
52 |
30
0
30 |
183
335
127 |
10
43
16 |
9
14
19 |
3
22
41 |
56
41
27 |
3
54
45 |
0
0
0 |
|
288
306
324 |
8
212
55 |
9
13
18 |
24
44
5 |
41
58
16 |
15
50
25 |
36
19
3 |
0
30
0 |
280
73
225 |
49
22
55 |
25
30
35 |
0
18
37 |
13
59
45 |
36
27
18 |
0
0
0 |
|
342
360
378 |
258
101
304 |
22
26
31 |
25
45
6 |
33
51
9 |
59
34
9 |
46
30
13 |
30
0
30 |
18
171
323 |
28
1
34 |
40
46
51 |
56
15
34 |
31
17
2 |
9
0
51 |
0
0
0 |
|
396
414
432 |
147
350
193 |
35
39
44 |
26
46
7 |
26
44
1 |
43
18
53 |
57
40
23 |
0
30
0 |
116
268
61 |
7
41
14 |
56
2
7 |
52
11
30 |
48
34
20 |
42
33
24 |
0
0
0 |
|
450
468
486 |
36
239
82 |
48
52
57 |
27
47
7 |
19
37
55 |
28
2
37 |
7
51
34 |
30
0
30 |
213
6
158 |
47
20
53 |
12
18
23 |
49
7
26 |
6
52
37 |
15
6
57 |
0
0
0 |
|
504
522
540 |
286
129
332 |
1
5
10 |
28
48
8 |
12
29
47 |
12
47
21 |
18
1
45 |
0
30
0 |
311
103
256 |
26
59
32 |
28
34
39 |
45
4
22 |
23
9
55 |
48
39
30 |
0
0
0 |
|
558
576
594 |
175
18
221 |
14
18
23 |
29
49
9 |
4
22
40 |
56
31
5 |
28
12
55 |
30
0
30 |
49
201
354 |
5
38
11 |
44
50
55 |
41
0
19 |
41
27
13 |
21
12
3 |
0
0
0 |
|
612
630
648 |
64
267
110 |
27
31
36 |
29
50
10 |
57
15
32 |
40
15
50 |
39
22
6 |
0
30
0 |
146
299
91 |
45
18
51 |
0
5
11 |
37
56
15 |
58
44
30 |
54
45
36 |
0
0
0 |
|
666
684
702 |
313
156
359 |
40
42
49 |
30
51
11 |
50
7
25 |
24
59
34 |
49
33
16 |
30
0
30 |
244
36
189 |
24
57
30 |
16
21
27 |
34
53
11 |
16
2
48 |
27
18
9 |
0
0
0 |
|
720
738
756 |
202
45
249 |
53
57
2 |
31
52
12 |
43
0
17 |
9
43
18 |
0
43
27 |
0
30
0 |
342
134
287 |
3
36
9 |
32
37
43 |
30
49
8 |
34
19
5 |
0
51
42 |
0
0
0 |
|
774
792
810 |
92
295
138 |
6
10
15 |
32
52
13 |
35
53
11 |
53
27
2 |
10
54
37 |
30
0
30 |
79
232
24 |
42
15
48 |
48
53
59 |
26
45
4 |
51
37
23 |
33
34
15 |
0
0
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Martis in annis expansis et horis longitudinis et diversitatis
♂
|
♂ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni expansi |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
191
22
213 |
16
33
50 |
54
48
43 |
27
55
22 |
38
17
55 |
35
11
47 |
45
30
15 |
168
336
145 |
28
57
25 |
30
0
30 |
17
35
53 |
42
25
7 |
32
5
38 |
50
40
30 |
|
4
5
6 |
45
236
67 |
7
24
41 |
37
32
26 |
50
18
45 |
34
12
51 |
23
58
34 |
0
45
30 |
313
122
290 |
54
22
51 |
1
31
1 |
10
28
46 |
50
32
15 |
11
44
17 |
20
10
0 |
|
7
8
9 |
258
90
281 |
58
15
32 |
21
15
10 |
13
41
8 |
30
8
47 |
10
46
21 |
15
0
45 |
99
167
76 |
19
48
16 |
32
2
32 |
3
21
39 |
57
40
22 |
49
22
55 |
50
40
30 |
|
10
11
12 |
112
304
135 |
49
5
22 |
4
59
53 |
36
4
37 |
25
4
43 |
57
33
9 |
30
15
0 |
244
53
221 |
45
13
42 |
2
33
3 |
57
14
32 |
5
48
30 |
28
1
34 |
20
10
0 |
|
13
14
15 |
326
157
349 |
39
56
13 |
47
42
36 |
59
27
54 |
21
0
38 |
44
20
56 |
45
30
15 |
30
198
7 |
10
39
7 |
33
4
34 |
50
7
25 |
13
55
38 |
6
39
12 |
50
40
30 |
|
16
17
18 |
180
11
203 |
30
47
4 |
31
25
20 |
22
49
17 |
17
56
34 |
32
7
43 |
0
45
30 |
175
344
152 |
36
4
33 |
4
35
5 |
43
1
18 |
20
3
45 |
45
18
51 |
20
10
0 |
|
Hore |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
0
0 |
1
2
3 |
18
37
55 |
36
13
49 |
32
4
36 |
14
29
43 |
38
17
56 |
0
0
0 |
1
2
3 |
9
18
27 |
14
28
42 |
10
21
32 |
48
36
25 |
22
45
7 |
|
4
5
6 |
0
0
0 |
5
6
7 |
14
33
51 |
26
2
39 |
8
41
13 |
58
13
27 |
35
14
53 |
0
0
0 |
4
5
6 |
36
46
55 |
56
10
26 |
43
54
4 |
13
1
50 |
30
52
14 |
|
7
8
9 |
0
0
0 |
9
10
11 |
10
28
47 |
15
52
28 |
45
17
50 |
42
57
11 |
32
11
49 |
0
0
0 |
8
9
10 |
4
13
23 |
39
53
7 |
15
26
37 |
38
26
15 |
36
59
22 |
|
10
11
12 |
0
0
0 |
13
14
15 |
6
24
43 |
5
41
18 |
22
54
26 |
26
41
55 |
28
7
46 |
0
0
0 |
11
12
13 |
32
41
50 |
21
35
50 |
48
58
9 |
3
52
40 |
44
7
29 |
|
13
14
15 |
0
0
0 |
17
18
19 |
1
20
39 |
54
31
8 |
59
31
3 |
10
25
39 |
25
4
43 |
0
0
0 |
15
16
17 |
0
9
18 |
4
18
32 |
20
31
42 |
28
17
5 |
51
14
36 |
|
16
17
18 |
0
0
0 |
20
22
23 |
57
16
34 |
44
21
57 |
35
8
40 |
54
9
23 |
22
0
39 |
0
0
0 |
18
19
20 |
27
37
46 |
46
1
15 |
52
3
14 |
53
42
30 |
59
21
43 |
|
19
20
21 |
0
0
0 |
24
26
27 |
53
12
30 |
34
10
47 |
12
44
17 |
38
52
7 |
18
57
36 |
0
0
0 |
21
23
24 |
55
4
13 |
29
43
57 |
25
36
46 |
19
7
55 |
6
28
51 |
|
22
23
24 |
0
0
0 |
28
30
31 |
49
8
26 |
23
0
37 |
49
21
53 |
22
36
51 |
15
54
33 |
0
0
0 |
25
26
27 |
23
32
41 |
11
26
40 |
57
8
19 |
44
32
20 |
13
36
58 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Martis in mensibus et diebus longitudinis et diversitatis
♂
|
♂ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
15
31
47 |
43
26
9 |
18
36
55 |
26
53
20 |
55
51
47 |
46
33
19 |
30
0
30 |
13
27
41 |
50
41
32 |
50
40
30 |
9
19
29 |
40
20
1 |
29
58
27 |
0
0
0 |
|
4
5
6 |
52
78
94 |
53
36
19 |
13
32
50 |
47
14
41 |
43
38
34 |
6
52
39 |
0
30
0 |
55
69
83 |
23
14
5 |
20
10
0 |
38
48
58 |
41
22
2 |
56
25
54 |
0
0
0 |
|
7
8
9 |
110
125
141 |
3
46
29 |
9
27
46 |
8
35
2 |
30
26
21 |
25
12
58 |
30
0
30 |
96
110
124 |
55
46
37 |
51
41
31 |
7
17
26 |
43
23
4 |
23
52
21 |
0
0
0 |
|
10
11
12 |
157
172
188 |
13
55
39 |
4
22
41 |
29
56
23 |
17
13
9 |
45
31
18 |
0
30
0 |
138
152
166 |
28
19
10 |
21
11
1 |
36
46
55 |
44
25
5 |
50
19
48 |
0
0
0 |
|
Dies |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
1
1 |
31
2
34 |
26
53
19 |
36
13
50 |
53
47
41 |
51
43
34 |
33
6
39 |
0
0
1 |
27
55
23 |
41
23
5 |
40
20
0 |
19
38
58 |
20
41
2 |
58
56
54 |
|
4
5
6 |
2
2
3 |
5
37
8 |
46
13
39 |
27
4
41 |
35
29
23 |
26
17
9 |
12
45
18 |
1
2
2 |
50
18
46 |
46
28
10 |
41
21
1 |
17
36
56 |
23
44
5 |
52
50
48 |
|
7
8
9 |
3
4
4 |
40
11
42 |
6
32
59 |
18
55
32 |
17
10
4 |
0
52
43 |
51
24
57 |
3
3
4 |
13
41
9 |
51
33
15 |
42
22
2 |
15
34
54 |
26
47
8 |
46
44
42 |
|
10
11
12 |
5
5
6 |
14
45
17 |
26
52
19 |
8
45
22 |
58
52
46 |
35
27
18 |
30
3
36 |
4
5
5 |
36
4
32 |
56
38
20 |
43
23
3 |
13
32
52 |
29
50
11 |
40
38
36 |
|
13
14
15 |
6
7
7 |
48
20
51 |
45
12
39 |
59
36
13 |
40
34
27 |
10
1
53 |
9
42
15 |
6
6
6 |
0
27
55 |
1
43
25 |
44
24
4 |
11
30
50 |
32
53
14 |
34
32
30 |
|
16
17
18 |
8
8
9 |
23
54
25 |
5
32
59 |
50
27
4 |
21
15
9 |
44
36
27 |
48
21
54 |
7
7
8 |
23
50
18 |
6
48
30 |
45
25
5 |
9
28
48 |
35
56
17 |
28
26
24 |
|
19
20
21 |
9
10
11 |
57
28
0 |
25
52
19 |
41
17
54 |
3
57
51 |
19
11
2 |
27
0
33 |
8
9
9 |
46
13
41 |
11
53
35 |
46
26
6 |
7
26
46 |
38
59
20 |
22
20
18 |
|
22
23
24 |
11
12
12 |
32
3
34 |
45
12
38 |
31
8
45 |
44
38
32 |
54
45
37 |
6
39
12 |
10
10
11 |
9
36
4 |
16
58
40 |
47
27
7 |
5
25
44 |
41
2
23 |
16
14
12 |
|
25
26
27 |
13
13
14 |
6
37
8 |
5
31
58 |
22
59
36 |
26
20
14 |
28
20
11 |
45
18
51 |
11
12
12 |
32
0
27 |
21
3
45 |
48
28
8 |
3
23
42 |
44
5
26 |
10
8
6 |
|
28
29
30 |
14
15
15 |
40
11
43 |
25
51
28 |
13
50
26 |
8
1
55 |
3
54
46 |
24
57
30 |
12
13
13 |
55
23
50 |
26
8
50 |
49
29
9 |
1
21
40 |
47
8
29 |
4
2
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Veneris in annis coniunctis longitudinis et diversitatis
♀
|
♀ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
18
36
54 |
355
351
346 |
37
14
52 |
25
51
16 |
36
12
49 |
20
41
1 |
34
9
43 |
30
0
30 |
90
180
271 |
27
55
23 |
44
29
13 |
34
8
43 |
23
47
11 |
46
33
19 |
30
0
30 |
|
72
90
108 |
342
338
333 |
29
7
44 |
42
8
33 |
25
1
38 |
22
42
3 |
12
52
27 |
0
30
0 |
1
92
182 |
50
18
46 |
58
42
27 |
17
51
25 |
35
58
22 |
6
52
39 |
0
30
0 |
|
126
144
162 |
329
324
320 |
21
59
36 |
59
24
50 |
14
50
17 |
24
45
5 |
1
36
10 |
30
0
30 |
273
3
94 |
14
41
9 |
12
56
41 |
0
35
9 |
46
10
33 |
25
12
58 |
30
0
30 |
|
180
198
216 |
316
311
307 |
14
51
29 |
16
41
7 |
3
39
16 |
25
46
6 |
45
19
53 |
0
30
0 |
184
275
5 |
37
5
32 |
25
10
54 |
43
18
52 |
57
21
45 |
45
31
18 |
0
30
0 |
|
234
252
270 |
303
298
294 |
6
43
21 |
32
58
24 |
52
28
5 |
27
48
8 |
28
3
37 |
30
0
30 |
96
186
276 |
0
28
56 |
39
24
8 |
27
1
35 |
9
32
56 |
4
51
37 |
30
0
30 |
|
288
306
324 |
289
285
281 |
58
36
13 |
49
15
40 |
41
17
54 |
29
49
10 |
12
46
21 |
0
30
0 |
7
97
188 |
23
51
19 |
53
37
22 |
10
44
19 |
20
43
7 |
24
10
57 |
0
30
0 |
|
342
360
378 |
276
272
268 |
51
28
5 |
6
32
57 |
30
6
43 |
30
51
12 |
55
30
4 |
30
0
30 |
278
9
99 |
47
14
42 |
6
51
36 |
53
27
2 |
31
55
19 |
43
30
16 |
30
0
30 |
|
396
414
432 |
263
259
254 |
43
20
58 |
23
48
14 |
19
55
32 |
32
53
13 |
39
13
48 |
0
30
0 |
190
280
11 |
10
38
5 |
20
5
49 |
36
11
45 |
43
6
30 |
3
49
36 |
0
30
0 |
|
450
468
486 |
250
246
241 |
35
13
50 |
40
5
31 |
8
44
21 |
34
54
15 |
22
57
31 |
30
0
30 |
101
192
282 |
33
1
29 |
34
18
3 |
19
54
28 |
54
18
41 |
22
9
55 |
30
0
30 |
|
504
522
540 |
237
233
228 |
27
4
42 |
56
22
48 |
57
33
10 |
36
56
17 |
6
40
15 |
0
30
0 |
12
103
193 |
56
24
52 |
48
32
17 |
3
37
11 |
5
29
53 |
42
28
15 |
0
30
0 |
|
558
576
594 |
224
219
215 |
20
57
35 |
13
39
4 |
46
22
59 |
37
58
18 |
49
24
58 |
30
0
30 |
284
14
105 |
20
47
15 |
1
46
30 |
46
20
55 |
17
40
4 |
1
48
34 |
30
0
30 |
|
612
630
648 |
211
206
202 |
12
49
27 |
30
56
21 |
35
12
48 |
38
0
20 |
33
7
42 |
0
30
0 |
195
286
16 |
43
11
38 |
15
0
44 |
29
3
38 |
28
52
15 |
21
7
54 |
0
30
0 |
|
666
684
702 |
198
193
189 |
4
42
19 |
47
13
38 |
24
1
37 |
41
1
22 |
16
51
25 |
30
0
30 |
107
197
288 |
6
34
1 |
29
13
58 |
12
47
21 |
39
3
27 |
40
27
13 |
30
0
30 |
|
720
738
756 |
184
180
176 |
57
34
11 |
4
29
55 |
13
50
26 |
43
3
24 |
0
34
9 |
0
30
0 |
18
108
199 |
29
57
25 |
42
27
12 |
55
30
4 |
51
14
38 |
0
46
33 |
0
30
0 |
|
774
792
810 |
171
167
163 |
49
26
4 |
21
46
12 |
2
39
15 |
44
5
25 |
43
18
52 |
30
0
30 |
289
20
110 |
52
20
48 |
56
41
25 |
39
13
47 |
2
26
49 |
19
6
52 |
30
0
30 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Veneris in annis expansis et horis longitudinis et diversitatis
♀
|
♀ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni expansi |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
359
359
359 |
45
30
16 |
24
49
14 |
45
30
16 |
21
42
3 |
8
17
25 |
35
10
45 |
225
90
315 |
1
3
4 |
32
4
37 |
28
57
25 |
34
9
43 |
39
18
57 |
15
30
45 |
|
4
5
6 |
359
358
358 |
1
46
32 |
39
3
28 |
1
46
32 |
24
45
6 |
34
42
51 |
20
55
30 |
180
45
270 |
6
7
9 |
9
42
14 |
54
22
51 |
18
53
27 |
37
16
55 |
0
15
30 |
|
7
8
9 |
358
358
357 |
17
3
48 |
53
18
42 |
17
2
48 |
28
49
10 |
0
8
17 |
5
40
15 |
135
0
225 |
10
12
13 |
46
19
52 |
20
48
17 |
2
37
11 |
34
14
53 |
45
0
15 |
|
10
11
12 |
357
357
357 |
34
19
4 |
7
32
56 |
33
18
4 |
31
52
13 |
25
34
43 |
50
25
0 |
90
315
180 |
15
16
18 |
24
57
29 |
45
14
42 |
46
21
55 |
32
11
51 |
30
45
0 |
|
13
14
15 |
356
356
356 |
50
35
21 |
21
46
11 |
49
34
20 |
34
56
17 |
51
0
8 |
35
10
45 |
45
270
135 |
20
21
23 |
2
34
7 |
11
40
8 |
30
5
39 |
30
9
48 |
15
30
45 |
|
16
17
18 |
356
355
355 |
6
52
37 |
36
0
25 |
5
50
36 |
38
59
20 |
17
25
34 |
20
55
30 |
0
225
90 |
24
26
27 |
39
12
44 |
37
5
34 |
14
49
23 |
28
7
46 |
0
15
30 |
|
Hore |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
0
0 |
2
4
7 |
37
55
23 |
50
41
32 |
43
26
9 |
3
6
9 |
1
2
3 |
0
0
0 |
1
3
4 |
32
4
27 |
28
57
25 |
34
9
44 |
42
25
8 |
58
57
56 |
|
4
5
6 |
0
0
0 |
9
12
14 |
51
19
47 |
22
13
4 |
52
25
18 |
12
15
18 |
5
6
7 |
0
0
0 |
6
7
9 |
9
42
14 |
54
22
51 |
18
53
28 |
51
34
17 |
54
53
52 |
|
7
8
9 |
0
0
0 |
17
19
22 |
14
42
10 |
55
45
36 |
1
44
27 |
21
24
27 |
9
10
11 |
0
0
0 |
10
11
13 |
47
19
52 |
20
48
17 |
3
37
12 |
0
43
26 |
50
49
48 |
|
10
11
12 |
0
0
0 |
24
27
29 |
38
6
34 |
27
17
8 |
10
53
36 |
30
33
36 |
12
14
15 |
0
0
0 |
15
16
18 |
24
57
29 |
45
14
42 |
46
21
56 |
9
52
35 |
47
45
44 |
|
13
14
15 |
0
0
0 |
32
34
36 |
1
29
57 |
59
50
40 |
19
2
45 |
39
42
45 |
16
18
19 |
0
0
0 |
20
21
23 |
2
34
7 |
11
40
8 |
31
6
40 |
18
1
44 |
43
41
40 |
|
16
17
18 |
0
0
0 |
39
41
44 |
25
53
21 |
31
22
12 |
28
11
54 |
48
51
54 |
20
21
23 |
0
0
0 |
24
26
27 |
39
12
44 |
37
5
34 |
15
50
24 |
27
10
53 |
38
37
36 |
|
19
20
21 |
0
0
0 |
46
49
51 |
49
16
44 |
3
54
45 |
37
21
4 |
57
0
3 |
24
25
27 |
0
0
0 |
29
30
32 |
17
49
22 |
2
31
0 |
59
34
9 |
36
19
2 |
35
33
32 |
|
22
23
24 |
0
0
0 |
53
56
59 |
12
40
8 |
35
26
17 |
47
30
33 |
6
9
12 |
28
29
31 |
0
0
0 |
33
35
36 |
54
26
59 |
28
57
25 |
43
18
53 |
45
28
11 |
31
29
28 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Veneris in mensibus et diebus longitudinis et diversitatis
♀
|
♀
|
|||||||||||||||
Longitudo |
Diversitas |
|||||||||||||||
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||
1
2
3 |
29
59
88 |
34
8
42 |
8
17
25 |
36
13
49 |
36
12
48 |
15
31
46 |
30
0
30 |
18
36
55 |
29
59
29 |
42
25
8 |
56
52
49 |
35
11
47 |
44
28
12 |
0
0
0 |
||
4
5
6 |
118
147
177 |
16
50
24 |
34
43
51 |
26
3
39 |
25
1
37 |
2
17
33 |
0
30
0 |
73
92
110 |
58
58
28 |
51
34
18 |
46
42
39 |
22
58
34 |
56
40
24 |
0
0
0 |
||
7
8
9 |
206
2
245 |
59
33
7 |
0
8
17 |
16
52
29 |
13
50
26 |
48
4
19 |
30
0
30 |
129
147
166 |
28
57
27 |
0
43
26 |
36
32
29 |
10
45
21 |
8
52
36 |
0
0
0 |
||
10
11
12 |
295
338
354 |
41
15
49 |
26
34
43 |
6
42
19 |
2
38
15 |
35
50
6 |
0
30
0 |
184
203
221 |
27
56
26 |
9
52
35 |
25
22
19 |
57
33
8 |
20
4
48 |
0
0
0 |
||
Dies |
Longitudo |
Diversitas |
||||||||||||||
1
2
3 |
0
1
2 |
59
58
57 |
8
16
24 |
17
34
51 |
13
26
39 |
12
25
37 |
31
2
33 |
0
1
1 |
36
13
50 |
59
58
58 |
25
51
17 |
53
46
39 |
11
22
34 |
28
56
24 |
||
4
5
6 |
3
4
5 |
56
55
54 |
33
41
49 |
8
26
43 |
52
6
19 |
50
2
15 |
4
35
6 |
2
3
3 |
27
4
41 |
57
57
56 |
43
9
35 |
32
25
19 |
45
57
8 |
52
20
48 |
||
7
8
9 |
6
7
8 |
53
53
52 |
58
6
14 |
0
17
34 |
32
45
58 |
27
40
52 |
37
8
39 |
4
4
5 |
18
55
32 |
56
55
54 |
1
27
52 |
12
5
58 |
20
31
43 |
16
44
12 |
||
10
11
12 |
9
10
11 |
51
50
49 |
22
31
39 |
52
9
26 |
12
25
38 |
5
17
30 |
10
41
12 |
6
6
7 |
9
46
23 |
54
53
53 |
18
44
10 |
51
45
38 |
54
6
17 |
40
8
36 |
||
13
14
15 |
12
13
14 |
48
47
47 |
47
56
4 |
43
1
18 |
51
4
18 |
42
55
7 |
43
14
45 |
8
8
9 |
0
37
14 |
52
52
51 |
36
2
28 |
31
24
17 |
29
40
52 |
4
32
0 |
||
16
17
18 |
15
16
17 |
46
45
44 |
12
20
29 |
35
52
9 |
31
44
57 |
20
32
45 |
16
47
18 |
9
10
11 |
51
28
5 |
50
50
49 |
54
20
45 |
11
4
57 |
3
14
26 |
28
56
24 |
||
19
20
21 |
18
19
20 |
43
42
41 |
37
45
54 |
27
44
1 |
10
24
37 |
57
10
22 |
49
20
51 |
11
12
12 |
42
19
56 |
49
48
48 |
11
37
3 |
50
43
37 |
37
49
0 |
52
20
48 |
||
22
23
24 |
21
22
23 |
41
40
39 |
2
10
18 |
18
36
53 |
50
3
17 |
35
47
0 |
22
53
24 |
13
14
14 |
33
10
47 |
47
46
46 |
29
55
21 |
30
23
16 |
12
23
35 |
16
44
12 |
||
25
26
27 |
24
25
26 |
38
37
36 |
27
35
43 |
10
27
44 |
30
43
56 |
12
25
37 |
55
26
57 |
15
16
16 |
24
50
38 |
45
45
44 |
47
13
38 |
9
2
56 |
46
58
9 |
40
8
36 |
||
28
29
30 |
27
28
29 |
35
35
34 |
52
0
8 |
2
19
36 |
9
23
36 |
50
2
15 |
28
59
30 |
17
17
18 |
15
52
29 |
44
43
42 |
4
30
56 |
49
42
35 |
21
32
44 |
4
32
0 |
||
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Mercurii in annis coniunctis longitudinis et diversitatis
☿
|
☿ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Anni coniuncti |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
18
36
54 |
355
351
346 |
37
14
52 |
25
51
16 |
36
12
49 |
20
41
1 |
34
8
43 |
30
0
30 |
251
142
33 |
0
1
2 |
45
31
17 |
45
31
17 |
53
47
41 |
45
30
15 |
0
0
0 |
|
72
90
108 |
342
338
333 |
29
6
44 |
42
8
33 |
25
1
38 |
22
42
3 |
18
52
27 |
0
30
0 |
284
175
66 |
3
3
4 |
3
48
34 |
3
49
35 |
35
28
22 |
0
45
30 |
0
0
0 |
|
126
144
162 |
329
324
320 |
21
59
36 |
58
24
50 |
14
50
27 |
24
45
5 |
1
36
10 |
30
0
30 |
317
208
99 |
5
6
6 |
20
6
51 |
21
7
53 |
16
10
3 |
15
0
45 |
0
0
0 |
|
180
198
216 |
316
311
307 |
14
51
28 |
16
41
7 |
3
39
16 |
25
46
6 |
45
19
54 |
0
30
0 |
350
241
132 |
7
8
9 |
37
23
9 |
38
24
10 |
57
51
45 |
30
15
0 |
0
0
0 |
|
234
252
270 |
303
298
294 |
6
43
21 |
32
58
24 |
52
28
5 |
27
48
8 |
28
3
37 |
30
0
30 |
23
274
165 |
9
10
11 |
54
40
26 |
56
42
28 |
38
32
26 |
45
30
15 |
0
0
0 |
|
288
306
324 |
289
285
281 |
58
36
13 |
49
15
40 |
41
17
54 |
29
49
10 |
12
46
21 |
0
30
0 |
56
307
198 |
12
12
13 |
12
58
43 |
14
0
46 |
20
13
7 |
0
45
30 |
0
0
0 |
|
342
360
378 |
276
272
268 |
51
28
5 |
6
32
57 |
30
6
43 |
30
51
12 |
55
30
4 |
30
0
30 |
89
340
231 |
14
15
16 |
29
15
1 |
32
17
3 |
1
55
48 |
15
0
45 |
0
0
0 |
|
396
414
432 |
263
259
254 |
43
20
58 |
23
48
14 |
19
55
32 |
32
53
13 |
39
13
48 |
0
30
0 |
122
13
264 |
16
17
18 |
46
32
18 |
49
35
21 |
42
36
30 |
30
15
0 |
0
0
0 |
|
450
468
486 |
250
246
241 |
35
13
50 |
40
5
31 |
8
44
21 |
34
54
15 |
22
57
31 |
30
0
30 |
155
46
297 |
19
19
20 |
4
49
35 |
7
53
39 |
23
17
11 |
45
30
15 |
0
0
0 |
|
504
522
540 |
237
233
228 |
27
5
42 |
57
22
48 |
57
33
10 |
36
56
17 |
6
40
15 |
0
30
0 |
188
79
330 |
21
22
22 |
21
7
52 |
25
10
56 |
5
58
52 |
0
45
30 |
0
0
0 |
|
558
576
594 |
224
219
215 |
20
57
35 |
13
39
4 |
46
22
59 |
37
58
18 |
49
24
58 |
30
0
30 |
221
112
3 |
23
24
25 |
38
24
10 |
42
28
14 |
46
40
33 |
15
0
45 |
0
0
0 |
|
612
630
648 |
211
206
202 |
12
49
27 |
30
56
21 |
35
12
48 |
39
0
20 |
33
7
42 |
0
30
0 |
254
145
36 |
25
26
27 |
56
41
27 |
0
46
32 |
27
21
15 |
30
15
0 |
0
0
0 |
|
666
684
702 |
198
193
189 |
4
42
19 |
47
13
38 |
24
1
37 |
41
1
22 |
16
51
25 |
30
0
30 |
287
178
69 |
28
28
29 |
13
59
44 |
18
4
49 |
8
2
56 |
45
30
15 |
0
0
0 |
|
720
738
756 |
184
180
176 |
57
34
11 |
4
29
55 |
13
50
26 |
43
3
24 |
0
34
9 |
0
30
0 |
320
211
102 |
30
31
32 |
30
16
2 |
35
21
7 |
50
43
37 |
0
45
30 |
0
0
0 |
|
774
792
810 |
171
167
163 |
49
26
4 |
21
46
12 |
2
39
15 |
44
5
25 |
43
18
52 |
30
0
30 |
353
244
135 |
32
33
34 |
47
33
19 |
53
39
25 |
31
25
18 |
15
0
45 |
0
0
0 |
|
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Mercurii in annis expansis et horis longitudinis et diversitatis
Tabula motuum stellarum quinque mediorum longitudinis et diversitatis
Motus Mercurii in mensibus et diebus longitudinis et diversitatis
☿
|
☿ |
||||||||||||||
Longitudo |
Diversitas |
||||||||||||||
Menses |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Partes |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
1
2
3 |
29
59
88 |
34
8
42 |
8
17
25 |
36
13
49 |
36
12
48 |
15
31
46 |
30
0
30 |
93
186
279 |
12
24
36 |
3
6
10 |
29
59
19 |
47
35
23 |
55
50
45 |
0
0
0 |
|
4
5
6 |
118
147
177 |
16
50
24 |
34
43
51 |
26
3
39 |
25
1
37 |
2
17
33 |
0
30
0 |
12
106
199 |
48
0
12 |
13
17
20 |
59
28
58 |
11
59
47 |
40
35
30 |
0
0
0 |
|
7
8
9 |
206
236
266 |
59
33
7 |
0
8
17 |
16
52
29 |
13
50
26 |
48
4
19 |
30
0
30 |
292
25
118 |
24
36
48 |
24
27
31 |
28
58
28 |
35
23
11 |
25
20
15 |
0
0
0 |
|
10
11
12 |
295
325
354 |
41
15
49 |
26
34
43 |
6
42
19 |
2
38
15 |
35
50
6 |
0
30
0 |
212
305
38 |
0
12
24 |
34
38
41 |
57
27
57 |
59
47
35 |
10
5
0 |
0
0
0 |
|
Dies |
Longitudo |
Diversitas |
|||||||||||||
1
2
3 |
0
1
2 |
59
58
57 |
8
16
24 |
17
34
51 |
13
26
39 |
12
25
37 |
31
2
33 |
3
6
9 |
6
12
19 |
24
48
12 |
6
13
20 |
59
59
58 |
35
11
47 |
50
40
30 |
|
4
5
6 |
3
4
5 |
56
55
54 |
33
41
49 |
8
26
43 |
52
6
19 |
50
2
15 |
4
35
6 |
12
15
18 |
25
32
38 |
36
0
24 |
27
34
41 |
58
57
57 |
23
59
35 |
20
10
0 |
|
7
8
9 |
6
7
8 |
53
53
52 |
58
6
14 |
0
17
34 |
32
45
58 |
27
40
52 |
37
8
39 |
21
24
27 |
44
51
57 |
48
12
37 |
48
55
2 |
57
56
56 |
10
46
22 |
50
40
30 |
|
10
11
12 |
9
10
11 |
51
50
49 |
22
31
39 |
52
9
26 |
12
25
38 |
5
17
30 |
10
41
12 |
31
34
37 |
4
10
16 |
1
25
49 |
9
16
23 |
55
55
55 |
58
34
10 |
20
10
0 |
|
13
14
15 |
12
13
14 |
48
47
47 |
47
56
4 |
43
1
18 |
51
4
18 |
42
55
7 |
43
14
45 |
40
43
46 |
23
29
36 |
13
37
1 |
30
37
44 |
54
54
53 |
45
21
57 |
50
40
30 |
|
16
17
18 |
15
16
17 |
46
45
44 |
12
20
29 |
35
52
9 |
31
44
57 |
20
32
45 |
16
47
18 |
49
52
55 |
42
48
55 |
25
49
14 |
51
58
5 |
53
53
52 |
32
9
45 |
20
10
0 |
|
19
20
21 |
18
19
20 |
43
42
41 |
37
45
54 |
27
44
1 |
10
24
37 |
57
10
22 |
49
20
51 |
59
62
65 |
1
8
14 |
38
2
26 |
12
19
26 |
52
51
51 |
20
56
32 |
50
40
30 |
|
22
23
24 |
21
22
23 |
41
40
39 |
2
10
18 |
18
36
53 |
50
3
17 |
35
47
0 |
22
53
24 |
68
71
74 |
20
27
33 |
50
14
38 |
33
40
47 |
51
50
50 |
8
44
20 |
20
10
0 |
|
25
26
27 |
24
25
26 |
38
37
36 |
27
35
43 |
10
27
44 |
30
43
56 |
12
25
37 |
55
26
57 |
77
80
83 |
40
46
52 |
2
27
51 |
54
1
8 |
49
49
49 |
55
31
7 |
50
40
30 |
|
28
29
30 |
27
28
29 |
35
35
34 |
52
0
8 |
2
19
36 |
9
23
36 |
50
2
15 |
28
59
30 |
86
90
93 |
59
5
12 |
15
39
3 |
15
22
29 |
48
48
47 |
43
19
55 |
20
10
0 |
|
〈IX.5〉 Capitulum quintum: De his quorum premissio est necessaria in modis quinque stellarum erraticarum
Et postquam posuimus que prediximus, oportet ut sequamur illud loquendo de diversitatibus stellarum quinque erraticarum que sunt in pertransitionibus earum in longitudine. In summa autem modorum secundum quod posuimus motus (namque simplices sufficientes in hac scientia) sunt duo motus, sicut diximus. Quorum unus est qui est super orbes egredientium centrorum a centro orbis signorum, et alter qui est super orbes quorum centra est centrum orbis signorum. Et ipsi revolvunt orbes revolutionis. Et similiter quod videtur cuiusque stellarum ex diversitate non est nisi due diversitates. Quarum una est que videtur apud partes orbis signorum, et altera que videtur propter figuras earum apud Solem. Sed in hac quidem inveniemus ex diversitatibus figurarum que sunt ex considerationibus continue sequentibus in partibus unis orbis signorum stellarum quinque erraticarum quod tempus quod est a motu maiore ad motum medium est semper longius tempore quod est a motu medio ad motum minorem. Quod autem accidit ex eo non est possibile ut sit secundum modum orbis centri egredientis, sed secundum ipsius contrarium, propterea quod est in hoc modo semper motus maior in longitudine propinquiore et erit arcus qui est a longitudine propinquiore ad punctum in quo est motus medius in ambabus partibus minor arcu qui pervenit ad longitudinem longiorem. Secundum modum vero orbis revolutionis possibile est illud cum non fuerit motus maior in longitudine propinquiore, sicut est in Luna, sed fuit in longitudine longiore, scilicet cum inceperit stella a longitudine longiore et non fuerit eius cursus ab oriente ad occidentem sicut Lune, sed fuerit ad successionem signorum. Et ex hoc dicimus quod hec diversitas non erit nisi secundum modos orbium revolutionum. In diversitate autem que videtur apud partes orbis signorum invenimus contrarium illius in arcubus qui sunt in ortibus unis aut figuris unis orbis signorum, scilicet invenimus tempus quod est a motu minore ad motum medium longius semper tempore quod est a motu medio ad motum maiorem. Et iam possibile est etiam ut contingat hoc in uno quoque duorum modorum, quemadmodum ostendimus in similitudine duorum modorum in principio nostri sermonis in Sole. Et narravimus quod proprior et convenientior Soli est modus centri orbis egredientis. Et secundum illud accepimus diversitatem eius. Modum vero alterum non invenimus nisi modum orbis revolutionis. Sed propter illud quod consideratur de transitionibus ad illud quod provenit ei ex commixtione duorum modorum et ex hoc quod nos consequenter consideravimus ipsum non invenimus esse possibile ut compleatur secundum illud, propterea quod superficies in quibus lineantur orbes egredientium centrorum non sunt fixe, non mote, et neque est linea recta descripta super duo centra duorum orbium, orbis signorum et orbis stelle, secundum longitudinem unam a punctis duarum equalitatum et duorum tropicorum super quam videntur longitudo longior et longitudo propinquior cuiusque stellarum et centra orbium revolutionis, neque revolvuntur super orbes hos centrorum egredientium quorum centra per motus suos revolvuntur revolutione equali et perambulant in temporibus equalibus angulos equales. Sed longitudo longior cuiusque eorum in orbibus centrorum egredientium habet motum localem parvum equalem etiam ad successionem signorum a duobus punctis duarum equalitatum super centrum orbis signorum, et est motus ille cuiusque stellarum secundum quantitatem motus quem invenimus sphere stellarum fixarum, scilicet qui in omnibus centum annis est pars una. Ex eo vero quod diximus scitur quod centra orbium revolutionis revolvuntur super orbes alios equales orbibus centrorum egredientium qui ponunt diversitatem et centra illorum non sunt centra eorum. Sed stellarum quidem quatuor que sunt preter Mercurium revolvuntur super orbes quorum centra secant lineas que sunt in eo quod est inter centrum orbis signorum et inter centrum orbis egredientis cuiusque earum in duo media. Et in Mercurio quidem quantitas longitudinis que est inter centrum ipsum, idest centrum super quod revolvitur, et inter centrum quod revolvit ipsum est quantitas que est inter illud centrum et inter illud quod ponit diversitatem apud longitudinem longiorem et inter hoc centrum et inter visus nostros. In hac namque stella solum invenimus, sicut reperimus in Luna, quod centrum orbis egredientis revolvit et reducit centrum orbis revolutionis quod prediximus ad contrarium successionis signorum revolutione una in omni anno. Quoniam Mercurius etiam in revolutione una videtur in longitudine propinquiore duabus vicibus, quemadmodum Luna vicibus duabus in longitudine propinquiore in mense uno videtur.
〈IX.6〉 Capitulum sextum: In declaratione diversitatis secundum duos modos
Declarabitur autem nobis quod aggregatur propter illud quod prediximus de duobus modis ita: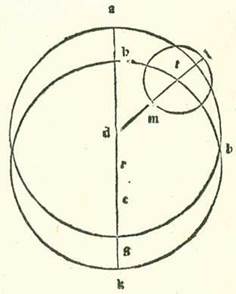 
Imaginemur in modo stellarum aliarum prius circulum orbis centri egredientis, super quem sint A, B, G super centrum D, et sit diametrus que transit super centrum orbis medii signorum et super punctum D diametri ADG, super quam sit centrum orbis signorum, scilicet locus visuum aspicientium, punctum E, et sit super punctum A longior longitudo, et sit punctum G longitudo propinquior, et secabo lineam DE in duo media super punctum R, et describam circulum super centrum R, et secundum longitudinem equalem DA manifestum est quod ipse erit equalis circulo ABG, super quem sint H, T, K, et describam super centrum T orbem revolutionis, supra quem sint L, M, et protraham lineam LTMD, et ponam primum ut sit superficies in qua sunt orbes centrorum egedientium declinata a superficie orbis signorum et quod sit superficies orbis revolutionis declinata a superficie orbium centrorum egredientium propter transitum stellarum in latitudine secundum quod declarabitur nobis in eo quod narrabimus de eis. Propter alleviationem autem transituum earum in longitudine imaginabimur ut sint omnes stelle in superficie una, que est superficies orbis signorum, propterea quod non est diversitas in longitudine ulla habens quantitatem propter has duas declinationes secundum quantitatem que declarabitur de diversitate que apparet cuiusque stellarum secundum seipsam. Et post illud dico quod superficies quidem tota movetur equaliter ad successionem signorum super centrum E et movet longitudinem longiorem et longitudinem propinquiorem cuiusque earum in omnibus centum annis parte una. Diametrus vero LTM, que est orbis revolutionis, revolvit etiam centrum D equaliter ad successionem signorum secundum quod sequitur reversio stelle in longitudine, et revolvit cum ea duo puncta L et M, que sunt orbis revolutionis, et revolvitur punctum T, quod est centrum orbis revolutionis, super orbem egredientis centri, supra quem sint H, T, K. Et movetur stella etiam supra circulum LM orbis revolutionis equaliter. Et ponit etiam eius reditionem ad diametrum que declinat semper ad centrum D secundum quod sequitur revolutio media, que est diversitatis eius que est propter Solem, et est eius motus localis a puncto L, quod est longitudo longior ad successionem signorum. Et illud est quod oportuit nos demonstrare.
Proprietas vero modi Mercurii declarabitur nobis ita: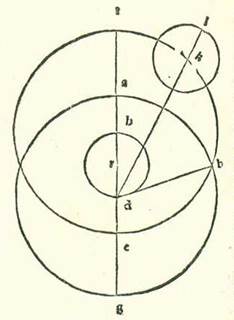 
Describam orbem centri egredientis qui est diversitatis, supra quem sint A, B, G, supra centrum D, et diametri quidem que transit super punctum D et super punctum E, centrum orbis signorum, et super punctum A, quod est longior longitudo, supra quam sint A, D, E, G, et assumam de linea AG lineam ad partem puncti A, quod est longitudo longior, equalem linee DE, supra quam sint D, R. Cum ergo fuerint res que sunt in forma secundum habitudinem suam, scilicet cum fuerit tota superficies revolvens longitudinem longiorem, et reduxerit eam super centrum E ad successionem signorum, et fuerit motus stelle in orbe revolutionis secundum quantitatem RDE sicut in aliis stellis, et fuerit linea DK revolvens orbem revolutionis super centrum D secundum equalitatem ad successionem signorum, et fuerit motus stelle in orbe revolutionis propinquus motui stellarum aliarum, erit hic centrum orbis egredientis alius. Et ipse est super quem semper est centrum orbis revolutionis in omni hora. Quoniam ipse etiam est equalis primo revolutum supra punctum R contra revolutionem orbis revolutionis, scilicet contra successionem signorum equaliter et secundum cursum equalem cursui eius. Et erit illud quod revolvit ipsum linea RHT donec sit reditio cuiusque duarum linearum DB et RHT ad puncta partium orbis signorum in anno uno vice una. Et manifestum est quod reditio cuiusque earum ad alteram erit duabus vicibus. Et erit longitudo semper centri orbis egredientis alius a puncto R cum linea equali cuique duarum linearum ED et DR, et est linea RH, donec sit circulus minor, quem describit per motum suum, qui est contra successionem signorum, supra centrum R et cum longitudine RH transiens semper per punctum D, quod est centrum egredientis orbis fixum primum, et sit orbis centri egredientis motus semper descriptus super centrum H et cum longitudine HT, que est equalis linee DA, sicut est hic orbis TK, et sit centrum orbis revolutionis semper super ipsum, sicut est hic punctum K. Et illud est quod nos oportuit demonstrare.
Et etiam poterimus consequi declarationem scientie eius quod edidimus ex eo quod diximus per id quod declarabitur quando sciemus quod est cuiusque stellarum ex quantitatibus. Et declarabuntur cum hoc manifestiore declaratione in locis pluribus cause que moverunt nos ad operandum secundum hunc modum. Et quia revolutionum que sunt in longitudine non sunt reditiones cum reditionibus partium orbis medii signorum et non cum longitudinibus longioribus et longitudinibus propinquioribus que sunt orbium centrorum egredientium propter motum eorum localem, tunc propter illud quod posuimus de motibus in longitudine secundum hunc modum quem posuimus non continet reditiones que videntur apud longissimam longitudinem, que sunt orbium centrorum egredientium, sed continet reditiones que sunt ad puncta duorum tropicorum et duarum equalitatum secundum quod sequitur tempus nostri anni. Demonstrabo autem prius secundum hos modos, cum fuerit longitudo transitus stelle medii in longitudine quantitatis unius a duobus lateribus longitudinum longiorum aut propinquiorum, quod tunc erit diversitas que videtur propter orbem signorum quantitatis unius in unaquaque duarum longitudinum et longitudo maior que est orbis revolutionis a transitu medio ad duas partes erit una.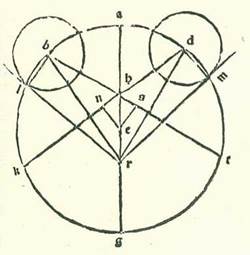 
Et describam ad exemplum illius circulum orbis egredientis, super quem sint A, B, G, D, super centrum E et diametrum AEG, et super ipsum ponam punctum quidem R centrum orbis signorum et centrum orbis centri egredientis qui ponit diversitatem, scilicet super quem est transitus orbis revolutionis medius secundum equalitatem, punctum H, et protraham lineas duas BHT et DHK secundum longitudinem unam, scilicet cuiusque duarum linearum a puncto A, quod est longitudo longior, donec sint duo anguli AHB et AHD equales, et protraham super punctum B et punctum D duos orbes revolutionis equales, et producam duas lineas BR et DR, et protraham a puncto aspectus nostrorum visuum ad partem unam duas lineas RL et RM contingentes duos orbes revolutionis. Dico ergo quod angulus RBH, qui est diversitatis que est propter orbem signorum, est equalis angulo HDR et angulus BRL, qui est longitudinis maioris que est orbis revolutionis, est equalis angulo DRM. Et similiter longitudinum maiorum que sunt ex commixtione erit quantitas elongationum a media equalis. Et producam duas perpendiculares a puncto quidem B et a puncto D ad duas lineas RL et RM, super quas sint BL et DM, et a puncto quidem E ad duas lineas BT et DK duas perpendiculares EN et ES. Et quia angulus SHE est equalis angulo NHE et duo anguli qui sunt apud N et apud S sunt recti et linea EH communis, erit linea NH equalis linee SH et perpendicularis EN erit equalis perpendiculari ES. Ergo erunt due elongationes duarum linearum BT et DK a centro puncti E equales. Ergo he due linee sunt equales, et etiam due medietates earum erunt equales, et etiam propter illud erunt due relique, que sunt BH et DH, equales. Sed HR communi existente et duobus angulis qui sunt sub lateribus equalibus, qui sunt angulus BHR et angulus DHR, qui sunt equales, erit basis BR equalis basi DR. Sed angulus HBR est equalis angulo HDR, et linea BL, que est medietas diametri orbis revolutionis, est equalis linee DM, et sunt duo anguli qui sunt apud duo puncta L et M recti. Ergo angulus BRL est equalis angulo DRM. Et illud est quod demonstrare voluimus.
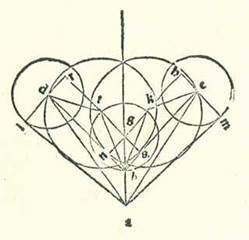Et sit etiam propter modum Mercurii diametri que transit super centra et super longitudinem longiorem que est orbium, supra quam sint A, B, G, et faciam punctum A centrum orbis signorum et punctum B centrum orbis centri egredientis qui ponit diversitatem et punctum G super quod revolvitur centrum orbis egrediens qui revolvit orbem revolutionis, et protraham etiam ad unumquodque duorum laterum duas lineas BD et BE, que sunt motus orbis revolutionis equalis ad successionem signorum, et sint due linee GR et GH revolutionis que est orbis centri egredientis contra successionem signorum equalis velocitatis. Erit ergo manifestum quod duo anguli qui sunt apud punctum G et punctum B sunt equales. Et erit linea BD equidistans linee GR, et linea BE equidistans linee GH. Et ponam centrum duorum orbium egredientium centrorum super duas lineas GR et GH, et sint duo puncta T et K, et revolvam circa ea duos orbes egredientium centrorum super quos sint duo orbes revolutionis super duo puncta D et E equales, et protraham duas lineas AD et AE, et protraham ad partem unam duas lineas AL et AM contingentes duos orbes revolutionis. Et ostendam quod ita etiam erit angulus ADB, qui est diversitatis que est propter orbem signorum, equalis angulo AEB et angulus DAL, qui est longitudo que est propter orbem revolutionis, est equalis angulo EAM. Et producam lineas BT et BK et TD et KE, et protraham perpendiculares a puncto G ad duas lineas BD et BE, super quas sint GN et GS, et producam etiam ab ad M. duobus punctis D et E ad duas lineas GR et GH duas perpendiculares DR et EH et ad duas lineas AL et AM duas perpendiculares DL et EM. Et quia angulus GBN est equalis angulo GBS et duo anguli qui sunt apud N et apud S sunt recti et linea GB est communis, erit linea GN equalis linee GS et etiam linea DR equalis linee EH, et linea TD est equalis linee KE, et duo anguli qui sunt apud R et apud H sunt recti. Et propter hoc erit angulus DTR equalis angulo EKH et angulus GTB est equalis angulo HKB. Quoniam linea TG est equalis linee GK, et linea GB est communis, et angulus TGB est equalis angulo KGB, et angulus BTD reliquus est equalis angulo BKE. Ergo basis BD est equalis basi BE. Et sit linea BA etiam communis. Ergo angulus BDA est equalis angulo BEA, et basis AD est equalis basi AE. Et quia linea DL est equalis linee EM et duo anguli qui sunt apud L et apud M sunt recti, erit angulus DAL equalis angulo EAM. Et illud est quod monstrare voluimus.
〈IX.7〉 Capitulum septimum: In scientia longitudinis longioris que est stelle Mercurii et motus eius localis
Et postquam scivimus quod premissum est, accepimus prius de partibus orbis medii signorum partem supra quam est longitudo longior stelle Mercurii secundum hunc modum: Quesivimus considerationes maiorum longitudinum in quibus fuerunt transitus matutinales equalis longitudinis cum transitibus vespertinis a transitu Solis medio, scilicet longitudo que est inter ipsum et inter stellam. Cum enim illud repertum fuerit, ex eo cuius premisimus declarationem necessarium erit ut sit locus longitudinis longioris orbis centri egredientis ipsum punctum quod est inter duos transitus. Accepimus ergo in hoc considerationes paucas, propterea quod huius applicationis rara est certificatio secundum veritatem et neque erit illud nisi in rarissimo tempore. Sed tamen istis considerationibus est possibile declarare hoc: Consideravimus nos in anno sextodecimo annorum Adriani sextodecimo die transacto mensis Phemenut, qui est unus mensium Egyptiorum, in vespere quod sequitur dies septimusdecimus stellam Mercurii cum instrumento stellarum, et invenimus tunc maiorem longitudinem eius a transitu medio Solis, et fuit visa tunc per duo foramina quando consideravimus ipsam cum stella Aldebaran lucida in parte una in longitudine Piscis. Sed in hoc tempore posito fuit locus transitus Solis medii novem partes et medietas et quarta partis Aquarii. Fuit ergo longitudo maior eius vespertina a loco transitus medii Solis 21 partes et quarta partis. Et consideravimus in anno decimooctavo annorum Adriani decimooctavo die transacto mensis Athica, qui est mensis Egyptiorum, mane diei deciminoni hora matutinali stellam Mercurii cum instrumento stellarum, et ipsa in longitudine maiore fuit visa subtilis occulta, et visa fuit tunc per ambo foramina quando consideravimus eam cum stella Aldebaran lucida in decimaoctava parte et medietate et quarta partis in longitudine Tauri. Sed in hoc tempore fuit locus transitus Solis medii decem partes Geminorum. Fuit ergo hic etiam longitudo eius maior matutinalis a transitu Solis medio equalis illis partibus, scilicet 21 partibus et quarte partis. Et quia transitus stelle medius fuit in una duarum considerationum in novem partibus et medietate et quarta partis Aquarii et in consideratione altera in decem partibus Geminorum et punctum quod est inter has duas considerationes de punctis orbis medii signorum est super partem decima Arietis diminuta octava parte unius, ergo super hunc locum fuit tunc diametrus que transit super longitudinem longiorem. Et etiam consideravimus in anno primo annorum Antonii viginti diebus preteritis de mense Athica, qui est ex mensibus Egyptiorum, mane die vigesimiprimi hora vespertina stellam Mercurii cum instrumento stellarum apud maiorem longitudinem eius que fuit a transitu Solis medio, et fuit visa tunc per duo foramina quando consideravimus eam cum stella cordis Leonis in septem partibus Cancri in longitudine. Sed in hoc tempore fuit locus transitus Solis medii decem partes et medietas partis Geminorum. Fuit igitur longitudo eius vespertina a transitu Solis medio vigintisex partes et medietas partis. Et similiter etiam consideravimus in anno quarto annorum Antonii decem et octo diebus preteritis mensis Phemenut, qui est ex mensibus Egyptiorum, matutino diei deciminoni hora matutinali stellam Mercurii cum instrumento stellarum, et ipsa etiam in longitudine sua maiore. Fuit ergo tunc visa per duo foramina quando consideravimus eam cum stella Anchus nominata cor Scorpionis in tredecem partibus et medietate partis Capricorni. Sed in hoc tempore fuit locus transitus Solis medii in undecim partibus Aquarii. Ergo hic etiam est longitudo maior matutinalis a transitu Solis medio equalis illis partibus, scilicet vigintisex partibus et medietate partis. Et quia fuit in una duarum considerationum transitus stelle medius in decem partibus et medietate partis Geminorum et in consideratione altera in decem partibus Aquarii et punctum quod est inter eas orbis medii signorum est in decem partibus et quarta partis Libre, ergo super hunc locum fuit tunc diametrus que transit super longiorem longitudinem. Ex istis autem considerationibus invenimus longiorem longitudinem super decem quidem partes Arietis et super decem partes libre fere. Sed ex considerationibus antiquis in quibus fuerunt longitudines maiores invenimus eam in septem partibus horum duorum signorum, sicut iam poterit qui voluerit ut meditetur in hoc et in eius simili ex eo quod diximus ante facere. In anno namque vigesimotertio secundum quod dixit Dionysius vigesimoprimo die transacto mensis Ydros fuit stelle splendide vehementer lucide que est orientalis in Capricorno et cuius longitudo ad septentrionem est quantitas trium diametrorum lunarium fixe locus secundum principia nostra, scilicet que sunt a punctis duorum tropicorum et duarum equalitatum in vigintiduabus partibus et tertia partis, scilicet in cauda Capricorni. Et manifestum est quod secundum quantitatem illius longitudinis fuit locus stelle Mercurii et fuit locus Solis medius decem et octo partes et sexta sexra M. partis Aquarii. Tempus namque quod fuit in anno quadringentesimo et octuagesimosexto annorum Nabuchodonosor decimoseptimo die transacto mensis Changuat, qui est ex mensibus Egyptiorum, in matutino diei decimioctavi ante diem parum. Et fuit longitudo maior matutinalis a loco Solis medio vigintiquinque partes et medietas et tertia partis. Et nos non invenimus secundum veritatem longitudinem magnam vespertinam equalem huic longitudini in aliqua considerationum que pervenerunt ad nos. Nos tamen invenimus longitudinem equalem huic longitudini per duas considerationes fere secundum hunc modum quem narro. In hoc namque anno vigesimotertio secundum verbum Dionysii in die quarto mensis Taurini in hora noctis prima fuit linea que transit super duo cornua Tauri diminuta quantitate trium diametrorum lunarium, et iam estimabatur in transitu eius quod longitudo eius ad meridiem fuit maior tribus diametris lunaribus donec fuit locus eius etiam secundum principia nostra in vigintitribus partibus et duabus tertiis partis Tauri. Fuitque tempus illud in anno quadringentesimo octuagesimosexto etiam Nabuchodonosor in mense Phemenut in matutino diei primi eius apud primam noctem. Et fuit locus Solis medius 29 partes et medietas partis Arietis. Ergo fuit longitudo maior vespertina a medio vigintiquatuor partes et sexta partis. Et in anno vigesimooctavo secundum sermonem Dionysii in die septimo mensis Geminalis fuit stella Mercurii obvia capiti Geminorum et fuit longitudo eius ad meridiem a capite meridiano quantitas tertie diametri Lune, scilicet minor duplo longitudinis que est inter caput Geminorum, donec fuit etiam locus stelle Mercurii tunc secundum principia nostra in vigintinovem partibus et tertia partis Geminorum. Et hoc etiam tempus fuit in anno quadringentesimo nonagesimoprimo annorum Nabuchodonosor quinque diebus transactis mensis Pharmeati ex mensibus Egyptiorum in vespere diei sexti hora noctis prima. Et fuit locus Solis medius due partes et medietas et tertia partis Geminorum. Fuit ergo hec longitudo vigintisex partes et medietas partis. Et quia transitus medius fuit in Ariete vigintinovem partes et medietas partis, et fuit longitudo maior vigintiquatuor partes et sexta partis, et in Geminis quidem fuit transitus medius due partes et medietas et tertia partis, et fuit longitudo maior vigintisex partes et medietas partis, et fuit longitudo matutinalis vigintiquinque partes et medietas et tertia partis fere, qua nos inquirimus partem applicationis, tunc nos invenimus ut sit longitudo vespertina propter vigintiquinque partes et medietatem et tertiam partis medias ex superfluitate que est in eo quidem inter duas considerationes positas. Aggregatur enim ut sit longitudo que est inter duos transitus maiores in unaquaque duarum considerationum trigintatres partes et tertia partis et superfluitas quidem que est inter duas longitudines maiores due partes et tertia partis. Accipiam igitur ex trigintatribus partibus et tertia partis quanta est quantitas partis et duarum tertiarum partis que est superfluitas que est inter vigintiquinque partes et medietatem et tertiam partis et inter vigintiquatuor partes et sextam partis de duabus partibus et tertia partis que sunt superfluitas que est inter duas longitudines maiores, invenimus ergo illud vigintiquatuor partes fere. Quas cum addiderimus super vigintinovem partes et medietatem partis Arietis, inveniemus transitum medium in quo erit longitudo maior vespertina equalis matutinali, scilicet vigintiquinque partes et medietas partis et tertia partis. Et erit illud in vigintitribus partibus et medietate partis Tauri. Et erit punctum medium inter decem et octo partes et sextam partis que sunt Aquarii et inter vigintitres partes et medietatem partis que sunt Tauri in quinque partibus et medietate et tertia partis Arietis. Et etiam in anno vigesimoquarto annorum Dionysii decem et octo diebus transactis mensis Leonini hora vespertina fuit Mercurius precedens Aschimech Alahazel ad conversionem signorum in eo quod probavit Abrachis plus tribus partibus parum. Ergo fuit locus eius tunc secundum principia nostra in decem et novem partibus Virginis et medietate partis. Et hoc tempus fuit in 486 anno annorum Nabuchodonosor 30 die mensis Beuni, qui est ex mensibus Egyptiorum. Et fuit in illa hora transitus Solis medius in vigintiseptem partibus et medietate et tertia partis Leonis. Fuit ergo longitudo maior vespertina a cursu medio 21 partes et due tertie partis, et est longitudo qua invenimus partem applicationis matutinalis secundum veritatem et etiam secundum duas considerationes positas. Quarum una fuit in anno septuagesimoquinto annorum Caldeorum et quartodecimo die Tisirim postremi. Et fuit stella Mercurii orientalis supra Lancem Libre meridionalem secundum quantitatem cubiti et medietatis cubiti. Fuit ergo locus eius tunc secundum principia nostra in quatuordecem partibus et sexta partis Libre. Et hoc tempus est annus quingentesimus et duodecimus annorum Nabuchodonosor novem diebus transactis mensis Thut in matutino diei decimi ante diem. Et fuit in illa hora locus Solis medius quinque partes et sexta partis Scorpionis. Fuit ergo longitudo maior matutinalis 21 partes. Altera vero consideratio fuit in anno sexagesimoseptimo annorum Caldeorum quinque diebus transactis mensis Chenun primi. Et fuit stella orientalis super frontis Scorpionis partem septentrionalem secundum quantitatem cubiti et medietatis cubiti. Et fuit tunc locus eius in duabus partibus et tertia partis Scorpionis. Et fuit hoc tempus annus quingentesimus et sexagesimusquartus annorum Nabuchodonosor vigintinovem diebus transactis mensis Thut ex mensibus Egyptiorum in matutino diei vigesimioctavi ante mane parum. Et fuit locus Solis medius tunc vigintiquatuor partes et medietas et tertia partis Scorpionis. Fuit ergo etiam hec longitudo maior vigintidue partes et medietas partis. Et quia etiam in his duabus considerationibus aggregatur ut sit quod est inter duos transitus Solis medios decem et novem partes et due tertie partis et superfluitas que est inter duas longitudines maiores est pars et medietas partis, propter hoc igitur accepimus ex decem et novem partibus et duabus tertiis partis, que sunt superfluitas que est inter duos transitus medios, quantum est quantitas duarum tertiarum partis, que est superfluitas que est inter 21 partem et duas tertias partis et inter 21 partem, de parte et medietate partis, que est superfluitas que est inter duas longitudines maiores. Invenimus ergo illud novem partes fere. Quas cum addiderimus super quinque partes et sextam partis que sunt Scorpionis, invenimus transitum medium in quo fuit longitudo maior matutinalis equalis alii longitudini vespertine vesperne M., que est 21 partes et due tertie partis, et locus eius quatuordecem partes et sexta partis Scorpionis. Et erit etiam punctum medium inter vigintiseptem partes et medietatem et tertiam partis Leonis et inter quatuordecem partes et sextam partis que est Scorpionis in sex partibus Libre fere. Ex eo igitur quod diximus et ex eo quod vidimus de convenientia que est in stellis aliis et in divisione earum invenimus in quinque stellis erraticis diametros que transeunt super longitudines longiores et propinquiores habere hahere M. motum localem ad successionem signorum super centrum orbis signorum et quod tempus huius localis motus est equale tempori localis motus sphere stellarum fixarum. Quoniam motus illius sphere ex eo quod premisimus est in centum annis pars una fere. Hoc ergo est tempus quod est ex considerationibus antiquis, in quibus fuit longitudo Mercurii longior in sex partibus, et est in tempore considerationum nostrarum, in quo fuit motus eius quatuor partes fere. Quoniam quod fuit inter duo tempora est quadringenti anni.
〈IX.8〉 Capitulum octavum: In demonstratione quod Mercurius est in longitudine propinquiore in revolutione una duabus vicibus
Et post illud quod diximus inquirimus quantitates longitudinum maiorum que sunt cum Sol fuerit in veritate loci longitudinis longioris que est stellarum et etiam cum fuerit in longitudine earum propinquiore. Et illud est quod non reperimus ex considerationibus antiquis, et neque reperimus ipsum nisi ex considerationibus nostris quas consideravimus per instrumentum stellarum. Et tunc declarabitur aspicienti bonitas decoris considerationis per ipsum, quamvis non videatur in eo quod appropinquat Soli de stellis consideratis aliquid stellarum quarum precessit scientia locorum. Et illud plurimum est quod accidit in stella Mercurii, propterea quod non est possibile ut videatur plurimum stellarum fixarum ex longitudine Solis que est equalis longitudini Mercurii nisi in raro tempore. Per instrumentum ergo in stellis que videntur plurime longitudinis est possibile comprehendere loca stellarum quesitarum secundum veritatem suam in longitudine et latitudine. In anno autem decimonono annorum Adriani in quartodecimo die transacto mensis Athus ex mensibus Egyptiorum in matutino diei quindecimi eius fuit Mercurius in longitudine longiore et fuit consideratus per instrumentum cum stella cordis Leonis. Fuit ergo visus orientalis in viginti partibus et quinta partis Virginis. Et fuit Sol per motum suum medium in novem partibus et quarta partis Libre. Fuit ergo longitudo eius maior decem et novem partes et vigesima partis unius. In illo autem anno etiam in decimonono die mensis Iachur ex mensibus Egyptiorum hora vespertina fuit Mercurius etiam in longitudine longiore per considerationem cum instrumento cum stella Aldebaran lucida, et locus eius quatuor partes et tertia partis Tauri, et locus Solis per motum suum medium undecem partes et duodecima partis Arietis. Fuit ergo longitudo maior vigintitres partes et quarta partis. Et ex hoc declaratur quod longitudinis longioris locus orbis centri egredientis non est nisi in Libra, et non in Ariete.
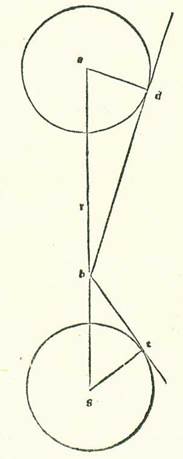Et postquam scivimus que diximus, describam diametrum super longitudinem longiorem, supra quam sint A, B, G, et sit in ea centrum orbis signorum, quod est aspectus visuum, supra quod sit punctum B, et super decem partes Libre sit punctum A, et super decem partes Arietis sit punctum G, et describam duos orbes revolutionis equales supra duo puncta A et G, supra unum quorum sit D et supra alterum E, et producam duas lineas a puncto B contingentes eos, que sint BD et BE, et producam a duobus centris ad duo loca contactus duas perpendiculares AD et GE. Et quia longitudo maior matutinalis que est in Libra fuit considerata a transitu medio decem et novem partes et vigesima partis, erit angulus ABD decem et novem partes et tria minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 38 partes et sex minuta, et erit arcus qui est super lineam AD 38 partes et sex minuta secundum quantitatem qua est circulus continens triangulum ABD ortogonium 360 partes, et erit chorda eius que est AD 39 partes et novem minuta fere secundum quantitatem qua est diametrus AB 120 partes. Et etiam quoniam longitudo maior vespertina considerata a transitu medio fuit 23 partes et quarta partis, erit angulus GBE 23 partes et 15 minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 46 partes et medietas. Quapropter erit arcus qui est super lineam GE 46 partes et 30 minuta secundum quantitatem qua est circulus continens triangulum GBE ortogonium 360 partes et erit chorda eius que est GE 47 partes et 22 minuta secundum quantitatem qua est diametrus GB 120 partes. Secundum quantitatem ergo qua est linea GE 39 partes et 9 minuta et linea AB 120 partes, propterea quod linea AD est equalis linee GE, que est a centro orbis revolutionis, erit linea BG 99 partes et 9 minuta. Et sit tota linea AG 219 partes et 9 minuta. Cum ergo dividitur in duo media super punctum R, est linea AR, que est medietas, 109 partes et 34 minuta. Ergo linea que est inter punctum B et inter punctum R est 10 partes et 25 minuta. Et illud est quod oportuit demonstrari.
Et manifestum est quod punctum R est aut centrum orbis egredientis centri, super quem est semper orbis revolutionis, aut contingit ut sit revolutio centri circuli quem diximus semper super ipsum. Ita enim tantum erit longitudo centri orbis revolutionis a puncto R equalis, quemadmodum iam declaratum est in unaquaque duarum stationum positarum oppositarum in forma. Si enim esset punctum R ipsum centrum orbis centri egredientis, super quem est semper centrum orbis revolutionis, esset hic orbis qui est orbis centri egredientis fixus et esset locus Arietis propinquior locis ad terram, quoniam linea BG est brevior omnibus lineis que protrahuntur a puncto B ad orbem descriptum supra punctum R. Non autem invenitur locus Arietis propinquior locis ad terram, sed locus Geminorum et Aquarii est propinquior ad terram loco Arietis, et ipsi sunt propinqui ad hoc ut sint equales. Manifestum est igitur quod revolutio centri orbis centri egredientis huius quem diximus est super punctum R econtra revolutionem orbis revolutionis, scilicet ad conversionem signorum, vice una in revolutione una et quod centrum orbis revolutionis in hac revolutione una fit in longitudine propinquiore duabus vicibus. Et declarabitur nobis quod orbis revolutionis, cum fuerit in Geminis aut in Aquario, erit locus eius propinquior terre loco Arietis ex eo quod premissum est de considerationibus. In hac namque consideratione que fuit in anno sextodecimo annorum Adriani decimosexto die mensis Phemenut fuit longitudo maior vespertina a cursu medio 21 partes et quarta partis. Et in consideratione que fuit in quarto anno annorum Antonii decimonono die mensis Phemenut ex mensibus Egyptiorum fuit longitudo maior matutinalis a medio 26 partes et medietas partis. Et fuit locus Solis per motum suum medium in ambabus considerationibus decem partes Aquarii. Fuit etiam in consideratione que fuit in anno decimooctavo annorum Adriani decimonono die mensis Athica longitudo maior matutinalis a medio 21 partes et quarta partis. Et fuit in consideratione que fuit in anno primo annorum Antonii vigesimo die mensis Athica longitudo maior vespertina a cursu medio 26 partes et medietas partis. Et fuit Sol per motum suum medium in his ambabus considerationibus in decem partibus Geminorum. Cum ergo aggregaverimus duas longitudines duorum diversorum cursuum in Aquario et in Geminis, erit 47 partes et medietas et quarta partis. Et cum aggregaverimus duas longitudines duorum diversorum cursuum in Ariete, erunt 46 partes et medietas partis. Quoniam vespertina fuit equalis matutine et fuit in consideratione eius 23 partes et quarta partis.
〈IX.9〉 Capitulum nonum: In scientia proportionis quantitatis magnitudinis diversitatum Mercurii
Post illud vero quod premissum est superest ut demonstrem super quod punctum linee AB erit reversio orbis revolutionis in anno ad successionem signorum secundum cursum medium et quanta sit longitudo centri orbis egredientis centri cuius cursus est ad conversionem signorum cum tempore reversionis equali tempori reversionis orbis revolutionis a puncto R. Assumam autem in hac inquisitione duas considerationes duarum longitudinum maiorum matutinalis et vespertine, longitudo cuiusque quarum medii cursus sit quarta circuli ad partem unam a longiore longitudine, et est locus in quo est plurimum diversitatis fere in orbe revolutionis. ‘In anno autem quartodecimo annorum Adriani decimooctavo die mensis Mesur hora vespertina’, sicut invenimus in considerationibus que sunt Taionis, inquit: ‘invenimus plurimum longitudinis eius a Sole diminutum a stella cordis Leonis tribus partibus et medietate et tertia partis’. Fuit ergo locus eius secundum principia nostra super sex partes et tertiam partis Leonis fere. Et fuit tunc locus Solis per motum suum medium decem partes et medietas sexte partis Cancri. Fuit ergo longitudo maior vespertina 26 partes et quarta partis. Et consideraverimus Probably corrupt for consideravimus, which is also the reading of Paris, BnF, lat. 14738 (154r, line 10 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 456, line 6 from the bottom). nos longitudinem eius maiorem cum instrumento stellarum in anno secundo annorum Antonii vigesimoprimo die mensis Mesure ante mane et consideravimus ipsum cum stella Aldebaran lucida et invenimus locum eius viginti partes et medietatem sexte partis Geminorum. Et fuit Sol per motum suum medium tunc etiam in decem partibus et tertia partis Cancri. Fuit ergo longitudo maior tunc matutinalis 20 partes et quarta partis.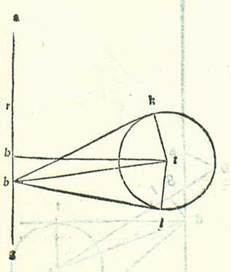 
Et postquam firmavimus hoc, sit diametrus transiens super decem partes Libre et Arietis, supra quam sint A, R, B, G, et sit, sicut est in forma que est ante istam, punctum quidem A locus super quem est centrum orbis revolutionis cum fuerit in decem partibus Libre, et punctum G locus super quem erit centrum orbis revolutionis cum fuerit in decem partibus Arietis, et sit punctum B centrum orbis signorum, et punctum R supra quod movetur localiter centrum orbis centri egredientis contra successionem signorum. Et inquiramus primum ut inveniamus quanta sit longitudo centri supra quod est motus equalis qui est orbis revolutionis ad successionem signorum a puncto B. Et sit illud centrum punctum H, et protraham lineam a puncto H secundum rectum angulum super lineam AG ut sit eius longitudo a longitudine longiore quarta circuli, et firmabo in hac linea centrum orbis revolutionis quod fuit in his duabus considerationibus positis, supra quod sit punctum T, quoniam longitudo huius etiam a longitudine longiore est quarta circuli, et sit Sol per cursum suum medium in decem partibus Cancri, et describam super punctum T orbem revolutionis, super quem sint K, L, et protraham a puncto B duas lineas contingentes ipsum, que sint BK et BL, et producam lineas TK et TL et BT. Et quia super hunc transitum medium positum fuit longitudo maior matutinalis a medio viginti partes et quarta partis et longitudo maior vespertina vigintisex partes et quarta partis, erit angulus KBL 46 partes et 30 minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes et erit medietas earum que est angulus KBT 46 partes et 30 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Erit ergo arcus qui est super lineam TK 46 partes et 30 minuta secundum quantitatem qua est circulus continens triangulum BTK ortogonium 360 partes et erit eius chorda, que est TK, 47 partes et 22 minuta secundum quantitatem qua est diametrus BT 120 partes. Ergo secundum quantitatem qua est linea TK, que est medietas diametri orbis revolutionis, 39 partes et 9 minuta et linea BR secundum quod ostensum est est 10 partes et 25 minuta erit linea BT 99 partes et 9 minuta. Et etiam quoniam augmentum unius harum duarum longitudinum super alteram est sex partes facte continentes duabus vicibus diversitatem que est propter orbem signorum et hanc diversitatem continet angulus BTH, tunc quia huius diversitatis iam precessit declaratio, erit angulus BTH tres partes secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit sex partes. Quapropter erit arcus qui est super lineam BH sex partes secundum quantitatem qua est circulus continens triangulum BTH ortogonium 360 partes et erit eius chorda que est BH sex partes et 17 minuta secundum quantitatem qua erit diametrus BT 120 partes. Ergo secundum quantitatem qua est linea BT 99 partes et 9 minuta et linea BR 10 partes et 25 minuta erit linea BH 5 partes et 12 minuta. Ergo linea BH est medietas linee BR fere et unaqueque duarum linearum BH et HR est 5 partes et 12 minuta fere secundum quantitatem qua est medietas diametri orbis revolutionis 39 partes et 9 minuta. Et hoc est quod oportuit nos declarare.
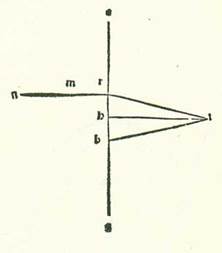Et protraham etiam in hac forma lineam super punctum R econtrario linee HT secundum angulum rectum linee AH, supra quem sint R, M, N. Manifestum est igitur quod erit supra ipsam tunc centrum egrediens supra quod erit centrum orbis revolutionis, scilicet punctum T, propter equalitatem duorum temporum reversionis que est econtra linee HT et linee RN simul. Et sit linea RA equalis linee RN donec sit unaqueque duarum linearum RN et AR composita ex medietate diametri orbis centri egredientis et ex eo quod est inter duo centra, centrum orbis centri egredientis et centrum puncti R, et sit nota centri orbis centri egredientis, supra quam est punctum M, et protraham lineam RT. Et quia angulus MRH est rectus et angulus TRH parum diversificatur a recto fere, ita ut linea NRT fortasse non diversificetur quando sit linea recta, et iam ostensum est quod secundum quantitatem qua est medietas diametri orbis revolutionis 39 partes et 9 minuta erit linea RN, que est equalis linee AR, 109 partes et 34 minuta et linea RT, que est equalis linee TB, 99 partes et 9 minuta, tunc erit tota linea NRT 208 partes et 43 minuta, et erit medietas illius, que est linea NM, et est medietas diametri orbis centri egredientis, 104 partes et 22 minuta fere, et linea reliqua que est in eo quod est inter duo centra, et est linea RM, 5 partes et 12 minuta. Et secundum illam quantitatem declaratum est quod unaqueque duarum linearum BH et HR est quinque partes et 12 minuta. Iam ergo aggregatur ut secundum quantitatem qua est medietas diametri orbis centri egredientis 104 gradus et 22 minuta sit unaqueque earum que sunt inter duo centra 5 partes et 12 minuta et sit diametrus orbis revolutionis 39 partes et 9 minuta. Ergo secundum quantitatem qua est medietas diametri orbis egredientis centri 60 partes erit unaqueque duarum longitudinum que sunt in eo quod est inter duo centra tres partes et cifre et erit medietas diametri orbis revolutionis 22 partes et 30 minuta. Et illud est quod nos oportuit declarare.
Postquam igitur iam affirmatum est hoc secundum quod diximus, erunt longitudines maiores que sunt in longitudine propinquiore convenientes ei quod fuit in considerationibus, scilicet cum fuerit transitus medius in decem partibus Aquarii aut Geminorum et fuerit longitudo eorum a longitudine longiore latus trianguli, erit angulus qui est apud visus nostros cui subtenditur orbis revolutionis 47 partes et medietas et quarta fere. Et ita sciemus illud: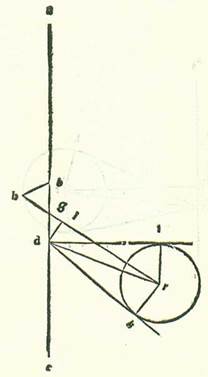 
Describam diametrum supra longitudinem longiorem, super quam sint A, B, G, D, E, et sit punctum A super diametrum locus longitudinis longioris, et punctum B locus super quem revolvitur centrum orbis egredientis centri in motu suo locali contra successionem signorum, et punctum G locus super quem revolvitur centrum orbis revolutionis per motum suum localem ad successionem signorum, et punctum D centrum orbis signorum, et perveniat quisque duorum motuum secundum proprietatem centri eorum equaliter et in duobus temporibus equalibus ad contrarium longitudinis longioris, que est punctum A ad latus trianguli, et sit linea que revolvit orbem revolutionis linea GR et ea que revolvit centrum orbis egredientis centri linea BH, et sit centrum orbis egredientis centri punctum H et centrum orbis revolutionis punctum R, et describam super ipsum orbem revolutionis, et protraham duas lineas DT et DK contingentes orbem revolutionis, et protraham lineas GH et DR et RT et RK, et protraham a D ad lineam GR perpendicularem super ipsam, que sit perpendicularis DL, et ostendam quod angulus TDK est 47 partes et medietas et quarta partis secundum quantitatem qua sunt quatuor anguli recti 360 partes. Et quia unusquisque duorum angulorum ABH et AGL subtenditur lateri trianguli et est 120 partes secundum quantitatem qua sunt duo anguli recti 180 partes, ergo unusquisque duorum angulorum HBG et DGL est 60 partes secundum illam quantitatem. Sed angulus BGH est equalis angulo BHG, quoniam linea BG est equalis linee BH. Et ipsi simul sunt quod minuitur ex complemento duorum angulorum rectorum, et est 120 partes. Unusquisque igitur eorum est 60 partes secundum illam quantitatem. Triangulus igitur BHG est equalium laterum et equalium angulorum. Sed angulus DGL est equalis angulo BGH. Puncta igitur H, G, L, R sunt super lineam rectam. Quapropter erit linea HR, que est medietas diametri orbis egredientis centri, 60 partes secundum quantitatem qua est GH, que est equalis linee GD, que est inter duo centra, tres partes. Et remanet ut sit linea GR secundum illam quantitatem 57 partes. Et etiam quia angulus DGL est 60 partes secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes est 120 partes, tunc erit arcus qui est super lineam DL 120 partes secundum quantitatem qua est circulus continens triangulum GDL ortogonium 360 partes, et erit arcus qui est super lineam GL reliquum complementi medietatis circuli 60 partes, et erit chorda DL tres partes et 55 minuta secundum quantitatem qua est diametrus GD 120 partes, et erit chorda GL secundum illam quantitatem 60 partes. Quapropter secundum quantitatem qua est GD tres partes et linea GR 57 partes erit linea DL due partes et 36 minuta, et linea GL secundum illam quantitatem erit pars una et 30 minuta, et linea LR residua erit 55 partes et 30 minuta. Et quia ex quadrata LR et DL, cum aggregantur, est quadratum DR, erit linea DR 55 partes et 34 minuta secundum quantitatem qua est medietas diametri orbis egredientis centri, scilicet linea RH, 60 partes. Et unaqueque linearum RT et RK est 22 partes et 30 minuta. Ergo secundum quantitatem qua est chorda DR 120 partes erit unaqueque duarum linearum RT et RK 48 partes et 35 minuta, et unusquisque duorum angulorum RDT et RDK erit 47 partes et 46 minuta secundum illam quantitatem qua sunt duo anguli recti 360 partes. Quapropter erit totus angulus TDK 47 partes et 46 minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes. Et illud est quod fuit demonstrandum.
〈IX.10〉 Capitulum decimum: In equatione motuum revolutionum Mercurii
Post illud autem quod diximus sequitur ipsum equatio motuum revolutionum Mercurii et locorum eius. Motus autem longitudinis, scilicet quod revolvit orbis revolutionis eius equaliter super punctum G, ex hoc sunt noti ex motu solari. Sed motus diversitatis, scilicet quos revolvit stella in orbe revolutionis super centrum suum, accepimus ex duabus considerationibus in quibus non est dubitatio. Quarum unam fecimus nos, et alteram ex considerationibus antiquis assumpsimus. Nos vero consideravimus stella Probably corrupt for stellam, which is also the reading of Paris, BnF, lat. 14738 (155v, line 3) and would correspond to the Greek text (see Toomer, loc. cit., p. 461, line 9). Mercurii in anno secundo annorum Antonii, qui fuit annus octingentesimus octuagesimussextus annorum Nabuchodonosor, duobus diebus transactis mensis Athica ex mensibus Egyptiorum in nocte quam sequitur dies eius tertius, et consideravimus ipsum per instrumentum stellarum, et non pervenit longitudo eius ad longitudinem eius maiorem vespertinam, et consideravimus ipsum cum stella cordis Leonis, et invenimus locum eius 17 partes et medietatem partis Geminorum. Et fuit tunc locus eius addens super centrum Lune partem unam et sextam partis. Et fuit illud tempus in Alexandria ante medietatem noctis futuram, cuius mane fuit dies tertius, quatuor horis et medietate hore equalis, quoniam medium celi fuit per instrumentum stellarum duodecem partes Virginis. Et fuit Sol in vigintitribus partibus Tauri. In illa autem hora fuit locus transitus Solis medii secundum modos quos demonstravimus 22 partes et 34 minuta Tauri, et fuit locus transitus Lune medii 12 partes et 14 minuta Geminorum, et fuit locus diversitatis que est a longitudine longiore orbis revolutionis 281 partes et 20 minuta. Colligitur ergo ex hoc ut sit locus transitus centri Lune veri 17 partes et 10 minuta Geminorum et locus transitus eius in quo videtur 16 partes et 20 minuta. Fuit ergo locus stelle Mercurii secundum hoc 17 partes et medietas partis Geminorum, quoniam fuit addens super centrum Lune partem unam et sextam partis.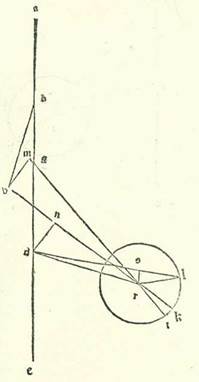 
Et postquam firmavimus hoc, describam diametrum super longitudinem longiorem et longitudinem propinquiorem, super quam sint A, B, G, D, E, et sit punctum diametri A locus iocus M. longitudinis longioris, et punctum B locus super quem revolvitur centrum orbis centri egredientis ad conversionem signorum, et punctum G locus super quem est revolutio relutio M. centri orbis revolutionis ad successionem signorum, et punctum D centrum orbis signorum, et moveatur quidem super punctum G punctum R, quod est centrum orbis revolutionis, sitque illud quod movet ipsum linea GR super angulum AGR, et super punctum B moveatur centrum orbis egredientis centri, quod est punctum H, et sit illud quod movet ipsum linea BH super angulum ABH, de quo manifestum est quod ipse est semper equalis angulo AGR propter equalitatem duorum temporum motuum eorum, et describam super punctum R orbem revolutionis, supra quem sint TKL, et sit stella super punctum L, et protraham lineas GH et HR et DR et HK et RL et DL, et producam perpendiculares ad lineam GRT a puncto H et a puncto D, que sint perpendiculares due HM et DN, et ad lineam DL a puncto R, que sit perpendicularis RS. Et sit inquisitum inventio arcus qui est a puncto T, et est longitudo longior ad punctum L, et est locus stelle orbis revolutionis. Et quia locus transitus Solis medii fuit tunc 22 partes et 34 minuta Tauri, et locus longitudinis propinquioris stelle fuit decem partes Arietis fere, et fuit locus transitus stelle medii in longitudine elongatus a loco longitudinis propinquioris 42 partibus et 34 minutis, erit angulus GBH 42 partes et 34 minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 85 partes et 8 minuta. Et unusquisque duorum angulorum BHG et BGH est 137 partes et 26 minuta secundum illam quantitatem, propterea quod linea BG est equalis semper linee BH. Et erunt circuli descripti super triangulum BGH, arcus quidem qui est super lineam GH 85 partes et 8 minuta secundum quantitatem qua est circulus 360 partes, et erit arcus qui est super lineam BG secundum illam quantitatem 137 partes et 26 minuta. Erunt ergo eorum chorde, chorda quidem GH 81 partes et 10 minuta secundum quantitatem qua est diametrus 120 partes, et chorda GB secundum illam quantitatem erit 111 partes et 49 minuta. Ergo secundum quantitatem qua est linea BG tres partes erit linea HG due partes et 11 minuta. Et etiam quia angulus BGH est 137 partes et 26 minuta secundum quantitatem qua sunt duo anguli recti 360 partes et angulus BGM secundum illam quantitatem est 85 partes et 8 minuta, erit angulus HGM, qui est ad complendum quod remansit, 52 partes et 18 minuta. Et propter illud erit arcus qui est super lineam HM 52 partes et 18 minuta secundum quantitatem qua est circulus continens triangulum HGM ortogonium 360 partes, et erit arcus qui est super lineam GM ad complendum quod remansit de semicirculo 127 partes et 42 minuta, et erunt chorde eorum, chorda quidem MH 52 partes et 53 minuta secundum quantitatem qua est diametrus GH 120 partes, et erit chorda GM 107 partes et 43 minuta. Ergo secundum quantitatem qua est linea GH due partes et 11 minuta et linea HR, que est medietas diametri orbis egredientis centri qui revolvit orbem revolutionis, 60 partes erit linea quidem HM pars 0 et 58 minuta et erit linea GM pars una et 58 minuta. Propter illud igitur erit linea MR, et est minor diametro HR absque multa diversitate, 60 partes secundum illam quantitatem et linea GR residua 58 partes et duo minuta. Et similiter quia angulus DGR est 85 partes et octo minuta secundum quantitatem qua sunt duo anguli recti 360 partes, erit arcus qui est super lineam DN 85 partes et 8 minuta secundum quantitatem qua est circulus continens triangulum DGN ortogonium 360 partes, et arcus qui est super lineam GN, residuum complementi semicirculi, 94 partes et 52 minuta, et erunt eorum chorde, chorda quidem DN 81 pars et 10 minuta secundum quantitatem qua est diametrus GD 120 partes, et erit chorda GN 88 partes et 23 minuta. Ergo secundum quantitatem qua est linea GD tres partes (et de linea GR iam ostensum fuit quod ipsa est 58 partes et duo minuta), erit linea quidem DN due partes et duo minuta, et linea GN due partes et 13 minuta, et erit linea NR residua 55 partes et 49 minuta. Quapropter erit diametrus DR 55 partes et 51 minutum fere secundum quantitatem qua est medietas diametri orbis revolutionis 22 partes et 30 minuta. Ergo secundum quantitatem qua est diametrus DR 120 partes erit linea DN 4 partes et 22 minuta et arcus qui est super eam 4 partes et 11 minuta secundum quantitatem qua est circulus continens triangulum DRN ortogonium 360 partes. Quapropter erit angulus DRN similiter quatuor partes et 11 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Totus ergo angulus EDR fit 89 partes et 19 minuta. Sed totus angulus EDL est 135 partes, propterea quod stelle longitudo fuit tunc a longitudine propinquiore 67 partes et 30 minuta. Et erit angulus RDL residuus 45 partes et 41 minutum. Arcus igitur qui est super lineam RS erit 45 partes et 41 minutum secundum quantitatem qua est circulus continens triangulum DRS ortogonium 360 partes. Et erit linea RS 46 partes et 35 minuta secundum quantitatem qua est diametrus DR 120 partes. Quapropter secundum quantitatem qua est linea DR 55 partes et 51 minutum et fuit linea RL medietas diametri orbis revolutionis 22 partes et 30 minuta erit RS 21 partes et 41 minutum. Et secundum quantitatem qua est diametrus RL 120 partes erit linea RS etiam 115 partes et 39 minuta, et arcus qui est super lineam RS erit 149 partes et duo minuta secundum quantitatem qua est circulus continens triangulum RLS ortogonium 360 partes, et erit angulus RLS 149 partes et duo minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Et secundum hoc ostenditur quod angulus RDL est 45 partes et 41 minutum et similiter etiam quod angulus TRK secundum illud exemplum erit quatuor partes et 11 minuta. Erit ergo totus angulus TRL 198 partes et 44 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et secundum quantitatem qua sunt quatuor anguli recti 360 partes erit 99 partes et 27 minuta. Fit ergo arcus TKL orbis revolutionis, qui fuit in hora considerationis ipsa longitudo stelle Mercurii a puncto T, quod est longitudo longior, 99 partes et 27 minuta. Et illud est quod nos oportuit demonstrare.
Et etiam in anno vigesimoprimo annorum Dionysii, quod fuit in anno quadringentesimo octuagesimoquarto annorum Nabuchodonosor, vigintiduobus diebus transactis de mense Alathrabi et decimooctavo die preterito mensis Thut ex mensibus Egyptiorum in mane diei deciminoni eius fuit stella splendida matutinalis et fuit longitudo eius a linea recta que transit super frontem septentrionalem Scorpionis et super stellam mediam stellarum frontis Scorpionis ad illud quidem quod minuitur quantitas diametri Lune et ad septentrionalem quidem a fronte septentrionali quantitas duarum diametrorum Lune. Sed stelle quidem medie stellarum frontis Scorpionis fuit locus tunc secundum principia nostra pars una et due tertie partis Scorpionis, et fuit secundum illam quantitatem etiam declinatio eius ad partem meridiei ab orbe medii signorum. Stelle autem septentrionalis stellarum frontis Scorpionis fuit locus due partes et tertia partis Scorpionis, et fuit declinatio eius ad septentrionem ab orbe medii signorum pars una et tertia partis. Fuit ergo locus Mercurii tunc tres partes et tertia partis Scorpionis fere. Manifestum est igitur quod non pervenit longitudo ad maiorem longitudinem matutinalem. Quoniam post quatuor dies in 26 diebus mensis Alathrabi fuit longitudo eius in eo quod invenimus scriptum ab hac linea ad illud quod minus est quantitas diametri integri et medietas diametri Lune. Fit ergo eius longitudo maior, propterea quod Sol movetur quatuor partibus fere et movetur stella quantitate medietatis diametri Lune. Et fuit locus Solis medius in decem et novem diebus mensis Thut ante mane secundum computationem nostram 20 partes et medietas et tertia partis Scorpionis. Et fuit longitudo longior Mercurii in sex partibus Libre, propterea quod anni qui fuerunt inter duas considerationes fuerunt quadringenti in quibus factus est motus localis longitudinis longioris quatuor partes fere.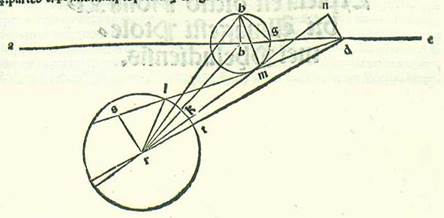 
Et postquam quod diximus fixum est secundum habitudinem suam, describam etiam formam similem forme superiori que est ante eam. Propter diversitatem igitur transituum in similitudine erunt anguli qui sunt apud punctum A, ubi est longitudo longior, acuti, et linee continue stelle erunt ad illud quod precedit de orbe revolutionis, et erit perpendicularis RS super lineam RL, que est medietas diametri orbis revolutionis. Et quia cursus stelle medii fuit longitudo a longitudine longiore 44 partes et 50 minuta, erit angulus ABH 44 partes et 50 minuta secundum quantitatem qua sunt quatuor anguli recti 360 partes, et secundum quantitatem qua sunt duo anguli recti 360 partes erit 89 partes et 40 minuta. Quapropter erit angulus HBG reliquus 270 partes et 20 minuta. Et unusquisque duorum angulorum BGH et BHG est 44 partes et 50 minuta. Et propter illud erunt chorde eorum, chorda quidem GH 84 partes et 36 minuta secundum quantitatem qua est diametrus circuli continentis triangulum BHG 120 partes, et unaqueque duarum chordarum BG et BH secundum illam quantitatem 45 partes et 46 minuta. Ergo secundum quantitatem qua est unaqueque duarum linearum BH et BG tres partes erit linea GH 5 partes et 33 minuta. Et etiam quia angulus AGR est 89 partes et 40 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et similiter angulus BGH 44 partes et 50 minuta, colligitur ut sit totus angulus GMH 134 partes et 30 minuta. Erit ergo arcus qui est super HM 134 partes et 30 minuta secundum quantitatem qua est circulus continens triangulum GHM ortogonium 360 partes, et arcus qui est super lineam GM residuum complementi semi circuli erit 45 partes et 30 minuta, et erunt chorde eorum, chorda quidem MH 110 partes et 40 minuta secundum quantitatem qua est diametrus GH 120 partes, et chorda quidem GM 46 partes et 24 minuta secundum illam quantitatem. Quapropter secundum quantitatem qua est linea GH 5 partes et 33 minuta, scilicet cum fuerit linea RH, que et medietas diametri orbis centri egredientis, 60 partes, erit linea MH quinque partes et septem minuta et linea GM due partes et 10 minuta. Et propter hoc colligitur ut sit longitudo linee RM 59 partes et 47 minuta secundum illam quantitatem, et tota linea RMG erit 61 partes et 57 minuta. Et similiter quia angulus DGN est 89 partes et 40 minuta secundum quantitatem quantatem M. qua sunt duo anguli recti 360 partes, erit arcus qui est super lineam DN 89 partes et 40 minuta secundum quantitatem qua est circulus continens triangulum DGN ortogonium 360 partes, et arcus qui est super lineam GN residuum complementi semicirculi erit 90 partes et 20 minuta, et erunt chorde eorum, chorda quidem DN 84 partes et 36 minuta secundum quantitatem qua erit diametrus GD 120 partes, et erit chorda GN secundum illam quantitatem 85 partes et sexta partis. Igitur secundum quantitatem qua est linea GD tres partes erit linea quidem DN due partes et septem minuta, et linea GN due partes et octo minuta, et tota linea RGN erit 64 partes et 5 minuta. Quapropter erit chorda RD secundum illam quantitatem 64 partes et septem minuta. Ergo secundum quantitatem qua est linea RD 120 partes erit linea DN tres partes et 58 minuta, et erit arcus qui est super eam tres partes et 48 minuta secundum quantitatem qua est circulus continens triangulum RDN ortogonium 360 partes. Et similiter erit angulus DRN tres partes et 48 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, et erit angulus RDN 176 partes et 12 minuta, et angulus ADR reliquus secundum illam quantitatem erit 85 partes et 52 minuta. Sed angulus ADL positus secundum illam quantitatem erit 54 partes et 40 minuta, propterea quod longitudo stelle fuit in consideratione a longitudine longiore 27 partes et 20 minuta donec fuit angulus LDR reliquus 31 partes et 12 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Erit ergo arcus qui est super lineam RS 31 partes et 12 minuta secundum quantitatem qua est circulus continens triangulum DRS ortogonium 360 partes, et erit linea RS ipsa eadem 32 partes et 16 minuta secundum quantitatem qua est diametrus DR 120 partes. Ergo secundum quantitatem qua est linea DR 64 partes et 7 minuta, scilicet qua mensura est linea RL, que est medietas diametri orbis revolutionis, 22 partes et 30 minuta, erit linea RS 17 partes et 15 minuta, et secundum quantitatem qua erit diametrus RL 120 partes erit linea RS 92 partes fere. Quapropter erit arcus qui est super lineam RS centum partes et octo minuta secundum quantitatem qua est circulus continens triangulum RLS ortogonium 360 partes, et erit angulus RLS centum partes et octo minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Et secundum illam quantitatem est declaratum quod angulus RDL est 31 partes et 12 minuta. Ergo erit angulus TRL 68 partes et 56 minuta et angulus TRK similiter tres partes et 48 minuta. Quapropter erit angulus KRL residuus secundum quantitatem qua sunt duo anguli recti 360 partes 65 partes et 8 minuta et secundum quantitatem qua sunt quatuor anguli recti 360 partes 32 partes et 34 minuta. Et illud est quod nos opportuit declarare.
〈IX.11〉 Capitulum undecimum: In positione motuum Mercurii qui sunt revolutionum eius
Et fuit etiam in hac consideratione longitudo stelle a puncto K, quod est longitudo propinquior orbis revolutionis, 32 partes et 34 minuta. Et manifestum est quod eius longitudo fuit a longitudine longiore 212 partes et 34 minuta. Et iam ostensum fuit quod in tempore considerationis nostre fuit longitudo eius a longitudine longiore orbis revolutionis 99 partes et 27 minuta. Et fuit tempus quod fuit inter duas considerationes anni Egyptii quadringenti et duo et ducenti et octuagintatres dies et tredecem hore et medietas fere. Et hoc tempus continet reversiones diversitatis integras huius stelle 1268. In viginti enim annis Egyptiis fuerunt revolutiones 63 fere. In quadringentis ergo annis aggregantur 1260 revolutiones, et in duobus annis reliquis cum eo quod consequitur eos de numero dierum et horarum revolvitur stella octo revolutionibus aliis. Iam ergo declaratum est nobis quod in quadringentis et duobus annis et ducentis et octuagintatribus diebus et tredecem horis et medietate hore pertransivit stella Mercurii post reversiones diversitatum integras, que sunt 1268 et 246 partes et 53 minuta. Et illud est quod fuit inter locum eius in consideratione nostra et inter locum eius in consideratione prima. Et similiter aggregatur nobis ex partibus que superfluunt in similitudine horum dierum quod diximus secundum quod premisimus eius positionem in tabulis. Ex hoc namque et eius simili posuimus equationem revolutionum motuum stelle Mercurii. Tempus quidem presens divisimus per dies, et revolutiones diversitatis cum superfluitate divisimus per partes. Cum ergo dividentur plures partes per plures dies, progredietur ex eo quod firmavimus in eo quod precessit de motu stelle Mercurii medio diei unius in diversitate sua. Quemadmodum autem fecimus in Sole et Luna, similiter faciemus in quinque stellis erraticis. Et posuimus loca earum in anno primo annorum Nabuchodonosor in primo die mensis Thut, qui est ex mensibus Egyptiorum, in medietate diei, scilicet fecimus simile illius, scilicet accepimus tempus quod est inter hoc tempus et tempus antiquum et quod est inter considerationem antiquam et considerationem modernam de annis Egyptiis et diebus et horis, scilicet 483 annis et 17 diebus et 18 horis. Et invenimus illud quod opponitur huic tempori secundum quod firmatur in tabulis de motu medio qui est stellarum diversitatis et quod superfluit stella de eo 190 partes et 39 minuta. Et illud est quod cum proiecerimus ex partibus longitudinis stelle in hora considerationis a longitudine longiore orbis revolutionis, scilicet ex 212 partibus et 34 minutis, inveniemus in primo anno annorum Nabuchodonosor in primo die mensis Thut, qui est ex mensibus Egyptiorum, in medietate diei diversitatem stelle que est a longitudine longiore sua in orbe revolutionis 21 partes et 55 minuta, et in longitudine quidem in parte Piscis, in qua fuit Sol tunc, et est 0 et 45 minuta, locum autem longitudinis longioris orbis egredientis centri in parte una et sexta partis Libre, quoniam pars centesima horum annorum fit quatuor partes et medietas et tertia partis fere, et secundum istas partes addunt sex partes Libre que fuerunt in tempore considerationis super partem unam et sextam partis Libre.
Expleta est dictio nona libri Almagesti Ptolemei Pheludiensis.