⟨V⟩
Claudii Ptolemei Pheludiensis dictio quinta libri Almagesti decem et novem capitulis huic loco redimita quadrat.
Capitulum primum: De artificio instrumenti armilarum, quo considerantur stelle et sciuntur loca earum in longitudine et latitudine
Capitulum secundum: De scientia modi diversitatis Lune duplicis
Capitulum tertium: De scientia quantitatis diversitatis Lune que est propter Solem
Capitulum quartum: De scientia proportionis que est inter duo centra, scilicet centrum orbis ecentrici Lune et centrum orbis signorum
Capitulum quintum: De scientia declinationis orbis revolventis lunaris et inclinationis eius in duabus partibus
Capitulum sextum: Quomodo sciatur cursus Lune verus per lineas mensurabiles propter motus revolutionum
Capitulum septimum: De scientia ponendi tabulas diversitatis Lune universalis
Capitulum octavum: De positione tabularum diversitatis Lune universalis
Capitulum nonum: De scientia numerationis universalis diversitatis lunaris
Capitulum decimum: Quod non est magna quantitas diversitatis que est in coniunctione et oppositione propter orbem centri egredientis lunaris
Capitulum undecimum: De diversitate aspectus que accidit in Luna
Capitulum duodecimum: De artificio instrumenti quo scitur quantitas diversitatis aspectus Lune
Capitulum tertiumdecimum: De declaratione et demonstrationibus longitudinum Lune
Capitulum quartumdecimum: De scientia eorum que videntur ex coniunctione et oppositione de quantitate diametri Solis et diametri umbre et diametri Lune
Capitulum quintumdecimum: De scientia umbre terre et longitudinis Solis et eorum que demonstrantur cum eis propter longitudinem Lune
Capitulum decimumsextum: De scientia magnitudinis Solis et Lune et terre
Capitulum decimumseptimum: De scientia divisionis diversitatis aspectus que est Solis et Lune
Capitulum decimumoctavum: De positione tabularum diversitatis aspectus
Capitulum decimumnonum: De scientia cognitionis diversitatum aspectus et comprehensione earum
⟨V.1⟩ Capitulum primum: De artificio instrumenti armillarum, quo considerantur stelle et sciuntur loca earum in longitudine et latitudine
Que vero accidunt ex applicatione Lune cum Sole in coniunctionibus et oppositionibus et que fiunt in eis ex eclypsibus, iam invenimus que sufficiant nobis in eis secundum modum quem narravimus de diversitate prima singulari, etsi non aliud fiat solummodo. Sed in divisione motuum Lune non in coniunctionibus et oppositionibus ex figuris non sufficit nobis in ea illud. Iam enim invenimus Lune diversitatem secundam, quemadmodum diximus, propter elongationem eius a Sole. Et hec quidem diversitas secunda iam redit et equatur cum diversitate prima in ambabus applicationibus, scilicet coniunctione et oppositione. Et maior erit hec diversitas secunda in ambabus quadraturis que sunt a duabus partibus impletionis. Et pervenimus ad sciendum illud et credendum per ea que posuit Abrachis de considerationibus scriptis revolutionum Lune et per ea que nos invenimus per instrumentum quod accepimus ad hoc et eius similia, cuius articium est sicut narrabimus. Accipiemus duas armillas mensurate magnitudinis sapienter et bene rasas quarum superficies quadrate equales similes omnimodo, et componemus unam earum in alteram in duobus locis oppositis ortogonaliter super superficies suas, et imaginabimur unam earum orbem signorum et alteram orbem meridiei, cum ipse est descriptus super polos duorum orbium, scilicet orbis equationis diei et orbis signorum. Postea accipiemus ex latere quadratorum duorum ipsorum duo puncta que determinant duos polos orbis signorum, in quibus infigemus duos paxillos rotundos equalium grossicierum equales transeuntes per duas superficies, scilicet apparentem et intrinsecam, fixos in eis, et componemus in eis armillam alteram super superficiem apparentem cuius superficies interior contingat duas superficies duarum armillarum compositarum apparentes in omni loco et ex omni parte tactu vero, et ponemus ipsam lenis revolutionis et cursus in longitudine super duos polos orbis signorum quos prediximus. Et similiter componemus armillam alteram in eis in superficie intrinseca, cuius superficies etiam apparens contingat duas superficies duarum armillarum compositarum interiores contactu vero in omni loco et ex omni parte lenis revolutionis et cursus sicut altera in longitudine et super duos polos super quos movetur armilla extrinseca, et dividemus hanc armillam intrinsecam et etiam armillam que est loco orbis signorum, unamquamque videlicet earum in 360 partes, scilicet divisione circuli, et secundum omnes partes partium secundum quas possibile est. Et componemus etiam armillam aliam parvam subtilem, in qua sint duo foramina opposita transeuntia in interiori armille intrinsece, ut sit revolutio eius et cursus in superficie interiori armille intrinsece ad unumquemque duorum polorum positorum propter considerationem latitudinis. Et postquam fient hee armille sicut prediximus, perveniemus ad arcum qui est inter duos polos, scilicet polum orbis signorum et polum equationis diei, quem declaravimus in his que precesserunt, et accipiemus quantitatem eius ab unoquoque duorum polorum orbis signorum in orbe meridiei, de quo imaginamur quod ipse sit descriptus super polos, et signabimus hic duas notas oppositas etiam, et componemus eas in duobus polis fixis in armilla alia simili armille orbis meridiei, quem declaravimus in principio libri Amagesti, in considerationibus arcus qui est inter duos tropicos orbis meridiei, ut cum hec armilla fuerit fixa in illo loco in quo fuerit illa armilla, scilicet cum fuerit erecta super superficiem horizontis et supra altitudinem poli propriam loci inhabitati, et fuerit etiam equidistans superficiei orbis qui est secundum naturam orbis meridiei, sit revolutio armillarum intrinsecarum in ea et cursus earum omnium omnino super duos polos equationis diei ab oriente ad occidentem sequentes localem motum totius primum. Cum ergo posuerimus instrumentum secundum hunc modum, tunc quotiens possibile erit ut sint Sol et Luna simul apparentes super terram, erigemus armillam extrinsecam currentem super duos polos orbis signorum super partem Solis repertam in illa hora fere et revolvemus armillam orbis descripti super polos, ut cum fuerit locus sectionis duarum armillarum, qui est supra partem Solis, cadens super Solem secundum veritatem, fiant due armille, scilicet armilla orbis signorum et armilla orbis descripti super duos polos, simul obumbrantes seipsas. Et si fuerit loco Solis aliqua stellarum visa loca quarum considerantur et sciuntur, tunc cum fuerit oculus aspicientis unius super alterum laterum armille extrinsece et super locum ex quo videtur stella qui est super partem orbis signorum in qua est stella, fit stella visa per latus et locum opposita et occurrentia illi lateri et loco armille, ac si connexa esset duobus lateribus, et in superficie eorum. Armillam vero alteram intrinsecam divisam huius instrumenti revolvemus tunc ad Lunam aut ad aliud eorum que inquirimus, ut nos videndo Solem aut aliam stellarum simul videamus Lunam aut aliud eorum que inquirimus ex duobus foraminibus ambobus que sunt in armilla composita in interiori armille intrinsece divise. Nos enim ita sciemus locum Lune aut alterius stellarum quas inquirimus in longitudine partium orbis signorum, scilicet partium armille quam imaginati fuimus orbem signorum et divisimus in potentia secundum divisiones eius, et sciemus quanta sit longitudo Lune aut stelle ab orbe signorum ad septentrionem aut ad meridiem in orbe descripto super duos polos orbis signorum ex partibus quas invenimus in armilla interiori divisa et per longitudinem que est inter medium foraminis quod est super terram in armilla parva que revolvitur et inter lineam que est medium cinguli signorum.
⟨V.2⟩ Capitulum secundum: De scientia modi diversitatis Lune duplicis
Per considerationem vero absolutam iam invenimus longitudines Lune a Sole ex considerationibus scriptis quas posuit Abrachis et ex considerationibus nostris secundum numerationem et modum positum quandoque convenientes aliis et convenientes inter se et quandoque diversas ab aliis et diversas inter se, et quandoque minoratur illud et quandoque augetur. Quia ergo prolongatur nostrum studium et nostra inquisitio de scientia ordinis huius diversitatis et neque abscinditur nostra inquisitio ab ea in tempore continuo, in applicatione quidem coniunctionis et oppositionis semper inveniemus eam aut absque diversitate sensibili aut cum diversitate parva secundum quantitatem qua possibile est ut sit illud ex diversitate aspectus Lune. In ambabus vero quadraturis que sunt a duabus partibus impletionis aut erit diversitas parva aut non erit ei diversitas omnino, et illud erit cum Luna fuerit aut in longitudine longiore sua aut in longitudine sua propinquiore in orbe revolvente. Maior autem diversitas tunc quidem crescit cum fuerit Luna in loco cursus sui medii qui est inter duas longitudines in medio duarum medietatum. Tunc enim diversitas que est propter diversitatem primam erit maior que unquam erit. Et quia diversitas prima est cum fuerit Luna in qualibet duarum quadraturarum et in medietate orbis revolventis, in qua est cursus diminutus, erit locus eius maioris diminutionis diminutione prima numerata non in duabus quadraturis. Et cum fuerit Luna in qualibet duarum quadraturarum et in medietate in qua est cursus augmentatus, erit locus eius etiam similiter maioris additionis secundum quantitatem multitudinis augmenti et diminutionis prime, donec nos propter id quod invenimus ex eo estimemus quod orbis revolvens Lunam habeat orbem egredientis centri supra quem revolvatur, et quod Luna, cum fuerit in coniunctione et impletione, erit in longitudine eius longiore, et cum fuerit in ambabus quadraturis, erit in longitudine eius propinquiore. Et accidit illud cum fuerit equatio modi primi sicut ego narrabo. Imaginabimur in superficie orbis Lune declivis orbem cuius centrum sit centrum orbis signorum, et sit eius premissio, sicut fuit prius, propter latitudinem super duos polos orbis signorum secundum quantitatem augmenti motus latitudinis super motum longitudinis, et sit cursus Lune etiam in orbe revolvente in arcu longitudinis eius longioris contra successionem signorum secundum quod sequitur reversionem diversitatis prime. Et in hac superficie que est in orbe Lune declivi sint duo motus in duabus partibus contrariis, quorum quisque sit in seipso equalis, et ambo sint super centrum orbis signorum. Et unus eorum revolvat centrum orbis revolventis secundum successionem signorum secundum quod sequitur motum latitudinis, et alter revolvat centrum orbis egredientis centri et longitudinem eius longiorem, que est in illa superficie super quam erit centrum orbis revolventis semper, et revolvat ipsum contra successionem signorum secundum quantitatem augmenti longitudinis que est inter Solem et Lunam duplicis super motum latitudinis. Per quod intelligi volumus augmentum quod est inter motum Lune medium in longitudine et motum Solis medium in longitudine, verbi gratia donec sit in die una motus centri orbis revolventis, qui est motus latitudinis, 13 partes et 14 minuta fere secundum successionem signorum, et sit ut cursus centri orbis revolventis videatur in orbe signorum ipse motus longitudinis, qui est 13 partes et 11 minuta, quoniam totus motus orbis declivis minuit ex motu latitudinis superfluitatem que est inter duos motus, scilicet tria minuta, et longitudo longior orbis centri egredientis movetur etiam contra successionem signorum 11 partibus et 9 minutis, et est augmentum quod addunt partes duplicis longitudinis que est inter Solem et Lunam, que est 24 partes et 23 minuta, super motum latitudinis, qui est 13 partes et 14 minuta. Propter oppositionem ergo duorum motuum diversorum qui sunt super centrum orbis signorum, sicut prediximus, precedit linea que transit super centrum orbis revolventis lineam que transit super centrum orbis egredientis centri per arcum compositum ex 13 partibus et 14 minutis et ex 11 partibus et 9 minutis, qui est duplum partium longitudinis, que est 12 partes et 11 minuta et medium fere. Quapropter secat orbis revolutionis orbem egredientis centri bis in mense lunari, et erit reversio centri orbis revolventis ad longitudinem longiorem in orbe centri egredientis in coniunctionibus et oppositionibus mediis.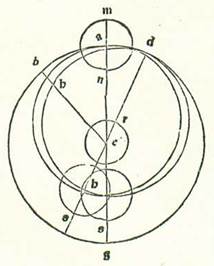 
Et ut illud declaretur nobis visibiliter, imaginemur etiam in superficie orbis Lune declivis orbem cuius centrum sit centrum orbis signorum, supra quem sint A, B, G, D supra centrum E, cuius diameter sit AEG, et ponam longitudinem longiorem, que est orbis centri egredientis, et centrum orbis revolventis et longitudinem longiorem septentrionis et principium Arietis et medium motum Solis simul super punctum A. Dico ergo quod in die una erit motus superficiei totus contra successionem signorum, quod est ab A ad D et supra centrum E tria minuta fere, donec sit longitudo septentrionis longior in vigesimanona parte et quinquagesimoseptimo minuto Piscis fere. Et sit linea que est similis linee EA revolvens duos motus diversos super centrum E etiam, quod est centrum orbis signorum, per motum suum equalem in die una. Linea vero que transit super centrum orbis egredientis centri, que est similis linee EA, revolvitur equaliter contra successionem signorum ad locum ED et revolvit quidem longitudinem longiorem que est orbis centri egredientis ab A ad D. Et describam super centrum R, quod est centrum orbis egredientis centri, orbem ecentricum DH et ponam arcum AD 11 partes et 9 minuta. Et linea que transit supra centrum orbis revolventis revolvitur etiam supra punctum E equaliter secundum successionem signorum ad locum EB et revolvit centrum orbis revolventis ad punctum H. Et ponam arcum AB 13 partes et 14 minuta, donec sit longitudo puncti H, quod est centrum orbis revolventis visa a puncto quidem A, quod est longitudo longior septentrionis, 13 partes et 14 minuta, que sunt latitudo, et a principio quidem Arietis 13 partes et 11 minuta, que sunt longitudo, quoniam punctum A, quod est longitudo longior septentrionis, in hoc tempore erit super vigesimamnonam partem et quinquagesimum septimum minutum Piscis, et erit elongatio eius a puncto D, quod est longitudo longior orbis egredientis centri scilicet aggregata ex duobus arcubus simul, scilicet ex arcu AB et ex arcu AD, 24 partes et 23 minuta, que sunt duplum longitudinis motus diei unius medii. Et similiter quia ambo motus, qui sunt linee que transit super punctum B et punctum D, faciunt revolutionem unam in medietate temporis medii mensurni, tunc manifestum est quod ipsi in quarta illius temporis et in medietate et quarta etiam necessario opponuntur. Per quod intelligi volo quod cum fuerint visi in duabus quadraturis mediis, erit linea centri orbis revolventis, que transit super EHB, opposita linee que transit super ED, que est longitudo longior in orbe centri egredientis et sit in longitudine eius propinqua. Manifestum est ergo, postquam hoc est quemadmodum diximus, quod non erit ex diversitate quod diversificet motum medium qui est linee EB propter orbem centri egredientis (per quod intelligi volo diversitatem similitudinis arcus DB apud arcum DH, qui est orbis centri egredientis), sed propter DAB, qui est orbis signorum, cum pertransierit ipsum Luna per motum medium equalem, quoniam eius revolutio non est supra punctum R, quod est centrum orbis centri egredientis, sed super punctum E. Neque eius diversitas est nisi propter orbem revolventem tantum, propter hoc quod cum fuerit orbis revolvens in longitudine propinquiore, erit semper addens in diversitate aut minuens ex ea equaliter, scilicet augmentum equale aut diminutionem equalem, quoniam angulus continens ipsum, qui est apud aspectum oculorum, erit maior cum fuerit in longitudine propinquiore. Universaliter ergo dico quod non erit diversitas nisi propter modum primum cum fuerit centrum orbis revolventis super punctum quod est longitudo longior, et neque erit illud nisi cum fuerit centrum orbis revolventis apud coniunctiones et oppositiones que videntur medie. 
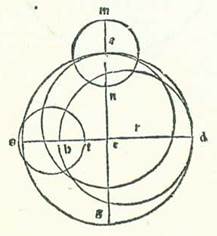Si ergo lineaverimus super punctum A orbem revolventem, supra quem sint M, N, erit proportio EA ad AM equalis proportioni quam declaravimus in eclypsibus. Et maior diversitas que erit erit cum fuerit transitus orbis revolventis super punctum H, quod est nota longitudinis propinquioris orbis centri egredientis, sicut orbis descriptus super H, super quem sunt duo puncta S et T, et illud est quod videtur apud duas quadraturas medias. Proportio igitur SH ad EH erit maior omnibus proportionibus que aggregantur ex locis aliis, quoniam linea SH, que est a centro orbis revolventis est una equalis semper. Quapropter erit linea EH, que est a centro terre minor omnibus lineis que progrediuntur ad orbem centri egredientis cum paribus combinatis.
⟨V.3⟩ Capitulum tertium: De scientia quantitatis diversitatis Lune que est propter Solem
Ut autem sciamus quantitatem diversitatis maioris cum fuerit transitus orbis revolventis in longitudine propinquiore orbis centri egredientis, consideravimus longitudines Lune a Sole in quibus est cursus Lune medius secundum propinquitatem. Maior enim diversitas Lune et longitudo Lune media a Sole quarta orbis erit fere cum fuerit orbis revolvens in longitudine propinquiore orbis centri egredientis. Et etiam cum fuerit ita, non erit Lune diversitas aspectus in longitudine. Illud namque erit cum fuerit sicut diximus et fuerit quod videtur ex consideratione apud elongationem in longitudine equale longitudini vere. Tunc enim erit inventio diversitatis secunde secundum veritatem. Et cum nos posuerimus nostram inquisitionem secundum has considerationes, inveniemus quod cum fuerit orbis revolvens in longitudine propinquiore, tunc erit diversitas maior apud transitum quidem medium septem partes et due tertie partis fere et apud diversitatem primam due partes et due tertie partis. Et exemplificabo illius exemplum, ut declaretur nobis illius comprehensio et cognitio. Consideravimus Solem et Lunam in anno secundo annorum Antonini 25 diebus mensis Camenut transactis, qui est unus ex mensibus Egyptiorum, et post ortum Solis et ante meridiem quinque horis et quarta hore equalibus. Et fuit Sol visus per considerationem in decimaoctava parte et medietate et tertia partis Aquarii. Et fuit medium celi in illa hora quarta pars Sagittarii. Et fuit Luna visa in nona parte et duabus tertiis partis Scorpionis. Et similiter fuit locus eius secundum veritatem. Et quia ipsa fuit in primis partibus Scorpionis, fuit eius elongatio in Alexandria a linea meridiei ad occidentem in longitudine circiter horam et medietatem hore. Et non fuit ei diversitas aspectus sensibilis. Et fuit tempus quod fuit inter locum Solis et Lune in primo annorum Nabuchodonosor usque ad hanc considerationem octingenti et octuagintaquinque anni et ducenti et tres dies et 18 hore et medietas et quarta hore equales absolute et vere. Et invenimus locum Solis per cursum eius medium decimamsextam partem et vigesimumseptimum minutum Aquarii et secundum veritatem decimamoctavam partem et quinquagesimum minutum, et illud est equale ei quod consideravimus per instrumentum. Et fuit locus Lune in illa hora secundum modum primum per medium cursum in longitudine decimaseptima pars et vigesimum minutum Scorpionis. Et fuit eius elongatio media a Sole circiter quartam circuli. Et fuit elongatio diversitatis a longitudine longiore in orbe revolvente 87 partes et 19 minuta, in quibus fuit etiam diversitas maior. Fuit ergo cursus Lune verus minor medio septem partibus et duabus tertiis partis loco quinque partium que fuerunt ex diversitate prima. Et etiam ut declaretur nobis in eis que demonstrabimus quantitas diversitatis et ex eis que posuit Abrachis ex considerationibus similibus horum motuum, ponam unam suarum considerationum, quam dicit fuisse in anno quinquagesimo revolutionis tertie Philippi sexdecem diebus transactis mensis Acthica, qui est ex mensibus Egyptiorum, supra duas tertias hore, scilicet hore prime diei. Et fuit cursus 241. Et fuit Sol visus per considerationem in octo partibus et medietate et medietate sexte partis Leonis. Et fuit locus Lune visus tunc in 12 partibus et tertia partis Tauri. Fuitque locus eius secundum veritatem in equalitate illarum partium fere. Erit ergo quod videtur ex longitudine que est inter Solem et Lunam secundum veritatem 86 partes et 15 minuta. Sed quia Sol fuit in primis partibus Leonis, erunt tempora horarum illius diei in Rhodo, ubi fuit consideratio 17 tempora et tertia temporis. Quinque ergo hore et tertia hore temporales que fuerunt ante meridiem erunt sex hore et sexta hore equales. Fuit ergo consideratio ante medium diem Iomin sextidecimi sex horis et sexta hore equalibus. Et fuit medium celi 9 partes Tauri. Et fit quod aggregatur ex tempore quod est inter duo loca Solis et Lune quasi essent in radice usque ad horam considerationis 619 anni Egyptii et 314 dies et 17 hore et medietas et tertia hore equales absolute, et secundum verificationem 17 hore et medietas et quarta hore. Et invenimus nos locum Solis usque ad illam horam secundum modos quos posuimus per cursum medium 10 partes et 27 minuta Leonis, et secundum verificationem octo partes et 20 minuta. Et invenimus locum Lune per cursum medium in longitudine 4 partes et 25 minuta Tauri. Quoniam orbis meridiei descriptus super Rhodum est descriptus super Alexandriam et est unus. Fuit ergo longitudo media que est inter Solem et Lunam circiter quartam circuli. Et fuit elongatio diversitatis a longitudine longiore in orbe revolvente 257 partes et 47 minuta. Sed in equalitate harum partium erit etiam maior diversitas fere, que est propter diversitatem orbis revolventis. Fit ergo quod est inter locum Lune per cursum medium et quod est inter veritatem loci Solis 93 partes et 55 minuta. Et fuit in consideratione quod fuit inter locum Lune secundum veritatem usque ad locum Solis secundum veritatem 86 partes et 15 minuta. Fit ergo quod addit veritas loci Lune qui videtur super locum suum per cursum medium etiam septem partes et due tertie partis loco quinque partium que fuerunt in modo primo. Iam ergo ostensum est per duas considerationes que fuerunt apud duas quadraturas quod nostram quidem considerationem invenimus diminutam a comprehensione diversitatis prime duabus partibus et duabus tertiis partis et per considerationem Abrachis augmentatam duabus partibus et duabus tertiis partis. Quoniam omnis diversitas secundum quod nos quidem posuimus minuitur et secundum quod Abrachis posuit augetur. Et nos quidem iam invenimus per considerationes alias multas equales istis quod plurimum quod erit diversitatis erit cum fuerit orbis revolvens in longitudine propinquiore orbis centri egredientis, sicut hec quam invenimus.
⟨V.4⟩ Capitulum quartum: De scientia proportionis que est inter duo centra, scilicet inter centrum orbis ecentrici Lune et inter centrum orbis signorum
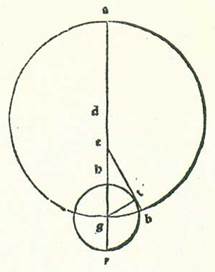Postquam ergo hoc ita est sicut diximus, describam orbem centri egredientis lunarem, supra quem sint A, B, G, supra centrum D, et sit eius diameter ADG, supra quam sit centrum orbis signorum supra punctum E, et sit punctum A nota longitudinis logitudinis M. longioris orbis centri egredientis et punctum G nota longitudinis propinquioris eius, et describam supra centrum G circulum orbis revolventis Lune, supra quem sint R, H, T, et protraham lineam contingentem orbem revolventem, supra quam sint E, T, B, et producam lineam GT. Et quia cum Luna fuerit in linea contingente orbem revolventem, erit diversitas maior, et iam ostensum est quod ipsa est septem partes et due tertie partis, erit angulus GET, qui est apud centrum orbis signorum, septem partes et due tertie partis secundum quantitatem qua erunt quatuor anguli recti 360 partes. Sed secundum quantitatem qua erunt duo anguli recti 360 partes erit 15 partes et 20 minuta. Et arcus qui est supra lineam GT erit 15 partes et 20 minuta secundum quantitatem qua erit circulus continens triangulum GET ortogonium 360 partes, et eius chorda, que est GT, erit 16 partes fere secundum quantitatem qua erit diameter EG 120 partes. Secundum quantitatem ergo qua erit GT, que est medietas diametri orbis revolventis, sicut iam demonstravimus, quinque partes et 15 minuta et EA, que est a centro orbis signorum ad longitudinem longiorem orbis centri egredientis, 60 partes erit linea EG scilicet ab illo eodem centro ad longitudinem propinquiorem orbis centri egredientis 39 partes et 22 minuta. Tota ergo diameter AG secundum illam quantitatem erit 99 partes et 22 minuta. Et DA, que est a centro orbis egredientis centri, erit 49 partes et 41 minuta. Et linea ED, que est inter duo centra, scilicet orbis signorum et orbis centri egredientis, erit 10 partes et 19 minuta. Iam ergo declaravimus proportionem que est inter duo centra. Et hoc est quod fuit demonstrandum.
⟨V.5⟩ Capitulum quintum: De scientia declinationis orbis Lune revolventis et inclinationis eius in duabus partibus
In eis quidem que videntur de figuris locorum Lune in coniunctionibus et oppositionibus et quadraturis iam sumus sufficientes per modos positos secundum orbes eius. In eis vero que videntur de divisione cursus eius in figuris suis aliis, in quibus sunt elongationes ipsius a Sole alie ab illis quando concavatur et quando fit gibbosa, quod est apud sextam mensis et tertiam eius, et illud plurimum erit cum fuerit orbis revolvens in eo quod est inter longitudinem longiorem et longitudinem propinquiorem orbis centri egredientis, invenimus accidens proprium quod accidit in Luna apud declinationem orbis revolventis et inclinationem eius. Et quia iam oportet ut sit in omnibus revolventibus orbibus locus unus ad hoc ut sint reversiones motuum eorum que in eis moventur semper ab eo et ad eum, necessario nominatur locus ille longitudo longior equalis.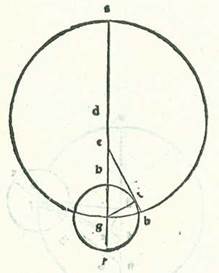 
A quo erunt principia reversionum motuum qui erunt super orbes revolventes, quemadmodum est in hac figura quam diximus ante punctum R. Linea autem que transit super omnia centra est quam terminat hoc punctum secundum quamlibet quantitatem loci orbis revolventis a longitudine longiore et longitudine propinquiore orbis centri egredientis, sicut linea ADEG. In omnibus vero modis aliis non videmus aliquid eorum que videntur contradicere et prohibere quin sit diameter que transit super hanc longitudinem longiorem orbis revolventis in motibus aliis qui sunt orbium revolventium. Per quod intelligi volo ut linea RGH sit semper in loco in quo est linea revolvens centrum orbis revolventis secundum equalitatem, sicut in hac forma est linea EG, et sit eius declinatio semper ad centrum linee revolventis, apud quod erunt in temporibus equalibus anguli equales motus equalis. Quod autem videtur in Luna contrarium est illius. Quoniam in transitu orbis revolventis in eo quod est inter duo puncta A et G non erit declinatio diametri RH ad punctum E, quod est centrum orbis signorum, neque sequetur locum linee EG. Iam ergo invenimus semper hanc declinationem positam comitantem locum unum diametri AG, sed eius declinatio non est ad punctum E, scilicet centrum orbis signorum, neque ad punctum D, scilicet centrum orbis centri egredientis, sed est eius declinatio ad lineam equalem linee DE, que est inter duo centra post punctum E ad partem longitudinis propinquioris orbis centri egredientis. Et ostendam etiam quod hoc est sicut diximus ex considerationibus pluribus et ponam duas considerationes ex quibus possibile erit declarare illud secundum plurimum quod possibile est, scilicet duas considerationes in quibus fuit orbis revolvens apud duas longitudines medias et fuit Luna apud longitudinem longiorem aut longitudinem propinquiorem orbis revolventis, propter hoc quod apud hec duo loca contingit ut sit maior diversitas huius declinationis posite. Iam ergo scripsit Abrachis quod ipse consideravit cum instrumento in Rhodo Solem et Lunam in anno centesimo nonagesimoseptimo post mortem Alexandri undecem diebus mensis Formiche transactis, qui est ex mensibus Egyptiorum, in principio hore secunde diei. Et dixit quod invenit Solem, cum consideravit ipsum cum instrumento, in septem partibus et medietate et quarta partis Tauri et vidit centrum Lune in 21 parte et duabus tertiis partis Piscis, et fuit secundum veritatem in vigesimaprima parte et tertia et octava partis. Fuit ergo longitudo Lune vera in illo tempore a loco Solis vero secundum successionem signorum 313 partes et 42 minuta fere. Et quia consideratio fuit in principio hore secunde, et fuit ante medium diem Iomin undecimi quinque horis temporalibus fere, et fuit tunc in Rhodo quinque horis et duabus tertiis hore equalibus fere, erit quod fuit inter locum Solis et Lune ac si essent in radice usque ad horam considerationis 620 anni Egyptii et 219 dies et 18 hore et tertia hore absolute equalis, et secundum veritatem 18 hore tantum. Et invenimus in illo tempore locum quidem Solis per cursum suum medium sex partes et 41 minuta Tauri et secundum verificationem 7 partes et 45 minuta. Et fuit locus Lune per cursum suum medium in longitudine quidem 22 partes et 13 minuta Piscis et in diversitate quidem a longitudine orbis revolventis longiore per cursum suum medium 185 partes et 30 minuta. Et fuit longitudo que fuit inter Lunam per cursum suum medium et inter locum verum Solis 314 partes et 28 minuta. 
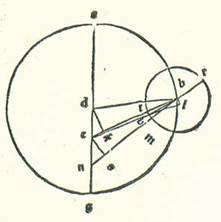Et postquam hoc est secundum quod diximus, describam circulum orbis centri egredientis lunaris, supra quem sint A, B, G, supra centrum D, sitque diameter ADG, in qua sit centrum orbis signorum super punctum E. Et super centrum B describam orbem revolventem Lune, supra quem sint R, H, T, sitque revolutio orbis revolventis secundum successionem signorum per motum suum a puncto B ad punctum A, et sit motus Lune super orbem revolventem a puncto R ad punctum H, postea ad punctum T, et protraham lineas DB et ETBR. Et quia in tempore medio mensurno erunt orbis revolventis due reversiones in orbe centri egredientis et ad hunc locum positum fuit longitudo que est inter Solem et Lunam per cursum eorum medium 315 partes et 32 minuta, cum nos duplaverimus has partes et proiecerimus ex eis unam revolutionem, scilicet 360 partes, erit radix longitudinis centri orbis revolventis tunc a longitudine longiore orbis centri egredientis secundum continuitatem signorum 271 partes et 4 minuta. Quapropter erit angulus AEB, qui est complementum quattuor angulorum rectorum, 88 partes et 56 minuta. Protraham ergo a puncto D super lineam EB perpendicularem DK. Et quia angulus DEK erit 88 partes et 56 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 177 partes et 52 minuta, erit arcus quidem qui est super lineam DK 177 partes et 52 minuta secundum quantitatem qua erit circulus continens triangulum DEK orthogonium 360 partes, et arcus qui est super lineam EK residuus ex complemento semicirculi erit due partes et octo minuta, et erunt chorde eorum, chorda quidem DK 119 partes et 59 minuta secundum quantitatem qua erit diameter DE 120 partes, et chorda quidem EK erit secundum illam quantitatem due partes et 14 minuta. Secundum quantitatem ergo qua erit linea DE, que est longitudo que est inter duo centra, 10 partes et 19 minuta, et linea quidem DB, scilicet medietas diametri orbis centri egredientis, 49 partes et 41 minuta, erit DK etiam 10 partes et 19 minuta fere. Et similiter erit linea EK 12 minuta. Et quia cum minuetur linea DK multiplicata in se ex linea BD multiplicata in se, erit residuum linea BK multiplicata in se, et erit linea BK secundum illam quantitatem 48 partes et 36 minuta, eritque tota linea EB 48 partes et 48 minuta. Et etiam quia elongatio Lune per cursum suum medium equalem a loco Solis vero fuit 314 partes et 28 minuta, et eius elongatio vera per considerationem 313 partes et 42 minuta, propter hoc ergo minuitur ex ea quantitas huius diversitatis, que est 46 minuta, et videtur cursus Lune medius super lineam EB. Et ponam Lunam super notam H, quoniam fuit in longitudine propinquiore orbis revolventis, et protraham duas lineas EHL et BH, et producam a puncto B super lineam EHL perpendicularem BL. Et quia angulus BEL continet diversitatem Lune, erit 46 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit pars una et 32 minuta. Et arcus qui est super lineam BL similiter erit pars una et 32 minuta secundum quantitatem qua erit circulus continens triangulum EBL othogonium 360 partes, et eius chorda, que est BL, pars una et 36 minuta secundum quantitatem qua erit diameter BE 120 partes. Secundum quantitatem ergo qua erit linea BE 48 partes et 48 minuta et medietas diametri orbis revolventis quinque partes et 15 minuta erit linea BL 39 minuta. Ergo secundum quantitatem qua erit linea BH, scilicet medietas diametri orbis revolventis, 120 partes erit linea BL 14 partes et 52 minuta, et arcus qui est super ipsam 14 partes et 14 minuta secundum quantitatem qua erit circulus continens triangulum BHL ortogonium 360 partes. Et similiter erit angulus BHL 14 partes et 14 minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Et erit angulus TBH reliquus 12 partes et 42 minuta, sed secundum quantitatem qua erunt quattuor anguli recti 360 partes erit sex partes et 21 minuta. Et ille sunt partes arcus HT orbis revolventis, qui quidem continet longitudinem que est inter Lunam et longitudinem propinquiorem veram orbis revolventis. Verum quia longitudo Lune fuit in hora considerationis a longitudine longiore media 185 partes et 30 minuta, tunc manifestum est quia propinquior longitudo media precedit Lunam, scilicet punctum H, et fit supra punctum M. Protraham autem lineam BMN et producam perpendicularem ES super eam a puncto E. Et quia iam ostensum est quod arcus TH est sex partes et 21 minuta et fuit arcus HMA longitudine propinquiore quinque partes et 30 minuta donec factus sit arcus totus TM 11 partes et 51 minuta, erit angulus EBS 11 partes et 51 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, sed secundum quantitatem qua erunt duo anguli recti 360 partes erit 23 partes et 42 minuta. Et similiter arcus qui est super lineam ES erit 23 partes et 42 minuta secundum quantitatem qua erit circulus continens triangulum BES ortogonium 360 partes. Et erit chorda ES 24 partes et 39 minuta secundum quantitatem qua erit diameter BE 120 partes. Secundum quantitatem ergo qua erit linea BE 48 partes et 48 minuta erit linea ES decem partes et duo minuta. Et etiam quia angulus AEB est 177 partes et 52 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et angulus EBS secundum illam quantitatem 23 partes et 42 minuta, erit angulus ENS reliquus secundum illam quantitatem 154 partes et 10 minuta. Et similiter erit arcus qui est super lineam ES 154 partes et 10 minuta secundum quantitatem qua erit circulus continens triangulum ENS ortogonium 360 partes, et chorda ES 116 partes et 58 minuta secundum quantitatem qua erit diameter EN 120 partes. Secundum quantitatem ergo qua erit linea ES decem partes et duo minuta, et linea DE, que est inter duo centra, 10 partes et 19 minuta erit linea EN 10 partes et 18 minuta. Declinatio ergo linee BM, que transit super longitudinem propinquiorem mediam ad punctum N, secat lineam EN equalem linee DE fere. Et illud est quod oportuit nos declarare.
Et similiter ut demonstremus ex locis orbis centri egredientis et orbis revolventis oppositis quod illud quod accidit in eis est equale, assumemus etiam ex longitudinibus quas consideravit Abrachis in Rhodo, quemadmodum diximus, considerationem quam ipse consideravit in illo anno, scilicet anno 197 post mortem Alexandri, 17 diebus transactis mensis Teguz One could equally read Tegum. Paris, BnF, lat. 14738 (79v, line 6) reads Tuz. The Greek text reads ‘Payni’ (see Toomer, loc. cit., p. 230, line 18 from the bottom)., qui est ex mensibus Egyptiorum, novem horis et tertia hore diei preteritis. Et fuit Sol, sicut ipse dixit in illa hora per instrumenta, in undecim partibus excepta decima partis Cancri. Et fuit locus visus Lune maior qui fuit 29 partes Leonis. Et similiter fuit secundum veritatem. Quoniam in Rhodo, cum Luna fuit in fine Leonis et fuit eius elongatio ab orbe meridiei in longitudine circiter unam horam, non fuit ei diversitas aspectus visibilis. Fuit ergo longitudo loci Lune veri in illa hora a Solis loco vero secundum successionem signorum 48 partes et 6 minuta. Et quia consideratio fuit post medietatem diei Iomin decimiseptimi mensis Thot, qui est ex mensibus Egyptiorum, tribus horis et tertia hore temporalibus, quod fuit in Rhodo illa hora quattuor horis equalibus fere, erit tempus quod fuit inter duo loca Solis et Lune ac si essent in radice usque ad horam huius considerationis etiam 620 anni Egyptii et 286 dies et 4 hore absolute equales, et erunt verificate tres hore et due tertie hore. Et similiter invenimus in hoc tempore locum Solis per cursum suum medium 12 partes et 5 minuta Cancri et secundum veritatem 10 partes et 40 minuta. Et invenimus locum Lune per cursum suum medium in longitudine 27 partes et 20 minuta Leonis. Fit ergo longitudo que est inter locum Lune per cursum suum medium et inter locum Solis secundum veritatem 46 partes et 40 minuta, et fit diversitas eius longitudinis longioris medie in orbe revolvente 333 partes et 12 minuta.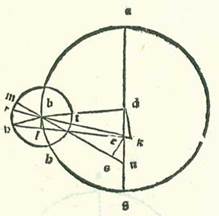 
Et postquam hoc inventum est et firmatum sic, tunc describam etiam orbem centri egredientis lunarem, supra quem sint A, B, G, supra centrum D et diametrum ADG, supra quam sit centrum orbis signorum supra punctum E, et describam supra centrum B orbem Lune revolventem, supra quem sint R, H, T, et producam lineam DB et lineam ETBR. Et quia longitudo que fuit inter locum Lune per cursum suum medium et locum Solis medium, cum duplicatur fuit, 90 partes et 30 minuta, erit propter illud cuius iam precessit scientia angulus AEB 90 partes et 30 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes. Sed secundum quantitatem qua erunt duo anguli recti 360 partes erit 181 partes. Si ergo nos protraxerimus lineam BE et super ipsam produxerimus a puncto D perpendicularem DK, erit angulus DEK residuus ex complemento duorum angulorum rectorum 179 partes, et erit arcus qui est super lineam DK 179 partes secundum quantitatem qua erit circulus continens triangulum DEK orthogonium 360 partes, et arcus qui est supra lineam EK est pars una residua ex complemento semicirculi. Erunt ergo chorde eorum, chorda quidem DK 119 partes et 59 minuta secundum quantitatem qua erit diameter DE 120 partes, et chorda quidem EK erit pars una et tria minuta fere. Quapropter secundum quantitatem qua erit linea DE, que est id quod est inter duo centra, 10 partes et 19 minuta et linea BD, que est medietas diametri orbis centri egredientis, 49 partes et 41 minuta erit linea quidem DK 10 partes et 19 minuta fere, et linea EK erit quinque minuta. Et quia cum minuitur linea DK multiplicata in se ex linea BD multiplicata in se, erit residuum linea BK multiplicata in se, et erit longitudo totius linee BK 48 partes et 36 minuta, remanebit ut sit linea EB secundum illam quantitatem 48 partes et 31 minuta. Et etiam quia longitudo Lune per cursum suum medium a loco Solis vero fuit 46 partes et 40 minuta et fuit longitudo Lune vera 48 partes et 6 minuta, addit quantitas diversitatis partem unam et 26 minuta. Ponam autem locum Lune quia ipsa fuit apud longitudinem longiorem in orbe revolvente super notam H. Cum ergo coniunxerimus lineam EH et lineam BH, protrahemus a puncto B super lineam EH perpendicularem BL. Et quia angulus BEL erit pars una et 26 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit due partes et 52 minuta, erit arcus qui est super lineam BL due partes et 52 minuta secundum quantitatem qua erit circulus continens triangulum BEL orthogonium 360 partes, et erit chorda BL due partes et 59 minuta secundum quantitatem qua erit diameter BE 120 partes. Secundum quantitatem ergo qua erit linea EB 48 partes et 31 minuta et linea quidem BH, que est medietas diametri orbis revolventis, 5 partes et 15 minuta erit linea BL pars una et 12 minuta. Ergo secundum quantitatem qua est linea diametri BH 120 partes erit linea BL 27 partes et 34 minuta, et arcus qui est super eam erit 26 partes et 34 minuta secundum quantitatem qua erit circulus continens triangulum BHL orthogonium 360 partes et arcus LH 152 partes et 26 minuta. Ergo angulus BHL erit 26 partes et 34 minuta secundum quantitatem qua sunt duo anguli recti 360 partes. Totus ergo angulus RBH erit secundum illam quantitatem 29 partes et 26 minuta, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erunt 14 partes et 43 minuta. He ergo partes sunt arcus HR orbis revolventis comprehendens longitudinem que est inter longitudinem longiorem veram et inter Lunam. Sed fuit eius longitudo a longitudine longiore media in tempore considerationis 333 partes et 12 minuta. Si ergo nos posuerimus longitudinem longiorem mediam super punctum M et protraxerimus lineam MBN et produxerimus super eam a puncto E perpendicularem ES, erit totus arcus MRH residuum complementi circuli 26 partes et 48 minuta. Et remanebit ut sit arcus RM 12 partes et 5 minuta. Quapropter erit angulus MBR, qui est equalis angulo EBS, 12 partes et 5 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 24 partes et 10 minuta. Et arcus qui est super lineam ES erit 24 partes et 10 minuta secundum quantitatem qua erit circulus continens triangulum BES orthogonium 360 partes. Et erit chorda ES 25 partes et 7 minuta secundum quantitatem qua erit linea BE 120 partes. Ergo secundum quantitatem qua erit linea BE 48 partes et 31 minuta et linea DE, que est id quod est inter duo centra, 10 partes et 19 minuta erit linea ES 10 partes et 8 minuta. Et etiam quia angulus AEB secundum quod positum est est 181 partes secundum quantitatem qua erunt duo anguli recti 360 partes, et iam ostensum est quod angulus EBN est 24 partes et 10 minuta, ergo propter hoc erit angulus ENB residuus secundum illam quantitatem 156 partes et 50 minuta. Et erit arcus qui est super lineam ES 156 partes et 50 minuta secundum quantitatem qua erit circulus continens triangulum ENS orthogonium 360 partes. Et erit chorda ES 117 partes et 32 minuta secundum quantitatem qua erit diameter EN 120 partes. Secundum quantitatem ergo qua erit linea ES 10 partes et 8 minuta et linea DE, que est inter duo centra, 10 partes et 19 minuta erit linea EN 10 partes et 20 minuta. Ex hoc ergo iam demonstratum est quod linea NB, que pervenit usque ad punctum M, quod est longitudo longior media, secat cum declinatione sua ad punctum N lineam EN equalem linee DE fere, que est id quod est inter duo centra. Et illud est quod oportuit nos declarare. Et iam invenimus illas proportiones aggregatas circiter ex considerationibus pluribus aliis, ita quod verificetur ex eis proprietas modi Lune qui est propter declinationem orbis revolventis, et erit ut centrum orbis revolventis revolvatur super punctum E, quod est centrum orbis signorum, et non erit declinatio diametri orbis revolventis, que terminat punctum longitudinis longioris medie orbis revolventis, ad punctum E, quod est centrum orbis revolutionis medie, sicut est in aliis, sed erit eius declinatio semper ad punctum N secundum longitudinem equalem linee DE, que est id quod est inter duo centra.
⟨V.6⟩ Capitulum sextum: De scientia accipiendi cursum Lune verum ex motibus revolutionum per lineas mensurabiles
Postquam hoc ita iam declaratum est, sequitur ut adiungamus ei quomodo in divisione revolutionum Lune, cum acceperimus loca eius per motus medios, inveniemus augmentum et diminutionem quod additur super locum eius per cursum eius medium in longitudine aut minuitur ex eo, quod est quantitas diversitatis ex numero longitudinis que est inter Solem et Lunam et que est inter longitudinem longiorem et inter locum Lune in orbe revolvente. Per lineas vero mensurabiles erit comprehensio huius cognitionis secundum capitula similia istis capitulis positis.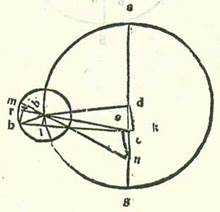 
Si enim exemplificaverimus exemplo similis forme precedenti postreme et posuerimus motus illarum revolutionum que sunt longitudinis et diversitatis, scilicet longitudinis quidem duplicis, que est 90 partes et 30 minuta, et diversitatis quidem que est a longitudine longiore media orbis revolventis, que est 333 partes et 12 minuta, et protraxerimus lineam supra quam sint N, S loco perpendicularis ES et lineam HL loco LB, tunc per illa capitula etiam, postquam iam scivisti angulos qui sunt apud centrum E et duas chordas DE et EN equales, declarabitur quod unaqueque duarum linearum DK et NS est 10 partes et 19 minuta fere secundum quantitatem qua erit DB, que est medietas diametri orbis centri egredientis, 49 partes et 41 minuta et BH, que est medietas diametri orbis revolventis quinque partes et 15 minuta. Et unaqueque duarum linearum EK et ES secundum illam quantitatem erit quinque minuta. Quapropter tota quidem linea BK, quemadmodum ostensum est in precedentibus, erit 48 partes et 36 minuta secundum illam quantitatem, et linea BE similiter erit 48 partes et 31 minuta, et linea BS residua erit 48 partes et 26 minuta. Et quia quod aggregatum est ex multiplicatione linee BS in se et linee NS in se equale erit multiplicationi linee BN in se, erit longitudo eius 49 partes et 31 minuta secundum quantitatem qua erit linea quidem NS 10 partes et 19 minuta. Secundum quantitatem ergo qua erit diameter BN 120 partes erit linea quidem NS 25 partes fere, et arcus qui est supra eam erit 24 partes et 3 minuta secundum quantitatem qua erit circulus continens triangulum NBS othogonium 360 partes. Quapropter erit angulus NBS, qui est equalis angulo RBM, 24 partes et tria minuta secundum quantitatem qua erunt duo anguli recti 360 partes. Sed secundum quantitatem qua erunt quattuor anguli recti 360 partes erit 12 partes et unum minutum fere. Similiter ergo erunt partes arcus RM, qui est orbis revolventis, 12 partes et unum minutum. Et quia puncti H, quod est locus Lune, fuit elongatio a puncto M, quod est longitudo longior media, que est residuum complementi circuli unius 26 partes et 48 minuta, erit arcus HR residuus 14 partes et 47 minuta. Quapropter erit angulus HBR 14 partes et 47 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, sed secundum quantitatem qua erunt duo anguli recti 360 partes erunt 29 partes et 34 minuta. Arcus igitur qui est super lineam HL erit 29 partes et 34 minuta secundum quantitatem qua erit circulus continens triangulum BHL orthogonium 360 partes, et arcus qui est super lineam LB residuus ad complendum semicirculum erit 150 partes et 26 minuta. Erunt ergo chorde eorum, HL quidem 30 partes et 37 minuta secundum quantitatem qua erit diameter BH 120 partes, et chorda quidem LB secundum illam quantitatem erit 117 partes et duo minuta. Ergo secundum quantitatem qua erit BH, scilicet medietas diametri orbis revolventis, quinque partes et 15 minuta et linea BE, quemadmodum iam ostensum est, 48 partes et 31 minuta erit linea quidem HL pars una et 21 minuta et linea quidem LB similiter quinque partes et 5 minuta. Tota ergo linea EBL erit 53 partes et 36 minuta secundum quantitatem qua fuit linea HL pars una et 21 minuta. Et quia aggregatum etiam ex multiplicatione cuiusque earum in se erit equale quadrato linee EH, erit longitudo linee EH secundum illam quantitatem 53 partes et 36 minuta fere. Secundum quantitatem ergo qua erit diameter EH 120 partes erit linea HL due partes et 59 minuta et arcus qui est super eam erit due partes et 52 minuta secundum quantitatem qua erit circulus continens triangulum EHL 360 partes. Arcus ergo diversitatis qui est sub HEL, qui est quantitas diversitatis, erit due partes et 52 minuta secundum quantitatem qua sunt duo anguli recti 360 partes, sed secundum quantitatem qua erunt quattuor anguli recti 360 partes erit pars una et 26 minuta. Et illud oportuit nos demonstrare.
⟨V.7⟩ Capitulum septimum: De positione tabularum diversitatis Lune universalis
Ut autem demonstremus brevi scientia cognitionem additionum et diminutionum secundum ipsarum divisiones ponendo tabulas, complevimus tabulam cuius iam premisimus positionem in modo singulari per tabulas quibus possibile est equare diversitatem compositam breviter et secundum operationem nostram, et per illa capitula et lineas etiam. Nos enim post duas tabulas primas, in quibus sunt numeri, posuimus tabulam tertiam, in qua sunt additiones et diminutiones que sunt secundum quantitatem numeri diversitatis, ut mutemus quod aggregatur ex motibus mediis qui sunt a longitudine longiore media, scilicet a puncto M ad longitudinem longiorem veram, scilicet ad punctum R. Nos namque, quemadmodum premisimus in hac longitudine posita, que est 90 partes et 30 minuta, quod arcus RM est 12 partes et 1 minutum, tunc, ut inveniremus partes longitudinis Lune, que est a puncto R, quod est longitudo longior vera, 333 et 30 minuta et cuius longitudo fuit a puncto M, quod est longitudo longior media, 333 partes et 12 minuta, adiunximus eis arcum RM, et facta est longitudo eius longior vera 345 partes et 13 minuta, que sunt partes quibus oportet assumere additionem aut diminutionem que sunt motus medii in longitudine propter orbem revolventem. Et similiter oportet ut assumantur numeri alii qui sunt longitudinis. Et assumamus quantitates additionum et diminutionum positarum que sunt cum illis portionibus quibus fuerunt portiones mensurate. Et ne prolongemus sermonem in omni hora, ponemus in tabula tertia proprietatem cuiusque modorum. Et ponemus in tabulis que sunt post ipsas, in tabula quidem quarta ponemus diversitates quarum positionem premisimus in tabula prima, que est propter diversitatem orbis revolventis, cuius maioris additionis et diminutionis summa est 5 partes fere secundum quantitatem proportionis 60 ad 5 partes et 15 minuta, et in tabula quinta ponemus superfluitatem diversitatum que est ex diversitate que est inter diversitatem secundam et diversitatem primam, et aggregatur ut sit diversitas additionis et diminutionis maior hic 7 partes et 12 minuta secundum proportionem 60 ad octo, ut sit tabula quarta locus orbis revolventis in applicationibus in longitudine longiore orbis centri egredientis, et ut sit tabula quinta eorum que aggregantur ex additionibus diversitatis que est ex loco orbis revolventis in longitudine propinquiore orbis centri egredientis in quadraturis. Et ut assumamus portiones augmentorum transitus orbis revolventis in eis que sunt inter hec duo loca, ponemus ad hoc tabulam sextam, in qua sunt minuta que oportet addi in unoquoque numerorum longitudinis que est diversitatis posite. Et oportet ut addatur super illud quod est in tabula quarta ex additione et diminutione quod est propter diversitatem primam positam. Et secundum hunc modum ponemus quod diximus.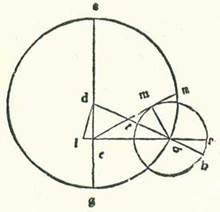 
Describam autem ad exemplum illius etiam orbem centri egredientis lunarem, supra quem sint A, B, G, supra centrum D, et sit diameter eius ADG et centrum orbis signorum super punctum E, et secabo arcum AB, et describam orbem revolventem supra centrum B, supra quem sint R, H, T, et protraham lineam EBR, et ponam hanc longitudinem a Sole verbi gratia 60 partes. Fiet ergo angulus AEB etiam propter ea quorum precessit iam declaratio, qui est duplum huius longitudinis posite 120 partes. Et producam a puncto D super lineam BE perpendicularem DL, et protraham etiam lineam DTBH, et fiet linea que producitur a centro E ad Lunam contingens orbem revolventem, ut sit maior diversitas super lineam EMN, et protraham perpendicularem BM. Et quia angulus AEB est 120 partes secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 240 partes, erit angulus DEL, qui est complementum eius quod remanet ex duobus rectis, 120 partes. Quapropter erit arcus qui est supra lineam DL 120 partes secundum quantitatem qua erit circulus continens triangulum DEL orthogonium 360 partes, et arcus qui est super lineam EL residuum complementi semicirculi erit 60 partes. Erunt igitur eorum chorde, chorda quidem EL 60 partes secundum quantitatem qua diameter DE est 120 partes, et chorda DL secundum illam quantitatem erit 103 partes et 55 minuta. Secundum quantitatem ergo qua erit linea DE 10 partes et 19 minuta et linea DB 49 partes et 41 minuta erit linea quidem EL quinque partes et 10 minuta fere et linea quidem DL 8 partes et 56 minuta. Et quia cum minuitur ex BD multiplicata in se DL multiplicata in se, erit residuum BL multiplicata in se, tunc erit longitudo totius BEL 48 partes et 53 minuta. Et erit EB residua secundum illam quantitatem 43 partes et 43 minuta secundum quantitatem qua erit BM, que est medietas diametri orbis revolventis quinque partes et 15 minuta. Secundum quantitatem ergo qua erit diameter EB 120 partes erit linea BM 14 partes et 25 minuta, et arcus qui est super eam erit 13 partes et 48 minuta secundum quantitatem qua erit circulus continens triangulum BEM orthogonium 360 partes. Angulus igitur BEM continens maiorem diversitatem erit 13 partes et 48 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, sed secundum quantitatem qua erunt quattuor anguli recti 360 partes erunt sex partes et 54 minuta. Et hoc debuimus ostendere.
⟨V.8⟩ Capitulum octavum: De positione tabularum diversitatis Lune universalis
Fit ergo superfluitas que est inter diversitatem que est propter hanc longitudinem et inter diversitatem que est propter longitudinem longiorem, que est quinque partes et unum minutum, pars una et 53 minuta. Sed tota diversitas que erit quousque perveniat ad longitudinem propinquiorem fit due partes et 39 minuta. Secundum quantitatem igitur qua erit diversitas maior 60 partes erit pars una et 53 minuta 42 partes et 38 minuta et unum secundum. Et ponam illud oppositum numero 120, qui est longitudinis in tabula sexta. Et similiter in portionibus reliquis etiam numerantur per illa capitula alia que assumuntur ex superfluitate que est inter duas diversitates. Et ponam coram proprietate cuiusque numerorum quod ipsum contingit ex minutis. Et manifestum est quod numerus 60 totus positus oppositus est duplo 90 partium quod est longitudinis, quod est 180 partes, que sunt longitudinis propinquioris orbis centri egredientis. Et iam ponemus tabulam septimam, in qua est transitus Lune in latitudine in ambabus partibus orbis signorum sicut orbis descriptus super polos eius, scilicet arcus qui separantur ex hoc orbe qui sunt inter orbem signorum et inter orbem Lune declivem, cuius revolutio est super centrum orbis signorum in unaquaque revolutionum particularium quam ipse revolvit in orbe Lune declivi. Et utemur in declaratione illius capitulo quo demonstrantur arcus qui sunt inter orbem equationis diei et inter orbem signorum orbis descripti super polos eorum. Hic vero non accipiemus nisi arcum qui est inter orbem signorum et inter longitudinem longiorem orbis Lune declivis in septentrione et longiorem longitudinem eius in meridie orbis magni descripti super polos eorum, qui est quinque partes. Quoniam ita declaratur nobis et Abrachi ex eis que videntur quod longitudo longior Lune in septentrione et longior longitudo eius in meridie ab orbe signorum est hec quantitas fere, et cuncta que videntur in Luna per considerationes lunares et ex eis que videntur ex stellis et que videntur per instrumentum similiter invenimus convenientiam longitudini transitus eius in latitudine, sicut declarabitur convenientia et communitas super ipsam per illud quod declarabitur post hec. Et hec est forma tabularum diversitatis Lune universalis:
Tabula diversitatis Lune universalis
Inclinationum orbis revolventis |
Tabule diversitatis prime singularis |
Tabula superfluitatum diversitatis secunde super primam |
Tabula proportionum et minutorum eius |
Partes latitudinis |
|||||||||||||
Additiones et divisiones |
Latitudo Lune in septentrione et meridie |
||||||||||||||||
Orbis centri egredientis |
Orbis revolventis |
Diversitates |
|||||||||||||||
Orbis revolventis |
Minutorum |
||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
|||||||||||
Partes |
Partes |
Partes |
Minuta |
Partes |
Minuta |
Partes |
Minuta |
Minuta |
Minuta |
Partes |
Minuta |
||||||
6
12
18 |
354
348
342 |
0
1
2 |
53
47
39 |
0
0
1 |
29
57
25 |
0
0
0 |
14
28
42 |
0
0
1 |
12
24
20 |
4
4
4 |
58
54
45 |
||||||
24
30
36 |
336
330
324 |
3
4
5 |
31
23
15 |
1
2
2 |
53
19
44 |
0
1
1 |
56
10
23 |
2
3
4 |
16
24
32 |
4
4
4 |
34
20
3 |
||||||
42
48
54 |
318
312
306 |
6
6
7 |
7
58
48 |
3
3
3 |
8
31
51 |
1
1
2 |
35
44
54 |
6
8
10 |
28
18
22 |
3
3
2 |
43
20
56 |
||||||
60
66
72 |
300
294
288 |
8
9
10 |
36
22
6 |
4
4
4 |
8
24
38 |
2
2
2 |
3
11
18 |
12
15
17 |
26
5
44 |
2
2
1 |
30
2
33 |
||||||
78
84
90 |
282
276
270 |
10
11
12 |
48
37
0 |
4
4
4 |
49
56
59 |
2
2
2 |
25
31
35 |
20
23
26 |
34
24
36 |
1
0
0 |
3
32
0 |
||||||
93
96
99 |
267
264
261 |
12
12
12 |
15
28
39 |
5
5
5 |
0
1
0 |
2
2
2 |
37
38
39 |
28
29
31 |
52
49
25 |
0
0
0 |
16
32
48 |
||||||
102
105
108 |
258
255
252 |
12
12
13 |
48
56
3 |
4
4
4 |
59
57
53 |
2
2
2 |
39
39
38 |
33
34
36 |
1
37
14 |
1
1
1 |
3
17
33 |
||||||
111
114
117 |
249
246
243 |
13
13
13 |
6
9
7 |
4
4
4 |
49
44
38 |
2
2
2 |
38
37
35 |
37
39
41 |
50
26
2 |
1
2
2 |
48
4
16 |
||||||
120
123
126 |
240
237
234 |
13
12
12 |
4
59
50 |
4
4
4 |
32
29
16 |
2
2
2 |
32
28
24 |
42
44
45 |
38
3
28 |
2
2
2 |
30
43
56 |
||||||
129
132
135 |
231
228
225 |
12
12
11 |
36
16
54 |
4
3
3 |
7
57
46 |
2
2
2 |
20
16
11 |
46
48
49 |
33
58
32 |
3
3
3 |
8
30
32 |
||||||
138
141
144 |
222
219
216 |
11
11
10 |
29
2
33 |
3
3
3 |
35
23
10 |
2
1
1 |
5
58
51 |
50
51
53 |
45
59
12 |
3
3
4 |
43
53
3 |
||||||
147
150
153 |
213
210
207 |
10
9
8 |
0
22
38 |
2
2
2 |
56
43
28 |
1
1
1 |
43
35
27 |
54
54
55 |
3
44
45 |
4
4
4 |
11
20
27 |
||||||
156
159
162 |
204
201
198 |
7
6
6 |
48
56
3 |
2
1
1 |
13
57
41 |
1
1
1 |
19
11
2 |
56
57
58 |
36
55
55 |
4
4
4 |
34
40
45 |
||||||
165
168
171 |
195
192
189 |
5
4
3 |
8
11
12 |
1
1
0 |
25
9
52 |
0
0
0 |
52
42
31 |
59
59
59 |
35
16
26 |
4
4
4 |
50
54
56 |
||||||
174
177
180 |
186
183
180 |
2
1
0 |
11
7
0 |
0
0
0 |
35
18
0 |
0
0
0 |
21
10
0 |
59
59
60 |
26
49
0 |
4
4
5 |
58
59
0 |
||||||
⟨V.9⟩ Capitulum nonum: De scientia numerationis diversitatis Lune universalis
Quotienscunque voluerimus numerare diversitatem Lune et locum eius verum ex eis que posuimus in tabulis, accipiemus motus medios ex tempore posito in Alexandria in longitudine Lune et elongatione eius et diversitatem ipsius et latitudinem eius secundum modum quem declaravimus, et duplabimus primum numerum elongationis semper in omni hora, et proiciemus revolutionem integram, si fuerit Probably necesse or something similar is missing here. Cf. Toomer, loc. cit., p. 239, line 3. Paris, BnF, lat. 14738 (82v, line 5) offers the same deficient text as M.. Postea mittemus comprehensum in tabulas diversitatis et accipiemus partes que opponuntur illi numero in tabula tertia. Tunc si fuerit ille numerus duplatus ab una parte usque ad 180 partes tantum, addemus illas partes super partes diversitatis medias, et si fuerit numerus ille maior 180 partibus, minuemus eas ex eis, et quod fuerit post augmentum aut diminutionem erit diversitas vera. Postea assumemus numerum diversitatis vere, que comprehensa fuit nobis post augmentum aut diminutionem, et mittemus ipsum in tabulas illas, et accipiemus quod opponitur ei ex augmento vel diminutione in tabula quarta, et etiam diversitatem que opponitur ei in tabula quinta, et servabimus unumquodque eorum per se. Deinde post hoc accipiemus numerum duplatum, qui est elongatio media, et mittemus ipsum in illas tabulas, et accipiemus quod opponitur ei ex minutis in tabula sexta. Deinde assumemus secundum quantitatem illorum minutorum ex diversitate quam servavimus et addemus illam semper super locum in tabula quarta additionis aut diminutionis. Postea considerabimus quod aggregabitur nobis ex partibus. Tunc si fuerit numerus diversitatis vere a parte una usque ad 180 partes, minuemus illas partes ex partibus longitudinis et latitudinis mediarum. Quod si fuerit maior 180 partibus, addemus illas partes super partes longitudinis et latitudinis mediarum. Deinde accipiemus comprehensum ex numero longitudinis et computabimus ipsum a parte que est locus Lune medius, et ubi provenerit nobis numerus ille, dicemus quod ille est locus Lune verus. Postea accipiemus numerum latitudinis, qui est longior longitudo septentrionis, et mittemus ipsum in illas tabulas, et considerabimus numerum partium que opponuntur ei in tabula septima, que est latitudinis, et dicemus quod ipse sunt elongatio centri Lune a linea medii cinguli signorum in orbe magno descripto super polos eius. Si ergo ceciderit numerus quem misimus in quindecim areas primas, dicemus quod latitudo Lune est in septentrione. Quod si ceciderit in eis que sunt post quindecim areas primas, dicemus quod latitudo est in meridie. In tabula namque numerorum prima est transitus Lune a septentrione ad meridiem, et in tabula secunda a meridie ad septentrionem.
⟨V.10⟩ Capitulum decimum, in quo ostenditur quod in applicationibus Lune, scilicet oppositione et coniunctione, non erit diversitas que est propter orbem centri egredientis magne quantitatis
Et quia sequitur ea que narravimus ut quidam homines dubitent, tunc dicimus quod iam erit diversitas manifesta in coniunctionibus et oppositionibus et in eclypsibus que sunt in eis propter orbem egredientis centri lunarem. Non enim est in omni hora neque necessario ut sit semper centrum orbis revolventis in veritate longitudinis longioris orbis centri egredientis. Sed iam possibile est ut elongetur ab eo secundum arcum magnum, propter hoc quod eius loca in longitudine longiore non erunt nisi in applicationibus que videntur medie. Coniunctiones autem et oppositiones vere erunt cum eo quod accidit unicuique duorum luminarium ex diversitate. Pensemus ergo ut ostendamus quod huius diversitatis non est quantitas faciens in aliquo eorum que videntur in applicationibus errorem cuius sit magna quantitas, quamvis non imaginemur cum ea diversitatem que erit propter orbem centri egredientis.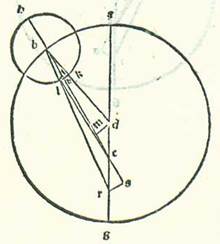 
Et faciam ad exemplum illius circulum orbis centri egredientis lunarem, supra quem sint A, B, G supra centrum D et diametrum ADG, in quo quidem sit centrum orbis signorum punctum E, et nota quidem declinationis que opponitur puncto D sit punctum R, et separabo arcum AB a puncto A, quod est longitudo longior, et lineabo super punctum B orbem revolventem, supra quem sint H, T, K, L, et protraham lineam BD et lineam BKE, et etiam lineam BLR. Et quia declaratur ex duobus modis possibile esse ut diversificetur quantitas diversitatis que est ex loco centri orbis egredientis in puncto A, quod est longitudo longior, propter hoc quod quando fuerit locus eius in longitudine propinquiore, fiet angulus qui est apud punctum E maior, et propter hoc quod declinatio diametri que erit a longitudine longiore media et longitudine propinquiore media non erit ad punctum E, quod est centrum signorum, sed ad punctum R. Et augebitur diversitas aut propter causam primam, cum fuerit diversitas Lune maior, aut propter causam secundam, cum fuerit locus Lune in longitudine longiore aut longitudine propinquiore orbis revolventis. Et cum acciderit ut sit diversitas que est propter causam primam maior, tunc erit diversitas que est propter causam secundam omnino insensibilis, propter hoc quod Luna erit super lineas contingentes orbem revolventem, et erit tunc diversitas additionis et diminutionis in tempore longo diversitas una, et erit possibile ut sit diversitas que est inter applicationem mediam et applicationem veram secundum illas ambas diversitates que sunt ex diversitate cuiusque duorum luminarium cum unum eorum augmentatum et alterum diminutum fuerit. Et cum acciderit ut sit diversitas declinationis maior ea que est propter causam secundam, erit etiam tunc diversitas que est propter causam primam insensibilis, propter hoc quod tota diversitas aut erit parva valde aut non erit omnino, et illud est cum fuerit Luna aut in longitudine longiore aut in longitudine propinquiore orbis revolventis, et erit diversitas que est inter applicationem mediam et applicationem veram ipsa diversitas que est propter Solem tantum. 
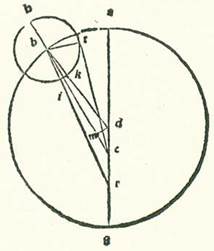Ponam autem ut sit Sol in maiore additionum suarum, que est due partes et 23 minuta, et Luna sit primum in maiore diminutione sua, que est quinque partes et unum minutum, ut sit angulus AEB continens duplum partium ambarum diversitatum septem partium et 24 minutorum, quarum duplum sunt 14 partes et 48 minuta, et protraham a puncto E lineam contingentem orbem revolventem supra quam sint E, T, et producam perpendicularem BT, et protraham etiam a puncto D super lineam BE perpendicularem DM. Et quia angulus AEB est 14 partes et 48 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erunt 29 partes et 36 minuta, erit arcus qui est supra lineam DM 29 partes et 36 minuta secundum quantitatem qua erit circulus continens triangulum DEM orthogonium 360 partes. Angulus ergo EDM, qui est arcus residui complementi semicirculi, erit 150 partes et 24 minuta. Et erunt eorum chorde, chorda quidem DM 30 partes et 39 minuta secundum quantitatem qua erit diameter DE 120 partes, et chorda EM secundum illam quantitatem 116 partes et unum minutum. Propter hoc ergo secundum quantitatem qua erit linea DE, que est id quod est inter duo centra, decem partes et 19 minuta, et linea BD, que est medietas diametri orbis centri egredientis, 49 partes et 41 minuta, erit linea DM due partes et 38 minuta, et linea EM similiter 9 partes et 59 minuta. Et quia cum ex quadrato linee BD minuitur quadratum linee DM, remanet quadratum linee BM, erit longitudo linee BM 49 partes et 37 minuta, et tota linea BME erit 59 partes et 36 minuta secundum quantitatem qua erit linea BT, que est medietas diametri orbis revolventis, quinque partes et 15 minuta. Secundum quantitatem ergo qua erit diameter EB 120 partes erit linea BT decem partes et 34 minuta. Et arcus qui est super eam erit decem partes et sex minuta secundum quantitatem qua erit circulus continens triangulum BET orthogonium 360 partes. Angulus ergo BET, qui est diversitas maior, erit decem partes et sex minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erunt quinque partes et tria minuta loco quinque partium et minuti unius, que erunt cum fuerit centrum orbis revolventis in puncto A, quod est longitudo longior. Fit enim tunc diversitas que est propter hanc causam duo minuta partis unius. Et hoc quidem est quod non pervenit ad hoc ut sit medietas octave hore unius. Et illud est quod oportuit nos demonstrare.
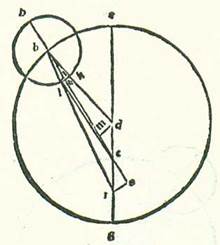Ponam etiam ut sit Luna in longitudine propinquiore media super punctum L, ad hoc ut sit angulus AEB continens fere duplum partium diversitatis Solis tantum, scilicet quattuor partium et 46 minutorum. Et in simili huius forme cum protraxerimus lineam EL et produxerimus super lineam EB duas perpendiculares, a puncto quidem L perpendicularem LI et a puncto R perpendicularem RS, tunc secundum similitudinem eorum que precesserunt, quoniam angulus qui est apud punctum E erit quattuor partes et 46 minuta secundum quantitatem qua quattuor anguli recti erunt 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit novem partes et 32 minuta, erit quisque duorum arcuum qui sunt super duas lineas DM et RS novem partes et 32 minuta secundum quantitatem qua erit quisque duorum circulorum continentium duos triangulos EDM et ERS orthogonios 360 partes, et erit quisque duorum arcuum qui sunt super duas lineas EM et ES existentium residuum complementi medietatis sui circuli 170 partes et 28 minuta. Ergo unaqueque duarum chordarum DM et RS erit novem partes et 58 minuta secundum quantitatem qua erit unaqueque duarum diametrorum DE et ER 120 partes. Et unaqueque duarum chordarum EM et ES secundum illam quantitatem erit 119 partes et 35 minuta. Secundum quantitatem ergo qua erit unaqueque duarum linearum DE et ER decem partes et 19 minuta et DB medietas diametri orbis egredientis centri 49 partes et 41 minuta erit unaqueque duarum linearum DM et RS 51 minuta, et unaqueque duarum linearum ME et ES secundum illam quantitatem erit decem partes et 17 minuta. Et quia cum ex quadrato linee DB minuitur quadratum linee DM, remanet quadratum linee BM secundum illam quantitatem 49 partes et 41 minuta fere, tunc fiet linea BE 59 partes et 58 minuta, et tota linea BS secundum illam quantitatem erit 70 partes et 15 minuta secundum quantitatem qua fuit linea RS 51 minuta. Quapropter erit chorda BR equalis illis partibus 70 partes et 15 minuta. Et sicut linea BR est apud unamquamque duarum linearum RS et BS, similiter erit linea BL apud unamquamque duarum linearum LI et BI. Secundum quantitatem ergo qua erit linea BL, scilicet medietas diametri orbis revolventis, quinque partes et 15 minuta, cum iam ostensum sit quod linea BE est 59 partes et 58 minuta, erit linea LI quattuor minuta et linea BI quinque partes et 15 minuta fere. Et remanet ut sit linea EI 54 partes et 43 minuta secundum quantitatem qua erit linea LI quattuor minuta. Et quia propter hoc quod diximus quod chorda LE non est diversa a 54 partibus et 43 minutis fit ut cum fuerit diameter LE 120 partes, erit linea LI octo minuta fere et arcus qui est super eam erit octo minuta secundum quantitatem qua erit circulus continens triangulum ELI orthogonium 360 partes, ergo angulus BEL, qui est diversitas que est inter Lunam et inter declinationem que est ad punctum R, erit octo minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit quattuor minuta. Iam ergo facta est etiam hic diversitas Lune quattuor minuta. Et illud est cuius error non est magne quantitatis in eis que videntur in applicationibus, quoniam non erit quantitas octave hore fere. Et non est extraneum ut cadat multotiens equale huic etiam in eis que videntur in considerationibus. Et illud est quod oportuit nos declarare.
Et nos non affirmavimus ea que narravimus ex eo nisi ad significandas istas diversitates que sunt propter orbem centri egredientis et dimisimus earum operationem, cum dimisimus eam apud inquisitionem nostram scientie applicationum, non quia sit impossibilis earum operatio, etsi sit parva, sed quia non affert nobis aliquid erroris sensibile in eis que demonstravimus de eclypsibus lunaribus cum dimisimus earum operationem. Ea vero que fiunt in inquisitione comprehensionis verificationis motuum Lune et locorum eius sunt que narravimus. Et quia accidit in Luna ut non sit cursus eius verus in sensu equalis cursui eius in visu, propter hoc quod, sicut diximus, non est quantitas terre apud quantitatem longitudinis eius in spera sua sicut punctum, fit propter ea que videntur in aliis modis, et precipue que videntur in eclypsibus Solis, ut sequatur ea que prediximus necessario narratio diversitatum aspectuum Lune propter quos possimus cognoscere motus Lune qui videntur per aspectum aspicientium eam ex superficie terre vel motus veros qui sunt a centro terre usque ad orbem signorum, et etiam econtrario cognoscere motus veros per motus qui videntur.
⟨V.11⟩ Capitulum undecimum: De scientia diversitatis aspectuum Lune
Et sequitur etiam hanc inquisitionem quod non est possibile scire quantitatem particularium diversitatum aspectuum quin sciatur longitudo Lune a terra neque est possibile scire longitudinem Lune quin sciatur aliqua diversitatum aspectuum, quoniam in eo in quo non est diversitas sensibilis, scilicet omni apud quantitatem longitudinis cuius in sphera sua est terra sicut punctum, ostendam non esse possibile invenire longitudinem eius. In eo autem cuius est diversitas aspectus sicut in Luna oportet tantum ut inveniatur eius longitudo prius propter diversitatem aspectus unam notam. Possibile est enim comprehendere illud per considerationem diversitatis unius solum. Et non est possibile comprehendere quantitatem longitudinis per considerationem. Abrachis vero non posuit plurimum inquisitionis huius nisi propter Solem. Quoniam ex eis que accidunt in Luna et in Sole, que narrabimus post hoc, sequitur illud ut cum scitur longitudo unius duorum luminarium, sciatur ex ea longitudo alterius. Et studuit ut sciret longitudinem Solis. Postea demonstravit ex ea longitudinem Lune. Prius autem posuit diversitatem visus Solis tantum minorem que sentitur, ut ex ea acciperet longitudinem eius. Deinde post illud demonstravit per eclypsim solarem quam ipse posuit, et posuit diversitatem visus Solis quandoque minorem que sentitur, quandoque posuit eam maiorem. Et ex hoc facta fuit longitudo Lune diversa apud eum in omni modorum quos posuit. Et omnino fuit longitudo in qua non est dubitatio, non tantum in mensura quantitatis diversitatis visionis Solis, sed in hoc utrum Solis sit diversitas visus.
⟨V.12⟩ Capitulum duodecimum: De artificio instrumenti quo scitur quantitas diversitatis aspectus Lune
Ut autem non uteremur in hac inquisitione aliqua causarum occultarum, preparavimus instrumentum quo possimus considerare secundum plurimum quo possibile est scire quanta erit diversitas aspectus Lune secundum verificationem et quanta sit longitudo loci eius a puncto summitatis capitum in orbe magno descripto supra duos polos horizontis et super centrum Lune. Accepimus duas regulas quattuor habentes angulos quarum quidem longitudo non sit minor quattuor cubitis, ut possimus dividere longitudinem in partes multas. Quantitas vero quam queque earum continet sit laudabilis media quantitatum et secundum quantitatem qua non flectantur propter longitudinem earum, sed ut sint vehementer plane et recte secundum quod subtilius et verius possibile est unumquodque laterum earum rectificari. Deinde lineavimus post illud in medio duarum superficierum latitudinalium cuiusque duarum regularum lineas rectas in longitudine, et composuimus in ambabus extremitatibus unius earum duas tabellas quadratas equales equidistantes erectas super superficiem quarum medium sit erectum super lineam que est in medio superficiei, et fecimus in medio cuiusque earum foramen, et posuimus medium cuiusque duorum foraminum super verificationem linee que est in medio regule, et posuimus foramen super quod ponitur oculus aspicientis minus et foramen quod sequitur Lunam maius secundum quantitatem qua cum aspiciens aspicit cum uno oculorum suorum per foramen minus, possit videre totam Lunam per foramen maius quod ei opponitur, et fecimus in unaquaque duarum regularum apud unam duarum extremitatum que est apud tabellam in qua est foramen maius in veritate medii linearum foramen equale, et composuimus in eis axem ordinantem duas regulas et constringentem unam earum cum alia sicut constringuntur linee cum centro, et fiximus regulam in qua non sunt due tabelle super basim fixione vehementi et sapiente, et posuimus regulam aliam, in qua sunt due tabelle lenis revolutionis ad omnem partem absque inclinatione et separatione a revolutione sua, et signavimus super veritatem medii duarum linearum que sunt in unaquaque duarum regularum apud duas extremitates que sequuntur basim duas notas quarum longitudo a centro in quo est axis sit equalis secundum quod magis possibile est esse equale, et divisimus lineam diffinitam que est in regula secunda in sexaginta partes, et divisimus unamquamque harum partium in partes secundum quod possibile fuit, et composuimus in duabus extremitatibus huius regule secunde retro ipsam duas tabellas sicut paxillos in quibus sint latera earum que sequuntur unamquamque partem super lineam illam adinvicem opposita. Et sit earum longitudo a linea media undique equalis, ut quando suspenditur perpendiculum et fit chorda eius contingens duas tabellas, sciatur quod regula secunda est fixa recte super superficiem horizontis absque declinatione. Et nos quidem iam premisimus et preparavimus lineam meridiei in superficie equidistante superficiei horizontis, et preparavimus super ipsam hoc instrumentum in loco lucido, non tenebroso, erectum, et posuimus angulos duarum regularum in quibus una earum alteri applicatur cum axe conversos ad meridiem, donec fiant due superficies supposite equidistantes linee meridiei posite, et posuimus regulam cui basis est erectam, non declinatam neque motam, sed sapienter fixam, et posuimus aliam lenis revolutionis super axem cum moderata equalitate in superficie orbis meridiei, et addidimus regulam aliam subtilem rectam, et composuimus eam in clavo parvo in extremitate linee divise que est apud basim, ut sit ipsa etiam lenis revolutionis super ipsum et perveniat ad maiorem revolutionem extremitatis linee que est in regula revoluta cuius longitudo est equalis longitudini linee que est in regula secunda, ut possibile sit nobis, cum fuerit eius revolutio in illa extremitate, declarare per ipsam longitudinem que est inter duas extremitates esse equalem. Et posuimus considerationes Lune secundum hunc modum quem dicam: Cum fuerit transitus Lune in veritate linee orbis meridiei et in duobus punctis duorum tropicorum orbis signorum (in habitudinibus namque istis similibus erunt orbes magni descripti super duos polos orbis horizontis et super centrum Lune ipsi orbes descripti super duos polos orbis signorum vere in quibus videtur transitus Lune in latitudine et eius longitudo vera a puncto summitatis capitum, et propter hoc declarabimus acceptionem eius), revolvamus regulam in qua sunt due tabelle ad Lunam apud transitum eius super lineam meridiei, donec aspiciens videat centrum Lune ab ambobus foraminibus in medio foraminis maioris et sciemus per regulam subtilem longitudinem que est inter duas extremitates duarum linearum que sunt in duabus regulis. Post ea ponam ipsam super lineam divisam in sexaginta partes in regula erecta secunda, et inveniemus numerum partium linee longitudinis quam prediximus secundum quantitatem qua erit medietas diametri orbis (quem lineat revolutio in superficie orbis meridiei) sexaginta partes. Postea accipiemus arcum cui subtenditur linea huius longitudinis, et dicam quod ipse est arcus longitudinis que fuit tunc inter centrum Lune quod videtur et inter punctum summitatis capitum in orbe magno descripto super duos polos horizontis et super Lunam. Et hic orbis fuit tunc ipse meridiei orbis descriptus super polos orbis equationis diei et orbis signorum. Et ut sciremus secundum verificationem maiorem transitum Lune qui erit in latitudine, consideravimus secundum speculationem in hora in qua fuit Luna in puncto tropici estivalis et in ultima longitudine septentrionis orbis Lune declivis. Cum enim fuerit in his duobus punctis, erit eius transitus in latitudine secundum sensum longe more tardi motus. Et quia Luna fuit tunc apud punctum summitatis capitum in linea equidistante descripta super Alexandriam in qua nos fecimus considerationem, fuit locus eius qui videtur equalis loco eius verificato fere. Invenimus ergo in pertransitionibus istis similibus longitudinem que est inter centrum Lune a puncto summitatis capitum duas partes et octavam partis fere, donec declaratur ex hac inquisitione quod maior longitudo Lune in latitudine ad duas partes orbis signorum est quinque partes. Et ipse sunt partes addite super partes que sunt inter punctum summitatis capitum et inter orbem equationis diei, que iam demonstrate sunt in Alexandria esse 30 partes et 58 minuta diminutis duabus partibus et octava partis, que sunt longitudo visionis. Iam vero ostensum fuit quod longitudo que est inter orbem equationis diei et inter punctum tropici estivi est 23 partes et 51 minuta. Et ut perscrutaremur diversitatem aspectus, consideravimus etiam Lunam secundum modum illi similem quando fuit in puncto tropici hyemalis, propter illud cuius iam premisimus narrationem. Et quia tunc Luna fuit maioris elongationis a puncto summitatis capitum, sicut transitus eius qui fuit in orbe meridiei, fuit diversitas aspectus eius maior et manifestior. Ut autem ponam ex diversitatibus aspectuum quas consideravimus in pertransitionibus istis similibus diversitatem aspectus unius, etiam demonstrabo per eam modum accipiendi et numerationem eius quod remanet ex diversitatibus aspectuum secundum quod sequitur.
⟨V.13⟩ Capitulum tertiumdecimum: De demonstrationibus longitudinum Lune
Consideravimus Lunam in anno vigesimo annorum Adriani in die tertiodecimo mensis Athus, qui est tertius ex mensibus Egyptiorum, post quinque horas et medietatem et tertiam hore equales a media die et iuxta occasum Solis. Et fuit visa elongatio que est inter centrum Lune et inter punctum summitatis capitum per instrumentum quinquaginta partes et medietas et tertia et medietas sexte partis. Et illud fuit quia longitudo chorde quam invenimus per regulam subtilem fuit 51 partes et medietas et medietas sexte partis secundum quantitatem qua diviserunt medietatem diametri orbis revolutionis in sexaginta partes, et ipsa est chorda arcus quinquaginta partium et medietatis et tertie et medietatis sexte partis secundum quantitatem qua erit circulus 360 partes. Fuit autem tempus quod fuit inter duo loca Solis et Lune in primo annorum Nabuchodonosor et inter horam huius considerationis octingenti et octuagintaduo anni Egyptii et septuagintaduo dies et quinque hore et medietas et tertia hore absolute equales, que secundum verificationem erunt quinque hore et tertia hore. Et invenimus Solem in hac hora per cursum suum medium in septem partibus et 31 minutis Libre, secundum verificationem vero in quinque partibus et 28 minutis eius, et locum Lune per cursum suum medium 25 partes et 44 minuta Sagittarii. Et fuit comprehensum quod fuit inter duo loca eorum per cursum medium 78 partes et 13 minuta. Et invenimus longitudinem que fuit inter longitudinem longiorem mediam in orbe revolvente et inter locum Lune per cursum suum medium 262 partes et 20 minuta, partes autem latitudinis que est ab ultima longitudine septentrionis 354 partes et 40 minuta. Et propter hoc addidit quantitas diversitatis super illud quod est proprium ei in tabulis septem partes et 26 minuta. Quapropter fuit verificatio loci Lune in illa hora in longitudine quidem tres partes et decem minuta Capricorni, et in latitudine in orbe quidem declivi ab ultima longitudine septentrionis due partes et sex minuta, et in orbe quidem lineato super duos polos orbis signorum, qui fuit tunc existens orbis meridiei fere, quattuor partes et 59 minuta ab orbe signorum ad septentrionem, et longitudo loci trium partium et decem minutorum Capricorni ab equatione diei in illo orbe ad partem meridiei 23 partes et 49 minuta. Et fuit elongatio equationis diei a puncto summitatis capitum in Alexandria ad partem meridiei 30 partes et 58 minuta. Ergo fuit longitudo vera centri Lune a puncto summitatis capitum 49 partes et 48 minuta. Fuitque visa eius longitudo 50 partes et 55 minuta. Ergo fuit diversitas aspectus Lune secundum quantitatem transitus eius hic positi pars una et septem minuta in orbe magno descripto super ipsam et super duos polos horizontis. Et fuit eius elongatio vera a puncto summitatis capitum 49 partes et 48 minuta.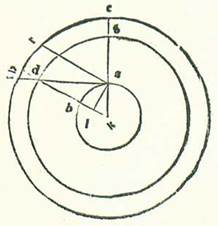 
Et postquam quod prediximus fit notum, lineabo in superficie orbis magni descripti super duos polos horizontis et super Lunam, videlicet super centrum eius, orbem terre magnum, supra quem sint A, B, et orbem quidem continentem lineam rectam que transit super centrum Lune apud considerationem, supra quem sint G, D, et orbem apud quem sit quantitas terre sicut punctum, supra quem sint E, R, H, T, sitque centrum omnium eorum commune punctum K, et linea que a centro progreditur et transit super punctum summitatis capitum sit KAGE, et sit Luna super punctum D, et eius longitudo vera a puncto summitatis capitum, quod est punctum G, est iste partes posite, scilicet 49 partes et 48 minuta. Protraham autem duas lineas KDH et ADT. Et etiam protraham a puncto A, quod erit aspectus aspicientium, perpendicularem super lineam KB, que sit perpendicularis AL, sitque linea AR equidistans linee KH. Manifestum est igitur aspicientibus a puncto A quod diversitas aspectus Lune est arcus HT, qui est pars una et septem minuta secundum quod comprehendimus per considerationem. Et quia arcus RT est maior arcu HT secundum id quod non computatur diversitas, quoniam tota terra est apud orbem ERHT sicut punctum, erit arcus RT circiter unam partem et septem minuta. Quapropter quoniam cum punctum A positum fuerit centrum orbis RHT, non erit in illo diversitas numerata, erit angulus RAT pars et septem minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erunt due partes et 14 minuta. Quapropter erit angulus ADK ei equalis due partes et 14 minuta, et arcus qui est super lineam AL erit due partes et 14 minuta secundum quantitatem qua erit circulus continens triangulum ADL orthogonium 360 partes. Chorda igitur AL erit due partes et 21 minuta secundum quantitatem qua erit diameter AD 120 partes. Sed linea DL est brevior diametro AD secundum id quod non numeratur diversitas. Ergo secundum quantitatem qua erit linea AL due partes et 21 minuta erit linea DL fere 120 partes. Et etiam quia arcus GD est 49 partes et 48 minuta, erit angulus GKD, qui est apud centrum orbis, 49 partes et 48 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, sed secundum quantitatem qua erunt duo anguli recti 360 partes erunt 99 partes et 36 minuta. Et propter hoc erit arcus qui est super lineam AL 99 partes et 36 minuta secundum quantitatem qua erit circulus continens triangulum ALK orthogonium 360 partes. Et arcus qui est supra lineam LK residuum semicirculi erit 80 partes et 24 minuta. Et chorde que subtenduntur arcubus, chorda quidem AL erit 91 partes et 39 minuta secundum quantitatem qua erit diameter AK 120 partes, et erit chorda LK 77 partes et 27 minuta. Secundum quantitatem ergo qua erit diameter AK, que est medietas diametri terre, pars una erit chorda quidem AL 46 minuta et chorda KL 39 minuta, sed secundum quantitatem qua fuit linea AL due partes et 21 minuta fuit declaratum quod linea LD est 120 partes fere. Ergo secundum quantitatem qua erit linea AL 46 minuta erit linea LD 39 partes et 6 minuta. Sed secundum quantitates illas fuit linea KL 39 minuta, et linea KA, que est medietas diametri terre, fuit pars una. Ergo secundum illam quantitatem erit tota linea KD continens longitudinem Lune, que fuit in hora considerationis 39 partes et 45 minuta. Et illud est quod ostendere voluimus.
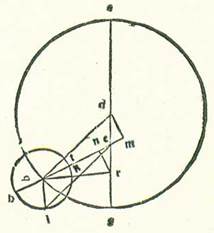Et post huius declarationem lineabo orbem Lune egredientis centri, supra quem sint A, B, G supra centrum D, et sit diameter eius ADG, et in diametro sit centrum orbis signorum, supra quod sit E, et nota declinationis orbis revolventis sit punctum R, et lineabo supra centrum B orbem revolventem, supra quem sint H, T, K, L, et protraham lineas HBTE et BD et BKR, sitque locus Lune in hac consideratione posita punctum L. Protraham autem duas lineas EL et LB, et producam lineam BE, et faciam ipsam pertransire, et protraham super ipsam duas perpendiculares, a puncto quidem D perpendicularem DM et a puncto R perpendicularem RN. Et quia in hora considerationis fuit numerus longitudinis 78 partes et 13 minuta, erit propter illud cuius iam precessit declaratio angulus AEB 156 partes et 26 minuta secundum quantitatem qua erunt quattuor anguli recti 360 partes, et unusquisque duorum angulorum REN et DEM, qui sunt residuum complementi duorum angulorum rectorum, erit 23 partes et 34 minuta. Et secundum quantitatem qua erunt duo anguli recti 360 partes erunt 47 partes et 8 minuta. Quapropter erit arcus qui est super unamquamque duarum linearum DM et RN 47 partes et 8 minuta secundum quantitatem qua erit quisque duorum circulorum continens duos triangulos DEM et REN positos ortogonios 360 partes, quoniam linea DE est equalis linee ER. Et arcus qui est super unamquamque duarum linearum EM et EN erit secundum illam quantitatem 132 partes et 52 minuta. Igitur unaqueque chordarum suarum, scilicet chorda DM et chorda RN, erit 47 partes et 59 minuta secundum quantitatem qua erit unaqueque duarum diametrorum DE et ER 120 partes. Et unaqueque duarum linearum EM et EN secundum illam quantitatem erit 110 partes. Et secundum illam quantitatem secundum quam erit unaqueque duarum linearum DE et ER decem partes et 19 minuta et linea DB medietas diametri orbis centri egredientis 49 partes et 41 minuta erit unaqueque duarum linearum DM et RN quattuor partes et octo minuta, et unaqueque duarum linearum EM et EN secundum illam quantitatem erit novem partes et 27 minuta. Et quia cum minuitur ex quadrato linee BD quadratum linee DM, remanet quadratum linee BM, erit longitudo linee BM secundum illam quantitatem 49 partes et 31 minuta. Et propter hoc erit linea BE 40 partes et 4 minuta. Et remanet ut sit linea BN secundum illam quantitatem 30 partes et 37 minuta secundum quantitatem qua fuit linea RN quattuor partes et octo minuta. Et quia cum aggregaverimus quadrata earum erit equale quadrato RB, erit longitudo chorde BR 30 partes et 54 minuta secundum quantitatem qua linea RN est quattuor partes et octo minuta. Ergo secundum quantitatem qua erit diameter BR 120 partes erit linea RN sexdecem partes et duo minuta. Et arcus qui est super eam erit 15 partes et 21 minuta secundum quantitatem qua erit circulus continens triangulum BRN orthogonium 360 partes. Angulus igitur RBN erit 15 partes et 21 minuta secundum quantitatem qua erunt duo anguli recti 360 partes, et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit septem partes et 40 minuta fere, que sunt arcus TK orbis revolventis. Et etiam quia longitudo Lune fuit in hora considerationis a longitudine longiore media 262 partes et 20 minuta et a puncto K, quod est longitudo propinquior media, et manifestum est quod est residuum longitudinis medietatis circuli maioris, 82 partes et 20 minuta, erit arcus KL 82 partes et 20 minuta et totus arcus TKL 90 partes. Ergo angulus TBL est rectus. Et quia linea BD, que est medietas diametri orbis centri egredientis, est 49 partes et 41 minuta, et linea BL, que est medietas diametri orbis revolventis, est quinque partes et 15 minuta, et secundum illam quantitatem fuit iam ostensum quod linea EB est 40 partes et 4 minuta et aggregatum ex quadratis earum est equale quadrato EL, erit longitudo linee EL secundum illam quantitatem 40 partes et 25 minuta. Longitudo ergo Lune in hora considerationis fuit 40 partes et 25 minuta secundum quantitatem qua fuit linea BL, que est medietas diametri orbis revolventis, quinque partes et 15 minuta. Et linea EA, que est a centro terre ad longitudinem longiorem orbis centri egredientis, est 60 partes. Et linea EG, que est a centro terre ad longitudinem propinquiorem orbis centri egredientis, est 39 partes et 22 minuta. Iam vero ostensum fuit quod in hora considerationis longitudo Lune, scilicet linea EL, fuit 39 partes et 45 minuta secundum quantitatem qua erit medietas diametri terre pars una. Ergo secundum quantitatem qua erit linea EL, que est longitudo Lune in hora considerationis, 39 partes et 45 minuta et medietas diametri terre pars una erit linea EA, que est longitudo Lune media que erit in hora applicationum, 59 partes, et linea EG, que est longitudo Lune media que erit in hora medietatis impletionis Lune, erit 38 partes et 43 minuta. Et medietas diametri orbis revolventis secundum illam quantitatem erit quinque partes et decem minuta. Et hoc est quod demonstrare intendimus.
⟨V.14⟩ Capitulum decimumquartum: De scientia eorum que videntur ex coniunctione et oppositione de quantitatibus diametrorum Solis et Lune et umbre
Et postquam declaravimus longitudines Lune secundum hunc modum, sequitur illud nunc ut demonstremus longitudines Solis. Et erit illud breviter per lineas cum nos addiderimus super longitudines Lune que erunt in hora applicationum quantitates angulorum qui proveniunt apud aspectum propter diametros Solis et Lune et umbre. Nos vero abhorruimus operari in inquisitione huius per capitula quorum quantitates reperiuntur per instrumenta aque aut instrumenta temporum elevationum equalitatis, quas estimavimus esse longitudinem diametrorum duorum luminarium et significant super ea et significant super ea: Corrupt passage? Cf. Toomer, loc. cit., p. 252, lines 4-7. Paris, BnF, lat. 14738 (86v, line 18 from the bottom) offers the same text., ideo quod non est possibile verificari illud per capitula istis similia et instrumenta. Sed nos operati sumus in eo per instrumenta duarum regularum quas declaravit Abrachis secundum longitudinem quattuor cubitorum. Cum ergo nos consideravimus per hoc instrumentum, invenimus diametrum Solis continere unum angulum fere in omni loco, et non est propter longitudinem Solis in eo diversitas cuius sit magna quantitas. Diameter vero Lune non continet illum angulum quem continet diameter Solis nisi cum fuerit longitudo eius a terra maxima, que erit in impletione Lune in longitudine longiore orbis revolutionis tantum, secundum quod simile est modis quibus operati sunt antiqui, et non cum fuerit Luna in longitudine media. Cum eo namque invenimus angulos minores angulis qui reperiuntur per instrumentum secundum quantitatem manifestam et non parvam. Et non per quantitates instrumenti duarum regularum invenimus illud, sed per quasdam eclypses lunares. Cum quidem subtenduntur queque duarum diametrorum angulo equali, scilicet quorum unus equalis est alteri, tunc iam fuit possibile accipere illud leviter per duas regulas. Non enim fit in illo aliquid ex numero partium. Quante vero quantitatis sit angulus, manifestum fuit nobis iam quod dubitatio est in eo magna. Quoniam apud considerationes nostras per duas regulas erit illud quod obumbrat latitudo in longitudine regule ex eo quod est inter oculos nostros et tabellam multus numerus. Et propter hoc non est possibile ut sit secundum veritatem. Et quia invenimus Lunam cum fuit in longitudine sua magna, sicut iam invenimus eam in considerationibus eclypsium lunarium que fuerunt in illa longitudine sua magna, fit angulus qui est apud visum aspicientis equalis etiam angulo Solis qui est apud visum aspicientis etiam. Cum ergo invenerimus quantitatem anguli qui subtenditur Lune, tunc ex hoc iam inveniemus angulum qui subtenditur Soli. Modi autem inveniendi quod diximus demonstrabimus scientiam in duabus eclypsibus etiam quas dicam. Fuit una earum in anno qui fuit quintus annorum Kalesen, qui est annus 127 annorum Nabuchodonosor, 27 die transacto mensis Athus, qui est unus ex mensibus Egyptiorum, in nocte cuius mane fuit dies vigesimusoctavus et in fine undecime hore noctis. Incepit Luna eclypsari in Babylonia, fuitque plurimum eclypsis eius a parte meridiei quarta diametri eius. Et quoniam eclypsis initium fuit post mediam noctem quinque horis temporalibus et fuit tempus medium post medietatem noctis sex horis fere, que fuerunt tunc in Babylonia quinque hore et medietas et tertia hore equales, quoniam locus Solis secundum verificationem fuit in illa hora 27 partes et tria minuta Arietis, manifestum est igitur quod eclypsis fuit tempus medium apud plurimum quod cecidit ex diametro eius in umbra in Babylonia quidem post medietatem noctis quinque horis et medietate mediate M. et tertia hore equalis et in Alexandria post medietatem noctis quinque horis tantum. Et fuit tempus aggregatum a primo annorum Nabuchodonosor usque ad horam medie eclypsis 126 anni et 86 dies et 17 hore equales absolute, et erunt cum equate fuerint per diversitatem dierum cum noctibus suis sexdecem hore et medietas et quarta hore. Et propter hoc fuit visus locus Lune per cursum suum medium in longitudine 25 partes et 32 minuta Libre, et fuit locus eius verus 27 partes et 5 minuta, et fuit longitudo partis in qua fuit Luna a longitudine longiore orbis revolutionis 340 partes et 7 minuta, fuitque longitudo illius partis in orbe suo declivi a longitudine longiore septentrionis 80 partes et 40 minuta. Manifestum est igitur quod cum fuerit longitudo centri ab uno duorum nodorum novem partes et tertia partis in orbe suo declivi cum fuerit in longitudine sua magna, et fuerit centrum umbre in orbe magno descripto supra illam longitudinem secundum angulum rectum orbis declivis in loco in quo erunt magne tenebre, quarta diametri Lune cadet in umbram. Et fuit eclypsis secunda in anno septimo annorum Chamersis, qui est annus ducentesimus et vigesimus quintus annorum Nabuchodonosor decem et septem diebus mensis Chamertuz One could equally read Chamertum. Paris, BnF, lat. 14738 (87r, line 18 from the bottom) reads Chameuit. The Greek text reads ‘Phamenoth’ (see Toomer, loc. cit., p. 253, line 4 from the bottom). transactis in nocte cuius mane fuit dies decimusoctavus ante medietatem noctis una hora. Et eclypsatum fuit ex Luna in Babylonia a parte septentrionis medietas diametri eius. Et fuit illa eclypsis in Alexandria ante medietatem noctis una hora et medietate et tertia hore equalis fere. Et fuit tempus aggregatum ducenti et vigintiquatuor anni Egyptii et centum et nonagintasex dies et decem hore et sexta hore absolute equales, que erunt secundum verificationem novem hore et medietas et tertia hore, quoniam Sol fuit in 18 partibus et 12 minutis Cancri. Et fuit locus Lune per cursum suum medium in longitudine 20 partes et 20 minuta Capricorni, et secundum verificationem 18 partes et 14 minuta. Et fuit longitudo eius a longitudine longiore orbis revolutionis 28 partes et 5 minuta. Fuitque longitudo illius partis a longitudine longiore septentrionis in orbe suo declivi 262 partes et 12 minuta. Iam ergo manifestum est quod ex hoc etiam cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe suo declivi septem partes et quattuor quinte partis, et fuerit Luna in illa longitudine magna, et fuerit centrum umbre eius in loco quem prediximus, medietas diametri Lune cadet in umbram. Sed cum fuerit longitudo centri Lune ab uno duorum nodorum in orbe declivi novem partes et tertia partis, erit longitudo eius a linea medii cinguli signorum quadragintaocto minuta et medietas minuti partis unius in orbe magno descripto super ipsum secundum angulum rectum orbis declivis. Et cum fuerit eius longitudo ab uno duorum nodorum in orbe declivi septem partes et quattuor quinte partis, erit elongatio eius a linea medii cinguli signorum 40 minuta et due tertie minuti partis unius in orbe magno descripto supra ipsum secundum angulum rectum orbis declivis. Et quoniam superfluitas que est inter duas eclypses non est nisi quarta diametri Lune et superfluitas que est inter longitudines earum a linea medii cinguli signorum, que est centrum umbre, est septem minuta et medietas et tertia minuti, tunc manifestum est quod tota diameter Lune subtenditur arcui orbis magni, qui erit 31 minuta et tertia unius minuti. Et propter hoc declaratur nobis quod medietas diametri umbre subtenditur 40 minutis et duabus tertiis minuti partis unius cum fuerit in longitudine Lune magna. Cum enim fuerit longitudo centri Lune a centro umbre iste partes, erit centrum Lune contingens circulum umbre, propter hoc quod illud quod eclypsatur de Luna est medietas diametri eius. Erit ergo medietas diametri umbre dupla medietati diametri Lune, que est quindecem minuta et due tertie minuti et tres quinte similis eius, excepta re parva, cuius non est magna quantitas. Cum ergo invenerimus has quantitates positas in considerationibus aliis pluribus et istis similibus convenientes fere, operabimur per eas in eis que videntur ex eclypsibus et operati sumus per eas in hoc loco in declaratione longitudinis Solis, quam ipse secutus est Abrachis. Et fuerunt circuli Solis et Lune et terre quos comprehendit figura pinealis minores circulis suis magnis descriptis in spheris eorum, et diametri eorum minores diametris eorum.
⟨V.15⟩ Capitulum decimumquintum: De scientia umbre terre et longitudinis Solis et eorum que declarantur cum eis propter longitudinem Lune
Postquam quod diximus fit notum et longitudo Lune magna, cum fuerit in applicationibus, erit 64 partes et 10 minuta secundum quantitatem qua erit medietas diametri terre pars una, quoniam iam ostensum est quod longitudo media est 59 partes et medietas diametri orbis revolutionis est 5 partes et 10 minuta, tunc considerabimus quanta erit longitudo Solis.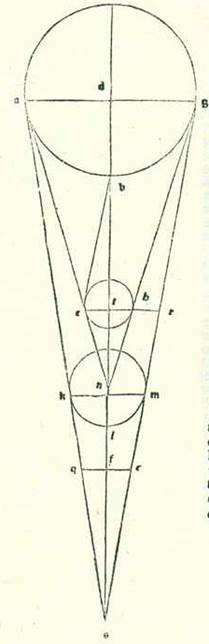 
Describam circulos orbium magnorum in superficie spherarum ipsorum, circulum quidem orbis Solis, supra quem sint A, B, G, supra centrum D, et circulum quidem orbis Lune in longitudine sua magna, supra quem sint E, H, supra centrum T, et circulum orbis terre, supra quem sint K, L, M, supra centrum N, sintque superficies eorum que sunt supra centra eorum superficies quidem continens terram et Solem, supra quam sint A, S, G, et continens Solem et Lunam, supra quam sint A, N, G, sitque axis communis supra quam sint D, T, N, S, et sint linee que transeunt per loca contactus linee contingentes de quibus manifestum est quod ipse erunt in sensu equales et equidistantes diametri, linea quidem contingens circulum orbis Solis, supra quam sint A, D, G, et linea contingens circulum orbis Lune, supra quam sint E, T, H, et linea contingens circulum orbis terre, supra quam sint K, N, M, et linea contingens circulum umbre in qua cadit Luna in longitudine sua magna, supra quam sint Q, F, C, et sit linea TN equalis linee NF, et unaqueque earum sit 64 partes et 10 minuta secundum quantitatem qua erit linea NL, que est medietas diametri terre pars una. Oportet igitur ut inveniamus proportionem linee ND, que est longitudinis Solis ad lineam NL, que est medietas diametri terre. Faciam igitur pertransire lineam EH usque ad R. Et quia iam declaravimus quod diameter Lune in eis que narravimus de longitudine eius magna in applicationibus subtenditur arcui orbis descripti super ipsam super centrum terre, qui erit 31 minuta et 20 secunda secundum quantitatem qua erit circulus 360 partes, ergo erit angulus ENH 31 minuta et 20 secunda secundum quantitatem qua erunt quattuor anguli recti 360 partes. Et eius medietas, que est angulus TNH, erit 31 minuta et 20 secunda secundum quantitatem qua erunt duo anguli recti 360 partes. Quapropter erit arcus qui est super lineam TH 31 minuta et 20 secunda secundum quantitatem qua erit circulus continens triangulum NHT orthogonium 360 partes, et arcus qui est super lineam TN residuum complementi semicirculi erit 179 partes et 28 minuta et 40 secunda, et chorde eorum erunt, chorda quidem TH 32 minuta et 48 secunda secundum quantitatem qua erit diameter NH 120 partes, et propter hoc erit chorda NT fere 120 partes. Cum autem fuerit linea NT 64 partes et 10 minuta, erit linea TH secundum illam quantitatem 17 minuta et 33 secunda, et secundum illam quantitatem erit linea NM, que est medietas diametri terre pars una. Sed quia proportio linee FC ad lineam TH est equalis proportioni duorum et trium quintarum fere ad unum, erit linea FC secundum illam quantitatem 45 minuta et 38 secunda. Ergo erunt due linee TH et FC pars una et tria minuta et undecem secunda secundum quantitatem qua erit linea MN pars una. Sed ambe linee FC et TR, scilicet totum, secundum illam quantitatem sunt due partes, quoniam ipse sunt equales duplo MN. Et quia omnes linee, quemadmodum diximus, sunt equidistantes et linea FN equatur linee NT, remanet ergo ut sit linea HR residua 56 minuta et 49 secunda secundum quantitatem qua erit linea NM pars una, et erit proportio NM ad HR sicut proportio NG ad GH, que est sicut proportio ND ad TD. Secundum quantitatem ergo qua erit linea ND pars una erit linea TD 56 minuta et 49 secunda, et linea TN residua secundum illam quantitatem erit tria minuta et undecem secunda. Ergo secundum quantitatem qua erit linea NT 64 partes et 10 minuta et linea NM pars una erit linea ND, que est longitudo Solis, 1210 partes fere. Et similiter quia secundum quantitatem qua erit linea MN pars una fuit declaratum quod linea FC est 45 minuta et 38 secunda, et quod sicut proportio linee NM ad lineam FC similiter proportio linee NS ad lineam SF, ergo secundum quantitatem qua erit linea NS pars una erit linea FS 45 minuta et 38 secunda, et linea FN residua erit secundum illam quantitatem 14 minuta et 22 secunda. Secundum quantitatem ergo qua erit linea FN 64 partes et 10 minuta et linea NM medietas diametri terre pars una erit linea SF 203 partes et 50 minuta fere. Et tota linea SN est 268 partes. Iam ergo aggregatum est nobis ut cum fuerit medietas diametri terre pars una, erit secundum illam quantitatem longitudo Lune quidem media in applicationibus 59 partes et longitudo Solis 1210 partes et longitudo extremitatis umbre a centro terre 268 partes. Et illud est quod voluimus demonstrare.
⟨V.16⟩ Capitulum sextumdecimum: De scientia magnitudinis corporum Solis et Lune et terre
Et ex hoc levior facta est nobis scientia magnitudinis corporum per id quod scivimus de proportionibus diametri Solis et Lune et terre. Iam enim declaratum est nobis quod secundum quantitatem qua erit linea NM, que est medietas diametri terre, pars una erit linea TH, que est medietas diametri Lune, 17 minuta et 33 secunda et linea NT 64 partes et 10 minuta. Et erit proportio NT ad TH sicut proportio ND ad DG. Ergo secundum illam quantitatem qua iam ostensum est quod linea ND est 1210 partes erit DG, que est medietas diametri Solis, quintuplum medietatis diametri terre et medietas eius fere. Erunt ergo proportiones diametrorum existentes ille proportiones invente. Secundum quantitatem igitur qua erit diameter Lune pars una erit diameter terre tres partes et due quinte fere et diameter Solis decem et octo partes et quattuor quinte partis. Diameter ergo terre erit in longitudine triplum diametri Lune et due quinte eius. Et erit diameter Solis decuplum et octuplum diametri Lune et quattuor quinte eius fere. Eritque diameter Solis quintuplum diametri terre et medietas eius fere. Et similiter quia cubus qui erit ex multiplicatione unius in se, deinde in se, non erit nisi unus secundum quantitatem unius, et cubus qui erit ex multiplicatione tripli et duarum quintarum eius in se et postea in se erit secundum illam quantitatem trigintuplum nonuplum et quarta eius fere, et cubus qui erit ex multiplicatione decupli et octupli et quattuor quintarum eius in se, deinde in se, erit sexies mille et sexcentuplum et quadragintuplum et quadruplum et medietas eius fere, tunc iam aggregatum est nobis ut secundum quantitatem qua erit magnitudo corporis Lune pars una erit magnitudo corporis terre trigintuplum et nonuplum et quarta eius fere, et quod magnitudo corporis Solis erit sexies mille et sexcentuplum et quadragintuplum et quadruplum et medietas eius, et est centuplum et septuagintuplum corporis terre fere.
⟨V.17⟩ Capitulum decimumseptimum: De scientia divisionis diversitatis aspectus que est Solis et Lune
Iam autem oportet, postquam fuit quod prediximus secundum quod narravimus, ut demonstremus etiam breviter quomodo accipiantur diversitates aspectuum particularium ex quantitatibus longitudinum Solis et Lune. Demonstrabimus autem primum diversitates que videntur in orbe magno descripto super eos et super punctum summitatis capitum.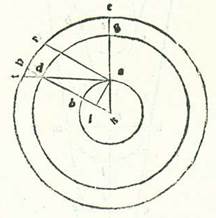 
Lineabo igitur in superficie huius orbis magni quem prediximus etiam orbem terre magnum descriptum, supra quem sint A, B, et orbem quidem Solis aut Lune, supra quem sint G, D, et orbem apud quem erit terra sicut punctum, supra quem sint E, R, H, T, et sit centrum omnium eorum commune punctum K, et diameter lineata supra punctum summitatis capitum sit KAGE. Cum ergo separaverimus arcum a puncto G, quod est summitas capitum, ad D, et erit arcus GD verbi gratia 30 partes secundum quantitatem qua erit orbis GD 360 partes, et protraxerimus etiam duas lineas KDH et ADT, et produxerimus a puncto A lineam equidistantem KH, que sit linea AR, et protraxerimus super eam perpendicularem LA, tunc quia longitudo non figitur secundum unam habitudinem in omni hora que est propter unumquodque duorum luminarium, igitur propter hoc erit diversitas diversitatum aspectuum que est propter Solem parvissima omnino et non sensibilis, quoniam longitudo centri orbis centri egredientis Solis et terre est parva et longitudo est magna. Diversitas autem diversitatum aspectuum Lune erit sensibilis et manifesta propter motum Lune in orbe revolutionis et motum orbis revolutionis in orbe centri egredientis, propter hoc quod demonstratur quod id quod facit motum in unaquaque duarum longitudinum diversitatum non est parvum. Diversitates autem aspectuum Solis declarabimus per proportionem longitudinis unius tantum, per quod volo intelligi proportionem 1210 partium ad unam. Diversitates vero aspectuum Lune demonstrabimus in longitudinibus quattuor, ut sint in capitulis que futura sunt levioris acceptionis. Assumam autem ex istis quattuor longitudinibus primum duas longitudines orbis revolutionis cum fuerit in longiore longitudine orbis centri egredientis. Et ex istis duabus longitudinibus assumam primum longitudinem que pervenit ad longitudinem longiorem orbis revolutionis, que facta fuit per illud cuius premisimus declarationem 64 partes et decem minuta secundum quantitatem qua erit medietas diametri terre pars una. Et longitudo secunda est que pervenit ad longitudinem propinquiorem orbis revolutionis, que fuit 53 partes et 50 minuta. Due vero relique longitudines sunt cum fit orbis revolutionis in longitudine propinquiore orbis centri egredientis. Et ex his duabus assumam etiam primum longitudinem que pervenit ad longitudinem longiorem orbis revolutionis, que fit propter id cuius iam premisimus declarationem 43 partes et 53 minuta secundum quantitatem qua erit medietas diametri terre pars una. Secunda vero longitudo est que pervenit ad longitudinem propinquiorem orbis revolutionis, et fit 33 partes et 33 minuta secundum illam quantitatem. Et quia arcus GD positus est 30 partes, erit angulus GKD 30 partes secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 60 partes. Quapropter erit arcus qui est super lineam AL 60 partes secundum quantitatem qua erit circulus continens triangulum AKL orthogonium 360 partes. Et arcus qui est super lineam KL residuum complementi semicirculi est 120 partes. Chorde ergo eorum, scilicet chorda AL est 60 partes secundum quantitatem qua erit diameter AK 120 partes, et erit chorda KL 103 partes et 55 minuta secundum illam quantitatem. Ergo secundum quantitatem qua erit linea AK pars una erit AL 30 minuta et linea KL 52 minuta. Et similiter erit quantitas linee KLD in longitudine quidem Solis 1210 partes, et in longitudinibus quidem Lune secundum terminum quidem primum 64 partes et 10 minuta, et secundum terminum quidem secundum 53 partes et 50 minuta, et secundum terminum quidem tertium 43 partes et 53 minuta, et secundum terminum quidem quartum 33 partes et 33 minuta. Ergo remanet linea LD reliqua, que est loco linee AD, non tamen diversificatur in hoc quin ipsa sit diversa, non equalis, que in longitudine quidem Solis erit 1209 partes et octo minuta, et in longitudinibus quidem Lune erit secundum terminum quidem primum 63 partes et 18 minuta, et secundum terminum secundum 52 partes et 58 minuta, et secundum terminum tertium 43 partes et minutum unum, et secundum terminum quartum 32 partes et 41 minuta. Secundum quantitatem ergo qua erit chorda AD 120 partes erit linea AL duo minuta et 59 secunda. Et ut non iteremus sermonem in omni hora, commendabimus memorie longitudines secundum ordines suos. Postea erit 56 minuta et 52 secunda, deinde erit pars una et septem minuta et 58 secunda, postea pars una et 23 minuta et 41 secunda, postea pars una et 50 minuta. Et arcus qui est super eam primo erit duo minuta et 52 secunda, postea erit 54 minuta et 18 secunda, postea erit pars una et 4 minuta et 54 secunda, et postea pars una et 20 minuta, postea ultimo erit pars una et 45 minuta fere secundum quantitatem qua erit circulus continens triangulum DLA orthogonium 360 partes. Et angulus ADB, qui est equalis angulo RAT, erit secundum quantitatem qua erunt duo anguli recti 360 partes in principio duo minuta et 52 secunda, postea erit 54 minuta et 18 secunda, postea erit pars una et quattuor minuta et 54 secunda, postea pars una et 20 minuta, postea tandem pars una et 45 minuta. Et secundum quantitatem qua erunt quattuor anguli recti 360 partes erit minutum unum et 25 secunda, postea 27 minuta et 9 secunda, postea 32 minuta et 27 secunda, postea 40 minuta tantum, postea 52 minuta et 30 secunda. Ergo quia punctum A non est diversum a centro, scilicet puncto K, et arcus RHT est maior arcu HT secundum quantitatem insensibilem, quoniam tota terra apud orbem ERHT fuit sicut punctum, erit arcus HT, qui est diversitas aspectus, secundum quantitatem qua erit circulus ERHT 360 partes in longitudine quidem Solis minutum unum et 25 secunda, sed in longitudinibus Lune secundum terminum primum 27 minuta et 9 secunda, et secundum terminum secundum 32 minuta et 27 secunda, et secundum terminum tertium 40 minuta, et secundum terminum quartum 52 minuta et 30 secunda. Et hoc est quod oportuit nos declarare.
Et secundum similitudinem illius in eis que remanent ex longitudinibus que sunt a puncto summitatis capitum numeravimus divisionem diversitatis aspectus secundum terminos quattuor, et posuimus eam omnibus sex partibus usque ad complementum nonaginta partium in tabulis quas lineavimus ad cognitionem diversitatis aspectus in quadragintaquinque areis etiam et in novem tabulis, et posuimus in prima tabularum earum numerum partium quarte, que sunt 90 partes (et manifestum est quod earum superfluitas est secundum duas et duas partes), et in tabula secunda portionem minutorum cuiusque portionum que sunt ex diversitate aspectus Solis, et in tabula tertia diversitatem aspectus Lune secundum terminum primum, et in tabula quarta superfluitatem que est inter terminum primum et terminum secundum diversitatis aspectus Lune, et in tabula quinta diversitates aspectuum Lune que sunt secundum terminum tertium, et in tabula sexta superfluitatem diversitatis aspectus Lune que est inter terminum quartum et terminum tertium, sicut verbi gratia illud quod posuimus in tabula prima Solis unum minutum et 25 secunda, et post illud 27 minuta et 9 secunda que sunt Lune secundum terminum primum, et quinque minuta et 18 secunda que sunt augmentum quod addit terminus secundus super terminum primum, deinde post illud etiam 40 minuta que sunt tertii termini, deinde post illud 12 minuta et 30 secunda que sunt augmentum quod addit terminus quartus super terminum tertium. Et ut sciremus diversitates aspectuum Lune in longitudinibus que sunt in eis que sunt inter longitudines que sunt longitudo longior et inter longitudines que sunt longitudo propinquior secundum quantitatem divisionis portionum sectionum partium breviter ex eis que posuimus in terminis quattuor de minutis positis, posuimus tabulas tres reliquas, ut produceremus ex eis has diversitates positas, quarum considerationes posuimus secundum modum quem dicam, si Deus voluerit.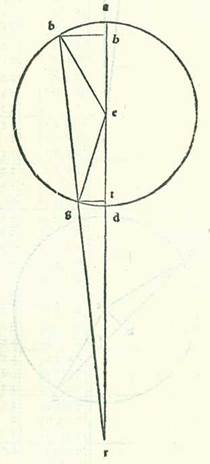 
Lineabo orbem revolutionis Lune, supra quem sint A, B, G supra centrum E, et sit punctum R centrum orbis signorum et centrum terre, et protraham lineam AER, et producam lineam RGB, et protraham duas lineas BE et GE, et producam super lineam AD duas perpendiculares, a puncto quidem B perpendicularem BH et a puncto G perpendicularem GT, et sit primum longitudo Lune a puncto A, quod est longitudo longior que videtur vere ad centrum R, arcus AB, et sit iste arcus verbi gratia 60 partes, ut sit angulus BEH 60 partes secundum quantitatem qua erunt quattuor anguli recti 360 partes, et secundum quantitatem qua erunt duo anguli recti 360 partes erit 120 partes. Et similiter erunt duo arcus, ille quidem qui est super lineam HB 120 partes secundum quantitatem qua erit circulus continens triangulum BEH orthogonium 360 partes, et arcus qui est super lineam EH, qui est ad complendam medietatem circuli, 60 partes. Erunt ergo chorde eorum, chorda quidem BH 103 partes et 55 minuta secundum quantitatem qua erit diameter EB 120 partes, et chorda EH secundum illam quantitatem erit 60 partes. Cum autem fuerit punctum E, scilicet centrum orbis revolutionis, in longitudine longiore orbis centri egredientis, erit proportio RE ad EB sicut proportio 60 ad quinque partes et 15 minuta. Secundum quantitatem ergo qua erit linea EB quinque partes et 15 minuta erit linea BH quattuor partes et 33 minuta, et linea EH due partes et 38 minuta, et tota linea HR erit 62 partes et 38 minuta. Et quia ex quadrato linee RH cum quadrato linee HB, quando ei coniungetur, erit quadratum linee RB, erit longitudo linee RB 62 partes et 38 minuta secundum quantitatem qua erit RA, que est longitudo que est in termino primo, 65 partes et 15 minuta, et erit linea RD, que est longitudinis que est secundum terminum secundum, 54 partes et 45 minuta, et linea AD, que est superfluitas que est inter duas longitudines horum duorum terminorum, erit decem partes et 30 minuta. Ergo secundum diversitatem que est in eis que sunt inter longitudinem que est in termino secundo et inter longitudinem que est in termino primo erit due partes et 27 minuta secundum quantitatem qua erit tota diversitas decem partes et 30 minuta. Quapropter secundum quantitatem qua erit tota diversitas 60 minuta erit diversitas 14 minuta. Illud ergo est quod iam fiximus in tabula septima in area in qua est ex numero medietas 60, per quod intelligitur 30, quoniam omnes partes fixe in tabula prima, que sunt 90 partes, sunt medietas 180 que sunt in eis que sunt inter terminum primum et quartum. Et similiter si nos posuerimus arcum GD secundum illam quantitatem 60 partes, declarabitur quod linea GT erit quattuor partes et 33 minuta secundum quantitatem qua erit linea GE, que est medietas diametri orbis revolutionis, quinque partes et 15 minuta. Et similiter erit linea ET due partes et 38 minuta, Et remanet ut sit linea RT secundum illam quantitatem 57 partes et 22 minuta. Quapropter erit chorda RG 57 partes et 33 minuta. Quas cum minuerimus etiam ex 65 partibus et 15 minutis que sunt termini primi, inveniemus residuum septem partes et 42 minuta, que sunt ex minutis diversitatis totius 44 minuta. Et ipsa ponemus in illa tabula, et opponemus ea numero 60, propterea quod arcus ABG est 120 partes. Et illud est quod oportuit nos demonstrare.
Et etiam figam hos arcus secundum habitudinem suam et imaginabor punctum E, quod est centrum, super longitudinem propinquiorem orbis centri egredientis, que est locus in quo est terminus tertius et quartus. Et quia in hoc loco erit proportio ER ad EB sicut proportio 60 ad octo, ergo secundum quantitatem qua erit BE octo partes aggregatur ut sit unaqueque duarum linearum BH et GT, cum fuerit unusquisque duorum arcuum AB et DG 60 partes, sex partes et 56 minuta secundum quantitatem qua erit linea RE 60 partes, et unaqueque duarum linearum EH et ET secundum illam quantitatem quattuor partes. Et propter hoc, cum fuerit RH secundum illam quantitatem 64 partes et RT 56 partes, propter illud aggregatur ut sit chorda RB 64 partes et 23 minuta, et erit chorda RG secundum illam quantitatem 56 partes et 26 minuta secundum quantitatem qua erit linea RA, que est termini tertii, 68 partes et linea AD, que est diversitatis termini quarti, sexdecem partes. Si ergo nos minuerimus 64 partes et 23 minuta ex 68 partibus, erit residuum tres partes et 37 minuta, que erunt ex minutis totius, scilicet sexdecem, 13 minuta 33 secunda. Et similiter ponam hec etiam opposita numero 30 partium in tabula octava. Et si nos minuerimus 56 partes et 26 minuta ex illis 68 partibus, erit residuum undecem partes et 34 minuta, quarum portio ex sexdecim, que est diversitas tota, erit 43 minuta et 24 secunda. Que similiter figemus in tabula octava opposita numero 60 partium. Que autem aggregantur ex diversitatibus que erunt propter motum Lune in orbe revolutionis sunt secundum modum quem diximus et posuimus.
Diversitatum vero que sunt propter revolutionem orbis revolutionis in orbe centri egredientis acceptio est sicut narrabo.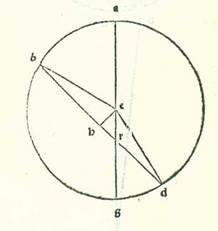 
Describam orbem centri egredientis Lune, supra quem sint A, B, G, D, supra centrum E et diametrum AEG, et imaginabor super hanc diametrum centrum orbis signorum supra notam R. Et cum protraxerimus lineam BRD et posuerimus etiam unumquemque duorum angulorum BRA et GRD 60 partes secundum quantitatem qua erunt quattuor anguli recti 360 partes, et illud est quod accidet si fuerit longitudo 60 partes, cum fuerit centrum orbis revolutionis super punctum B et cum fuerit centrum orbis revolutionis supra punctum D, erit longitudo 120 partes. Et cum protraxerimus duas lineas BE et ED et produxerimus a puncto E perpendicularem super lineam BRD supra quam sint E, H, tunc quia angulus BRA erit 120 partes secundum quantitatem qua erunt duo anguli recti 360 partes, erit arcus quidem qui est super lineam EH 120 partes secundum quantitatem qua erit circulus continens triangulum ERH orthogonium 360 partes, et arcus qui est super lineam RH 60 partes diminutas ex complemento semicirculi. Erunt ergo chorde que subtenduntur eis, chorda quidem EH 103 partes et 55 minuta secundum quantitatem qua erit diameter RE 120 partes, et chorda quidem RH secundum illam quantitatem 60 partes. Similiter ergo erit RE quidem, que est id quod est inter duo centra, decem partes et 19 minuta, et medietas quidem diametri orbis centri egredientis 49 partes et 41 minuta. Secundum ergo illam quantitatem erit linea EH octo partes et 56 minuta, et linea RH secundum illam quantitatem erit quinque partes et decem minuta. Et quia cum ex quadrato linee BE minuitur quadratum linee EH, erit residuum quadratum linee BH, erit unaqueque duarum linearum BH et DH secundum illam quantitatem 48 partes et 53 minuta. Erit ergo tota RB 54 partes et tria minuta secundum quantitatem qua erit linea RA, que est terminus primus, 60 partes, et linea RG, que est terminus secundus, 39 partes et 22 minuta, et superfluitas que est inter eas 20 partes et 38 minuta. Et remanet ut sit linea RD secundum illam quantitatem 43 partes et 43 minuta. Et quia 60 partes addunt super 54 partes et tria minuta quinque partes et 57 minuta, que sunt ex 20 partibus et 38 minutis, que sunt diversitatis totius, 17 minuta et 18 secunda, et super 43 partes quidem et 43 minuta addunt 16 partes et 17 minuta, que sunt etiam ex 20 partibus et 38 minutis 47 minuta et 21 secunda, ergo manifestum est quod oportet ut ponamus 17 minuta et 18 secunda in tabula nona opposita numero 30 partium, que sunt longitudinis longioris, et 47 quidem minuta et 21 secunda opponamus numero 60, qui est etiam 120, quoniam cum fuerit longitudo propinquior apud numerum 90, erit longitudo 60 et longitudo 120 equales in potentia. Et hoc est quod voluimus ostendere.
Et secundum hunc modum numerabimus in arcubus aliis quod erit ex minutis diversitatis secundum additiones tres positas super omnes duodecem portiones, que erunt etiam super omnes has sex portiones in numeris positis in tabulis, propter hoc quod 180 partes (que sunt a longiore longitudine ad propinquiorem longitudinem) complentur in tabulis super 90 partes. Posuimus ergo quod aggregatum fuit ex minutis secundum mensurationem cuiusque numerorum cuiusque portionis proprietatem. Declaravimus scilicet que sunt inter portiones ex superfluitate portionum que sunt super omnes sex partes. Posuimus ea secundum superfluitatem equalem. Quoniam diversitas in eis fere non mutat mensurationem secundum aliquid magnum nisi quod fuerit maius hac quantitate, neque in superfluitate neque in diversitate aspectus. Et hec est descriptio tabularum:
⟨V.18⟩ Capitulum decimumoctavum: De positione tabularum diversitatis aspectus
☉ |
☾ |
☽ |
|||||||||||||||||||||||
Numeri |
Diversitates aspectus Solis |
Tabule superfluitatum diversitatum aspectuum Lune |
Minuta longitudinis |
Minuta orbis centri egredientis |
|||||||||||||||||||||
Primi modi ☾ |
Secundi modi super primum |
Tertii modi ☽ |
Quarti modi super tertium |
longioris |
propinquioris |
||||||||||||||||||||
orbis revolutionis |
|||||||||||||||||||||||||
Prima |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Septima |
Octava |
Nona |
|||||||||||||||||
Partes |
Minuta |
Secunda |
Minuta |
Secunda |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Minuta |
Secunda |
Minuta |
Secunda |
Minuta |
Secunda |
Minuta |
Secunda |
||||||||
2
4
6 |
0
0
0 |
7
13
19 |
1
3
5 |
54
48
41 |
0
0
1 |
23
45
7 |
0
0
0 |
3
6
9 |
0
0
0 |
0
1
2 |
50
40
30 |
0
0
0 |
14
28
42 |
0
0
0 |
11
22
33 |
0
0
0 |
15
30
45 |
||||||||
8
10
12 |
0
0
0 |
25
31
37 |
7
9
11 |
34
27
19 |
1
1
2 |
29
51
12 |
0
0
0 |
11
14
17 |
40
20
0 |
3
4
5 |
20
10
0 |
1
2
2 |
22
2
42 |
1
1
2 |
7
41
15 |
1
2
3 |
13
21
9 |
||||||||
14
16
18 |
0
0
0 |
42
48
53 |
13
15
16 |
10
0
49 |
2
2
3 |
33
54
15 |
0
0
0 |
19
22
25 |
40
20
0 |
5
6
7 |
50
40
30 |
3
4
5 |
35
28
21 |
3
4
5 |
18
11
19 |
3
5
6 |
22
35
48 |
||||||||
20
22
24 |
0
1
1 |
58
4
9 |
18
20
23 |
36
22
6 |
3
3
4 |
36
54
18 |
0
0
0 |
27
30
33 |
40
20
0 |
8
9
10 |
20
10
0 |
6
7
9 |
39
57
15 |
6
7
8 |
25
41
57 |
8
10
11 |
22
4
39 |
||||||||
26
28
30 |
1
1
1 |
15
20
25 |
24
25
27 |
49
30
9 |
4
4
5 |
39
59
18 |
0
0
0 |
35
37
40 |
40
20
0 |
10
11
12 |
50
40
30 |
10
12
14 |
50
25
0 |
10
12
13 |
29
1
33 |
12
15
17 |
32
25
18 |
||||||||
32
34
36 |
1
1
1 |
30
35
40 |
28
30
31 |
46
21
54 |
5
5
6 |
37
55
13 |
0
0
0 |
42
44
47 |
40
20
0 |
13
14
15 |
20
10
0 |
15
17
19 |
52
44
36 |
15
17
19 |
22
11
0 |
19
21
23 |
23
28
33 |
||||||||
38
40
42 |
1
1
1 |
44
49
54 |
33
34
36 |
24
51
14 |
6
6
7 |
30
46
3 |
0
0
0 |
49
51
53 |
40
20
0 |
15
16
17 |
50
40
30 |
21
23
25 |
40
44
48 |
20
22
24 |
19
58
57 |
25
27
29 |
40
47
54 |
||||||||
44
46
48 |
1
2
2 |
58
3
8 |
37
38
40 |
37
55
14 |
7
7
7 |
20
25
49 |
0
0
0 |
55
57
59 |
40
20
0 |
17
18
19 |
20
10
0 |
27
29
31 |
52
56
0 |
27
29
31 |
1
5
9 |
32
34
36 |
0
6
12 |
||||||||
50
52
54 |
2
2
2 |
12
16
20 |
41
42
43 |
38
39
45 |
8
8
8 |
3
16
29 |
1
1
1 |
0
2
4 |
40
20
0 |
19
20
21 |
50
40
30 |
33
35
38 |
0
0
0 |
33
35
37 |
14
18
24 |
38
40
42 |
9
6
3 |
||||||||
56
58
60 |
2
2
2 |
23
26
29 |
44
45
46 |
48
48
46 |
8
9
9 |
42
53
3 |
1
1
1 |
5
6
8 |
40
20
0 |
21
21
22 |
20
10
0 |
40
42
44 |
50
40
0 |
39
41
43 |
24
24
24 |
43
45
47 |
49
35
21 |
||||||||
62
64
66 |
2
2
2 |
32
34
36 |
47
48
49 |
40
30
15 |
9
9
9 |
13
22
31 |
1
1
1 |
9
10
12 |
40
20
0 |
22
22
23 |
50
40
30 |
45
47
49 |
56
22
48 |
45
47
48 |
13
2
11 |
48
50
51 |
49
17
45 |
||||||||
68
70
72 |
2
2
2 |
38
40
42 |
49
50
51 |
57
36
11 |
9
9
9 |
39
46
53 |
1
1
1 |
13
14
15 |
40
20
0 |
23
23
23 |
20
10
0 |
50
52
53 |
56
22
48 |
50
51
53 |
24
57
30 |
52
54
55 |
57
9
21 |
||||||||
74
76
78 |
2
2
2 |
44
46
47 |
51
52
52 |
44
12
34 |
9
10
10 |
58
4
8 |
1
1
1 |
15
16
17 |
40
20
0 |
23
24
24 |
40
20
30 |
54
56
57 |
57
6
15 |
54
55
57 |
41
52
3 |
56
57
57 |
32
23
54 |
||||||||
80
82
84 |
2
2
2 |
48
49
50 |
53
53
53 |
13
19
21 |
10
10
10 |
11
14
16 |
1
1
1 |
17
17
18 |
40
20
0 |
24
24
24 |
40
50
0 |
57
58
59 |
57
39
21 |
57
58
59 |
47
31
35 |
58
58
59 |
26
58
30 |
||||||||
86
88
90 |
2
2
2 |
50
51
51 |
53
53
53 |
29
33
34 |
10
10
10 |
16
17
17 |
1
1
1 |
18
18
19 |
40
20
0 |
24
24
24 |
40
50
0 |
59
59
60 |
34
40
0 |
59
59
60 |
30
45
0 |
59
59
60 |
40
50
0 |
||||||||
⟨V.19⟩ Capitulum decimumnonum: De cognitione equandi diversitates aspectuum et equatione earum
Cum voluerimus scire quanta sit quantitas diversitatis aspectus Lune in omni revolutione primum que est in orbe magno descripto super Lunam et super punctum summitatis capitum, considerabimus quanta sit quantitas longitudinis que est inter Lunam in hoc orbe et inter orbem meridiei ex horis equalibus in climate quesito et mittemus eas in tabulas angulorum que sunt illius climatis et illius signi in quo est Luna. Postea accipiemus partes que opponuntur horis in tabula secunda et portionem que contingit partibus horarum ex eo si fuerint cum eis partes. Illud igitur est longitudo Lune a puncto summitatis capitum in orbe magno descripto super eas. Postea mittemus illud in tabulam diversitatum aspectuum et considerabimus in qua area tabule prime sit et que opponuntur illi numero in quattuor tabulis que sunt post tabulam diversitatis aspectus Solis, que sunt tabula tertia, quarta, quinta et sexta, et firmabimus quod erit in unaquaque earum per se. Demum post illud accipiemus numerum cursus diversitatis equate in illa hora que est longitudinis longioris equate vere, ipsummet augmentum quidem accipiemus si fuerit minus 180, et diminutum quidem a complemento 360 si fuerit plus 180. Postea semper accipiemus medietatem harum partium, et mittemus eas in lineam numerorum, et considerabimus quantum opponatur illi numero in tabula septima et in tabula octava ex minutis, et firmabimus unumquodque eorum per se, et accipiemus quod inveniemus ex minutis in tabula septima, que sunt diversitatis que est in tabula quarta, et addemus ea semper super diversitatem aspectus que est in tabula tertia, et accipiemus quod invenimus ex minutis in tabula octava ex eis que sunt diversitatis que est in tabula sexta, et addemus ea super diversitatem aspectus que est in tabula quinta, et firmabimus, idest scribemus, superfluitatem que est inter duas diversitates duorum aspectuum. Deinde post illud accipiemus partes longitudinis Lune per cursum suum medium, aut a parte Solis aut a parte opposita ei, et accipiemus longitudinem propinquiorem ad quamcunque duarum partium fuerit, et mittemus eam in tabulam numerorum primam, et considerabimus quod opponitur illi numero primo ex minutis in tabula nona, scilicet ultima, et accipiemus illa minuta ex superfluitate que est inter duas diversitates duorum aspectuum quam firmavimus, et addemus ea super minorem duarum diversitatum duorum aspectuum equatorum tabule tertie et quarte. Quod ergo aggregabitur erit diversitas aspectus Lune in orbe magno descripto super eam et super summitatem capitum. Et ex hoc videtur diversitas aspectus Solis expedite in loco illi simili propter eclypses solares ex eo quod est in tabula secunda ex partibus que opponuntur quantitati arcus qui est a puncto summitatis capitum.
Et ut equemus diversitatem aspectus que erit in illa hora in longitudine et latitudine, accipiemus illas horas equales etiam que sunt longitudinis Lune ab orbe meridiei, et mittemus eas in illum locum tabularum angulorum, et inquiremus partes que opponuntur numero horarum. Si ergo fuerit locus Lune ante meridiem, accipiemus partes que sunt in tabula tertia, et si fuerit locus eius post meridiem, acccipiemus partes que sunt in tabula quarta. Tunc si fuerint partes minus 90, firmabimus eas, et si fuerint plus 90, firmabimus partes que minuuntur ex complemento 180. Et illud est quantitas anguli parvi ex angulis qui sunt super hanc portionem secundum quantitatem qua erit angulus rectus 90 partes. Accipiemus ergo partes quas firmavimus, et duplabimus eas, et mittemus quod provenerit in tabulam chordarum arcuum, scilicet mittemus illas easdem partes et etiam que minuuntur ex complemento 180 partium. Erit ergo proportio chorde arcus qui est duplum harum partium ad chordam que subtenditur arcui diminuto ex complemento semicirculi sicut proportio diversitatis aspectus Lune in latitudine ad diversitatem eius in longitudine. Quoniam inter arcus orbium magnorum quorum hec fuerit quantitas et inter lineas rectas seu istas chordas non est diversitas. Quoniam quantitates arcuum istis similium orbium sunt quorum sunt diverse chorde. Multiplicabo igitur numerum harum chordarum in numerum chordarum arcuum diversitatis aspectus inventum, sicut verbi gratia diversitatis aspectus que erit in orbe descripto super punctum summitatis capitum, postea dividam quod aggregatur per centum et viginti, et partes que provenerint ex divisione sunt diversitas illius aspectus. Universaliter autem dico quod illud quod erit ex diversitate aspectus in latitudine tunc cum fuerit punctum summitatis capitum in orbe meridiei declinatum ad septentrionem a puncto quod est in medio celi orbis signorum, erit diversitas aspectus ad meridiem. Et cum fuerit punctum summitatis capitum declinatum a puncto quod est in medio celi orbis signorum ad meridiem, tunc diversitas aspectus in latitudine erit eo tempore ad septentrionem. Sed quod erit ex diversitate aspectus in longitudine, quia quantitates angulorum posite in tabulis non continent nisi angulum septentrionis ex duobus angulis quos continet portio orbis signorum ab occidente ad orientem a duabus partibus, tunc quidem cum fuerit diversitas aspectus in latitudine in parte septentrionis, tunc si fuerit angulus positus maior recto, erit diversitas aspectus in longitudine secundum conversionem successionis signorum, et si fuerit angulus minor recto, erit secundum successionem signorum. Et cum fuerit diversitas aspectus in latitudine ad partem meridiei, erit secundum conversionem illius, scilicet si fuerit angulus positus in tabulis angulorum maior recto, tunc diversitas aspectus in longitudine erit secundum successionem signorum, et si fuerit minor recto, tunc erit secundum contrarietatem successionis signorum. Et operati sumus cum illa diversitate aspectus Solis secundum quod iam precessit eius declaratio, etsi non sit sensibilis, sed ne simus ignari quod iam scimus quod ei est diversitas aspectus faciens accidere in eis que videntur aliquid propter quod immittitur aliquid erroris, non tamen quod immittat aliquid sensibile. Et similiter sufficimus nobis in diversitate aspectus Lune per arcus et angulos qui proveniunt in orbe signorum propter orbem magnum descriptum super duos polos horizontis. Et excusamur per illud ab eo quod accidit propter orbem Lune declivem. Quoniam diversitatem que provenit ex eo in applicationibus eclypsium non invenimus sensibilem. Et vehementer laborare ad ponendum hoc est difficile indigens declaratione multa in numeratione. Quoniam loca Lune in omni pertransitione eius in orbe signorum non sunt terminata, neque longitudo eius a duobus nodis, sed eius localis motus multe diversitatis est in magnitudine et in locis in quantitatibus et in sitibus eisdem.
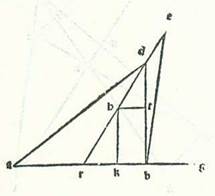Et ut levior fiat scientia eorum que prediximus, ponam portionem orbis signorum, supra quam sint A, B, G, et portionem orbis Lune declivis, supra quam sint A, D, et super nodum punctum A, et centrum Lune punctum D, et producam lineam erectam a puncto D ad orbem signorum, supra quam sint DB, et ponam punctum E polum horizontis, et lineabo super ipsum portiones orbis magni, super centrum quidem Lune portionem EDR et super punctum B portionem EB, et sit diversitas aspectus Lune arcus DH, et protraham a puncto H ad duas lineas rectas BA et BD duas lineas rectas, scilicet lineam HT et lineam HK, et sit longitudo Lune a nodo in longitudine quidem longitudo eius vera AB et longitudo eius que videtur KA, et longitudo eius ab orbe signorum in latitudine quidem vera BD et longitudo eius que videtur HK, et ex diversitatibus aspectus que videntur a D et H ad orbem signorum in longitudine quidem est equale linee TH et in latitudine equale linee DT. Et quia diversitas aspectus DH scietur ex eis quorum premisimus narrationem cum scitus erit arcus ED, et unaqueque duarum diversitatum aspectus DT et TH scietur cum fuerit angulus GRE notus, et nos iam declaravimus in precedentibus arcus et angulos qui erunt apud puncta orbis signorum nota in orbe magno descripto super punctum summitatis capitum, et nobis non est notum hic ex punctis orbis signorum nisi punctum B tantum, tunc manifestum est quod nos fecimus arcum EB loco arcus ED et fecimus angulum GBE loco anguli GRE. Abrachis vero iam incepit ut faceret equationem huic similem, sed non sapienter et secundum magnam diminutionem eorum quibus opus erat. Primum quidem non fecit nisi longitudinem unam, que est longitudo AD, et non fecit omnes longitudines neque plures eorum. Et illud est quod fuit necessarium ut operaretur ipse diligenti inquisitione subtilium rerum. Et postea illud oblitus est donec cecidit in errorem valde horrendum et fedum. Quoniam ipse etiam iam premisit et declaravit arcus et angulos qui videntur propter orbem signorum et quod DH scietur ex ED cum fuerit ED nota (ipse enim declaravit hoc in libro suo primo in diversitate aspectus) et fecit etiam inventionem arcus DE arcum ER et angulum ERG, ac si essent noti. Et similiter in libro suo secundo, cum ipse numeravit arcum DR, reperire voluit arcum ED residuum et non pervenit ad scientiam eius, quoniam punctum B est notum ex orbe signorum, et non punctum R, et similiter etiam noti ex arcubus quidem arcus EB, et non arcus ER, et ex angulis quidem angulus EBG, et non angulus ERG. Et illud est quod movit eum ad equationes particulares. Quoniam in pluribus locis erit diversitas que est inter arcum ED et arcum ER magne quantitatis in sensu, propterea quod ipsi sunt magis elongati ab hoc ut sint noti quam illi duo multum, plurimum autem diversitatis que est inter BE, que est nota secundum veritatem, et inter diversitatem que est ED, que erit secundum quantitatem magnam, est BD tantum, que est ex longitudine a nodo in omni hora. Et hoc oportuit demonstrari.
Equatio autem vera declarabitur nobis quemadmodum narrabo. 
Describam orbem signorum, supra quem sint A, B, G, et faciam transire super ipsum lineam aliam secantem ipsum orthogonaliter, supra quam sint D, B, E, et sit Luna aut super punctum D aut super punctum E, sitque longitudo eius in latitudine ab AG, scilicet orbe signorum, arcus notus, sicut BD aut BE, et arcus qui sunt apud orbem signorum, scilicet apud punctum B a puncto summitatis capitum, et anguli noti, et erunt arcus et anguli qui sunt apud punctum D aut punctum E quesiti noti. Et illud est quod nos oportuit demonstrare.
Et cum fuerit situs orbis signorum super rectum angulum orbis descripti super punctum R et ponemus punctum R polum horizontis et orbem magnum descriptum super duo puncta R et B, sicut verbi gratia RDBE, tunc manifestum est quod arcus DE obviabit orbi signorum et erit angulus qui videtur super punctum D et punctum E non diversus ab angulo qui est apud B. Ergo anguli qui erunt ex istis lineis descriptis super hec puncta orbis signorum erunt recti, et erit arcus RD minor arcu RB secundum arcum BD, et arcus RE est maior arcu RB secundum arcum BE, et ipsi sunt noti. Et illud est quod oportuit nos demonstrare.
Quod si concurrerint orbis signorum, supra quem sint A, B, G, et orbis magnus descriptus super punctum summitatis capitum, et posuerimus polum horizontis punctum A, et protraxerimus duos arcus AD et AE, erunt hi duo arcus diversi ab arcu AB, et duo anguli BAD et BAE diversi AB Probably corrupt for ab, which is also the reading of Paris, BnF, lat. 14738 (92v, line 13 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 269, line 1 from the bottom). angulo quod Probably corrupt for qui, which is also the reading of Paris, BnF, lat. 14738 (92v, line 13 from the bottom) and would correspond to the Greek text (see Toomer, loc. cit., p. 269, line 1 from the bottom). non erant Probably corrupt for erat, which would correspond to the Greek text (see Toomer, loc. cit., p. 269, line 1 from the bottom). Paris, BnF, lat. 14738 (92v, line 13 from the bottom) reads erat (corrected from erunt). ante, et erunt AD et AE noti, cum fuerit eorum proportio sicut proportio chordarum eorum propter parvitatem diversitatis que est inter illa. Cum ergo unusquisque horum AB et DB et BE fuerit datus, et ambo quadrata AB et BE fuerint equalia quadrato AE, et ambo quadrata AB et BD fuerint equalia quadrato AD, similiter duo anguli BAD et BAE erunt noti. Et hoc est quod oportuit nos declarare.
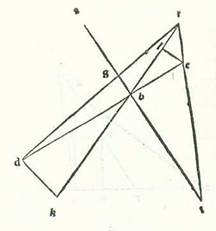Et cum fuerit situs orbis signorum declivis a capite et recto angulo et protraxerimus a puncto R, quod est polus horizontis, lineas coniunctas, que sint RB et RGD et RET, erit arcus RB notus et angulus ABR notus. Manifestum est igitur quod etiam oportet ut sint BD et BE note et duo arcus RD et RE et duo anguli AGR et ATR noti cum protraxerimus duas perpendiculares DK et EL super lineam RB. Et quia angulus ABR est datus et angulus ABE est rectus semper, erunt duo trianguli BDK et BLE rectanguli angulorum datorum, et erit proportio RB ad duas lineas continentes angulum rectum nota, et ad duas chordas DB et BE nota etiam. Et propter hoc erunt due chorde RD et RE date. Et propter hoc erunt duo anguli DRK et ERL, qui sunt additiones quesite, noti. Angulus autem AGR est maior angulo ABR secundum angulum DRB, et angulus ATR est minor angulo ABR secundum angulum ERL. Et illud est quod debuimus demonstrare.
Demonstrabo etiam quod cum fuerit longitudo in latitudine hec longitudo posita, erit diversitas maior in angulis quidem cum fuerit punctum B ipsum punctum summitatis capitum. Etenim cum non fuerit apud B neque unus angulus, erunt linee que protrahuntur a puncto summitatis capitum ad duo puncta D et E facientes angulos rectos super orbem signorum. Et in arcubus quidem, cum fuerint loca eorum locus unus et nec etiam fuerit apud punctum B neque arcus unus, erit quantitas duorum arcuum qui sunt apud duo puncta D et E equalis quantitati transitus Lune in latitudine. Et similiter etiam cum fuerit orbis descriptus super punctum summitatis capitum erectus super orbem signorum, erit diversitas que erit inter unumquemque duorum arcuum RD et RE et inter arcum RB tota diversitas transitus Lune in latitudine. Et cum fuerit declinatio DE ad RB in locis aliis, erit quod aggregabitur ex additionibus arcuum et angulorum ad minus quam ad totam latitudinem. Et cum fuerit longitudo Lune in latitudine ab orbe signorum quinque partes, erit plurimum quod diversificatur ex diversitate aspectuum decem minuta fere. Quinque enim partes que sunt diversitas maior arcuum non faciunt diversitatem aspectus quantitatem horum minutorum nisi in magnis additionibus et parvis longitudinibus. Per hoc volumus intelligi: Quando Luna fuerit in propinquiore propinquitate orbis revolutionis et orbis ecentrici, et cum fuerit longitudo Lune in eclypsibus solaribus maior transitus, qui est pars una et medietas partis fere, erit diversitas aspectus tantum unum minutum et medietas meditas M. minuti, scilicet equalis numero partium longitudinis Lune. Et illud non erit nisi in raritate temporis.
Acceptio autem capituli equandi angulos et arcus ab eo qui vult illud breviter et pauco sermone erit secundum modum quem narrabo. Omnino ergo dico quod accipiemus numerum anguli, et duplabimus ipsum, et mittemus ipsum in tabulas arcuum et chordarum, et accipiemus quod opponitur ei et quod opponitur etiam numero diminuto a complemento duorum angulorum rectorum, qui sunt 180, et ponemus unumquodque eorum per se, et multiplicabimus ipsum in partes latitudinis. Postea accipiemus ex unoquoque eorum partem centesimam et vicesimam et firmabimus et scribemus eam, et quod fit ex angulo primo, proiiciemus ex arcu qui est a puncto summitatis capitum cum fuerit Luna ad partem puncti summitatis capitum, et cum fuerit Luna ad contrarium puncti summitatis capitum, addemus ipsum super illum arcum, et quod comprehensum fuerit, multiplicabimus in se, et addemus ipsum super quadratum quod erit ex multiplicatione que provenit ex angulo diminuto a 180 in se ducto. Postea accipiemus radicem eius quod aggregatur, et ipsa erit chorda portionis arcus quesiti. Deinde post illud accipiemus quod firmavimus de angulo diminuto, et multiplicabimus ipsum in 120, et dividemus illud per arcus inventos, et quod provenerit ex divisione firmabimus secundum seipsum. Postea mittemus quod firmavimus in tabulas chordarum et arcuum et accipiemus ex arcubus ipsum quod sequitur. Postea accipiemus medietatem eius. Si ergo fuerit arcus equatus maior primo, addemus illud super id quod est anguli primi, et si fuerit minor, minuemus ipsum ex eo, et iam equavimus angulum etiam. Et ut exemplificemus illius exemplum, ponemus in hac forma posita arcum BR 45 partes, et angulum ABR 30 partes secundum quantitatem qua erit unus angulus rectus 90 partes, et unumquemque duorum arcuum DB et BE, qui sunt latitudinis, quinque partes. Et quia chorda que opponitur duplo 30 partium, scilicet 60, erit 60 et chorda que opponitur ei quod minuitur ex complemento duorum angulorum rectorum, scilicet 120, erit 104 partes fere, erit proportio BL ad LE sicut proportio 60 ad 104 partes. Et similiter erit proportio BK ad KD secundum quantitatem qua erit chorda BD 120 partes. Multiplicabo igitur unumquemque duorum numerorum in quinque partes que sunt chorde et accipiam cuiusque earum partem centesimam et vigesimam, et erit unaqueque earum, scilicet KB et BL, due partes et 30 minuta secundum illam quantitatem, et unaqueque harum DK et EL erit quattuor partes et 20 minuta. Si ergo fuerit Luna super punctum E, minuemus primum duas partes et 30 minuta ex quadragintaquinque partibus que sunt arcus RB, propter hoc quod longitudo Lune in latitudine erit ad partem summitatis capitum. Per quod intelligi volumus quod ambe erunt aut ad partem meridiei aut ad partem septentrionis orbis signorum. Erit ergo arcus RL 42 partes et 30 minuta. Quod si fuerit Luna super punctum D, addemus eas, propter hoc quod est contrarium illius. Erit ergo arcus RK 47 partes et 30 minuta. Postea aggregabo unumquodque duorum quadratorum RL et RK cum unoquoque duorum quadratorum DK et LE secundum se, scilicet aggregabo quadratum quattuor partium et 20 minutorum cum unoquoque duorum quadratorum, scilicet 42 partium et 30 minutorum et 47 partium et 30 minutorum, et eius quod provenit ex omnibus duobus quadratis secundum se accipiemus radicem. Ergo erit arcus RE 42 partes et 56 minuta fere, et erit arcus RD 47 partes et 54 minuta. Postea multiplicabo quattuor partes et 20 minuta in 120 et dividam ea per 42 partes et 56 minuta et per 47 partes et 54 minuta. Erit ergo EL duodecim partes et octo minuta fere secundum quantitatem qua erit chorda RE 120 partes, et erit DK decem partes et medietas et tertia partis fere secundum quantitatem qua erit diameter RD 120 partes, et erit arcus qui est super chordam duodecim partium et octo minutorum undecim partes et tres quinte partis fere, et erit arcus qui est super chordam decem partium et medietatis et tertie partis fere decem partes et tertia partis fere. Et assumam medietates earum. Quinque ergo partes et quattuor quintas partis que sunt anguli ERL minuam ex angulo ABR, qui est 30 partes, propter hoc quod arcus RE est minor arcu RB. Fit ergo angulus ATR 24 partes et quinta partis. Quinque vero partes et sextam partis que sunt anguli DRK addam super 30 partes, ideo quia arcus RD est maior arcu RB. Fit ergo angulus AGR 35 partes et sexta partis. Et hoc est quod debuimus demonstrare.
Expleta est dictio quinta libri Almagesti Ptolemei Pheludiensis.