Ptolemy
Almagesti (tr. Gerard of Cremona)
Venice, Petrus Liechtenstein, 1515
transcribed by Stefan Georges
How to cite this transcription?
This transcription is taken from the copy München, Deutsches Museum, 3000/1946 B 16 (henceforth abbreviated by the siglum ‘M’), which, as has become clear in the course of this work, represents one of at least three versions of the 1515 print (the other two being represented by the copies München, Bayerische Staatsbibliothek, Res/2 A.gr.b. 1000 and München, Bayerische Staatsbibliothek, 2 A.gr.b. 1001). Cf. for instance the differences in the geometrical figures on 22r and the difference in the last line on 31v.
Transcription rules
The transcription has been established on the basis of the transcription guidelines of the ‘Ptolemaeus Arabus et Latinus’ project. In addition to these remarks, the following are necessary:
The text is full of problematic passages, many of which seem to derive from difficulties Gerard had in understanding the Arabic text. Commenting on all of them would have exceeded the possibilities of this transcription. Therefore, only those passages have been commented on which are outright ungrammatical or nonsensical. In these cases, unless there was secondary literature, the text has regularly been compared with the 12th century manuscript ‘Paris, Bibliothèque nationale de France, lat. 14738’ and to G. J. Toomer’s English translation of the Almagest, established on the basis of Heiberg’s edition of the Greek text.
The abbreviations i., nāque and unamquāque can be resolved in two different ways, since the words for which they stand appear with two different spellings when they are not abbreviated: idest / id est, namque / nanque and unamquamque / unamquanque. As in each case the first alternative is the more frequent one, these have been chosen for resolving the abbreviations.
Similarly, measuring units often appear in the singular where by classical standards the plural would be required (e.g. invenimus locum Solis in illa hora 26 partem et 17 minutum Piscis), thus allowing for two alternative resolutions in cases where such units are abbreviated. As these cases are very numerous, they have not been counted to find a solution. Instead, they have been resolved as plural forms on the grounds that these appear to be used more frequently.
Further, there are six instances of the unusual abbrevation g̑, the sense of which is clearly that of ergo or igitur. Since the standard abbreviation for ergo would be go, and for igitur g~, gi or gr, and since M also uses a semicircle with a downward facing opening for ‑er in scienter, this abbreviation has been interpreted as g~ and therefore been resolved as igitur.
Further, the notes .e.l. and .e.m., which figure abundantly in the star catalogue on 78r-88v and look like abbreviations, are in fact not abbreviations. Rather, they were originally meant to be written as l above e and as e above m (cf. the explanation in the last four lines on 77v) and were apparently meant to replicate ل above ه and ه above م, which in the Arabic version of the catalogue is used to denote in stars a somewhat lower or higher luminosity than the one indicated by their class number.
Finally, M often prints the same figures two or more times in a row, apparently in order to keep them available for the reader in cases when the related text covers both the front and the back of a leaf. In these cases the repeated figures have been left out except when they appear alongside a new chapter.
Table of contents and links to chapters
〈Prooemium〉
Claudii Ptolemei Alexandrini astronomorum principis Almagesti seu magne constructionis liber omnium celestium motuum rationem clarissimis sententiis enucleans fausto sydere incipit. Et primo in eundem prefatio:
Quidam princeps nomine Albuguafe in libro suo quem Scientiarum electionem et verborum nominavit pulchritudinem dixit quod hic Ptolemeus fuit vir in disciplinarum scientia prepotens, preeminens aliis, in duabus artibus subtilis, idest geometria et astrologia, et fecit libros multos, de quorum numero iste est, qui Megasiti dicitur, cuius significatio est Maior perfectus, quem ad linguam volentes convertere Arabicam nominaverunt Almagesti. Hic autem ortus et educatus fuit in Alexandria maiori terra Egypti. Cuius tamen propago de terra Sem et de provincia que dicitur Pheuludia. Qui in Alexandria cursus syderum consideravit instrumentis tempore regis Adriani et aliorum et super considerationes quas Abrachis in Rhodo expertus est opus suum edidit. Ptolemeus vero hic non fuit unus regum Egypti qui Ptolemei vocati sunt, sicut quidam estimant, sed Ptolemeus fuit eius nomen ac si aliquis vocaretur Cosdrohe aut Cesar. Hic autem in statu moderatus fuit, colore albus, incessu largus, subtiles habens pedes, in maxilla dextra signum habens rubeum, barba eius spissa et nigra, dentes anteriores habens discoopertos et apertos, os eius parvum, loquele bone et dulcis, fortis ire, tarde sedabatur, multum spaciabatur et equitabat, parum comedebat, multum ieiunabat, redolentem habens anhelitum et indumenta nitida. Mortuus est anno vite sue septuagesimooctavo. Hec sunt de disciplinis et sapientiis Ptolemei huius: Conveniens est intelligenti pro Deo verecundari cum ea que ei sunt grata cogitat. Intelligens est qui semper linguam suam refrenat nisi ad hoc ut de Deo loquatur. Insipiens est qui suiipsius ignorat quantitatem. Cum aliquis sibi placet, ad hoc deductus est ut ira Dei sit super ipsum. In bono quod Deus operatur quasi bonitatem largi datoris attendere debes, et in malis adversis quasi purgationis et eterne remunerationis bonitatem. Quanto plus fini appropinquas, bonum cum augmento operare. Hominis disciplina sui intellectus socius est et apud homines intercessor. Non fuit mortuus qui scientiam vivificavit, nec fuit pauper qui intellectui dominatus est. Qui inter sapientes humilior est sapientior existit, sicut locus profundior magis abundat aquis aliis lacunis. Non disseras nisi cum eo qui veritatem concedit, nec respondeas nisi a te querenti consilium et cupide recipienti. Tuum consilium non committas nisi qui ipsum celaverit. Qui in mundo permanere voluerit cor patiens adversitatibus preparet. Parva domus est dolor minor. Plus gaudeas quod non dixisti errorem quam quod bene dicendo non tacuisti. Cum irasceris, non extendas manum ad peccandum, et cum dimissio vindicte non fuerit debilitas, parce. Ultime hominis promissiones cane sunt. On this sentence Charles Burnett comments: ‘The Arabic means: ›Old age is the last promise (or trust) in this world‹’ (see Charles Burnett, ›Ptolemaeus in Almagesto dixit‹: The Transformation of Ptolemy’s Almagest in its Transmission via Arabic into Latin, in: Georg Toepfer and Hartmut Böhme (eds.), Transformationen antiker Wissenschaften, Berlin/New York 2010, p. 115-140, p. 129). Iustorum corda secretorum sunt monumenta. Qui per alios non corrigitur, nec alii per ipsum corrigentur. Manus intellectuum animarum tenent habenas. Vulgi habenas regere melius est quam multos habere milites. Fiducia est socius consolans quam, licet non consequaris, eam tamen angariasti. On this sentence Charles Burnett comments: ‘The Latin translator seems to have read astamtaʿta (›you have enjoyed it‹) as ›astamnaʿta‹, which he has understood as deriving from root ›m-n-ʿ‹ (›constrain, prevent‹). The Arabic makes sense: ›Hope is a cheerful friend. Even if 〈what you hope for〉 does not come to you, you have enjoyed 〈its companionship〉‹’ (see Burnett, loc. cit., p. 129). Securitas solitudinis dolorem removet, et pavor multitudinis consolationem aufert. Inter homines altior existit mundo qui non curat in cuius manu sit mundus. Invido videtur quod ablatio boni alterius sit sibi bonum. Homines lucrantur census, et census lucrantur homines. Qui scientiam suam ultra astutiam que in ipso est extendit est sicut pastor debilis cum multis ovibus. Qui in dignitate sua multum extollitur in amissione eius multum deprimitur. Qui male operando vult celari satis discoopertus est. Qui in mendacio confidit, tempestive deficiet ei. Meditatio veritatis existit clavis. Intercessor est petentis ala. Anima non egredietur a fiducia usque ad mortem. Anima ignorans suo socio magis inimicatur. Quidam rex invitavit Ptolemeum ad prandium, qui rogans fore se excusatum dixit: ‘Regibus contingit fere quod contingit considerantibus picturas, que cum a longe videntur placent, propinque vero non dulcescunt’.
〈I〉
Liber hic Almagesti preclarissimi Ptolemei Pheludiensis universam celestium motuum rationem tredecem dictionibus seu partialibus libris centum et quadragintaquattuor capitulis constantibus aptissime complectitur. In quarum cuiusque dictionum fronte capitula quibus eadem contexta fuerit pari huic serie se offerent.
Dictio prima quattuordecim capitulis constat.
Capitulum primum, in quo scientie huius ad alias excellentiam et finis eius utilitatem dicam
Capitulum secundum: De ordinibus modorum huius scientie
Capitulum tertium: Quomodo scitur quod motus celi sit sphericus
Capitulum quartum: De eo quod indicat quod terra sit spherica
Capitulum quintum: De eo quod indicat quod terra sit in medio celi
Capitulum sextum: De eo quod indicat quod terra sit sicut punctum apud celum
Capitulum septimum: Quod terra localem motum non habeat
Capitulum octavum: Quod primi motus qui sunt in celo sunt duo
Capitulum nonum: De scientia quantitatis chordarum partium circuli
Capitulum decimum: Quomodo tabule chordarum partium circuli fiant
Capitulum undecimum: De positione arcuum et chordarum eorum in tabulis
Capitulum duodecimum: De arte instrumenti quo scitur quantitas arcus qui est inter duos tropicos
Capitulum tredecimum: De scientia quantitatum arcuum qui sunt inter orbem equationis diei et inter orbem medii signorum qui sunt declinationis
Capitulum quartumdecimum: De scientia quantitatum arcuum equationis diei qui elevantur in sphera directa cum arcubus orbis signorum datis
〈I.1〉 Capitulum primum: De scientie huius ad alias excellentia et finis eius utilitate
Bonum scire fuit quod sapientibus non deviantibus visum est cum partem speculationis a parte operationis diviserunt, que sunt due sapientie partes. Licet enim contingat ut operatione sit speculatio prius, inter eas tamen non parva existit differentia, non solum quia, etsi quorundam morum honestatem possibile sit pluribus hominibus inesse absque doctrina, non tamen totius scientiam absque doctrina comprehendere est possibile possibibile M., verum etiam quia plurimum utilitatis consistit in operatione quidem propter plurimam perseverantiam agendi in rebus et in scientia quidem propter augmentum in scientia. Quapropter nobis visum est expedire nobis ut sciamus metiri operationem cum doctrina principiorum eorum que reperiuntur in imaginatione et intellectu, ne quid desit ex inquisitione totius pulchre rei decentis forme secundum mensurationis bonitatem, neque in minimis rebus neque in vilibus, et ut expendamus plurimum nostri ocii et plurimum nostri studii in disciplina scientie magne et excelse, et precipue que proprie nominatur scientia. O quam bonum fuit quod Aristoteles divisit theoricam cum eam in tria prima genera distribuit, in naturale videlicet, doctrinale et theologicum. Generatio namque omnis generati ex materia est et forma et motu, neque est possibile ut in aliquo noto unumquodque horum trium solum per se sigillatim stans absque alio videatur. Possibile tamen est ut unum absque alio intelligatur. Quod si quis scire querit que sit prima causa primi motus, affirmabitur illi accuratius perscrutanti, cum illud secundum ordines suos fuerit declaratum, quod est Deus invisibilis et immobilis. Species autem theorice qua inquiritur perscrutatio qua scitur quod est in suprema altitudine ordinum mundi nominatur theologica. Et hec quidem intelligitur separatum esse a substantiis sensibilibus. Species vero theorice qua species materiales investigantur semper alterate in album et nigrum, et calidum et frigidum, et acetosum et dulce et que his assimilantur nominatur naturalis. Hec autem natura consistit in rebus antiquis, quarum plures sub orbe Lune moventur vel que corrumpuntur vel que finiuntur. Speciem vero indicantem demonstrationem specierum formarum et motus eorum que localiter moventur et quantitatem et magnitudinem et tempus et figuram et que his similia existunt sigillatim ponam, et vocabo eam proprie nomine scientie. Et hec quidem natura quasi medium tenet inter illas duas naturas, non tantum quoniam possibile est ut intelligatur secundum sensum, sicut species comprehenditur naturalis, et absque sensu etiam, quemadmodum species comprehenditur theologica, verumetiam quia cum in omnibus essentiis existit actu, ipsa etiam temperantia This word, which is not contained in the Greek text (see G. J. Toomer (transl.), Ptolemy’s ALMAGEST, Princeton 1998, p. 36, lines 10-11), does not seem to fit in here and is probably due to a corruption. In Paris, BnF, lat. 14738 (2r, lines 16-17) it is the subject of the subclause: ... verum etiam quia temperantia communiter existit in omnibus corporibus que corrumpuntur et que non corrumpuntur ... communiter existit in omnibus essentiis mortalibus et immortalibus et que corrumpuntur et que non corrumpuntur. In eis autem que corrumpuntur existit cum alteratione forme, que non separatur a materia, sed in eis que non corrumpuntur, scilicet in natura celesti, remanet in forma sua absque alteratione. Quapropter dico quod duo reliqua genera divisionis theorice sola estimatione cognoscuntur, et non scientie veritate comprehenduntur, theologicum videlicet quia nunquam videtur neque comprehenditur, naturale vero propter motionem materie et levitatem sui cursus et velocitatem sue alterationis et parvitatem sue more, quare convenientia sapientum nunquam in eis expectatur. Genus vero doctrinale ipsum solum replet eum qui ipsum studiose reponit et vehementi investigatione inquirit scientia permanente vera absque alteratione et contrarietate. Quoniam demonstrationes que in ipso sunt secundum vias sunt in quibus non est ambiguitas, cum assumantur ex scientia numeri et mensure. Nos autem volumus ut in tota hac scientia, inquantum possumus, desudemus, et precipue in scientia corporum celestium. In hac namque scientia semper fit investigatio et consideratio de rebus que semper sunt uno modo. Quapropter possibile est ut hec scientia per seipsam comprehendatur propter sui declarationem et sui ordinis bonitatem uno modo semper existentis, quod quidem proprium est scientie vere. Hec quoque non parum valet ad reliquorum duorum modorum scientie comprehensionem, et precipue scientie Dei excelsi. Ipsa namque est scientia et via ad sciendum Deum altissimum propter rationem cum perscrutatione et intellectu, que et eis similia vere et manifeste significant Deum, qui non alteratur et non movetur neque est accidens neque est factus, quia ipsa nostre scientie quam de Deo habemus altissimo vicina existit et quia ipsa est semita ducens ad eum. Ipsa namque sola tantum de rebus semper permanentibus perseveranter inquirit et est de rebus que sunt ex genere considerationis eius quod non alteratur, et estimatio ipsius absque opere vicinatur accidentibus que sunt in revolutionibus et ordinibus motuum qui sunt in substantiis sensibilibus moventibus et motis sempiternis, in quibus non existit diversitas. Ad genus quoque naturale non parvi extat iuvaminis. Universalitas enim proprietatis nature materialis non videtur neque comprehenditur nisi ex proprietate conversionis motus localis. Quapropter et quod corrumpitur et quod non corrumpitur per motum rectum et circularem sentitur. Grave quoque et leve et agens et patiens videntur per motum a medio et per eum qui est ad medium. Preterea in actionibus quoque et honestatibus morum laudabilium non est eius necessitas parva. Immo nihil est magis adiuvans ad acuendos oculos mentis nostre et intellectus ad considerandum ea que operibus similantur divinis propter bonitatem moderaminis et equalitatis et parvitatem arrogantie et quoniam ipsa facit eum qui perseveranter eam inquirit hanc celestem puchritudinem diligere et ducit eum ad perseverantiam divini studii et coniungit eum ipsi quod anime simile est propter bonitatem forme et assimilat eum creatori suo. Nos autem laborabimus ut in amore scientie sempiternorum manentium usque ad terminum quem eorum conditor eis imposuit in sequentibus huius nostri libri addamus. Ea vero huius scientie quorum comprehensio iam completa est a scientibus ea non deviantibus, scilicet habentibus hanc scientiam et inquirentibus eam cum investigatione et studio, addiscemus. Desideramus vero addere in eis ex declaratione secundum mensuram qua possibile fuerit secundum tempus quod fuit inter nos et eos. De omnibus vero huius scientie que iam estimamus fore manifesta et posita et certificata apud nos usque ad hoc nostrum presens tempus elaborabimus librum scribere compendiosum absque disputatione et quanto plus possibile est brevem, secundum mensuram tamen qua possibile sit subtiles in arte arithmetice eum intelligere. Quia vero tempora complere volumus, ponemus quicquid possibile est conferre et quo indigent ex scientia celesti in loco sibi proprio et secundum suos ordines. Ne autem liber prolongetur, quecunque verificata sunt ex eis que ab antiquis posita sunt simpliciter solum pertranseam. Que vero comprehendere non potuerunt aut aliter quam oportuit posuerunt elaborabo perficere et speculari secundum quantitatem nostre virtutis.
〈I.2〉 Capitulum secundum: De ordinibus modorum huius scientie
Quod prius de hac scientia est sciendum vel premittendum est summa scientie habitudinis mensure totius terre ad totum celum, quecunque fuerit hec mensura. Dico ergo quod primum oportet nos in sequentibus ex divisionibus eius et partibus sumere investigationem scientie loci declivis orbis per quem orbem signorum intelligimus, et post sciemus que accidunt locis orbis terre habitabilibus. Deinde post hec sequemur cum diversitate que est inter horizontas eorum ab eis inseparabilium inseparabilum M., que proveniunt propter declinationes secundum eorum ordines. Postquam igitur eorum que prediximus scientiam premiserimus, erit inquisitio eorum que sunt preter ista facilioris vie. Quod vero post hoc ad narrandum sumendum est est inquisitio scientie motus solaris et lunaris et que in eis contingunt. Impossibile namque est comprehendere scientiam stellarum et que de earum scientia explanare volumus ante horum scientie comprehensionem. Quia igitur sermo de stellis est postremum quod in ea sumendum est secundum quod ordinabiliter videtur, tunc vere oportet ut premittamus de orbe stellarum fixarum sermonem. Deinde consequetur hunc sermo de quinque stellis que planete dicuntur. Et laborabimus ut declaremus unumquodque eorum que prediximus sumendo mentionem instrumentorum et considerationum horum per res apparentes et manifestas in quibus non est dubitatio ex eis que antiqui tradiderunt. Et nos post ipsos experti sumus quasi fundamentum et principia et constituemus super ea quecunque ea sequuntur secundum semitas demonstrationum mensurabilium.
〈I.3〉 Capitulum tertium: Quo scitur quod celum sit sphericum et motus eius circularis
Summa vero eius quod narrando oportet nos preponere est quod referam. Dico quod celum sit sphericum et motus eius est sphericus, et quod etiam figura terre cum omnibus suis partibus secundum sensum sit spherica et locus eius in medio totius celi, et quod ipsa secundum magnitudinem et spacium est quasi punctum quantum ad orbem stellarum fixarum, et quod ipsa non habet motum localem. Et premittam paucos sermones secundum demonstrationem de unoquoque eorum que prediximus ad rememorandum. Primum quod intellexerunt antiqui de his que prediximus vere fuit hoc quod dicam ex considerationibus doctrinalium per instrumenta post longa tempora. Unde considerationes intelligi volumus quas doctrinales post longa tempora per instrumenta experti sunt. Videbant enim quod Sol et Luna et relique stelle movebantur semper ab oriente ad occidentem super orbes adinvicem equidistantes incipientes ab infimo inferiori et paulatim elevabantur ad supremam altitudinem ac si elevarentur a terra. Deinde post hoc uno moderamine ad infimum inferius descenderent donec essent quasi cadentes in terram et occiderent omnino in ea. Deinde parvo tempore post hoc morarentur occulte et elongate. Post etiam orirentur et occiderent ac si alterum haberent principium. Et inveniebant hec tempora que erant motuum earum ab oriente in occidentem et ab occidente in orientem cum mensuratione alternata. Plurimum vero quod perduxit eorum intellectus ad affirmandum figuram celi esse sphericam fuit revolutio stellarum semper apparentium que videntur in circulis suis revolvi super unum centrum. Necessario igitur oportet ut punctum illud quod est centrum sit polus sphere celestis. Et videbant quod quecunque stellarum magis appropinquant puncto in circulis revolvebantur brevioribus et quecunque earum sunt a puncto remotiores revolvebantur in circulis maioribus secundum mensuram propinquitatis et remotionis donec elongatio perveniat ad eas que occultantur. Et videbant quod earum que occultantur quecunque propinquiores existunt semper apparentibus minus morantur in occasu et que sunt remotiores magis morantur secundum quantitatem propinquitatis et remotionis. Hec ergo et eis similia sunt prima solum que eorum intentiones confirmaverunt et in eorum cogitationibus fixerunt quod figura celi esset spherica. Post hec vero reliqua indicantia hoc idem que sequuntur ista sunt que Probably corrupt for quod, which is also the reading of Paris, BnF, lat. 14738 (3r, line 7 from the bottom). The Greek text is somewhat different here (see Toomer, loc. cit., p. 38, line 5). nos scimus quod quecunque videmus in eo ex rebus apparentibus significant contrarium eius in quo contradicentium consistit opinio, et hoc est ut ponamus quod homo dicat quod motus stellarum sit secundum rectitudinem usque in infinitum, quemadmodum quidam estimaverunt. Possibile ergo nobis est ut dicamus: ‘Si ita est, quomodo possibile est ut quelibet earum singulis diebus super nos oriatur ab ortu cuiusque? Et quomodo est possibile ut ad ortum suum redeat cum eius motus sit secundum rectitudinem usque in infinitum? Et quomodo, si revertitur, non videmus secundum rectitudinem redire? Et quomodo non alteratur eius longitudo et non minuitur ex ipsius magnitudine et lumine paulatim et postea occidit? Nos vero huius contrarium videmus, quoniam apud occasum suum augmentatur, demum frustatim minuitur ac si a superficie terre secaretur.’ Verum quod etiam dicunt quod ipse accendantur a terra et post hoc extinguantur in ea, ostendam quod sermo hoc One could equally read hec. Either, however, is probably corrupt for hic, which is also the reading of Paris, BnF, lat. 14738 (3v, line 4) and would correspond to the Greek text (see Toomer, loc. cit., p. 39, line 9). omni ignorantia maior existit. Quod si nos concesserimus quod hec mensuratio magna et excelsa que est in magnitudine mensurarum earum et quantitatum et longitudinum et locorum et temporum sit vana et falsa, et quod sit natura quorundam finium terre accendens et quorundam extinguens, sed et locus quibusdam hominibus sit accensus, quibusdam extinctus, et quod quedam stelle ipsemet quibusdam hominibus sint accense et quibusdam extincte et quibusdam neutre, non accense nec extincte, erit hoc totum derisio et illusio dicentis ipsum. Quid ergo dicent de semper apparentibus que non oriuntur neque occidunt? Apparentes autem que non oriuntur et occidunt in quibusdam locis non semper apparent in omni loco supra terram. Et omnino manifestum est quod stelle ille in quibusdam locis oriuntur et occidunt et in quibusdam nec oriuntur nec occidunt. Ob quas causas non erunt stelle accendentes et extinguentes orientes et occidentes semper in omni loco supra terram. Universaliter autem dico quod quamcunque figuram aliquis dixerit motus esse celestis preter sphericam, necessarium erit ut sint spacia que sunt a terra usque ad loca altiora diversa ubicunque sit terra, sive in medio sive a medio totius remota. Quapropter oportebit ut videamus magnitudinem mensure stellarum et intervalla earum adinvicem diversa in loco uno in omni revolutione, eo quod quandoque sint in longitudine maiore et quandoque in longitudine minore. Et similiter oportebit ut sit declinatio signi in suo cursu quandoque remotioris intervalli quandoque vicinioris. Nos vero nihil horum videmus. Quod autem videmus ex augmento magnitudinis earum cum sunt apud horizontas non demonstrant nobis sic esse propinquitas earum et parvitas longitudinis earum ab horizonte. Sed est quasi simile ei quod in aqua ponitur. Videtur enim maius, et quanto plus in profundum mergitur, augmentatur eius magnitudo. Demonstrat etiam affirmandum esse figuram celi sphericam quoniam convenientia considerationum per instrumenta non est possibilis nisi secundum hunc modum et hanc figuram tantum. Nunc quoque dicemus secundum naturam sermonem. Celestis namque motus levior est omni motu et velocior absque tarditate et prohibitione. Et figurarum velocioris motus ex superficialibus est circulus, et ex corporeis est sphera. Et quia figure plurium laterum que sunt in circulis equalibus plures habentes angulos sunt eis maiores, est circulus maior figuris superficialibus et est sphera maior figuris corporeis. Celum igitur est maius corporibus que sunt preter ipsum. Ad hoc quoque sciendum reperimus semitam ex rebus naturalibus. Ether namque tenuior est et subtilior omnibus corporibus aliis et vehementius similis adinvicem. Cuius autem partes ad invicem sunt similes, eius superficies adinvicem similantur. Superficies vero quarum partes adinvicem assimilantur due tantum sunt: ex superficialibus circulus et ex solidis sphera. Quia igitur ether non est superficialis et neque est nisi corporeus, oportet tunc ut sit sphericus. Nos quoque reperimus corpora naturalia terrena, grossa, antiqua, spissa, corruptibilia, alterata, diversarum partium, facta secundum figuras et circulos non adinvicem similes, et reperimus celestia subtilia, similium partium, sempiterna, habitudinis unius, que consistit in ethere, facta secundum spheram. Si enim essent plana et ad modum rerum alia cooperientium facta, non quicunque ea viderent viderent ea in una hora, neque ex partibus terre diversis viderent ea rotunda. Quapropter oportet ut quia ether ea continens in sui natura est sphericus et quia eius partes sunt similes, sit ipsius motus circularis secundum equalitatem.
〈I.4〉 Capitulum quartum: De eo quod indicat quod terra sit spherica
Declaratur nobis quod terra cum omnibus partibus suis sit spherice figure secundum sensum quia videmus Solem et Lunam et reliquas stellas non in omni loco oriri et occidere in una hora. Immo oriuntur et occidunt prius apud orientales et postremo apud occidentales. Hoc autem scimus quoniam reperimus considerationes temporum eclypsium, et precipue lunarium, que sunt in momento uno, scriptas in libris antiquorum qui eas consideraverunt in horis diversis, non equalibus, incipientes omnes a meridie, et invenimus principium horarum que sunt in libris orientalium antiquorum qui consideraverunt eclypses ante principium earum que sunt in libris occidentalium. Postquam igitur invenimus diversitatem que est inter horas secundum quantitatem longitudinum que est inter loca, tunc verificatur nobis ut existimemus superficiem terre esse sphericam. Non enim hoc accideret nisi terra spherica foret. Gibbositas namque que est ab omnibus partibus eius adinvicem similibus est que cooperit lumen. Et fiunt tenebre. Deinde apparet augmentum et diminutio in eis que sequuntur partium ipsius secundum mensurationem unam. Quod si figura terre non foret spherica, non esset ita. Preterea possibile nobis est ut sciamus hoc ex eo quod dicam, quod est: Si terra foret concava, videremus stellas oriri prius apud occidentales. Et si esset plana, orirentur super omnes inhabitantes terram in una hora. Quod si esset triangulata aut quadrata aut alterius figure poligonie, orirentur stelle etiam super omnes inhabitantes in superficie una et super unam rectam lineam in una hora. Nos autem nihil horum videmus. Neque etiam est ut columna longitudinis unius circularis cuius rotunditas sit superficies plana ad orientem et occidentem cuius due superficies extremitatum eius sint super duos polos mundi, etsi hoc sit quod veritati similius existimetur. Si enim hoc ita foret, nullus habitantium super eius gibbositatem aliquam stellarum semper apparentium videret semper, et omnes stelle orirentur et occiderent semper super omnes homines, preter stellas equalis longitudinis ab utroque duorum polorum. Ipse namque essent apud omnes homines semper occulte. Nos autem videmus quod quanto plus imus ad plagam septentrionalem, secundum quantitatem nostri incessus in eam augmentatur quod occultatur a nobis ex stellis meridianis et quod apparet nobis ex stellis septentrionalibus. Declaratur igitur nobis per equalitatem eius quod gibbositas terre nobis occultat his duabus partibus cum adinvicem comparantur in omnibus earum plagis quod ipsa est rotunda. Similiter quoque cum nos in aqua imus ad montes aut ad loca alta que sint specule, a quibuscunque horizontibus veniamus et apud quoscunque fuerimus, videmus magnitudinem et quantitatem eorum paulatim elevari a mari et quasi ante hoc fuissent summersa. Ergo declaratur nobis quod hoc est propter gibbositatem superficiei aque.
〈I.5〉 Capitulum quintum: De eo quod indicat quod terra sit in medio celi
Postquam scimus et novimus hoc, tunc si scire cupierimus locum terre in his que narrabimus, non complebitur eius scientia per hoc quod apparet nobis in ea sicut videmus et reperimus nisi cum affirmaverimus locum eius medium celi sicut centrum in sphera tenere. Nisi enim ipsa sic fuerit, necessarium erit ut aut terra sit egressa ab axe equalis longitudinis ab utroque duorum polorum, aut sit super axem neque sit eius longitudo ab unoquoque duorum polorum equalis, aut sit egressa ab axe magis appropinquans uni polorum. Quod autem destruit sermonem dicentis quod locus eius sit primus trium est quod narrabo: Si imaginaremur eam cum hominibus ad superiora elevatam aut cum eis ad inferiora demersam a medio, comitaretur illos cum essent in orbe recto, ne noctis et diei equalitas semper apud eos esset, eo quod horizon secaret quod ex celo esset super terram et sub ea absque equalitate semper. Et cum essent in loco ubi est sphera declivis, accideret eis ut aut nullo modo apud eos dies et nox equarentur, aut, si apud eos esset equalitas, non fieret hoc in transitu medii inter tropicum estivalem et tropicum hyemalem, eo quod hec duo spacia necessario essent inequalia. Quoniam circulus quem horizon secaret tunc in duo media, non esset circulus equalitatis qui est maximus eorum qui revolvuntur super duos polos motus totius, sed esset unus circulorum qui equidistat ei, aut ex eis qui ab eo sunt septentrionales aut ex eis qui sunt ad meridiem. Apud vero omnes homines iam affirmatum est quod hec duo spacia in omni loco equalia existunt propter hoc quod invenerunt additionem diei equalis in longitudine sua quousque perveniatur ad illum cuius longitudo est longior in tropicis estivalibus esse equalem diminutioni in longitudine sua quousque perveniatur ad illum cuius brevitas est brevior in tropicis hyemalibus. Quod si imaginaremur terram inclinatam cum hominibus ad plagam orientalem vel occidentalem, contingeret eis ne viderent magnitudines stellarum neque earum longitudines equales et secundum unum modum in horizonte matutinali et horizonte vespertino, neque esset apud eos tempus quod est ab oriente ad medium celi equale tempori quod est a medio celi ad occidentem. Hoc autem totum diversum est ab eo quod videmus. Illud quoque quo annihilatur sermo dicentis quod locus terre est secundus trium, scilicet quod est super axem et inclinata est ad unum duorum polorum, est quod narrabo. Si hoc modo esset, superficies horizontis in omni climate non secaret quod est super terram neque quod est sub ea ex celo secundum equalitatem, sed semper secaret ipsum secundum diversitatem multis modis, quorum quisque in seipso diversificaretur et quorum quisque esset absque alio, neque esset possibile ut horizon secaret celum in duo media nisi tantum in orbe recto. In circulo autem declivi, qui propinquior est duorum polorum, semper faceret apparere quod minueretur quod esset super terram et augmentaretur quod esset sub terra semper. Quapropter superficies huius horizontis secaret circulum maiorem qui transit supra medium signorum absque equalitate. Hoc autem est quod non sic apparet. Omnes enim homines semper vident sex signa supra terram apparere et sex reliqua occultari et celari. Deinde post hoc apparent illa sex occulta super terram et occidunt alia sex residua. Propter hoc igitur declaratur quod horizon secat etiam partes orbis signorum in duo media. Quoniam unaqueque medietatum duarum orbis apparet integra supra terram semel et occultatur sub ea semel. Summa vero eius quod accideret nisi locus terre esset sub linea equationis diei, sed esset inclinata ad unum duorum polorum, ad septentrionem scilicet aut ad meridiem, est quod non esset umbra instrumentorum orientalium in equalitate diei cum umbra instrumentorum occidentalium supra unam lineam rectam super superficies equidistantes horizonti. Nos autem videmus eorum equalitatem supra unam lineam in omni loco. Et ex hoc demonstratur quod non affirmatur sermo dicentis quod locus terre est tertius trium quos diximus. Quicquid enim accidit contrarium ei quod videmus in duobus locis primis adunatur in tertio. Dico autem confidenter quod alteraretur et omnino mutaretur totum quod apparet ex mensuratione augmenti et diminutionis in nocte et die si locus terre non esset medium. Neque essent eclypses lunares in omnibus plagis celi in oppositione Solis et Lune supra diametrum. Multotiens enim non obumbraret eam terra in transitu oppositionis neque nisi in spaciis que essent minora medietate circuli.
〈I.6〉 Capitulum sextum: De eo quod indicat quod terra sit ut punctum apud celum
Maius quo scitur quod terra secundum sensum quantum ad spacium quod pervenit a centro totius ad orbem stellarum fixarum sit sicut punctum est quod magnitudines quantitatum stellarum et intervallorum que inter eas existunt videntur in omnibus plagis celi ubicunque terrarum in eadem hora equales et similes, quemadmodum invenimus considerationes que sunt in diversis climatibus non diversas neque in aliquo decipientes. Instrumentis quoque umbrarum que ponuntur in quibuslibet plagis terre et in centris orbium qui sunt ex armillis similibus vero centro terre in potentia apparent que videntur et revolutio umbre et motus eius ad omnem partem similia rebus apparentibus absque deceptione ac si ipsa transirent supra punctum medii terre. Manifestius autem indicium quod hoc sit sicut diximus est quod superficies que egrediuntur a nostris visibus ubique que nominantur horizontes semper secant spheram celi in duo media. Hoc autem impossibile esset si magnitudo terre sensibilis foret quantum ad celeste spacium. Neque nisi superficies que transit super centrum terre solum secaret orbem in duo media. Superficies vero que transiret super quemlibet locum superficiei terre alium faceret semper partes que essent sub terra maiores eis que supra ipsam essent. Sed non sic videtur. Ergo etcetera.
〈I.7〉 Capitulum septimum: De eo quod indicat quod terra motum localem non habeat
Quemadmodum in precedentibus ostendimus quod terra non egreditur a centro, ita declarabitur non esse possibile ut terra ad aliquam suarum plagarum moveatur et quod omnino non moveatur a loco centri. Eadem namque accidentia contingerent que evenirent si non medium locus eius esset. Quapropter estimavi quod investigare causas motus qui est ad medium superfluum est et vanum post illud quod iam semel ostensum est de hoc quod videtur quod terra sit in loco medii mundi et quod gravia omnia undique ad ipsam festinanter tendant. Facilius autem quod apparet ex eis que vicinius sumuntur ad inveniendum quod diximus cum eo quod iam ostensum est de hoc quod terre figura sit spherica et locus eius medium totius est quod declinatio et motus corporum gravium proprius et partes motus ad terram in omni hora et in omni loco sunt secundum rectos angulos super superficiem fixam contingentem rem cadentem. Manifestum est autem, postquam hoc est secundum quod diximus, quod tendentia ad terram motu suo pervenirent pervenenirent M. ad centrum nisi esset quod terre superficies recipit ea et secat ante hoc, et etiam quoniam linea recta que presecando pervenit ad centrum semper ortogonaliter existit supra superficiem sphere celestis contingentis lineam. Qui autem existimaverunt mirabile esse ut cum corpus terre supra rem aliquam non sit situm, stet et non summergatur nec inferius descendat propter sue gravitatis magnitudinem vel multitudinem, erraverunt, eo quod posuerunt considerationem secundum quod eis accidit, et non secundum quod proprietati totius accidit. Quod si concederent quod magnitudo terre, cum comparatur ad magnitudinem totius corporis ipsam continentis, est eius quantitas ad ipsum sicut punctum, non affirmaretur eorum miraculum. Viderent enim quod hoc modo est possibile ut illud quod est in ultimitate parvitatis secundum comparationem ad id quod est in ultimitate magnitudinis sit contentum donec in loco suo remaneat, propter hoc quod illud quod est in ultimitate magnitudinis sustentat quod in circuitu eius est quod est in ultimitate parvitatis undique et impellit equaliter et similiter. Mundus enim in seipso neque superius habet neque inferius. Quare nullum eorum que in ipso sunt dicendum est esse supra ipsum neque sub ipso, quemadmodum nihil eorum que in sphera sunt dicitur. Naturalium autem que in ipso sunt possibile est ut sit motus secundum quantitatem eorum nature propriam, videlicet levia et subtilia, cum sint ex eis que ascendunt et elevantur, sit eorum motus et intentio ad superiora sicut egredientis ad circumferentiam. Et omnis quod quidem ad superiora capitis nostri tendit, quod nominatur superius, est intentio et motus ad superficiem continentem. Spissorum vero et gravium intentio et motus sit ad medium et centrum. Et estimatur ut eorum intentio et casus sit ad inferiora. Quod enim pedibus nostris subest, quod nominatur inferius, est ad centrum terre. Quapropter motus vere fortiores sunt et aggregantur mota et stant fixa in medio ex sustentatione et coangustatione vel fulcimento et impulsione eorum adinvicem ab omnibus partibus equaliter et similiter. Quare fit ut res graves, etsi sint parve, consequantur terram, quamvis ipsius sit magna quantitas apud quantitatem eius quod ad ipsam tendit, cum ipsa sit fixa recipiens totum quod ad eam cadit ex omnibus partibus. Quod si terre et reliquorum corporum gravium que sunt preter eam esset motus unus communis, terra propter superfluitatem sue molis et gravitatis vinceret omnia gravia que sunt preter ipsam et inferius iret, et remanerent animalia et relique species gravium sita in aere, et terra velociter omnino caderet et pertransiret celum solum. Tamen imaginari hoc et eius simile est derisio et illusio imaginantis ipsum. Quidam vero hominum, cum estiment ab eis nihil bene responderi posse quod istorum refellat sermonem, concedunt et existimant quod si affirmaverint quod celum sit fixum, non motum, et quod terra moveatur super axem unum ab occidente ad orientem et revolvatur quaque die semel aut quod celum et terra simul moveantur quantum moventur, illud tamen sit supra axem unum tantum, quemadmodum diximus, et secundum quantitatem qua unum eorum consequitur alterum, non erit aliquid refellens eorum sermonem et destruens eorum testimonium. Ad hoc autem perducti fuerunt quoniam propter id quod in stellis apparet non est impossibile quin sit hoc secundum quod dixerunt secundum acceptionem absolutam. Propter hoc vero quod nobis contingit et in aere apparet declaratur quod eorum sermo est stultitia maior que esse potest. Quod si nos concederemus eis quod est contrarium nature, scilicet ut leve subtile similium partium aut nullo modo moveatur aut moveatur motu non diverso a motu qui secundum naturam ei est contrarius, tunc manifestissime declararetur quod motus eorum que sunt in aere sublimi subtili velocior esset omnibus terrenis. Et si concederemus eis etiam ut motus gravis, spissi, diversarum partium proprie sit velox equalis, tunc iam etiam declararetur quod terrena forsitan non possent et non essent preparata se adinvicem movere. Preter hec quoque affirmant quod motus terre velocior existat omnibus motibus qui sunt supra ipsam propter ipsius reversionem ad locum suum in tam brevi hora. Quod si ita esset, aer semper sentiretur moveri motu contrario motui terre neque videremus nubes semper transire ad orientem neque aliquam avium neque aliquid eorum que in aere iaciuntur, propterea quod terra consequeretur omnia semper et vinceret ea velocitate sui cursus ad orientem, et existimaretur quod omnia que sunt preter ipsam semper irent ad partem occidentis. Si autem dixerint aerem cum terra moveri motu ipsius velocitati equali, tunc existimatio tarditatis motus naturalium que sunt in eo a duobus motibus simul non erit minor existimatione prima. Quod si dixerint quod illa naturalia fixa aeri coniuncta ac si essent solidata cum eo moventur, tunc iam consequetur ea ne videantur antecedentia neque subsequentia, sed sint semper fixa et non habeant alterationem, neque in aere stantia alarum motione, neque moveantur localiter, neque in eorum motu neque in eorum volatu neque in eorum iactu et eorum casu. Nos autem videmus manifestissime quod nunquam alicui eorum est necessaria velocitas neque tarditas propter motum terre. Hos vero modos oportuit necessario antecedere divisiones doctrinalium et partes eorum et que consequentur ea post hoc. In eis autem que de eis diximus sicut capitula et principia sufficientia est. Et nos declarabimus ea et confirmabimus per ea que eis attestantur de his que videntur et demonstrabimus in sequentibus huius libri nostri per demonstrationes et ex convenientia eorum cum rebus apparentibus.
〈I.8〉 Capitulum octavum, quo declaratur quod primi motus qui sunt in celo sunt duo
Post hec que prediximus vere oportet ut ex summa que antecessit sint etiam primi motus celi duo. Quorum unus est qui movet totum semper ab oriente in occidentem uno modo et revolutionibus equalis velocitatis super orbes adinvicem equidistantes, quos duo poli sphere celestis revolvunt, qui totum secundum equalitatem revolvunt. Horum autem orbium maximus nominatur orbis equationis diei, propterea quod orbis horizontis maior ipsum secat solummodo in duo equa media semper in omni loco inter reliquos equidistantes. Cum ergo Sol super ipsum volvitur, equantur dies et nox et secundum sensum ubique terrarum equantur. Alter vero motus est qui movet orbem stellarum currentium contra motum primum, videlicet ab occidente in orientem supra duos alios polos, et non supra polos eius. Nos autem non affirmamus quod posuimus nisi quoniam cum consideramus omnia que in celo sunt quaque die, videmus ea sensibiliter in una die oriri et mediare celum et occidere super loca in forma similia et orbi equationis diei equidistantia. Et hec quidem est proprietas motus primi. Motum vero secundum intelligimus ex eis que post hoc videmus in considerationibus succedentibus. Videmus enim stellas que sunt preter currentes manentes proprietate locorum suorum, et intervalla que sunt inter eas sunt fixa cum motu primo. Solem vero et Lunam et stellas erraticas videmus habere cum motu primo motus diversos, non equales, et eos omnes ad orientem ad partes stellarum fixarum et spacia que sunt inter eas, quasi illud quod illas revolvit sit orbis unus. Quod si motus planetarum et Solis et Lune essent supra orbes equidistantes orbi equationis diei, scilicet supra duos polos motus primi, esset in affirmando motum unum ad totum movendum sufficientia. Nos quoque verisimile videremus ut eorum motus non dicerentur diversi nisi secundum existimationem, et non ut haberent motus diversos. Nos vero videmus eos cum motibus eorum ad orientem habere motus ad septentrionem et meridiem semper et videmus quantitatem intervallorum eorum que sunt in eis diversam et fere existimamus quod illa eorum declinatio que est in eis sit propter res impellentes eos et necessario ad eam ducentes. Propter hanc ergo existimationem sunt diversi absque mensuratione. Secundum affirmationem vero nostram quod hoc sit propter orbem declivem ab orbe equationis diei, in quo motus mensurantur, est possibile ut videamus eos habere motus diversos in eis que sentiuntur, ipsi tamen in se non sunt diversi. Quapropter scimus quod orbis hic declivis solus proprie secundum terminum currentibus est attributus et quod Sol motu suo ad orientem signat ipsum et verificat. Et ab utraque parte huius circuli et super ipsum est transitus Lune et quinque erraticarum et earum transitus a septentrione ad meridiem et a meridie ad septentrionem semper redeuntes. Neque aliqua earum quantitatem spacii sibi attributi in duabus partibus ab utraque parte orbis declivis parum etiam pertransit. Hic autem orbis non videtur nisi magnus, propterea quod Sol ipsum penetrat ab orbe equationis diei duobus spaciis equalibus ad septentrionem et meridiem. Motus ergo omnium stellarum currentium ad orientem sunt in orbe uno determinato quemadmodum diximus. Et necessarium est ut affirmetur quod hic motus qui est super duos polos orbis declivis cuius inventionem comprehendimus sit secundus a motu universali primo et quod ipse est contra ipsum. Quod et si imaginemur orbes magnos decriptos super polos horum duorum orbium quos prediximus, scilicet equationis diei et orbis declivis, tendentes in latitudinem a meridie ad septentrionem quos eorum poli revolvunt ab oriente ad occidentem et quos necessario convenit secare orbem equationis diei et declivem ab eo in duo media et duo media et ortogonaliter, reperiemus quatuor puncta super que secant declivem. Duo quorum sunt illa super que secat ipsum orbis equationis diei quorum unumquodque alteri opponitur, que vocantur equantia diem. Quorum unum est super quod transit Sol a meridie ad septentrionem, nominatum vernale, et alterum super quod transit Sol a septentrione in meridiem, et vocatur autumnale. Reliqua vero duo puncta sunt super que orbem declivem secat orbis magnus descriptus super polos duorum orbium, quorum etiam unumquodque alteri opponitur. Et unum eorum, quod est ad id quod sequitur meridiem ab orbe equationis diei, nominatur tropicus hyemalis, et alterum, quod est ad id quod sequitur septentrionem ab orbe equationis diei, nominatur tropicus estivalis. Sciamus autem quod motum unum primum universalem continentem omnes motus alios, qui est ille quem prediximus, comprehendit et determinat orbis magnus signatus supra polos duorum orbium motu suo, et movet omnia que sunt eius ab oriente ad occidentem super duos polos orbis equationis diei, qui sunt quasi fixi in orbe meridiano. Qui per hoc tantum quod narrabo differt ab orbe quem prediximus, quem poli duorum orbium revolvunt, quoniam nullo modo ipsum duo poli orbis declivis in aliqua hora volvunt et quoniam ipse ortogonaliter est supra horizonta. Et nominatur orbis meridiei quoniam ipse secat unamquamque duarum medietatum sphere celestis, que est super terram et que est sub ea, in duo media et mediat tempora noctis et diei et stat locus eius semper. Motum vero secundum plurium connexionum continet motus primus. Et ipse continet orbes stellarum currentium. Sed movet eos motus primus, quemadmodum diximus, ab oriente in occidentem. Et ipse movetur contra hoc supra duos polos orbis declivis, qui sunt fixi sicut duo centra semper in orbe qui comprehendit motum primum et terminat ipsum descriptus supra duos polos duorum orbium qui cum eo vere moventur, sed manent fixi in motu secundo, qui est contra primum, quorum loca sunt orbis magni ab eis revoluti declivis ab orbe equationis diei declinatione que semper una existit.
〈I.9〉 Capitulum nonum: De scientia quantitatis chordarum partium circuli
Summa vero principiorum que oportuit nos incipere et premittere est secundum quod narravimus. Quoniam vero volumus incipere a demonstrationibus que sunt super particulares, quarum prima est demonstratio qua reperitur quantitas arcus qui est inter duos polos quos nominavimus circuli magni signati supra polos duorum orbium, videmus quod necessario oportet nos prius loqui de scientia quantitatum chordarum partium circuli, postquam volumus declarare demonstrationem super hoc quod narraturi sumus per lineas, et facere post hoc, ut levior sit inventio, partis cuius volumus scire quantitatem per tabulas. Dividam itaque circuli circumferentiam per 360 partes, et ponam superfluum arcuum in eis secundum augmentum medietatis et medietatis partis et coram ipsis quantitatem chordarum que eis subtenduntur, et dividam diametrum circuli in 120 partes ad hoc ut nobis declaretur eius levitas in numeris. Prius tamen quam brevioribus capitulis potero ad protractionem vel inventionem eius quod volumus velocioribus demonstrabo qualiter per ea sciamus quantitatem chordarum, ad hoc ut non tantum sint posite nobis in tabulis et ignoremus de eis inventionem mensurationis et numerationis. Sed cum positione earum in tabulis demonstrabimus scientiam quantitatum earum, ut facilius fiat quod est ex capitulis scientie numerationis et mensurationis. Et assumemus numerum 60 in omnibus que operaturi sumus ex capitulis arithmetice, ut allevietur operatio in fractionibus, et sequemur in omni multiplicatione et divisione ad sciendum cuius quantitatis veritatem volumus ei propinquiorem et ita ne quod ex eo deest quantitatis sit sensibilis. 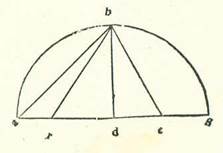 Sit itaque primum semicirculus ABG erectus supra diametrum ADG circumductus supra centrum D. Protraham autem a D supra lineam AG ortogonaliter lineam DB, et dividam DG in duo media supra punctum E, et producam lineam BE, sitque linea ER equalis linee EB, et protraham lineam BR. Dico ergo quod linea RD est latus decagoni et linea BR est latus pentagoni. Quod sic probatur: Quoniam DG dividitur in duo media super E et adiungitur ei linea DR, ergo ductus GR in RD cum quadrato ED equatur quadrato linee ER, que est equalis BE. Duo vero quadrata DB et ED simul equantur EB quadrato. Quapropter ductus GR in RD cum quadrato DE equatur duobus quadratis DE et DB simul. Cum ergo minuitur ex unoquoque eorum quadratum DE, remanet ductus GR in RD equale quadrato DB, que est equalis GD. Et quia cum latus hexagoni et latus decagoni, que sunt in circulo uno, sunt linea una, ipsa dividitur secundum proportionem habentem medium et duo extrema et DG, que est medietas diametri, est latus hexagoni, erit DR latus decagoni. Et similiter quoniam latus pentagoni potest supra latus hexagoni cum latere decagoni quod sunt in uno circulo potest ... circulo: Corrupt passage? Cf. Toomer, loc. cit., p. 49, lines 8-10. Paris, BnF, lat. 14738 (7r, lines 15-16 from the bottom) does not offer any better text. et angulus BDR trianguli BDR est rectus, erit quadratum BR equale quadrato BD, que est latus hexagoni, et quadrato DR, que est latus decagoni, simul, et erit BR latus pentagoni. Et quia diametrum circuli divisimus in 120 partes, ergo propter hoc quod premisimus erit linea DE 30 partes, et erit quadratum eius 900, et erit linea BD, postquam ipsa est medietas diametri, 60 partes, et eius quadratum 3600, et quadratum EB, quod est quadratum ER, que sunt in circulo uno, 4500. Propter hoc ergo erit ER 67 partes et 4 minuta et 55 secunda vicinius. Et remanebit linea DR secundum illas partes 37 partes et 4 minuta et 55 secunda vicinius. Ipsa vero est equalis lateri decagoni. Latus ergo decagoni, quod subtenditur arcui 36 partium secundum quantitatem qua circulus est 360 partes, erit 37 partes et 4 minuta et 55 secunda vicinius secundum quantitatem qua diameter est 120 partium. Et etiam quia linea DR est 37 partes et 4 minuta et 55 secunda, et eius quadratum est 1375 partes et 4 minuta et 14 secunda, et quadratum DB est 3600, et cum hec duo coniungentur, erit ex eis quadratum BR, quod est 4975 partes et 4 minuta et 14 secunda, ergo propter hoc erit longitudo linee BR secundum illam quantitatem 70 partes et 32 minuta et 3 secunda vicinius. Ipsa autem est equalis lateri pentagoni. Quapropter latus pentagoni, quod est chorda partium 72 secundum quantitatem qua circulus est 360, erit 70 partes et 32 minuta et 3 secunda secundum quantitatem qua diameter est 120. Iam ergo manifestum est quod latus hexagoni, quod subtenditur arcui 60 partium et est medietas diametri, est 60 partes. Et similiter etiam quia latus quadrati, quod subtenditur 90 partibus, est in potentia duplum medietatis diametri, et latus trianguli, quod subtenditur 120, est in potentia triplum medietatis diametri, et quadratum medietatis diametri est 3600, ergo fiet quadratum lateris quadrati 7200 et quadratum lateris trianguli 10800. Quapropter erit longitudo chorde arcus 90 partium 84 partes et 51 minuta et 10 secunda vicinius secundum quantitatem qua diameter est 120, et erit longitudo chorde arcus 120 secundum eandem mensuram 103 partes et 55 minuta et 23 secunda.
Sit itaque primum semicirculus ABG erectus supra diametrum ADG circumductus supra centrum D. Protraham autem a D supra lineam AG ortogonaliter lineam DB, et dividam DG in duo media supra punctum E, et producam lineam BE, sitque linea ER equalis linee EB, et protraham lineam BR. Dico ergo quod linea RD est latus decagoni et linea BR est latus pentagoni. Quod sic probatur: Quoniam DG dividitur in duo media super E et adiungitur ei linea DR, ergo ductus GR in RD cum quadrato ED equatur quadrato linee ER, que est equalis BE. Duo vero quadrata DB et ED simul equantur EB quadrato. Quapropter ductus GR in RD cum quadrato DE equatur duobus quadratis DE et DB simul. Cum ergo minuitur ex unoquoque eorum quadratum DE, remanet ductus GR in RD equale quadrato DB, que est equalis GD. Et quia cum latus hexagoni et latus decagoni, que sunt in circulo uno, sunt linea una, ipsa dividitur secundum proportionem habentem medium et duo extrema et DG, que est medietas diametri, est latus hexagoni, erit DR latus decagoni. Et similiter quoniam latus pentagoni potest supra latus hexagoni cum latere decagoni quod sunt in uno circulo potest ... circulo: Corrupt passage? Cf. Toomer, loc. cit., p. 49, lines 8-10. Paris, BnF, lat. 14738 (7r, lines 15-16 from the bottom) does not offer any better text. et angulus BDR trianguli BDR est rectus, erit quadratum BR equale quadrato BD, que est latus hexagoni, et quadrato DR, que est latus decagoni, simul, et erit BR latus pentagoni. Et quia diametrum circuli divisimus in 120 partes, ergo propter hoc quod premisimus erit linea DE 30 partes, et erit quadratum eius 900, et erit linea BD, postquam ipsa est medietas diametri, 60 partes, et eius quadratum 3600, et quadratum EB, quod est quadratum ER, que sunt in circulo uno, 4500. Propter hoc ergo erit ER 67 partes et 4 minuta et 55 secunda vicinius. Et remanebit linea DR secundum illas partes 37 partes et 4 minuta et 55 secunda vicinius. Ipsa vero est equalis lateri decagoni. Latus ergo decagoni, quod subtenditur arcui 36 partium secundum quantitatem qua circulus est 360 partes, erit 37 partes et 4 minuta et 55 secunda vicinius secundum quantitatem qua diameter est 120 partium. Et etiam quia linea DR est 37 partes et 4 minuta et 55 secunda, et eius quadratum est 1375 partes et 4 minuta et 14 secunda, et quadratum DB est 3600, et cum hec duo coniungentur, erit ex eis quadratum BR, quod est 4975 partes et 4 minuta et 14 secunda, ergo propter hoc erit longitudo linee BR secundum illam quantitatem 70 partes et 32 minuta et 3 secunda vicinius. Ipsa autem est equalis lateri pentagoni. Quapropter latus pentagoni, quod est chorda partium 72 secundum quantitatem qua circulus est 360, erit 70 partes et 32 minuta et 3 secunda secundum quantitatem qua diameter est 120. Iam ergo manifestum est quod latus hexagoni, quod subtenditur arcui 60 partium et est medietas diametri, est 60 partes. Et similiter etiam quia latus quadrati, quod subtenditur 90 partibus, est in potentia duplum medietatis diametri, et latus trianguli, quod subtenditur 120, est in potentia triplum medietatis diametri, et quadratum medietatis diametri est 3600, ergo fiet quadratum lateris quadrati 7200 et quadratum lateris trianguli 10800. Quapropter erit longitudo chorde arcus 90 partium 84 partes et 51 minuta et 10 secunda vicinius secundum quantitatem qua diameter est 120, et erit longitudo chorde arcus 120 secundum eandem mensuram 103 partes et 55 minuta et 23 secunda.
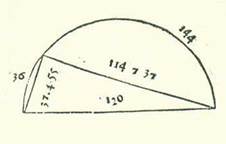 Iam ergo facile novimus harum chordarum quantitates in seipsis. Et declarabitur nobis quod cum he chorde scite fuerint, scietur per eas facile operatio chordarum que subtenduntur arcubus residuis semicirculi. Quoniam duo quadrata duarum chordarum simul equalia sunt quadrato diametri circuli. Verbi gratia iam ostensum est quod chorda arcus 36 partium est 37 partes et 4 minuta et 55 secunda, et quadratum eius est 1375 partes et 4 minuta et 14 secunda, et quadratum diametri 14400, et quadratum chorde residui semicirculi, quod est 144, et est residuum quadrati diametri, est 13024 partes et 55 minuta et 46 secunda. Longitudo ergo chorde residui semicirculi est 114 partes et 7 minuta et 37 secunda vicinius secundum illam quantitatem. Et similiter sciemus per chordas reliquas notas chordas arcuum reliquorum semicirculi.
Iam ergo facile novimus harum chordarum quantitates in seipsis. Et declarabitur nobis quod cum he chorde scite fuerint, scietur per eas facile operatio chordarum que subtenduntur arcubus residuis semicirculi. Quoniam duo quadrata duarum chordarum simul equalia sunt quadrato diametri circuli. Verbi gratia iam ostensum est quod chorda arcus 36 partium est 37 partes et 4 minuta et 55 secunda, et quadratum eius est 1375 partes et 4 minuta et 14 secunda, et quadratum diametri 14400, et quadratum chorde residui semicirculi, quod est 144, et est residuum quadrati diametri, est 13024 partes et 55 minuta et 46 secunda. Longitudo ergo chorde residui semicirculi est 114 partes et 7 minuta et 37 secunda vicinius secundum illam quantitatem. Et similiter sciemus per chordas reliquas notas chordas arcuum reliquorum semicirculi.
Et declarabitur in sequentibus qualiter per istas chordas sciatur inventio chordarum arcuum diversorum reliquorum, postquam nos premiserimus narrationem capituli valde perutilis in hac scientia. 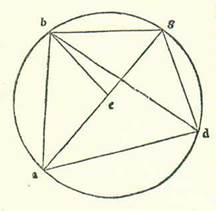 Sit itaque circulus ABGD in quo describam quadrilaterum supra quod sint A, B, G, D, et protraham duas lineas AG et BD, et ostendam quod ductus AG in BD equatur duobus ductibus AB in DG et AD in BG simul. Quod sic demonstratur: Ponam enim angulum ABE equalem angulo DBG. Et quia angulus DBG equatur angulo ABE, tunc si nos communicaverimus angulum EBD et addiderimus ipsum unicuique ipsorum, erit angulus ABD equalis angulo EBG. Angulus autem BDA est equalis angulo BGE, quoniam eorum chorda est arcus unius. Triangulus igitur ABD est equiangulus triangulo BGE. Quapropter proportio BG ad GE est sicut proportio BD ad DA. Ergo ductus BG in AD equatur ductui BD in GE. Et etiam quia angulus ABE est equalis angulo DBG et angulus BAE equatur angulo BDG, erit triangulus ABE equiangulus triangulo BGD. Ergo proportio BA ad EA est sicut proportio BD ad DG. Quadratum itaque BA in GD equatur quadrato BD in EA. Iam vero declaratum fuit quod ductus BG in AD est equalis ductui BD in GE. Ergo totus ductus AG in BD est equalis ductui AB in GD et AD in BG simul. Et illud est quod demonstrare voluimus.
Sit itaque circulus ABGD in quo describam quadrilaterum supra quod sint A, B, G, D, et protraham duas lineas AG et BD, et ostendam quod ductus AG in BD equatur duobus ductibus AB in DG et AD in BG simul. Quod sic demonstratur: Ponam enim angulum ABE equalem angulo DBG. Et quia angulus DBG equatur angulo ABE, tunc si nos communicaverimus angulum EBD et addiderimus ipsum unicuique ipsorum, erit angulus ABD equalis angulo EBG. Angulus autem BDA est equalis angulo BGE, quoniam eorum chorda est arcus unius. Triangulus igitur ABD est equiangulus triangulo BGE. Quapropter proportio BG ad GE est sicut proportio BD ad DA. Ergo ductus BG in AD equatur ductui BD in GE. Et etiam quia angulus ABE est equalis angulo DBG et angulus BAE equatur angulo BDG, erit triangulus ABE equiangulus triangulo BGD. Ergo proportio BA ad EA est sicut proportio BD ad DG. Quadratum itaque BA in GD equatur quadrato BD in EA. Iam vero declaratum fuit quod ductus BG in AD est equalis ductui BD in GE. Ergo totus ductus AG in BD est equalis ductui AB in GD et AD in BG simul. Et illud est quod demonstrare voluimus.
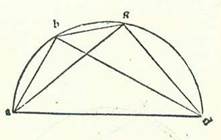 Et postquam premisimus capitulum, describam semicirculum, supra quem sint A, B, G, D, super diametrum AD, et protraham ab A duas chordas AB et AG, sitque cuiusque earum quantitas nota, et producam chordam BG. Dico ergo quod etiam chorda BG erit nota. Quod sic probatur: Protraham enim duas chordas BD et GD. Manifestum est igitur quod ipse etiam note sunt, quoniam quecunque earum est chorda residui semicirculi. Et quia in semicirculo est quadrilaterum super quod sunt A, B, G, D, ergo ductus BA in GD cum ductu AD in BG simul equantur ductui AG in BD. Et quoniam ductus AG in BD est scitus, et ductus AB in GD est scitus, et diameter AD est nota, erit chorda BG nota. Iam ergo ostensum est quod cum fuerint duo arcus noti notarum chordarum, chorda superflui quod est inter eos erit nota. Manifestum est etiam quod possibile est ut per hoc capitulum chorde plures superflui arcuum chordas secundum seipsas notas habentium producantur. Et similiter reperiemus chordam arcus 12 partium, propterea quod scimus chordam sexaginta et chordam septuagintaduarum partium.
Et postquam premisimus capitulum, describam semicirculum, supra quem sint A, B, G, D, super diametrum AD, et protraham ab A duas chordas AB et AG, sitque cuiusque earum quantitas nota, et producam chordam BG. Dico ergo quod etiam chorda BG erit nota. Quod sic probatur: Protraham enim duas chordas BD et GD. Manifestum est igitur quod ipse etiam note sunt, quoniam quecunque earum est chorda residui semicirculi. Et quia in semicirculo est quadrilaterum super quod sunt A, B, G, D, ergo ductus BA in GD cum ductu AD in BG simul equantur ductui AG in BD. Et quoniam ductus AG in BD est scitus, et ductus AB in GD est scitus, et diameter AD est nota, erit chorda BG nota. Iam ergo ostensum est quod cum fuerint duo arcus noti notarum chordarum, chorda superflui quod est inter eos erit nota. Manifestum est etiam quod possibile est ut per hoc capitulum chorde plures superflui arcuum chordas secundum seipsas notas habentium producantur. Et similiter reperiemus chordam arcus 12 partium, propterea quod scimus chordam sexaginta et chordam septuagintaduarum partium.
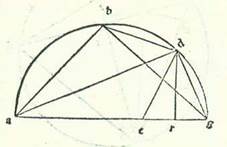 Quod si etiam arcus fuerit notus et chorda eius nota et voluerimus invenire chordam medietatis eius, tunc describemus semicirculum super quem sint A, B, G, sitque diameter AG, et sit arcus BG chordam habens notam quem in duo media supra D secabo, et protraham chordas AB et AD et BD et DG, et producam perpendicularem RD super diametrum AG erectam. Dico ergo quod RG est medietas superflui AG super AB. Quod sic probatur: Ponam enim lineam AE equalem linee AB et producam lineam DE. Et quia AB est equalis AE facta AD communi, erunt due linee AB et AD equales duabus lineis AE et AD, queque videlicet sue relative equalis, et angulus BAD equalis angulo EAD, ergo et basis BD equalis basi DE. Et quia BD equatur DG, erit DG equale DE. Quia igitur triangulus DEG duorum equalium existit laterum, erit perpendicularis DR dividens basim EG in duo media. Ergo ER equatur RG ac tota EG est superfluum AG super AB. Ergo RG est medietas superflui AG super AB. Et quoniam chorda arcus BG est nota, erit chorda residui semicirculi, que est AB, nota, que est equalis AE. Et quia diameter AG est nota, erit EG, que est residuum diametri, nota, et eius medietas, que est RG, nota, que est medietas superflui AG super AB. Quia igitur in triangulo ADG ortogonio egreditur ab eo perpendicularis DR, erit triangulus ADG ortogonius equiangulus triangulo DRG et erit proportio AG ad DG sicut proportio GD ad GR. Ductus igitur AG in GR equatur quadrato GD. Quapropter longitudo chorde GD est nota, que subtenditur medietati arcus BG. Per hoc ergo capitulum scientur chorde plures si mediaveris ea quorum precessit scientia. Quarum est sicut chorda arcus 12 partium et chorda arcus sex partium et chorda arcus trium partium et chorda arcus partis et semis et chorda arcus medietatis partis et quarte. Et hoc etiam modo inveniemus quod chorda arcus partis et semis est pars et 34 minuta et 15 secunda vicinius secundum quantitatem qua diameter est 120 partes, et chorda arcus medietatis et quarte partis secundum illam quantitatem est cifre et 47 minuta et 8 secunda fere.
Quod si etiam arcus fuerit notus et chorda eius nota et voluerimus invenire chordam medietatis eius, tunc describemus semicirculum super quem sint A, B, G, sitque diameter AG, et sit arcus BG chordam habens notam quem in duo media supra D secabo, et protraham chordas AB et AD et BD et DG, et producam perpendicularem RD super diametrum AG erectam. Dico ergo quod RG est medietas superflui AG super AB. Quod sic probatur: Ponam enim lineam AE equalem linee AB et producam lineam DE. Et quia AB est equalis AE facta AD communi, erunt due linee AB et AD equales duabus lineis AE et AD, queque videlicet sue relative equalis, et angulus BAD equalis angulo EAD, ergo et basis BD equalis basi DE. Et quia BD equatur DG, erit DG equale DE. Quia igitur triangulus DEG duorum equalium existit laterum, erit perpendicularis DR dividens basim EG in duo media. Ergo ER equatur RG ac tota EG est superfluum AG super AB. Ergo RG est medietas superflui AG super AB. Et quoniam chorda arcus BG est nota, erit chorda residui semicirculi, que est AB, nota, que est equalis AE. Et quia diameter AG est nota, erit EG, que est residuum diametri, nota, et eius medietas, que est RG, nota, que est medietas superflui AG super AB. Quia igitur in triangulo ADG ortogonio egreditur ab eo perpendicularis DR, erit triangulus ADG ortogonius equiangulus triangulo DRG et erit proportio AG ad DG sicut proportio GD ad GR. Ductus igitur AG in GR equatur quadrato GD. Quapropter longitudo chorde GD est nota, que subtenditur medietati arcus BG. Per hoc ergo capitulum scientur chorde plures si mediaveris ea quorum precessit scientia. Quarum est sicut chorda arcus 12 partium et chorda arcus sex partium et chorda arcus trium partium et chorda arcus partis et semis et chorda arcus medietatis partis et quarte. Et hoc etiam modo inveniemus quod chorda arcus partis et semis est pars et 34 minuta et 15 secunda vicinius secundum quantitatem qua diameter est 120 partes, et chorda arcus medietatis et quarte partis secundum illam quantitatem est cifre et 47 minuta et 8 secunda fere.
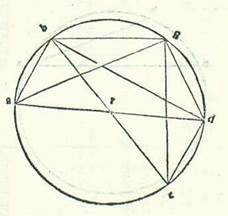 Describam etiam circulum ABGD supra diametrum AD, et sit centrum circuli R, et accipiam ab A duos arcus notos coniunctos duas chordas notas habentes, supra quos sint AB et BG, et copulabo unam chordam eorum alteri. Dico igitur quod si protraxerimus chordam AG, erit ipsa quoque nota. Quod sic probatur: Producam enim a B diametrum circuli, que sit BRE, et protraham lineas BD et GD et DE et GE. Manifestum est igitur quod ex scientia linee BG scietur linea GE, et ex noticia AB scietur BD, et ex ea DE. Et propter hoc quod iam premisimus, quoniam in circulo est quadrilaterum supra quod sunt BGDE et eius due diametri sunt BD et GE, erit ductus unius diametri eius in alterum equalis omnibus duobus ductibus omnium duorum laterum oppositorum cuiusque in alterum. Quia igitur ductus BD in GE est notus, erunt duo ductus BG in DE et GD in BE simul noti. Diameter vero BE est nota. Ergo linea GD reliqua est nota. Quapropter chorda arcus residui semicirculi, que est AG, est nota. Iam ergo novimus quod cum duo arcus coniuncti fuerint noti chordas habentes notas, erit eorum chorda simul iunctorum nota. Per hoc autem capitulum declaratur nobis quod quotiens composuerimus chordam arcus partis et semis cum qualibet chordarum notarum et totius eius quod erit ex earum compositione descripserimus in tabulis libri nostri chordam, continget ut cum arcus illarum chordarum duplabuntur, habeat arcus cuiusque illarum chordarum tertiam integram, et erunt chorde eorum omnes veraciter note, et remanebunt inter omnes duas chordas earum duo loca duarum chordarum tantum quarum perscrutabimur scientiam, eo quod posuimus arcus in tabulis libri nostri secundum superfluum medietatis partis.
Describam etiam circulum ABGD supra diametrum AD, et sit centrum circuli R, et accipiam ab A duos arcus notos coniunctos duas chordas notas habentes, supra quos sint AB et BG, et copulabo unam chordam eorum alteri. Dico igitur quod si protraxerimus chordam AG, erit ipsa quoque nota. Quod sic probatur: Producam enim a B diametrum circuli, que sit BRE, et protraham lineas BD et GD et DE et GE. Manifestum est igitur quod ex scientia linee BG scietur linea GE, et ex noticia AB scietur BD, et ex ea DE. Et propter hoc quod iam premisimus, quoniam in circulo est quadrilaterum supra quod sunt BGDE et eius due diametri sunt BD et GE, erit ductus unius diametri eius in alterum equalis omnibus duobus ductibus omnium duorum laterum oppositorum cuiusque in alterum. Quia igitur ductus BD in GE est notus, erunt duo ductus BG in DE et GD in BE simul noti. Diameter vero BE est nota. Ergo linea GD reliqua est nota. Quapropter chorda arcus residui semicirculi, que est AG, est nota. Iam ergo novimus quod cum duo arcus coniuncti fuerint noti chordas habentes notas, erit eorum chorda simul iunctorum nota. Per hoc autem capitulum declaratur nobis quod quotiens composuerimus chordam arcus partis et semis cum qualibet chordarum notarum et totius eius quod erit ex earum compositione descripserimus in tabulis libri nostri chordam, continget ut cum arcus illarum chordarum duplabuntur, habeat arcus cuiusque illarum chordarum tertiam integram, et erunt chorde eorum omnes veraciter note, et remanebunt inter omnes duas chordas earum duo loca duarum chordarum tantum quarum perscrutabimur scientiam, eo quod posuimus arcus in tabulis libri nostri secundum superfluum medietatis partis.
Quod si nos reperiremus chordam arcus medietatis partis, vere inveniremus cum ea per capitulum compositionis et capitulum superflui augmentorum quantitates chordarum reliquorum arcuum que sunt inter chordas notas quas nominavimus secundum veritatem numerationis linearum almisaat et tegdir et per hoc compleremus omnes chordas circuli secundum superfluum medietatis partis et medietatis partis. Hoc autem non secundum veritatem reperitur. Quoniam etsi chorda arcus partis et semis sit nota, tamen eius tertia non est reperta secundum veritatem numerationis almisaat et tegdir. Perscrutabor igitur inventionem chorde arcus unius partis per chordam arcus partis et semis et per chordam arcus medietatis et quarte et ponam capitulum de hoc. Quamvis enim non contineat vere quantitatem omnium chordarum, possibile tamen est ut per ipsum inveniatur quantitas chordarum parvorum arcuum, ita ut nihil veritatis eius cuius sentitur quantitas deficiat. Et ad hoc premittam hoc capitulum et dicam: Si descripte sint in circulo due chorde diverse, erit proportio chorde longioris ad chordam breviorem minor proportione arcus chorde longioris ad arcum chorde brevioris. 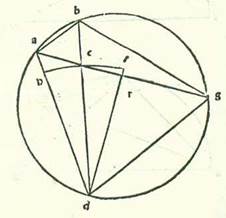 Et describam propter hoc circulum, supra quem sint A, B, G, D, in quo sint due chorde diverse, quarum brevior sit AB et earum longior sit BG. Dico ergo quod proportio chorde BG ad chordam BA est minor proportione arcus BG ad arcum BA. Quod sic probatur: Dividam enim angulum ABG in duo media linea BD et protraham lineas AEG et AD et GD. Et quoniam angulus ABG divisus est in duo media linea BED, erit linea GD equalis linee AD. Linea autem GE est longior linea AE. Producam autem a D ad lineam AEG perpendicularem DR. Et quia linea AD est longior linea ED et linea ED est longior DR, erit circulus descriptus supra centrum D cum longitudine DE secans AD et pertransiens DR. Igitur signabo circulum supra quem sint H, E, T et producam DR ad T. Et quia sector DET est maior triangulo DER et triangulus DEA est maior sectore DEH, erit proportio trianguli DER ad triangulum DEA minor proportione sectoris DET ad sectorem DEH. Proportio autem trianguli DER ad triangulum DEA est sicut proportio linee ER ad lineam EA, et proportio sectoris DET ad sectorem DEH est sicut proportio anguli RDE ad angulum ADE. Ergo proportio linee RE ad lineam EA est minor proportione anguli RDE ad angulum EDA. Cum ergo composuerimus, erit proportio linee RA ad lineam EA minor proportione anguli RDA ad angulum ADE, et erit proportio dupli AR, quod est GA, ad AE minor proportione anguli GDA, qui est duplus anguli ADR, ad angulum EDA. Et cum diviserimus, erit proportio linee GE ad AE minor proportione anguli GDE ad angulum EDA. Sed proportio linee GE ad EA est sicut proportio chorde GB ad chordam BA, et proportio anguli GDB ad angulum BDA est sicut proportio arcus GB ad arcum BA. Proportio igitur chorde GB ad chordam BA est minor proportione arcus GB ad arcum BA. Et hoc est quod voluimus demonstrare.
Et describam propter hoc circulum, supra quem sint A, B, G, D, in quo sint due chorde diverse, quarum brevior sit AB et earum longior sit BG. Dico ergo quod proportio chorde BG ad chordam BA est minor proportione arcus BG ad arcum BA. Quod sic probatur: Dividam enim angulum ABG in duo media linea BD et protraham lineas AEG et AD et GD. Et quoniam angulus ABG divisus est in duo media linea BED, erit linea GD equalis linee AD. Linea autem GE est longior linea AE. Producam autem a D ad lineam AEG perpendicularem DR. Et quia linea AD est longior linea ED et linea ED est longior DR, erit circulus descriptus supra centrum D cum longitudine DE secans AD et pertransiens DR. Igitur signabo circulum supra quem sint H, E, T et producam DR ad T. Et quia sector DET est maior triangulo DER et triangulus DEA est maior sectore DEH, erit proportio trianguli DER ad triangulum DEA minor proportione sectoris DET ad sectorem DEH. Proportio autem trianguli DER ad triangulum DEA est sicut proportio linee ER ad lineam EA, et proportio sectoris DET ad sectorem DEH est sicut proportio anguli RDE ad angulum ADE. Ergo proportio linee RE ad lineam EA est minor proportione anguli RDE ad angulum EDA. Cum ergo composuerimus, erit proportio linee RA ad lineam EA minor proportione anguli RDA ad angulum ADE, et erit proportio dupli AR, quod est GA, ad AE minor proportione anguli GDA, qui est duplus anguli ADR, ad angulum EDA. Et cum diviserimus, erit proportio linee GE ad AE minor proportione anguli GDE ad angulum EDA. Sed proportio linee GE ad EA est sicut proportio chorde GB ad chordam BA, et proportio anguli GDB ad angulum BDA est sicut proportio arcus GB ad arcum BA. Proportio igitur chorde GB ad chordam BA est minor proportione arcus GB ad arcum BA. Et hoc est quod voluimus demonstrare.
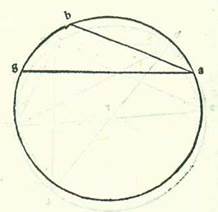 Postquam affirmavimus hanc precedentem figuram, describam circulum ABG et in eo duas chordas AB et AG. Et ponam primum ut AB subtendatur arcui medietatis et quarte partis circuli et AG subtendatur arcui partis unius. Et quia proportio chorde AG ad chordam AB est minor proportione arcus AG ad arcum AB et arcus AG est quantum AB et eius tertia, ergo, quia iam ostensum est quod chorda AB est cifre et 47 minuta et 8 secunda secundum quantitatem qua diameter est 120, erit chorda AG minus parte una et duobus minutis et 50 secundis secundum quantitatem illam, tertiis pretermissis, que non ponuntur in tabulis, que tamen sunt 40 secundum illam quantitatem. Hoc namque vicinius existit tanto et tertie tanti quantum sunt 47 minuta et 8 secunda. In hoc quoque circulo ponam ut chorda AB subtendatur arcui partis unius et chorda AG subtendatur arcui partis et semis. Secundum ergo quod narravimus, quoniam arcus AG est quantum arcus AB et semis, erit chorda GA minus quam quantum chorda AB et semis. Iam autem ostensum fuit quod chorda AG est pars et 34 minuta et 15 secunda secundum quantitatem qua diameter est 120. Chorda igitur AB est plus parte et duobus minutis et 50 secundis secundum quantitatem illam. Pars namque et 34 minuta et 15 secunda sunt tantum et medium tanti quantum est pars et duo minuta et 50 secunda. Postquam ergo chorda unius partis circuli quandoque est minus parte et 2 minutis et 50 secundis et quandoque maius parte et duobus minutis et 50 secundis, tunc manifestum est quod convenit nobis ut accipiamus chordam unius partis circuli partem unam chorde et duo minuta et 50 secunda secundum quantitatem qua diameter est 120. Et propter hoc quod iam ostensum est per id quod diximus erit chorda arcus medietatis partis fere cifre et 31 minuta et 25 secunda. Et per hoc complebitur residuum reliquarum chordarum quas prediximus que sunt inter chordas notas. Chordam enim arcus duarum partium sciemus per compositionem arcus partis et semis cum arcu medietatis partis. Sed chordam arcus duarum partium et semis sciemus propter superfluum, videlicet per superfluum arcus trium partium super arcum medietatis partis. Et similiter sciemus quantitatem reliquarum chordarum. Et illud est quod demonstrare voluimus.
Postquam affirmavimus hanc precedentem figuram, describam circulum ABG et in eo duas chordas AB et AG. Et ponam primum ut AB subtendatur arcui medietatis et quarte partis circuli et AG subtendatur arcui partis unius. Et quia proportio chorde AG ad chordam AB est minor proportione arcus AG ad arcum AB et arcus AG est quantum AB et eius tertia, ergo, quia iam ostensum est quod chorda AB est cifre et 47 minuta et 8 secunda secundum quantitatem qua diameter est 120, erit chorda AG minus parte una et duobus minutis et 50 secundis secundum quantitatem illam, tertiis pretermissis, que non ponuntur in tabulis, que tamen sunt 40 secundum illam quantitatem. Hoc namque vicinius existit tanto et tertie tanti quantum sunt 47 minuta et 8 secunda. In hoc quoque circulo ponam ut chorda AB subtendatur arcui partis unius et chorda AG subtendatur arcui partis et semis. Secundum ergo quod narravimus, quoniam arcus AG est quantum arcus AB et semis, erit chorda GA minus quam quantum chorda AB et semis. Iam autem ostensum fuit quod chorda AG est pars et 34 minuta et 15 secunda secundum quantitatem qua diameter est 120. Chorda igitur AB est plus parte et duobus minutis et 50 secundis secundum quantitatem illam. Pars namque et 34 minuta et 15 secunda sunt tantum et medium tanti quantum est pars et duo minuta et 50 secunda. Postquam ergo chorda unius partis circuli quandoque est minus parte et 2 minutis et 50 secundis et quandoque maius parte et duobus minutis et 50 secundis, tunc manifestum est quod convenit nobis ut accipiamus chordam unius partis circuli partem unam chorde et duo minuta et 50 secunda secundum quantitatem qua diameter est 120. Et propter hoc quod iam ostensum est per id quod diximus erit chorda arcus medietatis partis fere cifre et 31 minuta et 25 secunda. Et per hoc complebitur residuum reliquarum chordarum quas prediximus que sunt inter chordas notas. Chordam enim arcus duarum partium sciemus per compositionem arcus partis et semis cum arcu medietatis partis. Sed chordam arcus duarum partium et semis sciemus propter superfluum, videlicet per superfluum arcus trium partium super arcum medietatis partis. Et similiter sciemus quantitatem reliquarum chordarum. Et illud est quod demonstrare voluimus.
〈I.10〉 Capitulum decimum: Quomodo tabule chordarum partium circuli fiant
Ut autem sciatur quantitas chordarum arcuum circuli, hoc levius est quo fit et brevius et magis aggregatum. Et quoniam necesse est nobis scire numerum partium chordarum et quantitatem earum et ut sint preparate, faciam tabulas, et in unaquaque tabula 45 areas, eo quod in hoc mensurationis bonitas consistit. Et describam in prima tabula numerum partium arcuum superfluentium medietate partis et medietate partis, et in tabula secunda numerum partium chordarum et minutorum partium et secundorum earum que subtenduntur arcubus consequenter ex latere, ita quod queque chorda suum consequatur arcum secundum divisionem diametri circuli per 120, in tabula vero tertia partem tricesimam superflui quod est inter omnes duas chordas que subtenduntur arcubus superfluentibus medietate partis et medietate partis, ideo ut cum sciverimus numerum minutorum portionis medialis minuti unius non diverse a veritate secundum sensum, possimus scire levi opere portionem minutorum que sunt ab uno minuto usque ad 30 minuta ex eis que sunt inter omnes duas chordas. O quam bene quod declarabitur nobis, cum dubitaverimus de errore existente in aliquo numero alicuius chordarum descriptarum in tabulis, verificatio illius erroris. Quoniam poterimus per hec capitula rectificare illud et scire eius veritatem, aut per scientiam chorde que subtenditur duplo arcus dati aut per scientiam superflui quod est inter duos arcus notos duas notas habentes chordas aut per totius arcus scientiam, qui est ad complendum semicirculum cum arcu noto chordam habente notam. Et hec est tabularum descriptio:
〈I.11〉 Capitulum undecimum: De positione arcuum et chordarum eorum in tabulis
Prima |
Secunda |
|||||||||||||||||||
Tabula prima chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
Tabula secunda chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
|||||||||||||||||
Arcus |
Chorde |
Arcus |
Chorde |
|||||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
|||
0
1
1 |
30
0
30 |
0
1
1 |
31
2
34 |
25
50
15 |
0
0
0 |
0
0
0 |
2
2
2 |
50
50
50 |
23
23
24 |
0
30
0 |
23
24
24 |
55
26
56 |
27
13
58 |
0
0
0 |
1
1
1 |
1
1
1 |
32
30
26 |
|||
2
2
3 |
0
30
0 |
2
2
3 |
5
37
8 |
40
4
28 |
0
0
0 |
1
1
1 |
2
2
2 |
48
48
48 |
24
25
25 |
30
0
30 |
25
25
26 |
27
58
29 |
41
22
1 |
0
0
0 |
1
1
1 |
1
1
1 |
22
18
14 |
|||
3
4
4 |
30
0
30 |
3
4
4 |
39
11
42 |
52
16
40 |
0
0
0 |
1
1
1 |
2
2
2 |
48
48
48 |
26
26
27 |
0
30
0 |
26
27
28 |
59
30
0 |
38
14
48 |
0
0
0 |
1
1
1 |
1
1
1 |
12
8
4 |
|||
5
5
6 |
0
30
0 |
5
5
6 |
14
45
16 |
4
27
49 |
0
0
0 |
1
1
1 |
2
2
2 |
46
44
44 |
27
28
28 |
30
0
30 |
28
29
29 |
31
1
32 |
20
50
18 |
0
0
0 |
1
1
1 |
1
0
0 |
0
56
52 |
|||
6
7
7 |
30
0
30 |
6
7
7 |
48
19
50 |
11
33
54 |
0
0
0 |
1
1
1 |
2
2
2 |
44
42
42 |
29
29
30 |
0
30
0 |
30
30
31 |
2
33
3 |
44
8
30 |
0
0
0 |
1
1
1 |
0
0
0 |
48
44
40 |
|||
8
8
9 |
0
30
0 |
8
8
9 |
22
53
24 |
15
35
54 |
0
0
0 |
1
1
1 |
2
2
2 |
40
38
38 |
30
31
31 |
30
0
30 |
31
32
32 |
33
4
34 |
50
8
22 |
0
0
0 |
1
1
1 |
0
0
0 |
36
28
26 |
|||
9
10
10 |
30
0
30 |
9
10
10 |
56
27
58 |
13
32
49 |
0
0
0 |
1
1
1 |
2
2
2 |
38
34
32 |
32
32
33 |
0
30
0 |
33
33
34 |
4
34
4 |
35
46
55 |
0
0
0 |
1
1
1 |
0
0
0 |
22
18
12 |
|||
11
11
12 |
0
30
0 |
11
12
12 |
30
1
32 |
5
21
36 |
0
0
0 |
1
1
1 |
2
2
2 |
32
30
28 |
33
34
34 |
30
0
30 |
34
35
35 |
35
5
35 |
1
5
6 |
0
0
0 |
1
1
0 |
0
0
59 |
8
2
58 |
|||
12
13
13 |
30
0
30 |
13
13
14 |
3
35
6 |
50
4
16 |
0
0
0 |
1
1
1 |
2
2
2 |
28
24
22 |
35
35
36 |
0
30
0 |
36
36
37 |
5
35
4 |
5
1
55 |
0
0
0 |
0
0
0 |
59
59
59 |
52
48
44 |
|||
14
14
15 |
0
30
0 |
14
15
15 |
37
8
39 |
27
38
47 |
0
0
0 |
1
1
1 |
2
2
2 |
22
18
18 |
36
37
37 |
30
0
30 |
37
38
38 |
34
4
34 |
47
36
22 |
0
0
0 |
0
0
0 |
59
59
59 |
38
32
26 |
|||
15
16
16 |
30
0
30 |
16
16
17 |
10
42
13 |
56
3
9 |
0
0
0 |
1
1
1 |
2
2
2 |
14
12
10 |
38
38
39 |
0
30
0 |
39
39
40 |
4
33
3 |
5
46
24 |
0
0
0 |
0
0
0 |
59
59
59 |
22
16
12 |
|||
17
17
18 |
0
30
0 |
17
18
18 |
44
15
46 |
14
17
19 |
0
0
0 |
1
1
1 |
2
2
2 |
6
4
4 |
39
40
40 |
30
0
30 |
40
41
41 |
33
2
32 |
0
33
3 |
0
0
0 |
0
0
0 |
59
59
58 |
6
0
54 |
|||
18
19
19 |
30
0
30 |
19
19
20 |
17
48
19 |
21
21
19 |
0
0
0 |
1
1
1 |
2
1
1 |
0
56
54 |
41
41
42 |
0
30
0 |
42
42
43 |
1
30
0 |
30
54
15 |
0
0
0 |
0
0
0 |
58
58
58 |
48
42
36 |
|||
20
20
21 |
0
30
0 |
20
21
21 |
50
21
52 |
16
12
6 |
0
0
0 |
1
1
1 |
1
1
1 |
52
48
44 |
42
43
43 |
30
0
30 |
43
43
44 |
29
58
28 |
33
49
1 |
0
0
0 |
0
0
0 |
58
58
58 |
32
24
18 |
|||
21
22
22 |
30
0
30 |
22
22
23 |
22
53
24 |
58
49
39 |
0
0
0 |
1
1
1 |
1
1
1 |
42
40
36 |
44
44
45 |
0
30
0 |
44
45
45 |
57
26
55 |
10
16
19 |
0
0
0 |
0
0
0 |
58
58
58 |
12
6
0 |
|||
Residuum tabularum chordarum arcuum semicirculi una cum excessuum earundem parte tricesima, unius videlicet minuti arcuum portiuncule debita
Tertia |
Quarta |
|||||||||||||||||||
Tabula tertia chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
Tabula quarta chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
|||||||||||||||||
Arcus |
Chorde |
Arcus |
Chorde |
|||||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
|||
45
46
46 |
30
0
30 |
46
46
47 |
24
53
22 |
19
16
9 |
0
0
0 |
0
0
0 |
57
57
57 |
54
46
42 |
68
68
69 |
0
30
0 |
67
67
67 |
6
32
58 |
12
12
8 |
0
0
0 |
0
0
0 |
52
51
51 |
0
52
42 |
|||
47
47
48 |
0
30
0 |
47
48
48 |
51
19
48 |
0
47
30 |
0
0
0 |
0
0
0 |
57
57
57 |
34
26
22 |
69
70
70 |
30
0
30 |
68
68
69 |
23
49
15 |
59
45
27 |
0
0
0 |
0
0
0 |
51
51
51 |
32
24
14 |
|||
48
48
49 |
30
0
30 |
49
49
50 |
17
45
14 |
11
48
21 |
0
0
0 |
0
0
0 |
57
57
57 |
14
5
0 |
71
71
72 |
0
30
0 |
69
70
70 |
41
6
32 |
4
36
3 |
0
0
0 |
0
0
0 |
51
50
50 |
4
54
46 |
|||
50
50
51 |
0
30
0 |
50
51
51 |
42
11
39 |
51
18
42 |
0
0
0 |
0
0
0 |
56
56
56 |
57
48
36 |
72
73
73 |
30
0
30 |
70
71
71 |
57
22
47 |
26
44
56 |
0
0
0 |
0
0
0 |
50
50
50 |
36
24
16 |
|||
51
52
52 |
30
0
30 |
52
52
53 |
8
36
4 |
0
16
29 |
0
0
0 |
0
0
0 |
56
56
56 |
32
26
18 |
74
74
75 |
0
30
0 |
72
72
73 |
13
38
3 |
4
7
5 |
0
0
0 |
0
0
0 |
50
49
49 |
6
56
46 |
|||
53
53
54 |
0
30
0 |
53
54
54 |
32
0
28 |
38
43
44 |
0
0
0 |
0
0
0 |
56
56
55 |
10
2
56 |
75
76
76 |
30
0
30 |
73
73
74 |
27
52
17 |
58
46
29 |
0
0
0 |
0
0
0 |
49
49
49 |
36
26
16 |
|||
54
55
55 |
30
0
30 |
54
55
55 |
56
24
52 |
42
36
26 |
0
0
0 |
0
0
0 |
55
55
55 |
48
40
32 |
77
77
78 |
0
30
0 |
74
75
75 |
46
6
31 |
7
39
7 |
0
0
0 |
0
0
0 |
49
48
48 |
4
56
44 |
|||
56
56
57 |
0
30
0 |
56
56
57 |
20
47
15 |
12
54
33 |
0
0
0 |
0
0
0 |
55
55
55 |
24
18
8 |
78
79
79 |
30
0
30 |
75
76
76 |
55
19
43 |
29
46
58 |
0
0
0 |
0
0
0 |
48
48
48 |
34
24
14 |
|||
57
58
58 |
30
0
30 |
57
58
58 |
43
10
38 |
7
38
5 |
0
0
0 |
0
0
0 |
55
54
54 |
2
54
44 |
80
80
81 |
0
30
0 |
77
77
77 |
8
32
56 |
5
6
2 |
0
0
0 |
0
0
0 |
48
47
47 |
2
52
40 |
|||
59
59
60 |
0
30
0 |
59
59
60 |
5
32
0 |
27
45
0 |
0
0
0 |
0
0
0 |
54
54
54 |
36
30
22 |
81
82
82 |
30
0
30 |
78
78
79 |
19
43
7 |
52
38
18 |
0
0
0 |
0
0
0 |
47
47
47 |
32
20
8 |
|||
60
61
61 |
30
0
30 |
60
60
61 |
27
54
21 |
11
17
19 |
0
0
0 |
0
0
0 |
54
54
53 |
12
4
56 |
83
83
84 |
0
30
0 |
79
79
80 |
30
54
17 |
52
21
45 |
0
0
0 |
0
0
0 |
46
46
46 |
58
48
36 |
|||
62
62
63 |
0
30
0 |
61
62
62 |
48
15
42 |
17
10
0 |
0
0
0 |
0
0
0 |
53
53
53 |
46
40
30 |
84
85
85 |
30
0
30 |
80
81
81 |
41
4
27 |
3
15
22 |
0
0
0 |
0
0
|
46
46
46 |
24
14
4 |
|||
63
64
64 |
30
0
30 |
63
63
64 |
8
35
2 |
45
26
2 |
0
0
0 |
0
0
0 |
53
53
53 |
22
12
4 |
86
86
87 |
0
30
0 |
81
82
82 |
50
13
36 |
24
19
9 |
0
0
0 |
0
0
0 |
45
45
45 |
50
40
30 |
|||
65
65
66 |
0
30
0 |
64
64
65 |
28
55
21 |
34
1
24 |
0
0
0 |
0
0
0 |
52
52
52 |
54
46
38 |
87
88
88 |
30
0
30 |
82
83
83 |
58
21
44 |
54
33
6 |
0
0
0 |
0
0
0 |
45
45
44 |
18
6
56 |
|||
66
67
67 |
30
0
30 |
65
66
66 |
47
13
40 |
43
57
7 |
0
0
0 |
0
0
0 |
52
52
52 |
28
20
10 |
89
89
90 |
0
30
0 |
84
84
84 |
6
28
51 |
34
55
10 |
0
0
0 |
0
0
0 |
44
44
44 |
42
30
20 |
|||
Residuum tabularum chordarum arcuum semicirculi una cum excessuum earundem parte tricesima, unius videlicet minuti arcuum portiuncule debita
Quinta |
Sexta |
|||||||||||||||||||
Tabula quinta chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
Tabula sexta chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
|||||||||||||||||
Arcus |
Chorde |
Arcus |
Chorde |
|||||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
|||
90
91
91 |
30
0
30 |
85
85
85 |
13
35
57 |
20
24
23 |
0
0
0 |
0
0
0 |
44
43
43 |
8
58
44 |
113
113
114 |
0
30
0 |
100
100
100 |
3
21
38 |
59
16
26 |
0
0
0 |
0
0
0 |
34
34
34 |
34
20
4 |
|||
92
92
93 |
0
30
0 |
86
86
87 |
19
41
2 |
15
2
42 |
0
0
0 |
0
0
0 |
43
43
43 |
34
20
10 |
114
115
115 |
30
0
30 |
100
101
101 |
55
12
29 |
28
25
15 |
0
0
0 |
0
0
0 |
33
33
33 |
54
40
24 |
|||
93
94
94 |
30
0
30 |
87
87
88 |
24
45
7 |
17
45
7 |
0
0
0 |
0
0
0 |
42
42
42 |
56
44
34 |
116
116
117 |
0
30
0 |
101
102
102 |
45
2
19 |
57
33
1 |
0
0
0 |
0
0
0 |
33
32
32 |
12
56
42 |
|||
95
95
96 |
0
30
0 |
88
88
89 |
28
49
10 |
24
34
39 |
0
0
0 |
0
0
0 |
42
42
41 |
20
10
56 |
117
118
118 |
30
0
30 |
102
102
103 |
35
51
7 |
22
37
44 |
0
0
0 |
0
0
0 |
32
32
32 |
30
14
0 |
|||
96
97
97 |
30
0
30 |
89
89
90 |
31
52
13 |
37
29
15 |
0
0
0 |
0
0
0 |
41
41
41 |
44
32
20 |
119
119
120 |
0
30
0 |
103
103
103 |
23
39
55 |
44
37
23 |
0
0
0 |
0
0
0 |
31
31
31 |
46
32
18 |
|||
98
98
99 |
0
30
0 |
90
90
91 |
33
54
14 |
55
29
56 |
0
0
0 |
0
0
0 |
41
40
40 |
8
54
42 |
120
121
121 |
30
0
30 |
104
104
104 |
11
26
41 |
2
34
59 |
0
0
0 |
0
0
0 |
31
30
30 |
4
50
34 |
|||
99
100
100 |
30
0
30 |
91
91
92 |
35
55
15 |
17
32
40 |
0
0
0 |
0
0
0 |
40
40
40 |
30
16
4 |
122
122
123 |
0
30
0 |
104
105
105 |
57
12
27 |
16
26
30 |
0
0
0 |
0
0
0 |
30
30
29 |
20
8
52 |
|||
101
101
102 |
0
30
0 |
92
92
93 |
35
55
15 |
42
38
27 |
0
0
0 |
0
0
0 |
39
39
39 |
52
38
28 |
123
124
124 |
30
0
30 |
105
105
106 |
42
57
11 |
26
14
55 |
0
0
0 |
0
0
0 |
29
29
29 |
36
22
8 |
|||
102
103
103 |
30
0
30 |
93
93
94 |
35
54
14 |
11
47
17 |
0
0
0 |
0
0
0 |
39
39
38 |
12
0
48 |
125
125
126 |
0
30
0 |
106
106
106 |
26
40
55 |
29
56
15 |
0
0
0 |
0
0
0 |
28
28
28 |
54
38
24 |
|||
104
104
105 |
0
30
0 |
94
94
95 |
33
52
12 |
41
58
9 |
0
0
0 |
0
0
0 |
38
38
38 |
34
22
8 |
126
127
127 |
30
0
30 |
107
107
107 |
9
23
37 |
27
32
30 |
0
0
0 |
0
0
0 |
28
27
27 |
10
56
40 |
|||
105
106
106 |
30
0
30 |
95
95
96 |
31
50
9 |
13
11
2 |
0
0
0 |
0
0
0 |
37
37
37 |
56
42
28 |
128
128
129 |
0
30
0 |
107
108
108 |
51
5
18 |
20
2
37 |
0
0
0 |
0
0
0 |
27
27
26 |
24
10
56 |
|||
107
107
108 |
0
30
0 |
96
96
97 |
27
46
4 |
46
24
55 |
0
0
0 |
0
0
0 |
37
37
36 |
16
2
50 |
129
130
130 |
30
0
30 |
108
108
108 |
32
45
58 |
5
25
38 |
0
0
0 |
0
0
0 |
26
26
26 |
40
26
12 |
|||
108
109
109 |
30
0
30 |
97
97
97 |
23
41
59 |
20
38
49 |
0
0
0 |
0
0
0 |
36
36
36 |
36
22
10 |
131
131
132 |
0
30
0 |
109
109
109 |
11
24
37 |
44
42
32 |
0
0
0 |
0
0
0 |
25
25
25 |
56
40
26 |
|||
110
110
111 |
0
30
0 |
98
98
98 |
17
35
53 |
54
52
43 |
0
0
0 |
0
0
0 |
35
35
35 |
56
42
28 |
132
133
133 |
30
0
30 |
109
110
110 |
50
2
15 |
15
50
18 |
0
0
0 |
0
0
0 |
25
24
24 |
10
56
42 |
|||
111
112
112 |
30
0
30 |
99
99
99 |
11
29
46 |
27
5
35 |
0
0
0 |
0
0
0 |
35
35
34 |
16
0
48 |
134
134
135 |
0
30
0 |
110
110
110 |
27
39
51 |
39
52
57 |
0
0
0 |
0
0
0 |
24
24
23 |
26
10
54 |
|||
Residuum tabularum chordarum arcuum semicirculi una cum excessuum earundem parte tricesima, unius videlicet minuti arcuum portiuncule debita
Septima |
Octava |
|||||||||||||||||||
Tabula septima chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
Tabula octava chordarum arcuum medietate et medietate partis superfluentium |
Pars tricesima superflui quod est inter omnes duas chordas, et est portio arcus unius minuti |
|||||||||||||||||
Arcus |
Chorde |
Arcus |
Chorde |
|||||||||||||||||
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
Partes |
Minuta |
Partes |
Minuta |
Secunda |
Partes |
Minuta |
Secunda |
Tertia |
|||
135
136
136 |
30
0
30 |
111
111
111 |
3
15
27 |
54
44
26 |
0
0
0 |
0
0
0 |
23
23
23 |
40
24
10 |
158
158
159 |
0
30
0 |
117
117
117 |
47
53
59 |
43
39
26 |
0
0
0 |
0
0
0 |
11
11
11 |
52
34
20 |
|||
137
137
138 |
0
30
0 |
111
111
112 |
39
50
1 |
1
28
47 |
0
0
0 |
0
0
0 |
22
22
22 |
54
38
24 |
159
160
160 |
30
0
30 |
118
118
118 |
5
10
16 |
6
37
1 |
0
0
0 |
0
0
0 |
11
10
10 |
2
48
30 |
|||
138
139
139 |
30
0
30 |
112
112
112 |
12
24
35 |
59
3
0 |
0
0
0 |
0
0
0 |
22
21
21 |
8
54
36 |
161
161
162 |
0
30
0 |
118
118
118 |
21
26
31 |
16
23
22 |
0
0
0 |
0
0
0 |
10
9
9 |
14
58
42 |
|||
140
140
141 |
0
30
0 |
112
112
113 |
45
56
7 |
48
29
2 |
0
0
0 |
0
0
0 |
21
21
20 |
22
6
50 |
162
163
163 |
30
0
30 |
118
118
118 |
36
40
45 |
13
55
30 |
0
0
0 |
0
0
0 |
9
9
8 |
24
10
52 |
|||
141
142
142 |
30
0
30 |
113
113
113 |
17
27
37 |
27
44
54 |
0
0
0 |
0
0
0 |
20
20
20 |
34
20
4 |
164
164
165 |
0
30
0 |
118
118
118 |
49
54
58 |
56
14
24 |
0
0
0 |
0
0
0 |
8
8
8 |
36
20
4 |
|||
143
143
144 |
0
30
0 |
113
113
114 |
47
57
7 |
56
50
37 |
0
0
0 |
0
0
0 |
19
19
19 |
48
34
16 |
165
166
166 |
30
0
30 |
119
119
119 |
2
6
10 |
26
20
6 |
0
0
0 |
0
0
0 |
7
7
7 |
48
32
16 |
|||
144
145
145 |
30
0
30 |
114
114
114 |
17
26
36 |
15
46
9 |
0
0
0 |
0
0
0 |
19
18
18 |
2
46
30 |
167
167
168 |
0
30
0 |
119
119
119 |
13
17
20 |
44
13
34 |
0
0
0 |
0
0
0 |
6
6
6 |
58
42
26 |
|||
146
146
147 |
0
30
0 |
114
114
115 |
45
54
3 |
24
31
30 |
0
0
0 |
0
0
0 |
18
17
17 |
14
58
44 |
168
169
169 |
30
0
30 |
119
119
119 |
23
26
29 |
47
52
49 |
0
0
0 |
0
0
0 |
6
5
5 |
10
54
36 |
|||
147
148
148 |
30
0
30 |
115
115
115 |
12
21
29 |
22
6
41 |
0
0
0 |
0
0
0 |
17
17
16 |
28
10
56 |
170
170
171 |
0
30
0 |
119
119
119 |
32
35
37 |
37
17
49 |
0
0
0 |
0
0
0 |
5
5
4 |
20
4
48 |
|||
149
149
150 |
0
30
0 |
115
115
115 |
38
46
54 |
9
29
40 |
0
0
0 |
0
0
0 |
16
16
16 |
40
22
8 |
171
172
172 |
30
0
30 |
119
119
119 |
40
42
44 |
13
29
36 |
0
0
0 |
0
0
0 |
4
4
3 |
32
14
58 |
|||
150
151
151 |
30
0
30 |
116
116
116 |
2
10
18 |
44
40
28 |
0
0
0 |
0
0
0 |
15
15
15 |
52
36
20 |
173
173
174 |
0
30
0 |
119
119
119 |
46
48
50 |
35
26
8 |
0
0
0 |
0
0
0 |
3
3
3 |
42
24
10 |
|||
152
152
153 |
0
30
0 |
116
116
116 |
26
33
41 |
8
40
4 |
0
0
0 |
0
0
0 |
15
14
14 |
4
48
32 |
174
175
175 |
30
0
30 |
119
119
119 |
51
53
54 |
43
10
28 |
0
0
0 |
0
0
0 |
2
2
2 |
54
36
20 |
|||
153
154
154 |
30
0
30 |
116
116
117 |
48
55
2 |
20
28
28 |
0
0
0 |
0
0
0 |
14
14
13 |
16
0
44 |
176
176
177 |
0
30
0 |
119
119
119 |
55
56
57 |
38
39
32 |
0
0
0 |
0
0
0 |
2
1
1 |
2
46
32 |
|||
155
155
156 |
0
30
0 |
117
117
117 |
9
16
22 |
20
4
40 |
0
0
0 |
0
0
0 |
13
13
12 |
28
12
56 |
177
178
178 |
30
0
30 |
119
119
119 |
58
58
59 |
18
55
23 |
0
0
0 |
0
0
0 |
1
0
0 |
14
56
42 |
|||
156
157
157 |
30
0
30 |
117
117
117 |
29
35
41 |
8
28
40 |
0
0
0 |
0
0
0 |
12
12
12 |
40
24
6 |
179
179
180 |
0
30
0 |
119
119
120 |
59
59
0 |
44
56
0 |
0
0
0 |
0
0
0 |
0
0
0 |
24
8
0 |
|||
〈I.12〉 Capitulum duodecimum: De arte instrumenti quo scitur quantitas arcus qui est inter duos tropicos
Postquam demonstravimus quantitatem chordarum circuli et numerum partium earum, convenit ut declaremus primum, quemadmodum prediximus, quanta sit declinatio orbis signorum declivis ab orbe equationis diei et que sit proportio orbis magni quem duo poli revolvunt ad arcum qui est eius portio existens inter duos polos et secundum cuius quantitatem existit longitudo linee equationis diei ab utroque duorum tropicorum. Hoc autem declarabitur nobis per artificium instrumenti concavi, fusi, non coniuncti, cuius artificium est quemadmodum declarabo: Faciam armillam ex ere, mensurate quantitatis, bene planam et limatam, cuius superficies sint quadrate, et assumam eam lineam meridiei, et dividam eam per 360 sectiones secundum sectionem circuli maioris, et dividam unamquamque partium eius in quot minuta possibile fuerit. Deinde aliam armillam in interioribus huius armille competenti ordine statuam, et ponam earum latera in superficie una fixa, minorque armilla moveatur in interioribus maioris, ita tamen ne eius motus in illius superficie impediatur ad septentrionem et meridiem, et ponam in duobus locis oppositis unius laterum minoris duas regulas parvas equales facie ad faciem et faciebus centro duarum armillarum conversis, et ponam ubi vere medium est duarum regularum duas linguulas duas extremitates valde tenues habentes contingentes superficiem armille maioris, in qua partium existit divisio, et ponam has duas armillas, quotiens nobis necesse fuerit per eas considerare, super perpendicularem mensuratam, et figam basim perpendicularis sub celo in loco non moto a superficie horizontis, ita ut sit superficies duarum armillarum erecta supra superficiem horizontis ortogonaliter et sit equidistans superficiei orbis meridiei. Preparatio vero primi horum duorum modorum sic erit: Preparabimus enim ipsum cum perpendiculo quando suspendetur in puncto quod est in armilla super summitatem capitum et descendet ita ut transeat supra punctum quod ei opponitur nobis rectificantibus duas armillas per ea que eas firment et equent donec filum perpendiculi sit supra punctum quod opponitur puncto summitatis capitum, a quo eius incepit descensio. Secundi vero modi preparatio fiet per lineam rectam quam describemus in superficie supra quam perpendicularis est erecta. Et sit linea equidistans linee orbis meridiei, et movebimus duas armillas et inclinabimus eas ad partes donec fiat superficies duarum armillarum equidistans linee meridiei quam sub perpendiculari descripsimus. Cum ergo duas armillas ad hunc modum preparaverimus, inspiciemus in medietatibus dierum longitudines Solis in partibus meridiei et septentrionis nobis moventibus armillam interiorem ad partes meridiei et septentrionis donec obumbretur tota regula inferior tota umbra superioris. Cum enim hoc fecerimus, indicabunt nobis extremitates duarum linguarum numerum partium que sunt longitudo centri Solis a summitate capitum nostrorum in meridiei linea in omni tempore quo voluerimus. Accipiam etiam loco duarum armillarum aliquod aliud considerandi instrumentum, quod velocius fiat et levius et vicinius assumatur. Faciam enim laterem lapideum aut ligneum quadratum mensurate latitudinis et altitudinis, ut supra superficiem sue basis absque tortuositate et declinatione erigatur, sitque una superficierum eius vehementer plana et lenis et equalis. Ponam autem apud unum angulorum huius superficiei punctum quod constituam centrum, et describam supra ipsum quartam circuli, et protraham ab ipso duas lineas rectas ad duas extremitates quarte descripte continentes angulum rectum qui est sub quarta, et dividam angulum quarte in 90 partes, et dividam partes in partes suas. Deinde faciam duos paxillos parvos rotundos pyramidales cum torno equales in quantitate et grossicie, et figam eos in duabus extremitatibus unius duarum linearum rectarum erecte supra superficiem horizontis, et sit locus eius a latere ad partem meridiei, et ponam medium extremitatis unius duorum paxillorum supra medium puncti quod est in centro quarte, et ponam medium extremitatis alterius paxilli supra medium puncti quod est in extremitate altera inferiori linee. Deinde erigam hanc superficierum lateris in qua est hec linea supra lineam descriptam in terra equidistantem linee meridiei ut sit superficies equidistans linee meridiei et ponam lineam que est inter duos paxillos libratam cum perpendiculo erectam supra superficiem horizontis ortogonaliter nobis eam rectificantibus per ea que eam firment donec supra ipsam cadat filum quod descendit cum perpendiculo a paxillo superiori ad paxillum inferiorem. Postea considerabimus in medietatibus dierum umbram paxilli superioris, qui est in centro, et ponemus sub quarta descripta aliquid ut sit locus umbre vehementer manifestus, et considerabimus medium umbre super quas partes quarte cadat. Et per hoc indicabitur transitus Solis in linea orbis meridiei in terra. Per has ergo considerationes, precipue quas consideravimus in hora duorum tropicorum in pluribus revolutionibus, in tropicis estivalibus et hiemalibus, invenimus illas longitudines et illas partes que ad septentrionem sunt longiores et que ad meridiem sunt longiores non mutari. Et plurimum quod consideravimus a puncto summitatis capitum invenimus quod longior longitudo septentrionis a longiori longitudine meridiei, que est illud quod est inter duos tropicos, est semper 47 partes et plus duabus tertiis partis et minus medietate et quarta partis. Et hec quidem consideratio convenit considerationi quam consideravit Archusianus philosophus qua Abrachis operatus est. Illud enim quod est inter duos tropicos est fere 11 secundum quantitatem qua linea orbis meridiei est 83. His autem considerationibus vicinius sumitur declinatio locorum in quibus consideravimus, et hoc cum assumpserimus arcum qui est inter punctum quod est inter hec duo spacia quod est in linea orbis equationis diei et inter punctum quod est supra summitatem capitum, qui demonstratur esse equalis longitudini cuiusque duorum polorum ab horizonte.
Et quoniam sequitur ut demonstrem post hoc numerum partium quantitatum arcuum qui sunt orbium maiorum descriptorum super duos polos orbis equationis diei, et sunt arcus qui sunt inter lineam equationis diei et lineam medii orbis signorum, oportet ut premittam capitula pauca utilitatem afferentia quibus possimus demonstrare plurimum scientie demonstrationum sphericarum quam levius possibile est et sapientius. 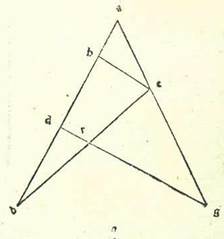 Describam ergo duas lineas AB et AG et protraham in eo quod inter illas duas lineas est BE et GD sese supra R secantes. Dico ergo quod proportio GA ad EA aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione RB ad BE. Quod sic probatur: Protraham ab E lineam EH equidistantem linee DG. Et quia EH et GD sunt equidistantes, fit proportio GA ad AE sicut proportio GD ad EH. Ponam autem RD mediam inter GD et EH. Manifestum est igitur quod proportio GD ad EH aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione DR ad EH. Quapropter proportio GA ad AE aggregatur ex proportione GD ad DR et ex proportione DR ad EH. Proportio vero DR ad EH est sicut proportio BR ad BE. Et quoniam due linee EH et RD sunt equidistantes, ergo proportio AG ad AE aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione BR ad BE. Et hoc est quod proposuimus.
Describam ergo duas lineas AB et AG et protraham in eo quod inter illas duas lineas est BE et GD sese supra R secantes. Dico ergo quod proportio GA ad EA aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione RB ad BE. Quod sic probatur: Protraham ab E lineam EH equidistantem linee DG. Et quia EH et GD sunt equidistantes, fit proportio GA ad AE sicut proportio GD ad EH. Ponam autem RD mediam inter GD et EH. Manifestum est igitur quod proportio GD ad EH aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione DR ad EH. Quapropter proportio GA ad AE aggregatur ex proportione GD ad DR et ex proportione DR ad EH. Proportio vero DR ad EH est sicut proportio BR ad BE. Et quoniam due linee EH et RD sunt equidistantes, ergo proportio AG ad AE aggregatur ex duabus proportionibus, ex proportione GD ad DR et ex proportione BR ad BE. Et hoc est quod proposuimus.
Similiter quoque declarabitur secundum modum dividendi quod proportio GE ad EA aggregatur ex duabus proportionibus, ex proportione GR ad RD et ex proportione DB ad BA. Quod sic probatur: 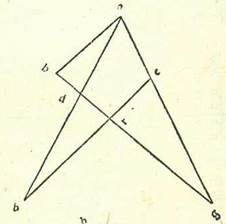 Producam enim AH equidistantem ER et protraham GD ad H. Et quia due linee AH et ER sunt equidistantes, fit proportio GE ad EA sicut proportio GR ad RH. Ponam autem DR mediam inter GR et RH. Manifestum est igitur quod proportio GR ad RH aggregatur ex duabus proportionibus, ex proportione GR ad RD et ex proportione RD ad RH. Verum proportio RD ad RH est sicut proportio DB ad BA, quoniam due linee BA et RH cadunt super duas lineas AH et BE equidistantes. Ergo proportio GR ad RH aggregatur ex duabus proportionibus, scilicet ex proportione GR ad RD et ex proportione BD ad BA. Proportio autem GE ad EA est sicut proportio GR ad RH. Ergo proportio GE ad EA aggregatur ex duabus proportionibus, ex proportione GR ad RD et ex proportione DB ad BA. Et hoc est quod voluimus ostendere.
Producam enim AH equidistantem ER et protraham GD ad H. Et quia due linee AH et ER sunt equidistantes, fit proportio GE ad EA sicut proportio GR ad RH. Ponam autem DR mediam inter GR et RH. Manifestum est igitur quod proportio GR ad RH aggregatur ex duabus proportionibus, ex proportione GR ad RD et ex proportione RD ad RH. Verum proportio RD ad RH est sicut proportio DB ad BA, quoniam due linee BA et RH cadunt super duas lineas AH et BE equidistantes. Ergo proportio GR ad RH aggregatur ex duabus proportionibus, scilicet ex proportione GR ad RD et ex proportione BD ad BA. Proportio autem GE ad EA est sicut proportio GR ad RH. Ergo proportio GE ad EA aggregatur ex duabus proportionibus, ex proportione GR ad RD et ex proportione DB ad BA. Et hoc est quod voluimus ostendere.
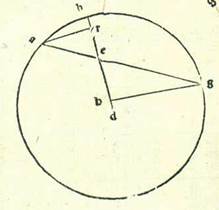 Describam etiam circulum, supra quem sint A, B, G, supra centrum D, et dividam ex circulo duos arcus AB et BG, et ponam unumquemque eorum semicirculo minorem. Et similiter dividentur omnes arcus in sequentibus. Hanc ergo exceptionem memorie commendemus. Et protraham duas lineas AG et DEB. Dico ergo quod proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG. Quod sic probatur: Protraham enim duas lineas perpendiculares a duobus punctis A et G ad lineam DB, que sint AR et GH. Et quia AR et GH equidistant et cadit super eas linea AEG, erit proportio AR ad GH sicut proportio AE ad EG. Proportio vero AR ad GH est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG, quoniam unaqueque est medietas chorde sui dupli. Ergo proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG. Et hoc est quod demonstrare voluimus.
Describam etiam circulum, supra quem sint A, B, G, supra centrum D, et dividam ex circulo duos arcus AB et BG, et ponam unumquemque eorum semicirculo minorem. Et similiter dividentur omnes arcus in sequentibus. Hanc ergo exceptionem memorie commendemus. Et protraham duas lineas AG et DEB. Dico ergo quod proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG. Quod sic probatur: Protraham enim duas lineas perpendiculares a duobus punctis A et G ad lineam DB, que sint AR et GH. Et quia AR et GH equidistant et cadit super eas linea AEG, erit proportio AR ad GH sicut proportio AE ad EG. Proportio vero AR ad GH est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG, quoniam unaqueque est medietas chorde sui dupli. Ergo proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG. Et hoc est quod demonstrare voluimus.
Hoc autem superest quod cum arcus AG totus fuerit notus et proportio chorde dupli arcus AB ad chordam dupli arcus BG nota, erit unusquisque duorum arcuum AB et BG notus. Verbi gratia: 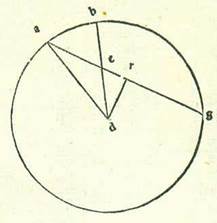 Reiterabo enim figuram, et protraham lineam AD, et producam perpendicularem AD ad lineam AEG, que sit DR. Et quoniam cum fuerit arcus AG notus, erit angulus ADR, cuius basis est medietas arcus, notus, erit et totus triangulus ADR notus. Et manifestum est quod cum fuerit tota chorda AG nota, et iam firmum est quod proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG, erit linea AE nota. Et post hoc sciemus RE. Et propter hoc quod DR est nota sciemus ex hoc angulum EDR trianguli EDR ortogonii, quoniam omnis trianguli ortogonii notorum laterum reliqui eius anguli sunt noti per illud quod premisimus in tabulis loci portionis cuiusque chorde arcus. Sciemus ergo totum angulum ADB. Et propter hoc sciemus arcum AB et sciemus arcum BG, qui est residuum arcus AG. Et hoc est quod oportuit nos declarare.
Reiterabo enim figuram, et protraham lineam AD, et producam perpendicularem AD ad lineam AEG, que sit DR. Et quoniam cum fuerit arcus AG notus, erit angulus ADR, cuius basis est medietas arcus, notus, erit et totus triangulus ADR notus. Et manifestum est quod cum fuerit tota chorda AG nota, et iam firmum est quod proportio AE ad EG est sicut proportio chorde dupli arcus AB ad chordam dupli arcus BG, erit linea AE nota. Et post hoc sciemus RE. Et propter hoc quod DR est nota sciemus ex hoc angulum EDR trianguli EDR ortogonii, quoniam omnis trianguli ortogonii notorum laterum reliqui eius anguli sunt noti per illud quod premisimus in tabulis loci portionis cuiusque chorde arcus. Sciemus ergo totum angulum ADB. Et propter hoc sciemus arcum AB et sciemus arcum BG, qui est residuum arcus AG. Et hoc est quod oportuit nos declarare.
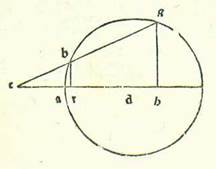 Describam etiam circulum, supra quem sint A, B, G, super centrum D, et sit unusquisque duorum arcuum AB et AG minor semicirculo, et similiter quisque arcus dividetur in sequentibus existens minor semicirculo, et protraham duas lineas HDA et GB et producam eas donec concurrant super E. Dico ergo quod proportio GE ad EB est sicut proportio chorde dupli arcus AG ad chordam dupli arcus AB. Huius autem demonstratio prime similis est. Protraham enim ad lineam HDA duas perpendiculares AB et AG, que sint BR et GH. Et quia ipse sunt equidistantes, erit proportio GE ad EB sicut proportio GH ad BR. Et propter hoc erit proportio GE ad EB sicut proportio chorde dupli arcus GA ad chordam dupli arcus AB. Et illud voluimus demonstrare.
Describam etiam circulum, supra quem sint A, B, G, super centrum D, et sit unusquisque duorum arcuum AB et AG minor semicirculo, et similiter quisque arcus dividetur in sequentibus existens minor semicirculo, et protraham duas lineas HDA et GB et producam eas donec concurrant super E. Dico ergo quod proportio GE ad EB est sicut proportio chorde dupli arcus AG ad chordam dupli arcus AB. Huius autem demonstratio prime similis est. Protraham enim ad lineam HDA duas perpendiculares AB et AG, que sint BR et GH. Et quia ipse sunt equidistantes, erit proportio GE ad EB sicut proportio GH ad BR. Et propter hoc erit proportio GE ad EB sicut proportio chorde dupli arcus GA ad chordam dupli arcus AB. Et illud voluimus demonstrare.
Sequitur vero hoc quoniam cum fuerit hic arcus GB solum notus et fuerit proportio chorde dupli arcus AG ad chordam dupli arcus AB nota, scietur arcus AB. Quod sic probatur: 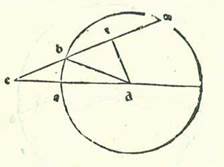 Protraham namque in figura simili huic forme etiam a puncto D semidiametrum DB et perpendicularem ad chordam BG, que sit DR. Angulus ergo BDR, cuius basis est medietas arcus BG, erit notus. Quapropter totus triangulus BDR ortogonius est notus. Et quia proportio GE ad EB est nota et chorda GB est nota, sciemus ex hoc EB et per consequens totam lineam EBR. Et quoniam DR est nota, erit angulus EDR trianguli EDR ortogonii notus et sciemus angulum EDB residuum, cuius quantitas est arcus AB, quem querebamus.
Protraham namque in figura simili huic forme etiam a puncto D semidiametrum DB et perpendicularem ad chordam BG, que sit DR. Angulus ergo BDR, cuius basis est medietas arcus BG, erit notus. Quapropter totus triangulus BDR ortogonius est notus. Et quia proportio GE ad EB est nota et chorda GB est nota, sciemus ex hoc EB et per consequens totam lineam EBR. Et quoniam DR est nota, erit angulus EDR trianguli EDR ortogonii notus et sciemus angulum EDB residuum, cuius quantitas est arcus AB, quem querebamus.
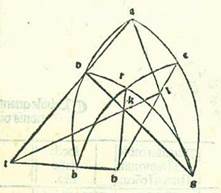 Et postquam premisimus hec antecedentia, describam in superficie spherica arcus orbium maiorum, qui sint arcus AB et AG et arcus BE et GD sese secantes supra R. Et sit quisque arcuum minor semicirculo. Hanc vero exceptionem commendabimus memorie in omnibus formis. Dico igitur quod proportio chorde dupli arcus GE ad chordam dupli arcus EA aggregatur ex proportionibus duabus, ex proportione chorde dupli arcus GR ad chordam dupli arcus RD et ex proportione chorde dupli arcus DB ad chordam dupli arcus BA. Quod sic probatur:
Et postquam premisimus hec antecedentia, describam in superficie spherica arcus orbium maiorum, qui sint arcus AB et AG et arcus BE et GD sese secantes supra R. Et sit quisque arcuum minor semicirculo. Hanc vero exceptionem commendabimus memorie in omnibus formis. Dico igitur quod proportio chorde dupli arcus GE ad chordam dupli arcus EA aggregatur ex proportionibus duabus, ex proportione chorde dupli arcus GR ad chordam dupli arcus RD et ex proportione chorde dupli arcus DB ad chordam dupli arcus BA. Quod sic probatur: 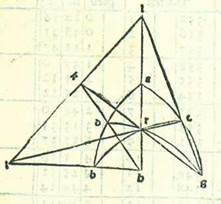 Ponam enim centrum sphere H, et protraham a centro ad puncta B et R et E, ubi se secant circuli lineas HB et HR et HE, et protraham chordam AD, et producam HB, que est medietas diametri, donec concurrant supra punctum T, et protraham duas lineas GA et GD secantes duas lineas HR et HE supra duo puncta K et L. Fiunt ergo in linea una recta tria puncta, que sunt T et K et L, quoniam ipsa ipfa M. simul sunt in superficie trianguli AGD et in superficie circuli BRE. He ergo due superficies se secant in linea LKT. Cum ergo hec linea protrahetur, due linee TL et GD se secabunt inter duas lineas TA et GA, et erit earum sectio supra K. Manifestum est ergo quod proportio GL ad AL aggregatur ex duabus proportionibus, ex proportione GK ad KD et ex proportione DT ad TA. Proportio autem GL ad LA est sicut proportio chorde dupli arcus GE ad chordam dupli arcus EA, sicut ostensum est in primo quattuor circulorum precedentium hanc figuram, et proportio GK ad KD est sicut proportio chorde dupli arcus GR ad chordam dupli arcus RD, et proportio DT ad TA est sicut proportio chorde dupli arcus DB ad chordam dupli arcus BA, quemadmodum ostensum est in tertio quattuor circulorum precedentium hanc figuram. Ergo proportio chorde dupli arcus GE ad chordam dupli arcus EA aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus GR ad chordam dupli arcus RD et ex proportione chorde dupli arcus DB ad chordam dupli arcus BA. Ex eo autem quod demonstratum est ex proportionibus linearum in forma superficiali precedente declaratur quod proportio chorde dupli arcus GA ad cordam dupli arcus AE aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus GD ad chordam dupli arcus DR et ex proportione chorde dupli arcus RB ad chordam dupli arcus BE. Et hoc intendimus probare.
Ponam enim centrum sphere H, et protraham a centro ad puncta B et R et E, ubi se secant circuli lineas HB et HR et HE, et protraham chordam AD, et producam HB, que est medietas diametri, donec concurrant supra punctum T, et protraham duas lineas GA et GD secantes duas lineas HR et HE supra duo puncta K et L. Fiunt ergo in linea una recta tria puncta, que sunt T et K et L, quoniam ipsa ipfa M. simul sunt in superficie trianguli AGD et in superficie circuli BRE. He ergo due superficies se secant in linea LKT. Cum ergo hec linea protrahetur, due linee TL et GD se secabunt inter duas lineas TA et GA, et erit earum sectio supra K. Manifestum est ergo quod proportio GL ad AL aggregatur ex duabus proportionibus, ex proportione GK ad KD et ex proportione DT ad TA. Proportio autem GL ad LA est sicut proportio chorde dupli arcus GE ad chordam dupli arcus EA, sicut ostensum est in primo quattuor circulorum precedentium hanc figuram, et proportio GK ad KD est sicut proportio chorde dupli arcus GR ad chordam dupli arcus RD, et proportio DT ad TA est sicut proportio chorde dupli arcus DB ad chordam dupli arcus BA, quemadmodum ostensum est in tertio quattuor circulorum precedentium hanc figuram. Ergo proportio chorde dupli arcus GE ad chordam dupli arcus EA aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus GR ad chordam dupli arcus RD et ex proportione chorde dupli arcus DB ad chordam dupli arcus BA. Ex eo autem quod demonstratum est ex proportionibus linearum in forma superficiali precedente declaratur quod proportio chorde dupli arcus GA ad cordam dupli arcus AE aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus GD ad chordam dupli arcus DR et ex proportione chorde dupli arcus RB ad chordam dupli arcus BE. Et hoc intendimus probare.
〈I.13〉 Capitulum tredecimum: De scientia quantitatum arcuum qui sunt inter orbem equationis diei et orbem medii signorum qui sunt declinationis
Et postquam premisimus hoc capitulum, ostendemus primum demonstrationes super hos arcus quemadmodum narrabo et exemplificabo. 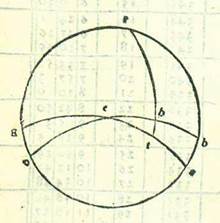 Describam ergo orbem quem revolvunt duo poli simul, polus orbis equationis diei et polus medii orbis signorum, et signabo super ipsum ABG, et decribam in eo medietatem orbis equationis diei, supra quam sint A, E, G, et medietatem orbis medii signorum, supra quam sint B, E, D, qui se secent supra punctum E, quod sit punctum equationis diei vernale, et sit tropicus hiemalis punctum B et tropicus estivalis punctum D, et ponam ut polus orbis equationis diei sit punctum R arcus ABG, et ponam ut arcus EH, qui est orbis signorum, sit triginta secundum quantitatem qua orbis maior est 360, et describam arcum RHT, qui sit orbis magni, et investigabo scientiam arcus HT. Et quia abhorreo iterare sermonem in omni hora, dico ergo quod cum nos nominamus in hoc loco et in omni eius simili qui est ex eis quos declaraturi sumus mus M. numerum partium arcuum aut partium chordarum, nolumus intelligere per partes arcuum nisi illas que sunt ex partibus maioris, scilicet circuli 360, et per partes chordarum nisi illas que sunt ex 120 partibus diametri circuli. Et quoniam in forma horum orbium maiorum inter duos arcus AR et AE sunt duo arcus RT et EB sese supra H secantes, fit ut proportio chorde dupli arcus RA ad chordam dupli arcus AB aggregetur ex duabus proportionibus, ex proportione corde dupli arcus RT ad chordam dupli arcus TH et ex proportione chorde dupli arcus HE ad chordam dupli arcus EB. Iam autem scivimus quod duplum arcus RA est 180, et chorda eius 120, et duplum arcus AB secundum quod consideravimus et convenimus supra ipsum secundum proportionem 11 ad 83 est 47 partes et 42 minuta et 40 secunda, et est eius chorda 48 partes et 31 minuta et 55 secunda, et duplum arcus HE est 60 partes, et eius chorda est 60 partes, et duplum arcus EB est 180 partes, et eius chorda 120 partes. Cum ergo nos proiecerimus ex proportione 120 partium ad quadragintaocto partes et 31 minuta et 55 secunda proportionem 60 ad 120, remanebit proportio chorde dupli arcus RT ad chordam dupli arcus TH, que est proportio 120 ad 24 partes et 15 minuta et 57 secunda. Duplum vero arcus RT est 180 et eius chorda 120. Linea ergo que subtenditur duplo arcus TH secundum illas partes est 24 partes et 15 minuta et 57 secunda. Et similiter erit duplum arcus TH 23 partes et 19 minuta et 59 secunda. Et erit arcus TH secundum illas partes undecim partes et 40 minuta vicinius.
Describam ergo orbem quem revolvunt duo poli simul, polus orbis equationis diei et polus medii orbis signorum, et signabo super ipsum ABG, et decribam in eo medietatem orbis equationis diei, supra quam sint A, E, G, et medietatem orbis medii signorum, supra quam sint B, E, D, qui se secent supra punctum E, quod sit punctum equationis diei vernale, et sit tropicus hiemalis punctum B et tropicus estivalis punctum D, et ponam ut polus orbis equationis diei sit punctum R arcus ABG, et ponam ut arcus EH, qui est orbis signorum, sit triginta secundum quantitatem qua orbis maior est 360, et describam arcum RHT, qui sit orbis magni, et investigabo scientiam arcus HT. Et quia abhorreo iterare sermonem in omni hora, dico ergo quod cum nos nominamus in hoc loco et in omni eius simili qui est ex eis quos declaraturi sumus mus M. numerum partium arcuum aut partium chordarum, nolumus intelligere per partes arcuum nisi illas que sunt ex partibus maioris, scilicet circuli 360, et per partes chordarum nisi illas que sunt ex 120 partibus diametri circuli. Et quoniam in forma horum orbium maiorum inter duos arcus AR et AE sunt duo arcus RT et EB sese supra H secantes, fit ut proportio chorde dupli arcus RA ad chordam dupli arcus AB aggregetur ex duabus proportionibus, ex proportione corde dupli arcus RT ad chordam dupli arcus TH et ex proportione chorde dupli arcus HE ad chordam dupli arcus EB. Iam autem scivimus quod duplum arcus RA est 180, et chorda eius 120, et duplum arcus AB secundum quod consideravimus et convenimus supra ipsum secundum proportionem 11 ad 83 est 47 partes et 42 minuta et 40 secunda, et est eius chorda 48 partes et 31 minuta et 55 secunda, et duplum arcus HE est 60 partes, et eius chorda est 60 partes, et duplum arcus EB est 180 partes, et eius chorda 120 partes. Cum ergo nos proiecerimus ex proportione 120 partium ad quadragintaocto partes et 31 minuta et 55 secunda proportionem 60 ad 120, remanebit proportio chorde dupli arcus RT ad chordam dupli arcus TH, que est proportio 120 ad 24 partes et 15 minuta et 57 secunda. Duplum vero arcus RT est 180 et eius chorda 120. Linea ergo que subtenditur duplo arcus TH secundum illas partes est 24 partes et 15 minuta et 57 secunda. Et similiter erit duplum arcus TH 23 partes et 19 minuta et 59 secunda. Et erit arcus TH secundum illas partes undecim partes et 40 minuta vicinius.
Ponam etiam ut arcus EH sit 60 partes et dimittam que sunt preter ipsum in forma secundum habitudinem suam. Fiet ergo duplum arcus EH 120 partes et chorda eius 103 partes et 55 minuta et 23 secunda. Cum ergo nos proiecerimus ex proportione 120 partium ad 48 partes et 31 minuta et 55 secunda proportionem 103 partium et 55 minutorum et 23 secundorum ad 120, remanebit proportio chorde dupli arcus RT ad chordam dupli arcus TH, que est proportio 120 ad 42 partes et minutum unum et 48 secunda. Chorda autem dupli arcus RT est 120. Quapropter erit chorda dupli arcus TH secundum illas partes 42 partes et minutum unum et 48 secunda. Ergo duplum arcus TH erit 41 partes et cifre et 18 secunda, et arcus TH secundum illas partes erit 20 partes et 30 minuta et novem secunda. Et illud est quod voluimus demonstrare. Similiter referemus partes arcuum et scribemus numerum earum in tabulis recipientibus numerum quarte, que est 90 partes, et scribemus post unumquemque arcum ex latere consequentem numerum partium declinationis ipsius. Tabularum autem descriptio erit sicut ego describam post hunc sermonem.
Tabule quantitatum arcuum orbis meridiei qui sunt inter orbem equationis diei et orbem medii signorum qui sunt declinationis
Partium orbis medii signorum numeri communes |
Declinationes |
Partium orbis medii signorum numeri communes |
Declinationes |
Partium orbis medii signorum numeri communes |
Declinationes |
|||||||||||||||||
Partes |
Partes |
Minuta |
Secunda |
Partes |
Partes | Minuta |
Secunda |
Partes |
Partes |
Minuta |
Secunda |
|||||||||||
359
358
357 |
1
2
3 |
0
0
1 |
24
48
12 |
16
31
47 |
329
328
327 |
31
32
33 |
12
12
12 |
1
22
43 |
21
31
29 |
299
298
297 |
61
62
63 |
20
20
21 |
42
55
7 |
55
18
19 |
||||||||
356
355
354 |
4
5
6 |
1
2
2 |
37
1
25 |
0
12
22 |
326
325
324 |
34
35
36 |
13
13
13 |
4
24
45 |
16
48
7 |
296
295
294 |
64
65
66 |
21
21
21 |
18
30
40 |
56
9
58 |
||||||||
353
352
351 |
7
8
9 |
2
3
3 |
49
13
37 |
30
35
37 |
323
322
321 |
37
38
39 |
14
14
14 |
5
25
44 |
13
4
42 |
293
292
291 |
67
68
69 |
21
22
22 |
51
50
11 |
23
24
0 |
||||||||
350
349
348 |
10
11
12 |
4
4
4 |
1
25
49 |
38
32
24 |
320
319
318 |
40
41
42 |
15
15
15 |
4
23
42 |
5
12
4 |
290
289
288 |
70
71
72 |
22
22
22 |
20
28
37 |
11
56
17 |
||||||||
347
346
345 |
13
14
15 |
5
5
6 |
13
36
0 |
11
53
30 |
317
316
315 |
43
44
45 |
16
16
16 |
0
18
37 |
40
59
2 |
287
286
285 |
73
74
75 |
22
22
22 |
45
52
59 |
11
40
42 |
||||||||
344
343
342 |
16
17
18 |
6
6
7 |
24
47
10 |
1
26
45 |
314
313
312 |
46
47
48 |
16
17
17 |
54
12
29 |
48
16
27 |
284
283
282 |
76
77
78 |
23
23
23 |
6
12
18 |
18
28
11 |
||||||||
341
340
339 |
19
20
21 |
7
7
8 |
33
57
20 |
57
3
0 |
311
310
309 |
49
50
51 |
17
18
18 |
46
2
19 |
19
53
7 |
281
280
279 |
79
80
81 |
23
23
23 |
23
28
32 |
27
16
38 |
||||||||
338
337
336 |
22
23
24 |
8
9
9 |
42
5
28 |
50
32
5 |
308
307
306 |
52
53
54 |
18
18
19 |
35
50
5 |
3
39
54 |
278
277
276 |
82
83
84 |
23
23
23 |
36
40
43 |
33
1
0 |
||||||||
335
334
333 |
25
26
27 |
9
10
10 |
50
12
34 |
29
43
48 |
305
304
303 |
55
56
57 |
19
19
19 |
20
35
49 |
50
25
38 |
275
274
273 |
85
86
87 |
23
23
23 |
45
47
49 |
33
38
15 |
||||||||
332
331
330 |
28
29
30 |
10
11
11 |
56
18
39 |
42
27
59 |
302
301
300 |
58
59
60 |
20
20
20 |
3
17
30 |
31
1
9 |
272
271
270 |
88
89
90 |
23
23
23 |
50
51
51 |
25
6
20 |
||||||||
〈I.14〉 Capitulum decimumquartum: De scientia quantitatis arcuum equationis diei qui elevantur in sphera directa cum arcubus orbis signorum datis
Et post hoc demonstrabo numerum quantitatum arcuum equationis diei quos separant orbes descripti super duos polos equationis diei et super partes datas orbis signorum. Et per hoc scies in quanto tempore temporum horarum equalium pertranseunt partes date orbis signorum orbem meridiei in omni loco et pertranseunt horizonta sphere recte. Et hoc est quoniam apud illum tantum est horizon descriptus supra duos polos equationis diei. 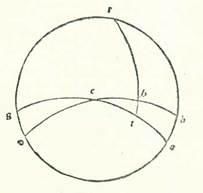 Ergo describam formam cuius declaratio precessit, et ponam primum arcum EH orbis signorum 30 partes, et perscrutabor inventionem arcus ET orbis equationis diei. Secundum illud ergo quod premisimus proportio chorde dupli arcus RB ad chordam dupli arcus BA aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus RH ad chordam dupli arcus TH et ex proportione chorde dupli arcus TE ad chordam dupli arcus EA. Duplum vero arcus RB est 132 partes et 17 minuta et 20 secunda, et chorda eius est 109 partes et 44 minuta et 53 secunda, et duplum arcus BA est 47 partes et 42 minuta et 40 secunda, et eius chorda 48 partes et 31 minuta et 55 secunda. Duplum quoque arcus RH est 156 partes et 40 minuta et duo secunda, et eius chorda est 117 partes et 31 minuta et 15 secunda, et duplum arcus HT est 23 partes et 19 minuta et 59 secunda, et chorda eius 24 partes et 15 minuta et 57 secunda. Cum ergo nos proiecerimus ex proportione 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda proportionem 117 partium et 31 minutorum et 15 secundorum ad 24 partes et 15 minuta et 57 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, et ipsa est proportio 54 partium et 52 minutorum et 26 secundorum ad 117 partes et 31 minuta et 15 secunda, et est etiam proportio 56 partium et unius minuti et 53 secundorum ad 120. Duplum vero arcus EA est 180, et eius chorda est 120. Ergo chorda dupli arcus TE secundum illas partes est 56 partes et minutum unum et 53 secunda. Quapropter erit duplum arcus TE 55 partes et 40 minuta vicinius, et TE secundum illas partes erit 27 partes et 50 minuta. Ponam etiam arcum EH 60 partes et dimittam reliqua que sunt in forma secundum suam habitudinem. Erit igitur duplum arcus RH 138 partes et 59 minuta et 42 secunda, et eius chorda 112 partes et 23 minuta et 56 secunda, et duplum arcus HT 41 partes et cifre et 18 secunda, et eius chorda 42 partes et minutum et 48 secunda. Ergo cum nos etiam proiecerimus ex proportione 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda proportionem 112 partium et 23 minutorum et 56 secundorum ad 42 partes et 1 minutum et 48 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, que est proportio 95 partium et 2 minutorum et 41 secundorum ad 112 partes et 23 minuta et 56 secunda, que est etiam sicut proportio 101 partium et 28 minutorum et 20 secundorum ad 120 partes. Chorda autem dupli arcus EA est 120. Quapropter erit chorda dupli arcus TE secundum illas partes 101 partes et 28 minuta et 20 secunda vicinius, et arcus TE secundum illas partes 57 partes et 44 minuta. Iam ergo declaratum est quod prime 12 partium orbis signorum tempus elevationis equatur tempori elevationis 27 partium et 50 minutorum partium orbis equationis diei secundum hunc modum. Et secunde 12 partium orbis signorum tempus elevationis equatur tempori elevationis 29 partium et 54 minutorum partium equationis diei. Iam enim ostensum est quod ipse simul sunt 57 partes et 44 minuta. Et manifestum est quod tertie 12 partium orbis signorum tempus elevationis equatur tempori elevationis residui quarte orbis equationis diei, quod est 32 partes et 16 minuta, propter hoc quod tempus elevationum cuiusque quarte orbis declivis equatur tempori elevationum cuiusque quarte orbis equationis diei cum fuerint elevationes orbium descriptorum supra duos polos orbis equationis diei. Secundum hunc vero modum et hanc declarationem sciemus numerum partium arcuum orbis equationis diei que elevantur cum omnibus decem partibus orbis declivis, eo quod arcus qui sunt minus decem partibus non multum diversificantur ab arcubus equalibus augmentis superfluentibus. Et affirmabo portionem partium orbis equationis diei debitam omnibus decem partibus orbis declivis pertransire cum omnibus decem partibus orbis declivis lineam orbis meridiei in omni loco et pertransire horizontem sphere recte. Et incipiam decem primas partes a puncto equationis diei. Igitur portio orbis equationis diei que debetur decem primis partibus orbis signorum est novem tempora et decem minuta, et secundarum decem portio est novem tempora et 15 minuta, et portio decem tertiarum est novem tempora et 25 minuta. Cum ergo aggregantur portiones decenarum prime 12 partium, sunt 27 tempora et 50 minuta. Portio vero decene quarte est novem tempora et 40 minuta, et portio decene quinte est novem tempora et 58 minuta, et portio decene sexte est decem tempora et 16 minuta. Cum ergo aggregantur decene partis secunde orbis declivis, sunt 29 tempora et 54 minuta. Portio autem decene septime est decem tempora et 34 minuta, et portio octave decene est 10 tempora et 47 minuta, et portio none decene est 10 tempora et 55 minuta. Quapropter cum aggregantur portiones decenarum tertie 12 partium, cuius finis est punctum tropici, sunt 32 tempora et 16 minuta. Et convenit ut sit portio 90, que est totius quarte portio, 90 tempora. Et propter hoc manifestum est quod relique quarte similiter sunt. Unamquamque enim quartam comitatur quod comitatur aliam, ideoque orbis equationis diei erigitur super horizontem hominum inhabitantium spheram rectam absque declinatione.
Ergo describam formam cuius declaratio precessit, et ponam primum arcum EH orbis signorum 30 partes, et perscrutabor inventionem arcus ET orbis equationis diei. Secundum illud ergo quod premisimus proportio chorde dupli arcus RB ad chordam dupli arcus BA aggregatur ex duabus proportionibus, ex proportione chorde dupli arcus RH ad chordam dupli arcus TH et ex proportione chorde dupli arcus TE ad chordam dupli arcus EA. Duplum vero arcus RB est 132 partes et 17 minuta et 20 secunda, et chorda eius est 109 partes et 44 minuta et 53 secunda, et duplum arcus BA est 47 partes et 42 minuta et 40 secunda, et eius chorda 48 partes et 31 minuta et 55 secunda. Duplum quoque arcus RH est 156 partes et 40 minuta et duo secunda, et eius chorda est 117 partes et 31 minuta et 15 secunda, et duplum arcus HT est 23 partes et 19 minuta et 59 secunda, et chorda eius 24 partes et 15 minuta et 57 secunda. Cum ergo nos proiecerimus ex proportione 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda proportionem 117 partium et 31 minutorum et 15 secundorum ad 24 partes et 15 minuta et 57 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, et ipsa est proportio 54 partium et 52 minutorum et 26 secundorum ad 117 partes et 31 minuta et 15 secunda, et est etiam proportio 56 partium et unius minuti et 53 secundorum ad 120. Duplum vero arcus EA est 180, et eius chorda est 120. Ergo chorda dupli arcus TE secundum illas partes est 56 partes et minutum unum et 53 secunda. Quapropter erit duplum arcus TE 55 partes et 40 minuta vicinius, et TE secundum illas partes erit 27 partes et 50 minuta. Ponam etiam arcum EH 60 partes et dimittam reliqua que sunt in forma secundum suam habitudinem. Erit igitur duplum arcus RH 138 partes et 59 minuta et 42 secunda, et eius chorda 112 partes et 23 minuta et 56 secunda, et duplum arcus HT 41 partes et cifre et 18 secunda, et eius chorda 42 partes et minutum et 48 secunda. Ergo cum nos etiam proiecerimus ex proportione 109 partium et 44 minutorum et 53 secundorum ad 48 partes et 31 minuta et 55 secunda proportionem 112 partium et 23 minutorum et 56 secundorum ad 42 partes et 1 minutum et 48 secunda, remanebit proportio chorde dupli arcus TE ad chordam dupli arcus EA, que est proportio 95 partium et 2 minutorum et 41 secundorum ad 112 partes et 23 minuta et 56 secunda, que est etiam sicut proportio 101 partium et 28 minutorum et 20 secundorum ad 120 partes. Chorda autem dupli arcus EA est 120. Quapropter erit chorda dupli arcus TE secundum illas partes 101 partes et 28 minuta et 20 secunda vicinius, et arcus TE secundum illas partes 57 partes et 44 minuta. Iam ergo declaratum est quod prime 12 partium orbis signorum tempus elevationis equatur tempori elevationis 27 partium et 50 minutorum partium orbis equationis diei secundum hunc modum. Et secunde 12 partium orbis signorum tempus elevationis equatur tempori elevationis 29 partium et 54 minutorum partium equationis diei. Iam enim ostensum est quod ipse simul sunt 57 partes et 44 minuta. Et manifestum est quod tertie 12 partium orbis signorum tempus elevationis equatur tempori elevationis residui quarte orbis equationis diei, quod est 32 partes et 16 minuta, propter hoc quod tempus elevationum cuiusque quarte orbis declivis equatur tempori elevationum cuiusque quarte orbis equationis diei cum fuerint elevationes orbium descriptorum supra duos polos orbis equationis diei. Secundum hunc vero modum et hanc declarationem sciemus numerum partium arcuum orbis equationis diei que elevantur cum omnibus decem partibus orbis declivis, eo quod arcus qui sunt minus decem partibus non multum diversificantur ab arcubus equalibus augmentis superfluentibus. Et affirmabo portionem partium orbis equationis diei debitam omnibus decem partibus orbis declivis pertransire cum omnibus decem partibus orbis declivis lineam orbis meridiei in omni loco et pertransire horizontem sphere recte. Et incipiam decem primas partes a puncto equationis diei. Igitur portio orbis equationis diei que debetur decem primis partibus orbis signorum est novem tempora et decem minuta, et secundarum decem portio est novem tempora et 15 minuta, et portio decem tertiarum est novem tempora et 25 minuta. Cum ergo aggregantur portiones decenarum prime 12 partium, sunt 27 tempora et 50 minuta. Portio vero decene quarte est novem tempora et 40 minuta, et portio decene quinte est novem tempora et 58 minuta, et portio decene sexte est decem tempora et 16 minuta. Cum ergo aggregantur decene partis secunde orbis declivis, sunt 29 tempora et 54 minuta. Portio autem decene septime est decem tempora et 34 minuta, et portio octave decene est 10 tempora et 47 minuta, et portio none decene est 10 tempora et 55 minuta. Quapropter cum aggregantur portiones decenarum tertie 12 partium, cuius finis est punctum tropici, sunt 32 tempora et 16 minuta. Et convenit ut sit portio 90, que est totius quarte portio, 90 tempora. Et propter hoc manifestum est quod relique quarte similiter sunt. Unamquamque enim quartam comitatur quod comitatur aliam, ideoque orbis equationis diei erigitur super horizontem hominum inhabitantium spheram rectam absque declinatione.
Expleta est dictio prima libri Almagesti Ptolemei.