〈III〉
I De magnitudine anni temporis
II Expositio canonum mediorum Solis motuum
III De his que secundum omalium et circularem motum ypothesibus.
IV De apparente Solis anomalia
V De ea que ad particulares portiones anomaliarum canonopiia consideratione
VI Canonium solaris anomalie
VII De ea que secundum medium Solis pergressum epochi
VIII De solari psiphophoria, idest compoto
IX De nictimerorum inequalitate
Assignatas Assignatas] assignatis V2F1 a nobis in ante hoc coordinatis et universaliter debentibus de celo et terra mathematice prelibari amplius et de inclinatione eius qui per media animalia solaris circuli et particulariter circa ipsum accidentibus et in recta spera et in secundum unamquamque habitationem inclinata, consequens arbitramur et deinceps que de Sole et Luna facere sermonem et circa ipsorum motus superaccidentia pertransire, eo quod nichil circa stellas apparentium absque istorum prelibatione ad plenum possit inveniri, et horum vero ipsorum precedens reperimus solaris motus negotium quo sine rursum nec ea que circa Lunam possibile utique fiet perfecte comprehendi.
〈III.1〉
Primum Primum] primo V2 igitur omnium circa Solem demonstrandorum existente annuum tempus invenire, antiquorum quidem circa sententiam huiusmodi et dissonantias et dubitationes dicemus extractatibus ipsorum et maxime ab Yparco viro studii laborem simul et veritatem diligente. Ducit enim maxime et hunc in huiusmodi ambiguitate per eos quidem que circa conversiones et equinoctia apparent restitutiones minus annuale tempus inveniri quarte super ccclxv dies adiectione, per ea vero que circa applanas stellas considerantur, maius. Unde conicitur et applanarum speram transitum quendam diuturnum facere et ipsam, quemadmodum et eas que planomenorum, in consequentia primam circundactionem circundactionem] circumactionem V2 circoactionem F1 fatientis lationis secundum scriptum per utrosque polos et equinoctialis et obliqui circulum. Nos autem hoc quidem et quoniam ita se habeat et quo fiat modo in eis que de applanis stellis ostendemus. Non enim que circa illas sine solari et lunari prelibatione possibile utique fiet ex toto considerari. Secundum presentem vero considerationem ad nichil aliud arbitramur oportere respitientes annuale Solis tempus attendere, quam ipsam ipsam] ipsius V2 Solis ad seipsum, hoc vel vel] est V2 eum qui ab ipso fit obliquum circulum, restitutionem et diffinire annuale tempus secundum quod ab aliquo immobili puncto huius circuli secundum deinceps in idem venit, sola principia propria huiusmodi restitutionis arbitrantes sub tropicis et equinoctialibus predictis punctis segregata puncta predicti circuli. Sive enim mathematice rationi institerimus, nec magis propriam restitutionem inveniemus in eadem figurationem ferente Solem et localiter, et temporaliter, vel ad oridentes, oridentes] orizontes V2 vel ad meridianum, vel magnitudines nictimerorum huiusmodi considerato, nec alia principia in eo qui per media animalia circulo, sola vero secundum accidens segregata sub tropicis et equinoctialibus punctis; sive magis phisicum quis attendat proprium, nec restitutionem rationabilem rationabilem] rationabiliorem V2F1 inveniet a simili circa aera catastimare catastimare] catastimate V2F1 in simile et eadem hora in eandem ferente Solem, nec alia principia quam ea sola secundum que hore maxime discernuntur, cum eo quod et ad applanas stellas considerata restitutio inconveniens videtur, et propter alia et maxime quoniam et ipsarum spera fatiens quendam ordinatum transitum in consequentia celi consideratur. Nichil enim his ita se habentibus prohibet dicere tantum esse annum Solis tempus in quanto Saturni stellam verbi gratia vel aliquem aliorum planomenorum Sol deprehendit. Multa vero sic et diversa fient annualia tempora. Propter hoc ergo competere extimamus inventum per observationes ut est maxime a plure distantia sumptas ab aliqua conversione vel equinoctio in idem et deinceps tempus arbitrari annuum Solis. Quoniam vero turbat quodam modo Iparcum et circa ipsam huiusmodi restitionem restitionem] restitucionem V2F1 suspecta per eas que secundum deinceps facte sunt continuas observationes inequalitas, temptabimus ostendere per brevia hoc nequaquam turbatione dignum, persuasionem quidem sumentes de eo quod minime sint inequalia tempora ista ex eis quas et ipsi per organa secundum deinceps summa summa] sumus V2F1 observantes et conversionibus et equinoctiis, nichilo enim cura digno differentia ipsa inveniemus ab ea que secundum quartam adiectionem, sed aliquotiens fere quanto penes et constructionem et positionem organorum contingit falli, coniectantes vero et ex eis quibus Yparcus ratiocinatur magis observationum eam esse que circa inequalitates fallatiam. Exponens enim primum in eo qui trasmotione tropicorum et equinoctialium punctorum visus visus] visas V2 sibi dilligenter et deinceps observari et estivas et hybernas conversiones, fatetur et ipse non tantam in ipsis esse dissonantiam, quare propter ipsas inequalitas arguatur annui temporis. Super ipsis enim dicit ita: ‘Ex his ergo observationibus manifestum quoniam exigue omnino facte sunt annorum differentie. Sed in conversionibus quidem non despero et nos et Archimedus Archimedus] Archimenidem V2 et in observatione et in sillogismo falli et usque quartam diei partem. Diligenter vero potuit intelligi anomalia annuorum temporum ex observatis in eo qui in Alexandrie iacet eneo crico in tetragono vocata porticu qui videtur designare equinoctialem diem in qua utique ex altera parte incipit cavam superfitiem illustrare’. Dehinc adiungit primum autupnalium equinoctiorum tempora, ut dilligenter observatorum, in xviio quidem anno tertie secundum Callippon periodi Mesori xxxa circa occasum Solis, post tres autem annos in xx anno neomedia neomedia] neomenia V2F1 epagomenon mane, oportet autem in meridie, quare discordare iiiia unius diei. Post annum vero in xxi anno hora sexta, quod erat et consequens ei que ante ipsam observationem. Post xi annos vero in xxxiio anno tertia epagomenon in iiiia mesonictii, oportet autem mane, quare quasi te quasi te] quarte V2F1 rursum differentiam esse. Post annum vero unum in xxxiiio anno iiii epagomenon mane, quod et erat consequens ei que ante ipsam observationi. Post tres autem annos in xxxvi anno, quarta epagomenon vespere, oportet autem mesonictii, quare quarta sola rursum discordare. Post vero exponit et similli dilligentia observata verna equinoctia: in xxxii quidem anno tertie secundum Calippon periodi Mechir xxvii mane. ‘Sed et cricus, inquit, qui in Alexandria equaliter ex utraque parte illuminatus est circa va horam, quare iam et idem equinoctium differenter observatum v horis ad proximum differre.’ Sed et ea que deinceps dicit usque xxxvii annos concordare ei que ad quartam adiectioni. Post xi autem annos in iiio et xlo anno Mechir xxixa post mesonictium quod in xxxa fieri dicit vernum equinoctium, quod et consequens erat que in xxxiio anno observationi et consonat, inquit, rursum et ad eas que in continuis annis observationes usque annos l. Fuit enim Phamenoth prima circa occasum Solis post unam diem et dimidium et quartam ad proximum ab ea que in xliiio anno, quod et attinet mediis vii annis. Nulla ergo his observationibus facta est cura digna differentia, quamvis possibili existente, non solum circa tropicas observationes, sed etiam circa equinoctiales, fieri aliquam preter ipsas fallaciam et usque quartam unius diei. Quamvis enim iiiadca sola parte eius qui per polos equinoctialis circuli permutetur exanunatione exanunatione] examinatione V2F1 positio vel etiam distinctio organorum, tantam secundum latitudinem recessionem corrigit Sol in equinoctialibus portionibus quartam unius gradus secundum longitudinem in obliquo circulo motus, quare et dissonantiam usque quartam unius diei ad proximum differre. Adhuc autem plus peccabitur in non semel stantibus et penes observationes ipsas examinatis, sed firmatis organis ab aliquo principio subiacentibus pavimentis ad manentem in multum habendam portionem, portionem] posicionem V2 facta aliqua circa ipsam sub tempora latenti transmotione, ut in eis que penes nos in palestra eneis cricis in equinoctialis epipedo visis habere positionem videat utique quis. Tanta enim nobis observantibus apparet perversio positionis ipsorum et maxime maioris et antiquioris, ut aliquotiens etiam bis in ipsis equinoctiis illuminentur cave ipsorum superfities. Sed enim talium quidem nichil nec ipse Yparcus arbitretur contingere dignum fide ad suspitionem inequalitatis annuorum temporum. A quibusdam vero Lune eclipsibus investigans invenire dicit quoniam anomalia annuorum temporum ad medium considerata non maiorem continet differentiam media et iiiia parte unius diei, quod utique esset iam quadam inquisicione dignum, si ita se haberet et non ex ipsis que profert falsum consideraretur. Ratiocinatur enim per quasdam prope applanas stellas observatas lunares eclipses, quantum secundum unamquanque ea que vocatur stachis antecedit autumpnale punctum, et per has reperire arbitratur, aliquotiens quidem plurimum ipsam distantem eis que secundum ipsum temporius gradibus vi et dimidio, aliquotiens vero minimum gradibus v et iiiia. Colligit autem hinc quod, quoniam quidem non possibille stachim in tam pauco tempore tantum trasmoveri, Solem oportet, a quo locos applanorum Yparcus investigat, non in equali tempore facere restitionem restitionem] restitucionem V2F1. Latuit autem ipsum quoniam, investigatione nequaquam volente volente] valente V2 procedere nec secundum eclipsim Solis locus subiaceat, ipse in hoc secundum unamquamque assumens diligenter in annis illis sub seipso observatas conversiones et equinoctia inde manifestum facit nullam circa comparationem annorum existentem penes quarte adiectionem differentiam. Ut enim in uno exemplo ex ea quidem que in xxxiio anno tertie secundum Callippon periodi apposita ecliptica observatione reperiri arbitratur stachim precedentem anuale anuale] autumpnale V2 puctum gradibus vi et dimidio, per eam vero que in xliii anno eiusdem periodi antecedentem gradibus v et iiiia, et similliter apponens in propositas ratiotinationes in annis istis obervata diligenter verna equinoctia, ut per hec quidem sumat in mediis temporibus eclipsium solares locos, ab his vero lunares, ab eis ante qui Lune eos qui stellarum, hoc quidem quod in xxxiio anno dicit factum fuisse Mechyr xxviia mane, illud autem quod in xliiio anno xxixa post mesonictium quod in xxx post ii et dimidium et iiii diei fere ab eo quod in quod in] om. add. s. l. V3 xxxii anno factum est, quot et facit iiiia sola assumpta unicuique mediorum xi annorum. Si ergo neque in maiori nec in minori tempore ea que secundum quartam adiectione Sol ad subiacentia equinoctia restitutionem fecit, neque stachim in tam paucis annis contingit unum gradum et iiiia moveri, quomodo non inconveniens ea que per subiacentia principia computata sunt assumere ad ipsorum construentium ea accusationem, et causam eius quod circa stichios tantos motus impossibiles nulli quidem alii adaptari, pluribus existentibus inferre tantam fallaciam valentibus, solis vero subiacentibus equinoctiis, ut simul diligenter et non diligenter observatis. Possibille enim utique videbitur magis vel in ipsis eclipsibus distantias Lune ad proximas stellarum universalius coniectari vel computationes, aut permutationum eius ad apparentium locorum considerationem, aut Solis motus ab equinoctiis in media eclipsium tempora vel non vere vel non diligenter sumi. Verum autumo et Yparcum cognoscere quidem et ipsum quoniam nichil in talibus inest dignum fide, ut secunda aliqua adaptetur Soli anomalia, voluisse vero solum ob amorem veritatis non tacere quid aliquos in suspitione quomodo eumque quomodo eumque] quomodocumque V2 valentium inferre. Usus est ergo et ipse ypothesibus Solis et Lune, ut una et eadem existente circa Solem anomalia conrestituta ei quod ad conversiones et equinoctia annuo tempori. Eoque minime quod equitemporales subiaceant exposite Solis periodi circa eclipses apparentia consideramus cura digno aliquo differentia ab eis que secundum expositas ypotheses computantur, quod utique sensibille valde contingent, contingent] contingeret V2 minime coassumpta circa inequalitatem annui temporis directione, si et unius solum esset gradus, duarum vero horarum ad proximum equinoctialium. Ex his ergo universis et ex quibus nos ipsi per deinceps nobis observatos Solis progressus assumimus restitutionum tempora, neque inequalem invenimus annuam magnitudinem, si ad unum quid et non aliquotiens quidem ad tropica et equinoctialia puncta, aliquotiens vero ad applanes stellas considerantur, nec aliam magis propriam restitutionem ad aliquo tropico vel equinoctiali puncto vel etiam aliquo alio puncto eius qui per media animalia circuli rursus meridie meridie] in idem V2 ferente Solem. Penitus autem arbitramur competere per simplitiores ut est maxime ypotheses apparentia demonstrare, in quantum utique nichil cura dignum ex observationibus adversari eidem proposito liquet. Quoniam ergo ad conversiones et equinoctia consideratum tempus annuum minus est quarte super ccclxv dies appositione, manifestum nobis factum est et per que Yparcus demonstravit. Quanto vero minus est omnino quidem sine fallatia non possibille utique fiet sumere, et quarte augmento in plures annos ad sensum inmutabili permanente propter parvitatem differentie, et propter hoc secundum eam que per longius tempus comparatione, valente inventa dierum adiectione, quam oportet mediis distantie annis distribuere, et in pluribus et in pautioribus annis eadem considerari. Sumatur autem ad proximum examinate huiusmodi restitutio, quanto utique medium conparatarum observationum tempus plus invenitur, et non solum in ista huiusmodi accidit, verum et in omnibus periodicis restitutionibus. Namque penes ipsarum observationum infirmitatem, quamvis dilligenter et artifitiose fiant, factum mendatium breve et idem ad proximum existens ut ad eum qui penes ipsas sensiter sensiter] sensum V2 et in per longum et in breve tempus apparentibus, in pautiores quidem distribuunt annos maiorem facit annuam fallaciam ex hoc secundum longius tempus collectam, in plures autem minus. Unde suffitiens competit arbitrari si, quantum medium tempus et nostrum et earum quas habemus antiquarum simul et diligentium observationum potest facere periodicarum ypothesium propinquitati, tantum et ipsi temptabimus conferre et non spontanei negligemus inquisitionem competentem. Eas ante ante] autem V2F1 que de toto seculo vel et longitudine aliqua multiplicato secundum observationes tempore affirmationes affirmationes] affirmiores V2F1 alienas a disciplina et veritate arbitremur. Itaque causa quidem antiquitatis et ab eis qui circiter Methona et Ectimona observante estive conversiones et que post istos ab eis qui circiter Aristarcum deberent utique in comparatione secundum nos factarum assumi. Verum quoniam universaliter conversionum observationes difficille discerni possunt et ad hec ab illis tradite unversalius sumpte, ut Yparco videtur, apparent, istas quidem refutabimus. Conversi autem sumus ad propositam comparationem equinoctiorum observationibus et harum diligentie causa et ab Yparco maxime designatis ut certissime sumptis ab ipso et a nobis per ea ipsis que in huiusmodi in principio sintaxeos demonstrata sunt organa indubitanter maxime observatis. Ex quibus reperimus ccc ad proximum annis una die prius factas conversiones et equinoctia eam que secundum quartam supra ccclxv dies adiectione. Namque in xxxiio quidem anno tertie secundum Callippon periodi, designavit maxime autumpnale equinoctium Yparcus ut diligetissime diligetissime] diligentissime V2F1 observatum et computari dicit ipsum fuisse factum tertia epagomenon, mesonictio in quartam ferente, et est annus clxxviiius ab Alexandri morte. Post annos autem cclxxxv in tertio anno Antonini, qui est cccclxiiius ab Alexandri morte, nos observavimus ut certissime rursum autumpnale equinoctium factum ixa Athir post unam horam ad proximum ab ortu Solis. Accepit ergo restitutio in integris egiptiacis cclxxxv annis, hoc est ana ccclxv, diebus lxx et iiiia et iiiia et xx ad proximum unius diei pro secunda quarta secunda quarta] secundum quarte V2 adiectionem pertinentibus propositis annis diebus lxxi et iiiia. Quare prius facta fuit restitutio ea que secundum quartam adiectione die uno defitienti parte xxa ad proximum. Similiter autem rursum Yparcus quidem dicit in proposi proposi] proposito V2F1 xxxii anno tertie secundum Calippon periodi vernum equinoctium diligentissime observatum factum fuisse xxvii Mechir mane, et est annus clxxviiius ab Alexandri morte. Nos autem post annos similiter cclxxxv, cccclxiii ab Alexandri morte vernum equinoctium reperimus factum vii Pachon post unam horam ad proximum a meridie, quare et istam periodum recepisse equales dies lxx et iiiiam et xxa ad proximum pro secundum iiiia pertinentibus cclxxxv annis diebus lxxi et iiiia. Prius ergo et hic facta est verni equinoctii restitutio ea que penes quartam adiectionem die uno deficienti xxa parte. Quare quoniam eandem habent proportionem et ccc anni ad cclxxxv et unus dies ad unum deficientem xxa parte, colligitur quoniam et in ccc annis ad proximum prius est ea que secundum quartam adiectione ad equinoctialia puncta facta Solis restitutio die uno. Et si ad ab eis qui circiter Methona et Ectimona observatam estivam conversionem ut universalius descriptam comparationem antiquitatis eam eam] causa F1 fecerimus, eius que a nobis ut est maxime indubitanter investigata idem ipsum inveniemus. Et enim illa quidem describitur facta sub Apseudo principante Athenis secundum Egiptios Phamenoth xxa mane. Nos autem eam que in proposito cccclxiii anno ab Alexandri morte sine fallacia investigavimus factam esse xia Mesori post ii horas prope ab eo quod in xiia mesonictium, et sunt a sub Apseudo descripta estiva conversione usque ab eis qui circiter Aristarcum observatam l anno prime secundum Calippon periodi, sicut et Yparcus dicit, anni clii. A proposito autem l anno qui erat secundum xliiii annum ab Alexandri morte usque cccclxiii qui secundum nostram observationem anni ccccxix. In intermediis ergo totius distantie dlxxi annis, si ab eis qui circiter Ectimona observata estiva conversio circa principium Phamenoth xxi sit facta, appositi sunt in integris Egipciacis annis dies cxl et dimidium et iiia ad proximum cxlii cxlii] pro cxlii V2 et dimidium et iiiia dlxxi annis secundum quarte adiectionem pertinentibus. Quare prius facta est exposita restitutio ea que secundum quartam adiectione duobus diebus defitientibus xiia unius diei. Manifestum ergo et ita factum est quoniam in dc integris annis duos plenos ad proximum dies annuum tempus precedit eam que secundum quartam adiectionem. Et per alias vero plures observationes et nos idem ipsum contingens reperimus et Yparcum videmus sepe in hoc consentientem. Et enim in eo qui de annua magnitudine comparans ab Aristarco observans observans] observatam V2 estivam conversionem l anno defitienti prime secundum Calippon periodi ab ipso rursum diligenter sumpte xliiio anno defitienti tertie secundum Calippon periodi dicit ita: ‘Manifestum ergo quoniam in cxlv annis velotius facta est conversio ea que secundum quartam adiectione meditate compositi ex die et nocte temporis’. Rursumque in eo qui de embolismis et mensibus et diebus predictis quoniam secundum illos quidem qui circiter Methona et Ectimona annuum tempus continet dies ccclxv et iiiia et lxxvi unius diei, secundum Calippon vero dies ccclxv et iiiia tantum adiungit secundum dictionem ita: ‘Nos autem menses totos reperimus contentos in xix annis, quot et illi, annum vero adhuc et iiiia minus ccca assumentem maxime parte unius diei, quare in ccc annis deficere secundum Methonem quidem dies quinque, secundum Calippon vero diem unam’. Sed et recapitulans sententias sui ipsius fere per descriptionem propriorum sintagmatum dicit ita: ‘Coordinavi autem et de annuo tempore in libro uno in quo demonstro quoniam qui secundum Solem annus hic autem fit tempus, in quo Sol a conversione in conversionem eandem venit vel ab equinoctio in idem equinoctium, continet dies ccclxv et minus quam quartam partem ccca ad proximum parte unius diei et noctis et non, sicut mathematici autumant, ipsam quartam superapponi dicte dierum multitudini’. Quoniam ergo huc usque huc usque] usque nunc V2 apparentia circa quantitatem annui temporis predicte ad tropicorum et equinoctialium punctorum restitutionem magnitudini concurrunt secundum eorum que nunc ad ea que prius consensum, manifestum reor factum esse. His vero ita se habentibus, si distribuerimus unam diem in ccc annos, contingunt cuique anno unius diei secunda xiia, quod, si dempserimus a a] add. secundum V2F1 om. in lac. V3 quarta adiectionis ccclxv et xv, habebimus inquisitum annuum tempus dierum ccclxv et xiiii et xlviii. Itaque tanta quidem multitudo dierum erit utique ad proximum nobis ut est maxime ex presentibus sumpta. Causa vero eius que et in Sole et in aliis ad penes singula factas ipsorum progressiones considerationis, quam promptam et velut expositam apta est prestare sintaxis particularis canonopiie, propositum quidem et intentionem arbitramur oportere esse mathematico demonstrare apparentia in celo omnia per equales et circulares motus consumata, competentem vero et consequenter tali proposito maxime canonopiiam distinguentem quidem particulares equales motus ab ea que propter circulorum ypotheses videtur contingere anomalia, rursum vero ex mistionem mistionem] mixtionem V2F1 et conggione conggione] congregacione V2F1 istorum amborum apparentes ipsorum progressiones demonstrantem. Ut ergo nobis talis figura commodior et secundum ipsas demonstrationes sub manu sumatur, faciemus hic expositionem particularium equalium Solis motuum modo tali. Una namque restitutione demonstrata dierum ccclxv et xiiii et xlviii, si distribuerimus in istas unius circuli gradus ccclx, habebimus diurnum medium motum Solis graduum o lix viii xvii xiii xii et xxxi ad proximum. Sufficit enim usque tantas lxa particionem particionem] portiones V2 istorum facere. Rursum diurni motus sumentes xxiiiia habebimus horarium graduum o ii xxvii l xliii iii i ad proximum. Similiter diurnum multiplicantes in unius quidem mensis dies xxx habebimus medium motum menstruum graduum xxix xxxiiii viii xxxvi xxxvi xv xxx. In unius autem anni egiptiaci ccclxv dies habebimus annuum medium motum graduum ccclix xlv xxiiii xlv xxi viii xxxv. Rursum annuum multiplicantes in annos xviii propter apparituram simmetriam canonographie et auferentes universos circulos habebimus xviii annorum collectionis epoysiam graduum ccclv xxxvii xxv xxxvi xx xxxiiii xxx. Ordinavimus ergo canonia plani motus Solis tria unumquodque in versus quidem rursum xlv, partes vero duas. Continebit vero primum quidem canonium xviii annorum collectionum medios motus, secundum autem primum annuos et sub ipsis horarios, tertium vero primum quidem menstruos, inferius autem diurnos, temporis quidem numeris in primis partibus ordinatis, eius vero que graduum appositionis in secundis secundum proprias singulorum superagregationes.
Et sunt canones huius modi.
〈III.2〉
| Medius cursus Solis in annis Egyptiis collectis sine bisexto Medius cursus Solis in annis expansis | |||||||||||||||
| Anni collecti | Anni ex pansi | ||||||||||||||
| gradus | minuta | secunda | tertia | quarta | quinta | sexta | gradus | minuta | secunda | tertia | quarta | quinta | sexta | ||
| xviii | ccclv | xxxvii | xxv | xxxvi | xx | xxxiiii | xxx | i | ccclix | xlv | xxiiii | xlv | xxi | viii | xxxv |
| xxxvi | cccli | xiiii | li | xvi | xli | o | o | ii | ccclix | xxx | xlix | xxx | xlii | xvii | x |
| liiii | cccxlvi | lii | xvi | xlix | i | xliii | xxx | iii | ccclix | xvi | xiii | xvi | iii | xxv | xlv |
| lxxii | cccxlii | xxix | xlii | xxv | xxii | xviii | o | iiii | ccclix | i | xxxix | i | xxiiii | xxxiiii | xx |
| xc | cccxxxviii | vii | viii | i | xlii | lii | xxx | v | ccclviii | xlvii | iii | xlvi | xxv | xlii | lv |
| cviii | cccxxxiii | xliv | xxxiii | xxxviii | iii | xxvii | o | vi | ccclviii | xxxii | xxviii | xxxii | vi | li | xxx |
| cxxvi | cccxxix | xxi | lix | xiiiii | l | i | xxx | vii | ccclviii | xvii | liii | xvii | xxviii | o | v |
| cxliiii | cccxxiiiii | lix | xxiiii | l | xliiii | xxxvi | o | viii | ccclviii | iii | xviii | ii | xlix | viii | xl |
| clxii | cccix | xxxvi | l | xxvii | v | x | xxx | ix | ccclvii | xlviii | xlii | xlviii | x | xvii | xv |
| clxxx | cccxvi | xliiii | xvi | iii | xxv | xlii | o | x | ccclvii | xiiii | vii | xxxiii | xxxi | xxv | v |
| cxcviii | cccxi | li | xli | xxxix | xlvi | xix | xxx | xi | ccclvii | xix | xxxii | xviii | lii | xxxiiii | xxv |
| ccxvi | cccvii | xxix | vii | xvi | vi | liiii | o | xii | ccclvii | iiii | lvii | iiii | xiii | xliii | o |
| ccxxxiiii | ccciii | vi | xxxii | lii | xxvii | xlviii | xxx | xiii | ccclvi | v | xxi | xlix | xxxiiii | li | xxxv |
| cclii | ccxviii | xliii | lviii | xxviii | xlviii | iii | o | xiiii | ccclvi | xxxv | xlvi | xxxiiii | lvi | o | x |
| cclxx | ccxciiii | xxi | xxiiii | v | viii | xxxvii | xxx | xv | ccclvi | xxi | xi | xx | xvii | viii | xxxv |
| cclxxxviii | cclxxxix | lviii | xlix | xli | xxix | xii | o | xvi | ccclvi | vi | xxxvi | v | xxxviii | xvii | xx |
| cccvi | cclxxxv | xxxv | xv | xvii | xlix | xlvi | xxx | xvii | ccclv | lii | o | l | lix | xxv | lv |
| cccxxiiii | cclxxxi | xiii | xl | liiii | x | xxi | o | xviii | ccclv | xxxvii | xxv | xxxvi | xx | xxxiiii | xxx |
| cccxlii | cclxxvi | li | vi | xxx | xxx | lv | xxx | Medius cursus Solis in horis | |||||||
| ccclx | cclxxii | xxviii | xxxii | vi | li | xxx | o | ||||||||
| ccclxxviii | cclxviii | v | lvii | xliii | xii | liii | xxx | hore | gradus | minuta | secunda | tertie | quarta | quinta | sexta |
| cccxcvi | cclxiii | xliii | xxiii | xix | xxxii | xxxix | o | i | o | ii | xxvii | l | xliii | iii | i |
| ccccxiiii | cclix | xx | xlviii | lv | liii | xiii | xxx | ii | o | iii | lv | xli | xxvi | vi | ii |
| ccccxxxii | ccliiii | lviii | xiiii | xxxii | xiii | xlviii | o | iii | o | vii | xxiii | xxxii | ix | ix | iii |
| ccccl | ccl | xxxv | xl | viii | xxxiiii | xxii | xxx | iv | o | ix | li | xxii | lii | xii | v |
| cccclxviii | ccxlvi | xv | v | xliiii | liiii | lvii | o | v | o | xii | xix | xiii | xxxv | xv | vi |
| cccclxxxvi | ccxli | l | xxxi | xxi | xv | xxxi | xxx | vi | o | xiiii | xlvii | iiii | xviii | xviii | vii |
| diiii | ccxxxvii | xxvii | lvi | lvii | xxxvi | vi | o | vii | o | xvii | xiiii | lv | i | xxi | ix |
| dxxii | ccxxxiii | v | xxii | xxxiii | lvi | xl | xxx | viii | o | xix | xli | xlv | xlii | xxiii | x |
| dxl | ccxxviii | xlii | xlviii | x | xviii | xv | o | ix | o | xxii | x | xxxvi | xxvii | xxvii | xi |
| dlviii | ccxxiiii | xx | xiii | xlvi | xxxvii | xlix | xxx | x | o | xxiiii | xxxviii | xxvii | x | xxx | xii |
| dlxxvi | ccxix | lvii | xxxix | xxii | lviii | xxiiii | o | xi | o | xxvii | vi | xvii | liii | xxxiii | xiiii |
| dxciiii | ccxv | xxxv | iiii | lix | xviii | lviii | xxx | xii | o | xxix | xxxiiii | viii | xxxvi | xxxvi | xv |
| dcxii | ccxi | xii | xxx | xxxv | xxxix | xxxiii | o | xiii | o | xxxii | i | lvii | xix | xxxix | xvi |
| dcxxx | ccvi | xlix | lvi | xii | o | vii | xxx | xiiii | o | xxxiiii | lxxix | l | ii | xlii | xviii |
| dcxlviii | ccii | xxvii | xxi | xlviii | xx | xlii | o | xv | o | xxxvi | lvii | xl | xlv | xlv | xix |
| dclxvi | cxcviii | iiii | xlvii | xxiiii | xli | xvi | xxx | xvi | o | xxxix | xxv | xxxi | xxviii | xlviii | xx |
| dclxxxiiii | cxciii | xlii | viii | i | i | li | o | xvii | o | xli | xxiii | xxii | xi | li | xxi |
| dccii | clxxxix | xix | xxxviii | xxxvii | xxii | xxv | xxx | xviii | o | xliiii | xxi | xii | liiii | liiii | xxiii |
| dccxx | clxxxiiii | lvii | iiii | xiii | xlii | lix | o | xix | o | xlvi | xlix | iii | xxxvii | lvii | xxiiii |
| dccxxxviii | clxxx | xxxiiii | xxix | l | iii | xxxiiii | xxx | xx | o | xlix | xvi | liiii | xxi | o | xxv |
| dcclvi | clxxvi | xi | lv | xxvi | xxiiii | ix | o | xxi | o | li | xliiii | xlv | iv | iii | xxvii |
| dcclxxxiiii | clxxi | xlix | xxi | ii | xliiii | xliii | xxx | xxii | o | liiii | xii | xxxv | xlvii | vi | xxviii |
| dccxcii | clxvii | xxvi | xlvi | xxxix | v | xviii | o | xxiii | o | lvi | xl | xxvi | xxx | ix | xxix |
| dcccx | clxiii | xii | xii | xv | xxv | lii | xxx | xxiiii | o | lix | v | xvii | xiii | xii | xxxi |
| MEDIS CURSUS SOLIS IN MENSIBUS | ||||||||
| menses | Nomina mensium | |||||||
| Gradus | Minuta | Secunda | Tertia | Quarta | Quinta | Sexta | ||
| xxx | xxix | xxxiiii | viii | xxxvi | xxxvi | xv | xxx | Pharmythios |
| lx | lix | viii | xvii | xiii | xii | xxxi | o | Pachon |
| xx | lxxxviii | xlii | xxv | xlix | xlviii | xlvi | xxx | Pauni |
| cxx | cxviii | xvi | xxxiiii | xxvi | xxv | ii | o | Epiphi |
| cl | cxlvii | l | xliii | iii | i | xvii | xxx | Mesori |
| clxxx | clxxvii | xxiiii | li | xxxix | xxxvii | xxxiii | o | Thoth |
| ccx | ccvi | lix | o | xvi | xiii | xlviii | xxx | Phaophi |
| cclxx | ccxxxvi | xxxiii | viii | lii | l | iiii | o | Athir |
| cclxx | cclxvi | vii | xvii | xxix | xxvi | xix | xxx | Chiac |
| ccc | ccxcv | xli | xxvi | vi | ii | xxxv | o | Tivi |
| cccxxx | cccxxv | xv | xxxiiii | xlii | xxxviii | l | xxx | Mechir |
| ccclx | cccliiii | xlv | xliii | xix | xv | vi | o | Phamenoth |
| MEDIUS CURSUS SOLIS IN DIEBUS | ||||||||
| Dies | Gradus | Minuta | Secunda | Tertie | Quarta | Quinta | Sexta | |
| i | o | lix | viii | xviii | xiii | xii | xxxi | |
| ii | i | lviii | xvi | xxxiiii | xxvi | xxv | ii | |
| iii | ii | lvii | xxiv | li | xxix | xxxvii | xxxiii | |
| iiii | iii | lvi | xxxiii | viii | lii | l | iiii | |
| v | iiii | lv | xli | xxvi | vi | ii | xxxv | |
| vi | v | liiii | xlix | xliii | xix | xv | vi | |
| vii | vi | liii | lviii | o | xxxii | xxvii | xxxvii | |
| viii | vii | liii | vi | xvii | xlv | xl | viii | |
| ix | viii | lii | xiiii | xxxiiii | lviii | xlii | xxxix | |
| x | ix | li | xxii | lii | xii | ix | x | |
| xi | x | l | xxxi | v | xxv | xvii | xli | |
| xii | xi | xlix | xxxix | xxvi | xxxviii | xxx | xii | |
| xiii | xii | xlviii | xlvii | xliii | li | xlii | xliii | |
| xiiii | xiii | xlvii | lvi | i | iiii | lv | xiiii | |
| xv | xiiii | xlvii | iiii | xviii | xviii | vii | xlv | |
| xvi | xv | xlvi | xii | xxxv | xxxi | viii | xvi | |
| xvii | xvi | xlv | xx | lii | xliiii | xxxii | xlvii | |
| xviii | xvii | xliiii | xxix | ix | lvii | xlv | xviii | |
| xix | xviii | xliii | xxxvii | xxvii | x | lvii | xlix | |
| xx | xix | xlii | xlv | xliiii | xxiiii | x | xx | |
| xxi | xx | xli | liiii | i | xxxvii | xxii | li | |
| xxii | xxi | xli | ii | xviii | l | xxxv | xx | |
| xxiii | xxii | xl | x | xxxv | iii | xlvii | liii | |
| xxiiii | xxiii | xxxix | xviii | liii | xvii | o | xxiiii | |
xxv |
xxiiii | xxxviii | xxvii | x | xxx | xii | lvi | |
xxvi |
xxv | xxxvii | xxxv | xxvii | xliii | xxv | xxvi | |
xxvii |
xxvi | xxxvi | xliii | xliiii | lvi | xxxvii | lvii | |
xxviii |
xxvii | xxxv | lii | ii | ix | l | xxviii | |
| xxix | xxviii | xxxv | o | xix | xxiii | ii | lix | |
| xxx | xxix | xxxiiii | viii | xxxvi | xxxvi | xv | xxx | |
〈III.3〉
Deinceps autem existentem existentem] existente F1 et apparentem anomaliam Solis demonstrare, prelibandum universaliter quoniam et planomenorum in consequentia celi transitiones, ut et in precedentia latio universorum, equales quidem sunt omnes et circulares natura, hoc est intellecte circumducere recte vel etiam circulos ipsarum in omnibus simpliciter in equalibus temporibus equales angulos suscipiunt ad centra uniuscuiusque periferiarum. Apparentes autem circa ipsas anomalie penes portiones et ordines eorum qui in speris ipsorum circulorum per quos faciunt motus perfitiuntur et nichil alienum ab ipsarum sempiternitate circa subintellectam apparentium inordinatione vere aptum est contingere. Causam autem anomalie fantasie secundum duas maxime primas et universales ypotheses contingit fieri. Motu enim ipsarum considerato ad et omocentricum mundo et in eppipedo eius qui per media animalia intellectum, intellectum] add. circulum V2 quasi non differre ad centrum eius nostrum visum, ipsas vel non secundum omocentricos mundo circulos equales suspicandum facere motus, vel secundum omocentricos quidem, non simpliciter autem in ipsis, sed in aliis super ipsis delatis vocatisque epiciclis. Secundum utrumque enim istarum ypothesium contingens apparebit in equis ipsos temporibus inequales videri visibus nostris transgredientes eius qui per media animalia circuli omocentrici mundo periferias. Si enim in ea que secundum ecentrotica ypothesium intellexerimus excentricum quidem, in quo plane stella movetur, ABGD circa centrum E et diametrum AED, punctum vero Z in ipsa nostrum visum, quare et A quidem apogiotaton fieri punctum, B B] D V2vero periguiotaton, assumentesque equales periferias AB et GD copulaverimus BE et BZ et GE et GZ. Inde manifestum erit quoniam AB et GD periferias utrumque in tempore equali progrediens stella inequales videbitur scripti circa Z centrum circuli pertransire periferias, propter, equali existente BEA angulo angulo GED, minorem quidem fieri BZA utroque ipsorum, maiorem vero eum qui est GZD.
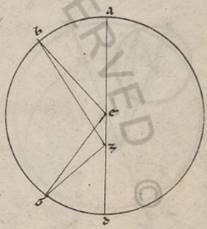 Et si in ea que secundum epiciclum ypothesi intellexerimus omocentricum quidem ei qui per media animalia circulum ABGD circa centrum E et diametrum AEG, in ipso vero delatum epiciclum, in quo movetur stella, ZITR circa centrum A, manifestum et ita inde erit quoniam, epiciclo plane pertranseunte ABGD circulum, ut ab A verbi causa in B, et stella epiciclum quando quidem secundum Z et T fit, stella indifferenter apparebit A centro epicicli, quando vero secundum alia, nequaquam. Sed secundum I quidem, ut ita dicatur, facta maiorem videbitur fecisse motum equali AI periferia, secundum R vero minorem similiter AR periferia. In huiusmodi ergo secundum excentrotica ypothesi semper contingit minimum quidem motum secundum apoguiotaton subsequi, maximum vero secundum periguiotaton, quoniam et semper AZB angulus minor est eo qui est DZG. In ea vero que secundum epiciclum ambo contingere possunt. Epiciclo enim in consequentia celi transitum faciente, ut verbi gratia ab A in B, siquidem stella ita in epiciclo faciat motum, quare ab apoguio transitionem in consequentia rursum perfici, hic est ab Z velut in I, secundum apoguion maximum transitum fieri continget propter in eadem et epiciclum tunc et stellam moveri. Si autem qui ab apoguio stelle motus in precedentia epicicli fiat, hoc est ab Z velut in R, R] K V2F1 secundum apoguion e contrario minimus transitus perfitietur, propter in contrariam contrariam] contraria V2F1 transitus epicicli stellam tunc moveri.
Et si in ea que secundum epiciclum ypothesi intellexerimus omocentricum quidem ei qui per media animalia circulum ABGD circa centrum E et diametrum AEG, in ipso vero delatum epiciclum, in quo movetur stella, ZITR circa centrum A, manifestum et ita inde erit quoniam, epiciclo plane pertranseunte ABGD circulum, ut ab A verbi causa in B, et stella epiciclum quando quidem secundum Z et T fit, stella indifferenter apparebit A centro epicicli, quando vero secundum alia, nequaquam. Sed secundum I quidem, ut ita dicatur, facta maiorem videbitur fecisse motum equali AI periferia, secundum R vero minorem similiter AR periferia. In huiusmodi ergo secundum excentrotica ypothesi semper contingit minimum quidem motum secundum apoguiotaton subsequi, maximum vero secundum periguiotaton, quoniam et semper AZB angulus minor est eo qui est DZG. In ea vero que secundum epiciclum ambo contingere possunt. Epiciclo enim in consequentia celi transitum faciente, ut verbi gratia ab A in B, siquidem stella ita in epiciclo faciat motum, quare ab apoguio transitionem in consequentia rursum perfici, hic est ab Z velut in I, secundum apoguion maximum transitum fieri continget propter in eadem et epiciclum tunc et stellam moveri. Si autem qui ab apoguio stelle motus in precedentia epicicli fiat, hoc est ab Z velut in R, R] K V2F1 secundum apoguion e contrario minimus transitus perfitietur, propter in contrariam contrariam] contraria V2F1 transitus epicicli stellam tunc moveri.
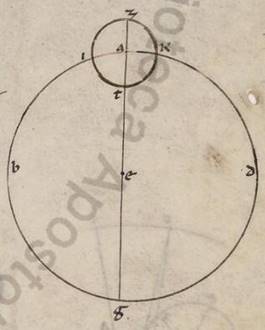 His autem ita se habentibus, deinceps et illa prelibandum et quoniam in duplices quidem facientibus anomalias ambas ypotheses istas contingit complicari, ut in eis que de ipsis demonstrabimus. In una ergo et eadem utentibus anomalia et una expositarum ypothesium sufficiet. Et quoniam omnia apparentia secundum utrumque earum immutabiliter perficientur, eisdem proporcionibus in utrisque contentis, hoc est quando, quam habet proportionem ea que inter centra in secundum ecentrotica ypothesi et visus et ecentrici circuli ad eam que ex centro excentrici, eam habet proportionem in secundum epiciclum ypothesi ea que ex centro centro] add. epicicli ad eam que ex centro V2 ferentis ipsum circuli, et adhuc in quanto tempore ecentricum circulum stella in consequentia faciens motum ametaptoton existentem perambulat, in tanto et epiciclus quidem omocentricum visui circulum pertransit, rursum ut in consequentia motus, stella vero epiciclum equali celeritate, ut tamen eo qui secundum apoguion transitu in antecedentia facto.
His autem ita se habentibus, deinceps et illa prelibandum et quoniam in duplices quidem facientibus anomalias ambas ypotheses istas contingit complicari, ut in eis que de ipsis demonstrabimus. In una ergo et eadem utentibus anomalia et una expositarum ypothesium sufficiet. Et quoniam omnia apparentia secundum utrumque earum immutabiliter perficientur, eisdem proporcionibus in utrisque contentis, hoc est quando, quam habet proportionem ea que inter centra in secundum ecentrotica ypothesi et visus et ecentrici circuli ad eam que ex centro excentrici, eam habet proportionem in secundum epiciclum ypothesi ea que ex centro centro] add. epicicli ad eam que ex centro V2 ferentis ipsum circuli, et adhuc in quanto tempore ecentricum circulum stella in consequentia faciens motum ametaptoton existentem perambulat, in tanto et epiciclus quidem omocentricum visui circulum pertransit, rursum ut in consequentia motus, stella vero epiciclum equali celeritate, ut tamen eo qui secundum apoguion transitu in antecedentia facto.
Quoniam ergo, his ita subiacentibus, eadem circa utramque ypothesium apparentia contingunt, breviter docebimus et per proportiones ipsas et post hec et per expositos in ipsis in Solis anomalie numeros. Dico ergo primum quoniam secundum utraque ipsarum maxima differentia fit plane motionis ad apparentem anomaliam, secundum quam et medius transitus stellarum intelligitur, quando apparens distantia ab apoguio tetartimorium recipit, et quoniam quod ab apoguiotato usque dictum medium medium] add. transitum V2 tempus maius est eo quod a medio in periguiotaton. Unde contingit secundum ecentricorum quidem ypothesim semper, secundum eam vero que epiciclorum, quando apoguis apoguis] ab apoguiis V2F1 ipsarum transitus in antecedentia fuerit, quod a minimo motu in medium tempus maius fieri eo quod a medio in maximum, propter secundum apoguium in utraque minimum motum perfici, at vero secundum in consequentia epicicli ab apoguio facientem circumductiones stellarum e contrario quod a maxima motione in mediam, tempus maius fieri eo quod a media in minimam, propter et hic secundum apoguion maximum transitum perfici. Esto ergo primum excentricus stelle circulus ABGD circa centrum E et diametrum AEG, in qua sumatur centrum zodiaci, hoc est secundum visum et sit Z, et per Z ad rectos angulos ei que est AEG protracta BZD subiaceat stella in B et D punctis, ut manifestum quoniam tetartimorio utrimque apparens distantia distat ab A apoquio; demonstrandum quoniam ad B et D puncta maxima fit distantia plani motus ad anomalon. Copulentur enim EB et ED. Quoniam ergo quam habet proportionem EBZ angulus ad quatuor rectos, eam habet proportionem eius que penes anomaliam differentie periferia ad totum circulum, inde fit manifestum: quoniam quidem AEB angulus plani motus subtendit periferiam, AZB vero apparentis anomali, superhabundatia vero ipsorum ipsorum] add. est V2 EBZ angulus. Dico ergo quoniam istorum 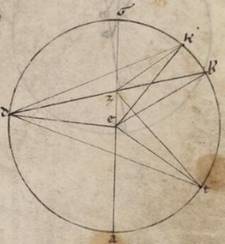 utroque alius angulus maior non constituetur ad ABGD circuli periferiam super EZ rectam. Constituantur enim anguli ad T et R puncta ETZ et EKZ et coniungantur TD et KD. Quoniam ergo omnis trigoni maius latus maiorem subtendit angulum, maius vero est TZ quam ZD, maior erit et TDZ angulus angulo DTZ. Equalis vero est EDT angulus angulo
utroque alius angulus maior non constituetur ad ABGD circuli periferiam super EZ rectam. Constituantur enim anguli ad T et R puncta ETZ et EKZ et coniungantur TD et KD. Quoniam ergo omnis trigoni maius latus maiorem subtendit angulum, maius vero est TZ quam ZD, maior erit et TDZ angulus angulo DTZ. Equalis vero est EDT angulus angulo 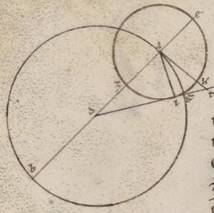 ETD, quoniam et ET ei que est ED est equalis. Et totus ergo EDZ angulus, hoc est EDB, maior est angulo ETZ. Rursum quoniam maior est DZ quam KZ, maior est et ZKD quam ZDK. Equalis vero est EKD toti EDK, quoniam et EK rursum ei que est ED est equalis et reliquus ergo EDZ, hoc est EBZ, quam EKZ maior est. Non ergo possibille alios maiores constitui angulos, secundum quem diximus modum, eis qui ad B et D puncta. Coostensum vero est quoniam et AB periferia, que continet illud quod a minima motione in mediam tempus, maior est quam BG, que continet illud quod a media motione in maximam tempus, duabus differentiam anomalie continentibus periferiis, quoniam quidem AEB angulus maior est quam rectus, hoc est quam EZB eo qui est EBZ, angulus BEG vero minor eodem.
ETD, quoniam et ET ei que est ED est equalis. Et totus ergo EDZ angulus, hoc est EDB, maior est angulo ETZ. Rursum quoniam maior est DZ quam KZ, maior est et ZKD quam ZDK. Equalis vero est EKD toti EDK, quoniam et EK rursum ei que est ED est equalis et reliquus ergo EDZ, hoc est EBZ, quam EKZ maior est. Non ergo possibille alios maiores constitui angulos, secundum quem diximus modum, eis qui ad B et D puncta. Coostensum vero est quoniam et AB periferia, que continet illud quod a minima motione in mediam tempus, maior est quam BG, que continet illud quod a media motione in maximam tempus, duabus differentiam anomalie continentibus periferiis, quoniam quidem AEB angulus maior est quam rectus, hoc est quam EZB eo qui est EBZ, angulus BEG vero minor eodem.
Rursus ut in altera ypothesi demonstretur idem contingens, esto omocentricus quidem mundo circulus ABG circa centrum D et diametrum ADB. In eadem vero epipedo delatus super ipsum epiciclus EZI circa centrum A et subiaceat stella in I, quando tetartimorio distans apparet ab eo quod secundum apoguion puncto et coniungantur AI et DIG; dico quoniam DIG contingit epiciclum. Tunc enim plurima fit differentia plani motus ad anomalium. Quoniam enim planus quidem ab apoguio motus continetur sub EAI angulo, – equali enim celeritate et stella epiciclum et epiciclus ABG circulum pertranseunt –, differentiam vero plani motus ad apparentem sub ADI angulo continetur. Manifestum quoniam et differentia EAI anguli ad ADI, hoc est AID angulus, apparentem stelle ab apoguio distantiam continet. Quare quoniam subiacet ipsa tetartimorii, rectus quidem erit et AID angulus, contingens vero propter hoc et DIG recta EZI epicicli, periferia ergo AG inter A centrum et contingentem maxima est differentia eius quod penes anomaliam. Et secundum eadem EI periferia, que continet et secundum hic subiacentem in epiciclo transitionem illud quod a minima motione in mediam tempus, maior est quam IZ, que continet quod a media motione in maximam tempus, duabus AG perferiis. Quoniam quidem si protraxerimus DIT et duxerimus ei que est EZ ad rectos angulos AKT, equales quidem fient KAI angulus angulo ADG et KI periferia ei quem est AG similis. Eadem vero uno tetartimorio maior quidem est EKI, minor vero ZI. Quare oportebat ostendere.
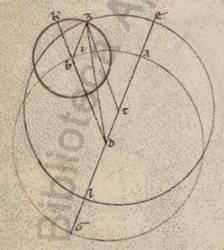 Quoniam vero et in particularibus motibus in utraque ypothesi in equalibus temporibus eadem fiunt omnia circa planos et apparentes motus et adhuc ipsorum superhabundantias, hoc est eam que penes anomaliam differentiam, hinc utique quidem maxime addiscet. Esto enim omocentricus quidem ei qui per media animalia circulus ABG circa centrum D, circulus autem ecentricus, equalis quidem omocentrico ABG, EZL circa centrum T, communis vero amborum diametrum per D et T centrum et EA apoguion EATD, et assumpta in omocentri quacumque periferia AB centro B B] corr. ex D V3 spatioque DT, scribatur BZ epiciclus et coniungantur K, B, D; dico quoniam stella quidem in utraque motionum in Z sectionem excentrici et epicicli omnino secundum equale tempus inferetur, hoc est tres periferie similles erunt invicem EZ ecentrici et AB omocentrici et KZ epicicli, differentia vero plani motus ad anomalon et apparens stelle progressio secundum utramque ypothesium similis et eadem continget. Copulentur ZT et BZ et adhuc DZ. Quoniam quadrilateri BDZT opposita latera equalia sunt utrumque utrique, ZT quidem ei que est BD, BZ vero ei quod est TD, parallilogramum erit BDZT quadrilaterum, equales ergo sunt anguli ETZ et ADB et ZBK, quare, quoniam ad centra sunt, et subtensas sub ipsis periferias similles invicem fieri EZ excentrici et AB omocentrici et KZ epicicli, itaque secundum utrosque motus in equali tempore in eundem punctum Z inferetur stella et eandem eius qui per media animalia circuli periferiam ab apoguio AI AI] AL V2 scilicet apparebit pertransiens. Quare consequenter et que ad anomaliam differentia eadem secundum utramque ypothesium, quoniam huiusmodi differentiam ostendimus contentam in ea quidem que secundum ecentrotica ypothesi sub DZT angulo, in ea vero que secundum epiciclum sub BDZ, et ipsi vero et equales et permutatim fuerit propter parallilam ostendi ZT ei que est BD. Manifestum vero quoniam et in omnibus distantiis eadem consequenter, paralillogramo semper facto TDZB quadrilatero et scripto ecentrico circulo ab ipsa que secundum epiciclum stelle transitione, quando proportiones secundum utramque ypothesium et similles et equales contingunt.
Quoniam vero et in particularibus motibus in utraque ypothesi in equalibus temporibus eadem fiunt omnia circa planos et apparentes motus et adhuc ipsorum superhabundantias, hoc est eam que penes anomaliam differentiam, hinc utique quidem maxime addiscet. Esto enim omocentricus quidem ei qui per media animalia circulus ABG circa centrum D, circulus autem ecentricus, equalis quidem omocentrico ABG, EZL circa centrum T, communis vero amborum diametrum per D et T centrum et EA apoguion EATD, et assumpta in omocentri quacumque periferia AB centro B B] corr. ex D V3 spatioque DT, scribatur BZ epiciclus et coniungantur K, B, D; dico quoniam stella quidem in utraque motionum in Z sectionem excentrici et epicicli omnino secundum equale tempus inferetur, hoc est tres periferie similles erunt invicem EZ ecentrici et AB omocentrici et KZ epicicli, differentia vero plani motus ad anomalon et apparens stelle progressio secundum utramque ypothesium similis et eadem continget. Copulentur ZT et BZ et adhuc DZ. Quoniam quadrilateri BDZT opposita latera equalia sunt utrumque utrique, ZT quidem ei que est BD, BZ vero ei quod est TD, parallilogramum erit BDZT quadrilaterum, equales ergo sunt anguli ETZ et ADB et ZBK, quare, quoniam ad centra sunt, et subtensas sub ipsis periferias similles invicem fieri EZ excentrici et AB omocentrici et KZ epicicli, itaque secundum utrosque motus in equali tempore in eundem punctum Z inferetur stella et eandem eius qui per media animalia circuli periferiam ab apoguio AI AI] AL V2 scilicet apparebit pertransiens. Quare consequenter et que ad anomaliam differentia eadem secundum utramque ypothesium, quoniam huiusmodi differentiam ostendimus contentam in ea quidem que secundum ecentrotica ypothesi sub DZT angulo, in ea vero que secundum epiciclum sub BDZ, et ipsi vero et equales et permutatim fuerit propter parallilam ostendi ZT ei que est BD. Manifestum vero quoniam et in omnibus distantiis eadem consequenter, paralillogramo semper facto TDZB quadrilatero et scripto ecentrico circulo ab ipsa que secundum epiciclum stelle transitione, quando proportiones secundum utramque ypothesium et similles et equales contingunt.
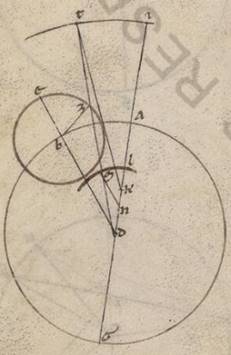 Quoniam vero, etsi similles tantum fuerint, inequales autem magnitudine, eadem rursum apparentia contingent, manifestum et ita fiet. Esto enim similiter omocentricus quidem mundo circulus ABG circa centrum D et diametrum, secundum quam apoguiotatos stella fit, ADG, epiciclus vero circa B distans ab A apoguio AB qualibet periferia, et moveatur stella EZ periferiam simillem factam manifestum quoniam ei que est AB propter equalium temporum esse circulorum restitutiones, et coniungantur DBE et BZ et DZ. Quoniam quidem ergo equales fiunt semper ADE angulus et ZBE et quoniam in DZ recta stella apparebit secundum istam ypothesim, inde est manifestum. Dico vero quoniam et per eam que secundum ecentrotica, sive maior, sive minor fuerit excentris omocentri ABG, et proportionum simillitudine sola subiacente et restitutionum equalitate secundum tempus, in eadem iterum recta DZ apparebit stella. Scribatur enim maior quidem ut diximus excentris IT circa centrum R R] K V2F1 in AG, minor vero LM circa centrum similiter N et, eductis DMZT et TLAI, copulentur TK et MN. Quoniam est sicut DB ad BZ, ita TK ad KD et MN ad ND, et angulus BZD angulo MDN equalis, propter parallilon esse DA ei que est BZ equiangula sunt trigona et qui sub proportionalibus lateribus anguli equales BDZ et DTK et DMN, paralille ergo sunt BD et TK et MN recte. Quare et anguli ADB et AKT et ANM sunt equales et, quoniam ad centra sunt circulorum, similes erunt et que super ipsos periferie AB et IT et LM. In equali ergo tempore non solum epiciclus AB periferia et stella EZ pertransierunt, sed et in excentribus stella et IT et LM pertransiens erit, et in eadem semper recta DMZT propter hoc considerabitur et secundum epiciclum quidem in Z puncto facta, secundum maiorem vero ecentricum intra, intra] in T V2 secundum minorem autem in M et in omnibus periferiis similiter.
Quoniam vero, etsi similles tantum fuerint, inequales autem magnitudine, eadem rursum apparentia contingent, manifestum et ita fiet. Esto enim similiter omocentricus quidem mundo circulus ABG circa centrum D et diametrum, secundum quam apoguiotatos stella fit, ADG, epiciclus vero circa B distans ab A apoguio AB qualibet periferia, et moveatur stella EZ periferiam simillem factam manifestum quoniam ei que est AB propter equalium temporum esse circulorum restitutiones, et coniungantur DBE et BZ et DZ. Quoniam quidem ergo equales fiunt semper ADE angulus et ZBE et quoniam in DZ recta stella apparebit secundum istam ypothesim, inde est manifestum. Dico vero quoniam et per eam que secundum ecentrotica, sive maior, sive minor fuerit excentris omocentri ABG, et proportionum simillitudine sola subiacente et restitutionum equalitate secundum tempus, in eadem iterum recta DZ apparebit stella. Scribatur enim maior quidem ut diximus excentris IT circa centrum R R] K V2F1 in AG, minor vero LM circa centrum similiter N et, eductis DMZT et TLAI, copulentur TK et MN. Quoniam est sicut DB ad BZ, ita TK ad KD et MN ad ND, et angulus BZD angulo MDN equalis, propter parallilon esse DA ei que est BZ equiangula sunt trigona et qui sub proportionalibus lateribus anguli equales BDZ et DTK et DMN, paralille ergo sunt BD et TK et MN recte. Quare et anguli ADB et AKT et ANM sunt equales et, quoniam ad centra sunt circulorum, similes erunt et que super ipsos periferie AB et IT et LM. In equali ergo tempore non solum epiciclus AB periferia et stella EZ pertransierunt, sed et in excentribus stella et IT et LM pertransiens erit, et in eadem semper recta DMZT propter hoc considerabitur et secundum epiciclum quidem in Z puncto facta, secundum maiorem vero ecentricum intra, intra] in T V2 secundum minorem autem in M et in omnibus periferiis similiter.
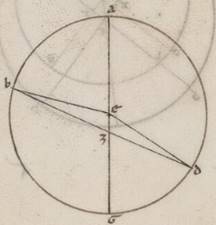 Superaccidit vero quoniam, et quando equalem periferiam stella sumens apparet et ab apoguio et a periguio, equalis erit secundum utramque positionem ad anomaliam differentia. Etenim in ea que secundum ecentrotica, si scripserimus ABGD excentrem circulum circa centrum E et diametrum AEZG per A apoguion, visu subiacente in ipsa secundum Z punctum, et per Z rectam BZD quacumque producentes copulavimus EB et ED, et apparentes transitus et equales et oppositi erunt, hoc est et AZB eius qui ab apoguio et GZD eius qui a periguio, et que penes anomaliam differentia eadem erit, propter equalem esse BE quidem ei que est ED, EBZ vero angulum angulo EDZ. Quare eadem differentia apparente perifferia, hoc est sub utroque AZB et EGZD EGZD] GZD V2 angulorum contenta, maior quidem fit ea que ab apoguio plani motus periferia, minor vero ea que ab G periguio plani motus periferia, propter et AEB quidem angulum maiorem esse angulo AZB, GED vero minorem angulo GZD.
Superaccidit vero quoniam, et quando equalem periferiam stella sumens apparet et ab apoguio et a periguio, equalis erit secundum utramque positionem ad anomaliam differentia. Etenim in ea que secundum ecentrotica, si scripserimus ABGD excentrem circulum circa centrum E et diametrum AEZG per A apoguion, visu subiacente in ipsa secundum Z punctum, et per Z rectam BZD quacumque producentes copulavimus EB et ED, et apparentes transitus et equales et oppositi erunt, hoc est et AZB eius qui ab apoguio et GZD eius qui a periguio, et que penes anomaliam differentia eadem erit, propter equalem esse BE quidem ei que est ED, EBZ vero angulum angulo EDZ. Quare eadem differentia apparente perifferia, hoc est sub utroque AZB et EGZD EGZD] GZD V2 angulorum contenta, maior quidem fit ea que ab apoguio plani motus periferia, minor vero ea que ab G periguio plani motus periferia, propter et AEB quidem angulum maiorem esse angulo AZB, GED vero minorem angulo GZD.
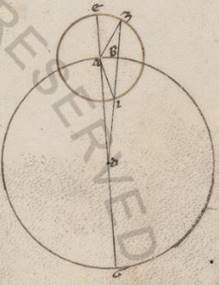 Et in ea que secundum epiciclum ypothesi, si scripserimus omocentrem quidem similiter circulum ABG circa centrum D et diametrum ADG, epiciclum vero EZI circa centrum A, et protrahentes DIBZ quacumque coniuncxerimus AZ et AI et eius quidem que penes anomaliam differentie periferia AB eadem rursum erit subiacenti secundum ambas portiones, hoc est sive secundum Z, sive secundum I fuerit stella. Equaliter vero distans apparebit et ab eo quod secundum apoguion puncto eius qui per media animalia, quando fiunt fiunt] fuerit V2 secundum Z punctum, et ab eo quod secundum periguion, quando fuerit secundum I, quoniam quidem ab apoguio apparens periferia continetur sub DZA angulo. Superhabundantia enim existens ostensus est et plani motus et eius que penes anomaliam differentie. A periguio vero apparens continetur sub ZLA ZLA] ZIA V2 angulo. Equalis enim est et ipse et ei qui a periguio plano motui et ei que ad anomaliam differentie. Equalis vero est et DZA angulus angulo ZIA, propter et AZ ei que est AI equalem esse, quare et hinc rursum colligi quoniam eadem differentia, hoc est ADI angulo, maior quidem est ei ei] qui V2 ad apoguion medius apparente, hoc est EAZ angulus angulo AZD, minor vero qui ad periguion medius apparente eodem existente, hoc est IAD angulus angulo AIZ. Quod propositum erat ostendere.
Et in ea que secundum epiciclum ypothesi, si scripserimus omocentrem quidem similiter circulum ABG circa centrum D et diametrum ADG, epiciclum vero EZI circa centrum A, et protrahentes DIBZ quacumque coniuncxerimus AZ et AI et eius quidem que penes anomaliam differentie periferia AB eadem rursum erit subiacenti secundum ambas portiones, hoc est sive secundum Z, sive secundum I fuerit stella. Equaliter vero distans apparebit et ab eo quod secundum apoguion puncto eius qui per media animalia, quando fiunt fiunt] fuerit V2 secundum Z punctum, et ab eo quod secundum periguion, quando fuerit secundum I, quoniam quidem ab apoguio apparens periferia continetur sub DZA angulo. Superhabundantia enim existens ostensus est et plani motus et eius que penes anomaliam differentie. A periguio vero apparens continetur sub ZLA ZLA] ZIA V2 angulo. Equalis enim est et ipse et ei qui a periguio plano motui et ei que ad anomaliam differentie. Equalis vero est et DZA angulus angulo ZIA, propter et AZ ei que est AI equalem esse, quare et hinc rursum colligi quoniam eadem differentia, hoc est ADI angulo, maior quidem est ei ei] qui V2 ad apoguion medius apparente, hoc est EAZ angulus angulo AZD, minor vero qui ad periguion medius apparente eodem existente, hoc est IAD angulus angulo AIZ. Quod propositum erat ostendere.
〈III.4.〉 De apparente Solis anomalia
Istis ergo ita preexpositis, presuspicandum et soles soles] del. F1 et circa Solem apparentem anomalia, propter et unam esse et a minimo motu in medium tempus maius facere semper eo quod a medio in maximum. Et hoc enim consonum existens invenimus apparentibus posse quidem et per utramque propositarum ypothesium perfici, per eam tamen que secundum epiciclum, quando secundum apoguiam eius periferiam Solis transitio in precedentia fit. Rationabilius autem utique erit adherere ei que secundum excentrotica ypothesi simplitiori existenti et sub uno et non sub duobus motibus consummate. Precedente ergo proportionem eius que circa solarem circulum excentroticos invenire, hoc est quam proportionem habet intermedia centrorum excentrici et eius quod secundum visum centri eius qui per media animalia circuli ad eam que e centro excentrici, et adhuc secundum quam maxime portionem eius qui per media animalia circuli apoguiotaton est excentrici punctum, ostensa sunt quidem hec et Iparco cum studio. 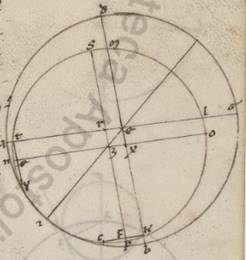 Supponens enim quod quidem a vernali equinoctio usque estivam conversionem tempus dierum xciiii et dimidii, quod non non] vero V2 ab estiva conversione usque autumpnale equinoctium dierum xcii et dimidii per sola hec apparentia demonstrat intermediam quidem predictorum centrorum rectam xxiiiam ad proximum partem existentem eius que e centro excentrici, apoguion vero eius precendens estivam conversionem portionibus xxiiii et dimidii ad proximum, qualium est qui per media animalia circulus ccclx. Et nos vero precedentium precedentium] preiacentium quidem V2 tetartimoriorum tempora et proportiones preiacentes easdem ad proximum et nunc existentes invenimus. Quoniam Quoniam] om. V2 quare propter hoc et quoniam eandem semper positionem excentricus Solis circulus conservat ad tropica et equinoctialia puncta, manifestum nobis fieri. Propter vero non obmissum esse talem locum, sed et per nostros numeros expositum adiacere theorema, faciemus et ipsi propsitorum ostensionem ut in excentrico circulo utentes eisdem apparentibus, hoc est, ut diximus, quod a verno quidem equinoctio usque estivam conversionem tempus continere dies xciiii et dimidium, quod autem ab estiva conversione usque autumpnale equinoctium xcii d et dimidium. Etenim per diligentissime observatas a nobis secundum cccclxiii annum ab Alexandri morte et equinoctialem et estivam conversionem consonam distantiarum multitudinem multitudinem] multidinem V3 dierum invenimus. Quoniam quidem, sicut diximus, autumpnale equinoctium factum est ixo Athir post Solis ortum, vernum vero vii Pachon post meridiem, quare colligi distantiam dierum clxxviii et iiii, estivam autem conversionem xio Mesori post illud quod in xii mesonictium, quare et istam quidem distantiam, hoc est eam que a vernali equinoctio in estivam conversionem, dies colligere xciiii et dimidium, reliqui vero in eam que ab estiva conversione in illud quod deinceps autumpnale equinoctium reliquos in annuum tempus dies ad proximum xcii et dimidium.
Supponens enim quod quidem a vernali equinoctio usque estivam conversionem tempus dierum xciiii et dimidii, quod non non] vero V2 ab estiva conversione usque autumpnale equinoctium dierum xcii et dimidii per sola hec apparentia demonstrat intermediam quidem predictorum centrorum rectam xxiiiam ad proximum partem existentem eius que e centro excentrici, apoguion vero eius precendens estivam conversionem portionibus xxiiii et dimidii ad proximum, qualium est qui per media animalia circulus ccclx. Et nos vero precedentium precedentium] preiacentium quidem V2 tetartimoriorum tempora et proportiones preiacentes easdem ad proximum et nunc existentes invenimus. Quoniam Quoniam] om. V2 quare propter hoc et quoniam eandem semper positionem excentricus Solis circulus conservat ad tropica et equinoctialia puncta, manifestum nobis fieri. Propter vero non obmissum esse talem locum, sed et per nostros numeros expositum adiacere theorema, faciemus et ipsi propsitorum ostensionem ut in excentrico circulo utentes eisdem apparentibus, hoc est, ut diximus, quod a verno quidem equinoctio usque estivam conversionem tempus continere dies xciiii et dimidium, quod autem ab estiva conversione usque autumpnale equinoctium xcii d et dimidium. Etenim per diligentissime observatas a nobis secundum cccclxiii annum ab Alexandri morte et equinoctialem et estivam conversionem consonam distantiarum multitudinem multitudinem] multidinem V3 dierum invenimus. Quoniam quidem, sicut diximus, autumpnale equinoctium factum est ixo Athir post Solis ortum, vernum vero vii Pachon post meridiem, quare colligi distantiam dierum clxxviii et iiii, estivam autem conversionem xio Mesori post illud quod in xii mesonictium, quare et istam quidem distantiam, hoc est eam que a vernali equinoctio in estivam conversionem, dies colligere xciiii et dimidium, reliqui vero in eam que ab estiva conversione in illud quod deinceps autumpnale equinoctium reliquos in annuum tempus dies ad proximum xcii et dimidium.
Esto ergo qui per media animalia circulus ABGD circa centrum E et protrahantur in ipso due diametri ad rectos adinvicem per tropica et equinoctialia puncta AG et BD. Subiaceat autem A quidem vernale punctum B vero estivum et que deinceps continentur. Quoniam ergo centrum excentrici circuli inter EA et EB rectas cadit, manifestum ex eo quod est semicirculum quidem ABG plus continere continere] add. tempus V2 dimidio annui temporis et propter hoc maiorem assumi excentrici portionem semicirculo, AB vero tetartimorium et ipsum plus continere tempus et maiorem periferiam deprehendere excentrici quam BG tetartimorion. Hoc autem ita se habente, subiaceat Z punctus excentrici centrum et protrahatur quidem per utraque centra et apoguion diametros EZI. Centro vero Z et spacio quocunque scribatur excentricus circulus Solis TKLM et per Z trahantur parallile ei quidem que est AG ea que est NXO, ei vero que est BD ea que est PRS et adhuc trahantur catheti ab T in NXO ETY, ab K vero in PRS ea que est KFC. Quoniam ergo Sol TKLM circulum plane perambulans TK quidem periferiam pertransit in diebus xciiii et dimidia, KL vero in diebus xxii et dimida movetur autem plane in diebus quidem xciiii et dimidia, gradus xciii et ix ad proximum, qualium est circulus ccclx in xcii vero et dimidio gradus xci et xi, erit utique TKL quidem portio graduum clxxxiiii et xx, coutraque vero NT et LO 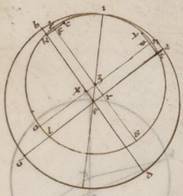 reliquorum post NPO semicirculum graduum iiii et xx, et utraque quidem ergo earum erit graduum ii et x, periferia vero TNY dupla eius que est TN eorumdem iiii et xx. Quare et que quidem sub ea recta TY talium erit iiii xxxii ad proximum, qualium est excentrici diametros cxx, dimidia vero eius que est ET, hoc est EX, eorumdem ii et xvi.
reliquorum post NPO semicirculum graduum iiii et xx, et utraque quidem ergo earum erit graduum ii et x, periferia vero TNY dupla eius que est TN eorumdem iiii et xx. Quare et que quidem sub ea recta TY talium erit iiii xxxii ad proximum, qualium est excentrici diametros cxx, dimidia vero eius que est ET, hoc est EX, eorumdem ii et xvi.
Rursum quoniam TNPK portio tota graduum est xciii et ix, est autem et TN graduum ii et x tetartimorium vero NP graduum xc et reliqua quidem est PK periferia graduum o et lix, dupla vero eius KPC periferia graduum i et lviii. Quare et que quidem sub ipsa recta KFE talium erit ii et iiii, qualium est excentrici diametros cxx, dimidia vero eius KF, hoc est ZX, portionum i et ii. Eorumdem vero ostensa est EX recta ii et xvi et quoniam que ab eis composita faciunt quod ab EZ erit et ipsa longitudine talium ii et xxxix et dimidii ad proximum, qualium est que ex centro excentrici lx. Que ergo ex centro ecentrici circuli vigintupla quadrupla est ad proximum eius que inter centra eius et zodiaci.
Rursum quoniam qualium EZ ostensa est ii et xxix et dimidii, talium erat et recta ZX unius et ii et qualium ergo est EZ ypotenusa cxx, talium erit et ZX quidem recta xlix et xlvi ad proximum. Que vero super eam periferia scripti circa EZX orthogonium circuli, talium xlix ad proximum, qualium circulus est ccclx. Itaque et angulus ZEX qualium quidem sunt ii recti ccclx, talium erunt xlix, qualium vero iiii recti ccclx, talium xxiiii et xxx. Quare quoniam ad centrum E zodiaci et BI periferia, qua precedit quod secundum I apoguion B estivum tropicum punctum, graduum est xxiiii et xxx. Relique vero quoniam quidem OS quidem tetartimorion et SN utrumque graduum est xc, est autem et OL quidem periferia et ipsa et TN utraque graduum iiorum et x, MS vero graduum o lix, et LM quidem perferia erunt graduum lxxxvi et li, MT MT] om. V2 vero graduum lxxxviii et xlix. Sed lxxxvi quidem gradus et li plane Sol pertransit in diebus lxxxviii et viii MT, gradus autem lxxxviii et xlix in diebus xc et viii minutis ad proximum. Quare et GD quidem periferiam, que est ab autumpnali equinoctio in hybernam conversionem, apparebit pertransiens Sol in diebus lxxxviii et viii, DA vero, que est ab yberna conversione in e e] om. V2F1 vernale equinoctium, in diebus xc et viii minutis ad proximum. Inventa sunt proposita nobis consona consona] consone V2 ab Iparco dictis.
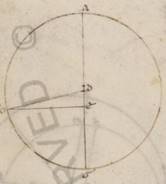 Secundum ergo has quantitates consideremus prius quanta est plurima differentia plani motus ad anomalon et ad que puncta huiusmodi continget. Esto ergo excentricus circulus ABG circa centrum D et diametroci diametroci] diametron V2F1 per A apoguion ADG, in qua sit centrum zodiaci E et ad rectos angulos ei que est AG trahatur AB AB] EB V2F1 et copulentur DB. Quoniam ergo qualium est BD que ex centro lx, talium est DE inter centra ii et xxx secundum xxiiii proportionem et qualium ergo est BD ypotenusa cxx, talium erit et DE quidem recta quinque, que vero super ipsam periferia talium iiii et xlvi ad proximum, qualium est qui circa BDE orthogonium circulus ccclx. Quare et DBE angulus, qui continet plurimam differentiam anomalie, qualium quidem sunt iio recti ccclx, talium erunt iiii et xlvi, qualium vero iiii recti ccclx, talium ii et xxiii. Eorumdem vero est et BED quidem rectus angulus xc, equalis vero duobus BDA manifestum quoniam xcii et xxiii, et quoniam ad centra sunt angulus quidem BDA excentrici, angulus vero BED zodiaci, habebimus plurimam quidem differentiam eius que penes anomaliam ii et xxiii, xxiii] corr. ex xxiiii V3 periferiarum vero ad quas hoc fit eam quidem que excentrici et planam graduum xcii et xxiii ab apoguio, eam vero que zodiaci et anomaliam apparentem tetartimorii, quemadmodum et prius demonstravimus, graduum xc. Manifestum vero ex preassignatis quoniam secundum contraiacentem portionem apparens quidem medius transitus et plurima differentia anomalie erit secundum cclxx gradus, planus autem et secundum excentricum secundum cclxxvii cclxxvii] cclxvii V2F1 et xxxvii.
Secundum ergo has quantitates consideremus prius quanta est plurima differentia plani motus ad anomalon et ad que puncta huiusmodi continget. Esto ergo excentricus circulus ABG circa centrum D et diametroci diametroci] diametron V2F1 per A apoguion ADG, in qua sit centrum zodiaci E et ad rectos angulos ei que est AG trahatur AB AB] EB V2F1 et copulentur DB. Quoniam ergo qualium est BD que ex centro lx, talium est DE inter centra ii et xxx secundum xxiiii proportionem et qualium ergo est BD ypotenusa cxx, talium erit et DE quidem recta quinque, que vero super ipsam periferia talium iiii et xlvi ad proximum, qualium est qui circa BDE orthogonium circulus ccclx. Quare et DBE angulus, qui continet plurimam differentiam anomalie, qualium quidem sunt iio recti ccclx, talium erunt iiii et xlvi, qualium vero iiii recti ccclx, talium ii et xxiii. Eorumdem vero est et BED quidem rectus angulus xc, equalis vero duobus BDA manifestum quoniam xcii et xxiii, et quoniam ad centra sunt angulus quidem BDA excentrici, angulus vero BED zodiaci, habebimus plurimam quidem differentiam eius que penes anomaliam ii et xxiii, xxiii] corr. ex xxiiii V3 periferiarum vero ad quas hoc fit eam quidem que excentrici et planam graduum xcii et xxiii ab apoguio, eam vero que zodiaci et anomaliam apparentem tetartimorii, quemadmodum et prius demonstravimus, graduum xc. Manifestum vero ex preassignatis quoniam secundum contraiacentem portionem apparens quidem medius transitus et plurima differentia anomalie erit secundum cclxx gradus, planus autem et secundum excentricum secundum cclxxvii cclxxvii] cclxvii V2F1 et xxxvii.
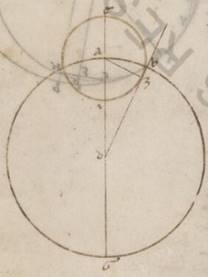 Ut autem et per numeros, ut diximus, easdem quantitates ostendamus collectas et in ea que secundum epiciclum ypothesi, quando eedem proportiones secundum quem diximus modum continentur, esto omocentricus quidem ei qui qui] add. per V2 media animalia circulus ABG circa centrum D et diametrum ADG, epiciclus vero EZI circa centrum A, et protrahatur ab D contingens epiciclum recta DZB et copulentur A, Z, fit ergo similiter in orthogonio ADZ xxiiiipli xxiiii] add. s. l. pla V2 : τετρακαιεικοσαπλασίων H 240.3 AD eius que est AZ. Quare et qualium est AD ypotenusa cxx, talium rursus et AZ quidem fieri v, eam vero que super ipsam periferiam talium iiii et xlvi, qualium est scriptus circa ADZ orthogonium circulus ccclx, et ADZ ergo angulus qualium quidem sunt ii recti ccclx, talium erunt iiii et xlvi, qualium vero iiii recti ccclx, talium ii et xxiii. Itaque plurima quidem differentia anomalie, hoc est AB periferia, et huic inventa est consone graduum ii et xxiii, anomalia vero, quoniam quidem sub AZD recto angulo continet, gradus xc, omala vero contenta sub EAZ angulo graduum rursus xcii et xxiii.
Ut autem et per numeros, ut diximus, easdem quantitates ostendamus collectas et in ea que secundum epiciclum ypothesi, quando eedem proportiones secundum quem diximus modum continentur, esto omocentricus quidem ei qui qui] add. per V2 media animalia circulus ABG circa centrum D et diametrum ADG, epiciclus vero EZI circa centrum A, et protrahatur ab D contingens epiciclum recta DZB et copulentur A, Z, fit ergo similiter in orthogonio ADZ xxiiiipli xxiiii] add. s. l. pla V2 : τετρακαιεικοσαπλασίων H 240.3 AD eius que est AZ. Quare et qualium est AD ypotenusa cxx, talium rursus et AZ quidem fieri v, eam vero que super ipsam periferiam talium iiii et xlvi, qualium est scriptus circa ADZ orthogonium circulus ccclx, et ADZ ergo angulus qualium quidem sunt ii recti ccclx, talium erunt iiii et xlvi, qualium vero iiii recti ccclx, talium ii et xxiii. Itaque plurima quidem differentia anomalie, hoc est AB periferia, et huic inventa est consone graduum ii et xxiii, anomalia vero, quoniam quidem sub AZD recto angulo continet, gradus xc, omala vero contenta sub EAZ angulo graduum rursus xcii et xxiii.
〈III.5〉 De ea que ad particulares portiones anomaliarum canonopiia
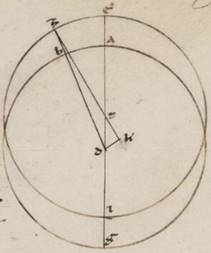 Ut autem et particulares anomali motus quaque vice possint discerni, ostendemus rursum in utraque ypothesium, quomodo utique, una expositarum periferiarum data, sumamus et reliquas. Esto ergo primum quidem omocentricus circulus zodiaco ABG circa centrum D, excentris autem EZI circa centrum T, per utraque vero centra et E apoguion diametros EATDI et, assumpta EZ periferia, copulentur ZD et ZT. Detur vero primum EZ periferia gradus existens verbi gratia xxx et, educta ZT, cathetos in ipsam protrahantur ab D, sitque DK. Quoniam ergo EZ periferia subiacet graduum xxx et ETZ ergo angulus, hoc est DTK, qualium quidem sunt iiii recti ccclx, talium est xxx, qualium vero duo recti ccclx, talium lx, ergo et que quidem super DK periferia talium est lx, qualium est qui circa DTK orthogonium circulus ccclx, que vero super KT reliquorum semicirculum cxx. Et que sub ipsis ergo recte erit DK quidem talium lx, qualium est DT ypothemusa ypothemusa] ypothenusa V2F1 cxx, KT vero eorumdem ciii et lv. Qualium Qualium] add. quare et V2 est ergo DT recta quidem ii et xxx, ZT vero que e centro lx, talium et DK quidem unius erit et xv, TK vero eorumdem ii et x, KTZ autem tota lxii et x. Et quoniam que ab eis composita fatiunt quod ab ZD, erit et ZD ypothenusa talium lxii et xi, et qualium ergo est ZD cxx, talium erunt erunt] erit V2F1 et DK quidem recta ii et xxv, que vero super eam periferiam talium ii xviii, qualium est qui circa ZDK orthogonium circulus ccclx. Quare et DZK angulus qualium quidem sunt duo recti ccclx, talium est ii et xviii, qualium vero iiii recti ccclx, talium unius et ix, tantorum ergo est que penes anomaliam tunc differentia, eorumdem vero erat ETZ angulus xxx et reliquus ergo ADB angulus, hoc est AB zodiaci periferia, graduum est xxviii et li.
Ut autem et particulares anomali motus quaque vice possint discerni, ostendemus rursum in utraque ypothesium, quomodo utique, una expositarum periferiarum data, sumamus et reliquas. Esto ergo primum quidem omocentricus circulus zodiaco ABG circa centrum D, excentris autem EZI circa centrum T, per utraque vero centra et E apoguion diametros EATDI et, assumpta EZ periferia, copulentur ZD et ZT. Detur vero primum EZ periferia gradus existens verbi gratia xxx et, educta ZT, cathetos in ipsam protrahantur ab D, sitque DK. Quoniam ergo EZ periferia subiacet graduum xxx et ETZ ergo angulus, hoc est DTK, qualium quidem sunt iiii recti ccclx, talium est xxx, qualium vero duo recti ccclx, talium lx, ergo et que quidem super DK periferia talium est lx, qualium est qui circa DTK orthogonium circulus ccclx, que vero super KT reliquorum semicirculum cxx. Et que sub ipsis ergo recte erit DK quidem talium lx, qualium est DT ypothemusa ypothemusa] ypothenusa V2F1 cxx, KT vero eorumdem ciii et lv. Qualium Qualium] add. quare et V2 est ergo DT recta quidem ii et xxx, ZT vero que e centro lx, talium et DK quidem unius erit et xv, TK vero eorumdem ii et x, KTZ autem tota lxii et x. Et quoniam que ab eis composita fatiunt quod ab ZD, erit et ZD ypothenusa talium lxii et xi, et qualium ergo est ZD cxx, talium erunt erunt] erit V2F1 et DK quidem recta ii et xxv, que vero super eam periferiam talium ii xviii, qualium est qui circa ZDK orthogonium circulus ccclx. Quare et DZK angulus qualium quidem sunt duo recti ccclx, talium est ii et xviii, qualium vero iiii recti ccclx, talium unius et ix, tantorum ergo est que penes anomaliam tunc differentia, eorumdem vero erat ETZ angulus xxx et reliquus ergo ADB angulus, hoc est AB zodiaci periferia, graduum est xxviii et li.
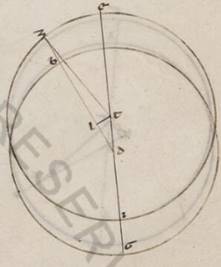 Quoniam vero, etsi alius quis angulorum detur, et reliqui dabuntur, manifestum inde erit, catheto TL protracta in eadem descriptione ab T super ZD. Sive enim AB zodiaci periferiam supposuerimus datam, hoc est TDL angulum, propter hoc erit et recte DT ad TL proportio data. Data autem et ea que recte DT ad TZ, dabitur et ea que recte TZ ad TL, propter hoc habebimus datos TZL angulum, hoc est eam que penes anomaliam differentiam, et ETZ angulum, hoc est EZ excentrici periferiam, sive que penes anomaliam differentiam supposuerimus datam, hoc est TZD angulum, e contrario eadem contingent, data quidem propter hoc recte TZ ad TL proportione, data vero a principio et ea que recte TZ ad TD, quare dari quidem propter hoc recte DT ad TL proportionem, dari vero propter hoc et TDL angulum, hoc est AB zodiaci periferiam, et ETZ angulum hoc est EZ excentrici periferiam.
Quoniam vero, etsi alius quis angulorum detur, et reliqui dabuntur, manifestum inde erit, catheto TL protracta in eadem descriptione ab T super ZD. Sive enim AB zodiaci periferiam supposuerimus datam, hoc est TDL angulum, propter hoc erit et recte DT ad TL proportio data. Data autem et ea que recte DT ad TZ, dabitur et ea que recte TZ ad TL, propter hoc habebimus datos TZL angulum, hoc est eam que penes anomaliam differentiam, et ETZ angulum, hoc est EZ excentrici periferiam, sive que penes anomaliam differentiam supposuerimus datam, hoc est TZD angulum, e contrario eadem contingent, data quidem propter hoc recte TZ ad TL proportione, data vero a principio et ea que recte TZ ad TD, quare dari quidem propter hoc recte DT ad TL proportionem, dari vero propter hoc et TDL angulum, hoc est AB zodiaci periferiam, et ETZ angulum hoc est EZ excentrici periferiam.
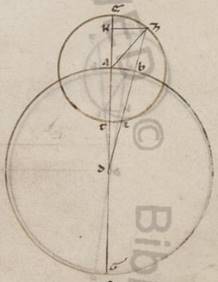 Rursus esto omocentricus quidem ei qui per media animalia circulus ABG centrum D et diametrum ADG, epiciclus vero secundum eadem proportionem EZIT circa centrum A et, assumpta EZ periferia, coniungantur ZBD et ZA. Subiaceat vero rursum EZ periferia eorumdem graduum xxx, et protrahatur ab Z cathetus KZ super AE. Quoniam ergo EZ periferia graduum est xxx, erit utique et EAZ quidem angulus, qualium quidem sunt iiii recti ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super ZK periferia talium est lx, qualium que circa AZK ortogonium circulus ccclx, que autem super AK reliquorum in semicirculum cxx; et que sub ipsis ergo recte erit KZ quidem talium lx, qualium est AZ diametros cxx, KA vero eorumdem ciii et lv. Qualium Qualium] Quare et qualium V2 ergo est AZ quidem ypothenusa ii et xxx, AD vero que e centro lx, talium erit et ZK quidem recta unius et xv, KA vero eorumdem ii et x, et KAD tota lxii et x. Et quoniam que ab eis composita fatiunt quod ab ZBD erit et ZD longitudine talium lxii et xi, qualium erat ZK i et xv, et qualium ergo est DZ ypothenusa cxx, talium erit et ZK quidem recta ii et xxv, que vero super ipsam periferia talium ii et xviii, qualium qui circa DZK ortogonium circulus ccclx. Quare et ZDK angulus, qualium quidem sunt duo recti ccclx, talium est ii et xviii, qualium vero iiii recti ccclx, talium unius et ix, tantorum ergo est rursus que penes anomaliam differentia AB periferie. Eorumdem autem erat et EAZ angulus xxx. Reliquus ergo AZD angulus, hoc est apparens zodiaci periferia, graduum est xxviii li consone demonstratis in excentrotice quantitatibus.
Rursus esto omocentricus quidem ei qui per media animalia circulus ABG centrum D et diametrum ADG, epiciclus vero secundum eadem proportionem EZIT circa centrum A et, assumpta EZ periferia, coniungantur ZBD et ZA. Subiaceat vero rursum EZ periferia eorumdem graduum xxx, et protrahatur ab Z cathetus KZ super AE. Quoniam ergo EZ periferia graduum est xxx, erit utique et EAZ quidem angulus, qualium quidem sunt iiii recti ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super ZK periferia talium est lx, qualium que circa AZK ortogonium circulus ccclx, que autem super AK reliquorum in semicirculum cxx; et que sub ipsis ergo recte erit KZ quidem talium lx, qualium est AZ diametros cxx, KA vero eorumdem ciii et lv. Qualium Qualium] Quare et qualium V2 ergo est AZ quidem ypothenusa ii et xxx, AD vero que e centro lx, talium erit et ZK quidem recta unius et xv, KA vero eorumdem ii et x, et KAD tota lxii et x. Et quoniam que ab eis composita fatiunt quod ab ZBD erit et ZD longitudine talium lxii et xi, qualium erat ZK i et xv, et qualium ergo est DZ ypothenusa cxx, talium erit et ZK quidem recta ii et xxv, que vero super ipsam periferia talium ii et xviii, qualium qui circa DZK ortogonium circulus ccclx. Quare et ZDK angulus, qualium quidem sunt duo recti ccclx, talium est ii et xviii, qualium vero iiii recti ccclx, talium unius et ix, tantorum ergo est rursus que penes anomaliam differentia AB periferie. Eorumdem autem erat et EAZ angulus xxx. Reliquus ergo AZD angulus, hoc est apparens zodiaci periferia, graduum est xxviii li consone demonstratis in excentrotice quantitatibus.
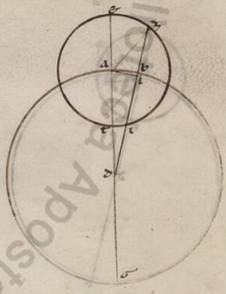 Similiter autem et hic, quamvis alius detur angulus, dati erit et reliqui, ducto catheto AL in eadem desciptione ab A super DZ. Sive enim rursum apparentem zodiaci periferiam dederimus, hoc est AZD angulum, data quidem erit propter hoc et recte ZA ad AL proportio, data vero ex principio et recte ZA ad AD proportione, dabitur et que recte DA ad AL. Propter hoc autem et ADB angulus dabitur, hoc est AB periferia eius que penes anomaliam differentie, et EAZ angulus, hoc est EZ epicicli periferia, sive eam que penes anomaliam differentiam supposuerimus datam, hoc est ADB angulum, e contrario similiter dabitur quidem propter hoc et recte AD ad AB AB] AL V2 proportio, data vero ex principio et recte DA et AZ proportione, dabitur et que recte ZA ad AL, propter hoc autem et AZD angulus datus erit, hoc est apparens zodiaci periferia, et angulus EAZ, hoc est EZ epicicli periferia.
Similiter autem et hic, quamvis alius detur angulus, dati erit et reliqui, ducto catheto AL in eadem desciptione ab A super DZ. Sive enim rursum apparentem zodiaci periferiam dederimus, hoc est AZD angulum, data quidem erit propter hoc et recte ZA ad AL proportio, data vero ex principio et recte ZA ad AD proportione, dabitur et que recte DA ad AL. Propter hoc autem et ADB angulus dabitur, hoc est AB periferia eius que penes anomaliam differentie, et EAZ angulus, hoc est EZ epicicli periferia, sive eam que penes anomaliam differentiam supposuerimus datam, hoc est ADB angulum, e contrario similiter dabitur quidem propter hoc et recte AD ad AB AB] AL V2 proportio, data vero ex principio et recte DA et AZ proportione, dabitur et que recte ZA ad AL, propter hoc autem et AZD angulus datus erit, hoc est apparens zodiaci periferia, et angulus EAZ, hoc est EZ epicicli periferia.
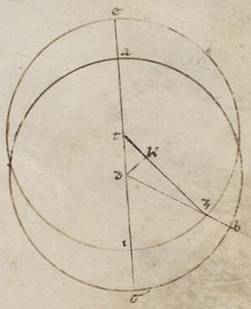 Rursum in preiacente excentris circuli descriptione assumatur ab I periguio excentrici IZ periferia subiacens eorumdem graduum xxx, et coniungantur DZB et ZT, et cathetus DLC DLC] DK V2 protrahatur ab D in TZ, et quoniam ZI periferia graduum est xxx, erit utique ZTI angulus, qualium quidem sunt iiii recti ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super DK rectam periferia talium est lx, qualium qui circa DTK ortogonium circulus ccclx, que vero super KT reliquorum in semicirculum portionum cxx, et subtendentes ergo ipsas recte erit DK quidem talium lx, qualium DT diametros cxx, KT vero eorumdem ciii et lv. Et qualium ergo est DT quidem ypotenusa ii et xxx, IZ vero que ex centro lx, talium est et DK quidem recta unius et xv, TK vero similiter ii et x, KZ autem reliquorum lvii et l. Et quoniam que ab eis composita faciunt quod ab DZ, erunt erunt] erit V2F1 et ipsa longitudine talium lvii et li ad proximum, qualium DK erat unius et xv, et qualium ergo est DZ ypothenusa cxx, talium et DK quidem erit ii et xxxv et xxxiiii, que vero super eam periferia talium ii et xxvii, qualium que circa DZK orthogonium circulus ccclx. Quare et DZK angulus, qualium quidem sunt duo recti ccclx, talium est ii et xxvii, qualium autem iiii recti ccclx, talium unius et xiiii ad proximum, tantorum ergo est que penes anomalium differentia. Et quoniam eorumdem subiacet et ZTI angulus xxx, erit et BDG totus, hoc est GD zodiaci periferia, graduum xxxi et xiiii.
Rursum in preiacente excentris circuli descriptione assumatur ab I periguio excentrici IZ periferia subiacens eorumdem graduum xxx, et coniungantur DZB et ZT, et cathetus DLC DLC] DK V2 protrahatur ab D in TZ, et quoniam ZI periferia graduum est xxx, erit utique ZTI angulus, qualium quidem sunt iiii recti ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super DK rectam periferia talium est lx, qualium qui circa DTK ortogonium circulus ccclx, que vero super KT reliquorum in semicirculum portionum cxx, et subtendentes ergo ipsas recte erit DK quidem talium lx, qualium DT diametros cxx, KT vero eorumdem ciii et lv. Et qualium ergo est DT quidem ypotenusa ii et xxx, IZ vero que ex centro lx, talium est et DK quidem recta unius et xv, TK vero similiter ii et x, KZ autem reliquorum lvii et l. Et quoniam que ab eis composita faciunt quod ab DZ, erunt erunt] erit V2F1 et ipsa longitudine talium lvii et li ad proximum, qualium DK erat unius et xv, et qualium ergo est DZ ypothenusa cxx, talium et DK quidem erit ii et xxxv et xxxiiii, que vero super eam periferia talium ii et xxvii, qualium que circa DZK orthogonium circulus ccclx. Quare et DZK angulus, qualium quidem sunt duo recti ccclx, talium est ii et xxvii, qualium autem iiii recti ccclx, talium unius et xiiii ad proximum, tantorum ergo est que penes anomalium differentia. Et quoniam eorumdem subiacet et ZTI angulus xxx, erit et BDG totus, hoc est GD zodiaci periferia, graduum xxxi et xiiii.
Secundum eadem vero et hic educta BL et catheto TL in ipsam tracta, et si GB zodiaci periferiam dederimus, hoc est TDL angulum, dabitur quidem propter hoc et rectae DT ad TL proportio, data vero ex principio et recte TD et TZ proportione, dabitur et que recte ZT ad TL. Propter hoc autem et habebimus datas TZD angulum, hoc est eam que ad anomaliam differentiam, atque ZTD, hoc est IZ excentrici periferiam, et si eam que adnomaliam adnomaliam] ad anomaliam V2F1 differentiam dederimus, hoc est TZD angulum, e converso dabitur quidem propter hoc et recte ZT ad TL proportio, data vero ex principio et ea que recte ZT ad TD, dabitur et que recte DT ad TL. Propter hoc autem datos habebimus TDL angulum, hoc est GB periferiam zodiaci, atque ZTI, hoc est IZ excentrici periferiam.
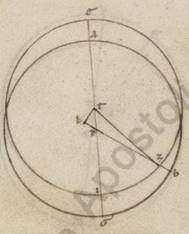 Similiter in preiacenti omocentrici et epicicli descriptione assumpta ab T periguio TI periferia eorumdem graduum xxx, copulentur quidem AI et DIB, cathetus vero IK ab I in AD trahatur. Quoniam ergo rursum TI periferia graduum est xxx, erit utique et TAL angulus, qualium quidem sunt iiii ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super IK periferia talium est lx, qualium que circa IKA orthogonium circulus ccclx, que vero super AK reliquorum in semicirculum cxx, et earum ergo que sub ipsis rectarum IK quidem erit talium lx, qualium est AI ypothenusa cxx, AK vero eorumdem ciii et lv et, qualium ergo est AI quidem recta ii et xxx, AD vero que e centro lx, talium et IK quidem erit unus et xv, AK vero similiter ii et x, KD autem reliquorum lvii et l. Et quoniam que ab eis composita faciunt quod ab DI, longitudine ergo erit et ipsa talium lvii et li ad proximum, qualium KI recta erat unius et xv et, qualium ergo est DI ypothenusa cxx, talium erit et IK quidem recta ii et xxiiii xxiiii] xxxiiii V2F1 et xxxvi, que vero super ipsam periferia talium ii et xxvii, qualium que circa DIK circulus ccclx. Quare et IDK angulus, qualium quidem sunt ii recti ccclx, talium est ii et xxvii, qualium vero iiii recti ccclx, talium unius et xiiii ad proximum, tantorum ergo est que penes adnomaliam adnomaliam] anomaliam V2F1 differentia et hic, hoc est AB periferia. Et quoniam eorumdem subiacet KAL KAL] KAI V2F1 angulus xxx, erit et BIA totus, qui continet apparentem zodiaci periferia, graduum xxxi et xiiii concorditer eis que in excentrico quantitatibus.
Similiter in preiacenti omocentrici et epicicli descriptione assumpta ab T periguio TI periferia eorumdem graduum xxx, copulentur quidem AI et DIB, cathetus vero IK ab I in AD trahatur. Quoniam ergo rursum TI periferia graduum est xxx, erit utique et TAL angulus, qualium quidem sunt iiii ccclx, talium xxx, qualium vero duo recti ccclx, talium lx. Quare et que quidem super IK periferia talium est lx, qualium que circa IKA orthogonium circulus ccclx, que vero super AK reliquorum in semicirculum cxx, et earum ergo que sub ipsis rectarum IK quidem erit talium lx, qualium est AI ypothenusa cxx, AK vero eorumdem ciii et lv et, qualium ergo est AI quidem recta ii et xxx, AD vero que e centro lx, talium et IK quidem erit unus et xv, AK vero similiter ii et x, KD autem reliquorum lvii et l. Et quoniam que ab eis composita faciunt quod ab DI, longitudine ergo erit et ipsa talium lvii et li ad proximum, qualium KI recta erat unius et xv et, qualium ergo est DI ypothenusa cxx, talium erit et IK quidem recta ii et xxiiii xxiiii] xxxiiii V2F1 et xxxvi, que vero super ipsam periferia talium ii et xxvii, qualium que circa DIK circulus ccclx. Quare et IDK angulus, qualium quidem sunt ii recti ccclx, talium est ii et xxvii, qualium vero iiii recti ccclx, talium unius et xiiii ad proximum, tantorum ergo est que penes adnomaliam adnomaliam] anomaliam V2F1 differentia et hic, hoc est AB periferia. Et quoniam eorumdem subiacet KAL KAL] KAI V2F1 angulus xxx, erit et BIA totus, qui continet apparentem zodiaci periferia, graduum xxxi et xiiii concorditer eis que in excentrico quantitatibus.
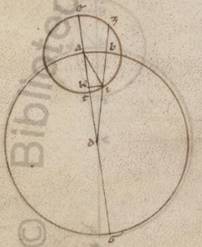 Secundum eadem vero et hic catheto AL protracta in DB, si zodiaci periferiam dederimus, hoc est AIL angulum, dabitur quidem propter hoc recte IA ad AL proportio, data vero ex principio et recte IA ad AD proportione, dabitur et que recte DA ad AL. Propter hoc autem datos habebimus et ADB angulum, hoc est AB periferiam eius que penes anomaliam differentie, et TAI, hoc est TI epicicli periferiam. Si autem rursum AB periferiam dederimus eius que penes anomaliam differentie, hoc est ADB angulum, e converso similiter dabitur quidem propter hoc recte DA ad AL proportio, data vero ex principio et recte DA ad AI proportione, dabitur et que recte AI ad AL. Propter hoc autem datos habebimus et AIL angulum, hoc est zodiaci periferiam, atque TAI, hoc est TI epicicli periferiam. Demonstrata sunt que proposuimus.
Secundum eadem vero et hic catheto AL protracta in DB, si zodiaci periferiam dederimus, hoc est AIL angulum, dabitur quidem propter hoc recte IA ad AL proportio, data vero ex principio et recte IA ad AD proportione, dabitur et que recte DA ad AL. Propter hoc autem datos habebimus et ADB angulum, hoc est AB periferiam eius que penes anomaliam differentie, et TAI, hoc est TI epicicli periferiam. Si autem rursum AB periferiam dederimus eius que penes anomaliam differentie, hoc est ADB angulum, e converso similiter dabitur quidem propter hoc recte DA ad AL proportio, data vero ex principio et recte DA ad AI proportione, dabitur et que recte AI ad AL. Propter hoc autem datos habebimus et AIL angulum, hoc est zodiaci periferiam, atque TAI, hoc est TI epicicli periferiam. Demonstrata sunt que proposuimus.
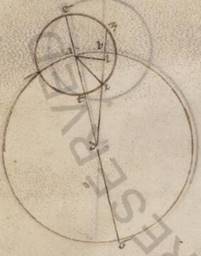 Varia ergo per hec theoremata potente constitui canonopiia canonopiia] corr. ex cononoperipiia V3 continentium portionum ex anomalia apparentium progressuum distinctiones ad ex promptu sumendum particularium directionum quantitates, placet nobis magis quam quam] que V2F1 omalis periferiis adiacentes habet eas que penes anomaliam differentias, et propter secundum ipsas ypotheses consequens, et propter simplicitatem et facilitatem eius que secundum singula computationis. Hinc consequentes primas et in numeris expositis theorematum et in particularibus portionibus investigavimus per lineas similiter demonstratis unicuique omalarum periferiarum pertinentes anomalie differentias. Universaliter ergo que quidem ad apoguia tetartimoria, distribuimus et in Sole et in aliis in portiones xv, quare et in his fieri appropositionem in ipsis per gradus vi, que vero a a] ad V2F1 periguia in portiones xxx, quare et in his fieri approportionem per gradus iii, quoniam quidem maiores sunt ad periguia differentie superhabundantie, penes omaliam omaliam] anomaliam V2 pertinentibus equalibus portionibus differentiis, ad apoguia factis. Ordinabimus ergo et Solis anomalie canonium in versus quidem rursus xlv, selidia vero tria, quorum quidem prima duo continent numeros eorum qui plani motus ccclx graduum, primis quidem xv versibus continentibus ea que ad apoguion tetartimoria duo, reliquis vero xxx ea que ad periguion, selidium vero unicuique planorum numerorum pertinentes gradus prostafereseos eius que penes anomaliam differentie. Et hoc est canonium.
Varia ergo per hec theoremata potente constitui canonopiia canonopiia] corr. ex cononoperipiia V3 continentium portionum ex anomalia apparentium progressuum distinctiones ad ex promptu sumendum particularium directionum quantitates, placet nobis magis quam quam] que V2F1 omalis periferiis adiacentes habet eas que penes anomaliam differentias, et propter secundum ipsas ypotheses consequens, et propter simplicitatem et facilitatem eius que secundum singula computationis. Hinc consequentes primas et in numeris expositis theorematum et in particularibus portionibus investigavimus per lineas similiter demonstratis unicuique omalarum periferiarum pertinentes anomalie differentias. Universaliter ergo que quidem ad apoguia tetartimoria, distribuimus et in Sole et in aliis in portiones xv, quare et in his fieri appropositionem in ipsis per gradus vi, que vero a a] ad V2F1 periguia in portiones xxx, quare et in his fieri approportionem per gradus iii, quoniam quidem maiores sunt ad periguia differentie superhabundantie, penes omaliam omaliam] anomaliam V2 pertinentibus equalibus portionibus differentiis, ad apoguia factis. Ordinabimus ergo et Solis anomalie canonium in versus quidem rursus xlv, selidia vero tria, quorum quidem prima duo continent numeros eorum qui plani motus ccclx graduum, primis quidem xv versibus continentibus ea que ad apoguion tetartimoria duo, reliquis vero xxx ea que ad periguion, selidium vero unicuique planorum numerorum pertinentes gradus prostafereseos eius que penes anomaliam differentie. Et hoc est canonium.
〈III.6〉
| NUMERI COMMUNES | PROSTAFE RESIS | ||
| Gradus | Gradus | Gradus | Minuta |
| vi | cccliiii | o | xiiii |
| xii | cccxlviii | o | xxviii |
| xviii | cccxlii | o | xlii |
| xxiiii | cccxxxvi | o | lvi |
| xxx | cccxxx | i | ix |
| xxxvi | cccxxiiii | i | xxi |
| xlii | cccxviii | i | xxxii |
| xlviii | cccxxi | i | xliii |
| liiii | cccvi | i | liii |
| lx | ccc | ii | i |
| lxvi | ccxciiii | ii | viii |
| lxxii | cclxxxviii | ii | xiiii |
| lxxviii | cclxxxii | ii | xviii |
| lxxxiiii | cclxxvi | ii | xxi |
| xc | cclxx | ii | xxiii |
| xciii | cclxvii | ii | xxiii |
| xcvi | cclxiiii | ii | xxiii |
| xcix | cclxi | ii | xxii |
| cii | cclviii | ii | xxi |
| cv | cclv | ii | xx |
| cviii | cclii | ii | xviii |
| cxi | ccxlix | ii | xvi |
| cxiiii | ccxlvi | ii | xiii |
| cxvii | ccxliii | ii | x |
| cxx | ccxl | ii | vi |
| cxxiii | ccxxxvii | ii | ii |
| cxxvi | ccxxxiiii | i | lviii |
| cxxix | ccxxxi | i | liiii |
| cxxxii | ccxxviii | i | xlix |
| cxxxv | ccxxv | i | xliiii |
| cxxxviii | ccxxii | i | xxxix |
| cxli | ccxix | i | xxxiii |
| cxliiii | ccxvi | i | xxvii |
| cxlvii | ccxiii | i | xxi |
| cl | ccx | i | xiiii |
| cliii | ccvii | i | vii |
| clvi | cciiii | i | o |
| clix | cci | o | liii |
| clxii | cxcviii | o | xlvi |
| clxv | cxcv | o | xxxix |
| clxviii | cxcii | o | xxxii |
| clxxi | clxxxix | o | xxiiii |
| clxxiiii | clxxxvi | o | xvi |
| clxxvii | clxxxiii | o | viii |
| clxxx | clxxx | o | o |
〈III.7〉 De ea que secundum medium in Solis progressum epochi
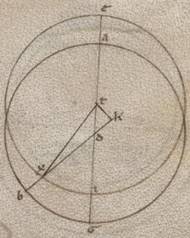 Reliquo vero existente epochim plani motus Solis constituere ad particularium quaque vice progressum considerationes, fecimus et huiusmodi expositionem, consequentes quidem universaliter rursum et in Sole et in aliis nobis ipsis diligentissime observatis progressibus, reducentes vero in ipsis epocharum constitutiones in principium Navonassari regni per demonstratos medios motus, a quo tempore et antiquis observationes habemus ut in universum usque nunc salvatas. Esto ergo omocentricus quidem ei qui per media animalia circulus ABG circa centrum D, excentricus vero Solis circulus EZI circa centrum T, per utraque vero centra et E apoguion diametros EAIG. Subiaceat vero B punctum zodiaci autumpnale, et copuletur BZD et ZT, cathetus autem TK ab T in ZD eductam protrahatur. Quoniam B autumpnale punctum continet Chelarum principium, G vero periguion Sagittarii v et dimidium, BG vero periferia graduum est lxv et xxx, et BDG ergo angulus, hoc est TDK, qualium quidem sunt iiii recti ccclx, talium lxv et xxx, qualium vero duo recti ccclx, talium cxxxi. Quare et que quidem super TK rectam periferia talium est cxxxi, qualium que circa DTK orthogonium circulus ccclx. Ipsam vero subtendens recta TK talium cix et xii, qualium est DT diametros cxx, qualium ergo est DT quidem recta v, ZT vero ypothenusa cxx talium et TK quidem erit iiii et xxxiii, que vero super ipsam periferia talium iiii et xx, qualium est qui circa TZK orthogonium circulus ccclx. Quare et TZK angulus, qualium quidem sunt duo recti ccclx, talium est iiii iet iet] et V2F1 xx, qualium vero iiii recti ccclx, talium ii et x. Eorumdem vero erat BDG angulus lxv et xxx, et reliquus ergo ZTI, hoc est ZI excentrici periferia, graduum est lxiii et xx. Quando ergo in autumpnali equinoctio est Sol, perigion, hoc est Sagittarii gradus v et dimidium, precedit medie motus gradus lxiii et xx ab apoguio vero, hoc est secundum Geminos gradibus v et xxx, distat medie in consequentia gradibus cxvi et xl.
Reliquo vero existente epochim plani motus Solis constituere ad particularium quaque vice progressum considerationes, fecimus et huiusmodi expositionem, consequentes quidem universaliter rursum et in Sole et in aliis nobis ipsis diligentissime observatis progressibus, reducentes vero in ipsis epocharum constitutiones in principium Navonassari regni per demonstratos medios motus, a quo tempore et antiquis observationes habemus ut in universum usque nunc salvatas. Esto ergo omocentricus quidem ei qui per media animalia circulus ABG circa centrum D, excentricus vero Solis circulus EZI circa centrum T, per utraque vero centra et E apoguion diametros EAIG. Subiaceat vero B punctum zodiaci autumpnale, et copuletur BZD et ZT, cathetus autem TK ab T in ZD eductam protrahatur. Quoniam B autumpnale punctum continet Chelarum principium, G vero periguion Sagittarii v et dimidium, BG vero periferia graduum est lxv et xxx, et BDG ergo angulus, hoc est TDK, qualium quidem sunt iiii recti ccclx, talium lxv et xxx, qualium vero duo recti ccclx, talium cxxxi. Quare et que quidem super TK rectam periferia talium est cxxxi, qualium que circa DTK orthogonium circulus ccclx. Ipsam vero subtendens recta TK talium cix et xii, qualium est DT diametros cxx, qualium ergo est DT quidem recta v, ZT vero ypothenusa cxx talium et TK quidem erit iiii et xxxiii, que vero super ipsam periferia talium iiii et xx, qualium est qui circa TZK orthogonium circulus ccclx. Quare et TZK angulus, qualium quidem sunt duo recti ccclx, talium est iiii iet iet] et V2F1 xx, qualium vero iiii recti ccclx, talium ii et x. Eorumdem vero erat BDG angulus lxv et xxx, et reliquus ergo ZTI, hoc est ZI excentrici periferia, graduum est lxiii et xx. Quando ergo in autumpnali equinoctio est Sol, perigion, hoc est Sagittarii gradus v et dimidium, precedit medie motus gradus lxiii et xx ab apoguio vero, hoc est secundum Geminos gradibus v et xxx, distat medie in consequentia gradibus cxvi et xl.
Hoc autem considerato, quoniam in primis a nobis observatis equinoctiis unum diligentissime sumptorum factum fuit equinoctium autumpnale xviio anno Adriani, secundum Egiptios Athir viia, post duas ad proximum horas equinoctiales a meridie manifestum quoniam, secundum illud tempus Sol medie delatus distabat ab apoguio secundum excentricum circulum in consequentia gradibus cxvi et xl. Verum a Navonassari quidem regno usque ad Alexandri mortem anni colligentur secundum Egiptios ccccxxiiii, ab Alexandri vero morte usque ad Augusti regnum autem ccxciiii. A primo autem anno Augusti secundum Egiptios eius que in Thot prima meridiei, quoniam epochas constituimus a meridie, usque xvii annum Adriani Athir viia post iius iius] duas V2 equinoctiales horas a meridie anni fiunt clxi et dies lxvi et hore equinoctiales ii. Et a primo ergo anno Navonassari secundum Egiptios Thot prima meridiei usque tempus expositi autumpnalis equinoctii, colligentur anni egiptiaci dccclxxix et dies lxvi et hore equinoctiales ii. Verum in tanto tempore Sol medie movetur post omnes circulos gradus ccxi et xxv ad proximum. Si ergo eis que secundum expositum autumpnale equinoctium distantie ab apoguio excentrici gradibus cxvi et xl apponamus unius circuli gradus ccclx et a factis dempserimus ccxi gradus et xxv eius que secundum medium tempus epoysie, habebimus in epochin medii motus primo anno Navonassari secundum Egyptios Thoth prima meridie distantem quidem ab apoguio Solem in consequentia secundum planum motus gradus cclxc et xv, obtinentem vero medie Priscium Priscium] Piscium V2F1 primi gradus lxa xlv.
〈III.8〉 De solari compoto
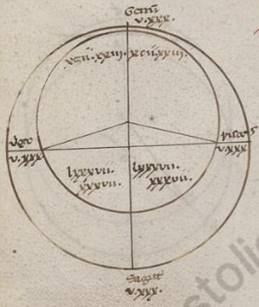 Quotienscumque ergo voluerimus secundum unumquodque inquisitorum temporum Solis motum dinoscere, collectum ab epochi tempus usque subiacens ad eam que in Alexandria horam inferentes in plani motus canonia, adiacentes propriis numeris gradus supercomponemus cum distantie ccxlv gradibus et xv, et a factis eacientes eacientes] eicientes V2F1 totos circulos reliquos numerabimus ab in Geminis gradibus v et xxx in consequentia animalium, et, ubicumque exciderit numerus, ibi medium Solis motum inveniemus. Deinceps vero eumdem numerum, hoc est qui ab apoguio usque medium motum, inferentes in anomalie canonium adiacentes numero gradus in tertio selidio, secundum primum quidem selidium numero cadente, hoc est usque clxxx gradus, gradus] add. existente V2F1 auferemus ab ea que secundum medium motum epochi, in secundum vero selidium incidente numero, hoc est excedente clxxx, adiungemus medio motui et ita examinatum et apparentem Solem inveniemus.
Quotienscumque ergo voluerimus secundum unumquodque inquisitorum temporum Solis motum dinoscere, collectum ab epochi tempus usque subiacens ad eam que in Alexandria horam inferentes in plani motus canonia, adiacentes propriis numeris gradus supercomponemus cum distantie ccxlv gradibus et xv, et a factis eacientes eacientes] eicientes V2F1 totos circulos reliquos numerabimus ab in Geminis gradibus v et xxx in consequentia animalium, et, ubicumque exciderit numerus, ibi medium Solis motum inveniemus. Deinceps vero eumdem numerum, hoc est qui ab apoguio usque medium motum, inferentes in anomalie canonium adiacentes numero gradus in tertio selidio, secundum primum quidem selidium numero cadente, hoc est usque clxxx gradus, gradus] add. existente V2F1 auferemus ab ea que secundum medium motum epochi, in secundum vero selidium incidente numero, hoc est excedente clxxx, adiungemus medio motui et ita examinatum et apparentem Solem inveniemus.
〈III.9〉 De nictimerorum inequalitate
Que vero circa Solem solum considerantur, fere hec sunt. Consequens autem utique erit his adiungere breviter et de nictimerorum inequalitate debentia prelibari, propter expositos quidem nobis secundum unumquodque simpliciter medios cursus universos secundum equales superhabundantias augmentum sumere, velut et nictimeris omnibus equitemporalibus existentibus, hoc autem non ita se habens consideratur. Universorum ergo conversione et plane consumata et circa equinoctialis polos et huiusmodi restitutionem secundum designatius, vel ad orizontem, vel ad meridianum sumpta, mundi quidem circuactio circuactio] circumactio V2 manifestum quoniam una est eiusdem puncti equinoctialis ab aliqua portione vel orizontis vel meridiani in id ipsum restitutio. Nictimeron vero simpliciter solum ab aliqua portione vel orizontis vel meridiani rusum in idem restitutio. Itaque planum quidem nictimerum fit propter ista quod continet motum eorum que unius conversionis equinoctialis temporum ccclx et adhuc unius temporis lxorum lix ad proximum, quot in tanto medie Sol supermovetur, anomalium vero quod continet transitum et eorum que unius conversionis equinoctialis circuli temporum ccclx et adhuc vel coascendentium vel celum medium cooptinentium anomalo Solis excessui. Hanc autem superascendentem equinoctialis portionem ccclx temporibus inequalem neccessarium est fieri, et propter apparentem Solis anomaliam, et propter equales eius qui per media animalia circuli portiones, neque in equalibus temporibus, neque orizontem, neque meridianum pertransire. Utrumque quidem istorum eam que in uno nictimero differentiam plane restitionis ad anomaliam anomaliam] anomalam V2 corr. in anomalam F1 insensibilem facit, ex pluribus autem nictimeris supercollectam, etiam valde sensibilem. Penes ergo solarem anomaliam plurima fit differentia, in eis que ab uno mediorum Solis motuum in alterum distantiis. Ita enim collectam nictimera differunt planorum quidem temporibus iiii et dimidio et iiiia ad proximum. Invicem duplicatis temporibus vero duplicatis … vero] vero duplicatis temporibus V2F1 ix et dimidio propter hoc et apparentem Solis transitum ad plenum secundum eum quidem qui ad apoguium semicirculus iiii et dimidium iiiia gradus deficere, secundum eum vero qui a a] ad V2 periguion, habundare eisdem. Penes autem coortum vel occasum occasum] cooccasum F1 anomaliam plurima fit differentia in sub tropicis punctis determinatis semicirculis. Et hic enim utriusque istorum semicirculorum coascensiones differunt aplane quidem consideratis temporibus clxxx, differentiis maxime vel minime diei penes equinoctialem, invicem vero quibus maxima dierum vel noctium a minima differt, differt] differet V2F1 simmesuraniseon inequalitatum plurima rursum fit differentia in duo precipiue dodecatimoria continentibus distantiis que utrimque simul vel tropicis vel equinoctialibus punctis. Et istorum enim que ad tropica coutraque aplane quidem consideratis differrunt temporibus iiii et dimidio ad proximum, ab eis vero que ad equinoctialia coutrisque rursum temporibus ix propter ista quidem deficere penes mediam epivolin, illa vero equali fere habundare; hinc et que in epochis principia nictimerorum a mesuranisibus constituimus et non ab ortibus vel occasibus Solis, propter ad orizontes quidem consideratam differentiam et usque multas horas posse contingere et non esse eadem ubique, coalterari vero ei que secundum unamquamque inclinationem spere superhabundantie maximorum vel nicmitimorum nicmitimorum] minimorum V2F1 dierum, eam vero que ad meridianum et eandem esse secundum omnem habitationem et nec ex solari anomalia collecta differentie tempora superare. Constituitur vero et ex ambarum istarum mixtione, eius videlicet que penes Solis anomaliam et eius que penes simesuranises simesuranises] summesuranises V2 simmesuranises F1 differentia in secundum utrasque dictas differentias vel appositis simul vel ablativis differentiis, ablativa quidem utrimque maxime facta que ab Aquario medio usque Chelas portione, appositam vero que a Scorpio usque medium Aquarium, propter utramque expositarum portionum plurimum vel apponere vel auffere penes solarem quidem anomaliam gradibus iii ad proximum et tertiam, penes vero simmesuranises tempora iiii et iii ad plurimum, quare plurima ex exposita mixtione colligi differentiam nictimerorum secundum utramque dictarum portionum, ad plana quidem temporibus viii et iii, hoc est unius hore et dimidii et xviiia, ad alterna vero duplis temporibus xvi et iiia, hoc est horam i et ix. Tantum vero in Sole quidem et aliis negglectum nullo utique forsan sensibili ledit circa ipsa apparentium considerationem, in Luna vero propter motus eius celeritatem cura dignam utique iam differentiam faceret et usque iii quintas unius gradus. Ut ergo et secundum quamcumque distantiam data nictimera, dico autem que a meridie vel mesonictio in meridie vel mesonictium, in plana nictimera universaliter resolvamus, consideremus et secundum priorem epochim et posteriorem date nictimerorum distantie, secundum quem est eius qui per media animalia circuli gradus Sol et plane motus et anomalie, postea eam que ab anomalo, idest apparente in apparentem differentiam eorum qui epoisie gradus, inferentes in eas que in recta spera ascensiones intuebimus quantis celum medium cooptinebunt temporibus equinoctialis qui anomalie distantie, ut diximus, gradus et sumentes superhabundantiam et inventorum temporum et eorum qui plane distantie graduum, computantesque contentam quantitatum hore equinoctialis sub superhabundantie temporibus istam, maiore quidem invento numero temporum omale distantie, apponemus date nictimerorum multitudini, minore vero, auferemus ab ipsa, et factum tempus habebimus in omala nictimera distinctum, – quo et utemur maxime ad superagregationes eorum qui in  canonibus Lune mediorum motuum. Facile vero intellligibile inde quoniam et ab omalorum nictimerorum substitutione temporalia et simpliciter considerata sumuntur, proposita horariorum temporum prostaferesi e contrario facta, optinebat quidem secundum nostram epochim Sol, hoc est primo anno Navonassari secundum Egyptios Thoth prima meridiei, omale quidem motus, ut paulo ante demonstravimus, Piscium graduum iii xlv, anomalie vero iiia graduum et viii ad proximum sexagesima Piscium.
canonibus Lune mediorum motuum. Facile vero intellligibile inde quoniam et ab omalorum nictimerorum substitutione temporalia et simpliciter considerata sumuntur, proposita horariorum temporum prostaferesi e contrario facta, optinebat quidem secundum nostram epochim Sol, hoc est primo anno Navonassari secundum Egyptios Thoth prima meridiei, omale quidem motus, ut paulo ante demonstravimus, Piscium graduum iii xlv, anomalie vero iiia graduum et viii ad proximum sexagesima Piscium.
Explicit liber tertius Claudii Ptolomei mathematicorum.