〈V〉
Primum de constructione astrolabii organi
Secundum de ea que ad duplam anomaliam Lune ypothesi
Tertium de quantitate eius que penes Solem anomalie Lune
Quartum de proportione excentroticos lunaris circuli
Quintum de prosnensi prosnensi] prosneusi V2F1 epicicli Lune
Sextum quomodo per lineas a periodicis motibus examinatus Lune progressus sumatur
Septimum negotium canonos universalis anomalie Lune
〈O〉ctavum de universali compoto Lune
Nonum quoniam cura nulla digna fuit differentia in sinzugiis penes encentricum encentricum] excentricum V2F1 Lune circulum
Decimum de permutationibus Lune
Undecimum de constructione organi paralictici
Duodecimum apodixis apostimatum Lune
Tertiumdecimum de quantitate apparentium in sizugiis diametrorum Solis et Lune et umbre
Quartumdecimum de solari apostimate eique coostensis
Quintumdecimum de magnitudinibus Solis et Lune et terre
Sextumdecimum de particularibus permutationibus Solis et Lune
Septimumdecimum canon paralacticus
Octavumdecimum de permutationibus distinctione
Incipit quintus
〈V.1〉 De constructione astrolabii organi
Causa vero earum que ad Solem sinzugiarum et sinodicarum vel panselinicarum et secundum ipsas conplectarum eclipsium suffitientem reperimus expositam in prima et simplici anomalia ypothesim, etsi ipsi solum ita nobis sumatur. Verum tamen ad particulares in aliis ad Solem figurationibus progressiones nequaquam utique suffitientem quis ipsam inveniet, propter et secundam, ut diximus, deprehendi Lune anomaliam penes eas que ad Solem distantias, restitivam restitivam] restitutam V2F1 vero in primam secundum utrasque sinzugias, maximam vero factam secundum utrasque dichothomias. Inducti vero sumus in huiusmodi congnitione congnitione] cognicionem V2F1 et fidem et et] add. ab V2F1 observatis sub Yparco et descriptis Lune progressionibus et ab nobis ipsis sumptis per ad huius huius] huiusmodi V2F1 nobis constructum organum, continens vero modum hunc. Duos enim circulos sumentes diligenter tornatos et tetragonos superfiticientibus, et simmetros quidem magnitudine, undique vero equales et similles, adinvicem coaptavimus secundum diametrum ad rectos angulos in eisdem superfitiebus, quare alterum quidem ipsorum intelligi eum qui per media animalia, alterum vero per polos ipsius et equinoctialis factum meridianum. In quo sumentes a tetragoni latere eius qui per media animalia circuli polos determinancta determinancta] determinantia V2F1 puncta et empolizantes utraque chilindriis prominentibus et ad exteriorem et ad interiorem superfitiem ad eam quidem que exterius empolizavimus alium circulum contingentem undique examinate cava ipsius superficie convexam coaptatorum duorum circulorum et potentem circumagi secundum longitudinem circa dictos polos eius qui per media animalia. Ad ea vero que interius similiter alium circulum empolizavimus contingentem quidem ipsum undique examinate convexa ipsius superficie cavam duorum circulorum, circumductum vero similiter secundum longitudinem circa ipsos polos ei qui exterius. Dividentes autem et istum qui interius circulum et adhuc pro eo qui per media animalia factum in subiacentes perimetri gradus ccclx et quot contingit ipsorum partes, subaptavimus diligenter alterum tenuem circuliscum foramina habentem secundum dyametrum eminentia sub eo qui intra duos circulos, ut possit preferri preferri] preterferri V2F1 secundum illud illi epipedum ut ad utrumque expositorum polorum causa eius que secundum latitudinem observationis. His vero ita factis, apostisantes in per utrosque polos intellecto circulo ab utroque polorum zodiaci mediam demonstravi demonstravi] demonstratam V2F1 periferiam duorum polorum eius qui per media animalia et equinoctialis factos terminos secundum diametrum rursus alterius, empolizavimus et ipsos ad similem meridianum in principio Sintaxeos demonstrato ad eius que inter tropica meridiani periferie observationem, quare, isto secundum eandem portionem illi constituto, hoc est et recta recta] recto V2F1 ad orizontis epipedum et secundum propriam elevationem poli subiacentis habitationis et adhuc equidistante eius qui natura meridiani epipedo, eorum qui interius circulorum circumductionem compleri circa equinoctialis polos ab orientibus in occidentes consequenter prime universorum lationi. Ad hunc ergo modum constituentes organum, quotienscumque super terram simul apparere poterant Sol et Luna, eum quidem que que] qui V2F1 exterius astrolabiorum circulum constituimus in secundum illam horam inventum ad proximum Solis gradum et circumducebamus eum qui per polos circulum, ut, secundum solarem gradum circulorum sectione ad Solem diligenter conversa, obumbrent seipsos simul circuli et qui per media animalia et qui per polos eius vel, si stella fuerit que perspicitur, ut, uno occulorum apposito alteri laterum constituti exterius circuli subiacentem ipsius secundum eum qui per media animalia circulum gradum, et per illud quod ex adverso et equidistantis circuli latus quasi adherens utrisque ipsorum superfitiebus stella in proposito ipsorum epipedo conspiciatur. Alterum vero et eorum qui interius astrolabiorum circulum preterferebamus ad Lunam vel ad aliud quidem quesitorum, ut simul quidem Solis vel et alterius subiacentis conspectui et Luna vel ad aliud quidem quesitorum per ea que secundum subaptarum subaptarum] subaptatum V2F1 circuliscum foramina utraque videatur. Sic enim et quam secundum longitudinem optinet eius qui per media animalia portionem cognoscimus ex secundum equipotentis ipsius circuli divisionem facta interioris circuli sectione et quot etiam gradibus distiterit vel ad arctos vel ad meridiem, ut in eo qui polos eius circulo, et per ipsius interioris astrolabii divisionem et inventam distantiam a medio quod super terram foramine eius qui sub ipsum circumducti circulisci in mediam lineam eius qui per media animalia circuli.
〈V.2〉 De ea que ad duplicem anomaliam Lune ypothesi
Igitur simpliciter quidem facta huiusmodi observatione, Lune ad Solem distantie et ex eis quas Iparcus describit et ex eis quas nos observavimus aliquotiens quidem consone deprehendebatur eis que secundum expositam ypothesim computationibus, aliquotiens autem dissone et differentes, aliquando quidem pauco, aliquando vero multo. Plure vero nobis et curiosiore instantia secundum continuum facta circa ordinem huiusmodi anomalie, deprehendimus quoniam circa sinodos quidem semper et panselinia vel nichil sensibile peccatur, vel parum, vel quantam utique permutationibus permutationibus] permutaciones V2F1 Lune possunt facere distantiam, distantiam] differentiam V2 circa dichothomias vero utrasque minimum quidem vel nichil peccatur, Luna secundum apoguion epicicli vel periguion contingente, plurimum autem, quando circa medios cursus existens plurimam penes primam anomaliam differentiam facit, et quoniam, ablativa quidem existente prima anomalia, in utralibet dichotomiarum adhuc minor locus eius invenitur ex prima ablatione computato, appositam vero, adhuc maior similiter et proportionaliter quantitati prime prostaphereseos, quasi per istum ordinem iam conspiceremus nos quoniam et epiciclum Lune in excentrico circulo fieri fieri] ferri V2F1 subsuspicandum, apoguiotaton quidem factum circa sinodos et panselinia, perguiotaton vero circa dichotomias utrasque. Contingit vero huiusmodi, prima ypothesi huiusmodi quadam directione sumente. Intelligatur enim omocentricus quidem ei qui per media animalia circulus in obliquo Lune epipedo precedens, quemadmodum et prius, causa latitudinis circa eius qui per media animalia polos tantum, quanto superhabundat longitudinis motui ille qui latitudinis. Luna vero vocatum epiciclum circuiens rursum, ut secundum apoguion eius periferiam in precedentia transicionem faciens consequenter prime anomalie restitioni. restitioni] restitucioni V2F1 In hoc ergo obliquo epipedo duos motus oppositos invicem supponimus planos et circa eius qui per media animalia centrum utrosque, quorum unum quidem circumduccentem epicicli centrum in consequentia animalium consequenter ei qui secundum latitudinem motui, alterum vero circumduccentem centrum et apoguion sumpti in eodem epipedo excentrici circuli in quo erit semper centrum epicicli, circumduccentem vero in precedentia animalia et tantum, quantum superhabundat superhabundat] superhabundit V3 ei qui secundum latitudinem motui duplicata remotio, hoc est superhandantia eius qui secundum longitudinem lunaris medii motus ad solarem, quare in una die verbi gratia epicicli quidem centrum motum facit latitudinis gradus xiii et xiiii ad proximum in consequentia animalium in eo qui per media animalia apparere transgrediens longitudinis gradus xiii et xi, propter totum obliquum circulum contraferie contraferie] contraferre V2 add. in precedencia V2F1 superhabundantie lxa iii, apoguion autem excentrici contracircumducci rursum in precedentia gradus xi et ix, quot superhabundant dupli distantie gradus xxiiii et xxiii latitudinis gradibus xiii et xiiii. Ita enim ex amborum motuum contraria circumductione circa centrum, ut diximus, eius qui per media animalia facta ea que per centrum excentrici recedet ad constitutam ex xiii gradibus et xiiii minutis et xi ix periferiam duplam factam eorum qui qui] add. ad V2 add. a F1 distantia graduum xii et xi et dimidio ad proximum. Ac propter hoc bis in medio menstruo tempore excentricus epiciclus pertransibit, ad apoguion excentrici intellecta restitutione in medie consideratis in in] et V2 sinodis et panseliniis supposita consumari. Ut autem magis nobis sub visum fiant que ypotheseos, intelligatur rursum in obliquo Lune epipedo ei qui per media animalia omocentricus circulus ABGD circa centrum E et diametrum AEG.  Subiaceant vero simul secundum A punctum et apoguion excentrici et centrum epicicli et borealis terminus et principium Arietis et medius Sol. In diurno ergo progressu totum quidem epipedum dico moveri in precedentia velut ab A in D circa E centrum lxis iii ad proximum, quare autem borealiorem terminum fieri secundum Piscium gradus xxix et lvii, duobus autem contrariis motibus sub similli ei que est EA recta circa E rursum eius qui per media animalia centrum plane consumatis; in diurno similiter dico motu per centrum quidem excentrici simillem ei qui qui] que V2F1 est EA circumtractam plane in precendentia animalia, velut in eam que est ED, apoguion quidem excentrici ferre in D et describere circa Z centrum DI excentricum, periferiam vero AD facere graduum xi et ix, eam vero que per centrum epicicli circa E rursum plane circumtractam in consequentia animalium, velut EB, ferre quidem in I centrum epicicli, periferiam AB vero facere graduum xiii et xiiii, quare I centrum epicicli ab A quidem boreali termino distans apparere gradibus xiii et xiiii latitudinis, a principio vero Arietis xiii et xi gradibus longitudinis, propter A borealiorem borealiorem] borealem V2 terminum in tanto fieri secundum Piscium gradus xxix et lvii, ab B B] D V2F1 animo animo] vero V2F1 apoguion excentrici collectiones coutramque coutramque] coutrarumque V2F1 AD et AB periferiarum gradus xxiiii et xxiii, qui sunt dupli eorum qui diurne medie remotionis. Ita ergo quoniam quidem coutrumque coutrumque] couterque V2F1 et qui per B et qui per D motus in dimidio medii menstrui temporis unam restitutionem faciunt ad invicem, manifestum quoniam in quarta eiusdem temporis et ad ad] adhuc V2F1 in dimidio et quarta semper diametrizant invicem, hoc est in medie consideratis dichotomiis, quod per EB rectam epicicli diametrizans quod per ED rectam apoguion excentrici secundum periguion eius fiet. Manifestum ergo quoniam, et his ita se habentibus, penes quidem ipsum excentricum, hoc est anomatita anomatita] anomiotuta V2 anomiotita F1 DB periferie ad DI nulla erunt erunt] erit que V2F1 differentia ad motum planum EB recte, non enim DI excentrici periferiam, sed DB eius qui per media animalia plane pertransiens, propter non circa centrum Z excentrici, circa E vero facere circumductionem, penes vero solam secundum ipsum epiciclum factam differentiam ex terre propinquiorem ipsum factum augere semper eam que penes anomaliam differentiam ex quo quo] equo F1 et secundum afferesim et secundum prosthesim deprehendentem deprehendentem] deprehendente V2 ipsum ad visum angulo in periguioteris positionibus maiore completo. Nulla ergo erit penes primam ypothesim universaliter differentia, quando secundum A apoguion erit centrum epicicli, facto huiusmodi circa medie consideratas sinodos et panselinia. Si enim scripserimus circa A MN epiciclum, eius AE ad AM proportio eadem fit ei que per eclipses demonstrata est. Plurima vero erit differentia, quando secundum I excentrici peringuiotaton punctum epiciclus faciet motum, velut descriptus per X, O puncta, quod rursum contingit secundum medie consideratas dichotomias. Maior enim eius que est XI ad IE proportio fit omnibus secundum alias positiones collectis, quoniam quidem, equali semper et eadem existente XI que e centro epicicli, EI que e centro
Subiaceant vero simul secundum A punctum et apoguion excentrici et centrum epicicli et borealis terminus et principium Arietis et medius Sol. In diurno ergo progressu totum quidem epipedum dico moveri in precedentia velut ab A in D circa E centrum lxis iii ad proximum, quare autem borealiorem terminum fieri secundum Piscium gradus xxix et lvii, duobus autem contrariis motibus sub similli ei que est EA recta circa E rursum eius qui per media animalia centrum plane consumatis; in diurno similiter dico motu per centrum quidem excentrici simillem ei qui qui] que V2F1 est EA circumtractam plane in precendentia animalia, velut in eam que est ED, apoguion quidem excentrici ferre in D et describere circa Z centrum DI excentricum, periferiam vero AD facere graduum xi et ix, eam vero que per centrum epicicli circa E rursum plane circumtractam in consequentia animalium, velut EB, ferre quidem in I centrum epicicli, periferiam AB vero facere graduum xiii et xiiii, quare I centrum epicicli ab A quidem boreali termino distans apparere gradibus xiii et xiiii latitudinis, a principio vero Arietis xiii et xi gradibus longitudinis, propter A borealiorem borealiorem] borealem V2 terminum in tanto fieri secundum Piscium gradus xxix et lvii, ab B B] D V2F1 animo animo] vero V2F1 apoguion excentrici collectiones coutramque coutramque] coutrarumque V2F1 AD et AB periferiarum gradus xxiiii et xxiii, qui sunt dupli eorum qui diurne medie remotionis. Ita ergo quoniam quidem coutrumque coutrumque] couterque V2F1 et qui per B et qui per D motus in dimidio medii menstrui temporis unam restitutionem faciunt ad invicem, manifestum quoniam in quarta eiusdem temporis et ad ad] adhuc V2F1 in dimidio et quarta semper diametrizant invicem, hoc est in medie consideratis dichotomiis, quod per EB rectam epicicli diametrizans quod per ED rectam apoguion excentrici secundum periguion eius fiet. Manifestum ergo quoniam, et his ita se habentibus, penes quidem ipsum excentricum, hoc est anomatita anomatita] anomiotuta V2 anomiotita F1 DB periferie ad DI nulla erunt erunt] erit que V2F1 differentia ad motum planum EB recte, non enim DI excentrici periferiam, sed DB eius qui per media animalia plane pertransiens, propter non circa centrum Z excentrici, circa E vero facere circumductionem, penes vero solam secundum ipsum epiciclum factam differentiam ex terre propinquiorem ipsum factum augere semper eam que penes anomaliam differentiam ex quo quo] equo F1 et secundum afferesim et secundum prosthesim deprehendentem deprehendentem] deprehendente V2 ipsum ad visum angulo in periguioteris positionibus maiore completo. Nulla ergo erit penes primam ypothesim universaliter differentia, quando secundum A apoguion erit centrum epicicli, facto huiusmodi circa medie consideratas sinodos et panselinia. Si enim scripserimus circa A MN epiciclum, eius AE ad AM proportio eadem fit ei que per eclipses demonstrata est. Plurima vero erit differentia, quando secundum I excentrici peringuiotaton punctum epiciclus faciet motum, velut descriptus per X, O puncta, quod rursum contingit secundum medie consideratas dichotomias. Maior enim eius que est XI ad IE proportio fit omnibus secundum alias positiones collectis, quoniam quidem, equali semper et eadem existente XI que e centro epicicli, EI que e centro 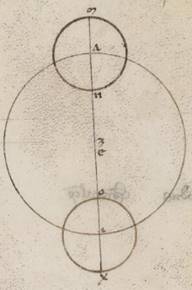 terre omnibus aliis in excentricum copulatis est minor.
terre omnibus aliis in excentricum copulatis est minor.
〈V.3〉 De quantitate eius eius] add. que penes Solem anomalie Lune F1
Ut autem videamus, quanta fiat plurima penes anomaliam differentia, quando secundum periguiotaton excentrici ferri contingit epiciclum, observavimus tales ad Solem consideratarum Lune distantiarum in quibus et cursus eius medii ad proximum contingebant. Tunc enim plurima differentia fit anomalie et ad Solem eius differentia medie sumpta tetartimorium ad proximum faciebat, quando et epiciclus circa periguiotaton fiebat excentrici et adhuc in quibus his ita se habentibus nec permutabatur quidem secundum longitudinem Luna. Istis enim contingentibus et apparente in perspectu secundum longitudinem distantia eadem facta examinate, sumetur utique sine fallacia et quesita anomalie secunde differentia. Ex huiusmodi ergo observationibus facientes considerationem reperimus, quando secundum periguiotaton erat epiciclus, plurimam differentiam anomalie factam ad medium quidem transitum graduum vii et Γo ad proximum, ad primam vero anomaliam graduum ii et Γo. Exempli enim causa, ut in una observatione vel duabus observationibus sub visum huiusmodi nobis distinctio fiat, perspeximus Solem et Lunam secundo anno Antonini, secundum Egiptios Phamenoth xxv, post ortum quidem Solis, ante v vero horas equinoctiales et quartam a meridie. Sole enim considerato secundum Aquarii gradus xviii et dimidium et iiia et medium tenente celum Sagittarii gradus iiii, Luna apparebat optinens Scorpii gradus ix et Γo, examinate vero totidem obtinebat, quoniam quidem circa primas partes Scorpii in Alexandria horas v et dimidium ad proximum distans ad occidentes a meridiano secundum longitudinem nichil sensibile permutatur. Et est quod ab epochis que secundum primum annum Navonassari usque observationem tempus annorum annorum] corr. in annuorum V3 Egiptiorum dccclxxxv et dierum cciii et horarum equinoctialium, et simpliciter, et examinate, xviii et dimidii et iiii, ad quod tempus Solem reperimus medie quidem optinentem Aquarii gradus xvi et xxvii, examinate vero gradus xviii et l, quemadmodum et in astrolabio prospiciebatur, et Luna vero secundum illam horam ex prima ypothesi optinens medie invenitur secundum longitudinem quidem Scorpii gradus xvii et xx, quare tetartimorii contingere ad proximum mediam distantiam Solis, anomalie vero ab apoguio epicicli gradus lxxxvii et xix, circa quas rursum plurima fit differentia anomalie. Minor ergo examinatus progressus fiebat omalo gradibus vii et Γo pro v qui secundum primam anomaliam.
Rursum ut et ex ab Yparco observatis huiusmodi progressibus manifesta nobis que in simillibus differentia fiat, apponemus et istarum unam quam dicit observasse l anno tertie secundum Calippon periodi et secundum Εgiptios Epiphi xvi diurno prime hore preterite. Cursus ergo, inquit, erat ccxli, Sole vero considerato secundum Leonis gradus viii et dimidium et xiia, Luna apparebat optinens Tauri gradus xii et iiia, examinate vero optinebat ad proximum eosdem. Fit ergo inter Solem et Lunam diligenter considerata differentia graduum lxxxvi et xv. Verum Sole existente circa primas partes Leonis in Rodo, ubi observatio fiat, diei hora temporum est xvii et iii, ante meridiem v hore temporales et iiia faciunt equinoctiales vi et viam, quare fieri observationem ante vi horas equinoctiales et viam ab ea que in xvia, meridie medium celum tenente Tauri gradus ix. Colligitur ergo et hic quod ab epochis in observationem tempus annorum egiptiacorum dcxix dierum cccxiiii et horarum equinoctialium simpliciter quidem xvii et dimidii et iiia, examinate vero xvii et dimidii et iiiia, ad quod tempus reperimus Solem secundum nostras ypotheses, quoniam quidem quidem] add. id V2 add. idem F1 est meridianus qui per Rodum et Alexandriam, medie quidem optinentem Leonis gradus x et xxvii, examinte vero gradus viii et xx, Lunam vero medie secundum longitudinem quidem optinentem Tauri gradus iiii et xxv, quare proprie esse rursum mediam distantiam tetartimorii, anomalie vero ab apoguio epicicli gradus cclvii et xlvii, ad quos rursum ad proximum fit plurima differentia eius que penes epiciclum anomalie. Colligitur ergo distantia que a media Luna in examinatum Solem graduum xciii et lv. Obervata est vero que ab examinata Luna in examinatum Solem graduum lxxxvi et xv. Plures ergo optinebat Luna examinate considerata omalo motu gradus rursum vii et Γο pro v qui secundum primam ypothesim. Manifestum vero factum est quoniam et istarum duarum observationum circa secundas dichotomias factarum que quidem secundum nos defitiens inventa est ea que secundum primam anomaliam distinctione duobus gradibus et dimirio, que vero secundum Yparcum superhabundans eisdem, quoniam quidem et tota que penes anomaliam secundum quidem nos ablativa contingebat, secundum Yparcum vero appositam appositam] appositiva F1 et ex aliis vero pluribus observationibus huiusmodi vii graduum et xl xl] Γo V2 ad proximum reperimus plurimam penes anomaliam differentiam, quando epiciclus secundum periguiotatam fuerit portionem excentrici.
〈V.4〉 De proportione excentrotitos lunaris circuli
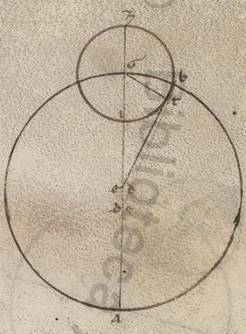 Hoc ergo ita se habente, esto excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua subiaceat eius qui per media animalia centrum E, quare A quidem fieri apoguiotaton excentrici, punctum G vero periguiotaton. Centro vero G scribatur epiciclus Lune ZIT, trahaturque contingens eius ETB, et copuletur GT. Quoniam ergo, secundum contingentem epicicli Luna facta, plurima anomalie differentia constituta est, hec autem ostensa est collecta graduum vii et Γo, erit utique et GET angulus ad centrum existens eius qui per media animalia, qualium quidem sunt iiii recti ccclx, talium viia et xl, qualium vero duo recti ccclx, talium xv et xx, et que quidem ergo super GT periferia talium est xv et xx, qualium qui circa GET orthogonium circulus ccclx, que vero sub ipsam recta GT talium xvi ad proximum, qualium est GE ypothenusa cxx. Quare et qualium GT quidem que e centro epicicli ostensa est v et xv, EA vero que a centro eius qui per media animalia in apoguion excentrici lx, talium erunt et EG quidem que ab eodem centro in periguion excentrici xxxix et xxii, et tota ergo AG quidem diametros eorumdem erit xcix et xxii, DA vero que e centro excentrici xlix et xli, ED autem media centrorum eius qui per media animalia et excentrici x et xix, et demonstrata est nobis et in excentrotide contenta proportio.
Hoc ergo ita se habente, esto excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua subiaceat eius qui per media animalia centrum E, quare A quidem fieri apoguiotaton excentrici, punctum G vero periguiotaton. Centro vero G scribatur epiciclus Lune ZIT, trahaturque contingens eius ETB, et copuletur GT. Quoniam ergo, secundum contingentem epicicli Luna facta, plurima anomalie differentia constituta est, hec autem ostensa est collecta graduum vii et Γo, erit utique et GET angulus ad centrum existens eius qui per media animalia, qualium quidem sunt iiii recti ccclx, talium viia et xl, qualium vero duo recti ccclx, talium xv et xx, et que quidem ergo super GT periferia talium est xv et xx, qualium qui circa GET orthogonium circulus ccclx, que vero sub ipsam recta GT talium xvi ad proximum, qualium est GE ypothenusa cxx. Quare et qualium GT quidem que e centro epicicli ostensa est v et xv, EA vero que a centro eius qui per media animalia in apoguion excentrici lx, talium erunt et EG quidem que ab eodem centro in periguion excentrici xxxix et xxii, et tota ergo AG quidem diametros eorumdem erit xcix et xxii, DA vero que e centro excentrici xlix et xli, ED autem media centrorum eius qui per media animalia et excentrici x et xix, et demonstrata est nobis et in excentrotide contenta proportio.
〈V.5〉 De prosneusi epicli
Causa ergo et circa sinzugiis et adhuc circa dichotomias Lune figurationes apparentium usque tanta utique quis insistat expositorum eius circulorum ypothesibus. Ex particulariter autem circa minoydes et amphicritas amphicritas] amphicirtas V2 distantias consideratis transitionibus, secundum quas maxime fit inter apoguion et periguion excentrici epiciclus, proprium quid circa epicicli prosneusim in Luna reperimus contingens. Quoniam enim unum aliquod et idem universaliter epiciclorum subiacere oportet punctum ad quod semper in ipsis motorum restitutiones neccessarium est consummari. Hoc ergo vocamus apoguion omalon, a quo et principia eius que secundum epiciclum motionis numerorum constituimus, velut in preiacente descriptione Z, et determinatur huiusmodi punctus secundum eam que in apoguiis et periguiis excentricorum epicicli positionem, sub per universa centra educta recta velut DEG. In aliis quidem ypothesibus omnibus simpliciter nichil videmus ex apparentibus contrarium accidens, propter secundum alias epiciclorum transitiones eam que per propositum apoguion epicicli diametrum, hoc est ZGI, eandem positionem semper conservare centrum eius plane circumduccenti recte, velut hic ei que est EG, et nuere, quod utique quis et consequens arbitretur, semper ad centrum circumductionis ad quod et in equalibus temporibus equales anguli omali motus deprehenduntur. In Luna vero adversantur apparentia, propter et in eis que inter A et G transitionibus epicicli ZI diametrum non ad E centrum circumductionis nuere et eamdem ei que est EG positionem salvare. Reperimus enim ad unum quidem aliquod et idem punctum eorum que in AG diametro expositam prosneusin semper conservatam, neque tamen ad E centrum eius qui per media animalia, neque ad D excentrici, sed ad secundum equalem recte DE que inter centra distans ab E, ut ad periguion excentrici. Et quoniam quoniam] om. add. s. l. V3 hoc ita se habet, ostendemus rursum a pluribus observationibus, exponentes duas maxime propositum declarare potentes, hoc est secundum quas et epiciclus circa medias distantias erat et Luna circa apoguion vel perguion epicicli, propter circa huiusmodi transitiones plurimam differentiam contingere expositarum prosneusium. Describit ergo Yparcus in Rodum Rodum] Rodo V2F1 observatum fuisse fuisse] add. per organa V2 add. marg. per organa F1 Solem et Lunam cxcviio anno ab Alexandri obitu, secundum Egyptios Pharmuti Pharmuti] Parmuthi V2 xia, hora secunda incipiente, et dicit enim Sole perspecto per organa secundum Tauri gradus vii et d et iiiia, Lune centrum apparebat optinens Piscium gradus xxi xl m et Γo, optinebat ergo examinate xxi et iiia et viii, secundum expositum ergo tempus distabat examinata Luna ab examinato Sole in consequentia gradibus cccxiii et xlii ad proximum. Verum quoniam, secunda hora incipiente facta, fuit observatio ante v ante horas ad proximum temporales ab ea que in xia meridie, iste vero faciunt in Rodo tunc equinoctiales horas v et bisse ad proximum, colligitur quod ab epochi nostra usque observatione tempus annorum egiptiacorum dcxx et dierum ccxix et horarum equinoctialium simpliciter quidem rursum xviii et iii, examinate vero xviii tantum, in quo tempore reperimus omalum quidem Solem optinentem Tauri gradus vi et xli, examinate vero gradus vii et xlv, Lunam vero omalam secundum longitudinem quidem optinentem Piscium gradus xxii et xiii, anomalie vero a medio apoguio epicicli gradus clxxxv et xxx, quare et omale Lune ab examinato Sole distantia colligeri graduum cccxiiii et xxviii.
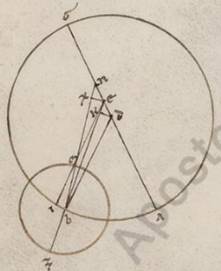 His ergo subiacentibus, esto excentricus Lune circulus ABG circa centrum D et diametrum ADG, in quo esto centrum eius qui per media animalia circuli E, et centro B describatur epiciclus Lune ZIT. Circumducatur autem epiciclus quidem in consequentia animalium motu ut ab B in A, Luna vero eo qui secundum epiciclum ut ab Z in I et T, et copulentur DB et ETBZ. Quoniam ergo in medio mentruo tempore due continentur restitutiones epicicli ad excentricum, secundum expositam vero positionem distabat media Luna a medio Sole gradibus cccxv et xxxii, si duplicantes istos dempserimus circulum, habebimus ab apoguio excentrici factam remotionem tunc epicicli in consequentia graduum cclxxi et iiii. Quare et AEB angulus in reliquorum in iiii rectos erit graduum lxxxviii et lvi. Trahatur autem cathetus DK ab D in EB. Quoniam ergo DEB, qualium quidem sunt iiii recti ccclx, talium est lxxxviii et lvi, qualium vero duo recti ccclx, talium clxxvii et lii erit utique, et que quidem super DK periferia talium clxxvii et lii, qualium est qui circa DEK orthogonium circulus ccclx, que vero super EK reliquorum in semicirculum ii et viii et earum ergo que sub ipsis rectarum DK quidem erit talium cxix et lix, qualium est DE diametros cxx, EK vero eorumdem ii et xiiii, et qualium ergo est DE quidem quidem] add. media V2F1 centrorum x et xix, DB vero que e centro excentrici xlix xli, talium et DK quidem erit x et xix rursum ad proximum, EK vero similiter o et xii. Et quoniam ab DK sumptum ab eo quod sub DB facit quod ab BK, habebimus et BK eorumdem xlviii et xxxvi, BE vero totam xlviii xlviii.
His ergo subiacentibus, esto excentricus Lune circulus ABG circa centrum D et diametrum ADG, in quo esto centrum eius qui per media animalia circuli E, et centro B describatur epiciclus Lune ZIT. Circumducatur autem epiciclus quidem in consequentia animalium motu ut ab B in A, Luna vero eo qui secundum epiciclum ut ab Z in I et T, et copulentur DB et ETBZ. Quoniam ergo in medio mentruo tempore due continentur restitutiones epicicli ad excentricum, secundum expositam vero positionem distabat media Luna a medio Sole gradibus cccxv et xxxii, si duplicantes istos dempserimus circulum, habebimus ab apoguio excentrici factam remotionem tunc epicicli in consequentia graduum cclxxi et iiii. Quare et AEB angulus in reliquorum in iiii rectos erit graduum lxxxviii et lvi. Trahatur autem cathetus DK ab D in EB. Quoniam ergo DEB, qualium quidem sunt iiii recti ccclx, talium est lxxxviii et lvi, qualium vero duo recti ccclx, talium clxxvii et lii erit utique, et que quidem super DK periferia talium clxxvii et lii, qualium est qui circa DEK orthogonium circulus ccclx, que vero super EK reliquorum in semicirculum ii et viii et earum ergo que sub ipsis rectarum DK quidem erit talium cxix et lix, qualium est DE diametros cxx, EK vero eorumdem ii et xiiii, et qualium ergo est DE quidem quidem] add. media V2F1 centrorum x et xix, DB vero que e centro excentrici xlix xli, talium et DK quidem erit x et xix rursum ad proximum, EK vero similiter o et xii. Et quoniam ab DK sumptum ab eo quod sub DB facit quod ab BK, habebimus et BK eorumdem xlviii et xxxvi, BE vero totam xlviii xlviii.
Rursum que quidem omale Lune ab examinato Sole distantia graduum erat cccxiiii et xxviii, que vero examinate ex observatione graduum cccxiii et xlii, quare aufferre quod penes anomaliam eius differentia differentia] differentiam V2 gradus o xlvi, consideratur autem omala transicio Lune in EB recta, subiaceat Luna, quoniam quidem circa periguion erat epicicli, secundum I punctum et, copulatis EI et BI, cathetus BL ad B trahatur in EI eductam. Quoniam ergo BEL angulus quod penes anomaliam Lune continet differentiam, erit utique, qualium sunt iiii recti ccclx, talium o xlvi, qualium vero duo recti ccclx, talium unius et xxxii. Quare et que quidem super BL rectam periferia talium erit unius et xxxii, qualium qui circa EBL orthogonium circulus ccclx, que vero sub ipsam rectam BL unius et xxxvi, qualium est EB ypothenusa cxx. Quare et qualium est BE quidem recta xlviii et xlviii, BI vero que e centro epicicli v et xv, talium erit et BL recta o xxxix, et qualium ergo est BL quidem recta erit xiiii et lii, que vero super ipsam periferia talium xiiii et xiiii, qualium est et qui circa BIL orthogonium circulus ccclx. Quare et BIL quidem angulus talium est xiiii et xiiii, qualium sunt ii recti ccclx. Reliquus vero EBI eorumdem quidem xii et xlii, qualium autem iiii recti ccclx, talium vi et xxi, tantorum ergo erit graduum IT epicicli periferia ea que a Luna in examinatum periguion continens differentiam. Sed quoniam a medio apoguio distabat Luna secundum tempus observationis gradibus clxxxv et xxx, manifestum quoniam et periguion medium precedit Lunam, hic hic] hoc V2F1 est I punctum. Esto ergo M, et protrahatur BMN et ab E cathetus in ipsam trahatur EX. Quoniam ergo TI quidem periferia ostensa est graduum vi et xxi, IM vero subiacet eorum qui a periguio graduum v et xxx, quare totam TM colligi graduum xi et li, erit utique et EBX angulus quidem, qualium sunt iiii recti ccclx, talium xi et li, qualium duo recti ccclx, talium xxiii et xlii, quare et que quidem super EX periferia talium est xxiii et xlii, qualium qui circa BEX orthogonium circulus ccclx, ipsa vero cx cx] EX V2 ex F1 recta talium xxiiii et xxxix, qualium est BE ypothenusa cxx, et qualium ergo est BE recta xlviii et xviii, talium et erit EX recta x et lxorum et iiorum. Rursum quoniam AEB quidem angulus talium erat clxxvii et lii, qualium vero recti ccclx, EBN vero eorumdem xxiii et xlii, erit utique et ENB reliquus angulus eorumdem cliiii et x. Quare et que quidem super EX periferiam periferiam] periferia V2 talium est cliiii et x, qualium quem quem] qui V2 circa ENX orthogonium circulus ccclx, ipsa vero EX recta talium cxvi et lviii, qualium est EN ypothenusa cxx, et qualium ergo est EX quidem recta x et lxorum iiorum, DE vero media centrorum x et xix, talium et EN erit x et xviii. Equalem ergo ad proximum ei que est DE eam que est EN assumit per medium periguion BM in N facta prosneusis.
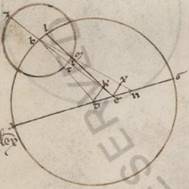 Similiter autem ut et ex contraiacentibus partibus et excentrici et epicicli idem contingens demonstremus, sumpsimus rursum ex ab Yparco observatis, ut diximus, in Rodo distantiis perspectam eorumdem cxcvii anno ab Alexandri morte, secundum Egiptios Pauni, xvii hora ix et iiia, secundum quem, diem, diem] dicit V2 Sole perspecto secundum Carcini gradus xi defitientes autem xxi xxi] xi V2F1 parte, Luna apparebat optinens Leonis xxix maxime gradus, totidem autem et examinate optinebat. Quoniam quidem in Rodo circa extrema Leonis post unam horam ad proximum a meridiano secundum longitudinem nichil Luna permutatur. Distabat ergo secundum expositum tempus examinata Luna ab examinato Sole gradibus in consequentia xlviii et vi. Verum quoniam facta est observatio post tres horas temporales et iiiam ab ea que in xviia Pauni meridiei, iste autem effitiunt in Rodo tunc equinoctiales horas iiii ad proximum, fit quod ab epochi nostra usque observatione observatione] observacionem V2F1 tempus annorum egiptiacorum rursus dcxx et dierum cclxxxvi et horarum equinoctialium, simpliciter quidem iiii, examinate vero iii et Γo, in quod tempus reperimus similiter omalon quidem Solem optinentem Carcini gradus xii et v, examinatum vero x et xl, omalin autem Lunam secundum longitudinem quidem optinentem Leonis gradus xxvii et xx, quare et eam que omale Lune ab examinato Sole distantiam colligi graduum xlvi et xl, anomalie vero a medio apoguio epicicli graduum cccxxxiii et xii.
Similiter autem ut et ex contraiacentibus partibus et excentrici et epicicli idem contingens demonstremus, sumpsimus rursum ex ab Yparco observatis, ut diximus, in Rodo distantiis perspectam eorumdem cxcvii anno ab Alexandri morte, secundum Egiptios Pauni, xvii hora ix et iiia, secundum quem, diem, diem] dicit V2 Sole perspecto secundum Carcini gradus xi defitientes autem xxi xxi] xi V2F1 parte, Luna apparebat optinens Leonis xxix maxime gradus, totidem autem et examinate optinebat. Quoniam quidem in Rodo circa extrema Leonis post unam horam ad proximum a meridiano secundum longitudinem nichil Luna permutatur. Distabat ergo secundum expositum tempus examinata Luna ab examinato Sole gradibus in consequentia xlviii et vi. Verum quoniam facta est observatio post tres horas temporales et iiiam ab ea que in xviia Pauni meridiei, iste autem effitiunt in Rodo tunc equinoctiales horas iiii ad proximum, fit quod ab epochi nostra usque observatione observatione] observacionem V2F1 tempus annorum egiptiacorum rursus dcxx et dierum cclxxxvi et horarum equinoctialium, simpliciter quidem iiii, examinate vero iii et Γo, in quod tempus reperimus similiter omalon quidem Solem optinentem Carcini gradus xii et v, examinatum vero x et xl, omalin autem Lunam secundum longitudinem quidem optinentem Leonis gradus xxvii et xx, quare et eam que omale Lune ab examinato Sole distantiam colligi graduum xlvi et xl, anomalie vero a medio apoguio epicicli graduum cccxxxiii et xii.
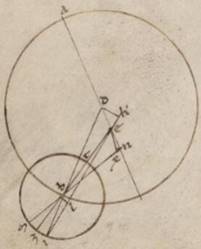 His subiacentibus, esto rursum excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua esto centrum eius qui per media animalia circuli E et scribatur circa B punctum ZIT epiciclus Lune et copulentur DB et ETBZ. Quoniam ergo media distantia Solis et Lune duplicata continet gradus xc et xxx, erit utique propter per considerata AEB angulus, qualium quidem sunt iiii recti ccclx, talium xc et xxx, qualium autem ii recti ccclx, talium clxxxi. Si ergo eitientes BE cathetum in ipsam adduxerimus ab D eam que est DK, fiet DEK angulus reliquorum in duos rectos clxxix, quare et que quidem super DK periferia talium est clxxix, qualium qui circa DEK orthogonium circulus ccclx, que autem super EK reliqui in semicirculum gradus unius, et earum ergo que sub ipsis rectarum DK quidem erit talium cxix et lix, qualium est DE ypothenusa cxx, EK vero eorumdem i et iii, quare et qualium est DE quidem media centrorum x et xix, BD vero que e centro excentrici xlix et xli, et DK quidem recta erit x et xix ad proximum, et EK similiter o v, et quoniam quod ab BD defitiens eo quod ab DK facit quod ab BK, habebimus et totam quidem BK rectam xlviii et xxxvi, reliquam autem EB eorumdem xlviii et xxxi. Rursum quoniam que quidem omale Lune ab examinato Sole distantia graduum erat xlvi et xl, que vero examinate graduum xlviii et vi, quare apponi que penes anomaliam differentiam gradus i et xxvi, subiaceat Luna, quoniam quidem circa apoguion erat epicicli, secundum I punctum et, copulatis EI et BI, cathetus BI BI] BL V2F1 ab B trahatur in EI. Quoniam ergo BEL angulus, qualium quidem sunt iiii recti ccclx, talium est ius xxvi, qualium autem ii recti ccclx, talium ii et lii, erit utique et que quidem super BE periferia talium ii et lii, qualium est qui circa BEL orthogonium circulus ccclx, ipsa vero BL recta talium ii et lix, qualium est EB ypothenusa cxx, et qualium ergo est EB quidem recta xlviii et xxxi, BI vero que e centro epicicli v et xv, talium erit et BL recta unius et xii. Quare et qualium est BI ypothenusa cxx, talium et BL erit xxvii et xxxiiii, et que super ipsam periferia talium xxvi et xxxiiii, qualium est qui circa BIL orthogonium circulus ccclx, et BIL ergo angulus talium est xxvi et xxxiiii, qualium sunt ii recti ccclx, et ZBI totus eorumdem quidem xxix et xxvi, qualium autem iiii recti ccclx, talium xiiii et xliii, tantorum ergo graduum est IIZ IIZ] IZ V2F1 epicicli periferia eam que a Luna in examinatum apoguium continens distantiam.
His subiacentibus, esto rursum excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua esto centrum eius qui per media animalia circuli E et scribatur circa B punctum ZIT epiciclus Lune et copulentur DB et ETBZ. Quoniam ergo media distantia Solis et Lune duplicata continet gradus xc et xxx, erit utique propter per considerata AEB angulus, qualium quidem sunt iiii recti ccclx, talium xc et xxx, qualium autem ii recti ccclx, talium clxxxi. Si ergo eitientes BE cathetum in ipsam adduxerimus ab D eam que est DK, fiet DEK angulus reliquorum in duos rectos clxxix, quare et que quidem super DK periferia talium est clxxix, qualium qui circa DEK orthogonium circulus ccclx, que autem super EK reliqui in semicirculum gradus unius, et earum ergo que sub ipsis rectarum DK quidem erit talium cxix et lix, qualium est DE ypothenusa cxx, EK vero eorumdem i et iii, quare et qualium est DE quidem media centrorum x et xix, BD vero que e centro excentrici xlix et xli, et DK quidem recta erit x et xix ad proximum, et EK similiter o v, et quoniam quod ab BD defitiens eo quod ab DK facit quod ab BK, habebimus et totam quidem BK rectam xlviii et xxxvi, reliquam autem EB eorumdem xlviii et xxxi. Rursum quoniam que quidem omale Lune ab examinato Sole distantia graduum erat xlvi et xl, que vero examinate graduum xlviii et vi, quare apponi que penes anomaliam differentiam gradus i et xxvi, subiaceat Luna, quoniam quidem circa apoguion erat epicicli, secundum I punctum et, copulatis EI et BI, cathetus BI BI] BL V2F1 ab B trahatur in EI. Quoniam ergo BEL angulus, qualium quidem sunt iiii recti ccclx, talium est ius xxvi, qualium autem ii recti ccclx, talium ii et lii, erit utique et que quidem super BE periferia talium ii et lii, qualium est qui circa BEL orthogonium circulus ccclx, ipsa vero BL recta talium ii et lix, qualium est EB ypothenusa cxx, et qualium ergo est EB quidem recta xlviii et xxxi, BI vero que e centro epicicli v et xv, talium erit et BL recta unius et xii. Quare et qualium est BI ypothenusa cxx, talium et BL erit xxvii et xxxiiii, et que super ipsam periferia talium xxvi et xxxiiii, qualium est qui circa BIL orthogonium circulus ccclx, et BIL ergo angulus talium est xxvi et xxxiiii, qualium sunt ii recti ccclx, et ZBI totus eorumdem quidem xxix et xxvi, qualium autem iiii recti ccclx, talium xiiii et xliii, tantorum ergo graduum est IIZ IIZ] IZ V2F1 epicicli periferia eam que a Luna in examinatum apoguium continens distantiam.
Sed quoniam a medio apoguio distabat secundum tempus observationis gradibus cccxxxiii et xii, si supposuerimus medium apoguium secundum M et copulantes MBN cathetum in ipsam adduxerimus a puncto est EX, erit IZM quidem tota periferia reliquorum in circulum graduum xxvi et xlviii. Reliqua vero ZM graduum xii et v, quare MBZ quidem angulus, hoc est ELIX ELIX] EBX V2F1, qualium quidem sunt iiii recti ccclx, talium est xii et v, qualium autem ii recti ccclx, talium xxiiii et x, et que quidem super EX periferia talium est xxiiii et x, qualium qui circa BEX orthogonium circulus ccclx. Ipsa vero EX recta talium xxv et vii, qualium est BE ypothenusa cxx, et qualium ergo est BE quidem recta xlviii et xxxi, DE vero que inter centra x et xix, talium et EX erit x et lxorum viii. Rursum quoniam AEB quidem angulus subiacet talium clxxxi, qualium ii recti ccclx, EBN vero ostensus est xxiiii et x, quare et reliquum ENB reliqui eorumdem clvi et l, fit et que quidem super EX periferia talium clvi et l, qualium est qui circa ENX orthogonium circulus ccclx. Ipsa vero EX talium cxvii et xxxiii, qualium est EN ypothenusa cxx, et qualium est ergo EX quidem recta x et lxorum viii, DE vero que inter centra x et xix, talium et EN erit x et xx, et ex his ergo equalem ad proximum recte DE que inter centra rectam EN rursum assumpsit que per M medium apoguium recte MB in N prosneusis. Et ex aliis vero pluribus observationis easdem proportiones ad proximum collectas reperimus, quare ex his confirmari quod circa ypothesim Lune secundum epicicli prosneusim proprium: centra centra] centri V2F1 quidem epicicli circumductione circa E centra centra] centrum V2F1 eius qui per media animalia completa, idem autem et secundum quod medium apoguium epicicli punctum determinate eius diametro non iam ad E centra omale circumductionis prosneusim, quemadmodum in aliis faciente, sed semper ad N secundum equalem altera distantiam DE que inter centra recte.
〈V.6〉 Quomodo per lineas a periodicis motibus examinatus Lune progressus sumatur
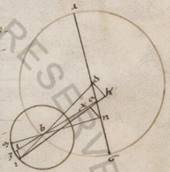 His autem ita demonstratis, consequenti que existente adiungere, quomodo et in particularibus Lune progressibus progressibus] add. motivorum V2F1 motuum epochas sumentes reperiemus et ab eo qui remotionis numero et ab eo qui secundum Lune epiciclum factam appositionem vel ablationem ei qui secundum longitudinem medio progressui eius que penes anomaliam differentie, per lineas quidem huiusmodi sumitur discretio a simillibus eis que exposita sunt theorematibus. Si enim exempli causa in posteriore preiacencium descriptionum eosdem supponamus periodicos motus remotionis et anomalie, hoc est remotionis quidem ex duplicatione congregatos gradus xc et xxx, anomalie vero a medio apoguio epicicli gradus cccxxxiii et xii, et pro EX quidem catheto NX adducemus, pro BL vero IL, per eadem quidem rursum exdari ad E centrum angulos et DE et EN ypothenusas equales existentes, utraque quidem rectarum DK et NX talium ostenditur x et xix ad proximum, qualium est DB quidem que e centro excentrici xlix et xli, BI vero que e centro epicicli v et xv. Utraque vero rectarum EK et EX eorumdem o v et propter hoc BK quidem tota erit, quemadmodum autem ostendemus, eorumdem xlviii et xxxvi, BE vero similiter xlviii et xxxi, BX autem reliquorum xlviii et xxvi. Quare quoniam et que a rectis BX et XN composita faciunt quod a recta BN et ipsum habebimus longitudine talium xlix et xxxi, qualium erat NX recta x et xix, et qualium ergo est BN ypothenusa cxx, talium erit et NX quidem recta xxv ad proximum, que vero super ipsam periferia talium xxiiii et iii, qualium est qui circa BNX orthogonium circulus ccclx. Quare et NBX angulus, hoc est ZBM, qualium quidem sunt ii recti ccclx, talium erit xxiiii et iii, qualium vero iiii recti ccclx talium xii et i ad proximum, tantorum ergo est ZM epicicli periferia. Sed quoniam I punctus Lune distat ab M medio apoguio reliquos in unum circulum gradibus xxvi et xlviii, et reliquam habebimus IZ periferiam graduum xiiii et xlvii. Quare et IBZ angulus qualium quidem sunt iiii recti ccclx, talium est xiiii et xlvii, qualium autem ii recti ccclx, talium xxix et xxxiiii et que quidem super IL periferia talium est xxix et xxxiiii, qualium qui circa IBL orthogonium circulus ccclx, que autem super LB reliquorum in semicirculum cl et xxvi et earum ergo que sub ipsis rectarum IL quidem erit talium xxx et xxxvii, qualium est BI ypothenusa ccxx, LB vero eorumdem cxvi et ii. Quare et qualium est BI quidem que e centro epicicli v et xv, BE vero ostensa est xlviii et xxxi, talium et IL quidem erit unius et xx, LB vero similiter v et v, et tota ergo EBL talium est liii et xxxvi, qualium et li erat unius et xx. Et quoniam rursum que ab eis composita fatiunt quod ab EI tetragonum habebimus et EI longitudine eorumdem liii et xxxvii ad proximum. Quare et qualium est EI ypothenusa cxx, talium et IL quidem erunt ii et lix, que vero super ipsam periferia talium ii et lii, qualium est qui circa EIL orthogonium circulus ccclx, et IEL ergo angulus eius que penes anomaliam differentie, qualium quidem sunt ii recti ccclx, talium est ii et lii, qualium autem iiii recti ccclx, talium unius et xxvi. Quod propositum erat demonstrare.
His autem ita demonstratis, consequenti que existente adiungere, quomodo et in particularibus Lune progressibus progressibus] add. motivorum V2F1 motuum epochas sumentes reperiemus et ab eo qui remotionis numero et ab eo qui secundum Lune epiciclum factam appositionem vel ablationem ei qui secundum longitudinem medio progressui eius que penes anomaliam differentie, per lineas quidem huiusmodi sumitur discretio a simillibus eis que exposita sunt theorematibus. Si enim exempli causa in posteriore preiacencium descriptionum eosdem supponamus periodicos motus remotionis et anomalie, hoc est remotionis quidem ex duplicatione congregatos gradus xc et xxx, anomalie vero a medio apoguio epicicli gradus cccxxxiii et xii, et pro EX quidem catheto NX adducemus, pro BL vero IL, per eadem quidem rursum exdari ad E centrum angulos et DE et EN ypothenusas equales existentes, utraque quidem rectarum DK et NX talium ostenditur x et xix ad proximum, qualium est DB quidem que e centro excentrici xlix et xli, BI vero que e centro epicicli v et xv. Utraque vero rectarum EK et EX eorumdem o v et propter hoc BK quidem tota erit, quemadmodum autem ostendemus, eorumdem xlviii et xxxvi, BE vero similiter xlviii et xxxi, BX autem reliquorum xlviii et xxvi. Quare quoniam et que a rectis BX et XN composita faciunt quod a recta BN et ipsum habebimus longitudine talium xlix et xxxi, qualium erat NX recta x et xix, et qualium ergo est BN ypothenusa cxx, talium erit et NX quidem recta xxv ad proximum, que vero super ipsam periferia talium xxiiii et iii, qualium est qui circa BNX orthogonium circulus ccclx. Quare et NBX angulus, hoc est ZBM, qualium quidem sunt ii recti ccclx, talium erit xxiiii et iii, qualium vero iiii recti ccclx talium xii et i ad proximum, tantorum ergo est ZM epicicli periferia. Sed quoniam I punctus Lune distat ab M medio apoguio reliquos in unum circulum gradibus xxvi et xlviii, et reliquam habebimus IZ periferiam graduum xiiii et xlvii. Quare et IBZ angulus qualium quidem sunt iiii recti ccclx, talium est xiiii et xlvii, qualium autem ii recti ccclx, talium xxix et xxxiiii et que quidem super IL periferia talium est xxix et xxxiiii, qualium qui circa IBL orthogonium circulus ccclx, que autem super LB reliquorum in semicirculum cl et xxvi et earum ergo que sub ipsis rectarum IL quidem erit talium xxx et xxxvii, qualium est BI ypothenusa ccxx, LB vero eorumdem cxvi et ii. Quare et qualium est BI quidem que e centro epicicli v et xv, BE vero ostensa est xlviii et xxxi, talium et IL quidem erit unius et xx, LB vero similiter v et v, et tota ergo EBL talium est liii et xxxvi, qualium et li erat unius et xx. Et quoniam rursum que ab eis composita fatiunt quod ab EI tetragonum habebimus et EI longitudine eorumdem liii et xxxvii ad proximum. Quare et qualium est EI ypothenusa cxx, talium et IL quidem erunt ii et lix, que vero super ipsam periferia talium ii et lii, qualium est qui circa EIL orthogonium circulus ccclx, et IEL ergo angulus eius que penes anomaliam differentie, qualium quidem sunt ii recti ccclx, talium est ii et lii, qualium autem iiii recti ccclx, talium unius et xxvi. Quod propositum erat demonstrare.
〈V.7〉 Negotium canonos universalis anomalie Lune
Ut autem rursum et per canonicam expositionem doceamus eam que ex promtu discretionem particularium prostaferesium, adimplevimus quod secundum simplicem ypothesim perexpositarum perexpositarum] perexpositorum V2F1 nobis canoniorum et duplam anomaliam prompta prompta] prompte V2F1 dirigere potentibus selidiis per easdem lineas rursus utentes ephodis. Post prima namque selidia duo continentia numeros inposuimus tertium selidium continens factas prostafereses ei qui anomalie numero, ad medio apoguio, hoc est M, congregatum ex mediis progressibus transferri ad examinatum apoguion, hoc est Z. Quemadmodum enim in exposita remotione xc graduum et xxx demonstravimus ZM periferiam graduum existentem xii et i, ut quoniam quidem ab M medio apoguio distabat Luna gradibus cccxxxiii et xii, ab Z examinato apoguio distantiam inveniemus eius congregatam graduum manifestum quoniam cccxlv et xiii, ad quos que propter epiciclum prosthapheresis eius qui secundum longitudinem medii motus debet sumi; ita et in aliis remotionis numeris, per quot commensurabilis erat portiones, factas preiacentis prostafereseos quantitates per eadem sumentes, ne secundum unumquodque longum sermonem faciamus, apposuimus proprie cuique numerorum in tertio selidio. Eorum autem que deinceps selidiorum quartum quidem continebit preexpositas in primo canonio differentias eius que penes epiciclum anomalie, velut maxima prostaferesi usque v gradus et i ad proximum contingente secundum eam que lx ad v et xv proportionem, quintum vero superhabundantias factarum differentiarum ex secunda anomaliarum penes primam, velut et hic maxima prostaferesi graduum congregata vii et Γο secundum eam que lx ad viii proportionem, ut quartum quidem selidium sit secundum apoguion excentrici circa sinzugias facta positione epicicli, quintum vero earum que congregatur congregatur] congregantur V2F1 superhabundantiarum ex secundum periguium excentrici dichothomias completa anomalia. Causa vero secundum intermedios duarum istarum positionum motus epicicli pertinentes partes adiacentium superhabundantiarum sumendi proportionaliter apposuimus vi selidium continens lx, quot oporteret secundum unumquemque remotionis numerum adiacentis differentie sumpta apponere ei que penes primam anomaliam exposite secundum quartum selidium prostaferesi, et hec utique nobis ordinata sunt ad hunc modum.
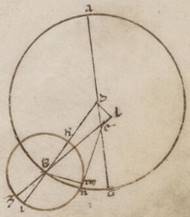 Esto enim rursum excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua subiaceat centrum eius qui per media animalia E, et assumpta AB periferia, scriptoque epiciclo B circa ZITK, protrahatur EBZ EBZ] add. dentur V2F1. autem verbi gratia remocionis gradus lx, quare propter easdem predemonstratis esse rursum AEB angulum duplicatorum subiacentis remotionis graduum cxx, et trahatur quidem cathetus DL in BE eductam a puncto D, et subiaceat ab E centro in Lunam eiecta recta contingens epiciclum, ut plurima fiat differentia anomalie, velut EMN, copuleturque BM. Quoniam ergo AEB angulus, qualium quidem sunt iiiior recti ccclx, talium subiaceat cxx, qualium autem duo recti ccclx, talium ccxl erit utique, et DEL angulus reliquorum in duos rectos cxx. Quare et que quidem super DL rectam periferiam talium cxx, qualium qui circa DEL orthogonium circulus ccclx, que vero super EL reliquorum in semicirculum lx, et earum ergo que sub ipsas rectarum EL quidem talium erit lx, qualium DE ypothenusa cxx, DL vero eorumdem ciii et lv. Et qualium ergo est DE quidem recta x et xix, DB vero similiter xlix et xli, talium erit et EL quidem recta v et xv ad proximum, DL vero similiter viii et lvi. Et quoniam quod ab BD deficiens eo quod ab DL facit quod ab BL, longitudine ergo erit et tota quidem BEL recta xlviii et liii, reliqua vero EB talium xliii et xliii, qualium est MB que e centro epicicli v et xv. Et qualium ergo est EB ypothenusa cxx, talium erit et BM quidem recta xiiii et xxv, que vero super eam periferia talium xiii et xlviii, qualium est qui circa BEM orthogonium circulus ccclx, et BEM ergo angulus qui continet plurimam differentiam anomalie, qualium quidem sunt ii recti ccclx, talium est xiii et xlviii, qualium vero iiii recti ccclx, talium vi et liiii. Distitit ergo secundum istam remocionis distantiam ea que penes anomaliam differentia differentia] add. a V2 secundum apoguion factis gradibus v et i uno gradu lxis liii. Est autem et tota usque periguion differentia graduum ii et xxxix. Et qualium ergo est maxima differentia lx, talium erit que unius gradus et liii lxorum xlii et xxxviii, que et apponemus cxx numero in vio selidio. Similiter autem et in reliquis portionibus computantes rursus per eadem ita sumptas partes eius que duarum anomaliarum superhabundantie, apposuimus propriis numeris pertinentia cuique adiacentis superhabundantie lxa, totis lx manifestum quoniam appositis duplicato xc graduum remotionis numero, qui est secundum clxxx a perguio excentrici, et vii vero apposuimus selidium continens secundum latitudinem factos progressus Lune in utrasque partes eius qui per media animalia, ut in eo qui per polos eius, hoc est asumptas huius circuli periferias inter eum qui per media animalia et eum qui circa ipsum centrum obliquum Lune circulum, sed sed] secundum V2F1 unumquemque particularium in obliquo progressuum. Usi autem sumus et ad hoc demonstratione huiusmodi per quam et eas que inter equinoctialem et eum qui per media animalia periferias eius qui per polos equinoctialis investigavimus, hic tamen velut ea que inter zodiacum et borealem vel australem terminum obliqui circuli periferia maximi per ambos polos ipsos scripti circuli v graduum existente, quoniam quidem et nobis quemadmodum et Iparco per circa borealissimos et australissimos progressus apparentia investigatus tantus ad proximum in utraque zodiaci progressus Lune plurimus deprehenditur et universa fere que circa observationes eius et eas que ad stellas et eas que per organa considerantur consone adaptantur tantis secundum latitudinem maximis progressionibus, ut per deinceps demonstrata confitebitur. Et est universalis Lune anomalie canonium huiusmodi.
Esto enim rursum excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua subiaceat centrum eius qui per media animalia E, et assumpta AB periferia, scriptoque epiciclo B circa ZITK, protrahatur EBZ EBZ] add. dentur V2F1. autem verbi gratia remocionis gradus lx, quare propter easdem predemonstratis esse rursum AEB angulum duplicatorum subiacentis remotionis graduum cxx, et trahatur quidem cathetus DL in BE eductam a puncto D, et subiaceat ab E centro in Lunam eiecta recta contingens epiciclum, ut plurima fiat differentia anomalie, velut EMN, copuleturque BM. Quoniam ergo AEB angulus, qualium quidem sunt iiiior recti ccclx, talium subiaceat cxx, qualium autem duo recti ccclx, talium ccxl erit utique, et DEL angulus reliquorum in duos rectos cxx. Quare et que quidem super DL rectam periferiam talium cxx, qualium qui circa DEL orthogonium circulus ccclx, que vero super EL reliquorum in semicirculum lx, et earum ergo que sub ipsas rectarum EL quidem talium erit lx, qualium DE ypothenusa cxx, DL vero eorumdem ciii et lv. Et qualium ergo est DE quidem recta x et xix, DB vero similiter xlix et xli, talium erit et EL quidem recta v et xv ad proximum, DL vero similiter viii et lvi. Et quoniam quod ab BD deficiens eo quod ab DL facit quod ab BL, longitudine ergo erit et tota quidem BEL recta xlviii et liii, reliqua vero EB talium xliii et xliii, qualium est MB que e centro epicicli v et xv. Et qualium ergo est EB ypothenusa cxx, talium erit et BM quidem recta xiiii et xxv, que vero super eam periferia talium xiii et xlviii, qualium est qui circa BEM orthogonium circulus ccclx, et BEM ergo angulus qui continet plurimam differentiam anomalie, qualium quidem sunt ii recti ccclx, talium est xiii et xlviii, qualium vero iiii recti ccclx, talium vi et liiii. Distitit ergo secundum istam remocionis distantiam ea que penes anomaliam differentia differentia] add. a V2 secundum apoguion factis gradibus v et i uno gradu lxis liii. Est autem et tota usque periguion differentia graduum ii et xxxix. Et qualium ergo est maxima differentia lx, talium erit que unius gradus et liii lxorum xlii et xxxviii, que et apponemus cxx numero in vio selidio. Similiter autem et in reliquis portionibus computantes rursus per eadem ita sumptas partes eius que duarum anomaliarum superhabundantie, apposuimus propriis numeris pertinentia cuique adiacentis superhabundantie lxa, totis lx manifestum quoniam appositis duplicato xc graduum remotionis numero, qui est secundum clxxx a perguio excentrici, et vii vero apposuimus selidium continens secundum latitudinem factos progressus Lune in utrasque partes eius qui per media animalia, ut in eo qui per polos eius, hoc est asumptas huius circuli periferias inter eum qui per media animalia et eum qui circa ipsum centrum obliquum Lune circulum, sed sed] secundum V2F1 unumquemque particularium in obliquo progressuum. Usi autem sumus et ad hoc demonstratione huiusmodi per quam et eas que inter equinoctialem et eum qui per media animalia periferias eius qui per polos equinoctialis investigavimus, hic tamen velut ea que inter zodiacum et borealem vel australem terminum obliqui circuli periferia maximi per ambos polos ipsos scripti circuli v graduum existente, quoniam quidem et nobis quemadmodum et Iparco per circa borealissimos et australissimos progressus apparentia investigatus tantus ad proximum in utraque zodiaci progressus Lune plurimus deprehenditur et universa fere que circa observationes eius et eas que ad stellas et eas que per organa considerantur consone adaptantur tantis secundum latitudinem maximis progressionibus, ut per deinceps demonstrata confitebitur. Et est universalis Lune anomalie canonium huiusmodi.
〈V.7〉 Canonium universalis anomalie Lune
| Canonium universalis anomalie LUNE | ||||||||||||
| Numeri communes | Prostaferesis Excentrica | Canonium universalis Anomalie Lune | Prostaferesis circuli revolutionis | Differentia minutorum | Latitudine | |||||||
| Gradus | Gradus | Gradus | Minuta | Gradus | Minuta | Gradus | Minuta | Gradus | Minuta | Gradus | Minuta | |
| vi | cccliiii | o | liii | o | xxix | o | xiiii | o | xii | iii | lviii | |
| xii | cccxlviii | i | xlvii | o | lvii | o | xxvii | o | xxxiiii | iiii | liiii | |
| xviii | cccxlii | ii | xxxix | i | xxv | o | xlii | i | xx | iiii | xlv | |
| xxiiii | cccxxxvi | iii | xxxi | i | liii | o | lvi | ii | xvi | iiii | xxxiiii | |
| xxx | cccxxx | iiii | xxiii | ii | xix | i | x | iii | xxiiii | iiii | xx | |
| xxxvi | cccxxiiii | v | xv | ii | xliiii | i | xxiii | iiii | xxxii | iiii | iii | |
| xliii | cccxviii | vi | vii | iii | viii | i | xxxv | vi | xxv | iii | xliii | |
| xlviii | cccxii | vi | lviii | iii | xxxi | i | xlv | viii | xviii | iii | xx | |
| liiii | cccvi | vii | xlviii | iii | li | i | liiii | x | xxii | ii | lvi | |
| lx | ccc | viii | xxxvi | iiii | viii | ii | iii | xii | xxvi | ii | xxx | |
| lxvi | ccxciiii | ix | xxii | iiii | xxiiii | ii | xi | xv | v | ii | ii | |
| lxxii | cclxxxviii | x | vi | iiii | xxxviii | ii | xviii | xvii | xliiii | i | xxxiii | |
| lxxviii | cclxxxii | x | xlviii | iiii | xlix | ii | xxv | xx | xxxiiii | i | iii | |
| lxxxiiii | cclxxvi | xi | xxvii | iiii | lvi | ii | xxxi | xxiii | xxiiii | o | xxxii | |
| xc | cclxx | xii | o | iiii | lix | ii | xxxvii | xxvi | xxxvi | o | o | |
| xciii | cclxvii | xii | xv | v | o | ii | xxxvii | xxviii | xii | o | xvi | |
| xcvi | cclxiiii | xii | xxviii | v | i | ii | xxxviii | xxix | xlix | o | xxxii | |
| xcix | cclxi | xii | xxxix | v | o | ii | xxxix | xxxi | xxv | o | xlviii | |
| cii | cclviii | xii | xlviii | iiii | lix | ii | xxxix | xxxiii | i | i | iii | |
| cv | cclv | xii | lvi | iiii | lvii | ii | xxxviii | xxxiiii | xxxvii | i | xviii | |
| cviii | cclii | xiii | ii | iiii | liii | ii | xxxviii | xxxvi | xiiii | i | xxxiii | |
| cxi | ccxlix | xiii | vi | iiii | xlix | ii | xxxvii | xxxvii | l | i | xlviii | |
| cxiiii | ccxlvi | xiii | ix | iiii | xliiii | ii | xxxiiii | xxxix | xxvi | ii | ii | |
| cxvii | ccxliii | xiii | vii | iiii | xxxviii | ii | xxxii | xli | ii | ii | xvi | |
| cxx | ccxl | xiii | iiii | iiii | xxxii | ii | xxxi | xlii | xxxviii | ii | xxx | |
| cxxiii | ccxxxvii | xii | lix | iiii | xxv | ii | xxviii | xliiii | iii | ii | xliii | |
| cxxvi | ccxxxiiii | xii | l | iiii | xvi | ii | xxiiii | xlv | xxviii | ii | lvi | |
| cxxviiii | ccxxxi | xii | xxxvi | iiii | vii | ii | xx | xlvi | xxxiii | iii | viii | |
| cxxxii | ccxxviii | xii | xvi | iii | lvii | ii | xvi | xlviii | xxxviii | iii | xxi | |
| cxxxv | ccxxv | xi | liiii | iii | xlvi | ii | xi | xlix | xxxii | iii | xxxii | |
| cxxxviii | ccxxii | xi | xxviiii | iii | xxxv | ii | v | l | xlv | iii | xliii | |
| cxli | ccxix | xi | ii | iii | xxiii | i | lviii | li | lix | iii | liii | |
| cxliiii | ccxvi | x | xxxiii | iii | x | i | li | lii | l | iii | iii | |
| cxlvii | ccxiii | x | o | ii | lvii | i | xliii | liiii | iii | iiii | xi | |
| cl | ccx | ix | xxii | ii | xliii | i | xxxv | lv | xiiii | iiii | xx | |
| cliii | ccvii | viii | xxxviii | ii | xxviii | i | xxvii | lv | xlv | iiii | xxvii | |
| clvi | cciiii | vii | xlviii | ii | xiii | i | xix | lvi | xlvi | iiii | xxxiiii | |
| clix | cci | vi | lvi | i | lvii | i | xi | lvii | xv | iiii | xl | |
| clxii | cxcviii | vi | iii | i | xli | i | ii | lvii | lv | iiii | xlv | |
| clxv | cxcv | v | viii | i | xxv | o | lii | lviii | xxxv | iiii | l | |
| clxviii | cxcii | iiii | xi | i | ix | o | xlii | lviii | xxxiiii | iiii | liiii | |
| clxxi | clxxxi | iii | xii | o | lii | o | xxxii | lix | xxvi | iiii | lvi | |
| clxxiiii | clxxxvi | ii | xi | o | xxxv | o | xxi | lix | xxxvii | iiii | lviii | |
| clxxvii | clxxxiii | i | vii | o | xviii | o | x | lix | xlix | iiii | lix | |
| clxxx | clxxx | o | o | o | o | o | o | lx | o | v | o |
〈V.8〉 De universali compoto Lune
Quotienscumque ergo voluerimus per expositionem canonii compotum lunaris anomalie facere, sumentes eos qui secundum subiacens in Alexandria tempus medios motus Lune et longitudinis et remotionis et anomalie et latitudinis secundum subobstensum subobstensum] corr. ex obtsensum V3 subostensum V2F1 modum collectum primum remocionis numerum duplicantes semper et aufferentes, si habuerimus, circulum inferentesque in anomalie canonium adiacentes ipsi gradui in iiio selidio, numero quidem duplicato usque clxxx graduum existente, apponemus anomalie gradibus mediis, excedente vero clxxx, auferemus ab ipsis et factum examinatum anomalie numerum inferemus in idem canonium, et adiacentem ipsi prosthaferesim in iiiio selidio et adhuc adiacentem in vo selidio differentiam describemus seorsum. Post hec vero et duplicatum medie revolucionis numerum inferentes in eadem selidia, quod utique adiacebunt ipsi lxa in vio selidio, totidem lxa sumentes eius, quam descripsimus differentie, apponemus semper exposite quarti selidii prosthaferesi et collectos gradus, si quidem anomalie examinatus numerus usque clxxx gradus fiunt, fiunt] fuerit V2F1 auferemus a longitudinis et latitudinis mediis gradibus, si autem super clxxx, apponemus ipsis, et factorum numerorum eum quidem qui longitudinis eitientes ab ea que secundum epochim moitothesia, moitothesia] moirothesia V2 ubi utique defecerit, ibi Lunam dicemus esse examinate, latitudinis quidem eum qui a boreali fine inferemus in idem canonium et, quotcumque fuerint adiacentes ipsi gradus in vii selidio latitudinis, totidem distabat ab eo qui per media animalia centrum, Lune in maximo per polos eius scripto circulo, et si quidem illatus numerus in primis fiunt fiunt] fuerit V2 v versibus, ut ad arctos, si autem in eis qui sub ipsos, ut ad meridiem, primo quidem numerorum selidio continente eum qui ab arctis ad meridiem eius progressum, si vero secundo Si vero secundo] secundo vero V2 eum qui a meridie ad arctos.
〈V.9〉 Quoniam cura nulla digna fuit differentia in sinzugiis penes excentricum Lune circulum
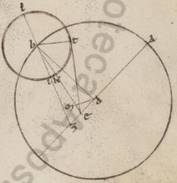 Quoniam vero consequens est dubitare aliquos, nunquando et circa sinodos et panselinia et eas que in ipsis eclipses cura digna aliqua differentia consequatur et per excentricum Lune circulum, propter non semper et omnino in ipsis in ipso apoguiotato centrum contingere epicicli, sed et distare ab ipso periferiam suffitientem dari, propter eas quidem que secundum apoguion positiones in medie consideratis sinzugiis compleri, examinatas vero sinodos et panselinia cum utriusque luminarium anomalia sumi, temptabimus ostendere huiusmodi differentiam nulla cura dignam fallaciam circa apparentia secundum sinzugias potentem operari, etsi non coinvestigetur que penes excentrotica circuli differentia. Esto enim excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua sumatur eius quidem qui per media animalia circuli centrum secundum E punctum, contraiacens vero ei quod est D prosneuseos punctum secundum Z, et assumpta ab A apoguio AB periferia, scribatur quidem circa B circulus ITKL, copulentur vero BD et IBKE et adhuc BLZ. Quoniam ergo secundum duos modos potest differre que penes anomaliam quantitas eius que secundum A apoguion posicionis epicicli, et propter periguioteron ipsum factum maiorem ad E angulum deprehendere, et propter prosneusim eius que secundum medium apoguion et periguion diametri nequaquam ad E centrum, sed ad Z punctum fieri, plurima autem constituitur que quidem penes primam causam differentia, quando que et penes anomaliam Lune plurima fiunt, fiunt] fuerit V2F1 que autem secundum secundam, quando circa apoguion vel periguion Luna fiunt fiunt] fuerit V2F1 epicicli, manifestum quoniam, quando ea quidem que penes primam causam differentia plurima contingit, tunc que quidem penes secundam insensibilis erit omnino, propter Lunam in contingentibus epiciclum rectis existentem in multum prostrapheresim indifferentem facere. Possibile autem erit examinatam sinzugiam a mediam differre coutrisque que penes anomaliam differentiis, utriusque luminum huius quidem secundum appositionem existente, illius vero secundum ablationem. Quando vero que penes secundam prosneuseos differentia plurima contingit, tunc que quidem penes primam rursus insensibilis est, propter et totam que penes anomaliam vel nullam vel parvam omnino fieri, Luna circa apoguion vel periguion epicicli contingente. Differt autem examinata sinzugia a medie considerata sola ea que penes solarem anomaliam differentia. Subiaceat ergo Sol quidem plurimam appositionem facies facies] faciens F1 ii graduum et xxiii, Luna vero primum et ipsa plurimam ablacionem faciens v graduum et i, ut et AEB angulus coutrorumque vii graduum et xxiiii duplicatos contineat xiiii et xlviii, tractaque ab E puncto contingente epicicli ET, copuletur BT cathetus, et adhuc ab D in BE cathetus trahatur DM. Quoniam ergo AEB angulus, qualium quidem sunt iiii recti ccclx, talium est xiiii et xlviii, qualium vero ii recti ccclx, talium xxix et xxxvi, erit utique et que quidem super DM periferia talium xxix et xxxvi, qualium est qui circa DEM orthogonium circulus ccclx, que vero super EM reliquorum in semicirculum cl et xxiiii, et earum ergo que sub ipsis rectarum DM quidem talium erit xxx et xxxix, qualium est DE ypothenusa cxx, EM vero eorumdem cxvi et i. Quare et qualium est DE quidem que inter centra x et xix, BD vero que e centro excentrici xlix et xli, talium et DM quidem erit ii et xxxviii, EM vero similiter ix et lix. Et quoniam ab BD deficiens eo quod ab DM facit quod ab BM, fit et BM quidem recta xlix et xxxvii, BME vero tota talium lix et xxxvi, qualium est et BT que e centro epicicli v et xv, et qualium ergo est EB ypothenusa cxx, talium et BT quidem recta erit x et xxxiiii, que vero super ipsam periferia talium x et lxorum, qualium est qui circa BET orthogonium circulus ccclx, et BET ergo angulus plurime differentie anomalie, qualium quidem sunt duo recti ccclx, talium erit x et lxorum vi, qualium vero iiii recti ccclx, talium v et iii pro v et i factis, secundum A apoguion existente epiciclo, distant ergo penes istam causam que penes anomaliam differentia lxis ii unius gradus, que nec xviam possunt unius hore metiri.
Quoniam vero consequens est dubitare aliquos, nunquando et circa sinodos et panselinia et eas que in ipsis eclipses cura digna aliqua differentia consequatur et per excentricum Lune circulum, propter non semper et omnino in ipsis in ipso apoguiotato centrum contingere epicicli, sed et distare ab ipso periferiam suffitientem dari, propter eas quidem que secundum apoguion positiones in medie consideratis sinzugiis compleri, examinatas vero sinodos et panselinia cum utriusque luminarium anomalia sumi, temptabimus ostendere huiusmodi differentiam nulla cura dignam fallaciam circa apparentia secundum sinzugias potentem operari, etsi non coinvestigetur que penes excentrotica circuli differentia. Esto enim excentricus Lune circulus ABG circa centrum D et diametrum ADG, in qua sumatur eius quidem qui per media animalia circuli centrum secundum E punctum, contraiacens vero ei quod est D prosneuseos punctum secundum Z, et assumpta ab A apoguio AB periferia, scribatur quidem circa B circulus ITKL, copulentur vero BD et IBKE et adhuc BLZ. Quoniam ergo secundum duos modos potest differre que penes anomaliam quantitas eius que secundum A apoguion posicionis epicicli, et propter periguioteron ipsum factum maiorem ad E angulum deprehendere, et propter prosneusim eius que secundum medium apoguion et periguion diametri nequaquam ad E centrum, sed ad Z punctum fieri, plurima autem constituitur que quidem penes primam causam differentia, quando que et penes anomaliam Lune plurima fiunt, fiunt] fuerit V2F1 que autem secundum secundam, quando circa apoguion vel periguion Luna fiunt fiunt] fuerit V2F1 epicicli, manifestum quoniam, quando ea quidem que penes primam causam differentia plurima contingit, tunc que quidem penes secundam insensibilis erit omnino, propter Lunam in contingentibus epiciclum rectis existentem in multum prostrapheresim indifferentem facere. Possibile autem erit examinatam sinzugiam a mediam differre coutrisque que penes anomaliam differentiis, utriusque luminum huius quidem secundum appositionem existente, illius vero secundum ablationem. Quando vero que penes secundam prosneuseos differentia plurima contingit, tunc que quidem penes primam rursus insensibilis est, propter et totam que penes anomaliam vel nullam vel parvam omnino fieri, Luna circa apoguion vel periguion epicicli contingente. Differt autem examinata sinzugia a medie considerata sola ea que penes solarem anomaliam differentia. Subiaceat ergo Sol quidem plurimam appositionem facies facies] faciens F1 ii graduum et xxiii, Luna vero primum et ipsa plurimam ablacionem faciens v graduum et i, ut et AEB angulus coutrorumque vii graduum et xxiiii duplicatos contineat xiiii et xlviii, tractaque ab E puncto contingente epicicli ET, copuletur BT cathetus, et adhuc ab D in BE cathetus trahatur DM. Quoniam ergo AEB angulus, qualium quidem sunt iiii recti ccclx, talium est xiiii et xlviii, qualium vero ii recti ccclx, talium xxix et xxxvi, erit utique et que quidem super DM periferia talium xxix et xxxvi, qualium est qui circa DEM orthogonium circulus ccclx, que vero super EM reliquorum in semicirculum cl et xxiiii, et earum ergo que sub ipsis rectarum DM quidem talium erit xxx et xxxix, qualium est DE ypothenusa cxx, EM vero eorumdem cxvi et i. Quare et qualium est DE quidem que inter centra x et xix, BD vero que e centro excentrici xlix et xli, talium et DM quidem erit ii et xxxviii, EM vero similiter ix et lix. Et quoniam ab BD deficiens eo quod ab DM facit quod ab BM, fit et BM quidem recta xlix et xxxvii, BME vero tota talium lix et xxxvi, qualium est et BT que e centro epicicli v et xv, et qualium ergo est EB ypothenusa cxx, talium et BT quidem recta erit x et xxxiiii, que vero super ipsam periferia talium x et lxorum, qualium est qui circa BET orthogonium circulus ccclx, et BET ergo angulus plurime differentie anomalie, qualium quidem sunt duo recti ccclx, talium erit x et lxorum vi, qualium vero iiii recti ccclx, talium v et iii pro v et i factis, secundum A apoguion existente epiciclo, distant ergo penes istam causam que penes anomaliam differentia lxis ii unius gradus, que nec xviam possunt unius hore metiri.
Rursum subiaceat secundum L medium periguium Luna, ut manifestum quoniam AEB angulus duplicatos ad proximum contineat solius solaris anomalie gradus iiii et xlvi, et copulata in simili descriptione EL recta, catheti trahantur in BE ab L quidem lii, lii] LN F1 ab Z vero eductam ZX; secundum eadem ergo eis que prius, quoniam quidem qui ad E angulus, qualium quidem sunt iiii recti ccclx, talium est iiii et xlvi, qualium vero duo recti ccclx, talium ix et xxxii, erit utique et que quidem super utrasque rectarum DM et ZX periferie talium ix et xxxii, qualium qui circa EDM et EZX sunt orthogonia circuli ccclx, que vero super utrasque rectarum EM et EX reliquorum in semicirculos clxx et xxviii, et earum ergo que sub ipsis rectarum utraque quidem rectarum DM et XZ talium erit ix lviii, qualium est utraque DE et EZ ypothenusarum cxx, utraque vero ME et EX rectarum eorumdem cxix et xxxv. Quare et qualium est utraque quidem DE et EZ rectarum x et xix, DB vero que e centro excentrici xlix et xli, erit et utraque quidem rectarum DM et ZX li, utraque autem rectarum ME et EX eorumdem x et xvii. Et quoniam ab BD defitiens eo quod ab DM facit quod ab BM, erit et BM longitudine eorumdem ad proximum 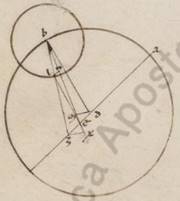 xlix et xli. Quare et BE quidem recta erit lix et lviii, BX autem tota talium lxx et xv, qualium et ZX erat li, propter eadem vero et BZ ypothenusa equalium erit ad proximum lxx et xv, et est sicut BZ ad utramque rectarum ZX et BX, ita BL ad utramque rectarum LN et BN. Quare et qualium est BL quidem que e centro epicicli v et xv, BE vero ostensa est lix et lviii, talium et LN quidem erit o et iiii, BN vero eorumdem ad proximum v et xv, reliqua autem NE talium liiii et xliii, qualium LN erat o et iiii. Quoniam autem propter preiacentia et EL ypothenusa non differt ab eisdem liiii et xliii, colligitur quoniam et qualium est EL ypothenusa cxx, talium et LN quidem recta erit o viii ad proximum, que vero super ipsam periferia talium o viii rursum, qualium est qui circa ELN orthogonium circulus ccclx, et BEL ergo angulus quem differebat Luna penes eam que in Z prosneusim, qualium quidem sunt iiii recti ccclx, talium o iiii, qualium autem ii recti ccclx, talium o viii. Quare et hic quod penes anomaliam Lune differebat lxis iiii, que nec ipsa faciunt aliquam cura dignam fallaciam circa sinzugias apparentia nec octavam ad proximum potentia unius hore, quantum et penes ipsas observationes minime minime] add. mirabile V2F1 erit sepe falli. Hoc tamen apposuimus, non quasi existente possibilli et ad sinzugiarum considerationes coinvestigari et has ipsas differentias, etsi brevissime contingant, sed tamquam nullo nobis sensibili peccato secundum eas que per expositas lunares eclipses apodixes, penes non couti ea que per excentrotica completa per ea que deinceps ypothesi.
xlix et xli. Quare et BE quidem recta erit lix et lviii, BX autem tota talium lxx et xv, qualium et ZX erat li, propter eadem vero et BZ ypothenusa equalium erit ad proximum lxx et xv, et est sicut BZ ad utramque rectarum ZX et BX, ita BL ad utramque rectarum LN et BN. Quare et qualium est BL quidem que e centro epicicli v et xv, BE vero ostensa est lix et lviii, talium et LN quidem erit o et iiii, BN vero eorumdem ad proximum v et xv, reliqua autem NE talium liiii et xliii, qualium LN erat o et iiii. Quoniam autem propter preiacentia et EL ypothenusa non differt ab eisdem liiii et xliii, colligitur quoniam et qualium est EL ypothenusa cxx, talium et LN quidem recta erit o viii ad proximum, que vero super ipsam periferia talium o viii rursum, qualium est qui circa ELN orthogonium circulus ccclx, et BEL ergo angulus quem differebat Luna penes eam que in Z prosneusim, qualium quidem sunt iiii recti ccclx, talium o iiii, qualium autem ii recti ccclx, talium o viii. Quare et hic quod penes anomaliam Lune differebat lxis iiii, que nec ipsa faciunt aliquam cura dignam fallaciam circa sinzugias apparentia nec octavam ad proximum potentia unius hore, quantum et penes ipsas observationes minime minime] add. mirabile V2F1 erit sepe falli. Hoc tamen apposuimus, non quasi existente possibilli et ad sinzugiarum considerationes coinvestigari et has ipsas differentias, etsi brevissime contingant, sed tamquam nullo nobis sensibili peccato secundum eas que per expositas lunares eclipses apodixes, penes non couti ea que per excentrotica completa per ea que deinceps ypothesi.
〈V.10〉 De permutationibus lune
Igitur ad conceptiones examinatorum Lune progressuum sumpta fere hec utique erit. Contingente vero in Luna et nec ad sensum eamdem fieri apparentem eius progressionem examinate, eo quod minime puncti rationem habeat, ut diximus, terra ad apostima spere eius, neccessarium utique erit et consequens et aliorum apparentium eam et eorum maxime que circa Solis eclipses considerantur de permutationibus ipsius facere sermonem, ex quibus possibile erit per eas que ad centrum terre et eius qui per media animalia circuli intelliguntur examinatas progressiones et a visu conspitientium, hoc est ab aliqua superfitie terre consideratas, discernere, et rursum e contrario ab apparentibus examinatas. Assequente vero huiusmodi considerationi neque particulares quantitates permutationum, nisi detur apostimatis proportio, posse tractari, neque ipsam apostimatis rationem, nisi detur aliqua permutatio, in nichil quidem sensibile permutatis, hec hec] hoc V2F1 est ad que utique terra puncti rationem habet, nec apostimatis proportionem manifestum quoniam possibile utique fiet sumere. In permutatis vero, quemadmodum in Luna, competit utique solum per aliquam primum datam permutationem apostimatis rationem invenire, propter aliquam quidem huiusmodi permutativam observationem et secundum seipsam posse concipi, apostimatis vero quantitatem nequaquam. Yparcus ergo a Sole maxime huiusmodi observationem facit. Quoniam enim a quibusdam aliis circa Solem et Lunam contigentibus, super quibus in eis que deinceps faciemus sermonem, consequitur, eo quod secundum alterum luminarium apostimate dato, et quod secundum alterum dari, temptat quod illud quod illud] inv. V2F1 Solis coniectans illud ita et illud … et] ita et illud V2F1 quod demonstrare demonstrare … Lune] inv. V2F1 Lune. Primum quidem supponens Solem minimum sensibile solum permutari, ut et apostima ipsius sumat, post hec vero et per appositam solarem eclipsim aliquotiens quidem quasi nichil sensibile, aliquotiens vero et quasi suffitiens Sole permutato, huic etiam ipsi et proportiones lunaris apostimatis differentes secundum unamquamque expositarum ypothesium apparebant, dubitato omnino circa Solem, non solum in quantum, sed et si quid omnino permutaretur.
〈V.11〉 De constructione organi paralictici
Nos autem, ut nichil immanifestorum in huiusmodi considerationem assumamus, construximus organum per quod possumus utique, ut est maxime, diligenter observare, quantum et a quanta eius qui secundum verticem differentia Luna permutatur, ut in maximo per polos orizontis et ipsam scripto circulo. Fecimus enim canones duos quadrilateros, longitudine quidem non minores iiii cubitis, ut divisiones in plures partes possunt fieri, continentia vero simmetros, quare et non converti propter longitudinem, sed extendi multum diligenter et in directo secundum unumquodque laterum. Deinde ascribentes lineas rectas in utroque secundum medium latius latus, apposuimus alteri canonium in extremitatibus ambabus recta prismatia tetragona circa mediam lineam et equalia parallila, foramen habens utrumque secundum medium diligenter factum, quod quidem in ad visum futurum subtile, quod vero ad Lunam maius, ita ut, apposito uno oculorum minus foramen habenti prismatio, per alterius et in directo foramen Lunam totam posse videri; perforantes ergo ex equo utrumque canonum secundum medias lineas in altero terminorum ad maius foramen habens prismatium et inaptantos inaptantos] inaptantes V2F1 per ambos axem, quare colligari quidem sub ipso ad lineas canonum latera velut sub centro, circumducci non non] vero V2 posse prismatia habentem ubique et indistorte, inclavantesque basi alterum canonum si si] non V2F1 habentem prismatia, sumpsimus in utriusque media linea puncta quedam ad eos qui ad basim terminos equaliter et plurimum ab eo quod secundum axem centro distantia, et divisimus determinatam lineam basim habentis canonis in partes lx et istarum etiam unamquamque in quot potuimus portiones. Apposuimus autem et post eumdem canonem ad terminos prismatia ea que in easdem partes latera ad eamdem lineam in directo invicem habentia et equalem distantia undique ab eodem et media linea, ut per ipsa cathetio dependente possit canon rectus et non inclinatus ad orizontis epipedum stare. Habentes autem et meridianam lineam anteductam in epipedo parallilo epipedo orizontis in aliquo non obscurato spatio constituamus organum rectum, quare latera canonum, secundum que iunguntur invicem sub axe, ad meridiem converti parallila facta adiacenti meridiane linee, et basim quidem habentem canonem rectum inacclinate et indistorte et firme stare, alterum vero circumagi commensurabiliter angustie circa axem in meridiani epipedo. Apposuimus autem alterum canonium subtile et rectum adaptatum quidem propter et ipsum circumagi clavo brevi secundum quid ad basim tantum divise linee, attingens vero usque plurimam preterlationem equaliter distantis termini alterius canonis linee, quare posse simul ipsi circumactum intermedium duorum terminorum factum in directo spatium ostendere.
Faciebamus ergo ad hunc modum Lune observationes secundum factas in ipso meridiano et circa tropica puncta eius qui per media animalia circuli progressiones. Quoniam quidem secundum tales habitudines et per polos orizontis et centrum Lune scripti maximi circuli eidem ad proximum fiunt per polos eius qui per media animalia scriptis, ad quos secundum latitudinem progressiones Lune considerantur, et examinata distantia puncti quod secundum verticem per hoc inde et prompte potest sumi, preterferentes ergo prismatia habentem canonem ad Lunam secundum ipsas que in meridiano progressiones, usque per ambo foramina secundum medium maioris foraminis centrum ipsius videatur, et signantes in subtili canonio intermediam extremarum que in canonibus rectarum distantiam et addentes ipsam divise in lx portiones linee recti canonis, reperimus quot est portionum predicte distantie recta, qualium est que e centro circumactione scripti in meridiani epipedo circuli manifestum quoniam lx, et sumentes a tanta recta subtensam periferiam, istam habuimus quam distabat tunc ab eo quod secundum verticem puncto apparens centrum Lune in maximo per polos orizontis et ipsum scripto circulo, qui idem faciebat faciebat] fiebat F1 tunc et per polos equinoctialis et eius qui per media animalia descripto meridiano. Itaque propter factam secundum latitudinem plurimam progressionem Lune examinate cognoscendam coutebamur perspectione, et circa estivum tropicum punctum maxime ipsa existente et adhuc circa ipsum obliqui eius circuli borealem terminum, et propter ista circa ista circa] inv. F1 puncta in suffitiens spatium eandem ad sensum secundum latitudinem progressionem determinari, et propter ad ipsum quod secundum verticem punctum tunc Lunam factam in eo qui per Alexandriam paralillo, secundum quem faciebamus observationes, eandem ad proximum facere apparentem portionem examinate. Deprehendebatur autem circa huiusmodi progressiones distans semper centrum Lune ab eo quod secundum verticem puncto ii et viiia ad proximum, quare et ex tali inquisitione v graduum demonstari plurimam ipsius secundum latitudinem in utraque eius qui per media animalia progressionem, quantis fere superhabundant qui ab eo quod secundum verticem puncto qui in equinoctialem in Alexandria ostensi gradus xxx et lviii defitientes apparentis distantie gradibus ii et viiia ab equinoctiali in estivum tropicum punctum demonstratis gradibus xxiii li. At vero et propter eam que ad permutationes inquisitionem faciendam, obervabamus rursum secundum eumdem modum Lunam circa quidem hyemale tropicum punctum contingentem et propter predicta et propter plurimum tunc ipsam distantem, ut in similli secundum meridianum progressione ab eo quod secundum verticem puncto permutationem et maiorem et notabiliorem dare. A pluribus ergo secundum huiusmodi progressiones observatis a nobis permutationibus unam rursum exponemus, per quam et computationis modum simul ostendemus et reliquorum demonstrationem secundum eam que deinceps consequentiam faciemus.
〈V.12〉 De apodixi apostimatum Lune
Observavimus enim xxo anno Adriani secundum Egiptios Athir xiii post v horas equinoctiales et dimidium et iii a meridie, futuro Sole secundum occidens, Lunam in meridiano factam et apparebat nobis per organum centrum eius distans ab eo quod secundum verticem puncto gradibus l et dimidio et xiiia et xiia. Que enim in subtili canonio distantia talium erat li et dimidii et xiia, inequalia divisa est que e centro circumactionis circuli lx. Tanta vero recta subtendit periferia talium l et dimidii et iiia et dimidii, qualium est circulus ccclx. Verum quod ab eis que in primo anno Navonassari epochis tempus usque quod secundum expositam observationem annorum egiptiacorum dccclxxxii et dierum lxxii et horarum equinoctialium simpliciter quidem v et dimidii et iiia, examinate vero v et iii. In quid quid] quod V2F1 tempus reperimus quidem Sole quid] quod V2F1 medie optinentem Chelarum vii gradus et xxxi, examinate vero v et xxviii, Lunam vero medie optinentem Sagitter Sagitter] Sagittarii V2 gradus xxv xliiii et apochim quidem graduum ccviii xiii, a medio autem apoguio epicicli cclxii xx, a boreali quoque termino latitudinis cccliiii xl. Adiungebat autem propter hec et que penes anomaliam differentiam undique ex proprio canone discretam graduum vii xxvi, quare et examinatam Lune positionem secundum illam horam optinere secundum longitudinem quidem Egoceri gradus iii et x, secundum latitudinem vero in obliquo quidem circulo a boreali fine gradus ii et vi, in eo autem qui per polos eius qui per media animalia, qui ipse ad proximum erat tunc meridiano, ab eo quidem qui per media animalia ad arctos gradus iiii lix. Distant vero et Egoceri quidem gradus iii et x ab equinoctiali ad meridiem in eodem circulo gradibus xxiii xlix, equinoctialis autem ab eo qui in Alexandria secundum verticem puncto ad meridiem similiter gradibus xxx et lviii. Itaque centrum Lune distabat examinate ab eo quod secundum verticem puncto gradibus xlix et xlviii, apparebat autem distans gradibus l et lv, permutata ergo est Luna secundum eam que circa expositum progressum distantiam gradibus i et lxis vii in maximo per ipsam et polos orizontis scripto circulo distans examinate ab eo qui secundum verticem puncto gradibus xlix et xlviii.
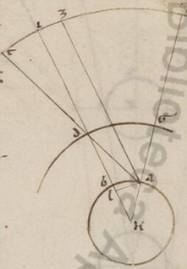 Hoc manifestato, scribantur in epipedo eius qui per polos orizontis et Lunam maximi circuli circa idem centrum terre quidem maximus circulus AB, qui vero per secundum observationem centrum Lune GD, ad quem vero terra puncti rationem habet EZIT, et centrum quidem commune omnium sit K, que autem per ea que secundum verticem puncta KAGE recta, subiaceat Luna secundum D punctum distans examinate ab eo quod secundum verticem puncto G preiacentibus gradibus xlix xlviii, et copulentur et KDI et ADT et adhuc ab A, quod sit visus videntium, cathetus quidem AB trahatur in KB, equidistans vero ei que est KI recta AZ. Quoniam ergo IT periferiam ab A conspitientibus permutata est Luna manifestum, quare erit utique unius gradus et lxorum vii ex observatione deprehensorum. Quoniam autem indifferenti maior est ZT periferia ea que est IT, eo quod terra tota puncti rationem habeat ad EZIT circulum, erit utique et ZIT periferia eorumdem ad proximum unius et vii. Quare et ZAT angulus, eo quod rursum non differat A punctum a centro ad ZT circulum, qualium quidem sunt iiii recti ccclx, talium est unius et vii, qualium vero ii recti ccclx, talium ii et xiiii. Eorumdem vero est et equalis ipsi angulus ADL ii et xiiii, et que super AL ergo rectam periferiam talium est ii et xiiii, qualium qui circa ADL orthogonium circulus ccclx. Ipsa vero AL recta talium ii et xxi, qualium est AD ypothesim ypothesim] ypothenusa V2F1 cxx. Ista autem indifferenti minor est LD, et qualium ergo est LA recta ii et xxi, talium est LD recta cxx ad proximum.
Hoc manifestato, scribantur in epipedo eius qui per polos orizontis et Lunam maximi circuli circa idem centrum terre quidem maximus circulus AB, qui vero per secundum observationem centrum Lune GD, ad quem vero terra puncti rationem habet EZIT, et centrum quidem commune omnium sit K, que autem per ea que secundum verticem puncta KAGE recta, subiaceat Luna secundum D punctum distans examinate ab eo quod secundum verticem puncto G preiacentibus gradibus xlix xlviii, et copulentur et KDI et ADT et adhuc ab A, quod sit visus videntium, cathetus quidem AB trahatur in KB, equidistans vero ei que est KI recta AZ. Quoniam ergo IT periferiam ab A conspitientibus permutata est Luna manifestum, quare erit utique unius gradus et lxorum vii ex observatione deprehensorum. Quoniam autem indifferenti maior est ZT periferia ea que est IT, eo quod terra tota puncti rationem habeat ad EZIT circulum, erit utique et ZIT periferia eorumdem ad proximum unius et vii. Quare et ZAT angulus, eo quod rursum non differat A punctum a centro ad ZT circulum, qualium quidem sunt iiii recti ccclx, talium est unius et vii, qualium vero ii recti ccclx, talium ii et xiiii. Eorumdem vero est et equalis ipsi angulus ADL ii et xiiii, et que super AL ergo rectam periferiam talium est ii et xiiii, qualium qui circa ADL orthogonium circulus ccclx. Ipsa vero AL recta talium ii et xxi, qualium est AD ypothesim ypothesim] ypothenusa V2F1 cxx. Ista autem indifferenti minor est LD, et qualium ergo est LA recta ii et xxi, talium est LD recta cxx ad proximum.
Rursum quoniam GD periferia subiacet graduum xlix et xlviii, erit utique et GKD angulus ad centrum existens circuli, qualium quidem sunt iiii recti ccclx, talium xlix et xlviii, qualium autem ii recti ccclx, talium xcx et xxxvi. Quare et que quidem super AL rectam periferia talium est xcix xxxvi, qualium qui circa ALK orthogonium circulus ccclx, que vero super LK reliquorum in semicirculum lxxx xxviiii, et subtendentium ergo ipsas rectarum AL quidem erit talium xci xxxix, qualium est AK ypothenusa cxx, LK vero eorumdem lxxvii xxvii. Quare et qualis unius est AK que e centro terre, talium et AL quidem erit o xlvi, KL vero similiter o xxxix. Sed et qualium erat AL recta ii xxi, talium LD ostensa est cxx, et qualium ergo est AL recta o xlvi talium erit et LD recta xxxix vi, eorumdem vero erat et KL quidem recta o xxxix, KA vero que e centro terre unius, unius terre] terre i V2F1 et qualis ergo est KA que e centro unius terre, talium erit et KLD tota continens vero illud quod secundum observationem Lune apostima xxxix xlv.
Hoc ostenso, esto Lune excentricus circulus ABG circa centrum D et diametrum ADG, in qua sumatur eius quidem qui per media animalia circuli centrum E, quod autem prosneuseos epicicli punctum Z et, scripto circa B punctum ITKL epiciclo, copulentur et IBTE et BD et BKZ. Subiaceat autem in preiacenti observatione Luna secundum L punctum, et copulentur quidem LE et LB. Catheti vero protrahantur in BE, ab D quidem educta, DM ab Z vero NZ. Quoniam ergo secundum tempus observationis apochis numerus erat lxxviii xiii, erit utique propter preconsiderata AEB quidem angulus, qualium sunt iiii recti ccclx, talium clvi xxvi, utraque utraque] uterque V2F1 vero angulorum ZEN et DEM reliquorum quidem in duos rectos xxiii xxxiiii, qualium vero sunt ii recti ccclx, talium xlvii viii. Quare et que quidem super utramque rectarum DM et ZN periferia talium erit xlvii viii, qualium sunt qui circa exposita orthogonia circuli ccclx, eo quod equalis sit DE ei que est EZ, que vero super utramque rectarum EM et EN eorumdem cxxxii lii, et earum ergo que sub ipsis rectarum utraque quidem rectarum DM et ZB ZB] ZN V2F1 talium est xlvii lix, qualium utraque DE et EZ ypothenusarum cxx, utraque vero rectarum EM et EN eorumdem cx et x. Quare qualium est utraque quidem DE et EZ rectarum x et xix, DB vero que e centro ecentrici xlix xli, talium et utraque quidem rectarum DM et ZN erit iiii viii, utraque vero rectarum EM et EN eorumdem ix et xxvii, et quoniam quod ab BD defitiens eo quod ab DM facit quod ab BM tetragonum, habebimus et BM quidem totam longitudinem longitudinem] longitudine V2F1 eorumdem xlix xxxi, BE vero similiter xliiii, reliqua vero BN talium xxx xxxvii, qualium et ZN erat iiii viii, et quoniam que ab ipsis composita faciunt quod ab BZ, habebimus et BZ ypothenusam longitudine eorumdem xxx liiii. Quare et qualium est BZ ypothenusa cxx, talium et ZB quidem erit xvi ii, que vero super ipsam periferia xv xxi, qualium est qui circa BZN orthogonium circulis ccclx, et ZBN ergo angulus, qualium quidem sunt duo recti ccclx, talium est xv xxi, qualium autem iiii recti ccclx, talium vii et xl ad proximum, tantorum ergo graduum est TK epicicli periferia.
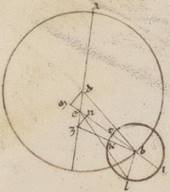 Rursum quoniam secundum tempus observationis distabat Luna a medio quidem apoguio epicicli gradibus cclxii xx, ab K vero medio periguio reliquis manifestum quoniam post semicirculum gradibus lxxxii xx, erit et KL quidem periferia graduum lxxxii xx, TKL vero tota graduum xc o, rectus ergo est TBL angulus. Quare quoniam qualium est DB quidem que e centro excentrici xlix xli, BL non non] vero V2F1 que e centro epicicli v xv, talium et EB ostensa erat xl et lxorum iiii, que vero ab eis composita faciunt quod ab EL tetragonum, habebimus et EL longitudine eorumdem xl xxv, que ergo secundum observationem apostima Lune talium est xl xxv, qualium est BL quidem que e centro epicicli subiacet v et xv, EA vero que a centro terre in apoguium excentrici lx, EG autem que a centro terre in periguium excentrici xxxix xxii. Verum ostensum est quod secundum observationem Lune apostima, hoc est EL recta, talium xxxix xlv, qualis est unius que e centro terre, et qualium ergo est EL quidem recta eius quod secundum observationem lunaris apostimatis xxxix xlv, que vero e centro terre unius, talium erit et EA quidem recta eius quod secundum sunzugias medii apostimatis lix o, EG vero eius quod secundum dichothomias medii apostimatis xxxviii xliii, que autem e centro epicicli eorumdem v x. Quod propositum erat demonstrare.
Rursum quoniam secundum tempus observationis distabat Luna a medio quidem apoguio epicicli gradibus cclxii xx, ab K vero medio periguio reliquis manifestum quoniam post semicirculum gradibus lxxxii xx, erit et KL quidem periferia graduum lxxxii xx, TKL vero tota graduum xc o, rectus ergo est TBL angulus. Quare quoniam qualium est DB quidem que e centro excentrici xlix xli, BL non non] vero V2F1 que e centro epicicli v xv, talium et EB ostensa erat xl et lxorum iiii, que vero ab eis composita faciunt quod ab EL tetragonum, habebimus et EL longitudine eorumdem xl xxv, que ergo secundum observationem apostima Lune talium est xl xxv, qualium est BL quidem que e centro epicicli subiacet v et xv, EA vero que a centro terre in apoguium excentrici lx, EG autem que a centro terre in periguium excentrici xxxix xxii. Verum ostensum est quod secundum observationem Lune apostima, hoc est EL recta, talium xxxix xlv, qualis est unius que e centro terre, et qualium ergo est EL quidem recta eius quod secundum observationem lunaris apostimatis xxxix xlv, que vero e centro terre unius, talium erit et EA quidem recta eius quod secundum sunzugias medii apostimatis lix o, EG vero eius quod secundum dichothomias medii apostimatis xxxviii xliii, que autem e centro epicicli eorumdem v x. Quod propositum erat demonstrare.
Demonstratis autem nobis secundum expositum modum Lune aposimatibus, consequens erit utique et illud quod Solis coostendere, prompto et huiusmodi facto per lineas, si simul dentur eis que secundum sinzugias Lune apostimatibus quantitates in ipsis constitutorum ad visum angulorum sub diametris Solis et Lune et umbre.
〈V.13〉 〈De quantitate apparentium in sinzugiis diametro Solis et Lune et umbre〉
〈Harum ergo que ad huiusmodi consideracionem ephodorum alias quidem, quante per ydrometria vel ea que secundum equinoctiales ortus tempora putantur luminarium facere mensuracionem, refutavimus, eo quod non sane possit per huiusmodi propositum sumi. Construentes autem et ipsi ostensam ab Ipparco per tetracubitum canonem dioptram et per istam facientes observaciones Solis quidem diametrum sub eodem ad proximum angulo ubique contentam invenimus, nulla semone digna facta differentia ex apostimatibus ipsius, ea vero que Lune tunc tantum et ipsam sub eodem Soli angulo contentam, quando in pleniluniis maximo apostimate a terra distat secundum apoguiotaton existens epicicli, et non quando medio, consequenter priorum ypothesibus. Ad hec autem et angulos ipsos aliquo cura digno minores deprehendimus traditis, nequaquam tamen per eam que in canone mensuracionem investigantes quod huiusmodi, sed per quasdam lunares eclipses. Quando enim equalem subtendit angulum utraque diametrorum, promptum ex canonis constructione poterat fieri, propter nullam consequi in huiusmodi mensuracionem. Sed et quantum multum nobis apparebat dubitabile, ea que investigacionibus superapposite latitudinis in longitudinem canonis que a visu in prismatium, plurima existente mensuracionem mensuracionem] mensuracione F1 mentiri a veritate potente. Quoniam vero semel Luna secundum maximum ipsius apostima equalem ad visum angulum apparebat faciens, per circa hoc apostima observatas lunares eclipses subtensi sub ipsa anguli magnitudinem investigantes et eum qui Solis coostensum habebimus inde. Modum autem huiusmodi investigacionis per duas rursum subordinatarum eclipsium bene investigabilem investigabilem] intelligibilem F1 faciemus.〉
〈Quinto enim anno Navopollasari qui est cxxviius annus a Navonassaro, secundum Egiptios Athir xxviia in xxviiia, hora xi desinente, in Babilone cepit Luna deficere, defecitque plurimum a notho iiiia diametri. Quoniam ergo principium quidem eclipseos factum fuit post v horas a mesonictio temporales, medium autem tempus post vi ad proximum, que erant in Babilone tunc equinoctiales v dimidium iiia, eo quod Sol examinate optineret Arietis gradus xxvii et lxorum iii, manifestum quoniam factum fuit medium tempus eclipseos, quando plurimum in umbra inciderat diametri, in Babilone quidem post v horas equinoctiales et dimidium et iiia a mesonictio, in Alexandria vero rursum post v solas et colligit quod ab epochis tempus annos egiptiacos cxxvi et dies lxxxvi horas equinoctiales, simpliciter quidem xvii, ad omalam vero nictimera xvi dimidium iiii. Quare et medius quidem secundum longitudinem Lune progressus obtinebat Chelarum gradus xxv xxxii, examinatus vero gradus xxxvii v, qui vero ab apoguio epicicli gradibus ccclx ccclx] cccxl F1 et lxis vii, qui autem a boreali termino in obliquo circulo gradibus lxxx xl, et manifestum quoniam, quando ix et iii distat a nodis centrum Lune in obliquo circulo circa maximum existentis apostima, et erit in scripto per ipsum ad rectos ei qui obliquo maximo circulo centrum umbre, secundum quam posicionem maxime fiunt obscuraciones, quarta ipsius in umbram incidit diametri.〉
〈Rursum vero septimo anno Cambisi qui est ccxxv annus a Navonassaro secundum Egiptios Phamenoth xviia in xviii ante unam horam a mesonictio in Babilone defecit Luna ab arctis medietate diametri. Facta est ergo et ista eclipsis in Alexandria ante i dimidium iii hore equinoctialis ad proximum a mesonocitio. Et colligit quod ab epochi tempus annos egiptiacos ccxxiiii et dies et cxcvi et horas equinoctiales simpliciter quidem x et via, examinate vero ix et dimidium iiia, eo quidem quidem] quod F1 Sol optineret Carchini gradus xviii xii. Quare et Luna secundum longitudinem medie quidem optinebat Egoceri gradus xx xxii, examinate vero xviii xiiii. Distabat autem et ab apoguio quidem epicicli gradibus xxviii v, a boreali vero termino obliqui circuli gradibus cclxii xii. Et hinc ergo manifestum quoniam, quando vii gradibus et iiii quintis a nodis distat centrum Lune in obliquo circulo circa idem maximum existentis apostima, centro umbre dictam habente ad ipsum posicionem, media pars in umbram incidit lunaris diametri. Sed siquidem ix et iii gradibus distat a nodis in obliquo circulo centrum Lune, xlviii et dimidio lxa unius gradus distat ab eo qui per media in ad rectos ei qui obliquus per ipsum scripto maximo circulo. Quando vero vii gradibus et iiii quintis distat a nodis in obliquo circulo xl et Γo xl unius gradus ab eo qui per media distat in ad rectos obliquo per ipsum scripto maximo circulo. Quoniam ergo duarum quidem eclipsium superhabundancia quartam continet lunaris diametri, que vero expositarum centri ipsius duarum distanciarum ab eo qui per media animalia, hoc est a centro umbre, sexagesima unius gradus vii dimidium iiia manifestum quoniam et tota diametros Lune subtendit maximi circuli periferiam sexagesimorum unius gradus xxxi iiia. Facile vero intellectu est inde quoniam et que e centro umbre que secundum idem apostima maximum Lune subtendit quidem unius gradus sexagesima xl Γo, quoniam quidem, quando tantis saxagesimis centrum Lune a centro umbre distabat, elevabatur a circulo umbre, eo quod medietatem lunaris diametri defecisset. Indifferenti autem minor est dupla et adhuc iii quintis maior ea que e centro Lune sexagorum existente xv Γo. Per plures vero huiusmodi observaciones consonas ad proximum expositas quantitates deprendentes et ad alia circa eclipses considerata cousi sumus sumus] add. ipsis F1 et nunc ad demonstracionem solaris apostimatis secundum eandem futuram, quam et Ypparcus consequtus consequtus] consecutus F1 est, et velut comprehensis sub conis circulis Solis et Lune et terre in differenti minoribus existentibus in speris ipsorum scriptis maximis circulis et diametris.〉
〈V.14〉 〈De solari apostimate eique coostensis〉
〈Istis ergo datis et quoniam secundum sinzugias maximum apostima Lune talium est lxiiii x, qualium est unius que e centro terre, eo quod medium quidem ostendatur eorumdem lix, ea vero que e centro epicicli v x, videamus quantum colligitur et Solis apostima. Sint enim maximi et in eodem epipedo sperarum circuli, solaris quidem ABG circa centrum D, lunaris vero secundum maximum eius apostima EZI circa centrum T, eius autem que secundum terram KLM circa centrum N; eorum vero que per centra epipedorum, terram quidem et Solem conprehendens AXG, Solem vero et Lunam ANG et axis quidem communis DTNX, que vero per contactus recte parallile manifestum quoniam facte et diametris equales ad sensum, solaris quidem circuli ADG, lunaris vero ETI, eius autem qui terre KNM, eius vero qui umbre in quam incidit secundum maximum apostima Luna OPR, quare et equalem esse TN ei que est NP et utraque talium lxiiii x, qualis est NL que e centro terre unius. Operti Operti] oportet F1 autem invenire, quam habet proporcionem ND recta solaris apostimatis ad NL que e centro terre. Educatur ergo EIC, et quoniam demonstravimus quoniam Lune diametros secundum expositum in sinzugiis maximum apostima subtendit periferiam secundum ipsam scripti circa centrum terre circuli, talium o xxxi xx, qualium est circulus ccclx, erit utique enim enim] ENI F1 angulus talium xxxi xx, qualium iiii recti ccclx, medietas vero ipsius TNI talium rursum o xxxi xx, qualium sunt duo recti ccclx. Quare et que quidem super TI periferia, talium est o xxxi xx, qualium qui circa NIT orthogonium circulus ccclx, que vero super TN reliquorum in semicirculum clxxix xxviii xl, et earum que sub ipsis rectarum IT quidem erit talium o xxxii xlviii, qualium NI diametros cxx, NT vero eorumdem cxx ad proximum. Quare et qualium est NT recta lxiiii x, talium et TI erit o xvii xxxiii, eiusdem vero est NM que e centro terre unius. Sed quoniam proporcio est recte PR ad TI, quam habent ii xxxvi ad proximum ad unum, fiet et PR eorumdem o xlv xxxlviii xxxlviii] xxxviii F1. Couterque Couterque] coutreque F1 ergo TI et PR talium sunt unius iii xi, qualis est NM unius. Couterque PR et TC tota eorumdem sunt ii, eo quod equales ipse sint duabus NM, et parallile enim, ut diximus, sunt omnes, equalis NP ei que est NT. Et reliqua ergo IC relinquetur talium o lvi xlix, qualium est NM recta unius, et est sicut NM ad IC, ita NG quidem ad IG, ND vero ad TD. Qualis ergo est ND unius, talium et DT quidem erit o lvi xlix, reliqua vero TN eorumdem o iii xi. Quare et qualium est NT quidem recta lxiiii x, NM vero unius, talium habebimus et ND solaris apostimatis L ccx ad proximum. Similiter autem, quoniam qualis est NM recta unius, talium PR ostensa est o xlv xxxviii. Sicut autem NM ad PR, ita NX ad XP, et qualis ergo NX recta unius, talium XP quidem erit o xlv xxxviii, reliqua vero PN eorumdem o xiiii xxii, et qualium ergo est PN quidem recta lxiiii x. NM vero que e centro terre unius, talium et XP quidem erit cciii l ad proximum, XN vero tota cclxviii. Collectum ergo nobis est quoniam, qualis est que e centro terre unius, talium est Lune quidem in sinzugiis medium apostima lix, Solis vero iccx, quod autem e centro terre usque verticem communi umbre cclxviii.〉
〈V.15〉 〈De magnitudinibus Solis et Lune et terre〉
〈Facilis vero intellectu fit hinc et solidarum quantitatum proporcio ab ea que diametrorum Solis et Lune et terre. Quoniam enim ostensum quidem est quoniam, qualis unius et NM que e centro terre, talium est TI quidem que e centro Lune xxxvi, NT vero recta lxiiii x, est autem et sicut NT ad TI, ita ND ad DG, eorumdem et ND ostensa iccx, habebimus et DG que e centro Solis eorumdem v et dimidii ad proximum, et diametrorum ergo tales erit proporciones. Quare et qualis est Lune diametros unius, talium et ea quidem que terre iii et duarum quintarum ad proximum, que vero Solis xviii et iiii quintarum. Itaque terre quidem diametros lunaris tripla est et adhuc duabus quintis maior, ea vero que Solis lunaris quidem decoctupla et adhuc iiii quintis maior, eius vero que terre quincupla et adhuc et adhuc medietate ad proximum maior, secundum eadem ergo quoniam et qui ab uno quidem cubus eiusdem est unius, qui vero a tribus et duabus quintis eorumdem ad proximum xxxix iiii, qui vero ab xviii et iiii quintis similiter vidcxliiii et dimidii ad proximum, collectum est nobis quoniam et qualis est unius Lune solida magnitudo, talium est terre quidem xxxix iiii, Solis vero vidcxliiii et dimidii, centupla et septuagintupla ergo ad proximum solaris quantitas terre.〉
〈V.16〉 De particularibus permutationibus Solis et Lune
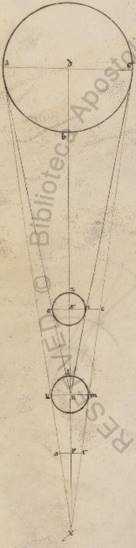 His ergo ita subiacentibus, consequens utique erat coostendere rursum per brevia, quo quis modo ex apostimatum quantitate Solis et Lune et secundum partem ipsorum factas permutationes investiget et primum in maximo per punctum quod secundum verticem et in ipsa scripto circulo consideratas.
His ergo ita subiacentibus, consequens utique erat coostendere rursum per brevia, quo quis modo ex apostimatum quantitate Solis et Lune et secundum partem ipsorum factas permutationes investiget et primum in maximo per punctum quod secundum verticem et in ipsa scripto circulo consideratas.
Sint ergo in dicti maximi circuli epipedo terre quidem rursum minimus minimus] maximus V2 circulus AB, qui vero secundum Solem et Lunam GD, ad quem vero terra puncti rationem habet EZIT, et centrum quidem omnium K, que vero per ea que secundum verticem puncta diametros KAGE, et assumpta a puncto G quod secundum verticem GD periferia talium verbi causa existente ut, ut] xxx V2F1 qualium est GD circulus ccclx, copulentur que que] quidem V2F1 rursum KDI et ADT, ab A vero parallilos quidem trahatur AZ ei que est KI, cathetus vero in ipsam AB; AB] AL V2F1 quoniam ergo, non manente semper eodem apostimate circa utrumque luminarium, circa Solem quidem futura propter hoc permutationum differentia brevis omnino et insensibilis erit, eo quod et excentrotis circuli eius parva sit et apostima magnum, que vero circa Lunam et multum utique fiet sensibilis, et eius qui in epiciclo motus ipsius causa et eius qui ipsius epicicli secundum excentricum non parvam facientis circa apostases differentia utrique, Solis quidem permutationes in una sole proportione ostendemus, dico autem ea que iccx ad unum. Eas vero que Lune in iiii maxime in eas que deinceps ephodos melioris vie futuris. Sumpsimus autem iiii istorum apostimatum prima quidem duo facta, epiciclo secundum appoguiotaton excentrici contingente, et istorum prius quidem quod usque apoguium epicicli, quod collectum est per demonstrata talium lxiiii x, qualis est que e centro terre unius, secundum autem quod usque periguium epicicli collectum, et hoc eorumdem liii l, reliqua vero ii facta, in epiciclo secundum periguiotaton excentrici contingente; et istorum vero rursum prius quidem usque apoguium epicicli collectum per predemonstrata talium xliii liii, qualis est que e centro unius, secundum vero usque periguion epicicli collectum et ipsum eorumdem xxxiii xxxiii. Quoniam ergo GD perifieria subiacet graduum xxx, erit utique et GKD angulus, qualium quidem sunt iiii recti ccclx, talium xxx, qualium vero ii recti ccclx, talium lx. Quare et que quidem super AL periferia talium est lx, qualium qui circa AKL orthogonium circulus ccclx, que vero super KL reliquorum in semicirculum cxx, et earum ergo que sub ipsis rectarum AL quidem talium erit lx, qualium est AK diametros cxx, KL vero eorumdem ciii lv, et qualis ergo est AK unius, talium, et AL quidem erit o xxx, KL vero recta o lii. Eorumdem vero est et KLD recta in solari quidem apostimate iccx. In lunaribus autem secundum primum quidem terminum lxiiii x iuxta, secundum vero liii l, secundum tertium autem xliii liii, secundum quartum vero xxxiii xxxiii, et reliqua ergo LD hoc est AD quoniam indifferenti sunt inequales, in solari quidem apostimate erit iccix viii. In lunaribus autem secundum primum quidem terminum lxiii xviii, iuxta secundum vero lii lviii, secundum iii autem xliii i, secundum quartum vero xxxii xli. Quare et qualium est AD ypothenusa cxx, talium erit AL recta, subaudito ne idem replicemus eodem ordine, o ii lix et o lvi lii et i vii lviii et i xxiii xli et i l ix et ea ergo que super ipsam periferia talium erit o ii l et o liiii xviii et i iiii liiii et i xx et l l] i V2F1 xlv ad proximum, qualium est qui circa DLA orthogonium circulus ccclx, ADB vero angulus, hoc est ZAT, qualium quidem sunt ii recti ccclx, talium o ii l et o liiii xviii et i iiii liiii et i xx et i xlv, qualium vero iiii recti ccclx, talium o i xxv et o xxvii ix et o xxxii xxvii et o xl o et o lii xxx. Quare quoniam A quidem punctum indifferens est K centro, ZIT vero periferia indifferenti maior est ea que est IT, eo quod terra tota puncti rationem habeat ad EZIT circulum, et IT permutationis periferia, qualium est EZIT circulus ccclx, talium in solari quidem apostimate erit o i xxv, in lunaribus vero secundum primum quidem terminum o xxvii ix, iuxta secundum autem o xxxii xxvii, secundum tertium vero o xl o, secundum quartum autem o lii xxx. Quod propositum erat demonstrare.
Eodem modo et in reliquis apostasibus ab eo quod secundum verticem puncto factas secundum unumquodque terminum permutationes investigantes per gradus vi usque tetartimorii gradus xc, descripsimus canonia ad distinctiones permutationum in versus quidem rursus xlv, selidia vero ix, quorum in primo quidem apposuimus tetartimorii gradus xc per duo manifestum quoniam augmentum ipsorum facientes, in secundo vero pertinentia cuique portioni lxa solarium permutationum, in tertio autem eas que secundum primum terminum Lune permutationes, in quarto vero superhabundantias earum que secundi termini permutationum ad eas que primi, in quinto autem eas que secundum tertium terminum permutationes, in sexto vero superhabundantias permutationum iiii termini ad eas que tertii, qualium ut in xxx graduum appositione o i xxv Solis, postea que deinceps o xxvii ix primi termini Lune, et deinceps o v xviii, quibus superat secundus terminus primum; postea rursum o xl tertii termini, et lxa o xii xxx, quibus et quartus terminus tertium superat. Causa vero et eas que in mediis apoguiorum et periguiorum apostimatibus permutationes proportionaliter eis que secundum partem portionibus ab eis que secundum expositos iiii terminos prompte docendi per lxorum appositionem reliqua nobis selidia tria copulata sunt ad appositionem talium differentiarum, quarum et ipsarum fecimus investigationem in hunc modum.
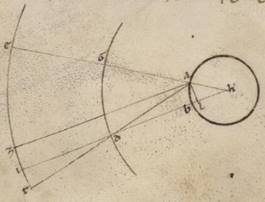 Esto enim epiciclus Lune ABGD circa centrum E, quod vero eius qui per media animalia et terre centrum Z, et copulata AEDZ, protrahatur ZGB, et copulentur quidem BE et GE. Catheti vero trahantur in AD, a puncto quidem B BI, a puncto vero G GT, et subiaceat primum Luna AB periferia distans ab eo quod secundum A examinato et ad centrum Z considerato apoguio graduum verbi causa existentem lx. Quare et BEI angulum, qualium quidem sunt iiii recti ccclx, talium esse lx, qualium vero ii recti ccclx, talium cxx; ac propter hoc eam quidem que super BI periferiam talium fieri cxx, qualium est qui circa BEI orthogonium circulus ccclx, eam vero que super EI reliquorum in semicirculum lx, et subtendentium ergo ipsas rectarum BI quidem erit talium ciii lv, qualium est EB diametros cxx,
Esto enim epiciclus Lune ABGD circa centrum E, quod vero eius qui per media animalia et terre centrum Z, et copulata AEDZ, protrahatur ZGB, et copulentur quidem BE et GE. Catheti vero trahantur in AD, a puncto quidem B BI, a puncto vero G GT, et subiaceat primum Luna AB periferia distans ab eo quod secundum A examinato et ad centrum Z considerato apoguio graduum verbi causa existentem lx. Quare et BEI angulum, qualium quidem sunt iiii recti ccclx, talium esse lx, qualium vero ii recti ccclx, talium cxx; ac propter hoc eam quidem que super BI periferiam talium fieri cxx, qualium est qui circa BEI orthogonium circulus ccclx, eam vero que super EI reliquorum in semicirculum lx, et subtendentium ergo ipsas rectarum BI quidem erit talium ciii lv, qualium est EB diametros cxx, 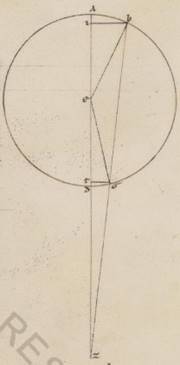 EI vero eorum lx. Verum quoniam E centrum epicicli in apoguio fuerit ecentrici, proportio est eius que est ZE ad EB que lx ad v xv, et qualium est ergo EB recta v xv, talium et BI quidem erit iiii xxxiii, EI vero recta ii xxxviii, tota autem IEZ lxii xxxviii, et quoniam quod ab ZI cum eo quod ab BI facit quod ab ZB, erunt et ipsa talium lxii xlviii, qualium est ZA quidem primi termini apostima lxv xv, ZD vero secundi termini liiii xlv, AD autem differentia duorum istorum terminorum superabundantie x xxx, et ea ergo que secundum B differentia ad primum terminum talium est ii xxvii, qualium est tota differentia x xxx. Quare et qualium est tota differentia lx, talium erit et que tunc differentia xiiii o, hec vero apponemus in viio selidio versu continenti medietatum lx numeri, hoc est ad xxx, propter et totos expositos in primo selidio canonis xc gradus medietatem continere eorum qui ab A in D graduum clxxx. Secundum eadem vero, etsi GD periferia supponamus eorumdem lx graduum, GT quidem ostendetur talium iiii xxxiii, qualium est EG que e centro v xv, atque ET similiter ii, reliqua vero ZT eorumdem lvii xxii, et propter eadem ZG ypothenusa lvii xxxiii, que aufferentes rursum ab eis qui primi termini lxv xv, reliqua vii xlii inveniemus lxa gradus gradus] om. V2 existentia totius differentie xliiii o, que et ipsa apponemus in eodem selidio ad lx numerum, eo quod et ABG periferia sit graduum cxx.
EI vero eorum lx. Verum quoniam E centrum epicicli in apoguio fuerit ecentrici, proportio est eius que est ZE ad EB que lx ad v xv, et qualium est ergo EB recta v xv, talium et BI quidem erit iiii xxxiii, EI vero recta ii xxxviii, tota autem IEZ lxii xxxviii, et quoniam quod ab ZI cum eo quod ab BI facit quod ab ZB, erunt et ipsa talium lxii xlviii, qualium est ZA quidem primi termini apostima lxv xv, ZD vero secundi termini liiii xlv, AD autem differentia duorum istorum terminorum superabundantie x xxx, et ea ergo que secundum B differentia ad primum terminum talium est ii xxvii, qualium est tota differentia x xxx. Quare et qualium est tota differentia lx, talium erit et que tunc differentia xiiii o, hec vero apponemus in viio selidio versu continenti medietatum lx numeri, hoc est ad xxx, propter et totos expositos in primo selidio canonis xc gradus medietatem continere eorum qui ab A in D graduum clxxx. Secundum eadem vero, etsi GD periferia supponamus eorumdem lx graduum, GT quidem ostendetur talium iiii xxxiii, qualium est EG que e centro v xv, atque ET similiter ii, reliqua vero ZT eorumdem lvii xxii, et propter eadem ZG ypothenusa lvii xxxiii, que aufferentes rursum ab eis qui primi termini lxv xv, reliqua vii xlii inveniemus lxa gradus gradus] om. V2 existentia totius differentie xliiii o, que et ipsa apponemus in eodem selidio ad lx numerum, eo quod et ABG periferia sit graduum cxx.
Rursum subiacentibus eisdem periferiis, intelligatur E centrum in periguio excentrici, secundum quam positionem et tertius terminus continetur et iiiius. Quoniam ergo secundum huiusmodi positionem proportio est eius que est ZE ad EB que lx ad viii, et qualium ergo BE fit viii, colligetur et utraque quidem BI et GT rectarum, quando et utraque AB et GD periferiarum lx graduum subiacet, talium vi lvi, qualium est ZE recta lx, utraque vero rectarum EI et ET eorumdem iiii o. Quare et ZI quidem facta eorumdem lxiiii, atque ZT similiter lvi, propter eadem et ZB quidem ypothenusam colligi lxiiii xxiii, ZG vero talium lvi xxvi, qualium est ZA quidem recta que tertii termini lxviii, que vero tertii ad quartum differentie AD recta xvi; si quidem ergo lxiiii xxiii dempserimus ab lxviii, reliquentur nobis iii xxxvii, que eorum que sunt xvi totius differentie sexagesima facta xiii xxxiii, apponemus similiter eorum que sunt xxx xxx xxx] om. V2 numero in viii selidio. Si autem lvi xxvi dempserimus ab eisdem lxviii reliquentur xi xxxiiii, que et ipsa eorum que sunt xvi totius differentie sexagesima facta xliii xxiiii, apponemus similiter eorum que sunt lx numero in eodem viiio selidio. Itaque propter eam quidem que in epiciclo fit transitionem Lune collecte differentie, hoc nobis modo exponentur, eas vero que propter ipsius epicicli in excentrico progressum docebimus ita.
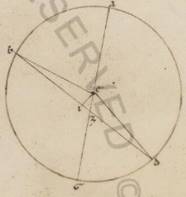 Esto enim excentricus Lune circulus ABG circa centrum E et diametrum AEG, in qua intelligatur centrum eius qui per media animalia circuli Z, et protracta BZD, subiaceat rursum uterque AZB et GZD angulorum talium lx, qualium sunt iiii recti ccclx, quod contingit, remotione, quando quidem in B fiunt fiunt] fuerit V2 centrum epicicli xxx graduum existente, quando vero in D, graduum cxx, et copulatis BE et ED, cathetus EI trahatur ab E in BZD. Quoniam ergo BZA angulus talium est cxx, qualium ii recti ccclx, erit utique et que quidem super EI periferia talium cxx, qualium est qui circa EZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum lx, et earum ergo que sub ipsis rectarum EI quidem erit talium ciii lv, qualium EZ ypothenusa cxx, IZ vero eorumdem lx. Quare et qualium est EZ quidem inter centra que x xix, que vero e centro excentrici xlix xli, tantum] talium V2F1 tantum erit et EI quidem recta viii lvi, ZI vero eorumdem v x, et quoniam quod ab BE defitiens eo quod ab EI facit quod ab BI, erit et utraque rectarum BI et DI eorumdem xlviii liii. Quare et tota quidem ZB talium est liiii iii, qualium est ZA quidem primorum terminorum lx, ZG vero secundum terminorum xxxix xxii, superhabundantiam autem ipsorum xx xxxviii, reliqua vero ZD eorumdem xliii xliii. Quoniam ergo lx ea quidem que sunt liiii iii superant eis que sunt v lvii, que eorum, que sunt xx xxxviii totius differentie, lx fiunt xvii xviii, ea vero que sunt xliii xliii eis que sunt xvi xvii, que et ipsa eorum, que sunt xx xxxviii, lxa fiunt xlvii xxi, et xvii quidem xviii manifestum quoniam apponemus in ix selidio ei qui est xxx numero remotionis, xlvii vero et xxi ei qui est cxx cxx] add. hoc est rursum ei qui V2F1 lx, eo quod, ad xc existente periguio, eque possit secundum apostima ea que lx remotio ei que cxx. Eodem ergo modo et in aliis periferiis facta sexagesimorum distantiarum distantiarum] differentiarum V2 investigantes secundum expositas tres superhabundantias per xii portiones, que fiunt rursus sex portiones in eis qui in canone numeris, propter et eos qui ab apoguiis in periguia gradus clxxx ad canonis xc gradus compleri, apposuimus in unoquoque demonstratorum numerorum proprie congregata per lineas lxa. Eam tamen que inter portiones apponere secundum omalum augmentum eius que vi graduum superhabundantie fecimus, nulla in ipsis cura digna facta differentia penes linearia usque per tantum sumptas superhabundantias, neque in sexagessimis, neque in ipsis permutationibus, et est canon qui positus est.
Esto enim excentricus Lune circulus ABG circa centrum E et diametrum AEG, in qua intelligatur centrum eius qui per media animalia circuli Z, et protracta BZD, subiaceat rursum uterque AZB et GZD angulorum talium lx, qualium sunt iiii recti ccclx, quod contingit, remotione, quando quidem in B fiunt fiunt] fuerit V2 centrum epicicli xxx graduum existente, quando vero in D, graduum cxx, et copulatis BE et ED, cathetus EI trahatur ab E in BZD. Quoniam ergo BZA angulus talium est cxx, qualium ii recti ccclx, erit utique et que quidem super EI periferia talium cxx, qualium est qui circa EZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum lx, et earum ergo que sub ipsis rectarum EI quidem erit talium ciii lv, qualium EZ ypothenusa cxx, IZ vero eorumdem lx. Quare et qualium est EZ quidem inter centra que x xix, que vero e centro excentrici xlix xli, tantum] talium V2F1 tantum erit et EI quidem recta viii lvi, ZI vero eorumdem v x, et quoniam quod ab BE defitiens eo quod ab EI facit quod ab BI, erit et utraque rectarum BI et DI eorumdem xlviii liii. Quare et tota quidem ZB talium est liiii iii, qualium est ZA quidem primorum terminorum lx, ZG vero secundum terminorum xxxix xxii, superhabundantiam autem ipsorum xx xxxviii, reliqua vero ZD eorumdem xliii xliii. Quoniam ergo lx ea quidem que sunt liiii iii superant eis que sunt v lvii, que eorum, que sunt xx xxxviii totius differentie, lx fiunt xvii xviii, ea vero que sunt xliii xliii eis que sunt xvi xvii, que et ipsa eorum, que sunt xx xxxviii, lxa fiunt xlvii xxi, et xvii quidem xviii manifestum quoniam apponemus in ix selidio ei qui est xxx numero remotionis, xlvii vero et xxi ei qui est cxx cxx] add. hoc est rursum ei qui V2F1 lx, eo quod, ad xc existente periguio, eque possit secundum apostima ea que lx remotio ei que cxx. Eodem ergo modo et in aliis periferiis facta sexagesimorum distantiarum distantiarum] differentiarum V2 investigantes secundum expositas tres superhabundantias per xii portiones, que fiunt rursus sex portiones in eis qui in canone numeris, propter et eos qui ab apoguiis in periguia gradus clxxx ad canonis xc gradus compleri, apposuimus in unoquoque demonstratorum numerorum proprie congregata per lineas lxa. Eam tamen que inter portiones apponere secundum omalum augmentum eius que vi graduum superhabundantie fecimus, nulla in ipsis cura digna facta differentia penes linearia usque per tantum sumptas superhabundantias, neque in sexagessimis, neque in ipsis permutationibus, et est canon qui positus est.
〈V.18〉 De permutationum distinctione
Quando ergo voluerimus sumere quantum Luna secundum unamquamque progressionum permutatur, primum in maximo per ipsam et punctum quod secundum verticem scripto circulo considerabimus, quot equinoctiales horas distat a meridiano secundum subiacens clima, et inventas inferentes in canonia angulorum proprii climatis et proprii dodecatimorii, adiacentes hore gradus in secundo selidio vel totos vel pertinentes parti hore habebimus quod distat ab eo quod secundum verticem puncto Luna in per ipsos scripto maximo circulo. Quos inferentes in permutationum canonem considerabimus, secundum quem versum sunt primi selidii et adiacentia numero in eis que deinceps post illud quod solarium permutationum iiii selidiis, hoc est iiio et iiiio et vo et vio, seorsum unumquodque scribemus. Postea secundum illam horam discretum anomalie numerum ad examinatum apoguium sumentes, vel ispum, vel si superat clxxx gradus, relictum in ccclx, medietatem semper ita sumptorum graduum inferentes in ipsos numeros, considerabimus, quot sexagesima adiacent numero seorsum in viio vel viiio selidio, et quot utique in viio selidio invenietur, tot sexagesima sumentes eius que in iiiio selidio differentie apponemus semper tertii selidii permutationi, quot vero in viiio selidio invenientur, tot sexagesima sumentes eius que in vio selidio differentie apponemus semper quinti selidii permutationi. Atque ita duarum factarum permutationum exponemus superhabundantiam. Deinceps vero sumentes quot distat medie Luna gradibus vel a solari vel ab ipsum diametrizanti secundum propinquiorem utrolibet ipsorum differentiam, inferemus et ipsos in eos qui in primo selidio numeros, et quotcumque adiacebunt rursum sexagesima in ixo et finali selidio, tot sexagesima sumentes eius quam exposuimus duarum permutationum superhabundantie, facta apponemus semper minori, hoc est ex tertio et iiiio selidio discrete, et composita habebimus que permutatur Luna in per ipsam et punctum quod secundum verticem scripto maximo circulo, considerata hinc simpliciter et solari permutatione secundum simillem positionem propter solares eclipses ex in secundo selidio adiacentibus gradibus quantitati eius que ab eo quod secundum verticem puncto periferie.
Ut ergo et eum qui per media animalia secundum secundum] om. V2 tunc factam permutationem discernamus et secundum longitudinem et secundum latitudinem easdem rursum equinoctiales horas, quasi quasi] quas V2 distat a meridiano Lune, inferentes in eadem partem angulorum canonis considerabimus adiacentis adiacentis] adiacentes V2F1 numero horarum gradus, ante siquidem meridianum fiunt fiunt] fuerit V2F1 Luna, eos qui in iiio selidio, si vero post meridianum, eos qui in iiiio, et si quidem inter xc fuerint gradus, ipsos scribemus, si vero super xc, deficientes clxxx. In tantorum enim erit minor eorum qui circa expositam sectionem angulorum, qualium est unus rectus xc. Scriptos itaque gradus duplicantes inferemus in earum que in circulo rectarum canonium et ipsos defitientes in clxxx, et quam utique proportionem habet duplicatorum graduum periferia subtendens recta ad subtendentem defitientem in semicirculum, eam habebit proportionem que secundum latitudinem permutatio ad eam que secundum longitudinem, quoniam quidem tante circulorum periferie non differtur differtur] differunt V2 a rectis. Multiplicantes ergo
〈V.17〉
| Canon Paralacti | |||||||||||||||||||
| Minuta distantie | Minuta distantie | Minuta circuli | |||||||||||||||||
| Numeri Communes | Differentia visionis Solis | Primus terminus | Secundus terminus | Tercius terminus | Quartus terminus | Maximum apostima | Minimum apostima | ||||||||||||
| Differentie visionis Lune | Differentie visionis Lune | Differentie visionis Lune | Differentie visionis Lune | circuli qui volvitur | circuli qui volvitur | Excentricus | |||||||||||||
| G | M | S | G | M | S | M | S | G | M | S | M | S | M | S | M | S | M | S | |
| ii | o | o | vii | o | i | liiii | o | xxviii | o | iii | o | o | l | o | xiiii | o | xi | o | xv |
| iiii | o | o | xiii | iii | xlviii | o | xlv | o | vi | o | i | xl | o | xxviii | o | xxii | o | xxx | |
| vi | o | o | xix | v | xli | i | vii | o | ix | o | ii | xxx | o | xlii | o | xxxiii | o | xlv | |
| viii | o | o | xxv | o | vii | xxxiiii | i | xxix | o | xi | xl | iii | xx | i | xxii | i | vii | i | xxxiii |
| x | o | o | xxxi | ix | xxviii | i | li | xiiii | xx | iiii | x | ii | ii | i | xli | ii | xxi | ||
| xii | o | o | xxxvii | xi | xix | ii | xii | xvii | o | v | o | ii | xlii | ii | xv | iii | ix | ||
| xiiii | o | o | xlii | o | xiii | x | ii | xxxiii | o | xix | xl | v | l | iii | xxxv | iii | xiii | iiii | xxii |
| xvi | o | o | xlviii | xv | o | ii | liiii | xxii | xx | vi | xl | iiii | xxviii | iiii | xi | v | xxxv | ||
| xviii | o | o | liii | xvi | xlix | iii | xv | xxv | o | vii | xxx | v | xxi | v | ix | vi | xliii | ||
| xx | o | o | lviii | o | xviii | xxxvi | iii | xxxvi | o | xxvii | xl | viii | xx | vi | xxxix | vi | xxv | viii | xxv |
| xxii | o | i | iiii | xx | xxii | iii | lvii | xxx | xx | ix | x | vii | lvii | vii | xli | x | ii | ||
| xxiiii | o | i | ix | xxii | vi | iiii | xviii | xxxiii | o | x | o | ix | xv | viii | lvii | xi | xxxix | ||
| xxvi | o | i | xiiii | o | xxiii | xlix | iiii | xxxix | o | xxxv | xx | x | l | x | l | x | xxix | xiii | xxxii |
| xxviii | o | i | xx | xxv | xxx | iiii | lix | xxxvii | xl | xi | xl | xii | xxv | xii | i | xv | xxv | ||
| xxx | o | i | xxv | xxvii | ix | v | xviii | xl | o | xii | xxx | xiiii | o | xiii | xxxiii | xvii | xviii | ||
| xxxii | o | i | xxx | o | xxviii | xlvi | v | xxxvii | o | xlii | xx | xiii | xx | xv | lii | xv | xxii | xix | xxiii |
| xxxiiii | o | i | xxxv | xxx | xxi | v | lv | xliiii | xl | xiiii | x | xvii | xliiii | xvii | xi | xxi | xxviii | ||
| xxxvi | o | i | xl | xxxi | liiii | vi | xiii | xlvii | o | xv | o | xix | xxxvi | xix | o | xxiii | xxxiii | ||
| xxxviii | o | i | xliiii | o | xxxiii | xxiiii | vi | xxx | o | xlix | o | xv | xl | xxi | xxxvi | xx | lix | xxv | xl |
| xl | o | i | xlix | xxxiiii | li | vi | xlvii | li | o | xvi | xx | xxiii | xxxvi | xxii | lviii | xxvii | xlvii | ||
| xlii | o | i | liiii | xxxvi | xiiii | vii | iiii | liii | o | xvii | o | xxv | xxxvi | xxiiii | lvii | xxix | liiii | ||
| xliiii | o | i | lviii | o | xxxvii | xxxvii | vii | xx | o | lv | o | xvii | xl | xxvii | xl | xxvii | i | xxxii | o |
| xlvi | o | ii | iii | xxxviii | lvii | vii | xxxv | o | lvii | o | xviii | xx | xxix | xliiii | xxix | v | xxxiiii | vi | |
| xlviii | o | ii | viii | xl | xiiii | vii | xlix | o | lix | o | xix | o | xxxi | xlviii | xxxi | ix | xxxvi | xii | |
| l | o | ii | xii | o | xli | xxviii | viii | iii | i | o | xl | xix | xl | xxxiii | lii | xxxiii | xiiii | xxxviii | ix |
| lii | o | ii | xvi | xlii | xxxix | viii | xvi | i | ii | xx | xx | xx | xxxv | lvi | xxxv | xix | xl | vi | |
| liiii | o | ii | xx | xliii | xlv | viii | xxix | i | iiii | o | xxi | o | xxxviii | o | xxxvii | xxiiii | xlii | iii | |
| lvi | o | ii | xxiii | o | xliiii | xlviii | viii | xlii | i | v | xx | xxi | xx | xl | o | xxxix | xxiiii | xliii | xlix |
| lviii | o | ii | xxvi | xlv | xlviii | viii | liii | i | vi | xl | xxi | xl | xlii | o | xli | xxiiii | xlv | xxxv | |
| lx | o | ii | xxix | xlvi | xlvi | ix | iii | i | viii | o | xxii | o | xliiii | o | xliii | xxiiii | xlvii | xxi | |
| lxii | o | ii | xxxii | o | xlvii | xl | ix | xiii | i | ix | xx | xxii | xx | xlv | l | xlv | xiii | xlviii | xlix |
| lxiiii | o | ii | xxxiiii | xlviii | xxx | ix | xxii | i | x | xl | xxii | xl | xlvii | xl | xlvii | ii | l | xvii | |
| lxvi | o | ii | xxxvi | xlix | xv | ix | xxxi | i | xii | o | xxiii | o | xlix | xxx | xlviii | li | li | xlv | |
| lxviii | o | ii | xxxviii | o | xlix | lvii | ix | xxxix | i | xiii | xl | xxiii | x | l | lvi | l | xxiiii | lii | lvii |
| lxx | o | ii | xl | l | xxxvi | ix | xlvi | i | xiiii | xx | xxiii | xx | lii | xxii | li | lvii | liiii | ix | |
| lxxii | o | ii | xlii | li | xi | ix | liii | i | xv | o | xxiii | xxx | liii | xlviii | liii | xxx | lv | xli | |
| lxxiiii | o | ii | xliiii | o | li | xliiii | ix | lix | i | xv | xl | xxiii | xl | liiii | lvii | liiii | xli | lvi | xii |
| lxxvi | o | ii | xlvi | lii | xii | x | iiii | i | xvi | xx | xxiii | l | lvi | vi | lv | liii | lvii | iii | |
| lxxviii | o | ii | xlvii | lii | xxxiiii | x | viii | i | xvii | o | xxiiii | o | lvii | xv | lvii | iii | lvii | liiii | |
| lxxx | o | ii | xlviii | o | lii | liii | x | xi | i | xvii | xx | xxiiii | x | lvii | lvii | lvii | xlvii | lviii | xxvi |
| lxxxii | o | ii | xlix | liii | ix | x | xiiii | i | xvii | xl | xxiiii | xx | lviii | xxxix | lviii | xxxi | lviii | lviii | |
| lxxxiiii | o | ii | l | liii | xxi | x | xvi | i | xviii | o | xxiiii | xxx | lix | xxi | lix | xv | lix | xxx | |
| lxxxvi | o | ii | l | o | liii | xxix | x | xvi | i | xviii | xx | xxiiii | xl | lix | xxxiiii | lix | xxx | lix | xl |
| lxxxviii | o | ii | li | liii | xxxiii | x | xvii | i | xviii | xl | xxiiii | l | lix | xlvii | lix | xlv | lix | l | |
| xc | o | ii | li | liii | xxxiii | x | xvii | i | xix | o | xxv | o | lx | o | lx | o | lx | o | |
numerum adiacentium rectarum in inventam ut in scripto per illud quod secundum verticem punctum circulo permutationem et factam distribuentes in cxx seorsum ex divisione collectas particulas habebimus proprie permutationis. Universaliter autem in eis que secundum latitudinem permutationibus, quando quidem quod secundum verticem punctum in meridiano borealius fiunt fiunt] fuerit V2F1 eo quod tunc tenet medium celum eius qui per media animalia circuli, permutatio erit ad meridiem ab ipso; quando vero australius fiunt fiunt] fuerit V2F1 quod secundum verticem medium tenente celum, ad arctos erit ea que secundum latitudinem permutatio. In eis vero que secundum longitudinem, quoniam quidem quantitates adiacentium in canone angulorum eum qui ab arctis continent duorum subcontinenti portione eius qui per media utrimque contentorum, ea quidem que secundum latitudinem permutatione ad arctos facta, si quidem maior fiunt fiunt] fuerit V2F1 recto expositus angulus, in precendentia animalium erit ea que secundum longitudinem permutatio, si vero minor recto, in consequentia; secundum latitudinem vero permutatione ad meridiem facta, e contrario, si quidem maior fiunt fiunt] fuerit V2F1 recto expositus angulus, in consequentia animalium secundum longitudinem erit permutatio, si vero minor recto, in precendentia. Cousi quidem sumus predemonstratis circa Solem, quasi nichil ipso sensibile permutato, non ignorantes quoniam faciet aliquam circa ipsam ipsam] ipsa V2 differentiam intellecta et circa ipsum ex eis que deinceps permutatio. Sed quoniam non ita cura dignum arbitramur circa apparentia propter hoc consequi peccatum, quoniam neccessarium esse movere aliqua sine huiusmodi inquisitione et brevi existente autem sumptorum. Similiter autem et ad permutationes Lune contenti fuimus ad eum qui per media animalia circulum factis sub maximo per polos orizontis scripto circulo et periferiis et angulis per per] pro V2F1 ad obliquum Lune consideratis, quoniam in eclipticis quidem sinzugiis futura penes hoc differentia insensibilis erat, et istas vero exponere et difficile demonstrationibus et operosum computationibus non diffinitis secundum unamquamque earum que in zodiaco progressionum Lune et eis que a nodo distantiis, sed et magnitudinibus et positionibus ipsis varias transitiones sumentibus.
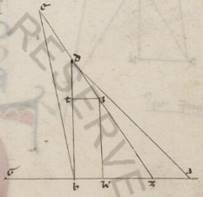 Ut autem bene intelligibile fiat quod dictum est, adiaceat eius eius] add. quidem V2F1 qui per media animalia circuli portio ABG, obliqui vero Lune AD, et nodus quidem subiaceat A punctus, Lune vero centrum D, et scribatur a puncto D in eum qui per media animalia circulum recta DB. Esto vero polus orizontis E punctus, et scribatur per ipsum maximi circuli porcio, per centrum quidem Lune EDZ, per B vero EB, permuteturque Luna DI periferiam et scribatur scribatur] scribantur V2F1 per ipsum ad BD et BZ recte IT et IK, quare earum quidem que secundum longitudinem remotionum a nodo examinatam quidem fieri AB, apparentem vero AK, earum vero que secundum latitudinem ab eo qui per media examinatam quidem BD, apparentem vero KI; et ad DI ad zodiacum consideratarum permutationum secundum longitudinem quidem equalem ei que est TI, secundum latitudinem vero equalem ei que est DT. Quoniam ergo DI quidem permutatio inventa est per preexposita, ED periferia data, utraque vero DT et TI permutationum GZE angulo dato, nos autem in eis quem prius demonstravimus ad data zodiaci puncta factos eius qui per punctum quod secundum verticem et arcus et angulos, solum autem habebimus hic datum eius qui per media punctorum B, manifestum quoniam EB quidem periferia coutimur pro ED, angulo autem GBE pro GZE. Iparcus ergo incepit quidem et huiusmodi directionem facere multum imperite et propter rationem ipsi apparet accedens. Primum enim una distantia eius que est AD cousus est et non omnibus vel pluribus quod erat consequens et de parvis examinate inquirere preeligenti. Postea et pluribus inconventioribus inconventioribus] inconvenientioribus V2F1 latuit incidens. Quoniam enim et ipse et periferias et angulos ad eum qui per media animalia consideratos contingebat predemonstrans et quoniam ab ED data DI sumitur, hoc enim in primo paralacticorum demostrat coutitur ad ED periferie dationem et EZ periferia et EZG angulo quasi datis. Ita enim in secundo eam que est ZD investigans et reliquam ED supponit. Preteriit enim tamen ipsum non inquirere, quoniam B et non Z punctus est eius qui per media datus, et propter hoc et periferiarum EB data est et non EZ et angulorum EBG et non EZG. Unde et ad faciendam quandam etsi particularem directionem motus est sepe, facta sensibili multum differentia ED periferiarum ad periferias EZ, propter multo magis illis ipsas non dari. Ea vero que est BE vere data, ea que ad ED differentia plurimum differunt differunt] differt V2F1 sola eius que est BD secundum unamquamque unamquamque] add. a nodo V2F1 differentiarum magnitudine. Quod tamen secundum sanum modum future directionis consequens fiet utique nobis sub visum ita.
Ut autem bene intelligibile fiat quod dictum est, adiaceat eius eius] add. quidem V2F1 qui per media animalia circuli portio ABG, obliqui vero Lune AD, et nodus quidem subiaceat A punctus, Lune vero centrum D, et scribatur a puncto D in eum qui per media animalia circulum recta DB. Esto vero polus orizontis E punctus, et scribatur per ipsum maximi circuli porcio, per centrum quidem Lune EDZ, per B vero EB, permuteturque Luna DI periferiam et scribatur scribatur] scribantur V2F1 per ipsum ad BD et BZ recte IT et IK, quare earum quidem que secundum longitudinem remotionum a nodo examinatam quidem fieri AB, apparentem vero AK, earum vero que secundum latitudinem ab eo qui per media examinatam quidem BD, apparentem vero KI; et ad DI ad zodiacum consideratarum permutationum secundum longitudinem quidem equalem ei que est TI, secundum latitudinem vero equalem ei que est DT. Quoniam ergo DI quidem permutatio inventa est per preexposita, ED periferia data, utraque vero DT et TI permutationum GZE angulo dato, nos autem in eis quem prius demonstravimus ad data zodiaci puncta factos eius qui per punctum quod secundum verticem et arcus et angulos, solum autem habebimus hic datum eius qui per media punctorum B, manifestum quoniam EB quidem periferia coutimur pro ED, angulo autem GBE pro GZE. Iparcus ergo incepit quidem et huiusmodi directionem facere multum imperite et propter rationem ipsi apparet accedens. Primum enim una distantia eius que est AD cousus est et non omnibus vel pluribus quod erat consequens et de parvis examinate inquirere preeligenti. Postea et pluribus inconventioribus inconventioribus] inconvenientioribus V2F1 latuit incidens. Quoniam enim et ipse et periferias et angulos ad eum qui per media animalia consideratos contingebat predemonstrans et quoniam ab ED data DI sumitur, hoc enim in primo paralacticorum demostrat coutitur ad ED periferie dationem et EZ periferia et EZG angulo quasi datis. Ita enim in secundo eam que est ZD investigans et reliquam ED supponit. Preteriit enim tamen ipsum non inquirere, quoniam B et non Z punctus est eius qui per media datus, et propter hoc et periferiarum EB data est et non EZ et angulorum EBG et non EZG. Unde et ad faciendam quandam etsi particularem directionem motus est sepe, facta sensibili multum differentia ED periferiarum ad periferias EZ, propter multo magis illis ipsas non dari. Ea vero que est BE vere data, ea que ad ED differentia plurimum differunt differunt] differt V2F1 sola eius que est BD secundum unamquamque unamquamque] add. a nodo V2F1 differentiarum magnitudine. Quod tamen secundum sanum modum future directionis consequens fiet utique nobis sub visum ita.
 Esto enim zodiacus ABG, et ad rectos ipsi DBE, Luna vero vel secundum D vel secundum E distans secundum latitudinem ab ABG qui per media animalia circulo datam periferiam sicut BD et BE, quare eos quidem qui ad B punctum zodiaci arcus ab eo quod secundum verticem et angulos dari, queri vero ad D vel E factos. Si quidem ergo huiusmodi habeat positionem zodiacus, quare ad rectos angulos ei esse qui per Z punctum, quod subiaceat polus orizontis, et per B scripto maximo circulo, ut ei qui est ZB, concidet iste manifestum quoniam DE periferie, et angulus quidem ad D et E consideratus indifferens erit ad B subiacenti. Recti enim et per hoc qui ad zodiacum fiunt, fiunt] fuerit V2F1 ea vero que est ZB periferia ZD quidem minor erit ea que est BD, ZE vero maior quam BE, datis et ipsis.
Esto enim zodiacus ABG, et ad rectos ipsi DBE, Luna vero vel secundum D vel secundum E distans secundum latitudinem ab ABG qui per media animalia circulo datam periferiam sicut BD et BE, quare eos quidem qui ad B punctum zodiaci arcus ab eo quod secundum verticem et angulos dari, queri vero ad D vel E factos. Si quidem ergo huiusmodi habeat positionem zodiacus, quare ad rectos angulos ei esse qui per Z punctum, quod subiaceat polus orizontis, et per B scripto maximo circulo, ut ei qui est ZB, concidet iste manifestum quoniam DE periferie, et angulus quidem ad D et E consideratus indifferens erit ad B subiacenti. Recti enim et per hoc qui ad zodiacum fiunt, fiunt] fuerit V2F1 ea vero que est ZB periferia ZD quidem minor erit ea que est BD, ZE vero maior quam BE, datis et ipsis.
Si autem concidat ABG zodiacus maximo per punctum quod secundum verticem scripto circulo, et supponentes polon orizontis A, coniunxerimus AD et AE, et ipse distabunt ab AB periferia et BAD et BAE anguli ante ente prius, dantur dantur] add. vero V2 quidem AD et AE, sermone existente velut in rectis propter indifferens et ab AB et BD et BE datis, que vero ab eis composita faciunt que ab AD et AE, consequenter autem ipsis et BAD et BAE anguli. Zodiaci vero positione inclinata, si a Z polo orizontis coniuncxerimus ZB et ZID et ZET, data quidem erit et ZB periferia, et ABZ angulus et rursum manifestum quoniam BD et BE. Debent vero dari Z Z] et V2F1 ZD et ZE periferie et AIZ et AZT anguli, dantur dantur] daretur V2 autem et isti, cathetis tractis in ZB et DK et EL. Quoniam enim ABZ angulus datus est, rectus vero semper ABE, dantur BKD et BLE orthogonia et proportio eius que est ZB ad eas que circa rectum, quoniam et ad BD et BE ypothenusas. Quare et ZD et ZE ypothenuse dabuntur, et propter hoc et DZK et EZL anguli superhabundantie existentes inquisitorum. Nam angulus quidem AIZ minor est quam ABZ angulo DZB, ATB vero minor quam ABZ angulo EZL. Manifestum vero quoniam et plurima fit differentia eadem secundum latitudinem subiacentem apochi, angulorum quidem, quando B punctus ipse erit qui secundum verticem, nullo enim ad B facto angulo, que in D et E ab eo quod secundum verticem rectos facient ad zodiacum angulos, periferiarum vero, quando ipsa eadem positio erit, nulla enim rursum ad B facta periferia, que ad D et E tante erit, erit] erint V2 quante utique fiunt et que secundum latitudinem progressionis Lune, et quando rectus fiunt fiunt] fuerit F1 ad zodiacum qui per illud quod secundum verticem. Tanta enim rursum secundum latitudinem progressione distabunt ad ZB ZD et ZE periferie.
In aliis autem positionibus inclinata DE ad ZB et periferiarum et angulorum et superhabundantie in minus colliguntur. Quare, et quando quidem v gradibus Luna secundum latitudinem distat ab qui per media, plurima differentia permutationum erit x ad proximum lx. Maxime namque differentie periferiarum gradus v tot faciunt lxa permutationis in maximis superhabundantiis et minimis apostimatibus, quando vero in solaribus eclipsibus maximam progressionem distat, ipsa autem fiet unius gradus ad proximum et medietatis, equalia sexagesima i et dimidium differentia erit permutationis, eo quod huiusmodi raro contingente.
Methodus tamen que ad huiusmodi directionem et angulorum et periferiarum fit utique promta volentibus ut in ita parvis proportionibus ad hunc modum. Universaliter enim angulorum numerum duplicantes et inferentes in earum que in circulo rectarum canonium adiacentia et ipsi relicto in duorum rectorum gradus clxxx seorsum multiplicantes in latitudinis gradus cxx utrorumque scribamus scribamus] scribemus V2 et ex primo angulo facta auferemus quidem a subiacente ab eo quod secundum verticem periferia, quando in eisdem fiunt fiunt] fuerit V2F1 ei quod secundum verticem Luna, apponemus vero, quando in contrariis, et facta facientes super eadem componentesque ex relicto angulo factis quadratis et ipsis collectorum latus habebimus proprie inquisitorum periferiam. Deinde ex relicto angulo descripta centies et vigesies facientes et distribuentes seorsum in inventas periferias earum que factis adiacent periferiarum in canone rectarum medietates, siquidem maior fiunt fiunt] fuerit V2F1 directa periferia quam prima, apponemus eis que primi anguli, si vero minor, auferemus, ab ipsis et habebimus angulum directum.
 Exempli vero causa subiaceat in preiacente descriptione ZB quidem periferia graduum xlv, angulus vero ABZ talium xxx, qualium unus rectus xc, utraque vero earum que sunt DB et BE latitudinis graduum v. Quoniam ergo duplis quidem xxx, hoc est lx, adiacet recta portionum lx, relictis vero in duos rectos, hoc est cxx, adiacet recta portionum ciiii ad proximum, fit portio eius que est BL ad LE que lx ad ciiii. Eadem vero et eius que est BK ad DK qualium ypothenusa cxx. Multiplicantes ergo utrumque numerorum in v gradus ypothenuse et cxx ipsorum sumentes habebimus utrumque utrumque] utramque V2 quidem earum que sunt KB et BL eorumdem ii et xxx, utramque vero earum que sunt DK et EL similiter iiii et xx. Ea vero ii et xxx primum, quidem quidem] siquidem V2F1 secundum E punctum Luna subiacet, auferentes ab ZB periferie gradibus xlv, propter in eisdem ei quod secundum verticem esse eam que secundum latitudinem apochin Lune, hoc est propter utramque vel australia vel borealia esse zodiaco, habebimus ZL graduum xlii xxx, si autem secundum D fiunt fiunt] fuerit V2F1 Luna, apponentes ipsis propter contrarium habebimus ZK graduum xlvii et xxx. Componentes ergo quod ab utraque earum que sunt ZL et ZK seorsum cum eo quod ab utraque DK et EL, hoc est quod a iiii xx et cum eo quod ab xlvii xxx et collectorum seorsum sumentes latus, habebimus et ZE quidem periferia graduum xlii xlvi ad proximum atque ZD similiter xlvii xliiiio. Reliquum vero iiii xx centies et vigesies facientes et comparantes seorsum et penes xlii xlvi et penes xlvii et xliiii, habebimus EL quidem talium xii xiii ad proximum, qualium est ypothenusa ZE cxx, DK vero talium x et dimidii et iiia ad proximum, qualium ZD ypothenusa cxx. Adiacet autem recte xii viii periferia graduum xi iii v. Ei vero que x et dimidii et iiia periferia graduum x iii ad proximum, quorum dimidio sumentes v quidem et iiii va EZL anguli abstulimus ab ABZ anguli gradus xxx, propter et ZE periferiam minorem esse ea que est ZB et habuimus ATZ angulum graduum xxiiii v. At vero v et dimidium
Exempli vero causa subiaceat in preiacente descriptione ZB quidem periferia graduum xlv, angulus vero ABZ talium xxx, qualium unus rectus xc, utraque vero earum que sunt DB et BE latitudinis graduum v. Quoniam ergo duplis quidem xxx, hoc est lx, adiacet recta portionum lx, relictis vero in duos rectos, hoc est cxx, adiacet recta portionum ciiii ad proximum, fit portio eius que est BL ad LE que lx ad ciiii. Eadem vero et eius que est BK ad DK qualium ypothenusa cxx. Multiplicantes ergo utrumque numerorum in v gradus ypothenuse et cxx ipsorum sumentes habebimus utrumque utrumque] utramque V2 quidem earum que sunt KB et BL eorumdem ii et xxx, utramque vero earum que sunt DK et EL similiter iiii et xx. Ea vero ii et xxx primum, quidem quidem] siquidem V2F1 secundum E punctum Luna subiacet, auferentes ab ZB periferie gradibus xlv, propter in eisdem ei quod secundum verticem esse eam que secundum latitudinem apochin Lune, hoc est propter utramque vel australia vel borealia esse zodiaco, habebimus ZL graduum xlii xxx, si autem secundum D fiunt fiunt] fuerit V2F1 Luna, apponentes ipsis propter contrarium habebimus ZK graduum xlvii et xxx. Componentes ergo quod ab utraque earum que sunt ZL et ZK seorsum cum eo quod ab utraque DK et EL, hoc est quod a iiii xx et cum eo quod ab xlvii xxx et collectorum seorsum sumentes latus, habebimus et ZE quidem periferia graduum xlii xlvi ad proximum atque ZD similiter xlvii xliiiio. Reliquum vero iiii xx centies et vigesies facientes et comparantes seorsum et penes xlii xlvi et penes xlvii et xliiii, habebimus EL quidem talium xii xiii ad proximum, qualium est ypothenusa ZE cxx, DK vero talium x et dimidii et iiia ad proximum, qualium ZD ypothenusa cxx. Adiacet autem recte xii viii periferia graduum xi iii v. Ei vero que x et dimidii et iiia periferia graduum x iii ad proximum, quorum dimidio sumentes v quidem et iiii va EZL anguli abstulimus ab ABZ anguli gradus xxx, propter et ZE periferiam minorem esse ea que est ZB et habuimus ATZ angulum graduum xxiiii v. At vero v et dimidium  DZK anguli apponentes eisdem xxx; propter et ZD periferiam maiorem esse ea que est ZB, habuimus et AIZ angulum graduum xxxv et dimidii. Que propositum erat demonstrare. Finit quintus.
DZK anguli apponentes eisdem xxx; propter et ZD periferiam maiorem esse ea que est ZB, habuimus et AIZ angulum graduum xxxv et dimidii. Que propositum erat demonstrare. Finit quintus.