〈IV〉
A quibus oportet observationibus que circa Lunam examinare
De periodicis temporibus Lune
De eis qui secundum partem omalis motibus Lune
Canonium expositio continentium medios progressus Lune
Quoniam et 〈in〉 simplici ypothesi Lune eadem apparentia faciunt et que secundum excentrotica et que secundum epiciclum
Apodisis Apodisis] apodixis V2F1 prime et simplicis anomalie Lune
De directione mediorum progressuum Lune et longitudinis et anomalie
De epochi omalorum Lune motuum et longitudinis et anomalie
De directione eorum qui secundum latitudinem mediorum progressuum Lune et epochi ipsorum
Compotum canoniorum prime et simplicis anomalie Lune
Quoniam non penes differentias ypothesium, verum penes epilogismos differt ea que secundum Yparcon quantitas lunaris anomalie
Claudii Ptolomei mathematicorum sintaxeos liber iiiius incipit
〈IV.1〉 〈A〉 quibus oportet observationibus que circa Lunam examinare
In eo quod ante hoc coordinantes quecumque utique quis videat contingentia circa Solis motum incipientesque secundum eam que deinceps consequentiam et de Luna sermonem primum arbitramur competere non simpliciter neque fortuito accedere earum que in hoc observationum usibus, verum ad universales quidem conceptiones illis maxime attendere demonstrationum quecumque non solum ex plure tempore, sed ab ipsis que secundum lunares eclipses observationibus sumuntur, – per has enim solas examinate utique loci Lune invenientur, aliis quecumque vel per eos qui ad applanas stellas progressus, vel per organa, vel per Solis eclipses considerantur, valde mentiri potentibus propter permutationes Lune –, ad particulariter autem superaccidentia et ab aliis iam observationibus facere considerationem. Distantia namque qua distitit spera Lune a centro terre non existente quemadmodum et ea que secundum zodiacum circulum tanta, ut puncti ad ipsam rationem habeat terre magnitudo, necesse est a centro terre in centrum Lune eductam rectam in eius qui per media animalia circuli partes, ad quam examinati motus omnium intelliguntur, minime vero ad sensum eandem fieri semper ab aliqua superfitie terre, hoc est visu conspitientium, in centrum Lune educte, ad quam apparens transitus eius consideratur; verum quando quidem secundum verticem fiunt fiunt] fuerit V2F1 observantis Luna, tunc tantum unam et eadem rectam fieri eam que a centro terre et visu conspitientis in centrum Lune et zodiacum educitur, quando vero nutum fecerit quomodocumque ab eo qui secundum verticem loco differentes quoque inclinationes propositarum rectarum compleri, ac propter hoc apparentem transitum non eandem eandem] eundem V2F1 fieri examinato, ad alias et alias positiones visu descendente eis que per centrum terre segregatis proportionaliter quantitatibus factorum sub inclinatione angulorum. Propter quod accidit solaribus quidem eclipsibus factis a lunari subcursu et appositione super appositione super] superapposicione V2 que incidens in eum qui a visu nostro in Solem conum facit usque transitionem obtenebrationem non ubique ipsas, neque quantitatibus, neque temporibus similiter perfici, neque omnibus similiter, propter quas diximus causas, obtenebrante Luna, neque secundum easdem partes Solis apparentes; in lunaribus autem eclipsibus nullam talem differentiam ex permutationibus consequi, factam factam] facta V2 circa Lunam ecliptica passione non coassumente conspitientium visum in causam sintomatis, illustrata namque Luna semper a solari fulgore, quotienscumque secundum diametricam habitudinem ipsi fit, alio quidem tempore apparet nobis tota illustrata propter totum illuminatur illuminatur] illuminatum V2F1 eius hemisperium simul et nobis tunc totum facere nutum, quando non non] vero V2F1 ita diametrizabitur, ut in umbre terre conum incidat contracircumactum semper Soli, tunc fit obtenebrata proportionaliter illapsionis quantitatibus, obscurante terra Solis fulgores. Inde similiter secundum omnes partes terre et quantitatibus et distantiarum temporibus defitiens apparet. Propter hoc ergo ad universalem considerationem examinatis locis Lune, non autem apparentibus debentibus assumi, quoniam quidem et ordinatum et simille inordinatis et dissimillibus neccessarium utique erit preiacere, aliis quidem observationibus dicimus non oportere couti eis que in ipsis locis per visum observantium deprehensis, solus solus] solis V2F1 vero eis que eclipsium eius, quoniam quidem in ipsis nichil ad locorum conceptionem visus conducit. Quod enim portionem eius qui per media animalia Sol optinens inveniatur secundum medium tempus eclipsis, in quo Lune centrum sub Sole secundum longitudinem examinate, ut est maxime, diametrizantur, huius manifestum quoniam quod secundum diametrum obtinebit et Lune centrum ad examinationem secundum idem tempus medium eclipseos.
〈IV.2〉 De periodicis temporibus Lune
A quibus ergo observationibus circa Lunam debentia universaliter sumi convenit considerare, propter hoc figurare nobis preexponatur. Modum vero et secundum quem antiqui apodixium investigationibus usi sunt et secundum quem utique nos ad apparentia concordium ypothesium discretionem commodiorem faciemus temptabibus pertransire. Quoniam ergo anomalie anomalie] anomale V2F1 quidem Luna apparet mota et secundum longitudinem et latitudinem et non equitemporaliter neque eum qui per media animalia circulum semper transiens, neque ad eum qui secundum latitudinem eius transitum restituta, sine inventione vero anomalie ipsius restituti temporis secundum neccessarium neque aliorum periodos sumere possibile utique fiet, secundum omnes partes tamen zodiaci et medias et maximas et minimas per particulares observationes apparet mota et secundum partes borealissimas et australissimas et secundum ipsum qui per media animalia circulum facta, querebant convenienter antiqui mathematici tempus aliquod, per quantum semper Luna equaliter moventur moventur] moveretur V2 secundum longitudinem, velut hoc solo anomaliam potente restituere. Apponentes ergo observationes lunarium eclipsium, propter quas diximus causas, considerabant que utique multitudinis mensium differentia et equitemporalis fiat semper eque multitudinis distantiis et equales circulos contineat secundum longitudinem, vel totos, vel cum aliquibus equalibus periferiis. Universalius ergo adhuc antiquiores tempus hoc suspicabantur omne omne] esse V2F1 dierum vidlxxxv et tertiam. Per tantum enim ad proximum videbant menses quidem completos ccxxiii, restitutiones autem anomalie quidem ccxxxix, latitudines autem ccxlii, circunciones vero latitudinis latitudinis] om. V2F1 longitudinis ccxli, et adhuc quot et Sol assumit xviii circulus circulus] circulis V2F1 in predicto tempore gradus x iii ii, velut restitutione ipsorum ad applanas stellas considerata. Vocaverunt autem tempus istud periodicum, velut primum in unam restitutionem ducens ad proximum differentias motuum et, ut ex totis diebus ipsum constituerunt, triplicaverunt vidlxxxv dies et iiia et habuerit habuerit] habuerunt V2F1 dierum numerum xixdcclvi, quem vocaverunt exeligmon, idest evolutionem, et alia vero similiter triplicantes, habuerunt menses quidem dclxix, restitutiones vero anomalie quidem dccxxvii, latitudines vero dccxxvi, circumcursus vero longitudinis dccxxiii, et adhuc quot et Sol assumit liiii circulis gradus xxxii. Iam tamen rursum Yparcus arguit et a Caldeacis et ab eis que secundum ipsum observationibus ratiocinans non habentia se hec examinate. Demonstrat enim per quas exposuit observationes quoniam primus numerus dierum per quot semper eclipticium tempus in equalibus mensibus et in equalibus motibus revolvitur cxx est adhuc etiam vivii dierum et unius hore equinoctialis, in quibus menses quidem perfectos invenit xxxcclxvii, totas vero anomalie restitiones restitiones] restituciones V2F1 iiiidlxxiii, zodiacos vero circulos iiiidcxii defitientes gradus vii et dimidium ad proximum, quot et Sol in cccxlv circulos deficit rursum, velut restitione restitione] restitucione V2F1 ipsorum ad applanas stellas considerata. Unde invenit et menstruum et medium tempus, distributa dierum preiacente multitudine in iiiicclxvii menses, dierum collectionem xxix xxxi lviii xx ad proximum. In tanto ergo tempore que ab eclipsi lunari in eclipsi simpliciter redditas equales distantias demonstrat, quare manifestum fieri restitui anomaliam ex semper, per tantum tempus tantosque menses contineri et equalibus secundum longitudinem periodis iiiidc xi assumi gradus equales ccclii et dimidium consequenter eis que ad Solem coniugationibus. Si quis autem non ab eclipsi lunari in eclipsi numerum mensium inquirat, solum vero eum qui a sinodo vel panselinio in similem sinzugiam, inveniet utique adhuc minorem restitutionem et anomalie et mensium numerum, sumens solum ipsorum communem mensuram xvii, que colligit menses quidem ccli, anomalie vero restitutiones cclxix. Nondum tamen preiacens tempus invenietur et eam que secundum latitudinem perfitiens restitionem restitionem] restitucionem V2F1. Redditio namque eclipsium dumtaxat et temporis et secundum longitudinem periodorum apparebat salvans equalitates, minime autem ad quantitates et simillitudines obscurationum a quibus et latitudo deprehenditur. Iam vero presumpto anomalie restitutio restitutio] restitutivo V2 tempore, apponens rusum Yparcus distantias mensium similles secundum omnia extremas eclipses habentium et quantitatibus et temporibus obscurationum, in quibus nulla facta est differentia penes anomaliam, quare propter hoc et secundum latitudinem transitum restitutum apparere, demonstrat et huiusmodi periodum perfectam in mensibus quidem vcccclviii, periodis vero latitudinariis vcccxxiii. Modus ergo quo ad tales conceptiones usi sunt qui ante nos talis erat. Quoniam vero neque simplex, neque facilis, secundum multa et non fortuita indiges indiges] indigens V2F1 instantia, ita utique intelligemus. Ut enim demus examinate equalia invicem distantiarum tempora inveniri, primum quidem nulla utilitas est quod huiusmodi, neque Sole eam que penes anomaliam differentiam vel nullam vel eamdem fatiente secundum utrumque utrumque] utramque V2F1 distantiarum. Si enim non hoc contingat, fiat autem adhuc, ut dixi, penes anomaliam eius differentia, neque ipse erit in equalibus temporibus equales circuitiones faciens, neque manifestum quoniam Luna. Si enim verbi causa utraque quidem comparatarum distantiarum post tota et equalia annua tempora assumat dimidium annui temporis, in tanto vero supermotus Sol contingat secundum primam quidem differentiam ab eo qui secundum Pisces medio motu, iuxta secundam vero ab eo qui secundum Virginem, secundum priorem quidem minus assumens erit Sol semicirculo gradibus iiiia et dimidio et iiiia ad proximum, iuxta secundam vero plus semicirculo eisdem gradibus, quare et Lunam in equalibus temporibus post totos circulos secundum priorem quidem differentiam assumere gradus clxxxv clxxxv] clxxv V2F1 et iiii, iuxta secundam vero clxxxiiii et dimidium et iiii. Opportere ergo dicimus hoc primum habere differentias circa Solem accidens, vel totos ipsum circulos continere, vel secundum alteram quidem distantiarum eum qui ab apoguio semicirculum supersumere secundum alteram vero eum qui a periguio, vel ab eadem portione incipere secundum utramque differentiarum, vel equaliter distare utrimque vel ab apoguio vel a periguio et secundum priorem eclipsim alterius distantiarum et iuxta secundam alterius. Ita enim utique dumtaxat vel nulla vel eadem fiet distantiam penes anomaliam ipsius secundum utramque distantiarum, quare et equales supersumptas fieri periferias, vel alterius alterius] alternis V2F1, vel et alternis et omalis. Secundum autem arbitramur oportere et circa cursus Lune simillem instantiam facere. Hoc enim indiscreto manente, contingens rursum apparebit et Lunam multotiens equales periferias secundum longitudinem in equalibus temporibus superassumere posse, non penitus et anomalia ipsius restituta. Continget autem huiusmodi, sive secundum utramque distantiarum ab eodem secundum appositionem vel eodem secundum ablationem cursu faciet principium et non in eundem desinet, sive secundum alteram quidem a maximo cursu incipiens in minimum cursum desinat, secundum alteram vero a minimo cursu in maximum, sive equaliter distent utrimque ab eodem minimo vel maximo cursu et alterius distantie primus cursus et alterius postremus, unde quodcumque istorum si contingat, vel nullam rursus, vel eadem faciet penes anomaliam ipsius differentiam. Ac propter hoc eas quidem que secundum longitudinem super assumptiones equales faciet, anomaliam vero nequaquam restituet. Nichil ergo neque istorum simptomatum habere oportet assumptas differentias, differentias] distantias V2 del. differentias add. distantias F1 si cherent cherent] deberent V2F1 inde restitutum anomalie tempus contentum ire. Contrarie autem utique deberemus eligere eas que maxime inequalitatem declarare valent, si non tote contineantur anomalie restitutiones, hoc est quando non solum differentibus cursibus principia habeant, verum et valde differentibus vel secundum magnitudinem vel secundum potentiam, secundum magnitudinem quidem, velut quando secundum alteram quod quod] quidem V2 differentiam differentiam] add. s. l. tanti V3F1 distantiam V2 a minimo cursu incipit et non in maximum desinet, secundum alteram vero, quando a maximo incipit et non in minimum desinit. Plurima enim ita erit eius que secundum longitudinem superassumptionis differentia, non totis circulis anomalie completis, quando precipue tetartimorium unum vel et tria unus unus] unius V2F1 anomalie superassumuntur, duabus tunc penes anomaliam differentiis inequalibus distantiis futuris, secundum potentiam vero, velut quando secundum utramque quidem distantiarum a medio cursu inchoaverit, non ab eodem vero medio, sed secundum alteram quidem ab eo qui secundum appositionem, secundum alteram vero ab eo qui secundum ablationem. Et ita enim plurimum distabunt adinvicem longitudinis apoysie, apoysie] epoysie V2 precipue non restituta anomalia, tetartimorio quidem uno rursum vel etiam tribus superassumptis unius anomalie, duabus penes anomaliam differentiis, semicirculi vero iiii. Propter hec ergo et Yparcum videmus observantissime, ut maxime autumabat, usum assumptarum in huiusmodi considerationem differentiarum differentiarum] distantiarum V2 ellectione, et cousum quidem Lunam secundum alteram differentiam a maximo cursu fecisse principium et non in minimum quievisse, secundum alteram vero a minimo cursu fecisse principium et non in maximum quievisse, sorigentem sorigentem] corrigentem V2F1 vero et penes anomaliam Solis factam differentiam, quamvis brevem existentem, propter iiiiam ad proximum unius dodecatimorii et non eiusdem vel equalem faciens differentiam anomalie secundum utramque distantiarum in totos circulos reliquisse Solis restitionem. restitionem] restitucionem V2F1 Hec vero diximus, non acusantes preiacentem investigationem periodicarum restitutionum restitionum] restitucionum V2F1 conceptionis, sed constituentes quoniam cum competenti quidem instantia et secundum consequens ratiocinatione facta dirigere potest propositum. Si autem aliqua et quod minimum expositorum simptomatum pretereat, frustrabitur omnino ab inquisita conceptione, et quoniam difficilis est perspicaciter facientibus talium observationum ellectionem ab examinationem omnium debentium ipsis inesse redditio. Igitur expositarum periodicarum restitionum secundum ab Yparco factas computationes ea quidem que mensium, ut diximus, sane ut maxime inerat investigata, nullo sensibili apparet inde tua inde tua] mentita V2F1 a veritate, que vero anomalie et latitudinis digno cura aliquo peccans, quare et nobis compedium compedium] compendium V2F1 factum fuisse ex in huiusmodi discrecionem secundum simplicius et commodius assumptis ephodis, quas statim demonstrabimus simul quantitati lunaris anomalie, preexponentes primum propter ad ea que deinceps commodum secundum partium factos medios cursus et longitudinis et anomalie et latitudinis, convenienter preiacentibus periodicorum motuum restitutivis temporibus et ex demonstranda ipsorum directione superagregata.
〈IV.3〉 De eis qui secundum partem omalis motibus Lune
Si ergo demonstratum medium Solis motum diurnum o lix viii xvii xiii xii xxxi ad proximum multiplicantes in unius mensis dies xxix xxxi l viii xx et factis apposuerimus unius circuli gradus ccclx, habebimus, quos in uno mense media Luna movetur secundum longitudinem, gradus ccclxxxix vi xxiiii i xxiiii ii xxx lvii ad proximum. Istos distribuentes in propositos mensis dies habebimus diurnum medium motum longitudinis gradus xiii x xxxiiii lviii xxxiii xxx xxx ad proximum.
Rursus cclxix circulos anomalie multiplicantes in unius circuli gradus ccclx habebimus multitudinem graduum xcvidccc xl. Istos dividentes in factos dies ccli mensium viiccccxii x xliiii li xl habebimus et anomalie diurnum medium motum gradus xiii iii liii lvi xxix xxxviii xxxviii.
Similiter vdcccc xxiii latitudinis restitutiones multiplicantes in unius circuli gradus ccclx habebimus multitudinem graduum ii cxxxiicclxxx. Istos distribuentes in vdc lviii mensium factos dies clxiclxxvii lviii minuta lviii secunda iii xx habebimus et latitudinis diurnum medium motum gradus xiii xiii xlv xxxix xl xvii xix.
Rursum a Lune secundum longitudinem diurno motu aufferentes Solis medium diurnum motum habebimus apochis medium diurnum motum gradus xii xi xxvi xli xx xvii lix. Per deinceps vero, ut diximus, nobis assumandas in huiusmodi consideracione ephodos longitudinis quidem diurnum motum fere inpermutabilem reperimus a preiacenti eum qui apochis manifestum quoniam, anomalie vero minorem gradibus o o o o xi xlvi xxxix, quare fieri graduum xiii iii liii lvi xvii li lix, latitudinis autem maiorem gradibus o o o o viii xxxix xviii, quare et ipsum fieri graduum xiii xiii xlv xxxix xlviii lvi xxxvii.
Secundum hec vero diurna sumentes uniuscuiusque xxiiii habebimus horarum medium motum, longitudinis quidem graduum o xxxii lvi xxvii xxvi xxiii xlvi, anomalie vero graduum o xxxii xxxix xliiii l xliiii xxxix lvii xxx, latitudinis vero graduum o xxxiii iiii xxiiii ix xxxii xxxi xxxii xxx, apochis autem graduum o xxx xxviii xxxvi xliii xx xliiii lvii xxx. Tricesies autem fatientes diurnos et auferentes circulos habebimus menstruam menstruam] mediam V2 add. mediam F1 epoysiam, longitudinis quidem graduum xxxv xvii xxix xvi xlv xv, anomalie vero graduum xxxi lvi lviii viii lv lix xxx, latitudinis autem graduum xxxvi lii xlix liiii xxviii xviii xxx, apochis autem graduum v xliii xx xl viii lix xxx.
Rursum diurnos multiplicantes in egiptiaci anni dies ccclxv et auferentes omnes circulos habebimus annuam mediam epoysiam, longitudinis quidem graduum cxxix xxii xlvi xiii l xxxii xxx, anomalie vero graduum lxxxviii xliii vii xxviii xli xiii lv, latitudinis autem graduum cxlviii xlii xlvii xii xliiii xxv v, apochis graduum cxxix xxxvii xxi xxviii xxix xxiii lv.
Dehinc deciesocties facientes annuos, per canonographiam sicut diximus commodum, et auferentes totos circulos habebimus xviii annorum spatii mediam epoysiam, longitudinis quidem graduum clxviii xlix lii ix ix xlv, anomalie vero gradum clvi lvi xiiii xxxvi xxii x xxx, latitudinis autem graduum clvi l viiii xlix xix xxxi xxx, apochis autem graduum clxxiii xii xxvi xxxii xlix x xxx.
Descripsimus ergo, quemadmodum et in Sole, canones tres in versus quidem rursum xlv, selidia vero secundum unumquemque v. Selidiorum autem prima quidem continebunt propria tempora, in primo quidem canone xviii annos, in secundo vero annos simplices et deinceps rursum horas, in tertio autem menses et deinceps rursum dies, reliqua autem iiiior proprias mensium appositiones, secunda quidem longitudinis, tertia anomalie, quarta latitudinis, quinta apochis. apochis] add. et est expositio canoniorum talis V2F1
〈IV.4〉
Motus Lune in longitudine |
Motus Lune in diversitate |
|||||||||||||||
Anni congregati |
Anni congregati |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
||||||||
xviii |
clxviii |
xlix |
lii |
ix |
ix |
xlv |
o |
xviii |
clvi |
lvi |
xiiii |
xxxvi |
xxii |
x |
xxx |
|
xxxvi |
cccxxxvii |
xxxix |
xviii |
xliiii |
xix |
xxx |
o |
xxxvi |
cccxiii |
lii |
xxix |
xii |
xliiii |
xxi |
o |
|
liiii |
cxlvi |
xxix |
xxvii |
xxxvi |
xxix |
xv |
o |
liiii |
cx |
xlviii |
xliii |
xlix |
vi |
xxxi |
xxx |
|
lxxii |
cccxv |
xix |
xxxvi |
xxviii |
xxxix |
o |
o |
lxxii |
cclxvii |
xliiii |
lviii |
xxv |
xxviii |
xlii |
o |
|
xc |
cxxiiii |
ix |
xlv |
xx |
xlviii |
xlv |
o |
xc |
lxiiii |
xli |
xiii |
i |
l |
lii |
xxx |
|
cviii |
cxcii |
lix |
liiii |
xii |
lviii |
xxx |
o |
cviii |
ccxxi |
xxxvii |
xxvii |
xxxviii |
xiii |
iii |
o |
|
cxxvi |
ci |
xlix |
iiii |
v |
viii |
xv |
o |
cxxvi |
xviii |
xxxiii |
xlii |
xiiii |
xxxv |
xiii |
xxx |
|
cxliiii |
cclxx |
xxxviii |
xiii |
lvii |
xviii |
o |
o |
cxliiii |
clxxv |
xxix |
lvi |
l |
lvii |
xxiiii |
o |
|
clxii |
lxxix |
xxviii |
xxii |
xlix |
xxvii |
xlv |
o |
clxii |
cccxxxii |
xxvi |
xi |
xxvii |
xix |
xxxiiii |
xxx |
|
clxxx |
ccclviii |
xviii |
xxxi |
xli |
xxxvii |
xxx |
o |
clxxx |
cxxix |
xxii |
xxvi |
iii |
xli |
xlv |
o |
|
cxcviii |
lvii |
viii |
xl |
xxxii |
xlvii |
xv |
o |
cxcviii |
cclxxxvi |
xviii |
xl |
xl |
iii |
lv |
xxx |
|
ccxvi |
ccxxv |
lviii |
xlix |
xxv |
lvii |
o |
o |
ccxvi |
lxxxiii |
xiiii |
lv |
xvi |
xxvi |
vi |
o |
|
dclxvi |
cxxvi |
xlv |
xxxix |
ix |
o |
xlv |
o |
dclxvi |
xlvi |
xli |
o |
xxv |
xl |
xxviii |
xxx |
|
dclxxxiiii |
ccxcv |
xxxv |
xlviii |
i |
x |
xxx |
o |
dclxxxiiii |
cciii |
xxxvii |
xxxvii |
xv |
ii |
ii |
o |
|
dccii |
ciiii |
xxiiii |
lvii |
liii |
xx |
xv |
o |
dccii |
o |
xxxiii |
xxix |
xxxviii |
xxiiii |
xlix |
xxx |
|
dccxx |
cclxxiii |
xiiii |
vi |
xlvi |
xxx |
o |
o |
dccxx |
clvii |
xxix |
xliiii |
xiiii |
xlvii |
o |
o |
|
dccxxxviii |
lxxxii |
iiii |
xv |
xxxviii |
xxxix |
xlv |
o |
dccxxxviii |
cccxiiii |
xxv |
lviii |
li |
ix |
x |
xxx |
|
dcclvi |
ccl |
liiii |
xxiiii |
xxii |
xlix |
xxx |
o |
dcclvi |
cxi |
xxii |
xiii |
xxvii |
xxxi |
xxi |
o |
|
dcclxxiiii |
lix |
xliiii |
xxxiii |
xxii |
lix |
xv |
o |
dcclxxiiii |
cclxviii |
xviii |
xxviii |
iii |
liii |
xxxi |
xxx |
|
dccxcii |
ccxxviii |
xxxiiii |
xiiii |
xliii |
ix |
o |
o |
dccxcii |
lxv |
xiiii |
xlii |
xl |
xv |
xlii |
o |
|
dcccx |
xxxvii |
xxiiii |
xii |
vi |
xviii |
xlv |
o |
dcccx |
ccxxii |
x |
lvii |
xvi |
xxxvii |
lii |
xxx |
|
Motus Lune in latitudine |
Motus Lune in loco suo a Sole |
|||||||||||||||
Anni congregati |
Anni congregati |
|||||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||
xviii |
clvi |
i |
ix |
xlix |
xix |
xxxi |
xxx |
xviii |
clxxiii |
xii |
xxvi |
xxxii |
xlix |
x |
xxx |
|
xxxvi |
cccxiii |
xl |
xix |
xxxviii |
xxxix |
iii |
o |
xxxvi |
cccxlvi |
xxiiii |
liii |
v |
xxxviii |
xxi |
o |
|
liiii |
cx |
xxx |
xxix |
xxviii |
lviii |
xxxiiii |
xxx |
liiii |
clix |
xxxvii |
xix |
xxxviii |
xxvii |
xxxi |
xxx |
|
lxxii |
cclxvii |
xx |
xxxix |
xvii |
xviii |
vi |
o |
lxxii |
cccxxxii |
xlix |
xlvi |
xi |
xvi |
xlii |
o |
|
xc |
lxiiii |
x |
xlix |
vi |
xxxvii |
xxxvii |
xxx |
xc |
cxlvi |
ii |
xii |
xliiii |
v |
lii |
xxx |
|
cviii |
ccxxi |
o |
lviii |
lv |
lvii |
ix |
o |
cviii |
cccxix |
xiiii |
xxxix |
xvi |
lv |
iii |
o |
|
cxxvi |
xvii |
li |
viii |
xlv |
xvi |
xl |
xxx |
cxxvi |
cxxxii |
xxvii |
v |
xlix |
xliiii |
xiii |
xxx |
|
cxliiii |
clxxiiii |
xli |
xviii |
xxxiiii |
xxxvi |
xii |
o |
cxliiii |
cccv |
xxxix |
xxxii |
xxii |
xxxiii |
xxiiii |
o |
|
clxii |
cccxxxi |
xxxi |
xxviii |
xxiii |
lv |
xliii |
xxx |
clxii |
cxviii |
li |
lviii |
lv |
xxii |
xxxiiii |
xxx |
|
clxxx |
cxxviii |
xxi |
xxxviii |
xiii |
xv |
xv |
o |
clxxx |
ccxcii |
iiii |
xxv |
xxviii |
xi |
xlv |
o |
|
cxcviii |
cclxxxv |
xi |
xlviii |
ii |
xxxiiii |
xlvi |
xxx |
cxcviii |
cv |
xvi |
lii |
i |
o |
lv |
xxx |
|
ccxvi |
lxxxii |
i |
lvi |
li |
liiii |
xviii |
o |
ccxvi |
cclxxviii |
xxix |
xviii |
xxxiii |
l |
vi |
o |
|
ccxxxiiii |
ccxxxviii |
lii |
vii |
xli |
xiii |
xlix |
xxx |
ccxxxiiii |
xci |
xli |
xlv |
vi |
xxxix |
xvi |
xxx |
|
cclii |
xxxv |
xlii |
xvii |
xxx |
xxxiii |
xxi |
o |
cclii |
cclxiiii |
liiii |
xi |
xxxix |
xxviii |
xxvii |
o |
|
cclxx |
cxcii |
xxxii |
xxvcii |
xix |
lii |
lii |
xxx |
cclxx |
lxxviii |
vi |
xxxviii |
xii |
xvii |
xxxvii |
xxx |
|
cclxxxviii |
cccxlix |
xxii |
xxxvii |
ix |
xiii |
xxiiii |
o |
cclxxxviii |
ccli |
xix |
iiii |
xlv |
vi |
xlviii |
o |
|
cccvi |
cxlvi |
xii |
xlvi |
lviii |
xxxi |
lv |
xxx |
cccvi |
lxiiii |
xxxi |
xxxi |
xvii |
lv |
lviii |
xxx |
|
cccxxiiii |
ccciii |
ii |
lvi |
xlvii |
li |
xxvii |
o |
cccxxiiii |
ccxxxvii |
xliii |
lvii |
l |
xlv |
ix |
o |
|
cccxlii |
xcix |
liii |
vi |
xxxvii |
x |
lviii |
xxx |
cccxlii |
l |
lvi |
xxiiii |
xxiii |
xxxiiii |
xix |
xxx |
|
ccclx |
cclvi |
xliii |
xvi |
xxvi |
xxx |
xx |
o |
ccclx |
ccxxiiii |
viii |
l |
lvi |
xxiii |
xxx |
o |
|
ccclxxviii |
liii |
xxxiii |
xxvi |
xv |
i |
l |
xxx |
ccclxxviii |
xxxvii |
xxi |
xvii |
xxix |
xii |
xl |
xxx |
|
Motus Lune in longitudine |
Motus Lune in diversitate |
|||||||||||||||
Menses |
Menses |
|||||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||
xxx |
xxxv |
xvii |
xxix |
xvi |
xlv |
xv |
o |
xxx |
xxxi |
lvi |
lviii |
viii |
lv |
lix |
xxx |
|
lx |
lxx |
xxxiiii |
lviii |
xxxiii |
xxx |
xxx |
o |
lx |
lxiii |
liii |
lvi |
xvii |
li |
lix |
o |
|
xc |
cv |
lii |
xxvii |
l |
xv |
xlv |
o |
xc |
xcv |
l |
liiii |
xxvi |
xlvii |
lviii |
xxx |
|
cxx |
cxli |
ix |
lvii |
vii |
i |
o |
o |
cxx |
cxxvii |
xlvii |
lii |
xxxv |
xliii |
lviii |
o |
|
cl |
clxxvi |
xxvii |
xxvi |
xxiii |
xlvi |
xv |
o |
cl |
clix |
xliiii |
l |
xliiii |
xxxix |
lvii |
xxx |
|
clxxx |
ccxi |
xliiii |
lv |
xl |
xxxi |
xxx |
o |
clxxx |
cxci |
xli |
xlviii |
liii |
xxxv |
lviii |
o |
|
ccx |
ccxlvii |
ii |
xxiiii |
lvii |
xvi |
xlv |
o |
ccx |
ccxxiii |
xxxviii |
xlvii |
ii |
xxxi |
lvi |
xxx |
|
cclx |
cclxxxii |
xix |
liiii |
xiiii |
ii |
o |
o |
ccxl |
cclv |
xxxv |
xlv |
xi |
xxvii |
lvi |
o |
|
cclxx |
cccxvii |
xxxvii |
xxiii |
xxx |
xlvii |
xv |
o |
cclxx |
cclxxxviii |
xxxii |
xliii |
xx |
xxiii |
lv |
xxx |
|
ccc |
ccclii |
liiii |
lii |
xlvii |
xxxii |
xxx |
o |
ccc |
cccxix |
xxix |
xli |
xxix |
xix |
lv |
o |
|
cccxxx |
xxviii |
xii |
xxii |
iiii |
xvii |
xlv |
o |
cccxxx |
cccli |
xxvi |
xxxix |
xxxviii |
xv |
liiii |
xxx |
|
ccclx |
lxiii |
xxix |
li |
xxi |
iii |
o |
o |
ccclx |
xxiii |
xxiii |
xxxvii |
xlvii |
xi |
liiii |
o |
|
Motus Lune in longitudine |
Motus Lune in diversitate |
|||||||||||||||
Dies |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Dies |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
i |
xiii |
x |
xxxiiii |
lviii |
xxxiii |
xxx |
xxx |
i |
xiii |
iii |
liii |
lvi |
xvii |
li |
lix |
|
ii |
xxvi |
xxi |
ix |
lvii |
vii |
i |
o |
ii |
xxvi |
vii |
xlvii |
lii |
xxxv |
xliii |
lviii |
|
iii |
xxxix |
xxxi |
xliiii |
lv |
xl |
xxxi |
xxx |
iii |
xxxix |
xi |
xli |
xlviii |
liii |
xxxv |
lvii |
|
iiii |
lii |
xlii |
xix |
liiii |
xiiii |
ii |
o |
iiii |
lii |
xv |
xxxv |
xlv |
xi |
xxvii |
lvi |
|
v |
lxv |
lii |
liiii |
lii |
xlvii |
xxxii |
xxx |
v |
lxv |
xix |
xxix |
xli |
xxix |
xix |
lv |
|
vi |
lxxix |
iii |
xxxix |
li |
xxi |
iii |
o |
vi |
lxxviii |
xxiii |
xxiii |
xxxvi |
xlvii |
xi |
liiii |
|
vii |
xcii |
xiiii |
iiii |
xlix |
liiii |
xxxiii |
xxx |
vii |
xci |
xxvii |
xvii |
xxxiiii |
v |
iii |
liii |
|
viii |
cv |
xxiiii |
xxxix |
xlviii |
xxviii |
iiii |
o |
viii |
ciiii |
xxxi |
xi |
xxx |
xxii |
lv |
lii |
|
ix |
cxviii |
xxxv |
xiiii |
xlvii |
i |
xxxiiii |
xxx |
ix |
cxvii |
xxxv |
v |
xxvi |
xl |
xlvii |
li |
|
x |
cxxxi |
xlv |
xlix |
xlv |
xxxv |
v |
o |
x |
cxxx |
xxxviii |
lix |
xxii |
lviii |
xxxix |
l |
|
xi |
cxliiii |
lvi |
xxiiii |
xliiii |
viii |
xxxv |
xxx |
xi |
cxliii |
xlii |
liii |
xix |
xvi |
xxxi |
xlix |
|
xii |
clviii |
vi |
lix |
xlii |
xlii |
vi |
o |
xii |
clvi |
xlvi |
xlvii |
xv |
xxxiiii |
xxiii |
xlviii |
|
xiii |
clxxi |
xvii |
xxxiiii |
xli |
xv |
xxxvi |
xxx |
xiii |
clxix |
l |
xli |
xi |
lii |
xv |
xlvii |
|
xiiii |
clxxxiiii |
xxviii |
ix |
xxxix |
xlix |
vii |
o |
xiiii |
clxxxii |
liiii |
xxxv |
viii |
x |
vii |
xlvi |
|
xv |
cxcvii |
xxxviii |
xliiii |
xxxviii |
xxii |
xxxvii |
xxx |
xv |
cxcv |
lviii |
xxix |
iiii |
xxvii |
lix |
xlv |
|
xvi |
ccx |
xlix |
xix |
xxxvi |
lvi |
viii |
o |
xvi |
ccix |
ii |
xxiii |
o |
xlv |
li |
xliiii |
|
xvii |
ccxxiii |
lix |
liiii |
xxxv |
xxix |
xxxviii |
xxx |
xvii |
ccxxii |
vi |
xvi |
lvii |
iii |
xliii |
xliii |
|
xviii |
ccxxxvii |
x |
xxix |
xxxiiii |
iii |
ix |
o |
xviii |
ccxxxv |
x |
x |
liii |
xxi |
xxxv |
xlii |
|
xix |
ccl |
xxi |
iiii |
xxxii |
xxxvi |
xxxix |
xxx |
xix |
ccxlviii |
xiiii |
iiii |
xlix |
xxxix |
xxvii |
xli |
|
xx |
cclxiii |
xxxi |
xxxix |
xxxi |
x |
x |
o |
xx |
cclxi |
xvii |
lviii |
xlv |
lvii |
xix |
xl |
|
xxi |
cclxxvi |
xlii |
xiiii |
xxix |
xliii |
xl |
xxx |
xxi |
cclxxiiii |
xxi |
lii |
xlii |
xv |
xi |
xxxix |
|
xxii |
cclxxxix |
lii |
xlix |
xxviii |
xvii |
xi |
o |
xxii |
cclxxxvii |
xxv |
xlvi |
xxxviii |
xxxiii |
iii |
xxxviii |
|
xxiii |
ccciii |
iii |
xxiiii |
xxvi |
l |
xli |
xxx |
xxiii |
ccc |
xxix |
xl |
xxxiiii |
l |
lv |
xxxvii |
|
xxiiii |
cccxvi |
xiii |
lix |
xxv |
xxiiii |
xii |
o |
xxiiii |
cccxiii |
xxxiii |
xxxiiii |
xxxi |
vii |
xlvii |
xxxvi |
|
xxv |
cccxxix |
xxiiii |
xxxiiii |
xxxiii |
lvii |
xlii |
xxx |
xxv |
cccxxvi |
xxxvii |
xxviii |
xxvii |
xxvi |
xxxix |
xxxv |
|
xxvi |
cccxlii |
xxxv |
ix |
xxii |
xxxi |
xiii |
o |
xxvi |
cccxxxix |
xli |
xxii |
xxiii |
xliiii |
xxxi |
xxxiiii |
|
xxvii |
ccclv |
xlv |
xliiii |
xxi |
iiii |
xliii |
xxx |
xxvii |
ccclii |
xlv |
xvi |
xx |
ii |
xxiii |
xxxiii |
|
xxviii |
viii |
lvi |
xix |
xix |
xxxviii |
xiiii |
o |
xxviii |
v |
xlix |
x |
xvi |
xx |
xv |
xxxii |
|
xxix |
xxii |
vi |
liiii |
xviii |
xi |
xliiii |
xxx |
xxix |
xviii |
liii |
iiii |
xii |
xxxviii |
vii |
xxxi |
|
xxx |
xxxv |
xvii |
xxix |
xvi |
xlv |
xv |
o |
xxx |
xxxi |
lvi |
lviii |
viii |
lv |
lix |
xxx |
|
Motus Lune in latitudine |
Motus Lune in distantia loci eius a Sole |
|||||||||||||||
Menses |
Menses |
|||||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||
xxx |
xxxvi |
lii |
xlix |
liiii |
xxviii |
xviii |
xxx |
xxx |
v |
xliii |
xx |
xl |
viii |
lix |
xxx |
|
lx |
lxxiii |
xlv |
xxxix |
xlviii |
lvi |
xxxvii |
o |
lx |
xi |
xxvi |
xli |
xx |
xvii |
lix |
o |
|
xc |
xc |
xxxviii |
xxix |
xliii |
xxiiii |
lv |
xxx |
xc |
xvii |
x |
ii |
o |
xxvi |
lviii |
xxx |
|
cxx |
cxlvii |
xxxi |
xix |
xxxvii |
liii |
xiiii |
o |
cxx |
xxii |
liii |
xxii |
xl |
xxxv |
lviii |
o |
|
cl |
clxxxiiii |
xxiiii |
ix |
xxxii |
xxi |
xxxii |
xxx |
cl |
xxviii |
xxxvi |
xliii |
xx |
xliiii |
lvii |
xxx |
|
clxxx |
ccxxi |
xvi |
lix |
xxvi |
xlix |
li |
o |
clxxx |
xxxiiii |
xx |
iiii |
o |
liii |
lvii |
o |
|
ccx |
cclviii |
ix |
xlix |
xxi |
xviii |
ix |
xxx |
ccx |
xl |
iii |
xxiiii |
xli |
ii |
lvi |
xxx |
|
ccxl |
ccxcv |
ii |
xxxix |
xv |
xlvi |
xxviii |
o |
ccxl |
xlv |
xlvi |
xlv |
xxi |
xi |
lvi |
o |
|
cclxx |
cccxxxii |
lv |
xxix |
x |
xiiii |
xlvi |
xxx |
cclix |
li |
xxx |
vi |
l |
xx |
lv |
xxx |
|
ccc |
viii |
xlviii |
xix |
iiii |
xliii |
v |
o |
ccc |
lvii |
xiii |
xxvi |
xli |
xxix |
lv |
o |
|
cccxxx |
xlv |
xli |
viii |
lix |
xi |
xxiii |
xxx |
cccxxx |
lxii |
lvi |
xlvii |
xxi |
xxxviii |
liiii |
xxx |
|
ccclx |
xxxiii |
lviii |
liii |
xxxix |
lxxii |
xlii |
o |
ccclx |
lxviii |
xl |
viii |
i |
xlvii |
liiii |
o |
|
Motus Lune in latitudine |
Motus Lune in distantia loci eius a Sole |
|||||||||||||||
Dies |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Dies |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|
i |
xiii |
xiii |
xlv |
xxxix |
xlviii |
lvi |
xxxvii |
i |
xii |
xi |
xxvi |
xli |
xx |
xvii |
lix |
|
ii |
xxvi |
xxvii |
xxxi |
xix |
xxxvii |
liii |
xiiii |
ii |
xxiiii |
xxii |
liii |
xxii |
xl |
xxxv |
lviii |
|
iii |
xxxix |
xli |
xvi |
lix |
xxvi |
xlix |
li |
iii |
xxxvi |
xxxiiii |
xx |
iiii |
o |
liii |
lvii |
|
iiii |
lii |
lv |
ii |
xxxix |
xv |
xlvi |
xxviii |
iiii |
xlviii |
xlv |
xlvi |
xlv |
xxi |
xi |
lvi |
|
v |
lxvi |
viii |
xlviii |
xix |
iiii |
xliii |
v |
v |
lx |
lvii |
xiii |
xxvi |
xli |
xxix |
lv |
|
vi |
lxxix |
xxii |
xxxiii |
lviii |
liii |
xxxix |
xlii |
vi |
lxxiii |
viii |
xl |
viii |
i |
xlvii |
liiii |
|
vii |
xcii |
xxxvi |
xix |
xxxviii |
xlii |
xxxvi |
xix |
vii |
lxxxv |
xx |
vi |
xlix |
xxii |
v |
liii |
|
viii |
cv |
l |
v |
xviii |
xxxi |
xxxii |
lvi |
viii |
xcvii |
xxxi |
xxxiii |
xxx |
xlii |
xxiii |
lii |
|
ix |
cxix |
iii |
l |
lviii |
xx |
xxix |
xxxii |
ix |
cix |
xliii |
o |
xii |
ii |
xli |
li |
|
x |
cxxxii |
xvii |
xxxvi |
xxxviii |
ix |
xxvi |
x |
x |
cxxi |
liiii |
xxvi |
liii |
xxii |
lix |
l |
|
xi |
cxlv |
xxxi |
xxii |
xvii |
lviii |
xxii |
xlvii |
xi |
cxxxiiii |
v |
liii |
xxxiiii |
xliii |
xvii |
xlix |
|
xii |
clviii |
xlv |
vii |
lvii |
xlvii |
xix |
xxiiii |
xii |
cxlvi |
xvii |
xx |
xvi |
iii |
xxxv |
xlviii |
|
xiii |
clxxi |
lviii |
liii |
xxxvii |
xxxvi |
xvi |
i |
xiii |
clviii |
xxviii |
xlvi |
lvii |
xxiii |
liii |
xlvii |
|
xiiii |
clxxxv |
xii |
xxxix |
xvii |
xxv |
xii |
xxxviii |
xiiii |
clxx |
xl |
xiii |
xxxviii |
xliiii |
xi |
xlvi |
|
xv |
cxcviii |
xxvi |
xxiiii |
lvii |
xiiii |
ix |
xv |
xv |
clxxxii |
li |
xl |
xx |
iiii |
xxix |
xlv |
|
xvi |
ccxi |
xl |
x |
xxxvii |
iii |
v |
lii |
xvi |
cxcv |
iii |
vii |
l |
xxiiii |
xlvii |
xliiii |
|
xvii |
ccxxiiii |
liii |
lvi |
xvi |
lii |
ii |
xxix |
xvii |
ccvii |
xiiii |
xxxiii |
xlii |
xlv |
v |
xliii |
|
xviii |
ccxxxviii |
vii |
xli |
lvi |
xl |
lix |
vi |
xviii |
ccxix |
xxvi |
o |
xxiiii |
v |
xxiii |
xlii |
|
xix |
ccli |
xxi |
xxvii |
xxxvi |
xxix |
lv |
xliii |
xix |
ccxxxi |
xxxvii |
xxvii |
v |
xxv |
xli |
xli |
|
xx |
cclxiiii |
xxxv |
xiii |
xvi |
xviii |
lii |
xx |
xx |
ccxliii |
xlviii |
liii |
xlvi |
xlv |
lix |
xl |
|
xxi |
cclxxvii |
xlviii |
lviii |
lvi |
vii |
xlviii |
lvii |
xxi |
cclvi |
o |
xx |
xxviii |
vi |
xvii |
xxxix |
|
xxii |
ccxci |
ii |
xliiii |
xxxv |
lvi |
xlv |
xxxiiii |
xxii |
cclxviii |
xi |
xlvii |
ix |
xxvi |
xxxv |
xxxviii |
|
xxiii |
ccciiii |
xvi |
xxx |
xv |
xlv |
xlii |
xi |
xxiii |
cclxxx |
xxiii |
xiii |
l |
xlvi |
liii |
xxxvii |
|
xxiiii |
cccxvii |
xxx |
xv |
lv |
xxxiiii |
xxxviii |
xlviii |
xxiiii |
ccxcii |
xxxiiii |
xl |
xxxii |
vii |
xi |
xxxvi |
|
xxv |
cccxxx |
xliiii |
i |
xxxv |
xxiii |
xxxv |
xxv |
xxv |
ccciiii |
xlvi |
vii |
xiii |
xxvii |
xxix |
xxxv |
|
xxvi |
cccxliii |
lvii |
xlvii |
xv |
xii |
xxxii |
ii |
xxvi |
cccxvi |
lvii |
xxxiii |
liiii |
xlvii |
xlvii |
xxxiiii |
|
xxvii |
ccclvii |
xi |
xxxii |
lv |
i |
xxviii |
xxxix |
xxvii |
cccxxix |
ix |
o |
xxxvi |
viii |
v |
xxxiii |
|
xxviii |
x |
xxv |
xviii |
xxxiiii |
l |
xxv |
xvi |
xxviii |
cccxli |
xx |
xxvii |
xvii |
xxviii |
xxiii |
xxxii |
|
xxix |
xxiii |
xxxix |
iiii |
xiiii |
xxxix |
xxi |
liii |
xxix |
cccliii |
xxxi |
liii |
lviii |
xlviii |
xli |
xxxi |
|
xxx |
xxxvi |
lii |
xlix |
liiii |
xxviii |
xviii |
xxx |
xxx |
v |
xliii |
xx |
xl |
viii |
lix |
xxx |
|
Motus Lune in longitudine |
Motus Lune in diversitate |
|||||||||||||||
Anni simplices |
Anni simplices |
|||||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Secunda |
|||
i |
cxxix |
xxii |
xlvi |
xiii |
l |
xxxii |
xxx |
i |
lxxxviii |
xliii |
vii |
xxviii |
xli |
xiii |
lv |
|
ii |
cclviii |
xlv |
xxxii |
xxvii |
xli |
v |
o |
ii |
clxxvii |
xxxvi |
xiiii |
lvii |
xxii |
xxvii |
l |
|
iii |
xxviii |
viii |
xviii |
xli |
xxxi |
xxxvii |
xxx |
iii |
cclxvi |
ix |
xxii |
xvi |
iii |
xli |
xlv |
|
iiii |
clvii |
xxxi |
iiii |
lv |
xxii |
x |
o |
iiii |
cccliiii |
lii |
xxix |
liiii |
xliiii |
lv |
xl |
|
v |
cclxxxv |
liii |
li |
ix |
xii |
xlii |
xxx |
v |
lxxxiii |
xxxv |
xxxvii |
xxiii |
xxvi |
ix |
xxxv |
|
vi |
lvi |
xvi |
xxxvii |
xxiii |
iii |
xv |
o |
vi |
clxxii |
xviii |
xliiii |
lii |
vii |
xxiii |
xxx |
|
vii |
clxxxv |
xxxix |
xxiii |
xxxvi |
liii |
xlvii |
xxx |
vii |
cclxi |
i |
lii |
xx |
xlviii |
xxxvii |
xxv |
|
viii |
cccxv |
ii |
ix |
l |
xliiii |
xx |
o |
viii |
cccxlix |
xliiii |
lix |
xlix |
xxix |
li |
xx |
|
ix |
lxxxiiii |
xxiiii |
lvi |
iiii |
xxxiiii |
lii |
xxx |
ix |
lxxviii |
xxviii |
vii |
xviii |
xi |
v |
xv |
|
x |
ccxiii |
xlvii |
xlii |
xviii |
xxv |
xxv |
o |
x |
clxvii |
xi |
xiiii |
xlvi |
lii |
xix |
x |
|
xi |
cccxliii |
x |
xxviii |
xxxii |
xv |
lvii |
xxx |
xi |
cclv |
liiii |
xxii |
xv |
xxxiii |
xxxiii |
v |
|
xii |
cxii |
xxxiii |
xiiii |
xlvi |
vi |
xxx |
o |
xii |
cccxliiii |
xxxvii |
xxix |
xliiii |
xiiii |
xlvii |
o |
|
xiii |
ccxli |
lvi |
o |
lix |
lvii |
ii |
xxx |
xiii |
lxxiii |
xx |
xxxiii |
xii |
lvi |
o |
lv |
|
xiiii |
xi |
xviii |
xlvii |
xiii |
xlvii |
xxxv |
o |
xiiii |
clxii |
iii |
xliiii |
xli |
xxxvii |
xiiii |
l |
|
xv |
cxl |
xli |
xxxiii |
xxvii |
xxxviii |
vii |
xxx |
xv |
ccl |
xlvi |
lii |
x |
xviii |
xxviii |
xlv |
|
xvi |
cclxx |
iiii |
xix |
xli |
xxviii |
xl |
o |
xvi |
cccxxxix |
xxix |
lix |
lxxxviii |
lix |
xlii |
xl |
|
xvii |
xxxix |
xxvii |
v |
lv |
xix |
xii |
xxx |
xvii |
lxviii |
xiii |
vii |
vii |
xl |
lvi |
xxxv |
|
xviii |
clxviii |
xlix |
lii |
ix |
ix |
xlv |
o |
xviii |
clvi |
lvi |
xiiii |
xxxvi |
xxii |
x |
xxx |
|
Ho
re |
Motus Lune in longitudine |
Ho
re |
Motus Lune in diversitate |
|||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Secunda |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Secunda |
|||
i |
o |
xxxii |
lvi |
xxvii |
xxvi |
xxiii |
xlvi |
i |
o |
xxxii |
xxxix |
xliiii |
l |
xliiii |
xl |
|
ii |
i |
v |
lii |
liiii |
lii |
xlvii |
xxxii |
ii |
i |
v |
xix |
xxix |
xli |
xxix |
xx |
|
iii |
i |
xxxviii |
xlix |
xxii |
xix |
xi |
xviii |
iii |
i |
xxxvii |
lix |
xiiii |
xxxii |
xiiii |
o |
|
iiii |
ii |
xi |
xlv |
xlix |
xlv |
xxxv |
v |
iiii |
ii |
x |
xxxviii |
lix |
xxii |
lviii |
xl |
|
v |
ii |
xliiii |
xlii |
xvii |
xi |
lviii |
li |
v |
ii |
xliii |
xviii |
xliiii |
xiii |
xliii |
xx |
|
vi |
ii |
xvii |
xxxviii |
xliiii |
xxxviii |
xxii |
xxxvii |
vi |
iii |
xv |
lviii |
xxix |
iiii |
xxviii |
o |
|
vii |
iii |
l |
xxxv |
xii |
iiii |
xlvi |
xxiiii |
vii |
iii |
xlviii |
xxxviii |
xiii |
lv |
xii |
xl |
|
viii |
iiii |
xxiii |
xxxi |
xxxix |
xxxi |
x |
x |
viii |
iiii |
xxi |
xvii |
lviii |
xlv |
lvii |
xx |
|
ix |
iiii |
lvi |
xxviii |
vi |
lvii |
xxxiii |
lvi |
ix |
iiii |
liii |
lvii |
xliii |
xxxvi |
xlii |
o |
|
x |
v |
xxix |
xxiiii |
xxxiiii |
xxiii |
lvii |
xlii |
x |
v |
xxvi |
xxxvii |
xxviii |
xxvii |
xxvi |
xl |
|
xi |
vi |
ii |
xxi |
i |
l |
xxi |
xxix |
xi |
v |
lix |
xvii |
xiii |
xviii |
xi |
xx |
|
xii |
vi |
xxxv |
xvii |
xxix |
xvi |
xlv |
xv |
xii |
vi |
xxxi |
lvi |
lviii |
viii |
lvi |
o |
|
xiii |
vii |
viii |
xiii |
lvi |
xliii |
ix |
i |
xiii |
vii |
iiii |
xxxvi |
xlii |
lix |
xl |
xxxix |
|
xiiii |
vii |
xli |
x |
xxiiii |
ix |
xxxii |
xlvii |
xiiii |
vii |
xxxvii |
xvi |
xxvii |
l |
xxv |
xix |
|
xv |
viii |
xiiii |
vi |
li |
xxxv |
lvi |
xxxiii |
xv |
viii |
ix |
lvi |
xii |
xli |
ix |
lix |
|
xvi |
viii |
xlvii |
iii |
xix |
ii |
xx |
xx |
xvi |
viii |
xlii |
xxxv |
lvii |
xxxi |
liiii |
xxxix |
|
xvii |
ix |
xix |
lix |
xlvi |
xxviii |
xliiii |
vi |
xvii |
ix |
xv |
xv |
xlii |
xxii |
xxxix |
xix |
|
xviii |
ix |
lii |
lvi |
xiii |
lv |
vii |
lii |
xviii |
ix |
xlvii |
lv |
xxvii |
xiii |
xxiii |
lix |
|
xix |
x |
xxv |
lii |
xli |
xxi |
xxxi |
xxxviii |
xix |
x |
xx |
xxxv |
xii |
iiii |
viii |
xxxix |
|
xx |
x |
lviii |
xlix |
viii |
xlvii |
lv |
xxv |
xx |
x |
liii |
xiiii |
lvi |
liiii |
liii |
xix |
|
xxi |
xi |
xxxi |
xlv |
xxxvi |
xiiii |
xix |
xi |
xxi |
xi |
xxv |
liiii |
xli |
xlv |
xxxvii |
lix |
|
xxii |
xii |
iiii |
xlii |
iii |
xl |
xliii |
lviii |
xxii |
xi |
lviii |
xxxiii |
xxvi |
xxxvi |
xxii |
xxxix |
|
xxiii |
xii |
xxxvii |
xxxviii |
xxxi |
vii |
vi |
xliiii |
xxiii |
xii |
xxxi |
xiiii |
xi |
xxviii |
vii |
xix |
|
xxiiii |
xiii |
x |
xxxiiii |
lviii |
xxxiii |
xxx |
xxx |
xxiiii |
xiii |
iii |
liii |
lvi |
xvii |
li |
lix |
|
Motus Lune in latitudine |
Motus Lune in distantia loci eius a Sole |
|||||||||||||||
Anni simplices |
Anni simplices |
|||||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Secunda |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Secunda |
|||
i |
cxlviii |
xlii |
xlvii |
xii |
xliiii |
xxv |
v |
i |
cxxix |
xxxvii |
xxi |
xxviii |
xxix |
xxiii |
lv |
|
ii |
ccxcvii |
xxv |
xxxiiii |
xxv |
xxviii |
l |
x |
ii |
cclix |
xiiii |
xlii |
lvi |
lviii |
xlvii |
l |
|
iii |
lxxxvi |
viii |
xxi |
xxxviii |
xiii |
xv |
xv |
iii |
xxviii |
lii |
iiii |
xxv |
xxviii |
xi |
xlv |
|
iiii |
ccxxxiiii |
li |
viii |
l |
lvii |
xl |
xx |
iiii |
cxviii |
xxix |
xxv |
liii |
lvii |
xxxv |
xl |
|
v |
xxiii |
xxxiii |
lvi |
iii |
xlii |
v |
xxv |
v |
cclxxxviii |
vi |
xlvii |
xxii |
xxvi |
lix |
xxxv |
|
vi |
clxxii |
xvi |
xliii |
xvi |
xxvi |
xxx |
xxx |
vi |
lvii |
xliiii |
viii |
l |
lvi |
xxiii |
xxx |
|
vii |
cccix |
lix |
xxx |
xxix |
x |
xv |
xxxv |
vii |
clxxxvii |
xxi |
xxx |
xix |
xxv |
xlvii |
xxv |
|
viii |
cix |
xlii |
xvii |
xli |
lv |
xx |
xl |
viii |
cccxvi |
lviii |
li |
xlvii |
lv |
li |
xx |
|
ix |
cclviii |
xxv |
iiii |
liiii |
xxxix |
xlv |
xlv |
ix |
lxxxvi |
xxxvi |
xiii |
xvi |
xxiiii |
xxxv |
xv |
|
x |
xlvii |
vii |
lii |
vii |
xxiiii |
x |
l |
x |
ccxvi |
liii |
xxxiiii |
xliiii |
liii |
lix |
x |
|
xi |
cxcv |
l |
xxxix |
xx |
viii |
xxxv |
lv |
xi |
cccxlv |
l |
lvi |
xiii |
xxiii |
xxiii |
v |
|
xii |
cccxliiii |
xxxiii |
xxvi |
xxxii |
xiii |
i |
o |
xii |
cxv |
xxviii |
xvii |
xli |
lii |
xlvii |
o |
|
xiii |
cxxxiii |
xvi |
xiii |
xlv |
xxxvii |
xxvi |
v |
xiii |
ccxlv |
v |
xxxix |
x |
xxii |
x |
lv |
|
xiiii |
cclxxxi |
lix |
o |
xviii |
xxi |
li |
x |
xiiii |
xiiii |
xliii |
o |
xxxviii |
li |
xxxiiii |
l |
|
xv |
lxx |
xli |
xlviii |
xi |
vi |
xvi |
xv |
xv |
cxliiii |
xx |
xxii |
vii |
xx |
lviii |
xlv |
|
xvi |
ccxix |
xxiiii |
xxxv |
xxiii |
l |
xli |
xx |
xvi |
cclxxiii |
lvii |
xliii |
xxxv |
l |
xxii |
xl |
|
xvii |
viii |
vii |
xxii |
xxxvi |
xxv |
vi |
xxv |
xvii |
xliii |
xxxv |
v |
iiii |
xix |
xlvi |
xxxv |
|
xviii |
clvi |
l |
ix |
xlix |
xix |
xxxi |
xxx |
xviii |
clxxiii |
xii |
xxvi |
xxxii |
xlix |
x |
xxx |
|
Hores |
Motus Lune in latitudine |
Hores |
Motus Lune in diversitate |
|||||||||||||
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
Gradus |
Minuta |
Secunda |
Tertia |
Quarta |
Quinta |
Sexta |
|||
i |
o |
xxxiii |
iiii |
xxiiii |
ix |
xxxii |
xxii |
i |
o |
xxx |
xxviii |
xxxvi |
xliii |
xx |
xlv |
|
ii |
i |
vi |
viii |
xlviii |
xix |
iiii |
xliii |
ii |
i |
o |
lvii |
xiii |
xxvi |
xli |
xxx |
|
iii |
i |
xxxix |
xiii |
xii |
xxviii |
xxxvii |
v |
iii |
i |
xxxi |
xxv |
l |
x |
ii |
xv |
|
iiii |
ii |
lii |
xvii |
xxxvi |
xxxviii |
ix |
xxx |
iiii |
ii |
i |
liiii |
xxvi |
liii |
xxii |
lix |
|
v |
ii |
xlv |
xxii |
o |
xlvii |
xli |
xlii |
v |
ii |
xxxii |
xxiii |
iii |
xxxvi |
xliii |
xlvii |
|
vi |
iii |
xviii |
xxvi |
xxiiii |
lvii |
xiiii |
x |
vi |
iii |
ii |
li |
xl |
xx |
iiii |
xxx |
|
vii |
iii |
li |
xxx |
xlix |
vi |
xlvi |
xxxi |
vii |
iii |
xxxiii |
xx |
xviii |
iii |
xxv |
xv |
|
viii |
iiii |
xxiiii |
xxxv |
xiii |
lvi |
xviii |
lii |
viii |
iiii |
iii |
xlviii |
liii |
xlvi |
xlvi |
lix |
|
ix |
iiii |
lvii |
xxxix |
xxxvii |
xxv |
li |
xiiii |
ix |
iiii |
xxxiiii |
xvii |
xxx |
xxx |
vi |
xlv |
|
x |
v |
xxx |
xliiii |
l |
xxxv |
xxiii |
xxxv |
x |
v |
iiii |
xlv |
vii |
xiii |
xxvii |
xxx |
|
xi |
vi |
iii |
xlviii |
xxv |
xliiii |
lv |
lvii |
xi |
xxxv |
xix |
xliii |
lvi |
xlvii |
xiiii |
v |
|
xii |
vi |
xxxvi |
lii |
xlix |
liiii |
xxviii |
xviii |
xii |
vi |
v |
xliii |
xx |
xl |
viii |
lix |
|
xiii |
vii |
ix |
lvii |
xiiii |
iiii |
o |
xl |
xiii |
vi |
xxxvi |
xi |
lvii |
xxiii |
xxix |
xliiii |
|
xiiii |
vii |
xliii |
i |
xxxviii |
xiii |
xxxiii |
i |
xiiii |
vii |
vi |
xl |
xxxiiii |
vi |
l |
xxix |
|
xv |
viii |
xvi |
vi |
ii |
xxiii |
v |
xxiii |
xv |
vii |
xxxvii |
ix |
x |
l |
xi |
xiiii |
|
xvi |
viii |
xlix |
x |
xxvii |
xxii |
xxxvii |
xlv |
xvi |
viii |
vii |
xxxvii |
xlvii |
xxxiii |
xxxi |
lix |
|
xvii |
ix |
xxii |
xiiii |
l |
xlii |
x |
vii |
xvii |
viii |
xxxviii |
vi |
xxiiii |
xvi |
lii |
xliiii |
|
xviii |
ix |
lv |
xix |
xiiii |
li |
xlii |
xxviii |
xviii |
ix |
viii |
xxxv |
i |
o |
xiii |
xxix |
|
xix |
x |
xxviii |
xxiii |
xxxix |
i |
xiiii |
l |
xix |
ix |
xxxix |
iii |
xxxvii |
xliii |
xxxiiii |
liiii |
|
xx |
xi |
i |
xxviii |
iii |
x |
xlvii |
xi |
xx |
x |
ix |
xxxii |
xiiii |
xxv |
liiii |
xix |
|
xxi |
xi |
xxxiiii |
xxxii |
vii |
xx |
xix |
xxxii |
xxi |
x |
xl |
o |
li |
x |
xv |
xliiii |
|
xxii |
xii |
l |
xxxvi |
xxi |
xxix |
li |
liiii |
xxii |
xi |
x |
xxix |
xxvii |
liii |
xxxv |
xxix |
|
xxiii |
xii |
xl |
xli |
xv |
xv |
xxxix |
xxiiii |
xxiii |
xi |
xl |
lix |
iiii |
xxxvi |
lvii |
xiiii |
|
xxiiii |
xiii |
xiii |
xlv |
xxxix |
xlviii |
lvii |
xxxviii |
xxiiii |
xii |
xi |
xxvii |
xli |
xx |
xvii |
lix |
|
〈IV.5〉 Quoniam et in simplici ypothesi Lune eadem apparentia faciunt et que secundum excentrotica et que secundum epiciclum
Consequente vero his demonstrare et modum et quantitatem lunaris anomalie, nunc primum faciemus super hoc sermonem, velut una ista existente, cui soli et omnes fere qui ante nos adherentes apparent, dico vero secundum expositum tempus restitutionem consumante. Post hec vero ostendemus quoniam facit quandam et secundam anomaliam Luna penes eas que ad Solem distantias, maximam quidem factam circa dichotomias utrasque, restitutam vero his his] bis V2F1 in menstruo tempore circa ipsas et sinodos et panselinia. Ita vero ordine demonstrationis ad secundam utemur, propter istam quidem sine prima complicata ipsi semper numquam reperiri posse, illam vero et sine secunda, quoniam quidem a lunaribus eclipsibus sumitur, secundum quas nulla sensibillis fit differentia ex penes Solem contingente. In precendente vero demonstratione et sequamur theorematis ephodis quibus et Iparcum videmus cousum. Sumentes enim et ipsi tres eclipses lunares ostendemus et quanta plurima fiat differentia penes medium motum et eam que secundum apoguiotaton apochin, velut huiusmodi anomalia secundum seipsam considerata et per eam que secundum epiciclum ypothesim consumata, quidem eisdem rursum futuris et per eam que secundum excentrotica ypothesim, proprius autem utique copulanda que huiusmodi secundum mixtionem ambarum anomaliarum secunde et penes Solem contingenti. Quoniam quidem talia rursum et hic fiunt apparentia per utramque expositarum ypothesium, quamvis non equalia sint invicem, quemadmodum in Sole ostendimus, tempora restitutionum ambarum eius scilicet que secundum anomaliam et eius que ad eum qui per media animalia circulum consideratur, sed, quemadmodum in Luna, inequalia, proportionibus rursum solis subiacentibus eisdem, ita utique intelligemus rursum in ipsa simplici anomalia Lune exposita facientes considerationem. Quoniam ergo celius celius] celeri V2 celerius F1 facit Luna ad eum qui per media animalia circulum restitutionem restitutionem] restitucionem V2F1 ea que ad subiacentem anomaliam, in equalibus temporibus manifestum quoniam secundum eam que secundum epiciclum ypothesim maiorem quam secundum simille periferiam epiciclus semper movebitur in eo qui omocentricus zodiaco ea que a Luna secundum epiciclum conprehenditur. In ea vero vero] add. que V2F1 secundum excentrotica Luna quidem simillem ei que in epiciclo et in excentrotico movebitur periferiam, excentricus vero in eadem Lune circa centrum zodiaci tantam, quanta maior est que secundum longitudinem progressio ea que secundum anomaliam, hoc est facta omocentrici periferia ea que epicicli. Ita enim non solum proportionum, sed etiam temporum temporum] add. utriusque V2F1 motuum simillitudines in ambabus ypothesibus salvabuntur.
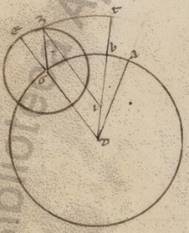 His ergo secundum consequens inde neccessario subiacentibus, esto omocentricus quidem ei qui per media animalia circulus ABG circa centrum D et diametrum AD, epiciclus vero EZ circa centrum G. Subiaceat autem, quando quidem erat epiciclus secundum A et Luna secundum E, apoguion epicicli facta, in equali vero tempore epiciclus quidem AG periferiam transiens, Luna vero EZ, et copulentur ED, ZG. Et quoniam maior est quam secundum simille AG periferia quam EZ, assumatur BG simillis eius que est EZ et coniungantur BD. Quoniam ergo in equali tempore et excentricus ADB angulum transituum ambarum superhabundantie motus est et factum est eius et centrum et apoguion in BD, manifestum. Hoc autem ita se habente, iaceat ei que est GZ equalis DI, et copulentur ZI, et centro I spatioque IZ scribatur excentricus circulus ZT; dico quoniam et eius quidem que est ZL ZL] ZI V2 ad ID proportio eadem erit proportioni eius que est DG ad GZ, et secundum istam vero ypothesim Luna secundum Z punctum erit, hoc est similis et ZT periferia erit ei que est EZ. Quoniam enim equalis est BDG angulus angulo EGZ, parallilos est GZ ei que est DI, et ZI ergo ei que est GD et equalis est et parallilos, et eius que est ZI ad ID proportio eadem proportioni eius que est DG ad GZ. Rursum quoniam paralillos est DG ei que est IZ, equalis est GDB angulus angulo ZIT. Subiaceat autem et GDB angulus angulo EGZ equalis. Quare et ZT periferia ei que est EZ simillis est. In equali ergo tempore secundum utramque ypothesium secundum Z punctum facta est Luna, quoniam quidem et ipsa EZ epicicli et TZ excentrici periferias similles ostensas mota est, epicicli vero centrum AG periferiam, quod vero excentrici AB superhabundantiam eius que est AG ad EZ. Quod oportebat ostendere.
His ergo secundum consequens inde neccessario subiacentibus, esto omocentricus quidem ei qui per media animalia circulus ABG circa centrum D et diametrum AD, epiciclus vero EZ circa centrum G. Subiaceat autem, quando quidem erat epiciclus secundum A et Luna secundum E, apoguion epicicli facta, in equali vero tempore epiciclus quidem AG periferiam transiens, Luna vero EZ, et copulentur ED, ZG. Et quoniam maior est quam secundum simille AG periferia quam EZ, assumatur BG simillis eius que est EZ et coniungantur BD. Quoniam ergo in equali tempore et excentricus ADB angulum transituum ambarum superhabundantie motus est et factum est eius et centrum et apoguion in BD, manifestum. Hoc autem ita se habente, iaceat ei que est GZ equalis DI, et copulentur ZI, et centro I spatioque IZ scribatur excentricus circulus ZT; dico quoniam et eius quidem que est ZL ZL] ZI V2 ad ID proportio eadem erit proportioni eius que est DG ad GZ, et secundum istam vero ypothesim Luna secundum Z punctum erit, hoc est similis et ZT periferia erit ei que est EZ. Quoniam enim equalis est BDG angulus angulo EGZ, parallilos est GZ ei que est DI, et ZI ergo ei que est GD et equalis est et parallilos, et eius que est ZI ad ID proportio eadem proportioni eius que est DG ad GZ. Rursum quoniam paralillos est DG ei que est IZ, equalis est GDB angulus angulo ZIT. Subiaceat autem et GDB angulus angulo EGZ equalis. Quare et ZT periferia ei que est EZ simillis est. In equali ergo tempore secundum utramque ypothesium secundum Z punctum facta est Luna, quoniam quidem et ipsa EZ epicicli et TZ excentrici periferias similles ostensas mota est, epicicli vero centrum AG periferiam, quod vero excentrici AB superhabundantiam eius que est AG ad EZ. Quod oportebat ostendere.
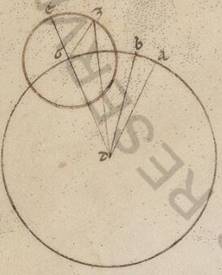 Quoniam vero et si similles tantum sint proportiones et non equales, neque ipse, neque excentricus omocentrico idem rursum contingit, et ita nobis erit manifestum. Describatur enim seorsum utraque ypothesium et esto omocentricus quidem ei qui per media animalia circulus ABG circa centrum D et diametrum AD, epiciclus autem EZ circa centrum G, Luna vero Z, et rursus excentricus quidem circulus ITK circa centrum L et diametrum TLM, in qua zodiaci centrum esto M, punctum vero K Luna. Et copuletur illic quidem DGE, GZ, DZ, hic autem IM, KM, KL. Subiaceat autem eius que est DG ad GE proportio eadem proportioni eius que est TL ad LM, et moveantur in equali tempore epiciclus quidem ADG angulum, et Luna rursum EGZ, excentricus autem IMT angulum, et Luna rursum TLK. Equalis ergo est per subiacentes ergo motuum proportiones EGZ quidem angulus ei qui est TLK, angulus autem ADG coutrisque IMT et TLK. Hoc autem ita se habente, dico quoniam rursum secundum utramque ypothesium in equali tempore equalem periferiam Luna apparebit transiens, hoc est quoniam equalis est ADZ angulus angulo IMK. Quoniam secundum principium quidem distantie et apoguiis existens Luna secundum DA et MI rectus apparebat, secundum finem vero in Z et K punctis existens per ZD et MK. Iaceat autem utrique TK et EZ periferiarum similis rursum BG, et copulentur BD. Quoniam ergo est sicut DG ad GZ, ita KL ad LM, et circa equales angulos qui ad G, L puncta latera proportionalia, equiangulum est GDZ trigonium trigono KLM et sub proportionalibus lateribus anguli equales, equalis ergo est GZD angulus angulo LMK. Sed et BDZ angulo GDZ equalis, eo quod paralille sint GZ et BD, equalibus subiacentibus ZGE et BDG angulis, equalis ergo est et ZBD ZDB angulus angulo LMK. Subiaceat autem et ADB angulus superhabundancie motuum ei qui sub IMT excentrici progressui equalis et totus ergo ADZ equalis est toti KMI. Quod propositum erat demonstrare.
Quoniam vero et si similles tantum sint proportiones et non equales, neque ipse, neque excentricus omocentrico idem rursum contingit, et ita nobis erit manifestum. Describatur enim seorsum utraque ypothesium et esto omocentricus quidem ei qui per media animalia circulus ABG circa centrum D et diametrum AD, epiciclus autem EZ circa centrum G, Luna vero Z, et rursus excentricus quidem circulus ITK circa centrum L et diametrum TLM, in qua zodiaci centrum esto M, punctum vero K Luna. Et copuletur illic quidem DGE, GZ, DZ, hic autem IM, KM, KL. Subiaceat autem eius que est DG ad GE proportio eadem proportioni eius que est TL ad LM, et moveantur in equali tempore epiciclus quidem ADG angulum, et Luna rursum EGZ, excentricus autem IMT angulum, et Luna rursum TLK. Equalis ergo est per subiacentes ergo motuum proportiones EGZ quidem angulus ei qui est TLK, angulus autem ADG coutrisque IMT et TLK. Hoc autem ita se habente, dico quoniam rursum secundum utramque ypothesium in equali tempore equalem periferiam Luna apparebit transiens, hoc est quoniam equalis est ADZ angulus angulo IMK. Quoniam secundum principium quidem distantie et apoguiis existens Luna secundum DA et MI rectus apparebat, secundum finem vero in Z et K punctis existens per ZD et MK. Iaceat autem utrique TK et EZ periferiarum similis rursum BG, et copulentur BD. Quoniam ergo est sicut DG ad GZ, ita KL ad LM, et circa equales angulos qui ad G, L puncta latera proportionalia, equiangulum est GDZ trigonium trigono KLM et sub proportionalibus lateribus anguli equales, equalis ergo est GZD angulus angulo LMK. Sed et BDZ angulo GDZ equalis, eo quod paralille sint GZ et BD, equalibus subiacentibus ZGE et BDG angulis, equalis ergo est et ZBD ZDB angulus angulo LMK. Subiaceat autem et ADB angulus superhabundancie motuum ei qui sub IMT excentrici progressui equalis et totus ergo ADZ equalis est toti KMI. Quod propositum erat demonstrare.
〈IV.6〉 Apodixis prime et simplicis anomalie
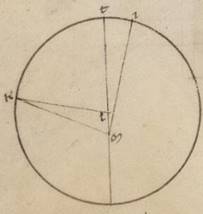 Hec ergo usque tanta nobis preconsiderentur. Faciemus autem demonstrationem exposite lunaris anomalie, in ea que secundum epiciclum ypothesim, propter quam diximus causam; primum quidem earum quas habemus principalissimas eclipsium tribus indubitanter visis describi coutentes, deinceps vero et earum que in presenti tempore tribus rursum a nobis ipsis diligentissime observatis. Ita enim utique et examinatio nobis erit, per quantum maxime possibille erat longum tempus, et aliter manifestum erit quoniam et que penes anomaliam differentia eadem ex ambobus ostensionibus ad proximum exibit, et mediorum motuum epoysia consona semper invenietur secundum exposita periodica tempora secundum nostram directionem supercollecte. Ad ostensionem ergo prime et quasi secundum seipsam considerate anomalie ea que secundum epiciclum ypothesis, ut diximus, contineat modum hunc. Intelligatur enim in Lune spera circulus omocentricus et in eodem epipedo iacens ei qui per media animalia, adhuc vero alter inclinatus proportionalis quantitati eius qui secundum latitudinem motus Lune, delatus plane in precedentia circa centrum qui per media animalia circuli tantum, quantum qui secundum latitudinem motus superabundat illi qui secundum longitudinem. In isto ergo obliquo circulo ferri supponimus eum qui vocatur epiciclus plane rursus in consequentia mundi consequenter ei que secundum latitudinem restitutioni, que manifestum quoniam ad ipsum qui per media animalia consideratum secundum longitudinem facit motum. In ipso autem epiciclo Lunam velut secundum apoguiam periferiam in precedentia mundi transitionem facientem consequenter ei que anomalie restitutioni. Ad subiacentem tamen ostensionem nichil utique impediemur, neque ea que per latitudinem precessione, neque obliquatione lunaris circuli coassumpta, nulla cura digna differentia ei qui secundum longitudinem progressui accedente ex ea que in tantum inclinatione. Earum ergo quas sumpsimus antiquarum trium eclipsium ex in Babilone obversatis prima quidem descripta est primo anno Mardokempadi secundum Egipitios Thot xxixa in xxxa. Incepit autem, inquit, deficere post ortum, una hora sufficienter preterita, et defecit tota. Quoniam ergo Sol circa postrema Piscium erat et nox horarum equinoctialium xii ad proximum, principium quidem eclipseos factum fuit manifestum quoniam ante iiiior horas equinoctiales et dimidium a mesonictio, medium vero tempus, quoniam perfecta erat eclipsis, ante duas horas et dimidium. In Alexandria ergo, quoniam quidem ad eum qui per ipsam meridianum epochas constituimus horarias, precedit vero qui per ipsam meridianus eum qui per Babilonem dimidia et tracta tracta] tercia V2F1 ad proximum hore unius equinoctialis, medium tempus fuit preiacentis eclipseos ante tres horas equinoctiales et iiia a mesonictio, secundum quam horam Sol secundum preexpositas ratiocinationes nobis obtinebat examinate Piscium gradus xxiiiia et dimidium ad proximum.
Hec ergo usque tanta nobis preconsiderentur. Faciemus autem demonstrationem exposite lunaris anomalie, in ea que secundum epiciclum ypothesim, propter quam diximus causam; primum quidem earum quas habemus principalissimas eclipsium tribus indubitanter visis describi coutentes, deinceps vero et earum que in presenti tempore tribus rursum a nobis ipsis diligentissime observatis. Ita enim utique et examinatio nobis erit, per quantum maxime possibille erat longum tempus, et aliter manifestum erit quoniam et que penes anomaliam differentia eadem ex ambobus ostensionibus ad proximum exibit, et mediorum motuum epoysia consona semper invenietur secundum exposita periodica tempora secundum nostram directionem supercollecte. Ad ostensionem ergo prime et quasi secundum seipsam considerate anomalie ea que secundum epiciclum ypothesis, ut diximus, contineat modum hunc. Intelligatur enim in Lune spera circulus omocentricus et in eodem epipedo iacens ei qui per media animalia, adhuc vero alter inclinatus proportionalis quantitati eius qui secundum latitudinem motus Lune, delatus plane in precedentia circa centrum qui per media animalia circuli tantum, quantum qui secundum latitudinem motus superabundat illi qui secundum longitudinem. In isto ergo obliquo circulo ferri supponimus eum qui vocatur epiciclus plane rursus in consequentia mundi consequenter ei que secundum latitudinem restitutioni, que manifestum quoniam ad ipsum qui per media animalia consideratum secundum longitudinem facit motum. In ipso autem epiciclo Lunam velut secundum apoguiam periferiam in precedentia mundi transitionem facientem consequenter ei que anomalie restitutioni. Ad subiacentem tamen ostensionem nichil utique impediemur, neque ea que per latitudinem precessione, neque obliquatione lunaris circuli coassumpta, nulla cura digna differentia ei qui secundum longitudinem progressui accedente ex ea que in tantum inclinatione. Earum ergo quas sumpsimus antiquarum trium eclipsium ex in Babilone obversatis prima quidem descripta est primo anno Mardokempadi secundum Egipitios Thot xxixa in xxxa. Incepit autem, inquit, deficere post ortum, una hora sufficienter preterita, et defecit tota. Quoniam ergo Sol circa postrema Piscium erat et nox horarum equinoctialium xii ad proximum, principium quidem eclipseos factum fuit manifestum quoniam ante iiiior horas equinoctiales et dimidium a mesonictio, medium vero tempus, quoniam perfecta erat eclipsis, ante duas horas et dimidium. In Alexandria ergo, quoniam quidem ad eum qui per ipsam meridianum epochas constituimus horarias, precedit vero qui per ipsam meridianus eum qui per Babilonem dimidia et tracta tracta] tercia V2F1 ad proximum hore unius equinoctialis, medium tempus fuit preiacentis eclipseos ante tres horas equinoctiales et iiia a mesonictio, secundum quam horam Sol secundum preexpositas ratiocinationes nobis obtinebat examinate Piscium gradus xxiiiia et dimidium ad proximum.
Secunda vero eclipsium scripta est facta secundo anno eiusdem Mardokempadi secundum Egiptios Thot xviii in xixa, defecitque, inquit, a notho digitos iii in ipso mesonicti. Quoniam ergo medium tempus in Babilone apparet factum secundum ipsum mesonictium, in Alexandria debet fieri ante dimidium et tertiam partem unius hore a mesonictio, secundum quam horam Sol obtinebat examinate Piscium gradus xiii et dimidium et iiii.
Tertia vero eclipsium descripta est facta eodem secundo anno Mardokempadi secundum Egiptios Phamenoth xva in xvia. Incepit autem, inquit, deficere post ortum et defecit ab arctis plus dimidia. Quoniam ergo Sol circa principium erat Virginis, noctis que magnitudo in Babilone xi ad proximum horarum contingenbat contingenbat] contingebat V2F1 equinoctialium, dimidium autem noctis v horarum et dimidii, et principium ergo eclipseos fuit ante quinque maxime horas equinoctiales a mesonictio, eo quod post ortum esse incepit, medium vero tempus ante tres horas et dimidium. Quoniam totum tempus tante quantitatis obscurationis trium ad proximum horarum debet fieri, in Alexandria rursum ergo medium tempus eclipseos complebitur ante iiiior horas equinoctiales et iiia a mesonictio, secundum quam horam Sol optinebat examinate Virginis gradus iii et iiiia ad proximum. Manifestum ergo quoniam a medio quidem tempore prime eclipseos in medium tempus secunde, motus est Sol, hoc est et Luna, post omnes circulos gradibus cccxlix et xv, a secunde vero eclipsis tempore medio in medium tempus tertie gradibus clxix et xxx. Sed et intermediorum temporum distantia a primo quidem in secundum dies continet cccliiii et horas equinoctiales, simpliciter quidem ita contemplantibus duas et dimidium, ad equalium vero nictimerorum rationationem duas et dimidium et xva; a secundo autem in tertium dies clxxvi et horas equinoctiales similliter quidem rursum xx et dimidium, examinate vero xx et va. Movetur autem Luna plane, – ad tantum enim tempus nullo sensibili distabit, etsi eis que prope periodos examinatas quis consequatur –, in diebus quidem ccc liiii et horis equinoctialibus ii et dimidio et xva, anomalie quidem post integros circulos gradibus cccvi et xxv, longituinis vero gradibus cccxlv et li; in diebus autem clxxvi et horis equinoctialibus xx et va, anomalie quidem cl et xxvi, longitudinis vero gradibus clxx vii ad proximum. Manifestum ergo quoniam prime quidem distantie epicicli cccvi et xxv apposuerit apposuerit] apposuerunt F1 medio motui Lune gradus iii et xxiiii, distantie vero secunde gradus cl et xxvi dempserunt a medio motu gradus o et xxxvii.
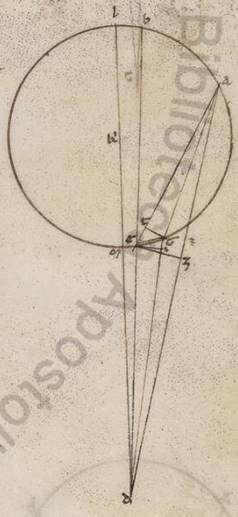 Istas Istas] Istis V2 ergo subiacentibus, esto Lune epiciclus ABG et A quidem punctus esto secundum quem erat Luna in medio tempore prime eclipseos, B vero secundum quem erat in medio tempore secunde eclipsis, G autem secundum quem erat in medio tempore tertie eclipsis. Intelligatur autem Lune in epiciclo transitus, ut a puncto B in A et ab A in G factus, quare ABG quidem periferiam, quam progressa est a prima eclipsi in secunda, graduum existente existente] existentem V2F1 cccvi et xxv, apponere medio gradus iii et xxiiii, BAG vero, quam mota est a secunda ecplisi in terciam, graduum existentem cl et xxvi, auferre a medio gradus o xxxvii, propter hoc autem a puncto quidem B in A transitum, graduum existentem liii et xxxvi, auferre a medio eosdem gradus iii et xxiiii, eum autem qui ab A in G, graduum existentem xcvi et li, apponere medio gradus ii et xlii. Quoniam ergo non possibile in BAG perferia periguiotaton esse epicicli manifestum ex ablativam ipsam ipsam] add. esse V2 et minorem semicirculo, maximo motu secundum periguion subiacente, quoniam vero omnino in BEG, sumatur centrum et eius qui per media animalia circuli et ferentis centrum epicicli et esto D, et copulentur ab ipso in tria eclipsium puncta recte DA, DEB, DG. Universaliter ergo, ut et similles ostensiones facilem traductionem theorematis faciamus, sive per eam que secundum epiciclum ypothesim ipsas, ut nunc ostendamus, sive per eam que secundum excentrotica, D centro tunc intus sumpto, una quidem copulatarum trium rectarum educatur in contraiacentem periferiam, ut hic DEB, NT NT] M V2 inde F1 habebimus perductam in E punctum ab B secunde eclipseos. Reliqua autem duo puncta eclipsium copulet recta, ut hic AG, et a facta sectione ab educta, quemadmodum E, copulentur quidem in reliqua duo puncta recte, ut hic AE, EG. Catheti vero ducantur in a reliquis duobus punctis in zodiaci centrum copulatas rectas super AD quidem EZ et super GD EI, et adhuc ab altero duorum dictorum punctorum, ut hic ab G, cathetus ducatur in ab altero ipsorum, ut A, in factam abiectione superfluam sectionem, quale E, copulatam rectam, velut hic in rectam AE ea que est GT. Undecumque enim utique utemur descriptionis ductu, easdem inveniemus procedentes rationes per ostensionis numeros, ellectione ad commodum tantummodo relicta. Quoniam ergo BA periferia subtendens ostensa est eius qui per media animalia circuli iii et xxiiii, erit utique et BDA angulus ad centrum eius existens, qualium quidem sunt iiii recti ccclx, talium iii et xxiiii, qualium vero duo recti ccclx, talium vi et xlviii. Quare et que quidem super EZ rectam periferia talium vi et xlviii, qualium qui circa DEZ orthogonium scriptus circulus ccclx, ipsa vero EZ recta talium vii et vii, qualium DE ypothenusa cxx; similiter quoniam BA periferia graduum est liii et xxxv, erit utique et BEA angulus ad periferiam existens talium liii et xxxv, qualium sunt ii recti ccclx. Eorumdem vero erat et BDA angulus vi et xlviii et reliquus ergo EAZ angulus eorumdem est xlvi et xlvii. Quare et que quidem super EZ periferia talium est xlvi et xlvii, qualium est qui circa EAZ orthogonium circulus ccclx. Ipsa vero EZ recta talium xlvii et xxxviii et xxx, qualium est EA ypothenusa cxx, et qualium est ergo EZ recta vii et vii et ED cxx, talium erit et AE recta xvii lv et xxxii.
Istas Istas] Istis V2 ergo subiacentibus, esto Lune epiciclus ABG et A quidem punctus esto secundum quem erat Luna in medio tempore prime eclipseos, B vero secundum quem erat in medio tempore secunde eclipsis, G autem secundum quem erat in medio tempore tertie eclipsis. Intelligatur autem Lune in epiciclo transitus, ut a puncto B in A et ab A in G factus, quare ABG quidem periferiam, quam progressa est a prima eclipsi in secunda, graduum existente existente] existentem V2F1 cccvi et xxv, apponere medio gradus iii et xxiiii, BAG vero, quam mota est a secunda ecplisi in terciam, graduum existentem cl et xxvi, auferre a medio gradus o xxxvii, propter hoc autem a puncto quidem B in A transitum, graduum existentem liii et xxxvi, auferre a medio eosdem gradus iii et xxiiii, eum autem qui ab A in G, graduum existentem xcvi et li, apponere medio gradus ii et xlii. Quoniam ergo non possibile in BAG perferia periguiotaton esse epicicli manifestum ex ablativam ipsam ipsam] add. esse V2 et minorem semicirculo, maximo motu secundum periguion subiacente, quoniam vero omnino in BEG, sumatur centrum et eius qui per media animalia circuli et ferentis centrum epicicli et esto D, et copulentur ab ipso in tria eclipsium puncta recte DA, DEB, DG. Universaliter ergo, ut et similles ostensiones facilem traductionem theorematis faciamus, sive per eam que secundum epiciclum ypothesim ipsas, ut nunc ostendamus, sive per eam que secundum excentrotica, D centro tunc intus sumpto, una quidem copulatarum trium rectarum educatur in contraiacentem periferiam, ut hic DEB, NT NT] M V2 inde F1 habebimus perductam in E punctum ab B secunde eclipseos. Reliqua autem duo puncta eclipsium copulet recta, ut hic AG, et a facta sectione ab educta, quemadmodum E, copulentur quidem in reliqua duo puncta recte, ut hic AE, EG. Catheti vero ducantur in a reliquis duobus punctis in zodiaci centrum copulatas rectas super AD quidem EZ et super GD EI, et adhuc ab altero duorum dictorum punctorum, ut hic ab G, cathetus ducatur in ab altero ipsorum, ut A, in factam abiectione superfluam sectionem, quale E, copulatam rectam, velut hic in rectam AE ea que est GT. Undecumque enim utique utemur descriptionis ductu, easdem inveniemus procedentes rationes per ostensionis numeros, ellectione ad commodum tantummodo relicta. Quoniam ergo BA periferia subtendens ostensa est eius qui per media animalia circuli iii et xxiiii, erit utique et BDA angulus ad centrum eius existens, qualium quidem sunt iiii recti ccclx, talium iii et xxiiii, qualium vero duo recti ccclx, talium vi et xlviii. Quare et que quidem super EZ rectam periferia talium vi et xlviii, qualium qui circa DEZ orthogonium scriptus circulus ccclx, ipsa vero EZ recta talium vii et vii, qualium DE ypothenusa cxx; similiter quoniam BA periferia graduum est liii et xxxv, erit utique et BEA angulus ad periferiam existens talium liii et xxxv, qualium sunt ii recti ccclx. Eorumdem vero erat et BDA angulus vi et xlviii et reliquus ergo EAZ angulus eorumdem est xlvi et xlvii. Quare et que quidem super EZ periferia talium est xlvi et xlvii, qualium est qui circa EAZ orthogonium circulus ccclx. Ipsa vero EZ recta talium xlvii et xxxviii et xxx, qualium est EA ypothenusa cxx, et qualium est ergo EZ recta vii et vii et ED cxx, talium erit et AE recta xvii lv et xxxii.
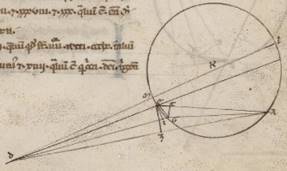 Rursum quoniam BAG periferia subtendit zodiaci gradus o et xxxvii, erit utique et BDG angulus ad centrum eiusdem existens, qualium quidem sunt iiiior recti ccclx, talium o xxxvii, qualium vero ii recti ccclx, talium unius et xiiii. Quare et que quidem super EA periferia talium est unius et xiiii, qualium est qui circa DEI trigonum circulus ccclx, ipsa vero EI recta talium unius et xvii et xxx, qualium est DE ypothenusa cxx. Similiter quoniam BAG periferia graduum est cl et xxvi, erit utique et BEG angulus ad periferiam existens talium cl et xxvi, qualium sunt duo recti ccclx. Eorumdem vero erat et BDG angulus unius et xiiii. Et reliquus ergo EGD eorumdem est cxlix et xii. Quare et que quidem super EI periferia talium est cxlix et xii, qualium que circa GEI orthogonium circulus ccclx, ipsa vero EI recta talium cxv et xli et xxi, qualium est GE ypothenusa cxx, et qualium ergo est EI quidem recta unius et xvii et xxxviii et DE cxx, talium est GE recta unius et xx et xxiii, eorumdem vero ostensa est et EA recta xvii et lv et xxxii.
Rursum quoniam BAG periferia subtendit zodiaci gradus o et xxxvii, erit utique et BDG angulus ad centrum eiusdem existens, qualium quidem sunt iiiior recti ccclx, talium o xxxvii, qualium vero ii recti ccclx, talium unius et xiiii. Quare et que quidem super EA periferia talium est unius et xiiii, qualium est qui circa DEI trigonum circulus ccclx, ipsa vero EI recta talium unius et xvii et xxx, qualium est DE ypothenusa cxx. Similiter quoniam BAG periferia graduum est cl et xxvi, erit utique et BEG angulus ad periferiam existens talium cl et xxvi, qualium sunt duo recti ccclx. Eorumdem vero erat et BDG angulus unius et xiiii. Et reliquus ergo EGD eorumdem est cxlix et xii. Quare et que quidem super EI periferia talium est cxlix et xii, qualium que circa GEI orthogonium circulus ccclx, ipsa vero EI recta talium cxv et xli et xxi, qualium est GE ypothenusa cxx, et qualium ergo est EI quidem recta unius et xvii et xxxviii et DE cxx, talium est GE recta unius et xx et xxiii, eorumdem vero ostensa est et EA recta xvii et lv et xxxii.
Rursum quoniam AG periferia graduum ostensa est xcvi et li, erit utique et AEG angulus ad periferiam existens talium xcvi et li, qualium sunt duo recti ccclx. Quare et que quidem super GT periferia talium est xcvi et li, qualium qui circa GET trigonum circulus ccclx et que super ET periferia reliquorum in semicirculum lxxxiii et ix. Subtendentes ergo ipsas recte erit GT quidem talium lxxxix et xlvi et xiiii, qualium est GE ypothenusa cxx, et ET eorumdem lxxix et xxxvii et lv, et qualium ergo est GE recta unius et xx et xxiii, talium erit et GT quidem recta unius o et viii, ET vero similiter o liii et xxi. Eorumdem vero erat EA tota xvii et lv et xxxii, et reliqua ergo TA talium est xvii et ii et xi, qualium GT ostensa est unius o viii et est, quod quidem ab AT tetragonum ccxc et xiiii et xix, quod vero ad GT similiter unius o et xviii, que coniuncta faciunt quod ab AG tetragonum ccxcii et xiiii et xxxvi. Longitudine ergo est AG talium xvii iii et lvii, qualium est DE quidem recta recta] add. cxx GE vero eorumdem i et xx et xxiii. Est autem et qualium epicicli diametros cxx, talium AG recta V2 lxxxix et xlvi et xiiii. Subtendit enim AG periferiam existentem xcvi et li, et qualium ergo est AG quidem recta lxxxix et xlvi et xiiii atque epicicli diametros cxxi, cxxi] cxx V2 talium erit et DE recta dcxxxi et xiii et xlviii atque GE eorumdem vii et ii et l. Quare et que quidem super eam periferiam GE talium vi et xliiii et unius, qualium est epiciclus ccclx. Eorumdem vero subiacet et BAG periferia cl et xxvi et tota ergo BGE periferia graduum est clvii et x i, que vero sub ipsa recta BE talium cxvii et xxxvii et xxxii, qualium est epicicli diametros cxx, ED autem recta dcxxxi et xiii et xlviii. Si ergo BE recta equalis erat invente diametro epicicli, in ipsa utique continget manifestum quoniam centrum eius, et inde utique apparet diametros proportio. Quoniam vero minor est ipsa, minor vero et BGT BGT] BGE V2F1 periferia semicirculo manifestum quoniam centrum epicicli cadet extra BAGE proportionem. Subiaceat ergo K punctum et copuletur a D centro eius qui per media animalia circuli per K recta DMKL, quare L punctum fieri apoguiotaton epicicli, M vero periguiotaton. Quoniam ergo sub DB et DE contentum orthogonium equale est sub LD et DM contento orthogonio, ostensum autem 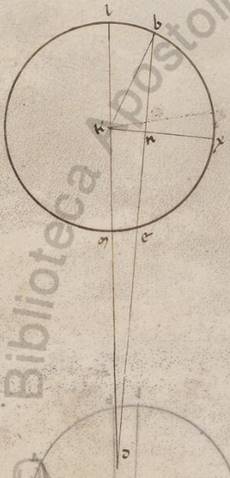 nobis quoniam qualium est epicicli diametros, hoc est LKM recta, cxx, talium est BE recta cxvii et xxxvii et xxxii, CD CD] ED V2F1 vero eorumdem dcxxxi et xiii et xlviii. Tota vero BD manifestum quoniam dccxlviii et li et xxiii fit quod sub BD et DE, hoc est quod sub DL et DM contentum orthogonium cccclxxiidcc et sesagessimorum v et xxxii.
nobis quoniam qualium est epicicli diametros, hoc est LKM recta, cxx, talium est BE recta cxvii et xxxvii et xxxii, CD CD] ED V2F1 vero eorumdem dcxxxi et xiii et xlviii. Tota vero BD manifestum quoniam dccxlviii et li et xxiii fit quod sub BD et DE, hoc est quod sub DL et DM contentum orthogonium cccclxxiidcc et sesagessimorum v et xxxii.
Rursum quoniam et quod sub LD et DM cum eo quod ab KM facit quod ab DK tetragonum, KM autem e centro existens epicicli eorumdem est lx, si iiidc eius quod ab ipsa tetragoni apposuerimus que cccclxxiidcc v xxxii, habebimus quod ab DK tetragonum eorumdem viccc v xxxii et longitudine erit ergo DK e centro existens ferens epiciclum omocentrici eius qui per media animalia circuli talium dcxc et sexagesimorum viii xlii, qualium est KM e centro existens epicicli lx. Quare et qualium est que e centro ferentis epiciclum omocentrici in sui in sui] visui V2 circuli lx, talium erit et que e centro epicicli v et xiii ad proximum.
Trahatur ergo in sensibili sensibili] simili V2F1 descriptione e centro K cathetus in BE, sitque KUX KUX] KNX V2F1, copuleturque BK. Quoniam ergo qualium est DK dcxc portionum viii minutorum et xlii, talium erat et DE recta dcxxxi et xiii et xlviii et NE dimidia existens eius que est BE eorumdem lviii et xlviii et xlvi, et quare et totam DEN eorumdem fieri dcxc et sexagesimorum ii et xxxiiii, et qualium ergo DK ypothenusa est cxx, talium et DN erit cxix et lviii et lvii et que supra eam periferia talium clxxviii et ii ad proximum, qualium est qui circa DNK orthogonium circulus ccclx, qualium vero iiiior recti ccclx, talium lxxxix et unius et XM ergo epicicli periferia graduum est lxxxix et unius, at vero LBX reliquorum in semicirculum xc et lix. Eordumdem vero est XB periferia dimidia existens eius que est BXE graduum lxxviii et xxxv, quoniam quidem BE tota demonstrata est graduum clvii et x ad proximum, et reliqua ergo LB epicicli periferia, quam abstabat Luna ab apoguiotato secundum expositum medium tempus secunde eclipseos, graduum est xii et xxiiii.
Similiter autem quoniam DKN angulus ostensus est talium lxxxix et uinus, qualium sunt iiiior recti ccclx, et reliquus erunt erunt] erit V2F1 KDN angulus, qui subtendit ablatam secundum longitudinem progressionis periferiam ex ea que est penes LB epicicli facta anomalia, reliquorum in unum rectum graduum o lix, et secundum longitudinem ergo medie obtinebat Luna secundum medium tempus secunde eclipseos Virginis graduum graduum] gradus V2 xiiii et xliiii, quoniam quidem examinate obtinebat gradus xiii et xlv, quot et Sol in Piscibus.
Rursum earum quas sumpsimus trium eclipsium ex curiosissime nobis in Alexandria observatis, prima quidem facta fuit xviio anno Adriani secundum Egiptios autem Payui Payui] Payni V2F1 xxa xxa] add. in xxi V2F1. Medium vero tempus diligenter ratiocinati sumus fieri ante medietatem et quartam unius hore equinoctialis a mesonictio et defecit tota, secundum quam horam examinate defecit defecit] obtinebat V2F1 Sol Tauri gradus xiii et iiii ad proximum. Secunda vero facta fuit xixo anno Adriani secundum Egiptios Chiach iia in iiia. Medium vero tempus ratiocinati sumus fieri ante unam horam aequinoctialem a mesonictio et defecit ab arctis dimidio et iiia diametri, secundum quam horam Sol optinebat examinate Chelarum gradus xxv et viam ad proximum. Tertia vero eclipsium facta fuit xxo anno Adriani secundum Egiptios Pharmothi Pharmothi] Pharmoythi V2F1 xixa in xxa. Medium vero tempus ratiotinati sumus fieri post iiiior horas equinoctiales a mesonictio, et defecit medietate diametri ab arctis. Optinebat autem et secundum illam horam Sol Piscium gradus xiiii et xii ad proximum. Manifestum ergo quoniam et hic mota est Luna post omnes circulos a medio quidem tempore prime eclipseos in medium tempus secunde eclipseos, quot et Sol, gradus clxi et lv, ab eo vero quod secunde in illud quod tertie, gradus cxxxviii et lv. Est autem et quod in medio tempus prime quidem distantie anni Egiptiaci unius et dierum clxvi et horarum equinoctialium simpliciter quidem xxiii et dimidii et viii, secunde vero distantie anni rursus Egiptiaci unius et dierum cxxxvii et horarum equinoctialium simpliciter quidem v, examinate autem v et dimidii. Movetur autem Luna medie post omnes circulos in uno quidem anno et diebus clxvi et horis equinoctialibus xxiii et dimidio et viiia, anomalie quidem gradus cx et xxi, longitudinis vero gradus clxix et xxxvii ad proximum; in uno autem anno et diebus cxxxvii et horis equinoctialibus v et dimidia, anomalie quidem gradus lxxxi et xxxvi, longitudinis autem gradus cxxxvii et xxxiiii ad proximum. Manifestum ergo quoniam et prime quidem distantie epicicli gradus cx et xxi dempserunt ab eo qui secundum longitudinem medio progressu gradus vii xlii, secunde autem distantie gradus lxxxi et xxxvi apposuerimus apposuerimus] apposuerunt V2F1 ei qui secundum longitudinem medio progressui gradus i et xxi.
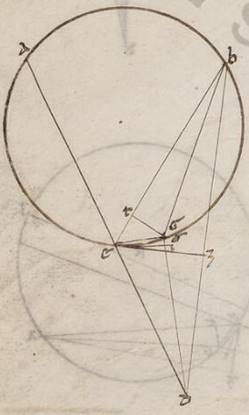 Istis ergo subiacentibus, esto rursus epiciclus Lune ABG, et A quidem punctus subiaceat secundum quem erat Luna in medio tempore prime eclipsis, B vero qui secunde eclipsis, G autem qui tertie. Intelligatur autem similiter transitus Lune ut ab per A G factus, quare AB quidem periferiam graduum existentem cx et xxi auffere, ut diximus, ab eo qui secundum longitudinem medio progressu gradus vii et xvii, BG vero graduum existentem lxxxi et xxxvi apponere longitudini gradus i et xxi, reliqua reliqua] reliquam V2F1 vero GA graduum existentem clxviii et iii apponere longitudini reliquos gradus vi et xxi. Quoniam ergo I ab I ab] in AB V2F1 periferia apoguiotaton esse oportet, manifestum ex neque in BG esse posse neque in GA, propter utramque ipsarum et appositivam esse et minorem semicirculo. Sumatur tamen, quasi non subiacente hoc, centrum zodiaci et circuli in quo fertur epiciclus et sit D, copulenturque ab ipso in tria eclipsium puncta recte DEA et DB et DG, et, copulata BG, trahantur ab E puncto recte in puncta quidem B, G EB et EG, in BD autem et DG rectas catheti EZ et EI, et adhuc ab G in BE cathetus trahatur GT. Quoniam ergo AB periferia subtendit eius qui per media animalia circuli gradus vii et xlii, erit utique et ADB angulus ad centrum existens zodiaci, qualium quidem sunt iiii recti ccclx, talium vii et xlii, qualium autem duo recti ccclx, talium xv et xxiiii. Quare et que quidem super EZ periferia talium est xv et xxiiii, qualium que circa DEZ trigonum circulus ccclx, ipsa vero EZ recta talium xvi iiii et xlii, qualium est DE ypothenusa cxx.
Istis ergo subiacentibus, esto rursus epiciclus Lune ABG, et A quidem punctus subiaceat secundum quem erat Luna in medio tempore prime eclipsis, B vero qui secunde eclipsis, G autem qui tertie. Intelligatur autem similiter transitus Lune ut ab per A G factus, quare AB quidem periferiam graduum existentem cx et xxi auffere, ut diximus, ab eo qui secundum longitudinem medio progressu gradus vii et xvii, BG vero graduum existentem lxxxi et xxxvi apponere longitudini gradus i et xxi, reliqua reliqua] reliquam V2F1 vero GA graduum existentem clxviii et iii apponere longitudini reliquos gradus vi et xxi. Quoniam ergo I ab I ab] in AB V2F1 periferia apoguiotaton esse oportet, manifestum ex neque in BG esse posse neque in GA, propter utramque ipsarum et appositivam esse et minorem semicirculo. Sumatur tamen, quasi non subiacente hoc, centrum zodiaci et circuli in quo fertur epiciclus et sit D, copulenturque ab ipso in tria eclipsium puncta recte DEA et DB et DG, et, copulata BG, trahantur ab E puncto recte in puncta quidem B, G EB et EG, in BD autem et DG rectas catheti EZ et EI, et adhuc ab G in BE cathetus trahatur GT. Quoniam ergo AB periferia subtendit eius qui per media animalia circuli gradus vii et xlii, erit utique et ADB angulus ad centrum existens zodiaci, qualium quidem sunt iiii recti ccclx, talium vii et xlii, qualium autem duo recti ccclx, talium xv et xxiiii. Quare et que quidem super EZ periferia talium est xv et xxiiii, qualium que circa DEZ trigonum circulus ccclx, ipsa vero EZ recta talium xvi iiii et xlii, qualium est DE ypothenusa cxx.
Similiter quoniam AB periferia graduum est cx et xxi, erit utique ACB angulus ad periferiam existens talium cx et xxi, qualium sunt iio recti ccclx. Eorumdem vero erat et ADB angulus xv et xxiiii, reliquus ergo EBD angulus eorumdem est xciiii et lvii. Quare et que quidem super EZ periferia talium est xciiii et lvii, qualium qui circa BEZ orthogonium circulus ccclx, ipsa vero EZ recta talium lxxxviii et xxvi et xvii, qualium est BE ypothenusa cxx, et qualium ergo EZ quidem recta xvi et iiii et xlii, DE vero cxx, talium est BE recta xxi et xlviii et lix. Rursum quoniam GEA periferia subtendens ostensa est eius qui per media animalia circuli graduum vi et xxi, erit utique et ADG angulus ad centrum existens zodiaci qualium quidem sunt iiii recti ccclx, talium vi et xxi, qualium vero ii recti ccclx, talium xii et xlii. Quare et que quidem EI  periferia talium est xii et xlii, qualium que circa DEI orthogonium circulus ccclx, ipsa vero EI recta talium xiii et xvi et xix, qualium est DE ypothenusa cxx. Similiter quoniam ABG periferia colligitur graduum cxci et lvii, erit utique et AEG angulus ad periferiam existens talium cxci et lvii, qualium sunt ii recti ccclx. Eorumdem vero erat et ABG angulus xii et xlii, et reliquus ergo EGD eorumdem est clxxix et xv. Quare et que quidem super EI periferia talium est clxxix et xv, qualium qui circa GEI orthogonium orthogonium] trigonum V2 circulus ccclx. Ipsa vero EI recta talium cxix et lix l, qualium est GE ypothenusa cxx et qualium ergo est ei quidem recta xiii et xvi et xix, DE autem ostensa est cxx, talium erit et GE recta xiii et xvi et xx, eorumdem vero ostensa est cxx, talium erit et GE recta xiii et xvi et xx. Eorumdem vero ostensa est et BE recta xxi et xlviii et lii. lii] lix V2F1 Rursum quoniam BG periferia est lxxxia et xxxvi erit utique et BEG angulus ad periferiam existens talium lxxxi et xxxvi, xxxvi] add. erit utique et BEG angulus ad periferiam existens talium lxxxi et xxxvi V2 qualium sunt ii recti ccclx. Quare et que quidem super GT periferia talium est lxxxi et xxxvi, qualium est qui circa GET trigonum circulus ccclx. Que vero super ET reliquorum in semicirculum xcviii et xxiiii, et earum ergo que sub ipsis rectarum GT quidem erit talium lxxviii et xxiiii et xxxvi, qualium est EG ypothenusa cxx, ET autem eorumdem xc l et xxii, et qualium ergo est GE recta xiii et xvi et xx, talium et GT quod quod] quidem V2F1 erit viii et xl et xx, ET vero similiter x ii xlix. Eorumdem vero erat EB tota xxi et xlviii et lix, et reliqua ergo TB talium erit xi et xlvi et x, qualium et GT erat viii et xi et xx. Et enim enim] est V2 quod quidem ab TB tetragonum cxxxviii et xxxi et xi, quod vero ab GT eorumdem lxxv et xii et xxvii, que composita faciunt quod ab BG tetragonum ccxiii et xlvi et xxxviii. Longitudine ergo est BG talium xiiii et xxxvii et x, qualium est DE quidem recta cxx, atque GE similiter xiii et xvi et xx. Est autem et qualium epicicli diametros cxx, talium GB recta lxxviii et xxiiii et xxxvii. Subtendit enim BG periferia periferia] periferiam V2F1 graduum existentem lxxxi et xxxvi, et qualium ergo est BG quidem recta lxxviii et xxiiii et xxxvii, epicicli vero diametros cxx, talium erit et DE quidem recta dcxliii et xxxvi et xxxix, EG vero eorumdem lxxi et xi et iiii. Quare et que super eam periferia GE talium est lxxii et xlvi et x, qualium epiciclus ccclx. Eorumdem vero GEA subiacet clxviii et iii et reliqua ergo EA quidem periferia graduum est xcv et xvi l, que vero sub ipsam recta AE talium est lxxxviii et xl et xvii, qualium quidem epicicli diametros cxx, DE vero recta dcxliii et xxxvi et xxxix.
periferia talium est xii et xlii, qualium que circa DEI orthogonium circulus ccclx, ipsa vero EI recta talium xiii et xvi et xix, qualium est DE ypothenusa cxx. Similiter quoniam ABG periferia colligitur graduum cxci et lvii, erit utique et AEG angulus ad periferiam existens talium cxci et lvii, qualium sunt ii recti ccclx. Eorumdem vero erat et ABG angulus xii et xlii, et reliquus ergo EGD eorumdem est clxxix et xv. Quare et que quidem super EI periferia talium est clxxix et xv, qualium qui circa GEI orthogonium orthogonium] trigonum V2 circulus ccclx. Ipsa vero EI recta talium cxix et lix l, qualium est GE ypothenusa cxx et qualium ergo est ei quidem recta xiii et xvi et xix, DE autem ostensa est cxx, talium erit et GE recta xiii et xvi et xx, eorumdem vero ostensa est cxx, talium erit et GE recta xiii et xvi et xx. Eorumdem vero ostensa est et BE recta xxi et xlviii et lii. lii] lix V2F1 Rursum quoniam BG periferia est lxxxia et xxxvi erit utique et BEG angulus ad periferiam existens talium lxxxi et xxxvi, xxxvi] add. erit utique et BEG angulus ad periferiam existens talium lxxxi et xxxvi V2 qualium sunt ii recti ccclx. Quare et que quidem super GT periferia talium est lxxxi et xxxvi, qualium est qui circa GET trigonum circulus ccclx. Que vero super ET reliquorum in semicirculum xcviii et xxiiii, et earum ergo que sub ipsis rectarum GT quidem erit talium lxxviii et xxiiii et xxxvi, qualium est EG ypothenusa cxx, ET autem eorumdem xc l et xxii, et qualium ergo est GE recta xiii et xvi et xx, talium et GT quod quod] quidem V2F1 erit viii et xl et xx, ET vero similiter x ii xlix. Eorumdem vero erat EB tota xxi et xlviii et lix, et reliqua ergo TB talium erit xi et xlvi et x, qualium et GT erat viii et xi et xx. Et enim enim] est V2 quod quidem ab TB tetragonum cxxxviii et xxxi et xi, quod vero ab GT eorumdem lxxv et xii et xxvii, que composita faciunt quod ab BG tetragonum ccxiii et xlvi et xxxviii. Longitudine ergo est BG talium xiiii et xxxvii et x, qualium est DE quidem recta cxx, atque GE similiter xiii et xvi et xx. Est autem et qualium epicicli diametros cxx, talium GB recta lxxviii et xxiiii et xxxvii. Subtendit enim BG periferia periferia] periferiam V2F1 graduum existentem lxxxi et xxxvi, et qualium ergo est BG quidem recta lxxviii et xxiiii et xxxvii, epicicli vero diametros cxx, talium erit et DE quidem recta dcxliii et xxxvi et xxxix, EG vero eorumdem lxxi et xi et iiii. Quare et que super eam periferia GE talium est lxxii et xlvi et x, qualium epiciclus ccclx. Eorumdem vero GEA subiacet clxviii et iii et reliqua ergo EA quidem periferia graduum est xcv et xvi l, que vero sub ipsam recta AE talium est lxxxviii et xl et xvii, qualium quidem epicicli diametros cxx, DE vero recta dcxliii et xxxvi et xxxix.
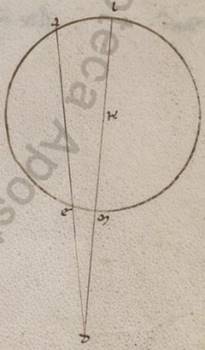 Quoniam ergo rursum EA periferia minor ostensa est semicirculo, manifestum quoniam centrum epicicli cadet extra portionem EA. Sumatur ergo sitque K, et copuletur DMKL, quare rursum quidem I punctum fieri apoguiotaton, M vero periguiotaton. Quoniam ergo sub AD et DE contentum orthogonium equale est ei qui sub LD et DM, ostensum autem nobis est quoniam, qualium est LKM epicicli diametros cxx, talium est AE quidem recta lxxxviii et xl et xvii, ED vero eorumdem dcxliii et xxxvi et xxxix, AD autem tota manifestum quoniam dccxxxii et xvi lvi, fit quod sub AD et DE, hoc est quod sub LD et DM, eorumdem graduum cccclxxiccciiii et xlvi et xvii. Rursum quod sub LDM cum eo quod ab ab] add. KM facit quod ab V2F1 DK tetragonum, KM vero e centro existens epicicli lx facit quod ab ipsa iiidc. Si iiidc addiderimus propositis cccclxxiccciiii et xlvi et xvii, habebimus quod ab DK tetragonum eorumdem cccclxxiiiidcccciiii et xlvi et xvii, et longitudine ergo erit DK e centrum existens ferentis epiciclum omocentrici ei qui per media animalia talium dclxxxix et viii, qualium est KM e centro existens epicicli lx, lx] add. quare et qualium est que inter centra eius qui per media animalia et epicicli lx V2 F1 talium erit et que e centro epicicli v et xiiii, et est eadem ad proximum proporcio per antiquiores eclipses paulo ante demonstrata.
Quoniam ergo rursum EA periferia minor ostensa est semicirculo, manifestum quoniam centrum epicicli cadet extra portionem EA. Sumatur ergo sitque K, et copuletur DMKL, quare rursum quidem I punctum fieri apoguiotaton, M vero periguiotaton. Quoniam ergo sub AD et DE contentum orthogonium equale est ei qui sub LD et DM, ostensum autem nobis est quoniam, qualium est LKM epicicli diametros cxx, talium est AE quidem recta lxxxviii et xl et xvii, ED vero eorumdem dcxliii et xxxvi et xxxix, AD autem tota manifestum quoniam dccxxxii et xvi lvi, fit quod sub AD et DE, hoc est quod sub LD et DM, eorumdem graduum cccclxxiccciiii et xlvi et xvii. Rursum quod sub LDM cum eo quod ab ab] add. KM facit quod ab V2F1 DK tetragonum, KM vero e centro existens epicicli lx facit quod ab ipsa iiidc. Si iiidc addiderimus propositis cccclxxiccciiii et xlvi et xvii, habebimus quod ab DK tetragonum eorumdem cccclxxiiiidcccciiii et xlvi et xvii, et longitudine ergo erit DK e centrum existens ferentis epiciclum omocentrici ei qui per media animalia talium dclxxxix et viii, qualium est KM e centro existens epicicli lx, lx] add. quare et qualium est que inter centra eius qui per media animalia et epicicli lx V2 F1 talium erit et que e centro epicicli v et xiiii, et est eadem ad proximum proporcio per antiquiores eclipses paulo ante demonstrata.
Trahatur ergo rursum in eadem descriptione ab K centro cathetus in DEA et KNX, et copuletur AK. Quoniam ergo qualium DK ostensa est dclxxxix et viii, talium erat et DE quidem recta dcxliii et xxxvi et xxxix, NE vero dimidia existens eius que est AE eorumdem est xliiii et xx viii. Quare et tota DEN eorumdem dclxxxvii et lvi et xlvii, et qualium ergo est DK ypothenusa cxx, talium et DN erit cxix et xlvii et xxxvi, et que super ipsam periferia talium clxxiii et xvii ad proximum, qualium est qui circa DKN orthogonium circulus ccclx. Quare et DKN angulus, qualium quidem sunt ii recti ccclx, talium est clxxiii et xvii, qualium vero iiii recti ccclx, talium est lxxxvi et xxxviii et dimidii, et MEX ergo epicicli periferia graduum est lxxxvi et xxxviii et dimidii, dimidii] add. atque V2F1 LAX reliquorum in semicirculum xciii et xxi et dimidii, eorumdem vero est AX periferia, dimidia existens eius que est AE, graduum xlvii et xxxviii et dimidii ad proximum, et reliqua ergo AL periferia graduum est xlv et xliii. Subiacebat autem AB tota eorumdem cx et xxi, et reliqua ergo LB periferia, quam distabat Luna ab apoguiotato secundum expositum medium tempus secunde eclipseos, graduum est lxiiii et xxxviii. Similiter quoniam DKN quidem angulus demonstratus est talium lxxxvi et xxxviii ad proximum, qualium iiiior recti ccclx, KDN vero sint reliquorum in unum rectum iii et xxii. Subiacebat autem et ADB totus eorumdem vii et xlii, et reliquus ergo LDB angulus, qui subtendit ablatam medii secundum longitudinem progressus eius qui per media animalia circuli periferiam ex ea que penes LB facta epicicli anomalia, graduum erit iiii et xx, et secundum longitudinem ergo medie obtinebat Luna secundum medium tempus secunde eclipsis Arietis gradus xxix et xxx, quoniam quidem examinate obtinebat gradus xxv et x, quot et Sol Chelarum.
〈IV.7〉 De directione mediorum progressuum Lune et longitudinis anomalie
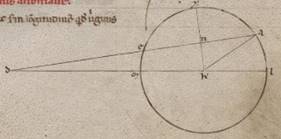 Quoniam ergo in secunda quidem antiquorum eclipsium demonstravimus Lunam secundum medium tempus optinentem omale secundum longitudinem quidem Virginis gradus xiiii et xliiii, anomlie vero ab apoguio epicicli gradus xii et xxiiii; in secunda autem earum que secundum nos trium eclipsium similiter optinens medie ostensa est secundum longitudinem quidem Arietis gradus xxix et cxxx, cxxx] xxx V2 anomalie autem ab apoguio gradus lxiiii xxxviii, manifestum quoniam et intermedio tempore propositarum eclipsium recepit medie Luna post omnes circulos, longitudinis quidem gradus ccxxxiiii ccxxxiiii] ccxxiiii F1 et xlvi, anomalie vero gradus lii et xiiii. Medium vero tempus secundi anni Mardokempadi Thothe Thothe] Thoth V2F1 xviii in xixa autem autem] ante V2F1 dimidium et iiia unius hore equinoctialis a mesonictio et xix anni Adriani chiak iia in tertiam autem autem] ante V2F1 unam horam equinoctialem a mesonictio continet egyptiacos annos dcccliiii et dies lxxiii et horas equinoctiales simpliciter quidem rursum xxiii et dimidium et iii, examinate vero et ad equalia nictimera xxiii et iiia, omnis autem dies cccxidcclxxxiii et horas equinoctiales xxiii et iii. Quibus reperimus superadiectas post omnes circulos epoysias ex preexpositis nobis diurnis motibus secundum prime directionis ypotheses, longitudinis quidem gradus ccxxiiii et xlvi, anomalie vero gradus lii et xxxi, quare longitudinis quidem epoysiam inpermutatam, ut diximus, inveniri per expositas observationes a nobis collecte, eam vero que anomalie superfluere lxis xvii. Unde autem canoniorum expositionem causa diurnorum motuum directionis xvii lxa distribuentes in propositam dierum multitudinem, unicuique diei pertinentia o o o o xi et xlvi et xxxix auferentes ab ante directionem deprehenso anomalie diurno medio motu, invenimus directum graduum xiii et iii et lvi et xvii et li et lix. Quibus consequenter et reliquas canonicorum esintheses esintheses] episintheses V2F1 fecimus.
Quoniam ergo in secunda quidem antiquorum eclipsium demonstravimus Lunam secundum medium tempus optinentem omale secundum longitudinem quidem Virginis gradus xiiii et xliiii, anomlie vero ab apoguio epicicli gradus xii et xxiiii; in secunda autem earum que secundum nos trium eclipsium similiter optinens medie ostensa est secundum longitudinem quidem Arietis gradus xxix et cxxx, cxxx] xxx V2 anomalie autem ab apoguio gradus lxiiii xxxviii, manifestum quoniam et intermedio tempore propositarum eclipsium recepit medie Luna post omnes circulos, longitudinis quidem gradus ccxxxiiii ccxxxiiii] ccxxiiii F1 et xlvi, anomalie vero gradus lii et xiiii. Medium vero tempus secundi anni Mardokempadi Thothe Thothe] Thoth V2F1 xviii in xixa autem autem] ante V2F1 dimidium et iiia unius hore equinoctialis a mesonictio et xix anni Adriani chiak iia in tertiam autem autem] ante V2F1 unam horam equinoctialem a mesonictio continet egyptiacos annos dcccliiii et dies lxxiii et horas equinoctiales simpliciter quidem rursum xxiii et dimidium et iii, examinate vero et ad equalia nictimera xxiii et iiia, omnis autem dies cccxidcclxxxiii et horas equinoctiales xxiii et iii. Quibus reperimus superadiectas post omnes circulos epoysias ex preexpositis nobis diurnis motibus secundum prime directionis ypotheses, longitudinis quidem gradus ccxxiiii et xlvi, anomalie vero gradus lii et xxxi, quare longitudinis quidem epoysiam inpermutatam, ut diximus, inveniri per expositas observationes a nobis collecte, eam vero que anomalie superfluere lxis xvii. Unde autem canoniorum expositionem causa diurnorum motuum directionis xvii lxa distribuentes in propositam dierum multitudinem, unicuique diei pertinentia o o o o xi et xlvi et xxxix auferentes ab ante directionem deprehenso anomalie diurno medio motu, invenimus directum graduum xiii et iii et lvi et xvii et li et lix. Quibus consequenter et reliquas canonicorum esintheses esintheses] episintheses V2F1 fecimus.
〈IV.8〉 De epochi omalorum Lune motuum
Ut autem et epochas ipsarum constituamus in eundem primum annum Navonassari secundum Egiptios Thot prima meridiei, sumpsimus quidem hinc tempus usque medium secunde eclipseos primarum et propinquiorum trium, que, ut diximus, fuit anno iio Mardokempadi secundum Egiptios Thot xviii in xixa ante dimidium et iiiam unius hore equinoctialis a mesonictio. Colligitur autem istud annorum egiptiacorum xxvii et dierum xvii et horarum et simpliciter et examinate ad proximum xi et vi, et adiacent tanto tempori post omnes circulos epoysie, longitudinis quidem gradus cxxiii et xxii, anomalie vero gradus ciii et xxxv. Quos si dempsimus ab eis qui in medio tempore secunde eclisis eclisis] eclipses V2 eclipsis F1 epochis utraque ab utraque proprie, habebimus in primo anno Navonassari secundum Egiptios Thot prima meridiei obtinentem medie Luna, secundum longitudinem quidem Tauri gradus xi et xxii, anomalie vero ab apoguio epicicli cclxviii et xlix, apochis autem manifestum quoniam gradus lxx et xxxvii. Quoniam quidem et Sol in eodem tempore demonstratus est obtinens Piscium gradus o xlv.
〈IV.9〉 De directione eorum qui secundum latitudine mediorum progressuum Lune et epochi ipsorum
Longitudinis ergo anomalie periodicos motus et adhuc epochas ipsorum per huiusmodi ephodos constituimus, in eis autem qui secundum latitudinem prius quidem peccabamus et ipsi coutentes secundum Yparcum Lunam secenties et les ad proximum dimetiri proprium circulum, bis autem et dimidies eum qui umbre dimetiri secundum illam que in coniugationibus mediam distantiam. His enim subiacentibus et quantitate inclinationis obliqui circuli Lune, particularium eius eclipsium termini dantur. Sumentes ergo distantias eclipticas, et a magnitudine earum que secundum media tempora obscurationum examinatos secundum latitudinem in obliquo circulo progressus ab utrolibet nodorum computantes, et per demonstratam secundum anomaliam differentiam ab examinatis progressibus preiodicos discernentes, ita et eas que secundum media tempora eclipsium epochis periodice latitudinis reperimus et eam que in intermedio tempore post omnes circulos epoysiam. Nunc autem utentes gratioribus ephodis et nullo prius subiacentium indigentibus ad inquisitorum comprehensionem et per illam illam] illa F1 computant computant] computatum F1 latitudinis progressum reperimus mendacem et a nunc sine illis deprehenso et ypotheses ipsas circa magnitudines et distantias non ita se habentes arguentes correximus. Simile vero fecimus et in Saturni et Mercurii ypothesibus, moventes quedam priorum non multum diligenter sumptorum, propter posterius certiores observationes invenisse. Competit enim vere amore veritatis et inquisitive huiusmodi theorie accedentibus, non ad solam antiquarum ypothesium correctionem couti novitate ad indubitalius inventarum ephodorum, verum et ad eam que propriarum, si ita se habeant, nec turpe cogitare, magna quadam et divina existente lectione, etsi ab aliis, et non solum ab ipsis sexaminarius sexaminarius] in examinatius V2F1 suscipiant correctionem. Quo ergo modo unumquodque istorum demonstramus, in eis que deinceps secundum propria loca reddamus. Convertemur vero in presenti consequentie causa in secundum latitudinem progressus ostensionem, que habet ephodum talem. Itaque primum quidem in eiusdem medii progressus directionem quesivimus eclipses lunares ab indubitanter descriptis, per quantum maxime inerat plurimum tempus, secundum quas et magnitudines observationum facte sunt et circa eundem nobis nobis] nodum V2F1 et utrasque vel ab arctis vel a meridie et adhuc Luna circa equalem erat differentiam. His ergo ita se habentibus, neccesse est centrum Lune equaliter distare secundum utramque eclipsium in eisdem partibus ab eodem nodo et propter hoc examinatum progressum eius totos secundum latitudinem circulos in intermedio obscurationum tempore continere.
Sumpsimus ergo primam quidem eclipsim sub Dario primo observatam in Babilone xxxi eius anno secundum Egiptios Tybi iiia in quarta, hora via media, secundum quam declaratur quoniam Luna defecit ab notho digitos ii.
Secundum autem observatam in Alexandriam Alexandriam] Alexandria V2F1 ixo anno Adriani secundum Egiptios Pachon xviia in xviiia ante tres horas equinoctiales et tres quintas unius hore a mesonictio, secundum quam similiter defecit Luna via parte diametri a meridie.
Erat autem et secundum latitudinem progressus Lune circa descendentem nodum in utraque eclipsium, huiusmodi namque et ex universalioribus ypothesibus occipitur. Apostima vero ad proximum equale et paulo medio periguioteron, et hoc enim ex predemonstratis de anomalia fiet manifestum. Quoniam ergo, quando defecit Luna a notho, borealius est centrum eius eo qui per media, manifestum quoniam et secundum utramque eclipsium equaliter precedebat descendentem nobis nobis] nodum V2F1 Lune centrum. Sed secundum primam eclipsim distabat Luna ab apoguio epicli gradibus clx xix. Medium enim tempus in Babilone factum est ante emyorium a mesonictio, in Alexandria autem ante primam et tertiam hore equinoctialis, et quod ab epochi que sub Navonassaro tempus colligit annos cclvi cxxii et horas equinoctiales simpliciter siquidem x et iiia, ad equalia autem nictimera x et iiiia et propter hoc minor erat examinatus motus periodico v gradibus. In secunda vero eclipsi distabat Luna ab apoguio epicicli gradibus ccli et liii. Et hic enim quod ab epochi tempus usque medium eclipseos colligit annos dccclxxxi et dies cclvi et horas equinoctiales simpliciter quidem viii et ii quintas, examinate vero viii et xiia, et propter hoc autem et examinatus progressus maior erat medio gradibus iiii et liii. In intermedio ergo tempore duarum eclipsium continenti annos egiptiacos dcxv et dies cxxxiii et horas equinoctiales xxi et dimidium et iiiam, examinatus quidem secundum latitudinem progressus Lune totos continet circulos, periodicos periodicos] periodicus F1 vero defecit in totos circulos ex ambabus anomaliis collectis ergo ix et liii, defitiunt autem ex preexpositis secundum Yparcum ypotheses mediorum motuum in tanto tempore in integras restitutiones gradibus x et sexagesima ad proximum duo. Maior ergo factus est secundum ypotheses medius secundum latitudinem progressus lxis ix. Ista ergo distribuentes in multitudine ex preiacente tempore collectorum dierum xiiiidc ix ad proximum et ex comparatione facta o o o o viii et xxxix et xviii apponentes secundum illas ypotheses predemonstrato medio divino motui, invenimus directum graduum xiii xiii et xlv et xxxix et xlviii et lvi et xxxvii, quibus rursum consequenter et reliquas canoniorum episintheses negotiati sumus. Demonstrato vero semel ad modum hunc periodico secundum latitudinem motu, deinceps et in epocharum ipsius constitutionem quesivimus rursum distantiam indubitalium eclipsium duarum, secundum quas alia quidem eadem his que prius contingebat, hoc est et distantie Lune ad proximum equales fiebant et obscurationes equales et vel ad arthos arthos] arctos V2F1 vel ad meridiem ambe, nodus vero nequaquam idem, sed compositus compositus] oppositus V2.
Et istarum vero eclipsium prima quidem est qua usi sumus et adnomalie adnomalie] ad anomalie V2F1 apodixim, facta vero secundo anno Mardokempadi secundum Egyptios Thoth xviii in xixa, in Babilone quidem mesonictii, in Alexandria vero ante dimidium et iii unius hore equinoctalis, secundum quam declaratur deficiens Luna a notho digitos iii.
Secunda vero qua et Iparcus cousus est facta xxo anno Darii eius qui post Kamuysin Cambisem, secundum Egyptios Epyphi xxviiia in xxixa, nocte preterita equinoctiales horas vi et iiia, secundum quam similiter defecit Luna a notho quartam diametri, et erat medium tempus in Babilone quidem ante duas quintas unius hore equinoctialis a mesonictio, quoniam eminictium erat tunc horarum equinoctialium vi et dimidii et iiiia ad proximum, in Alexandria vero ante unam et quartam hore equinoctialis a mesocitio. Facta vero est et istarum eclipsium utraque, Luna circa maximam existente distantiam, verum prior quidem circa ascendentem nodum, secunda vero circa descendentem, quare et hic equali borealius esse eo qui per media in ipsis centrum Lune.
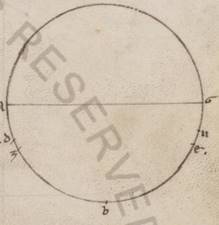 Esto ergo obliquus eius circulus ABG circa diametrum AG, et subiaceat A quidem punctus ascendens nodus, G vero descendens, atque B borealissimus terminus, et assumantur equales periferie ab utraque A et G nodorum, ut ad B borealem terminum, Sintque AD et GE, quare secundum priorem quidem eclipsim secundum D esse centrum Lune, in secunda vero secundum E. Verum quidem in priorem eclipsim ab apochis tempus annorum est egiptiacorum xxvii et dierum xvii et horarum equinoctialium et simpliciter et examinate xi et via, et propter hoc distabat Luna ab apoguio epicicli gradibus xii et xxiiii, maiorque erat periodicus progressus examinato lxis lix. Quod autem in secunda eclipsim similiter annorum egiptiacorum ccxlv et dierum cccxxvii et horarum equinoctialium simpliciter quidem x et dimidii et iiiia, examinate vero x et iiii, et propter hoc distabat Luna ab apoguio epicicli gradibus ii et xliiii, maiorque erat periodicus progressus examinato lxis xiii. Et quod inter observationes tempus continens egiptiacos annos ccxviii et dies cccix et horas equinoctiales xxiii et xii colligit secundum demonstrationem demonstrationem] demonstratum V2F1 latitudinis medium motum epoysiam gradus clx et lxa et iiii. Esto ergo rursum perexposita et medius progressus centri Lune in priori quidem eclipsi secundum Z, in secunda secundum N. Et quoniam ZBN quidem periferia graduum est clx et lxorum iiii, DZ vero lxorum lix, EN autem lxorum xiii, colligetur et DE periferia graduum clx et l, et coutreque igitur AD et EG quidem reliquorum in semicirculum sunt graduum xix et x, utraque non non] vero V2F1 earum, quoniam equales sunt, eorumdem ix et xxxv, quantis examinatus progressus Lune secundum priorem quidem eclipsim defitiebat ab ascendente nodo, secundum alteram vero descendentem precedebat. Et tota ergo AZ quidem periferia graduum est x et xxxiiii, reliqua vero NG graduum ix et xxii. Quare et periodicus transitus Lune secundum priorem quidem eclipsim defitiebat ab ascendente nodo gradibus x et xxxiiii et distabat ab B boreali termino gradibus cclxxx et xxxiiii, iuxta secundam vero precedebat descendentem gradibus ix et xxii et distabat ab eodem boreali termino gradibus lxxx et xxxviii. Reliquum ergo, quoniam quidem ab epochi tempus usque medium prioris eclipseos epoysiam continet latitudinis graduum cclxxxvi et xix, istos si dempserimus ab eis qui secundum epochim prioris eclipseos gradus cclxxx et xxxiiii, apponentes ipsis unum circulum, habebimus et in primo anno Navonassari, secundum Egiptios Thoth prima meridiei periodice latitudinis epochim a boreali termino graduum cccliiii et xv. Et ad discretiones vero ipsorum que circa sinodos et panselinia fiunt compotorum, quoniam secundum huiusmodi progressus nichil indigebimus demonstranda secunda anomalia, exponemus particularium portionum canonium per lineas rursum, quemadmodum et in Sole, negotium ipsarum fatientes et coutentes quidem ea que lx ad v et iiiia proportione, pertranseuntes autem similiter que ad apoguium tetartimoria per gradus vi, que vero ad periguium per gradus iii, quare rursum canonii descriptionem simillem fieri ei que in Sole versuum xlv, selidiorum vero trium, primis quidem duobus continentibus numeros anomalie graduum, tertio vero proprie unicuique portioni adiacentes prostafereses, ablatione quidem facta secundum compotum et in longitudine et in latitudine, quando anomalie ab apoguio epicicli collectus numerus usque clxxx gradus erit, appositione vero, quando clxxx gradus superat. Et est canonium huiusmodi.
Esto ergo obliquus eius circulus ABG circa diametrum AG, et subiaceat A quidem punctus ascendens nodus, G vero descendens, atque B borealissimus terminus, et assumantur equales periferie ab utraque A et G nodorum, ut ad B borealem terminum, Sintque AD et GE, quare secundum priorem quidem eclipsim secundum D esse centrum Lune, in secunda vero secundum E. Verum quidem in priorem eclipsim ab apochis tempus annorum est egiptiacorum xxvii et dierum xvii et horarum equinoctialium et simpliciter et examinate xi et via, et propter hoc distabat Luna ab apoguio epicicli gradibus xii et xxiiii, maiorque erat periodicus progressus examinato lxis lix. Quod autem in secunda eclipsim similiter annorum egiptiacorum ccxlv et dierum cccxxvii et horarum equinoctialium simpliciter quidem x et dimidii et iiiia, examinate vero x et iiii, et propter hoc distabat Luna ab apoguio epicicli gradibus ii et xliiii, maiorque erat periodicus progressus examinato lxis xiii. Et quod inter observationes tempus continens egiptiacos annos ccxviii et dies cccix et horas equinoctiales xxiii et xii colligit secundum demonstrationem demonstrationem] demonstratum V2F1 latitudinis medium motum epoysiam gradus clx et lxa et iiii. Esto ergo rursum perexposita et medius progressus centri Lune in priori quidem eclipsi secundum Z, in secunda secundum N. Et quoniam ZBN quidem periferia graduum est clx et lxorum iiii, DZ vero lxorum lix, EN autem lxorum xiii, colligetur et DE periferia graduum clx et l, et coutreque igitur AD et EG quidem reliquorum in semicirculum sunt graduum xix et x, utraque non non] vero V2F1 earum, quoniam equales sunt, eorumdem ix et xxxv, quantis examinatus progressus Lune secundum priorem quidem eclipsim defitiebat ab ascendente nodo, secundum alteram vero descendentem precedebat. Et tota ergo AZ quidem periferia graduum est x et xxxiiii, reliqua vero NG graduum ix et xxii. Quare et periodicus transitus Lune secundum priorem quidem eclipsim defitiebat ab ascendente nodo gradibus x et xxxiiii et distabat ab B boreali termino gradibus cclxxx et xxxiiii, iuxta secundam vero precedebat descendentem gradibus ix et xxii et distabat ab eodem boreali termino gradibus lxxx et xxxviii. Reliquum ergo, quoniam quidem ab epochi tempus usque medium prioris eclipseos epoysiam continet latitudinis graduum cclxxxvi et xix, istos si dempserimus ab eis qui secundum epochim prioris eclipseos gradus cclxxx et xxxiiii, apponentes ipsis unum circulum, habebimus et in primo anno Navonassari, secundum Egiptios Thoth prima meridiei periodice latitudinis epochim a boreali termino graduum cccliiii et xv. Et ad discretiones vero ipsorum que circa sinodos et panselinia fiunt compotorum, quoniam secundum huiusmodi progressus nichil indigebimus demonstranda secunda anomalia, exponemus particularium portionum canonium per lineas rursum, quemadmodum et in Sole, negotium ipsarum fatientes et coutentes quidem ea que lx ad v et iiiia proportione, pertranseuntes autem similiter que ad apoguium tetartimoria per gradus vi, que vero ad periguium per gradus iii, quare rursum canonii descriptionem simillem fieri ei que in Sole versuum xlv, selidiorum vero trium, primis quidem duobus continentibus numeros anomalie graduum, tertio vero proprie unicuique portioni adiacentes prostafereses, ablatione quidem facta secundum compotum et in longitudine et in latitudine, quando anomalie ab apoguio epicicli collectus numerus usque clxxx gradus erit, appositione vero, quando clxxx gradus superat. Et est canonium huiusmodi.
〈IV.10〉
| Canonium prime et simplicis anomalie Lune | |||
| Communes numeri | Prosthaferesis | ||
| Gradus | Gradus | Gradus | Minuta |
| vi | cccliiii | o | xxix |
| xii | cccclviii | o | lvii |
| xviii | cccxlii | i | xxv |
| xxiiii | cccxxxvi | i | liii |
| xxx | cccxxx | ii | xix |
| xxxvi | cccxxiiii | ii | xliiii |
| xlii | cccxviii | iii | viii |
| xlviii | cccxii | iii | xxxi |
| liiii | cccvi | iii | li |
| lx | ccc | iiii | viii |
| lxvi | ccxciiii | iiii | xxiiii |
| lxxii | cclxxxviii | iiii | xxxviii |
| lxxviii | ccclxxxii | iiii | xlix |
| lxxxiiii | cclxxvi | iiii | lvi |
| xc | cclxx | iiii | lix |
| xciii | cclxvii | v | o |
| xcvi | cclxiiiic | v | i |
| xcix | clxi | v | o |
| cii | clviii | iiii | lix |
| cv | cclv | iiii | lvii |
| cviii | cclii | iiii | liii |
| cxi | ccxlix | iiii | xlix |
| cxiiii | ccxlivi | iiii | xliiii |
| cxvii | ccxliii | iiii | xxxviii |
| cxx | ccxl | iiii | xxxi |
| cxxiii | ccxxxvii | iiii | xxv |
| cxxvi | ccxxxiiii | iiii | xvi |
| cxxix | ccxxxi | iiii | vii |
| cxxxii | ccxxviii | iii | lvii |
| cxxxv | ccxxv | iii | xlvi |
| cxxxviii | ccxxii | iii | xxxv |
| cxli | ccxix | iii | xxiii |
| cxliiii | ccxvi | iii | x |
| cxlvii | ccxiii | ii | lvii |
| cl | ccx | ii | xliii |
| cliii | ccvii | ii | xxviii |
| clvi | cciiii | ii | xiii |
| clix | cci | i | lvii |
| clxii | cxcviii | i | xli |
| clxv | cxcv | i | xxv |
| clxviii | cxcii | i | ix |
| clxxi | clxxxix | o | lii |
| clxxiiii | clxxxvi | o | xxxv |
| clxxvii | clxxxiii | o | xviii |
| clxxx | clxxx | o | o |
〈IV.11〉 Quoniam non penes differentias ypothesium, verum penes epilogissmos differt ea que secundum Yparcon quantitas lunaris anomalie
His ita demonstratis, congrue utique quis inquiret propter quam causam ex ab Yparco appositis lunaribus eclipsibus ad huiusmodi anomalie considerationem, neque eadem fit proportio a nobis demonstrate, neque consona prima et per eam que excentrotica ypothesim est est] om. V2F1 ostensa secunde et per eam que secundum epiciclum ypothesim investigare. investigare] investigate V2 Namque secundum primam quidem demonstrationem colligit proportionem eius que ex centro excentrici ad intermediam centro eius et illius qui per media animalia, quam habent iiicxliiii ad ccxxvii xl ad proximum, cui proportioni eadem est que lx ad vi et xv, iuxta secundum vero colligit proportionem eius que e centro eius qui per media animalia usque centrum epicicli ad eam que e centro epicicli, quam habent iiicxxii et dimidium ad ccxlvii et dimidium, cui proportioni eadem est que lx ad iiii et xlvi. Facit autem plurimam anomalie differentiam ea quidem que lx ad vi et iiii proportio v graduum et xlix, que vero lx et ad iiii et xlvi graduum iiii et xxxiiii, secundum nos lx ad v et iiiiam proportione v graduum ad proximum fatiente expositam differentiam.
Quoniam ergo non penes ypothesium discordiam, ut quidam autumant, huiusmodi consequutum est peccatum, et rationem paulo ante manifestum factum est ex secundum utramque ipsarum eadem apparentia inpermutabiliter contingere, et per numeros vero si voluerimus computationes facere, eandem utique reperimus factam proportionem ex ambabus ypothesibus, si eisdem quidem apparentibus sequamur in utraque, et non diversis, quemadmodum Yparcus. Possibile enim ita erit, non eisdem suppositis eclipsibus, vel penes ipsas observationes, vel penes distantiarum computationes fallaciam accidere. Inveniemus ergo et in ipsis eclipsibus coniugationes quidem sane observatas et consone factas a nobis demonstratis et plani et anomali motus ypothesibus, distantiarum vero computationes, per quas quantitas eius demonstrata est, non solicite, ut est maxime, factas. Ostendemus vero ipsorum ipsorum] istorum V2F1 utrumque a primis tribus eclipsibus inchohantes. Igitur has quidem tres eclipses apponi dicit ab ex Babilone deportatis velut ibi observatas, factam vero fuisse primam, principante Athenis Phanostrato, mense Possideone, et defecisse Lunam brevi parte circuli ab estivo ortu, noctis reliquo existente hemiorio, et adhuc dicit: ‘defitiens occidit’. Fit ergo istud tempus secundum ccclxvi annum a Navonassaro, secundum Egiptios autem, ut ipse dicit, Thot xxvi in xxvii, post v horas temporales et dimidium a mesonictio, quoniam quidem reliquum erat noctis hemihorium. Sed Sole existente circa extrema Sagittarii, in Babilone noctis hora temporum et xviii, nox enim est horarum equinoctialium xiiii et iiarum quintarum, quoniamque quoniamque] quinque V2F1 ergo hore temporales et dimidii colligunt equinoctiales horas vi et iii quintas. Principium ergo ecplipsis factum est post xviii horas equinoctiales et iii quintas ab ea que in xxvi meridie. Quoniam autem parva pars inumbrata est, totum quidem tempus eclipseos debet fieri una hora et dimidii ad proximum. Medium vero manifestum quoniam post xix horas equinoctiales et iiiam. In Alexandria ergo rursum factum est medium tempus eclipseos post xviii horas equinoctiales et dimidium ab ea vero que in xxvia meridie, et est quod ab ea que secundum primum annum Navonassari epochi tempus usque subiacentem annorum egiptiacorum ccclxv et dierum xxv et horarum simpliciter quidem xviii et dimidii, examinate vero xviii et iiiia. Ad quod tempus computantes secundum expositas nobis ypotheses, Sole Sole] Solem V2F1 quidem reperimus examinate obtinentem Sagittarii gradus xxviii et xviii, Lunam vero medie quidem Geminorum gradus xxiiii et xx, examinate vero xxviii et xvii, quoniam quidem et secundum anomaliam distat ab apoguio apoguio] corr. ex apogovio V3 epicicli gradibus ccxxvii et xliii. Rursum eam que deinceps eclipsim dicit factam fuisse, principante Athenis Phanostrato, chiroforione mense, secundum Egyptios autem Phamenoth xxiiiia in xxv. ‘Defecit vero, dicit, ab estivo ortu, prima hora preterita’. Fit ergo et istud tempus secundum ccclxvim annum a Navonassaro Phamenoth xxiiiia in xxv ante v horas et dimidium maxime temporales a mesonictio. Sed Sole existente circa postrema Geminorum, noctis hora est in Babilone temporum xii. Quinque ergo hore temporales et dimidium faciunt equinoctiales iiii et duas quintas et principium ergo eclipseos factum est post vii horas equinoctiales et iii quintas ab ea que in xxiiii meridie. Sed quoniam totum tempus eclipseos horarum trium describitur, medium manifestum quoniam factum est post ix horas equinoctiales et xa. In Alexandria ergo debet fieri post viii et iiiia ad proximum horas equinoctiales ab ea que in xxiiii meridie, et est rursum quod ab epochis tempus annorum egiptiacorum ccclxv et dierum cciii et horarum equinoctialium simpliciter viii et iiiia, examinate vero vii et dimidii et iiia, ad quod tempus reperimus Solem quidem examinate optinentem Geminorum gradus xxi et xlvi, Lunam autem medie quidem Sagittarii gradus xxiii et lviii, examinate vero gradus xxi et xlviii, quoniam quidem secundum anomaliam distabat ab apoguio epicicli gradibus xxvii et xxxvii. Colligit autem et distantia a prima eclipsi in secunda dierum clxxvii et horarum xiii et iii quintarum equinoctialium, graduum vero, quos Sol motus est, clxxiii et xxviii, Yparco faciente demonstrationem velut distantia dierum existente clxxvii et horarum equinoctialium xiii et dimidii et iiiia, graduum vero clxxiii deficientium viiia parte unius gradus. Tertiam autem dicit factam fuisse, principante Athenis Evandro, mense Possideone priore, secundum Egiptios Thoth xvia in xviia, ‘defecit autem, dicit, tota incipiens ab estivalibus ortibus iiii horis preteritis’. Fit ergo et istud tempus secundum ccclxvii annum a Navonassaro, Thot xvia in xviia, ante duas horas et dimidium maxime a mesonictio. Verum Sole existente circa duas partes Sagittarii, in Babilone noctis hora temporum est xviii ad proximum, quare due et dimidium hore temporales faciunt equinoctiales horas iii. Quare principium eclipseos fuit post ix horas equinoctiales ab ea que in xvia meridie. Verum quoniam tota defecit, totum quidem tempus ad proximum fuit horarum iiii equinoctialium, medium vero tempus manifestum quoniam post xi horas a meridie, in Alexandria ergo medium tempus eclipseos debet fieri post x et vi horas equinoctiales ab ea que in xvia meridie. Et est quod ab epochis tempus annorum egiptiacorum ccclxv ccclxv] ccclxvi V2F1 add. marg. al. man. 366 V3 et dierum xv et horarum equinoctialium simpliciter quidem rursum x et vi, vi] corr. ex xci V3 examinate vero ix et dimidii et iiia, ad quod tempus reperimus Solem quidem optinentem examinate Sagittarii gradus xvii et xxx, Lunam vero medie quidem Geminorum gradus xvii et xxi, examinate vero xvii et xxviii, propter secundam anomaliam distare ab apoguio epicicli gradibus clxxxi et xii. Colligitur autem a secunda in tertiam eclipsim distantia dierum quidem clxxvii et equinoctialium horarum ii, gradus gradus] graduum V2 vero clxxvii clxxvii] clxxv V2F1 et xliiii, Yparco rursum ponente et istam distantiam dierum quidem clxxvii et hore unius et Γo, graduum autem clxxv et viii. Apparet ergo in distantiarum computationibus mentitus in diebus quidem vi et iiia unius hore equinoctialis, in gradibus autem tribus quintis ad proximum secundum utramque unius gradus, que non quacumque in quantitate proportionis operari dissonantiam possunt.
Transibimus ergo et in posterius expositas illi tres eclipses, quas dicit observatas in Alexandria. Istarum vero primam dicit factam fuisse liiiio anno secunde secundum Calippon periodi secundum Egiptios Mesori xvi, secundum quam incepit quidem deficere Luna ante hemiorium ab ortu, ad extremum vero completa est tertia hora media. Medium ergo tempus factum fuit, hora quidem secunda incipiente, ante v vero horas temporales a mesonictio ante totidem autem et equinoctiales, quoniam quidem Sol circa extema erat Virginis. Quare post vii horas equinoctiales ab ea que in xvia meridie in Alexandria factum fuit tempus medium eclipseos. Est autem et quod ab eis que secundum primum annum Navonassari epochis tempus annorum egyptiacorum dxlvi et dierum cccxlv et horarum equinoctialium simpliciter quidem vii, examina examina] examinate V2 vero vi et dimidii, secundum quod tempus rursum reperimus Solem quidem optinentem examinate Virginis gradus xxvi et via, Lunam vero medie quidem Piscium gradus xxii, examinate gradus autem xxvi et viiam, propter secundum anomaliam distare ab apoguio epicicli gradibus ccc et lxis xiii. Eam vero quam deinceps eclipsim dicit factam fuisse lvo anno eiusdem periodi secundum Egiptios Mechir ix. Incepit autem noctis preteritis horis v et tritimorio et defecit tota. Factum est ergo principium quidem eclipseos post xi et iii horas equinoctiales ab ea que in ixa meridie, quoniam quidem rursum Sol circa extrema erat Piscium. Medium autem tempus post xiii et iii horas equinoctiales, propter Lunam totam defecisse, et est quod ab epochis usque hoc tempus annorum egiptiacorum dxlvii et dierum clviii et horarum equinoctialium tam simpliciter quam examinate examinate] add. ad proximum xiii et iii, ad quod tempus similiter reperimus Solem quidem examinate V2F1 optinentem Piscium gradus xxvi et xvii, Lunam vero medie quidem Chelarum gradus et vii, examinate vero Virginis xxvi et xvi, quoniam quidem secundum anomaliam distabat ab apoguio gradibus cix et xxviii. Colligitur autem et a prima eclipsi in secunda distantia dierum clxxviii et horarum equinoctialium vi et dimidii et iiia, graduum vero clxxx et xi, Iparco faciente demonstrationem velut distantia ista dierum quidem existente clxxviii et horarum vi equinoctialium, graduum vero clxxx et xx.
Tertiam vero dicit eclipsim factam fuisse eodem lvo anno secunde periodi, secundum Egiptios Mesori v. Incepit autem noctis preteritis horis vi ideo, et defecit tota. Medium vero eclipsis tempus dicit factum fuisse circiter horas maxime viii et tritimorion, hoc est post duas horas temporales et iiia a mesonictio. Verum Sole existente circa media Virginis, in Alexandria noctis hora temporum est xiiii et iiarum quintarum. Due ergo hore temporales et iiia faciunt equinoctiales ad proximum duas et iiiiam, quare factum fuit medium tempus tempus] add. post V2F1 xiiii horas equinoctiales et iiiiam ab ea que in vo meridie, et est rursum quod a epochis usque hoc tempus annorum egiptiacorum dxlvii et dierum cccxxxiiii et horarum equinoctialium simpliciter quidem xiiii et iiii, examinate vero xiii et dimidii et iiii, ad quod tempus reperimus Solem quidem obtinentem examinate Virginis xv gradus et xii, Lunam vero medie quidem Piscium gradus x et xxiiii, examinate vero gradus xv et xiii, quoniam quidem secundum anomaliam distabat ab apoguio epicicli gradibus cxlix cxlix] ccxlix V2F1 et ix. Colligitur autem et a secunda eclipsi in tertiam distantia dierum quidem clxxvi et duarum quintarum unius hore equinoctialis, graduum vero clxviii et lv, Iparco rursum supponente et istam differentiam dierum clxxviii et unius tertie hore equinoctialis, graduum vero clxviii et xxxiii. Et hic ergo apparet mentitus in gradibus quidem vi et iiia ad proximum unius gradus, in diebus autem dimidio et iiia et xiia ad proximum unius hore equinoctialis, que et in ipsa possunt differentiam cura dignam circa ypotheseos proportionem operari. Facta est ergo nobis sub visum et preiacentis dissonantie causa, et quoniam confidentes utique adhuc magis coutemur secundum nos demonstrata ratione anomalie in coniugationibus Lune, et istis ipsis eclipsibus consonis maxime nostris ypothesibus inventis.
Claudi Ptolomei mathematicarum quartus liber explicit.