〈IX〉
De ordine sperarum Solis et Lune et quinque erraticorum
De ea que secundum ypotheses erraticorum propositione
De periodicis restitutionibus quinque planomenorum
De expositio canonica mediorum motuum quinque planomenorum
Presumpta in ypotheses quinque erraticarum
De modo et differentia ypothesium
Demonstratio apoguii stelle Mercurii et transmotionis ipsius
Quoniam bis et Mercurii stella periguiotatos in uno circulo fit
De proportione et quantitate anomaliarum Mercurii
De periodicis Mercurii motibus
De epochi periodicorum periodicorum] corr. ex periodorum V3 motuum
Incipit nonus
〈IX.1〉 De ordine sperarum Solis et Lune et quinque erraticorum
Igitur quecumque quidem quis et de fixis stellis velut in capitulis commermorat, secundum quantum usque nunc apparentia processum conceptionis suggerunt, fere hoc hoc] hec F1 erunt. Relicto autem in hanc coordinationem quinque erraticorum negotio, faciemus de ipsis expositionem, propter non idem dicere secundum comune, in quantum contingit, ephodorum singulas superadiungentes. Primum ergo de ordine speram ipsorum que et ipse positiones habent quasi circa obliqui et eius qui per medias imagines animalium circuli polos, et omnes quidem terre propinquiores esse ea que fixarum, a terra vero lunari remotiores, et tres eam scilicet que Saturni maiorem existentem et eam que Iovis ut in terre propinquiora secundum et eam que Martis sub illam, a terra remotiores esse et reliquis et ea que Solis fere penes omnes primos mathematicos videmus consonantia, eam autem que Veneris et eam que Mercurii penes antiquiores quidem suppositas solari, at penes aliquos eorum qui post hec et ipsas superpositas, eo quod sub ipsis numquam Sol obscuratur. Nobis vero iuditium quidem huiusmodi infirmitatem habere videtur, eo quod possint alique esse quidem sub Sole nondum vero omnino et in aliquo eorum que per ipsum et visum nostrum epipedo, sed in alio, et propter hoc non appareant superobiecte ipsi, quemadmodum et in coniunctionibus Lune subcursibus multotiens non fiunt obscurationes. Non valente vero neque secundum alium modum huiusmodi conceptione procedere, eo quod nulla stellarum aliquam transmutationem faciat sensibilem, a quo solo apparente distancie sumuntur, credibilior magis antiquorum ordinatio apparet segregans naturalius Sole medio omni distantia distans ab ipso ante ita se habentibus, sed circa ipsum semper motis, in quantum non ea usque removet ipsas in id quod terre propinquius, quantum cura dignam aliquam transmotionem operari possit.
〈IX.2〉 De ea que secundum ypotheses erraticorum prepositione
Quod ergo secundum ordines sperarum huiusmodi utique erit. Proposito vero nobis et in quinque erraticis stellis, quemadmodum in Sole et Luna, apparentes ipsarum anomalias omnes demonstrare per planos et circulares motus completas, his quidem propriis existentibus natura divinorum, inordinatione vero et dissimillitudine aliorum, magnum quidem reputari decet quod secundum huiusmodi preportionem offitium et finem tamquam vere eius qui in philosophia mathematice theorie, difficille vero propter multa et convenienter a nullo prius adimpletum: nam et in eis que circa periodicos uniuscuiusque motus inquisitionibus, eo quod secundum comparatas observationes sub visu considerari ad subtilius potest velociter quidem sensibilem facientes secundum quod deinceps tempus differentiam, quando in minori distantia fiunt inquisitum, tarde vero, quando ab ampliore, tempus autem quo erraticorum observationes habemus descriptas breve existens ut ad ita magnam conceptionem eam in que tempus longo multiplicatum prefationem infirmam construit. Atque in anomaliarum inquisitione non parvam ingerit turbationem et duas secundum unumquodque ipsorum apparere factas anomalias et ipsas inequales quidem et magnitudinibus et restitutionum temporibus, quarum hec quidem ad Solem, illa vero ad zodiaci partes proportionem habens consideratur, mixtas autem ubique ambas, quod secundum utramque proprium hinc diffitile discerni possit, et antiquorum observationes indiligenter simul et confuse describi. Nam et magis continue ipsarum stricigmoys stricigmoys] corr. ex stricigmoysis V3 continent et illuminationes. Virtus vero istarum proprietatum non est sine dubitatione conceptio, stationibus quidem non potentibus exanimatum tempus declarare, propter secundum multos dies locali transitione insensibili facta et prius et posterius ipsa statione, illuminationibus nec non nec non] corr. marg. ex vero nec F1 solum loca statim simul disparere facientibus primum vel postremum visis, sed et secundum tempora peccare potentibus causa et differentie aeris et visus observationum; et universaliter ad aliquam stellarum fixarum e spatio longiore facte observationes, nisi quis omnium causa et perspicaciter et artifitiose eis intendat, difficile comprehensibilem et magna attentione indigentem habent quantitatem dimensionis, non solum propter medias observatarum stellarum lineas differentes angulos ad eum qui per medias imagines animalium facere et non omnino rectos, unde convenit multum consequi errorem propter multimodum inclinationis zodiaci circa discretionem et eius quem secundum longitudinem et eius quem secundum latitudinem optenti loci, sed et propter distantias easdem ad orizontes quidem maiores visibus apparere, ad mensuranises mensuranises] mesuranises F1 vero minores, et propter hoc manifestum quoniam aliquotiens quidem velut maiores, aliquotiens non non] vero F1 velut minores subiecto vere spatio mensurari posse. Unde et Ipparco estimo amicum veritatis dictum et propter hec omnia et maxime pro eo quod numquam tantas antea causas examinatarum observationum receptas esse, quantas ipse nobis tradidit, Solis quidem et Lune ypotheses et querere et ut inest demonstrare omni artifitio per planos et circulares motus completas, eis vero que quinque erraticatum per eas que in nos venerunt commemorationes nec principium inmittere, solum vero observationes ipsorum ab utilius coordinare et ostendere per ipsas dissonantia ea que apparent ab eorum qui tunc mathematorum ypothesibus. Non enim solum reputabatur conveniens, ut videtur enuntiare, quoniam duplam queque ipsarum facit anomaliam, vel quoniam secundum unamquamque inequales et tante fiunt precessiones, aliis mathematicis quasi de una et eadem et anomalia et precessione eas que per lineas demonstrationes facientibus, neque quoniam ipsas vel per excentricos vel per omocentricos quidem zodiaco, epiciclos vero circumferentes nova propter secundum coutramque compleri contingit, zodiaca quidem anomalia existente tam magna, ea vero que ad Solem tanta. His enim instuduerunt fere, quanti per vocatam secularem canonopiiam planum et circularem motum voluerunt ostendere, falso non non] vero F1 simul et demonstrabiliter, hii quidem nequaquam penitus, illi vero aliquantulum consentientes propositum. Reputatum est autem quoniam usque tantam et diligentiam et amorem veritatis provectio per omnia mathematica non sufficit usque tanta stare, quemadmodum aliis nichil distitit, sed neccessarium utique erunt futuro persuadere et seipsum et ad hec pertingentes et utriusque anomaliarum quantitatum et periodos per apparentia manifesta et confessa demonstrare, et miscenti rursum ambas et portionem et ordinem circulorum, per quos ipse fiunt, et modum motionis ipsorum invenire, et fere omnia quod reliquum coaptare apparentia ypothesis circulorum ydiotropie. Hoc autem puto et ipsi difficile apparebat. Hec autem diximus non ostensionis causa, sed sic ut ab ipsa re constringimur vel uti aliquo preter rationem, ut quando verbi gratia velut in nudis speris in qui speris … qui] qui in speris F1 ipsarum describentur a motu circulis et quasi secundum idem epipedum existentibus ei qui per medias imagines animalium propter facilem consequentiam demonstrationes faciemus vel suppponere aliqua prima nobis nobis] om. F1 non ab apparente principio, sed secundum continuum usum et coaptationem incipientia conceptionem vel non in omnibus eumdem et inpermutatum modum motionis vel inclinationis circulorum supponi concedimus, scientes quoniam neque uti aliquo talium, in quantum nulla de hoc debere debere] debet F1 consequi cura digna differentia, derogabit quidem propositum neque inprobabiliter supposita, si semel consona apparentibus deprehendentur, preter artem aliquam et instantiam reperiri poterunt, si difficile tractabilis erit modus conceptionis ipsorum. Quoniam quidem et universaliter primorum principiorum vel nichil vel difficile interpretabilis est natura causa, neque differre alicui modum ypotheseos circulorum mirabile et irrationabile satis quis putet, et circa ipsas stellas apparentibus difficillibus deprehensis, quando cum secundum omnes simpliciter planum et circularis motus salvatione et apparentium singula secundum universalius simillitudinis ypothesium demonstrabuntur. Utimur tamen observationum ad eas que secundum unumquodque demonstrationes eis que indubitabilibus esse maxime possunt, hoc est et secundum coniunctionem vel magnam apropinquationem stellarum vel et Lune observatis et maxime per astrolabica organa deprehensis, erecto quodam modo visu per in circulis diametrizantia foramina et equalia spatia ubique per similles periferias vidente et ad eum qui per media cuiusque progressiones et secundum longitudinem et secundum latitudinem examinate intelligere potente per ad observata differentiam et eius qui secundum zodiacum in astrolabio circuli et que secundum illos qui per polos ipsius circulos diametrizantium foraminium.
〈IX.3〉 De periodicis restitutionibus quinque planomenorum
His ita prelibatis, exponemus primum computatas ab Ipparco periodicas et minimas uniuscuiusque quinque planomenorum ad proximum conrestitutiones, correctas quidem a nobis ex post anomaliarum apodyces apodyces] apodixes F1 considerata locorum que optinent comparatione, ut ibi manifestum fecimus, preordinatas vero nobis, propterea ut ad anomaliarum computationes prompte expositas habeamus vel eos qui secundum partem cuiusque medios motus et longitudinis et anomalie, nullo hic differente cura digno, etsi universalius quis mediis progressionibus utetur. Ad Ad] om. F1 audiendum vero universaliter longitudinis quidem motum eum qui centri epicicli circa excentricum, anomaliam vero eum qui stelle circa epiciclum. Itaque Saturni quidem lvii anomalias reperimus completas in annis quidem solaribus qui secundum nos, hoc est a conversionibus equinoctialibus in easdem, lix et adhuc die uno et dimidio et quarta ad proximum, circumcisionibus circumcisionibus] circumcursionibus F1 vero stelle duabus et gradu i et duabus partibus et xxa, quoniam quidem in semper circadeprehensis a Sole tribus stellis tantos semper circulos Sol pertransit in restitutio restitutio] restitutivo F1 secundum unamquamque tempore, quante sunt simul et secundum longitudinem circumcisiones circumcisiones] circumcursiones F1 stelle et anomalie restitutiones composite. Iovis vero lxv anomalias reperimus completas in annis quidem solaribus simpliciter sumptis lxxi minus habentibus dies iiii et dimidio et iiia et xva ad proximum, circumcursibus vero stelle a conversionibus in easdem conversiones vi defitientibus gradibus iiii dimidio iiia; atque Martis xxxvii anomalias in annis quidem solaribus qui secundum nos lxxix et diebus iii et via et xxa ad proximum, circumcursibus vero stelle qui a conversionibus in easdem conversiones xlii et gradibus iii et via; Veneris autem quinque anomalias in annis quidem solaribus qui secundum nos viii minus habentibus dies ii et iiiia et xxa ad proximum, circumcursibus vero stelle numero paribus eis qui viii Solis defitientibus ii et iiiia; Mercurii vero clxv anomalias in annis quidem eisdem xlvi et die uno et xxxa ad proximum, circumcursibus vero numero paribus Soli rursus xlvi et gradu i. Sed si resolverimus in unoquoque restitutionis quidem tempus in dies consequenter demonstrato a nobis annuo tempori, multitudinem vero anomaliarum in eos qui secundum unum circulum gradus ccclx habebimus: in Saturno quidem dies xxi xviii et gradus anomalie xx dxx, in Iove autem dies xxv dccc xxvii xxxvii, gradus vero anomalie xxvii cccc, in Marte vero dies quidem xxviii dccclvii liii, gradus vero anomalie xiii ccc xx, in Venere vero dies quidem ii dcccc xix xl, gradus vero anomalie i dccc, in Mercurio autem dies quidem xvi dcccii xxiiii, gradus vero anomalie lii cc.
Distribuentes ergo secundum unumquoque proprie multitudinem graduum anomalie in multitudinem dierum habebimus anomalie diurnum medium motum: Saturni quidem gradus t lvii vii xliii xli xliii xl ad proximum, Iovis autem gradus o liiii ix ii xlvi xxvi, Martis vero gradus o xxvii xli xl xviiii xx lviii, Veneris vero gradus t xxxvi lix xxv liii xi xxviii, Mercurii autem gradus iii vi xxiiii vi lix xxxv l.
Istorum autem sumentes secundum unumquodque xxiiii habebimus horarum anomalie medium motum: Saturni quidem gradus o ii xxii xlix xix xiiii xix x, Iovis autem gradus o ii xv xxii xxxvi lvi v, Martis vero gradus o i ix xiiii x xlviii xxii xxv, Veneris autem gradus o i xxxii xxviii xxxiiii xlii lviii l, l] xl F1 Mercurii vero gradus o vii xlvi o xvii xxviii lix xxxv.
Rursum tricesies quidem facientem diurnos cuiusque habebimus anomalie menstruum medium motum: Saturni quidem gradus xxviii xxxiiii li l li l o, Iovis autem gradus xxvii iiii xxxi xxiii xiii o o, Martis vero gradus xiii l l ix xl xxix o, Veneris autem gradus xviii xxix xlii lvi xxxv xliiii o o, Mercurii vero gradus xciii xii iii xxix xlvii lv o.
Multiplicantes vero similiter diurnos in dies unius anni egiptiaci ccclxv habebimus annuum anomalie medium motum: Saturni quidem gradus cccxlvii xxxii o xlviii l xxxviii xx, Iovis autem gradus cccxxix xxv i lii xxviii x o, Martis vero gradus clxviii xxviii x o. Martis vero gradus clxviii xxviii xxx xvii xlii xxxii l, Veneris autem gradus ccxxv i xxxii xxviii xxxiiii xxxix xv, Mercurii vero gradus supergressionis, idest epoysie, liii lvi xlii xxxii xxxii lix x.
Similiter autem et annorum unumquemque decies octies fatientes, quemadmodum et in luminarium canonopiia, habebimus xviii annorum egiptiacorum collectorum mediam anomalie supergressionem: Saturni quidem gradus cxxxv xxxvi xiiii xxxv xi xxx o, Iovis vero gradus clxix xxx xxxiii xliiii xxvii o o, Martis autem gradus clii xxxiii v xviii xlv li o, Veneris autem gradus xc xxvii xliiii xxxiiii xxiii xlvi xxx, Mercurii vero gradus ccli o xlv xlv liii xlv o.
Consequenter vero his et secundum longitudinem medios motus, ut non etiam circumcursuum multitudinem resolventes in gradus distribuamus in expositum in unoquoque tempus, quidem Veneris et Mercurii manifestum quoniam eosdem habebimus in Sole preexpositis, reliquarum vero trium stellarum defitientes eis qui anomalie in completionem solarium secundum unumquodque proprie numerorum. Etiam propter hec habebimus diurni quidem secundum longitudinem medii motus: Saturni quidem gradus o ii o xxxiii xxxi xxviii li, Iovis autem gradus o iiii lix xiiii xxvi xlvi xxxi, Martis vero o xxxi xxvi xxxvi liii li xxxiii.
Horarii vero Saturni quidem gradus o o v i xxiii xlviii xlii vii xxx, Iovis autem gradus o o xii xxviii vi vi lvi xvii xxx, Martis vero gradus o i xviii xxxvi xxxii xiiii xxxix.
Menstrui autem Saturni quidem gradus i o xvi xlv xliiii xxv xxx, Iovis autem gradus ii xxix xxxvii xiii xxiii xv xxx, Martis vero gradus xv xliii xviii xxvi lv xlvi xxx.
Annui vero Saturni quidem gradus xii xiii xxiii lvi xxx i xv, Iovis vero gradus xxx xx xxii lii xxxv, Martis autem gradus cxci xvi liiii xxvii xxxviii xxxv xlv.
Annorum vero xviii: Saturni quidem medium motum gradus ccxx i x lvii ix iiii xxx, Iovis autem supergressionem gradus clxxxvi vi li li liii xxxiiii xxx, Martis autem epoysia gradus cciii iiii xx xvii xxxiiii xliii xxx.
Ordinabimus ergo iterum utilitatis causa cuiusque secundum ordinem stellarum canones superagregationis preiacentium mediorum motuum, in versus quidem similiter aliis xlv, partes autem tres, quarum quidem priore continebunt xviii annorum collectionis superagregationis, superagregationis] superagregaciones F1 secunde vero et annuas et horarias, tertie vero et menstruas et diurnas; et canones quidem sunt hii.
〈IX.4〉 Expositio canonica mediorum motuum quinque planomenorum
Nos autem brevitati desinentes tabulas diversitatum que a quibusdam dicuntur tabule argumentorum sive portionum pretermittimus tabulas siquidem longitudinum sive mediorum cursuum trium superiorum subscribimus, nec fuit necesse, ut ait Albategni, tabulas diversitatum apponere. Habetur namque diversitas cuiuslibet trium superiorum subtracto eius medio a medio solari. Item tabulas mediorum cursuum Veneris et Mercurii non est necesse cum medius eorum cursus idem sit qui et Solis. Ponimus autem tabulas diversitatum eorum que non possunt haberi per subtractionem mediorum eorum a medio Solis ut reliquorum.
CANONES MEDIORUM SATURNI |
|||||||||||||||
| Anni collecti | Medius cursus Saturni in annis collectis | Dies |
|||||||||||||
| G | M | S | T | Q | Q | S | mensium |
G |
M |
S |
T |
Q |
Q |
||
| xviii | ccxx | i | x | lvii | ix | iiii | xxx | xxx |
i |
o |
xvi |
xlv |
xliiii |
xxv |
|
| xxxvi | lxxx | ii | xxi | liiii | xviii | ix | o | lx |
ii |
o |
xxxiii |
xxxi |
xxviii |
li |
|
| liiii | ccc | iii | xxxii | li | xxvii | xiii | xxx | xc |
iii |
o |
l |
xvii |
xiii |
xvi |
|
| lxxii | clx | iiii | xliii | xlviii | xxxvi | xviii | o | cxx |
iiii |
i |
vii |
ii |
lvii |
xlii |
|
| xc | xx | v | liiii | xlv | xlv | xxii | xxx | cl |
v |
i |
xxiii |
xlviii |
xlii |
vii |
|
| cviii | ccxl | vii | v | xlii | liiii | xxvii | o | clxxx |
vi |
i |
xl |
xxxiiii |
xxvi |
xxxiii |
|
| dccxx | clx | xlvii | xviii | vi | iii | o | o | ccx |
vii |
i |
lvii |
xx |
x |
lviii |
|
| dccxxxviii | xx | xlviii | xxix | iii | xii | iiii | xxx | ccxl |
viii |
ii |
xiiii |
v |
lv |
xxiiii |
|
| dcclvi | ccxl | xlix | xl | o | xxi | i | o | cclxx |
ix |
ii |
xxx |
li |
xxxix |
xlix |
|
| dcclxxiiii | c | l | l | lvii | xxx | xiii | xxx | ccc |
x |
ii |
xlvii |
xxxvii |
xxiiii |
xv |
|
| dccxcii | cccxix | lii | i | liiii | xxxix | xviii | o | cccxxx |
xi |
iii |
iiii |
xxiii |
viii |
xl |
|
| dcccx | clxxx | liii | xii | li | xlviii | xxii | xxx | ccclx |
xii |
iii |
xxi |
viii |
liii |
vi |
|
| Anni simplices | G | M | S | T | Q | Q | S | Dies | G | M | S | T | Q | Q | |
| i | xii | xiii | xxiii | lvi | xxx | xxx | xv | 〈i〉 | 〈o〉 | 〈ii〉 | o | xxxiii | xxxi | xxix | |
| ii | xxiiii | xxvi | xlvii | liii | i | o | xxx | 〈ii〉 | 〈o〉 | iiii | i | vii | ii | lviii | |
| iii | xxxvi | xl | xi | xlix | xxxi | xxx | xlv | 〈iii〉 | 〈o〉 | vi | i | xl | xxxiiii | xxvi | |
| iiii | xlviii | liii | xxxv | xlvi | ii | i | o | iiii | o | viii | ii | xiiii | v | lv | |
| v | lxi | vi | lix | xlii | xxxii | xxxi | xv | v | o | x | ii | xlvii | xxxvii | xxiiii | |
| vi | lxxiii | xx | xxiii | xxxix | iii | i | xxx | vi | o | xii | iii | xxi | viii | liii | |
| vii | lxxxv | xxxiii | xlvii | xxxv | xxxiiii | xxxi | xlv | vii | o | xiiii | iii | liiii | xl | xxii | |
| viii | xcvii | xlvii | xi | xxxii | iiii | ii | o | viii | o | xvi | iiii | xxviii | xi | li | |
| ix | cx | o | xxxv | xxviii | xxxiiii | xxxii | xv | ix | o | xviii | v | i | xliii | xx | |
| x | cxxii | xiii | lix | xxv | v | ii | xxx | x | o | xx | v | xxxv | xiiii | xlvii | |
| xi | cxxxiiii | xxvii | xxiii | xxi | xxxv | xxxii | xlv | xi | o | xxii | vi | viii | xlvi | xvii | |
| xii | cxlvi | xl | xlvii | xviii | vi | iii | o | xii | o | xxiiii | vi | xlii | xvii | xlvi | |
| xiii | clviii | liiii | xi | xiiii | xxxvi | xxxiii | xv | xiii | o | xxvi | vii | xv | xlix | xv | |
| xiiii | clxxi | vii | xxxv | xi | vii | iii | xxx | xiiii | o | xxviii | vii | xlix | xx | xlv | |
| xv | clxxxiii | xx | lix | vii | xxxvii | xxxiii | xlv | xv | o | xxx | viii | xxii | lii | xiii | |
| xvi | cxcv | xxxiiii | xxiii | iiii | viii | iiii | o | xvi | o | xxxii | viii | lvi | xxiii | xlii | |
| xvii | ccvii | xlvii | xlvii | o | xxxviii | xxxiiii | xv | xvii | o | xxxiiii | ix | xxix | lv | x | |
| xviii | ccxx | i | x | lvii | ix | iiii | xxx | xviii | o | xxxvi | x | iii | xxvi | xxxix | |
| Hore i | o | o | v | i | xxiii | xlviii | xlii | xix | o | xxxviii | x | xxxvi | lviii | viii | |
| ii | o | o | x | ii | xlvii | xxxvii | xxiiii | xx | o | xl | xi | x | xxix | xxxvii | |
| iii | o | o | xv | iiii | xi | xxvi | vi | xxi | o | xlii | xi | xliiii | i | vi | |
| iiii | o | o | xx | v | xxxv | xiiii | xlviii | xxii | o | xliiii | xii | xvii | xxxii | xxxv | |
| v | o | o | xxv | vi | lix | iii | xxxi | xxiii | o | xlvi | xii | li | iiii | iii | |
| vi | o | o | xxx | viii | xxii | lii | xiii | xxiiii | o | xlviii | xiii | xxiiii | xxxv | xxxii | |
| vii | o | o | xxxv | ix | xlvi | xl | lv | xxv | o | l | xiii | lviii | vii | i | |
| viii | o | o | xl | xi | x | xxix | xxxvii | xxvi | o | lii | xiiii | xxxi | xxxviii | xxx | |
| ix | o | o | xlv | xii | xxxiiii | xviii | xix | xxvii | o | liiii | xv | v | ix | lix | |
| x | o | o | l | xiii | lviii | vii | i | xxviii | o | lvi | xv | xxxviii | xli | xxviii | |
| xi | o | o | lv | xv | xxi | lv | xliii | xxix | o | lviii | xvi | xii | xii | lvii | |
| xii | o | i | o | xvi | xlv | xliiii | xxv | xxx | i | o | xvi | xlv | xliiii | xxv | |
| MEDIUS CURSUS IOVIS | |||||||||||||||
Anni collecti |
Gradus longitudinis |
Menses dies | Medius cursus Iovis ad menses | ||||||||||||
G |
M |
S |
T |
Q |
Q |
S |
G | M | S | T | Q | ||||
xviii |
clxxxvi |
vi |
li |
li |
liii |
xxxiiii |
xxx |
xxx | ii | xxix | xxxvii | xiii | xxiii | ||
xxxvi |
xii |
xiii |
xliii |
xliii |
xlvii |
ix |
o |
lx | iiii | lix | xiiii | xxvi | xlvii | ||
liiii |
cxxviii |
xx |
xxxv |
xxxv |
xl |
xliii |
xxx |
xc | vii | xxviii | li | xl | x | ||
lxxii |
xxiiii |
xxvii |
xxvii |
xxvii |
xxxiiii |
xviii |
o |
cxx | ix | lviii | xxviii | liii | xxxiii | ||
xc |
ccx |
xxxiiii |
xix |
xix |
xxvii |
lii |
xxx |
cl | xii | xxviii | vi | vi | lvi | ||
cviii |
xxxvi |
xli |
xi |
xi |
xxi |
xxvii |
o |
clxxx | xiiii | lvii | xliii | xx | xx | ||
dccxx |
ccxliiii |
xxxiiii |
xxxiiii |
xxxv |
xliii |
o |
o |
ccx | xvii | xxvii | xx | xxxiii | xlii | ||
dccxxxviii |
lxx |
xli |
xxvi |
xxvii |
xxxvi |
xxxiiii |
xxx |
ccxl | xix | lvi | lvii | xlvii | vi | ||
dcclvi |
cclvi |
xlviii |
xviii |
xix |
xxx |
ix |
o |
cclxx | xxii | xxvi | xxxv | o | xxix | ||
dcclxxiiii |
lxxxii |
lv |
x |
xi |
xxiii |
xliii |
xxx |
ccc | xxiiii | lvi | xii | xiii | lii | ||
dccxcii |
cclxix |
ii |
ii |
iii |
xvii |
xviii |
o |
cccxxx | xxvii | xxv | xlix | xxvii | xvi | ||
dcccx |
xcv |
viii |
liii |
lv |
x |
lii |
xxx |
ccclx | xxix | lv | xxvi | xl | xxxix | ||
| Anni simplies | G | M | S | T | Q | Q | 〈S〉 | 〈Dies〉 | 〈G〉 | 〈M〉 | 〈S〉 | 〈T〉 | 〈Q〉 | ||||||
| i | xxx | xx | xxii | lii | lii | lviii | 〈xxxv〉 | 〈i〉 | 〈o〉 | 〈iiii〉 | 〈lix〉 | 〈xiiii〉 | xxvi | ||||||
| ii | lx | xl | xlv | xlv | xlv | lvii | x | 〈ii〉 | 〈o〉 | 〈ix〉 | 〈lviii〉 | xxviii | liii | ||||||
| iii | xci | i | viii | xxxviii | xxxviii | lv | xlv | iii | o | 〈xiiii〉 | lvii | xliii | xx | ||||||
| iiii | cxxi | xxi | xxxi | xxxi | xxx | liiii | xx | iiii | o | xix | lvi | lvii | xlvii | ||||||
| v | cli | xli | liiii | xxiiii | xxiiii | lii | lv | v | o | xxiiii | lvi | xii | xiiii | ||||||
| vi | clxxxii | ii | xvii | xvii | xvii | li | xxx | vi | o | xxix | lv | xxvi | xl | ||||||
| vii | ccxii | xxii | xl | x | x | l | v | vii | o | xxxiiii | liiii | xli | vii | ||||||
| viii | ccxlii | xlii | iii | iii | iii | xlviii | xl | viii | o | xxxix | liii | lv | xxxiiii | ||||||
| ix | cclxxiii | iii | xxv | lv | lvi | xlvii | xv | ix | o | xliiii | liii | x | i | ||||||
| x | ccciii | xxiii | xlviii | xlviii | xlix | xlv | l | x | o | xlix | lii | xxiiii | xxvii | ||||||
| xi | cccxxxiii | xliiii | xi | xli | xlii | xliiii | xxv | xi | o | liiii | li | xxxviii | liiii | ||||||
| xii | iiii | iiii | xxxiiii | xxxiiii | xxxv | xliii | o | xii | o | lix | l | liii | xxi | ||||||
| xiii | xxxiiii | xxiiii | lvii | xxvii | xxvii | xli | xxxv | xiii | i | iiii | l | vii | xlviii | ||||||
| xiiii | lxiiii | xlv | xx | xx | xxi | xl | x | xiiii | i | ix | xlix | xxii | xv | ||||||
| xv | xcv | v | xliii | xiii | xiiii | xxxviii | xlv | xv | i | xiiii | xlviii | xxxvi | xli | ||||||
| xvi | cxxv | xxvi | vi | vi | vii | xxxvii | xx | xvi | i | xix | xlvii | li | viii | ||||||
| xvi | clv | xlvi | xxviii | lix | o | xxv | lv | xvii | i | xxiiii | xlvii | v | xxxv | ||||||
| xviii | clxxxvi | vi | li | li | liii | xxxiiii | xxx | xviii | i | xxix | xlvi | xx | ii | ||||||
| Hore i | o | o | xii | xxviii | vi | vi | lvi | xix | i | xxxiiii | xlv | xxxiiii | xxix | ||||||
| ii | o | o | xxiiii | lvi | xii | xiii | lii | xx | i | xxxix | xliiii | xlviii | lv | ||||||
| iii | o | o | xxxvii | xxiiii | xviii | xx | xlviii | xxi | i | xliiii | xliiii | iii | xxii | ||||||
| iiii | o | o | xlix | lii | xxiiii | xxvii | xlv | xxii | i | xlix | xliii | xvii | xlix | ||||||
| v | o | i | ii | xx | xxx | xxxiiii | xli | xxiii | i | liiii | xlii | xxxii | xv | ||||||
| vi | o | i | xiiii | xlviii | xxxvi | xli | xxxvii | xxiiii | i | lix | xli | xlvi | xlii | ||||||
| vii | o | i | xxvii | xvi | xlii | xlviii | xxxiiii | xxv | ii | iiii | xli | i | ix | ||||||
| viii | o | i | xxxix | xliiii | xlviii | lv | xxx | xxvi | ii | ix | xl | xv | xxxvi | ||||||
| ix | o | i | lii | xii | lv | ii | xxvi | xxvii | ii | xiiii | xxxix | xxx | iii | ||||||
| x | o | ii | iiii | xli | i | x | xxi | xxviii | ii | xix | xxxviii | xliiii | xxix | ||||||
| xi | o | ii | xvii | ix | vii | xvi | xix | xxix | li | xxiiii | xxxvii | lviii | lvi | ||||||
| xii | o | ii | xxix | xxxvii | xiii | xxiii | xv | xxx | ii | xxix | xxxvii | xiii | xxiii | ||||||
CANONES MEDIORUM CURSUUM MARTE |
|||||||||||||||||||
Anni
collecti |
Medius cursus Martis in longitudine |
Menses |
Medius cursus Martis ad menses |
||||||||||||||||
G |
M |
S |
T |
Q |
Q |
S |
G |
M |
S |
T |
Q |
Q |
|||||||
xviii |
cciii |
iiii |
xx |
xvii |
xxxiiii |
xliii |
xxx |
xxx |
xv |
xlvii |
xviii |
xxvi |
lv |
xlvi |
|||||
xxxvi |
xlvi |
viii |
xl |
xxxv |
ix |
xxvii |
o |
lx |
xxxi |
xxvi |
xxxvi |
liii |
li |
xxxiii |
|||||
liiii |
ccxlix |
xiii |
o |
lii |
xliiii |
x |
xxx |
xc |
xlvii |
ix |
lv |
xx |
xlvii |
xix |
|||||
lxxii |
xcii |
xvii |
xxi |
x |
xviii |
liiii |
o |
cxx |
lxii |
liii |
xiii |
xlvii |
xliii |
vi |
|||||
xc |
ccxci |
xxi |
xli |
xxvii |
liii |
xxxvii |
xxx |
cl |
lxxviii |
xxxvi |
xxxii |
xiiii |
xxxviii |
lii |
|||||
cviii |
cxxxviii |
xxvi |
i |
xlv |
xxviii |
xxi |
o |
clxxx |
xciiii |
xix |
l |
xli |
xxxiiii |
xxxix |
|||||
dccxx |
ccii |
liii |
xxxi |
xliii |
ix |
o |
o |
ccx |
cx |
iii |
ix |
viii |
xxx |
xxv |
|||||
dccxxxviii |
xlv |
lvii |
lii |
o |
xliii |
xliii |
xxx |
ccxl |
cxxv |
xlvi |
xxvii |
xxxv |
xxvi |
xii |
|||||
dcclvi |
ccxlix |
ii |
xii |
xviii |
xviii |
xxvii |
o |
cclxx |
cxli |
xxix |
xlvi |
ii |
xxi |
lviii |
|||||
dcclxxiiii |
xcii |
vi |
xxxii |
xxxv |
liii |
x |
xxx |
ccc |
clvii |
xiii |
iiii |
xxix |
xvii |
xlv |
|||||
dccxcii |
ccxcv |
x |
lii |
liii |
xxvii |
liiii |
o |
cccxxx |
clxxii |
lvi |
xxii |
lvi |
xiii |
xxxi |
|||||
dcccx |
cxxxviii |
xv |
xiii |
xi |
ii |
xxxvii |
xxx |
ccclx |
clxxxviii |
xxxix |
xli |
xxiii |
ix |
xviii |
|||||
| 〈Anni simplices〉 | 〈G〉 | 〈M〉 | 〈S〉 | 〈T〉 | 〈Q〉 | 〈Q〉 | 〈S〉 | 〈Dies〉 | G | M | S | T | Q | Q | |
| i | cxci | xvi | 〈liiii〉 | 〈xxvii〉 | 〈xxxviii〉 | 〈xxxv〉 | 〈xlv〉 | 〈i〉 | o | xxxi | xxvi | xxxvi | liii | li | |
| ii | xxii | xxxiii | 〈xlviii〉 | 〈lv〉 | 〈xvii〉 | 〈xi〉 | 〈xx〉 | ii | i | ii | liii | xiii | xlvii | xliii | |
| iii | ccxiii | l | xliii | xxii | lv | xlvii | xv | iii | i | xxxiiii | xix | l | xli | xxxv | |
| iiii | xlv | vii | xxxvii | l | xxxiiii | xxiii | o | iiii | ii | v | xlvi | xxvii | xxxv | xxvi | |
| v | ccxxxvi | xxiiii | xxxii | xviii | xii | lviii | xlv | v | ii | xxxvii | xiii | iiii | xxix | xviii | |
| vi | lxvii | xli | xxvi | xlv | li | xxxiiii | xxx | vi | iii | viii | xxxix | xli | xxiii | ix | |
| vii | cclviii | lviii | xxiiii | xiii | xxx | x | xv | vii | iii | xl | vi | xviii | xvii | o | |
| viii | ix | xv | xv | xli | viii | xlvi | o | viii | iiii | xi | xxxii | lv | x | lii | |
| ix | cclxxxi | xxxii | x | viii | xlvii | xxi | xlv | ix | iiii | xlii | lix | xxxii | iiii | xliii | |
| x | cxii | xlix | iiii | xxxvi | xxv | lvii | xxx | x | v | xiiii | xxvi | viii | lviii | xxxv | |
| xi | ccciiii | v | lix | iiii | iiii | xxxiii | xv | xi | v | xlv | lii | xlv | lii | xxvii | |
| xii | cxxxv | xxii | liii | xxxi | xliii | ix | o | xii | vi | xvii | xix | xxii | xlvi | xviii | |
| xiii | cccxxvi | xxxix | xlvii | lix | xxi | xliiii | xlv | xiii | vi | xlviii | xlv | lix | xl | x | |
| xiiii | clvii | lvi | xlii | xxvii | o | xx | xxx | xiiii | vii | xx | xii | xxxvi | xxxiiii | ii | |
| xv | cccxlix | xiii | xxxvi | liiii | xxxviii | lvi | xv | xv | vii | li | xxxix | xiii | xxvii | liii | |
| xvi | clxxx | xxx | xxxi | xxi | xvii | xxxii | o | xvi | viii | xxiii | v | l | xxi | xv | |
| xvii | xi | xlvii | xxv | xlix | lvi | vii | xlv | xvii | viii | liiii | xxxii | xxvii | xv | xxxvi | |
| xviii | cciii | iiii | xx | xvii | xxxiiii | xliii | xxx | xviii | ix | xxv | lix | iiii | ix | xxviii | |
| Hore i | o | i | xviii | xxxvi | xxxii | xiiii | xxxix | xix | ix | lvii | xxv | xli | iii | xix | |
| ii | o | ii | xxxvii | xiii | iiii | xxix | xvii | xx | x | xxviii | lii | xvii | lvii | xi | |
| iii | o | iii | lv | xlix | xxxvi | xliii | lvi | xxi | xi | o | xviii | liiii | li | iii | |
| iiii | o | v | xiiii | xxvi | viii | lviii | xxxv | xxii | xi | xxxi | xlv | xxxi | xliiii | liiii | |
| v | o | vi | xxxiii | ii | xli | xiii | xiiii | xxiii | xii | iii | xii | viii | xxxviii | xlvi | |
| vi | o | vii | li | xxxix | xiii | xxvii | liii | xxiiii | xii | xxxiiii | xxxviii | xlv | xxxii | xxxvii | |
| vii | o | ix | x | xv | xlv | xlii | xxxii | xxv | xiii | vi | v | xxv | xxvi | xxix | |
| viii | o | x | xxviii | lii | xvii | lvi | xi | xxvi | xiii | xxxvii | xxxi | lix | xx | xx | |
| ix | o | xi | xlvii | xxviii | l | xi | xlix | xxvii | xiiii | viii | lviii | xxxvi | xiiii | xi | |
| x | o | xiii | vi | v | xxii | xxvi | xxviii | xxviii | xiiii | xl | xxv | xiii | viii | iii | |
| xi | o | xiiii | xxiiii | xli | liiii | xli | vii | xxix | xv | xi | li | l | i | lv | |
| xii | o | xv | xliii | xviii | xxvi | lv | xlvi | xxx | xv | xliii | xviii | xxvi | lv | xlvi | |
CANONES DIVERSITATIS VERNERIS |
|||||||||||||||
Anni collecti |
Medius cursus diversitatis Veneris |
Menses |
Diversitas Veneris ad menses |
||||||||||||
G |
M |
S |
T |
Q |
Q |
S |
G |
M |
S |
T |
Q |
Q |
|||
xviii |
xc |
xxvii |
xliiii |
xxxiiii |
xxiii |
xlvi |
xxx |
xxx |
xviii |
xxix |
xlii |
lvi |
xxxv |
xliiii |
|
xxxvi |
clxxx |
lv |
xxix |
viii |
xlvii |
xxxiii |
o |
lx |
xxxvi |
lix |
xxv |
liii |
xl |
xxviii |
|
liiii |
cclxxi |
xxiii |
xiii |
xliii |
xi |
xix |
xxx |
xc |
lv |
xxix |
viii |
xlix |
xlvii |
xii |
|
lxxii |
i |
l |
lviii |
xvii |
xxxv |
vi |
o |
cxx |
lxxiii |
lviii |
li |
xlvi |
xxii |
lvi |
|
xc |
xcii |
xviii |
xlii |
li |
lviii |
lii |
xxx |
cl |
xcii |
xxviii |
xxxiiii |
xlii |
lviii |
xl |
|
cviii |
clxxxii |
xlvi |
xxvii |
xxvi |
xxii |
xxiii |
o |
clxxx |
cx |
lviii |
xvii |
xxxix |
xxxiiii |
xxiiii |
|
dccxx |
xviii |
xxix |
xlii |
lv |
li |
o |
o |
ccx |
cxxix |
xxviii |
o |
xxxvi |
x |
viii |
|
dccxxxviii |
cviii |
lvii |
xxvii |
xxx |
xiiii |
xlvi |
xxx |
ccxl |
cxlvii |
lvii |
xliii |
xxxii |
xlv |
lii |
|
dcclvi |
cxcix |
xxv |
xii |
iiii |
xxxviii |
xxxiii |
o |
cclxx |
clxvi |
xxvii |
xxvi |
xxix |
xxi |
xxxvi |
|
dcclxxiiii |
cclxxxix |
lii |
lvi |
xxxix |
ii |
xix |
xxx |
ccc |
clxxxiiii |
lvii |
ix |
xxv |
lvii |
xx |
|
dccxcii |
xx |
xx |
xli |
xiii |
xxvi |
vi |
o |
cccxxx |
cciii |
xxvi |
lii |
xxii |
xxxiii |
iiii |
|
dcccx |
cx |
xlviii |
xxv |
xlvii |
xlix |
lii |
xxx |
ccclx |
ccxxi |
lvi |
xxxv |
xix |
viii |
xlviii |
|
| Anni simplices | G | M | S | T | Q | 〈Q〉 | 〈S〉 | 〈Dies〉 |
〈G〉 |
〈M〉 |
〈S〉 |
〈T〉 |
〈Q〉 |
〈Q〉 |
|
| i | ccxxv | i | xxxii | xxviii | xxxiiii | 〈xxxix〉 | 〈xv〉 | 〈i〉 |
〈o〉 |
〈xxxvi〉 |
〈lix〉 |
〈xxv〉 |
〈liii〉 |
〈xi〉 |
|
| ii | xc | iii | iiii | lvii | ix | xviii | 〈xxx〉 | 〈ii〉 |
〈i〉 |
〈xiii〉 |
〈lviii〉 |
〈li〉 |
〈xlvi〉 |
xxiii |
|
| iii | cccxv | iiii | xxxvii | xxv | xliii | lvii | xlv | 〈iii〉 |
〈i〉 |
〈l〉 |
〈lviii〉 |
xvii |
xxxix |
xxxiiii |
|
| iiii | clxxx | vi | ix | liiii | xviii | xxxvii | o | iiii |
ii |
xxvii |
lvii |
xliii |
xxxii |
xlv |
|
| v | xlv | vii | xlii | xxii | liii | xvi | xv | v |
iii |
iiii |
lvii |
ix |
xxv |
lvii |
|
| vi | cclxx | ix | xiiii | li | xxvii | lv | xxx | vi |
iii |
xli |
lvi |
xxxv |
xix |
ix |
|
| vii | clxxxv | x | xlvii | xx | ii | xxxiiii | xlv | vii |
iiii |
xviii |
lvi |
i |
xii |
xx |
|
| viii | o | xii | xix | xlviii | xxxvii | xiiii | o | viii |
iiii |
lv |
lv |
xxvii |
v |
xxxii |
|
| ix | cxxv | xiii | lii | xvii | xi | liii | xv | ix |
v |
xxxii |
liiii |
lii |
lviii |
xliii |
|
| x | xc | xv | xxiiii | xlv | xlvi | xxxii | xxx | x |
vi |
ix |
liiii |
xviii |
li |
liiii |
|
| xi | cccxv | xvi | lvii | xiiii | xxi | xi | xlv | xi |
vi |
xlvi |
liii |
xliiii |
xlv |
vi |
|
| xii | clxxx | xviii | xxix | xlii | lv | li | o | xii |
vii |
xxiii |
liii |
x |
xxxviii |
xviii |
|
| xiii | xlv | xx | ii | xi | xxx | xxx | xv | xiii |
viii |
o |
lii |
xxxvi |
xxxi |
xxix |
|
| xiiii | cclxx | xxi | xxxiiii | xl | v | ix | xxx | xiiii |
viii |
xxxvii |
lii |
ii |
xxiiii |
xli |
|
| xv | cxxxv | xxiii | vii | viii | xxxix | xlviii | xlv | xv |
ix |
xiiii |
li |
xxviii |
xvii |
lii |
|
| xvi | o | xxiiii | xxxix | xxxvii | xiiii | xxviii | o | xvi |
ix |
li |
l |
liiii |
xi |
iiii |
|
| xvii | ccxxv | xxvi | xii | v | xlix | vii | xv | xvii |
x |
xxviii |
l |
xx |
iiii |
xv |
|
| xviii | xc | xxvii | xliiii | xxxiiii | xxiii | xlvi | xxx | xviii |
xi |
v |
xlix |
xlv |
lvii |
xxvi |
|
| Hore i | o | i | xxxii | xxviii | xxxiiii | xlii | lviii | xix |
xi |
xlii |
xlix |
xi |
l |
xxxvii |
|
| ii | o | iii | iiii | lvii | ix | xxv | lvii | xx |
xii |
xix |
xlix |
xxxvii |
xliii |
xlix |
|
| iii | o | iiii | xxxvii | xxv | xliiii | viii | lvi | xxi |
xii |
lvi |
xlviii |
iii |
xxxvii |
i |
|
| iiii | o | vi | ix | liiii | xviii | li | liiii | xxii |
xiii |
xxxiii |
xlvii |
xxix |
xxx |
xii |
|
| v | o | vii | xlii | xxii | liii | xxxiiii | liii | xxiii |
xiiii |
x |
xlvi |
lv |
xxiii |
xxiiii |
|
| vi | o | ix | xiiii | li | xxviii | xvii | lii | xxiiii |
xiiii |
xlvii |
xlvi |
xxi |
xvi |
xxxv |
|
| vii | o | x | xlvii | xx | iii | ix | l | xxv |
xv |
xxiiii |
xlv |
xlvii |
ix |
xlvi |
|
| viii | o | xii | xix | xlviii | xxxvii | xliii | xlix | xxvi |
xvi |
i |
xlv |
xiii |
ii |
lviii |
|
| ix | o | xiii | xlii | xvii | xii | xxvi | xlviii | xxvii |
xvi |
xxxviii |
xliiii |
xxxviii |
lvi |
ix |
|
| x | o | xv | xxiiii | xlv | xlvii | ix | xlvi | xxviii |
xvii |
xv |
xliiii |
iiii |
xlix |
xxi |
|
| xi | o | xvi | lvii | xiiii | xxi | lii | xlv | xxix |
xvii |
lii |
xliii |
xxx |
xlii |
xxxiii |
|
| xii | o | xviii | xxix | xlii | lvi | xxxv | xliiii | xxx |
xviii |
xxix |
xlii |
lvi |
xxxv |
xliiii |
|
CANONES MEDIORUM CURSUUM DIVERSITATIS MERCURII |
|||||||||||||||
Anni collecti |
Medius cursus longitudinis Mercurii |
Menses |
Diversitas Mercurii |
||||||||||||
G |
M |
S |
T |
Q |
Q |
S |
G |
M |
S |
T |
Q |
Q |
|||
xviii |
ccli |
o |
xlv |
xlv |
liii |
xlv |
o |
xxx |
xciii |
xii |
iii |
xxix |
xlvii |
lv |
|
xxxvi |
cxlii |
i |
xxxi |
xxxi |
xlvii |
xxx |
o |
lx |
clxxxvi |
xxiiii |
vi |
lix |
xxxv |
l |
|
liiii |
xxxii |
ii |
xvii |
xvii |
xli |
xv |
o |
xc |
cclxxix |
xxxvi |
x |
xxix |
xxiii |
xlv |
|
lxxii |
cclxxxii |
iii |
iii |
iii |
xxxv |
o |
o |
cxx |
xii |
xlviii |
xiii |
lix |
xi |
xl |
|
xc |
clxxv |
iii |
xlviii |
xlix |
xxviii |
xlv |
o |
cl |
cvi |
o |
xvii |
xxviii |
lix |
xxxv |
|
cviii |
lxvi |
iiii |
xxxiiii |
xxxv |
xxii |
xxx |
o |
clxxx |
cxcix |
xii |
xx |
lviii |
xlvii |
xxx |
|
dccxx |
cccxx |
xxx |
xxx |
xxxv |
l |
o |
o |
ccx |
ccxcii |
xxiiii |
xxiiii |
xxviii |
xxxv |
xxv |
|
dccxxxviii |
ccxi |
xxxi |
xvi |
xxi |
xliii |
xlv |
o |
ccxl |
xxv |
xxxvi |
xxvii |
lviii |
xxiii |
xx |
|
dcclvi |
cii |
xxxii |
ii |
vii |
xxxvii |
xxx |
o |
cclxx |
cxviii |
xlviii |
xxxi |
xxviii |
xi |
xv |
|
dcclxxiiii |
cccliii |
xxxii |
xlvii |
liii |
xxxi |
xv |
o |
ccc |
ccxii |
o |
xxxiiii |
lvii |
lix |
x |
|
dccxcii |
ccxliiii |
xxxiii |
xxxiii |
xxxix |
xxv |
o |
o |
cccxxx |
cccv |
xii |
xxxviii |
xxvii |
xlvii |
v |
|
dcccx |
cxxxv |
xxxiiii |
xix |
xxv |
xviii |
xlv |
o |
ccclx |
xxxviii |
xxiiii |
xli |
lvii |
xxxv |
o |
|
〈Anni simplices〉 |
〈G〉 |
〈M〉 |
〈S〉 |
〈T〉 |
〈Q〉 |
〈Q〉 |
〈S〉 |
〈Dies〉 |
G |
M |
S |
T |
Q |
Q |
|
〈i〉 |
〈liii〉 |
〈lvi〉 |
〈xlii〉 |
〈xxxii〉 |
〈xxxii〉 |
〈lix〉 |
〈x〉 |
i |
iii |
vi |
xxiiii |
vi |
lix |
xxxvi |
|
ii |
cvii |
〈liii〉 |
〈xxv〉 |
〈v〉 |
〈v〉 |
〈lviii〉 |
〈xx〉 |
ii |
vi |
xii |
xlviii |
xiii |
lix |
xi |
|
iii |
clxi |
l |
vii |
xxxvii |
xxxviii |
lvii |
xxx |
iii |
ix |
xix |
xii |
xx |
lviii |
xlvii |
|
iiii |
ccxv |
xlvi |
l |
x |
xi |
lvi |
xl |
iiii |
xii |
xxv |
xxxvi |
xxvii |
lviii |
xxiii |
|
v |
cclxix |
xliii |
xxxii |
xlii |
xliiii |
lv |
l |
v |
xv |
xxxii |
o |
xxxiiii |
lvii |
lix |
|
vi |
cccxxiii |
xl |
xv |
xv |
xvii |
lv |
o |
vi |
xviii |
xxxviii |
xxiiii |
xli |
lvii |
xxxv |
|
vi |
xvii |
xxxvi |
lvii |
xlvii |
l |
liiii |
x |
vii |
xxi |
xliiii |
xlviii |
xlviii |
lvii |
x |
|
viii |
lxxi |
xxxiii |
xl |
xx |
xxiii |
liii |
xx |
viii |
xxiiii |
li |
xii |
lv |
lvi |
xlvii |
|
ix |
cxxv |
xxx |
xxii |
lii |
lvi |
lii |
xxx |
ix |
xxvii |
lvii |
xxxvi |
ii |
lvi |
xxii |
|
x |
clxxix |
xxvii |
v |
xxv |
xxix |
li |
xl |
x |
xxxi |
iiii |
i |
ix |
lv |
lviii |
|
xi |
ccxxxiii |
xxiii |
xlvii |
lviii |
ii |
l |
l |
xi |
xxxiiii |
x |
xxv |
xvi |
lv |
xxxiiii |
|
xii |
cclxxxvii |
xx |
xxx |
xxx |
xxxv |
l |
o |
xii |
xxxvii |
xvi |
xlix |
xxiii |
lv |
x |
|
xiii |
cccxliiii |
xvii |
xii |
iii |
viii |
xlix |
x |
xiii |
xl |
xxiii |
xiii |
xxx |
liiii |
xlvi |
|
xiiii |
xxxv |
xiii |
lv |
xxxv |
xli |
xlviii |
xx |
xiiii |
xliii |
xxix |
xxxvii |
xxxvii |
liiii |
xxii |
|
xv |
lxxxix |
x |
xxxviii |
viii |
xiiii |
xlvii |
xxx |
xv |
xlvi |
xxxvi |
i |
xliiii |
liii |
lvii |
|
xvi |
cxliii |
vii |
xx |
xl |
xlvii |
xlvi |
xl |
xvi |
xlix |
xlii |
xxv |
li |
liii |
xxxiii |
|
xvii |
cxcvii |
iiii |
iii |
xiii |
xx |
xlv |
l |
xvii |
lii |
xlviii |
xlix |
lviii |
liii |
ix |
|
xviii |
ccli |
o |
xlv |
xlv |
liii |
xlv |
o |
xviii |
lv |
lv |
xiiii |
v |
lii |
xlv |
|
Hore i |
o |
vii |
xlvi |
o |
xvii |
xxviii |
lix |
xix |
lix |
i |
xxxviii |
xii |
lii |
xxi |
|
ii |
o |
xv |
xxxii |
o |
xxxiiii |
lvii |
lix |
xx |
lxii |
ix |
ii |
xix |
li |
lvii |
|
iii |
o |
xxiii |
xviii |
o |
lii |
xxvi |
lviii |
xxi |
lxv |
xiiii |
xxvi |
xxvi |
li |
xxxii |
|
iiii |
o |
xxxi |
iiii |
i |
ix |
lv |
lviii |
xxii |
lxviii |
xx |
l |
xxxiii |
li |
viii |
|
v |
o |
xxxvii |
l |
i |
xxvii |
xxiiii |
lvii |
xxiii |
lxxi |
xxvii |
xiiii |
xl |
l |
xliiii |
|
vi |
o |
xlvi |
xxxvi |
i |
xliiii |
liii |
lvii |
xxiiii |
lxxiiii |
xxxiii |
xxxviii |
xlvii |
l |
xx |
|
vii |
o |
liiii |
xxii |
ii |
ii |
xxii |
lvii |
xxv |
lxxvii |
xl |
ii |
liiii |
xlix |
lv |
|
viii |
i |
ii |
viii |
ii |
xix |
li |
lvi |
xxvi |
lxxx |
xlvi |
xxvii |
i |
xlix |
xxxii |
|
ix |
i |
ix |
liiii |
ii |
xxxvii |
xx |
lvi |
xxvii |
lxxxiii |
lii |
li |
viii |
xlix |
vii |
|
x |
i |
xvii |
xl |
ii |
liiii |
xlix |
lv |
xxviii |
lxxxvi |
lix |
xv |
xv |
xlviii |
xliii |
|
xi |
i |
xxv |
xxv |
iii |
xii |
xviii |
lv |
xxix |
xc |
v |
xxxv |
xxii |
xlviii |
xix |
|
xii |
i |
xxxiii |
xii |
iii |
xxix |
xlvii |
lv |
xxx |
xciii |
xii |
iii |
xxix |
xlvii |
lv |
〈IX.5〉 Presumpta in ypotheses quinque erraticorum
Deinceps vero existente istorum expositioni sermone de anomaliis que fiunt in ea que secundum longitudinem progressione quinque erraticarum, ea quidem que secundum integritatem comformationis investigatio facta fuit nobis per huiusmodi. Simplissimis enim simul et sufficientibus ad propositum motibus duobus existentibus, ut diximus, eo videtur qui per excentricos circulos ut ad zodiacum completur et eo qui per omocentricos quidem epiciclos aut circumferentes, similiter autem et secundum unamquamque stellam apparentibus anomaliis duabus existentibus, ea videlicet que penes zodiaci partes consideratur et ea que penes eam que ad Solem figurationes, in ista quidem reperimus ex continuis et circa easdem partes zodiaci obervatis differentibus figurationibus et in quinque erraticis illud quod a maxima motione in medium tempus maius semper factum eo quod a media in minima, huiusmodi accidente in ea quidem que secundum excentrotica ypothesi consequi non potente, sed contrario propter quod semper quidem ipsis maxima progressio secundum id quod terre proximum compleatur, minor vero sit et in ambabus ypothesibus ea que a periguio usque ad illud quod secundum mediam progressionem punctum periferia ea que ab isto usque apoguion, secundum eam vero que epicilorum potente contingere, quando maxima tamen progressio non secundum periguion, quemadmodum in Luna, sed secundum apoguion compleatur, hoc est quando stella incipiens ab apoguio non ut in precedentia mundi Lune similiter, sed ut in consequentia facit transitionem. Unde et huiusmodi anomaliam per epiciclos supposuimus contingere. In ea vero que ad zodiaci partes consideratur anomalia contrarium reperimus, per in easdem illuminationes vel easdem figurationes deprehensas zodiaci periferias, illud quod a minima motione in mediam tempus maius factum semper eo quod a media in maximam, huiusmodi rursum simptomate et secundum utramque quidem ypothesium potente consequi, quemadmodum in eis quidem simillitudine ipsarum in principio eius que de Sole sintaxeos tractavimus, proprio vero existente magis eius que secundum excentrotica, secundum quam et supposuimus talem anomaliam compleri, et propter alteram solius eius que secundum epiciclon quasi propriam inveniri. Iam vero per secundum partem observatarum progressionum in constitutos ductus ex commixtione ambarum ypothesium additionem et inquisitionem continuam non ita simpliciter reperimus potens procedere, neque epipeda in quibus excentricos circulos scribentia mobilia esse, manente semper secundum easdem a tropicis vel equinoctialibus punctis distantias ea que per ambos ipsos et eum qui per media recta secundum quam et apoguia et periguia considerantur, neque epiciclos in istis excentricis habere mota centra ipsarum, quorum sunt centra est quibus eum qui in consequentia motum plane circumagentes equales in equalibus temporius angulos comprehendunt. Sed et apoguia excentricorum facientes quandam brevem in consequentia tropicorum punctorum transitionem et planam rursum velut circa zodiaci centrum et fere secundum unamquamque stellam, quantam et applanorum spera deprehenditur faciens, in c annis unum gradum et, in quantum est ex presentibus conspicere, et centra epiciclorum in equalibus quidem circulis eis qui anomaliam faciunt excentricis mota, non in eisdem vero centris descriptis, sed in aliis quidem stellis in duo equa dividentibus medias centrorum rectas et illorum et zodiaci. In solo autem Mercurio eo quod tantum distat a circumagente ipsum centro, quantum et illud ab anomaliam faciente, faciente] corr. ex faciens V3 velut ab apoguion distat et hoc a secundum visum supposito. Etenim in ista stella sola, quemadmodum et in Luna reperimus, et excentricum circulum a predicto centro contra circumactum epiciclo rursum in precedentia unam in anno circumcisionem, circumcisionem] circumversionem F1 quoniam quidem et ipsa bis in uno circumcursu perguiotatos apparet facta, quemadmodum et Luna bis in uno mense.
〈IX.6〉 De modo et differentia ypothesium
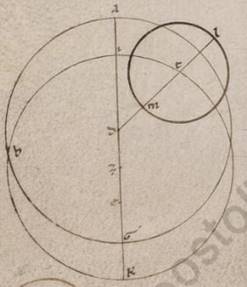 Fiat autem magis bene intelligibillis collectarum per precendentia ypothesium modus talis. Intelligatur enim in aliorum ypothesi primum excentricus circulus ABG circa centrum D, per D autem et centrum zodiaci diametros ADG, in qua zodiaci centrum, hoc est visus videntium E, faciat A quidem punctum apoguiotaton, G vero periguiotaton. Divisa vero DE in duo equa secundum Z, scribatur centro Z et spatio DA circulus equalis manifestum quoniam ei qui est ABG videlicet ITK, et centro T scribatur epiciclus LM, et copulentur LTMD. Supponimus ergo primum obliquari quidem excentricorum circulorum epipedum ad illud quod zodiaci et adhuc illud quod epicicli ad illud quod excentricorum causa eius que secundum latitudinem transitionis stellarum secundum de his nobis demonstrata, ad eas autem que secundum longitudinem transitiones utilitatis causa in uno zodiaci epipedo intelligi omnes nullius in longitudine future cura digna diaffore preter tam magnas inclinationes, quante secundum unumquodque astrorum apparebunt. Postea epipedum quidem totum plane in consequentia animalium dicimus circumagi circa E centrum et transferentem apoguia et periguia per annos c gradu i, diametrum vero LIM LIM] LTM F1 epicicli circumducci quidem sub D centro rursum plane in consequentia animalium consequenter ei que secundum longitudinem stelle restitutioni simul vero circumduccere L et M puncta epicicli et T centrum delatum semper per ITK excentricum, stellam vero ipsam motam in LM epiciclo rursum equaliter et ad in D centrum facientem nutum super diametrum facientem restitutiones consequenter medie periodo eius que ad Solem anomalie, et quasi ea que secundum L apoguion transitione ut in consequentia animalium completa.
Fiat autem magis bene intelligibillis collectarum per precendentia ypothesium modus talis. Intelligatur enim in aliorum ypothesi primum excentricus circulus ABG circa centrum D, per D autem et centrum zodiaci diametros ADG, in qua zodiaci centrum, hoc est visus videntium E, faciat A quidem punctum apoguiotaton, G vero periguiotaton. Divisa vero DE in duo equa secundum Z, scribatur centro Z et spatio DA circulus equalis manifestum quoniam ei qui est ABG videlicet ITK, et centro T scribatur epiciclus LM, et copulentur LTMD. Supponimus ergo primum obliquari quidem excentricorum circulorum epipedum ad illud quod zodiaci et adhuc illud quod epicicli ad illud quod excentricorum causa eius que secundum latitudinem transitionis stellarum secundum de his nobis demonstrata, ad eas autem que secundum longitudinem transitiones utilitatis causa in uno zodiaci epipedo intelligi omnes nullius in longitudine future cura digna diaffore preter tam magnas inclinationes, quante secundum unumquodque astrorum apparebunt. Postea epipedum quidem totum plane in consequentia animalium dicimus circumagi circa E centrum et transferentem apoguia et periguia per annos c gradu i, diametrum vero LIM LIM] LTM F1 epicicli circumducci quidem sub D centro rursum plane in consequentia animalium consequenter ei que secundum longitudinem stelle restitutioni simul vero circumduccere L et M puncta epicicli et T centrum delatum semper per ITK excentricum, stellam vero ipsam motam in LM epiciclo rursum equaliter et ad in D centrum facientem nutum super diametrum facientem restitutiones consequenter medie periodo eius que ad Solem anomalie, et quasi ea que secundum L apoguion transitione ut in consequentia animalium completa.
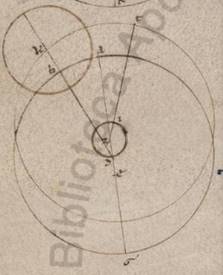 Quod autem in Mercurii ypothesi proprium sumemus utique sub visum ita. Esto enim anomalie quidem excentricus circulus ABG circa centrum D. Que vero per D et E centrum zodiaci per A apoguion diametros ADEG. Sumaturque in AG ei que est DE ut ad A apoguion equalis recta DZ. Aliis ergo manentibus eisdem, hoc est et toto epipedo circa E centrum in consequentia apoguion transferente, quantum et in aliis stellis, et epiciclo circa D centrum plane in circumsequentia circumsequentia] consequentia F1 circumducto velut sub DB recta, et adhuc stella in epiciclo mota similiter aliis, ubi autem centrum alterius excentrici, in quo semper equalia rursum existente ad primum centrum E epicicli, circumduccetur quidem circa Z Z] del. centrum V3 punctum in contraria epiciclo, hoc est in precendentia imaginum animalium et plane et equali velocitate ipsi, ut sub ZIT recta, quare ad zodiaci quidem puncta semel utramque DB et ZIT rectarum in anno restitui, bis autem manifestum quoniam ad alternas. Distabit autem semper ab Z puncto et ipsum secundum equalem utriuslibet rectarum ED et DZ sicut rectam ZI, quare scriptum ad in precedentia motu eius circulum parvulum centro Z et spatio ZI per totum determinari et sub D centro primi et manentis excentrici, et describi quidem eum qui movetur excentricum semper centro I et spatio IT equali existente ei quod est DA ut hic TK, epiciclum vero in ipso centrum semper habere ut hic secundum K punctum. Sed magis utique adhuc persequemur supposita ex secundum unamquamque in quantitates ipsorum demonstrandis, in quibus et moventia quodam modo ad investigationes ypothesium figuratius multipliciter apparebunt.
Quod autem in Mercurii ypothesi proprium sumemus utique sub visum ita. Esto enim anomalie quidem excentricus circulus ABG circa centrum D. Que vero per D et E centrum zodiaci per A apoguion diametros ADEG. Sumaturque in AG ei que est DE ut ad A apoguion equalis recta DZ. Aliis ergo manentibus eisdem, hoc est et toto epipedo circa E centrum in consequentia apoguion transferente, quantum et in aliis stellis, et epiciclo circa D centrum plane in circumsequentia circumsequentia] consequentia F1 circumducto velut sub DB recta, et adhuc stella in epiciclo mota similiter aliis, ubi autem centrum alterius excentrici, in quo semper equalia rursum existente ad primum centrum E epicicli, circumduccetur quidem circa Z Z] del. centrum V3 punctum in contraria epiciclo, hoc est in precendentia imaginum animalium et plane et equali velocitate ipsi, ut sub ZIT recta, quare ad zodiaci quidem puncta semel utramque DB et ZIT rectarum in anno restitui, bis autem manifestum quoniam ad alternas. Distabit autem semper ab Z puncto et ipsum secundum equalem utriuslibet rectarum ED et DZ sicut rectam ZI, quare scriptum ad in precedentia motu eius circulum parvulum centro Z et spatio ZI per totum determinari et sub D centro primi et manentis excentrici, et describi quidem eum qui movetur excentricum semper centro I et spatio IT equali existente ei quod est DA ut hic TK, epiciclum vero in ipso centrum semper habere ut hic secundum K punctum. Sed magis utique adhuc persequemur supposita ex secundum unamquamque in quantitates ipsorum demonstrandis, in quibus et moventia quodam modo ad investigationes ypothesium figuratius multipliciter apparebunt.
Prelibandum tamen quoniam, eis que secundum longitudinem periodis non simul rectitutis et eius qui per medias imagines animalium circuli punctis et excentricorum apoguiis vel periguiis propter subiacentem transcasionem secundum preiacentem modum nobis exposite secundum longitudinem motiones, non eas ad que apoguia excentricorum considerantur restitutiones continent, sed eas que ad tropica et equinoctialia puncta fuerit fuerit] fiunt F1 consequenter secundum nos anno tempori. Ostensum est ergo primum quoniam et secundum et secundum] iter. V3 istas ypotheses, quando secundum longitudinem medius transitus stelle equaliter utrumque utrumque] utrimque F1 distat ab apoguiis vel periguiis, tunc que penes zodiacam anomaliam differentia equalis constituitur secundum utramque distantiam et secundum epiciclum in easdem partes medii transitus maxima distantia.
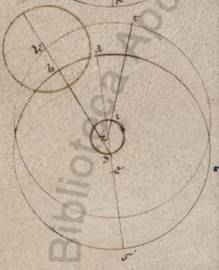 Esto enim excentricus quidem circulus in quo fertur epicicli centrum ABGD circa centrum E et diametrum AEG, in qua subiaceat zodiaci quidem centrum Z, quod vero anomaliam facientis excentrici, hoc est circa quod medium dicimus epicicli transitum plane perfici I, et protrahatur BIT et DIK equaliter utraque distans ab A apoguio, quare equales esse eos qui sub AIB et AID angulos, scribanturque circa B et D puncta equales epicicli et copulentur quidem recte BZ et DZ, trahantur vero ab Z visu in easdem partes contingentes epiciclorum ZL et ZM; dico quoniam angulus quidem qui sub ZBI eiusque penes anomaliam zodiacam differentie equalis est angulo qui sub IDZ, qui vero sub BZL eius que penes epiciclum maxime remotionis, ei qui sub DZM similiter. Ita enim et ex coniunctione maximarum medie remocionum quantitates equales erunt. Trahantur ergo ab B quidem et D in rectas ZL et ZM catheti BL et DM ab E vero in rectas BT et DK EN et EX. Quoniam equalis est qui sub XIE angulus ei qui sub NIE, recti vero et qui ad N et X, et communis equiangulorum trigonorum recta EI, equalis est recta quidem NI ei que est XI, EN vero cathetus ei que est EX. Recte ergo BT et DK equaliter distant ab E centro, equales ergo sunt et ipse et dimidie. Quare et relique BI et DI equales sunt. Sed et recta quidem IZ communis, angulus autem qui sub equalibus lateribus secundum qui sub BIZ ei qui sub DIZ equalis. Itaque et basis quidem BZ basi DZ equalis est, angulus autem qui sub IBZ angulo qui sub IDZ equalis. Esto autem et recta BL que e centro epicicli ei que est DM equalis et recti qui ad L et M anguli, et ille ergo qui sub BZL angulus angulo qui sub DZM equalis est. Quod propositum erat demonstrare.
Esto enim excentricus quidem circulus in quo fertur epicicli centrum ABGD circa centrum E et diametrum AEG, in qua subiaceat zodiaci quidem centrum Z, quod vero anomaliam facientis excentrici, hoc est circa quod medium dicimus epicicli transitum plane perfici I, et protrahatur BIT et DIK equaliter utraque distans ab A apoguio, quare equales esse eos qui sub AIB et AID angulos, scribanturque circa B et D puncta equales epicicli et copulentur quidem recte BZ et DZ, trahantur vero ab Z visu in easdem partes contingentes epiciclorum ZL et ZM; dico quoniam angulus quidem qui sub ZBI eiusque penes anomaliam zodiacam differentie equalis est angulo qui sub IDZ, qui vero sub BZL eius que penes epiciclum maxime remotionis, ei qui sub DZM similiter. Ita enim et ex coniunctione maximarum medie remocionum quantitates equales erunt. Trahantur ergo ab B quidem et D in rectas ZL et ZM catheti BL et DM ab E vero in rectas BT et DK EN et EX. Quoniam equalis est qui sub XIE angulus ei qui sub NIE, recti vero et qui ad N et X, et communis equiangulorum trigonorum recta EI, equalis est recta quidem NI ei que est XI, EN vero cathetus ei que est EX. Recte ergo BT et DK equaliter distant ab E centro, equales ergo sunt et ipse et dimidie. Quare et relique BI et DI equales sunt. Sed et recta quidem IZ communis, angulus autem qui sub equalibus lateribus secundum qui sub BIZ ei qui sub DIZ equalis. Itaque et basis quidem BZ basi DZ equalis est, angulus autem qui sub IBZ angulo qui sub IDZ equalis. Esto autem et recta BL que e centro epicicli ei que est DM equalis et recti qui ad L et M anguli, et ille ergo qui sub BZL angulus angulo qui sub DZM equalis est. Quod propositum erat demonstrare.
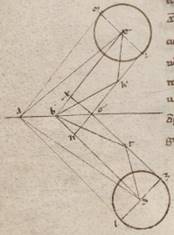 Esto ergo rursum et eius que Mercurii ypotheseos causa per centra et apoguion circulorum diametros ABG, et A quidem subiaceat centrum zodiaci, B vero centrum anomaliam facientis excentrici, G autem punctus circa quod centrum excentrici movetur ferentis epiciclum, et protrahantur in utrasque partes rursum et recte BD et BE plane et in consequentia epicicli motionis atque recte GZ et GI eque celeris et in precedentia excentrici circumactionis, quare manifestum et eos qui ad B et G angulos equales esse atque equidistantes BD quidem rectam ei que est GZ, rectam vero BE ei que est GI, sumanturque in rectis GZ et GI centra excentricorum, sintque T et K, veniant quod quod] que F1 circa ipsa scripti excentrici in quibus sunt epicicli per D et E puncta; scriptisque rursum circa D et E puncta equalibus epiciclis, copulentur quidem recte AD et EA, trahantur vero et in easdem partes epiciclorum contingentes AL et AM. Ostendendum ergo quoniam et ita ille quidem qui sub ADB angulus eius que penes zodiacam anomaliam ei qui sub AEB est equalis, qui vero sub DAL eius que penes epiciclum maxime remocionis ea ea] ei F1 qui sub EAM. Copulentur enim recte BT et BK et TD et KE et trahantur a puncto quidem G in rectas BD et BE catheti GN et GX, a punctis vero D et E in rectas quidem GZ et GI recte DZ et EI, in rectas autem AL et AM recte DL et EM. Quoniam ergo equalis est qui sub GBN angulus ei qui sub GLX GLX] GBX F1 et recte quidem qui ad N et X anguli, communis vero GB recta equalis est, et GN recta recte GX, hoc est recta DZ ei que est EI. Est autem et recta quidem TD ei que est KE equalis, recti vero et qui ad Z et I anguli. Quare et DIZ angulus angulo EKI equalis est, atque GTB angulo ZKB, propter et GT quidem rectam ei que est KG equalem subiacere, vero communem GB, angulum autem TGB angulo KGB equalem. Quare et reliquus quidem BTD angulo BKE equalis est, basis vero BD basi BE. Sed et BA quidem recta rursum communis, angulus vero DBA angulo DBA DBA] EBA F1 equalis. Quare et basis quidem AD basi AE equalis est, angulus vero ADB angulo AEB. Per eadem vero, quoniam et DL quidem recta ei que est EM est equalis. Recti vero. vero] add. qui ad L et M anguli et DAL angulus angulo EAM equalis est. Quod oporteat demonstrare F1
Esto ergo rursum et eius que Mercurii ypotheseos causa per centra et apoguion circulorum diametros ABG, et A quidem subiaceat centrum zodiaci, B vero centrum anomaliam facientis excentrici, G autem punctus circa quod centrum excentrici movetur ferentis epiciclum, et protrahantur in utrasque partes rursum et recte BD et BE plane et in consequentia epicicli motionis atque recte GZ et GI eque celeris et in precedentia excentrici circumactionis, quare manifestum et eos qui ad B et G angulos equales esse atque equidistantes BD quidem rectam ei que est GZ, rectam vero BE ei que est GI, sumanturque in rectis GZ et GI centra excentricorum, sintque T et K, veniant quod quod] que F1 circa ipsa scripti excentrici in quibus sunt epicicli per D et E puncta; scriptisque rursum circa D et E puncta equalibus epiciclis, copulentur quidem recte AD et EA, trahantur vero et in easdem partes epiciclorum contingentes AL et AM. Ostendendum ergo quoniam et ita ille quidem qui sub ADB angulus eius que penes zodiacam anomaliam ei qui sub AEB est equalis, qui vero sub DAL eius que penes epiciclum maxime remocionis ea ea] ei F1 qui sub EAM. Copulentur enim recte BT et BK et TD et KE et trahantur a puncto quidem G in rectas BD et BE catheti GN et GX, a punctis vero D et E in rectas quidem GZ et GI recte DZ et EI, in rectas autem AL et AM recte DL et EM. Quoniam ergo equalis est qui sub GBN angulus ei qui sub GLX GLX] GBX F1 et recte quidem qui ad N et X anguli, communis vero GB recta equalis est, et GN recta recte GX, hoc est recta DZ ei que est EI. Est autem et recta quidem TD ei que est KE equalis, recti vero et qui ad Z et I anguli. Quare et DIZ angulus angulo EKI equalis est, atque GTB angulo ZKB, propter et GT quidem rectam ei que est KG equalem subiacere, vero communem GB, angulum autem TGB angulo KGB equalem. Quare et reliquus quidem BTD angulo BKE equalis est, basis vero BD basi BE. Sed et BA quidem recta rursum communis, angulus vero DBA angulo DBA DBA] EBA F1 equalis. Quare et basis quidem AD basi AE equalis est, angulus vero ADB angulo AEB. Per eadem vero, quoniam et DL quidem recta ei que est EM est equalis. Recti vero. vero] add. qui ad L et M anguli et DAL angulus angulo EAM equalis est. Quod oporteat demonstrare F1
〈IX.7〉 Demonstratio apoguii stelle Mercurii
His consideratis, sumpsimus primum secundum quas partes est eius qui per medias imagines animalium circuli apoguion stelle Mercurii ad hunc modum. Quesivimus enim maximarum apostasium observationes, in quibus orientales progressiones occidentalibus equaliter a solari media progressione, hoc est ea que stelle, distiterit. Hoc enim invento, ex quibus demonstravimus neccessarium est medium duarum progressionum punctum eius qui per media apoguion excentrici continere. Sumpsimus ergo in hoc observationes paucas quidem, propter raro huiusmodi coniunctionem diligenter inveniri, potentes tamen sub visum ducere propositum, quarum noviores quidem hee sunt. Observavimus enim nos xvi anno Adriani secundum Egiptios mensis Phamenoth xvia in xviia vespere Mercurii stellam per astrolabii constitutionem plurimum distantem a media Solis progressione. Tunc vero et perspecta ad lucentem yada optinens apparebat secundum longitudinem Piscium gradum i dimidium. Verum secundum expositum tempus Solis progressio media obtinebat Aquarii gradus ix dimidium iiiia. Maxima ergo a media distantia occidentalis facta est xxi et iiiia graduum. Et xviiio anno Adriani secundum Egiptios mensis Epiphi xviii in xixa mane in maxima existens distantia stella Mercurii valde subtilis et obscura apparens, conspectaque ad lucentem yada optinens apparebat Tauri gradus xviii dimidium iiiia. Sed et secundum illud tempus optinebat medius Sol Geminorum gradus x et hoc ergo maxima a media distantia orientalis facta est equalium xxi et iiiia graduum. Quare, quoniam secundum alteram quidem observationum medie stelle progressio optinebat Aquarii gradus ix et dimidium iiiia, at vero secundum alteram Geminorum gradus x. Medius autem istorum punctus eius qui per media continet Arietis gradus x minus habentem viiiam partem unius gradus, secundum hanc utique erit tunc portionem per apoguii diametros. Rursum nos observavimus per astrolabium primo Antonini anno secundum Egiptios xxa mensis Epiphi in xxia vespere Mercurii stellam plurimum distantem a Solis media progressione. Conspecta autem tunc ad eam que in corde Leonis optinens apparebat Cancri gradus vii. Sed et secundum expositum tempus medius Sol optinebat Geminorum gradus x et dimidium. Facta est ergo maxima a media distantia occidentalis graduum xxvi et dimidii. Similiter autem in iiiio anno Antonini mensis Phamenoth xviiia in xixa mane rursum in maxima existens differentia et conspecta ad vocatam Antarim optinens apparebat Capricorni gradus xiii et dimidium, medio Sole optinente Aquarii gradus x; et hic ergo a maxima distantia media orientalis facta est xxvi et dimidii graduum. Quare, quoniam secundum alteram quidem observationum optinebat media progressio stelle Geminorum gradus x et dimidium, secundum vero alteram Aquarii gradus x. Medius vero ipsorum punctus eius qui per media continet Chelarum gradus x et iiiia, secundum hanc utique erit tunc positionem per apoguium diametros. Itaque ex istis quidem observationibus circa x gradus ad proximum Arietis vel Chelarum apoguion excidens reperimus. Per antiquas autem que circa maximas apostases observate sunt circa vi gradus eorum dodecatimoriorum, ex talibus utique quis colliget. Anno enim xxiii secundum Dionisium mensis Ydronos xxix eous stilbon a lucentissima cauda in Capricorno pertransibat in eas que ad arctos Lunas iii. Optinebat autem tunc dicta fixa secundum nostra principia, hoc est ea que a tropicis et equinoctialibus punctis, Capricorni gradus xxii iii quartas. Manifestum quoniam et Mercurii stella et medius manifestum quoniam Sol optinebat Aquarii gradus xviii via. Erat enim tempus secundum cccclxxxvi annum annavoanassaro annavoanassaro] a Navonassaro F1 secundum Egiptios mensis Chiat xviia in xviiia mane. Facta est ergo maxima a media distantia eoa graduum xxv et dimidii iiia. Itaque equalem quidem examinate ipsam maximam esperiam distantiam non invenimus in eis que in nos venerunt observationibus, per duas vero que ad proximum equalem supputavimus ad hunc modum. Nam eodem quidem xxiiio anno secundum Dionisium Tauronos iiiia vespere ab ea que per Tauri cornua recta relinquebatur tres Lunas. Videbatur autem pertransiens a stella communi distare ad meridiem plus tribus Lunis, quare optinere rursum secundum nostra principia Tauri gradus xxiii et bisse, et erat tempus secundum cccclxxxvi annum rursum a Navonassaro secundum Egiptios Phamenoth xxxa in prima vespere, quando medius Sol optinebat Arietis gradus xxix et dimidium, facta est ergo maxima a media ypostasis ypostasis] apostasis F1 esperia graduum xxiiii via. In xxviii vero anno secundum Dionisium Didimonos viia vespere secundum rectam erat maxime capitibus Geminorum ad meridiem vero ab australi distabat iiia parte Lune minus quam duplum eius quo capita distabant, quare optinebat rursum tunc Mercurii stella secundum nostra principia Geminorum xxix et iiia. Est autem et istud tempus secundum ccccxci annum a Navonassaro secundum Egiptios Pharmouthi va in via vespere secundum quod medius Sol optinebat Geminorum gradus ii et dimidium iiia. Facta est ergo et ipsa distantia graduum xxvi et dimidii. Quoniam ergo, medio existente in Ariete quidem xxix et dimidii, maxima apostasis facta est graduum xxiiii via, in Geminis autem graduum ii et dimidii iiia distantia facta est graduum xxvi et dimidii. Erat autem eoa ad quam querebamus coniungentem graduum xxv et dimidii iiia. Sumpsimus ubi media existente, et esperia distantia graduum xxv et dimidii iiia erit ex superhabundantia subordinatarum duarum observationum. Colligetur enim mediarum quidem progressionum secundum utramque superhabundantiam superhabundantiam] superhabundantia F1 graduum xxxiii iiia, maximarum vero distantiarum graduum ii iiia, quare et gradui uni et tertiis duabus quo superhabundant gradus xxv et dimidium iiia gradus xxiiii via pertinere gradus xxiiii ad proximum, quos, si apposuerimus Arietis gradus xxix et dimidium, habebimus mediam progressionem, secundum quam maxima hesperia distantia equalium colligetur eoe graduum xxv et dimidii iiia, continentem Tauri gradus xxiii et dimidium; et est punctum quod inter Aquarii et gradus xviii et via et Tauri gradus xxiii et dimidium circa v et dimidium et iiia gradus Arietis.
Rursum anno xxiiiio secundum Dionisium Leontonos xxviiia vespere precedebat Spicam ex eis que Yparcus computat paulo plus iii gradibus. Quare optinebat tunc secundum nostra principia Virginis gradus xix et dimidium. Est autem tempus secundum cccclxxxvi annum a Navonassaro secundum Egiptios Pauni xxxa vespere secundum quod medius Sol optinebat Leonis gradus xxvii et dimidium iiia. Facta est ergo maxima medie distantia hesperia graduum xxi bisse ex qua examinate coniungentem eoam computavimus rursum per duas subiacentes. Nam anno quidem lxxvo secundum Caldeos Dion Dion] Diou F1 xiiii eoa erat super australem Libram cubiti dimidio, quare optinere tunc secundum nostra principia Chelarum gradus xiiii via; et est tempus secundum dxii annum a Navonassaro secundum Egiptios mensis Thoth ixa in xa mane, secundum quod medius Sol optinebat Scorpii gradus v via. Facta est ergo eoa maxima distantia graduum xxi. Anno vero lxviio secundum Caldeos Appelleon va eoa erat superstationem borealem Scorpii cubiti dimidio. Quare optinebat tunc secundum nos Scorpii gradus ii iiia. Est autem et hoc tempus secundum diiii annum a Navonassaro secundum Egiptios mensis Thoth xxvii in xxviiia mane, secundum quod medius Sol optinebat Scorpii gradus xxiiii et dimidium iiiia. Facta est ergo et ipsa distantia graduum xxii et dimidii. Quoniam ergo rursum in duabus istis observationibus mediarum quidem progressionum superhabundantie colliguntur graduum xix bisse, maximarum autem distantiarum gradus i et dimidii, propter hoc autem et duabus partibus unius gradus quibus superhabundant quesite distantie gradus xxi bisse minoris xxi gradus, superaddunt gradus ix ad proximum. Istas, si apposuerimus Scorpii gradus v et dimidii, habebimus mediam progressionem, secundum quam maxima eoa distantia equalis sit sit] fit F1 hesperie gradibus xxi bisse, continentem Scorpii gradus xiiii via; et est rursum punctus que inter Leonis gradus xxvii et dimidii iiia et Scorpii xiiii via circa vi maxime gradus Chelarum. Et ex istorum ergo et ex eorum que circa alias stellas apparent particulari coaptatione consonum reperimus et facere quandam transitionem in consequentia imaginum animalium circa zodiaci centrum eas que per apoguia et periguia diametros in quinque erraticis, et transitionem istam equitemporalem esse ei que spere fixarum. Quoniam quidem illa transgrediente ex eis que demonstravimus in c annis gradum i ad proximum et hic quidem ab antiquis observationibus tempus, secundum quod Mercurii apoguion circa sextos erat gradus, in tempus earum que secundum nos observationum, in quo iiiior ad proximum processit gradus, propter eos quod decimos optineat, circiter cccc continens annos deprehenditur.
〈IX.8〉 Quoniam bis et Mercurii stella periguiotatos in uno circulo fit
His autem consequenter quesivimus quantitates factarum maximarum distantiarum, quando media Solis progressio in ipso apoguiotato contingit et rursum quando secundum diametricam ipsius stationem. Quod autem huiusmodi ex antiquis quidem non reperimus observationibus, sed ex eis que a nobis per astrolabium facte sunt. Hic enim et maxime valitatum huiusmodi perspectionis utique quis intelliget, quoniam quidem etsi non prope observatas stellas apparent quedam presumptas habentium positiones, quemadmodum in Mercurii stella secundum plurimum contingit, propter raro ab equali ipsius a Sole distantia distantia] corr. ex distantias V3 multas applanarum posse apparere et per multum distantium perspectionem competunt quesitorum positiones examinate et secundum longitudinem et secundum latitudinem comprehendi.
 Itaque xo ix quidem anno Adriani secundum Egiptios mensis Athir xiiiia in xva eoa Mercurii stella circa maximam distantiam et perspecta ad eam que in corde Leonis optinens apparebat Virginis gradus xxv, medio Sole circa ix ix] corr. ex x V3 et iiiia gradus existente Chelarum, quare effici maximam distantiam xviiii gradus et adhuc xxam partem unius gradus. Eodem vero anno mensis Pachon xixa vespere circa maximam rursus existens distantiam et perspecta ad lucidam yadam optinens apparebat Tauri gradus iiii iiia, medio Sole xi et xiia gradus Arietis optinente, quare et hic constitui maximam distantiam xxiii graduum et iiiia. Et manifestum hinc fieri circa Chelas et non circa Arietem esse apoguion excentrici. His autem datis, esto que per apoguion diametros ABG, et subiaceat quidem zodiaci centrum, in quo visus B, punctus vero A qui sub decimum gradum Chelarum, G autem quod sub decimum gradum Arietis; et descriptis equalibus epiciclis circa A et G et eo in quo D et eo in quo E, educantur a puncto B contingentes ipsos recte BD et BE, trahantur a centris in contactus AD et GE catheti. Quoniam ergo que in Chelis eoa maxima distantia a media observata est gradibus xix et xxa, erit utique ABD angulus, qualium quidem sunt iiiior recti, ccclx talium xix iii, qualium vero ii recti ccclx, talium xxxviii vi. Quare et que quidem super AD rectam periferia talium est xxxviii vi, qualium que que] qui F1 circa ABD orthogonium circulus ccclx. Que vero sub ipsam rectam AD talium est xxxix ix ad proximum, qualium AB ypothenusa cxx.
Itaque xo ix quidem anno Adriani secundum Egiptios mensis Athir xiiiia in xva eoa Mercurii stella circa maximam distantiam et perspecta ad eam que in corde Leonis optinens apparebat Virginis gradus xxv, medio Sole circa ix ix] corr. ex x V3 et iiiia gradus existente Chelarum, quare effici maximam distantiam xviiii gradus et adhuc xxam partem unius gradus. Eodem vero anno mensis Pachon xixa vespere circa maximam rursus existens distantiam et perspecta ad lucidam yadam optinens apparebat Tauri gradus iiii iiia, medio Sole xi et xiia gradus Arietis optinente, quare et hic constitui maximam distantiam xxiii graduum et iiiia. Et manifestum hinc fieri circa Chelas et non circa Arietem esse apoguion excentrici. His autem datis, esto que per apoguion diametros ABG, et subiaceat quidem zodiaci centrum, in quo visus B, punctus vero A qui sub decimum gradum Chelarum, G autem quod sub decimum gradum Arietis; et descriptis equalibus epiciclis circa A et G et eo in quo D et eo in quo E, educantur a puncto B contingentes ipsos recte BD et BE, trahantur a centris in contactus AD et GE catheti. Quoniam ergo que in Chelis eoa maxima distantia a media observata est gradibus xix et xxa, erit utique ABD angulus, qualium quidem sunt iiiior recti, ccclx talium xix iii, qualium vero ii recti ccclx, talium xxxviii vi. Quare et que quidem super AD rectam periferia talium est xxxviii vi, qualium que que] qui F1 circa ABD orthogonium circulus ccclx. Que vero sub ipsam rectam AD talium est xxxix ix ad proximum, qualium AB ypothenusa cxx.
Rursum quoniam que in Ariete esperia a media maxima distantia observata est graduum xxiii et iiiia erit utique GBE angulus, qualium quidem sunt iiiior recti ccclx, talium xxiii et xv, qualium vero iio recti ccclx, talium xlvi xxx. Quare et que quidem super GE periferia talium xlvi xxx, qualium que circa GBE orthogonium circulus ccclx, que vero sub ipsa recta GE talium xlvii xxii, qualium est BG ypothenusa cxx, et qualium est ergo GE quidem recta xxxix ix, AB vero recta cxx, propter equalem esse rectam AD recte GE e centro epicicli, talium et BG quidem erit xcix ix, tota vero ABG recta ccxix ix. Quare et ipsa in duo equalia divisa secundum Z punctum et AZ quidem medietas erit eorumdem cixxxxiiii, media vero punctorum B, Z x xxv. Quoniam ergo vel Z punctum centrum est excentrici, in quo est semper centrum epicicli, vel circa ipsum fertur centrum dicti circuli, manifestum. Itaque enim utique solum equaliter distet a puncto Z, sicut demonstratum est, centrum epicicli secundum utramque expositarum diametricarum stationum. Verum quoniam, si ipsum quidem Z centrum esset excentrici in quo semper est centrum epicicli et stabilis utique esset excentricus iste, et omnium portionum ea que secundum Arietem periguiotati, propter et rectam BG omnium a puncto B in circa Z scriptum circulum copulatarum minimam esse. Non invenitur autem ea que secundum Arietem positio periguiotati aliarum. Sed adhuc ille que secundum Geminos et Aquarii periguiotete et adinvicem ad proximum equales, manifestum quoniam circa Z punctum predicti excentrici fertur in contraria circumductioni epicicli, hoc est in precedentia animalium, semel et ipsum in una periodo. Bis enim ita in ipsa secundum periguiotaton erit centrum epicicli. Quoniam vero et secundum Geminos et Aquarium periguiotetos epiciclus fit ea que secundum Arietem positione, et hinc facile intelligibille ex preexpositis observationibus. In ea enim que secundum xvi annum Adriani mensis Phamenoth xv observatione esperia maxima distantia a media graduum erat xxi iiiia. In ea vero que secundum iiii annum Antonii mensis Phamenoth xviii eoa maxima a media distantia graduum erat xxvi et dimidii, medio Sole secundum ambas observationes circa x gradus existente Aquarii. Et rursum in ea que secundum xviii annum Adriani mensis Epiphi xixa observatione eoa maxima a media distantia graduum erat xxi iiiia et in ea que secundum primum annum Antonii mensis Epiphi xxa esperia maxima a media distantia graduum erat xxvi et dimidii et in istis ambe medii Solis circa x gradus Geminorum, ut et in Aquario et in Geminis compositas que in contraria maximas distantias faciunt gradus xlvii et dimidium, eis que secundum Arietem coutrisque distantiis continentibus graduum xlvi et dimidium, propter esperiam equalem existentem eoe observatam fuisse graduum xxiii iiiia.
〈IX.9〉 De proportione et quantitate anomaliarum Mercurii
His autem preexpositis, reliquum utique erit demonstrare circa quale punctum AB recte in consequentia animalium fit epicicli secundum planum motum annua restitutio et quantum distat ab Z puncto centrum excentrici in precedentia equitemporalem restitutionem sumentis. Coutemur ergo in huiusmodi consideratione duabus observationibus maximarum distantiarum, eoe scilicet et esperie, ab ambabus quidem media tetartimorion distante in easdem partes apoguiotaton secundum quam portionem ad proximum plurima fit differentia zodiace anomalie.
Etenim xiiiio quidem anno Adriani secundum Egiptios mensis Mesori xviiia vespere velut in a Theone sumptis observationibus invenimus: plurimum, inquit, distitit a Sole relicto ab ea que in corde Leonis gradus iii et dimidium iiia, quare optinere secundum nostra principia Leonis gradus vi iiia ad proximum, medio Sole tunc existente circiter Cancri gradus x et xiia, quare fieri esperiam maximam distantiam graduum xxvi iiiia.
Secundum vero anno Antonini secundum Egiptios mensis Mesori xxiii in xxiiiia mane nos per astrolabium observantes maximam ipsius distantiam et perspicientes eum ad lucidam Yada invenimus optinentem Geminorum gradus xx et xiiam, medio Sole iterum existente circiter Cancri gradus x et iiia, quare fieri et eoam maximam distantiam graduum xx et iiiia.
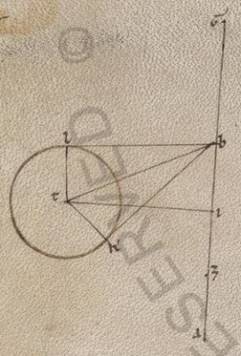 Istis ergo subiacentibus, esto rursum per x gradum Chelarum et Arietis diametros AZBG et subiaceat quemadmodum in priori descriptione A quidem secundum quod fit centrum epicicli, quando sub x gradus erat Chelarum, G vero secundum quod fit, quando sub x gradus erat Arietis, B autem centrum zodiaci. At vero Z circa quod centrum excentrici in precedentia facit transitionem, et proponatur primum invenire quantum distat ab B puncto centrum circa quod planum et in consequentia diximus fieri motum epicicli. Sit ergo I, et protrahatur quedam per I recta ad rectos angulos ei que est AG, ut tetartimorio distet ab apoguio, sumaturque in ipsa quod secundum expositas observationes epicicli centrum T, propter et secundum ipsas tetartimorio distare ab apoguio medium progressum Solis existentis circa x gradus Cancri, et scripto circa T epiciclo KL, trahantur quidem a puncto B contingentes ipsum recte BK et BL, copulentur vero recte TK et TL et BT. Quoniam ergo secundum expositum medium motum eoa quidem maxima media distantia subiacet graduum xx et iiiia, esperia vero graduum xxvi et iiiia, erit utique KBL angulus, qualium sunt iiii recti ccclx, talium xlvi et xxx et medietas ergo ipsius KBT angulus eorumdem est xlvi xxx, qualium ii recti ccclx. Quare et que quidem super TK rectam periferia talium est xlvi et xxx, qualium qui circa BTK orthogonium circulus ccclx, que vero sub ipsam rectam TK talium xlvii et xxii, qualium est BT ypothenusa cxx, et qualium est ergo recta quidem TK que e centro epicicli xxxix et ix, recta vero BZ ostensa est x et xxv, talium et BT erit xcix et ix. Rursum quoniam preiacentium maximarum distantiarum differentia graduum vi existens bis continet eam que penes zodiacam anomaliam differentiam, hec autem sub BTI angulo continetur. Hoc enim nobis predemonstratum est, erit utique BTI angulus, qualium quidem sunt iiiior recti ccclx, talium iii, qualium vero ii recti ccclx, talium vi, quare et que quidem super BI rectam periferia talium est vi, qualium qui circa BIT orthogonium circulus ccclx. Ipsa vero BI recta talium vi et xvii, qualium est BT ypothenusa cxx, et qualium est ergo BT quidem recta xcix et et] om. add. s. l. V3 ix, BZ vero similiter x et xxv, talium et BI erit v et xii. Medietas ergo est ad proximum recta BI eius que est BZ et utraque rectarum BI et IZ talium v et xii ad proximum, qualium est que e centro epicicli xxxix et ix.
Istis ergo subiacentibus, esto rursum per x gradum Chelarum et Arietis diametros AZBG et subiaceat quemadmodum in priori descriptione A quidem secundum quod fit centrum epicicli, quando sub x gradus erat Chelarum, G vero secundum quod fit, quando sub x gradus erat Arietis, B autem centrum zodiaci. At vero Z circa quod centrum excentrici in precedentia facit transitionem, et proponatur primum invenire quantum distat ab B puncto centrum circa quod planum et in consequentia diximus fieri motum epicicli. Sit ergo I, et protrahatur quedam per I recta ad rectos angulos ei que est AG, ut tetartimorio distet ab apoguio, sumaturque in ipsa quod secundum expositas observationes epicicli centrum T, propter et secundum ipsas tetartimorio distare ab apoguio medium progressum Solis existentis circa x gradus Cancri, et scripto circa T epiciclo KL, trahantur quidem a puncto B contingentes ipsum recte BK et BL, copulentur vero recte TK et TL et BT. Quoniam ergo secundum expositum medium motum eoa quidem maxima media distantia subiacet graduum xx et iiiia, esperia vero graduum xxvi et iiiia, erit utique KBL angulus, qualium sunt iiii recti ccclx, talium xlvi et xxx et medietas ergo ipsius KBT angulus eorumdem est xlvi xxx, qualium ii recti ccclx. Quare et que quidem super TK rectam periferia talium est xlvi et xxx, qualium qui circa BTK orthogonium circulus ccclx, que vero sub ipsam rectam TK talium xlvii et xxii, qualium est BT ypothenusa cxx, et qualium est ergo recta quidem TK que e centro epicicli xxxix et ix, recta vero BZ ostensa est x et xxv, talium et BT erit xcix et ix. Rursum quoniam preiacentium maximarum distantiarum differentia graduum vi existens bis continet eam que penes zodiacam anomaliam differentiam, hec autem sub BTI angulo continetur. Hoc enim nobis predemonstratum est, erit utique BTI angulus, qualium quidem sunt iiiior recti ccclx, talium iii, qualium vero ii recti ccclx, talium vi, quare et que quidem super BI rectam periferia talium est vi, qualium qui circa BIT orthogonium circulus ccclx. Ipsa vero BI recta talium vi et xvii, qualium est BT ypothenusa cxx, et qualium est ergo BT quidem recta xcix et et] om. add. s. l. V3 ix, BZ vero similiter x et xxv, talium et BI erit v et xii. Medietas ergo est ad proximum recta BI eius que est BZ et utraque rectarum BI et IZ talium v et xii ad proximum, qualium est que e centro epicicli xxxix et ix.
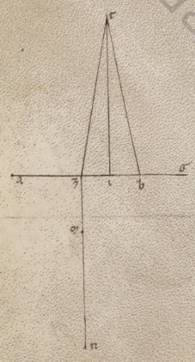 Rursum trahatur in eadem descriptione et per Z in contraria ei que est IT ad rectos angulos ei que est AG recta ZMN, in qua erit tunc manifestum quoniam propter equitemporalem earum que sunt IT et ZN in contraria conrestitutionem centrum excentrici, super quod est T centrum epicicli, iaceatque ei que est ZA equalis recta ZN, quare et ZN quemadmodum et AZ componi et ex ea que e centro excentrici et ex intermedia centrorum ipsius et Z puncti, sumaturque in ipsa centrum excentrici, sitque M, et copuletur recta ZT. Quoniam ergo MZI quidem angulus rectus est, indifferens vero est ad proximum et TZI a recto, quare et NZT indifferentem esse a recta. Ostentum vero est quoniam, et qualium est que e centro epicicli xxxix et ix, talium est NZ quidem equalis existens AZ recte cix et xxxiiii, at vero ZT equalis existens ei que est BT eorumdem xcix et ix, et tota quidem NZT erit ccviii et xliii, dimidia autem eius NM e centro excentrici ciiii et xxxii ad proximum, reliqua vero ZM que inter centra v et xii, eorumdem vero ostensa est et utraque BI et IZ rectarum v et xii. Collectum est ergo nobis quoniam, qualium est que e centro excentrici ciiii et xxii, talium est unaqueque quidem earum que inter centra v et xii, que vero e centro epicicli xxxix et ix, et qualium est ergo que est est] e F1 centro excentrici lx, talium et unaqueque quidem earum que inter centra earum earum] corr. s. l. al. man. erunt V3 erit F1 iii, que vero e centro epicicli xxii et xxx. Quod oportuit ostendere. Quoniam vero, his subiacentibus, et que secundum perguiotata maxime distantie consone fuerit observatis, hoc est quando medius motus fuerit secundum x gradus Aquarii vel Geminorum et trigoni latere distat ab apoguio, ille qui ad visum epiciclum subtendit angulus graduum est xlviii et dimidii et iiiia ad proximum, sciemus utique ita.
Rursum trahatur in eadem descriptione et per Z in contraria ei que est IT ad rectos angulos ei que est AG recta ZMN, in qua erit tunc manifestum quoniam propter equitemporalem earum que sunt IT et ZN in contraria conrestitutionem centrum excentrici, super quod est T centrum epicicli, iaceatque ei que est ZA equalis recta ZN, quare et ZN quemadmodum et AZ componi et ex ea que e centro excentrici et ex intermedia centrorum ipsius et Z puncti, sumaturque in ipsa centrum excentrici, sitque M, et copuletur recta ZT. Quoniam ergo MZI quidem angulus rectus est, indifferens vero est ad proximum et TZI a recto, quare et NZT indifferentem esse a recta. Ostentum vero est quoniam, et qualium est que e centro epicicli xxxix et ix, talium est NZ quidem equalis existens AZ recte cix et xxxiiii, at vero ZT equalis existens ei que est BT eorumdem xcix et ix, et tota quidem NZT erit ccviii et xliii, dimidia autem eius NM e centro excentrici ciiii et xxxii ad proximum, reliqua vero ZM que inter centra v et xii, eorumdem vero ostensa est et utraque BI et IZ rectarum v et xii. Collectum est ergo nobis quoniam, qualium est que e centro excentrici ciiii et xxii, talium est unaqueque quidem earum que inter centra v et xii, que vero e centro epicicli xxxix et ix, et qualium est ergo que est est] e F1 centro excentrici lx, talium et unaqueque quidem earum que inter centra earum earum] corr. s. l. al. man. erunt V3 erit F1 iii, que vero e centro epicicli xxii et xxx. Quod oportuit ostendere. Quoniam vero, his subiacentibus, et que secundum perguiotata maxime distantie consone fuerit observatis, hoc est quando medius motus fuerit secundum x gradus Aquarii vel Geminorum et trigoni latere distat ab apoguio, ille qui ad visum epiciclum subtendit angulus graduum est xlviii et dimidii et iiiia ad proximum, sciemus utique ita.
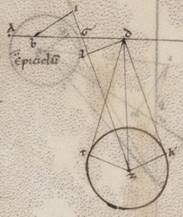 Esto enim per apoguium diametros ABGDE, cuius A quidem punctum subiaceat quod ad apoguion, B vero circa quod centrum excentrici in precedentia facit transitionem, G vero circa quod centrum epicicli in consequentia facit motum, D autem centrum zodiaci, et compleantur utrique motus circa propria centra plane et equitemperaliter in contraria ab A apoguio secundum trigoni latus; sitque epiciclum angulus recta GZ, que vero agit centrum excentrici BI; sitque excentrici quidem centrum in epicicli vero Z, et scripto circa ipsum epiciclo, educantur DT et DK contingentes epiciclum, et copulentur quidem recte GI et DZ et ZT et GK, GK] ZK F1 katetus autem a puncto D in GZ trahatur DL; demonstrandum est quoniam TDK angulus talium est xlvii et dimidii et iiiia, qualium iiiior sunt recti ccclx. Quoniam ergo utrumque ABI et AGL angulorum trigoni latus subtendit talium est cxx, qualium duo recti clxxx, quare et utrumque angulorum GBI et DGL eorumdem esse lx, equalis vero angulus BIG angulo BGI, propter et recte BG ei que est BI equalem subiacere. Coutrique vero reliquorum sunt, in duos rectos cxx, et utrumque ipsorum erit equalium lx. Equiangulum ergo et equilaterum est BGI trigonum, equalis vero et DGL angulus angulo BGI. In directo ergo sunt I, G, Z puncta. Quare et IZ quidem e centro existens excentrici talium est lx, qualium recta GI equalis existens ei que est GD que inter centrum centrum] centra F1 iii, reliqua vero GZ eorumdem lvii. Rursum quoniam DGL angulus, qualium quidem sunt iiii recti ccclx, talium est lx, qualium vero ii recti ccclx, talium cxx, erit utique et que quidem super DL rectam periferia talium cxx, qualium que circa GDL orthogonium circulus ccclx, que vero super GI GI] GL F1 reliquorum in semicirculum lx. Et earum ergo que sub ipsis rectarum DL quidem talium est ciii et lv, qualium GD ypothenusa cxx, at vero GL eorumdem lx. Quare, et qualium est GD quidem recta iii GZ vero similiter lvii, talium et DL quidem erit ii xxvi atque GL eorumdem i xxx, at vero LZ reliquorum lv xxx. Et quoniam quod ab ipsa et quod a recta DL composita faciunt quod a recta DZ, erit et DZ longitudine talium lv xxxiiii, qualium et que a centro epicicli, hoc est utraque rectarum ZT et ZB subiacet xxii xxx, et qualium ergo est DZ DZ] corr. ex DEZ F1 ypothenusa cxx, talium et utraque quidem rectarum RZ et ZK erit xlviii et xxxv, utrumque vero ZDT et ZDK angulorum talium xlvii xlvi, qualium sunt iio recti ccclx. Quare et totus TDK angulus eorumdem xlvii xlvi, qualium sunt iiiior recti ccclx. Quod oportet demonstrare.
Esto enim per apoguium diametros ABGDE, cuius A quidem punctum subiaceat quod ad apoguion, B vero circa quod centrum excentrici in precedentia facit transitionem, G vero circa quod centrum epicicli in consequentia facit motum, D autem centrum zodiaci, et compleantur utrique motus circa propria centra plane et equitemperaliter in contraria ab A apoguio secundum trigoni latus; sitque epiciclum angulus recta GZ, que vero agit centrum excentrici BI; sitque excentrici quidem centrum in epicicli vero Z, et scripto circa ipsum epiciclo, educantur DT et DK contingentes epiciclum, et copulentur quidem recte GI et DZ et ZT et GK, GK] ZK F1 katetus autem a puncto D in GZ trahatur DL; demonstrandum est quoniam TDK angulus talium est xlvii et dimidii et iiiia, qualium iiiior sunt recti ccclx. Quoniam ergo utrumque ABI et AGL angulorum trigoni latus subtendit talium est cxx, qualium duo recti clxxx, quare et utrumque angulorum GBI et DGL eorumdem esse lx, equalis vero angulus BIG angulo BGI, propter et recte BG ei que est BI equalem subiacere. Coutrique vero reliquorum sunt, in duos rectos cxx, et utrumque ipsorum erit equalium lx. Equiangulum ergo et equilaterum est BGI trigonum, equalis vero et DGL angulus angulo BGI. In directo ergo sunt I, G, Z puncta. Quare et IZ quidem e centro existens excentrici talium est lx, qualium recta GI equalis existens ei que est GD que inter centrum centrum] centra F1 iii, reliqua vero GZ eorumdem lvii. Rursum quoniam DGL angulus, qualium quidem sunt iiii recti ccclx, talium est lx, qualium vero ii recti ccclx, talium cxx, erit utique et que quidem super DL rectam periferia talium cxx, qualium que circa GDL orthogonium circulus ccclx, que vero super GI GI] GL F1 reliquorum in semicirculum lx. Et earum ergo que sub ipsis rectarum DL quidem talium est ciii et lv, qualium GD ypothenusa cxx, at vero GL eorumdem lx. Quare, et qualium est GD quidem recta iii GZ vero similiter lvii, talium et DL quidem erit ii xxvi atque GL eorumdem i xxx, at vero LZ reliquorum lv xxx. Et quoniam quod ab ipsa et quod a recta DL composita faciunt quod a recta DZ, erit et DZ longitudine talium lv xxxiiii, qualium et que a centro epicicli, hoc est utraque rectarum ZT et ZB subiacet xxii xxx, et qualium ergo est DZ DZ] corr. ex DEZ F1 ypothenusa cxx, talium et utraque quidem rectarum RZ et ZK erit xlviii et xxxv, utrumque vero ZDT et ZDK angulorum talium xlvii xlvi, qualium sunt iio recti ccclx. Quare et totus TDK angulus eorumdem xlvii xlvi, qualium sunt iiiior recti ccclx. Quod oportet demonstrare.
〈IX.10〉 De periodicis Mercurii motibus
His autem consequenti contingenti et periodicos Mercurii motus et epochis ipsius constituere, eos quidem qui longitudinis, hoc est epiciclum plane circa G ferentes, inde habemus datos a solaribus, eos autem qui anomalie, hoc est stellam secundum epiciclum circa centrum ipsius ferentes, sumpsimus a duabus observationibus indubitabilibus: una quidem ex secundum nos descriptis, altera vero ex antiquis. Nam nos quidem observavimus Mercurii stellam secundo anno Antonini, qui erat secundum dccclxxxvi annum a Navonassaro secundum Egiptios mensis Epiphi iia in iiia per astrolabicum organum nondum in maximam esperiam distantiam venientem. Et perspecta ad eam que in corde Leonis ipsa optinens apparebat Geminorum gradus xvii et dimidium. Tunc autem centrum Lune relinquebat gradus i et vi et erat tempus in Alexandria ante iiii et dimidium horas equinoctiales ab eo quod in tertiam mesonictio, quoniam quidem celi mediabat in astrolabio Virginis gradibus xii, Sole circiter xxiii gradus Tauri existente. Sed in illam horam Solis quidem medius progressus secundum demonstratas nobis ypotheses obtinebat Tauri gradus xxii xxxiiii, qui vero Lune Geminorum gradus xii xiiii, anomalie vero ab apoguio epicicli gradus cclxxxi xx, quare ex his colligi examinatum quidem 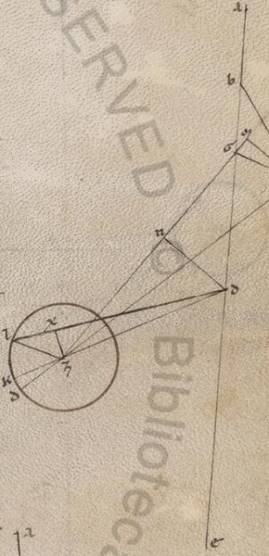 progressum centri Lune in Geminorum graduum xvii x, apparentem vero xvi xx. Itaque Mercuii stella et ita optinebat, quoniam quidem relinquebat centrum Lune gradus i et via, Geminorum gradus xvii et dimidium. Hoc ergo subiacente, esto per apoguion et periguion diametros ABGDE, et A quidem punctus ipsius subiaceat apoguium, B vero circa quod centrum excentrici in precedentia facit transitionem, G A DZ] corr. ex DEZ F1 circa quod centrum epicicli in consequentia facit transitionem, D vero centrum zodiaci. Et moveatur circa G quidem punctum Z centrum epicicli in eo que est GZ AGZ angulum, circa B vero sub ea que est BI moveatur I centrum excentrici ABI angulum equalem existentem semper manifestum quoniam propter equitemporalitatem motuum ei qui est AGZ; et scripto circa Z epiciclo TKL, subiaceat stella secundum L; et copulentur quidem recte GI et IZ et DZ et ZL et DL, catheti vero trahatur in rectam quidem GZT educatam a punctis I et D ille qui super IM et DN, in rectam vero DL a puncto Z ea que est ZX; et proponatur inveniente inveniente] invenire F1 eam que est ab T apoguio in eam que secundum L stellam epicicli periferiam. Quoniam ergo medius quidem Sol optinebat tunc Tauri gradus xxii xxxiiii, periguion autem stelle x gradus ad proximum Arietis, quare mediam ipsius secundum longitudinem progressionem distare ab ipso periguio gradibus xlii et xxxiiii, erit utique GBI quidem angulus, qualium sunt iiii recti ccclx, talium xlii xxxiiii, qualium vero ii recti ccclx, talium lxxxv viii. Utrumque vero angulorum BIG et BGI, propter equalem esse semper rectam BG ei que est BI, eorumdem cxxxvii cxxxvii] corr. ex cxxxviii V3 xxvi. Quare, et scripto circulo circa BGI trigonum, que quidem super IG rectam periferia talium est lxxxv viii, qualium circulus ccclx, que vero super BG eorumdem cxxxvii xxvi. Et earum ergo que sub ipsis rectarum GI quidem talium erit lxxxi x, qualium est circuli diametros cxx, BG vero eorumdem cxi xlix. Quare et qualium est BG recta iii, talium et GI erit ii xi.
progressum centri Lune in Geminorum graduum xvii x, apparentem vero xvi xx. Itaque Mercuii stella et ita optinebat, quoniam quidem relinquebat centrum Lune gradus i et via, Geminorum gradus xvii et dimidium. Hoc ergo subiacente, esto per apoguion et periguion diametros ABGDE, et A quidem punctus ipsius subiaceat apoguium, B vero circa quod centrum excentrici in precedentia facit transitionem, G A DZ] corr. ex DEZ F1 circa quod centrum epicicli in consequentia facit transitionem, D vero centrum zodiaci. Et moveatur circa G quidem punctum Z centrum epicicli in eo que est GZ AGZ angulum, circa B vero sub ea que est BI moveatur I centrum excentrici ABI angulum equalem existentem semper manifestum quoniam propter equitemporalitatem motuum ei qui est AGZ; et scripto circa Z epiciclo TKL, subiaceat stella secundum L; et copulentur quidem recte GI et IZ et DZ et ZL et DL, catheti vero trahatur in rectam quidem GZT educatam a punctis I et D ille qui super IM et DN, in rectam vero DL a puncto Z ea que est ZX; et proponatur inveniente inveniente] invenire F1 eam que est ab T apoguio in eam que secundum L stellam epicicli periferiam. Quoniam ergo medius quidem Sol optinebat tunc Tauri gradus xxii xxxiiii, periguion autem stelle x gradus ad proximum Arietis, quare mediam ipsius secundum longitudinem progressionem distare ab ipso periguio gradibus xlii et xxxiiii, erit utique GBI quidem angulus, qualium sunt iiii recti ccclx, talium xlii xxxiiii, qualium vero ii recti ccclx, talium lxxxv viii. Utrumque vero angulorum BIG et BGI, propter equalem esse semper rectam BG ei que est BI, eorumdem cxxxvii cxxxvii] corr. ex cxxxviii V3 xxvi. Quare, et scripto circulo circa BGI trigonum, que quidem super IG rectam periferia talium est lxxxv viii, qualium circulus ccclx, que vero super BG eorumdem cxxxvii xxvi. Et earum ergo que sub ipsis rectarum GI quidem talium erit lxxxi x, qualium est circuli diametros cxx, BG vero eorumdem cxi xlix. Quare et qualium est BG recta iii, talium et GI erit ii xi.
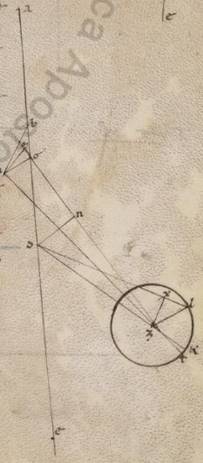 Rursum quoniam BGI quidem angulus talium est cxxxvii xxvi, qualium ii recti ccclx, angulus autem BGM eorumdem lxxxv viii, erit utique et angulus IGM reliquorum lii xviii. Quare et que quidem super rectam IM periferiam talium est lii xviii, qualium qui circa GIM orthogonium circulus ccclx, que vero super GM reliquorum in semicirculum cxxvii xlii; et earum ergo que sub ipsis rectarum IM quidem talium est lii liii, qualium GI ypothenusa cxx, GM vero eorumdem cvii xliii. Quare et qualium est GI quidem recta ii xi, IZ vero que e centro excentrici ferentis epiciclum lx, talium et IM quidem erit o lviii, GM vero similiter i lviii, propter hoc autem et MZ quidem indifferenti minor existens quam IZ recta subtendente eorumdem lx, reliqua vero GZ recta lviii ii.
Rursum quoniam BGI quidem angulus talium est cxxxvii xxvi, qualium ii recti ccclx, angulus autem BGM eorumdem lxxxv viii, erit utique et angulus IGM reliquorum lii xviii. Quare et que quidem super rectam IM periferiam talium est lii xviii, qualium qui circa GIM orthogonium circulus ccclx, que vero super GM reliquorum in semicirculum cxxvii xlii; et earum ergo que sub ipsis rectarum IM quidem talium est lii liii, qualium GI ypothenusa cxx, GM vero eorumdem cvii xliii. Quare et qualium est GI quidem recta ii xi, IZ vero que e centro excentrici ferentis epiciclum lx, talium et IM quidem erit o lviii, GM vero similiter i lviii, propter hoc autem et MZ quidem indifferenti minor existens quam IZ recta subtendente eorumdem lx, reliqua vero GZ recta lviii ii.
Similiter quoniam quidem DGN angulus talium est lxxxv viii, qualium ii recti ccclx, erunt erunt] erit F1 utique et que quidem super recta DN periferia talium lxxxv viii, qualium qui circa GDN orthogonium circulus ccclx, que vero super GN reliquorum in semicirculum xciiii lii. Quare et earum que sub ipsas rectarum DN quidem erit talium lxxxi x, qualium est GD ypothenusa cxx, GN vero eorumdem lxxxviii xxiii, et qualium est ergo recta quidem GD iii, GZ vero ostensa est lviii ii, talium et DN quidem erit ii ii, GN vero similiter ii xiii, NZ autem reliquorum lv xlix. Propter hoc autem et DZ ypothenusa talium lv li ad proximum, qualium est et que e centro epicicli xxii xxx, et qualium est ergo DZ ypothenusa cxx, talium et DN quidem erit iiii xxii, que vero super ipsam periferia talium iiii xi, qualium est qui circa DZN orthogonium circulus ccclx. Quare et DZN quidem angulus talium est iiii xi, qualium ii recti ccclx, totus autem EDZ lxxxix xix. Est autem et EDL quidem totus eorumdem cxxxv, propter stellam tunc distantem a periguio apparere gradibus lxvii xxx, angulus autem ZDL reliquorum xlv xli. Itaque et ea quidem que super terram ZX periferia talium est xlv xli, qualium qui circa DEX orthogonium circulus ccclx. Ipsa vero ZX recta talium est xlvi xxxv, qualium est DZ ypothenusa cxx. Quare et qualium quidem est DZ recta lv li, ZL vero que e centro epicicli xxii xxx, talium ZX erit xxi xli. Qualium vero ZL ypothenusa cxx, talium est ZX rursum cxv xxxix et ea ergo que quidem super rectam ZX periferia talium est cxlix ii, qualium qui circa ZLX orthogonium circulus ccclx, angulus autem ZLX talium est cxlix ii, qualium ii recti ccclx, eorumdem vero ostensus est et DZL quidem angulus xlv xli, angulus autem TZK similiter iiii xi. Quare et totus TZL, qualium quidem sunt ii recti ccclx, talium est cxcviii liii, qualium vero iiii recti ccclx, talium xcix xxvii; et TKL ergo periferia epicicli qua distabat secundum observationem Mercurii stella ab T apoguio graduum est xcix xxvii. Quod propositum erat demonstrare.
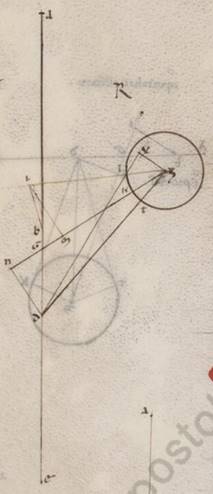 Cursum Cursum] rursum F1 vero et xxi anno secundum Dionisium qui erat secundum cccclxxxiiii annum a Navonassaro mensis Scorpionios xxii secundum Egyptios mensis Thoth xviii xviii] iter. del. V3 in xixa eous stilbon ab ea que per borealem frontem Scorpii et mediam recta distabat in relicta Lunam, ad arctos vero a boreali fronte distabat ii Lunas. Verum media quidem earum que in fronte Scorpii secundum nostra principia optinebat tunc Scorpii gradum i xl et australior est eo qui per media equali. Borealissima vero optinebat Scorpii gradus ii iiia et borealior eo est qui per media gradu i et iiia. Mercurii itaque stella optinebat Scorpii gradus iii et iiia ad proximum. Manifestum vero fit et quoniam nondum in maximam eoam distantiam veniat, propter post iiii dies in xxvi Scorpionos describi, quoniam ad eadem recta distabat in consequentia totam et dimidiam Lunam. Maior enim facta est distantia, Sole quidem iiii ad proximum gradus progressio, stella vero dimidiam Lunam; et optinebat medius Sol xix mensis Thoth mane secundum nos Scorpii gradus xx et dimidium iiia, apoguion vero stelle vi gradus Chelarum, propter medios observationum annos circa cccclxx iiii graduum ad proximum facere apoguii transitionem.
Cursum Cursum] rursum F1 vero et xxi anno secundum Dionisium qui erat secundum cccclxxxiiii annum a Navonassaro mensis Scorpionios xxii secundum Egyptios mensis Thoth xviii xviii] iter. del. V3 in xixa eous stilbon ab ea que per borealem frontem Scorpii et mediam recta distabat in relicta Lunam, ad arctos vero a boreali fronte distabat ii Lunas. Verum media quidem earum que in fronte Scorpii secundum nostra principia optinebat tunc Scorpii gradum i xl et australior est eo qui per media equali. Borealissima vero optinebat Scorpii gradus ii iiia et borealior eo est qui per media gradu i et iiia. Mercurii itaque stella optinebat Scorpii gradus iii et iiia ad proximum. Manifestum vero fit et quoniam nondum in maximam eoam distantiam veniat, propter post iiii dies in xxvi Scorpionos describi, quoniam ad eadem recta distabat in consequentia totam et dimidiam Lunam. Maior enim facta est distantia, Sole quidem iiii ad proximum gradus progressio, stella vero dimidiam Lunam; et optinebat medius Sol xix mensis Thoth mane secundum nos Scorpii gradus xx et dimidium iiia, apoguion vero stelle vi gradus Chelarum, propter medios observationum annos circa cccclxx iiii graduum ad proximum facere apoguii transitionem.
His ergo subiacentibus, adiaceat rursum simillis superiori descriptio, tamen propter progressionum dissimillitudinem et qui ad A apoguion anguli acuti describantur et stellam copulantes recte in precendentia epicicli et ZX cathetus ex centro epicicli super DL. Quoniam ergo media stelle progressio distabat ab apoguio gradibus xliiii l, erit utique ABI angulus, qualium quidem sunt iiii recti ccclx, talium xliiii l, qualium vero ii recti ccclx, talium lxxxix xl. Quare reliquus quidem GBI erit cclxx xx, utrumque vero eorum qui sunt BGI et BIG eorumdem xliiii l. Propter eadem vero et earum que sub ipsas rectarum GI quidem erit talium lxxxiiii xxxvi, qualium est eius qui circa BGI trigonum circuli diametros cxx. Utrumque vero BG et BI rectarum eorumdem xlv xlvi, et qualium est ergo utraque BG et BI rectarum iii, talium et GI erit v et xxxiii.
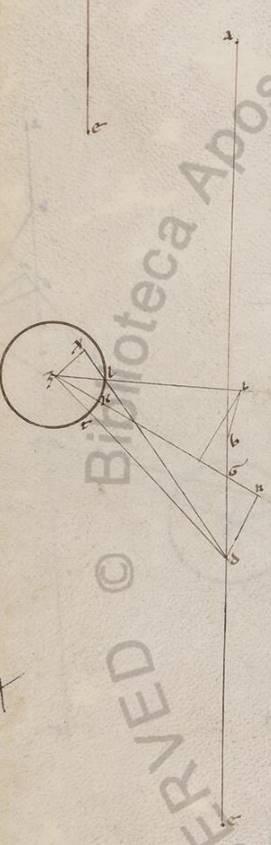 Rursum, quoniam AGZ quidem angulus subiacet talium lxxxix xl, qualium ii recti ccclx, angulus autem BGI similiter xliiii l, totus vero ZGI colligitur cxxxiiii xxx, erit utique et que quidem sub IM periferia talium cxxxiiii xxx, qualium est qui circa GM orthogonium circulus ccclx, que vero super GM reliquorum in semicirculum xlv xxx. Et earum ergo que sub ipsis rectarum MI quidem talium erit cx xl, qualium GI ypothenusa cxx, GM vero eorumdem xlvi xxiiii. Quare et qualium est GI recta v xxxiii, hoc est ZL ZL] ZI F1 que e centro excentrici lx, talium et IM quidem erit v et vii, GM vero similiter ii x. Propter hoc autem et ZM quidem colligitur longitudine eorumdem lix xlvii tota vero ZMG lxi lvii. Similiter quoniam et DGN angulus talium est lxxxix xl, qualium ii recti ccclx, erit utique et que quidem super DN periferia talium lxxxix xl, qualium qui circa GDN orthogonium circulus ccclx, que vero super GN reliquorum in semicirculum xc xx et earum ergo que sub ipsis rectarum DN quidem talium est lxxxiiii xxxvi, qualium est GN ypothenusa cxx, GN vero eorumdem lxxxv vi. Quare et qualium est GD recta iii, talium et DN quidem erit ii vii, GN vero similiter ii viii, tota autem ZGN lxiiii v. Propter hoc autem et ZD ypothenusa eorumdem lxiiii vii, et qualium ergo est ZD recta cxx, talium et DN quidem erit iii lviii, que vero super ipsam periferia talium iii xlviii, qualium est qui circa ZDN orthogonium circulus ccclx. Quare et DZN quidem angulus talium est iii xlviii, qualium ii recti ccclx, reliquus vero ADZ eorumdem lxxxv lii. Sed et ADL angulus eorumdem subiacet liiii xl, propter distare ab apoguio stellam secundum observationem gradibus xxvii xx, ut et reliquum ZDL angulum talium reliqui xxxi xii, qualium ii recti ccclx, et que quidem super ZX periferia talium est xxxi xii, qualium qui circa ZDX orthogonium circulus ccclx. Ipsa vero ZX recta talium xxxii xvi, qualium est DZ ypothenusa cxx, et qualium quidem est ergo DZ recta lxiiii vii, hoc est ZL ex centro epicicli xxii xxx, talium et erit XZ recta xvii xv iii, qualium vero ZL ypothenusa cxx, talium et ZX xcii ad proximum. Quare et que quidem super ZX periferia talium c et sexagesimorum viii, qualium qui circa ZLX orthogonium circulus ccclx. Angulus autem ZLX talium c viii, qualium ii recti ccclx. Eorumdem vero ostensus est et ZDL quidem angulus xxxi xii, angulus autem TZK similiter iii xlviii. Quare et reliquus KZL, qualium quidem sunt ii recti ccclx, talium est lxv viii, qualium vero iiii recti ccclx, talium xxxii xxxiiii. Distabat ergo et secundum istam observationem stella a periguio quidem epicicli K gradibus xxxii xxxiiii, ab apoguio vero manifestum quoniam gradibus ccxii xxxiiii. Ostensa Ostensa] corr. ex ostensus V3 est autem distans et secundum nostre observationis tempus similiter ab apoguio epicicli gradibus xcix xxvii et est medium quidem duarum observationum tempus annorum egiptiacorum ccccii et dierum cclxxxiii et horarum xiii et dimidii ad proximum. Continet autem tempus istud totas anomalie restitutiones stelle icclxviii, quoniam quidem, xx egiptiacis annis facientibus periodos ad proximum lxiii, anni quidem cccc colligunt i cclx, reliqui vero ii anni cum comprehensis diebus totas alias viii. Manifestum ergo nobis factum est quoniam in annis egipciacis ccccii et diebus cclxxxiii et horis xiii et dimidio stella Mercurii post totas anomalie restitutiones icclxviii sumpsit gradus ccxlv liii, quantis ea que secundum nos epochi priorem superat. Tante vero fere epoysie colliguntur gradus et ex preexpositis nobis canonibus, quoniam quidem ab his ipsis directionem periodicorum Mercurii motuum fecimus, propositum quidem tempus resolventes in dies, circulos autem anomalie cum epoysia in gradus. Distributa enim multitudine graduum in multitudinem dierum, colligitur in precendentibus expositus nobis in Mercurio diurnus anomalie medius motus.
Rursum, quoniam AGZ quidem angulus subiacet talium lxxxix xl, qualium ii recti ccclx, angulus autem BGI similiter xliiii l, totus vero ZGI colligitur cxxxiiii xxx, erit utique et que quidem sub IM periferia talium cxxxiiii xxx, qualium est qui circa GM orthogonium circulus ccclx, que vero super GM reliquorum in semicirculum xlv xxx. Et earum ergo que sub ipsis rectarum MI quidem talium erit cx xl, qualium GI ypothenusa cxx, GM vero eorumdem xlvi xxiiii. Quare et qualium est GI recta v xxxiii, hoc est ZL ZL] ZI F1 que e centro excentrici lx, talium et IM quidem erit v et vii, GM vero similiter ii x. Propter hoc autem et ZM quidem colligitur longitudine eorumdem lix xlvii tota vero ZMG lxi lvii. Similiter quoniam et DGN angulus talium est lxxxix xl, qualium ii recti ccclx, erit utique et que quidem super DN periferia talium lxxxix xl, qualium qui circa GDN orthogonium circulus ccclx, que vero super GN reliquorum in semicirculum xc xx et earum ergo que sub ipsis rectarum DN quidem talium est lxxxiiii xxxvi, qualium est GN ypothenusa cxx, GN vero eorumdem lxxxv vi. Quare et qualium est GD recta iii, talium et DN quidem erit ii vii, GN vero similiter ii viii, tota autem ZGN lxiiii v. Propter hoc autem et ZD ypothenusa eorumdem lxiiii vii, et qualium ergo est ZD recta cxx, talium et DN quidem erit iii lviii, que vero super ipsam periferia talium iii xlviii, qualium est qui circa ZDN orthogonium circulus ccclx. Quare et DZN quidem angulus talium est iii xlviii, qualium ii recti ccclx, reliquus vero ADZ eorumdem lxxxv lii. Sed et ADL angulus eorumdem subiacet liiii xl, propter distare ab apoguio stellam secundum observationem gradibus xxvii xx, ut et reliquum ZDL angulum talium reliqui xxxi xii, qualium ii recti ccclx, et que quidem super ZX periferia talium est xxxi xii, qualium qui circa ZDX orthogonium circulus ccclx. Ipsa vero ZX recta talium xxxii xvi, qualium est DZ ypothenusa cxx, et qualium quidem est ergo DZ recta lxiiii vii, hoc est ZL ex centro epicicli xxii xxx, talium et erit XZ recta xvii xv iii, qualium vero ZL ypothenusa cxx, talium et ZX xcii ad proximum. Quare et que quidem super ZX periferia talium c et sexagesimorum viii, qualium qui circa ZLX orthogonium circulus ccclx. Angulus autem ZLX talium c viii, qualium ii recti ccclx. Eorumdem vero ostensus est et ZDL quidem angulus xxxi xii, angulus autem TZK similiter iii xlviii. Quare et reliquus KZL, qualium quidem sunt ii recti ccclx, talium est lxv viii, qualium vero iiii recti ccclx, talium xxxii xxxiiii. Distabat ergo et secundum istam observationem stella a periguio quidem epicicli K gradibus xxxii xxxiiii, ab apoguio vero manifestum quoniam gradibus ccxii xxxiiii. Ostensa Ostensa] corr. ex ostensus V3 est autem distans et secundum nostre observationis tempus similiter ab apoguio epicicli gradibus xcix xxvii et est medium quidem duarum observationum tempus annorum egiptiacorum ccccii et dierum cclxxxiii et horarum xiii et dimidii ad proximum. Continet autem tempus istud totas anomalie restitutiones stelle icclxviii, quoniam quidem, xx egiptiacis annis facientibus periodos ad proximum lxiii, anni quidem cccc colligunt i cclx, reliqui vero ii anni cum comprehensis diebus totas alias viii. Manifestum ergo nobis factum est quoniam in annis egipciacis ccccii et diebus cclxxxiii et horis xiii et dimidio stella Mercurii post totas anomalie restitutiones icclxviii sumpsit gradus ccxlv liii, quantis ea que secundum nos epochi priorem superat. Tante vero fere epoysie colliguntur gradus et ex preexpositis nobis canonibus, quoniam quidem ab his ipsis directionem periodicorum Mercurii motuum fecimus, propositum quidem tempus resolventes in dies, circulos autem anomalie cum epoysia in gradus. Distributa enim multitudine graduum in multitudinem dierum, colligitur in precendentibus expositus nobis in Mercurio diurnus anomalie medius motus.
〈IX.11〉 De epochi periodicorum ipsius motuum
Ut ergo quemadmodum et in Sole et in Luna et in quinque erraticis eopchas in primo anno Navonassari secundum Egiptios mensis Thot primo ad meridiem constituamus, sumpsimus tempus medium et antiquioris et propioris observationum. Colligitur autem ita annorum egiptiacorum cccclxxxiii et dierum xvii et horarum xviii iiia ad proximum et adiacet tempori huic medii motus epoysia anomalie gradus cxc xxxix. Quos si auferamus ab eis qui secundum observationem ab apoguio gradibus ccxii xxxiiii, habebimus epochin in primo anno Navonassari secundum Egiptios mensis Thoth prima ad meridiem, anomalie quidem ab apoguio epicili gradus xxi lv, longitudinis vero eamdem Soli, hoc est Piscium gradus o xlv, apoguion vero excentrioticis circiter Chelarum gradum i vi. Quoniam quidem centenarii propositorum annorum faciunt gradus iiii et dimidium iii ad proximum, tantis vero i et vi superant Chelarum gradus qui secundum observationem.
Claudii Ptolemei mathematici sintaxeos liber nonus explicit.