〈II〉
De universali positione eius que penes nos habitabilis
Quomodo, data maxime diei quantitate, deprehense ab equinoctiali et obliquo circulo orizontis periferie dantur
Quomodo, eisdem subiacentibus, elevatio poli datur et e converso
Quomodo investigandum quibus et quando et quotiens Sol ad verticem fit
Quomodo ab eis que exposita sunt propositiones gnomonum ad equinoctiales et tropicas in meridiebus umbras summuntur
Expositio eorum que secundum parallilon ydiomatum
De eis que in inclinata spera eius qui per media animalia circuli et equinoctialis coascensionibus
Expositio eorum que canoniorum secundum decamirias in uno quoque parallilo accessionum
De eis que particulariter anaphoras consequuntur
De angulis ab eo qui per media animalia circulo et meridiano factis
De angulis ab eodem obliquo circulo et orizonte factis
De eis qui ad eundem circulum fiunt eius qui per polos orizontis angulis atque periferiis
Expositio secundum parallilum propositorum angulorum ac perferiarum
Liber secundus
〈II.1〉
Pertranseuntes in primo sintaxeos de totorum positione capitulatim debentia prelibari et quecumque quis eorum que in recta spera ad subiacentium contemplationem utilia arbitretur, temptabimus deinceps et eorum que circa inclinatam speram accidunt principaliora rursus ut est maxime facile edocere. Et hic ergo quod quidem universaliter oportet prelibari, hoc est quoniam terra in iiii divisa cetartimoria cetartimoria] tetartimoria V2F1 facta ab eo qui secundum equinoctialem circulum et uno eorum qui per polos ipsius describuntur, eiusque penes nos habitabilis magnitudo sub altero borealium ad proximum continetur. Hoc autem maxime fiet manifestum in latitudine quidem, idest a meridie ad arctos transitu, eo quod ubique in equinoctiis facte gnomonum meridiales umbre ad arctos semper fatiunt nutus et nunquam ad meridiem; in longitudine vero, idest eo qui ab oriente in occidente occidente] occidentem V2F1 transitu, eo quod eedem eclipses maximeque lunares apud eos qui in ultimis orientalibus eius partibus que penes nos habitabilis et apud eos qui in extremis eiusdem occidentalibus habitant eodem tempore vise non pluribus quam xii prius posteriusve appareant horis equinoctialibus, ipso secundum longitudinem terre tetartimorio xii horarum spatium continente, quoniam ab uno eorum qui equinoctialis semicirculorum determinatur. Eorum vero qui qui] que V2F1 particulariter oportet considerari precipue utique quis propositum ad negotium putet attinere ea que secundum unumquemque magis borealium equinoctiali circulo parallilorum ipsi et subiacentibus habitationibus secundum principaliora accidunt ydiomatum. Hec autem sunt quantum poli primi motus ab orizonte vel quantum punctus qui ad verticem ab equinoctiali circulo in meridionali distet, et quibus Sol in vertice fiat, et quando et quotiens hoc contingat, que etiam proportiones equinoctialium et tropicarum in meridiebus umbrarum ad gnomones, quante quoque maximarum vel minimarum dierum ad equinoctiales differentie et quecumque alia circa particulares auxomioses nictimerorum, amplius autem et circa coortus et occasus equinoctialis et obliqui circuli et circa ydiomata quantitatesque factorum a principalioribus et maximis circulis angulorum superaccidentia considerantur.
〈II.2〉 Quomodo, data maxime diei quantitate, deprehense ab equinoctiali et obliquo circulo orizontis periferie dantur
Preiacet universaliter exemplorum causa per Rodum scriptus equidistans equinoctiali circulus, ubi elevatio quidem poli graduum est xxxvi, maxima vero dies horarum est equinoctium equinoctium] equinoctialium V2F1 xiiii et dimidii, sitque meridianus quidem circulus ABGD, orizontis vero orientalis semicirculus BED et equinoctiali quidem circuli semicirculus similiter AEG, australis vero ipsius polus Z, subiaceat etiam eius qui per media animalia circuli yemale tropicum punctum oriens per N, describaturque per Z, N puncta maximi circuli tetartimorion ZNT. Detur ergo primum maxime diei quantitas, proponaturque EN orizontis periferiam invenire. Quoniam ergo spere conversio circa equinoctialis polos completur, manifestum quoniam tempore in eodem N punctus et T in ABGD meridiano erit, et quod ab ortu quidem usque super terram mensuranisim N puncti 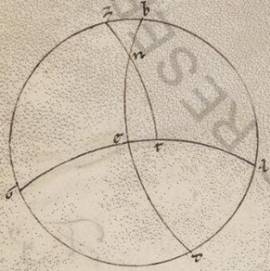 tempus idest quod sub TA equinoctialis periferia continetur, quod autem a sub terra mesuranisi ad ortum usque idest quod sub GT. Consequens vero est quoniam et diei tempus quod duplum est contenti sub TA, noctis vero quod duplum est sub GT contenti. Quoniam quidem et seorsum et que super terram et que sub terra portiones equidistantium equinoctiali circulorum omnium in duo equa a meridano dividuntur. Propter hoc autem et ET quidem periferia medietas existens differentie minime seu maxime diei ad equinoctialem unius quidem hore et quarte fiet in parallilo subiacenti, temporum vero manifestum quoniam xviii xlv minutorum, reliqua vero in tetartimorio periferia TA eorumdem lxxi xv minutorum. Quoniam ergo secundum eadem premonstratis in duas maximorum circulorum periferias AE et AZ due scripte sunt EB et ZT secantes seinvicem ad punctum N, eius que sub dupla periferie TA ad eam que sub dupla periferie EA proportio composita est ex proportione eius que sub dupla periferie NB ad eam que sub dupla periferie BE et proportione eius que sub dupla periferie TZ ad eam que sub dupla perferie ZN. Sed TA quidem periferie dupla graduum est cxlii xxx minutorum et que sub ea recta portionum cxiii xxxvii minutorum liiii secundorum, que vero perferie AE graduum clxxx et que sub ea recta portionum cxx, et rursus TZ quidem periferie dupla graduum clxxx et que sub ipsa recta portionum cxx. Que vero periferie ZN graduum cxxxii xvii minutorum xx secundorum et que sub ipsa recta portionum cviiii xliiii minutorum liii secundorum. Si ergo a proportione eorum que sunt cxiii xxxvii minutorum liiii secundorum ad cxx abstulerimus proportionem eorum que sunt cxx ad cix xliiii minuta liii secunda, relinquetur nobis proportio eius que sub dupla periferie NB ad eam que sub dupla periferie BE, que eorum que sunt ciii lv xxvi ad cxx. Est autem que sub dupla periferie BE, quoniam tetartimorii contingit, portionum cxx, et ea ergo que sub dupla periferie NB eorumdem est ciii lv minutorum xxvi secundorum. Quare et dupla quidem periferie BN erunt erunt] erit V2F1 graduum cxx ad proximum, ipsa vero BN eorumdem lx, et reliqua ergo NE talium relinquetur xxx, qualium est orizon ccclx.
tempus idest quod sub TA equinoctialis periferia continetur, quod autem a sub terra mesuranisi ad ortum usque idest quod sub GT. Consequens vero est quoniam et diei tempus quod duplum est contenti sub TA, noctis vero quod duplum est sub GT contenti. Quoniam quidem et seorsum et que super terram et que sub terra portiones equidistantium equinoctiali circulorum omnium in duo equa a meridano dividuntur. Propter hoc autem et ET quidem periferia medietas existens differentie minime seu maxime diei ad equinoctialem unius quidem hore et quarte fiet in parallilo subiacenti, temporum vero manifestum quoniam xviii xlv minutorum, reliqua vero in tetartimorio periferia TA eorumdem lxxi xv minutorum. Quoniam ergo secundum eadem premonstratis in duas maximorum circulorum periferias AE et AZ due scripte sunt EB et ZT secantes seinvicem ad punctum N, eius que sub dupla periferie TA ad eam que sub dupla periferie EA proportio composita est ex proportione eius que sub dupla periferie NB ad eam que sub dupla periferie BE et proportione eius que sub dupla periferie TZ ad eam que sub dupla perferie ZN. Sed TA quidem periferie dupla graduum est cxlii xxx minutorum et que sub ea recta portionum cxiii xxxvii minutorum liiii secundorum, que vero perferie AE graduum clxxx et que sub ea recta portionum cxx, et rursus TZ quidem periferie dupla graduum clxxx et que sub ipsa recta portionum cxx. Que vero periferie ZN graduum cxxxii xvii minutorum xx secundorum et que sub ipsa recta portionum cviiii xliiii minutorum liii secundorum. Si ergo a proportione eorum que sunt cxiii xxxvii minutorum liiii secundorum ad cxx abstulerimus proportionem eorum que sunt cxx ad cix xliiii minuta liii secunda, relinquetur nobis proportio eius que sub dupla periferie NB ad eam que sub dupla periferie BE, que eorum que sunt ciii lv xxvi ad cxx. Est autem que sub dupla periferie BE, quoniam tetartimorii contingit, portionum cxx, et ea ergo que sub dupla periferie NB eorumdem est ciii lv minutorum xxvi secundorum. Quare et dupla quidem periferie BN erunt erunt] erit V2F1 graduum cxx ad proximum, ipsa vero BN eorumdem lx, et reliqua ergo NE talium relinquetur xxx, qualium est orizon ccclx.
〈II.3〉 Quomodo, eisdem subiacentibus, elevatio poli detur et e converso
Proponatur ergo rursus, hoc dato, et elevationem poli sumere, idest BZ meridiani periferiam. Fit ergo in eadem descriptione proportio eius que sub dupla periferie ET ad eam que sub dupla periferie TA conposita ex proportione eiusque sub dupla periferie EN ad eam que sub dupla periferie NB et proportione eius que sub dupla perferie BZ ad eam que sub dupla periferie ZA. At dupla quidem periferie ET graduum est xxxvii xxx minutorum et que sub ipsa recta portionum xxxviii xxxiiii minutorum xxii secundorum. Dupla vero perferie TA graduum cxlii 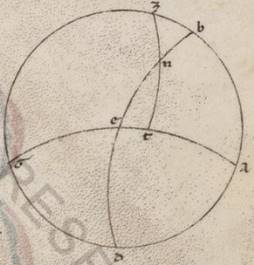 xxx minutorum; estque sub ea recta portionum cxiii xxxvii liiii et rursum dupla quidem periferie EN graduum est lx et que sub ipsa recta portionum lx, dupla vero periferie NB graduum cxx et que sub ea recta portionum ciii lv minutorum xxiii secundorum. Si ergo a proportione eorum que sunt xxxviii portionum xxxiiii minutorum xxii secundorum ad cxiii portiones xxxvii minuta liiii secunda abstulerimus proportionem eorum que sunt lx ad ciii porciones lv minuta xxiii secunda, relinquitur proportio eius que sub dupla periferie BZ ad eam que sub dupla periferie ZA, que est eorum que sunt lxx portionum xxxiii minutorum ad proximum ad cxx; et est rursum que sub dupla periferie ZA portionum cxx et ea ergo que sub dupla periferie BZ eorumdem est lxx portionum xxxiii minutorum. Quare dupla quidem BZ periferie erunt graduum lxxii i minuti, ea vero que est BZ eorumdem xxxvi ad proximum.
xxx minutorum; estque sub ea recta portionum cxiii xxxvii liiii et rursum dupla quidem periferie EN graduum est lx et que sub ipsa recta portionum lx, dupla vero periferie NB graduum cxx et que sub ea recta portionum ciii lv minutorum xxiii secundorum. Si ergo a proportione eorum que sunt xxxviii portionum xxxiiii minutorum xxii secundorum ad cxiii portiones xxxvii minuta liiii secunda abstulerimus proportionem eorum que sunt lx ad ciii porciones lv minuta xxiii secunda, relinquitur proportio eius que sub dupla periferie BZ ad eam que sub dupla periferie ZA, que est eorum que sunt lxx portionum xxxiii minutorum ad proximum ad cxx; et est rursum que sub dupla periferie ZA portionum cxx et ea ergo que sub dupla periferie BZ eorumdem est lxx portionum xxxiii minutorum. Quare dupla quidem BZ periferie erunt graduum lxxii i minuti, ea vero que est BZ eorumdem xxxvi ad proximum.
Rursum in eadem descriptione cum sub] add. del. dupla V3 e contrario BZ quidem periferia elevationis poli detur observata graduum xxxvi, proponatur autem invenire differentia differentia] differentiam V2F1 maxime vel minime diei ad equinoctialem, idest duplam periferie ET. Fit ergo propter eadem proportio eius que sub dupla periferie ZB ad eam que sub dupla periferie BA composita ex proportione eius que sub dupla periferie ZN ad eam que sub dupla periferie NT et proportione eius que sub dupla periferie TE ad em que sub dupla periferie EA. At dupla quidem periferie ZB graduum est lxxii et que sub ea recta portionum lxx xxxii minutorum iii secundorum, dupla vero periferie BA graduum cviii, et que sub ea recta portionum xcvii iiii minutorum lvi secundorum; et rursum dupla quidem periferie ZN graduum est cxxxii xvii minutorum xx secundorum et que sub ea recta portionum cix xliiii minutorum liii secundorum, dupla vero perferie NT graduum xlvii xlii minutorum xl secundorum et que sub ea recta portionum xlviii xxxi minutorum lv lv] corr. ex liii V3 secundorum. Si ergo a proportione eorum que sunt lxx portionum xxxii minutorum iii secundorum ad xcvii portiones iiii minuta lvi secunda abstulerimus proportionem eorum que sunt cix portionum xliiii minutorum liii secundorum ad xlviii portiones xxxi minuta lv secunda, relinquetur proportio eius nobis que sub dupla periferie TE ad eam que sub dupla periferie EA, que eorum que sunt xxxi portionum xv xv] xl V2 minutorum xxiii secundorum ad xcvii iiii lvi. Et quoniam eadem proportio est ad proximum et eorum que sunt xxxviii portionum xxxiiii minutorum ad cxx portiones, ea vero que sub dupla periferie EA portionum est cxx, colligiturque colligiturque] colligitur et que V2F1 sub dupla periferie ET eorumdem xxxviii xxxiiii minutorum. Quare et dupla periferie ET graduum quidem erit xxxvii xxx ad proximum, horarum vero equinoctialium ii et dimidii. Quod oportet demonstrare.
Secundum eadem vero dabitur et EN orizontis periferia, eo quod et eius que sub dupla perferie ZA ad eam que sub dupla periferie ZA … periferie] iter. V3 iter. del. F1 AB proportio detur componi ex proportione eius que sub dupla periferie ZT ad eam que sub dupla periferie TN et proportione eius que sub dupla periferie NE ad eam que sub dupla periferie EB. Quare, et EB data, relinquetur et eius que est EN magnitudo. Manifestum autem quoniam, licet vero vero] non V2 hyemale tropicum punctum ponamus N, sed aliarum aliquam eius qui per media animalia circuli portionum, secundum eadem rursus 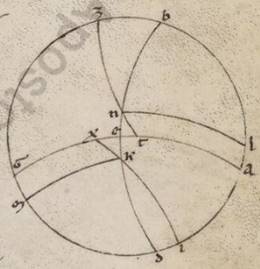 periferiarum ET et EN dabitur utraque, et preexpositis nobis per obliquationis canonium deprehensis meridiani periferiis ab unaquaque porcione eius qui per media animalia circuli et equinoctialis, hoc est simillibus NT periferie, et consequente quidem inde sub eisdem parallilis factas portiones eius qui per media, hoc est equaliter ab eodem tropico distare distare] distans V2 puncto, easdem et in eisdem partibus ab equinoctiali facere orizontis sectiones et nictimerorum quantitates equales utrasque utrisque simillium, coostenso vero et sub equalibus parallilis factas, hoc est equaliter distantes ab eodem equinoctiali puncto, et orizontis periferias equales utrimque equinoctiali facere et nictimerorum permutatim equales dissimillium quantitates. Si enim in exposita descriptione supposuerimus et K punctum secundum quod secat BED orizontis semicirculum ille qui equalis et parallilos per N scripto, et compleverimus NL et KM parallilorum portiones permutatim, et equales manifestum quoniam factas et per K polumque borealem I tetartimorion IKX descripserimus, equales quidem erunt TA quidem periferia XG periferie, eo quod utraque utrique earum que sunt LN et MK simillis fit, relinquetur autem et reliqua ET et reliqua EX equalis. Fient autem et duorum simillium trilaterorum que sunt ENT et EKX duo quidem latera duobus equalia, ET quidem ei quod est EX, at vero NT ei quod est KX. Rectus vero uterque eorum qui ad T et X angulorum, quare et basis EN basi KE fit equalis.
periferiarum ET et EN dabitur utraque, et preexpositis nobis per obliquationis canonium deprehensis meridiani periferiis ab unaquaque porcione eius qui per media animalia circuli et equinoctialis, hoc est simillibus NT periferie, et consequente quidem inde sub eisdem parallilis factas portiones eius qui per media, hoc est equaliter ab eodem tropico distare distare] distans V2 puncto, easdem et in eisdem partibus ab equinoctiali facere orizontis sectiones et nictimerorum quantitates equales utrasque utrisque simillium, coostenso vero et sub equalibus parallilis factas, hoc est equaliter distantes ab eodem equinoctiali puncto, et orizontis periferias equales utrimque equinoctiali facere et nictimerorum permutatim equales dissimillium quantitates. Si enim in exposita descriptione supposuerimus et K punctum secundum quod secat BED orizontis semicirculum ille qui equalis et parallilos per N scripto, et compleverimus NL et KM parallilorum portiones permutatim, et equales manifestum quoniam factas et per K polumque borealem I tetartimorion IKX descripserimus, equales quidem erunt TA quidem periferia XG periferie, eo quod utraque utrique earum que sunt LN et MK simillis fit, relinquetur autem et reliqua ET et reliqua EX equalis. Fient autem et duorum simillium trilaterorum que sunt ENT et EKX duo quidem latera duobus equalia, ET quidem ei quod est EX, at vero NT ei quod est KX. Rectus vero uterque eorum qui ad T et X angulorum, quare et basis EN basi KE fit equalis.
〈II.4〉 Quomodo investigandum quibus et quando et quotiens Sol ad verticem fit
Promptum vero his datis est coinvestigare quibus et quando et quotiens Sol ad verticem fit. Cum sit inde manifestum quoniam habitantibus quidem sub plus distantibus ab equinoctiali parallilis quam totius distantie estivi tropici puncti gradibus xxiii li minutis xx secundis ad proximum nullatenus Sol ad verticem fit, eis autem qui sub equidistantibus habitant semel in ipsa estiva conversione manifestum quoniam fit ad verticem, eis vero que sub minus distantibus bis, – que autem promptum facit canonii obliquationis expositio. Quot enim gradibus parallilus inquisitus distiterit ab equinoctiali eorum scilicet qui intra tropicum punctum, totidem in secundas selidiorum partes inferentes, adiacentes ipsis ex tetartimorio gradus in primis partibus selidiorum habebimus quot ab utroque punctorum Sol equinoctialium distans, ut ad estivum tropicum eis qui super super] sub V2F1 illo exposito parallilo fit ad verticem.
〈II.5〉 Quomodo ab eis que exposita sunt proportiones gnomonum ad equinoctiales et tropicas in meridiebus umbras sumantur
Quoniam vero et proposite umbrarum ad gnomonas gnomonas] corr. ex gnomonias V3 proportiones simplicius sumuntur, datis semel ea que inter tropica periferia et ea que inter orizontem et polos, ita utique fiet manifestum. Esto enim meridianus circulus ABGD circa centrum E, positoque quod ad verticem puncto A, protrahatur AEG diametros cui cui] ciii V3 ad rectos ducatur angulos in meridiani epipedo GKZN, equidistans manifestum quoniam facta a a] om. V2F1 communi orizontis et meridiani sectioni. Et quoniam tota terra puncti ac centri ad sensum et et] om. V2F1 rationem habet ad Solis speram, quare minime differt E centrum a gnomonis vertice, intelligatur quidem gnomon GE, recta vero GKZN in quam in meridiebus umbrarum ex creata ex creata] extrema V2 cadatur, protrahanturque per E equinoctialis et tropici radiique meridiani. Esto vero equinoctialis quidem BEDZ, estivus vero IETK, yemalis autem LEMN, quare et GK quidem estivam fieri umbram, GZ vero equinoctialem, GN hybernam. Quoniam ergo GD quidem periferia, cui equale est poli borealis ab orizonte elevatio in climate subiacenti, talium est xxxvi, qualium est ABG meridianus ccclx, utraque vero earum que sunt TD et DM eorumdem xxiii li minutorum xx, manifestum quoniam et reliqua quidem GT periferia, portionum erunt erunt] erit V2 xii viii minutorum xl secundorum, tota vero GM eorumdem lix li minutorum xx secundorum. Quare et eorum qui sub ipsis angulorum, qualium quidem sunt quatuor recti ccclx, talium KEG quidem angulus xii portionum viii minutorum xl secundorum, angulus vero ZEG eorumdem xxxvi, at vero NEG similiter lix portionum li minutorum xx secundorum. Qualium vero duo recti ccclx, talium angulus quidem KEG xxiiii xvii minutorum xx secundorum, at vero ZEG eorumdem lxxii, angulus autem NEG similiter cxix xlii minutorum xl secundorum. Et eorum ergo qui circa KEG et ZEG et NEG trigona orthogonia circuli describuntur que quidem super GK rectam periferia graduum est xxiiii xvii minutorum xx secundorum, et que super GE relictaque in semicirculo eorumdem clv xlii minutorum xl secundorum, que vero super GZ graduum lxxii et que super GE similiter eorumdem cviii, que autem super GN graduum cxix xlii minutorum xl secundorum, et que super GE reliquorum rursus in semicirculo lx xvii minutorum xx secundorum. Quare et earum que sub ipsis rectarum GE colligitur, qualium quidem GK est xxv xiiii minutorum xliii, talium cxvii xviii minutorum lix secundorum; qualium vero GZ rursus lxx xxxii minutorum iiii secundorum, talium xcvii iiii minutorum lvi secundorum; qualium autem GN similiter ciii xlvi minutorum xvi secundorum, talium lx xv minutorum xlii secundorum; et qualium ergo GE gnomon lx, talium et GK estiva umbra colligetur xii lv minutorum, equinoctialis autem GZ xliii xxxvi, hyemalis vero GN ciii xx minutorum ad proximum.
Manifestum autem inde quoniam et e converso, etsi due sole proportiones dentur qualescumque ab expositis tribus GE gnomonis ad umbras, et poli elevacio dabitur et que in tropica, quoniam quidem, et duobus datis quibuslibet ad E angulis, datur et reliquus, eo quod equales sint ED ED] TD V2 et DM periferie. Propter eam tamen que circa ipsas observationes diligentiam, illa quidem indubitanter utique sumetur secundum quem demonstravimus modum. Expositarum autem umbrarum ad gnomonas proportiones non similiter, eo quod equinoctialium quidem tempus indeterminatum quodam modo secundum seipsum est, hyemalium vero verticum extrema difficile congnosci congnosci] discerni V2 agnosci F1 possunt.
〈II.6〉 Expositio eorum que secundum ydiomatum parallilum
Eodem autem modo his et in aliis parallilis sumentes universalia expositorum ydiomatum, quarta unius hore equinoctialis utpote suffitienti differentias inclinationum adaugentes, faciemus universalem eorum expositionem ante eam que particulariter superaccidentium. Principium vero ab eo qui sub ipsum equinoctialem parallilo faciemus. Qui determinat quidem ad proximum eam que ad meridiem totius partem tetartimorii eius que penes nos habitabilis. Solus vero habet dies et noctes universas equales invicem. Omnes enim qui in spera circulo parallili equinoctiali ibi tantum in duo equa ab orizonte dividuntur, quare que super terram eorum portiones et similes invicem et equales eis que super terra per singulos, hoc in nulla inclinationum contingente, sed solo quidem rursus equinoctiali ubique et in duo equa ab orizonte diviso et dies qui secundum ipsum noctibus equales ad sensum fatiente, quoniam et ipse maximorum est circulorum, reliquis vero in non equalia divisis, et secundum nostre habitationis inclinationem, australioribus quidem ipso et eas que super terram portiones eis que sub terra minores et dies noctibus breviores fatientibus, borealioribus vero e converso et que super terram portiones maiores et dies longiores. Est autem et amphischios iste parallilus. Bis enim sub eo existentibus fit Sol ad verticem secundum equinoctialis et obliqui circuli sectiones, 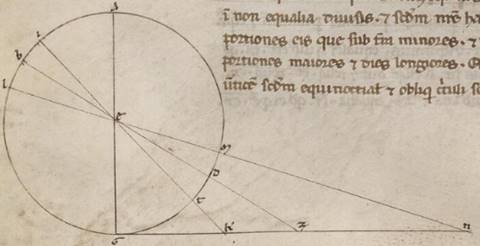 quare tunc tantum gnomones in mensuranisibus mensuranisibus] mesuranisibus V2F1 aschii fiunt. Sole vero borealem quidem semicirculum perambulante, gnomonum umbre declinant ad meridiem, australem vero ad arctas. arctas] arctos V2F1 Et est hic qualium gnomon lx, talium utraque et estiva umbra et hiberna xxvi et dimidii ad proximum. Dicimus autem universaliter umbras que in meridiebus fiunt et ut nullo cura digni differentes, eo quod non omnino in ipsis meridiebus et equinoctia et conversiones compleantur. Eis autem qui sub equinoctiali ad verticem quidem fiunt astrorum quecumque in ipso equinoctiali circumlationes periforas faciunt, cuncta vero et orientia apparent et occidentia, spere polis in ipso orizonte existentibus nullumque circulum facientibus, neque parallilorum semper apparentem semper ne semper ne] semperve V2 disparentem, neque meridianorum colurum. Habitationis ante ante] autem V2F1 esse quidem sub equinoctiali contingere aiunt, ut valde eucrato, eo quod Sol eis que ad verticem punctis minime immoretur, veloci facta circa equinoctiales portiones secundum latitudinem recessione, unde utique estas eucrata sit, neque in conversionibus multum distat ab eo quod ad verticem, quare neque hyemem validam facit. Que vero sint habitationes, non utique habemus persuasibiliter dicere. Inpenetrabiles enim sunt usque in presens eis qui in ea que penes nos habitabili et oppinionem magis utique quis quam hystoriam arbitretur ea que dicuntur de ipsis. Propria ergo eius quidem qui sub equinoctiali parallili, concolligenti dicere, hec utique erunt. De reliquis vero, a quibus et habitationes estimant aliqui comprehendi, adnectemus illa communius, ne in unoquoque dicamus idem, quoniam videlicet eorum qui deinceps uniuscuiusque in verticem fiunt astrorum, quecumque equali periferia distiterint ab equinoctiali in eo qui per polos ipsius circulo, qua et ipse subiectus parallilus distat, et quoniam apparens quidem semper fit is circulus qui polo quidem boreali polo equinoctialis, spatio vero poli elevatione describitur, stelleque sub isto deprehense semper apparentes, disparens vero semper circulus qui polo quidem australi, australi] add. polo V2 spatio vero eodem scribitur et que in isto stelle semper disparentes.
quare tunc tantum gnomones in mensuranisibus mensuranisibus] mesuranisibus V2F1 aschii fiunt. Sole vero borealem quidem semicirculum perambulante, gnomonum umbre declinant ad meridiem, australem vero ad arctas. arctas] arctos V2F1 Et est hic qualium gnomon lx, talium utraque et estiva umbra et hiberna xxvi et dimidii ad proximum. Dicimus autem universaliter umbras que in meridiebus fiunt et ut nullo cura digni differentes, eo quod non omnino in ipsis meridiebus et equinoctia et conversiones compleantur. Eis autem qui sub equinoctiali ad verticem quidem fiunt astrorum quecumque in ipso equinoctiali circumlationes periforas faciunt, cuncta vero et orientia apparent et occidentia, spere polis in ipso orizonte existentibus nullumque circulum facientibus, neque parallilorum semper apparentem semper ne semper ne] semperve V2 disparentem, neque meridianorum colurum. Habitationis ante ante] autem V2F1 esse quidem sub equinoctiali contingere aiunt, ut valde eucrato, eo quod Sol eis que ad verticem punctis minime immoretur, veloci facta circa equinoctiales portiones secundum latitudinem recessione, unde utique estas eucrata sit, neque in conversionibus multum distat ab eo quod ad verticem, quare neque hyemem validam facit. Que vero sint habitationes, non utique habemus persuasibiliter dicere. Inpenetrabiles enim sunt usque in presens eis qui in ea que penes nos habitabili et oppinionem magis utique quis quam hystoriam arbitretur ea que dicuntur de ipsis. Propria ergo eius quidem qui sub equinoctiali parallili, concolligenti dicere, hec utique erunt. De reliquis vero, a quibus et habitationes estimant aliqui comprehendi, adnectemus illa communius, ne in unoquoque dicamus idem, quoniam videlicet eorum qui deinceps uniuscuiusque in verticem fiunt astrorum, quecumque equali periferia distiterint ab equinoctiali in eo qui per polos ipsius circulo, qua et ipse subiectus parallilus distat, et quoniam apparens quidem semper fit is circulus qui polo quidem boreali polo equinoctialis, spatio vero poli elevatione describitur, stelleque sub isto deprehense semper apparentes, disparens vero semper circulus qui polo quidem australi, australi] add. polo V2 spatio vero eodem scribitur et que in isto stelle semper disparentes.
Secundus vero vero] om. V2F1 fit parallilus, secundum quem maxima dies horarum est equinoctialium xii et quarte. Iste vero distat ab equinoctiali gradibus iiii et quarta et scribitur per Talbanen Talbanen] Taprobanen V2 insulam. Est autem et iste amphischiorum, Sole rursum bis sub eo habitantibus facto ad verticem et gnomones in mensuranibus mensuranibus] mesuranisibus V2F1 aschios faciente, quando distat ab estiva conversione in utraque parte gradibus lxxix et dimidio. Quare, clix ipso perambulante, gnomonum umbre declinant in australia, reliquos autem cci, in borealia. Et est hic qualium gnomon lx, talium equinoctialis quidem umbra iiii iii xi, estiva vero xxi iii, hyemalis autem xxxii.
Tertius est parallilus, secundum quem fit maxima dies horarum equinoctialium xii et dimidii, distatque iste ab equinoctiali gradibus viii xxv et describitur per Abalitum sinum. Est autem et amphischiorum iste, Sole bis his qui sub eo facto supra verticem et gnomonas in mesuranibus mesuranibus] mensuranisibus V2F1 aschios fatiente, quando ab estiva conversione distat in utraque parte gradibus lxix. Quare, cxxxviii quidem ipso perambulante, gnomonum umbre declinant ad meridiem, reliquos autem ccxxxii, ad arctos. Et est hic qualium gnomonum lx, talium quidem equinoctialis umbra viii et dimidii et tertie, estiva vero xvi dimidii iii, hyemalis autem xxxvii dimidii iii xv ii.
Quartus parallilus est, secundum quem fit longissima dies horarum equinoctialium xii dimidii et iiiia, distatque iste ab equinoctiali gradibus xii et dimidio. Et scribitur per Adolitum Adolitum] Adoliticum V2 calpum. Est vero et ipse amphischiorum, Sole rursum bis eis qui sub ipso facto in vertice gnomonasque in mesuranisibus fatiente aschios, quando conversione distat ab estiva in utraque parte gradibus lvii xii iiia. Quare cxv iiia ipso perambulante, gnomonum umbre declinant ad meridiem, reliquos autem ccxliiii xii ad arctos. Et est qualium gnomon lx, talium equinoctialis quidem umbra xiii iiia, estiva vero xii, hyemalis autem xliiii dimidii via.
Quintus est parallilus, secundum quem fit dies productissima horarum equinoctialium xiii, distatque iste ab equinoctiali gradibus xvi xxvii vel xxxvii et scribitur per Meroem insula. insula] insulam F1 Est vero et ipse amphischiorum, Sole bis sub eo habitantibus facto ad verticem gnomonasque in mesuranisibus aschios faciente, quando distat ab estiva conversione in utraque parte gradibus xlv. Quare, xc quidem eo percurrente, gnomonum umbre declinant ad meridiem, reliquos vero cclxx, ad arctos. Et est hic qualium gnomon lx, talium equinoctialis quidem umbra xvii dimidii iiiia, estiva vero vii et dimidii iiiia, hyemalis autem li.
Sextus est parallilus, secundum quem fit maxima dies horarum equinoctialium xiii et quarte. Distat autem ab equinoctiali gradibus xx xiiii minutis describiturque per Anapaton. Est vero et ipse amphischiorum, Sole eis qui sub ipso bis facto supra verticem gnomonasque in meridiebus aschios faciente, quando conversione distat ab estiva in utraque parte gradibus xxxi. Quare, lxii quidem ipso perambulante, gnomonum umbre declinant ad meridiem, reliquos autem ccxcviii, ad arctos. Et est hic qualium gnomon lx, talium equinoctialis quidem umbra xxii via, estiva vero iii dimidii iiiia, hyemalis autem lviii via.
Septimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xiii et dimidii distatque iste ab equinoctiali gradibus xxiii li minutorum. Scribiturque per Sienem. Primus vero est iste parallilus eorum qui eteroschii nominantur. Numquam enim sub eo habitantibus in meridiebus gnomonum umbre declinant ad meridiem, sed in ipsa quidem sola estiva conversione Sol eis fit ad verticem gnomonesque aschii conspitiuntur. Tantum enim distat ab equinoctiali, quantum et estivum tropicum punctum. Omni vero alio tempore gnomonum umbre declinant ad arctos. Et hic est qualium gnomon lx, talium equinoctialis quidem umbra xxvi et dimidii, hyemalis autem lxv dimidii iiia, estiva vero aschios est. Sed et omnes isto borealiores parallili eum usque qui nostram deteriat habitabilem etheroschii sunt. Nunquam enim secundum ipsos gnomones in meridiebus neque aschii fiunt, neque umbras faciunt ad meridiem, sed semper ad arctos, eo quod numquam supra verticem Sol eis fiat.
Octavus est parallilus, secundum quem fit maxima dies horarum equinoctalium xiii et dimidii iiiia. Distat autem hic ab equinoctiali gradibus xxvii xii. Scribiturque per Ptholomaidem que in Thebaide, que et Mercurii vocatur. Et est hic qualium gnomon lx, talium estiva quidem umbra iii et dimidii, equinoctialis autem xxvi dimidii et iiiia, hiemalis vero lxx iiii et via.
Nonus est parallilus, secundum quem fit maxima dies horarum equinoctialium xiiii. Distat autem iste ab equinoctiali gradibus xxx xxii minutis. Scribiturque per inferiorem provintiam Egipti. Et hic est qualium gnomon lx, talium estiva quidem umbra vi et dimidii iiia, equinoctialis autem xxxv xii, hyberna vero lxxxiii xii.
Decimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xiiii iiiia. Distat autem ab equinoctiali gradu gradu] gradibus V2 xxxiii xviii scribiturque per Phenitiam mediam. Et est hic qualium gnomon lx, talium estiva quidem umbra x, equinoctialis autem xxxix et dimidii, hyemalis vero xciii et xii.
Undecimus est parallilus, secundum quem longissima dies horarum est equinoctialium xiiii et dimidii. Distat autem ab equinoctiali gradibus xxxvi et descibitur per Rodum. Et est hic qualium gnomon lx, talium estiva quidem umbra xii et dimidii iiia xiia, equinoctialis autem xliii et dimidii, hyberna vero ciii iia.
Duodecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xiiii et dimidii et iiiia. Distat autem iste ab equinoctiali gradibus xxxviii xxxv, scribiturque per Smirnam. Et est hic qualium gnomon lx, talium estiva quidem umbra xv iii ii, equinoctialis autem xlvii dimidii iiia, hyberna vero cxiiii dimidii iiia xiia.
Tertiusdecimus est parallilus, secundum quem longissima dies fit horarum equinoctialium xv. Distat autem iste ab equinoctiali gradibus xl lvi minutis et descibitur per Ellespontum. Et est hic qualium gnomon lx, talium estiva quidem umbra xviii et dimidii, equinoctialis autem lii via, hyberna hyberna] add. vero V2 cxx dimidii iiia.
Quartusdecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xv iiiia, distat autem distat autem] distatque V2F1 iste ab equinoctali gradibus xliii iiii minutis, et describitur per Massaliam. Et est hic qualium gnomon lx, talium estiva quidem umbra xx et dimidii et iii, equinoctialis autem lv dimidii iiia xiia, hyberna vero cxl iiiia.
Quintusdecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xv et dimidii, distatque iste ab equinoctiali gradibus xlv et unius minuti et … minuti] xxx minutis V2F1 et describitur per medium Pontum, estque hic qualium gnomon lx, talium estiva quidem umbra xxiii iiiia, equinoctialis autem eorumdem lx, atque hyberna clv x iiii vel ii.
Sextusdecimus est parallilus, secundum quem fit longissima dies horarum equinoctialium xv et dimidii et iiiia, distatque iste ab equinoctiali gradibus xlvi li et descibitur per fontes Histri fluminis, est hic que hic que] inv. V2F1 qualium gnomon lx, talium estiva quidem umbra xxv et dimidii, equinoctialis autem lxiii et dimidii iiia xiia, hiemalis clxxi iiii ii via ii.
Septimusdecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvi. Distat autem iste ab equinoctiali gradibus xlviii xxxii, scribiturque per emissiones Boristenis, estque hic qualium gnomon lx, talium estiva quidem xxvii et dimidii, equinoctialis autem lxvii et dimidii iii, atque hyberna clxxxviii et dimidii xii.
Octavusdecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvi iiiia, distatque iste ab equinoctiali gradibus l. Et describitur per medium Meotidis paludis, estque hic qualium gnomon lx, talium estiva quidem umbra xxix dimidii iii xiia, equinoctialis autem lxxi iii, atque hyberna ccviii iii.
Nonusdecimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvi et dimidii. Distat autem iste ab equinoctiali gradibus li dimidio via, scribiturque per australissima Britannie, estque hic qualium gnomon lx, talium estiva quidem umbra xxxi iii xii, equinoctialis autem lxxv iii xii, atque hyberna ccxxxix ccxxxix] ccxxix V2 iii.
Vicessimus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvi dimidii iiii, distatque iste ab equinoctiali gradu gradu] gradibus V2 lii l, et describitur per Reni emissiones, estque hic qualium gnomon lx, talium estiva quidem xxxii xxxii] xxxiii V2 iiia, equinoctialis autem lxxix xii, atque hyberna ccliii via.
Vicessimus primus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvii. Distat autem iste ab equinoctiali gradibus liiii i. Scribiturque per Tanaidis emissiones, Estque hic qualium gnomon lx, talium estiva quidem umbra xxxiiii dimidii iii xiia, equinoctialis autem lxxxii et dimidii, hyberna cclxxviii dimidii iiiia.
Vicessimus secundus est parallilus, secundum quem fit maxima dies horarum equinoctialium xvii iiiia, distatque iste ab equinoctiali gradibus lv et describitur per Brigantium magne Britannie, Estque hic qualium gnomon lx, talium estiva quidem umbra xxxvi iiiia, equinoctialis autem lxxxv iii, hyberna ccciiii dimidii.
Vicessimus tercius est parallilus, secundum quem fit maxima dies horarum equinoctialium xvii dimidii, distatque iste ab equinoctiali gradibus lvi, et decribitur per medium Britannie magne, estque hic qualium gnomon lx, talium estiva quidem umbra xxxvii iii, equinoctialis autem lxxxviii dimidii iii, hiberna vero cccxxxv et iiiia.
Vicessimus quartus est parallilus, secundum quem fit longissima dies horarum equinoctialium xvii dimidii iiie. Distat autem ab equinoctiali iste gradibus lvii, scribiturque hic per Catouractonium Britannie, et est hic qualium gnomon lx, talium estiva quidem umbra xxxix iii, equinoctialis autem xcii iii x ii, hiberna vero ccclxxii x ii.
Vicessimus quintus est parallilus, secundum quem fit maxima dies horarum equinoctialium xviii, distatque iste ab equinoctiali gradu gradu] gradibus V2 lviii, et describitur per autralia parve Britannie, estque hic qualium gnomon lx, talium estiva quidem umbra xlii x, equinoctialis autem xcvi, hyberna vero ccccxix xii.
Vicessimus sextus est parallilus, secundum quem fit maxima dies horarum equinoctialium xviii dimidii. Distat autem iste ab equinoctiali gradu gradu] gradibus V2 lix et dimidio, scribiturque per media parve Britannie. Non sumus autem hic usi quarte horarum augmento, quod et continui iam fiant parallili et ellevacionum differentia nec unius totius gradus colligatur, quodque non similiter in nobis in nobis] inv. V2F1 amplius borealibus studium intendere intendere] impendere V2F1 competit, propter quod et umbrarum ad gnomonas proportiones, ut in segregatas segregatas] segregatis V2F1 locis, superfluum diximus apponere.
Ubi ergo maxima dies horarum est equinoctialium xix, ille parallilus distat ab equinoctiali gradibus lxi, scribitur quoque scribitur quoque] scribiturque V2 per borealia parve Britannie.
Ubi vero maxima dies horarum est equinoctialium xix et dimidii, ille parallilus distat ab equinoctiali gradibus lxii et describitur per eas que Ebode insule appellantur.
Ubi vero longissima dies horarum est equinoctialium xx, ille parallilus distat ab equinoctiali gradibus lxiii et describitur per Thilem insulam.
Ubi autem maxima dies horarum est equinoctialium xxi, ille parallilus distat ab equinoctiali gradibus lxiiii et dimidio, scribiturque per Sciticas gentes ignotas.
Ubi vero maxima dies horarum est equinoctialium xxii, distat ille parallilus ab equinoctiali gradibus lxv et dimidio.
Ubi autem maxima dies horarum est equinoctialium xxiii, distat ille parallilus ab equinoctiali gradibus lxvi.
Ubi maxima dies horarum est equinoctialium est est] om. V2F1 xxiiii, parallilus ille distat ab equinoctiali gradibus lxvi viii minutis xl secundis. Et est iste paraschiorum primus. In sola enim estiva conversione Sole ibi minime occidente, gnomonum umbre super omnes orizontis partes nutus faciunt. Estque hic estivus quod quod] quidem V2F1 tropicus parallilus semper apparens, tropicus autem parallilus disparens semper, eo quod ambo permutatim contingant orizontem. Fit vero et in obliquis quique per media animalia circulus idem orizonti, quando ipsius punctus vernalis oritur.
Si vero quis aliter contemplationis causa et de adhuc borealioribus inclinationibus quedam universaliorum siptomatum siptomatum] sinptomatum V2F1 inquisierit, inveniet utique ubi elevatio est graduum lxvii ad proximum, ibi non occidentes omnino ex utraque conversionis eius qui per media animalia circuli gradus xv. Quare maxima dies et umbrarum super omnes orizontis partes circumductio fere menstrua fit. Erunt enim et hec facile intelligibilia per expositum obliquationis canonium. Quot enim gradibus invenerimus ab equinoctiali distantem parallilum deprehendentem verbi gratia in utraque tropici puncti gradus xv, factum vero tunc vel semper apparentem vel semper disparentem, cum deprehensa eius qui per media animalia circuli portionem, totidem gradibus manifestum quoniam deficiet a tetartimorii porcionibus xc poli borealis elevatio.
Itaque et ubique ubique] ubi V2F1 quidem elevatio poli graduum est lxix et dimidii, ibi utique quis inveniet omnino non occidentes ex utraque parte estive conversionis gradus xxx. Quare fere mensibus ad proximum duobus et macxima dies et gnomones perischii fiunt.
Ubi vero elevatio poli graduum est lxxiii iii, ibi utique quis reperiet non occidentes in utraque estive conversionis gradus xlv. Quare et maxima dies et gnomones perischii tribus ad proximum mensibus extenduntur.
Ubi vero elevacio poli graduum est lxxviii iii, ibi utique quis inveniet non occidentes in utraque eiusdem conversionis gradus lx, quare iiii fere mensium et maximam diem et umbrarum circumductionem fieri.
Ubi elevatio poli graduum est lxxxiiii, ibi quis reperiet non occidentes in utraque parte estive conversionis gradus lxxv, quare v rursus mensium fere longissimam diem fieri et gnomonas tempore perischios equali.
Ubi totius tetartimorii gradibus xc borealis polus ab orizonte elevatur, ibi borealiorum quidem equinoctiali eius qui per media animalia semicirculus totus nunquam sub terra fit, australiorum autem totus nunquam super terram. Quare unam quidem diem cuiusque anni unaqueque nox utraque ad proximum vi mensium fit, gnomonesque semper perischii contingunt. Propria vero sunt et huiusmodi inclinationes inclinationes] inclinationis V2 borealem polum super verticem fieri et equinoctialem et semper apparentis et semper disparentis, amplius quoque orizontis positionem deprehendere, super terram quidem facientem semper totum borealius ab eodem hemisperium, sub terra vero australius.
〈II.7〉 De his que inclinata inclinata] in inclinata F1 spera eius qui per media animalia circuli et equinoctialis coascensionibus
Expositis ergo que universaliter circa inclinationes considerantur, deinceps utique erit demonstrare quomodo sumantur secundum unamquamque inclinationem et conscendentia conscendentia] coascendentia V2F1 equinoctialis tempora eius qui per media animalia circuli periferiis, a quibus et alia omnia particularium consequenter nobis docebuntur. Utemur vero nominibus animalium et in ipsis obliqui circuli dodecatimoriis, et quasi principiis ipsorum a tropicis et equinoctialibus punctis sumptis, quod quidem a vernali equinoctio ut in consequentia motus universorum primum dodecatimorium Arietem appellantes, secundum Taurum et in eis que deinceps eodem modo secundum traditum nobis ordinem xii animalium. Demonstrabimus vero primum quoniam equidistantes ab eodem equinoctiali puncto eius qui per media animalia circuli periferie equalibus semper equinoctialis circuli periferiis coascendunt. Esto enim meridianus quidem circulus ABGD, orizontis vero semicirculus BED, equinoctialis vero circuli AEG et obliqui circuli due portiones ZI et TK, ut utrumque quidem punctorum Z et T vernale ad equinoctium supponatur, equales vero in utraque ipsius deprehense periferie ZI et TK per K et I puncta oriantur: dico quoniam et utreque eis coasscendentes equinoctialis periferie, hoc est ZE et TE, equales sunt. Sint enim pro polis equinoctialis L et M puncta, scribanturque per ea maximorum portiones circulorum que sunt LEM et LT, ampliusque LK et ZM et MI. Quoniam ergo equalis est ZI ei que est TK et per K et I scripti parallili equidistant in utraque ab 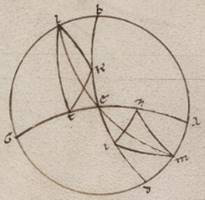 equinoctiali, quare et LK LK] add. quidem V2 ei que est MI fit equalis, EK vero ei que est EI, equilatera ergo sunt LKT quidem ei quod est MIZ, at vero LEK ei quod est MEI. Et angulus ergo KLE quidem equalis est angulo IME, angulus vero KLT totus angulo IMZ toti, quare et reliquus ELT reliquo EMZ equalis erit, et basis ergo ET basi EZ equalis est. Quod oportet demonstrare.
equinoctiali, quare et LK LK] add. quidem V2 ei que est MI fit equalis, EK vero ei que est EI, equilatera ergo sunt LKT quidem ei quod est MIZ, at vero LEK ei quod est MEI. Et angulus ergo KLE quidem equalis est angulo IME, angulus vero KLT totus angulo IMZ toti, quare et reliquus ELT reliquo EMZ equalis erit, et basis ergo ET basi EZ equalis est. Quod oportet demonstrare.
Rursus vero demonstrabimus quoniam coasscendentes equinoctialis periferie equalibus et equidistantibus ab eodem tropico puncto eius qui per media animalia circuli coutreque coutrisque ipsarum eis que in recta spera ascensionibus sunt equales. Adiaceat enim meridianis meridianis] meridianus V2F1 ABGD et semicirculorum BED orizontis et AEG equinoctialis scribanturque due et equales et equidistantes ab hyberno puncto obliqui circuli periferie ZI et TI, puncto quidem Z autumpnali, T vero puncto vernali subiacente, quare I quidem punctus communis ortus ipsarum et orizontis, eo quod sub eodem parallilo circulo equinoctiali comprehendantur ZI et TI periferie. Coascendere vero manifestum TE quidem ei que est TE TE] TI V2F1, at vero EZ ei que est 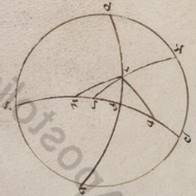 ZI. Manifestum ergo fit inde quoniam et tota TEZ equalis est eis que in recta spera periferiarum ZI et TI ascensionibus. Si enim supponentes australem equinoctialis polum K punctum descripserimus per ipsum et I maximi circuli tetartimorium KIL equipotens ei qui in recta spera orizonti, fit rursum TI TI] TL V2F1 quidem coascendens ei que est TI in recta spera LZ vero coascendens ei que est ZI similiter, quoque et coutrasque TLZ coutrisque TEZ et equales esse et sub una eadem contineri que est IZ. IZ] TZ V2F1 Quod oportet ostendere.
ZI. Manifestum ergo fit inde quoniam et tota TEZ equalis est eis que in recta spera periferiarum ZI et TI ascensionibus. Si enim supponentes australem equinoctialis polum K punctum descripserimus per ipsum et I maximi circuli tetartimorium KIL equipotens ei qui in recta spera orizonti, fit rursum TI TI] TL V2F1 quidem coascendens ei que est TI in recta spera LZ vero coascendens ei que est ZI similiter, quoque et coutrasque TLZ coutrisque TEZ et equales esse et sub una eadem contineri que est IZ. IZ] TZ V2F1 Quod oportet ostendere.
Et factum est nobis manifestum per hec quoniam etsi in uno solo tetartimorio secundum unamquamque inclinationem particulares coascensiones ostenderimus, coostensas habebimus et eas que reliquorum trium tetartimoriorum. His ergo ita se habentibus, subiaceat rursus qui per Rodum parallilus, ubi maxima quidem dies horarum est equinoctialium xiiii et dimidii, borealis vero polus elevatus est ab orizonte gradibus xxxvi; sitque meridianus circulus ABGD et orizontis quidem similiter semicirculus BED, equinoctialis vero circuli AEG; eius autem qui per media animalia ZIT ita se habens, ut I subiaceat vernale punctum; sumptoque boreali polo equinoctialis ad K punctum, scribatur per ipsum et eam que ad L sectionem eius qui per media animalia circuli et orizontis maximi circuli tetartimorion KLM, proponatur vero, IL periferia data, coascendentem ipsi equinoctiali, hoc est IE, invenire, contineatque primum IL Arietis dodecatimorion. Quoniam ergo rursus in descriptione maximorum circulorum in duas EG et GK scripte sunt ED et KM secantes seinvicem ad L, proportio eius que sub dupla periferie KD ad eam que sub dupla periferie DG composita est ex proportione eius que sub dupla periferie 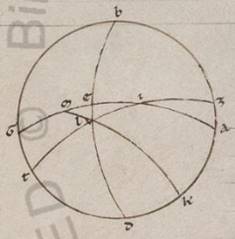 KL ad eam que sub dupla periferie LM et proportione eius que sub dupla periferie ME ad eam que sub dupla periferie EG. At dupla quidem periferie KD graduum est lxxii et que sub ipsa recta portionum lxx xxx xxx] xxxii V2F1 minutorum iiii secundorum, que vero periferie GD graduum est cviii et que sub ea recta portionum xcvii iiii minutorum lvi secundorum; et rursus quidem dupla periferie KL graduum est clvi xli minutorum et que sub ea recta porcionum cxvii xxxi minutorum xv secundorum. Dupla vero periferie LM graduum xxiii xix minutorum lix secundorum et que sub ea recta porcionum xxiiii xv minutorum lvii secundorum. Si ergo a proportione eorum que sunt lxx xxxii minutorum iiii secundorum ad xcvii portiones iiii minuta lvi secunda abstulerimus proportionem eorum que sunt cxvii portionum xxxi minutorum xv secundorum ad xxiiii portiones xv minuta lvii secunda, relinquetur proportio eius que sub dupla periferie periferie] add. ME ad eam que sub dupla periferie V2F1 EG, que eorum que sunt xvii portionum o minuti v secundorum ad cxx portiones; et est que sub dupla periferie EG portionum cxx, que ergo sub dupla perferie ME eorumdem xviii portionum o minuti v secundorum. Quare et dupla quidem periferie ME graduum erit xvii ad proximum, ipsa vero ME eorumdem viii xxxviii xxviii. At quoniam tota IM periferia periferie IL in recta spera coascendit, predemonstratorum est graduum xxvii l, et reliqua ergo EI graduum est xix xxii xii. Et coostensum est quoniam et Piscium quidem dodecatimorium eisdem temporibus coascendit xix xii, utrumque vero et quod Virginis et quod chelarum in relictis ad in duplam eius que in recta spera ascensionem temporibus xxxvi xxviii minutis. Quod oportet demonstrare.
KL ad eam que sub dupla periferie LM et proportione eius que sub dupla periferie ME ad eam que sub dupla periferie EG. At dupla quidem periferie KD graduum est lxxii et que sub ipsa recta portionum lxx xxx xxx] xxxii V2F1 minutorum iiii secundorum, que vero periferie GD graduum est cviii et que sub ea recta portionum xcvii iiii minutorum lvi secundorum; et rursus quidem dupla periferie KL graduum est clvi xli minutorum et que sub ea recta porcionum cxvii xxxi minutorum xv secundorum. Dupla vero periferie LM graduum xxiii xix minutorum lix secundorum et que sub ea recta porcionum xxiiii xv minutorum lvii secundorum. Si ergo a proportione eorum que sunt lxx xxxii minutorum iiii secundorum ad xcvii portiones iiii minuta lvi secunda abstulerimus proportionem eorum que sunt cxvii portionum xxxi minutorum xv secundorum ad xxiiii portiones xv minuta lvii secunda, relinquetur proportio eius que sub dupla periferie periferie] add. ME ad eam que sub dupla periferie V2F1 EG, que eorum que sunt xvii portionum o minuti v secundorum ad cxx portiones; et est que sub dupla periferie EG portionum cxx, que ergo sub dupla perferie ME eorumdem xviii portionum o minuti v secundorum. Quare et dupla quidem periferie ME graduum erit xvii ad proximum, ipsa vero ME eorumdem viii xxxviii xxviii. At quoniam tota IM periferia periferie IL in recta spera coascendit, predemonstratorum est graduum xxvii l, et reliqua ergo EI graduum est xix xxii xii. Et coostensum est quoniam et Piscium quidem dodecatimorium eisdem temporibus coascendit xix xii, utrumque vero et quod Virginis et quod chelarum in relictis ad in duplam eius que in recta spera ascensionem temporibus xxxvi xxviii minutis. Quod oportet demonstrare.
Rursum IL perferia contineat duum dodecatimoriorum Arietis et Tauri gradus lx per subiacentia ergo aliis manentibus eisdem, dupla quidem periferie KL graduum est est] om. V2F1 fit cxxxviii lix minutorum xlii secundorum et que sub ea recta portionum portionum] add. cxii xxiii lvi, dupla vero periferie LM graduum xli o xviii et que sub recta portionum V2F1 xlii et minuti xlviii secundorum. Si ergo rursum a proportione eorum que sunt lxx portionum xxxii minutorum iiii secundorum ad xviii portiones iiii minuta lvi secunda abstulerimus proportionem eorum que sunt cxii portionum xxiii minutorum lvi secundorum ad xlii portiones i minutum xlviii secunda, reliquetur proportio eius que sub dupla periferie ME ad eam que sub dupla periferie EG, que eorum que sunt xxxii xxxvi iiii ad cxx. Et est que sub dupla periferie EG portionum cxx, que ergo sub dupla periferie ME eorumdem est xxxii xxxvi iiii. Quare dupla quidem periferie ME graduum est xxxi xxxii ad proximum, ipsa vero ME eorumdem xv xlvi. Sed tota MI secundum eadem premonstrata est graduum lvii xliiii minutorum, et reliqua ergo IE graduum est xli lviii. Aries ergo et Taurus ascendunt ambo in temporibus xli lviii, quorum ostensus est Aries coascendens 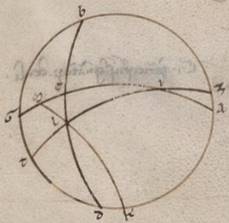 temporibus xix xii, et solum ergo Tauri dodecatimorium coascendit temporibus xxii xlvi. Propter eadem vero rursum et Aquarii quidem dodecatimorium coascendit temporibus xxii xlvi, utrumque vero quod scilicet Leonis et quod Scorpii defitientibus in duplam eius que in recta spera ascensionem temporibus xxxvii ii. Quoniam vero et maxima dies horarum est equinoctialium xiiii et dimidii, minima vero ix et dimidii, manifestum quoniam et qui quidem a Cancro usque ad Sagittarium semicirculus coascendet equinoctialis temporibus ccxvii xxx, que vero a Capricorno usque Geminos temporibus cxlii xxx. Quare utrumque et quidem eorum que ex utraque parte vernalis puncti tetartimoriorum coascendet temporibus lxxi xv, utrumque vero eorum que ex utraque autumpnalis puncti temporibus cviii xlv. Quare et reliquum quidem Geminorum et Egoceri dodecatimorium utrumque coascendet temporibus xxix xvii defitientibus in tetartimorii tempora lxxi xv. Reliquum vero Cancri et Sagittarii utrumque temporibus xxxv xv defitientibus rursum in huius tetartimorii tempora cviii xlv. Et manifestum quoniam eodem utique modo his sumemus et minorum portionum eius qui per media animalia circuli coortus.
temporibus xix xii, et solum ergo Tauri dodecatimorium coascendit temporibus xxii xlvi. Propter eadem vero rursum et Aquarii quidem dodecatimorium coascendit temporibus xxii xlvi, utrumque vero quod scilicet Leonis et quod Scorpii defitientibus in duplam eius que in recta spera ascensionem temporibus xxxvii ii. Quoniam vero et maxima dies horarum est equinoctialium xiiii et dimidii, minima vero ix et dimidii, manifestum quoniam et qui quidem a Cancro usque ad Sagittarium semicirculus coascendet equinoctialis temporibus ccxvii xxx, que vero a Capricorno usque Geminos temporibus cxlii xxx. Quare utrumque et quidem eorum que ex utraque parte vernalis puncti tetartimoriorum coascendet temporibus lxxi xv, utrumque vero eorum que ex utraque autumpnalis puncti temporibus cviii xlv. Quare et reliquum quidem Geminorum et Egoceri dodecatimorium utrumque coascendet temporibus xxix xvii defitientibus in tetartimorii tempora lxxi xv. Reliquum vero Cancri et Sagittarii utrumque temporibus xxxv xv defitientibus rursum in huius tetartimorii tempora cviii xlv. Et manifestum quoniam eodem utique modo his sumemus et minorum portionum eius qui per media animalia circuli coortus.
Amplius autem commodius et artifitiosius ipsos investigabimus sic. Esto enim primum meridianus circulus ABGD, et orizontis quidem semicirculus BED, equinoctialis vero AEG, eius autem qui per media animalia ZEI, sectione E vernale ad punctum subiacente et assumpta in ipso ET periferia quecumque, scribatur TK portio eius qui per T parallili circulo equinoctiali; sumptoque L polo equinoctialis, per ipsum maximorum tetartimoria circulorum describantur LTM et LKN, amplius autem LE. Manifestum ergo inde est quoniam et ET proportio eius qui per media animalia in recta quidem spera EM periferie equinoctialis coascendit, in inclinata vero spera equali eius que est NM, quoniam KT quidem parallili periferia, cui coascendit ET porcio, similis est NM periferie equinoctialis. Similles autem periferie parallilorum in equalibus 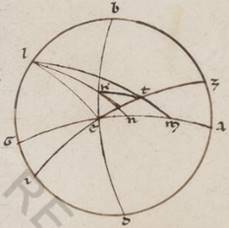 ubique temporibus ascendunt, et NE ergo periferia minor est que in inclinata spera ET porcionis ascensio ea que in recta spera. Et demonstratum est quoniam universaliter, si describantur quedam ita periferie maximorum circulorum, ut LTM et LKN, portio EN continebit differentiam earum que in recta et inclinata spera ascensionum deprehensarum eius qui per media animalia circuli periferiarum ab E et descripto per K parallilo. Quod oportet ostendere.
ubique temporibus ascendunt, et NE ergo periferia minor est que in inclinata spera ET porcionis ascensio ea que in recta spera. Et demonstratum est quoniam universaliter, si describantur quedam ita periferie maximorum circulorum, ut LTM et LKN, portio EN continebit differentiam earum que in recta et inclinata spera ascensionum deprehensarum eius qui per media animalia circuli periferiarum ab E et descripto per K parallilo. Quod oportet ostendere.
Hoc preconsiderato, adiaceat descriptio solorum meridiani et eorum que que] qui V2F1 orizontis et equinoctialis semicirculorum, ac per Z australem equinoctialis polum duo tetartimoria maximorum scribantur circulorum, sintque ZIT et ZKL. Subiaceat autem I quidem punctus communis per hybernum tropicum punctum scripti parallili et orizontis, at vero K communis descripti per principium verbi gratia Pistium vel et alterius alicuius tetartimorii portionum date. In duas ergo rursum maximorum circulorum periferias ZT et ET scripte sunt ZKL et EKI secantes seinvicem ad K. Et est proportio eius que sub dupla periferie TI ad eam que sub dupla periferiae ZI composita ex proportione eius que sub dupla periferie TE ad eam que sub dupla periferie EL et proportione eius que sub dupla periferie KL ad eam que sub dupla periferie KZ. Verum in omnibus inclinationibus dupla TI periferie eadem data est, est enim que inter tropica. Ac propter hoc et reliqua dupla scilicet IZ periferie et similiter in eisdem eius qui per media animalia portionibus et LK periferie dupla secundum omnes inclinationes eadem et data est per obliquationis canonium, et reliqua propter hoc rursum que dupla periferie KZ. Quare et eius que sub dupla periferie TE ad eam que sub dupla periferie EL reliquitur proportio eadem in omnibus inclinationibus in eisdem tetartimorii portionibus. Si ergo, his ita se habentibus, KL periferie differentiam per x portiones eius quod a vernali equinoctio ut ad hybernum tropicum punctum tetartimorii adauxerimus, tantas usque periferias divisione suffitienti secundum usum futurum, TI quidem periferie duplam habebimus semper graduum xlvii xlii xl et eam que sub ipsa rectam portionum xlviii xxxi lv, duplam vero periferie IZ graduum cxxxii xvii xx et eam que sub ipsa rectam portionum cix xliiii liii, eodemque modo et in decamiria quidem distante a vernali puncto ut ad hybernum tropicum periferia duplam quidem periferie KL graduum viii iii xvi et eam que sub ipsa rectam portionum viii xxv xxxix, duplam vero periferie KZ graduum clxxi lvi xliiii et eam que sub ipsa rectam portionum cxix xlii xiiii; in xx vero gradibus eodem modo distante periferia KL quidem periferie duplam graduum xv liiii vi et que sub ea rectam portionum xvi xxxv lvi, duplam vero periferie KZ graduum clxiiii v liiii et que sub ea rectam portionum cxviii l xlvii; in gradibus vero xxx distante periferia LK quidem periferie duplam graduum xxiii xix viii et eam que sub ipsa rectam portionum xxiiii xv lvi, duplam vero periferie KZ graduum clvi xli et que sub ipsa rectam portionum cxvii xxxiiii xv; in gradibus autem xl distante periferia duplam quidem periferie LK graduum xxx viii et que sub ea rectam porcionum 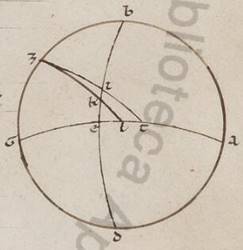 xxxi xi xliiii, xliiii] xliii V2F1 eius vero que est KZ duplam graduum cxlix li lii et eam que sub ipsa rectam portionum cxv lii xix; in ea vero que gradibus l periferia distat LK quidem periferie duplam graduum xxxvi v xlvi et que sub ipsa rectam portionum xxxvii x xxxix, eius vero que est KZ duplam graduum cxliii liiii xiiii et que sub ipsa rectam portionum cxiiii v xliiii; in gradibus vero lx distante periferia LK quidem periferie duplam graduum xli o xviii et eam que sub ipsa rectam portionum xlii i xlviii, periferie vero KZ duplam graduum xxxviii lix xlii et eam que sub ipsa rectam portionum cxii xxiii lvii; in gradibus autem lxx distante periferia LK quidem periferie duplam graduum xliiii xl xxii et eam que sub ipsa rectam portionum xlv xxxvi xviii, duplam vero periferie KZ graduum cxxxv xix xxxviii et eam que sub ipsa rectam portionum cx lix xlvii.
xxxi xi xliiii, xliiii] xliii V2F1 eius vero que est KZ duplam graduum cxlix li lii et eam que sub ipsa rectam portionum cxv lii xix; in ea vero que gradibus l periferia distat LK quidem periferie duplam graduum xxxvi v xlvi et que sub ipsa rectam portionum xxxvii x xxxix, eius vero que est KZ duplam graduum cxliii liiii xiiii et que sub ipsa rectam portionum cxiiii v xliiii; in gradibus vero lx distante periferia LK quidem periferie duplam graduum xli o xviii et eam que sub ipsa rectam portionum xlii i xlviii, periferie vero KZ duplam graduum xxxviii lix xlii et eam que sub ipsa rectam portionum cxii xxiii lvii; in gradibus autem lxx distante periferia LK quidem periferie duplam graduum xliiii xl xxii et eam que sub ipsa rectam portionum xlv xxxvi xviii, duplam vero periferie KZ graduum cxxxv xix xxxviii et eam que sub ipsa rectam portionum cx lix xlvii.
In gradibus lxxx vero lxxx vero] inv.V2 distante periferia LK quidem periferie duplam graduum xlvi lvi xxxii et que sub ipsa rectam portionum xlvii xl xl, dupla dupla] duplam V2 vero periferie KZ cxxxiii iii xxviii et eam que sub ipsa rectam portionum cx iiii xvi. Ac propter preiacentia, si ab eius que sub dupla periferie TI ad eam que sub dupla periferie IZ proportione, hoc est ab ea que xlviii xxxi lv ad cix xliiii liii, abstulerimus unamquamque secundum decamiriam expositarum eius que sub dupla periferie LK ad eam que sub dupla periferie KZ proportionum, relinquetur nobis et eius que sub dupla periferie TE ad eam que sub dupla periferie EL proportio secundum omnes inclinationes eadem ei que lx in x quidem gradibus distante periferia, ut diximus, ad ix xxxiii, in ea vero que xx ad xviii lvii, in ea autem que xxx ad xxviii i, in ea vero que xl ad xxxvi xxxiii, in ea autem que l ad xliiii xii, in ea vero que lx ad l xliiii, in ea autem que lxx ad lv xlv, in ea vero que lxxx ad lviii lv. Manifestum autem inde quoniam et secundum unaquamque unaquamque] unamquamque V2F1 inclinationum datam habentes duplam periferie TE, quoniam quidem tot est graduum, quot temporibus minimam diem superat ea que equinoctialis et que sub ipsa rectam et proportionem huius ad duplam EL periferie habebimus et ipsa datam et duplam EL periferie. Cuius dimidiam, hoc est ipsam EL, continentem predictam differentiam subtrahentes ab eis que in recta spera exposite eius qui per media periferie ascensionibus, eam que secundum subiacens clima eiusdem periferie ascensionem inveniemus. Adiaceat enim exempli causa rursus inclinatio eius qui per Rodum parallili, secundum quem duplam quidem ET periferie graduum est xxxvii xxx, que vero sub ea recta portionum xxxviii et xxxiiii ad proximum. Quoniam ergo eadem proportio est lx ad xxxviii et xxxiiii, et ix xxxiii ad vi et viii, et xviii lvii ad xii et xi, et xxviii i ad xviii o, atque xxxvi et xxxiii ad xxiii et xxix, et xliiii et xii ad xxviii et xxv, et l et xliiii ad xxii xxiii] xxxiii V2 et xxxvii, atque lv xlv ad xxxv lii, et lviii et lv ad xxxvii et lii, fit et que quidem sub dupla periferie EL periferie secundum unamquamque x graduum differentiarum expositarum proprie portionum, dimidia vero eius que sub ipsa periferie, hoc est ipsa EL, graduum in prima quidem decamiria ii et lvi, in secunda vero v l, in tertia vero viii et xxxviii, in quarta vero xi et xvii, in quinta xiii et xlii, in sexta xv et xlvi, in septima xvii et xxviii, in octava xviii et xxiiii, et in nona manifestum quoniam ipsorum xviii et xlv. Quare quoniam quidem et in recta spera que quidem usque primam decamiriam periferia coascendit temporibus ix et x, que vero usque secundam xviii et xxv, que vero usque tertiam xxvii et l, que vero usque quartam xxxvii et xxx, que vero usque quintam xlvii et xxviii, que autem usque sextam lvii et xliiii, que vero usque septimam lxviii et xviii, et que usque octavam lxxix et v, et que usque nonam totius tetartimorii temporibus xc. Manifestum quoniam, etsi subtraxerimus ab unaquaque expositarum in recta spera ascensionum propriam quantitatem eius que secundum EL periferiam differentie, habebimus et que in subiacenti climate earumdem ascensiones et coascendet que quidem usque primam decamiriam periferia reliquis temporibus vi et xiiii, que vero usque secundam xii et xxxv, que autem usque tertiam xix et xii, et que usque quartam xxvi et xiii, que usque quintam xxiii xxii] xxxii V2F1 xlvi, que usque sextam xli et lviii, que usque septimam l et liiii, que usque octavam lx et xli, que usque nonam, hoc est que totius tetartimorii, ex medietate magnitudinis diei collectis temporibus lxxi et xv. Et ipsarum ergo decamiriarum prima quidem coascendet temporibus vi et xiiii, secunda vero vi et xxi, tertia vi et xxxvii, quarta vii et i, quinta vii et xxxiii, sexta viii et xii, septima viii lvi, octava ix et xlvii, nona x et xxxiiii. Quibus demonstratis, inde erunt rursus per ante considerata coostense et reliquorum tetartimoriorum secundum consequentiam ascensiones. Eodem vero modo investigantes et aliorum parallilorum in unamquamque decamiriam ascensiones, in quotcumque eum qui penes singula usum attingere competit, et exponemus ipsas canonice ad eam que in reliqua methodum, incipientes quidem ab eo qui sub ipso equinoctiali, pertingentes vero usque fatientem horarum xvii maximam diem et augmentum eorum dimidiam horam fatientes, eo quod cura digna minime fiat in emiorium penes omala differentia. Preordinantes igitur circuli xxxvi decamirias, apponemus cuique secundum deinceps proprie asscensionis climatis tempora et ipsorum superaggregationem hoc modo.
〈II.8〉 Expositio earum que canoniorum secundum decamirias in unoquoque parallilo ascensionum
| CANONIUM SECUNDUM DECAMIRIAM ANAPHORARUM | ||||||||||||||||||
| Signa | Spere recte hore xii | Abaliti sinus | Meroys | |||||||||||||||
| de ca mi rie | hore xii et de latitudine viii xxii | hore xiii latitudinis g xvi xxvii | ||||||||||||||||
| Ascensiones singularum decamiriarum | Tempora aggregata | Ascensiones singularium decamiriarum | Tempora aggregata | Ascensiones | Aggregationes | |||||||||||||
| G | M | G | M | G | M | G | M | G | M | G | M | |||||||
| Aries | x | ix | x | ix | x | viii | xxxv | viii | xxxv | vii | lviii | vii | lviii | |||||
| xx | ix | xv | xviii | xxv | viii | xxxix | xvii | xiiii | viii | v | xvi | iii | ||||||
| xxx | ix | xxv | xxvii | l | viii | lii | xxvi | vi | viii | xvii | xxiiii | xx | ||||||
| Taurus | x | ix | xl | xxxvii | xxxx | ix | viii | xxxv | xiiii | viii | xxxvi | xxxii | lvi | |||||
| xx | ix | lviii | xlvii | xviii | ix | xxix | xliiii | xliiii | ix | i | xli | lvii | ||||||
| xxx | x | xvi | lvii | xliiii | ix | li | liiii | xxxiiii | ix | xxvii | li | xxiiii | ||||||
| Gemini | x | x | xxxiiii | lxviii | xviii | x | xv | lxiiii | xlix | ix | lvi | lxi | xx | |||||
| xx | x | xlvii | lxxix | v | x | xxxv | lxxv | xxiiii | x | xxiii | lxxi | xliii | ||||||
| xxx | x | lv | xc | o | x | li | lxxxvi | xv | x | xlvii | lxxxii | xxx | ||||||
| Cancer | x | x | lv | c | lv | x | lix | xcvii | xiiii | xi | iii | xciii | xxxiii | |||||
| xx | x | xlvii | cxi | xlii | x | lix | cviii | xiii | xi | xi | ciiii | xliiii | ||||||
| xxx | x | xxxiiii | cxxii | xvi | x | xxxiii | cxix | vi | xi | xii | cxvi | lvi | ||||||
| Leo | x | x | xvi | cxxxii | xxxii | x | xli | cxxix | xlvii | xi | v | cxxvii | l | |||||
| xx | ix | lviii | cxlii | xxx | x | xxvii | cxl | xiiii | x | lv | cxxxvii | lvi | ||||||
| xxx | ix | xl | clii | x | x | xii | cl | xxvi | x | xliiii | cxlviii | xl | ||||||
| Virgo | x | ix | xxv | clxi | xxxv | ix | lviii | clx | xxiiii | x | xxxiii | clix | xiii | |||||
| xx | ix | xv | clxx | l | ix | li | clxx | xv | x | xxv | clxix | xxxviii | ||||||
| xxx | ix | x | clxxx | o | ix | xlv | clxxx | o | x | xxii | clxxx | o | ||||||
| Libra | x | ix | x | clxxxix | x | ix | xlv | clxxxix | xlv | x | xxii | cxc | xxii | |||||
| xx | ix | xv | cxcviii | xxv | ix | li | cxcix | xxxvi | x | xxv | cc | xlvii | ||||||
| xxx | ix | xxv | ccvii | l | ix | lviii | ccix | xxxiiii | x | xxxiii | ccxi | xx | ||||||
| Scorpius | x | ix | xl | ccxvii | xxx | x | xii | ccxix | xlvi | x | xliiii | ccxxii | iv | |||||
| xx | ix | lviii | ccxxvii | xxviii | x | xxvii | ccxxx | xiii | x | lv | ccxxxii | lix | ||||||
| xxx | x | xvi | ccxxxvii | xliiii | x | xli | ccxl | liiii | xi | v | ccxliiii | iv | ||||||
| Sagittarius | x | x | xxxiiii | ccxlviii | xviii | x | liii | ccli | xlvii | xi | xii | cclv | xvi | |||||
| xx | x | xlvii | cclix | v | x | lix | cclxii | xlvi | xi | xi | cclxvi | xvii | ||||||
| xxx | x | lv | cclxx | o | x | lix | cclxxiii | xlv | xi | iii | cclxxvii | xxx | ||||||
| Capricornius | x | x | lv | cclxxx | lv | x | li | cclxxxiiii | xxxvi | x | xlvii | cclxxxviii | xvii | |||||
| xx | x | xlvii | ccxci | xlii | x | xxxv | ccxcv | x | x | xxii | ccxcviii | xl | ||||||
| xxx | x | xxxiiii | cccii | xvi | x | xv | cccv | xxvi | ix | lvi | cccviii | xxxvi | ||||||
| Aquarius | x | x | xvi | cccxii | xxxii | ix | li | cccxv | xvii | ix | xxvii | cccxviii | iii | |||||
| xx | ix | lviii | cccxxii | xxx | ix | xxix | cccxxiiii | xlvi | ix | i | cccxxvii | iiii | ||||||
| xxx | ix | xl | cccxxxii | x | ix | viii | cccxxxiii | liiii | viii | xxxvii | cccxxxv | xl | ||||||
| Pisces | x | ix | ix | cccxli | xxxv | viii | lii | cccxlii | xlvi | viii | xvi | cccxliii | lvii | |||||
| xx | ix | xv | cccl | l | viii | xxxix | cccli | xxv | viii | v | ccclii | ii | ||||||
| xxx | ix | x | ccclx | o | viii | xxxv | ccclx | o | vii | lviii | ccclx | o | ||||||
| CANONIUM SECUNDUM DECAMIRIAM ANAPHORARUM | ||||||||||||||||||
| Signa | Signis | Inferiora | Egipti | Rodi | ||||||||||||||
| hore xiii et dimidii latitudinis graduum xxiii li | hore xiiii | latitudinis xxx xxii | hore xiiii et | dimidii latitudinis xxxvi o | ||||||||||||||
| De ca mi rie | Anaphore singularum decamiriarum | Aggregationes | Ascensiones | Aggregationes | Ascensiones | Aggregationes | ||||||||||||
| G | M | G | M | G | M | G | M | G | M | G | M | |||||||
| Aries | x | vii | xxiii | vii | xxiii | vi | xlviii | vi | xlviii | vi | xiiii | vi | xiiii | |||||
| xx | vii | xxix | xiiii | lii | vi | lv | xiii | xliii | vi | xxi | xii | xxxv | ||||||
| xxx | vii | xlv | xxii | xxxvi | vii | x | xx | liii | vi | xxxvii | xix | xii | ||||||
| Taurus | x | viii | iiii | xxx | xli | vii | xxxiii | xxviii | xxvi | vii | i | xxvi | xiii | |||||
| xx | viii | xxxi | xxxix | xii | viii | ii | xxxvi | xxviii | vii | xxxiii | xxxiii | xlvi | ||||||
| xxx | ix | iii | xlviii | xv | viii | xxxvii | xlv | v | viii | xii | xli | lviii | ||||||
| Gemini | x | ix | xxxvi | lviii | li | ix | xvii | liii | xxii | viii | lvi | l | liiii | |||||
| xx | x | xi | lxviii | ii | x | o | lxiiii | xxii | ix | xlvii | lx | xli | ||||||
| xxx | x | xliii | lxxviii | xlv | x | xxxviii | lxxv | o | x | xxxiiii | lxxi | xv | ||||||
| Cancer | x | xi | vii | lxxxix | lii | xi | xii | lxxxvi | xii | xi | xx | lxxxii | xxxi | |||||
| xx | xi | xxiii | ci | xv | xi | xxxiiii | xcvi | xlvi | xi | xlvii | xciiii | xviii | ||||||
| xxx | xi | xxxii | cxii | xlvii | xi | li | cix | xxxvii | xii | xii | cvi | xxx | ||||||
| Leo | x | xi | xxix | cxxiiii | xvi | xi | lv | cxxi | xxxii | xii | xx | cxviii | l | |||||
| xx | xi | xxv | cxxxv | xli | xi | liiii | cxxxiii | xxvi | xii | xxiii | cxxxi | xiii | ||||||
| xxx | xi | xvi | cxlvi | lvii | xi | xlvii | cxlv | xiii | xii | xix | cxliii | xxxviii | ||||||
| Virgo | x | xi | v | clviii | ii | xi | xl | clvi | liii | xii | xiii | clv | xlv | |||||
| xx | xi | i | clxix | iii | xi | xxxv | clxviii | xxviii | xii | ix | clxvii | liiii | ||||||
| xxx | x | lvii | clxxx | o | xi | xxxii | clxxx | o | xii | vi | clxxx | o | ||||||
| Libra | x | x | lvii | cxc | lvii | xi | xxxii | cxci | xxxii | xii | vi | cxcii | vi | |||||
| xx | xi | i | cci | lviii | xi | xxxv | cciii | vii | xii | ix | cciiii | xv | ||||||
| xxx | xi | v | ccxiii | iii | xi | xl | ccxiv | xlvii | xii | xiii | ccxvi | xxviii | ||||||
| Capricornus | x | xi | xvi | ccxxiv | xix | xi | xlvii | ccxxvi | xxxxiiii | xii | xix | ccxxviii | xlvii | |||||
| xx | xi | xxv | ccxxxv | xliiii | xi | liiii | ccxxxviii | xxviii | xii | xxiii | ccxli | x | ||||||
| xxx | xi | xxix | ccxlvii | xiii | xi | lv | ccl | xxiii | xii | xx | ccliii | i | ||||||
| Sagittarius | x | xi | xxxii | cclviii | xlv | xi | li | cclxii | xiiii | xii | xii | cclxv | xlii | |||||
| xx | xi | xxiii | cclxx | viii | xi | xxxiiii | cclxxiii | xlviii | xi | xlvii | cclxxvii | xxix | ||||||
| xxx | xi | vii | cclxxxi | xv | xi | xii | cclxxxv | o | xi | xvi | cclxxxviii | xlv | ||||||
| Capricornus | x | x | xliii | ccxci | lviii | x | xxxviii | ccxcv | xxxviii | x | xxxiiii | ccxcix | xix | |||||
| xx | x | xi | cccii | ix | x | o | cccv | xxxviii | ix | xlvii | cccix | vi | ||||||
| xxx | ix | xxxvi | cccxi | xlv | ix | xviii | cccxiiii | lv | viii | xlvi | cccxviii | ii | ||||||
| Aquarius | x | ix | iii | cccxx | xlviii | viii | xxxvii | cccxxiii | xxxii | viii | xii | cccxxvi | xiiii | |||||
| xx | viii | xxxi | cccxxx | xix | viii | ii | cccxxxi | xxxiiii | vii | xxxiii | cccxxxiii | xlvii | ||||||
| xxx | viii | iiii | cccxxxvii | xxiii | vii | xxxiii | cccxxxix | vii | vii | i | cccxl | xlviii | ||||||
| Pisces | x | vii | xlv | cccxlv | l | vii | x | cccxlvi | xvii | vi | xxxvii | cccxlvii | xxv | |||||
| xx | vii | xxix | ccclii | xxxvii | vi | lv | cccliii | xii | vi | xxi | cccliii | xxvi | ||||||
| xxx | vii | xxiii | ccclx | o | vi | xlviii | ccclx | o | vi | xiiii | ccclx | o | ||||||
| ASCENSIONES SIGNORUM AD DECENOS GRADUS | |||||||||||||||
| signa | decene | Ellesponti | Medii ponti | Boristhenis emissiones | |||||||||||
| hore xv latitudinis xl lvi | hore xv et dimidii latitudinis xlv i | hore xvi latitudinis xlvi xxxii | |||||||||||||
| Ascensiones decenorum graduum | Tempora superaggregata | Ascensiones | Aggregationes | Ascensiones | Aggregationes | ||||||||||
| G | M | G | M | G | M | G | M | G | M | G | M | ||||
| Aries | x | v | xl | v | xl | v | viii | v | viii | iiii | xxxvi | iiii | xxxvi | ||
| xx | v | xlvii | xi | xxvii | v | xiiii | x | xxii | iiii | xliii | ix | xix | |||
| xxx | vi | v | xvii | xxxii | v | xxxiii | xv | lv | v | i | xiiii | xx | |||
| Taurus | x | vi | xxix | xxiiii | i | v | lviii | xxi | liii | v | xxvi | xix | xlvi | ||
| xx | vii | iiii | xxxi | v | vi | xxxiv | xxviii | xxiii | vi | v | xxv | li | |||
| xxx | vii | xlvi | xxxviii | li | vii | xx | xxxv | xlvii | vi | lii | xxxii | xliii | |||
| Gemini | x | viii | xxxvii | xlvii | xxix | viii | xv | xliiii | ii | vii | liii | xl | xxxvi | ||
| xx | ix | xxxii | lvii | i | ix | xix | liii | xxi | ix | v | xlix | xli | |||
| xxx | x | xxx | lxvii | xxx | x | xxiiii | lxiii | xlv | x | xix | lx | o | |||
| Cancer | x | xi | xxi | lxxviii | li | xi | xxvi | lxxv | xi | xi | xxxi | lxxi | xxxi | ||
| xx | xii | ii | xc | liii | xii | xv | lxxxvii | xxvi | xii | xxix | lxxxiiii | o | |||
| xxx | xii | xxx | ciii | xxiii | xii | liii | c | xix | xiii | xv | xcvii | xv | |||
| Leo | x | xii | xlvi | cxvi | ix | xiii | xii | cxiii | xxxi | xiii | xl | cx | lv | ||
| xx | xii | lii | cxxix | li | xiii | xxii | cxxvi | liii | xiii | li | cxxiiii | lvi | |||
| xxx | xii | li | cxli | lii | xiii | xxii | cxl | xv | xiii | liiii | cxxxviii | xl | |||
| Virgo | x | xii | xlv | cliiii | xxxvii | xiii | xvii | cliii | xxxii | xiii | xlix | clii | xxix | ||
| xx | xii | xliii | clxviii | xx | xiii | xvi | clxvi | xlviii | xiii | xlvii | clxvi | xvi | |||
| xxx | xii | xl | clxxx | o | xiii | xii | clxxx | o | xiii | xliiii | clxxx | o | |||
| Libra | x | xii | xl | cxcii | xl | xiii | xii | cxciii | xii | xiii | xlvii | cxciii | xliiii | ||
| xx | xii | xliii | ccv | xxiii | xiii | xvi | ccvi | xxviii | xiii | xlvii | ccvii | xxxi | |||
| xxx | xii | xlv | ccxviii | viii | xiii | xvii | ccxix | xlv | xiii | xlix | ccxxi | xxi | |||
| Scorpius | x | xii | li | ccxxx | lix | xiii | xxii | ccxxxiii | vii | xiii | liv | ccxxxv | xiiii | ||
| xx | xii | lii | ccxliii | li | xiii | xxii | ccxlvi | xxix | xiii | li | ccxlix | v | |||
| xxx | xii | lvi | ccliii | xxxvii | xiii | xii | cclix | xli | xiii | xl | cclxii | xlv | |||
| Sagittarius | x | xii | xxx | cclxix | vii | xii | liii | cclxxii | xxxiiii | xiii | xv | cclxxvi | o | ||
| xx | xii | ii | cclxxxi | ix | xii | xv | cclxxxiiii | xlix | xii | xxix | cclxxxviii | xxix | |||
| xxx | xi | xxi | ccxcii | xxx | xi | xxvi | ccxcvi | xv | xi | xxxi | ccc | o | |||
| Capri cornus | x | x | xxix | cccii | xxxix | x | xxiiii | cccvi | xxxix | x | xix | cccx | xix | ||
| xx | x | xxxii | cccxii | xxxi | x | xix | cccxv | lviii | ix | v | cccxix | xxiiii | |||
| xxx | viii | xxxviii | cccxxi | ix | viii | xv | cccxxiiii | xiii | vii | liii | cccxxvii | xvii | |||
| Aquarius | x | vii | xlv | cccxxviii | lv | vii | xx | cccxxxi | xxxiii | vi | lii | cccxxxiiii | xix | ||
| xx | vi | xxix | cccxlii | xxxviii | v | lviii | cccxliiii | v | vi | v | cccxl | xxiiii | |||
| xxx | vi | xxix | cccxlii | xxxviii | v | lviii | cccxliiii | v | v | xxvi | cccxlv | xvii | |||
| Pisces | x | vi | v | cccxlviii | xxxiii | v | xxxiii | cccxlix | xxxvii | v | i | cccl | xli | ||
| xx | v | xlvii | cccliiii | xx | v | xxxiii | cccliiii | lii | iiii | xliii | ccclv | xxiiii | |||
| xxx | v | xl | ccclx | o | v | viii | ccclx | o | iiii | xxxvi | ccclx | o | |||
| CANONIUM SECUNDUM DECAMIRIAM ANAPHORARUM | ||||||||||
| signa | decene | Australissima | Britanie | Tanaidos | emissionum | |||||
| hore xvi et | dimidii latitudinis li xl | hore xvii latitudinis | liiii i | |||||||
| Ascensiones decenarum | Aggregationes | Ascensiones decenarum | Aggregata | |||||||
| G | M | G | M | G | M | G | M | |||
| Aries | x | iiii | v | iiii | v | iii | xxxvi | iii | xxxvi | |
| xx | iiii | xii | viii | xvii | iii | xliii | vii | xix | ||
| xxx | iiii | xxxi | xxxi | xlviii | iiii | o | xi | xix | ||
| Taurus | x | iiii | lvi | xvii | xliii | iiii | xxvi | xv | xlv | |
| xx | v | xxxiiii | xxiii | xviii | v | iiii | xx | xlix | ||
| xxx | vi | xxv | xxix | xliii | v | lvi | xxvi | xlv | ||
| Gemini | x | vii | xxix | xxxvii | xii | vii | v | xxxiii | l | |
| xx | viii | xlix | xlvi | i | viii | xxxiii | xlii | xxiii | ||
| xxx | x | xiiii | lvi | xv | x | vii | lii | xxx | ||
| Cancer | x | xi | xxxvi | lxvii | li | xi | xliii | lxiiii | xiii | |
| xx | xii | xlv | lxxx | xxxvi | xiii | l | lxxviii | xiiii | ||
| xxx | xiii | xxxix | xcvii | xv | xiv | iii | xci | xvii | ||
| Leo | x | xiiii | vii | cviii | xxii | xiiii | xxxvi | cv | liii | |
| xx | xiiii | xxii | cxxii | xliii | xiiii | lii | cxx | xlv | ||
| xxx | xiiii | xxiiii | cxxxvii | vii | xiiii | liiii | cxxxv | xxxix | ||
| Virgo | x | xiiii | xix | cli | xxvii | xiiii | l | cl | xxix | |
| xx | xiiii | xviii | clxv | xlv | xiiii | xlviii | clxv | xvi | ||
| xxx | xiiii | xv | clxxx | o | xiiii | xliiii | clxxx | o | ||
| Libra | x | xiiii | xv | cxciiii | xv | xiiii | xliiii | cxciiii | xliiii | |
| xx | xiiii | xviii | ccviii | xxxiii | xiiii | xlvii | ccix | xxxi | ||
| xxx | xiiii | xix | ccxxii | lii | xiiii | l | ccxxiiii | xxi | ||
| Scorpius | x | xiiii | xxiiii | ccxxxvii | xvi | xiiii | liiii | ccxxxix | xv | |
| xx | xiiii | xxii | ccli | xxxviii | xiiii | lii | ccliiii | vii | ||
| xxx | xiiii | vii | cclxv | xlv | xiiii | xxxvi | cclxviii | xliii | ||
| Sagittarius | x | xiii | xxxix | cclxxix | xxiiii | xiiii | iii | cclxxxii | xlvi | |
| xx | xii | xlv | ccxcii | ix | xiii | l | ccxcv | xlvii | ||
| xxx | xi | xxxvi | ccciii | xlv | xi | xliii | cccvii | xxx | ||
| Capricorus | x | x | xiiii | cccxiii | lix | x | vii | cccxvii | xxxvii | |
| xx | viii | xlix | cccxxii | xlviii | viii | xxxvi | cccxxvi | x | ||
| xxx | vii | xxix | cccxxx | xvii | vii | v | cccxxxiii | xv | ||
| Aquarius | x | vi | xxv | cccxxxvi | xlii | v | lvi | cccxxxix | xi | |
| xx | v | xxxiiii | cccxlii | xvi | v | iiii | cccxliiii | xv | ||
| xxx | iiii | lvi | cccxlvii | xii | iiii | xxvi | cccxlviii | xli | ||
| Pisces | x | iiii | xxxi | cccli | xliii | iiii | o | ccclii | xli | |
| xx | iiii | xii | ccclv | lv | iii | xliii | ccclvi | xxiiii | ||
| xxx | iiiii | v | ccclx | o | iii | xxxvi | ccclx | o | ||
〈II.9〉
Quoniam vero, ascensionum temporibus preiacenti modo nobis expositis, facile intelligibilia reliqua omnia fient partem in hanc pertinentium, et neque linearibus demonstrationibus ad singula ipsorum indigebimus, neque canonographya superflua, per has suppositas ephodos manifestum erit. Primum enim date diei vel noctis sinnitur sinnitur] sumatur V2 sumitur F1 quantitas, numeratis temporibus proprii climatis, in die quidem a solari gradu eum usque qui e diametro Solem respicit, ut in consequentia dodecatimoriorum, in nocte vero a Solis opposito in ipsum solarem gradum. Collectorum enim temporum xv sumentes, habebimus quot est horarum equinoctialium subiacens clima, xii vero sumentes, habebimus quot temporum est temporalis hora eiusdem spatii. Invenitur autem et promptius horaria quantitas, sumpta ex preiacente canonio ascensionum differentia adiacentium superagregationum, die quidem solari gradui, nocte vero diametrizanti et in eo qui sub equinoctiali parallilo et in eo qui subiacentis climitatis. climitatis] climatis V2 Invente enim differentie sextam sumentes, et in boreali quidem semicirculo illatu illatu] illato V2 gradu existente, adiunges adiunges] adiungentes V2 ipsam equinoctialis unius hore xv temporibus, in australi vero, auferentes ab eisdem xv temporibus, faciemus multitudinem temporum subiacentis hore temporalis. Deinceps autem datas quidem temporales horas resolvimus in equinoctales, multiplicantes duricias duricias] diurnas V2 duritias F1 quidem in diei illius proprii climatis horaria tempora, nocturnas autem in ea que noctis. Collectorum enim xv sumentes, habebimus multitudinem horarum equinoctialium. E contrario vero datas equinoctiales horas resolvemus in temporales, multiplicantes ipsas in xv et partientes in subiacentia proprii diostimatis diostimatis] diastimatis V2 horaria tempora.
Rursum dato nobis tempore et hora qualicumque temporali, primum quidem orientem tunc graduum graduum] gradum V2 eius qui per media animalia circuli sumemus, multiplicantes multitudinem horarum, diei quidem earum que ab ortu Solis, noctis vero earum que ab occasu, in propria horaria tempora. Collectum enim numerum dirigemus diei quidem a solari gradu, noctis vero a diametrizante, ut in consequentia animalium, secundum subiacentis climatis ascensiones, et in quemcumque inciderit gradum numerus, illum dicemus tunc oriri. Si vero medium tenentem celum super terram voluerimus sumere, temporales horas semper que a meridie preterita usque data multiplicantes in propria horaria tempora, factum numerum dirigemus a solari gradu in consequentia secundum ea ea] eas V2 que in recta spera ascensiones, et in quemcumque ceciderit gradum numerus, ille tunc super terram celum medium tenet. Similiter aut ab oriente quidem gradu celum medium tenentem super terram sumemus, contemplantes orientem orientem] orienti V2 adiacentem superagregationis numerum in proprii climatis canonio. Aufferentes enim ab ipso semper tetartimorii tempora xc, adiacentem numero gradum ex superagregatione eius que in recta spera selidii tunc super terram celum medium tenentem inveniemus, e contrario vero ab eo quod super terram celum medium tenet orientem rursum sumemus, considerantes celum tenenti medium gradui adiacentem superagregationis numerum recte spere selidio. Apponentes enim ipsi semper rursus eadem xc tempora, intuebimur ex superagregatione subiacentis climatis, quamvis quamvis] quis V2 gradus adiacet numero, et cum cum] eum V2 tunc orientem inveniemus. Manifestum autem et quoniam sub eodem quidem meridiano habitantibus Sol equalibus equinoctialibus horis abstat a meridie vel mesonictio, eum eum] eis V2F1 vero qui minime ab eodem meridiano tot equinoctialibus temporibus differt, quot utique gradibus meridianus a meridiano penes utrosque distat.
〈II.10〉
Relique Relique] reliquo V2F1 vero existente in subiacentem speculationem de angulis facere rationem, dico vero ad eum qui per media animalia circulum factis, prelibandum quoniam rectum angulum sub maximis circulis diximus contineri, quando, poli poli] polo V2F1 communi sectione circulorum et spectio spectio] spatio V2 quolibet scripto circulo, deprehensa ipsius periferia sub angulum continentibus portionibus tetartimoriorum tetartimoriorum] tetartimorium V2 scripti circuli facit, et universaliter quoniam quam utique habet proportionem deprehensa periferia ad scriptum circulum secundum quem diximus modum, eam habet proportionem contentus angulus sub inclinatione eppipedorum, ad quatuor rectos. Quare quoniam quidem perimetrum supposuimus portionum ccclx, quot utique invenietur portionum deprehensa periferia, tot erunt erunt] erit V2F1 et subtendens ipsam angulus, qualium unus rectus xc. Ad reliquum reliquum] obliquum V2 autem circulum factorum angulorum maxime utiles ad subiacentem specculationem illi sunt qui sub sectione ipsius et meridiani continentur et qui sub sectione ipsius et et] add. orizontis secundum unamquamque et similiter qui sub sectione ipsius et V2 per polos orizontis scripti maximi circuli, coostensis eisdem angulis et deprehensis huius circuli periferiis sub sectione et polo orizontis, hoc est eo eo] add. quod V2F1 ad vertice puncto. Singula enim expositorum demonstrata et ad speculationem ipsam suffitientissimum habet habet] habent V2 locum et ad ea que circa permutationes Lune inquiruntur maxime conferrunt plurimum, nequaquam huius huius] huiusmodi V2 conceptione potente precedere absque illorum preconceptione. Quoniam vero et quatuor existentibus angulis contentis sub duorum circulorum sectione, hoc est eius qui per media animalia et unius ei complacitorum, de uno vero secundum portionem similli sermonem facere deberemus. Prediffiniendum quoniam universaliter duorum angulorum qui circa consequentem comuni sectioni circulorum periferia periferia] periferiam V2 eius qui per media animalia eum qui ab arctis subaudiendus, subaudiendus] subaudiendum V2 quare accidentia et quantitates demonstrandas esse ita se habentibus angulis. Simplitiori vero demonstratione existente ad meridianum circulum consideratorum obliqui angulorum, ab his incipiemus.
Demonstrabimus primum quoniam equidistantia ab eodem equinoctiali puncto eius qui per media animalia circuli puncta expositos angulos equales alternis fatiunt. Esto enim equinoctialis quidem circuli periferia ABG, eius vero qui per media animalia DBE, polus autem equinoctialis Z punctum et, assumptis equalibus periferiis BL et BT in utrasque B puncti equinoctialis, scribantur per Z polum et I, T puncta meridianorum circulorum periferie et ZKI et ZTL. Dico quoniam equalis est RIB RIB] KIB V2 angulus angulo ZTE. Et est inde manifestum: equiangulum enim fit BIR BIR] BIK V2F1 trilaterum ei quod est BIL, quoniam tria latera tribus lateribus equalia habent singula, IB quidem ei quod est BT, IR IR] IK V2F1 vero ei quod est TL, et BK ei quod est BL. Demonstrata enim sunt huius omnia in eis que ante et angulus ergo RIB RIB] KIB V2F1 add. angulo BTI (BTL F1), hoc est ei qui est ZTE, est equalis. Quod oportebat ostendere V2F1
 Rursus demonstrandum quoniam eque distantium eque … distantium] corr. ex eque distandum V3 equidistancium V2 equidistantium F1 punctorum eius qui per media animalia circuli ab eodem tropico puncto ad meridianum facti anguli ambo simul duobus rectis sint equales. Esto enim eius qui per media animalia circuli periferia ABG, ABG] add. B V2 subiacente tropico puncto et assumptis in utrasque eius periferiis equalibus BD et BE, scribantur per D et E puncta et Z polum equinoctialem meridianorum circulorum periferie ZB ZB] ZD V2F1 et ZE; dico quoniam ZBB ZBB] ZDB V2F1 angulus et ZEG ambo simul duobus rectis sint equales. Est autem et hoc manifestum inde: quoniam enim D et E puncta equidistant ab eodem tropico puncto, equalis est DZ periferia periferia] add. ei V2F1 que est ZE et angulus ergo ZDB ZDB] add. angulo ZEB equalis est. Verum ZEB et V2 cum cum] om. V2 ZEG duobus rectis equales sunt. Quod oportebat ostendere.
Rursus demonstrandum quoniam eque distantium eque … distantium] corr. ex eque distandum V3 equidistancium V2 equidistantium F1 punctorum eius qui per media animalia circuli ab eodem tropico puncto ad meridianum facti anguli ambo simul duobus rectis sint equales. Esto enim eius qui per media animalia circuli periferia ABG, ABG] add. B V2 subiacente tropico puncto et assumptis in utrasque eius periferiis equalibus BD et BE, scribantur per D et E puncta et Z polum equinoctialem meridianorum circulorum periferie ZB ZB] ZD V2F1 et ZE; dico quoniam ZBB ZBB] ZDB V2F1 angulus et ZEG ambo simul duobus rectis sint equales. Est autem et hoc manifestum inde: quoniam enim D et E puncta equidistant ab eodem tropico puncto, equalis est DZ periferia periferia] add. ei V2F1 que est ZE et angulus ergo ZDB ZDB] add. angulo ZEB equalis est. Verum ZEB et V2 cum cum] om. V2 ZEG duobus rectis equales sunt. Quod oportebat ostendere.
 His preconsideratis, esto meridianus quidem circulus ABGD, eius autem qui per media animalia semicirculus AEG, puncto A subiacente hiberno tropico, atque polo A, spatio vero tetragoni latere scribatur ABD ABD] BED V2 semicirculus. Quoniam ergo ABGD meridianus et per eius qui est ABG ABG] AEG V2 polos et per eius qui est BED scriptus est, tetartimorii ED periferia. Rectus est ergo DAE angulus, rectus autem premoncrate premoncrate] per premonstrata V2F1 et sub estivo tropico puncto factus. Quare oportebat ostendere.
His preconsideratis, esto meridianus quidem circulus ABGD, eius autem qui per media animalia semicirculus AEG, puncto A subiacente hiberno tropico, atque polo A, spatio vero tetragoni latere scribatur ABD ABD] BED V2 semicirculus. Quoniam ergo ABGD meridianus et per eius qui est ABG ABG] AEG V2 polos et per eius qui est BED scriptus est, tetartimorii ED periferia. Rectus est ergo DAE angulus, rectus autem premoncrate premoncrate] per premonstrata V2F1 et sub estivo tropico puncto factus. Quare oportebat ostendere.
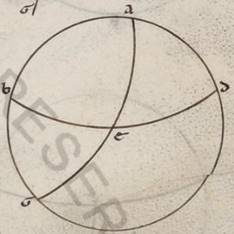 Rursus esto esto] add. meridianus V2F1 quidem circulus ABGD, equinoctialis vero semicirculus AEG, et scribatur eius qui per media animalia AZG semicirculus ita, ut A punctum sit autupnale equinoctiale, poloque A spatioque tetragoni latere scribatur BZED semicirculus. Propter eadem ergo, quoniam ABGD et per eius qui est AEG et per eius qui est BED polo polo] polos V2F1 scriptus est, tetartimorii ZAZ ZAZ] et AZ V2F1 et ED. Quare et Z quidem punctum erunt erunt] erit V2 hibernum tropicum, periferia vero ZE demonstratorium demonstratorium] demonstratorum V2 graduum xxiii et li ad proximum. Et tota ergo ZED quidem periferia graduum est cxiii et li, angulus autem DAZ talium cxiii et li, qualium est unus rectus xc. Premonstrata Premonstrata] Propter premonstrata V2 vero rursum et qui sub vernali vernali] unali V3 equinoctiali puncto fit angulus reliquorum in duos rectos erunt erunt] erit V2 graduum lxvi xi xi] ix V2.
Rursus esto esto] add. meridianus V2F1 quidem circulus ABGD, equinoctialis vero semicirculus AEG, et scribatur eius qui per media animalia AZG semicirculus ita, ut A punctum sit autupnale equinoctiale, poloque A spatioque tetragoni latere scribatur BZED semicirculus. Propter eadem ergo, quoniam ABGD et per eius qui est AEG et per eius qui est BED polo polo] polos V2F1 scriptus est, tetartimorii ZAZ ZAZ] et AZ V2F1 et ED. Quare et Z quidem punctum erunt erunt] erit V2 hibernum tropicum, periferia vero ZE demonstratorium demonstratorium] demonstratorum V2 graduum xxiii et li ad proximum. Et tota ergo ZED quidem periferia graduum est cxiii et li, angulus autem DAZ talium cxiii et li, qualium est unus rectus xc. Premonstrata Premonstrata] Propter premonstrata V2 vero rursum et qui sub vernali vernali] unali V3 equinoctiali puncto fit angulus reliquorum in duos rectos erunt erunt] erit V2 graduum lxvi xi xi] ix V2.
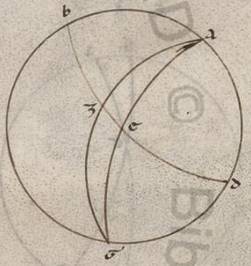 Rursus esto meridianus quidem circulus ABGD, equinoctialis quidem semicirculus AEG, eius vero qui per media animalia BZD, ut Z quidem punctum subiaceat autumpnale, periferia autem BZ primum unius dodecatimorii eius, scilicet quod Virginis, et B punctum principium manifestum quoniam Virginis. Polo autem rursus B, spatio vero tetragoni latere scribatur ITR ITR] ITEK V2 semicirculus et at iaceat at iaceat] adiaceat V2 RBT RBT] KBT V2 angulum invenire. Quoniam ergo ABGD meridianus et per eius qui est AEG et per eius qui est IER IER] IEK V2F1 polos scriptus est, tetartimorii quidem fit unaquaque BL BL] BI V2 et BT et SI SI] ei V2 EI F1 periferiarum. Propter descriptionem vero proportio eius que sub dupla periferiae BA ad eam que sub dupla periferie AI composita est ex proportione eius que sub dupla periferie BZ ad eam que sub dupla periferie TZ et proportione eius que sub dupla periferie TE ad eam que sub dupla periferie EI. Sed dupla quidem eius BA propter premonstrata graduum est xxiii, et que sub ipsa recta portionum xxiiii et xvi, dupla vero eius que est AI graduum clvi et xl, et que sub ea recta portionum cxvii et xxxi, et rursum quidem dupla eius que est ZB graduum lx, et que sub ea recta portionum lx, dupla eius que est ZT graduum cxx, et que sub ea recta portionum ciii et lv et xxiii. Si ergo rursum a proportione eorum que sunt xxiiii et xvi ad cxvii et xxxi dempserimus proportione lx ad ciii et lv xxiii, relinquetur proportio eius que sub dupla periferie TE ad eam que sub dupla periferie EI, que xlii et lviii ad proximum ad cxx, et est que sub dupla periferie EI portionum cxx, et ea ergo que sub dupla periferie TE eorumdem est xlii et lviii. Quare et dupla quidem periferie TE graduum est xlii ad proximum, ipsa vero TE eorumdem xxi, et tota ergo TER TER] TEK V2F1 quidem et ipsa et RBT RBT] KBT V2F1 angulus graduum cxi, propter preostensa vero et sub principio quidem Scorpii factus angulus equalium erunt erunt] erit V2 graduum cxi, utrumque autem eorum que sub principio Tauri et principio Piscium reliquorum in duos rectos graduum lxix. Quod oportebat ostendere.
Rursus esto meridianus quidem circulus ABGD, equinoctialis quidem semicirculus AEG, eius vero qui per media animalia BZD, ut Z quidem punctum subiaceat autumpnale, periferia autem BZ primum unius dodecatimorii eius, scilicet quod Virginis, et B punctum principium manifestum quoniam Virginis. Polo autem rursus B, spatio vero tetragoni latere scribatur ITR ITR] ITEK V2 semicirculus et at iaceat at iaceat] adiaceat V2 RBT RBT] KBT V2 angulum invenire. Quoniam ergo ABGD meridianus et per eius qui est AEG et per eius qui est IER IER] IEK V2F1 polos scriptus est, tetartimorii quidem fit unaquaque BL BL] BI V2 et BT et SI SI] ei V2 EI F1 periferiarum. Propter descriptionem vero proportio eius que sub dupla periferiae BA ad eam que sub dupla periferie AI composita est ex proportione eius que sub dupla periferie BZ ad eam que sub dupla periferie TZ et proportione eius que sub dupla periferie TE ad eam que sub dupla periferie EI. Sed dupla quidem eius BA propter premonstrata graduum est xxiii, et que sub ipsa recta portionum xxiiii et xvi, dupla vero eius que est AI graduum clvi et xl, et que sub ea recta portionum cxvii et xxxi, et rursum quidem dupla eius que est ZB graduum lx, et que sub ea recta portionum lx, dupla eius que est ZT graduum cxx, et que sub ea recta portionum ciii et lv et xxiii. Si ergo rursum a proportione eorum que sunt xxiiii et xvi ad cxvii et xxxi dempserimus proportione lx ad ciii et lv xxiii, relinquetur proportio eius que sub dupla periferie TE ad eam que sub dupla periferie EI, que xlii et lviii ad proximum ad cxx, et est que sub dupla periferie EI portionum cxx, et ea ergo que sub dupla periferie TE eorumdem est xlii et lviii. Quare et dupla quidem periferie TE graduum est xlii ad proximum, ipsa vero TE eorumdem xxi, et tota ergo TER TER] TEK V2F1 quidem et ipsa et RBT RBT] KBT V2F1 angulus graduum cxi, propter preostensa vero et sub principio quidem Scorpii factus angulus equalium erunt erunt] erit V2 graduum cxi, utrumque autem eorum que sub principio Tauri et principio Piscium reliquorum in duos rectos graduum lxix. Quod oportebat ostendere.
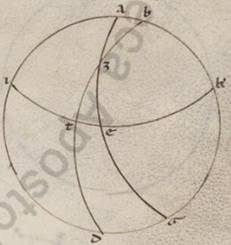 Rursum in eadem descriptione ZB periferia subiaceat duorum dodecatimorum, dodecatimorum] dodecatimoriorum V2 ut punctus B principium sit Leonis, eisdem subiacentibus, dupla quidem eius que est BA graduum fit xli et que sub ea recta portionum xlii ii, dupla vero periferie AI graduum cxxxix et que sub ea recta portionum cxii xxiiii, et rursum quidem dupla periferie ZB graduum cxx et que sub ea recta portionum ciii lv et xxiii, dupla vero periferie ZT graduum lx et que sub ea recta portionum lx. Si ergo rursum a proportione eorum que sunt xlii et ii ad cxii et xxiiii dempserimus proportionem eorum que sunt ciii et lv xxiii ad lx, relinquetur proportio eius que sub dupla periferie TE ad eam que sub dupla periferie EI, que eorum que sunt xxv et liii ad cxx. Que ergo sub dupla periferie TE fit eorumdem xxv liii. Quare et dupla quidem eius que est TE graduum erunt erunt] erit V2F1 xxv ad proximum, ipsa vero TE eorumdem xii et dimidii. Tota ergo TR TR] TEK V2 quidem et ipsa et KBT angulus graduum cii et dimidii. Propter eadem ergo et ille quidem qui sub principio Sagittarii angulus continetur equalium cii et dimidii. Uterque eorum qui sub principio Geminorum et principio Aquarii in duos rectos graduum lxxvii et dimidii. Et demonstrata sunt nobis proposita, eodem quidem futuro ductu in amplius minoribus obliqui circuli portionibus, suffitiente vero ad ipsum negotii usum et ea que secundum unumquodque dodecatimoriorum expositione.
Rursum in eadem descriptione ZB periferia subiaceat duorum dodecatimorum, dodecatimorum] dodecatimoriorum V2 ut punctus B principium sit Leonis, eisdem subiacentibus, dupla quidem eius que est BA graduum fit xli et que sub ea recta portionum xlii ii, dupla vero periferie AI graduum cxxxix et que sub ea recta portionum cxii xxiiii, et rursum quidem dupla periferie ZB graduum cxx et que sub ea recta portionum ciii lv et xxiii, dupla vero periferie ZT graduum lx et que sub ea recta portionum lx. Si ergo rursum a proportione eorum que sunt xlii et ii ad cxii et xxiiii dempserimus proportionem eorum que sunt ciii et lv xxiii ad lx, relinquetur proportio eius que sub dupla periferie TE ad eam que sub dupla periferie EI, que eorum que sunt xxv et liii ad cxx. Que ergo sub dupla periferie TE fit eorumdem xxv liii. Quare et dupla quidem eius que est TE graduum erunt erunt] erit V2F1 xxv ad proximum, ipsa vero TE eorumdem xii et dimidii. Tota ergo TR TR] TEK V2 quidem et ipsa et KBT angulus graduum cii et dimidii. Propter eadem ergo et ille quidem qui sub principio Sagittarii angulus continetur equalium cii et dimidii. Uterque eorum qui sub principio Geminorum et principio Aquarii in duos rectos graduum lxxvii et dimidii. Et demonstrata sunt nobis proposita, eodem quidem futuro ductu in amplius minoribus obliqui circuli portionibus, suffitiente vero ad ipsum negotii usum et ea que secundum unumquodque dodecatimoriorum expositione.
〈II.11〉
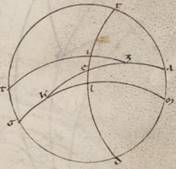 Deinceps autem demonstrabimus quomodo utique sumamus I I] in V2F1 dato climate ad orizontem eius qui per media animalia circuli factos angulos simplitiorem et ipsos habentes in ethodum in ethodum] methodum V2F1 reliquis. Quoniam ergo qui ad meridianum fuerit idem sunt eis qui ad eum qui a recta spera orizontem, manifestum. Causa vero sumendi et eos qui in climata in climata] inclinata V2F1 spera monstrandum rursus primum quoniam equidistantia puncta eius qui per media animalia circuli ab eodem equinoctiali puncto factos ad eundem orizontem angulos equales alterius alterius] alternis V2F1 faciunt. Esto enim meridianus circulus ABGD et isimerini idest equinoctialis idest equinoctialis] quidem V2 semicirculus AEG, orizontis vero BED, atque scribantur obliqui circuli due portiones ZIT et KIM KIM] KLM V2 ita se habentes, ut utrumque quidem punctorum que sunt Z et R R] K V2F1 subiaceat autumpnale equinoctiale, periferia vero ZI ei que est KI KI] KL V2F1 equalis; dico quoniam et EIT angulus equalis est angulo DLR DLR] DLK V2F1 et est inde manifestum: equiangulum enim rursum fit EZI trilaterum ei quod est ERL. ERL] EKL V2F1 Quoniam et propter premonstrata et tria latera tribus lateribus equalia habet singula singulis, ZI quidem ei quod est KL, at vero IE sectionis orizontis ei quod est EL, atque EZ ascensionis ei que est ER ER] EK V2. Equalis ergo est angulus quidem ERZ ERZ] EIZ V2F1 angulo EIR, EIR] EIZ V2 EIK F1 reliquas vero EIT reliquo DLR DLR] DLK V2F1 est equalis. Quod oportebat ostendere.
Deinceps autem demonstrabimus quomodo utique sumamus I I] in V2F1 dato climate ad orizontem eius qui per media animalia circuli factos angulos simplitiorem et ipsos habentes in ethodum in ethodum] methodum V2F1 reliquis. Quoniam ergo qui ad meridianum fuerit idem sunt eis qui ad eum qui a recta spera orizontem, manifestum. Causa vero sumendi et eos qui in climata in climata] inclinata V2F1 spera monstrandum rursus primum quoniam equidistantia puncta eius qui per media animalia circuli ab eodem equinoctiali puncto factos ad eundem orizontem angulos equales alterius alterius] alternis V2F1 faciunt. Esto enim meridianus circulus ABGD et isimerini idest equinoctialis idest equinoctialis] quidem V2 semicirculus AEG, orizontis vero BED, atque scribantur obliqui circuli due portiones ZIT et KIM KIM] KLM V2 ita se habentes, ut utrumque quidem punctorum que sunt Z et R R] K V2F1 subiaceat autumpnale equinoctiale, periferia vero ZI ei que est KI KI] KL V2F1 equalis; dico quoniam et EIT angulus equalis est angulo DLR DLR] DLK V2F1 et est inde manifestum: equiangulum enim rursum fit EZI trilaterum ei quod est ERL. ERL] EKL V2F1 Quoniam et propter premonstrata et tria latera tribus lateribus equalia habet singula singulis, ZI quidem ei quod est KL, at vero IE sectionis orizontis ei quod est EL, atque EZ ascensionis ei que est ER ER] EK V2. Equalis ergo est angulus quidem ERZ ERZ] EIZ V2F1 angulo EIR, EIR] EIZ V2 EIK F1 reliquas vero EIT reliquo DLR DLR] DLK V2F1 est equalis. Quod oportebat ostendere.
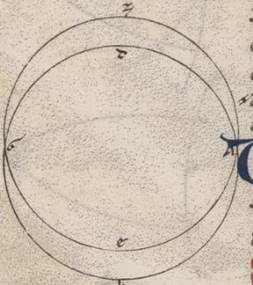 Dico quoniam et punctorum diametrizantium alterius orientalis angulus cum alterius occidentali, duobus rectis sunt equales. Si autem scripserimus orizontem quidem circulum ABGD, eum vero qui per media animalia AEGZ secantes se invicem ad A et G puncta, ambo quidem simul anguli ZAD et DAE duobus rectis equales esse. esse] fiunt V2 Equalis vero angulus ZAD angulo ZGD. Quare et ambo simul anguli ZGD et DAE duos rectos faciunt. Quod oportebat ostendere.
Dico quoniam et punctorum diametrizantium alterius orientalis angulus cum alterius occidentali, duobus rectis sunt equales. Si autem scripserimus orizontem quidem circulum ABGD, eum vero qui per media animalia AEGZ secantes se invicem ad A et G puncta, ambo quidem simul anguli ZAD et DAE duobus rectis equales esse. esse] fiunt V2 Equalis vero angulus ZAD angulo ZGD. Quare et ambo simul anguli ZGD et DAE duos rectos faciunt. Quod oportebat ostendere.
Superaccidet autem, his ita se habentibus, quoniam demonstrati sunt et equidistantium ab eodem equinoctiali puncto ad eumdem orizontem considerati anguli equales et equidistantium ab eodem tropico puncto alterius orientalem et alterius occidentalem ambos simul duobus rectis equales esse. Quare et propter hoc sub sub] si ab V2F1 Ariete usque ad chelas factos orientales angulos invenerimus, coostensi erunt et orientales alterius semicirculi, ampliusque duorum 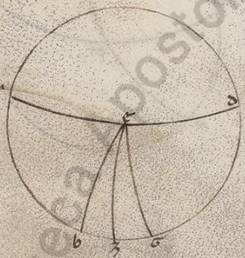 semicirculorum occidentales. Quo vero modo ostenditur, breviter exponemus utentes rursum exempli causa eodem parallilo, hoc est secundum quem borealis polus elevatur ab orizonte gradibus xxxvi. Sub equinoctialibus ergo punctis eius qui per media animalia circuli ad orizontem facti anguli promte possunt sumi. Si enim scripserim scripserim] scripserimus V2F1 meridianum quidem circulum ABGD, subiacentis vero orizontis orientalem semicirculum AED et equinoctialis quidem tetartimorio tetartimorio] tetartimorion V2 EZ, eius vero qui per media animalia duo, EB scilicet ZEG, ZEG] et EG V2 ita se habenti, habenti] habentia V2 ut E punctus ad EB quidem tartimorion tartimorion] tetartimorion V2 intelligatur autupnale, ad EG vero vernale, et B quidem fiat hibernum tropicum, G autem estivum: colligitur quoniam DZ quidem periferia subiacente graduum liiii cl scilicet perfectio altitudinis poli scilicet … poli] om. V2, utraque vero periferiarum que sunt BZ et ZG equalium xxiii et li ad proximum, et GB GB] GD V2 quidem fit graduum xxx ix, BD vero eorumdem lxxvii li. Quare quoniam E polus est ABGD meridianus meridianus] meridiani V2F1 et DEG angulus factus sub principio Arietis talium est xxx ix, qualium est unus rectus xc, angulus vero factus DEB sub principio chellarum eorumdem lxxvii et li.
semicirculorum occidentales. Quo vero modo ostenditur, breviter exponemus utentes rursum exempli causa eodem parallilo, hoc est secundum quem borealis polus elevatur ab orizonte gradibus xxxvi. Sub equinoctialibus ergo punctis eius qui per media animalia circuli ad orizontem facti anguli promte possunt sumi. Si enim scripserim scripserim] scripserimus V2F1 meridianum quidem circulum ABGD, subiacentis vero orizontis orientalem semicirculum AED et equinoctialis quidem tetartimorio tetartimorio] tetartimorion V2 EZ, eius vero qui per media animalia duo, EB scilicet ZEG, ZEG] et EG V2 ita se habenti, habenti] habentia V2 ut E punctus ad EB quidem tartimorion tartimorion] tetartimorion V2 intelligatur autupnale, ad EG vero vernale, et B quidem fiat hibernum tropicum, G autem estivum: colligitur quoniam DZ quidem periferia subiacente graduum liiii cl scilicet perfectio altitudinis poli scilicet … poli] om. V2, utraque vero periferiarum que sunt BZ et ZG equalium xxiii et li ad proximum, et GB GB] GD V2 quidem fit graduum xxx ix, BD vero eorumdem lxxvii li. Quare quoniam E polus est ABGD meridianus meridianus] meridiani V2F1 et DEG angulus factus sub principio Arietis talium est xxx ix, qualium est unus rectus xc, angulus vero factus DEB sub principio chellarum eorumdem lxxvii et li.
〈U〉t autem autem] add. et reliquorum V2 effodos manifesta fiat, preiaceat exempli causa invenire factum orientalem angulum sub principio Tauri et orizonte. Sitque meridianus quidem circulus ABGD, subiacentis vero orizontis orientalis semicirculus BED, et scribatur eius qui per media animalia AEG semicirculus, ut punctus E principium sit Tauri, et quoniam in hoc climate, principio Tauri oriente, in medio celi sub terra fuerit Cancri gradus xvii et xli, demonstravimus enim qualiter 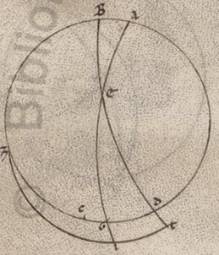 talia de facili sumantur per expositas nobis ascensiones, minor fit EG periferia tetartimorio. Scribatur ergo polo E spatioque tetragoni latere maximi circuli porcio TIZ, et adimpleatur et EGI tetartimorium et EDT. Fit autem e DGZ et ZIT utraque tetartimorii, eo quod BET orizonti sit per polos et ZGD meridiani et ZIT maximi circuli. Rursus quoniam Cancri quidem gradus xvii et xli distant ab equinoctiali ad arctos in eo qui per polos ipsius maximo circulo gradibus xxii et xl, – exposita enim sunt et hec –, equinoctialis autem distat a Z polo orizontis in eadem periferia ZGD gradibus xxxvi, colligitur et ZG periferia graduum lviii et xl; his manifestatis, fit reliquum propter descriptionem proportio eius que sub dupla periferiae GD ad eam que sub dupla periferie DZ composita ex proportione eius que sub dupla periferie GE ad eam que sub dupla periferie EI et proportione eius que sub dupla periferie IT ad eam que sub dupla periferie ZT. Verum propter periacentia dupla quidem periferie GD graduum est lxii et xl et que sub ea recta portionum lxii xxiiii, dupla vero eius que est DZ graduum clxxx et que sub ea recta portionum cxx, et rursum dupla quidem eius que est GE graduum clv xxii et que sub ea recta portionum cxvii xiiii, dupla vero eius que est EI graduum clxxx et que sub ea recta portionum cxx. Si ergo a proportione eorum que sunt lxii xxiiii ad cxx subtraxerim proportionem eorum que sunt cxvii xiiii ad cxx, relinquetur nobis proportio eius que sub dupla periferie TI ad eam que sub dupla periferie TZ, que lxiii lii ad cxx et est que sub dupla periferie ZT proportioni cxx et ea ergo que sub dupla periferie IT eorumdem lxiii lii. Quare et dupla quidem quidem] add. del. periferie V3 eius que est IT graduum est lxiiii xx, item item] IT V2 vero et ipsa et IET angulus eorumdem xxxii x. Quod oportet ostendere. Idem modus, ne secundum unumquodque eundem sermonem revolventes extendamus commentarium sintareos, sintareos] sintaxeos V2F1 et in reliquis et dodecatimoriis et climatibus nobis intelligetur.
talia de facili sumantur per expositas nobis ascensiones, minor fit EG periferia tetartimorio. Scribatur ergo polo E spatioque tetragoni latere maximi circuli porcio TIZ, et adimpleatur et EGI tetartimorium et EDT. Fit autem e DGZ et ZIT utraque tetartimorii, eo quod BET orizonti sit per polos et ZGD meridiani et ZIT maximi circuli. Rursus quoniam Cancri quidem gradus xvii et xli distant ab equinoctiali ad arctos in eo qui per polos ipsius maximo circulo gradibus xxii et xl, – exposita enim sunt et hec –, equinoctialis autem distat a Z polo orizontis in eadem periferia ZGD gradibus xxxvi, colligitur et ZG periferia graduum lviii et xl; his manifestatis, fit reliquum propter descriptionem proportio eius que sub dupla periferiae GD ad eam que sub dupla periferie DZ composita ex proportione eius que sub dupla periferie GE ad eam que sub dupla periferie EI et proportione eius que sub dupla periferie IT ad eam que sub dupla periferie ZT. Verum propter periacentia dupla quidem periferie GD graduum est lxii et xl et que sub ea recta portionum lxii xxiiii, dupla vero eius que est DZ graduum clxxx et que sub ea recta portionum cxx, et rursum dupla quidem eius que est GE graduum clv xxii et que sub ea recta portionum cxvii xiiii, dupla vero eius que est EI graduum clxxx et que sub ea recta portionum cxx. Si ergo a proportione eorum que sunt lxii xxiiii ad cxx subtraxerim proportionem eorum que sunt cxvii xiiii ad cxx, relinquetur nobis proportio eius que sub dupla periferie TI ad eam que sub dupla periferie TZ, que lxiii lii ad cxx et est que sub dupla periferie ZT proportioni cxx et ea ergo que sub dupla periferie IT eorumdem lxiii lii. Quare et dupla quidem quidem] add. del. periferie V3 eius que est IT graduum est lxiiii xx, item item] IT V2 vero et ipsa et IET angulus eorumdem xxxii x. Quod oportet ostendere. Idem modus, ne secundum unumquodque eundem sermonem revolventes extendamus commentarium sintareos, sintareos] sintaxeos V2F1 et in reliquis et dodecatimoriis et climatibus nobis intelligetur.
〈II.12〉
 Restante igitur effodo secundum quam utique sumemus factos quoque ad eum qui per polos orizontis secundum unamquamque inclinationem et secundum unamquamque positionem eius qui per media animalia circuli angulos, coostensa, ut iam sepe diximus, periferia quoque circuli qui per polos orizontis sub eo quod ad verticem puncto et ea que ad obliquum circulum eius sectione deprehensa, exponemus rursum et que in hanc partem sunt prelibanda, et ostendemus primum quoniam, equidistantibus ab eodem tropico puncto eius qui per media animalia circuli punctis equalia tempora deprehendentibus in utraque meridiani, hoc quidem ad orientem, illo vero ad occidentem, et que ab eo quod ad verticem in ipsa periferie maximorum circulorum alternis sunt equales et qui ad ipsa sunt anguli, secundum quem distincximus modum, duobus rectis equales. Esto enim meridiani portio ABG, et subiaceat in ipsa punctum quidem quod ad verticem B, isimerini vero polus G, et scribantur eius qui per media animalia portiones due ADE et AZI ita se habentes, ut D et Z puncta et eque distent ab eodem tropico et equales deprehendant periferias eius qui per ipsa parallili in utraque ABG meridiani. Scribantur vero et maximorum circulorum periferie per D Z puncta, ab equinoctialis quidem polo G et GD et GZ, ab eo vero quod ad verticem puncto quod est G et BD et BZ; dico quoniam BD quidem periferia ei que est BZ est equalis, angulus vero RDE RDE] BDE V2F1 cum BZA duobus rectis equales. Quoniam enim D et Z puncta secundum equales eius qui per ipsa parallili periferias distant ab ABG meridiano, equalis est est] add. BGD angulus ei qui est V2F1 BGZ. Duo ergo trilatera sunt BGD et BGZ duo latera duobus lateribus equa habentia utriusque utrique GA GA] GD V2 quidem ei quod est GZ, communem vero BG et angulum angulo qui sub equis lateribus continentur BGD ei qui est
Restante igitur effodo secundum quam utique sumemus factos quoque ad eum qui per polos orizontis secundum unamquamque inclinationem et secundum unamquamque positionem eius qui per media animalia circuli angulos, coostensa, ut iam sepe diximus, periferia quoque circuli qui per polos orizontis sub eo quod ad verticem puncto et ea que ad obliquum circulum eius sectione deprehensa, exponemus rursum et que in hanc partem sunt prelibanda, et ostendemus primum quoniam, equidistantibus ab eodem tropico puncto eius qui per media animalia circuli punctis equalia tempora deprehendentibus in utraque meridiani, hoc quidem ad orientem, illo vero ad occidentem, et que ab eo quod ad verticem in ipsa periferie maximorum circulorum alternis sunt equales et qui ad ipsa sunt anguli, secundum quem distincximus modum, duobus rectis equales. Esto enim meridiani portio ABG, et subiaceat in ipsa punctum quidem quod ad verticem B, isimerini vero polus G, et scribantur eius qui per media animalia portiones due ADE et AZI ita se habentes, ut D et Z puncta et eque distent ab eodem tropico et equales deprehendant periferias eius qui per ipsa parallili in utraque ABG meridiani. Scribantur vero et maximorum circulorum periferie per D Z puncta, ab equinoctialis quidem polo G et GD et GZ, ab eo vero quod ad verticem puncto quod est G et BD et BZ; dico quoniam BD quidem periferia ei que est BZ est equalis, angulus vero RDE RDE] BDE V2F1 cum BZA duobus rectis equales. Quoniam enim D et Z puncta secundum equales eius qui per ipsa parallili periferias distant ab ABG meridiano, equalis est est] add. BGD angulus ei qui est V2F1 BGZ. Duo ergo trilatera sunt BGD et BGZ duo latera duobus lateribus equa habentia utriusque utrique GA GA] GD V2 quidem ei quod est GZ, communem vero BG et angulum angulo qui sub equis lateribus continentur BGD ei qui est 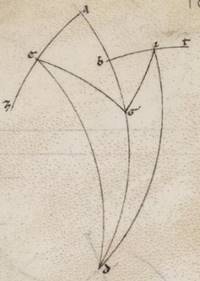 BGZ, et basim ergo BD basi BZ equalem habebunt et angulum BZG angulo BDG. Sed quoniam demonstratum est paulo ante quoniam equidistantium ab eodem tropico puncto facti ad eum qui per polos equinoctialis anguli ambo simul duobus rectis equales sunt, ambo ergo simul GDE et GZA duobus rectis sunt equales. Ostensus est autem et angulus BDG ei que est BZG equalis et ambo igitur simul BDE et BZA duobus rectis sunt equales. Quod oportebat ostendere.
BGZ, et basim ergo BD basi BZ equalem habebunt et angulum BZG angulo BDG. Sed quoniam demonstratum est paulo ante quoniam equidistantium ab eodem tropico puncto facti ad eum qui per polos equinoctialis anguli ambo simul duobus rectis equales sunt, ambo ergo simul GDE et GZA duobus rectis sunt equales. Ostensus est autem et angulus BDG ei que est BZG equalis et ambo igitur simul BDE et BZA duobus rectis sunt equales. Quod oportebat ostendere.
Rursum vero demonstrandum quoniam, eisdem punctis eius qui per media animalia circuli secundum equalia tempora distantibus in utraque meridiani, et ab eo qui ad verticem in ipsa scripte maximorum circulorum periferie sibi invicem sunt equales, et qui ad ipsas fiunt anguli ambo simul, quorum unus ad orientem, alter ad occidentem, duobus sub meridiano et ad idem puctum factis sunt equales, quando in utraque positione medium tenentia celum ambo, vel borealiora, vel australiora eo quod ad verticem puncto contingunt. Primum vero subiaceant ambo australiora, sitque meridiani portio ABGD, in ipsa vero quod quidem ad verticem punctum G, polus vero isimerini D, scribanturque due portiones eius qui per media animalia circuli AEZ et BIT ita se habentes, ut E punctum et I idem subiacens equali in utraque eius qui 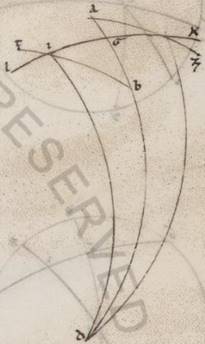 per ipsum parallili periferia distet ab ARGD GA] GD V2 meridiano, scribanturque rursum per ipsa portiones maximorum circulorum ab eodem eodem] eo V2F1 quidem quod est G et GE et GI, ab eo vero quod est D et DE et DI. Propter eadem ergo eis que ante, quoniam est est] E V2 et I puncta eundem facientia parallilum equales ipsius periferias in utraque faciunt meridiani, et equilaterum et equiangulum fit DE DE] GDE V2F1 trilaterum ei quod est GDI. Quare Z Z] om. V2F1 et GE ei que est GI fit equalis. Dico ergo quoniam et ambo simul GEZ et GIB duobus qui sunt BEZ BEZ] DEZ V2 et DIB sunt equales. Quoniam enim angulus quidem DEZ idem est ei qui est DIB, angulus autem GED equalis est ei qui est DIG et ambo igitur simul GED et GIB sunt equales ei qui est DEZ. Quare ambo simul GEZ totus et GIB duobus qui sunt DEZ et DIB sunt equales. Quod oportebat ostendere.
per ipsum parallili periferia distet ab ARGD GA] GD V2 meridiano, scribanturque rursum per ipsa portiones maximorum circulorum ab eodem eodem] eo V2F1 quidem quod est G et GE et GI, ab eo vero quod est D et DE et DI. Propter eadem ergo eis que ante, quoniam est est] E V2 et I puncta eundem facientia parallilum equales ipsius periferias in utraque faciunt meridiani, et equilaterum et equiangulum fit DE DE] GDE V2F1 trilaterum ei quod est GDI. Quare Z Z] om. V2F1 et GE ei que est GI fit equalis. Dico ergo quoniam et ambo simul GEZ et GIB duobus qui sunt BEZ BEZ] DEZ V2 et DIB sunt equales. Quoniam enim angulus quidem DEZ idem est ei qui est DIB, angulus autem GED equalis est ei qui est DIG et ambo igitur simul GED et GIB sunt equales ei qui est DEZ. Quare ambo simul GEZ totus et GIB duobus qui sunt DEZ et DIB sunt equales. Quod oportebat ostendere.
Describantur rursum cedere cedere] eedem V2F1 portiones expositorum circulorum ita tamen, ut A punctum et B borealiora fiant puncto G; dico quoniam idem et sic continget, hoc est ambo simul REZ REZ] KEZ V2F1 angulus et LIB, duobus qui sunt DEZ sunt equales. Quoniam enim angulus quidem DEZ idem est angulo DIB equalis vero DER DER] DEK V2F1 angulo DIL et totus ergo LIB equalis est ambobus simul DEZ et DER DER] DEK V2F1 angulis. Quare et ambo simul LIB et REZ REZ] KEZ V2F1 duobus qui sunt DEZ sunt equales.
Adiaceat rursum descriptio similis ita tamen, ut orientalis quidem portionis medium celi tenens punctus, hoc est A australior sit G puncto qui ad verticem, eius vero que ad occidentem porcionis qui celi medium tenet, hoc est B, borealior sit eodem; dico quoniam ambo simul anguli GEZ et LIB duobus DEZ maiores sunt duobus rectis. Quoniam enim angulus quidem DIG equalis est angulo DEG, ambo autem simul DIG et DIL duobus rectis equales sunt, et ambo igitur simul DEG et DIL anguli duobus rectis sunt equales. Sunt autem et DEZ angulus  idem angulo DIB. Quare et ambo simul GEZ et LIB anguli duobus simul DEZ et DIB angulis, hoc est bis eo qui est DEZ, maiores sunt ambobus simul DEG et DIL angulis qui sunt duobus rectis equales. Quod oportebat ostendere.
idem angulo DIB. Quare et ambo simul GEZ et LIB anguli duobus simul DEZ et DIB angulis, hoc est bis eo qui est DEZ, maiores sunt ambobus simul DEG et DIL angulis qui sunt duobus rectis equales. Quod oportebat ostendere.
Adiaceat autem quod relinquitur secundum simillem descriptionem eius quidem que ad orientem portionis medium celum tenens punctus A borealior factus puncto G, eius vero que ad occidentem portionis medium celum tenens punctus B australior; dico quoniam ambo simul KEZ et GIB duobus DEZ minores sunt duobus rectis. Propter eadem enim rursum ambo quidem simul REZ REZ] KEZ V2F1 et GIR GIR] GIB V2 anguli anguli] iter. V3 ambobus simul DEZ et DIB angulis, hoc est duobus qui sunt DEZ, minores sunt ambobus simul DER DER] DEK V2F1 et DIG angulis. Ipsi vero duobus rectis equales. equales] add. eo quod ambo quidem simul DEK et DEG anguli duobus rectis sint equales V2 Equales vero et DEG angulus angulo DIG. Quod oportebat ostendere.
Quoniam vero ex promtu possunt sumi illi eorum qui fiunt sub obliquo circulo ad maximum per punctum verticis scriptum circulum et angulorum et arctuum, arctuum] arcuum V2F1 secundum quem diximus modum, et que in meridiano et qui in orizonte fiunt, et inde utique erit ita manifestum. Si enim scripsimus meridianum circulum ABGD et orizontis quidem semicirculum BED, eius vero qui per media animalia circuli ZEI quomodocumque se habens, quando quidem per ipsum medii celi punctum Z intellexerimus maximum per punctum verticis A scriptum circulum, idem fiet meridiano ABGD et erit angulus DZE inde nobis datus, eo quod et Z punctus et eius ad meridianum factus angulus detur et ipsa AZ periferia, eo quod habeamus quot gradibus in meridiano et Z punctus distat ab equinoctiali et equinoctialis ab A puncto verticis. Quando vero per orientem ipsum punctum E, intelligemus maximum per A scriptum circulum ut AEG, inde  et ita fiet manifestum quoniam AE quidem periferia semper fiet tetartimorii, eo quod A punctus polus sit BED orizontis, recto vero existente semper propter eamdem causam AED angulo et dato eo qui obliqui circuli ad orizontem, hoc est DEI, dabitur et totus AEI angulus. Quod oportebat ostendere.
et ita fiet manifestum quoniam AE quidem periferia semper fiet tetartimorii, eo quod A punctus polus sit BED orizontis, recto vero existente semper propter eamdem causam AED angulo et dato eo qui obliqui circuli ad orizontem, hoc est DEI, dabitur et totus AEI angulus. Quod oportebat ostendere.
Quare manifestum quoniam, his ita se habentibus, si in unaquaque inclinatione eos qui ante meridianum solos et angulos et arcus eorum tantum que a principio Cancri usque principium Capricorni dodecatimoriorum supputaverimus, coostensos habebimus et eos qui post meridianum ipsorum et angulos et arcus et adhuc reliquorum et eos qui ante meridianum et eos qui post meridianum. Ut autem et in his secundum unamquamque inclinationem efodos manifesta fiat, exempli rursus causa exponemus futuram universaliter ostensionem per unum theorema, supponentes secundum eandem inclinationem, hoc est secundum quam borealis polus ab orizonte elevatur gradibus xxxvi, principium Cancri verbi gratia una hora equinoctiali distare ad orientem a meridiano, secundum quam positionem in preiacenti parallilo medium quidem celi tenentem tenentem] tenent V2 tenente F1 Geminorum gradus xvi xii, oriuntur vero Virginis gradus xvii xxxvii. Esto autem meridianus circulus ABGD, et orizontis quidem semicirculus BED, eius autem qui per media animalia ZIT ita se habens, ut I quidem punctus principium sit Cancri, Z vero obtineat Geminorum gradus xvi xii, T vero Virginis gradus xvii xxxvii, scribaturque et per A punctum verticis et per I principium Cancri maximi circuli portio AIEG, preiaceat autem primum AI periferia periferia] periferiam V2F1 invenire. Manifestum ergo quoniam ZT quidem periferia gridi gridi] graduum V2F1 est xci xxv, item item] IT V2 vero graduum lxxvii xxxvii. Similiter autem quoniam quidem Geminorum quidem gradus xvi xii assumunt meridiani ab equinoctiali ad arctos gradus xxiii vii, equinoctialis vero circulus ab 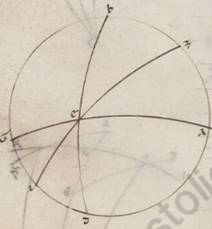 A quod secundum verticem puncto gradus xxxvi, erunt erunt] erit V2 et AZ periferia graduum xii liii, ZB vero reliquorum in tetartimorium graduum lxxvii vii; hic hic] his V2 datis, fit rursum propter descriptionem proporcio eius que sub dupla periferie periferie] add. ZB ad eam que sub dupla periferie V2F1 BA composita ex proportione eius que sub dupla periferie ZT ad eam que sub dupla periferie TI et ex proportione eius que sub dupla periferie IE ad eam que sub dupla periferie EA. Verum dupla quidem eius que est ZB graduum est cliiii xiiii et que sub ea recta portionum cxvi lix, dupla vero eius quem est BA graduum est clxxx et que sub ea recta portionum cxx; et rursum dupla quidem eius que est ZT graduum est clxxxii l et que sub ea recta portionum cxix lviii, que vero eius que est TI graduum clv xiiii et que sub ea recta portionum cxvii xii. Si ergo a proportione eorum que sunt cxvi lix ad cxx minuerimus proportionem eorum que sunt cxix lviii ad cxvii xii, reliquetur nobis proportio eius que sub dupla periferie EI ad eam que sub dupla periferie EA, que cxiiii xvi proxime ad cxx et est que sub dupla periferie periferie] add. EA portionum cxx V2F1 et ea ergo que sub dupla periferie EI eorumdem est cxiiii xvi. Quare et dupla quidem EI periferiae graduum est cxliiii xxvi ad proximum, ipsa vero IE eorumdem lxxii xiii, et reliqua ergo AI restantium in tetartimorium est graduum xvii xlvii. Quod oportebat ostendere.
A quod secundum verticem puncto gradus xxxvi, erunt erunt] erit V2 et AZ periferia graduum xii liii, ZB vero reliquorum in tetartimorium graduum lxxvii vii; hic hic] his V2 datis, fit rursum propter descriptionem proporcio eius que sub dupla periferie periferie] add. ZB ad eam que sub dupla periferie V2F1 BA composita ex proportione eius que sub dupla periferie ZT ad eam que sub dupla periferie TI et ex proportione eius que sub dupla periferie IE ad eam que sub dupla periferie EA. Verum dupla quidem eius que est ZB graduum est cliiii xiiii et que sub ea recta portionum cxvi lix, dupla vero eius quem est BA graduum est clxxx et que sub ea recta portionum cxx; et rursum dupla quidem eius que est ZT graduum est clxxxii l et que sub ea recta portionum cxix lviii, que vero eius que est TI graduum clv xiiii et que sub ea recta portionum cxvii xii. Si ergo a proportione eorum que sunt cxvi lix ad cxx minuerimus proportionem eorum que sunt cxix lviii ad cxvii xii, reliquetur nobis proportio eius que sub dupla periferie EI ad eam que sub dupla periferie EA, que cxiiii xvi proxime ad cxx et est que sub dupla periferie periferie] add. EA portionum cxx V2F1 et ea ergo que sub dupla periferie EI eorumdem est cxiiii xvi. Quare et dupla quidem EI periferiae graduum est cxliiii xxvi ad proximum, ipsa vero IE eorumdem lxxii xiii, et reliqua ergo AI restantium in tetartimorium est graduum xvii xlvii. Quod oportebat ostendere.
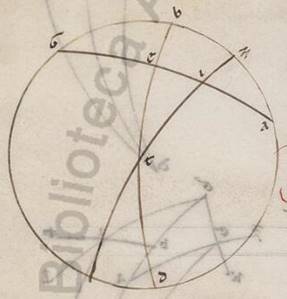 Deinceps vero et AIT angulum inveniemus ita. Adiaceat enim eadem descriptio et polo I, spatioque tetragoni latere scribatur maximi circuli porcio KLM. Quare quoniam AIE circulus et per eius qui est ETM et per eius qui est KLM polos scriptus est, utraque EM et RM RM] KM V2F1 periferiarum tetartimorii fit. Rursus ergo propter descriptionem erit proportio eius que sub dupla periferie IE ad eam que sub dupla periferie EK composita ex proportione eiusque sub dupla periferie IT ad eam que sub dupla periferie TL et proportione eius que sub dupla periferie LM ad eam que sub dupla periferie RM. RM] KM V2F1 Sed dupla quidem eius que est IE graduum cxliiii xxvi et que sub ea recta portionum cxiiii xvi, dupla vero eius que est ER ER] EK V2F1 graduum xxxv xxxiiii, et que sub ea recta portionum xxxvi xxxviii; et rursum dupla quidem eius que est TI graduum est clv xiiii et que sub ea recta portionum cxvii xii, dupla vero eius que est TL graduum xxiiii xlvi, et que sub ea recta portionum xxv xliiii. Quare si a proportione eorum que sunt cxiiii xvi ad xxxvi xxxviii subtraximus proportionem eorum que sunt cxvii xii ad xxv xliiii, relinquetur nobis proportio eorum que sub dupla periferie LM ad eam que sub dupla periferie MK, que lxxxii xi proxime ad cxx; et est que sub dupla periferie KM KM] MK V2 portionum cxx et ea ergo que sub dupla periferie LM eorumdem est lxxxii xi. Quare et dupla periferie LM graduum lxxxvi xxviii, ipsa vero LM eorum xliii xiiii, et reliqua ergo LR LR] LK V2F1 periferia et ipsa et LIK angulus porcionum est xlvi xlvi minutorum. Quare et AIT angulus reliquorum in duos rectos graduum erit cxxxiii xiiii. Quod oportebat ostendere.
Deinceps vero et AIT angulum inveniemus ita. Adiaceat enim eadem descriptio et polo I, spatioque tetragoni latere scribatur maximi circuli porcio KLM. Quare quoniam AIE circulus et per eius qui est ETM et per eius qui est KLM polos scriptus est, utraque EM et RM RM] KM V2F1 periferiarum tetartimorii fit. Rursus ergo propter descriptionem erit proportio eius que sub dupla periferie IE ad eam que sub dupla periferie EK composita ex proportione eiusque sub dupla periferie IT ad eam que sub dupla periferie TL et proportione eius que sub dupla periferie LM ad eam que sub dupla periferie RM. RM] KM V2F1 Sed dupla quidem eius que est IE graduum cxliiii xxvi et que sub ea recta portionum cxiiii xvi, dupla vero eius que est ER ER] EK V2F1 graduum xxxv xxxiiii, et que sub ea recta portionum xxxvi xxxviii; et rursum dupla quidem eius que est TI graduum est clv xiiii et que sub ea recta portionum cxvii xii, dupla vero eius que est TL graduum xxiiii xlvi, et que sub ea recta portionum xxv xliiii. Quare si a proportione eorum que sunt cxiiii xvi ad xxxvi xxxviii subtraximus proportionem eorum que sunt cxvii xii ad xxv xliiii, relinquetur nobis proportio eorum que sub dupla periferie LM ad eam que sub dupla periferie MK, que lxxxii xi proxime ad cxx; et est que sub dupla periferie KM KM] MK V2 portionum cxx et ea ergo que sub dupla periferie LM eorumdem est lxxxii xi. Quare et dupla periferie LM graduum lxxxvi xxviii, ipsa vero LM eorum xliii xiiii, et reliqua ergo LR LR] LK V2F1 periferia et ipsa et LIK angulus porcionum est xlvi xlvi minutorum. Quare et AIT angulus reliquorum in duos rectos graduum erit cxxxiii xiiii. Quod oportebat ostendere.
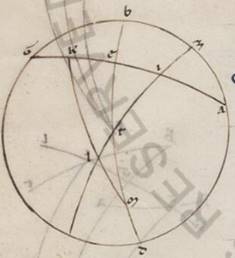 Modus ergo inventionis preiacentium in reliquis idem colligitur. Nos autem et alios et angulos et arcus, quantorum convenit neccessitatem particularibus considerationibus fore, promte habeamus expositos, supputabimus et ipsos lineariter, incipientes quidem ab eo qui per Meroen parallilo secundum quem maxima dies horarum est equinoctialium xiii, pertingentes vero eum usque qui super parallilum parallilum] Pontum V2F1 scriptum est per emissiones Borestenis, ubi maxima horarum est equinoctialium xvi. Si Si] usi V2F1 autem sumus secundum unamquamque augmento in climatibus quidem eo quod secundum emiorium rursus, quemadmodum et in ascensionibus; in eius vero qui per media animalia circuli portionibus, eo quod per unum dodecatimorium; in eis autem que ad orientem vel et ad occidentem meridiani positionibus, eo quod per unam horam equinoctialem. Faciemus vero et istorum expositionem canonice secundum unamquam unamquam] unumquodque et V2 unamquamque F1 clima et dodecatimorium, apponentes in primis quidem partibus quantitatem earumque distantie in utraque meridiani post eam que secundum ipsum positionem equinoctialium horarum, in secundis autem quantitates earum que ab eo quod ad verticem puncto usque principium expositi dodecatimorii fiunt, ut diximus, periferiarum, in tertiis vero et in quartis quantitates eorum qui sub preiacente sectione secundum diffinitum nobis modus modus] modum V2 continentur angulorum, in tertiis quidem eos qui earum que ad ad] add. orientem meridiani posicionum, in quartis autem eos qui earum et que ad V2 occidentem, sicut et in principio tamen distinximus. Reminisci oportet quoniam duorum qui sub continenti portione eius qui per media animalia circuli continetur angulorum eum qui ab artus artus] arctis V2 eiusdem porcionis semper assumpsimus, tales tales] talium V2 in unoquoque ipsorum quantitatem adiungentes, qualium est unus
Modus ergo inventionis preiacentium in reliquis idem colligitur. Nos autem et alios et angulos et arcus, quantorum convenit neccessitatem particularibus considerationibus fore, promte habeamus expositos, supputabimus et ipsos lineariter, incipientes quidem ab eo qui per Meroen parallilo secundum quem maxima dies horarum est equinoctialium xiii, pertingentes vero eum usque qui super parallilum parallilum] Pontum V2F1 scriptum est per emissiones Borestenis, ubi maxima horarum est equinoctialium xvi. Si Si] usi V2F1 autem sumus secundum unamquamque augmento in climatibus quidem eo quod secundum emiorium rursus, quemadmodum et in ascensionibus; in eius vero qui per media animalia circuli portionibus, eo quod per unum dodecatimorium; in eis autem que ad orientem vel et ad occidentem meridiani positionibus, eo quod per unam horam equinoctialem. Faciemus vero et istorum expositionem canonice secundum unamquam unamquam] unumquodque et V2 unamquamque F1 clima et dodecatimorium, apponentes in primis quidem partibus quantitatem earumque distantie in utraque meridiani post eam que secundum ipsum positionem equinoctialium horarum, in secundis autem quantitates earum que ab eo quod ad verticem puncto usque principium expositi dodecatimorii fiunt, ut diximus, periferiarum, in tertiis vero et in quartis quantitates eorum qui sub preiacente sectione secundum diffinitum nobis modus modus] modum V2 continentur angulorum, in tertiis quidem eos qui earum que ad ad] add. orientem meridiani posicionum, in quartis autem eos qui earum et que ad V2 occidentem, sicut et in principio tamen distinximus. Reminisci oportet quoniam duorum qui sub continenti portione eius qui per media animalia circuli continetur angulorum eum qui ab artus artus] arctis V2 eiusdem porcionis semper assumpsimus, tales tales] talium V2 in unoquoque ipsorum quantitatem adiungentes, qualium est unus 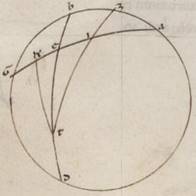 rectus xc et est expositio canoniorum talis.
rectus xc et est expositio canoniorum talis.
S〈upraposita auctoris demonstracio locum non habet, nisi arcus IT sit minor tetartimorio.〉 Potest autem esse equalis et maior. Nichil〈ominus tamen noti erit anguli septentrionales orientales qui sunt ante〉 meridiem. Sit primo IT equalis tetartimorio. Dico quoniam qui sub AIT x〈c graduum est. Constat itaque IT maiorem esse quam IE, eo quod totum AE〉 sit tetartimorion, ergo polo quidem I et spatio IT tetragoni latere scribatur maximi circuli po〈rcio TK. Quoniam ergo circulus AIEK〉 transit per polos TE et TK utraque TE et TK tetartimorion, fit igitur angulus KIT x x] xc V2F1 graduum est et reliquus AIT similiter xc.
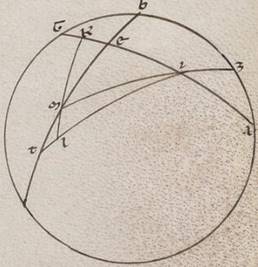 Sit item periferia IT maior tetartimorio et sit superhabundatia TL et polo I spatioque IL tetragoni latere scribatur maximi circuli portio LEIK. Quare quoniam AIEK circulus per eius qui est EM et KM polo scriptus est utraque EM et KM periferia tetartimorion fit, erit ergo proportio eius que sub dupla periferie IE ad eam que sub dupla periferie EK composita ex proportione eius que sub dupla periferie IT ad eam que sub dupla periferie TL et proportione eius que sub dupla periferie LM ad eam que sub dupla periferie KM. Quoniam ergo periferie IE nota est et EK nota et utraque IT et TL nota et KM nota erit LM nota, protrahatur arcus IM, tetartimorion erit angulus KIM xc graduum et reliquus MLA xc graduum. Si ergo abstulerimus angulum MIL, iam nota xc remanet angulus AIT notus.
Sit item periferia IT maior tetartimorio et sit superhabundatia TL et polo I spatioque IL tetragoni latere scribatur maximi circuli portio LEIK. Quare quoniam AIEK circulus per eius qui est EM et KM polo scriptus est utraque EM et KM periferia tetartimorion fit, erit ergo proportio eius que sub dupla periferie IE ad eam que sub dupla periferie EK composita ex proportione eius que sub dupla periferie IT ad eam que sub dupla periferie TL et proportione eius que sub dupla periferie LM ad eam que sub dupla periferie KM. Quoniam ergo periferie IE nota est et EK nota et utraque IT et TL nota et KM nota erit LM nota, protrahatur arcus IM, tetartimorion erit angulus KIM xc graduum et reliquus MLA xc graduum. Si ergo abstulerimus angulum MIL, iam nota xc remanet angulus AIT notus.
CANCRI |
LIBRE |
|||||||||||||
eius qui per Meroen hore xiii graduum xvi mintorum xxvii |
||||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
minuta |
Auster |
Boreas |
Gradus |
minuta |
Auster |
Auster |
|||||||
meridies
i
ii |
vii
xv
xxix |
xxvii
lv
iii |
xc
xxv
ix |
o
xvi
xv |
cliiii
clix |
xliiii
xlv |
meridies
i
ii |
xvi
xxvii
xxvii |
xxvii
viii
l |
cxiii
cliiii
clxxiii |
li
liii
xvii |
lxxii
liiii |
xlix
xxv |
|
iii
iiii
v |
xlii
lvi
o |
xlii
xxv
ii |
i
clxxv
clxx |
xxxviii
vii
xviii |
cxxviii
xxx
ix |
xxii
liii
xlii |
iii
iiii
v |
xlvii
lxi
lxxv |
xx
xxii
xxxix |
i
v
vii |
xxiii
viii
ix |
xlvi
xlii
xl |
xix
xxxiiii
xxxiii |
|
vi
vi xxx |
lxxxiii
xc |
xxvi
o |
clxiiii
clxi |
xli
lvii |
xv
xviii |
xix
iii |
vi |
xc |
o |
vii |
xxiiii |
xl |
xviii |
|
Leonis |
Scorpii |
|||||||||||||
Boreas |
Boreas |
Auster |
Auster |
|||||||||||
meridies
i
ii |
iiii
xiiii
xxviii |
iii
xx
xlii |
cii
xxvi
xv |
xxx
iii
xxviii |
clxviii
ix |
lvii
xxxii |
meridies
i
ii |
xviii
xxxi
xl |
vii
xlv
lii |
cxi
cxxxix
clvii |
o
o
lix |
lxxxiii
lxiiii |
o
i |
|
iii
iiii
v |
xlii
xlvi
o |
xliii
xlix
xxxviii |
x
v
ii |
v
xix
xxxiii |
xiiii
xviii
xxii |
lv
xli
xxvii |
iii
iii
v |
lii
lxxv
lxxix |
xxx
xl
xviii |
cxlix
clxxvi
l |
xxiii
xli
xli |
lii
xlv
xl |
xxxvii
xix
xix |
|
vi
vi xxv |
lxxxii
xc |
xvii
o |
clxxvii
clxxiiii |
o
li |
xxviii
xxx |
o
ix |
v xlvi |
xc |
o |
iiii |
ix |
xxxvii |
li |
|
Virginis |
Sagittarii |
|||||||||||||
Auster |
Auster |
Auster |
Auster |
|||||||||||
meridies
i
ii |
iiii
xv
xxix |
xlvii
xx
xxviii |
cx
o
viii |
o
o
o |
o
xlii
xxxiiii |
o
o
o |
meridies
l
ii |
xxxv
xxxix
xlvii |
lvii
xlvi
xv |
cii
cxxv
cxliii |
xxx
xii
v |
lxxix
lxi |
xlix
lii |
|
iii
iiii
v |
xliii
lviii
lxxii |
xl
xiii
xxxvi |
ix
viii
vi |
xv
xxxix
liii |
xxxii
xxxiii
xxxv |
xlv
xxi
vii |
iii
iiii
v |
lvii
lxix
lxxxii |
xxxiii
xxx
xviii |
clvi
clxiiii
clxxi |
iii
xlviii
xliii |
xlviii
xl
xxxiii |
lvii
xviii
xvii |
|
v
vi xiiii |
lxxxvi
xc |
xli
o |
v
xxx |
xxxvii
ix |
xxxvi
xxxvii |
xxiii
li |
v xxxv |
xc |
o |
clxxiiii |
li |
ix |
||
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Auster |
Auster |
Auster |
Auster |
|||||||||||
meridies
i
ii |
x
xlii
xlix |
xviii
liiii
xlviii |
ix
cxi
cxxviii |
o
xxiiii
li |
lxviii
li |
xxxvi
ix |
meridies
i
ii |
xvi
xxii
xxxiii |
xxvii
viii
l |
lxvi
cvii
cxxv |
ix
xi
xxxv |
xxv
vi |
vii
xliii |
|
iii
iiii
v |
lix
lxxi
lxxxiii |
xxxv
iiii
xxxi |
cxli
cli
clviii |
xlix
xxv
lviii |
xxxviii
xxviii
xxi |
xi
xxxv
xii |
iii
iiii
v |
xlvii
lxi
lxxv |
xx
xxii
xxxix |
cxxxiii
cxxxvii
cxxxix |
xli
xxvi
xxvii |
clxxviii
clxxxiiii
clxxii |
xxxvii
lii
li |
|
v xxx |
xc |
o |
clxi |
lvii |
xviii |
iii |
vi |
xc |
o |
cxxxix |
xlii |
clxxii |
xxxvi |
|
AQUARII |
TAURI |
|||||||||||||
Auster |
Auster |
Auster |
Boreas |
|||||||||||
meridies
i
ii |
xxxvi
xxxix
xlvii |
lvii
xlvi
xv |
lxxvii
c
cxviii |
xxx
xii
v |
liiii
xxxvi |
xlv
lv |
meridies
i
ii |
iiii
xv
xxix |
xlvii
xx
xxviii |
lxix
cxxxviii
cxlvi |
o
o
o |
clxxx
clxxii |
o
o |
|
iii
iiii
v |
lvii
lxix
lxxxii |
xxxiii
xxx
xviii |
cxxxi
cxxxix
cxlvi |
iii
xlviii
xliii |
xxiii
xv
vii |
lvii
xii
xvii |
iii
iii
v |
xliii
lviii
lxxii |
xl
xiii
xxxvi |
cxlvii
cxlvi
cxliii |
xv
xxxix
liii |
clxx
clxxi
clxxiii |
xlv
xxi
vii |
|
v xxv |
xc |
o |
cxcix |
li |
v |
ix |
vi
vi iiii |
lxxxvi
xc |
xli
o |
cxliii
cxlii |
xxxvii
ix |
clxxiiii
clxxv |
xxiii
li |
|
PISCES |
GEMINORUM |
|||||||||||||
Auster |
Auster |
Boreas |
Boreas |
|||||||||||
meridies
i
ii |
xxviii
xxxi
xl |
vii
xlvi
lii |
lxix
xcvii
cxv |
o
o
lii |
xli
xxi |
o
i |
meridies
l
ii |
iiii
xiiii
xxviii |
iii
xx
xlvi |
lxxvii
i
clxx |
xxx
iii
xxviii |
cliii
clxiiii |
xvii
xxxii |
|
iii
iiii
v |
lii
lxv
lxxix |
xxx
xl
xviii |
cxxvii
cxxxiiii
cxxxix |
xxiii
xli
xli |
x
iii
clxxviii |
xxxvii
xix
xix |
iii
iiii
v |
xli
lvi
lxx |
xliii
xlix
xxxviii |
clxi
clxi
clvii |
v
xix
xxxiii |
clxix
clxxiii
clxxvii |
lv
xli
xxvii |
|
v xlvi |
xc |
o |
cxlii |
ix |
clxxv |
li |
vi
vi xxx |
lxxxiiii
xc |
xvii
o |
clii
cxlix |
o
li |
iii
v |
o
ix |
|
CANCRI |
LIBRE |
|||||||||||||
eius qui per Sienen hore xiii et dimidii graduum xxiii minutorum li |
||||||||||||||
Hore |
||||||||||||||
Hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
meridies
i
ii |
o
xiii
xxvii |
o
xliii
xxiii |
xc
clxxvi
clxxiii |
o
xv
li |
o
iii
vi |
o
xlv
ix |
meridies
i
ii |
xxiii
xxvii
xxxvii |
liiii
lvi
xxxvi |
cxiii
cxliiii
clxii |
li
x
xiii |
lxxiii
lxv |
xxxii
xxix |
|
iii
iiii
v |
xl
liiii
lxvii |
xx
xxvii
xlii |
clxviii
clxvi
clxi |
xv
li
xlii |
xi
xiii
xvii |
xlv
ix
xviii |
iii
iiii
v |
xlix
lxii
lxxvi |
xlii
xlvii
xx |
clxxi
clxxvi
clxxix |
xlv
lix
iii |
lv
l
xlviii |
lvii
xliii
xxxviiii |
|
vi
vi xlv |
lxxx
xc |
xxxvi
o |
clvii
cliii |
lix
xlvi |
xxii
xxvi |
i
xiiii |
vi |
xc |
o |
clxxx |
o |
xlvii |
xlii |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
iii
xiiii
xxvii |
xxi
xviii
lvi |
cii
clxxvi
clxxx |
xxx
iiii
o |
xxviii
xxv |
lvi
o |
meridies
i
ii |
xxxv
xxxviii
xlvi |
xxxi
xxv
ii |
cxi
cxxxiii
cl |
o
xv
xviii |
lxxxviii
lxxi |
xlv
xlii |
|
iii
iiii
v |
xli
lv
xlviii |
xliiii
xiiii
xliii |
clxxv
clxxvii
clxxxiii |
iii
xviii
xl |
xxv
xxvii
xxxi |
lxxvii
xlii
xx |
iii
iiii
v |
lvi
lxviii
lxxxi |
xxx
xxxi
xxii |
clxi
clxix
clxxiiii |
xli
v
xxx |
lx
lii
xlvii |
xix
lv
xxx |
|
vi
vi xxxviii |
lxxxi
xc |
lii
o |
clxviii
clxvi |
lvi
liii |
xxxvi
xxxviii |
iiii
vii |
v xxxix |
xc |
o |
clxxvi |
xli |
xlv |
xix |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xii
xviii
xxx |
xi
xlii
lvii |
cxi
clviii
clxxiii |
o
xl
xliiii |
lxiii
xlviii |
xx
xvi |
meridies
i
ii |
xliiii
xlvi
liii |
xxi
xl
iiii |
cii
cxxi
cxxxvii |
xxx
xxx
xvi |
lxxxiii
lxvii |
xxx
xliiii |
|
Iii
iiii
v |
xliiii
lviii
lxxi |
xxii
i
xliii |
clxxviii
clxxx
clxxv |
iii
o
xv |
xliii
xlii
xlii |
lvii
o
xlv |
iii
iiii
v |
lxii
lxxiii
lxxxv |
xviii
xx
xxiii |
cxlix
clvii
clxi |
xxv
lviii
xlvi |
lv
xlvii
xl |
xxxv
ii
xiiii |
|
V
vi xxi |
lxxxv
xc |
xx
o |
clxxvii
clxxvi |
xxxix
o |
xliiii
xlv |
xxi
xix |
v xxii |
xc |
o |
clxvi |
liii |
xxxviii |
vii |
|
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
meridies
i
ii |
xlvii
xlix
lv |
xlvi
lii
lii |
xc
cl
cxxiii |
xxx
xxx
xvi |
lviii
xlii |
xxx
xliiii |
meridies
i
ii |
xxiii
xxvii
xxxvii |
li
lvi
xxxvi |
lxvi
xcvi
cxiiii |
ix
xxviii
xxxi |
xxxv
xvii |
l
xlvii |
|
iii
iiii
v |
lxiiii
lxxv
lxxvi |
xxxvii
xii
liiii |
cxxxv
cxliiii
clii |
xxv
lviii
xlvi |
xxx
xxxii
xv |
xxxv
ii
xiiii |
iii
iiii
v |
xlix
lxii
lxvi |
xlii
xlvii
xx |
cxxiiii
cxxix
cxxxi |
xxx
vii
xxi |
viii
iii
o |
xv
i
lvii |
|
v xv |
xc |
xc |
cxli |
liii |
xiii |
viii |
vi |
xc |
o |
cxxxii |
xviii |
o |
o |
|
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
xliiii
xlvi
liii |
xxi
xl
iiii |
lxxvii
xcvi
cxii |
xxx
xxx
xvi |
lviiii
xlii |
xxx
xliiii |
meridies
i
ii |
xii
xviii
xxx |
xi
xlii
lvii |
lxix
cxvi
cxxxi |
o
xl
xliiii |
xxi
vi |
xx
xvi |
|
iii
iiii
v |
lxii
lxxiii
lxxxv |
xviii
xx
xxiii |
cxxiiii
cxxxii
cxxxix |
xxv
lviii
xlvi |
xxx
xxii
xv |
xxxv
ii
xiiii |
iii
iii
v |
xliii
lviii
lxxi |
xxii
i
xliii |
cxxxvi
cxxxviii
cxxxvii |
iii
o
xv |
i
o
o |
lvii
o
xlv |
|
v xxv |
xc |
o |
cxli |
liii |
xiii |
vii |
vi
vi xxi |
lxxxv
xc |
xx
o |
cxxxv
cxxxiiii |
xxxix
xli |
ii
iii |
xxi
xix |
|
PISCIUM |
GEMINORUM |
|||||||||||||
meridies
i
ii |
xxv
xxxviii
xlvi |
xxxi
xxv
ii |
lxix
xci
cviii |
o
xv
xvii |
xlvi
xxix |
xlv
xlii |
meridies
l
ii |
iii
xiiii
xxvii |
xxxi
xviii
lvi |
lxxvii
cli
clv |
xxx
iiii
o |
iii
o |
lvi
o |
|
iii
iiii
v |
xlvi
lxviii
lxxxi |
xxx
xxxi
xxii |
cxvix
cxxvii
cxxxii |
xli
v
xxx |
xviii
x
v |
xix
lv
xx |
iii
iiii
v |
xli
lv
lxviii |
xliiii
xiiii
xliii |
cliiii
clii
cxliii |
iii
xviii
xlvi |
o
ii
vi |
lvii
xlii
xx |
|
v xxxix |
xc |
o |
cxxxiiii |
xli |
vi |
xix |
vi
vi xxxviii |
lxxxi
xc |
lii
o |
cxliii
cxli |
lvi
liii |
xi
xiii |
iiii
vii |
|
CANCRI |
LIBRE |
|||||||||||||
eius qui per inferiorem regionem Egipti hore xiiii graduum xxx minutorum xxii |
||||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
G |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
vi
xiiii
xxvii |
xxxi
lvi
xxiii |
xc
cl
clix |
o
o
xxxviii |
xxx
xx |
o
xxii |
meridies
i
ii |
xxx
xxxiii
xli |
xxii
xxxv
xxxix |
cxiii
cxxxvii
cliiii |
li
xxxii
xix |
xc
lxxiii |
x
xxiii |
|
iii
iiii
v |
xl
liii
lxv |
xix
xiiii
lv |
clx
clviii
clvi |
xxx
li
o |
xix
xxi
xxiiii |
xxx
ix
o |
iii
iiii
v |
lii
lxiiii
lxxvii |
xxv
xxviii
vi |
clxiiii
clxix
clxxii |
x
xlvii
xxi |
lxiii
lvii
lv |
xxxii
lv
xxi |
|
vi
vii |
lxxviii
xc |
xv
o |
cli
cxlvi |
xlix
xxviii |
xxviii
xxxiii |
xi
xxxii |
vi |
xc |
o |
clxxiii |
xxix |
liiii |
xiii |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
ix
xvi
xxviii |
lii
xlv
xliiii |
cii
cliii
clxvi |
xxx
xiii
xxii |
li
xxxviii |
xlvii
xxxviii |
meridies
i
ii |
xlii
xliiii
l |
ii
xxvi
xlviii |
cxi
cxxix
cliiii |
o
xxxii
xxxviii |
xcii
lxxvii |
xxviii
xxii |
|
iii
iiii
v |
xli
liiii
lxvii |
xxxi
xxvii
xvii |
clxix
clxix
clxvii |
xxvi
viii
i |
xxxv
xxxv
xxxvii |
xxxiiii
lii
lix |
iii
iii
v |
lx
lxxi
lxxxiii |
xix
xx
xix |
clv
clxii
clxvii |
xxxiii
lvi
liiii |
lxvi
lix
liiii |
xxvii
iiii
vi |
|
vi
vi li |
lxxix
xc |
xlviii
o |
cxliii
clix |
xlvi
xlix |
xli
xlv |
xiiii
xi |
v xxxii |
xc |
o |
clxxix |
lv |
lii |
v |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xviii
xxiii
xxxiii |
xlii
xviii
xxx |
cxi
cxlv
clxii |
o
xviii
xxv |
lxxvi
lix |
xlii
xxxv |
meridies
l
ii |
l
lii
lviii |
lii
liii
xxvii |
cii
cxviii
cxxii |
xxx
xxxix
li |
lxxxvi
lxxii |
xxi
ix |
|
iii
iiii
v |
xlv
lviii
lxxi |
xxvi
xxi
xv |
clxix
clxxii
clxxii |
xxxiiii
x
xxviii |
lii
xlix
xlix |
xxvi
l
xxxii |
iii
iiii
v |
lxvi
lxxvi
lxxxviii |
xliiii
li
ix |
cxliiii
clii
cliii |
i
xxxvii
xliii |
lx
lii
xlvi |
lix
xxiii
xvii |
|
v
vi xxviii |
lxxxiiii
xc |
vii
o |
clxxi
clxix |
v
lv |
l
lii |
lv
v |
v ix |
xc |
o |
clix |
xlix |
xlv |
xi |
|
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
G |
M |
G |
M |
G |
M |
G |
M |
G |
M |
G |
M |
|||
meridies
i
ii |
liiii
lvi
lxii |
xiii
vi
xxii |
xc
cv
cxix |
o
xxiiii
xxiii |
lxxiiii
lx |
xxxvi
xxxvii |
meridies
i
ii |
xxx
xxxiiii
xli |
xxii
xxxv
xxxix |
lxvi
lxxxix
cvi |
ix
xi
xxxv |
xlii
xxv |
xxviii
xli |
|
iii
iiii
v |
lxix
lxxviii
xc |
xvii
lix
o |
cxxx
cxxxix
cxlvi |
xlvi
xxx
xxviii |
xlix
xl
xxxiii |
xiiii
xxx
xxxii |
iii
iiii
v |
lii
lxiiii
lxxvii |
xxv
xxviii
vi |
cxvi
cxxii
cxxiiii |
xxviii
v
xxxix |
xv
x
vii |
l
xiii
xxxix |
|
v |
xc |
o |
cxxxix |
xlvii |
vi |
xxxi |
||||||||
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
l
lii
lviii |
lii
liii
xxvii |
lxxvii
cxciii
cvii |
xxx
xxxv
li |
lxi
xlvii |
xxi
ix |
meridies
i
ii |
xviii
xxiii
xxxiii |
xlii
xviii
xxx |
lxix
ciii
cxx |
o
xviii
xxv |
xxxiiii
xvii |
xlii
xxxv |
|
iii
iiii
v |
lxvi
lxxvii
lxxxviii |
xliiii
li
ix |
cxix
cxxvii
cxxxiii |
i
xxxvii
xliii |
xxxv
xxvii
xxi |
lix
xxiii
xvii |
iii
iii
v |
xxlv
lviii
lxxi |
xxxvi
xxi
xv |
cxxvii
cxxx
cxxx |
xxxiiii
x
xxviii |
x
vii
vii |
xxxvi
l
xxxii |
|
v ix |
xc |
o |
cxxxiiii |
xlix |
xx |
xi |
vi
vi xxviiii |
lxxxv
xc |
vii
o |
cxxix
cxxvii |
v
lv |
l
x |
lv
v |
|
PISCES |
GEMINORUM |
|||||||||||||
Auster |
Auster |
Boreas |
Boreas |
|||||||||||
meridies
i
ii |
xlii
xliiii
l |
ii
xxvi
lviii |
lxix
lxxxvii
cii |
o
xxxii
xxxviii |
l
xxxv |
xxviii
xxii |
meridies
l
ii |
ix
xvi
xxviii |
lii
xlv
xliiii |
lxxvii
cxxviii
cxli |
xxx
xiii
xxii |
xxvi
xiii |
xlvii
xxxviii |
|
iii
iiii
v |
lx
lxxi
lxxxiii |
xix
xx
xix |
cxiii
cxx
cxxv |
xxxiii
lvi
liiii |
xxiiii
xvii
xii |
xxvii
iiii
vi |
iii
iiii
v |
xli
liiii
lxvii |
xxxi
xxvii
xvii |
cxliiii
cliiii
cxlii |
xxvi
viii
i |
x
x
xii |
xxxiiii
lii
lix |
|
v xxxii |
xc |
o |
cxxvii |
lv |
x |
v |
vi
vi li |
lxcix
xc |
xlviii
o |
cxxxviii
cxxxiiii |
xlvi
xlix |
xvi
xx |
xiiii
xi |
|
eius qui per Rhodum hore xiiii et dimidii gradus xxxvi minutum o |
||||||||||||||
CANCRI |
LIBRE |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
xii
xvii
xxviii |
ix
xlvii
xxviii |
xc
cxxxiii
cxlvii |
o
xiiii
xlv |
xlvi
xxxii |
xl vi
xv |
meridies
i
ii |
xxxvi
xxxviii
xlv |
o
xxxvii
xxxi |
cxiii
cxxxiii
cxlviii |
li
xxiii
xxiii |
xciiii
lxxix |
xix
xix |
|
iii
iiii
v |
xl
lii
lxiiii |
xxvii
xvi
xxxvi |
cli
cli
cxlix |
xlvi
lii
liiii |
xxviii
xxviii
xxx |
xiiii
viii
vi |
iii
iiii
v |
lv
lxvi
lxxvii |
vi
ix
lvi |
clviii
clxvi
clxvi |
ix
lviii
xxxvi |
lxix
lxiii
lxi |
xxxiii
xliiii
vi |
|
vi
vii
vii xv |
lxxvi
lxxxvii
xc |
xvi
xxiii
o |
cxlvi
cxli
cxl |
xxv
xxx
i |
xxxiii
xxxviii
xxxix |
xxxv
xxx
lix |
vi |
xc |
o |
cxlvii |
li |
lix |
li |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
xv
xx
xxx |
xxx
xx
xxviii |
cii
cxxxix
clv |
xxx
xxxii
xix |
lxv
xlix |
xxviii
xli |
meridies
i
ii |
xlvii
xlix
v |
xl
xlii
xxvi |
cxi
cxxvi
cxl |
o
l
xx |
xcv
lxxxi |
x
xl |
|
iii
iiii
v |
xlii
liiii
lxvi |
vi
xii
xvii |
clx
clxii
clxi |
xxxvi
xi
v |
xliiii
xlii
xliii |
xxiiii
xlix
lv |
iii
iii
v |
lxiii
lxxiii
lxxxv |
xlviii
xlv
v |
cl
clvii
clxii |
xxxiiii
li
xxviii |
lxxi
lxiiii
lix |
xxvi
ix
xxxii |
|
vi
vi
vii iiii |
lxxviii
lxxxix
xc |
vii
xxvii
o |
clviii
cliii
cliii |
x
xxxix
xxxvi |
xlvi
li
li |
i
xxi
xxiiii |
v xxxv |
xc |
o |
clxiiii |
vii |
lvii |
liii |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xxiiii
xxvii
xxxvi |
xx
li
xxiiii |
cxi
cxxxvii
cliii |
o
xxxviii
lix |
lxxxiiii
lxviii |
xxii
i |
meridies
l
ii |
lvi
lviii
lxiii |
xxx
xiiii
xiii |
cii
cxvi
cxxix |
xxx
xxxix
xxiii |
lxxxviii
lxxv |
xxi
xxxvii |
|
iii
iiii
v |
xlvii
lix
lxxi |
xiiii
o
v |
clxii
clxv
clxvi |
x
xl
xxxiiii |
lix
lvi
lv |
l
xx
xxvi |
iii
iiii
iiii lvi |
lix
lxxx
xc |
xli
ii
o |
clxxxix
cxlvii
cliii |
xlvii
xlvii
xxxvi |
lxv
liii
li |
xiii
xiii
xxiiii |
|
v
vi xxv |
lxxxiii
xc |
ix
o |
clxv
clxiiii |
xxx
vii |
lvi
lvii |
xxx
liii |
||||||||
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
lix
lxi
lxvi |
li
xxx
xii |
xc
ciii
cxvi |
o
xlv
x |
lxxvi
lxiii |
xv
l |
meridies
i
ii |
xxxvi
xxxviii
xlv |
o
xxxvii
xxxi |
lxvi
lxxxv
c |
ix
xli
xli |
xlvi
xxxi |
xxvii
xxxi |
|
iii
iiii
iiii xlv |
lxxiii
lxxxii
xx |
xxiii
xxiii
o |
cxxvi
cxxxiiii
cxl |
xxxvi
lvi
i |
liii
xlv
xxxix |
xxiiii
iiii
lix |
iii
iiii
v |
lv
lxvi
lxxvii |
vi
ix
lvi |
cx
cxvi
cxviii |
xxvii
xvi
liiii |
xxi
xvi
xiii |
li
ii
xxiiii |
|
vi |
xc |
o |
cxx |
ix |
xii |
ix |
||||||||
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
lvi
lviii
lxiii |
xxx
xiiii
xiii |
lxxvii
xci
ciiii |
xxx
xxxix
xxiii |
lxiii
l |
xxi
xxvii |
meridies
i
ii |
xxiiii
xxvii
xxxvi |
xx
li
xxiiii |
lxix
xcv
cxi |
o
xxxviii
xxvi |
xlii
xxvi |
xxii
i |
|
iii
iiii
iiii lvi |
o
lxxx
xc |
xli
ii
o |
cxiiii
cxxii
cxxviii |
xlvii
xlvii
xxxvi |
xl
xxxii
xxvi |
xiii
xiii
xxiiii |
iii
iii
v |
xlvii
lix
lxxi |
xiiii
o
v |
cxx
cxxiii
cxxiiii |
x
xl
xiii |
xvii
xiiii
xxvi |
l
xx
xxxiiii |
|
vi
vi xxxv |
lxxxviii
xc |
ix
o |
cxxiii
cxxii |
xxx
vii |
xiiii
xv |
xxx
liii |
||||||||
PISCIUM |
GEMINORUM |
|||||||||||||
Auster |
Auster |
Boreas |
Boreas |
|||||||||||
meridies
i
ii |
xlvii
lix
lv |
xl
xlii
xxvi |
lxix
lxxxiiii
xcviii |
o
l
xx |
liii
xxxix |
x
xl |
meridies
l
ii |
xv
xx
xxx |
xxx
xx
xxviii |
lxxvii
cxiiii
cxxx |
xxx
xxxii
xix |
xl
xxiiii |
xxviii
xli |
|
iii
iiii
v |
lxiii
lxxiii
lxxxv |
xlviii
lv
v |
cviii
cxv
cxx |
xxxiiii
li
xxviii |
xxix
xxii
xvii |
xxvi
xx
xxxii |
iii
iiii
v |
xlii
liiii
lxvi |
vi
xii
xvii |
cxxxv
cxxxviicxxxvi |
xxxvii
xi
v |
xix
xvii
xviii |
xxiii
xlix
lv |
|
v xxxii |
xc |
o |
cxxii |
vii |
xv |
liii |
vi
vii
vii iiii |
lxxxviii
lxxxix
xc |
vii
xvii
o |
cxxxiii
cxxviii
cxxviii |
x
xxxix
xxxvi |
xxi
xxvi
xxvi |
i
xxi
xxiiii |
|
Eius qui per Hellespontum |
hore xv latitudinis gradus xl minuta lvi |
|||||||||||||
CANCRI |
LIBRE |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
xvii
xxi
xxx |
v
xviii
xvii |
xc
cxxii
cxxxviii |
o
xxxii
xxix |
lvii
xli |
xxviii
xxxi |
meridies
i
ii |
xl
xliii
xlix |
lvii
l
vii |
cxiii
cxxix
cxliii |
li
lvii
xxxviii |
xcvii
lxxxiiii |
xlv
iiii |
|
iii
iiii
v |
xli
lii
lxiii |
xxxvii
xxv
xlvii |
cxliiii
cxlv
cxliiii |
xviii
xxxvii
xxviii |
xxxv
xxxiiii
xxxv |
xlii
xxii
xxxii |
iii
iiii
v |
lvii
lxvii
lxxviii |
xlii
l
xlv |
cliii
clviii
clxi |
viii
xlvii
lix |
lxxiiii
lxviii
xv |
xxxiiii
lv
xliii |
|
vi
vii
vii xxx |
lxxiiii
lxxxv
xc |
xlviii
ix
o |
cxli
cxxxvii
cxxxiiii |
xxx
v
xvi |
xxxviii
xlii
xlv |
xxx
xlv
xliiii |
vi |
xc |
o |
clxii |
lv |
lxiiii |
xlvii |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
xx
xxiiii
xxxii |
xxvi
v
xxxvii |
cii
cxxxi
cxlvii |
xxx
vi
o |
lxxiii
xlviii |
liiii
o |
meridies
i
ii |
lii
liiii
lix |
xxxvi
xxiii
xxv |
cxi
cxxiiii
cxxxvi |
o
xlvi
lv |
xcvii
lxxxv |
xiiii
v |
|
iii
iiii
v |
xliii
liiii
lxv |
viii
xix
xxxvi |
cliii
clvi
clv |
l
v
viii |
li
xlviii
xlix |
x
lv
lii |
iii
iii
v |
lxvi
lxxvi
lxxxvi |
lviii
xv
xxxviii |
cxlvi
cliii
clvii |
xxiiii
x
xlv |
lxxv
lxviii
lxiiii |
xxxvi
l
xv |
|
vi
vii
vii xvi |
lxxvi
lxxxvii
xc |
xlvi
xxiiii
o |
cliii
cxlix
cxlviii |
xxiiii
vi
vi |
li
lv
lvi |
xxxvi
liiii
liiii |
v xviii |
xc |
o |
cxlviii |
lix |
lxiii |
i |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xxix
xxxii
xxxix |
xvi
v
xxii |
cxi
cxxxii
cxlvii |
o
xxx
xxx |
lxxxix
lxxiiii |
xxx
xxx |
meridies
i
ii |
lxi
lxiii
lxvii |
xxvi
o
xxiiii |
cii
cxv
cxxvi |
xxx
v
xxix |
lxxxix
lxxviii |
lv
xxxi |
|
iii
iiii
v |
xlix
lix
lxxi |
iii
l
v |
clvi
clx
clxi |
o
vii
xxiiii |
lxvi
lxi
lx |
o
liii
xxxvi |
iii
iiii
iiii xliiii |
lxxiiii
lxxxii
xc |
xiii
xlviii
o |
cxxxvi
cxliii
cxlviii |
x
xlv
vi |
lxviii
xlxi
lvi |
l
xv
liiii |
|
vi
vi xlii |
lxxxii
xc |
xxii
o |
clx
clviii |
xl
lix |
lxi
lxiii |
xx
i |
||||||||
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
lxiiii
lxvi
lxx |
xlvii
xv
xxx |
xc
cii
cxiii |
o
xxviii
xxxv |
lxxvii
lxvi |
xxxiii
xxv |
meridies
i
ii |
xl
xliii
xlix |
lvi
l
vii |
lxvi
lxxxii
xcv |
ix
xv
lvi |
l
xxxvi |
iii
xxii |
|
iii
iiii
iiii xxx |
lxxvii
lxxxv
xc |
iiii
xviii
o |
cxxii
cxxx
cxxxiiii |
lv
lviii
xvi |
lvii
xlix
xlv |
v
ii
xliiii |
iii
iiii
v |
lvii
lxviii
lxxviii |
xlii
l
xlv |
cv
cxi
cxiiii |
xxvi
v
xvii |
xxxvi
xxi
xviii |
lii
xiii
i |
|
vi |
xc |
o |
cxv |
xiii |
xvii |
v |
||||||||
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
lxi
lxiii
lxvii |
xcvi
o
xxiiii |
lxxvi
xc
ci |
xxx
v
xxix |
lxiii
liii |
lv
xxxi |
meridies
i
ii |
xxix
xxxii
xxxix |
xvi
v
xxii |
lxix
xc
cv |
o
xxx
xxx |
xlvii
xxxii |
xxx
xxx |
|
iii
iiii
iiii lvi |
lxxiiii
lxxxii
xc |
xiii
xlvii
o |
cxi
cxviii
cxxiii |
x
xlv
vi |
xliii
xxxvi
xxxi |
l
xv
liiii |
iii
iii
v |
xlix
lix
lxxi |
iii
l
v |
cxiiii
cxviii
cxix |
o
vii
xxiiii |
xxiiii
xix
xviii |
o
liii
xxxvi |
|
vi
vi xlii |
lxxxii
xc |
xxii
o |
cxviii
cxvi |
xl
lix |
xix
xxi |
xx
i |
||||||||
PISCIUM |
GEMINORUM |
|||||||||||||
Boreas |
||||||||||||||
meridies
i
ii |
lii
liiii
lix |
xxxvi
xxiii
xxv |
lxix
lxxxii
xciiii |
o
xlvi
lv |
lv
xliii |
xiiii
v |
meridies
l
ii |
xx
xxiiii
xxxii |
xxvi
v
xxxvii |
lxxvii
cvi
cxxii |
xxx
vi
o |
xlviii
xxxiii |
liiii
o |
|
iii
iiii
v |
lxvi
lxxvii
lxxxvi |
lviii
xv
xxxviii |
ciiii
cxi
cxv |
xxiiii
x
xlv |
xxxiii
xxvi
xxii |
xxxvi
l
xv |
iii
iiii
v |
xliii
liiii
lxv |
viii
xix
xxxvi |
cxxviii
cxxxi
cxxx |
l
v
viii |
xxvi
xxiii
xxiiii |
x
lv
lii |
|
v xviii |
xc |
o |
cxvi |
lix |
xxi |
i |
vi
vii
vii xvi |
lxxxvi
lxxvii
xc |
xlvi
xxiiii
o |
cxxviii
cxxiiii
cxxiii |
xxiiii
vi
vi |
xxvi
xxx
xxxi |
xxxvi
liiii
liiii |
|
Eius qui per medium pontum |
hore xv et dimidiie latitudinis gradus xlv minuta i |
|||||||||||||
CANCRI |
CHELARUM |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
xxi
xxiiii
xxxii |
x
xxxii
xii |
xc
cxvi
cxxxi |
o
v
xxx |
lxiii
xlviii |
lv
xxx |
meridies
i
ii |
xlv
xlvi
lii |
i
lv
xvii |
cxiii
cxxviii
cxl |
li
xix
xxvi |
xcix
lxxxvii |
xxiii
xvi |
|
iii
iiii
v |
xlii
lii
lxiii |
i
xxix
iiii |
cxxxvii
cxl
cxl |
xvii
xxxi
ii |
xli
xxxix
xxxix |
xliii
xxix
lviii |
iii
iiii
v |
lx
lxix
lxxix |
i
xix
xxviii |
cxlix
cliiii
clvii |
iiii
xlviii
lv |
lxxviiii
lxxii
lxix |
xxxviii
liiii
xlvii |
|
vi
vii
vii xxx |
lxxiii
lxxxiii
xc |
xxiiii
xvii
o |
cxxxvii
cxxxiii
cxxix |
xxxii
xxvi
xxi |
xlii
xlvi
l |
xxviii
xxxiiii
xxxix |
vi |
xc |
o |
clviii |
l |
lxviii |
lii |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
xxiiii
xxvii
xxxiiii |
xxxi
xxix
xlviii |
cii
cxxiiii
cxl |
xxx
xlix
xlvii |
lxxx
lxiiii |
xi
xiii |
meridies
i
ii |
lvi
lviii
lxii |
xli
xix
xlix |
cxi
cxxiiii
cxxxiiii |
o
xxxi
xvi |
xcviii
lxxxvii |
xxix
xliiii |
|
iii
iiii
v |
xliiii
liiii
lxv |
xx
xxxvii
xv |
cxlviii
cli
cli |
v
v
vii |
lvi
liii
liii |
lv
lv
liii |
iii
iii
v |
lxix
lxxviii
lxxxvii |
xlii
xvi
lvi |
cxliii
cxlix
cliiii |
xii
xxxi
vi |
lxxviii
lxxii
lxvii |
xlviii
xxix
liiii |
|
vi
vii
vii xxxviii |
lxxv
lxxxv
xc |
xxxix
xxxix
o |
cxlix
cxlv
cxliii |
xx
xxxix
xxv |
lv
lix
lxi |
xl
xxi
xxxv |
v xii |
xc |
o |
cliiii |
xliii |
lxvii |
xvii |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xxxiii
xxxv
xlii |
xxi
xliii
iiii |
cxi
cxxix
cxlii |
o
xv
l |
xcii
lxxix |
xlv
x |
meridies
i
ii |
lxv
lxvi
lxx |
xxxi
lv
lviii |
cii
cxiii
cxxiiii |
xxx
l
xxi |
xci
lxxx |
x
xxxix |
|
iii
iiii
v |
l
lx
lxxi |
xlvi
xliiii
xii |
cli
clv
clvii |
ix
xxxi
iii |
lxx
lxvi
lxiiii |
li
xxix
lvii |
iii
iiii
iiii xxxii |
lxxvii
lxxxv
xc |
xiiii
l
o |
cxxxiii
cxl
cxliii |
xix
xix
xxv |
lxxi
lxiiii
lxi |
xli
xl
xxxv |
|
vi
vi xlviii |
lxxxi
xc |
xlvi
o |
clvi
cliiii |
xxxi
xliii |
lxv
lxvii |
xxix
xvii |
||||||||
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
lxviii
lxx
lxxiiii |
lii
xiiii
v |
xc
ci
cxi |
ō
xi
xxx |
lxviii
lxviii |
xlix
xxx |
meridies
i
ii |
xlv
xlvi
lii |
i
lv
xvii |
lxvi
lxxx
xcii |
ix
xxxvii
xliiii |
li
xxxix |
xli
xxxiiii |
|
iii
iiii
iiii xv |
lxxx
lxxxvii
xc |
vi
xlii
ō |
cxx
cxxviii
cxxix |
xxix
xiii
xxi |
lix
li
l |
xxxi
xlvii
xxxix |
iii
iiii
v |
lx
lxix
lxxix |
i
xix
xxviii |
ci
cvii
cx |
xxii
vi
xiii |
xxx
xxv
xxii |
lvi
xii
v |
|
vi |
xc |
ō |
cxi |
viii |
xxi |
x |
||||||||
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
lxv
lxvi
lxx |
xxxi
lv
lviii |
lxxvii
lxxxviii
xcix |
xxx
viii
xxi |
lxvi
lv |
x
xxxix |
meridies
i
ii |
xxxiii
xxxv
xlii |
xxi
xliii
iiii |
lxix
lxxxvii
c |
ō
xv
l |
l
xxxvii |
xlv
x |
|
iii
iiii
iiii xxxii |
lxxvii
lxxxv
xc |
xiiii
x
ō |
cviii
cxv
cxviii |
xix
xx
xxv |
xlvi
xxxix
xxxvi |
xli
xl
xxxv |
iii
iiii
v |
l
lx
lxxi |
xlvi
xliiii
xii |
cix
cxiii
cxv |
ix
xxxi
iii |
xxviii
xxiiii
xxiii |
li
xxix
lvii |
|
vi xlviii |
xc |
ō |
cxii |
xliii |
xxv |
xvii |
||||||||
PISCIUM |
GEMINORUM |
|||||||||||||
Boreas |
||||||||||||||
meridies
i
ii |
lvi
lviii
lxii |
xli
xix
xlix |
lxix
lxxxi
xcii |
ō
xxxi
xvi |
xlvi
xlv |
xxix
xliiii |
meridies
i
ii |
xxiiii
xxix
xlviii |
xxxi
v
xxxvii |
lxxvii
xcix
cxv |
xxx
xlix
xlvii |
lv
xxxix |
xi
xiii |
|
iii
iiii
v |
lxix
lxxviii
lxxxvii |
xlii
xvi
lvi |
ci
cvii
cxii |
xii
xxxi
vi |
xxxvi
xxx
xxv |
xlviii
xxix
liiii |
iii
iiii
v |
xliiii
liiii
lxv |
xx
xxxvii
xv |
cxxiii
cxxvi
cxxvi |
v
v
vii |
xxxi
xxviii
xxviii |
lv
lv
liii |
|
v xii |
xc |
ō |
cxii |
xliii |
xxv |
xvii |
vi
vii
vii xxviii |
lxxv
lxxxv
xc |
xxxix
xxxix
ō |
cxxiiii
cxx
cxviii |
xx
xxxix
xxv |
xxx
xxxiiii
xxxvi |
xl
xxi
xxxv |
|
Eius qui per Boristhenem |
hore xvi latitudinis gradus xlviii minuta xxxiv |
|||||||||||||
CANCRI |
CHELARUM |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
xxiiii
xxviii
xxxiiii |
xli
xxx
ix |
xc
cxi
cxxvi |
o
xliiii
vii |
lxviii
liii |
xvi
liii |
meridies
i
ii |
xlviii
l
liii |
xxxii
xxvi
lix |
cxiii
cxxvi
cxxxviii |
li
xxx
xl |
ci
xc |
xii
ii |
|
iii
iiii
v |
xliii
lii
lxii |
ii
xliiii
xl |
cxxxiii
cxxxvi
cxxxvi |
xviii
vi
iiii |
xlvi
xliii
xliii |
xlii
liiii
lvi |
iii
iiii
v |
lxii
lxx
lxxx |
v
xli
viii |
cxlv
cli
cliiii |
xlvi
xviii
xxiii |
lxxxi
lxxvi
lxxiii |
lvi
xxiiii
xix |
|
vi
vii
viii |
lxxii
lxxxi
xc |
xxiiii
xxxviii
o |
cxxxiiii
cxxx
cxxiiii |
o
xvi
lviii |
xlvi
xlix
lv |
o
xliiii
ii |
vi |
xc |
o |
cl |
xix |
lxxii |
xxiii |
|
LEONIS |
SCORPII |
|||||||||||||
meridies
i
ii |
xviii
xxx
xxxvi |
ii
xxxii
lv |
cii
cxxii
cxxxv |
xxx
ix
liiii |
lxxxii
lxix |
li
vi |
meridies
i
ii |
lx
lxi
lxv |
ii
xxxviii
xxxvi |
cxi
cxxii
cxxxii |
o
v
x |
xcix
lxxxix |
lv
l |
|
iii
iiii
v |
xlv
lv
lxiiii |
xxx
iii
lix |
cxliii
cxlvi
cxlvii |
xxviii
l
xix |
lxi
lviii
lvii |
xxxii
x
xli |
iii
iii
v |
lxxii
lxxx
lxxxix |
v
iii
iii |
cxl
cxlvi
cli |
xxvi
xxviii
ii |
lxxxi
lxxv
lxx |
xxxiiii
xxxii
lviii |
|
vi
vii
vii xl |
lxxiiii
lxxxiiii
xc |
xlvii
x
o |
cxlv
cxlii
cxxxix |
xlvi
xxvii
xx |
lix
lxii
lxv |
xiiii
xxxiii
xl |
v vi |
xc |
o |
cli |
xxii |
lix |
xxxviii |
|
VIRGINIS |
SAGITTARII |
|||||||||||||
meridies
i
ii |
xxxv
xxxviii
xliiii |
lii
lvi
xxxi |
cxi
cxxvi
cxxxix |
o
xlv
vii |
xcv
lxxxii |
xv
liii |
meridies
i
ii |
lxix
lxx
lxxiiii |
ii
xx
ii |
cii
cxii
cxxii |
xxx
xlix
xxxi |
xcii
lxxxii |
xi
xxix |
|
iii
iiii
v |
lii
lxi
lxxi |
xxv
xxxv
xxii |
cxlvii
cli
cliii |
ix
xxxvi
xxiii |
lxxiiii
lxx
lxviii |
li
xxiiii
xxxvii |
iii
iiii
iiii xx |
lxxix
lxxxvii
xc |
xliiii
xiiii
o |
cxxx
cxxxvii
cxxxix |
xlix
xxv
xx |
lxxiiii
lxvii
lxv |
xi
xxxv
xl |
|
vi
vi liiii |
lxxxi
xc |
xvii
o |
clii
cli |
lviii
xxii |
lxix
lxx |
ii
xxxviii |
||||||||
CAPRICORNI |
ARIETIS |
|||||||||||||
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
hore |
periferie |
Anguli
orientales |
Anguli
occidentales |
|||||||
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
Gradus |
M |
|||
meridies
i
ii |
lxxii
lxxiii
lxxvii |
xxiii
xxxviii
x |
ix
c
cix |
ō
xv
xlvii |
lxxix
lxx |
xlv
xiii |
meridies
i
ii |
xlviii
l
liiii |
xxxii
xxi
lix |
lxvi
lxxviii
lxxxix |
ix
xlviii
xlviii |
liii
xli |
xxx
xx |
|
iii
iiii |
lxxxii
xc |
xliiii
ō |
cxviii
cxxiiii |
iii
liii |
lxi
lv |
lvii
ii |
iii
iiii
v |
lxii
lxx
lxxx |
v
xliiii
ix |
xcviii
ciii
cvi |
iiii
xxxvi
xli |
cxxxiiii
xxviii
xxv |
xiiii
xlii
xxxvii |
|
vi |
xc |
o |
cvii |
xxxvii |
xxiiii |
xli |
||||||||
AQUARII |
TAURI |
|||||||||||||
meridies
i
ii |
lxix
lxx
lxxiiii |
ii
xx
ii |
lxxvii
lxxxvii
xcvii |
xxx
xlix
xxxi |
lxiii
lvii |
xi
xxix |
meridies
i
ii |
xxxvi
xxxviii
xliiii |
lii
lvi
xxxi |
lxix
lxxxiiii
xcvii |
ō
xliii
vii |
liii
xl |
xv
liii |
|
iii
iiii
iiii xx |
lxxix
lxxxviii
xc |
xlviii
xiiii
ō |
cv
cxii
cxiiii |
xlix
xxv
xx |
xlix
xlii
xl |
xi
xxxv
xl |
iii
iii
v |
lii
lxi
lxxi |
xxv
xxxv
xxii |
cv
cv
cxi |
ix
xxxvi
xxiiii |
xxxii
xxviii
xxvi |
li
xxiiii
xxxvii |
|
vi
vi liiii |
lxxxi
xc |
xvii
ō |
cx
cix |
lviii
xxii |
xxvii
xxviii |
ii
xxxviii |
||||||||
PISCIUM |
GEMINORUM |
|||||||||||||
Boreas |
||||||||||||||
meridies
i
ii |
lx
lxi
lxv |
xii
xxxviii
xxxvi |
lxix
lxxx
xc |
ō
v
xvi |
lvii
xlvii |
lv
liiii |
meridies
i
ii |
xxviii
xxx
xxxvi |
ii
xxxii
lv |
lxxvii
xcvii
cx |
xxx
ix
liiii |
lvii
xliiii |
li
vi |
|
iii
iiii
v |
lxxii
lxxx
lxxxix |
v
iii
iii |
xcviii
ciiii
cix |
xxvi
xxviii
ii |
xxxix
xxxiii
xxviii |
xxxiiii
xxxii
lviii |
iii
iiii
v |
xlv
lv
lxiiii |
xxx
iii
lix |
cxviii
cxxi
cxxii |
xxviii
l
xix |
xxxvi
xxxiii
xxxii |
xxxii
x
xli |
|
v vi |
xc |
ō |
cix |
xxii |
xxviii |
xxxviii |
vi
vii
vii xl |
lxxiiii
lxxxiiii
xc |
xlvii
x
ō |
cxx
cxvii
cxiii |
xlvi
xxvii
xx |
xxxiiii
xxxvii
xl |
xiiii
xxxiii
xl |
|
Exposito ergo et angulorum negocio, deficiente vero suppositis epochas earum que secundum unamquamque regionem designatione dignarum civitatum considerari secundum longitudinem et latitudinem ad in ipsis apparentium investigationes, huiusmodi quidem expositionem egregio et geographico habitam negocio secundum se ipsam sub visum faciemus, consequentes tractantium ut est maxime hanc figuram historiis et ascribentes quot gradus distat ab equinoctiali civitatum unaquaque secundum eum qui per ipsam scriptus est meridianum et quot iste a scripto per Alexandriam meridiano ad orientes vel occidentes in equinoctiali, eo quod ad istum nobis constituta sint tempora. Nunc vero tantum, velut subiacentibus positionibus, superaddere consequens duximus quoniam, quotienscumque voluerimus in aliquo subiacentium locorum determinatam horam considerare que erat secundum idem tempus in altero aliquo inquisitorum, quando differunt qui per ipsos meridiani, sumere debemus quot differunt invicem isti gradibus in equinoctiali, et uter uter] uterque V2 eorum orientalior est vel occidentalior, totidemque temporibus equinoctialibus augere vel minuere eam que secundum subiacentem locum horam, ut faciamus eam que in inquisito secundum idem tempus consideratur, augmento quidem constituto, quando inquisitus locus orientalior fuerit, minutione vero quando occidentalior subiacens.