Ptolemaeus Arabus et Latinus

⟨VI⟩

Primum de sinodis et panseliniis

Secundum negotium canoniorum madiarum madiarum] mediarum V₂F₁ sinzugiarum

Tercium expositio canoniorum

Quartum quomodo oporteat et periodicas et examinatas sinzugias inquirere

Quintum de eclipticis terminis Solis et Lune

Sextum de distantia eclipticorum mensium

Septimum negotium canoniorum eclipticorum

⟨O⟩ctavum expositio eclipticorum canonium

Nonum lunarium eclipsium discretio

Decimum solarium eclipsium discretio

Undecimum de eis que in eclipsibus prosneusibus

Duodecimum expositio earum que ad prosneuses perscriptionum

Tertiumdecimum discretio prosneusium

Claudii Ptolomei mathematicorum sintaxeos sextus incipit

⟨VI.1⟩ De sinodis et panseliniis

Deinceps ergo contingente eo quod circa eclipticas sinzugias Solis et Lune negotio, cuius precedit rursum examinate consideratarum sinodorum et panselinarum consideratio, sufficere quidem extimamus ad talium primam conceptionem demonstratas secundum utramque utramque] utrumque V₂ luminarium et periodicos et anomalos motus, possibilique per hoc facto, non pigritantibus particulares ipsorum epochas quaque vice, computare et loca et tempora futurarum sinzugiarum et ad medios motus sumptarum et cum anomalia examinatarum. Et non Et non] tamen V₂ ut promptius nobis et ipse doceantur, preexpositis ex promtu et eis que secundum periodicas sinodos et panselinia temporibus et locis et eis que secundum media tempora epochis et latitudinis et anomalie Lune, per quas et que ad sinzugias examinatas directio fit, et ab ipsis que ad eclipticas fecimus ad huiusmodi considerationem canonia continentia modum hunc.

⟨VI.2⟩ Negotium canoniorum mediarum sinzugiarum

Primum enim, ut cursus et mensium epochas, quemadmodum et alias, a primo anno Navonassari constituamus, demonstratam in anno istho istho] isto V₂F₁ Thot neomenia secundum Egiptios meridiei epoysiam distantie graduum existentem lxx xxxvii comparantes penes diurnum medium motum distantie invenimus dies v xlvii xxxiii, quasi autem tatos tatos] tantos V₂F₁ factam fuisse ei que in neomenia Thoth meridiei ante factam mediam sinodon, et que deinceps ergo facta est post dies xxiii xliiii xvii ad proximum ab eadem meridie, hoc est post lx^as diei unius xxxiiii xxxiiii] xliiii V₂F₁ xvii ab ea que in xxiiii meridie. In diebus autem xxiii xliiii xvii Sol quidem movetur medie gradibus xxiii xxiii viii, Luna vero anomalie quidem gradibus cccxviii et xv latitudinis autem gradibus cccxiiii ii xxi. Optinebat autem in neomene meridie Thot medie Sol quidem Piscium gradus o xlv, ab apoguio vero proprio propter utile gradus cclxv et xv, Luna vero anomalie quidem ab apoguio epicicli gradus cclxviii xlix, latitudinis vero a boreali termino obliqui circuli gradus cccliiii et xv; et in preiacente ergo tempore eius que post neomeniam medie sinodi Sol quidem et Luna medie distabant ambo a solari apoguio, hoc est ab in Geminis gradibus v xxx, cclxxxviii xxxviii l, Luna vero anomalie ab apoguio gradibus cxviii lvii xv, latitudinis vero a boreali termino gradibus cccviii xvii xxi.

Ordinabimus ergo primum canonium sinodicum versuum quidem rursum xlv, selidiorum vero v, et apponemus in primis versibus in primo quidem selidio primum annum Navonassari, in secundo vero Thot dies xxiiii xliiii xvii, quoniam quidem lx^a consequentia eius que in xxiiii sunt meridiei, in tertio autem medie epochis ab apoguio Solis gradus cclxxxviii xxxviii l, in quarto vero apoguio lunaris anomalie gradus ccxviii lvii xv, in quinto autem a boreali termino latitudinis gradus cccviii xvii xxi. Quoniam vero et in dimidio medii menstrui temporis dies quidem continentur xiiii xlv lv ad proximum, gradus autem solaris quidem epochis xiiii xxxiii xii, lunaris autem anomalie cxcii liiii xxx, latitudinis vero cxcv xx vi, aufferentes istos numeros ab eis qui exposite sinode, reliquos preordinabimus et ipsos in secundo et similiter habenti canonio, panseliniaco utique futuro secundum eumdem primum modum. Reliquuntur autem dies quidem ix lviii xxii, gradus autem ab apoguio quidem solari cclxxiiii v xxxviii, anomalie vero ab apoguio Lune xxvi ii xlv, latitudinis autem a boreali termino cxii lvii xv. Quoniam vero et in xxv annis egiptiacis minus habentibus uno die lx^a duo xlvii v totique menses ad proximum complentur et recipit post omnes circulos medie Sol quidem gradus cccliii lii xxxiiii xiii, Luna vero anomalie quidem gradus lvii xxi xliiii i, latitudinis autem gradus cxvii xii xlix liiii, prima quidem selidia duorum canoniorum adaugebimus adaugebimus] add. xxv annis, secundum autem minuemus lxii xlvii. Reliquorum autem tercia quidem adaugebimus V₂F₁ cccliii lii xxxiiii xiii, quarta vero lvii xxi xliiii i, quinta vero cxvii xii xlix liiii. His autem deinceps ordinabimus canonium annuum in versus xxiiii et aliud menstruum in versus xii, selidiorum autem utramque utramque] utrumque V₂F₁ primis equalium, et in menstruo quidem apponentes in primis versibus in primo quidem selidio primum mense, in secundo vero mensis dies xxix xxxi l viii xx, in tertio autem in tanto tempore agregatos Solis gradus xxix vi xxiii i, in quarto vero eos qui anomalie Lune xxv xlix o viii, in quinto latitudinis gradus xxx xl xiiii ix. Adaugebimus autem et ista eisdem numeris et in primis versibus expositis. In annuo autem apponentes et in primis versibus in primo quidem selidio primum annum, in secundo autem comprehensos in xiii mensibus dies xviii liii lii xlviii, in tertio in tanto tempore solaris epoysie gradus xviii xxii lix xviii, in quarto vero lunaris anomalie gradus cccxxxv xxxvii i li, in quinto latitudinis gradus xxxviii xliii iii li. Adaugebimus autem et ista aliquotiens quidem expositis xiii mensium epoysis, aliquotiens vero xii mensium, que colligunt dies quidem cccliiii xxii i xl, gradus autem solaris quidem epochis cccxlix xvi xxxvi xvi, lunaris autem anomlie cccix xlviii i xlii, latitudinis autem viii ii xlix xlii ad primam in totis egiptiacis annis sinzugiam nobis exponi appositiones, que sufficit usque secunda sexagesima facere.

Et hoc est canonium. canonium] canoniorum descriptio talis V₂

⟨VI.3⟩

⟨VI.4⟩ Quomodo oporteat et periodicas et examinatas sinsiguias sinsiguias] sinzugias F₁ inquirere

Quando ergo voluimus voluimus] voluerimus V₂F₁ secundum aliquem inquisitorum amorum medie consideratas sinziguias sinziguias] sinzygias V₂ sinzugias F₁ sumere, computatur computatur] computantes V₂F₁ quotus est subiacens annus a primo anno Navonassari et considerantes quales numerum annorum versus continent, et ex eis que in utrolibet primorum duorum canoniorum xxv etiridibus, et ex eis que secundum tercium canonium annus adiacentia versibus ambobus in eis que deinceps selidiis superconponemus proprie, in sinodieis quidem sinzyguiis ea que ex primo canone et ea que ex tercio, in panseliniacis vero ea que ex secundo et ea que ex tertio similiter, et ex iuxta secundum quidem selidium compositis habebimus quod a principio illius anni sinzyguie tempus, quale si colligantur dies xxxiiii xliiii post xliiii sexagesima ab ea que in xxiiii^a Thoth meridie, et rursum si xxxiiii xliiii post equalia sexagesima ab ea que in xiiii^a Phaophi meridie, ex eis autem que secundum tertium eos qui ab apoguio Solis gradus, ex eis que autem secundum quartum eos qui ab apoguio anomalie Lune, ex eis autem que secundum quintum eos qui a boreali termino latitudinis, et deinceps vero consequenter, sive omnis, sive quosdam, sumere voluerimus, per eas que in menstruo et quarto canonio secundum proprium supercompositos ex promtu computabimus; translatis in unoquoque temporum propter utile diei sexagesima sexagesima] sexagesimis V₂F₁ in horas equinoctiales. Erit tamen collecta horarum epoysia velut nictimeris omalis existentibus, non eadem existente semper temporaliter deprehensa, sed alia que velut anomalis factis nictimeris. Dirigemus ergo et quod huiusmodi inquirentes, velut demonstratum est, eam que penes hoc differentiam, et si quidem maior fiunt fiunt] fuerit V₂F₁ que ad anomaliam distantiam epoysia temporum, aufferentes ipsum ab omale collecta, si vero minor, ipsi apponentes.

Sumpto ergo ad hunc modum ad medias progressiones considerato sinodico vel panseliniaco tempore et eis que secundum ipsum anomaliis in utroque luminarium, facile comprehensibile erit et examinate sinzugie et tempus et locus et adhuc ea que secundum latitudinem Lune progressio ex comparatione ambarum anomaliarum. Etenim secundum utramque ipsarum considerantes eam que in exposito periodico tempore per inventam prosthaferesim examinatam progressionem et Solis et Lune et latitudinis, si quidem et ita ysomayri ysomayri] ysomoiri V₂ ysomosyri F₁ vel diametrizantes inveniuntur, ideo habebimus idem tempus et examinate sinzugie, si vero non, sumentes distantie ipsorum gradus et apponentes ipsis duodecimam ipsorum pro quo Sol ad proximum supermovetur considerabimus in quantis horis equinoctialibus Luna tantos gradus tunc anomalie anomalie] anomale F₁ movebuntur, movebuntur] movebitur V₂F₁ et factas horas, si quidem minor fiunt fiunt] fuerit F₁ exanimata Lune progressio ea que Solis, apponemus tempori periodico, si vero maior, aufferemus ab ipso. Similiter et ipsos distantie iporum gradus cum xii^a rursum ipsorum, si quidem minor fiunt fiunt] fuerit V₂F₁ que secundum periodicum tempus examinata progressio Lune solari, apponentes ipsi, si vero maior, aufferentes ab ea, et secundum longitudinem et latitudinem examinate sinzugie habebimus tempus et eam que in obliquo circulo Lune examinatam progressionem ad proximum. Sumitur tamen quaque vice qui secundum sinzugias Lune horarius anomalus motus ad hunc modum. Inferentes enim eum qui secundum subiacens tempus anomalie graduum graduum] add. numerum V₂F₁ in anomaliem anomaliem] anomalie V₂F₁ Lune canonium sumemus ex adiacentium ipsi prosthaferesium superhabundantiam contingentem differentiam uni anomalie portioni et multiplicantes ipsam in horarum horarum] horarium F₁ anomalie medium motum o xxxii xl o facta, si quidem anomalie numerus in eis qui supra maximam prosthaferesim versibus fuerint, auferemus ab eo qui secundum longitudinem horario medio motu o xxxii lvi o, si vero in eis qui infra, apponemus eisdem, et facta habebimus que tunc Luna secundum longitudinem anomalie movebitur in una hora equinoctiali. Itaque in Alexandria quidem factum tempus examinatarum sinzugiarum ita nobis methodice invenientur, eo quod et epoche omnes ad eum qui per Alexandriam meridianum horariorum temporum constitutionem sumant. Facile vero ab eis que in Alexandria temporibus et in qualicumque climate futura eiusdem sinzugie tempora invenire, data que sunt secundum ipsum multitudine equinoctialium horarum eius que a meridiano differre. Ab habitationum namque differentia considerantes eum qui per inquisitam regionem meridianum, quot gradibus differt ab eo qui per Alexandriam, si quidem qui per inquisitam regionem meridianus ab orientibus fiunt fiunt] fuerit V₂F₁ ei qui per Alexandriam, tantis temporibus ibi posterius videbitur observari apparens, si vero ab occidentibus, prius eisdem xv rursum temporibus unam manifestum quoniam facientibus horam equinoctialem.

⟨VI.5⟩ De eclipticis terminis Solis et Lune

His ita expositis, consequens utique erit apponere pertinentia ad eclipticos terminos et earum que Solis et earum que Lune contraportionum, ut etsi non omnes periodicas sinzugias investigare eligemus, solas vero potentes in ecliptica signa incidere, prompta nobis huiusmodi sit discretio ex adiacente cuique periodicarum sinzugiarum media Solis latitudinem progressione Lune. Itaque in eo quidem quod ante hoc sintagmari sintagmari] sintagmati V₂F₁ demonstravimus. Quem Lune diametros subtendit periferiam maximi circuli secundum maximum ipsius apostima scripti circa centrum zodiaci unius gradus sexagesimorum xxxi xx, per duas eclipses factas circa apoguion ipsius epicicli huiusmodi ratiocinantes. Ex Ex] et V₂ nunc vero quoniam maximos eclipticorum sinzugiarum terminos sumere, isti vero sunt qui fiunt, Luna circiter periguiotaton existente epicicli, demonstrabimus per duas rursum circa periguion observatas eclipses, quoniam quidem per apparentia ipsorum firmius utique erit talia ostendere, quantam et hic periferiam similiter Lune diametros comprehendit.

Septimo itaque anno Philomitorios Philomitorios] Philomitoios V₂ Philomitoros F₁ qui dlxxiiii^us a Navonassaro secundum Egiptios Phamenoth xxvii^a in xxviii^a ab hora viii^a incipiente usque x^am completam in Alexandria defecit Luna plurimum ab arctis datilos datilos] dactilos V₂F₁ vii. Quoniam ergo medium tempus factum post duas horas temporales et dimidium a mesonictio, que fiunt fiunt] fuerit V₂F₁ equinoctiales ii et iii^a, eo quod Sol optineret examinate Tauri gradus vi et iiii^a et colligitur quod ab epochi tempus usque medium eclipseos annorum egiptiacorum dlxxiii et dierum ccvi et horarum equinoctialium simpliciter quidem xiiii et iii^a, ad anomala anomala] omala V₂ vero nictimera xiiii solum, secundum quod tempus centrum Lune medie optinebat Scorpii gradus vii lix, examinate vero gradus vi xvi, et ab apoguio quidem epicicli gradus clxiii xl, a boreali vero termino obliqui circuli gradus xcviii xx; manifestum quoniam, quando gradibus viii xx distabat a nobis nobis] nodis V₂F₁ centrum Lune in obliquo circulo circa minimum existentis apostima et erit in in] iter. V₃ maximo circulo scripto per ipsum ad rectos obliquo circulo centrum umbre, secundum quam progressionem maxime obscurationum conplentur, dimidio et xii^a ipsius in umbram incidit diametri.

Rursum vero xxxvii anno tertie secundum Callippon periodi, qui est dcvii^us annus a Navonassaro, secundum Egiptios Tybi ii^a in iii^a hora v^a incipiente in Rodo incepit deficere Luna et obscurata est plurimum a notho dactilos iii. Quoniam ergo et rursum hic principium quidem eclipseos factum est ante duas horas temporales a mesonictio, que fuere equinoctiales et in Rodo et in Alexandria ii et dimidium et iii^a, eo quod Sol optineret examinate Aquarii gradus v et viii. Medium vero tempus in quo plurimum obscurata est ante unam horam equinoctialem et dimidium et iii^a ad proximum a mesonictio, et colligitur quod ab epochi usque medium eclipseos tempus annorum egiptiacorum dcvi et dierum cxxi et horarum equinoctialium et simpliciter et ad omala nictimera x et vi^a, secundum quod tempus centra centra] centrum V₂F₁ Lune medie quidem optinebat Leonis gradus v et xvi, examinate vero v et viii, et ab apoguio quidem epicicli gradus clxxviii xlvi, a boreali vero termino in obliquo circulo gradus cl xxxvi. Manifestum quoniam et hinc, quando gradibus x xxxvi distabat a nodis Lune centrum in obliquo circulo circa idem maximum existentis apostima, centro umbre communem sectionem optinente et eius qui per media et per centrum Lune ad rectos obliquo scripti maximi circuli, tunc quarta pars in umbram incidet lunaris diametri. Sed, si quidem viii et iii^a gradibus distat a coniunctionibus in obliquo circulo centrum Lune, xliii et xx sexagesima unius gradus in per polos ipsius scripto maximo circulo distat ab eo qui per media, quando vero x gradibus iii quintas a coniunctionibus distat secundum obliquum circulum, liiii et dimidium et iii^a sexagesima unius gradus in per polos ipsius scripto maximo circulo distat ab eo qui per media. Quoniam ergo duarum quidem eclipsium superhabundantia tertiam continet lunaris diametri, que vero expositi centri ipsius in eodem maximo circulo duarum distantiarum ab eodem puncto eius qui per media, hoc est centro umbre sexagesima unius gradus xi xlvii, manifestum quoniam et diametros tota Lune subtendit secundum nunium nunium] minimum V₂F₁ ipsius apostima scripti circa centrum zodiaci scripti … zodiaci] om. add. marg. V₃ maximi circuli periferiam sexagssimorum gradus unius xxxv et iii^a ad proximum. Quoniam vero in secunda eclipsium secundum, quam quarta defecerat lunaris diametri, distat centrum Lune a centro quidem umbre sexagesima liiii et dimidium et iii^a, a puncto vero secundum quod secat umbre periferiam ea que contingit ipsorum centra quartam diametri lunaris, que est sexagesima viii et dimidium et iii. Manifestum huic huic] hinc V₂F₁ et que e centro umbre secundum minimum Lune apostima relinquitur lx^orum xvi, et est indifferenti maior ea que est dupla et tribus quintis maior ea que e centro Lune sexagesimorum existente xvii Γ_o. Sed ea que e centro Solis subtendit periferiam similiter secundum ipsi scripti circa centra centra] centrum V₂F₁ zodiaci maximi circuli sexagesimorum xv xl, equaliter enim demonstrati fuerunt dimetientes proprios circulos et Sol et Luna secundum quod in sinzugiis maximum apostima. Quando ergo apparens centra centra] centrum V₂F₁ Lune distat a centro Solis in utraque eius qui per media unius gradus o xxxii xx, tunc primum possibille erit apparentem positionem Lune secundum contactum fieri Solis.

Quale, si intelligamus eius quidem qui per media animalia circuli perferiam AB, obliqui vero Lune GD, equidistantes ad sensum factos usque eas que secundum ecliptica tempora progressiones, et per obliqui polos scribemus maximi circuli perferiam AEG, intelligemus autem et circa A punctum Solis semicirculum, circa E vero apparentem Lune, quare contingere primum solarem secundum Z punctum, AE periferia, quam distitit E apparens centra centra] centrum V₂F₁ Lune ab A solari, potest aliquotiens fieri expositorum o xxxii xxxii] xxxiii V₂F₁ xxi. Sed in eis que a Meroe locis, ubi maxima dies est horarum equinoctialium xiii, usque ad effluxiones Boristenis, ubi maxima dies horarum est equinoctialium xvi, ad arctos quidem plurimum Luna permutatur secundum sinzugiarum minimum apostima, supputata Solis transmutatione, o viii ad proximum, ad meridiem vero similiter plurimum o lviii. Permutatur autem et secundum longitudinem plurimum, quando quidem o viii ad arctos permutatur, circa Leonem et Geminos o xxx ad proximum, quando vero o lviii ad meridiem, circa Scorpium et Pisces o xv ad proximum. Si ergo examinatum Lune centrum supposuerimus secundum D et coniuncxerimus DE totius permutationis, DG quidem eius que secundum longitudinem ad proximum erit permutationis, GE vero eius que secundum latitudinem. Quare, quando quidem ab arctis fiunt fiunt] fuerit V₂F₁ Luna a Sole et permutatur plurimum ad meridiem, DG quidem erit o xv, AEG vero gradus unius xxxi ad proximum; et quoniam proportio eius que a coniunctione in G periferie ad GA secundum mediam eclipticorum terminorum diastima quam habent xi et dimidium ad i, facile enim intelligibille hec fit per demonstrata in inclinatione lunaris circuli et ipsa quidem que a coniunctione in G erit graduum xvii xxxvi est GD vero eorumdem xvii xli, quando vero a meridie existens a Sole plurimum ad arctos permutatur, DG quidem erit o xxx, tota vero AEG o xli, et propter eadem que quidem a coniunctione in G graduum vii lii, que vero est GD tota eorumdem viii xxii. Quando ergo centrum Lune examinate distat ab utralibet coniunctionum in obliquo circulo ad arctos quidem gradibus xvii xli, ad meridiem vero gradibus viii xxii, tunc primum in expositis locis eius que secundum nos habitate possibille erit apparentem ipsius positionem secundum contactum fieri Solis.

Rursum quoniam solaris quidem anomalie plurima differentia monstrata est graduum ii xxiii, lunaris vero circa sinzugias graduum vii, possibille erit aliquotiens Lunam distare a Sole secundum periodicas sinzugias examinate gradibus vii xxiiii. Sed in quanto pertransit eos Luna, Sol quidem progredietur xiii^am ipsorum ad proximum, hoc est o xxxiiii, in quantum vero rursum Luna o xxxiiii supermovetur, progredietur et Sol xiii^am ipsorum o iii ad proximum, quorum nequaquam fit xiii^a cura digna. Si ergo que in idem o xxxvii, que fiunt eorum que ex principio vii xxiiii pars xii^a, apposuerimus solaris anomalie gradibus ii xxiii, habebimus gradus iii, quibus plurimum different ab eis que in periodicis sinzugiis progressionibus et longitudinis et latitudinis ad proximum ille que examinate; et quando ergo media progressio centri Lune distabat a coniunctionibus in obliquo circulo ad arctos quidem gradibus xx xli, ad meridiem vero gradibus xi xxii, tunc primum in expositis locis possibile erit apparentem ipsius positionem secundum contactum fieri Solis; et propter eadem quando a boreali termino obliqui circuli Lune adiacens periodicis sinzugiis graduum numerus vel eis que a lxix xix usque ci xxii vel eis que a cclviii xxxviii usque ccxc xli concidit, tunc tantum in eclipticis locis possibile erunt accidere propositum.

Rursum et Lune eclipticorum terminorum causa, quoniam que quidem e centro Lune secundum minimum ipsius apostima subtendens demonstrata est periferiam graduum o xvii xl, que vero e centro umbre dupla existens et adhuc tribus quintis maior ad proximum ea que e centro Lune colligitur eorumdem o xlv lvi, manifestum quoniam, et quando centrum Lune examinate distat a centro umbre in maximo quidem per ipsa et polos obliqui scripto circulo in utrasque eius qui per media gradu i iii xxxvi, in obliquo autem circulo Lune ab utralibet coniunctionum secundum i^us et et​] ad V₂ xi et dimidium proportionem gradibus xii xii ad proximum, tunc primum possibile erit Lunam contingere umbram. Propter eadem vero circa anomaliam demonstratis, et quando secundum mediam progressionem sumptum centrum Lune distabat a coniunctionibus in obliquo circulo gradibus xv xii, quare rursum incidere secundum eos qui a boreali termino numeros et in eos qui a lxxiiii xlviii usque cv xii et in eos qui a ccliiii xlviii usque cclxxxv xii, primum possibile erit Lunam contingere umbram. Apponemus ergo preiacentibus sinzuguiarum canoniis et solarium et lunarium terminorum latitudinis Lune numeros, ut et potentium in eclipsim incidere discretionem ex promptu faciamus.

⟨VI.6⟩ De distantia eclipticorum mensium

Et per quot vero ut in universum menses possibile erit sinzugias eclipticas fieri, utile utique erit his apponere, assumentes unam epochim ecliptice sinzugie, non omnes rursum eas que deinceps, sed eas que per tot utique contingens erunt erunt] erit V₂F₁ menses eclipsim fieri, ad terminorum conspectionem comprehendere. Itaque per vi quidem menses possibile esse et Solem et Lunam deficere, hinc utique erunt erunt] erit V₂F₁ manifestum: quoniam media quidem secundum latitudinem progressio Lune in vi mensibus colligit clxxxi gradus et xxv, que vero inter eclipticos terminos periferie et in Sole et in Luna, alie quidem intra semicirculum minores ipsis gradus continent, alie vero supra semiciculum maiores. Etenim solaribus terminis ad arctos comprehendentibus ab utralibet coniunctionum in obliquo circulo Lune demonstratos gradus xx xli, ad meridiem vero xi xxii, et que quidem ab arctis non ecliptica periferia fit graduum cxxxviii xxxviii, que vero a meridie graduum clvii xvi. Lunaribus vero deprehendentibus in utrasque partes eius qui per media in eodem circulo gradus a coniunctionibus xv xii, et utraque non eclipticarum periferiarum colligitur graduum cxlix xxxvi. Quoniam vero et per istas ypotheses possibile erit Lune eclipsim compleri per maximam pentaminiam, hoc est secundum quam Sol quidem maximam facit progressionem, Luna vero minimam, videbimus utique ita. Quoniam quidem enim in media pentaminia eam quidem que secundum longitudinem utriusque luminarium progressionem reperimus comprehendentem medie gradus cxxxv xxxii, Lunam vero anomalie in epiciclo gradus cxxix v, istorum autem graduum cxlv xxxii Solis secundum in utrasque periguii maximam progressionem assumunt penes mediam gradus iiii xxxviii, qui vero epicicli Lune cxxix gradus v secundum in utrasque apoguii minimam progressionem auferunt a media gradus viii xl. In tempore ergo medie pentaminie, quando Sol quidem maximam facit progressionem, Luna vero minimam, amplius precedens erunt erunt] erit V₂F₁ Solem Luna, collectis ex ambabus anomaliis gradibus xiii xviii. Quorum rursum xii^am sumentes propter demonstratam demonstratam] demonstrata V₂F₁ habebimus gradum i sexagesima vi ad proximum, que Sol supermovetur usque dum comprehendatur a Luna. Quoniam ergo ex propria quidem anomalia sumpserat gradus iiii et sexagesima xxxviii, ex ea vero que usque examinatam sinzugiam comprehensione alium gradum i et sexagesima vi, erit et maxima pentaminia penes mediam summens secundum longitudinem v et sexagesima xliiii. Tantos ergo ad proximum et secundum latitudinem in obliquo circulo progressio Lune sumens erit gradus, secundum mediam pentaminiam collectis latitudinariis portionibus cliii xxi ad proximum. Quare et examinate considerata secundum latitudinem progressio in maxima pentaminia colligetur gradus clix et sexagesimorum v; alii quid quid] quidem V₂ in utrasque eius qui per media ecliptici secundum medium apostima Lune termini continent in maximo quidem per polos obliqui scripto circulo gradum i ad proximum, eo quod secundum minimum quidem sit gradus i iii iii] corr. ex iiii V₃ xxxvi, secundum maximum vero colligatur o o] t V₃ lvi xxiiii, in obliquo autem circulo a coniunctionibus portiones xi xxx. Que vero inter ipsos et non ecliptica periferia propter hoc colligitur graduum clvii o, qui minores sunt secundum maximam pentaminiam sumptis obliqui circuli gradibus clix et v sexagesimis portionibus duabus et sexagesimis v. Manifestum ergo ex his quoniam possibile erit Luna Luna] Lunam V₂F₁ in maxima pentaminia secundum primam panseliniam deficientem secundum ea que in utralibet coniunctionum remotionem et in finali panselinia rursum deficere secundum eam que in contrariis coniunctionibus prosodon, ab eisdem partibus eius qui per media in ambabus eclipsibus obscuratione facta et nunquam a contrariis. Quoniam ergo ergo] add. maxima V₂F₁ pentaminia eptiminias] eptamenias V₂ potest duas fecisse lunares eclipses, ita nobis manifestum factum est. Quoniam vero per eptiminias inpossibile erit hoc accidere, etsi minimam eptaminiam supposuerimus, hoc est secundum quam Sol quidem minimam facit progressionem, Luna vero maximam, videbimus utique eodem modo docentes preexpositis. Quoniam enim rursum in media eptaminia media quidem utriusque luminarium secundum longitudinem progressio assumit gradus cciii xlv, que vero in epiciclo Lune gradus clxxx xliii, istorum autem graduum quidem cciii xlv Solis secundum eam qua in utrasque apoguii minimam progressionem aufferunt a medio motu gradus iiii xlii, qui vero epicicli Lune clxxx xliii secundum eam que in utrasque periguii maximam progressionem addunt medie gradus ix lviii. In tempore ergo minime eptaminie, quando Sol quidem minimam facit progressionem, Luna vero maximam, pertransiens erit Solem Luna collectis ex ambabus anomaliis gradibus xiiii xl. Quorum propter eadem xii^am sumentes et apponentes ex solari anomalia deficientibus gradibus iiii xlii collectos gradus v lv ad proximum habebimus, quantis et que secundum longitudinem progressio in minima eptaminia deficiet ab ea que in media, et que secundum latitudinem similiter deficiet collectis secundum mediam eptaminam portionibus ccxiiii xlii. In minima ergo eptaminia assumens erunt erunt] erit V₂F₁ Luna secundum latitudinem in obliquo circulo portiones ccviii xlvii, tota que inter eclipticos secundum medium apostima Lune terminos obliqui circuli maxima periferia et eius que secundum accessionem alterius coniunctionum et eius que secundum recessionem contrarie coniunctionis portionum existente cciii o. Non ergo possibile erit Lunam neque in minima eptaminia defitientem secundum primam panseliniam qualitercumque et secundum extrema deficere.

Demonstrandum ergo rursum quoniam et Solem possibile erit in eisdem bis deficere in maxima pentaminia et secundum omnes partes eius que secundum nos habitabilis. Quoniam quidem enim in maxima pentaminia eam que secundum latitudinem progressionem Lune demonstravimus portionum clix v, non ecliptica periferia in Sole secundum medium apostima Lune eorumdem facta clxvii xxxvi, propter et eclipticos terminos ipsius qui per media distare in eo quidem qui per polos ipsius circulo portiones o xxxii xx, in obliquo vero Lune gradus vi xii ad proximum, manifestum quoniam, nichil transmutata Luna, inpossibile erit propositum, propter maiorem esse non eclipticam periferiam ea que in maxima pentaminia progressione portionibus in obliquo quidem circulo viii xxxi, in eo vero qui ad rectos ei qui per media o xlv ad proximum. Ubi vero potest permutari ita, quare eas que in utralibet extremarum sinodorum vel et eas que coutrasque simul permutationes o xlv habundare, ibi possibile erit et extremas sinodos ambas eclipticas fieri. Quoniam ergo demonstravimus in tempore maxime pentaminie, quando Luna quidem minimam facit progressionem, Sol vero maximam, a duabus partibus Virginis usque duas partes Aquarii procurentem adhuc Soli Lunam eis qui ex ea que ambarum anomaliarum gradibus xiii xviii, istos autem et adhuc xii^a ipsorum Luna movetur medie in die uno et horis ii et iiii, manifestum quoniam, tempore medie quidem pentaminie contingente dierum cxlvii et horarum ad proximum xv et d et iiii^a, maxime pentaminie tempus erit dierum cxlviii et horarum xviii; et propter hoc prima et circa duas partes Virginis facta sinodo, extrema et circa duas partes Aquarii facta prius erit in totos dies defitientibus horis vi. Querendum est ergo ubi et quando potest Luna permutari vel in altero preiacentium dodecatimoriorum vel in ambobus secundum eam que in Aquario ab ea que in Virgine ante vi horas stationem plus expositis xlv sexagesimis. Itaque ad arctos quidem nusquam eius que penes nos habitabilis, secundum quem diximus modum, reperitur tantum permutata Luna. Unde impossibile fit in maxima pentaminia bis deficere Solem, secundum eam que a meridie ab eo qui per mediam Lune progressionem, hoc est quando secundum primam quidem sinodon descendit a descendente coniunctione, secundum extrema vero accedit asscendenti. Ad meridiem vero fere a post equinoctialem habitantibus ut ad arctos potest tamen in ambobus expositis dodecatimoriis secundum eam que ante vi horas portionem permutari, quando due quidem Virgines partes secundum primam sinodon in occasu subiacent, ille vero que Aquarii secundum secundam sinodon in meridiano. Etenim secundum huiusmodi portiones reperimus Lunam in medio apostimate ad meridiem permutatam, supputata solari permutatione, sub equinoctiali quidem in Virginis portione graduum o xxii ad proximum, in ea vero que Aquarii o xiiii. Ubi vero maxima dies horarum est xii et dimidii secundum Virginis quidem portionem gradus o xxvii, secundum eam autem que Aquarii gradus o xxii, velut hinc iam coutrasque permutationes sexagesimis iiii^or superare preiacentia o xlv. Plure ergo secundum borealiores semper locos ea que ad meridiem permutatione facta, manifestum quoniam et magis semper possibile erunt erunt] erit V₂F₁ in ipsis habitantibus bis in ipsa pentaminia apparere Solem defitientem secundum solam tamen ab arctis ab eo qui per media Lune progressionem, hoc est quando in prima eclipsi discedit ab ascendente coniunctionum, in secunda vero ascedit ascedit] om. V₂ corr. in accedit F₁ descendenti.

Dico ergo rursum quoniam et in minima eptaminia possibile erit bis Solem penes eosdem deficere. Quoniam quidem enim et in minima eptaminia eam que secundum latitudinem Lune progressionem demonstravimus portionum ccviii xlvii, maxima vero inter eclipticos terminos deprehensa periferia obliqui circuli ea que ab eo quod secundum accessionem alterius coniunctionis illud usque quod secundum disscessionem contrarie coniunctionis, colligitur et in Sole huiusmodi distantia in medio Lune apostimate portionum cxcii xxiiii, manifestum quoniam, nichil rursum quidem permutata Luna, inpossibile erit propositum, propter maiorem esse eam que minime eptaminie obliqui circuli periferiam ea que sub eclipticis terminis Solis maxima deprehenditur portionibus in obliquo quidem circulo xvi xxiii, in eo vero qui per polos zodiaci i xxv. Ubi vero potest permutari ita, quare eas que in utralibet et finalium sinodorum vel et eas que coutrarumque simul permutationes superare i gradibus et xxv, ibi possibile erit et finales sinodos ambas eclipticas fieri. Quoniam quidem ergo demonstravimus in tempore medie eptaminie, quando Luna quidem maximam facit progressionem, Sol vero minimam, ab extremis Aquarii usque media Virginis procurentem Lunam Soli examinate gradus xiiii xl, tantos autem gradus et adhuc xii^am ipsorum Luna movetur in die i horis v, manifestum quoniam, tempore medie eptaminie continente dies ccvi et horas xvii ad proximum, minime eptaminie tempus erit dierum ccv et horarum xii, et propter hoc extreme et circa media Virginis sinodi tempus post xii^a horas erit ab eo quod prime et circa extrema Aquarii. Querendum est ergo ubi et quotiens potest Luna plus i xxv gradus permutari, vel in altero propositorum dodecatimoriorum vel in ambobus secundum eam que per xii horas positionem, hoc est quando alterum quidem occidit, alterum vero oritur, eo quod nullo modo aliter possint eclipses ambe super terram fieri, ad arctos quidem rursum nusquam eius que secundum nos habitabilis secundum nullam positionem tantum reperitur permutata Luna, neque ispis qui sub equinoctiali magis sexagesimis xxiii ea que secundum maximum apostima facta secundum latitudinem permutatione. Unde inpossibile fit in minima eptaminia bis deficere Solem secundum eam que a meridie ab eo qui per media Lune progressionem, hoc est quando secundum priorem quidem sinodum accedit asscendenti coniunctioni, secundum extremam vero disscedit a descendenti. Ad meridiem vero tantam permutationem reperimus completam fere ab eo qui per Rodum parallilo, quando extrema quidem Aquarii oriuntur, media vero Virginis occidunt, permutatur in Rodo et eis qui sub eodem parallilo locis secundum utramque istarum positionum Luna secundum medium apostima, solari permutatione sublata, ad meridiem ana o xlvi ad proximum, quare eas que in ambobus sinodis permutationes hinc iam maiores fieri uno gradu et xxv sexagesimis. Plure ergo facta ea que ad meridiem permutatione in amplius isto parallilo borealioribus, manifestum quoniam possibile erit secundum ipsos habitantibus bis in minima eptamina eclipsim Solis apparere, secundum solam tamen rursum eam que ab arctis ab eo qui per media Lune progressionem, hoc est quando in prima quidem eclipsi accedit descendenti coniunctioni, in secunda vero discedit ab ascendente.

Restat autem adhuc demonstrare et quoniam per mensem unum inpossibile erit bis Solem deficere in ea que secundum nos habitabili, neque in eodem climate, neque in diversis, et omnia quis simul supponat non potentia quidem concurrere, concepta vero aliter posse facere propositum, dico vero, etsi Lunam quidem secundum minimum apostima supposuerimus, ut plus permutetur, mensem autem minimum, ut quanto possibile minimo maior ea que secundum latitudinem menstrua progressio fiat quam que sub eclipticis terminis Solis continetur, etsi indifferenter et terminis et dodecatimoriis utemur, secundum quem maximas apparet permutationes fatiens. Quoniam ergo in medio mense que quidem secundum longitudinem utriusque luminarium progressio comprehendit medie gradus xxix vi, que vero secundum epiciclum Lune gradus xxv xlix, istorum vero Solis quidem xxix vi. secundum eam que in utrasque apoguii minimam progressionem aufferent a media gradum i viii, qui vero epicicli Lune xxv gradus et xlix secundum eam que in utrasque periguii maximam progressionem apposuerit medie gradus ii xxviii, si consequentur predemonstratis componentes eas que ex ambobus anomaliis prostafereses factorum iii xxxvi xii^a videlicet o xviii apposuerimus quibus Sol defecerat, faciemus portiones i xxvi et tantis habebimus minorem minimi mensis progressionem ea que in medio mense et secundum longitudinem et secundum latitudinem. Quare quoniam quidem medii mensis secundum latitudinem progressio graduum est xxx xl eam que minimi progressionem fieri graduum xxix xiiii, que faciunt in eo qui ad rectos zodiaco maximo circulo portiones ii xxxiii ad proximum. Verum omnis eclipticorum terminorum Solis progressio colligitur, secundum minimum apostima Luna existente, portionum i vi, quare maiorem fieri minimi mensis progressionem portionibus i xxvii. Oportebit ergo omnino, si in uno mense bis Sol defecerit, vel secundum alteram quidem sinodorum nichil permutari Lunam, secundum alteram vero plus i xxvii, vel secundum utramque quidem rursum sinodorum in easdem permutari, superhabundantiam vero permutationis maiorem esse i xxvii, vel coutrasque permutationes plures eisdem colligi portionibus, quando que quidem alterius sinodi fit ad arctos, que vero alterius ad meridiem. Verum nusquam terre in sinzugiis, neque secundum minimum apostima plus Luna secundum latitudinem permutatur, solari permutatione supputata, i gradu. Non erit ergo hoc inpossibile in uno minimo mense bis deficere Solem, quando vel secundum alteram quidem sinodorum nichil Luna permutatur, vel secundum ambas in easdem permutatur, superhabundantia ipsarum non plure facta gradu i, indigens i et xxvii. Solum ergo propositum potest contingere, si, in contraria facta utraque permutatione, ex ambabus plures in xxvii portiones colligantur. Hoc autem in diversa quidem habitata contingens erit, eo quod possit penes borealiores quidem ab equinoctiali eorum qui in secundum nos habitata ad meridiem permutari Luna, penes australiores vero ab equinoctiali antichenorum vocatorum ab arctos permutari post Solis permutationem ab o xxv usque gradum i. In eadem vero habitata numquam continget, eo quod plurimum Luna permutetur similiter penes eos quidem sub ipso qui sub … qui] qui sub ipso V₂F₁ equinoctiali non plus sexagesimis xxv et ad arctos et meridiem, penes autem borealissimos vel australissimos ipsorum non plus in contraiacentia preiacente i gradu, quare et ita adhuc minores colligi coutrasque permutationes i xxvii portionibus. Multo vero minore in eis qui inter equinoctialem et alterum terminum utraque contraiacentium permutationum semper facta, procedit utique adhuc magis penes ipsos possibile. Penes eosdem ergo nusquam terre in uno mense possibile erit bis Solem deficere, penes diversos autem nusquam eiusdem habitate. Quod nobis propositum erat demonstrare.

⟨VI.7⟩ Negotiorum canoniorum eclipticorum

Quales ergo diastases sinzugiarum in considerationibus eclipsium debemus assumere, per hoc nobis factum est clarum. Ut autem et eis que secundum ipsas mediis temporibus discretis et eis que in ipsis progressionibus Lune computatis in sinodicis quidem sinzugiis apparentibus, in panseliniacis vero examinatis per eas que secundum latitudinem per per​] om. V₂F₁ epochas Lune promte considerare valeamus et omnino futuras eclipticas sinzugiarum et istarum et magnitudines et tempora obscurationum, composuimus canonia ad huiusmodi discretionem: duo quidem solarium eclipsium causa, duo vero lunarium secundum et maximum et minimum Lune apostima, supponentes augmentum obscurationum per xii partem obscurate diametri utriusque luminarium. Itaque quidem primum canonium solarium eclipsium, quod continet eos qui secundum maximum apostima Lune eclipticos terminos, hat hat] om. V₂F₁ ordinabimus in versus quidem xxv, selidia vero iiii. Istorum autem duo quidem prima continebunt eam que secundum latitudinem Lune in obliquo circulo apparentem progressionem in unaquamque obscurationum. Quoniam enim Solis quidem diametros sexagesimorum est xxi xxi] xxxi V₂F₁ xx, ea vero que Lune et ipsa secundum maximum apostima ostensam ostensam] ostensa V₂ est eorumdem xxxi xx et propter eadem, quando apparens centrum Lune distabat a solari quidem centro in eo qui per centra amborum maximo circulo sexagesimis xxxi xx, a coniunctione vero in obliquo circulo gradibus vi secundum preexpositam proportionem que est xi xxx ad i, tunc enim primum secunudm contactum erit Solis, secundum primos quidem versus selidiorum ordinabimus primi quidem lxxxiiii gradus, secundi vero cclxxvi, secundum postremos autem primi rursum xcvi, secundi vero cclxiiii; cclxiiii] add. secundum postremos autem primi rursum lxxxvi secundi vero cclxiiii V₂ et quoniam xii^e solaris diametri pertinent obliqui circuli unius gradus sexagesima xxx ad proximum, tantis augebimus et minuemus preiacentia duo selidia ab extremis incipientes ea usque qui circiter medios versus. In mediis enim ordinabimus et xc gradus et cclxx. Tertium vero selidium continebit quantitates obscurationum in extremis quidem versibus, appositis eis que contactus o o, in eis autem que deinceps ipsorum uno digito propter xii^am diametri et ita in reliquis uni digito augmento facto usque medium versum in quem xii digitorum numerus perveniet. Quartum autem selidium continebit factas centri Lune progressiones secundum unamquamque obscurationum, ut minime coinvestigatis tamen nondum nec supermotibus Solis neque supertransmutationibus Lune.

Secundum autem solarium eclipsium canonium quod continet eos qui secundum minimum apostima Lune eclipticos terminos ordinabimus alia quidem similiter primo, in versus autem xxvii et selidia iiii, propter eam quidem que e centro Lune in minimo apostimate talium ostendi xvii et sexagesimorum xl, qualium est que e centro Solis xv et sexagesimorum xl. Quando vero primum secundum contactum fit Solis Luna, tunc apparens centrum ipsius distare a solari quidem centro et rursum unius gradus et sexagesima xxxiii et secunda xx, a coniunctionibus autem in obliquo circulo gradibus vi xxiiii. Fiunt enim in extremis versibus apparentis latitudinis numeri et qui lxxxiii xxxvi et qui cclxvi. cclxvi] cclxxvi V₂F₁ Et rursum qui xcvi xxiiii et qui cclxiii xxxvi. Qui vero in medio digitorum propter et simillem superhabundantiam xii digitorum et amplius unius pentimoriorum iiii, Secundum quem et sola fit progressio.

Lunarium autem canoniorum utrumque ordinabimus in versus quidem xlv, selidia vero v; et primo quidem latitudinis numeros apponemus, ut in maximo apostimate existente Luna. Quoniam enim que quidem e centro Lune ostensa est secundum maximum apostima sesagesimorum xv xl, que vero e centro umbre eorumdem xl xliiii, quare, quando primum contingit umbram Luna, tunc centrum ipsius distare a centro umbre in eo qui per ambo centra maximo circulo sexagesima lvi xxiiii, a coniunctionibus autem in obliquo circulo gradum i et sexagesima xlviii, secundum primos quidem versus ordinabimus et eum qui eorum que sunt lxxix xii numerum et eum qui sunt cclxxx xlviii, secundum extremos autem et eum qui c et sexagesimorum xlviii et eum qui eorum que sunt cclix xii; et propter eadem primis auxomiosim ipsorum fatiemus pertinentibus xii^e eius que tunc lunaris diametri xxx sexagesimis. Secundo autem canonio latitudinis numeros apponemus, velut in minimo apostimate existente Luna, secundum quod apostima que quidem e centro ipsius ostensa est sexagesimis xvii xl, que vero e centro umbre eorumdem xlv lvi, quare, quando primum contingit umbram Luna, tunc centrum ipsius distare a centro quidem umbre rursum similiter gradu i et sexagesimis iii xxxvi, a nodo vero in obliquo circulo gradibus xii et sexagesimis xii. Propter hoc ergo secundum primos quidem versus ordinantes et eorum que sunt lxxvii xlviii numerum et eum qui eorum que sunt cclxxxii xii, secundum extremos vero et eum qui eorum que sunt cii xii et eum qui eorum que sunt cclvii xlviii, rursum auxomiosim ipsorum faciemus pertinentibus xii eius que tunc lunaris diametri xxxiiii sexagesimis, digitorum autem tertia selidia eumdem modum continent solaribus et similiter ea que deinceps et continentia progressiones Lune secundum unamquamque obscurationum et utrasque et casus et complectionis et adhuc eos qui medietatis more. Investigavimus Investigavimus] add. autem V₂F₁ secundum unamquamque obscurationum expositas progressiones Lune lineariter, cautentes cautentes] coutentes V₂F₁ tamen demonstrationibus quasi in uno epidedo et quasi in rectis, eo quod usque tantam magnitudinem periferie vero differant ad sensum ab eis que sub ipsas rectis, et amplius quasi nullo rursum cura digno differente ea que in obliquo circulo progressione Lune penes ad eum qui per media animalia consideratam. Non enim suspicetur quis nos ignorare quoniam et universaliter ad eam que secundum longitudinem progressionem Lune fit quedam differentia penes couti obliqui circuli periferiis pro eis que eius qui per media et adhuc sinzyguiarum tempora non sequar sequar] sequitur V₂F₁ eadem inpermutabiliter esse mediis eclipsium.

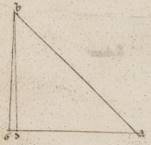Si enim assumamus ab A coniunctione duorum preiacentium circulorum equales periferias AB et AG et copulantes BG rectam a puncto B ad AG scripserimus BD, manifestum hinc erit Luna quidem in B supposita, quando quando] quoniam V₂F₁ AG eius qui per media periferia coutentibus nobis pro AD, propter ad eos qui per polos zodiaci circuli eas que ad ipsum progressiones considerari, ea que est GD differet que penes inclinationem lunaris circuli differentia. Sole vero rursum vel centro umbre in B intellecto, sinzuguie quidem tempus erit secundum indifferentiam circulorum, quando et Luna secundum G fiet, medium vero eclipseos, quando secundum D, eo rursum quod media tempora obscurationum ad eos qui per polos lunaris circuli considentur; considentur] considerentur V₂F₁ et differet sinzugie tempus a medio eclipsis GD periferiam. periferiam] periferia V₂ Verum causa, ut non et istas nos coinvestigemus periferias in particularibus negotiis, parvas esse et insensibiles ipsarum differentias, et quoniam ignorare quidem aliquid talium inconveniens, at vero propter eam que in penes singula methodos kataskeliam spontaneum despicere aliquid tantorum, quanta et penes ypotheses et penes observationes ipsas competit considerari, eius quidem que secundum simplitius utilitatis plurimum infert sensum, eius vero quod circa apparentia peccati vel nullum vel omnino parvum. Itaque similem GD periferie universaliter quidem minime maiorem reperimus sexagesimis v unius gradus, – demonstratum est enim hoc per idem thehorema thehorema] theorema V₂F₁ per quod et differentias investigavimus periferiarum equinoctialis ad periferias eius qui per media animalia, ut in per polos equinoctialis scriptis circulis –, in eclipsibus autem non maiorem duabus sexagesimis, quoniam qualium quidem est utraque AB et AG periferiarum xii, fere enim usque tantas pertingent que secundum eclipses Lune progressiones, qualis est BD unius ad proximum. Propter hoc autem et AD eorumdem xi lviii ad proximum et reliquatur GD reliqua duorum sexagesimorum, que nec xvi^am faciunt unius hore equinoctialis. In tantum vero examinare varie varie] vane V₂F₁ gloriosi magis quam veritatem amantis utique erit. Propter ea ergo et expositas obscurationum progressiones Lune, velut non differentibus ad sensum circuli, circuli] circulis V₂F₁ composuimus.

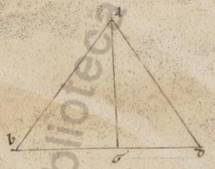Facta Facta] Sacta V₃ vero est nobis huiusmodi investigatio, velut in uno vel duobus rursum exemplis, continens ita. Esto enim Solis quidem vel umbre centrum A, que vero pro periferia lunaris circuli recta BGD, et subiaceat B quidem centrum Lune, quando accedens primum contingit Solem vel umbram, D vero, quando discedens, et copulatis AB et AD, trahatur ab A in BD cathetos AG. Quoniam ergo, quando secundum G fiet centrum, et medium tempus fiet eclipseos et maxima obscuratio, manifestum et ex AB quidem ei que est AD equalem esse, propter hoc autem et BG progressionem ei que est GD et ex AG omnibus minorem esse in ea que est BD duo centra copulantibus. Manifestum autem quoniam et utraque quidem earum que sunt AB et AD coutrasque continet que e centris Lune et Solis et umbre, AG vero minor est utraque ipsarum ea que sub obscuratione deprehenditur parte diametri eius quod deficit. His ergo ita se habentibus, fiat exempli causa obscuratio digitorum iii, et subiaceat primum A Solis centrum. Itaque in maximo quidem apostimate existente Luna, AB quidem fit sexagesimorum xxxi xx et quod ab ipsa dcccclxxxi xlvii, AG vero eorumdem xxxiii xxx. Minor enim est quam AB tribus xii^is solaris diametri, hoc est vii l, quod autem ab ipsa dlii xv. Quare et quod quidem ab BG erit eorumdem ccccxxix xxxii, ipsa vero BG longitudine xx xliii ad proximum, que et apponemus primo canonio tribus digitis solarium secundum quartum selidium. In minimo autem apostimate Lune AB quidem rursum fit sexagesimorum xxxiii xx et quod ab ipso mcxi vii, AG vero eorumdem xxv xxx, et quod ab ipsa dcl xv. Reliquum autem quod ab BG sexagesimorum cccclx lii et longitudine ergo BG erit eorumdem xxi xxviii, que et ipsa apponemus in secundo canonio solarium tribus digitis secundum quartum selidium.

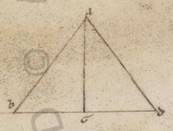Rursum subiaceat A centrum umbre et obscuratio eiusdem iiii^a lunaris diametri. Itaque in maximo quidem apostimate Lune AB quidem sit sexagesimorum lvi xxiiii, et quod ab ipsa iiiclxxx lviii, AG vero eorumdem xlviii xxxiiii. Minor enim est quam AB iiii^a lunaris diametri, hoc est eis que in maximo apostimate vii l, quod autem ab ipsa iiccclviii xliii. Quare et que quidem ab BG relinquetur dcccxxii xv, ipsa vero BG erit longitudine eorumdem xxviii xli, que et apponemus in primo lunarium canoniorum tribus digitis secundum quartum selidium, continentia casus progressionem eandem existentem ad sensum ei que complectionis. In minimo autem apostimate AB quidem fit sexagesimorum lxiii xxxvi, et quod ab ipsa iiiixliiii lviii, AG vero eorumdem liiii lvi. Ea enim que superhabundantie viii l quarta sunt rursum eius que secundum minimum apostima lunaris diametri, quod autem ab ipsa iidccccxcix xxiii. Quare et quod quidem ab BG relinquetur ixlv xxxv, ipsa vero BG longitudine eorumdem xxxii xxi, que et ipsa apponemus similiter tribus digitis secundum quartum selidium quod in secundo lunarium canoniorum.

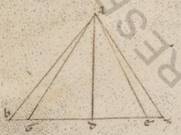Rursum propter et more tempus habentes lunares obscurationes esto centrum quidem umbre A punctum, que vero pro periferia obliqui Lune circuli recta BGDEZ, atque B quidem subiaceat secundum quod centrum erit Lune, quando adducte primum exterius continget umbram, G vero secundum quod erit centrum Lune, quando primum tota defitiens interius continget circulum umbre, E autem secundum quod erit rursum centrum Lune, quando discendens primum interius continget circulum umbre, Z vero secundum quod erit centrum Lune, quando educta ad extremum continget exterius umbram, et trahatur rursum ab A in BZ cathetos AD. Manentibus ergo et hic premonstratis, amplius et hoc manifestum quoniam et utraque AG et AE rectarum continet superhabundantiam qua superat eam que e centro Lune eam que e centro umbre, quare et GD quidem progressionem equalem ei que est DE fieri et continere utramque dimidium more, reliqua vero BG rectam casus relique EZ recte completionis equalem esse. Subiaceat ergo eclipsis secundum quam adiacent xv digiti Lune, hoc est secundum quam D centrum ipsius interius fit eo qui secundum eclipticos terminos fine una lunari diametro, et adhuc quarta parte ipsius, hoc est quando AD minor erit utraque quidem rectarum AB et AZ preiacente una lunari diametro, et amplius quarta ipsius parte, utraque vero rectarum AG et AE quarta parte unius diametri lunaris. Itaque in maximo quidem apostimate existente Luna, AB quidem fit preiacentium sexagesimorum lvi xxiiii et quod ab ipsa iiiclxxx lviii, AG vero eorumdem xxv iiii, Lune enim diametros in maximo apostimate sexagesimorum est xxxi xx, et quod ab ipsa dcxxviii xx, AD vero similiter xvii xiiii, et quod ab ipsa ccxcvi lix. Quare et quod quidem ab BD relinquitur iidccclxxxiii lix, et ipsa longitudine erit eorumdem liii xlii, quod autem ab GD relinquitur cccxxxi xxi, et ipsa longitudine erit eorumdem xviii xii, reliqua vero et BG eorumdem xxxv xxx. Apponemus ergo xv digitorum numero primi canonii lunarium eclipsium secundum quartum quidem selidium casus sexagesimorum xxxv xxx equalia existentia eis que completionis, secundum quintum vero dimidii tempora solius xviii xii. In minimo vero apostimate existente Luna AB quidem fit rursum preiacentium lxiii xxxvi, et quod ab ipsa iiiixliiii lviii, AG autem eorumdem xxviii xvi, Lune enim diametros in minimo apostimate ostensa est lx^orum xxxv xx, et quod ab ipsa dccxc ix o, AD vero similiter xix xx, et quod ab ipsa ccclxxvii xxxix. Quare et quod quidem ab BD relinquitur iiidclxvii xix, et ipsa BD longitudine erit eorumdem lx et xxxiiii, quod autem ab GD relinquitur ccccxxi xxi, et ipsa longitudine erit eorumdem xx xxxii, reliqua vero et BG eorumdem xl ii. Apponemus ergo in secundo canonio lunarium eclipsium xv digitorum numero secundum quartum quidem selidium casus sexagesima xl ii equalia rursum existentia eis que completionis, secundum quintum vero selidium ea que dimidii Solis xx xxxii.

Ut autem et in eis que inter maximum et minimum apostima Lune in epiciclo progressionibus pertinentes singulis superhabundantias totius differentie per sexagesimorum methodum promte sumamus, subordinavimus preiacentibus canoniis aliud canonium breve continens et progressionis que secundum epiciclum numeros et pertinentia sexagesima cuique apparentium superhabundantiarum ex primis et secundis canoniis eclipsium. Composita vero nobis est istorum sexagesima quantitas in paralactico Lune canonie exposita secundum vii selidium, velut epiciclo secundum apoguiam excentrici propter coniunctiones subiacente. Quoniam vero plurimi observantium eclipticas significaciones nequaquam diametris circulorum dimetiuntur quantitates obscurationum, verum ut in universum totis ipsorum epipedis visu secundum simplex prosbolis apparens ipsum totum non apparenti comparante, apposuimus his et alium breve canonium in versus quidem xii, selidia vero iii^a. Istorum autem in primo quidem xii digitos ordinavimus, velut unoquoque digito continente, quemadmodum et in ipsis eclipticis canoniis, xii^a diametri cuiusque luminarium, in eis vero que deinceps pertinentes ipsis rursum duodecimas totarum immissionum, in secundo quidem eas que solaris, in tertio vero eas que lunaris. Investigavimus autem et huiusmodi additiones in solis factis quantitatibus, secundum medium apostima Luna existente. Eadem enim ad proximum proportio in tanta diametrorum auxomiosi constituta est, et velut proportione perimetrorum ad diametros existente, quam habent iii viii xxx ad unum. Ista enim proportio media est ad proximum et triplitium vii^a parte et triplitium x septuagessimis solis, quibus Archimenides secundum simplitius usus est.

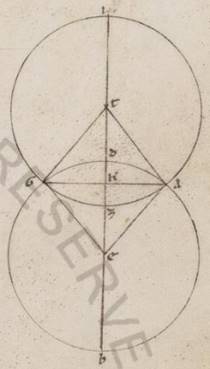Esto enim primum propter solares eclipses Solis circulus ABGD circa centrum E, qui vero secundum medium apostima Lune AZIG circa centrum T seccans Solis circulum secundum A et G puncta, et copulata BETI, subiaceat quartam deficere diametri solaris, quare ZD quidem talium esse iii, qualium est BD diametros xii, ZI vero Lune diametrum eorumdem xii xx ad proximum secundum eorum que sunt xv xl ad xvi xl proportionem, propter hoc autem et ET colligi eorumdem ix x, et perimetrorum ergo secundum i^us ad iii viii xxx proportionem que quidem solaris circuli fit portionum xxxvii xlii, que vero lunaris eorumdem xxxviii xlvi. Similiter autem et totarum immissionum, quoniam quidem que e centro in perimetrum multiplicata duo embada circuli facit quod quidem solaris circuli colligetur graduum cxiii vi, quod autem circuli Lune eorumdem cxix xxxii.

His ergo ita se habentibus, preiaceat invenire quantorum est contentum sub ADGZ embadum, qualium est totum solaris circuli embadum xii. Copulentur ergo AE et AT et GE et GT et adhuc AKG cathetus. Quoniam ergo qualium est ET recta ix x, talium utraque quidem rectarum AE et EG subiacet vi, utraque vero rectarum AT et TG eorumdem vi x, et rectus est qui ad K angulus, si superhabundatiam qua superhabundat quod ab TA ei quod ab AE, hoc est duo et sexagesima duo, comparabimus penes ET, habebimus EK et KT rectarum superhabundantiam eorumdem sexagesimorum xiii iii^a, quare et EK quidem colligi iiii xxviii, KT vero eorumdem iiii xlii, propter hoc autem et utraque earum que sunt AK et KG, quoniam equales sunt, eorumdem iiii ad proximum. His autem consequenter et quod quidem AEG trigoni embadum habebimus xvii lii, quod vero trigoni ATG eorumdem xviii xlviii.

Rursum quoniam qualium est BD quidem diametros xii, ZI vero similiter xii xx talium et AG colligitur viii, qualium quidem est BD diametros cxx, talium AG erit lxxx, qualium vero ZI diametros cxx, talium lxxvii l, et earum ergo que super ipsam periferiarum ADG quidem talium est lxxxiii xxxvii iiii, qualium ABGD circulus ccclx, AZG vero talium lxxx lii, qualium AZGI circulus ccclx. Quare quoniam eadem est proportio circulorum ad periferias et embadorum ipsorum ad ea que eorum que ipsis sectorum periferiis et quod quidem AEGD sectoris embadum habebimus talium xxvi xvi, qualium ostensum est quod ABGD circuli cxiii vi, quod autem ATGZ sectoris eorumdem xxvi li, quoniam et quod AZGI circuli eorumdem erat cxix xxxii. Demonstrabatur autem quod quidem AEG trigoni embadum eorumdem xvii lii, quod autem ATG similiter xviii xlviii, et reliquum erat ergo quod quidem ADGK portionis embadum habebimus viii xxiiii, quod autem AZGK eorumdem l iii, et totum ergo sub AZGD contentum embadum talium est xvi xxvii, qualium quod quod] quidem V₂ ABGD circuli subiacet cxiii vi. Quare et qualium est solaris circuli embadum xii, talium sub defitiente est unius et dimidii et iiii^a ad proximum, que et apposuimus in dicto canonio versui trium digitorum in secundo selidiorum.

Rursum subiaceat et lunarium eclipsium causa in eadem descriptione Lune quidem circulus ABGD, qui vero eius qui secundum medium apostima umbre AZGI, et defitiat similiter quarta lunaris diametri. Quare qualium est BD diametros xii, talium ZD quidem eclipseos unius unius] om. V₂ iii, ZI vero umbre diametrum secundum i^us ad ii xxxvi proportionem eorumdem xxxi xii, propter hoc et EKT colligi xviii xxxvi. Itaque perimetrorum quidem rursum que quidem lunaris circuli fit portionum xxxvii xlii, que vero eius qui umbre xcviii eorumdem i, embadorum autem quod quidem lunaris circuli cxiii vi, quod vero eius qui umbre eorumdem dcclxiiii xxxii. Quoniam ergo et hic, qualium est ET rectarum xviii xxxvi, talium utraque quidem rectarum AE et EG subiacet vi, utraque vero rectarum AT et EG eorumdem xv xxxvi, si similiter superhabundantiam qua superat quod ab TA illud quod ab AE comparabimus penes ET, habebimus rectarum EK et KT superhabundantiam eorumdem xi viii, quare et EK quidem colligi iii xliiii, KT vero eorumdem xiiii lii, propter hoc autem et utramque earum que sunt AK et KG eorumdem iiii xlii. Consequenter vero his et AEG quidem trigoni embadum, habebimus xvii xxxiii, quod autem trigoni ATG eorumdem lxix lii.

Rursum quoniam qualium est BD diametros xii ZI vero similiter xxxi xii, talium et AG colligitur ix xxxiiii et qualium quidem est BD diametros cxx, talium AG erit xciiii, qualium vero ZI diametros cxx, talium xxxvi ix xiii, et earum ergo que super ipsam periferiarum ADG quidem talium est ciii viii, qualium ABGD circulus ccclx, AZG vero talium xxxv iiii, qualium AZGI circulus ccclx. Quare propter predicta et AEGD quidem sectoris embadum talium habebimus xxxii xxiiii, qualium ostensum est ABGD circuli cxiii vi, quod autem AGEZ AGEZ] AGTZ V₂ sectoris eorumdem lxxiiii xxviii. Quoniam et quod AGZI circuli erat dcclxiiii xxxii. Demonstrabatur autem et AEG quidem trigoni embadum eorumdem xvii xxxiii, quod autem ATG similiter lxix lii, et reliquum ergo quod quidem ADGK portionis embadum habebimus xiiii li, quod autem AZGK eorumdem iiii xxxvi, et totum ergo sub AZ, GD contentum embadum talium est xviii xxvii, qualium quod ABGD circuli subiacet cxiii vi. Quare, et qualium est lunaris circuli embadum xii, talium contentum sub defitiente ipsius portionem erit ii et amplius xv^a partis ad proximum, que et apposuimus in eodem canonio versui trium digitorum in tertio lunari selidio. Et est canoniorum expositio talis.

⟨VI.8⟩

⟨VI.9⟩ Lunarium eclipsium discretio

His ergo preexpositis preexpositis] corr. al. man. ex expositis V₃, lunarium quidem eclipsium considerationem faciemus ad hunc modum. Exponentes enim inquisite panselinie collectum numerum secundum eam que in Alexandria medii temporis sinzugie horam et eum qui ab apoguio epicicli vocate anomalie graduum et eorum qui a boreali termino latitudinis post eam que ex prosthaferesi discretionem eum quidem qui latitudinis primum inferemus in lunarium eclipsium canonia, et si coincidet primorum duorum selidiorum numeris, adiacentia latitudinis numero secundum utrumque canoniorum et in eis que progressionum selidiis et in eis que digitorum scribemus seorsum singula. Deinde et anomalie numerum inferentes in directionis canonium, quantacumque fuerit adiacentia ipsi sexagesima, tanta sumentes superhabundantie secundum utrumque canoniorum descriptorum et digitorum et sexagesimorum apponemus ex primo canonio sumptis. Si tamen contingat latitudinis numerum in secundum solum canonium cadere, in ipso solo adiacentium digitorum et particularum reperta sexagesima exponemus, et quantos quidem reperiemus ex tali directione contingentes digitos, tot xii^a continere dicemus obscurationem lunaris diametri secundum medium tempus eclipsis. Sexagesimis autem factis secundum eamdem directionem apponentes semper xii^am ipsorum, pro quibus Sol supermovetur, et distribuentes in eum qui tunc Lune anomalum horarium motum, quotienscumque excidet distributio, tot equinoctiales horas habebimus cuiuscumque progressionariorum temporum eclipsis, ex quarto quidem selidio collectas seorsum et eius quod casus et eius quod completionis temporis, eas vero que ex quinto selidio eius quod medie more temporis, manifestis inde factis et eis que secundum principia et fines coituum et disscessionum horariis epochis ex ad medium more, hoc est examinate ad proximum panselinie tempus cuiusque secundum partem inventorum, prosthaferesi. Inde vero et diametri duodecimis illatis in omnino breve canonium, et xii^a totorum embadorum reperiemus ex adiacentibus in tertio selidio, similiter autem et ea que solarium ex in secundo selidio adiacentibus. Itaque ratio quidem habet non semper illud quod a principio eclipseos tempus usque medium equale fieri ei quod a medio usque in finem, propter ea que et circa Solem et circa Lunam anomaliam equalium progressionum propter huiusmodi in inequalibus temporibus complerum complerum] completarum V₂. At vero propter sensum nullam utique cura dignam operatur ad apparentia fallaciam non inequalia tempora hoc hoc] hec V₂F₁ supponi, eo quod, etsi circa medios cursus fuerint, ubi maiores sunt augmentorum superhabundantie, ea que usque tot horas progressio, quot est omne perfecte eclipseos tempus, nullam omnino sensibilem fatiat superhabundantie differentiam. Quoniam vero et competenter falsam reperimus ab Yparco demonstratam latitudinis Lune periodum secundum illam quidem ypothesim, minore apparente ea que inter expositas eclipses epoysia, maiore vero secundum nostras investigationes sumpta, ab eisdem utique rursum insistentes intelligemus. Sumens enim in huiusmodi demonstrationem eclipses duas lunares per menses viiclx factas, in quibus ambabus quarta lunaris diametri secundum eandem ab ascendente coniunctione progressionem defitiens contingebat, quarum primam quidem in secundo anno Mardokempadi observatam, secundam vero in xxxvii anno tertie secundum Callippon periodi, coutitur quidem eandem secundum latitudinem in utraque eclipsium progressionem ex omala contineri ad restitutionis demonstrationem ex priorem quidem eclipsim factam fuisse, secundum apoguiotaton epicicli Luna existente, secunda vero secundum periguiotaton; et propter hoc, sicut putabat, nullam sicut … nullam] nullam, sicut putabat V₂ contingere differentiam ex anomalia. Fallitur autem et secundum hoc ipsum, quoniam quidem et ex anomalia fiebat quedam cura digna differentia, penes non equali maiorem omalam progressionem inveniri quam examinatam, secundum ambas eclipses, sed in priore quidem uno gradu ad proximum, in secunda vero octava unius gradus, quare secundum hoc difficile latitudinis periodum in totas restitutiones dimidio et iiii^a et viii^a unius gradus, qualium est obliquus Lune circulus ccclx. Postea neque propter Lune apostima contingentem circa quantitates obscurationum differentiam coinvestigabat plurimam maxime factam in ipsis eclipsibus, propter priorem quidem secundum maximum apostima Lune existente fuisse factam, secundam vero secundum minimum. Neccesse est enim eiusdem quarte partis obscurationem consequi secundum priorem quidem eclipsim a minore distantia asscendentis coniunctionis, iuxta secundam vero a maiore. Quare differentiam demonstravimus unius gradus et pentimorii collectam, quare et hic tanto habundare latitudinis periodum post totas restitutiones. Itaque tantum quidem in ipso errore collectis ex ambabus fallatiis duobus ad proximum gradibus peccaret utique periodica latitudinis restitutio, si contigerent ambe ad minus vel ad maius ferentes differentiam. Quoniam vero hec quidem deficere faciebat restitutionem, vero illa vero illa] inv. V₂F₁ habundare secundum aliquem casum, quem forsitan et Iparcus completam quodam modo intellexit sola superhabundantie fallaciarum tertia parte unius gradus, apparebat maior existens comprehensio restitutionis.

⟨VI.10⟩ Solarium eclipsium discretio

Itaque lunarium quidem eclipsium consideratio solum utique propter hoc fiet sane, secundum quos exposuimus modos investigationum examinatarum. Deinde autem solarium eclipsium discretionem diffitilliorem existentem propter permutationes Lune faciemus ad hunc modum. Considerantes enim illud quod in Alexandria examinate sinodi tempus, ante quot vel post quot horas excidit equinoctiales a meridie, postea, si alterum fuerit subiacens clima inquisite habitationis, hoc est si non sub eodem fuerit meridiano ei qui per Alexandriam, apponentes vel aufferentes eam que secundum longitudinem differentiam in duobus meridianis ab equinoctialibus horis et scientes ante quot vel post quot equinoctiales horas et in illis excidit examinate sinodi tempus, in inquisito climate idem ad proximum futurum discernemus primum et apparentis sinodi tempus in inquisito climate idem ad proximum futurum medie eclipseos a circa permutationes exposita nobis in precedentibus ephodo. Sumentes enim et ex angulorum canone et eo qui permutationum proprie et climati et horarum distantie a meridiano et adhuc sinodice parti zodiaci et adhuc Lune apostimati factam primum ipsius permutationem, ut in maximo per punctum quod secundum verticem et centrum Lune scripto circulo, et ab ista auferentes semper secundum eundem versum adiacentem solarem permutationem, a reliqua discernemus, velut demonstratum est, per inventum circa sectionem zodiaci et maximi per punctum quod secundum verticem scripti circuli angulum collectam ad solem solem] solam V₂F₁ secundum longitudinem progressionem permutationem; et ipsi apponentes semper pertinentem contentis sub ispa temporibus equinoctialibus super transmutationis differentiam, hoc est in eodem canone deprehense superhabundantie adiacentium duarum permutationum et prime puncti quod secundum verticem distantie et ei que cum appositione equinoctialium temporum, ei que secundum longitudinem soli rursum contingentia permutationi cum tota parte ipsorum, si sensibilis fit, fit] sit V₂F₁ quota et ipsa pars sunt prime permutationis, et ita collectis eius totius que secundum longitudinem permutationis particulis apponemus rursum xii^am ipsorum, pro qua Sol supermovetur, et collecta resolvemus in horas equinoctiales ex distributione eorum circa sinodum Lune anomalorum horariorum cursuum, etsi quidem in consequentia animalium ea que secundum longitudinem permutatio fuerit facta, – demonstravimus enim in precedentibus qualiter huiusmodi nobis discretio sumatur –, in equinoctiales quidem horas resolutas particulas aufferentes a secundum examinatum sinodi tempus prediscretis Lune gradibus seorsum cuiusque et longitudinis et latitudinis et anomalie, habebimus in tempore apparentis sinodi examinatas progressionem Lune. Ipsas vero horas erimus invenientes, quantis prius apparens sinodos fiet quam examinata. Si vero in precendentia animalium ea que secundum longitudinem permutatio fuerit particulas quidem apponemus e contrario secundum examinate sinodi tempus prediscretis progressionibus cuiusque et longitudinis rursum et latitudinis et anomalie, horas vero habebimus, quantis posterius apparens sinodus erit quam examinata. Rursum secundum apparentis sinodi equinoctialium horarum a meridiano differentia considerantes per easdem ephodos, quantum primum Luna permutatur ad maximum per ipsam et punctum quod secundum verticem scriptum circulum, et auferentes ab inventis eidem numero adiacentem Solis permutationem a reliquis similiter ex eo qui tunc circa circulorum sectionem invenietur angulo, discernemus eam que secundum latitudinem, ut in eo qui ad rectos zodiaco circulo, factam permutationem et collectas particulas transmutantes in secundum obliquum circulum contingente portiones, hoc est duodecies ipsas facientes, factas gradus, si quidem eam que secundum latitudinem permutatio ut ad arctos fuerit ab eo qui per media completa, circa quidem asscendentem coniunctionem Luna existente, apponemus ei que secundum tempus apparentis sinodi predistincte latitudinarie progressioni, circa descendentem vero aufferemus similiter; si vero ea que secundum latitudinem permutatio ut ad meridiem completur a zodiaco secundum contrarium, circa ascendentem quidem coniunctionem existente Luna, aufferemus eos qui ex permutatione a a] om. V₂ gradus a predistinctis in tempore apparentis sinodi latitudinis graduum, circa descendentem vero apponemus similiter; et ita habebimus eum qui in tempore apparentis sinodi apparentis latitudinis numerum, quod inferentes in solarium eclipsium canonia, si coinciderit primorum duorum selidiorum numeris, eclipsim Solis fore dicemus, cuius medium ad proximum tempus quod apparentem sinodum continet. Exponentes ergo quantitatem adiacentium apparentis latitudinis numero et digitorum et particularum et earum que casus et earum que mundationis seorsum ex utroque canoniorum, inferemus et eum qui ab apoguio secundum apparentem sinodum anomalie numerum Lune in directionis canonium et adiacentia ipsi sexagesima, quotcumque fuerint, tanta sumentes superhabundantie cuiusque descriptorum, apponemus semper ex primo canonio sumptis et factos quidem ex huiusmodi directione digitos, habebimus in quot duodecimis rursum diametri solaris obscuratio erit secundum medium ad proximum tempus eclipseos. Utriusque vero progressionis particulis apponentes rursum xii^am ipsarum, pro quibus Sol supermovetur, et facta ad Lune anomalum motum facientes horas equinoctionales, tantum habebimus tempus utriusque et casus et mundationis, quasi nulla tamen circa tempora ista super contingente propter permutationes differentia. Quoniam vero fit quedam inequalitas sensibilis circa ipsa permutationum tantum tantum] tamen V₂F₁ Lune gratia et non anomalie luminarium, secundum quam et maiora complentur seorsum utraque preexpositorum semper et ut sepius inequalia invicem, neque istam indisscusam relinquimus, etsi brevis existens contingat. Consequitur hoc ergo simptoma, propter fieri quasdam in apparenti Lune progressione semper permutationum eum, eum] causa V₂ eam F₁ velut precessivas quasdam fantasias, si nichil proprie in consequentia percipiatur mota. Sive enim ante meridianum progrediens apparet, paulatim asscendens et minus semper preterito permutata ad orientes, tardius apparet in consequentia transitionem faciens, sive post meridianum progrediatur, descendens rursum paulatim et plus semper preterito permutata ad ocidentes, similiter tardiorem in consequentia transitionem apparebit faciens. Huius itaque rei causa predicta tempora semper maiora erunt simplititer ita sumptis. Maiore vero semper differentia in superhabundantiis permutationum facta in propinquioribus meridiani progressionibus, neccesse est et ea que ad meridianum eclipsium tempora tardius compleri; et propter istam causam, quando quidem in ipsam meridiem medium tempus eclipseos excidit, tunc tantum equale ad proximum fieri tempus casus ei quod completionis, equali in utraque contingente ad proximum tunc et ex permutationibus precessiva fantasia; quando vero ante meridiem, tunc illud quod completionis propinquius existens meridiano maius fieri; quando vero post meridiem, tunc illud quod casus propinquius existens meridiano maius fieri. Ut ergo et huiusmodi temporum directionem faciamus, considerabimus, secundum quem demonstavimus modum, et ante istam directionem collectum tempus utriusque expositarum progressionum et eam que secundum medium tempus eclipseos ab eo qui secundum verticem apostatim.

Ego Ego] Esto F₁ vero verbi gratia temporis quidem utrumque unius hore equinoctialis, eius vero qui secundum verticem distantia graduum lxxv. Considerabimus ergo in paralactico canonio adiacentia lxxv numero permutationis sexagesima, tamquam secundum maximum apostima verbi gratia existente Luna, ad quod apostima in tertio selidio adiacentia summuntur. Reperimus autem pertinentia lxxv gradibus sexagesima lii; et casus et quoniam utrumque tempus et completionis subiacet medie consideratum unius quidem hore equinoctialis, temporum vero xv, ista aufferentes quidem ab lxxv distantie gradibus, invenimus reliquis lx gradibus adiacentia permutationis sexagesima in eodem selidio xlvii, tamquam secundum medium ad meridianum progressionem ex permutatione precessionem sexagesimorum v colligi, apponentes autem ipsa eis que sunt lxxv et, collectis xc gradibus, invenimus in eodem selidio adiacentia totius permutationis sexagesima liii et dimidium, tamquam et hic precessionem eius que prope orizontem colligi progressionis eorumdem sexagesimorum i et dimidii. Inventarum ergo differentiarum longitudini pertinentia sumentes et utrumque rursum resolventes ex Lune anomalo motu in partem hore equinoctialis, sicut demonstratum est, collectum ab utroque apponemus proprie utrique medie et simpliciter sumptorum temporum et casus et completionis, maius quidem ei quod secundum propinquiorem meridiano progressionem, minus autem ei quod secundum propinquiorem orizonti. Manifestum autem quoniam et preiacentium temporum superhabundantiam particularum quidem facta est iii et dimidium et ix^a ad proximum unius hore equinoctialis, in quanto tanta sexagesima medie Lune movebitur. Relinquitur vero ex promptu et equinoctiales horas, si voluerimus, secundum unamquamque differentiam resolvere in eas que secundum partes temporales secundum demonstratum in preordinatis nobis modum.

⟨VI.11⟩ De eis que in eclipsibus prosneusis prosneusis] prosneusibus F₁

Deinceps autem existente et factas obscurationum prosneuses considerare, constat quidem huiusmodi conceptio et ex earumdem obscurationum ad eum qui per media animalia circulum prosneusi et ex ea que ipsius qui per media ad orizontem. Istorum autem utrumque in unoquocumque eclipticorum temporum plurimam et inconprehensibilem tribuet circa transmutationes variationem, si quis per totum tempus fiendas prosneuses inquirere voluerit, non multum quidem ea que in tantum prefatione neccessaria vel utili existente. Etenim zodiaci quidem ad orizonta habitudine considerata ex orientium vel occidentium ipsius punctorum secundum orizontem epochi, neccesse est secundum eclipseos tempus, differentibus continue factis orientibus et occidentibus partibus zodiaci, et sub ipsis completa orizontis sectiones continue differentes fieri. Similiter autem et ad ipsum qui per media obscurationum prosneusi considerata in maximo per ambo centra et eius qui Lune et eius qui umbre vel Solis scripto circulo, rursum neccesse est propter eam que in tempore eclipsis centri Lune progressionem et per ambo centra scriptum circulum portionem aliam semper ad zodiacum sumere et sub sectione ipsorum contentos angulos continue inequales facere. Suffitienti ergo futura huiusmodi consideratione, si in solis significatione aliquam habentibus obscurationibus sumetur, et secundum universalius ad orizonta consideratarum periferiarum possibile quidem erat et tamen factam passionem sub visum sumentibus conicere per eam que secundum ambas inclinationes considerationem eas que in tempora prosneusium, suffitienti in talibus existente et ea que secundum oloscheriam, ut diximus, perceptione. Verum tamen ut non transeamus locum, temptabimus et ad huiusmodi ephodum exponere quosdam modus ut est maxime promptos.

Obscurationum ergo cepimus et nos velut significationes dignas et eam que primi defitientis, que in principio totius temporis eclipseos fit, et eam que extremi defitientis, que in principio temporis more fit, et eam que plurimi defitientis, que in medio tempore eclipseos sine mora fit, et eam que primi completi, que in fine totius temporis more fit, et eam que extremi completi, que in fine totius eclipseos temporis fit. Sed et prosneusium rursum tamquam et rationabiliores et apparentiores cepimus determinatas sub meridiano et eius qui per media et orientibus et occidentibus et equinoctialibus et estivalibus et yemalibus, ventorum principio differenter quidem multis multotiens audiendo potente vero, si quis voluerit, ab expositis orizontis angulis declarari. Itaque factarum quidem sub meridiano sectionum orizontis borealem quidem audimus arctos, australem vero meridiem, orientalium autem et occidentalium sub principio quidem Arietis et Chelarum factas orizontis sectiones semper equale tetartimorium distans a sub meridiano factis equinoctialem orientem et occidentem, eas vero que sub principio Egoceri ybernum orientem et occidentem, eas vero que sub principio Cancri estivum orientem et estivum occidentem, eis quidem que secundum istas distantiis secundum clima differentibus factis, suffitienti vero prosneusium apostasi, quando vel secundum aliquem, vel inter aliquos preiacentium terminorum ostendetur. Itaque propter eam quidem que quaque vice zodiaci ad orizontem habitudinem investigavimus secundum in primis sintaxeos demonstratum modum factas sub orizonte orientibus sub principio cuiusque dodecatimoriorum distantias in utraque factarum ab equinoctiali sectionum secundum unumquodque eorum que a Meroe usque Boristhenem climati; in quibus et angulos exposuimus et perscripsimus secundum bene considerabile pro canonio circulos viii circa idem centrum in orizontis epipedo intellectos ei continentes vii climatum distantias et nominationes. Postea ascribentes rectas duas per omnes circulos ad rectos angulos invicem alteram quidem et obliquam, velut communem sectionem epipedorum et orizontis et equinoctialis, alteram vero et rectam, velut communem sectionem epipedorum et orizontis et meridiani, designavimus secundum eos qui ad interiorem circulum terminos, obliqua quidem linea et equinoctialem orientem et equinoctialem occidentem, recta vero et ad arctos et ad meridiem. Similiter ascribentes utrimque equinoctialis recte secundum ipsius equalem distantiam per omnes rursum circulos, apposuimus et secundum hec in mediis quidem septem distantiis inventas secundum unumquodque clima tropicorum punctorum ab equinoctiali distantias in orizonte, velut tetartimorio graduum existente xc. In eis autem qui ad interius circulorum terminis eis eis] add. quidem F₁ qui ad meridiem hyemalem orientem et hyemalem occidentem, eis autem qui ad arctos estivum orientem et estivum occidentem, causa vero eorum que inter dodecatimoriorum coordinantes inter unumquodque iiii^or diastimatum alias duas lineas, apposuimus et secundum ista propriorum dodecatimoriorum in orizonte distantias ab equinoctiali, nominatione cuiusque secundum exteriorem circulum superscripta. Designavimus autem et circa meridianam lineam et nominationes parallilorum et horarias magnitudines et polorum elevationes, et borealissimorum supersciptionem a maiore et continente circulo facientes. Qualiter autem et ipsarum obscurationum ad eum qui per media apparentes prosneuses expositas habeamus, hoc est factos angulos, in unaquaque factarum significationum sub sectione zodiaci et maximi per ambo demonstrata centra scripti circucli, et ipsas investigavimus secundum unamquamque uno digito obscurationis differentium progressionum Lune, in moris tamen, propter suffitiens secundum medium apostima factis, et velut parallilis ad sensum existentibus eis que in obscurationibus periferiis et eius qui per media animalia circuli et obliqui Lune.

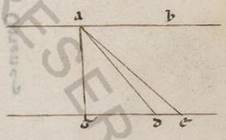Esto enim exempli causa que quidem pro periferia eius qui per media animalia recta AB, in qua Solis centrum vel umbre subiaceat A, que vero pro obliquo circulo Lune GDE, et punctus quidem G secundum quem centrum Lune secundum medium tempus fit eclipseos, D vero secundum quem rursum erit centrum ipsius, quando primum tota deficit vel primum incipit mundari, hoc est quando interius contingit umbre circulum, E autem, secundum quem fit centrum ipsius, quando primum incipit deficere vel extremum compleri Sol et Luna, hoc est quando exterius contingunt se invicem circuli, et copulentur AG et AD et AE. Quoniam ergo BAG quidem et AGE anguli medium tempus continentes eclipsium recti sunt ad sensum, angulus autem autem] add. BAE continet factam et in primo deficiente et in extremo completo. Angulus autem F₁ BAD eam que in extremo defitiente et primo completo, manifestum. Clarum autem inde, quoniam et AE quidem rursum eas que e centris amborum circulorum continet; AD vero superhabundantiam ipsarum. Subiaceat ergo exempli causa eclipsis, secundum quam in medio tempore medietas diametri Solis obscurabitur, et esto A centrum Solis, quare AE quidem semper, propter medium subiacere Lune apostima, colligi particularum xxxii xx, AG vero relictam ab illa dimidium solaris diametri eorumdem xvi xl. Quoniam ergo qualium est EA ypothenusa xxxii xx, talium colligitur et AG secundum expositam obscurationis quantitatem xvi xl, et qualium ergo est AE ypothenusa cxx, talium et AG quidem erit lxi li, que vero super ipsam periferiam talium lxii ii, qualium est qui circa AGE orthogonium circulus ccclx. Quare et angulus AEG, hoc est BAE, qualium quidem sunt duo recti ccclx, talium est lxii ii, qualium vero iiii recti ccclx, talium xxxi i.

Rursum et lunarium eclipsium causa esto A umbre centrum, quare, quoniam medium similiter subiacet Lune apostima, eorumdem semper colligi AE quidem rectam lx, AD vero similiter xxvi xl, et defitiat Luna secundum xviii digitorum progressionem, quare diametri dimidium rursus minorem esse AG quam AD, et reliqua eorumdem x o. Quoniam ergo, qualium est AE ypothenusa cxx, talium et AG quidem fit xx o, que vero super ipsam periferia talium erit xix xii, qualium est qui circa trigonum orthogonium circulus ccclx, erit utique et AEG angulus, hoc est BAE, qualium sunt ii recti ccclx, talium xix xii, qualium vero iiii recti ccclx, talium ix xxxvi. Similiter autem quoniam, et qualium est AD ypothenusa cxx, talium et AG quidem fit, fit] add. xlv F₁ que vero super ipsam periferiam talium xliiii ii, qualium est qui circa AGD orthogonium circulus ccclx, erit utique et ADG, hoc est BAD, qualium sunt ii recti ccclx, talium xliiii ii, qualium vero iiii recti ccclx, talium xxii i. Eodem ergo modo et in aliis digitis sumentes quantitates minorum recto angulo, ut in uno portionum existente xc, quot et orizontis tetartimorion subiacet, ordinavimus canonium in versus quidem xxii, selidia vero iiii, quorum primum quidem continebit inventos ipsius qui secundum diametrum obscurationis digitos in medio tempore eclipseos, secundum vero in solaribus eclipsibus factos angulos et in primi defitientis tempore et in extremi completi, tertium vero in lunaribus factos angulos et secundum primi defitientis tempus et extremi completi, quartum autem factos angulos in lunaribus rursum eclipsibus et secundum extremi defitientis temporis et primi completi.

⟨VI.12⟩

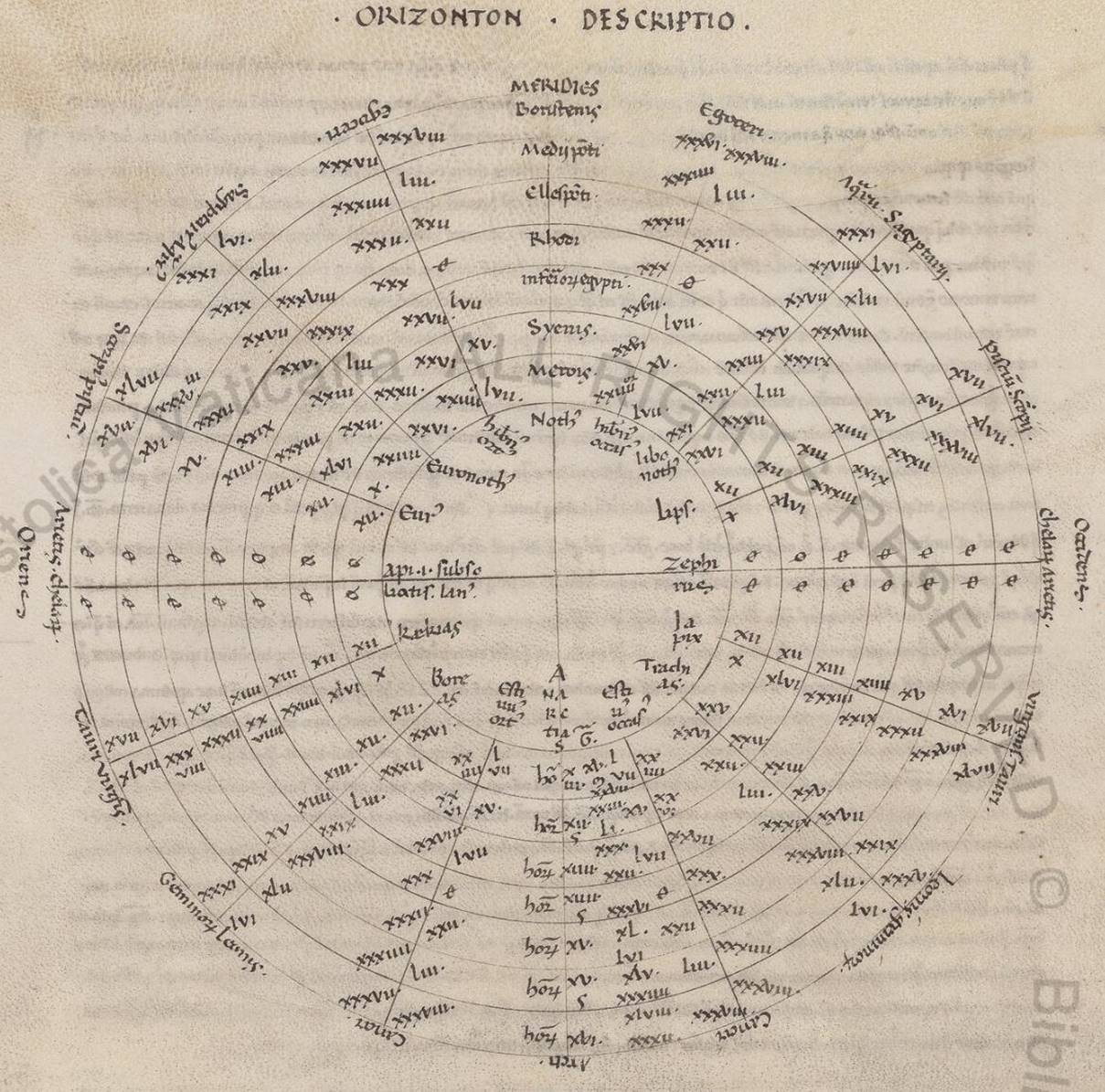
⟨VI.13⟩ Discretio prosneusium

Habentes ergo predescreta, predescreta] prediscreta F₁ quo demonstravimus modo, tempora cuiusque expositarum significationum et a temporibus manifestum quoniam secundum ipsa orientes et occidentes partes eius qui per media et a descriptione eas que secunudm orizontem portione ipsorum, quoniam quidem secundum ipsum qui per media centrum Lune vel apparens ut in solaribus eclipsibus vel examinatum ut in lunaribus, eam quidem que secundum primum defitiens Solis prosneusim et adhuc eam que secundum extremum et defitiens et completum Lune habebimus ab ipsius quod tunc occidentis secundum orizonta portione, eam vero que secundum extremum completum Solis et amplius eam que secundum primum et defitiens et completum Lune ab ipso oriente; quando vero non secundum eum qui per media fuerit centrum Lune, sumentes ex canonio proprios quantitati digitorum adiacentes angulorum numeros, eitiemus et ipsos a communibus sectionibus et orizontis et eius qui per media, si quidem borealius fuerit ipso centrum Lune, in primo quidem defitiente Solis, et extremo defitiente Lune, ut ad arctos ab occidentali sectione, in extremo autem completo Solis et primo completo Lune, ut ad arctos ab orientali, et rursum in primo quidem defitiente Lune, ut ad meridiem ab orientali sectione, in extremo autem completo Lune, ut ad meridiem ab occidentali, sed sed] si F₁ autem australius fiunt fiunt] fuerit F₁ eo qui per media centrum Lune, in primo quidem defitiente Solis et extremo defitiente Lune, ut ad meridiem ab occidentali sectione, in ex postremo autem completo Solis et primo completo, completo] add. Lune F₁ ut ad meridiem ab orientali, et rursum in primo quidem defitiente Lune, ut ad arctos ab orientali sectione, in extremo autem completo Lune, ut ad arctos ab occidentali; et constitutam ex huiusmodi directione partem orizontis habebimus, quo facient prosneusim, sicut diximus, universalius recipientes lunarium partes primas et extremas eclipsium et completionum significationes.