Ptolemaeus Arabus et Latinus

⟨XI⟩

Demonstratio excentroticis Iovis

Demonstratio magnitudinis epicicli Iovis

De directione periodicorum Iovis motuum

De epochi periodicorum Iovis motuum

Demonstratio excentroticos et apoguii Saturni

Demonstratio magnitudinis epicicli Saturni

De directione periodicorum stelle Saturni motuum

De epochi periodicorum Saturni motuum

Quomodo a periodicis motibus examinata progressus lineariter sumantur

Negotium anomaliarum canonopiie

De eo quod secundum longitudinem quinque erraticorum compoto

Incipit undecimus

⟨XI.1⟩ Demonstratio excentroticis Iovis

Demonstratis circa Martis stellam periodicis motibus et anomaliis et epochis, deinceps et eas que circa Iovis stellam negotiabimus secundum eundem modum, sumentes rursum primum in demonstratione et apoguii et excentroticis tres acronictoys diametros ad mediam Solis progressionem, quarum primam quidem observavimus per astrolabicum organum xvii^o anno Adriani secundum Egiptios Epiphi i^a in ii^a unam horam autem mesonictium circiter Scorpii gradus xxii iii xi, secundam vero xxi anno Phaophi xiii^a in xiiii^a duas horas autem autem] ante F₁ mesonictium circa Piscium gradus vii liiii, tertiam autem primo anno Antonini mensis Athir xx^a in xxi^a post horas quinque a mesonictio circa Arietis gradus xiiii xxiii. Duarum ergo distantiarum ea quidem que a prima acronicto in secundam annos quidem egiptiacos continet iii et dies cvi et horas xxiii, gradus autem apparentis stelle progressionis ciii xliii, que vero a secunda in tertiam annum quidem egiptiacum unum et dies xxxvii et horas vii, gradus autem similiter xxxvi xxix. Colligiturque et media secundum longitudinem progressio eius quidem quod prime distantie temporis graduum xcix lv, eius vero quod secunde graduum xxiii xxiii] xxxiii F₁ xxvi. Ab his autem distantiis consequenter consequenter] add. eis que F₁ in Marte nobis exposite sunt ephodis faciemus primum demonstrationem propositarum nobis inveniri, velut uno rursum existente excentrico circulo, ad hunc modum.

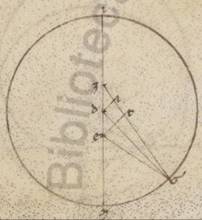
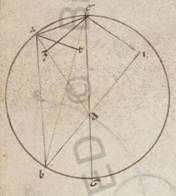Esto enim excentricus circulus ABG et subiaceat A quidem punctus in quo erat centrum epicicli secundum primam acronicton, B vero quod secunde acronicti, G vero quod tertie; sumptoque intra ABG excentricum D centro zodiaci, copulentur recte AD et BD et GD et educta recta GD, copulentur AE et EB et AB. Trahantur autem ab E quidem in AD et BD catheti OZ OZ] EZ F₁ et EI ab A vero in EB AT. Quoniam ergo BG excentrici periferia subiacet subtendens zodiaci gradus xxxvi et xxix, erit utique et BDG angulus, hoc est EDI ad centrum existens zodiaci, qualium quidem sunt iiii recti ccclx, talium xxxvi xxix, qualium autem ii recti ccclx, talium lxxii lviii. Quare et que quidem super EI periferia talium est lxxii lviii, qualium qui circa EDI orthogonium circulus ccclx, recta vero EI talium lxxi xxi, qualium est DE ypothenusa cxx. Similiter quoniam BG periferia graduum est xxxiii xxvi, erit utique et BEG quidem angulus ad periferia existens talium xxxiii xxvi, qualium sunt ii recti ccclx, reliquus autem EBI eorumdem xxxix xxxii. Quare et que quidem sunt DI EI periferia talium est xxxix xxxii, qualium qui circa BEI orthogonium circulus ccclx, EI vero recta talium xl xxxv, qualium est BE ypothenusa cxx, et qualium ergo EI quidem ostensa est lxxi xxi, ED vero recta cxx, talium et BE erit ccx lviii. Rursum quoniam ABG tota periferia excentrici subtendens subiacet zodiaci collectos ambarum distantiarum gradus cxli xii, erit utique et ADG angulus ad centrum existens zodiaci, qualium quidem sunt iiii recti ccclx, talium cxli xii, qualium vero ii recti ccclx, talium cclxxxii xxiiii, qui vero deinceps ipsi ADE angulus eorumdem lxxvii xxxvi. Quare et que quidem super EZ periferia talium est lxxvii xxxvi, Quare … xxxvi] iter. V₃ qualium est qui circa DEZ orthogonium circulus ccclx, EZ vero recta talium lxxv xii, qualium est DE ypothenusa cxx. Similiter quoniam ABG excentrici periferia collecta est graduum cxxxiii xxi, erit utique et AEG angulus ad periferiam existens cxxxiii xxi, qualium sunt ii recti ccclx. Eorum vero erat et ADE angulus lxxvii xxxvi, et reliqua ergo EAZ eorumdem erit cxlix iii. Quare et que quidem super EZ periferia talium est cxlix iii, qualium qui circa AEZ orthogonium circulus ccclx, EZ vero recta talium est cxv xxxix, qualium est EA ypothenusa cxx, et qualium ergo EZ quidem ostensa est lxxv xii, ED vero subiacet cxx, talium et EA erit lxxviii ii. Rursum quoniam AB excentrici periferia graduum est xcix lv, erit utique et AEB angulus ad circumferentiam existens talium xcix lv, qualium sunt ii recti ccclx. Quare et que quidem super AT periferia talium xcix lv, qualium qui circa AET orthogonium circulus ccclx, que vero super ET reliquorum in semicirculum lxx v. lxx] lxxx F₁ Et earum ergo que sub ipsis rectarum AT quidem erit talium xci lii, qualium est EA ypothenusa cxx, ET vero eorumdem lxxvii xii. Quare et qualium AE quidem ostensa est lxxviii ii, DE vero recta cxx talium et EIT quidem erit lix xliiii, ET non non] vero F₁ similiter l xii. Eorumdem vero ostendebatur et EB tota ccx lviii, et reliqua ergo TB talium erit clx xlvi, qualium est et AT recta lix xliiii, et est quidem quod a recta TB tetragonum xxvdcccxlv lv, quod autem a recta TA similiter iiidlxviii iiii, que composita faciunt quod ab AB tetragonum xxixccccxiii lix. Longitudine ergo erit AB talium clxxi xxx, qualium ED quidem erat cxx, EA vero similiter lxxviii ii. Est autem et qualium excentrici diametros cxx, talium AB recta xci lii. Subtendit enim periferiam graduum xcix lv, et qualium ergo est AB quidem recta xci lii, excentrici vero diametros cxx, talium et ED quidem erit lxiiii xvii, EA EA] add. vero F₁ recta xli xlvii. Quare et que quidem super EA periferia excentrici graduum est xl xlv, tota vero EABG graduum clxxiiii vi. Propter hoc autem et EDG recta talium cxix l ad proximum, qualium est excentrici diametros cxx.

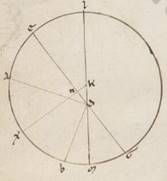Quoniam ergo minor est EABG portio semicirculo et propter hoc extra ipsam cadit centrum excentrici, subiaceat K, et protrahatur per ipsum et D que per utraque centra diametros LKDM, et a puncto K in GE tracta educatur cathetos KNX. Quoniam ergo, qualium est LM diametros cxx, talium EG quidem tota ostensa est cxix l, ED vero recta lxiiii xvii, et reliquam habebimus GD eorumdem lv xxxiii. Quare quoniam sub rectis ED DG contentum orthogonium equale est sub rectis LD DM contento orthogonio, habebimus et quod sub rectis LD DM talium iiidlxx lvi, qualium est LM diametros cxx. Verum quod sub rectis LD, MD cum eo quod a recta DK tetragono facit illud quod a medietate diametri, hoc est recta LK tetragonum. Si ergo ab medietatis diametri tetragono, hoc est factis iiidc, dempserimus quod sub LD DM, hoc est iiidlxx lvi, relinquetur nobis quod a recta DK tetragonum eorumdem xxix iiii. Et longitudine ergo habebimus DK mediam centrorum talium v xxiii ad proximum, qualium est KL que ex centro excentrici lx. Rursum quoniam medietas quidem eius que est GE, hoc est GN, talium est lix lv, qualium LM diametros cxx, eorumdem vero ostensa est et GD recta lv xxxiii, et reliqua ergo DN talium est iiii cxxii, cxxii] xxii F₁ qualium DK erat v xxiii. Quare et qualium est DK ypothenusa cxx talium et DN quidem erit xcvii xxviii, que vero super ipsam periferia talium cviii xxiiii, qualium est qui circa DKN orthogonium circulus ccclx, et DKN ergo angulus, qualium quidem sunt ii recti ccclx, talium est cviii xxiiii, qualium vero iiii recti ccclx, talium liiii xii, et quoniam ad centrum est excentrici, habebimus et MX periferiam liiii xii. Est autem et GMX tota medietas existens eius que est GXE graduum lxxxvii iii. Et reliqua ergo MG que a periguio in iii acronicton graduum erunt erunt] erit F₁ xxxii li. Manifestum vero quoniam, et BG quidem distantia subiacente graduum xxxiii xxvi, et reliquam habebimus BM periferiam que ab iia acronicto in periguion sexagesimorum xxxv, AB vero distantia subiacente graduum xcix lv, et reliquam LA habebimus que ab apoguio in primam acronicton graduum lxxix xxx. Itaque si quidem in hoc excentrico centrum ferebatur epicicli, istis utique suffecisse quantitatibus permutabilibus couti. Quoniam autem secundum consequens ypotheseos in altero circulo movetur, hoc est eo qui scribitur duo centro equalia duo … equalia] centro in duo equalia F₁ dividenti recta DK spatioque KL, oportebit rursum, quemadmodum et in Marte, supputare primum factas differentias apparentium distantiarum et demonstrare quante quedam utique erant, ut his ad proximum existentibus proportionibus, si non in altero excentrico, sed in primo et zodiacam anomaliam continente ferebatur centrum epicicli, hoc est circa K centrum scripti.

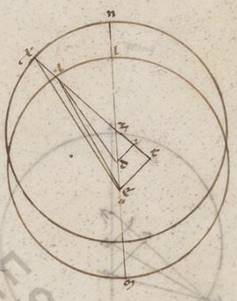Esto ergo centrum quidem epicicli ferens excentricus LM circa centrum D, qui vero plani eius motus circulus NX circa centrum Z equalis ei que est LM, et copulata ea que per centra diametro NLM, sumatur in ipsa et zodiaci centrum E, et subiaceat primum in prima acronicto centrum epicicli secundum A punctum, et copulentur quidem recte DA et EA et ZAX et EX. Protrahatur vero a punctis D et E in AZ ductam catheti DI et ET. Quoniam ergo NZX angulus plane secundum longitudinem progressionis talium est lxxix xxx ostensus, qualium sunt iiii recti ccclx, erit utique et que secundum verticem ipsius DZI angulus, qualium quidem sunt iiii recti ccclx, talium lxxix xxx, qualium vero ii recti ccclx, talium clix. Quare et que quidem super rectam DI periferia talium est clix, qualium qui circa DZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum xxi. Et earum ergo que sub ipsis rectarum DI quidem talium erit cxvii lix, qualium est DZ ypothenusa cxx, at vero ZI eorumdem xxi lii. Quare et qualium est DZ quidem dimidia existens EZ recte ii xlii ad proximum, DA vero que ex centro excentrici lx, talium et DI quidem erit ii xxxix, ZI vero similiter o xxx, et quoniam quod a recta DI sumptum sub eo quod a recta DA facit quod a recta AI, et rectam AI habebimus eorumdem lix lvi. Similiter autem quoniam ZI quidem ei que est IT est equalis, dupla vero ET eius que est DI, et AT tota erit talium lx xxvi, qualium est ET recta v xviii. Propter hoc autem et AE ypothenusa eorumdem lx xl, et qualium est ergo AE recta cxx, talium et ET quidem erit x xxix, que vero super ipsam periferia talium x et sexagesimi unius ad proximum, qualium qui circa AET orthogonium circulus ccclx. Quare et EAT angulus talium est x et sexagesimi unius, qualium sunt ii recti ccclx. Rursum quoniam qualium est ET recta v xviii, talium est et ZX quidem que ex centro excentrici lx, at vero ZT recta unius, tota autem XT clarum quoniam lxi, habebimus et EX ypothenusa eorumdem lxi xiiii. Quare et qualium est EX recta cxx, talium et ET quidem erit x xxiii, que vero super ipsam periferiam talium ix lv, qualium est qui circa TEX orthogonium circulus ccclx, et EXT ergo angulus talium est est ix lv. Qualium ii recti ccclx. Eorumdem vero ostensus est et EAT angulus x et sexagesimi unius. Et reliquus ergo AEX angulus inquisite differentie, qualium quidem sunt ii^o recti ccclx, talium erit o vi, qualium vero iiii recti ccclx, talium o iii. Verum apparebat secundum i acronicton stella in EA recta considerata optinens Scorpii gradus xxiii xi. Manifestum ergo quoniam, si non in LM excentrico centrum ferebatur epicicli, sed in NX, erat quidem secundum X ipsius punctum, apparebat autem stella in EX recta differens tribus sexagesimis et optinens Scorpii gradus xxiii et sexagesima xiiii.

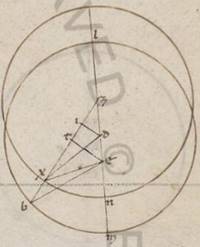Rursum in simili scemate adiaceat et secunde acronicti descriptio parum in precedentia periguii figurata. Quoniam NX periferia excentrici ostensa est sexagesimorum xxxv, erit utique et XZN angulus, qualium quidem sunt iiii recti ccclx, talium o xxxv, qualium vero iio recti ccclx, talium i x. Quare et que quidem super rectam D D] DI F₁ periferia talium est i x, qualium est qui circa DZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum clxxviii l. Et earum ergo que sub ipsis rectarum DI quidem talium erit v xiii, qualium est DZ ypothenusa cxx, ZI vero eorumdem ad proximum cxx. Quare et qualium est DZ quidem recta ii xlii, DB vero que ex centro excentrici lx, talium et DI quidem erit o ii, ZI vero similiter ii xlii. Similiter autem et IB, quoniam quidem indifferens est ab BD ypothenusa eorumdem lx et quoniam rursum TI ei que est IZ equalis est, at vero ET eius que est DI dupla, et reliquam TB habebimus talium lvii xviii, qualium est ET recta o iiii propter hoc autem et EB ypothenusa eorumdem lvii xviii. Quare et qualium est EB recta cxx, talium et ET quidem erit o viii ad proximum, que vero super ipsam periferia talium o viii rursum, qualium est qui circa BET orthogonium circulus ccclx, et EBT ergo angulus talium est o viii, qualium ii recti ccclx. Similiter quoniam qualium est ZX que ex centro excentrici lx, talium et ZT tota ostensa est v xxiiii, habebimus et reliquam TX talium liiii xxxvi, qualium et ET erat o iiii. Propter hoc autem et EX ypotenusa eorumdem liiii xxxvi, et qualium est ergo EX recta cxx, talium et ET erit o x ad proximum, que vero super ipsam periferia talium o x, qualium qui circa EIX orthogonium circulus ccclx. Quare et EXT quidem angulus talium o x, qualium sunt ii recti ccclx, reliquus vero BEX eorumdem quidem o ii, qualium autem iiii recti ccclx, talium o i. Manifestum ergo et hic quoniam quidem secundum secundam acronicton stella in EB apparens optinebat Piscium gradus vii liiii, si in EX rursum apparebat optinebat utique solos Piscium gradus lx liii.

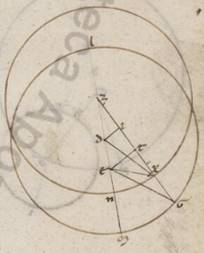Adiaceat ergo et tertie acronciti descriptio in consequentia periguii figurata. Quoniam ergo NX periferia excentrici subiacet gradus xxxii li, erit utique et NZX angulus, qualium quidem sunt iiii recti ccclx, talium xxxii li, qualium vero ii recti ccclx, talium lxv xlii. Quare et que quidem super DI periferia talium est lxv xlii, Quare … xlii] iter. V₃ qualium qui circa DZI orthogonium circulus ccclx, Que vero super ZN reliquorum in semicirculum cxiiii, et earum que sub ipsis rectarum DI quidem erit talium lxv vi, qualium est DZ ypothenusa cxx, ZI vero eorumdem c quidem et sexagesimorum xlix. Quare et qualium quidem est DZ recta ii xlii, DG vero que ex centro excentrici lx, talium et DI quidem erit i xxviii, ZI vero similiter ii xvi. Et quoniam quod ab recta DI sumptum sub eo quod a recta GD facit illud quod ab recta GI, habebimus et ipsam eorumdem lix ad proximum. Similiter autem quoniam TI quidem ei que est IZ est equalis, ET vero eius que est DI dupla, et reliquam GT habebimus talium lvii xliii, qualium est ET recta ii lvi. Propter hoc autem et EG ypothenusa eorumdem lvii xlvii, et qualium est ergo EG recta cxx, talium et ET quidem erit vi v, que vero super ipsam periferia talium v xlviii ad proximum, qualium est qui circa GET orthogonium circulus ccclx. Quare et EGT angulus talium v xlviii, qualium sunt ii recti ccclx. Similiter quoniam, qualium est ZX que ex centro excentrici lx, talium et ZT tota collecta est iiii xxxii, et reliquam XT habebimus talium lv xxviii, qualium et ET erat ii lvi. Propter hoc autem et EX ypothenusa eorumdem lv xxxiii. Quare et qualium est EX recta cxx, talium et ET quidem erit vi xx, que vero super ispam periferia talium vi ii, qualium est qui circa ETX orthogonium circulus ccclx. Itaque et EXT quidem angulus talium est vi ii, qualium sunt ii recti ccclx, reliquus vero GEX eorumdem o xiiii, qualium vero ii recti ccclx, talium o vii. Quare quoniam secundum tertiam acronicton stella in EG considerata optinebat Arietis gradus xiiii xxiii, manifestum rursus quoniam, si in EX recta contingebat, optinebat utique Arietis gradus xiiii xxx. Ostensum vero est quoniam et secundum primam quidem acronicton optinebat Scorpii gradus xxiii xiiii, iuxta secundam vero 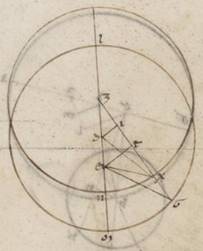Piscium gradus vii liii. Colliguntur ergo apparentes stelle distantie, si non ad ferentem centrum epicicli excentricum considerentur, sed ad equalem ipsius continentem motum, a prima quidem acronicto in iiam gradus ciiii xxxix, a secunda vero in tertiam gradus xxxvi xxxvii. Quibus assequentes in predemonstrato thehoremate reperimus quidem mediam centrorum zodiaci et equalem motum epicicli continentis excentrici talium v xxx ad proximum, qualium est excentrici diametros cxx, excentrici vero periferarum eam quidem que ab apoguio in primam acroniction graduum lxxvii xv, eam que vero a secunda acronicto in periguium graduum ii l, eam autem que a periguio in tertiam acronicton graduum xxx xxxvi. Quoniam vero et hinc diligenter sumpte contingunt exposite quantitates, propter differentias distantiarum easdem ad proximum eis que prius et per hec colligi, manifestum ex eo quod et apparentes stelle distantie per inventas rationes heedem inveniantur observatis, ut ex hix nobis erit manifestum.

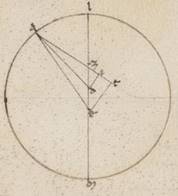Adiaceat enim prime rursum acronicti descriptio solum habens excentricum ferentem centrum epicicli. Quoniam LZA angulus, qualium quidem sunt iiii recti ccclx, talium ostensus est lxxvii xv, qualium vero ii recti ccclx, talium et ipse et qui secundum verticem ipsius DZI angulus cliiii xxx, erit utique et que quidem super DI periferia talium cliiii xxx, qualium qui circa DZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum xxv xxx. Et earum ergo que sub ipsis rectarum DI quidem talium est cxvii ii, qualium est DZ ypothenusa cxx, ZI vero eorumdem xxvi ix. Quare et qualium est ZD quidem recta ii xlv, DA vero que ex centro excentrici lx, talium et DI quidem erit ii xli, ZI vero similiter o xxxvi. Propter eadem vero predemonstratis et AI quidem erit eorumdem lix lvi, tota vero AT talium lx xxxii, qualium est ET dupla existens DI recte v xxii, quare et AE ypothenusa eorumdem colligi lx xlvi. Et qualium est ergo AE recta cxx, talium et ET quidem erit x xxxvi, que vero super ipsam periferia talium x et sexagesimorum viii, qualium qui circa AET orthogonium circulus ccclx, et EAT ergo angulus talium est x viii, qualium sunt ii recti ccclx, reliquus que LEA eorumdem quidem cxliiii xxii, qualium vero iiii recti ccclx, talium lxxii xi. Tot ergo gradibus distabat stella secundum primam acronicton ab apoguio zodiaci.

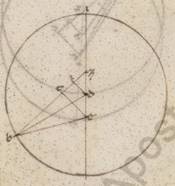Rursum adiaceat secunde acronicti descriptio. Quoniam BZM angulus, qualium quidem sunt iiii recti ccclx, talium ii l, qualium vero ii recti ccclx, talium v xl, erit utique et que quidem super DI periferia talium v xl, qualium qui circa DZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum clxxiiii xx. Et earum ergo que sub ipsis rectarum DI quidem erit talium v lv, qualium est DZ ypothenusa cxx, ZI vero eorumdem cxix li. Quare et qualium est DZ recta ii xlv atque DB que ex centro excentrici lx, talium et DI erit o viii, at vero ZI similiter ii xlv ad proximum. Propter eadem vero et BI eorumdem est lx ad proximum, reliquaque BT talium lvii xv, qualium est ET recta o vi, quare et EB ypothenusa eorumdem colligi lvii xv. Et qualium est ergo EB recta cxx, talium et ET erunt o xxxiii, et que super ipsam periferiam talium o xxxii, qualium est qui circa BET orthogonium circulus ccclx. Quare et EBT angulus talium est o xxxii, qualium ii recti ccclx, totusque BEM eorumdem quidem vi xii, qualium vero iiii recti ccclx, talium iii vi. Distabat ergo et secundum secundam acronicton stella in precedentia periguii gradibus iii vi. Ostensa est autem et secundum primam distans in consequentia gradibus lxxii xi. Colligitur ergo et a prima acronicto in secundam apparens distantia reliquorum in semicirculum graduum ciiii xliii con con] consone F₁ ex observationibus deprehense distantie.

Adiaceat ergo et tertie acronicti descriptio. Quoniam MZG angulus, qualium quidem sunt iiii recti ccclx, talium ostensus est xxx xxxvi, qualium vero ii recti ccclx, talium lxi xii, erit utique et que super DI periferia talium lxi xii, qualium est qui circa DZI orthogonium circulus ccclx, que vero super ZI reliquorum in semicirculum cxviii xlviii. Et earum ergo que sub ipsis rectarum DI quidem talium erit lxi vi, qualium est DZ ypothenusa cxx, ZI vero eorumdem ciii xvii. Quare et qualium est DZ recta ii xlv, GD vero que ex centro excentrici lx, talium et DI erit i xxiiii, atque ZI similiter ii xxii. Propter eadem vero et GI erit eorumdem lix lix, reliquaque GT talium lvii xxxvii, qualium et ET colligitur ii xlviii, quare et EG simul ypothenusa eorumdem lvii xli. Et qualium est ergo recta cxx, talium et ET erit v lviii et que super ipsam periferia talium v xxxiiii, qualium est qui circa GET orthogonium circulus ccclx. Quare et EGT angulus talium est v xxxiiii, qualium ii recti ccclx, totusque MEG eorumdem lxvi xlvi, qualium vero iiii recti ccclx, talium xxxiii xxiii. Tot ergo gradibus et secundam tertiam acronicton distabat stella in consequentia periguii. Ostensa est autem distans et secundum iiam in precedentia eiusdem periguii gradibus iii vi. Colligitur ergo et que a secunda acronicto in tertiam apparens distantia eorum que in idem graduum xxxvi xxix consone rursum observatis.

Manifestum vero hinc quod, et quoniam quidem secundum tertiam acroniton optinebat stella observatos Arietis gradus xiiii xxiii distans, velut ostensa est, in consequentia periguii gradus xxxiii xxiii, periguium quidem eius tunc optinebat excentroticis Piscium gradus xi, apoguion vero secundum diametrum Virginis gradus xi. Et si scripserimus circa G centrum ITK epiciclum, eum quidem qui ab eo quod secundum L apoguio excentrici medium secundum longitudinem motum habebimus inde graduum ccx xxxvi, propter MZG angulum demonstrari talium xxx xxxvi, qualium sunt iiii recti ccclx, TK vero epicicli periferiam que a periguio T in eam que secundum K stellam graduum ii xlvii, propter et EGZ angulum talium ostendi v xxxiiii, qualium sunt ii recti ccclx, qualium vero iiii recti ccclx, talium ii xlvii. Si ergo tempore iiie acronicti, hoc est primo anno Antonini secundum Egiptios mensis Athir xx in xxi post v horas a mesonictio Iovis stella ad progressiones medias considerata secundum longitudinem quidem distabat ab apoguio excentrici gradibus ccx xxxvi, hoc est optinebat Arietis gradus xi xxxvi, anomalie vero ab I apoguio epicicli gradibus clxxxii xlvii.

⟨XI.2⟩ Demonstratio magnitudinis epicicli Iovis

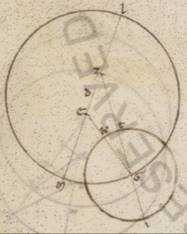Rursum deinceps in demonstrationem quantitatis epicicli sumemus observationem quam perspeximus secundo anno Antonini secundum Egiptios Mesori xxvia in xxviia primo Solis ortu, hoc est post v horas ad proximum equinoctiales a mesonictio. Quoniam quidem media Solis progressio optinebat Carcini gradus xvi xi, medium vero celum tenebat in astrolabio ii gradus Arietis, tunc autem ad lucentem quidem Yada considerata stella Iovis, optinens apparebat Geminorum gradus xv et dimidii iiii^a, centro vero Lune australioris existentis exequali apparebat. Verum in illam horam per preexpositas supputationes reperimus Lunam medie quidem optinente optinente] optinentem F₁ Geminorum gradus ix o, anomalie vero ab apoguio epicicli gradus cclxxii v, propter hoc autem et examinatum quidem progressum eius circa xiiii l gradus Geminorum. In Alexandria vero apparentem circa xv xlv. Itaque Iovis stella et ita optinebat xv et dimidium iiii^a gradus Geminorum. Rursum quoniam quod a tertia acronicto usque preiacentem observationem tempus anni est Egiptiaci unius et dierum cclxxvi, continet autem tempus istud, – nullo enim sensibili distat, etsi integrius quidem huiusmodi sumatur –, longitudinis quidem gradus liii xvii, anomalie vero gradus ccxviii xxxi, si apposuerimus istos secundum tertiam acronicton demonstratis epochis, habebimus et in huius observationis tempus longitudinis quidem ab eodem ad proximum apoguio gradus cclxiii liii, anomalie vero ab apoguio epicicli gradus xli xviii.

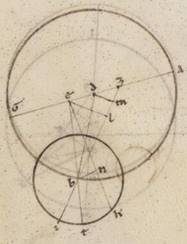His ergo subiacentibus, adiaceat rursum similis demonstrationis in Marte descriptio Iovis epicicli quidem portionem portionem] positionem F₁ habens ad consequentes partes periguii excentrici, eam vero que stelle ad eas que post apoguion epicicli consequenter expositis hic mediis progressionibus et longitudinis et anomalie. Quoniam ergo ab apoguio excentrici secundum longitudinem media progressio graduum est cclxiii liii, erit utique et BZG angulus, qualium quidem sunt iiii recti ccclx, talium lxxxiii liii, qualium vero duo recti ccclx, talium clxvii xlvi. Quare et que quidem super DM periferia talium est clxvii xlvi, qualium qui circa DZM orthogonium circulus ccclx, que vero super ZM reliquorum in semicirculum xii xiiii. Et earum ergo que sub ipsis rectarum DM quidem talium est cxix xix, qualium est DZ ypothenusa cxx, ZM vero eorumdem xii xlvii. Quare et qualium est DZ recta ii xlv, atque DB que ex centro excentrici lx, talium et DM erit ii xliiii ad proximum, atque ZM similiter o xviii, et quoniam quod ab DM sumptum sub eo quod ab DB facit quod ab MB, erit et MB eorumdem lix lvi. Similiter autem quoniam ZM ei que est ML equalis est, atque EL eius que est DM dupla, et reliqua LB erit talium lix xxxviii, qualium et EL collecta est v xxviii. Propter hoc autem et EB ypothenusa eorumdem lix lii. Et qualium est ergo EB recta cxx, talium et EL erit x lviii ad proximum, et que super ipsam periferia talium x xxx, qualium qualium] add. qualium qui circa F₁ BEL orthogonium circulus ccclx. Quare et EBZ angulus talium est x xxx, qualium duo recti ccclx, eorumdem vero erat et BZG angulus clxvii xlvi. Totus ergo BEG eorumdem erit clxxviii xvi. Rursum quoniam quidem G periguion optinet Piscium gradus xi ad proximum, stella vero apparebat in recta EK optinens Geminorum gradus xv xlv, erit utique et KEG angulus, qualium quidem sunt iiii recti ccclx, talium xxiiii xlv, qualium vero duo recti ccclx, talium clxxxix xxx, reliquusque BEK eorumdem xi xiiii. Quare et que super BN periferia talium est xi xiiii, qualium qui circa BEN orthogonium circulus ccclx, atque BN talium recta xi xliiii, qualium est EB ypothenusa cxx, et qualium ergo est EB lix lii, et que ex centro excentrici lx, talium et BN erit v l. Similiter autem quoniam IK periferia graduum est xli xviiii, erit utique et IBK angulus qualium sunt iiii recti ccclx, talium xli xviii, qualium vero ii recti ccclx, talium lxxxii xxxvi. Eorumdem vero erat et EBZ, hoc est IBT angulus, x xxx, reliquus ergo TBK erit lxxii vi. Ostensus est autem et KET angulus eorumdem xi xiiii, et reliquus ergo BKN eorumdem est lx lii. Quare et que super BN periferia talium est lx lii, qualium qui circa BKN orthogonium circulus ccclx, at vero BN recta talium est clx xlvii, qualium est BK ypothenusa cxx. Et qualium est ergo BN recta v l et que ex centro excentrici lx, talium et BK que ex centro epicicli erunt xi xxx ad prixmum. Quod oportebat demonstrare.

⟨XI.3⟩ De directione periodicorum ipsius motuum

Deinceps vero et periodicorum motuum causa sumemus rursum unam indubitantium descriptarum antiquarum observationum secundum quam declaratur quoniam xlv anno secundum Dionisium Parthenonos iii, Iovis stella eoa operuit australem asinum. Itaque tempus quidem est secundum lxxxiii annum ab Alexandri morte secundum Egiptios Epiphi xviia in xviiia mane, in quo Sole reperimus secundum mediam progressionem optinentem Virginis gradus ix lvi. Verum et vocatus australis Asinus eorum que circa nubeculam Cancri secundum nostre quidem observationis tempus obtinebat Cancri gradus xi iii, secundum exposita vero observationem manifestum quoniam gradus vii xxxiii, quoniam rursum eis qui inter observationes ccclxxviii annis pertinent gradus iii xlvii. Et Iovis itaque stella tunc, propter operuisse stellam, vii xxxiii gradus optinebat Cancri. Similiter autem et quoniam apoguion erat secundum nos circa Virginis gradus xi, secundum observationem debuit optinere Virginis gradus vii xiii, et manifestum quoniam apparens quidem stella distabat ab eo quod tunc apoguio excentrici gradibus ccc et sexagesimis xx, medius autem Sol ab eodem apoguio ii xliiii.

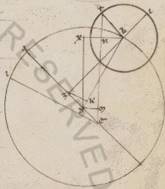Istis subiacentibus, adiaceat rursum similis eius que in Marte demonstrationis descriptio solum consequenter hic secundum observationem datis progressionibus eam quidem que circa B epicicli positionem habens ad I apoguion, eam vero que secundum L medie epochis Solis post breve ab eodem ab … eodem] iter. V₃ apoguion, propter hec vero et eam que secundum T stelle post i apoguion epicicli, copulatis quidem simpliciter semper recta ZBI et DB et BT et adhuc ET, cathetis vero ductis in DB quidem ea que est ZK in ET vero quidem ea que est DM et BN, in eam vero que est NB eductam hic ea que est DX et facientem DMNX parallilum orthogonium. Quoniam ergo AET quidem angulus continens reliquum in unum zodiaci circulum post ccc gradus et sexagesima xx talium est lix xl, qualium iiii recti ccclx, AEL vero angulus eorumdem ii xliii, erunt erunt] erit F₁ utique et LET totus, hoc est BRE BRE] BTE F₁, qualium quidem sunt iiii recti ccclx, talium lxii xxiii, qualium vero ii recti ccclx, talium cxxiiii xlvi. Quare et que quidem super BN periferia talium est cxxiiii xlvi, qualium qui circa BTN orthogonium circulus ccclx, BN vero recta talium cvi xx, qualium est BT ypothenusa cxx et qualium est ergo que ex centro epicicli xi xxx, talium et BN erunt erunt] erit F₁ x xii. Rursum quoniam DEM quidem angulus, qualium sunt iiii recti ccclx, talium subiacet lix xl, qualium vero ii recti ccclx, talium cxix xx, reliquus reliquus] corr. ex reliquum V₃ vero MDE eorumdem lx xl, erit utique et que quidem super DM periferia talium cxix xx, qualium qui circa DEM orthogonium circulus ccclx, at vero DM recta talium ciii xxxiiii, qualium est ED ypothenusa cxx. Et qualium est ergo ED quidem recta ii xlv, DB vero que ex centro excentrici lx, talium et DM erit ii xxiii, atque BNX tota eorumdem xii xxxv. Quare et qualium est DB ypothenusa cxx, talium et BX erit xxv x, et que super eam periferia talium xxiiii xiiii, qualium est qui circa BDX orthogonium circulus ccclx, et BDX ergo angulus talium est xxiiii xiiii, qualium sunt ii recti ccclx, reliquusque BDM eorumdem clv xlvi, totus vero BDE similiter ccxvi xxvi, reliquus vero rursum BDZ eorumdem cxliii xxxiiii. Quare et que quidem super ZK periferia talium est cxliii xxxiiii, qualium est qui circa ZDK orthogonium circulus ccclx, que vero super DK reliquorum in semicirculum xxxvi xxvi. Propter hoc vero et earum que sub ipsis rectarum ZK quidem talium erit cxiii lix, qualium est DZ ypothenusa cxx, DK vero eorumdem xxxvii xxxi. Et qualium est ergo DZ recta ii xlv, atque DB que ex centro excentrici lx, talium et KZ erit ii xxxvii, atque DK similiter o lii, reliqua vero KB eorumdem lix viii, propter hoc autem et ZB ypothenusa eorumdem ix xii. Quare et qualium est ZB recta cxx, talium et ZK erit v xviii, et que super eam periferia talium v iiii, qualium est qui circa BZK orthogonium circulus ccclx. Et ZBD ergo angulus talium est v iiii, qualium iio recti ccclx, atque AZB totus equalem longitudinem continens eorumdem quidem cxlviii xxxviii, qualium vero iiii recti ccclx, talium lxxiiii xix. Quoniam vero et IBT angulus cum BZG angulo et semicirculi compositus, hoc est relinquens nunc AZB angulum facit AEL angulum eorumdem existentem ii xliiii, habebimus et IBT angulum qui continet eam que ab apoguio epicicli transitionem stelle eorumdem lxxvii ii.

Demonstratum est ergo nobis quoniam secundum tempus preiacentis observationis Iovis stella secundum medium progressum considerata secundum longitudinem quidem distabat ab apoguio excentrici gradibus cclxxxv xli, hoc est optinebat medie Geminorum gradus xxii liiii, anomalie vero ab apoguio epicicli gradibus lxvii ii. Ostendebatur vero nobis et in tempore iii acronicti distans ab apoguio epicicli gradibus clxxxii xlvii. Supersumpsimus ergo in medio duarum observationum tempore continenti annos Egiptiacos ccclxxvii et dies cxxviii defitientes ad proximum hora ia post totos circulos anomalie cccxlv gradus cv xlv, quanta rursum fere et ex negotiatis nobis mediis motibus colligitur graduum anomalie supergressio, propter et ab ipsis istis diurni constitutionem nos facere, distributis ex multitudine circulorum et supergressionis collectis gradibus in multitudinem dierum ex tempore collectorum.

⟨XI.4⟩ De epochi periodicorum Iovis motuum

Ut hoc ergo rursum quoniam quod a primo anno a Navonassari secundum Egiptios mensis Thoth ia ad meridiem usque expositam antiquam observationem tempus annorum Egiptiacorum est dvi et dierum cccxvi et dimidii iiii^a ad proximum, continet vero istud tempus supergressionis longitudinis quidem gradus cclviii xiii, anomalie vero gradus ccxc lviii, si istos dempserimus ab expositis secundum observationem propriis epochibus, habebimus in idem aliis epochis tempus Iovis stellam medie secundum longitudinem quidem optinentem Chelarum gradus iiii xli, anomalie vero ab apoguio epicicli gradus cxlvi iiii, propter eadem vero et apoguion ipsius excentroticis optinebit gradus Virginis ii ix.

⟨XI.5⟩ Demonstratio excentrocitos et apoguii Saturni

Relicto vero in hunc locum et circa Saturni stellam consideratas et anomalias et epochas demonstrare, primum in apoguii et excentroticos considerationem sumemus, quemadmodum et in aliis, tres acronictoys staciones stelle ad medium Solis progressum diametros, quarum primam quidem per astrolabica organa observavimus xi anno Adriani secundum Egiptios mensis Pochon vii^a in viii^a vesperi circa Chelarum gradum i et sexagesima xiii, secunda vero xviii anno similiter Adriani secundum Egiptios epiphi xviii^a. Examinate vero diametrizationis tempus et locum consupputavimus per eas que circa ipsam observationes post iiii horas a meridie que in xviii^a circa Sagittarii gradus xx xl, tertia vero acronicton observantes xx anno rursum Adriani secundum Egiptios Mesori xxiiiia tempus quidem examinate diamtrizationis similiter supputavimus fuisse secundum ipsam que in xxiiii meridiem, locum vero circiter Capricorni gradus xiiii xiiii. Istarum ergo duarum distantiarum ea quidem que a prima acronicto in secundam annos quidem Egiptiacos continet vi et dies lxx et horas xxii, gradus vero apparentis stelle progressionis lxviii xxvii, que vero a secunda in tertiam annos quidem Egiptiacos iii et dies xxxv et horas xx, gradus vero similiter xxxiiii xxxiiii. Colliguntur autem et medie secundum longitudinem progressionis secundum integrius eius quidem prime distantie temporis gradus lxxv xliii, eius vero quod secunde gradus xxxvii lii.

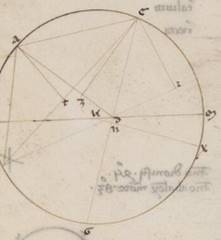His ergo distantiis subiacentibus, ostendemus rursum proposita per idem theorema, ut in uno prius excentrico ad modus hunc. Adiaceat enim, ut non idem replicemus, similis eis que eiusdem demonstrationis descriptio, et quoniam BG excentrici periferia subiacet subtendens zodiaci gradus xxxiiii xxxiiii, erit utique et BDG angulus, hoc est EDI ad centrum existens zodiaci, qualium sunt iiii recti ccclx, talium xxxiiii xxxiiii, qualium vero ii recti ccclx, talium lxix viii, qualium qui circa DEI orthogonium circulus ccclx, atque EI recta talium lxviii v, qualium est DE ypothenusa cxx; similiter quoniam BG periferia graduum est xxxvii lii, erit utique et BEG angulus ad periferiam existens talium xxxvii lii, qualium sunt ii recti ccclx, reliquus EBI eorumdem xxxi xvi. Quare et que super EI periferia talium est xxxi xvi, qualium est qui circa EBI orthogonium circulus ccclx, EI vero recta talium xxxii xx, qualium est BE ypothenusa cxx. Et qualium ergo EI ostensa est lxviii v, atque ED recta cxx, talium et BE erit cclii xli. Rursum quoniam ABG periferia tota subtendit zodiaci collectos ambarum distantiarum gradus ciii i, erit utique et ADG angulus ad centrum existens zodiaci talium ciii i, qualium sunt iiii recti ccclx, propter hoc autem et qui deinceps ei ADE eorum quidem lxxvi lix, qualium vero ii recti ccclx, talium cliii lviii. Quare et que super periferia EZ talium est cliii lviii, qualium est qui circa DEZ orthogonium circulus ccclx, atque EZ recta talium cxvi lv, qualium est DE ypothenusa cxx. Similiter quoniam ABG excentrici periferia collecta est graduum cxiii xxxv, erit utique et AEG angulus ad periferiam existens talium cxiii xxxv, qualium sunt ii recti ccclx. Eorumdem vero erat et ADE angulus cliii lviii, et reliquus ergo ZAE eorumdem erit xcii xxvii. Quare et que super EZ periferia talium est xcii xxvii, qualium est qui circa AEZ orthogonium circulus ccclx atque EZ recta talium lxxxvi xxxix, qualium est AE ypothenusa cxx. Et qualium ergo EZ EZ] corr. ex EX V₃ ostensa est cxvi lv, atque ED recta cxx, talium et EA erit clxi lv. Rursum quoniam AB excentrici periferia graduum est lxxv xliii, erit utique et AEB angulus ad periferiam existens talium lxxv xliii, qualium sunt ii recti ccclx. Quare et que super AT periferia talium lxxv xliii, qualium qui circa AET orthogonium circulus ccclx, et que super ET reliquorum in semicirculum ciiii xvii. Et earum ergo que sub ipsis rectarum AT quidem erunt erunt] erit F₁ talium lxxiii xxxix, qualium est EA ypothenusa cxx, ET vero eorumdem xciiii xlv. Quare et qualium AE quidem ostensa est clxi lv, DE vero recta cxx, talium et AT erit xcix xliii, ET vero similiter cxxvii li. Eorumdem autem ostendebatur et EB tota cclii xli. Et reliqua ergo TB talium est cxxiiii l, qualium et AT recta xcix xliii. Et est quod quidem a recta TB tetragonum xvdlxxxiii xxii, quod autem a recta AT similiter ixdccclxxvii iii, que composita faciunt quod a recta AB tetragonum xxvcccclx xxv. Longitudine ergo erit AB talium clix xxxiiii, qualium ED erat cxx, et EA similiter clxi lv. Est autem et qualium excentrici diametros cxx, talium AB recta lxxiii xxxix. Subtendit enim periferiam gradibus lxxv xliii. Et qualium est ergo AB recta lxxiii xxxix, atque excentrici diametros cxx, talium et ED quidem erit lv xxiii, atque EA recta lxxiiii xliii. Quare et EA periferia excentrici graduum est lxxvii i atque EABG tota graduum cxc xxxvi, reliquaque GE manifestum quoniam graduum est clxix xxiiii, propter hoc autem et GDE recta talium est cxix xxviii ad proximum, qualium est excentrici diametros cxx. Sumatur ergo excentrici centrum intra EAG portionem, quoniam maior est semicirculo, et sit K, et protrahatur per ipsum et D que per utraque centra diametros excentrici LKDM, et a puncto K in GE tracta educatur cathetus KNX. Quoniam ergo, qualium est LM diametros cxx, talium EG tota ostensa est cxix xxviii, et ED recta lv xxiii, et reliquam habebimus DG eorumdem lxiiii v. Quare quoniam quod sub rectis ED, DG contentum orthogonium equalem equalem] equale F₁ est sub rectis LD, DM contento, habebimus et quod sub rectis LD, DM talium iiidxlix ix, qualium est LM diametros cxx. Verum et quod sub rectis LD, DM cum eo quod a recta DK tetragono facit illud quod a medietate diametri, hoc est LK recta tetragonum. Si ergo a medietatis tetragono, hoc est factis iiidc, dempserimus iiidxlix ix, reliquetur nobis quod a recta DK tetragonum eorumdem l li. Et longitudine ergo habebimus DK mediam centrorum talium vii viii ad proximum, qualium est excentrici diametros cxx. 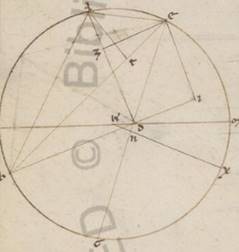Rursum quoniam medietas quidem eius que est GE, hoc est EN, talium est lix xlix, quoniam LM diametros cxx, eorumdem vero ostensa est et ED recta lv xxiii, et reliquam habebimus DN talium iiii xxi, qualium DK erat vii viii. Quare et qualium est DK ypothenusa cxx, talium et DN erit lxxiii xi, et que super ipsam periferia talium lxxv x, qualium est qui circa DKN orthogonium circulus ccclx. Et DKN ergo angulus, qualium sunt ii recti ccclx, talium est lxxv x, qualium vero iiii recti ccclx, talium xxxvii xxxv; et quoniam ad centrum est excentrici, habebimus et XM periferia graduum xxxvii xxxv. Est autem et GX dimidia existens eius que est GXE graduum lxxxiiii xlii, et reliqua ergo GL que ab apoguio in iiiam acronicton erit lvii xliii. Eorumdem vero et BG subiacet xxxvii lii, et reliqua ergo LB que ab apoguio in ii^am acronicton erit graduum xix li. Similiter autem quoniam AB subiacet graduum lxxv xliii, et reliquam habebimus AL que ab acronicto prima in apoguion graduum lv lii. Quoniam ergo rursum neque in hoc excentrico feretur centrum epicicli sed in eo qui scribitur centro puncto medio recte DK spatioque KL, investigavimus secundum consequens, quemadmodum in aliis, factas differentias in zodiaco apparentium distantiarum, velut his ad proximum existentibus proportionibus, si quis ad expositum excentricum et zodiacam anomaliam facientem transferant epicicli progressionem.

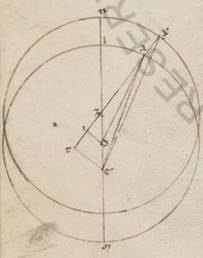Adiaceat enim in similli demonstratione in prima acronicto descriptio in precedentia L apoguii figurata. Quoniam ergo NZX angulus equalis secundum longitudinem progressionis, hoc est DZI, qualium sunt iiii recti ccclx; talium ostensus est lv lii, qualium vero duo recti ccclx, talium cxi xliiii, erit utique et que super DI periferia talium cxi xliiii, qualium est qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum lxviii xvi. Et earum ergo que sub ipsis rectarum DI quidem talium est xcix xx, qualium est DZ ypothenusa cxx, atque ZI eorumdem lxvii xx. Quare qualium est DZ media centrorum iii xxxiiii atque DA que ex centro excentrici lx, talium et DI erit ii lvii atque ZI similiter ii o. Et quoniam quod a recta DI sumptum sub eo quod a recta DA facit quod a recta AI, habebimus et AI eorumdem lix lvi. Similiter autem quoniam ZI ei que est TI equalis est atque TE eius que est ID dupla, et AT tota erunt talium lxi lvi, qualium est ET recta v liiii. Propter hoc autem et AE ypothenusa erit eorumdem lxii xiii. Quare et qualium est AE ypothenusa cxx, talium et ET erit xi xxi, et que super ipsam periferia talium x li ad proximum, qualium est qui circa AET orthogonium circulus ccclx, et EAT ergo angulus talium est x li, qualium ii recti ccclx. Rursum quoniam qualium est recta ET v liiii, talium est ZX que ex centro excentrici lx, atque ZT recta iiii, totaque TX manifestum quoniam lxiiii, habebimus et EX ypothenusa eorumdem lxiiii xvi. Et qualium est ergo EX ypothenusa cxx, talium et TE erit xi ii, que vero super ipsam periferia talium x xxxiii, qualium est qui circa ETX orthogonium circulus ccclx. Quare et EXT angulus talium est x xxxiii, qualium ii recti ccclx. Eorumdem vero et EAT ostensus est x li, et reliquum ergo AEX angulus inquisite differentie, qualium sunt ii recti ccclx, talium est o xviii, qualium vero iiii recti ccclx, talium o ix. Verum apparebat secundum primam acronicton stella in AE recta optinens Chelarum gradum i et sexagesima xiii. Manifestum ergo, si non in AL centrum ferebatur epicicli, sed in NX, erat quidem secundum X eius punctum. Apparebat vero stella in EX recta precedens eam que secundum A positionem ix sexagesimis et optinebat Chelarum 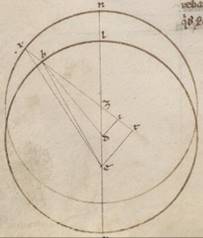gradum i et sexagesima iiii.

Rursum adiaceat et secunde acronicti secundum eamdem demonstrationem descriptio in consequentia apoguii figurata. Quoniam NX periferia excentrici ostensa graduum xix xl, xl] li F₁ erunt erunt] erit F₁ utique et NZX angulus et ipse et qui secundum verticem eius DZI, qualium sunt iiii recti ccclx, talium xix li, qualium vero ii recti ccclx talium xxxix xlii. Quare et que quidem super DI periferia talium est xxxix xlii, qualium qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum cxl xviii. Et earum ergo que sub ipsis rectarum DI talium est xl xlv, qualium DZ ypothenusa cxx, atque ZI eorumdem cxii lii. Quare et qualium est DZ recta iii xxxiiii atque DB que ex centro excentrici lx, talium et DI erit i xiii atque ZI similiter iii xxi. Et quoniam quod a recta DI sumptum sub eo quod a recta DB facit quod a recta BI, erit et BI eorumdem lix lix ad proximum. Similiter autem quoniam ZI ei que est IT est equalis atque ET eius que est DI dupla, et totam BT habebimus talium lxiii xx, qualium est ET recta ii xxvi, propter hoc autem et EB ypothenusam eorumdem lxiii xxiii. Et qualium est ergo BE ypothenusa cxx, talium ET erit iiii xxxvi, que vero super ipsam periferiam talium iiii xxiiii, qualium est qui circa BET orthogonium circulus ccclx. Quare et EBT angulus talium est iiii xxiiii, qualium iio recti ccclx. Similiter quoniam, qualium est XZ que ex centro excentrici lx, talium ZT collecta est vi xlii, habebimus XT totam talium lxvi xlii, qualium et ET subiacebat ii xxvi, propter hoc autem et EX ypothenusa eorumdem lxvi xlv. Quare, et qualium est EX ypothenusa cxx, talium et ET erit iiii xxiii, que vero super ipsam periferia talium iiii xii, qualium est qui circa ETX orthogonium circulus ccclx. Et EXT ergo angulus talium est iiii xii, qualium ii recti ccclx. Eorumdem vero demonstrabatur et EBT angulus iiii xxiiii, et reliquum ergo BEZ eorumdem quidem erunt o xii, qualium vero iiii recti ccclx talium o vi. Manifestum ergo et hic quod, quoniam quidem et secundum secundam acronicton stella in recta EB apparens optinebat Sagittarii gradus ix xl, si ergo in NX rursum apparebat, optinebat utique Sagittarii gradus ix xlvi. Demonstratum vero est quoniam et secundum primam acronicton optinebat utique similiter Chelarum gradum i et sexagesima iiii. Manifestum ergo quoniam et que a prima acronicto in secunda apparens distantia collecta est utique, si ad NX excentricum considerabatur, zodiaci graduum lxviii xlii.

Similiter adiaceat et tertie acronicti descriptio secundum eamdem figurationem ei que in secunda exposita est. Quoniam NX periferia graduum ostensa est lvii xliii, erit utique et NZX angulus, hic hic] hoc F₁ est DZI, qualium sunt iiii recti ccclx, talium lvii xliii, qualium vero ii recti ccclx, talium cxv xxvi. Quare et que quidem super DI periferia talium cxv xxvi, qualium qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum lxiiii xxiiii. xxiiii] xxxiiii F₁ Et earum ergo que sub ipsis rectarum DI talium est ci xxvii, qualium est DZ ypothenusa cxx, atque ZI eorumdem lxiiii vi. Quare et qualium est DZ iii xxxiiii atque DG que ex centro excentrici lx, talium et DI erit iii i atque ZI similiter i liiii. Et quoniam rursum quod a recta DI sumptum sub eo quod a recta DG facit illud quod a recta GI, habebimus et rectam GI eorumdem lix lvi. Similiter autem quoniam et recta ZI ei que est IT equalis, est atque ET eius que est DI dupla, et GT totam habebimus talium lxi l, qualium et ET collecta est vi ii, propter hoc A et EG ypothenusa eorumdem lxii viii, et qualium est ergo GE ypothenusa cxx, talium et ET erit xi xxxix, que super vero super vero] inv. F₁ ipsam periferia talium xi ix ad proximum, qualium est qui circa GET orthogonius orthogonus] orthogonum F₁ circulus ccclx. Quare et EGT angulus talium est xi ix, qualium ii recti ccclx. Similiter quoniam qualium est XZ que ex centro excentrici lx, talium et ZT collecta est iii xlv, xlv] xlviii F₁ et totam XT habebimus talium lxiii xlviii, qualium et ET erat vi ii, propter hoc autem et EX ypothenusa eorumdem lxiiii v, et qualium est ergo EX ypothenusa cxx, talium et ET erit xi xviii, que vero super ipsam periferiam talium x xlix, qualium qui circa EXT orthogonium circulus ccclx. Quare et EXT angulus talium est x xlix, qualium duo recti ccclx. Eorumdem vero ostensus est et EGT angulus xi ix. Reliquus ergo GEX eorumdem quidem est o xx, qualium vero iiii recti ccclx, talium o x. Quare et quoniam secundum tertiam acronicton in EG recta apparens stella optinebat Capricorni gradus xiiii xiiii, manifestum quoniam, si in EX recta contingent, optinent utique Capricorni gradus xiiii xxiiii et fiebat rursum a secunda acronicto in tertiam apparens distantia ad NX excentricum considerata graduum xxxiiii xxxviii.

Istis ergo distantiis assecuti in eodem thehoremate reperimus eam quidem que inter centra zodiaci et equalem epicicli motum continentis excentrici, hoc est equalem ei que est EZ, talium vi l ad proximum, qualium est excentrici diametros cxx. Earum ergo que eiusdem excentrici periferiarum eam quidem que a prima acronicto in apoguion graduum lvii v, eam vero que ab apoguio in in] add. secunda acronicton graduum xviii xxxviii, atque ea que ab apoguio in F₁ tertiam acronicton graduum lvi xxx. Et sunt hinc examinate rursum exposite quantitatis sumpte, propter differentias periferiarum zodiaci easdem ad proximum eis que prius et per hec colligi eas et consonas reperiri apparentes stelle distantias observatis, velut ex similibus nobis erit manifestum.

Adiaceat enim prime acronicti figuratio in solo excentrico ferente centrum epicicli. Quoniam ergo AZL angulus subtendens excentrici gradus lvii v, qualium quidem sunt iiii recti ccclx, talium est lvii v, qualium vero ii recti ccclx, talium et ipse qui secundum verticem ipsius DZI angulus cxiiii x, erit utique et que super rectam DI periferia talium cxiiii x, qualium est qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum lxv l. Et earum ergo que sub ipsis rectarum DI quidem talium est c et sexagesimorum xliiii, qualium est DZ ypothenusa cxx, atque ZI eorumdem lxv xiii. Quare et qualium est DZ media centrorum iii xxv atque DA que ex centro excentrici lx, talium et DI erit ii lii atque ZI similiter i li. Et quoniam quod rursum a recta DI sumptum sub eo quod a recta AD facit illud quod a recta AI, habebimus et AI eorumdem lix lvi. Similiter autem quoniam et ZI ei que est IT equalis est atque ET eius que est DI dupla, et totam AT habebimus talium lxi xlvii, qualium et ET collecta est v xliiii, propter hoc autem et AE ypothenusa eorumdem lxii iii, et qualium est ergo AE ypothenusa cxx, talium et ET erit xi v, que vero super ipsam periferia talium x xxxvi, qualium qui circa AET orthogonium circulus ccclx. Quare et EAZ angulus talium est x xxxvi, qualium ii recti ccclx, eorumdem vero et AZL subiacebat cxiiii x, et reliquus ergo AEL eorumdem quidem erit ciii xxxiiii, qualium vero iiii recti ccclx, talium li xlvii, tot ergo gradibus stella secundam primam acronicton precedebat apoguion.

Rursum adiaceat secundum simille secunde acronicti descriptio. Quoniam BZL angulus, qualium sunt iiii recti ccclx, talium ostensus est xviii xxxviii, qualium vero ii recti ccclx, talium et ipse et qui secundum verticem eius DZI angulus xxxvii xvi, erit utique et que super DI periferia talium xxxvii xvi, qualium qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum cxlii xliiii. Et earum ergo que sub ipsis rectarum DI quidem talium est xxxviii xx, qualium DZ ypothenusa cxx et ZI eorumdem cxiii xliii. Quare et qualium est DZ recta iii xxv atque DB que ex centro excentrici lx, talium et DI erit xxx v et ZI similiter iii xiiii. Et quoniam quod a recta DI sumptum sub eo quod a recta DB facit quod a recta BI, habebimus et BI eorumdem lix lix. Similiter autem quoniam et ZI ei que est IT equalis est et ET eius que est DI dupla, et totam BT habebimus talium lxiii xiii, qualium et ET collecta est ii x, propter hoc autem et EB ypothenusa eorumdem lxiii xv, et qualium ergo est EB ypothenusa cxx, talium et TE erit iiii vii, et que super ipsam periferia talium iii lvi, qualium est qui circa BET orthogonium circulus ccclx. Quare et EBZ angulus talium iii lvi, qualium iio recti ccclx. Eorumdem vero et BZL subiacebat xxxvii xvi, et reliquus ergo BEL erit eorumdem quidem xxxiii xx, qualium vero iiii recti ccclx, talium xvi xlvi. Iuxta secundam ergo acronicton relicta apparebat stella apoguii gradibus xvi xl. Ostensa est autem et secundum primam acronicton precedens idem apoguium gradus li xlvii. Colligitur ergo a prima acronicto in secunda apparens distantia in idem expositorum graduum lxviii xxvii consone eis qui ex observationibus deprehensi sunt.

Adiaceat autem et tertie acronicti descriptio quoniam GZL angulus qualium quidem sunt iiii recti ccclx, talium ostensus est lvi xxx. Qualium vero ii recti ccclx, talium et ipse et qui secundum verticem ipsius DZI angulus cxiii o, erit utique et que super DI periferia talium cxiii, qualium est qui circa DZI orthogonium circulus ccclx, et que super ZI reliquorum in semicirculum lxvii. Et earum ergo que sub ipsis rectarum DI quidem talium est c et sexagesimorum iiii, qualium est DZ ypothenusa cxx, atque ZI eorumdem lxvi xiiii. Quare et qualium est DZ recta iii xxv atque DG que ex centro excentrici lx, talium et DI erit ii li et ZI similiter i liii. Et quoniam rursum quod a recta DI sumptum sub eo quod a recta DG facit illud quod a recta GI, habebimus et GI eorumdem lix lvi. Similiter autem quoniam et recta quidem ZI ei que est IT est equalis, ET vero eius que est DI dupla, et totam GT habebimus talium lxi xlix, qualium et ET collecta est v xlii, propter hoc autem et EG ypothenusa eorumdem lxii v, et qualium est ergo GE ypothenusa cxx, talium et ET erit xi x, et que super ipsam periferiam talium x xxxii, qualium est qui circa GET orthogonium circulus ccclx. Quare et EGT angulus talium est x xxxii, qualium ii recti ccclx. Eorumdem vero et GZL subiacet cxiii, et reliquus ergo GEL eorumdem quidem erit cii xxviii, qualium vero iiii recti ccclx, talium li xiiii. Totus Totus] tot F₁ ergo gradibus et secundam secundam] secundum F₁ tertiam acronicton relicta stella apparebat apoguii. Demonstrata vero est et secundum secundam acronicton relicta eiusdem apoguii gradibus xvi xl, quare et colligi et a secunda acronicto in tertiam apparentem distantiam eorum qui superhabundantie graduum xxxiiii xxxiiii consone rursum eis qui ex observationibus deprehensi sunt.

Manifestum vero hinc quoniam quidem secundum tertiam acronicton optinebat stella Capricorni gradus xiiii xiiii, relicta ab apoguio, velut demonstratum est, gradibus li xiiii, apoguion quidem ex centroticis eius optinebat Scorpii gradus xxiii, periguion vero secundum diametrum Tauri gradus xxiii. Similiter autem, et si descripserimus circa G centrum IT epiciclum, eam quidem que ad apoguio excentrici mediam secundum longitudinem progressionem epicicli demonstratorum hinc habebimus graduum lvi xxx, at vero TK epicicli periferiam graduum v xvi, propter et EGZ angulum ostendi talium x xxxii, qualium sunt ii recti ccclx, quare et reliquam IT periferiam que ab apoguio epicicli in stellam relinqui o clxiiii xliii. In tempore ergo iii acronicti, hoc est xx anno Adriani secundum Egiptios Mesori xxiiii ad meridiem, Saturni stella ad medias progressiones considerata secundum longitudinem quidem distabat ab apoguio excentrici gradibus lvi xxx, hoc est optinebat Capricorni gradus xix xxx, anomalie vero ab apoguio epicicli gradus clxxiiii xliiii. Que aper procheito curin. ἅπερ προέκειτο εὐρεῖν H 413.20

⟨XI.6⟩ Demonstratio magnitudinis epicicli Saturni

Rursum vero deinceps in demonstrandam epicicli quantitate quantitate] quantitatem F₁ sumemus observationem quam nos observavimus secundo anno Antonini secundum Egiptios mensis Mechir via in viia iiii horas equinoctiales ante mesonictium, quoniam quidem celum medium optinebat secundum astrolabium extremus graduum Arietis, medio Sole optinente Sagittarii gradus xxviii xli. Tunc autem Saturni stella ad lucentem quidem Yada considerata optinens apparebat Aquarii gradus ix xv, a centro vero Lune relinquebatur dimidio ad proximum unius gradus, tantum enim ipsius distabat a boreali termino. Verum in illam horam Luna secundum mediam progressionem optinebat Aquarii gradus viii lv et anomalie ab apoguio epicicli gradus clxxiii xv, propter hoc autem et examinata quidem eius progressio debuit optinere Aquarii gradus ix xl, ea vero que in Alexandria apparens gradus viii xxxiiii. Et ita ergo Saturni stella, quoniam quidem relinquebatur a centro eius dimidio ad proximum unius gradus, debuit optinere Aquarii gradus ix xv et distabat ab apoguio excentrici ipsius, propter nichil sermone dignum in tantum tempus ipsam transmoveri lxxv lxxv] lxxvi F₁ iiii. Quoniam quidem ergo et quod a tertia acronicto usque istam observationem tempus annorum egiptiacorum est ii et dierum clxvii et horarum viii movetur integrius in tanto tempore rursum Saturni stella longitudinis quidem gradibus xxx et sexagesima iii, anomalie vero cxxxiiii xxiiii, si apposuerimus istos secundum tertiam acronicton expositis epochis, habebimus et in preiacentis observationis tempus longitudinis quidem ab apoguio excentrici gradus lxxxvi xxxiiii, xxxiiii] xxxiii F₁ anomalie vero ab apoguio epicicli gradus cccix viii.

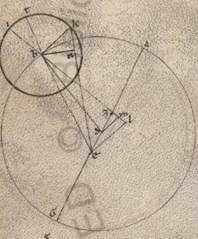Istis ergo subiacentibus, adiaceat rursum similis demonstrationis descriptio epicicli quidem positionem habens ad consequentia apoguii excentrici, eam vero que stelle in eis que apoguium epicicli subiacentibus ipsorum progressionibus consequenter. Quoniam ergo AZB angulus, hoc est DZM, qualium sunt iiii recti ccclx, talium subiacet lxxxvi xxxiii. Qualium vero ii recti ccclx talium clxxiii vi erit utique et que super DM periferia talium clxxiii vi, qualium est qui circa DZM orthogonium circulus ccclx, et que super ZM reliquorum in semicirculum vi liiii. Et earum ergo que sub ipsis rectarum DM quidem talium erit cxix xlvii, qualium est DZ ypothenusa cxx, atque MZ eorumdem vii xiii. Quare et qualium est DZ media centrorum iii xxv atque DM que ex centro excentrici lx, talium et DM quidem erit ad proximum iii xxv, ZM vero similiter lxx xii. Et quoniam quod a recta DM sumptum sub eo quod a recta DB facit illud quod a recta BM, habebimus et BM eorumdem lix liiii. Similiter autem quoniam et ZM recta ei que est ML equalis est et EL eius que est DM dupla, habebimus et totam BL talium lx et sexagesimorum vi, qualium et EL collecta est vi l, propter hoc autem et EB ypothenusa eorumdem lx xxix, et qualium est ergo EB ypothenusa cxx, talium et EL erit xiii xxxiii, et que super ipsam periferia talium xii lviii, qualium est qui circa BEL orthogonium circulus ccclx. Quare et EBZ angulus talium est xii lviii, qualium ii recti ccclx, eorumdem vero subiacet et DZB angulus clxxiii vi. Et reliquus ergo AEB eorumdem erit clx et sexagesimorum viii. Verum et AEK angulus continens ab apoguio apparentem distantiam stelle, qualium quidem sunt iiii recti ccclx, talium subiacebat lxxvi iiii, qualium vero ii recti ccclx, talium clii viii. Et reliquum ergo KEB habebimus eorumdem viii o. Quare et que super BN periferia talium est viii, qualium qui circa BEN orthogonium circulus ccclx, atque BN recta talium viii xxii, qualium est EB ypothenusa cxx. Et qualium est ergo EB recta lx xxix et que ex centro excentrici 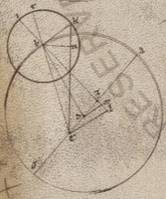lx, talium et BN erit iiii xiii. Rursum quoniam distabat stella ab apoguio I epicicli gradibus cccix viii, erit utique et reliqua IK periferia graduum l lii. Et IBK ergo angulus, qualium sunt iiii recti ccclx, talium est l lii, qualium vero ii recti ccclx, talium ci xliiii. Eorumdem vero erat et EBZ, hoc est IBT angulus, xii lviii. Et reliquus ergo TBK erit eorumdem lxxxviii xlvi, qualium KEB qualium KEB] iter. V₃ ostensus est viii. Et reliquum ergo BKN habebimus eorumdem lxxx xlvi. Quare et que super BN periferia talium est lxxx xlvi, qualium est qui circa BKN orthogonium circulus ccclx, atque BN recta talium lxxvii xlv, qualium est BK ypothenusa cxx. Et qualium ergo BN ostensa est iiii xiii et que ex centro excentrici lx, talium et BK que ex centro epicicli habebimus vi et dimidii ad proximum. Et collectum est nobis quoniam apoguion quidem Saturni secundum ea que circiter principium regni Antonini tempora optinebat Scorpii gradus xxiii, qualium vero que ex centro excentrici ferentis epiciclon est lx, talium et que media centrorum zodiaci et equale motum facientis excentrici collecta est vi l, que vero ex centro epicicli eorumdem vi xxx. Quod oportebat demonstrare.

⟨XI.7⟩ De directione periodicorum Saturni motuum

Relicta vero demonstrari periodicorum motuum directione, sumemus et in hoc unam rursum indubitanter descriptarum antiquarum observationum secundum quam declaratur quoniam lxxxii anno secundum Chaldeos Xanthiki v vesperi Saturni stella subtus erat australi humero Virginis digitos ii. Tempus Tempus] add. ergo F₁ est secundum dxix annum a Navonassaro secundum Egiptios Tybi xiiiia vesperi in quo medium Solem reperimus optinentem Piscium gradus vi x. Verum et que in australi humero Virginis fixa secundum nostre quidem observationis tempus optinebat Virginis gradus xiii vi, at vero secundum illud quod exposite observationis, propter intermediis ccclxvi annis adiungi motionis fixarum gradus iii bisse ad proximum, Virginis manifestum quoniam gradus ix et dimidium, quot et Saturni stella, quoniam quidem australior quam fixa duobus digitis. Similiter autem et quoniam apoguion eius secundum nos ostensum est circiter xxiii gradus Scorpii secundum expositam observationem debuit optinere xix iii gradus Scorpii et colligitur propter hoc quoniam secundum preiacens tempus apparens stella distabat ab eo quod tunc apoguio gradibus in zodiaco ccxc x, medius autem Sol ab eodem apoguio gradibus cvi l.

Istis subiacencibus, adiaceat rursum in similli demonstratione descriptio epicicli quidem positionem habens precedentem apoguium excentrici, eam vero que Solis precedentem periguium et equidistantem ipsi eam que a centro epicicli in stellam. Quoniam ergo Saturni stella precedens apparebat apoguium relictos in unum circulum gradibus lixix lixix] lxix F₁ l erit utique et AET angulus ad centrum existens zodyaci, qualium sunt iiii recti ccclx, talium lxix l, qualium vero duo recti ccclx, talium cxxxix xl. Subiacet autem et AEL angulus solaris distantie, qualium sunt iiii recti ccclx, talium cvi l, qualium vero duo recti ccclx talium ccxiii xl. Et totus ergo TL, TL] TEL F₁ hoc est BTE, propter equidistantes esse rectas BT et EL, talium est cccliii xx, qualium ii recti ccclx, reliquusque BTN eorumdem vi xl. Quare et que super BN periferia talium est vi xl, qualium qui circa BTN orthogonium circulus ccclx, atque BN recta talium vi lviii, qualium est BT ypothenusa cxx. Et qualium ergo est BT que ex centro epicicli vi xxx, et BN erit t xxiii. Similiter quoniam AET angulus talium cxxxix xl, qualium duo recti ccclx, et EDM eorumdem xl xx, erit utique et que super DM periferia talium cxxxix xl, qualium qui circa DEM orthogonium circulus ccclx. Ipsaque DM recta talium est cxii xxxix, qualium ED ypothenusa cxx. Et qualium est ergo ED media centrorum iii xxv atque DB que ex centro excentrici lx, talium et DM, hoc est XN recta, erit iii xii, atque BNX tota talium iii xxxv, qualium est DB ypothenusa lx. Et qualium est ergo DB recta cxx, talium et BX erit vii x, et que super ipsam periferia talium vi lii, qualium qui circa BDX orthogonium circulus ccclx. Quare et BDX angulus talium est vi lii, qualium ii recti ccclx, reliquusque BDM eorumdem clxxiii viii, 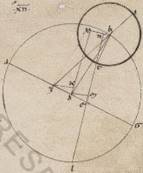totusque BDE similiter ccxiii xxviii. Reliquus vero BDA eorumdem cxlvi xxxii. Quare et que super ZK periferia talium est cxlvi xxxii, qualium qui circa DZK orthogonium circulus ccclx, et que super DK reliquorum in semicirculum xxxiii xxviii. Et earum ergo que sub ipsis rectarum ZK quidem erit talium cxiiii lv, qualium est DZ ypothenusa cxx, atque DK eorumdem xxxiiii xxxiii. Et qualium est ergo DZ media centrorum iii xxv atque DB que ex centro excentrici lx, talium et ZK erit iii xvii et DK similiter o lix, reliquaque KB talium lix i, qualium et ZK iii xvii, propter hoc autem et ZB ypothenusa eorumdem lix vi. Quare et qualium est qui circa BZK est] add. ZB ypothenusa cxx, talium et ZK erit vi xl, et que super ipsam periferia talium vi xxii, qualium est F₁ orthogonium circulus ccclx. Et ZBK ergo angulus talium et vi xxxii, xxxii] xxii F₁ qualium ii recti ccclx. Eorumdem vero erat et ADB angulus cxlvi xxxii, et totum ergo AZB angulum qui continet equalem secundum longitudinem progressionem habebimus eorumdem quidem clii liiii, qualium vero iiii recti ccclx, talium lxvi xxvii. Distabat ergo secundum exposite observationis tempus stella Saturni secundum medium longitudinis progressum ab apoguio cclxxxiii xxxiii, hoc est optinebat Virginis gradus ii liii. Quoniam vero et Solis medius progressus subiacet graduum cvi l, si apposuerimus ipsis unius circuli gradus ccclx et a factis cccclxvi l dempserimus longitudinis gradus cclxxxiii xxxiii, habebimus in idem tempus et anomalie ab apoguio epicicli gradus clxxxiii xvii. Quoniam ergo in tempore quidem preiacentis observationis existenti secundum dxix annum a Navonassaro Tybi xiiii vesperi ostensus est distans ab apoguio epicicli clxxxiii xvii, in eo vero quod tertie acronicti existenti secundum dccclxxxiii annum a Navonassaro Mesori xxiiii ad meridiem gradibus clxxiiii xliiii, manifestum quoniam in medio observationum tempore continenti annos Egiptiacos ccclxiiii gradus et dies ccxix dimidii iiii^a progressa est stella Saturni post totos circulos anomalie gradus cccli xxvii, quanta ferme rursum ex negotiatis rursum mediis motibus colligitur graduum supergressio, propter hec ipsa et diurno medio progressu constituto distributis collectis gradibus ex multitudine circulorum et supergressione in multitudine collectorum ex tempore dierum.

⟨XI.8⟩ De epochi periodicorum Saturni motuum

Quoniam vero et quod a primo anno Navonassari mensis Thoth prima ad meridiem usque expositam antiquam observationem tempus annorum est egiptiacorum dxiii et dierum cxxxiii iiii^a. Continet autem tempus istud tempus supergressionis longitudinis quidem gradus ccxvi, anomalie gradus cxlix xv. Si istos dempserimus a secundum observationem expositis epochis, habebimus rursum in idem epoche tempus et Saturni stellam medie secundum longitudinem continentem Egoceri gradus xxvi xliii et anomalie ab apoguio epicicli gradus xxxiiii ii, propter hec vero et apoguion eius excentroticis circiter Scorpii gradus xiiii i. Quod oportebat demonstrare.

⟨XI.9⟩ Quomodo a periodicis motibus examinati progressus lineariter sumantur

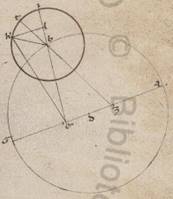Quoniam vero et e converso, periodicis periferiis et equalem motum continentis excentrici et epicicli datis, et apparentes progressus stellarum promte per lineas sumantur, per eadem nobis erit clarum. Si enim in simplici descriptione et excentrici ZBT et EBI copulaverimus, dato quidem secundum longitudinem medio progressu, hoc est AZB angulo, dabitur et secundum ambas ypotheses ex antedemonstratis et AEB angulus et EBZ, hoc est IBT, et adhuc EB recte ad eam que ex centro epicicli proportio. Supposita autem et stella verbi causa secundum K punctum epicicli, et copulatis rectis EK et BK, dataque TK periferia, si non iam, quemadmodum in ea que e contrario demonstratione, a puncto B centro epicicli cathetum duxerimus in rectam EK, sed ab K stella in EB rectam, velut hic KL, datus quidem erit et totus IBK angulus, propter hoc autem et earum que sunt KL et LB et ad BK et ad EB manifestum quoniam proporcio dabitur. Dabitur autem consequenter et que totius EBL ad LK, quare, et LEK angulo dato, et totum nobis colligi AEK angulum continentem eam que ab apoguio stelle apparentem distantiam.

⟨XI.10⟩ Negotium anomaliarum canonopiie

Ut tamen nobis nobis] non F₁ semper per lineas apparentes progressus supputemus, tali modo solo quidem examinantem propositum, ut ad promtum considerationum contingente, faciemus ut est maxime et commode simul et proxime examinationi canonem secundum unamquamque stellarum quinque continentem ipsarum secundum partem comparatas anomalias, ut per ipsarum examinationem periodicorum motuum a propriis apoguiis datis apparentes usque quamque progressione supputemus

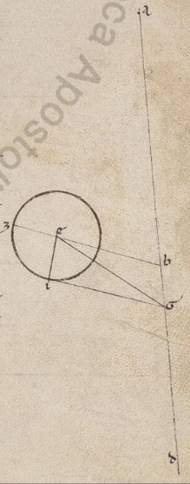Ordinatus est nobis canonum unusquisque in versus quidem rursus commoditatis causa xlv, selidia vero viii. Selidiorum autem primum quidem quidem] del. prima F₁ continebit duos mediarum progressionum numeros, quemadmodum in Sole et Luna, in primo quidem ordinatis superius eis qui ab apoguio graduum clxxx, in secundo vero inferius reliquus semicirculi graduum clxxx, quare clxxx quidem graduum numerum in ambobus ordinari in extremis versibus, augmentum vero ipsorum in superioribus quidem primis xv versibus fieri per gradus vi, in eis vero que sub ipsis xxx reliquis versibus per gradus iii, quoniam et anomalie portionum superhabundantie ab apoguio quidem in multum a seinvicem differentes sunt, ad periguia vero velotiorem sumunt transmutationem. Eorum autem que deinceps duorum selidiorum, tertium quidem continebit factas secundum propriorum versuum numeros medie secundum longitudinem progressionis, propter maiorem excentrotica prostafereses, sumptas tamen secundum simplex, ut utique si secundum ipsum equalem motum continentem excentricum centrum ferebatur epicicli, quartum vero collectas differentias prostaferesium penes non in predicto circulo, sed in altero centrum fieri epicicli. Modus vero secundum quem utrumque istorum et simul et seorsum per lineas sumitur per multa preexposita thehoremata factus est bene intelligibilis. Itaque hic quidem, ut in sintaxi competens erat huiusmodi discretionem zodiace anomalie sub visum facere, et propter hoc in duobus selidiis exponi, in usu tamen ipsius sufficiet et unum selidium ex ambarum istarum prostaferesi supercollectum. Eorum vero que deinceps trium selidiorum unumquodque continebit factas penes epiciclum prostafereses simpliciter iterum sumptas et velut illis que in ipsis apoguiis vel periguiis ad illud quod a visu nostro apostima consideratis, et huiusmodi demonstrationis modo secundum preexposita thehoremata facto nobis intellectu facili. Itaque medium quidem trium istorum selidiorum, sextum autem a primo, continebit secundum proportiones mediorum apostimatum collectas prostafereses, quintum vero ex eisdem portionibus factas superhaundantias earum que in maxima distantia prostaferesium penes eas que in media, septimum autem factas superhabundantias earum que in minima distantia prostaferesium penes eas que in media. Demonstratum est enim nobis quoniam, qualium est que ex centro epicicli in stella quidem Saturni, – bene enim utique se habet reliquum ab eis que superius principium facere –, vi xxx, in Iovis vero stella xi xxx, in Marte autem xxxix xxx, in Venere vero xliii x, in Mercurio vero xxii xxx, talium et medium quidem apostima omnium est lx, hoc est quod ad eam que ex ex] corr. ex a V₃ centro ferentis epiciclon excentrici consideratum, maximum vero ut ad zodiaci centrum, in Saturni quidem stella lxiii xxv, in ea vero que Iovis lxii xlv, in Marte autem lxvi, in Venere lxi xv, in Mercurio lxviiii, minimum vero in Saturni quidem stella lvi xxxv, in Iovis lvii xv, in Martis liiii, in Veneris lviii xlv, in Mercurio lv xxxiiii. Reliquum vero et viiium selidium ordinatum est ad sumendum pertinentes partes expositarum superhabundantiarum, quando non secundum ipsarum media vel maxima vel minima aposimata contingerint epicicli stellarum, sed in mediis istorum progressionibus. Coordinata est autem nobis et huiusmodi supputatio ad solas secundum unumquodque mediorum apostimatum sub eis que a visu nostro contingentibus epiciclum factas maximas prostafereses, velut nulla cura digno differente superhabundantiarum adiectione in particularibus epicicli portionibus ad eas que in maximis prostaferesibus. Propterea vero ut et quod dictum est manifestius fiat et ephodus ipsa adiectionum manifesta constituatur, adiaceat recta quem quem] que F₁ per utraque centra et zodiaci et equalem epicicli motum continentis excentrici ABGD, et subiaceat zodiaci quidem centrum G, quod vero equalis epicicli motus B, et educta BEZ, scribatur circa E centrum ZL ZL] ZI F₁ epiciclus, et trahatur a puncto G contingens ipsum GI recta. Copulentur vero et GE et EI cathetus. Subiaceat que exempli causa in unaquaque v stellarum centrum epicicli distans equaliter ab apoguio excentoticis gradibus xxx. Quoniam ergo, ut non eadem ostendentes longam faciamus supputationem, ostensum est per multa in precedentibus et in ea que Mercurii et in ea que reliquorum ypothenusi ypothenusi] ypothesi F₁, quoniam, dato ABE angulo, data est et eius que est GE ad eam que ex centro epicicli, hoc est IE, proporcio, colligitur vero et hec per eas que secundum unamquamque supputationes, ABE angulo subiacente talium xxx, qualium sunt iiii recti ccclx, in Saturno quidem que lxiii ii ad vi xxx, in Iove que lxii xxvi ad xi xxx, in Marte vero que lxv xxiiii ad xxxix xxx, in Venere quod lxi xxvi ad xliii x, in Mercurio que lxvi xxxv ad xxxii xxx, et EGI utique angulum habebimus qui continet eam que tunc maxima penes epiciclum prostaferesim, qualium sunt iiii recti ccclx, talium in Saturno quidem v lv dimidii, in Iove vero x xxxvi et dimidii, in Marte xxxvii ix, in Venere xliiii lvi et dimidii, in Mercurio xix xlv. Colliguntur autem que in mediis distantiis maxime prostefereses secundum paulo ante expositas rationes proprie conpetenti ordini stellarum, ut non idem replicemus, gradus vi xiii et xi iii et xli x et xlvi o et xxii ii, que vero in maximis aposimatibus gradus v liii et x xxxiiii et xxxvi et xlv et xliiii xlviii et xix ii, que autem in minimus apostimatibus gradus vi xxxvi et xi xxxv et xlvii i et xlvii xvii et xxiii liii, ut differant ab eis que in mediis apostimatibus ille quidem que in maximis gradus o xx et o xxix et iiii xxv et i xii et iii o, ille vero que in minimis gradus o xxiii et o xxxii et v li et i xvii et i li. Quoniam qui inquisitorum apotimatum prostafereses et minores sunt eis que secundum media apostimata et differunt ab ipsis gradibus o xvii et dimidio et o xxvi et dimidio et iiii i et i iii et dimidio et ii xvii. Istarum vero expositarum omnium differentiarum mediarum apostasium ad maximas sexagesima fuerit in Saturno quidem lii xxx, in Iove vero liiii l, in Marte autem liiii xxxiiii, in Venere lii lv, in Mercurio xlv xl, tot sexagesima apponemus in viii selidiis secundum unumquemque canonem ad versum continentem xxx graduum periodice longitudinis numerum. In apostimatibus vero maiores habentibus prostefereses penes eas que in mediis apostimatibus factas ipsarum superhabundantias similiter quidem in sexagesima rursum resolvemus, ut ad totas tamen superhabundantias eorum que in minimis apostimatibus et non adhuc earum que in maximis. Eodem vero modo et in aliis epochibus propter vi gradus medie longitudinis supputantes facta sexagesima totarum superhabundantiarum apponemus propriis numeris, eadem, ut diximus, ad sensum facta differentiarum epiboli, etsi non in ipsis maximis prostaferesibus epicicli progressiones fiant stellarum, sed in aliis eius partibus. Et est quinque canonum expositio talis.

⟨XI.11⟩ De eo quod secundum longitudinem quinque erraticarum compoto

Quando ergo propositorum negocium a periodicis motibus et longitudinis et anomalie apparentes cuiusque stellarum voluerimus progressiones cognoscere, faciemus compoti supputationem unam et eandem existentem in quinque stellis modo tali. Colligentes enim ex medii motus canonibus factas inquisitum tempus post omnes circulos planas epochas et longitudinis et anomalie eos quidem qui ab eo quod tunc apoquio excentrici usque mediam secundum longitudinem progressionem gradus, primum inferemus in proprium stelle canonem anomalie et adiacentia numero in tercio selidio eius que secundum longitudinem discretionis cum ea que in quarto selidio collecta sexagesimorum prostaferesi, si quidem expositus longitudinis numerus secundum primum fuerit selidium, auferemus quidem a longitudinis gradibus, apponemus vero eis qui anomalie; si vero secundum secundum] add. secundum F₁ apponemus eis qui longitudinis, auferemus vero ab eis qui anomalie, ut habeamus ambas progressiones discretas. Deinde eum quidem qui ab apoguio anomalie discretum numerum inferentes rursum in prima duo selidia adiacentem ipsi secundum viium selidium medie apostasis prostaferesim ascribemus. Ex principio vero per illatum omale longitudinis similiter inferentes in eosdem numeros, siquidem in primis et apoguioteris fuerit versibus eius qui secundum mediam apostasim, quod ex eis que in viii selidio sexagessimis fit manifestum, adiacentia ipsi in ipso viiio selidio, quotcumque fuerint, tot sumentes adiacentis differentie versui ascripte medie prostafereseos in maxime apostasis v selidio, facta aufferemus ab eis que ascripsimus. Si autem dicte longitudinis numerus in eis qui inferius et periguioteris fuerit versibus eius qui secundum mediam apostasim, adiacentia similiter ipsi sexagesima in viiio selidio, quotcumque fuerint, tot sumentes adiacentis differentie ascripte medie prostaferesi in minime aposis vii selidio facta apponemus eis qui ascripsimus, et collectos gradus discrete prostaphereseos, si quidem discretus anomalie numerus secundum primum fuerit selidium, apponemus discrete longitudinis gradibus, si vero secundum secundum, auferemus ab ipsis, et collectum graduum numerum dementes ab eo quod tunc apoguio stelle in apparentem ipsius progressionem incuremus.

Claudii Ptholomei mathematicorum sintaxeos liber nonus finit.