Ptolemaeus Arabus et Latinus

⟨XIII⟩

Claudii Ptolomei mathematicorum sintaxeos liber xiii^us incipit

Hec continentur in xiii^o mathematicorum Ptolomei.

Primum de ypothesibus in eas que secundum latitudinem progressionis quinque planetarum

Secundum de modo motionis earum que secundum ypotheses inclinationum et obliquationum

Tertium de ea que secundum unamquamque inclinationum et obliquationum quantitate

Quartum negotium canonicorum in particulares latitudinis progressus

Quintum expositio canoniorum eius qui secundum latitudinem negotii

Sextum compotus eius que secundum latitudinem recessionis quinque planetarum

Septimum de apparitionibus et absconsionibus quinque planetarum

Octavum quoniam consonant ypothesibus et proprie pertinentia apparitiones et absconsiones Veneris et Mercurii

Nonum ephodos in particulares in apparitionibus et absconsionibus a Sole distantias

Decimum expositio canoniorum continentium apparitiones et absconsiones quinque planetarum

Undecimum epilogus sintaxeos

⟨XIII.1⟩ De ypothesibus in eas que secundum latitudinem progressionis quinque planetarum

Delictis Delictis] relictis F₁ autem in eam que de quinque erraticis coordinationem adhuc duobus his et secundum latitudinem ipsorum facto ad eum qui per medias imagines animalium circulum progressu et eo quod secundum distantias ad Solem apparitionum et absconsionum negotio presumi quoque debentibus et hic latitudinariis cuiusque distantiis, quoniam quidem et penes hoc fiunt quedam sermone digne circa apparitiones et absconsiones differentie, preexponemus primum rursum, quanta communia circa circulorum ipsorum inclinationes supposuimus. Itaque propter duplam quidem apparere faciens unumquodque et eam que secundum latitudinem differentiam, quemadmodum et eam que secundum longitudinem anomaliam, eam quidem que ad partes zodiaci penes excentricum, eam vero que ad Solem penes epiciclum, inclinationes in omnibus supponimus et excentricum ad eius qui per media epipedum et epiciclum ad illud quod excentrici, nulla, ut diximus, propter hoc facta sermone digna permutatione circa eam que secundum longitudinem progressionem vel demonstrationes anomaliarum usque tantas inclinationes, ut in eis que deinceps ostendemus. At vero propter et per particulares observationes secundum unumquodque ipsorum, quando et qui discrete longitudinis et qui discrete anomalie numerus utrumque simul tetartimorio ad proximum distat, hic quidem boreali termino excentrci, ille vero a proprio apoguio, secundum ipsum qui circa illud quod per media epipedum apparere stellas, et excentricorum inclinationes circa zodiaci centrum, quemadmodum et in Luna et ad eas que per boreales vel australes terminos diametros, supponimus et eos qui epiciclorum ad in centrum zodiaci nuentes ipsorum diametros in quibus apparentia et apoguia et periguia considerantur.

Rurum vero in tribus quidem erraticis Saturno scilicet et Iove et Marte observavimus quoniam, quando quidem circiter apoguiotaton portionem excentrici contingerint ille secundum longitudinem ipsorum progressiones, borealiores plurimum semper eo qui per media apparent et plurimo tunc borealiores secundum eas que in periguiis epiciclorum progressiones eis que in apoguiis. Quando vero circiter terre propinquiorem portionem excentrici contingerint illi qui secundum longitudinem ipsorum progressus secundum contrarium ordinem, australiores apparent eo qui per media, et quoniam borealissimi termini excentricorum in Saturno quidem et Iove circiter principia sunt dodecatimorii Chellarum, in Marte vero circa extrema Cancri et ferme circiter ipsum apoguiotaton, quare ex his colligi quoniam excentroticorum quidem ipsorum hec quidem secundum dictas partes zodiaci ad arctos inclinantur, illa vero diametra equali ad meridiem, epiciclorum vero semper periguia in easdem excentricorum inclinationi, ad rectos angulos diametris eis que per apoguia ipsorum parallilis semper manentibus ei qui per media epipedo. In Venere autem et Mercurio observavimus quoniam, quando quidem secundum apoguia vel periguia excentrici contingerint ille que secundum longitudinem ipsorum progressiones, tunc ille quidem qui secundum periguia epiciclorum motus nulli secundum latitudinem differunt his que secundum apoguia, sed similiter vel borealiores eo qui per media sunt vel australiores, in Venere quidem semper borealiores, in Mercurio vero e contrario semper australiores.

Que vero secundum maximas distantias ipsorum progressiones a seinvicem quidem plurimo differunt, hoc est eoe ab esperiis, earum vero que secundum apoguia et periguia epiciclorum, hoc est eius que penes excentricum differentie in contrarium rursum equali consequentis et esperia maxima distantia, in Venere quidem secundum apoguion excentrici borealiori facta et secundum periguion australiori, in Mercurio vero e contrario secundum apoguion australiori et secundum periguion borealiori. Quando vero secundum coniunctos fuerint ille et que secundum longitudinem ipsarum discrete progressionis, tunc que quidem in utraque epiciclorum ab apoguiis vel periguiis tetartimorie distantie in eo quod per media epipedo contingunt ambe, que vero secundum periguia progressiones plurimo differunt ab eis que secundum apoguia, et in Venere quidem faciunt inclinationem in ea quidem que secundum ablativum semicirculum coniunctionem ad meridiem, in contrario vero ad arctos, in Mercurio vero contrarium rursus, in ea quidem que secundum ablativum semicirculum coniunctione ad arctos, in contrario vero ad meridiem, quare et ex hoc colligi quoniam excentricorum quidem inclinationes mote et ipse conrestituuntur periodis epiciclorum, circa coniunctiones quidem existentibus ipsis, in eodem epipedo facte ei qui per media, circa apoguia vero et periguia plurima, in Venere quidem borealiorem facientes epiciclum, in Mercurio vero australiorem. Epicicli autem duas faciunt differentias: has quidem per apparentia apoguia diametros plurimum inclinantes secundum conventus excentricorum, illas vero ad rectos ipsis plurimum obliquantes, – isto enim nobis nomine eadem inclinatio distinguatur –, secundum apoguia et periguia excentricorum, contrarium vero illas quidem in epipedo excentrici facientes secundum apoguia ipsius et periguia, istas vero in epipedo eius qui per media secundum dictos conventus.

⟨XIII.2⟩ De modo motionis earum que secundum ypotheses inclinationum et obliquationum

Colligitur ergo universale ypothesium huiusmodi quoniam excentrici quidem circuli quinque erraticorum inclinati contingunt ad illius qui per media epipedum circa centrum zodiaci. Verum in tribus quidem Saturno Iove Marte manent, quare eas secundum diametrum progressionem epiciclorum in contraria fieri latitudinis, in Venere autem et Mercurio transmutatis epiciclis in eandem latitudinem, in Venere quidem semper ad arctos, in Mercurio vero semper ad meridiem. Epiciclorum vero que quidem per apparentia apoguia diametri ab aliquo principio in epipedo excentrici facte transferuntur sub circellis adiacentibus, ut ita dicam, periguiis ipsorum terminis commensurabilibius quidem tante secundum latitudinem recessioni, rectis vero ad excentricorum epipeda et centra habentibus in ipsis, circumversis autem equaliter et consequenter eis que secundum longitudinem progressionibus ab altero eorum que secundum sectiones epipedorum et ipsorum et epiciclorum principio, ut ad arctos secundum ypothesim, simulque transducentibus epipeda epiciclorum secundum eam quidem que in primum tetartimorium conversione in borealissimum manifestum quoniam terminum, at vero secundum eam que deinceps in excentrici rursum epipedum, at secundum eam que in tertium in australissimum terminum, atque secundum eam que in reliquum restitutionem in principii epipedum; et quoniam illud quod huiusmodi afeseos et principum et restitutio in Saturno et Iove et Marte ab ea que secundum asscendentem coniunctione sectione constituuntur, in Venere vero a periguio excentrici, in Mercurio vero ab apoguio excentrici. Ille vero que ad rectos angulos diametri eis que ante dicte sunt in tribus quidem stellis manent, ut diximus, semper equidistantes eius qui per media epipedo vel nullo cura digno ad ipsum obliquante contingunt. In Mercurio autem et Venere et ipse facte rursum ab aliquo principio in eius qui per media epipedo transferuntur sub circellis adiacentibus consequentibus, ut ita dicam, ipsorum terminis conmensurabilibus quidem rursum tante secundum latitudinem recessioni, rectis vero ad eius qui per media epipedum et centra habentibus in diametris equidistantibus eius qui per media epipedo circumversus vero equali celeritate aliis ab altero eorum secundum sectiones epipedorum et ipsorum et epiciclorum principio, ut ad arctos rursum secundum ypothesim, simulque transducentibus ad vesperum terminos expositarum diametrorum secundum eundem ordinem manifestum quoniam ei qui ante ductus est et adhuc et in his similis afeseos et principium et restitio restitio] restitucio F₁, in Veneris quidem stella ab ea que secundum apositum semicirculum coniunctione constituitur, in Mercurio vero ab ea que circa ablativum. Oportet tamen circa dictos circellos, sub quibus translationes epiciclorum complentur, hic hic] hoc F₁ presumere, quoniam in duo quidem equalia dividuntur sub epipedis et ipsi, circa que translationem inclinationum fieri dicimus. Ita enim utique Solis equales in utrasque secundum latitudinem ipsorum progressiones constitui accidit. Eos tamen que ad equales motus circumlationes non circa proprium centrum habent completas, sed circa quoddam alteram alteram] alterum F₁ quod faciat eandem excentrotica ad circellum ei que secundum longitudinem stelle ad eum qui per media animalia circulum. Restitutionibus enim equitemporalibus subiacentibus et in zodiaco et in circello et adhuc eis que in utroque tetartimoriis progressionibus sibi invicem secundum apparens congruentibus, siquidem circa proprium centrum circulatio circelli fiat, propositum numquam continget, eis quidem secundum circellum progressionibus unumquodque tetartimoriorum equitemporali pertranseuntibus, eis autem que ad zodiacum epicicli consideratur nequaquam, propter secundum unumquodque subiacente excentrotica. Si vero circa positionem simille ei quod excentrici et tetartimoriorum coaptantia et zodiaci et parvuli circuli, secundum equalia tempora ille que inclinationum restitutionem pertransibunt. Et neque in tales ypothesium operosas putet intendens eorum que penes nos artificiorum dificultatum. Non enim competit humana divinis comparare, neque eas que de tantis fides a dissimillimis exemplis sumere, – quid enim difficilius semper semper] add. et eodem modo se habentibus F₁ ad illa que numquam et ab omni retinendis ad ea que nec a seipsis? –, verum temptare quidem ut est maxime simplitiores ypothesium coaptare eis qui in celo motibus. Si vero hoc non procedat, contigetes contigetes] contingentes F₁, si enim semel singula apparentium secundum consequens ypothesium salventur, quid utique adhuc mirabile aliquibus putetur posse tales contricationes celestium motibus contingere nulla existente penes ipsa natura prohibente, sed commensurabili procedere et recedere eis qui secundum naturam singulorum motibus, quamvis contrarii contingant, quare omnia per omnes simpliciter dispersiones attingere et apparere posse, non solum circa particulares circulos tale quidem procedere, sed et circa speras ipsas et axes circulationum.

Quare et ipsarum eam que in differentibus motibus contricationem et alternitatem in ordinatis quidem penes nos figuris videmus operosam et inventum difficillem ad motum in prohibitionem, in celesti vero nusquam nullo modo sub tali mixtione impedita. Magis autem et ipsum simplex celestium neque a penes nos ita se habere putatis competit iudicare, quando neque in nobis idem omnibus similiter est simplex. Ita enim considerantibus nichil videbitur eorum que secundum celum fiunt simplex, neque ipsum prime lationis inpermutabile, quoniam et hoc ipsum omne tempus similiter se habere in nobis est non difficile, sed omnino impossibile, ab earum vero que in ipso celo naturarum et motuum inpermutabilitate. Ita enim utique omnes apparebunt simplices et magis quam penes nos ita habere putata, nullo labore neque difficultate aliqua circa periodos ipsorum subintelligi potentibus.

⟨XIII.3⟩ De ea que secundum unamquamque inclinationum et obliquationum quantitate

Itaque universaliter quidem positionem et ordinem inclinationis circulorum ab his utique quis supputet, particulares vero in unaquaque stellarum quantitates periferiarum, quas inclinationes deprehendunt per polos inclinati et recti ad eius qui per media epipedum scripti maximi circuli, ad quem ille que secundum latitudinem progressiones considerantur. In Venere quidem et Mercurio tribuunt facile investigabiles ille que secundum expositas positiones apparent latitudinis progressiones. Nam quando quidem secundum apoguia et periguia excentricorum illi qui secundum longitudinem ipsorum fuerint motus, circa periguia quidem et apoguia epiciclorum progredientes stelle, ut diximus, a propinquis observationibus epiboli nobis facta, equali borealiores vel australiores apparent eo qui per media. Que quidem Veneris sexta maxime unius gradus semper borealior, que vero Mercurii dimidio et quarte quarte] quarta F₁ parte semper australior, quare ex his et excentricorum circulorum inclinationes utriusque tantas fieri. Circa vero maximas Solis distantias ambo v gradibus secundum mediam rationem borealiores vel australiores apparent contrariis maximis distantiis, quoniam quidem que quidem Veneris indifferenti v gradibus, minoribus quidem in apoguio excentrici, pluribus in periguio apparent dictam secundum latitudinem contrarietatem faciens, qui vero Mercurii dimidio maxime unius gradus. Quare eas que in altera eorum que secundum excentroticos epipedorum obliquationes epicicli secundum mediam rationem duo et dimidium gradus subtendunt circuli qui ad rectos zodiaco, a quibus et quantitates angulorum factorum in epicicli obliquatione ad excentricorum epipeda sumuntur, quemadmodum in eis que deinceps de ipsis demonstrata sunt erit manifestum, ut non secundum presens eam que de inclinationibus communiter in quinque planetis rationem. Quando vero secundum coniunctiones et medias ad proximum distantias illi qui secundum longitudinem discreti motus fuerint, que quidem Veneris circa apoguion quidem epicicli progressionem faciens borealior et australior apparet eo qui per media gradu i, at vero circa periguion gradibus vi et iii^a ad proximum, quare ex his et inclinationem epicicli ii dimidium gradus deprehendere per polos ipsius ipsius] add. secundum F₁ quem diximus modum scripti circuli. Tantos enim reperimus ex ea que secundum epiciclum anomalia circa media apostimatum secundum apoguion quidem epicicli ypothenusas ad visum angulum gradus unius et sexagesimorum ii, secundum periguion vero graduum vi et sexagesimorum xxii. Que vero Mercurii circa apoguion quidem epicicli progressionem faciens, ut ex proximis apparitionibus utique quis supputet, australior et borealior fit eo qui per media gradu i et dimidio et quarta, circa periguion vero gradibus iiii ad proximum, quare ex hoc scilicet et inclinationem epicicli graduum vi et iiii^a constitui. Tantos enim rursus reperimus ex ea que secundum epiciclum anomalia circiter maximarum inclinationum apostimata, hoc est quando discreta longitudo tetartimorio distat ab apoguio, secundum apoguion quidem epicicli subtendentes ad visum angulum gradum i et sexagesima xlvi, at vero secundum periguion gradus iiii et sexagesima v. In reliquis autem Saturno, Iove, et Marte, hinc quidem non utique quis superaddat quantitatibus inclinationum, mixtis ambabus semper et ea que secundum secundum] add. excentricum et ea que secundum F₁ epiciclum completur. Ab eis autem que secundum et periguia et apoguia excentricorum et epiciclorum observantur rursum secundum latitudinem progressionibus segregamus utraque inclinationum modo tali.

Esto enim in eo quod ad rectos ei quidem per media animalia epipedo ad ipsum communis sectio epipedi quidem eius qui per media recta AB, epipedi vero excentrici recta GD, atque E punctum centrum zodiaci, in communi sectione epipedorum, scribaturque que circa G apoguion excentrici et circa D periguion in subiacenti epipedo equales circuli ZITK LMNX, ut qui per polos epiciclorum, in quibus inclinentur epiciclorum epipeda, et in ea que est IGK et ea que MDX ad equales manifestum quoniam qui ad puncta G et D angulos, et copulentur ab E centro zodiaci, in quo est visus, in apoguia et periguia epiciclorum recte, in apoguia quidem EI et EM, in periguia vero EK et EX, et punctis quidem K et X acronictas manifestum quoniam progressiones continentibus, at vero I et M coniunctionales.

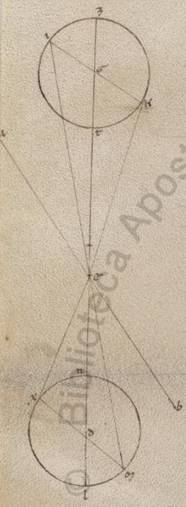In Martis quidem stella sumpsimus factas secundum latitudinem progressiones et circa eas que secundum apoguion excentrici constitute sunt acronictas, hoc est que circa K punctum epicicli, et circa eas que secundum periguion excentrici, hoc est circa X punctum epicicli, propter valde sensibilem ipsorum esse differentiam. Distat autem in eis que circa apoguion acronictis ad arctos ab eo qui per media gradibus iiii iii, in eis autem que secundum periguion ad meridiem gradibus vii ad proximum, quare et AEK angulum constitui talium iiii iii, qualium sunt iiii recti ccclx, at BEX angulum eorumdem vii.

Talibus autem subiacentibus, reperimus sub excentrici inclinatione contentum angulum, hoc est AEG, et eum qui sub ea que epicicli, hoc est IGZ, modo tali. Quoniam enim ex eis quas demonstravimus Martis anomaliis facile intellectu est quoniam subtendentis ad visum angulis sub equalibus et ad periguia epicicli periferiis que circa eas que secundum apoguion excentrici progressiones ad eas que secundum periguion proportionem habent quam vi vi] v F₁ ad proximum ad ix. Equales autem TK et NX periferie, proporcio utique erit et GEK anguli ad DEX que v ad ix. Quare, quoniam quidem dati sunt AEK et BEX anguli, anguli] corr. ex angulus V₃ data est autem et GEK anguli ad DEX proporcio, et equalis est AEG angulus angulo BED, si quanta pars est superhabundantiam superhabundantiam] superhabundantia F₁ totarum quantitarum superhabundantie proporcionum, tantam partem cuiusque proporcionum sumemus, habebimus habebimus] add. eam F₁ que sub propriam proportionem quantitatum. Ostenditur enim hoc per limatium quoddam arizmeticum. Quoniam ergo quantitates sunt iiii iii vii, superhabundantia vero istorum bisse, proportio vero eorum que sunt v ad ix et superhabundantia istorum iiii. At vero ii bisse eorum que sunt iiii pars sunt dimira, tantam sumentes partem eorum que sunt v et eorum que sunt ix, GEK angulum habebimus iii iii^a graduum atque DEX eorumdem vi, reliqui vero consequenter utrumque eorum qui sunt AEG et BED inclinationis excentrici gradus unius, ex his autem et TK periferiam epicicli inclinationis graduum ii iiii^a propter propter] corr. ex per V₃ tantas secundum anomalie canonem contineri ad proximum inventas quantitates GEK et DEX angulorum.

In Saturno autem et Iove, quoniam quidem ad sensum indifferentes reperimus circa apoguias excentricorum portiones factas progressiones ab eis que circa periguia et secundum diametrum secundum utrumque modum ex earum circa apoguia epiciclorum ad eas que circa periguia conparatione investigavimus propositum. Distant autem, ut ex particularibus observationibus factum est nobis facile intelligibille, in eis quidem que circa apparitiones et absconsiones progressionibus plurimum ad arctos et meridiem que quidem Saturni ii gradibus ad proximum, que vero Iovis i, in eis autem que circa acronictois que quidem Saturni circa tres gradus, que vero Iovis circa ii, quoniam quidem ergo et ex istorum anomalia fit manifestum quoniam, subtentis ad visum angulis sub equalibus circa apoguia et periguia epicicli periferiis, sub eis que circa apoguia constituti proporcionem habent ad eos qui sub circa periguia factis in Saturno quidem quam xviii ad xxiii, in Iove vero xxix ad xliii. Equales vero ZI et TK epicicli periferie, proporcio erit et ZEI anguli ad ZEK, in Saturno quidem que xviii ad xxiii, in Iove vero que ad xxix ad xliii. Verum et IEK angulus superhabundantia existens duarum secundum latitudinem progressionum in ambabus stellis relinquitur gradus i. Secundum expositas ergo proportiones diviso i gradu, habebimus et ZEI angulum in Saturno quidem sexagesimorum xxvi, in Iove autem xxiiii, atque ZEK angulus in Saturno sexagesimorum xxxiiii, in Iove xxxvi. Quare et reliquus AEG inclinationis excentrici reliquetur, in Saturno quidem graduum ii xxvi, in Iove vero gradus i xxiiii, pro quibus propter commensurabilius cousi sumus ii dimidio i et dimidio totis. Autem hinc et TK periferia inclinationis epiciclorum colligitur in Saturno iiii dimidii, in Iove ii dimidii. Tante enim secundum utrumque in anomalie canonibus continent rursum ad proximum inventas quantitates ZEI et ZEK angulorum. Quod oportebat ostendere.

⟨XIII.4⟩ Negotium canoniorum in particulares latitudinis progressiones

Ex his quidem nobis constituantur universales quantitates maximarum inclinationum et excentricorum et epiclorum. Ut autem et particularium distantiarum latitudinarias progressiones quaque vice possimus prompte invenire, negotiati sumus negotia negotia] canonia F₁ quinque erraticorum, versuum quod quod] quidem F₁ unumquodque quot et ea que anomalie, selidiorum autem v. Istorum autem prima quidem duo continent numeros, quemadmodum et in illis, tertia vero pertinentes secundum latitudinem distantias ab eo qui per media particularibus epiciclorum portionibus in ipsis maximis inclinationibus, quod quidem Veneris et quod Mercurii eis que secundum coniunctiones excentricorum, que vero reliquarum iii stellarum eis que circa boreales terminos excentricorum. In his autem et iiii selidia continebunt eas que circa australes fines excentricorum similes adiectiones, consupputate in tribus istis et ipsorum excentricorum et ad arctos et ad meridiem plurima a recessione. Factum est autem nobis negocium proportionum in Venere quidem et Mercurio per unum rursum theorema modo tali.

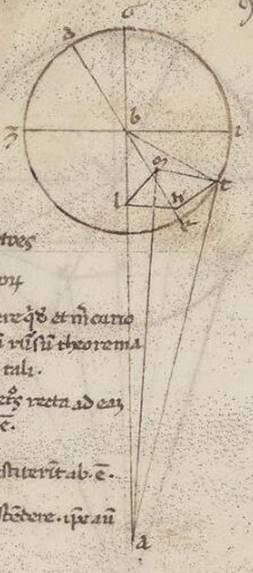Esto enim in eo quod ad rectos angulos angulos] add. ei F₁ quod per media animalia epipedo ABG quidem communis sectio ad ipsum epipedi zodiaci, DBE DBE] add. vero F₁ communis sectio epipedi epicicli, et esto zodiaci quidem centrum A, epicicli vero B, atque AB eorum que circa maximas inclinationes apostimatum epiciclorum; et scripto circa B punctum DZEI epiciclo, copuletur ZBI diametros recta ad eam que est DE. Subiaceat autem et epicicli epipedum subiacens rectum, quare ei que est DE ad rectos angulos ductarum in ipso alias quidem omnes equidistantes esse eius qui per media epipedo, ZI vero solam in ipso; et proponatur, datis et proportione eius que est AB ad BE et quantitate inclinationis, hoc est ABE angulo, invenire eas que secundum latitudines latitudines] latitudinem F₁ stellarum progressiones, quando exempli causa destiterint ab E periguio epicicli xlv gradibus, qualium est epiciclus ccclx, quoniam quidem et factas differentias eis que secundum longitudinem progressionibus propter huiusmodi inclinationes preoptamus coostendere, ipse autem circa eas que inter E periguium et ZI progressuum plurimum deberet deberet] debent F₁ differre, propter eas que in dictis punctis easdem fieri et seorsum inclinatione completis. 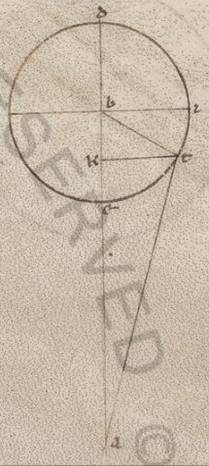Assumatur autem periferia dictorum xlv graduum ET, et catheti trahantur in BE quidem TK. In eius autem qui per media epipedum LK et TM copulentur que TB et LM et AT, quoniam LKTM quadrilaterum est et orthogonium et parallilogramum, propter KT equidistantem esse eius qui per media epipedo, et quoniam eam quidem que secundum longitudinem prostaferesim LAM angulus continet, eam vero que secundum latitudinem progressionem ille qui est TAM, ALM et AMT angulis rectis et ipsis constitutis, propter et rectam AM in eius qui per media epipedo cadere hinc utique erit manifestum. Quante vero inquisite progressionis colligantur secundum utramque predictarum stellarum, iam ostendendum prius in stella Veneris. Quoniam ergo ET periferia talium est xlv, qualium epiciclus ccclx, erit utique EBT angulus ad centrum existens epicicli, qualium sunt iiii recti ccclx, talium xlv, qualium vero ii recti ccclx, talium xc. Quare et utraque earum que super BK et KT periferiarum talium est xc, qualium BTK orthogonium circulus ccclx. Et earum ergo que sub ipsis rectarum utraque talium est lxxxiiii lii, qualium est BT ypothenusa cxx. Quare et qualium est BT que ex centro epicicli xliii x atque AB medii apostimatis lx, propter circa hoc maxime maximam inclinationem fieri epicicli, talium et utraque BK et KT rectarum erit xxx xxxii. Rursum quoniam ABE angulus inclinationis, qualium sunt iiii recti ccclx, talium subiacet ii xxx, qualium vero ii recti ccclx, talium v, erit utique et que super LK periferia talium v, qualium est qui circa BLK orthogonium circulus ccclx, et que super BL reliquorum in semicirculum clxxv. Et earum ergo que sub ipsis rectarum KL quidem talium erunt v xiiii, qualium BK ypothensa cxx, atque BL eorumdem cxix liii. Quare et qualium est BK ypothenusa xxx xxxii atque AB recta lx et KL erit i xx atque BL eorumdem xxx xxx atque AL reliquorum xxix xxx. Eorumdem vero est et LM equalis existens ei que est KT recta xxx xxxii, quare et AM ypothenusa colligi eorumdem xlii xvii, et qualium est ergo AM ypothenusa cxx, talium et LM erit lxxxvi xix atque angulus LAM eius que tunc secundum longitudinem prostafereseos, qualium sunt ii^o recti ccclx, talium xcii o, qualium vero iiii recti ccclx, talium xlvi o. Similiter autem quoniam, et qualium est AM recta xlii xxvii, talium est TM equalis existens ei que est KL recta i xx, et que ab ipsis composita faciunt quod ab AT, erit et AT longitudine eorumdem xlii xxix. Et qualium est ergo ypothenusa AT cxx, talium TM erit iii xxxvi atque TAM angulus eiusque secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium iii xxxvi, qualium vero iiii recti ccclx, talium i xlviii, que et apposuimus in iii selidio stelle Veneris secundum versum canonis continentem cxxxv graduum numerum.

Causa vero comparandi factam differentiam eius que secundum longitudinem prostafereseos adiaceat simul descriptio inclinatum habens epiciclum. Et quoniam ostendimus utramque BK et KT rectarum talium xxx xxxii, qualium est AB recta lx, quare et AK fieri reliquorum xxix et xxviii, quod autem ab ipsa et quod ab xxix composita faciunt quod ab AT, erit et AT longitudine eorumdem xlii xxvi, et qualium est ergo AT ypothenusa cxx, talium et KT erit lxxxvi xxi atque TAK angulus eius que secundum longitudinem prostafereseos, qualium sunt ii recti ccclx, talium xcii iii, quare vero iiii recti ccclx, talium xlvi ii ad proximum. Ostendebatur autem in inclinatione eorumdem xlvi, deficiebat ergo ea que secundum longitudinem prostaferesis propter inclinationem epicicli unius gradus sexagesimis ii. Quod oportebat demonstrare.

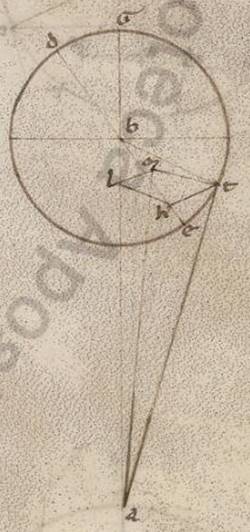Rursum ut eas que in Mercurio progressiones ostendamus, adiaceat similis ei que ante istam descriptio, ET periferia eorumdem subiacente xlv graduum, quare et BK et KT utramque talium rursum colligi lxxxiiii lii, qualium est BT ypothenusa cxx, et qualium ergo est BT que ex centro epicicli xxii xxx atque AB recta eius quod secundum maximas inclinationes apostimatis lvi xl, – hec enim omnia nobis predemonstrata sunt –, talium et utraque earum que sunt BK et KT erit xv lv. Rursum quoniam ABE angulus inclinationis epicicli, qualium sunt iiii recti ccclx, talium subiacet vi xv, qualium vero sunt ii recti ccclx, talium xii xxx, erit utique et que super LK periferia talium xii xxx, qualium qui circa BKL orthogonium circulus ccclx, et que super BL reliquorum in semicirculum clxvii xxx. Et earum ergo que sub ipsis rectarum KL quidem talium est xiii iiii, qualium BK ypothenusa cxx, atque BL eorumdem cxix xvii. Quare et qualium BK ostensa est xv lv atque AB subiacet lvi xl, talium et KL erit i xliiii atque BL similiter xv xlix, reliqua AL eorumdem xl lix li. Est autem et LM equalis existens ei que est KT eorumdem xv lv, et quoniam quod ab AL cum eo quod ab LM facit quod ab AM, habebimus et ipsam longitudine talium xliii l, qualium est LM recta xv lv. Et qualium est ergo AM ypothenusa cxx, talium et LM erit xliii xxxiiii atque LAM angulus eius que secundum longitudinem prostafereseos, qualium sunt ii recti ccclx, talium xlii xxxiiii, qualium vero iiii recti ccclx, talium xxi xvii. Similiter autem quoniam, qualium est AM recta xliii l, talium et TM equalis existens ei que est KL fit i xliiii, et que ab ipsis composita faciunt quod ab AT, istam habebimus longitudine eorumdem xliii lii. Et qualium est ergo AT ypothenua cxx, talium et TM erit xliiii i atque TAM angulus eius que secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium xliiii xliiii] iiii F₁ xxxii, qualium vero iiii recti ccclx, talium ii xvi, que et apponemus rursum in iii selidio Mercurii canonis secundum eundem versum, hoc est continentem cxxxv graduum numerum.

Rursum et comparationis prostafereseos causa adiaceat et seorsum inclinatione descriptio, et quoniam ostensum est quoniam, qualium AB recta lvi xl, talium est utraque TK et KB rectarum xv lv, reliquaque AK eorumdem manifestum quoniam xl xlv, et quod ab AK cum eo quod ab KT facit quod ab AT, longitudine ergo et ipsam habebimus talium xliii xlv, qualium erat et TK recta xv lv. Et qualium est ergo AT recta ypothenusa cxx, talium et TK erit xliii xxxix, atque KAT angulus eius que secundum longitudinem prostafereseos, qualium sunt ii recti ccclx, talium xlii xl, qualium vero iiii recti ccclx, talium xxi xx. Ostendebatur autem inclinatione eorumdem xxi xvii. Defitiebat ergo et hic ea que secundum longitudinem prostaferesis propter inclinationem epicicli unius gradus sexagesimis iii. Quod oportebat ostendere.

⟨XIII.5⟩ Expositio canoniorum eiusque secundum latitudinem negotii

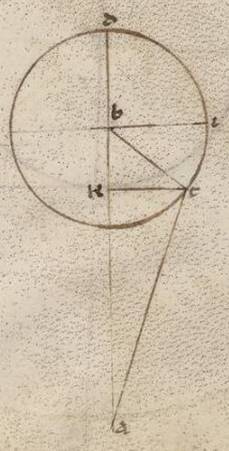Itaque harum duarum stellarum eas que in maximis inclinationibus secundum latitudinem progressiones exposito modo negotiati sumus, propter constituere ipsas, quando et excentricus in eodem epipedo contingit ei qui per media animalia, eas autem que reliquarum trium stellarum per alterum a descriptione theorema, quoniam ergo qui secundum maximas excenticorum inclinationes et maxime epiciclorum constituuntur, et previationis utique erunt erunt] erit F₁ coinvestigatas habere ex ambabus inclinationibus collectas latitudinarias progressiones.

Esto enim rursum in eo quod ad rectos angulos epipedo ei qui per media animalia communis ad ipsum sectio epipedi eius qui per media recta AB, epipedi vero excentrici AG, epipedi vero epicicli DGE; subiaceatque zodiaci centrum A, epicicli vero G, et scribatur circa G punctum DZEI epiciclus ita rursum, quare ei que est DE ad rectos angulos ductarum, ZGI quidem diametrum in excentrici quidem esse epipedo, ei autem quod eius qui per media equidistantem, reliquas autem equidistantes ambobus dictis epipedis; assumaturque ET similiter periferia eorumdem subiacens xlv graduum, et ab T secundum stella puncto catheto tracta TK et adhuc a punctis T et K in eius qui per media epipedum eis que super KB et TL, copulentur recte BL et AL, et AT proportionem quem proportionem quem] proponaturque F₁ invenire et eam que secundum longitudinem prostaferesim contentam sub BAL angulo et eam que secundum latitudinem progressionem 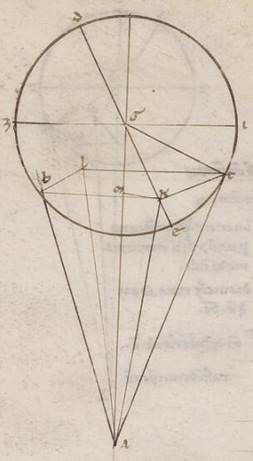contentam sub LAT angulo. Trahatur ergo in AG a puncta puncta] puncto F₁ K cathecus KM, et copulentur GT et AK et AT; subiaceatque rursum per preostensa earum que sunt GK et KT utraque talium lxxxiiii lii, qualium est GT ypothenusa cxx. Quoniam ergo Saturni primum ea que ex centro epicicli epicicli] add. demonstrata est F₁ talium vi xxx, qualium est medium apostima lx, erit et utraque GK et KT rectarum talium iiii xxxvi qualium est GT ypothenusa vi xxx. Et quoniam AGE angulus inclinationis epicicli subiaceat, qualium sunt iiii recti ccclx, talium iiii xxx qualium vero duo recti ccclx, talium ix, erit utique que super KM periferia talium ix, qualium est qui circa GKM orthogonium circulus ccclx, et que super GM reliquorum in semicirculum clxxi. Et earum ergo que sub ipsis rectarum KM quidem erit talium ix xxv, qualium est GK ypothenusa cxx, atque GM eorumdem cxix xxxviii, et qualium est ergo GK recta iiii xxxvi, talium et KM erit o xxii et GM similiter iiii xxxv. Verum in ea que secundum apoguioteron semicirculum maxima inclinatione AG eius quod circa principia Chellarum apostimatis ex preexpositis in anomaliis theorematibus colligitur eorumdem lxii x, quare et reliquam AM talium relinqui lvii xxxv, qualium est MK recta o xxii, propter hoc autem et AK ypothenusam eorumdem lvii xxxv. Et qualium est ergo AK ypothenusa cxx, talium et KM erit o xlvi atque KAM angulus talium o xliiii, qualium sunt ii recti ccclx. Subiacet autem et BAG inclinationis excentrici, qualium sunt iiii recti ccclx, talium ii xxx, qualium vero ii recti ccclx, talium v. Et totus ergo BAK angulus talium est v xliiii, qualium ii recti ccclx. Quare et que super BK periferia talium v xliiii, qualium qui circa BAK orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxiiii xvi et earum ergo que sub ipsis rectarum BK quidem talium vi o, qualium est AK ypothenusa cxx, atque AB cxix li. Quare et qualium est AK recta lvii xxxv, talium BK erit ii liii, et AB similiter lvii xxxi. Eorumdem vero et BL equalis existens ei que est KT fit iiii xxxvi. Et quoniam quod ab AB cum eo quod ab BL facit quod ab AL, et istam habebimus longitudine eorumdem lvii xlii. Similiter autem quoniam et LT equalis existens ei que BK fit eorumdem ii liii, quod autem ab AL cum eo quod ab LT facit quod ab AT longitudine, et istam habebimus eorumdem lvii xlvi. Quare et qualium est AT ypothenusa cxx, talium et TL erit v lix atque TAL angulus eius que secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium v xliiii, qualium vero iiii recti ccclx, talium ii lii, que et apponemus in tertio selidio stelle Saturni secundum canonii cxxxv. In ea vero que secundum periguioteron semicirculum maxima inclinatione, quoniam quidem AG eius quod secundum principia Arietis apostimatis talium colligitur lvii xl, qualium KM ostensa est o xxii atque GM similiter iiii xxxv, et propter hoc reliqua quidem AM fit liii v, eorumdem vero et AK ypothenusa, propter indifferenti maius esse quam AM recta, liii v. Et qualium est ergo AK ypothenusa cxx; talium et KM erit o l et KAM angulus talium o xlviii, qualium sunt ii recti ccclx, eorumdem vero subiacet et BAG angulus v. Et totus ergo BAK angulus talium est v xlviii, qualium sunt ii recti ccclx. Quare et que super BK periferia talium est v xlviii, qualium qui circa BAK orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxiiii xii. Et earum ergo que sub ipsis rectarum BK fit talium vi iiii, qualium est AK subtendens cxx, atque AB eorumdem cxix li. Quare et qualium est AK recta liii v, talium et BK ii xli, at vero AB similiter liii i. Et quoniam quod ab AB cum eo quod ab BL facit quod ab AL, eorumdem vero ostensa est et BL iiii xxxvi, habebimus et AL longitudine eorumdem liii xiii, et qualium est ergo AL ypothenusa cxx, talium et BL erit x xxiii, atque BAL angulus eius que secundum longitudinem prostafereseos, qualium quidem sunt ii recti ccclx, talium ix lvi, qualium vero iiiior recti ccclx, talium iiii lviii. Rursum quoniam, qualium est AL recta liii xiii, talium et TL equalis existens ei que est KL fiet ii xli, et que ab ipsis composita faciunt quod ab AT, et et​] add. s. l. V₃ istam habebimus longitudinem eorumdem liii xvii. Et qualium est ergo AT ypothenusa cxx, talium et TL erit vi iii, atque TAL angulus eius que secundum latitudinem recessionis, qualium quidem sunt ii recti ccclx, talium v xlvi, qualium vero iiii recti ccclx, talium ii liii, que et ipsa apponemus in iiii selidio canonii secundum cxxv graduum.

Ut ergo et comparationem earum que secundum longitudinem prostaferesium in periguiotera inclinatione faciamus, describatur rursum nullam inclinationem habens figura. Et quoniam, qualium est recta AG eius quod tunc apostimatis lvii xl, talium utraque quidem earum que sunt GK et KT subiacet iiii xxxvi, reliqua vero AK eorumdem liii iiii, quod autem ab ipsa cum eo quod ab KT facit quod ab AT, habebimus et AT longitudine liii xvi. Quare et qualium est AT ypothenusa cxx, talium et KT erit x xxii, atque TAK angulus eius que secundum longitudinem prostafereseos, qualium quidem sunt ii recti ccclx, talium ix liiii, qualium vero iiii recti ccclx, talium iiii lvii. Demonstrabatur autem in inclinationibus eorum iiii lviii, adimpleta est ergo penes utrasque inclinationes ea que secundum longitudinem prosteferesis sexagesimo i. Quod oportebat invenire.

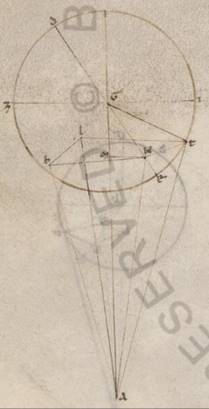Rursum adiaceat primum in inclinationibus descriptio continens in stella Iovis demonstratas rationes, quare, qualium est GT que ex centro epicicli xi xxx, talium utraque earum que sunt GK et KT colligi viii viii. Quoniam ergo AGE angulus eius que epicicli inclinationis, qualium sunt iiii recti ccclx, talium subiacet ii xxx, qualium vero ii recti ccclx, talium v, erit utique et que super KM periferia talium v, qualium qui circa GKM orthogonium circulus ccclx, et que super GM reliquorum in semicirculum clxxv. Et earum ergo que sub ipsis rectarum KM talium est v xiiii, qualium GK ypothenusa cxx, atque GM eorumdem cix liii. Quare et qualium est GK recta viii viii atque AG eius quod circa principia chelarum apostimatis lxii xxx, talium et KM erit o xxi atque GM similiter viii viii, reliqua vero MA recta liiii xxii, propter hoc autem et AK ypothenusa, quoniam indifferenti maior est ea que est MA, eorum liiii xxii, et qualium est ergo ypothenusa cxx, talium et KM erit o xlvi, atque KAM angulus talium o xliiii, qualium ii recti ccclx. Subiacet autem et BAG angulus eius qui excentrici inclinationis, qualium sunt iiii recti ccclx, talium i xxx, qualium vero ii recti ccclx, talium iii. Et totus ergo BAK angulus talium est iii xliiii, qualium ii recti ccclx. Quare et que super KB periferia talium est iii xliiii, qualium qui circa BAK orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxvi xvi. Et earum ergo que sub ipsis rectarum KB talium est iii liiii, qualium AK ypothenusa cxx, atque AB eorumdem cxix lvi. Quare et qualium est AK recta liiii xxii, talium et KB erit i xliiii, atque AB similiter liiii xx, eorumdem vero est per predemonstrata et BL recta viii viii. Et quoniam que ab ipsis composita faciunt quod ab AL, habebimus ipsam longitudine eorumdem liiii lvi. Similiter autem quoniam et LT eorumdem est i xlvi, que vero ab ipsis composita faciunt quod ab AT, et istam habebimus eorumdem liiii lviii. Quare et qualium est AT ypothenusa cxx, talium et LT erit iii lii, atque TAL angulus eius que secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium iii lii, qualium vero iiii recti ccclx, talium i li, que et apponemus tertio selidio canonii stelle Iovis secundum cxxxv gradus.

Similiter autem quoniam rursum AG eius quod secundum principia Arietis apostimatis talium colligitur lvii xxx, qualium ostendemus KM rectam o xxi atque GM similiter viii viii, quare et reliquam AM, hoc est AK, indifferenti maiorem existentem eorumdem relinqui xlix xxii. Propter hoc autem, et qualium est AK ypothenusa cxx, talium et KM fit o li, li] corr. ex xli V₃ atque KAM angulus talium o xlix, qualium sunt ii recti ccclx, colligetur et totus BAK angulus eorumdem iii xlix. Quare et que super KB periferia talium est iii xlix, qualium qui circa AKB orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxvi xi. Et earum ergo que sub ipsis rectarum BK talium est iii lix, qualium AK ypothenusa cxx, atque AB eorumdem cxix lvi. Quare et qualium est AK recta xlix xxii, talium et KB erit i xxxix, atque AB similiter xlix xx. Propter hoc autem quoniam BL eorumdem est lviii, que vero ab eis composita faciunt quod ab AL, et istam habebimus longitudinem l o. Quare et qualium est AL ypothenusa cxx, talium et BL erit xix xxxi, atque BAL angulus eius que secundum longitudinem prostafereseos, qualium sunt ii recti ccclx, talium xviii xliiii, qualium vero iiii recti ccclx, talium ix xxii. Rursum quoniam qualium est AL recta l o, talium et TL fit i xxx et que ab ipsis composita faciunt quod ab AT, et istam habebimus longitudine eorumdem l et sexagesimis ii, et qualium est ergo AT ypothenusa cxx, talium et LT erit iii lvii, atque TAL angulus eius que secundum latitudinem distantie, qualium sunt ii recti ccclx, talium iii xlvi, qualium vero iiii recti ccclx, talium i liii, que et apponemus in iiii selidio canonii secundum eosdem cxxxv gradus.

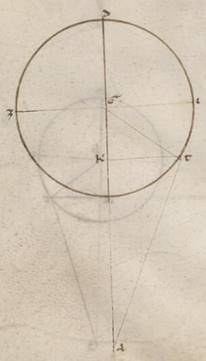Et comparationis vero earum que secundum longitudinem prostaferesium causa adiaceat seorsum inclinationum descriptio. Et quoniam secundum expositum apostima, qualium est utraque TK et GK rectarum viii viii, talium et AG est tota lvii xxxi, reliquaque AK eorumdem xlix xxii, quod autem ab ipsa cum eo quod ab KT facit quod ab AT, et istam habebimus longitudine eorumdem viii et sexagesimis ii. Quare et qualium est AT ypothenusa cxx, talium et TK erit xix xxxviii, atque TAK angulus eius que secundum longitudinem prostafereseos, qualium quidem sunt ii recti ccclx, talium xviii xlii, qualium vero iiii recti ccclx, talium ix xxi. Ostendebatur autem in inclinationibus eorumdem ix xxii, adimpleta est ergo rursum penes utrasque inclinationes ea que secundum longitudinem prostaferesis uno solo sexagesimo. Quod oportebat demonstrare.

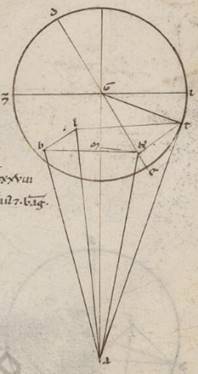Deinceps autem et Martis rationum causa adiaceat primum inclinationum descriptio et colligatur rursum utraque earum que sunt GK et KT talium xxvii lvi, qualium est GT que ex centro epicicli xxxix xxx. Quoniam ergo AGE angulus eius que epicicli inclinationis subiacet, qualium sunt iiii recti ccclx, talium ii xv, qualium vero ii recti ccclx, talium iiii xxx, erit utique et que super KM periferia talium iiii xxx, qualium qui circa GMK orthogonium circulus ccclx, que vero super GM reliquarum in semicirculum clxxv et xxx. Et earum ergo que sub ipsis rectarum KM talium iiii xliii, qualium est GK ypothenusa cxx, atque GM eorumdem cxix liiii. Quare et qualium est GK recta xxvii lvi atque AG maximi apostimatis lxvi, talium et KM erit iiii vi, atque GM similiter xxvii liiii atque AM reliquorum xxxviii vi. Propter hoc autem et AK ypothenusa eorumdem xxxviii vii. Et qualium est ergo AK ypothenusa cxx, talium et KM erit iii xxviii, atque KAM angulus talium iii xix, qualium sunt duo recti ccclx. Subiacet autem et BAG angulus eius que excentrici inclinationis, qualium sunt iiii recti ccclx, talium i, qualium vero ii recti ccclx, talium ii. Et totus ergo BAK angulus talium colligitur v xix, qualium vero sunt ii recti ccclx. Quare et que super KB talium est v xix, qualium qui circa BAK orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxiiii xli. Et earum ergo que sub ipsis rectarum BK quidem talium est v xxxiiii, qualium AK ypothenusa cxx, atque AB eorumdem cxix lii. Quare et qualium est AK recta xxxviii vii, talium et KB erit i xlvi atque AB similiter xxxviii v, eorumdem vero est et BL recta xxvii lvi. Et quoniam quod ab AB cum eo quod ab BL facit quod ab AL, et istam habebimus longitudine xlvii xiiii. Similiter autem quoniam TL eorumdem i xlvi, quod autem ab AL cum eo quod ab LT facit quod ab AT, et istam habebimus longitudine eorumdem xlvii xvi. Quare et qualium est AT ypothenusa cxx, talium et TL erit iiii xxix, atque TAL angulus eius que secundum latitudinem distantie, qualium sunt ii recti ccclx, talium iiii xviii, qualium vero iiii recti ccclx, talium ii ix, que et apponemus in iii selidio canonii Martis secundum cxxxv gradus.

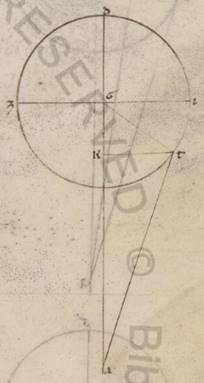Similiter autem in eis que secundum minimum apostima inclinationibus, quoniam talium est AG recta liiii, qualium KM ostensa est i vi atque GM similiter xxvii liiii, quare et AM relinqui reliquorum xxvi vi atque AK ypothenusa colligi eorumdem xxvi vii, et qualium est AK ypothenusa cxx, talium et KM erit v iii, atque KAM angulus talium iiii xlix, qualium sunt ii recti ccclx, propter hoc autem et totus BAK eorumdem vi xlix. Quare et que super BK periferia talium est vi xlix, qualium qui circa ABK orthogonium circulus ccclx, et que super AB reliquorum in semicirculum clxxiii xi. Et eorum ergo que sub ipsis rectarum BK quidem erit talium vii viii, qualium est AK ypothenusa cxx, atque AB eorumdem cxix xlvii. Quare et qualium est AK recta xxvi vii, talium et BK erit i xxxiii atque AB similiter xxvi iiii, eorumdem vero est rursum et BL recta xxvii lvi. Et quoniam quod ab AB cum eo quod ab BL facit quod ab AL, et istam habebimus longitudine xxxviii xii. Quare et qualium est AL ypothenusa cxx, talium et BL erit lxxxvii xlv atque BAL angulus eius que secundum longitudinem prostafereseos, qualium sunt ii recti ccclx, talium xciiii, qualium vero iiii recti ccclx, talium xlvii. Similiter autem quoniam, qualium est AL recta xxxviii xii, talium et LT fit i xxxiii, et que ab ipsis composita faciunt quod ab AT tetragonum, et istam habebimus longitudine eorumdem xxxviii xiiii. Quare et qualium est AT ypothenusa cxx, talium et LT erit iiii lii atque TAL angulus eius que secundum latitudinem distantie, qualium sunt ii recti ccclx, talium iiii xl, qualium vero iiii recti ccclx, talium ii xx, que et apponemus in quinto selidio canonis secundum eosdem cxxxv gradus.

Et comparationis ergo rursum eam earum que secundum longitudinem prostaferesium, si exponamus eam que seorsum inclinationum descriptionem, fit secundum minimum apostima, ubi maxime differentiam sensibilem neccessarium contingere, proportio recte AG ad utramque earum que sunt GK et KT que eorum que sunt liiii ad xxvii lvi, quare propter hoc AK relinqui reliquorum xxvi iiii atque AT ypothenusam colligi eorumdem xxxviii xii, propter hoc autem et qualium est AT ypothenusa cxx, talium et TK rectam fieri rursum lxxxvii xlv atque TAK angulum eius que secundum longitudinem prostefereseos, qualium sunt ii recti ccclx, talium xciiii, qualium vero iiii recti ccclx, talium xlvii. Tantorum autem ostendebatur et ab eis que secundum inclinationes supputionibus, supputionibus] supputacionius F₁ nullo ergo in Marte differt penes inclinationes circulorum ea que secundum longitudinem prostaferesis. Quod oportebat demonstrare.

Quatuor vero selidia duorum canoniorum stelle Veneris et stelle Mercurii continebunt que sub maximis obliquationibus epiciclorum ipsarum que circa apoguia et periguia excentricorum constituuntur contentas latitudinarias progressiones factas nobis tam tam] tamen F₁ secundum ipsas, seorsum ea que penes excentricorum inclinationes facta differentia, quoniam quidem et plurimum utique indigeret canoniorum et compoto commodiori, inequalibus et et] om. add. s. l. V₃ non omnino in easdem eius qui per media constitui debentibus et esperiis et eois progressionibus et aliter inclinatione excentricorum non manente, earum que penes maximas inclinationes et diminutionum superhabundantie dissonare debent ad earum que penes maximas obliquationes diminutionum. Seorsum tamen posita differentia, singula nobis promptius docebuntur, ut ex his erit manifestum.

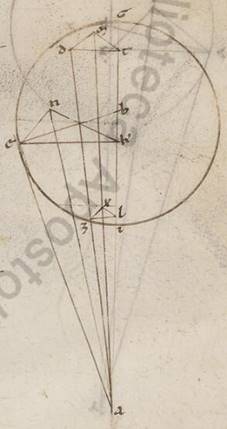Esto ergo AB communis sectio epipedorum et eius qui per media animalia et epicicli, et A quidem punctum subiaceat centrum zodiaci, B vero centrum epicicli; scribaturque circa ipsum GDEZI epiciclus obliquus ad eius qui per media epipedum, hoc est quare ductas in ipsis lineas rectas ad GI communem sectionem equales facere angulos omnes qui ad ipsius GI puncta constitutos; protrahanturque AE contingens epiciclum atque AZD secans ipsum ut acccidit; et trahantur ab D, E, Z punctis catheti in GI quidem DT et EK et ZL, in eius vero qui per media epipedum DM et EN et ZX; et copulentur TM et KN et LX et adhuc AN et AXM, recta enim AXM est, quoniam quidem in duobus epipedis sunt iii puncta et eo quod eius qui per media et illo quod per AZD recta ad illud quod per media. Quoniam ergo in exposita obliquatione eas quidem que secundum longitudinem stellarum prostafereses continetur et TAM angulus et KAM, eas autem que secundum latitudinem et angulus DAM et angulus EAN, manifestum. Demonstrandum vero primum quoniam et que sub EAN secundum latitudinem progressio secundum contactum constituta omnibus est maior, quemadmodum et quem quem] que F₁ secundum longitudinem prostaferesis. Quoniam enim EAK angulus maior est omnibus, KE ad EA maiorem proportionem habet quam utraque earum que sunt TD et LZ ad utramque earum que sunt DA et AZ. Verum sicut EK ad EN, ita et TD ad DM et LZ ad ZX. Equiangula enim omnia sunt, ut diximus, ita consituta trigona et recti qui ad puncta N, M, X anguli. Et NE ergo ad EA maiorem proportionem habet quam utraque que sunt MD et XZ ad utramque earum que sunt DA et ZA, et sunt rursum recti DMA et ENA et ZXA anguli. Maior est ergo et EAN angulus DAM angulo et omnibus manifestum quoniam eodem modo constitutis. Manifestum autem hinc quoniam et factarum in eis que secundum longitudinem prostaferesibus ex obliquatione differentiarum maior est ea que ad secundum E maiores progressiones completa, quoniam continent quidem ipsas subtendentes anguli superhabundantias earum que sunt TD et KE et LZ ad TM et KN et LX. Eadem vero ratione secundum unamquamque ipsarum manente et ad superhabundantias, consequetur et superhabundantiam earum que sunt EK et KN maiorem rationem habere ad EA quam eas que reliquarum ad similles ei que est AD. Manifestum vero hinc quoniam, et quam utique habet proportione ea que secundum longitudinem maxima prostaferesis ad eam que secundum latitudinem maximam progressionem, eam habent proportionem et in omnibus epicicli portionibus ille que secundum longitudinem in unoquoque prostafereses ad secundum latitudinem progressiones, quoniam ut recta KE ad EN ita et omnes similles eis que sunt LZ et TD ad similles eis que sunt ZX et DM. Quod oportebat ostendere.

Istis autem preexpositis, videamus primum quartus angulus secundum utramque stellarum sub obliquatione epipedorum contineatur, supponentes secundum in principio presumpta quoniam circa media maximi et minimi apostimatis v graduum utraque ipsarum plurimum borealior vel australior fit contrariis secundum epiciclum progressionius, quoniam quidem Veneris indifferenti maiorem et minorem v graduum eam que secundum periguion et apoguion excentrici recessionem apparet faciens, que vero Mercurii unius ad proximum gradus dimidii.

Esto ergo rursum ABG communis sectio et eius qui per media animalia et epicicli, et scripto circa B punctum GD epiciclo obliquo ad eius qui per media animalia epipedum, secundum quem exposuimus modum, copuletur ab A centrum zodiaci contingens epiciclum AD, trahanturque a puncto D catheti in GBE quidem DZ. In eius vero qui per media epipedum DI, et copulentur BD et ZI et AI. Subiaceat autem et DAI angulus continens medietatem exposite secundum latitudinem recessionis secundum utramque stellarum existentem talium ii dimidii, qualium sunt iiii recti ccclx, et proponatur quantitatem obliquationis utriusque epipedorum invenire, hoc est quantitatem DZI anguli.

Itaque in stella quidem Veneris, quoniam quidem, qualium est que ex centro epicicli xliii x, talium maximum apostima lxi xv, minimum vero lviii xlv et quod inter hec fit lx, AB vero recta ad DB proportionem habebit quam lx ad xliii x. Et quoniam quod ab BD sumptum ab eo quod ab AB facit quod ab AD, et istam habebimus longitudinem eorumdem xli xl. Similiter quoniam, ut BA ad AD, et BD ad DZ, eorumdem et DZ habebimus xxix lviii. Rursum quoniam DAI angulus subiacet, qualium sunt iiiior recti ccclx, talium ii xxx, qualium vero duo recti ccclx, talium v erit utique, et que super DI periferia talium v, qualium qui circa ADI orthogonium circulus ccclx, que vero sub ipsa recta DI talium v xiiii, qualium est AD ypothenusa cxx, et qualium est ergo AD recta li xl, talium DI erit i l, eorumdem vero et DZ ostendebatur xxix lviii. Quare et qualium est DZ ypothenusa cxx, talium et DI erit vii xx; atque DZI obliquationis, qualium sunt duo recti ccclx, talium vii, qualium vero iiii recti ccclx, talium iii xxx. Sed quoniam et superabundantia DAZ anguli ad IAZ angulum continet factam eius que secundum longitudinem prostafereseos differentiam, hinc et istam coinvestigandum a deprehensa ipsorum quantitate. Quoniam enim ostensa est, qualium est DI recta i l, talium AD ypothenusa xli xl, atque DZ similiter xxix lviii, et quidem ab DI sumptum ab eis que ab utraque earum que sunt AD ad ZD facit quod ab utraque earum que sunt AI et IZ, habebimus et AI longitudine eorumdem xli xxxvii, atque IZ similiter xxix lv. Quare et qualium est AI ypothenusa cxx, talium et ZI, erit lxxxvi xvi, atque ZAI angulus, qualium sunt duo recti ccclx, talium xci lvi, qualium vero iiii recti ccclx, talium xlv lviii. Similiter autem quoniam, et qualium est AD ypothenusa cxx, talium et DZ fit lxxxvi xviii, atque DAZ angulum habebimus, qualium sunt duo recti ccclx, talium xci lviii, qualium vero iiii recti ccclx, talium xlv lix. Deficiebat ergo penes obliquationem ea que secundum longitudinem prostaferesis sexagesimo i^o.

In Mercurio vero quoniam, qualium est que ex centro epicicli xxii xxx, talium maximum apostima ostensum est lxix et quod diametron lvii et quod inter hec colligitur eorumdem lxiii, atque recta AB ad BD proportionem habet quam lxiii ad xxii xxx, et quoniam quod ab DB sumptum ab eo quod ab AB facit quod ab AD, et istam habebimus longitudine lviii li. Similiter autem quoniam sicut AB ad AD et BD ad DZ, eorumdem et DZ erit xxi i. Rursum quoniam DAI angulus talium subiacet v, qualium sunt ii recti ccclx, erit utique et que super DI periferia talium v, qualium qui circa ADI orthogonium circulus ccclx, et que super ipsam recta DI talium v xiiii, qualium AD ypothenusa cxx. Et qualium est ergo AD recta lviii li, talium et DI erit ii xxxiiii. Eorumdem vero et DZ demonstrabatur xxi i. Qualium est ergo DZ ypothenusa cxx, talium et DI erit xiiii xl atque DZI angulus obliquationis, qualium sunt ii recti ccclx, talium xiiii, qualium vero iiii recti ccclx, talium vii.

Similiter autem et sigkriseos eorum qui prostafereseos angulorum causa, quoniam quidem rursum, qualium est DI recta ii xxxiiii, talium et AD ypothenusa ostensa est lviii li, atque DZ similiter xxi i, quod autem a recta DI sumptum sub eis que ab utraque earum que sunt DA et DZ facit quod ab utraque earum que sunt AI et IZ, habebimus et AI longitudine lviii lvii atque ZI eorumdem xx liii. Qualium est ergo AI ypothenusa cxx, talium et IZ erit xlii xxxviii atque ZAI angulus, qualium sunt ii recti ccclx, talium xli xxxviii, qualium vero iiii recti ccclx, talium xx xlix. Secundum hec vero quoniam, et qualium est AD ypothenusa cxx, talium et DZ colligitur xlii l, et DAZ angulum habebimus, qualium sunt ii recti ccclx, talium xli l, qualium vero iiii recti ccclx, talium xx lv. Deficiebat ergo et in hoc penes obliquationem ea que secundum longitudinem prostaferesis sexagesimis vi. Quod oportebat demonstrare.

His autem deinceps videamus, si istas supponentes obliquationum quantitates consonas reperiamus eas que secundum maxima et minima apostimata maximas secundum latitudinem progressiones eis que ex observationibus comprehense sunt. Subiaceatque rursum in eadem descriptione maximum apostima primum stelle Veneris, hoc est eius que est AB ad BD proportionem que eorum que sunt lxi xv ad xliii x, quare quoniam quod a recta BD sumptum sub eo quod ab AB facit quod ab AD, et istam colligi eorumdem xliii xxvii. Verum sicut AB ad AD et BD ad DZ, et DZ ergo recta eorumdem erit xxx xxxvii. Rursum quoniam DZI angulus obliquationis subiacet talium vii, qualium ii recti ccclx, atque DI recta talium vii xx, qualium DZ ypothenusa cxx, et qualium est ergo DZ recta xxx xxxvii atque AD similiter xliii xxvii, talium et DI erit i lii. Quare et qualium est AB ypothenusa cxx, talium et DI erit v ix, atque DAI angulus maxime secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium iiii liiii, qualium vero iiii recti ccclx, talium ii xxvii. At vero secundum minimum apostima, quoniam qualium est BD que ex centro epicicli xliii x, talium et AB subiacet lviii xlv, quod vero ab DB sumptum sub eo quod ab AB facit quod ab AD, et istam habebimus longitudine eorumdem xxxix li. Similiterque quoniam sicut AB ad AD et BD ad DZ erit eorumdem xxix xvii. Verum eius que est DZ ad DI proportio subiacet que cxx ad vii xx. Et qualium est ergo DZ recta xxix xvii atque AD similiter xxxix li, talium et DI fit i xlvii. Quare et qualium est AD ypothenusa cxx, talium et DI erit v xxii atque DAI angulus maxime secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium v viii, qualium vero sunt iiii recti ccclx, talium ii xxxiiii. Indifferenti ergo ad sensum ea que secundum mediam proportionem secundum latitudinem recessione ii dimidii graduum subiacente, minor quidem facta est ea que secundum apoguion, maior autem que secundum periguion, quoniam quidem ea que secundum maximum apostima tribus solis deficiebat sexagesimis, que vero secundum minimum iiii sexagesimis aucta est, que ex observationibus facile intelligibilia fieri omnino non contingebat.

Rursum subiaceat maximum apostima stelle Mercurii, hoc est eius que est AB ad AD proportio, que lxix ad xxii xxx, quare propter eadem eis que supra colligi AD eorumdem lxv xiiii atque DZ similiter xxi xvi. Verum et hic DZI angulum habemus obliquationis subiacentem talium xiiii, qualium sunt ii recti ccclx, atque DI rectam propter hoc talium xiiii xl, qualium est DZ ypothenusa cxx. Et qualium est ergo DZ recta xxi xvi atque AD similiter lxv xiiii, talium et DI erit ii xxxvi. Quare et qualium est AD ypothenusa cxx, talium et DI erit iiii xlvii atque DAI angulus maxime secundum latitudinem recessionis, qualium sunt ii recti ccclx, talium iiii xxxiiii, qualium vero iiii recti ccclx, talium ii xvii. In minimo autem apostimate eius que est AB ad BD proportio subiacet que lvii ad xxii xxx, propter hec vero rursum recta AD eorumdem lii xxii atque DZ similiter xx xl. Quoniam vero propter eandem obliquationem subiacet eius que est ZD ad DI proportio que cxx ad xiiii xl, et qualium est ergo DZ xx xl atque AD similiter lii xxii, talium et DI est ii xxxii. Quare et qualium est AD ypothenusa cxx, talium et DI erit v xlviii atque DAI angulus, qualium sunt ii recti ccclx, talium v xxxii, qualium vero iiii recti ccclx, talium ii xlvi. Distitit ergo ab ea que secundum mediam proportionem maxima recessione secundum latitudinem ii dimidii et hic graduum subiacentis ea quidem que secundum apoguion in minimum xiii sexagesimis, que vero secundum periguion in plurimum xvi sexagesimis, pro quibus in eam que in compoto penes mediam rationem directionem iiii^a i^us gradus secundum observationum ad sensum differentiam cousi sumus.

His autem demonstratis, et quoniam, sicut maxime secundum longitudinem prostafereses ad maximas secundum latitudinem progressiones, ita et in reliquis epicicli portionibus ad particulares longitudinis prostafereses latitudinis progressiones, hinc nobis prompte facta est in expositis iiii selidiis et eius que Veneris et eius que Mercurii, earum que ex obliquatione secundum latitudinem precessionum appositio tamen penes ipsam solam obliquationem epiciclorum et a media adiectione, ut diximus, collectarum ea que penes excentricorum inclinationem et adhuc penes apoguion et periguion eius que Mercurii differentia, propter bene compositum, ex agendo compoto directionem receptam.

Quoniam enim secundum expositas medias rationes ea quidem que secundum latitudinem ambarum stellarum ex obliquatione in utraque eius qui per media maxima progressio ostensa est graduum ii xxx, que vero secundum longitudinem maximam prosteferesis in Venere quidem xlvi graduum, in Mercurio vero xxii ad proximum, habemus autem expositas in anomalie ipsorum canonibus pertinentes particularibus portionibus epiciclorum prostafereses, quarta quarta] quanta F₁ utique fuerint pars ipse totarum secundum longitudinem maximarum prostaferesium, totam partem sumentes in utraque stellarum proprie ii xxx graduum, facta apponemus in iiii selidiis canoniorum latitudinis eisdem numeris.

Quinta vero selidia facta sunt nobis, propter et in aliis excentricorum progressionibus constitutas secundum latitudinem recessiones discerni ex apositorum sexagesimorum methedias methedias] methodias F₁. Quoniam enim, ut diximus, proportionaliter excentricorum restitutioni et epiciclorum e inclinationes et obliquationes augmenti et diminutionis restitutionem faciunt per parvorum circulorum appositionem, quantitates autem inclinationum et obliquationum omnium non maiores utique sunt ea que secundum obliquum Lune circulum, et proportionaliter quidem se habent ad proximum rursum ille que usque totas inclinationes secundum partem recessiones, factas autem habemus lineariter eas que Lune duodecies unamquamque earum que ibi appositionum facientes, propter maximam epibolem ibi quidem esse graduum v ad proximum, nunc vero nos facere ipsam lx, facta apposuimus propriis numeris in unoquoque quintorum selidiorum; et est canoniorum expositio talis.

EXPOSITIO CANONIORUM EIUS QUOD SECUNDUM LATITUDINEM NEGOCII. Tabula Saturni debet precedere tabula Iovis.

⟨XIII.6⟩ Compotus eius que secundum latitudinem recessionis quinque planetarum

His ita se habentibus, docebimus et eam que secundum latitudinem quinque stellarum psiphophoriam ad hunc modum. In tribus enim Saturno, Iove et Marte discretam longitudinem inferentes in proprii canonis numeros, eam quidem que Martis secundum se, eam vero que Iovis cum ablatione xx graduum, eam autem que Saturni cum appositione l graduum, adiacentia ipsi sexagesima per se scribemus. Et similiter discretum anomalie numerum inferentes in eosdem numeros adiacentem ipsi latitudinariam differentiam, si quidem discreta longitudo in primis fuerit xv versibus, eam quidem que in iiio selidio, si vero in eis que deinceps, eam que in iiiio multiplicantes in expositam sexagesima factis habebimus stellam eo qui per media, si quidem ex iii^o selidio latitudinariam differentiam fuerimus sumentes, borealiorem, si vero ex iiii^to, australiorem. In Venere autem et Mercurio discretum anomalie numerum primum inferentes in numeros proprii canonii adiacentia ipsi in iiio et iiiio selidio latitudinis scribemus seorsum, eam quidem que in aliis selidiis ipsa secundum ipsa, ea vero que in iiiio Mercurii, in primis quidem xv versibus existente discreta longitudine cum ablatione decime ipsorum partis, in eis vero que sub ipsas cum appositione eiusdem partis deinceps apponentes discrete longitudini semper in Venere quidem gradus xc, in Mercurio vero gradus cclxx, sive auferentes xc habemus circulum, factas inferemus in eosdem numeros, et quotcumque fuerint numeris adiacentia sexagesima in vo selidio, tot sumentes eorum que ex iiio selidio per se descriptorum, facta exponemus, ea quidem que cum exposita appositione longitudine in primis xv versibus existente, si quidem discrete anomalie numerus in primis xv versibus fuerit, ut in australia, si vero in eis que deinceps, ut in borealia. Dicte vero longitudinis numero in eis que sub primis xv versibus excidente, si quidem dicte anomalie numerus in primis xv versibus fuerit, ut in borealia, si vero in eis que deinceps, ut in australia. Deinceps vero rursum discretam longitudinem in Venere quidem ipsam simpliciter, in Mercurio vero cum appositione clxxx graduum inferentes in eosdem numeros, quotcumque adiacent et huic sexagesima in v^o selidio, tanta sumentes eorum que in iiii^o selidio seorsum scripto sunt, facta exponemus, illata enim quidem, ut diximus, longitudine in primis xv versibus excidente, si quidem usque clxxx graduum fuerit discretus anomalie numerus, ut in borealia, si vero supra clxxx, ut in australia. Divisa autem longitudine sub xv versus excidente, si quidem anomalie numerus usque clxxx graduum fuerit, ut in australia, si vero supra clxxx, ut in borealia. Reliquorum vero et ipsorum istorum ex secundum longitudinis inductione inventorum sexagesimorum sumentes tantam partem, quanta et ipsa erat lx, factorum in Venere quidem viam preexponemus semper ut in borealia, in Mercurio dimidium et iiii^a semper ut in australia. Et ita ex mistione trium expositionum apparentem ad eum qui per media animalia circulum secundum latitudinem ipsorum progressionem cognoscemus.

⟨XIII.7⟩ De apparitionibus et absconsionibus quinque planetarum

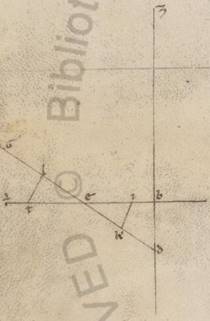Facta ergo et ea que secundum latitudinem quinque stellarum recessione, relinquitur adimplere et circa apparitiones et absconsiones isti ipsarum ad Solem factas debentia considerari. Accidit enim, quemadmodum in fixarum stellarum coordinatione pertransivimus, in equales fieri differenter eas que in eo qui per media animalia circulo distantias ipsarum ad Solem et in apparitionibus et absconsionibus propter multas causas, quarum prima quidem est penes inequalitatem magnitudinum ipsarum, secunda vero penes dissimillitudinem inclinationum zodiaci ad orizontes, tercia vero penes eas que secundum latitudinem ipsarum progressiones.

Si enim rursum intellexerimus maximorum circulorum portiones orizontis quidem AB, eius autem qui per media animalia maximi circuli GD; et E punctum supposuerimus communem eorum sectionem orientalem vel occidentalem, puncta vero G, A ad meridiem inclinata, atque D punctum centrum Solis; et per ipsum et polum orizontis scripserimus maximi circuli rursum portionem DBZ, stellamque supposuerimus oriri vel occidere in AEB orizonte, quando quidem in eo qui per media fuerit, manifestum quoniam secundum E punctum, quando vero borealior fuerit eo qui per media, secundum I, quando autem australior, secundum T; et adduxerimus in eum qui per media ab I et T punctis cathetos IK et TL, eam que est BD rursum habebimus, cui equalem distante Sole semper periferiam sub terra eadem stella primum videbitur vel disparebit. Namque ad ita scriptum maximum circulum equalibus sub terra distantiis eedem illuminationes radiorum Solis fiunt. Ista ergo primum in aliis inequalibus stellis in equali secundum consequens constituta, neccessarium, etsi alia omnia eadem sunt, et rectum angulum subtendentes zodiaci periferias, hoc est similles ei que est ED distantias differentes esse, et maior quidem stellarum minores manifestum quoniam, minorum maiores. Similiter autem et si BD quidem eadem erit in eadem stella, at vero BED angulus inclinationis eius qui per media vel penes dodecatimoriorum differentias vel penes eas que habitationum inequalis fit rursum et ED differentie periferia differet et maior quidem erit expositio, angulo diminuto, minor vero, augmentato; similiter si autem et hoc affuerit primo, et inclinationem esse eandem, stella vero non erit in eo qui per media, sed vel secundum I borealior vel secundum T australior, nondum DE periferiam distans apparebit vel abscondetur primum, sed quando quidem borealior erit eo qui per media, DK minorem existentem, quando vero australior, DEL maiorem existentem. Neccessarium est ergo ad particularium investigationem dare primum, in unaquaque quinque stellarum erraticarum universales quantitates DL DL] DB F₁ periferiarum a cercioribus cercioribus] certioribus F₁ observatis apparitionibus. Ipse autem erunt estivales et circa Cancrum, et propter illam que in hora illa subtilitatem et serenitatem aerum et commensurationem zodiaci ad orizontes inclinationum. Reperi Reperi] reperimus F₁ ergo per talem orientalium observationum investigationem quoniam circa principium Cancri oritur, ut in universum Saturni quidem stella distans ab examinato Sole gradibus xiiii, Iovis vero distans similiter gradibus xii dimidio iiiia, Martis vero gradibus xiiii dimidio, Veneris vero esperia distans v bisse, Mercurii autem esperia distans gradibus xi dimidio. His autem ita subiacentibus, describatur preiacentis descriptionis figura, nullo differente in tantis periferiis, si velut in eis que sub ipsas rectis differentibus ad sensum existentibus causa commoditatis faciamus rationes.

Et esto E quidem punctum communis sectionis eius qui per media et orizontis E punctum, preiacentibus apparitionibus secundum principium Cancri oriens quidem in tribus orientalibus, Saturno, Iove et Marte, occidens vero manifestum quoniam in esperiis Venere et Mercurio. Clima vero subiacet subiacet] add. quod F₁ per Phenices, ubi maxima dies horarum est equinoctialium xiiii et iiii, quoniam quidem secundum istum maxime vel circa istum parallilum plurimum et fide digne facte sunt observationum secundum ipsum fere caldaice, circa ipsum vero que circa Ellada et Egiptum. Quoniam ergo ex predemonstrato quidem angulorum negotio, quando principium Carchini oritur secundum subiacens clima, BED angulum reperimus talium ciii, qualium ii recti ccclx, et proportionem propter hoc eorum que circa rectos angulos eam que xciiii ad lxxv ad proximum, talium vero et ypothenusas cxx, per latitudinis vero negotium circa principia Carchini facientibus ortus tribus stellis solis, hoc est circa apoguia epicicli progressionem facientibus secundum quantamcumque apoguii distantiam non maiorem dodecatimoria, reperimus indifferenter ad sensum eam quidem que Saturni et eam que Iovis in ipso fere qui per media, eam vero que Martis borealiorem eius qui per media vam partem maxime unius gradus, DE quidem erit quam distabunt a Sole secundum eum qui per media que Saturni et que Iovis, at vero DK quam distabat a Sole que Martis, propter borealiorem esse ei que est KI sexagesimorum existenti xii. Quoniam vero proportio est eius que est KI ad KE que xciiii ad lxxv, eorumdem KE erit sexagesimorum x ad proximum. Subiacet autem et DK in Marte xiiii et dimidii graduum, quare et totam DE colligi graduum xiiii xl. Est autem et in Saturni stella xiiii graduum, in Iovis vero xii dimidii iiii^a. Quare quoniam rursum proportio est eius que est ED ad BD que cxx ad xciiii, habebimus et DB periferiam maximi per polos orizontis scripti circuli, in Saturno quidem xi graduum, in Iove vero x, in Marte autem xi dimidii ad proximum.

Similiter autem in Venere et Mercurio, quoniam, et quando occidit principium Carcini, eundem preiacenti angulum et inclinationem ad orizontem facit, subiacet autem circa hanc partem eius qui per media oriri esperia Veneris quidem stella distans ab examinato Sole gradibus v bisse, stella vero Mercurii xi gradibus dimidio, obtinebit ergo in ortibus ipsorum examinatus quidem Sol in stella quidem Veneris Geminorum gradus xxiiii iii^a, in Mercurii vero gradus xviii dimidium, medius vero in Venere quidem gradus xxv, in Mercurio autem xi x gradus ad proximum. Ipsos ergo gradus optinebat ea que secundum longitudinem media motio stellarum. Quando vero, ita se habente longitudine, ipsi in principio carchini apparent, Stella quidem Veneris distans reperitur ab apoguio epicicli circa xiiii gradibus, Mercurii vero circa xxxii. Ostenditur enim hoc per ea que de anomalia ipsorum preexposita sunt htheoremata. htheoremata] theoremata F₁ 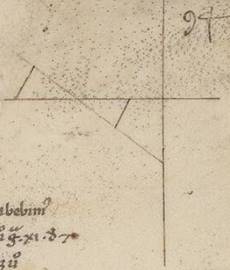Consequenter autem in his progressionibus stella quidem Veneris borealior invenitur eo qui per media gradu i, Mercurii vero gradibus i et bisse ad proximum, quantorum est manifestum quoniam ea que est KI. Quare quoniam et proprior proprior] proporcio F₁ ipsius que ad EK est que xciiii ad lxxv, eadem vero proprior proprior] proporcio F₁ est et i quidem ad dimidium iiii^a, unius vero et bisse ad i iii ad proximum, habebimus et EK in Venere quidem dimidii iiii^a partis unius gradus, in Mercurio vero i iii. Eorumdem vero subiacet et DK, quam apparebat utraque distans a Sole, in Venere quidem gradibus v bisse, in Mercurio vero gradibus xi dimidio, et totam ergo DKE habebimus Veneris graduum vi et ii quintarum, in Mercurio vero graduum xii dimidii iii^a ad proximum. Quare quoniam rursum et ED ad BD proportio est que cxx ad xciiii, eadem vero isti proportio est et vi et ii quintarum ad v atque xii dimidii iii^a ad x ad proximum, habebimus et eam que est DB universalis distantie quantitatem, in Venere quidem graduum v, in Mercurio vero x. Que propositum erat invenire.

⟨XIII.8⟩ Quoniam consonant ypothesibus et proprie pertinentia apparitiones et absconsiones Veneris et Mercurii

Quoniam vero expositis ypothesibus consequentia constituuntur circa apparitiones et stelle Veneris et et​] iter. V₃ stelle Mercurii extranee convenientia, hoc est quoniam stelle quidem Veneris quod ab esperio occasu in orientalem ortum tempus quidem circa principia Piscium ii maxime dierum fit, at vero circa principia Virginis xvi dierum, stelle vero Mercurii esperie quidem apparitiones defitiuntur, quando circa principia debet apparere Scorpii, eoe vero, quando circa principia Tauri, intelligemus utique ita, et primum in stella Veneris. Adiaceat enim simillis preiacenti apparitionum descriptio, et subiaceat primum E quidem punctum eius qui per media circa principia Piscium, ubi secundum periguion epicicli contingens Veneris stella borealior est eo qui per media gradibus vi et iiia ad proximum, scema vero hesperii occasus, secundum quem BED quidem angulus in subiacenti climate colligitur talium cliiii, qualium sunt ii recti ccclx, qualium vero ypothenusa cxx, talium maior quidem eorum que circa rectum cxvii, minor vero xxvii ad proximum. Propter hoc ergo, et qualium est BD universalis differentie v, talium et DE fit v viii. Sed quoniam borealior est stella eo qui per media graduum vi et iii^a, quantorum est KI periferia, eadem vero proportio est cxvii ad xxvii et vi iii^a ad i ad proximum, ea quidem que est KE erit gradus unius dimidii, reliqua vero KD, quam distabat stella in esperio occasu in consequentia a Sole, graduum iii xxxviii.

Rursum in similli descriptione, quoniam quidem secundum eoum ortum BED quidem fit talium lxix, qualium sunt ii recti ccclx, propter hoc autem, qualium ypothenusa cxx, talium minor quidem eorum que circa rectum lxviii, maior vero xcix ad proximum, eedem vero proportiones colliguntur lxviii quidem ad cxx et eorum qui sunt v ad viii xlix, eorum vero que sunt lxviii ad xcix et vi iiia ad ix xiii, eam quidem est DE habebimus eorumdem viii xlix, eam vero que est KE eius que penes latitudinem differentie ix xiii, Reliqua que DK, ut in consequentia manifestum quoniam Solis, sexagesimorum xxiiii.

Distat autem secundum esperium occasum similiter in consequentia gradibus iii xxxviii, minus ergo movetur in in] om. add. s. l. V₃ eo quod ab esperio occasu in eoum ortum tempore Solis motu, hoc est proportio ad proximum secundum longitudinem progressu eam que propter eam … propter] propter eam que V₃ penes epiciclum precessionem gradibus iii xiiii. Quoniam ergo tantis gradibus in predentia tansit stella, ut ex animalie canone facile intellectu fit, quando secundum periguion epicicli movetur gradus i et iiii^a, ita vero pertransit medie stella in diebus ad proximum duobus, manifestum quoniam tantum utique fiet preiacenti preiacenti] preiacentis F₁ distantie tempus consequenter apparentibus.

Rursum in simili descriptione subiaceat E quidem punctum circa principia Virginis, ubi secundum periguion epicicli contingens Veneris stella australior apparet eo qui per media equalibus ad proximum gradibus vi et iiia; et preiaceat primum esperia absconsio, quando BED quidem angulus talium erit lxix, qualium ii recti ccclx, qualium vero ypothenusa cxx, talium minor quidem earum que circa rectum lxviii, maior vero xcix ad proximum. Quoniam ergo eedem fiunt proportiones eius que circa eoam apparitionem Piscium, et eius que secundum latitudinem distantie existentis equalis, habebimus eorum ED quidem periferiam viii xlix, eam vero que est LE eius que penes latitudinem differentie ix xiii, totamque DL, quam distabat stella in consequentia a Sole, graduum xviii ii. Per anomalie vero canonem, ut diximus, tantis gradibus eius que penes medium Solis et stelle secundum longitudinem motum precessionis pertinent a periguio epicicli gradus vii dimidium ad proximum.

Similiter autem quoniam et secundum eoum ortum qui circa principia Virginis, quando BED quidem angulus talium erit cliiii, qualium sunt ii recti ccclx, qualium vero ypothenusa cxx, talium maior quidem earum que circa rectum angulum cxvii, minor vero xxvii, eedem vero proportiones colligentur rursum in esperia absconsione Piscium expositis, habebimus eorumdem DE quidem periferia v viii, EL vero eius que penes latitudinem differentie i xxx, totamque DL, quam distabat stella in precendentia a Sole, graduum vi xxxviii, quantis secundum eundem modum pertinet ea que a periguio epicicli gradus ii dimidium ad proximum. Omnes ergo Veneris stella ab esperia absconsione in eoum ortum movebitur epicicli gradus x, quo quo] quot F₁ in preiacentibus ad proximum xvi diebus consequenter apparentibus pertransit.

His autem demonstratis, considerandum et circa eclipticas apparitiones stelle Mercuii contingentia, et primum quoniam secundum principia Scorpii, etsi maximam in consequentia a Sole faciat distantiam, esperia non potest apparere. Adiaceat enim ea que in apparitionius descriptio, E puncto eius qui per media subiacente circa principia Scorpii, ubi secundum occasum BED quidem angulus talium est lxix, qualium ii recti ccclx, qualium vero ypothenusa cxx, talium minor earum que circa rectum lxviii, maior vero xcix. Et qualium est ergo BD universalis distantie x, talium et DE erit xvii xxxix. Verum quando preiacentem portionem habet stella, australior fit eo qui per media gradibus iii ad proximum. Quare quoniam secundum expositas rationes, et qualium est ea que est LT latitudinis iii, talium et LE quidem fit iiii xxii, DEL vero tota eorumdem xxii ad proximum, tantas differentie oportet stellam ab examinato Sole, ut possit apparere primum. Quare quoniam quidem solos distat ab examinato Sole plurimum in principiis existens Scorpii gradibus xx lviii, hoc enim nobis preostensum est per eam que circa maximas distantias exposita sunt, manifestum quoniam eedem apparitionum convenienter defitiunt.

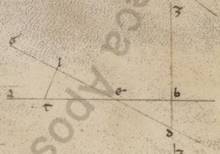Si autem, rursum exposita similli apparitionum descriptione, E punctum supposuerimus principium Tauri secundum eoum ortum, quando stella quidem secundum expositas progressiones australior erit eo qui per media gradibus iii et via ad proximum, earum vero que circa rectos angulos proportiones preiacentibus fuerunt eedem, eam quidem que est DE eorumdem habebimus xvii xxxix, eam vero que est LE talium iiii xxxvii, qualium est ea que est TL latitudinis iii x, totamque DEL eorumdem xxii xvi, quare et hic tantos quidem distare ab examinato Sole oportebit stellam, ut primum videatur. Non distante vero plurimum super predemonstratos xxii xiii gradus, convenienter et tales apparitionum defitient. Et demonstrata sunt nobis proposita consona et apparentibus et expositis ypothesibus.

⟨XIII.9⟩ Efodos in particulares in apparitionibus et absconsionibus a Sole distans distans] distantias F₁

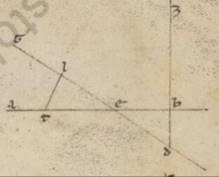Manifestum vero hinc quoniam, et universaliter BD periferiis subiacentibus in unaquaque stellarum et secundum E sectionem dato principio dodecatimoriorum, propter hoc et BED angulo, dabitur quidem ea que est DKE et ea que secundum talem stelle distantiam secundum latitudinem progressio, hoc est ea que est KI erit TL, propter hoc autem et KE erit EL et adhuc apparens distantia que est DK erunt DL. Hoc ergo modo in omnibus dodecatimoriis supputantes rursum, ne longam sintaxim faciamus, secundum unamquamque quinque stellarum, in uno tamen propter suffitiens preiacenti climate medio apparentes ortuum et absconsionum ab examinato Sole distantias, velut ipsis stellis in principiis dodecatimoriorum subiacentibus, subordinavimus et istas facilitatis usus causa in v canoniis v stellarum quaque 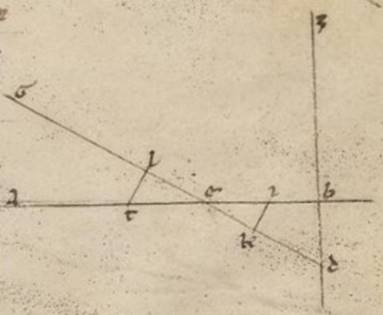vice continentibus versus xii. Istorum autem prima quidem tria et Saturni et Iovis et Martis ordinavimus in selidia iiia, primis quidem selidiis continentibus dodecatimorioum principia, secundis vero orientalium ortuum distantias, terciis vero eas que esperiorum occasuum, duo vero que deinceps canonia stelle Veneris et stelle Mercurii in v selidia, primis quidem similiter continentibus dodecatimoriorum principia, secundis autem esperiorum ortuum distantias, terciis vero eas que esperiorum occasuum, et rursum quartis quidem eas que eoorum ortuum, quintis vero eas que eoorum occasuum. Et est canonii expositio talis.

⟨XIII.10⟩

⟨XIII.11⟩ Epilogus sintaxeos

Adimpletis ergo et huiusmodi, O Syre, et fere omnibus secundum meum intellectum tractatis in huiusmodi coordinationem debentibus considerari, in quantum et quod usque presens tempus ad inventionem vel correctionem examinationem examinationem] examinaciorem F₁ cooperabatur et que ad commmoditatem solam contemplationis, sed non ad ostentationem, commemoratio suggerebat, proprium utique nobis hic et commensurabilem recipiat finem presens negotium.