Ptolemy
Almagesti (tr. Sicily c. 1150)
Vatican, BAV, Vat. lat. 2056
transcribed by Colette Dufossé
How to cite this transcription?
The transcription is based on MS Vatican, BAV, Vat. lat. 2056 (V3), which is the only complete copy of the text. When V3 has a corrupt or incorrect reading (also judging from the Greek text as edited by Heiberg), the correct reading is reported in footnotes from the other witnesses: Bologna, BCA, A. 1855 (B); Florence, BNC, Conv. Soppr. A.V.2654 (F1); Vatican, BAV, Ottob. lat. 1826 (V1); Vatican, BAV, Pal. lat. 1371 (V2); Venice, BNM, lat. VIII.10 (3266) (V4); and Wolfenbüttel, HAB 147 Gud. Lat. 4° (4451) (W). The text of V.12–15, absent from V3, is taken from V2. In Books VII–XIII, where V3 is damaged and has blank spaces in the tables, values have been added between 〈 〉 from F1.
The transcription follows the Project’s guidelines, with the following exceptions: (1) Greek mathematical signs are kept where they are used by the Latin scribe: ō for zero, ϛ for ½ and Γo for ⅔; (2) the unit fractions, e.g. ¾ expressed as a sum of ½ and ¼, written ϛ′ δ′ in Greek, et dimidium et iiiia in Latin, are left unchanged; (3) only the usually lacking endings of ‘dimidium’, ‘sexagesima’ and ‘gradus’ have been supplied.
Table of contents and links to chapters
〈Proemium translatoris〉
Iam Iam] Eam V2BW pingendi Gratias antiqui feruntur habuisse consuetudinem, ut unam quidem vultum aversam due, quibus illa manum porrigeret, aspectarent. Cuius misterii non ignarus dudum moriter moriter] memoriter V2BW teneo gratiam simplam profectam duplam reverti opportere. Tui ergo boni muneris memoror memoror] memor V2 quo earum quas Aristotiles acrivestatas vocat artium doctrina, quasi haustu aque vive, animum sitientem liberaliter imbuisti, olim quidem anxie queritabam quid tue dignum benivolentie possem referre. Nec enim eis que philosophie tardus asecla longo pauperis exertitio exertitio] add. vene W conquisiveram purus ingenii torrens fons et domus artium pectus indigebat. Opes quoque aput earum contemptorem minimum promerri promerri] promereri V2W non dubius intelligebam. Angebatur ergo in dies magis ac magis animus meus eo molestius sustinens votum, quo complendi voti absolutius facultas negabatur. Verum diutini clamorem desiderii superna tandem pietas exaudivit dignum, ut arbitror, plene tribuens remunerationis instrumentum quod tuum tanto, ut tua pace loquar, minus precedit, quanto finis eo quod ad finem laudabilius. Nec enim tuum latet acumen quod omni sapienti liquet, numerorum mensurarumque scientiam ad eam que astrorum quasi quandam introductionis pontem prestruere. Huius vero eam partem que siderum motus specculatur veterum lima, specculum modernorum, Claudius Ptolomeus astrorum scientie peritissimus xiii perscripsit libris qui a Grecis quidem Mathematica seu Meguisti Sintaxis, a Saracenis vero Elmeguisti corrupto nomine appellantur. Hos autem cum Salerni medicine insudassem audiens quendam ex nuntiis regis Scicilie quos ipse Constantinopolim miserrat nomine Aristipum largicione susceptos imperatoria Panormum transvexisse rei diu desiderate spe succensus, Scilleos latrattus non exhorui, Caripdim permeavi, ignea Ethene fluenta circuivi, eum queritans a quo mei finem sperabam desiderii. Quem tandem inventum Perguse prope Perguse prope] prope Pergusam V2W inv. B fontem Ethnea miracula satis cum perriculo perscrutantem, cum occulte quidem alia, manifeste vero mens scientie siderum expers prefatum michi transferre opus prohiberent, grecis ego litteris diligentissime preinstructus, primo quidem in Euclidis Dedomenis, Opticis et Catoptricis Phisicaque Procli Elementatione prelusi, dehinc vero prefatum Ptolomei opus aggressus, expositorem propitium divina michi gratia providente Eugenium, virum tan grece quam arabice lingue peritissimum, latine quoque non ignarum, illud contra viri discoli voluntatem latine dedi orationi. In quo nimirum mens mea infando pressa labore inceptum sepe destituisset opus, nisi superande difficultatis auctor potentissimus amor tui tuumque munus animum crebra mutui repetitionem repetitionem] repeticione V2 repetitione B repetitioni W pulsarent. Neque enim questus spe motus aut gloria istum potui laborem substinere, cum liquido constet spei locum artifici non relinqui, ubi ars ludibrio est et decori decori] dedecori B. Neque enim artificem mirari potest qui artem non miratur. Sensisti vero et tu non ullos non ullos] nonnullos WV2B his in temporibus cause quam ignorant iudices audacissimos, qui ne minus scientes videantur, quecumque nesciunt inutilia predicant aut profana, – iuxta quod arabes dicunt: nullus maior artis inimicus quam qui expers est ipsius –, eoque pertinatius criminandis instant artibus, quo ab earum laude imperitie probrum certius sibi conspitiunt imminem. Eos omitto qui honestatis zelo honesta quoque studia persequuntur, quos pie peccare recte dixerim dum nocivam curarum putredinem recidere concedentes, a sanarum altrice curarum philosophia manum minime continent indiscretam, sed et eam ipsius partem gravi criminatione persequuntur que ingeniis exquisita clarissimis et exculta, quo defecatior ac purior est, eo sapientie vocabulo dignior, eo gratiori quadam compede specculationis iocundissime animos hominum continet alligatos. Horum siquidem error, sive coloratus honesto, malitioso quoque predictorum testimonio fretus, apud imperitos, quorum maxima est multitudo, in bonarum negglectum artium efficacissime peroravit, ut iam numerorum quidem mensurarumque scientia omnino superflua et inutilis, astronomie vero studium ydolatria estimetur. Ita nimirum sentiebat vir religiosus ac prudens, cum dicebat: ‘hoc est igitur illud quadruvium quo his iuvandum est qui a sensibus procreatis nobiscum ad certiora intelligentie perduci volunt’, eisdem quoque Remigius attestatur dicens: cum omnes artes pensundate essent, aput Egiptios Abraam eos astrologiam docuisse, sed et sanctum Moysem sanctumque Danielem Dominus credo ob astrorum scientiam reprobavit, stultum quippe creatoris opera contemplari, eorumque specculatione ineffabilem ipsius potentiam ac sapientiam detestabilius ammirari, nefarium quoque penitusque liquet illicitam illicitam] illicitum V2 B W ad conditoris cognitionem conditorum cognitione animum sublevare, creatorem insensibilem sensibilium specculatione sibi quodam modo sensibilem comparare? O mentes cecas viamque philosophandi penitus ignorantes! A creatura siquidem mundi invisibilia Dei intellecta conspitiuntur, nec satis insensibilium veritatem percipere potest mens humana nisi ad eam preludio sensibilium sibi viam facultatemque preexcuderit. Hinc a sapientibus constitutus est ac diligenter observatus hic studiorum ordo, ut primo quidem ingenite nebulas ruditatis diligenti creatorum disquisitione serenaretur, serenaretur] serenarent V2 B W omnibus quidem sed eis potissimum invigilando disciplinis, que ipsam sine omni erroris devio sine omni scrupulo dubitationis veritatem contemplantes occulum mentis, Boetio teste, rursus illuminantur, deinde vero robore hoc animati in theologica exercitatione mentis atiem fiducialiter intendebant, unde et ab ordine docendi et discendi theologiam methaphysicam nominabant. Verum nostri nimirum aquile hoc quasi quodam volimine giganteo minime indigent omni creaturarum aminiculo radiis summe lucis occulos infigere potentissimi atque summe secreta veritatis efficaciter penetrare vix rudimentis a puerilibus celum involvant terrasque habitare dedignantur, super nubes eorum conversatio, atque in ipso summe sinu sapientie sese requiescere gloriantur, mundanam despiciunt sapientiam, eique vacantium deliramenta subsannant.
Tibi vero vir mentis serenissime, longe alia mens est: tu sacras artes et propter se appetendas, scientibus dulces, insciis adorandas rectissime arbitraris. Nec vero tuum fallit acumen quoniam perfectio habitudinis in plenitudine existit congnitionis, quo sciendo proficimus, hoc accessum ad beatitudinem fieri, presertim cum otio quidem mens corrumpatur, studium vero virtutis sit amicum, predarum Predarum] preclarum V2 quoque tibi, credo, videtur, in quo prestat homo ceteris animantibus hominem homini prenittere, hinc insurgendum summisque viribus iudicas incubendum ut omni scientie genere mens illustretur, ad beatitudinem preparetur, suo proprio bono decoretur. Tui ergo tibique simillium gratia presentem ego laborem hunc suscepi. Quibus si placeo intentio quoque mea michi perfecta est. Rideant et exultent artium inimici, ignota iudicent, astrorum studium insaniam predicent, mihi confiteor hec insania dulcis, mihi dulce clamare cum Nasone:
‘Felices anime quibus hoc cognoscere primum,
Inque domos superas scandere cura fuit!’
Faveas ergo summisque tibi vigiliis opus elaboratum benignus, queso, suscipias, illud tamen unum super omnia moneo ac rogo, ut ea qua et in geometricis usus esse docendis discretione collaudanda ad huius operis lectionem dignos admittas, indignos abicias: suam quippe rebus dignis adimet dignitatem, siquis eam communicaverit indignis.
1. Proemium
2. De ordine theorematum
3. Quoniam sperice celum fertur
4. Quoniam et terra sperica est ad sensum secundum omnes partes
5. Quoniam media celi est terra
6. Quoniam puncti rationem rationem] iter. V3 habet ad celestia tellus
7. Quoniam nullum motum transitivum facit terra
8. Quoniam due differentie primorum motuum sunt in celo
9. De particularibus conceptionibus
10. De quantitate earum que in circulo rectarum
11. Canonium earum que in circulo rectarum
12. De ea que inter tropica periferia
13. Prelibata in spericas demonstrationes
14. De eis que inter equinoctialem et obliquum circulum periferiis
15. Canonum obliquationis
16. De eis que in recta spera asscensionibus
〈I〉
〈I.1〉 Proemium auctoris
Valde bene qui proprie philosophati sunt, O Sire, videntur mihi sequestrasse theoreticum philosophie a practico. Etenim si accidit et practico prius hoc ipsum theoreticum esse, nichilominus utique quis inveniet magnam existentem in ipsis differentiam, non solum quod moralium quidem virtutum quedam multis et sine disciplina inesse possunt, eam vero que universorum speculationem absque doctrina consequi inpossibile, sed et eo quod ibi quidem ex ea que in ipsis rebus est continua operatione, hic autem ex eo qui in theorematibus processu, plurima utilitas fiat. Inde nobis ipsis duximus conpetere actus quidem in ipsarum imaginationum investigationibus ordinare, ut nec in minimis eius que ad bonum et bene dispositum statum considerationis obliviscamur, scole vero dare plurimum in theorematum multorum et bonorum existentium doctrinam, precipue vero in eam que eorum que proprie mathematica nominantur.
Etenim rursus et theoreticum Aristotiles diligentissime in tria prima genera dividit, phisicum, mathematicum, theologicum. Entibus enim universis ex materia, specie et motu habentibus existentiam, et cum seorsum quidem horum unumquodque secundum subiectum considerari minime possit, intelligi vero solum et absque reliquis, omnium quidem primi motus primam causam si quis excipiat secundum simplex, Deum invisibilem et immobilem utique estimabit, huiusque species quesitiva theologicum sursum alicubi circa elevatissima mundi, huiusmodi operatione intellecta utique solum semelque a sensibilibus substantiis segregata. Materialis vero semperque mote qualitatis scrutativa species, que circa album et calidum et dulce et molle et similia versatur, phisica utique nominabitur, huiuscemodi in essentia in coruptibilibus, ut in pluribus, et sub lunari spera conversante. Verum eius que secundum species motusque transitorios attenditur qualitatis declarativa species, figure, scilicet multitudinis et magnitudinis, ampliusque loci et temporis et similium quesitiva existens, quasi mathematica determinabitur, huiuscemodi essentia quasi inter illa duo cadente, non solum eo quod et b b] om. V2V4B per sensum et sine sensu intelligi possit, sed et eo quod omnibus simpliciter existentibus accidat tan mortalibus quam immortalibus, his quidem semper secundum speciem inseparabilem variatis coalterata, illis autem que sempiterna ethereeque nature coobservans immobilem speciei immutabilitatem. Ex quibus attendentes quoniam alia quidem duo genera theoretici potius utique quis oppinionem quam conceptionem scientialem dicat, – theologicum quidem propter omnifariam inapparens ipsius et incomprehensibile, phisicum vero propter materie instabile et inmanifestum –, quasi propter hoc utique desperandum de his concorditer intelligere philosophantes, solum autem mathematicum, si quis huic diligentiam exibeat inquisitionis, firmam stabilemque fide intendentibus notitiam dabit, velut utique demonstratione per indubitales vias facta, aricmeticam scilicet et geometriam, omnis quidem huiusmodi specculationis maxime pro viribus curam agere propulsi sumus, verum eius que specialiter que specialiter] inv. V2V4B circa divina et celestia intelligitur, eo quod hec sola circa semper se semper se] inv. V2V4B eodem modo habentium considerationem versatur et, propter hoc, potens et ipsa circa propriam quod quod] quidem V2V4B conceptionem neque inmanefestam neque inordinatam existentem semper eodem modo se habere, quod est proprium sciencie, ad alias vero non minus illis ipsis cooperari. Speciei quippe theologice hec utique potissimum viam preparabit, sola potens bene coniectare immutabilem ac segregatam operatione ab eorum que circa sensibiles quidem et moventes atque motas, sempiternas vero et impossibiles impossibiles] impassibiles V4B substantias propinquitate accidentium circaque lationes et ordines motuum.
Ad phisicam quoque non minimum utique confert, fere enim universale materialis essentie proprium ab ea que circa transituum transituum] transitivum V2 motum ydiotropia declaratur, ut corruptibile quidem ipsum et incorruptibile a recto et circulari, ponderosum vero et leve sive passivum et activum ab eo qui in medium et eo qui a medio.
Ad eam quoque que secundum actus et mores bonitatem omnium hec utique maxime vel conponet perspicaces a circa divina contemplata similitudine et bono ordine et mediocritate et modestia, amatores quidem faciens assequentes divini decoris huius, assuefaciens autem et quasi natura tribuens ad similem anime constitutionem. Hunc ergo semper et eodem modo se habentium contemplationis amorem temptamus et ipsi continue exaugere, discentes quidem iam talium mathematum comprehensa a proprie et inquisitive ipsa accedentibus, volentes vero et ipsi tantam appositionem conferre, quantam fere usque ad nos ab illis anteactum tempus sunggere sunggere] suggere V2 suggerere V4B poterit. Et quanta ergo impsenti impsenti] in presenti V2V4B arbitramur nobis venisse in lumen, per brevia ut est maxime, et ut illi qui ian aliquantum incubuere his assequi valeant, temptabimus memorare, perfectionis quidem negotii causa universa ad celestium utilia contemplationem ordine proprio exponentes, ne vero longum sermonem faciamus, a veteribus quidem examinata pertranseuntes solum, que vero sive nullatenus comprehensa sive non ut inerat commode, hec pro facultate pertractantes.
〈I.2〉 De ordine theorematum
Proposite vero nobis coordinationis antecedit quidem universalem totius terre ad totum celum videre habitudinem. Eorum vero que secundum partem iam et deinceps primum quidem erit de positione obliqui circuli et locis eius que penes nos habitabilis rationem pertransire, amplius et de ipsorum adinvicem secundum unumquenque orizontem penes inclinationes facta in ordinibus differentia, – premissa enim istorum consideratio consideratio] contemplacio V2 reliquorum contemplationem contemplationem] consideracionem V2 facilioris exhibet vie –; secundum vero de solari motu et lunari, et his superaccidentibus pertractare, – absque enim istorum preconceptione nec ea que circa stellas attenduntur possibile utique fiet ad plenum contemplari. Ultima vero existente, ut ad ipsam efodum, de stellis ratione, preordinabuntur quidem congrue et hic que de fixarum spera; sequentur vero que de quinque planetis dicenda videbuntur.
Istorum vero singula demonstrare temptabimus, principiis quidem et quasi fundamentis in adinventionem adinventionem] adventionem V2 utentes evidentem apparentibus et indubitatis et antiquarum et earum que secundum nos observationum, conceptionum autem eas que deinceps adaptande per eas que in linearibus efodis demonstrationes. Universalis ergo prelibacio talis utique erit, quoniam celum et spericum est et sperice fertur et quoniam terra figura quidem et ipsa sperica est ad sensum ut secundum omnes partes sumpta; positione vero media totius celi iacet centro similiter, magnitudine autem distantia et distantia et] inv. V2B puncti rationem optinet ad fixarum speram, ipsa nullum motum faciens transitivum. De horum autem unoquoque commemorationis causa breviter pertransibimus.
〈I.3〉 Quoniam sperice celum fertur
Igitur primas quidem sententias de his a tali quadam observatione probabile veteribus advenisse. Videbant enim et Solem et Lunam et alia sidera ab ortu semper in occasum ferri secundum equidistantes alternis circulos, et inchoantia quidem de deorsum ab imo et quasi ex ipsa terra sursum ferri, elata vero paulatim in excelsum, deinde rursum proportionaliter et circumire et in imo ferri et usque quo perfecte quasi terre incidentia disparerent, dehinc rursum manentia tempus quoddam in disparentia quasi alio a principio et orientia et occidentia atque tempora hec ampliusque ortuum et occasuum locos et ordinate et similiter quasi omnino reddentia. Maxime vero ipsos in spericam sententiam egit semper apparentium circumversio siderum considerata circularis atque centro uni et eidem circumcluta. circumcluta] circumvoluta V2B Polus enim uterque necessario punctus ille fiebat celestis spere, ei quidem magis propinquantibus secundum minores circulos replicatis, remocioribus autem ad distantie proportionem maiores in circumscriptione circulos fatientibus, quo ad abstantia et usque disparentia perveniat. Et horum vero que quidem prope stellas semper manifestas pacum pacum] paucum V2B tempus, que vero a longe proportionaliter item plus manentia videbant in disparentia. Quare principium quidem propter sola huiusmodi predictam ipsos sententiam summe, iam vero secundum eam que deinceps contemplationem et reliqua his intellexerunt consequentia, omnibus similiter similiter] simpliciter V2B apparentibus sententiis alterius opinionis contratestantibus. Age enim, si quis siderum supponat lationem in directo factam in infinitum ferri, quemadmodum quibusdam visum est, quis utique modus intelligetur secundum quem ad eodem printipio singula cotidie ferri videbuntur? Qui enim reflecti possent astra in infinitum ruentia? Vel quomodo reflectentia non apparent, apparent] add. vel qualiter non paulatim magnitudinibus in minutis propter a nobis crescentem distanciam disparerent V2B e contra vero maiora quidem ad ipsas visa disparentias paulatim vero abscondita et quasi a telluris abscissa superfitie? Sed et ipsa a terra reaccendi et iterum in hanc extingui et irrationabillissimorum utique penitus apparebit. Ut enim tantum ordinem in quantitatibus et qualitatibus eorum, amplius vero distantiis et locis et temporibus ita vane et ut accidit compleri quis concedate; et hanc quidem totam terre partem accesivam habere naturam, illam vero extinctivam; amplius vero eandem his quidem accendere, illis vero extinguere; et astrorum eadem his quidem iam extincta, vel accensa contingere, illis vero nondum, si quis, inquam, hec omnia concedat sic ridicula existentia, quid utique de semper manifeste manifeste] manifestis V2B habebimus dicere neque orientibus neque occidentibus? Vel propter quam causam que quidem et accenduntur et extinguntur non ubique et oriuntur et occidunt, que vero istud minime patiuntur sunt semper ubique super terram? Non enim eadem his quidem semper accendentur et extingentur, his vero nichil unquam horum patiuntur, cum omnino sit evidens, stellas easdem penes hos quidem et oriri et occidere, penes alios vero neutrum. Colligenti vero dicere, etsi qualemcumque quis aliam figuram celestium lationis supponat preter spericam, distantias a tellure in partes elevatorum neccesse est fieri inequales, ubicumque ipsa fit et qualitercumque subiaceat. Quare et magnitudines et ad seinvicem stellarum distantias eisdem secundum unamquamque circulationem inequalia oportet apparere, ut utique aliquotiens quidem in maiori, aliquotiens vero in minori spatio facta, quod nequaquam accidere videtur. Sed enim et ad orizontes maiores apparere magnitudines non distantia minor existens, sed humidi terram continentis exalatio facit inter nostrum visum et ipsas facta, ut et in aquam missa maiora apparent et, quanto utique inferius cedunt, tanto maiora.
Adducunt autem in spericam formam formam] sententiam V2 et que huiusmodi, et quoniam aliam secundum ypothesim quam solam istam horoscopiorum minime possunt fabrice consonare; et quoniam, celestium lacione et inprohibita et omnium mobilissima existente, figurarum quoque mobilissima est planarum planarum] add. quidem V2 circularis, solidarum quoque quoque] vero V2 sperica; similiter autem quoniam, equalem circumferentiam habentibus figuris differentibus, quoniam quidem maiores sunt que plures angulos habent: planarum quidem circulus fit maior, solidarum vero spera, maius vero et celum aliis corporibus.
Nec non et et] add. a V2B phisicis quibusdam est ad huiusmodi moveri intellectum: ut quoniam corporibus universis subtilior pars est ether, similium partibus vero similes partibus superfities, similles partibus vero superfities superfities] add. sole V2 in planis circularis et in solidis sperica, – ethere autem non plano sed solido existente, reliquitur ipsum spericum esse –, et similiter quoniam natura corpora omnia terrestria quidem et corruptibilia omnino ex circularibus dissimilium partium atque spericis, quoniam quidem plana entia vel concava non utique omnibus diversis ex terre locis tempore sub eodem conspitientibus figura apparerent circulari, propter hoc autem probabile esse et continentem ea ethera nature simillis existentem et spericum esse et propter simillitudinem partium et circulariter ferri et equaliter.
〈I.4〉 Quoniam terra sperica est ad sensum ut secundum omnes partes
Quoniam vero et terra sperica est ad sensum, ut secundum universas partes sumpta, ita utique maxime intelligemus. Solem enim rursus et Lunam et alta sidera est videre non secundum idem omnibus qui in terra et occidentia et orientia, sed primi moribus primi moribus] prioribus V2 pluribus B quidem eis semper qui ad orientem, posterioribus vero eis qui habitant ad occidentem. Consummatas enim tempore sub eodem eclipticas apparitiones, et maxime lunares, non in horis eisdem, hoc est equaliter distantibus a meridie, penes universos reperimus scriptas, sed semper eas que penes magis orientales observantium posteriores eis que penes magis occidentales describuntur et, horarum quidem differentia proportionali distantiis regionum inventa, spericam terre superfitiem quis competenter itaque suspicetur ea que secundum convexitatem secundum omnes sumpta partes partium simillitudine proportionaliter semper obiectiones eis qui deinceps fatiente. Si autem figura altera esset, non utique contingeret hoc, sicut videbit quis utique et ex his. Cava enim siquidem siquidem] quidem V2 ea existente, prioribus utique magis accidentalibus astra orientia apparerent ; plana vero simul et secundum idem omnibus qui in terra et orirentur et occiderent; trigona autem seu tetragona sive alicuius alius figure multiangularum, universis utique rursus similiter et secundum idem recta in eadem habitantibus, quod minime videtur fieri. Quoniam vero neque chilidroides chilidroides] chilindroides V2 chylindroydes B erit ut circularis quidem superfities ad ortus conversa sit et occasus planarum autem basium latera ad mundi polos, – quod utique quasi persuasibilius aliqui suspicentur –, inde manifestum. Nulli enim convexa in superfitie habitantium nullum semper manifestum fieret astrorum, sed vel omnibus omnia et orirentur et occiderent, vel eadem et equaliter obstantia ab utroque polorum cunctis semper inmanifesta permanerent. Nunc autem quanto utique magis ad arctos procedimus, tanto australiorum quidem astrorum plura absconduntur, borealiorum vero apparent. Quare manifestum, quoniam et hec terre convexitas, et in obliquas partes obiectiones proportionaliter faciens, undique formam speroydem monstrat. Cum eo quod, etsi adnavigaverimus mortibus vel aliquibus excelsis locis a quocumque angulo et ad quemcumque, paulatim ipsorum augmentari magnitudines considerantur, quasi ex ipso mari consurgentium, prius vero submensorum propter convexitatem superfitiei aque.
〈I.5〉 Quoniam media celi est terra
Hoc autem considerato, si quis deinceps et de terre inquirat positione, intelliget utique ita solum consumanda apparentia circa ipsam, si celi mediam, quasi centrum spere, substituerimus. Hoc enim minime ita se habente, oporteret vel axem quidem esse extra terram, ab utroque vero polorum equaliter abstare, vel in axe existentem ad alterum polorum accedere, vel neque in axe esse, neque polorum ab utroque distare equaliter. Ad primam ergo trium positionem illa pugnant, quoniam, si in id quidem quod sursum et deorsum aliquorum accedens intelligatur, his utique coaccidet in recta quidem spera nunquam equinoctium fieri inequalia, semper divisis ab orizonte quidem quod super terram et quod sub terra, in inclinata vero, vel minime fieri equinoctium rursus omnino, vel non in estive conversionis et yberne transitu intermedio, spatiis his ex neccessitate factis inequalibus propter equinoctialem et macximum equidistantium scriptorum polus circulationis circulorum non amplius in duo equa dividi ab orizonte, sed unum equidistantium ei et vel magis borealium, vel magis australium. Concessum est autem ab omnibus simpliciter quoniam hec spatia equa contingunt ubique, eo quod et penes equinoctium diei maxime incrementa in estivis conversionibus sint equalia minimorum dierum detrimentis in hyemalibus conversionibus. Si autem in eas que ad orientem vel ad occidentem partes aliquorum rursus accessio supponatur, et his utique accidet, neque magnitudines astrorumque distantias equales et easdem ad eoum et ad hesperium orizonta apparere, neque ab ortu usque medii celi obtentum eo quod a medii celi optentu in occasum tempus equale perfici, que evidenter omnino apparentibus adversantur. Ad secundam autem positionem, secundum quam in axe existens ad alterum polorum accedens intelligetur, rursus itaque quis obiuvabit quoniam, si hoc ita se haberet, secundum climatum unumquodque orizontis planum inequale differenter faceret semper celi quod super terram et quod sub terra secundum aliam et aliam accessionem et ad seipsa et adinvicem sola quidem recta spera inequalia duo dividere ipsam potente orizonte, in inclinatione vero faciente propinquiorem polorum semper manifestum, quod quidem super terram semper minuente, augente vero quod sub terra, quare accidere et maximum qui per medium animalium circulum ab orizontis plano in inequalia dividi, quod minime sic se habens consideratur, sex quidem semper et apud omnes apparentibus signis super terram, sex vero reliquis disparentibus deinceps rursum, illis quidem totis secundum idem apparentibus super terram, reliquis vero simul non apparentibus. Quare manifestum contingere quoniam et zodiaci portiones ab orizonte inequalia duo dividuntur, ex eo quod idem semicirculi toti, aliquotiens quidem super terram, aliquotiens vero sub terra, comprehendantur. Sed et universaliter utique contingeret, si non sub ipso equinoctiali haberet terra positionem, positionem] corr. ex supositionem V3 ad arctos vero aut meridiem declinaret ad alterum polorum, non amplius neque ad sensum in equinoctiis orientales gnomonum umbras secundum equidistantiam equidistantiam] equidistantia V2B orizonti epipeda occidentalibus in directo fieri, quod utique palam videtur assequi. Manifestum autem inde quoniam neque tertiam positionum possibile est procedere, utrisque contrarietatibus que in primis in ipsa contingentibus. Colligenti vero dicere, omnis utique penitus ordo confundetur circa noctis et diei spatiorum augmenta atque diminutiones consideratus, non media subiacente terra, cum eo quod neque Lune eclipses secundum omnes celi partes ad eam que secundum diametrum Soli stationem poterunt consummari, terra multotiens vero vero] non V2 in transitibus secundum diametrum oppositionis interposita ipsis, sed in minoribus semicirculo spatiis.
〈I.6〉 Quoniam puncti rationem habet ad celestia tellus
Quoniam vero puncti etiam rationem habet ad sensum tellus ad illud quod usque eorum que aplana vocantur speram apostima, magnum quidem signum ab omnibus eius partibus astrorum et magnitudines et distantias secundum eadem tempora equales et similles ubique apparere, quemadmodum climatibus a diversis que in eis observationes nec minimum dissonantes inveniuntur. Nec non illud assumendum gnomones in quacumque telluris parte positos, amplius autem cirthotarum centrum sperarum ei quod secundum veritatem terre centrum idem posse et salvare perspectiones et umbrarum circumductiones ita consequentes ypothesibus apparentium, sicut utique si per medium terre punctum factam factam] facte V2B contingerent. Evidens autem signum hoc ita se habere et ubique per visus educta epipeda, que orizontes appellamus, in equalia duo semper totam celi dividere speram, quod utique non contingeret, si terre magnitudo sensibilis esset ad celestium distantiam, sed solum quidem per illud quod in centro punctum eductum epipedum in duo equalia speram dividere posset, que vero per quamcumque terre superficiem maiores utique semper sub terra faceret portiones eis que super terram.
〈I.7〉 Quoniam nullum motum transitivum facit terra
Secundum eadem vero eis que ante ostendetur quoniam nec quemcumque motum in predictas obliquas partes terram passibile passibile] possibile V2B facere, penitusve transire aliquando ab eo qui secundum centum loco. Eadem enim acciderent utique, que et si positionem aliam preter medium habens contingeret. Quare mihi videtur utique superflue utique superflue] inv. V2 quis et eius que in medium lationis inquirere causas, semel quoniam et tellus medium optinet locum mundi, et in ipsam pondera feruntur universa, ita existente evidente ex ipsis apparentibus. Et illud vero solum promtissimum utique in huiusmodi conceptione fiat, sperica et media universi, ut diximus, tellure demonstrata, in omnibus simpliciter eius partibus et nutus et pondus habentium corporum laciones, dico autem proprias eorum, ad rectos angulos semper et ubique fieri educto per eum qui secundum illapsum fit contactum indeclinato epipedo. Manifestum enim propter hoc ita se habere, quoniam et, nisi reciderentur a telluris superfitie, laciones omnino utique in ipsum centrum pervenirent, quoniam et in centrum ducens recta ad rectos angulos semper fit per eam que secundum contactum sectionem contingenti speram epipedo. Quicumque non non] vero V2B preter oppinionem autimant autimant] autumant V2B neque sedere alicubi neque ferri tantum terre pondus mihi viderentur ad eas que secundum ipsos passiones et minime ad universi proprium aspitientes comparationem fatientes falli. Non enim utique mirabille puto eis amplius hoc appareat, si sciant quoniam hec terre magnitudo toti continenti corpori comparata ad ipsum puncti rationem habet. Possibille enim ita extimabitur id, quod secundum proportionem minimum ab eo quod omnino est maximum et omimeron omimeron] omiomeron V2 sustineri et obfirmari undique equaliter et similli inclinatione, deorsum quidem vel sursum ad ipsam nichillo existente in mundo, quemadmodum nec in spera tale quid utique quis intelliget, earum vero que in ipsis concreationum concreationum] concretionum V2 quantum in propria et secundum naturam earum latione levibus quidem et leptomeris in id quod extra et quasi ad circumferentiam flagellatis, visis vero in id quod penes singulos sursum motum facere, eo et quod et quod] inv. V2B omnium nostrum quod super caput sursum vero vocatum, ipsum quoque quasi ad continentem nutum habeat superfitiem, gravibus autem et pachimeris in medium et quasi ad centrum delatis, visis vero in id deorsum cadere, eo quod et omnium rursus nostrum quod ad pedes vocatum autem deorsum, ipsum quoque nutum habeat ad centrum terre, concessum quoque convenienter circa medium sumentibus sub adinvicem undique equali et similli retentione et obfirmatione. Ideo et competenter deprehenditur totum stereoma terre, maximum ita ens ut ad ea que feruntur in ipsam et sub valde minimorum ponderum motu quoniam undique inconcussa utique universa utique universa] om. V2B et quasi concidentia recipiens. Si vero et ipsius esset utique latio communis et una et eadem ponderibus aliis, manifestum quoniam precedet utique universa propter tantam magnitudinis yperbolem deorsum lata et reliquerentur quidem et animalia et particularia ponderum in aere equitantia, hec vero vellocissime omnino utique excederet et ab ipso celo. Verum talia quidem, cogitata etiam solum, omnium utique ridiculosissima apparebunt. Iam vero aliqui, sicut existimabant existimabant] existimant V2B persuasibilius, his quidem non habentes quod contradicant assentiuntur, putant vero ipsis nichil contratestari, si celum quidem immobile supponant verbi gratia, terram autem circa ipsum axem versam ab occidente in orientem quaque quaque] itaque V2 die una ad proximum circumversione, vel et ambo moveantur quamque quamque] quantumcumque V2 quantumque B tantum et circa eundem axem, ut diximus, et commetibiliter ei que ad alterna circumprehensioni. Latuit autem ipsos quoniam propter ea quidem que circa astra apparent nichil utique forsan prohiberet sed sed] secundum V2B simplitiorem intellectum hec ita se habere, ab eis vero que circa nos ipsos et aera accidentibus valde siquidem ridiculum apparebit quod huiusmodi. Ut enim concedamus eis quidem preter naturam ita subtillissima quidem et levissima vel omnino non moveri, vel indifferenter eis que contrarie sunt nature, eis quoque que circa aera minusque subtilibus evidenter ita celeriores terrestrioribus universis facientibus lationes, grossisima vero et gravissima motum proprium acutum sic et equalem facere, terrestribus rursum, ut fatentur, nec ad eum qui ab aliis motum apte interdum se habentibus, attamen terre siquidem conversionem omnium simpliciter motuum qui circa ipsam vallidissimam fieri fatebuntur, velut utique tantam brevi in tempore fatientem restitutionem, quare universa utique in ipsa minime iaccentia unum semper contrarium motum terre fatientia apparentur, et neque nubes neque aliud volitantium vel proiectorum aliquid progrediens ad orientem aliquotiens ostenderetur, precedente semper omnia terre et ad orientem motum presumente, quare reliqua universa in ea que ad occidentem et relicta videri cedere. Si enim et aera dicant simul ipsi circumduci secundum eadem et equali velocitatem, nichilominus secundum ipsam facte concrectiones concrectiones] concreciones V2 semper utique videbuntur ab utrorumque motu derelinqui, vel si et ipsa quasi unita simul aeri circumagentur, neutrum iam utique neque precedentia neque derelicta apparerent, verum manentia semper et neque in volitationibus neque in proiectionibus trasmutationem aliquam fatientia seu transitum; que omnia ita videmus aperte consumata, quasi neque tarditate aliqua omnino, neque celeritate ab eo quod non stet ipsis tellus consequente.
〈I.8〉 Quoniam due differentie primorum motuum sunt in celo
Has quidem ypotheses in particulares tradictiones hisque consequentes neccessario prelibatas sufficiet et usque tanta velut in capitulis substitui, confirmandas et perfecte testificandas ex ipsa consequenter ac deinceps demonstrandorum ad apparentia simphonia. Ad hec vero amplius et illud universalium iuxte iuxte] iuste B quis utique prelibandum arbitretur, quoniam due differentie primorum motuum sunt in celo: una quidem sub qua ab oriente in occidentem feruntur universa, semper eodem modo et equa celeritate circumductionem fatiente secundum equidistantes sibi invicem circulos, huius equaliter universa circumagentis manifestum quoniam scriptos spere polis, quorum maximus circulus equinoctialis appellatur, eo quod ipse solus a maximo ente orizonte semper in equa duo dividatur et ad ipsum solum facta circunversio ad sensum ubique faciat equinoctium; altera vero secundum quam stellarum spere secundum contraria predicte lationis circa polos alteros et non eosdem eis qui prime circumductionis quasdam faciunt transmotiones. Et hec vero ita se habere supponimus, eo quod ex ea quidem que secundum unamquamque diem contemplatione universa omnino que in celo secundum uniformes et equiditantes equinoctiali circulo locos et ortus et mensurases mensurases] mesuranises V2 B et occasus ad sensum facientia conspitiantur, – hoc primi motus proprio existente –; ex ea vero que deinceps et magis continua observatione, alia quidem astrorum omnia et ad seinvicem diastimata et que ad proprios prime lationis locos plurimum ydiomata appareant observantia, Sol autem et Luna et erratica sidera transitiones quasdam fatiant varias quidem et inequales adinvicem, cunctas autem ut ad universalem motum in eas que ad orientem et derelictas partes distantias alternos alternos] alternas V2 B conservantium et quasi sub una spera circumductorum astrorum.
Si ergo et hic errantium transitus secundum equidistantes equinoctiali circulos fieret, idest circa prima fatientes polos circumductionem, suffitiens utique fieret unam autumare et eandem omnium periforam universorum primae consequentem. Persuasibile enim ita appareret et factam ipsorum transitionem secundum derelictos differentes et non secundum oppositum motum consummari. Nunc autem simul eis que ad orientem transitionibus accidentes apparent et ad arctos et ad meridiem, nec omala considerata progressionis huiusmodi quantitate, quare videre per expulsiones quasdam circa ea fieri hoc sinptoma, verum anomala quidem, ut ad talem intelligentiam, ordinata vero, ut sub obliquo ad equinoctialem circulo consummata. Unde et huiusmodi circulus et unus et idem et errantium propius deprehenditur, examinatus vero et scriptus quasi scriptus quasi] inv. V2 B a Solis motu, circumvagatus autem et a Luna et ab errantibus semper circa ipsum conversantibus atque determinata secundum unumquodque in utrasque partes ab illo nec minimum excedentibus recessione. Quoniam vero et maximus iste circulus consideratur eo quod eque et borealior et australior equinoctiali fiat Sol et circum unum eundem, ut diximus, cunctorum errantium ad orientem transitiones consummentur; hanc secundam motus universalis differentia differentia] differentiam V2 B neccesse erat constituere circa polos deprehensi obliqui circuli et in contraria prime lationis consummantam. consummantam] consummatam V2 consumata B Si autem per utrorumque polos predictorum circulorum maximum circulum scriptum intellexerimus, qui ex neccessitate illorum utrorumque, idest et equinoctialem et eum qui ad ipsum inclinatur et in duo equa et ad rectos angulos secat, quatuor quidem erunt obliqui puncta circuli: duo quidem in equinoctiali secundum diametrum sibi invicem facta, vocata vero equinoctia, equinoctia] equinoctialia V2 quorum quod quidem ad arctos a meridie transitum habet vernale dicitur, quod autem oppositum autumpnale, duo autem facta sub per utrosque polos scripto circulo, et ipsa manifestum quoniam secundum diametrum sibi invicem, appellata vero tropica, quorum quod quidem equinoctiali a meridie hybernum dicitur, quod autem ab arctis estivale.
Intelligetur autem una quidem et prima latio aliasque continens universas, circumscripta et quasi determinata a maximo per utrosque polos scripto circulo et circumducto et reliqua omnia circumagente simul ab oriente in occidentem circa polos equinoctialis quasi in eo qui vocatur meridianus equitantes, qui hoc solo a predicto differt, quod et per obliqui polos circuli non semper describitur, amplius quoniam et ad rectos angulos orizonti continue intelligitur, meridianus autem appellatur, quoniam positio talis utrumque et quod super terram et quod sub terra hemisperium in duo equalia seccans, media quoque nictimerorum tempora continet; secunda vero ac multiplex contenta quidem a prima, continens vero errantium omnium speras, lata quidem a predicta ut diximus, revoluta vero in contraria circa obliqui circuli polos, qui et ipsi delati semper in primam circumscriptionem fatiente, idest descripto polos per utrosque, circulo et cum eo convenienter circumaguntur et secundum eum qui in contraria secunde lationis motum eandem semper servant positionem scripti per ipsos maximi et obliqui circuli ad equinoctialem.
〈I.9〉 De particularibus conceptionibus
Universalis itaque prelibatio ut in capitulis talem utique habeat expositionem eorum que opportet presubiacere. Debentes autem eas que secundum partem demonstrationes inchoare, quare primam arbitramur per quam predictorum polorum inter mediam maximi per eos inscripti circuli periferiam quantam contingat esse deprehenditur, earum que in circulo rectarum quantitatis negotium preexpositionem preexpositionem] preexponere V2 preexpositione B videmus necessarium, lineariter semel singula demonstraturi.
〈I.10〉 De quantitate earum que in circulo rectarum
Ad eum igitur usum qui ex promtu canonicam quandam post hec earum quantitatis expositionem faciemus, perimetrum quidem in ccclx portiones dividentes, apponentes vero secundum emimirion augmenta periferiarum subtendentes rectas, hoc est quot sint portionum quasi diametro, eo quod ex computationibus appareat in numeris utile, in cxx divisa portiones. Prius autem ostendemus quomodo utique maxime ut est per pauca et eadem theoremata brevem ac facilem ad earum quantitates epibolem fatiamus, ut non solum rectarum magnitudines sine insistentia expositas habeamus, sed et per eam que ex lineis methodicam ipsarum constitutionem elenchum ex levi percipiamus. Numerorum tamen efodis utemur universaliter secundum sexagenarii modum propter fractionem fractionem] fractionum V2B difficultatem. Amplius autem multiplicationes sequemur atque divisiones proximum semper intuentes, ut nullo cura utique digno differrat reliquum ab eo quod ad sensum examinatum est.
Esto ergo primum semicirculus ABG super diametrum ADG circa centrum D et a centro D recte AG ad rectos angulos protrahatur recta DB et dividatur in duo equalia recta DG ad punctum est est] E V2B et copuletur EB, iaceatque ipsi equalis recta EZ, copuleturque ZB; dico quoniam recta quidem ZD decagoni latus est, recta vero BZ pentagoni. Quoniam enim recta linea DG in duo equa dividitur ad E et adiacet ei quedam recta DZ, quod a rectis GZ et ZD continetur orthogonium cum eo quod a recta 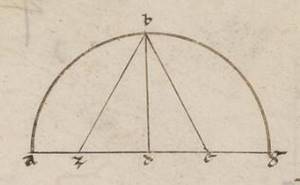 ED tetragono equale est ei quod a recta BE, quoniam equalis est recta EB recte ZE. Verum ei quod a recta EB tetragono equalia sunt que a rectis ED et DB tetragona. Sub rectis ergo GZ et ZD contentum orthogonium cum eo quod a recta DE tetragono, equale est eis que a rectis ED et DB tetragonis et, ablato communi quod a recta ED tetragono, reliquum quod sub GZ et ZD equale est ei quod a recta DB, hoc est ei quod a recta DG. Recta ergo ZG divisa est secundum proportionem habentem medium et duo extrema ad punctum D. Quoniam ergo exagoni et decagoni eidem circulo inscriptorum latera in eadem recta secundum proportionem habentem medium et duo ex ex] extrema B dividuntur, rectaque GD e centro existens exagoni latus continet, recta DZ lateri decagoni equalis est. Similiter autem quoniam pentagoni latus potest illud quod exagoni et illud quod decani decani] decagoni V2 eidem circulo inscriptorum, orthogonii autem BDZ quod a recta BZ tetragonum equale est ei quod a recta BD, que est exagoni latus, et ei quod a recta DZ, que decagoni latus est. Recta ergo BZ pentagoni lateri equalis est.
ED tetragono equale est ei quod a recta BE, quoniam equalis est recta EB recte ZE. Verum ei quod a recta EB tetragono equalia sunt que a rectis ED et DB tetragona. Sub rectis ergo GZ et ZD contentum orthogonium cum eo quod a recta DE tetragono, equale est eis que a rectis ED et DB tetragonis et, ablato communi quod a recta ED tetragono, reliquum quod sub GZ et ZD equale est ei quod a recta DB, hoc est ei quod a recta DG. Recta ergo ZG divisa est secundum proportionem habentem medium et duo extrema ad punctum D. Quoniam ergo exagoni et decagoni eidem circulo inscriptorum latera in eadem recta secundum proportionem habentem medium et duo ex ex] extrema B dividuntur, rectaque GD e centro existens exagoni latus continet, recta DZ lateri decagoni equalis est. Similiter autem quoniam pentagoni latus potest illud quod exagoni et illud quod decani decani] decagoni V2 eidem circulo inscriptorum, orthogonii autem BDZ quod a recta BZ tetragonum equale est ei quod a recta BD, que est exagoni latus, et ei quod a recta DZ, que decagoni latus est. Recta ergo BZ pentagoni lateri equalis est.
Quoniam ergo, ut dixi, supponimus diametrum circuli portionum cxx fit per periacencia recta quidem DE cum sit medietas eius que a centro portionum xxx et quod ab ea dcccc, recta ergo DB que e centro portionum lx et quod ab ipsa iiidc. Quod autem ab recta EB, hoc est quod ab EZ que in idem iiiid longitudine est igitur recta EZ portionum lxvii iiii minutorum lv secundorum ad proximum, at DE xxx et reliqua DZ eorumdem xxxvii portionum iiii minutorum lv secundorum. Decagoni ergo latus submersa ergo vero periferie talium xxxvi qualium est circulus ccclx talium erit xxxvii portionum iiii minutorum lv secundorum, qualium diametros cxx. Kursum Kursum] rursum V2B quoniam DZ portionum est xxxvii iiii lv et quod ab ea in ccclxxv portionum et iiii et xv. Est autem et quod a recta BD eorumdem iiidc, que composita fatiunt quod a recta BZ tetragonum iiiidcccclxxv iiii xv, longitudine igitur erit BZ portionum lxx xxxii iii ad proximum. Que ergo pentagoni latus subtensa autem gradibus lxxii, qualium est circulus ccclx, talium est lxx xxxii iii, qualium diametros cxx. Manifestum vero inde quoniam et que exagoni latus subtendens vero gradus lx et equalis ei que e centro portionum est lx. Similiter autem, quoniam quidem que tetragoni latus subtendens autem gradus xc potentia dupla est eius que a centro, que autem trigoni latus submensa vero gradibus cxx potentia eiusdem tripla est, quod autem ab ea que e centro portionum est iiidc, colligetur quod quidem a tetragoni latere viicc, quod a trigoni autem xdccc. Quare et longitudine que quidem xc gradibus subtenditur recta talium erit lxxxiiii li x ad proximum, qualium diametros cxx; que autem cxx, eorumdem ciii lv xxiii.
Hec Hec] hee V2 ergo ita vobis ex promtu et secundum se ipsas sumantur et erit manifestum hinc quoniam, datis his rectis, ex facili dantur et que relictis in semicirculo periferiis subtenduntur, quoniam que ab ipsis composita fatiunt quod a diametro quadratum et quoniam que gradibus subtenditur xxxvi portionum ostensa est xxxvii iiii lv et quod ab ipsa iccclxxv iiii minutorum xv secundorum, quod autem a diametro portionum est xiiiicccc, erit et quod quidem ad relictos in semicirculo gradus cxliiii subtendente, subtendente] subtenditur B reliquorum xiiixxiiii lv xlv, ipsa longitudine cxiiii vii xxxvii ad proximum et in aliis similiter. Quomodo autem ab his et relique particulares dentur, deinceps ostendemus, ad presens negotium valde utile limatium preexponentes.
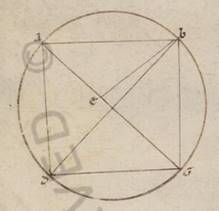 Esto enim circulus inscriptum habens utrumque utrumque] utcumque V2 quadrilaterum ABGD, copulenturque AG et BD, demonstrandum quoniam sub AG et BD contentur orthonium orthonium] orthogonium B ei quod sub AB et DG et ei quod sub AD et BG simul acceptis equale est. Iaceat enim angulo DBG angulus ABE equalis quoniam ergo equalis est angulus DBG angulo ABE, si communem apposuerimus angulum EBD, erit et angulus ABD equalis angulo EBG. Est autem et angulus BDA angulo BGE equalis. Eidem enim portioni subtenduntur. Equiangulus igitur est trigonus ABD trigono BGE. Quare et proportionaliter est, sicut BG ad GE, ita BD ad DA. Quod ergo sub BG et AD equale est ei quod sub DB et GE. Rursus quoniam equalis est ABE angulus angulo DBG, est autem et BAE angulus equalis angulo BDG, equiangulus igitur est BAE trigonus trigono BDG, proportionaliter ergo est, sicut BA ad AE, ita BD ad DG. Quod ergo sub BA et DG equale est ei quod sub BD et AE. Demonstratum est autem et quod sub BG et AD equale ei quod sub BD et GE et totum ergo quod sub AG et BD equale est ei quod sub AB et DG et ei quod sub AD et BG simul acceptis. Quod oportebat ostendere.
Esto enim circulus inscriptum habens utrumque utrumque] utcumque V2 quadrilaterum ABGD, copulenturque AG et BD, demonstrandum quoniam sub AG et BD contentur orthonium orthonium] orthogonium B ei quod sub AB et DG et ei quod sub AD et BG simul acceptis equale est. Iaceat enim angulo DBG angulus ABE equalis quoniam ergo equalis est angulus DBG angulo ABE, si communem apposuerimus angulum EBD, erit et angulus ABD equalis angulo EBG. Est autem et angulus BDA angulo BGE equalis. Eidem enim portioni subtenduntur. Equiangulus igitur est trigonus ABD trigono BGE. Quare et proportionaliter est, sicut BG ad GE, ita BD ad DA. Quod ergo sub BG et AD equale est ei quod sub DB et GE. Rursus quoniam equalis est ABE angulus angulo DBG, est autem et BAE angulus equalis angulo BDG, equiangulus igitur est BAE trigonus trigono BDG, proportionaliter ergo est, sicut BA ad AE, ita BD ad DG. Quod ergo sub BA et DG equale est ei quod sub BD et AE. Demonstratum est autem et quod sub BG et AD equale ei quod sub BD et GE et totum ergo quod sub AG et BD equale est ei quod sub AB et DG et ei quod sub AD et BG simul acceptis. Quod oportebat ostendere.
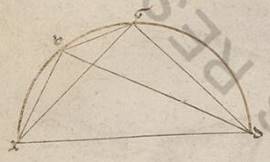 Hoc exposito, esto semicirculus ABGD super diametrum AD et a puncto A due protrahantur AB et AG, sitque utraque earum data magnitudine, qualia in diametro data cxx, copuleturque BG; dico quoniam et ipsa data est. Copulentur enim BD et DG, manifestum ergo quoniam et ipse date sunt, eo quod et in semicirculo relinquantur. Quoniam ergo in circulo quadrilaterum est ABGD, quod sub AB et GD cum eo quod sub AD et BG equale est ei quod sub AG et BD. Est autem et quod sub AG et BD datum et quod sub AB et GD et reliquum ergo quod sub AD et BG datum est et est AD diametros data data ergo est et BG recta. Ac manifestum ergo nobis factum est, quoniam, si date fuerint due periferie et que sub ipsis recte date, et duarum differentia differentia] differentiam V2B periferiarum subtendens recta. Manifestum vero quoniam per hoc theorema et alias non paucas rectas inscribemus ab in eis que secundum seipsas datis differentiis et eam ergo que sub xii gradibus, quoniam habemus et eam que sub lx et eam que sub lxxii.
Hoc exposito, esto semicirculus ABGD super diametrum AD et a puncto A due protrahantur AB et AG, sitque utraque earum data magnitudine, qualia in diametro data cxx, copuleturque BG; dico quoniam et ipsa data est. Copulentur enim BD et DG, manifestum ergo quoniam et ipse date sunt, eo quod et in semicirculo relinquantur. Quoniam ergo in circulo quadrilaterum est ABGD, quod sub AB et GD cum eo quod sub AD et BG equale est ei quod sub AG et BD. Est autem et quod sub AG et BD datum et quod sub AB et GD et reliquum ergo quod sub AD et BG datum est et est AD diametros data data ergo est et BG recta. Ac manifestum ergo nobis factum est, quoniam, si date fuerint due periferie et que sub ipsis recte date, et duarum differentia differentia] differentiam V2B periferiarum subtendens recta. Manifestum vero quoniam per hoc theorema et alias non paucas rectas inscribemus ab in eis que secundum seipsas datis differentiis et eam ergo que sub xii gradibus, quoniam habemus et eam que sub lx et eam que sub lxxii.
Rursum proponatur, data aliqua recta in circulo, eam que sub dimidio subtense periferie rectam invenire. Esto ergo semicirculus ABG super diametrum AG atque data recta GB periferia secetur in duo equa ad punctum D, copulenturque AB et AD, BD et DG, et a puncto D super AG cathetus protrahatur DZ; dico quoniam ZG rectarum AB et AG differentie medietas est. Iaceat enim recte AB equalis recta AE et copulentur DE et quoniam equalis est recta AB recte AE, communis autem AD, due quoque AB et AD duabus AE et AD sunt equales utraque utrique et angulus BAD angulo EAD equalis equalis] add. est ergo basis BD basi DE equalis B et recta ergo DG recte DE equalis est. Quoniam ergo cum ysocheles sit trigonus DEG et a vertice in basim ducta sit cathetus DZ equalis est recta EZ recte ZG. Verum recta 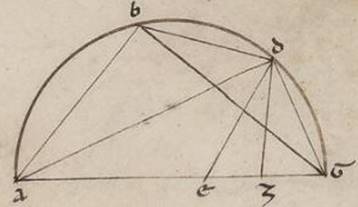 EG tota rectarum AB et AG differentia. differentia] add. est V2 Recta ergo ZG earumdem differentie medietas est. Quare quoniam data est que BG periferie subiacet, inde data est et relicta in semicirculo scilicet AB, dabitur et ZG, cum sit rectarum AG et AB differentie medietas. At quoniam, in orthogonio AGD catheto ducta DZ, equiangulum fit ADG orthogonium ei quod est DGZ et est sicut AG ad GD, ita DG ad GZ, contentum ergo sub AG et GZ orthogonium equale est ei quod a recta GD tetragono. Datum vero quod sub AG et GZ datum ergo est et quod a recta GD tetragonum. Quare et longitudine dabitur recta GD medietati BG subtensa periferie.
EG tota rectarum AB et AG differentia. differentia] add. est V2 Recta ergo ZG earumdem differentie medietas est. Quare quoniam data est que BG periferie subiacet, inde data est et relicta in semicirculo scilicet AB, dabitur et ZG, cum sit rectarum AG et AB differentie medietas. At quoniam, in orthogonio AGD catheto ducta DZ, equiangulum fit ADG orthogonium ei quod est DGZ et est sicut AG ad GD, ita DG ad GZ, contentum ergo sub AG et GZ orthogonium equale est ei quod a recta GD tetragono. Datum vero quod sub AG et GZ datum ergo est et quod a recta GD tetragonum. Quare et longitudine dabitur recta GD medietati BG subtensa periferie.
Ac per hoc item theorema alie quoque summuntur plurime secundum preexpositarum medietates, et a xii subtensa gradibus recta et que vi et que tribus et que uni et dimidio subtenditur, et que dimidio et quarte unius. Reperimus autem expilogismis expilogismis] ex epilogismis V2B eam quidem que sub uno gradu et dimidio talium unius et a a] om. V2B xxxiiii et xv ad proximum, qualium est diametros cxx, eam vero que sub dimidio et quarta, eorumdem o xlvii l.
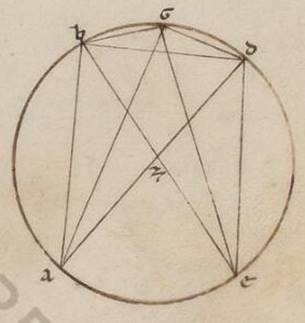 Rursum esto circulus ABGD circa diametrum quidem AD AD] ad V2 centrum vero Z et a puncto A summantur due periferie secundum date secundum date] date secundum V2B deinceps AB scilicet et BG, copulenturque AB et AG sub ipsis recte et ipse date, dico quoniam, si copulaverimus rectam AG, dabitur et ipsa. Ducatur enim per punctum B diametros circuli sitque BZE, copulenturque BD, DG, GE, DE. Manifestum vero inde quoniam propter rectam quidem BG dabitur et GE, ac propter AB dabitur et BD et DE. Et ex his que ante dicta sunt, quoniam in circulo quadrilaterum est BGDE atque in eo protracte sunt BD et GE, contentum sub eis orthogonium eisque sub contrapositis simul acceptis est equale. Quare quoniam, dato quod sub BD et GE, datum est et quod sub BG et DE, datum est ergo et quod sub BE et GD. Data est autem et BE diametros et reliqua GD erit data, quamobrem et relicta in semicirculum recta GA. Quare si detur due periferie et que sub eis recte, dabitur et coutrisque periferiis secundum compositionem subtensa recta per hoc theorema. Manifestum vero quoniam semper cum preexpositis omnibus eam que sub uno gradu et dimidio componentes et compositas computantes universas simpliciter inscribemus, quecumque bis facte tertiam partem habebunt, et sole adhuc comprehenduntur ana unius et dimidii gradus spatiorum intermedie due secundum unumquodque future, quoniam quidem secundum emimirion facimus inscriptionem. Quare si eam que sub emimirio rectam invenerimus, ipsam ipsam] ipsa V2B secundum compositionem et habundantiam ad spatia continentes et datas rectas reliquas quoque intermedias omnes nobis coadimplebit. Quoniam vero, data aliqua recta ut ea que sub uno gradu et dimidio, tertie que tertie que] inv. V2B eiusdem periferie subtenditur, per lineas nullo modo datur, – si vero possibile esset, haberemus utique inde et eam que sub emimirio –, prius eam que sub uno gradu docebimus ab ea que sub uno gradu et dimidio, et ea que sub dimidio et quarta limatium supponentes, quod, quamvis non universaliter possit quantitates diffinire, in ita minimis tamen id quod ad diffinitas inpermutabile poterit conservare. Dico enim quoniam, si in circulo due recte inequales protrahantur, maior ad minorem minorem habet proportionem quam que super maiorem rectam periferia ad eam que super minorem.
Rursum esto circulus ABGD circa diametrum quidem AD AD] ad V2 centrum vero Z et a puncto A summantur due periferie secundum date secundum date] date secundum V2B deinceps AB scilicet et BG, copulenturque AB et AG sub ipsis recte et ipse date, dico quoniam, si copulaverimus rectam AG, dabitur et ipsa. Ducatur enim per punctum B diametros circuli sitque BZE, copulenturque BD, DG, GE, DE. Manifestum vero inde quoniam propter rectam quidem BG dabitur et GE, ac propter AB dabitur et BD et DE. Et ex his que ante dicta sunt, quoniam in circulo quadrilaterum est BGDE atque in eo protracte sunt BD et GE, contentum sub eis orthogonium eisque sub contrapositis simul acceptis est equale. Quare quoniam, dato quod sub BD et GE, datum est et quod sub BG et DE, datum est ergo et quod sub BE et GD. Data est autem et BE diametros et reliqua GD erit data, quamobrem et relicta in semicirculum recta GA. Quare si detur due periferie et que sub eis recte, dabitur et coutrisque periferiis secundum compositionem subtensa recta per hoc theorema. Manifestum vero quoniam semper cum preexpositis omnibus eam que sub uno gradu et dimidio componentes et compositas computantes universas simpliciter inscribemus, quecumque bis facte tertiam partem habebunt, et sole adhuc comprehenduntur ana unius et dimidii gradus spatiorum intermedie due secundum unumquodque future, quoniam quidem secundum emimirion facimus inscriptionem. Quare si eam que sub emimirio rectam invenerimus, ipsam ipsam] ipsa V2B secundum compositionem et habundantiam ad spatia continentes et datas rectas reliquas quoque intermedias omnes nobis coadimplebit. Quoniam vero, data aliqua recta ut ea que sub uno gradu et dimidio, tertie que tertie que] inv. V2B eiusdem periferie subtenditur, per lineas nullo modo datur, – si vero possibile esset, haberemus utique inde et eam que sub emimirio –, prius eam que sub uno gradu docebimus ab ea que sub uno gradu et dimidio, et ea que sub dimidio et quarta limatium supponentes, quod, quamvis non universaliter possit quantitates diffinire, in ita minimis tamen id quod ad diffinitas inpermutabile poterit conservare. Dico enim quoniam, si in circulo due recte inequales protrahantur, maior ad minorem minorem habet proportionem quam que super maiorem rectam periferia ad eam que super minorem.
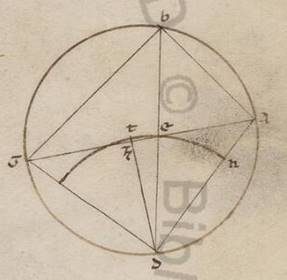 Esto enim circulus ABGD et pertrahantur in ipso due recte inequales, minor quidem AB, maior vero BG; dico quoniam BG recta ad BA rectam minorem habet proportionem quam BG periferia ad BA periferiam. Dividatur enim ABG angulus in duo equa a recta BD, copulenturque AEG et AD et GD et quoniam ABG angulus in duo equa divisus est a recta BED, equalis quidem est GD recta recte AD, maior vero GE recta quam EA. Ducatur autem a puncto D cathetus DZ in rectam AEG. Quoniam ergo maior est AD quidem quam ED, ED vero quam DZ, centro quidem D spatio vero DE descriptus circulus AD quidem secabit, cadet vero super AZ. Describatur ergo circulus NET et educatur recta DZT et quoniam sector quidem DET maior est trigono DEZ, trigonus autem DEA maior est sectore DEN, trigonus ergo DEZ ad DEA trigonum minorem proportionem habet quam DET, sector ad DEN sectorem. Verum sicut trigonus DEZ ad trigonum DEA, ita EZ ad EA; ut autem sector DET ad sectorem DEN, ita ZDE angulus ad angulum EDA. Recta ergo ZE ad AE rectam minorem habet proportionem quam ZDE angulus ad angulum EDA. Quare et componenti recta ZA ad EA rectam minorem proportionem habet quam ZDA angulus ad angulum ADE et antecedentium dupla GA recta ad AE rectam minorem habet proportionem quam GDA angulus ad angulum EDA. Et dividenti recta GE ad rectam EA minorem proportionem habet quam GDE angulus ad angulum EDA. Verum ut recta quidem GE ad rectam EA, ita recta GB ad BA; ut autem GDB angulus ad BDA, ita periferia GB ad periferiam BA. Recta ergo GB ad BA minorem proportionem habet quam GB periferia ad BA periferiam.
Esto enim circulus ABGD et pertrahantur in ipso due recte inequales, minor quidem AB, maior vero BG; dico quoniam BG recta ad BA rectam minorem habet proportionem quam BG periferia ad BA periferiam. Dividatur enim ABG angulus in duo equa a recta BD, copulenturque AEG et AD et GD et quoniam ABG angulus in duo equa divisus est a recta BED, equalis quidem est GD recta recte AD, maior vero GE recta quam EA. Ducatur autem a puncto D cathetus DZ in rectam AEG. Quoniam ergo maior est AD quidem quam ED, ED vero quam DZ, centro quidem D spatio vero DE descriptus circulus AD quidem secabit, cadet vero super AZ. Describatur ergo circulus NET et educatur recta DZT et quoniam sector quidem DET maior est trigono DEZ, trigonus autem DEA maior est sectore DEN, trigonus ergo DEZ ad DEA trigonum minorem proportionem habet quam DET, sector ad DEN sectorem. Verum sicut trigonus DEZ ad trigonum DEA, ita EZ ad EA; ut autem sector DET ad sectorem DEN, ita ZDE angulus ad angulum EDA. Recta ergo ZE ad AE rectam minorem habet proportionem quam ZDE angulus ad angulum EDA. Quare et componenti recta ZA ad EA rectam minorem proportionem habet quam ZDA angulus ad angulum ADE et antecedentium dupla GA recta ad AE rectam minorem habet proportionem quam GDA angulus ad angulum EDA. Et dividenti recta GE ad rectam EA minorem proportionem habet quam GDE angulus ad angulum EDA. Verum ut recta quidem GE ad rectam EA, ita recta GB ad BA; ut autem GDB angulus ad BDA, ita periferia GB ad periferiam BA. Recta ergo GB ad BA minorem proportionem habet quam GB periferia ad BA periferiam.
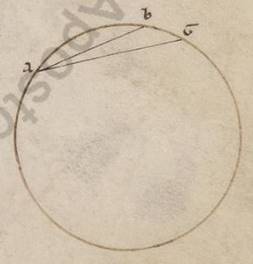 Hoc ita subiacente, esto circulus ABG et protrahatur protrahatur] protrahantur V2B in ipso due recte AB et AG. Subiaceat autem AB quidem primum AB … primum] primum AB quidem V2 subtendi unius gradus dimidio et quarte, AG vero uni gradui. Quoniam AG rectam AG rectam] inv. V2 ad BA rectam minorem habet proportionem quam AG periferia ad AB, periferia vero AG epitritos eius est que est AB recta, ergo GA eius que est BA minor est quam epitritos. Verum AB recta ostensa est talium lxvii lxvii] xlvii V2 47 B minutorum et vii secundorum, qualium est cxx diametros. Recta ergo GA minor est eorumdem uno duobus minutis et l secundis. Hec enim epitrita sunt ad proximum xlvii minutorum et vii secundorum.
Hoc ita subiacente, esto circulus ABG et protrahatur protrahatur] protrahantur V2B in ipso due recte AB et AG. Subiaceat autem AB quidem primum AB … primum] primum AB quidem V2 subtendi unius gradus dimidio et quarte, AG vero uni gradui. Quoniam AG rectam AG rectam] inv. V2 ad BA rectam minorem habet proportionem quam AG periferia ad AB, periferia vero AG epitritos eius est que est AB recta, ergo GA eius que est BA minor est quam epitritos. Verum AB recta ostensa est talium lxvii lxvii] xlvii V2 47 B minutorum et vii secundorum, qualium est cxx diametros. Recta ergo GA minor est eorumdem uno duobus minutis et l secundis. Hec enim epitrita sunt ad proximum xlvii minutorum et vii secundorum.
Rursus in eadem descriptione recta quidem AB subiaceat uni subtensa gradui, AG vero uni et dimidio. Secundum eadem ergo quoniam AG periferia periferie AB est emiolia, recta ergo GA recte BA minor est quam emiolia. Verum AG demonstravimus rectam talium esse unius xxxiiii et xv, qualium est diametros cxx. Recta ergo AB maior est eorumdem uno duobus min. et l sec. Horum enim emiolia sunt preiacentia unius xxxiiii minutorum dxv dxv] xv V2 15 B secundorum. Quare quoniam eisdem demonstrata est et maior et minor uni subtensa gradui recta, manifestum est quoniam hanc habebimus talium unius ii minutorum et l secundorum ad proximum, qualium est diametros cxx. Ac propter preostensa eam, quoque que sub emimirio que invenitur eorundem xxxi minutorum et xxv secundorum ad proximum et coadimplebuntur reliqua, ut diximus, spatia: ex ea quidem que ad unum et dimidium gradum, verbi gratia, ut in primo spatio, compositione emimirii ea que sub duobus gradibus demonstrata est, ex habundantia vero que ad tres gradus ea quoque que sub duobus gradibus et dimidio data, eodem vero modo et in reliquis. Negotium vero rectarum que in circulo, sicut utique reor, facile pertractabitur. Ut autem, sicut dixi, in necessitatum unaquaque rectarum quantitates ex promptu habeamus, canonia subordinabimus ana versuum xlv simmetrie causa, quorum prime quidem partes periferiarum quantitates continebunt secundum emimirion accrescentes, secunde vero adiacentium periferiis rectarum magnitudines, velut diametro cxx portionum subiacente, tertie autem eius quod secundum unumquodque emimirion rectarum incrementi partem tricesimam, ut et unius sexagesime mediam habentes epybolam indifferentem ad sensum examinate et in in] om. V2 eis que infra dimidium partibus pertinentes invenire possimus quantitates. Facile vero intelligi quoniam per eadem et preiacentia theoremata, etsi in ambiguitate simus descriptive fallacie circa quedam adiacentium in canonio rectarum, facilem faciemus et inquisitionem et correctionem, sive ab ea que sub dupla inquisite, sive ab ea que datarum ad aliquas alias differentia, sive ab ea que relicta relicta] relicte V2 B in semicirculo periferie recta subtenditur. Et est canonii descriptio talis.
〈I.11〉 Canonium earum que in circulo rectarum
Perife
riarum |
rectarum |
sexagessimarum |
perife
ria |
rectarum |
sexagessimarum |
|||||||||
G |
M |
S |
M |
S |
T |
G |
M |
S |
M |
S |
T |
|||
Dimid g |
o |
xxxi |
xxv |
i |
ii |
l |
xxiii |
xxiii |
lv |
xxvii |
i |
i |
xxxiii |
|
i |
i |
ii |
l |
i |
ii |
l |
xxiii.ϛ |
xxiiii |
xxvi |
xiii |
i |
i |
xxx |
|
i et d |
i |
xxxiiii |
xv |
i |
ii |
l |
xxiiii |
xxiiii |
lvi |
lviii |
i |
i |
xxvi |
|
ii |
ii |
v |
xl |
i |
ii |
l |
xxiiii.ϛ |
xxv |
xxvii |
xli |
i |
i |
xxii |
|
ii et d |
ii |
xxxvii |
iiii |
i |
ii |
xlviii |
xxv |
xxv |
lviii |
xxii |
i |
i |
xix |
|
iii |
iii |
viii |
xxviii |
i |
ii |
xlviii |
xxv et d |
xxvi |
xxix |
i |
i |
i |
xv |
|
iii et d |
iii |
xxxix |
lii |
i |
ii |
xlviii |
xxvi |
xxvi |
lix |
xxxviii |
i |
i |
xi |
|
iiii |
iiii |
xi |
xvi |
i |
ii |
xlvii |
xxvi.ϛ |
xxvii |
xxx |
xiiii |
i |
i |
viii |
|
iiii.ϛ |
iiii |
xlii |
xl |
i |
ii |
xlvii |
xxvii |
xxxviii |
o |
xlviii |
i |
i |
xiiii |
|
v |
v |
xiiii |
iiii |
i |
ii |
xlvi |
xxvii.ϛ |
xxxviii |
xxxi |
xx |
i |
i |
o |
|
v.ϛ |
v |
xlv |
xxvii |
i |
ii |
xlv |
xxviii |
xxix |
i |
l |
i |
o |
lvi |
|
vi |
vi |
xvi |
xlix |
i |
ii |
xliiii |
xxviii.ϛ |
xxix |
xxxii |
xviii |
i |
o |
lii |
|
vi.ϛ |
vi |
xlviii |
xi |
i |
ii |
xliii |
xxix |
xxx |
ii |
xliiii |
i |
o |
xlviii |
|
vii |
vii |
xix |
xxxiii |
i |
ii |
xlii |
xxix.ϛ |
xxx |
xxxiii |
viii |
i |
o |
xliiii |
|
vii.ϛ |
vii |
l |
liiii |
i |
ii |
xli |
xxx |
xxxi |
iii |
xxx |
i |
o |
xl |
|
viii |
viii |
xxii |
xv |
i |
ii |
xl |
xxx.ϛ |
xxxi |
xxxiii |
l |
i |
o |
xxxv |
|
viii.ϛ |
viii |
liii |
xxv |
i |
ii |
xxxix |
xxxi |
xxxii |
iiii |
viii |
i |
o |
xxxi |
|
ix |
ix |
liiii |
li |
i |
ii |
xxxviii |
xxxi.ϛ |
xxxii |
xxxiiii |
xxii |
i |
o |
xxvii |
|
ix.ϛ |
ix |
lvi |
xiii |
i |
ii |
xxxvii |
xxxii |
xxxiii |
iiii |
xxxv |
i |
o |
xxii |
|
x |
x |
xxvii |
xxxii |
i |
ii |
xxxv |
xxxii.ϛ |
xxxiii |
xxxi |
xlvi |
i |
o |
xvii |
|
x.ϛ |
x |
lviii |
xlix |
i |
ii |
xxxiii |
xxxiii |
xxxiiii |
iiii |
lv |
i |
o |
xii |
|
xi |
xi |
xxx |
v |
i |
ii |
xxxii |
xxxiii.ϛ |
xxxiiii |
xxxv |
i |
i |
o |
viii |
|
xi.ϛ |
xii |
i |
xxi |
i |
ii |
xxx |
xxxiiii |
xxxv |
v |
v |
i |
o |
iii |
|
xii |
xii |
xxxii |
xxxvi |
i |
ii |
xxviii |
xxxiiii et d |
xxxv |
xxxv |
vi |
o |
lix |
lvii |
|
xii.ϛ |
xiii |
iii |
l |
i |
ii |
xxvii |
xxxv |
xxxvi |
v |
v |
o |
lix |
lii |
|
xiii |
xiii |
xxxv |
iiii |
i |
ii |
xxv |
xxxv.ϛ |
xxxvi |
xxxv |
i |
o |
lix |
xlviii |
|
xiii.ϛ |
xiiii |
v |
xvi |
i |
ii |
xxiii |
xxxvi |
xxxvii |
iiii |
lv |
o |
lix |
xliii |
|
xiiii |
xiiii |
xxxvii |
xxvii |
i |
ii |
xxi |
xxxvi.ϛ |
xxxvii |
xxxiiii |
xlvii |
o |
lix |
xxxviii |
|
xiiii.ϛ |
xv |
viii |
xxxviii |
i |
ii |
xix |
xxxvii |
xxxviii |
iiii |
xxxvi |
o |
lix |
xxxii |
|
xv |
xv |
xxxix |
xlvii |
i |
ii |
xvii |
xxxvii.ϛ |
xxxviii |
xxxiiii |
xxii |
o |
lix |
xxvii |
|
xv.ϛ |
xvi |
x |
lvi |
i |
ii |
xv |
xxxviii |
xxxix |
iiii |
v |
o |
lix |
xxii |
|
xvi |
xvi |
xlii |
iii |
i |
ii |
xiii |
xxxviii.ϛ |
xl |
xxxiii |
xlvi |
o |
lix |
xvi |
|
xvi.ϛ |
xvii |
xiii |
ix |
i |
ii |
x |
xxxix |
xl |
iii |
xxv |
o |
lix |
xi |
|
xvii |
xvii |
xiii |
ix |
i |
ii |
vii |
xxxix.ϛ |
xl |
xxxiiii |
o |
o |
lix |
v |
|
xvii.ϛ |
xviii |
xv |
xvii |
i |
ii |
v |
xl |
xli |
ii |
xxxiii |
o |
lix |
o |
|
xviii |
xviii |
xlvi |
xix |
i |
ii |
ii |
xl.ϛ |
xli |
xxxii |
iii |
o |
lviii |
liiii |
|
xviii.ϛ |
xix |
xvii |
xxi |
i |
ii |
o |
xli |
xlii |
i |
xxx |
o |
lviii |
xlviii |
|
xix |
xix |
xlviii |
xxi |
i |
i |
lvii |
xli.ϛ |
xlii |
xxx |
liiii |
o |
lviii |
xlii |
|
xix.ϛ |
xx |
xix |
xix |
i |
i |
liiii |
xlii |
xliii |
o |
xv |
o |
lviii |
xxxvi |
|
xx |
xx |
l |
xvi |
i |
i |
li |
xlii.ϛ |
xliii |
xxix |
xxxiii |
o |
lviii |
xxxi |
|
xx.ϛ |
xxi |
xxi |
xi |
i |
i |
xlviii |
xliii |
xliii |
lviii |
xlix |
o |
lviii |
xxv |
|
xxi |
xxi |
lii |
vi |
i |
i |
xlv |
xliii.ϛ |
xliiii |
xxviii |
i |
o |
lviii |
xviii |
|
xxi.ϛ |
xxii |
xxii |
xlviii |
i |
i |
xlii |
xliiii |
xliiii |
lvii |
x |
o |
lviii |
xii |
|
xxii |
xxii |
liii |
xlix |
i |
i |
xxxix |
xliiii.ϛ |
xlv |
xxvi |
xvi |
o |
lviii |
vi |
|
xxii.ϛ |
xxiii |
xxi |
xxxix |
i |
i |
xxxvi |
xlv |
xlv |
lv |
xix |
o |
lviii |
o |
|
perifer
iarum |
Rectarum sexagesimarum |
periferi
arum |
Rectarum |
sexagessimarum |
||||||||||
G |
M |
S |
M |
S |
T |
G |
M |
S |
M |
S |
T |
|||
xlv.ϛ |
xlvi |
xxiiii |
xix |
o |
lvii |
liiii |
lxviii |
lxvii |
vi |
xii |
o |
lii |
i |
|
xlvi |
xlvi |
xxiii |
xvi |
o |
lvii |
xlvii |
lxviii.ϛ |
lxvii |
xxxii |
xii |
o |
li |
lii |
|
xlvi.ϛ |
xlvii |
xxii |
ix |
o |
lvii |
xli |
lxix |
lxvii |
lviii |
l |
o |
li |
xliii |
|
xlvii |
xlvii |
li |
o |
o |
lvii |
xxxiiii |
lxix.ϛ |
lxviii |
xxiii |
lix |
o |
li |
xxxiii |
|
xlvii.ϛ |
xlviii |
xix |
xlvii |
o |
lvii |
xxvii |
lxx |
lxviii |
xlix |
xlv |
o |
li |
xxiii |
|
xlviii |
xlviii |
xlviii |
xxx |
o |
lvii |
xxi |
lii.ϛ |
lxix |
xv |
xxvii |
o |
li |
xiiii |
|
xlviii.ϛ |
xlix |
xvii |
xi |
o |
lvii |
xiiii |
lxxi |
lxix |
xli |
iiii |
o |
li |
iiii |
|
xlix |
xlix |
xlv |
xlviii |
o |
lvii |
vii |
lxxi.ϛ |
lxx |
vi |
xxxvi |
o |
l |
lv |
|
xlix.ϛ |
l |
xiiii |
xxi |
o |
lvii |
o |
lxxii |
lxx |
xxxii |
iii |
o |
l |
xlv |
|
l |
l |
xlii |
li |
o |
lvi |
liii |
lxxii.ϛ |
lxx |
li |
xxvi |
o |
l |
xxxv |
|
l.ϛ |
li |
xi |
xviii |
o |
lvi |
xlvi |
lxxiii |
lxxi |
xxii |
xliiii |
o |
l |
xxv |
|
li |
li |
xxxix |
xlii |
o |
lvi |
xxxix |
lxxiii.ϛ |
lxxi |
xlvii |
lvi |
o |
l |
xvi |
|
li.ϛ |
lii |
viii |
o |
o |
lvi |
xxxii |
lxxiiii |
lxxii |
xiii |
iiii |
o |
l |
vi |
|
lii |
lii |
xxxvi |
xvi |
o |
lvi |
xxv |
lxxiiii.ϛ |
lxxii |
xxxviii |
vii |
o |
xlix |
lvi |
|
lii.ϛ |
liii |
iiii |
xxix |
o |
lvi |
xviii |
lxxv |
lxxiii |
iii |
v |
o |
xlix |
xlvi |
|
liii |
liii |
xxxii |
xxxviii |
o |
lvi |
x |
lxxv.ϛ |
lxxiii |
xxvii |
lviii |
o |
xlix |
xxxvi |
|
liii.ϛ |
liiii |
o |
xliii |
o |
lvi |
iii |
lxxvi |
lxxiii |
lii |
xlvi |
o |
xlix |
xxvi |
|
liiii |
liiii |
xxviii |
xliiii |
o |
lv |
lv |
lxxvi.ϛ |
lxxiiii |
xvii |
xxix |
o |
xlix |
xvi |
|
liiii.ϛ |
liiii |
lvi |
xlii |
o |
lv |
xlviii |
lxxvii |
lxxiiii |
xlii |
vii |
o |
xlix |
vi |
|
lv |
lv |
xxiiii |
xxxvi |
o |
lv |
xl |
lxxvii.ϛ |
lxxv |
vi |
xxxix |
o |
xlviii |
lv |
|
lv.ϛ |
lv |
lii |
xxvi |
o |
lv |
xxxiii |
lxxviii |
lxxv |
xxxi |
vii |
o |
xlviii |
xlv |
|
lvi |
lvi |
xx |
xii |
o |
lv |
xxv |
lxxviii.ϛ |
lxxv |
lv |
xxix |
o |
xlviii |
xxxiiii |
|
lvi.ϛ |
lvi |
xlvii |
liiii |
o |
lv |
xvii |
lxxix |
lxxvi |
xix |
xlvi |
o |
xlviii |
xxiiii |
|
lvii |
lvii |
xv |
xxxiii |
o |
lv |
ix |
lxxix.ϛ |
lxxvi |
xliii |
lviii |
o |
xlviii |
xiii |
|
lvii.ϛ |
lvii |
xliii |
vii |
o |
lv |
l |
lxxx |
lxxvii |
viii |
v |
o |
xlviii |
iii |
|
lviii |
lviii |
x |
xxxviii |
o |
liiii |
liii |
lxxx.ϛ |
lxxvii |
xxxii |
vi |
o |
xlvii |
lii |
|
lviii.ϛ |
lviii |
xxxviii |
v |
o |
liiii |
xlv |
lxxxi |
lxxvii |
lvi |
ii |
o |
xlvii |
xli |
|
lix |
lix |
v |
xxvii |
o |
liiii |
xxxvii |
lxxxi.ϛ |
lxxviii |
xix |
lii |
o |
xlvii |
xxxi |
|
lix.ϛ |
lix |
xxxii |
xlv |
o |
liiii |
xxix |
lxxxii |
lxxviii |
xliii |
xxxviii |
o |
xlvii |
xx |
|
lx |
lx |
o |
o |
o |
liiii |
xxi |
lxxxii.ϛ |
lxxix |
vii |
xviii |
o |
xlvii |
ix |
|
lx.ϛ |
lx |
xxvii |
xi |
o |
liiii |
xxii |
lxxxiii |
lxxix |
xxx |
lii |
o |
xlvi |
lviii |
|
lxi |
lx |
liiii |
xvii |
o |
liiii |
iiii |
lxxxiii.ϛ |
lxxix |
liiii |
xxi |
o |
xlvi |
xlvii |
|
lxi.ϛ |
lxi |
xxi |
xix |
o |
liii |
lvi |
lxxxiiii |
lxxx |
xvii |
xlv |
o |
xlvi |
xxxvi |
|
lxii |
lxi |
xlviii |
xvii |
o |
liii |
xlvii |
lxxxiiii.ϛ |
lxxx |
xli |
iii |
o |
xlvi |
xxv |
|
lxii.ϛ |
lxii |
xv |
x |
o |
liii |
xxxix |
lxxxv |
lxxxi |
iiii |
xv |
o |
xlvi |
xiiii |
|
lxiii |
lxii |
xlii |
o |
o |
liii |
xxx |
lxxxv.ϛ |
lxxxi |
xxvii |
xxii |
o |
xlvi |
iii |
|
lxiii.ϛ |
lxiii |
viii |
xlv |
o |
liii |
xxii |
lxxxvi |
lxxxi |
l |
xxiiii |
o |
xlv |
lii |
|
lxiiii |
lxiii |
xxxv |
xxv |
o |
liii |
xiii |
lxxxvi.ϛ |
lxxxii |
xvii |
xix |
o |
xlv |
xl |
|
lxiiii.ϛ |
lxiiii |
ii |
i |
o |
liii |
iiii |
lxxxvii |
lxxxii |
xxxvi |
ix |
o |
xlv |
xxix |
|
lxv |
lxiiii |
xxviii |
xxxiiii |
o |
lii |
lv |
lxxxvii.ϛ |
lxxxii |
lviii |
liiii |
o |
xlv |
xviii |
|
lxv.ϛ |
lxiiii |
lv |
i |
o |
lii |
xlvi |
lxxxviii |
lxxxiii |
xxi |
xxxiii |
o |
xlv |
vi |
|
lxvi |
lxv |
xxi |
xxiiii |
o |
lii |
xxxvii |
lxxxviii.ϛ |
lxxxiii |
xli |
iiii |
o |
xliiii |
lv |
|
lxvi.ϛ |
lxv |
xlvii |
xliii |
o |
lii |
xxviii |
lxxxix |
lxxxiiii |
vi |
xxxii |
o |
xliiii |
xliii |
|
lxvii |
lxvi |
xiii |
lvii |
o |
lii |
xix |
lxxxix.ϛ |
lxxxiiii |
xxviii |
liiii |
o |
xliiii |
xxxi |
|
lxvii.ϛ |
lxvi |
xl |
vii |
o |
lii |
x |
xc |
lxxxiiii |
li |
x |
o |
xliiii |
xx |
|
periferi
arum |
rectartum |
sexagessimarum |
periferi
arum |
rectarum |
sexagessimarum |
|||||||||
G |
M |
S |
M |
S |
T |
G |
M |
S |
M |
S |
T |
|||
xc.ϛ |
lxxxv |
xiii |
xx |
o |
xliiii |
viii |
cxiii |
c |
lix |
lix |
o |
xxxiiii |
xxxi |
|
xci |
lxxxv |
xxxv |
xxiiii |
o |
xliii |
lvii |
cxiii.ϛ |
c |
xxi |
xvi |
o |
xxxiiii |
xx |
|
xci.ϛ |
lxxxv |
lvii |
xxiii |
o |
xliii |
xlv |
cxiiii |
c |
xxxviii |
xxvi |
o |
xxxiiii |
vi |
|
xcii |
lxxxvi |
xix |
xv |
o |
xliii |
xxxiii |
cxiiii.ϛ |
c |
lv |
xxviii |
o |
xxxiii |
lii |
|
xcii.ϛ |
lxxxvi |
xli |
ii |
o |
xliii |
xxi |
cxv |
ci |
xii |
xxv |
o |
xxxiii |
xxxix |
|
xciii |
lxxxvii |
ii |
xlii |
o |
xliii |
ix |
cxv.ϛ |
ci |
xxix |
xv |
o |
xxxiii |
xxv |
|
xciii.ϛ |
lxxxvii |
xxiiii |
xvii |
o |
xlii |
lvii |
cxvi |
ci |
xlv |
lvii |
o |
xxxiii |
xi |
|
xciiii |
lxxxvii |
xlv |
xlv |
o |
xlii |
xlv |
cxvi.ϛ |
cii |
ii |
xxxiii |
o |
xxxii |
lvii |
|
xciiii.ϛ |
lxxxviii |
vii |
vii |
o |
xlii |
xxxiii |
cxvii |
cii |
xix |
i |
o |
xxxii |
xliii |
|
xcv |
lxxxviii |
xxviii |
xxiiii |
o |
xlii |
xxi |
cxvii.ϛ |
cii |
xxxv |
xxii |
o |
xxxii |
xxix |
|
xcv.ϛ |
lxxxviii |
xlix |
xxxiiii |
o |
xlii |
ix |
cxviii |
cii |
li |
xxxvii |
o |
xxxii |
xv |
|
xcvi |
lxxxix |
x |
xxxix |
o |
xli |
lvii |
cxviii.ϛ |
ciii |
vii |
xli |
o |
xxxii |
o |
|
xcvi.ϛ |
lxxxix |
xxxi |
xxxvii |
o |
xli |
xlv |
cxix |
ciii |
xxiii |
xliiii |
o |
xxxi |
xlvi |
|
xcvii |
lxxxix |
lii |
xxvii |
o |
xli |
xxxiii |
cxix.ϛ |
ciii |
xxxix |
xxxvii |
o |
xxxi |
xxxii |
|
xcvii.ϛ |
xc |
xiii |
xv |
o |
xli |
xxi |
cxx |
ciii |
lv |
xxiii |
o |
xxxi |
xviii |
|
xcviii |
xc |
xxxiii |
lv |
o |
xli |
viii |
cxx.ϛ |
ciiii |
xi |
ii |
o |
xxxi |
iiii |
|
xcviii.ϛ |
xc |
liiii |
xxix |
o |
xl |
lv |
cxxi |
ciiii |
xxxi |
xxxiiii |
o |
xxx |
xlviiii |
|
xcix |
xci |
xiiii |
lvi |
o |
xl |
xlii |
cxxi.ϛ |
ciiii |
xli |
lix |
o |
xxx |
xxxv |
|
xcix.ϛ |
xci |
xxxv |
xvii |
o |
xl |
xxx |
cxxii |
ciiii |
lvii |
xvi |
o |
xxx |
xxi |
|
c |
xci |
lv |
xxxii |
o |
xl |
xvii |
cxxii.ϛ |
cv |
xii |
xxvi |
o |
xxx |
vii |
|
c.ϛ |
xcii |
xv |
xl |
o |
xl |
iiii |
cxxiii |
cv |
xxvii |
xxx |
o |
xxix |
lii |
|
ci |
xcii |
xxxv |
xlii |
o |
xxxix |
lii |
cxxiii.ϛ |
cv |
xlii |
xxvi |
o |
xxix |
xxxvii |
|
ci.ϛ |
xcii |
lv |
xxxviii |
o |
xxxix |
xxxix |
cxxiiii |
cv |
lvii |
xiiii |
o |
xxix |
xxiii |
|
cii |
xciii |
xv |
xxvii |
o |
xxxix |
xxvi |
cxxiiii.ϛ |
cvi |
xi |
lv |
o |
xxix |
viii |
|
cii.ϛ |
xciii |
xxxv |
xi |
o |
xxxix |
xiii |
cxxv |
cvi |
xxvi |
xxix |
o |
xxviii |
liiii |
|
ciii |
xciii |
liiii |
xxxvii |
o |
xxxix |
o |
cxxv.ϛ |
cvi |
xl |
lvi |
o |
xxviii |
xxxix |
|
ciii.ϛ |
xciiii |
xiiii |
xvii |
o |
xxxviii |
xlvii |
cxxvi |
cvi |
lv |
xv |
o |
xxviii |
xxiiii |
|
ciiii |
xciiii |
xxxiii |
xli |
o |
xxxviii |
xxxiiii |
cxxvi.ϛ |
cvii |
ix |
xxvii |
o |
xxviii |
x |
|
ciiii.ϛ |
xciiii |
lii |
lviii |
o |
xxxviii |
xxi |
cxxvii |
cvii |
xxiii |
xxxii |
o |
xxvii |
lvi |
|
cv |
xcv |
xii |
ix |
o |
xxxviii |
viii |
cxxvii.ϛ |
cvii |
xxxvii |
xxx |
o |
xxvii |
xl |
|
cv.ϛ |
xcv |
xxxi |
xiii |
o |
xxxvii |
lv |
cxxviii |
cvii |
li |
xx |
o |
xxvii |
xxv |
|
cvi |
xcv |
l |
xi |
o |
xxxvii |
xlii |
cxxviii.ϛ |
cviii |
v |
ii |
o |
xxvii |
x |
|
cvi.ϛ |
xcvi |
ix |
ii |
o |
xxxvii |
xxix |
cxxix |
cviii |
xviii |
xxxvii |
o |
xxvi |
lvi |
|
cvii |
xcvi |
xxvii |
xlvii |
o |
xxxvii |
xvi |
cxxix.ϛ |
cviii |
xxxii |
v |
o |
xxvi |
xli |
|
cvii.ϛ |
xcvi |
xlvi |
xxiiii |
o |
xxxvii |
iii |
cxxx |
cviii |
xlv |
xxv |
o |
xxvi |
xxvi |
|
cviii |
xcvii |
iiii |
lvi |
o |
xxxvi |
l |
cxxx.ϛ |
cviii |
lviii |
xxxviii |
o |
xxvi |
xi |
|
cviii.ϛ |
xcvii |
xxiii |
xx |
o |
xxxvi |
xxxvi |
cxxxi |
cix |
xi |
xliiii |
o |
xxv |
lvi |
|
cix |
xcvii |
xli |
xxxviii |
o |
xxxvi |
xxiii |
cxxxi.ϛ |
cix |
xxiiii |
xlii |
o |
xxv |
xli |
|
cix.ϛ |
xcvii |
lix |
xlix |
o |
xxxvi |
ix |
cxxxii |
cix |
xxxvii |
xxxii |
o |
xxv |
xxvi |
|
cx |
xcviii |
xvii |
liiii |
o |
xxxv |
lvi |
cxxxii.ϛ |
cix |
l |
xv |
o |
xxv |
xi |
|
cx.ϛ |
xcviii |
xxxv |
lii |
o |
xxxv |
xlii |
cxxxiii |
cx |
ii |
l |
o |
xxiiii |
lvi |
|
cxi |
xcviii |
liii |
xliii |
o |
xxxv |
xxix |
cxxxiii.ϛ |
cx |
xv |
xviii |
o |
xxiiii |
xli |
|
cxi.ϛ |
xcix |
xi |
xxvii |
o |
xxxv |
xv |
cxxxiiii |
cx |
xxvii |
xxxix |
o |
xxiiii |
xxvi |
|
cxii |
xcix |
xxix |
v |
o |
xxxv |
i |
cxxxiiii.ϛ |
cx |
xxxix |
lii |
o |
xxiiii |
x |
|
cxii.ϛ |
xcix |
xlvi |
xxxv |
o |
xxxiiii |
xlviii |
cxxxv |
cx |
li |
lvii |
o |
xxiii |
lv |
|
Periferi
arum |
Rectarum |
Sexagesimarum |
Periferi
arum |
Rectarum |
Sexagessimarum |
|||||||||
G |
M |
S |
M |
S |
T |
G |
M |
S |
M |
S |
T |
|||
cxxxv.ϛ |
cxi |
iii |
liiii |
o |
xxiii |
xl |
clviii |
cxvii |
xlvii |
xliii |
o |
xi |
li |
|
cxxxvi |
cxi |
xv |
xliiii |
o |
xxiii |
xxv |
clviii.ϛ |
cxvii |
liii |
xxxix |
o |
xi |
xxxv |
|
cxxxvi.ϛ |
cxi |
xxvii |
xxvi |
o |
xxiii |
ix |
clix |
cxvii |
lix |
xxvii |
o |
xi |
xix |
|
cxxxvii |
cxi |
xxxix |
i |
o |
xxii |
liiii |
clix.ϛ |
cxviii |
v |
vii |
o |
xi |
iii |
|
cxxxvii.ϛ |
cxi |
l |
xxviii |
o |
xxii |
xxxix |
clx |
cxviii |
x |
xxxvii |
o |
x |
xlvii |
|
cxxxviii |
cxii |
xxx |
xlvii |
o |
xxii |
xxiiii |
clx.ϛ |
cxviii |
xvi |
i |
o |
x |
xxxi |
|
cxxxviii.ϛ |
cxii |
xii |
l |
o |
xxii |
l |
clxi |
cxviii |
xxi |
xvi |
o |
x |
xiiii |
|
cxxxix |
cxii |
xxiiii |
iii |
o |
xxi |
liii |
clxi.ϛ |
cxviii |
xxvi |
xxiii |
o |
ix |
lviii |
|
cxxxix.ϛ |
cxii |
xxv |
o |
o |
xxi |
xxxvii |
clxii |
cxviii |
xxxi |
xxii |
o |
ix |
xlii |
|
cxl |
cxii |
xlv |
xlviii |
o |
xxi |
xxii |
clxii.ϛ |
cxviii |
xxxvi |
xiii |
o |
ix |
xxv |
|
cxl.ϛ |
cxii |
lvi |
xxix |
o |
xxi |
vii |
clxiii |
cxviii |
xl |
lv |
o |
ix |
ix |
|
cxli |
cxiii |
vii |
ii |
o |
xx |
li |
clxiii.ϛ |
cxviii |
xlv |
xxx |
o |
viii |
liii |
|
cxli.ϛ |
cxiii |
xvii |
xxv |
o |
xx |
xxxvi |
clxiiii |
cxviii |
xlix |
lvi |
o |
viii |
xxxiii |
|
cxlii |
cxiii |
xxvii |
xliiii |
o |
xx |
xix |
clxiiii.ϛ |
cxviii |
liiii |
xv |
o |
viii |
xx |
|
cxlii.ϛ |
cxiii |
xxxvii |
liiii |
o |
xx |
iiii |
clxv |
cxviii |
lviii |
xxv |
o |
viii |
iiii |
|
cxliii |
cxiii |
xlvii |
xxvi |
o |
xix |
xlix |
clxv.ϛ |
cxix |
ii |
xxvi |
o |
vii |
xlviii |
|
cxliii.ϛ |
cxiii |
lvii |
l |
o |
xix |
xxxiii |
clxvi |
cxix |
vi |
xx |
o |
vii |
xxxi |
|
cxliiii |
cxiiii |
vii |
xxxvii |
o |
xix |
xvii |
clxvi.ϛ |
cxix |
x |
vi |
o |
vii |
xv |
|
cxliiii.ϛ |
cxiiii |
xvii |
xv |
o |
xix |
ii |
clxvii |
cxix |
xiii |
xliiii |
o |
vi |
lix |
|
cxlv |
cxiiii |
xxvi |
xlvi |
o |
xviii |
xlvi |
clxvii.ϛ |
cxix |
xvii |
xiii |
o |
vi |
xlii |
|
cxlv.ϛ |
cxiiii |
xxxvi |
ix |
o |
xviii |
xxx |
clxviii |
cxix |
xx |
xxxiiii |
o |
vi |
xxvi |
|
cxlvi |
cxiiii |
xlv |
xxiiii |
o |
xviii |
xiiii |
clxviii.ϛ |
cxix |
xxiii |
xlvii |
o |
vi |
x |
|
cxlvi.ϛ |
cxiiii |
liiii |
xxxi |
o |
xvii |
lix |
clxix |
cxix |
xxvi |
lii |
o |
v |
liii |
|
cxlvii |
cxv |
iii |
xxx |
o |
xvii |
xliii |
clxix.ϛ |
cxix |
xxix |
xlix |
o |
v |
xxxvii |
|
cxlvii.ϛ |
cxv |
xii |
xxii |
o |
xvii |
xxvii |
clxx |
cxix |
xxxii |
xxxvii |
o |
v |
xx |
|
cxlviii |
cxv |
xxi |
vi |
o |
xvii |
xi |
clxx.ϛ |
cxix |
xxxv |
xvii |
o |
v |
iiii |
|
cxlviii.ϛ |
cxv |
xxix |
xli |
o |
xvi |
lv |
clxxi |
cxix |
xxxvii |
xlix |
o |
iiii |
xlviii |
|
cxlix |
cxv |
xxxviii |
ix |
o |
xvi |
xl |
clxxi.ϛ |
cxix |
xl |
xiii |
o |
iiii |
xxxi |
|
cxlix.ϛ |
cxv |
xlvi |
xxix |
o |
xvi |
xxiiii |
clxxii |
cxix |
xlii |
xxviii |
o |
iiii |
xiiii |
|
cl |
cxv |
liiii |
xl |
o |
xvi |
l |
clxxii.ϛ |
cxix |
xli |
xxxv |
o |
iii |
lviii |
|
cl.ϛ |
cxvi |
ii |
xliiii |
o |
xv |
lii |
clxxiii |
cxix |
xlvi |
xxxv |
o |
iii |
xlii |
|
cli |
cxvi |
x |
xl |
o |
xv |
xxxvi |
clxxiii.ϛ |
cxix |
xlviii |
xxv |
o |
iii |
xxvi |
|
cli.ϛ |
cxvi |
xviii |
xxviii |
o |
xv |
xx |
clxxiiii |
cxix |
l |
viii |
o |
iii |
ix |
|
clii |
cxvi |
xxvi |
viii |
o |
xv |
xl |
clxxiiii.ϛ |
cxix |
li |
xliii |
o |
ii |
liii |
|
clii.ϛ |
cxvi |
xxxiii |
xl |
o |
xiiii |
xlviii |
clxxv |
cxix |
liii |
x |
o |
ii |
xxxiii |
|
cliii |
cxvi |
xli |
iiii |
o |
xiiii |
xxxii |
clxxv.ϛ |
cxix |
liiii |
xxvii |
o |
ii |
xx |
|
cliii.ϛ |
cxvi |
xlviii |
xx |
o |
xiiii |
xvi |
clxxvi |
cxix |
lv |
xxxviii |
o |
ii |
iii |
|
cliiii |
cxvi |
lv |
xxviii |
o |
xiiii |
o |
clxxvi.ϛ |
cxix |
lvi |
xxxix |
o |
i |
xlvii |
|
cliiii.ϛ |
cxvii |
ii |
xxviii |
o |
xiii |
xliiii |
clxxvii |
cxix |
lvii |
xxxii |
o |
i |
xxx |
|
clv |
cxvii |
ix |
xx |
o |
xiii |
xxviii |
clxxvii.ϛ |
cxix |
lviii |
xviii |
o |
i |
xiiii |
|
clv.ϛ |
cxvii |
xvi |
iiii |
o |
xiii |
xii |
clxxviii |
cxix |
lviii |
lv |
o |
o |
lvii |
|
clvi |
cxvii |
xxii |
xl |
o |
xii |
lvi |
clxxviii.ϛ |
cxix |
lix |
xxiiii |
o |
o |
xli |
|
clvi.ϛ |
cxvii |
xxix |
viii |
o |
xii |
xl |
clxxix |
cxix |
lix |
xliiii |
o |
o |
xxv |
|
clvii |
cxvii |
xxxv |
xxviii |
o |
xii |
xxiiii |
clxxix.ϛ |
cxix |
lix |
lvi |
o |
o |
ix |
|
clvii.ϛ |
cxvii |
xii |
xl |
o |
xii |
vii |
clxxx |
cxx |
o |
o |
o |
o |
o |
|
〈I.12〉 De ea que inter tropica periferia. Istrumentum ad idem.
Rectarum ergo que in circulo exposita quantitate, primum utique, sicut diximus, erit ostendere, quantum obliquus et qui per media animalia circulus declinat ab equinoctiali, hoc est quam proportionem habet maximus qui per utrosque expositos polos circulus ad deprehensam ipsius inter polos periferiam, cuius equali manifestum quoniam et tropicorum ab utroque punctorum distat quod ad equinoctialem. Inde vero nobis hoc instrumentaliter deprehenditur per huiusmodi quamdam fabricam simplicem. Faciemus enim circulum ereum, simetrum magnitudine, tornatum diligenter, tetragonum superfitiem, quo utemur meridiano dividentes ipsum in subiacentes maximi circuli portiones ccclx et harum unamquamque in quot recipit partes. Deinde alterum circulum circulum] circellum V2 subtiliorem sub predicto adaptantes, ita ut latera quidem eorum in una maneant superfitie, circumduci vero sine inpedimento sub maiore minor circulus possit in eodem epipedo et ad arctos et ad meridiem, apponemus in duabus aliquibus que secundum diametrum minoris circuli portionibus in altero laterum pigmatia parvula equalia nutum facientia et ad seinvicem et ad centrum circulorum examinate, apponentes secundum medium latitudinis ipsorum gnomonia subtilia maioris atque divisi circuli latus contingentia. Hunc ergo et firme coadaptantes in ad singula necessitatibus super stiliscum simmetrum et in ypetro stilisci basim statuentes in indeclinato ad orizontis epipedum pavimento, observabimus ut epipedum circulorum ad illud quidem quod orizontis rectum sit, ei vero quod meridiani parallilum. Horum vero primum quidem per cathetium investigabitur, suspensum ab ad verticem futuro puncto, observatum vero usque quo ex suppositionum directione in id quod secundum diametrum nutum faciat, secundum vero meridiana certo sumpta signo linea in eo quod sub stilisco epipedo ac preterlatis in obliqua circulis, usque quo linee parallilum eorum epipedum videatur. Tali vero positione facta, Solis ad arctos et meridiem progressionem observabimus interiorem circulum in meridiebus transferentes, usque quo totum inferius a toto superiore pigmatio adumbretur, et, hoc facto, significabunt nobis extrema gnomoniorum, quot portionibus ab eo quod ad verticem undique Solis centrum distiterit in meridiano. Item. Item] om. V2
Amplius autem commodiorem faciebamus observationem, huiusmodi lapideam sive ligneam plineida plineida] plincida V2 pro circulis construentes tetragonam et involubilem, in simmetra latitudine et altitudine altitudine] add. ut attingat secundum tempora V2 planum quidem et extensum habentem examinate alterum laterum, in qua centro quodam utentes puncto, ad unum angulorum scripsimus circuli tetartimorion, copulantes ab eo quod ad centrum puncto usque scriptam scriptam] add. periferiam V2 rectum sub tetartimorio angulum continentes rectas et similiter dividentes periferiam in gradus xc et eorum partes. Post Post] add. hec V2 vero in una rectarum et ad orizontis epipedum debente recta fore et ad meridiem habituram habituram] habitura V2 positionem empolizantes recta et equalia undique chilindria duo parvula tornata secundum simille, hoc quidem in ipso quod ad centrum puncto circa ipsum ipsum] add. medium V2 examinate, illud vero ad inferiorem terminum recte, deinde erigentes hoc descriptum plincidos latus iuxta protractam in epipedo subiacente lineam meridianam, ut et ipsa meridiani epipedo parallilam positionem possideret, et in in] om. V2 cathetio per chillindria et indeclinatam, et rectam ad orizontis epipedum, eam que per ipsa rectam examinantes, suppositionibus rursum quibusdam subtilibus id quod opportet corrigentibus, observabamus eodem modo in meridiebus ab eo quod ad centrum chillindro factam umbram, ad descriptam periferiam, ut manifestior ipsius appareret locus, aliquid apponentes et huius signantes medium, eam que ad ipsum tetartimorii periferie portionem sumebamus, designantem scilicet eum qui secundum latitudinem in meridiano progressum Solis.
Ex huiusmodi ergo observationibus eisque maxime que circa conversiones ipsas nobis examinate sunt in plures periodos, equales et easdem meridiani circuli portiones et secundum estivas conversiones et secundum ymbernas ymbernas] hybernas V2 designationem, designationem] designacione V2 ut omnino, ab eo quod ad verticem deprehendente puncto, comprehendebamus eam que a borealismo borealismo] borealissimo V2 termino in australissimum periferiam, que est tropicarum intermedia portionum, semper factam xlvii et maioris quidem dimirio portionis, minoris vero dimidio et quarta, per quod colligitur fere eadem ratio ei que Exatostonis, Exatostonis] Eratostenis V2 qua et Yparcus cousus est. Fit enim que inter tropica talium xi ad proximum qualium est meridianus lxxxiii. Inde vero facilia cognitu ex preiacente observacione fuerit et habitationum in quibus observationes faciemus inclinamenta, sumptis duorum medio terminorum puncto, quod ad equinoctialem fit, intermediaque huius et illius quod ad verticem periferia, cuius equali manifestum quoniam et poli ab orizonte distant.
Cum sit aut aut] autem V2 consequens demonstrare et que particulariter attenduntur quantitates comprehensarum inter equinoctialem et eum qui per media animalia periferiarum eorum qui per equinoctialis polos maximi circuli describuntur, preexponemus limatia brevia et commoda commoda] add. per V2 que plurimas fere demonstationes eorum que sperice considerantur, ut est maxime simplicius et artificiosius faciemus.
〈I.13〉 Prelibata in spericas demonstrationes
In duas ergo rectas AB et AG protracte due recte BE et GD secent seinvicem ad Z punctum; dico quoniam recte GA ad AE proporcio composita est ex proportione recte GD ad DZ, et proportione recte ZB ad BE. Ducatur enim per E recte GD equidistans EN. Quoniam ergo equidistantes sunt recte GD et EN, proporcio recte GA ad EA eadem est ei que recte GD ad EN. Ab extrinsecus vero recta GD GD] ZD V2F1, que ergo recte GD ad EN proporcio composita erit ex ea que recte GD ad DZ et ea que recte DZ ad NE. Quare et recte GA ad AE proportio componitur ex ea que recte GD ad DZ et ea que recte DZ ad NE. Est autem et recte DZ ad NE proportio eadem ei que recte ZB ad BE, quoniam rursum equidistantes sunt EN et GD GD] ZD V2F1 recte, ergo GA ad AE proportio componitur ex ea que recte GD ad DZ et ea que recte ZB ad BE. Quod propositum erat demonstrare.
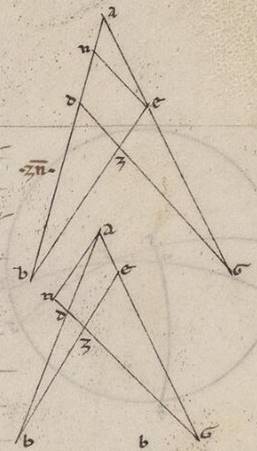 Secundum eadem vero demonstrabitur quoniam et secundum divisionem recte GE ad EA proportio composita est ex ea que recte GZ ad DZ et ea que recte DB ad BA, per punctum A recte EB equidistante ducta et educta in ipsam recta GDN. Quoniam enim rursum parallilos est recta AN, recte EZ est sicut GE ad EA, ita GZ ad ZN. Verum recta ZD ab extrinsecus sumpta, recte GZ ad ZN proportio componitur ex ea que recte GZ ad ZD et ea que recte DZ ad ZN. Est autem recte DZ ad ZN proportio eadem ei que recte DB ad BA, quoniam in equidistantes AN et ZB protracte sunt BA et ZN. Recte ergo GZ ad ZN proportio composita est ex ea que recte GZ ad DZ et ea que recte DB ad BA. Verum recte GZ ad ZN proportioni eadem est recte GE ad EA proportio. Quare componitur ex ea que recte GZ ad DZ et ea que recte DB ad BA. Quod oportebat demonstrare.
Secundum eadem vero demonstrabitur quoniam et secundum divisionem recte GE ad EA proportio composita est ex ea que recte GZ ad DZ et ea que recte DB ad BA, per punctum A recte EB equidistante ducta et educta in ipsam recta GDN. Quoniam enim rursum parallilos est recta AN, recte EZ est sicut GE ad EA, ita GZ ad ZN. Verum recta ZD ab extrinsecus sumpta, recte GZ ad ZN proportio componitur ex ea que recte GZ ad ZD et ea que recte DZ ad ZN. Est autem recte DZ ad ZN proportio eadem ei que recte DB ad BA, quoniam in equidistantes AN et ZB protracte sunt BA et ZN. Recte ergo GZ ad ZN proportio composita est ex ea que recte GZ ad DZ et ea que recte DB ad BA. Verum recte GZ ad ZN proportioni eadem est recte GE ad EA proportio. Quare componitur ex ea que recte GZ ad DZ et ea que recte DB ad BA. Quod oportebat demonstrare.
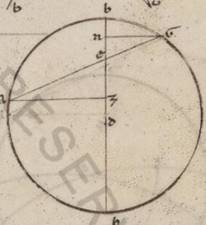 Rursum esto circulus ABG, cuius centro D, summanturque in ipsius circumferentia quelibet tria puncta A, B, G ita, ut utraque periferiarum AB et BG semicirculo fit fit] sit V2F1 minor, – et in deinceps sumptis periferiis simile subaudiatur –, copulenturque AG et DB; DB] DEB V2 dico quoniam est sicut que sub dupla periferie AB ad eam que sub dupla periferie AB … periferie] iter. V3 BG, ita AE recta ad EG. EG] add. rectam V2F1 Ducantur enim catheti ab A et G punctis in DB, sintque AZ et GN. Quoniam equidistans est recta AZ recte GN et protracta est in ipsas recta AEG est ut AZ ad GN ita AE ad EG. Verum eadem proportio est recte AZ ad GN et eius que sub dupla periferie BA ad eam que sub dupla periferie BG, – dimidia enim utraque utriusque –, et ea ergo que recte AE ad EG proportio eadem est proportioni eius que sub dupla periferie AB ad eam que sub dupla periferie BG. Quod oportebat demonstrare.
Rursum esto circulus ABG, cuius centro D, summanturque in ipsius circumferentia quelibet tria puncta A, B, G ita, ut utraque periferiarum AB et BG semicirculo fit fit] sit V2F1 minor, – et in deinceps sumptis periferiis simile subaudiatur –, copulenturque AG et DB; DB] DEB V2 dico quoniam est sicut que sub dupla periferie AB ad eam que sub dupla periferie AB … periferie] iter. V3 BG, ita AE recta ad EG. EG] add. rectam V2F1 Ducantur enim catheti ab A et G punctis in DB, sintque AZ et GN. Quoniam equidistans est recta AZ recte GN et protracta est in ipsas recta AEG est ut AZ ad GN ita AE ad EG. Verum eadem proportio est recte AZ ad GN et eius que sub dupla periferie BA ad eam que sub dupla periferie BG, – dimidia enim utraque utriusque –, et ea ergo que recte AE ad EG proportio eadem est proportioni eius que sub dupla periferie AB ad eam que sub dupla periferie BG. Quod oportebat demonstrare.
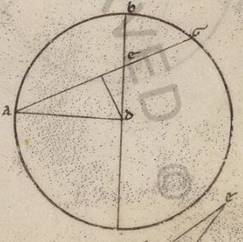 Consequitur autem inde quoniam, etsi date sint tota AG periferia et eius que sub dupla periferie AB ad eam que sub dupla periferie BG proporcio, dabitur et utraque AB et BG periferiarum. Eadem enim exposita descriptione, copulentur A D ducaturque a puncto D cathetus DZ super AEG. Quoniam ergo, AG periferia data, et ADZ angulus dimidio eius subtensus datus erit et totus ADZ trigonus, manifestum quoniam vero, et recta AG tota data, subiacet et recte AE ad EG, proportio eadem proportioni eius que sub dupla periferie AB ad eam que sub dupla periferie BG et que est AE erit data et reliqua ZE. Ac propter hoc, et DZ data, dabitur et angulus EDZ orthogonii EDZ et totus ADB angulus. Quare et AB periferia dabitur et reliqua BG. Quod oportebat oportebat] oportet V2F1 demonstrare.
Consequitur autem inde quoniam, etsi date sint tota AG periferia et eius que sub dupla periferie AB ad eam que sub dupla periferie BG proporcio, dabitur et utraque AB et BG periferiarum. Eadem enim exposita descriptione, copulentur A D ducaturque a puncto D cathetus DZ super AEG. Quoniam ergo, AG periferia data, et ADZ angulus dimidio eius subtensus datus erit et totus ADZ trigonus, manifestum quoniam vero, et recta AG tota data, subiacet et recte AE ad EG, proportio eadem proportioni eius que sub dupla periferie AB ad eam que sub dupla periferie BG et que est AE erit data et reliqua ZE. Ac propter hoc, et DZ data, dabitur et angulus EDZ orthogonii EDZ et totus ADB angulus. Quare et AB periferia dabitur et reliqua BG. Quod oportebat oportebat] oportet V2F1 demonstrare.
Rursus esto circulus ABG circa centro D atque in ipsius periferia summantur tria puncta A, B, G ita, ut utraque periferiarum AB et AG sit semicirculo minor, – et in deinceps sumptis periferiis simille subaudiatur –, copulateque DA et GB educantur et concurrant ad punctum E; dico quoniam est sicut que sub dupla periferie GA ad eam que sub dupla periferie AB, ita GE recta ad BE. Similiter limatio priori, si a punctis B et G cathetos duxerimus in DA, sintque BZ et GN, erit enim eo quod ipse sint equidistantes, sicut GN ad BZ, ita GE ad EB, quare et sicut que sub dupla periferie GA ad eam que sub dupla periferie AB, ita GE ad EB.
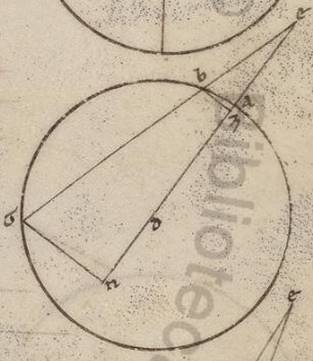 Consequitur autem inde et hic quoniam, etsi GB periferia sola detur et eius que sub dupla periferie GA ad eam proportio que sub dupla periferie AB detur, dabitur et AB periferia. Rursum enim in simili descriptione copulata DB et catheto DZ ducta in BG, angulus quidem BDZ dimidie subtensus periferie BG erit datus, quare et totum BDZ orthogonium. Quoniam vero et GE ad EB proportio data est, et etiam GB recta dabitur et EB et etiam EBZ. Quare et quoniam DZ data est, dabitur et EDZ angulus eiusdem orthogonii et reliquus EDB. Quare et AB periferia erit data est. est] om. V2F1
Consequitur autem inde et hic quoniam, etsi GB periferia sola detur et eius que sub dupla periferie GA ad eam proportio que sub dupla periferie AB detur, dabitur et AB periferia. Rursum enim in simili descriptione copulata DB et catheto DZ ducta in BG, angulus quidem BDZ dimidie subtensus periferie BG erit datus, quare et totum BDZ orthogonium. Quoniam vero et GE ad EB proportio data est, et etiam GB recta dabitur et EB et etiam EBZ. Quare et quoniam DZ data est, dabitur et EDZ angulus eiusdem orthogonii et reliquus EDB. Quare et AB periferia erit data est. est] om. V2F1
 His prelibatis, scribantur in sperica superfitie maximorum periferie circulorum ita, ut in duas AB et AG due scripte BE et GD seinvicem secent ad punctum Z. Sit autem earum unaqueque semicirculo minor, – idem vero et in omnibus descriptionibus subaudiatur –; dico ergo quoniam eius que sub dupla periferie GE ad eam que sub dupla periferie EA proportio composita est ex eius que sub dupla periferie GZ ad eam que sub dupla periferie ZD proportione et proportione eius que sub dupla periferie DB ad eam que sub dupla periferie BA. Summatur enim centrum spere sitque I et ducantur ab I in B, Z, E sectiones circulorum sintque IB et IZ et IE, copulataque AD educatur et concurrat ei que est IB educte et ipsi ad punctum T. Similiter autem copulate DG et AG secent IZ et IE ad K et L puncta. In una ergo sunt recta T, K et L puncta, eo quod in duobus simul sunt epipedis, trigoni scilicet AGD atque circuli BZE. Que copulata facit in duas rectas TA et GA protractas TL et GD secantes seinvicem ad K punctum. Recte ergo GL ad LA proportio composita est ex recte GK ad KD proportione et ea que recte DT proportione ad TA. Verum sicut GL quidem ad LA, ita que sub dupla periferie GE ad eam que sub dupla periferie EA. Sicut autem GK ad KD ita que sub dupla periferie GZ ad eam que sub dupla periferie ZD. Ut vero DT ad TA, ita que sub dupla periferie DB ad eam que sub dupla periferie BA. Et proportio igitur eius que sub dupla periferie GE ad eam que sub dupla periferie EA composita est ex proportione eius que sub dupla periferie GZ ad eam que sub dupla periferie ZD et proportione eius que sub dupla periferie DB ad eam que sub dupla periferie BA. Secundum eadem vero et quemadmodum in epipeda descriptione rectarum ostenditur quoniam et eius que sub dupla periferie GA ad eam que sub dupla periferie EA proportio composita est ex eius que sub dupla periferie GD ad eam que sub dupla periferie DZ proportione et proportione eius que sub dupla periferie ZB ad eam que sub dupla periferie BE. Quod propositum erat demonstrare.
His prelibatis, scribantur in sperica superfitie maximorum periferie circulorum ita, ut in duas AB et AG due scripte BE et GD seinvicem secent ad punctum Z. Sit autem earum unaqueque semicirculo minor, – idem vero et in omnibus descriptionibus subaudiatur –; dico ergo quoniam eius que sub dupla periferie GE ad eam que sub dupla periferie EA proportio composita est ex eius que sub dupla periferie GZ ad eam que sub dupla periferie ZD proportione et proportione eius que sub dupla periferie DB ad eam que sub dupla periferie BA. Summatur enim centrum spere sitque I et ducantur ab I in B, Z, E sectiones circulorum sintque IB et IZ et IE, copulataque AD educatur et concurrat ei que est IB educte et ipsi ad punctum T. Similiter autem copulate DG et AG secent IZ et IE ad K et L puncta. In una ergo sunt recta T, K et L puncta, eo quod in duobus simul sunt epipedis, trigoni scilicet AGD atque circuli BZE. Que copulata facit in duas rectas TA et GA protractas TL et GD secantes seinvicem ad K punctum. Recte ergo GL ad LA proportio composita est ex recte GK ad KD proportione et ea que recte DT proportione ad TA. Verum sicut GL quidem ad LA, ita que sub dupla periferie GE ad eam que sub dupla periferie EA. Sicut autem GK ad KD ita que sub dupla periferie GZ ad eam que sub dupla periferie ZD. Ut vero DT ad TA, ita que sub dupla periferie DB ad eam que sub dupla periferie BA. Et proportio igitur eius que sub dupla periferie GE ad eam que sub dupla periferie EA composita est ex proportione eius que sub dupla periferie GZ ad eam que sub dupla periferie ZD et proportione eius que sub dupla periferie DB ad eam que sub dupla periferie BA. Secundum eadem vero et quemadmodum in epipeda descriptione rectarum ostenditur quoniam et eius que sub dupla periferie GA ad eam que sub dupla periferie EA proportio composita est ex eius que sub dupla periferie GD ad eam que sub dupla periferie DZ proportione et proportione eius que sub dupla periferie ZB ad eam que sub dupla periferie BE. Quod propositum erat demonstrare.
〈I.14〉 De periferiis que inter equinoctialem et obliquum circulum
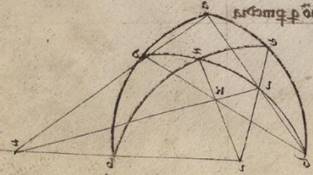 Isto ergo theoremate preexposito, prima propositarum periferiarum apodixem faciemus hoc modo. Esto enim qui per utrosque polos equinoctialis et eius qui per media animalia circulus ABGD et equinoctialis quidem emiciclion AEG, eius vero qui per media animalia BED, punctusque est Est]E V2F1 ea que secundum vernum equinoctium eorum sectio, ut B quidem sit hibernum, tropicum D vero estivale. Summatur vero in ABG periferia polus AEG equinoctialis, sitque Z punctus et assumatur EN periferia eius qui per media animalia circuli xxx subiacens portionum, qualium est maximus circulus ccclx. ccclx] corr. ex ccc xlx V3 Atque per puncta Z, N scribatur maximi circuli periferia ZNT sitque proponitur proponitur] propositum V2F1 NT scilicet invenire. Preiacet autem et hic et in omnibus simillibus demonstrationibus universaliter, – ne secundum unamquamque revolvamus idem –, quoniam, quando quantitates periferiarum dicimus aut rectarum, quot sint graduum portionumve, in periferiis quidem talium dicimus, qualium circuli
Isto ergo theoremate preexposito, prima propositarum periferiarum apodixem faciemus hoc modo. Esto enim qui per utrosque polos equinoctialis et eius qui per media animalia circulus ABGD et equinoctialis quidem emiciclion AEG, eius vero qui per media animalia BED, punctusque est Est]E V2F1 ea que secundum vernum equinoctium eorum sectio, ut B quidem sit hibernum, tropicum D vero estivale. Summatur vero in ABG periferia polus AEG equinoctialis, sitque Z punctus et assumatur EN periferia eius qui per media animalia circuli xxx subiacens portionum, qualium est maximus circulus ccclx. ccclx] corr. ex ccc xlx V3 Atque per puncta Z, N scribatur maximi circuli periferia ZNT sitque proponitur proponitur] propositum V2F1 NT scilicet invenire. Preiacet autem et hic et in omnibus simillibus demonstrationibus universaliter, – ne secundum unamquamque revolvamus idem –, quoniam, quando quantitates periferiarum dicimus aut rectarum, quot sint graduum portionumve, in periferiis quidem talium dicimus, qualium circuli 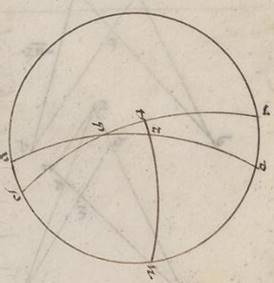 periferia portionum ccclx, in rectis vero vero] add. del. talium V3 qualium circuli diametros cxx. Quoniam ergo in maximorum descriptione circulorum in duas AZ et AE periferias scripte sunt due ZT et EB secantes seinvicem ad N, proportio eius que sub dupla periferie ZA ad eam que sub dupla periferie AB composita est ex eius que sub dupla periferie ZT ad eam que sub dupla periferie TN proportione et proportione eius que sub dupla periferie NE ad eam que sub dupla periferie EB. At periferie quidem ZA dupla graduum est clxxx et que sub ipsa recta portionum cxx, periferie vero vero] corr. ex dupla V3 AB dupla secundum constitutam nobis lxxxiii ad xi proportionem graduum xlvii xlii minutorum xl secundorum, que vero sub ipsa recta portionum xlviii xxxi minutorum lv secundorum. Et rursum periferie quidem NE dupla graduum lx et que sub ipsa recta portionum lx; EB vero periferie dupla graduum clxxx et que sub ipsa recta portionum cxx. Si ergo a proportione eorum que sunt cxx ad xlviii xxxi lv abstulerimus proportionem eorum que sunt lx ad cxx, relinquitur proportio eius que sub dupla periferie ZT ad eam que sub dupla periferie TN que scilicet cxx ad xxiiii xv lvii. Et est dupla quidem periferie ZT graduum cxxx, cxxx] clxxx V2F1 que vero sub ipsa recta portionum cxx. Et ea ergo que sub dupla periferie TN eorundem est xxiiii xv lvii. Quare et dupla quidem periferie TN graduum est xxiii xix lix, ipsa vero TN eorundem xi minutorum xl ad proximum.
periferia portionum ccclx, in rectis vero vero] add. del. talium V3 qualium circuli diametros cxx. Quoniam ergo in maximorum descriptione circulorum in duas AZ et AE periferias scripte sunt due ZT et EB secantes seinvicem ad N, proportio eius que sub dupla periferie ZA ad eam que sub dupla periferie AB composita est ex eius que sub dupla periferie ZT ad eam que sub dupla periferie TN proportione et proportione eius que sub dupla periferie NE ad eam que sub dupla periferie EB. At periferie quidem ZA dupla graduum est clxxx et que sub ipsa recta portionum cxx, periferie vero vero] corr. ex dupla V3 AB dupla secundum constitutam nobis lxxxiii ad xi proportionem graduum xlvii xlii minutorum xl secundorum, que vero sub ipsa recta portionum xlviii xxxi minutorum lv secundorum. Et rursum periferie quidem NE dupla graduum lx et que sub ipsa recta portionum lx; EB vero periferie dupla graduum clxxx et que sub ipsa recta portionum cxx. Si ergo a proportione eorum que sunt cxx ad xlviii xxxi lv abstulerimus proportionem eorum que sunt lx ad cxx, relinquitur proportio eius que sub dupla periferie ZT ad eam que sub dupla periferie TN que scilicet cxx ad xxiiii xv lvii. Et est dupla quidem periferie ZT graduum cxxx, cxxx] clxxx V2F1 que vero sub ipsa recta portionum cxx. Et ea ergo que sub dupla periferie TN eorundem est xxiiii xv lvii. Quare et dupla quidem periferie TN graduum est xxiii xix lix, ipsa vero TN eorundem xi minutorum xl ad proximum.
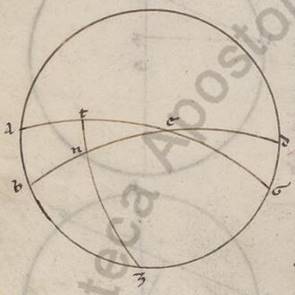 Rursum subiaceat EN periferia graduum lx, quare, aliis manentibus eisdem, dupla quidem EN periferie fiat graduum cix, cix] cxx V2F1 que vero sub ipsa recta portionum ciii lv xxiii. Si ergo rursum a proportione cxx ad xlviii xxxi lv auferamus eam que ciii lv xxiii ad cxx, relinquetur proportio eius que sub dupla periferie ZT ad eam que sub dupla periferie TN scilicet que cxx ad xlii i minutum xlvii secunda et est que sub dupla periferie ZT portionum cxx. Quare et que sub dupla periferie TN eorundem erit xlii i minuti xlvii. Unde et dupla quidem periferie TN graduum est xli o minuti xviii secundorum, TN vero eorundem xx xxx ix. Quod oportet demonstrare.
Rursum subiaceat EN periferia graduum lx, quare, aliis manentibus eisdem, dupla quidem EN periferie fiat graduum cix, cix] cxx V2F1 que vero sub ipsa recta portionum ciii lv xxiii. Si ergo rursum a proportione cxx ad xlviii xxxi lv auferamus eam que ciii lv xxiii ad cxx, relinquetur proportio eius que sub dupla periferie ZT ad eam que sub dupla periferie TN scilicet que cxx ad xlii i minutum xlvii secunda et est que sub dupla periferie ZT portionum cxx. Quare et que sub dupla periferie TN eorundem erit xlii i minuti xlvii. Unde et dupla quidem periferie TN graduum est xli o minuti xviii secundorum, TN vero eorundem xx xxx ix. Quod oportet demonstrare.
Eodem vero modo et in particularibus periferiis investigantes quantitates, exponemus canonium xc tetartimorii graduum adiacentes habens quantitates simillium demonstratis periferiarum.
Et est canonium huismodi.
〈I.15〉 Canonium obliquationis
Canonium |
Obliquationis |
||||||
Periferie
meridiani |
Periferie
Meridiani |
||||||
Gradus |
G |
M |
S |
Gradus |
G |
M |
S |
i |
o |
xxiiii |
xvi |
xlvi |
xvi |
liiii |
xlvii |
ii |
o |
xlviii |
xxxi |
xlvii |
xvii |
xii |
xvi |
iii |
i |
xii |
xlvi |
xlviii |
xvii |
xxix |
xxvii |
iiii |
i |
xxxvii |
o |
xlix |
xvii |
xlvi |
xx |
v |
ii |
i |
xii |
l |
xviii |
ii |
liii |
vi |
ii |
xxv |
xxii |
li |
xviii |
xix |
xv |
vii |
ii |
xxix |
xxx |
lii |
xviii |
xxxv |
v |
viii |
iii |
xiii |
xxxv |
liii |
xviii |
l |
xli |
ix |
iii |
xxxvii |
xxxvii |
liiii |
xix |
v |
lvii |
x |
iiii |
i |
xxxviii |
lv |
xix |
xx |
lvi |
xl |
iiii |
xxv |
xxxii |
lvi |
xix |
xxxv |
xxviii |
xii |
iiii |
xlix |
xxi |
lvii |
xix |
xlix |
xlii |
xiii |
v |
xiii |
xi |
lviii |
xx |
iii |
xxxi |
xiiii |
v |
xxxvi |
liii |
lix |
xx |
xvii |
iiii |
xv |
vi |
o |
xxxi |
lx |
xx |
xxx |
ix |
xvi |
vi |
xxiiii |
i |
lxi |
xx |
xlii |
lviii |
xvii |
vi |
xlvii |
xxvi |
lxii |
xx |
lv |
xxiiii |
xviii |
vii |
x |
xlv |
lxiii |
xxi |
vii |
xxi |
xix |
vii |
xxxiii |
lvii |
lxiiii |
xxi |
xviii |
lviii |
xx |
vii |
lvii |
iii |
lxv |
xxi |
xxx |
xi |
xxi |
viii |
xx |
o |
lxvi |
xxi |
xli |
o |
xxii |
viii |
xlii |
l |
lxvii |
xxi |
li |
xxv |
xxiii |
ix |
v |
xxxii |
lxviii |
xxii |
i |
xxv |
xxiiii |
ix |
xxviii |
v |
lxix |
xxii |
xi |
xi |
xxv |
ix |
l |
xxix |
lxx |
xxii |
xx |
xi |
xxvi |
x |
xii |
xlvi |
lxxi |
xxii |
xxviii |
lvii |
xxvii |
x |
xxxiiii |
lvii |
lxxii |
xxii |
xxxvii |
lvii |
xxviii |
x |
lvi |
xliii |
lxxiii |
xxii |
xlv |
xi |
xxix |
xi |
xviii |
xxv |
lxxiiii |
xxii |
lii |
xxxix |
xxx |
xi |
xxxix |
lv |
lxxv |
xxii |
lix |
xli |
xxxi |
xii |
i |
xx |
lxxvi |
xxiii |
vi |
xvii |
xxxii |
xii |
xxii |
xxx |
lxxvii |
xxiii |
xii |
xxvii |
xxxiii |
xii |
xliii |
xxviii |
lxxviii |
xxiii |
xviii |
xi |
xxxiiii |
xiii |
iiii |
xiiii |
lxxix |
xxiii |
xxiii |
xxviii |
xxxv |
xiii |
xxiiii |
xlvii |
lxxx |
xxiii |
xxviii |
xvi |
xxxvi |
xiii |
xlv |
vi |
lxxxi |
xxiii |
xxxii |
xxx |
xxxvii |
xiiii |
v |
xi |
lxxxii |
xxiii |
xxxvi |
xxxv |
xxxviii |
xiiii |
xxv |
ii |
lxxxiii |
xxiii |
xl |
ii |
xxxix |
xiiii |
xliiii |
xxxix |
lxxxiiii |
xxiii |
xliii |
ii |
xl |
xv |
xxx |
iiii |
lxxxv |
xxiii |
xlv |
xxxiiii |
xli |
xv |
xxiii |
x |
lxxxvi |
xxiii |
xlvii |
xxxix |
xlii |
xv |
xlii |
ii |
lxxxvii |
xxiii |
xlix |
xvi |
xliii |
xvi |
o |
xxxviii |
lxxxviii |
xxiii |
l |
xxv |
xliiii |
xvi |
xviii |
lviii |
lxxxix |
xxiii |
li |
vi |
xlv |
xvi |
xxxvii |
xx |
xc |
xxiii |
li |
xx |
〈I.16〉 De his que in recta spera ascensionibus
Deinceps autem erit coostendere equinoctialis periferiarum factas quantitates a circulis per eius polos et datas obliqui circuli portiones scriptis. Ita enim habebimus, in quot temporibus equinoctialibus eius qui per media animalia portiones pertransibunt et meridianum ubique et in recta spera orizontem, eo quod et ipse tunc tantum per polos equinoctialis describatur. Adiaceat ergo descriptio premonstrata, dataque rursus EN periferia obliqui circuli prius portionum xxx, propositum esto ET equinoctialis periferiam invenire. Ex eis ergo que ante dicta sunt eiusque sub dupla periferie BZ proportio ad eam que sub dupla periferie BA composita est ex proportione eius que sub dupla periferie ZN ad eam que sub dupla periferie NT, et ea que eius 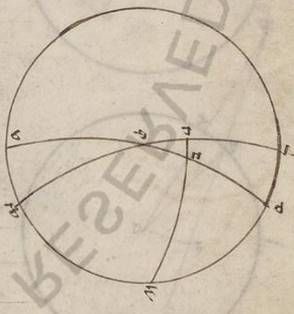 que sub dupla periferie TE ad eam que sub dupla periferie EA. At dupla quidem periferie ZB graduum est cxxxii xvii minutorum xx secundorum et que sub ipsa recta porcionum cix xliiii minutorum liii secundorum; que vero periferie quidem BA dupla graduum xlvii xlii minutuorum xl secundorum et que sub ipsa recta portionum xlviii xxxi minutorum lv secundorum; et rursus periferie quidem ZN dupla graduum clvi xli minutorum et que sub ipsa recta portionum cxvii xxxi minutorum xv secundorum; que vero periferie quidem NT dupla graduum xxiii xix minutorum lix secundorum et que sub ipsa recta portionum xxiiii xv minutorum lviii secundorum. Si ergo a proportione eorum que sunt cix xliiii minutorum liii secundorum ad xlviii xxxi minuta lv secunda auferemus proportionem eorum que sunt cxvii xxxi minutorum xv secundorum ad xxiiii xv minuta lvii secunda, relinquetur nobis eius que sub dupla periferie TE proportio ad eam que sub dupla periferie EA, que portionum liiii lii minutorum xxvi secundorum ad cxvii xxxi minuta xv secunda. Eadem vero proportio est eorum que sunt lvi i xxv ad cxx, et est dupla quidem periferie EA graduum clxxx et que sub ipsa recta portionum cxx, et ea ergo que sub dupla periferie TE portionum earundem lvi i minuti xxv secundorum. Quare et dupla quidem periferie TE TE] add. erit graduum lv xl ad proximum, que vero periferie TE V2F1 earundem xxvii l minutorum.
que sub dupla periferie TE ad eam que sub dupla periferie EA. At dupla quidem periferie ZB graduum est cxxxii xvii minutorum xx secundorum et que sub ipsa recta porcionum cix xliiii minutorum liii secundorum; que vero periferie quidem BA dupla graduum xlvii xlii minutuorum xl secundorum et que sub ipsa recta portionum xlviii xxxi minutorum lv secundorum; et rursus periferie quidem ZN dupla graduum clvi xli minutorum et que sub ipsa recta portionum cxvii xxxi minutorum xv secundorum; que vero periferie quidem NT dupla graduum xxiii xix minutorum lix secundorum et que sub ipsa recta portionum xxiiii xv minutorum lviii secundorum. Si ergo a proportione eorum que sunt cix xliiii minutorum liii secundorum ad xlviii xxxi minuta lv secunda auferemus proportionem eorum que sunt cxvii xxxi minutorum xv secundorum ad xxiiii xv minuta lvii secunda, relinquetur nobis eius que sub dupla periferie TE proportio ad eam que sub dupla periferie EA, que portionum liiii lii minutorum xxvi secundorum ad cxvii xxxi minuta xv secunda. Eadem vero proportio est eorum que sunt lvi i xxv ad cxx, et est dupla quidem periferie EA graduum clxxx et que sub ipsa recta portionum cxx, et ea ergo que sub dupla periferie TE portionum earundem lvi i minuti xxv secundorum. Quare et dupla quidem periferie TE TE] add. erit graduum lv xl ad proximum, que vero periferie TE V2F1 earundem xxvii l minutorum.
Rursum subiaceat EN periferia graduum lx, ut aliis manentibus eisdem, dupla quidem periferie ZN graduum fiat cxxxviii lix minutorum xlii secundorum et que sub ipsa recta portionum cxii xxiii minutorum lvi secundorum; dupla vero periferie NT graduum xli o minutorum xviii secundorum et que sub ipsa recta portionum xlii i minuti xlviii secundorum. Si ergo a proportione eorum que sunt cix xliiii minutorum liii secundorum ad xlviii xxxi minuta lv secunda abstulerimus proportionem eorum que sunt cxii xxiii minutorum lvi secundorum ad xlii i minutum xlviii secunda, relinquetur eius proportio que sub dupla periferie TE ad eam que sub dupla periferie EA, que eorum que sunt xcv ii minutorum xl secundorum ad cxii xxiii 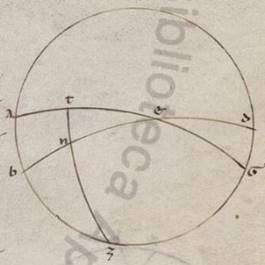 minuta lvi secunda. Eadem vero proportio huic est et que ci xxviii minutorum ii secundorum. ad cxx. Est vero que sub dupla periferie EA recte portionum cxx. Quare et que sub dupla periferie TE portionum earundem est ci xxviii ii. Quare et dupla quidem periferie TE graduum erit cxv xxviii minutorum ad proximum, ipsa vero TE eorundem lvii xliiii minutorum. Demonstratum est autem quoniam primum quidem ab equinoctiali puncto dodecatimorion eius qui per media animalia circuli commoratur equinoctialis secundum expositum modum portionibus xxvii l minutis, secundum portionibus xxix liiii minutis, quoniam quidem ambo demonstrata sunt graduum lvii xliiii m. Sed et tertium dodecatimorion manifestum quoniam reliquis in tetartimorio gradibus xxxii xvi minutis commorabitur, eo quod et totum obliqui circuli tetartimorium toti ei quod equinoctialis eque moretur, ut ad eos qui per polos equinoctialis circulos describuntur. Eodem ergo modo preiacentem demonstrationem consequentes et cuique obliqui circuli decamirie commorantes equinoctialis periferias investigavimus, eo quod amplius his minores nullo cura digno differant ab eis que ad equale augmentum superhabundantiis. Exponemus ergo et has, ut, in quot temporibus earum unaqueque et meridianum, ut diximus, ubique et in recta spera transeat orizontem, in promptu habeamus. Principium vero ab ea que ad equinoctiale punctum decamiria faciemus. Itaque prima continet tempora ix x minuta, secunda vero tempora ix xv minuta, tertia vero tempora ix xxv minuta, quare in idem primi dodecatimorii tempora colliguntur xxvii l minuta; quarta tempora ix xl minuta, quinta tempora ix lviii minuta, sexta tempora x xvi minuta, quare et secundi dodecatimorii tempora colliguntur xxix liiii minuta; septima tempora x xxxiiii minuta, octava tempora x xlvii minuta, nona tempora x lv minuta, ut rursus et tertii quidem atque ad tropica puncta dodecatimorii tempora colligantur xxxii xvi minuta, totius autem tetartimorii xc consone. Atque inde manifestum est quoniam et reliquorum tetartimoriorum ordinatio contingit eadem, omnibus in unoquoque eisdem contingentibus, propter rectam speram, idest equinoctialem sine declinatione ad orizontem subiacere.
minuta lvi secunda. Eadem vero proportio huic est et que ci xxviii minutorum ii secundorum. ad cxx. Est vero que sub dupla periferie EA recte portionum cxx. Quare et que sub dupla periferie TE portionum earundem est ci xxviii ii. Quare et dupla quidem periferie TE graduum erit cxv xxviii minutorum ad proximum, ipsa vero TE eorundem lvii xliiii minutorum. Demonstratum est autem quoniam primum quidem ab equinoctiali puncto dodecatimorion eius qui per media animalia circuli commoratur equinoctialis secundum expositum modum portionibus xxvii l minutis, secundum portionibus xxix liiii minutis, quoniam quidem ambo demonstrata sunt graduum lvii xliiii m. Sed et tertium dodecatimorion manifestum quoniam reliquis in tetartimorio gradibus xxxii xvi minutis commorabitur, eo quod et totum obliqui circuli tetartimorium toti ei quod equinoctialis eque moretur, ut ad eos qui per polos equinoctialis circulos describuntur. Eodem ergo modo preiacentem demonstrationem consequentes et cuique obliqui circuli decamirie commorantes equinoctialis periferias investigavimus, eo quod amplius his minores nullo cura digno differant ab eis que ad equale augmentum superhabundantiis. Exponemus ergo et has, ut, in quot temporibus earum unaqueque et meridianum, ut diximus, ubique et in recta spera transeat orizontem, in promptu habeamus. Principium vero ab ea que ad equinoctiale punctum decamiria faciemus. Itaque prima continet tempora ix x minuta, secunda vero tempora ix xv minuta, tertia vero tempora ix xxv minuta, quare in idem primi dodecatimorii tempora colliguntur xxvii l minuta; quarta tempora ix xl minuta, quinta tempora ix lviii minuta, sexta tempora x xvi minuta, quare et secundi dodecatimorii tempora colliguntur xxix liiii minuta; septima tempora x xxxiiii minuta, octava tempora x xlvii minuta, nona tempora x lv minuta, ut rursus et tertii quidem atque ad tropica puncta dodecatimorii tempora colligantur xxxii xvi minuta, totius autem tetartimorii xc consone. Atque inde manifestum est quoniam et reliquorum tetartimoriorum ordinatio contingit eadem, omnibus in unoquoque eisdem contingentibus, propter rectam speram, idest equinoctialem sine declinatione ad orizontem subiacere.
Claudii Ptolomei Mathematice Syntaxeos libri primi explicit.