⟨X⟩
Demonstratio apoguii stelle Veneris
De epicicli ipsius quantitate
De proportionibus excentroticos stelle
De directione periodicorum stelle motuum
De epochi periodicorum ipsius motuum
Presumpta in eas que de reliquis stellis demonstrationes
Demonstratio excenticos excenticos] excentroticos F1 et apoguii Martis
Demonstratio quantitatis epicicli Martis
De directione periodicorum ipsius motuum
De epochi periodicorum Martis motuum
⟨X.1⟩ Demonstratio apoguii stelle Veneris
Igitur stelle quidem Mercurii ypotheses et quantitates anomaliarum, amplius autem quantitates periodicorum motuum et epoche ad hunc nobis sumpta sunt modum. In Veneris autem stella primum rursus quesivimus, secundum quas partes est eius qui per medias imagines animalium circuli et apoguion et periguion excentroticos ab equalibus et in eadem partes maximis distantiis. In quod antiquos observationes convenientes non invenimus, ex his autem quas nos observationibus fecimus investigationem huiusmodi. Nam in eis quidem que a theonematico theonematico] Theone mathematico F1 date sunt nobis invenimus descriptam observationem xvio anno Adriani secundum Egiptios Pharmoyti xxi in xxii, secundum quam, dicit, Veneris stella esperia plurimum distabat a Sole precedens medium Pliados longitudine, videbatur autem et paulo australior ipsam pertransire. Quoniam ergo medium Pliados tunc secundum nostra principia obtinebat Tauri gradus iii. Longitudo vero ipsius unius et dimidii est ad proximum gradus, Veneris stella manifestum quoniam optinebat tunc Tauri i et dimidium. Quare quoniam et Sol medius obtinebat tunc Piscium gradus xiiii iiii, facta est a medio esperia maxima distantia graduum xlvii iiiia. Nos autem observavimus xiiii anno Antonini secundum Egiptios mensis Thoth xia in xiia stellam Veneris eoam plurimum distantem a Sole et distabat a medio genu Geminorum ad arctos et orientes Lunam unam dichominon. Optinebat autem stella quidem fixa tunc secundum nos Geminorum xviii iiiia, quare Veneris stellam circa xviii et dimidium gradus ad proximum contingere, medius autem Sol Leonis gradus v et dimidium iiiia. Facta est ergo eoa maxima distantia eorumdem xlvii iiii graduum. Quoniam ergo secundum priorem quidem observationem media progressio optinebat Piscium gradus xiiii iiiia, iuxta secundam vero Leonis gradus v et dimidium iiiia, quod autem inter ipsam eius qui per media punctum in xxv gradus excidit Tauri et Scorpii, secundum hec utique erit que per apoguion et periguion diametros.
Similiter in eis quidem que a Theone invenimus quoniam xiio anno Adriani secundum Egiptios mensis Athir xxi in xxiia Veneris eoa stella plurimum distitit a Sole, relicta ab ea que in extrema australi ale Virginis Pliadis longitudine vel minus suiipsius magnitudine. Videbatur autem borealior pertransire stellam Luna una. Quoniam ergo stella quidem fixa tunc secundum nos optinebat Leonis gradus xxviii et dimidium iiia xiia, quare et stellam Veneris optinere tertiam ad proximum unius gradus Virginis. Medius autem Sol zigoy graduum xvii et dimidii iiia xxxa facta est maxima a media eoa distantia graduum xlvii et dimidii xxx.
Nos autem xxi anno Adriani secundum Egiptios mensis Mechir ix in xa vespere observavimus Veneris stellam plurimum distantem a Sole et precedebat borealissimam earum iiii que velut in quidem latero post eam que consequens et in directo boubasi Aquarii duabus partibus ad proximum Lune dichomene et videbatur illuminare stellam. Quare quoniam rursum stella quidem fixa tunc secundum nos optinebat Aquarii gradus xx et propter hoc et stella Veneris erat circa xix gradus et et] om. add. s. l. V3 iii pentimoria. Medius autem Sol optinebat Capricorni gradus ii xva hic facta est esperia maxima distantia eorumdem xlvii et dimidii xxxa graduum et sunt puncta zodiaci intermedia et eorum qui secundum primam observationem Libre graduum xvii et dimidii iii xxxa et eorum qui iuxta secundam Capricorni graduum ii xv secundum xxv gradus ad proximum rursum Scorpii et Tauri.
⟨X.1bis⟩ Demonstratio apoguii stelle Veneris
Itaque quod quidem in eis que secundum nos temporibus apoguion excentroticos secundum xxv gradus esse et Tauri et Scorpii, per hec nobis sumptum est. Consequenter autem inquisivimus rursum factas maximas distantias medie Solis circa xxv gradus Tauri contingentes in circa xxv gradus Scorpii.
Nam in eis quidem que a Theone nobis date sunt reperimus quoniam xiii anno Adriani secundum Egiptios mensis Epiphi iia in iiia eoa Veneris stella plurimum distitit a Sole, rectam que per precedentem earum trium que in capite Arietis et eam que in posteriore crure precedens gradu i et duabus quintis. Ad precendentem autem earum que in capite diastima duplex faciebat eius quod ad eam que in crure. Optinebat autem tunc secundum nos precendens quidem earum trium que in capite Arietis gradus vi et iii quintas. Et borealior est eo qui per media gradibus vii iiia. Que autem in posteriore crure Arietis gradus xiiii et dimidium et iiiia et australior est eo qui per media gradibus v et iiiia. Stella ergo Veneris optinebat Arietis gradus x et iii quintas et australior erat eo qui per media gradu i et dimidio. Quare et quoniam medius Sol optinbat tunc Tauri gradus xxv et ii quintas, fit maxima distantia a medio graduum xliiii et et] om. add. s. l. V3 iiii et et] om. F1 quintarum.
Nos autem observavimus xxi anno Adriani secundum Egiptios mensis Tybi iia in iiia vespere Veneris stellam plurimum distantem a Sole, et perspecta ad eas que in cornibus Capricorni optinens apparebat gradus Capricorni xii et dimidium iiia, medio Sole optinente Scorpii gradus xxv et dimidium, quare hic maximam medio distantiam colligi graduum xlvii iiia et fieri manifestum quoniam et apoguion quidem secundum xxv gradus est Tauri, periguion vero secundum xxv gradus est Scorpii. Manifestum autem factum est nobis quoniam et stabilis est ferens epiciclum stelle Veneris excentricus circulus, propter hoc nequaquam eius qui per media ambas simul in utraque a medio maximas distantias neque minores inveniri coutrisque que secundum Taurum, neque maiores coutrisque que secundum Scorpium.
⟨X.2⟩ De epicicli ipsius quantitate
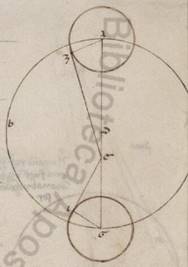His ergo subiacentibus, esto excentricus circulus in quo fertur semper Veneris epiciclus ABG circa diametrum AG, in qua excentrici quidem centrum subiaceat D, quod autem zodiaci E, punctum autem A quod sub xxv gradus Tauri, et scribantur circa A et G puncta equales epicicli, in quibus Z et I, et protractis contingentibus EZ et EI copulentur recte AZ et GI. Quoniam ergo AEZ angulus ad centrum existens zodiaci subtendit eam que secundum apoguion stelle maximam distantiam subiacentem graduum xliiii et iiiior quintarum, erit utique, qualium quidem sunt iiii recti ccclx, talium xliiii xlviii, qualium vero ii recti ccclx, talium lxxxix xxxvi. Quare et que quidem super AZ rectam periferia talium est lxxxix xxxvi, qualium qui circa AEG orthogonium circulus ccclx, que vero sub ipsam recta AZ talium lxxxiiii xxxiii ad proximum, qualium est AE ypothenusa cxx. Similiter quoniam GEI angulus subtendit eam que secundum maximam perguion distantiam subiacentem et ipsam graduum xlvii iiia, erit utique, qualium quidem sunt iiii recti ccclx, talium xlvii xx, qualium vero ii recti ccclx, talium xciii xciii] xciiii F1 xl. Quare et que quidem super rectam GI periferia talium xciii xciii] xciiii F1 xl, qualium qui circa GEI orthogonium circulus ccclx, que vero sub ipsam recta GI talium lxxxviii xiii ad proximum, qualium est EG ypothenusa cxx. Et qualium ergo est GI quidem, hoc est AZ recta que ex centro epicicli, lxxxiiii xxxiii, recta vero AE cxx, talium et EG quidem erit cxv i. Tota vero AG manifestum quoniam ccxxxv i, medietas vero eius AD cxiiii xxx ad proximum, reliqua vero recta DE inter centra ii xxix. Quare et qualium est AD que e centro lx, talium et que inter recta DE erit i iiii ad proximum, recta vero AZ que ex centro epicicli xliii vi.
⟨X.3⟩ De proportionibus excentroticos stelle
Quoniam autem non manifestum si circa D punctum equalis epicicli motio completur, sumpsimus et hic duas maximas distantias in contraria, medie Solis tetartimorio in utraque distantis ab apoguio. Quarum alteram quidem observavimus viii anno Adriani secundum Egiptios Pharmoyti iia in iiia, secundum quam eoa Veneris stella plurimum distitit a Sole et perspecta ad eam que vocatur Antari optinebat Capricorni gradus xi et dimidium iiia xiia, medio Sole tunc optinente Aquarii gradus xxv et dimidium, quare fieri eoam a medio maximam distantiam graduum xliii et dimidii et xiia. Altera vero observavimus iiio anno Antonini secundum Egiptios Pharmoyti iiiia in va vespere, secundum quam plurimum stella Veneris distabat a Sole et perspecta ad lucentem Yada optinebat Arietis gradus xiii xiii] om. add. s. l.V3 et dimidium iiia, a a] om. F1 medio Sole optinente rursum Aquarii gradus xxv et dimidium, quare et hic esperiam a medio maximam distantiam fieri graduum xlviii iiia.
His subiacentibus, esto per apoguion et periguion excentricos diametros ABG, et subiaceat A quidem punctum quod sub xxv gradus Tauri, B vero centrum zodiaci. Proponatur autem invenire centrum circa quod planam diximus motionem compleri epicicli. Esto ergo D punctum et trahatur per ipsum recta ad rectam AG linea DE, ut tetartimorio distet quemadmodum in observationibus media epicicli progressio ab apoguio. Sumatur autem in ipsa quod secundum expositas observationes epicicli centrum E et scripto circa ipsum ZI epiciclo, trahantur quidem a puncto B contingentes ipsum recte BZ et BI, copulentur vero BE et EZ et EI. Quoniam ergo secundum mediam progressionem eoa quidem maxima a medio distantia subiacet graduum xliii et dimidii xiia, esperia vero graduum xlviii iiia, erit utique et ZBI angulus totus talium xci lv, qualium sunt iiii recti ccclx, et medietas ergo ipsius ZBE eorumdem est xci lv, qualium sunt ii recti ccclx. Quare et que quidem super rectam EZ periferia talium est xci lv, qualium qui circa BEZ orthogonium circulus ccclx. Ipsa vero EZ recta talium lxxxvi xvi, qualium est BE ypothenusa cxx, et qualium ergo est EZ que e centro epicicli xliii x, talium et BE erit lx et sexagesimorum iiia.
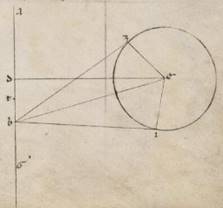Rursum quoniam propositarum maximarum distantiarum superhabundantia graduum existens iiii xlv bis continet eam que tunc penes zodiacam anomaliam differentiam que sub BED angulorum continetur, erit utique BED angulus, qualium quidem sunt iiii recti ccclx, talium ii xxii et dimidii, qualium ii recti ccclx, talium iiii xlv. Quare et que quidem super rectam BD periferia talium est est] add. iiii xlv qualium F1 qui circa BDE orthogonium circulus ccclx, ipsa vero BD recta talium iiii lix ad proximum, qualium est BE ypothenusa cxx. Et qualium est ergo BE quidem recta lx et sexagesimorum iii, que vero ex centro epicicli xliii et x, talium et recta BD erit ii et dimidii ad proximum.
Ostensa est autem et que inter B centrum zodiaci et centrum excentrici in quo semper est centrum epicicli eorumdem i iiiia. Quare et medietas est recte BD. Si ergo in duo equa diviserimus rectam BD secundum T, habebimus demonstratum quoniam, qualium est recta TA que ex centro excentrici ferentis epiciclum lx, talium est utraque quidem earum que sunt BT et TD inter centrum i iiiia, recta vero EZ que ex centro epicicli xliii x. Quod propositum erat demonstrare.
⟨X.4⟩ De directione periodicorum stelle motuum
Itaque modus quidem ypotheseos et proportiones anomaliarum ad hunc nobis sumpta sunt modum. Rursum vero et periodicorum motuum stelle et epocharum eam, eam] causa F1 sumpsimus duas observationes indubitabiles et ex eis que secundum nos et ex antiquis. Igitur nos quidem observavimus secundo anno Antonini secundum Egiptios mensis Tybi xxixa in xxxa per astrolabium Veneris stellam post maximam eoam distantiam ad Spicam et apparebat optinens Scorpii gradus vi et dimidium. Tunc autem et inter et in directo erat et borealissime earum que in fronte Scorpii et apparente centro Lune. Centrum vero Lune precedebat ipsam emiolio eius quo deficiebat a borealissima earum que in fronte. Verum stella quidem fixa optinebat tunc secundum nostra principia Scorpii gradus vi xx et borealior est ea qui per media gradu i xx. Tempus autem erat post iiii et dimidium iiii horas equinoctiales a mesonictio, quoniam quidem, Sole circiter xxiii graduum existente Sagitarii, celum medium optinebat in astrolabio Virginis gradus ii, secundum quod tempus Sol quidem medius optinebat Sagittarii gradus xxii ix, Luna vero Scorpii gradus xi xxiiii. Anomalie vero ab apoguio gradus lxxxvii xxx, latitudinis vero a boreali termino gradus xii xxii et propter hec examinate quidem optinebat centrum ipsius Scorpii gradus v xlv. Borealius autem erat eo qui per media gradibus v. Apparebat autem in Alexandria secundum longitudinem quidem optinens Scorpii gradus vi xlv. Borealius autem eo qui per media gradibus iiii xl. Stella itaque Veneris propter ista optinebat Scorpii gradus vi xxx et borealior erat eo qui per media gradibus ii xl.
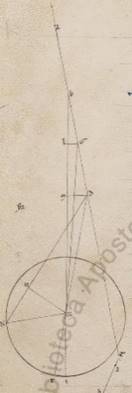His subiacentibus, esto per apoguion diametros ABGDE, et A quidem subiaceat secundum xxv gradus Tauri, B vero circa quod movetur epiciclus plane, G A A] autem F1 centrum excentrici in quo fertur centrum epicicli, D vero centrum zodiaci. Et quoniam medius Sol optinebat in observatione Sagittarii gradus xxii ix, quare et mediam epicicli progressionem distare in consequentia ab eo quod secundum E periguio gradibus xxvii ix, subiaceat centrum ipsius secundum Z, et scripto circa ipsum ITK epiciclo, copulentur quidem recte DZI et GZ et BZT. Catheti vero trahatur a punctis G et D in BZ que sunt GL et DM, et subiacente stella secundum K punctum, copulentur quidem recte DK et KZ, cathetus autem trahatur ZN. Proponatur autem invenire TK periferiam, quam distabat stella a puncto T apoguio epicicli. Quoniam ergo EBZ angulus, qualium quidem sunt iiiior recti ccclx, talium est xxvii ix, qualium ii recti ccclx, talium liiii xviii, erit utique et que quidem super rectam GL periferia talium liiii xviii, qualium est qui circa BGL orthogonium circulus ccclx, TI vero super rectam BL reliquorum in semicirculum cxxv xlii. Et earum ergo que sub ipsis rectarum GL quidem erunt talium liiii xlvi, qualium est BG ypothenusa cxx, recta vero BL eorum cvi xlvii. Quare et qualium BG quidem recta i xv, recta vero GZ que ex centro excentrici lx, talium et ZL quidem erit o xxxiiii. Recta vero BL similiter i vii. Et quoniam quod a recta ZG defitiens quod a recta GL facit quod a recta GL, erit et ipsa eorumdem ad proximum lx. Est autem et ML quidem ei que est LB equalis, recta vero DM eius que est GL dupla, propter equalem esse et rectam BG ei que est GD. Quare et ZM quidem erit reliquorum lviii liii, recta vero DM eorumdem i viii. Propter hoc autem et ZD ypothenusa lviii liiii ad proximum; et qualium est ergo ZD recta cxx, talium et DM quidem erit ii xviii, que vero super ipsam periferia talium ii xii, qualium qui circa DZM orthogonium circulus ccclx. Quare et BZD angulus talium est ii xii, qualium sunt ii recti ccclx. Totus vero EDZ eorumdem lvi xxx. Est autem et EDK, qualium quidem sunt iiii recti ccclx, talium xviii xxx, propter tantos precedere stellam gradus secundum observationem illud quod secundum E periguium, hoc est xxv gradus Sorpii, qualium vero ii recti ccclx, talium xxxvii. Itaque et totus quidem KDZ angulus talium est xciii xxx, qualium ii recti ccclx. Que vero super ipsam ZN periferia talium xciii xxx, qualium qui circa DZN orthogonium circulus ccclx, et ea ergo que sub ipsam recta ZN, qualium quidem est cxx ea que est ZD, talium est lxxxvii xxv, qualium vero lviii liiii, hoc est qualium recta ZK que ex centro epicicli xliii x, talium xlii liiii. Quare et quorum est ZK ypothenusa cxx, talium et ZN quidem erit cxix xviii. Que vero super ipsam periferia talium clxvii xxxviii, qualium est qui circa ZKN orthogonium circulus ccclx. Itaque et ZKD quidem angulus eorumdem clxvii xxxviii, qualium angulus ZDK subiacet xciii xxx, totus vero KZI cclxi viii. Ostensus est autem et BZD, hoc est IZT, eorumdem ii xii. Et reliquus ergo TZK angulus, qualium quidem sunt ii recti ccclx, talium talium] add. erit cclviii lvi. Qualium vero iiiior recti ccclx talium F1 cxxix xxviii. Distabat ergo Veneris stella secundum expositum tempus a puncto E apoguio epicicli in precendentia quidem expositos gradus cxxix xxviii, in consequentia vero secundum consequentem ypothesi motum reliquos in unum circulum gradus ccxxx xxxii. Quod oportet demonstrare.
Antiquarum autem observationum sumpsimus eam quam describit Thimocharis ita: ‘xiii et dimidio anno Philadelphi secundum Egiptios Mesori xviia in xviiia hora xiia stella Veneris apparebat occupans eam que contraiacet protriguitiri examinate’. Et est stella ista secundum nos post eam que in extrema australi ala Virginis. Optinebat autem secundum primum Antonini annum Virginis gradus viii iiiia. Quoniam ergo observationis quidem annus cccclxxvi est a Navonassaro, qui vero usque Antonini regnum dccclxxxiiii, quare superaddere mediis ccccviii annis fixarum et apoguiorum motionis gradus iiii xiia ad proximum, manifestum quoniam Veneris quidem stella optinebat Virginis gradus iiii via, periguion vero excentrici Scorpii gradus xx et dimidium iiia xiia. Transit autem et hic Veneris stella maximam eoam differentiam. Post iiii enim dies proposite observationis xxi Mesori in xxii ex eis que dicit Thimocharis optinebat secundum nostra principia Virginis gradus viii et dimidium iiia. Media autem Solis progressione secundum priorem quidem observationem optinente Chelarum gradus xvii iii, at vero secundum eam que deinceps Chelarum gradus xx lix, quare et prioris quidem observationis distantiam colligi graduum xlii liii, eius vero que deinceps graduum xlii ix.
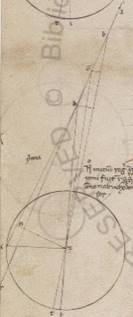His ergo datis, adiaceat rursum simillis descriptio in precendentia quidem periguii epiciclum habens, propter mediam quidem epicicli progressionem optinere Chelarum gradus xvii iii, periguion vero Scorpii gradus xx lv. Quoniam ergo propter hoc EBZ angulus, qualium quidem sunt iiiior recti ccclx, talium est xxxiii lii, qualium vero ii recti ccclx, talium lxvii xliiii, erit utique et que quidem super GL periferia talium lxvii xliiii, qualium est qui circa BGL orthogonium circulus ccclx, que vero super BL reliquorum in semicirculum cxii xvi, et earum ergo que sub ipsis rectarum GL quidem talium est lxvi lii, qualium BG ypothenusa cxx, recta vero BL eorumdem xcix xxxviii. Quare et qualium est BG quidem recta i xv, recta vero GZ que ex centro excentrici lx talium, et GL quidem erit o xlii, BL vero similiter i ii, et quoniam quod a recta ZG defitiens quod a recta GL facit quod a recta ZL, erit et ipsa longitudine eorumdem ad proximum lx. Est autem propter eadem et recta quidem BL ei que est LM equalis, recta vero DM eius que est GL dupla. Quare et reliqua quidem ZM erit lviii lviii, recta vero DM eorumdem i xxiiii. Propter hoc autem et ZD ypothenusa lviii lix ad proximum; et qualium est ergo cxx ea que est ZD, talium et recta quidem DM erit ii li, que vero super ipsam periferia talium ii xliiii, qualium est qui circa ZDM orthogonium circulus ccclx. Quare et BZD quidem angulus talium est ii xliiii, qualium ii recti ccclx. Totus vero EDZ eorumdem lxx xxviii. Est autem et EDK angulus quo distabat stella in precedentia a periguio, qualium sunt iiii recti ccclx, talium lxxvi xlv, qualium vero ii recti ccclx, talium cliii xxx. Quare et reliquus quidem ZDK angulus eorumdem est lxxxiii ii, que vero super rectam ZN periferia talium lxxxiii ii, qualium est qui circa DZN orthogonium circulus ccclx, et que sub ipsa ergo recta ZN, qualium quidem est DZ ypothenusa cxx, talium erit lxxix xxxiii, qualium vero lviii lix, hoc est, qualium ZK que ex centro epicicli xliii x, talium xxxix vii. Quare et qualium est ZK ypothenusa cxx, talium et ZN quidem recta erit cviii xlv, que vero super ipsam periferia talium cxxx ad proximum, qualium est qui circa ZKN orthogonium circulus ccclx, et angulus ergo DKZ talium est cxxx, qualium et ZDK subiacet lxxxiii ii, totus vero TZK eorumdem ccxiii ii ostensus est ante et BZD, hoc est IZC, IZC] IZT F1 eorumdem ii xliiii. Et totus ergo IZK angulus qualium quidem sunt duo recti, ccclx talium ccxv xlvi, qualium vero iiii recti ccclx, talium cvii liii. Et secundum hoc ergo tempus Veneris stella distabat ab I apoguio epicicli in consequentia defitientibus in unum circulum gradibus cclii vii. Quod oportet demonstrare.
Quoniam ergo distabat et hoc nostre observationis tempus similiter ab apoguio epicicli gradibus ccxxx xxxii, quod autem inter duas observationes tempus continet annos quidem Egiptiacos ccccix et dies clxvii ad proximum, anomalie vero restitutiones totas cclv, quoniam quidem, viii Egiptiacis annis facientibus ad proximum v periodos, anni quidem ccccviii colligunt periodos cclv, reliquus autem annus cum comprehensis diebus non complet tempus unius restitutionis, manifestum nobis factum est quoniam in annis egiptiacis ccccix et diebus clxvii Veneris stella sumit post totas anomaliarum restitutiones cclv gradus in epiciclo cccxxxviii xxv, quantis ea que secundum nos epochi priori superhabundabat. Tanti vero fere supergressionis colliguntur gradus et in preexpositis nobis mediorum motuum canonibus, propter et directionem ipsorum ab inventa periodorum supergressione constitui, tempore quidem resoluto in dies, restitutionibus vero cum supergressione in gradus. Distributa enim multitudine graduum in multitudine dierum, constituitur preexpositis preexpositis] preexpositus F1 nobis in Veneris stella diurnus anomalie medius motus.
⟨X.5⟩ De epochi periodicorum ipsius motuum
Relicto autem et hic epochas periodicorum motuum in primum annum regni Navonassari secundum Egiptios mensis Thoth io ad meridiem constituere, sumpsimus rursum medium tempus et huius et eius quod secundum antiquiorem observationem. Colligitur autem illud annorum egiptiacorum cccclxxv et dierum cccxlvi et dimidii iiiia ad proximum. Que adiacet tempori huic secundum anomalie selidia medii motus supergressio graduum clxxxi ad proximum. Quos si dempserimus ab eis qui secundum observationem gradibus cclii vii, habebimus epochin in primum annum Navonassaro secundum Egiptios mensis Thoth io ad meridiem anomalie ab apoguio epicicli gradus lxxi vii, Media longitudinis eadem rursum subiacente ei que Solis, hoc est optinente Piscium gradus lxx xlv. Manifestum autem quoniam et eo quod secundum observationem apoguie contigente circa Tauri gradus xx lv, intermediis autem cccclxxvi annis ad proximum pertinentibus gradibus iiii et dimidio iiiia, secundum expositum tempus epochis erit apoguion circa xvi x gradus Tauri.
⟨X.6⟩ Presumpta in eas que de reliquis stellis demonstrationes
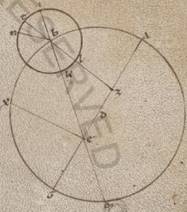Itaque in his quidem duabus stellis Mercurii scilicet et Veneris talibus epochis utentes contigimus et ad investigationes ypothesium et ad demonstrationes anomaliarum. In reliquis autem tribus, Marte, Iove et Saturno ypothesim quidem motionis unam et simillem reperimus eius que circa Veneris stellam deprehensa est, hic hic] hoc F1 est secundum quam excentricus circulus in quo semper fertur epicicli centrum scribitur in duo equa dividenti puncto inter mediam centrorum eius scilicet quod zodiaci et eius qui equalem facit epicicli circumductionem, quoniam quidem et in unoquoque istorum secundum integrius investigationis constitute excentroticos ex quantitate earum que circa maximas et minimas distantias epicicli proiguiseton per maximam distantiam eius que penes zodiacum anomalie reperta dupla ad proximum deprehenditur.
Demonstrationes autem per quas quantitates utrasque anomaliarum et apoguia constituimus non valentes ad eumdem modum duobus illis et in istis tradi, propter omnem ipsas a Sole facere distantiam et non fieri manifestum ex observationibus quemadmodum in maximis distantiis Mercurii et Afroditis, quando secundum contactum stella fit educte recte a visu nostro contingentis epiciclum. Eo ergo quod huiusmodi non procedente, cousi sumus ad mediam Solis progressionem observatis ipsorum diametricis stationibus, a quibus primum excentroticos proportiones et apoguia ostendimus, quoniam quidem in sole ita consideratis progressionibus disterminatam reperimus secundum seipsam zodiacam anomaliam, nulla facta tunc penes eam que ad Solem anomaliam differentia.
Esto enim excentricus circulus stelle in quo fertur centrum epicicli ABG circa centrum D, et que quidem apoguion diametros AG, in ipsa vero E punctum quidem centrum zodiaci, punctus vero Z excentrici, ad quem que secundum longitudinem media progressio epicicli consideratur, et scripto circa B epiciclo ITKL, copulentur et recta ZLBT et recta IBKEM; dico primum quoniam, quando stella secundum rectam EI per B centrum epicicli apparet, et media semper Solis progressio in eadem recta erit, et secundum I quidem punctum facta stella coniungitur medie Solis progressioni et ipsi ad I considerate, at vero secundum K punctum diametros ipsa fiet ad M punctum considerata. Quoniam enim ab apoguiis in unaquaque harum stellarum medie distantie et longitudinis et anomalie composite faciunt eam que ab eodem principio mediam Solis progressionem, eius vero qui ad Z centrum anguli qui continet eum qui secundum longitudinem stelle planum motum et eius qui ad E qui continet apparentem, superhabundantiam semper fit ille qui ad B angulus continens planum secundum epiciclum ipsius progressum, manifestum quoniam, quando secundum I quidem punctum fuerit stella, defitiet ab ea que in T apoguion restitutionem restitutionem] restitucione F1 IBT angulum, qui compositus cum angulo AZB, hoc est sumptus sub ipso, facit contentum sub solari medio progressu angulum AEI eumdem existentem apparenti stelle. Quando vero secundum K punctum fuerit mota, rursum erit secundum epiciclum TBK angulum, qui compositus est cum AZB fatiet ab A apoguio mediam Solis progressionem continentem et semicirculum et adhuc AZB angulum defitientem LBK angulum, hoc est GEM, rursum secundum diametrum existentem apparenti stelle. Propter hoc autem et in talibus quidem figurationibus et ab B centro epicicli in stella educta recta et que ab E quod secundum visum nostrum in mediam progressionem Solis secundum unam et eamdem rectam concidunt ambe. In omnibus autem aliis distantiis distantes quidem faciunt acclinationes, equidistantes autem seinvicem semper. Si enim quacumque positionem in exposita descriptione a puncto quidem B in stella duxerimus rectam velut BN, ab E vero in mediam Solis progressionem velut EX, equalis quidem erit propter predicta AEX angulus coutrisque AZT et NBT, equalis autem et AZT coutrisque AEI et IBT. Communi vero ablato AEI, et reliquus IEX reliquo IBN equalis erit, parallilos ergo est EX recta ei que est BN.
Quoniam ergo secundum dictas figurationes et coniunctionales et acronictoys ad mediam Solis progressionem consideratos per centrum epicicli stellam consideratam reperimus, quemadmodum utique sive quaquam sive quaquam] si nequaquam F1 secundum epiciclum motum haberet, sed ipsam in ABG circulo portionem habens sub ZB recta plane circumageretur ad eumdem modum centro epicicli, manifestum quoniam quidem possibille per tales erit progressiones eas que penes excentrotica zodiace anomalie proportiones secundum seipsas demonstrare. Non apparentibus autem coniunctionalibus figurationibus, reliquitur per acronictias efodos demonstrationem facere.
⟨X.7⟩ Demonstratio excentroticos et apoguii Martis
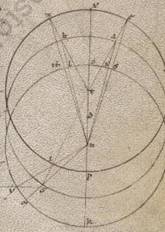Quemadmodum ergo in Luna sumentes trium panselinicarum eclipsium et loca et tempora demonstravimus per lineas et anomalie rationem et apoguii locum, eodem modo et hic trium acronicton ad mediam Solis progressionem diametrorum secundum unamquamque stellarum istarum et locos observantes ut est maxime diligenter per astrolabica organa et ab eis que secundum observationes mediis Solis progressionibus ad subtilius distantie et tempus et locus adinvestigantes ab his ostendimus excentrotitis rationem et apoguion. In prima ergo stella Martis sumpsimus tres acronictoys, quarum primam quidem observavimus xvo anno Adriani secundum Egiptios mensis Tybi xxvi in xxvii post unam horam equinoctialem a mesonictio circiter Geminorum gradus xxi, secundam vero xixo anno Adriani secundum Egiptios Pharmoythi vi in vi ante horas iii a mesonictio circiter Leonis gradus xxviii l, tertiam autem sub anno Antonini secundum Egiptios Epiphi xiia in xiiia ante duas horas equinoctiales a mesonictio circiter Sagittarii gradus ii xxxiiii. Itaque tempora quidem distantiarum continet a prima quidem acronicto in secundam annos Egiptiacos iiii et dies lxix et horas equinoctiales xx, a secunda vero in tertiam annos iiii similiter et dies xcvi et horam equinoctialem unam. Colliguntur vero ex primo quidem distantie tempore post totos circulos longitudinis motus gradus lxxxi xliiii, ex eo vero quod secunde gradus xcv xxviii. Nullo enim cura digno difereret, quamvis ab integrius expositis periodicis restitutionibus in tanto tempore medios motus supputemus. Manifestum vero quoniam et secundum primam quidem differentiam apparens stella mota est post totos circulos gradus lxvii l, at vero iuxta secundam gradus xciii xliiii.
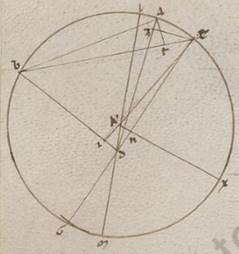Describantur ergo in zodiaci epipedo tres equales circuli quorum ille quidem qui fert centrum epicicli Martis esto ABG circa centrum D, qui vero plani motus excentricus EZI circa centrum T, qui autem omocentricus zodiaco KLM circa centrum N, que vero per MA centra diametros XOPR. Subiaceat autem A quidem secundum quod erat epicicli centrum in prima acronicto, B vero secundum quod erat in secunda acronicto, acronicto] add. G autem secundum quod erat in iiia acronicto F1 et copulentur recte TAE et TBZ et TIG et NKA et NLB et NGM, quare et EZ quidem excentrici periferiam graduum esse qui prime periodice distantie lxxxi xliiii, eam vero que est ZI eorum qui secunde xcv xxviii, et rursum KL quidem periferiam zodiaci eorum qui apparentis prime distantie graduum lxvii l, eam vero que est LM eorum qui secunde xciii xliiii. Itaque siquidem EZ et ZI excentrici periferie sub KL et LM zodiaci periferiis subtendebantur, nichil utique aliud ad demonstrationem amplius excentroticos querebamus. Quoniam vero ipse quidem eas que sunt AB et BG medii excentrici subtendunt non datas, si autem copulavimus rectas NSE et NTHZ et NIY, rursum EZ et ZI excentrici periferias ille que sunt STH et TY zodiaci subtendunt, neque ipse manifestum quoniam date, oportebit priores dari KZ et LTH et MI differentes portiones, ut a coniugantibus periferiis que sunt EZI et STHY ad examinationem excentroticos proportio demonstretur. Quoniam autem neque istas possibile est examinate sumere prius excentroticos proportione et apoguio, dabuntur tamen ad proximum, etiam si non examinate illa persumantur, propter non magnas ipsarum fieri differentias, faciemus prius investigationem quasi nullo cura digno differentibus penes eas que sunt KLM STHY periferiis.
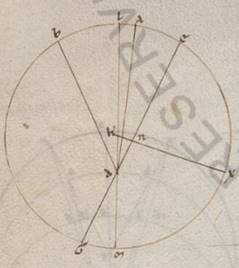Esto enim plane progressionis Martis excentricus circulus ABG, et subiaceat A quidem punctum prime acronicti, B vero secunde, G autem tertie. Sumatur autem in ipso centrum zodiaci in quo visus videtur D, et copulentur recte semper ab tribus punctis acronictorum in illud quod visionis velut nunc recta AD et BD et GD, et ducatur quidem universaliter una copulatarum trium rectarum in contrariam excentrici periferiam velut hic recta GDE. Reliqua vero duo puncta acronictorum copulet recta velut in his ea que est AB. Deinde facta a sectione excentrici sub educta recta quale E, copulentur quidem recte in reliqua duo puncta acronictorum velut hic et EA et EB, catheti vero ducantur in rectas a dictis duobus punctis in zodiaci centrum copulatos velut in istis in AD quidem EZ, in BD vero EI, et adhuc ab altero dictorum duorum punctorum cathetus ducatur ad rectam ab altero ipsorum in factum excentrici superfluum punctum copulatam velut hic ab A in BE rectam AT b b] igitur F1 hec quidem semper observantes in tali descriptione secundum quem utique voluerimus modum easdem rationes in numeris inveniemus delatas, reliqua autem demonstrato a preiacentibus in stella Martis periferiis erit manifestum modo tali.
Quoniam enim BG excentrici periferia subiacet subtendens zodiaci gradus xciii xliiii, erit utique BDG quedem quedem] quidem F1 angulus ad centrum existens zodiaci, qualium quidem super iiiior recti ccclx, talium xciii xliiii, qualium vero ii recti ccclx, talium clxxxvii xxviii, qui vero deinceps ipsi EDI eorumdem clxxii xxxii. Quare et que quidem super rectam EI periferia talium est clxxii xxxii, qualium qui circa DEI orthogonium circulus ccclx, recta vero EI talium erunt cxix xlv, qualium est DE ypothenusa cxx. Similiter quoniam BG periferia est graduum xcv, erunt erunt] erit F1 utique et BEG angulus ad periferiam existens talium xcv xxviii, qualium ii recti ccclx, eorumdem vero erat et BDE angulus clxxii xxxii, et reliquus ergo EBI eorumdem erit xcii. Quare et que quidem super EI periferia talium xcii, qualium qui circa BEI orthogonium circulus ccclx, recta vero EI talium lxxxvi xix, qualium est BE ypothenusa cxx. Et qualium ergo EI quidem ostensa est cxix xlv, recta vero ED similiter cxx, talium et BE erit clxvi xxix.
Rursum quoniam ABG tota periferia excentrici subiacet subtendens zodiaci collectos utrarumque distantiarum gradus clxi xxxiiii, erit utique et ADG quidem angulus talium clxi xxxiiii, qualium sunt iiii recti ccclx, reliquus autem ad ADE eorumdem quidem xviii xxvi, qualium vero ii recti ccclx, talium xxxvi lii. Quare et que quidem super EZ periferia talium est xxxvi lii, qualium qui circa DEZ orthogonium circulus ccclx, recta vero EZ talium xxxvii lvii, qualium est DE subtendens cxx. Similiter quoniam ABG excentrici periferia colligitur graduum clxxvii xii, erit utique et AEG angulus talium clxxvii xii, qualium sunt ii recti ccclx. Eorumdem vero erat et ADE angulus xxxvi lii, et reliquus ergo DAE eorumdem est cxlv lvi. Quare et que quidem super rectam EZ periferia talium est cxlv lvi, qualium qui circa DEZ orthogonium circulus ccclx, recta vero EZ talium cxiiii xliiii, qualium est AE ypothenusa cxx, et qualium ergo EZ quidem ostensa est xxxvi lvii, recta vero ED cxx, talium et AE erunt erunt] erit F1 xxxix xlii.
Rursum quoniam AB excentrici periferia graduum est lxxxi xliiii, erit utique et AEB angulus talium lxxxi xliiii qualium sunt iio recti ccclx. Quare et que quidem super AT periferia talium est lxxxi xliiii, qualium qui circa AET orthogonium circulus ccclx, que vero super rectam ET reliquorum in semicirculum xcviii xvi. Et earum ergo que sub ipsas rectarum AT quidem erit talium lxxviii xxxi, qualium est AE ypothenusa cxx. Recta vero eorumdem xc xlv. Quare et qualium est ostensa AE quidem xxxix xlii DE vero subiacet cxx, talium et TA quidem erit xxv lviii ET vero similiter xxx et sexagesimorum iiorum, eorum vero demonstrata est et EB tota clxvi xxix. Et reliqua ergo TB talium est cxxxvi xxvii, qualium TA erat xxv lviii, et est quod quidem a recta TB tetragonum dcxv xvi, quod autem a a] om. add. s. l. V3 recta TA similiter dclxxiiii xvi, que composita faciunt quod a recta AB tetragonum xixcclxxxix xxxii. Longitudine ergo recta AB talium est cxxxviii liii, qualium ED quidem erat cxx, recta vero AE xxxix xlii. Est autem et qualium excentrici diametros cxx, talium AB recta lxxviii xxxi. Subtendit enim periferia graduum lxxxi xliiii. Et qualium est ergo AB quidem recta lxxviii xxxi excentrici vero diametros cxx, talium et ED quidem erit lxvii l, recta vero AE eorumdem xxii xliiii. Quare et que quidem super ipsam periferia excentrici graduum est xxi xli, tota vero EABG graduum cxcviii liii, et reliqua ergo GE quidem periferia graduum est clxi vii. Que vero sub ipsam recta GDE talium cxviii xxii, qualium est excentrici diametros cxx. Itaque siquidem GE recta equalis erat invente diametro excentrici, manifestum quoniam et in ipsa utique contingeret centrum ipsius et hinc utique apparent excentroticos ratio. Quoniam vero non est facta equalis, maiorem autem et EABG portionem fecit semicirculo, manifestum quoniam ad hanc cadet centrum excentrici. Subiaceat ergo K, et protrahatur per istud et punctum D, que per utrumque centrum diametros LKDM, et a puncto K in GE cathetus trahatur KNX. Quoniam ergo EG recta ostensa est talium cxviii xxii, qualium est LM diametros cxx, eorumdem vero erat et DE recta lxxvii lxxvii] lxvii F1 l, et reliqua ergo GD eorumdem erunt l xxxii. Quare quoniam sub rectis ED DG contentum orthogonium equale est sub rectis LD DM contento, talium habebimus sub LD DM contentum orthogonium iiiccccxxvii li. Verum et quod sub rectis LD DM cum ea que a recta DK tetragono facit quod a dimidia totius, hoc est recta LK, tetragonum. Si ergo ab eo quod a dimidia tetragono factis iiidc, dempserimus sub LD DM facta ccccxxvii ccccxxvii] iiiccccxxvii F1 li relinquetur nobis quod a recta DK tetragonum eorumdem clxxii ix. Et longitudine ergo habebimus DK inter centra existentem talium xiii vii ad proximum, qualium est recta KL que ex centro excentrici lx.
Rursum quoniam dimidia quidem eius que est GE, hoc est GN, talium est lix xi, qualium LM diametros cxx, eorumdem vero ostensa est et GD recta l xxxii, et reliqua ergo DN talium est viii xxxix, qualium DK inventa est xiii vii. Quare et qualium est DK ypothenusa cxx, talium et DN quidem erit lxxix viii, que vero super ipsam periferia talium lxxxii xxx, qualium qui circa DKN orthogonium circulus ccclx, et DKN ergo angulus, qualium quidem sunt ii recti ccclx, talium est lxxxii xxx, qualium vero iiii recti ccclx, talium xli xv. Et quoniam ad centrum est excentrici, habebimus et MX periferiam graduum xli xv. Est autem et GMX tota dimidia existens eius que est GXE lxxx xxxiiii, et reliqua ergo GM que ab iiia eorumdem acronicto in periguion graduum est xxxix xix. Manifestum vero quoniam, et BG quidem subiacente xcv xxviii, et reliqua LB que ab apoguio in ii acronicton graduum erit xlv xiii, AB vero subiacente graduum lxxxi xliiii, et reliqua AL que prima acrinicto in apoguion graduum xxxvi xxxi.
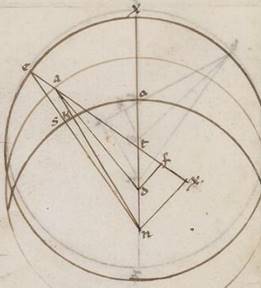His ergo subiacentibus, consideremus collectas ab ipsis differentias quesitarum secundum unamquamque acronicton zodiaci periferiarum modo tali. Adiaceat enim ex iiium acronictorum preiacente figura unius acronicti solius descriptio, et copulata recta AD, trahantur a punctis D et N in AT eductam catheti DF et XN. Quoniam ergo XE periferia graduum est xxxvi xxxi, erit utique et ETX angulus, qualium quidem sunt iiii recti ccclx, talium xxxvi xxxi, qualium vero ii recti ccclx, talium et ipse qui et secundum verticem ipsius DTF lxxiii ii. Quare et que quidem DF periferia talium est lxxiii ii, qualium qui circa DTF orthogonium circulus ccclx, que vero super TF reliquorum in semicirculum cvi lviii. Et earum ergo que sub ipsis rectarum DF quidem talium est lxxi xxv, qualium DT ypothenusa cxx, FT vero eorumdem xcvi xxvii. Quare et qualium est DT quidem recta vi xxxiii et dimidii, DA vero que e centro excentrici lx, talium et DF quidem erit iii liiii, FT vero similiter v xvi, et quoniam quod a recta DF sumptum ab eo quod a recta DA facit quod a recta FA, erit erit] add. et recta AF F1 quidem longitudine lix lii, tota vero XA, quoniam equalis est recta XF ei que est FT, talium lxv viii, qualium et NX dupla existens eius que est DF colligitur vii xlviii. Propter hoc autem et NA ypothenusa eorumdem erit lxv xxxvi, et qualium est ergo NA recta cxx, talium et NX quidem erit xiiii xvi, que vero super ipsam periferia talium xiii xl, qualium qui circa ANX orthogonium circulus ccclx. Quare et NAX angulus talium est xiii xl, qualium iio recti ccclx.
Rurusm quoniam qualium est TE que ex centro excentrici lx, talium est et NX quidem ostensa est vii xlviii, recta vero XT similiter x xxxii, et tota quidem erit XTE eorumdem lxx xxxii, propter hoc autem et NE ypothenusa lxxi ad proximum, et qualium est ergo NE recta cxx, talium et XN quidem recta erit xiii x, que vero super ipsam periferia talium xii xxxvi, qualium qui circa ENX orthogonium circulus ccclx. Quare et NEX angulus talium est xii xxxvi, qualium ii recti ccclx, eorumdem vero erat et NAX angulus xiii xl, et reliquus ergo ANE angulus, qualium quidem sunt duo recti ccclx, talium est i iiii, qualium vero iiii recti ccclx, talium o xxxii, tantorum ergo est et KS zodiaci periferia.
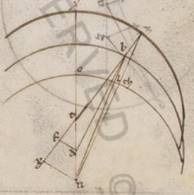Adiaceat ergo simul figura continens secunde acronicti descriptionem. Quoniam ergo ZX graduum subiacet xlv xiii, erit utique et XTZ angulus, qualium qualium quidem sunt iiiior recti ccclx, talium xlv xiii, qualium vero duo recti ccclx, talium et ipse et qui secundum verticem ipsius DTF angulus xc xxvi. Quare et que quidem super DF periferia talium est xc xxvi, qualium qui circa DTF orthogonium circulus ccclx, que vero super FT reliquorum in semicirculum lxxxix xxxiiii. Et earum ergo que sub ipsis rectarum DF quidem talium lxxxv x, qualium DT ypothenusa cxx, recta vero FT eorumdem lxxxiiii xxxii. Quare et qualium est DT quidem recta vi xxxiii et dimidii, DB vero que ex centro excentrici lx, talium et DF quidem erit iiii xxxix, recta vero FT similiter iiii xxxviii, et quoniam quod a recta DF sumptum sub eo quod a recta DB facit quod a recta BF tetragonum, erit et FB quidem longitudine lix xlviii, tota vero XB, propter equalem esse FX ei que est FT, talium lxiiii xxvii, qualium et NX dupla existens eius que est DF colligitur ix xviii. xviii] corr. ex lxviii V3F1 Propter hoc autem et NB ypothenusa eorumdem erit lxix vi, et qualium est ergo cxx recta NB, talium et NX quidem erit xvii ix, que vero super ipsam periferia talium xvi xxvi, qualium est qui circa BNX orthogonium circulus ccclx. Quare et NBX angulus talium est xvi xxvi, qualium ii recti ccclx. Rursum quoniam qualium est ZT que e centro excentrici lx, talium et NX quidem ostensa est ix xviii, ZT vero similiter ix xvi, et tota quidem erit XTZ eorumdem lxix xvi. Propter hoc autem et NZ ypothenusa lxix lii, et qualium est ergo NZ ypothenusa cxx, talium et NX quidem erit xvi ad proximum, que vero super ipsam periferia talium xv xx, qualium est qui circa ZNX orthogonium circulus ccclx. Quare et NZX quidem angulus talium est xv xx, qualium ii recti ccclx, eorumdem vero erat et NBX angulus xvi xxvi, et reliquus ergo BNZ eorumdem quidem i vi, qualium vero iiii recti ccclx, talium o xxxiii. Tantorum ergo est et LTH zodiaci periferia. Quoniam ergo et in prima acronicto eam que est KS invenimus o xxxii, manifestum quoniam ambarum periferiarum portionibus AE maior erit ad excentricum considerata prima datam datam] distantia F1 apparente et continebunt gradus lxviii lv.
Adiaceat autem et tertie acronicti descriptio. Quoniam ergo DPI DPI] et PI F1 periferia subiacet graduum xxxix xix, erit utique et PTI angulus, qualium quidem sunt iiii recti ccclx, talium xxxix xix, qualium vero iio recti ccclx, talium lxxviii xxxviii. Quare et que quidem super rectam DF periferia talium est lxxviii xxxviii, qualium qui circa DTF orthogonium circulus ccclx, que vero super rectam TF reliquorum in semicirculum ci xxvii, xxvii] xxii F1 et earum ergo que sub ipsis rectarum DF quidem talium lxxvi ii, qualium DT ypothenusa cxxi, DF vero eorumdem xcii l. Qualium ergo est DT quidem inter centra vi et xxxiii et dimidii, recta vero DG que ex centro lx, talium et DF quidem erit iiii ix, recta vero FT similiter v iiii. Et quoniam quod a recta DF sumptum sub ea quod a recta GD facit quod a recta GF, erit GF quidem recta lix li, reliqua vero GX, propter equalem esse TF ei que est FX talium liiii xlvii, qualium et XN dupla existens eius que est DF colligitur viiii xviii. Propter hoc autem et NG ypothenusa sit sit] fit F1 eorumdem lv xxv, et qualium est ergo cxx recta NG, talium et NX erit quidem xvii lix, que vero super ipsam periferia talium xvii xiiii, qualium est qui circa GNX orthogonium circulus ccclx. Quare et UGX UGX] NGX F1 angulus talium est xvii xiiii, qualium ii recti ccclx. Rursum quoniam, qualium est TI que ex centro excentrici lx, talium et NX quidem ostensa est viii xviii, recta vero TX similiter xviii, et reliqua quidem XI erit eorumdem xlix lii. Propter hoc autem et NI ypothenusa l xxxiii, et qualium ergo est cxx, NI recta, talium et NX quidem erit xlix xlii, que vero super ipsam periferia talium xviii liiii, qualium qui circa INX orthogonium circulus ccclx. Quare et NIX angulus talium est xviii liiii, qualium sunt ii recti ccclx, eorumdem vero ostensus est et NGX angulus xvii xiiii, et reliquus ergo GUI GUI] GNI F1 eorumdem quidem est i xl, qualium vero iiii recti ccclx, talium o l tantorum est ergo et MY zodiaci periferia.
Quoniam ergo et in secunda acronicto invenimus LTH portionum o xxxiii, manifestum quoniam coutrarumque periferiarum portionibus i xxiii minor erit apparente ad excentricum considerata secunda differentia et continebit gradus xcii xxi.
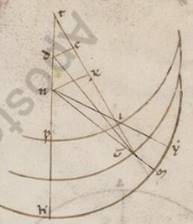Secundum has autem ergo congregatas ii distantiarum zodiaci periferias et eas que natura rursum secundum excentricum subiacent assequentes preostenso istorum theoremati per quod et apoguion et excentroticos rationem demonstramus reperimus, ut non per eandem longam faciamus commemorationem, eam quidem que inter centra scilicet DK talium facta xi l, qualium est que ex centro excentrici lx, GM vero excentrici periferiam, hoc est eam que a tertia acronicto in periguion, graduum xlv xxxiii, a qua rursum et LB quidem fit graduum xxxviii lix, AL vero similiter xlii xlv. Istis autem similiter assequentes in eis que secundum unamquamque acronictio demonstrationibus invenimus reliquum examinatas quantitates cuiusque quesitarum periferiarum, eius quidem que est KS sexagesima xxviii, eius vero que est LTH equalia ad proximum similiter xxviii, eius autem que est MY sexagesima xl. Quorum ea quidem que prime et que secunde acronictoy componentes et facta sexagesima lvi apponentes eis que prime distantie zodiaci gradibus lxvii l ad excentricum examinate consideratam distantiam habebimus graduum lxviii xlvi. Ea vero que secunde et iiie acronicty componentes et factum gradum i viii auferentes ab eis que iuxta secundam differentiam apparent zodiaci gradibus xciii xliiii, ad excentricum rursum diligentur consideratam distantiam invenimus graduum xcii xxxvi, a quibus reliqui eadem demonstratione utentes et rationem excentroticis et apoguion examinavimus. Et invenimus quidem eam que inter centra que est DK talium xii ad proximum, qualium est KL que ex centro excentrici lx, GM vero excentrici periferia graduum 
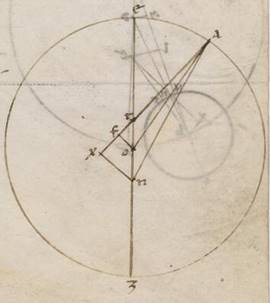xliiii xxi. A qua rursum et LB quidem fit graduum xl xi, AL vero similiter xli xxxiii. Quoniam autem istis reliquum quantitatibus et observate prius trium acronictorum apparentes distantie consone deprehenduntur, per eadem faciemus manifestum. Adiaceat enim primi acronicti descriptio solum habens EZ excentricum, in quo semper fertur centrum epicicli. Quoniam ergo ATE angulus, qualium quidem sunt iiii recti ccclx, talium est xli xxxiii, qualium vero iio recti ccclx, talium et ipse et qui secundum verticem ipsius DTF angulus lxxxiii vi, erit utique et que quidem super DF periferia talium lxxxiii vi, qualium est qui circa DTF orthogonium circulus ccclx, que vero super FT reliquorum in semicirculum xxvi liiii. Et earum ergo que sub ipsas rectarum DF quidem talium est lxxix xxxv, qualium est DT ypothenusa cxx, 
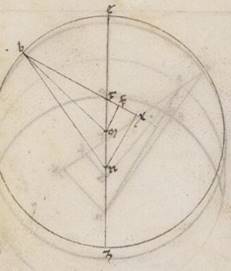FT vero eorumdem lxxxix l. Quare et qualium est est] add. DT F1 quidem recta vi, DA vero ypothenusa lx, talium et DF quidem erit iii lviii et dimidii, FT vero similiter iiii xxx. Et quoniam quidem ab recta DF sumptum sub eo quod a recta DA facit quod a recta FA, erit et ipsa longitudine eorumdem lix l. Rursum quoniam FT quidem ei que est FX equalem, recta vero UX UX] NX F1 eius que est DF dupla, totam AX habebimus talium lxiiii xx, qualium est NX recta vii lvii. Propter hoc autem et NA ypothenusa erit eorumdem lxiiii lii. Quare et qualium est NA recta cxx, talium et NX quidem erit xiiii xliiii, que vero super ipsam periferia talium xiiii vi, et qualium est qui circa ANX orthogonium circulus ccclx, et NAX ergo angulus, qualium quidem sunt ii recti ccclx, talium est xiiii vi, qualium vero iiii recti ccclx talium vii iii, eorumdem vero erat et ATE angulus xli xxxiii. Et reliquus ergo ANE angulus apparentis progressionis graduum erit ad proximum xxxiiii xxx, quibus precedebat apoguium stella secundum primam acronicton.
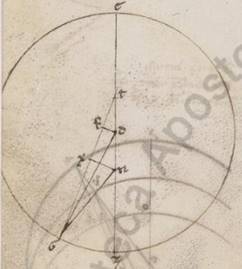Rursus adiaceat simul ii acronicti descriptio. Quoniam ergo BTE angulus medie epicicli progressionis, qualium quidem sunt iiii recti ccclx, talium est xl xi, qualium vero ii recti ccclx, talium et ipse et qui secundum verticem ipsius FTD angulus lxxx xxii, erit utique et que quidem super DF periferia periferia] add. talium F1 lxxx xxii, qualium est qui circa DTF orthogonium circulus ccclx, que vero super FT reliquorum in semicirculum xcix xxxviii. Et earum ergo que sub ipsis rectarum DF quidem talium est lxxvii xxvi, qualium DT ypothenusa cxx, recta vero FT eorumdem xci xli. Quare et qualium est DT quidem recta vi, DB vero ypothenusa lx, talium et DF quidem erit iii lii, FT vero similiter iiii xxxv. Et quoniam quod a recta DF sumptum ab eo quod a recta DB facit quod a recta BF, erit et ipsa longitudine eorumdem lix liii. Secundum ista vero quoniam TF quidem ei que est FX equalis est, recta vero NX eius que est DF dupla, et BX tota erit talium lxiiii xxviii, qualium est NX recta vii xliiii. Propter hoc autem et BN ypothenusa eorumdem erit lxiiii xlvi. Et qualium est ergo NB ypothenusa cxx, talium et NX quidem erit xiiii xix, que vero super ipsam periferiam talium xiii xlii, qualium est qui circa BNX orthogonium circulus ccclx. Quare et NBX angulus, qualium quidem sunt ii recti ccclx, talium est xiii xlii, qualium vero iiii recti ccclx, talium vi li, eorumdem vero erat et BTE angulus xl xi. Et reliquus ergo ENB angulus apparentis progressionis eorumdem est xxxiii xx, tot ergo gradus relinquens apparebat apoguium stella secundum ii acronicton. Demonstrata est autem et in prima acronicto precedens apoguium gradibus xxxiiii xxx, tota ergo que a prima acronicto in secunda distantia colligitur graduum lxvii viii, consone eis qui ab observationibus comprehensi sunt.
Adiaceat ergo similiter et iii acronicti descriptio. Quoniam ergo et hic GTZ angulus plane epicicli progressionis, qualium quidem sunt iiii recti ccclx, talium est xliiii xxi, qualium vero ii recti ccclx, talium lxxxviii xlii, erit utique et que quidem super DF rectam periferia talium lxxxviii xlii, qualium qui circa DTF orthogonium circulus ccclx, que vero super FT reliquorum in semicirculum xci xviii. Et earum ergo que sub ipsis rectarum DF quidem talium est lxxxiii liii, qualium DT ypothenusa cxx, recta vero FT eorumdem lxxxv xlix. Quare et qualium est DT quidem recta vi, DG vero que ex centro excentrici lx, talium et DF quidem erit iiii xi et dimidii, FT vero similiter iiii xvii. Et quoniam quod a recta DF sumptum sub eo quod a recta DG facit quod a recta GF tetragonum, habebimus et istam longitudine eorumdem lix li.
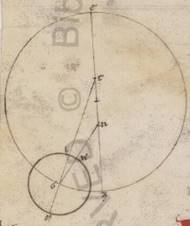Rursum vero quoniam et FT quidem ei que est FX equalis est, NX vero eius que est DF dupla, et reliqua XG habebimus talium lv xxxiiii, qualium est NX recta viii xxiii. Propter hoc autem et GN ypothenusam eorumdem habebimus lvi xii, et qualium est ergo GN ypothenusa cxx, talium et NX quidem erit xvii lv, que vero super ipsam periferia talium xvii x, qualium est qui circa GNX orthogonium circulus ccclx. Quare et TGN angulus, qualium quidem sunt ii recti ccclx, talium xvii x, qualium vero iiii recti ccclx, talium viii xxxv. Eorumdem vero erat et GTZ angulus xliiii xxi. Et totus ergo GNZ angulus eorumdem est lii lvi, tot ergo gradibus apparebat precedens periguium secundum tertiam acronicton stella. Ostensa est autem et in secunda acronicto relinquens apoguium gradus xxxiii xx, et reliqui quidem ab iia acronicto rursum in iiia collecti gradus xciii xliiii consoni invenientur in ii differentia observatis. Manifestum autem et quoniam quod in GN quidem recta considerata stella secundum tertiam acronicton obtinebat observatos Sagittarii gradus ii xxxiiii, angulus autem GNX ad centrum existens zodiaci ostensus est talium lii lvi, qualium sunt iiii recti ccclx, et periguion quidem excentroticos quod secundum Z punctum optinebat Capricorni gradus xxv xxx, apoguion vero secundum diametrum Cancri gradus xxv xxx. Sed et si scripserimus circa G centrum KLM epiciclum Martis, et eiciemus TG rectam, habebimus in tempore iii acronicti ab apoguio quidem excentrici mediam progressionem epicicli gradus cxxxv xxxix, quoniam et GTZ quidem angulus reliquorum in semicirculum ostensus est graduum xliiii xxi, a puncto vero M apoguio epicicli mediam Martis progressionem, hoc est MK periferiam, gradus clxxi xxv, propter, TGN angulo ostenso talium viii xxxv, qualium sunt iiii recti ccclx, et ad centrum existente epicicli, et KL quidem periferiam que ab K stella in L periguion eorumdem fieri graduum viii xxxv, eam vero que ab apoguio M in eam que secundum K stellam reliquorum in semicirculum, ut preiacet, clxxi xxv. Et factum est nobis cum aliis manifestum quod secundum iii tempus acronicti, hoc est secundo Antonini secundum Egiptios Epiphi xiia in xiiia ante duas horas equinoctiales mesonictii, Martis stellam stellam] stella F1 secundum appellatam quidem longitudinem distabat medie ab apoguio excentrici gradibus cxxxv xxxix, secundum anomaliam vero ab apoguio epicicli gradibus clxxi xxv. Quod oportet ostendere.
⟨X.8⟩ Demonstratio quantitatis epicicli Martis
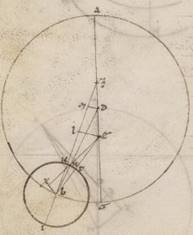Deinceps autem existente et quantitatis epicicli rationem demonstrare, summemus in hoc observationem quam perspeximus tres ad proximum dies post iii acronictum, hoc est secundo anno Antonii secundum Egiptios Epiphi xva in xvia tres horas equinoctiales ante mesonictium, quoniam quidem celimediebat secundum astrolabium xx gradus Chelarum, Sole secundum mediam progressionem optinente tunc Geminorum gradus v xxvii. Itaque eo quod in Spica perspecto ad propriam positionem, Martis stella apparebat optinens Sagittarii gradus i et iii quintas partes secundum etiam idem tempus et centrum Lune distans apparebat in consequentia eumdem gradum unum et iii quintas partes et erat media quidem progressio tunc Lune circa Sagittarii gradus iiii xx, examinata vero Scorpii circa xxix xx, quoniam quidem et secundum anomaliam distabat ab apoguio epicicli gradibus xcii. Apparens autem circa principium Sagittarii, quasi et hinc optinere tunc consone stellam Martis, quemadmodum et perspitiebatur, Sagittarii gradum gradum] add. i F1 xxxvi et distare manifestum quoniam a periguio in precedentia gradibus liii liiii. Continentur autem et in medio tempore iii acronicti et istius observationis longitudinis quidem gradum i xxxii, anomalie vero gradum i xxi ad proximum. Quos si apposuerimus secundum subiacentem iii acronicton demonstratis epochis, habebimus et in tempore huius observationis distantem stellam Martis longitudinis quidem ab apoguio excentrici gradibus cxxxvii xi, anomalie vero ab apoguio epicicli gradibus clxxii xlvi.
Istis ergo subiacentibus, esto centrum epicicli ferens excentricus circulus ABG circa centrum D et diametrum ADG, in qua zodiaci quidem centrum subiaceat E, quod autem maioris excentroticos Z, et scripto circa B punctum ITK epiciclo, protrahantur recte ZKBI et ETB et adhuc DB, et trahantur a punctis D et E in ZB catheti EL et DM. Subiaceat autem et stella secundum N punctum epicicli et copulatis rectis EN et BN, trahatur in EN eductam a puncto B cathetus BX. Quoniam ergo stella cxxxvii xi distat ab apoguio excentrici, quare et BZG angulum, qualium quidem sunt iiii recti ccclx, talium esse xlii xlix, qualium vero ii recti ccclx, talium lxxxv xxxviii, erit utique et que quidem super rectam DM periferia talium lxxxv xxxviii, qualium et qui circa DZM orthogonium circulus ccclx, que vero super ZM reliquorum in semicirculum xciiii xxii. Et earum ergo que sub ipsas rectarum DM quidem erit talium lxxxi xxxiiii, qualium est DZ ypothenusa cxx, recta vero ZM eorumdem lxxxviii i. Quare et qualium est DZ quidem inter centra vi, DB vero que ex centro excentrici lx, talium et DM quidem erit iiii v, ZM vero similiter iiii xxiiii. Et quoniam quidem a recta DM sumptum sub eo quod a recta DB facit quod a recta BM tetragonum, erit et BM recta eorumdem lix lii. Similiter autem et ZM quidem ei que est ML est equalis, EL vero eius que est DM dupla, et reliqua quidem BL erit lv xxviii, EL vero eorumdem viii x. Propter hoc autem et EB ypothenusa lvi iiii, et qualium est ergo EB recta cxx, talium et EL quidem erit xvii xxviii, que vero super ipsam periferia talium xvi xliiii, qualium est qui circa BEL orthogonium circulus ccclx. Quare et ZBE angulus talium est xvi xliiii, qualium sunt ii recti ccclx.
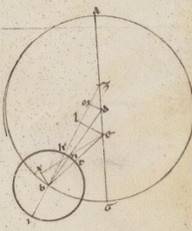Rursum quando quando] quoniam F1 GEX angulus quem apparebat precedens Martis stella G periguium, qualium quidem sunt iiii recti ccclx, talium subiacet liii liiii, qualium vero iio recti ccclx, talium cvii xlviii, eorumdem vero est et GEB angulus cii xxii, propter equalem ipsam esse coutrisque angulis ZBE ostenso talium xvi xliiii et GZB subiacenti eorumdem lxxxv xxxviii, erit utique et reliquus quidem BEX angulus eorumdem v xxvi, que vero super BX periferia talium est v xxvi, qualium est qui circa BEX orthogonium circulus ccclx. Propter hoc autem et BX recta talium est v xliiii, qualium est EB ypothenusa cxx, et qualium ergo EB quidem ostensa est lvi iiii, que vero e centro excentrici lx, talium et BX erit ii xxxix. Similiter quoniam quidem N punctum distabat ab I apoguio epicicli gradibus clxxii xlvi, a periguio vero K gradibus vii xiiii, erit utique et KBN angulus, qualium quidem sunt iiii recti ccclx, talium vii xiiii, qualium vero ii recti ccclx, talium xiiii xxviii. Eorumdem vero erat et KBT angulus xvi xliiii, et reliquus quidem NBT angulus ii xvi, totus vero XNB eorumdem vii xlii. Quare et que quidem super XB periferia talium vii xlii, qualium qui circa BNX orthogonium circulus ccclx. Ipsa vero BX recta talium viii iii, qualium est BN ypothenusa cxx, et qualium est ergo BX quidem recta ii xxxix, que vero ex centro excentrici lx, talium et BN que e centro epicicli erit xxxix xxx ad proximum, et proportio ergo eius que ex centro excentrici ad eam que ex centro epicicli que lx ad xxxix xxx. Quod oportebat demonstrare.
⟨X.9⟩ De directione periodicorum Martis motuum
Et directionis causa vero periodicorum mediorum motuum sumemus et antiquarum observationum unam, secundum quam declaratur quoniam xiii anno secundum Dionisium Egonos xxv eoa stella Martis boreali fronte Scorpii videbatur obici. Itaque observationis quidem tempus fit secundum lii annum ab Alexandri morte, hoc est secundum cccclxxvi annum a Navonassaro, secundum Egiptios mensis Athir xx in xxi mane, in quo Solem reperimus secundum mediam progressionem optinentem Capricorni xxiii liiii. Que autem in boreali fronte Scorpii observata est secundum nos optinens Scorpii gradus vi iii. Quare quoniam rursum illi qui ab observatione usque Antonini regnum ccccix anni faciunt transitionis fixarum gradus iiii et sexagesima v ad proximum et secundum tempus exposite observationis debet optinere fixa Scorpii gradus ii iiiia, eosdem autem manifestum quoniam et Martis stella. Similiter autem, quoniam et secundum nos, hoc est secundum principium regni Antonini, apoguion optinebat Martis Cancri gradus xxv xxx, secundum observationem debet optinere gradus xxi xxv. Et manifestum quoniam apparens quidem stella distabat tunc ab apoguio gradibus c et sexagesimis l, medius autem Sol ab eodem apoguio gradibus clxxxii xxix, a periguio vero manifestum quoniam gradibus ii xxix.
Istis subiacentibus, esto centrum epicicli ferens excentricus circulus ABG circa centrum D et diametrum ADG, in qua subiaceat zodiaci quidem centrum E, quod autem maioris excentroticos Z, et scripto circa centrum B IT epiciclo, protrahantur quidem recte ZBI et DB, a puncto vero Z in DB rectam trahatur cathetus ZK. Subiaceat autem stella in T puncto epicicli, et copulata recta BT, trahatur ipsi equidistans a puncto E recta EL, in qua manifestum quoniam propter predemonstrata media Solis progressio considerabitur, et copulata recta ET, in ipsam trahantur a punctis D et B catheti DM et BN, et adhuc puncto puncto] a puncto F1 D in rectam BN trahatur cathetus DX, quare et DMNX scema fieri parallilogramum orthogonium. Quoniam ergo AET quidem angulus eius que ab apoguio apparentis stelle progressionis talium est c et sexagesimorum l, qualium sunt iiiior recti ccclx, angulus autem GEL medie Solis progressionis eorumdem ii xxix, erit utique et TEL, hoc est BTE angulus, qualium quidem sunt iiiior recti ccclx, talium lxxxi xxxix, qualium vero ii recti ccclx, talium clxiii xviii. Quare et que quidem super BN periferia talium est clxiii xviii, qualium est qui circa BTN orthogonium circulus ccclx, ipsa vero BN recta talium cxviii xliii, qualium est BT ypothenusa cxx, et qualium est ergo BT quidem que ex centro epicicli xxxix xxx, ED vero intermedia centrorum vi, talium et BN erit xxxix iii.
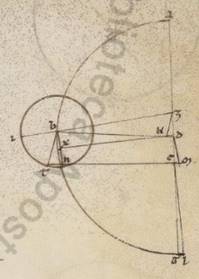Rursum quoniam AET angulus, qualium quidem sunt iiii recti ccclx, talium est c et sexagesimorum l, qualium vero ii recti ccclx, talium cci xl. Propter hoc autem et qui deinceps huic scilicet DEM angulus eorumdem clviii xx, erit utique et que quidem super rectam DEI periferia talium clviii xx, qualium est qui circa DEM orthogonium circulus ccclx, ipsa vero DM recta talium cxvii lii, qualium est DE ypothenusa cxx. Et qualium est ergo DE quidem recta vi, BN vero ostensa est xxxix iii, talium et DM quidem, hoc est NX, erit v liiii, reliqua BX talium xxxiii ix, qualium est et BD que ex centro excentrici lx, et qualium est ergo BD ypothenusa cxx, talium et BX erit lxvi xviii, que vero super ipsam periferia talium lxvii iiii ad proximum, qualium est qui circa BDX orthogonium circulus ccclx. Quare et BDX quidem angulus talium est lxvii iiii, qualium sunt ii recti ccclx, totus autem BDM ccxlvii iiii, eorumdem vero est et EDM angulus xxi xl, propter DEM angulum ostendi clviii xx. Itaque et reliquus quidem BDE angulus colligitur ccxxv xxiiii, qui vero deinceps ipsi angulus BDA similiter cxxxiiii xxxvi. Quare et que quidem super ZK periferia talium est cxxxiiii xxxvi, qualium est qui circa DZK orthogonium circulus ccclx, que vero super DK reliquorum in semicirculum xlv xxiiii. Et earum ergo que sub ipsis rectarum ZK quidem erit talium cx xlii, qualium est DZ ypothenusa cxx, DK vero eorumdem xlvi xviii. Et qualium est ergo DZ quidem recta vi, DB vero que ex centro excentrici lx talium, et ZK quidem erit v xxxii, DK vero similiter ii xix, reliqua autem KB recta lvii li. Propter hoc autem et BZ ypothenusa eorumdem lvii lvii ad proximum, et qualium est ergo BZ recta cxx, talium et KZ quidem erit xi xxviii, que vero super ipsam periferia talium x lviii, qualium qui circa BKZ orthogonium circulus ccclx. Quare et ZBD angulus talium est x lviii, qualium sunt ii recti ccclx, eorumdem vero erat et BDE angulus cxxxiiii xxxvi. Et totus ergo BZA angulus eorumdem quidem est cxlv xxxiiii, qualium vero iiii recti ccclx, talium lxxii xlvii. Distabat ergo secundum tempus exposite observationis media secundum longitudinem progressio stelle, hoc est B centrum epicicli, ab apoguio gradibus lxxii xlvii et propter hoc optinebat Chelarum gradus iiii xii. Quoniam vero et GEL angulus eorumdem subiacet ii xxix, qui cum ABG semicirculi duobus rectis equalis sit coutrisque eis qui sunt AZB angulus medie longitudinis et IBT angulus anomalie, hoc est eius que secundum epiciclum stelle motionis, et reliquum habebimus IBT angulum eorumdem cix xlii. Distabat ergo secundum quod observationis tempus et stella ab apoguio epicicli expositis anomalie gradibus cix xlii. Quod oportet ostendere.
Ostensa est autem nobis et in tempore iii acronicti secundum anomaliam distans ab apoguio epicicli gradibus clxxi xxv, supersumpsit ergo intermedio observationum tempore continenti annos egiptiacos ccccx et dies ccxxxi bisse ad proximum post omnes circulos cxcii gradus lxi xliii. Quantam fere progressionem reperimus negotiatis nobis mediorum ipsius motuum canonibus, quoniam quidem et diurnus nobis ab istis constitutus est, distributis eis qui ex multitudine circulorum supergressione collecti sunt gradibus in eos qui ex intermedio tempore duarum observationum collecti sunt dies.
⟨X.10⟩ De epochi periodicorum ipsius motuum
Rursum ergo, quoniam quod a primo anno Navonassari secundum Egiptios mensis Thoth io ad meridiem usque expositam observationem tempus est annorum Egiptiacorum cccclxxv et dierum lxxix dimidii iiiia ad proximum. Continet autem istud tempus supergressiones longitudinis quidem gradus clxxx xli, anomalie vero gradus cxlii xxix, si istos dempserimus ab utraque utraque] add. del. parte V3 priore earum que secundum observatione exposite sunt epocharum, hoc est et ab eis qui longitudinis in Chelis iiii xii et ab eis qui anomalie cix xlii, habebimus in primum annum Navonassari secundum Egyptios mensis Thoth io ad meridiem epochin periodicorum Martis motuum secundum longitudinem quidem Arietis gradus iii xxxii, sed anomaliam vero ab apoguio epicicli gradus cccxxvii xiii. Propter eamdem eamdem] eadem F1 vero, quoniam et transitionis apoguiorum in cccclxxv annis colliguntur gradus iiii dimidium iiia, iiia] iiiia F1 erat autem apoguion Martis secundum observationem circiter Cancri gradus xxi xxv, optinebit manifestum quoniam et secundum expositum epochis tempus Cancri gradus xvi xl.
Claudii Ptolemei mathematici sintaxeos liber decimus explicit.