〈X〉
Incipit liber X Magne Compositionis Ptolomei
〈X.1〉 〈Capitulum I :〉 Demonstratio maxime longitudinis stelle Veneris
Sed Mercurii quidem suppositionis inequalitatumque magnitudines et periodicorum motuum quantitates locique obtenti hoc modo nobis capti sunt. In Veneris autem stella primum rursus quesivimus in qua parte circuli per medium signorum maxima et minima excentricitatis longitudo inveniretur per equales et ad eandem partem maximas distantias, quam quidem ad rem priscas observationes non potuimus exquisitas habere, sed ab observationibus nostri temporis hec nobis investigata sunt.
Invenimus enim conscriptam observationem in his quas Theon mathematicus nobis dedit in 16 anno Adriani Pharmothi secundum Egyptios die 21 sequente 22, quando, inquit, vespertina Venus plurimum distabat a Sole, mediamque Vergiliarum Vergiliarum] corr. ex Virgiliarum G precedebat per ipsarum Vergiliarum longitudinem, videbatur autem paulo australior quam ipse sint. Quoniam igitur Vergiliarum media tunc secundum nostra principia tres gradus Tauri Tauri] corr. ex Thauri G obtinebat, estque longitudo ipsarum gradus unius 30que proxime sexagesimarum, patet quia stella Veneris unum gradum 30que sexagesimas Tauri Tauri] corr. ex Thauri G tunc obtinebat. Quare quoniam medius Sol in 14 15′ gradibus Piscium erat, vespertina maxima a medio motu distantia 47 15′ graduum fuit.
Nos quoque observavimus anno Antonini 14 Thoth secundum egyptios die xi sequente 12 stellam Veneris matutinam maxime distare a Sole, et aberat a medio Geminorum genu ad septentrionem atque orientem per mediam Lunam. Erat autem stella fixa tunc secundum nos in gradibus Geminorum 18 15′, Veneris itaque stella in 18 30′ gradibus proxime fuit, quare matutina quoque maxima distantia 47 15′ graduum fuit. Quoniam igitur in priore observatione medius motus erat in 14 15′ gradibus Piscium, in posteriore in 5 45′ gradibus Leonis, et punctum circuli per medium quod inter hos gradus est in 25 gradibus Tauri atque Scorpionis invenitur, ad hec puncta diameter que per maximam et minimam longitudinem est certe perveniet.
Similiter in observationibus Theonis invenimus quod in 12 anno Adriani Athir secundum Egyptios die 21 sequente 22 distabat stella Veneris matutina plurimum a Sole, distabatque a stella que est in summitate australis ale Virginis per longitudinem Vergiliarum, vel tanto minus quanto est magnitudo sua, videbaturque borealior per Lunam unam. Quoniam igitur stella fixa 28 55′ gradus Leonis tunc secundum nos obtinebat, ut stella Veneris 20 proxime unius gradus sexagesimas Virginis obtineret, et medius Sol Libre 17 52′ maxima distantia matutina a a] add. s. l. G medio motu graduum fuit 47 32′.
Nos antem 21 anno Adriani Mechir secundum egyptios a nono a nono] add. marg. G sequente 10o vesperi observavimus stellam Veneris maxime distare a Sole, precedebatque borealissima earum que in quadrilatera sunt figura post succedentem que ad rectam lineam est cum stellis que sunt in inguinibus Aquarii duabus Lune plene partibus, videbaturque splendore suo stellam obtegere. Quoniam igitur rursus stella 20 gradus Aquarii tunc secundum nos obtinebat, stellaque propterea Veneris in 19 36′ gradibus Cancri erat, medius autem Sol in Capricorni gradibus 12 15′, facta fuit etiam hic maxima vespertina a medio motu distantia graduum 47 32′. Sunt autem puncta circuli per medium inter hos gradus 17 52′ Libre secundum primam observationem et 12 15′ Capricorni secundum alteram in 25 gradu proxime rursus Tauri atque Scorpionis
〈X.2〉 Capitulum II : De epicycli Veneris magnitudine
Quod igitur nostris temporibus maxima et minima excentricitatis longitudo in 27 gradibus Tauri et Scorpionis sit per hoc nobis perceptum est sed quesivimus rursum consequenter maximas distantias que fiunt cum Sol medius in 25 gradibus Tauri et in 25 Scorpionis circiter sit.
In observationibus igitur quas Theon nobis tradidit invenimus quod in 13 anno Adriani secundum Egyptios Epiphi die secunda sequente tertia stella Veneris matutina plurimum distabat a Sole precedens lineam que est per antecedentem de tribus que sunt in capite Arietis et per eam que est in posteriore crure crure] post corr. G per gradum 1 et sexagesimas 24, faciebatque distantiam ad precedentem earum que sunt in capite duplam ad illam que fuit ad fixam que est in crure. Obtinebat autem tunc precedens quidem de tribus que sunt in capite Arietis gradus 6 36′ et est boralior circulo per medium gradibus 7 20′, stella vero que est in posteriore Arietis crure gradibus 9 45′, et est australior circulo per medium gradibus 5 15′. Veneris ergo stella 10 gradus et 36 sexagesimas Arietis obtinebat, et erat autralior circulo per medium gradu 1 30. Quoniam igitur medius etiam Sol tunc obtinebat gradus Tauri 25 24′, colligitur maxima a medio motu distantia graduum 44 48′.
Nos etiam observavimus 21 anno Adriani Tibi secundum Egyptios die 2 sequente 3 vesperi stellam Veneris plurimum a Sole distantem, que ad eas perspecta fixas que sunt in cornubus Capricorni obtinere cernebatur gradus Capricorni 12 5′, eratque medius Sol tunc in gradibus Scorpionis 25 30′, ut hic maxima a medio motu distantia colligatur graduum 47 20′, perspicuumque factum sit quod maxima longitudo in 25 gradibus Tauri est et minima in 25 Scorpionis. Hinc etiam nobis patuit quod stabilis est ad sensum excentricus qui epicyclum Veneris defert, propterea quod in nullo circuli per medium puncto ambe utrinque a medio motu distantie minores inveniantur ambabus que in Tauro fiunt, sed nec maiores alicubi ambabus que fiunt in Scorpione.
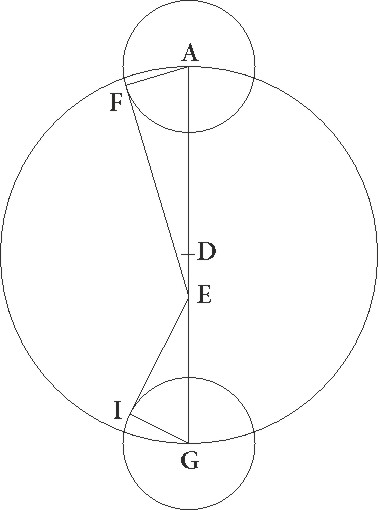His ita presuppositis, presuppositis] corr. ex presupositis G sit circulus excentricus ABG in quo semper Veneris epicyclus circumfertur , eiusque diameter sit AG, in qua excentrici quidem centrum sit D, zodiaci vero sit E, A vero punctum sit sub ipso gradu Tauri 25, describanturque in A et G punctis equales epicycli in quibus F et I, protractisque tangentibus EF et EI lineis, coniungantur linee AF et GI. Quoniam igitur angulus EF AEF] corr. ex AF G qui est in centro zodiaci subtendit maximam distantiam stelle que in maxima longitudine invenitur queque quaeque] post corr. G graduum est 44 48′, erit profecto ipse talium 44 48′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 89 36′. Quare arcus etiam corde AF talium erit 89 36′ qualium est circulus qui EAF rectangulo circumscribitur 360, corda vero eius AF talium 84 33′ proxime qualium est E que rectum angulum subtendit 120. Similiter quoniam angulus GEI subtendit maximam distantiam que est in minima longitudine queque quaeque] corr. ex quae G graduum esse supponitur 47 20′, erit profecto ipse talium 47 20′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 94 40′. Quare arcus etiam corde GI talium erit 94 40′ qualium est circulus qui GEI rectangulo circumscribitur 360. Ipsa vero corda GI talium 88 13′ proxime qualium est EG que rectum angulum subtendit 120. Qualium est igitur GI, hoc est AF epicycli semidiameter, 84 33′ et E linea 120, talium erit EG 115 1′. Tota vero AG 235 1′, medietas autem eius AD 117 30′ proxime. Quare qualium est AD semidiameter excentrici 60, talium erit DE que est inter centra 1 15′ proxime, AF autem semidiameter epicycli 43 10′.
〈X.3〉 Capitulum III : De proportionibus excentricitatis stelle Veneris
Verum quoniam non patet utrum ad D punctum equalis epicycli motus efficiatur, duas etiam hic cepimus maximas distantias ad contraria, cum medius Solis motus quartam utrinque partem a maxima longitudine distaret. Quarum alteram observavimus in anno 18 Adriani Pharmothi secundum Egyptios die secundo sequente tertio, quando stella Veneris matutina plurimum distabat a Sole, perspectaque ad fixam que vocatur Antares obtinebat gradus Capricorni 11 55′, medius vero Sol erat in gradibus 25 30′ Aquarii, ut maxima a medio motu matutina distantia fuerit graduum 43 55′. Alteram autem tertio tertio] post corr. G Antonini observavimus anno Pharmothi secundum Egyptios die 4 sequente 5, quando Veneris stella plurimum distabat a Sole, perspectaque ad fulgentem Succularum obtinebat 13 50′ gradus Arietis. Erat autem medius Sol in gradibus Aquarii rursum 25 30′, itaque vespertina a medio motu distantia maxima graduum fuit 48 20′.
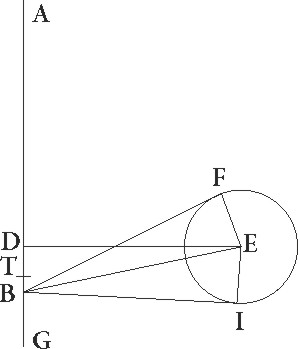His suppositis, sit per per] add. s. l. G maximam et minimam longitudinem excentricitatis diameter ABG, sitque A punctum sub ipso 25 gradu Tauri, B vero sit centrum zodiaci, propositumque sit id centrum invenire ad quod equalem epicycli motum fieri asserimus, sitque punctum D, et protrahatur ab ipso DE perpendicularis ad AG, ut medius epicycli motus quartam partem a maxima longitudine distet, sicut etiam in observationibus, capiaturque in ipsa secundum expositas observationes E centrum epicycli, circa quod descripto FI epicyclo, protrahantur a puncto B tangentes ipsum BF et BI linee, et coniungantur linee BE et EF et EI. Quoniam igitur secundum expositum medium motum matutina quidem maxima a medio motu distantia graduum erat 43 35′, vespertina vero 48 20′, erit totus FBI angulus talium 91 55′ qualium quatuor recti sunt 360. Medietas ergo eius, hoc est angulus FBE, talium est 91 55′ qualium duo recti sunt 360. Quare arcus corde EF talium est 91 55′ qualium est circulus qui rectangulo BEF circumscribitur 360. Ipsa vero linea EF talium 86 16′ qualium est BE qua rectus angulus subtenditur 120. Qualium igitur est EF semidiameter epicycli 43 10′, talium erit BE 60 3′.
Rursus quoniam propositarum maximarum distantiarum excessus 4 45′ bis continet differentiam que tunc penes zodiaci erat inequalitatem, queque ab angulo BED continetur, erit profecto ipse BED angulus talium 2 22′ 30′′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 4 45′. Quare arcus linee BD talium erit 4 45′ qualium est circulus qui rectangulo BED circumscribitur 360. Ipsa vero linea BD talium 4 79′ proxime qualium est BE qua rectus angulus subtenditur 120, qualium est ergo BE linea 60 sexagesimarumque trium et semidiameter epicycli 43 10′, talium et BD erit 2 30′ proxime. Demonstrata est autem linea etiam que est inter centra zodiaci et excentrici in quo semper centrum epicycli est 1 15′ earundem, medietas ergo est linee BD. Si ergo in duo equalia BD lineam in puncto T dividamus, demonstratum habebimus, qualium est TA TA] corr. ex A G semidiameter deferentis epicyclum excentrici 60, talium esse utranque BT et TD que sunt inter centra 1 15′, semidiameter vero epicycli EF 43 10′, que erant nobis demonstranda.
〈X.4〉 Capitulum IIII: De emendatione periodicorum Veneris motuum
Sed modus quidem suppositionis proportionesque inequalitatum hoc modo nobis capte sunt. Rursus autem propter periodicos stelle motus locosque ipsorum duas non ambiguas cepimus observationes, alteram de nostris, alteram de priscis.
Observavimus enim nos secundo anno Antonini Tibi secundum Egyptios 29 sequente 30 per astrolabium stellam Veneris ad fixam que vocatur Spica post matutinam maximam distantiam, perspiciebaturque obtinere 6 30′ gradus Scorpionis, erat etiam tunc inter borealissimam fixarum que sunt in fronte Scorpii et centrum Lune apparens, eratque ad rectam cum istis lineam, precedebatque praecedebatque] post corr. G ipsa Lune centrum per sesqualteram proportionem spacii quo borealissima in Scorpii fronte ipsam precedebat. Erat autem fixa secundum nostra principia in gradibus Scorpionis 6 20′, borealior circulo per medium gradibus 1 20′. Tempus vero erat post mediam noctem horis equalibus 4 15′. Nam cum Sol in 23o gradu Sagittarii esset, erat secundum astrolabium in medio celo 2 graduum Capricorni, quo quidem in tempore Sol 22 9′ Sagittarii gradus medie obtinebat, Luna vero 11 24′ Scorpionis, inequalitatis autem a maxima longitudine gradus 87 30′ et latitudinis a boreali termino 12 22′, centrum itaque ipsius 5 45′ Scorpionis gradus exacte obtinebat, et borealius circulo per medium erat gradibus 5, perspiciebatur autem in Alexandria per longitudinem quidem 6 45′ Scorpionis gradus obtinere, borealius vero esse circulo per medium gradibus 4 40′. Erat igitur etiam propter hec stella Veneris in 6 30′ gradibus Scorpii, eratque borealior circulo per medium gradibus 2 40′.
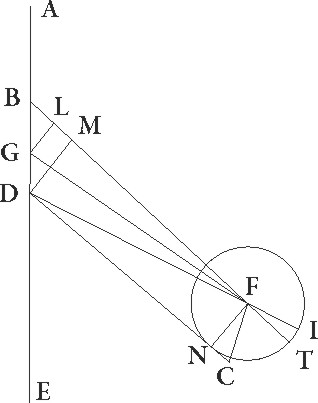
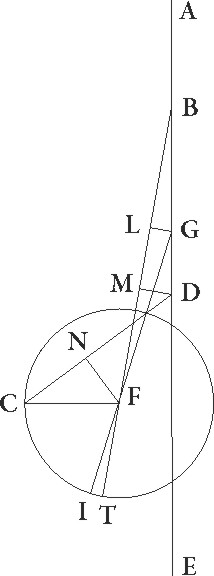
His suppositis, sit ABGDE diameter per maximam longitudinem et A quidem sit sub ipso gradu Tauri 25, B vero sit centrum ad quod epicyclus equaliter movetur, G autem sit centrum excentrici in quo centrum epicycli defertur, et D sit centrum zodiaci. Quoniam igitur medius Sol Sol] sit add. et del. AG in observatione obtinebat Sagittarii gradus 22 9′, et sic medius etiam epicycli motus distabat a minime longitudinis puncto ad successionem gradibus 27 9′, supponatur centrum eius esse in F, descriptoque circa ipsum epicyclo ITC, coniungantur linee DFI et GF et BFT, deinde a punctis G et D ad lineam BF perpendiculares GL et DM producantur, stellaque ipsa supposita in C puncto, coniungantur DC et FC linee, et deducatur ad lineam DC perpendicularis FN, propositumque sit invenire arcum TC quo stella a puncto T, hoc est a maxima epicycli longitudine, distabat. Quoniam ergo angulus EBF talium est 27 9′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 54 18′, erit etiam arcus linee GL talium 54 18′ qualium est circulus qui BGL rectangulo circumscribitur 360, arcus vero linee BL reliquarum ad semicirculum 125 42′. Corde igitur etiam sue GL quidem talium erat 54 46′ qualium est BG qua rectus angulus subtenditur 120, BL autem 106 47′ earundem. Qualium igitur est BG linea 1 15′ et GF semidiameter excentrici 60, talium GL quidem quidem] corr. ex qualium G erit 0 34′, BL autem 1 7′. Et quoniam, si quadratum linee GL subtrahatur a quadrato linee GF, relinquitur quadratum linee FL, erit etiam ipsa FL 60 proxime earundem. Est autem etiam linea ML equalis linee LB, linea vero DM dupla ad lineam GL, propterea quod BG quoque linea equalis est linee GD. Erit igitur etiam FM reliquarum 58 53′, DM autem 1 8′ earundem. Quapropter etiam FD qua rectus angulus subtenditur 58 54′ proxime. Qualium igitur est FD linea 120, talium etiam DM erit 2 18′ et arcus suus talium 2 12′ qualium est circulus qui triangulo DFM circumscribitur 360, quare angulus etiam BFD talium erit 2 12′ qualium duo recti sunt 360, quare totus angulus EDF erit 56 30′ earundem. Est autem angulus quoque CDE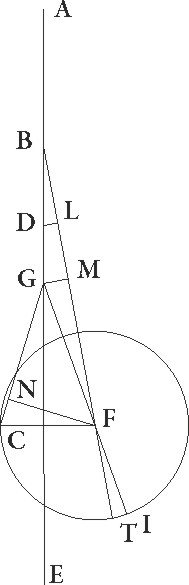 
talium 18 30′ qualium quatuor recti sunt 360. Totidem enim gradibus stella secundum observationem E minime longitudinis punctum, hoc est 25m Scorpionis gradum precedebat. Qualium vero duo recti sunt 360, talium 37, quare totus etiam angulus CDF talium est 93 30′, qualium duo recti sunt 360. Arcus vero linee FN talium 93 30′ qualium est circulus qui rectangulo DFN circumscribitur 360. Corda igitur etiam FN talium est 87 25′ qualium est FD linea 120, qualium vero 58 54′, idest qualium est FC semidiameter epicycli 43 10′, talium 42 54′. Ita qualium est FC qua rectus angulus subtenditur 120, talium etiam FN erit 119 18′ et arcus suus talium 167 38′ qualium est circulus qui rectangulo FCN circumscribitur 360. Quare angulus quoque FCD talium est 167 38 qualium FDC angulus supponitur 93 30′, angulus vero CFI totus 261 8′. Sed angulus quoque BFD, idest angulus IFT, demonstratus est earundem esse 2 12′. Reliquus igitur etiam angulus TFC talium erit 258 56′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 129 28′. Quare stella Veneris in proposito tempore distabat a puncto T maxime longitudinis epicycli ad precedentia quidem gradibus dictis 129 28′, ad successionem vero secundum motum qui ad suppositionem sequitur reliquis ad circulum unum 290 32′, quod nobis erat inveniendum.
De priscis autem observationibus illam cepimus quam Timocharis sic conscribit: ‘tertiodecimo anno cum dimidio Philadelphi’, ait, ‘Messori secundum Egytios die 17 sequente 18 hora 12 Veneris stella cernebatur exacte obscurasse oppositum Previndemiatrici’, que fixa secundum nos est post illam que est in extremitate australis hale Virginis, hec erat in primo anno Antonini in gradibus Virginis 8 15′. Quoniam igitur annus observationis erat 476 a Nabonassaro et usque ad imperium Antonini 884, ut annis 408 qui fuerunt interea 4 5′ proxime gradus secundum fixarum sphere et maximarum longitudinum motum congruant, perspicuum est quia stella Veneris 4 10′ gradus Virginis tunc obtinebat, minima vero excentrici longitudo Scorpionis graduum 20 55′. Fuit autem etiam hic Veneris stella ultra maximam distantiam matutinam progressa. Diebus enim quatuor post observationem 21 Messori sequente 22 secundum verba Timocharis Timocharis] corr. ex Thimocharis G obtinebat secundum principia nostra gradus Virginis 8 50′, medius vero Solis motus in priore quidem observatione 17 20′ gradus Libre obtinebat, in posteriore autem Libre 20 55′, quare distantia prime observationis 42 53′ graduum colligitur, secunde vero 49 9′.
His datis, similis rursus proponatur descriptio que tamen ad precedentia minime longitudinis habeat epicyclum, propterea quod medius epicycli motus 17 3′ Libre gradus obtinebat, et minima longitudo erat in gradibus Scorpionis 20 55′. Quoniam ergo idcirco angulus EBF talium est 33 52′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 67 44′, erit profecto etiam arcus linee GL talium 67 44′ qualium est circulus qui rectangulo BGL circumscribitur 360, arcus vero linee BL 112 16′ reliquarum ad semicirculum. Corde igitur etiam sue GL quidem talium 66 52′ qualium est BG qua rectus angulus subtenditur 120, BL vero 99 38′ earundem. Qualium igitur est BG linea 1 15′ et GF semidiameter excentrici 60, talium erit GL 0 42′ et BL 1 2′. Et quoniam, si a quadrato linee GF subtrahatur quadratum linee GL, relinquitur quadratum linee FL, erit etiam ipsa per longitudinem 60 proxime earundem. Est autem propter eadem BL linea LM linee equalis et DM linea ad lineam GL dupla. Erit ergo reliqua etiam FM 58 58′, linea vero DM 1 24′ earundem, propter hoc etiam FD qua rectus angulus subtenditur erit 58 59′ proxime. Quare qualium est FD 120, talium quoque erit corda DM 2 51′ et arcus eius talium 2 44′ qualium est circulus qui rectangulo FDM circumscribitur 360. Angulus igitur etiam BFD talium est 2 44′ qualium duo recti sunt 360, angulus vero EDF EDF] corr. ex DF G 70 28′ earundem. Est autem angulus etiam EDC per quem stella distabat ad precedentia minime longitudinis E talium 76 46′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 153 30′, quare FDC quoque reliquus angulus 83 2′ earundem est, arcus vero linee FN talium 83 2′ qualium est circulus qui rectangulo DFN circumscribitur 360. Corda igitur etiam sua FN talium est 79 33′ qualium FD qua rectus angulus subtenditur 120, qualium vero 58 59′, hoc est qualium FC semidiameter epicycli 43 10′ talium 39 7. Quare qualium est FC qua rectus angulus subtenditur 120, talium erit FN linea 108 45′ et arcus eius talium 130 proxime, qualium est circulus qui rectangulo FCN circumscribitur 360. Quare angulus quoque FCN talium est 130 qualium FDC angulus supponitur esse 83 2′, angulus vero IFC totus 213 2′ earundem. Sed angulus quoque BFD, hoc est IFT, demonstratus est 2 44′ earundem, totus ergo angulus CFT talium est 215 46′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 107 53′. Distabat igitur in hoc tempore stella Veneris a puncto T maxime epicycli longitudinis ad successionem 252 7′ gradibus ad unum circulum reliquis.
Quoniam igitur in tempore quoque nostre observationis distabat similiter a maxima epicycli longitudine gradibus 230 32′, et tempus inter duas observationes 409 annos egyptiacos et dies proxime 167 continet, inequalitatis autem restitutiones integras 255, —nam cum octo anni egyptiaci 5 proxime periodos faciant et 400 et 8 egiptiaci anni 255 et annus qui restat una cum diebus 167 non compleat unius restitutionis tempus perspicuum nobis, hinc factum est quod in annis egyptiacis 409 et diebus 167 stella Veneris post integras inequalitatum restitutiones 255 intercipit in epicyclo gradibus 338 25′—, quot quidem gradibus nostra observatio primam excedebat, totidem autem ferme post integros circulos per tabulas mediorum motuum nobis expositas gradus colliguntur, propterea quod emendatio ipsorum ab invento numero graduum facta est, tempore quidem in dies resoluto, restitutionibus autem in gradus additis etiam gradibus qui superfuerant, nam cum multitudinem graduum per multitudinem dierum partiti simus, medius inequalitatis diurnusque Veneris motus nobis inventus est.
〈X.5〉 Capitulum V : De locis periodicorum motuum stelle Veneris
Verum cum reliquum hic etiam sit locos periodicorum motuum in primo Nabonassari anno in meridie diei prime Thoth secundum egyptios constituere tempus, rursum cepimus cepimus] post corr. G quod fuit inter diem dictam et antiquissimam observationum, quod colligitur 475 egyptiacorum annorum et dierum 46 45′ proxime. Cui tempori secundum inequalitatis inequalitatis] corr. ex in qualitatis G tabulas post integros circulos medii motus gradus adiacent 181 proxime, quos si subtraxerimus a gradibus observationis 252 7′, habebimus locum inequalitatis a maxima epycicli longitudine graduum 71 7′ in primo Nabonassari anno in meridie diei prime Thoth mensis secundum Egyptios. Medius autem longitudinis motus idem Veneris etiam et Solis esse supponitur, obtinet enim gradum Piscium 0 45′, patet etiam, cum maxima longitudo in tempore observationis in 20 55′ gradibus Tauri fuerit, congruantque 476 annis qui proxime interfuerant gradus 4 45′, quod in tempore proposito in quo locos et quasi radices constituimus in eiusdem signi gradibus 16 10′ fuerat.
〈X.6〉 Capitulum VI : Hec premittuntur ad ad] post corr. G ea que de reliquis planetis demonstrantur
In duabus igitur Veneris et Mercuri stellis huiusmodi ratione ac via usi sumus, tum ad suppositiones, tum ad inequalitatum demonstrationes inveniendas. In reliquis autem tribus, Martis, Iovis Saturnique stellis rationem motus eandem invenimus quam de Veneris stella percepimus, hoc est secundum quam circulus excentricus, in quo semper fertur centrum epicycli, describitur centro illo puncto quod equaliter dividit lineam que est inter duo centra, zodiaci dico et eius quod epicycli circumductionem equalem facit. In singulis enim etiam istorum secundum universalem considerationem excentricitatis que constituitur ex magnitudine regressuum qui fiunt in maximis et minimis centri epicycli longitudinibus queque per maximam inequalitatis zodiaci differentiam invenitur dupla proxime esse percipitur, sed demonstrationes quibus utriusque inequalitatis magnitudines et maximas longitudines constituimus, cum non possint ut in illis duabus ita in his etiam adhiberi, propterea quod omnem a Sole distantiam possunt iste distare, ac ideo non possit perspicuum ab observationibus fieri, sicut in maximis a medio motu Mercurii Venerisque distanciis, quando stella in contactu reperitur perducte a visu nostro linee ad epicyclum ipsumque tangentis. Cum igitur hoc non procedat, usi sumus diametralibus ipsarum oppositionibus ad medium Solis motum observatis, unde primum excentricitatis proportiones et maximas longitudines demonstramus. In motibus enim solummodo qui hoc pacto considerantur inequalitatem zodiaci separatam seorsum per seipsam invenimus, cum nulla nulla] post corr. G tunc penes inequalitatem ad Solem differentia fiat.
Sit enim excentricus stelle circulus ABG in quo centrum epicycli defertur cuius centrum D, et diameter que per maximam longitudinem est sit AG, in qua E quidem punctum zodiaci centrum, sit F autem centrum excentrici ad quem medius epicycli secundum longitudinem motus consideratur, descriptoque circa B centrum ITCL epicyclo, coniungantur FLBT et IBCM linee; dico igitur quod, quando stella secundum EI lineam que est per B centrum epicycli cernitur, semper etiam medius Solis motus in eadem linea erit, cunque stella fuerit in I, tunc medio motui Solis coniungitur, quoniam et ipse ad punctum I perspicitur, cum vero fuerit in C, diametraliter sibi opponetur, quoniam ad punctum M percipiatur. Nam quoniam in singulis stellis istis medie longitudinis inequalitatisque distantie simul capte medium Solis motum qui ab initio fuit efficiunt, estque anguli qui est in F centro qui equalem longitudinis stelle motum continet et anguli qui est in E qui apparentem continet excessus semper angulus qui fit in B qui continet equalem stelle motum qui fit in epicyclo, patet quia, quando stella est in I puncto,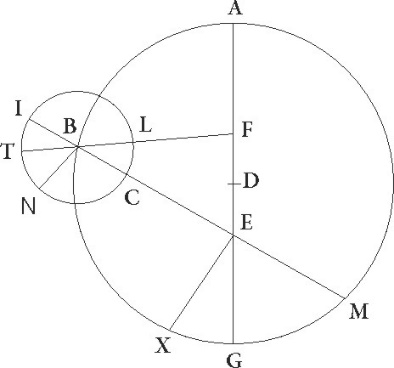 
deficiet a restitutione que est in puncto maxime longitudinis T per angulum IBT, qui subtractus ab angulo AFB facit angulum EI qui continetur a medio motu Solis et idem est angulo apparentis stelle, quando vero in C puncto est, tunc mota erit rursus in epicyclo per angulum TBC, qui compositus cum angulo AFB faciet medium Solis motum a puncto A maxime longitudinis, is motus semicirculum continet et amplius AFB angulum, deficiente angulo LBC, hoc est angulum GEM.
Idcirco in talibus quidem aspectibus tum linea que a centro epicycli B ad stellam protrahitur, tum linea que a puncto E, hoc est a visu nostro, ad medium Solis motum educitur in unam et eandem utreque utraeque] post corr. G lineam concidunt, in ceteris autem omnibus distanciis, quamvis differentes faciant declinationes, semper tamen equidistantes inter se sunt.
Nam si in quovis situ in posita descriptione lineam a centro B ad stellam protraxerimus, ut lineam BN, a centro autem E ad medium Solis motum lineam EX, erit propter predicta angulus EX utrisque angulis AFT et NBT equalis. Est autem etiam AFT utrisque EI et IBT equalis, quare subtracto EI angulo communi, reliquus IEX reliquo IBN equalis erit. Equidistans ergo est linea EX linee BN. Quoniam igitur in predictis aspectibus, coniunctionalibus dico atque oppositionalibus, qui ad medium Solis motum considerantur stellam ita invenimus per centrum epicycli perspectam, tanquam si non moveretur in epicyclo, sed situm in ipso ABG circulo haberet, et a linea FB equaliter eodem modo quo centrum epicycli circumduceretur, patet quia possibile erit per huiusmodi motus demonstrare proportiones inequalitatis zodiaci que propter excentricitatem fiunt, cum autem aspectus coniunctionales cerni non possint, reliquum est ut per oppositiones demonstrationum doctrinam faciamus.
〈X.7〉 Capitulum VII: Demonstratio excentricitatis et maxime longitudinis Martis
Quemadmodum igitur in Luna tribus eclipsibus captis lunaribus et locos et tempora et ad hec proportionem inequalitatis et maxime longitudinis locum per lineas demonstravimus, eodem modo hic etiam trium ad medium Solis motum oppositionum in singulis harum stellarum captis et locos quam exactissime fieri potest per astrolabica instrumenta observavimus, et a mediis Solis motibus qui fuerunt in observationibus tam tempus quam locum distantie subtilius computavimus, et ab istis tum proportionem excentricitatis tum maximam longitudinem demonstravimus.
Primum igitur in Marte tres cepimus observationes quarum prima quintodecimo anno Adriani observavimus Tibi secundum Egyptios die 26o sequente 27o post mediam noctem una equali hora et erat in gradu Geminorum Geminorum] 20 add. et del. A 21o, alteram anno Adriani 19o Pharmuthi secundum Egyptios die sexto sequente septimo ante mediam noctem horis tribus, et erat in gradibus Leonis 28 50′, tertiam anno Antonini secundo Epiphi secundum Egyptios die 12 sequente 13 ante mediam noctem duabus equalibus horis, et erat in gradibus Sagittarii 2 34′. Tempora igitur distantiarum a prima quidem ad alteram oppositionem quatuor egyptiacos annos et dies 69 et horas equales 20 continent, a secunda vero ad tertiam annos similiter 4 dies 96 et horam equalem unam. Colliguntur igitur ex tempore prime distantie post integros circulos gradus longitudinis 81 44′, ex secunde vero gradus 95 28′. Nulla enim diferentia erit de qua curandum sit, si a periodicis restitutionibus universalius expositis in tanto tempore medios motus computamus, patet etiam quod in prima quidem distantia mota est apparens stella 67 50′ gradus post integros circulos, in secunda vero 93 44′.
Designentur igitur tres circuli equales in zodiaci superficie de quibus ille a quo centrum epicycli Martis defertur sit ABG cuius centrum D, excentricus autem equalis motus sit EFI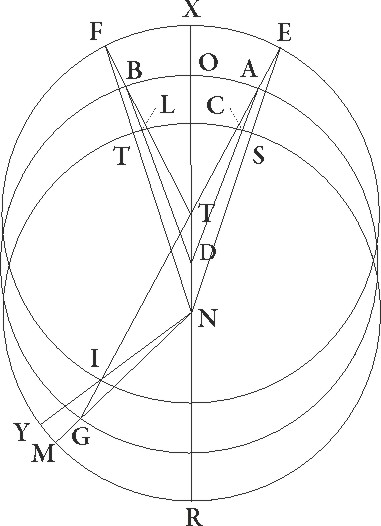 
cuius centrum T, zodiaco vero concentricus sit CLM cuius centrum N, diameter vero que per omnia transit centra sit XOPR. Supponatur autem A quidem punctum esse ubi centrum epicycli erat in prima oppositione, B autem ubi erat in secunda, G vero ubi in tertia, et coniungantur TE et TBF et TIG et NCA et NLB et NGM linee, ut excentrici arcus EF 81 44′ prime periodice distantie graduum sit, arcus vero FI 95 28′ graduum secunde, et rursus CL zodiaci arcus 67 50′ apparentis prime distantie graduum sit, et LM similiter arcus 93 44′ secunde distantie graduum. Si ergo arcus excentrici EF et FI subtenderentur ab arcubus zodiaci CL et LM, nihil aliud ad demonstrationem excentricitatis quereremus. Verum quoniam ipsi medii excentrici arcus AB et BG non datos subtendunt et, si coniunxerimus NSE et NTF et NIY, rursum excentrici arcus EF et FI subtenduntur ab arcubus zodiaci ST et TY, nec ipsis etiam datis, opus erit ut antea CS et LT et MY varii arcus dentur, ut ab arcubus coniugatis EFI et STY proportio excentricitatis exquisite demonstretur. Verum quoniam, antea quam excentricitatis et maxime longitudinis proportio habeatur, exquisite istos capere possibile non est, darique proxime possunt, etiam si non exquisite illi presupponantur, propterea quod differentie ipsorum non magne sunt, computationem prius faciemus, tamquam si nulla differentia de qua curandum sit ST et TY arcus differant ab arcubus CL et LM.
Sit enim ABG circulus excentricus equalis motus Martis, et supponatur A punctum prime oppositionis esse, B secunde, G autem tertie, et capiatur intra excentricum D zodiaci centrum in quo visus noster sit, et coniungantur semper a tribus oppositionum punctis linee ad visum, sicut modo AD et BD et GD linee, producaturque una coniunctarum trium linearum ad oppositum excentrici arcum, ut hic linea GDE, reliqua vero duo puncta oppositionum linea quedam coniungat, ut hic linea AB, deinde ab excentrici sectione factam per eductam lineam in puncto E coniungantur ad reliqua duo puncta oppositionum linee, ut hic E et EB, deducanturque ad lineas que sunt a dictis duobus punctis ad zodiaci centrum perpendiculares, ut hic in lineam AD perpendicularis EF et ad lineam BD perpendicularis EI, ad hec ab uno duum dictorum punctorum ad lineam que est ab altero ipsorum ad punctum excentrici postremo factam perpendicularis ducatur, ut hic a puncto A in lineam BE perpendicularis AT. Hec si semper in hac descriptione, sicuti placuerit, servabimus, easdem in numeris proportiones inveniemus, reliqua vero demonstratio a propositis in Marte arcubus hoc modo aperietur.
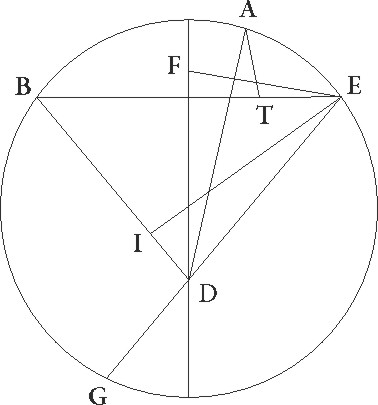Nam quoniam excentrici arcus BG 93 44′ zodiaci gradus subtendere supponitur, erit profecto angulus BDG qui fit in centro zodiaci talium 187 28′, qualium quatuor recti sunt 360, angulus vero EDI qui deinceps est 172 32′ earundem. Quare arcus etiam corde EI talium erit 172 32′ qualium est circulus qui qui] add. s. l. G rectangulo DEI circumscribitur 360, ipsa vero EI linea talium 119 45′ qualium est DE qua rectus angulus subtenditur 120. Similiter quoniam BG arcus 95 28′ graduum est, erit etiam angulus BEG qui est in circumferentia talium 95 28′ qualium duo recti sunt 360. Erat autem etiam BDE angulus 172 32′ earundem. Reliquus igitur etiam EBI earumdem erit 92, quare arcus quoque corde EI talium est 92 qualium est circulus qui rectangulo BEI circumscribitur 360, ipsa vero linea EI talium 86 19′ 
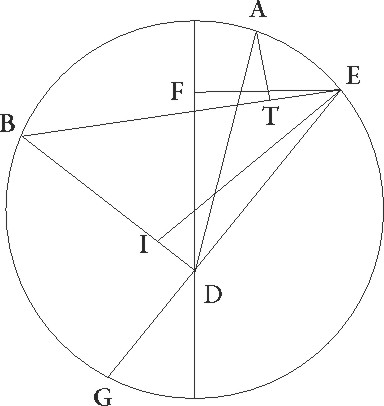qualium est EB qua rectus angulus subtenditur 120. Qualium ergo EI linea demonstrata est 119 45′ et ED 120, talium etiam BE erit 166 29′.
Rursus quoniam arcus excentrici totus ABG collectos zodiaci gradus 161 34′ utrarunque distantiarum subtendere supponitur, erit angulus quoque ADG talium 161 34′ qualium quatuor recti sunt 360, reliquus vero ADE 18 26′ earundem, qualium vero duo recti sunt 360, talium 36 52′. Quare arcus etiam corde EF talium est 36 52′ qualium est circulus qui rectangulo DEF circumscribitur 360, linea vero EF talium 37 57′ qualium est DE qua rectus angulus subtenditur 120. Similiter quoniam arcus excentrici ABG 177 12′ graduum colligitur, erit angulus quoque EG talium 177 12′ qualium duo recti sunt 360. Erat autem etiam angulus ADE 36 52′ earundem, erit ergo reliquus etiam DE 145 56′ earundem. Quare arcus corde EF talium est 145 56′ qualium est circulus qui rectangulo EF circumscribitur 360, linea vero EF talium 114 44′ qualium est E qua rectus angulus subtenditur 120. Qualium igitur demonstrata est linea EF 37 57′ et ED 120, talium E linea etiam erit 39 42′.
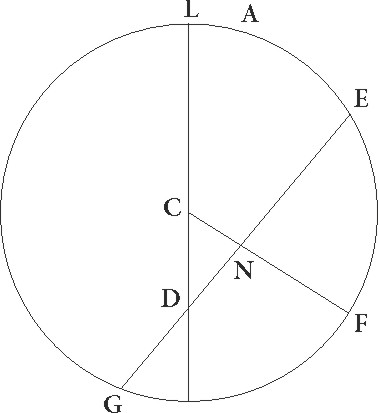Rursus quoniam arcus excentrici AB 81 44′ graduum est, erit angulus quoque EB talium 81 44′ qualium duo recti sunt 360. Quare arcus etiam corde AT talium est 81 44′ qualium est circulus qui rectangulo ET circumscribitur 360, arcus autem linee ET 98 16′ reliquarum ad semicirculum. Corde igitur etiam sue AT quidem talium erit 78 31′ qualium est E qua rectus angulus subtenditur 120, ET autem 90 45′ earundem. Qualium igitur E linea demonstrata est 39 42′ et DE 120 esse supponitur, talium etiam TA erit 25 58′, ET vero 30 2′ similiter. Erat autem etiam tota EB linea 166 29′ earundem demonstrata. Erit igitur reliqua etiam TB talium 136 27′ qualium TA erat 25 58′. Sed quadratum linee TB est 18615 16′, quadratum autem linee TA 674 16′, hec simul composita faciunt quadratum linee AB 19289 32′. Erit igitur AB linea talium per longitudinem 138 53′ qualium erat ED 120 et E 39 42′. Est autem AB linea talium 78 31′ qualium excentrici diameter est 120. Subtendit enim arcum graduum 81 44′. Qualium ergo est AB linea 78 31′ et diameter excentrici 120, talium erit ED 67 50′ et E 22 44′. Quare arcus etiam excentrici suus graduum est 21 41′, totus autem EABG arcus 198 53′ graduum est. Reliquus igitur etiam GE graduum est 161 7′ et corda sua GDE 118 22′ talium qualium est diameter excentrici 120.
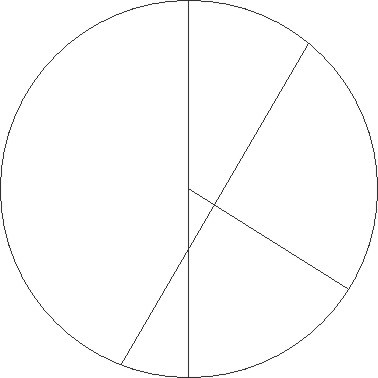Si ergo linea GE diametro excentrici equalis esset esset] corr. ex esse G inventa, patet quia in ipsa centrum excentrici esset, esset] corr. ex esse G et inde proportio excentricitatis aperte haberetur. Quoniam vero equalis non est, est autem etiam EABG EABG] corr. ex EADBG G portio maior semicirculo, perspicuum est quia in ea centrum excentrici erit. Supponatur igitur in puncto C, et ducatur per ipsum et per punctum D diameter LCDM que est per utraque centra, protrahaturque a puncto C ad lineam GE perpendicularis CNX. Quoniam ergo linea EG talium demonstrata est 118 22′ qualium est LM diameter 120, erat autem etiam DE linea 67 50′ earundem, erit etiam reliqua DG 50 32′ earundem. Quare quoniam rectangulum quod a lineis lineis] post corr. G ED et DG constituitur equale illi est quod constituitur ex lineis LD et DM, habebimus etiam rectangulum quod fit a lineis LD et DM 3427 51′. Sed rectangulum quod sub LD et DM continetur cum quadrato linee DC facit quadratum medietatis totius; hoc est quadratum linee LC. Si ergo a quadrato LC, hoc est a 3600, subtraxerimus rectangulum linearum LD et DM, hoc est 3427 51′, relinquetur nobis quadratum linee DC 172 9′ earundem. Habebimus ergo DC lineam que est inter centra talium per longitudinem 13 7′ proxime qualium est CL 
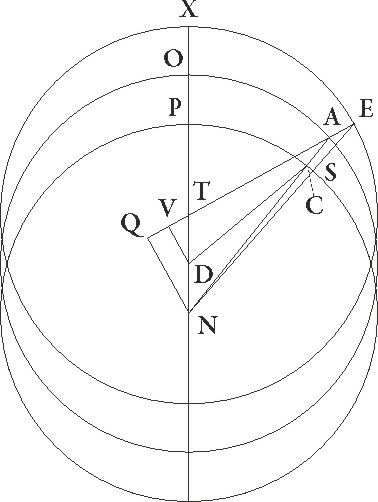semidiameter excentrici 60.
Rursus quoniam medietas linee GE, hoc est linea GN, 59 11′ talium est qualium LM diameter 120, est autem GD quoque linea 53 2′ earundem, demonstrata erit reliqua DN talium 8 39′ qualium DC inventa est 13 7′. Qualium igitur est DC que rectum angulum subtendit 120 talium etiam erit DN 79 8′, arcus vero suus talium 82 30′ qualium est circulus qui rectangulo DCN circumscribitur 360. Angulus igitur etiam DCN talium est 82 30′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 41 15′. Et quoniam in centro excentrici est, habebimus arcum etiam MX graduum 41 15′. Est autem totus quoque arcus GMX 80 3′, cum sit medietas arcus GXE. Reliquus ergo arcus GM qui est a tertia oppositione ad minimam longitudinem graduum est 39 19′. Patet autem, cum BG arcus 95 28′ graduum supponatur, quod reliquus quoque LB qui est a maxima longitudine ad secundam oppositionem graduum erit 45 13′. Sed cum etiam AB arcus 81 44′ graduum supponatur, erit reliquus quoque AL qui est a prima oppositione ad maximam longitudinem graduum 36 31′.
His igitur suppositis, consideremus iam collectas ab istis quesitorum in omni oppositione zodiaci arcuum differentias hoc modo.
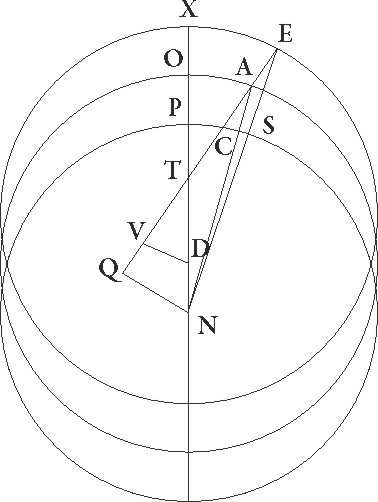Describatur ex figura trium oppositionum solius prime oppositionis descriptio, et coniuncta linea AD, deducantur a punctis D et N ad AT lineam protractam DU et NQ perpendiculares. Quoniam igitur arcus XE 36 31′ graduum est, erit etiam angulus ETX talium quidem 36 31′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium et ipse et oppositus ei DTN 73 2′, quare arcus etiam DU talium erit 73 2′ qualium est circulus qui rectangulo DTU circumscribitur 360, arcus vero UT 106 58′ ad semicirculum reliquorum. Corde igitur quoque sue DU quidem talium est 71 25′ qualium est DT qua rectus angulus subtenditur 120, UT autem 96 27′ earundem. Quare qualium est DT linea 6 33′ 30′′ et DA semidiameter excentrici 60, talium etiam erit DV 3 54′ et VT 5 16′. Et quoniam quadratum linee DU subtractum a quadrato linee DA facit quadratum linee UA, erit etiam AU linea 59 52′ per longitudinem, tota vero linea QA, quoniam equalis est QV linea linee VT, talium 65 8′ qualium NQ que dupla est ad DV colligitur 7 48′. Idcirco etiam NA qua rectus angulus subtenditur erit 65 36′. Quare qualium est NA linea 120, 120] post corr. G talium NQ erit 14 16′ et arcus suus talium 13 40′ qualium est circulus qui rectangulo ANQ circumscribitur 360. Angulus igitur etiam NAQ talium est 13 40′ qualium duo recti sunt 360. Rursus quoniam qualium est TE semidiameter excentrici 60, talium etiam QN demonstrata est 7 48′ et QT similiter 10 32′, erit etiam tota linea QTE 70 32′ et propterea etiam NE qua rectus angulus subtenditur 71 proxime. Qualium igitur est NE linea 120 talium QN quoque erit 73 10′ et arcus suus talium 12 36′ qualium est circulus qui rectangulo ENQ circumscribitur 360. Quare angulus etiam NEQ talium est 12 36′ qualium duo recti sunt 360, erat autem earumdem angulus quoque NAQ 13 40′. Quare reliquus etiam ANE angulus talium quidem est 1 4′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 0 32′. Totidem igitur zodiaci quoque arcus ES continet.
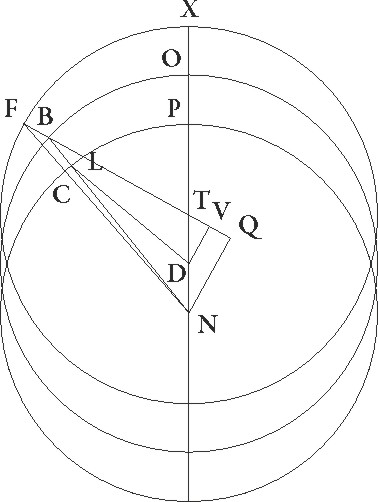Describatur rursum similis figura que secunde oppositionis descriptionem contineat. Quoniam igitur XF 45 13′ graduum supponitur, erit etiam angulus XTF talium quidem 45 13′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et qui sibi opponitur DTU angulus 90 26′. Quare arcus etiam DU linee talium est 90 26′ qualium est circulus qui DTV rectangulo circumscribitur 360, arcus vero UT 89 34′ ad semicirculum reliquorum. Corde igitur etiam sue DV quidem talium est 85 10′ qualium est DT qua rectus angulus subtenditur 120, linea vero UT 84 32′ earundem. Ergo qualium est DT linea 6 33′ 30′′ et DB semidiameter excentrici 60, talium etiam erit linea DU 4 39′ et UT 4 38′ similiter. Et quoniam si quadratum linee DV subtrahatur a quadrato linee DB facit quadratum linee BV, erit etiam linea BU 59 49′ per longitudinem, tota vero QB, quoniam VQ linea equalis est linee UT, talium est 64 27′ qualium NQ, que dupla est ad DU, colligitur 9 18′. Idcirco etiam NB que rectum angulum subtendit 69 6′ earundem erit. Quare qualium est NB 120, talium erit NQ 17 9′ et arcus suus talium 16 20 qualium est circulus qui BNQ rectangulo circumscribitur 360. Ergo etiam angulus NBQ talium est 16 26′, qualium quatuor recti sunt 360.
Rursus quoniam qualium est FT semidiameter excentrici 60, talium NQ quoque linea demonstrata est 9 18′ et QT similiter 9 16′, erit tota linea QTF 69 16′ earundem, et propterea linea quoque NF que rectum angulum subtendit 69 52′. Quare qualium est NF qua rectus angulus subtenditur 120, talium erit NQ linea 16 proxime, et arcus suus talium 15 20′ qualium est circulus qui FNQ rectangulo circumscribitur 360. Erit igitur etiam angulis NFQ talium 15 20′ qualium duo recti sunt 360, erat autem etiam angulus NBQ 16 26′ et reliquus ergo BNF 1 6′ earundem est. Qualium vero quatuor recti sunt 360, talium 0 33′, totidem ergo est etiam arcus zodiaci LT. Quoniam igitur in prima oppositione arcus CS 0 32′ inventus est, patet quoniam utrorunque simul arcuum portionibus 1 5′ maior erit prima distantia que ad excentricum consideratur quam apparens et continebit gradus 68 55′.
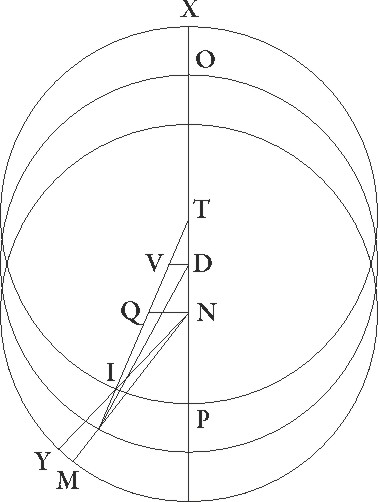Designetur etiam tertie oppositionis descriptio. Quoniam ergo arcus PI 39 19′ graduum supponitur, erit etiam angulus PTI talium quidem 39 19′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 78 38′. Quare arcus quoque DV talium erit 78 38′ qualium est circulus qui DTV rectangulo circumscribitur 360, arcus vero TU reliquorum ad semicirculum 101 22′. Corde igitur etiam sue DV quidem talium est 76 2′ qualium est DT qua rectus angulus subtenditur 120, et TV linea 92 50′ earundem. Quare qualium est linea DT que inter centra est 6 33′ 30′′ et DG semidiameter excentrici 60, talium DV quoque linea erit 4 9′ et VT 5 4′ similiter. Et quoniam si quadratum linee DU subtrahatur a quadrato linee DG facit quadratum UG, erit etiam linea VG 59 51′, reliqua vero linea GQ, quoniam equalis est TV linea linee VQ, talium 54 47′ qualium NQ que dupla est ad lineam DV colligitur 8 18′. Idcirco etiam NG que rectum angulum subtendit 55 25′ earundem est. Qualium igitur est NG 120, talium erit NQ 17 59′ et arcus suus talium 17 14′ qualium est circulus qui rectangulo GNQ circumscribitur 360, quare angulus quoque NGQ talium est 17 14′ qualium duo recti sunt 360. Rursus quoniam qualium est TI semidiameter excentrici 60, talium etiam NQ linea demonstrata est 8 18′ et TQ similiter 10 8′, erit etiam reliqua QI 49 52′ earundem. Idcirco linea quoque NI que rectum angulum subtendit 50 33′, quare qualium est ipsa NI qua rectus angulus subtenditur 120, talium etiam erit NQ linea 19 42′ et arcus suus talium 18 54′ qualium est circulus qui rectangulo INQ circumscribitur 360, ergo etiam angulus NIQ talium est 18 54′ qualium duo recti sunt 360. Sed angulus etiam NGQ 17 14′ earundem demonstratus est. Reliquus igitur ING 1 40′ earundem est. Qualium vero quatuor recti sunt 360, talium 0 50′, totidem ergo est MY arcus zodiaci.
Quoniam igitur in secunda etiam oppositione LT arcus 0 33′ inventus fuit, patet quia utrorunque simul arcuum portionibus 1 23′ minor erit prima distantia que ad excentricum consideratur quam apparens et continebit gradus 92 21′. Secundum hos ergo duarum distantiarum zodiaci arcus nobis collectos et eos qui rursus natura secundum excentricum suppositi fuerant premissa theoremata secuti, quibus maxima longitudo et excentricitatis proportio demonstrata demonstrata] corr. ex demonstra G nobis est, invenimus, ne repetentibus longior nobis doctrina fiat, lineam DC que est inter centra talium esse 11 50′ qualium est semidiameter excentrici 60, GM autem arcum excentrici qui est a tertia oppositione ad minimam longitudinem graduum 45 35′, unde rursus arcus etiam LB 38 59′ graduum colligitur, arcus autem AL 42 45′ similiter, hec in demonstrationibus singularum oppositionum secuti quesitorum magnitudines arcuum exacte in singulis invenimus arcus quidem CS magnitudinem sexagesimarum 28, LT vero t〈o〉tidem totidem] titidem A proxime 28, arcus autem MI sexagesimarum 40. Prime igitur secundeque oppositionis huiusmodi quantitates composuimus et factas inde 56 sexagesimas addidimus 67 50′ prime distantie zodiaci gradibus, et sic exacte invenimus consideratam ad excentricum distantiam graduum esse 68 46′, secunde similiter et tertie oppositionis quantitates composuimus, factamque inde quantitatem gradus 1 8′ subtraximus ab apparentibus gradibus secunde distantie zodiaci graduum graduum] add. marg. G 93 44′, et sic rursus exacte invenimus consideratam ad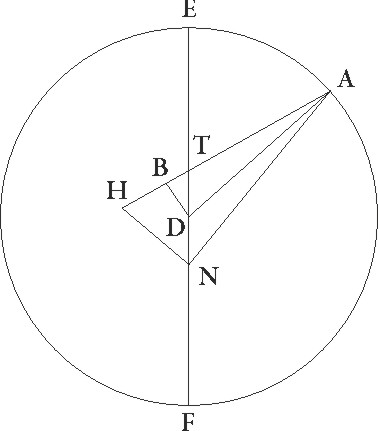 
excentricum distantiam graduum esse 92 36′. Ex quibus iam eadem demonstratione usi et proportionem excentricitatis et maximam longitudinem exquisite habuimus, invenimusque lineam DC que est inter centra talium 12 proxime qualium est CL semidiameter excentrici 60, GM vero excentrici arcum graduum 44 21′, a qua rursus LB quidem arcus graduum fit 40 11′, AL autem 41 33′ similiter. Quod autem his magnitudinibus apparentes observateque trium oppositionum distantie congruunt, perspicuum per eadem faciemus.
Proponatur enim prime oppositionis descriptio que solum excentricum EF habeat in quo epicycli centrum semper fertur. Quoniam ergo angulus ATE talium est 41 33′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et oppositus sibi angulus DTV 83 6′, erit etiam arcus corde DV talium 83 6′, qualium est circulus qui rectangulo DTV circumscribitur 360, arcus vero UT 96 54′ ad semicirculum reliquorum. Corde igitur etiam sue DV quidem talium erit 79 35′ qualium est DT que rectum subtendit subtendit] post corr. G 120, VT vero 89′ 50 earundem. Qualium igitur est DT linea 6 et DA semidiameter excentrici 60, talium erit DU quidem 3 58′ 30′′, UT autem 4 30′. Et quoniam quadratum linee DV subtractum a quadrato linee DA facit quadratum linee UA, erit etiam ipsa UA 59 50′ per longitudinem earundem. Rursus quoniam UT equalis est linee UQ et NQ dupla est ad DV, habebimus etiam totam AQ talium 64 20′ qualium est NQ linea 7 57′. Idcirco etiam NA que rectum subtendit 64 52′ earundem erit. Quare qualium qualium] erit add. et del. A est NA que rectum angulum subtendit 120, talium etiam erit NQ 14 44′ et arcus suus talium 14 6′ qualium est circulus qui rectangulo ANQ circumscribitur 360. Ergo angulus quoque NAQ talium est 14 6′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 7 3′. Erat autem etiam angulus ATE 41 33′ earundem. Erit igitur reliquus quoque ANE apparentis motus graduum 34 30′, quibus stella maximam longitudinem in prima oppositione precedebat.
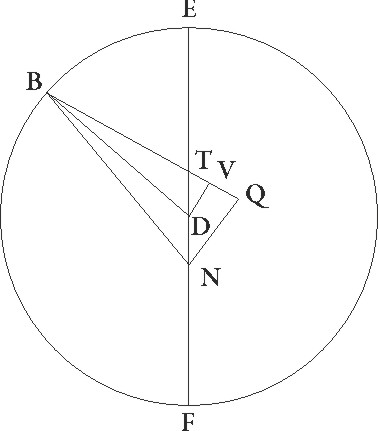Designetur rursum similis secunde oppositionis descriptio. Quoniam ergo medii motus epicyli angulus BTE talium 40 11′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et oppositus angulus UTN 80 22′, erit etiam arcus DU talium 80 22′ qualium est circulus qui DTU rectangulo circumscribitur 360, arcus vero UT 99 38′ ad semicirculum reliquorum. Corde igitur etiam sue DU quidem talium erit 77 26′ qualium est DT que rectum angulum subtendit 120, UT vero 91 41′ earundem. Qualium ergo est DT linea 6 et DB semidiameter excentrici 60, talium etiam DU erit 3 52′ et UT 4 35′. Et quoniam quadratum linee DU subtractum a quadrato linee DB facit quadratum linee BU, erit etiam ipsa BU 59 53′ earundem per longitudinem, eodem modo, quoniam TU linea equalis est linee UQ et NQ dupla linee DU, erit etiam BQ tota talium 64 28′ qualium est NQ 7 44′. Idcirco etiam BN que rectum subtendit 64 56′ erit earundem, quare qualium est BN que rectum angulum subtendit 120 talium etiam erit NQ 14 19′ et arcus suus talium 13 42′ qualium est circulis qui rectangulo BNQ circumscribitur 360. Angulus ergo etiam NBQ talium est 13 42′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 6 51′. Erat autem angulus quoque BTE 40 11′, et reliquus igitur ENB angulus apparentis motus 33 20′ earundem est, totidem ergo gradibus a maxima longitudine ad successionem stella in secunda oppositione distabat. Fuit autem demonstrata in prima oppositione 34 30′ gradibus maximam longitudinem precedere, quare tota distantia a prima oppositione ad secundam 67 50′ graduum colligitur, quemadmodum per observationes etiam habuimus.
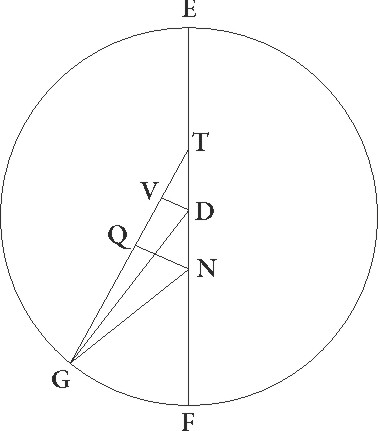Designetur similiter tertie oppositionis descriptio. Quoniam ergo etiam hic angulus GTF qui est ipsius equalis motus epicycli talium est 44 21′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 88 42′, erit etiam arcus linee DV talium 88 42′, qualium est circulus qui rectangulo DTF circumscribitur 360. Arcus vero linee UT 91 18′ reliquorum ad semicirculum. Corde Cordae] corr. ex Corda G igitur etiam sue DV quidem talium erit 83 83] corr. ex 33 G 53′ qualium et DT que rectum angulum subtendit 120, VT autem 85 49′ earundem. Qualium igitur est DT linea 6 et DG semidiameter excentrici 60, talium etiam erit DV quidem 4 11′ 30′′, UT vero 4 17′. Et quoniam quadratum linee DV subtractum a quadrato linee DG facit quadratum linee GV, habebimus etiam hanc 59 51′ earundem per longitudinem. Rursus quoniam UT linea equalis est linee VQ et NQ dupla est ad DU, habebimus etiam reliquam QG talium 55 34′ qualium est NQ 8 23′, ideo etiam GN que rectum subtendit earundem 56 12′. Qualium ergo est GN que rectum angulum subtendit 120, talium etiam erit NQ 17 55′ et arcus suus talium 17 10′ qualium est circulus qui rectangulo GNQ circumscribitur 360. Angulus igitur etiam TGN talium quidem est 17 10′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 8 35′. Erat autem etiam angulus GTF 44 21′, totus ergo etiam GNF 52 56′ eorundem est. Quasobres totidem etiam gradibus precedere minimam longitudinem stella in tertia oppositione videbatur, sed in secunda quoque oppositione demonstrata est ad successionem maxime longitudinis fuisse per gradus 33 20′, et reliqui ergo a secunda oppositione rursus ad tertiam collecti gradus 93 44′ inventi sunt convenienter illis qui in secunda distantia fuerant observati. Verum quoniam, quando stella in tertia oppositione per lineam GN perspiciebatur, tunc observatos obtinebat Sagittarii gradus 2 34′ et GNF angulus qui est in centro zodiaci 52 56′ talium demonstratus est qualium quatuor recti sunt 360, patet quod etiam minima excentricitatis longitudo, que est in puncto F, 25 30′ Capricornii gradus obtinebat, maxima vero 25 30′ Cancri per oppositionem.
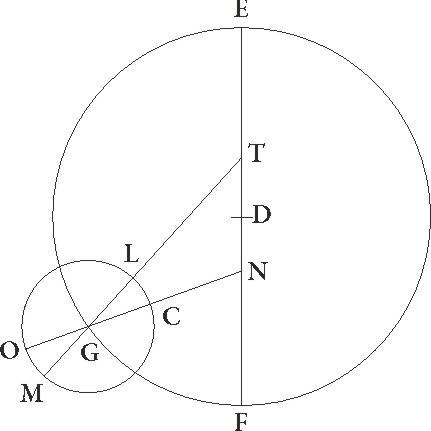Si ergo descripserimus in G centro CLM Martis epiciclum et produxerimus TG lineam, habebimus in tempore tertie oppositionis medium quidem epicycli a maxima excentrici longitudine motum 135 39′ graduum, propterea quod GTF angulus reliquorum ad semicirculum demonstratus est graduum 44 21′, medium vero stelle motum a maxime longitudinis puncto epicycli M, hoc est arcum MC, graduum 171 25′, propterea quod angulus TGN demonstratus est talium 8 35′ qualium quatuor recti sunt 360, cum sit in centro epicycli, et sic arcus quidem CL ex stella C ad minimam longitudinem L eorundem fit graduum 8 35′, arcus vero a maxima longitudine M ad stellam C reliquorum ad semicirculum 171 25′, ut propositum est.
Et ita factum nobis una cum aliis perspicuum est quod in tempore tertie oppositionis, hoc est in secundo anno Antonini Epiphi secundum Egyptios die 12o sequente 13o ante mediam noctem duabus horis equalibus distabat stella Martis secundum longitudinem quidem medie a maxima excentrici longitudine gradibus 135 39′, secundum inequalitatem vero a maxima epiycli longitudine gradibus 171 25′.
〈X.8〉 Capitulum VIII: Demonstratio magnitudinis epicycli Martis
Cum autem consequens sit ut magnitudinis etiam epicycli proportionem demonstremus, observavimus ad hoc stellam Martis post tertie oppositionis tempus tribus diebus proxime, hoc est secundo Antonini anno Epiphi secundum Egyptios die 15o sequente 16o ante mediam noctem tribus horis equalibus. Erat enim secundum astrolabium in medio celi 20us Libre Libre] corr. ex Libere G gradus et Sol medio motu 5 27′ Geminorum gradus tunc obtinebat. Spica igitur stella in suo situ perspecta, Mars cernebatur in gradibus Sagittarii 1 36′. In eodem vero tempore a centro quoque Lune distare ad successionem similiter videbatur gradibus 1 36′, et erat medius Lune motus tunc in 4 20′ gradibus Sagittarii, verus autem in 29 gradibus Scorpionis. Secundum enim inequalitatem 92 gradibus a maxima epicycli longitudine stabat. Apparens autem erat in principio Sagittarii, ut etiam hinc Mars, sicuti perspiciebatur, 1 36′ gradus Sagittarii obtinuisse ostendatur. Patet igitur quod distabat a minima longitudine ad precedentia gradibus 53 54′. Continentur autem in tempore quod fuit inter tertiam oppositionem et hanc observationem longitudinis gradus 1 32′ et inequalitatis 1 21′ proxime. Quos si addiderimus demonstratis tertie oppositionis motibus, habebimus in huius observationis tempore distantem Martis stellam a maxima excentrici longitudine gradibus quidem longitudinis 137 11′, inequalitatis vero a maxima epicycli longitudine gradus 172 46′.
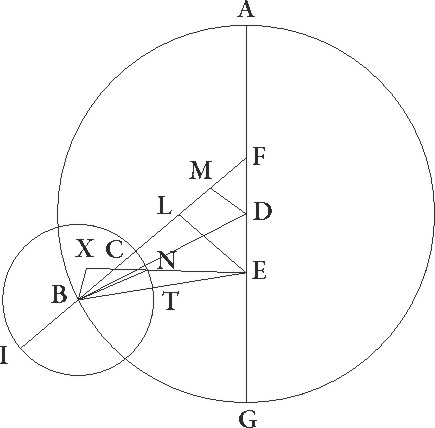His ita suppositis sit ABG deferens centrum epicycli excentricus cuius centrum D, et diameter ADG in qua zodiaci centrum sit E, maioris vero excentricitatis centrum sit F, et descripto in puncto B epycylo ITC, protrahantur FCBI et ETB et DB linee, et a punctis D et C deducantur ad FB lineam perpendiculares EL et DM, et supponatur stella esse in puncto epicycli N, et coniunctis lineis EN et BN, ducatur ad lineam EN protractam a puncto B perpendicularis BX. Quoniam igitur stella 137 11′ gradibus a maxima excentrici longitudine distat, estque angulus BFG talium 42 49′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 85 38′, erit etiam arcus linee DM talium 85 38′ qualium est circulus qui DFM rectangulo circumscribitur 360, arcus vero FM 94 22′ ad semicirculum reliquorum. Corde igitur etiam sue DM quidem talium erit 81 34′ qualium est DF que rectum angulum subtendit 120, FM autem 81 1′ earundem. Quare qualium est DF que inter centra est 6 et DB semidiameter excentrici 60, talium etiam erit DM 4 5′ et FM 4 24′. Et quoniam, si quadratum linee DM subtractum fuerit a quadrato linee DB, facit quadratum BM, erit etiam linea BM 59 52′ earundem. earundem] corr. ex eas G Similiter autem linea quoque FM equalis est linee ML, linea vero EL dupla est ad lineam DM. Reliqua igitur linea BL erit 55 28′ et EL 8 10′ earundem. Idcirco etiam EB que rectum angulum subtendit 56 4′ earundem est. Qualium igitur est EB que rectum subtendit 120, talium etiam erit EL 17 28′, et arcus suus talium 16 44′ qualium est circulus qui rectangulo BEL circumscribitur 360. Quare angulus quoque FBE talium est 16 44′ qualium duo recti sunt 360.
Rursus quoniam angulus GEX quo Martis stella minimam longitudinem G precedere cernebatur talium supponitur 53 54′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 107 48′, estque angulus etiam GEB 102 22′ earundem, propterea quod equalis utrisque simul angulis sit FBE demonstrato 16 44′ earundem et BFE 85 38′ supposito earundem, erit etiam reliquus angulus BEX 5 26′ earundem. Arcus vero linee BX talium 5 26′, qualium est circulus qui rectangulo BEX circumscribitur 360. Quapropter etiam linea BX talium est 5 41′ qualium est EB que rectum angulum subtendit 120. Qualium igitur ipsa EB 56 4′ demonstrata est et semidiameter excentrici 60, talium BX linea erit 2 39′.
Eodem modo, quoniam N punctum a maxima quidem epicycli longitudine, hoc est a puncto I, distabat gradibus 172 46′ et a minima longitudine C gradibus 7 14′, erit etiam angulus CBN talium 7 14′ qualium quatuor recti sunt. 360, qualium vero duo recti sunt 360 talium 14 28′, erat autem etiam angulus CBT 16 44′ earundem, et reliquus igitur NBT angulus erit 2 16′, sed angulus etiam BEX 5 26′ demonstratus earundem est. Erit igitur etiam augulus XNB 7 42′ earundem, quare arcus quoque linee XB talium erit 7 42′ qualium est circulus qui rectangulo BNX circumscribitur 360. Ipsa vero linea BX talium 8 3′ qualium est BN que rectum angulum subtendit 120. Qualium igitur est BX linea 2 39′ et semidiameter excentrici 60, talium etiam erit BN epicycli semidiameter 39 30′ proxime. Quare proportio etiam semidiametri excentrici ad semidiametrum epicycli proportio est quam 60 habent ad 39 30′.
〈X.9〉 Capitulum VIIII : De emendatione periodicorum motuum Martis
Sed gratia etiam emendationis periodicorum motuum unam cepimus de priscis observationibus qua declaratur quod anno 13o secundum Dionysium Capricornionis 25 stella Martis Martis] corr. ex Maris G matutina cernebatur boreali Scorpionis incumbere fronti, et est tempus observationis in anno 52 a morte Alexandri, hoc est annus 476us a Nabonassaro Athyr secundum Egyptios die 20o sequente 21o in mane. In quo tempore medium motum Solis invenimus Capricorni gradus obtinentem 23 54′. Fixa vero que est in boreali fronte Scorpionis a nobis observata est etiam in gradibus eiusdem 6 20′. Quoniam igitur anni 409 qui fuerunt ab observatione usque ad Antoninum progressum fixarum faciunt graduum quatuor et 5 sexagesimarum proxime, fixa quam diximus in tempore illius observationis 2 15′ gradus Scorpionis obtinuisse debet, totidem ergo etiam stella Martis obtinuit. Similiter quoniam etiam tempore nostro, idest in principio Antoniani imperii, maxima longitudo Martis 25 30′ Cancri gradus obtinebat, debet in tempore observationis 21 25′ obtinuisse. Patet igitur quod stella quidem apparens 100 gradibus et sexagesimis 50 tunc a maxima longitudine distabat, medius autem Sol ab eadem maxima longitudine distabat gradibus 182 29′, et ab opposita minimaque longitudine 2 29′.
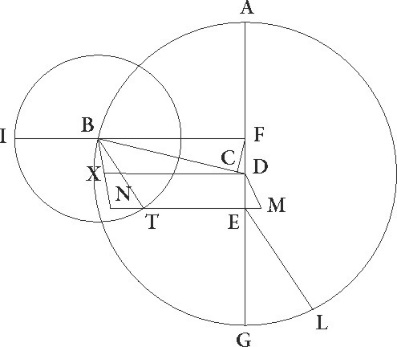His ita suppositis, sit ABG centrum epicycli deferens excentricus cuius centrum D, et diameter ADG in qua zodiaci centrum sit E, maioris autem excentricitatis sit F, et descripto in centro B epicyclo IT, protrahantur FBI et DB linee et a puncto F ad lineam DB ducatur perpendicularis FC et supponatur stella esse in T puncto epicycli, et coniuncta linea BT, trahatur a puncto E ipsi equidistans linee EL in qua per ea que iam demonstrata sunt medius motus Solis erit, coniunctaque linea ET, ducantur ad ipsam a punctis D et B perpendiculares DM et BN, et similiter a puncto D ad lineam BN perpendicularis DX, ut figura DMNX rectangulum paralellogrammum fiat. Quoniam igitur angulus ACT apparentis motus stelle a maxima longitudine talium est partium 100 et sexagesimarum 50 qualium quatuor recti sunt 360, angulus vero medii motus Solis GEL 2 29′ earundem, erit etiam angulus TEL, hoc est angulus BTE, talium 81 39′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 163 18′. Quare arcus etiam linee BN talium est 163 18′ qualium est circulus qui rectangulo BTN circumscribitur 360, ipsa vero linea BN talium 118 43′ qualium est TB que rectum angulum subtendit 120. Quare qualium est BT semidiameter epicycli 39 30′ et ED que est inter centra 6, talium etiam BN erit 39 3′. Rursus quoniam angulus ET talium est 100 et sexagesimarum 50 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 201 40′, ac ideo qui deinceps est angulus DEM 158 20′ earundem, erit etiam arcus DM talium 158 20′ qualium est circulus qui DEM rectangulo circumscribitur 360, ipsa vero linea DM talium 117 52′ qualium est DE que rectum angulum subtendit 120. Quare qualium est DE linea 6 et BN 39 3′, talium etiam erit DM, hoc est NX, 5 54′ et reliqua BX talium 33 9′ qualium est BD semidiameter excentrici 60. Quare qualium est BD que rectum angulum subtendit 120, talium etiam erit BX 66 18′ et arcus suus talium 67 4′ proxime qualium est circulus qui rectangulo BDX circumscribitur 360. Et angulus igitur BDX talium est 67 4′ qualium duo recti sunt 360, totus vero BDM 247 4′, est autem etiam EDM angulus 21 40′ earundem, propterea quod DEM angulus demonstratus est esse 158 20′ et reliquus igitur BDE angulus 225 24′ esse colligitur et qui deinceps est angulus BDA 134 36′ similiter. Quare arcus etiam FC talium est 134 36′ qualium est circulus qui rectangulo DFC circumscribitur 360, et arcus DC 45 24′ reliquorum ad semicirculum. Corde igitur etiam sue FC quidem talium erit 110 42′ qualium est DF que rectum angulum subtendit 120, DC vero 46 18′ earundem. Quare qualium est DF linea 6 et DB semidiameter excentrici 60, talium FC erit 5 32′ et DC 2 19′ et reliqua CB 57 41′, ideo etiam BF que rectum angulum subtendit 57 57′ proxime earundem. Qualium igitur est BF 120, talium FC quidem erit 11 28′ et arcus suus 10 58′ talium qualium est circulus qui rectangulo BCF circumscribitur 360. Quare angulus etiam FBD talium est 10 58′ qualium duo recti sunt 360. Sed erat etiam angulus BDA 134 36′ earundem. Totus igitur BFA angulus earundem est 145 34′. Qualium vero vero] add. s. l. G quatuor recti sunt 360, talium est 72 47′. Quare medius secundum longitudinem stelle motus, hoc est B centrum epicycli, distabat in tempore observationis proposite a maxima longitudine gradibus 72 47′, et propterea 4 12′ Libre gradus obtinebat. Verum quoniam etiam GEL angulus 2 29′ earundem supponitur, qui cum duobus rectis semicirculi ABG equalis efficitur utrisque simul AFB medie longitudinis angulo et IBT inequalitatis, hoc est angulo motus stelle in epicyclo, habebimus reliquum angulum IBT 109 42′ earundem. Quare in eodem observationis tempore stella distabat a maxima epiycli longitudine dictos inequalitatis gradus 109 42′, qui nobis erant inveniendi.
Sed demonstratum etiam fuit quod in tempore tertie oppositionis distabat secundum inequalitatem ab eadem maxima epicycli longitudine gradibus 171 25′. Addidit ergo in interiecto inter observationes tempore quod 410 egyptiacos annos et dies 341 40′ proxime continet, post 192 integros circulos addidit, in quam gradus 61 43′ quantam ferme additionem invenimus per tabulas quas de mediis motibus ipsius conscripsimus. Ab istis enim diurnus nobis motus constitutus est, divisa multitudine graduum que per circulos et additionem colligitur in dies qui inter duas observationes fuisse colliguntur.
〈X.10〉 Capitulum X : De locis periodicorum Martis motuum in tempore Nabonassari
Rursus ergo quoniam a primo Nabonassari anno Thot secundum Egyptios die prima in meridie tempus usque ad propositam observationem 475 egyptiacorum annorum et dierum 79 45′ proxime colligitur quod tempus post integros circulos longitudinis quidem 180 40′ gradus continet, inequalitatis vero 142 29′, si hos gradus ab utroque observationis loco congrue subtraxerimus, hoc est in longitudine quidem a 4 12′ gradibus Libre, in inequalitate autem a gradibus 109 42′, habebimus in primo Nabonassari anno Thot secundum Egyptios die prima in meridie locos periodicorum motuum Martis longitudinis quidem in gradibus Arietis 3 32′, inequalitatis vero a maxima epicycli longitudine in gradibus 327 13′. Per easdem autem rationes, quoniam in 475 annis colliguntur colliguntur] corr. ex colligitur G 4 45′ gradus maximarum longitudinum motus, eratque maxima longitudo Martis in tempore observationis in gradibus Cancri 21 25′, obtinebit profecto in dicto constitutionis locorum tempore gradus Cancri Cancri] corr. ex Tauri G 16 40′.