Ptolemaeus Arabus et Latinus

〈XII〉

Incipit liber XII Magne Compositionis Ptolomei

〈XII.1〉 〈Capitulum I :〉 De iis que premittuntur ad regressus planetarum demonstrandos

His demonstratis, sequitur ut regressus etiam qui singulis quinque planetarum accidunt tam minimos quam maximos consideremus, ac magnitudines ipsorum ab expositis suppositionibus quam maxime fieri potest congruos ostendamus iis que per observationes capiuntur. Ad huius rei ergo intelligentiam et ceteri mathematici et Apollonius Pergensis demonstrant in una inequalitate solari quod, sive supposito epicyclo accidat cum epicyclus in circulo qui concentricus zodiaco sit motu longitudinis ad successionem signorum progrediatur et stella in epicyclo ad centrum ipsius motu inequalitatis ad successionem maxime longitudinis, producaturque a visu nostro linea sic epicyclum secans, ut partis eius que intra epicyclum est medietas ad reliquam que est a visu nostro usque ad sectionem que fit in in] add. s. l. G minima epicycli longitudine proportionem habeat eam quam habet epicycli velocitas ad velocitatem stelle, punctum quod ab huiusmodi linea in circumferentia epicycli fit progressus et regressus ita dividit, ut cum stella in ipso sit stare videatur, sive per suppositionem excentricitatis inequalitas Solis accidat, que suppositio suppositio] post corr. G in reliquis etiam tribus stellis solummodo que per omnem a Sole distantiam distant procedere potest, si centrum excentrici circa circa] post corr. G centrum zodiaci ad successionem signorum equaliter Soli moveatur et stella in excentrico circa centrum ipsius ad precedentia signorum inequalitatis motui equaliter, producaturque in excentrico circulo huiusmodi a zodiaci centro, hoc est a visu nostro, linea huiusmodi, ut medietas totius linee ad minorem partem earum partium que a visu fiunt eam proportionem habeat quam habet velocitas excentrici ad stelle velocitatem, quando in illo puncto fuerit stella ubi linea 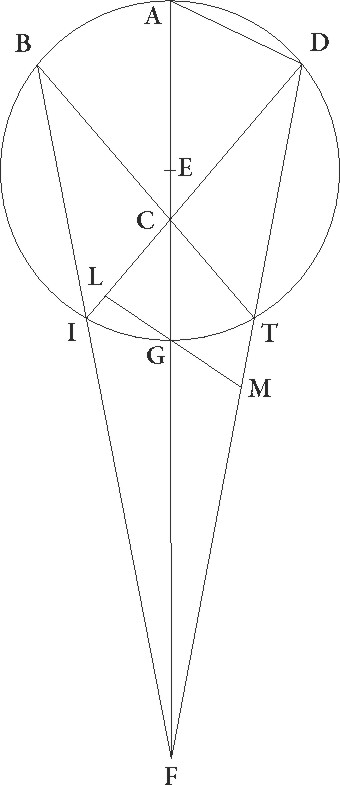minime longitudinis arcum secat, tunc standi phantasiam faciet. Sed nos et brevius et facilius propositum demonstrabimus, utemur autem communi permixtaque de utrisque suppositionibus demonstratione, ut etiam hinc similitudo et convenientia utrarunque rationum confirmetur.

Sit ergo epicyclus ABGD cuius centrum E, et diameter EG, hec usque ad F centrum zodiaci, hoc est ad visum nostrum, producatur, interceptisque ex utraque parte G minime longitudinis puncti equalibus arcubus GI et GT, protrahantur a puncto F per I et T puncta FIB et FTD linee, et coniungantur DI et BT linee secantes seipsas in puncto C, quod videlicet in AG diametro erit. Dico igitur primum quod AF linea sic se habet ad lineam FG, sicut AC linea ad lineam CG. Coniungantur enim AD et DG linee, et ducatur per punctum G linea LGM equidistans linee AD AD] post corr. G, hec, quoniam ADG angulus rectus est, perpendicularis erit ad lineam DG. Quoniam igitur angulus GDI equalis est angulo GDT, erit etiam linea GL equalis linee GM. Quare AD linea eandem habebit ad utranque proportionem, sed sicut se habet AD linea ad lineam GM, sic se habet etiam AF ad FG, et sicut se habet AD ad LG, sic se habet AC ad CG, sicut ergo AF ad FG, sic AC ad CG. Si ergo circulum ABGD in suppositione excentricitatis ipsum excentricum esse intellexerimus, erit C punctum zodiaci centrum et dividetur ab eo diameter AG in eandem proportionem suppositionis secundum epicyclum. Demonstravimus enim iam eam proportionem habere AC maximam in excentrico distantiam ad CG minimam quam habet in epicyclo AF maxima distantia ad FG minimam.

Dico etiam quod proportio DF linee ad lineam FT est proportio BC linee ad CT. Coniungatur enim in simili descriptione linea BND, hec perpendiculariter incidet ad diametrum AG, et a puncto T ducatur equidistans ei linea TXI. Quoniam igitur BN linea equalis est linee ND, eandem utraque ipsarum ad lineam XT habebit proportionem. Sed sicut se habent ND ad XT, sic etiam DF ad FT, et sicut BN ad XT, sic BC ad CT, quare sicut DF ad FT, sic BC ad CT, et coniunctim ergo sicut DF et FT ad FT, sic BT ad TC, et disiunctim perpendicularibus deductis sicut OF ad FT, sic PT ad TC, et iterum disiunctim sicut OT ad TF, sic PC ad CT. Si ergo in epicycli suppositione ita DF protrahatur, ut OT linea eam habeat proportionem ad lineam TF, quam epicycli velocitas ad stelle velocitatem, eandem habebit etiam proportionem in suppositione excentricitatis PC linea ad lineam CT. Causa vero est, ne hic quoque hac proportione disiuncta, hoc est proportione PC linee ad lineam CT, ad stationes utamur, sed proportione coniuncta ea videlicet quam habet PT linea ad lineam CT, quod velocitas epicycli eam habet ad velocitatem stelle proportionem, quam solus longitudinis motus ad solum inequalitatis motum, velocitas autem excentrici eam habet ad velocitatem stelle proportionem, 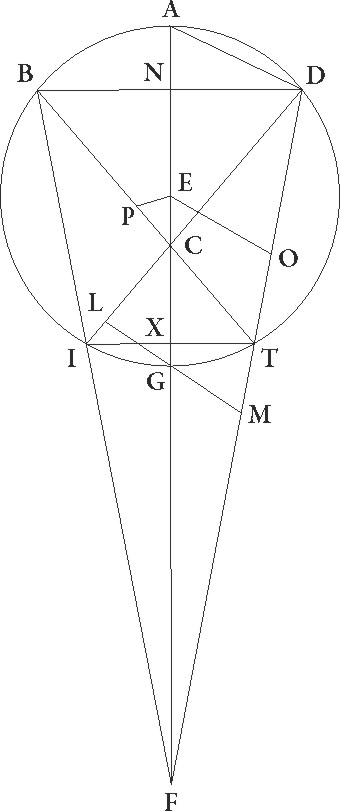quam habet medius motus Solis, hoc est longitudinis et inequalitatis stelle motus simul, ad motum inequalitatis solum, sicut exempli gratia in stella Martis proportio velocitatis epicycli ad stelle velocitatem est proportio 42 proxime ad 37. 37] corr. ex 34 A Proportio enim motus longitudinis ad motum inequalitatis hec proxime nobis demonstrata est, idcirco etiam linea OT hanc habet proportionem ad lineam TF. Proportio vero velocitatis excentrici ad velocitatem stelle illam que est utrorunque simul 73 ad 37, hoc est coniunctim proportionem PT ad TC. Proportio enim per disiunctionem videlicet proportio PC ad CT eadem erat proportioni linee OT ad lineam TF, hoc est eius que inveniuntur in 42 ad 37. Sed hec nobis ad hoc usque premissa premissa] post corr. G sint.

Cum autem reliquum sit quod linearum captarum que in huiusmodi proportionem dividuntur in utraque suppositione I et T puncta standi phantasiam contineant, et arcus quidem IGT regressuum sit, reliquus vero progressuum, huiusmodi ad hoc premittit Appolinius theorema: sit triangulus, inquit, ABG cuius latus BG maius sit quam AG, et intercipiatur de linea GB linea GD non minor quam linea AG, dico, inquit, GD lineam maiorem proportionem habere ad BD quam angulum ABG ad angulum BGA, hoc ita demonstrat. Compleatur, inquit, paralellogrammum ADGE, protracteque linee BA et GE concurrant in puncto F. Quoniam igitur E linea non est minor quam AG, circulus qui centro A et spatio E describitur aut per G punctum aut super super] corr. ex per G G pertransibit. Describatur ergo per G circulus IEG, et quoniam triangulus EF maior est sectore EI, triangulus vero EG minor est sectore EG, habebit EF triangulus maiorem proportionem ad triangulum EG quam sector EI ad sectorem EG. Sed sicut se habet sector EI ad sectorem 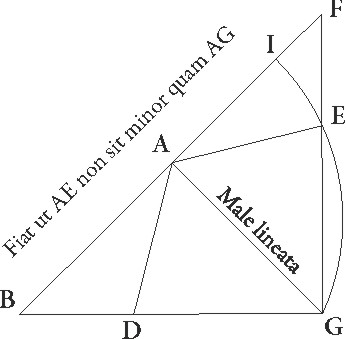EG, sic se habet angulus EAF ad angulum EAG, et sicut triangulus EF ad triangulum EG, sic FE basis ad basim EG. Maiorem ergo habet proportionem linea FE ad lineam EG quam angulus FE ad angulum EAG, sed sicut linea FE ad lineam EG, sic GD ad DB. Est autem angulus FE equalis angulo ABG et angulus EAG angulo AGD. Habebit ergo GD linea maiorem proportionem ad DB quam angulus ABG ad angulum AGB. Est autem perspicuum maiorem multo futuram proportionem, si GD linea, hoc est E, non non] add. s. l. G supponatur equalis linee 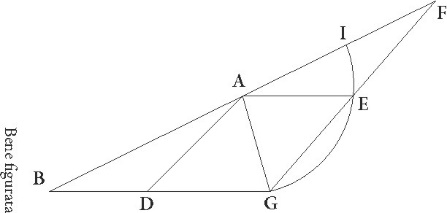AG sed maior.

Hoc premisso, premisso] post corr. G sit ABGD epicyclus cuius centrum E et diameter EG que producatur usque ad F visus nostri punctum, ut aperte pateat pateat] post corr. G quod EG semidiameter maiorem ad GF lineam habeat proportionem quam epicycli velocitas ad stelle velocitatem. Possibile igitur est sic ducere lineam FIB, ut medietas linee BI eam proportionem habeat ad lineam IF quam habet velocitas epycycli ad velocitatem stelle, et si per ea que iam demonstrata sunt. interceperimus AD arcum equalem arcui AB et coniunxerimus DTI lineam, erit profecto in suppositione excentricitatis visus noster in T puncto et medietas DI linee sic se habebit ad TI lineam, sicut velocitas excentrici ad stelle velocitatem. Dico igitur quod, quandocunque in utraque suppositione stella erit in puncto I, standi phantasiam faciet, et quantumcunque arcum ex utraque parte I puncti ceperimus, arcus qui versus maximam longitudinem intercipietur progressum, qui vero versus minimam regressum stelle continebit.

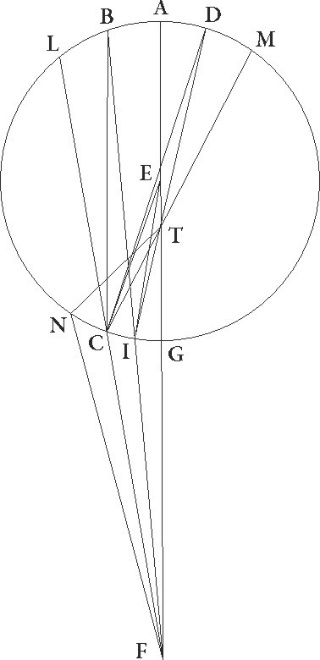Intercipiatur primo versus maximam, ut forte contigerit arcus CI, et protrahantur FCL et CTM linee, et coniungantur BC et DC et EC et EI linee. Quoniam igitur BI latus trianguli BCF maius est quam latus BC, maiorem BI linea ad IF habebit proportionem quam angulus IFC ad angulum IBC. Quare medietas etiam linee BI ad lineam IF maiorem habebit proportionem quam angulus IFC ad angulum dupplum anguli CBI, hoc est ad angulum CEI. Est autem proportio medietatis linee BI ad lineam IF proportio velocitatis epicycli ad stelle velocitatem. Quare angulus qui eam habet proportionem ad angulum CEI quam velocitas epicycli ad velocitatem stelle maior est angulo IFC. Sit igitur angulus IFN. Quoniam igitur in tempore in quo stella CI arcum epicycli transit, in eo tempore centrum epicycli pertransivit ad contrarium equalem arcum distantie que est ab FI ad FN, patet quia in eo tempore per minorem angulum ad visum nostrum CI epicycli arcus ad precedentia stellam traduxit, traduxit] corr. ex traducit G hoc est per angulum IFC, angulo per quem ipse epicyclus motu suo ad successionem transtulit, hoc est angulo IFN, et sic stella ad successionem facta est per angulum CFN.

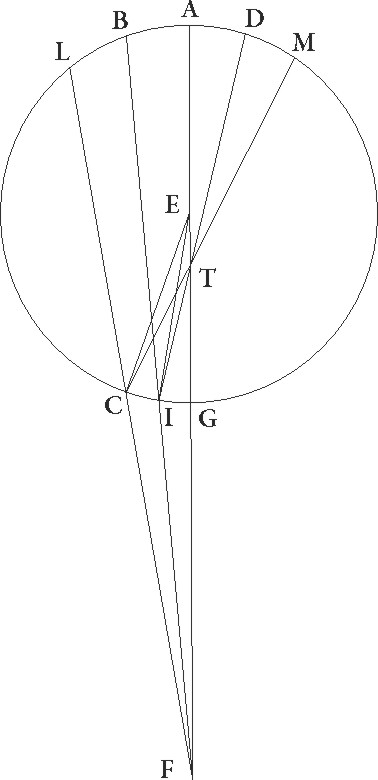Similiter si hec in excentrico ratiocinemur, quoniam BI linea ma〈i〉orem maiorem] maorem A proportionem habeat ad lineam IF quam angulus IFC ad angulum CBI, et coniunctim ergo linea BF maiorem habebit proportionem ad lineam FI quam angulus BCL ad angulum IBC. Sed sicut BF ad FI, sic DT ad TI. Est autem etiam BCL angulus equalis angulo DCM et angulus IBC angulo IDC. Maiorem ergo etiam DT habebit proportionem ad TI quam angulus DCM ad angulum IDC, quare coniunctim quoque DI linea maiorem habebit proportionem ad IT quam angulus ITC ad angulum IDC, et disiunctim ergo medietas linee DI maiorem habebit proportionem ad lineam IT quam angulus ITC ad angulum duplum anguli IDC, hoc est ad angulum IEC. Est autem proportio medietatis linee DI ad TI velocitatis excentrici ad stelle velocitatem. Minorem igitur habebit proportionem angulus ITC ad angulum IEC quam excentrici velocitatis ad stelle velocitatem. Angulus ergo qui eandem habet proportionem ad angulum IEC quam habet velocitas excentrici ad velocitatem stelle maior est angulo ITC. Sit rursum angulus ITN. Quoniam igitur in eodem tempore stella quidem per CI arcum ad precedentia mota fecit angulum CEI et a motu excentrici ad successionem translata est per angulum ITN maiorem angulo CTI, perspicuum est quod etiam sic ad successionem per angulum CTN pertransisse stella videbitur.

Facile autem intellectu est quod per eadem contrarium quoque demonstrabitur, si in eadem descriptione medietatem quidem LC linee ad lineam CF eam habere proportionem supposuerimus, quam habet epicycli velocitas ad stelle velocitatem, ut medietas etiam linee MC sic se habeat ad lineam TC, sicut velocitas excentrici ad stelle velocitatem, arcum vero CI versus minimam longitudinem ab LF linea interceptum intellexerimus. Nam si coniuncta fuerit linea LI feceritque triangulum LFI in quo intercepta sit FC linea maior quam FI habebit LC minorem proportionem ad CF quam angulus IFC ad angulum ILC. Quare medietas etiam linee LC ad lineam CF minorem habebit proportionem quam angulus IFC ad angulum duplum anguli ILC, hoc est ad angulum CEI, conversim quam antea demonstratum est, et sic per eadem colligetur contrarium quod videlicet angulus CEI ad angulum quidem IFC minorem habet proportionem quam velocitas stelle ad velocitatem epicycli, ad angulum vero ITC minorem quam velocitas stelle ad excentrici velocitatem. Quare cum angulus CEI qui eandem proportionem habebat maior fiat regrediendi quoque motus motu progrediendi maior fiet, perspicuum etiam est quod in quibuscunque longitudinibus non habet linea EG maiorem proportionem ad lineam GF quam velocitas epicycli habeat ad stelle velocitatem, non erit in in] ipsa add. et del. A ipsis possibile aliam lineam in proportione equali perducere, stellaque nec stare nec regredi unquam videbitur. Nam quoniam in triangulo ECF intercepta est linea EG non minore quam linea EC, minorem angulus GFC habebit proportionem ad angulum GEC quam EG linea ad lineam GF. Proportio autem ipsius EG ad ipsam GF non est maior quam proportio velocitatis epicicli ad stelle velocitatem. Minorem igitur etiam angulus GFC habebit proportionem ad angulum GEC quam velocitas epicycli ad stelle velocitatem. Quoniam igitur demonstratum est nobis, ubicunque id accidit, stellam progredi nec epicycli nec excentrici ullum inveniemus arcum ubi stella regredi videatur.

〈XII.2〉 Capitulum II: Demonstratio regressuum Saturni

Cum hec ita se habeant, reliquum est est] add. s. l. G ut per singulos planetas consequenter ad demonstratas suppositiones regressuum computationes faciamus initium a Saturno facientes hoc modo.

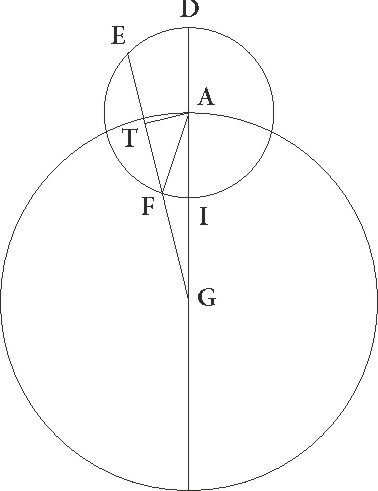
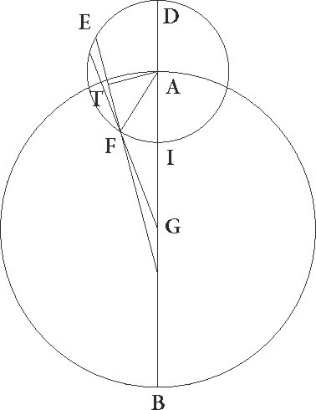Sit circulus AB qui centrum epicycli deferat cuius diameter AGB in qua centrum zodiaci, hoc est visus noster, supponatur esse in puncto G, descriptoque circa centrum A epicyclo DEFI, perducatur sic linea GFE, ut, cum ad eam deducatur perpendicularis AT, medietas linee EF, hoc est linea TF, proportionem habeat ad lineam FG quam habet velocitas epicycli ad stelle velocitatem, supponaturque primum situm epicycli esse in media longitudine, ut periodici longitudinis et inequalitatis motus equales proxime motibus fiant illis qui ad centrum zodiaci considerantur. Quoniam igitur in stella Saturni, qualium est medie longitudinis linea GA 60, talium AD semidiameter epicycli demonstrata est 6 30′, ita ut tota DG fiat 66 30′ et reliqua GI 53 30′ earundem, sitque rectangulum quod sub ipsis DG et GI continetur 3557 45′, quod est equale rectangulo sub EG et GF lineis contento, contento] post corr. G habebimus etiam ipsum rectangulum quod fit a lineis EG et GF 3557 45′ earundem. Rursus quoniam consequenter ad medios motus qualis unius est velocitas epicycli hoc est linea TF, talium est stelle velocitas, hoc est linea FG, 28 25′ 46′′ proxime, ut tota etiam EG linea 30 25′ 46′′ colligatur, rectangulum autem quod sub EG et GF lineis continetur 865 5′ 32′′ earundem, si per 865 5′ 32′′ partiemur 3557 45′ et numeri ex partitione facti 4 6′ 45′′ radicem 2 1′ 40′′ seorsum in TF, hoc est in unum, et in FG, hoc est in 28 25′ 46′′ multiplicaverimus, habebimus etiam TF talium 2 1′ 40′′ qualium est rectangulum sub EG et GF lineis contentum 3557 45′ et lineam FG 57 38′ 55′′. Quoniam igitur, si AF lineam coniunxerimus, talium est FT linea 2 1′ 40′′ qualium AF 6 30′, qualium vero 120, talium 37 26′ 9′′, erit profecto arcus quoque linee TF talium 36 21′ 15′ qualium est circulus qui rectangulo AFT circumscribitur 360, angulus autem FAT talium 36 21′ 15′′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 18 10′ 38′′ proxime. Rursus quoniam GFT tota talium colligitur 59 40′ 35′′ qualium est GIA que rectum angulum subtendit 60, qualium vero 120 talium 119 21′ 10′′, erit etiam arcus linee GT talium 168 5′ 39′′ qualium est circulus qui rectangulo AGT circumscribitur 360, angulus autem GAT talium 168 5′ 39′′ qualium duo recti sunt 360, qualium vero duo recti sunt 360, talium 84 2′ 50′′ proxime. Idcirco habebimus angulum quoque AGT reliquorum ad unum rectum 5 57′ 10′′, angulum autem FAI, remoto angulo FAT, habebimus 65 52′ 12′′. Quoniam igitur in prima quidem statione per GF lineam stella videtur, in oppositione vero Solis per lineam GI, patet quia, si centrum epicycli non moveretur ad successionem, tunc 65 52′ 12′′ gradus ipsius arcus FI continerent gradus anguli AGF 5 57′ 10′′ regressionis. Verum quoniam secundum expositam proportionem velocitatis epicycli ad velocitatem stelle gradibus inequalitatis iam dictis 65 52′′ 12′ congruunt longitudinis gradus 2 19′ proxime, habebimus regressum quidem ab altera statione ad Solis oppositionem reliquorum graduum 3 38′ 10′′ et dierum 69 in quibus proxime 2 19′ periodice longitudinis gradibus stella movetur, totum vero regressum graduum 7 16′ 20′′ et dierum 138.

Sed magnitudines etiam que in maxima longitudine fiunt per eadem consideremus, hoc est quando media inter stationes ad Solem oppositio in ipso maxime longitudinis excentrici puncto centrum epicycli sistit, stationum vero utraque in distantia propinqua demonstratis secundum mediam rationem gradibus 2 19′ ab oppositione, hoc est a maxima distantia excentrici secundum equatam longitudinem, in quo situ AG istius longitudinis linea indifferens esse a maxima per theoremata theoremata] corr. ex theoreumata G iam demonstrata invenitur, additio autem subtractiove que uni longitudinis gradui congruit 6 30′ sexagesimarum proxime reperitur, et sic equata longitudo ad inequalitatem equatam, hoc est apparens tunc epicycli velocitas ad apparentem stelle velocitatem, eam habet proportionem quam 0 53′ 30′′ ad 28 32′ 16′′.

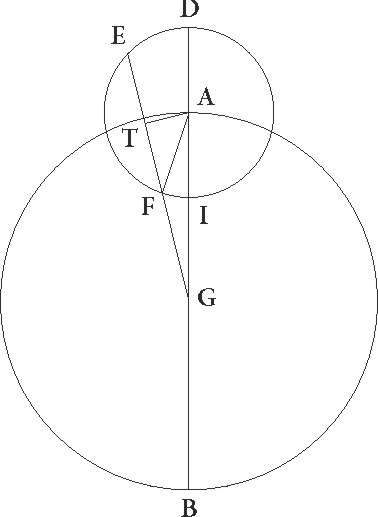Hac igitur eadem figura descripta, qualium est DA semidiameter epicycli 6 30′, talium erit GA indifferens a maxima longitudine 63 25′. Idcirco tota DG 69 55′ colligitur et reliqua GI 56 55′ et quod ab ipsis fit, hoc est quod sub EG et GF, rectangulum continetur est 3979 25′ 25′′. Est autem etiam, qualium FT linea velocitatis epicycli supponitur 0 53′ 30′′, talium GF velocitas stelle 28 32′ 16′′ et tota EG linea 30 19′ 12′′, rectangulum autem quod continetur sub EG et GF lineis talium 865 17′ 50′′. Si ergo rursum 3979 25′ 25′′ partiemur per 865 17′ 50′′ et facti ex partitione numeri 4 35′ 56′′ radicem capiemus, hoc est 2 8′ 40′′, eamque seorsum multiplicabimus in lineam TF, hoc est in 0 53′ 30′′, et in lineam FG similiter, hoc est in 28 32′ 16′′, habebimus lineam quidem TF talium 1 54′ 44′′ qualium AF linea est 6 30′ et AG 63 25′, lineam vero GF 61 11′ 52′′ earundem, totam autem GT 63 6′ 36′′. Quare qualium est AF que rectum angulum subtendit 120, talium erit TF 35 18′ 9′′, et qualium GA que rectum subtendit 120, talium GT linea 119 25′ 11′′. Idcirco arcus a linee TF talium erit 34 13′ 4′′ qualium est circulus qui rectangulo AFT circumscribitur 360, arcus autem linee GT talium 168 43′ 38′′ qualium est circulus qui rectangulo AGT circumscribitur 360, qualium ergo recti duo sunt 360 talium angulus quidem FAT erit 34 13′ 4′′, angulus vero GAT 168 43′ 38′′, qualium autem quatuor recti sunt 360, talium angulus FAT 17 6′ 32′′ et angulus GAT 84 21′ 49′′, et sic reliquum quidem AGT angulum qui est ab altera stationum ad oppositionem, si epicyclus non moveretur, graduum haberemus 5 38′ 11′′, reliquum vero FAI FAI] corr. ex FIAI G angulum qui est apparentis in eadem longitudine motus in epicyclo graduum 67 15′ 17′′, quibus quoniam secundum proportiones velocitatum in maxima longitudine gradus equate longitudinis congruunt 2 6′ 6′′, habebimus medietatem totius regressus reliquorum graduum 3 32′ 5′′ et dierum 70 20′, in quibus proxime stella movetur periodicos gradus 2 21′ 35′′ congruentes expositis equate longitudinis gradibus 2 6′ 6′′, totum autem regressum graduum 7 4′ 10′′ et dierum 140 40′.

Sed minime quoque longitudinis magnitudines modo per similia in eadem descriptione consideremus, quando media inter stationes oppositio in ipsa minima excentrici longitudine accidit, et utraque stationum in exposita secundum motum motum] post corr. G longitudinis distantia ab oppositione, hoc est a minima excentrici longitudine, in quo situ AG quidem linea longitudinis istius indifferens similiter a minima reperitur, additio autem subtractiove que gradui congruit uni sexagesimarum 7 20′ proxime. Quare hic etiam apparens epicycli velocitas eam habet proportionem ad apparentem stelle velocitatem quam 1 7′ 20′′ ad 28 18′ 26′′, et idcirco qualium est TF linea 1 7′ 20′′, talium GF quidem colligitur 28 18′ 26′′, tota vero EG talium 30 33′ 6′′, rectangulum autem quod sub EG et GF lineis continetur 864 49′ 58′′. Et quoniam qualium est DA semidiameter epicycli 6 30′, talium etiam est AG que est indifferens a minima longitudine 56 35′, et propterea tota DG 63 5′ earundem colligatur, et GI reliqua 50 et sexagesimarum 5, rectangulumque sub ipsis hoc est sub EG et GF contentum 3159 25′ 25′′, si partiemur similiter 3159 25′ 25′′ per 864 49′ 58′′ et facti ex partitione numeri 3 39′ 12′′ radicem que est 1 54′ 45′′ seorsum multiplicabimus tum in lineam TF, hoc est in 1 7′ 20′′, tum in lineam FG, hoc est in 28 18′ 26′′, habebimus lineam quidem TF talium 2 8′ 43′′ qualium est AF semidiameter epicycli 6 30′ et AG longitudinis istius linea 56 35′, lineam vero GF 54 6′ 22′′ earundem, totam autem GT 56 15′ 5′′. Qualium igitur est AF que rectum angulum subtendit 120, talium TF erit 39 36′ 18′′, qualium vero GA que rectum similiter subtendit 120, talium GT 119 17′ 46′′. Idcirco arcus etiam linee FT talium erit 38 32′ 34′′ qualium est circulus qui AGT rectangulo circumscribitur 360. Quare qualium duo recti sunt 360 talium FAT quoque angulus erit 38 32′ 34′′, angulus vero GAT 167 34′ 54′′, qualium autem quatuor recti sunt 360, talium angulus FAT 19 16′ 17′′ et angulus GAT 83 47′ 27′′, et reliquum igitur AGT angulum ab altera stationum ad oppositionem regressus penes velocitatem stelle partium habebimus 6 12′ 33′′, reliquum autem FAI angulum apparentis in epicyclo in eadem longitudine motus partium 64 31′ 10′, quibus, quoniam secundum proportionem velocitatum que in minima longitudine fiunt 2 33′ 28′′ gradus equate longitudinis congruunt, medietatem quidem totius regressus graduum habebimus 3 39′ 5′′ et dierum 68 in quibus proxime stella medie medie] add. s. l. G movetur, congruentes expositis equate longitudinis gradibus 2 33′ 28′′ gradus periodicos 2 16′ 45′′, totum vero regressum 7 18′ 10′′ et dierum 136

〈XII.3〉 Capitulum III : Demonstratio regressuum Iovis

In stella vero Iovis secundum computationes que in media longitudine fiunt proportio quidem TF ad GF ea colligitur que est unius ad 10 10] 59 add. et del. AG 51′ 29′′, proportio autem EG ad FG 12 51′ 29′′ ad 10 51′ 29′′, rectangulum vero quod sub ipsis continetur est 139 37′ 39′′, et rursus proportio linee GA ad AD est 60 ad 11 30′ et proportio GD ad GI est 71 30′ ad 48 30′, et rectangulum sub ipsis contentum 3467 55′. Facti autem ex partitione numeri 24 59′ radix 4 59′ 1′′ multiplicata in prepositam linee TF ad FG proportionem facit lineam quidem TF ad expositas GA et AF magnitudines 4 59′ 1′′, lineam vero GF 54 6′ 44′′ earundem, totam autem GT 59 5′ 45′′, et idcirco ad proportionem etiam partium 120 utriusque AF et AG linearum que rectum angulum subtendunt TF quidem linea erit 52 0′ 10′′, GT vero 118 11′ 4′′, et arcus sui linee quidem FT graduum 51 21′ 41′′, linee autem GT 164 55′′. Consequenter autem angulus etiam FAT talium 25 40′ 50′′ proxime colligitur qualium quatuor recti sunt 360, angulus vero GAT 8 2′ 28′′ earundem, et angulus FGA ipsius regressus penes velocitatem stelle reliquorum 9 57′ 32′′, angulus autem FAI apparentis inequalitatis graduum 54 21′ 38′′, quibus cum secundum expositas ipsius per longitudinem motus proportiones gradus congruant 5 1′ 24′′, fit regressus medietas graduum 4 56′ 8′′ et dierum 60 30′ proxime, totus vero regressus graduum 9 52′ 16′′ et dierum 121. Longitudo autem que est in quinque graduum distantia a maxima et a minima longitudine indifferenti quodam minor est quam maxima et maior quam minima.

Secundum vero computationes que in maxima longitudine fiunt additio quidem atque subtractio equationis 5 10 sexagesimarum invenitur, et idcirco linee quoque TF ad GF lineam proportio est 0 54′ 50′′ ad 10 56′ 39′′, rectangulum vero quod sub ipsis continetur est 139 46′ 42′′, et rursum proportio GA linee ad AD lineam est 62 45′ ad 11 30′, proportio autem DG ad GI est 74 15′ ad 51 15′, et rectangulum quod sub ipsis continetur 3805 18′ 45′′. Radix vero numeri 27 13′ 26′′ qui ex partitione fit, que est 5 13′ 4′′, multiplicata in expositam TF et FG linearum proportionem lineam quidem FT facit ad expositas GA et AF linearum magnitudines 4 46′ 6′′, lineam vero GF 57 6′ 19′′ earundem, GT autem 61 52′ 25′′, idcirco etiam ad proportionem 120 utriusque linearum AF et AG que rectum angulum subtendunt FT quidem linea est 49 45′ 23′′, GT autem 118 19′ 27′′ et arcus sui FT quidem graduum 48 59′ 34′′, GT vero 160 49′ 36′′. Ad has lineas consequenter angulus quoque FAT talium est 24 29′ 47′′ qualium quatuor recti sunt 360, angulus vero GAT 80 24′ 48′′ earundem, earundem] corr. ex eorundem G et reliquorum FGA quidem angulus ipsius regressus penes stelle velocitatem graduum est 9 35′ 12′′, FAI vero angulus apparentis inequalitatis 55 55′ 1′, quibus cum secundum proportiones maxime distantie 4 40 35′′ equate longitudinis gradus congruant, et periodice 5 6′ 35′′, colligitur regressus medietas graduum 4 50′ 37′′ et dierum 61 30′ proxime, totus autem regressus graduum 9 49′ 18′′ et dierum 123.

Secundum vero computationes que in minima distantia fiunt additio equationis atque subtractio 5 40′ sexagesimarum invenitur, idcirco etiam proportio linee EF ad lineam FG est 1 5′ 40′′ ad 10 45′ 49′′ et proportio EG ad GF 12 57′ 9′′ ad 10 45′ 45′′, rectangulum vero sub ipsis contentum 135 24′ 56′′. Rursus proportio linee GA ad AD lineam est 57 15′ ad 11 30′, et proportio DG ad GI 68 45′ ad 45 45′, et rectangulum sub ipsis contentum 3145 18′ 45′′, numeri vero ex partitione facti 22 33′ 39′′ radix 4 45′ 0′′ multiplicata in prepositam proportionem TF et FG linearum facit ad expositas GA et AF linearum magnitudines lineam quidem TF partium 5 11′ 55′′, lineam autem FG 51 7′ 38′′ earundem, et totam GT 56 19′ 33′′. Idcirco ad rationem etiam 120 utriusque linearum FA et AG que rectum subtendunt FT quidem est 54 14′ 47′′, GT autem 118 3′ 46′′, arcuum autem FT quidem arcus graduum est 53 45′ 4′′, GT vero 159 22′ 40′′, ad hos arcus consequenter FAT quoque angulus talium est 26 52′ 39′′ qualium quatuor recti sunt 360, angulus vero GAT 79 41′ 20′′, et reliquorum FGA quidem angulus ipsius regressus propter velocitatem stelle graduum est 10 18′ 40′′, FAI autem angulus apparentis inequalitatis 52 48′ 48′′, quibus cum secundum proportiones minime distantie equate quidem longitudinis 5 21′ 20′′ gradus congruant, periodice autem 4 54′ 20′′ colligitur, regressus graduum 9 54′ 40′′ et dierum 118.

〈XII.4〉 Capitulum IIII : Regressuum Martis demonstratio

In stella vero Martis secundum medie longitudinis conputationes proportio quidem FT linee ad FG ea colligitur que est unius ad 0 52′ 51′′, proportio vero EG linee ad GF 2 52′ 51′′ ad 0 52′ 51′′ et rectangulum sub ipsis contentum 2 32′ 15′′, et rursum GA linee ad lineam AD proportio est 60 ad 39 30′, proportio vero DG linee ad GI 99 30′ ad 20 30′, et rectangulum sub ipsis contentum 2039 45′. Facti autem ex partitione numeri 803 50′ 50′′ radix 28 21′ 8′′ multiplicata ad prepositam TF et FG linearum proportionem facit ad expositas GA et AF linearum magnitudines lineam quidem TF 28 21′ 8′′, lineam vero GF 24 58′ 25′′ earundem, et totam GT 53 19′ 33′′. Idcirco etiam ad rationem 120 utriusque AF et AG linearum que rectum angulum subtendunt FT quidem linea colligit 86 8′ 0′′, GT autem 106 39′ 6′′, et suorum arcuum FT quidem graduum 91 44′ 34′′, GT autem 125 26′ 10′′, ad quos consequenter angulus quidem FAT talium est 45 52′ 17′′ qualium quatuor recti sunt 360, GAT vero angulus 62 43′ 5′′ earundem, earundem] corr. ex eorundem G et reliquorum FGA quidem angulus ipsius regressus qui est propter stelle velocitatem graduum 27 16′ 55′′, FAI autem inequalitatis angulus 16 50′ 48′′, quibus cum secundum expositam motus longitudinis proportionem gradus congruant 19 7′ 33′′, fit regressus medietas graduum 8 9′ 22′′ et dierum 36 30′ proxime, totus vero regressus graduum 16 18′ 44′′ et dierum 73. Longitudo autem que est in hac distantia maxime minimeve longitudinis a stationibus 20 sexagesimis minor est quam maxima et maior quam minima. Secundum vero computationes que in maxima distantia fiunt additio equationis atque subtractio que uni congruit gradui 10 20 sexagesimarum invenitur. Idcirco etiam proportio linee TF ad lineam FG est 0 49′ 40′′ ad 1 3′ 11′′, proportio vero EG ad GF 2 42′ 31′′ ad 1 3′ 11′′, et rectangulum sub ipsis contentum 2 51′ 8′′. Et rursum proportio linee GA ad AI lineam est 65 44′ ad 39 30′, et DG ad GI 105 10′ ad 26 10′, et rectangulum sub ipsis contentum 2751 51′ 40′′, et numeri 964 48′ 47′′ ex partitione facti radix 31 3′ 41′′ multiplicata ad prepositam TF et FG linearum proportionem facit ad expositas GA et AF linearum magnitudines lineam quidem TF partium 25 42′ 43′′, lineam vero FG 32 42′ 34′′ earundem, et totam GT 58 25′ 17′′. Idcirco etiam ad rationem 120 utriusque AF et AG linearum que rectum angulum subtendunt FT quidem linea est 78 6′ 44′′, GT vero 106 45′ 36′′ similiter, arcuum autem suorum FT quidem graduum est 81 13′ 28′′, GT autem 125 39′ 46′′, ad quos arcus consequenter angulus etiam FAT talium erit 40 36′ 34′′ qualium quatuor recti sunt 360, angulus vero GAT 62 49′ 53′′ earundem, earundem] corr. ex eorundem G et reliquorum angulus quidem FGA ipsius regressus qui est propter velocitatem stelle graduum est 27 17′, angulus autem FAI inequalitatis apparentis 22 13′ 19′′. 19''] quibuscum et ex add. et del. G Quibus cum secundum proportiones maxime longitudinis 17 13′ 21′′ equate longitudinis gradus congruant et periodice 20 58′ 21′′, colligitur regressus medietas graduum 9 56′ 46′′ et dierum 40 proxime, totus vero regressus graduum 19 53′ 32′′ et dierum 80.

Secundum autem computationes que in minima longitudine fiunt additio atque subtractio equationis 12′ 12'] 48 add. et del. A 40′′ sexagesimarum invenitur. Idcirco etiam proportio TF linee ad FG est 1 12′ 40′′ ad 0 40′ 11′′, proportio autem EG ad GF est 3 5′ 37′′ ad 0 40′ 11′′, et rectangulum quod sub ipsis continetur est 2 4′ 14′′. Rursus proportio GA ad AD est 54 20′ ad 39 30′, et proportio DG ad GI 93 50′ ad 18 50′ et rectangulum sub ipsis contentum 1397 51′ 40′′, radix autem numeri 672 23′ ex partitione facti que est 25 55′ 38′′ multiplicata in proportionem expositam TF et FG linearum facit lineam quidem TF ad expositas G et AF linearum magnitudines 31 24′ 3′′, lineam vero GF 17 21′ 51′′ earundem, totam vero GT 48 45′ 54′′. Idcirco ad rationem etiam 120 utriusque linearum AF et AG que rectum angulum subtendunt FT quidem est 95 23′ 42′′, GT vero 107 42′ 7′′, arcuum autem suorum FT quidem graduum est 105 18′ 10′′, GT vero 127 40′ 22′′, ad hos arcus consequenter angulus quoque FAT talium est 52 39′ 5′′ qualium quatuor recti sunt 360, angulus vero GAT 63 50′ 11′′ earundem, earundem] corr. ex eorundem G et reliquorum FGA quidem angulus ipsius regressus propter stelle velocitatem graduum est 26 9′ 49′′, FAI autem angulus apparentis inequalitatis graduum 11 11′ 6′′. Quibus cum secundum proportiones minime longitudinis 20 33′ 42′′ gradus equate longitudinis congruant et periodice 16 52′ 52′′, colligitur medietas ipsius regressus graduum 5 36′ 7′′ et dierum 32 15′ proxime, totus vero regressus graduum 11 12′ 14′′ et dierum 64 30′.

〈XII.5〉 Capitulum V : Regressuum Veneris demonstratio

In stella autem Veneris secundum medie quidem longitudinis computationes proportio linee TF ad FG lineam colligitur ea que est unius ad 0 37′ 31′′, et proportio EG ad GF 2 37′ 31′′ ad 0 37′ 31′′, et rectangulum sub ipsis contentum 1 38′ 30′′, et rursum proportio linee GA ad lineam AD est 60 ad 43 10′, et proportio DG ad GI 103 10′ ad 16 50′, et rectangulum sub ipsis contentum 1736 38′ 20′′. Numeri autem 1057 56′ ex partione facti radix 32 31′ multiplicata in expositam proportionem TF et FG linearum facit lineam quidem TF ad expositas GA et AF linearum magnitudines 32 31′ 29′′, lineam vero GF 20 20′ 11′′ et totam GT 52 51′ 40′′. Idcirco ad rationem etiam 120 utriusque linearum AF et AG que rectum angulum subtendunt linea quidem FT 90 24′ 58′′ partium est, GT vero 105 43′ 20′′, arcuum autem TF quidem graduum est 97 47′ 0′′, 〈G〉T GT] T A vero 123 31′ 49′′, ad hos arcus consequenter FAT quoque angulus talium est 48 53′ 30′′ qualium quatuor recti sunt 360, angulus vero GAT 61 45′ 54′′ proxime earundem, earundem] corr. ex eorundem G et reliquorum angulus quidem FGA ipsius regressus qui est propter stelle velocitatem graduum est 28 14′ 6′′, Angulus vero FAI inequalitatis 12 52′ 24′′. Quibus cum secundum expositam mediam motus longitudinis proportionem gradus congruant 20 35′ 19′′, medietas regressus colligitur gradum 7 38′ 47′′ et dierum 20 50′ proxime, totus autem regressus graduum 15 17′ 34′′ et dierum 41 40′.

Longitudo autem que est in hac distantia maxime minimeve longitudinis a stationibus 5 sexagesimis proxime minor est quam maxima et maior quam minima. Secundum vero computationes que in maxima longitudine fiunt additio subtractiove equationis 2 20′ sexagesimarum invenitur. Idcirco etiam proportio linee TF ad lineam FG est 0 57′ 40′′ ad 0 39′ 51′′, et proportio EG ad GF 2 35′ 11′′ ad 0 39′ 51′′, rectangulum vero sub ipsis contentum 1 43′ 4′′. Rursus proportio GA ad AD est 61 10′ ad 43 10′, et DG ad GI 104 20′ ad 18 0′ et quadrangulum sub ipsis contentum 1878. Facti autem ex partitione numeri 1093 16′ 23′′ radix 33 3′ 53′′ multiplicata in proportione TF et FG linearum expositam facit TF quidem lineam ad magnitudines dictas GA et AF linearum partium 31 46′ 44′′, lineam vero GF 21 57′ 38′′ earundem, et totam GT 53 44′ 22′′, et idcirco ad proportionem etiam 120 utriusque linearum AF et AG que rectum angulum subtendunt FT quidem linea est 88 20′ 30′′, GT autem 105 25′ 44′′, et arcuum suorum FT quidem graduum est 94 48′ 54′′, arcus vero GT 122 56′ 27′′ ad hos arcus consequenter angulus quoque FAT talium erit 47 24′ 27′′ qualium quatuor recti sunt 360, angulus vero GAT 61 28′ 14′′ eorundem, et reliquorum FGA quidem angulus regressus propter velocitatem stelle graduum est 28 31′ 46′′, angulus autem FAI apparentis inequalitatis 14 3′ 47′′ quibus cum secundum proportiones maxime longitudinis congruant equate equatae] corr. ex equate G quidem longitudinis gradus 20 19′ 3′′, periodice vero 21 9′ 3′′, medietas quidem regressus colligitur graduum 8 12′ 43′′ et dierum 21 30′ proxime, totus vero regressus graduum 16 25′ 26′′ et dierum 43.

Secundum autem computationes que fiunt in minima longitudine additio equationis subtractiove sexagesimarum 2 20′ invenitur, propterea etiam proportio quidem FT ad FG est 12 20′ ad 0 35′ 11′′, proportio autem EG ad GF 2 39′ 51′′ ad 0 35′ 11′′ et rectangulum sub ipsis contentum 1 33′ 44′′, et rursus proportio GA ad AD est 58 50′ ad 43 10′ et DG ad GI 102 0′ ad 15 40′ et rectangulum sub ipsis contentum 1558 0′. Numeri vero ex partitione facti 1022 54′ 7′′ radix 31 58′ 58′′ multiplicata in proportione linearum TF et FG facit lineam TF ad suppositas GA et AF magnitudines 33 13′ 36′′, lineam vero GF 18 45′ 16′′ earundem, et totam GT 51 58′ 52′′, idcirco etiam ad proportionem 120 utriusque AF et AG linearum que rectum angulum subtendunt FT quidem linea erit 92 22′ 3′′, GT autem 106 1′ 23′′, de arcubus vero FT quidem linee arcus graduum est 100 39′ 34′′, GT autem 124 8′ 22′′, et consequenter FAC angulus talium 50 19′ 47′′ qualium quatuor recti sunt 360, et angulus GAT 62 4′ 11′′ eorundem, et reliquorum FGA quidem angulus regressus propter velocitatem stelle graduum erit 27 55′ 49′′, FAI autem apparentis inequalitatis angulus 11 44′ 24′′, quibus cum secundum proportiones minime distantie equate quidem longitudinis gradus congruant 20 53′ 30′′, periodice vero 20 et sexagesime 4′ 30′′, medietas regressus graduum consequenter colligitur 7 2′ 19′′ et dierum 20 20′ proxime, totus autem regressus graduum 14 4′ 38′′ et dierum 40 40′.

〈XII.6〉 Capitulum VI : Regressuum Mercurii demonstratio

In Mercurio etiam rursus secundum computationes que in media longitudine fiunt TF quidem linee ad FG lineam proportio ea colligitur que est unius ad 3 9′ 8′′, EG vero ad GF 5 9′ 8′′ ad 3 9′ 8′′, et rectangulum sub ipsis contentum 16 14′ 27′′. Rursus GA linee ad GI 60 ad 22 30′, et DG ad GI 82 30′ ad 37 30′, et rectangulum sub ipsis contentum 30 93′ 45′′ et numeri vero 190 29′ 31′′, ex partitone facti radix 13 43′ 7′′′ multiplicata in proportione linearum TF et FG facit lineam TF ad suppositas GA et AF magnitudines 13 48′ 7′′, et lineam FG 43 30′ 24′′, totam vero GT 57 18′ 31′′. Propterea etiam ad rationem 120 utriusque AF et AG linearum que rectum angulum subtendunt FT quidem erit 73 36′ 37′′, GT autem 114 37′ 2′′, et arcuum suorum FT quidem graduum 73 40′ 28′′, arcus vero linee GT 145 32′ 52′′, et consequenter angulus etiam AFT talium erit 36 50′ 14′′ qualium quatuor recti sunt 360, angulus autem TAG 72 46′ 26′′ eorundem, et reliquorum angulus quidem FGA ipsius regressus qui est propter velocitatem stelle graduum graduum] corr. ex gradum A erit 17 13′ 34′′, angulus vero FAI graduum inequalitatis 34 56′ 12′′, quibus cum secundum expositam longitudinis motus proportionem congruant gradus 11 4′ 59′′, medietas quidem regressus relinquitur graduum 6 8′ 35′′ et dierum 11 15′ proxime, totus autem regressus graduum colligitur 12 17′ 10′′ et dierum 22 30′.

Secundum autem computationes que in maxima longitudine fiunt, hoc est quando equata longitudo 11 gradibus distat a maxima longitudine quibus equales atque medii congruunt 11 30′ proxime, equationis additio subtractiove que uni gradui congruit 2 20′ sexagesimarum proxime invenitur, et propterea TF etiam linee proportio ad FG est 0 57′ 40′′ ad 3 11′ 28′′, linee vero EG ad GF 5 6′ 48′′ ad 3 11′ 28′′, et rectangulum sub ipsis contentum 16 19′ 2′′ et rursus GA quidem linee ad ED proportio est 68 36′ ad 22 30′, DG autem ad GI 91 6′ ad 46 6′, et rectangulum sub ipsis contentum 4199 42′ 36′′, numeri autem 257 22′ 44′′ ex partitione facti radix 16 2′ 35′′ multiplicata in expositam TF et FG linearum proportionem facit IF quidem lineam ad suppositas GA et AF linearum magitudines 15 25′ 9′′, lineam vero FG 51 13′ 43′′, et totam GT 66 36′ 52′′, idcirco etiam ad rationem 120 utriusque linearum FA et AG que rectum angulum subtendunt FT quidem partium est 82 14′ 8′′, GT autem 116 31′ 36′′, et arcus FT graduum 86 31′ 4′′, et TG arcus 152 27′ 56′′, ad quos consequenter FAC angulus talium est 43 15′ 32′′ qualium quatuor recti sunt 360, angulus autem TAG 76 13′ 52′′ eorundem, et et] add. s. l. G reliquorum angulus quidem FGA ipsius regressus qui est propter stelle velocitatem graduum erit 13 46′ 2′′, angulus vero FAI apparentis inequalitatis graduum 32 52′ 26′′, quibus cum secundum maxime longitudinis proportiones congruant equate quidem longitudinis gradus 9 48′ 51′′, periodice vero 10 16′ 51′′, medietas quidem regressus relinquitur graduum 3 57′ 11′′ et dierum 10 30′ proxime, totus totus] add. s. l. G autem regressus graduum 7 54′ 22′′ et dierum 21.

Secundum autem proportiones que in minimis longitudinibus fiunt que longitudines sunt in distantiis 120 periodicorum graduum a maxima longitudine additio equationis subtractiove que colligitur ex eo quod congruit 11 gradibus qui ex utraque parte minimarum longitudinum sunt invenitur 0 1′ 30′′ proxime, et propterea etiam TF ad FG proportio est 1 1′ 30′′ ad 3 7′ 38′′, EG autem ad GF 5 10′ 38′′ ad 3 7′ 38′′, et rectangulum sub ipsis contentum 16 11′ 25′′. Et rursus GA ad AD proportio est sicut 55 42′ proxime ad 22 30′, et DG ad GI sicut 78 12′ ad 32 12′, et rectangulum sub ipsis contentum 2594 14′ 24′′, et numeri 160 21′ 29′′ ex partitione facti radix 12 39′ 48′′ multiplicata seorsum in proportione TF et FT linearum prepositam facit lineam quidem TF ad suppositas GA et AF linearum magnitudines 12 58′ 47′′, lineam vero FG 39 36′ 4′′, et totam GT 52 34′ 51′′ earundem, et propterea etiam ad rationem 120 utriusque AF et AG linearum que rectum angulum subtendunt TF linea quidem erit 69 13′ 31′′, TG vero 113 16′ 48′′, et arcus linee IF graduum 70 27′ 44′′, TG vero arcus graduum 181 28′ 14′′, et consequenter TAF quidem angulus talium est 35 13′ 52′′ qualium quatuor recti sunt 360, angulus vero TAG 70 44′ 7′′ eorundem, et reliquorum angulus quidem FAG ipsius regressus qui est propter stelle velocitatem graduum erit 19 15′ 53′′, angulus autem FAI apparentis inequalitatis graduum 35 30′ 15′′, quibus cum secundum prepositas proportiones equate quidem longitudinis gradus congruant 11 39′ 30′′, periodice vero 11 31′ 30′′, medietas quidem regressus relinquitur graduum 7 36′ 23′′ et dierum 11 30′ proxime, totus autem regressus 15 12′ 46′′ et dierum 23. 23] corr. ex 25 A

Et sic demonstrate magnitudines conveniunt proxime cum illis que per apparentia in singulis planetarum inveniuntur. Cepimus autem congruentias motuum longitudinis que fiunt in maximis et minimis longitudinibus hoc modo. Nam, gratia exempli, quoniam in motibus maxime longitudinis Martis demonstravimus arcum epicycli apparentem qui est ab altera statione ad oppositionem, hoc est qui ad centrum zodiaci percipitur, graduum 22 13′ 19′′ et congruentes istis periodice longitudinis gradus secundum proportionem unius ad 1 3′ 11′′ sunt 21 10′ proxime, etsi precise non totidem sint, propterea quod proportiones velocitatum in stationibus exposite non eedem sunt per totos regressus, non tamen adeo multum a veritate differunt, ut congruens additio subtractiove que est graduum 3 45′ proxime sensibili aliquo differat de quo curandum sit, his subtractis a gradibus epicycli 22 13′ 19′′, —in maximis enim longitudinibus maiores sunt apparentes in epicyclo motus quam periodici—, invenimus congruentem ipsis periodicum inequalitatis motum ab altera stationum ad oppositionem graduum 18 28′ 19′′. Quibus quoniam per proportionem mediorum motuum congruunt gradus periodici motus 20 48′ 21′′, his quoniam precise capti sunt pro 21 10′ usi sumus. Additionis autem subtractionisve gradus 3 45′, —totidem enim proxime hic quoque sunt, quoniam in maximis longitudinibus apparentes secundum longitudinem motus minores sunt quam periodici—, subtraximus ab ipsis, et sic apparentem preposite longitudinis motum secundum longitudinem invenimus graduum 17 13′ 21′′.

〈XII.7〉 Capitulum VII : Computatio tabule stationum

Verum ut etiam in m〈e〉diis mediis] corr. ex mdiis G longitudinibus que sunt inter mediam et maximam minimamve facile possimus invenire in quibus particulis epicycli singuli planete standi phantasiam faciunt, tabulam composuimus versuum 31 31] corr. ex 30 A et ordinum 12, quorum primi duo numeros periodice longitudinis continent per sex gradus omnes adauctos, reliqui vero decem distantias equate inequalitatis singulorum quinque ab aparentibus maximis epicyclorum longitudinibus primi quidem in singulis ordines primarum stationum et secundi secundarum, harum magnitudines a predemonstratis de mediis minimis maximisque longitudinibus et ab excessibus qui sunt in intermediis longitudinibus cepimus de quibus dictum est in iis que de tabulis inequalitatum exposita nobis sunt, cum de appositione sexagesimarum octavi ordinis sermo haberetur. In singulis enim periodice longitudinis motibus una cum magnitudine maxime differentie inequalitatis distantie quoque in epicyclo in quibus stationum perspicitur differentia demonstrantur. Sed primum quoniam demonstrati regressus qui fiunt in maximis minimisque longitudinibus non continent stationes que ibi fiunt quando centra epicyclorum in ipsis maximis minimisque longitudinibus sunt, sed quando determinatam quandam distantiam in singulis planetis habent, cepimus cepimus] post corr. G etiam ab istis eas magnitudines que ipsis maximis et minimis longitudinibus congruunt hoc modo.

Primum in stellis Saturni ac lovis, quoniam nullo sensibili de quo curandum sit distantie epicyclorum que sunt in ipsis minimis et maximis longitudinibus differunt ab expositorum expositorum] post corr. G locis distantiis, inventos in eis inequalitatis numeros qui colliguntur ab apparentibus maximis epicyclorum longitudinibus in versibus suis congruenter apposuimus, hoc est maximarum quidem longitudinum in versibus qui 360 numerum continent, minimarum vero in versibus qui 180 numerum continent. Demonstratum autem est in stella Saturni quod distantia que fit in maxima excentricitatis longitudine a minima epicycli graduum est 67 15′ proxime, que autem fit in minima longitudine 64 31′. In stella vero Iovis distantia quidem que fit in maxima longitudine graduum est 55 55′, que vero in minima 52 49′. Congruentes igitur his a maximis epicyclorum longitudinibus numeros, ut facilius capiantur, in quatuor ordinibus qui deinceps ad longitudinis motum sunt in propriis versibus apposuimus, in versu quidem qui 360 maxime longitudinis numerum continet in tertio quidem ordine gradus prime stationis Saturni 112 45′, in quarto vero gradus secunde stationis 247 15′, et similiter in quinto gradus stationis p〈r〉ime primae] pimae A Iovis 124 5′, in sexto secunde stationis 235 55′. In versu autem qui minime longitudinis numerum 180 continet eodem ordine similiter gradus 115 29′ et 244 31′, eodemque modo gradus 127 11′ et 232 47′.

In Marte autem quoniam demonstratum est, quando 20 58′ periodicis gradibus centrum epicycli a maxima distat excentrici longitudine, tunc standi phantasiam a stella fieri distareque ab apparente minima epicycli longitudine gradibus 22 13′, quoniamque motus qui fit in media distantia gradus continet 16 51′, erit excessus graduum 5 22′. Est autem maxima longitudo talium 66 qualium media 60 et excessus iparum 6, longitudo vero in preposita a maxima longitudine distantia graduum erat 65 40′ et excessus eius ad mediam 5 40′. Multiplicavimus igitur 6 in 5 22′, factumque numerum per 5 40′ partiti invenimus excessum qui est ad mediam distantiam in ipsa maxima longitudine graduum 5 41′ proxime, et sic ab apparente minima epicycli longitudine gradus colliguntur 22 32′, a maxima vero longitudine prime quidem stationis 157 28′, quos in ordine septimo in versu qui continet numerum 360 ponemus, secunde vero stationis gradus 202 32′ in ordine octavo eodemque versu.

Similiter quoniam quando 16 53′ periodicis gradibus distat centrum epicycli in minima longitudine, tunc standi phantasiam facit, distatque ab apparente apparente] corr. ex aparente G minima epicycli gradibus 11 11′, fitque sic excessus ad mediam distantiam graduum 5 40′, et longitudinum minima quidem est 54 earundem secundum excessum 6 ad mediam, que vero est preposite distantie a minima excentrici longitudine 54 20′, et excessus eius ad mediam 5 40′, habebimus totum excessum qui fit in ipsa minima longitudine graduum 6, et idcirco motum quidem qui est ab aparente minima epicycli graduum 10 51′, qui vero est a maxima prime quidem stationis graduum 169 9′, secunde autem 190 51′, quos apponemus in versu qui habet numerum 180 in congruentibus ordinibus.

In Stella autem Veneris quoniam demonstratum est, quando per longitudinem 21 9′ periodicis gradibus centrum epicycli distat a maxima excentrici excentrici] corr. ex centrici G longitudine, tunc stellam phantasiam standi facere, distareque ab apparente minima epicycli 14 4′ gradibus, et motum qui fit in longitudine media 12 52′ graduum esse, itaque fieri ut excessus sit gradus unius et sexagesimarum 12 et ad hec maximam longitudinem talium 61 15′ qualium media 60, ut excessus ad mediam sit 1 15′, et longitudinem in presupposita a maxima longitudine distantia 61 10′, et excessus ad mediam mediam] corr. ex medium G sit 1 10′, multiplicavimus rursum 1 10′ in 1 12′, factumque numerum per 1 10′ partiti invenimus excessum ad mediam distantiam in ipsa maxima longitudine 1 17′, et sic ab apparenti minima epicycli gradus colliguntur 14 9′, a maxima vero prime quidem stationis 165 51′, quos in ordine nono et in versu numeri 360 conscribemus, secunde vero stationis gradus 194 9′, quos in ordine 10 eodemque versu apponemus.

Similiter quoniam quando 20 proxime gradus secundum medium longitudinis motum a minima excentrici epicyclus epicyclus] add. s. l. G longitudine distat, tunc stella phantasiam standi facit, distatque ab aparente minima epicycli gradibus 11 44′, ita ut excessus ad mediam unius gradus sexagesimarumque octo colligatur, estque longitudinum minima quidem talium 58 45′ qualium media 60, excessusque harum 1 15′, longitudo autem in preposita a minima longitudine distantia earundem 58 50′, et huius ad mediam excessus 1 10′, multiplicavimus 1 15′ in 1 8′, factumque numerum per 1 10′ partiti invenimus excessum 1 13′ qui fit in ipsa minima longitudine ad mediam. Et propterea motum quidem qui est ab apparente minima epicycli habuimus graduum 11 39′, motum vero a maxima usque ad primam stationem 168 21′ et usque ad secundam 191 39′, quos in eisdem ordinibus ad numerum 180 conscribemus.

In stella vero Mercurii quoniam demonstratum est quod, quando epicyclus 10 17′ periodicis gradibus a maxima excentrici distat, tunc stella standi phantasiam facit, distatque a minima epicycli gradibus 32 52′, motusque qui fit in media longitudine gradus continet 34 56′, ut excessus 2 4′ graduum colligatur, estque maxima longitudo talium 69 qualium media 60, et excessus earum 9, et longitudo in preposita a maxima longitudine distantia 68 36′, et excessus eius ad mediam 8 36′, multiplicavimus similiter 9 in 2 4′, factumque numerum per 8 36′ partiti invenimus excessum in ipsa maxima longitudine ad mediam graduum 2 10′ proxime, et sic ab apparente minima epicicli gradus colliguntur 32 46′, a maxima vero prime quidem stationis 147 14′, quos in ordine 11 penes numerum 360 conscribemus, secunde vero stationis gradus 212 46′, quos in ordine 12^o in eodem versu apponemus.

Similiter quoniam, quando 11 22′ periodicis epicyclus gradibus distat a minima, tunc standi phantasiam stella facit, distatque ab apparente minima epicycli gradibus 35 30′, et sic excessus ad mediam fit gradus 1 et sexagesimarum 34, longitudinum vero minima quidem talium est 55 34′ qualium media 60, harumque excessus 4 26′, longitudo autem in preposita a minima longitudine distantia 55 52′ proxime earumdem, et excessus eius ad mediam 4 18′, multiplicatis rursum 4 26′ in 0 34′, factumque numerum per 4 18′ partiti invenimus excessum qui fit in ipsa minima ad mediam 0 35′, ac idcirco motum quidem ab apparente minima epicycli graduum 35 31′, a maxima vero prime quidem stationis 144 29′, secunde autem 215 31′, quos in eisdem quidem ordinibus sed non penes 180 numerum apponemus, sed penes 120 et 240, propterea quod in his minime excentricitatis Mercurii longitudines demonstrate sunt.

His ita expositis, consequenter ad hanc doctrinam motuum quoque qui inter hos sunt differentie colliguntur. Proponatur enim exempli causa invenire apparentis inequalitatis motus qui in primis stationibus fiunt, quando medius secundum longitudinem motus 30 gradibus a maxima longitudine distat, in quo situ distantia epicycli qualium media omnium est 60 talium in Saturno quidem, ut diximus, colligitur 63 2′, in Iove autem 62 26′, in Marte 65 24′, in Venere 61 6′, in Mercurio 66 35′, et sic singularum excessus ad mediam secundum expositum ordinem, ne sepe repetamus, est 3 2′ et 2 26′ et 5 24′ et 1 6′ et 6 35′. Sunt autem etiam excessus ipsarum maximarum longitudinum ad medias, propterea quod maiores in omnibus proposite longitudinis quam ipsius medie numeri sint, earundem 3 25′ et 2 45′ et 6 0′ et 1 15′ et 2 9′. Quoniam igitur graduum apparentis inequalitatis integri excessus maximarum longitudinum ad medias secundum eundem ordinem colligunt gradus 1 23′ et 1 33′ et 5 41′ et 1 17′ et 2 10′, multiplicatis singulis congruenter in excessum date tunc distantie singularum stellarum ad medium, ut verbi gratia 1 23′ in 3 2′, factum hinc numerum per excessum maxime distantie, ut per 3 25′, partiti habuimus excessus graduum inequalitatis in proposito longitudinis motu ad excessus medie distantie 1 14′ et 1 22′ et 5 7′ et 1 8′ et 1 35′. Sunt autem in mediis distantiis ab aparente maxima epicycli longitudine gradus 114 8′ et 125 38′ et 163 9′ et 167 8′ et 145 4′, in maximis vero in ceteris quidem paucio〈r〉es pauciores] pauciones A istis, in Mercurio autem plures. Subtractis igitur collectis excessibus in data distantia in ceteris a gradibus mediarum distantiarum, in Mercurio autem additis, habebimus gradus qui 30 gradibus periodice longitudinis apponuntur in ordinibus primarum stationum apparentis inequalitatis a maxima epicycli longitudine, in Saturno quidem 112 54′, in Iove autem 124 16′, in Marte 158 2′, in Venere 166 0′, in Mercurio 146 39, secundarum vero stationum ordines hinc absolvemus apponentes reliquos ad 360 gradus in quolibet versu ad numeros primarum stationum in eisdem versibus et in ordinibus secundarum stationum, ut in data longitudine, gradus 247 6′ et 235 44′ et 201 58′ et 194 0′ et 213 21′.

Facile autem intellectu est, quod si etiam non ad apparentem maximam epicycli longitudinem perspectos inequalitatis gradus apponere apponere] post corr. G voluerimus, sed, ut facilius fiat, eos qui ad periodicum perspiciuntur et adhuc inequatos hinc nobis hoc quoque constituetur, subtracta additione subtractioneve que numero periodice singulorum longitudinis in tabulis inequalitatis apponitur a gradibus apparentis inequalitatis usque ad numerum graduum a maxima excentrici longitudine 180, addita vero ipsis in numero graduum maiori quam 180. Est autem tabularum compositio hec.

〈XII.8〉 Capitulum VIII: Tabule stationum quinque planetarum planetarum] Hec tabula scribatur post eam que sequitur, etsi potest fieri, copulentur in unam faciem chartae, ut ordinum numerus ostendit, ita ut numeri communes semel scribantur add. G

Hec tabula scribatur primo et copuletur cum antecedente, ita ut hec precedat, ut ordines ostendunt add. G

〈XII.9〉 Capitulum VIIII: Maximarum a Sole distantiarum Veneris atque Mercurii demonstratio

Expositis iam omnibus que de regressibus considerantur, sequitur ut maximas Veneris atque Mercurii in singulis signis a Sole distantias que ab expositis suppositionibus constituuntur demonstremus, has ad apparentem Solis motum explanavimus, stellasque in ipsis signorum principiis posuimus secundum maximas nostri temporis longitudines que ad solstitialia et equinoctialia puncta ita site sunt, ut Veneris quidem in 25 gradu Tauri sit, Mercurii vero in 10 Libre. Mutatio enim maximarum huiusmodi distantiarum propter maximarum longitudinum progressum facta facile per hanc ipsam viam ac rationem a posterioribus emendabitur, que tamen in longo tempore indifferenter se habebit. Verum ut modus demonstrationum facilis intellectu fiat, demonstrande sunt exempli gratia primo maxime, ut diximus, matutine et 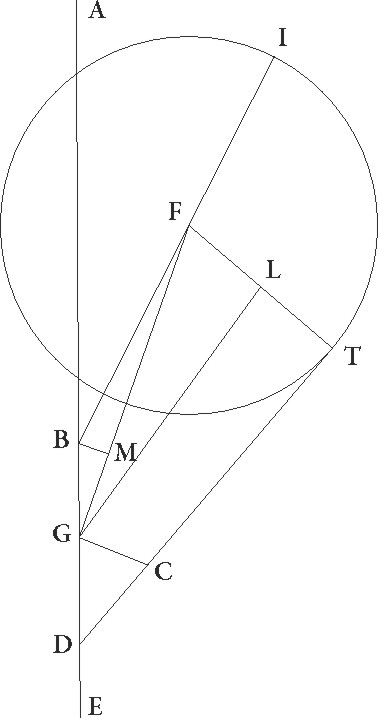vespertine Veneris distantie, quando in verno equinoctio et in principio Arietis est.

Sit ergo ABGDE linea excentricitatis per A punctum maxime longitudinis, in qua sit B centrum equalis motus, et G centrum excentrici qui epicyclum defert, et D zodiaci centrum, protractaque a centro excentrici linea GF, describatur circa F epicyclus IT, producaturque a puncto D linea DT tangens matutinas antecedentesque partes ipsius, et coniungantur BFI et FT linee, deducanturque GC et GL et BM perpendiculares. Quoniam igitur DA linea in 25 gradu Tauri est, linea vero DT in principio Arietis, erit profecto angulus ADT talium 55 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium ipse quidem 110. Angulus vero DGC reliquorum ad unum rectum 70. Quare arcus etiam linee GC talium erit 110 qualium est circulus qui GDC rectangulo circumscribitur 360, linee vero GC talium 98 18′ qualium est GD que rectum angulum subtendit 120, quare qualium est GD linea 1 15′ et FT semidiameter epicycli 43 10′, talium etiam GC, hoc est LT, erit 1 1′ et reliqua FL talium 42 9′ qualium GF semidiameter excentrici esse supponitur 60. Qualium igitur est GF que rectum subtendit 120, talium etiam erit FL 84 18′ et arcus suus talium 89 16′ qualium est circulus qui GFL rectangulo circumscribitur 360. Quare angulus quoque FGL talium est 89 16′ qualium duo recti sunt 360, sed angulus quoque DGC 70 eorundem est, et LGC rectus. Totus igitur FGD colligitur graduum 339 16′ et reliquus AGF 20 44′ eorundem. Quare arcus etiam linee BM talium erit 20 44′ qualium est circulus qui rectangulo BGM circumscribitur 360, arcus vero linee GM 159 16′ ad semicirculum reliquorum. Corde igitur etiam sive BM quidem talium est 21 35′ qualium BG que rectum subtendit 120, GM autem 118 2′ earundem. Quare qualium est BG linea 1 15′ et GF semidiameter excentrici 60 talium etiam BM erit 0 13′ et GM 1 14′ et reliqua MF 58 46′, idcirco etiam BF que rectum subtendit earundem erit 58 48′. Quare qualium est BF 120, talium BM erit 0 27′, et arcus suus talium 0 26′ qualium est circulus qui rectangulo BFM circumscribitur 360, et angulus igitur BFG talium est 0 26′ qualium duo recti sunt 360, sed angulus quoque AGF demonstratus est 20 44′ eorundem, et totus igitur ABF angulus ipsius equalis secundum longitudinem motus talium erit 21 10′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 10 35′. Quare medius quoque Solis motus distabit a puncto A maxime longitudinis ad precedentia gradibus 10 35′, obtinebitque videlicet 14 25′ Tauri gradus, verus autem 15 14′. Stella igitur etiam, quando in principio Arietis Arietis] iter. et del. AG est, maxime maxime] longitudinis add. et del. A a vero Sole distabit gradibus 45 14′.

Designetur rursus similis descriptio, ut linea tangens ad partes epicycli vespertinas atque succedentes ducatur, stellaque similiter in principio Arietis esse supponatur. Per ea igitur que demonstrata sunt, ADT angulo eodem manente, colligetur angulus DGC talium 70 qualium duo recti sunt 360, et linea GC, hoc est LT, talium 1 1′ qualium GF semdiameter excentrici est 60, et FT semidiameter epicicli 43 43] post corr. G 10′, et sic tota FL linea 44 11′ earundem. Perspicuum autem est talium esse ipsam lineam FL 88 22′ qualium est GF que rectum subtendit 120, et arcum ipsius FL talium 94 51′ qualium est circulus qui rectangulo GFL circumscribitur 360. Quare 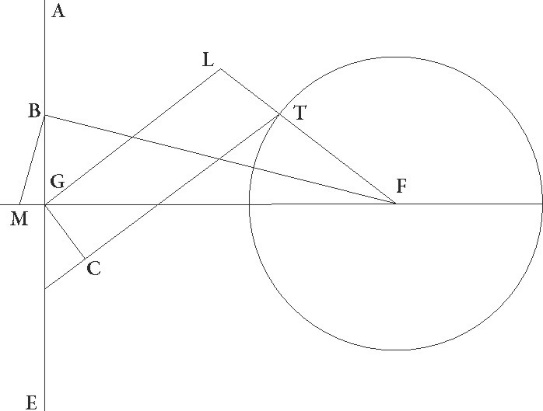angulus etiam FGL talium est 94 51′ qualium duo recti sunt 360, angulus autem FGC 85 9′ ad unum rectum reliquorum, et totus FGD, hoc est BGM, 155 9 eorundem, idcirco etiam arcus linee BM talium est 155 9′ qualium est circulus qui BGM rectangulo circumscribitur 360, arcus autem linee GM 24 51′ ad semicirculum reliquorum. Corde igitur etiam sue BM quidem talium est 117 11′ qualium est BG que rectum subtendit 120, GM autem 25 49′ earundem. Quare qualium est BG linea 1 15′, talium et BM erit 1 13′, MG autem 0 16′, tota vero MF 60 16′, ideo BF

quoque que rectum angulum subtendit 60 17′ earundem erit. Qualium igitur est BF que rectum subtendit 120, talium etiam BM erit 2 25′ et arcus suus talium 12 19′ qualium est circulus qui BFM rectangulo circumscribitur 360. Angulus igitur etiam BFM talium est 2 19′ qualium duo recti sunt 360, sed angulus quoque BGF 204 51′ eorundem est, propterea quod DGF angulus 155 9′ eorundem demonstratus est. Et totus igitur ABF angulus ipsius secundum longitudinem motus talium colligitur 207 10′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 103 35′. Quare medius Solis motus 11 25′ gradus Aquarii obtinebit, verus autem 13 38′. Quare stella quoque vespertina plurimum in principio Arietis a vero Sole distabit gradibus 46 22′.

In stella vero Mercurii propter faciliorem additum ad futuras de eclipticis eius apparitionibus propositum sit modo invenire quantum maxime a vero Sole vespertinus quidem in principio Scorpionis, matutinus vero in principio Tauri a vero Sole distare potest. Quoniam ergo secundum ea que de Mercurio supponuntur, apparente motu stelle dato, medius secundum longitudinem non habetur, propterea quod linea GF non equalis semper nec eadem ad semidiametrum excentrici permaneat sicut in aliorum suppositione, equali autem motu secundum longitudinem dato, apparens inde demonstratur, duobus longitudinis locis suppositis in singulis signis, unde possit ad principium eius quod queritur stella pervenire altero ad precedentia altero ad successionem, computatisque distantiis que in adinventis huiusmodi motibus fiunt, per eas etiam distantiam que maxima in principio signi fieri potest invenimus, sicut per ea que dicentur facile intelligitur.

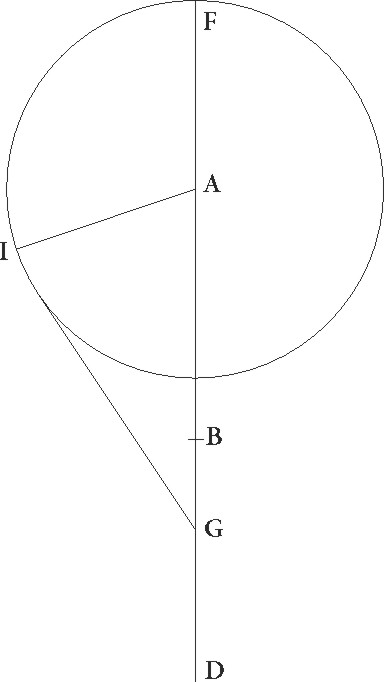Sit enim ABGD per maximam longitudinem diameter, in qua zodiaci centrum sit G, punctum vero B sit centrum ipsius equalis motus epicycli, et supponatur primo centrum epicycli in ipsa maxima esse longitudine, ut medius Solis secundum longitudinem motus 10^m gradum Libre obtineat, verum autem octavum, descriptoque circa punctum A epiciclo FI, ducatur a puncto G linea GI vespertinam eius partem contingens, iungaturque perpendicularis AI. Quoniam igitur per premissa demonstratum est talium esse AI semidiametrum epicycli 22 30′ qualium est GA linea maxime longitudinis 69, erit etiam profecto AI linea talium 39 38′ qualium est AG que rectum angulum subtendit 120. Quare arcus etiam linee AI talium est 38 4′ qualium est circulus qui rectangulo AGI circumscribitur 360, angulus vero AGI talium 38 4′ qualium duo recti sunt 360, qualium autem quatuor recti sunt 360, talium 19 2′, sed GA linea in gradu 10^o Libre est. Stella ergo 29 2′ eiusdem signi gradus obtinebit maxime a vero Sole distans gradibus 21 2′.

Supponatur rursus media longitudo a maxima distantia graduum 3, ut medius Sol 13 gradum Libre obtineat, verus autem 11 4′, perductaque linea BE describatur circa E centrum epicyclus FI, tractaque similiter GI tangente, coniungantur EG et EI linee. Quoniam igitur secundum hunc situm in quo ABE angulus talium 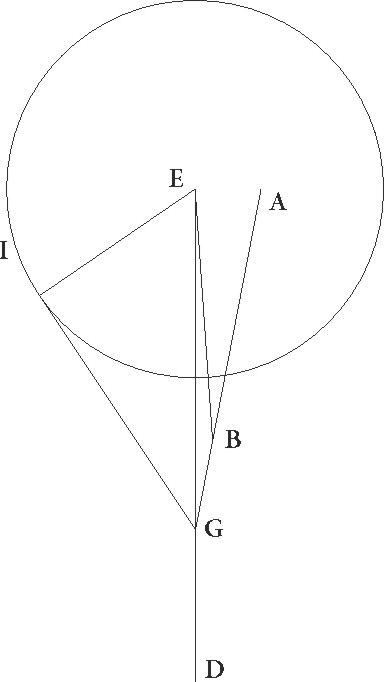supponitur 3 qualium quatuor recti sunt 360, demonstratur per premissa AGE quidem angulus differentie excenticitatis 2 52′ eorundem, linea vero EG distantie epicycli in hoc situ talium 68 58′ proxime qualium est EI semidiameter epicycli 22 30′, erit etiam linea EI talium 39 9′ qualium est EG que rectum subtendit 120. Quare arcus etiam EI linee talium erit 38 5′ qualium est circulus qui GEI rectangulo circumscribitur 360, angulus autem EGI 38 5′ talium qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 19 3′ proxime, idcirco etiam totus AGI angulus erit 21 55′ eorundem. Quare quando stella 1 55′ gradus Scorpionis obtinebit, tunc maxime a vero Sole distabit gradibus 20 51′. Fuit autem etiam demonstratum quod, quando 29 2′ Libre gradus obtinet, tunc maxima a vero Sole distare potest 21 2′. Quoniam igitur excessus locorum quos obtinebat est graduum 2 53′ et maximarum distantiarum excessus sexagesimarum 11, suntque a primo loco ad principium Scorpionis sexagesime 58 quibus congruunt sexagesime quatuor proxime, has si subtraxerimus a gradibus 21 2′, habebimus in ipso Scorpionis principio maximam stelle vespertinam a Sole distantiam graduum 20 58′.

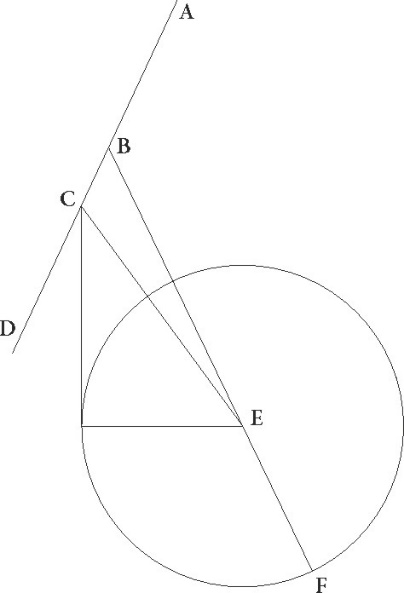Verum ut etiam matutinam distantiam, que maxima in principio Tauri fit inveniamus, supponatur primo medius per longitudinem motus distare ad successionem minime longitudinis gradibus 39, ut medius Sol 19 Tauri gradum obtineat et verus 19 38′, describaturque similis figura que habeat epicyclum ad successionem minime longitudinis et tangentem lineam ad matutinam epicycli partem productam. Quoniam igitur secundum expositum motum angulus DBF talium supponitur 39 qualium quatuor recti sunt 360, per premissaque demonstratur DGE quidem angulus 40 57′ eorundem, GE autem linea distantie istius talium 55 59′ qualium est EI epicycli semidiameter 22 30′, erit etiam EI EI] post corr. G linea talium 48 14′ qualium est GE que rectum subtendit 120, et arcus suus talium 47 24′ qualium est circulus qui rectangulo GEI circumscribitur 360. Quare angulus quoque EG talium erit 47 24′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 22 42′, reliquus autem IGD 17 15′ eorundem. Stella igitur Mercurii, cum 27 15′ Arietis gradus obtineat, maxime matutina a vero Sole 22 23 gradibus distabit.

Superponatur rursum medius longitudinis motus ad eandem minime longitudinis partem 42 gradibus distare, ut Sol quoque medius 22 Tauri, verus autem 22 31′ gradus obtineat. Quoniam igitur secundum hunc motum talium DBF angulus supponitur 42 qualium quatuor recti sunt 360, et DGE angulus 44 4′ demonstratur, et linea GE istius longitudinis talium 55 55′ qualium est EA epiycli semidiameter 22 30′, erit etiam EI linea talium 44 19′ qualium est EG que rectum subtendit 120, et arcus suus talium 47 30′ qualium est circulus qui rectangulo EGI circumscribitur 360. Quare angulus etiam EGI talium erit 47 30′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 23 45′, reliquus autem IGD 20 19′ eorundem. Quando igitur stella Mercurii 19 sexagesimis a primo Tauri gradu distat, maxime a vero Sole ad matutinas partes distabit gradibus 22 12′. Demonstratum autem fuit quod, quando obtinet 27 15′ gradus Arietis, tunc maxime similiter distare potest gradibus 22 23′. Quoniam igitur excessus locorum quos obtinere suppositus est graduum colligitur 3 4′, et et] add. s. l. G maximarum distantiarum 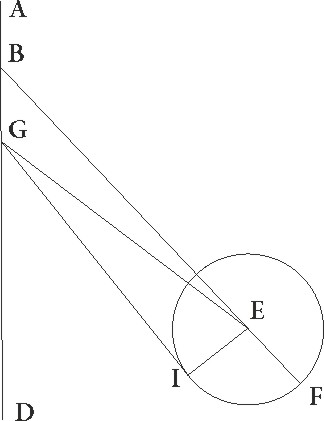excessus sexagesimarum 11, congruuntque gradibus 2 45′ qui sunt a primo loco ad principium Tauri 10 sexagesime proxime, si has subtraxerimus a gradibus 22 23′, habebimus maximam matutinam a vero Sole in ipso principio Tauri distantiam graduum 22 13′.

Eodem modo in ceteris quoque signis maximas distantias et matutinas et vespertinas utrarunque stellarum computavimus, tabulamque illarum constituimus in versibus duodecim secundum signorum numerum et ordinibus quinque, in quorum primo principia signorum posuimus ab Ariete facto initio, in reliquis vero quatuor computatas maximas a vero Sole distantias, ita ut secundus quidem matutinas, tertius vespertinas Veneris contineat, et rursum quartus matutinas Mercurii, quintus vespertinas. Est autem tabula hec.

〈XII.10〉 Capitulum X: Tabula maximarum a vero Sole distantiarum Veneris atque Mercurii