PAL: Ms/446/616/Text/4

`_`	(the underscore) is the placeholder for exactly one character.
`%`	(the percent sign) is the placeholder for no, one or more than one character.
`%%`	(two percent signs) is the placeholder for no, one or more than one character, but not for blank space (so that a search ends at word boundaries).

〈IV〉

Incipit liber quartus Ptolomei Magne Compositionis

〈IV.1〉 〈Capitulum I:〉 A quibus observationibus observationibus] corr. ex observanti G Lune accidentia examinanda sunt

Cum iam in precedenti libro que Solis motui accidunt investigaverimus, sitque nobis consequenter de Luna dicendum, illud apprime monere debemus quod non simpliciter neque casu observationibus que ad Lunam pertinent utendum est, sed ad universales quidem apprehensiones illis precipue demonstrationibus est attendendum que non solum ex maiori tempore, verum etiam ab ipsis observationibus lunarium eclipsium capiuntur. Istis enim dumtaxat exquisite loci Lune poterint inveniri. Nam alie, sive per transitus iuxta stellas fixas, sive per instrumenta, sive per eclipsis solares considerentur, propter Lune aspectuum diversitates non parum fallere possunt. Ad particulariora vero accidentia etiam ab aliis observationibus considerandum est. Nam cum distantia qua Lune globus distat a centro terre non sit tanta, quanta est ad zodiacum ut instar puncti magnitudo terre ad eam habeat, necesse est ut recta linea que a centro terre ad partes obliqui circuli protrahitur, qua veri motus omnium comprehenduntur, ne ad sensum quidem eadem illi fiat que a quavis terre superficie, hoc est a visu videntium, ad centrum Lune protrahitur, qua motus eius apparens conspicitur, sed tunc solum a centro terre visuque visuque] corr. ex visu usque A videntium per centrum Lune ad zodiacum una eademque recta linea protrahitur, quando super verticem observantis Luna invenitur. Quando autem a vertice quomodocunque declinaverit, tunc linearum quoque declinationes diverse fiunt, et hac de causa motus apparens non idem vero motui efficitur, cum visus ad alios atque alios situs traducatur, quoniam anguli qui per centrum terre determinantur proportionaliter declinationis quantitatibus fiant.

Idcirco accidit, cum eclipses Solis obiectu Lune fiant, que in eum conum incidens qui a visu nostro ad Solem est obumbrationem, donec transeat, facit, nec ubique ipsas aut magnitudine aut temporibus similiter fieri, nec eodem omnibus modo, nec in eisdem partibus Solis fieri propter causas dictas, in lunaribus vero eclipsibus nullam huiusmodi differentiam ex diversitatibus sequi. Nam passioni ipsius defectus Lune nullam diversitas visus causam affert. Cum enim semper a solari splendore Luna illuminetur, illuminetur] post corr. G quando diametraliter ipsi opposita fuerit, tuncque aliis temporibus, quoniam totum semispherium eius a Sole illuminatum ad nos declinatur tota lucere cernebatur, tunc, inquam, quando sic opposita Soli fuerit ut in terrestris umbre incidat conum qui ex opposito Solis una cum eo circumducitur, proportionaliter incidentie quantitatibus lumine privatur. Terra Terra] post corr. G enim solaribus obiicitur radiis hinc fit ut in omnibus terrarum partibus tam magnitudinibus quam distantiarum temporibus similiter deficere videatur. His de causis ad universalem non apparentium, sed verorum Lune locorum considerationem defectus eius accipi debent, accipi debent] corr. ex accipient G et ad hec, quoniam quod ordinatum et simiter est necesse est ut inordinato atque dissimili anteponatur. Quare aliis quidem observationibus in quibus visu observantium stellarum loca capiuntur non esse utendum asserimus, solis autem ipsius Lune defectibus, quoniam nihil ad deprehensionem locorum visus in ipsis conducit. Nam quancunque portionem obliqui Sol circuli medio lunaris eclipsis tempore obtinere invenitur, in quo tempore Lune centrum absolute secundum longitudinem, quantum fieri potest, diametraliter Soli opponitur, eius oppositam portionem in eodem medio eclipsis tempore Lune centrum obtinebit.

〈IV.2〉 Capitulum II: De 〈per〉riodicis periodicis] riodicis A temporibus Lune

Sic igitur breviter a quibus observationibus Lune accidentia universaliter consideranda sunt expositum nobis sit. Nunc explanare conabimur conabimur] post corr. G quomodo prisci demonstrationum accomodationibus usi sunt et quomodo nos utilius faciliusque consequenter ad aparentia suppositionum distinctionem faciemus.

Quoniam igitur Luna et per longitudinem et per latitudinem inequaliter moveri cernitur, nec per obliquum semper circulum, nec per latitudinem eius equali tempore revolvi, neque sine inventione temporis quo inequalitas eius necessario restituitur aliorum restitutiones invenire possibile sit, cunque per omnes zodiaci partes et per medium et per minimum et per maximum motum particularibus observationibus moveri cognoscatur, et in omnibus partibus borealissima et australissima in ipso quoque circulo qui per medium signorum est fiat, non absque causa tempus prisci mathematici quoddam querebant quo Luna semper equaliter per longitudinem movebitur, quasi hoc solum possit inequalitatem restituere. Itaque observationes lunarium eclipsium propter causas dictas reservantes considerabant, quenam multitudinis mensium distantia equalis in tempore semper fieret eiusdem multitudinis distanciis, equalesque secundum longitudinem revolutiones aut integras cum quibusdam equalibus arcubus contineret.

Prisci ergo admodum tempus hoc esse putabant directum 6585 et tertiam unius diei partem. In tanto enim tempore proxime 223 menses colligi videbant, revolutiones autem inequalitatis quidem 239, latitudinis autem 242, longitudinis vero revolutiones 241 et ad hec gradus 10 40′ quos in 18 revolutionibus in predicto tempore Sol pertransivit restitutione ipsorum ad fixas stellas considerata; idque tempus periodicum appellarunt, quia primum primum] corr. ex post modum G differentias motuum ad unam proxime restitutionem reducat; utque diebus id integris constituerent dies 6585 partemque tertiam triplicarunt, et sic habuerunt dierum numerum 19756, quem absolutam restitutionem vocaverunt. Ceteris quoque similiter triplicatis, habuerunt menses quidem 669, restitutiones vero inequalitatis quidem 717, latitudinis vero 726, circuitus autem longitudinis 723, et ad hec 32 gradus quos Sol in 54 revolutionibus pertransivit.

Sed iam Hiparchus tum a Chaldaicis Chaldaicis] corr. ex Caldaicis G tum etiam a suis observationibus non absolute ista se habere redarguit. Per observationes enim quas exposuit demonstrat quia primus dierum numerus per quem semper tempus eclipsium in mensibus ac motibus equalibus revolvitur 126007 dierum et hore unius equalis est, in quibus menses invenit absolvi 4267, integras vero inequalitatis restitutiones 4573, circulos autem zodiacos 4612 minus 7 30′ gradibus proxime, quibus et Sol ad 345 circulos rursum deficit et restitutio ipsorum ad fixas stellas perspiciatur. Vnde propositam dierum multitudinem in 4267 menses partiens mensis medii tempus invenit 29 31′ 58″ 20″′ proxime colligi. In tanto igitur tempore distantias ab eclipsi lunari ad eclipsim simpliciter redeuntes equales esse demonstrat, ut ideo manifestum fiat inequalitatem restitui, quod semper et in tanto tempore tot menses continentur et equalibus per longitudinem revolutionibus 4611 totidem gradus comprehenduntur, scilicet 352 30′ consequenter ad coniunctiones et oppositiones solares.

Siquis vero numerum mensium non ab eclipsi lunari ad eclipsim querat, sed solummodo illum qui a coniunctione lunari vel plenilunio ad similem respectum est, is minorem adhuc restituentem inequalitatis et mensium numerum inveniet, si solum 17 numerum communem ipsorum mensuram ceperit. Hic enim menses quidem 251 colligit, inequalitatis vero restitutiones 269. Sed hoc tempus latitudinis quoque restitutionem absolvere non inveniebatur. Eclipsium enim reditus ipse solum ad temporis et revolutionum per longitudinem distantias equalitatem servare videbatur, nequaquam vero ad magnitudines similitudinesque observationum, unde latitudo quoque comprehenditur.

Sed iam tempore quo inequalitas restituitur sic deffinito, cum rursus distantias mensium similes quibus exquisite in omnibus et magitudinibus et temporibus observationum eclipses extreme continebatur Hipparchus apposuerit in quibus eclipsibus nulla differentia penes inequalitatem fiebat, ut hac ratione latitudinis quoque motus restitutus videretur, hanc quoque restitutionem absolvi demonstrat in mensibus quidem 5458, revolutionibus vero latitudinariis 5923.

Ac modus quidem quo ad inventionem harum rerum prisci usi sunt huiusmodi erat. Quod vero neque simplex neque intellectu facilis, sed magna diligentique indigens consideratione, sic profecto videbimus. Nam si dederimus equalia distantiarum tempora exacte inveniri, primum nihil hoc prodest, nisi vel nullam Sol quoque inequalitatis differentiam vel eandem in utraque distantia faciat. Nam nisi hoc accidat, sed nonnulla penes inequalitatem eius differentia fiat, nec ipse in temporibus equalibus nec Luna equales fecisse circuitus videbitur. Nam si verbi gratia utraque distantiarum que comparantur mediam anni partem post integra equaliaque annua tempora superaccipiat, et Sol in hoc tempore progressus in prima quidem distantia a medio transitu Piscium fuerit, in secunda vero a medio transitu Virginis, in prima quidem Solis locus erit minus quam in semicirculo gradibus 4 45′ proxime, in secunda vero plus quam in semicirculo eisdem gradibus, ut Luna quoque in temporibus equalibus post integras restitutiones in prima quidem distantia 175 15′ gradus obtineat, in secunda vero 184 45′. Oportere igitur primum asserimus ut hoc distantie habeant quod in Sole accidit, ut videlicet vel integre revolutiones suas absolvat, vel in altera distantia maximam in altera minimam longitudinem attingat, vel ab eadem portione utraque distantia incipiat, vel equaliter utrinque aut a maxima aut a minima longitudine distet, ita ut in eclipsi priore ab altera distantia et in posteriore ab altera equaliter distet. Sic enim solum vel nulla vel eadem penes inequalitatem eius in utraque distantia erit differentia. Quare circumferentie quoque partes quas progressus comprehendit equales erunt vel inter se solum vel inter se et equalibus.

Deinde putamus etiam oportere simili attentione Lune cursus considerare. Nam nisi hoc discernatur accidere poterit ut sepius ipsa quoque Luna equalibus in temporibus equales secundum longitudinem arcus optineat, nondum eius inequalitate restituta, quod accidet sive in utraque distantia vel ab eodem per additionem cursu vel ab eodem per subtractionem initium fecerit, nec in eundem desiverit, sive in altera quidem a maximo cursu inceperit et in minimum devenerit, in altera vero a minimo cursu ad maximum, sive utrinque primus alterius distantie cursus et alterius ultimus equaliter ab eodem minimo aut maximo cursu distent. Quicquid enim horum accidat, vel nullam rursus vel eandem inequalitatis Lune differentiam faciet. Ac ideo motus quidem longitudinis equales efficiet, inequalitatem vero nequaquam restituet. Nihil igitur horum accepte debent habere differentie, si tempus quo inequalitas Lune restituitur contenture sint. Immo vero illas contra eligere debemus que inequalitatem maxime possint ostendere, si restitutiones inequalitatis integre non contineantur, hoc est quando non solum a diversis principia cursibus habeant, verum etiam a valde diversis aut secundum magnitudinem aut secundum virtutem: secundum magnitudinem quidem, quando in altera distantia a minimo cursu incipiat, nec in maximum desinat, in altera quando a maximo incipiat, nec in minimum desinat. Sic enim maxima secundum longitudinem motus differentia erit, cum inequalitatis revolutiones integre non absolvantur, quando maxime unam quartam aut etiam tres unius inequalitatis superaccipiet. Duabus enim tunc penes inequalitatem differentiis inequales distantie future sunt, secundum virtutem autem, quando in utraque distantia a cursu medio incipiat, sed non ab eodem medio, sed in altera ab eo qui per additionem, in altera ab eo qui per subtractionem efficitur. Nam etiam sic longitudinis progressus plurimum inter se different maxime, inequalitate non restituta. Nam cum una rursus quarta vel tres unius inequalitates inequalitates] corr. ex in qualitates A comprehenduntur, duabus penes inequalitatem differentiis different, cum vero semicirculi differentiis quatuor. Quapropter Hipparchum etiam videmus observantissime, quam maxime poterat, elegisse distantias quibus in hac consideratione usus est. Usus enim eis est in quibus Luna in altera distantia a maximo cursu principium fecit, nec in minimum desivit, in altera incepit a minimo, et in maximum non desivit. Ad hec etiam emendavit differentiam que fit penes Solis inequalitatem, quamvis parva sit, propterea quod quarta proxime parte unius signi nec eiusdem nec eius quod equalem inequalitatis differentiam in utraque utraque] post corr. G distantiarum faciat ad integros Solis restitutio circulos defficit.

Hec diximus non quia restitutionum modum reprehendemus, sed quia ostendere voluimus voluimus] corr. ex volumus A quod, si attente is modus rationeque consequenti adhibeatur, propositam rem totam in ordinem potest certum redigere, sin vero parvum aliquid de tam multis pretermiserit, longe admodum a proposito aberraturum, utque intelligatur quam difficilis sit horum omnium restitutio, siquis perspicaciter harum observationum electionem adhibeat.

Ab expositis enim revolutionum restitutionibus secundum Hipparchi calculos mensium quidem, ut diximus, restitutio recte sane computata nulla re sensibili a veritate aberrat, inequalitatis vero atque latitudinis longe abest a veritate, que res nos impulit ut ut] add. s. l. G simpliciorem facilioremque ad harum rerum investigationem viam et rationem quereremus, quam paulo post una cum inequalitate lunari demonstrabimus, si prius, ut facilior ad cetera ingressus sit, medios particulariter motus longitudinis inequalitatis distantie latitudinis consequenter ad exposita restitutionum tempora et cum eis que ab emendatione ipsarum colliguntur exposuerimus.

〈IV.3〉 Capitulum III: De Lune motibus equalibus aequalibus] corr. ex qualibus G secundum partes suas

Si ergo diurnum Solis medium motum 0 59′ 8″ 17′′′ 13′′′′ 12′′′′′ 31′′′′′′ proxime in dies unius mensis 29 31′ 58′′ 20′′′ multiplicaverimus et summe addiderimus unius circuli gradus 360, habebimus quot in mense uno Luna medie per longitudinem movetur gradus 389 6′ 23′′ 1′′′ 24′′′′ 2′′′′′ 30′′′′′′ 51′′′′′′′ proxime, hos si partiti fuerimus in expositos mensis dies, habebimus medium diei secundum longitudinem graduum 13 1′ 34′′ 58′′′ 33′′′′ 30′′′′′ 31′′′′′′ proxime.

Et rursus si 269 inequalitatis revolutiones in 360 unius circuli gradus multiplicaverimus, habebimus multitudinem graduum 96840; hos si per 7412 10′ 44′′ 51′′′ 40′′′′ dies mensium 251 partiamur, medium diurnum inequalitatis motum habebimus graduum 13 3′ 53′′ 56′′′ 29′′′′ 38′′′′′ 38′′′′′′.

Similiter si 5923 latitudinis revolutiones in 360 unius circuli gradus multiplicaverimus, habebimus graduum multitudinem 2132280, hos partientes partientes] post corr. G per 5458 mensium dies 161177 58′ 58′′ 3′′′ 25′′′′, habebimus latitudinis quoque medium diurnum motum 13 13′ 45′′ 39′′′ 40′′′′ 17′′′′′ 19′′′′′′.

Rursus si a diurno longitudinis Lune motu medium Solis motum subtraxerimus, habebitur etiam distantie medius diurnus graduum 12 11′ 26′′ 41′′′ 20′′′′ 17′′′′′ 59′′′′′′, quamvis per demonstrationes quas postea, ut diximus, ad considerationem hanc adducemus eosdem ferme diurnum longitudinis et distantie motus eis inveniamus quos modo exposuimus. Inequalitatis vero minorem gradibus 0 0′ 0′′ 0′′′ 11′′′′ 46′′′′′ 39′′′′′′, ut fiat graduum 13 3′ 53′′ 56′′′ 17′′′′ 51′′′′′ 59′′′′′′, latitudinis vero maiorem gradibus 0 0′ 0′′ 0′′′ 8′′′′ 39′′′′′ 18′′′′′′, ut hic quoque fiat graduum 13 13′ 45′′ 39′′′ 48′′′′ 56′′′′′ 37′′′′′′.

Horum diurnorum motuum si vigesimamquartam in singulis ceperimus partem, habebimus medium unius hore motum longitudinis quidem graduum 1 32′ 56′′ 27′′′ 26′′′′ 23′′′′′ 46′′′′′′ 15′′′′′′, inequalitatis vero graduum 0 32′ 39′′ 44′′′ 50′′′′ 44′′′′′ 39′′′′′′ 57′′′′′′′ 30′′′′′′′, latitudinis autem graduum 0 33′ 4′′ 24′′′ 9′′′′ 32′′′′′ 21′′′′′′ 32′′′′′′′ 30′′′′′′′′, distantie vero graduum 0 30′ 28′′ 36′′′ 43′′′′ 20′′′′′ 44′′′′′′ 57′′′′′′′ 30′′′′′′′′.

Multiplicato deinde diurno motu trigesies circulisque reiectis, habebimus mensis medium unius motum longitudinis quidem 35 17′ 29′′ 16′′′ 45′′′′ 15′′′′′, inequalitatis autem graduum 31 56′ 58′′ 55′′′′ 59′′′′′ 30′′′′′′, longitudinis autem graduum 36 52′ 49′′ 54′′′ 28′′′′ 18′′′′′ 31′′′′′′, distantie autem graduum 5 43′ 20′′ 48′′′ 59′′′′′ 30′′′′′′.

Si rursum diurnos motus in 365 anni egiptiaci dies multiplicaverimus circulosque reiecerimus, habebimus medium anni motum longitudinis graduum 129 22′ 46′′ 13′′′ 50′′′′ 2′′′′′ 30′′′′′′, inequalitatis vero graduum 188 43′ 47′′ 28′′′ 41′′′′ 13′′′′′ 55′′′′′′, latitudinis vero graduum 148 42′ 47′′ 12′′′ 44′′′′ 25′′′′′ 5′′′′′′, distantie autem graduum 129 31′ 21′′ 28′′′ 29′′′′ 23′′′′′ 55′′′′′.

Decies octies deinde propter tabularum, ut diximus, commoditatem annuis annuis] post corr. G motibus multiplicatis circulisque reiectis, habebimus etiam decem et octo annorum medium motum longitudinis quidem graduum 168 49′ 52′′ 9′′′ 9′′′′ 45′′′′′, inequalitatis vero graduum 156 56′ 14′′ 36′′′ 22′′′′ 10′′′′′ 30′′′′′′, latitudinis vero graduum 156 50′ 9′′ 49′′′ 19′′′′ 31′′′′′ 30′′′′′′, distantie autem graduum 173 12′ 26′′ 32′′′ 49′′′′ 10′′′′′ 30′′′′′′.

Conscribemus igitur sicut etiam Sole tabulas tres in versibus rursum 45, in ordinibus autem 5 per singulas, quorum ordinum primi tempora continebunt, ita ut primus prime tabule ordo collectos annos contineat, secunde expansos et horas deinceps, tertie menses et dies rursum deinceps, reliqui vero quatuor gradus singulis convenientes, secundi quidem longitudinis, tercii autem inequalitatis, quarti vero latitudinis, quinti autem distantie. Est autem tabularum expositi hec:

〈IV.4〉 〈Capitulum IIII〉

Tabule mediorum equaliumque motuum Lune

	Tabula longitudinis							Tabula inequalitatis
Anni collecti	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a
18	168	49	52	9	9	45	0	156	56	14	36	22	10	30	0
36	337	39	44	18	19	30	0	313	52	29	12	44	21	0	0
54 54] corr. ex 44 A	146	29	36	27	29	15	0	110	48	43	49	6	31	30	0
72	315	19	28	36	39	0	0	267	44	58	25	28	42	0	0
90	124	9	20	45	48	45	0	644	41	13	1	50	52	30	0
108	292	59	12	54	58	30	0	221	37	27	38	13	3	0	0
126	101	49	5	4	8	15	0	18	33	42	14	35	13	30
144	270	38	57	13	18	0	0	175	29	57	50	57	24	0
162	79	28	49	22	27	45	0	332	25	11	27	19	34	30
180	248	18	41	31	37	30	0	129	22	26	3	41	45	0
198	57	8	33	40	47	15	0	286	18	40	40	3	55	30
216	225	58	25	49	57	0	0	83	15	55	16	26	6	0
234	34	48	17	59	6	45	0	240	11	9	52	48	16	30
252	203	38	10	8	16	30	0	37	7	24	29	10	27	0
270	12	28	2	17	26	15	0	194	3	39	5	32	37	30
288	181	17	54	26	36	0	0	350	59	53	41	54	48	0
306	350	7	46	35	45	45	0	147	56	8	18	16	58	30
324	158	57	38	44	55	30	0	304	52	22	54	39	9	0
342	127	47	30	54	5	15	0	101	48	37	31	1	19	30
360	136	37	23	3	15	0	0	258	44	52	7	23	30	0
378	305	27	15	12	24	45	0	55	41	6	43	45	40	30
396	114	17	7	21	34	30	0	212	37	21	20	7	51	0
414	283	6	59	30	44	15	0	9	33	35	56	30	1	30
432	91	56	51	39	54	0	0	166	29	50	32	52	12	0
450	260	46	43	49	3	45	0	323	26	5	9	14	22	30
468	69	36	35	58	13	30	0	120	22	19	45	36	33	0
486	238	26	28	7	23	15	0	277	18	34	21	58	43	30
504	47	16	20	16	33	0	0	74	14	48	58	20	54	0
522	216	6	12	25	42	45	0	231	11	3	34	43	4	30
540	24	56	4	34	52	30	0	28	7	18	11	5	15	0
558	193	45	56	44	2	15	0	185	3	32	47	27	25	30
576	2	35	48	53	12	0	0	341	59	47	23	49	36	0
594	171	25	41	2	21	45	0	138	56	2	0	11	46	30
612	340	15	33	11	31	30	0	295	52	16	36	33	57	0
630	149	5 5] corr. ex 25 G	25	20	41	15	0	92	48	31	12	76	7	30
648	317	55	17	29	51	0	0	249	44	45	49	18	18	0
666	126	45	9	39	0	45	0	46	41	0	25	40	28	30
684	295 295] corr. ex 255 G	35	1	48	10	30	0	203	37	15	2	2	39	0
702	104	24	53	57	20	15	0	0	33	29	38	24	45	30
720	273	14	46	6	30	0	0	157	29	44	14	47	0	0
738	82	4	38	15	39	45	0	314	25	58	51	9	10	30
756	250	34	30	24	49	30	0	111	22	13	27	31	21	0
774	59	44	22	33	59	15	0	268	18	28	3	53	31	30
782	228	34	14	43	9	0	0	65	14	42	4	15	2	0
810	37	24	6	52	18	45	0	222	10	56	16	37	52	30
Longitudinis radix Tauri xi xxii								Inequalitatis radix 268 49

Tabula latitudinis radix 354 15								Tabula medie distantie a Sole radix 0 37
Anni collecti	Grad us	P^a	2^a	3^a	4^a	5^a	6^a	Grad us	P^a	2^a	3^a	4^a	5^a	6^a
18	156	50	9	49	19	31	30	173	12	26	32	49	10	30
36	313	40	19	38	39	3	0	146	24	53	5	38	21	0
54	110	30	29	27	78	34	30	159	37	19	38	27	31	30
72	267	20	39	17	18	6	0	332	49	46	11	16	42	0
90	64	10	49	6	37	37	30	146	2	12	44	5	52	30
108	221	0	58	55	57	9	0	319	14	39	16	55	3	0
126	17	51	8	45	16	4	30	132	27	5	49	44	13	30
144	174	41	18	34	36	12	0	305	39	32	22	33	24	0
162	331	31	28	23	74	45	30	118	51	58	55	22	34	30
180	128	21	38	13	15	15	0	252	4	25	28	11	45	0
198	285	11	48	2	34	46	30	105	16	52	1	0	55	30
116	202	1	57	51	54	18	0	278	29	18	33	50	6	0
234	238	52	7	41	13	49	30	91	41	45	6	37	16	30
252	35	42	17	40	33	21	0	264	54	11	39	28	27	0
270	192	32	27	19	52	52	30	98	6	38	12	17	37	30
288	349	22	37	9	12	24	0	251	19	4	45	6	48	0
306	146	12	46	58	31	55	30	64	31	31	17	55	58	30
324	303	2	76	47	51	27	0	237	43	57	50	45	9	0
342	99	53	6	37	10	58	30	50	56	24	23	34	19	30
360	256	43	16	26	30	30	0	24	8	50	56	23	30	0
378	53	33	26	15	59	1	30	37	21	17	29	12	40	30
396	210	23	36	5	9	33	0	210	33	44	1	1	51	0
414	7	13	45	54	29	4	30	23	46	10	34	71	1	30
432	164	3	55	43	48	36	0	196	78	37	7	40	12	0
450	320	54	5	33	8	7	30	10	11	3	4	29	22	30
468	117	44	15	22	27	39	0	183	23	30	13	18	33	0
486	274	34	25	11	47	10	30	356	35	76	46	7	43	30
504	71	24	35	1	6	42	0	169	48	23	18	56	54	0
522	228	14	44	50	26	13	30	343	0	49	51	46	4	30
540	25	4	54	39	45	45	0	156	13	16	24	35	15	0
558	181	55	4	29	5	16	30	329	25	42	57	24	25	30
576	338	45	14	18	24	48	0	142	38	9	30	13	36	0
594	355	35	24	7	44	19	30	315	50	36	2	2	46	30
612	292	25	34	57	3	51	0	129	30	2	35	51	57	0
630	89	15	43	46	23	22	30	302	15	29	8	41	7	30
648	246	5	53	35	42	54	0	115	27	55	41	30	18	0
666	42	56	3	25	2	25	30	228	40	22	14	19	28	30
684	199	46	13	14	21	57	0	101	52	48	47	8	39	0
702	356	36	23	3	41	28	30	275	5	15	19	57	49	30
720	373	26	33	73	1	0	0	88	17	41	52	47	0	0
738	310	16	42	42	20	31	30	261	30	8	35	36	10	30
756	107	6	52	31	40	3	0	74	42	34	58	25	21	0
774	263	77	2	20	59	34	30	247	55	1	31	14	31	30
792	60	47	12	10	19	6	0	61	7	28	30	3	42	0
810	217	37	21	59	38	37	30	234	19	54	36	52	52	30

	Longitudinis							Inequalitatis
Anni simplices	Gra dus	Pⁱ	2^a	3^a	4^a	5^a	6^a	Gra dus	Pⁱ	2^a	3^a	4^a	5^a	6^a
1	129	22	46	13	50	32	30	88	43	7	28	41	13	55
2	258	45	32	27	41	5	0	177	26	14	57	22	27	50
3	28	8	18	41	31	37	30	166	9	22	26	3	41	45
4	157	31	4	55	22	10	0	354	52	29	54	44	55	40
5	286	53	51	4	12	42	30	83	35	37	23	26	9	35
6	56	16	37	23	3	15	0	172	18	44	52	7	23	30
7	185	39	23	36	53	47	30	261	1	52	20	48	37	25
8	315	2	9	50	44	20	0	349	44	79	49	29	51	20
9	84	24	56	4	34	52	30	78	28	7	18	11	5	15
10	213	47	42	18	25	25	0	167	11	14	46	52	19	10
11	343	10	28	32	15	57	30	255	74	22	15	33	33	5
12	112	33	14	46	6	30	0	344	37	29	44	14	47	0
13	241	56	0	59	57	2	30	73	20	37	12	56	0	55
14	11	18	47	13	47	35	0	162	3	44	41	37	14	50
15	140	81	33	27	38	7	30	250	46	52	10	18	28	45
16	270	4	19	41	28	40	0	339	29	59	38	59	42	40
17	39	27	5	55	19	12	30	68	13	7	7	40	56	35
18	168	49	52	9	9	45	0	156	56	14	36	22	10	30
	Horarum tabule
Hore	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a
1	0	32	56	27	26	23	46	0	32	39	44	50	44	40
2	1	5	52	54	52	47	32	1	5	19	29	41	29	20
3	1	38	49	22	19	11	18	1	37	59	14	32	14	0
4	2	11	45	49	45	35	5	2	10	38	59	22	58	40
5	2	44	42	17	11	58	71	2	43	18	44	13	43	20
6	3	17	38	44	38	22	37	3	15	58	29	4	28	0
7	3	5	35	12	4	46	23	3	48	38	13	55	12	40
8	4	23	31	39	31	10	10	4	21	17	58	45	57	20
9	4	56	28	6	57	33	56	4	53	57	43	36	42	0
10	5	29	24	34	23	57	42	5	26	37	28	27	26	40
11	6	2	21	1	50	21	28	5	59	17	13	18	11	20
12	6	35	17	29	16	45	15	6	31	56	58	8	56	0
13	7	8	13	56	43	9	1	7	4	36	42	59	40	39
14	7	41	10	24	9	32	47	7	37	16	27	50	25	19
15	8	14	6	51	35	56	33	8	9	56	12	41	9	59
16	8	47	3	19	2	20	20	8	42	35	57	31	54	39
17	9	19	59	46	28	44	6	9	15	15	42	22	39	19
18	9	52	56	13	55	7	52	9	47	55	27	13	23	59
19	10	25	52	41	21	31	38	10	20	35	12	4	8	39
20	10	58	49	8	47	55	25	10	53	14	56	54	53	19
21	11	31	45	36	14	19	11	11	25	54	41	45	37	59
22	12	4	42	3	40	42	57	11	58	34	26	36	22	39
23	12	37	38	31	7	6	43	12	31	14	11	27	7	19
24	13	10	34	58	33	30	30	12	3	53	56	17	51	59
	Longitudinis							Inequalitatis

Latitudinis								Distantie
Anni simplices	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a
1	148	42	47	12	44	25	5	129	37	21	28	29	23	55
2	197	25	34	25	28	50	10	259	14	42	56	58	47	50
3	88	8	21	38	13	15	15	28	72	4	25	28	11	45
4	234	51	8	50	57	40	20	158	29	25	53	57	35	40
5	23	33	56	30	42	7	25	288	6	47	22	26	59	35
6	172	16	43	16	26	30	30	57	44	8	50	56	23	30
7	320	79	30	29	10	55	35	187	21	30	19	25	47	25
8	109	42	17	41	55	20	40	316	58	51	47	55	11	20
9	258	25	40	74	39	45	45	86	36	13	16	24	35	15
10	47	7	52	7	24	10	70	216	13	34	44	53	59	10
11	197	50	39	20	8	35	55	345	50	56	13	23	23	5
12	344	33	26	32	53	1	0	115	28	17	41	52	47	0
13	133	16	13	45	37	26	5	245	5	39	10	22	10	55
14	281	59	0	58	21	51	10	14	43	0	38	51	34	50
15	70	41	48	11	6	16	15	144	20	22	7	20	58	45
16	219	24	35	23	50	41	20	273	57	43	35	50	22	40
17	8	7	22	36	35	6	25	43	35	5	4	19	46	35
18	156	50	9	49	19	31	30	173	12	26	32	49	10	30
Hore	Horarum tabule
1	0	33	4	24	9	32	22	0	30	28	36	43	20	45
2	1	6	8	48	19	4	43	1	0	57	13	26	41	30
3	1	39	13	12	28	37	5	1	31	25	50	10	2	15
4	2	12	17	36	38	9	26	2	1	54	26	53	23	0
5	2	45	22	0	47	41	48	2	32	23	3	36	43	45
6	3	18	26	24	57	14	9	3	2	51	40	20	4	30
7	3	51	30	49	6	46	31	3	33	20	17	3	25	15
8	4	24	35	13	16	18	52	4	3	48	53	46	46	0
9	4	57	39	37	25	51	14	4	34	17	30	30	6	45
10	5	30	44	1	35	23	35	5	4	46	7	13	27	30
11	6	3	48	25	44	55	57	5	35	14	43	56	48	15
12	6	36	52	49	54	28	19	6	5	43	20	40	9	0
13	7	9	57	14	4	0	40	6	36	11	57	23	29	44
14	7	43	1	38	13	33	2	7	6	40	34	6	50	29
15	8	16	6	2	23	5	23	7	37	9	10	50	11	18
16	8	49	10	26	32	37	45	8	7	37	47	33	31	59
17	9	22	14	50	42	10	6	8	38	6	24	16	52	44
18	9	55	19	14	51	42	28	9	8	35	1	0	13	29
19	10	28	23	39	1	14	49	9	39	3	37	43	34	14
20	11	1	28	3	10	47	11	10	9	32	14	26	54	59
21	11	34	32	27	20	19	32	10	40	0	51	10	15	44
22	12	7	36	51	29	51	54	11	10	29	27	73	36	29
23	12	40	41	15	39	24	15	11	40	58	4	36	57	14
24	13	13	45	39	48	56	37	12	11	26	51	20	17	59
	Latitudinis							Distantie

Mensium secundum Egyptios

	Longitudinis							Inequalitatis
Menses	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a
30	35	17	29	16	45	15	0	31	56	58	8	55	59	30
60	70	34	58	33	30	30	0	63	153	56	17	51	59	0
90	105	52	27	50	15	45	0	95	50	54	26	37	58	30
120	141	9	57	7	1	0	0	127	47	52	35	43	58	0
150	176	27	26	23	46	15	0	159	44	50	44	39	57	30
180	211	44	55	40	31	30	0	191	41	48	53	35	57	0
210	247	2	24	57	16	45	0	123	38	47	2	31	56	30
240	282	19	54	14	2	0	0	255	35	45	11	27	56	0
270	317	37	23	30	47	15	0	287	32	43	20	23	55	30
300	352	54	52	47	32	30	0	319	29	41	29	19	55	0
230	28	12	22	4	17	45	0	351	26	39	38	15	54	30
260	63	29	51	21	3	0	0	23	23	37	47	11	54	0

Dies	Dierum longitudinis							Inequalitatis
1	13	10	34	58	33	30	30	13	3	53	56	17	51	59
2	26	21	9	57	7	1	0	26	7	47	52	35	43	58
3	39	31	44	55	40	31	30	39	11	41	48	53	35	57
4	52	42	19	54	14	2	0	52	15	35	45	11	27	56
5	65	52	74	52	47	32	30	65	19	29	41	29	19	55
6	79	3	29	51	21	3	0	78	23	23	37	47	11	54
7	92	14	4	49	54	33	30	91	27	17	34	5	3	53
8	105	24	39	48	28	4	0	104	31	11	30	22	55	52
9	118	35	14	47	1	34	30	117	35	5	26	40	47	51
10	131	45	49	45	35	5	0	103	38	59	22	58	39	50
11	144	56	24	44	8	35	30	143	42	53	19	16	31	49
12	158	6	59	42	42	6	0	156	46	47	15	34	23	48
13	171	17	34	41	15	36	30	169	50	41	11	52	15	47
14	184	28	9	39	49	7	0	182	54	35	8	10	7	46
15	197	38	44	38	22	37	30	195	58	29	4	27	59	45
16	210	49	19	36	56	8	0	209	2	23	4	45	51	44
17	223	59	54	35	29	38	30	222	6	16	57	3	43	43
18	237	10	29	34	3	9	0	235	10	10	53	21	35	42
19	250	21	4	32	36	39	30	248	14	4	49	39	27	41
20	263	31	39	31	10	10	0	261	17	58	45	57	19	40
21	276	42	14	29	43	40	30	274	21	52	42	15	11	39
22	289	52	49	28	17	11	0	287	25	46	38	33	3	38
23	303	3	24	26	50	41	30	300	29	31	34	50	55	37
24	316	13	59	25	24	12	0	313	33	34	31	8	47	36
25	329	24	34	23	57	42	30	326	37	28	27	26	39	35
26	342	35	9	22	31	13	0	339	41	22	23	44	31	34
27	355	45	44	21	4	43	30	352	45	16	20	2	23	33
28	8	56	19	19	38	14	0	5	49	10	16	20	19	32
29	22	6	54	18	11	44	30	18	53	4	12	38	7	31
30	35	17	29	16	45	15	0	31	56	58	8	55	59	30

Longitudinis									Distantie
Men ses	Gra dus	P^a	2^a	3^a	4^a	5^a	6^a		Gra dus	P^a	2^a	3^a	4^a	5^a	6^a
30	36	52	49	54	28	18	30		7	43	20	40	8	59	30
60	73	45	39	48	56	37	0		11	26	41	20	17	59	0
90	110	38	29	43	24	55	30		17	10	2	0	26	58	30
120	147	31	19	37	53	14	0		22	53	22	40	35	58	0
150	184	24	9	32	21	32	30		28	36	43	20	44	57	30
180	221	16	59	26	49	11	0		34	20	4	0	53	57	0
210	258	9	49	21	18	9	30		40	3	24	41	2	56	30
240	295	2	39	15	46	28	0		45	46	45	21	11	56	0
270	331	55	29	10	14	46	30		51	30	6	1	20	51	30
300	8	48	19	4	43	5	0		57	13	26	41	29	55	0
330	45	41	8	59	11	23	30		62	56	47	21	38	54	30
360	82	33	58	53	39	42	0		68	40	8	1	47	54	0
Dies latitudinis								Dierum	distantie
1	13	13	47	39	48	56	37		12	11	26	41	20	17	59
2	26	27	31	19	37	53	14		24	22	53	22	40	35	58
3	39	41	16	59	26	49	51		36	34	20	4	0	53	57
4	52	55	2	39	15	46	28		48	45	46	45	21	11	56
5	66	8	48	19	4	43	5		60	57	13	26	41	29	55
6	79	22	33	58	53	39	42		73	8	40	8	1	47	54
7	92	36	19	38	42	36	19		85	20	6	49	22	5	53
8	105	50	5	18	31	32	16		97	31	36	30	42	23	52
9	119	3	50	58	20	29	33		109	43	0	12	2	41	51
10	132	17	36	38	9	26	10		121	54	26	53	22	59	50
11	145	51	22	17	58	22	47		134	5	53	34	43	17	49
12	158	45	7	57	47	19	24		146	17	20	16	3	35	48
13	171	78	53	37	36	16	1		158	28	46	57	23	53	47
14	185	12	39	17	25	12	38		170	40	13	38	44	11	46
15	198	26	24	57	14	9	15		182	51	40	20	4	29	45
16	211	40	10	37	3	5	52		195	3	7	1	24	47	44
17	224	73	56	16	52	2	29		207	14	33	42	45	5	43
18	238	7	41	56	40	50	6		219	26	0	24	5	23	42
19	251	21	27	36	29	55	43		231	37	27	5	25	41	41
20	264	35	13	16	18	52	20		243	48	53	46	45	59	40
21	277	48	58	56	7	48	57		256	0	20	28	6	17	39
22	291	2	44	35	56	48	34		268	11	47	9	26	35	38
23	304	16	30	15	45	42	11		280	23	13	50	46	53	37
24	317	30	15	55	34	38	48		292	34	40	32	7	11	36
25	330	44	1	35	23	35	25		304	46	7	13	27	29	35
26	341	57	47	15	12	32	2		316	54	33	54	47	47	34
27	357	11	32	55	1	38	39		329	9	0	36	8	5	33
28	10	25	18	34	52	25	16		341	20	27	17	28	23	32
29	23	39	4	14	39	21	53		353	31	53	58	48	41	31
30	36	52	49	54	28	18	30		5	43	20	40	8	59	30

〈IV.5〉 Capitulum V: Quod etiam in simplici suppositione lunari eadem tam excentricitatis quam epicycli suppositio apparentia facit

Cum autem consequens sit tum modum cum quantitatem lunaris inequalitatis ostendere, nunc quidem ita de his loquemur, quasi una solummodo inequalitas sit quam solam omnes ferme qui ante nos fuerunt intellexisse videntur, eam dico que secundum exposita restitutionum absolvitur tempora. Postea vero demonstrabimus quod etiam aliam et secundam inequalitatem quandam Luna facit penes distantias quibus abest a Sole, hec maxima quidem fit in utroque semilunio. semilunio] corr. ex plenilunio A Restituitur autem bis in tempore menstruo in ipsis coniunctionibus atque pleniluniis.

Hoc autem demonstrationum ordine utemur, quoniam hec secunda ita prime semper coniungitur, ut nunquam absque illa possit inveniri, illa vero absque hac secunda inveniatur. Capitur enim ab eclipsibus lunaribus penes quas nulla sensibilis ex ea que propter Solem accidit fit differentia. In prima igitur demonstranda ea via utemur qua Hipparchum etiam usum fuisse videmus. Nam tres nos quoque lunares capiemus eclipsis, demonstrabimusque quanta maxima differentia penes medium motum et penes distantiam a maxima longitudine fiat. Hec enim inequalitas seorsum per se inspicitur et per epicycli suppositionem absolvitur, et quamvis eadem rursus apparentia per excentrici quoque suppositionem cernantur, commodius tamen hec inequalitas que fit per utrarumque inequalitatum compositionem secunde que propter Solem accidit coniungetur. Quod autem eadem etiam hic ex utraque prepositarum suppositionum appareant, quamvis tempora restitutionum utrarunque, inequalitatis videlicet et eius que ad obliquum circulum inspicitur non sint equalia, sicut in Sole, demonstravimus, sed inequalia, sicut in Luna, dum dum] add. s. l. G eedem proportiones rursum solummodo supponatur, sic profecto intelligemus in ipsa proposita Lune simplicique inequalitate considerationem facientes. Nam quoniam Luna restitutionem illam que ad zodiacum cernitur citius facit quam illam que ad expositam inequalitatem, est per maiorem certe in temporibus equalibus in epicycli suppositione arcum epicyclus in concentrico zodiaci semper movebitur quam similem ei arcui quem Luna in epicyclo pertransivit, in suppositione autem excentricitatis Luna quidem similem in excentrico arcum epicycli arcui pertransibit, excentricus vero ad easdem partes quas Luna circa centrum zodiaci tantum, quantum longitudinis motus motu inequalitatis maior est. Sic enim non solum proportionum sed temporum etiam utriusque motus similitudines in utraque suppositione servabuntur.

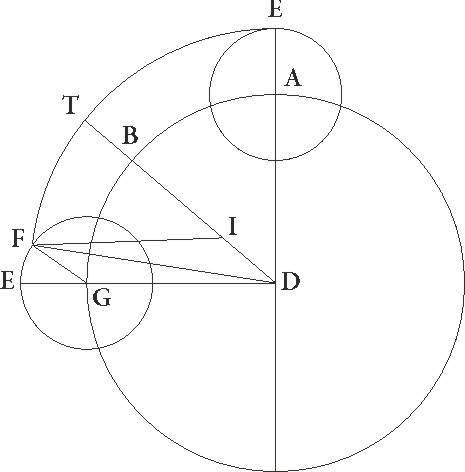His His] Commentary to the diagram: In haec figura ABG arcus minor sit quam una et BG arcus similis capiam arcui EF G ita necessario consequenterque suppositis, sit ABG concentricus zodiaco circulus, cuius centrum D et diameter AD, et sit epicyclus EF, cuius centrum G, et supponatur, quando epiyclus erat in A, tunc Lunam fuisse in E maxima epicycli epicycli] corr. ex epicicli G longitudine, equalique in tempore epicyclum quidem AG, Lunam autem EF arcum pertransisse, et iungantur ED et GF, et quoniam AG arcus maior est arcu EF quam similis, capiatur arcus BG arcui EF similis, et iungatur BD. Quod igitur equali tempore angulum ADB excessus utriusque motuum excentricus quoque pertransibit et tum centrum tum maxima longitudo eius ad DB lineam pervenit, perspicuum est. Id cum ita se habeat, sit linea GF equalis linee DI, et iungatur FI, et centro quidem I, spatio autem IF, describatur excentricus FT: dico eandem esse proportionem FI linee ad ID que est DG ad GF. Erit autem etiam secundum hanc positionem Luna in puncto F, idest similis erit arcus FT arcui EF. Nam quoniam BDG angulus equalis est angulo EGF, erunt GF et DI linee equidistantes. Sed GF et DI equales sunt, ergo FI etiam linea equidistans equalisque est linee GD et proportio FI ad ID eadem erit proportioni DG ad GF. Rursus quoniam DG et IF equidistantes sunt, erit angulus EDB equalis angulo FIT. Sed suppositus suppositus] corr. ex suppositus G etiam erat angulus GDB angulo EGF equalis, quare arcus quoque FT arcui EF similis est. In tempore igitur equali utraque in suppositione Luna pervenit ad punctum F. Ipsa enim et EF epicycli et TF excentrici arcus similes demonstratos pertransibit. Centrum autem epicicli arcum AG, excentrici vero centrum AB arcum, qui est excessus arcus AG ad arcum EF, quod erat demonstrandum.

Q 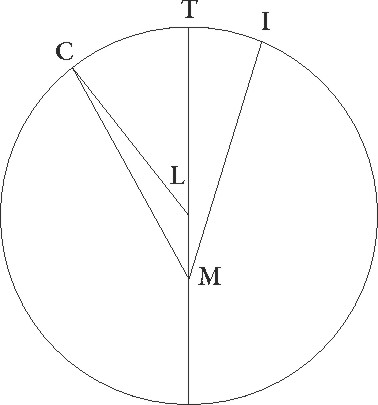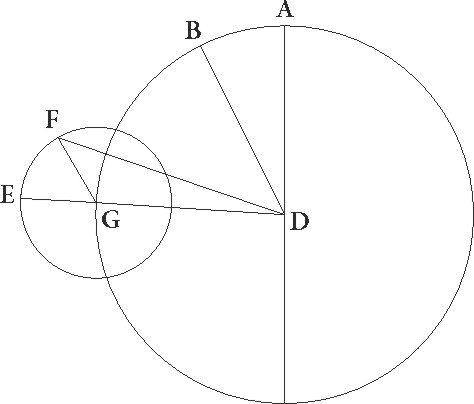uod autem, si solummodo proportiones similes fuerint, quamvis neque ipse neque in per se excentricus concentrico equales sint, idem tamen rursus eveniat, sic nobis erit perspicuum. Describatur enim utraque suppositionum seperatim, et sit concentricus quidem zodiaco ABG circulus, cuius centrum D et diameter AD, epicyclus autem sit EF circa centrum G, Luna vero sit in F, et rursum sit ITC circulus excentricus, cuius centrum sit L, et diameter TLM, in qua zodiaci centrum sit in puncto M, et Luna in puncto C, et coniungantur ibi quidem DGE et GF, hic vero TIM et CM et CL linee, supponaturque eandem esse DG proportionem ad GE que est TL ad LM, equalique in tempore pertranseant epicyclus quidem ADG angulum, Luna vero EGF, excentricus autem IMT, et Luna rursus angulum TLC. Erit igitur propter suppositas motuum proportiones angulus quidem EGF equalis angulo TLC, angulus autem ADG utrisque angulis IMT et TLC equalis. Hec cum ita se habeant, dico quod in utraque suppositione rursus equalem in tempore equali arcum Luna pertransibit, id ita fit, quia ADF angulus equalis est angulo IMC. Nam cum in principio distantie in maxima longitudine Luna esset, per lineas DA et MI cernebatur, in fine autem, cum esset in F et C punctis, per lineas DF et MC. Sit ergo utrique arcui TC et EF similis rursum arcus BG, et iungatur linea BD. Quoniam igitur ita se habet DG ad GF, sicut CL ad LM, suntque ista latera quibus G et L equales anguli continentur proportionalia, erit GDF triangulus equiangulus triangulo CLM et anguli proportionalibus lateribus contenti equales. Est ergo angulus GFD angulo LMC equalis. Sed angulus etiam BDF equalis est angulo GFD, propterea quod equedistantes sunt GF et BD. Anguli enim FGE et BDG equales esse supponuntur, quare angulus etiam FDB angulo LMC equalis est. Fuit autem etiam ADB angulus ipsius excessus motuum angulo IMT per motum excentrici constituto equalis, quare totus etiam ADF toti CMI equalis est, quod erat demonstrandum.

〈IV.6〉 Capitulum VI: Prime ac simplicis lunaris inequalitatis demonstratio

Verum hec ad hec usque nobis perspecta sint, nunc exposite lunaris inequalitatis demonstrationum in epicycli suppositione propter causam dictam faciemus, utemurque primum tribus eclipsibus quas exacte putamus ab antiquissimis esse conscriptas, deinde quibusdam etiam quas temporibus nostris exquisitissime nos ipsi observavimus. Sic enim inquisitio hec nobis per quam maxime longa tempora procedet, eritque alioquin manifestum quod et differentia que penes inequalitatem est eadem proxime ex utrisque demonstrationibus eveniet, et mediorum motuum progressus semper conveniet progressui qui in temporibus revolutionum expositis secundum emendationem nostram colligitur. Ad demonstrationem igitur prime inequalitatis que per seipsam inspicitur hoc modo epicycli suppositio, ut diximus, se habeat.

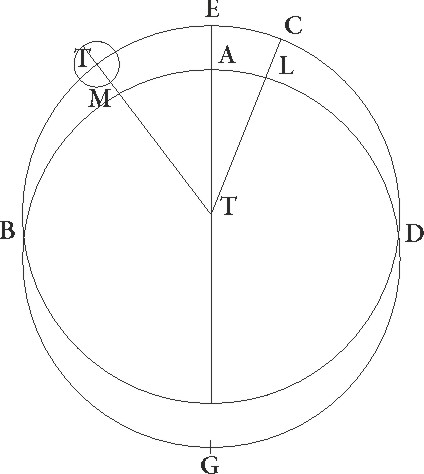Intelligatur enim in sphera Lune circulus et concentricus et in eadem superficie situs cum zodiaco circulo et alius secundum quantitatem latitudinis motus Lune proportionaliter ad hunc declinatus, is equaliter ad precedentia signorum circa obliqui centrum tamen moveatur quanto latitudinis motus longitudinis motum excedit. In hoc igitur obliquo circulo epicyclum equaliter rursus ad successionem signorum supponimus consequenter circumferri ad latitudinis restitutionem que ad zodiacum ipsum relata motum longitudinis facit, in hoc autem epicyclo Lunam esse supponimus, ita ut in arcu maxime longitudinis ad precedentia totius moveatur consequenter ad restitutionem inequalitatis, quamvis nihil ad propositam demonstrationem impediamur, etiam si neque latitudinis progressus neque lunaris circuli obliquatio supponatur. Nulla enim de qua curandum sit differentia ex tanta declinatione ad longitudinis motum accedit.

Prima Prima] Perima A igitur antiquissimarum eclipsium apud Babilonios observatarum primo anno Mardocempadi vigesimanona Thoth mensis egyptiaci die quam trigesima sequebatur facta conscribitur, et incepit, inquit, deficere post ortum eius una hora bene transacta, defecitque tota. Quoniam ergo Sol circa finem Piscium erat et nox equalium horarum proxime xii patet, quia eclipsis quidem initium ante mediam noctem 4 30′ equalibus horis fuit. Tempus autem medium quoniam eclipsis perfecta fuit 2 30′. Horis ergo Alexandrie ad meridianum cuius horarum motum consideramus, consideramus] post corr. G cuiusque meridianus 50′ unius equalis hore sexagesimas Babylonis Babylonis] corr. ex Babilonis G meridianum precedit, medium illius eclipsis tempus fuit ante mediam noctem horis equalibus 3 20′, in qua hora secundum expositos nobis calculos verus motus Solis erat in Piscium gradibus 24 30′ proxime.

Secunda eclipsium secundo anno eiusdem Mardocempadi fuisse conscribitur die Thot 18^o, 19^o consequente, defecitque ab austro digitis, inquit, 3 in ipsa media nocte. Quoniam igitur tempus medium in ipsa media nocte apud Babilonios fuisse conscribitur, debet in Alexandria fuisse ante mediam noctem 50′ hunius hore sexagesimis, in qua hora verus Solis motus erat in Piscium gradibus 13 45′.

Tertia eclipsium fuisse scribitur eodem secundo anno Mardocempadi quintodecimo die Phamenoth, sextodecimo veniente, incepitque deficere, inquit, post ortum, et defecit a septentrione plusquam medietas. Quoniam igitur Sol in principio Virginis erat, erat] post corr. G magnitudo quidem noctis apud Babylonios xi horarum fuit, cuius medietas est hore 5 30′. Quare ante mediam noctem 5 maxime horis equalibus eclipsis initium fuit. Cepit enim, inquit, deficere post ortum, medium vero tempus 3 30′ horis mediam noctem antecessit. Totum enim tempus tante tantae] corr. ex ante G obscurationis trium proxime horarum fuisse debet, quare Alexandrie rursus medium eclipsis tempus fuit ante mediam noctem horis equalibus 4 20′, in qua hora verus Solis motus erat in gradibus Virginis 3 15′ proxime.

Patet ergo ab eclipsis prime medio tempore ad medium secunde Solem, Lunamque videlicet, integris circulis reictis, motos fuisse gradibus 349 15′, a medio vero secunde ad medium tertie gradus 169 30′. Distantia etiam interiacentium temporum a primo quidem ad secundum 354 dies continet et horas insuper simpliciter quidem considerantibus 2 30′, ad equales autem naturales dies reducentibus 2 34′. A secundo vero ad tertium dies 176 et horas equales, simpliciter quidem 20 30′, exquisite vero 20 12′. Movetur autem Luna equaliter (nulla enim sensibilis in tanto tempore differentia erit, etiam si proximos verorum redituum sequemur) in diebus quidem 354 et horis 2 34′ equalibus, inequalitatis quidem reiectis circulis gradus 306 25′, longitudinis autem gradus 345 51; at vero in diebus 176 et equalibus horum 20 12′, inequalitatis quidem gradibus 150 26′, longitudinis autem gradus 170 7′ proxime. Patet igitur quod 306 25′ gradibus epicycli in prima distantia addiderunt ad medium Lune motum gradus 3 24′, secunde autem distantie gradus 150 26′ 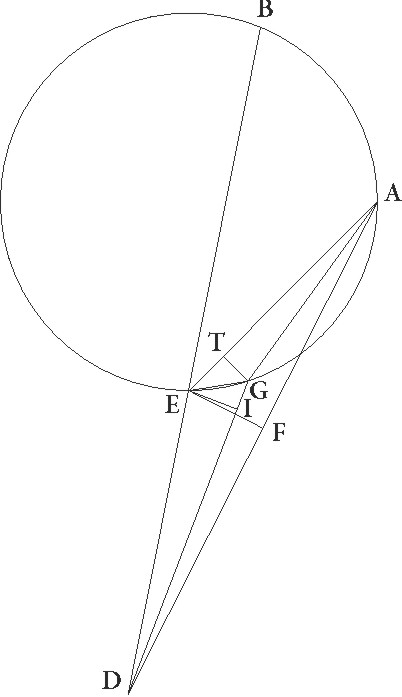subtraxerunt a medio motu gradus 0 37′.

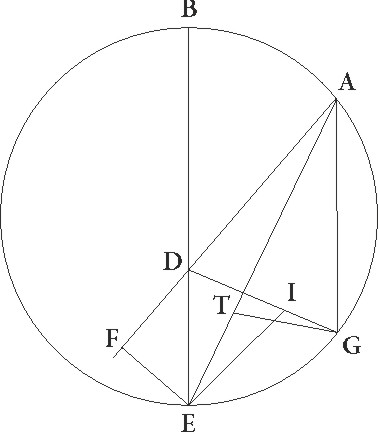His suppositis, sit epicyclus Lune ABG circulus, et sit A punctum in quo Luna erat in medio tempore prime eclipsis, B vero in quo erat in medio tempore secunde eclipsis, G autem in quo similiter erat in medio tempore tertie eclipsis. Intelligatur autem Lune in epicyclo transitus ex B ad A et ex A ad G fieri, ut arcus quidem AGB quem a prima eclipsi ad secundam pertransivit, qui 306 25′ graduum est addat ad medium motum gradus 3 24′. Arcus vero BAG, quem a secunda eclipsi ad tertiam pertransivit, quique graduum est 150 26′ subtrahat a medio gradus 0 37′, et propterea motus etiam ex B ad A qui graduum est 53 35′ sub〈t〉rahat subtrahat] subrahat A a medio eosdem 3 24′ gradus, arcus autem ex A ad G qui graduum est 96 51′ addat ad medium motum 2 47′. Quod igitur non est possibile minimam epicycli longitudinem esse in arcu BAG, inde perspicuum est, quod et subtrahendi vim hic arcus habet et minor semic〈i〉rculo semicirculo] semicurculo A sit. Maximus enim motus in minima longitudine necessario esse supponitur. Quoniam ergo in arcu BEG omnino est, accipiatur centrum tam circuli qui per medium signorum est quam eius qui defert centrum epicycli, et sit illud D, et protrahantur ab eo ad trium eclipsium puncta linee DA et DEB et DG. Universaliter ergo ut etiam ad similes demonstrationes traductionem huius speculationis facilem faciamus, sive per epicycli ut modo, sive per excentricitatis suppositionem demonstremus, centro D tunc intus accepto, una quidem protrahendarum trium linearum ad oppositum arcum producatur, ut hic DEB linea ex B secunde eclipsis puncto protractam habemus ad E. Reliqua vero duo eclipsium puncta linea quedam coniungat, ut hic linea GA, et a sectione que per productam lineam fit, ut ex puncto E, linee ad reliqua duo puncta protrahantur sicut hic EA et EG linee. Perpendiculares autem deducantur ad lineas que a reliquis punctis duobus ad centrum zodiaci protrahuntur ad lineam quidem AD perpendicularis EF, ad lineam vero GD perpendicularis EI, et ad hec ab altero duorum que diximus punctorum, ut hic ex G, perpendicularis ad eam ducatur lineam que ab altero ipsorum, ut a puncto A, ad sectionem a producta factam in puncto E protracta est, ut hic ad lineam E perpendicularis GT deducitur. Quacunque enim descriptionis huius lineatione utamur, easdem provenire per numerorum demonstrationem proportiones videbimus, ita ut ad faciliorem solummodo usum alteram deligamus. Quoniam ergo arcus BA 3 24′ zodiaci gradus subtendere demonstratus est, erit etiam angulus BDA, cum sit in centro eius, talium quidem 3 24′, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 6 48′. Quare arcus etiam corde EF talium erit 6 48′, qualium circulus qui describitur circa rectangulum DEF 360, ipsa vero linea EF talium 7 7′, qualium est DE corda 120. Similiter quoniam arcus BA graduum est 53 35′, erit etiam angulus BEA, cum sit in circunferentia, talium 53 35′, qualium duo recti sunt 360. Erat autem etiam angulus BDA 6 48′ eorundem. Erit igitur etiam reliquus angulus EAF 46 47′ eorundem. Quare arcus etiam corde EF talium erit 46 47′, qualium est circulus qui circa rectangulum EF describitur 360, ipsa vero linea EF talium 47 38′ 30′′, qualium est corda EA 120. Quare qualium est EF quidem linea 7 7′, linea vero ED 120, talium etiam E linea erit 17 55′ 32′′. Rursus quoniam arcus BAG 0 37′ gradus zodiaci subtendit, erit etiam angulus BDG, cum in centro ipsius sit, talium 0 37′, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 1 14′. Quare arcus quoque per EI cordam tensus talium est 1 14′, qualium est circulus qui describitur circa rectangulum DEI 360, ipsa vero linea EI talium 1 17′ 30′′, qualium est DE corda 120. Similiter quoniam arcus BAG graduum est 150 26′, erit etiam angulus BEG, cum sit in circumferentia, talium 150 26′, qualium duo recti sunt 360. Erat autem etiam angulus BDG 1 14′. Erit ergo etiam reliquus EGD 149 12′ eorundem. Quare arcus quoque corde EI talium est 149 12′, qualium est circulus qui circa GEI rectangulum describitur 360, ipsa vero linea EI talium 115 41′ 21′′, qualium est corda GE 120. Quare qualium EI quidem linea est 1 17′ 30′′, DE vero 120, talium est linea GE 1 20′ 23′′, sed EA quoque linea 17 55′ 32′′ eorundem demonstrata est.

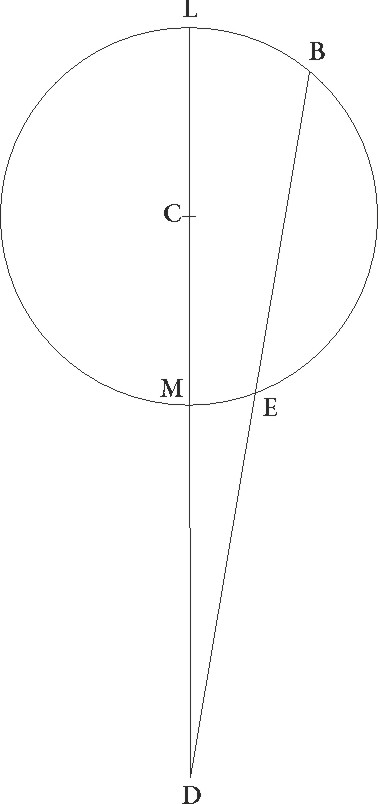Rursus quoniam arcus AG graduum esse dictus est 96 51′, erit etiam angulus EG, cum sit in circumferentia, talium 96 51′, qualium duo recti sunt 360. Quare arcus quoque corde GT talium erit 96 51′, qualium est circulus qui circa GET triangulum describitur 360, arcus vero corde ET reliquorum ad semicirculum 83 9′. Quare linee etiam quibus tenduntur GT quidem talium 89 46′ 14′′, ET autem 79 37′ 55′′, qualium est GE corda 120. Qualium ergo est GE linea 1 20′ 23′′, talium GT quidem linea erit 1 0′ 8′′, ET autem similiter 0 53′ 21′′. Erat autem etiam tota EA eorundem 17 55′ 23′′. Est igitur reliqua etiam TA talium 17 2′ 11′′, qualium GT esse demonstrata est 1 0′ 8′′. Est autem quadratum quod fit ex AT 290 14′ 19′′, quod vero similiter fit ex GT 1 0′ 1 0'] post corr. G 17″, que si componantur, faciunt quadratum quod fit ex AG, hoc est 291 14′ 36′′. Quare AG talium per longitudinem est 17 30′ 57′′, qualium est DE quidem linea 120, GE autem 1 20′ 23′′ eorundem. Est autem etiam qualium epicycli diameter 120, talium AG linea 89 46′ 14′′. Per eam enim arcus AG subtenditur qui est graduum 96 51′, qualium ergo est AG quidem linea 89 46′ 14′′, epicycli autem diameter 120, talium erit DE quidem linea 631 13′ 48′′, GE autem eorundem 7 2′ 50′′, quare arcus etiam GE qui ab ea subtenditur talium est 6 44′ 1′′, qualium est epicyclus 360. Sed arcus quoque BAG supponitur esse eorundem 150 26′, quare totus quoque arcus BGE graduum est 157 11′ corda vero sua BE talium 117 37′ 32′′, qualium epicycli quidem diameter est 120, linea vero DE 631 13′ 48′′.

Si ergo BE linea equalis epicycli diametro esset inventa, in ipsa profecto centrum eius esset, et hinc diametrorum proportio caperetur. Verum quoniam minor est et arcus etiam BGE semicirculo minor, perspicuum est quia extra BAGE portionem centrum epicycli cadit.

Sit ergo E punctum, et protrahatur ex D obliqui circuli centro per C linea DMCL, ita L quidem punctum maxima, M vero minima epicycli fit longitudo. Quoniam igitur rectangulum quod est ex BD et DE equale illi rectangulo est quod ex LD et DM continetur, estque nobis demonstratum, qualium epicycli diameter, hoc est linea LCM, est 120, talium esse lineam quidem BE 117 37′ 32′′, ED autem lineam 631 48′′ earundem, totam vero BD 748 51′ 20″, ideo certe fit quod ex BD et DE hoc est ex LD et DM rectangulum continetur eorundem 472700 et sexagesimarum 5′ 32′′. Rursum quoniam quod fit ex LD et DM cum quadrato CM facit quadratum quod est ex DC cumque CM, quia est a centro epicycli, 60 eorundem eorundem] post corr. G sit, si quadratum quod ex ipsa fit hoc est 3600 addamus ad 472700 5′ 32′′, habebimus quadratum quod est ex DC earundem earundem] post corr. G 476300 5′ 32′′. Quare DC quoque, cum sit a centro differentis epicyclum qui est 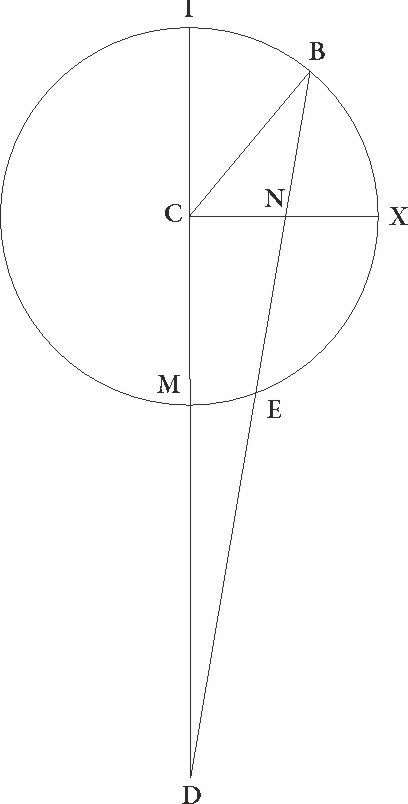concentricus zodiaco, talium erit 690 et sexagesimarum 8′ 42′′, qualium est CM que est a centro epicycli 60. Quare qualium est semidiameter deferentis epicyclum concentrici zodiaco 60, talium est etiam epicycli semidiameter 5 13′ proxime.

Producatur igitur in simili descriptione perpendicularis CNX a centro C ad lineam BE, et coniungatur BC. Quoniam ergo qualium est DC 690 8′ 42′′, talium etiam erant linee DE quidem 631 13′ 48′′, NE autem, cum medietas sit ipsius BE, 58 48′ 46′′ earundem, erit tota quoque DEN earundem earundem] post corr. G 690 et sexagesimarm 2′ 34′′, et qualium ergo DC diameter est 120, talium DN erit 119 58′ 57′′, arcus vero ab ea subtensus 178 2′ proxime talium, qualium est circulus qui DNC rectangulo circumscribitur 360. Quare angulus quoque DCN talium est 178 2′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 89 1′. Quare XM etiam epicycli arcus graduum est 89 1′, reliquus autem LBX reliquorum ad semicirculum 90 59′. Est autem etiam arcus XB, cum sit medietas partis circumferentie BXE, graduum 78 35′. Totus enim EB 157 10′ proxime graduum demonstratus est. Quare reliquus etiam LB arcus epicicli quo Luna a maxima longitudine in exposito medio secunde eclipsis tempore distabat graduum graduum] corr. ex gradum G est 12 24′. Similiter quoniam DCN angulus 89 1′ talium demonstratus est, qualium quatuor recti sunt 360, erit etiam CDN reliquus angulus qui subtendit arcum a medio longitudinis motu auferendum prope inequalitatem que fit penes LB arcum epiycli reliquorum ad rectum angulum graduum 0 59′. Quare Lune per longitudinem in medio secunde eclipsis tempore medius motus in gradibus 14 44′ Virginis fuit. Verus enim in gradibus 13 45′ fuit, sicut et Solis verus motus in Piscibus.

Rursus prima trium eclipsium de illis quas accuratissime in Alexandria observavimus fuit in xvii anno Adriani Pauni mensis secundum egyptios die 20^o quem xxi^us sequebatur, cuius tempus medium fuisse computavimus 45 sexagesimis unius equalis hore ante mediam noctem, et defecit tota, eratque verus locus Solis in Thauri gradibus 13 4′ proxime.

Secunda vero fuit in xix^o anno Adriani Chiac die secundo tertio sequente, cuius tempus medium fuisse computavimus ante mediam noctem una hora equali, defecitque a septentrione medietas et tertia diametri pars, in qua hora verus Solis locus fuit in Libra gradibus 25 6′ proxime.

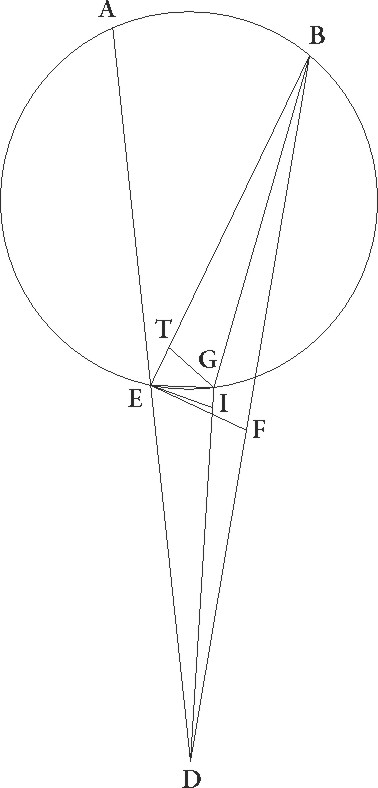Tertia fuit xx^o anno Adriani die Pharmothi secundum Egyptios Egyptios] corr. ex Egiptios G xix^o quem sequebatur vigesimus, cuius medium tempus fuisse computavimus quatuor equalibus horis post mediam noctem, et defecit defecit] corr. ex fecit G medietas diametri a septentrione. Fuit autem Sol in ea hora in gradibus Piscium 14 12′ proxime.

Patet igitur quia etiam hic integris reiectis circulis tot gradibus Lunam motam fuisse, quot Sol quoque motus fuit, a medio quidem prime ad medium secunde eclipsis tempus gradibus 161 55′, a medio vero secunde ad medium tertie gradus 138 55′. Est autem interiacens tempus prime quidem distantie anni unius egyptiaci et dierum 166 et horarum equalium simpliciter quidem 23 45′, exacte autem 23 39′, secunde vero distantie anni rursus egyptiaci unius et dierum 137 et horarum equinoctialium simpliciter quidem quinque, exacte vero 5 30′. Movetur autem rursus Luna medie reiectis circulis in anno quidem uno et diebus 166 et horis equalibus 23 39′ inequalitatis quidem gradus 110 21′, longitudinis autem gradus 169 37′ proxime, in anno vero uno et diebus 137 et horis equalibus 5 30′, inequalitatis quidem gradus 81 36′, longitudinis autem 137 34′ proxime. Patet ergo quia gradus 110 21′ epicycli in prima distantia subtraxerunt a medio motu longitudinis gradus 7 42′, secunde autem distantie gradus 81 36′ addiderunt addiderunt] corr. ex ad dierum G medio longitudinis motui gradus 1 21′.

His ita suppositis, sit rursum ABG epicyclus Lune, et A quidem punctum sit in quo Luna fuit in medio prime eclypsis tempore, B autem in quo in secunde, G vero in quo in tertie, intelligaturque similiter Lune transitus ex A ad B fieri et ex B ad G, ut AB quidem arcus cum sit graduum 110 21′ auferat, auferat] post corr. G ut diximus, a medio longitudinis motu gradus 7 42′, BG autem arcus, cum sit graduum 81 36′, addat longitudini gradus 1 21′, reliquus vero arcus GA, cum sit graduum 168 3′, addat longitudini reliquos gradus 6 21′.

Quod igitur in arcu AB maximam esse oportet longitudinem, perspicuum inde est, quod neque in BG arcu neque in GA esse potest. Nam uterque ipsorum et vim addendi habet et minor semicirculo est, et et] add. s. l. G tamen, hoc non supposito, capiatur centrum zodiaci et eius circuli in quo epicyclus fertur, et sit punctum D, et ab eo ad trium eclipsium puncta DEA et DB et DG linee protrahantur, et coniuncta BG, protrahantur etiam ex E puncto ad puncta quidem B, G linee EB et EG ad lineas vero BD et DG perpendiculares EF et EI, preterea ex G puncto ad BE lineam perpendicularis GT producatur. Quoniam ergo AB arcus 7 42′ gradus circuli qui per medium signorum est subtendit, erit etiam angulus ADB, cum sit in centro zodiaci, talium 7 42′, qualium quatuor quidem recti sunt 360, qualium vero duo recti sunt 360, erit 15 24′. Quare arcus etiam corde EF talium est 15 24′, qualium est circulus qui triangulo DEF circumscribitur 360. Ipsa vero linea EF 16 4′ 42′′ talium, qualium est diameter DE 120. Similiter quoniam AB arcus graduum est 110 21′, erit angulus quoque EB, AEB] corr. ex EAEB G cum sit in circumferentia, talium 110 21′, qualium duo recti sunt 360. Erat autem etiam ADB angulus 15 24′ eorundem. Quare reliquus et EBD angulus 94 57′ est eorundem. Est igitur etiam arcus corde EF talium 94 57′, qualium est circulus qui triangulo BEF circumscribitur 360. Ipsa vero linea EF 88 26′ 17′′ talium, qualium est corda BE 120, quare qualium EF quidem linea est 16 4′ 42′′, DE vero 120, talium etiam BE linea erit 21 48′ 59′′.

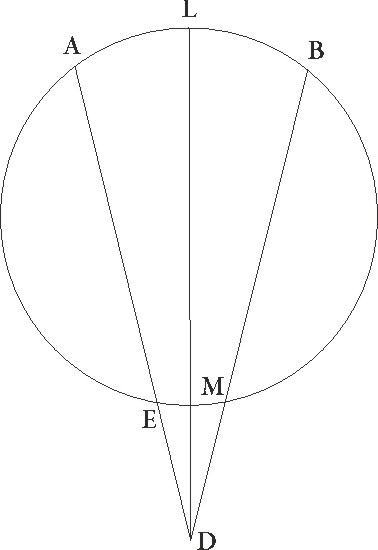Rursus quoniam GE arcus 6 21′ gradus circuli qui per medium signorum est subtendere demonstratus est, erit angulus quoque ADG, cum sit in centro zodiaci, talium 6 21′, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 12 42′, quare arcus quoque linee EI talium erit 12 42′, qualium est circulus qui DEI rectangulo circumscribitur 360. Ipsa vero linea EI talium 13 16′ 19′′, qualium est corda DE 120. Similiter quoniam ABG arcus graduum esse colligitur 191 57′, erit angulus quoque EG, cum sit in circunferentia, talium 191 57′, qualium duo recti sunt 360. Erat autem etiam ADG angulus 12 42′ eorundem. Erit ergo etiam reliquus EGD 179 15′ eorundem, quare arcus quoque corde ei talium erit 179 15′, qualium est circulus qui GEI triangulo circumscribitur 360. Ipsa vero linea EI talium erit 119 59′ 50′′, qualium est diameter GE 120, quare qualium est EI quidem linea 13 16′ 19′′, DE vero 120, talium erit etiam linea EG 13 16′ 20′′. Sed linea etiam BE 21 48′ 59′′ eorundem demonstrata est.

Rursus quoniam arcus BG graduum est 81 36′, erit etiam angulus BEG, cum sit in circumferentia, 81 36′ talium, qualium duo recti sunt 360, quare arcus etiam corde quidem GT talium erit 81 36′, qualium est circulus qui GET triangulo circumscribitur 360. Corde autem ET arcus reliquorum ad semicirculum 98 24′. Erunt igitur etiam corde sue GT quidem talium 78 24′ 37′′, qualium est diameter EG 120, ET autem 90 50′ 22′′ earundem. earundem] post corr. G Quare qualium est linea GE 13 16′ 20′′, talium erit GT quidem 8 40′ 20′′, ET autem similiter 2 49′. Erat autem etiam tota linea EB 21 48′ 59′′, ergo reliqua etiam TB talium erit 11 46′ 10′′, qualium erat GT 8 40′ 20′′. Est autem autem] add. s. l. G etiam quadratum linee BT 138 31′ 11′′ et quadratum linee GT 75 12′ 27′′ eorundem, que composita faciunt quadratum linee BG, hoc est 213 43′ 48′′. Quare BG talium per longitudinem est 14 37′ 10′′, qualium DE quidem linea est 120, GE autem similiter 13 16′ 20′′. Est autem etiam ipsa BG talium 78 24′ 37′′, qualium est epicycli diameter 120. Subtendit enim arcum arcum] corr. ex archum G BG qui est graduum 81 36′. Quare qualium BG quidem linea est 78 24′ 37′′, diameter vero epicycli 120, talium ED quidem linea erit 643 36′ 39′′, GE autem 71 11′ 4′′ eorundem. Erit igitur etiam arcus corde GE talium 72 46′ 10′′, qualium est epicyclus 360. Sed suppositus etiam est arcus GEA 168 3′, et reliquus igitur EA graduum est 95 16′ 50′′, et corda sua talium 88 40′ 17′′, qualium epicycli quidem diameter est 120, ED autem linea 643 36′ 39′′.

Quoniam igitur rursum arcus EA minor semicirculo demonstratus est, patet quia centrum epicycli extra EA portionem cadet. Capiatur igitur, et sit C, et coniungantur DM et CL, ut rursus L quidem punctum maxima, M vero minima fiat longitudo. Quoniam igitur rectangulum quod fit ex AD et ED equale illi rectangulo est quod ex LD et MD producitur, demonstratumque nobis est, qualium est LCM epicycli diameter 120, talium EA quidem lineam esse 88 40′ 17′′, ED autem 643 36′ 39′′ eorundem, eorundem] post corr. G totam vero AD 732 16′ 56′′, ideo certe fit quod ex AD et DE, hoc est quod ex LD et DM, producitur eorundem eorundem] post corr. G 471304 46′ 17′′. Rursus quoniam quod fit ex LD et DM cum eo quod est ex CM illud quadratum facit quod est ex DC, quoniam que CM, cum a centro epicycli sit, 60 partium sit, estque quadratum eius 3600, si istis 471304 46′ 17′′ addiderimus, habebimus quadratum DC 474904 46′ 17′′ eorundem. eorundem] post corr. G Quare DC que a centro concentrici zodiaci epicyclumque deferentis est talium erit 689 8′, qualium est CM que a centro epicycli est 60, quare qualium est linea que est inter centra zodiaci et epicycli 60, talium etiam erit que est a centro epicycli 5 14′, que proportio eadem est proxime illi proportioni quam per antiquissimas eclipses paulo ante demonstravimus.

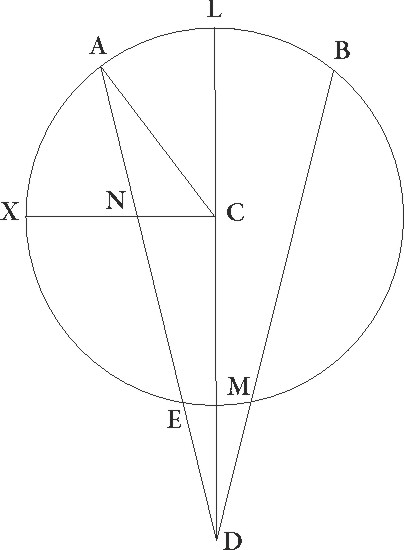Ducatur igitur rursus in eadem descriptione a centro C ad lineam DEA perpendiculis CNX, et protrahatur AC linea. Quoniam igitur qualium DC linea demonstrata est 689 8′, talium erat etiam DE quidem linea 643 36′ 39′′, NE autem, cum sit medietas ipsius E, 44 28′ eorundem, eorundem] post corr. G et erit etiam tota DEN eorundem eorundem] post corr. G 687 56′ 47′′. Quare qualium DC corda est 120, talium erit DN 119 47′ 36′,′ et arcus suus talium 173 17′ proxime, qualium est circulus qui DCN triangulo circumscribitur 360. Quare angulus quoque DCN talium est 173 17′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 86 38′ 30′′. Quare arcus etiam epicycli MEX est 86 38′ 30′′, reliquus autem LAX 93 17′ 30′′ reliquorum ad semicirculum. Est autem etiam arcus AX, cum sit medietas ipsius arcus E, 47 38′ 30′′ proxime eorundem. Erit ergo etiam reliquus AL graduum 45 43′. Sed totus AB supponebatur esse 110 21′ eorundem, erit ergo etiam reliquus LB arcus quo Luna in medio secunde eclipsis tempore a maxima longitudine distabat graduum 64 38′.

Similiter quoniam DCN angulus 86 38′ proxime talium demonstratus est, qualium quatuor recti sunt 360, angulus vero CDN reliquorum ad unum rectum 3 22′, supponebatur autem totus ADB angulus 7 42′ eorundem esse, erit ergo reliquus angulus LDB qui subtendit arcum a medio longitudinis motu auferendum propter inequalitatem que fit penes LB arcum epicycli reliquorum graduum 4 20′. Quare Luna secundum longitudinem in medio secunde eclipsis tempore medie mota obtinebat gradus Arietis 29 30′, nam exquisite 25 10′ Arietis, tot scilicet, quot etiam Sol Libre gradus obtinebat.

〈IV.7〉 Capitulum VII: De emendatione mediorum longitudinis et inequalitatis motuum Lune

Quoniam igitur demonstravimus Lunam in secunda quidem antiquarum eclipsium in medio ipsius eclipsis tempore equaliter secundum longitudinem quidem 14 44′ gradus Virginis obtinuisse, inequalitatis autem a maxima epicycli longitudine gradus 12 24′, in secunda vero nostri temporis eclipsium medie similiter secundum longitudinem 29 30′ gradus Arietis obtinuisse, inequalitatis vero a maxima longitudine gradus 64 38′, patet quia in tempore quod inter predictas eclipsis interfuit reiectis integris circulis mota medie Luna est longitudinis quidem gradibus 21 4′ 46′′, inequalitatis vero gradibus 52 14′. Sed tempus a secundo anno Mardocempadi Thot 18 sequente decimonono ante mediam noctem media et tertia hore unius equalis parte usque ad xviiii^m Adriani annum Chiach die secundo sequente tertio ante mediam noctem hora una equali annorum est egyptiacorum 854 et dierum 73 et horarum simpliciter quidem 23 50′, exquisite autem et ad equales dies naturales 23 3′, estque totus dierum numeris 311783 et horarum equalium 23 3′, quibus per diurnos diurnos] corr. ex diuarnos A medios motus sine equatione iam nobis expositos convenire integris reiectis circulis invenimus longitudinis quidem gradus 224 46′, inequalitatis vero gradus 52 31′, et sic longitudinis motus idem invenitur illi qui per expositas observationes a nobis collectus est, inequalitatis vero 17 sexagesimis excedit. Quare antequam tabulas conscriberemus, ut diurni motus emendarentur, 17 sexagesimas per multitudinem dictarum dierum partiti et uni diei convenientes partes 0 0′ 0′′ 0′′′ 11′′′′ 46′′′′′ 39′′′′′′ subtraximus a diurno medio motu inequalitatis qui ante emendationem habebatur, et sic invenimus emendatum esse graduum 13 3′ 53′′ 56′′′ 15′′′′ 51′′′′′ 59′′′′′′, et his consequenter reliquam tabularum compositionem absolvimus.

〈IV.8〉 Capitulum VIII: De locis equalium Lune motuum longitudinis et inequalitatis in tempore Nabonassari

Verum ut etiam motus eorum in eundem primum Nabonassari Nabonassari] corr. ex Nabonasari G annum et in prime diei Thot secundum Egyptios meridiem reducamus, cepimus tempus quod est inde usque ad medium secunde antiquarum eclipsium tempus que, ut diximus, fuit secundo Mardocempadi anno Thoth xviii^a decimanona sequente 50′ equalis hore sexagesimis ante mediam noctem. Id tempus colligitur esse annorum egyptiacorum egyptiacorum] corr. ex egiptiacorum G 27 dierum 17 et horarum simpliciter simul et exacte 11 6′ proxime cui adiacent integris circulis reiectis longitudinis quidem gradus 123 22′, inequalitatis vero gradus 103 35′. Hos si a gradibus locorum medii temporis eclipsis secunde alteros ab alteris convenienter subtraxerimus, habebimus quod in primo Nabonasari anno Thoth secundum Egyptios prima in meridie Luna medie fuit secundum longitudinem quidem 11 22′ gradus Thauri, inequalitatis vero a maxima epicycli longitudine habebimus gradus 268 49′, distantie autem gradus 70 37′. Sol enim in eodem tempore 0 45′ Piscium gradus obtinuisse demonstratus est.

〈IV.9〉 Capitulum VIIII: De emendatione mediorum motuum latitudinis Lune et de locis ipsorum in primo Nabonassari anno

At longitudinis quidem et inequalitatis periodicos motus et locos ipsorum his rationibus constituimus, in latitudinis autem motu antea quidem etiam ipsi errabamus eo quod utebamur secundum Hyparchum illa proportione ex Luna sexcentis quinquagintaque proxime vicibus circulum suum mensuraret, bis autem atque semis umbram secundum mediam in pleniluniis distantiam. His enim suppositis, et ad hec quantitate inclinationis obliqui circuli Lune, particularium eclipsium ipsius termini dantur, capiebamus igitur eclipsium distantias, et a magnitudine obscurationum in temporibus mediis motum latitudinis in obliquo circulo ab altero nodorum computabamus, et per demonstratam inequalitatis differentiam periodicos motus a veris discernebamus, et sic periodicos latitudinis motus in mediis eclipsium temporibus et locum quo in interiecto tempore pervenit, circulis integris semper reiectis, inveniebamus. Nunc autem faciliore usi via que suppositionibus eisdem ad invenienda quesita non indiget, et motum latitudinis per computationem illorum factum factum] corr. ex factam G falsam invenimus, et ab hoc absque illis percepto rationes rationes] post corr. G quoque ipsas de magnitudinibus atque distantiis tanquam falsas redarguimus ac emendavimus, id ipsum in Saturni quoque atque Mercurii rationibus fecimus. Mutavimus enim nonnulla non exacte percepta, quoniam veriores postea observationes in nos pervenerunt. Quippe decet omnes qui amore veritatis impulsi has speculationes suscipiunt non solum ad priscorum emendationem certiore novaque uti via, verum etiam ad sui isporum, nec id turpe sibi putare, si non solum a se ipsis verum etiam ab aliis ad exactiora revocantur, presertim cum magna hec atque divina professio sit. Sed quomodo singula horum demonstrantur, in propris locis explanabimus. In presentiarum autem, ut consequenter progrediamur, ad demonstrandum latitudinis motum revertamur, hec demonstratio sic se habet.

Nam primum ad huius medii motus emendationem defectus Lune quam diligentissme conscriptos quam remotissimi temporis inveniri potuerunt quesivimus, in quibus et obscurationum magnitudines equales fuerunt, in eodemque nodo facte et in utrisque aut a septentrione aut a meridie similiter et ad hec Luna in distantia erat equali. Hec enim cum ita se habeant, necesse est ut centrum Lune equaliter in utroque defectu ipsius et ad easdem distet nodi partes, et idcirco verus motus eius integros in medio tempore observationum circulos latitudinis contineat.

Primam igitur eclipsim cepimus que primo et trigesimo primi Darii anno in Babylone fuit observata Tibi secundum Egyptios tertio sequente quarto ante mediam noctem hora media, diciturque Luna defecisse ab austro duobus digitis.

Secundam que Alexandrie nono Adriani anno fuit observata Pachon secundum egyptios die xvii sequente 18 ante mediam noctem horis 3 36, quando similiter sexta pars lunaris diametri a meridie defecit.

Erat autem etiam motus latitudinis Lune in utraque eclipsi iuxta descendentem nodum, quod per universaliores quoque rationes comprehenditur, distantia etiam equalis proxime et paulo propinquior terre quam media, quod etiam ab iis que de inequalitate demonstrata sunt perspicuum est. Quoniam ergo, quando ab austro Luna deficit, tunc centrum eius borealius ecliptico circulo est, patet quia in utraque eclipsi centrum Lune descendentem nodum equaliter precedebat. Sed in prima quidem eclipsi Luna 100 19′ gradus a maxima epicycli longitudine distabat. Medium enim tempus media hora mediam noctem in Babilone precessit, in Alexandria vero tertia unius equalis hore parte et sunt a statuto loco Lune in tempore Nabonasari anni 256 dies 122 et equales hore simpliciter quidem 10 20′, ad dies vero equatos 10 15′. Idcirco verus motus gradibus quinque medio minor fuit. In secunda vero eclipsi Luna 251 53′ gradibus maxima epicycli longitudine distabat. Sunt enim etiam hic a statu〈to〉 a statuto] astatur A loco Lune usque ad medium eclipsis anni 871 dies 256 et equales hore simpliciter quidem 8 24′, exacte autem 8 5.′ Quapropter etiam verus motus 4 53′ gradibus maior medio erat. In tempore igitur quod inter utrasque fuit eclipsis annorum egyptiacorum 615 dierum 133 et horarum equalium 21 50′ verus Lune motus secundum latitudinem integros circulos absolvit, medius vero gradibus 9 53′ qui ex utraque inequalitate colliguntur ad integros circulos defecit. Sed a mediis motibus qui secundum Hyparchi viam in tanto tempore colliguntur decem gradus et due sexagesime proxime ad integras restitutiones deficiunt. Quare motus latitudinis novem sexagesimis per eam viam excedit.

Has igitur in multitudinem dierum predicti temporis 224609 proxime partiti quod factum est 0 0′ 0′′ 0′′′ 8′′′′ 39′′′′′ 18′′′′′, addidimus diurno medio motui iam demonstrato, et sic emendatum diurnum motum invenimus gradum 13 13′ 45′′ 39′′′ 48′′′′ 56′′′′′ 37′′′′′′, consequenterque postea reliquas tabulas composuimus.

Ita ergo semel motu latitudinis demonstrato, deinceps ad locorum eius constitutione duarum rursus eclipsium distantiam quesivimus, in quibus cetera quidem superioribus conveniebant. Nam et distantie Lune equales proxime inveniebantur et obscurationes similiter et utreque vel ad septentionem vel ad meridiem, nodus vero idem non erat sed oppositus.

Harum eclipsium prima est, qua ad demonstrandam inequalitatem fuimus usi, facta secundo anno Mardocempadi Thot secundum Egyptios die xviii^o sequente xix in media nocte apud Babylonios, Allexandrie autem 50′ unius hore sexagesimis precessit, asseriturque Luna tribus digitis ab austro defecisse.

Secunda est, qua Hipparchus etiam usus fuit, facta xx^o eius Darii anno qui Cambysse successit Epiphi secundum egyptios egyptios] corr. ex egiptios G die 28^o sequente 29^o in horis equalibus post occasum Solis 6 20′, in qua similiter Luna quarta diametri parte ab austro defecit, eratque medium tempus in Babylone ante mediam noctem 24′ unius equalis hore sexagesimis, fuit enim tunc media nox in horis 6 45′ proxime, in Allexandria vero ante mediam noctem 1 15′ equalibus, factaque est eclipsis utraque, cum Luna in maxima distantia esset, sed prima iuxta ascendentem nodum altera iuxta descendentem, ut etiam in ispis equaliter borealius circulo qui per medium signorum est centrum Lune fuisse inveniatur.

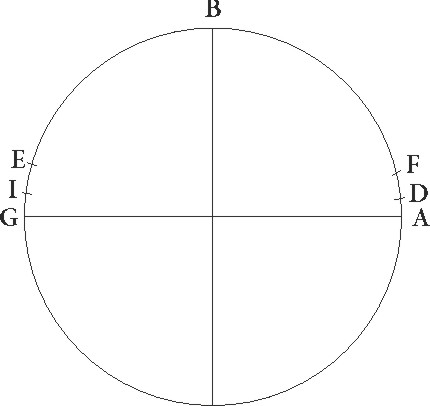Sit igitur AB obliquus circulus eius, cuius diameter AG, et supponatur A punctum nodum esse ascendentem, G vero descendentem, B autem borealissimum terminum, et intercipiantur a punctis A et G, idest ab utroque nodorum versus B borealem terminum AD et GE arcus equales, ita ut in prima quidem eclipsi centrum Lune in puncto D, in secunda vero in E fuerit. Sed tempus a statuto loco Lune ad primam eclipsim annorum fuit egyptiacorum 27 et dierum 17 et horarum equinoctialium tam simpliciter quam exacte xi 6′, atque hac de causa a maxima epicycli longitudine Luna distabat gradus 12 24′ et medius motus eius maior erat quam verus 59 sexagesmis, tempus autem usque ad secundam eclipsim similiter egyptiacorum annorum 245 et dierum 327 et horarum equinoctialium, simpliciter quidem 1 45′, exacte autem 1 15′, et hac de causa Luna a maxima epycicli epycicli] corr. ex epicicli G longitudine distabat gradibus 2 44′, eratque medius motus maior quam verus 13 sexagesimis, tempus etiam quod inter has observationes interfuit quodque 218 egyptiacos annos continet et dies 309 et horas equales 23 12′ secundum latitudinis motum medium iam expositum colligit, reiectis integris circulis, gradus 160 et 4 sexagesimas.

Sit ergo propter hec medius etiam centri Lune motus in prima quidem eclipsi in puncto F, in secunda vero in I, et quoniam CBI arcus gradum gradum] corr. ex gradus G est 160 4′, DF autem sexagesimarm 59′, EI vero sexagesimarum 13, colligetur etiam arcum DE graduum esse 160 50′. Quare utrique simul AD et EG arcus reliquorum ad semicirculum sunt gradum 19 10 et uterque isporum per se quoniam equales sunt 9 35′ eorundem, quibus vere Lune motus in prima quidem eclipsi a nodo descendente deficiebat, in secunda vero descendentem precedebat. Quare totus etiam arcus AF graduum est 10 34 et reliquus IG graduum 9 22′. Ergo medius quoque Lune motus in prima quidem eclipsi ab ascendente nodo deficiebat gradibus 10 34′, distabatque a boreali termino gradibus 280 34′, in secunda vero 9 22′ gradibus descendentem precedebat, distabatque ab eodem boreali termino gra-dibus 80 38′. Quare, quoniam tempus a loco Lune statuto usque ad eclipsis prime medium continet, reiectis circulis, gradus 286 19′, si hos a loco eclipsis prime, hoc est a gradibus 280 34′, adiecto circulo, subtraxerimus, habebimus locum medii motus latitudinis a boreali termino gradus 354 15′ in primo Nabonassari anno primo die Thot secundum Egyptios Egyptios] corr. ex Egiptios G in meridie.

〈IV.10〉 Capitulum X: Expositio tabule prime ac simplicis inequalitatis Lune

Verum quoniam ad discernendas coniunctiones et oppositiones calculosque ipsorum secunda quam demonstraturi sumus inequalitate non indigemus, particularium partium tabulam fecimus, quarum computationem per lineas sicut etiam in Sole adinvenimus, usique sumus proportione 60 ad 5 et et] add. s. l. A 14′ sexagesimas proxime, partitique sumus similiter quartas quidem partes illas que maxime longitudini adherent per gradus 6, eas vero que minime longitudini adherent per gra-dus 3, ut rursus tabule descriptio huius solari similis sit, versusque habeat 45, ordines 3, quorum duo primi numeros graduum inequalitatis continent, tertius addendos subtrahendosve gradus qui singulis partibus accommodantur. Ita subtractio quidem tam in longitudinis quam in latitudinis calculo fit, quando inequalitatis numerus qui a maxima epicycli longitudine colligitur usque ad 180 gra-dus ascendit, additio vero, quando 180 gradus excedit, et est tabula huiusmodi: huiusmodi] volve cartam add. A

Tabula prime simplicisque inequalitatis Lune Numeri communes
Primus	2^us	3^us
6	354	0	29
12	348	0	57
18	342	1	25
24	336	1	53
30	330	2	19
36	324	2	44
42	318	3	8
48	312	3	31
54	306	3	51
60	300	4	8
66	294	4	24
72	288	4	32
78	282	4	49
84	276	4	56
90	270	4	59
93	267	5	0
96	264	5	1
99	261	5	0
102	258	4	59
105	255	4	57
108	252	4	53
111	249	4	49
114	246	4	44
117	243	4	38
120	240	4	31
123	237	4	24
126	234	4	16
129	231	4	7
132	228	3	57
135	225	3	46
138	222	3	35
141	219	3	23
144	216	3	10
147	213	2	57
150	210	2	43
153	207	2	28
156	204	2	13
159	201	1	57
162	298	1	41
165	294	1	25
168	292	1	9
171	189	0	52
174	186	0	35
177	185	0	18
180	180	0	0

〈IV.12〉 Capitulum XII: Quod non penes suppositionum, sed penes computationum sed … computationum] add. marg. A differentias lunaris inequalitatis quantitas diversa est secundum Hipparchum

His ita iam demonstratis, non iniuria quispiam quereret quamnam quamnam] post corr. G ob causam per expositas ab Hipparcho ad huius inequalitatis considerationem lunaris eclipsis nec eadem proportio illi colligitur quam nos demonstravimus, nec prima excentricitatis suppositio secunde que per epicyclum est consonare convenireque, ut demonstravimus, invenitur. In prima enim suppositione ex computationibus colligit eam esse semidiametri excentrici ad lineam que inter centra ipsius et zodiaci est quam habent 3144 ad 327 50′ proxime, que proportio eadem est proportioni 60 ad 6 15′. In secunda vero colligit proportionem semidiametri zodiaci circuli usque ad epicycli centrum ad semidiametrum epicycli eam esse quam habent 3122 30′ ad 347 30′, que proportio eadem est proportioni 60 ad 4 46′. Facit autem maximam inequalitatis differentiam: proportio quidem 60 ad 6 15′ graduum 5 49′, proportio autem 60 ad 10 46′ graduum 4 34′ cum secundum nos proportio 60 ad 5 14′ differentiam predictam 5 graduum proxime faciat. faciat] corr. ex faciant G

Quod autem non propter suppositionum differentiam, ut aliqui putarent, hic error secutus est tum ratione paulo ante patuit, quoniam utroque modo eadem penitus accidere apparentia demonstratum est, tum si per numeros computationem facere voluerimus, eandem ex utraque suppositione fieri proportionem inveniemus, dummodo eisdem apparentibus in utraque utamur, nec diversa, sicut Hypparchus, accipiamus. Possibile enim sic est, cum non eedem eclipsis capiantur, errorem vel penes ipsas observationes vel penes distantiarum computationes accidere. Inveniemus igitur etiam in illis eclipsibus recte oppositiones observatas fuisse convenienterque factas positionibus equalis et inequalis motus a nobis demonstratis, computationes autem distantiarum quibus proportionis quantitas demonstratur non diligenter factas fuisse, quorum utrunque a primis tribus eclipsibus initium capientes demonstrabimus.

Tres igitur eclipsis a Babylone delatas ibique observatas ait, primamque fuisse in Phanostrati magistratu apud Athenienses mense Posideone, defecisseque Lune parvam circuli partem ab ortu estivo et occidit, inquit, adhuc deficiens hic annus 366 a Nabonassaro fit secundum Egyptios, ut ipse ait, Thot 26 sequente 27 post mediam noctem horis 5 30′, media enim pars hore ad diem restabat. Verum cum Sol circa finem Sagittarii sit, nocturne hore hore] vel add. et del. AG unius tempora in Babilonia 18 sunt. Nox enim horarum 14 10′ equalium est, temporales igitur hore 5 30′ colligunt equales horas 6 15, principium igitur eclipsis fuit post horas equales 18 15′ post meridiem diei 26′. Sed quoniam parva pars obscurata fuit, totum eclipsis tempus fuisse debet horis 1 30′ proxime, medium vero eclipsis post meridiem horis equalibus 19 20′. Quare in Allexandria rursus medium huius eclipsis tempus fuit post meridiem diei vigesimisexti horis 18 30′. Est autem tempus a dato loco Lune in primo Nabonassari Nabonassari] corr. ex Nabonasari G anno usque ad expositum 365 egyptiacorum annorum et dierum 25 et horarum equalium simpliciter quidem 18 30′ exacte vero 18 4′, ad quod tempus computantes secundum expositas nobis rationes verum Solis motum invenimus optinuisse Sagittarii gradus 28 18′, Lune autem medie quidem Geminorum 24 20′, vere autem 28 17′, secundum inequalitatem enim 227 43′ gradus a maxima epicycli longitudine distabat.

Sequentem deinceps eclipsim ait in magistratu Phanostrati apud Athenienses Stirophorionis mensis fuisse. Phamenoth secundum Egyptios die 24 sequente 25, defecitque, ut ait, ab ortu estivo, prima hora transacta, hoc tempus colligitur esse a Nabonassaro Nabonassaro] corr. ex Nabonassario G annorum 366 Phamenoth die 24 sequente 25 ante mediam noctem horis temporalibus 5 30′ proxime. Quoniam igitur Sol iuxta finem Geminorm fuit una noctis hora in Babilone temporum 12 est, quare 5 30′ hore temporales faciunt equales 4 24′. Principium igitur eclipsis fuit horis 7 36′ equalibus post post] add. s. l. G meridiem diei xxiiii. Sed quoniam totum eclipsis tempus trium scribitur horarum fuisse, medium videlicet fuit post horis equalibus 9 10′, debuit ergo Allexandrie Allexandriae] corr. ex Alexandriae G post meridiem diei vigesime quarte horis equalibus 8 15′ proxime facta fuisse. Anni ergo a constituto loco rursus sunt 365 et dies 203 et equales hore simpliciter quidem 8 15′, exacte vero 7 50′, quo in tempore invenimus Solem exacte optinuisse Geminorum gradus 21 46, Lunam autem Sagitarii medie quidem gradus xxiii 58′, exacte vero 21 48′, secundum inequalitatem enim 27 37′ a maxima epicycli longitudine distabat. Colligitur autem distantia a prima ad secundam eclipsim dierum 177 et horarum equalium 13 36′, in quibus Sol motus fuit graduum 173 28′. Sed Hypparchus demonstravit quasi numerus dierum distantie fuisset 177 et horarum equalium 13 461′ et graduum 173 octava unius gradus parte minus.

Tertiam ait fuisse in magistratu Evandri apud Athenienses mense primo Possideone Thoth secundum Egyptios die xvi sequente 17 et defecit, ut ait, tota incipiens ab ortu estivo quatuor horis transactis, quod tempus etiam a Nabonassaro colligitur annorum 367 Thot die xvi sequente xvii^o ante mediam noctem horis 2 30′. Sed cum Sol duas Sagittarii peregerit partes, hora noctis in Babilone temporum est 18 proxime, quare 2 30′ hore temporales tres equales horas faciunt, et sic principium eclypsis fuit post meridiem diei 16 horis 9 equalibus, et quoniam tota defecit, totum quidem tempus quatuor horarum equalium fuit et medium tempus videlicet post meridiem horis xi, quare medium tempus in Allexandria debet fuisse post eandem meridiem horis equalibus 70 10′. Est autem tempus a locis constitutis annorum 366 dierum 15 et horarum equalium simpliciter quidem 10 10′, exacte vero 9 50′, in quo tempore invenimus Solem exacte, hoc est vero suo motu, obtinuisse Sagittarii gradus 17 30′ et Lunam medie quidem Geminorm gradus 17 21′, exacte vero 17 28′, secundum inequalitatem enim 181 12′ gradus a maxima epicycli longitudine distabat. Colligitur autem etiam a secunda ad tertiam eclipsim tempus dierum 177 et horarum equalium 2, graduum vero 175 44′. Sed hanc distantiam Hypparchus rursum supposuit dierum 177 et horarum equalium 1 40′, graduum vero 175 8′. Apparet igitur in comptutationibus distantiarum errasse: in tempore quidem sextam et tertiam hunius equalis hore partem, in gradibus vero 36 sexagesimis gradus unius proxime in utraque distantia, que non parvam in quantitate proportionis differentiam facere possunt.

Sed transeamus nunc ad tres eclipses postremo sibi positas et Allexandrie observatas, ut ait, quarum primam asserit fuisse anno 54 secunde secundum Calippum periodi periodi] pereriodi A Messori secundum Egyptios die 16, et incepit Luna deficere ante ortum suum per mediam horam, repletaque rursus fuerat in tertie hore medio , quare medium tempus fuit hora secunda incipiente ante mediam noctem horis tam temporalibus quam equalibus 5. Sol enim circa Virginis finem fuit, quare post meridiem diei 16 horis equalibus septem medium eclipsis tempus Allexandrie fuit. Est autem tempus a constitutis locis et anno Nabonassari primo annorum egyptiacorm 546 dierum 345 et horarum equalium simpliciter quidem 7, exacte vero 6 30′, in quo tempore Solem exacte obtinuisse invenimus Virginis gradus 26 6 et Lunam medie quidem Piscium gradus 22, exacte vero 26 7′, secundum inequalitatem enim gradibus 313 a maxima epycicli longitudine distabat.

Sequentem autem deinceps eclipsim 55 anno eiusdem periodi facta asserit Mechir secundum Egyptios die 12, et incepit 5 20 noctis hora transacta, defecitque tota. Fuit ergo eclipsis principium post meridiem diei none horis 11 20. Sol enim iuxta finem Piscium erat, medium vero tempus fuit post meridiem horis 13 20′, tota enim Luna defecit, estque a locis constitutis usque ad eclipsim tempus annorum egyptiacorum 147 dierum 158 et horarum equalium tam simpliciter quam exacte 13 20′, in quo tempore Solem 26 17′ gradus Piscium exacte obtinuisse invenimus, et Lunam medie quidem 1 7′ Libre gradus exacte autem et vero motu suo 26 16′ Virginis gradus. Secundum inequalitatem enim 109 28′ gradibus a summa epicycli longitudine distabat. Colligitur autem distantie tempus a prima ad secundam eclipsim dierum quidem 178 et horarum equalium 6 50′, gra-duum autem 180 11′, sed Hypparcus demonstrationem hanc fecit quasi huius distantie tempus tempus] add. marg. G fuerit dierum 178 et horarum equalium 6, graduum vero 180 20′.

Tertiam eclipsim fuisse ait eodem 55 anno secunde periodi Messori secundum Egyptios die 5^a et incepit transacta noctis hora 6 et 40 sexagesimis, defecitque tota. Medium autem tempus asserit fuisse in horis 8 20′ proxime, hoc est post mediam noctem horis temporalibus 2 20′. Sed cum Sol iuxta medietatem Virginis fuerit, noctis in Allexandria hora 18 24′ temporum est. Hore igitur 2 20′ temporales faciunt horas equales 2 15′ proxime. Quare medium tempus fuit post meridiem diei quinte horis equalibus 14 15′. Est autem a constitutis locis tempus annorum egyptiacorum 547 dierum 334 et horarum equalium simpliciter quidem 14 15′, exacte vero 13 45′, in quo tempore Solem 15 12′ Virginis gradus exacte obtinuisse invenimus, Lunam aut medie quidem 10 24′ Piscium, exacte vero 15 13′. Secundum inequalitatem enim 249 9′ gradibus a maxima epicycli longitudine distabat. Colligitur autem etiam distantie a secunda eclipsi ad tertiam tempus dierum 176 et 24 sexagesimarum hore unius equalis, graduum vero 168 55′. Sed hanc etiam distantiam Hypparchus 176 dierum et 20 sexagesimarum unius equalis hore supposuit et gradum 168 33′. Quare hic quoque videtur errasse in gradibus quidem sextam et tertiam partem proxime gradus unius, in diebus autem 55 sexagesimis sexagesimis] post corr. G proxime hore unius equalis, que similiter magnam exposite proportionis differentiam faciunt.

Ante oculos igitur causa dissonantie posita iam est, quare magis confidentes proportione inequalitatis, quam ipsi demonstravimus, in oppositionibus coniunctionibusque Lune utemur, cum etiam eclipsis iste, quas Hypparchus conscripsit, summopere rationibus nostris convenire videamus.

Finis quarti libri.