PAL

Ptolemaeus Arabus et Latinus

_ (the underscore) is the placeholder for exactly one character.
% (the percent sign) is the placeholder for no, one or more than one character.
%% (two percent signs) is the placeholder for no, one or more than one character, but not for blank space (so that a search ends at word boundaries).

At the beginning and at the end, these placeholders are superfluous.

〈IX〉

Liber VIIII Magne Compositionis Ptholomei incipit

〈IX.1〉 Capitulum I : De ordine globorum Solis, Lune, ceterorumque stellarum erraticarum

Verum que de fixis summatim quantum ab apparentibus atque ad hunc diem hunc diem] iter. et del. A cognitis intelligendum iuvamur dici possunt, hec ferme sunt. Cum autem ad compositionem istam quinque planetarum negotium restet, quantum fieri potest singulas speculationes ipsorum coniungemus. Nam ne sepius eadem repetantur, communiter prius de ipsis dicemus.

Primum igitur de spherarum ipsorum ordine que similiter situm habent quasi ad polos obliqui solaris qui per medium signorum est, quod omnes propinquiores terre sint quam sphera fixarum, et remotiores a terra quam sphera lunaris, quamque tres, Saturni, que maior est, et Iouis, que secunda et terre propinquior, et Martis sub ipsa remotiores a terra reliquis sunt, solari etiam ipsa, eodem fere modo ab omnibus primis mathematicis dicitur. Veneris autem atque Mercurii sphere a priscis quidem sub solari collocantur, a nonnullis autem iuniorum ipse quoque idcirco superponuntur, quoniam nunquam ab istis planetis defici Sol visus est. Sed hec ratio infirma nobis videtur. Possunt enim planete aliqui esse sub Sole, nec tamen in aliqua penitus superficie ipsarum que per ipsum et visum nostrum sunt, sed in alia atque idcirco obiici sibi non posse, sicut et in coniunctionalibus Lune obiectionibus, ut plurimum nullus Solis defectus efficitur.

Verum cum rei huius intelligentia nequeat aliter haberi, propterea quod nulla stellarum sensibilem diversitatis aspectum facit, a quo solo apparente distantie capiuntur, verisimilior priscorum mihi ordo videtur, naturalius per medium Solem eos disseparans planetas qui qui] corr. ex quae G quavis possunt ab eo distantia removeri ab illis que non ita se habent, sed circa ipsum semper circumducuntur, cum tamen non adeo ipsos ab eo versus terram removeat, ut aspectus diversitas de qua curandum sit fieri possit.

〈IX.2〉 Capitulum II : De difficillimo suppositionum modo modo] in quibus add. et del. A in quinque planetis

Sed de ordine spherarum hec dicta sint. Cum vero propositum nobis sit, sicut de Sole ac Luna fecimus, sic de quinque quoque planetis apparentes ipsorum inequalitates omnes equalibus circularibusque motibus fieri demonstrare, —hii enim divinorum corporum nature conveniunt, unde inordinatio et dissimilitudo longe abest—, magni facere oportet quicquid in hac re assequemur, que finis speculationis mathematice philosophie profecto est. Est autem negotium hoc multis de causis difficilimum, primum quia nundum a prioribus recte consideratum, deinde, cum in considerationibus periodicorum in singulis motuum possit in observationibus per instrumenta minutus error fieri qui citius sensibilem in posterum facit differentiam, quando minore temporis spatio facta observatio sit, tardius, quando maiore, tempus ex quo planetarum observationes habemus conscriptas adeo breve est ad magnitudinem rerum collatum, ut longi temporis predictionem infirmam faciat. Preterea non parum turbat quod in consideratione inequalitatum due in singulis inequalitates fieri videntur, ipseque inequales tum magnitudine tum restitutionum temporibus, quarum, quamvis ad Solem altera altera ad zodiaci partes perspiciatur, tamen sic inter se penitus confunduntur, ut neutre proprietas facile descernatur, ab hec priscorum observationes minore cura et universalius conscripte sunt. Nam que crebriores sunt stationes et apparitiones continent, quarum utriusque ambigua nimium perceptio perceptio] post corr. G est, stationes enim verum ostendere tempus non possunt, cum in multis ante stationem et post stationem diebus localis progressus insensibilis fiat. Apparitiones autem non solum locos ipsos ubi prius vel posterius vise sunt statim delere videntur, verum etiam errorem in temporibus afferunt, tum ex differentia eris, tum ex differentia visus cernentium; et universaliter observationes ad aliquam fixarum stellarum longiore distantia facte, nisi quis genera omnium diligenter ac scite animadvertat, difficile atque coniecturaliter mensurationis magnitudinem ostendunt, non solum quoniam linee que inter observatas stellas inveniuntur varios ad obliquum solarem faciunt angulos nec penitus rectos, unde magnus error consequitur propter variam zodiaci declinationem quam habent in ipsa longitudinis atque latitudinis observatione, verum etiam quoniam ipse quoque distantie maiores ad orizontem visibus apparent, et minores in medii celi locationibus; et propterea modo quasi maiores modo quasi minores ipsa vera subiecta distantia mensurantur.

Quas ob res puto Hipparcum veritatis amicum, qui propter hec omnia et maxime quia non habuit tot veras observationes a priscis quot ipse nobis prebuit, negotium quidem Solis ac Lune et investigasse et ut possibile erat per equales et circulares motus fieri demonstrasse, quinque autem planetarum negotium, quantum commentarii sui quos nos vidimus ostendunt, ne suscepisse quidem, sed solum observationes ipsorum commodius congregasse, ostendisseque per ipsas non convenire apparentia suppositionibus mathematicorum illius temporis. Non enim putavit ut videtur affirmandum tantummodo esse quod duppl〈i〉cem dupplicem] dupplcem A singuli quinque planetarum inequalitatem faciant, vel quod inequales tantosque unusquisque progressus habeat, cum ceteri mathematici quasi de una eademque et inequalitate et progressu linearum demonstrationibus usi sint, neque quod circulis excentricis aut concentricis quidem zodiaco, sed epicyclos habentibus aut certe utrisque ista efficiantur, quod inequalitas zodiaci tanta sit et tanta illa que ad Solem habetur. Quibus omnes ferme qui per tabulas quas perpetuas appellant equalem circularemque motum ostendere voluerunt quidem, sed alii nihil omnino demonstrarunt, demonstrarunt] post corr. G alii ad finem usque non pervenerunt. Sed cogitavit quod, cum per omnes disciplinas exquisite vereque processisset, non debebat sicuti ceteri incipere quod ad exitum deduci posse non videbatur. Intelligebat enim et utriusque inequalitatis magitudinem et periodos ipsas per apparentia certa nec ulli dubitata esse demonstrandas, ac rursus coniungendo utrasque tam positionem quam ordinem circulorum quibus ipse fuerit et modum motus ipsarum inveniendum, omniaque apparentia proprietati suppositionis circulorum accomodanda. Id igitur etiam ipsi difficilimum arbitror visum fuisse. Hec non ostentationis causa diximus, sed ut, si rebus ipsis cogamur aut preter rationem aliquibus abuti, ut verbi gratia quando quasi in circulis fictis atque in spheris per motum ipsorum descriptis et quando quando] add. s. l. G quasi in eadem superficie cum obliquo solari sint, demonstrationes propter commoditatem facimus, aut quando prima quedam supponimus non a principio quoddam apparente, sed crebra experientia et accomodatione intellecta, aut quando non eundem atque immutabilem motus modum vel declinationi circulorum in omnibus supponi volumus. Scimus enim neque huiusmodi abusum ex quo nulla sequitur differentia de qua curandum sit nostro posse obesse proposito, neque illa que sine demonstratione supponuntur, si apparentibus omnino conveniunt, inventa esse absque diligenti animadversione viaque posse, etiam si modus intelligentie sue vix possit exponi, presertim cum universaliter primorum principiorum cause aut nulle sint aut exponi vix possint, neque varii suppositionis circulorum modi quasi minus rationabiles putandi sunt, presertim cum ipsa etiam apparentia dissimilia in stellis esse percipiantur, et maxime quoniam equalis et et​] add. s. l. G circularis motus simpliciter in omnibus conservetur et apparentium singula ex similitudine suppositionum proprie atque universaliter demonstrentur.

Usi autem sumus ad singulas demonstrationes observationibus de quibus minime ambigitur, hoc est que per coniunctionem aut maximam stellarum propinquitatem aut etiam Lune habite sunt, et maxime iis quas per astrolabica instrumenta invenimus, in quibus per foramina circulorum visus dirigitur, et tum equales distantias undique per similes arcus cernere, tum transitus singulorum qui ad obliquum solarem fuerint et per longitudinem et per latitudinem exquisite potest percipere per accommodationem zodiaci in astrolabio circuli et diametralium foraminum que sunt in circulis per polos ipsius transeuntibus.

〈IX.3〉 Capitulum III : De periodicis restitutionibus quinque planetarum

His ita dictis, exponemus periodicas minimasque quinque planetarum proxime restitutiones ab Hipparcho expositas et a nobis ex colatione locorum que quae] add. s. l. G per demonstrationes inequalitatum emergit correctas quod loco suo apertius faciemus. Has autem restitutiones preponimus, preponimus] post corr. G ut inequalitatum computationibus expositos iam medios singulorum longitudinis atque inequalitatis motus habeamus, nec erit differentia de qua curandum sit ulla, si quis universalius medios motus exposuerit. Universaliter autem longitudinis motum dicimus centri epicycli in excentrico motum, inequalitatem vero stelle motum in epicyclo.

Invenimus ergo 57 inequalitates Saturni in solaribus annis, sicuti nos exposuimus, hoc est a solstitialibus vel equinoctialibus punctis ad eadem ipsa, 59 et die uno sexagesimisque 45 proxime fieri, revolutionibus autem stelle duabus et gradu uno et sexagesimis 43. Nam in tribus stellis quibus Sol velocior semper est tot semper circulos ipse Sol in tempore restitutionis stelle pertransivit, quot sunt revolutiones stelle secundum longitudinem et restitutiones inequalitatis simul composite. Iovis autem 65 inequalitates in solaribus similiter invenimus annis fieri 71, diebus quatuor et sexagesimis 54 proxime deficientibus, revolutionibus autem stelle a solstitialibus punctis ad eadem ipsa sex gradibus quatuor et sexagesimis 50 deficientibus; Martis vero 37 inequalitates in annis solaribus similiter 79 et diebus 3 et sexagesimis 13 proxime, revolutionibus autem stelle ab eodem solstitio ad idem 42 et gradibus 3 10′; quinque vero inequalitates Veneris in annis similiter solaribus octo, diebus 2 et sexagesimis 18 proxime deficientibus, revolutionibus autem stelle equalibus numero revolutionum Solis octo, deficientibus gradibus 2 15′; Mercurii autem 145 inequalitates in annis similiter 46 die uno et duabus sexagesimis proxime, revolutionibus vero equalibus numero rursus revolutionum Solis 46, gradu addito uno.

Si ergo in singulis restitutionis tempus in dies resolverimus et multitudinem inequalitatum in gradus per singulos circulos 360, habebimus in Saturno quidem 21551 18′ et gradus inequalitatis 20520, in Iove autem dies 25927 37′ et gradus inequalitatis 27400, in Marte vero dies 28857 53′ et gradus inequalitas 13320, in Venere autem dies quidem 2919 40′, gradus vero inequalitatis 1800, in Mercurio vero dies 46802 24′ et gradus inequalitatis 52200.

Mutitudinem igitur graduum inequalitatis per multitudinem dierum accommodate per singulos partiti habuimus medium diurnum motum inequalitatis, in Saturno quidem graduum 0 57′ 7′′ 43′′′ 41′′′′ 43′′′′′ 40′′′′′′ proxime, Iovis vero graduum 0 54′ 9′′ 2′′′ 46′′′′ 26′′′′′ 0′′′′′′, Martis autem graduum 0 27′ 41′′ 40′′′ 19′′′′ 20′′′′′ 58′′′′′′, Veneris vero 0 36′ 59′′ 25′′′ 53′′′′ 11′′′′′ 28′′′′′′, Mercurii autem graduum 3 6′ 24′′ 6′′′ 6'''] corr. ex 26 G 59′′′′ 35′′′′′ 50′′′′′′.

Captaque vigesima quarta parte singulorum, habuimus medium inequalitatis motum hore unius, Saturni quidem graduum 0 2′ 22′′ 49′′′ 19′′′′ 14′′′′′ 19′′′′′′ 10′′′′′′′, Iovis vero graduum 0 2′ 15′′ 22′′′ 36′′′′ 56′′′′′ 5′′′′′′, Martis autem 0 1′ 9′′ 14′′′ 10′′′′ 48′′′′′ 22′′′′′′ 25′′′′′′′, Veneris vero 0 1′ 32′′ 28′′′ 39′′′′ 42′′′′′ 58′′′′′′ 40′′′′′′′, Mercurii autem 0 7′ 46′′ 0′′′ 17′′′′ 28′′′′′ 59′′′′′′ 35′′′′′′′.

In triginta vero diurnos motus singulorum multiplicavimus, et sic habuimus unius mensis medium inequalitatis motum, Saturni quidem graduum 28 33′ 51′′ 50′′′ 51′′′′ 50′′′′′ 0′′′′′′, Iovis vero 27 4′ 31′′ 23′′′ 13′′′′ 0′′′′′ 0′′′′′′, Martis autem 13 50′ 50′′ 9′′′ 40′′′′ 29′′′′′ 0′′′′′′, Veneris vero 18 29′ 42′′ 56′′′ 35′′′′ 44′′′′′ 0′′′′′′, Mercurii autem graduum 93 12′ 3′′ 29′′′ 47′′′′ 55′′′′′′ 0′′′′′′.

Similiter diurnos singulorum motus in 365 unius egyptiaci anni dies multiplicavimus, et sic habuimus habuimus] post corr. G medium inequalitatis annuum motum. Saturni quidem g〈ra〉duum graduum] garduum A 347 32′ 0′′ 48′′′ 50′′′′ 38′′′′′ 20′′′′′′, Iovis vero 329 25′ 1′′ 52′′′ 28′′′′ 10′′′′′ 0′′′′′′, Martis autem 168 28′ 30′′ 17′′′ 42′′′′ 32′′′′′ 50′′′′′′, Veneris vero 225 1′ 32′′ 28′′′ 34′′′′ 39′′′′′ 15′′′′′′, Mercurii autem reiectis circulis graduum 53 56′ 42′′ 32′′′ 32′′′′ 59′′′′′ 10′′′′′′.

Similiter annorum motuum singulos in 18 multiplicavimus, et sic habuimus 18 egyptiacorum annorum inequalitatis motum reiectis circulis, Saturni quidem graduum 135 36′ 14′′ 39′′′ 11′′′′ 30′′′′′ 0′′′′′′, Iovis vero 169 30′ 33′′ 44′′′ 27′′′′ 0′′′′′ 0′′′′′′, Martis autem 152 33′ 5′′ 18′′′ 45′′′′ 51′′′′′ 0′′′′′′, Veneris autem 90 27′ 44′′ 34′′′ 23′′′′ 46′′′′′ 30′′′′′′ Mercuri vero 251 0′ 45′′ 45′′′ 53′′′′ 45′′′′′ 0′′′′′′.

Ad hos consequenter medios etiam motus longitudinis, ne revolutionum quoque multitudinem in gradus resolutam in exposito in singulis tempore partiamur, Veneris quidem atque Mercurii eosdem habuimus quos iam in tabula Solis conscripsimus, reliquarum vero stellarum trium residuum subtracta inequalitate a medio motu solari, et sic habuimus diurnum secundum longitudinem medium motum Saturni quidem graduum 0 2′ 0′′ 33′′′ 31′′′′ 28′′′′′ 51′′′′′′, Iovis vero 0 4′ 59′′ 14′′′ 26′′′′ 46′′′′′ 31′′′′′′, Martis autem 0 31′ 26′′ 36′′′ 53′′′′ 51′′′′′ 33′′′′′; unius autem hore motum Saturni quidem graduum 0 0′ 5′′ 1′′′ 23′′′′ 48′′′′′ 42′′′′′′ 7′′′′′′′ 30′′′′′′′′, Iovis vero 0′ 10′ 12′′ 28′′′ 6′′′′ 6′′′′′ 56′′′′′′ 17′′′′′′′ 30′′′′′′′′, Martis autem 0 1′ 18′′ 36′′′ 32′′′′ 14′′′′′ 39′′′′′′; mensis vero unus Saturni quidem graduum 1 0′ 16′′ 45′′′ 44′′′′ 25′′′′′ 30′′′′′′, Iovis autem 2 29′ 37′′ 13′′′ 23′′′′ 15′′′′′ 30′′′′′′, Martis vero 15 43′ 18′′ 26′′′ 55′′′′ 46′′′′′ 30′′′′′′, anni autem unius Saturni quidem graduum 12 13′ 23′′ 56′′′ 30′′′′ 30′′′′′ 15′′′′′′, Iovis vero 30 20′ 22′′ 52′′′ 52′′′′ 58′′′′′ 35′′′′′′, Martis autem 101 16 54 27 38 35 45; decem et octo autem annnorum Saturni quidem medium motum graduum 220 1′ 10′′ 57′′′ 9′′′′ 4′′′′′ 30′′′′′′, Iovis vero reiectis circulis graduum 186 6′ 51′′ 51′′′ 53′′′′ 34′′′′′ 30′′′′′′, Martis vero reiectis circulis graduum 203 4′ 20′′ 17′′′ 34′′′′ 33′′′′′ 30′′′′′′.

Scribemus igitur facilioris gratia usus singularum stellarum tabulas per ordinem mediorum quos exposuimus motuum in versibus similiter ut in aliis 45 et partibus tribus, quarum prime tabule mediorum motuum longitudinis longitudinis] temporis add. et del. G et inequalitatis quinque planetarum tabule … planetarum] add. marg. G decem et octo annorum reiectis circulis motum continebunt, secunde annos et singularum horarum tertie menstruos atque diurnos. Sunt autem tabule iste.

〈IX.4〉 Capitulum IIII: Tabule mediorum motuum longitudinis et et] add. s. l. A inequalitatis quinque planetarum
Anni longitudinis Saturni
Saturni anni collecti per 18
Inequalitatis motus Saturni
Gra
dus
P
2
3
4
5
6
18
220
1
10
57
9
4
30
145
36
14
39
11
30
0
36
80
2
21
54
18
9
0
271
12
29
18
23
0
0
54
300
3
32
51
27
13
30
46
48
43
57
34
30
0
72
160
4
43
48
36
18
0
182
24
58
36
46
0
0
90
20
5
54
45
45
22
30
318
1
13
15
57
30
0
108
240
7
5
42
54
27
0
93
37
27
55
9
0
0
126
100
8
16
40
3
31
30
229
13
42
34
20
30
0
144
320
9
27
37
12
36
0
4
49
57
13
32
0
0
162
180
10
38
34
21
40
30
140
26
11
52
43
30
0
180
40
11
49
31
30
45
0
276
2
26
31
55
0
0
198
260
13
0
28
39
49
30
51
38
41
11
6
30
0
216
120
14
11
25
48
54
0
187
14
55
50
18
0
0
234
340
15
22
22
57
58
30
322
51
10
29
29
30
0
252
200
16
33
20
7
3
0
98
27
25
50
41
0
0
270
60
17
44
17
16
7
30
234
3
39
47
52
30
0
288
280
18
55
14
25
12
0
9
39
54
27
4
0
0
306
240
20
6
11
34
16
30
145
16
9
6
15
30
0
324
0
21
17
8
43
21
0
280
52
23
45
27
0
0
342
220
22
28
5
52
25
30
56
28
38
24
38
30
0
360
80
23
39
3
1
30
0
192
4
53
3
50
0
0
378
300
24
50
0
10
35
30
327
41
7
43
1
30
0
396
160
26
0
57
19
39
0
103
17
22
22
13
0
0
414
20
27
11
54
28
43
30
238
53
27
1
24
30
0
432
240
28
22
51
37
48
0
14
29
51
40
36
0
0
450
100
29
33
48
46
52
30
150
6
6
19
47
30
0
468
320
30
44
45
55
57
0
285
42
25
58
58
0
0
486
180
31
55
43
5
1
30
61
18
35
38
10
30
0
504
40
33
6
40
14
6
0
196
54
50
17
27
0
0
522
260
34
17
37
23
10
30
332
31
4
56
33
30
0
540
120
35
28
34
32
15
0
150
7
19
35
45
0
0
558
340
36
39
31
41
19
30
243
43
34
14
56
30
0
576
200
37
50
28
50
24
0
19
19
48
54
8
0
0
594
60
39
1
25
59
28
30
154
56
3
33
19
30
0
612
280
40
12
23
8
33
0
290
32
18
12
31
0
0
630
140
41
23
20
17
37
30
66
8
32
51
42
30
0
648
0
42
34
17
26
42
0
201
44
47
30
54
0
0
666
220
43
45
14
35
46
30
337
21
2
10
5
30
0
684
80
44
56
11
44
51
0
112
57
16
49
17
0
0
702
300
46
7
8
53
55
30
288
33
31
28
28
30
0
720
160
47
18
6
3
0
0
24
9
46
7
40
0
0
738
20
48
29
3
12
4
30
159
46
0
46
51
30
0
756
240
49
40
0
21
9
0
295
22
15
26
3
0
0
774
100
50
50
57
30
13
30
70
58
30
5
14
30
0
792
320
52
1
54
39
18
0
206
34
44
44
26
0
0
810
180
53
12
51
48
22
30
342
10
59
23
37
30
0

Radices longitudinis Capricorni 26 46, maxime longitudinis Scorpii 14 10, graduum 34 12

Anni expansi Saturni
Inequalitatis
Gra
dus
Pri
ma
2
3
4
5
6
Gra
dus
Pri
ma
2
3
4
5
6
1
12
13
23
56
30
30
15
347
32
0
48
50
38
20
2
24
26
47
53
1
0
30
335
4
1 1] corr. ex 12 G
37
41
16
40
3
36
40
11
49
31
30
45
322
36
2
26
31
55
0
4
48
53
36
46
2
1
0
310
8
3
15
22
33
20
5
61
6
59
2
32
31
15
297
40
4
4
13
11
40
6
73
20
23
39
3
1
30
285
12
4
53
3
50
0
7
85
33
47
35
33
31
45
372
44
5
41
54
28
20
8
97
47
11
32
4
2
0
260
16
6
30
45
6
40
9
110
0
35
28
34
32
15
247
48
7
19
35
45
0
10
125
13
59
25
5
2
30
235
20
8
40
26
23
20
11
134
27
23
21
35
32
45
222
52
8
57
17
1
40
12
146
40
47
18
6
3
0
210
24
9
46
7
40
0
13
158
54
11
14
36
33
15
197
56
10
34
58
18
20
14
171
7
35
11
7
3
30
185
28
11
33
48
56
40
15
183
20
59
7
37
33
45
173
0
12
12
39
35
0
16
195
34
23
4
8
4
0
160
32
13
1
30
13
20
17
207
47
47
0
38
34
15
148
4
13
50
20
51
40
18
220
1
10
56
9
4
30
135
36
14
39
11
30
0
Hore
Longitudinis Saturni
Inequalitatis Saturni
1
0
0
5
1
23
48
42
0
2
22
49
19
14
19
2
0
0
10
2
46
37
24
0
4
45
38
38
28
38
3
0
0
15
40
11
26
6
0
7
8
27
57
42
57
4
0
0
20
5
35
14
48
0
9
31
16
16
57
17
5
0
0
25
6
59
3
31
0
11
54
6
36
11
36
6
0
0
30
8
22
52
13
0
14
16
55
55
25
55
7
0
0
35
9
46
4
55
0
16
39
45
14
40
14
8
0
0
40
11
10
29
37
0
19
2
34
33
54
33
9
0
0
45
12
34
18
19
0
21
25
23
53
8
52
10
0
0
50
13
58
7
1
0
23
48
13
12
23
12
11
0
0
55
15
21
55
43
0
26
11
2
31
37
31
12
0
1
0
16
45
44
25
0
28
33
51
50
51
50
13
0
1
5
18
9
33
8
0
30
56
41
10
6
9
14
0
1
10
19
33
21
50
0
33
19
30
27
20
28
15
0
1
15
20
57
10
32
0
35
42
19
48
34
47
16
0
1
20
22
20
59
14
0
38
5
9
7
49
7
17
0
1
25
23
44
47
56
0
40
27
58
27
3
26
18
0
1
30
25
8
36
38
0
42
50
47
46
17
45
19
0
1
35
26
32
25
20
0
45
13
36
5
32
4
20
0
1
40
27
56
14
2
0
47
36
26
24
46
23
21
0
1
45
29
20
2
45
0
49
59
15
44
0
42
22
0
1
50
30
43
51
27
0
52
22
5
3
15
2
23
0
1
55
32
7
40
9
0
54
44
55
22
29
21
24
0
1
0
33
31
28
51
0
57
7
43
41
43
40

Menses
Longitudinis Saturni
Saturni inequalitatis
Gra
dus
Pri
ma
2a
3a
4a
5a
6a
Gra
dus
Pri
ma
2a
3a
4a
5a
6a 6a] et ceteris similiter add. G
30
1
0
16
45
44
25
30
28
33
51
50
51
50
0
60
2
0
36
31
28
51
0
57
7
43
41
43
40
0
90
3
0
50
17
13
16
30
85
41
35
32
35
30
0
120
4
1
7
2
57
42
0
114
15
27
23
27
20
0
150
5
1
23
48
42
7
30
142
49
19
14
19
10
0
180
6
1
40
34
26
33
0
171
23
11
5
11
0
0
210
7
1
57
20
10
58
30
199
57
2
56
2
50
0
240
8
2
14
5
55
24
0
228
30
54
46
54
40
0
270
9
2
1
51
39
49
30
257
4
46
37
46
30
0
300
10
2
47
37
24
15
0
285
38
38
38
38
20
0
330
11
3
7
23
8
40
30
314
12
30
19
30
10
0
360
12
3
21
8
53
6
0
342
46
22
10
22
0
0
Dies
Longitudinis Saturni
Inequalitatis
1
0
2
0
33
31
28
51
0
57
7
43
41
43
40
2
0
4
1
7
2
57
42
1
54
15
27
23
27
20
3
0
6
1
40
34
26
33
2
51
23
11
5
11
0
4
0
8
2
14
5
55
24
3
48
30
54
46
54
40
5
0
10
2
47
37
24
15
4
45
38
38
28
38
20
6
0
12
3
21
8
53
6
5
42
46
22
10
22
0
7
0
14
3
54
40
21
57
6
39
57
5
52
5
40
8
0
16
4
28
11
50
48
7
37
4
49
33
49
20
9
0
18
5
1
43
19
39
8
34
9
33
15
33
0
10
0
20
5
35
14
48
30
9
31
17
16
57
16
40
11
0
22
6
8
46
17
21
10
28
25
0
39
0
20
12
0
24
6
42
17
46
12
11
25
32
44
20
44
0
13
0
26
7
15
49
15
3
12
22
40
28
2
27
40
14
0
28
7
49
20
44
54
13
19
48
11
44
11
20
15
0
30
8
22
12
12
45
14
16
55
55
25
55
0
16
0
32
8
56
23
41
36
15
14
3
39
7
38
40
17
0
34
9
29
55
10
27
16
11
11
22
49
22
20
18
0
36
10
3
26
39
18
17
8
19
6
31
6
0
19
0
38
10
36
58
8
9
18
5
26
50
12
49
40
20
0
40
11
10
29
37
0
19
2
34
33
54
33
20
21
0
42
11
44
1
5
51
20
59
42
17
36
17
0
22
0
44
12
17
32
34
42
21
56
50
1
18
0
40
23
0
46
12
51
4
3
33
22
53
57
44
59
44
20
24
0
48
13
24
37
32
24
23
51
5
28
41
28
0
25
0
50
13
58
7
1
15
24
48
13
12
23
11
40
26
0
52
14
31
38
30
6
25
45
20
56
4
55
20
27
0
54
15
5
9
58
57
26
42
28
39
46
39
0
28
0
56
15
38
41
27
48
27
39
36
23
28
22
40
29
0
58
16
12
12
56
39
28
36
44
7
10
6
20
30
0
0
16
45
44
25
30
29
33
51
50
51
50
0

Anni collecti per 18
Longitudinis Iovis
Inequalitatis
18
186
6
51
51
53
34
30
169
30
33
44
27
0
0
36
12
13
43
43
47
9
0
339
1
7
28
54
0
0
54
198
20
35
35
40
43
30
148
31
41
13
21
0
0
72
24
27
27
27
34
18
0
318
2
14
57
48
0
0
90
210
34
19
19
27
52
30
127
32
48
42
15
0
0
108
36
41
11
11
21
27
0
297
3
22
26
42
0
0
126
222
48
3
3
15
1
30
106
33
56
11
9
0
0
144
48
54
54
55
8
36
0
276
4
29
55
36
0
0
162
235
1
46
47
2
10
30
85
35
3
40
3
0
0
180
61
8
38
38
55
45
0
255
5
37
23
30
0
0
198
247
15
30
30
49
19
30
64
36
11
50
57
0
0
216
73
22
22
22
42
54
0
234
6
41
53
24
0
0
234
259
29
14
14
36
28
30
43
37
18
37
51
0
0
252
85
36
6
6
30
3
0
213
7
52
22
18
0
0
270
271
42
57
78
23
37
30
22
38
26
6
45
0
0
288
97
49
49
50
17
12
0
192
8
59
51
12
0
0
306
283
56
41
42
10
46
30
1
39
33
35
39
0
0
324
110
3
33
34
4
21
0
171
10
7
20
6
0
0
342
296
10
25
25
57
55
30
340
40
41
4
33
0
0
360
122
17
17
17
51
30
0
150
11
14
49
0
0
0
378
308
24
9
9
45
4
30
319
41
48
33
27
0
0
396
134
31
1
1
38
39
0
129
12
28
17
54
0
0
414
320
37
52
53
32
13
30
298
42
56
2
21
0
0
432
146
44
44
45
25
48
0
250
13
29
46
48
0
0
450
332
51
36
37
19
22
30
276
44
3
31
15
0
0
468
158
58
28
29
12
57
0
87
14
37
15
42
0
0
486
345
5
20
21
6
31
30
256
45
11
0
9
0
0
504
171
12
12
13
0
6
0
66
15
47
44
36
0
0
522
357
19
4
4
53
40
30
235
45
18
29
3
0
0
540
183
25
55
56
47
15
0
45
16
52
13
30
0
0
558
9
32
47
48
40
49
30
214
47
25
57
57
0
0
576
195
39
39
40
34
24
0
24
17
59
42
24
0
0
594
21
46
31
32
27
58
30
193
48
33
46
51
0
0
612
207
53
23
24
21
33
0
3
19
7
11
18
0
0
630
34
0
15
16
15
7
30
172
49
40
55
45
0
0
648
220
7
7
8
8
42
0
342
20
14
40
12
0
0
666
46
13
59
0
2
16
30
151
50
48
24
39
0
0
684
232
20 20] corr. ex 120 G
50
51
55
51
0
321
21
22
9
6
0
0
702
58
27
42
43
49
25
30
101
51
55
53
33
0
0
720
254
34
34
35
43
0
0
300
22
29
38
0
0
0
738
70
41
26
27
36
34
30
109
53
3
22
27
0
0
756
256
48
18
19
30
9
0
279
23
37
6
54
0
0
774
82
55
10
11
23
43
30
88
54
10
51
21
0
0
792
269
2
2
3
17
17
0
257
24
44
35
48
0
0
810
95
8
53
55
10
52
30
67
55
18
20
15
0
0

Radices Libre 4 14 maxime longitudinis Virginis 2 9, 146 4.

Anni expansi
Longitudinis Iovis
Inequalitatis
1
30
20
22
52
52
58
35
329
25
1
52
28
10
0
2
60
40
45
45
45
57
10
298
50
3
44
56
20
0
3
91
1
8
38
38
55
45
268
15
5
37
24
30
0
4
121
21
31
31
31
54
20
237
40
7
29
52
40
0
5
151
41
51
24
24
52
55
207
50
9
22
20
50
0
6
182
2
17
17
17
51
30
176
30
11
14
49
0
0
7
212
22
40
10
10
50
5
145
55
13
7
17
10
0
8
242
43
3
3
3
48
40
115
20
14
59
45
20
0
9
273
3
25
55
56
47
15
214
45
16
52
13
30
0
10
303
23
48
48
49
45
50
54
10
18
44
41
40
0
11
333
44
11
41
42
44
25
23
35
20
37
9
50
0
12
4
4
34
34
35
43
0
353
0
22
29
38
0
0
13
34
24
57
27
28
41
35
322
25
24
22
6
10
0
14
64
45
20
20
21
40
10
291
50
26
14
34
20
0
15
95
5
43
13
14
38
45
261
15
28
7
2
30
0
16
125
26
6
6
7
37
20
230
40
29
59
30
40
0
17
155
46
28
58
0
35
55
200
5
31
52
58
50
0
18
186
6
51
51
53
34
30
169
30
33
44
27
0
0
Hore
Longitudinis Iovis
Inequalitatis
1
0
0
12
28
6
6
56
0
2
15
22
36
56
5
2
0
0
24
56
12
13
52
0
4
30
45
13
52
10
3
0
0
37
24
18
20
48
0
6
46
7
50
48
15
4
0
0
49
52
24
27
45
0
9
1
30
27
44
20
5
0
1
2
20
30
34
41
0
11
16
53
4
4
25
6
0
1
14
48
36
41
37
0
13
32
15
41
36
30
7
0
1
27
16
42
48
34
0
15
47
38
18
32
35
8
0
1
39
44
48
55
30
0
18
3
0
55
28
40
9
0
1
52
12
55
2
26
0
20
18
23
32
28
45
10
0
2
4
41
1
9
22
0
22
33
46
9
20
50
11
0
2
17
9
7
16
19
0
24
49
8
46
16
55
12
0
2
29
37
13
23
15
0
27
4
31
23
13
0
13
0
2
42
5
19
30
11
0
29
19
54
0
9
5
14
0
2
54
33
25
37
8
0
31
35
16
37
5
10
15
0
3
7
1
31
44
4
0
33
50
39
34
1
15
16
0
3
19
29
37
51
0
0
36
6
1
50
57
20
17
0
3
31
57
43
57
56
0
38
21
24
27
53
25
18
0
3
44
25
50
4
53
0
40
36
47
4
49
30
19
0
3
56
53
56
11
49
0
42
52
9
41
45
35
20
0
4
9
22
2
18
45
0
45
7
32
18
41
40
21
0
4
21
50
8
25
42
0
47
22
54
55
35
45
22
0
4
34
18
14
32
38
0
49
38
17
32
33
50
23
0
4
46
46
20
37
34
0
51
53 53] corr. ex 43 A
40
9
29
55
24
0
4
59
14
26
46
31
0
54
9
2
46
26
0

Menses
Longitudinis Iovis
Inequalitatis
30
2
29
27
13
23
15
30
27
4
31
23
13
0
0
60
4
59
14
25
46
31
0
54
9
2
46
26
0
0
90
7
28
51
40
9
46
30
81
13
34
9
39
0
0
120
9
58
28
53
2
2
0
108
18
5
32
52
0
0
150
12
28
6
6
17
17
30
135
22
36
56
60
0
0
180
14
57
43
20
33
33
0
162
27
8
19
18
0
0
210
17
27
20
33
48
48
30
189
31
39
42
31
0
0
240
19
56
57
47
4
4
0
216
36
11
5
44
0
0
270
22
26
35
0
19
19
30
243
40
42
28
57
0
0
300
24
56
12
30
36
36
0
270
45
13
52
10
0
0
350
27
25
49
27
50
50
30
297
49
45
15
23
0
0
360
29
55
26
40
6
6
0
324
34
16
38
33
0
0
Dies
Longitudinis Iovis
Inequalitatis
1
0
4
59
14
26
46
31
0
54
9
2
46
26
0
2
0
9
58
28
53
33
2
1
48
18
5
32
52
0
3
0
14
57
43
20
19
33
2
42
27
8
19
18
0
4
0
19
56
57
47
6
4
3
36
36
11
5
44
0
5
0
24
56
12
13
52
35
4
30
45
13
52
10
0
6
0
29
55
26
40
39
6
5
24
54
16
38
36
0
7
0
34
54
41
7
25
37
6
19
3
19
25
2
0
8
0
39
53
55
34
12
8
7
13
12
22
11
28
0
9
0
44
53
10
0
58
39
8
7 7] corr. ex 17 G
21
24
57
54
0
10
0
49
52
24
27
45
10
9
1
30
37
47
20
0
11
0
54
51
38
54
31
41
9
55
39
30
30
46
0
12
0
59
50
53
21
18
12
10
49
48
33
19
12
0
13
1
4
50
7
48
4
42
11
43
57
36
3
32
0
14
1
9
49
22
14
51
14
12
38
6
38
50
4
0
15
1
14
48
36
41
37
45
13
32
15
41
36
30
0
16
1
19
47
51
8
24
16
14
26
24
44
22
56
0
17
1
24
47
5
36
10
47
15
20
33
47
9
22
0
18
1
29
46
20
1
57
18
16
14
42
49
55
48
0
19
1
34
45
34
28
43
49
17
8
51
52
42
14
0
20
1
39
44
48
55
30
20
18
3
0
55
28
40
0
21
1
44
44
3
22
16
51
18
57
9
58
15
6
0
22
1
49
43
17
49
3
22
19
51
19
1
1
32
0
23
1
54
42
32
15
49
53
20
45
28
3
47
58
0
24
1
59
41
46
42
36
24
21
39
37
6
34
24
0
25
2
4
41
1
9
22
55
22
33
46
9
20
50
0
26
2
9
40
15
36
9
26
23
27
55
12
7
16
0
27
2
14
39
30
2
55
57
24
22
4
14
53
42
0
28
2
19
38
44
29
42
28
25
16
13
17
40
8
0
29
2
24
38
58
56
28
59
26
10
22
20
26
54
0
30
2
29
37
13
23
15
30
27
4
31
23
13
0
0

Anni
collecti
Longitudinis Martis
Inequalitatis
Gra
dus
P
2
3
4
5
6
Gra
dus
P
2
3
4
5
6
18
203
4
20
17
34
43
30
152
33
5
18
45
51
0
36
46
8
40
36
9
27
0
305
6
10
37
31
42
0
54
249
13
0
52
44
10
30
97
39
15
55
17
33
0
72
92
17
21
10
18
54
0
250
12
21
14
3
24
0
90
295
21
41
27
53
37
30
42
45
26
33
49
15
0
108
138
26
1
45
28
21
0
195
18
31
52
35
6
0
126
341
30
22
3
3
4
30
347
51
37
11
20
57
0
144
184
34
42
20
37
48
0
140
24
42
30
6
48
0
162
27
39
2
38
12
31
30
292
57
47
48
52
39
0
180
230
32
22
55
47
15
0
85
30
53
7
38
30
0
108
73
47
43
13
21
58
30
238
3
58
26
24
21
0
216
276
52
3
30
56
42
0
30
37
3
45
10
12
0
234
119
56
23
48
31
25
30
183
10
9
3
56
3
0
252
323
0
44
6
6
9
0
335
43
14
22
41
54
0
270
166
5
4
23
40
52
30
128
16
19
41
27
45
0
288
9
9
24
41
15
36
0
280
49
25
0
13
36
0
306
212
13
44
58
50
19
30
73
22
30
18
59
27
0
324
55
18
5
16
25
3
0
225
55
35
37
45
18
0
342
258
22
25
33
59
46
30
18
28
40
56
31
9
0
360
101
26
45
51
34
30
0
171
1
46
15
17
0
0
378
304
31
6
9
9
13 13] corr. ex 16 A
30
323
34
51
34
2
51
0
396
147
35
26
26
43
57
0
116
7
56
52
48
42
0
414
350
39
46
44
28
40
30
268
44
2
11
34
33
0
432
193
44
7
1
52
24
0
61
14
7
30
20
24
0
450
36
48
27
19
37
7
30
213
47
12
49
6
15
0
468
239
52
47
37
1
51
0
6
20
18
7
52
6
0
486
82
57
7
54
46
34
30
158
53
23
26
37
57
0
504
286
1
28
12
11
18
0
311
26
28
45
23
48
0
522
129
5
48
29
55
1
30
103
59
34
4
9
39
0
540
332
10
8
47
20
45
0
256
32
39
22
55
30
0
555
175
14
29
5
55
28
30
49
5
44
41
41
21
0
576
18
18
49
22
30
12
0
201
38
50
0
27
12
0
594
221
23
9
40
4
55
30
354
11
55
19
13
3
0
612
64
27
29
57
39
39
0 0] corr. ex 30 A
146
45
0
37
58
54
0
630
267
31
50
15
24
22
30
299
18
5
56
44
45
0
648
110
36
10
32
49
6
0
91
51
11
15
30
36
0
666
313
40
30
50
33
47
30
244
24
16
34
16
27
0
684
156
44
51
8
58
33
0
36
57
21
53
2
18
0
702
359
49
11
25
43
16
30
189
30
27
11
48
9
0
720
202
53
31
43
8
0
0
341
3
32
30
34
0
0
738
45
57
52
0
42
43
30
134
36
37
49
19
51
0
756
249
2
12
18
17
27
0
287
9
43
8
5
42
0
774
92
6
32
36
53
10
30
79
42
48
26
51
33
0
792
295
10
52
53
26
54
0
232
15
53
45
37
24
0
810
138
15
13
11
11
34
30
24
48
59
1
23
15
0

Radices Arietis 3 37, maxime longitudinis Cancri 16 40, 327 13

Anni expansi
Longitudinis Martis
Inequalitatis
1
191
16
54
27
38
35
45
168
28
30
17
42
32
50
2
22
33
48
55
17
11
30
336
57
0
35
25
5
40
3
213
50
43
22
55
47
15
145
25
30
53
7
38
30
4
45
7
37
50
34
23
0
313
54
1 1] corr. ex 31 G
10
50
11
20
5
236
29
32
18
12
58
45
122
22
31
28
32
44
10
6
67
41
26
45
51
34
30
290
51
1
46
15
17
0
7
258
58
24
13
30
10
15
99
19
32
3
57
49
50
8
90
15
15
41
8
46
0
267
48
2
21
40
22
40
9
281
32
10
8
47
21
45
76
16
32
39
22
55
30
10
12
49
4
36
25
27
30
244
45
2
57
5
28
20
11
304
5
59
4
4
33
15
53
13
33
14
45
1
10
12
135
22
53
31
43
9
0
221
42
3
32
30
34
0
13
326
39
47
59
21
44
45
30
10
33
50
13
6
50
14
157
56
42
27
0
20
30
198
39
4
7
55
39
40
15
349
13
36
54
38
56
15
7
7
34
25
38
72
30
16
180
30
31
22
17
32
0
175
36
4
43
20
45
20
17
11
47
25
49
56
7
45
344
4
35
1
3
18
10
18
203
4
20
17
34
43
30
192
33
5
18
45
51
0
Hore
Longitudinis Martis
Inequalitatis
1
0
1
18
36
32
14
39
0
1
9
14
10
48
22
2
0
2
37
13
4
29
17
0
2
18
28
21
36
44
3
0
3
55
49
36
43
56
0
3
26
42
32
25
7
4
0
5
14
26
8
58
35
0
4
36
56
43
13
29
5
0
6
33
2
41
13
14
0
5
46
10
54
1
52
6
0
7
51
39
13
27
53
0
6
55
25
4
50
14
7
0
9
10
15
45
42
32
0
8
4
39
15
38
36
8
0
10
28
52
17
57
11
0
9
13
53
26
26
59
9
0
11
47
28
50
11
49
0
10
23
7
37
15
21
10
0
13
6
5
22
26
28
0
11
32
21
48
3
44
11
0
14
24
41
54
41
7
0
11
41
35
58
52
6
12
0
15
43
18
26
55
46
0
13
50
50
9
40
29
13
0
17
1
54
59
10
25
0
15
0
4
20
28
51
14
0
18
20
31
31
25
4
0
16
9
18
31
17
13
15
0
19
39
8
3
39
43
0
17
18
32
42
5
36
16
0
20
57
44
35
54
22
0
18
27
46
52
53
58
17
0
22
16
21
8
9
0
0
19
37
1
3
42
21
18
0
23
34
57
40
23
39
0
20
46
15
14
30
43
19
0
24
53
34
12
38
18
0
21
55
29
25
19
5
20
0
26
12
10
44
52
54
0
23
4
43
36
7
28
21
0
27
30
47
17
7
36
0
24
13
54
46
55
50
22
0
28
49
23
49
22
15
0
25
23
11
57
44
13
23
0
30
8
0
21
36
54
0
26
32
26
8
32
35
24
0
31
26
36
53
51
33
0
27
41
40
19
20
58

Menses
Longitudinis Martis
Inequalitatis
Gra
dus
P
2
3
4
5
6
Gra
dus
P
2
3
4
5
6
30
15
43
18
26
55
46
30
13
50
50
9
40
29
0
60
31
26
36
53
51
33
0
27
41
40
19
20
58
0
90
47
9
55
20
47
19
30
41
32
30
29
1
27
0
120
62
53
13
47
43
6
0
55
23
20
38
41
56
0
150
78
36
32
14
38
52
30
68
14
10
48
22
25
0
180
94
19
50
41
34
39
0
83
5
0
58
2
54
0
210
110
3
9
8
30
25
30
96
56
51
7
43
23
0
240
125
46
27
35
26
12
0
110
46
41
17
23
52
0
270
141
29
46
2
21
58
30
124
37
31
27
4
21
0
300
157
13
29
29
17
45
0
138
28
21
36
44
50
0
334
172
56
56
56
13
31
30
152
19
11
46
25
19
0
360
188
39
23
23
9
18
0
166
10
1
56
5
48
0
Dies
Longitudinis Martis
Inequalitatis
1
0
31
26
36
53
51
33
0
27
41
40
19
20
58
2
1
2
53
13
47
43
6 6] corr. ex 36 G
0
55
23
20
38
41
56
3
1
34
19
50
41
34
39
1
23
5
0
48
2
54
4
2
5
46
27
35
26
12
1
50
46
41
17
23
52
5
2
37
13
4
29
17
45
2
18
21
21
36
44
50
6
3
8
39
41
23
9
18
2
46
10
1
56
5
48
7
3
40
6
18
17
0
51
3
13
51
42
15
26
46
8
4
11
32
55
10
52
24
3
41
33
22
34
47
44
9
4
42
59
32
4
43
57
4
9
15
2
54
8
42
10
5
14
26
8
58
35
30
4
36
56
43
13
29
40
11
5
45
52
45
52
27
3
5
4
38
23
32
50
38
12
6
17
19
22
46
18
36
5
32
20
3
52
11
36
13
6
48
45
59
40
10
9
6
0
1
44
11
32
34
14
7
20
12
36
34
1
42
6
27
43
24
30
53
32
15
7
51
39
13
27
53
15
6
55
23
4
50
14
30
16
8
23
5
50
21
44
48
7
23
6
45
9
36
28
17
8
54
32
27
15
36
21
7
50
48
25
28
56
26
18
9
25
59
4
9
27
54
8
18
30
5
48
17
24
19
9
57
25
41
3
19
27
8
46
11
46
7
38
22
20
10
28
52
17
57
11
0
9
13
53
26
26
59
20
21
11
0
18
54
51
2
33
9
41
35
6
46
20
18
22
11
31
45
31
44
54
6
10
9
16
47
5
41
16
23
12
3
12
8
38
45
39
10
36
58
27
25
2
14
24
12
34
38
45
32
37
12
11
4
40
7
4
23
12
25
13
5
5
22
26
28
45
11
32
21
48
3
44
10
26
13
37
31
59
20
20
18
12
0
3
28
23
5
8
27
14
8
58
36
14
11
51
12
27
45
8
42
26
6
28
14
40
25
13
8
3
24
12
55
26
49
1
47
4
29
15
11
51
50
1
54
57
13
23
8
29
21
8
2
30
15
43
18
26
55
46
30
13
50
50
9
40
29
0

Anni collecti
Longitudinis Veneris
Inequalitatis
18
355
37
25
36
20
34
30
90
27
44
34
23
46
30
36
351
14
51
12
41
9
0
180
55
29
8
47
33
0 0] corr. ex 30 G
54
346
51
16
49
1
43
30
271
23
13
43
11
19
30
72
332
29
42
25
22
18
0
1
50
58
17
35
6
0
90
338
7
8
1
43
52
30
92
18
42
51
58
52
30
108
333
44
33
38
3
27
0
182
46
27
26
22
39
0
126
329
21
59
14
24
1
30
173
14
12
0
46
25
30
144
324
59
24
50
44
36
0
3
49
56
35
10
12
0
162
320
36
50
27
5
10
30
94
9
41
9
33
58
30
180
316
14
16
3
25
45
0
184
37
25
43
57
45
0
198
311
51
41
39
46
19
30
275
5
10
18
21
31
30
216
307
29
7
16
6
54
0
5
32
54
52
45
18
0
334
303
6
32
52
27
28
30
96
0
39
27
9
4
30
252
298
43
58
28
48
3
0
186
28
24
1
32
51
0
270
294
21
24
5
8
37
30
276
56
8
35
56
37
30
288
289
51
49
41
29
12
0
7
23
53
10
20
24
0
306
285
36
15
17
49
46
30
97
51
37
44
44
10
30
324
281
13
40
54
10
21
0
188
19
22
19
7
57
0
342
276
51
6
30
30
55
30
278
47
6
53
31
43
30
360
272
28
32
6
51
30
0
9
14
51
27
55
30
0
378
268
5
57
43
12
4
30
99
42
36
2
19
16
30
396
263
43
23
19
32
39
0
190
10
20
36
43
3
0
414
259
20
48
55
53
13
30
280
38
5
11
6
49
30
432
254
58
14
32
13
48
0
11
5
49
45
30
36
0
450
250
35
40
8
34
22
30
101
33
34
19
54
22
30
468
246
13
5
44
54
57
0
192
1
18
54
18
9
0
486
241
50
31
21
15
31
30
282
29
3
28
41
55
30
504
237
27
56
54
36
6
0
12
56
48
3
5
42
0
522
233
5
22
33
56
40
30
103
24
32
37
29
28
30
540
228
42
48
10
12
15
0
193
52
17
11
53
15
0
558
224
20
13
46
37
49
30
284
20
1
46
17
1
30
576
219
57
39
22
58
24
0
14
47
46
20
40
48
0
544
215
35
4
59
18
58
30
105
15
30
55
4
37
30
612
211
12
30
35
39
33
0
195
43
15
29
28
21
0
630
206
49
56
12
0
7
30
286
11
0
3
52
7
30
648
202
27
21
48
20
42
0
16
38
44
38
15
54
0
666
198
4
47
24
41
16
30
107
6
29
12
39
40
30
684
193
48
13
1
1
51
0
197
34
13
47
3
27
0
702
189
19
38
37
22
25
30
288
1
58
21
27
13
30
720
184
57
4
13
42
0
0
18
29
42
55
51
0
0
738
180
34
29
50
3
34
30
108
57
27
30
14
46
30
756
176
11
55
26
24
9
0
199
25
12
4
38
33
0
774
171
49
21
2
44
43
30
289
52
56
39
2
19
30
792
167
26
46
39
5
18
0
20
20
41
13
26
6
0
810
163
4
12
15
25
52
30
110
48
25
47
49
52
30

Radices Piscium 0 45, longitudinis maxime Tauri 16 10, 71 graduum 7 primi.

Anni expansi
Longitudinis Veneris
Inequalitatis
1
359
45
24
45
21
8
35
225
1
32
28
34
39
15
2
359
30
49
30
42
17
10
90
3
4
57
9
18
30
3
359
16
14
16
3
25
45
315
4
37
25
43
57
45
4
359
1
39
1
24
34
20
180
6
9
54
18
37
0
5
358
47
3
46
45
42
55
45
7
42
22
53
16
15
6
358
32
28
32
6
51
30
170
9
14
51
27
55
30
7
358
17
53
17
28
0
5
135
10
47
20
2
34
45
8
358
3
18
2
49
8
40
0
12
19
48
37
14
0
9
357
48
43
48
10
17
15
225
13
52
17
11
53
15
10
357
34
7
33
31
25
50
90
15
24
45
46
32
30
11
357
19
32
18
52
34
25
315
16
54
14
21
11
45
12
357
4
57
4
13
43
0
180
18
29
42
55
51
0
13
356
50
21
49
34
51
35
145
20
2
11
30
30
15
14
356
35
46
34
56
0
10
270
21
34
40
5
9
30
15
356
21
11
20
17
8
45
135
23
7
8
39
48
45
16
356
6
36
5
38
17
20
0
44
39
37
14
28
0
17
355
52
0
50
59
25
55
225
26
12
5
49
7
15
18
355
57
25
36
20
34
30
90
27
44
34
23
46
30
Hore
Longitudinis Veneris
Inequalitatis
1
0
2
27
50
43
3
1
0
1
32
28
34
42
58
2
0
4
55
41
26
6
2
0
3
10
57
9
25
57
3
0
7
23
32
9
9
3
0
4
37
25
44
8
56
4
0
9
51
22
52
12
5
0
6
9
54
18
51
54
5
0
12
19
13
35
15
6
0
7
42
22
53
34
53
6
0
14
47
4
18
18
7
0
9
14
51
28
17
52
7
0
17
14
55
1
21
9
0
10
47
20
3
0
50
8
0
19
42
45
44
24
10
0
12
19
48
37
43
49
9
0
22
10
36
27
27
11
0
13
52
17
12
26
48
10
0
24
38
27
10
30
12
0
15
24
45
47
9
46
11
0
27
6
12
53
33
14
0
16
57
14
21
52
45
12
0
29
34
8
36
36
15
0
18
29
42
56
35
44
13
0
32
1
59
19
39
16
0
20
2
11
31
18
42
14
0
34
29
50
2
42
18
0
21
34
40
6
1
41
15
0
36
57
40
45
45
19
0
23
7
8
40
44
40
16
0
39
25
31
28
48
20
0
24
39
37
15
27
38
17
0
41
53
22
11
51
21
0
26
12
5
50
10
37
18
0
44
21
12
54
54
23
0
27
44
34
24
53
36
19
0
46
49
3
37
57
24
0
29
17
2
59
36
34
20
0
49
16
54
21
0
25
0
30
49
31
34
19
33
21
0
51
44
45
4
3
27
0
32
22
0
9
2
32
22
0
54
12
35
47
6
28
0
33
54
28
43
45
30
23
0
56
40
26
30
9
29
0
35
26
57
18
28
29
24
0
59
8
17
13
12
31
0
36
59
25
53
11
28

Menses
Longitudinis Veneris
Inequalitatis
30
29
34
8
36
36
15
30
18
29
42
56
35
44
0
60
59
8
17
13
12
31
0
36
59
25
53
11
28
0
90
88
42
25
49
48
46
30
55
29
8
49
47
12
0
120
118
16
34
26
25
2
0
73
58
51
46
22
56
0
150
147
50
43
3
1
17
30
92
28
34
42
58
40
0
180
177
24
51
39
37
33
0
110
58
17
49
34
24
0
210
206
59
0
16
13
48
30
129
28
0
36
10
50
0
240
236
33
8
52
50
4
0
147
57
43
32
45
52
0
270
266
7
17
29
26
19
30
166
27
26
29
21
36
0
300
295
41
25
6
2
35
0
184
57
9
25
57
20
0
330
325
15
34
42
38
50
30
203
26
52
22
33
4
0
360
354
49
43
19
15
6
0
221
56
35
19
8
48
0
Dies
Gra
dus
P
2
3
4
5
6
Gra
dus
P
2
3
4
5
6
1
0
59
8
17
13
12
31
0
36
59
25
53
11
28
2
1
58
16
34
26
25
2
1
13
58
51
46
22
56
3
2
57
24 24] corr. ex 4 G
51
39
37
33
1
50
58
17
39
34
24
4
3
56
33
8
52
50
4
2
27
57
43
32
45
52
5
4
55
41
26
6
2
35
3
4
57
9
25
57
20
6
5
54
49
43
19
15
6
3
41
56
35
19
8
41
7
6
53
58
0
32
27
37
4
18
56
1
12
20
16
8
7
53
6
17
45
40
8
4
55
55
27
5
31
44
9
8
52
14
34
58
52
39
5
32
54
52
58
43
12
10
9
51
22
52
12
5
10
6
9
54
18
51
54
40
11
10
50
31
9
25
17
41
6
46
53
44
45
6
8
12
11
49
39
26
38
30
12
7
23
53
10
38
17
36
13
12
48
47
43
51
42
43
8
0
52
36
31
29
4
14
13
47
56
1
4
55
14
8
37
52
2
24
40
32
15
14
47
4
18
18
7
45
9
14
51
28
17
52
0
16
15
46
12
35
31
20
16
9
51
50
54
11
3
28
17
16
45
20
52
44
32
47
10
28
50
20
4
14
56
18
17
44
29
9
57
45
18
11
5
49
45
57
26
24
19
18
43
37
27
10
52
49
11
42
49
11
50
37
52
20
19
42
45
44
24
10
20
12
19
48
37
41
49
20
21
20
41
54
1
37
22
51
12
56
48
3
37
0
48
22
21
41
2
18
50
35
22
13
33
47
29
30
12
16
23
22
40
10
36
3
47
53
14
10
46
55
23
23
44
24
23
39
18
53
17
0
24
14
47
46
21
16
35
12
25
24
38
20
10
30
12
55
15
24
45
47
9
46
40
26
25
37
35
27
43
25
26
16
1
45
13
2
58
8
27
26
36
43
44
56
37
57
16
38
44
38
56
9
36
28
27
35
52
2
9
50
28
17
15
44
4
49
21
4
29
28
35
0
19
23
2
59
17
52
43
30
42
32
32
30
29
34
8
36
36
15
30
18
29
42
56
35
44
0

Anni collecti
Longitudinis Mercurii
Inequalitatis
18
355
37
25
36
20
39
30
251
0
45
45
53
45
0
36
351
14
51
12
41
9
0
142
1
31
31
47
30
0
54
344
52
16
49
1
43
30
33
2
17
17
41
15
0
72
342
29
42
25
22
18
0
284
3
3
3
35
0
0
90
338
7
8
1
42
52
30
175
3
48
49
28
45
0
108
333
44
33
38
3
27
0
66
4
34
35
22
30
0
126
329
21
59
14
24
30
30
317
5
20
21
16
15
0
144
324
59
24
50
44
36
0
208
6
6
7
10
0
0
162
320
36
50
27
5
10
30
99
6
51
53
3
45
0
180
316
14
16
3
25
45
0
350
7
37
38
57
30
0
198
311
51
41
39
46
19
30
241
8
23
24
51
15
0
216
307
29
7
16
6
54
0
132
9
9
10
45
0
0
234
303
6
32
52
27
28
30
23
9
54
56
38
45
0
252
328
43
58
28
48
3
0
274
10
40
42
32
30
0
270
394
21
24
5
8
37
30
165
11
26
28
76
15
0
288
289
58
49
41
29
12
0
56
12
12
14
20
0
0
306
285
35
15
17
49
46
30
307
12
58
0
13
45
0
324
281
13
40
54
10
21
0
178
13
43
46
7
30
0
342
276
51
6
30
30
55
30
89
14
29
32
1
15
0
360
272
28
32
6
51
30
0
340
15
15
17
55
0
0
378
268
5
57
43
12
4
30
231
16
1
3
48
45
0
396
263
43
23
19
32
39
0
122
16
46
49
42
30
0
414
259
20
48
55
53
13
30
13
17
32
35
38
15
0
434
254
58
14
32
13
48
0
264
18
18
21
30
0
0
450
250
35
40
8
34
22
30
155
19
4
7
23
45
0
468
246
13
5
44
54
57
0
46
19
49
53
17
30
0
426
241
50
31
21
15
34
30
297
20
35
39
11
15
0
504
237
27
56
57
36
6
0
188
21
21
35
5
0
0
522
233
5
22
33
56
40
30
79
22
7
10
58
45
0
540
228
42
45
10
17
15
0
330
22
12
56
52
30
0
558
224
20
13
46
37
49
30
221
23
38
42
46
15
0
576
219
57
39
22
58
24
0
112
24
24
28
40
0
0
594
215
35
4
59
18
58
30
3
25
10
14
33
45
0
612
211
12
30
35
39
33
0
274
25
56
0
27
30
0
630
206
49
56
12
0
7
30
145
26
41
46
21
15
0
648
202
27
24
48
20
42
0
36
27
27
32
15
0
0
666
198
4
47
24
41
16
30
227 227] corr. ex 224 G
28
13
18
8
45
0
684
193
42
13
1
1
51
0
178
28
59
4
2
30
0
702
189
19
38
37
22
25
30
69
29
44
49
56
15
0
720
184
57
4
13
43
0
0
320
30
30
35
50
0
0
738
180
34
29
50
3
34
30
211
31
16
21
46
45
0
756
176
11
55
26
24
9
0
102
32
2
7
37
30
0
774
171
49
41
2
44
43
30
353
32
47
53
31
15
0
792
167
26
46
39
5
18
0
244
33
33
39
25
0
0
810
163
4
12
15
25
52
30
135
34
19
25
18
45
0

Radices Piscium 0 45, maxime longitudinis Libre 1 10, graduum 21 55

Anni expansi
Longitudinis Mercurii
Inequa〈lita〉tis
1
359
45
24
45
21
8
35
53
56
42
32
32
59
10
2
359
30
49
30
42
17
10
107
53
25
5
5
58
20
3
359
16
14
16
3
25
45
161
50
7
37
38
57
30
4
359
1
39
1
24
31
20
215
46
50
10
11
56
40
5
358
47
3
46
46
42
55
269
43
32
42
44
55
50
6
358
32
28
32
6
51
30
323
40
15
15
17
55
0
7
358
17
53
17
28
0
5
17
36
57
47
50
54
10
8
358
3
18
2
49
8
40
71
33
40
20
23
53
20
9
357
48
42
48
10
17
15
125
30
22
52
56
52
30
10
357
34
7
33
31
25
50
179
27
5
25
29
51
40
11
357
19
32
18
52
34
25
233
23
47
58
2
50
50
12
357
4
57
4
13
42
0
287
20
30
30
35
50
0
13
356
50
21
49
34
51
35
341
16
13
3
8
49
10
14
356
35
46
34
56
0
10
35
13
55
35
41
48
20
15
356
21
11
20
17
8
45
89
10
38
8
14
47
30
16
356
6
36
5
38
17
20
143
7
20
40
47
46
40
17
355
52
0
50
59
25
55
197
4
3 3] corr. ex 30 G
13
20
45
50
18
355
37
25
36
20
34
30
251
0
45
45
53
45
0
Hore
Longitudinis Mercurii
Inequalitatis
1
0
2
27
50
43
3
1
0
7
46
0
17
28
59
2
0
4
55
41
26
6
2
0
15
32
0
34
57
59
3
0
7
23
32
9
9
3
0
23
8
0
52
26
58
4
0
9
51
22
52 52] corr. ex 53 G
12
5
0
31
4
1
9
55
58
5
0
12
19
13
35
15
6
0
38
8
1
27
24
57
6
0
14
47
4
18
18
7
0
46
36
1
44
53
57
7
0
17
14
55
1
21
9
0
54
22
2
2
22
57
8
0
19
42
45
44
24
10
1
2
8
2
19
51
56
9
0
22
10
36
27
27
11
1
9
54
2
37
20
56
10
0
24
38
27
10
30
12
1
17
40
2
54
49
55
11
0
27
6
17
53
33
14
1
25
26
3
12
18
55
12
0
29
34
8
36
36
15
1
33
12
3
29
47
55
13
0
32
1
59
19
39
16
1
4
58
3
47
16
54
14
0
34
29
50
2
42
18
1
48
44
4
4
45
54
15
0
36
57
40
45
45
19
1
56
30
4
22
14
53
16
0
39
25
31
28
48
20
2
4
16
4
39
43
53
17
0
41
53
22
11
51
21
2
12
2
4
57
12
52
18
0
44
21
12
54
54
23
2
19
48
5
14
41
52
19
0
46
49
3
37
57
24
2
27
34
5
32
10
52
20
0
49
16
54
21
0
25
2
35
20
5
49
39
51
21
0
51
44
45
4
3
27
2
43
6
6
7
8
51
22
0
54
12
35
47
6
28
2
50
52
6
24
37
50
23
0
56
40
26
30
9
29
2
58
38
6
42
6
50
24
0
59
8
17
13
12
31
3
6
24
6
59
35
50

Menses
Longitudinis Mercurii
Inequalitatis
G
P
2
3
4
5
6
G
P
2
3
4
5
6
30
29
34
8
36
36
15
30
93
12
3
29
47
55
0
60
59 59] corr. ex 58 G
8
17
13
12
31
0
186
24
6
59
35
50
0
90
88
42
25
49
48
46
30
279
36
10
29
23
45
0
120
118
16
34
26
25
2
0
12
48
13
59
11
40
0
150
148
50
43
3
1
17
30
106
0
17
28
59
35
0
180
177
24
51
39
37
33
0
199
12
20
58
47
30
0
210
206
59
0
16
13
48
30
299
24
24
28
35
25
0
240
236
33
8
52
50
4
0
25
36
27
58
23
20
0
270
266
7
17
29
26
19
30
118
48
31
28
11
15
0
300
295
41
25
6
2
35
0
212 212] corr. ex 312 G
0
34
57
59
10
0
330
325
15
34
42
38
50
30
305
12
38
27
47
5
0
360
354
49
43
19
15
6 6] corr. ex 60 G
0
38
24
41
57
35
0
0
Dies
Inequalitatis
1
0
59
8
17
13
12
31
3
6
24
6
59
35
50
2
1
58
16
34
26
25
2
6
12 12] corr. ex 19 G
48
13
59
11
40
3
2
57
24
51
39
37
33
9
19
12
20
58
47
30
4
3
56
33
8
52
50
4
12
25
36
27
58
23
20
5
4
55
41
26
6
2
35
15
32
0
34
57
59
10
6
5
54
49
43
19
15
6
18
38
24
41
57
35
0
7
6
53
58
0
32
27
37
21
44
48
48
57
10
50
8
7
53
6
17
45
40
8
24
51
12
55
56
46
40
9
8
52
14
34
58
52
39
27
57
37
2
56
22
30
10
9
51
22
52
12
5
10
31
4
1
9
55
58
20
11
10
50
31
9
25
17
41
34
10
25
16
55
34
10
12
11
49
39
26
38
30
12
37
16
49
23
55
10
0
13
12
48
47
43
51
42
43
40
23
13
30
54
45
50
14
13
47
56
1
4
55
14
43
29
37
37
54
21
40
15
14
47
4
18
18
7
45
46
36
1
44
53
57
30
16
15
46
12
35
31
20
16
49
42
25 25] corr. ex 20 A
51
53
33
20
17
16
45
20
52
44
32
47
52
48
49
58
53
9
10
18
17
44
29
9
57
45
18
55
55
14
5
52
45
0
19
18
43
37
27
10
57
49
59
1
38
12
52
20
50
20
19
42
45
44
27
10
20
62
8
2
19
51
56
40
21
20
41
54
1
37
22
51
65
14
26
26
51
32
30
22
21
41
2
18
50
55
22
68
20
50
33
51
8
20
23
22
40
10
35
3
47
53
71
27
14
40
50
44
10
24
23
39
18
53
17
0
24
70
33
38
47
50
20
0
25
24
38
27
10
30
12
55
77
40
2
54
49
55
50
26
25
37
35
27
43
25
26
80
46
27
1
49
31
40
27
26
36
43
44
56
37
57
83
52
51
8
49
7
30
28
27
35
52
2
9
50
28
86
59
15
15
48
43
20
29
28
35
0
19
23
2
59
90
5
39
22
48
19
10
30
29
34
8
36
36
15
30
93
12
3
29
47
55
0

〈IX.5〉 Capitulum V : De iis que premittuntur ad doctrinam motuum quinque planetarum

Cum autem sequatur deinceps ut de inequalitatibus que fiunt in motu longitudinis quinque planetarum verba faciamus, universalior quidem expositio his rationibus facta est nobis.

Nam cum simplicissimi atque sufficientes ad demonstrandum duo motus sint, ut diximus, alter qui per excentricos ad zodiacum circulos fit, alter qui per concentricos quidem, sed in quibus epicycli circumducuntur, cunque similiter inequalitates que in singulis planetis conspiciuntur due sint, altera que penes zodiaci partes consideratur, altera que penes aspectus solares, in hac quidem per crebros atque diversos et in eisdem zodiaci partibus consideratos quinque planetarum aspectus tempus quod est a maxima ad mediam semper maius tempore quod est a media ad minimam invenimus, quod accidens in excentricitatis suppositione fieri non potest, sed huius contrarium, propterea quod semper in ipsa maximus motus in minima longitudine fit et in utrisque suppositionibus arcus qui a minima longitudine usque ad punctum medii transitus est minor fit quam arcus ab hoc ipso puncto usque ad maximam longitudinem. Secundum vero epicyclorum suppositionem tunc potest accidere, quando maximus motus non in minima longitudine, sicut in Luna, sed in maxima efficitur, hoc est quando stella moveri a maxima longitudine incipiens non ad precedentia mundi, ut Luna, sed ad succedentia progreditur. Hac de causa inequalitatem huiusmodi per epicyclos fieri supponimus.

In inequalitate inequalitate] corr. ex equalitate G autem que ad partes zodiaci consideratur per apparitionum ad easdem vel aspectuum ad eosdem interceptos zodiaci arcus contra invenimus tempus a motu minimo ad medium maius semper esse quam a medio ad maximum, quod rursus accidens, quamvis utrique suppositioni accomodari possit, sicuti cum de Sole ac de similitudine ipsarum ageremus dictum est, magis tamen excentricitatis suppositioni convenit, qua et fieri hanc inequalitatem supponimus, quoniam et altera suppositioni alteri accomodari proprie invenitur.

Iam autem per crebram observatorum particulariter motuum examinationem atque comperationem ad locos qui ex utrarunque suppositionum compositione constituuntur non ita simpliciter fieri posse percepimus, neque quod superficies in quibus excentricos describimus immobiles sint, permanente semper in eisdem distantiis a tropicis vel equinoctialibus punctis linea que est inter utraque centra ipsorum et obliqui solaris in qua maxime et minime longitudines considerantur, neque quod epicycli in iis excentricis habeant centra sua, quorum sunt illa centra ad que circumducti equaliter ad successionem equales in temporibus equalibus angulos intercipiunt, sed maxime longitudines excentricorum quoque circulorum parvum quendam ad successionem punctorum solstitialium progressum facere equalem rursus et quasi ad zodiaci centrum tantumque ferme in singulis quinque quantum sphera fixarum facere reperitur, hoc est gradum unum in centum annis, quantum ex presentibus conspicere possumus, centra etiam epicyclorum in circulis ferri qui equales quidem facientibus inequalitatem excentricis sunt, sed non in eisdem centris descripti, descripti] corr. ex descipti G sed in ceteris quidem in centris que dividunt equaliter lineas que sunt inter centra illorum et zodiaci, in solo autem Mercurio in centro quod tantum distat a circumducto centro, quantum et ipsum a faciente inequalitatem centro quasi versus maximam longitudinem distat, et hoc a centro ubi visus esse supponitur. In hac enim etiam stella solum modo, sicut etiam in Luna, invenimus excentricum quoque circulum circumduci a predicto centro contra epicyclum in precedentia rursus unam in anno revolutionem, quoniam ipsa quoque bis in una revolutione proxima terre fieri cernitur, veluti et Luna bis in mense uno.

〈IX.6〉 Capitulum VI: De modo et differentia suppositionum

detail Sed modus iste suppositionum que propter predicta colliguntur, sic intellectu facilior erit. Intelligatur enim in suppositione quidem ceterorum primum ABG circulus excentricus cuius centrum D, et diameter per D atque per zodiaci centrum sit ADG, in qua centrum zodiaci, hoc est cernentium visus, sit E punctum, quod faciat, ut A quidem maxima sit a terra longitudo, G vero minima, et equaliter divisa linea DE in puncto F, centro F et spatio equali DA describatur circulus ITC circulo ABG equalis, deinde centro T describatur LM epicyclus, et coniungatur LTMD.

detail Primum igitur supponamus excentricorum superficiem circulorum obliquam esse ad superficiem circuli per medium signorum et similiter superficiem epicycli ad superficiem excentricorum propter motum stellarum secundum latitudinem, ut loco suo demonstrabimus, et tamen quantum ad motus longitudinis gratia facilitatis in una omnes zodiaci superficie sitas esse, nulla differentia de qua curandum sit penes tantas declinationes quante in singulis perspicientur futura. Deinde totam quidem superficiem equaliter ad successionem signorum circa E centrum dicimus circumduci, traducereque maximam et minimam longitudinem uno gradu in centum annis, epicycli vero diametrum LTM circumduci a centro D equaliter rursus ad successionem signorum consequenter ad restitutionem motus longitudinis stelle, circumducereque L et M epicycli puncta et centrum quod semper fertur per excentricum excentricum] corr. ex centricum G ITC, stellam quoque ipsam in epicyclo LM equaliter rursus moveri, restitutionesque ad diametrum semper ad D centrum declinatam facere equaliter medio motui inequalitatis ad Solem, et quasi progressus maxime longitudinis L puncti ad successionem signorum efficatur.

Proprietatem autem suppositionis Mercurii sic ante oculos ponemus. Sit enim circulus ABG inequalitatis excentricus cuius centrum D, et diameter per D et E zodiaci centrum et a maxima longitudine sit ADEG, sumaturque in AG diametro versus A maxime distantie punctum linea DF linee DE equalis. Ceteris igitur eisdem permanentibus, hoc est quod tota superficies circa E centrum ad successionem maximam longitudinem traducat tantum, quantum et in ceteris stellis, et quod epicyclus circa D centrum equaliter a linea DT ad successionem circumducatur, et ad hec quod stella in epicyclo moveatur similiter ceteris, hic centrum alterius excentrici qui semper equalis primo ponitur et in quo centrum epicyli erit circumducetur circa F punctum in contrarium epicycli, hoc est in precedentia signorum, equaliter equalique velocitate ipsi tanquam a linea FIT, ut ad zodiaci quidem puncta semel utraque linearum DB et FIT in anno restituatur, bis vero inter se videlicet, distabitque semper etiam ipsum ab F puncto per lineam equalem alterutri linearum ED et DF sicut per lineam FI, ut parvus circulus qui a motu ipsius ad precedentia centro F et spatio FI describitur semper etiam per D centrum primi stabilisque excentrici terminetur, semperque mobilis excentricus centro I et spatio IT equali DA describatur, ut hic excentricus TC, utque semper epicyclus centrum in ipso habeat, ut hic in puncto T.

Sed magis supposita hec assequemur ex demonstrandis de magnitudinibus ipsarum per singulos, unde etiam que quodam modo ad intelligendas has suppositiones induxerunt per figuras passim apparebunt.

detail Premittendum tamen quod, cum motus secundum longitudinem non restituantur ad puncta circuli per medium signorum, nec ad maximas minimasve excentricorum distantias propter suppositam eorum transgressionem, motus longitudinis modo predicto nobis expositi non continent restitutiones que ad maximas longitudines excentricorum considerantur, sed eas que ad solstitialia et equinoctialia puncta fiunt consequenter ad annuum temporis secundum nos spatium. Primum igitur demonstrandum quod secundum etiam has suppositiones, quando medius stelle motus secundum longitudinem equaliter utranque a maximis et minimis longitudinibus distat, tunc differentia que fit penes inequalitatem zodiaci equalis in utraque distantia colligitur et maxima distantia que fit in 〈e〉piciclo epiciclo] piciclo A ad easdem medii transitus partes.

Sit enim excentricus ABGD circulus cuius centrum E et diameter EG in qua zodiaci centrum sit F, centrum autem excentrici facientis inequalitatem circa quod medium epicycli motum equaliter fieri asserimus sit I, et protrahantur BIT et DIC linee equaliter utraque distans ab A maxime longitudinis puncto ut AIB et AID anguli equales sint, et describantur in B et D punctis epicycli equales, coniunganturque BF et DF linee, et ducantur ab F cernentium visu ad easdem partes que tangant epicyclos linee FL et et] add. s. l. G FM. Dico FBI FBI] corr. ex FB G angulum 〈d〉ifferentie differentiae] fifferentiae A que penes inequalitatem zodiaci fit equalem esse angulo IDF et angulum BFL maxime distantie que penes epiciclum est equalem esse similiter angulo DFM. Sic enim magnitudines etiam ex compositione a medio motu distantiarum commutatim captarum captarum] post corr. G equales erunt. Protrahantur preterea ex B quidem et D ad lineas FL et FM perpendiculares BL et DM, ex puncto autem E ad lineas BT et DC perpendiculares EN et EX. Quoniam igitur angulus XIE equalis est angulo NIE, suntque recti anguli N et X, estque triangulorum equiangulorum latus EI commune, equalis est NI quidem linea linee XI, perpendicularis vero EN perpendiculari EX. Linee igitur BT et DT ab E centro equaliter distant. Equales igitur sunt et ipse et dimidie ipsarum. Quare BI reliqua DI relique equalis est. Est autem etiam linea IF comunis et anguli qui sunt sub equis lateribus BIF et DIF equales. Quare basis quoque BF equalis est basi DF et angulus IBF angulo IDF equalis. Est autem etiam BL semidiameter epicicli DM semidiametro equalis et anguli qui sunt in L et in M recti. Quare angulus quoque BFL angulo DFM equalis est.

Sit etiam gratia mercurialis suppositionis ABG diameter per centra et per maxima circulorum longitudinem, et A quidem centrum zodiaci esse supponatur, B autem centrum excentrici facientis inequalitatem, G vero punctum sit circa quod centrum excentrici deferentis epicyclum moveatur, et perducantur rursus ad utranque partem BD et BE linee motus equalis et ad successionem epycycli, et GF ac GI circumductionis equaliter velocis velocis] Nota quod GT debet poni equalis GB et similiter GC, nota etiam quod BD et GF debent esse equidistantes et similiter BE et GI, BA vero et BG equales add. G ad excentrici precedentia, ut anguli qui sunt in G et in B fiant fiant] corr. ex fiunt G equales et BD fiat equidistans linee GF et similiter BE linee GI. Sumantur autem in lineis GF et GI excentricorum centra, sintque ipsa T et C, et descripti in his centris excentrici in quibus epicycli sunt transeant per puncta D et E, descriptisque rusum circa D et E puncta equalibus epicyclis, coniungantur AD et E linee, detail producenturque tangentes epicyclos ad easdem partes linee AL et AM. Demonstrandum igitur est quod etiam sic ADB angulus differentie que est propter inequalitatem zodiaci equalis est angulo EB, angulus vero DAL maxime penes epicyclum distantie angulo EAM. Coniungantur enim linee BT et BC et TD et CE, deducanturque ex G quidem puncto ad BD et BE perpendiculares GN et GX, a punctis vero D et E ad lineas quidem GF et GI perpendiculares DF et EI, ad lineas vero AL et AM perpendiculares DL et EM. Quoniam igitur GBN angulus equalis est angulo GBX, suntque anguli in N et in X recti et linea GB communis, erit linea quoque GN linee GX equalis, hoc est linea DF linee EI. Est autem etiam DT linea equalis CE, angulique in F et in I recti. Erit ergo angulus detail quoque DTF equalis angulo ECI, et angulus GTB angulo GCB, propterea quod linea quoque TG equalis esse supponitur linee GC, et linea GB communis, et angulus TGB angulo CGB equalis. Et reliquus ergo angulus BTD angulo BCE equalis est, et basis BD basi BE equalis. Sed BA linea communis rursum est, angulusque DBA angulo EBA equalis, quare basis quoque AD basi E equalis, et angulus ADB angulo EB. Quapropter quoniam DL quoque linea equalis est linee EM et anguli qui sunt in L et in M equales, erit etiam DAL angulus equalis angulo EM, que nobis erant demonstranda.

〈IX.7〉 Capitulum VII: Demonstratio maxime Mercurii longitudinis et motus eius

His ita perspectis, primo cepimus in quibus partibus circuli per medium signorum maxima Mercurii longitudo invenitur hoc modo investigavimus, invenimusque maximarum distantiarum observationes in quibus matutini motus equaliter sicut et vespertini a Solis medio motu, hoc est a medio ipsius stelle distabant. Hoc enim invento, necesse est propter predemonstrata ut punctum zodiaci quod est inter duos motus maximam excentrici longitudinem contineat. Cepimus igitur ad hoc observationes paucas quidem, propterea quod raro huiusmodi coniugationem exquisite possumus assequi, sed quibus possit ante oculos propositum poni quarum posteriores iste sunt.

Observavimus enim nos ipsi per astrolabium sextodecimo Adriani anno Phamenoth secundum Egiptios xvi sequente decima septima vesperi Mercuri stellam maxime a medio Solis motu distantem. Que perspecta ad fulgentem Succularum cernebatur primum primum] add. marg. G gradum Piscium per longitudinem obtinere. Obtinebat autem tunc Sol medio suo motu 9 45′ gradus Aquarii. Quare vespertina maxima a medio motu distantia 21 15′ graduum erat. erat] add. marg. G

Decimo etiam octavo anno Adriani Ephiphi secundum Egiptios die 18 sequente 19 in mane, cum Mercurius esset in maxima distantia ac valde tenuis et exiguus videretur, perspiciebatur ad fulgentem Succularum similiter 18 45′ Tauri gradus obtinere. Erat autem medie tunc Sol in x gradibus Geminorum. Quare hic quoque maxima distantia matutina 21 15′ graduum equaliter fuit. Quoniam igitur in altera observatione medius stelle motus 9 45′ gradus Aquarii, in altera Geminorum gradus 10 obtinebat et punctum circuli per medium inter hos gradus est in 9 52′ 39′′ 39''] add. s. l. G Arietis. Arietis] 30 add. et del. AG In hoc situ profecto erat dyameter que per maximam longitudinem est.

Observavimus rursum per astrolabium primo Antonini anno die 20 Epiphi sequente xxi vesperi stellam Mercurii maxime a medio Solis motu distantem. Que perspecta tunc ad cor Leonis videbatur 7 gradus Cancri obtinere. Erat autem in eo tempore Sol in gradu Geminorum 10 30′. Quare maxima a medio motu distantia vespertina graduum fuit 26 30′.

Similiter in quarto etiam anno Antonini Phamenoth 18 sequente 19 in mane, cum maxima rursus esset distantia, perspeximus ipsam ad stellam fixam que vocatur Antares eratque in 13 30′ gradibus Capricorni, medius autem Sol erat in 10 gradibus Aquarii. Quare hic quoque maxima a medio motu distantia matutina 26 30′ graduum equaliter erat. Quoniam igitur in altera observationum medius stelle motus 10 30′ Geminorum, in altera 10 Aquarii gradus obtinebat, punctum autem quod inter hec est 10 15′ Libre gradus obtinet, in hoc profecto situ diameter que per maximam longitudinem est tunc inveniebatur. Ex his igitur observationibus in x gradibus proxime vel Arietis vel Libre maximam longitudinem esse invenimus, ex priscis vero que in maximis distantiis fuerant capte in 6 proxime gradibus eorundem signorum, ut hinc facile quispiam computaverit.

Anno enim vigesimo tertio secundum Dionisium Aquarionis die 29 Mercurius matutinus distabat a fulgentissima caudula Capricorni ad septentrionem lunas tres, sed hec fixa stella secundum principia nostra que sunt a tropicis et equinoctialibus punctis obtinebat gradus Capricorni 22 20′, quot et Mercurii stella, medius autem Sol 18 10′ gradus Aquarii. Aquarii] post corr. G Erat enim tempus 486 annorum a a] add. s. l. G Nabonassaro Chiac secundum Egyptios 17 sequente 18 in mane. Fuit ergo maxima matutina a medio motu distantia graduum 25 50′.

Huic equalem exacte maximam vespertinam distantiam in observationibus que ad nos pervenerunt non invenimus. Per duas autem equales proxime hoc modo equalem computavimus.

Nam eodem 23 anno secundum Dionisium Thauronis die quarto vesperi distabat ad successionem Mercurius a linea cornuum Tauri per tres lunas, videbaturque pertransiens habiturus distantiam a communi a communi] A communi. Communem appellat stellam fixam que est in cornu Tauri et in extremitate dexteri pedis Aurige add. marg. G ad meridiem maiorem quam trium lunarum, ut rursus secundum principia nostra 23 40′ gradus Tauri obtineret, et erat tempus annorum rursus a Nobonassaro 486 Phamenoth secundum Egyptios 30 sequente prima Pharmothy vesperi, quando medius Sol obtinebat 29 30′ Arietis. Fuit ergo maxima a medio motu vespertina distantia graduum 24 10′.

Anno autem 28 secundum Dionisium Geminionis 7o vesperi per rectam lineam erat maxime ad capita Geminorum, in meridie autem distabat ab australi tertia lunari parte minus quam duplum illius quo capita inter se distant. Rursus igitur Mercurii tunc stella secundum principia nostra 29 20′ Geminorum gradus obtinebat, et est tempus annorum 491 a Nabonassaro Pharmothy secundum Egyptios die 5 sequente sexto, quando Sol medius in 2 50′ Geminorum gradibus erat. Fuit ergo hec quoque distantia graduum 26 30′.

Quoniam igitur, cum medius motus esset in 29 30′ graduum Arietis, maxima distantia fuit graduum 24 10′, cum vero esset in Geminorum gradibus 2 50′, tunc distantia fuit graduum 26 30′, eratque matutina cuius coniugatam 25 50′ graduum querebamus, invenimus ubi, existente medio motu vespertina distantia graduum 25 50′, erit per excessum duarum observationum quas modo subiecimus. Colligitur enim mediorum quidem motuum excessus graduum 33 20′, maximarum vero distantiarum graduum 2 20′, ita uni gradui et sexagesimis 40 quibus 24 10′ gradus exceduntur a 25 50′ gradibus 24 proxime gradus congruunt. Quos si 29 30′ gradibus Arietis addiderimus, habebimus medium motum in quo maxima distantia vespertina equaliter sicut matutina colligetur graduum 25 50′ in 23 30 gradibus Tauri, et est punctum inter 18 10′ gradus Aquarii et 23 30′ Tauri in 5 50′ gradibus Ar〈i〉etis. Arietis] Aretis A

Anno rursus 24 secundum Dionisium Leonionis die 28 vesperi vesperi] post corr. G precedebat Spicam Mercurius, ut Hipparcus computavit, paulo plus quam per tres gradus, ut secundum principia nostra 19 30′ Virginis gradus tunc obtineret, et est tempus 366 annorum a Nabonassaro Pauni secundum Egyptios die 30 vesperi, quando medius Sol erat in gradibus Leonis 27 50′. Fuit ergo maxima a medio motu distantia vespertina graduum 21 40′, cui exacte correspondentem matutinam per duas rursum observationes conputavimus.

Anno enim 57 die 14 Dii mensis secundum Caldeos matutinus Mercurius erat superior quam fixa que est in extremitate australis forficalis Libre medietate unius brachii, ut secundum nostra principia 14 10′ Libre gradus tunc obtineret, et est tempus annorum 512 a Nabonassaro Nabonassaro] corr. ex Nabonasaro G Thot secundum Egyptios die 9 sequente decimo in mane, quando medius Sol erat in gradibus Scorpionis 5 10′. Fuit ergo matutina maxima distantia graduum 21.

Anno etiam 67 Apelei secundum Chaldeos die quinto matutinus superior erat boreali fronte Scorpionis medietate brachii. Erat ergo secundum principia nostra in gradibus Scorpionis 2 20′, et est tempus anni 504 a Nabonassaro Thot secundum Egyptios 27 sequente 28 in mane, quando sol medius erat in Scorpionis gradibus 24 50′. Fuit ergo etiam hec maxima distantia graduum 22 30′.

Quoniam ergo in his etiam duabus observationibus mediorum quidem motuum excessus graduum est 19 40′, maximarum autem distantiarum 1 30′, sexagesimis vero 40 unius gradus quibus 21 minoris distantie gradus exceduntur a 21 40′ maioris distantie gradibus congruunt gradus 9 proxime. Hos si 5 10′ Scorpionis gradibus addiderimus, habebimus medium motum in quo matutina distantia equalis efficitur gradibus vespertine 21 40′ obtinentem 14 10′ gradus Scorpionis, et est rursus punctum inter 27 50′ gradus Leonis et 14 10′ Scorpionis in 6 proxime gradibus Libre.

Ex istis igitur et ex illis que in aliis planetis particulariter consideravimus similiter in quinque planetis invenimus diametros que per maximas et minimas longitudines sunt ad successionem signorum circa zodiaci centrum moveri et motum hunc equevelocem esse motui sphere fixarum. Nam, ut demonstravimus, uno proxime gradu in centum annis illa movetur, sed hic tempus a priscis observationibus in quo maxima Mercurii longitudo in 6 gradibus Arietis erat que nunc decem eiusdem gradus obtinet 400 fere annorum est, in quo quatuor graduum proxime longitudins motus reperitur.

〈IX.8〉 Capitulum VIII: Quod Mercurii quoque stella bis proxima terre in una revolutione fit

Post hec consequenter magnitudines maximarum distantiarum quesivimus que fiunt, quando medius Solis locus in ipsa maxima longiudine invenitur et quando diametraliter ipsi opponitur. Id Id] post corr. G vero non per priscas observationes, sed per nostras invenimus. Hic enim maxime instrumentalis perspectionis utilitas intelligitur. Nam etiam si non prope observandas stellas certos iam habentes locos fixe cernuntur, quod in Mercurio ut plurimum accidit, propterea quod raro que nobis conscripte de fixis sunt equaliter Mercurio distant a Sole, possunt tamen etiam per multo distantium perspectionem exquisite querendarum stellarum situs tam per longitudinem quam per latitudinem capi.

Anno igitur Adriani 19 Athir secundum Egyptios die 14. sequente 15 Mercurius matutinus et in maxima distantia perspiciebatur ad fixam que est in corde Leonis, obtinebatque gradus Virginis 20 12′, Sol autem medius erat in 9 15′ gradibus Libre ut maxima distantia fuerit graduum 19 3′.

Eodem anno Pachon 19 vesperi in maxima rursus erat distantia perspectusque ad fulgentem de Succulis obtinere cernebatur gradus Tauri 4 20′. Sol autem medius 11 5′ Arietis gradus obtinebat, ita etiam hic maxima distantia 23 15′ graduum invenitur, unde perspicuum fit maximam mercurialis excentrici longitudinem non in Ariete, sed in Libra esse.

His enim datis, sit diameter ABG que per maximam longitudinem est, et sit zodiaci centrum B in quo est visus, A vero punctum sub ipso decimo Libre gradu, G autem sub decimo Arietis, descriptisque equalibus epicyclis in A et in G centris, unus in quo D et alter in quo E, producantur a puncto B recte tangentes epicyclos linee BD et BE, et deducantur a centris ad contactus perpendiculares AD et GE. Quoniam ergo maxima matutina a medio motu distantia que in Libra fuit fuisse observata est graduum 19 3′, erit angulus ABD, qualium quidem quatuor recti sunt 360, talium 19 3′, qualium vero duo recti sunt 360, talium 38 6′. Quare arcus quoque corde AD talium erit 38 6′ qualium est circulus qui circa ABD rectangulum describitur 360. Corda vero eius AD talium 39 9′ proxime qualium est AB qua rectus angulus subtenditur 120.

detail Rursus quoniam vespertina maxima a medio motu distantia que in Ariete fuit observata est fuisse graduum 23 15′, erit etiam angulus GBE talium 23 15′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 46 30′. Quare arcus quoque corde GE talium erit 46 30′ qualium est circulus qui circa GBE rectangulum describitur 360, et corda eius GE talium 47 22′ qualium est BG qua rectus angulus subtenditur 120. Quare qualium est GE linea 39 9′ AB autem 120, equales enim sunt AD et GE, cum sint a centro epicycli, talium etiam erit BG 99 9′, tota vero ABG linea 219 9′. Quare si equaliter dividatur, in F puncto erit AF quidem medietas 109 34′ earundem, linea vero que est inter puncta B F 10 25′.

Quod igitur F punctum aut centrum est excentrici in quo semper epicycli centrum est aut circa dicti circuli centrum fertur, perspicuum est. Sic enim solummodo centrum epicycli equaliter ab F puncto distabit, sicuti demonstratum est, in utraque diametralium distantiarum. Verum quoniam si F punctum centrum esset eius excentrici in quo epicycli centrum semper invenitur, stabilis esset excentricus hic, et situs qui est in Ariete minime omnium situum esse longitudinis, propterea quod BG linea omnium linearum que ab ipso B ad circumferentiam circuli in puncto F descripti protrahuntur minima est, nec invenitur situs qui in Ariete est minime ceterorum omnium longitudinis, cum situs qui sunt in Geminis et Aquario minoris sint longitudinis ipso et equales proxime inter se, patet quod centrum dicti excentrici circa F punctum fertur ad contrarium quam epycylus circumducitur, hoc est ad precedentia signorum semel etiam ipsum in una revolutione. Sic enim bis in ipsa centrum epicycli erit in minima longitudine.

Quod autem in Geminis et in Aquario propinquior terre fit epicyclus quam in Arietis situ ab expositis observationibus facile intelligitur. Nam in observatione quam quam] Nota quod qualium est semidiameter deferentis 60 talium erit AB minima distantia 49 22 proxime 33 32 minima dico quae erat in Geminis et Aquario add. marg. G fecimus in anno 16 Adriani Phamenoth xvi vespertina maxima a medio motu distantia graduum erat 21 15′ et in observatione quam fecimus in quarto anno Antonini Phamenoth xviii maxima matutina a medio motu distantia graduum erat 26 30′, eratque medius Sol in utrisque observationibus in xo. gradu Aquarii, et rursus in observatione quam fecimus in anno Adriani 18 Epiphi 19 matutina maxima a medio motu distantia graduum erat 21 15′ et in observatione in primo anno Antonini Epiphi 20 vespertina maxima a medio motu distantia erat 26 30′, eratque medius in utrisque similiter Sol in 10 gradibus Geminorum ut maxime distantie que in oppositis sunt Aquario atque Geminis simul capte faciant gradus 47 45′, cum utreque distantie que in Ariete fuerunt gradus contineant 46 30′. Nam, cum vespertina equalis sit matutine, observata est fuisse graduum 23 15′.

〈IX.9〉 Capitulum VIIII : De proportione ac magnitudine inequalitatum Mercurii

His ita premissis, demonstrandum iam sequitur in quo puncto linee AB annua restitutio epicicli per equalem motum ad successionem signorum fiat et quantum distat a puncto F centrum excentrici qui equalis temporis restitutionem ad precedentia facit. Usi autem sumus a〈d〉 ad] ab G hanc considerationem duabus maximarum distantiarum matutine vespertineque observationibus, cum ab utrisque distanciis medius motus quartam partem distaret ad eandem maxime longitudinis partem, in quo situ maxima proxime differentia inequalitatis zodiaci fit.

Quartodecimo ig〈it〉ur igitur] igur A anno Adriani Messori secundum Egiptios die xviii vesperi, sicut in observationibus Theonis invenimus, maxime a Sole distabat Mercurius remotior ad precedentia a stella que in corde Leonis est gradibus 3 50′, ut secundum nostra principia 6 20′ proxime Leonis gradus obtineret. Erat autem tunc medius Sol in gradibus Cancri 10 5′, ut maxima distantia vespertina fuerit graduum 26 15′.

In secundo autem anno Antonini Messori 23 sequente 24 in mane nos per astrolabium maximam eius distantiam observantes perspicientesque ipsum ad splendidam Succularum invenimus eum in 20 5′ gradibus Geminorum. Medius autem Sol erat in Cancri gradibus 10 20′, ut maxima distantia inveniatur graduum 20 15′.

detail His suppositis, sit per 10m gradum Libre diameter AFBG, ponaturque sicut in antecedente descriptione A quidem punctum ubi centrum epicycli sit, quando est in decimo Libre gradu, B autem sit centrum zodiaci, F vero punctum circa quod centrum excentrici ad precedentia circumducitur, primumque proponatur inveniendum quantum distet a puncto B centrum circa quod equalem motum epicycli ad sucessionem fieri dicimus.

Sit igitur illud I, et protrahatur per ipsum I linea que rectos ad AG lineam angulos faciat, ut per quartam partem a maxima longitudine distet, et in ipsa capiatur T centrum epicycli secundum observationes premissas, propterea quod etiam in ipsis medius Solis locus qui erat decimus Cancri gradus per quartam partem a maxima longitudine distat, descriptoque circa T centrum CL epicyclo, protrahantur a puncto B tangentes ipsum linee BC et BL, et coniungantur TC et TL et BT. Quoniam igitur in proposito medio loco matutina quidem maxima ab ipso distantia graduum esse supponitur 20 15′, vespertina vero 26 15′, erit angulus CBL talium 46 30 qualium quatuor recti sunt 360. Quare medietas etiam eius hoc est angulus CBT talium erit 46 30′ qualium duo recti sunt 360. Arcus ergo corde CT talium est 46 30′ qualium est circulus qui BTC rectangulo circumscribitur 360, et corda sua TC talium 47 22′ qualium est BT que rectum angulum subtendit 120. Quas ob res, qualium est TC semidiameter epycycli 39 9′ et BF demonstrata 10 25′, talium etiam erit BT 99 9′.

Rursus quoniam excessus prepositarum maximarum distantiarum qui est graduum 6 differentiam inequalitatis zodiaci bis continet, que differentia continetur ab angulo BTI, ut iam demonstravimius, erit angulus BTI talium quidem 3 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 6. Quare arcus etiam corde BI talium erit 6 qualium est circulus qui BIT rectangulo circumscribitur 360, ipsa vero corda BI talium 6 17′ qualium est BT que rectum angulum subtendit 120. Qualium igitur est BT linea 99 9′ et BF similiter 10 25′, talium BI etiam erit 5 12′. Est igitur BI linea medietas proxime ipsius BF, et erit utraque linearum BI et IF talium 5 12′ proxime qualium est semidiameter epicycli 39 9′.

detail Rursus protrahatur in eadem descriptione etiam per F punctum in contrariam partem linee IT ad AG lineam perpendicularis FMN in qua erit profecto propter equalis temporis restitutionem linearum IT et FN ad contraria centrum excentrici, in quo T centrum epicycli est, et supponatur FA equalis esse linee FN, ut etiam FN linea componatur sicut et AF ex semidiametro excentrici et linea que est inter centra ipsius, dico, et puncti F, capiaturque in ipsa centrum excentrici et sit M, coniungaturque linea FT. Quoniam igitur angulus MFI rectus est, est autem proxime indifferens recto angulus etiam TFI, erit linea quoque NFT indifferens a recta. Est autem demonstratum, qualium est semidiameter epicycli 39 9′, 39 9'] post corr. G talium etiam esse lineam FN que est equalis linee AF 109 34′, lineam vero FT que est equalis linee BT 99 9′ earundem. Erit igitur tota linea in FT 208 43′, et medietas eius linee NM que est semidiameter excentrici 104 22′ proxime, et et] add. s. l. G reliqua FM que est inter centra 5 12′. Est autem demonstrata etiam utraque linearum BI et IF 5 12′. Collectum igitur nobis est, qualium est semidiameter excentrici 104 22′, talium esse utranque ipsarum que inter centra sunt 5 12′ et semidiametrum epicyli 39 9′. Qualium igitur est semidiameter excentrici 60 talium erit utraque linearum que sunt inter centra 3 0′ et semidiameter epicycli 22 30′, quod erat demonstrandum.

Quod autem, his ita demonstratis, maxime quoque a minimis longitudinibus distantie observationibus conveniant, hoc est quando medius motus est in decimo Aquarii vel Geminorum gradu et latere trianguli distet a maxima longitudine, tunc angulus quo epicyclus in visu subtenditur graduum est 47 45′ proxime, sic perdiscemus.

Sit enim per maximam longitudinem diameter ABGDE, cuius punctum A sit in maxima longitudine, B autem sit circa quod centrum excentrici ad precedentia circumfertur, D vero sit centrum zodiaci, et intercipiant ambo hi motus regulariter equalique velocitate a maxima longitudine ad contraria in propris centris facti latus trianguli, et sit linea GF qua epicyclus circumducitur, BI autem qua centrum excentrici circumfertur, et sit I centrum excentrici, F autem centrum epicycli, destriptoque circa ipsum epicyclo, producantur DT et DC linee tangentes epycyclum, et coniungantur GI et DF et FT et FC linee, deducaturque a puncto D ad GF lineam perpendicularis DL. Demonstrandum igitur quod angulus TDC talium est 47 45′ qualium quatuor recti sunt 360.

Quoniam ergo uterque angulorum ABI et AGL trianguli latus subtendit et talium est 120 qualium duo recti sunt 180, ut uterque etiam angulus GBI et et] add. s. l. G DGL earundem sit 60, sitque angulus BIG angulo BGI equalis, propterea quod linea BG linee BI equalis supponitur, sintque utrique simul reliquorum ad duos rectos 120, erit uterque ipsorum earundem 60, quare triangulus BGI et angulorum et laterum equalium est. Est autem etiam angulus DGL equalis angulo BGI. 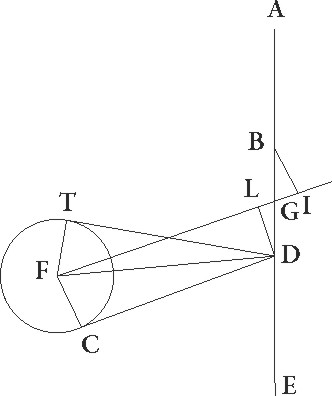detail Ad rectam igitur lineam sunt puncta I G F, quare linea IF que est semidiameter excentrici talium est 60 qualium est GI equalis linee GD que est intra centra 3, et reliqua GF 57 earundem.

Rursus quoniam angulus DGL talium est 60 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 120, erit etiam arcus corde DL talium 120 qualium est circulus qui GDL rectangulo circumscribitur 360, arcus vero corde GL reliquorum 60 ad semicirculum. Corde igitur etiam sue DL quidem talium est 103 55′ qualium GD que rectum angulum subtendit 120, GL vero earundem 60. Qualium igitur est GD linea 3, et GF similiter 57, talium erit DL 2 36′ et GL 1 30′ earundem, LF autem reliquarum 55 30′, et quoniam quidem ab ipsa et quod a DL fuerit, si componantur, faciunt quadratum quod fit a linea DF, erit etiam DF 55 54′ talium per longitudinem qualium semidiameter epicicli, hoc est utraque linearum FT et FC, supponebatur 22 30′. Qualium igitur est DF que rectum angulum subtendit 120, talium etiam erit utraque quidem linearum TF et FC 48 35′. Vterque vero angulorum FDT et FDC talium 47 46′ qualium duo recti sunt 360. Quare totus etiam angulus TDC 47 46′ talium est qualium quatuor recti sunt 360, quod erat demonstrandum.

〈IX.10〉 Capitulum X : De periodicis Mercurii motibus

Cum ad hec sequatur ut periodicos Mercurii motus ad inveniendos locos eius constituamus, longitudinis quidem motus, hoc est quibus equaliter circa G punctum epicyclus fertur, a solaribus iam datos habemus, motus autem inequalitatis, idest quibus stella in epicyclo circa centrum eius circumducitur, a duabus observationibus minime ambiguis cepimus, quarum alteram nos ipsi ipsi] corr. ex ipsius G observavimus, alteram a priscis accepimus.

Ipsi enim perspeximus stellam Mercurii secundo Antonini anno qui fuit annus 886 a Nabonassaro Epiphi secundum Egiptios die secundo sequente tertio per astrolabicum instrumentum, cum nondum ad maximam distantiam vespertinam pervenisset, perspectusque ad stellam qui est in corde Leonis cernebatur 7 30′ Geminorum gradus obtinere, quando etiam a centro Lune per gradum 1 sexagesimas 10 posterior erat. Erat autem tempus in Alexandria ante mediam noctem diei tertie horis equalibus 4 30′. Duodecimus enim gradus Capricorni in medio celo secundum astrolabium collocabatur. Erat enim Sol in 23 gradibus Tauri, obtinebatque medius motus eius in illa hora secundum demonstratas nobis suppositiones 22 24′ Tauri gradus, Lune vero gradus Geminorum 12 14′, inequalitatis inequalitatis] corr. ex in qualitatis G autem a maxima epicycli longitudine gradus 181 20′, ut ex istis verus quidem motus centri Lune in 17 10′ Geminorum esse colligatur, apparens autem in 16 20′ quare stella Mercurii, quoniam Luna ipsam uno gradu et 10 sexagesimis precedebat, in 17 30′ Geminorum gradibus erat.

detail Hoc ita supposito, sit per maximam et minimam longitudinem diameter ABGDE, cuius cuius] post corr. G A punctum in maxima sit longitudine, B autem sit punctum circa quod excentrici centrum ad precedentia circumfertur, G vero ad quod epicicli centrum ad successionem signorum progreditur, et D sit centrum zodiaci, motumque sit F epicycli centrum circa G punctum a linea GF per angulum AGF, circa B autem I centrum excentrici a linea BI per angulum ABI qui semper propter equalitatem motuum equalis est angulo AGF, descriptoque circa F epiciclo TCL, supponatur stella esse in L, et coniungantur GI et IF et DF et FL et DL linee, et deducantur ad lineam quidem GFT productam a punctis I et D perpendiculares IM et DN, ad lineam vero DL perpendicularis FX, propositumque sit invenire archum epicycli a puncto T maxime longitudinis ad stellam.

Quoniam igitur medius Sol 22 34′ gradus Tauri, minima vero stelle longitudo decimum Arietis gradum tunc obtinebat, ut medius stelle secundum longitudinem motus distaret a minima longitudine gradibus 42 34′, erit GBI angulus talium 42 34′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 85 8, uterque autem angulorum BIG et BGI, quoniam BG linea semper equalis est linee BI, earundem 137 26′. Quare descripti circa BGI triangulum circuli arcus quidem corde IG talium est 85 8′ qualium ipse circulus 360, arcus vero corde BG 137 26′ earundem, corde quoque sue GI quidem talium erit 81 10′ qualium est ipsius circuli diameter 120, BG autem 111 49′ earundem. Ergo GI quoque linea talium erit 2 11′ qualium est BG trium. Rursus quoniam BGI angulus talium est 137 26′ qualium duo recti sunt 360, angulus vero BGM 85 8′ earundem, erit etiam angulus IGM reliquarum 52 18′. Quare arcus quidem corde IM talium est 52 18′ qualium est circulus qui GIM GIM] corr. ex GM G rectangulo circumscribitur 360, arcus vero corde GM reliquarum ad semicirculum 127 42′. Corde igitur etiam sue IM quidem talium est 52 53′ qualium est GI que rectum angulum subtendit 120, GM vero 107 43′ earundem. Quare qualium est IG linea 2 11′′ et IF semidiameter differentis epiciclum 60, talium etiam est IM 0 58′ et GM 1 58′. Idcirco etiam linea MF que indifferente aliquo est minor quam IF earundem erit 60, et reliqua GF linea 58 2′.

detail Similiter quoniam DGN angulus talium est 85 8′ qualium duo recti sunt 360, erit etiam arcus corde DN talium 85 8′ qualium est circulus qui GDN rectangulo circumscribitur 360, arcus vero corde GN reliquarum ad semicirculum 94 52′. Corde igitur etiam sue DN quidem talium erit 81 10′ qualium est GD qua rectus angulus subtenditur 120, GN vero 88 23′ earundem. Qualium igitur est GD quidem 3 et GF 58 2′ demonstrata, talium erit DN 2 2′ et GN 2 13′ et NF 55 49′ reliquarum, et propterea DF quoque qua rectus angulus subtenditur talium 55 51′ proxime qualium est epicycli etiam semidiameter 22 30′. Qualium ergo est DF linea qua rectus angulus subtenditur 120, talium etiam erit DN corda 4 22′ et arcus suus talium 4 11′ qualium est circulus qui DNF rectangulo circumscribitur 360. Quare angulus quoque DFN talium erit 4 11′ qualium duo recti sunt 360, totus vero angulus EDF 89 19′. Est autem ad hec angulus quoque totus EDL 135 earundem, propterea quod stella tunc 67 30′ distare a maxima longitudine apparebat, angulus vero FDL reliquarum partium 45 41′. Quare arcus quoque corde FX talium est 45 41′ qualium est circulus qui DFX rectangulo rectangulo] 360 add. et del. AG circumscribitur 360. Ipsa vero linea FX talium 46 35′ qualium est DF que rectum angulum subtendit 120. Qualium ergo est DF linea 55 51′ et FL semidiameter epicycli 22 30′ talium FX erit 21 41′, qualium vero FL qua rectus angulus subtenditur est 120, talium rursus FX erit 115 39′. Quare arcus etiam corde FX talium est 149 2′ qualium est circulus qui rectangulo FLX circumscribitur 360, et angulus FLX talium 149 2′ qualium duo recti sunt 360. Demonstratus autem est etiam angulus FDL 45 41′ et angulus TFC 4 11′. Quare totus TFL talium quidem est 198 54′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 99 27′. Quare arcus epicycli TCL quo in observatione Mercurii stella distabat a puncto T maxime longitudinis graduum est 99 27′.

Rursus 21 anno secundum Dionsium quod tempus est annus 484 a Nabonassaro Nabonassaro] corr. ex Nabonasaro G Scorpionis die 22 secundum Egyptios Thot 18 sequente 19 Mercurius matutinus distabat a linea que est per borealem frontem Scorpii et per medium ad precedentia Lunam unam, ad septentrionem vero distabat a fronte boreali per duas Lunas. Sed media stellarum que sunt in fronte Scorpii secundum nostra principia obtinebat tunc gradus Scorpionis 1 40′, quantum etiam est australior a circulo per medium signorum, borealissima vero erat in gradibus Scorpii 2 20′, et est borealior quam circulus per medium gradibus 1 20′ proxime. Patet autem quod nondum in maximam distantiam matutinam pervenerat, propterea quod post quatuor dies 26 mensis Scorpionis distabat, ut conscribitur, ab eadem linea ad successionem unam integre Lunam et dimidiam. Maior igitur est facta distantia, cum Sol quatuor proxime gradibus motus sit, et stella per unam lunam et dimidiam. Obtinebat autem medius Sol die 19 Thot in mane secundum nos 20 50′ gradus Scorpii, maxima vero stelle longitudo sextum Libre gradum. Anni enim fere 470 qui fuerunt inter observationes quatuor proxime graduum maxime longitudinis motum faciunt.

His ita suppositis, describatur figura superiori similis. Sit tamen ut propter motuum dissimlitudinem et anguli qui sunt ad A maximam longitudinem acuti describantur et linee quibus stella coniungitur sint ad epicycli precedentia, et perpendicularis FX supra FL epicycli semidiametrum.

Quoniam igitur medius stelle motus 44 50′ gradibus distabat a maxima longitudine, erit profecto ABI angulus talium 44 50′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 89 40′. Reliquus igitur GBI etiam erit 270 20′, uterque autem angulorum BGI et BIG 44 50′ earundem. Quapropter corde quoque sue GI quidem talium erit 84 36′ qualium est diameter circuli BGN triangulo descripti 120, utraque vero linearum BG et BI 45 46′ earundem. Qualium igitur utraque linearum BG et BI 3um, talium GI erit 5 33′. Rursus quoniam angulus AGF talium esse suppositus est 89 40′ qualium duo recti sunt 360, et BGI 45 50′ similiter, totus autem FGI 134 30′ colligitur, erit profecto arcus corde IM talium 134 30′ qualium est circulus qui rectangulo GIM circumscribitur 360, arcus vero corde GM reliquarum ad semicirculum 45 30′. Corde igitur etiam sue IM quidem erit talium 110 40′ qualium est GI qua rectus angulus subtenditur 120, GM autem 46 24′ earundem. Qualium igitur est GI linea 5 33′, hoc est FN semidiameter excentrici 60, talium etiam IM erit 5 7′ et GM 2 10′. Idcirco etiam FM colligitur 59 47′ earundem per longitudinem, tota autem linea FMG 61 57′.

detail Similiter quoniam angulus quoque DGN talium est 89 40′ qualium duo recti sunt 360, erit etiam arcus corde DN talium 89 40′ qualium est circulus qui GDN rectangulo circumscribitur 360, arcus autem corde GN reliquorum ad semicirculum graduum 90 20′. Corde igitur quoque sue DN quidem talium est 84 36′ qualium GD qua rectus angulus subtenditur 120, GN autem 85 6′ earundem. Qualium ergo est GD linea 3 talium est DN 2 7′ et GN 2 2] post corr. G 8′ et FGN tota 64 5′. Idcirco etiam FD que rectum angulum subtendit 64 7′. Quare qualium est FD linea 120, talium erit DN 3 58′, et arcus eius talium 3 48′ qualium est circulus qui FDN rectangulo circumscribitur 360. Angulus etiam DFN talium est 3 48′ qualium duo recti sunt 360, et reliquus ADF 85 52′ earundem, sed angulus quoque ADL 54 40′ earundem esse suppositus est, propterea quod stella in observatione 27 20′ gradibus a maxima longitudine distabat, ut reliquus etiam angulus FDL 31 12′ talium relinquatur qualium duo recti sunt 360. Quare arcus etiam corde FX talium est 31 12′ qualium est circulus qui FDX rectangulo circumscribitur 360, ipsa vero linea FX talium 32 16′ qualium est DF qua rectus angulus subtenditur 120. Qualium igitur est DF linea 64 7′, hoc est FL epicycli semidiameter 22 30′, talium XF linea erit 17 15′ 3′′. Qualium vero FL qua rectus angulus subtenditur 120, talium erit ipsa FX 92 proxime. Arcus igitur etiam corde FX talium est 100 et sexagesimarum 8 qualium est circulus qui FLX rectangulo cirumscribitur 360. Sed angulus etiam FDL 31 12′ earundem demonstratus est et TFC 3 48′ similiter. Quare CFL quoque reliquus talium quidem est 65 8′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360. talium 32 34′.

Distabat ergo etiam secundum hanc observationem Mercurius ex C quidem minima epicycli longitudine gradibus 32 34′, a maxima vero longitudine gradibus 212 34′. Demonstratus autem est distare a maxima similiter epicycli longitudine in tempore nostre observationis gradibus 99 27′ et fuit tempus inter duas observationes egyptiacorum annorum quatuor et dierum 283 et horarum 13 30′ proxime, quod tempus integras inequalitatis restitutiones stelle huius 1268 continet. Nam cum 20 egyptiaci anni 63 proxime contineant restitutiones, colliguntur in annis quadringentis 1260. Reliqui autem duo anni simul cum dierum numero alias octo integras continent. Quare perspicuum nobis factum est quod annis egyptiacis 402 et diebus 283 et horis 13 30′ Mercurii stella ad integras 1268 restitutiones 246 53′ gradus addidit, quot gradibus observatio nostra priscam excedebat. Totidem autem ferme post integros circulos per tabulas nobis expositas gradus colliguntur. Ab his enim ipsis periodicos Mercurii motus emendavimus, dato tempore in dies resoluto, inequalitatis vero circulis in gradus gradibus etiam additis qui post integros circulos superfuerant, multitudine nanque graduum per multitudinem dierum divisa, diurnus medius inequalitatis Mercurii motus ille coligitur qui nobis expositus est. est] De locis periodicorum motuum Mercurii add. et del. AG

〈IX.11〉 Capitulum XI : De locis periodicorum motuum Mercurii

Ut igitur, sicut in Sole ac Luna, sic etiam in quinque planetis locos ipsorum ad primum Nabonassari Nabonassari] corr. ex Nabonasari G annum Thot Thot] corr. ex Tot G secundum egyptios die primo in meridie constituamus, cepimus tempus ab anno illo ad antiquiorem et propinquiorem observationem: id annorum egyptiorum 483 dierum 17 et horarum 18 20′ proxime colligitur, cui tempori post integros circulos in medio inequalitatis inequalitatis] post corr. G motu ascribuntur gradus 190 39′. Quos si subtraxerimus a gradibus maxime longitudinis 212 34′, quos in tempore observationis invenimus, habebimus in primo Nabonassari anno Thot secundum Egyptios die prima in meridie inequalitatis quidem a maxima epicycli longitudine gradus 21 55′, longitudinis vero sicut et in Sole Piscium 0 45′, maximam vero excentricitatis longitudinem in 1 10′ gradibus Libre. Centesima enim pars propositorum annorum partium est 4 50′ proxime quibus 1 10′ exceduntur ab observationis gradibus Libre sex.