Ptolemaeus Arabus et Latinus

〈XI〉

Liber XI Magne compositionis Ptolomei incipit

〈XI.1〉 〈Capitulum I:〉 Demonstratio excentricitatis et maxime longitudinis stelle Iovis

Demonstratis iam motibus periodicis et locis et inequalitatibus Martis, deinceps eodem modo de Iove nobis dicendum est. Capiemus igitur rursum ad demonstrandam excentricitatem et maximam longitudinem tres oppositiones ad medium Solis motum, quarum prima astrolabicis observavimus instrumentis anno Adriani Adriani] Nota quod a vigesimo primo anno Adriani ad primum Antonnini interfuit annus unus et dies 35 sicut scribit a secunda observatione ad tertiam add. marg. G 17^o secundum Egyptios Epiphi die primo sequente 2^o ante mediam noctem hora una, invenimusque lovis stellam in 23 11′ gradibus Scerpionis, alteram anno 21^o Pheophi 13^o sequente 14^o ante mediam noctem horis duabus, invenimusque in gradibus Piscium 7 54′, tertiam primo Antonini anno die 20^o sequente 21^o post mediam noctem horis 5, invenimusque in gradibus Arietis 14 23′. Duarum igitur distantiarum a prima quidem oppositione ad secundam tempus egyptiacos continet annos 3 et dies 106 et horas 23 et gradus apparentis stelle motus 104 43′, a secunda vero ad tertiam annum egyptiacum unum et dies 37 et horas 7 et gradus similiter 36 29′, medius autem secundum longitudinem motus temporis prime distantie gradus 99 55′, secunde vero 33 26′. Per has igitur distantias, quemadmodum et in Marte, fecimus propositorum que volumus invenire demonstrationem primum, quasi rursum unus excentricus sit hoc modo.

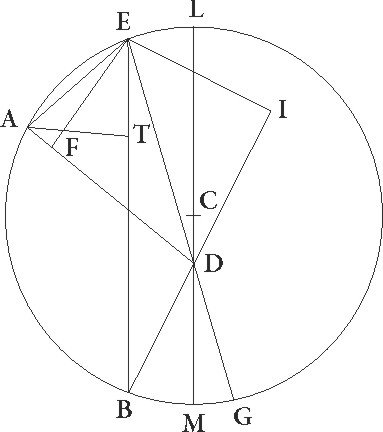
Sit ABG circulus excentricus, et sit A punctum ubi centrum epycycli erat in prima oppositione, B autem ubi in secunda, G vero ubi in tertia, captoque D zodiaci centro intra circulum excentricum ABG, coniungantur AD et BD et GD linee, et protracta GD usque ad E, coniungantur linee E et EB, deducanturque a puncto E ad AD et BD lineas perpendiculares EF et EI, a puncto vero A ad lineam EB perpendicularis AT. Quoniam igitur BG arcus excentrici 36 29′ zodiaci gradus subtendere supponitur, erit etiam BDG angulus, hoc est angulus angulus​] iter. et del. G BG arcus nota pro figura add. marg. G (commentary to the diagram) EDI, talium quidem 36 29′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 72 58′, et reliquus DEI 107 2′ earundem. Quare arcus quoque linee EI talium erit 72 58′ qualium est circulus qui EDI rectangulo circumscribitur 360, ipsa vero linea EI talium 71 21′ qualium est DE que rectum angulum subtendit 120. Similiter quoniam BG arcus graduum est 33 26′, erit etiam angulus BEG qui in circumferentia constituitur talium 33 26′ qualium duo recti sunt 360. Totus vero BEI 140 28′ earundem et reliquus igitur EBI 39 32′ earundem erit. Quare arcus etiam EI talium erit 39 32′ qualium est circulus qui rectangulo BEI circumscribitur 360 , et ipsa linea EI talium 40 35′ qualium est BE que rectum angulum subtendit 120. Qualium igitur EI linea demonstrata est 71 21′ et ED 120, talium etiam BE linea erit 210 58′. Rursus quoniam totus ABG arcus excentrici 141 12′ gradus utrarumque distantiarum simul subtendere in zodiaco supponitur, erit etiam angulus ADG in centro zodiaci constitutus talium 141 12′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 282 24′, angulus vero ADE qui deinceps ad ipsum sequitur 77 36′ earundem. earundem] Nota quod BM arcus MX 30^a pars est ipsius arcu MIG similter in sequente add. marg. G Quare arcus quoque linee EF talium est 77 36′ qualium est circulus qui DEF rectangulo circumscribitur 360, ipsa vero linea EF talium 75 12′ qualium est DE que rectum angulum subtendit 120. Similiter quoniam ABG arcus excentrici 133 21′ graduum colligitur, erit etiam angulus EG, cum sit in in] add. s. l. G circumferentia, talium 133 21′ qualium duo recti sunt 360, erat autem angulus quoque ADE 77 36′ earundem, et reliquus igitur EAF 149 3′ earundem erit. Quare arcus etiam linee EF talium est 149 3′ qualium est circulus qui EF rectangulo circumscribitur 360, linea vero EF talium 115 39′ qualium est EA que rectum angulum subtendit 120. Qualium igitur EF linea demonstrata est 75 12′ et ED supponitur 120, talium etiam EA linea erit 78 2′.

Rursum quoniam AB arcus excentrici 99 55′ graduum est, erit profecto etiam EB angulus, cum in circumferentia constituatur, 99 55′ talium qualium duo recti sunt 360, quare arcus quoque linee AT talium est 99 55 qualium est circulus qui ET rectangulo circumscribitur 360, et arcus linee ET 81 5′ reliquorum ad semicirculum. Corde igitur etiam sue AT quidem talium erit 91 52′ qualium est EA que rectum angulum subtenditur 120, ET vero 77 12′ earundem. Qualium igitur E linea 78 2′ demonstrata est et DE 120, talium etiam AT erit 59 44 et ET 50 12′. Demonstrata est autem linea quoque tota EB 210 58′ earundem, et reliqua igitur BT talium erit 160 46′ qualium est AT 59 44′. Est autem quadratum linee TB 25845 55′ et quadratum linee TA 3568 4′, que simul capta faciunt quadratum linee ab 29413 59′. Erit igitur linea AB talium per longitudinem 171 30′ qualium erit linea ED 120 et EA 78 2′. Est autem ipsa linea AB talium 91 52′ qualium est excentrici diameter 120, arcum enim subtendit graduum 59 55′. Qualium igitur est AB linea 91 52′ et excentrici diameter 120, talium etiam erit ED linea 64 17′ et EA 41 47′. Quare arcus quoque ipsius EA linee 40 45′ graduum est, totus vero arcus EABG graduum 144 6′. Quapropter etiam linea EDG talium est 119 50′ proxime, qualium est excentrici diameter 120.

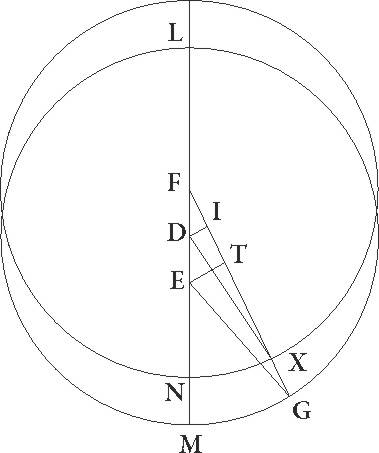
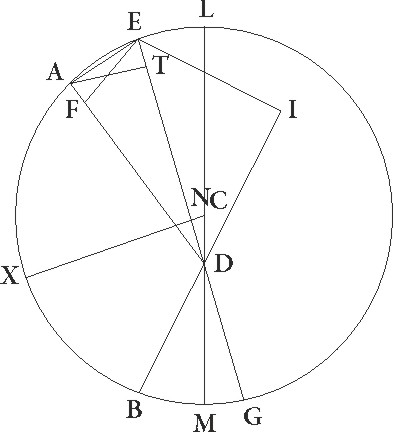Quoniam igitur EABG circuli portio minor est quam semicirculus atque ideo centrum excentrici extra ipsam invenitur, supponatur esse in C, ducaturque per ipsum et per D diameter LCDM que est per utraque centra, et ab ipso ad lineam GE ducta perpendicularis CN protrahatur usque ad X. Quoniam igitur qualium est LM diameter 120, talium demonstrata est EG linea 119 50′ et ED 64 17′, habebimus reliquam GD 55 33′ earundem. Quare quoniam rectangulum quod sub ED et DG lineis continetur equale est rectangulo quod sub LD et DM lineis, habebimus etiam rectangulum quod sub LD et DM lineis continetur talium 3570 56′ qualium est LM diameter 120, sed rectangulum quod fit a lineis LD et MD cum quadrato linee DC facit quadratum semidiametri, hoc est linee CL. Si ergo a quadrato semidiametri, hoc est a a] add. s. l. G 3600, subtraxerimus rectangulum sub lineis LD et DM contentum, hoc est 3570 56′, relinquetur quadratum linee DC 29 4′ earundem. Habebimus ergo ipsam lineam DC que est inter centra talium 5 23′ proxime qualium est CL excentrici semidiameter 60.

Rursus quoniam medietas linee GE, hoc est linea GN, talium est 59 55′ qualium LM diameter 120, demonstrataque est linea GD 55 33′ earundem, et reliqua ergo linea DN talium est 4 22′ qualium erat linea DC 5 23′. Qualium igitur est DC que que] add. s. l. G rectum angulum subtendit 120, talium etiam DN erit 97 28′ et arcus suus talium 108 24′, qualium est circulus qui rectangulo DCN circumscribitur 360. Angulus igitur etiam DCN talium quidem est 108 24′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 54 12′. Et quoniam in centro excentrici est, habebimus etiam arcum in 4 54 12′. Est autem totus etiam arcus GMXT graduum 87 3′, cum sit medietas totius GXE, reliquus ergo arcus MG qui est a minima longitudine ad tertiam oppositionem graduum erit 32 51′. Cum autem BG distantia 33 26′ graduum supponatur, patet quod reliquum quoque arcum BM qui est a secunda oppositione ad minimam longitudinem habebimus sexagesimarum 35, cunque AB distantia 99 55′ graduum supponatur, habebimus etiam reliquam LA que est a maxima longitudine ad primam oppositionem graduum 79 30′.

Si ergo in hoc excentrico epicycli centrum deferretur, satis esset his magnitudinibus tanquam certis peruti. Verum quoniam secundum suppositionis consequentiam in alio circulo movetur qui describitur centro dividenti puncto lineam DC equaliter et spatio CL, oportebit rursus, sicut in Marte factum est, primum apparentium distantiarum differentias computare, demonstrareque quantenam essent quasi proportiones excentricitatis iste proxime sint, si non in altero excentrico, sed in primo qui zodiaci continet inequalitatem quique ad centrum C circumscribitur epicycli centrum deferretur.

S 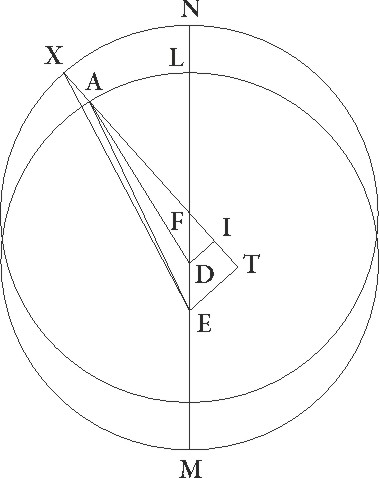it ergo LM excentricus qui centrum defert epicicli cuius centrum D, excentricus vero qui epicicli motum facit equalem sit NX cuius centrum F, et sit equalis excentrico LM, coniunctaque NLM diametro que per centra est, capiatur in ipsa zodiaci centrum et sit E, et supponatur primum in prima oppositione centrum epicycli esse in puncto A, et coniungantur DA et E et FAX et EX linee, deducanturque a punctis D et E ad lineam AF productam perpendiculares DI et ET. Quoniam igitur angulus NFX equalis secundum longitudinem motus talium 79 30′ demonstratus est qualium quatuor recti sunt 360, erit etiam contra se positus angulus DFI talium quidem 79 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 159. Quare arcus quoque DI talium est 159 qualium est circulus qui DFI rectangulo circumscribitur 360, arcus autem FI 21 reliquorum ad semicirculum. Corde igitur etiam sue DI quidem talium erit 117 59′ qualium est DF que rectum angulum subtendit 120, FI autem 21 52′ earundem. Quare qualium est linea DF que est medietas linee EF 2 42′ proxime, et DA semidiameter excentrici 60, talium etiam erit DI 2 39′ et FI 0 30′. Et quoniam quadratum linee DI subtractum a quadrato linee DA facit quadratum linee AI, habebimus etiam lineam AI 59 56′ earundem. Similiter quoniam linea FI equalis est linee IT, et ET dupla ad EI, erit tota linea AT talium 60 26′ qualium est ET 5 18′, et propterea etiam E que rectum angulum subtendit 60 40′ earundem. Quare qualium est E que rectum subtendit 120, talium erit ET 10 19′ et arcus suus talium 10 1′ proxime qualium est circulus qui rectangulo ET circumscribitur 360. Angulus igitur etiam EAT talium est 10 1′ qualium duo recti sunt 360. Rursus quoniam qualium est ET linea 5 18′ talium est FX excentrici semidiameter 60 et FT linea unius, tota vero FT 61, habebimus etiam EX que rectum angulum subtendit 61 14′ earundem. Qualium igitur est EX que rectum subtendit 120, talium etiam erit ET 10 23′ et arcus suus 9 55′ talium qualium est circulus qui rectangulo ETX circumscribitur 360. Quare angulus etiam EXT talium est 9 55′ qualium duo recti sunt 360, sed angulus quoque EAT 10 1′ earundem demonstratus est, et reliquus igitur EX angulus differentie quam querimus talium quidem erit 0 6′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 0 3′. Cernebatur autem in prima oppositione Iovis stella perspecta per lineam EA 23 11′ gradus Scorpionis obtinere, quare perspicuum est quod, si non in excentrico LM, sed in excentrico NX epicycli centrum deferretur, esset profecto in p〈u〉ncto puncto] poncto A eius X et stella per EX lineam perspiceretur tribus sexagesimis differens obtinensque gradus Scorpionis 23 14′.

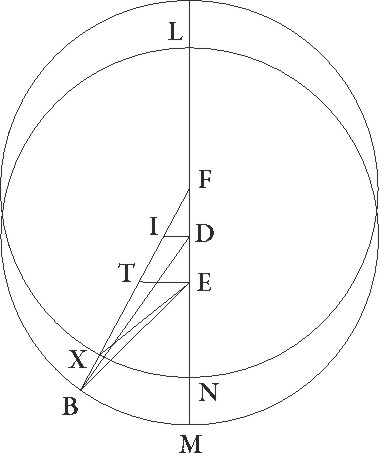
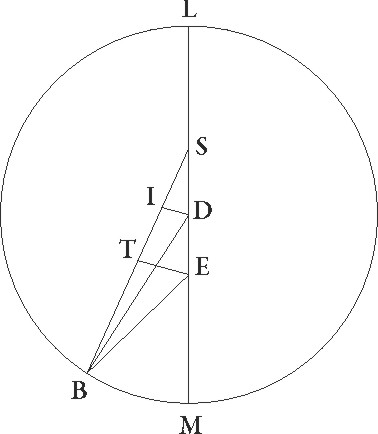
Rursus in simili figura designetur secunde oppositionis descriptio parum ad minime longitudinis precedentia designata. Et quoniam excentrici arcus XN 35 sexagesimarum demonstratus est, erit profecto etiam angulus XFN talium 0 35′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 1 10′. Quare arcus etiam DI talium erit 1 10′ qualium est circulus qui DIF rectangulo circumscribitur 360 et FI 178 50′ reliquorum ad semicirculum. Corde igitur etiam sue DI quidem talium erit 1 13′ qualium est DF que rectum angulum subtendit 120, FI autem earundem 120 proxime. Qualium igitur est DF linea 2 42′ et DB excentrici semidiameter 60, talium erit DI 0 2′ et FI 2 42′, et similiter IB earundem 60, cum sit indifferens a linea BD que rectum subtendit. Et quoniam rursus IT linea equalis est linee IF, et ET dupla est ad DI, habebimus etiam reliquam TB talium 57 18′ qualium est ET 0 4′, et idcirco etiam lineam EB 57 18′ earundem. Qualium igitur est EB que rectum angulum subtendit 120, talium quoque erit ET 0 8′ proxime, et arcus suus talium 0 8′ qualium est circulus qui rectangulo BET circumscibitur 360. Quare angulus etiam EBT talium est 0 8′ qualium duo recti sunt 360. Similiter quoniam qualium est FX excentrici semidiameter 60, talium FT tota demonstrata est 5 24′, habebimus etiam reliquam TX talium 54 36′ qualium erat ET 0 4′, et idcirco etiam lineam EX 54 36′ earundem. Qualium igitur est EX que rectum angulum subtendit 120, talium ET quoque erit 0 10′ proxime, et arcus suus talium 0 10′ qualium est circulus qui rectangulo ETX circumscribitur 360. Quare angulus etiam EXT talium erit 0 10′ qualium est circulus qui triangulo ETX circumscribitur 360 et reliquus BEX angulus 0 2′ earumdem, qualium vero quatuor recti sunt 360, talium 0 1′. Perspicuum igitur etiam hic est quod stella que in secunda oppositione per EB lineam perspecta 7 54′ Piscium gradus obtinebat, si per EX perspiceretur, 7 53′ Piscium solumodo obtineret.

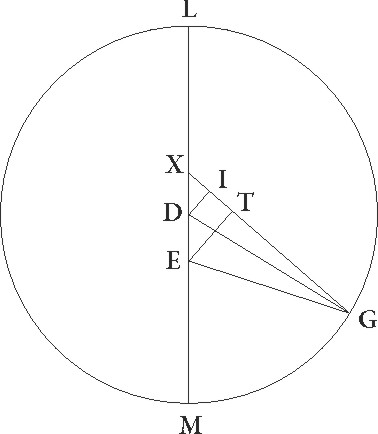
Proponatur etiam tertie oppositionis descriptio ad successionem minime longitudinis designata, et quoniam NX arcus excentrici graduum esse supponitur 32 51′, erit profecto etiam angulus NFX talium 32 51′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 65 42′. Quare arcus quoque DI talium erit 65 42′ qualium est circulus qui DFN rectangulo circumscribitur 360, arcus vero linee FI 114 18′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 65 6′, qualium est DF que rectum angulum subtendit 120, FI autem 100 49′ earundem. Qualium igitur est DF linea 2 42′ et DG excentrici semidiameter 60, talium DI quoque erit 1 28′ et FI 2 16′. Et quoniam quadratum linee DI subtractum a quadrato linee DG facit quadratum linee GI, habebimus etiam ipsam lineam GI 59 59′ proxime earundem. Similiter quoniam TI linea equalis est linee IF, et ET dupla ad DI, habebimus etiam reliquam GT talium 57 43′ qualium est ET linea 2 56′, et propterea etiam EG que rectum angulum subtendit 57 47′ earundem. Qualium igitur est EG que rectum subtendit 120, talium etiam ET linea erit 6 5′ et arcus suus talium 5 48′ 48'] post corr. A proxime qualium est circulus qui GET rectangulo circumscribitur 360. Quare angulus etiam EGT talium est 5 48′, qualium duo recti sunt 360. Eodem modo quoniam qualium est FX excentrici semidiametri 60, talium tota FT colligitur 4 32′, habebimus etiam reliquam XT talium 55 28′ qualium erat ET 2 56′, et propterea etiam EX que rectum angulum subtendit earundem 55 33′. Quare qualium est ipsa EX que rectum subtendit 120, talium etiam erit ET 6 20′ et arcus suus talium 6 2′ qualium est circulus qui rectangulo ETX circumscribitur 360. Quare angulus quoque EXT talium erit 6 2′, qualium duo recti sunt 360 et reliquus GEX 0 14′ earundem, qualium vero quatuor recti sunt 360, talium 0 7′. Quas ob res quoniam stella in tertia oppositione per EG lineam perspecta 14 23′ gradus Arietis obtinebat, perspicuum rursus est, si per lineam EX fuisset perspecta quod 14 30′ gradus Arietis obtinuisset. Demonstratum autem est ipsam 23 14′ Scorpionis gradus in prima oppositione obtinuisse, et in secunda 17 53′ gradus Piscium. Apparentes igitur iste Iovis distantie, si non ad excentricum qui epicycli centrum defert, sed ad eum qui equalem eius motum continet considerentur, a prima quidem oppositione ad secundam 104 39′ colligitur gradus, a secunda vero ad tertiam 36 37′, has in demonstrato iam theoreumate secuti lineam quidem que quae] post corr. G est inter centra zodiaci et eius excentrici qui equalem epicycli continet motum talium 5 30′ proxime invenimus qualium excentrici diameter est 120, illum vero arcum excentrici qui a maxima longitudine ad primam oppositionem est graduum 77 15′, arcum autem qui est a secunda oppositione ad minimam longitudinem graduum 2 50′, et arcum tandem qui est a minima longitudine ad tertiam oppositionem graduum 30 36′

Quod vero etiam hinc exacte exposite magnitudines capte sint, propterea quod differentie distantiarum eedem proxime prioribus per hec quoque colliguntur, inde patet quod apparentes etiam stelle distantie per inventas proportiones eedem inveniuntur illis que per observationes capte fuerunt, quod nobis ita perspicuum erit.

D 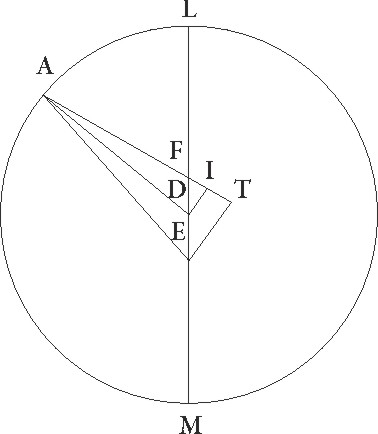esignetur enim rursus prime oppositionis descriptio que excentricum deferentem epicycli centrum solum modo habeat. Quoniam igitur angulus LFA talium demonstratus est est 67 15′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et qui sibi oppositus est angulus DFI 154 30′ earundem, erit etiam arcus linee DI talium 154 30′ qualium est circulus qui rectangulo DFI circumscribitur 360, arcus autem linee FI 25 30′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 117 2′ qualium est DF que rectum angulum subtendit 120, FI autem 26 9′ earundem. Quare qualium est FD linea 2 45′ et DA excentrici semidiameter 60, talium quoque erit DI linea 2 41′ et FI 0 36′, et per eadem superiorbus AI quidem linea erit 59 56′ earundem. Tota vero AT talium 60 32′ qualium est ET que dupla est ad DI 5 22′, sic E quoque, cum rectum subtendit angulum, 60 46′ earundem colligitur. Qualium igitur est E que rectum angulum subtendit 120, talium etiam erit ET 10 36′, et arcus suus talium 10 8′ qualium est circulus qui rectangulo ET circumscribitur 360, et angulus igitur EAT talium est 10 8′ qualium duo recti sunt 360, et reliquus ergo LEA angulus 144 22′ earundem erit, qualium vero quatuor recti sunt 360, talium 72 11′. Tot ergo gradibus stella a maxima longitudine in prima oppositione in zodiaco distabat.

Designetur rursum secunde oppositionis descriptio. Quoniam igitur angulus BFM BFM] corr. ex BXFM G talium supponitur esse 2 50′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 5 40′, erit etiam arcus linee DI talium 5 40′ qualium est circulus qui rectangulo DFI circumscribitur 360, arcus vero linee FI 174 20′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 5 55′ qualium est DF que rectum angulum subtendit 120, FI autem 119 51′ earundem. Qualium igitur est AF linea 2 45′ et DB excentrici semidiameter 60, talium etiam erit linea DI 0 8′ et IF 2 45′ proxime. Per eadem vero linea etiam IB 60 proxime earundem erit, et reliqua BT talium 57 15′ qualium est ET linea 0 16′, sic EB quoque que rectum angulum subtendit 57 15′ earundem colligitur. Qualium igitur est EB que rectum subtendit 120, talium ET quoque erit 0 33′ et arcus suus talium 0 32′, qualium est circulus qui BET rectangulo circumscribitur 360. Quare angulus etiam EBT talium est 0 32′ qualium duo recti sunt 360, totus autem BEM 6 12′ earundem, qualium vero quatuor recti sunt 360 talium 3 6′, distabat ergo etiam a minima longitudine ad precedentia in secunda oppositione stella Iovis gradibus 3 6′, demonstrataque fuit distare ad successionem in prima oppositione 72 11′. Colligitur ergo a prima oppositione ad secundam apparens distantia reliquorum ad semicirculum graduum 104 43′, sicut per observationes perspectum est.

Designetur etiam tertie oppositionis descriptio. Quoniam igitur MFG angulus talium demonstratus est 30 36′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 61 12′, erit etiam arcus linee DI talium 61 12′ qualium est circulus qui rectangulo DFI circumscribitur 360. Arcus vero linee FI reliquorum ad semicirculum 118 48′ et corde igitur etiam sue DI quidem talium erit 61 6′ qualium est DF que rectum angulum subtendit 120, et FI 103 17′ earundem. Qualium igitur est DF linea 2 45′ et GD excentrici semidiameter 60, talium erit DI linea 1 24′ et FI 2 22′, et per eadem GI quidem linea 59 59′ earundem erit, et reliqua GT 57 37′ talium qualium etiam ET colligitur 2 48′, sic etiam EG que rectum angulum subtendit 57 41′ earundem colligitur. Quare qualium est EG que rectum subtendit 120, talium ET erit 5 50′ et arcus suus talium 5 34′ qualium est circulus qui rectangulo EGT circumscribitur 360. Quare angulus etiam EGT talium est 5 34′ qualium duo recti sunt 360, totus vero MEG MEG] corr. ex MG G 66 46′ earundem. Qualium vero quatuor recti sunt 360 talium 33 23′. Totidem ergo gradibus in tertia oppositione ad successionem a minima longitudine stella distabat, demonstrataque est ab eadem minima longitudine ad precedentia 3 6′ gradibus in secunda oppositione distare. Quare apparens a secunda ad tertiam oppositionem distantia componendorum graduum est 36 29′, ut per observationes etiam habuimus.

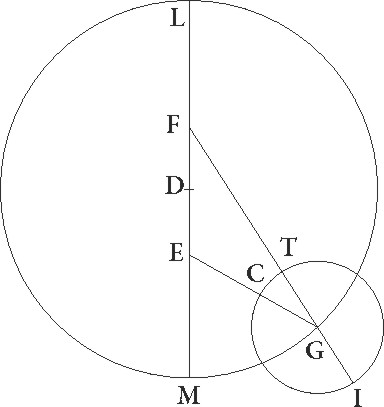Hinc patet, quoniam in tertia oppositione observatos 14 23′ gradus Arietis stella obtinebat, distabatque, ut demonstratum est, a minima longitudine ad successionem gradibus 33 23′, quod minima excentricitatis eius longitudo 11 gradus Piscium tunc obtinebat, maxima vero ex opposito 11 Virginis. Quare si centro G epicyclum ITC descripserimus, medium quidem per longitudinem motum a puncto L maxime longitudinis excentrici graduum habebimus 210 36′, angulus enim MFG talium demonstratus est 30 36′ qualium quatuor recti sunt 360, arcum vero epicycli TC qui est a T minima epicycli longitudine ad punctum C, ubi stella supponitur, graduum 2 47′. Nam etiam angulus EGF talium demonstratus est 5 34′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 2 47′. Quapropter oppositionis tertie, hoc est in primo anno Antonini Athir secundum Egyptios die 20 sequente 21 post mediam noctem horis 5, stella Iovis ad medios motus perspecta per longitudinem quidem a maxima excentrici longitudine distabat gradibus 210 36′ et obtinebat 11 36′ gradus Arietis, per inequalitatem vero a puncto L, hoc est a maxima epicycli longitudine, gradibus 182 47′.

〈XI.2〉 Capitulum II: Demonstratio magnitudinis epicycli Iovis

Consequenter postea ad demonstrandam epicycli magnitudinem observationem cepimus quam in secundo anno Antonini observavimus Messori secundum Egyptios die 26 sequente 27 ante ortum Solis, hoc est post mediam noctem quinque proxime horis equalibus. Medius enim motus Solis 16 11′ gradus Cancri obtinebat et erat in medio celo secundum astrolabium secundus gradus Arietis, quando stella Iovis ad splendidam Succularum perspecta cernebatur esse in gradibus Geminorum 15 45′, perspiciebaturque eundem cum centro Lune que australior erat locum obtinere, quo quidem in tempore per expositas nobis computationes Lunam medie 9 gradum Geminorum obtinuisse invenimus, inequalitatis vero a maxima epicycli longitudine gradus 272 5′, et propterea verum quidem motum eius in 14 50′ gradus Geminorum, apparentem vero in Alexandria in 15 45′. Iovis igitur stella 15 45′ gradus Geminorum similiter obtinebat. Rursus quoniam a tertia oppositione usque ad expositam modo observationem unus egyptiacus annus interfuit et dies 276, quod tempus nulla enim sensibilis erit differentia, si hoc universalius capiamus, longitudinis quidem gradus continet 53 17′, inequalitatis vero 218 31′. Si ergo gradibus tertie oppositionis accomodate hos addiderimus, habebimus ad tempus huius observationis longitudinis quidem ab eadem proxime maxima longitudine 263 53′, inequalitatis vero a maxima epicycli longitudine 41 18′.

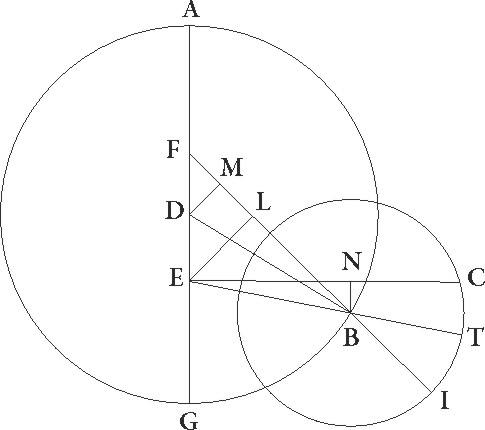His suppositis, designetur rursum descriptio similis demonstrationis quam de Marte, premisimus premisimus] corr. ex premissimus G ubi epicycli situs ad successionem minime excentrici longitudinis habetur, stelle autem ipsius ad partem que est post maximam epicycli longitudinem congrue accomodateque mediis motibus longitudinis et inequalitatis quos hic exposuimus. Quoniam igitur medius a maxima excentrici longitudine secundum longitudinem motus graduum est 263 53′, erit etiam angulus BFG talium 83 53′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 167 46′. Arcus igitur etiam linee DM talium est 167 46′ qualium est circulus qui rectangulo DFM circumscribitur 360, arcus vero linee FM 12 14′ ad semicirculum reliquorum. Corde igitur etiam sue DM quidem talium erit 119 19′ qualium est DF que rectum angulum subtendit 120, FM autem 12 47′ earundem. Quare qualium est DF linea 2 45′ et DB excentrici semidiameter 60, talium etiam erit DM 2 44′ proxime et FM 0 18′. Et quoniam quadratum linee DM subtractum a quadrato linee DB facit quadratum linee MB, erit etiam linea MB 59 56′ per longitudinem earundem. Similiter quoniam linea FM equalis est linee ML, et EL dupla est ad DM, erit etiam reliqua LB talium 59 38′ qualium linea EL colligitur 5 28′. Idcirco etiam EB que rectum angulum subtendit 59 52′ earundem erit. Quare qualium est EB que rectum subtendit 120 talium erit EL 10 58′ proxime, et et] add. s. l. G arcus suus talium 10 30′ qualium est circulus qui rectangulo BEL circumscribitur 360. Quare angulus quoque EBF talium est 10 30′ qualium duo recti sunt 360. Erat autem etiam angulus BFG 167 46′ et totus igitur BEG angulus 178 16′ earundem erit.

Rursus quoniam G minima longitudo 11 gradus proxime Piscium obtinet, et stella perspiciebatur in linea EC 15 45′ Geminorum gradus obtinere. Erit etiam angulus CEG talium 94 45′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 189 30′ et reliquus BEC 11 14′ earundem. Quare arcus quoque linee BN talium erit 11 14′ qualium est circulus qui BEN rectangulo circumscribitur 360, et ipsa linea BN talium 11 44′ qualium est EB que rectum angulum subtendit 120. Qualium igitur est EB linea 59 52′ et excentrici semidiameter 60, talium etiam BN erit 5 50′.

Similiter quoniam arcus IC 41 18′ graduum est, erit etiam angulus IBC talium quidem 41 18′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 82 36′. Erat autem etiam EBF angulus, hoc est IBT 10 30′, et reliquus igitur TBC erit 72 6′ earundem, sed angulus quoque CET 11 14′ earundem demonstratus est, et reliquus igitur BCN 60 52′ earundem erit. Quare arcus quoque linee BN talium erit 60 52′ qualium est circulus qui BCN rectangulo circumscribitur 360, BN autem corda talium 60 47′ qualium est BC que rectum angulum subtendit 120. Quare qualium est BN linea 5 50′ et et] add. marg. G excentrici semidiameter 60, talium etiam BC epicycli semidiameter erit 11 30′ proxime, quod nobis querebatur:

〈XI.3〉 Capitulum III: De emendatione periodicorum motuum Iovis

Consequenter autem periodicorum motuum gratia unam rursus de priscis observationibus que non ambigue conscripta est accepimus, per quam aperitur quod anno 45 secundum Dionysium Virginionis decima matutina Iovis stella australem obtexit Asinum, et est tempus annorum 83 a morte Alexandri Epiphi secundum Egiptios 17 sequente 18 in in] iter. et del. AG mane, quando Solem medio motu 9 56′ gradus Virginis obtinuisse invenimus, sed stella que vocatur australis Asinus, cum sit in nebula Cancri, in tempore quidem observationis nostre 11 3′ gradus Cancri obtinebat. Obtinuit ergo in observatione dicta gradus 7 33′. Annis enim 378 qui interfuerunt 3 47′ congruunt gradus, quare stella quoque Iovis que tunc fixam obtexerat 7 33′ gradus Cancri obtinebat. Similiter quoniam maxima longitudo in Virginis gradibus 11 tempore nostro reperitur, tempore observationis 7 13′ gradus eiusdem obtinere debebat. debebat] corr. ex debeat G Unde patet apparentem stellam 300 gradibus et 20 sexagesimis a maxima excentrici longitudine tunc remotam fuisse, medium vero Solem ab eadem longitudine ad successionem gradibus 2 43′.

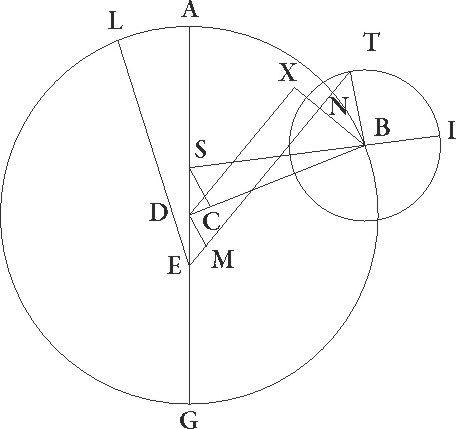His suppositis, designetur rursum descriptio similis demonstrationi quam de Marte habuimus consequenter dumtaxat motibus qui per observationes dati sunt. Que situm quidem epicycli in B puncto ante A maximam longitudinem habeat, situm autem medii Solis motus parum post eandem longitudinem in puncto L, et propter hec situm quoque stelle in T puncto post I maxime longitudinis epicycli punctum, coniunctis semper eodem modo FBI et DB et BT et ET lineis, deductisque ad lineam quidem DB perpendiculari FC, ad lineam vero ET perpendicularibus DM et BN, ad lineam autem BN protractam hic perpendiculari DX, que faciat DMNX paralellogramum rectangulum. Quoniam igitur angulus ET qui reliquos ad circulum zodiaci unum post gradus 300 et sexagesimas 20 continet talium est 59 40′ qualium quatuor recti sunt 360, et angulus EL 2 43′ similium, erit etiam LET totus, hoc est BTE, talium 62 23′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 124 46′. Quare arcus quoque linee BN talium erit 124 46′ qualium est circulus qui BTN rectangulo circumscribitur 360. Ipsa vero BN linea talium 106 20′ qualium est BT que rectum angulum subtendit 120. Qualium igitur est epicycli semidiameter 11 30′ talium erit BN linea 10 12′. Rursus quoniam angulus DEM talium esse supponitur 59 40′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 119 20′, et reliquus MDE 60 40′ earundem, erit etiam arcus linee DM talium 119 20′ qualium est circulus qui DEM DEM] corr. ex DM G rectangulo circumscribitur 360, et linea DM talium 103 34′ qualium est ED que rectum angulum subtendit 120. Qualium igitur est ED linea 2 45′ et DB excentrici semidiameter 60, talium erit DM 2 23′ et BNX tota 12 35′ earundem. Quare qualium est BD que rectum angulum subtendit 120, talium erit BX linea 25 10′ et arcus suus talium 24 14′ qualium est circulus BDX qui rectangulo circumscribitur 360. Quare angulus quoque BDX talium erit 24 14′ qualium duo recti sunt 360 et reliquus BDM 155 46′ earundem, totus autem BDE 216 26′ similium, et reliquus rursum BDF 143 34′ earundem. Quare arcus etiam linee FC talium erit 143 34′ qualium est circulus qui FDC rectangulo circumscribitur 360, arcus vero linee DC 36 26′ ad semicirculum reliquorum. Quapropter corde quoque sue FC quidem talium 113 59′ qualium est DF que rectum angulum subtendit 120, DC autem 37 31′ earundem. Qualium igitur est DF linea 2 45′ et DB excentrici semidiameter 60, talium etiam erit CF 2 37′ et DC 0 52′ et reliqua CB 59 8′, et propterea etiam FB que rectum angulum subtendit 59 12′ earundem. Quare qualium est FB que rectum subtendit 120, talium etiam FC erit 5 18′ et arcus suus talium 5 4′ qualium est circulus qui BFC rectangulo circumscribitur 360. Quare angulus quoque FBD talium est 5 4′ qualium duo recti sunt 360, totus vero AFB quo motus longitudinis medius continetur earundem 148 38′ erit, qualium vero quatuor recti sunt 360, talium 74 19′. Verum quoniam, si angulus IBT compositus fuerit cum angulo BFG et semicirculo simul, hoc est si ab eo subtractus fuerit angulus DFB facit angulum IBT quo motus stelle a maxima epicycli longitudine continetur 77 2′ earundem, demonstratum itaque nobis est quod in tempore observationis proposite stelle stelle] post corr. G Iovis medie moveri considerata distabat per longitudinem a maxima excentrici longitudine gradibus 285 41′, obtinebatque medie 22 54 gradus Geminorum, inequalitatis autem a maxima epicycli longitudine 77 2′, fuitque nobis etiam demonstratum quod in tempore tertie oppositionis distabat ab eadem epicycli longitudine gradibus 182 47′. Addidit ergo in tempore quod inter duas fuit observationes, hoc est in annis egyptiacis 377 et diebus 128 una proxime hora minus, post 345 integros inequalitatis circulos gradibus 105 45′, quot nobis ferme post integros circulos per tabulas mediorum motuum iam expositas colliguntur, propterea quod ab istis diurnum constituimus motum ex partitione multitudinis graduum que ex circulis resolutis et additis gradibus congregatur per multitudinem dierum qui ex omni tempore colliguntur.

〈XI.4〉 Capitulum IIII : De locis periodicorum motuum Iovis

Quoniam igitur hic rursum a primo Nabonassari anno secundum Egyptios die prima in meridie usque ad priscam observationem quam exposuimus anni egyptiaci sunt 506 et dies 316 45′ proxime, quod tempus continet post integros circulos longitudinis quidem gradus 258 13′, inequalitatis vero 290 58′, si hos acomodate a locis observationum subtraxerimus, habebimus locos stelle Iovis in eodem cum aliis tempore mediorum motuum longitudinis quidem in gradibus Libre 4 41′, inequalitatis vero a maxima epicycli longitudine 146 4′, et per eadem maximam longitudinem excentricitatis ipsius in gradibus Virginis 2 9′.

〈XI.5〉 Capitulum V : Demonstratio excentricitatis Saturni et maxime longitudinis eius

Sed iam cum reliquum ad pertractandum hunc locum sit, ut stelle Saturni inequalitates et locos demonstremus, primum rursus ad maxime longitudinis et excentricitatis considerationem tres, tres] sunt add. et del. A sicut etiam in aliis, stelle situs stationesque ad medium Solis motum diametraliter oppositas cepimus, quarum primam astrolabicis observavimus instrumentis anno Adriani 1^o Parchon secundum Egyptios die 7^o sequente 8^o vesperi, fuitque fuitque] post corr. G in Libre gradu uno et sexagesimis 13, alteram anno Adriani 17 Epiphi secundum Egyptios 18^o, exacte autem oppositionis et tempus et locum per observationes precedentes sequentesque cepimus, invenimusque fuisse post meridiem diei 18^e quatuor horis in gradibus Sagittarii 9 40′, tertiam oppositionem 20 anno Adriani Messori secundum Egyptios die 24^a observavimus, tempusque oppositionis exacte fuisse similiter computavimus in ipsa meridie diei 24^e locum etiam in Capricorni gradibus 14 14′.

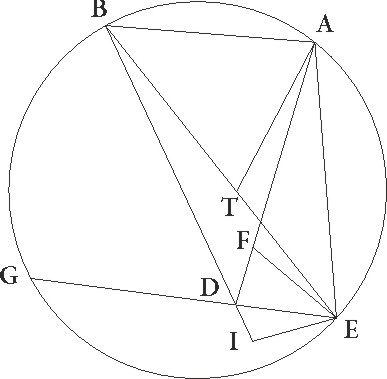Prima igitur harum distantiarum que est a prima oppositione ad secundam annos continet egyptiacos 6 et dies 70 et horas 22 et gradus apparentis stelle motus 68 27′, a secunda vero ad tertiam annos similiter egyptiacos 3 et dies 53 et horas 20 et gradus similiter 34 34′. Colliguntur autem medii secundum longitudinem motus universalius considerati temporis quidem prime distantie graduum 75 43′, secunde vero 37 52′. His distanciis suppositis, que proposita rursus sunt per idem theoreuma, ut in uno prius excentrico, demonstramus hoc modo.

Designetur enim, ne sepius eadem repetamus, similis eiusdem demonstrationis descriptio. Et quoniam BG arcus excentrici 34 34′ zodiaci gradus subtendere supponitur, erit profecto etiam angulus BDG, hoc est EDI, qui est in centro zodiaci talium 34 34′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 69 8′. Quare arcus quoque linee EI talium erit 69 8′ qualium est circulus qui DEI rectangulo circumscribitur 360, linea vero EI talium 68 5′ qualium est DE que rectum angulum subtendit 120. Similiter quoniam arcus linee BG 37 52′ graduum est, erit etiam angulus BEG qui est in circumferentia talium 37 52′ qualium duo recti sunt 360, et reliquus EBI angulus 31 16′ earundem. Quare arcus linee EI talium erit 31 16′ qualium est circulus qui EBI rectangulo circumscribitur 360, linea vero EI talium 32 20′ qualium est BE que rectum angulum subtendit 120. Qualium igitur EI linea demonstrata est 68 5′ et ED 120, talium etiam BE erit 252 41′.

Rursus quoniam arcus ABG totus 103 gradus et sexagesimam unam ex utraque distantia collectos zodiaci subtendit, erit etiam ADG angulus qui est in centro zodiaci talium 103 1′ qualium quatuor recti sunt 360. Quapropter angulus quoque ADE qui deinceps est 76 59′ earundem erit, qualium vero duo recti sunt 360 talium 153 58′. Quare arcus etiam linee EF talium erit 153 58′, qualium est circulus qui DEF rectangulo circumscribitur 360. Ipsa vero linea EF talium 116 55′, qualium est DE que rectum angulum subtendit 120. Similiter quoniam ABG arcus excentrici 113 35′ graduum colligitur, erit etiam EG angulus qui est in circumferentia talium 113 35′ qualium duo recti sunt 360. Erat autem etiam angulus ADE 153 58′ earundem, et reliquus igitur FE earundem erit 52 27′. Quare arcus quoque linee EF talium erit 52 27′ qualium est circulus qui EF rectangulo circumscribitur 360. Ipsa vero linea EF talium 86 39′, qualium est E que rectum angulum subtendit 120, quare qualium EF linea 116 55′ demonstrata est et ED 120, talium etiam erit EA 161 55′.

Rursus quoniam AB arcus excentrici graduum est 75 43′, erit etiam angulus EB qui est in circumferentia talium 75 43′ qualium duo recti sunt 360. Quare arcus etiam linee AT talium erit 75 34′ qualium est circulus qui ET rectangulo circumscribitur 360, arcus vero linee ET 104 17′ ad semicirculum reliquorum. Corde igitur etiam sue AT quidem talium erit 73 39′ qualium est EA que rectum angulum subtendit 120, ET autem 94 45′ earundem. Quare qualium E linea demonstrata est 161 55′ et DE 120, talium et AT erit 99 43′ et ET 127 51′. Fuit autem etiam tota EB linea demonstrata 252 41′ et reliqua ergo TB talium erit 124 50′ qualium est AT 99 43′. Est autem quadratum linee TB 15583 22′ et quadratum linee AT similiter 9877 3′, que composita faciunt quadratum linee AB 25460 25′. Erit ergo talium AB linea per longitudinem 159 34′ qualium erit ED 120, et EA 161 55′ similiter. Est autem ipsa linea AB talium etiam 73 39′ qualium excentrici diameter 120, propterea quod subtendit arcum graduum 75 43′. Qualium igitur est AB linea 73 39′ et excentrici diameter 120, talium etiam erit ED linea 55 23′ et EA 74 43′. Quare EA quoque arcus excentrici graduum est 77 1′, totus vero EABG 190 36′, reliquus autem GE 169 24′. Idcirco linea quoque GDE talium erit 119 28′ proxime qualium est excentrici diameter 120.

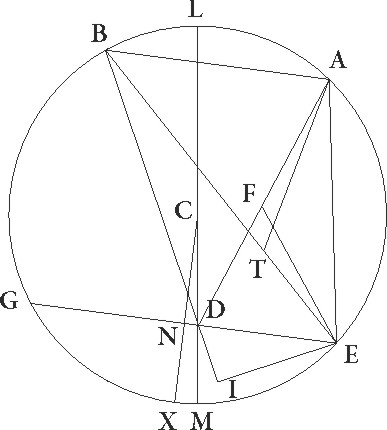Capiatur igitur excentrici centrum intra portionem EAG que maior semicirculo est, et sit punctum C, et ducatur per ipsum et D centrum LCDM diameter que est per utraque centra, et ducatur a puncto C ad lineam GE perpendicularis ad circumferentiam usque protracta C NX. Quoniam igitur qualium est LM diameter 120, talium tota linea EG demonstrata est 119 28′ et ED 55 23′, habebimus etiam reliquam DG 64 5′ earundem. Quare quoniam rectangulum quod continetur a lineis ED et DG equale illi rectangulo est quod fit a lineis LD et DM, habebimus etiam rectangulum LD et DM linearum 3549 9′ talium qualium est LM diameter 120. Sed rectangulum linearum LD et DM cum quadrato linee DC facit quadratum semidiametri, hoc est linee LC. Si ergo a semidiametri quadrato, hoc est 3600, subtraxerimus 3549 9′, relinquetur nobis quadratum linee DC 50 51′ earundem. Erit ergo linea DC que est inter centra 7 8′ proxime per longitudinem talium qualium est excentrici dyameter 120. Rursus quoniam medietas linee GE, hoc est linea EN, talium est 59 44′ qualium LM diameter 120, demonstrata est autem ED quoque linea 55 23′ earundem, habebimus etiam etiam] earundem add. et del. A reliquam DN talium 4 21′ qualium erat DC 7 8′. Quare qualium est DC que rectum angulum subtendit 120, ta〈l〉ium talium] taium A erit ipsa DN 73 11′ et arcus suus talium 75 10′ qualium est circulus qui rectangulo DCN circumscribitur 360. Angulus igitur etiam DCN talium erit 75 10′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 37 35′. Et quoniam in centro excentrici est, habebimus etiam arcum XM graduum 37 35′. Est autem etiam arcus GX que est medietas totius GXE graduum 84 42. Reliquus igitur etiam GL qui est a minima longitudine ad tertiam oppositionem graduum erit 57 43′. Sed BG quoque arcus 37 52′ eorundem supponitur, et reliquus igitur LB qui est a maxima longitudine ad secundam oppositionem graduum erit 19 51′. Similiter quoniam arcus ABG supponitur 75 43′, habebimus etiam reliquum AL qui est a prima oppositione ad maximam longitudinem graduum 55 52′. Quoniam ergo rursus centrum epicycli non in hoc excentrico fertur, sed in eo qui describitur centro quo DC linea equaliter dividitur et spatio linee CL, computavimus consequenter sicut et in ceteris differentias distantiarum que in zodiaco apparent, tamquam proportiones eedem proxime sint, si qui epicicli motum ad predesignatum excentricum qui zodiaci inequalitatem facit traduceret.

Designetur enim in simili demonstratione prime oppositionis descriptio ad precedentia L maxime longitudinis figurata. Quoniam ergo NFX angulus equalis secundum longitudinem motus, hoc est angulus DFI, talium quidem 55 52′ demonstratus est qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 111 44′, erit etiam arcus linee DI talium 111 44′ qualium est circulus qui DFI rectangulo circumscribitur 360, arcus vero linee FI 68 16′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 99 20′, qualium est DF que rectum angulum subtendit 120, FI autem 67 20′ earundem. Quare qualium est linea DF que inter centra est 3 34′ et DA excentrici semidiameter 60, talium etiam erit DI 2 57′ et FI 2 0′. Et quoniam quadratum linee DI subtractum a quadrato linee DA facit quadratum linee AI, habebimus etiam ipsam AI 59 56′ earundem. Similiter quoniam FI linea equalis est linee 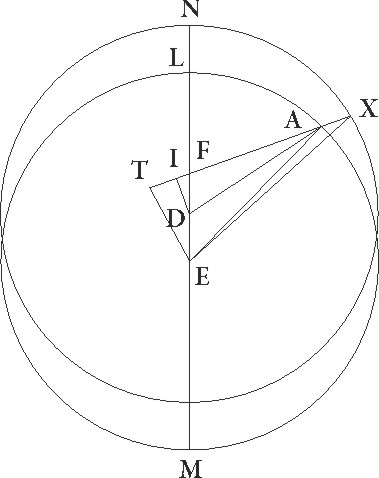TI, et TE dupla ad ID, erit AT tota talium 61 56′ qualium est ET 5 54′, idcirco etiam E que rectum angulum subtendit 62 13′ erit earundem. Quare qualium est E que rectum subtendit 120, talium etiam erit ET 11 21′, et arcus suus talium 10 51′ proxime qualium est circulus qui ET rectangulo circumscribitur 360. Angulus igitur etiam EAT talium est 10 51′ qualium duo recti sunt 360. Rursus quoniam qualium est ET linea 5 54′, talium FX quoque semidiameter excentrici 60, et FT linea 4, et tota TX 64, habebimus etiam EX que rectum angulum subtendit 64 16′ earundem. Qualium igitur est ipsa EX que rectum subtendit 120, talium erit TE 11 2′, et arcus suus talium 10 33′ qualium est circulus qui rectangulo ETX circumscribitur 360. Quare angulus etiam EXT talium est 10 33′ qualium duo recti sunt 360. Fuit autem etiam angulus EAT demonstratus 10 51′. Erit igitur etiam reliquus EX differentie que queritur angulus talium 0 18′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 0 9′. Sed stella in prima oppositione apparebat in E linea gradum unum et 13 sexagesimas Libre obtinens. Patet igitur, si centrum epicicli non deferretur deferretur] corr. ex defferretur G in circulo AL, sed in NX, quod esset in puncto X ipsius circuli NX, appareretque in EX linea precedens situm A puncti 9 sexagesimis. Obtineret igitur unum gradus Libre et sexagesimas quatuor.

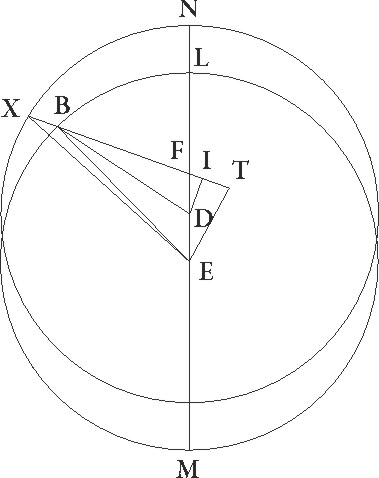Designetur rursum secunde oppositionis in simili demonstratione descriptio ad successionem maxime longitudinis figurata. Quoniam igitur NX arcus excentrici 19 51′ graduum demonstratus est, erit etiam angulus NFX tum ipse tum DFI, qui est in vertice ipsius, talium 19 51′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 39 42′. Quare arcus quoque linee DI talium erit 39 42′ qualium est circulus qui rectangulo DFI circumscribitur 360, arcus vero linee FI 140 18′ reliquorum ad semicirculum. Corde igitur etiam sue DI quidem talium est 40 45′ qualium DF que rectum angulum subtendit 120, corda vero FI 112 52′ earundem. Qualium igitur est DF linea 3 34′ et DB semidiameter excentrici 60, talium etiam DI erit 1 13′ et FI 3 21′. Et quoniam quadratum linee DI subtractum a quadrato linee DB facit quadratum linee BI, erit etiam ipsa BI 59 59′ proxime earundem. Et similiter quoniam FI linea equalis est linee IT, et ET dupla ad DI, habebimus etiam lineam TB totam talium 63 23′ qualium est ET 2 26′, idcirco etiam EB que rectum angulum subtendit 63 23′ earundem est. Quare qualium est ipsa BE que rectum subtendit 120, talium erit ET 4 36′ et arcus suus talium 4 24′ qualium est circulus qui BET rectangulo circumscribitur 360, et sic angulus quoque EBT talium erit 4 24′, qualium duo recti sunt 360. Similiter quoniam qualium est XF semidiameter excentrici 60, talium FT linea colligitur 6 42′, erit tota linea XT talium 66 42′ qualium ET supponebatur 2 26′, idcirco etiam EX que rectum angulum subtendit 66 45′ earundem erit. Qualium igitur est EX que rectum subtendit 120, talium ET erit 4 23′ et arcus suus talium 4 12′ qualium est circulus QETX rectangulo circumscribitur 360. Quare angulus quoque EXT talium est 4 12′ qualium duo recti sunt 360. Est autem demonstratus angulus etiam EBTX 24 earundem, et reliquus igitur BEX 0 12′ earundem erit, qualium vero quatuor recti sunt 360, talium 0 6′. Patet igitur etiam hic, quoniam in secunda oppositione stella apparens in EB linea 9 40′ gradus Sagittarii obtinebat, quod, si in linea EX appareret, 9 46′ eiusdem gradus obtineret. Fuit autem demonstratum quod etiam in prima oppositione gradus 1 et sexagesimas quatuor Libre similiter obtinuisset. Quare perspicuum est quod apparens distantia que est a prima oppositione ad secundam, si ad excentricum NX consideraretur, colligeret profecto 68 42′ gradus zodiaci.

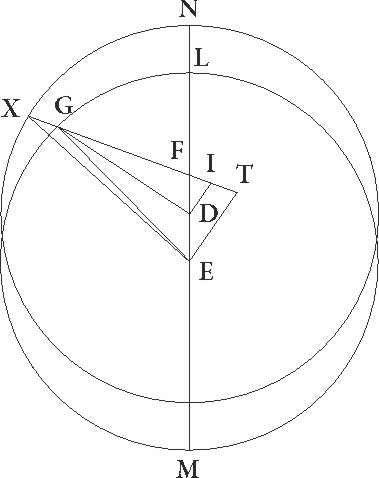Designetur similiter tertie oppositionis descriptio in eadem cum secunda lineatione. Quoniam igitur arcus NX 57 43′ graduum demonstratus est, erit etiam angulus NFX, hoc est DFI, talium 57 43′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 115 26′. Quare arcus quoque linee DI talium erit 115 26′ qualium est circulus qui DFI rectangulo circumscribitur 360, arcus vero linee FI 64 34′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 101 27′ qualium est DF que rectum angulum subtendit 120, FI autem 64 6′ earundem. Qualium igitur est DF linea 3 34′ et DG semidiameter excentrici 60, talium quoque DI quidem erit 3 1′, FI autem 1 54′. Et quoniam rursum quadratum linee DI subtractum a quadrato linee DG facit quadratum linee GI, habebimus etiam ipsam GI 59 56′ earundem. Similiter quoniam FI linea equalis est linee TI, et ET dupla ad DI, habebimus etiam totam GT talium 61 50′ qualium ET linea colligitur 6 2′, idcirco etiam EG que rectum angulum subtendit 62 8′ earundem erit. Quare qualium est GE que rectum subtendit 120, talium etiam erit ET 11 39′ et arcus suus talium 11 9′ proxime qualium est circulus qui GET rectangulo circumscribitur 360. Quare angulus quoque EG talium erit 11 9′ qualium duo recti sunt 360. Similiter quoniam qualium est XF semidiameter excentrici 60, talium FT quoque colligitur 3 48′, habebimus totam quoque lineam XT talium 63 48′ qualium erat ET 6 2′, idcirco etiam EX rectum angulum subtendentem 64 5′ earundem. Qualium igitur est EX que rectum subtendit 120, talium erit ET 11 18′ et arcus suus talium 10 49′ qualium est circulus qui rectangulo ETX circumscribitur 360. Quare angulus quoque EXT talium erit 10 49′ qualium duo recti sunt 360. Demonstratus autem est etiam EGT angulus 11 9′ earundem. Erit ergo reliquus quoque GEX 0 20′ earundem, qualium vero quatuor recti sunt 360 talium 0 10′. Quare quoniam in tertia oppositione stella in EG apparens linea 14 14′ Capricorni gradus obtinebat, patet quia, si fuisset in linea EX, 14 24′ eiusdem signi gradus obtinuisset, essetque rursus apparens a secunda oppositione usque ad tertiam distantia ad excentricum NX considerata graduum 34 38′.

Has distantias in eodem theoremate secuti invenimus lineam que est inter centra zodiaci et eius excentrici qui equalem epicycli motum continet, continet] 6 40 ad add. et del. A id est id est] post corr. G lineam EF, id … EF] Similis est antecedenti nisi quod loco B habet iste G et ibi arcus NX est graduum 19 51 hic gra 57 43 fiat ergo maior illo; NX arcus istius debet esse maius quam in antecedente fiat et tamen fecisti minorem quam ad hec que scribis ita habes suasimus ad lyram, fiat ergo ille minor quam medietas quam est, iste paulo maior quam est, ut autem semper consideras ut proportionaliter fiat, nam in exemplari istius satis bene se ista habent, iste fecit circulos maiores et non servavit proportiones add. marg. G (commentary to the diagram) talium 6 50′ proxime qualium est excentrici semidiameter 60, arcus autem eiusdem excentrici illum quidem qui est a prima oppositione ad maximam longitudinem graduum 57 5′, illum vero qui est ab eadem longitudine ad secundam quidem oppositionem graduum 18 38′, ad tertiam vero 56 30′, suntque rursum etiam hinc exacte magnitudines exposite adinvente, propterea quod differentie arcuum arcuum] corr. ex arcum G zodiaci eedem proxime superioribus per hec quoque colliguntur, et apparentes distantie stelle cum observationibus congrue inveniuntur, sicut a similibus aperte nobis patebit.

Designetur enim prime oppositionis figura in excentrico solum quo epycyclus defertur. Quoniam ergo AFL angulus 57 5′ gradus excentrici subtendens talium est 57 5′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et DFI angulus 114 10′, erit etiam arcus linee DI talium 114 10′ qualium est circulus qui DFI rectangulo circumscribitur 360, arcus vero linee FI 65 50′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 100 44′ qualium est DF que rectum angulum subtendit 120, FI autem 65 13′ earundem. Quare qualium est DF linea que inter centra est 3 25′ et DA excentrici semidiameter 60, talium etiam erit linea DI 2 52′ et FI 1 51′. Et quoniam rursum quadratum linee DI subtractum a quadrato linee DA facit quadratum linee AI, habebimus etiam ipsam AI 59 56′ earundem. Similiter quoniam linea FI equalis est linee IT, et ET dupla ad DI, habebimus etiam totam AT talium 61 47′ qualium ET colligitur 5 44′, idcirco etiam E lineam que rectum angulum subtendit 62 3′ earundem. Qualium igitur est E que rectum subtendit 120, talium etiam erit ET 11 5′, et arcus suus talium 10 36′ qualium est circulus qui ET rectangulo circumscribitur 360. Quare angulus quoque EAF talium erit 10 36′ qualium duo recti sunt 360. Sed AFL angulus 114 10′ supponebatur, et reliquus igitur EL 103 34′ earundem erit. Qualium vero quatuor recti sunt 360 talium 51 47′, totidem ergo gradibus in prima oppositione maximam 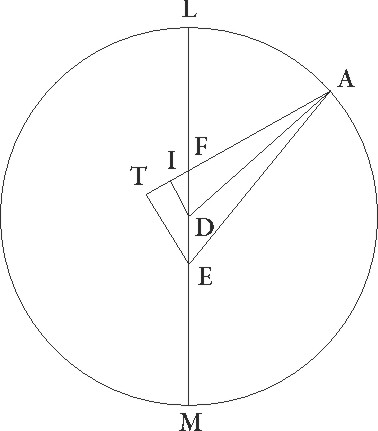longitudinem stella precedebat.

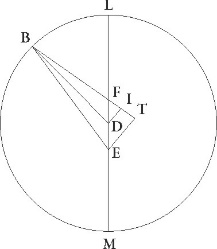Designetur rursum similis secunde oppositionis figura. Quoniam igitur angulus BFL talium est demonstratus 18 38′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et angulus DFI 37 16′, erit etiam arcus DI talium 37 16′ qualium est circulus qui DFI rectangulo circumscribitur 360, arcus vero linee FI 142 44′ ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium erit 38 20′ qualium est DF que rectum angulum subtendit 120, FI autem 113 43′ earundem. Qualium igitur est DF linea 3 25′ et DB semidiameter excentrici 60 talium etiam erit ID 1 5′ et FI 3 14′. Et quoniam quadratum linee DI subtractum a quadrato linee DB facit quadratum linee BI, habebmus etiam lineam BI 59 59′ earundem. Similiter quoniam IF linea equalis est linee IT, et ET dupla est ad lineam DI, habebimus etiam totam BT talium 63 13′ qualium ET colligitur 2 3′, et idcirco etiam lineam EB qua rectus angulus subtenditur 63 15′ earundem. Qualium igitur est ipsa EB que rectum subtendit 120, talium etiam erit TE 4 7′, et arcus suus talium 3 56′ qualium est circulus qui BET rectangulo circumscribitur 360. Quare angulus etiam EBF talium erit 3 56′ qualium duo recti sunt 360, sed angulus etiam BFL 37 16′ earundem suppositus fuit, et reliquus ergo BEL earundem erit 33 20′, qualium vero quatuor recti sunt 360, talium 16 40′. Quare in secunda etiam oppositione 16 40′ distare ad successionem a maxima longitudine stella profecto apparebat. Fuit autem demonstrata etiam in prima oppositione 51 57′ gradibus eandem longitudinem precedere. Colligitur ergo apparens a prima oppositione ad secundam distantia graduum qui ad eandem partem capiuntur 68 27′, sicut etiam per observationes habuimus. habuimus] post corr. G

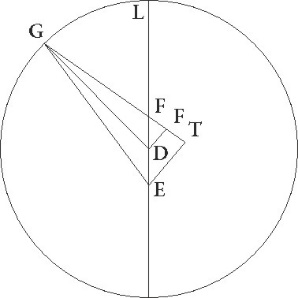Describatur etiam tertie oppositionis figura. Quoniam igitur angulus GFL talium 56 30′ demonstratus est qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium et ipse et DFI 113, erit etiam arcus linee DI talium 113, qualium est circulus qui DFI rectangulo circumscribitur 360, arcus vero linee FI 67 ad semicirculum reliquorum. Corde igitur etiam sue DI quidem talium est 100 sexagesimarumque 4 qualium est DF que rectum angulum subtendit 120, arcus vero FI 66 14′ eorundem. Quare qualium est DF linea 3 25′ et DG excentrici semidiameter 60, talium DI quoque linea erit 2 51′ et IF 1 53′. Et quoniam rursus quadratum linee DI subtractum a quadrato linee DG facit quadratum linee GI, habebimus etiam ipsam IG 59 56′ earundem. Similiter quoniam FI linea equalis est linee IT, et ET dupla ad DI, habebimus totam GT talium 61 49′ qualium GT quoque linea colligitur 5 42′, idcirco etiam EG que rectum angulum subtendit 62 5′ earundem est. Qualium igitur est ipsa GE qua rectus angulus subtenditur 120 talium etiam erit ET 11 10′ et arcus suus talium 10 32′ qualium est circulus qui GET rectangulo circumscribitur 360. Quare angulus etiam EGT talium est 10 32′ qualium duo recti sunt 360. Sed angulus quoque GFL 113 earundem supponitur, et reliquus reliquus] angulus add. et del. A igitur GEL 102 28′ earundem erit, qualium vero quatuor recti sunt 360, talium 51 14′. Tot ergo gradibus etiam in tertia oppositione stella distabat a maxima longitudine ad successionem, sed in secunda quoque oppositione ab eadem longitudine similiter distabat distabat] ergo add. et del. A gradibus 16 40′, quare apparens a secunda oppositione ad tertiam distantia 34 34′ ipsius excessus graduum est, sicut rursum per observationes habetur. Verum quoniam in tertia quoque oppositione 14 14′ Capricorni gradus stella obtinebat, distabatque a maxima longitudine ad successionem gradibus 51 14′, perspicuum hinc est quod maxima excentricitatis eius longitudo 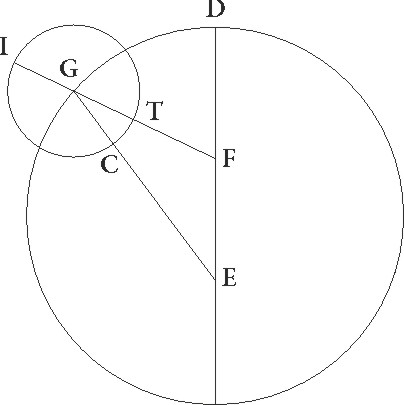23 gradus Scorpionis obtinebat, minima vero vero] obtinebat add. et del. A 23 Tauri per oppositionem.

Quare si centro G epicyclum TI descripserimus, habebimus hinc medium a maxima excentrici longitudine motum epicycli secundum longitudinem demonstratorum graduum 56 30′, TC vero arcum epicycli graduum 5 16′, propterea quod EGF quoque angulus talium 10 32′ demonstratus sit qualium duo recti sunt 360. Quare IT quoque arcus a maxima epicyli longitudine ad stellam 174 44′ graduum relinquitur. In tempore igitur tertie oppositionis, hoc est in 20^o anno Adriani Messori secundum Egyptios die 24, stella Saturni secundum medios motus considerata per longitudinem quidem distabat a maxima excentrici longitudine gradibus 56 30′, obtinebatque Cancri gradus 19 30′, inequalitatis autem a maxima epicycli longitudine gradibus 174 44′, que nobis erant invenienda.

〈XI.6〉 Capitulum VI: Demonstratio magnitudinis epicycli Saturni

Consequenter rursus ad demonstrandam epicycli magnitudinem cepimus observationem quam ipsi observavimus secundo Antonini anno Mechir secundum Egyptios die 6^o sequente 7^o ante mediam noctem horis quatuor. Erat enim in medio celi secundum astrolabium ultimus Arietis gradus, et medius Sol 28 41′ Sagittarii gradus obtinebat. Tunc igitur stella Saturni ad splendidam Succularum Succularum] corr. ex Sccularum G perspecta 9 15′ Aquarii gradus obtinebat. Distabat autem a centro Lune ad successionem medietate unius gradus proxime, tantum enim a boreali cornu ipsius distabat. Sed Luna secundum medium motum suum obtinebat tunc gradus Aquarii 8 55′ et inequalitatis a maxima epicycli longitudine 174 15′. Quare verus quoque motus suus 9 40′ Aquari gradus obtinere debebat, apparens autem in Allexandria motus 8 34′ graduum erat. Quare sic quoque stella Saturni, quoniam a centro ipsius ad successionem medio gradu proxime distabat, 9 15′ Aquarii gradus obtinere debebat, distareque ab eadem excentrici longitudine que in tam brevi tempore nullo motu de quo curandum sit progessa est gradibus 76 4′. Quoniam vero tempus quoque a tertia oppositione ad hanc usque observationem duorum est egyptiacorum annorum et dierum 167 et horarum 8, in quo tempore tempore] post corr. G Saturni stella universalius movetur per longitudinem quidem 30 gradibus et sexagesimis 3, inequalitatis autem gradibus 134 24′, si hos gradus predictis oppositionis tertie locis addiderimus, habebimus in tempore huius observationis longitudinis quidem a maxima excentrici longitudine gradus 86 33′, inequalitatis autem a maxima epicycli longitudine 309 8′.

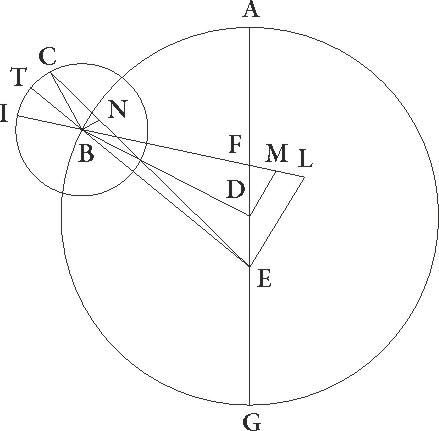His ita suppositis, designetur rursus similis demonstrationis figura que habebat epicyli quidem situm ad ad] post corr. G successionem maxime longitudinis excentrici, stelle vero ad precedentia maxime longitudinis epicycli consequenter ad expositos ipsorum motus. Quoniam ergo AFB angulus, hoc est DFM, talium esse supponitur 86 33′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 173 6′, erit arcus linee DM talium 173 6′ qualium est circulus qui DFM rectangulo circumscribitur 360, arcus vero linee FM 6 54′ ad semicirculum reliquorum. Corde igitur etiam sue DM quidem talium erit 119 47′ qualium est DF que rectum angulum subtendit 120, MF autem 7 13′ earundem. earundem] corr. ex eorundem G Quare qualium est DF linea que inter centra est 3 25′ et DB semidiameter excentrici 60, talium DM quoque linea erit 3 25′ proxime et FM 0 12′. Et quoniam quadratum linee DM subtractum a quadrato linee DB facit quadratum linee BM, habebimus etiam ipsam BM 59 54′ earundem. Similiter quoniam linea FM equalis est linee ML, et EL dupla ad DM, habebimus etiam totam BL talium 60 sexagesimarumque 6 qualium ipsa EL colligitur 6 50′, idcirco etiam lineam EB que rectum angulum subtendit 60 29′ earundem. Quare qualium est EB que rectum subtendit 120, talium etiam erit EL linea 13 33′, et arcus suus talium 12 58′ qualium est circulus qui BEL rectangulo circumscribitur 360. Angulus igitur etiam EBF talium est 12 58′ qualium duo recti sunt 360. Sed angulus quoque AFB 173 6′ earundem supponitur, et reliquus igitur EB 160 sexagesimarumque octo earundem erit. Sed angulus EC qui apparentem stelle a maxima longitudine distantiam continet 76 4′ talium suppositus est qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 152 8′, et reliquum igitur CEB angulum 8 0′ earundem habebimus. Arcus igitur etiam linee BN talium erit 8 qualium est circulus qui BEN rectangulo circumscribitur 360, ipsa vero linea BN talium 8 22′ qualium est EB que rectum angulum subtendit 120. Quare qualium est EB linea 60 29 et semidiameter excentrici 60, talium etiam erit BN 4 13′.

Rursum quoniam stella distabat a maxima epicycli longitudine gradibus 309 8′, erit reliquus quoque arcus IC graduum 50 52′. Angulus igitur etiam IBC talium est 50 52′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 101 44′. Erat autem etiam EBF, hoc est IBT, angulus 12 58′, et reliquus igitur TBC talium erit 88 46′ qualium angulus CEB demonstratus est 8. Reliquum ergo etiam BCN angulum 80 46′ earundem habebimus. Quare arcus quoque linee BN talium erit 80 46′ qualium est circulus qui BCN rectangulo circumscribitur 360, ipsa vero linea BN talium 77 45′ qualium est BC que rectum angulum subtendit 120. Qualium igitur BN linea 4 13′ demonstrata est, et semidiameter excentrici 60, talium habebimus BC semidiametrum epicycli 6 30′ proxime, collectumque ita nobis est quod maxima Saturni longitudo 23 gradus Scorpionis in principio imperii Antonini obtinebat, quodque Quodque] corr. ex quod G qualium est semidiameter defferentis epiciclum excentrici 60, talium etiam est que est inter centra zodiaci et excentrici qui motum equalem facit 6 50′ et semidiameter epicycli 6 30′ earundem, que nobis erant invenienda.

〈XI.7〉 Capitulum VII: De periodicorum Saturni motuum emendatione

Cum autem reliquum sit, ut emendationem periodicorum motuum demonstremus, cepmius ad hoc rursus unam de priscis observationibus quam non ambigue conscriptam reperimus, in qua declaratur quod in 20^o anno secundum Chaldeos Xanthyci die quinto vesperi fuit Saturni stella sub australi Virginis humero digitis duobus, et est annus a Nabonassaro 519 Tybi secundum Egyptios die 14 vesperi, in quo Solem medium invenimus in 6 10′ gradibus Piscium fuisse, sed fixa etiam que est in australi Virginis humero in nostro quidem observationis tempore in 13 6′ Virginis gradibus erat. In tempore autem observationis exposite, quoniam annis 366 congruunt fixarum motui gradus 3 40′, in Virginis gradibus 9 30′, totidem igitur Saturni stella etiam obtinebat, propterea quod australior erat quam ipsa fixa duobus digitis. Similiter quoniam maxima eius longitudo in 23^o gradu Scorpionis tempore nostro esse demonstrata est, debebat tempore observationis exposite 19 20′ Scorpionis gradus obtinuisse. Unde colligitur quod apparens stella tunc a maxima illius temporis longitudine distabat in zodiaco gradibus 290 10′, medius vero Sol ab eadem longitudine gradibus 106 50′.

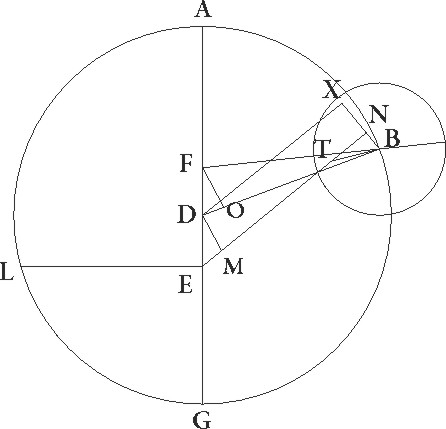His suppositis, designetur rursum similis demonstrationis figura que epicycli situm ad precedentia maxime longitudinis excentrici habeat, Solis vero ad precedentia minime longitudinis equidistantemque ipsi lineam a centro epicycli ad stellam. Quoniam igitur Saturni stella precedere maximam longitudinem cernebatur reliquis ad unum circulum gradibus 69 50′, erit etiam ET angulus, cum sit in centro zodiaci, talium 69 50′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 139 40′. Sed EL solaris distantie angulus talium 106 50′ esse supponitur qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 113 40′. Totus igitur angulus LET, hoc est ETB, equidistantes enim sunt LE et TB linee, talium est 353 20′ qualium duo recti sunt 360, et reliquus BTN 6 40′ earundem. Quare arcus etiam linee BN talium est 6 40′ qualium est circulus qui BTN rectangulo circumscribitur 360, corda vero BN talium 6 58′ qualium est BT que rectum angulum subtendit 120. Qualium igitur est BT semidiameter epicycli 6 30′, talium erit linea BN 0 23′. Similiter quoniam angulus ET talium est 139 40′ qualium duo recti sunt 360, et EDM angulus 40 20′ earundem, erit etiam arcus linee DM talium 139 40′ qualium est circulus qui DEM rectangulo circumscribitur 360, ipsa vero linea DM talium 112 39′ qualium est ED que rectum angulum subtendit 120. Quare qualium est ED linea que inter centra est 3 25′ et DB semidiameter excentrici 60, talium erit DM hoc est XN 3 12′, tota vero BNX linea 3 35′ talium qualium est EB que rectum angulum subtendit 60. Qualium igitur est DB que rectum angulum subtendit 120, talium etiam erit BX 7 10′ et arcus suus 6 52′ talium qualium est circulus qui BDX rectangulo circumscribitur 360. Quare angulus etiam BDX talium est 6 52′ qualium duo recti sunt 360, et reliquus BDM 173 8′ earundem, totus vero angulus BDE 213 28′ similiter, et reliquus BDA 146 32′ earundem. Quare arcus etiam linee FC talium erit 146 32′ qualium est circulus qui DFC rectangulo circumscribitur 360, arcus autem linee DC 33 28′ ad semicirculum reliquorum. Corde igitur etiam sue EF quidem talium erit 114 55′ qualium est EF que rectum angulum subtendit 120, DC vero 34 33′ earundem. Quare qualium est DF que inter centra est 3 25′ et DB semidiameter excentrici 60, talium FC quoque erit 3 17′ et DC 0 59′, reliqua vero linea CB talium 59 1′ qualium FC est 3 17′, idcirco etiam FB que rectum angulum subtendit 59 6′ earundem. Quare qualium est FB que rectum subtendit 120, talium etiam erit FC 6 40′, et arcus suus talium 6 22′ qualium est circulus qui BFC rectangulo circumscribitur 360. Quare angulus quoque FBC talium est 6 22′ qualium duo recti sunt 360. Erat autem etiam ADB angulus 146 32′, totum igitur AFB angulum qui medium secundum longitudinem motum continet 152 54′ earundem habebimus, qualium vero quatuor recti sunt 360, talium 76 27′. Quas ob res Saturni stella in observationis exposite tempore distabat secundum medie longitudinis motum a maxima longitudine gradibus 283 33′ et obtinebat gradus Virginis 2 53′. Verum quoniam Solis etiam medius motus graduum supponitur 106 50′, si 360 unius circuli gradus eis addiderimus et a factis 466 50′ longitudinis gradus 283 33′ subtraxerimus, habebimus in eodem tempore gradus et inequalitatis a maxima epicycli longitudine 183 17′.

Quoniam igitur in tempore observationis exposite quod fuit in 519 anno a Nabonassaro Tybi die 14^a vesperi demonstrata est Saturni stella distare a maxima epicycli longitudine gradibus 183 17′, in tempore vero tertie oppositionis, hoc est in anno 883 a Nabonassaro Mesori 24 in meridie, gradibus 174 44′, patet quod in tempore annorum egyptiacorum 364 et dierum 219 mota est post 357 integros circulos gradibus inequalitatis 351 27′, quot fere ab expositis mediis motibus rursum colliguntur. Hinc enim etiam diurnum medium motum constituimus divisa multitudine graduum in multitudinem dierum.

〈XI.8〉 Capitulum VIII : De locis periodicorum Saturni motuum in tempore Nabonassari

Quoniam igitur a primo etiam Nabonassari anno Thot secundum Egyptios die primo in meridie usque ad expositam priscam observationem tempus interfuit egyptiacorum annorum 518 et dierum 113 15′, quo tempore reiectis integris circulis continetur motus secundum longitudinem graduum 216 et inequalitatis 149 15′, si hos gradus a locis in observatione habitis subtraxerimus, habebimus in tempore Nabonassari stellam Saturni medie secundum longitudinem in gradibus Capricorni 26 43′, inequalitatis autem a maxima epicycli longitudine habebimus gradus 34 2′ et per eadem maximam quoque excentricitatis longitudinem in Scorpionis gradus 14 10′, que nobis erant invenienda.

〈XI.9〉 Capitulum VIIII : Quomodo a periodicis motibus apparentes ac veri per lineas capiuntur

Quod vero etiam conversim, datis periodicis arcubus tum eo qui equalem excentrici motum contineat tum arcum epicycli, apparentes hinc quoque stellarum motu facile per lineas capiantur, per eadem nobis perspicuum erit.

Si enim in simplici excentrici et epicycli descriptione coniunxerimus lineas FBT et EBI, dato medio motu longitudinis, hoc est angulo AFB, dabuntur secundum utrasque suppositiones per ea que demonstrata sunt tam angulus EB et EBF, hoc est IBT, quam proportio linee EB ad semidiametrum epycicli. Stella enim exempli gratia in C puncto epicycli superposita, coniunctisque lineis EC et BC, datoque arcu TC, si non quemadmodum in conversa demonstratione a centro epicycli ad lineam EC, sed a puncto C, ubi stella est, ad lineam EB duxerimus perpendicularem CL, erit etiam totus angulus IBC datus, et idcirco proportio quoque CL et LB linearum ad lineas EB et BC, et consequenter totius ELB linee proportio ad lineam LC dabitur. Quare angulus quoque CEL dato, totus angulus EC nobis collectus erit, continebitque apparentem stelle a maxima longitudine distantiam.

〈XI.10〉 Capitulum X : De faciendis inequalitatum tabulis

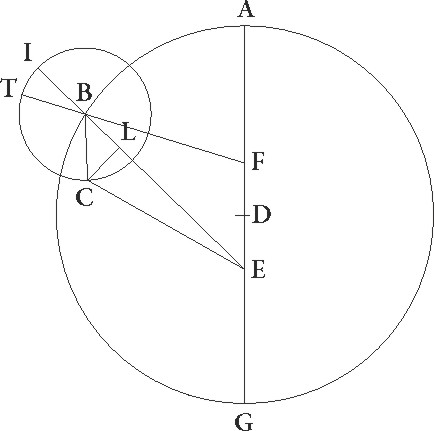Verum, ne semper apparentes motus per lineas computemus, —hic enim modus propositum quidem exquisite demonstrat, sed durior atque difficilior ad computationes est—, composuimus quam utiliter et quam proxime veritati potuimus tabulam per singulos quinque planetarum, que inequalitates eorum particulariter collatas continet, ut, datis periodicis motibus a maxima singulorum longitudine, apparentes quoque motus facile per eas computemus.

Est autem una quoque tabula rursum mediocritatis causa versuum 45 et ordinum octo, quorum duo primi numeros mediorum motuum, sicut etiam in Sole ac Luna, continebunt, ita ut in primo 180 gradibus a maxima longitudine conscribantur, in secundo reliqui ad semicirculum 180 ab inferioribus ad superiora, sic numerus graduum 180 in ultimo utriusque ordinis versu conscribetur. Fecimus autem incrementa in ipsis in quindecim quidem primis versibus per sex gradus, in 30 vero sequentibus per tres. Nam excessus etiam arcuum inequalitatis iuxta quidem maximas longitudines minus inter se differunt, iuxta vero minimas citius differentiam inter se accipiunt. De duobus autem ordinibus qui deinceps sunt tertius quidem continebit additiones subtractionesque factas propter excentricitatem maiorem in numeris congruentibus medii secundum longitudinem motus, simpliciter tamen captas quasi centrum epicycli deferretur in excentrico quo motus equalis continetur, quartus autem et quintus et quintus] add. marg. G collectas additionum subtractionumve differentias, propterea quod non in dicto excentrico, sed in alio centrum epicycli defertur. Modus vero per quem utrunque istorum et simul et seorsum per lineas invenitur per multa iam nobis exposita theoreumata facilis intellectu est. Hic tamen, ut hec inequalitatis zodiaci equatio ante oculis ponatur, in duobus ordinibus exposita est, quamvis ad usum usum] post corr. G etiam unus ordo ex additione subtractioneve collectus sufficeret. Singuli autem ordines de tribus qui qui] que add. et del. AG deinceps sequuntur factas penes epicyclum additiones subtractionesque continebunt continebunt] post corr. G que rursum simpliciter capte sunt, et quasi maxime minimeque longitudines in quibus capte sunt ad visus nostri distantiam considentur, qui etiam demonstrationis modus facilis intellectu factus est per theoremata theoremata] corr. ex theoreumata G nobis exposita. Medius igitur horum trium ordinum sextus autem a primo additiones subtractionesve que per proportiones mediarum longitudinum colliguntur continebit, quintus vero excessus additionum subtractionumque qui fiunt in eisdem eisdem] post corr. G arcubus maxime longitudinis ad mediam, septimus autem excessus minime longitudinis ad mediam qui in additionibus atque subtractionibus similiter fiunt. Demonstratum enim nobis est, qualium semidiameter epiycli est in Saturno quidem, —rectius enim iam a superioribus incipiemus—, 6 30′, In Iove autem 11 30′, in Marte vero 39 30′, in Venere 43 10′ et in Mercurio 22 30′, talium omnium omnium] corr. ex olim G mediam longitudinem esse 60, que scilicet ad semidiametrum deferentis epicyclum excentrici consideratur, maximam vero que ad centrum zodiaci consideratur in Saturno quidem 63 25′, in Iove autem 62 45′, in Marte 66, in Venere 61 15′, in Mercurio 69, minimam similiter in Saturno quidem 56 35′, in Iove autem 57 15′, in Marte 54, in Venere 58 45′, in Mercurio 55 54′. Ultimus autem octavusque ordo positus nobis est ad capiendas proportionales exponendorum excessuum partes, quando epicycli non sunt in ipsis mediis aut maximis aut minimis longitudinibus, sed in mediis inter eas transitibus. Facta vero huius etiam equationis computatio nobis est ad solas additiones subtractionesve maximas que fiunt in singulis intermediis longitudinibus a lineis que a visu nostro ad epicycli contactum exeunt. Nulla enim differentia de qua curandum sit differt excessuum magnitudo in particularibus epicycli arcubus ab excessibus qui fiunt in additionibus atque subtractionibus maximis.

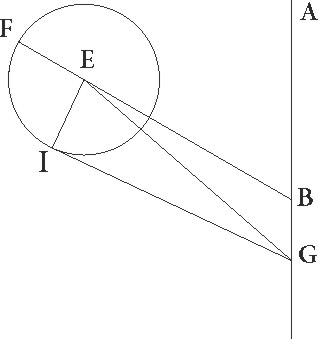Verum, ut clarius fiat quod dicitur, utque via doctrine huius apperiatur, ducatur recta linea que est per utraque centra, zodiaci videlicet et eius excentrici qui equalem epicycli continet motum, sitque ABGD linea, et sit G quidem zodiaci centrum, B autem excentrici qui facit epicycli motum equalem, et protracta protracta] corr. ex propterea G linea BEF, describatur circa E centrum epicyclus FI, producaturque a puncto G tangens ipsum linea GI, et coniungantur linea GE et perpendicularis EI, supponaturque gratia exempli centrum epicycli in omnibus quinque planetis distare a maxima excentricitatis longitudine secundum medium motum gradibus 30. Quoniam igitur, ne sepius eadem repetentes longior nobis computatio hec fiat, in superioribus per multa nobis theoremata theoremata] corr. ex theoreumata G et cum de Mercurio et cum de reliquis diceremus demonstratum est quod, dato angulo ABE, datur etiam proportio GE linee ad semidiametrum epicycli, hoc est ad lineam IE, que proportio colligitur per computationes factas in singulis, supposito nunc angulo ABE talium 30 qualium quatuor recti sunt 360, in Saturno quidem 63 2′ ad 6 30′, in Iove autem 62 26′ ad 11 30′, in Marte 65 24′ ad 39 30′, in Venere 61 26′ ad 43 10′, in Mercurio 66 35′ ad 22 30′, habebimus angulum etiam EGI qui maximam additionem subtractionemve que tunc penes epicyclum fit continet, qualium quatuor recti sunt 360, talium in Saturno 5 55′ 30′′, in Iove 10 36′ 30′′, in Marte 37 9′, in Venere 44 56′ 30′′, in Mercurio 19 45′. Colliguntur autem etiam maxime additiones subtractionesve que in mediis longitudinibus fiunt secundum proportiones paulo ante positas congruenter ad expositum stellarum ordinem, ne eadem repetamus, graduum 6 13′ et 11 3′ et 41 10′ et 46 0′ et 22 2′, in maximis vero longitudinibus graduum 5 53′ et 10 34′ et 36 45′ et 44 48′ et 19 2′, in minimis autem graduum 6 36′ et 11 35′ et 47 1′ et 47 17′ et 23 53′, et sic que fiunt in maximis longitudinibus differunt ab iis que in mediis fiunt gradibus 0 20′ et 0 29′ et 4 25′ et 1 12′ et 3 0′, que vero in minimis fiunt gradibus 0 23′ et 0 32′ et 5 51′ et 1 17′ et 1 51′.

Quoniam ergo quesitarum longitudinum additiones subtractionesve minores sunt iis que fiunt in mediis longitudinibus, differuntque ab ipsis gradibus 0 17′ 30′′ et 0 26′ 30′′ et 4 1′ et 1 3′ 30′′ et 2 17′, he autem differentie integrorum excessuum qui expositi sunt mediarum longitudinum ad maximas sexagesime sunt in Saturno quidem 52 30′, in Iove autem 54 50′, in Marte 54 34′, in Venere 52 55′, in Mercurio 45 40′ totidem sexagesimas. In octavis singularum tabularum ordinibus in versu qui habet numerum 30 graduum periodice longitudinis apposuimus. In longitudinibus autem que maiores additiones subtractionesve habent quam mediarum longitudinum sint collectos ipsarum excessus in sexagesimas similiter similiter] iter. et del. A rursum resolvimus, respectu tamen ad integros excessus qui in minimis longitudinibus et non in maximis fiunt. Eodem modo in ceteris etiam planetarum locis per sex gradus medie longitudinis sexagesimas integrorum excessuum computavimus, et congruentibus apposuimus numeris. Eadem enim ad sensum, ut diximus, differentiarum accomodatur proportio, etiam si motus stellarum non in maximis epicycli additionibus subtractionibusve fiant, sed in aliis etiam partibus suis. Est autem quinque tabularum conpositio hec.

〈XI.10〉 Capitulum X: Tabula inequalitatum quinque planetarum

〈XI.11〉 Capitulum XI : De computatione motus longitudinis quinque planetarum

Quandocunque igitur a periodicis longitudinis inequalitatisque motibus apparentes cuiusvis stellarum motus invenire voluerimus, computationem calculi uno et eodem modo in quinque planetis faciemus.

Nam cum a tabulis mediorum motuum equales longitudinis et inequalitatis motus integris semper reiectis circulis in tempore posito habeamus, gradus qui tunc a maxima excentrici longitudine sunt usque ad locum motus medie longitudinis in tabula inequalitatis stelle queremus, et appositos numero in ordine tertio gradus equationis longitudinis cum additione subtractioneve que in ordine quarto colligitur, si numerus graduum longitudinis in ordine primo invenitur, subtrahemus a gradibus longitudinis et addemus gradibus inequalitatis, sin vero in secundo longitudinis tunc gradibus addemus et subtrahemus a gradibus inequalitatis, et sic utrosque motus equatos habebimus. Deinde numerum inequalitatis a maxima longitudine iam equatum queremus rursum in duobus primis ordinibus, et appositam ei additionem subtractionemve in ordine sexto, qui est medie distantie, conscribemus. Et similiter numerum medie longitudinis quo primum intravimus queremus rursum in eisdem numeris, et si in primis versibus qui maioris longitudinis quam media sunt, quod a sexagesimis octavi ordinis perspicuum est, appositas ei sexagesimas in ordine in ordine] corr. ex longitudine G ipso octavo quotquot sint totidem capiemus, a differentia posita in versu conscripte iam medie additionis subtractionisve in ordine quinto qui maxime longitudinis est et quod factum erit subtrahemus ab illis que conscripsimus, sin autem numerus longitudinis in inferioribus minorisque longitudinis versibus quam longitudo media invenitur, sexagesimas ei in octavo similiter appositas ordine quotquot fuerint totidem ab apposita differentia additioni subtractionive medie conscripte in ordine septimo qui minime longitudinis est capiemus, quodque factum fuerit illis addemus que iam conscripsimus, collectosque gradus additionis subtractionisve iam equate, si numerus equate inequalitatis in ordine primo inveniatur, addemus longitudinis primum equate gradibus, sin vero in secundo, subtrahemus ab ipsis, collectumque graduum numerum a maxima que tempus ipsius planete sit longitudo connumerantes ad apparentem eius locum perveniemus.