Ptolemaeus Arabus et Latinus

〈XIII〉

Incipit XIII liber et ult〈i〉mus ultimus] ultmus A Magne Compositionis Pto〈lomei〉

〈XIII.1〉 〈Capitulum I:〉 De suppositionibus que ad motus latitudinis quinque planetarum pertinent

Verum cum ad absolvendum quinque planetarum doctrinam duo hec restent: primum ut motus ipsorum qui secundum latitudinem ad circulum qui per medium signorum est accipitur, deinde ut distantie a Sole quibus apparent ocultanturve cognoscantur, cumque latitudinales distantie preponende sint, quoniam etiam propter eas sensibiles differentie in apparitionibus et ocultationibus nonnulle fiunt, primo rursus quecunque de declinationibus circulorum suorum supponimus exponenda sunt.

Quoniam igitur omnes cernuntur latitudinis quoque habere differentiam, sicut et longitudinis alteram ad partes zodiaci propter circulum excentricum, alteram ad Solem propter epicyclum, idcirco inclines in omnibus supponimus excentricum quidem ad superficiem circuli per medium, epicyclum autem ad excentrici superficiem, nec ulla, ut diximus, de qua curandum sit propter hoc differentia in motu longitudinis aut in demonstrationibus inequalitatum propter tantam declinationem, ut paulo post post] post corr. G demonstrabimus, accidit. Verum quoniam per particulares in singulis observationes, quando equate longitudinis et equate inequalitatis numerus uterque simul per quartam proxime distat partem alter a boreali australive termino excentrici, alter a propria longitudine maxima, tunc in ipsa superficie circuli per medium stelle cernuntur, ideo excentricorum quidem quidem] qui A -dem add. marg. G inclinationes ad zodiaci centrum, sicut etiam in Luna, et ad diametros borealium aut australium terminorum, epicyclorum autem ad diametros ad zodiaci centrum inclinatas inclinatas] corr. ex inclinatos G in quibus apparentes ipsorum maxime minimeque longitudines considerantur, inclinari supponimus.

Ad hec in tribus quidem supperioribus, Saturno, Iove, Marte observavimus quod, quando motus longitudinis ipsorum in remotiore a terra excentrici arcu sunt, borealiores semper circulo per medium esse stelle cernuntur, tuncque borealiores maxime quando in minimis epicyclorum longitudinibus quam quando in maximis inveniuntur, quando autem motus longitudinis ipsorum in propinquiore arcu ad terram terram] corr. ex teram G excentrici sunt, e contra australiores circulo per medium perspiciuntur, preterea quod borealissimi excentricorum termini, in Saturno quidem et Iove, in principio Libre inveniuntur, in Marte vero, in exitu Cancri in ipsa ferme maxima longitudine. Ex quibus colligitur quod excentricorum partes que in dictis signis zodiaci sunt ad septentrionem declinantur et diametraliter diametraliter] post corr. G eis opposite ad meridiem equaliter, epicyclorum vero minime longitudines ad easdem cum excentricorum declinatione partes, ita ut diametri que rectos faciunt faciunt] corr. ex fiunt G angulos cum iis que per maximas eorum longitudines sunt equidistantes semper ad superficiem circuli per medium sint. In Venere autem atque Mercurio nobis observatum est quod, quando motus longitudinis earum in maximis aut minimis excentrici longitudinibus sunt, tunc motus quidem qui sunt in minimis epicyclorum nihil secundum latitudinem ab iis differunt qui sunt in maximis, sed similiter vel borealiores vel australiores circulo per medium inveniuntur, et in Venere quidem semper borealiores, in Mercurio autem contra semper australiores. Motus vero qui in maximis ipsorum distantiis fiunt inter se quidem maxime differunt, hoc est matutini a vespertinis, ab iis autem qui in maximis et minimis epicyclorum fiunt, hoc est a differentia propter excentricum equaliter ad contrarias, rursus enim succedens vespertinaque maxima distantia in Venere quidem borealior in maxima excentrici fit in minima australior, in Mercurio autem contra australior in maxima et borealior in minima. Quando autem equali motus longitudinis ipsorum in nodis sunt, tunc distantie quidem quarte partis in utraque epicyclorum parte a maximis et minimis epicyclorum longitudinibus utreque in superficie circuli per medium sunt, motus vero qui fiunt in minimis longitudinibus maxime differunt a motibus qui fiunt in maximis, et in Venere, quando quidem sunt in subtrahentis semicirculi nodo ad meridiem, quando vero in opposito ad septentrionem inclinantur, in Mercurio autem contra in subtrahentis quidem semicirculi nodo ad septentrionem, in contrario autem ad meridiem. Quare hinc etiam colligitur excentricorum quidem inclinationes ipsas quoque moveri et una restitui cum revolutionibus epicyclorum, cum quidem in nodis sint in eadem superficie circuli per medium, cum vero in maximis vel minimis longitudinibus, in Venere quidem maxime borealiorem faciunt epicyclum, in Mercurio autem australiorem. Epicycli vero duas faciunt differentias, nam diametros quidem que sunt per apparentes maximas longitudines maxime a nodis excentricorum inclinant, eas vero que ad rectos illis sunt maxime obliquant, —hoc enim nobis in maximis ac minimis excentricorum longitudinibus vocabulo hec inclinatio distinguitur—, contra vero illas quidem in excentrici superficie in maximis et minimis eius longitudinibus faciunt, has autem in superficie circuli per medium constituunt, quando in nodis sunt.

〈XIII.2〉 Capitulum II: De modo motus latitudinis secundum suppositiones inclinationum atque obliquationum

Est autem suppositionum summa hec: excentrici quinque planetarum circuli ad superficiem circuli per medium in centro zodiaci inclinantur, sed in tribus Saturno, Iove, Marte stabiliter eodemque modo, ut motus epicyclorum diametraliter oppositi ad contrarias latitudines ferantur, in Venere autem atque Mercurio simul cum epicyclis ad eandem latitudinem traducantur, in Venere quidem ad Septentrionem semper, in Mercurio autem ad meridiem. Epicyclorum vero diametri que per apparentes maximas longitudines sunt in excentrici superficie in aliquo principio constitute traducuntur a parvulis circulis qui minimarum longitudinum terminis, ut sic dicam, apponuntur mediocres ad tantum latitudinis transitum et recti ad excentricorum superficies in quibus centra eorum sunt. Revolvuntur autem equaliter consequenterque ad motus longitudinis ab altero principio eorum que sunt in sectionibus superficierum suarum et epicyclorum ad septentrionem ex suppositione, ducuntque secum superficies epicyclorum in versione quidem que in prima quarta fit ad borealissimum terminum, in ea vero que in secunda ad excentrici rursum superficiem, in ea que in tertia ad australissimum terminum, in ea que in ultima que restitutionis est ad primam principii superficiem. Huius autem motus initium atque restitutio, in Saturno quidem et Iove et Marte a sectione que in nodo ascendente fit constituitur, in Venere vero a minima excentrici longitudine, in Mercurio autem a maxima similiter. Diametri vero que rectos angulos ad predictas faciunt in tribus quidem superioribus equedistantes ad superficiem circuli per medium semper, ut diximus, sunt aut tantum oblique ad ipsum, ut nullius ea obliquatio cure digna sit, in Mercurio autem atque Venere ipsi quoque in principio quodam in superficie circuli per medium constitute traducuntur a parvulis circulis sequentibus, ut ita dicam, terminis ipsorum appositis, ii mediocres rursum sunt ad tantum latitudinis motum et recti ad superficiem circuli ad medium centraque sua in diametris habent equidistantibus a superficie circuli per medium, volvuntur autem equaliter cum aliis ab altero principio eorum que sunt in sectionibus superficierum suarum et epicyclorum ad septentrionem per suppositionem rursum, ducuntque secum vespertinos expositarum diametrorum terminos eodem modo, ut dictum est, in istis etiam motus principium atque restitutio in Venere quidem a nodo addentis semicirculi constituitur, in Mercurio autem ab aufferentis. aufferentis] corr. ex auferentis G

Ilud preterea de parvulis parvulis] corr. ex paulis G his circulis a quibus epicycli transferuntur dicendum est quod equaliter etiam ipsi a superficiebus ad quas declinationum traductiones fieri afferimus dividuntur. Sic enim solummodo motus suos secundum latitudinem equales in utraque fieri parte accidit. Revolutiones autem suas ad motum equalem non circa suum, sed circa aliud faciunt centrum quod possit facere eandem ad parvulum circulum excentricitatem quam habet motus longitudinis stelle ad circulum qui per medium signorum est. Nam cum restitutiones tam in zodiaco quam in parvulo circulo equalis temporis supponantur, et ad hec motus qui fiunt in utraque parte quarta alter alteri secundum apparentia coaptentur, si circuli parvuli circumductio ad centrum fieret suum, nullo modo posset propositum evenire, cum motus parvorum circulorum equali in tempore singulas pertranseant quartas, motus vero epicycli qui ad zodiacum considerantur nequaquam, idque propter excentricitatem que in singulis supponitur, sin vero circa centrum similis cum centro excentrici positionis fiat, etiam restitutiones declinationum equali in tempore pertransibunt.

Nemo autem multiplex atque arduum nostrarum excogitationum instrumentorumque considerans difficiles huiusmodi suppositiones arbitretur, nec enim decet corporibus divinis humana conferre nec rationes rerum ita magnarum a dissimillimis exemplis petere, quid enim dissimilius rebus perpetuis eodemque se modo semper habentibus quam ea que nunquam eodem modo se habent, aut quod dissimilius dissimilius] corr. ex dissimili G his que a quavis causa impediuntur quam illa que nec a se ipsis quidem impediuntur, sed niti quidem quam maxime simpliciores motibus celestium suppositiones accomodare, et si hoc non procedit, eas que possibiles sint. Nam si apparentium singula consequenti suppositionum ordine ad unguem servantur, cur mirum videbitur posse huiusmodi varietatem celestium motibus accidere, presertim cum nulla ibi prohibitiva natura sit, sed tota commoda ad cedendum naturalibus singularum motibus, etiam si contrarii esse videantur, ut omnia per omnia illa simpliciter corpora late liquideque fusa et pertransire et perfici possint, nec solum in circulis id recte procedat, verum etiam in ipsis globis atque axibus circumductionum. Quorum etiam varietatem alternationemque quam in diversitate motuum habent sic arduam atque difficilem in constructis a nobis imaginibus videmus, ut motus sine prohibitione in his fieri non possint. In celestibus autem hec varietas ac alternatio a seipsa non impeditur. Oportet igitur simplicitatem ipsam celestium non ab iis que simplicia esse apud nos videantur iudicare, cum nihil apud nos inveniatur quod similiter simplicitatem habere omnibus hominibus videatur. Nam qui ita considerat, is nihil in celo simplex esse putabit, nec ipsam quidem primi motus stabilem simplicemque naturam. Nan cum ea quoque eodem semper modo se habeat, non modo difficile est, sed omnino impossibile ymaginem eius apud nos inveniri. Non igitur hinc, sed a natura ipsorum celestium incommutabilitateque motuum id iudicandum. Sic enim omnes illi motus simplices videbuntur et quidem multomagis quam que apud nos simplicissima esse iudicantur, cum nihil difficultatis nihilque laboris in motibus illorum possit excogitari.

〈XIII.3〉 Capitulum III : De singularum inclinationum magnitudine

Sed universalem quidem situm seriemque declinationis circulorum hinc ratiocinari quilibet potest, magnitudines vero interceptorum a declinationibus in quolibet planeta particulariter arcuum maximi circuli descripti per polos inclinati circuli et erecti ad superficiem per medium ad quem motus latitudinis perspiciuntur, in Venere quidem atque Mercurio, a latitudinis motibus qui secundum expositos situs apparent faciles intellectu fiunt. fiunt] post corr. G Nam quando in maximis vel minimis excentricorum longitudinibus motus longitudinis ipsorum sunt, si etiam prope minimas vel maximas epicyclorum longitudines stelle, ut diximus, reperiantur, equaliter borealiores aut australiores, ut ex proximis observationibus adinvenimus, circulo per medium perspiciuntur, Venus quidem sexta fere unius gradus parte semper borealior, Mercurius vero 45 sexagesimis semper australior. Quare hinc excentricorum utriusque declinationem tantam esse percepimus. In maximis autem a Sole distantiis 5 fere gradibus utrique secundum mediam rationem borealiores aut australiores oppositis maximis apparent distantiis. Nam Venus Venus] corr. ex Vnus G quidem insensibili pene pene] post corr. G aliqua quinque gradibus differentia minus in maxima excentrici, plus vero in minima dictam secundum latitudinem facere oppositionem perspicitur, Mercurius vero medietate unius gradus maxime ut oblicationes epicycli ad utranque superficierum excentricorum partem 2 30′ gradus proxime in circulo qui rectos ad zodiacum angulos facit subtendant. A quibus magnitudines etiam angulorum qui ab epicyclorum obliquatione ad excentricorum superficies fiunt capiuntur, sicut in sequentibus dilucide demonstrabitur, ne in presentiarum communem sermonis cursum de quinque planetarum declinatione retardemus. Quando autem equatur equatur] post corr. G longitudinis motus in nodis et in mediis proxime distantiis sunt, Venus Venus] corr. ex Vnus G quidem, si in maxima epicycli longitudine est, uno gradu australior aut borealior circulo per medium invenitur, sin autem in minima, 6 20′ gradibus proxime, ut sic declinatio epicycli 2 30′ gradus circuli per polos ipsius descripti modo quo diximus intercipiat, totidem enim ex epicycli inequalitate invenimus in mediis distanciis, in maxima quidem epicycli subtendentes in visu angulum gradus unius et sexagesimarum 2, in minima vero graduum 6 et sexagesimarum 22, Mercurius autem, cum in maxima epicycli est, ut a proximis apparitionibus quispiam ratiotinabitur, australior borealiorve uno gradu et et] add. s. l. G sexagesimis 45 circulo per medium fit, cum vero in minima, gradibus quatuor proxime, ut hinc epicycli declinatio colligatur graduum 6 15′, totidem enim rursus ex inequalitate epicycli in distantiis maximarum declinationum invenimus, hoc est quando equata longitudo per quartam partem a maxima excentrici distat, hi in maxima epicycli angulum in visu gradus unius et sexagesimarum 46 subtendunt, in minima vero graduum quatuor et sexagesimarum 5.

In reliquis autem Saturno videlicet Iove ac Marte seorsum quidem non poterit quispiam magnitudines declinationum congruenter intelligere, cum utreque utreque] post corr. G inter se, hoc est que penes excentricum est et que penes epicyclum, commisceantur, sed a motibus rursum excentricorum et epicyclorum qui secundum latitudinem tum in minimis, tum in maximis longitudinibus observantur alteram declinationem hoc modo ab altera seperabimus.

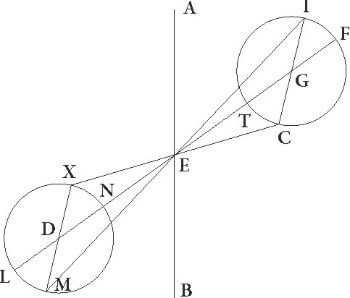Sit enim in superficie que recta est ad circulum per medium signorum communis ad ipsam sectio superficiei quidem circuli per medium AB linea, superficiei vero excentrici linea GD, zodiaci autem centrum sit E, describanturque in communi super〈fi〉cierum superficierum] supercierum A sectione in IG maxima excentrici et MD minima in subiecta superficie circuli equales FITC et LMNX qui per polos epicyclorum esse supponantur in quibus declinentur epicyclorum superficies tum ad lineam IGC tum ad linem MDX MDX] post corr. G ad equales videlicet videlicet] videlilicet A angulos in G et D punctis factos, et coniungantur a centro zodiaci E in quo visus est ad maximam et minimam epicyclorum longitudinem linee ad maximam quidem EI et EM, ad minimam vero EC et EX, ut C et X puncta motus medio Soli Soli] post corr. G oppositos contineant, puncta vero I et M coniunctionales.

In Marte igitur motus latitudinis eos cepimus qui fiunt in oppositionibus que in maxima excentrici longitudine, hoc est in puncto epicycli C, constituuntur. et eos qui in minima excentrici, hoc est in puncto X epicycli, fiunt, propterea quod differentia ipsorum valde sensibilis est. In oppositionibus enim quas in maxima longitudine facit removetur a circulo per medium ad septentrionem gradibus 4 20′, in iis autem quas in minima facit ad meridiem gradibus 7 proxime, ut angulus etiam EC talium 4 20′ colligatur qualium quatuor recti sunt 360, angulus vero BEX 7 eorundem.

His ita suppositis, tam angulum EG qui ab excentrici quam angulum IGF qui ab epicycli declinatione continetur hoc modo invenimus. Nam ab iis que de de] add. s. l. G inequalitatibus Martis demonstravimus facile intellectu est quod angulorum in visu constitutorum qui subtenduntur ab 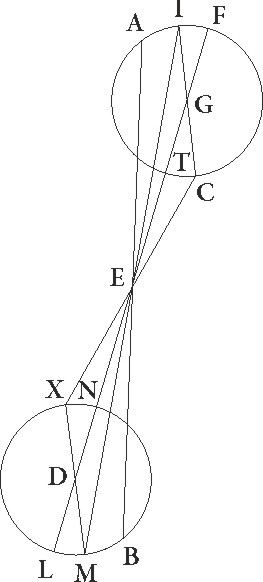arcubus equalibus qui sunt ad minimam epicycli longitudinem qui fiunt in motibus maxime longitudinis excentrici eam p〈ro〉portionem proportionem] perportionem A habent ad motus factos in minima quam quinque proxime ad novem. Sed arcus TC et NX equales sunt, quare proportio etiam anguli GEC ad angulum DEX erit, sicut 5 ad 9. Quoniam igitur dati sunt anguli EC et BEX et proportio GEC ad DEX, estque equalis angulus EG angulo BED, si quota pars est excess〈u〉s excessus] excessis A totarum magnitudinum ipsius excessus proportionis totam partem de utrisque utrisque] corr. ex trisque G terminis proportionis capiemus, habebimus quesitam quoque proportionis magnitudinem, id enim per arith[e]meticam arithmeticam] arithemeticam A propositionem quandam demonstratur. Quoniam ergo magnitudines quidem sunt 4 20′ et 7, et excessus earum 2 40′, proportio vero sicut 5 ad 9, horumque excessus quatuor, sunt autem 2 40′ pars ipsorum quatuor tertie due, si tantam partem ipsorum 5 et 9 ceperimus, habebimus GEC angulum 3 20′ graduum et DTX 6 eorundem, et utrunque reliquum consequenter EG et BED declinationis excentrici gradus unius, et ex istis TC quoque arcum declinationis epicycli graduum 2 15′, propterea quod totidem proxime secundum tabulas inequalitatis GEC et DEX inventas angulorum magnitudines continent.

In Saturno autem ac in Iove, quoniam indifferentes ad sensum inveniuntur motus in arcubus maximarum excentricorum longitudinum facti facti] post corr. G a motibus qui in minimis fiunt diametraliterque oppositis, alio modo ex collatione motuum qui fiunt in maximis epicyclorum ad eos qui fiunt in minimis eorum propositum computavimus. Removetur autem, ut ex particularibus observationibus facile intelleximus, in motibus quidem qui fiunt in apparitionibus et occultationibus maxime ad septentrionem atque meridiem Saturnus quidem gradibus 2 proxime, Iupiter autem 1, in oppositionibus vero ad Solem Saturnus gradibus 3, Iupiter 2. Quoniam igitur ex inequalitate quoque istorum perspicuum est quod angulorum in visu ab equalibus epicycli arcubus in maximis et minimis longitudinibus factorum qui in maximis constituuntur proportionem habentur habentur] post corr. G ad illos qui in minimis in Saturno quidem sicut 18 ad 23, in Iove autem sicut 29 ad 43, suntque arcus epicycli FI et TC equales, erit proportio anguli FEI ad angulum TEC in Saturno quidem sicut 18 ad 23, in Iove autem sicut 29 ad ad] add. s. l. G 43, sed angulus etiam IEC, qui est excessus duorum secundum latitudinem motuum, gradus unius in utrisque stellis relinquitur. Quare si secundum expositas proportiones unus gradus dividatur, habebimus angulum FEI in Saturno quidem sexagesimarum 26, in Iove autem 24, et angulum FEC in Saturno sexagesimarum 34, in Iove 36. Quare totus etiam EG angulus declinationis excentrici erit in Saturno quidem graduum 2 26′, in Iove autem 1 24′, pro quibus commodius enim est abusi sumus gradibus 2 30′ et 1 30′, hinc TC quoque arcus declinationis epicyclorum colligitur in Saturno quidem graduum 4 30′, in Iove autem 2 30′, totidem enim in tabulis inequalitatis utriusque continent rursum inventas proxime magnitudines angulorum FEI et FEC.

〈XIII.4〉 Capitulum IIII : De componendis particularium latitudinis motuum tabulis

Ex istis igitur nobis integre maximarum declinationum tam excentricorcum quam epiciclorum magnitudines constitute sunt. Verum ut particularum quoque distantiarum latitudinales quottidie motus facile possimus invenire, quinque planetarum quinque tabulas composuimus, totidem singulas versuum quot et inequalitatis tabule sunt, ordinum autem quinque, quorum duo primi numeros similiter similiter] corr. ex simili G ut illi etiam continent, tertii tertii] add. marg. G distantias secundum latitudinem circuli per medium congruentes particularibus epicyclorum arcubus in ipsis declinationibus maximis, que in Venere quidem atque Mercurio in nodis excentricorum fiunt, in reliquis autem tribus in borealibus excentricorum terminis. In his quarti etiam ordines similes congruentias que fiunt in australibus excentricorum terminis continebunt, computata in his tribus maxima ipsorum etiam excentricorum tum ad septentrionem tum ad meridiem remotione. Invenimus autem hos arcus in Venere quidem atque Mercurio per unum rursus theorema theorema] corr. ex theoreuma G hoc modo.

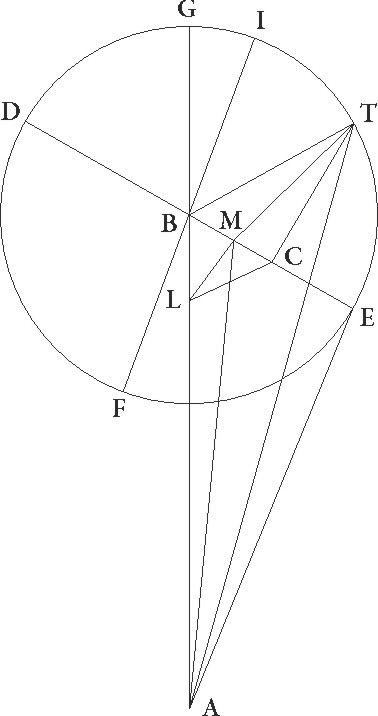Sit enim in superficie que rectos facit cum circulo per medium angulos ABG quidem linea communis ipsius et zodiaci section, linea vero DBE communis sectio superficiei epicycle, et sit A centrum zodiaci, B autem centrum epicycli, linea vero AB sit epicyclorum distantia que in maximis declinationibus fit, descriptoque circa B centrum epicyclo DFEI, coniungatur FBI diameter recta ad lineam DE, supponatur autem etiam epicycli superficies recta ad subiectam superficiem, ut linee que ducte in ipsa rectos angulos ad lineam DE faciunt, omnes quidem cetere equidistantes sint ad superficiem per medium, linea vero FI sola in ipsa sit, propositumque sit, data proportione AB linee ad BE et magnitudine declinationis, hoc est angulo ABE, invenire motus stellarum secundum latitudinem, quando exempli gratia distant a puncto E minime longitudinis epicycli gradibus 45 talium qualium est epicyclus 360. Nam differentias etiam que fiunt in motibus longitudinis propter has declinationes simul intendimus demonstrare, hec autem differentie in motibus qui fiunt inter minimam longitudinem et F et I puncta maxime sunt, propterea quod in dictis punctis iidem sunt cum illis qui absque inclinationibus fiunt.

Intercipiatur igitur arcus ET graduum, ut diximus, 45, ducanturque ad lineam quidem BE perpendicularis TC, ad superficiem vero circuli per medium perpendiculares CL et CM, et coniungantur TB et LM et AM et AT linee. Quod igitur LCTM quadrilatera figura paralellogramma et rectangula est, propterea quod CT equidistans est ad superficiem circuli per medium, et quod additionem subtractionemve longitudinis LAM angulus continet, motum vero latitudinis angulus TAM, cum anguli ALM et AMT recti sint, ideo quod AM quoque linea in superficie circuli per medium invenitur, perspicuum est. Nunc autem quanti colliguntur motus quos querimus in utraque dictarum stellarum demonstrandum est, et primum in Venere.

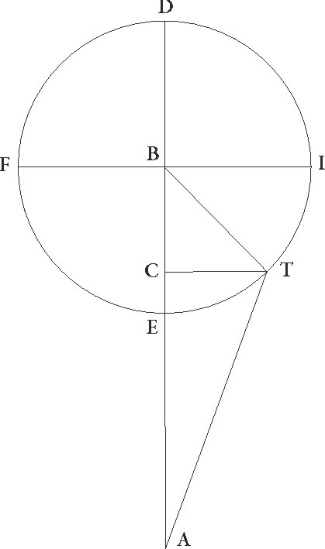Quoniam igitur arcus ET talium est 45 qualium est epicyclus 360, erit etiam angulus EBT qui est in centro epicycli talium 45 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 90. Quare uterque arcus BC et CT linearum talium est 90 qualium est circulus qui BTC rectangulo circumscribitur 360. Utraque igitur corda talium est 45 52′ qualium est BT que rectum subtendit 120. Qualium igitur est BT semidiameter epicycli 43 10′ et AB medie distantie 60, in hac enim maxime declinatio epicycli maxima fit, talium erit utraque linearum BC et CT 30 32′. Rursus quoniam ABE angulus declinationis talium supponitur 2 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 5, erit etiam arcus linee LC talium 5 qualium est circulus qui BLC rectangulo circumscribitur 360, arcus vero linee BL 175 ad semicirculum reliquorum. Corde igitur etiam sue CL quidem talium erit 5 14′ qualium est BC que rectum subtendit 120 et BL 119 53′ earundem. Quare qualium est BC que rectum subtendit 30 32′ et AB linea 60, talium CL quoque erit 1 20′ et BL 30 30′ earundem et AL 29 30′ reliquarum. Est autem etiam LM, cum sit equalis linee CT, 30 32 earundem. Quare AM etiam que rectum subtendit 42 27′ earundem colligitur. Qualium igitur est AM que rectum subtendit 120, talium erit etiam LM 86 19′, et angulus LAM additionis subtractionisve secundum longitudinem in hoc situ talium erit 92 0′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, qualium … 360​] add. marg. G talium 46 0′.

Similiter quoniam qualium est AM linea 42 27′, talium etiam est TM, cum sit equalis linee CL, 1 20′, et quadrata ipsarum composita faciunt quadratum linee AT, erit linea quoque AT 42 29′ earundem per longitudinem. Qualium igitur est AT que rectum subtendit 120, talium etiam erit EM 3 46′ et TAM angulus recessus secundum latitudinem talium 3 36′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 1 48′ hos gradus apponemus in ordine tertio tabule Veneris in versu qui continet numerum graduum 135.

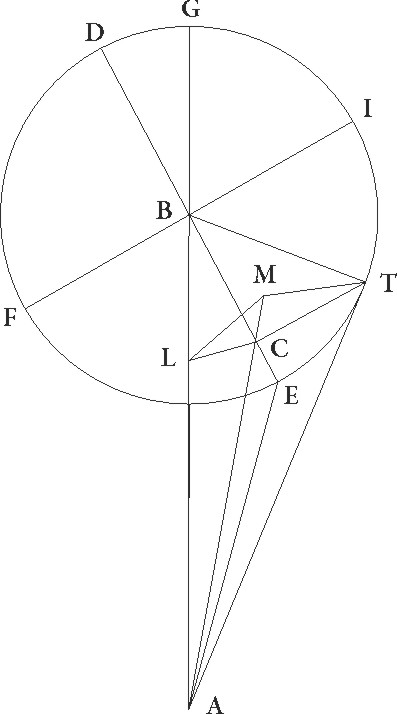Verum ut factam additionis subtractionisve longitudinis differentiam computaremus, describatur similis figura in qua epicyclus declinatus non sit. Et quoniam utranque linearum BC et CT talium demonstravimus 30 32′ qualium est AB 60, fit AC quoque reliquarum 29 28′, cuius quadratum compositum cum quadrato linee CT facit quadratum linee AT, erit igitur etiam AT 42 26′ per longitudinem earundem. Qualium igitur est AC que rectum subtendit 120, talium CT quoque erit 86 21′, angulus vero TAC additionis subtractionisve secundum longitudinem talium 92 4′ proxime qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 46 2′. Fuit autem in declinatione demonstratus 46 earundem, deficit igitur additio subtractiove secundum longitudinem idque propter declinationem epicycli duabus unius gradus sexagesimis.

Rursus ut motus quoque Mercurii demonstremus, describatur figura superiori similis, supponaturque arcus ET graduum similiter 45, ut utraque rursus BC et CT linearum talium colligatur 84 52′ qualium est BT que rectum subtendit 120. Qualium est igitur BT epicycli semidiameter 22 et AB linea distantie que fit in maximis declinationibus 56 40′. Hec enim nobis omnia demonstrata sunt, talium etiam utraque BC et CT linearum erit 15 55′. Rursus quoniam ABE angulus declinationis epicycli talium supponitur 6 15′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 12 30′, erit etiam arcus LC linee talium 12 30′ qualium est circulus qui BCL rectangulo circumscribitur 360, arcus autem linee BL 167 30′ ad semicirculum reliquorum. Quare sue quoque corde CL quidem talium erit 13 4′ qualium BC que rectum angulum subtendit 120, BL vero 119 17′ eorundem. Quare qualium BC linea demonstrata est 15 55′ et AB supponitur 56 40′, talium CL quoque erit 1 44′ et BL 15 49′ et reliqua AL 40 51′ earundem. Est autem etiam LM, cum sit equalis linee CT, 15 55′ earundem. Et quoniam quadratum linee AL cum quadrato linee LM facit quadratum linee AM, habebimus ipsam quoque talium per longitudinem 43 50′ qualium est LM linea 15 55′. Quare qualium est AM que rectum subtendit 120, talium LM quoque erit 43 34′ et LAM angulus additionis subtractionisve secundum longitudinem talium 42 34′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 21 17′.

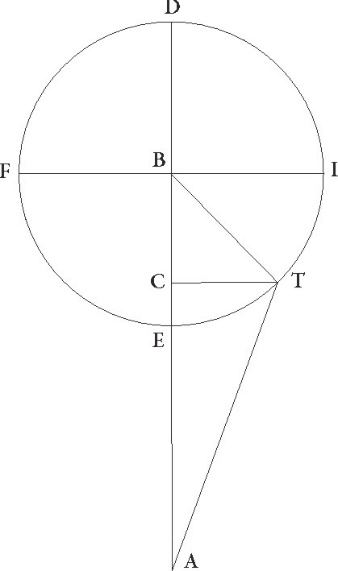Similiter quoniam qualium est AM linea 43 50′ talium TM que est equalis linee TL colligitur 1 44′ et quadrata ip〈s〉arum ipsarum] ipsarum A composita faciunt quadratum linee AT, habebimus hanc quoque 43 52′ per longitudinem earundem. Qualium igitur est AT que rectum subtendit 120, talium etiam TM erit 4 41′ et TAM angulus ipsius remotionis secundum latitudinem talium 4 32′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 2 16′. Hos gradus rursum in tertio tabule Mercurii ordine in eodem versu apponemus, hoc est in versu qui continet numerum graduum 135.

Rursus propter collationem additionis subtractionisque describatur figura absque ulla declinatione. Et quoniam demonstratum est talium esse utranque TC et CB linearum 15 55′ qualium est AB 56 40′ et reliqua AC 40 45′ earundem, quoniamque quadratum AC linee cum quadrato linee CT facit quadratum linee AT, habebimus etiam ipsam talium per longitudinem 43 45′ qualium erat TC 15 55′. Qualium ergo est AT rectum angulum subtendens 120, talium etiam CT erit 43 39′ et CAT angulus additionis subtrationisque longitudinis talium 42 40′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 21 20′. Fuit autem demonstrata graduum 21 17′ in declinatione, minor ergo etiam hic additio subtractiove longitudinis tribus unius gradus sexagesimis propter declinationem inventa est.

Motus igitur latitudinis harum duarum stellarum qui fiunt in maximis declinationibus hoc modo nobis tractati sunt, propterea quod tunc fiunt, quando excentricus in eadem cum circulo per medium signorum est superficie, reliquarum vero trium stellarum per aliud th〈e〉orema, theorema] thorema A propterea quod in maximis excentricorum declinationibus epicyclorum quoque maxime sunt. Quare opere pretium erit computatos habere motus latitudinis qui ex utraque declinatione colliguntur.

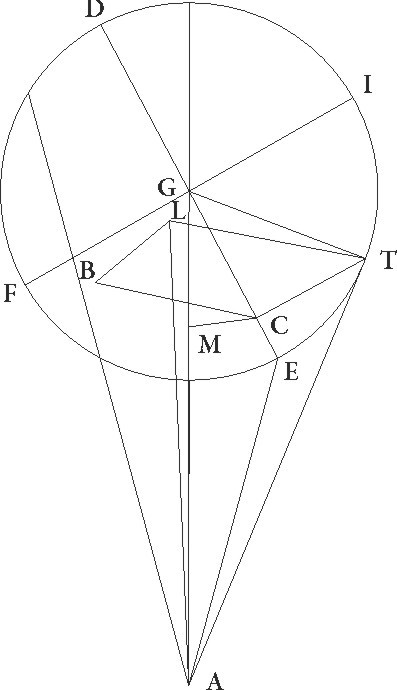
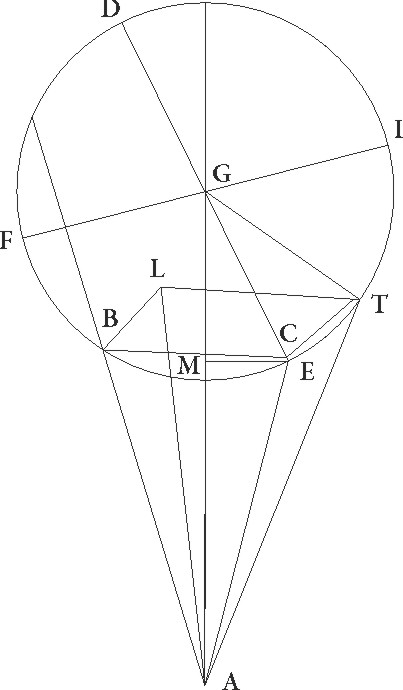Sunt igitur rursum in superficie que ad rectos angulos ad superficiem circuli per medium signorum est communis ad ipsam sectio superficiei quidem circuli per medium linea AB, superficiei autem excentrici linea AG, superficiei vero epicycli linea DG, et sic punctum A zodiaci centrum, epicicli vero G, et describitur circa G epicyclus DFEI, sic rursus ut linearum que dicte ad DE lineam rectos angulos faciunt diameter quidem FGI et in excentrici superficie sit et equidistans equidistans] post corr. G ad superficiem circuli per medium, relique autem utrisque superficiebus dictis equidistantes, et intercipiatur similiter arcus ET eorundem supposita graduum 45, et a puncto T, ubi stella est, TC perpendicularis ducatur, similiter a punctis T T] add. marg. G et C ad superficiem circuli per medium perpendiculares CB et TL, et coniungantur BL et AL linee, propositumque sit tum longitudinis additionem subtractionemve ab angulo BAL contentam tum latitudinis motum ab angulo LAT contentum invenire. Ducatur igitur etiam ad AG lineam a puncto C perpendicularis CM, coniunganturque GT et AC et AT linee, supponaturque propter predemonstrata utraque rursus linearum GC et CT talium 48 52′ qualium est GT que rectum subtendit 120. Quoniam igitur primum in Saturno semidiameter epicycli talium demonstrata est 6 30′ qualium media longitudo est 60, erit etiam utraque linearum GC et CT talium 4 36′ qualium est GT que rectum subtendit 6 30′, et quoniam AGE angulus declinationis epicycli talium supponitur 4 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 9, erit etiam arcus linee CM talium 9 qualium est circulus qui GCM rectangulo circumscribitur 360, arcus vero linee GM 171 ad semicirculum reliquorum. Corde igitur etiam sue CM quidem talium erit 9 25′ qualium est GT que rectum subtendit 120, GM vero 119 38′ earundem. Quare qualium est GC linea 4 36′, talium quoque CM erit 0 22′ et GM 4 35′. Sed in maxima declinatione semicirculi longioris distantie AG linea distantie que in principio Libre fit ut a predemonstratis in theorematibus theorematibus] corr. ex theorema G inequalitatis colligitur 62 10′ earundem est. Reliqua igitur AM 57 35′ talium relinquitur qualium est MC 0 22′, et propterea etiam AC que rectum subtendit 57 35′ earundem. Quare qualium est AC que rectum subtendit 120, talium erit etiam CM 0 46′ et angulus CAM talium 0 44′ qualium duo recti sunt 360. Supponitur autem etiam BAG BAG] corr. ex ABAG G angulus declinationis excentrici 2 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 5, et totus ergo angulus BAC talium erit 5 44′ qualium duo recti sunt 360. Quare arcus quoque linee BC talium est 5 44′ qualium est circulus qui BAC rectangulo circumscribitur 360, arcus vero linee AB 174 16′ ad semicirculum reliquorum. Corde igitur etiam sue BC quidem talium est 6 0′ qualium AC que rectum subtendit 120, AB autem 119 51′ earundem. Quare qualium est AC linea 57 35′, talium BC quoque erit 2 53′ et AB 57 31′. Est autem etiam BL linea, cum sit equalis linee CT, 2 36′ earundem. Et quoniam quadratum linee AB cum quadrato linee BL facit quadratum linee AL, habebimus etiam hanc 57 42′ per lungitudinem earundem. Similiter quoniam linea LT, cum sit equalis linee BC, 2 53′ earundem est et quadratum linee AL cum quadrato linee LT facit quadratum linee AT, habebimus etiam longitudinem huius 57 46′ earundem. Quare qualium est AT que rectum subtendit 120, talium LT quoque erit 5 59′ et TAL angulus remotionis secundum latitudinem talium 5 44′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 2 52′, quos gradus in tertio tabule Saturni ordine in numero graduum 135 apponemus.

In maxima vero declinatione que in semicirculo minime longitudinis est, quoniam AG linea distantia que in principio Arietis est talium colligitur 57 40′ qualium CM 0 22′ demonstrata est, et GM similiter 4 35′, atque ideo reliqua AM sit 53 5′ et AC que rectum subtendit, quoniam indifferenti quodam maior est quam AM, 53 5′, erit etiam CM talium 0 50′ qualium est AC que rectum subtendit 120, et angulus CAM talium 0 48′ 48'] corr. ex 848 G qualium duo recti sunt 360. Eorundem vero etiam angulus BAG supponitur 5, et totus igitur BAC talium est 5 48′ qualium quatuor recti sunt 360. Quare arcus quoque linee BC talium erit 5 48′ qualium est circulus qui BAC rectangulo circumscribitur 360. Arcus vero linee AB 174 12′ ad semicirculum reliquorum. Corde igitur etiam sue BC quidem talium erit 6 4′ qualium est AC que rectum subtendit 120, et AB 119 51′ earundem. Quare qualium est AC linea 53 5′, talium etiam BC erit 2 41′ et AB 53 1′. Et quoniam quadratum linee AB cum quadrato linee BL facit quadratum linee AL, demonstrataque est linea BL 4 36′ earundem, habebimus etiam longitudinem linee AL 53 13′ earundem. Quare qualium est AL que rectum subtendit 120 talium etiam BL erit 10 23′ et BAL angulus additionis subtractionisque secundum longitudinem talium 9 56′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 4 58′. Rursus quoniam qualium est AL linea 53 13′, talium etiam TL, cum sit equalis linee BC est 2 41′, et quadrata istarum simul faciunt quadratum linee AT, habebimus huius quoque longitudinem 53 17′ earundem. Quare qualium est AT que rectum subtendit 120, talium TL quoque erit 6 3′, et TAL angulus remotionis secundum latitudinem talium 5 46′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 2 53′, quos etiam gradus in quarto eiusdem tabule ordine ad numerum graduum 135 apponemus.

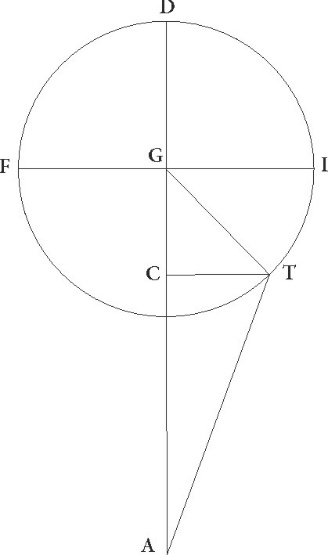Verum ut collationem etiam additionis subtractionisque secundum longitudinem in declinatione minoris distantie faciamus, describatur rursus figura in qua nulla sit declinatio. Et quoniam, qualium est AG huius distantie linea 57 40′, talium utraque linearum GC et CT supponitur 4 36′, et reliqua AC 53 4′ earundem, et quadratum suum cum quadrato linee CT facit quadratum linee AT, habebimus etiam longitudinem huius partium 53 16′. Quare qualium est AT que rectum subtendit 120, talium etiam CT erit 10 22′ et TAC angulus additionis subtractionisque secundum longitudinem talium 9 54′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 4 57′. Sed demonstratus fuit 4 58′ eorundem in declinationibus fuisse, additio igitur subtractiove secundum longitudinem una sexagesima propter utrasque declinationes subaucta est.

Describatur rursus figura declinationum demonstratas in stella Iovis continens proportiones, ut qualium est semidiameter epicycli 11 30′, talium utraque linearum GC et CT colligatur 8 8′. Quoniam ergo AGE angulus declinationis epicycli talium supponitur 2 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 5, erit etiam arcus linee EM talium 5 qualium est circulus qui rectangulo GCM circumscribitur 360, arcus vero linee GM 175 ad semicirculum reliquorum. Corde igitur etiam sue CM quidem talium erit 5 14′, qualium GC que rectum subtendit 120, et GM 119 53′. Quare qualium est GC linea 8 8′ et AG linea longitudinis que in principio Libre fit 62 30′, talium etiam CM erit 0 21′ et GM 8 8′ similiter, et reliqua MA 54 22′, et propterea etiam AC que rectum 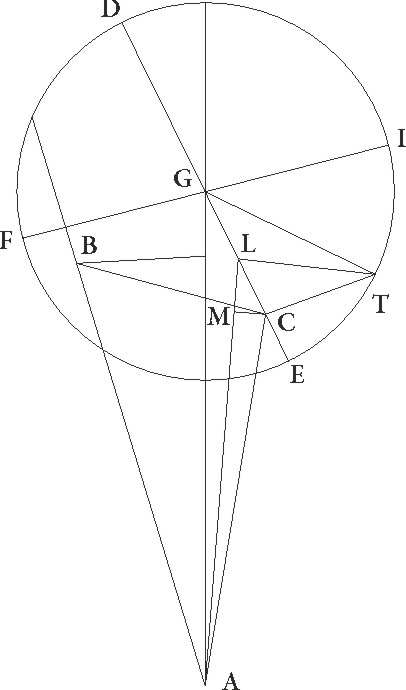subtendit, quoniam indifferenti quodam maior est quam linea MA, earundem erit 54 22′. Quare qualium est AC que rectum subtendit 120, talium CM quoque erit 0 46′ et angulus CAM talium 0 44′, qualium duo recti sunt 360. Sed BAG quoque angulus declinationis excentrici talium supponitur 1 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 3, et totus igitur BAC angulus talium est 3 44′ qualium duo recti sunt 360. Quare arcus quoque linee CB talium erit 3 44′ qualium est circulus qui BAC rectangulo circumscribitur 360, arcus vero linee AB 176 16′ ad semicirculum reliquorum. Corde igitur etiam sue CB quidem talium erit 3 54′ qualium AC que rectum subtendit 120, AB autem 119 56′ earundem. Quare qualium AC linea est 54 22′, talium CB quoque erit 1 46′ et AB 54 20′. Sed per demonstrata iam linea BL 8 8′ earundem est. Et quoniam quadrata sua simul faciunt quadratum linee AL, habebimus huius quoque longitudinem 54 56′ earundem. Similiter quoniam LT linea 1 46′ earundem est, et quadrata sua simul faciunt quadratum linee AT, habebimus hanc quoque 54 58′. Quare qualium est AT que rectum subtendit 120 talium LT quoque erit 3 52′ et TAL angulus remotionis secundum latitudinem talium 2 42′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 1 51′, quos gradus in ordine tabula Iovis tertio ad numerum 135 apponemus.

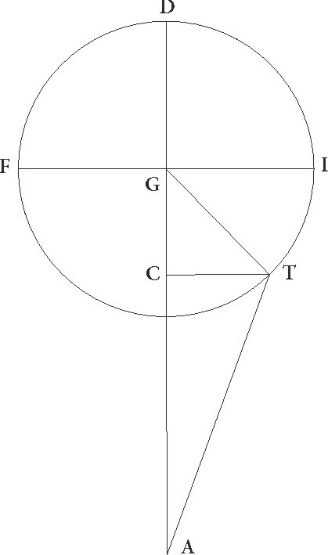Similiter quoniam rursus AG linea longitudinis que fit in principio Arietis talium colligitur 57 30′ qualium demonstravimus CM lineam 0 21′, et GM 8 8′, et sic reliqua etiam AM, hoc est AC, que indifferenti quodam maior relinquitur, 49 22′ earundem, et propterea qualium est AC que rectum subtendit 120, talium EM quoque est 0 51′ et angulus CAM talium 0 49′ qualium duo recti sunt 360, colligetur totus etiam angulus BAC 3 49′ eorundem. Quare arcus etiam linee CB talium erit 3 49′ qualium est circulus qui rectangulo ACB circumscribitur 360, arcus autem linee AB 176 11′ ad semicirculum reliquorum. Corde igitur etiam sue BC quidem talium erit 3 59′ qualium est AC que rectum subtendit 120, AB autem 119 56′ earundem. Quare qualium qualium] post corr. G est AC linea 49 22′, talium etiam CB erit 1 39′, et AB 49 20′, et propterea quoniam BL linea 8 8′ earundem est, et quadrata sua simul sumpta faciunt quadratum linee AL, habebimus huius quoque longitudinem 50 0′. Quare qualium est AL que rectum subtendit 120, talium BL quoque erit 19 31′ et BAL angulus additionis subtractionisque secundum longitudinem talium 18 44′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 9 22′. Rursus quoniam qualium est AL linea 50 0′, talium TL quoque colligitur 1 39′, quadrataque sua simul faciunt quadratum linee AT, habebimus huius quoque longitudinem earundem 50 et sexagesimarum duarum. Qualium igitur est AT que rectum subtendit 120, talium erit LT 3 57′, et angulus TAL remotionis secundum latitudinem talium 3 46′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 1 53′, quos gradus in quarto tabule ordine ad numerum 135 graduum apponemus.

Sed collationis etiam additionum subtractionumve longitudinis causa sine declinationibus figura rursum describatur. describatur] corr. ex describitur G Et quoniam in proposita distantia, qualium est utraque linearum TC et GC 8 8′, talium tota quoque AG 57 30′, et reliqua AC 49 22′ earundem, et quadratum suum cum quadrato linee TC facit quadratum linee AT, habebimus huius quoque longitudinem earundem 50 et sexagesimarum duarum. Quare qualium est AT que rectum subtendit 120, talium etiam TC erit 19 30′, et TAC angulus additionis subtractionisve secundum longitudinem talium 18 42′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 9 21′. Fuit autem in declinationibus 〈e〉tiam etiam] atiam A demonstratus 9 22′, addidit ergo rursum additio subtractiove secundum longitudinem propter utrasque declinationes sexagesimam unam.

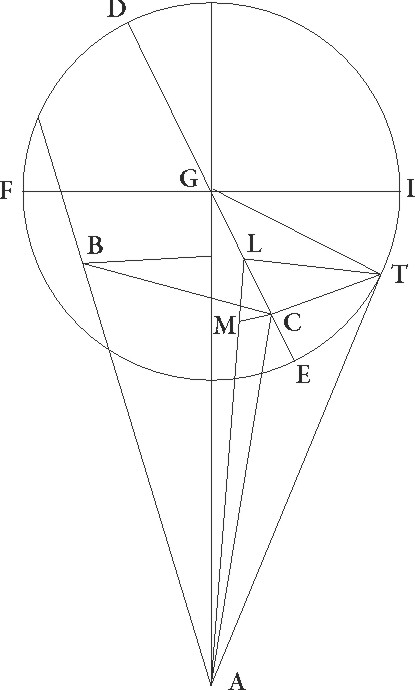Deinceps propter Martis quoque proportiones designetur primum declinationum descriptio, colligaturque rursum utraque linearum GC et CT talium 27 56′, qualium est GT semidiameter epicicli 39 30′. Quoniam igitur AGE angulus declinationis epicycli talium supponitur 2 15′, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 4 30′, erit etiam arcus linee CM talium 4 30′ qualium est circulus qui GMC rectangulo circumscribitur 360, et arcus linee GM 175 30′ ad semicirculum reliquorum. Corde igitur etiam sue CM quidem talium erit 4 43′ qualium est GT que rectum subtendit 120, GM autem 119 54′ earundem. Quare qualium est GC 27 56′, et AG maxime distantie linea 66 talium etiam CM erit 4 6′, et GM 27 54′, et AM 38 6′ reliquarum, idcirco AC etiam que rectum subtendit 38 7′ earundem. Quare qualium est AC que rectum subtendit 120, talium CM quoque erit 3 28′, et angulus CAM talium 3 19′ qualium duo recti sunt 360. Sed BAG quoque angulus declinationis excentrici talis unius est qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 2, et totus igitur BAC angulus talium colligitur 5 19′ qualium duo recti sunt 360. Ergo arcus quoque linee CB talium erit 5 19′, qualium est circulus qui BAC rectangulo circumscribitur 360, et arcus linee AB 174 41′ ad semicirculum reliquorum. Corde igitur etiam sue BC quidem talium est 5 34′, qualium AC que rectum subtendit 120, AB autem 119 52′ earundem. Quare qualium est AC linea 38 7′, talium etiam CB erit 1 46′, et AB 38 5′. Est autem BL quoque linea 27 56′, cunque quadratum linee AB cum quadrato linee BL faciat quadratum linee AL, habebimus huius quoque longitudinem 47 14′. Similiter quoniam TL linea 1 46′ earundem est, et quadratum linee AL cum quadrato linee TL facit quadratum linee AT, erit huius quoque longitudo 47 16′ earundem. Qualium ergo est AT que rectum subtendit 120, talium talium] corr. ex qualium G etiam TL erit 4 29′, et TAL angulus remotionis secundum latitudinem talium 4 18′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 2 9′, quos gradus in tertio tabule Martis ordine ad numerum 135 graduum apponemus.

Eodem modo in declinationibus minime longitudinis, quoniam talium est AG linea 54 qualium CM demonstrata est 1 6′ et GM 27 54′ et AM 26 6′ reliquarum colligitur et AC que rectum subtendit 26 7′ earundem, erit etiam CM talium 5 3′ qualium est AC que rectum subtendit 120, et angulus CAM talium 4 49′ qualium duo recti sunt 360, idcirco totus quoque BAC angulus 6 49′ eorundem. Quare arcus etiam linee BC talium erit 6 49′ qualium est circulus qui ABC rectangulo circumscribitur 360 et arcus linee AB 173 11′ ad semicirculum reliquorum. Corde igitur etiam sue BC quidem talium erit 7 8′ qualium est AC que rectum subtendit 120, et AB 119 47′. Quare qualium est AC linea 26 7′, talium BC quoque erit 1 33′ et AB 26 4′. Est autem rursum BL quoque linea 27 56′ earumdem. Et quoniam quadratum linee AB cum quadrato linee BL facit quadratum linee AL, erit huius quoque longitudo 38 12′. Qualium ergo est AL que rectum subtendit 120, talium BL quoque erit 87 45′, et BAL angulus additionis subtractionisve secundum longitudinem talium 94 qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 47. Similiter quoniam qualium est AL linea 38 12′, talium LT colligitur 1 33′, et quadrata sua simul faciunt quadratum linee AT, habebimus huius quoque longitudinem 33 18′ earundem. Quare qualium AT que rectum subtendit 120, talium LT quoque erit 4 52′ et TAL angulus remotionis secundum latitudinem talium 4 40′ qualium 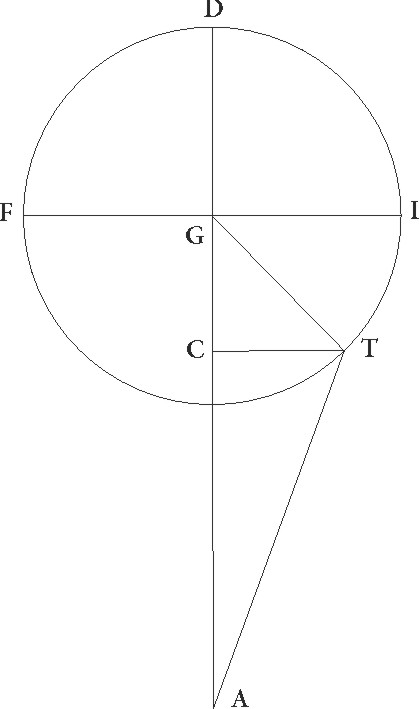duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 2 20′, quos gradus in quarto tabule ordine ad numerum graduum 135 apponemus.

Sed si collationis rursum additionis subtractionisve secundum longitudinem causa sine declinationibus figuram in minima distantia, ubi maxime sensibilis differentia fit, descripserimus, colligitur proportio linee AG ad utranque linearum GC et CT sicut 54 ad 27 56′, idque circo AC linea 26 4′ reliquarum erit, et AT que rectum angulum subtendit 38 12′ earundem, et propterea qualium est AT que rectum subtendit 120, talium rursum TC colligitur 87 45′, et TCA additionis subtractionisve secundum longitudinem angulus talium 94, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 47, totidem vero demonstratus ex proportionibus etiam declinationum fuit. Additio ergo subtractiove secundum longitudine nullam in Marte propter declinationes differentiam habuit.

Quarti autem duum duum] corr. ex durum G Veneris atque Mercurii tabularum ordines latitudinales continent motus qui a maximis ipsorum epicyclorum oblicationibus que in extremis excentricorum longitudinibus fiunt continentur. Quos motus per se absque differentia que fit propter excentricorum declinationes consideravimus. Plurimis enim illo modo tabulis opus nobis fuisset, computationisque calculus multo difficilior inde fieret, cum vespertini matutinique motus inequales nec omnino ad easdem circuli per medium partes fiant, nec alioquin excentricorum declinatio maneat, unde diminutionum excessus ad maximas inclinationes differentiam ab excessibus diminutionum ad maximas obliquationes essent habituri. Differentia vero separata, facilius singula nobis procedent, ut a sequentibus patebit.

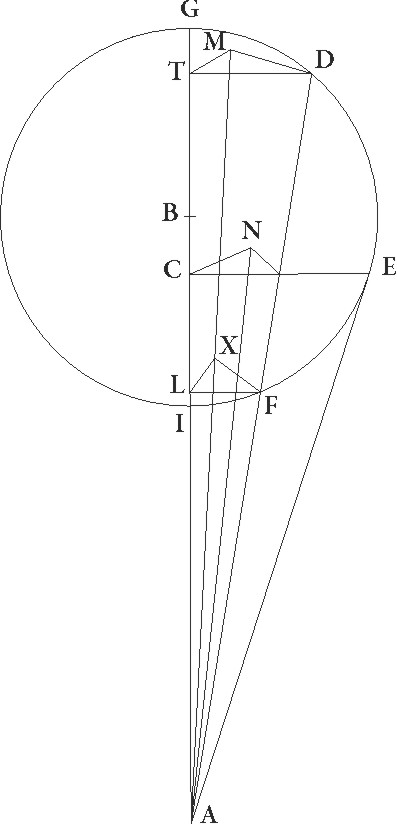Sit ergo AB linea superficierum circuli per medium et epicicli communis sectio, et sit B centrum epicycli, describaturque circa ipsum epicyclus GDEFI obliquus ad superficiem circuli per medium, hoc est ut ducte in ipsis linee perpendiculariter ad GI communem sectionem equales equales] corr. ex quales G faciant omnes angulos qui in ipsius GI linee punctis constituuntur, et protrahantur E quidem linea ad epicycli contactum, linea vero AFD, sic ut secet epicyclum sicuti contigerit et deducantur a tribus punctis D, E, F ad lineam GI perpendiculares DT et EC et FL, ad superficiem vero circuli per medium DM et EN et FX, et coniungantur TM et CN et LX linee, et preterea AN et AXM, nam AXM recta linea est. In duabus enim superficiebus omnia tria puncta sunt, hoc est in superficie circuli per medium et in superficie que per AFD lineam recta est ad zodiacum. Quod igitur in proposita obliquatione additiones quidem subtractionesve stellarum secundum longitudinem tum TAM tum CAN angulus continet, latitudinales vero angulus DAM et EAN, perspicuum est. Sed demonstrandum primo est quod etiam EAN anguli motus secundum latitudinem qui est in ipso contactu maior omnibus est, sicut etiam additio additio] corr. ex aditio G subtractioque secundum longitudinem. Nam quoniam EAC angulus maior est omnibus, maiorem CE linea ad E proportionem habebit quam utraque linearum TD et LF ad utranque DA et FA. Sed sicut EC linea ad EN, sic et TD ad DM et LF ad FX. Equalium enim trianguli omnes, ut diximus, qui sic constituuntur 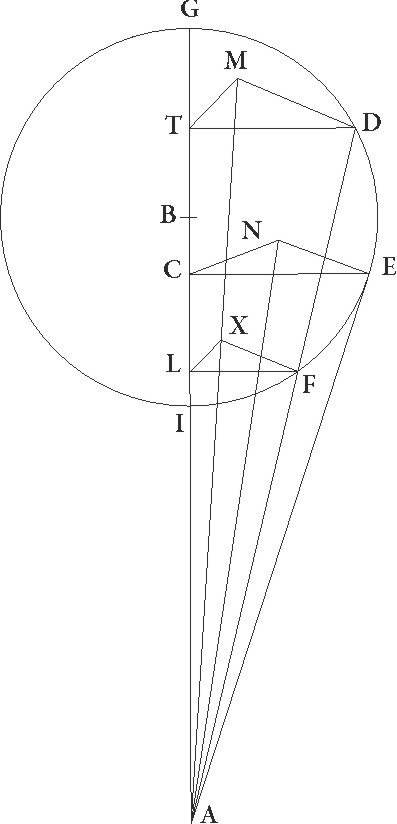sunt angulorum, et anguli qui fiunt in punctis M N X recti sunt. Quare linea NE ad lineam EA maiorem habet proportionem quam utraque linearum MD et XF ad utranque DA et FA, suntque rursum anguli DMA et ENA et FXA recti. Maior igitur est etiam EAN angulus angulo DAM ceterisque videlicet omnibus qui eodem modo constituuntur. Perspicuum autem hinc est quod differentiarum que fiunt ex obliquatione in additionibus subtractionibusve secundum longitudinem maior illa ceteris est que colligitur in motibus maximis qui fiunt in puncto E, propterea quod ipsas anguli continent quibus subtenduntur TD et CE et LF linearum excessus ad lineas TM et CN et LX. Cum vero in singulis ipsarum eadem proportio maneat et ad excessus, sequitur ut excessus etiam EC et CN linearum maiorem proportionem habeat ad lineam EA quam ipsi excessus reliquarum ad lineas similes linee AD, AD] iter. et del. G hinc etiam patet quod, quamcunque proportionem maxima additio subtractiove secundum longitudinem ad maximum latitudinis motum habuerit, hanc in omnibus epicycli particulis additiones subtractionesve secundum longitudinem ad motus latitudinis habebunt, propterea quod sicut se habet CE linea ad lineam EN, sic omnes linee similes lineis LF et TD ad similes lineis FX et DL.

His ita demonstratis, videamus nunc quantus nam angulus in utraque stellarum ab obliquatione superficierum continetur. Supponatur ergo, ut iam dictum est, quod inter maximam et minimam longitudinem quinque utraque ipsarum gradibus maxime borealior et australior fit fit] corr. ex fiat A motibus qui sunt secundum epicyclum contrarii. Stella contrarii Stella] add. marg. G enim Veneris indifferenti quodam maiorem atque minorem quam quinque graduum remotionem que fit in minima et maxima excentrici longitudine cernitur facere, stella vero Mercurii 30 proxime unius gradus sexagesimis.

Sit ergo rursum ABG linea circuli per medium signorum et epicycli communis sectio, descriptoque in B puncto epiciclo GDE obliquo obliquo] corr. ex obliqo G ad superficiem circuli per medium, ut iam explanavimus, coniungatur a centro zodiaci A tangens epicyclum linea AD, et protrahantur a puncto D, et ad lineam quidem GBE perpendicularis DF, ad superficiem autem circuli per medium perpendicularis DI, et coniunguntur BD et FI et AI linee, et supponatur DAI angulus continere in utraque stella medietatem proposite remotionis secundum longitudinem que medietas est talium 2 30′ qualium quatuor recti sunt 360, sitque propositum invenire magnitudinem obliquationis utriusque superficierum, hoc est magnitudinem anguli DF.

In Venere igitur, quoniam, qualium est epicycli semidiameter 43 10′, talium maxima quidem longitudo est 61 15′, minima vero 58 45′ et media inter eas 60, linea pro facto AB eam proportionem habebit ad lineam BD quam habent 60 ad 43 10′. Et quoniam quadratum linee BD subtractum a quadrato linee AB facit quadratum linee AD, habebimus etiam huius longitudinem 41 40′ earundem. Similiter quoniam sicut BA ad AD, sic et BD ad DF, habebimus etiam DF lineam 29 58′ earundem. Rursus quoniam angulus DAI talium supponitur 2 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 5, erit etiam arcus linee DI talium 5 qualium est circulus qui rectangulo ADI circumscribitur 360, et corda sua DI talium 5 14′ qualium est AD que rectum subtendit 120. Quare qualium est AD linea 41 40′, talium erit DI linea 1 50′. Fuit autem etiam DF 29 58′ earundem demonstrata. Quare qualium est DF que rectum subtendit 120, talium etiam DI erit 7 20′, et DFI angulus obliquationis talium 7 qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 3 30′. Sed quoniam excessus anguli DAF ad angulum IAF differentiam continet additionis subtractionisve secundum longitudinem, hinc etiam ipsam ratione simili ex ipsorum magnitudine consequemur. Nam quoniam demonstratum est talium esse AD que rectum angulum subtendit 41 40′ qualium est DI linea 1 50′, et DF linea 21 58′, subtractumque DI linee quadratum a quadrato utriusque linearum AD et FD facit quadrata utriusque linearum AI et IF, habebimus etiam longitudinem AI linee 41 37′ earundem, et longitudinem IF 29 55′. Quare qualium est AI que rectum subtendit 120, talium etiam FI erit 86 16′, et angulus FAI talium 91 56′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 45 58′. Similiter quoniam qualium est AD que rectum angulum subtendit 120, talium DF etiam est 86 18′, habebimus DAF quoque angulum talium 91 58′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 45 59′. Deficit ergo additio subtractiove secundum longitudinem sexagesima una.

In Mercurio autem, quoniam, qualium est epicycli semidiameter 22 30′, talium maxima longitudo demonstrata est 69, et opposita 57, et media inter has 63, habebit AB eam ad BD proportionem quam habent 63 ad 22 30′. Et quoniam quadratum linee DB subtractum a quadrato linee AB facit quadratum linee AD, habebimus etiam huius longitudinem 58 51′ earundem. Similiter quoniam sicut AB ad AD, sic et BD ad DF, erit etiam linea DF 21 1′. Rursum quoniam angulus DAI talium supponitur 5, qualium duo recti sunt 360, erit arcus DI talium 5 qualium est circulus qui rectangulo ADI circumscribitur 360, et corda eius DI talium 5 14′ qualium est AD que rectum subtendit 120. Quare qualium est AD 58 51′, talium etiam erit DI 2 34′. Demonstrata est autem etiam DF 21 1′, quare qualium est DF que rectum 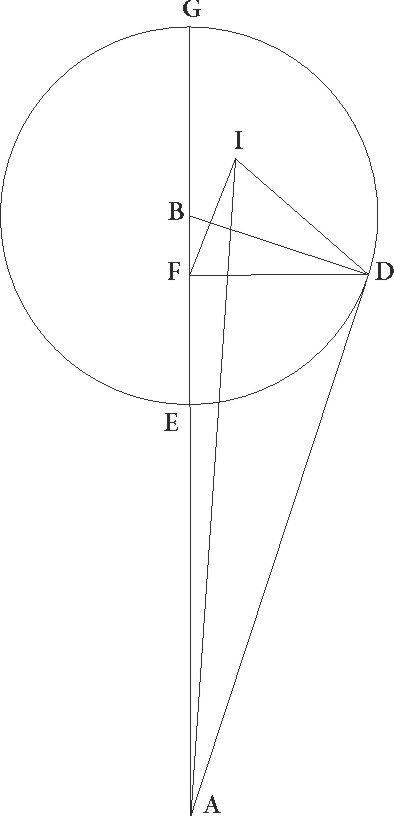subtendit 120, talium DI quoque erit 14 44′, et DFI angulus obliquationis talium 14 qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 7.

Similiter gratia etiam collationis angulorum additionis subtractionisque, quoniam rursum qualium est DI linea 2 34′, taliumque AD que rectum subtendit demonstrata est 58 41′ et DF 21 1′, et quadratum linee DI subtractum a quadrato utriusque linearum DA et DF facit quadratum utriusque AI et IF, habebimus linee quidem AI longitudinem 58 47′, linee vero FI 20 53′ earundem. Quare qualium est AI que rectum subtendit 120, talium IF etiam erit 42 38′, et angulus FAI talium 41 38′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 20 49′, et per eadem quoniam qualium est AD que rectum subtendit 120, qualium DF quoque colligitur 42 50′, habebimus etiam angulum DAF, idest idest] add. s. l. A talium 41 50′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 20 55′. Deficit ergo etiam in hoc additio subtractiove secundum longitudinem propter obliquationem sexagesimis sex, que nobis erant inveniende.

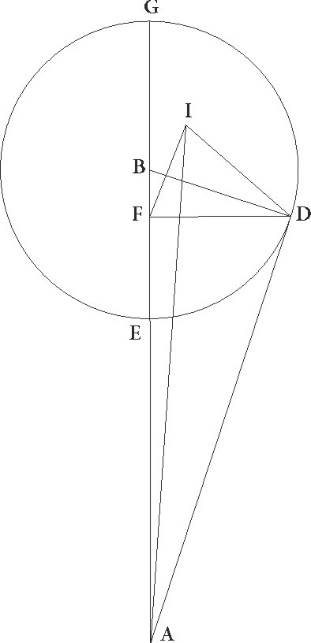Sed consideremus nunc si, suppositis his obliquationum magnitudinibus, maximi motus latitudinis qui fiunt in maximis minimisque longitudinibus congruere cum illis inveniuntur qui per observationes habentur, supponaturque rursum in eadem figura maxima Veneris longitudo, hoc est ut AB linea sit ad BD, sicut 61 15′ ad 43 10′. Quoniam igitur quadratum linee DB subtractum a quadrato linee AB facit quadratum linee AD, colligitur etiam hec 43 27′ earundem, sed sicut AB linea ad AD, sic et BD ad DF. Erit igitur etiam DF 30 37′ earundem. Rursus quoniam DFI obliquationis angulus talium supponitur 7 qualium duo recti sunt 360, et DI linea talium 7 20′ qualium DF que rectum subtendit 120, erit etiam DI linea talium 1 22′ qualium DF est 30 37′ et AD 43 27′. Quare qualium est AD que rectum subtendit 120, talium DI quoque erit 5 9′, et DAI angulus maxime secundum latitudinem remotionis talium 4 54′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 2 27′. In minima vero longitudine, quoniam qualium est BD epicycli semidiameter 43 10′, talium AB supponitur 58 45′, et quadratum linee DB subtractum a quadrato linee AB facit quadratum linee AD, habebimus huius quoque longitudinem 39 51′ earundem. Similiter quoniam, sicut AB linea ad AD, sic et BD ad DF, erit etiam DF 29 17′ earundem, sed proportio linee DF ad DI supponitur esse sicut 120 ad 7 20′, ergo qualium est DF linea 29 17′ et AD 39 51′, talium etiam DI colligitur 1 47′. Quare qualium est AD que rectum subtendit 120, talium DI quoque erit 5 22′ et DAI angulus maxime secundum latitudinem remotionis talium 5 8′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 qualium​ … 360] add. marg. G, talium 2 34′, indifferenti ergo quodam ad sensum minor factus est motus latitudinis qui fit in maxima longitudine et maior qui fit in minima quam remotio secundum latitudinem media que 2 30′ graduum supponitur. Nam motus quidem qui fit in maxima tribus solummodo sexagesimis, qui vero in minima quatuor sexagesimis excessit, quas per observationes capere nequaquam possibile erat.

Supponatur rursum maxima Mercurii longitudo, hoc est proportio AB linee ad BD que est sicut 69 ad 22 30′, ut per ea que in superioribus dicta sunt AD quidem linea 65 14′ earumdem colligatur et DF 21 16′ similiter. Habemus autem etiam hic DFI angulum obliquationis talium suppositum 14 qualium duo recti sunt 360, et idcirco lineam quoque DI talium 14 40′ qualium est DF que rectum subtendit 120. Qualium igitur est DF linea 21 16′ et AD 65 14′, talium etiam DI erit 2 36′. Quare qualium est AD que rectum subtendit 120, talium DI quoque erit 4 47′, et DAI angulus maxime secundum latitudinem remotionis talium 4 34′, qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 2 17′. In minima vero longitudine proportio quidem AB ad BD supponitur, sicut 57 ad 22 30′, AD vero linea per hec eadem 52 22′ earundem, et DF 20 40′ similiter. Et quoniam propter eandem obliquationem proportio linee DF ad lineam DI supponitur, sicut 120 ad 14 40′, estque DI linea talium 2 32′ qualium DF 20 40′ et AD 52 22′, erit etiam DA linea 5 48′ talium, qualium est AD que rectum subtendit 120, et DAI angulus talium 5 32′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 2 46′. Quare remotio secundum latitudinem que in maxima longitudine fit 13 ad minus, que vero in minima 16 ad plurimum sexagesimis excessit maximam latitudinis remotionem, que secundum mediam rationem etiam hic 2 30′ graduum supponitur, pro quibus in computationibus propter emendandam mediam rationem quarta unius gradus parte utemur, nam in observationibus id indifferens ad sensum est.

His demonstratis, et ad hec quod sicut maxime additiones subtractionesque secundum longitudinem ad maximos latitudinis motus se habent, sic et in reliquis partibus epicycli particulares longitudinis additiones subtractionesve ad particulares latitudinis motus, facilis nobis hinc in quartis Veneris atque Mercurii tabularum ordinibus appositio motuum obliquationis secundum latitudinem facta est, eorum tamen quoniam penes solam epicyclorum obliquationem et secundum mediam, ut diximus, rationem colliguntur, differentia que tum propter inclinationem excentricorum tum propter maximam et minimam Mercurii longitudinem colligitur in futuro calculo sic enim commodius est emendabitur.

Nam quoniam secundum propositas proportiones medias maximus quidem latitudinis utrarunque stellarum motus qui fit ex obliquatione ad utranque circuli per medium partem graduum demonstratus est 2 30′, additio vero subtractiove secundum longitudinem in Venere quidem graduum est 46, in Mercurio autem 22 proxime, habemus que in tabulis inequalitatis ipsarum congruentes particularibus epicyclorum arcubus additiones subtractionesque, quota pars iste integrarum maximarumque secundum longitudinem additionum subtractionumve sint, tantam in utraque stellarum capiemus congrue ad gradus 2 30′, factosque numeros eisdem numeris in quartis ordinibus tabularum latitudinis apponemus.

Quinti autem ordines nobis compositi sunt, ut remotiones secundum latitudinem que fiunt in aliis excentricorum motibus per appositas sexagesimas equare possimus. Nam quoniam, ut diximus, proportionaliter ad restitutionem que ad excentricum fit epicyclorum quoque inclinationes obliquationesque restitutionem incrementi decrementique per parvulorum appositionem faciunt circulorum, nec inclinationum obliquationumque omnium magnitudines longe sunt a magnitudine obliquationis circuli Lune, habentque se rursum proxime proportionaliter particulares tantarum inclinationum remotiones, demonstravimusque per lineas huiusmodi Lune remotiones duodecies unamquanque appositionem illarum multiplicando, propterea quod maxima ibi latitudo graduum est 5 proxime, nunc vero ipsam 60 facimus, eas que fiunt congruentibus singulorum quinque ordinum numeris apposuimus. Est autem tabularum compositio hec.

〈XIII.5〉 Capitulum V: Tabule latitudinum quinque planetarum

〈XIII.6〉 Capitulum VI : Calculus remotionis quinque planetarum secundum latitudinem

Hec cum ita se habeant, calculum etiam latitudinis stellarum hoc modo faciemus.

In tribus superioribus in congruentes tabule numeros per longitudinem equatam intrabimus, sed in Marte quidem ipsam longitudinem capiemus equatam, in Iove autem 20 ab ea gradus subtrahemus, in Saturno vero 50 addemus, appositasque in quinto latitudinis ordine sexagesimas conscribemus. Similiter inequalitatis equate numerum in eisdem numeris queremus, et appositam ei latitudinalem differentiam, si equata longitudo in primis 15 versibus fuerit, ex ordine tertio capiemus, sin autem in sequentibus, ex ordine quarto, multiplicabimusque in conscriptas sexagesimas, et facto numero stellam distare a circulo per medium dicemus, borealioremque esse, si latitudinalem differentiam ex ordine tertio cepimus, sin vero ex quarto, australiorem.

In Venere autem atque Mercurio per equatum inequalitatis numerum in tabulam intrabimus, appositasque ipsi in tertio et quarto latitudinis ordine seorsum conscribemus easdem quidem ipsas que in aliis tribus ordinibus sunt, que vero in quarto Mercurii ordine, si equatus longitudinis numerus in primis 15 versibus fuerit, cum decime partis earum subtractione, sin vero in reliquis, cum eiusdem partis additione, deinde longitudini equate semper in Venere quidem 90, in Mercurio autem 270 gradibus additis reiectisque circulis, si habentur, collectum numerum in eisdem duobus primis ordinibus queremus, et quotquot erunt sexagesime huiusmodi numero in ordine quinto apposite, tot de conscriptis ex ordine tertio capientes conscribemus, quando quidem longitudo una cum additione predicta in primis 15 versibus est, si equate etiam inequalitatis numerus in ipsis primis sit, ad austrum, sin vero in reliquis, ad boream, quando autem dictus longitudinis numerus ad inferiores ultra 15 versus excidit, si equate inequalitatis numerus in primis rursum versibus sit, ad septentrionem, sin vero in reliquis ad austrum.

Deinde rursum equatam longitudinem ipsam quidem simpliciter in Venere, in Mercurio autem cum additione 180 graduum in eisdem ordinibus inveniemus, et quotquot etiam in ordine quinto sexagesime apponuntur, tot de conscriptis ex ordine quarto capientes conscribemus, quando, sicut diximus, longitudinis numerus quo intravimus in primis 15 versibus invenitur, si equate inequalitatis numerus 180 gradus non excedit, ad septentrionem, sin vero excedit, ad austrum, quando autem dicte longitudinis numerus ultra 15 versus excidit, si rursum inequalitatis numerus 180 gradus non excedit, ad austrum, sin autem excedit, ad septentrionem. Deinde harum etiam sexagesimarum que per longitudinem ultimo invente sunt tantam partem capiemus, quota ipse erant de 60^a, et numeri sic facti in Venere quidem sextam partem ad septentrionem semper ponemus, in Mercurio autem m〈e〉dietatem medietatem] mdietatem A et quartam semper ad austrum, et sic ex compositione trium conscriptarum latitudinum apparentem ipsarum a circulo per medium singulorum secundum latitudinem motum cognoscemus.

〈XIII.7〉 Capitulum VII: De aparitionibus atque ocultationibus quinque planetarum

Verum cum etiam de remotione quinque stellarum secundum latitudinem iam dictum sit, reliquum est illa quoque addere que de apparitionibus ocultationibusque ipsarum respectu Solis factis considerantur. Accidit enim, sicut de non erraticis etiam dicebamus, multis modis distantias ipsarum ad Solem que in circulo per medium tam in apparitionibus quam in occultationibus considerantur inequales multis modis et multis de causis fieri, quarum prima est propter inequalitatem magnitudinum suarum, altera propter dissimilitudinem inclinationum zodiaci ad orizontas, tertia propter motum latitudinis ipsarum.

Nam si rursus maximorum arcus circulorum capiemus, orizontis quidem arcum AB, circuli vero maximi per medium signorum arcum GD, et E quidem punctum communem ipsorum sectionem orientalem vel occidentalem esse supposuerimus, puncta vero G et A ad austrum inclinata, et D punctum centrum sit Solis, ac per ipsum et per polum orizontis maximi rursum circuli arcum 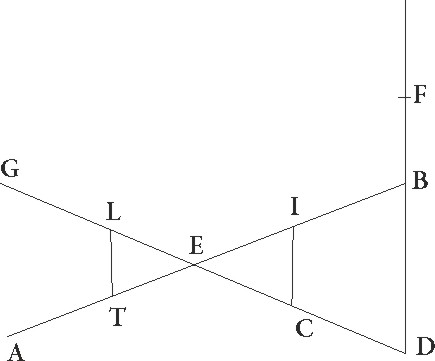DBF descripserimus, stellamque stellamque] corr. ex stellam G oriri aut occidere in orizonte EB, quando quidem in circulo per medium fuerit, in puncto E, quando autem borealior ipso, in puncto I, quando vero australior, in puncto T, deduxerimusque a punctis I et T ad circulum per medium perpendiculares IC et TL, habebimus rursum per BD arcum aut per equalem, distante Sole sub terra, primo apparere stellam aut occultari. Ad maximum enim circulum sic descriptum eedem equalium sub terra distantiarum illuminationes radiorum Solis fiunt. Hac ergo primum in aliis inequalibus stellis inequali consequenter constituta, necesse est etiam, si cetera omnia eadem sint, ut arcus zodiaci quibus rectus subtenditur angulus, hoc est distantias ED arcui similes, multum inter se differre, et minores esse in maioribus stellis, maiores autem in minoribus.

Similiter etiam, si BD linea eadem sit in eadem stella et BED angulus declinationis circuli per medium vel propter duodecim signorum vel propter diversarum habitationum differentias inequalis efficiatur, arcus quoque distantie ED differens atque diversus erit, maiorque fiet, quando angulus imminuitur, et minor, quando angulus augetur. Eodem modo, si id quoque similiter cum primo se habeat, ut videlicet declinatio etiam eadem sit, sed stella non sit in circulo per medium, sed vel borealior, ut in puncto I, vel australior, ut in puncto T, non apparebit primo, neque ocultabitur secundum DE arcus distantiam, sed quando borealior est circulo per medium, in distantia DC arcus qui minor est, quando autem australior, in distantia LED arcus qui maior est.

Quapropter necesse est ad particulariorem considerationem, ut primum in singulis quinque planetis magnitudines arcuum BD universaliter per minus ambiguas observationes habeantur. Tales vero sunt estive et in Cancro proxime observate, propterea quod in eo tempore et er tenuis magis est, certiusque per eum perspicitur et zodiaci ad orizontis orizontis] post corr. G inclinationes pene mediocres. Per hanc igitur orientalium observationum considerationem invenimus Saturni stellam semper oriri, quando a vero Sole 14 gradibus distat, Iovis autem similiter 12 45′, Martis 14 30′, Veneris vespertinam, quando 5 40′ gradibus distat, Mercurii similiter vespertinam, quando 11 30′.

His hoc modo suppositis, suppositis] post corr. G describatur antecedens figura, nihil enim differt, si in tam parvis arcubus quasi de cordis suis rectisque lineis, cum indifferentes ab arcubus ad sensum sint, gratia commoditatis verba faciamus, et sit E punctum communis sectionis circuli per medium et et] add. s. l. G orizontis, idque in propositis apparitionibus in principio Cancri oriatur in tribus matutinis Saturno, Iove, Marte, et occidat in vespertinis Venere atque Mercurio. Clima vero supponatur quod per Phenicem scribitur, ubi maxima dies horarum equalium est 14 15′. In hoc enim aut iuxta hunc paralellum plurime certioresque observationes facte sunt. Nam Chaldaice in eo ferme observate sunt et similiter quecunque in Gretia et in Egypto.

Quoniam igitur per doctrinam angulorum demonstrationesque illius negotii, quando Cancri principium in hoc climate oritur, talium 103 invenimus angulum BED, qualium duo recti sunt 360, idque circo proportionem linearum quibus recti anguli continentur sicut 94 ad 75 proxime et eas que rectos angulos subtendunt 120 similium. Per doctrinam autem de stellarum latitudine, quando tres superiores solum in principio Cancri oriuntur, et in maximis epicyclorum longitudinibus sunt, quantumcunque a maximis excentricorum distent, modo non magis quam per duodecim gradus, tunc indifferenter ad sensum Saturni quidem Iovisque stellas in ipso ferme circulo per medium, Martis vero quinta maxime unius gradus parte borealiorem. Quoniam igitur hec invenimus, erit DE linea per quam distabunt a Sole, cum sint in circulo per medium Saturnus et in Iupiter, DC autem per quam Martis stella distabit, propterea quod borealior est per lineam CI que est sexagesimarum 12. Quoniam autem proportio CI linee ad CE est sicut 94 ad 75, erit etiam CE linea sexagesimarum 101 proxime. Sed DC quoque 14 30′ graduum in Marte supposita est; quare tota DE graduum colligitur 14 40′. Est autem in Saturno quidem graduum 14, in Iove autem 12 45′. Quare quoniam rursus proportio linee ED ad DB est sicut 120 ad 94, habebimus etiam DB arcum circuli qui maximus per polos orizontis describitur, in Saturno quidem graduum xi, in Iove autem 10, et in Marte 11 30′ proxime.

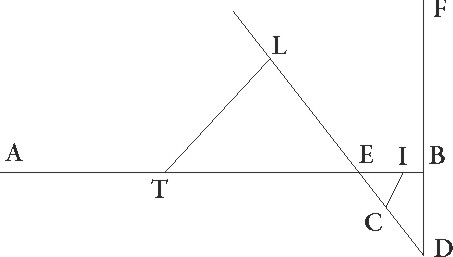Similiter in Venere atque Mercurio, quoniam etiam, quando Cancri principium occidit, eundem cum exposito augulum inclinationemque ad orizontem facit, supponiturque in hac circuli per medium parte stella Veneris vespertina tunc oriri, quando a vero Sole 5 40′ gradibus distat, Mercurii vero 11 30′ obtinebit in ortibus ipsarum, Sol apparens in Venere quidem 24 20′ gradus Geminorum, in Mercurio autem 18 30′, medius vero Sol in Venere gradus Geminorum 25, in Mercurio 19 proxime. Hos ergo gradus medius quoque longitudinis stellarum motus obtinebit. Quando autem ita se habet longitudo et stelle ipse in principio Cancri cernuntur, tunc stella quidem Veneris a maxima epicycli logitudine 14 pene gradibus distare invenitur, Mercuri vero 32 proxime, quod per theoreumata de inequalitate ipsorum habita demonstratur, consequenterque in his motibus Venus quidem borealior circulo per medium invenitur uno gradu, Mercurius vero 1 40′ proxime, quot videlicet graduum est arcus CI, quare quoniam eius quoque proportio ad arcum EC est sicut 94 ad 75, eademque eademque] post corr. G ipsa est unius gradus ad sexagesimas 45 et unius sexagesimarumque 40 ad unum et et] add. s. l. G sexagesimas 20 proxime, habebimus etiam arcum EC in Venere quidem 45 sexagesimarum, in Mercurio gradus unius et sexagesimarum 20. Sed earundem DC quoque arcus per quem distare a Sole utraque stella cernebatur, in Venere quidem 5 40′ graduum supponitur, in Mercurio autem 11 30′, quare totum quoque DCE in Venere 6 25′ habebimus, in Mercurio 12 50′ proxime. Quoniam ergo rursus proportio ED ad BD est sicut 120 ad 94, estque eadem huic proportio 6 25′ ad 5 et 12 50′ ad 10 proxime, habebimus etiam DB universalis distantie magnitudinem in Venere graduum quinque, in Mercurio graduum 10.

〈XIII.8〉 Capitulum VIII: Quod etiam apparitionum Veneris atque Mercurii propria cum suppositionibus ad unguem conveniunt

Quod autem consequenter ad expositas iam suppositiones illa etiam accidant que in apparitionibus ocultationibusque Veneris atque Mercurii mira solent videri, quia videlicet tempus a vespertino Veneris occasu ad matutinum ortum in principio quidem Piscium duorum maxime, in principio autem Virginis sexdecim dierum est, et Mercurii vespertine quidem apparitiones, cum in principio Scorpionis debet apparere, deficiunt, matutine autem, quando in principio Tauri, hinc profecto intelligemus, et primum in stella Veneris.

Designetur enim similis precedenti apparitionum figure descriptio, supponaturque primum E punctum circuli per medium in principio Piscium, ubi, quando in minima epicycli longitudine Veneris stella est, borealior circulo per medium 6 20′ gradibus proxime invenitur, figura vero vespertini occasus in qua BED angulus colligitur in proposito climate talium 154 qualium duo recti sunt 360, qualium vero que rectum angulum subtendit est 120, talium maius recti anguli latus 117 et minus 27 proxime, idcirco qualium etiam est DB arcus totius distantie 5, talium DE quoque invenitur 5 8′. Verum quoniam stella borealior est circulo per medium gradibus 6 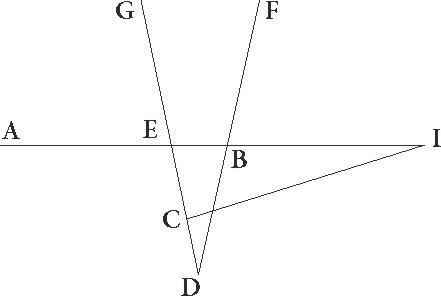20′, quot graduum est arcus CI, estque proportio eadem 117 ad 27 et 6 20′ ad 1 30′ proxime, erit arcus CE graduum 1 30′ et reliquus CD per quem stella in occasu vespertino ad successionem Solis distabat gradium 3 38′.

Rursus in simili descriptione, quoniam in ortu matutino BED angulus talium est 69 qualium duo recti sunt 360, ideoque qualium est que rectum angulum subtendit 120, talium minus recti anguli latus 68 et maius 99 proxime, colligunturque proportiones eedem 68 ad 120 et 5 ad 8 49′ et similiter 68 ad 99 et 6 20′ ad 9 13′, habebimus etiam lineam DE 8 49′, et CE differentie penes latitudinem 9 13′ eorundem, et reliquam DC ad successionem videlicet Solis sexagesimarum 24. Obtinebat autem in occasu vespertino ad successionem similiter gradus 3 38′. Minus ergo in tempore ab occasu vespertino ad matutinum ortum Solis motu, hoc est suo ipsius proxime longitudinis transitu propter regressum in epicyclo, 3 14′ gradibus mota est. Quoniam igitur totidem gradibus ad precedentia stella traducitur, ut ut] post corr. G ex tabula inequalitatis facile intellectu est, quando apud minimam epicycli longitudinem 1 15′ gradibus mota fuerit, quos medie pertransit in duobus diebus proxime, patet quia tantum erit tempus predicte distantie consequenter ad apparentia.

S 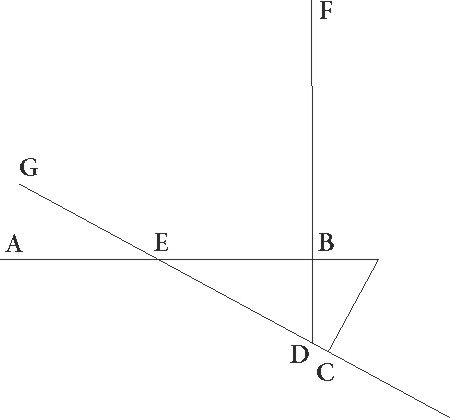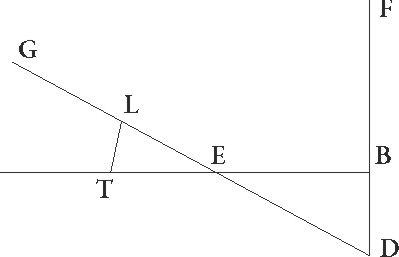it rursum simili descriptione E punctum in principio Virginis, ubi, quando in minima epicycli longitudine Venus est, australior apparet quam circulus per medium totidem proxime gradibus 6 20′, proponaturque primum vespertina ocultatio, quando angulus BED talium est 69 qualium duo recti sunt 360, qualium vero que rectum subtendit 120, talium minus recti anguli latus 68 et maius 99 proxime. Quoniam igitur eedem sunt proportiones cum proportionibus matutine apparitionis que fit in Piscibus, estque latitudinis distantia equalis, habebimus ED similiter arcum 8 49′ eorundem; et LE arcum differentie penes latitudinem 9 13′, totum vero DL per quem ad successionem Solis stella distabat graduum 18 2′, et per tabulam inequalitatis, ut diximus, totidem gradibus ipsius regressus penes medium Solis et stelle per longitudinem motum congruunt a minima epicycli longitudine gradus 7 30′ proxime.

Similiter quoniam in ortu matutino in principio Virginis, quando BED angulus talium est 154 qualium duo recti sunt 360, qualium vero que rectum subtendit 120, talium maius recti anguli latus 117 et minus 27, colligunturque rursum eedem proportiones cum proportionibus expositis in ocultatione que fit in Piscibus, habebimus arcum DE 5 8′, arcum vero EL differentie penes latitudinem 1 30′, et totum DL, per quem stella ad precedentia Solis distabat, graduum 6 38′, quibus eodem modo a minima epicycli congruunt 2 30′ gradus proxime. Omnes ergo quibus stella Veneris a vespertina ocultatione ad matutinum ortum transit epicycli gradus 10 inveniuntur per quos in dictis 16 diebus proxime consequenter ad apparentia movetur.

His demonstratis, illa iam que de apparitionibus Mercurii eclipticis accidunt consideranda sunt, et primo quod in principio Scorpionis, etiam si maximam ad successionem Solis distantiam faciat, faciat] corr. ex facit G vespertinus tamen apparere non potest. Lineetur Lineetur] post corr. G enim apparitionum 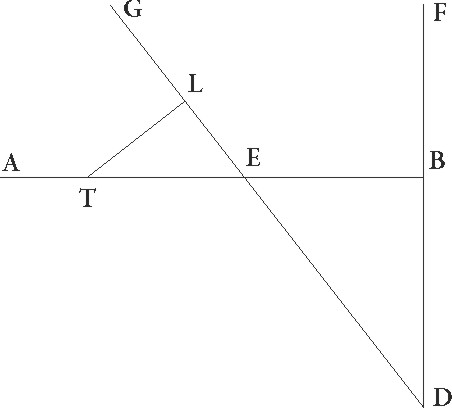descriptio, supponaturque E punctum circuli per medium in principio esse Scorpionis, in quo situ in occasu BED angulus talium est 69 qualium duo recti sunt 360, qualium vero que rectum subtendit 120, talium minus anguli recti latus 68 et maius 99. Quare qualium est BD universalis distantie arcus 10, talium etiam DE erit 17 39′, sed, quando stella dictum habet situm, australior est circulo per medium gradibus 3 proxime. Quare quoniam secundum expositas proportiones, qualium est LT latitudinis arcus 3, talium LE est 4 22′ et DEL 22 proxime eorundem, necesse est totidem removeri a vero Sole stellam, ut possit primo apparere. Quoniam ergo 20 58′ gradibus solum, quando in principio Scorpionis est, maxime a vero Sole distare 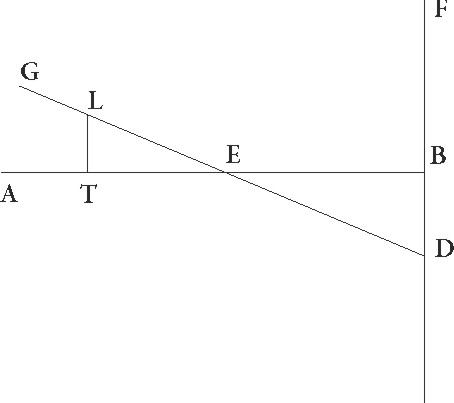potest, —id enim nobis per ea que de maximis a Sole distantiis tractavimus iam demonstratum est—, patet quia convenienter huiusmodi apparitiones deficiunt.

Deinde rursum simili apparitionum descriptione lineata, si E punctum in principio Tauri supposuerimus, matutinumque ortum ceperimus, quando stella secundum expositos motus 3 10′ proxime gradibus australior circulo per medium sit, et proportiones laterum que rectos angulos ambeant eedem sint, tunc habebimus arcum DE 17 39′ eorundem, et LE talium 4 37′ qualium est TL latitudinis arcus 3 10′, totum vero DEL 22 16′ eorundem. Quare hic etiam totidem gradibus distare a vero Sole stellam oportebit, ut primo apparere possit. Cum autem non ultra quam 22 13′ gradibus maxime possit in hoc situ, ut demonstravimus, distare, consequenter huiusmodi etiam apparitiones deficiunt, demonstrataque sunt nobis que proposuimus tam apparentibus quam expositis suppositionibus convenire

〈XIII.9〉 Capitulum VIIII : Doctrina ad particulares a Sole distantias apparitionum atque ocultationum

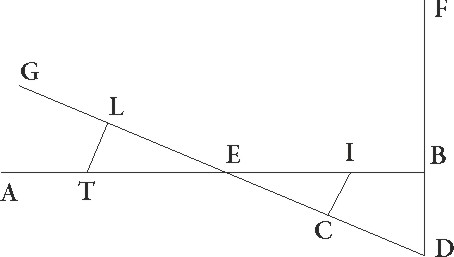Hinc perspicuum est quod, etiam universaliter suppositis BD arcubus in singulis stellarum, datoque signorum principio quod est in puncto E, et propterea etiam angulo BED dabitur arcus quoque DCE, et motus latitudinis, hoc est CI aut TL arcus, in huiusmodi stelle distantia, et propterea etiam arcus CE aut EL, et ad hec apparens distantia DC aut DL. Hoc igitur modo in omnibus signis, ne longiores simus, et in singulis quinque planetis hec computavimus, et in solo proposito climate medio, —sufficiens enim id est—, apparentes ortuum ocultationumque a Sole distantias, stellis ipsis in principio signorum locatis, facilioris usus gratia in quinque tabulis quinque stellarum conscripsimus quarum singule duodecim continent versus, et prime quidem Saturni, dico, Iovis, Martisque post primum ordinem qui signorum habet principia ex duobus ordinibus constant, quorum primi matutinorum ortuum, alteri vespertinorum occasuum distantias continent. Sequentes autem due Veneris atque Mercurii tabule quatuor ordinibus constant, quorum primi vespertinorum ortuum distantias, alteri vespertinorum occasuum continent, tercii matutinorum ortuum, rursus quarti matutinorum occasuum. Est autem tabularum compositio hec.

〈XIII.10〉 Capitulum X: Tabule apparitionum et occultationum quinque planetarum

〈XIII.11〉 Capitulum XI : Conclusio totius voluminis

Sed his etiam, o Syre, mihi expositis, fermeque omnibus que ad hanc tantarum rerum considerationem pertinent breviter mea quidem sententia, quantum ad hodiernum usque diem aut ad inveniendum aut ad emendandum exquisitius et tempora conferebant et docendi modus ad commoditatem speculationis non ad ostentationem accomodatus petebat, pertractatis, idoneum hic modum ac finem hec est compositio consecuta.