Ptolemaeus Arabus et Latinus

〈V〉

Incipit liber V Magne Compositionis Claudii Ptholomei

〈V.1〉 〈Capitulum I :〉 De constructione instrumenti quod astrolabium vocant

Verum ad oppositiones quidem atque coniunctiones et eclipsis que in eis in eis] iter. et del. G fiunt prime simplicisque inequalitatis rationem sufficere invenimus, etiam si ipsa nobis sola capiatur, sed ad particulares motus in aliis ad Solem aspectibus non sufficientem aliquis ipsam inveniet. Secunda enim etiam, ut diximus, inequalitas inequalitas] corr. ex in qualitas G Lune penes solares distantias comprehenditur, hec in oppositione atque coniunctione ad primam restituitur. Maxima vero est in utraque quadratura id animadvertimus, credidimusque tam a progressibus Lune quos Hypparchus conscripsit quam ab aliis quos nos per instrumentum ad hec nobis constructum accepimus.

Hoc ita se habet : duas armillas armillas] corr. ex armilas G exquisite tornatas superficiebusque quadratas ac magnitudine mediocres et undique similes equalesque inter se secundum diametrum ad rectos angulos in ispis superficiebus aptavimus, ita ut altera eorum circulus per medium signorum esse intelligeretur, altera circulus qui per polos ipsius et equinoctialis est hic meridianus appellatur. In quo ab una sectionum utrinque per quadrati latera cepimus puncta quibus poli circuli qui per medium signorum est disseperantur, et in utrisque cylindrulos tam ad interiorem quam ad exteriorem superficiem extantes coaptavimus. Deinde ad exteriorem armillam aliam coaptavimus, que undique concava sui superficie connexe duarum coaptatarum armillarum sic undique quadrabat, ut circa predictos polos circuli qui per medium signorum est posset per longitudinem circumduci, interiorem quoque aliam aliam] corr. ex alium G similiter armillam adaptavimus, cuius connexa superficies concavam duarum armillarum ubique tangebat, ita ut similiter secundum longitudinem circa eosdem polos exteriori circumduceretur, hanc interiorem armillam et eam que pro zodiaco est in 360 circumferentie gradus divisimus, partesque graduum quotquot potuimus. Deinde aliam armillulam exquisite adaptavimus, in qua foramina sunt diametraliter eminentia sub interiore duarum armillarum, ut in eadem illi superficie ad utrunque predictorum polorum gratia observande latitudinis possit transferri. His ita factis, arcum qui inter duos polos zodiaci videlicet atque equinoctialis in circulo qui per utrosque polos esse intelligitur ab utrisque zodiaci polis elongavimus et extremitates diametraliter rursum inter se oppositas coaptavimus ad meridianum illi similem quem in principio compositionis ad observationes arcuum meridiani qui inter solstitia sunt explanavimus. Hoc igitur secundum positionem illius statuto, idest recto ad superficiem orizuntis et secundum elevationum poli habitationis proposite et ad hec parallelo ad superficem naturalis naturalis] naturalalis A orizontis, interiorum circumductio armillarum ab ortu ad occasum fiat in polis equinoctialis consequenter ad primam totius lationem.

Sic instrumento constituto, quandocunque Sol et Luna super terram videri poterant exteriorem quidem astrolabii armillam in illo gradu in quo Sol proxime tunc inveniebatur constituebamus, et armillam que per pollos est circumducebamus, ut, sectione armillarum que ad solarem erat gradum exacte ad Solem versa, utreque armille, que per medium signorum et que per polos eius est simul, se ipsas obumbrarent, vel si stella perspiceretur, in uno oculorum in altero laterum exterioris armille sub gradu qui opponitur in armilla que per medium signorum est posito, per oppositum atque parallelum circuli latus, quasi utrisque superficiebus ipsorum stella sit conglutinata, in eorum superficie superficie] corr. ex sperficie G perspiciatur. Alteram vero armillam que intra astrolabium astrolabium] corr. ex astrolabum G est ad Lunam vel ad illud quod queritur vertimus, ut simul Solem aut aliud quod … aliud] add. marg. G quodvis prospiciendo Luna quoque vel quicquid queritur per utraque foramina que in adaptato minore circulo sunt perspiciatur.

Sic enim et quem gradum circuli qui per medium signorum est per longitudinem obtineat, invenimus a sectione interioris circuli que fit per divisionem equipollentis ipsi circuli, et quot gradus ad septentrionem vel ad meridiem ab ipso distet, non ignoramus sicut in circulo qui est per polos eius tum per divisionem ipsius interioris astrolabii tum per inventam distantiam a medio foramine quod super terram est eius armillule que ad mediam lineam circuli signorum traducitur.

〈V.2〉 Capitulum II : De suppositione que ad duplicem Lune inequalitatem pertinet

Huiusmodi ergo simpliciter facta observatione distantie Lune ad Solem, tum ex illis que Hypparthus conscripsit, tum ex eis que nos observabamus, modo consone computationibus preposite suppositionis comprehendebantur, modo dissone, dissone] corr. ex disone G differebantque nunc pauco, nunc multo, sed cum magis atque magis et diligentius frequentiusque huius inequalitatis ordinem animadverteremus, intelleximus quod in coniunctionibus quidem atque oppositionibus semper aut nihil sensibile aut admodum parum erratur tantumque, quantum diversitates aspectus lunaris possent efficere. In quadraturis vero utrisque in minimo vel in nullo erratur, cum Luna vel in maxima vel in minima epicycli longitudine sit, in maximo autem, quando est in medio cursu, et prime inequalitatis differentiam maximam facit, et ad hec quando prima inequalitas in quavis quadratura subtrahendi vim habet, tunc etiam minor Lune locus invenitur, quam si primam solummodo subtractionem computares, quando autem addendi, maior similiter proportionaliterque ad quantitatem prime additionis subtractionisve, ut ex hoc ordine perspicatur quod etiam epicyclus Lune in excentrico ferratur remotissimusque in coniunctionibus et oppositionibus a terra fiat, proximus autem in utrisque quadraturis, quod accidere potest, si prima suppositio talem emendationem accipiat.

Intelligatur concentricus circulo qui per medium signorum est in obliqua Lune superficie precedere, sicut et antea, gratia latitudinis circa polos zodiaci tanto, quanto latitudinis motus longitudinis motum excedit, Luna vero epicyclum ita pertransire, ut in arco eius remotissimo a terra ad precedentia moveatur consequenter ad restitutionem prime inequalitatis. In hac igitur obliqua superficie duos motus equales et inter se contrarios supponimus et ambos circa centrum circuli qui per medium signorum est: unum qui centrum epicycli ad successionem signorum circumducat consequenter ad resti〈tu〉tionem restitutionem] restitionem A latitudinis, alterum qui centrum et maximam longitudinem excentrici circuli qui in eadem superficie accipitur, in quo centrum epicycli semper erit, circumducat ad precedentia signorum tanto, quanto latitudinis motum distantia duplicata excedit, hoc est excessus medii lunaris per longitudinem motus ad solarem, ita ut in uno, verbi gratia, die centrum quidem epicycli, cum 13 14′ proxime latitudinis gradus ad succesionem signorum pertransierit, videatur in circulo qui per medium signorum est 13 11′ gradus pertransisse, propterea quod totus obliquus circulus tres sexagesimas ad precedentia inde auferat, maxima vero excentrici longitudo contraducatur rursum ad precedentia gradibus 11 9′, quibus 24 23′ duplicate distantie gradus latitudinis gradus 13 14′ excedunt. Sic enim ex utriusque motus contraria circunductione que, ut diximus, circa zodiaci centrum fit, motus quem centrum epicycli facit distabit a motu qui fit a centro excentrici per arcum compositum ex gradibus 13 14′ et 11 9′ duplum illi qui 12 11′ 30′′ proxime distantie gradus habet. Idcirco bis in mensis medii tempore excentricum epicyclus pertransibit, et restitutio que ad maximam intelligitur excentrici longitudinem fieri in coniunctionibus atque oppositionibus mediis absolvetur.

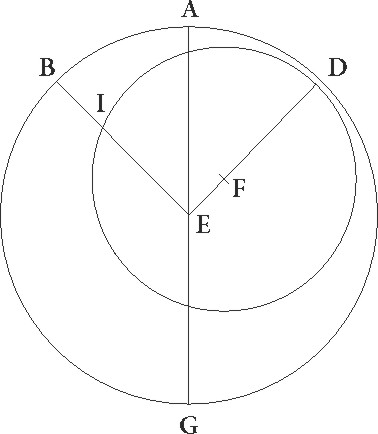Verum ut pre oculis hec suppositio fiat, intelligatur rursus in obliqua Lune superficie circulo qui per medio signorum est concentricus ABGD circulus, cuius centrum E et diameter EG, et supponantur simul esse in A puncto maxima excentrici longitudo, centrum epiycli, borealis terminus, principium Arietis, et Solis medius motus. In diurno igitur motu totam superficiem assero ab A puncto ad D circa centrum E tribus sexagesimis proxime ad precedentia moveri, ut borealis terminus in gradus 29 57′ Piscium pervenerit. Cum autem etiam duo etiam contrarii motus a linea simili linee EA circa E rursus zodiaci centrum equaliter fiant, in diurno similiter dico motu lineam quidem que est per centrum excentrici similem linee E equaliter ad precedentia signorum circumductam ad lineam ED maximam quidem excentrici longitudinem ad D punctum deferre et circa F centrum describere DI excentricum, ita ut faciat arcum AD graduum 11 9′, eam vero lineam que per centrum epicycli est equaliter rursum ad successionem signorum versus EB circumductam centrum quidem epicycli deferre ad I, arcum vero AB facere graduum 13 14′, ut I centrum epicycli a boreali quidem termino 13 14′ latitudinis gradibus distare perspiciatur, a principio autem Arietis 13 11′ longitudinis gradibus, eo quod A borealis terminus interea in 29 57′ Piscium gradus pervenerit, ex puncto vero D, hoc est a maxima excentrici longitudine, collectos utriusque AD et AB arcuum gradus 24 23′, qui distantie diurne duplices sunt. Sic igitur quoniam utrique motus qui est per B et qui est per D in medietate medii temporis menstrui unam restitutionem adinvicem faciunt, patet quod in quarta eiusdem temporis parte et ad hec in media et quarta diametraliter omnino inter se opponentur, idest in mediis quadraturis, centrum epicycli quod est in EB diametraliter opponetur ED maxime longitudini excentrici in minima eius longitudine factum.

Cum hec ita se habeant, perspicuum est quod penes excentricum quidem, hoc est penes dissimilitudinem DB arcus ad arcum DI, nulla differentia erit penes equalem motum linee EB. Non enim DI excentrici, excentrici] corr. ex centrici G sed DB circuli qui per medium signorm est arcum equaliter pertransit, quoniam non circa F excentrici centrum, sed circa E circumducitur, penes autem solam differentiam que per epicyclum ipsum efficitur: nam, eo quod propinquior terre fiat, auget semper inequalitatis differentiam equaliter secundum subtractionem et additionem anguli ipsum intercipientis iuxta visum qui angulus in propinquioribus terre positionibus maior efficitur. Nulla igitur omnino penes suppositionem primam differentia erit, quando centrum epicyli in A longitudine maxima erit, quod fit in coniunctionibus et oppositionibus Lune 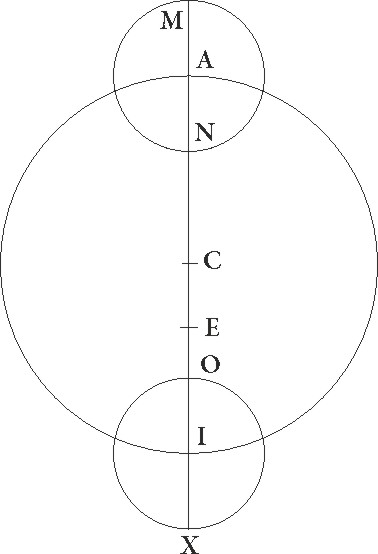mediis.

Si etiam circa centrum A epicyclum MN descripserimus, fiet proportio E linee ad lineam AM que per eclipsis demontrata est. Maxima vero differentia erit, quando epicyclus per I minimam excentrici longitudinem transitum facit, sicut epicyclus qui describitur per puncta X O, quod rursus in mediis accidit quadraturis. Maior enim fit proportio XI linee ad IE lineam ceteris omnibus que in aliis positionibus colliguntur. Nam cum linea XI equalis semper et eadem sit, a centro enim est epicycli linea EI, cum sit a centro terre, omnibus aliis que ad excentricum protrahuntur minor esse cognoscitur.

〈V.3〉 Capitulum III: De quantitatibus inequalitatis Lune que penes distantiam suam a Sole accidit

Sed, ut quanta maxima inequalitatis differentia fiat, perspiceremus, perspicieremus] post corr. G quando in minima excentrici longitudine epiciclus invenitur, observavimus in his Lune ad Solem distantiis in quibus et cursus eius medii proxime fuerunt, —tunc enim maxima inequalitatis differentia fit—, et distantia eius a Sole medie accepta quartam proxime partem faciebat, quando etiam epicyclus in longitudine minima excentrici erat et ad hec in quibus in quibus] in quibus supple Lune distantiis add. marg. G istis sic se habentibus nullam diversitatem aspectus per longitudinem Luna faciebat. Nam his ita se habentibus, si etiam distantia secundum longitudinem que observatione instrumentali apparuit eadem vere distantie sit, tuto certe differentia etiam secunde inequalitatis quam querimus capietur. His igitur observationibus facta consideratione, inveniebamus quando in minima longitudine erat epicyclus maximam inequalitatis differentiam fieri ad medium quidem progressum graduum 7 40′ proxime, ad primam vero equalitatem 2 40′.

Sed ut exempli gratia una vel altera observatione ante oculos hec diiudicatio ponatur, secundo anno Antonini Phamenoth secundum Egyptios die xxv post ortum Solis ante meridiem horis equalibus 5 15′ Solem in Lunam instrumentali observatione perspeximus. Sol igitur in Aquarii gradibus 18 50′ prospiciebatur, cunque quartus quartus] igitur add. et del. A Sagittarii gradus in medio esset celo, Luna perspiciebatur 9 40′ Scorpions gradus obtinere. Obtinebat autem totidem vero etiam motu suo. Nam cum esset in prima parte Scorpionis et distaret a meridiano per longitudinem versus occasum horis 1 30′, nullum sensibilem diversitatis aspectum faciebat. Est autem a locis in primo anno Nabonasari constitutis usque ad observationem tempus annorum egptiacorum 885 885] post corr. G et dierum 203 et horarum equalium simpliciter exacteque 18 45′, in quo tempore Solem invenimus medie obtinuisse 16 27′ gradus Aquarii, exacte autem 18 50′, sicut et per astrolabium perspiciebatur. Luna quoque in illa hora ex prima suppositione medie obtinuisse inveniebatur secundum longitudinem quidem Scorpionis gradus 17 20′, et sic distantia Solis medie quarte proxime partis erat, inequalitatis autem a maxima epicycli longitudine graduum 87 19′ iuxta quas rursum maxima inequalitatis differentia fit. Erat igitur verus motus medio minor gradibus 7 40′ pro 5 qui ex prima inequalitate inveniebantur.

Rursus ut etiam per observatos ab Hipparcho tales progressus differentia in similibus pateat, unam eius apponemus observationem quam ait anno 50 tertie secundum Calippum Calippum] corr. ex Chalippum G periodi observasse, Epiphi secundum Egiptios die sexto decimo, 40 sexagesimis prime hore transactis. Cursus igitur ait fuerat graduum 24 et Sol perspiciebatur esse in gradibus Leonis 8 42′, Luna vero videbatur in gradibus Tauri 12 3′, quas etiam proxime vero motu obtinebat. Fit igitur exacta inter Solem et Lunam distantia graduum 86 15′. Sed cum Sol in prima parte Leonis in Rhodo sit, ubi observatio fiebat, una hora diei temporum est 17 3′, quare hore 5 20′ temporales ante meridiem faciunt equales 6 6′. Facta fuit igitur observatio ante meridiem diei sextedecime horis equalibus 6 6′, eratque in medio celi Tauri gradus nonus. Colligitur ergo a statutis similiter locis ad observationem tempus annorum egyptiacorum 619 et dierum 314 et horarum equalium simpliciter quidem 17 50′, exacte vero 17 45′ in quo tempore secundum demonstrata, quoniam idem meridianus est per Rhodum et Allexandriam per … Allexandriam] postilla: add. marg. G in geographicis libris longitudinem Alexandrie graduum dicit esse 60 30, Rhodi 58 40 add. marg. A proxime, invenimus Solem medie obtinuisse 10 27′ gradus Leonis, exacte autem 8 20′, Lunam etiam medie secundum longitudinem quidem 4 25′ gradus Tauri, ut media rursus distantia quarte partis proxime esset, secundum inequalitatem vero maxima epicycli longitudine gradus 257 47′ in quibus proxime fit maxima penes epicyclum inequalitatis differentia. Colligitur ergo a media Luna usque ad Solem verum distantia 93 55′ gradus, observataque fuit a vera Luna ad verum Solem graduum 86 15′. Plures igitur Luna secundum verum quam secundum medium motum habebat gradus 7 40′ pro 5 qui sunt secundum primam suppositionem, ad apertumque est, cum iste due observationes in secunda quadratura facte sint, nostram quidem a prima inequalitate gradibus 2 40′ defecisse, Hipparchi autem totidem excessisse. Nam tota etiam inequalitas vim subtrahendi habebat in nostra, in Hipparchi vero addendi, sed ex aliis quoque pluribus observationibus 7 40′ proxime, quando epyciclus prope minimam excentrici longitudinem est, maximam inequalitatis invenimus differentiam.

〈V.4〉 Capitulum IIII: De proportione excentricitatis lunaris circuli

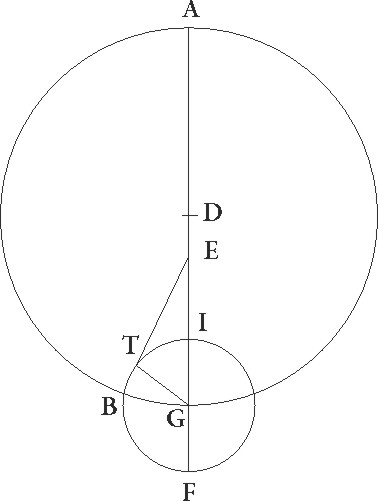Hec cum ita se habeant, sit ABG excentricus Lune circulus, cuius centrum D et diameter ADG, in qua E zodiaci centrum esse supponatur, ita ut A quidem punctum maxima longitudo excentrici sit, G vero minima, describaturque circa centrum G Lune epyciclus FIT FIT] corr. ex fit G et ducatur tangens ipsum linea ETB et coniungatur GT. Quoniam igitur, cum ad tangentem epicyclum lineam Luna pervenerit, maxima inequalitatis differentia fit que demonstrata est graduum esse 7 40′, erit etiam angulus GET, cum sit in centro zodiaci, talium 7 40′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 15 20′. Quare arcus quoque GT talium erit 15 20′ qualium est circulus qui triangulo GET circumscribitur 360, et corda sua GT talium 16 proxime qualium GE diameter 120, quare qualium etiam semidiamiter epicycli GT demonstrata est 5 15′, E vero que est a centro circuli qui per medium signorum est ad maximam excentrici longitudinem 60, talium etiam erit EG que est ab eodem centro ad minimam excentrici longitudinem 39 22′. Quare tota AG diameter erit earundem 99 22′, DA vero que est a centro excentrici 49 41′, ED autem que est inter centra zodiaci et excentrici 10 19′, et sic demonstrata nobis est proportio que ab excentricitate continetur.

〈V.5〉 Capitulum V: De lunaris epicycli declinatione

Sed gratia quidem apparentium in aspectibus coniunctionis coniunctionis] Lunae add et del. A ac oppositionis Lune quadraturarumque ad hec usque circulorum expositorum suppositiones quispiam inveniet. A particularibus autem motibus qui inter has distantias sunt in quibus maxime inter minimam et maximam excentrici longitudinem epicyclus invenitur proprium quidam Lune in declinatione sui epicycli accidere invenimus. Nam cum unum et idem universaliter in in] add. s. l. G epicyclis supponi punctum oporteat, ad quod semper restitutiones eorum que moventur in ipsis fieri necesse sit, quod maximam longitudinem mediam appellamus, unde principia quoque numerorum motus epicycli statuimus, ut punctum F in proposita descriptione. Quod punctum determinatur secundum situm maxime minimeque longitudinis excentricorum a linea, que per omnia centra educitur sicut linnea DEG.

In aliis quidem omnibus simpliciter suppositionibus nihil ex apparentibus obiici posse videmus, propterea quod diameter epicycli que per maximam longitudinem transit, hoc est FGI, in epicyclorum progressibus eundem semper situm conservet linee que centrum eius equaliter circumducit, sicut hic linee EG, declinetque semper, quod certe consequens quispiam arbitrabitur, ad circumductionis centrum in quo in temporibus equalibus equalis motus equales anguli intercipiuntur. In Luna vero apparentia his opponuntur. Nam etiam in progressibus epicycli qui sunt inter A et G diameter FI non dedinat ad E centrum circumductionis, nec eundem situm EG linee conservet. Invenimus enim ad unum quidem et idem AG diametri punctum dictam declinationem semper servari, sed neque ad E centrum zodiaci neque ad D excentrici centrum, sed ad punctum quod ab E versus minima excentrici longitudine tantum distat quanta est linea DE, id ita se habere a pluribus rursum observationibus demonstrabimus, duas tamen exponemus quibus propositum maxime potest declarari, hoc est in quibus in mediis distantiis erat epicyclus et Luna in maxima vel minima eius longitudine. In huiusmodi enim progressibus dictarum declinationum maxima differentia solet fieri.

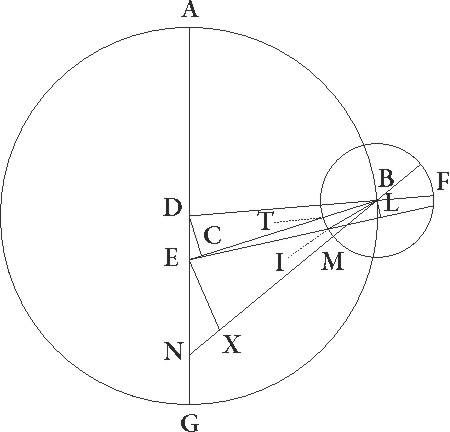Observasse igitur Hypparchus in Rhodo per instrumenta tam Solem quam Lunam conscribit anno 197 a morte Alexandri Pharmuthi secundum Egyptios 11 incipiente hora secunda, et Sol quidem ait perspiciebatur esse in Tauri gradibus 7 45′, Luna vero in Piscium 21 40′, erat autem exacte in 21 28′. In tempore igitur dicto vera Luna distabat a vero Sole ad sucessionem signorum gradibus 313 42′ proxime. Verum quoniam secunda incipiente hora observatio fuit ante meridiem diei undecime horis proxime 5 temporalibus, que in Rhodo tunc faciebant 5 40′ equales proxime, colliguntur a constituto nobis tempore usque ad observationis tempus anni egyptiaci 620 et dies 219 et equales hore simpliciter quidem 18 20′, exacte autem 18 solum. In quo tempore invenimus Solem medium in Tauri gradibus 6 41′, verum autem 7 45′, Lunam vero mediam secundum longitudinem quidem in Piscium gradibus 22 13′, secundum inequalitatem autem a maxima epicycli longitudine media distabat gradibus 22 … gradibus] add. marg. G 185 30′ et sic medie Lune a vero Sole distantia colligitur fuisse graduum 314 28′.

His ita suppositis, sit ABG excentricus Lune circulus cuius centrum D et dyameter ADG in qua sit E centrum zodiaci, et describatur circa B centrum FIT Lune epicyclus, et circunducatur epicyclus quidem ad successionem signorum sicut ex B ad A, Luna vero in epicyclo sicut ex F ad I et T, et coniungantur DB et ETBF. Quoniam igitur in medio tempore menstruo due restitutiones epicycli ad excentricum continentur et in proposita figuratione media Luna 315 32′ gradibus a medio Sole ad successionem signorum distabat, his dupplicatis integroque subtracto circulo, habebimus distantiam epicycli a maxima excentrici longitudine ad successionem signorum factam graduum 271 4′, quare EB quoque angulus reliquarum ad quatuor rectos partium erit 88 56′. Ducatur igitur ex D puncto ad EB lineam perpendicularis perpendicularis] corr. ex pependicularis G DC. Quoniam ergo DEB angulus talium est 88 56′ qualium quatuor recti sunt 360, qualium vero duo recti 360, talium 177 52′, erit etiam arcus DC talium 177 52′, qualium est circulus qui triangulo DEC circumscribitur 360, arcus autem EC reliquarum ad semicirculum 2 8′, quare corde quoque sue DC quidem talium erit partium 119 59′, qualium est DE diameter 120, EC vero 2 14′ eorundem, quare qualium est DE que inter centra est 10 19′ et DB que est a centro excentrici 49 41′, talium etiam est DC rursum 10 19′ proxime, EC autem similiter 0 72′. Et quoniam si quadratum DC auferas a quadrato DB fit quadratum BC, habebimus etiam BC quidem 48 36′ earundem, totam vero BE 48 48′. Rursus quoniam medie Lune a vero Sole distantia graduum erat 314 24′, vere autem Lune sicut observatio demonstrat 313 42′, ut differentia inequalitatis eius subtrahat gradus 0 46′, consideraturque medius Lune motus per lineam EB, supponatur Luna, quoniam in minima epicycli longitudine erat, in I puncto, coniunctisque lineis EI et BI, protrahatur ex B ad EI lineam productam perpendicularis BL. Quoniam igitur angulus BEL inequalitatis lunaris differentiam continet, erit talium quidem 0 46′, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 1 32′, 1 32'​] post corr. G quare arcus quoque BL talium est 1 32′, qualium est circulus qui triangulo EBL circumscribitur 360, et corda sua BL talium 1 36′ ,qualium EB semidiameter est 120, quare qualium est BE quidem linea 48 48′, BI vero que a centro epicycli est 5 15′ talium etiam erit BL linea 0 39′. Qualium igitur est BI que a centro epicycli est 120, talium BL linea erit 14 52′ et arcus per eam subtensus 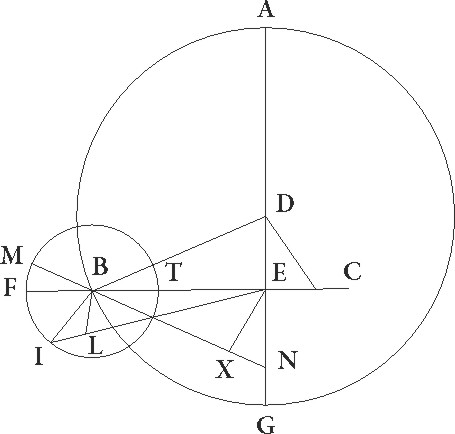talium 14 14′, qualium est circulus qui rectangulo BIL circumscribitur 360. Erit ergo etiam angulus BIL talium 14 14′, qualium duo recti sunt 360, et reliquus EBI earundem quidem 12 42′, 42'] totidem add. et del. G qualium vero quatuor recti sunt 360, talium 6 21′, totidem ergo graduum erit IT arcus epicycli quo distantia que est a Luna ad vere minimam longitudinem continetur. Verum quoniam a media maxima longitudine in tempore observationis 185 30′ gradibus Luna distabat, patet quia media etiam minima longitudo Lunam, hoc est I punctum, precedit.

Sit ergo in puncto M, et protrahatur linea MBN , et a puncto E ad ipsam perpendicularis ducatur EX. EX] post corr. G Quoniam ergo TI arcus 6 21′ graduum demonstratus est, et et] post corr. G IM supponitur esse graduum 5 30′ qui sunt a minima longitudine, ut totus TIM totus TIM] post corr. G colligatur graduum 11 51′, erit etiam angulus EBX talium xi 51′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 23 42′, quare arcus EX talium erit 23 42′, qualium est circulus qui rectangulo BEX circumscribitur 360, ipsa vero EX linea talium 24 39′, qualium est BE diameter 120, quare qualium est ipsa BE linea 48 48 talium etiam erit EX 10 2′. Rursus quoniam EB angulus talium erat 177 52′ qualium duo recti sunt 〈3〉60, 360] 260 A angulus vero EBN 23 42′ earundem, erit etiam reliquus angulus ENB 154 10′ earundem, quare arcus etiam EX talium erit 154 10′ qualium est circulus qui triangulo ENX circumscribitur 360, ipsa vero linea EX talium 116 58′ qualium est EN diameter 120. Qualium ergo est EX quidem linea x 2′, DE autem que est inter centra 10 19′, talium etiam erit EN 10 18′, quare declinatio linee BM per mediam minimam longitudinem ad punctum N facta intercepit lineam EN linee DE proxime equalem.

Verum ut similiter ab oppositis etiam excentrici et epicycli partibus idem evenire ostenderemus, cepimus rursum de de] add. s. l. A distanciis ab Hipparcho in Rhodo observatis eam quam in eodem 157 anno ab Alexandri morte perspexit secundum Egyptios Pauny 17 horis 9 20′. In quo tempore, ut ait, Sol perspiciebatur esse in gradibus Cancri 10 54′, Luna vero in Leonis 29 proxime, totidem etiam exacte obtinebat. In Rhodo enim, cum Luna sit in fine Leonis, post meridiem una proxime hora nullum diversitatis aspectum secundum longitudinem habet. Vera ergo Luna hoc modo distabat a vero Sole ad sucessionem signorum gradibus 48 6′ et quoniam post meridiem diei decimeseptime Pauny 3 20′ horis temporalibus facta observatio fuit, que tunc in Rhodo Rhodo] corr. ex Rhodio G quatuor proxime faciebant equales, fit ex tempore nobis constituto usque ad observationem tempus annorum egyptiacorum 620 et dierum 286 et horarum equalium simpliciter quidem 4, exacte autem 3 40′. In quo tempore similiter invenimus medium Solem in gradibus Cancri 12 5′ et verum 10 40′, mediam vero Lunam secundum longitudinem quidem in Leonis gradibus 27 20′. Quare distantia etiam a media Luna ad verum Solem 46 40′ graduum colligitur, inequalitatis autem a maxima longitudine media epycicli graduum 333 12′.

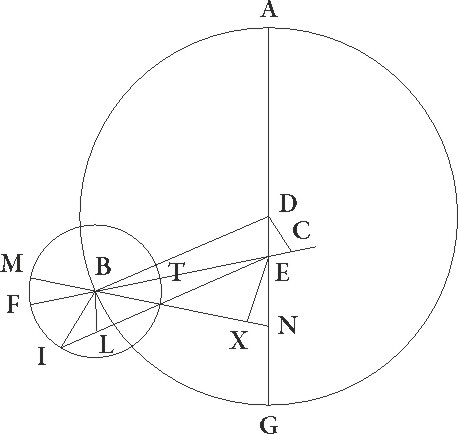His ita suppositis, sit rursum ABG excentricus Lune circulus cuius centrum D et diameter ADG in qua zodiaci centrum sit E, et describatur circa B punctum FIT Lune epicyclus, et protrahantur linee DB et ETBF. Quoniam ergo distantia Lune ad Solem dupplicata dupplicata] corr. ex duplicata A 90 30′ gradus continet, erit profecto per predicta angulus quoque EB talium 90 30′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 181. Si ergo BE lineam produxerimus et ad eam a puncto D perpendicularem DC protraxerimus, fit etiam angulus DEC reliquarum ad duos rectos partium 179, quare arcus quoque DC talium est 179 qualium est circulus qui DEC rectangulo circumscribitur 360, arcus vero EC reliqui ad semicirculum gradus unius. Corde igitur etiam sue DC quidem talium erit 119 59′ qualium est DE diameter 120, EC autem earundem 1 3′. Qualium ergo est DE que inter centra est 10 19′ et BD que est a centro excentrici 49 41′, talium etiam erit DC quidem 10 19′ proxime, EC autem similiter 0 5′. Et quoniam quadratum DC subtractum a quadrato BD facit quadratum BC, habebimus totam BC lineam partium 48 36′ et reliquam EB 48 31′ earundem. Rursum quoniam distantia medie Lune a vero Sole graduum erat 46 40′, vere autem 48 6′, ut differentia inequalitatis addat addat] post corr. G gradus 1 26′, supponatur Luna que iuxta maximam epicycli longitudinem erat esse in I puncto, tractisque lineis EI et BI, producatur ex puncto B ad lineam EI perpendicularis BL. Quoniam ergo BEL angulus talium est 1 26′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 2 52′, erit etiam arcus BL talium 2 52′ qualium est circulus qui hortogonio BEL triangulo circumscribitur 360, ipsa vero linea BL talium 2 59′ qualium est EB diameter 120, quare qualium EB est 48 31′, BI autem que a centro epicycli 5 15′, talium etiam erit BL linea 1 12′. Qualium ergo BI diameter est 120 talium, etiam erit BL 27 34′, arcus autem suus talium 26 34′ qualium est circulus qui BIL triangulo circumscribitur 360. Quare angulus quoque BIL talium erit 26 34′ qualium duo recti sunt 360, totus vero angulus FBI earundem quidem 29 26′, qualium vero quatuor recti 360, talium 14 43′. Totidem ergo est graduum IF epicycli arcus quo distantia a Luna ad exactam veramque maximam longitudinem continetur.

Verum quoniam in tempore observationis 333 12′ a media maxima longitudine distabat, si hanc mediam maximam longitudinem in M puncto esse supposuerimus et lineam MBN coniunxerimus et ad ipsam a puncto E perpendicularem EX deduxerimus, erit totus quidem arcus IFM reliquorum ad semicirculum graduum 26 48′, reliquus vero FM graduum 12 5′. Quare angulus etiam MBF, hoc est EBX, talium est 12 5′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 24 10′ et arcus quidem EX talium erit 24 10′ qualium est circulus qui BEX triangulo circumscribitur 360, ipsa vero EX linea talium 25 7′ qualium est diameter BE 120. Qualium ergo est BE quidem linea 48 31′, DE autem que inter centra est 10 19′, talium etiam erit EX 10 8′. Rursus quoniam angulus EB 181 talium esse suppositus est qualium duo recti sunt 360, angulus vero EBN demonstratus est esse 24 10′, ut reliquus etiam ENB earundem relinquatur 156 50′, fit ut et arcus EX talium sit 156 50′ qualium est circulus qui ENX triangulo circumscribitur 360, ipsa vero linea EX talium 117 33′ qualium est diameter EN 120. Qualium ergo est EX quidem linea 10 8′, DE autem que est inter centra 10 19′, talium etiam erit EN 10 20′. Quare hinc etiam patet quod declinatio MB linee per M punctum medie longitudinis maxime ad N punctum facta intercepit rursus EN lineam equalem proxime DE linee que inter centra est.

Sed ex aliis etiam observationibus quam pluribus easdem proxime proportiones colligi adinvenimus, ita ex his proprium lunaris suppositionis declinatio epicycli esse confirmatur, ut circumductio quidem centri epicycli circa E centrum circuli qui per medium signorum est fiat. Diametri vero que hoc ipsum et punctum medie longitudinis maxime epicycli disseparat non ad E centrum equalis circumductionis sicut in aliis, sed semper ad N per equalem linee DE que inter centra est ad alteram partem distantiam.

〈V.6〉 Capitulum VI : Quomodo per lineas a motibus periodicis verus Lune motum invenitur

His ita demonstratis, iam consequens est dicere, quo pacto, in particularibus Lune progressibus mediorum motuum captis captis] corr. ex capitis G locis, et a numero distantie et a numero qui est secundum epicyclum Lune additionem aut subtractionem eius eius] post corr. G inveniemus differentie, differentiae] post corr. G que penes inequalitatem colligitur queque medio secundum longitudinem progressui apponitur. Per lineas igitur a similibus theorematibus huius rei cognitionem accepimus.

Si enim exempli gratia in ultima prepositarum descriptionum eosdem periodicos motus distantie inequalitatisque supposuerimus, idest distantie quidem gradus 90 30′ qui per dupplicationem colligebantur, inequalitatis vero a media longitudine maxima epicycli gradus 333 12′ et pro EX et BI perpendicularibus perpendiculares NX et IL protraxerimus per eadem similiter, quoniam dati sunt anguli qui sunt ad E centrum et quoniam DE et EN linee equales sunt, utraque linearum DE et NX talium 10 19′ proxime demonstrabitur, qualium est DB que est a centro excentrici 49 41′ et BI que est a centro epicycli 5 15′, utraque vero linearum EC et EX 0 5′ earumdem, et propterea BC quidem tota erit, sicut demonstravimus, earundem 48 36′, BE autem similiter 48 31′ et BX reliquarum 48 26′. Quare quoniam quadrata BX et XN composita faciunt quadratum BN, hanc etiam habebimus talium 49 49] post corr. G 31′ qualium erat linea NX 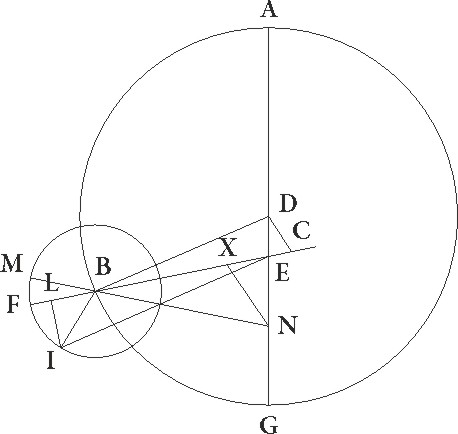10 19′. Qualium ergo est BN diamenter 120, talium etiam erit erit] post corr. G linea NX 25 proxime et arcus suus talium 24 3′ qualium est circulus qui hortogonio triangulo BNX circumscribitur. 360, quare angulus etiam NBX, idest FBM, talium erit 24 3′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 12 1′ proxime. Tot ergo graduum est arcus epicyli FM.

Verum quoniam I punctum Lune distat ab M media longitudine maxima 26 48′ reliquis ad unum circulum gradibus, habebimus etiam IF reliquum arcum graduum 14 47′, quare angulus quoque IBF talium erit 14 47′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 29 34′, et arcus IL talium 29 34′ et … 34'​] iter. A (and then deleted by G) qualium circulus qui rectangulo IBL circumscribitur 360, arcus vero LB reliquorum ad semicirculum 150 26′, quare corde quoque sue IL quidem talium erit 30 34′ qualium est BI diameter 120, LB autem 116 2′ earundem. Quare qualium BI quidem que est a centro epicycli est 5 15′, BE autem 48 31′ demonstrata, talium erit IL quidem 1 20′, LB vero similiter 5 5′. Quare tota etiam EBL talium erit 53 36′, qualium LI erat 1 20′. Et quoniam, si componantur que ab ipsis fiunt, reddunt quadratum linee EI, habebimus etiam ipsam EI earundem esse per longitudinem 53 37′ proxime. Quare qualium est ipsa EI diameter 120, talium etiam erit IL 2 59′ et arcus suus talium 2 52′ qualium est circulus qui EIL rectangulo circumscribitur 360. Quare angulus etiam IEL differentie penes inequalitatem talium est 2 52′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 1 26′, quod erat demonstrandum.

〈V.7〉 Capitulum VII : Expositio universalis tabule lunaris inequalitatis

Verum ut rursus per tabularem expositionem paratam particularium additionum subtractionumve cognitionem pre oculis poneremus, tabulam suppositionis simplicis iam habitam adimplevimus ordinibus additis quibus dupplex quoque inequalitas emendatur, usique sumus sumus] summus A similiter linearum doctrina. Post igitur duos ordines primos quibus numeri continentur, tertium ordinem connexuimus qui additiones subtractionesque continet numero inequalitatis, sic correspondentes, ut qui a media longitudine maxima, hoc est a puncto M, per medios progressus colligitur ad veram longitudinem maximam, idest ad punctum F, traducatur. Nam quemadmodum in proposita 90 30′ graduum distantia FM arcus 12 1′ graduum nobis demonstratus est, ut Lune, que 333 12′ gradibus ab M media longitudine maxima distabat, distantiam ab F vera longitudine maxima 345 13′ graduum colligi ostenderemus, per quos invenitur additio subtractiove que per epicylum facta medio secundum longitudinem motui apponitur, sic et in aliis distantie numeris eodemmodo quantitates additionis atque subtractionis per tot partes cepimus, per quot mediocriter commodeque fieri putavimus, accomodavimusque per tertium ordinem singulis numeris. Quartus deinde ordo expositas iam in prima tabula differentias inequalitatis que penes epicyclum est continebit quarum differentiarum maxima ad 5 1′ gradus gradus] quoque add. A (then deleted by G) proxime secundum proportionem 60 ad 5 15′ pervenit. Quintus autem ordo excessus differentiarum prime secundeque inequalitatis continebit, colligeturque maxima etiam etiam] add. s. l. A hic additio vel subtractio graduum 7 40′ secundum proportionem 60 ad 8, ita quartus ordo est positionis epicycli in maxima excentrici longitudine, que quidem positio fit in oppositionibus atque coniunctionibus, quintus vero collectorum excessuum ex inequalitate facta in quadraturis iuxta minimam excentrici longitudinem.

Verum ut partes excessuum proportionaliter pertinentes ad motus epicycli qui sunt inter duas huiusmodi positiones capiantur, sextum etiam addidimus addidimus] corr. ex addimus G ordinem quo sexagesime ille continentur quas per singulos distantie numeros apposite differentie captas prime additioni subtractionive, que penes primam inequalitatem in ordine quarto est, semper oportet addere: hec nobis sic adinventa sunt.

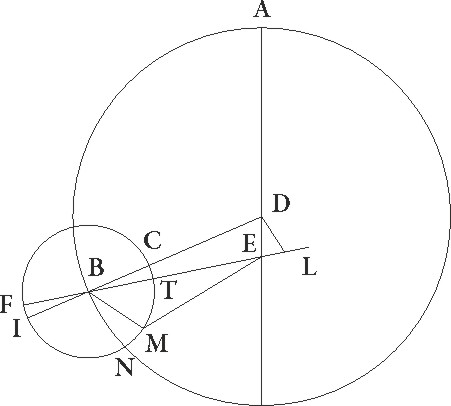Sit enim ABG Lune rursum excentricus cuius centrum D et diameter ADG in qua centrum zodiaci sit E et intercepto arcu AB describatur circa B punctum FIT epicyclus, et coniungatur linea EBF, deturque verbi gratia distantia graduum 60, ut similiter, sicut in superioribus, EB angulus duplicatorum graduum distantie sit 120, deducaturque ex D puncto ad BE lineam productam perpendicularis DL, et et​] add. s. l. G coniungatur linea BCD, et supponatur linea producta a centro E ad Lunam epicyclum tangere, ut maxima differentia inequalitatis fiat, sitque linea EMN, et coniungatur linea BM. Quoniam igitur EB angulus talium supponitur esse 120, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 240, erit etiam angulus DEL reliquorum ad duos rectos 120. Quare arcus etiam DL talium erit 120 qualium est circulus qui DEL rectangulo circumscribitur 360, arcus vero EL reliquorum ad semicirculum 60, corde quoque sue EL quidem talium 60 qualium DE diameter 120, DL vero 103 55′ earundem. Quare qualium est DE linea 10 19′ et DB similiter 49 41′, talium erit etiam EL linea 5 10′ proxime, DL autem similiter 8 56′. Et quoniam, si a quadrato linee BD quadratum DL subtraxeris, redditur quadratum BL, erit tota BL linea 48 53′ secundum longitudinem, longitudinem] between longitu and dinem talium qualium add. et del. A et reliqua EB 43 43′ talium qualium est MB que est a centro epicycli 5 15′. Qualium igitur est EB diameter 120, talium erit BM linea 14 25′, et arcus suus 13 48′ talium qualium est circulus qui BEM rectangulo cirumscribitur 360. Quare angulus etiam BEM quo maxima inequalitatis differentia continetur talium erit 13 48′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 6 54′. Differt ergo in hoc distantie spatio inequalitatis differentia gradibus 1 53′ a gradibus qui a maxima longitudine colliguntur 5 1′. Est autem tota usque ad minimam longitudinem differentia graduum 2 39′. Qualium ergo est maxima differentia 60, erit etiam differentia graduum 1 53′ talium sexagesimarum 42 38′, quas et apponimus in sexto ordine ad numerum distantie 120.

Similiter in reliquis etiam partibus computantes rursum eodem modo cepimus duarum inequalitatum excessum et apposuimus ad convenientes numeros sexagesimas que unicuique congruunt, totum vero numerum 60 numero distantie 90 graduum duplicate necessario accommodavimus qui est in gradibus 180 minime excentrici longitudinis. Septimum etiam addidimus addidimus] corr. ex addimus G ordinem quo progressus Lune secundum latitudinem ad utranque circuli qui per medium signorum est partem, sicut in circulo qui per polos eius est, continentur, hoc est intercepti huius circuli arcus inter circulum qui per medium signorum est et obliquum Lune circulum cuius centrum ipsum idem est per singulos particularesque in obliquo progressus, usique sumus etiam ad hoc eadem demonstratione per quam etiam arcus computavimus qui sunt inter equinoctialem et circulum qui per medium signorum est eius circuli qui est per polos equinoctialis ipsius, sic tamen ut hic inter circulum qui per medium signorum est et borealem aut australem obliqui circuli terminum arcus circuli qui maximus per utrosque polos ipsorum describitur 5 graduum sit. Nam et nobis, sicut et Hypparco, computantibus per apparentia borealissimorum atque australissimorum progressuum, tantus proxime ad utranque zodiaci partem maximus Lune progressus inventus est. Omnia etiam fere que in observationibus Lune videmus sive per stellas sive per instrumenta captis his maximis secundum latitudinem progressibus ad unguem conveniunt, sicut per ea que postea demonstrabimus confimabitur. Est autem tabula inequalitatis Lune universaliter talis.

Tabula universalis inequalitatis Lune Headings entirely corrected by George of Trebizond

〈V.9〉 Capitulum VIIII : De universali calculo lunari

Quandocunque igitur lunaris inequalitatis per hanc tabulam computationem facere voluerimus, capiemus medios Lune motus longitudinis, distantie, distantiae] in add. et del. A inequalitatis, ac denique latitudinis in proposito tempore in Alexandria modo iam pridem dicto. Denique duplicatum distantie numerum, integris inde subtractis circulis, queremus in tabula inequalitatis et correspondentes ipsi gradus in ordine tertio, si numerus dupplicatus usque ad 180 gradus fuerit, addemus inequalitatis medie gradibus, sin vero ultra 180 est, subtrahemus ab ipsis, et hunc exactum inequalitatis numerum rursus in eadem tabula queremus et quod ipsi correspondet in ordine quarto seorsum scribemus et similiter differentiam que est in ordine quinto. Postea ipsum dupplicatum numerum numerum] add. marg. G medie distantie nimirum in eisdem ordinibus queremus, et quot apponuntur in sexto ordine sexagesime, tot sexagesimas eius differentie sumentes quam seorsum scripsimus illi semper addemus quam in quarto inventam ordine seorsum posuimus, collectosque hinc gradus, si vere inequalitatis numerus 180 gradus non excedit, subtrahemus a gradibus mediorum motuum longitudinis atque latitudinis, sin autem excedit, addemus, et collectos numeros longitudinis quidem a gradibus constituti longitudinis loci computabimus et Lune verum motum ibi esse dicemus, latitudinis autem a boreali termino in eadem tabula queremus et gradus in ordine septimo conscriptos capiemus, totque gradibus dicemus Lune centrum a circulo per medium signorum distare in maximo circulo per polos eius descripto, ad septentereonem quidem, si numerus quo intravimus in primis 15 versibus invenitur, sin vero in sequentibus, ad meridiem, ita ut primus numerorum ordo progressum Lune qui est a septentrione ad meridiem contineat, secundus vero econtra ex meridie ad septentrionem.

〈V.10〉 Capitulum X: Quod nulla differentia de qua curandum sit fiat in coniunctionibus atque oppositionibus penes excentricum Lune circulum

Verum quoniam dubitare aliqui possent, ne forte in coniunctionibus etiam ac oppositionibus et in eclipsibus que in ipsis accidunt digna cure differentia etiam propter excentricum Lune circulum accidat, propterea quod in ipsis non semper in ipsa maxima longitudine centrum epicycli epicycli] corr. ex epicicli G precise inveniatur, sed possit ab eo satis magno arcu distare, cum situs qui in ipsa maxima longitudine sunt in mediis coniunctionibus et oppositionibus fieri perspiciantur, vere autem coniunctiones atque oppositiones simul cum inequalitate utriusque luminarium capiantur, conabimur ostendere nullum errorem de quo curandum sit iuxta apparentia hinc accidere, etiam si omnino differentia excentrici circuli negligatur.

Sit igitur ABG excentricus Lune circulus cuius centrum D et diameter ADG in qua centrum zodiaci sit E, et oppositum D puncto sit F punctum declinationis, et intercepto ab A maxima longitudine arcu AB, describatur circa B epicyclus ITCL, et coniungantur BD et IBCE et BLF. Quoniam ergo duobus modis magnitudo inequalitatis que accidit propter epicycli in A maxima longitudine situm differentiam facere potest, vel quoniam propiquior terre factus maiorem angulum in E centro constituat, vel quoniam diameter in media longitudine maxima et in minima similiter non ad E centrum, sed ad F punctum flectatur, fuitque maxima propter primam causam differentia, quando etiam penes inequalitatem Lune maxima differentia est, propter secundam autem, autem] quoniam add. et del. A quando in maxima vel minima epicycli longitudine longitudine] est add. et del. A Luna est, patet quia, quando maxima differentia penes primam causam accidit, tunc que penes secundam fiebat 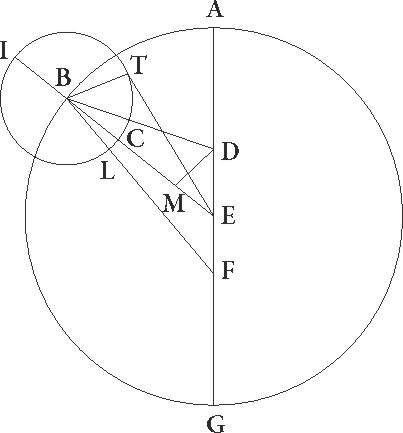insensibilis omnino est. Nam cum Luna in tangentibus epicyclum lineis sit, additionem subtractionemve valde indifferentem facit. Fieri autem potest ut oppositio vera coniunctiove utraque inequalitatis differentia utriusque luminarium a media differat, si altera subtrahitur altera additur. Quando vero differentia que propter declinationem accidit maxima est, tunc contra differentia que penes primam causam provenit insensibilis est. Nulla enim inequalitatis vel brevis omnino differentia fit, quando Luna in maxima vel minima epicycli longitudine invenitur. Sed oppositio vera coniunctiove sola differentia que penes solarem inequalitatem capitur a media differet. Supponatur igitur 2 23′ maxime differentie gradus Solem addere, Lunam vero primum etiam ipsam 5 1′ maxime differentie gradus gradus] Solem addere Lunam vero primum etiam add. et del. A subtrahere, ut angulus EB ad utriusque differentie 7 24′ duplices gradus 14 48′ contineat, productaque ab E puncto linea ET que epicyclum tangat, trahatur perpendicularis BT, et similiter a puncto D ad lineam BE perpendicularis DM deducatur. Quoniam ergo angulus EB talium est 14 48′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 29 36′, erit profecto etiam arcus DM talium 29 36′ qualium est circulus qui DEM rectangulo circumscribitur 360. Arcus vero EM reliquorum ad semicirculum 150 24′. Corde igitur etiam sue DM quidem talium erit 30 31′ qualium est DE diameter 120, EM autem 116 1′ earundem. Quare qualium etiam est DE que inter centra est est​] D add. et del. A 10 19′, BD vero que est a centro excentrici 49 41′, talium quoque erit DM quidem 2 38′, EM autem 9 59′. Similiter et quoniam, si a quadrato BD linee subtraxeris quadratum DM, relinquitur relinquitur] post corr. G quadratum linee BM, fit etiam linea BM 49 37′ et linea BME tota talium 59 36′ qualium etiam est BT que est a centro epicycli 5 15′. Qualium Qualium] est add. et del. A ergo est diameter EB 120, talium etiam erit BT linea 10 34′ et arcus suus talium 10 6′ qualium est circulus qui BET rectangulo circumscribitur 360. Quare EBT maxime inequalitatis differentie angulus talium erit 10 6′ qualium duo recti sunt 360, qualium vero 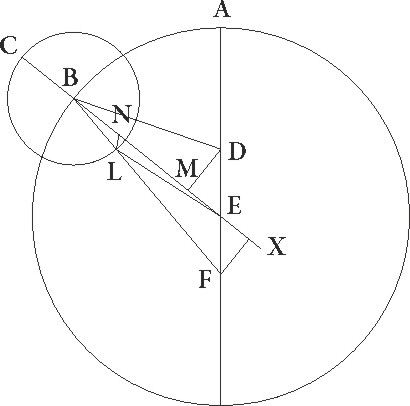quatuor recti sunt 360, talium 5 3′ pro 5 1′, que fiunt cum epicyclus in A maxima longitudine sit. Inequalitatis ergo differentia duabus sexagesimis unius gradus propter hanc causam differt, quibus ne sextadecima quidem unius hore pars continetur.

Supponatur rursum Luna esse in L media longitudine minima, ut angulus EB duplices solaris inequalitatis gradus 4 46′ contineat, et coniuncta in simili descriptione linea EL, deducantur ab L quidem puncto perpendicularis LN, ex puncto autem D perpendicularis DM, ab F autem puncto ad lineam BE protractam perpendicularis FX. Similiter ergo quoniam angulus qui est in E talium est 4 46′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 9 32′ erunt etiam utrique arcus DM et FX talium 9 32′ qualium sunt circuli qui rectangulis EDM et EFX circumscribuntur 360, et uterque similiter arcus EM et EX reliquorum ad semicirculos 170 28′. Corde igitur etiam sue DM quidem et FX utraque talium erit 9 58′ qualium est utraque diameter DE et EF 120, utraque vero linea ME et EX 119 35′ earundem. Quare qualium est utraque linearum DE et EF 10 19′, DB autem que est a centro excentrici 49 41′, talium etiam erit utraque DM et FX linea 0 51′, utraque vero ME et EX 10 17′ earundem. Et quoniam, si a quadrato linee BD subtraxeris quadratum linee DM , relinquitur quadratum linee BM, erit etiam ipsa BM per longtudinem 49 41′ earundem proxime. Quare BE quoque linea erit 59 58′ et BX tota talium 70 15′, qualium linea FX erat 0 51′, et propter hoc etiam BF que angulo recto subtenditur erit 70 15 proxime. Est autem sicut BF ad utranque linearum FX et BX, sic BL ad utranque LN et BN. Quare qualium est BL que est a centro epicycli 5 15′ et BE 59 58′, ut demonstratum est, talium etiam erit LN 0 4′ et BN earundem 5 15′ proxime. Reliqua vero NE talium 54 43′ qualium erat LN 0 4′. Verum quoniam propter exposita EL etiam qua rectus subtenditur angulus non differt ab eisdem 54 43′, colligitur hinc quod, qualium etiam est ipsa EL diameter 120, talium erit linea LN 0 8′ proxime, et et] post corr. G arcus suus talium rursus 0 8′ qualium est circulus qui rectangulo ELN circumscribitur 360. Quare angulus quoque BEL quo Luna differt penes declinationem ad F talium erit 0 8′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 0 4′. Ita etiam hic quatuor sexagesimis differentia penes inequalitatem Lune differt, que nullum errorem de quo curandum sit in apparentibus coniunctionis appositionisque faciunt, cum vix octavam unius hore partem colligere possint, quantum in ipsis etiam observationibus sepius errare mirum non est.

Hec diximus, non quia possibile non sit has etiam differentias, quamvis minime sint, in oppositionibus et coniunctionibus computare, sed quia ostendere voluimus voluimus] corr. ex volumus G non commisisse nos in expositis lunarium eclipsium demonstrationibus errorem sensibilem, propterea quod non sumus usi excenticitatis ratione quam adimplevimus postea.

〈V.11〉 Capitulum XI : De aspectibus diversitatis Lune

Hec ferme sunt que ad inveniendos veros Lune progressus adhibentur. Verum cum accidat ut neque ad sensum quidem apparens Lune progressus idem cum vero sit, quoniam terra non sit, ut diximus, quasi punctum ad distantiam orbis eius, consequens necessariumque profecto est cum aliorum apparentium causa tum maxime illorum que in solaribus apparent eclipsibus de diversitate aspectuum eius dicere, unde poterimus per veros progressus qui ad terre et zodiaci circuli centrum intelliguntur eos qui sunt a visu cernentium, hoc est qui ab aliqua terre superficie aspiciuntur, diiudicare, et contrarium rursus veros ab apparentibus. Cum autem ad hanc considerationem sequatur ut nec particulares diversitatis aspectuum quantitates possint inveniri, nisi distantie proportio detur, nec distantie proportionis, nisi aliquis diversitatis aspectus habeatur, in iis quidem que nullum diversitatis aspectum sensibilem habent, ad que videlicet terra quasi punctum est distantie proportionem capere possibile non est, in iis autem in quibus diversitas aspectuum est, sicut in Luna, solummodo fit ut diversitate aliqua primum aspectus habita distantie proportio inveniatur, propterea quod diversitas huiusmodi etiam per se ipsam per observationes accipitur, distantie vero quantitatis minime, quamvis Hypparcus a Sole id conetur invenire. Nam quoniam a quibusdam aliis Soli Luneque accidentibus de quibus postea verba faciemus sequitur, data unius luminaris distantia, alterius etiam distantiam dari, ideo conatur quasi per coniecturas habita Solis distantia Lune distantiam demonstrare, et primo quidem minimum sensibilem diversitatis aspectum in Sole fieri supponit, ut hinc distantiam eius capiat. Deinde per eclipsim etiam quam exponit, modo quasi nullus sensibilis sit in Sole diversitatis aspectus, modo quasi magnus sit verba facit, unde proportiones quoque distantie Lune diverse secundum varietatem suppositionum inventas sibi videmus, cum dubium de Sole penitus sit, non solum quantum diversitatis aspectum habeat, verum etiam si omnino aliquem habeat.

〈V.12〉 Capitulum XII : De constructione instrumenti quo aspectus diversitas capitur

Nos vero, ne aliquid in hac consideratione incerti assumemus, instrumentum construximus quo quam exactissime observari potest quantum et a quanta distantia verticis aspectus Lune variatur in maximo circulo qui per polos orizontis et Lune Lunae] piscius add. et del. A ipsius describitur.

Duas enim regulas quadrilateras fecimus non minores per longitudinem quatuor cubitis, ut plures possint in eis partes signari, crossitudine mediocres, ne propter longitudinem flectantur, sed optime recteque per quodlibet latus tendantur. Deinde rectas descripsimus lineas per medium latioris lateris utriusque regule, addidimusque in utrisque extremitatibus alterius regule tabellas quadratas rectas in ipsa media linea equales atque paralellas, quarum utraque in medio exactum habet foramen, alterum minus ad quod visus accomodatur, alterum quod ad Lunam est ita maiusculum, ut, cum unus oculus tabelle que minus habet foramen apponatur, possit per alterum foramen foramen​] post corr. G recte oppositum tota perspici Luna. Equaliter igitur utranque regulam per medium linearum in extremitatibus alterius iuxta tabellam que maius foramen habet perforavimus perforavimus] post corr. G et clavum ita per utrasque inmissimus, ut et regularum latera que ad lineas sunt quasi a centro ab ipso connecterentur et regula que tabellas habet recte possit undique circunduci, circunduci] post corr. G alteram vero que tabellas non habet in basi sua firmavimus, deinde in media utriusque linea ad extremitates iuxta basim puncta cepimus equaliter et quam plurimum a centro quod est in clavo distantia, lineamque regule basim habentis determinatam in 60 partes partiti sumus, harumque quamlibet in quam plures potuimus portiones. Apposuimus autem post hanc ipsam regulam ad extremitates paxillos ad earundem partium latera in eadem linea recta inter se positos positos] post corr. G et equaliter ab eadem media linea undique distantes, ut perpendiculum per ipsos dependens possit regula recta et indeclinabilis ad orizontis superficiem collocari, captaque meridiana linea et in paralella orizontis superficie protracta, instrumentum in loco non tenebroso rectum ita statuimus, ut regularum latera quibus inter se ipsas a clavo connectuntur ad meridiem converterentur, paralellaque fierent linee meridiane iam capte et regula que basim habet recta absque ulla declinatione ac firmiter staret, altera vero mediocriter clavo cohartata in superficie meridiani circumducetur. Apposuimus autem etiam aliam regulam parvulam subtilem et rectam acommodatam parvo clavo ad extremitatem divise linee iuxta basim, ita ut circumducatur que pervenire possit usque ad maximam remotionem equaliter distantis extremitatis linee alterius regule, ut quando circumducitur possit ostendere distantiam que inter duas extremitates facta est.

Deinde hoc modo Lune observationes in progressibus qui fiunt in ipso meridiano et iuxta solstitialia puncta circuli qui per medium signorum est faciebamus. Circuli enim qui in huiusmodi habitudine per orizontis et centri Lune polos maximi describuntur iidem proxime fiunt illis qui per polos polos] corr. ex pollos G zodiaci describuntur, ad quos progressus lunaris latitudinis perspiciuntur et vera a puncto verticis distantia per hoc per se ac facile potest haberi. Moventes igitur regulam que tabellas habet ad Lunam in ipsis meridianis progressibus, donec per utraque foramina per medium maioris foraminis centrum eius perspiceretur, et notantes in tenui regula distantiam que fit inter extremitates linearum que in regulis sunt et ipsam distantiam conferentes cum linea recte regule que in 60 partes fuit divisa, invenimus quot portionum est linea predicte distantie talium qualium est que est a centro circuli qui a circumductione in meridiani superficie describitur 60, captoque arcu qui per tantam subtenditur lineam, habebamus perspectum Lune centrum a puncto verticis per hunc arcum distare in circulo qui per polos orizontis et ipsius maximus describitur qui tunc idem etiam meridiano fiebat qui meridianus per equinoctialis polos et zodiaci describitur.

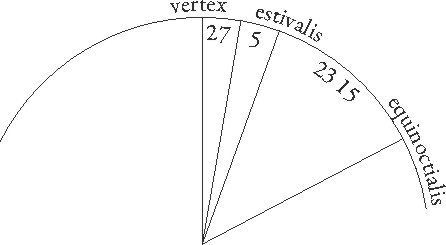Ut igitur maximum Lune latitudinis progressuum quam exactissime sciremus, usi tunc hac perspectione instrumentali sumus, quando maxime in estivali tropico ipsa fuit fuit] add. s. l. G et ad hec in ipso obliqui circuli borealissimo termino, tum quasi in his punctis per satis magnam distantiam idem secundum sensum Lune progressus determinatur, tum quia, cum Luna ad ipsum verticis punctum proxime tunc pervenisset, eundem proxime in Alexandrie paralello, ubi observationes nobis facte sunt, apparentem situm cum vero faciebat. Inveniebatur igitur in huiusmodi progressibus centrum Lune semper a puncto verticis distare duobus gradibus et octava proxime parte unius gradus, ut etiam per hanc investigationem quinque graduum maximus eius secundum latitudinem ad utranque circuli partem qui per medium signorum est progressus esse demonstretur, quibus fere fere] post corr. G qui sunt a puncto verticis ad equinoctialem in Alexandria demonstrati gradus 30 58′ excedunt eos qui sunt ab equinoctiali ad estivalem tropicum gradus 23 51′, duobus et octava inde parte subtracta.

Verum ut ut] post corr. G etiam considerationem diversitatis aspectuum faceremus, observabamus rursum eodem modo Lunam, cum in brumali puncto tropico esset, partim propter predicta, partim quia cum maxime tunc sicut in simili in meridiano progressu a puncto verticis distet, diversitatem etiam aspectus maiorem facilioremque cognitu facit. Sed a pluribus diversitatis aspectibus quos in huismodi progressibus observavimus unum rursus exponemus per quem et modum computationis aperiemus et reliquorum demonstrationem consequenter ad futura faciemus.

〈V.13〉 Capitulum XII〈I〉: Lunarium distantiarum demonstratio

Observavimus igitur in vigesimo Andriani anno Athyr secundum Egyptios 13 post meridiem horis equalibus 5 50′, Sole iam occidente, Lunam in meridiano fuisse, perspiciebaturque nobis per instrumentum gradibus 50 55′ a puncto verticis centrum eius distare. Distantia enim que in tenui regula fuit talium erat 51 35′ qualium circulus est 360. Sed a tempore constituto a primo Nabonasari anno usque ad expositam observationem tempus annorum est egyptiacorum 882 et dierum 72 et horarum equalium simpliciter quidem 5 50′, exacte vero 5 20′. In quo tempore Solem invenimus medie quidem in gradibus Libre 7 31′, exacte vero 5 28′, Lunam autem medie medie] corr. ex mediae G in Sagitarii gradibus 25 44′ et distantiam graduum 78 13′, gradus autem a media longitudine maxima epiycli 262 20′, a boreali vero latitudinis termino gradus 254 40′. Quapropter differentia etiam inequalitatis undique diligenterque collecta 7 26′ gradus addebat. Sic itaque verus etiam Lune situs ea hora obtinebat per longitudinem quidem Capricorni gradus 3 10′, per latitudinem autem in obliquo quidem circulo a boreali termino gradus 2 6′, in eo autem qui est per polos zodiaci qui idem proxime cum cum] in add. et del. G meridiano tunc erat a circulo qui per medium signorum est ad septentrionem gradus 4 59′. Distant autem Capricorni quidem gradus 3 10′ ab equinoctiali ad meridiem in eodem circulo gradibus 23 49′, equinoctialis vero a puncto Alexandrini verticis ad meridiem similiter gradibus 30 58′. Quare centrum Lune Lunae] post corr. G distabat exacte a puncto verticis gradibus 49 48′ et perspiciebatur distare 50 55′. Luna ergo secundum distantiam progressus expositi unius gradus et septem sexagesimarum diversitatis aspectum habuit in circulo maximo qui per polos orizontis et ipsam describitur, cum exacte a puncto verticis gradibus 49 48′ distaret.

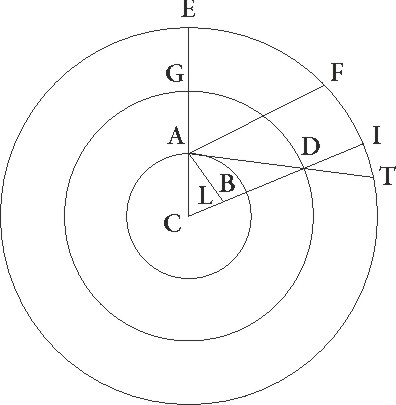His hoc modo expositis, describantur in superficie illius qui per polos Lune ac orizontis est maximi circa idem centrum circuli terre quidem maximus circulus AB, circulus vero per centrum Lune in observatione GD, et ille ad quem terra quasi punctum est FIT, sitque commune omnium centrum punctum C, et sit linea que per puncta verticis transit CAGE, et supponatur Luna esse in puncto D distans exacte a G puncto verticis expositis gradibus 49 48′, et coniungantur linee CDI et ADT, et ad hec a puncto A quo visus perspicientium est deducantur perpendicularis quidem ad lineam CB linea AL, equidistans vero linee CI linea AF. Perspicuum igitur est quod Luna per arcum IT aspectum ex A perspicientium inmutavit. Erit igitur hic arcus gradus unius et sexagesimarum septem, ut per observationem perspeximus, sed quoniam FT arcus insensibili differentia maior est quam arcus TI, propterea quod tota terra quasi punctum est ad EFIT circulum, erit etiam arcus FIT eorundem 1 7ʹ proxime. Quare angulus quoque FAT, quoniam rursus A punctum non habet sensibilem differentiam, sed quasi centrum est ad circulum FT talium erit 1 7′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 2 14′. Est autem isti equalis angulus ADL eorundem 2 14′, erit ergo arcus AL talium 2 14′ qualium est circulus qui ADL rectangulo circumscribitur 360, ipsa vero linea AL talium 2 21′ qualium est AD diameter 120. Sed hac indifferenter LD linea minor est, quare qualium est LA linea 2 21′, talium etiam erit LD linea 120 proxime. Rursus quoniam GD arcus graduum esse supponitur 49 48′, erit etiam GED angulus qui est in centro circuli talium 49 48′ qualium quatuor recti sunt 360, qualium vero duo recti sunt 360 talium 99 36′. Quare arcus etiam AL talium est 99 36′ qualium est circulus qui ALC rectangulo circumscribitur 360, arcus vero LC reliquorum ad semicirculum 80 24′. Ergo corde quoque sue AL quidem talium erit 99 31′ qualium est AC diameter 120, LC autem earundem 77 27′. Quare, si posuerimus AC lineam que est a centro terre esse unius qualis ipsa unius est talium erit AL 0 46′ et CL similiter 0 39′, sed qualium erat AL linea 2 21′, talium LD linea fuit demonstrata esse 120. Quare qualium est AL linea 0 46′, talium erit etiam linea LD 39 6′. Erat autem etiam earundem CL quidem linea 0 39′, CA vero que est a centro terre unius. Quare qualis unius est CA que est a centro terre talium etiam erit CLD tota que 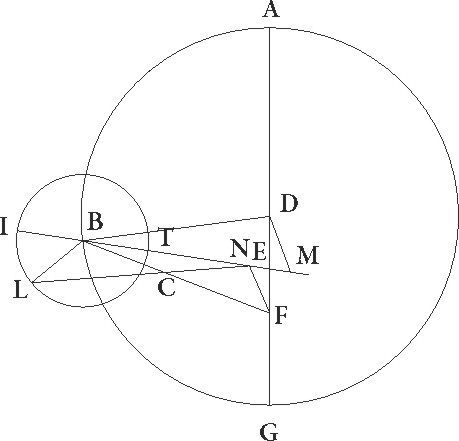Lune distantiam in ea observatione continebat 39 45′. 45'] Arcus AB capiatur maior aliquantulum et fiet figura medius similiter dictus IL maior adeo ut angulus TBL fit rectus add. marg. A (commentary to the diagram)

His ita ita] add. s. l. G demonstratis, sit ABG excentricus Lune circulus cuius centrum D et diameter ADG, in qua capiatur E punctum pro centro circuli qui per medium signorum est, et F pro declinationis declinationis] post corr. G epicycli puncto, descriptoque circa B punctum ITCL epicyclo, coniungantur linee IBTE et BD et BCF, supponaturque Luna in exposita observatione fuisse in puncto L, et coniungantur linee LE et LB, deducanturque ad BE lineam productam ex D quidem puncto perpendicularis DM, ex F autem perpendicularis FN. Quoniam igitur in tempore observationis distantie graduum numerus erat 78 13′, erit etiam propter predicta angulus quidem EB talium 156 26′ qualium quatuor recti sunt 360, uterque vero angulus FEN et DEM reliquarum ad duos rectos 23 24′, qualium vero duo recti sunt 360, talium 47 8′, quare arcus quoque uterque DM et FN talium erit 47 8′, qualium sunt circuli qui rectangulis dictis circumscribuntur 360, propterea quod equalis est linea DL linee EF, arcus vero uterque EM et EN 132 52′ eorundem. Quare corde etiam sue utrique DM et FN talium sunt 47 59′ qualium utraque diameter DE et F 120, utraque vero EM et EN 111 earundem. Quare qualium est utraque linea DE et EF 10 19′ et DB que est a centro excentrici 49 41′, talium etiam erit utraque quidem linea DM et FN 4 8′, utraque vero EM et EN 9 27′ earundem. Et quoniam, si a quadrato BD subtraxeris quadratum DM, relinquitur quadratum BM, habebimus etiam totam BM earundem per longitudinem 49 31′ et BE similiter 40 4′ et reliquam etiam lineam BN talium 30 37′ qualium erat linea FN 4 8′. Et quoniam que ab ipsis fiunt quadrata, si componantur, faciunt quadratum BF, habebimus etiam lineam BF qua rectus subtenditur angulus earumdem 30 54′ per longitudinem. Quare qualium est BF diameter 120 talium erit linea FN 16 2′ arcus vero suus talium 15 21′, qualium est circulus qui rectangulo BFN circumscribitur 360. Quare angulus quoque FBN talium erit 15 21′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360 talium 7 40′ proxime tot ergo TC arcus epicycli graduum est.

Rursus quoniam Luna in tempore observationis distabat a media longitudine maxima epicycli gradibus 262 20′, e C autem media longitudine minima reliquos videlicet post semicirculum gradus 82 20′, erit etiam arcus quidem CL graduum 82 20′. Totus vero TCL 90, rectus ergo est angulus TBL. Quare quoniam qualium est est​] corr. ex BDB G DB que est a centro centro] fiat D centrum circuli ABG ut E sit signorum add. marg. G (commentary to the diagram) excentrici 49 41′, BL vero que est a centro epicycli 5 15′ talium etiam EB fuit demonstrata 40 4′. Et quoniam quadrata istarum composita faciunt quadratum EL, habebimus etiam L per longitudinem 40 25′ earundem, distantia ergo Lune in observatione talium fuit 40 25′ qualium BL que est a 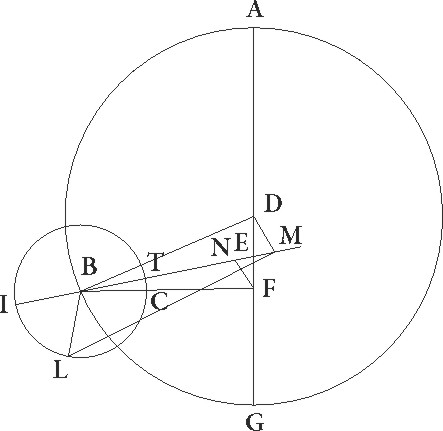centro epicycli 5 15′, et EA que est a centro terre ad maximam excentrici longitudinem 60, et EG que est a centro terre ad minimam excentrici longitudinem 39 22′. Sed distantia Lune in observatione, hoc est linea EL talium demonstrata est 39 45′ qualis est unius que est a centro tere. Ergo qualium est EL linea lunaris in observatione distantie 39 45′ et que est a centro terre unius, talium etiam erit E quidem linea distantie medie coniunctionum atque appositionum 59 0′, EG vero medie quadraturarum distantie 38 43′, et linea que est a centro epicycli 5 10′ earundem. Que nobis erant demonstranda.

Hoc modo lunaribus distanciis demonstratis, sequitur iam ut solarem etiam distantiam demonstremus, quod facile per lineas demonstratur, si ad distantias lunares in oppositionibus et coniunctionibus quantitates quoque angulorum qui constituuntur tempore ipsarum in visu a diametris Solis ac Lune et umbre dabuntur.

〈V.14〉 Capitulum XIIII : De quantitate diametrorum Solis et Lune et umbre que in coniunctionibus et oppositionibus perspiciuntur

Ceteras ergo huius considerationis vias que aut aque mensuris aut per tempora equinoctialium ortuum luminarium mensuram venantur, quoniam non integre potest per eas propositum inveniri, repulimus. Construximus autem etiam ipsi dioptram quadricubitalis regule quam Hipparchus Hipparchus] corr. ex Hipparcus G subostendit, per eamque o〈b〉servantes observantes] oservantes A Solis quidem diametrum ab eodem angulo proxime ubique contineri invemimus, nulla sensibili differentia de qua curandum sit a distanciis eius facta, Lune vero tunc solummodo ab eodem angulo contineri quo Solis comprehendimus, quando in oppositionibus per maximam a terra distantiam distat, cum in maxima epicycli et non in media sit longitudine, congrue consequenterque ad superiores rationes. Ad hec angulos quoque ipsos non parum minores quam traditi sint invenimus, non tamen regule mensura, sed per quasdam lunaris eclipsis hec computavimus. Nam quando quidem equalis angulus ab utraque diametro subtenditur, facile per regule constructionem potest cognosci, nulla enim in hoc mensuratione opus est, quantus vero subtendatur, ambiguum valde nobis videtur. Mensuratio enim que fit in pluribus huc et illuc remotionibus obiecte latitudinis super regule longitudines que est a visu ad tabellam in errorem potest ab exacta veritate abducere. Verum quoniam semel Luna in maxima eius distantia perspiciebatur equalem in visu angulum solari angulo facere, per eclipsis lunares in hac distantia observatas magnitudinem anguli ab ea subtensi computantes hinc et solarem demonstratum tenebamus. Cuius inquisitionis modum duabus rursum eclipsibus facilem intelectu faciemus.

Quinto igitur anno Nabopollassari qui est vigesimus septimus a Nabonassaro Athyr secundum Egiptios die 27^a vigesima octava sequente iuxta hore 12^e finem cepit Luna in Babilone difficere et defecit quarta maxime pars diametri ab austro. Quoniam igitur eclipsis initium post mediam noctem quinque horis temporalibus fuit, medium vero tempus sex horis proxime que tunc sunt in Babilone 5 50′ equales, Sol enim erat in 27 3′ gradibus Arietis, patet quia medium eclipsis tempus fuit, quando plurimum diametri Lune in umbram incidit in Babylone quidem post mediam noctem horis 5 5] corr. ex 1 A 50′ equalibus, in alexandria vero 5 solummodo. Et est tempus a locis constitutis annorum egiptyacorum 126 et dierum 86 et horarum equalium simpliciter quidem 17, exacte vero si ad dies equatos reduxeris 16 45′, quare medius secundum longitudinem Lune motus 25 32′ Libre gradus obtinebat, verus autem 27 5′. At vero ille qui est a maxima epicycli longitudine graduum erat 340 7′, a boreali vero termino in obliquo circulo graduum 80 40′. Perspicuum Perspicuum] corr. ex Perspicum G ergo est quia quando gradibus 9 3′ centrum Lune distat a nodis in obliquo circulo, quoniam in maxima sit distantia, sitque centrum umbre in maximo circulo qui per centrum Lune ad rectos angulos obliquo describitur, —secundum quem situm maxime fiunt obtenebrationes—, tunc quarta pars diametri Lune in umbram incidit.

Rursus in septimo anno Cambysse qui est a Nobonassaro Nobonassaro] corr. ex Nobonasaro G 225 Phamenoth secundum Egyptios die 17^a sequente 18^a ante mediam noctem hora 1 defecit in Babylone media pars diametri Lune a septentrione, fuit ergo in Allexandria Allexandria] corr. ex Alexandria G hec eclipsis ante mediam noctem horis equalibus 1 50′ proxime et sunt anni a constituto constituto] post corr. G tempore 224 egyptiaci et dies 196 et equales hore simpliciter quidem 10 10′, exacte vero 9 50′. Sol enim erat in Cancri gradibus 18 12′, quare Luna quoque secundum longitudinem medie quidem 20 22′ Capricorni gradus obtinebat, exacte vero 18 14′. Distabat autem etiam a maxima epicycli longitudine gradibus 28 5′, a boreali vero obliqui circuli termino gradibus 222 12′, quare hinc quoque patet quia, quando centrum Lune 7 48′ a nodo distat in obliquo circulo, cum in eadem maxima longitudine Luna sit umbreque centrum eundem situm ad ipsam habeat, media tunc lunaris diametri pars in umbram incidit.

Sed quando centrum Lune 9 3′ gradibus in obliquo circulo distat a nodo, tunc distat a circulo qui per medium signorum est in maximo circulo qui ad rectos obliquo angulos per ipsum centrum describitur unius gradus sexagesimas 48 30′, quando vero 7 48 gradibus in obliquo circulo distat a nodo, tunc distat a circulo qui per medium signorum est in maximo circulo qui per ipsum Lune centrum ad rectos obliquo describitur sexagesimas unius gradus 40 40′. Quoniam igitur excessus duarum eclipsium quartam lunaris diametri partem continet, excessus autem duarum distantiarum quas proposuimus quibus centrum eius a circulo qui per medium signorum est, hoc est ab umbre centro, distabat 7 50′ sexagesimis unius gradus, gradus] quod maior est semidiameter umbre quam dupla et tribus quintis semidiametro Lune bis enim 15 40 fiunt 31 20 adde tres quintas hoc est 9 21 fiunt 40 44 et ita superfluunt 4 secunda et sic est dupla super tripartiens quintas add. marg. A patet quia tota Lune diameter subtendit arcum maximi circuli 31 20′ sexagesimarum gradus unius.

Hinc etiam facile intellectu est quod linea que est a centro umbre que fit in eadem maxima longitudine Lune 40 40′ unius gradus sexagesimas subtendit. Nam quando centrum Lune totidem sexagesimis distabat ab umbre centro, tunc umbre circulum tangebat, propterea quod media lunaris diametri pars defecit. Insensibili autem atque indifferenti minor est quam dupla et ad hec tribus quintis maior semidiametro Lune, que est sexagesimarum 15 40′. Sed pluribus etiam hiusmodi observationibus consonas proxime invenimus expositas quantitates atque ideo tum ad alia que ad eclipsis pertinent ipsis usi sumus tum etiam nunc ad demonstrationem solaris distantie. Tantam enim fere invenimus quantam etiam Hiparchus secutus est. Nam circuli Solis Lune terreque qui a conis continentur indifferente quodam minores sunt quam circuli qui maximi in in] add. s. l. G his spheris ipsorum describuntur et diametri quam diametri similiter.

〈V.15〉 Capitulum XV : De solari distantia et iis que simul cum ea demonstrantur

His datis et etiam quod maxima Lune in coniunctionibus atque oppositionibus distantia talum est 64 10′, qualis est unius semidiameter terre, media enim distantia 59 earundem demonstrata est, semidiameter autem epycicli 5 10′, consideremus nunc quanta solaris distantia colligatur.

Sint igitur maximi sperarum et in eadem superficie circuli solaris quidem spere ABG circulus circa centrum D, lunaris vero in maxima Lune distantia circulus EFI circa centrum T, terre autem CLM circa centrum N et superficierum que sunt per centra superficies quidem que Solem et terram continet sit AXG, que vero Solem et Lunam amplectitur ANG, axis vero communis sit DTNX. Linee autem que per contactus sunt queque equidistantes fiunt et diametris ad sensum equales solaris quidem circuli sit ADG, lunaris vero ETI, terre autem CNM, umbre vero in quam in maxima sua longitudine Luna incidit OPR, OPR] corr. ex OPQR G ita ut TN linea equalis sit linee NP, et utraque 64 10′ talium, qualis est unius que est a centro terre. Oportet igitur invenire quam ND solaris distantie linea proportionem habeat habeat] corr. ex habebat G ad NL que est a centro terre.

Producatur igitur linea EI usque ad S et quoniam iam demonstravimus a diametro Lune in maxima distantia que est in oppositionibus et coniunctionibus subtendi arcum circuli qui per ipsam circa centrum terre describitur talium 0 31′ 20′′, qualium est ipse circulus 360, erit angulus ENI talium 0 31′ 20′′, qualium quatuor recti sunt 360, et medietas eius TNI talium 0 31′ 20′′, qualium duo recti sunt 360, quare arcus quoque TI talium est 0 31′ 20′′, qualium est circulus qui NIT rectangulo circumscribitur 360. Arcus vero TN reliquorum ad semicirculum 179 28′ 40′′ et corde sue IT quidem talium 0 32′ 48′′, qualium est NI diameter 120. NT autem 120 proxime earundem, quare qualium est NT linea 64 10′, talium erit TI 0 17′ 33′′, est autem talis etiam NM que est a centro terre unius et, quoniam proportio PR ad TI est proportio 2 36′ proxime ad unum, fit etiam PR 0 45′ 38′′, quare utreque utraeque] post corr. G simul TI et PR talium sunt 1 3′ 11′′, qualis est NM unius, sed utreque utreque] post corr. G simul PR et TS tota 2 earundem sunt, propterea quod equales sunt duabus NM. Equedistantes enim omnes ut diximus sunt et NP linea equalis est linee NT, reliqua ergo etiam IS talium remanet 0 56′ 49′′, qualis est linea NM unius, et est sicut NM ad IS sic NG ad IG et ND ad TD. Qualis ergo est ND unius talium est etiam TD 0 56′ 49′′ et reliqua TN 0 3′ 11′′ earundem, quare qualium est NT linea 64 10′ et NM unius, talium habebimus ND solaris solaris] post corr. G distantie lineam 1210 proxime.

Et similiter quoniam qualis est unius linea NM talium PR demonstrata est 0 45′ 38′′, est autem sicut NM ad PR sic NX ad XP . Qualis ergo unius NX linea est, talium XP erit 0 45′ 38′′, et reliqua PN 0 14′ 22′′ earundem, quare qualium est PN 64 10′ et NM que est a centro terre unius, talium etiam XP erit 203 50′ proxime, XN autem tota 268.

Colligitur ergo quod , qualis est unius linea que est a centro terre, talium est media Lune in coniunctionibus et oppositionibus distantia 59, Solis vero 1210, a centro autem terre usque ad verticem coni sunt umbre partes huiusmodi 368.

〈V.16〉 Capitulum XVI : De magnitudine Solis, Lune et terre

Facilis Facilis] corr. ex Facilius G antem hinc intellectu fit solidarum etiam magnitudinum proportio a diametris Solis, Lune et terre. Nam quoniam demonstratum est qualis est unius linea NM que est a centro terre, talium esse TI que est a centro Lune 0 17′ 33′′ et NT lineam 64 10′, est autem etiam sicut NT ad TI sic ND ad DG, estque ND demonstrata esse earundem 1210, habebimus etiam DG que est a centro Solis 5 30′ earundem proxime, quare diametrorum quoque eedem eedem] post corr. G erunt proportiones. Qualis igitur est Lune diameter unius talium erit terre 3 cum duabus quintis proxime, Solis vero 18 cum quatuor quintis, quare terre quidem diameter tripla est ad hec duabus quintis maior quam Lune, Solis vero decupla octuplaque quam Lune et ad hec quatuor quintis maior, quincupla vero ad diametrum terre et et] add. s. l. G ad hec medietate proxime maior, eodem modo, quoniam cubus qui est ab uno ipsius unius est, qui vero est a tribus duabusque quintis 39 4′ proxime earundem, qui autem est a 18 et quatuor quintis similiter 6644 30′ proxime, colligitur, qualis unius est solida Lune magnitudo, talium esse solidam terre magnitudinem 39 4′, Solis vero 6644 30′. Quare magnitudo Solis centies et septuagesies proxime terre magnitudinem continet.

〈V.17〉 Capitulum XVII : De particularibus aspectuum diversitatibus Solis et Lune

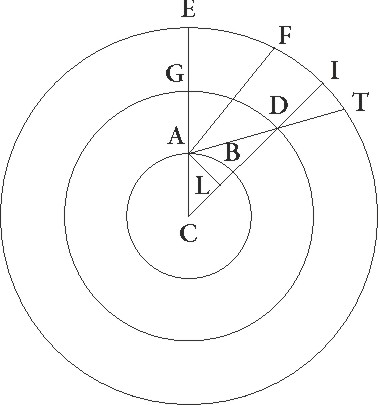His ita demonstratis, consequens est breviter declarare quomodo quispiam ex quantitate distantiarum Solis ac Lune particulares etiam ipsorum diversitates aspectuum computabit, et primum eas que in maximo circulo qui per punctum verticis et ipsas describitur perspiciuntur.

Sint ergo in superficie maximi huius circuli maximus quidem terre circulus AB, Solis autem vel Lune GD, ille vero ad quem terra puncti proportionem habet EFIT, centrumque omnium sit C, et diameter que est per puncta verticis CAGE, interceptoque a puncto verticis arcu GD talium verbi gratia supposito 30 qualium est GD circulus 360, coniungantur linee CDI et ADT, et a puncto A ducatur linea AF equidistans linee CI, perpendicularis etiam ad ipsam CI deducatur AL, et quamvis non eadem semper in utroque luminarium distantia permanet, differentia tamen diversitatis aspectuum que propter hoc in Sole accidit parva nimium et insensibilis est, presertim cum excentricitas etiam circuli eius parva sit et distantia magna, que vero Lune propter hoc accidit eam sensibilem valde esse necesse est, tum quia motus eius in epicyclo, tum quia epicycli etiam in excentrico motus non parvam in utrisque distanciis differentiam faciat. Diversitatem ergo aspectus solaris in una solum proportione demonstrabimus in proportione videlicet 1210 ad unum, Lune vero in quatuor que maxime faciliorem viam ad futuras demonstrationes prestabunt. Cepimus autem primo quidem duas distantias que fiunt cum epicyclus in maxima excentrici longitudine sit, quarum prima est usque ad maximam epicycli longitudinem quam colligi demonstavimus 64 10′ talium qualis unius est linea que est a centro terre, secunda vero usque ad minimam epicycli longitudinem que colligitur earundem 53 50′, deinde reliquas duas, cum epicyclus in minima excentrici longitudine sit, quarum prima usque ad maximam epicycli longitudinem colligitur per demonstrata talium esse 43 53′ qualis est linea que est a centro terre unius, altera usque ad minimam epicycli longitudinem colligitur earundem 33 33′.

Quoniam igitur arcus GD graduum 30 supponitur, erit etiam angulus GCD talium 30 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 60. Quare arcus quoque AL talium est 60 qualium est circulus qui ACL rectangulo circumscribitur 360. Arcus vero CL reliquorum ad semicirculum 120, quare corde quoque sue AL quidem talium erit 60 qualium est AC diameter 120, CL vero 103 55′ earumdem. Qualis ergo est AC unius, talium AL erit 0 30′ et CL 0 52′. Earundem autem est CLD linea in solari quidem distantia 1210, in lunaribus vero in primo quidem termino 64 10′, in secundo autem 53 50′, in tertio 43 53′, in quarto 33 33′. Reliqua ergo linea LD, hoc est AD, —inequales enim indifferente quodam sunt—, in solari quidem distantia erit 1209 8′, in lunaribus vero in primo termino 63 18′, in secundo 52 58′, in 3^o 43 1′, in quarto 32 41′. Quare qualium est AD diameter 120, talium erit AL linea eodem semper, ne longiores simus, ordine intelecto, 0 2′ 59′′ et 0 56′ 52′′ et 1 7′ 58′′ et 1 23′ 41′′ et 1 50′ 9′′. Quare arcus quoque suus talium erit 0 2′ 50′′ et 0 54′ 18′′ et 1 4′ 54′′ et 1 20′ et 1 45′ proxime qualium est circulus qui DLA rectangulo circumscribitur 360, angulus vero ADB, idest FAT, talium erit 0 2′ 50′′ et 0 54′ 18′′ et 1 4′ 54′′ et 1 20′ et l 45′ qualium duo recti sunt 360, qualium autem quatuor recti sunt 360 talium 0 1′ 25′′ et 0 27′ 9′′ et 0 32′ 27′′ et 0 40′ et 0 52′ 30′′. Quoniam igitur etiam A punctum indifferens est a centro C et FIT arcus indifferente quodam maior est quam IT, propterea quod universa terra instar puncti est ad circulum EFIT, erit etiam IT diversitatis arcus talium in solari distantia 0 1′ 25′′ qualium est EFIT circulus 360, in lunaribus vero in primo quidem termino 0 27′ 9′′, in secundo 0 32′ 27′′ in tertio 0 40′, in quarto 0 52′ 30′′, que nobis erant demonstranda.

〈V.18〉 Capitulum XVIII: De de] add. marg. G tabula diversitatis aspectuum

Eodem modo in reliquis a puncto verticis distanciis diversitates que fiunt per sex gradus usque ad nonaginta computavimus, tabulamque diversitatis aspectuum in quadraginta quinque rursum versibus et ordinibus novem conscripsimus, in quorum primo quarte partis gradus nonaginta posuimus per singulos binos facto incremento, in secundo que unicuique portioni ex diversitate aspectus solaris conveniunt, in tertio diversitatem Lune in primo termino, in quarto excessus quibus secundus terminus primum excedit, in quinto tercii termini diversitatem, in sexto excessus quibus quartus terminus tertium excedit, ut verbi gratia in trigesimo gradu 0 1′ 25′′ diversitatis solaris in secundo ordine congrue apposuimus, deinde 0 27′ 9′′ primi lunaris termini, et postea 0 5′ 18′′ quibus secundus terminus primum excedit, et deinde rursum 0 40′ tercii termini, et postea 0 12′ 30′′ quibus quartus terminus tertium excedit. Verum ut etiam in 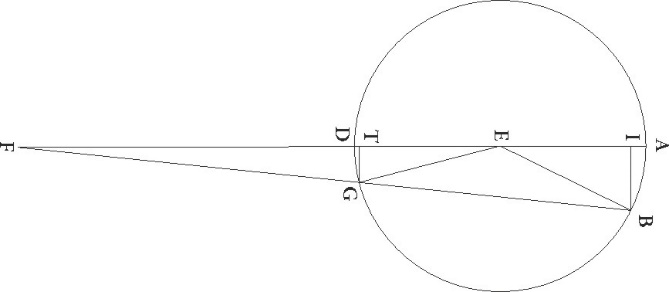distanciis que sunt inter maximas et minimas longitudines proportionaliter particularibus partibus diversitates aspectuum ab iis iis] post corr. G que inventa sunt in expositis quatuor terminis per sexagesimarum appositionem facile computare possimus, possimus] corr. ex possumus G tres nobis reliqui ordines ad appositionem huiusmodi differentiarum additi sunt, quarum computatio hoc nobis modo facta est.

Sit ABGD Lune epicyclus circa centrum E, circuli autem qui per medium signorum est et terre ipsius centrum sit F, et coniuncta EDF linea protrahatur linea FGB, et coniungantur linee BE et GE, et deducantur ad AD lineam ex puncto quidem B perpendicularis BI, ex puncto autem G perpendicularis GT, et supponatur primo Luna distare per arcum AB ab A maxima longitudine exacta et ad centrum F capta, qui verbi gratia sit graduum 60, ut etiam angulus BEI talium sit 60 qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 120. Erit igitur hac de causa BI arcus talium 120 qualium est circulus qui BEI rectangulo circumscribitur 360, EI vero reliquorum ad semicirculum 60. Corde igitur etiam sue BI quidem talium erit 103 55′ qualium est EB diameter 120, EI vero 60 earundem. Sed quando E centrum epicycli in maxima excentrici longitudine est, tunc FE ad EB proportio est quam 60 habent ad 5 15′, quare qualium est EB linea 5 15′, talium BI erit 4 33′ et EI linea 2 38′, IF autem tota 62 38′. Et quoniam, si componantur quadrata linearum FI et IB, faciunt faciunt] fiaciunt A quadratum linee FB, erit etiam ipsa talium 62 48′ qualium est FA FA] corr. ex AFA G primi termini distantia 65 15′, et FA secundi termini 54 45′, et AD differentia excessus harum duarum distantiarum 10 30′, et differentia ergo que in B ad primum terminum fit talium est 2 27′ qualium est tota differentia 10 30′, quare qualium tota differentia est 60, talium erit tunc differentia 14 0′. Hanc igitur in septimo ordine apponemus in versu qui medietatem sexaginarii numeri, hoc est triginta, continet, propterea quod omnes nonaginta gradus qui in primo ordine conscribuntur medietatem continent graduum eorum eorum] add. marg. G qui 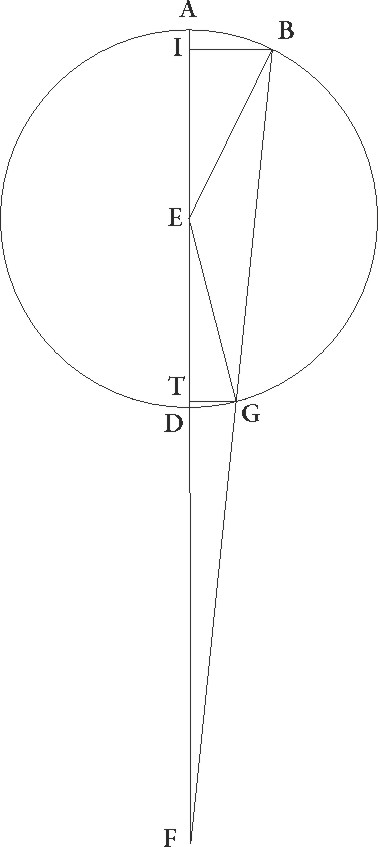sunt ex A ad D idest graduum 180.

Eodem modo, si supposuerimus GD arcum eorundem esse 60, demonstrabitur GT quidem talium 4 33′ qualium est EG semidiameter 5 15′, ET autem similiter 2 38′, et reliqua FT 57 22′ earundem. Quapropter etiam FG qua rectus angulus subtenditur erit 57 33′. Quas rursum, si a primi termini 65 15′ subtraxerimus, reliquas 7 42′ inveniemus esse esse] add. s. l. G totius differentie sexagesimas 44 0′. Quas similiter in eodem ordine ad sexagenarium numerum apponemus, propterea quod ABG arcus gradum est 120.

Rursus eisdem arcubus suppositis, intelligatur E centrum in minima longitudine excentrici esse, in quo situ tertius et quartus teriminus continetur. Quoniam ergo in hoc situ FE ad ad​] iter. et del. A EB proportionem habet 60 ad 8 et qualium ergo BE est octo, colligetur etiam utraque quidem BI et GT linea, quando etiam arcus utreque utreque] post corr. G AB et GD 60 graduum supponuntur talium 6 56′, qualium est linea FE 60, utraque vero linea EI et ET 4 0′ earundem, quare cum FI earundem fiat 64, FT vero similiter 56, colligetur etiam FB que rectum angulum subtendit 64 23′, FG autem talium 56 26′ qualium est tercii quidem termini linea FA 68, AD vero linea differentie tercii ad quartum 16. Si ergo 64 23′ a 68 subtraxeris, relinquuntur 3 37′ que totius differentie 16 sexagesime fiunt 13 33′ quas apponemus similiter in ordine octavo ad numerum 30. Sin autem 56 26′ a 68 subtraxerimus, remanebunt 11 34′ que similiter totius differentie 16 sexagesime fiunt 43 24′ quas apponemus similiter in eodem ordine ad numerum 60. Sed differentias quidem que colliguntur propter Lune in epicyclo progressum hoc modo exponemus, que vero propter ipsius epicycli in excentrico motum sic nobis invenientur.

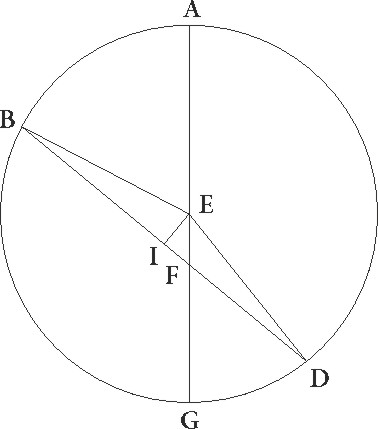Sit ABGD excentricus Lune circulus circa centrum E et diametrum EG in qua centrum zodiaci circuli sit F, protractaque BFD, supponatur rursum uterque angulus AFB et GFD talium 60 qualium quatuor recti sunt 360, quod accidit si distantia, quando quidem centrum epicycli fuerit in B puncto, 60 graduum sit, quando vero in D, D] corr. ex GD G graduum 120, coniunctisque lineis BE et ED, deducatur ex E puncto ad lineam BFD perpendicularis EI. Quoniam ergo angulus BFA talium est 120 qualium duo recti sunt 360, erit etiam arcus EI talium 120 qualium est circulus qui rectangulo EFI circumscribitur 360. Arcus vero FI reliquorum ad semicirculum 60. Corde igitur etiam sue EI quidem talium erit 103 55′ qualium est EF recto angulo subtensa 120, IF autem 60 earundem. Qualium ergo est EF linea que inter centra est 10 19′ et linea que est a centro excentrici 49 49′, talium erit EI quidem 8 56′, FI autem 5 10′ earundem, et quoniam, si a quadrato EB linee EI linee quadratum subtraxeris, redditur quadratum BI, erit etiam utraque BI et ID 48 53′. Quare tota etiam FB linea talium erit 54 3′, qualium est FA primorum terminorum 60, et FG secundorum 39 22′, et excessus harum 20 38′, et reliqua FD 43 43′ earundem. Quoniam ergo 60 numerus excedit 54 3′ quidem per 5 57′, que fiunt totius differentie 20 38′ sexagesime 17 18′, at vero at vero] post corr. G 43 43′ excedit per 16 17′ que similiter 20 38′ totius differentie sexagesime fiunt 47 21′, apponemus in nono ordine ad 30 quidem numerum distantie 17 18′, ad numerum autem 120, hoc est rursus ad numerum 60, ponemus 47 21′, propterea quod cum minima longitudo ad nonaginta gradus sit sexaginta graduum distantia distantie 120 graduum equipolet.

Eodem modo in ceteris quoque arcubus sexagesimas differentiarum computantes secundum expositos tres excessus per duodecim partes que rursum fiunt in numeris tabule partes sex, propterea quod 180 gradus qui sunt a maximis ad minimas longitudines 90 gradibus tabule continentur, apposuimus congrue in quolibet demonstratorum numerorum sexagesimas lineis collectas, partium autem interiacentium numeros incremento equali in excessu sex partium fecimus, nulla enim in tanto excessu differentia de qua curandum sit a numeris per lineas demonstratis invenitur, nec in sexagesimis, nec in ipsa diversitate aspectuum.

〈V.19〉 〈Capitulum〉 XVIIII: Tabula diversitatis aspectuum

Diversitas solaris et lunaris in maximo circulo qui per ipsa luminaria et verticem describitur.

〈V.20〉 Capitulum XX: De diversitatibus aspectuum discernendis

Quando igitur volumus invenire quantam Lune per singulos progressus diversitatem aspectus in circulo habet qui per ipsam et punctum verticis describitur, considerabimus quot equalibus horis in proposito climate distat a meridiano, et has queremus in angulorum eiusdem climatis tabula, et appositos hore gradus in signo in quo Luna est in ordine secundo aut omnes aut hore parti congruentes habebimus illos quibus a puncto verticis Luna distat in circulo qui per eam et punctum verticis describitur. Quibus cum intrantes in tabulam diversitatis aspectuum queremus eos in primo ordine et correspondentes eis numeros in ordinibus quatuor qui post ordinem solarium diversitatem deinceps sequuntur, hoc est in tertio, quarto quinto et sexto, seorsum singulos conscribemus. Deinde capiemus inequalitatis in illa hora exquisite numerum ad exactam maximam longitudinem aut ipsum, aut, si 180 excederet, reliquum ad 360, et huiusmodi numeri graduum medietatem semper in eisdem numeris queremus, sexagesimasque ipsi correspondentes seorsum in septimo et octavo ordine capiemus, et quotquot sexagesime septimi ordinis sunt, totidem a differentia quarti ordinis capiemus, easque tercii ordinis diversitati semper addemus, quotquot autem in octavo ordine inveniuntur, totidem a differentia sexti ordinis sumemus, et diversitati quinti ordinis semper rursum addemus, et duarum diversitatum ita congregatarum excessum scribemus. Demum considerabimus quot gradibus Luna a solari gradu vel a diametraliter opposito distat, propinquiorisque distantie gradus in primi ordinis numero inveniemus, et quotquot sexagesime in nono ac ultimo ordine ipsi correspondent, totidem ab excessu duarum diversitatum iam scripto sumentes, que fiunt minori semper addemus, hoc est illi quam ex tertio et quarto ordine exactam habuimus, et secundum congregatum hinc numerum aspectus lunaris mutatur in circulo qui maximus per ipsam et verticis punctum describitur, hinc simpliciter solaris quoque diversitas in simili situ solarium eclipsium gratia ex gradibus qui in secundo ordine appositi sunt per quantitates arcus qui in … qui] add. marg. G a vertice distat perspicitur.

Verum ut etiam diversitatem que tunc fit ad circulum qui ad medium signorum est tam per longitudinem quam per latitudinem discernamus, easdem rursum horas equales quibus a meridiano Luna distat in eadem parte tabule angulorum inveniemus, capiemusque gradus numero horarum appositos ex ordine tertio, si ante meridianum Luna invenitur, sin vero post meridianum, ex ordine quarto eosdemque ipsos conscribemus, si pauciores sint quam 90, sin vero plures, reliquos ad 180. Totidem enim erit taliumque angulus minor alter de duobus angulis qui fiunt in huiusmodi sectione, qualium unus rectus est 90. Gradus ergo istos duplicatos queremus in tabula cordarum tum ipsos tum reliquos ad 180, et quam proportionem habet corda arcus duplicatorum graduum ad cordam reliqui arcus ad semicirculum, hanc proportionem diversitas aspectus secundum latitudinem habebit ad diversitatem que per longitudinem est. Tanti enim circulorum arcus indifferentes a cordis sunt. Si ergo multiplicaverimus appositarum cordarum numerum in diversitatem captam in circulo qui per punctum verticis describitur et factum numerum per 120 seorsum parciemur, habebimus partes congrue diversitatis aspectuum eas que a partitione facte sunt.

Universaliter autem in diversitatibus aspectus secundum latitudinem quidem, si punctum vercicis in meridiano borealius sit quam pars circuli qui per medium signorum est que tunc erit in medio celi, diversitas aspectus ad meridiem eius erit, sin vero australius, diversitas aspectus secundum latitudinem ad septentrionem erit. In diversitatibus autem aspectus secundum longitudinem, quoniam quantitates angulorum que in tabula conscribuntur illum continent de duobus angulis a sequente portione obliqui utrinque contentis qui ad septentrionem est, quando quidem diversitas aspectus aspectus] add. s. l. G secundum latitudinem ad septentrionem est, si angulus inventus maior est recto, erit diversitas aspectus per longitudinem ad antecessionem, sin vero recto minor, ad successionem signorum, quando vero diversitas aspectus secundum latitudinem ad meridiem est, e e] add. s. l. G converso, si angulus maior est recto, ad successionem signorum diversitas aspectus secundum longitudinem erit, sin autem minor, ad antecessionem.

Usi autem sumus iis que de Sole iam pridem demonstravimus quasi sensibilis diversitas aspectus eius non sit, non quia nesciebamus quanta in his futura esset differentia ex diversitate aspectus quam de ipso eramus demonstraturi, verum quoniam non ita magnum errorem hinc ad apparentia putavimus accessurum, ut necesse fuerit nonnulla illorum movere que sine hac brevi diversitate preponebantur, similiter etiam in diversitatibus aspectuum lunarium satis nobis fuerunt arcus et anguli qui ad circulum qui per medium signorum est fiunt a circulo qui maximus per polos orizontis describitur loco illorum qui ad obliquum Lune conspiciuntur. Differentia enim que penes hanc rem in eclipsibus fit insensibilis est et expositio illorum omnium multiplex in demonstrationibus et difficilis in computationibus, computationibus] corr. ex compotaionibus G cum singuli Lune in zodiaco motus distantieque a nodo determinate non sint, sed tum per magnitudines tum per situs accipiant varios varios] add. marg. G multiplicesque progressus.

Quod ut facile intelligatur, sit portio circuli qui per medium signorum est ABG, obliqui vero lunaris AD, et supponatur A punctum nodus esse Lune quoque centrum esse in D, et trahatur ex D puncto ad circulum qui per medium signorum est recta DB, et sit E punctum polus orizontis, et describatur per ipsum maximi circuli per centrum quidem Lune portio EFD, per punctum autem B portio EB, sitque diversitatis aspectus in Luna arcus DI, et deducantur a puncto I ad lineas BD et BF recte IT et IC, ut distantia secundum longitudinem a nodo vera quidem sit AB, apparens autem AC, distantia vero a circulo qui per medium signorum est vera quidem sit BD, apparens autem CI. Earum vero diversitatum que ad zodiacum ex DI conspiciuntur secundum longitudinem quidem TI arcui equalis, per latitudinem autem equalis DT. Quoniam igitur DI aspectus diversitas, dato arcu ED, per ea que exposita sunt invenitur, utraque autem diversitas DT et TI, dato angulo GFE, nos vero in superioribus arcus et angulos circuli qui per verticem est ad data zodiaci puncta rectos demonstravimus, habemus vero hic solum B punctum datum in circulo qui per medium signorum est, patet quia EB arcu arcu​] corr. ex arcum G abutimur pro arcu ED et angulo GBE pro angulo GFE.

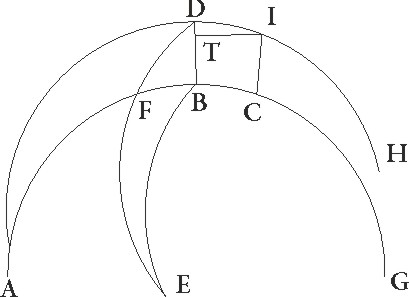Id hipparcus voluit quidem emendare, sed parum scite preterque rationem ipsam aggressus fuisse videtur. Nam primum una distantia arcus AD usus est, et non omnibus aut pluribus quod illi facere necesse est qui minuta diligenter rimari proposuit. Deinde nesciens in plura inconvenientia incidit. Predemonstraverat enim etiam ipse arcus et angulos qui ad circulum per medium signorum perspiciuntur et ad hec quia ED arcu dato DI arcus invenitur, —id enim in primo de diversitatibus ab eo demonstratur—, utitur autem ad habendum arcum ED tum EF arcu tum EFG angulo quasi datis. Sic enim in secundo FD arcum computavit et reliquum ED supposuit. Deceptus Deceptus] post corr. G autem fuit, quoniam non animadvertit B punctum circuli signorum, non F datum esse, unde fit ut arcus EB, non EF, datus sit, et angulus EBG, non EFG. Sed sepius ad emendationem aliquam faciendam incitatus fuit, cum valde sensibilem arcuum ED ad arcus EF differentiam fieri videret. videret] corr. ex videt G Isti namque multo magis quam illi dati non sunt. Ipsius autem arcus BE qui vere datus est ad arcum ED differentia sola magnitudine BD linee in singulis a nodo distanciis differet. Verum quomodo emendatio recte fiat sic, sic] corr. ex sit A ante oculos ponetur.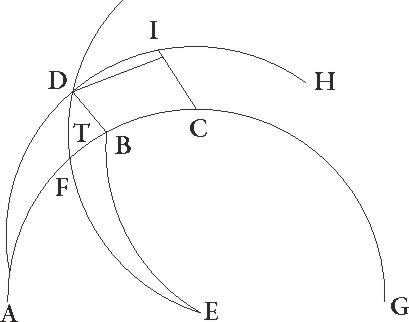

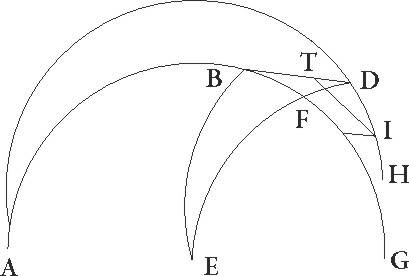
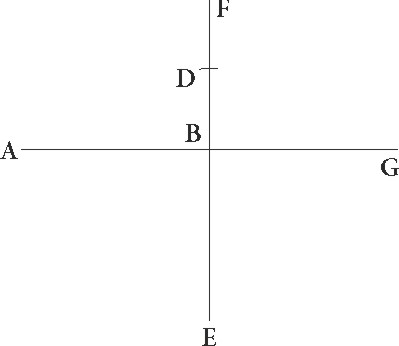Sit zodiacus ABG, ipsique ad rectos sit circulus DBE, Luna vero sit aut in D aut in E distans secundum latitudinem a circulo signorum ABG per arcum BD vel BE datum, ut arcus qui sunt a vertice ad B zodiaci punctum et anguli dati sint, et solum querantur qui ad D vel ad E fiunt.

Si ergo talem habeat zodiacus situm, ut ad rectos angulos sit illi qui per F punctum quod orizontis polus esse supponatur, et per B maximus describitur circulus, ut puta FB, concurret iste certe cum arcu DE, et sic angulus qui ad D et E puncta conspicitur indifferens erit ab angulo qui supponitur esse in B. Recti enim etiam per hec anguli ad zodiacum fiunt. Arcu vero FB arcus quidem FD minor erit per arcum BD, arcus vero FE maior per BE, qui etiam ipsi dati sunt.

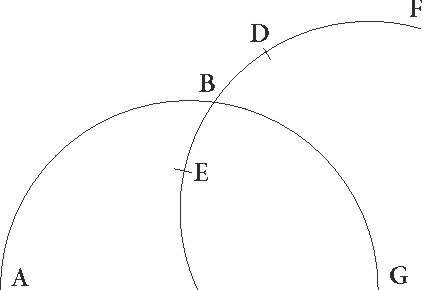Sin autem ABG zodiacus cum maximo circulo qui per punctum verticis describitur concurrat, supposito quod A punctum polus orizontis sit, et coniunctis AD et E; different isti quoque ab arcu AB, et anguli BAD et BE ab angulo qui prius non erat. Dantur autem arcus AD et E per proportionem rectarum linearum propter indifferentiam ex lineis AB et BD et BE datis. Quadrata enim ipsarum composita faciunt quadrata linearum AD et E consequenter etiam anguli BAD et BE.

Q 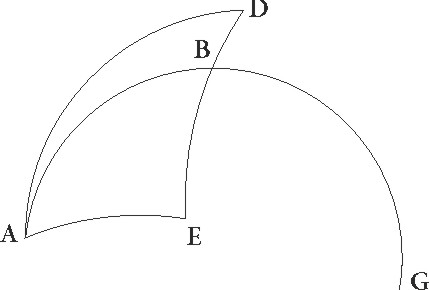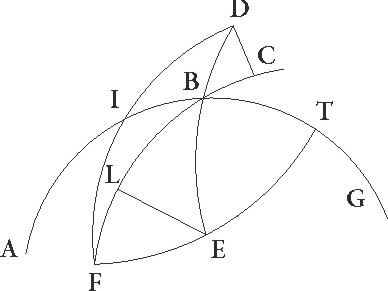uando vero situs zodiaci declinatur, si ex F orizontis polo FBC et FID et FET arcus coniunxerimus, erit arcus FB et angulus ABF datus, et similiter BD et BE. Queruntur autem tum arcus FD et FE tum anguli AIF et ATF qui dantur deductis ad arcum FBE perpendicularibus DC et EL. Nam quoniam ABF angulus datus est, estque angulus ABE semper rectus, dantur profecto rectangula BCD et BLE, proportio etiam FB ad eos arcus qui rectum ambeunt angulum, quoniam etiam ad DB et BE quibus rectus subtenditur angulus. Quare FD quoque et FE rectum subtendentes angulum dabuntur, quapropter etiam anguli DFC et EFL qui quesitorum excessus sunt. Nam angulus AIF maior est quam angulus ABF angulo DFB. At vero angulus ATF minor est quam angulus ABF angulo EFL. P〈er〉spicuum Perspicuum] Prespicuum A autem est maximam tunc fieri differentiam, quamvis eadem secu〈n〉dum secundum] secumdum A latitudinem distantia supponatur angulorum quidem, quando B punctum idem sit puncto verticis, —nam cum nullus ad B angulus constituatur, arcus qui sunt ex vertice ad D et E puncta rectos ad zodiacum angulos faciunt—, arcuum vero, quando idem similiter situs sit, —nam cum nullus ad B arcus fiat tanti erunt arcus ad D et ad E quanti sunt arcus progressus lunaris secundum latitudinem—, et quando qui per verticem est rectus est ad zodiacum, tunc enim arcus FD et FE toto rursus progressu latitudinis ab FB FB] Primos angulos appellat eos qui capiuntur ex tabula arcuum et angulorum add. marg. G arcu different. In aliis autem sitibus cum DE DE] corr. ex D G arcus ad FB arcum declinetur tam arcuum quam angulorum excessus ad minus contrahentur. Quare quando quinque gra-dibus Luna secundum latitudinem a circulo qui per medium signorum est distat, tunc maxima diversitatis aspectuum differentia erit sexagesimarum 10 proxime. Nam quinque maxime differentie arcuum gradus tot diversitatis aspectuum sexagesimos in maximis excessibus et minimis distantiis faciunt. Quando autem maximo progressu qui in solaribus eclipsibus est distat, qui est gradus 1 30′ proxime, tunc differentia diversitatis aspectuum totidem sexagesimarum erit, hoc est 1 30′, quod raro accidit.

Via tamen ratioque ad huiusmodi angulorum et arcuum emendationem hoc modo facilis volenti volenti] post corr. G breviter fiet. Universaliter enim dupplicatum angulorum numerum in tabula cordarum et arcuum queremus et correspondentes tum ipsi tum residuo ad 180 duorum rectorum gradus seorsum in latitudinis gradus multiplicabimus, et partem centesimam atque vigesimam utrorumque conscribemus, et numerum ex primo angulo factum subtrahemus a supposito circuli per verticem arcu, si Luna in eadem cum verticis puncto parte sit, sin vero in opposita, addemus, et numerum huic huic] corr. ex hinc G factum in se ipsum multiplicabimus, eique addemus quadratum ex numero relicti anguli factum, et totius radicem congrue dicemus arcum esse quem querebamus. Post hec numerum reliqui anguli iam conscriptum in 120 multiplicabimus, seorsumque per inventos arcus partiemur, et mediam arcuum qui facto numero in tabula cordarum adiacent partem, si arcus equatus maior primo fuerit, addemus primi anguli partibus, sin vero minor, subtrahemus ab ipsis, et sic angulum equatum habebimus.

Sit in preposita descriptione gratia exempli arcus FB graduum 45, angulus vero ABF talium 30 qualium unus rectus est 90, uterque autem DB et BE latitudinis arcus graduum 5. Quoniam igitur 30 gradibus dupplicatis hoc est 60 adiacet linea linea] post corr. G partium 60, reliquis vero ad duos rectos, hoc est 120, adiacet linea partium 104 proxime, idciro proportio BL ad LE fit ea que est 60 ad 104; eadem autem est etiam proportio BC ad DC, qualium est que rectum angulum subtendit 120. Utrunque igitur numerum in quinque gradus subtendentis multiplicabimus, et facti ex multiplicatione numeri centesimam et vigesimam partem capiemus, et sic habebimus utranque CB et BL earundem 2 30′, et utranque DC et EL similiter 4 20′. Si ergo Luna in E puncto esse supponitur, hanc quantitatem 2 30′ a 45 gradibus arcus FB auferemus, propterea quod ad eandem cum vertice partem distantia latitudinis Lune sit, hoc est quoniam utraque vel 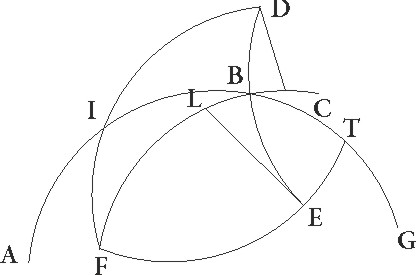australiora vel boraliora zodiaco sint, et sic habebitur FL graduum 42 30′, sin vero Luna in puncto D sit propter contrariam causam, addemus, et sic habebitur FC graduum 47 30′. Si ergo quadratum utriusque FL et FC seorsum composuerimus cum quadrato utriusque DC et EL, hoc est quadratum quod fit ex 4 20′ cum quadrato quod fit ex 42 30′, et cum eo quod fit ex 47 30′, et congregatorum numerorum latus seorsum inveniemus, habebitur etiam arcus FE graduum 42 46′ proxime, et arcus FD similiter 47 44′, deinde 4 20′ in 120 multiplicabimus, seorsumque per 42 46′ et 47 44′ partiemur, et sic habebimus EL quidem talium 12 8′ proxime qualium est FE que rectum angulum subtendit 120, DC autem 10 50′ proxime qualium FD que rectum angulum subtendit 120. Verum cum corde partium 12 8′ arcus 11 36′, corde vero partium 10 50′ arcus graduum 10 20′ proxime accomodetur. accomodetur] post corr. G Quorum medietate capta, gradus quidem 5 48′ anguli EFL subtraximus a 30 gradibus anguli ABF, propterea quod FE arcus minor est arcu FB, et sic habetur angulus ATF graduum 24 12′, gradus autem 5 10′ anguli DFC eisdem 30 addidimus, addidimus] corr. ex addimus G propterea quod arcus FD maior est arcu FB, et sic habetur etiam angulus AIF graduum 35 10′, que via rationeque nobis erant invenienda.