Ptolemaeus Arabus et Latinus

〈VI〉

Incipit liber VI Magne compositionis Ptolomei

〈VI.1〉 〈Capitulum I:〉 De coniunctionibus atque oppositionibus Solis et Lune

Cum vero deinceps de coniunctionibus atque oppositionibus eclipticis Lune ac Solis Lunae … Solis] iter. A dicendum sit, precedatque ad hoc coniunctionum et oppositionum verarum consideratio, quamvis ad primam istarum intelligentiam periodicos et inequales motus quos de utrisque demonstravimus luminaribus sufficere arbitramur, cum possibile per eos sit, si non tedeat quottidie ac diligenter inquirere, futuarum oppositionum et coniunctionum locos locos] post corr. G et tempora invenire, tam earum que in mediis motibus quam illarum que vere cum inequalitate considerantur. Tamen ut etiam hec nobis faciliora sint, tum temporibus et locis periodicarum coniunctionum et oppositionum expositis, tum mediorum temporum locis inequalitatis et latitudinis Lune, quibus et verarum coniunctionum ac oppositionum equatio fit et ab istis ea que eclipsium est, composuimus tabulas ad hanc considerationem hoc modo.

〈VI.2〉 Capitulum II: Quomodo mediarum coniunctionum atque oppositionum componende tabule sunt

Primum enim ut mensium etiam locos, sicut et ceterorum, a primo Nabonasari anno constituamus, inventum in eo in eo] add. s. l. G anno in callendis Thoth secundum Egyptios in meridie motum distantie graduum 70 37′ ad medium diurnumque distantie motum conferentes invenimus dies 5 47′ 33′′. Totidem igitur diebus ante meridiem kalendarum Thoth media coniunctio fuit. Quare post eiusdem diei meridiem diebus 23 44′ 17′′ proxime facta deinceps fuit, hoc est post meridiem diei vigesime quarte sexagesimis diei unius 44 17′, in diebus autem 23 44′ 17′′ medie Sol quidem movetur gradus 23 32′ 50′′, Luna vero inequalitatis quidem gradus 318 15′, latitudinis autem 314 2′ 21′′, obtinebat autem in meridie kalendarum Thoth medie Sol quidem Piscium gradus 0 45′ et a sua maxima longitudine, —facilior enim sic fit consideratio—, gradus 265 15′, Luna vero inequalitatis quidem quidem​] add. marg. G a maxima epicycli longitudine gradus 268 49′, latitudinis autem a boreali obliqui circuli termino gradus 354 15′ In proposito igitur tempore medie coniunctionis post kalendas Sol et Luna medie a solari maxima longitudine, hoc est a gradibus Geminorum 5 30′, utrique distabant gradibus 288 38′ 50′′, Luna vero inequalitatis quidem a maxima longitudine gradibus 218 57′ 15′′, latitudinis autem a boreali termino gradibus 308 17′ 21′′.

Statuemus igitur primam tabulam coniunctionalem versuum rursus 45 ordinum 5, apponemusque in primo versu et primo ordine primum Nabonassari annum, in secundo autem ordine et versu eodem Thoth mensis dies 24 44′ 17′′ sexagesime, —nanque que supersunt post meridiem diei 24^e sunt—, in tertio autem medie a maxima Solis longitudine distantia gradus 288 38′ 50′′, in quarto eiusdem versus ordine lunaris inequalitatis gradus 218 57′ 15′′, in quinto latitudinis a boreali termino gradus 308 17′ 21′′. Et quoniam in medii mensis lunaris medietate dies sunt 14 45′ 55′′ proxime, gra-dus autem solaris quidem motus 14 33′ 12′′, lunaris vero inequalitatis 192 54′ 30′′ et latitudinis 195 20′ 6′′, his numeris subtractis a proposite coniunctionis numeris, reliquos similiter in secunda tabula que oppositionalis erit conscribemus. Relinquuntur autem dies 9 58′ 22′′ et gradus a maxima solari longitudine 274 5′ 38′′, inequalitatis a maxima Lune longitudine 26 2′ 45′′, latitudinis a boreali termino 112 57′ 15′′. Et quoniam in 25 annis egyptiacis integri menses proxime absolvuntur, deficientibus unius diei sexagesimis 0 2 47′ 5′′, et Sol quidem reiectis integris circulis obtinet gradus 353 52′ 34′′ 13′′′, Luna vero inequalitatis quidem gradus 57 21′ 44′′ 1′′′, latitudinis autem gradus 117 12′ 49′′ 54′′′, primos quidem ordines duarum tabularum per 25 annos augebimus, secundos vero per 0 2′ 47′′ 5′′′ diminuemus, tertios tertios] post corr. G per 353 52′ 34′′ 13′′′ augebimus, quartos per 57 21′ 44′′ 1′′′, quintos per 117 12′ 49′′ 54′′′.

Deinde annuam tabulam 24 versuum faciemus et aliam sub ipsa ipsa] corr. ex ipsam G menstruam versuum 12. Habebit autem utraque totidem ordine quot prima, et in menstrua quidem tabula primum mensem in primo ordine versus primi ponemus, in ordine secundo eiusdem semper versus primi mensis dies 29 31′ 5′′ 8′′′ 20′′′′, in tertio Solis in hoc tempore collectos gradus 29 6′ 23′′ 1′′′, in quarto inequalitatis lunaris gradus 25 49′ 0′′ 8′′′, in quinto latitudinis gradus 30 40′ 14′′ 9′′′, quos augebimus eisdem muneris qui in primis versibus scripti sunt. In tabula vero annua in primo quidem ordine primi versus primum annum ponemus, in secundo ressiduos 13 mensium dies 18 53′ 52′′ 48′′′, in tertio solaris motus in tanto tempore gradus 18 22′ 59′′ 18′′′, in quarto lunaris inequalitatis gra-dus 335 37′ 1′′ 51′′′, in quinto latitudinis gradus 38 43′ 3′′ 51′′′, quos etiam augebimus nunc expositis tresdecim mensium quantitatibus nunc duodecim mensium, et colliguntur dies 354 22′ 1′′ 40′′′, solaris motus gradus 349 16′ 36′′ 16′′′, lunaris inequalitatis 309 48′ 1′′ 42′′′, latitudinis 8 2′ 49′′ 42′′′ qui numeri in ultimo mensium tabule versu in quatuor ordinibus conscripti sunt, quoniam prima que sequitur coniunctio sive oppositio post integros annos egyptiacos ponitur. Sufficiet autem ad secundas usque sexagesimas in tabulis progredi.

〈VI.3〉 Capitulum III: Tabula coniunctionum

Annui loci coniunctionum et oppositionum

Solares termini a gradibus 65 19 usque ad 101 22 et a gradibus 258 38 usque ad 290 41

Lunares termini a gradibus 74 48 usque ad 105 12 et a gradibus 258 48 usque ad 285 12

〈VI.4〉 Capitulum IIII: Quomodo et periodicas et veras coniunctiones et oppositiones considerare oportet

Quando igitur volumus in aliquo tempore medias coniunctiones atque oppositiones invenire, queremus annorum numerum, quotus a primo Nabonassari anno sit, et singulos quidem vigintiquinque annos in primo prime et secunde tabule ordine, simplices vero in primo tertie, inveniamus, inveniamus] corr. ex invenimus G et que annorum numeris in sequentibus ordinibus eodem in versu correspondent in coniunctionibus quidem ex prima et tertia tabula, in oppositionibus autem ex secunda et tertia similiter sumemus, congrueque congregabimus, et ex collectis ex ordine secundo habebimus tempus a principio anni coniunctionis illius, ut puta, si collecti fuerint dies 24 44′, post meridiem diei 24^e Thoth sexagesimis 44 medium tempus fore dicemus, sin vero 34 44′, post meridiem diei 4^e Phaophi totidem sexagesimis. Ex tertio autem gradus Solis a maxima sua longitudine habebimus, ex quarto gradus inequalitatis Lune a maxima longitudine, ex quinto gradus latitudinis a boreali termino, reliquos etiam consequenter, sive omnes, sive aliquas invenire voluerimus, facile ex menstrua quartaque tabula inventos computabimus numeros, diei sexagesimis ad horas equales propter faciliorem usum reductis, ita ut horarum numerus equatorum dierum sit, —temporalis enim hora non eadem semper comprehenditur, cum dierum inequalium sit—, hanc rem equabimus sic, quemadmodum dictum est, differentiam eius inveniemus. Nam si maior sit temporum quantitas que ad inequalem distantiam erit, subtrahemus differentiam a distantia equaliter collecta, sin vero minor, addemus.

Hoc igitur modo coniunctionis aut oppositionis mediorum motuum tempore capto et et] add. s. l. G inequalitatibus utriusque luminarium in eodem tempore facilius et tempus et locus verus invenietur, et ad hec motus latitudinis Lune per comperationem ambarum inequalitatum. inaequalitatum] corr. ex inequalitatem G Nam per additionem subtractionemque in eo tempore in utroque inventam motum Solis et Lune et latitudinis verum habebimus, et si in eodem gradu aut in oppositis luminaria sint, id ipsum tempus vere coniunctionis aut oppositionis esse dicemus, sin autem non, distantie gradibus duodecimam eorum ipsorum graduum partem quam Sol proxime in die progreditur addentes, considerabimus quot equalibus horis Luna tunc totidem gradus inequaliter movebitur, et factam horarum quantitatem periodico tempori addemus, si verus Lune motus solari minor sit motu, sin autem maior, subtrahemus ab ipso. Similiter ipsos quoque distantie gradus simul cum duodecima eorum parte vero lunari motui addemus, si minor erit solari, sin autem maior, subtrahemus ab ipsa tam per longitudinem quam per latitudinem, et tum tempus vere coniunctionis aut oppositionis, tum verum proxime in obliquo circulo Lune motum habebimus.

Invenitur autem semper inequalis unius hore Lune motus in oppositionibus atque coniunctonibus hoc pacto: inequalitatis graduum numerum in proposito tempore datum in tabula inequalitatis Lune queremus, capiemusque ab excessu appositarum additionum aut subtractionum congruam uni inequalitatis parti differentiam, ipsamque in medium hunius hore inequalitatis motum, hoc est in 0 32′ 40′′, multiplicabimus, et quod fiet, si numerus inequalitatis in superioribus versibus sit qui sunt supra maximam additionem subtractionemve, subtrahemus a medio unius hore per longitudinem motu, hoc est a 0 32′ 56′′, sin vero inferioribus, addemus eisdem, et quod fiet, id Luna tunc secundum longitudinem in una equali hora inequaliter movetur.

Sed tempus quidem verarum coniunctionum oppositionumque in Allexandria hoc nobis modo capietur. Ad Allexandrie namque meridianum horarum nobis tempora constituta sunt a quibus non est difficile coniunctionum oppositionumque tempora in quovis climate invenire, dato equalium horarum numero quibus ab Alexandrie meridiano differt. A differentia enim habitationum habebimus quot gradibus dati loci meridianus a meridiano Allexandrie distat, et si orientalior fuerit quam allexandrinus, tot temporibus postea ibi quam in Allexandria erit, sin autem occidentalior, totidem prius, ita ut quindecim tempora unam equalem faciant horam.

〈VI.5〉 Capitulum V: De eclipticis Solis et Lune terminis

His ita dictis, sequitur eorum expositio que ad eclipticos Solis et Lune terminos pertinent, ut si non omnes coniunctiones atque oppositiones computare velimus, sed solum illas que possint in eclipticos terminos incidere, facilis nobis ex apposito medio Lune per latitudinem motu in periodiocis coniunctionibus atque oppositionibus hec consideratio sit.

In antecedente igitur libro demonstratum a nobis est quod Lune diameter subtendit arcum circuli qui in maxima Lune distantia in centro zodiaci maximus describitur sexagesimarum unius gradus 31 20′, idque per duas eclipsis in maxima epicycli longitudine factas computavimus. Nunc vero quoniam maximos eclipticarum coniunctionum atque oppositionum terminos invenire volumus qui fiunt, quando Luna in minima epicycli longitudine est, per duas rursum eclipsis in minima longitudine observatas, —tutius enim est, per ea que apparent ista demonstrari—, quantum etiam hic arcum diameter Lune subtendat similiter demonstrabimus.

In 57^o igitur anno Philometoris qui est 574 a Nabonassaro Phamenoth secundum Egiptios die 27^o sequente 28 ab incipiente octava hora ad decimam usque desinentem Allexandrie Luna defecit plurimum a septentrione digitis 7. Quoniam igitur medium tempus fuit post mediam noctem horis temporalibus 2 30′, que fuerunt equales 2 20′, Sol enim exacte 6 4′ Tauri gradus obtinebat, colligiturque colligiturque] a Constantino add. et del. A a constituto tempore usque ad mediam eclipsim tempus annorum egiptiacorum 573 dierum 206 et horarum equalium, simpliciter quidem 14 3′, ad dies autem equatos 14 solum, in quo tempore Lune centrum medie 7 49′ Scorpionis gradus obtinebat, exacte autem 6 16′, et a maxima epicycli longitudine gradus 163 40′, a boreali autem obliqui circuli termino gradus 98 20′, perspicuum est quia quando Lune Lunae] post corr. G centrum 8 20′ a nodo gradibus in obliquo circulo distat, cum sit ipsa ipsa] post corr. G in minima distantia umbreque centrum sit in circulo maximo qui per ipsam distantiam per rectos angulos ad obliquum circulum describitur, in quo transitu maxime Lune obscuritates efficiuntur, tunc media et duodecima diametri eius pars in umbram incidit.

Trigesimo septimo rursus anno tertia secundum Calippum per〈i〉odo periodo] perodo A qui est 607 a Nabonassaro Tybi secundum Egyptios die die] 20 add. et del. A 2^o sequente 3^o incipiente hora quinta in Rhodo Luna cepit deficere, obscurataque fuit plurimum ab ab] aut add. et del. A austro digitis tribus. Quoniam igitur etiam hic eclipsis initium ante mediam noctem fuit per duas horas temporales que in Rhodo et in Allexandria fuerunt equales 2 20′, propterea quod Sol 5 8′ gradus Aquarii exacte obtinebat, et medium tempus in quo maxima obscuratio fuit ante mediam noctem horis 1 50′ equalibus proxime, colligitur a tempore nobis constituto usque ad mediam eclipsum tempus annorum egyptiacorum 606 et dierum 121 et horarum equalium tam simpliciter quam ad dies equatos 10 10′, in quo tempore Lune centrum medie 5 16′ et exacte 5 8′ Leonis gradus obtinebat, et a maxima epycicli longitudine gradus 178 46′, a boreali autem obliqui circuli termino gradus 280 36′, perspicuum etiam hinc est quia, quando 10 36′ gradibus centrum Lune in obliquo circulo distat a nodo, cum ipsa sit in eadem minima distantia et umbre centrum communem obtineat sectionem circuli qui per medium signorum est et circuli qui per centrum Lune maximus ad rectos angulos obliquo describitur, tunc quarta pars diametri lunaris in umbram incidit.

Sed quando 8 20′ gradibus a nodo centrum Lune in obliquo circulo distat, tunc distat a medio signorum sexagesimis 43 20′′ unius gradus in circulo qui per polos eius maximus describitur, quando autem gradibus 10 36′ in obliquo circulo distat a nodo, tunc distat a circulo qui per medium signorum est 54 50′′ unius gradus sexagesimis in circulo qui per polos eius maximus describitur. Quoniam igitur duarum eclipsium excessus tertiam lunaris diametri partem continet excessus autem expositarum distantiarum centri eius in eodem maximo circulo a puncto circuli qui per medium est ab umbre videlicet centro sexagesimarum unius gradus est 11 47′′, patet quod etiam tota diameter Lune subtendit arcum maximi circuli qui circa centrum zodiaci in minima eius distantia describitur sexagesimarum unius gradus 35 20′′ proxime. Verum quoniam in secunda etiam eclipsi in qua lunaris diametri pars quarta defecit centrum Lune a centro quidem umbre distabat sexagesimis 54 50′′, a puncto vero quo linea centra coniungens arcum umbre secat quarta lunaris diametri parte, hoc est sexagesimis 8 50′′, perspicuum hinc est quia etiam linea que est a centro umbre in minima Lune distantia relinquitur sexagesimarum 46, et est indifferente quodam maior quam dupla et tribus quintis quam illa que est a centro Lune que est sexagesimarum 17 40′′. Sed linea etiam que est a centro Solis subtendit similiter arcum circuli qui per ipsum circa centrum zodiaci maximus describitur sexagesimarum 15 40′′, equaliter enim et Sol et Luna proprios circulos in maxima distantia coniunctionum atque oppositionum metiri demonstrati sunt. Quando ergo apparens Lune centrum in utraque parte circuli qui per medium signorum est distat a centro Solis unius gradus sexagesimis 33 20′′ que sunt a centro utriusque luminaris, tunc primum possibile est apparentem situm Lune in tactu tactu] corr. ex actu G Solis fieri.

Veluti si intelligamus circuli quidem qui per medium signorum est arcum AB, obliqui vero lunaris arcum GD equidistantes ad sensum pervenire usque ad eclipticorum temporum transitus, describamusque EG maximi circuli arcum per polos obliqui, intelligamusque Solis semicirculum esse circa punctum A et apparens Lune centrum esse in E, ut primum solaris semicirculus in F puncto a lunari tangatur arcus E quo E apparens Lune centrum ex A solari distat, potest aliquando fieri partium dictarum 0 33′ 20′′. Sed a Meroe, Meroe] corr. ex Merore A ubi maximus dies 13 horarum equalium est, usque ad hostia Borysthonis, ubi maximus dies est horarum equalium 16, ad septentrionem quidem maxima Lune in minima coniunctionum oppositionumque distantia aspectus diversitas est 0 8′ proxime, solari diversitate simul computata, ad meridiem vero maxima similiter 0 58′. Est autem etiam maxima secundum longitudinem diversitas, quando quidem ad arcus diversitas est 0 8′, in Leone et in Geminis 0 30′ proxime, quando autem ad meridiem, 0 58,′ in Scorpione atque in Piscibus 0 15′ proxime. Si ergo verum Lune centrum in D puncto esse supposuerimus et protraxerimus protraxerimus] corr. ex protaxerimus G lineam DE totius diversitatis, erit linea DG diversitatis secundum longitudinem proxime, linea vero GE diversitatis secundum latitudinem. Quare quando Luna est septentrionalis a Sole, habetque ad meridiem maximam diversitatem, DG quidem erit 0 15′, 15'] et add. et del. A EG autem graduum 1 31′ proxime. Et quoniam proportio arcus a nodo ad punctum G ad arcum GA qui est per eclipticorum terminorum distantiam est proportio quam habent 11 30′ ad unum, quod facile intelligitur per demonstrationes de lunaris circuli declinatione factas, erit etiam hic ipse a nodo ad punctum G graduum 17 26′, cum ipso vero DG 17 41′ eorundem. Quando autem meridionalis est a Sole maximamque ad septentrionem habet diversitatem, tunc DG quidem erit 0 30′, EG vero tota 0 41′ et propter hec arcus a nodo ad punctum G graduum 7 52′ et cum arcu GD toto 8 22′ eorundem, quando igitur exacte centrum Lune a quovis nodo in obliquo circulo ad septentrionem quidem distat gradibus 17 41′, ad meridiem vero gradibus 8 22′, tunc primum in expositis nostri orbis regionibus possibile erit apparentem eius situm ad contactum Solis fieri.

Rursus quoniam maxima solaris inequalitatis differentia 2 23′ graduum demonstrata est, lunaris vero que in oppositionibus et coniunctionibus accedit graduum 5 1′, possibile erit Lunam aliquando secundum periodicas coniunctiones atque oppositiones 7 24′ gradibus distare a Sole.Sed in quo tempore hos gradus Luna pertransit in eo Sol tertiam decimam partem istorum proxime, hoc est 0 34′, pertransibit. In quo autem Luna rursus 0 34′ pertransit, in eo etiam Sol tertiam decimam istorum partem, hoc est 0 3′ proxime, pertransibit quorum tertia decima pars non est digna de qua queramus. Si ergo hec ad idem congre〈ga〉verimus et facta 0 37′, que sunt duodecima pars graduum a principio sumptorum 7 24′, solaris inequalitatis gradibus 2 23′ addiderimus, habebimus gradus tres quibus maxime veri longitudinis et latitudinis motus proxime different a motibus mediis coniunc〈t〉ionum coniunctionum] coniuncionum A atque oppositionum. Quare quando medius centri Lune motus in obliquo circulo distabit a nodis ad septentrionem quidem gradibus 20 41′, ad meridiem vero 11 22′, tunc primum in expositis regionibus possibile erit apparentem eius situm ad contactum Solis accedere; et propter hec quando a boreali obliqui Lune circuli termino graduum numerus qui periodicis coniunctionibus atque oppositionibus adiacet incidit in gradus qui sunt aut a 69 19′ usque ad 101 22′ aut a 258 38′ usque ad 290 41′, tunc solum in expositis regionibus possibile erit accidere quod diximus.

Rursus gratia etiam eclipticorum Lune terminorum, quoniam semidiameter Lune in minima eius distantia subtendere demonstrata est arcum graduum 0 17′ 40′′, semidiameter autem umbre que dupla est demonstrata et tribus proxime quintis maior semidiametro Lune colligitur earundem 0 45′ 56′′, patet quia, quando exacte centrum Lune distat ab umbre centro in maximo quidem circulo qui per ipsam et polos obliqui describitur in utranque circuli qui per medium est partem gradibus 1 3′ 36′′, in obliquo autem Lune a quovis nodo secundum proportionem unius ad 11 30′ gradibus 12 12′ proxime, tunc primum possibile erit tangi umbram a Luna; et propter illa que de inequalitate sunt demonstrata, quando etiam centrum Lune quod in medio motu capitur distat a nodo in circulo obliquo gradibus 15 12′, ut in borealis termini numeros a 74 48′ usque ad 105 12′ et a 254 48′ usque ad 285 12′ incidat, tunc primum possibile erit umbram tangi a Luna. Apponemus igitur expositis coniunctionum et oppositionum tabulis solarium etiam lunariumque terminorum latitudinis Lune numeros, ut facile discernamus quenam coniunctiones oppositionesque possint in eclipsim incidere.

〈VI.6〉 Capitulum VI: De distantia eclipticorum mensium

Sed utile etiam erit istis addere per quot quot] post corr. G universaliter menses oppositiones et coniunctiones possibile sit eclipticas fieri, ne cum unam eclipticam habeamus per omnes rursum deinceps eclipsim queramus, quaeramus] post corr. G sed per illas que tot mensibus distant ut possibile sit eclipsim fieri.

Quod igitur per sex menses tam Sol quam Luna deficere possint hinc manifestum est. Medius enim Lune secundum latitudinem motus colligit in sex mensibus gradus 184 17′ 25′′. Arcus autem qui sunt inter eclipticos terminos tam in Sole quam in Luna citra quidem semicirculum pauciores, ultra vero semicirculum plures continent gradus. Nam cum solares termini a quovis nodo in obliquo circulo Lune ad septentrionem quidem demonstratos gradus 20 41′, ad meridiem vero 11 21′ intercipiant, fit arcus non eclipticus a septentrione quidem gra-duum 138 38′, a meridie autem 157 16′. Cum vero lunares ad utranque medii circuli partem in eodem obliquo a quovis nodo gradus 15 12′ intercipiant, colligitur uterque arcus non eclipticus 149 36′. Quod autem his etiam suppositis possibile sit Lune defectum per maximorum quinque quinque] post corr. G mensium fieri spatium, hoc est in quo Sol quidem maximum faciat transitum, Luna vero minimum, hoc modo videbimus.

Nam quoniam in mediorum quinque quinque] post corr. G mensium spatio motum longitudinis medium utriusque luminarium 145 32′ gradus invenimus, inequalitatis vero lunaris in epicyclo gradus 129 5′, quorum 145 32′ solis gradus in maximo transitu qui est ad utranque minime longitudinis partem preter medium motum 4 38′ gra-dus accipiunt et 129 5′ gradus epicycli lunaris in minimo transitu qui est ad utranque maxime longitudinis partem subtrahunt a medio motu gra 8 40′, certe in mediorum quinque quinque] post corr. G mensium spatio, quando Sol maximum facit motum et Luna minimum, in antecedentibus adhuc Solis Luna erit per gradus ex utraque inequalitate collectos 13 18′. Quorum rursus duodecimam propter predemonstrata capientes partem habebimus gradus 1 6′ proxime quibus Sol Sol] uterimus add. et del. A ulterius movebitur, donec ad eum Luna perveniat. Quoniam ergo ex propria inequalitate gradus 4 38′ accepit et, antequam ad eum Luna perveniret gradus 1 et sexagesimas sex, habebit etiam maximorum mensium spatium ultra mediorum per longitudinem motum gradus 5 44′, totidem ergo proxime latitudinis etiam in obliquo circulo Lune motus obtinebit ultra 153 21′ proxime gradus latitudinis qui colliguntur in quinque mediorum mensium spatio. Verus igitur secundum latitudinem motus in maximis quinque mensibus colligitur gradus 159 5′, sed ecliptici termini ad utranque circuli qui per medium est partem continent in media longitudine Lune in circulo quidem qui maximus per polos obliqui describitur gradus unum proxime, in minima enim distantia 1 3′ 36′′, in maxima 0 56′ 24′′ colliguntur, in obliquo autem circulo gra 11 30′ a quovis nodo. Intermedius Intermedius] corr. ex Intermedium G autem et non eclipticus arcus graduum colligitur 157 qui pauciores sunt quam gradus per quinque maximos menses in obliquo circulo collecti 159 5′ duabus partibus et sexagesimis quinque. Perspicuum igitur est ex istis possibile esse Lunam in quinque maximorum mensium spatio, cum in prima oppositione in recessu a quovis nodo defecerit, in ultima rursum in accessu ad oppositum nodum deficere, fietque in utrisque eclipsibus obscuratio ab eiusdem circuli qui per medium est partibus et nunquam a contrariis. Verum quod maximi quinque menses duas possint lunares eclipsis continere, sic nobis perspicuum est.

Quod vere in septem mensibus impossibile est id accidere, etiam si minimorum mensium septem spatium supposuerimus, hoc est in quo Sol minimum faciet motum, Luna vero maximum, hoc modo similiter investigantes videbimus. Nam in mediorum rursus septem mensium spatio medius secundum longitudinem utriusque luminarium motus graduum est 203 45′, Lune autem in epicyclo 180 43′, quorum 203 45′ Solis gradus secundum minimum motum qui ad utranque maxime distantie partem est subtrahunt a medio motu gradus 4 42′, epicycli autem Lune gradus 180 43′ secundum maximum motum ad utranque minime longitudinis partem addunt medio motui gradus 9 58′. In spatio igitur mediorum mensium septem, quando Sol quidem minimi motus sit, Luna vero maximi, ultra Solem Luna 14 40′ gradibus ex utraque inequalitate collectis progredietur. Quorum duodecimam partem 4 42′ gradibus qui ab inequalitate solari defecerunt addemus et collectos 5 55′ proxime habebimus quot gradibus motus longitudinis in minimo septem mensium spatio prior erit motu mediorum septem, et motus similiter latitudinis deficiet a mediorum septem mensium motu collectis gradibus 214 42′. In minimis ergo septem mensibus per latitudinem Luna in obliquo circulo 208 47′ gradus movebitur. Sed totus inter eclipticos terminos in media Lune longitudine obliqui circuli maximus arcus tam in accessu nodi alterius quam in recessu contrarii graduum est 203, non erit igitur possibile Lunam in septem mensium spatio nec in minimorum quidem, si quoquo modo in prima oppositione defecerit, in ultima quoque deficere.

Sed demonstrandum est quod possibile sit etiam Solem apud eosdem in universis nostri orbis regionibus bis in maximorum quinque mensium spatio deficere. Nam quoniam in quinque maximis mensibus latitudinis Lune motum 159 5′ partium demonstravimus, fitque non eclipticus in Sole arcus in media Lune distantia 167 36′ eorundem, propterea quod ecliptici termini eius in circulo quidem qui per polos ipsius est distant a medio partibus 0 32′ 20′′, in obliquo vero Lune 6 12′ proxime, patet quia, si nulla lunaris aspectus diversitas est, impossibile erit quod queritur, propterea quod non eclipticus arcus maior est quam motus mensium quinque maximorum in obliquo quidem circulo partibus 8 31′, in circulo vero qui ad rectos zodiaco angulos describitur 0 45′ proxime. Ubi autem aspectus eius tanta diversitas est, ut alterius extremarum extremarum] corr. ex extremorum G coniunctionum aut utraque simul aspectus diversitas excedet excedet] corr. in excedat G gradus dictos 0 45′, ibi possibile est utrasque coniunctiones extremas eclipticas fore.

Quoniam igitur demonstratum est in tempore maximorum quinque mensium, quando Luna minimo motu, Sol autem maximo movetur, a duabus Virginis partibus usque ad duas Aquarii partes cum adhuc Luna utrorunque luminarium inequalitatis gradibus 13 18′ in antecedentibus Solis sit, quos Luna et ad eos duodecimam eorum partem in die uno et horis 2 15′ medie pertransit, patet, cum tempus mediorum quinque mensium dierum sit 147 et horarum 15 45′ proxime, quod tempus quinque maximorum mensium erit dierum 148 et horarum 18. Propterea, cum prima coniunctio in duabus circiter Virginis partibus fiat, ultima que circa duas partes Aquarii fit prior sex horis erit que ad integros dies deficiunt. Quare querendum ubi et quando Lune aspectus poterit immutari vel scilicet in altero duorum signorum que dicta sunt, vel in utrisque, ut locus Aquarii sex horis locum Virginis precedat pluribus quam dictis 45 sexagesimis.

Ad septentrionem ergo, ut diximus, nullibi Lune tanta diversitas aspectus invenitur. Quare impossibile est bis in maximorum quinque mensium spatio Solem dificere secundum Lune motum qui est in meridie circuli per medium signorum, hoc est quando in prima coniunctione a descendente nodo recedit et in ultima ad ascendentem accedit. Ad meridiem vero fere in in] ab add. et del. A regionibus que sunt post equinoctialem versus septentrionem potest tanta in utrisque signis dictis secundum precedentem sex horis situm diversitas fieri, quando due Virginis partes in prima coniunctione occidere et due Aquarii partes in meridiano secunde coniunctionis tempore supponuntur. In his enim sitibus invenitur Lune in media distantia diversitas ad meridiem, solari diversitate subtracta, sub ipso quidem quidem] post corr. G equinoctiali in Virginis situ gradus 0 22′ proxime, in Aquarii 0 14′, ubi autem dies maximus 12 30′ horarum est, in Virginis quidem situ gradus 0 27′, in Aquarii vero 0 22′, ut hee diversitates simul quatuor sexagesimis dictas 45 sexagesimas excedant. Cum igitur in borealioribus locis maior diversitas quam in meridionalibus fiat, patet quia magis semper erit possibile bis in quinque maximorum mensium spatio huiusmodi locorum incolis defectum aspici Solis, in solo tamen Lune motu septentrionali, hoc est quando in prima eclipsi ab ascendente nodo recedit et in secunda ad descendentem accedit.

Sed dico etiam rursus quod in septem quoque minimorum mensium spatio possibile est bis apud eosdem Solem deficere. Nam quoniam in hoc temporis spatio motum latitudinis Lune 208 47′ partium demonstravimus, maximusque obliqui circuli arcus inter eclipticos terminos intercipiatur qui est ab accessu nodi unius usque ad recessum oppositi, colligitur hec distantia in Sole in media Lune longitudine partium 192 24′. Quare perspicuum est quia, si nulla rursum diversitas Lune fuerit, non poterit esse quod queritur, propterea quod arcus obliqui circuli qui fit in spatio minimorum septem mensium maior est arcu qui ab eclipticis Solis terminis maximus intercipitur partibus in obliquo quidem circulo 16 23′, in circulo vero qui est per polos zodiaci 1 25′. Ubi autem tanta diversitas est ut vel alterius coniunctionum extremarum vel utriusque diversitates simul excedant gradu 1 25′, ibi possibile est utrasque coniunctiones extremas eclipticas fore. Quoniam ergo demonstratum est in tempore mediorum septem mensium, quando Luna maximo et Sol minimo motu movetur ab extremitate Aquarii usque ad mediam Virginem, Lunam iam ultra verum Solem antecessisse gradibus 14 40′, cum totidem gradus et adhuc duodecimam partem ipsorum in una die et horis 5 medie Luna pertranseat, patet quia, cum mediorum septem mensium tempus 206 dies et horas 17 proxime contineat, tempus minimorum septem mensium erit 205 dierum et horarum 12. Propterea extreme coniunctionis que in medio Virginis fit tempus erit post primam que fuit in extremitate Aquarii horis 12. Querendum igitur est ubi et quando maior quam gradus 1 25′ Lune diversitas potest fieri aut videlicet in altero dictorum signorum aut aut] add. s. l. G in utrisque secundum situm per 12 horas, hoc est quando alterum in occasu alterum in ortu est. Non enim aliter utrasque super terram eclipsis fieri possibile est. Ad septentrionem ergo rursus in orbe habitabili nostro nullo in situ tanta Lune diversitas invenitur, nec sub ipso quidem equinoctiali maior 23 sexagesimis que secundum latitudinem in maxima distantia fit. Quare impossibile est in septem minimorum mensium spatio bis Solem deficere secundum Lune transitum qui est a meridie circuli per medium, hoc est quando in prima quidem coniunctione ad ascendentem accedit, in secunda vero a descendente nodo recedit. Ad meridiem autem tantam ferme fieri diversitatem in paralello per Rhodum invenimus, quando extrema pars Aquarii oritur et media Virginis occidit. In locis enim huius paralelli in utroque horum situum subtracta diversitate solari Luna in media eius longitudine diversitatem habet ad meridiem sexagesimarum 46, ut ambarum coniunctionum diversitates excedant gradum gradum] corr. ex graduum A unum et sexagesimas 25. Cum igitur maior ad meridiem in borealioribus hoc paralello fiat diversitas, perspicuum est quia possibile sit bis ab incolis earum regionum in minimorum septem mensium spatio Solem deficientem videri, cum tamen in septentrione septentrione] corr. ex septentrionem A solummodo circuli qui per medium signorum est Luna inveniatur, hoc est quando in prima quidem eclipsi ad descendentem nodum accedat, in secunda vero ab ascendente recedat.

Restat nunc illud demonstrandum quod in nostro terrarum orbe non est possibile bis in uno mense Solem deficere neque in eodem climate neque in diversis etiam, si quis cuncta supponat que, quamvis concurrere non possunt, cum tamen concurrerint, conducunt ad possibilitatem propositi. Dico autem, etiam si Lunam in minima supposuerimus longitudine, ut maior eius diversitas sit, et mensem minimum, ut quam maxime possibile sit minimo maior menstruus latitudini motus fiat arcu qui ab eclipticis solaribus continetur, etiam si indifferenter tum horis tum signis signis] corr. ex figuris G abutamur, in quibus Luna maximas videtur diversitates aspectus facere.

Quoniam igitur in medio mense utriusque luminarium motus gradus obtinet 29 6′ et motus Lune in epicyclo 25 49′, quorum 29 6′ in minimo Solis motu ad utranque maxime longitudinis partem subtrahunt a medio motu gradus 1 8′, epicycli autem Lune gradus 25 49′ in maximo eius motu ad utranque minime longitudinis partem addunt medio motui 2 28′, si predemonstrata sequentes inequalitates ambas composuerimus, et gradus qui fiunt 3 36′ 12^〈am〉 12^am] 13 add. s. l. G partem, hoc est 0 18′, inequalitati qua Sol deficiebat addiderimus, faciemus gradus 1 26′, quibus minimi mensis motus minor erit motu medii mensis tam per longitudinem quam per latitudinem. Quare, quoniam medii mensis per latitudinem motus graduum est 30 40′, erit minimi mensis motus graduum 29 14′, qui faciunt in circulo qui ad rectos angulos zodiaco maximus est graduum 2 33′ proxime. Sed totus eclipticorum Solis terminorum transitus in minima Lune distantia gra-dus colligitur 1 6′, ut maior minimi mensis transitus fiat gradibus 1 27′. Oporteret igitur omnino ut in uno mense Sol bis posset deficere, vel nullam esse in altera coniunctionum Lune diversitatem et in altera maiorem quam 1 27′, vel ad eandem in utraque coniunctione partem Lune fieri diversitatem et excessum utrarumque diversitatum maiorem esse quam 1 27′, vel utrasque diversitates plurium esse gradibus quam 1 27′, quando alterius coniunctionis diversitas ad septentrionem alterius ad meridiem fieret. Sed nullibi terrarum in coniunctionibus ne in minima quidem longitudine maior Lune diversitas est solari diversitate subtracta quam gradus unus. Non erit igitur possibile bis in minimo mense Solem deficere, quando vel in altera coniunctione nulla vel ad eandem partem in utrisque Lune diversitas est, cum excessus earum uno gradu maior non fiat, oporteretque vel ipsis 1 27′ maiorem fieri. Solummodo igitur quod proposuimus accidere posset, si utraque diversitate in oppositis partibus facta plures gradus colligerentur quam 1 27′. Id vero in diversis quidem orbis terrarum partibus possibile erit, cum possit apud boreales ad equinoctialem in orbe nostro ad meridiem et apud australes ultra equinoctialem qui antipodes nominantur, Solis diversitate subtracta, ad septentrionem Lune diversitas esse a 0 25′ usque ad gradum unum. In eandem autem orbis terrarum parte nunquam accidere poterit, propterea quod maxima Lune diversitas est similiter sub ipso ipso] g add. et del. A quidem equinoctiali non magis quam 25 sexagesimarum tam ad septentrionem quam ad meridiem, apud autem borealissimos aut australissimos non magis quam per gradum unum in partes oppositas, ut etiam sic utreque simul diversitates minores inveniantur quam 1 27′. Cum autem multo minor utraque oppositarum diversitatum semper fiat apud interiacentia loca inter equinoctialem et utramque extremitatem, erit magis impossibile in illis quod queritur. Apud eosdem ergo nullibi terrarum bis in eodem mense Solem deficere possibile est, sed nec apud diversos in eadem orbis terrarum parte. Que nobis erant demonstranda.

〈VI.7〉 Capitulum VII: De tabulis eclipticis

Que igitur coniunctionum distantie in eclipsium consideratione accipiende nobis sint, per ea que dicta sunt ad apertum est. Ut autem et media ipsarum tempora discernere, motusque Lune computare in coniunctionibus quidem apparentes, in oppositionibus autem veros per locos Lune secundum latitudinem, facileque considerare possimus futuras omnino eclipticas coniunctiones atque oppositiones et magnitudines atque tempora obscurationum, tabulas ad huiusimodi cognitionem componemus: duas solarium eclipsium gratia et duas lunarium in maxima et minima Lune distantia incrementumque obscurationum per duodecimam utriusque luminarium partem supponemus.

Primam igitur solarium eclipsium tabulam qua ecliptici termini in maxima Lune longitudine continentur, 25 versuum et ordinum quatuor faciemus, quorum duo primi apparentem Lune transitum in obliquo circulo secundum latitudinem in singulis obscurationibus continebunt. Nam quoniam Solis diameter sexagesimarum est 31 20′′, Luneque in maxima distantia totidem esse demonstrata est, ac ideo, quando apparens Lune centrum a centro solari in circulo qui maximus per centra utrorumque describitur distat sexagesimis 31 20′ et a nodo in obliquo circulo gradibus 6 secundum expositam proportionem 11 30′ ad unum, tunc primum in contactu Solis Luna fit. Propterea in primis versibus ordinum ponemus in primo quidem ordine gradus 84, in 2^o vero gradus 276, in ultimis autem versibus in primo rursus ordine gradus 96, in secundo vero gradus 264. Et quoniam duodecime parti solaris diametri ab obliquo circulo 30 proxime sexagesime dantur, per totidem minuemus augebimusve binos propositos ordines ab extremitatibus incipientes, ita ut in mediis versibus 90 gradus et 270 collocemus. Tertius autem ordo magnitudines obscurationum continebit, ita ut in extremis versibus 0 0 primi contactus initia ponantur, et deinceps digitus unus pro duodecima diametri parte, similiterque incremento per unum facto usque ad medium versum, ad quem duodecim digitorum numerus perveniet. Quartus autem ordo transitus Lune continebit qui fiunt in singulis obscurationibus, nunquam tamen computatis neque Solis interea motibus neque Lune diversitatibus. Secundam vero solarium eclipsium tabulam qua ecliptici Lune termini in minima longitudine continentur sicuti primam in ceteris ordinabimus, sed 27 versuum et quatuor ordinum similiter faciemus, propterea quod semidiameter Lune in hac distantia talium sexagesimarum demonstrata est 17 40′′, qualium est solaris semidiameter 15 40′′. Quando igitur primum ad Solis contactum venit, tunc centrum eius a solari rursus centro 33 20′′ sexagesimis distat et a nodis in obliquo circulo gradus 6 24′. Fiunt itaque in extremis versibus apparentes latitudinis numeri 83 36′ et 276 24′ et rursum 96 24′ et 263 36′. Digitorum autem numerus in medio versuum similem duodecim digitorum excessum et aduc quatuor quintas continebit, quoniam more quoque transitus fit.

Utrasque autem lunares tabulas 45 versuum et quinque ordinum faciemus, et in prima numeros latitudinis Lune, prout in maxima longitudine est, apponemus. Nam quoniam semidiameter Lune in hac longitudine 15 40′ demonstrata est, umbre vero semidiameter 40 44′ earundem, ut, quando primum a Luna tangitur umbra, tunc centrum Lune a centro quidem umbre in circulo qui per centra utrarumque maximus describitur 56 24′′ sexagesimis distet, a nodis autem in obliquo circulo gradibus 10 48′, ideo in primis versibus 79 12′ numerum et 280 48′ conscribemus, in ultimis vero 100 48′ et 259 12′, et eodem modo ut prius augebimus minuemusve ipsos sexagesimis que dantur duodecime parti lunaris diametri que est sexagesimarum 30. In secunda vero vero] parte add. et del. A tabula numeros latitudinis Lune, quando in minima distantia ipsa est, conscribemus in qua distantia semidiameter eius 17 40′′ sexagesimarum demonstrata est et semidiameter umbre 45 56′′ earundem. Quare, quando primum Luna umbram tangit, tunc centrum eius ab umbre centro distat gradibus similter 1 3′ 36′′, a nodo autem in obliquo circulo gradibus 12 12′. Quocirca in primis versibus numerum 77 48′ et 282 12′ conscribemus, in extremis vero 102 12′ et 257 48′, et rursum augebimus diminuemusve ipsos sexagesimis que tunc dantur duodecime parti lunaris diametri, que est sexagesimarum 34. Tercii vero ordines qui sunt digitorum ita se habent, ut in Sole, et similiter qui secuntur quibus transitus Lune in singulis obscurationibus continentur tum incidentie tum repletionis et ad hec medii more temporis.

Computavimus autem positos Lune transitus per lineas in singulis obscurationibus sic tamen, ut usi demonstrationibus simus quasi in una superficie in rectis lineis, propterea quod arcus harum magnitudinum non differunt ad sensum a cordis suis, et ad hec quasi nullo sensibili digno cura motus Lune in obliquo circulo differat a motu qui est in circulo per medium signorum. Nemo enim nos ignorasse putet differentiam quandam ad motum Lune per longitudinem fieri, quoniam obliqui circuli arcubus pro arcubus eius qui per medium signorum est abusi sumus, nec etiam quod oppositionum coniunctionumque tempora non sunt eadem precise cum mediis eclipsium temporibus.

Si enim equales duos horum circulorum arcus ab A nodo acceperimus arcum scilicet scilicet] post corr. G AB et AG et BG lineam coniunxerimus perpendicularem que BD ex B ad AG lineam deduxerimus, perspicuum hinc erit, Luna in B puncto supposita, quia, cum AG arcu circuli qui per medium signorum est pro AD abusi simus, simus] post corr. G propterea quod ad circulos qui sunt per polos zodiaci motus qui ad ad​] post corr. G eum fiunt considerantur, per GD lineam differet inequalitatis differentia que est penes lunaris circuli declinationem. Sole vero aut umbre centro in B supposito, oppositionis quidem aut coniunctionis tempus erit per indifferentiam circulorum, quando Luna erit in G, medium autem eclipsis tempus, quando erit in D, propterea quod media obscurationum tempora ad circulos qui describuntur per polos lunaris circuli capiuntur, ita tempus medie coniunctionis atque oppositionis differet a medio eclipsis tempore per arcum GD.

Causa vero est, ne hos etiam arcus in particularibus tractatibus una computemus, quoniam parvas atque insensibiles differentias faciunt, et quoniam ignorare aliquid horum turpe 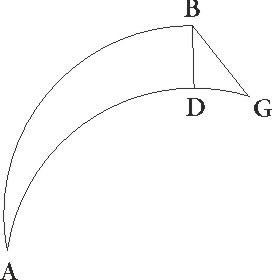professori putamus, putamus] post corr. G si vero gratia difficultatis que in particularium demonstrationibus est sponte aliquid ita parvorum despiciat, presertim quando et penes suppositiones et penes observationes ipsas illud negligi potest, universaliter quidem sensum maxime quod negligitur collectum facit, errorem vero in apparentibus, si non colligitur, aut nullum aut minimum inducit. Arcum igitur arcu GD similem universaliter quidem non maiorem quinque unius gradus sexagesimis invenimus, quod per theorema illud demonstratur quo differentias arcuum equinoctialis ad arcus circuli qui per medium signorum est quasi in circulis qui per polos equinoctialis describuntur computavimus. In eclipsibus autem non invenimus eam maiorem duobus sexagesimis. Qualium enim est uterque arcus AB et AG 12, ad tot enim fere Lune in eclipsibus transitus pervenit, talis BD linea est unius. Ac ideo etiam AD xi 58′ proxime eorundem. Reliquus ergo GD arcus sexagesimarum duarum est que nec sextamdecimam quidem partem unius equinoctialis faciunt hore. De tanta vero differentia multum curare ostentationis magis est quam veritatis. Quapropter transitus Lune in obscurationibus ita consideravimus, quasi nihil ad sensum isti circuli differant. Facta est autem nobis consideratio hec, ut uno aut duobus exemplis totam rursus rem aperiamus hoc modo.

Sit punctum A Solis aut umbre centrum, pro arcu arcu] corr. ex arcus A autem lunaris circuli sit recta linea BGD, et supponatur centrum Lune tunc esse in B, quando accedens primum Solem vel umbram tangit, in D autem, quando recedens, coniunctisque lineis AB et AD, deducatur ex A ad lineam BD perpendicularis AG. Quod igitur, quando Lune centrum in G puncto erit, tunc et medium eclipsis tempus et maxima obscuratio erit, patet partim ex eo quod AB et AD linee equales sunt, et propterea etiam transitus BG transitui GD equalis sit, partim ex eo quod AG linea minor illis omnibus est quibus duo centra in BD linea coniunguntur. Perspicuum autem est quod etiam utraque linearum AB et AD utrasque simul semidiametros Lune atque Solis aut umbre continet et quod AG utraque ipsarum minor est particula diametri deficientis luminaris que ab obscuratione intercipitur.

Hec cum ita se habeant, fiat obscuratio exempli gratia digitorum trium, et primum supponatur centrum Solis esse in A. Quando igitur Luna est in maxima sua distantia, tunc AB 31′ 20′′ sexagesimarum fit et quadratum suum 181′ 47′′, linea vero AG 23 30′′ earundem. Minor enim est quam AB tribus solaris diametri duodecimis, hoc est 7 50′ et quadratum eius 552′ 15′′, quare quadratum etiam linee BG erit earundem 429′ 32′′, ipsa vero BG per longitudinem 20′ 43′′ proxime. Quas in quarto prime solaris tabule ordine ad tres digitos apponemus. In minima vero Lune distantia AB linea rursus fit 33′ 20′′ sexagesimarum et quadratum suum 1111′′ 7′′′, AG vero 25′ 30′′ et quadratum suum 650′′ 15′′′ et reliquum quadratum linee BG sexagesimarum 460′′ 52′′′. Quare linea ipsa BG 21′ 28′′ erit earundem, quas similiter in quarto tabule solarium eclipsium ordine ad tres digitos apponemus.

Supponatur rursus A punctum umbre centrum esse et obscuratio eiusdem quar〈t〉e quarte] quare post corr. G partis lunaris diametri. In maxima ergo Lune longitudine 56 24′ AB linea sexagesimarum fit et quadratum suum 3180′ 58′′, AG vero linea 48 34′ earundem. Minor enim est quam AB quarte lunaris diametri parte, idest 7 50′, in maxima longitudine et quadratum eius 2358′ 43′′. Quare quadratum BG linee relinquitur 822′ 15′′, ipsa vero linea BG erit per longitudinem 28 41′ earundem. Quas in quarto prime tabule lunarium eclipsium ad tres digitos apponemus transitum incidentie continentes qui ad sensum transitui replectionis idem est, in minima vero longitudine AB quidem linea 63 36′ sexagesimarum fit et quadratum suum 4044′ 58′′, AG vero 54 46′ earundem. Excessus enim 8 50′ quarta rursus pars est lunaris diametri in distantia minima, eius quadratum est 2959′ 23′′. Quare relinquetur quadratum BG linee 1045′ 35′′, ipsa vero linea BG 32 21′ per longitudinem earundem. Quas similiter in quarto secunde tabule lunarium eclipsium ad tres digitos apponemus.

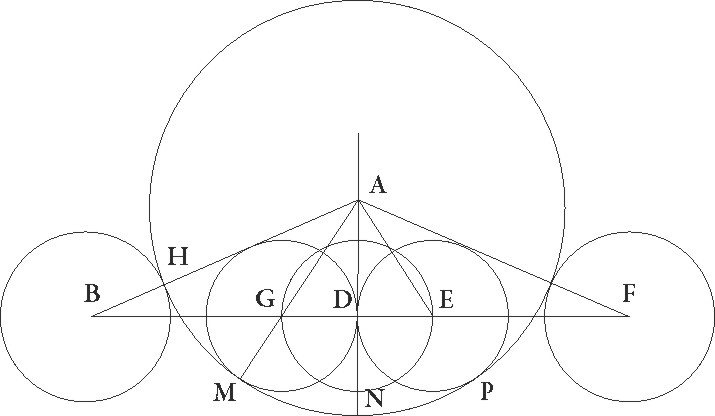Sed gratia temporis more que in lunaribus obscurationibus invenitur sit umbre centrum in puncto A, et recta linea BGDF sit pro arcu obliqui lunaris circuli, et B quidem punctum centrum esse Lune supponatur, quando primum deforis accedens umbram tangit, G vero ubi centrum Lune futurum sit, quando primo tota deficiens ab interiori parte umbre circulum tanget, E autem ubi rursus centrum Lune sit, quando recedens primum ab interiori parte umbre circulum tangit, F autem ubi erit centrum Lune, quando tandem recedens deforis umbram tanget. Predemonstratis igitur etiam hic servatis, illud preterea patet, quod utraque linearum AG et E excessum continet quo semidiameter umbre Lune semidiametrum excedit. Quare GD transitus DE transitui equalis fit et uterque medietatem continet more et reliqua BG transitus incidentie transitui replectionis EF equalis est. Supponatur ergo eclipsis digitorum Lune quindecim, hoc est in qua D centrum interius interius] corr. ex interus G ab extremitate eclipticorum terminorum fit tota semel lunari diametro et adhuc quarta ipsius parte, idest quando AD linea utraque quidem linearum AB et AF minor est per positam lunarem diametrum semel et adhuc per quartam ipsius partem, utraque vero linearum AG et E per quartam lunaris diametri solummodo partem. Quando igitur Luna est in maxima longitudine, tunc AB linea fit dictarum sexagesimarum 56 24′ et quadratum suum 3180′ 58′′, AG vero 25 4′ earundem. Lunaris enim diameter in maxima distantia sexagesimarum est 31 20′, et quadratum eius 628′ 20′′, AD autem linea similiter 17 14′, et quadratum eius 296′ 59′′. Quare quadratum etiam linee BD relinquetur 2883′ 59′′, ipsa vero BD 53 42′ earundem per longitudinem erit, quadratum autem linee GD relinquetur 331′ 21′′, et ipsa erit per longitudinem 18 12′ earundem, reliqua etiam BG linea earundem erit 35 30′. Quare ad numerum 15 digitorum in prima lunarium eclipsium tabula in quarto quidem ordine incidentie sexagesimas 35′ 30′′, quot etiam replectionis sunt, apponemus, in quinto autem medii more temporis sexagesimas 18 ′12′′. Quando vero Luna est in minima distantia, tunc AB linea fit expositarum sexagesimarum 63 36′ et quadratum eius 4000 44′ 58′′, AG autem linea 28′ 16′′ earundem. Lune namque diameter in minima distantia demonstrata est sexagesimarum 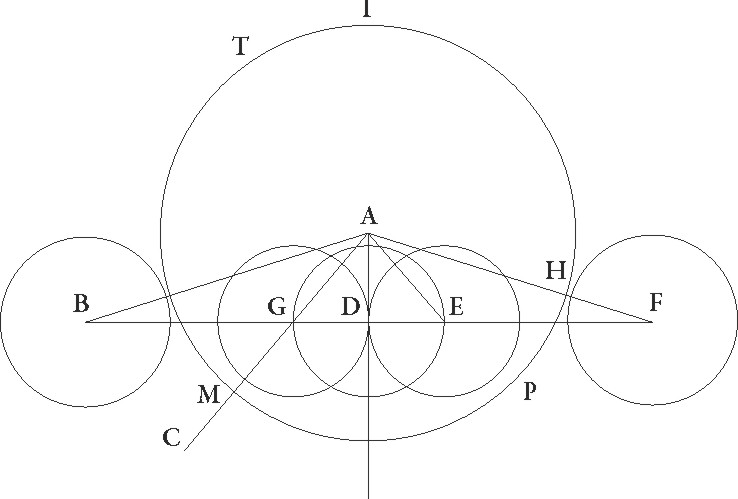35 20′ et quadratum eius 799′ 4′′, AD vero etiam similiter 19 20′ et quadratum suum 377′ 39′′, quare quadratum linee BD relinquetur 3667′ 19′′. Ipsa vero linea BD erit per longitudinem earundem 60 34′, quadratum autem linee GD relinquetur 421′ 21′′, et ipsa GD per longitudinem erit 20 32′ earundem, reliqua vero linea BG 40 2′ earundem. Quare ad numerum etiam digitorum 15 secunde lunarium eclipsium tabule, in quarto quidem ordine sexagesimas incidentie 40 2′, quot rursus replectionis sexagesime sunt, apponemus, in quinto autem sexagesimas sexagesimas] corr. ex sexagesimarum G medii more temporis 20 32′.

Verum ut ut] add. s. l. G etiam in motibus qui in epicyclo inter maximam et minimam Lune distantiam sunt congruentes singulis excessus totius differentie per sexagesimarum viam et rationem facile capiamus, parvam aliam superioribus tabulam apposuimus, qua et ipsius motus in epicyclo epicyclo] lunari add. et del. A numeri et congruentes sexagesime apparentibus singulis excessibus ex primis et secundis eclipsium tabulis continentur. Harum vero sexagesimarum quantitas in diversitatis lunaris aspectus tabula in septimo posita ordine nobis est, ita ut epicyclus in maxima excentrici longitudine propter oppositiones atque coniunctiones suppositus sit.

Verum quoniam plurimi eorum qui eclipticas significationes observant non per diametros circulorum magnitudines obscurationum metiuntur, sed per totas ipsarum superficies, quoniam visus secundum simplicitatem obiectionis totum ipsum quod apparet comperat non apparenti, aliam etiam parvam istis duodecim versuum et ordinum trium addidimus tabulam, et in primo quidem ordine duodecim digitos collocavimus, ita ut veluti in eclipticis tabulis duodecimam diametri utriusque luminarium partem quilibet digitus contineat, in reliquis autem duobus congruentes ipsis rursum totarum arearum duodecimas, in secundo quidem solaris, in tertio vero lunaris, hec in magnitudinibus solum quem in media longitudine Lune fiunt computavimus. Eadem enim proxime proportio fit in tantula diametrorum differentia. Consideravimus autem hec quasi proportio circumferentiarum ad diametros sit quam habent 3 8′ 30′′ ad unum. Hec enim proportio proxime est inter triplam septima parte adiecta et inter triplam decies septuagesima prima parte adiecta, quibus Archimedes simplicius usus est.

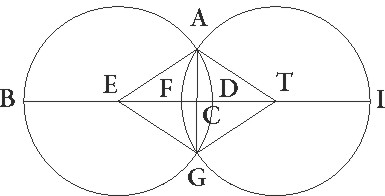Sit igitur primum solarium eclipsium gratia ABGD Solis circulus, cuius centrum sit E, circulus autem Lune in media distantia sit AFGI circa centrum T qui secet circulum Solis in punctis A et G, et coniuncta BETI linea, supponatur quartam solaris diametri partem defecisse, ut FD linea talium sit 3 qualium est BD diameter 12, diameter vero Lune IF 12 20′ proxime earundem secundum proportionem 15 40′ ad 16 14′, et propterea etiam ET lineam colligi earundem 9 10′. Quare circumferentiarum etiam secundum unius ad 3 8′ 30′′ proportionem solaris quidem circuli partium fit 37 42′, lunaris vero 38 46′ earundem. Similiter autem et arearum arcarum] corr. ex earum G totarum, quoniam linea que a centro ad circumferentiam est in circunferentiam multiplicata duas areas circuli facit, solaris quidem circuli area colligetur partium 113 6′, lunaris vero 119 32′ earumdem.

Hec cum ita se habeant, querendum est quot partium est area que continetur ab ADGF talium qualium tota solaris circuli area est 12. Coniungantur igitur linee E et AT et GE et GT et perpendicularis ACG. Quoniam igitur utraque linearum EA et EG talium esse supponitur 6 qualium est ET linea 9 10′ et utraque AT et TG 6 10 earundem et est C angulus rectus, si excessum quo quadratum linee TA excedit quadratum linee E, hoc est partes duas et sexagesimas duas, partiemur per lineam ET, habebimus excessum linearum EC et CT 13′ 3′′ sexagesimarum earundem. Quare EC quoque linea 4 28′ et CT 4 42′ earundem colligitur. Et propterea etiam utranque linearum AC et CG, —equales enim sunt—, 4 proxime earundem. Consequenter igitur EG quidem trianguli aream habebimus 17 52′, aream vero trianguli ATG 18 48′ earundem. Rursus quoniam qualium est BD diameter 12 et FI similiter 12 20, talium AG linea colligitur 8, erit AG talium 80 qualium BD diameter 120. Qualium vero FI diameter 120, talium AG 77 50′. Erunt igitur arcus quoque sui ADG quidem talium 83 37′ qualium ABGD circulus 360, AFG autem talium 80 52′ qualium est AFG circulus 360. Quare quoniam eadem proportio est circulorum ad arcus et arearum ipsorum circulorum ad areas sectorum qui sub eisdem arcubus sunt, habebimus etiam EGD quidem sectoris aream talium 26 16′ qualium demonstrata est area circuli ABGD 113 6′, ATGF autem sectoris aream 26 51′ earundem. Erat enim etiam area circuli AFGI 119 32′ earundem. Sed area trianguli EG demonstrata est 17 52′, area vero trianguli ATG similiter 18 48′, et reliquam ergo ADGC portionis aream 8 24′ partium habebimus, portionis vero AFGC 8 3′ earundem. Quare tota que ab AFGD area continetur talium est 16 27′, qualium ABGD circuli area supponitur 113 6′. Qualium ergo est solaris circuli area 12, talium erit quod per eclipsim continetur 1 45′ proxime, que in dicte tabule tertio versu et in ordine secundo apponemus.

Supponatur rursum lunarium etiam eclipsium gratia in eadem descriptione lunaris quidem circulus BGD, umbre autem in media distantia circulus AFGI, et deficiat deficiat] post corr. G similiter quarta lunaris diametri pars, ut qualium est BD diameter 12, talium talium] est add. et del. A sit defectus quidem linea FDZ, umbre vero diameter secundum proportionem unius ad 2 36′ earundem 31 12′, et propterea etiam ECT linea 18 36′ colligatur. Quare circumferentia rursus lunaris quidem circuli partium fit 37 42′, umbre autem circuli 98 1′ earundem, aree quoque lunaris quidem circuli 113 6′, umbre autem circuli 764 32′ earundem colliguntur. Quoniam igitur hic, qualium est ET linea 18 36′, talium utraque quidem linearum E et EG supponitur 6, utraque vero AT et TG 15 36′ earundem, si excessum similiter quo quadratum linee TA excedit quadratum linee E 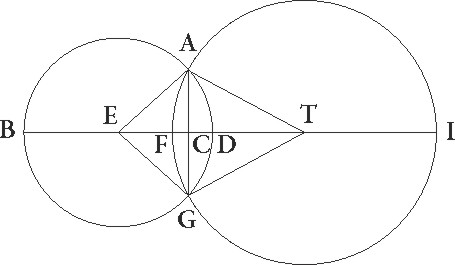partiemur per lineam ET, ET] post corr. A habebimus excessum linearum EC et CT 11 8′ earundem, ita EC quidem 3 44′, CT autem 14 52′, earundem colligitur, et propterea utraque etiam linearum AC et CG 4 42′ earundem. Quare consequenter aream quidem trianguli EG habebimus partium 17 33′, aream aream] corr. ex earundem G vero trianguli ATG 69 52′ earundem. Rursus quoniam, qualium est BD diameter 12 et FI similiter 31 12′, talium AG colligitur 9 24′, erit AG linea talium 94 qualium est BD diameter 120 et talium 36 9′ qualium est FI diameter 120. Quare arcus quoque sui ADG quidem talium erit 113 8′ qualium ABGD circulus 360, arcus vero AFG talium 35 4′ qualium AFGI circulus 360. Quare per predicta sectoris quoque EGD aream talium habebimus 32 24′ qualium area circuli ABGD demonstrata est 113 6′, aream vero sectoris AGTF 74 28′ earundem. Erat enim etiam area circuli AFGI 764 32′ earundem. Fuit autem area quoque trianguli EG 17 33′ earundem demonstrata, et trianguli similiter ATG area 69 52′, et reliquam ergo ADGC quidem portionis aream habebimus 14 51′, portionis autem AFGC 4 36′ earundem. Quare tota area que ab AF, GD continetur talium est 19 27′ qualium ABGD circuli area supponitur 113 6′. Qualium ergo est lunaris circuli area 12, talium erit deficientis portionis area 2 4′ proxime, que in eiusdem tabule ordine tertio atque lunari ad tres digitos apponemus. Sunt autem tabule iste.

〈VI.8〉 Capitulum VIII. Eclipsium tabule

〈VI.9〉 Capitulum VIIII : Lunarium eclipsium computatio

His ita expositis, lunarium eclipsium considerationem hoc modo faciemus: cum oppositionis quam querimus numerum qui colligitur in hora medii temporis in Allexandria tam graduum qui sunt a maxima epicycli longitudine qui gradus inequalitatis vocantur quam latitudinis qui sunt a boreali termino post equationem que per additionem subtractionemve fit, conscripserimus, primum cum latitudinis numero in lunarium eclipsium tabulas intrabimus, et si coincidit coincidit] post corr. G cum primorum duorum ordinum numeris, ea que numero latitudinis in utraque tabula apponuntur tam in transituum quam in digitorum ordinibus seorsum conscribemus, deinde cum inequalitatis etiam numero in tabulam equationis intrabimus, et quotquot sexagesimas inde assumemus, totidem capiemus ab excessu digitorum et sexagesimarum quas ex utraque tabula conscriptas habuimus, habuimus] post corr. G ipsasque illis addemus que a prima tabula sumpte sunt. Si tamen accideret ut latitudinis numerus in secundam solummodo tabulam incideret, que in ea sola de digitis partibusque sexagesime inveniuntur eas conscribemus, et quot ex huiusmodi equatione digiti fiunt, totidem duodecimas lunaris diameteri partes obscurationem in medio eclipsis tempore habituram dicemus. Deinde numero equato huiusmodi duodecimam semper suiipsius pro motu Solis qui interea fit partem addemus, partiemurque per motum Lune hunius hore inequalem inequalem] corr. ex equalem G qui tunc fuerit et numerus qui per partitionem emerget horarum erit equalium quas quelibet eclipsis tempora continebunt incidentie quidem repletionisque tempus eas que seorsum ex ordine quarto colliguntur, eas vero que ex quinto medietas temporis more. Hinc etiam singularum horarum motus qui fiunt in principio et in exitu incidentie atque replectionis ex subtractione additioneve ipsorum que in singulis inveniuntur ad medium more tempus, hoc est ad tempus vere oppositionis proxime inveniuntur. Postremo cum diametri digitis in brevissimam tabulam intrabimus, et duodecimas totarum arearum partes in ordine quarto conscriptas inveniemus, et similiter solarium quoque in ordine secundo.

Sed quamvis ratio quidem demonstrat non semper tempus quod a principio eclipsis usque ad medium ipsius est equale illi tempori esse quod est a medio usque ad extremum, propterea quod equales transitus in temporibus inequalibus propter Solis et Lune inequalitatem fiunt, tantum, quantum ad sensum pertinet, nullus dignus cura in apparentibus error fiet quod equalia hec tempora esse supposuimus. Nam etiam si in medio cursu fuerint ubi additiones maiores fiunt, transitus tamen ad tot horas, quot horarum totum eclipsis tempus est, differentiam excessus facit minime sensibilem.

Quod autem lunaris latitudinis periodus ab Hipparco demonstrata sine errore non sit, quoniam minor secundum illas rationes esse videtur intermedius expositarum eclipsium motus, maior autem que per computationem nostram percipitur, ex eisdem rursus animadvertentes intelligemus. Nam cum ad huiusmodi demonstrationem duas lunaris eclipsis per 7160 menses factas acceperit, in quibus quarta lunaris diametri pars in eodem ex ascendente nodo transitu defecit, quarum prima in secundo Mardocempadi anno altera in trigesimo septimo tertie secundum Calippum periodi fuit observata, observata] post corr. G accipit ad demonstrandam restitutionem quod idem secundum latitudinem transitus equaliter in utraque continetur eclipsi, eo quod prima facta fuerit, cum Luna esset in maxima, secunda, cum esset in minima epicycli longitudine, et propterea putavit nullam ex inequalitate accidisse differentiam. Sed in hoc ipso primum erravit, quoniam etiam non contemnenda differentia quedam ex inequalitate facta est, eo quod medius motus non equaliter maior quam verus in utrisque inveniatur eclipsibus, sed in prima per unum gradum proxime, in secunda vero per octavam unius gradus partem, ut secundum hoc latitudinis periodus ad integras restitutiones deficiat 52′ 52'] corr. ex 0 52' G 30′′ sexagesimis unius partis qualium est obliquus Lune circulus 360. Deinde nec differentiam que propter distantias Lune obscurationum magnitudinibus accidit computasse invenitur, que maxima in illis eclipsibus fuit. Prima enim in maxima, secunda in minima Lune distantia facta fuit. Necesse enim est eiusdem quarte partis obscurationem in prima quidem eclipsi a minore ascendentis distantia nodi accidisse, in altera vero a maiore. Quarum distantiarum differentiam unius gradus et quinte proxime partis colligi demonstravimus ut etiam hic per tantam differentiam latitudinis revolutio post integras restitutiones excedat. Quantum igitur ad errorem ipsum pertinet duobus proxime gradibus qui utrinque utrinque] post corr. G colliguntur periodica latitudinis restitutio a veritate aberrasset, si forte utreque utreque] corr. ex uterque G ad minus aut ad maius differentiam collegissent. Verum quoniam altera deficere restitutionem forte faciebat altera excedere, unde fortassis etiam Hipparchus alteram ex altera compensavit sola tertia parte unius gradus, hoc est per excessum eroris utriusque, maior motus quam restitutio invenitur.

〈VI.10〉 Capitulum X : Solarium eclipsium computatio

Sed lunarium quidem eclipsium consideratio modis expositis recte solummodo computabitur, solarium vero computationem que propter diversitates aspectus Lune difficilior est sic faciemus. Primo enim quot vere coniunctionis tempus horis equalibus ante vel post meridiem erit, inveniemus, deinde si querimus in alio climate, idest in regione que non sit sub Allexandrie meridiano, additione subtractioneve subtractioneve] corr. ex subtradictioneve G differentie horarum equalium que in duabus meridianis secundum longitudinem sunt inveniemus quot horis equalibus etiam ibi ante vel post meridiem vere coniunctionis tempus erit, primumque apparentis coniunctionis tempus in climate ubi queritur equabimus. Id idem proxime futurum est cum medio eclipsis tempore, idque faciemus via et ratione que nobis iam cum de diversitatibus diceremus exposita est. Nam cum ceperimus ex angulorum diversitatumque tabula convenienter tum climati tum horarum a meridiano distantie, et preterea parti zodiaci ubi coniunctio fiet, et ad hec lunari distantie diversitatem aspectus Lune que primo fit in circulo per punctum verticis et centrum Lune maximo descripto, ab hac semper subtrahentes solarem diversitatem in eodem versu conscriptam discernemus a reliqua, sicut demonstratum est, per angulum qui invenitur in sectione zodiaci et circuli maximi per punctum verticis descripti et que colligitur longitudinis solum diversitas erit. Cui semper addentes congruentem contentis ab ipsa equinoctialibus temporibus superdiversitatis differentiam, hoc est ipsius excessus duarum adiacentium diversitatum qui in eadem tabula invenitur diversitatis dico distantie que est a puncto verticis et illius que est cum equinoctialium temporum additione, que rursus diversitati soli secundum longitudinem conveniunt cum tota earum parte, si sensibilis sit, quota pars prime diversitatis ipse sunt, tandem partibus totius per longitudinem diversitatis que ita colligentur duodecimam rursus partem suam pro solari motu addemus, et totum collectum numerum in horas equales per partitionem inequalium huius hore Lune motuum qui in ipsa coniunctione fiunt resolvemus, et si diversitas secundum longitudinem ad successionem signorum fit, —iam enim demonstravimus quomodo id discernendum est—, tunc partes quidem que in horas equales fuerant resolute a vero Lune loco qui tempore coniunctionis equatus est aufferemus seorsum a a] corr. ex ad G longitudinis et latitudinis atque inequalitatis, et sic habebimus veros Lune motus in tempore apparentis coniunctionis, ipsis autem horis dicemus prius apparentem coniunctionem quam veram fore. Sin autem diversitas longitudinis ad precedentia signorum sit, tunc partes quidem econtra addemus motibus Lune in vere coniunctionis tempore equatis longitudinis rursum et latitudinis et inequalitatis seorsum, horas vero habebimus quot apparens posterior erit quam vera. Rursus igitur per horas equales quibus apparens coniunctio distat a meridiano eisdem viis primum quanta sit diversitas Lune ad circulum qui maximus per punctum verticis et ipsam describitur investigabimus, subtrahemusque a diversitate inventa Solis diversitatem que ipsi eidem numero adiacet, et ab ea que relinquitur similiter ex angulo qui tunc in sectione circulorum invenitur diversitatem latitudinis que fit quasi in circulo qui ad rectos zodiaci angulos describitur diligenter capiemus, partesque collectas in duodecim multiplicantes ad congruentes obliquo circulo gradus reducemus, gradusque collectos, si latitudinis diversitas ad septentrionem circuli per medium sit, cum Luna in eodem ascendente nodo inveniatur, inveniatur] corr. ex invenitur G addemus latitudinis motui quem in tempore apparentis coniunctionis equavimus, cum vero in descendente, similiter subtrahemus, sin autem diversitas latitudinis ad meridiem zodiaci fiat econtra, quando Luna est in ascendente nodo, tunc diversitatis gradus subtrahemus a gradibus latitudinis equatis in tempore apparentis coniunctionis, quando vero in descendente, addemus similiter, et sic habebimus apparentis latitudinis numerum in tempore apparentis coniunctionis, et cum hoc in tabula solarium eclipsium intrabimus. Et si inter numeros primorum ordinum invenitur, Solis eclipsim futuram asseremus, eiusque medium tempus apparentis coniunctionis proxime dicemus. Deinde conscriptis iam digitis et incidentie ac replectionis partibus que apparentis latitudinis numero adiacent seorsum ex ordine utroque, intrabimus etiam cum numero inequalitatis Lune qui est a maxima longitudine in tempore apparentis coniunctionis in tabulam equationis, et adiacentes illi sexagesimas quotquot sint tot capientes a singulorum conscriptorum excessu addemus semper his quas a prima tabula cepimus, et factos ex hac equatione digitos habebimus, quot duodecimarum rursus solaris diametri partium obscuratio in medio proxime tempore ipsius eclipsis erit. Partibus autem utriusque transitus duodecima rursum earum parte pro solari motu addita et facto inde numero ad horas equales per inequalem unius hore Lune motum reducto, habebimus tam incidentie quam replectionis tempus, quasi tamen in his temporibus nulla differentia propter diversitates accidat.

Sed quoniam inequalitas quedam sensibilis in his temporibus non inequalitatis luminarium, sed diversitatum Lune gratia per quam maiora etiam seorsum utraque superius positis semper inveniuntur et ut plurimum inter se inequalia, quamvis parva sit, diligenti tamen ipsam cura scrutabimur. Accidit igitur hoc, propterea quod quasi precedentium motuum quedam phantasie, si nihil proprie ad successionem moveri comprehendatur, in apparente Lune motu semper gratia diversitatum fiant. Nam sive ante meridianum moveri appareat paulatim ascendens minoremque semper ad ortus diversitatem faciens, tardius ad successionem videtur progredi, sive post meridianum moveatur descendens paululum rursum maioremque semper ad occasum diversitatem faciens, tardiorem similiter ad successionem progressum facere videtur. Cuius rei gratia predicta tempora maiora semper sic quam simpliciter capta erunt. Cum autem maior semper differentia propter hos diversitatum excessus in propinquioribus meridiano motibus fiat, necesse est ut tempora quoque eclipsium que meridiano magis propinquant tardius transeant. Hac de causa, quando medium eclipsis tempus in ipsa meridie invenitur, tunc solummodo incidentie tempus replectionis tempore equale proxime est, cum ad utranque partem tunc precedens diversitatum phantasia equalis proxime fiat. Quando autem ante meridiem tunc replectionis tempus, cum sit meridiano propinquius, maius efficitur.

Ut igitur hec quoque tempora congruentem equationem suscipiant, considerandum est modo quo diximus, tum tempus utriusque dictorum transituum quod ante hanc equationem erit, tum distantia a puncto verticis que in medio eclipsis tempore futura est.

Sit verbi gratia tempus utriusque una hora equalis et distantia a puncto verticis graduum 75. Queremus igitur in diversitatis tabula sexagesimas diversitatis 75 gradibus adiacentes, Luna in maxima longitudine supposita, in qua distantia ex ordine tertio sexagesime sumuntur. Inveniuntur autem sexagesime 52 gradibus 75 apposite. Et quoniam utrunque tum incidentie tum repletionis tempus medie perspectum unius equalis hore ac temporum quindecim supponitur, hec, si a 75 gradibus distantie subtraxerimus, inveniuntur reliquis 60 gradibus sexagesime diversitatis 47 in eodem ordine adiacere, ita in m〈e〉dio medio] mdio A ad meridianum transitu 5 sexagesimarum progressus ex diversitate colligitur. Rursus autem hec ipsa tempora 75 gradibus addentes invenimus 90 collectis gradus 53 30′ totius diversitatis sexagesimas in eodem ordine adiacere, ut etiam hic progressum motus ad orizontem 1 30′ earundem colligi pateat, et utrunque rursus per inequalem Lune motum in partes equalis hore, ut dictum est, resolventes que ab utroque numero pars colligitur congruenter addetur utrique temporum incidentie atque replectionis que medie atque simpliciter capta fuerunt, maior quidem tempori quod est ad meridianum, minor autem tempori quod est ad orizontem. Perspicuum autem est quod quod] add. s. l. G excessus etiam predictorum temporum sexagesimarum est 3 30′, hoc est pars nona proxime unius equalis hore, dum medie tot sexagesimas Luna pertransit. Relinquitur autem ut facile equales horas, si volumus, in qualibet distantia in temporales congruenter resolvere modum inquiramus qui nobis expositus in superioribus est.

〈VI.11〉 Capitulum XI: De inclinationibus que in eclipsibus fiunt

Sequitur modo ut inclinationes quoque obscurationum consideremus, quarum intelligentia constat ex intelligentia declinationis tum earundem obscurationum ad circulum qui per medium signorum est tum ipsius circuli qui per medium est ad ad] add. s. l. G orizontem. Quorum utrunque in singulis temporibus temporibus] corr. ex partibus G eclipticis maximam et incomprensibilem in transgressionibus facit mutationem, si quis futuras per totum eclipsis tempus inclinationes inutili cura scrutari scrutari] post corr. G voluerit, cum minuta hec predictio nec necessaria nec utilis sit. Nam cum zodiaci habitudo ad orizontem ex locis punctorum zodiaci que in orizonte aut oriuntur aut occidunt perspiciatur, necesse est, quoniam continue orientia et occidentia puncta zodiaci per totum eclipsis tempus mutentur, sectiones quoque orizontis que in eisdem punctis fiunt diversas fieri. Similiter cum etiam obscurationum inclinatio ad circulum qui per medium signorum est perspiciatur in circulo qui per utraque centra Lune et umbre aut Solis maximus describitur, necesse rursum est propter centri lunaris in eclipsis tempore motum ut circulus quoque qui per utraque centra describitur alium atque alium semper situm ad zodiacum accipiat ac angulos a sectione ipsorum continue factos inequales faciat. Hec igitur consideratio sufficienter fieri videtur, si solummodo in his obscurationibus capiatur que supersignationem aliquam habent et universaliter eorum arcuum qui ad orizontem perspiciuntur. Possibile namque hinc erit illi qui passionem huiusmodi pre oculis ponit per utriusque declinationis considerationem omnes supersignatas declinationes coniicere. Ne igitur pretermisisse penitus hunc locum videamur, modos quosdam quam facilimos poterimus ad hanc rem inveniendam explanare conabimur.

Accepimus ergo supersignatas dignasque predictione esse, tum obscurationem primi deficientis que in totius ecliptici temporis principio fit, tum extremi deficientis que in principio more temporis fit, tum maximi deficientis que in medio tempore more fit, tum eius quod primum repletur que in fine totius more temporis fit, tum eius quod extremum repletur que in fine totius eclipsis temporis fit. De inclinationibus autem illas rursum probatas magis et signantius notatas accepimus, que a meridiano et circuli qui per medium est ortu et occasu equinoctialibus estivis hyemalibusque constituuntur. Nam eadem ventorum principia differenter sepe ad diversos se habent possuntque, si quis ita velit ab expositis angulis orizontis facile percipi. De sectionibus igitur orizontis que a meridiano fiunt borealem quidem dicimus, que septentrionalis est, australem vero, que meridionalis, de orientalibus vero atque occidentalibus sectionibus orizontis eas quidem que a principio Libre atque Arietis fiunt, queque semper per equalem quartam partem ab illis distant que a meridiano fiunt, equinoctialem et ortum et occasum nominamus, eas vero que a principio Capricorni, tam ortum quam occasum brumalem. Sed cum in his differentes distantie per climata fiant, determinatio inclinationum sufficienter habetur, quando aut in aliquo dictorum terminorum aut inter aliquos esse demonstratur.

Ut igitur in singulis zodiaci ad orizontem habitudo habeatur, modo et via quam incipientes docuimus distantias que in orizonte in ortu et occasu a principio singulorum signorum fiunt consideravimus in utraque parte sectionum que ab equinoctiali fiunt in singulis a Meroes climate usque ad Boreistenis, in quibus nobis etiam anguli expositi sunt. Et ut facilius hec perspiciantur, loco tabule octo circulos in eodem centro descripsimus quos in superficie orizontis intelligi volumus, qui septem climatum distantias et nomina continent. Deinde duas rectas lineas per omnes circulos ad rectos inter se angulos, alteram que et lateralis est quasi communem sectionem superficierum orizontis et equinoctialis, alteram que recta stat communem superficierum orizontis atque meridiani sectionem, protraximus, ascripsimusque in extremitatibus exterioris circuli ad lateralem quidem lineam occasum et ortum equinoctialem, ad eam autem que recta stat septentrionem atque meridiem. Similiter ex utraque equinoctialis linee parte per equalem ab ipsa distantiam per omnes circulos lineas deduximus, et in septem circulorum spaciis distantias orizontis que in singulis climatibus ab equinoctiali inveniuntur conscripsimus, quasi quarta pars graduum sit 90. In extremitate autem circulorum interiore ad meridiem quidem ortum brumalem et occasum occasum] corr. ex ccasum G brumalem inscripsimus, ad septentrionem vero estivalem ortum et estivalem occasum. Sed propter signorum signorum] post corr. G numerum inter quatuor spatia alias duas addidimus lineas, et in his conscriptorum signorum in orizonte ab equinoctiali distantias apposuimus, nominibus singulorum ad circulum exteriorem conscriptis, circa etiam meridianam lineam tum paralellorum nomina et multitudinem horarum, tum elevationes poli signavimus, borealissimosque in maioris continentisque circuli spatio posuimus. Verum ut etiam obscurationum apparentes ad circulum qui per medium est inclinationes expositas habeamus, hoc est angulos qui a sectione zodiaci et circuli maximi per utraque dicta centra descripti in qualibet supersignatione fiunt, computavimus invenimusque istos per singulos Lune transitus uno obscurationis digito differentes solummodo tamen in eis, —satis enim est—, que in media media] corr. ex meda G distantia fiant et quasi arcus zodiaci et obliqui lunaris qui 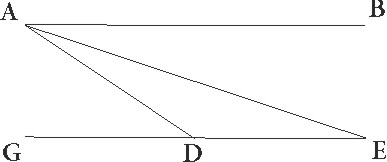obscurationibus continentur paralelli ad sensum sint.

Sit ergo rursus gratia exempli AB recta linea pro arcu zodiaci in qua Solis vel umbre centrum A esse supponatur. Recta vero linea GDE sit pro arcu obliqui lunaris, et G ubi centrum Lune in medio eclipsis tempore reperiatur, D vero ubi centrum eius sit quando primo tota deficit aut primo repleri incipit, hoc est quando ab interiore parte umbre circulum tangit, E autem ubi centrum ipsius sit quando primum deficere incipit aut extremum repleri aut Sol aut Luna, hoc est quando circuli alter alterum deforis tangunt, et protrahantur AG et AD et E linee. Quod igitur BAG BAG] corr. ex ABAG G et AGE anguli quibus medium eclipsis tempus continetur recti ad sensum sint et quod BE quidem angulus tum primum deficiens tum ultimum quod repletur continet, BAD autem tum ultimum deficiens tum primum quod repletur, perspicuum est. Hinc etiam patet quod E linea rursum semidiametros utrorumque continet circulorum, AD vero excessum ipsarum.

Supponatur igitur eclipsis exempli gratia in qua in medio tempore medietas solaris diametri obscuretur, et sit A centrum Solis, ut E linea, quoniam media longitudo Lune supponitur, 32 20′ particularum semper colligatur, AG vero medietate solaris diametri minor quam ipsa 16 40′ earundem. Quoniam igitur qualium est E qua rectus angulus subtenditur 32 20′, talium AG in supposita obscurationis magnitudine 16 40′ colligitur, profecto qualium est E que rectum angulum subtendit 120, talium etiam erit AG 61 51′ et arcus suus talium 62 2′ qualium est circulus qui triangulo AGE rectangulo circumscribitur 360. Quare angulus quoque EG, hoc est angulus BE, talium erit 62 2′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 31 1′.

Sed lunarium rursus eclipsium gratia sit A umbre centrum, ut, quoniam media similiter Lune longitudo supponitur, earundem semper colligatur E quidem linea 60, AD vero 26 40′ similiter, et deficiat Luna per 18 digitorum transitum, ut AG linea rursus minor sit quam AD medietate diametri et colligatur colligatur] post corr. G 10 0′ earundem. Quoniam igitur EA rectum angulum subtendens est 120, taliumque AG fit 20 0′ et arcus suus talium 19 12′ qualium est circulus qui triangulo AGE circumscribitur 360, erit profecto EG quoque angulus, hoc est BE, talium 19 12′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 9 36′. Similiter quoniam qualium est AD qua rectus subtenditur 120, fitque talium AG 45 et arcus suus talium 44 2′ qualium est circulus qui AGD rectangulo circumscribitur 360, erit profecto etiam angulus ADG, hoc est BAD, talium 44 2′ qualium duo recti sunt 360, qualium vero quatuor recti sunt 360, talium 22 1′.

Eodem modo in aliis quoque digitis magnitudines minorum recto angulorum cepimus, prout rectus unus partium est 90, quot partium orizontis etiam pars quarta supponitur, tabulamque fecimus 22 versuum et quatuor ordinum, quorum primus digitos diametri obscurationis qui in medio eclipsis tempore inveniuntur continebit, alter angulos qui in solaribus fiunt eclipsibus tum in tempore prime deficientis particule tum in tempore ultimi que repletur, tertius angulos qui in lunaribus eclipsibus fiunt tum in tempore prime deficientis particule tum in tempore ultime que repletur, quartus angulos que rursum in lunaribus fiunt eclipsibus tum in tempore ultime deficientis tum in tempore prime que repletur. Sunt autem tam tabule quam circulorum descriptiones iste.

〈VI.12〉 Capitulum XII: Tabula et circularis orizontum descriptio

〈VI.13〉 Capitulum XIII: Inquisitio inclinationum

Cum igitur singularum expositarum supersignationum equata modo quo diximus tempora et a temporibus orientes occidentesque circuli qui per medium signorum est partes et ex descriptione positiones ipsarum in orizonte habeamus, quando quidem centrum Lune aut apparens, ut in solaribus eclipsibus, aut verum, ut ut​] add. s. l. G in lunaribus, in ipso circulo sit qui per medium signorum est, inclinationem quidem in prima Solis deficiente particula et in ultima Lune tum deficiente tum repleri desinente habebimus ab ipso situ occidentis tunc partis in orizonte, inclinationem vero que est in ultima Solis que repletur et in Lune prima deficiente et prima que repletur ab ipsius tunc orizontis; quando autem Lune centrum non est in circulo per medium capiemus et tabula convenientes multitudini digitorum appositos angulorum numeros, proiiciemiusque ipsos a communibus orizontis et circuli qui per medium est sectionibus, si centrum Lune ipso borealius est in prima deficiente Solis, et in ultima deficiente Lune, tanquam occidentalis sectio ad septentrionem sit, in ultima vero Solis que repletur et prima similiter Lune, tamquam orientalis sectio ad septentrionem sit. Et rursus in prima deficiente Lune, tanquam orientalis sectio ad meridiem sit, in ultima vero Lune que repletur, tanquam occidentalis ad meridiem sit, sin vero Lune centrum australius sit circulo qui per medium signorum est, in prima deficiente Solis et in ultima deficiente Lune, tanquam occidentalis sectio ad meridiem sit, in ultima vero Solis que repletur et in prima Lune que repletur, tanquam ad meridiem orientalis sit, et rursum in prima deficiente Lune, tanquam ad septentrionem orientalis sectio sit, in ultima vero Lune que repletur tamquam ad septemtrionem occidentalis sit, et partem orizontis ex hac directione constitutam habebimus quo universalius, ut diximus, luminarium partes que primas et ultimas eclipsium atque replectionum signationes recipiunt inclinationem facture sint.