Ptolemaeus Arabus et Latinus

〈II〉 〈LIBER II〉

Incipit liber secundus Ptolomei Magne Compositionis

〈II.1〉 Capitulum I: De universali orbis terrarum situ qui a nobis habitatur

Quoniam iam in primo huius constitutionis libro ea perstrinximus que summatim de habitudine totorum debebant premitti et que, quamvis ad rectam spheram pertineant, non inutilia tamen ad propositam nobis speculationem quispiam arbitrabitur, conabimur deinceps accidentia quoque oblique sphere que principaliora sunt quam facillime rursus fieri potest docere. Hic etiam illud universaliter premitti oportet quod, cum terra in quatuor partes dividatur, que fiunt a circulo equinoctiali et altero eorum qui per polos ipsius equinoctialis describuntur, magnitudo eius quam nos habitamus ab altera borealium proxime continetur. Id inde maxime manifestum fit, quoniam in altitudine quidem, idest in transitu a meridie in septentrionem, ubique in equinoctiis meridiales gnomonum umbre ad septentrionem semper et nunquam ad meridiem tendunt, in longitudine vero, hoc est in transitu ab oriente ad occidens, eedem eclipsis et maxime lunares eodem conspecte tempore tam ab illis qui extremas orientales nostre habitabiles partes incolunt, quam ab aliis qui occidentales ultimas habitant, non plures quam duodecim equinoctialibus horis prius posteriusve fieri cernuntur, cum ipsa quarta pars terre duodecim horarum spatium contineat, quod ab uno equinoctialis semicirculorum determinetur. Eorum vero que particularius inspicienda sunt illa maxime ad propositum negotium quispiam pertinere putabit que per singulos borealiores equinoctiali circulo parallelos ipsi equinoctiali et subiectis habitationibus secundum principaliores accidunt proprietates ea sunt, quantum primi motus poli ab orizunte distent vel quantum punctum verticis ab equinoctiali per meridianum circulum distet, et quoniam Sol in vertice quibusdam fiat, quando et quotiens id accidit, et que tropicarum et equinoctialium in meridiebus umbrarum proportiones ad gnomonas sint, quantus etiam maximorum minimorumque dierum ultra equinoctiales dies excessus, et quecunque alia particularius in incremento dierum ac noctium decrementoque considerantur, et ad hec que de coortibus coortibus] corr. ex cohortibus G et occasibus equinoctialis atque obliqui circuli et que de proprietatibus et magnitudinibus angulorum, qui a principalioribus maximisque circulis fiunt accidentia, inspiciantur.

〈II.2〉 Capitulum II: Quomodo, maxime diei data magnitudine, dantur orizontis arcus qui ab equinoctali et obliquo circulo intercipiuntur

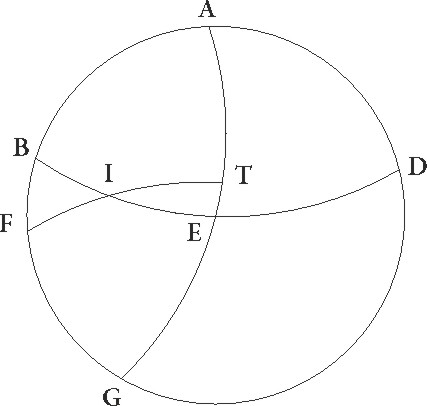Proponatur igitur universaliter gratia exempli paralellus equinoctiali circulus per Rhodum descriptus, ubi elevatio polli graduum est 36 et dies maximus equinoctialium horarum 14 ½, et sit meridianus quidem circulus ABGD. Orizuntis autem orientalis medietas BED equinoctialis etiam similiter medietas EG cuius australis polus sit F, et supponatur brumale tropicum circuli qui per medium signorum est punctum oriri per I, et per F, I describatur maximi circuli pars FIT. Sed primum data sit maxime diei magnitudo, sitque propositum EI orizuntis arcum invenire. Quoniam igitur circumductio sphere in polis equinoctialis efficitur, patet quia in eodem tempore I et T punctum erunt in ABGD meridiano, et tempus quod est ab ortu I puncti quousque ad medium celi super terram perveniat illud est quod ex TA parte circumferentie equioctialis continetur, tempus autem quod a subteraneo angulo usque ad ortum est illud quod ex GT continetur. Quare sequitur ut diei tempus duplum sit eius quod abs TA noctis vero duplum eius quod quod] abs TA add. et del. A per GT continetur.

N 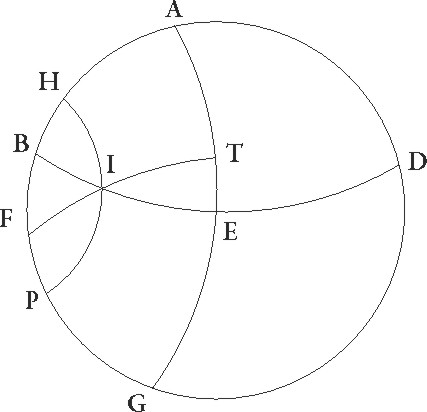am etiam seorsum parallelorum, idest equidistantium, equinoctiali circulorum portiones omnium que super terram et que sub terra sunt equaliter a meridiano dividuntur. Idcirco et arcus ET, cum sit minimi aut maximi diei ad equinoctialem differentie medietas, hore unius quarteque partis in hoc erit parallelo, temporum vero 18 45′ et residuum igitur ad quartam circuli partem eorundem 71 15′. et … 77 15ꞌ] add. marg. G Quoniam igitur per ea que prius demonstrata sunt in duos] corr. ex duobus A duos maximorum circulo arcus E et AF duo inscripti sunt EB et FT in I puncto seipsos secantes, proportio corde dupli arcus TA ad cordam dupli arcus E composita est ex proportionibus cordarum dupli arcus TF ad dupli arcus FI et dupli arcus IB ad dupli BE. Sed duplus TA partis circumferentie arcus 142 30′ graduum est, et corda ei subtensa partium 113 37′ 54′′. E vero partis circumferentie duplus graduum 180, et corda sua partium 120, et rursum duplus TF partis circumferentie arcus graduum est 180, et corda eius partium 120. FI autem partis circumferentie duplus graduum est 132 17′ 20″ et corda eius partium 109 44′ 53′′. Si ergo a proportione 113 37′ 54″ ad 120 auferamus proportionem 120 ad 109 44′ 53″, relinquetur nobis proportio corde dupli arcus IB ad cordam dupli BE hec est 103 55′ 26″ ad 120. Est autem corda dupli arcus BE, quoniam quarta circuli pars est, partium 120. Quare corda etiam dupli arcus IB erit eorundem 103 55′ 26″. Quare duplus etiam arcus BI partis circumferentie 120 graduum proxime erit, ipse vero BI eorundem 60. Relinquitur ergo reliqua etiam EI talium 30 qualium est orizon 360, quod erat demonstrandum.

〈II.3〉 Capitulum III: Quommdo, eisdem ipsis suppositis, elevatio poli datur

Hoc igitur dato, propositum sit ut poli elevationem, idest BF meridiani arcum, inveniamus. In eadem igitur descriptione proportio corde dupli arcus ET ad cordam dupli TA composita est ex proportionibus cordarum dupli arcus EI ad dupli arcus IB et dupli BF ad dupli FA. Sed duplus ET partis circumferentie arcus 37 30′ graduum est: et corda ei subtensa partium 38 34′ 22″. Duplus vero TA graduum est 142 30′, et et] add. s. l. G corda eius partium 113 37′ 54″ et rursum duplus EI graduum 60 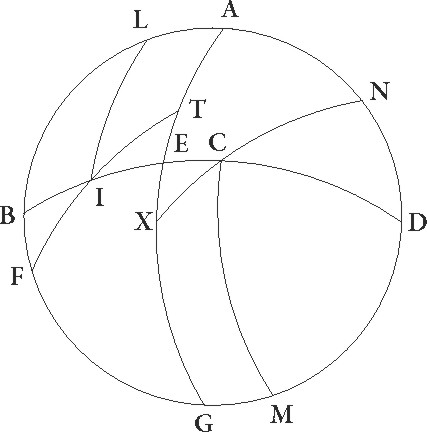et corda eius partium 60, duplus vero IB graduum 120 et corda eius partium 103 55′ 23″. Si ergo a proportione 38 34′ 22″ ad 113 37′ 54″ auferamus proportionem 60 ad 103 55′ 23″, relinquetur proportio corde dupli arcus BF ad cordam dupli arcus FA, ea est 70 33′ proxime ad 120, estque rursum corda dupli arcus FA partium 120. Quare corda dupli BF 70 33′ eorundem est, ita ipse arcus BF circumferentie duplus 72 1′ graduum erit. Ipse vero BF eorundem proxime 36. Sed in eadem rursus descriptione sit FB poli elevatio data graduum 36 propositumque sit invenire maxime aut minime diei ad equinoctialem differentiam, hoc est duplum ET circumferentie arcum. Eisdem igitur rationibus fit, ut proportio corde dupli arcus FB ad cordam dupli BA composita sit ex proportionibus cordarum dupli arcus FI ad dupli arcus IT et dupli arcus TE ad dupli arcus EA. Sed duplus FB partis circumferentie arcus graduum est 72, et corda eius partium 70 32″ 3″. Duplus vero BA graduum est 108 et corda eius partium 97 4′ 56″, et rursum duplus FI graduum est 132 17′ 20″ et corda eius partium 109 44″ 53″. Duplus autem IT graduum 47 42′ 40″ et corda eius partium 48 31′ 55″. Si ergo a proportione 70 32′ 3″ ad 97 4′ 56″ auferamus proportionem 109 44′ 53″ ad 48 31′ 55″, relinquetur nobis proportio corde dupli arcus ET ad cordam dupli EA que est 31 11′ 23″ ad 97 4′ 56″, et quoniam eadem proxime proportio est 38 34′ ad 120, corda vero dupli arcus EA partium est 120 colligitur etiam corda dupli arcus ET eorundem esse 38 34′. Quare duplus etiam arcus ET partis circumferentie graduum erit 37 30′ proxime, horarum autem equinoctialium duarum cum media quod erat demonstrandum. Eisdem rationibus EI quoque orizuntis arcus dabitur. Proportio enim corde dupli arcus FA ad cordam dupli AB composita est ex proportionibus cordarum dupli arcus FT ad dupli arcus TI, que data est, et dupli arcus EI ad dupli EB. Quare, cum EB data sit, 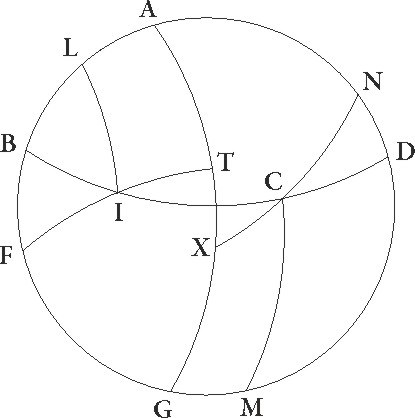relinquitur ut magnitudo etiam EI habeatur. Perspicuum autem est, quia, si non brunale tropicum punctum I esse supponeremus, sed quendam alium eius circuli gradum qui per medium signorum describitur, eisdem rationibus tam ET quam EI arcus dabitur. Iam enim nobis per obliquationis tabulam expositi sunt arcus meridiani qui a singulis eius eius] qui add. et del. A circuli gradibus qui per medium signorum est et equinoctiali circulo intercipiuntur, ii sunt similes arcui IT. Hinc etiam sequitur ut partes signiferi que ab eisdem equidistantibus fiunt, hoc est que equaliter a tropico puncto distant, easdem sectiones orizuntis et ad easdem partes equinoctiales faciant et dierum noctiumque similium magnitudines alteras alteris equales. Sed cum istis una etiam demonstratur quod partes que ab equalibus parallelis fiunt, hoc est que ab eodem equinoctialis puncto equaliter distant, equales ex utraque equinoctialis parte faciunt arcus et dierum ac noctium permutatim permutatim] corr. ex permutanti G equales dissimilium magnitudines. Nam si in eadem descriptione supposuerimus supposuerimus] corr. ex supposuimus G C quoque punctum ubi BED semicirculus orizuntis ab equale equidistantique illi qui per I descriptus est secatur et compleverimus IL et CM equedistantium partes permutatim equalesque factas et per C polumque borealem XCN quartam circuli descripserimus, erit arcus TA equalis arcui XG, quoniam LI et MC alter alteri similis est. Relinquetur autem ut et reliqua ET relique EX sit equalis, fient etiam duorum similium trilaterorum EIT et ECX duo latera duobus lateribus equalia, ET quidem ipsi EX, IT autem ipsi CX, est etiam uterque angulorum qui in T et X sunt rectus. Quare bassis etiam EI bassi CX erit equalis.

〈II.4〉 Capitulum IIII: Quomodo inveniendum quibus et quando et quotiens Sol in vertice fit

Facile autem, his datis, est quibus, quando, et quotiens Sol in vertice fiat invenire. Nam, cum perspicuum per se sit nunquam ad verticem illorum qui sub parallelis parallelis] qui add. et del. A ultra totum estivalis tropici spatium, idest ultra gradus 23 51′ 20″ proxime, habitant, semel autem in ipso estivali solstitio super verticem illorum qui sub parallelis per hoc ipsum, idest pertantum distantibus, distantibus] habitant add. et del. A et bis super verticem illorum Solem pervenire qui sub parallelis minus distantibus habitant, obliquationis tabula, quando id fiat, facillime ostendit. Nam numerum graduum quibus parallelus de quo querimus ab equinoctiali distat, si citra estivalem tropicum est, in secundo versu inveniemus et appositos ei quarte partis circuli gradus qui recte in primo scribuntur ordine summentes, tot gradibus dicemus ab utroque puncto equinoctiali Solem versus tropicum estivalem tunc distare, quando super verticem illorum fit qui sub illo habitant parallelo:

〈II.5〉 Capitulum V: Quomodo ab iis que iam exposita sunt gnomonum equinoctiales tropicumque umbre in meridiebus capiuntur

Quod autem, arcu qui inter tropicos est et eo qui inter orizontem et polos intercipitur datis, proportiones quoque umbrarum ad gnomonas simplicius sumuntur, sic profecto patebit:

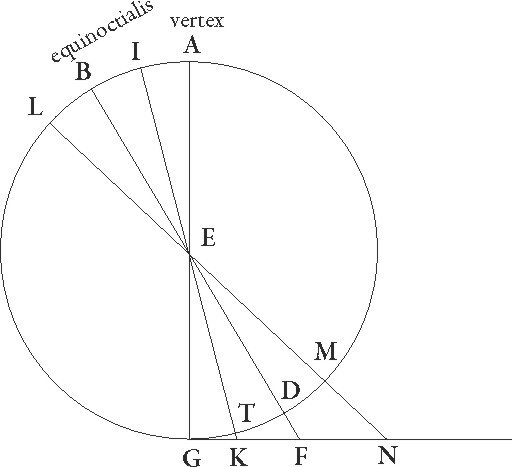sit ABGD meridianus circulus circa centrum E circumductus, sitque A punctum super verticem a quo, ducta diametro EG, ad rectos ipsi angulos in meridiani superficie linea GCFN protrahatur, hec meridiani atque orizontis comuni sectioni equedistans erit. Et quoniam tota terra puncti centrique rationem ad spheram Solis habere ad sensum videtur, ut minime centrum E a gnomonis vertice differat, animo percipitur GE quidem gnomonem, GCFN vero lineam esse super quam in meridie umbrarum extremitates deveniant, ducanturque per E meridiani radii tam equinoctiales quam tropici, et sit equinoctialis quidem radius BEDF, estivalis autem IETC, brumalis vero LEMN, ut GC quidem estivalis sit umbra, GF autem equinoctialis, brumalis vero GN. Quoniam ergo GD arcus cui equalis est arcus quo polus borealis ab orizunte in climate supposito elevatur talium est 36 graduum, qualium ABG meridianus 360, uterque vero TD et DM simul 23 51′ 20″ eorundem, patet quia reliquus etiam GT graduum erit 12 8′ 40″, totus vero GM 59 51′ 20″ eorundem. Quapropter angulorum etiam qui sub ipsis sunt CEG quidem 12 8′ 40″ talium est, qualium quatuor recti sunt 360, FEG autem 36 earundem partium, NEG vero 59 51′ 20″ similiter. Qualium autem duo recti sunt 360, talium CEG quidem angulus 24 17′ 20″, FEG autem 72 earundem, NEG vero 119 42′ 40″. Quare circulorum etiam qui circa CEG et FEG et NEG orthogonios triangulos describunt, arcus quidem qui super GC cordam est talium talium] post corr. G erit 24 17′ 20″, qui vero super GE que ad semicirculum semicirculum] corr. ex semiculum G residua est 155 42′ 40″ eorundem, qui autem super GF 72 et qui super GE 108 similiter earundem, qui vero super GN 119 42′ 40″, et qui super GE reliquorum rursus ad semicirculum 60 17′ 20″. Quare cordarum etiam que subsunt GE talium colligitur 117 18′ 51″, qualium est GC 25 14′ 43″, qualium vero GF 70 32′ 4″, talium 97 4′ 56″, sed qualium GN similiter 103 46′ 16″, talium 60 15′ 42′′. Quasobres qualium est GE gnomon 60, talium estivalis quidem umbra 21 55′ esse colligitur, GF autem equinoctialis umbra 43 36′, brumalis vero GN 103 20′ proxime. Hinc per se patet quia etiam conversim, si due due] corr. ex duo G dumtaxat date fuerint quevis proportiones de tribus expositis GE gnomonis ad umbras, tam poli elevatio quam arcus qui est inter tropicos dabitur. Nam, duobus etiam quibusvis angulis qui sunt ad E datis, reliquus etiam datur, propterea quod TD et DM arcus equales sunt, quamvis exquisite observationis gratia illa quidem modo quo docuimus sine dubitatione aliqua capientur, dictarum autem umbrarum proportiones ad gnomonas non similiter, quoniam equinoctialium quidem tempus per se ipsum indeterminatum quodammodo est, brumalium vero verticum extrema difficile cognoscuntur.

〈II.6〉 Capitulum VI: Expositio proprietatum per singulos parallelos

Eodem modo in ceteris quoque parallelis universales propositasque proprietates summentes, quarto unius equinoctialis hore declinationum excessibus adauctis (sufficiens enim id est), faciemus universalem earum expositionem antequam ad particularia descendamus.

Initium igitur a parallelo qui sub ipso equinoctiali est capiamus: is disseperat proxime a totius quarte nostri orbis parte illam que ad meridiem est, solusque dies et noctes universas equales inter se habet. Ibi enim solummodo omnes qui in sphera sunt paralleli ad equinoctialem circulum in duo equalia dividuntur, ita ut partes que super terram sunt et inter se similes et equales subterraneis partibus singule singulis sint, quod in nulla prorsus declinatione accidit. Solus enim equinoctialis rursum ubique equaliter ab orizunte divisus dies qui per ipsum fiunt equales ad sensum noctibus facit. De maximis enim ipse quoque circulis est. Reliqui vero, cum inequaliter et secundum nostri orbis declinationem dividantur, australiores quidem ipso partes qui super terram sunt minores subterraneis et dies noctibus breviores faciunt, borealiores autem econtra maiores super terram partes longioresque dies; hic parallelus umbre quoque duplicis est. Sol enim bis super verticem habitantium sub eo fit secundum equinoctialis obliquique circuli partes, quare tunc solum in meridie gnomones nullam umbram reddere possunt. Cum vero Sol per borealem semicirculum feratur, tunc ad meridiem, cum autem per australem, tunc ad septentrionem umbre a gnomonibus redduntur, redduntur] corr. ex reduntur G in his regionibus, qualium partium gnomon est 60, talium utraque tam estivalis quam hyemalis hyemalis] corr. ex hiemalis G umbra 26 30′ proxime est. Dicimus autem universaliter de illis umbris que in meridiebus fiunt, nec enim, quia non omnino in ipsis meridiebus equinoctia et solstitia efficiantur, nulla re de qua curandum sit differunt. Super verticem vero eorum qui sub equinoctiali habitant ille stelle perveniunt, que in ipso equinoctiali volvuntur, et omnes tam oriri quam occidere videntur.

Nam sphere poli, cum in ipso sint orizunte, nullum parallelorum circulum aut semper apparentem aut nunquam apparentem nullum etiam meridianorum collurum faciunt.

Habitationes autem posse sub equinoctiali esse quasi in regione nimium temperata multi contendunt; nam Solem nec in punctis super verticem inmorari, quoniam recessus secundum latitudinem velociter ab equinoctialibus punctis defiat, defiat] add. marg. G unde temperatam reddi estatem, nec in solsticiis multum a vertice distare, quare lenissimas hyemes fieri. Que vero iste sint habitationes verisimiliter dicere non possumus. Nam ad hunc usque diem nostri orbis homines minime illo penetrarunt. Quare coniecturam magis quam veram historiam ea que de ipsis narrantur quispiam existimabitur, sed sed] add. G de propriis quidem paralleli paralleli] corr. ex parallelis G qui sub equinoctiali est hec breviter dicta sint. De reliquis vero a quibus et habitationes nonnuli estimant comprehendi, illa ne in singulis repetetantur, addemus quod super verticem in singulis ille stelle fiunt que arcu equali eius circuli qui per polos equinoctialis est ab ipso distant, equali inquam arcui quo suppositus quoque paralelus similiter distat, et quod semper ille apparet circulus qui polo equinoctialis boreali polo et elevatione poli spatio describitur, a quo que intercipiuntur stelle omnes semper apparent. Contra vero nunquam ille apparet circulus qui polo australi polo et eodem describitur spatio, a quo que intercipiuntur stelle nunquam apparent.

Secundus est parallelus parallelus] corr. ex paralelus G in quo maximus dies horarum est equinoctialium 12 15′ hic ab equinoctiali 4 15′ gradibus distat et describitur per insulam Taprobanem; hic etiam umbre duplicis est. Sol enim bis super verticem illorum fit qui sub eo habitant et gnomonas in meridiebus umbra tunc privat, quando ab estivali solstitio in utraque parte 79 30′ gradibus distat. Ita dum per hos 159 gradus fertur, ad australia, dum vero per reliquos 201, ad borealia gnomonum umbre protenduntur; hic qualium gnomon est 60, talium est equinoctialis umbra 4 25′, estivalis 21 20′, brumalis 32.

Tertius parallelus est ubi maximus dies equinoctialium est horarum 12 ½; hic 8 25′ ab equinoctiali gradibus distat et describitur per sinum Avalitum; umbre duplicis hic quoque est. Sol enim bis super verticem illorum fit, qui sub eo habitant, et gnomonas in meridiebus umbra tunc privat, quando ab estivali solstitio in utraque parte 69 partibus distat. Ita dum per hos 138 gradus fertur, ad meridiem gnomonum umbre protenduntur; dum vero per reliquos 222, ad septentrionem; hic qualium gnomon est 60, talium equinoctialis quidem umbra est 8 50′, estivalis vero 12 50′, brumalis autem 27 54′.

Quartus est parallelus in quo maximus dies est horarum equinoctialium 12 45′; hic distat ab equinoctiali gradibus 12 30′ et describitur per sinum Aduliticum; hic quoque duplicis umbre est. Bis enim Sol super verticem fit, et gnomonas in meridiebus umbra tunc privat, quando ab equinoctiali solstitio in utraque parte 57 50′ gradibus distat. Ita dum per hos 115 40′ gradus fertur, ad meridiem umbre gnomonum protrahuntur; dum vero per reliquos 244 20′, ad septentrionem; hic qualium gnomon est 60, talium equinoctialis umbra 13 20′, estivalis 12, brumalis 44 10′.

Quintus est parallelus sub quo maximus dies est horarum equinoctialium 13; hic ab equinoctiali 16 27′ gradibus distat, et describitur per Meroem insulam; hic quoque umbre duplicis est, et Sol bis super verticem fit, gnomonasque umbra in meridiebus tunc privat, quando in utraque parte parte] corr. ex partem G ab estivali solstitio 45 gradibus distat. Ita dum per hos 90 gradus fertur, gnomonum umbre ad meridiem tendunt; dum vero per reliquos 270, ad septentrionem; hic qualium gnomon est 60, talium est equinoctialis umbra 17 45′, estivalis 7 45′, brumalis 51.

Sextus est parallelus sub quo maximus dies est 13 15′ horarum equinoctialium; hic ab equinoctiali 20 14′ gradibus distat, et describitur per Napata, et est etiam iste duplicis umbre; Sol enim bis super verticem fit et gnomonas in meridiebus umbra tunc privat, quando ab estivali solstitio ex utraque parte 31 gradibus distat; ita dum per hos hos] corr. ex os G 62 gradus fertur, gnomonum umbre ad meridiem protrahuntur; dum vero per reliquos 298 ad septentrionem; hic qualium gnomon est 60, talium equinoctialis umbra 22 10′, estivalis 3 45′, brumalis 58 10′.

Septimus est parallelus ubi maximus dies est horarum equinoctialium 13 ½; hic ab equinotiali 23 51′ gradibus distat et describitur per Syenem; hic parallelus primus eorum est qui simplicis umbre nominantur: nunquam enim sub ipso gnomonum in meridiebus umbre ad australia protenduntur, sed in ipso estivali dumtaxat solstitio super verticem habitantium sub eo Sol fit, et gnomones tunc absque umbra esse cernuntur: tantum enim ab equinoctiali distant, quantum estivale tropicum punctum. Reliquo vero tempore universo ad septentrionem umbram mittunt; hic qualium gnomon est 60, talium est equinoctialis umbra 26 30′, brumalis 65 50′, estiva vero umbra gnomones carent. Omnes quoque isto borealiores paralleli usque ad eum qui nostrum orbem disseperat disseperat] corr. ex disseptaret A simplicis umbre sunt: nunquam enim sub ipsis in meridiebus sine umbra penitus gnomones cernuntur, nec ad meridiem eas, sed ad septentrionem semper mittunt. Nunquam enim Sol super verticem in istis fit.

Octavus est parallelus sub quo maximus dies est 13 45′ horarum equinoctialium; hic ab equinoctiali 27 12′ gradibus distat, et scribitur per Ptolomaydem que in Thebayde est queque Mercurii appellatur; hic qualium gnomon est 60, talium estivalis umbra 3 30′, equinoctialis 36 50′, brumalis. 74 10′.

Nonus est parallelus ubi maximus dies est 14 horarum equinoctialium; hic ab equinoctiali 30 22′ gradibus distat, et scribitur per inferiorem Egypti regionem; hic qualium gnomon est est] corr. ex sunt A 60, talium estivalis umbra 6 50′, equinoctialis 35 12′, brumalis 83 5′.

Decimus est parallelus in quo maximus dies 14 15′ horarum equinoctialium est; hic ab equinoctiali 33 18′ gradibus distat, et scribitur per mediam Phenicem; hic qualium gnomon est 60, talium estivalis umbra 10, equinoctialis 39 30′, brumalis 93 5′.

Vndecimus est parallelus sub quo maximus dies 14 30′ horarum equinoctialium est; hic 36 ab equinoctiali gradibus distat, et scribitur per Rhodum; hic qualium gnomon est 60, talium est estivalis umbra 12 55′, equinoctialis 43 50′, brumalis 103 20′.

Duodecimus est parallelus in quo 14 45′ maximus dies horarum equinoctialium est; hic ab equinoctiali 38 35′ gradibus distat, et scribitur per per] add. marg. G Smirnem; hic qualium gnomon est 60, talium estivalis umbra 15 20′, equinoctialis 47 50′, brumalis 114 55′.

Tertiusdecimus est parallelus in quo maximus dies horarum quindecim equinoctialium est; hic ab equinoctiali 40 56′ gradibus distat, et scribitur per Elespontum; hic qualium gnomon est 60, talium estivalis umbra est 18 ½, equinoctialis 52 10′, brumalis 127 50′.

Quartusdecimus est parallelus ubi maximus dies est 15 15′ equinoctialium horarum; hic distat ab equinoctiali gradibus 43 4′, et scribitur per Massiliam; hic qualium gnomon est 60, talium est estiva umbra 20 50′, equinoctialis 55 55′, brumalis 140 15′.

Quintusdecimus est parallelus ubi maximus dies est 15 30′ equinoctialium horarum, distatque ab equinoctiali gradibus 45 1′, et scribitur per medium Puntum; hic qualium gnomon est 60, talium estivalis umbra est 23 15′, equinoctialis vero eorundem 60, brumalis 155 5′.

Sextusdecimus est parallelus sub quo maximus dies 15 45′ horarum equinoctialium est; hic ab equinoctiali 46 51′ gradibus distat, et scribitur per Danubii amnis fontes; hic qualium gnomon est 60, talium estivalis umbra est 25 30′, equinoctialis 60 55′, brumalis 171 35′.

Decimus septimus parallelus ubicumque maximus dies 16 horarum equinoctialium est; hic ab equinoctiali 48 32′ gradibus distat, et scribitur per hostia Borosthenis; hic qualium gnomon est 60, talium est estivalis umbra 27 ½, equinoctialis 67 50′, brumalis 188 35′.

Decimus octavus parallelus est ubicunque maximus dies 16 15′ horarum equinoctialium est; hic ab equinoctiali 54 gradibus distat, et scribitur per mediam Meotida paludem; hic qualium gonomon est 60, talium est estivalis umbra 29 55′, equinoctialis 71 20′, brumalis 208 20′.

Decimus nonus parallelus est in quo maximus dies 16 horarum equinoctialium est; hic ab equinoctiali 51 35′ gradibus distat, et scribitur per australissima Britanie; hic qualium gnomon est 60, talium est estivalis umbra 31 25, equinoctialis 75 25′, brumalis 229 20′.

Vigesimus est parallelus sub quo 16 45′ horarum equinoctialium maximus dies est; hic ab equinoctiali 52 50′ gradibus distat, et scribitur per Renni fluvii hostia; hic qualium est gnomon est 60, talium estiva umbra 33 20′, equinoctialis 79 5′, brumalis 253 10′.

Vigesimus primus est parallelus ubi maximus dies 17 horarum equinoctialium est; iste ab equinoctiali 54 1′ gradibus distat, et scribitur per Thanaydos fluvii hostia; hic qualium gnomon est 60, talium est estivalis umbra 34 55′, equinoctialis 82 35′, brumalis 218 45′.

Vigesimus secundus parallelus est in quo maximus dies 17 15′ horarum equinoctialium est; iste 55 gradibus distat ab equinoctiali, et scribitur per Brigatium magne Britanie; hic qualium gnomon est 60, talium est estivalis umbra 36 15′, equinoctialis 85 20′, brumalis 304 ½.

Vigesimus tertius est parallelus ubi maximus dies 17 ½ horarum equinoctialium est; iste ab equinoctiali 56 gradibus distat, et scribitur per mediam Britaniam magnam; hic qualium gnomon est 60, talium estivalis umbra est 37 20′, equinoctialis 88 50′, brumalis 30 35 15′.

Vigesmusquartus parallelus est sub quo maximus dies 17 45′ horarum equinoctialium est; iste ab equinoctiali 51 gradibus distat, et scribitur per Caturactonium Britanie; hic qualium gnomon est 60, talium est estivalis umbra 39 20′, equinoctialis 52 25′, brumalis 372 40′.

Vigesimus quintus parallelus est ubi maximus dies 18 equinoctialium horarum est; iste ab equinoctiali 58 gradibus distat, et scribitur per parve Britanie australia; hic qualium gnomon est 60, talium est estivalis umbra 40 44′, equinoctialis 56, brumalis 419 5′.

Vigesimus sextus parallelus est ubi maximus dies horarum est equinoctialium 18 ½; iste ab equinoctiali 59 30′ gradibus distat, et scribitur per mediam Britaniam parvam.

Non sumus hic usi quarta unius hore parte incremento, tum quoniam crebriores hic paralleli fiant, tum quoniam elevationum differentia ne ne] corr. ex nec A integri quidem huius gradus colligatur, et ad hec quia non similiter nobis in borealioribus borealioribus] corr. ex boralioribus G scrutanda sunt omnia, propterea et proportiones umbrarum et gnomones superfluum putavimus in seperatis reconditisque locis apponere.

Ubi ergo dies maximus 19 horarum equinoctialium est, ille parallelus 61 61] corr. ex 16 G ab equinoctiali gradibus distat, et scribitur per borealia parve Britanie.

Ubi autem maximus dies 19 ½ equinoctialium horarum est, ille parallelus 62 gradibus ab equinoctiali distat, et scribitur per insulas quas Ebudas nominant.

Ubi autem maximus dies 20 horarum equinoctialium est, ille parallelus 63 gradibus distat ab equinoctiali, et scribitur per Tylem Insulam.

Ubi vero maximus dies xxi horarum equinoctialium est, ille parallelus 64 30′ gradibus distat ab equinoctiali, et scribitur per Scythicas gentes ignotas.

Ubi maximus dies horarum est equinoctialium 22, ille parallelus 65 30′ gradibus distat ab equinoctiali.

Ubi maximus dies horarum est equinoctialium 23, ille parallelus ab equinoctiali 66 gradibus distat.

Ubi autem maximus dies 24 horarum equinoctialium est, ille parallelus distat ab equinoctiali gradibus 66 8′ 40′′; hic primus eorum est qui periscii, hoc est latine circumbratiles appellantur. In estivali enim solstitio dumtaxat, Sole non occidente, ad omnes orizuntis partes gnomonum umbre vertuntur; hic estivalis tropicus parallelus semper, brumalis vero nunquam apparet, ambo enim permutatim orizuntem tangunt. Obliquus autem circulus qui per medium signorum est, quando verum equinoctiale punctum oritur, idem fit cum orizunte. Siquis vero contemplationis causa universaliora borealiorum declinationum accidentia querat, is inveniet, ubi elevatio poli 67 proxime graduum est, ibi nequaquam 15 zodiaci gradus ad utranque estivalis solsticii partem occidere, ita ut dies maxima et umbrarum ad omnes orizuntis partes circumductio menstrua ferme fiat. Hec quoque facile per iam expositam obliquationis tabulam intelliguntur.

Nam quotcunque distare ab equinoctiali gradibus parallelum inveniemus qui verbi gratia 15 gradus ex utraque tropici parte intercipiat, quique tunc aut semper aut nunquam appareat cum intercepta eius circuli parte qui per medium signorum est, tot profecto gradibus a 90 unius quarte partibus borealis poli elevatio deficiet.

Ubi autem elevatio poli 69 ½ graduum est, ibi 30 gradus ex utroque solsticii estivalis parte non occidere quisquam inveniet, ita ut duorum proxime mensium maximus dies et gnomones circumumbrales eodem tempore fiant.

Vbi elevatio poli 73 20′ graduum est, ibi 45 gradus ex utraque solsticii estivalis parte non occidere quispiam inveniet, ita ut et maximus dies et gnomones periscii ad trium mensium proxime spatium extendantur.

Vbi elevatio poli 78 20′ graduum est, ibi ex utraque solsticii estivalis parte 60 gradus non occidere quispiam inveniet, ita ut et maximus dies et umbrarum circumductio ad mensium quatuor spatium procedat.

Vbi elevatio poli 84 graduum est, ibi ex utraque solsticii estivalis parte 75 gradus non occidere quispiam inveniet, ita ut quinque maximus dies mensium ferme fiat et gnomonum umbre eodem tempore circumducantur.

Vbi vero totius quarte partis 90 gradibus borealis polus elevatur ab orizonte ibi borealior borealior] corr. ex borialior G equinoctiali semicirculus signiferi, hoc est circuli qui per medium signorum est, nunquam sub terra fit, australior nunquam super terram, ita ut dies unus et nox una annui spacii sint sex utraque proxime mensium et gnomones semper perischii sint; huius declinationis propria sunt, ut borealis polus super verticem sit et obliquus quidem tum semper tum nunquam apparentis situm accipiat et borealius borealius] corr. ex borialius G semispherium sui super terram australius sub terra semper efficiat; equinoctialis vero situm habeat orizontis.

〈II.7〉 Capitulum VII: De coascensionibus circuli qui per medium signorum est et equinoctialis in sphera declivi

Quoniam que universaliter in delinationibus considerantur breviter exposita sunt, sequitur iam ut quomodo simul ascendentia in qualibet declinatione equinoctialis tempora capiantur demonstrare simul dico ascendentia cum eius circuli arcubus qui per medium signorum est, per quos cetera quoque omnia que particularia sunt consequenter exponentur. Abutemur autem signorum nominibus in ipsis duodecimis obliqui circuli partibus, et quasi eorum initia a tropicis equinoctialibusque punctis capiantur, sic duodecimam partem que ab equinoctio vernali ad totius sphere sequentia est Arietem, secundum Taurum apellabimus, similiterque deinceps secundum traditum signorum nobis duodecim ordinem.

Primum autem demonstrabimus quod arcus circuli qui per medium signorum est equaliter ab eodem equinoctiali puncto distantes cum equalibus semper equinoctialis circuli arcubus ascendunt.

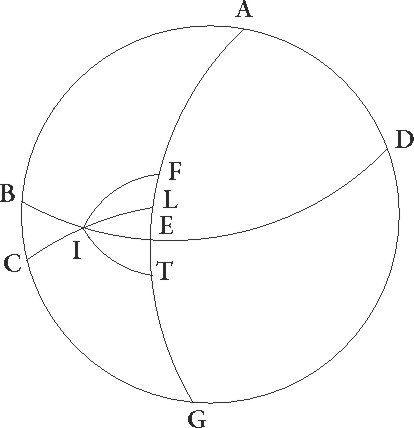Sit enim meridianus circulus ABDG, orizuntis autem semicirculus BED, equinoctialis vero EG, obliqui quoque circuli due portiones FI et TC, ita ut utrunque F et T punctum vernalis equinoctii esse supponatur et ex utraque ipsius parte arcus equales capti FI et TC per C et I puncta ascendere intelligantur. Dico quia ipsius equinoctialis arcus qui cum utroque istorum ascendunt, idest FE et ET, equales sunt: sint polorum polorum] corr. ex pollorum G ipius equinoctialis puncta L et M, describanturque per ipsa LEM et LT et LC et FM et MI maximorum circulorum portiones. Quoniam ergo FI et TC equales sunt et paralleli LC et MI qui per C et I describuntur utrinque ab equinoctiali equidistant, ipsi etiam equales sunt et EC et EI similiter equalium equalium] corr. ex qualium G erunt laterum LCT et MIF, et similiter LEC et MEI equalium laterum erunt. Quare angulus CLE angulo IME equalis est, similiter CLT totus IMF toti equalis est. Quamobrem etiam reliquus ELT reliquo EMF equalis est. Bassis ergo etenim ET bassi EF equalis est, quod erat demonstrandum.

Rursus autem demonstrabimus quod equinoctialis circuli arcus, qui simul ascendunt cum circuli qui per medium signorum equalibus arcubus equaliterque ab eodem tropico distantibus puncto, utrique utrisque ipsorum recte sphere assensionibus sunt equales. Designetur enim ABGD meridianus, et describantur equales duo equaliterque a brumali puncto distantes obliqui circuli arcus FI et TI, ita ut F autumnale, T vernum esse punctum presupponatur. Sic enim I punctum ortus ipsorum et orizontis erit commune, propterea quod ab eodem circulo parallelo ad equinoctialem FI et TI arcus comprehenduntur, sic etiam TE cum ipso TI et EF cum ipso FI simul ascendunt, ita per se patet quia etiam totus TEF TEF] corr. ex TF G recte sphere equalis est assensionibus arcuum FI et TI. Si enim C punctum australem equinoctialis polum esse supposuerimus, ac per ipsum et punctum I quartam maximi circuli descripserimus partem que sit CIL equipollens recte sphere orizunti, fit rursum ut TL simul ascendat cum TI in sphera recta et LF simul ascendat cum FI similiter. Quare utrique simul TLF utrisque simul TEF equales sunt et ab uno atque eodem TF continentur, quod erat demonstrandum.

Per hec nobis perspicuum factum est quia, si in una solummodo per singulas declinationes quarta particulares coascensiones computaverimus, reliquarum etiam trium quartarum simul erunt demonstrate.

Cum igitur hec ita se habeant, rursum nobis parallelus per[i] per] peri A Rhodum suppositus sit, ubi maxima dies horarum est equinoctialium 14 ½ et borealis polus 36 gradibus elevatur ab orizonte, sitque meridianus circulus ABDG, et orizuntis similiter semicirculus BED, ipsius vero equinoctialis EG, eius autem qui per medium signorum est FIT, sic ut I vernale punctum esse presupponatur, capiaturque ipsius equinoctialis borealis polus in puncto C, describaturque per ipsum et per L orizuntis et circuli qui per medium signorum est sectionem maximi circuli pars ipsa scilicet CLM, propositumque sit, dato arcu IL, invenire arcum equinoctialis EI qui cum illo simul ascendit, et primum quidem IL duodecimam circuli partem, Arietem scilicet, contineat. Quoniam ergo maximis descriptis circulis in duos arcus EG et GC duo ED et EM describuntur in L puncto se ipsos secantes, proportio corde dupli arcus CD ad cordam dupli DG composita est ex proportionibus cordarum dupli arcus CL ad dupli LM et dupli ME ad dupli EG. Sed arcus CD partis circumferentie duplus graduum est 72 et corda ei subtensa partium 70 32′ 4″.

Duplus uero GD graduum 108 et corda sua partium 97 4′ 56″, et rursum duplus LC partis circumferentie arcus graduum est 156 40′ 1″, et corda sua partium 117 31′ 15″, duplus vero LM graduum 23 19″ 50″, et corda sua partium 24 15′ 57″. Si ergo a proportione 70 32′ 4″ ad 97 4′ 56″ auferamus proportionem 117 31′ 15′′ ad 24 15′ 57′′, relinquetur proportio corde dupli arcus ME ad cordam dupli EG, que est proportio 18 0′ 5″ ad 120. Sed corda dupli arcus EG partium est 120, ergo corda etiam dupli arcus ME eorundem est 18 0′ 5″. Quare duplus etiam ME partis circumferentie arcus graduum erit 17 16′ proxime, ipse vero ME 8 38′ eorundem. Sed quoniam totus arcus IM qui cum ipso IL in orbe recto similiter ascendit, graduum demonstratus est esse 27 50′, idcirco reliquus EI graduum est 19 12′ et habemus una demonstratum quia etiam Pisces duodecima pars eisdem temporibus 19 12′ coascendit. Utraque vero Virgo et Libra residuis ad duplam in recto circulo ascensionem ascensionem] in add. et del. A temporibus 36 28′, quod erat demonstrandum.

Rursus autem IL arcus duarum duodecimarum spatium Arietis et Tauri 60 gradus contineat. Ceteris ergo eisdem manentibus per ea que exposita sunt, duplus quidem CL partis circumferentie arcus 138 59′ 42″ graduum est et corda sua partium 112 23′ 56′′. Duplus autem LM graduum 41 9′ 18′′, et corda sua partium 42 1′ 48′′. Si ergo rursus a proportione 70 32′ 4′′ ad 97 4′ 56″ subtrahamus proportionem 112 23′ 56″ ad 42 1′ 48″, relinquetur proportio corde dupli arcus ME ad dupli arcus EG que est proportio 32 36′ 4″ ad 120. Sed corda dupli arcus EG 120 partium est. Corda ergo dupli ME earundem est 32 36′ 4″. Quare duplus etiam ME partis circumferentie arcus graduum est 31 32′ proxime, ipse vero ME 15 46′ eorundem. Sed totus MI predemonstratus est esse graduum 57 44′ et reliquus ergo IE graduum est 41 58′. Quare Aries atque Taurus in temporibus 41 58′ utrique simul ascendunt. Sed Aries in temporibus 19 12′ conscendere demonstratus est. Taurus ergo solus 22 46′ temporibus conscendit, et per eadem rursus Aquarius equalibus temporibus 22 46′ conscendet, et uterque Leo et Scorpio residuis ad duplam in recto circulo ascensionem temporibus 37 2′. Verum quoniam maximus dies 14 ½, minimus autem 9 ½ horarum equinoctialium est, patet quia semicirculus a Cancro usque ad Sagittarium in 217 30′ ipsius equinoctialis temporibus conscendet, a Capricorno vero usque ad Geminos in temporibus 142 30′. Quare utraque quarta ex utraque vernalis puncti parte simul ascendet ascendet] corr. ex attendet G in temporibus 71 15′, utraque vero ex utraque autumnalis 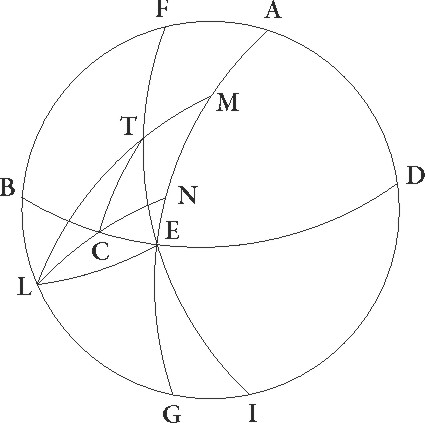puncti parte in temporibus 108 45′. Reliqua ergo duodecima que Geminorum est et similiter Capricorni utraque per se in temporibus 29 17′ ascendet, residuis videlicet ad tempora quarte 71 15′; reliqua etiam Cancri et Sagitarii in temporibus utraque similiter 35 15′ residuis rursum ad tempora huius quarte 108 45′.

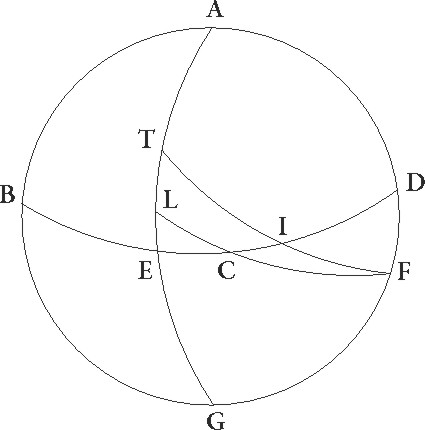Perspicuum autem est quod eodem modo minorum etiam circuli qui per medium signorum est portionum coortus et et] corr. ex ex A ascensiones capiemus, sed commodius faciliusque sic etiam ipsas computabimus. Sit enim primum meridianus circulus ABGD, et orizuntis semicirculus BED, equinoctialis vero EG, circuli autem qui per medium signorum est FEI, FEI] corr. ex EFEI G et E sectio vernale punctum esse presupponatur, et ab eo arcus ET contingenter capiatur, et equidistans ab equinoctiali portio TC per T describatur, captoque L polo equinoctialis, designentur per ipsum quarte maximorum circulorum partes LTM et LCN et etiam LE. Patet igitur hinc quia ET circuli qui per medium signorum est portio in recta quidem sphera cum EM ipsius equinoctialis arcu simul ascendit, in declivi vero cum equali ipsius NM. Arcus enim equidistantis CT, quacum simul ET portio ascendit, similis est ipsius equinoctialis arcui NM. Similes autem parallelorum arcus equalibus ubique in temporibus conscendunt. Quare ascensus ET portionis minor est in sphera declivi quam in sphera recta ipso arcu EN, demonstratumque est quod universaliter quoque, si arcus quidam maximorum circulorum sic describantur, sicut LTM et LCN, portio EN ascensionum declivis et recte sphere excessum continebit arcuum videlicet circuli qui per medium signorum est qui arcus per E et per parallelium qui per C describitur intercipiuntur, quod erat demonstrandum.

Cum igitur hec ita inspecta sint, proponatur sola meridiani circuli et orizuntis ac equinoctialis semicirculorum descriptio, et per F australem equinoctialis polum due quarte maximorum circulorum partes FIT et FCL describantur, et sit I quidem punctum commune paralleli qui per punctum brumalis solsticii describitur et orizuntis, C vero commune paralleli qui per initium, verbi gratia, Piscium aut cuiusvis portionis date de portionibus quarte. In duos igitur rursum FT et ET maximorum circulorum arcus descripti sunt FCL et ECI in puncto C se ipsos secantes, et est proportio corde dupli arcus TI ad cordam dupli arcus IF composita ex portionibus cordarum dupli arcus TE ad dupli EL et dupli LE ad dupli CF. Sed duplus TI partis circumferentie arcus, cum sit in omnibus declinationibus idem, —est enim inter tropicos—, datus est, ac ideo etiam reliquus videlicet est … videlicet] add. marg. G IF partis circumferentie duplus, et similiter in eisdem circuli qui per medium signorum est portionibus arcus LC partis circumferentie duplus, cum idem in omnibus declinationibus sit, per obliquationis tabulam datur, quapropter etiam duplus CF, quare proportio corde dupli arcus TE ad dupli arcus EL eadem in omnibus declinationibus relinquitur in eisdem quarte partis proportionibus.

Si ergo, cum ita se habeant, differentiam arcus CL per denos a verno equinoctio gradus quarte partis usque ad brumalis solsticii punctum adauxerimus, —sufficit enim huiusmodi arcuum ad usum divisio—, habebimus semper duplum IT partis circumferentie arcum 47 42′ 40″ graduum et cordam ei subtensam partium 48 31′ 55″, arcum vero IF partis circumferentie duplum 132 17′ 20″ graduum et cordam suam partium 109 44′ 53″. Similiter autem et in arcu qui per 10 versum brumale solstitium gradus a vernali puncto abest CL quidem duplum 8 3′ 16″ graduum, cordamque ipsi subtensam 8 25′ 39″ partium, CF autem duplum 171 56′ 44′′ graduum et cordam suam 119 42′ 14″. In arcu vero qui similiter 20 gradibus abest duplum CL 15 54′ 6″ graduum et cordam suam 16 35′ 56′′ partium, duplum vero CF graduum 164 5′ 54″ et cordam suam partium 118 50′ 47″. In arcu qui 30 gradibus abest duplum quidem CL graduum 23 19′ 58″, cordamque suam 24 15′ 56″ partium, duplum vero CF graduum 156 41′ et cordam suam partium 117 31′ 15″. In arcu qui 40 gradibus abest duplum quidem CL 30 8′ 8″ graduum et cordam suam 31 11′ 43′′, duplum vero CF graduum 149 51′ 52″, cordamque suam partium 115 52′ 19″. In arcu qui per 50 gradus abest CL quidem duplum graduum 36 5′ 46′′, cordamque suam partium 37 10′ 39″, duplum vero CF graduum 143 54′ 14″, cordamque suam partium 114 5′ 44′′. In arcu qui 60 gradibus abest, duplum quidem LE 41 0′ 18″ graduum, cordamque suam 42 1′ 48′′ partium, duplum vero CF graduum 138 59′ 42′′, cordamque suam 112 23′ 57′′. In arcu qui 70 gradibus abest duplum quidem LC graduum 44 40′ 22′′, cordamque suam partium 45 36′ 18′′, duplum vero CF graduum 135 19′ 38′′, cordamque suam partium 110 59′ 47′′. In arcu qui 80 gradibus abest duplum quidem LC graduum 46 56′ 32′′, cordamque suam partium 47 47′ 40″, duplum vero TF 133 3′ 28″ graduum, cordamque suam 114 16′ partium; et per illa que iam dicta sunt, si a proportione corde dupli arcus TI ad cordam dupli IF, hoc est a proportione 48 31′ 55′′ ad 109 44′ 53′′, subtrahamus singulas proportiones que per 10 gradus sunt cordarum dupli arcus LC ad dupli CF, relinquetur nobis proportio corde dupli arcus TE ad cordam dupli EL in omnibus declinationibus eadem proportioni 60: in arcu quidem qui 10 ut diximus gradibus abest ad 9 33′, in 20 vero gradibus ad 18 56′, in 30 ad 28 1′, in 40 ad 36 33′, in 50 ad 44 12′, in 60 ad 50 44′, in 70 ad 55 45′, in 80 ad 58 55′.

Hinc patet quia in singulis etiam declinationibus, cum duplum TE partis circumferentie arcum datum habeamus, habeamus] corr. ex habemus G —tot enim graduum est, quot temporibus temporibus] corr. ex partibus G equinoctialis dies minimum diem excedit—, cordam quoque suam et proportionem eius ad cordam dupli arcus EL, ipsum quoque arcum EL partis circumferentie duplum datum habebimus, habebimus] post corr. G cuius medietatem, idest ipsum EL qui predictum excessum continet, si de ascensionibus in recta sphera arcus circuli qui per medium signorum est subtraxerimus, inveniemus ascensionem eiusdem partis circumferentie in proposito climate.

Proponatur enim rursus exempli gratia paralleli per Rhodum declinatio, ubi duplus ET partis circumferentie arcus 37 30′ graduum est, corda vero sua partium 38 34′ proxime. Quoniam ergo eadem proportio est 60 ad 38 34′, et 9 33′ ad 6 8′, et similiter 18 57′ ad 12 11′, et 28 1′ ad 18 0′, et 36 33′ ad 23 29′, et 42 12′ ad 28 25′, et 50 44′ ad 32 37′, et 55 45′ ad 35 52′ et 58 55′ ad 37 52′, fit dupli quidem EL partis circumferentie arcus in singulis denorum denorum] post corr. G graduum excessus expositarum accommodatarum accommodatarum] post corr. G partium. Medietas vero eius ipsius arcus, idest ipsa EL: in prima quidem graduum decade decade] post corr. G graduum 2 56′, in secunda vero 5 50′, in tertia 8 38′, in quarta xi 17′, in quinta 13 42′, in sexta 15 46′, in septima 17 28′ 4″, in octava 18 24′, in nona ipsorum 18 45′. Quare quoniam etiam in recta sphera arcus prime graduum decadis 9 10′ temporibus simul conscendit, secunde 18 25′, tertie 27 50′, quarte 37 30′, quinte 47 28′, sexte 57 47′, septime 68 18′, octave 79 5′, none totius quarte partis temporibus 90, patet quia, si a singulis ascensionibus recte sphere convenientem secondum EL partis circumferentie quantitatem excessus subtraxerimus, ascensiones etiam eorundem in proposito climate habebimus, conscendetque simul prime decadis partis circumferentie reliquis temporibus 6 14′, usque ad secundam 12 35′, usque ad tertiam 19 12′, usque ad quartam 26 13′, usque ad quintam 33 46′, usque ad sextam 41 58′, usque ad septimam 50 57′, usque ad octavam 60 41′, usque ad nonam, idest totius quarte partis arcus, temporibus 71 15′ que coliguntur subtracta diurne magnitudinis medietate. diurnae … medietate] add. G

lpsarum ergo etiam decadum prima temporibus 6 14′ conscendet, secunda 6 21′, tertia 6 37′, quarta 7 1′, quinta 7 33′, sexta 8 12′, septima 8 56′, octava 9 47′, nona 10 34′.

His demonstratis, per ea que iam inspecta sunt reliquarum etiam quartarum ascensiones una erunt demonstrate. Modo igitur eodem ceterorum quoque parallelorum ad quos usus potest pervenire ascensiones per singulos denos gradus considerabimus et in tabulis, ut ad reliqua faciliorem prebeant viam, conscribemus, incipiemusque ab ipso equinoctiali et perveniemus ad eum usque qui maximum diem 17 reddit horarum, incrementumque ipsorum medio unius hore parte faciemus. Nullius enim cure digna differentia fit que preter equale incrementum inter mediam horam invenitur. Primo igitur circuli 36 decadas exponemus, deinde consequenter ipsius ascensus climatis tempora temporumque aggregationem hoc pacto, tabula sequitur.

〈II.8〉 Capitulum VIII: Tabule ascensionum per denos gradus gradus] incipiunt add. A (then deleted by G)

〈II.9〉 Capitulum VIIII: De iis que particulariter ad ascensiones secuntur

Quod autem, ascensionum temporibus hoc pacto nobis expositis, facilia intellectu omnia erunt que ad hanc partem pertinent, nec lineari ad singula ipsorum demonstratione nobis opus erit, nec longa tabularum compositione ex iis que dicentur, perspicuum erit.

Nam primum date diei aut noctis magnitudo numeratis propositi climatis temporibus capietur: in die quidem temporibus que a solari gradu ad eum usque qui ad sequentia signorum diametraliter opponitur, in nocte vero temporibus que a gradu diametraliter Soli opposito ad ipsum gradum solarem sunt. Collectorum enim una temporum quintadecima parte capta habebimus quot equalium horarum propositum spatium est, duodecima vero parte capta habebimus quot temporalis hora eiusdem spacii partium est.

Sed facilius quoque unius hore magnitudo invenietur, si ex proposita ascensionum tabula excessum scriptarum aggregationum capiemus, in die quidem in gradu solari, in nocte autem in diametraliter opposito tam in equinoctiali parallelo quam in proposito climate. Sexta enim parte inventi excessus capta, et si in boreali quidem semicirculo gradus quo intravimus est addita 15 unius hore temporibus, si vero in australi ab eisdem 15 temporibus temporibus​] corr. ex partibus G subtracta, multitudinem partium temporalis proposite hore inveniemus.

Datas etiam temporales horas in horas equales reducemus, si diurnas diurnas] corr. ex diuernas A quidem in partes horarum illius diei, nocturnas vero in partes horarum noctis propositi climatis multiplicaverimus. Quintadecima enim huiusmodi temporum parte capta, multitudinem equalium horarum habebimus. Equales autem horas in temporales econtra, si multiplicaverimus ipsas in 15 et per partes horarum proprii spacii parciemur.

Dato nobis rursum tempore horaque qualibet temporali, sic orientem gradum circuli qui per medium signorum est capiemus: multitudinem horarum ab hortu Solis in die, in nocte vero ab occasu in correspondentes horarum partes multiplicabimus, et factum numerum a Solis gradu in die, in nocte autem ab opposito ei diametraliter gradu, ad sequentia signorum secundum ascensiones climatis dirrigemus, illumque gradum oriri oriri] corr. ex horiri G tunc dicemus ad quem numerus pervenerit.

Si vero medii celi super terram gradum capere voluerimus, temporales super horas a transacta meridie ad datam usque in correspondentes horarum partes multiplicabimus, factumque numerum a solari gradu secundum ascensiones recte sphere dirigemus, et illum gradum in medio celi esse dicemus ad quem numerus pervenerit.

Similiter autem ab oriente gradu eum qui medium celi tenet inveniemus, si collectum numerum qui orienti gradui in tabula climatis ascribitur tenebimus. Nam si semper ab eo quarte partis 90 tempora subtrahemus, correspondentem numero illi gradum in versu collectionis graduum recti orbis tunc in medio celi esse inveniemus; econtra etiam a gradu qui super terram in medio celi est orientem rursus gradum habebimus, si collectum numerum gradui qui medium celi tenet appositum in recte sphere tabula capiemus, ipsique super eadem 90 addiderimus tempora. Facto enim numero correspondentem in collectione graduum climatis gradum oriri tunc oriri tunc] post corr. G inveniemus.

Perspicuum etiam est quia Sol totidem equaliter horas equales abest a media nocte meridieque omnium qui sub eodem meridiano habitant. Tot autem equalium horarum temporibus differt in omnibus qui non sub eodem meridiano habitant, quot gradibus meridianus a meridiano distat.

〈II.10〉 Capitulum X: De angulis atque arcubus que ab obliquo zodiaci circulo et meridiano fiunt

Verum cum ad propositam speculationem reliquum sit ut de angulis disseramus qui penes circulum quem per medium signorum dicimus fiunt, illa prius exponenda exponenda] corr. ex experienda G sunt quod rectum a maximis circulis contineri angulum dicimus, quando, communi circulorum sectione pro polo capta, spatio autem quolibet, descripti circuli arcus interceptus a portionibus que angulum continent quartam descripti circuli partem facit, et quod universaliter, que proportio est inter interceptum arcum ad circulum ita descriptum, ea etiam est anguli qui sub declinatione superficierum continetur ad quatuor rectos. Quare cum totam circumferentiam 360 partium esse supponamus, quot arcus interceptus partium erit, tot etiam angulus a quo ipse subtenditur erit, talium videlicet qualium unus rectus 90. Angulorum igitur qui penes obliquum circulum fiunt illi maxime ad hanc speculationem conferunt qui ab eius meridianique aut orizontis in omni situ sectione continentur, similiter qui ab eius et descripti per polos orizuntis maximi circuli sectione continentur. Cum huiusmodi autem angulis simul arcus etiam huius circuli qui intercipiuntur intersectionem et polum orizuntis, hoc est puncti super verticem, demonstrantur.

Horum enim singula demonstrata tam ad ipsam speculationem plurimum conferunt, quam ad alia que in Lune diversitatis aspectibus queruntur maxime conducunt. Nullo enim pacto progredi potest investigatio illa, nisi recte que diximus habeantur. Verum cum quatuor sint anguli qui a sectione duorum circulorum continentur, id est obliqui circuli et alicuius alicuius] corr. ex aliquibus A eorum a quibus secatur, nosque de uno qui secundum positionem similis sit verba facturi sumus, declarandum quod universaliter de duobus angulis qui fiunt ab arcu obliqui circuli sequente communem duorum 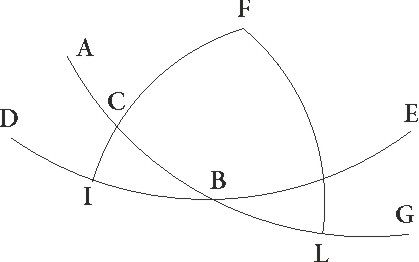circulorum sectionem illum qui est a septentrione intelligere debemus, ut accidentia quantitatesque quas demonstrabimus huiusmodi esse angulorum non dubitemus, sed, cum demonstratio angulorum obliqui circuli ad meridianum apertior sit, inde incipiemus, primoque demonstrabimus quod puncta obliqui circuli que ab eodem equinoctiali puncto equaliter distant equales dictos inter se angulos faciunt.

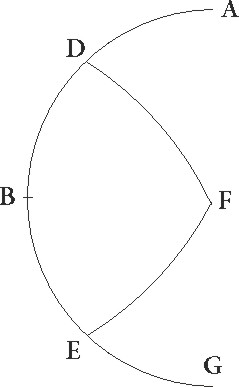Sit enim equinoctialis circuli arcus ABG, obliqui vero DBE, sitque equinoctialis circuli polus in puncto F, interceptisque arcubus equalibus BI et BT ad utranque B puncti equinoctialis partem, describantur per F polum et per I et T puncta meridianorum circulorum arcus FCI et FTL: dico quod angulus CIB equalis est angulo FTE, quod perspicuum est. Nam trilatere figure BIC et BTL equilatere sunt. Tria enim latera unius tribus lateribus alterius singula singulis equalia sunt, idest IB et BT, IC et TL, BC et BL, que omnia in superioribus demonstrata sunt. Quare angulus quoque CIB angulo BTL, idest angulo FTE, equalis est, quod erat demonstrandum.

Deinde quod anguli punctorum obliqui circuli equaliter ab eodem solstitiali puncto distantium qui anguli ad meridianum fiunt utrique simul capti duobus rectis equales sunt.

Sit enim obliqui circuli arcus ABG, sitque B punctum solstitiale et, interceptis ab utraque ipsius parte equalibus arcubus BD et BE, describantur per D et E puncta et F equinoctialis circuli polum meridianorum circulorum arcus FD et FE: dico quod anguli FDB et FEG duobus rectis simul utrique capti equales sunt, quod etiam perspicuum est. Nam quoniam D et E puncta equaliter ab eodem solstitiali distant puncto, arcus DF et FE equales sunt. Quare anguli quoque FDB et FED equales sunt Sed anguli FEB et FEG duobus rectis equales sunt. Quare anguli etiam FDB et FEG duobus rectis equales sunt quod erat demonstrandum.

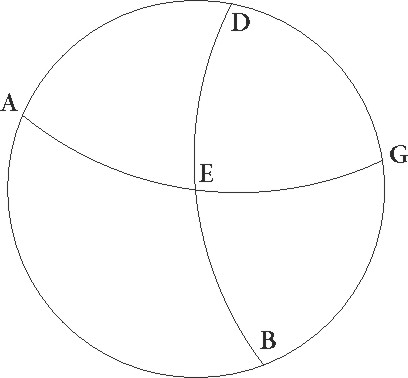His iam inspectis, sit meridianus circulus ABGD, et obliqui circuli semicirculus EG, presupponaturque A punctum brumalis solsticii esse, et polo ipso A spatio autem latere quadrati describatur BED semicirculus. Quoniam ergo ABGD meridianus per polos EG et BED circulorum descriptus est, arcus ED pars circuli quarta est. Quare angulus DE rectus est. Rectus autem propter predemonstrata est etiam ille qui in estivalis solsticii puncto efficitur, quod erat demonstrandum.

Sit rursus meridianus circulus ABGD, equinoctialis vero circuli semicirculus EG, et describatur AFG obliqui circuli semicirculus sic, ut A autumnalis equinoctii punctum sit, poloque ipso A et spatio latere quadrati BFED semicirculus describatur. Similiter igitur, quoniam ABDG per polos EG et BED circulorum descriptus est, tam AF arcus quam ED quarta pars circuli est. Quare F brumalis solsticii punctum erit et FE arcus graduum, ut iam demonstravimus, 23 51′ proxime. Erit igitur etiam totus FD arcus graduum 113 51′. Angulus vero DAF talium 113 51′, qualium unus rectus est 90, et propter demonstrata iam angulus etiam qui in verno equinoctiali puncto fit residuorum 66 9′ ad duos rectos graduum erit.

Sit rursus meridianus circulus ABDG, et equinoctialis circuli semicirculus EG, obliqui autem BFD, sic ut F quidem punctum autumnale esse presupponatur, BF autem arcus primum unius duodecime partis solummodo, idest Virginis, cuius Virginis principium B punctum sit, et rursum polo ipso B, spatio vero latere quadrati, semicirculus ITEC describatur, propositumque sit CBT angulum invenire. Quoniam ergo ABGD meridianus per polos EG et IEC circulorum descriptus est, BI et BT et EI arcus quarte portionis singuli sunt. Per figuram autem sectoris proportio corde dupli arcus BA ad cordam dupli arcus AI composita est ex proportionibus cordarum dupli arcus BF ad dupli FT et dupli TE ad dupli EI. Sed duplus BA partis circumferentie arcus 23 20′ graduum demonstratus est, et corda sua partium 24 16′, duplus vero AI graduum 156 40′, et corda sua partium 117 31′.

Rursum duplus FB graduum est 60, et corda sua partium 60, duplus vero FT graduum 120, et corda sua partium 103 55′ 23′′. Si ergo rursus a proportione 24 16′ ad 117 31′ subtraxerimus proportionem 60 ad 103 55′ 23″, relinquetur nobis proportio corde dupli arcus TE ad cordam dupli CI que est proportio 42 58′ proxime ad 120. Est autem corda dupli arcus EI partium 120, quare corda etiam dupli arcus TE 42 58′ eorundem. Est igitur etiam duplus TE partis circumferentie arcus graduum 42 proxime, ipse vero ET 21 eorundem. Quare totus CET arcus tam ipse quam EBT angulus 111 graduum est. Sed propter perdemonstrata etiam angulus qui a principio Scorpionis fit 111 graduum equaliter est. Vterque autem qui a principio Thauri et qui a principio Piscium fit residuorum ad duos rectos graduum 69, quod erat demonstrandum.

Supponatur in eadem rursus descriptione duarum esse duodecimarum portionum arcus BF, ita ut B punctum principium Leonis sit, eisdemque suppositis, duplus BA partis circumferentie arcus graduum erit 41, et corda sua partium 42 2′. Duplus vero AI graduum 139, et corda sua partium 112 74′, et rursum duplus FB graduum 120, et corda ipsi subtensa partium 103 55′ 23′′, duplus vero FT graduum 60, et corda sua partium 60. Si ergo rursus a proportione 42 2′ ad 112 24′ subtraxerimus proportionem 103 55′ 23′′ ad 60, relinquetur proportio corde dupli arcus TE ad dupli arcus EI que est proportio 25 53′ ad 120. Quare corda dupli arcus TE fit eorundem 25 53′. Duplus ergo etiam TE partis circumferentie arcus 25 proxime graduum erit, ipse vero TE 12 30′ eorundem, quarte totus TEC tam ipse quam angulus CBT graduum erit 102 30′. Propter hec etiam angulus qui a principio Sagittarii continetur 102 30′ equaliter erit. Uterque autem qui a Geminorum principio et qui a principio Aquarii continetur residuorum ad duos rectos graduum 77 30′, et demonstrata sunt nobis que proposuimus, eadem in minoribus etiam obliqui circuli portionibus deductio est, sed quantum ad usum et presentis negotii et singulorum descriptionis signorum, sufficienter dictum est.

〈II.11〉 Capitulum XI: De angulis atque arcubus qui ab eodem obliquo atque orizonte fiunt

Deinceps autem demonstrabimus, quomodo in data nobis declinatione angulos etiam quos obliquus ad orizuntem facit inveniemus, faciliore namque via ista reliquis capiuntur. Quod igitur qui ad meridianum fiunt iidem illis sunt qui ad recti orbis orizuntem fiunt, perspicuum est. Sed, ut in declivi 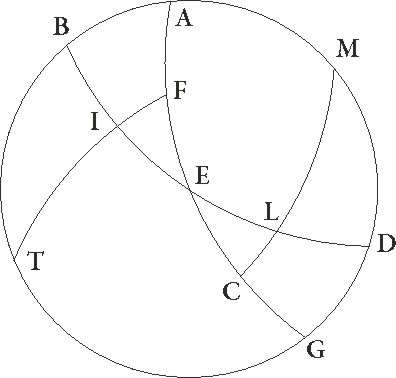etiam orbe capiantur, primum demonstrandum est puncta obliqui circuli que ab eodem equinoctiali puncto equaliter distant angulos qui ad eundem orizuntem constituuntur equales faciunt.

Sit enim meridianus circulus ABGD et equinoctialis circuli semicirculus EG, orizuntis vero circulus BED, et describantur due oblique circuli portiones FIT et CLM sicut F et T puncta autumnalis equinoctii punctum esse supponatur, et FI et CL arcus equales: dico angulos etiam EIT et DLE equales esse, quod inde apertum est. Nam EFI et ECL trilatere figure equales sunt, quoniam per ea que demonstrata sunt tria latera unius tribus lateribus alterius singula singulis equalia sunt FI et CB, preterea IE orizontis portio et EL equales sunt, et similiter EF ascensus EC EC] post corr. G ascensui. Quare angulus quoque EIF angulo ELC equalis est et reliquus EIT reliquo DLT equalis, quod erat demonstrandum.

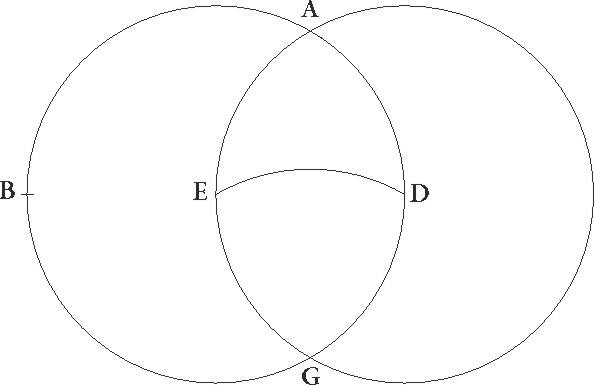Dico etiam quod punctorum diametraliter oppositorum orientalis angulus unius cum occidentali angulo alterius duobus rectis equalis est. Nam si circulum orizontis ABGD descripserimus, obliquum etiam circulum EGF in A et G puncta seipsos intersecantes intersecantes] corr. ex intersectantes G utrique simul FAD et DE duobus rectis equales sunt, sed FAD ipsi FGD equalis est, utrique igitur simul FGD et DE duos rectos faciunt.

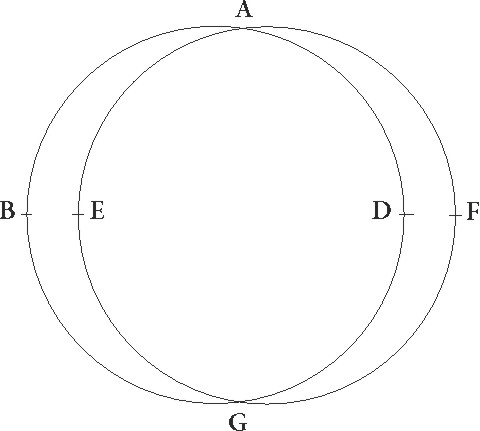Hec cum ita se habeant, quoniam etiam anguli qui ad eundem orizontem inspiciuntur, quique ab eodem equinoctiali signo equaliter distant equales demonstrati sunt, et punctorum que equaliter ab eodem solstitiali solstitiali] corr. ex solstitia G puncto distant alterius orientalis angulus alterius occidentalis duobus simul rectis equales; eveniet eveniet] corr. ex evenit G propter hec ut, si angulus orientalis ab Ariete usque ad Libram factos inveniemus, alterius etiam semicirculi orientales una erunt demonstrati et ad hec duorum semicirculorum occidentales. Quomodo autem id demonstretur breviter exempli gratia usi parallelo in quo borealis polus 36 ab orizunte gradibus elevatur, exponemus.

Anguli ergo qui ab equinoctialibus obliqui puncti ad orizuntem fiunt facile capientur, si meridianum ABGD circulum descripserimus. Propositi autem orizuntis ED orientalem semicirculum, equinoctialis vero quartam portionem EF, obliqui autem duas EB et EG sic se habentes, ut E punctum ad quartam quidem EB portionem autumnale intelligatur, at vero ad EG vernale, et B quidem hibernum fiat solstitiale, G autem estivale. Colligitur enim, cum arcus DF graduum 54 esse suppositus sit, et uterque BF et FG equaliter 23 51′ proxime, ut et GD graduum sit 30 9′, et BD 77 51′. Quare, quoniam E punctum ABGD meridiani polus est, angulus DEG qui a principio Arietis fit talium erit 30 9′, qualium unus rectus 90. Angulus vero DEB qui a principio Libre fit erit 77 51′ eorundem.

V 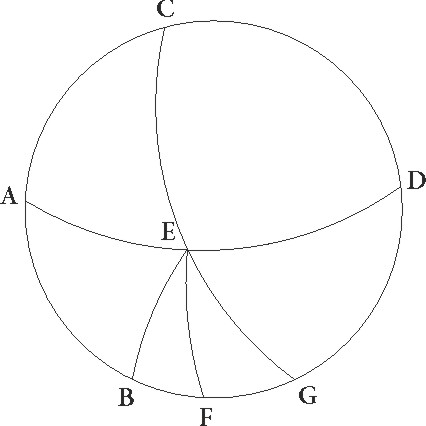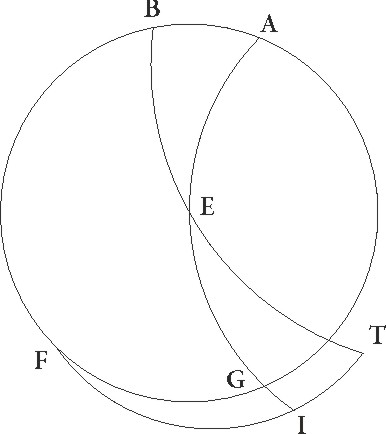erum ut etiam ad reliquos via pateat, proponatur exempli gratia, ut orientalis angulus qui a principio Tauri et orizunte fit nobis inveniendus sit, et sit ABGD circulus meridianus, BED propositi orizuntis semicirculus orientalis, et describatur EG obliqui semicirculus, ita ut E punctum Tauri principium sit, et quoniam principio Tauri in hoc climate oriente in medio celi sub terra 17 41′ Cancri gradus inveniuntur (ut ab expositis nobis assensionibus facile ista invenire docuimus), fit arcus EG quarta portione minor polo igitur E et latere quadrati spatio TIF maximi circuli portio describatur, et suppleantur tam EGI quam EDT quarte portiones, sic etiam DGF et FIT uterque quarta portio fit. Nam BET orizon per FGD meridiani et FIT maximi circuli polus est. Rursus quoniam 17 41′ Cancri gradus distant ab equinoctiali versus septentrionem in circulo maximo per polos eius gradibus 22 40′, (hec enim etiam exposita nobis sunt), equinoctialis autem ABF orizontis polo in eodem arcu FGD distat gradibus 36, colligitur ut arcus FG 58 40′ graduum sit. His datis, per figuram sectoris fit, ut proportio corde dupli arcus GD ad cordam dupli DF composita sit ex proportionibus cordarum dupli arcus GE ad dupli arcus EI et dupli IT ad dupli TF. Sed duplus GD propter preposita graduum est 62 40′, et corda sua partium 62 24′, duplus autem DF graduum 180, et corda sua partium 120, et rursum duplus GE graduum 155 22′, et corda sua partium 117 14′, duplus autem EI graduum 180, et corda sua partium 120. Si ergo a proportione 62 24′ ad 120 subtraxerimus proportione 117 14′ ad 120, relinquetur nobis proportio corde dupli arcus TI ad cordam dupli arcus TF que est proportio 63 52′ ad 120. Sed corda dupli arcus TF partium est 120, quare corda etiam dupli arcus IT 63 52′ eorundem erit. Duplus igitur IT partis circumferentie arcus 64 20′ graduum est, arcus vero IT tam ipse quam IET angulus 32 10′ eorundem, quod erat demonstrandum.

Hic modus, ne in singulis eadem dicentes longiorem huius negotii doctrinam faciamus, in reliquis et signis et climatibus nobis intelligitur.

〈II.12〉 Capitulum XII: De angulis atque arcubus qui ad eundem circulum ab illo fiunt qui est per polos orizontis

Illa iam nobis exponenda via et ratio restat qua etiam factos angulos obliqui circuli in omni declinatione atque situ ad eum qui per polos orizunti describitur capiamus, cum, ut diximus, arcus etiam circuli qui per orizuntis polos est a signo verticis et a sectione sui ad obliquum circulum interceptus una semper demonstratur.

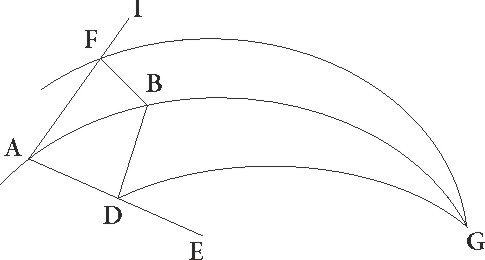Exponemus igitur rursum que huic parti premittenda sunt, primumque demonstrabimus quod, punctis obliqui circuli equaliter ab eodem solstitiali solstitiali] corr. ex solstitii G puncto distantibus, equaliaque intercipientibus tempora ex utraque meridiani parte altero ad ortum, altero ad occasum, et arcus maximorum circulorum a puncto verticis ad ipsa equales inter se sunt, et anguli qui ad ipsa fiunt modo quo distinximus duobus rectis equales.

Sit enim ABG meridiani portio, et supponatur in ipso B quidem verticis punctum, G vero ipsius equinoctialis polus, et describantur ADE et AFI obliqui 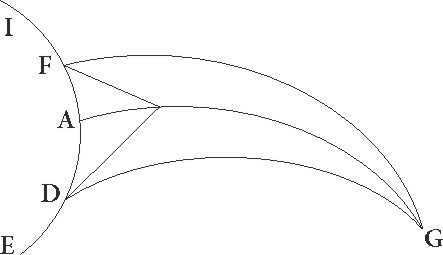circuli portiones sic se habentes, ut D et F puncta et equaliter ab eodem tropico distant et ex utraque ABG meridiani parte equos arcus paralleli qui per ipsa est intercipiant. Describantur etiam per D, F puncta maximorum arcus circulorum ex G quidem equinoctialis polo GD et GF, ex B vero verticis puncto BD et BF: dico BD et BF arcus equales esse et angulos BDE et BFA simul duobus rectis equales. Cum enim D D] corr. ex B G et F puncta equalibus paralleli qui per ipsa est arcubus ab AG meridiano distent, distent] post corr. G angulus BGD equalis est angulo BGF. Due igitur BGD et BGF trilatere figure duo latera duobus lateribus alterum alteri equalia habent. Nam GD et GF equalia sunt, BG autem commune est, angulus quoque BGD angulo BGF ab equalibus lateribus contento equalis, quare bassis quoque BD bassi BF et angulus BFG angulo BDG equalis est. Et quoniam paulo ante demonstratum est quod anguli punctorum equaliter ab eodem solstitiali puncto distantium qui ad circulum per polos equinoctialis descriptum fiunt utrique simul duobus rectis equales sunt, erunt utrique GDE et GFA simul duobus rectis equales. Sed angulus quoque BDG angulo BFG equalis est. Quare BDE et BFA utrique simul duobus rectis equales sunt, quod erat demonstrandum.

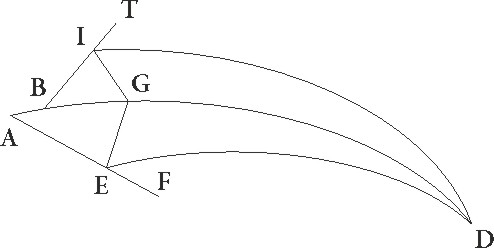Rursus demonstrandum quod, cum eadem obliqui circuli puncta per equalia tempora ex utraque meridiani meridiani] corr. ex meridiane G parte distent, et arcus maximorum circulorum qui a puncto verticis ad ipsa describuntur equales sunt inter se et duo anguli qui ab ipsa fiunt orientalis et occidentalis duobus angulis qui a meridiano ad ipsum punctum fiunt equales sunt, quando in utroque situ ambo medii celi puncta aut australiora aut borealiora puncto verticis sunt. Sed supponatur primum quod sint australiora et sit ABGD meridiani portio, et in ipso sit G verticis punctum, polus autem equinoctialis sit D, et describantur EF et BIT due obliqui circuli portiones sic se habentes, ut E et I punctum, cum idem esse supponatur, per equalem ad utramque utramque] corr. ex uramque G partem paralleli qui per ipsa est arcum arcum] s add. et del. G distet a meridiano, describanturque rursus rursus] corr. ex rursum G per ipsa maximorum circulorum portiones ab ipso quidem G portio GE et GI, ab ipso autem D portiones DE et DI. Propter eadem ergo superioribus quoniam E, I puncta eundem facientia parallelum equales ipsius ad utranque partem meridiani faciunt arcus, equalium tam angulorum quam laterum GDE et GDI trilatere fiunt figure, quare arcus etiam GE arcui GI equalis est. Dico autem quod etiam GEF et GIB duo anguli duobus DEF et DIB sunt equales. Nam quoniam DEF angulus idem est angulo DIB, et angulus GED angulo DIG equalis equalis] pluri hec desunt GED et GIB angulus AEF equales. Quare utrique simul add. marg. G erunt, utrique simul GEF totus et GIB duobus DEF et DIB sunt equales, ut quod erat demonstrandum.

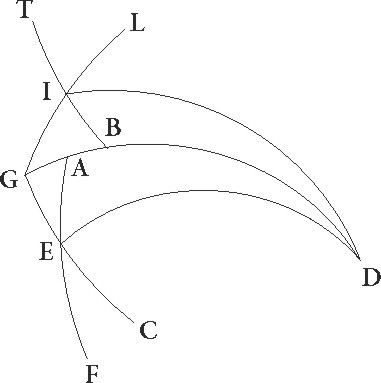Describantur deinde propositorum circulorum eedem portiones, ita ut A et B puncta borealiora G puncto sint. Dico etiam sic idem accidere, idest quod utrique simul anguli CEF et LIB duobus angulis DEF et DIB equales sunt. Nam quoniam angulus DF idem est angulo DIB et anguli DEC et DIL sunt equales, totus LIB duobus simul DEF et DEC equalis erit, quare utrique simul LIB et CEF duobus simul DEF et DIB equales sunt.

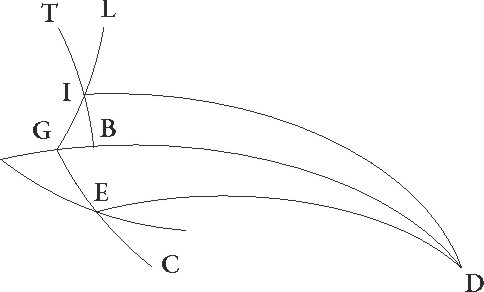Designetur rursus similis descriptio, ita ut punctum A quod in medio celi orientalis portionis est australius G puncto verticis sit, B autem quod est in medio celi occidentalis portionis eodem ipso borealius: dico quod utrique simul anguli GEF et LIB maiores sunt quam DEF et DIB duo anguli duobus rectis. Nam quoniam DIG angulus angulo DEG equalis est et ambo simul DIG et DIL duobus rectis equales, erunt utrique simul DEG et DIL duobus rectis equales. Sed angulus quoque DEF idem est angulo DIB. Quare utrique simul GEF et LIB maiores sunt quam utrique simul DEF et DIB, hoc est quam ipse DEF bis ambobus simul angulis DEG et DIL qui duobus rectis equales sunt, quod erat demonstrandum.

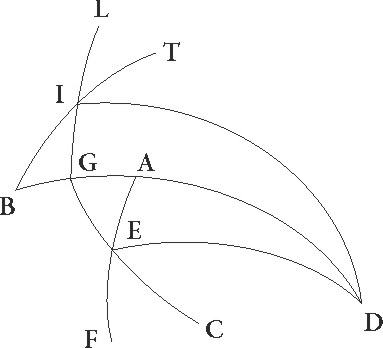Proponatur etiam quod restat in simili descriptione punctum quidem A quod medii celi punctum orientalis obtinet portionis borealius quam G, punctum autem B quod est in medio celi occidentalis portionis australius: dico quod utrique simul anguli CEF et GIB minores sunt quam duo simul DEF et DIB duobus rectis. Nam propter eadem rursus utrique simul anguli CEF et GIB minores sunt quam utrique simul DEF et DIB, hoc est quam DEF bis ambobus simul DEC et DIG. Ipsi vero duobus rectis equales sunt. Nam et ambo simul anguli DEC et DEG duobus rectis equales sunt et etiam DEG angulus angulo DIG equalis est, quod erat demonstrandum.

Quod autem quantitates tam angulorum quam arcuum qui ab obliquo circulo ad eum fiunt qui per punctum verticis maximus est, quique modo quo diximus in meridiano ac orizunte fiunt, facile inveniri possint, hinc ita erit perspicuum.

Nam si ABGD meridianum circulum descripserimus et BED orizontis semicirculum obliquique circuli portionem FEI, quomodocunque se habeat, quando quidem per F punctum in medio celi positum circulum maximum qui per A verticis punctum est descriptum esse intelligimus, tunc idem ipse fiet cum ABGD meridiano, et erit DFE angulus hinc nobis ideo datus, quoniam et F punctum et angulus eius qui ad meridianum fit datus est, sed ipse quoque arcus AF. Habemus enim quot gradibus in meridiano et F punctum distat ab equinoctiali et equinoctialis ab A puncto verticis. Quando autem maximum circulum EG qui per A describitur per E punctum oriens intelligimus, sic etiam hinc perspicuum est. Nam arcus E, quoniam A punctum BED orizuntis polus est, quarte semper erit portionis, et cum eadem de causa ED angulus rectus sit, et IED obliqui circuli ad orizuntem angulus datus, dabitur etiam totus EI, quod erat demonstrandum.

C 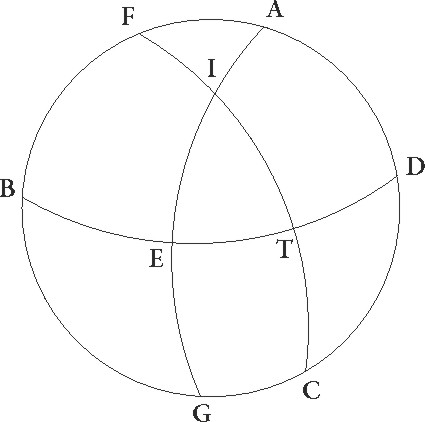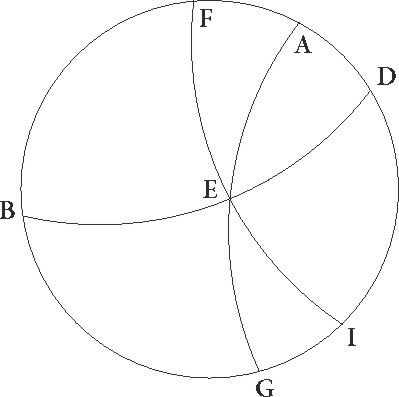um igitur hec ita se habeant, si in omni declinatione angulos atque arcus qui meridianum antecedunt a principio solummodo Cancri usque ad principium Capricorni computaverimus, eosque angulos arcusque simul qui post meridianum sunt una demonstratos habebimus, et ad hec ceteros qui fiunt tam ante quam post meridianum. Verum ut etiam in singulis sitibus via et ratio istorum pateat, exempli rursus gratia, demonstrationem universaliter per unum exponemus theorema, supponemusque in eadem declinatione, ubi videlicet borealis orizuntis polus 36 gradibus elevatur, Cancri principium una equali hora distare a meridiano versus orientem, in quo situ in hoc parallelo 16 12′ Geminorum gradus in medio celi sunt et 17 37′ gradus Virginis oriuntur.

Sit igitur ABGD meridianus circulus et BED orizuntis semicirculus obliqui autem FITC sic se habens, ut I quidem punctum Cancri principium sit, F autem 16 12′ Geminorum gradus obtineat, T vero 17 37′ Virginis gradus, et describatur per A punctum verticis, et per I Cancri principium AIEG maximi circuli portio, propositumque sit primo AI arcum invenire.

Patet ergo quod arcus TF 91 27′ graduum est, IT vero 77 37′. Similiter etiam quoniam 16 12′ Geminorum gradus 23 7′ ab equinoctiali equinoctiali] corr. ex quinoctiali G versus septentrione meridiani gradus intercipiunt et equinoctialis ab A verticis puncto 36 gradibus distat, erit arcus AF AF] corr. ex AEF G graduum 12 53′, arcus vero FB reliquorum ad quartam portionem gradum 77 7′. His datis, rursum per figuram sectoris proportio corde dupli arcus FB ad cordam dupli arcus BA composita est ex proportionibus cordarum dupli arcus FT ad dupli arcus TI et dupli arcus IE ad dupli EA. Sed duplus FB partis circumferentie arcus 154 14′ graduum est, et corda sua partium 116 59′, duplus vero BA graduum 180, et corda sua partium 120.

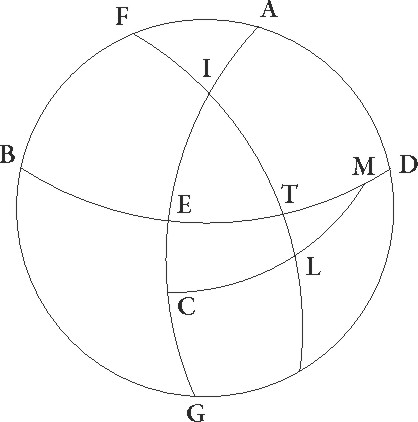Et rursus duplus FT partis circumferentie arcus graduum est 182 50′, et corda sua partium 119 58′, TI autem duplus graduum 155 14′, et corda sua partium 117 12′. Si ergo a proportione 116 59′ ad 120 subtraxerimus proportionem 119 58′ ad 117 12′, relinquetur nobis proportio corde dupli arcus EI ad cordam dupli EA que est proportio 114 16′ proxime ad 120. Sed corda dupli arcus EA partium est 120, erit ergo etiam corda dupli EI arcus 114 16′ partium earundem. earundem] corr. ex eorundem G Quare duplus etiam EI partis circumferentie arcus graduum erit 144 26′ proxime. Ipse vero EI 72 13′ eorundem. Quare reliquus quoque AI reliquorum ad quartam portionem graduum 77 47′, quod erat demonstrandum.

Deinde angulum etiam AIT sic inveniemus. Eadem enim descriptione posita et polo I, spatio vero latere quadrati CLM maximi circuli portio designetur. Quoniam ergo AIE circulus per polos ETM et TLM cirulorum descriptus est, uterque arcus EM et CM quarte portionis fit. Rursum igitur per figuram sectoris proportio corde dupli arcus IE ad cordam dupli arcus EC composita est ex proportionibus cordarum dupli arcus IT ad dupli TL et dupli LM ad dupli CM. Sed duplus IE partis circumferentie arcus graduum est.144 26′, et corda sua partium 114 16′, duplus autem EC graduum 35 34′, et corda sua partium 36 38′, et rursus duplus arcus TI graduum est 157 14′, et corda sua partium 117 12′, duplus vero TL graduum 24 46′, et corda sua partium 25 44′.

Quare si a proportione 114 16′ ad 36 38′ subtraxerimus proportionem 117 12′ ad 25 44′, relinquetur nobis proportio corde dupli arcus LM ad cordam dupli MC, que est proportio 82 11′ proxime ad 120. Sed corda dupli MC partium est 120, et corda ergo dupli LM eorundem est 82 11′. Quare duplus quoque LM partis circumferentie arcus graduum est 86 28′, ipse vero LM 43 14′ eorundem, et reliquus igitur arcus LC tam ipse quam LIC angulus graduum est 46 46′. Quare angulus quoque AIT 133 14′ reliquorum ad duos rectos est, quod erat demonstrandum.

Modus igitur inventionis eorum que proposita sunt idem et in ceteris colligitur, et nos, ut ceteros quoque et arcus et angulos quorum in particularibus considerationibus opus erit expositos paratosque habeamus, lineari doctrina ipsos adinvenimus, incepimusque a parallelo per Meroem, ubi maximus dies 13 horarum equalium est, et pervenimus ad eum usque qui ultra Puntum per hostia Borysthenis fluvii describitur, ubi maximus dies 16 horarum equalium est, usique sumus incremento in climatibus quidem medietatis rursum hunius hore sicut et in ascensionibus fecimus.

ln portionibus vero circuli obliqui unius signi hoc est partis duodecime, in situ autem meridiani tam ad ortum quam ad occasum hore unius equalis, fecimusque horum expositionem in tabulis per singula et signa et climata: et in primis partibus numerum equalium horarum secundum distantiam ad utranque meridiani partem post situm ipsius posuimus, in secundis quantitates arcuum qui a puncto verticis ad principium propositi signi fiunt, ut diximus, in terciis et quartis quantitates angulorum qui a proposita sectione modo quo distinximus continentur, in terciis quidem eorum qui ad ortum, in quartis vero eorum qui ad occasum, in variis positionibus fiunt. Sed, ut incipientes diximus, tenendum memoriter est quod de duobus angulis qui a sequente portione obliqui circuli continentur septentrionalem semper accipimus, quantitatemque ipsorum talium partium apponimus qualium unus rectus est 90. Est autem tabularum expositio huiusmodi Sequitur expositio tabularis.

〈II.13〉 Capitulum XIII: Tabularis arcuum atque angulorum per septem climata expositio

Climatis per Meroem. Horarum 13. Latitudinis graduum 16 27.