Ad sanctissimum dominum nostrum Sixtum Quartum Pontificem Maximum Andree Trapezuntii Georgii filii in paternam Almagesti Ptolomei traductionem prefatio

Evolventi mihi nuper libros patris mei, Georgii trapezuntii, viri optimi et omni doctrinarum genere insignis, Beatissime Pater, obtulit se Magna illa Ptolomei Compositio, quem Almagestum vocant, ab eo in Latinum e Greco conversa, sed inimici factione atque odio ex invidia conflato nondum emissa. Quam, ut attigi, statim percussit animum acerbus ille et pene sopitus ac evulsus dolor vetustate, qui omnem mihi veterem calamitatem atque miseriarum acerbitatem cumulumque renovavit. Nam felicissimum illud Trapezuntii ingenium vitaque omnis sanctissime acta laboresque sui et studia pro communi eruditione sponte suscepta, quo tempore fructu aliquo recreari debebant, in eo perditissime animorum declarationes ac iniuriarum moles ab his quos summis beneficiis devinxerat extiterunt. Non enim eos reliquis in artibus pervagata iam Trapezuntii fama eruditorum consensu celebrata adeo solicitabat, sed Ptolomei operis omnium difficillimi eisque minime cogniti splendor plurimum agitabat, cum trapezuntiana industria in gloriam nominis sempiternam Latinis hominibus tum primum refulgeret, atque cum ipsi et literarum ubertate et ingenii acumine doctis illa etate viris prestare se arbitrarentur, ea vero conversione ab uno Trapezuntio se facile superari viderent, omne eorum studium factionemque omnem ad acerbissimas in eum vexationes comportarunt. Ita partim sua ipsi potentia partim mercenariorum conductu non libros trapezuntianos obruere modo cupiverunt, sed communem quoque illum innocentissimi hominis spiritum de hominum genere optime meritum per summum scelus omnibus presidiis interclusis eripere tentaverunt. Quorum compresso odio, diu ex invidia collecto, iam erumpente nisi in articulo temporis concidere maluissemus a cervicibus nostris furorem illum scythicum omni ratione depellere oportuit. Has invidie tempestates per potentes inimicos concitatas, divus ille Alfonsus, Regum omnium quos presens hominum memoria longius repetere potest prestantissimus, cum accepisset, statim Trapezuntium per litteras ad se Neapolim commune doctorum refugium portiumque tutissimum accersivit et desponsa in annos singulos non mediocri pecunia comiter benigneque suscepit. Tot igitur tantisque calamitatibus ex familie cura oppressus dilaceratusque Trapezuntius traductionem ipsam plurimis annis elaboratam compressit, cuius editio ab eo eximebatur ut, remissa aliquando vel secessu invidia vel humanitate sopita vel vetustate consumpta, sua tandem cum animi tranquillitate et fortunarum redintegratione nostris hominibus divulgaretur. Sed decurtata potentis inimici factione vita, morte antea preventus est quam inscribere cuique posset. Quo mortuo, varia ipse rei familiaris cura distractus non adhibere in libri dicationem animum potui. Sed cum iam omnis ea solicitudo studiumque huiusmodi deferbuisse videatur, converti me tandem ad litteras longo intervallo revocatas. Atque quotidiano convicio hominum qui a me hoc munus non postulabant, sed efflagitabant, non sum passus debere diutius: quin iam iam attrectandum eis retinendumque dimitterem. Cum sepe igitur diuque ipse mecum cogitatem cui potissimum id laboris dedicarem, unus tu ex omnibus principibus quos nostra etas alit dignissimus occurristi cui paternas vigilias merito desponderem. Digna enim mihi visa res est, et summo certe digna pontifice, ut hec celestium corporum inferiora turbantium divina Ptolomei demonstratio tibi inscriberetur, qui humanarum rerum omnium pariter et divinarum administrationem et modum contineres. Nam etsi divina providentia summum pontificatum inieris, tue virtutes tamen singularisque religio ac pietas tanta, quanta Dei optimi maximi vicarium decet, eam tibi dignitatem iam pridem promittebat, ad quam celestium contemplationum videtur dedicanda esse doctrina. Quod si vel totius philosophie vel actionis vite vel preclarissimarum tuarum laudum gloria mihi nunc non explicanda, sed recensenda esset, omnibus liqueret profecto naturam ipsam te unum ex omnibus delegisse, in quo ornando omnes suas vires dotesque suas omnis effunderet. Ea enim in te bonitas est, is fidei cultus, ea iustitia, id religionis studium, ea denique vite sanctimonia, ut, cum nullus tibi non anteferri, sed ne comparari quidem possit, video te in horum temporum felicitatem divinitus pontificem maximum esse declaratum, qui tua singulari virtute propeque divina solus effecisti, ut, dum omnium horum genera sperneres, omnium tamen dignitatum culmen pro summis tuis virtutibus adipiscerere, ut non ad summam imperii maiestatem ambitione et studio, sed cunctis apostolici senatus suffragiis, omnium preterea gentium atque populorum consensu et desiderio vocarere. Quo quidem tuo facto, ceteris ad veram virtutis laudem aspirantibus divinum imitandi tui exemplum prescripsisti atque ad dignitates sectandas easdemque pure casteque adipiscendas viam formamque contulisti. Ac cum singulare illud tuum ingenium ad veritatis studium contulisses, omnemque tue vite tempus ad rerum divinarum rationes exquirendas transmisisses, brevi adeo tempore omnem philosophie ac theologie cognitionem absolutissime atque locupletissime hausisti, ut neque nostra, neque maiorum nostrorum etate aut ingenii acumine et celeritate aut disputatione et memoria aut subtilissimarum rerum et pene incomprehensibilium perceptione quisquam tibi proxime accesserit. Quibus artibus et disciplina apud omnes ita fama floruisti, ut, cum nihil iam tibi ad decus, nihil ad laudem operis superesset, quo illustrior et acceptior per omnes populos volitares, vitam tamen intergerrimam adiunxisti publicam utilitatem privato usui pretulisti. Que omnia etsi clarissima in te uno fuerunt quam in singulis singula, multo tamen fateor tua vite institutione fuisse clariora a teque illa magis tua virtute augeri quam tu ab illis auctus inveniaris. Iam vero, si benignitatem, clementiam, liberalitatem, innocentiam, magnificentiam attingere licebit, quis te ullo laudis genere prestantior aut splendidior invenietur, quo uno litterarum sacrario et virtutum officina, non solum Romana ecclesia placate tranquilleque regitur, sed ipsa quoque urbs tuis auspiciis et meritis aucta et illustrata pristinam dignitatem sibi restitutam letatur? Quis enim non iure letabitur, tantam in te animi magnitudinem, tantos erga deorum immortalium templa ac in urbis elegantiam tantos pecuniarum acervos esse profusos, cum hec tua edificia studio singulari, splendore admirabili, multitudine infinita tam celeriter et expleveris et inornaveris, qui plura brevi tempore magnificentius effeceris effeceris] corr. ex expleveris A quam ceteri memoria nostra pontifices in tanta rerum diuturnitate affecerint? Testis est divi Petri ad Vincula in veteri curia templum, parietibus et sarcto tecto tecto] corr. ex templo A in admirabilem iocunditatem sumptuoso opere exedificatum, Testis ipsa duodecim apostolorum ecclesia, diruta antea, nunc tua ope ad amplitudinem mecenatisque operis splendorum renovata, testis terre celique moderatoris divi Petri Basilica, que tuo ductu et impensa auro irradiatur et elegantiore ornatu illustrata circumspicitur, testis divi Stephani et Vitalis reliquorumque deorum edes et delubra urbis etiam solitudine obsoleta tua unius opera et impensa locata collocuplectata et ornatiora quam erant in hominum oculis collocata, testis sacrarium illud Matris Dei ad portam flaminiam novo opere fornicibus marmoratis instructum, cuius aditus divini numinis religionem, immo religionem ipsam pre se fert. Pontem vero illum tuum felicibus auspiciis Sixtium, excitatis ab aqua fundamentis, murmuri Tiberino, impositum, adeo Tiburtino lapide prestantem, ut tanta mole nihil antiquitati remittatur, cum non Ianiculum modo ipsum, verum urbs tota et artificio et impensa et utilitate illustretur: quis satis digne efferre poterit, presertim cum Valentianum pontem, Ianiculum et urbis insulam continentem tantopere antecellat? Valitudinariam vero illam Sancti Spiritus hospitalemque egrotorum sedem coctili latere ad Tiberis ripam tam elegantissime atque lautissime edificatam, qua nihil ad usum melius, ad speciem pulchrius, ad gloriam diuturnius desideratur, quantam tui animi amplitudinem, misericordiam, caritatemque denotat. Sed quid ego aut viarum descriptionem aut arearum laxitatem aut edificiorum et templorum totius totius] iter et del. A urbis splendorem iam sue vetustatis amplitudinem ac suavitatem agnoscentis pluribus exequar, aut singula memorem, cum ipsius civitatis urbs tota tantam eiusmodi in rebus profusionem ac studium tuum in primis adeo circumferat ut deformata antea, nunc per te luculentissime exornata non letari modo de tuo pontificatu, sed gestire prope omnibus videatur, et quo diuturnius id ei in hac summa tranquillitate pacis et ocii per te sit, diis presidibus ac omnium rectori et moderatori deo pientissime comprecatur? Ad hanc igitur tui gloriam recognoscendam et litterarum monumentis immortalitati commendandam omnes qui grati esse volent, quicquid studii ab eis impendi poterit, navare operam pro viribus debent, ne officio in te suo et quidem cum vitio defuisse videantur. Quod si cui vel facultas defuerit vel tempora denegaverint vel domestica cura retardaverit, vel ratio alia traduxerit, nihilo tamen minus voluntate et mente, que bono cuique presto est, referre tibi pro benemeritis gratias debet. Ego vero, ne in quo ceteros commoneo accuser ipse, et ne longius mea vagetur oratio, ad officium tandem revertar meum. Alexandriam, Pater Beatissime, Ptolomei nostri urbem totius Egypti opulentissimam sedemque provincie maxime claruisse ferunt, que, tametsi rerum omnium iocunditate et ubertate abundaret, conditorisque sui nobilitate urbes omnes anteiret, liberalium tamen artium studio et doctrina, deflorescente iam Grecia, adeo floruit, ut vel in medicina is doctior haberetur, qui Alexandrie operam se dedisse fateretur. Multos tulit ea civitas doctissimos homines glorie celebritate a scriptoribus scriptoribus] scriporibus A exornatos: Aristarchum grammaticum, Herodianum, Dydimum, Amenium, Stoicum Antipatrum, Diogenem, Archelaum, Diodorum, morum etiam gravitate ac vita Anthenodorum, Cesaris preceptorem, et alterum quem Cordylon appellant, qui cum Catone et vixit diutissime et apud eum placidissime functus est vita, Nestorem item Achademicum, Marcelli octavie pedagogum, complures preterea alios in omni doctrinarum genere perfacundos et pereruditos. Sed bona omnium venia dixerim, eduxit Antonino Imperante hunc Ptolemeum, regia stirpe oriundum, oriundum] corr. ex orundum A omnium sane philosophorum, quos illa aluit et litteris et ingenio et virtute facile principem, qui, cum in Cleopatram Ptolemeorum regnum sub Octaviano, redacta in provinciam Egypto, desiisset, privatus ipse regio, tamen animo et ingenio non ad sordida artificia, non ad vitam desidiosam, non ad secessum in solitudinem se addixit, verum in illo tunc celeberrimo Alexandrino orbis gymnasio haud obscuris facultatibus totum se ab litteras contulit atque in primis in philosophia, humane preclara societatis parente, auctore illo suo nature interprete Aristotele contenta, deinde in mathematicis disciplinis etatem omnem contrivit: ut mathematicis tamen, quibus vagantia celo sidera cognoscuntur et quibus succurendum videbat, potius insudaret. Nam cum ipse veri investigandi amore raperetur, illudque in hoc corporato et aspectabili mundo agitatione continua et dispari fluitante non inveniretur, supera illa complexus est, que ratis ordinibus immutabilique constantia et demonstratione rectissime cognoscuntur et perfectissime sciuntur, ubi perpetuorum corporum intervalla, magnitudines, conversiones, anfractus, varii multiplicesque nature perinde animo et ratione cernuntur atque illa que oculis subiecta perspiciuntur, ut vivere in terris homines et cum diis ipsis in tanto divino celi ornatu versari videantur. Quarum celestium rerum motuumque scientiam prisci illi exquisito ingenio viri, agitatione certa et veritate commoti, et primam omnium quesiverunt et omnium ultimam invenerunt. Explicuit vero et penitus absolvit Ptolomeus, unus omnium doctissimus et ingenii subtilitate usque eo acerrimus, ut in astrorum speculatione e nature sinu naturam ipsam extorserit, provocaverit, in certamenque deduxerit. Is, cum Solis Luneque magnitudinem, volutiones, proportiones, incrementa, detrimentaque satis a maioribus commode tradita extitissent, errantium vero fixarumque stellarum ratio et motus non institutis certis et doctrina, sed instrumentis etiam ab Hypparcho perquisitus, non ratam et perpetuam demonstrationis viam afferret, voluit huic quoquam parti homo non sibi, sed aliis natus ita consulere quo deinceps nihil ad astrorum consumationem discipline esset amplius a quoquam postulandum. Itaque his suis libris ambitus, stationes, cursusque siderum ac eorum motum omnem et statum, rem cognitu dignam omniumque difficillimam, subtilissime agressus investigavit, recte ab aliis inventa comprobavit, depravata correxit, infinita invenit ut solus de admirabilitate celestium rerum nullis angustiis aut concisis disputationibus illigatus commodissime scripserit, acute enodaverit, cumulatissime satisfecerit. Atque certam disciplinam Grecis hominibus, quos nondum ea celestis scientie gloria attigerat, non ipsius scientie terminis, sed sui ingenii finibus absolutissime importaverit, et cum nihil diminuti, nihil supervacui, nihil preter rem ab eo scriptum sit, nullus ad eius inventa et scripta potuerit aspirare. Harum igitur tantarum maximarumque rerum momenta et rationes Grecis litteris ab eo explicatas, a patre vero meo, ut diximus, in eius tantis calamitatibus latinas editas, tue sanctitudini despondeo, ut sub tui numinis tutela consecrate ardorem invidie restinguant, et in communem utilitatem, propter quam tanti labores suscepti sunt, felicibus tuis auspiciis divagentur. Ac si quando tibi ab hac rerum omnium procuratione et mole animum vendicare recreareque licuerit, possis novo hoc opere numeris lineisque interstincto divinum Ptolomei ingenium divinis in rebus cognoscere. Quamobrem, si labores nostri a tua Sanctitate probabuntur, enitar profecto reliquis Trapezuntianis libris nondum cuique inscriptis mee in te pietati, rursum tuorum in nos meritorum rationem presentibus posterisque constare. Quod si pro acceptis beneficiis parem gratiam referre non potero, id saltem quod implere possum, profiteor et repromitto, nullum, scilicet susceptorum beneficiorum officium apud me intermoriturum, quorum magnitudinem memoria colam sempiterna. Accipiat ergo tua sanctitudo benigne, ut solet, opus multis lucubrationibus a patre meo elaboratum, quod etsi aliquibus pre tua pontificia dignitate non dignum forte videbitur tui, animum tamen offerentis et abditarum scientiam rerum his evolutam libris minime abs te aspernari scio. Non enim hominibus crimini aut fraudi fuit Deum immortalem samiis vasis, cultuque tenuissimo coluisse, et simul me non preterit Magnum illum Alexandrum, Antigonum, Arthaxerxem offerentis studium magnopere comprobasse.

Magne Compositionis Ptolomei libri a Georgio Trapezuntio e Greco conversi incipiunt

〈I〉

〈I.1.〉 〈Capitulum I: Prefatio auctoris〉

Peroptime mihi videntur, o Syre, qui bene philosophati sunt speculativam philosophie partem ab activa separasse: nam etsi active accidat parti ut prius speculativa sit, magnam tamen differentiam in ipsis invenies, non solum quia nonnulle virtutes morales absque disciplina etiam multis inesse possunt, cum speculativam scientam sine doctrina consequi impossibile sit, verum etiam quia maxima utilitas in altera ex frequenti actione, que in ipsis rebus habetur, in altera ex progressu speculationum fieri solet. Hinc opus esse nobis putavimus, ut actiones quidem cogitandi motibus sic temperemus, quod ne in minimis quidem considerationis eius obliviscamur, que ad pulchram ordinatamque mentis constitutionem perducat, otium autem maxime ad doctrinam theorematum que plurima pulcherrimaque sunt et precipue illorum que proprie mathematica dicuntur convertamus. Commode namque admodum Aristotiles speculativam partem in tria rursus genera partitur physicum, mathematicum, theologicum. Nam cum res omnes ex materia et forma et motu constent quorum singula quamvis minime seorsum a subiecto inspici possint, intelligi tamen sine reliquis possunt, primam quidem primi omnium motus causam siquis in summa simplicitate accipiat, Deum invisibilem atque immobilem esse arbitrabitur et doctrine genus quod in hoc versatur theologicum appellabit. Altissima enim mundi actus hic superat et a sensibilibus omnino substantiis seperatus super illa penitus intelligitur. Genus autem quo materiales qualitates que semper moventur inquirimus, quodque circa molle ac dulce, album et callidum, et similia versatur, iure physicum nuncupabit, cum eius substantia incorruptibilibus plerunque et sublunari orbe inveniatur. Quod autem formarum progressivorumque motuum naturam ostendit, figure, insuper ac magnitudinis, et, ad hec, multitudinis, loci, temporis, atque similium scientiam scrutatur, id doctrine genus mathematicum esse diffiniet. Quipe res iste inter duas superiores consistunt, non solum quia et sensu et absque sensu percipi possunt, verum etiam quia omnibus simpliciter rebus tam mortalibus quam immortalibus accedunt, cum in iis iis] corr. ex his G quidem que semper mutantur secundum seperabilem formam commutentur, in iis vero que perpetue nature ac etheree sunt incommutabilitatem forme immobilem servent. Quia igitur hinc intelleximus duo speculationis genera coniecture magis quam certioris scientie nomine appelari posse, cum theologicum incomprehensibile penitus atque invisibile sit, naturale autem propter instabilitatem materie vix percipi possit, atque propterea nunquam de ipso convenire posse philosophantes arbitremur, solum vero mathematicum, si quis recte ipso utatur, utatur] corr. ex uetatur A firmam et imutabilem scientiam afferat, quoniam demonstratio arithmetica geometricaque via et ratione procedit, a a] add. G quibus dubitatio longe abest, placuit huic generi pro viribus maxime subvenire ac precipue illi eius parti que de divinis atque celestibus corporibus est. Sola enim hec de perpetuis que semper eodem modo se habent considerat, et propter ea ipsa quoque potest sine confusione semper eodem se modo habere ac percipi, quod proprium scientie est, ad cetera quoque genera non minus quam illa ipsa conferre videtur. Hec enim ad theologicum genus viam maxime preparat. Nam sola recte 〈propter〉 propinquitatem accidentium sensibilibus substantiis et moventibus quidem, motisque perpetuis vero atque impasibilibus, motibus quoque ipsis motuumque ordinibus immobilem et seperatum actum intelligere quodam modo potest, ad naturale quoque genus non parum conducit, quum conformis totius materialis substantie proprietas a progressivi motus conditionibus appreendatur, appreendatur] corr. ex apprendatur A veluti corruptibile quidem atque atque] add. G incorruptibile a recta recta] corr. ex recto G atque circulari, grave autem atque leve aut passivum atque activum ab eo quod est ad medium atque a medio. Vivendi autem agendique morum hec maxime omnium propter divinarum rerum similitudinem et mensuram faciet perspicaces, amoresque divine huius pulchritudinis studiosis iniiciet et ad simile anime statum quasi natura propter speculandi consuetudinem deducet. Hos igitur ipsi quoque amores speculationis rerum sempiternarum continue augere volentes que quidem inventa hactenus sunt, ab iis didicimus qui vere ac exquisite his disciplinis inheserunt et ipsi tantum afferre atque addere conamur quantum fere tempus quod inter nos et illos interfuit addere potest. Que igitur ad presens luce clarius perspeximus, ea omnia quam breviter aperteque ut vel qui aliquantulum in doctrinis pregressi sunt queant percipere, commentari conabimur. Verum ut absolute negotium hoc habeatur, cuncta que cuncta quae] corr. ex cunctaque G ad inspicienda celestia conferunt serie sua exponemus, sed ne sed ne] post corr. G longa nobis oratio contexatur, contexatur] corr. ex contexitur G que quidem a priscis exacte inventa sunt, ea brevius brevius] corr. ex brevis G enarrabimus, que vero vel nundum vel non commode tradita sunt, ea pro facultate nostra latius exponemus.

〈I.2〉 Capitulum II: De ordine huius doctrine

Propositi autem negotii huius illud precedit ut universalem terre totius habitudinem ad totum celum perspiciamus. Particularium vero que deinde secuntur primum est, ut de obliqui circuli situ et locorum habitabilium consideremus et ad hec de differentia que in ordine penes inclinationes per unumquenque orizonta alterius loci ad alterum fit, —hec enim consideratio, si precesserit, faciliorem ad consideranda reliqua viam prebebit—, alterum, ut de solari motu atque lunari et de accidentibus suis doctrinam afferamus. Nam nisi quis hec prius tenuerit, non erit possibile stellarum percipere accidentia, ita cum ad extremum fiat sermo de stellis, que quidem ad orbem stellarum pertinent quas fixas appellare solent, iure precedent, sequentur autem que ad erraticas quinque accomodantur. Horum singula principiis ad inveniendum et quasi fundamentis usi partim iis que perspicue apparent partim certis priscorum nostrisque observationibus demonstrare conabimur. Apprensiones vero que secuntur lineari demonstrationum via ac ratione accommodabimus. Universale igitur quod precedit huiusmodi est: quod celum sphericum sphericum] corr. ex spericum A est et globi modo pervolvitur, quod terra secundum secundum] corr. ex secumdum A figuram quidem, si partibus universis capiatur, ipsa quoque ad sensum spherica est atque globosa, situ situ] corr. ex situs A vero in medio totius celi centro simillima collocatur, magnitudine autem atque distantia ad fixarum stellarum spheram tamquam punctum se habet, quodque nullo progressivo motu movetur, de quorum singulis pauca breviter ut in memoriam reducantur nobis perstringenda sunt.

〈I.3〉 Capitulum III: Quod sphere ac globi modo celum convolvitur

Prima igitur principia ab huiusmodi observatione verisimiliter a priscis mihi hominibus inventa videntur. Solem enim et Lunam aliasque stellas ab ortu semper ad occasum in equidistantibus inter se circulis ferri videbant, ita ut incipientes ab inferioribus quasi ab ipsa terra sursum ferantur, paulatimque in altiora conscendere videantur, rursusque proportionaliter circumvolvi atque descendere quousque omnino quasi in terram inciderint pereant, temporeque aliquo interiecto, rursum perspiciebant quasi ab alio principio oriri atque occidere et hec tempora et ad hec ortuum occasuumque loca similiter atque ordine certo in universum redire. Sed stellarum que semper cernuntur circumvolutio que circa idem semper vertitur centrum, ut celum spericum esse crederent, maxime illos compellebat. Necessario enim punctum illud celestis sphere polus efficitur, cum stellarum que ipsi propinquiores sunt in minoribus circulis pervolvantur, que vero remotiores secundum proportionem distantie maiores circulos faciant, donec ad eas que occidunt occidunt] post corr. G distantia veniat quarum etiam propinquiores illis que semper cernuntur breviori tempore occultari videbant, remotiores autem proportionaliter maiore. Propter hec igitur sola predictam opinionem primo habuerunt, deinde reliqua quoque consequenter intellexerunt, quum omnia simpliciter que apparent contra〈r〉iis contrariis] contratiis A opinionibus suo testimonio repugnent. Nam si quis stellarum motum recte ad infinitum ferri supposuerit, veluti nonnulli putarunt, quenam via et que ratio excogitari poterit quare ab eodem quottidie initio ferri cernantur, quo enim pacto stelle in infinitum profecte regredi possent, aut quomodo regressus earum non cerneretur, aut quomodo magnitudines earum ita sensim non minuerentur, ut tandem nulle viderentur? Nunc vero contra maiores quidem in ipso videntur occasu et sensim ita occultantur, ut terre superficie quasi obice obtegi videantur. Incendi autem ipsas a terra rursusque in terram extingui absurdum omnino atque irrationabile videtur. Nam siquis tantam in magnitudinibus et quantitatibus earum et in distantiis locis atque temporibus seriem casu et absque ratione fieri concederet, preterea partem quidem aliam terre incendendi naturam habere, aliam vero extinguendi, immo autem eandem aliis incendendi aliis extinguendi etiam stellarum easdem aliis incensas iam aut extinctas esse aliis nondum, siquis, inquam, hec omnia redicula concederet, quid de apparentibus semper diceremus, que nec oriuntur nec occidunt, aut qua de causa que incenduntur et extinguntur non ubique illico oriuntur vel occidunt, que vero id minime patiuntur semper super terram ubique sunt? Nam eedem non possunt aliis incendi extinguique semper aliis nunquam istorum aliquid pati. Aperte namque patet easdem stellas apud alios quidem oriri atque occidere, apud alios autem neutrum istorum facere, et, ut breviter perstringam, quamcunque aliam motus celestium figuram figuram] corr. ex fuguram A preter globosam quisquam supposuerit, necesse erit inequales distantias a terra ad superiorum partes corporum fieri, ubicunque et quomodocunque situm ipsius posueris, ut et magnitudines et distantie stellarum adinvicem inequales eisdem in singulis circumductionibus videantur, quasi modo magis modo minus distarent, quod accidere nequaquam videmus. Nam quod iuxta orizontes maior maior] add. marg. A magnitudo stellarum videatur non distantie parvitas id facit, sed huiusmodi terram obeuntis evaporatio cum inter visum nostrum et stellas ipsas exalet, veluti maiora in aquis submersa videntur, et quidem tanto maiora, quanto profundiora petierint. Sed illa quoque, ut spherica esse celestia sentiamus, compelunt: quod nulla alia figura supposita preter istam structure instrumentorum convenire possunt, quod, quum celestium motus nulla re prohibeatur et facillime omnium volvatur, figurarum quoque omnium in superficiebus quidem circularis, in solidis vero spherica facillime movetur, quodque, cum capaciores ex diversis figuris equalem habentibus ambitum ille sint que plures angulos habent, circulis quidem planis, spera vero solidis capacior omnibus invenitur, celum autem ceteris omnibus corporibus capacius est. Sed ad hanc sententiam naturalia etiam quedam impellunt: veluti quod corporibus universis subtiliorum partium magisque similium ether est. Superficies autem corporum que similium partium sunt similes partes habent. Sole vero superficies in planis quidem circularis, in solidis autem spherica similium partium sunt. Quum igitur ether solidus sit globosum esse necesse est. Preterea terrestria quidem corruptibiliaque corpora ex rotundis universaliter natura, quamvis ex dissimilium partium figuris constituit, ethera vero divinaque omnia ex similium partium atque sphericarum. Nam si plana vel concava essent, non omnibus qui ex diversis terre locis in eodem tempore conspiciunt circularis esse figure viderentur. Quas ob res, cum ether etiam qui hec continet nature similis similiumque partium sit, rationabile est, ut et sphericus sit et circulariter equaliterque feratur.

〈I.4〉 Capitulum quartum: Quod terra quoque spherica est ad sensum quantum ad universas partes

Quod vero etiam terra secundum omnes partes accepta spherica sit ad sensum, sic maxime intelligemus. Solem enim et Lunam aliasque stellas videre licet non secundum idem in omnibus terris oriri atque occidere, sed prius semper orientalibus posterius autem occidentalibus. Nam que in eodem tempore fiunt eclipsis et maxime lunares non in eisdem horis idest equaliter a meridie distantibus apud omnes conscribi inveniemus, sed semper apud orientaliores observatas conscriptasque horas posteriores illas fuisse, que ab occidentalibus observate sunt. Cunque horarum etiam differentia terrarum distantie proportionalis inveniatur, non absurde terre superficiem globosam esse quispiam affirmabit, quoniam similitudo partium que per omnes partes partes] add. s. l. G propter rotunditatem accipitur proportionaliter proportionaliter] corr. ex proportionater A semper iis qui deinceps sunt se ipsam obiicit. quod accidere non posset, si alia quam spherica terre figura esset, quod etiam inde patet. Nam si cava esset, occidentalioribus orientes stelle prius viderentur, si plana, in eodem tempore omnibus simul qui in terra sunt orirentur atque occiderent.

Triangularis vero si esset aut aut] add. s. l. G quatuor angulorum vel cuiusvis plurium angulorum figure, omnibus similiter qui eandem rectam lineam habitant, quod nullibi fieri videtur. Quod autem nec cylindri quidem formam habet, ita quod rotunda quidem superficies ad ortum atque ad occasum versa sit, planarum vero basium latera ad mundi polos, quod quasi verisimilius aliqui putarent, inde perspicuum est, quod nulla unquam stella semper connexam habentibus superficiem cerneretur, sed aut omnes omnibus orirentur atque occiderent, aut eedem et equaliter ab utroque polo distantes omnibus semper apparerent, nunc vero quanto magis ad septentrionem progredimur, tanto plures australiorum quidem stellarum occultantur, boraliorum autem cernuntur, ut hinc pateat quod etiam hic terre globositas obices proportionaliter ad laterales faciens partes sphericam figuram undique ostendit. Ad hec si omnibus aut quibusdam altioribus locis a quovis et ad quemvis angulum navigantes accedimus, paulatim magnitudines eorum accrescere videntur, quasi ab ipso mari emergant que antea submersa propter connexam aque superficiem videbantur.

〈I.5.〉 Capitulum V: Quod terra in medio celi sita est

Hac re perspecta, si quis deinceps de situ terre certius dicere vellit, sic profecto que iuxta ipsam ipsam] corr. ex ipsum G apparent accidere solummodo intelliget, si eam in medio celi quasi sphere centrum posuerit. Nam si sic se res non habeat, aut oportebit quod ipsa sit extra axem et equaliter ab utroque polorum distet, aut in axe ita ut ad unum polorum magis accedat, aut nec in axe nec ab utroque pollorum equaliter distet. Ad primum igitur ex his tribus situm illa maxime pugnant. Nam si sursum aut deorsum extra axem intelligatur, accidet ut, quum in duo semper inequalia quod supra terram et quod sub terra est ab orizonte disseperentur, nunquam in recta sphera equinoctium fiat, in obliqua vero sphera, vel nunquam vel non in medio transitu ab altero solstitiorum estivo dico atque hyemali ad alterum. Nam hec spacia inequalia necessario fierent. Non enim equinoctialis maximusque parallelorum circulorum qui in polis circulationis describuntur divideretur ab orizunte in duo equaliter, sed unus equidistantium ei vel borealium magis vel australium. Sed apud omnes simpliciter constat hec spatia equalia esse ubique, quoniam et diei ab equinoctio incrementa, donec ad maximum diem in estivalibus solsticiis perveniatur, equalia sunt dierum decrementis ad infimum infimum] corr. ex immum G usque solstitiorum hyemalium diem. Si vero ad ortum vel occasum, idest ad aliquorum partes, rursus accedere supponatur, nec magnitudines et spatia stellarum secundum orientalem et occidentalem orizonta equalia eademque eisdem erunt, nec ab ortu ad meridiem tempus equale illi erit tempori quod a meridie ad occasum est, que omnia iis que apparent omnino repugnant. Ad secundam autem oppinionem qua sic in axe ponitur, ut ad alterum polorum magis accedere intelligat, ita rursus quispiam responderet, quia, si sic res se haberet, in singulis climatibus orizontis superficies celi partes duas que super terram et que sub terra est secundum alium atque alium accessum et ad seipsas et adinvicem semper inequales differenter efficeret, nec nisi in recta solummodo sphera in duas equales posset seperare. In obliquatione autem que propinquiorem polum semper facit manifestum, partem que super terram est semper minueret et subterraneam augeret. Vnde accideret ut maximus quoque circulus qui per medium signorum est inequaliter ab horizuntis planitie divideretur, quod minime ita se habere videtur. Sex enim semper omnibus super terram apparent signa et sex reliqua tunc non apparent, deinde rursus, cum illa super terram integre apperuerint, tunc reliqua non videntur, ut hinc perspicuum fiat portiones quoque zodiaci in duo equalia dividi ab horizunte, quoniam iidem semicirculi modo super terram modo sub terra integre sunt. Et omnino nisi terra sub ipso equinoctiali sita esset, sed ad septentrionem septentrionem] corr. ex semptentrionem A vel meridiem ad alterum polum apropinquaret, eveniret ut nec ad sensum quidem in equinoctialibus diebus orientales gomonum umbre in equidistantibus ab horizonte superficiebus ad rectam cum occidentalibus lineam fierent, quod ubique consequi aperte perspicitur. Hinc autem patet nullum etiam tertiam opinionem locum habere. Nam que primis repugnant ipsi quoque repugnant et, ut breviter perstringam, universa series que in decrementis incrementisque dierum et noctium perspicitur, nisi medium terra situm optinere ponatur, penitus confunderetur, et ad hec Lune quoque defectus eclipsisque, in quibuscunque partibus celi acciderent, non possent in opposito Solis loco fieri, cum sepius terra non in oppositione, sed in minoribus semicirculo spaciis seipsam illis opponeret.

〈I.6〉 Capitulum VI: Quod terra quasi punctum est ad celestia comparata

Quod vero puncti, quantum ad sensum pertinet, proportionem habet terra ad spatium quod est usque ad stellarum que fixe vocantur spheram, magno illud argumento est quod ab omnibus terre partibus magnitudines stellarum atque distantie in eisdem temporibus equales similesque videntur, quemadmodum observationes in diversis climatibus facte ostendunt, quibus nec minima quidem discrepantia invenitur. Accedit quod gnomones, in quacunque terre parte ponantur, et armilatarum centra spherarum idem possunt centro terre veraci. Perspectiones enim et circumductiones umbrarum ita convenientes suppositionibus apparentium conservant, quemadmodum si a puncto quod in media terra est fierent.

Hec ita se habere illud etiam signo est quod superficies que undique a visibus nostris educuntur, quas orizontes appellamus, totam celi spheram in partes equales dividunt semper, quod non fieret, si ad distantiam celestium sensibilis esset terre magnitudo. Sola enim superficies que per terre centrum educeretur spheram dividere posset equaliter, a quacunque autem duceretur planicie terre semper subterraneas portiones maiores his faceret que super terram inveniuntur.

〈I.7〉 Capitulum VII: Quod terra nullo motu progressivo movetur

Per eadem vero demonstrabitur nullo motu terram ad predictas laterales partes moveri aut unquam centri locum mutare. Eadem enim evenirent que, si alium situm preter medium haberet, acciderent. Quare, siquis causas motus gravium ad medium querat, frustra id mihi facere videtur, cum re ipsa manifestissimum sit et terram medium mundi locum posidere, et ponderosa omnia ferri ad ipsam. Illud autem ad istius rei intelligentiam facillimum est atque paratissimum, quod, quum spherica terra et in medio totius, ut diximus, demonstrata sit, in omnibus simpliciter partibus eius gravium corporum inclinationes et motus proprios ad rectos ad illam semper et ubique superficiem angulos fieri que per descendentium contactum equaliter educitur. Patet enim quoniam sic se res habet. Idcirco, si a superficie terre non repercuterentur, omnino ad ipsum centrum pervenirent, presertim quia linea etiam que recte ad centrum ducit ad rectos se illi planiciei planitiei] corr. ex planitei A semper angulos accommodat que in ipso incisionis contactu spheram attingit. Qui autem incredibile putant nec herere alicubi nec ferri tantum terre pondus, ii mihi videntur non ad proprietatem totius, sed ad passiones suas ipsorum respicientes, hec comperare atque ita plurimum aberrare. Non enim mirum eis visum iri hoc putarem, si animadverterent hanc terre magnitudinem universo continenti comparatam corpori puncti proportionem habere. Ita enim possibile videbitur quod proportione minimum est a vere maximo quod similium partium est sustineri equaliter undique inclinatione simili compulsum, quum nihil deorsum aut sursum in mundo ad ipsam sit, veluti nec in sphera unquam tale quid intelligere quispiam poterit, quamvis que in ipsa creantur quantum ad proprium naturalemque motum suum levia quidem et que subtilium partium sunt ad exteriora et quasi ad circumferentiam eleventur videanturque motum ad singulorum superiora facere, quod ideo ita fit, fit] add. s. l. G quoniam quod super caput nostrum est, quodque sursum vocatur, ipsum quoque quasi ad continentem superficiem tendit, gravia vero grossarumque partium omnia autem ad medium et quasi ad centrum ferantur ad inferiora cadere cernuntur, idque ideo, quoniam e contra quod sub pedibus nostris est deorsumque vocatur, ipsum quoque tendit ad centrum terre, ideo non absque causa circa medium hec ab incursu alterius ad alterum et simili undique atque equali collisione compensantur. Quas ob res non irrationabiliter totum terre firmamentum ita maximum respectu eorum esse percipitur que ad eam etiam minimi ponderis impetu feruntur, ut quiescens undique cadentia in ipsam recipiat. Quod si communis ceteris ponderibus singularisque motus ipsi quoque inesset, patet quia propter tantum sui magnitudinis excessum universa, dum deferretur, preveniret, ceterisque caeterisque] corr. ex caeteri A relictis in ere animalibus, dico aliisque ponderibus, ipsa velocissime extra celum quoque ipsum excideret. Verum hec ridiculosissima omnium intellectu videntur. Nonnulli autem, quum nihil verisimilius obiici istis arbitrentur, hec quidem concedunt, nihil vero putant sibi resistere posse, si celum verbi gratia immobile supponant, et terram ab occasu ad ortum in eodem axe revolvi singulis diebus diebus] corr. ex debus A una pene revolutione, aut etiam utraque quantocunque moveant dummodo circa eundem axem, ut diximus, et utriusque motui convenienter. Hos quippe fugit quantum ad aparentia quidem in stellis pertinet nihil forsam prohibere, siquis simplicius consideret sic ista se habere. Ab accidentibus vero que circa nos et in ere accidunt ridiculosum valde id videbitur. Nam ut eis concedamus quod que subtilissimarum partium ac levissima levissima] corr. ex leussima A sunt aut nulomodo moveri quod preter naturam est, aut non aliter quam ea que contrarie sunt nature, quum que in ere fiant minusque subtilium partium sint, aperte atque preoculis velocius quam terrestria omnia ferantur, cunque gravissima grosissimarumque partium proprium motum sic velocem equalemque faciat, cunque ipsa terrestria rursus nec ab aliis quidem vi apte non nunquam moveri posse omnes concedant, illud negare non possunt revolutionem terre, si sic volveretur, omnium simpliciter motuum que circa ipsam fiunt velocissimam fore, quippe que tantam in brevi tempore revolutionem absolveret, ut cuncta que in ipsa non sunt uno semper motu terre contrario moveri viderentur, ita nec nubes unquam nec aliud quicquam volitantium aut proiectorum ad ortum ferri cerneretur, sed omnia ipsa terra preveniret, motuique ad ortum ita resisteret, ut cetera universa progredi ad occasum derelicta viderentur. Nam etsi era dicant similiter equalique velocitate quum ipsa circunduci, non minus tamen que in ipso ere concrescunt semper posterius ab utriusque motu relinquerentur, vel si etiam ipsa quasi eri coniuncta una cum ipso circunducerentur, nullum tamen prevenire aliunde aut pene sequi cerneretur, sed manere semper ita ut nec in volatu nec in iactu aliud ab alio preveniretur, que omnia sic aperte fieri oculis cernimus, ut nulla tarditas omnino, nullaque velocitas, quoniam terra fixa non stet, accidere ipsis videatur.

〈I.8〉 Capitulum VIII: Quod duplex in celo primorum motuum differentia est

Has suppositiones necessario ad particulares doctrinas ipsarumque consequentia prelibasse ac ad hec usque summatim dixisse sufficiat. Ab ipsa enim eorum que consequenter et deinceps demonstrabuntur ad ea que apparent convenientia sic confirmabuntur comprobabunturque, ut refutari nequeant. Sed ad hec illud quoque ut universalium quiddam putaret quispiam non iniuria prelibandum quod due primorum motuum in celo differentie sunt: altera qua omnia in occasum ab ortu feruntur similiter semper et eque velociter in equidistantibus inter se circulis qui a polis scilicet sphere describuntur illius que omnia equaliter circumducit (horum maximus circulus equinoctialis vocatur, quoniam solus ipse ab orizunte qui etiam maximus est in duo equalia semper dividitur et Solis revolutio que in ipso fit equinoctium ubique ad sensum facit), altera qua stellarum sphere contra predictum motum in aliis quam in polis prime circumductionis progressus faciunt quosdam.

Hec ita se habere supponimus, quia ex quotidiano quidem aspectu universa simpliciter celestia in uniformibus et equidistantibus equinoctiali circulo locis ipsis oculis ortus mediique celi ascensus et tandem occasus facere cernuntur, que res ipsius primi motus proprium est. Ex frequentiori autem observatione atque continua cetere omnes stelle eas distantias quas inter se habent conservare videntur et proprietates suas quas habent ad loca primi motus propria eodem modo maxime, Solem autem atque Lunam erraticasque stellas progressiones facere quasdam cernimus, etsi varias atque inter se inequales omnes, tamen universaliter ad ortus relictasque partes a servantibus easdem distantias stellis et ab una quasi sphera circumductis. Si ergo huiusmodi erraticarum progressus stellarum in equidistantibus ab equinoctiali circulis fieret, idest circa eos polos a quibus prima efficitur circumductio, satis recte putare quispiam posset unam eandemque omnium esse circumvolutiom que primam sequeretur.

Credibile nanque videretur progressum earum non propter oppositum motum, sed quoniam relinquerentur fieri. Nunc vero simul cum progressibus ad ortum ad septentrionem etiam vel meridiem accedunt, ita ut ne quantitas quidem huius accessus equalis conspiciatur, ut hoc accidens per pulsiones quasdam in ipsis fieri videatur, quoniam quantum ad hanc existimationem inequaliter fit, quamvis ordinate quod ab obliquo ad equinoctialem circulo efficitur. Unde is circulus unus atque idem et erraticarum proprius esse comprehenditur, quamvis quasi exquisitius a motu Solis describitur, in quo semper et Luna et erratice quinque versantur, nec minimum ab interciso per ipsum ad utranque partem accessu excidant. Verum quoniam maximus hic circulus esse cognoscitur, —nam et in equinoctiali et borealior et australior ipso Sol fit—, et in uno eodemque illo, ut diximus, erraticarum omnium progressus ad ortum sunt, necesse fuit alterum ab universali motu hunc constituere qui circa polos obliqui circuli sic intellecti et contra primum motum moveretur. Si ergo describi per utrosque predictorum circulorum polos maximum circulum intellexerimus necessario utrunque illorum, equinoctialem dico atque obliquum, in duo equalia et ad rectos secabit, angulos quatuor in obliquo circulo puncta fient: duo quidem ab equinoctiali opposita inter se, que vocantur equinoctialia, quorum quod ad septentrionem a meridie procedit vernale, quod huic oppositum est autumnale nuncupatur, et duo que fiunt a circulo inter utrosque polos descripto et ipsa opposita inter se, hec solstitialia nominantur, quorum quod ab equinoctialis meridie est hiemale, quod a septentrione estivale vocatur. Intelligitur autem unus ille primusque motus qui ceteros continet omnes quasi descriptus atque determinatus a maximo circulo, qui per utrosque polos describitur, circumductusque reliqua omnia in occasum ab ortu circumducit, nixusque est in equinoctialis circuli polis, quasi in eo quem meridianum appellant, qui ea re solum differt ab illo, quod non semper per obliqui circuli polos describitur, et ad hec quia continue rectos ad horizontem angulos facere intelligitur. Meridianus autem vocatur quoniam hec positio utrunque quod super terram et quod sub terra est semispherium in duo equalia secans media dierum ac noctium tempora continet. Secundus vero atque multiplex continetur quidem a primo, ipse vero erraticarum spheras omnium continet, hic fertur quidem a predicto, ut diximus, revolvitur autem in contraria in obliqui circuli polis, qui etiam semper nixi in circulo a quo prima descriptio descriptio] corr. ex descripsio G fit, hoc est in eo qui per utrunque polos est, rationabiliter una cum ipso circumducuntur et penes motum secunde latitudinis in contraria eundem semper situm quum descripto per ipsos circulo maximo ad equinoctialem obliquo conservant. Sed universalis quidem prelibatio summatim atque per capita ita breviter que premittenda erant exposuit.

Nunc vero particulares demonstrationes aggressuri quarum primam esse arbitramur eam, qua arcus inter predictos polos medius maximi per eos descripti circuli quantus sit comprehnditur, necessarium esse videmus ut prius quantitatis rectarum linearum negotium que in circulo perducuntur ponamus, presertim quum nobis cure sit lineis singula demonstrare.

〈I.9〉 Capitulum VIIII: De quantitate rectarum linearum que in circulo perducuntur

Sed ad faciliorem usum quantitatis earum postea tabulas faciemus, et circumferentiam circuli totam in 360 portiones dividemus, et arcuum medium gradum incrementis rectas subtensas lineas accommodabimus, idest quot portionum sunt ita exponemus, quasi diameter propter computationis numerorum commoditatem in 120 partes dividatur. Prius autem demonstrabimus quomodo quam maxime possibile sit per eadem paucaque theoremata brevem ac facilem intelligentiam quantitatum cordarum faciemus, ut non solum earum magnitudines certius habeamus, verum etiam per linearum demonstrabilem viam facile possimus errata comprehendere. Vtemur autem universaliter numerorum via secundum sexagenarii numeri modum, ne fractionum difficultas nobis impedimento sit. Multiplicationes vero atque divisiones sic faciemus, ut proximum semper semper] se add. et del. A assequamur, ne quod relinquitur ulla de qua curandum sit differentia differat ab eo quod a sensu exquisite habetur.

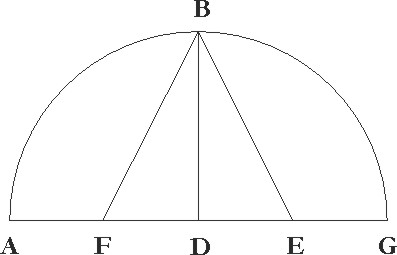Sit ergo semicirculus ABG cuius centrum D, diameter vero AG, et ex centro D per rectos angulos ad AG diametrum DB linea producatur. dividaturque DG in duo equalia per punctum E et coniungatur EB cui EF constituatur equalis, et coniungatur FB, dico FD quidem lineam decagoni BF autem pentagoni latus esse. Nam quoniam DG recta linea in duo equalia per punctum E divisa est, et ipsi DF linea recta in longum additur, quadrangulum quod sub GF et FD continetur una cum quadrato linee ED quadrato illi equale est quod ex EF linea in se ducta efficitur, quare illi etiam quod est ex EB, equalis enim posita est EB linea ipsi FE. Sed quadrato ipsius EB quadrata ED et DB linearum equalia sunt. Rectangulum ergo quod sub GF et FD continetur simul cum quadrato linee DE equale illis quadratis est que ex BD et DE lineis constituuntur. Quare, si ED linee quadratum commune utrinque auferas, reliquum quod ex GF et FD rectangulum constituitur quadrato DB equale est, quare quadrato etiam DG. Linea ergo FG secundum proportionem habentem medium et duo extrema in puncto D divisa est. Quoniam ergo sex anguli et decagoni que in eodem circulo intra describuntur latera, si eandem rectam continuamque faciunt lineam, secundum proportionem habentem medium et duo extrema dividuntur, estque linea GD cum a centro sit sex anguli latus, erit profecto linea DF decagoni lateri equalis, similiter quoniam pentagoni latus tantum potest quantum sex anguli et decagoni que in eodem circulo intra descripta sunt, estque BF lateris rectanguli trianguli BDF quadratum equale duobus quadratis BD linee, que sex anguli, et DF, que decagoni latus est, relinquitur necessario, ut BF equalis lateri pentagoni sit. Quoniam ergo, ut diximus, circuli diametrum 120 portionum portionum] corr. ex pro A esse supponimus, erit propter illa que modo demunstrata sunt DE linea cum eius que a centro est medietas medietas] add. marg. G sit partium 30 et quadratum eius 900, BD autem que a centro sit partium erit 60 et quadrato eius 900 … eius] add. marg. G 3600, quadratum vero EB linee, idest quadratum EF, earundem 4500. Quare EF linee longitudo erit proxime partium 67 4′ 55″ et reliqua DF earundem 37 4′ 55″, decagoni ergo latus quod 36 huiusmodi portionum arcui subtenditur, quales circulus habet 360, erit 37 4′ 55″ talium, quales diameter habet 120. Rursus quoniam DF partium est 37 4′ 55″, et quadratum eius 1375 4′ 15″. Est autem etiam quadratum linee DB 3600 earundem qui numeri, si componantur quadratum linee BF, constituunt quod est 4975 4′ 15″, erit BF linee longitudo partium proxime proxime] add. marg. A 70 32′ 3″. Quare latus quoque pentagoni quod talibus 72 gradibus subtenditur, quales circulus habet 360, talium est 70 32′ 3″, qualium diameter 120. Patet autem per se exagoni quoque latus, quod 60 subtenditur gradibus et semidiametro equale est, portionum esse 60. Similiter quoniam quadrati latus quod 90 gradibus subtenditur potentia semidiametro duplum est et trianguli latus quod 120 gradibus subtenditur triplum eiusdem potentia est, cum semidiametri quadratum sit 3600, colligetur quadrati lateris quadratum 7200, lateris vero trianguli 10800. Quare longitudo corde qua 90 gradus subtenduntur talium erit proxime 84 51′ 10″, qualium diameter 120, que vero 120 gradibus subtenditur erit earundem 103 55′ 23″.

Sed iste nobis ita facile ac per seipsas accepte sint, unde perspicuum est, datis quibusdam lineis, facile illas etiam dari, que reliquis ad semicirculum arcubus subtenduntur, cum quadrata ipsarum composita diametri quadratum efficiant. Nam quoniam verbi gratia que 36 gradibus subtenditur 37 4′ 55″ portionum esse demonstrata est et quadratum eius 1375 4′ 50″, diametri vero quadratum portionum 14400, erit corde qua reliqui ad semicirculum gradus 144 subtenduntur quadratum 1300 24′ 55″ et longitudo eius earundem 114 7′ 37″ proxime, in reliquis quoque similiter. Sed quemadmodum ab istis relique particulares etiam dabuntur, deinceps demontrabimus, si primus perutile ad hoc negotium theorema exposuerimus.

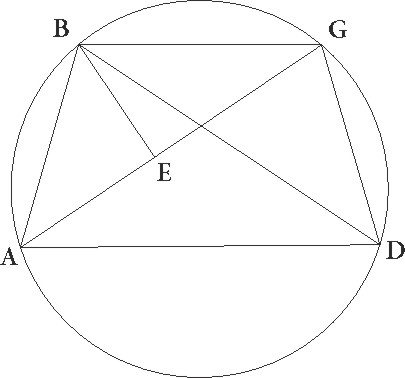/ 11r/ Sit enim in circulo ABGD quadrilatera, prout forte contigerit figura descripta, et protrahantur AG et BD; demonstrandum quia quod sub AG et BD lineis continetur equale utrisque simul illis est que ex AB in DG et ex AD in BG et … BG] iter et del. A BG] ex AD in BG add. et del. A constituuntur. Sit enim angulo DBG angulus EBA equalis. Si ergo communem addamus angulum EBD, erit totus angulus ABD toti angulo EBG equalis. Sed angulus quoque BDA equalis est angulo BGE, eundem enim arcum subtendunt. Trianguli ergo ABD et BGE equalium inter se angulorum sunt. Quare proportionalis se habent sicut BG ad GE, sic BD ad DA. Quare quadrangulum quod est ex BG in AD equale illi quadrangulo est, quod ex BD et GE constituitur. Rursus quoniam ABE angulus angulo GBD equalis est, et similiter BE ipsi BDG, idcirco triangulus ABE equalium est angulorum quum triangulo BGD.

Quare proportionaliter sicut AB ad E, sic BD ad DG. Est igitur quadrangulum quod ex AB et DG lineis constituitur equale quadrangulo linearum BD et E. Sed BG et AD linearum quadrangulum quadrangulo illi equale demonstratum est quod ex BD et GE lineis constituitur. Erit ergo totum etiam quadrangulum quod est ex AG in BD equale utrisque que sunt ex AB in DG et ex AD in BG, quod erat erat] corr. ex erit G demonstrandum.

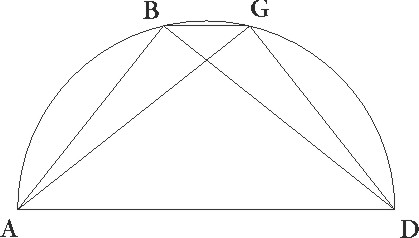Hoc ita exposito, exposito] corr. ex expositio A sit semicirculus ABDG super diametrum AD et due linee AB et AG ab A puncto protrahantur, sitque utraque ipsarum date magnitudinis taliumque portionum, quales in diametro dantur 120, et coniungatur BG; dico ipsam quoque lineam BG datam esse. Ducantur enim linee BD et GD quas etiam datas esse necesse est, quoniam residuis ad semicirculum arcubus subtenduntur. Quoniam ergo in semicirculo quadrangulum ABGD inscriptum est, erit quadrangulum quod fit ex AB in GD una cum eo quadrangulo quod est ex AD in BG equale quadrangulo illi quod ex AG in BD constituitur. Est autem quadrangulum quod fit ex AB in DG datum, ergo reliquum etiam quod est ex AD in BG datum est. Sed diameter quoque AD data est, data ergo etiam linea BG.

Hinc manifestum est, si duo arcus et linee que illos subtendunt dabuntur, dabitur etiam linea que duorum illorum arcuum excessus subtenditur, ex hoc theoromate patet quod alias quoque lineas nec paucas a datis excessibus inscribemus, et illam etiam qua duodecim gradus subtenduntur, cum habeamus 60 graduum arcus cordam et etiam que 72 gradus subtendit. Sit rursus propositum, data in circulo linea, medii subtensi arcus cordam invenire, sitque semicirculus ABG super diametrum AG et data linea sit GB. Arcus vero GB in duo equalia per punctum D dividatur, et ducantur linee AD, BD, DG, ex D autem ad AG perpendicularis DF deducatur; dico FG medietatem esse excessus AB et AG linearum. Ponatur enim E linea linee AB equalis, et protrahatur DE, et quoniam AB linea equalis est ipsi E, si AD communis accipiatur, erunt due linee AB et AD duabus E et AD 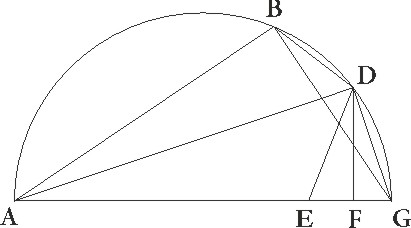altera alteri equalis.

Est autem et angulus BAD angulo EAD equalis. Quare basis quoque BD equalis erit bassi DE. Est autem ipsa BD ipsi DG et equalis erit ergo DG ipsi DE equalis. Quoniam igitur a vertice DEG trianguli duorum equalium laterum ad bassim eiusdem DF perpendicularis deducta est, erit EF linea ipsi FG equalis. Sed EG tota linearum AB et AG excessus est, et FG igitur excessus ipsarum medietas est. Quare, quum BG arcu corda data sit, et AB similiter quum ad semicirculum residua sit, dabitur etiam FG, que AG et AB linearum excessus medietas est. Verum quoniam in orthogonio triangulo AGD deducta perpendiculari DF duo trianguli ADG et DGF equalium angulorum efficiuntur, estque sicut AG ad GD, sic GD ad GF, erit etiam quod sub AG et GF rectangulum continetur equale quadrato linee DG, quare longitudo quoque ipsius DG, qua BG arcus medietas subtenditur, data erit; et ita per hoc theorema et alie multe per mediationem propositarum dabuntur et medietatis duodecim partium corda, que 6 subtendit et que tres et que unam quum dimidio, et que dimidium unius partis et quartum. Est autem nobis per computationem inventum unius partis quum dimidio cordam talium esse proxime 1 34′ 15″, qualium est diameter 120, et medietatis quarte que simul earundem 0 47′ 8″.

Sit rursum circulus ABGDE super diametrum AD et in centro F circumductus, et de puncto A duo deinceps dati arcus accipiantur qui sint AB et BG, et protrahantur AB et BG linee ipse quoque similiter date; dico, si AG coniuncta fuerit, ipsam quoque haberi. Ducatur enim ex B diameter circuli que sit BFE, et protrahantur linee BD, DG, GE, DE, patet ergo ex se ipso, quia propter lineam BG dabitur linea GE et propter AB dabitur BD et DE, et quoniam, ut in superioribus dictum est, BGDE quadrangulum in circulo constituitur, et BD, GE due linee ab angulis ad angulos eius deducte sunt, rectangulum quod sub istis continetur equale est utrisque simul que ex oppositis lateribus efficiuntur. Quare, quoniam rectangulum linearum BD et GE datum est, et similiter quod est ex BG et DE, dabitur etiam quod ex BE et GD constituitur. Sed diameter quoque BE data est, reliqua ergo etiam GD data erit, et propter hec etiam GA que ad semicirculum residua est. Quare si duo arcus et corde sue date fuerint, dabitur etiam per hoc theorema corda qua duo arcus illi per compositionem subtenduntur. Perspicuum autem est quia, si ad prepositas semper omnes eam componamus que unum gradum quum dimidio subtendit et compositas computemus, omnes simpliciter inscribemus que duplicate tertiam partem habebunt, et sole relinquentur que inter spatia unius gradus cum dimidio sunt due in singulis, quoniam per medietatem gradus incrementa facimus, future. Quare, si medii gradus cordam inveniemus, ipsa tum per compositionem datarum linearum quibus spatia continentur, tum per excessum, universas nobis que inter duas sunt facile replebit. Verum quoniam, data corda qua unius ac medie partis arcus subtenditur, que tertiam eiusdem arcus partem subtendit non datur per lineas, nam, si possibile id esset, medii gradus cordam hinc haberemus, idcirco a corda unius ac medii gradus et a corda medii simul atque quarte gradus unius cordam inveniemus theoremate uno preposito quod, etsi non universaliter quantitates possit determinare, attamen attamen] corr. ex atamen G in tam minimis nullam ad determinatas habeat mutationem. Dico igitur quia, si due inequales linee in circulo perducantur, maior ad minorem minorem proportionem habebit quam arcus maioris ad arcum minoris.

Sit enim circulus ABGD, et perducantur in eo due inequales linee, quarum minor sit AB, maior vero BG; dico GB lineam minorem proportionem habere ad BA quam BG arcum ad arcum BA. Dividatur enim ABG angulus in duo equalia per lineam BD, et coniungantur EG et AD et GD linee. Quoniam igitur ABG angulus in duo equalia per BED lineam divisus est, linea quidem GD equalis est linee AD, linea vero GE maior est quam linea EA. Deducatur igitur a puncto D ad EG lineam DF perpendicularis, et quoniam AD maior est quam ED, et ED quam EF, circulus qui centro D et spatio DE circumscribitur, AD quidem lineam dividet, DF vero lineam superexcidet. Designetur ergo circulus IET et producatur DF ad T. Quoniam igitur DET sector DEF triangulo maior est, triangulus autem DEA sectore DEI maior, habebit DEF triangolus minorem proportionem ad triangulum DEA quam DET sector ad DEI sectorem. Sed sicut se habet triangolus DEF ad triangulum DEA, sic se habet EF linea ad lineam EA; sicut etiam DET sector ad sectorem DEI se habet, sic se habet angulus FDE ad angulum EDA. Quare linea FE minoris est proportionis ad EA lineam quam FDE angulus ad angulum EDA. Quare coniunctim quoque linea FA minoris est proportionis ad lineam EA quam angulus FDA ad angulum ADE, antecedentium quoque dupla GA linea minorem habet proportionem ad lineam EA quam angulus GDA ad angulum EDA, disiunctim etiam linea GE ad lineam EA minorem habet proportionem quam angulus GDE ad angulum EDA, sed sicut se habet linea GE ad lineam EA, sic se habet linea GB ad lineam BA, et sicut se habet angulus GDB ad angulum BDA, sic se habet arcus GB ad arcum BA. Linea igitur GB minorem habet proportionen ad lineam BA quam arcus GB ad arcum BA.

Hoc ita preposito, describatur circulus circulus] add. marg. A ABG, et perducantur in eo due inequales linee AB et AG, supponaturque dimidiam partem gradus unius et quartam unam subtendi per lineam AB, per lineam vero AG gradus unus subtendatur, et quoniam AG linea minorem proportionem habet ad lineam AB quam AG arcus ad arcum AB, estque AG arcus in sesquitertia proportione ad arcum AB, erit GA linea ad lineam BA minor quam sesquitertia. Demonstrata est autem AB linea 0 47′ 8″ talium portionum, quales diameter habet 120. Linea igitur GA minor est quam 1 2′ 70″ earundem. Hec enim in sesquitertia proportione sunt ad 0 47′ 8″. Rursum in eadem descriptione supponamus unum gradum BA et unum atque dimidium AG linea subtendi. Similiter ergo quoniam AG circumferentie pars sesqualtera est ad AB arcum, erit GA linea minor quam sesqualtera ad lineam BA. Sed AG linea demonstrata est talium esse 1 34′ 15′, qualium diameter est 120. Linea igitur AB maior est quam portiones similes 1 2′ 50″. Ad has enim sesqualteram habent proportionem 1 34′ 15″ particule. Quare quoniam que unum gradum subtendit linea et maior et minor eisdem monstratur, ipsa quoque habebit de talibus partibus 1 2′ 50″ proxime, qualium est diameter 120. Itaque medium gradum subtendit ex istis habetur, inveniturque habere 0 31′ 27″ proxime de diametri partibus.

Hoc igitur modo, ut diximus, reliqua spatia replebuntur. Nam verbi gratia primum spatium duorum graduum arcus cordam inveniemus, compositione medii gradus ad unum et dimidium demonstrata, per excessum autem qui est ad tres gradus duorum cum dimidio graduum corda dabitur, et similiter in ceteris. Sed negotium de rectis in circulo lineis, sic ut puto, facillime pertractatum est. Verum ut paratas linearum quantitates, cum opus fuerit, habeamus, tabulas 45 versuum mediocritatis causa subiecimus, quarum prime partes arcuum quantitates medio gradu ad auctorum continebunt, secunde cordarum quantitates arcubus accommodatas, prout diameter 120 partium supponitur, tertie trigesimam cordarum in singulis semigraduum incrementis partem, ut unius quoque sexagesimi corda latius habita facile pertinentes usque ad 30 quantitates computemus. Hinc etiam si error in scribendis tabulis accidet, facilis et inquisitio et emendatio fiet, vel dupli arcus ad eum quem querimus corda, vel ab excessu aliarum que date sunt, vel a residui ad semicirculum arcus corda. Est autem tabularum descriptio hec

〈I.10〉 Capitulum X: Tabula cordarum et arcuum

〈I.11〉 Capitulum XI: De arcu qui est inter tropicos

Sic igitur quantitate linearum circuli exposita, primo demonstrandum est, ut diximus, quantum obliquus circulus qui per medium signorum intelligitur ab equinoctiali declinat, idest quam circulus qui per utrosque dictorum circulorum polos maximus describitur proportionem habet ad eum sui arcum qui inter polos interiacet, cui equali spatio equinoctiale punctum ab utroque solstitiali distare perspicuum est. Hoc autem nobis organice huiusmodi simplici fabricatione instrumenti comprehendetur. Circulum enim hereum magnitudine mediocrem exquisite tornatum et quadratum superficie faciemus quo pro meridiano utemur, sed prius ipsum in 360 maximi circuli suppositas portiones dividemus, harumque singulas in quotcunque partes possibile sit. Deinde alterum subtiliorem circulum sic sub predicto coaptabimus, ut eorum latera in una superficie maneant, circumducique sine impedimento minor circulus sub maiore ad septentrionem atque meridiem in eadem superficie superficie] corr. ex superfice A possit; addemusque in duabus quibusvis diametraliter oppositis in minori circulo portionibus in altero laterum equales parvasque regulas, que tum ad seipsas tum ad circulorum centrum exquisite declinentur, apponemusque in medio latitudinis ipsorum tenues lingulas que maioris divisique circuli latus attingant. Quem tuto ad singulos usus coaptabimus statuentesque in sereno super mediocre sustentaculum in pavimento equali ad orizuntis planitiem sustentaculi basim, observabimus ut circulorum planities ad orizuntis quidem planitiem recta sit, ad meridiani vero equidistans, quorum primum perpendiculo invenitur a puncto futuro in vertice suspenso observatoque, donec ex directictione suppositorum ad oppositum diametraliter punctum faciat declinationem, alterum merdiana linea que sub planitie sustentaculi est certo signo notata, circulisque ad obliquum circumductis, donec planities eorum equidistare linee perspiciatur. Ita igitur posito, ad septentrionem et meridiem Solis accessum observabamus interiorem circulum in meridiebus transferentes, quousque tota inferior regula a tota superiore fuerit inumbrata. Quo facto, extremitates linguarum nobis significarunt quot portionibus Solis centrum in meridiano a vertice in dies distabat. Sed illa etiam commodiore observatione usi sumus laterem pro circulis lapideum vel ligneum quadratum et involubilem in mediocri latitudine atque altitudine, ut firmius maneat, fabricati sumus, qui alterum latus planum exacte ac extensum habet in quo centrum ad unum angulorum cepimus, quartamque circuli partem designavimus, coniunximusque lineas omnes a centro ad descriptum descriptum] corr. ex scriptum G arcum que sub quarta circuli parte rectum angulum angulum] corr. ex agulum A continent, ipsumque arcum in 90 similiter gradus divisimus. Post hec in una linea recta que ad orizuntis planitiem recta futura erat et situm ad meridiem habitura duos rectos et equales undique cylindros parvulos, similiterque tornatos coaptavimus, alterum in ipso centro et in ipso medio exquisitissime, alterum ad inferiorem linee terminum, erigentesque descriptum hoc latus laterculi iuxta meridianam lineam in subiecta planitie ita protractam, ut ipsa quoque ad planiciem meridiani equidistantem habeat situm, et perpendiculo per cylindrulos indeclinatam rectamque per ipsos ad orizuntis planitiem, lineam diligenter comprehendentes, supositis rursus quibusdam subtilibus, quibus directio, ut oportet, fiebat, factam a cylindrulo qui ad centrum est umbram in meridiebus similiter observabamus, non nihil ad descriptam descriptam] corr. ex scriptam G circumferentiam, ut ut] add. s. l. G certius locus ipsius teneretur, apponentes, huius umbre medio signato, portionem arcus in ipsa circuli quarta cepimus, que portio Solis progressum secundum latitudinem in meridiano significavit. His observationibus ac maxime illis quas in multis annis in ipsis solstitialibus diebus examinavimus, cum designatio semper a puncto verticis intercipiat equales easdemque meridiani circuli partes quam in hyemalibus tam in estivis solsticiis, comprehendimus arcum qui est a boreali extremo termino ad australem similiter ultimum inter tropicos graduum semper esse 47 et portionis maioris quidem duabus tertiis, minoris vero quam medietate simul et quarta. Unde eadem ferme proportio nobis collecta est ei, quam Eratosthenes reperit, quaque Hipparchus etiam usus est. Nam circumferentia que inter solstitialia puncta est xi proxime talium portionum fit, qualium est meridianus 83. Ab hac preposita observatione habitationum quoque declinationes, in quibuscunque observationes fiant, facile inveniuntur, si ceperimus tum punctum quod inter duos terminos in ipso equinoctali necessario fit, tum arcum qui inter hoc et punctum punctum] corr. ex punctunctum A verticis est, cui arcus equalis scilicet est ille quo poli distant ab orizonte.

〈I.12〉 Capitulum XII: Theoremata que ad sphericas sphaericas] corr. ex spericas G demonstrationes premittuntur et ipsa figura sectoris spherica

Nunc cum sequatur ut particulares magnitudines eorum arcuum demonstremus, qui inter equinoctialem et circulum qui per medium signorum est interiacent, circulorum illorum, qui maximi per polos equinoctialis designantur, pauca breviter utiliaque theoremata preponemus, quibus plurimas pene demonstrationes eorum que spherice considerantur quam simplicissime atque artificiosissime faciemus.

In duas ergo lineas AB et AG due linee BE et GD protracte altera alteram in puncto F secent; dico quod GA linee ad E lineam proportio componitur componitur] corr. ex compatur G ex proportionibus GD ad DF et FB ad BE. Protrahatur enim a puncto E linea EI equidistans linee GD. Cum ergo equidistantes GD et EI linee sint, proportio GA linee ad EA lineam eadem est proportioni GD ad EI. Deforis autem FD proportio igitur GD ad EI lineam composita est ex proportione GD ad DF et DF ad EI. Quare proportio etiam linee GA ad E composita est ex proportionibus linearum GD ad DF et DF ad IE. Est autem etiam proportio linee DF ad IE eadem proportioni FB ad BE, cum equedistantes rursum sint EI et FD linee. Proportio ergo GA linee ad E composita est ex proportionibus linearum GD ad DF et FB ad BE. quod erat demonstrandum.

Eodem modo demonstrabitur quia etiam dividendo proportio GE linee ad EA lineam componitur ex proportionibus GF ad FD et DB ad BA, ducta a puncto A equidistante ad lineam EB productaque ad ipsam linea GDI. Rursum enim, quoniam AI, AI] et add. et del. G EF equidistantes sunt, erit sicut GE ad EA, sic GF ad FI. Sed FD assumpta deforis, erit GF linee proportio ad FI composita ex proportionibus linearum GF ad FD et DF ad FI. Est autem proportio DF ad FI eadem proportioni DB ad BA, quoniam in AI et FB equidistantes lineas BA et FI linee inciderunt. Quare proportio linee GF ad FI ex proportionibus linearum GF ad DF et DB ad BA coniuncta est. Sed proportioni GF linee ad FI eadem est proportio linee GE ad EA, erit ergo proportio linee GE ad EA composita ex proportionibus linearum GF ad FD et DB ad BA, quod erat demonstrandum.

Sit rursum circulus circulus] post corr. G ABG cuius centrum D, et accipiantur quevis quaevis] corr. ex quamvis G tria puncta in circumferentia eius. sintque ipsa A, B, G, A … G] corr. ex AG G ita tamen ut uterque arcus AB et BG minor semicirculo sit, quod in accipiendis etiam deinceps arcubus similiter erit intelligendum, protrahantque AG et DEB linee; dico quod, sicut se habet que duplum arcus AB subtendit ad eam que subtendit duplum arcus ABG, ABG] corr. ex BG G sic se habet E linea ad EG lineam. Deducantur enim AF et GI perpendiculares a punctis A et G ad DB lineam. Quoniam ergo AF et GI equidistantes sunt et in ipsas EG linea incidit, sic etiam AF ad GI, sicut E ad EG.

Sed proportio AF ad GI eadem est proportioni linee que est sub arcu duplo AB partis circumferentie ad eam que est sub dupla BGI. Dimidia enim est utraque utriusque. Quare proportio etiam E linee ad EG eadem est proportioni eius que est sub duplo ipsius arcus AB ad eam que est sub duplo BG, quod erat demonstrandum.

Hinc sequitur, si AG totus arcus et proportio corde que est sub duplo ipsius AB ad eam que est sub duplo arcus BG dabuntur, uterque arcus etiam AB et BG dabitur. Eadem enim descriptione proposita, coniungatur AD, et a puncto D perpendicularis DF ad EG lineam deducatur. Quod ergo, ABG arcu dato, angulus etiam ADF, quo medietas eius subtenditur, et ipse totus triangulus ADF datus erit, perspicuum est. Et quoniam, AG tota linea data, suppositum est proportionem E ad EG eandem esse proportioni illius que est sub duplo AB ad eam que est sub duplo BG, erit etiam E data et reliqua FE similiter. Quapropter, data etiam DF, angulus quoque EDF orthogonii trianguli EDF dabitur, totus etiam angulus ADB similiter. Quare AB quoque arcus dabitur et reliquus BG similiter.

Sit rursum circulus ABG super centrum D, accipianturque in circumferentia eius puncta tria que sint ABG, ita ut uterque arcuum AB et AG minor sit semicirculo, quod similiter et de arcubus deinceps accipiendis intelligendum est. Postea DA et GD ducte protrahantur, quousque coincidant in puncto E; dico quia, sicut se habet corda que subtendit duplum arcus GA ad eam que est sub duplo arcus AB, sic se habet linea GE ad EB. Nam, si, ut in precedenti, a punctis B et G perpendiculares BF et GI ad lineam DA deduxerimus, quia equidistantes sunt, erit sicuti GI ad BF, sic GE ad EB Quare sicut se habet que est sub duplo arcus GA ad eam que duplum AB arcus subtendit, sic se habet GE ad EG.

Hinc etiam sequitur quia, si solus GB arcus dabitur et proportio corde que duplum arcus GA subtendit ad eam que subtendit duplum arcus AB data fuerit, dabitur etiam AB arcus. In simili enim descriptione si DB coniungatur et DF perpendiculariter ad GB lineam deducatur, erit BDF angulus, quo medietas BG arcus subtenditur, datus, quare totus quoque triangulus orthogonius BDF, et quoniam proportio etiam linee GE ad EB data est, et insuper GB linea, dabitur etiam EB, et tota insuper EBF. Quare, cum DF etiam data sit, dabuntur similiter tam angulus EDF eiusdem orthogoni quam rel〈i〉quus reliquus] relquus A angulus EDB quare arcus etiam AB datus erit.

His premissis, describantur in spherica superficie maximorum arcus circulorum, circulorum] B add. et del. A ita ut in duos AB et GA duo inscripti BE et GD seipsos in puncto F secent, sitque ipsorum uterque semicirculo minor, quod de omnibus descriptionibus intelligendum est; dico quia proportio corde dupli arcus GE ad cordam dupli arcus EA composita est ex proportione corde dupli arcus GF ad cordam dupli FD et corde dupli DB ad cordam dupli BA. Capiatur enim sphere centrum, et sit I, ducanturque ab I ad B, F, E circulorum sectiones IB et IF et IE linee. Linea quoque AD coniuncta protrahatur et cum IB IB] inv. G linea ipsa etiam protracta concurrat in puncto T, similiter DG et AG producte lineas IF et IE secent in puncto C et in puncto L. In una ergo recta linea sunt tria hec puncta T, C, L. In duabus enim AGD trianguli et BFE circuli simul sunt superficiebus.

Hec ergo producta linea facit, ut TL et GD linee protracte duas TA et GA secent seipsas in puncto C. Quare proportio GL recte linee ad LA composita est ex proportionibus linearum GC ad CD et DT ad TA. Sed sicut se habet GL ad LA, sic se habet corda dupli arcus GE ad cordam dupli EA, et sicut GC ad CD, sic corda dupli arcus GF ad cordam dupli FD, et sicut DT ad TA, sic corda dupli DB ad cordam dupli BA. Quasobres proportio etiam corde dupli arcus GE ad cordam dupli E composita est ex proportionibus cordarum dupli arcus GF ad dupli FD et dupli DB ad dupli BA. Per eadem et sicut in plana rectarum descriptione linearum demonstratur quia etiam proportio corde dupli arcus GA ad cordam dupli E composita est ex proportionibus corde dupli arcus GD ad cordam dupli DF et corde dupli FB ad cordam dupli BE, que demonstranda erant.

〈I.13〉 Capitulum XIII: De arcubus qui sunt inter equinoctialem atque obliquum circulum

H 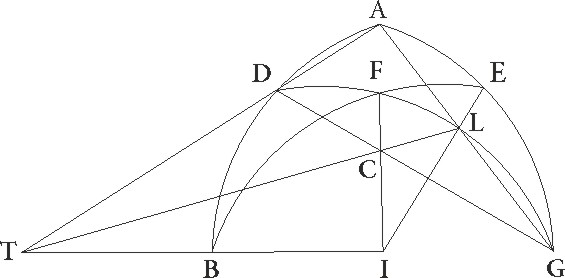oc theoromate premisso, primam propositorum arcuum demonstrationem sic faciemus: sit per utrosque utrosque] corr. ex utroque G polos equinoctialis circuli et eius qui per medium signorum est circulus ABGD, equinoctialisque circuli medietas sit semicirculus EG, eius vero qui est per medium signorum semicirculus sit BED. Sit autem punctum E vernalis equinoctii sectio, ut B quidem hyemale hyemale] corr. ex hiemale G tropicum fiat, D autem estivale, et capiatur polus equinoctialis EG in arcu ABG, sitque ipse in puncto F, et decidatur EI arcus eius circuli qui per medium signorum est, supponaturque talium esset 30 partium, qualium maximus circulus est 360, describaturque per F, I maximi circuli arcus FIT, sitque propositum nostrum IT arcum invenire.

Sed illud universaliter, ne in singulis repetatur, hic hic] corr. ex hec G dictum sit, quod qandocunque arcuum aut cordarum quantitates dicimus et gradus aut partes numero complectimur, in arcubus quidem tales intelligimus gradus quales maximi circumferentia circuli habet 360, in cordis vero tales partes quales circuli diameter habet 120. Quoniam ergo in maximorum descriptione circulorum in duos AF et E arcus duo descripti sunt FT et EB in puncto I seipsos secantes, proportio corde dupli arus FA ad cordam dupli arcus AB composita est ex proportionibus cordarum dupli arcus FT ad dupli arcus TI TI] corr. ex IE et dupli arcus IT G et dupli arcus IE ad dupli arcus EB.

Sed duplus FA partis circumferentie arcus graduum graduum] corr. ex gradum G est 180 et corda ei subtensa partium est 120. Arcus vero AB partis circumferentie duplus secundum proportionem 83 ad 41 in qua convenimus graduum est 47 42′ 40″, corda vero ei subtensa 48 31′ 55″. Et rursum duplus arcus EI partis circumferentie graduum est 60 et corda eius 60, arcus vero EB partis circumferentie duplus 180 et corda eius 120. Si ergo a proportione 120 ad 48 31′ 55′′ traximus proportionem 60 ad 120, relinquetur proportio corde dupli arcus FT que est proportio 120 ad 24 15′ 57″. Sed arcus FT partis circumferentie duplus graduum est 180 et corda eius 120, ergo corda etiam dupli arcus TI partium est 24 15′ 57″. Quare duplus arcus TI partis circumferentie graduum est 23 19′ 59″, ipse vero arcus TI 11 40′ graduum proxime. Sed supponatur rursum IE IE] corr. ex EIE G arcus graduum esse 60, sic igitur ceteris non mutatis, duplus IE partis circumferentie arcus graduum erit 120 et corda eius partium 103 55′ 23″. Si ergo rursus a proportione 120 ad 48 31′ 55′′ auferamus proportionem 103 55′ 23′′ ad 120, relinquetur proportio corde dupli arcus FT ad cordam dupli arcus TI, que est proportio 120 ad 42 1′ 48″, et est corda dupli arcus FT partium 120. Quare corda dupli arcus IT partium erit 42 1′ 48″. Duplus ergo IT partis circumferentie arcus graduum est 41 0′ 18″, ipse vero arcus IT 20 30′ 9″, que nobis erant demonstranda. Hoc modo in particularibus quoque arcubus quantitates computando, quarte partis, idest 90 graduum, tabulam faciemus, que arcuum partibus circumferentiarum demonstratis similium quantitates continebit et est hoc.

〈I.14〉 Capitulum XIIII: Tabula solaris obliquationis

〈I.15〉 Capitulum XV: De ascensionibus in recta sphera

Sequitur ut una cum istis demonstremus arcuum equinoctialis circuli quantitates factas a descriptis per polos eius circulis et a datis obliqui circuli partibus. Sic enim habebimus in quot equinoctialibus temporibus eius circuli gradus qui per medium signorum est et meridianum ubique et recte sphere orizuntem pertransibunt, ideoque etiam ipse tunc solummodo per polos equinoctialis describitur. Presupponatur Praesupponatur] corr. ex Presuponatur A igitur eadem descriptio, datoque rursus obliqui circuli arcu IE, IE] post corr. G triginta graduum, prius propositum sit ET arcum equinoctalis invenire

Similiter ergo ut in superioribus, proportio corde dupli arcus FB ad cordam dupli arcus BA composita est ex proportionibus cordarum dupli arcus FB … arcus​] add. marg. G arcus​] add. marg. A FI ad dupli arcus IT et dupli arcus TE ad dupli arcus EA. Sed arcus FB partis circumferentie duplus graduum est 132 17′ 20″ et corda eius partium 109 44′ 53″, duplus vero arcus BA 47 42′ 40″ et corda eius 48 31′ 55′′, et rursus duplus FI partis circumferentie arcus graduum est 156 40′ 1″ et corda eius partium 117 31′ 15′′. Duplus vero arcus IT partis circumferentie 23 19′ 79″ et corda eius 24 15′ 57″. Si ergo a proportione 109 44′ 53′′ ad 48 31′ 55″ auferamus proportionem 117 31′ 15′′ ad 24 15′ 57′′, remanebit nobis proportio corde dupli arcus TE ad cordam dupli arcus EA, que est proportio 54 52′ 26′′ ad 117 31′ 15′′, eadem proportio est etiam 56 1′ 25′′ ad 120, et est arcus quidem EA partis circumferentie duplus graduum 180, corda vero eius partium 120. Quare corda etiam dupli arcus ET 56 1′ 25″ partium est. Erit igitur duplus ET partis circumferentie arcus 55 40 graduum proxime, ipse vero ET 27 50. Supponatur rursum EI arcus graduum 60, sic igitur ceteris non mutatis, duplus FI partis circumferentie arcus graduum erit 138 19′ 42″ et et] add. s. l. G subtensa ei corda partium 112 23′ 56″, duplus autem IT partis circumferentie graduum 41 0′ 18″ et corda eius 42 1′ 48″ partium. Si ergo a proportione 109 44′ 73′′ ad 48 31′ 55′′ auferamus proportionem 112 23′ 56″ ad 42 1′ 48″, relinquetur proportio corde dupli arcus TE ad cordam dupli arcus TA, que est proportio 95 2′ 40″ ad 112 23′ 56′′. Sed eadem proportio est 101 28′ 20″ ad 120 et est corda dupli arcus EA partium 120. Quare corda etiam dupli arcus TE partium erit 101 28′ proxime. Erit igitur duplus ET partis circumferentie arcus graduum 115 20′, ipse vero TE 57 44′ earundem. Demontratum est igitur quia prima duodecima pars circuli qui per medium signorum describitur ab equinoctiali puncto accepta equaliter equinoctialis circuli gradibus 27 50′ secundum positum modum pertransit, secunda gradibus 29 54′. Nam uterque simul graduum demonstate sunt 57 44′. Tertia vero duodecima pars, quoniam tota obliqui circuli pars quarta toti equinoctialis quarte, sicut ad circulos qui per polos equinoctialis describuntur, equaliter compertransit, residuis ad quartam partem gradibus 32 16′ equaliter compertransibit. Eodem modo expositam demonstrationem prosequentes singulis etiam decem gradibus obliqui circuli contraseuntes equinoctialis gradus computavimus. His enim minores nulla quantitate que digna cura sit differunt ab excessibus qui equaliter adduntur, has decades exponemus, ut, in quot temporibus utraque ipsarum et meridianum, ut diximus, ubique et recte sphere orizontem pertranseat, paratum habeamus, initiumque a decima parte que ab equinoctiali puncto incipit faciemus. Prima igitur continet tempora 9 10′, secunda 9 15′, tertia 9 25′, ita prime duodecime partis partis] corr. ex partes A 27 50′ tempora colliguntur, quarta temporum est 9 40′, quinta 9 58′, sexta 10 16′, ita secunde quoque duodecime tempora colliguntur 29 54′, septima tempora continet 10 34′, octava 10 47′, nona 10 55′, ut rursus tertie duodecime partis que ad tropica signa exit 32 16′. Totius vero quarte partis 90 convenienter tempora colligantur. Est autem per se manifestum quia reliquarum quoque quartarum ordo idem poenitus est, nam quoniam sphera recta, idest equinoctialis sine declinatione ad orizontem, supponitur poenitus omnibus accidunt.

Finis primi libri feliciter.