Ptolemaeus Arabus et Latinus

〈III〉

Incipit liber tertius

〈III.1〉 Capitulum primum: De magnitudine anni anni] corr. ex annui G temporis

Cum in superioribus que universaliter ac mathematice de celo ac terra et ad hec de declinatione obliqui solarisque circuli ac de accidentibus ei particulariter tam in orbe recto quam in declivi per singulas habitationes doctrina iam scripta sit, sequi deinceps arbitramur ut de Sole ac Luna verba faciamus et accidentia motuum suorum investigemus. Nam aparentia que ceteris stellis accidere cognoscuntur, nisi prius de Sole ac Luna dicamus, absolute inveniri nequeunt, sed de his etiam negotium de motu Solis precedit, sine quo que Lune accidunt latius tractare non possumus.

〈III.2〉 Capitulum II: De magnitudine annui annui] corr. ex anni G temporis et de particularibus Solis equalibusque motibus

Cum igitur ceterorum omnium que de Sole demonstantur inquisitio annui temporis prima sit, priscorum quidem hac de re dubitationes diversasque sententias ab illis ipsis discere convenit et precipue ab Hipparco viro et industrie magne et veritatis amico, quem maxime in dubitationem impellit, quoniam per restitutiones quidem que in solsticiis et equinoctiis fiunt minus invenitur tempus annuum 365 diebus cum quarte unius additione, per eas vero que a fixis stellis considerantur maius, unde coniicit fixarum quoque stellarum orbem quam tardissime ad sequentia progredi, sicut et erraticarum, ad sequentia eius motus a quo prima fit circumductio per illum circulum qui per utrorunque polos equinoctialis dico atque obliqui describitur: quod ita se habere et quomodo fiat quando de fixis dicemus, tunc demonstrabimus.

Nam que illis etiam accidunt, nisi de Sole ac Luna prius dixerimus, penitus perspici nequeunt. In presenti autem consideratione nihil aliud respiciendum ut annuum Solis tempus inveniatur putamus quam ipsius Solis ad seipsum, idest ad obliquum, obliquum] corr. ex aliquum G a seipso factum circulum restitutionem. Diffiniendum enim tempus annuum est quo ab aliquo immobili huius circuli puncto ad sequentia Sol motus ad idem rediit, ita huius restitutionis principia predicti circuli puncta putamus que a solstitialibus et equinoctialibus punctis determinantur. Nam sive mathematice rationem consideramus, nec convenientiorem restitutionem inveniemus quam illam que ad eundem aspectum tam localiter quam temporaliter Solem reducit qui aspectus vel ad orizontas vel ad meridianum vel ad magnitudines dierum ac noctium perspicitur, nec alia initia in obliquo circulo, sed sola que per accidens a solstitialibus et equinoctialibus punctis determinatur, sive naturalius coniicere quispiam vult, nec idoneam magis restitutionem quam illam reperiet que a simili eris temperie ad similem et ab iisdem temporibus ad eadem Solem reducit, nec alia principia quam ea sola quibus tempora maxime discernuntur. Accedit quod restitutio que ad fixas stellas inspicitur et propter alia multa inconveniens videtur, et maxime quia etiam orbis suus ad ipsius celi sequentia ordinate ordinate] corr. ex ordine G progredi conspicitur, que cum ita se habeant nihil prohiberet tantum esse Solis annuum tempus dicere in quanto ad Saturni verbi gratia vel aliam erraticam stellam Sol motu suo rediret, et sic multarum diversarumque magnitudinum tempus annuum erit. Quas ob res convenire arbitramur ut id annuum Solis tempus existimemus quod ab observationibus quam maxime antiquis a solstitio vel equinoctio ad idem invenitur.

Verum quoniam Hipparthus perturbari etiam ab hac restitutione videtur propter continuarum inequalitatem observationum, conabimur breviter ostendere nullam hinc merito perturbationem fieri, firmam quidem rationem quod annua tempora non sint inequalia inde cepimus, quod etiam ipsi per instrumenta continua solstitia et equinoctia observavimus, nec differre annos quantitate que cura digna sit adinvenimus, sed tantum ferme quantum penes instrumentorum constructionem atque positionem errare possibile est. Coniecturam autem ab Impparchi computationbus fecimus quod hic inequalitatum error magis observationum quam rei sit. Nam primum in libro de mutatione solstitialium et equinoctialium punctorum, cum estiva brumaliaque solstitia que continue atque diligenter observata putabat exposuisset, fatetur non tantam in illis esse differentiam, ut propterea inequalitas in annuo tempore ponenda sit, his verbis: ′ex his observationibus patet parvas admodum horum differentias annorum fuisse, sed in solstitialibus spero nec nos nec Archimedem in observatione atque computatione ad quartam usque partem diei errasse. exacte tamen inequalitas annui temporis ab armilla herea que in fornice quadrata, sic enim vocatur, Alexandrie collocata est intelligi potest: dies enim in ea equinoctialis significari videtur ille in quo incipit ab altera parte cava eius superficies illuminari′.

Post hec autumnalium equinoctiorum tempora exactissime observatorum exponit. In 17^o quidem anno tertie secundum Calippum periodi 30^o die Mesori circa Solis occasum et post tres annos in anno xx^o in primo dierum intercalarium in mane, cum in meridie oportuisset, ita quarta diei parte dissonare videtur et post annum, idest in vigesimo primo anno hora diei sexta, quod quod] post corr. G etiam ad priores anni observationem sequebatur. Deinde post annos xi xi] corr. ex xxi A anno videlicet 32^o tertio intercalarium die in media nocte quam dies quartus sequebatur, cum mane oportuisset, ita quarta rursus diei parte discrepavit, quod ad antecedentem observationem sequebatur: Post annum vero unum videlicet in xxxiii^o quarta intercalarium die in mane, quod erat consequens ei observationi que illam antecedebat Post … antecedebat] add. s. l. G et post tres annos 36^o anno quarto intercalarium die die] corr. ex diem G vesperi, cum in media nocte oportuisset, ita quarta solummodo parte discrepavit.

Post hec verna etiam equinoctia simili diligentia observata exponit. In 30^o quidem et secundo anno tertie secundum Calippum periodi 27^o die Mechir in mane armilla, inquit, que in Alexandria est circa quintam horam equaliter ex utraque fuit parte illuminata, ut istud etiam equinoctium differenter observatum v horis proxime differat. Sequentia quoque, ait, usque ad trigesimum septimum annum quarte partis additioni convenisse, et post xi annos anno quadragesimo tertio tertio] corr. ex quarto A Mechir vigesima nona post mediam noctem ad quam trigesima sequebatur vernale asserit equinoctium fuisse, quod tum observationi trigesimi secundi anni conveniebat, tum ceteris quoque observationibus que inde usque ad quinquagesimum annum secute sunt. Factum enim prima Famenoth die in occasu Solis equinoctium fuit post unum diem cum dimidio et quartam proxime quam in quadragesimo tertio anno, quod intermediis septem annis proportionaliter convenit, nec ergo in his observationibus magna differentia facta est, cum tamen posset non solum in tropicis observationibus verum etiam in equinoctialibus error aliquis accidere usque ad quartam unius diei partem. Nam si ter millesima et sexcentesima solum particula circuli qui per polos equinoctialis describitur situs aut divisio instrumentorum ab exacta ratione diversificabitur, hanc secundum latitudinem accessum Sol iuxta equinoctiales proportiones quarta parte gradus unius in obliquo circulo secundum longitudinem motus adequat, ut discrepantia usque ad quartam proxime diei unius fiat. Preterea maior error accidere potest, quando per instrumenta fiunt observationes que non in observationum ipsarum tempore exquisite posita sunt, sed iam olim a certo principio sic constituta, ut ad longum tempus firma permaneant. Solet enim fieri longitudine temporis oculta instrumentorum huiusmodi commotio, ut in armillis eneis apud nos in palestra que videntur equinoctialis circuli superficie positionem habere perspicere quispiam poterit. Adeo enim diligenter nobis observantibus situs earum lapsus esse videtur et maxime maioris atque vetustioris, ut non nunquam etiam bis in eisdem equinoctiis cave superficies ipsarum iluminate sint.

Sed talium nihil etiam Hipartus ipse dignum fide argumentum quo de inequalitate annui temporis suspicari possumus afferre putat. A quibusdam autem Lune defectibus invenisse computando, ait, quod inequalitas annui temporis, cum ad medium perspicitur, non maiorem habet differentiam die dimediata et quarta ipsius parte. Id si sic se haberet, neque a verbis ipsius falsum inveniretur, examinatione indigeret. Per quosdam enim defectus Lune prope stellas fixas factos computavit quantum stella que Spica vocatur in singulis annis autumnale punctum precedit et per hec arbitratur invenisse quod aliquando in vita sua 6 30′ ad summum graduum, aliquando 5 15′ differentia eius fuerit. Hinc autem colligit quoniam non sit possibile Spicam in tam brevi tempore tantum progressum fecisse, necessarium esse Solem a quo fixarum loca ipse considerabat non equali restitutionem in tempore facere. Sed fugit ipsum quod, cum nullo modo progredi computatio possit, nisi locus Solis quem in eclipsi tenuit supponatur, ipse ad hoc accipiens semper solstitia et equinoctia exquisite in illis annis observata manifestum facit nullam preter quarte partis additionem in comparatione annorum esse differentiam.

Nam ut uno exemplo pateat ab observatione quidem eclipsis que fuit in trigesimo secundo anno tertie periodi secundum Calippum comprehendisse putat Spicam 6 30′ equinoctium autumnale, ab eclipsi autem que fuit in anno quadragesimo tertio eiusdem periodi 5 15′ gradibus precesisse. Et similiter ad propositas computationes vernalia equinoctia que fuerant in illis annis exquisite observata conferens ut ab equinoctiis quidem loca Solis in mediis eclipsium temporibus capiat et ab istis loca Lune et a locis Lune stellarum loca fixarum equinoctium quidem trigesimi secundi anni in mane vigesima septima die Mechir fuisse asserit. Equinoctium vero anni quadragesimi tertii die 29^o post mediam mediam] corr. ex merdieim G noctem ad quam dies trigesima sequebatur post duos cum dimidio dies et quartam fere diei partem quam in trigesimo secundo anno fuerat, quot certe facit quarta pars sola singulis undecim annis qui interfuerant addita. Si ergo nec maiori nec minori tempore quam additione quarte Sol ad proposita equinoctia rediit, nec Spicam in tam in tam] iter. et del. A paucis annis per 1 15′ gradum motam fuisse possibile, quomodo non est absurdum subiectis computata principiis ad refutationem eorum accipere a quibus confirmata sunt et causam, quod impossible sit tantum motum Spicam fecisse, quamvis plura sint que poterant tantum errorem attulisse, nulli tamen alii accomodare quam solis expositis equinoctiis tanquam simul exacte et non exacte observatis. Magis enim possibile videbitur vel Lune in ipsis eclipsibus ad proximas stellarum distantias simplicius fuisse coniectas quam vel computationes aut diversitatum ipsius Lune ad apparentium locorum considerationem aut motus solaris ab equinoctialibus ad media eclipsium tempora, vel non vere, vel non exquisite captos captos] post corr. G fuisse.

Sed arbirtror ipsum cognovisse nullam in istis causam tanti esse, ut secundam secundam] esse add. et del. A possit inequalitatem Soli adiungere, amore autem veritatis dumtaxat noluisse quicquam tacere quod in huiusmodi suspitionem possit iniicere. Ita enim suppositionibus istis in Sole ac Luna utitur quasi una eademque sit in Sole inequalitas, que ad solstitia et equinoctia simul cum annuo tempore restituatur, nec enim, quoniam equalium temporum expositi Solis reditus supponuntur, videmus ea que in eclipsibus apparent ullo cura digno differe a computatis secundum expositas positiones, quod certe sensibile admodum fieret, nisi equatio inequalitatis annui temporis adhiberetur, etiam si unius solummodo gradus et horarum proxime duarum equinoctialium esset.

Ex his igitur omnibus et ab eis que nos in continuis equinoctiis comprehendimus nec magnitudinem annui temporis inequalem invenimus, si ad unum quidam, nec modo ad solstitialia et equinoctialia puncta modo ad erraticas stellas perspiciatur, nec idoneum magis reditum eo qui ab aliquo solstitiali vel equinoctiali vel etiam quodam alio puncto circuli obliqui ad idem rursus deferat Solem, convenireque omnino putamus ut quam maxime simplicissimis suppositionibus apparentia demonstremus, dummodo nihil dignum cura huic nostro proposito per observationes repugnet. Quod igitur tempus annuum quod ad solstitia et equinoctia collatum perspicitur minus est quam 365 dies quartaque parte diei, ad apertum nobis est etiam per ea que Hipparchus demonstravit, quanto autem minus est, non possumus exactissime accipere, cum additio quarte partis ad plures annos immutabilis propter minimam eius differentiam permanere videatur, et propterea longoris temporis comparatione poterit adinveniri, eam annis qui intererunt distribuere oportebit, quoniam tam in multis quam in paucis annis eadem esse cognoscitur, que tamen restitutio tanto exquisitius capietur, quanto longius maiusque inter observationes fuerit tempus, quod non huic solum verum etiam ceteris restitutionibus accidit. Nam qui propter observationum, etiam si exquisite adhibeantur, instabilitatem error fit, quamvis parvus et nullus fere statim ad sensum esse videatur tam in longo quam in brevi tempore apparentibus. In pauciores enim divisus annos maior in uno anno efficitur et qui in longiore hinc a tempore colligitur similiter, in plures autem minor.

Quare satis esse censemus si, quantum quod inter nostras et exquisitas priscorum observationes interfuit tempus restitutionibus istis afferre potest, tantum ipsi quoque afferre conemur, nec sponte exactam exanimationem negligamus. nec … negligamus] add. marg. G Veritatem autem que a tota temporis perpetuitate aut a multiplici tempore observationum haberi potest aliis relinquendam putamus. Vetustatis igitur gratia estiva solstitia Metonis et Euctemonis et postea in Aristarchi temporibus observata his conferenda sunt que nostris fuerunt temporibus. Sed quoniam solstitiorum observationes difficile discernuntur et ad hec quoniam quas illi tradiderunt non exquisite capte videntur, quod quod] post corr. G etiam Hipparchi iudicio comprobatur, eas quidem pretermissimus. Usi Usi] corr. ex Visi A autem sumus equinoctiorum observationibus et maxime Hipparchi, quas exquisitissime ab ipso captas putamus, et nostris, quas instrumentis cepimus quorum quorum] post corr. G constructionem in primo libro docuimus, quibus invenimus uno die, priusquam additio quarte partis ad 365 dies postulat, in trecentis proxime annis solstitia et equinoctia facta fuisse. Nam in trigesimo secundo anno tertie secundum Calippum periodi autumnale Hipparcus equinoctium exquisitissime observatum significavit computasse, quod ait factum fuisse tertia intercalarium die in media nocte ad quam dies quartus sequebatur, et fuerunt anni 178 ab Alexandri morte. Deinde post 285 annos tertio Antonini anno qui est 463 a morte Alexandri exactissime ipsi observavimus autumnale rursus equinoctium 19 Athir post unam proxime horam a Solis ortu factum. Antecessit igitur restitutio in 285 annis Egyptiis quorum singuli 365 dies solummodo habent diebus 70 et quarta et vigesima proxime unius diei particula pro diebus 71 15′ que pro quarta parte predictis annis adduntur. Quare prius factum est quam additio quarte flagitat partis uno die vigesima proxime parte minus.

Rursum in predicto 32^o anno tertie secundum Calippum periodi equinoctium vernale ait Hipparchus exactissime observatum 27^o Mechir in mane factum fuisse, et sunt anni ab Alexandri morte 168. Deinde post 285 similiter annos in 463 anno ab Alexandri morte equinoctium vernale nos invenimus septimo die Pachon post meridiem una proxime hora, ut hic etiam redditus 70 et quarta vigesimaque proxime totidem videlicet diebus antecesserit pro 71 15′ diebus quas pro quarta 285 anni flagitabant. Prius ergo etiam hic vernalis equinoctii revolutio uno die fuit vigesima parte minus. Quare quoniam eadem proportio est 300 annorum annorum] add. s. l. G ad 285 et diei unius ad unam vigesima parte minus, colligitur quod in tercentis proxime annis redditus Solis ad equinoctialia puncta uno die additionem quarte partis precedat.

Quod si etiam ad solstitium estivale quod Metonis Euctemonisque temporibus simplicius fuerat observatum vetustatis gratia exquisitam observationem nostram contulerimus, idem inveniemus. Illud enim Apseude magistratum Athenis gerente 21 die Famenoth secundum Egiptios in mane fuit. Nos autem in dicto 463 anno ab Alexandri morte exactissime computavimus xi^a die Messori post mediam noctem quam xii^a sequebatur proxime factum, et sunt a solstitio estivali capto in magistratu Apseudis usque ad observatum ab Aristarco in anno 50^o prime secundum Calippum periodi, ut etiam Hipparchus asserit, anni 152. A dicto autem 50 anno qui est xliiii^us annus a morte Alexandri usque ad 463^um nostre observationis annum sunt anni 419. In omnibus igitur totius distantie 571 annis, si estivale solstitium ab Euctemone observatum sub magistratu Apseudis 21^a die Famenoth factum fuit, in annis Egyptiacis 571 accesserunt dies 140 50′ proxime pro 142 45′ quos 571 anni additione quarte partis postulabant. Quare dicta restitutio prius facta est quam additio quarte flagitat duabus minus duodecima parte diebus. Unde sic quoque patet in sexcentis annis duos plenos proxime dies quarte additionem solstitium precessisse, multis quoque aliis observationibus idem accidere nos invenimus, et Hipparchum quoque videmus sepenumero huic consentire. Nam in libro de magnitudine anni, cum estivale observatum ab Aristarcho solstitium 50^o anno prime secundum Calippum periodi exeunte illi comparasset solstitio quod ipse 43^o anno tertie secundum Calippum periodi exeunte cepit, sic ait: ′Perspicuum igitur est quod 145 annis citius quam additio quarte postulat solstitium factum est media parte nocturni diuturnique temporis simul′. Rursus in libro de intercalaribus mensibus et diebus, cum predixisset secundum Metonem Euctemonemque spatium anni 365 dies quartam et 76^am partem unius diei contineri, secundum Calippum vero 365 cum quarta solum, his verbis prosequitur: ′Nos vero menses quidem totidem in 19 annis solaribus contineri comperimus quot etiam illi. Annum autem etiam quarta parte minus precedere trecentesima diei parte invenimus, ita secundum Methonem quidem in trecentis annis 5 dies desunt, secundum Calippum vero una solummodo′. Deinde opiniones suas per librorum suorum titulos repetens sic ait: ′Scripsi etiam de annuo spatio librum unum in quo demonstro solarem annum, idest tempus quo a solstitio ad solstitium vel ab equinoctio ad equinoctium redit, continere dies 365 et minus quarta parte 300^a diurni nocturnique temporis parte, nec, ut mathematici arbitrantur, quartam solummodo partem ad dictam dierum mutitudinem addi′.

Quod igitur que ad hunc diem de magitudine anni percepta sunt predicte magnitudini restitutionis ad tropica et equinoctialia puncta consentiunt, perspicuum est. Que cum ita se habeant, si diem unam per trecentos annos partiemur, inveniemus singulis annis 12″ secunda distribui, hec si subtraxerimus a 365 15′ habebimus spatium anni 365 14′ 48″. Tanta igitur multitudo dierum anni erit quam proxime nobis ab observationibus quas habuimus adinventa.

Verum propter considerationem progressus Solis aliarumque stellarum ad singula loca, quem promptum et quasi expositum expositum] corr. ex expropositum A particularis tabularum series prebet, illam esse oportere mathematico intentionem arbitramur, ut cuncta que in celo apparent equalibus circularibusque motibus fieri ostendat, putetque illam tabularum compositionem huic intentioni maxime commodam qua motus equales singulorum seperantur ab inequalitate que propter suppositiones circulorum videtur accidere et qua rursus ex horum utrorunque congregatione apparentes progressus invenietur ac demonstrantur. Quod genus ut nobis commodius etiam in ipsis demonstrationibus paratum sit, faciemus equalium Solis particulariumque motuum expositionem hoc modo.

Nam cum restitutio una 365 14′ 48″ dierum sit, si per has 360 unius circuli gradus partiti fuerimus, habebimus diurnum solis motum 0 59′ 8″ 17′′′ 13′′′′ 12′′′′′ 31′′′′′′ proxime, —satis enim erit ad hec usque minuta partiendo descendere—, huius diurni motus, si vigesimam quartam ceperimus partem, habebimus hore unius motum graduum 0 2′ 27′′ 50′′′ 43′′′′ 3′′′′′ 1′′′′′′ proxime. Similiter si hunc diurnum motum multiplicaverimus in triginta mensis unius dies, habebimus medium mensis unius motum 29 34′ 8′′ 36′′′ 36′′′′ 15′′′′′ 30′′′′′′ proxime. Sin vero in unius egyptiaci anni dies 365 habebimus medium motum annuum 359 45′ 24′′ 45′′′ 21′′′′ 35′′′′′ graduum proxime.

Rursus si annuum motum in decem et octo annos propter emersuram in condendis tabulis commoditatem multiplicaverimus, habebimus integris tamen tamen] corr. ex in G subtractis circulis medium decem et octo annorum motum graduum 355 37′ 25′′ 36′′′ 20′′′′ 34′′′′′ 30′′′′′′. Tres igitur tabulas equalis motus Solis condidimus 45 versuum singulas et partium duarum: harum prima decem et octo collectorum annorum medium motum continebit, secunda primum annuos motus deinde horarum, tertia mensium primo deinde dierum continebit, et numerus quidem temporis in prima collocabitur parte, graduum vero in sequenti secundum convenientes singulis collectiones. Sunt autem tabule iste: iste] corr. ex infra ab alio latere cartae habentur G

〈III.3〉 Capitulum III: De suppositionibus equalis circularisque motus

Cum autem sequatur ut inequalitatem in solari motu apparentem demonstremus, universaliter predicendum est quod erraticarum quoque stellarum ad successionem singulorum motus, sicut et universa totius latio ad precedentia, equales omnes sunt circularesque natura, idest omnes linee que stellas aut circulos earum earum] corr. ex eorum G circumducere intelliguntur in omnibus in … omnibus] add. marg. A simpliciter equalibus temporibus equales angulos ad centra cuiuslibet circulationis intercipiunt. Que autem inequalitates in ipsis apparent, ee penes positiones atque ordines circulorum quibus moventur quique sunt in spheris earum efficiuntur, nec alienum a perpetuitate ipsorum propter apparentium confusum ordinem ullo modo ipsa re accidit. Causa vero, ut inequaliter moveri videantur, duabus maxime primis simplicibusque suppositionibus potest accidere. Nam, cum motus ipsarum ad concentricum 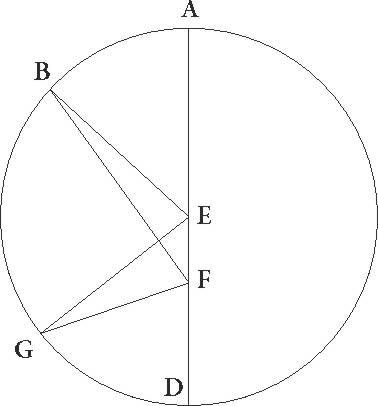mundo et in superficie circuli qui per medium signorum est sic aspiciatur, ut noster aspectus a centro eius non differat, ipsas aut aut] corr. ex autem G non in concentricis mundo circulis equaliter moveri credendum aut in concentricis quidem non autem in ipsis simpliciter, sed in aliis qui ab ipsis deferuntur quique epicycli vocantur. Utraque enim istarum suppositionum possibile erit, ut ut] post corr. G equalibus in temporibus inequales inequales] corr. ex in equales G obliqui circuli mundo concentrici arcus aspectibus nostris pertransiri videantur.

Nam sive in excentricitatis suppositione intellexerimus excentricum quidem in quo stella equaliter movetur movetur] add. s. l. G ABGD, ipsiusque centrum E, et diametrum ED, punctum autem F in ipsa et et​] add. s. l. G nostrum aspectum ut punctum quidem A maxima longitudo sit, D vero minima, cum AB et DG arcus equales ceperimus coniunxerimusque, tractis lineis BE et BF et GE et GF, manifestum hinc erit quod, quamvis per utrosque AG et GD arcus equali tempore stella moveatur, inequales tamen circa F centrum descripti circuli arcus pertransisse videbitur. Nam cum angulus BEA angulo GED equalis sit, angulus quidem BFA utroque ipsorum minor est, angulus vero GFD maior.

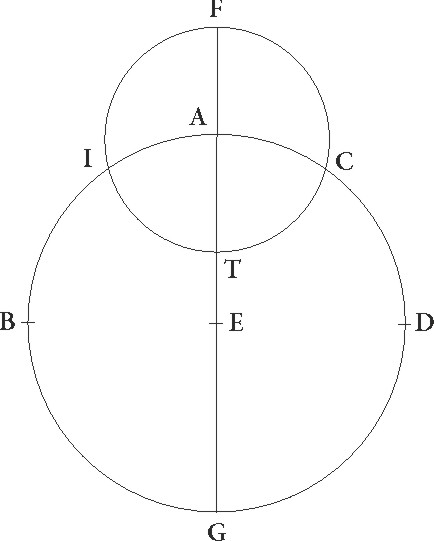
Sive in epicycli epicycli] corr. ex epicicli G suppositione concentricum quidem obliquo ABGD circulum intellexerimus, cuius centrum sit E, diameter EG, epicyclum vero in eo delatum in quo stella movetur FITC circa centrum A, perspicuum quoque sic erit, quamvis epicyclus epicyclus] corr. ex epiciclus G equaliter per ABGD circulum moveatur, a puncto A verbi gratia ad punctum B, B] corr. ex G A et stella quoque ipsa per epicyclum, tamen quanto quidem in F et T punctis stella est, nullam facere ad A centrum epicycli videbitur differentiam, quando vero in aliis non ita, sed cum erit verbi gratia in I puncto, per AI arcum equalem et medium motum excessisse, quando vero erit in puncto C minus medio motu per AC arcum mota videbitur.

Sed in suppositione quidem excentricitatis semper evenit ut minimus motus in maxima longitudine fiat, maximus vero in minima. Semper enim angulus AFB minor est angulo DFG. In ea vero que per epyciclum est utrunque fieri potest. Nam cum epicyclus ad successionem signorum moveatur, ut verbi gratia a puncto A ad punctum B, si stella quidem sic in epicyclo moveatur ut maxima longitudine ad successionem rursus signorum motus fiat, idest ab ab] post corr. G F ad I, maximus transitus in maxima longitudine fieri videbitur. Sic enim fit ut et epicyclus et stella ad eandem partem moveantur. Sin vero stelle motus maxima longitudine ad precedentia epicycli fiat, idest ab F puncto ad C, tunc e contra minimus transitus in longitudine maxima efficietur. Stella enim contrarium epicycli motum habebit.

Hec cum ita se habeant, illa deinceps prelibanda sunt, quod in erraticis que dupliciter inequalem facere motum videntur uterque suppositiones iste, ut in tractatu ipsarum demonstrabimus, connecti possunt, in illis vero que simplici uti inequalitate videntur una istarum suppositionum sufficiet. sufficiet] corr. ex sufficiat G Omnia enim que apparent exacte per utranque fieri possunt, cum eadem in utrisque proportio conservetur, id est quando in excentricitatis suppositione quam habet proportionem que inter centra est excentrici circuli et visus ipsius ad eam que est a centro excentrici, hanc in epicycli suppositione habeat, que a centro epicycli est ad eam que est a centro circuli deferentis ipsum, et ad hec quanto stella tempore ad successionem signorum mota circulum excentricum qui non moveatur pertransit, tanto etiam epiciclus quidem visui concentricum circulum ad sucessionem ipse quoque signorum motus pertranseat et stella epicyclum simili velocitate, ita tamen ut motus a maxima longitudine ad precedentia fiat.

Quod autem, his ita suppositis, eadem ex utraque suppositione accident breviter docebimus tum per proportiones ipsas tum postea in exponendis ipsis per numeros in Solis inequalitate. Dico igitur primum quod per utranque positionem maxima differentia inter equalem motum et eum qui videtur inequalis secundum quem medius etiam transitus stellarum intelligitur tunc fit, quando apparens a maxima longitudine distantia quartam circuli partem intercipiat intercipiat] corr. ex intercipit G et quod tempus a maxima longitudine ad dictum usque medium transitum maius est quam tempus a medio transitu ad longitudinem minimam. Unde in excentrici quidem quidem] corr. ex quod G suppositione semper accidit, in epicycli autem, quando motus stellarum a minima longitudine ad precedentia fit, ut tempus a motu minimo ad medium maius fiat fiat] corr. ex fit G quam a medio ad maximum, idque ideo quoniam in utraque minimus transitus in longitudine maxima efficitur. Quando autem stelle ad successionem epicyclorum a maxima longitudine circumduci supponuntur, tunc a motu maximo ad medium maius est tempus quam a medio ad minimum, idque ideo quoniam e contra hic in maxima longitudine maximus transitus fit.

Sit igitur primum ABGD stelle circulus excentricus, cuius centrum sit E, et diameter EG, in qua centrum zodiaci, hoc est visus ipsius, capiatur, et sit F, a puncto F ad rectos angulos diametri EG protrahatur linea BFD, supponaturque stella in B et D punctis esse, ut videlicet apparens distantia distantia] corr. ex distantiam A per quartam utrinque partem ab A longitudine maxima distet, demonstrandum est quod in B et D punctis maxima inter equalem et inequalem motum differentia fit. Coniungantur enim EB et ED. Quod igitur quam EBF angulus ad quatuor rectos habet habet] corr. ex habeat G proportionem, eam habet arcus differentie inequalitatis ad totum circulum, inde patet, quoniam EB angulus equalis motus arcum subtendit, angulus vero AFB arcum motus qui inequalis apparet, estque ipsorum excessus angulus EBF. Dico igitur quod neutro ipsorum maior alius angulus super circumferentiam circuli ABGD in linea EF constitui potest.

Constituantur enim in T et C punctis anguli ETF et ECF et coniungantur TD et ED, quoniam igitur in omni triangulo longius latus maior angulo subtenditur. Est autem maior TF linea quam linea FD, maior etiam erit angulus TDF angulo TDF, sed EDT angulus equalis est angulo ETD, quoniam ET et ED equales sunt. Erit igitur totus EDF angulus, hoc est ipse EBF maior angulo ETF. Rursum quoniam DF maior est quam CF, angulus quoque FCD maior est angulo FDC. FDC] corr. ex FCDC G corr. ex FCD A Sed angulus ECD toti angulo EDC equalis est. Nam et EC rursus et ED equales sunt, et reliquus ergo EDF, hoc est EBF, maior est angulo ECF.

Non enim ergo possibile maiores alios constitui angulos modo quo diximus quam sint anguli in B et D punctis constituti. Cum istis una demonstratur quod etiam AB arcus qui tempus a motu minimo ad medium continet maior est arcu BG quo tempus a medio motu ad maximum continetur duobus arcubus quibus inequalitatis differentia continetur. Angulus enim EB AEB] corr. ex AB G maior est recto, idest maior quam angulus EFB angulo EBF, angulus vero BEG minor quam rectus eodem.

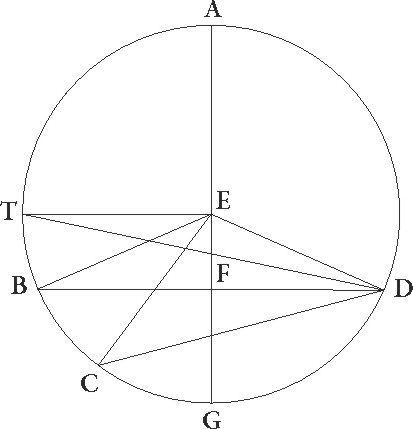
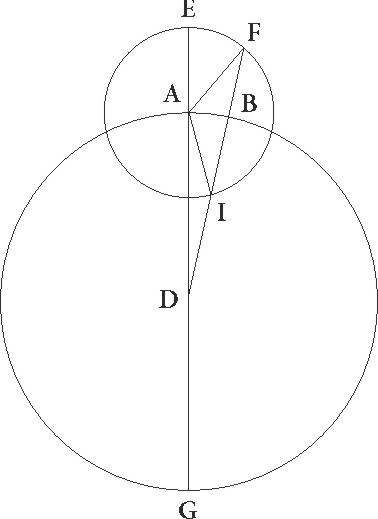
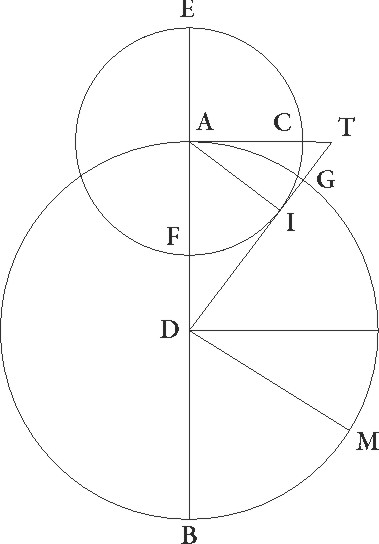Sed ut etiam in alia positione id accidere demonstremus, sit ABG concentricus mundo circulus, cuius centum D, et diameter ADB, circulus vero qui defertur in eo in eadem superficie sit EFI, cuius centrum sit A, supponaturque stella esse in I, quando per quartam videtur a maxime longitudinis puncto partem distare, et coniungatur AI et DIG, dico quod IG linea tangit epicyclum. Tunc enim maxima differentia a motu equali ad inequalem fit. Nam quoniam equalis a maxima longitudine motus sub angulo EAI continetur, —equali enim velocitate et stella epicyclum et epicyclus ABG circulum pertranseunt—, et differentia equalis motus ad apparentem sub angulo ADI continetur, patet quia excessus etiam EAI anguli ad ADI, hoc est angulus AID, apparentem a maxima longitudine stelle distantiam continebit. Quare quoniam ipsa quarte partis esse supponitur, rectus erit angulus AID et hac de causa DIG linea EFI circulum tanget. Quare arcus AG qui est inter A centrum et lineam tangentem maxima inequalitatis differentia est et per eadem arcus EI quo secundum suppositum nunc motum in epiciclo tempus a motu minimo ad medium continetur maior est quam IF quo tempus a medio motus ad maximum continentur duobus AG arcubus. Nam si DI ad T producamus et TCA lineam perpendiculariter ad EF protrahamus, fient anguli CAI et ADG equales et arcus CI arcui AG similis quo maior est EI quam una pars quarta, minor autem FI, quod erat demonstrandum.

Quod autem etiam in particularibus motibus in utraque suppositione eadem omnia equalibus temporibus fiunt tam in motibus equalibus quam in apparentibus et ad hec in ipsorum excessibus, idest in inequalitatis differentia, hinc maxime quispiam intelliget.

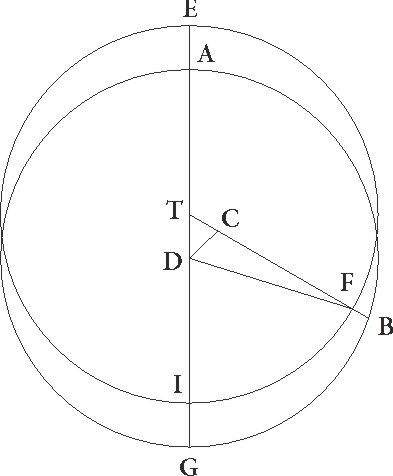
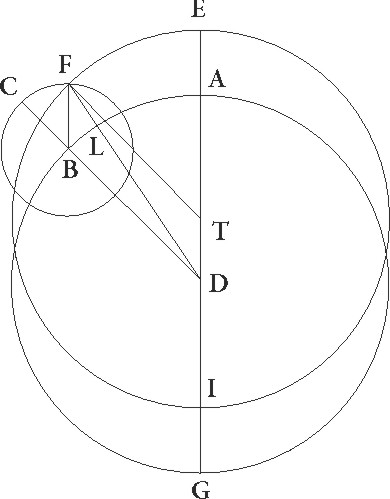Sit enim ABG circulus obliquo concentricus, cuius centrum sit D, excentricus autem et equalis ABG concentrico sit EFI, et centrum eius sit T, sitque communis utriusque diameter ATD transiens per E maximam longitudinem et per D, T centra, captoque contingenter in excentrico arcu AB, centro ipso B, describatur circulus CF secundum quantitatem DT, et protrahatur protrahatur] corr. ex protrahatur A linea CBD: dico quod stella quidem sub utroque motu ad F excentrici et epicycli sectionem in tempore omnino equali perveniet, hoc est quod tres arcus EF excentrici et AB concentrici et CF epicicli alteri alteris similes erunt, differentia vero equalis motus ad inequalem et apparens transitus stelle similis etiam ipse in utraque fit suppositione. Iungantur enim FT et BF et DF, et quoniam quadrilatere figure BDTF latera ex adverso collocata alterum alteri equalia sunt, BDFT quadrilatera figura parallelogramum erit et anguli similiter oppositi equales. Quare tres etiam anguli ETF et ADB et FBC equales sunt. Quoniam igitur in centris sunt, arcus quoque ipsis subtensi EF excentrici et AB concentrici et CF epicycli epicycli] corr. ex epicicli G similes inter se sunt. Equali ergo in tempore ad idem punctum F secundum utrosque motus stella 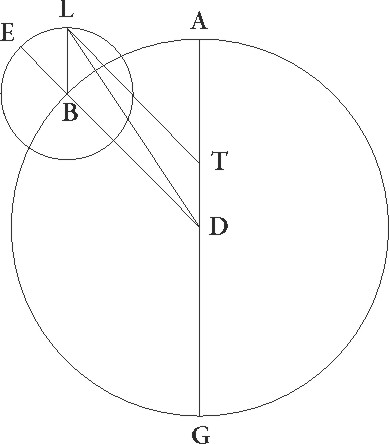perveniet, eundemque obliqui AL a maxima longitudine arcum pertransisse apparebit, et erit consequenter inequalitatis quoque differentia eadem in utraque suppositione. Eandem enim differentiam in positione quidem excentricitatis abs abs] post corr. G DFT angulo, in epicycli epicycli] corr. ex epicicli G autem abs BDF contineri demonstravimus, et ipsi quoque ex adverso equales quoniam FT et BD equidistantes esse demonstratum est.

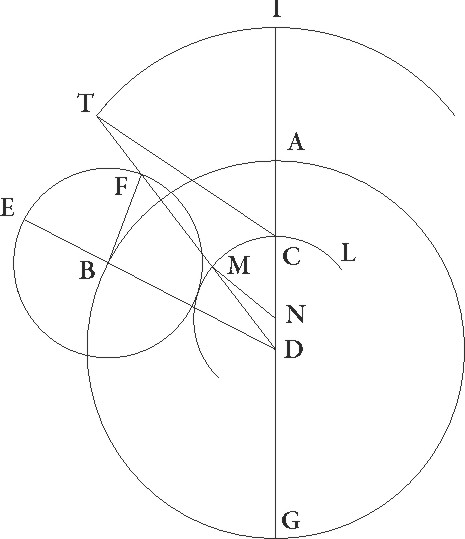Patet autem quod eadem in omnibus etiam distantiis consequentur, cum semper TDFB quadrilatera figura parallelogramum fiat, describaturque circulus excentricus sub ipso stelle motu qui est in epicyclo, epicyclo] corr. ex epiciclo G dummodo in utraque suppositione similes equalesque fiant proportiones, quamvis si solummodo similes, magnitudine vero inequales sint, eadem rursus apparere continget, quod perspicuum erit. Sit enim similiter ABG circulus mundo concentricus, cuius centrum D et diameter ADG, in qua stella maxime minimeque longitudinis fiat. fiat] post corr. G Sit autem EF epicyclus circa B qui distet ab A longitudine maxima per per] iter. et del. G AB arcum contingenter captum, sitque stella iam mota per totum EF arcum AB arcui videlicet similem, idque ideo quoniam revolutiones circulorum equali fiunt in tempore, et copulentur DBE et BF et DF. Quod igitur anguli ADE et FBE semper equales sunt, quodque stella in DF secundum hanc suppositionem linea apparebit, perspicuum est. Dico autem quod etiam in excentricitatis positione sive maior sive minor excentricus sit quam ABG concentricus, dummodo similitudo proportionum revolutionumque temporis equalitas solum supponantur in eadem rursus linea DF stella apparebit. Designetur enim enim] add. s. l. G IT maior ut diximus excentricus, cuius centrum sit C in AG linea, minor vero LM, cuius centrum sit N similiter, et producantur DMFT et DLAI, iunganturque TC et MN. Quoniam igitur sicut DB se habet ad BF sic TC ad TD et MN ad ND et angulus BFD angulo MDN equalis, idque ideo quoniam DA et BF equidistantes sunt, equalium angulorum tres trianguli sunt et anguli BDF et DTC et DMN proportionalibus contenti lateribus equales. Linee igitur BD et TC et TC] post corr. G quare anguli quoque ADB et ACT et ANM equales sunt, et quoniam in centris circulorum sunt, arcus AB et IT et LM a quibus subtenduntur similes erunt. Equali ergo in tempore non solum epicyclus epicyclus] corr. ex epiciclus G arcum AB et stella EF arcum pertransierunt, verum etiam in excentricis stella IT et LM arcum transibit, et semper in eadem linea DMFT propter hec apparebit, in epiciclo quidem cum in F puncto, in maiore vero excentrico cum in T, in minore autem cum in M fuerit, et in omni positione similiter.

Ad hec etiam accidit ut, quando per equalem a maxima et a minima longitudine arcum stella distare appareat, equalis in utraque suppositione inequalitatis differentia sit. Nam si primum ABGD excentricum in excentricitatis suppositione descripserimus, circa centrum E et diametrum EG per A longitudinem maximam, supposuerimusque visum esse in puncto F in ipsa diametro, et, per F punctum BFD contingenter protracta, coniunxerimus EB et ED, tam 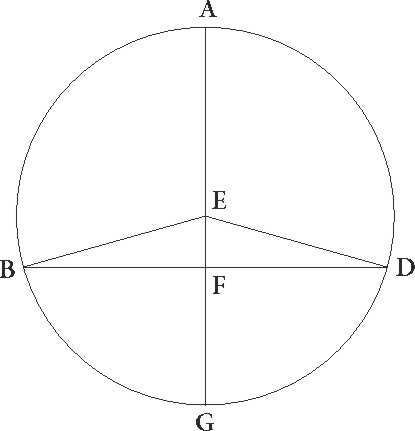apparentes transitus equales ex opposito erunt, hoc est AFB angulus ex parte maxime longitudinis et GFD ex parte minime, quam differentia inequalitatis eadem erit, idque ideo quoniam BC et ED equales sunt et angulus EBF angulo EDF equalis. Quare eadem differentia apparentis arcus, hoc est contenti ab utroque angulo AFB et GFD, maior quidem arcus ex A longitudine maxima ipsius motus equalis fit, minor autem ex AG minima longitudine, propterea quod EB angulus maior est quam AFB angulo FBE, angulus vero GED minor quam GFD angulo EFD.

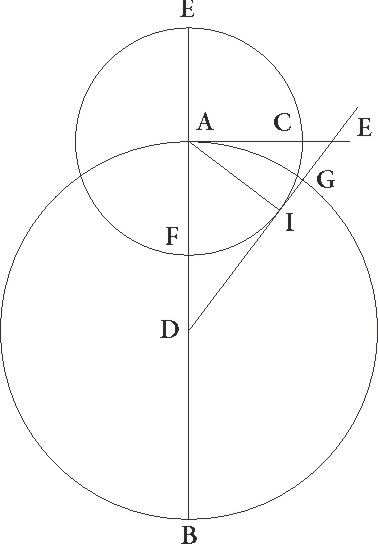
In epicycli epicycli] corr. ex epicicli G deinde suppositione, si ABG concentricum similiter circulum circa centrum D et diametrum ADG descripserimus, epicyclum epicyclum] corr. ex epiciclum G autem EFI circa centrum A, protractaque DIBF contingenter, coniunxerimus AF et AI, erit rursum arcus AB differentia inequalitatis eadem in utrisque supposita positionibus, positionibus] post corr. G hoc est sive in F puncto sive in I stella esse supponatur, et tam a maxime longitudinis obliqui circuli puncto cum fuerit in F, quam a minime cum fuerit in I equaliter distare apparebit, propterea quod arcus a maxima longitudine apparens sub angulo DFA continetur. Excessus enim esse demonstratus est motus equalis et differentie que penes inequalitatem est. Qui vero a minima longitudine apparens est sub angulo FIA continetur, hic enim etiam equali a maxima longitudine motui et differentie que penes inequalitatem est equalis esse cognoscitur. Sed angulus DFA angulo FIA equalis est, propterea quod AF et AI equales sunt. Quare hinc quoque rursus colligitur, quia eadem differentia, idest angulo ADI, maior quidem est medius qui a maxima longitudine est quam apparens, idest EAF angulus quam angulus AFD, minor autem medius qui est ad minimam longitudinem quam apparens qui idem est videlicet IAD angulus quam angulus AIF, quod erat demonstrandum.

〈III.4〉 Capitulum IIII: De apparente inequalitate solari

His ita expositis, existimandum est eam quoque inequalitatem que in motu Solis apparet, quoniam una est et quoniam maius semper a minimo ad medium motum tempus facit quam a medio ad maximum, id enim iis que apparent consonum invenimus utraque prepositarum suppositionum fieri posse, ita tamen ut in epicyclo epicyclo] corr. ex epiciclo G motus Solis ad precedentia a maxima longitudine fiat. Rationabilius autem est excentricitatis positioni que simplicior est et uno non duobus motibus peragitur id attribuere. Precedit autem ut excentricitatis solaris circuli proportionem inveniamus, hoc est quam proportionem habeat que inter duo centra est ad eam que a centro excentrici est, et ad hec in qua maxime portione obliqui remotissimum a terra punctum excentrici est, hec Hiparcho Hiparcho] corr. ex Hipacho G quoque demonstrata sunt. Nam cum supposuisset 94 30′ dierum tempus esse a verno equinoctio ad estivum solstitium et ab estivo solstitio ab equinoctium autumnale dierum 92 30′, ex his apparentibus solis demonstrat lineam quidem inter predicta centra vigesimam quartam proxime partem esse illius que a centro excentrici est, remotissimum vero eius a terra punctum 24 30′ proxime estivum solstitium talibus gradibus precedere, qualium est obliquus 360. Nos autem, quamvis predictarum quartarum tempora expositasque proportiones easdem proxime nunc etiam invenimus, ut hac de causa nobis perspicuum fiat eandem semper positionem ab excentrico Solis circulo ad solstitialia et equinoctialia puncta servari, tamen, ne hic locus desertus a nobis videatur et ut etiam numeris nostris theorema hoc expositum sit, ipsi quoque sicut in excentrico circulo prepositorum demonstrationem faciemus eisdem apparentibus usi, hoc est, ut diximus, quod quod] corr. ex qud G a verno equinoctio ad estivale usque solstitium 94 30′ dierum tempus intersit, ab estivali autem solstitio ad equinoctium usque autumnale dierum 92 30′. Consonam enim dierum multitudinem invenimus inter equinoctia ac estivale solstitium que a nobis 463 anno a morte Alexandri exactissime observata sunt. Nam, ut diximus, autumnale quidem equinoctium in 9^o Athyr die post ortum Solis fuit, vernum autem in die 7^o Pathon post meridiem, ut tota distantia 178 15′ dierum colligatur, solstitium vero estivale xi^o die Messori post mediam noctem que ad xii diem ferebat, ut hec quoque a verno equinoctio ad estivale solstitium distantia dierum esse colligatur 94 30′, relinquanturque ab estivali solstitio ad autumale consequens equinoctium dies ad tempus annuum 92 30′ proxime.

Sit igitur ABGD circulus obliquus, cuius centrum sit E, et protrahantur in ipso due diametri perpendiculariter inter se per tropica et equinoctialia signa AG et BD, sitque A quidem vernum, vernum] corr. ex verum G B vero estivale, et reliqua consequenter. Quod igitur excentrici circuli centrum inter EA et EB lineas cadit, inde perspicuum est, quod ABG semicirculus maius medietate annua tempus continet et hac de causa maiorem excentrici portionem intercipit quam semicirculum, et quod AB quarta pars maius etiam tempus continet et maiorem excentrici arcum intercipit quam quarta BG.

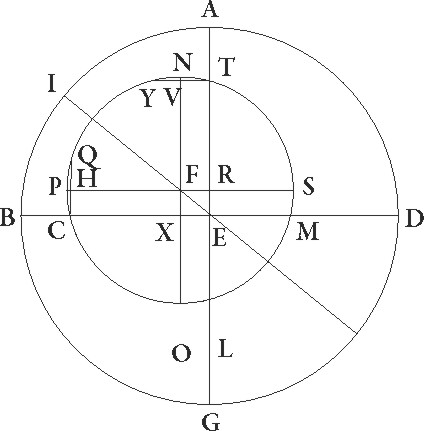
Hec cum ita se habeant, sit F punctum excentrici centrum, protrahaturque IFE diameter per utraque centra et per maximam longitudinem, et centro ipso F puncto, spatio autem contigenti, describatur TCLM circulus Solis excentricus, et ducantur equidistantes equidistantes] corr. ex equidistanti G per ipsum F ad AG quidem linea NXO, ad BD autem linea PRS, et ad hec perpendiculares quoque deducantur a puncto quidem T ad lineam NXO perpendicularis TUY, a puncto autem C ad lineam PRS perpendicularis CHQ. Quoniam ergo Sol, cum per TCLM circulum equaliter moveatur, arcum quidem TC in diebus 94 15′ petransit, arcum vero CL in diebus 92 30′, movetur autem equaliter in 94 30′ diebus gradus 93 9′ proxime tales, qualium obliquus est 360, in diebus vero 92 30′ gradus 91 xi′, erit arcus TCL 184 20′ graduum, utrique autem arcus NT et LO reliquorum, detractis 180 gradibus semicirculi, erunt graduum 4 20′, et duplus arcus TN, idest arcus TNY, eorundem 4 20′ Quare TY etiam corda sibi subtensa talium erit 4 32′ proxime, qualium est excentrici diameter 120, medietas vero eius idest TU, hoc est EX, eorundem 2 16′. Rursus quoniam TNPC portio tota graduum est 93 9′, et TN graduum 2 10′, et NP quarta pars graduum 90, relinquitur ut PC arcus graduum sit 0 59′ et duplus eius, idest arcus CPQ, graduum 1 58′. Quare corda quoque sibi subtensa talium erit 2 4′, qualium est excentrici diameter 120, medietas vero eius, hoc est CH, idest FX, partium 1 2′ earundem quarum linea EX demonstrata est 2 16′, et quoniam ab istis composita reddunt illud quod fit ex EF, erit ipsius quoque longitudo talium 2 29′ 30′′ proxime, qualium est semidiameter excentrici 60. Quare semidiameter excentrici vigintupla et quadrupla proxime illius est que est inter duo centra excentrici et obliqui.

Rursum quoniam qualium EF demonstrata est 2 29′ 30′′, talium etiam FX linea erat 1 2′, idcirco qualium est EF corda 120, talium erit FX linea 49 46′ proxime et super eam tensus arcus circuli qui circa EFX rectangulum describitur talium 49 proxime, qualium circulus est 360. Quare angulus etiam FEX talium erit 49, qualium duo recti sunt. 360, talium vero 24 30′, qualium quatuor recti sunt 360. Quoniam igitur in centro zodiaci est, erit etiam BI arcus quo I remotissimum a terra punctum estivalis solsticii punctum precedit graduum 24 30′. Verum quoniam OS quarta pars et reliqua SN graduum est utraque 90′, est autem G autumnale, etiam OL arcus 2 10′ et TN similiter, MS vero graduum 0 59′, erit arcus quidem LM graduum 86 51′, arcus vero MT 88 49′. Sed 86 51′ gradus Sol equali motu pertransit in diebus 88 8′, gradus vero 88 49′ in diebus 90 8′ proxime. Quare GD quoque arcum qui est ab equinoctio autumnali ad brumale solstitium in diebus 88 8′ pertransire 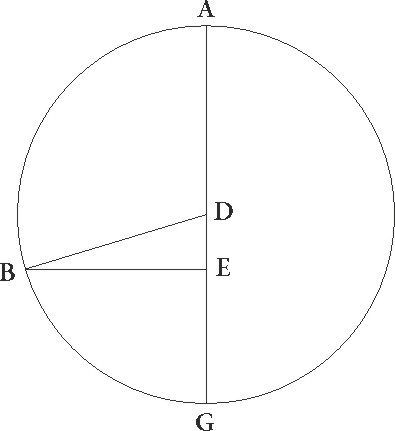videbitur, arcum vero DA qui est ab hyemali hyemali] corr. ex hiemali G solstitio ad equinoctium vernum in in] add. s. l. G diebus 90 8′ proxime. Inventa igitur nobis sunt que proposuimus consone illis que ab Hipparcho dicuntur. Per has igitur quantitates considerabimus, quanta est maxima equalis motus ad inequalem differentia et in quibus hec punctis accidit.

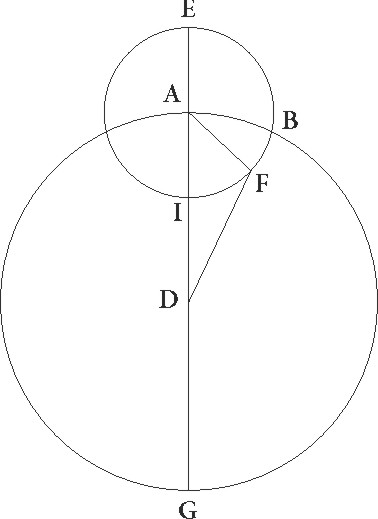Sit igitur ABG circulus excentricus, cuius centrum sit D et diameter per A remotissimum a terra punctum ADG, in qua centrum zodiaci sit E, et deducatur ad AG perpendicularis EB, protrahaturque protrahaturque] corr. ex protrahantur G BD, et quoniam, qualium est BD cum a centro sit 60, talium est DE que inter centra est 2 30′ secundum vigentuplam quadruplamque proportionem, ideo qualium est BD corda 120, talium erit DE quidem linea 5, arcus vero ab ea subtensus talium 4 46′ proxime, qualium est BDE circa rectangulum circulus 360. Quare angulus etiam DEB quo maxima inequalitatis differentia continetur, qualium quidem duo recti sunt 360, talium erit 4 46′, qualium vero 4 recti sunt 360, talium erit 2 23′. Earundem vero est etiam BED rectus angulus 90, equalis autem duobus, hoc est angulus BDA, 92 23′, et quoniam in centris sunt BDA quidem excentrici, BED autem zodiaci, habebimus maximam quidem inequalitatis differentiam graduum 2 23′, arcuum vero in quibus hec fit excentrici quidem et equalis motus arcum graduum 92 23′ a remotissimo a terra puncto, zodiaci autem et inequalis apparentisque motus arcum quarte unius, ut etiam antea demonstratum est, graduum 90. His demonstratis, manifestum est quod in opposita portione apparens quidem medius transitus et maxima inequalitatis differentia erit in gradibus 270, qualis autem qui in excentrico est in gradibus 267 37′.

Verum ut etiam, ut diximus, easdem quantitates colligi in epicycli epicycli] corr. ex epicicli G quoque suppositione per numeros demonstremus, quando eedem, ut diximus, proportiones continentur, sit ABG concentricus obliquo circulus, cuius centrum D et diameter ADG, epicyclus epicyclus] corr. ex epiciclus G autem sit EFI, cuius centrum A, et protrahantur a puncto D linea DFB tangens epiciclum, et coniungatur AF. Fit igitur similiter in ADF orthogonio vigintupla et quadrupla AD linea ad lineam AF. Quare qualium est AD corda 120, talium rursus AF quidem fiet 5, arcus vero suus 4 46 talium, qualium est circulus circa FDA descriptus 360. Quare angulus quoque ADF, qualium duo recti quidem sunt 360, talium erit 4 46′, qualium vero quatuor recti sunt 360, talium 2 23′. Maxima ergo inequalitatis differentia, hoc est arcus AB, hinc etiam concorditer graduum 2 23′ inventa est, arcus vero inequalitatis, quoniam sub angulo AFD recto continetur, graduum 90, equalitatis autem qui sub angulo EAF continetur graduum rursus 92 23′.

〈III.5〉 Capitulum V: De particularibus inequalitatis solaris portionibus

Verum ut particulares etiam inequales motus possumus in singulis discernere, in utraque rursum suppositione demonstrabimus quomodo, uno expositorum arcuum dato, reliquos capiemus.

S 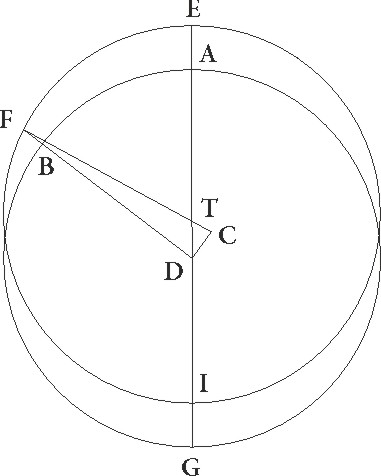it igitur primum ABG concentricus zodiaco circulus, cuius centrum D, excentricus autem sit EFI, cuius centrum T, diameter vero per utraque centra et E maximam longitudinem sit EATDIG, interceptoque arcu EF, coniungantur FD et FT, datusque sit primum arcus EF, sitque verbi gratia graduum 30, et protracta in longius FT, perpendicularis ad ipsam ex D puncto DC deducatur. Quoniam igitur arcus EF 30 graduum esse supponitur, erit etiam angulus ETF, hoc est DCT, talium triginta, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 60, quare arcus etiam corde DC talium erit 60, qualium circulus qui circa DTC rectangulum describitur est 360. Arcus vero corde TC reliquorum ad semicirculum 120, quare corde quoque eis subtense, DC quidem talium erit 60, qualium TD corda 120, CT vero 103 55′ eorundem. Quare qualium est DT quidem linea 2 30′, FT autem que est a centro 60, talium et erit DC quidem 1 15′, TC vero 2 10′ eorundem, tota vero CTF 62 10′, et quoniam que ab ipsis sunt, si componantur, illud reddunt quod fit ex FD, erit etiam FD corda 62 11′ proxime. Quare qualium est FD 120, talium DC quidem linea erit 2 25′, arcus vero super eam tensus 2 18′ talium, qualium est circulus qui circa FDC rectangulum describitur 360. Quare angulus quoque DFC talium erit 2 18′, qualium duo recti sunt 360, qualium vero 4 recti sunt 360, talium 1 9′. Tanta ergo est inequalitatis tunc differentia. Erat autem ETF angulus 30. Quare ADB reliquus angulus, hoc est est] add. s. l. G zodiaci arcus AB, graduum graduum] corr. ex gradum G erit 28 51′.

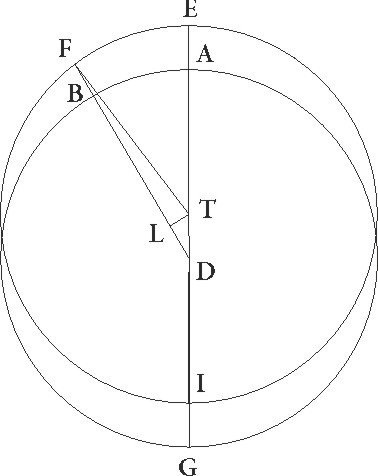
Quod vero etiam, si alius quidam angulorum dabitur, reliqui quoque dabuntur, manifestum erit, si perpendicularis TL in eadem descriptione ex T ad FD deducatur. Nam sive AB zodiaci arcum, hoc est ADB angulum, datum supposuerimus, erit hac de causa proportio quoque DT ad TL data, cunque etiam data sit proportio DT ad TF, dabitur etiam proportio FT ad TL. Quapropter datos etiam habebimus angulos TFL, hoc est inequalitatis differentiam, et ETF, hoc est excentrici arcum, sive inequalitatis differentiam, id est TFD angulum, datum supposuerimus, accident eadem econverso. Nam idcirco et proportio TF ad TL data erit. Fuit autem et a principio TF ad TD proportio data, quare proportio quoque DT ad TL data erit, et hac de causa dantur etiam anguli DTL, hoc est AB zodiaci arcus, et ETF, idest EF excentrici arcus.

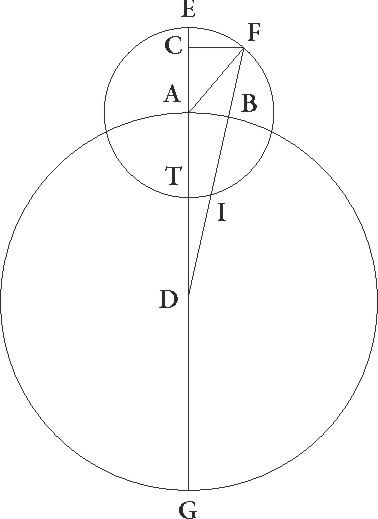
Sit rursus ABG circulus obliquo comcentricus, eius centrum sit D et diameter ADG, epicyclus autem in eadem proportione sit EFIT cuius centrum A, et intercepto arcu EF, coniungantur FBD et FA. Supponatur autem arcum EF 30 eorundem graduum esse, et deducatur FC perpendicularis ab F ab F] corr. ex ABF G ad lineam E. Quoniam igitur arcus EF graduum est 30, erit etiam angulus EAF talium 30, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 60. Quare arcus etiam corde CF talium erit 60, qualium est AFC circulus qui circa rectangulum describitur 360, AC vero arcus reliquorum ad semicirculum 120. Quare corde quoque sue erunt FC quidem talium 60, qualium est diameter 120, CA vero 103 55′ eorundem. Quare 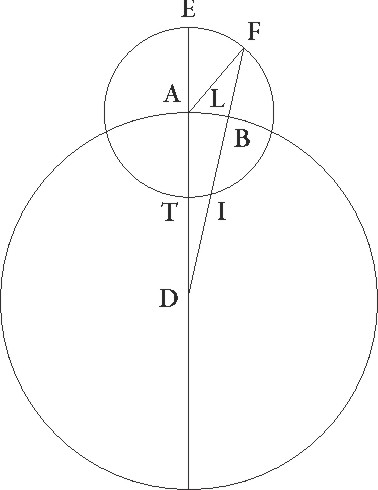qualium est AF quidem corda 2 30′, AD autem que est a centro 60, talium erit FC quidem linea 1 15′, CA vero 2 10′ eorundem, sed tota CAD 62 10′ et quoniam que ab ipsis sunt, si componantur, illud faciunt quod fit ex FBD, erit etiam ipsa FBD talium 62 11′, qualium erat FC 1 15′.

Quare qualium est corda DF 120, talium erit FC quidem linea 2 25′, arcus vero super eam tensus talium 2 18′, qualium erit circulus qui circa DFC rectangulum describitur 360. Quare angulus etiam EFDC talium quidem erit 2 18′, qualium 2^o recti sunt 360, qualium vero quatuor recti sunt 360, talium 1 9′. Tanta igitur rursus est inequalitatis differentia. Erat autem EAF etiam angulus eorundem 30, erit igitur etiam reliquus AFD angulus, hoc est apparens zodiaci arcus, graduum 28 51′, que omnia demonstratis quantitatibus excentricitatis concordant.

Similiter autem hic quoque, si alius dabitur angulus, reliqui etiam, perpendiculari AL ex A ad DF in eadem descriptione deducta, dabuntur. Nam sive apparentem rursus zodiaci arcum, idest AFD angulum, dederimus, erit hac de causa proportio etiam AF ad AL data, cunque proportio quoque AF ad AD a principio data sit, dabitur etiam proportio AD ad AL. Quapropter et angulus ADB, idest AB differentie inequalitatis arcus, dabitur et EAF, idest epicycli epicycli] corr. ex epicycli G arcus EF, sive inequalitatis inequalitatis] post corr. G differentiam, hoc est angulum ABD, datum supposuerimus, dabitur propterea similiter econverso proportio etiam AD ad AL, cunque a principio proportio DA ad AF data sit, dabitur etiam proportio AF ad AL, quapropter angulus etiam AFD, hoc est apparens zodiaci arcus, datus erit, et angulus EAF, idest epicycli epicycli] corr. ex epicycli G arcus EF.

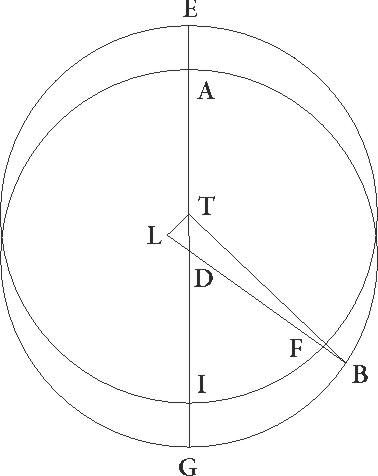Intercipiatur rursum in preposita excentrici circuli descriptione a puncto I minima excentrici longitudine arcus IF qui 30 eorumdem graduum esse supponatur, et coniungantur DFB et FT, et deducatur DC perpendicularis ex D ad linea TF, et quoniam arcus FI graduum graduum] corr. ex gradum G est 30, erit etiam angulus FTI talium 30, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 60. Quare arcus etiam corde DC talium erit 60, qualium est circulus qui circa DTC rectangulum describitur 360, arcus vero corde CT reliquorum ad semicirculum graduum 120, quapropter corde etiam quibus subtenduntur erunt DC quidem talium 60, qualium est DT diameter 120, CT vero 103 55′ eorundem. Quare qualium est DT quidem corda 2 30′, TF autem que est a centro 60, talium est DC quidem linea 1 15′, CT autem similiter 2 10′, CF vero reliquorum 57 50′, et quoniam, si componantur que ab ipsis sunt, illud facient quod est EDF, erit etiam ipsa talium 57 51′ proxime, qualium erat DC 1 15′, quare qualium est DF corda 120, talium erit DC 2 34′ 36′′. Arcus vero super eam tensus talium 2 27′, qualium est DFC circulus qui circa rectangulum describitur 360, quare DFC quoque angulus talium erit 2 27′, qualium duo recti sunt 360, qualium vero quattuor recti 360, talium 1 14′ proxime. Tanta igitur est inequalitatis differentia, et quoniam angulus FTI talium etiam 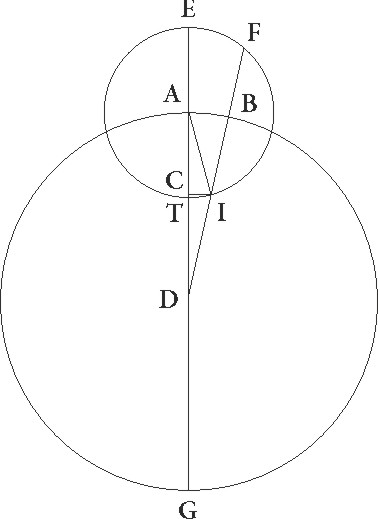suppositus est 30′, erit totus quoque angulus BDG, idest GB zodiaci arcus, graduum 31 14′.

Per eadem vero hic quoque, BD linea in longius tracta et TL perpendiculari ad ipsum deducta, sive GB zodiaci arcum, hoc est TDL angulum, dederimus, dabitur etiam hac de causa proportio TD ad TL, cunque proportio quoque ipsius TD ad TF in principio data sit, dabitur etiam proportio FT ad TL, quapropter et angulos TFD, idest inequalitatis differentiam, et FTD, hoc est IF excentrici arcum, datos habebimus, sive inequalitatis diferentiam, hoc est angulum FD, FD] corr. ex TFD A dederimus, dabuntur etiam hac de causa econverso proportio FT ad TL, cunque a principio proportio quoque FT ad TD data sit, dabitur etiam proportio DT ad TL, quare tam angulum TDL, hoc est GB zodiaci arcum, quam angulum FTI, hoc est IF excentrici arcum, datos habebimus.

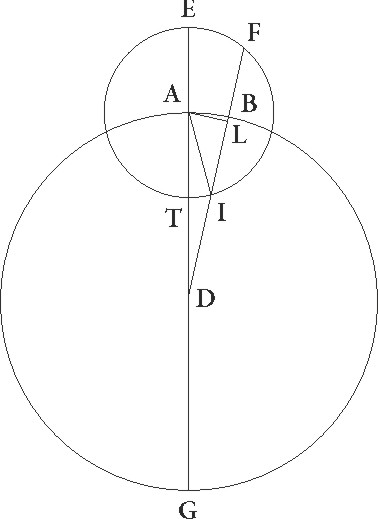Similiter in proposita expicycli expicycli] corr. ex picicli G atque concentrici descriptione, intercepto ex T minima longitudine arcu TI eorundem graduum 30 et coniunctus IA et DIB lineis, perpendicularis IC ad AD lineam deducatur. Quoniam igitur rursus TI arcus graduum est 30, erit TAI angulus talium 30, qualium quatuor recti sunt 360, qualium vero duo recti sunt 360, talium 60, quare arcus et corde IC talium erit 60, qualium est circulus qui circa ICA rectangulum describitur 360. Arcus vero corde AC reliquorum ad semicirculum 120, quare corde quoque quibus subtenduntur IC quidem talium erit 60, qualium est AI corda 120, AC vero 103 55′ eorundem, quare qualium AI quidem linea est 2 30′, AD vero, cum sit a centro 60, talium erit IC quidem 1 15′, AC autem similiter 2 10′ et CD 57 50′ reliquorum, et quoniam que ab ipsis composita sunt illud reddunt quod fit ex DI, erit hec etiam longitudinis talium 57 51′ proxime, qualium CI linea erat 1 15′. Quare qualium DI corda est 120, talium IC quidem linea erit 2 34′ 36′′, et arcus super eam tensus talium 2 27′, qualium est circulus qui circa DIC triangulum describitur 360, quare angulus quoque IDC, qualium quidem duo recti sunt 360, talium est 2 27′, qualium vero quatuor recti sunt 360, talium 1 14′ proxime. Tot ergo etiam hic AB arcus, idest inequalitatis differentia, continetur, et quoniam angulum CA 1 30′ eorundem esse supposuimus, erit totus angulus BIA quo apparens zodiazi arcus continetur graduum 31 14′, que omnia quantitatibus excentrici ad unguem concordant.

Per eadem vero hic quoque AL perpendiculari ad DB lineam deducta, sive obliqui arcum, idest AIL angulum, dederimus, dabitur etiam hac de causa proportio IA linee ad AL, cunque a principio IA quoque ad AD proportio data sit, dabitur etiam DA proportio ad AL, et idcirco angulos etiam ADB, hoc est AB inequalitatis differentie arcum, et TAI, hoc est TI epicicli arcum, datos habebimus, sive rursum AB inequalitatis differentie arcum, idest ADB angulum, dederimus, dabitur similiter hac de causa econverso proportio DA ad DL, cunque a principio proportio quoque DA ad AI data sit, dabitur etiam proportio AI ad AL, et idcirco tam angulum AIL, hoc est zodiaci arcum, quam TIA, idest TI arcum epicycli, epicycli] corr. ex epicicli G datos habebimus, et sic demonstrata nobis sunt que proposuimus.

〈III.6〉 Capitulum VI: De tabularum differentie inequalitatis solaris compositione

Cum igitur varia multiplexque tabule illarum portionum quibus inequalitatis distinctiones apparentium mortuum continentur per hec theoreumata theoreumata] corr. ex theoremata G compositio possit fieri, ut quantitates particularium equationum facile capiantur, ille modus magis nobis comprobatur, quo ad singulos motus equalis arcus differentie inequalitatis accomodantur, tum quoniam consequenter ad supposita fit, tum quoniam simplex et facilis intellectu singulorum calculus redditur. Quare prima et per numeros exposita theoremata secuti singularum proportionum singulas inequalitatis differentias que singulis arcubus motus equalis distribuuntur per lineas simili demonstratione computavimus. Partiti autem sumus tam in Sole quam universaliter in aliis quartas que sunt ad maximam longitudinem in 15 portiones, ut per sex gradus in eis additio subtractiove subtractiove] fiat add. et del. A differentie fiat, quartas vero que sunt ad minimam longitudinem in portiones 30, ut per tres gradus in istis additio subtractiove differentie fiat. Maior etenim est excessus differentiarum que ad minimam fiunt quam excessus earum que ad maximam longitudinem penes inequalitatem portionibus equis accommodantur.

Fecimus igitur solaris inequalitatis tabulam versuum quidem rursus 45, ordinum vero trium, quorum primi duo numerum 360 graduum motus equalis continent, ita ut 15 primi versus duas ad maximam longitudinem quartas contineant, reliqui vero 30 reliquas que sunt ad minimam longitudinem, tertius autem gradus differentie inequalitatis qui singulis equalis motus numeris conveniunt addendos subtrahendosve continet. Est autem tabula ipsa huiusmodi:

〈III.7〉 Capitulum VII: Tabula inequalitatis solaris

〈III.8〉 Capitulum VIII: De inveniendo loco medii motus Solis

Cum autem restet ut equalis motus solaris loca ad quottidianos progressus constituamus, id quoque ita fecimus, ut universaliter rursus tam in Sole quam in aliis eos motus sequamur, qui nobis exactissime observati sunt, et ab istis per medios motus iam demonstratos ad initium regni Nabonassaris, ex quo tempore priscas habemus observationes continue ad hoc usque tempus conservatas, locorum radices reducamus.

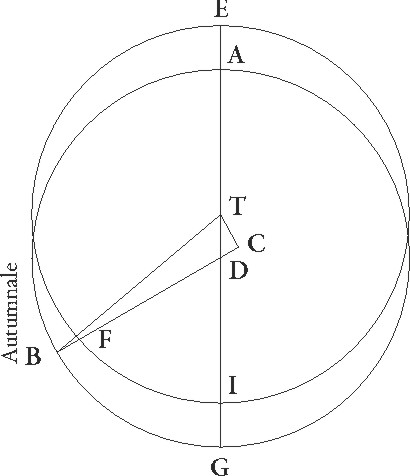Sit igitur ABG concentricus obliquo circulus, cuius centrum D, excentricus autem Solis sit circulus EFI, cuius centrum T, diameter vero per utraque centra et E maximam longitudinem sit EAIG, et supponatur quod B sit autumnale zodiaci punctum, et coniungantur BFD et FT perpendicularis etiam DC ex T puncto ad FD protractam lineam deducatur. Quoniam igitur B autumnale punctum Libre principium est, G vero minima longitudo in 5 30′ gradibus Sagitarii est, erit arcus BG graduum 65 30′. Quare BDG, hoc est TDC angulus, qualium quidem quatuor recti sunt 360, talium est 65 30′, qualium vero duo recti sunt 360, talium 131. Quare arcus etiam per TC lineam tensus talium est 131, qualium est circulus qui circa rectangulum DTC describitur 360, corda vero TC qua tenditur talium 109 12′, qualium est diameter DT 120. Quare qualium DT quidem linea est 5, FT autem corda 120, talium etiam erit TC 4 33′, et arcus per eam tensus talium 4 20′, qualium est circulus circa FTC rectangulum circumscriptus 360, quare angulus etiam TFC, qualium quidem duo recti sunt 360, talium est 4 20′, qualium vero quatuor recti 360, talium 2 10′. Erat autem angulus quoque BDG 65 30′ eorundem, quare reliquus etiam angulus FTI, hoc est FI excentrici arcus, graduum est 63 20′. Quando ergo Sol in autumnali equinoctio est, tunc minimam longitudinem, idest 5 30′ gradus Sagitarii, medio motu motus 63 20′ gradibus antecedit, a maxima vero longitudine, idest ex 5 30′ Geminorum gradibus, ad successionem signorum medie similiter motus 116 40′ gradibus distat.

His ita demonstratis, quoniam de observatis primo equinoctiis unum exquisitissime inter alia in autumno cepimus anno Adriani 17 Athyr secundum Egiptios die septima post meridiem duabus proxime horis equalibus, patet quia Sol illo tempore medie motus distabat a maxima longitudine in excentrico ad sequentia gradibus 116 40′. Sed a regno Nabonassaris usque ad Alexandri mortem colliguntur anni 424, a morte autem Allexandri usque ad regnum Augusti 294, et a primo Augusti anno primaque in Thoth egiptio mense meridie (dies enim a meridie incipere volumus) ad 17 Adriani annum 7^o die Athir duabus post meridiem horis equalibus anni sunt 161 dies 66 et hore due equales. Quare a primo Nabonassaris anno, primaque meridie Thoth mensis secundum Egiptios usque ad expositum nobis equinoctium autumnale colligentur anni 879 et dies 76 et equales hore due. Sed in tanto tempore Sol medie integris revolutionibus reiectis 211 25′ proxime gradibus movetur.

Si ergo gradibus distantie a maxima excentrici longitudine 116 40′ que distantia fuit in exposito nobis equinoctio 360 unius circuli gradus addiderimus, et a tota summa 211 25′ gradus subtraxerimus, habebimus in primo anno Nabonasaris Thoth secundum Egyptios die primo in meridie Solem a maxima longitudine ad sequentia secundum equalem motum distare gradibus 265 15′ et medie retinentem 45′ sexagesimas primi Piscium gradus.

〈III.9〉 Capitulum VIIII: De motus solaris computatione

Quandocunque igitur voluerimus in tempore dato motum Solis invenire, totum a loco Solis dato tempus usque ad illud in quo motum eius querimus ad Allexandrie meridiani horam in tabulis equalis motus queremus, et correspondentes numeris gradus addemus 265 15′ gradibus a quibus distantia est et a summa revolutionibus integris proiectis reliquos ex 5 30′ Geminorum gradibus ad successionem signorum enumerabimus et quo numerus perveniet ibi medium motum Solis tandem esse sciemus. Eundem deinde, hoc est numerum qui est a maxima longitudine ad hunc medii motus terminum, in tabula inequalitatis queremus, correspondentesque sibi gradus in ordine tertio, siquidem numerus quo intravimus in ordine primo idest usque ad 180 gradus ascendit, subtrahemus ipsum a loco medii motus, sin vero 180 gradus excedit, addemus medio motui et sic verum apparentemque Solis motum inveniemus.

〈III.10〉 Capitulum X: de diei naturalis inequalitate

Verum que de Sole solo considerantur hec ferme sunt, sequitur autem breviter ad hec ea dicere que dierum naturalium inequalitatem ostendunt, nec enim preponenda sunt, quoniam motus stellarum medii omnes simpliciter sic nobis expositi sunt sic … sunt] add. marg. G quasi cuncti naturales dies equales sint, equaliaque incrementa recipiant. Dies vero naturales non perspiciuntur omnes equales. Nam cum totius revolutio equaliter in polis equinoctialis circuli fiat et hec revolutio signantius aut in orizonte aut in meridiano capiatur, capiatur] corr. ex capiantur A totius quidem revolutio una est eiusdem puncti equinoctialis circuli ab aliquo vel orizontis vel meridiani puncto rursus ad idem reductio. Quare equalis dies naturalis est que unius equinoctialis circuli revolutionis 360 tempora continet et ad hec 59′ proxime unius temporis sexagesimas quas Sol medie motus in diei naturalis tempore pertransivit. Inequalis vero dies naturalis est, que unius revolutionis 360 graduum equinoctialis progressum continet et ad hec coascensiones in orizonte vel in medio celi que inequali Solis motui correspondent.

Hec igitur equinoctialis circuli portio que 360 temporibus accedit inequalis necessaro fit, tum propter inequalem Solis motum, tum quia obliqui circuli portiones tam orizontem quam meridanum equalibus temporibus non transeunt. Quorum tamen neutrum differentiam unius diei equalis ad alterum inequalem sensibilem facit, collectam vero per dies plures valde sensibilem.

Penes igitur inequalem Solis motum maxima differentia fit ex distantiis ab uno medio motu Solis ad alterum. Dies enim naturales ita reducti differunt ab equalibus 4 45′ temporibus proxime. Inter se autem 9 30′ duplatis temporibus, idque ideo quoniam apparens Solis motus in semicirculo quidem, qui a maxima longitudine est 4 45′ gradibus ab equali defficit motu, in semicirculo vero qui a minima longitudine capitur eisdem habundat. Penes autem coortuum aut cooccasuum inequalitatem maxima differentia fit in semicirculis qui a solstitialibus punctis disseperantur. Nam etiam hic utrorumque huiusmodi semicirculorum coascensiones a temporibus quidem 180 que conspiciuntur equaliter per maximi aut minimi diei ad equinoctialem differentiam differunt, inter se autem per differentiam qua maxima dierum vel noctium a minima differt. Penes autem meridiani transitus inequalitatem maxima rursum differentia fit in distantiis precipue quibus duo signa que utrinque simul aut solstitialium aut equinoctialium punctorum sunt continentur. Nam in his etiam etiam] post corr. G utraque que ad solstitialia sunt 4 30′ proxime temporibus differre ab equalibus conspiciuntur, que vero ad equinoctialia utraque rursus temporibus 9, hec enim a medio equalique deficiunt, illa vero tantundem ferme excedunt. Hac de causa diei naturalis principium non ab ortu Solis aut occasu, sed a meridie constituimus. Nam differentia que ad orizuntas inspicitur et ad multas horas ascendere potest et eadem ubique non est. Sed secundum excessum maximorum minimorumve dierum aut noctium qui propter declinationem sphere fit commutatur. Que vero ad meridianum perspicitur et eadem ubique est et tempora differentie que ab inequalitate Solis colliguntur non excedit. Statuitur autem maxima different〈i〉a differentia] differenta A per compositionem utrarunque distantiarum eius, dico que penes inequalitatem Solis et eius que penes transitum quo tempora tempora] post corr. G meridianum pertranseunt in utrisque dictis differentiis aut addendis aut subtrahendis, fitque utrinque maxime portio a medio Aquario usque ad Libram subtrahenda, a Scorpione vero usque ad medium Aquarium addenda, propterea quod utraque istarum portionum plurimum vel addit vel subtrahit penes solarem quidem inequalitatem 3 40′ proxime, proxime] ut maxima ex dicta add. A penes autem meridiani transitum tempora 4 40′ proxime, ut maxima ex dicta compositione ambarum inequalitatum eius dico que ab inequali Solis motu accidit et eius que ab inequalitate transitus quo meridianum tempora equinoctialis pertranseunt consurgit, naturalium dierum differentia colligatur penes utrarunque huiusmodi portionum ad dies quidem equales temporibus 8 20′, hec est pars hore unius media et decima octava, inter se autem duplicatis temporibus 16 40′, que faciunt horam unam et partem hunius hore nonam. Hec autem differentia in Sole quidem ceterisque neglecta non sensibiliter forsam aparentium considerationi nocebit, in Luna vero propter velocitatem eius dignum cura et usque ad tres unius gradus quintas errorem facient.

Ut ergo naturales dies in quantacunque distantia dentur, sive a meridie sive a media nocte ad equalitatem omnino reducamus, diligenter considerabimus in quo gradu obliqui circuli Sol est tam equaliter quam inequaliter motus tum in priore tum in posteriore dato dato] post corr. G tempore. Deinde ab inequali motu, idest ab apparenti, ad apparentem distantiam gradus loci Solis in ascensionum tabule recte sphere inveniemus, considerabimusque quot tempora equinoctialis in meridiano gradibus distantie, ut diximus, correspondent, et temporum que inveniemus ad gradus equalis distantie excessum capientes computabimus contentam ab excessu temporum equalis hore magnitudinem, et hanc si numerus temporum maior sit quam equalis distantie, date dierum multitudini addemus, sin vero minor, subtrahemus ab ea, et tempus in factum equalium naturalium dierum exacte habebimus, quo maxime in tabulis mediorum motuum Lune utemur. Facile autem hinc intellectu est quod equales etiam naturales dies ad temporales simpliciterque inspectas reducuntur, si exposita temporum hore additio subtractiove fiat econverso.

Optinebat autem secundum calculum nostrum Sol in primo Nabonassaris anno secundum Egyptios Thot in prima meridie equaliter quidem, ut paulo ante diximus, motus 0 4′ 5″ Piscium gradus, inequaliter vero gradus 3 Piscium et sexagesimas octo proxime. proxime] in anno Adriani 17 arbym 7 ut in 7 c^o. huius dicit medie distabat a longitudine magna 116 40, hoc est 2 10 in equaliter 0 0 add. et del. A

Finis tertii libri M〈agne〉 C〈ompositionis〉 P〈tolomei〉.