Demonstrationes astrolabii a Ptholomeo editae, correctae et rectificatae per magistrum Hisaac Hebreum

〈1〉

Scripsit Ptholomeus ad Sirum: Postquam possible est ut circuli secantes spheram appareant in superficie plana, et pluries necessario inducimur ad eos, ideo apparuit mihi, iuxta veritatem sapientie, quod si quis voluerit hoc scire, intelligat hunc tractatum: ut demonstret quomodo debeant circuli paralelli equinoctiali describi, et quomodo circulus declivis inter duos paralellos describatur, ita ut secet equinoctialem in duo media, prout scilicet apparet in figura spherica. Huiusmodi autem dispositio cogit nos ponere rectam lineam pro meridiano.

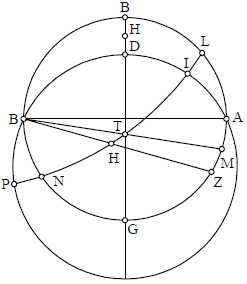
Describamus igitur equinoctialem ABGD super centro E, cuius duo diametri se invicem secent super angulos rectos, et sint AG et BD, quarum una locum meridiani teneat. E autem sit polus septentrionalis; polus enim meridionalis non debet dessignari, ut postea declarabitur, ea etiam causa quod septentrionalis semper apparet in terra habitabili, ideo designandus est. Et oportet ut describamus septentrionales equinoctiali paralellos intra dictum circulum; meridionales autem extra. Cum autem voluerimus hoc facere praecise et exquisite, extrahemus lineam AG utrinque, et secemus de circulo ABGD, ab ipso puncto G, utrinque duos arcus equales, scilicet GH et GN. Et coniungemus punctum D cum H et N duabus lineis rectis, ita ut DH secet AG lineam in puncto C, DN autem in puncto T. Deinde ponemus E centrum, et secundum distantiam EC describemus circulum cuius diameter sit CM. Describamus item super eodem centro E circulum in distantia ET super diametro TL. Postea dividemus lineam TM in duo equa in puncto R, super quo describemus circulum. Secundum medietatem huius lineae, scilicet TM, dico quod hi duo circuli LT et MC equidistant equinoctiali, et quod tertius circulus descriptus super puncto Z est ipse declivis, ita ut linea TM dividit ipsum circulum in duo equa, contingens duos praedictos paralellos, unum in puncto M, alterum in puncto T, et eque dividit etiam equinoctialem in duobus punctis oppositis B D. Coniungamus enim D cum M, linea DM, quae quidem linea secabit equinoctialem in puncto Z. Ergo post speculationem factam manifestabitur quod arcus AZ est equalis arcui HG, qui positus est equalis GN. Nam ME est equalis EC, et angulus MED CED sunt recti, et latus ED est commune duobus triangulis MED CED. Ergo DM erit equale DC, et extrahemus lineam DA et DG, quae sunt equales, quia sunt o corde quartae circuli. Sed AM est equale CG, ergo angulus ADM erit equalis angulo GDH. Ergo arcus AZ 〈equalis〉 arcui GH; ergo arcus ZDN erit semicirculus, et propterea angulus MDT erit rectus per 30 tertii. Quapropter circulus descriptus super diametro TM transibit super puncto D, aliter enim sequeretur contra 16 primi Euclidis. Similiter declarabitur quod transibit super puncto B. Igitur oportet ut secet equinoctialem per equa, et est inter duos paralellos equinoctiali. Et secundum huiusmodi viam poterimus extrahere paralellos equinoctiali ad libitum. Et est manifestum quod si secuerimus de circulo ABGD a duabus partibus G duos arcus equales, secundum quantitatem maximae declinationis, et descripserimus circulos, erit intrinsecus paralellus Cancri et exterior paralellus Capricorni. Et circulus signorum transibit super punctum Cancri et Capricorni, secando equinoctialem in duo media. Circulus quoque signorum dividetur in quatuor partes, quarum duae quaelibet proximae erunt equales, non autem quatuor inter se. Et erit caput Arietis B, et caput Librae D, et initium Capricorni T, Cancri autem M. BT autem erit equalis DT et BM MD. Qui autem voluerit dividere ipsum adunguem ut oportet, faciat hoc modo: Accipiat de ipso equinoctiali, ab ipso puncto G, arcum equalem declinationis gradus alicuius signi propositi, et circumscribat circulum secundum modum praedictum. Et punctus circuli signorum in quo transibit ille circulus erit gradus quaesitus. Postquam autem diviserimus unam praedictarum quatuor partium, non erit necesse vacare in divisione alterius partis oppositae. Quaelibet enim linea transiens per polum equinoctialis quae locum meridiani obtinet, secabit circulum signorum in duobus punctis oppositis.

〈2〉

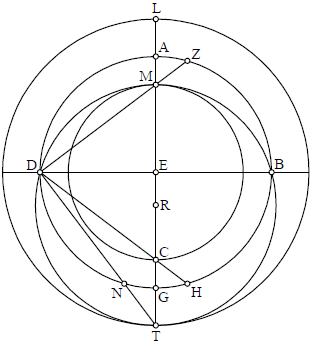
Secundum sphericam figuram, iuxta igitur huiusmodi dispositionem, poterimus dividere, scilicet circulum signorum, per singulos gradus. Postea autem describeamus orizontem secundum quod descripsimus circulum signorum. Qui quidem oz orizon secabit equinoctialem in duo equa secabit quoque circulum signorum in duas partes equales in potentia, id est quod denotant partes equales in sphera mundi, licet ipse partes non sint equales in figuram ipsam superficiali. Sed quidem, ut demonstrationem faciamus de eo quod diximus de divisione circuli signorum per dictam lineam, describamus equinoctialem ABGD super centro E. Declivis sit ZBHD, dividens equinoctialem in equa in punctis B D. Et extrahamus super polo E lineam rectam, quomcumque cadat, AZEGH, quae locum meridiani teneat. Dico quod duo puncta Z H sunt opposita in sphera. Secundum quod praediximus, id est quod paralelli equinoctiali transeuntes super his punctis secant de circulo signorum duos equales arcus a duabus partibus equinoctialis modo iam dicto.

Extrahamus enim a puncto E perpendicularem super lineam AG, quam continuemus usque ad T. Postea extrahemus lineas rectas TZC TA TG TLH. Quoniam per 30 tertii angulus ATG est in medietate circuli, erit de necessitate rectus. Et quoniam id quod fit ex ZE in EH est equale per 34 tertii ei quod fit ex ED in se, et ED est equalis ET, ergo erit equale ei quod fit ex ET in se. Igitur per 16 sexti proportio ZE ad ET erit ut proportio ET ad EH. Ergo per conversam 8 sexti angulus ZTH rectus. Sed angulus ATG est etiam rectus. Ergo si dempserimus ab eis ZTG commune, remanebit angulus ATC equalis angulo GTL. Quapropter arcus AC et GL erunt per 25 sexti equales. Ex hoc itaque clarum est quod lineae TC et TL secant duos arcus equales abde equinoctiali, et intersecantdeterminatos per ipsum punctum T, qui distat a duobus punctis AG oppositis per quartam, et pervenientes ad circulum signorum in duobus punctis Z H, super quibus oportet circumscribi duos paralellos equinoctiali invicem equales per equalem distantiam. [Ergo] Ergo linea ZEH cadit super duo puncta diametraliter opposita in sphera.

〈3〉

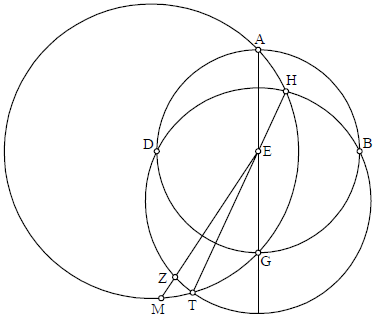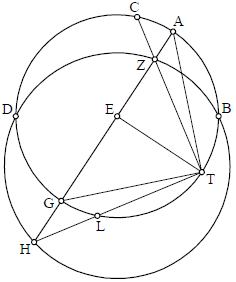
Deinde autem describamus circulum alium declinantem ab equinoctiali, qui locum orizontis teneat, ita ut eque secet equinoctialem. EtDico quod ipse quidem secabit circulum signorum in duobus punctis diametraliter oppositis in sphera, modo praedicto, id est quod linea coniungens huiusmodi duo puncta transit per polum, qui est centrum equinoctialis. Sit ergo equinoctialis ABGD super centro E, et circulis signorum HBTD. Diameter equinoctialis coniungens puncta sectionis sit linea BED, orizon HATG, qui quidem eque secat equinoctialem super diametro AEG et circulum signorum in duobus punctis H T. Dico quod si coniunxerimus H cum E per lineam rectam quae locum meridiani obtinet, et continuemus ipsam usque ad orizontem, necessario transibit super puctum T. Extrahamus igitur HE usque ad orizontem, in puncto T. Dico quod punctus T est communis orizonti et circulo signorum. Nam, quoniam in circulo HATG intersecantur duae lineae AG et HT, per 34 tertii, quod fit ex AE in EG erit equale ei quod fit ex EH in ET, ei etiam quod fit ex BE in ED. Igitur necessario BD et HT erunt in eodem circulo. Ergo punctus T erit super circulo signorum. Sed idem punctus erat super circulo orizontis, scilicet HATG. Ergo orizon secat circulum signorum in duobus punctis diametraliter oppositis secundum spheram. Aliter: Dico quod impossibile est ut HE secet orizontem nisi in puncto T. Si enim possibile est secet ipsum in puncto M, et secet circulum signorum in puncto Z. Quoniam id quod fit ex AE in EG est equale ei quod fit ex HE in EM et BE in ED, et BE in ED est equale ei quod fit ex HE in EM EZ. Ergo quod fit ex HE in EM est equale ei quod fit ex HE in EZ. Ergo EM et EZ sunt equales, quod est impossibile. Ergo impossibile est ut EH continuata secet orizontem nisi in puncto T. Ex hoc manifestum est quod quilibet circulus secans alterum horum circulorum, scilicet equinoctialem etvel circulum signorum, per equa secat quoque et reliquum per equum.

〈4〉

Cum autem hoc ita manifestum sit, inveniemus proportionem semidiametrorum paralellorum equinoctiali descriptorum super circulo declivi ad semidiametrum equinoctialis. Hoc et enim medio inveniemus ascensionem signorum et exquisite cognoscemus quantitatem ascensionis eorum, sicuti apparet et in sphera recta et in obliqua. Describamus igitur equinoctialem ABGD super centro E, cuius duae 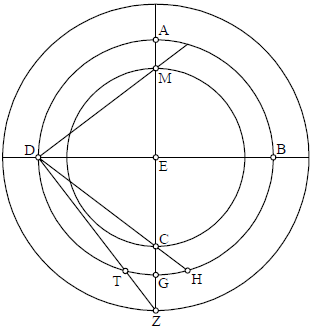diametri, intersecantes invicem ad angulos rectos in puncto E, sint AG DB. Et continuamus lineam AG usque ad Z, et secemus a puncto G utrinque duos arcus equales, scilicet GH GT, extrahamusque duas lineas DCH DTZ, et describamus duos paralellos equinoctiali, septentrionalem scilicet et meridionalem, super centro E. Et septentrionalis sit secundum quantitatem EC, meridionalis vero secundum quantitatem EZ. Dico igitur quod proportio EZ ad ED est ut ED ad EC. Nam, quoniam GH GT arcus sunt equales, erunt arcus BH et DT equales. Igitur arcus BH et BT simul erunt equales semicirculo; etergo de necessitate, angulus BDT et BDH erunt simul sumpti equales uni recto. Sed angulus HDB et ECD simul sumpti sunt equales uni angulo recto. Igitur duo trianguli rectanguli, scilicet EDC et EDZ, sunt similes. Ergo proportio EZ ad ED est ut ED ad EC. Cum autem hoc declaratum sit, accipiemus proportionem arcuum BT et TD et eorum cordarum. Quoniam itaque manifestum est quod proportio anguli BDT ad angulum BDH est ut proportio arcus BT ad arcum TD, cum arcus TD sit equalis arcui BH. Quae quidem proportio est [ut] ut proportio arcus BZ EZ ad arcum ED de circulo descripto super triangulum EDZ. Et hoc, propterea quod angulus BDH est equalis angulo EZD. Idcirco manifestum, arcus enim ad arcum ut corda ad cordam, est quod proportio EZ ad ED et ED ad EC est ut proportio corde arcus BT ad cordam arcus TD. Postquam igitur hoc totum ita manifestum sit, ponamus primo arcum GH et GT 23 partium, 51 minutorum, 2 secundorum, de partibus quibus universus circulus est 360, et est maxima declinatio. Iuxta igitur hoc, arcus BC BT erit 113 gradus, 51 minutorum, 2 secundorum, et BH, residuus de semicirculo, erit 66 gradus, 8 minutorum, 58 secundorum. Et linea recta quae est corda arcus BT, est 100 partes, 33 minutorum, 58 secundorum, de partibus quibus semidiameter est 120, prout positum est in Almagesto. Et corda arcus BH erit 25 partes, 29 minutorum. Huiusmodi itaque proportio est ut proportio EZ ad lineam ED, et ut ED ad EC. Et quoniam linea ED, quae est semidiameter equinoctialis est 60 partium, erit EZ 92 8′ 15′′, et est semidiameter paralelli hiemalis, scilicet initii Capricorni. Sed semidiameter circuli estivalis, scilicet initii Cancri, erit 39 4′ 19′′. Ex hoc autem decla〈ra〉bitur quod medietates harum duarum diametrorum simul sumptae erunt ipsa diameter circuli signorum, scilicet 131 12′ 34′′, cuius medietas est 65 36′ 17′′. Distantia autem centri circuli signorum a centro equinoctiali erit 26 31′ 58′′.

〈5〉

Amplius ponamus arcus GH GT 20 39′, iuxta scilicet distantiam paralellorum equinoctiali, qui distant a duobus tropicis per unum signum utrinque. Erit igitur: Arcus BT 100 30′ 9′′, cuius corda est 98 55′ 59′′, et arcus BH 69 20′ 61′′, cuius corda 68 23′ 51′′. Et quoniam proportio 98 35′ 59′′ ad 68 23′ 51′′ est ut proportio EZ ad ED lineam, et ut ED ad EC, ergo oportet quod: Linea EZ sit 66 29′ 42′′, et EC 41 39′ 15′′.

〈6〉

Iterum, ponamus arcus GH et GT 11 39′ 59′′, in distantia scilicet paralellorum equinoctiali qui distant 60 gradus a duobus tropicis, scilicet duobus signis. Erit itaque: BT 41 39′ 51′′, cuius corda est 93 20′ 14′′, et arcus BH erit 78 51′, cuius corda 75 47′ 23′′. Et quoniam proportio 93 20′ 14′′ ad 75 47′ 23′′ est ut proportio EZ ad ED, et ut ED ad EC, oportet igitur ut ex partibus quibus ED est 60, linea EZ habeat 73 39′ 17′′, et linea EC 48 52′ 42′′.

〈7〉

Ergo si posuerimus arcus GH et GT 54, iuxta scilicet distantiam equinoctialis eta paralellis qui tanguntur ab orizonti climatis Rodi, quarti scilicet, erit arcus BT 144 partium, cuius corda 94 7′ 37′′, et arcus BH 36 partium, cuius corda 36 4′ 55′′. Et quoniam proportio 94 7′ 37′′ ad 36 4′ 55′′ est ut proportio EZ ad ED et ut proportio ED ad EC, oportet ut EZ sit 183 39′ 48′′, et EC 19 42′. Et iam declaratum est quod hae due lineae simul sumptae sunt diameter praedicti orizontis, quemadmodum diameter circuli signorum est duae semidiametri circulorum tropicorum. Et Est itaque scilicet diameter circuli orizontis 204 partium, cuius medietas est 102. Et distantia eius centri a centro equinoctialis est 82 partium et 3 secundorum. Nunc autem volumus declarare quod polus meriodinalis non debet dessignari in astrolabio. Quoniam enim linea DT et DH monstrant distantiam paralellorum equinoctiali ab ipso equinoctiali, et semidiameter meridionalis circuli est a puncto E usque ad locum ubi lineae DT et EG, ut puta in Z, intersecantur. Exempli gratia: Si posuerimus arcum GT 89 partium, DT necessario ocurret linee EG in extremitate semidiametri paralelli equinoctiali, qui distat ab ipso equinoctiali 89 partibus. Sed distantia poli meridionalis est 90 partium, iuxta scilicet quantitatem arcus GD. Cum igitur ita sit, impossibile est designare polum meridionalem septentrionali iam dessignato. Si enim extraxerimus has duas lineas, scilicet EG et coniungentemcontangentem in puncto D etiam in infinitum, numquam concurrent, cum equidistent. Si autem imaginati fuerimus polum dessignatum esse, scilicet ipsum meridionalem, impossibile erit designare septentrionalem.

〈8〉

Cum autem huiusmodi res declarate sint, oportet demonstremus quod possumus numerare et cognoscere ascensionem signorum in sphera plana, ut et in corporea. Sit equinoctialis ABGD super centro E, et circulus signorum sit ZBHD super puncto centro T, et duarum diametrorum intersecantium invicem ad angulos rectos in puncto E, una coniungat puncta sectionisum equinoctialis scilicet B et D; altera autem transeat super duo centra, scilicet linea AZ et GH; punctaque H Z sint tropica. Manifestum itaque est quod arcus HB et HD, qui sunt due quarte circuli declivis, ascendunt cum arcubus GB et GD, quae sunt duo quarta equinoctialis. Oportet quoque quod simul transeant medium celi et quod simul descendant. Cuius demonstratio est quoniam diameter ZG dividit BD per equa ad angulos rectos in puncto E. Et quoniam intentio est declarare ascensionem signorum in orizonte recto, qui scilicet est tanquam meridianus, qui est linea recta transiens per polum equinoctialis E, idcirco oportet nos accipere duos arcus equales in circulo signorum, scilicet CB et DL.

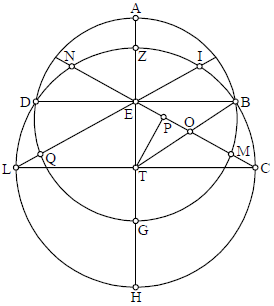Extrahamus enim lineas CMEN LQEI. Et quoniam in punctis C L I N transeunt paralelli equidistantes equaliter distantes ab equinoctiali, ita ut punctus C opponitur puncto N in potentia, et similiter L puncto I opponitur. Si posuerimus arcum CB signum Piscium, erit LD Libra, similiter BI Aries et ND Virgo. Extrahemus igitur lineas CT LT. Quoniam triangulus CTE est equalium laterum et angulorum triangulo LTE, erit per 4 primi angulus CET equalis angulo LET. Similiter quoque reliqui anguli CEB LED erunt equales, quia sunt residui duorum rectorum. Similiter quoque anguli oppositi erunt equales, quia reliquum est duorum rectorum. Sed huiusmodi anguli sunt super centro equinoctialis. Igitur arcus equinoctialis subtensi his angulis ascendentes cum his 4 signis erunt equales. Postquam autem demonstravimus quod sunt equales, investigabimus quantitatem cuiusque eorum. Erigamus enim perpendicularem super lineam CE, quae sit TP. Quoniam igitur de partibus quibus EG semidiameter equinoctialis est 60 partium linea TC, semidiameter scilicet scilicet circuli signorum, est 65 partium 36 minutorum 17 secundorum, et linea ET quae interiacet duo centra horum circulorum est 26 partium et 31 minutorum. Linea denique EC, quae est semidiameter paralelli descripti super initium Piscium et Scorpionis, scilicet puncta C L, est 72 39′ 7′′. Ideo erit triangulus TCE notus. Ergo per duodecimum primam et tertiam secundi Euclidis: Si diviserimus per lineam EC quadratum TC, postquam extraxerimus ab eo quadratum TE, remanebit superantia CP super EP. Si enim assumpserimus lineam PO equalem PE et continuaverimus ipsam ipsum O cum T, erit TO equalis TE. Sed per 12 secundi Euclidis quadratum TC est equale duobus quadratis TO et OC et ei quod fit ex CO in OP bis. Et per primam secundi, OC in OP bis est equale ei quod fit ex CO in OE. Ergo si auferemus ex quadrato TC quadratum TO sive TE, remanebit quadratum CO et quadrangulum factum ex CO in OE. Sed per tertiam secundi quod fit ex CE in OC est equale quadrato CO una cum quadrangulo facto ex CO in OE. Ergo si diviserimus quadratum TC, post extractionem quadrati TE per linea TC,EC, resultabit linea CO, quae est superantia,excessus, linee CP super lineam PE. Similiter quoqueAliter quoque huiusmodi excessus inveniemus: Nam, cum fuerint duo circuli inequales quorum maior eque secat minorem, si a quadrato semidiametri maioris extraxerimus quadratum lineae quae est inter duo centra, remanebit quadratum semidiametri minoris. Itaque, quoniam declivis secat eque equinoctialem, quadratum semidiametri maioris circuli, scilicet lineae TB, superat quadratum lineae TE, quae est distantia centrorum, per quadratum semidiametri equinoctialis scilicet EB, propterea quod angulus BET est rectus. Linea autem TB est equalis lineae CT. Linea autem EB, semidiameter scilicet equinoctialis est 60 partium, cuius quadratum est 36000. De quibus linea EC est 73 39′ 4′′. Igitur quadratum EB equivaleat, per 47 primi et 12 secundi, quadrato CO una cum eo quod fit ex CO in OP bis. Sive AB 〈quadratum〉 EB equivaleat, per 2 et 3 secundi, CE in CO. Igitur si diviserimus per lineam CE quadratum EB, resultabit superantia CP super PE, scilicet 48 22′ 42′′. EtQuod si minuerimus huiusmodi superantiamexcessum a linea CE, relinquentur 52 47′ 25′′, cuius medietas est linea PE, scilicet 12 23′ 42′′. Quibus partibus linea ET est 26 31′ 51′′. Igitur hoc patebit per tabulas de corda et arcu: De partibus quibus arcus ET est 180 de circulo descripto circa triangulum EPT, oportet ut arcus situatus super lineam PT sit 124 2′, et arcus qui est super cordam PE 55 40′. Ergo de partibus quibus 360 correspondent quatuor angulis rectis, angulus PTE erit 27 50′. Qui quidem angulus, cum angulo PET, per sicut unum angulum rectum, similiter quoque cum angulo BEM. Itaque, si auferemus communem angulum, remanebit angulus BEM equalis angulo PTE. Ergo angulus BEM est 27 50′. Et quoniam est super centro equinoctialis arcus subtensus, scilicet BM, erit 27 50′ de partibus quibus totus circulus est 360. Igitur ascensiones quatuor signorum apud initium Librae et Arietis inventae sunt in sphera plana, quemadmodum et in corporea. Possumus etiam hoc idem demonstrare via faciliori: Nam quod fit ex BE in ED est equale ei quod fit ex CE in EN, per 34 tertii, quod est 3600. Quae si diviserimus per lineam EC, resultabit quantitas EN nota. Sed CE superat ipsam EN per duplum PE. Ergo PE erit nota. Quoniam TP, linea perpendicularis super NC, eque dividit ipsum CN. ET autem est nota, quae opponitur angulo P recto. Erit ergo angulus PTE notus, qui est equalis angulo BEC, quia PET angulus et ETP simul sumpti equantur uni recto. Similiter, TEP et BEM simul sumpti equantur uni recto. Ergo angulo communi ablato, scilicet TEM, alii duo remanebunt invicem equales. Et propterea arcus BM notus.

〈9〉

Per ipsam itaque viam, qua numeravimus ascensionem horum quatuor signorum, numerabimus ascensiones reliquorum signorum. Ponemus enim arcum CB, duo signa, ita ut C sit initium Aquarii et L initium Sagittarii, N initium Leonis et I initium Geminorum. Et erit, prout iam declaratum est linea EC, quae est semidiameter paralelli descripti super initium Aquarii et Sagittarii: 86 29′ 42′′. Si igitur diviserimus 3600 per hunc numerum, resultabit superantia lineae CP super lineam PE, scilicet 41 28′ 18′′. Quam si abstulerimus a linea CE, remanebit 44 51′ 24′′, cuius medietas est 22 25′ 12′′, que est linea PE, de partibus quibus ET est 26 31′ 58′′. Igitur de partibus quibus ET est 120, PE erit 101 28′; et arcus corde PE erit 115 29′, de partibus quibus universus circulus est 360. Igitur de partibus quibus 360 faciunt 4 angulos rectos, angulus PTE erit 57 44′, cui quidem angulus BEC est equalis. Et propterea quod est super centro equinoctialis oportet ut arcus BM sit iuxta eandem quantitatem. A quo autem arcu, si auferemus partem Piscium, remanebit ascensio Aquarii: 29 54′; secundum quam quidem quantitatem est etiam ascensio reliquorum trium signo〈rum〉, quae equaliter distant a puncto equinoctiali. Cum extraxerimus 〈totum〉 hoc a 90, remanebit ascensio unius cuiusque 4 reli〈quorum〉 signorum, scilicet Geminorum, Cancri, Sagittarii et Capricorni.

〈10〉

Quum fuerint duo circuli equales invicem secantes, punctaque sectionum per lineam rectam coniungantur, dico quod linea coniungens duo centra eorum secabit praefatam lineam per equum ad angulos rectos; secabitur quoque ab ipsam per equa ad angulos rectos.

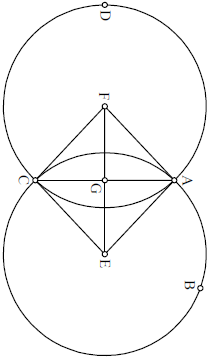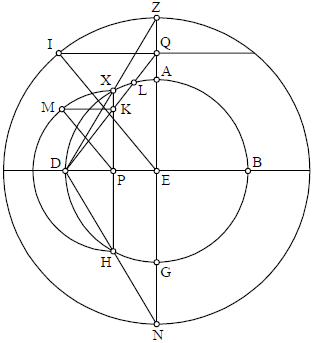
Sint duo circuli equales ABC ADC, secantes invicem in punctis A et C, quorum centra sint E et F. Deinde extrahantur due linee intersecantes invicem in puncto G: FE et AC. Dico quod AG equatur GC, et EG GF, et quod anguli ad G sunt recti. Nam, quoniam AE et AF trianguli AEF equantur CE et CF trianguli FCE, quia a centro ad circumferentiam, et FE est commune, ideo angulus AEF est equalis angulo FEC; similiter AFE ipsi CFE. Et quoniam duo latera continentia angulum AEG equantur duobus lateribus continentibus angulum GEC, equalem scilicet ipsi AEG, ideo per quartam prima, AG equatur ipsi GC, et angulus EGC ipsi AGE. Ergo tam EGC quam AGE, per diffinitionem, sunt recti; similiter oppositi. Similiter, quoniam AE et EC trianguli ACE equantur AF et FC trianguli AFC, et AC est communis, ergo angulus FCG equatur angulo ECG, per 4 quartam igitur Euclidis. EG equale ipsi GF, quod est secundum propositum. Postquam autem declaratum est hoc, investigabimus utrum ascensiones in sphera obliqua sint equales ascensionibus spherae rectae an non; et sequemur in hoc exemplum positum in Almagesti, de orizonte Rodi, in quo polus septentrionalis elevatur 36 partibus, et eius diameter, iuxta praedicta, est 150 partium et 4 minutorum 44 secundorum, et distantia eius centri a centro equinoctialis est 82 35′ 3′′. Ponamus ergo equinoctialem ABGD super centro E, circulum que signorum ZBHD super centro T, et imaginemur motum sphere super puncto E fixo, quod est polus septentrionalis, a puncto D ad punctum G, et a puncto B ad punctum A. Et describamus duos arcus orizontis transeuntes super puncta tropicorum, scilicet ZH, quorum arcuum unus sit ZCHL, alter ZMHN. Cum igitur situs spherae fuerit secundum orizontem ZCHL, oportebit ut Z ascendat cum puncto C, punctaque opposita, scilicet HL, una condescendant. Cum autem sphera fuerit situata secundum orizontem ZMHN, oportebit ut NH simul ascendant, et in ipso eodem tempore MZ simul descendant, imaginando scilicet spheram moveri super punctum E, quod est polus septentrionalis. Dicamus itaque: Quoniam non solum circulus signorum non eque secat equinoctialem, sed etiam omnis orizon eque secat equinoctialem, ideo oportet ut lineae rectae coniungentes puncta sectionum, scilicet CL et MN, transeant per punctum E. Ergo manifestum est quod arcus MN est equalis arcui CL, et AG similiter AM ipsi GN, quia opposita. Et relinquetur arcus LG equalis arcui AC. Assignemus ergo duo centra horum orizontium, Q et I, et extrahamus lineas QT TI QE EI. Ideo 〈op〉ortet ut linea †…† QTI sit una linea dividens ZH per equum ad an〈gulos〉 rectos. Similiter, linea QE erit perpendicularis super lineam CL, †…† 〈su〉per MN, per 3 tertii. Cum autem ita sit, manifestum est per [penul] penultimam primi et 8 eiusdem, quod angulus QET est equalis angulo IET; et duo anguli QEC et IEM sunt recti. Reliqua quoque anguli, scilicet AEM et AEC, sunt equales. Nam anguliis QEL et IEM sunt invicem equales, quia recti, ut iam patuit. Ergo angulo NEL communi ablato ab utrisque, relinquentur anguli QEN et IEL invicem equales. Sed monstratum est quod QET et IET sunt invicem equales. Ergo angulis QEN IEL invicem equalibus demptis ab ipsis QET et IET, relinquentur NET et LET invicem equales. Igitur anguli AEM et AEC oppositi erunt equales invicem. Similiter quoque, propter angulos equales, arcus AM AC et LG GN invicem equales, quia opposita prioribus. Igitur quoniam arcus HB ascendit cum arcu NB, et BZ cum arcu CB, qui est equalis BN, similiter arcus ZD cum arcu DC, et DH cum DN, qui equatur DC. Ex hoc manifestum est quod arcus circuli declivis, equaliter distantes utrinque ab altero puncto equinoctio, habent ascensiones equales. Manifestum quoque est quod arcus DZ habet ascensionem in sphera obliqua minorem quam in sphera recta per quantitatem CA; et arcus oppositus, scilicet HB, habent maiorem ascensionem in sphera obliqua quam in recta, per arcum GN, equalem scilicet arcui MA et AC. Et oportet ut ascensionem si arcus circuli signorum, qui est ex parte Arietis, sint minores in sphera obliqua quam in recta, per tantum, quantum ascensiones arcus oppositi sunt maiores in sphera obliqua quam in recta. Et est manifestum quod dies brevissima in praedicto climate est minor die mediocri per quantitatem duorum arcuum AC et GN, et longissimus est maior mediocri ipsam eadem quantitate.

〈11〉

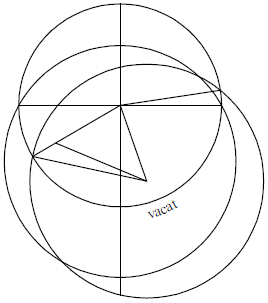Deinceps autem perscrutemur an differentia horum dierum in praefato climate sit concors cum differentia quae reperitur in sphera corporea. Et pingamus ad hoc ipsam eandem figuram quam supra, nisi quod horizon non transeat nisi super punctis Z C H L. Et ut deveniamus ad intentum nostrum, ponamus Q centrum horizontis, et extrahamus lineas QT QE, perpendiculares super lineas ZH CL. Quoniam itaque iam dictum est quod linea QE, distantia scilicet centrorum equinoctialis et horizontis, est 82 35′ 3′′, de partibus quibus ET, distantia scilicet centrorum equinoctialis et circuli signorum, est 26 35′ 58′′: Igitur de partibus quibus linea EQ, opposita angulo recto, fuerit 120, linea ET erit 38 53′, cuius arcus est 37 30′, de partibus quibus circulus circumscriptus triangulo est 360. Ergo angulus EQT: 18 45′. Angulus autem QET, qui praeficit angulus rectus, est 70 15′. Ergo angulus AEC erit 18 45′, quapropter arcus AC erit eiusdem quantitatis. Cum autem ita sit, quaelibet quarta circuli signorum que est ad punctum vernale ascendit cum 71 15′, et quarta opposita ascendit cum 108 45′. Et propterea, differentia inter diem longissimum et aut brevissimum et ipsum mediocrem est 37 30′, quae duas horas et mediam equales efficiunt, quemadmodum et in sphera corporea apparet.

〈12〉

Post hoc autem investigabimus ascensionem signorum in praefato climate. Pingamus ergo equinoctialem ABGD super centro E, et circulum signorum HDZB. Deinde secemus de circulo signorum arcum BT, signum Piscium, et coniungamus puncta T E L per lineam unam. Pingamus quoque horizontem, secundum altitudinem 36 partium, ita ut transeat super puncta T L, et secet equinoctialem in punctis M N. Extrahamusque lineam NEM. Similiter extrahamus a puncto Q, centro scilicet horizontis, lineas rectas QE et QT. Deinde lineam QI perpendicularem super lineam TL. Igitur prout super memoratum est arcus MS erit differentia qua ascensio Arietis vel Piscium in hoc climate minuit ab ascensione eiusdem in sphera recta. Secundum hanc ipsam quoque quantitatem erit additamentum ascensionis duorum signorum oppositos super ascensionem eiusdem eorundem in sphera recta. Et est manifestum quod linea ET, quae est semidiameter paralelli descripti super initium Piscium, est 73 39′ 7′′, de partibus quibus EQ est 82 35′ 3′′. Sed quoniam quadratum TQ superat quadratum EQ per 3600, scilicet per quadratum semidiametri equinoctialis si diviserimus huiusmodi numerum per lineam ET, evenient nobis res omnes eodem ordine quo evenerunt in sphera recta, et inveniemus lineam EI: 12 22′ 12′′. Nam accipiamus lineam OI equalem IE, et extrahamus lineas QO QM, et tunc quadratum TQ equivalet, per 12 secundi, quadratis TO et OQ, et ei quod fit ex TO in OI bis, seu TO in OE. OE enim duplum est ipsius OI. Sed TQ et QM sunt equales, quia a centro ad circumferentiam, et QO equalis, per 47 primi, EQ. Ergo quod fit ex quadrato QM equum est quadratis TO et OQ, seu EQ, et ei quod fit ex TO in OI bis, seu TO in OE. Sed quod fit ex quadrato TO et ex TO in OE equum est ei quod fit ex ET in TO, per 3 secundi. Ergo quadratum quoniam equum est quadrato OQ seu EQ et EQ quod fit ex ET in TO et quum quadratum MQ idem equivaleat, per 3 tertii et 47 primi, duobus scilicet quadratis EQ et EM, remoto quadrato EQ communi, quadratum ME equivalebit ei quod fit ex ET in TO. Divide igitur quadratum ME per lineam TE iam notam: Prodabit linea TO, quae subtracta a linea TE remanebit OE, quae iam divisa in duo equa, OI et IE, nota erit linea IE, quam quaerebamus. Sed de partibus quibus linea EQ, subtensa angulo recto, est 120, linea EI erit 18 partium et unius minutorum, cuius arcus est 17 16′, de partibus quibus universus circulus descriptus circa triangulum EQI est 360. Ergo angulus EQI: 8 38′. Qui quidem angulus EQI est equalis MES, si enim extraxeris lineam QI usque ad lineam EM in puncto Y, probabis, ex 8 sexti Euclidis, angulum EQI equari angulo MES, ex hoc scilicet quod angulus QEM est rectus.

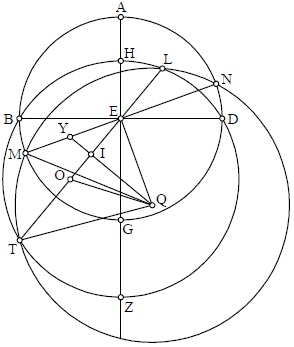Quod autem ita sit, patet: Nam linea MEN divisa est per equum in puncto E, et est corda arcus MLN. Et a centro huius arcus, scilicet Q, procedit linea QT, dividens ipsam cordam MEN per equum, ergo ad angulos rectos, per 3 tertii. Et propterea quod quodlibet quatuor signorum quae sunt apud equinoctia ascendit in sphera recta cum 27 50′. Si extraxerimus ab hac summa 8 38′, remanebit ascensio Arietis et LibraePiscium in hoc climate: 19 12′. Si autem addiderimus 8 38′ ascensioni eius in sphera recta, proveniet ascensio Virginis et Librae: 36 28′.

〈13〉

Iuxta autem huiusmodi dispositionem poterimus mensurare ascensionem duorum signorum, scilicet Piscium et Aquarii. Nam linea ET, semidiameter scilicet paralelli descripti super initium arcui, erit 86 partium 29′ 42′′. Per quem numeratur, si diviserimus 3600, scilicet quadratum EM, et fecerimus reliqua omniam ut super, inveniemus lineam EI: 22 25′ 42′′. Ergo de partibus quibus EQ fuerit 120, linea EI erit 31 32′, cuius arcus est 31 32′, de circulo descripto circa triangulum EQI. Ergo de partibus quibus 360 partes correspondent quatuor angulis rectis, erit angulus EQI: 15 partium et 46 minutorum, et propterea quod est equalis angulo TEM, per 8 sexti erit arcus SM: 15 6′, differentia scilicet inter ascensionem obliquam horum duorum signorum et ascensionem eorum rectam, quae est ut supra diximus, 57 48′. A quibus, si dempserimus 15 46′, remanebit ascensio Aquarii et Piscium simul: 41 58′. A quibus, si de dempserimus ascensionem Piscium, remanebit ascensio Aquarii: 22 46′. Si autem addiderimus 15 46′ ascensioni rectae Virginis et Leonis, scilicet 57 48′, proveniet ascensio obliqua Leonis et Virginis: 73 34′. A quibus, si dempserimus ascensionem obliquam Virginis, scilicet 36 28′, remanebit ascensio obliqua Leonis: 37 6′. Et est manifestum quod ascensio Tauri est equalis ascensioni Aquarii, et ascensio Scorpionis ascensioni Leonis. Et quoniam Gemini et Capricornus ascendunt cum residuo ascensionis correspondentis unicuique quarte Geminorum et Capricorni, similiter quoque Cancer et Sagittarius ascendit cum residuo ascensionis obliquae correspondentis unicuique quartae Cancri et Sagittarii. Ideo Gemini et Capricornus habebunt ascensionem 29 partium et 17 minutorum; Cancer autem et Sagittarius, unusquisque eorum, 35 15′, de partibus scilicet quibus equinoctialis est 360. Talis itaque est computatio ascensionis signorum in climate quarto Rodi, qui est in medio habitationis, et secundum hanc exemplificationem possumus fas facere in omni climate.

〈14〉

Huc usque, in hac prima parte huius tractatus, tractavimus de circulis paralellis equinoctiali et de ascensionibus signorum. Deinceps autem tractabimus de paralellis ipsi circulo signorum, ut inveniamus situs stellarum fixarum et dessignemus eos in ipsa re〈c〉tae. Accipiamus itaque, de circulis dessignatis, circulum exteriorem, qui scilicet continet reliquos circulos, et sit circulus ABGD super centro E, qui locum meridiani obtineat; et eius diametri, intersecantes invicem ad angulos rectos, sint AG BD. Deinde secemus, a puncto D, arcum DZ 66 partium, secundum scilicet distantiam initii Capricorni a polo equinoctialis; et extrahamus, a puncto G, lineam equidistantem lineae ED, quae sit GH. Et coniungemus D cum Z per lineam HD; et a puncto H erigamus perpendicularem HT super lineam ED; coniungamusque G cum D per lineam secantem, sit in puncto K. Dico quod si secuerimus de linea EG lineam equalem TK, scilicet EL, et super centro E descripserimus circulum QLM secundum quantitatem distantiam EL, circulus ABGD distabit a circulo QLM secundum quantitatem arcus similis arcui DZ. Sed ut hec rectae demonstremus, iungamus G Q cum M per lineam secantem circulum QLM in puncto N. Et ideo erit arcus MN similis arcui DZ; similiter, arcus GZ, residuus de quarta circuli, erit similis arcui LN, residuo de una quarta. 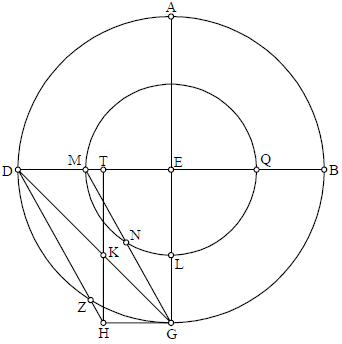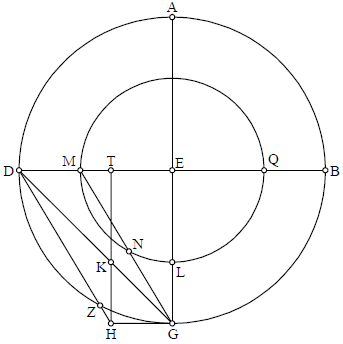Hoc autem manifestum est et clarum ex hoc: Nam proportio, per 2 sexti DE ad EG est ut DT ad TK, quoniam TK equidistat EG. Ergo per secundam sexti sequetur consequentia. Sed DE equatur EG; igitur DT equatur ipsi TK, et TK equatur EM; ergo EM equatur DT. Ergo si posuerimusauferemus TM commune, erit ET equalis MD. Sed ET est equalis et equidistans ipsi GH, MD quoque erit equalis et equidistans ipsi GH. Quapropter HD et GM erunt equales et equidistantes; ergo angulus GME erit equalis angulo ZDE, et propterea arcus QLN similis est arcui BGZ. Similiter quoque, residuus de semicirculo, scilicet MN, erit similis reliquo residuo de semicirculo, scilicet DZ. Ergo si supposuerimus circulum QLM locum equinoctialis obtinere, circulus ABGD erit descriptus distans ab eo per quantitatem LN, similem GZ. Alio modo faciliori: Si enim coniunxerimus D cum Z et extraxerimus, a puncto G, equidistantem lineae DZ, scilicet GM, deinde descripserimus circulum secundum distantiam EM, erit circulus equinoctialis; quoniam angulus NME est equalis angulo ZDE. Ex hoc enim arcus BGZ assimilatur arcui QLN; et per consequens, residuus arcus NL similis arcui GZ, quod est intentum.

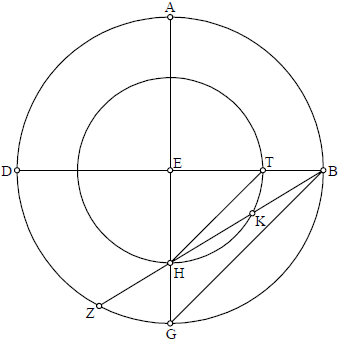Alio quoque modo, hoc idem quam facilime probabitur. Ponamus enim circulum maiorem ABGD super centro E, et extrahamus duas eius diametros secantes invicem ad angulos rectos. Et describamus intra ipsum alium circulum, qui distet a primo secundum distantiam arcus similis arcui GZ. Coniungamus enim B cum Z per lineam secantem lineam EG in puncto H, et ponamus E centrum, super quo describamus circulum secundum distantiam EH, qui sit HKT. Dico quod arcus KT similis est arcui ZG; nam, coniungamus G cum B et H cum T, erit, per 2 sexti HT equidistans GB. Ergo angulus KHT erit equalis angulo GBZ; sed quolibet eorum est super circumferentiam circuli. Igitur arcus KT assimilatur arcui GZ. Si itaque circulus HTK suppositus fuerit equinoctialis erit circulus ABGD descriptus secundum distantiam KT, similem arcui GZ, quidem est intentum.

〈15〉

Volumus nunc declarare quomodo describantur circuli paralelli ipsis circulo signorum, ut cognoscamus situs stellarum fixarum respectu circuli signorum, absque eo quod cognoscas eorum situm respectu equinoctialis. Ponamus itaque equinoctialem ABGD super centro E, et circulum signorum LBHD, lineaque transiens per ambo centra sit LAHG. Linea denique coniunges sectiones horum circulorum sit BD, et secemus arcum BT secundum distantiam quae i〈n〉ter polum equinoctialis et polum circuli signorum; et transeat linea super puncta D N T. Punctum igitur N erit, per primam huius, polus circuli signorum in potentia. Manifestum igitur est quod si huiusmodi distantia exquisite accipiatur, circulus transiens super huiusmodi polum, scilicet N, duoque puncta circuli signorum diametraliter opposita, secabit equinoctialem per equa.

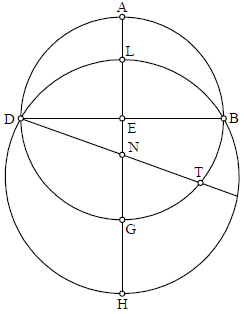Dixit Mesulam: Si huiusmodi circulus descriptis in astrolabio transibit per gradum stellae, necessario quoque transibit per stellam ipsam. Similiter, si transeat per ipsam stellam, transibit quoque per gradum ipsius. Similiter quoque, quaelibet linea recta transiens per polum equinoctialis assignatum in astrolabio, si transit per ipsam stellam, necessario quoque transibit per gradum cum quo mediat celum; et si transit per gradum cum quo mediat celum, necessario quoque transibit per stellam ipsam.

〈16〉

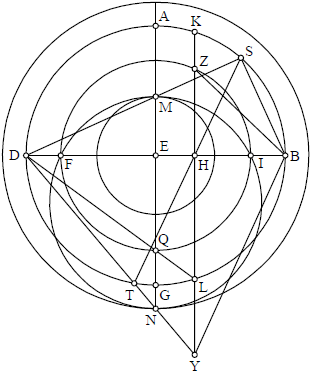Post hec autem notificemus descriptionem paralellorum ipsi circulo signorum. Et primo, describamus meridianum circulum transeuntem per polos equinoctialis ABGD super centro E, et imaginemur quod diameter sphere sit linea DEB, punctumque D polum meridionalem. Imaginemur quoque diametrum equinoctialis AEG, et diametrum paralelli circulo signorum, quem volumus dessignare in astrolabio, lineam SHT. Et extrahamus per punctum H lineam KL, equidistantem linee AG, occur〈r〉entem scilicet extremitatibus lineae DTN in puncto Y. Et extrahemus DMZS DQL et DTN. Dico igitur quod diameter, cuius circulus cuius diameter est ST, potest describi super diametrum MN: Nam huiusmodi circulus continget duos circulos paralellos equinoctiali, quorum distantiae ab eo erunt secundum quantitatem arcuum AS GT. Et propterea, quum descripserimus ipsum in her hos duos circulos per distantiam EN et EM, secabit quoqueper equum circulum paralellum equinoctiali, cuius diameter est LK, in superficie meridiani, cuius diameter est BD. Describatur igitur paralellus LK secundum distantiam QE, qui sit QIF. Dico quod circulus descriptus super diametrum MN secabit per equum circulum QIF, transiens per puncta I F, sicut et in sphera corporea apparet. Coniungantur enim per lineam rectam BS et BZ, et continuentur KL et DT quousque concurrant in puncto Y, quod quidem Y coniungatur cum B. Itaque, quoniam duo anguli BSD et BHZ sunt recti, oportet ut puncta B H Z S sint, per 5 quarti, in circumferentia eiusdem circuli. Quapropter angulus BZH erit, per 20 tertii, equalis angulo BSH, qui est equalis, per 20 tertii, angulo BDT, eo quod supponuntur eidem arcui. Igitur per 34 tertii, angulus BZH equalis angulo BDN; ergo BYDZ sunt in circumferentia eiusdem circuli. Nam circulus descriptus super triangulum ZBY necessario transibit super punctum B.D. Propterea quod angulus BZY est equalis angulo BDY; aliter enim sequeretur contra 16 primi. Igitur quod fit ex BH in HD equum est ei quod fit ex HY in HY, HZ, per 34 tertii. Sed quod fit ex BH in HD equum est ei quod fit ex HL in HK, seu HL in se. Igitur quod fit ex HY in HZ est equale ei quod fit ex HL in se. Sed YZ equidistat ipsi NM; ergo quod fit ex EQ in se est equale ei quod fit ex EM in EN. Nam, quoniam NM equidistat ZY, erit proportio ZH ad ME, per 2 sexti ut proportio DH ipsi DE; similiter per eandem, ut HL ipsi EQ. Igitur ZH ad HL ut ME ad EQ. Sed propter hanc ipsam equidistantiam, HY ad EN ut DH ad DE; ergo HY ad D EN ut ut HL ad EQ. Igitur HL ad HY ut EQ ad EN. Sed HL ad HY, per 16 sexti est ut ZH ad HL, quae quidem proportio est ut EM ad EQ; igitur EM ad EQ ut EQ ad EN. Ergo quod fit ex EM in EN equum est ei quod fit ex EQ in se. Et quoniam EQ equatur ei et EF, puncta N I M F erunt, per 35 tertii, necessario in circumferentia eiusdem circuli. Ergo puncta F I sunt in circumferentia eorundem duorum circulorum, scilicet circuli MN et circuli IQF. Quapropter, circulus descriptus super lineam MN secat circulum IQF per equa in punctis I F, quemadmodum et in sphera corporea apparet. Et nota, ut dixit Mesulam, quod distantia paralelli circulo signorum signorum mensurat latitudinem stellae. Igitur si extraxerimus a puncto N, quod est polus circuli signorum, arcum transeuntem super gradum ipsius stellae, secantem circulum signorum in duo equa potentialiter, punctus ubi secabit paralellum circulo signorum erit locus ipsius stellae in astrolabio. Hac autem eadem via qua descripsimus paralellos circulo signorum, poterimus describere paralellos horizonti, qui quidem dicuntur Almucantarat.

〈17〉

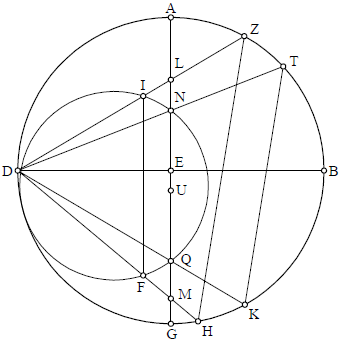Dicimus autem quod necessarium est ut centra circulorum equidistantium circulo signorum sint diversa. Et ad hoc demonstrandum, sit meridianus circulus ABGD super centro E, cuius diameter transiens per polos sit BED, diameter equinoctialis sit linea AG. Diametri autem paralellorum circulo signorum sint ZH TK, et extrahamus lineas DLZ DMH DNT DQK. Deinde circumscribemus circa triangulum DNQ circulum DIF, et extrahamus lineam IF; dividemusque lineam LM per equum in puncto U. Et est manifestum quod circulus, cuius diameter est ZH, potest describi, per praecedentem, super diametrum LM; similiter, circulus cuius diameter est TK potest describi super diametrum NQ. Et quoniam arcus ZT equalis est arcui KH, ex hoc quod ZH equidistat TK, erit arcus IN equalis arcui FQ, nam equales habent angulos in circumferentia eiusdem circuli. Quapropter, lineae LM FI equidistat. Igitur ex secunda sexti proportio LD ad LI ut DM ad MF. Sed proportio DL ad LI, ex prima sexti ut proportio quadrati DL ad quadrangulum factum ex DL in LI; similiter ut proportio quadrati DM ad quadrangulum factum ex DM in MF. Quadrangulum autem factum ex DL in LI, ex 36 tertii, est equale quadrangulo LQ in LN; similiter quoque, per eandem, quadrangulum DM in MF est equale quadrangulo NM in QM. Idcirco erit proportio quadrati DL ad quadrangulum QL in LN ut proportio quadrati DM ad quadrangulum NM in QM. Ergo permutatim, proportio quadrati DL ad quadratum DM ut proportio quadranguli QL in LN ad quadrangulum NM in QM. Sed quadratum DM maius est quadrato DL, ex hoc quod linea DM maior est linea DL; ergo quadrangulum NM in QM maius est quadrangulo QL in LN. Si autem posuerimus quadrangulum LN in QM commune, erit, ex prima secundi, quadrangulum NM in QM cum quadrato quadrangulo LN in MQ equale quadrangulo LM in MQ; et quadrangulum QL in LN cum quadrangulo LN in MQ est equale quadrangulo ML in LN. Ergo quadrangulum LM in MQ erit maius quadrangulo ML in LN. Quapropter MQ erit maior NL. Sed iam supposita est MU equalis LU; igitur UQ minor est UN, et propterea punctum U non potest esse in medio NQ. Cum autem dividat diametrum ML per medium, ideo impossibile est ut paralelli scilicet circulo signorum idem centrum possideant.

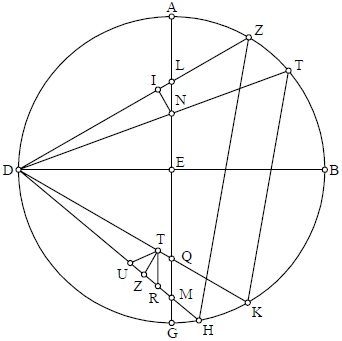Dixit Mesulam: Ptholomeus non demonstravit quod centra non sunt in eodem puncto nisi postquam monstravit quod linea MQ maior est linea LN, quod quidem faciliori modo demonstrabimus. Describamus enim circulum ut super, et extrahamus a puncto N perpendicularem super DL, quae sit NI. Cum autem manifestum sit quod DN est minor DQ (cum DN linea sit proximor centro E quam linea DQ, ergo DN minor est DQ) et DL ipsam DM, igitur secemus de linea DQ lineam equalem DN, quae sit DT. Secemus quoque de linea DM lineam equalem lineae DL, quae sit DZ. Igitur per 4 primi, triangulus DTZ erit equalis triangulo DNZ DNL. Cadat autem perpendicularis TU, sicut et perpendicularis M, erit que angulus DNI equalis angulo DTU; et propterea quod linea DQ longior est linea DN, erit angulus DNQ maior angulo DQN. Et ideo reliquus angulus DQG erit maior angulo DNL, qui est equalis angulo DTZ. Si igitur extraxerimus a puncto T equidistantem lineae MQ, ipsa cadet infra punctum Z. Ea autem equidistans sit TK; ergo proportio QD ad TD est ut MQ ad TK. Ergo linea QM est maior TK, et TK maior TZ, quae est equalis NL. Quod autem TK sit maior TZ, patet ex hoc: Nam, cum angulus DZT equalis angulo DLN sit acutus, ex hoc quod in triangulo DLE angulus DEL est rectus, angulus TZK erit obtusus, et propterea linea KT erit maior ZT, nam maiori angulo subtenditur maior linea. Ex hac autem figura patet quod portiones ipsius lineae GA, determinatae per lineas exeuntes a puncto D super ipsam GA secundum equales arcus, sunt inequales; et quanto propinquiores centro, tanto breviores.

〈18〉

Cum autem paralellus circulo signorum, secans paralellos equinoctiali qui numquam apparent et sunt versus polum meridionalem, non adhuc descriptus est in astrolabio, ideo ponamus meridianum ABGD super centro E, et imaginemur quod polus meridionalis sit punctus D. Diameter transiens per ambos polos equinoctialis sit linea DB, diameter equinoctialis AG, diameter paralelli ipsi equinoctiali sempiterne occultationis sit linea XH. Diameter autem paralelli circulo signorum, qui secat praefatum paralellum equinoctiali, sit TKL. Deinde describamus super lineam XH semicirculum XMH, et extrahamus a puncto K lineam KM, equidistantem DE; et cum extraxerimus lineas DHN DLQ et DTU, erit circulus descriptus secundum quantitatem EN, per puncta N I Z, de circulis qui numquam apparent. Et circulus descriptus secundum lineam QU, paralellus circulo signorum, erit necessario transibit per punctum Q, secans circulum NIZ per portiones similes portionibus HM et NZ MX. Faciamus autem in puncto E, super lineam EA, angulum equalem angulo MFK, qui sit IEN; erit que arcus IZ similis arcui MX (MF et IE sunt equidistantes, et DE cadit super eas; ergo angulus extrinsecus DFM intrinseco DEI est equalis; ergo et residuum MFK residuo IER). Dico igitur quod circulus descriptus secundum lineam TKL equidistans circulo signorum secabit paralellos equinoctiali qui sunt sempiternae occultationis secundum huiusmodi proportionem, id est quod transibit per puncta I Q U, secans circuli NIZ in puncto I. IgiturNam, iuxta additionem Mesulam, extrahamus lineam DX usque ad punctum Z; necessario enim perveniet ipsam linea usque ad Z, quemadmodum linea DH pervenit usque ad punctum N. Et est manifestum ex praecedentibus quod quemadmodum circulus cuius diameter est XH potest describi super diametro ZN, ita etiam circulus cuius diameter est TKL potest describi super diametro QU. Extrahamus autem lineam RKD; similiter quoque continuemus lineam XH usque ad punctum C, et a puncto T ad punctum Y vadat equidistans ipsi HC. Linea igitur UN divisa est ad similitudinem divisionis lineae HC equidistantis. Angulus autem DTY est equalis angulo DLT, ex hoc quod arcus DT est equalis arcui DY; sed angulus DTY equalis est angulo DCH. Ergo puncta L C T O sunt in circumferentia eiusdem circuli. Si enim extraxeris lineam TO, et circumscripseris circulum super triangulum TOL, ipse circulus transibit necessario super puncto C; aliter enim sequeretur contra 16 primi. Igitur quod fit ex CK in KE equale est ei quod fit ex KT in KL. Sed quod fit ex KT in KL est equale ei quod fit ex KX in KH; igitur quod fit ex KX in KH est equale ei quod fit ex KC in KO. Similiter quoque declarabitur quod id quidem fit ex ZR in RN est equale ei quod fit ex UR in RQ. Itaque coniungamus R cum I. Ergo triangulus REI similis est triangulo KFM, quoniam ex suppositionem angulus F est equalis angulo E, et latera continentia hos duos angulos sunt proportionales (sunt enim proportionales quia EN et FH equidistant; igitur erit proportio ED ad FD sicut EN ad FH, et ut ER ad FK, ergo permutatim ER ad EN vel ad ei ut FK ad FH aut ad FM, quae est equalis ipsi FH). Ergo reliqui anguli erunt equales. Cum autem angulus MKF sit rectus, angulus ERI erit etiam rectus; etergo ZR in RN esterit equale ei quod fit ex RI in se per 34 tertii. Sed ZR in RN equale est UR in RQ; igitur UR in RQ equum est RI in se. Et quoniam linea RI est perpendicularis super lineam QU, necesse est per conversam 34 tertii quod puncta I Q U sit in circumferentia eiusdem circuli. Ratio autem qua probatur ut quod fit ex ZR in RN equum sit ei quod fit ex QR in RU est: Quoniam in triangulo DZR linea XK equidistat ipsi ZR, ideo per secundam sexti erit proportio ZR ad XK ut DR ad DK. Item ex eadem secunda sexti QR ad OK est ut DR ad DK; ergo permutatim ZR ad QR ut KX ad OK. Rursus ex eadem secunda 〈sexti〉 proportio ZU ad CK ut DX ad DK; item DN ad RN ad KH ut DR ad DK; ergo permutatim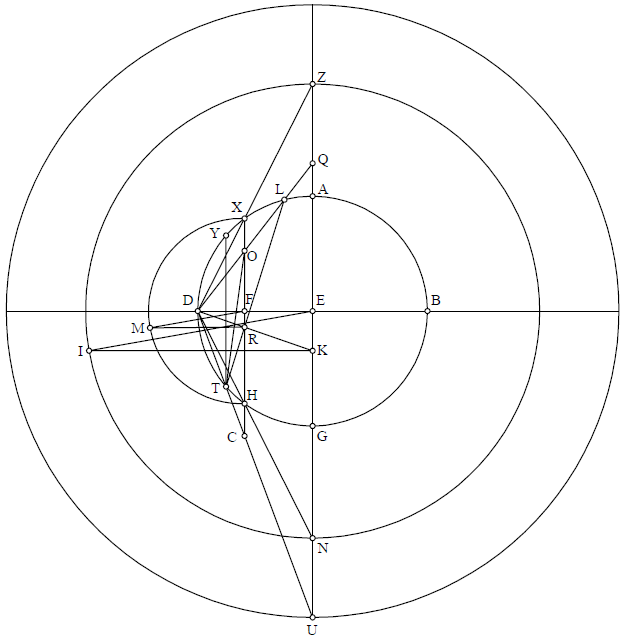

RU ad RN ut KC ad KH. Sed ex eo quod quadrangulum XK in KH equum est quadrangulo ex CK in KO, ut propter probatum est ergo per 15 sexti proportio XK ad KO ut KC ad KH. Ergo proportio ZX ad RQ ut RU ad RN. Ergo quod fit ex ZR in RN equum est ei quod fit ex QR in RU.

〈19〉

Per ipsum eundem modum quo super praecessimus, procedemus quoque in discriptionem paralelli circulo signorum, qui est super diametro DL, transiens per polum meridionalem. Extrahamus enim per punctum Q perpendicularem super lineam AEN, quae quidem perpendicularis obtinebit in sphera plana locum circuli cuius diameter est DL. Huiusmodi enim linea secat paralellos equinoctiali eadem divisionem qua est i〈n〉, et in sphera corporea secantur. Ad hoc autem monstrandum, sit diameter paralelli equinoctiali, qui est sempiternae occultationis linea XH; sitque circulus descriptus secundum distantiam AX sempiternae o occultationis, et fiat semicirculus super lineam XH, et procedat a puncto K linea KM, equidistans ipsi ED. Igitur quemadmodum paralellus circulo signorum, cuius diameter est DL, secatdividit praefatum paralellum equinoctiali in puncto M, in arcus HM et MX, ita etiam linea QI secat circulum NIZ in portiones NI et IZ, similes portionibus HM et MX. Coniungamus enim E cum I, et P cum M; ergo quoniam linea PH equidistat lineae NE, erit proportio NE ad EQ ut PH ad PK, per 2 sexti et per modum superius dictum in praecedenti.

Sed NE est equalis ipsi IE, et PH ipsi PM; igitur proportio IE ad EQ ut MP ad PK. Angulus autem IQE est rectus, similiter angulus MKP; ergo triangulus MPK similis est per 7 sexti triangulo IEQ. Et per consequens angulus IEQ angulo MPK est equalis; ergo arcus M similis est arcui HM, et portiones residuae de semicirculo similes residuis portionibus de semicirculo, quem scilicet dividit paralellus circulo signorum in sphera corporea. Et quoniam praefatus paralellus circulo signorum transit per polum equinoctialis meridionalem, qui quidem non potest assignari in sphera plana, ideo non potest describi in astrolabio. Ex hocEt 〈est〉 manifestum est quod paralellus equinoctiali, divisus per equa a paralello circulo signorum transeunte per polum equinoctialis necessario transit per polum circuli signorum.

〈20〉

His ergo viis et modis describendi sunt in sphera plana circuli, qui sunt in sphera corporea, scilicet: equinoctialis et paralelli eius, circuli meridiani, circulus signorum et eius paralelli, similiter horizon et paralelli eius. Et propterea quod secundum huiusmodi ordinem, locus poli equinoctialis est etiam centrum eius et omnium circulorum ipsi paralellorum, oportet ut paralelli equinoctiali septentrionales quidem sint minores, eo scilicet equinoctiali, meridionales vero maiores. Oportet quoque ut septentrionales gradatim minuantur secundum eorum distantiam ab ipso equinoctiali, meridionales vero gradatim augeantur secundum eorum distantiam ab eo. Necesse est etiam ut meridiani sint lineae rectae, et polus circuli signorum non est centrum eius, neque centrum alicuius paralellorum eius, neque etiam centrum unius est centrum alterius. Circuli autem magni transeuntes per polum equinoctialis estsunt lineae rectae. Circulus quoque transiens per ambos polos est linea recta, super quam quidem sunt centra paralellorum circulo signorum secundum inequales distantias. Possumus autem assignare stellam quamcumque in sphera plana, si erit in corporea, per paralellum equinoctiali aut per paralellum scilicet circulo signorum, et per eandem viam qua monstratum est in climate Rodi. Oportet quoque demonstrare in singulo climate; et non oportet divideredessig〈nare〉 circulos per singulos gradus, sed sufficit dividere eos per 30 gradus.Et des[s]ignentur per 30 gradus; at paralelli Cancri et Capricorni debent dessignari per 24 gradus, iuxta scilicet declinationem.

Sequens capitulum non est Ptolomei, sed est Abo Alcasis Mesulam filii Alchamad

Dixit Ptolomeus: Docuit in hoc tractatu quomodo debeamus describere orizontem et paralellos eius, qui dicuntur almucantarat. Similiter quoque circulus signorum et eius paralellos docuit. Etiam quomodo debeamus dividere circulum signorum per singulos gradus. Qui quidem divisio tribus modis potest fieri. Primus est quod faciamus paralellum equinoctiali secundum quantitatem declinationis unius gradus; similiter alium secundum quantitatem declinationis duorum graduum, et sic procedendo usque ad divisionem totius circuli. Alius modus est quod extrahamus lineas rectas per centrum equinoctialis secantes de equinoctiali portiones secundum ascensionem duorum vel plurium graduum ipsius circuli signorum. Huiusmodi enim lineae rite divident circulum signorum, et hic quidem modus est clarior. Alium quoque in hoc habemus modum: Nam, eum fuerint duo circuli magni in sphera, secantes invicem per equum, transierit que per puncta sectionis tertius magnus circulus, dividens per equum arcum declinationis eorum. Si exar extraxerimus quartum circulum magnum per polos tertii circuli, ille quartus circulus secabit equales arcus de duobus primis a punctis sectionum.

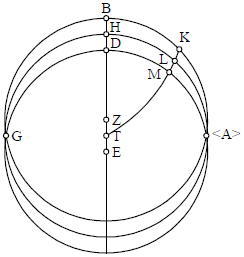Sint duo circuli magni ABG ADG, secantes invicem in punctis A G, quorum ab invicem declinatio sit arcus BD. Deinde alius circulus AHG transeat per puncta A G, dividens arcum BD per equum super punctum H, cuius polus sit punctum T, situatus scilicet inter E et Z, qui sunt poli circulorum ABG et ADG. Postea extrahamus a puncto T arcum TMLK. Dico quod arcus AK est equalis arcui AM, cuius demonstratio est: Nam angulus ALK et ALM sunt recti, ex hoc quod T est polus circuli ALHG, et anguli KAL et MAL sunt equales, ex hoc quod arcus DH equalis est arcui HB. Cum autem arcus AH dividat angulum KAM per equum, et arcus AL sit o communis, ergo per 14 primi Milei Euclidis] read Milei M, arcus AM est equalis arcui AK, quidem est intentum. Cum autem hoc ita declaratum sit, faciamus equinoctialem ABG, et ideo accipiamus arcum AZ equalem distantiae ipsius equinoctialis et tropici hiemalis, et coniungamus Z cum B. Erit, iuxta doctrinam Ptolomei, H polus circuli signorum. Igitur si diviserimus arcum AZ per equum in puncto M, et coniunxerimus B cum M, erit T polus circuli magni, divisi ab equinoctiali in punctis A B, et dividentis arcum interiacentem ipsum equinoctialem et punctum tropicum per equum. Igitur si assumpserimus de equinoctiali, a punctis A E T B, arcus AL et BN, equales 30 graduum, et extraxerimus per puncta L N et T arcum LIN LITNP, necesse est ut arcus AI sit signum Arietis et BP signum Librae. Itaque, iuxta huiusmodi viam, dividere poterimus circulum signorum per singulos gradus vel per alias partitiones ad libitum. Modus autem partitionis horizontis idem est cum modo partitionis circuli signorum, quem scilicet docuimus. Facta autem partitionem horizontis, describemus arcus transeuntes per puncta partitionis diametraliter opposita et per ipsum polum horizontis. Huiusmodi enim arcus eque divident horizontem et omnes eius paralellos. Finis.

כבודך ה' י"ט תשרי רע"ט לע"כ