PAL

Ptolemaeus Arabus et Latinus

_ (the underscore) is the placeholder for exactly one character.
% (the percent sign) is the placeholder for no, one or more than one character.
%% (two percent signs) is the placeholder for no, one or more than one character, but not for blank space (so that a search ends at word boundaries).

At the beginning and at the end, these placeholders are superfluous.

Ptolemy, Almagesti (tr. Gerard of Cremona)

Venice, Petrus Liechtenstein, 1515 · 51v

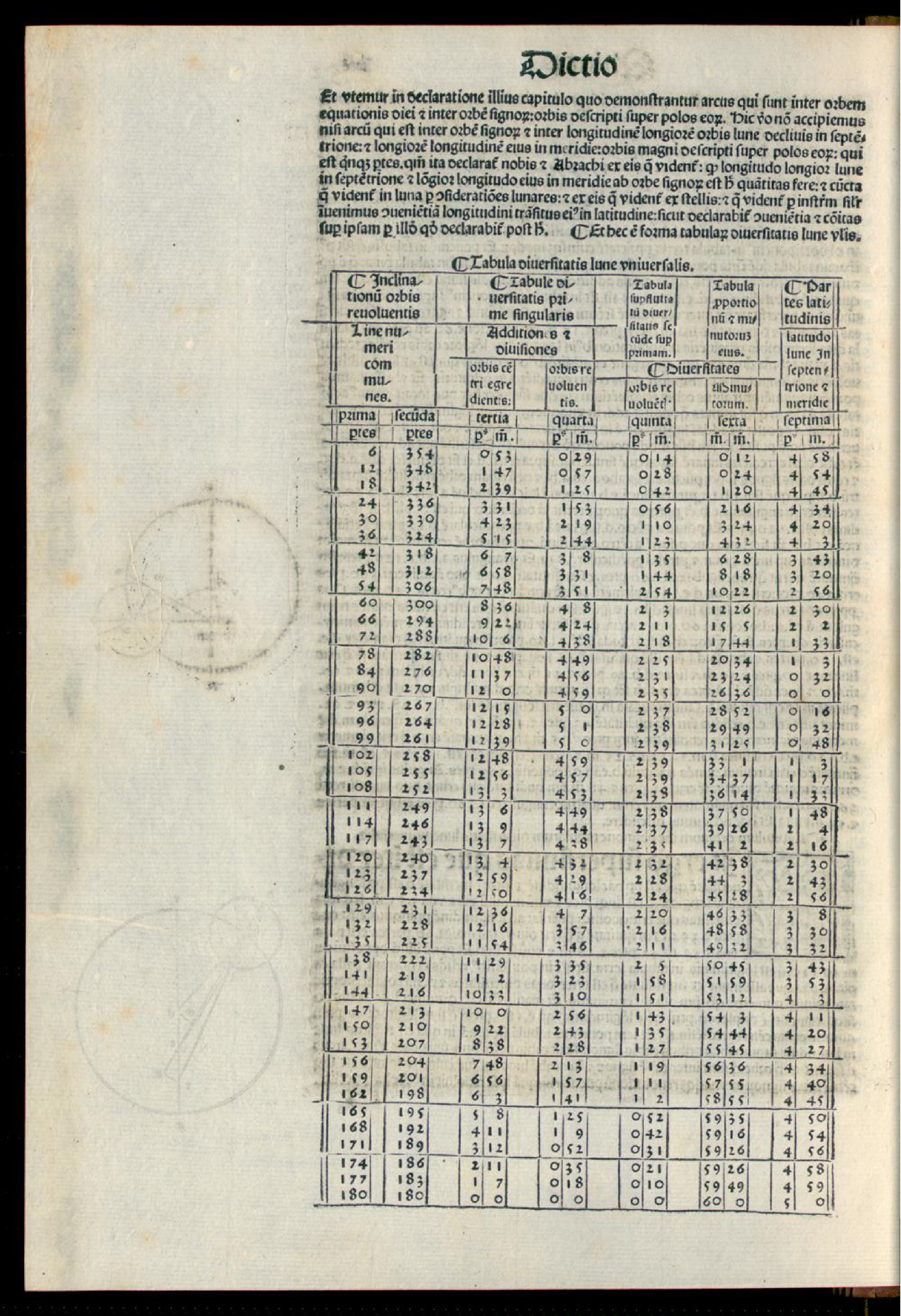
Facsimile

Et utemur in declaratione illius capitulo quo demonstrantur arcus qui sunt inter orbem equationis diei et inter orbem signorum orbis descripti super polos eorum. Hic vero non accipiemus nisi arcum qui est inter orbem signorum et inter longitudinem longiorem orbis Lune declivis in septentrione et longiorem longitudinem eius in meridie orbis magni descripti super polos eorum, qui est quinque partes. Quoniam ita declaratur nobis et Abrachi ex eis que videntur quod longitudo longior Lune in septentrione et longior longitudo eius in meridie ab orbe signorum est hec quantitas fere, et cuncta que videntur in Luna per considerationes lunares et ex eis que videntur ex stellis et que videntur per instrumentum similiter invenimus convenientiam longitudini transitus eius in latitudine, sicut declarabitur convenientia et communitas super ipsam per illud quod declarabitur post hec. Et hec est forma tabularum diversitatis Lune universalis:

Tabula diversitatis Lune universalis

Inclinationum orbis revolventis
Tabule diversitatis prime singularis
Tabula superfluitatum diversitatis secunde super primam
Tabula proportionum et minutorum eius
Partes latitudinis
Line numeri communes Line numeri communes: Paris, BnF, lat. 14738 reads Linee numeri communis. The sense of the Greek text is ‘common numbers’ (see Toomer, loc. cit., p. 238).
Additiones et divisiones
Latitudo Lune in septentrione et meridie
Orbis centri egredientis
Orbis revolventis
Diversitates
Orbis revolventis
Minutorum
Prima
Secunda
Tertia
Quarta
Quinta
Sexta
Septima
Partes
Partes
Partes
Minuta
Partes
Minuta
Partes
Minuta
Minuta
Minuta
Partes
Minuta
6
12
18
354
348
342
0
1
2
53
47
39
0
0
1
29
57
25
0
0
0
14
28
42
0
0
1
12
24
20
4
4
4
58
54
45
24
30
36
336
330
324
3
4
5
31
23
15
1
2
2
53
19
44
0
1
1
56
10
23
2
3
4
16
24
32
4
4
4
34
20
3
42
48
54
318
312
306
6
6
7
7
58
48
3
3
3
8
31
51
1
1
2
35
44
54
6
8
10
28
18
22
3
3
2
43
20
56
60
66
72
300
294
288
8
9
10
36
22
6
4
4
4
8
24
38
2
2
2
3
11
18
12
15
17
26
5
44
2
2
1
30
2
33
78
84
90
282
276
270
10
11
12
48
37
0
4
4
4
49
56
59
2
2
2
25
31
35
20
23
26
34
24
36
1
0
0
3
32
0
93
96
99
267
264
261
12
12
12
15
28
39
5
5
5
0
1
0
2
2
2
37
38
39
28
29
31
52
49
25
0
0
0
16
32
48
102
105
108
258
255
252
12
12
13
48
56
3
4
4
4
59
57
53
2
2
2
39
39
38
33
34
36
1
37
14
1
1
1
3
17
33
111
114
117
249
246
243
13
13
13
6
9
7
4
4
4
49
44
38
2
2
2
38
37
35
37
39
41
50
26
2
1
2
2
48
4
16
120
123
126
240
237
234
13
12
12
4
59
50
4
4
4
32
29
16
2
2
2
32
28
24
42
44
45
38
3
28
2
2
2
30
43
56
129
132
135
231
228
225
12
12
11
36
16
54
4
3
3
7
57
46
2
2
2
20
16
11
46
48
49
33
58
32
3
3
3
8
30
32
138
141
144
222
219
216
11
11
10
29
2
33
3
3
3
35
23
10
2
1
1
5
58
51
50
51
53
45
59
12
3
3
4
43
53
3
147
150
153
213
210
207
10
9
8
0
22
38
2
2
2
56
43
28
1
1
1
43
35
27
54
54
55
3
44
45
4
4
4
11
20
27
156
159
162
204
201
198
7
6
6
48
56
3
2
1
1
13
57
41
1
1
1
19
11
2
56
57
58
36
55
55
4
4
4
34
40
45
165
168
171
195
192
189
5
4
3
8
11
12
1
1
0
25
9
52
0
0
0
52
42
31
59
59
59
35
16
26
4
4
4
50
54
56
174
177
180
186
183
180
2
1
0
11
7
0
0
0
0
35
18
0
0
0
0
21
10
0
59
59
60
26
49
0
4
4
5
58
59
0