PAL

Ptolemaeus Arabus et Latinus

_ (the underscore) is the placeholder for exactly one character.
% (the percent sign) is the placeholder for no, one or more than one character.
%% (two percent signs) is the placeholder for no, one or more than one character, but not for blank space (so that a search ends at word boundaries).

At the beginning and at the end, these placeholders are superfluous.

Ptolemy, Almagesti (tr. Gerard of Cremona)

Venice, Petrus Liechtenstein, 1515 · 58r

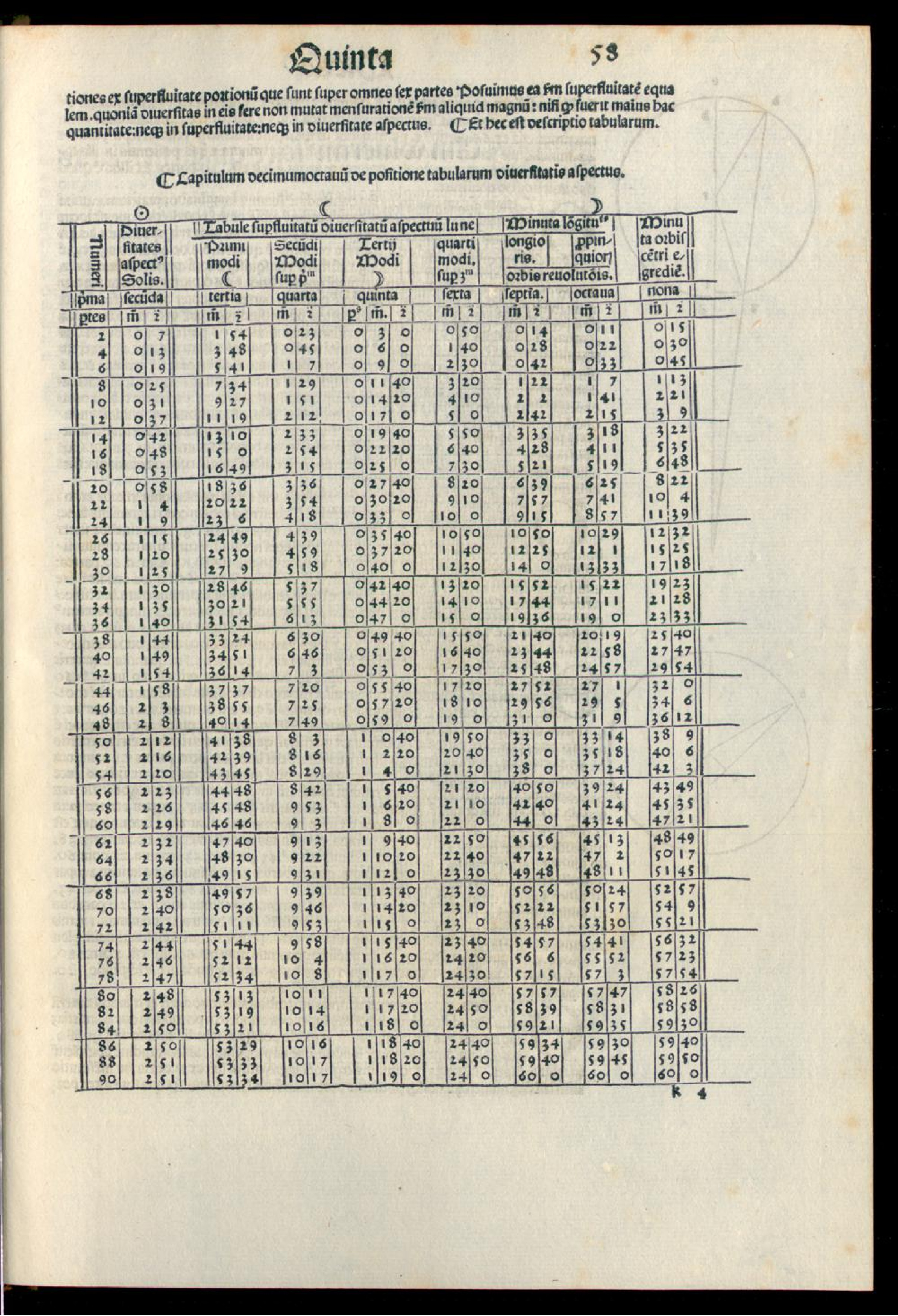
Facsimile

tiones ex superfluitate portionum que sunt super omnes sex partes. Posuimus ea secundum superfluitatem equalem. Quoniam diversitas in eis fere non mutat mensurationem secundum aliquid magnum nisi quod fuerit maius hac quantitate, neque in superfluitate neque in diversitate aspectus. Et hec est descriptio tabularum:

⟨V.18⟩ Capitulum decimumoctavum: De positione tabularum diversitatis aspectus
☉
☾
☽
Numeri
Diversitates aspectus Solis
Tabule superfluitatum diversitatum aspectuum Lune
Minuta longitudinis
Minuta orbis centri egredientis
Primi modi ☾
Secundi modi super primum
Tertii modi ☽
Quarti modi super tertium
longioris
propinquioris
orbis revolutionis
Prima
Secunda
Tertia
Quarta
Quinta
Sexta
Septima
Octava
Nona
Partes
Minuta
Secunda
Minuta
Secunda
Minuta
Secunda
Partes
Minuta
Secunda
Minuta
Secunda
Minuta
Secunda
Minuta
Secunda
Minuta
Secunda
2
4
6
0
0
0
7
13
19
1
3
5
54
48
41
0
0
1
23
45
7
0
0
0
3
6
9
0
0
0
0
1
2
50
40
30
0
0
0
14
28
42
0
0
0
11
22
33
0
0
0
15
30
45
8
10
12
0
0
0
25
31
37
7
9
11
34
27
19
1
1
2
29
51
12
0
0
0
11
14
17
40
20
0
3
4
5
20
10
0
1
2
2
22
2
42
1
1
2
7
41
15
1
2
3
13
21
9
14
16
18
0
0
0
42
48
53
13
15
16
10
0
49
2
2
3
33
54
15
0
0
0
19
22
25
40
20
0
5
6
7
50
40
30
3
4
5
35
28
21
3
4
5
18
11
19
3
5
6
22
35
48
20
22
24
0
1
1
58
4
9
18
20
23
36
22
6
3
3
4
36
54
18
0
0
0
27
30
33
40
20
0
8
9
10
20
10
0
6
7
9
39
57
15
6
7
8
25
41
57
8
10
11
22
4
39
26
28
30
1
1
1
15
20
25
24
25
27
49
30
9
4
4
5
39
59
18
0
0
0
35
37
40
40
20
0
10
11
12
50
40
30
10
12
14
50
25
0
10
12
13
29
1
33
12
15
17
32
25
18
32
34
36
1
1
1
30
35
40
28
30
31
46
21
54
5
5
6
37
55
13
0
0
0
42
44
47
40
20
0
13
14
15
20
10
0
15
17
19
52
44
36
15
17
19
22
11
0
19
21
23
23
28
33
38
40
42
1
1
1
44
49
54
33
34
36
24
51
14
6
6
7
30
46
3
0
0
0
49
51
53
40
20
0
15
16
17
50
40
30
21
23
25
40
44
48
20
22
24
19
58
57
25
27
29
40
47
54
44
46
48
1
2
2
58
3
8
37
38
40
37
55
14
7
7
7
20
25
49
0
0
0
55
57
59
40
20
0
17
18
19
20
10
0
27
29
31
52
56
0
27
29
31
1
5
9
32
34
36
0
6
12
50
52
54
2
2
2
12
16
20
41
42
43
38
39
45
8
8
8
3
16
29
1
1
1
0
2
4
40
20
0
19
20
21
50
40
30
33
35
38
0
0
0
33
35
37
14
18
24
38
40
42
9
6
3
56
58
60
2
2
2
23
26
29
44
45
46
48
48
46
8
9
9
42
53
3
1
1
1
5
6
8
40
20
0
21
21
22
20
10
0
40
42
44
50
40
0
39
41
43
24
24
24
43
45
47
49
35
21
62
64
66
2
2
2
32
34
36
47
48
49
40
30
15
9
9
9
13
22
31
1
1
1
9
10
12
40
20
0
22
22
23
50
40
30
45
47
49
56
22
48
45
47
48
13
2
11
48
50
51
49
17
45
68
70
72
2
2
2
38
40
42
49
50
51
57
36
11
9
9
9
39
46
53
1
1
1
13
14
15
40
20
0
23
23
23
20
10
0
50
52
53
56
22
48
50
51
53
24
57
30
52
54
55
57
9
21
74
76
78
2
2
2
44
46
47
51
52
52
44
12
34
9
10
10
58
4
8
1
1
1
15
16
17
40
20
0
23
24
24
40
20
30
54
56
57
57
6
15
54
55
57
41
52
3
56
57
57
32
23
54
80
82
84
2
2
2
48
49
50
53
53
53
13
19
21
10
10
10
11
14
16
1
1
1
17
17
18
40
20
0
24
24
24
40
50
0
57
58
59
57
39
21
57
58
59
47
31
35
58
58
59
26
58
30
86
88
90
2
2
2
50
51
51
53
53
53
29
33
34
10
10
10
16
17
17
1
1
1
18
18
19
40
20
0
24
24
24
40
50
0
59
59
60
34
40
0
59
59
60
30
45
0
59
59
60
40
50
0