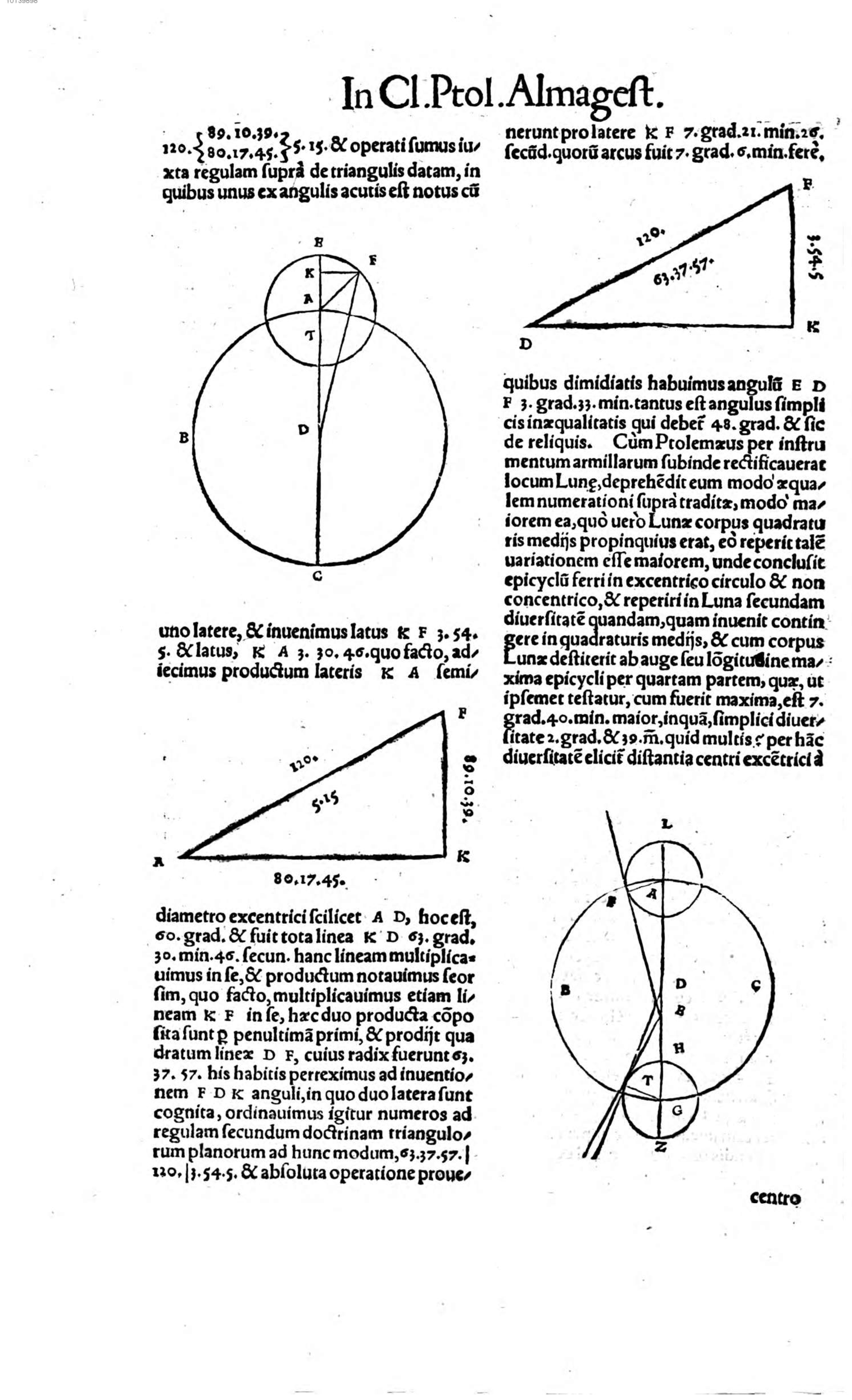
120° |
89° 10ʹ 39ʹʹ |
5° 15ʹ |
||
80° 17ʹ 45ʹʹ |
et operati sumus iuxta regulam supra de triangulis datam, in quibus unus ex angulis acutis est notus cum
uno latere, et invenimus latus KF, 3° 54ʹ 5ʹʹ, et latus KA, 3° 30ʹ 46ʹʹ, quo facto, adiecimus productum lateris KA
semidiametro excentrici, scilicet AD, hoc est 60 gradus, et fuit tota linea KD 63 gradus 30 minuta 46 secundae. Hanc lineam multiplicavimus in se et productum notavimus seorsim, quo facto, multiplicavimus etiam lineam KF in se, haec duo producta composita sunt per penultimam primi, et prodiit quadratum lineae DF, cuius radix fuerunt 63° 37ʹ 57ʹʹ. His habitis, perreximus ad inventionem FDK anguli, in quo duo latera sunt cognita, ordinavimus igitur numeros ad regulam secundum doctrinam triangulorum planorum ad hunc modum: 63° 37ʹ 57ʹʹ | 120° | 3° 54ʹ 5ʹʹ, et absoluta operatione provenerunt pro latere KF 7 gradus 21 minuta 26 secundae, quorum arcus fuit 7 graduum 6 minutorum fere,
quibus dimidiatis habuimus angulum EDF 3 graduum 33 minutorum. Tantus est angulus simplici inaequalitatis, qui debetur 48 gradus, et sic de reliquis. Cum Ptolemaeus per instrumentum armillarum subinde rectificaverat locum Lunae, deprehendit eum modo aequalem numerationi supra traditae, modo maiorem ea; quo vero Lunae corpus quadraturis mediis propinquis erat eo reperit talem variationem esse maiorem, unde conclusit epicyclum ferri in excentrico circulo et non concentrico, et reperiri in Luna secundam diversitatem quandam, quam invenit contingere in quadraturis mediis, et cum corpus Lunae destiterit ab auge seu longitudine maxima epicycli per quartam partem, quae, ut ipsemet testatur, cum fuerit maxima est 7 graduum 40 minutorum, maior, inquam, simplici diversitate 2 graduum et 39 minutorum. Quid multis? Per hanc diversitatem elicitur distantia centri excentrici a