Bernhardus Chorner
Almagesti Ptolomei abreviatum
Prague, APH, L. XLVIII (1292)
transcribed by Hanna Reidenbach
How to cite this transcription?
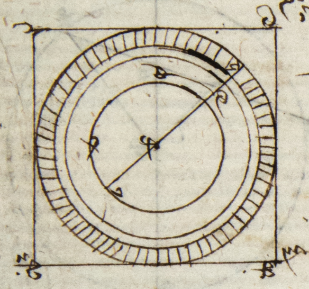
This transcription has been made from the only known witness, MS Prague, APH, L. XLVIII (1292). The transcription follows the Project’s guidelines. Note the variations in spelling in the words ‘adcedere’ / ‘accedere’, ‘Chancri’ / ‘Cancri’, ‘cenik’ / ‘cenic’, ‘Euclydis’ / ‘Euclidis’, ‘meridyanus’ / ‘meridianus’, ‘seccare’ / ‘secare’ and ‘zodyacus’ / ‘zodiacus’. The scribe also writes ‘Ptolomey’ and ‘semidyameter’. Some figures are empty (f. 61r, 66v) or unfinished (f. 65v, 66r, 67r, 68v and 69v). The latter were left unfinished because the scribe realised that he would not have enough space and redrew the same figure elsewhere. The empty and unfinished figures are ignored. Numbers in angular brackets are the proposition numbers of the Almagesti minor as in Zepeda’s edition.
〈I〉
〈I.3〉
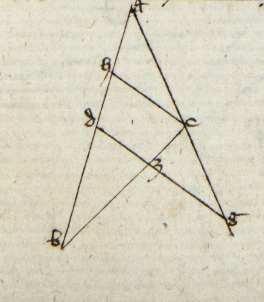
Sint AB et AG note. Erunt quoque per secundum corollarium prime huius corde BD et GD note. Cum igitur ex DB in GA tantum fiat quantum ex DG in AB, et ex AD in BG per premissam. Sed quod fit ex DB in AG est notum; quia tam AG quam DB est notum. Erunt illa duo que fiunt ex DG in AB et ex AD in GB nota secundum quod fit DG in AB notum. Quia tam DG quam AB est notum, erit id quod fit ex AD in BG notum. Sed AD est notum. Igitur BG erit notam, quod est intentum.
〈I.4〉 Quarta Quarta] i. m. P (proposition numbers are always given in the margin). Si in semicirculo corda alicuius arcus nota fuerit, corda quoque que eiusdem medietati subtenditur nota erit.
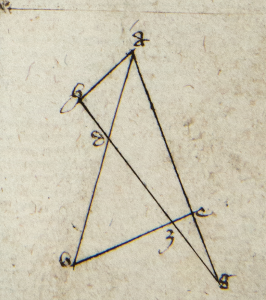
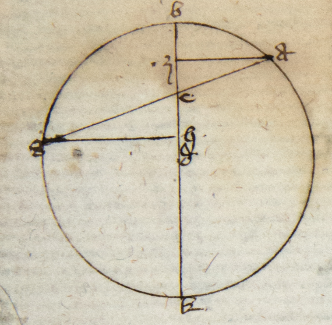
Ex ypothesi BG est nota. Igitur per secundum corollarium prime huius AB erit nota. Sit igitur D medius punctus arcus BG et sit AE equalis AB; et cum angulus BAD equus sit angulo DAG per 26 tertii et ultimam sexti Euclydis, erit per quartam primi eiusdem BD equalis DE; et coassumpta 28a tertii Euclidis erit DE equalis DG. Descendat igitur DZ perpendicularis AG que non cadat ad punctum E nec G quia oporteret per quintam primi Euclydis esse triangulum habentem tres angulos rectos, quod est inconveniens per 16am eiusdem. Sit igitur per 26am primi Euclidis Euclidis] corr. ex. est P Z punctus medius in linea EG. Cum igitur AG sit notum et AE notum quia AB est notum erit EG notum. Quare ZG erit notum. Cum igitur illud quod fit ex AG in ZG sit equale quarto DG per 30am tertii et corollarium secundum octave sexti Euclidis erit quartum DG et corda DG nota et hoc est quod propositio ista asserit.
〈I.5〉 Quinta. Si due corde duorum arcuum in semicirculo fuerint note, corda quoque que toti subtenditur arcui composito ex duobus arcubus illis erit nota.
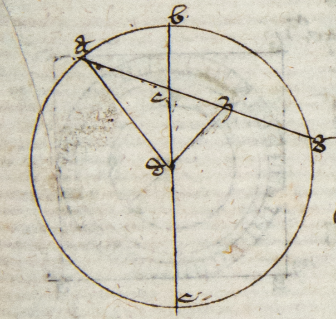
Sint AB et BG corde note. Protrahantur igitur due dyametri que sint AZD et BZE. Erunt igitur per corollarium secundum prime huius BD et GE corde note. Vides igitur quadrilaterum BGDE. Quare per secundam huius illud quod fit ex EG in BD quod est notum quia tam BD quam GE est notum equum est hiis que fiunt ex GD in BE et ex GB in DE que similiter erunt nota. Et cum ED sit notum per corollarium secundum prime huius quia BD est notum et BG ex yptothesi erit illud quod fit ex ED in GB notum. Quare illud quod fit ex BE in GD erit notum cumque BE sit notum erit GD notum. Quare per corollarium secundum prime huius erit AG notum, quod est propositum. Ad demonstrandum sequentem premittam hoc antecedens. Primum antecedens Primum antecedens] i. m. P: Si fuerit fuerit] sup. lin. P proportio primi ad secundum sicud proportio tertii ad quartum et proportio secundi ad quintum maior quam proportio quarti ad sextum, erit primi ad quintum maior quam tertii ad sextum. Sit enim A ad B ut C ad D. Item B ad E maior quam D ad F. Erit A ad E maior quam C ad F sitque B ad G ut D ad F. Quare B ad E maior quam B ad G. Igitur E minor est G per decimam quinti Euclidis. Quare A ad E maior proportio quam A ad G per octavam eiusdem. Sed proportio A ad G est proportio C ad F per 22am eiusdem quinti Euclidis seu da equam proportionalitatem per illud quod est demonstratum in 12 quinti Euclidis. Videlicet si primi a〈d〉 secundum sit sicud tertii ad quartum et tertii ad quartum minor et cetera, erit igitur proportio A ad E maior videlicet proportione C ad F, quod est propositum.
〈I.6〉 Sexta. Due inequales linee si in circulo protrahantur maioris ad minorem quam arcus longioris ad arcum breviorem, minor erit proportio.
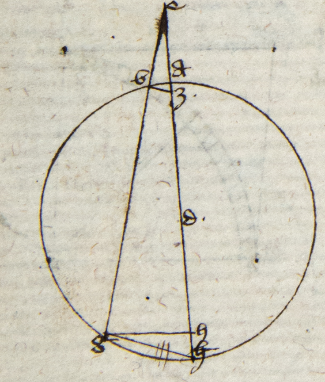
Adhuc demonstratum primam. Premittam primam. Secundum antecedens: Secundum antecedens] i. m. P Si proportio primi ad secundum maior fuerit quam tertii ad quartum et tertii ad quartum maior quam quinti ad sextum, erit proportio primi ad secundum maior quam quinti ad sextum. Sit enim A ad B maior quam C ad D et C ad D maior quam E ad F et sit A ad G ut C ad D et A ad H ut E ad F. Erit per duodecimam et decimam quinti Euclidis et animi conceptionem quicquid est maius maiore est maius minore. Quare per octavam quinti Euclidis A ad B est maior quam A ad H. Sed A ad H est E ad F. Igitur per 12 quinti Euclidis A ad B maior quam E ad F, quod est intentum. Rectum autem in ita argumentatione sit petitio principii partim ad quintum elementorum Euclydis. Sed credo quod non sit. Igitur corda BG maior corda BA erit, arcus BG maior arcui BA per 21am tertii Euclidis. Quod si ponitur, erit corda BG maior corda BA arguendo indirecte ex 27a et 28a tertii Euclidis. Quodcumque igitur ponatur, dico quod maior erit proportio arcus BG ad arcum BA quam corde BG ad cordam BA. Dividatur enim angulus GBA in duo equalia per lineam BD per nonam primi Euclidis. Et ductis lineis AG, AD et DG erit GE maior EA per tertiam sexti Euclidis et AD equalis DG per 25 tertii vel per ultimam seu 32am sexti Euclidis. Dividatur igitur in equali puncto Z per decimam primi Euclidis et erit punctus Z in linea EG. Erit etiam per octavam primi Euclidis linea DZ perpendicularis linee AG. Quare per 32 et 18 primi Euclidis DE maior erit DZ. Similiter per 16 primi Euclidis angulus DEA erit obtusus. Quare iterum per 32 et 18 primi Euclidis AD maior erit DE. Quare si arcus supra centro D secundum DE describatur, secabit AD in puncto H et transibit DZ ad punctum T ita ut DZT sit linea recta. Tunc sit proportio sectoris TDE ad sectorem EDH maior maior] followed by an unclear letter or symbol P quam trianguli ZDE ad triangulum EAD EAD] followed by one word crossed out by the scribe: per P totum per octavam quinti Euclydis. Per secundum igitur premissum antecedens proportio sectoris TDE ad sectorem EDH maior est quam trianguli ZDE ad triangulum EDA. Sed proportio sectoris ad sectorem est sicud anguli TDE ad angulum EDA, quod potest probari probari] followed by one word crossed out by the scribe: sicud P ut ultima sexti Euclidis. Et proportio trianguli ad triangulum est sicud basis ZE ad basim EA per primam sexti Euclidis. Igitur proportio anguli ZDE ZDE] corr. ex ZDA P ad angulum EDA maior est quam linee ZE ad lineam EA. Igitur coniunctim proportio anguli ZDA ad angulum EDA est maior quam linee AZ ad lineam EA per 28am quinti Euclidis. Numerando aditiones Campani et cum proportio AG AG] corr. ex AZG P ad ZA et anguli ADG ad angulum ADZ sit eadem quia utrobique dupla per octavam primi Euclidis, sequitur per premissum primum antecedens quod proportio proportio] followed by two letters crossed out by the scribe: AG P anguli ADG ad angulum ADE maior sit quam linee AG ad lineam AE; igitur disiunctim per 29 quinti Euclidis. Numerando additiones Campani proportio EDG ad angulum EDA maior erit quam proportio linee GE ad lineam EA. Sed proportio anguli GDE GDE] corr. ex GED P ad angulum EDA est proportio arcus BG ad arcum BA per ultimam sexti Euclidis et proportio linee GE ad lineam EA est proportio corde BG ad cordam BA per tertiam sexti 〈Euclidis〉. Sequitur quod proportio arcus BG ad arcum BA maior erit erit] followed by one letter crossed out by the scribe: t P quam proportio corde BG ad cordam BA et per consequens proportio corde BG ad cordam BA minor erit quam arcus BG ad arcum BA et hoc est quod intendimus. Et sic finitur capitulum nonum.
Capitulum decimum ostendens quomodo tabule arcuum circuli et cordarum eius fiant. Capitulum…fiant] i. m. P
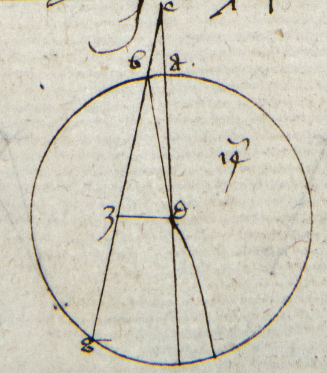
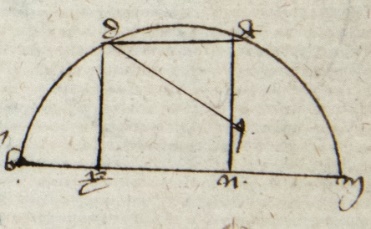
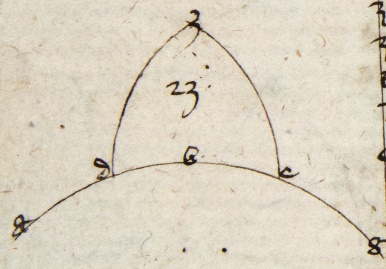
Centrum autem locum ostendit quomodo quelibet corda cuiuscumque arcus fuerit poterit notificari et per consequens quomodo adhuc possit fieri tabula, unde multe corde perpendiculares. Sex conclusiones possunt notificari quod non cura resumere exceptis paucis. Unde per primam conclusionem habetur corda arcus 60 graduum. Quare per quartam presentis corda 30 graduum erit nota. Similiter corda 36 graduum erit nota. Per primam huius corda 6 graduum erit nota et per consequens corda trium graduum erit nota per quartam huius et corda 1 gradus et 30 minutorum que erit unius puncti et 34 minutorum et 15 secundorum et intellige dyametrum esse 120 punctorum. Similiter per eandem erit corda 45 minutorum nota et erit novem puncta, 47 minuta, 8 secunda. Sed nulla nulla] followed by one word crossed out by the scribe: secunda P ratio precipue potest comprehendi quantitatem corde gradus. Quod tamen prope verum sit potest investigari. Sit arcus AB unius gradus, AC 45 minutorum, AD 90 minutorum et erit arcus AD sexquialterus ad AB et AB sexquitertius ad AC. Quare per sextam huius corda AB est maior quam sexquialtera et minor quam sexquitertia AC; et cum corda AD sit 1 punctum, 32 minuta, 15 secunda et AC 0 punctum, 47 minuta, 8 secunda erit. Corda AB que est unius gradus maior est quam 1 punctum, 2 minuta, 50 secunda et minor quam 1 punctum, 2 minuta, 50 secunda, 40 tertia. Quare non est inconveniens ut corda corda] followed by one word crossed out by the scribe: unius P AB unius gradus ponatur 1 punctum, 2 minuta, 50 secunda, quia error minor erit quam in duabus tertiis unius secundi. Et erit corda 30 minutorum, 0 punctum, 31 minuta, 25 secunda per quartam huius, quia sit semper per cordam arcus compositi ex arcu nota et arcu 30 graduum. Per quintam huius facies tabulam, quod est quod volumus.
Capitulum 11 de positione arcuum et cordarum est in tabulis. Duodecimum capitulum ostendit maximam declinationem nobis declivis seu arcum coluri interemptum inter tropicum Cancri et Capricorni et habet solam conclusionem.
〈I.15〉 Maximam declinationem per instromenti artificium et considerationem reperire.
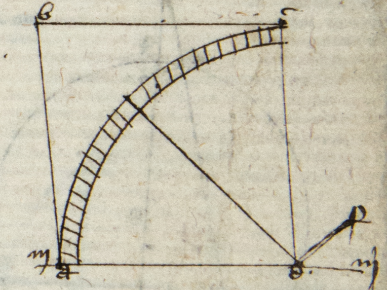
Capiatur superficies quarti ad cuius centrum describantur circuli duo quorum circumferentie in 360 partes dividantur et partes in partes quantum possibile est. Postea capitur ista superficies secundum ultimum circulum ut sit armilla divisa in 360 partes et ad internum ponatur alius circulus seu rota volubilis cuius dyamete sit HE et a punctis H et E erigantur due pinnule HG et EF orthogonales super rotam volubiles et exiat denticulus HK a medio pinnule ad armillam. Quo facto erigatur hoc totum supra superficiem †nm† †nm†] unclear: n written above m P equidistantem orizonti orthogonaliter et supra lineam MN meridyanam. Quo facto capiatur maxima Solis altitudo meridiana et minimam differentiam inter has erit arcus coluri intercepti inter tropicum Cancri et Capricorni cuius medietas est maxima declinatio. Aliter levius et melius fiat quadrans et per regulam DHK volubilem habebitur illud quod prius. Sciendum tamen quod diversi diversimode maximam Solis declinationem invenerunt. Nam Yndi invenerunt eam 24 graduum, Ptolomeus vero 23 graduum, 51 minutorum et 20 secundorum, et Arzahel 23 graduum, 33 minutorum et 30 secundorum. Ideo sollerter adhuc est inspiciendum et magis visui quam auditui credendum. Capitulum 13m docet finaliter declinationem cuiuslibet puncti 30ti invenire et habet conclusiones novem.
〈I.7〉 Septima. Duabus rectis lineis ab angulo uno descendentibus aliis duabus sese secantibus ab earumdem descentium reliquis in easdem reflexis, utralibet reflexarum alterius conterminalem sic figit ut portio ipsius fixe ad eam sui partem que supra fixionem producatur ex duabus proportionibus, ex una dico proportione quam habet sibi conterminalis reflexa ad eam sui partem que sectioni interiacet et fixioni, et alia proportione quam habet alterius reflexe inferior sub sectione portio ad eam totam cuius pars est lineam.
Exempli gratia sic: Proportio linee GA ad lineam EA componitur ex proportione linee GD ad lineam ZD et BZ ad BE. Sit enim EH equidistans DG per 31 primi Euclidis. Quare proportio GA ad EA est tanquam proportio GD ad HE per 29 et 32 32] corr. ex 22 P primi Euclidis et 4 sexti Euclidis; inter quas ZD linea constituatur media cuius proportio ad HE est sicud BZ ad BE per easdem 29 et 32 et 4 sexti 〈Euclidis〉, ex quo patet intentum.
〈I.8〉 Octava. Duabus lineis rectis ab angulo uno descendentibus aliisque duabus sese secantibus ab earum descendentium reliquis terminis in easdem reflexis, utralibet reflexarum alterius conterminalem sic figit proportio portionis fixe, inferioris dico partis ad superiorem partem, producatur ex duabus proportionibus, ex una inquam proportionem quam habet sibi conterminalis reflexe inferior sub sectione portio ad reliquam partem que sibi sectioni interiacet et fixioni, et alia proportione quam habet reliqua inferior descendens sub fixione portio ad eam totam cuius pars est lineam.
Exempli causa proportio GE ad EA producitur ex proportionibus GZ ad ZD et BD ad BA. Ducatur enim AH equidistans BE per 31 primi Euclydis; et cum anguli ZEG et ZGE sint minores duobus rectis per 16 primi Euclidis et angulus ZEG equalis sit HAE, erunt anguli HAG et AGD minores duobus rectis. Quare per petitionem DG et AH versus partem D et H, si protrahantur, concurrunt. Concurrunt igitur in puncto per 29 et 31 primi et 4 sexti Euclidis. Igitur proportio, scilicet GE ad EA, ut GZ ad Z. Inter quas statuatur media ZD cuius proportio Z ad DH sicud BD ad DA per 29 et 15 primi et quartam sexti Euclidis. Igitur per conversam coniunctam et iterum conversam proportionalitatem ZD ad ZH ut BD ad AB, unde habemus propositum.
〈I.9〉 Nona. Si in circulo continui summantur arcus et uterque minor semicirculo, dyametrus producta a communi eorum termino lineam rectam reliquos eorumdem terminos continuantem secabit secundum proportionem corde dupli arcus unius ad cordam dupli arcus alterius.
Sint GB et BA arcus propositi et ductis perpendicularibus AZ et GH supra dyametrum BK per 12 primi 〈Euclidis〉 que erunt sinus recti predictorum arcuum per 3 tertii, 8 primi, 25 tertii. Vides igitur triangulos similes per 27, 29, 15 primi et quartam sexti. Quare concludo propositum ex 15 quinti Euclidis. Si Si] followed by one word crossed out by the scribe: ad P autem adversarius dicat unam unam] followed by one word crossed out by the scribe: partem P perpendicularium cadere extra circulum ducta corda AB vel AK vel GB vel GA, per 30 30] followed by one word crossed out by the scribe: primi P tertii et 16 primi 〈Euclidis〉 probabitur angulum acutum maiorem esse recto.
〈I.10〉 10. Si unus arcus notus minor semicirculo in duos dividitur fueritque nota proportio corde duple arcus unius eorum ad cordam dupli arcus alterius, ambo ipsi erunt noti.
Sit DZ perpendicularis ad cordam arcus AG minoris semicirculo noti. Quare per tabulam arcuum et cordarum ultimam sexti et 46am sextam primi Euclidis totus triangulus, scilicet AZD, lineis et angulis erit notus. Item proportio GE ad EA per prescientiam et ypothesim erit nota. Igitur proportio coniuncta GA ad DA addita unitate proportionis disiuncte denominationi erit nota. Ergo cum AG sit notum, AE erit nota. Igitur EAZ et ZD erunt note. Quare per 46am primi 〈Euclidis〉 DE erit notum in circumscribendo igitur triangulo cuius dyameter per 30 tertii Euclidis erit DE. Erunt per ultimam sexti Euclidis omnes anguli noti. Quare cum angulus EDZ sit notus, tum angulo ADZ erit angulus ADE notus; quare arcus AB per ultimam sexti 〈Euclidis〉 et ideo arcus B, quod est intentum.
〈I.11〉 11. Si ab uno termino arcus semicirculo minoris linea ipsum arcum secans educatur docet cum dyametro per reliquum eiusdem arcus terminum extracta concurrat, fiet proportio linee preter centrum transeuntis ad partem extrinsecam sicud proportio corde dupli arcus de quo est sermo ad cordam dupli arcus illius quam educte linee includunt.
Esto GH sinus rectus GA arcus propositi et BZ sinus rectus arcus interclusi BA. Videris igitur triangulos GHE totalem et BEZ partialem ex quibus habemus propositum.
〈I.12〉 12. Si arcus predicto modo divisi lineis ut prescriptum est duce donec concurrant eductis portio nota inclusa inter lineas eductis eductas nota fuerit et portio corde dupli arcus lineis eductis inclusi constiterit, ipse arcus inclusus notus erit.
Sit DZ perpendicularis corde BG. Quare triangulus BZD lineis et angulis erit notus. Item cum proportio GE ad BE sit nota ex ypothesi et premissa erit proportio disiuncta nota, scilicet GB ad BE; et cum GB sit notum erit et BE notum; et cum etiam BZ sit notum EZ erit notum. Sed ZD etiam est notum. Quare triangulus totus EDZ lineis et angulis erit notus. Quare EDZ notus cumque BDZ sit notus erit BAD notus; quare arcus BA, quod est intentum.
〈I.13〉 13.14. In superficie spere duobus arcubus magnorum orbium semicirculo divisum minoribus ab uno communi termino descendentibus aliisque duobus duobus] sup. lin. P non minorum orbium ab illorum reliquis terminis in eosdem sese secando reflexis, uterque reflexorum alterius conterminalem arcum sic figit ut portio corde arcus duplicantis duplicantis] followed by three words crossed out by the scribe: superiorem eiusdem fixi P inferiorem portionem arcus fixi ad cordam arcus duplicantis superiorem eiusdem fixi portionem producatur ex gemina proportione, ex ea scilicet proportione quam habet corda arcus duplicantis inferiorem arcus reflexi portionem qui ipsi fixo conterminalis est ad cordam arcus duplica〈n〉tis reliquam eiusdem reflexi portionem, et ea proportione quam habet corda arcus duplicantis inferiorem alterius descendentis partem ad cordam duplicantem duplicantem] i. m. P arcum ipsum cuius pars est totalem.
Nota quod haec propositio bis posita fuit in exemplari. Si erga necesse fuerit, repete eam. Nota…eam] i. m. P
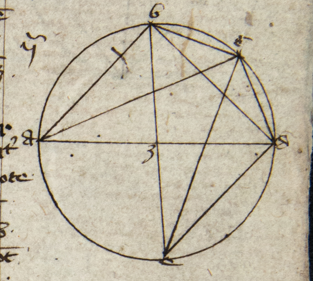
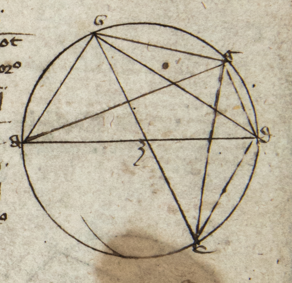
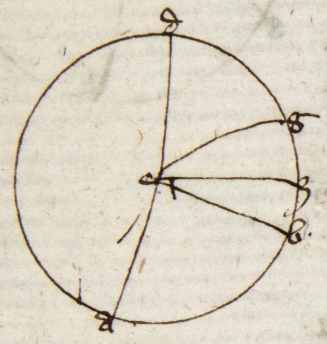
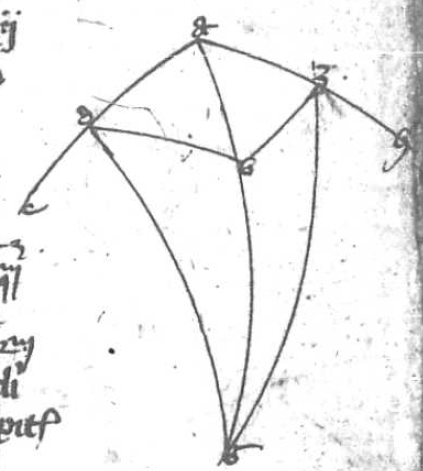
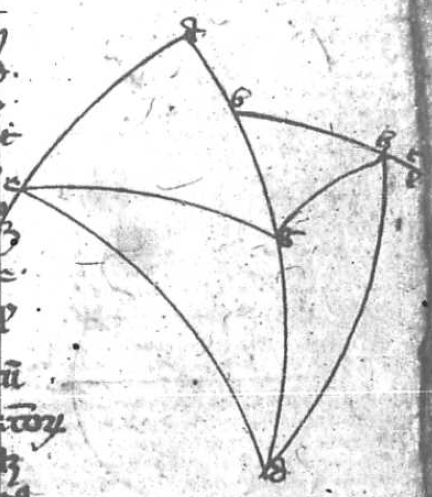
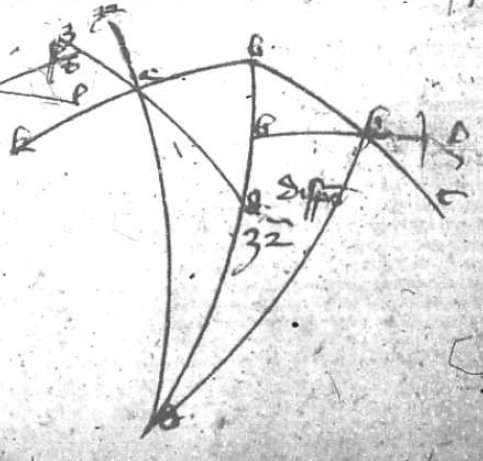
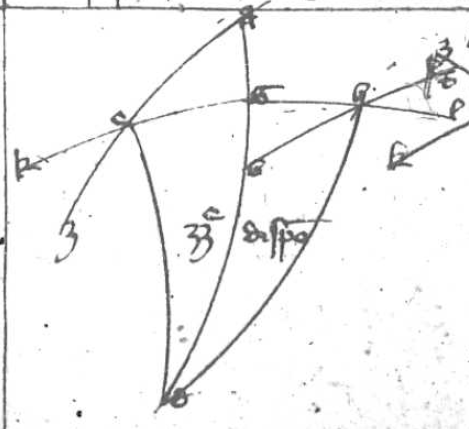
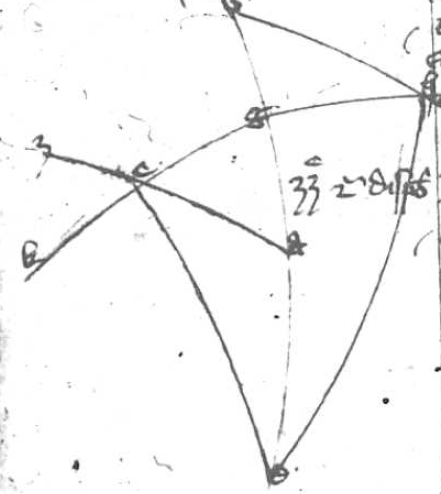
Descendant a communi termino A duo arcus AB et AG inter quos sint arcus BE GD secando se in Z sinus descendentes arcus orbium magnorum. Dico quod proportio corde corde] i. m. P dupli arcus GE ad cordam dupli arcus EA componitur ex proportione corde dupli arcus GZ ad cordam dupli arcus ZD et ex proportione corde dupli arcus BD ad cordam dupli arcus B B] followed by one letter crossed out by the scribe: q PA quod hinc constat. Sit H centrum spere et ducantur linee HE, HZ, GLA, GD et secet GA HE in L et GD HZ in K. Deinde ducatur ADT quousque concurrat cum HBT quod tamen non semper necesse est, sed solum cum arcus quo AB deficit a semicirculo est maior DB et tunc demonstratio Ptolomey que sequitur sufficiens est. Sed si predicti arcus essent equales, predicte linee essent equidistantes, et si DB fuerit maior eorum, concurrerent versus A et H et illis duobus demonstratio que sequitur non procederit et oportet recurrere ad figuram sectoris Campani. Sit igitur quod concurrat in puncto T. Quia igitur tria puncta T, K, L sunt in superficie trianguli GAD et in superficie trianguli arcus BZE, sequitur per tertiam undecimi Euclydis quod T, K, L 3 puncta erunt in una linea recta. Ducatur igitur linea TKL. Videris igitur duas lineas AG et AT inter quas duas lineas sese secantes GD et DL. Quare per katham disiunctam solet nonam istius dictionis: Proportio GL ad LA que est corde dupli arcus GE ad AD corda dupli arcus EA per 10 huius componetur ex proportione GK GK] corr. ex AGK P ad KD que per eadem decimam est proportio corde dupli arcus GZ ad cordam arcus ZD et proportione TD ad TA que per duodecimam huius est proportio corde dupli arcus BD ad cordam dupli arcus BA sicque patet intentum. Quod autem demonstratio Ptolomey que precessit non universalis ut predictum hac additione patet.
15. Si linea in semicirculo ex nulla parte aput dyametrum terminata arcum resecaret, si arcus inter ipsam et dymetrum fuerit equalis, ipsam dyametro equidistare necesse est; si autem inequales, ex qua parte fuerit arcus minor eas concurrere necesse est.
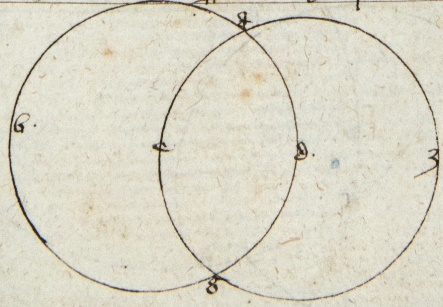
Sit primo DB equalis AM. Dico quod DA et BM sunt equidistantes. Ducantur enim perpendiculares DX et AN super dyametrum per 12 primi Euclidis que cadunt intra semicirculum. Alioquin sequitur quod angulus acutus sit maior recto per 16 primi et 30 tertii Euclidis ducta linea DB et AM. Hee igitur perpendiculares erunt sinus recti DB et AM per tertiam tertii et octavam primi et 25 tertii 〈Euclidis〉. Si Si] followed by one letter crossed out by the scribe: d P igitur DB et AM sunt equales, erunt DX et AN equales equales] uncertain reading P et equidistantes per 28 primi et per 33 primi 〈Euclidis〉 et DA et et] sup. lin. P XN equales et equidistantes, quod est primum. Si autem DB minor sit AM, et DX minor erit AN. Sitque equalis NQ ducaturque DQ que ut prius erit equalis et equidistans XN. Quare per 29 primi et ex ypothesi Euclidis Euclidis] followed by one word crossed out by the scribe: arcu P angulus QDX rectus. Quare duo anguli ADX et DXN maiores duobus rectis. Ergo per petitionem et 13am primi Euclidis DA et XN concurrunt versus DB, quod est secundum.
〈I.14〉 16. In superficie spere quatuor arcubus predicto modo depictis, fiet ut proportio arcus unum duplicantis descendentium totalem ad cordam arcus duplicantis superiorem eiusdem descendentis portionem componatur ex gemina proportione, scilicet ex ea quam habet corda arcus duplicantis totalem reflexum eiusdem descendentis conterminalem ad cordam arcus duplicantis eiusdem reflexi superiorem portionem et ex ea quam habet corda arcus duplicantis inferiorem sub sectione alterius reflexi portionem ad cordam arcus duplicantis eundem reflexum cuius pars est totum.
Istam conclusionem non credo in Almagesti minori vel maiori demonstratam esse, quare eam hic non demonstrare. Sed velit eam demonstrare, recurrat ad figuram sectionis Campani.
〈I.16〉 17. Cuiuslibet puncti in circulo declivi cuius distantia ab equinoctiali est nota declinationem invenire. Unde manifesta est hec regula: si sinus portionis ab equinoctiali inchoate inchoate] i. m. P cuius finalis puncti declinatio queritur ducatur in sinum maxime declinationis productum dividatur per sinum quadrantis, exibit sinus quesite declinationis.
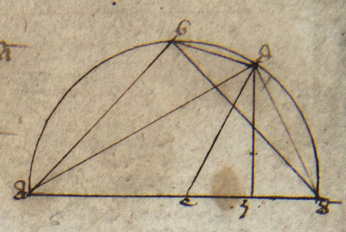
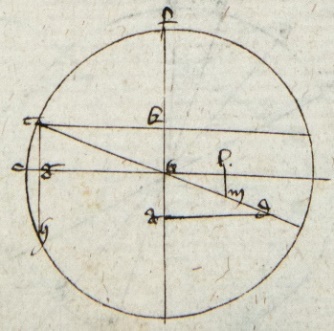
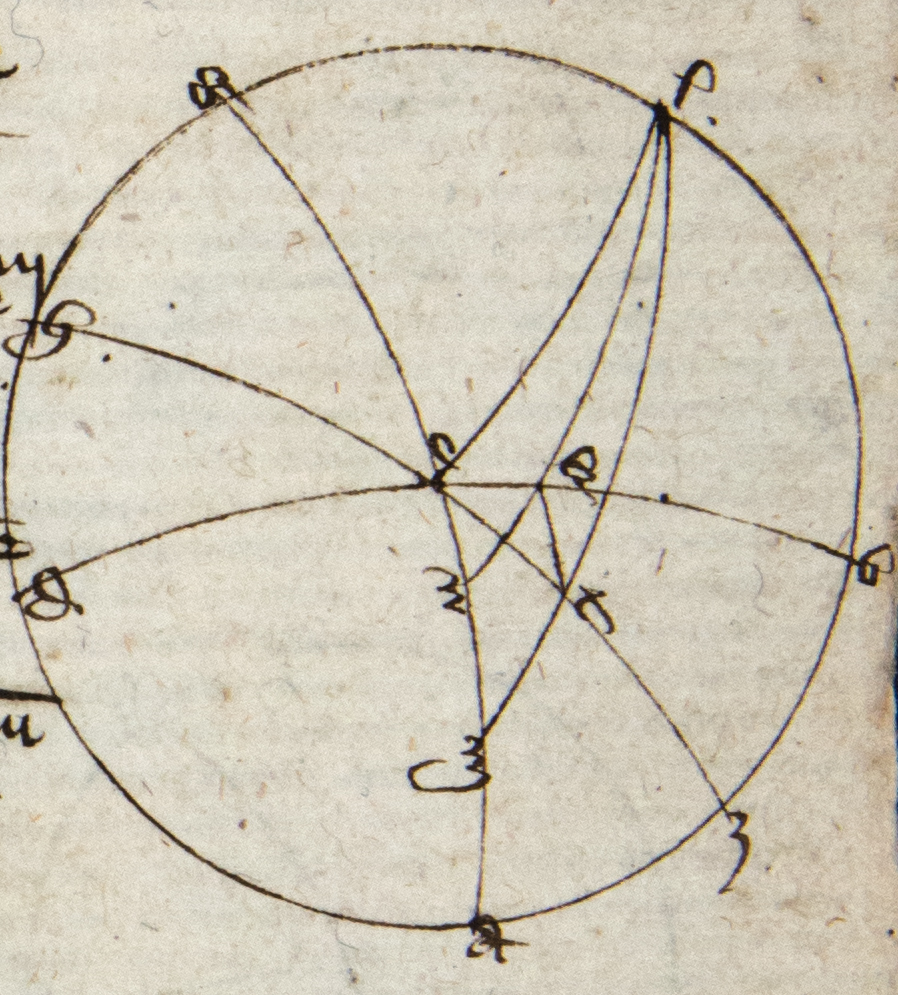
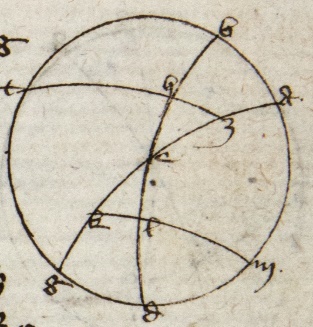
Sit ABG circulus magnus transiens per polos zodyaci et equinoctialis per 29 primi Theodosii, AEG vero equinoctialis et BED zodyacus, Z vero polus equinoctialis et E principium Arietis et punctus H finis noti arcus GEH cuius declinationem quero. Igitur cuius describo circulum magnum per 29 primi Theodosii ZH secantem AEG super T. Volo igitur scire arcum HT quam dico sic invenire: Ducatur sinus arcus EH noti in sinum arcus AB maxime declinationis. Productum dividatur per sinum arcus AZ quadrantis et exibit sinus arcus HT cuius quere arcum per tabulam arcuum et cordarum et scies arcum HT. Totus autem processus sic patet. Cum enim a puncto A communi duo arcus AZ et AE descendant inter quos duo alii sese secantes super H, scilicet T et EB. Igitur per premissam proportio sinus ZA ad sinum BA componitur ex proportione sinus ZT ad sinum HT et sinus EH ad sinum EB. Sed ZT equalis ZEB quia uterque est quarta circuli magni ZT per 23 primi Theodosii et 27 tertii Euclidis, EB vero per 15 primi et 12 secundi Theodosii et quarte circulorum magnorum sunt equales per 15 primi Theodosii. Igitur proportio sinus ZA ad sinum BA componitur ex sinu EB ad sinum HT sinu EH ad sinum EB. Sed due proportiones qualitercumque transponantur componunt eandem proportionem per 21 et 22 quinti Euclidis. Igitur proportio sinus ZA ad sinum BA componitur ex sinu EH ad sinum EB et sinu EB ad sinum HT. Sed sinus EH ad HT conponitur ex eisdem. Igitur sinus EH ad HT sicud sinus ZA ad BA. Ergo per 15 sexti Euclidis tantum provenit ex sinu EH in sinum BA sicud ex sinu ZA in sinum HT. Quare si illud quod provenit ex sinu EH in sinum BA dividatur per sinum ZA, exibit sinus HT, quod est intentum. Visum est etiam quod EB est quarta circuli magni; quare BZ principium Cancri et eadem ratione DZ principium Capricorni. Sed adhuc restat probare quod AB sit maxima declinatio quod sic patet cum DEB non transeat per polos GEA. Sequitur quod sit inclinatus super ipsum, alioquin per 17 primi Theodosii transierit per polos eius. Ergo per 10 secundi Theodosii DEB contingit duos circulos equidistantes GEA qui erunt super polos circuli GEA per primam secundi Theodosii. Igitur per 5 eiusdem B est punctus contactus circuli versus Z et omnis arcus circuli magni AZ ad circumferentiam istius circuli sunt equales per diffinitionem poli et 15 primi Theodosii et 27 tertii Euclidis. Ergo declinatio AB deficit a quarta circuli magni solum per arcum BZ et quelibet alia per arcum BZ, autem sibi equalem et arcum interceptum inter zodyacum et tropicum per 23 et 15 primi Theodosii et 27 tertii Euclidis. Igitur ABZ est maxima declinatio, quod intendebam.
Capitulum 14m est de assen〈s〉io〈ni〉bus assensionibus] asseniobus preceded by declinationis P signorum in circulo recto et habet solam conclusionem.
〈I.17〉 18. Si cuiuslibet portionis circuli declivi elevationem in spera recta invenire. Unde hec regula: si sinus perfectionis maxime declinationis ducatur in sinum declinationis portionis inchoate ab equinoctiali linea cuius portionis queritur elevatio, productum dividatur per sinum perfectionis declinationis illius portionis, et quod exierit ducatur iterum in sinum elevationis unius quadrantis, productum dividatur per sinum maxime declinationis, exibit sinus quesite declinationis.
Stante dispositione premisse et ypothesi volo notificare arcum ET et dico quod si sinus ZB perfectionis maxime declinationis ducatur in sinum HT declinationis EH arcus cuius elevatio queritur et productum dividatur per sinum ZH perfectionis declinationis arcus cuius elevatio queritur et quod exierit ducatur in sinum EA elevationis quadrantis et productum dividatur per sinum AB maxime declinationis, exibit sinum ET quesite declinationis. Quod sic patet quia enim duo arcus AZ AE descendunt a communi termino inter quos ZHT EHB intersecantes se in H. Igitur per 14 presentis proportio sinus ZB ad sinum componitur ex proportionibus sinus ZH ad sinum HT et sinus ET ad sinum sinum] followed by two letters crossed out by the scribe: AG P EA. Igitur si sinus ZB primus ducatur in sinum HT quartum productumque dividatur per sinum ZH ZH] corr. ex ZT P tertium, exibit linea que vocetur K, ad quam per 15 sexti 〈Euclidis〉 habet se sinus ZB sicud sinus ZH ad sinum HT. Igitur proportio sinus ZB ZB] corr. ex ZK P ad sinum BA componitur ex sinu ZB ad K et sinum ET ad sinum EA. Sed eadem componitur ex sinu ZB ad K et K ad sinum BA. Ergo ille simul sumpte sunt illis simul sumptis. Ergo per conceptionem si ab equalibus idem commune dematur vel saltem per equam proportionalitatem, erit K ad sinum BA ut sinus ET ad sinum EA. Ergo per 15 sexti Euclidis ex K in sinum EA tantum quantum ex sinu AB in sinum ET. Quare si illud dividatur per sinum AB, exibit sinus ET, quod est intentum.
Et sic finitur prima dictio Almagesti.
Secunda dictio Almagesti Ptolomey habet capitula 12. In primo ostenditur que et quanta pars terre sit habitabilis quia solum una quarta intercepta in in] corr. ex inter P circulum suppositum equinoctiali et duobus orthogonaliter sese secantibus in polo artico; et hinc patet quia semper umbre meridiane et equinoctiales proiciuntur et ad septentrionem nec umquam eclypsis lunaris in eadem hora apparet occidentalisbus, prius etiam et plus quam 12 12] followed by one word crossed out by the scribe: hore P horis.
Capitulum secundum ostendit qualiter sciatur arcus cuiuslibet diei et arcus orizontis obliqui qui est inter equinoctialem et quemlibet punctum zodyaci et 〈habet〉 conclusiones duas.
〈II〉
〈II.1〉 19. Arcum die minimi vel maximi in quovis clymate per nota〈m〉 poli altitudinem cognoscere. Unde manifestum est quod si sinus altitudinis poli ducatur in sinum maxime declinationis, et productum dividatur per sinum perfectionis maxime declinationis, et quod exierit ducatur in semidyametrum, productumque dividatur per sinum perfectionis altitudinis poli, exibit differentia mediata minimi diei ad equinoctialem diem et sic quilibet arcus diei potest investigari.
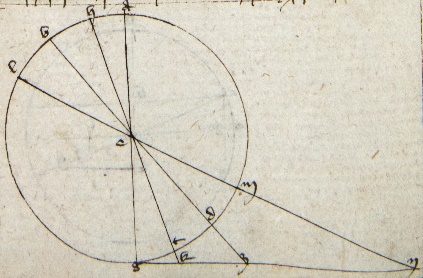
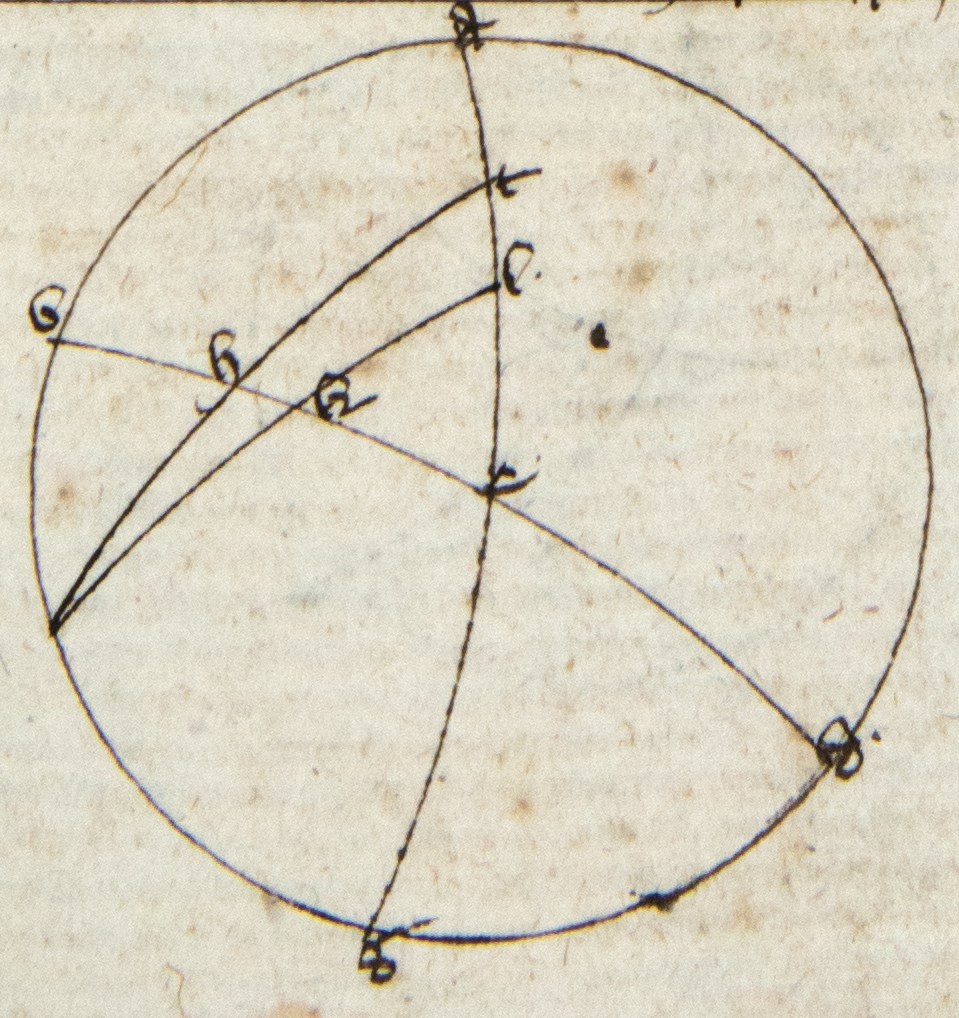
Sit ABG meridyanus et AEG equinoctialis, BED orizon, Z polus antarticus, H punctus orizontis vero oritur. Principium Capricorni intersecat orizontem et transeat circulus magnus per 29 primi Theodosii ZH usque ad T. Circulus igitur meridiei seccabit omnes arcus diurnos [omnes] in duo equa per 12 et primam secundi Theodosii si ymaginentur paralelli equinoctiali transeuntes per quelibet puncta zodyaci. Quare arcus tropici hyemalis ab H usque ad meridianum Z medietas arcus minimi diei, supposito quod arcus diei tropici hyemalis sit minimus, quod patebit. Quare cum AT sit similis arcui tropici AH usque ad meridianum per 14 secundi Theodosii, erit AT arcus minimi diei medietas et TE differentia mediata minimi diei ad equinoctialem diem. Cum EA sit medietas equinoctialis diei per prius probata, ultra HT erit maxima declinatio per 14 secundi Theodosii. Cum tropicus hyemalis secet maximam declinationem ut patuit in 16 prime dictionis et cum etiam maxima declinatio hyemalis sit EH vel maxime estivalis per animi conceptionem si ab equalibus idem commune demas et cetera, hiis premissis ducatur sinus ZB altitudinis poli in HT maxime declinationis et productum dividatur per HZ perfectionis maxime declinationis et exeat K, et erit ZB ad K ut ZH ad HT et per 15 sexti Euclidis - de sinibus semper loquor. Hoc dico igitur quod si K ducatur in sinum AE qui est semidyametrum productumque dividatur per sinum AB perfectionis poli, exibit sinus TE differentie medietate minimi diei ad equinoctialem diem. Per katham enim disiunctam erit ZB ad BA compositam ex ZH ad HT et ET ad EA. Sed ZH ad HT ut ZB ad K. Igitur quod ZB ad BA constat ex ZB ad K et ET ad EA. Sed ZB ad BA constat etiam ex ZB ad K et K ad BA. Igitur ille illis equales, igitur si ab equalibus idem commune demas. Si dematur ZB ad K ab utrisque, remanet K ad BA equalis ET ad EA. Quare per 15 6 Euclidis si[t] K ducatur in sinum EA productumque dividatur per AB, exibit ET, quod est intentum potesque si vis regulam universali particulari sic: si sinus altitudnis poli ducatur in sinum declinationis puncti cuius arcum diurnum queris productumque si diviseris per sinum perfectionis eiusdem declinationis et cetera ut prius, et finaliter differentia mediata arcus diei puncti cuius arcum queris ad equinoctialem diem exibit et erit demonstratio ut prius. Erit punctum H vero oritur punctus datus et HT eius declinatio et TE differentia quam queris. Hoc tamen intellige quod eadem est altitudo poli artici et antartici quod ex hac patet, si ab equis idem commune demas et cetera. Si protrahantur duo arcus circuli ymaginatorum a polis per terminos arcus diei hyemalis tropici et per terminos omni aliorum ostendentes similes in equinoctiali, per 14 secundi Theodosii erit arcus illis equinoctialis correspondens arcu tropici hyemalis que omni est minor.
〈II.2〉 20. Arcum orizontis in quovis clymate qui est inter ortum tropici et equinoctialem per assignatum minimi diei arcum investigare. Unde patet quod si ducatur sinus dimidii arcus diei minimi in sinum perfectionis arcus orizontis qui est inter ortum utriusque tropicorum et equinoctialem. Simili quoque ratione inveniri potest distantia ortus cuiuslibet signi vel gradus ab equinoctiali.
Manente dispositione premissa. Volo invenire arcum HE. Cum enim proportio conversa componatur ex conversis, erit per katham coniunctam AT ad AE composita ex BH ad BE et TZ ad HZ. Sed BE et ZT sunt equales ex 23 primi et 12 secundi et 15 primi Theodosii et 27 tertii Euclidis. Igitur AT ad AE constat ex BH ad BE et BE ad HZ. Sed BH ad HZ constat ex eisdem. Igitur AT ad AE ut BH ad HZ. Igitur per 15 sexti Euclidis si AT AT] corr. ex ATE P sinus medietatis arcus diei minimi primum ducatur in HZ quartum quartum] i.m. P sinum perfectionis maxime declinationis productumque dividatur per AE sinum quadrantis secundum, exibit BH sinus perfectionis arcus orizontis inter tropicum et equinoctialem tertium, quod est intentum. Potes quoque si vis hanc universalisari ut premissam et demonstrare eodem modo sicud innuitur in utraque.
Capitulum tertium ostendit quomodo sciatur altitudo poli per quamcumque arcum dyurnum notum et quomodo arcus orizontis inter equinoctialem et aliquam paralellorum per notam altitudinem poli notificetur quodque hii inter equinoctialem et paralellos equidistantes ab equinoctiali sunt equales et quod alternatim nox unius paralelli sit equalis diei alterius sibi equalis et habet tres conclusiones:
〈II.3〉 21. Altitudinem poli per arcum diei minimi invenire. Unde regula: Si sinus differentie medie diei minimi ad equinoctialem diem ducatur in sinum perfectionis arcus orizontis inter tropicum et equinoctialem productumque dividatur per sinum arcus orizontis qui est inter tropicum et equinoctialem, atque exierit ducatur in sinum quadrantis, productumque dividatur per sinum arcus medii diei minimi, exibit sinus altitudinis poli.
Si enim ET sinus differentie medie diei minimi ad equinoctialem †tracta† †tracta†] unclear reading P ducatur in BH sinum perfectionis arcus orizontis inter tropicum et equinoctialem productumque dividatur per HE sinum arcus orizontis inter tropicum et equinoctialem et exiat K, eritque per 15 sexti Euclidis ET ad K ut EH ad HB; et quia per katham disiunctam ET ad TA constat ex EH ad HB, et ZB ad ZA constabit et ex ET ad K et ZB ad ZA. Sed eadem constat ex ET ad TK et K ad TA. Igitur ille illis eque. Igitur si ab equis equa demas vel idem commune et cetera, erit K ad TA ut ZB ad ZA. Ergo per 15 sexti Euclidis si K ducatur ZB sinum quadrantis productumque dividatur per TA sinum arcus medii diei minimi, exibit ZB sinus altitudini poli, quod volui. Hoc autem ut premisse potest universalisari.
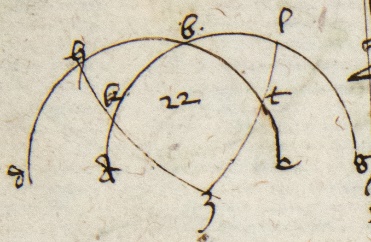
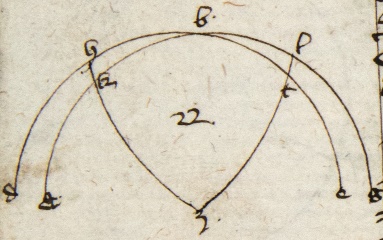
〈II.4〉 22. Arcum orizontis qui est inter tropicum et equinoctialem per altitudinem poli notam repereri. Unde patet: si sinum maxime declinationis ducatur in sinum quadrantis productumque dividatur per sinum perfectionis altitudinis, exibit sinus arcus orizontis qui est inter tropicum et equinoctialem deprehensus.
Quia enim eadem figura manente per katham coniunctam conversis proportionibus AB ad AZ constat ex TH ad TZ et ex EB vel TZ, quia sibi equale AHE, sed TH ad HE constat ex eisdem, igitur TH ad HE ut AB AB] corr. ex HB P ad AZ. Quare per 15 sexti Euclidis si TH sinus maxime declinationis ducatur in AZ sinum quadrantis productumque dividatur per AB sinum perfectionis altitudinis poli, exibit [exibit] HE sinus arcus inter tropicum et equinoctialem, quod volebam. Hec quoque potest ampliari.
〈II.5〉 23. Quilibet duo circuli paralelli circulo equinoctiali eiusdem longitudinis a duobus tropicis seu ab equinoctiali equales arcus orizontis ex utraque parte equinoctialis resecant, et fit coalternatim nox unius diei alterius equalis.
Sine figura prehabita trahantur duo paralelli et equaliter distantes ab equinoctiali qui sint HL et KM sitque Q polus articus et trahatur QK, scilicet arcus circuli magni. Cum igitur Q Z sint poli equinoctialis et suorum paralellorum per primam secundi Theodosii et orizon non transeat super illos polos, sequitur quod Z inclinatus paralellos alioquin per 17 primi Theodosii transierit per polos eorum. Quare sequitur per 22 secundi Theodosii et duodecimam eiusdem arcum KM equales esse arcui HL et sic arcus nocturnus superioris paralelle equalis arcui diurno inferioris, quod est secundum. Primum autem statim patet ex sexta primi et ypothesi et 21 secundi Theodosii. Sed Ptolomeus sic arguit: cum enim KM et HL sint equales sequitur per 14 Theodosii SG et TA esse equales. Quare TE et ES equales cumque ypothesi SK sit equalis TH et angulus T equalis S per 19 primi Theodosii. Igitur per 4 primi Milei HE equalis erit EK, quod est propositum.
Capitulum quartum ostendit quas terras inhabitent illi super quorum summitatem Sol transit et quando et quotiens. Capitulum quintum ostendit quomodo sciantur proportiones umbrarum ad res facientes umbras per altitudinem poli et econtrario et habet solam conclusionem:
〈II.6〉 24. Nota Solis altitudine proportionem umbre recte et verse ad rem facientem vel umbram invenire et econtra nota proportione umbre recte vel verse ad faciens altitudinem Solis invenire sicque ex notitia maxima altitudine Solis meridiana minimam umbram meridianam reperire et ex minima altitudine maximam umbram et econtra ex minima et maxima umbra meridiana maximam et minimam Solis.
Altitudinem invenire sicque maximam declinationem et altitudinem poli notam facere ex umbraque recta versam invenire et econtra ex versa rectam. Unde patent regule. Prima: Si sinus perfectionis altitudinis ducatur in rem facientem umbram productumque per sinum altitudinis dividatur, exibit umbra recta. Secunda: Et econtra si umbra recta cum nota sit in semidyametrum ducatur productumque per radicem quadratam aggregati ex duobus quartis, scilicet umbre recte et rei facientis umbram, dividatur, exibit sinus perfectionis altitudinis. Tertia: Similiter si res faciens umbram in semidyametrum ducatur productumque per radicem ante statim dictam dividatur, exibit sinus quesite altitudinis. Quarta: Et si sinus altitudinis Solis cum nota sit ducatur in rem facientem umbram productumque per sinum perfectionis altitudinis dividatur, exibit umbra versa. Quinta: Et econtra si umbra[m] versa[m] cum nota sit in semidyametrum ducatur productumque dividatur per radicem quadratam aggregati e quadrato umbre verse et rei facientis umbram, exibit sinus altitudinis quesite. Sexta: Similiter si res faciens umbram ducatur in semidyametrum productumque per radicem de qua statim mentio fiebat dividatur, exibit sinus perfectionis altitudinis quesite. Septima: Et si simul quod sit ex ductu rei facientis umbram rectam in rem facientem umbram versam per umbram rectam dividatur, exibit versa. Octava: Si autem per versam, exibit recta.
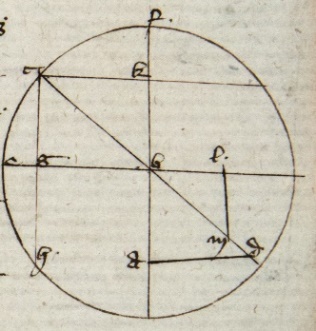
Inprimis scire oportet quod res faciens umbram ymaginetur dividi in 12 partes equales et notantur puncta et ideo idem est res faciens umbram et 12 puncta. Secundo notandum quod umbra recta debet esse in superficie sub orizonte equidistante ei super quam sit res faciens umbram orthogonaliter erecta, ita ut summitas rei sit in centro orizontis. Umbra autem versa est in superficie orthogonaliter intersecante orizontem in qua res faciens umbram perpendiculariter ita quod unus eius terminus sit in centro orizontis. Sed quia quantitas terre respectu celi est ut punctum, possumus umbram rectam rectam] followed by one word crossed out by the scribe: facere P capere in superficie equidistante equidistante] followed by one letter crossed out by the scribe: Z P orizonti super eum. Ymaginandi semper summitatem rei facientis umbram centrum orizontis quia insensibiliter respectu celi distat, umbram autem versam in superficie orthogonaliter istam intersecante in qua faciens sit, ut unus eius terminus sit cum summitate rei facientis umbram rectam. Sic igitur patet quod per umbram nos possumus videre. Non possumus altitudinem Solis super orizontem invenire nec ex ea illas invenire, sed superficiem equidistantem orizonti transeuntem per summitatem rei facientis umbram rectam que est in centrum circuli altitudinis in qua etiam terminatur res faciens umbram versam exiens in illa superficie. Sed tum insensibilis error erit et hoc totum statim clarius patebit. Sit igitur circulus altitudinis ABG cuius centrum E summitas rei facientis umbram rectam et est terminus rei facientis umbram versam orthogonaliter intersecans superficiem transeuntem per E supra quam habemus altitudinem vel volumus scire ita ut si sit illa superficies orizon quod transeat per 17 primi Theodosii per polos eius qui sunt A L. Communis autem sectio huius circuli et huius superficiei per 3 ultimi Euclidis sit recta linea BEK et volo illam superficiem vocari orizontem eritque ob hoc per 12 primi Theodosii AL perpendicularis superficiem orizontis et E centrum eius. Sit autem HG communis differentia circuli altitudinis et superficiei equidistantis orizonti DE subtus in qua res faciens umbram rectam stet perpendiculariter. Quia illa debet terminari in E oportet quod sit HE. Alias per conversam 14e ultimi Euclidis due essent perpendiculares super superficiem orizontis ex eadem parte in E, quod est inconveniens per 13 eiusdem et non est cura si EH sit minor, maior vel equalis EL. Sit autem BC altitudo Solis et CEG eritque HG umbra recta. Longitudo umbre saltim finite est linea recta intercepta inter rem facientem umbram que in ea stat orthogonaliter et inter inter] followed by two words crossed out by the scribe: umbram invenitur P lineam ducatam a centro luminosi per summitatem rei facientis umbram que cum ea concurrit. Et illa umbra invenitur per altitudinem luminosi super lineam equidistantem tali umbre transeuntis per summitatem rei facientis umbram. Et econtrario per umbram invenitur talis altitudo altitudo] followed by two words crossed out by the scribe: distans umbre P et debet centrum circuli altitudinis esse summitas rei facientis umbram umbram] followed by nine words crossed out by the scribe: distans umbre et transiens per summitatem rei facientis umbram P et hoc clare patebit. Unde patet quod per umbram non potest inveniri altitudo luminosi super orizonte〈m〉 nec econtra nisi linea illa equistans umbre et transiens per summitatem rei facientis umbram esse in superficie orizontis et res faciens umbras pendetur perpendiculariter in superficie orizontis. Sed quia altitudo supra orizontem et altitudo per quam invenitur umbra et econtra in insensibili differunt, saltim si res faciens umbram sit orthogonaliter erecta super orizontem vel superficiem equidistantem ei cum terra sit tanquam punctum respectu celi ut habitum est in prima dictione, ideo possumus capere unam per alia sine sensibili errore. Dyameter umbre est linea recta a summitate rei facientis umbram ad finem longitudinis umbre ducta. Aliqui disti〈n〉guunt de umbra recta et versa et credo quod umbra recta et versa solum differunt ut basis et kathetus. Unde umbra cuiuslibet rei prius diffinite potest vocari recta et umbra alicuius rei statutis statutis] followed by one word crossed out by the scribe: versa P super summitatem illius orthogonaliter versa. Unde patet quod si habeatur perfecta scientia de umbra recta, habetur etiam de versa. Tamen si quis voluerit specialem mentionem facere de umbra versa, capiat perfectionem altitudinis umbre recte et per eam inveniet versam sicud per altitudinem rectam et econtra et hoc statim patebit. Sciendum tamen quod antonomasice umbra rei erecte orthogonaliter super orizontem vel superficiem equidistantem orizonti vocatur recta et umbra rei erecte super summitatem illius equidistantis umbre eiusdem vocatur versa.
Sit AB faciens umbram rectam, C luminosum, CBD linea a centro luminosi ad concursum linee AD perpendicularis ad AB, BE autem equidistans AD. Quia igitur 3 linee AB, DBC, BE cum AD sunt in superficie una per 2 ultimi Euclidis, ponatur EB equalis CB, protrahatur AB usque ad F et ponatur BF predictis equalis et supra centro B secundum quantitatem BB BB] sic P in superficie predictarum quatuor linearum describatur circulus altitudinis ECF. Quia igitur BAD rectus erit ex ypothesi et 27 primi Euclidis, EBA rectus. Quare EBF rectus. Quare ex corollario 13 vel 15 primi et 25 tertii Euclidis EF est quarta circuli. Si igitur ducatur CGH corda dupli arcus altitudinis altitudinis] followed by one word crossed out by the scribe: ut P ita ut EH sit equalis EC quod potest fieri ex prima quarti adiuncta 27 tertii Euclidis, erit per 26 tertii et 8 primi Euclidis et diffinitionibus CG sinus altitudinis perpendicularis EB et eadem ratione CK perpendicularis BF et sinus CF. Quare per 28 primi 〈Euclidis〉 CBGK superficies equidistantium laterum atque per 34 eiusdem CK equale GB. Quia igitur duo trianguli CGB et BAD sunt equianguli per 28 primi et ypothesi ipsi per 4 sexti 〈Euclidis〉, habebit latera proportionalia prout respiciunt equales angulos. Quare GB ad AD ut GC ad AB. Igitur per 15 sexti Euclidis si GB sinus perfectionis altitudinis ducatur in AB faciens umbra〈m〉 productumque dividatur per GC sinum altitudinis, exibit AD umbra umbra] followed by one word crossed out by the scribe: quod P recta, quod est regula prima. Item AD ad GB ut DB DB] preceded by L or l〈inea?〉 P ad BC. Igitur per eadem si AD umbra recta ducatur in BC semidyametrum productumque dividatur per BD radicem quadrata aggregati ex quadrato AB facientis umbram et quadrato AD umbre recte per 46 primi Euclidis, exibit GB sinus perfectionis altitudinis, quod est regula secunda. Item AB ad GC ut DB 〈ad〉 BC. Quare illud quod sit AB in BC dividatur per DB, exibit GC, quod est regula tertia. Sequentes autem 3 regule patent sicud ille: Si EB ducatur usque ad latera ut BL sit res faciens umbram versam et LM umbra versa per triangulos CBK et BML et non mirum si LM ponatur umbra recta, CF est altitudo per quod invenitur hec altitudo et econtra, ut CE est altitudo per quam invenitur umbra AD et econtra. Ultime etiam duo trianguli BLM et BAD per 27 et 28 primi et 4 6 Euclidis habent latera proportionalia, igitur BL ad AD ut LM ad BA. Igitur per 15 sexti Euclidis patent ultime due regule. Et ad huc dico quod omnes umbre stante equali altitudine suis rebus facientibus umbras esse proportionales, quod sic patet, quia omnes trianguli contenti a dyametro umbrarum et a rebus facientibus umbras et a longitudinibus umbrarum habent latera proportionalia ex quarta sexti 〈Euclidis〉 et ex hoc quilibet talium habet unum rectum et unum compositum angulo qui supponitur perfectioni altitudinis. Per illam igitur scientiam potest ex notitia maxime et minime umbre meridiana haberi minima et maxima altitudo quarum differentia est duplum ad maximam declinationem; et si tunc a maxima altitudine subtrahatur maxima declinatio, remanebit altitudo equinoctialis maximam que si dematur a 90 90] uncertain reading P, remanet latitudo regionis que est equalis altitudini poli et ad huius Ptolomeus ponit talem figuram.
Capitulum sextum est de proportionibus orbium equidistantium equinoctiali ut de umbris umbris] preceded by an unclear letter or symbol P et de aliis et habet solum 7 conclusiones demonstratas:
〈II.7〉 Sub equinoctiali omnes dies sunt equales noctibus et sibi invicem, et omnes stelle habent ortum et occasum, et umbre meridiane quandoque quandoque] corr. ex quandocumque P ad meridiem quandoque ad septentrionem quandoque nusquam declinant.
Prima pars patet per primam secundi et 19 primi Theodosii, secunda ex hoc quod omnes circuli sunt equidistantes equinoctiali et medietates eorum eorum] followed by one word crossed out by the scribe: equinoctiali P equali tempore circumvolvuntur. Tertia sicud prima. Ex hac parte declinant et aliquando est in cenik.
〈II.8〉 Sub omni alia equidistante equinoctiali bis tantum in anno dies fit equali〈s〉 nocti; et dies estivi himi himi] sic for hibernis P prolixiores; et quanto ab equinoctiali distantiores dies estivi prolixiores seu productiores, himber himber] sic for hiberni P vero correptiores; et quedam stelle apparentes semper, quedam occulte semper; et distantia cenik ab equinoctiali equalis altitudini poli.
Prima pars patet si ymaginetur circulus orthogonaliter intersecans meridianum in polis mundi qui circulus orientis et occidentis vocantur. Circulus igitur occidentis et orientis cum meridiano dividunt equinoctialem in quartas per 15 et 17 primi et 12 secundi Theodosii. Cum autem orizon cum meridiano faciat hoc idem per 12 secundi Theodosii, oportet quod circulus orientis et occidentis seccent orizontem ubi principium Arietis vel Libre oriuntur. Quia igitur arcus diurnus principii Arietis vel Libre est equalis nocturno per 15 primi Theodosii, sequitur bis in anno diem equalem esse nocti. Quia etiam circulus occidentis et cetera secat omnes paralellos in equa per 1 secundi et 19 primi Theodosii, sequitur omnes dies a principio Arietis usque ad finem Virginis esse maiores suis noctibus et econverso in altera medietate quod ex hoc patet quod medietas orizontis super equinoctialem declinat a medietate circuli orientis et cetera supra eundem equinoctialem versus septentrionem et contra de medietatibus sub equinoctiali. Quare patet prima et secunda pars. Et quia orizon rectius rectius] preceded by an unclear letter or symbol P poli sunt equinoctiali et poli equinoctiali in orizonte recto per 19 et 17 primi Theodosii, sequitur quod quanto cenik removetur ab equinoctiali tanto orizon removetur a polis, tanto etiam crescunt arcus paralellorum inter orizontem et circulum orientis et cetera. Econtrario patent tertia et quarta pars. Et quia orizon est inclinatus super equinoctialem, aliquando enim transierit per polos eius per 17 primi Theodosii, sequitur per 10 secundi Theodosii quod ipse contingit duos circulos equidistantes equinoctiali. Qui cum sint super eiusdem polos per primam secundi Theodosii, sequitur quod quelibet stelle que sunt in polum apparentem et circulum sibi proximum semper apparent. Stelle autem inter circulum alium et polum alium semper sunt occulte, quod est residuum proportionis nostre. Non oportet autem demonstrare quod habentes eandem altitudinem poli habeant omnes dies equales quia hoc patet ex prima huius.
〈II.9〉 Sub remotiori linea ab equinoctiali maior est inequalitas dierum et noctium, et maior pars celi apparet et maior pars celi occulta semper.
Prima pars patet ex ex] followed by one word crossed out by the scribe: premissa P demonstratione premisse; secunda et tertia ex hoc quod quanto orizon adcedit ad equinoctialem tanto circuli paralelli quos contingit orizon accedunt ad equinoctialem. Et sic ut premissa patet propositum.
〈II.10〉 Sub omni linea cuius distantia ab equinoctiali minor maxima declinatione, umbre meridiane ad ultimamque partem alternatim declinant et bis in anno declinatione carent.
Patet quia Sol ad utramqe partem cenic declinat et bis in anno est in cenik cum sit bis in illo paralello.
〈II.11〉 Sub linea cuius discessus ab equinoctiali equalis est maxime declinationi, umbra semel declinatione caret, et umbra meridiana numquam declinat ad meridiem.
Prima patet quia Sol nec semel est in principio Cancri. Secunda oportet quia oportet quod Sol esset magis septentrionalis quam cenic eorum.
〈II.12〉 Sub linea circuli artici vel antartici umbra in aliquo die ad omnem partem flectitur et fit dies 24 horarum et dies sine nocte, et ex opposito nox sine die, et quanto distantia cenik ab hac linea maior versus polum tanto maius tempus abiit sine nocte et ex opposito sine die.
Prima patet si Sol in principio Canri ponatur. Ex eo zodiaci et orizontis aliquando sunt idem. Ex quo sequitur quod orizon contingit duos tropicos et sic etiam patent secunda, tertia, quarta. Et quia etiam quanto cenic appropinquat a circulo artico versus polum tanto orizon appropinquat equinoctiali a tropicis et tanto maior pars zodia〈ci〉 est semper super orizontem et alia sub equo patet, patet quinta et sexta pars.
〈II.13〉 Sub polo eadem medietas celi est apparens semper et eadem occulta semper et anni spatium et dies una cum nocte sua.
Hoc patet quia equinoctialis est illorum orizon.
Capitulum septimum est de ascensionibus signorum in circulo obliquo et habet quinque conclusiones:
〈II.14〉 In spera declivi quilibet duo arcus equales circuli declivis et equaliter distantes a puncto equinoctiali equales habent ascensiones.
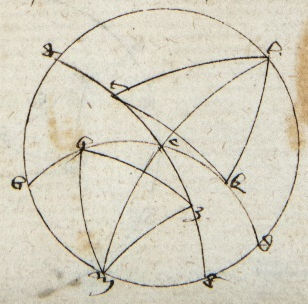
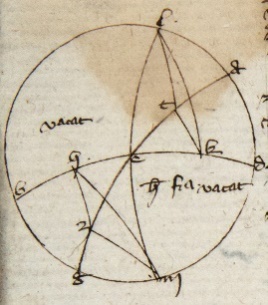
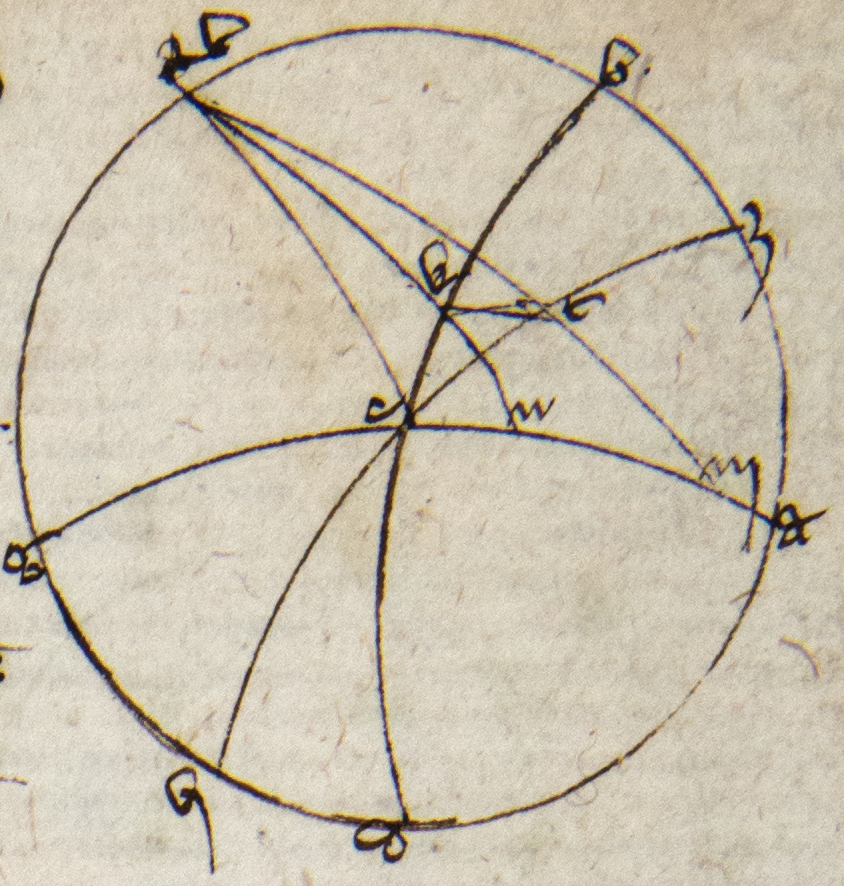
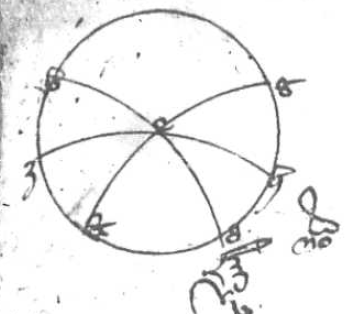
Sit meridianus ABGD, medietas orizontis BED, equinoctialis AEG, polus articus L, antarticus M. Sit autem articus ZH zodiaci incipiens ab equinoctiali ita ut Z sit principium Arietis vel Libre sitque gratia exempli ZH Pisces ita ut principium Piscium, scilicet H, sit in contactu orizontis, Z autem finis in equinoctiali. Manifestum igitur quod est E oritur in orizonte obliquo cum ZH. Quoniam simul incipiunt et desinunt oriri et punctus Z semper in equinoctiali AEG, oriatur ZH et ascendat Z principium Arietis usque ad C. Quousque totus Aries qui est equalis Piscibus sit per ortus sit TK manifestumque ut prius quod TE oritur cum TK quod ut plane pateat. Ymaginor duos equinoctiales, unum super alium, unum mobilem, alium inmobilem. Hoc dico igitur quod TE equum est EZ. Sic patet quia MZ, ME, LT, LE sunt omnes equales per 23 et 6 primi Theodosii et 27 tertii Euclidis. Vides igitur duos triangulos MZH LTK quorum duo latera unius, scilicet ZH et ZM, sunt equalia duobus alterius, scilicet TK TK] followed by one word crossed out by the scribe: et P et TL ; et anguli equis lateribus contenti equales quia contra se positi cum Z et T sunt idem punctum quamvis in diversis locis successive; et HZ et TL, scilicet Pisces et Aries, sunt arcus continui et MZ et TL, scilicet arcus circulorum magnorum a polis ad principium Arietis transeuntium, sicud etiam arcus continui. Alioquin concluditur quod circuli magni secent se per inequalia, quod est contra 15 primi Theodosii. Sic igitur per quartam primi Milei MH equum est LK. Igitur declinationes puncti H et K sunt equales. Igitur per 5 presentis HE est equale EK, tunc sic per secundam partem quarte primi Milei cum triangulis MHE et LEK. Per eandem partem erit angulus HME equus ELK et eadem ratione HMZ equus TLK. Igitur per communem scientiam EMZ equus ELT. Igitur iterum per quartam primi Milei EZ equale ET, quod est intentum. Nota Nota] vacat a nota ad finem illius (?) 9ti (?) add. i. m. P quod hec est figura Ptolomey et in ea ymaginentur motus a dextra ad sinistram et non est cura de hoc quia vertendo figuram habebis motum a sinistris ad dextram vel si velis ymaginari TK esse Pisces et M polum articum. Secunda figura ymaginatur motum a sinistra a〈d〉 dextram et non est cura quam recipies. Intellige quod idem erit iudicium si TZ sit principium Libre. Intellige etiam si arcus zodiaci non incipiat ab equinoctiali, probabitur per arcus inter illos interceptos et equinoctialem et per aggregatis ex illis et illis et communem scientiam.
〈II.15〉 Quilibet duo arcus circuli declivis equales et inequaliter distantes ab altero punctorum tropicorum habent in spera obliqua ascensiones coniunctas equas eis ascensionibus quas idem arcus habent in spera recta coniunctis. Ex qua et premissa manifestum est quod si note fuerint ascensiones unius quarte in spera obliqua, note erunt note] nocte or notte P ascensiones omnium.
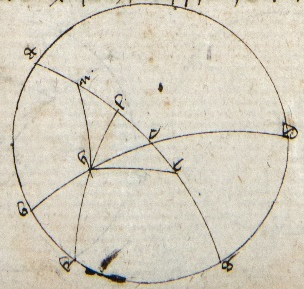
Sit ABDG meridianus circulus, BED medietas orizontis et AEG equinoctialis, idest ZH sit Libra ex toto super orizontem cuius finis H sit in contactu orizontis. Manifestum igitur ut in premissa quod est E oritur cum HZ in spera obliqua. Sit autem K polus antarticus et producatur circulus magnus KHL per 29 primi Theodosii qui ponatur orizon rectus. Patet igitur ut prius quod EL oritur in spera recta cum ZH. Si igitur ymaginemur paralellum transeuntem per H, ipse per 17 secundi Theodosii transibit per principium Piscium. Quare caput Piscium oritur in H puncto. Revolvetur igitur spera quousque caput Piscium veniat ad ad] sup. lin. P MH sitque HT ita ut T sit principium Arietis et H Piscium. Manifestum igitur igitur] followed by one word crossed out by the scribe: quod P ut prius quod TE oritur cum TH in spera obliqua et TL cum eodem in spera recta. Cum igitur TE et EZ sint ascensiones Libre et Piscium in spera obliqua et TL et LZ coniuncte ascensiones eorumdem in spera recta et TE et EZ coniuncte equales. Sit TL et LZ coniunctis, sequitur quod ascensiones coniuncte Libre et Piscium in spera obliqua sunt equales ascensionibus eorumdem in spera recta, quod est intentum. Intellige quod demonstratio est universalis sive cenic sit in circulo artico vel citra, non autem si ultra de quo dubitavi. Ex hiis concluditur corollarie quod in regionibus ubi cenik non est ultra circulum articum ascensiones signorum a principio Libre, idest portionis a principio Librem incipientis et circa finem Piscium terminate usque in finem Piscium in spera obliqua sunt maiores ascensionibus eorumdem in spera recta in alia medietate. Econtra in regionibus autem ubi cenik est ultra circulum articum non est ita. Hoc corollarium ex demonstratione prehabita cum figura sine obice concluditur. Corollarium autem conclusionis sic patet, sed debet intellegi de quarta incipiente ab aliquo solstitiorum vel equinoctiorum. Si igitur ascensiones quarte vernalis in spera obliqua fuerint note, erunt et hyemales note per premissam. Cum igitur ascensiones quarte vernalis et estivialis in spera recta adequantur per 17 prime dictionis vel quarte primi Milei, scilicet per secundam et primam eius partem, et similiter quarte hyemalis et autumpnalis. Igitur per presentem si ascensiones cuiuslibet portionis in quarta hyemali vel vernali in spera obliqua subtrahatur ab ascensionibus eiusdem portionis in spera recta duplicatis que note sunt, relinquentur ascensiones in spera obliqua portiones equales et equaliter distantes a puncto solstitii in quarta estivali vel autumpnali. Sic patebit propositum. Intellige quantum ad questionem: si arcus zodyaci non incipiant ab equinoctiali, argue ut in premissa. Nota quod hec precedens demonstratio ponitur in maiori Almagesti, sed in minori ponitur alia. Ibi enim disponuntur due figure omnino tales ut ista cum eisdem ypothesibus excepto quod in una ponitur ZH et non TH et in alia TH et non ZH et tunc probatur quod LE in una sit equalis LE in alia, quod patet cum angulus HLE in utraque sit rectus et HLE in utraque idem, scilicet contentus ab orizonte et equinoctiali, et HL unius equale HL alterius propter equales declinationes principii Piscium et finis Libre. Igitur per 16 primi Milei LE unius equale LE alterius. Quare excessus ascensionis HZ in spera obliqua super ascensionem eiusdem in spera recta equalis est excessui ascensionis HT in spera recta super ascensionem eiusdem in spera obliqua, ex quo concluditur propositum.
〈II.16〉 Cuiuslibet portionis circuli declivis ascensionem in spera declivi invenire. Regula operationis: si sinum altitudinis poli duxeris in sinum declinationis inchoate ab equinoctiali puncto cuius elevationem queris et productum dividas per sinum perfectionis eiusdem declinationis et quod exierit iterum ducas in semidyametrum et productum dividas per sinum perfectionis altitudinis poli, exibit sinus differentie elevationum sumpte in spera recta et declivi.
In Almagesto abbreviato queritur arcus EL in figura precedente qui per katham disiunctam cum arcubus AK et AE et aliis duobus reflexis per modum demonstrationis prime huius satis notficatur, sed in maiore describitur meridianus ABGD, equinoctialis AEG, orizon BED, zodyacus THLZ et ponatur H principium Arietis et veniat circulus magnus per 29 primi Theodosii a polo septentrionali AK per LK LM. Cum arcu igitur HL in spera obliqua elevatur HE et in spera recta HM. Erit igitur EM differentia elevationum HL in spera recta et obliqua qui ut in minori investigatur per GE GK KM ED arcus.
In parte sequenti Ptolomeus investigat quod in precedenti compendiosius, facilius et opere sapientiori ut ipse ayt.
〈II.17〉 Differentiam ascensionum in spera recta et declivi eiusdem portionis per arcum circuli magni vel principium in equinoctiali terminate a polo venientis terminare. Unde manifestum quod arcus circuli magni a polo venientis per punctum communem orizontis et paralelli transeuntis per finem portionis ab equinoctiali incepte terminat differentiam ascensionum eiusdem portionis in spera recta et declivi incepta a communi puncto orizontis et equinoctialis.
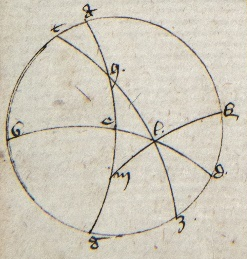
Sit meridianus ABGD, medietas equinoctialis AEG, orizontis BED, zodyaci HEZ ita ut E sit commune trium circulorum sitque punctum vernale G. Sit autem ET arcus zodyaci ad placitum et L polus equinoctialis et et] followed by three words crossed out by the scribe: dividatur per 29 P ducatur per 29 primi Theodosii arcus circuli magni LT in LE. Manifestum igitur quod EM oritur in spera recta cum ET. Deinde super polum B secundum quantitatem LT describatur arcus. Quousque secet orizontem super K sit TK qui per 2 secundi Theodosii equidistans erit equinoctiali. Deinde producatur arcus circuli magni LKN. Erit igitur KT similis NM per 14 secundi Theodosii. Portiones autem similes in quacumque spera circulorum equidistantium equinoctiali simul oriuntur, quod de spera recta patet per 14 et de obliqua per 17 secundi Theodosii. Si dubitas de spera obliqua, intellige quia orizon non transit per polos. Igitur per 17 primi Theodosii inclinatus super equinoctialem aliquando aliquando] corr. ex alioquin P sequitur contra eam. Quare per 10 secundi Theodosii contingit duos paralellos inter se equales et semper eosdem propter immobilitatem poli et secat paralellos inter istos. Si igitur principium alicuius paralelli arcus sit in orizonte, intellige duos orizontes, unum inmobilem, alium volubilem cum celo. Quando igitur arcus paralelli totus fuerit super orizontem, tunc inter medietates non concurrentes duorum orizontum erunt arcus paralellorum simul orientium similes, manifeste per 17 secundi Theodosii. Sic igitur patet quod in omni orizonte arcus paralellorum similes simul oriuntur. Igitur KT oritur cum NM in spera obliqua. Sed idem KT oritur ET in eadem spera. Igitur ET in spera obliqua oritur cum NM et sic differentia elevationum ET in spera recta et obliqua erit EN terminata per LKN arcum circuli magni a polo venientis, ut proponitur.
〈II.18〉 Cuiuslibet portionis circuli declivis elevationem in spera obliqua alia via rationis invenire. Unde manifestum erit quod si sinus differentie medie equalis diei ad minimum ducatur in sinum elevationis sumpte partis in spera recta et quod exierit dividatur per sinum quadrantis, exibit sinus differentie elevationum sumpte portionis in spera recta et obliqua.
Sit ABDG meridianus, AEG medietas equinoctialis, BED orizontis, Z polus, E punctum vernale et per premissam ZHT terminans differentiam ET elevationum totius quarte hyemalis. Manifestum igitur ex demonstratione prime huius quod ET est differentia mediata minimi diei ad medium et HT maxima declinatio et ZH perfectio eiusdem. Sit autem ZKL terminans iterum per premissam differentiam elevationum cuiuscumque minoris ut Piscium que sit EL et erit iterum ex demonstratione prime huius KL declinatio eius et ZK perfectio eiusdem. Ex katha igitur disiuncta proportio sinus ZH ad HT componitur ex proportione ZK ad KL et EL et ET. Sed eadem proportio, videlicet sinus perfectionis maxime declinationis ad sinum maxime declinationis, componitur ex proportione ZK ad KL, scilicet sinus perfectionis declinationis Piscium ad sinum declinationis eiusdem, et ex proportione sinus elevationis sumpte partis in spera recta ad sinum quadrantis, ut ex demonstratione ultime prime dictionis. Si eam bene inspexeris, clare patet igitur quod EL sinus ad ET sinum ut sinus elevationis sumpte partis in spera recta ad sinum quadrantis. Igitur per 15 sexti Euclidis si sinus ET differentie mediete minimi diei ad equalem ducatur in sinum elevationis sumpte partis in spera recta productumque dividatur per sinum quadrantis, exibit sinus ET differentie elevationum sumpte portionis in spera recta et obliqua, quod volui. Item intellige quod quelibet istarum viarum docet nisi de una quarta quia habita ista habentur alie.
Capitulum octavum docet ex premissis constituere tabulam ascensionum signorum in circulo obliquo et recto.
Capitulum nonum est de hiis que secuntur scientiam premissarum et habet solum duas conclusiones:
〈II.19〉 Per notas ascensiones et locum Solis notum quantitatem arcus diei et quantitatem arcus noctis et numerum equalium horarum diei vel noctis et tempora inequalium ascendensque et medium celi in omni hora invenire.
Pone Solem in occidente. Tunc oportet per 15 primi Theodosii ut nadir sit in oriente. Scias igitur asciensionem arcus a Sole in nadir in orizonte tuo et habebis arcum diurnum, quod est primum. Quam a toto circulo 360 demas et remanet arcus nocturnus, quod est secundum. Si autem arcum diei vel noctis per 15 diviseris, exibunt hore equales diei vel noctis, quod est tertium. Si autem arcum diei vel noctis per 12 diviseris, exibit tempus hore inequalis diei vel noctis, quod est quartum. Si autem horas ab ortu vel ocasu Solis vel a meridie vel media nocte ad gradus reduxeris et illos gradus ad gradus zodyaci reduxeris, habebis ascendens occidens medium celi et medium noctis, quod est residuum.
〈II.20〉 Datas horas temporales ad equales vertere et econtra. Hec satis clara est de se. Ergo non indiget ostensione.
Capitulum decimum de scientia angulorum provenientium ex zodyaco et meridiano et habet conclusiones sex:
〈II.21〉 Proportio speralis anguli supra polum alicuius circuli consistentis ad quatuor rectos est sicud arcus eiusdem circuli qui ei subtenditur ad totam circumferentiam.
Hec ut ultima sexti Euclidis ex diffinitione in continue proportionalitatis adiuncto corollario prime primi Milei concluditur evidenter sicque patet quod proportio angulorum supra polum alicuius circuli consistentem est sicud arcuum eiusdem circuli eis subpositorum.
〈II.22〉 Omnes duo anguli ex duobus meridianis cum circulo signorum ad eandem distantiam a puncto equinoctiali provenientes quorum alter intrinsecus alter vero extrinsecus ex eadem parte sibi oppositis fient equales.
Sit ABG equinoctialis, DBE zodyacus, Z polus, ZKH et ZTL meridiani, HB equale BT. Quia igitur duo anguli ad B sunt equales quia contra se positi et anguli HKB et BLT quia recti per 19 primi Theodosii et arcus HB equus BT, sequitur per 16 primi Milei KH equum esse TL. Cum autem ZK et ZL compleant semicirculum per 23 15 primi Theodosii et 27 tertii Euclidis sequitur [sequitur] ZH et ZT facere semicirculum. Quare per primam partem 10 prime Milei angulus ZTE equus est ZTH ZTH] uncertain reading P vel ZHD ZTH, quod est intentum. Sed Ptolomeus arguit ex hoc quod trianguli BKH et BTL sunt equilateri tum propter ypothesim, tum propter equales ascensiones, tum propter equales declinationes. Quare angulus hic equatur angulo BTL per quartam primi Milei qui ulterius equatur ZTE, ex quo sequitur intentum.
〈II.23〉 Omnes duo anguli ex duobus meridianis cum circulo signorum ad eandem distantiam a puncto tropico provenientis quorum alter intrinsecus alter vero extrinsecus extrinsecus] followed by one word crossed out by the scribe: ea P ex eadem parte sibi oppositi equantur duobus rectis.
Sit ABG zodiacus, B punctus tropici, Z polus, BD BE arcus equales, duo meridiani ZD ZE. Quia igitur ex premissis ZD et ZE sunt equales, sequitur per secundam primi Milei angulum ZED equum esse ZDE ZDE] corr. ex ZED P. Sed duo ad E sunt equales duobus rectis. Ergo E extrinsecus cum D intrinseco sunt equales duobus rectis, quod est intentum.
〈II.24〉 Angulus ex circulo meridiano cum circulo signorum aput punctum tropicum proveniens rectus esse necessario probatur.
Quia enim meridianus transiens per puncta tropica transit per polos zodiaci per 13 secundi Theodosii, sequitur intentum ex 19 primi eiusdem. Sed Ptolomeus depingit meridianum ABG et AEG zodiacum ponitque A punctum tropicum super quod depingit circulum magnum BED. Quia igitur ABG transit super polos AEG et BED, sequitur per 12 secundi et 15 primi Theodosii BE esse quartam circuli sui. Igitur per diffinitionem que puncta est est] uncertain reading P in principio secundi Almagesti abbreviati videlicet angulus rectus speralis est angulus speralis contentus ab arcubus circulorum magnorum supra polum alicuius circuli cui subponitur quarta eiusdem circuli sequitur BAE esse rectum, quod est intentum.
〈II.25〉 Maxima declinatione nota angulum ex meridiano et circulo signorum aput punctum equinoctii provenientem notum esse oportet. Unde patet si maximam declinationem addas vel subtrahas a quarta, remanet angulus quesitus.
Sit ABG meridianus, AZG zodyacus, B D poli mundi, AG equinoctialis, BZED colurus distinguens equinoctia eritque ZE maxima declinatio que si addatur ED quartam vel subtrahit ABG, notificabitur angulus ZAD vel ZAB. Tota questio patet per 29 primi, 12 secundi, 15 primi Theodosii et 21 presentis.
〈II.26〉 Quantitatem cuiuslibet anguli ex meridiano cum circulo signorum provenientis aput quodlibet punctum per notam puncti declinationem invenire. Unde liquet quod si declinationis puncti cuius angulus queritur sinum ducas in sinum perfectionis sumpte portionis a puncto equinoctiali et productum dividas per sinum ipsius portionis et exiens multiplices in semidyametrum atque quod provenerit dividas per sinum perfectionis declinationis, exibit sinus differentie anguli quesiti ad rectum cuius angulum si recto addideris vel recto subtraxeris, habebis angulum quesitum.
Sit ABGD meridianus, AEG equinoctialis, BZTE zodyacus. Sit autem ZB ad libitum, supra polum autem B secundum latus quadrati magni circuli describatur HTEK. Proportio igitur sinus BA ad AH per katham disiunctam constat ex BZ ad ZT et ET ad EH. Quare si sinus BA ducatur in ZT sinum perfectionis BZ ex ypothesi et productum dividatur per BZ et exeat M quod habebit se ad sinum AH ut ET ad EH EH] followed by one word crossed out by the scribe: quare P, quod patet ex demonstratione simili prime et tertie huius. Quare per 15 sexti Euclidis si M ducatur in sinum EH quadrantis per 12 secundi et 15 primi Theodosii cum ABG transeat per polos HEK et AEG productumque dividatur per sinum AH perfectionis declinationis cum BH et BT ex ypothesi et 27 tertii Euclidis sint quarte, exibit ET sinus differentie TH vel EK ad quartam. Quare per 21 huius anguli HBT vel TBK ad rectum, quod est intentum.
Capitulum undecimum est de scientia angulorum provenientium ex orizonte declivi et orbe signorum et habet quatuor conclusiones:
〈II.27〉 Omnes duo anguli ex ipso ex ipso] i. m. P ex orizonte declivi declivi] followed by three words crossed out by the scribe: et orbe signorum P provenientes cum circulo signorum ad eandem distantiam a puncto equinoctiali quorum unus intrinsecus alter vero extrinsecus ex eadem parte oppositi equales esse necesse est.
Sit ABG meridianus, AEG equinoctialis, BED orizon et sit KL Virgo ita ut K sit punctum autumpnale et principium Virginis in orizonte ascendat. Igitur Virgo et Libra ita ut K moveatur usque ad ZT. ZH sit Libra. Quia igitur trianguli EZH et EKL sunt equilateri ex 14a eiusque demonstratione quarta huius et ypothesi, sequitur per quartam primi Milei angulum ZHE equum esse angulo ELK. Cum autem duo anguli ZHE EHT simul sumpti sunt equales duobus angulis ELK et KLD quod et similia possunt haberi ex prima. Prima Milei eiusque demonstratione sequitur angulum EHT equum esse angulo DLK sicque patet propositum.
〈II.28〉 Omnes duo anguli ex uno orizonte obliquo cum circulo signorum aput puncta orientis et occidentis provenientes extrinsecus cum intrinseco ex eadem parte equantur duobus rectis. Unde colligitur quod duo quilibet angulo ad eandem distantiam a tropico puncto, unus orientalis alter occidentalis, unus intrinsecus alter extrinsecus ex eadem parte duobus rectis sunt equales. Quapropter notis angulis orientalibus unius medietatis incipientis a puncto equinoctiali, noti erunt orientales in alia et occidentales in utraque.
Sit ABGD orizon, AEGZ zodyacus. Quia igitur angulus ZA D] followed by one letter crossed out by the scribe: G PD equus est angulo ZGD ut patet ex demonstratione prime primi Milei et duo anguli ZAD DAE sunt equales duobus rectis ut patet ibidem, sequitur angulum DAE cum DGZ valere duos rectos quod est proportio. Quia igitur duo anguli orientales intrinsecus et extrinsecus ex eadem parte equaliter distantes a puncto equinoctiali ex premissa sunt equales et oppositi ex hac et 15a primi Theodosii sint equales, scilicet orientalis et occidentalis, sequitur corollarium primum. Si autem noti sint anguli orientales unius medietatis, noti erunt anguli orientales unius per premissam. Si autem noti sint anguli orientales alicuius medietatis incipientis a puncto equinoctiali, noti erunt occidentales eiusdem per primum corollarium et alterius per propositionem sicque patet tota nostra intentio.
Nota si esset magnus homo habens habens] followed by one letter crossed out by the scribe: p P caput in polo artico et pedes in polo antartico cum expansis brachiis movens celum primo primo] corr. ex primum P motu quo iam movetur ipse moveret celum a sinistris per ante ad dextram et a dextra per retro ad sinistram. Et ideo ad similitudinem huius motus debemus nos habere in nostris metibus, scilicet ita ire per ecclesiam, et etiam ita movere speram materialem cum per motum eius motum primum designare velimus ultra nota si alius in regionibus nostris stet vertens ante versus meridiem.
Ille habebit oriens a sinistris, meridiem ab ante, occidens a dextris, septentrionem a retro. Ideo si alius habeat aliquam figuram ante se que tota sit in superficie una, ponat oriens a sinistris, meridiem ab ante et cetera. Sed si alius habeat speram materialem ante se, non potest ita convenienter fieri quia si ponatur oriens ibi ubi signa oriuntur super orizontem a sinistris et velimus movere speram materialem ad modum primi mobilis oportet ut medietas spere materialis sub orizonte sit contra nos. Igitur ut medietas spere materialis supera orizontem sit contra nos et moveamus hanc speram ad motum primum ponendum erit habenti speram materialem in manu oriens a dextris meridiem a retro spere, quod est contra eum et cetera. Sic igitur si alius habeat figuram ante se que tota non sit in superficie una ut ubi signati sunt duo circuli in spera qui non sunt in superficie una in qua motum primum velit ymaginari, ponat oriens a dextris meridiem a retro figure quod debet ymaginari in aere contra hominem et cetera. Polos mundi autem si contingat signare, ponatur articus †s〈...〉† †s〈...〉†] unclear reading P sive ab ante circuli meridiani, antarticus autem econtra. Sic concordabimus nos modo figurandi antiquorum de dubitavi.
〈II.29〉 Nota poli altitudine et tropicorum distantia angulum ex concursu orizontis declivis et signorum circuli aput utrumque punctum equinoctii notum esse necesse est. Unde constat quod si differentiam que est inter regionis latitudinem et maximam declinationem cum latitudo maior fuerit a quarta circuli diminuas vel cum minor fuerit addicias, relinquitur angulus sub capite Libre. A quo si quantitatem distantie inter duos tropicos abieceris, residuum erit sub capite Arietis.
Sit ABGD meridianus, EZ quarta equinoctialis eritque per 19 et 23 primi Theodosii et 27 tertii Euclidis E polus meridiani. Sint autem EB et EG duo portiones zodyaci eruntque per diffinitionem poli et 15 primi Milei et 27 tertii Euclidis quarte. Sit igitur E ipsius EB principium Libre et E ipsius EG principium Arietis eritque ob hoc G principium Canri et B principium Capricorni. R autem sit nadir cenic eritque per communem scientiam si ab equalibus idem 〈et cetera〉 et 12 sextam et 15 primi Theodosii R est latitudo regionis. Cum autem BZ sit maxima declinatio et BG distantia tropicorum per 15 primi Theodosii et communem scientiam si ab equalibus idem commune et cetera et etiam E sit polus ABGD, ut propositum est, et RD quarta circuli magni per 23 et 15 primi Theodosii et 27 tertii Euclidis, sequitur per 21 huius intentum.
〈II.30〉 Quantitatem anguli anguli] followed by two words crossed out by the scribe: ex contingentia P ex concidentia orizontis et zodiaci aput quodlibet punctum per notum celi medium et eius declinationem notam investigare. Regula: si diametrum multiplices in sinum altitudinis gradus celi medii sub terra vel super terram terram] followed by four words crossed out by the scribe: prout contingat illam portionem P productumque dividas per sinum portionis que est inter orizontem et celi medium sub terra vel super terram prout contingat illam portionem esse minorem vel maiorem quarta, exibit sinus quesiti arcus et anguli.
Sit meridianus ABGD, orizon BED, orbis signorum AEG et sit E caput Chancri veniens ad orientem eritque per 19 huius medium celi sub terra que est punctus G notum et per eandem haberi potest quod EG est minus quarta. Describatur igitur super polum E secundum latus quarti arcus ZHT eritque ob hoc quod orizon transit per polos meridiani et ZHT et 12 secundi et 15 primi Theodosii ZT quarta et similiter ZD. Sic igitur per katham coniunctam erit sinus ZT ad HT ut EG ad GD quod transpositis proportionibus componentibus per 21 22 quinti Euclidis et ex diffinitione proportio proportio] corr. ex proportione P extremorum et cetera patet 15 sexti Euclidis. Patet nostra intentio. Si autem EG fuerit maius quarta, ut si E sit alius punctus zodyaci, fiat argumentum ex parte EA quod tunc erit minus quarta per 15 primi Theodosii ita ut ZHT describatur ex parte AB. Sed si placet possemus proponere propositionem nostram sic: si semi et cetera et productum et cetera portio[rtio]nis inter orizontem et celi medium sine disiunctione que sequitur et tunc probaretur conclusio ex hiis que prius et ex 11 meo proportionum descripto arcu ZHT super ZGD si EG fuerit maius quarta. Si autem EG fuerit quarta, autem tunc ZHT erit idem cum meridiano, autem secabit eum solum in A. Et igitur si primum, erit E polus meridiei, quare punctus equinoctialis per 19 et 27 primi Theodosii. Patet igitur ut in premissa intentum. Si secundum, erunt per 12 secundi et 15 primi Theodosii G et A poli orizontis. Quare 〈per〉 19 primi Theodosii angulus GED rectus. Quare iterum intentum.
〈12〉 Capitulum undecimum undecimum] sic for duodecimum P est de scientia arcuum et angulorum provenientium ab orbe signorum et orbe descripto super polos orizonti dati et habet conclusiones sex:
〈II.31〉 Omnes bini arcus binorum orbium altitudinis egressi a polo orizontis ad duo puncta circuli signorum eiusdem a puncto tropico distantie cum ipsa etiam a circulo medii diei ante et post secundum equalia tempora disteterint sunt equales et faciunt angulos cum circulo signorum extrinsecum et intrinsecum ex eadem parte sibi oppositum equales duobus rectis.
Sit ABG meridianus, B cenik, G polus equinoctialis, AD et AZ arcus zodyaci equales et distent debet puncta equaliter a meridiano et puncto tropico. Protrahantur igitur arcus magnorum circulorum BD BZ GD GZ. Quia igitur GD et GA protracti usque ad equinoctialem sunt equales, GA et GZ protractis tantumdem et arcus equinoctialis hic et ibi interceptus sunt equi. Sequitur per 4 primi Milei DGA equum esse AGZ et cum DG sit equalis ZG per 16 prime dicitionis sequitur facta GB communi. Sequitur per eandem quartam primi Milei BD equum esse BZ, quod est primum, et angulum GDB angulo GZB. Sed angulus EDG cum AZG valet duos rectos per 23 huius. Igitur anguli EDB et AZB valent duos rectos, quia illi et isti communicant in eisdem et equalibus sicque patet secundum.
〈II.32〉 Omnes bini arcus binorum orbium altitudinis a cenic egressi usque ad unum punctum circuli signorum cum ipsum a linea meridionali ante vel post secundum equalia tempora disteterit et cenik capitis ab ambobus punctis declivi mediantibus celum septentrionalem fuerit vel quod ipsum ab ambobus meridionale fuerit sunt equales et faciunt duos angulos coniunctim equales duplo angulo ex concidentia meridiani et circuli signorum ad idem punctum proveniente.
Meridianus sit ABGD, AE E] sup. lin. PZ et BHT positiones zodyaci et E et H idem punctum equaliter distans ex utraque parte ABG. Vero cenik primo ab ambobus punctis zodyaci mediantibus celum septentrionale et producatur arcus circulorum magnorum DE DH GE GH. Ex ypothesi igitur et quarta primi Milei bis assumpta sequitur arcum GE equum esse GH, quod est primum, et angulum DEG angulo GHD. Sic igitur duo anguli ZEG et BHG valent ZED angulum cum angulo DEG et BHG qui valent angulum DHB cum DEG equus sit DHG angulus autem BHG idem est angulo ZED. Igitur duo anguli ZEG et BHG coniunctim sunt equales duplo ZED, quod est secundum. Si vero G sit meridionale ab ambobus punctis A et B ut patet in secunda dispositione, sequitur ut prius GE equum esse GH quod est primum et angulum DEG angulo DHG. Quare angulus DEK equus DHL per conceptionem et ex eo quod duo anguli ex parte E valent duos rectos et similiter duo ex parte H. Anguli igitur ZEK et BHL valent BHD qui est idem ZED et DHL et ZEK qui valent ZED cum DHL equus sit KED. Igitur duo anguli ZEK et BHL valent duplum ZED.
〈II.33〉 Quod si unum punctorum celum mediantium sive orientalis portionis fuerit sive occidentalis meridianum fuerit a cenic capitum septentrionaleque alterum, anguli qui proveniunt ad punctum dictum superat duplum anguli ex meridiano arcu ad idem punctum facti quantitate duorum rectorum. Ex quibus omnibus colligitur quod si noti fuerint anguli et arcus ante meridianam lineam in omni declinatione a principio Cancri usque ad principium Capricorni, noti erunt et arcus et anguli eorum signorum post meridianam et una anguli reliquorum signorum et arcus ante et post meridianam lineam.
Sine dubio propositio sicud hic proponitur falsa est omnino et sic tamen invenimus eam in Almagesti abreviato quod tunc vidi et nescio utrum sit vitium scriptoris vel abreviatoris, sed debet sic poni: Si punctum medians celum orientalis portionis meridionale fuerit septentrionaleque alterum, anguli qui proveniunt ad punctum dictum superant duplum anguli ex meridiano arcu ad idem punctum facti quantitate duorum rectorum. Si vero punctum celum medians orientalis portionis septentrionale fuerit meridionaleque alterum, anguli qui proveniunt ad punctum dictum superantur a duplo anguli ex meridiano ad idem punctum facti quantitate duorum rectorum. Sit inprimis ut prius meridianus DBGA, G cenic, A celum medians meridionale, AG orientialis portionis, B vero septentrionale, cetera vero ut prius eritque ut prius angulus GED equus GHD cumque GHD cum DHL faciat duos rectos valebit GED cum DHL duos rectos angulos. Anguli autem ZEG et BHL valent ZED et BHD qui sunt idem et GED et DHL valentes duos rectos. Igitur isti superat duplum istius quantitate duorum rectorum. Si vero A fuerit septentrionale et B econtra, continebunt ZED et BHD et sunt idem angulus 〈et〉 angulus ZEK et BHG et angulos KED et GHD qui ut statim valent duos rectos. Igitur isti, scilicet ZEK et BHG, superantur ab duplo ZED quantitate duorum rectorum hocque Z. Nota quando sit mentio de aliquo angulo debet hoc intelligi de orientali septentrionali.
Corollarium vero patet quia si noti sint arcus et anguli medietatis a principio Cancri usque ad principium Capricorni in quacumque distantia a meridionali linea, erunt per 31 huius arcus et anguli alterius medietatis in quacumque distantia a meridionali linea noti. Quare per 32 et 33 huius adiuncta 19 huius arcus et anguli utriusque medietatis et in quacumque distantia a meridionali linea erunt noti.
〈II.34〉 Quemlibet angulum ex concidentia circuli altitudinis cum circulo signorum aput punctum medians celum vel ad punctum orizontis et arcum quoque a summitate capitum ad utrumlibet notum esse oportet.
Sit ABG meridianus, BED orizon, ZEH orizon qualitercumque cadat, A cenic. Si igitur latitudo regionis est nota et declinatio puncti Z etiam sit nota per 16 prime dictionis et cum Z sit notum per 19 huius, erit et AZ notum et angulus AZE notus per 26 huius. AE autem est quarta per 23 primi Theodosii et 27 tertii Euclidis notum. Item angulus AED notus quia rectus per 19 primi Theodosii et cum HED sic notus per 30 huius, erit HEA notus sicque patet correlarium.
Explicit Almagesti Ptolomey abreviatum Bernhardi Chorner quondam Iacobi de Tyrnavia.