عونك يا واحد
جمل ما في مقالة الرابعة من كتاب بطلميوس المنسوب إلى التعاليم
الأولى: من أيّ الأرصاد ينبغي أن يكون البحث عن أمور القمر منها؛ الثانية: في أزمان القمر الدوريّة؛ الثالثة: في حركات القمر المستوية الجزئيّة؛ الرابعة: في وضع جداول تقيّد بها مجازات القمر الوسطى؛ الخامسة: في أنّ الأصل البسيط أيضاً للقمر الأشياء التي تظهر واحدة بأعيانها من قبل الأصل الذي يوضع فيه فلك خارج المركز ومن قبل الأصل الذي يوضع فيه فلك تدوير؛ السادسة: في تبيين اختلاف القمر الأوّل البسيط؛ السابعة: في تصحيح حركات القمر الوسطى في الطول وفي الاختلاف؛ الثامنة: {في حا}صل حركات القمر الوسطى في الطول وفي الاختلاف؛ التاسعة: في تصحيح مجازات القمر الوسطى في العرض وحاصلها؛ العاشرة: حساب دور اختلاف القمر الأوّل البسيط وجداوله. الحادية عشرة: في أنّ الخلاف الذي وقع لأبرخس في مقدار الاختلاف الذي يلحق القمر لم يقع من قبل الخلاف في الأصول التي عليها يعمل بل من قبل الحساب.
〈IV〉 ابتداء المقالة الرابعة من كتاب بطلميوس المنسوب إلى التعاليم This phrase is not included in the English translation.
〈IV.1〉 آ: من أيّ الأرصاد ينبغي أن يكون البحث عن أمور القمر منها
إنّا لمّا آتينا في المقالة التي قبل هذه على جميع ما يوجد لازماً في حركة الشمس، أخذنا في هذه المقالة فيما يتّبع ذلك ويتّصل به من الكلام في القمر. فأوّل ه – خ: وأوّل ما رأينا أنّه يجب أن نبدأ به من القول في ذلك هو أنّه ليس ينبغي أن يكون استعمالنا للأرصاد في هذا المعنى جزافاً ولا كيف ه – خ: ما اتّفق لكن ينبغي أمّا في الأمور الكليّة التي يطلب إدراكها فيه فأن نقصد خاصّة من البراهين لما ه – خ: إلى ما كان منها متقادم العهد وكان مع ذلك مأخوذاً من الأرصاد أنفسها التي كانت في كسوفات القمر. فإنّ بهذه وحدها يقدر الطالب أن يجد مواضع القمر على الحقيقة وذلك أنّ سائر المواضع التي تعلم لمسير القمر بقياسه إلى الكواكب الثابتة ه: أو بالآلات أو بكسوفات الشمس قد يمكن أن يقع فيه خطاء كثير لاختلاف المنظر التي يلحق القمر. وأمّا فيما يلحقه من الأمور الجزئيّة فقد ينبغي أن يستعان على البحث عن أموره بسائر الأرصاد. فإنّ بعد كرة القمر من مركز الأرض لمّا لم يكن مبلغه كمبلغ بعد فلك البروج من مركز الأرض الذي من قبله صارت منزلة مقدار الأرض عند هذا البعد منزلة نقطة، وجب ضرورة في الخطّ المستقيم الذي يخرج من مركز الأرض، أعني من مركز فلك البروج، فيمرّ بمركز القمر ويصل إلى أجزاء ه – خ: نواحي فلك البروج وهو الخطّ الذي بالقياس إليه يعقل ه – خ: يعلم المسير الحقيقيّ لجميع الكواكب إلّا يكون عند الحسّ فضلاً عن {...} مطابقاً أبداً للخطّ المستقيم الذي يخرج من موضع ما من بسيط الأرض، أعني من ناظر الأبصار، إلى مركز القمر، وهو الخطّ الذي بقياسه يوجد مسيره الذي يرى. لكن متى كان القمر على سمت رأس الراصد له فحينئذ فقط يكون الخطّ الذي يخرج من مركز الأرض مطابقاً للخطّ الذي يخرج من بصر الناظر إلى مركز القمر ثمّ إلى فلك البروج. فأمّا إذا مال عن سمت الرأس إلى جهة من الجهات، أيّ جهة كانت، فإنّ هذه الخطوط التي وصفناها يكون لها ميول مختلفة، ومن أجل ذلك يكون المسير الذي يرى ليس هو والمسير الحقيقيّ واحداً بعينه إذ كان البصر ينحطّ عن المواضع التي تفرزها الخطوط التي تمرّ بمركز القمر ه – صح: الأرض إلى موضع بعد موضع على قياس أقدار الزوايا التي تحدث عن الميل.
ولذلك وجب في كسوفات الشمس إذ كانت أنّما تكون عن ممرّ القمر تحتها وستره لها، وذلك أنّه إذا وقع في المخروط الذي بين بصرنا وبين الشمس ستر نورها عنّا إلى أن تجوزها ألّا يكون في جميع النواحي واحدة بأعيانه، ولا يكون مقادير الكسوف وأزمانه على مثال واحد في جميع النواحي. وذلك أنّ القمر لا يستر ضوء الشمس عن الناس جميعاً على مثال واحد للأسباب التي ذكرناها، ولا الناس جميعاً يرونه بمكان واحد من الشمس. ووجب في كسوفات القمر ألّا يلحقها شيء من هذه الاختلاف من قبل اختلاف المناظر، لأنّ العلّة الحادثة في القمر الموجبة للكسوف ليست تحتاج في السبب المحدث لهذا العارض إلى معاضدة من نظر الناظرين. وذلك أنّ القمر أنّما يستضيء أبداً بوقوع شعاع الشمس عليه. ه – خ – صح: {...} والشمس أبداً يشرق على نصف كرته المقابل للشمس. فمتى كان القمر قياسه إلى الشمس قياس ما هو مقاطر ↑مقاطر↑: صح لها، فإنّه في سائر الزمان غير زمان الكسوف يرى كلّه مضيئاً، وذلك أنّ نصف كرته إذا استضاء كلّه كان أيضاً كلّه في ذلك الوقت مقبلاً علينا ه – صح: {...} مائلاً إلينا. {...} كانت مقاطرته للشمس مقاطرة يقع معها في مخروط ظلّ الأرض الذي هو أبداً دائر إلى ضدّ الجهة التي تدور إليها الشمس عدم حينئذ الضوء بأنّ الأرض تستر عنه من شعاع الشمس بقدر دخوله في هذا المخروط. ولذلك يرى في نواحي الأرض كلّها منكسفاً على مثال واحد في المقادير وفي أزمان المدد.
فمن قبل ذلك لمّا كان قد يحتاج في البحث الكلّي عن أمور القمر إلى استعمال مواضعه الحقيقيّة، لا التي أنّما يدركها بالعيان؛ إذ كان المنتظم والمتشابه يجب أن يقدّم وضعه ه – خ: وصفه على المختلط المتفنّن. ه – صح: المختلف التقدير فلنا أنّه ينبغي أن نترك استعمال الأرصاد التي أنّما أخذت مواضع القمر فيها بأبصار الرصّاد ونقتصر على استعمال المواضع التي وجد فيها في أوقات كسوفاته إذ كان البصر ليس له في هذه مدخل في استخراج مواضع القمر. وذلك أنّ الجزء من فلك البروج الذي توجد الشمس نازلة به في وسط زمان الكسوف، وهو الوقت الذي يكون فيه مركز القمر في استقبال ↑استقبال↑: مقاطراً الشمس في الطول بغاية ما يمكن من الحقيقة، فمن البيّن أنّ مركز القمر أيضاً يكون منزله في الجزء المقاطر لذلك الجزء بالحقيقة في ذلك الزمان الوسط من الكسوف. ه – خ – صح: في زمان وسط الكسوف.
〈IV.2〉 ب: في ه – خ: معرفة أزمان القمر الدوريّة
فهذا ما تقدّمه على طريق الرسم في الأرصاد التي منها ينبغي أن ينظر فيما يحتاج إلى أن يوقف عليه بالجملة من أمر القمر. ونحن ملتمسون الآن الأخبار بالطريق الذي سلكه القدماء في إقامة البراهين في ذلك والطريق الذي به نسير نحن فنحصل الأصول الموافقة للأمور الظاهرة بأسهل مأخذ.
فنقول إنّه لمّا كان القمر يتحرّك على اختلاف في الطول وفي العرض وليس قطعه أبداً لفلك لبروج في زمان سواء، ولا عودة في سيره ه – خ: عودته في مسيره في العرض إلى الموضع الذي منه ابتدأ في زمان سواء. وكان متى لم يوقف على الزمان الذي فيه يعود اختلافه، فواجب ضرورة ألّا يكون يمكن الوقوف ولا على سائر أدواره. وكان ه – خ: قد يوجد بالأرصاد الجزئيّة يتحرّك في أقسام فلك البروج كلّها أوسط حركاته وأعظمها وأصغرها، ويصير في جميع أجزاء فلك البروج في غاية بعده عنه في الشمال وفي غاية بعده عنه في الجنوب وعليه نفسه. فبالواجب جعل القدماء أصحاب التعاليم يطلبون زماناً في مثله يتحرّك القمر أبداً في الطول حركة سواء، لأنّ هذا الزمان وحده هو الذي يمكن به الوقوف على عودة اختلاف القمر. فقصدوا قصد أرصاد كسوفات القمر للأسباب التي ذكرناها وجعلوا يطلبون أن يجدوا فيها ه – خ: منها مدّة ما لعدّة من الشهور زمانها أبداً مساو للمدّة التي لمثل تلك العدّة من الشهور وتحيط بدوائر ه: في الطول عدّتها متساوية إمّا كاملة، وإمّا مع قسيّ ما متساوية.
فمن تقادم عهده من القدماء كانوا يظنّون على ظاهر النظر أنّ هذا الزمان هو ستّة آلاف وخمس مائة وخمسة وثمانون يوماً وثلث يوم. وذلك أنّهم كانوا يرون أنّ في قريب من هذه العدّة من الأيّام يستكمل من الشهور مائتا شهر وثلاثة وعشرون شهراً، ومن عودات الاختلاف مائتا عودة وتسع وثلاثون عودة، ومن عودات العرض مائتان واثنتان وأربعون عودة، ومن دورات السير في الطول مائتان وإحدى وأربعون دورة ومع ذلك الأجزاء التي تزيد الشمس فتقطّعها في هذا الزمان الذي ذكرناه على الدوائر الثمان عشرة ه – خ: (التي لها في هذه المدّة) وهي عشرة أجزاء وثلثا جزء على أنّ عودة هذه الدورات أنّما ه – خ: و يعمل فيها على القياس إلى الكواكب الثابتة. وسمّوا هذا الزمان الزمان الدوريّ من قبل أنّه أوّل زمان يكاد أن يكون يعود فيه أصناف الحركات عودة واحدة. ولمّا أرادوا أن يجعلوه من أيّام تامّة ضاعفو الستّة الآلاف اليوم والخمس المائة والخمسة والثمانين اليوم الثلث يوم ثلاث مرّات فصار عدد الأيّام تسعة عشر ألفاً وسبع مائة وستّة وخمسين يوماً، فسمّوا هذا العدد ه – خ: العدد المستخرج. ↑المستخرج↑: صح وضاعفوا أيضاً على هذا المثال سائر تلك الأشياء ثلاث مرّات، فخرج لهم من الشهور ستّ مائة وتسعة وستّون شهراً، ومن عودات الاختلاف سبع مائة وسبع عشرة عوره، ه: عود{ة} ومن عودات العرض سبع مائة وستّ وعشرون عودة، ومن دورات السير في الطول سبع مائة وثلاث وعشرون دورة ومع ذلك الأجزاء التي تزيد فتقطّعها الشمس في الأربع والخمسين الدائرة وهي اثنان وثلاثون جزءاً.
ثمّ إنّ أبرخس عاد بفسخ ه – خ: ففسخ ذلك وبيّن لما حسبه بأرصاد الكلذانيين وبالأرصاد التي كانت على عهده أنّ هذه الأشياء ليست صحيحة. وذلك أنّه تبيّن ه – خ: بيّن بالأرصاد التي وضعها أنّ أوّل عدد الأيّام التي في مثلها يدور أبداً فيعود زمان الكسوف في شهور سواء وحركات سواء هو مائة ألف يوم وستّة وعشرون ألف يوم وسبعة أيّام وساعة واحدة من ساعات الاستواء. ويجد أنّه في هذه الأيّام تستكمل من الشهور أربعة آلاف ومائتان وسبعة وستّون شهراً، ومن عودات الاختلاف التامّة أربعة آلاف وخمس مائة وثلاث وسبعون عودة، ومن أدوار فلك البروج أربعة آلاف وستّ مائة واثنتا عشرة دورة إلّا سبعة أجزاء ونصف ه: جزء بالتقريب، وهي الأجزاء التي تنقصها الشمس في الثلاث مائة والخمس والأربعين الدائرة ه: الدورة هذا أيضاً على أنّ عودات هذه الأشياء أنّما يعمل فيها على القياس إلى الكواكب الثابتة. ومن هناك وجد الزمان الأوسط للشهر إذا قسمت العدّة التي ذكرناها للأيّام على الأربعة الألف والمائتين والسبعة والستّين الشهر، يحصل من الأيّام تسعة وعشرون يوماً وإحدى وثلاثون دقيقة وخمسون ثانية وثمان ثوالث وعشرون رابعة ه – صح: في نقل الحجّاج وتسع روابع وعشرون خامسة بالتقريب. فهو بيّن أنّ المدد ه: {...} المتساوية التي من كسوف القمر إلى كسوف القمر أنّما تعود فتتكافئ ه: يقال يتكافأ على الإطلاق في هذا المقدار من الزمان حتّى أنّه يكون بيّنّا أنّ الاختلاف يعود من قبل أنّ هذا المقدار من الزمان أبداً ه – خ: أنّما يحيط بشهور متساوية ه – صح: وإنّ الأدوار في الطول المتساوية التي هي أربعة آلاف وستّ مائة وأحد عشر تلحقها أجزاء متساوية. وهي ثلاث مائة واثنان وخمسون جزءاً ونصف وهي الأجزاء التي تقطّعها حتّى تتّصل بالشمس.
فإن ه – خ: فإنّا إن لم يجعل الحساب لعدّة الشهور ه – خ: ولعدّة عودة الاختلاف من كسوف القمر إلى كسوف القمر لكن اقتصر ه: {...} على عدّة الشهور من اجتماع أو استقبال إلى مثل ذلك الاتّصال، ↑الاتّصال↑: خ الاجتماع أو الاستقبال وجد عدد عودة ↑: دات الاختلاف والشهور أقلّ وذلك بأن يوجد العدد الذي هو وحده مشترك لهما وهو سبعة عشر ه – خ: الواحد فقط المشترك لهذين العددين العاد لهما الذي يوجد هو سبعة عشر من كلّ واحد منهما. ، فيحصل منه من الشهور مائتان واحد وخمسون شهراً، ومن عودات الاختلاف مائتان وتسع وستّون عودة.
لكن لم يوجد هذا الزمان الذي وصف يكمّل أيضاً العودة في العرض. وذلك أنّ تكافيء الكسوفات أنّما وجد حافظاً للتساوي في المدد فقط التي للزمان وللأدوار في الطول، ولم يوجد حافظاً للتساوي في مقادير ستر الضوء، وتشابهه وهي الأشياء التي من قبلها يستخرج علم العرض. ولكن لمّا كان قد تقدّم استخراج زمان عودة الاختلاف، فإنّ أبرخس عاد فأضاف إلى ذلك مدداً من شهور الكسوفين اللذين هما طرفاها متشابهان من جميع الوجوه في مقادير ستر الضوء وأزمانه لم يكن فيها فرق من قبل الاختلاف، لأنّ المجاز أيضاً في العرض يوجد بذلك قد عاد. وبيّن ه – خ: فوجب لذلك فقد عاد أيضاً وبيّن. أنّ هذا الدور يكمّل من الشهور في خمسة آلاف شهر وأربع مائة وثمانية وخمسين شهراً ومن أدوار العرض في خمسة آلاف دورة وتسع مائة وثلاث وعشرين دورة.
فهذا هو الطريق الذي سلكه من كان قبلنا في استخراج هذه الأشياء. وقد يمكنك أن تعلم أنّ هذا الطريق ليس بسهل المرام ولا قريب المأخذ، بل يحتاج فيه إلى تأمّل شديد وتحصيل مستقصى ممّا أنّا واصفه. فلننزّل أنّ أزمان المدد تؤخذ متساوية بالصحّة. أقول أوّلاً أنّه ليس ينتفع بذلك ما لم يكن الفضل الذي من قبل اختلاف الشمس أيضاً إمّا لا ه – خ: ألّا يكون أصلاً في كلّ واحدة من المدّتين وإمّا أن يكون واحداً بعينه فيهما جميعاً. وذلك أنّ هذا إن ↑إن↑: إذا لم يقع هكذا، بل كان للشمس كما قلت فضل ما من قبل الاختلاف لم تكن الشمس نفسها تسير في الأزمان المتساوية مسيرات متساوية؛ وبيّن أنّ القمر أيضاً هذه تكون حالة. وإن كلّ واحدة من المدّتين اللتين يقاس بينهما إن لحقت فيها مثلاً مدّة أزمان سنين تامّة متساوية زيادة نصف زمان سنة وكانت الشمس قد زادت فتحرّكت في هذا المقدار من الزمان {أمّا} في المدّة الأولى فمن المسير الوسط في الحوت، وأمّا في ه – خ: من المدّة الثانية فمن المسير الوسط في العذراء. فإنّ الشمس أمّا في المدة الأولى فتكون قد زادت فقطعت أقلّ من نصف دائرة بأربعة أجزاء ونصف وربع بالتقريب، وأمّا في المدّة الثانية فتكون قد زادت فقطعت أكثر من نصف دائرة بهذه الأجزاء بأعيانها. Toomer, p. 177: Then over the first interval the sun will have traversed about 4¾° less than a semi-circle [beyond complete revolutions], but over the second about 4¾° more than a semi-circle. فيكون القمر أيضاً في أزمان متساوية قد زاد فقطع بعد الأدوار التامّة أمّا في المدّة الأولى فمائة وخمسة وسبعون جزءاً وربع جزء، وأمّا في المدّة الثانية فمائة وأربعة وثمانون جزءاً ونصف وربع. فنقول إنّه يجب أوّلاً أن يكون موجوداً في المدد ممّا قد وقع في الشمس: إمّا أن تكون ه – خ: تحيط بأدوار تامّة، وإمّا أن تكون في إحدى المدّتين تزيد فتقطّع نصف الدائرة الذي من البعد الأبعد ه – خ: (إلى البعد الأقرب) وفي المدّة الأخرى تزيد فتقطّع نصف الدائرة الذي من القرب الأقرب، ه – خ: (إلى البعد الأبعد) وإمّا أن تكون تبتدئ من قطع واحد بعينه في كلّ واحدة من المدّتين، وإمّا أن يكون بعدها سواء من جنبتي البعد الأبعد أو البعد الأقرب في الكسوف الأوّل من إحدى المدتّين وفي الكسوف الثاني من المدّة الأخرى. فإنّ الأمر متى جرى هذا المجرى فقط فإنّ الفضل الذي من قبل اختلاف الشمس إمّا إن لا يكون أصلاً وإمّا إن يكون واحداً بعينه في كلّ واحدة من المدّتين حتّى تكون القسيّ التي تلحق زائدة متساوية أيضاً إمّا بعضها لبعض وإمّا بعضها لبعض والقسيّ المستوية ه – خ: وللقسيّ المتساوية .
ثمّ نرى أنّه يجب ثانياً أن ننظر مثل هذا النظر أيضاً في سير القمر، فإنّ سيره متى ترك فلم يميّز فقد نرى أنّه ممكن أن يكون القمر أيضاً كثيراً ما ممكن أن يقطّع في الطول قسيّاً متساوية في الأزمان المتساوية من غير أن يكون اختلافه يعود لا محالة. وذلك يعرض إن كان ابتداؤه في كلّ واحدة من المدّتين من سير واحد بعينه بحيث الزيادة أو من سير واحد بعينه بحيث النقصان ه – خ: والنقصان ثمّ لم ينتهي ↑ينتهي↑: ينته إلى ذلك السير بعينه، و ه – خ: ذلكإن كان ابتداؤه في إحدى المدّتين من أعظم السير ثمّ انتهى إلى أقلّ السير وكان ابتداؤه في المدّة الأخرى من أقلّ السير ثمّ انتهى إلى أعظم السير، وإن كان سير إحدى المدّتين الأوّل وسير المدّة الأخرى الأخير بعدهما سواء عن جنبتي مسير واحد بعينه إمّا أقلّ المسير وإمّا أكثره.
وذلك أنّ كلّ واحد من هذه الأشياء متى وقع ه – خ: هكذا فإنّ الفضل الذي من قبل اختلاف القمر إمّا ألّا يكون أصلاً وإمّا أن يكون واحداً بعينه، ومن أجل ذلك تجعل ه – خ: تكون الزيادات ه – خ: (الفاضلة) التي في الطول متساوية إلّا أنّه ليس يكون به أصلاً إثبات له اختلاف يعود ه – خ: يكون أصلاً إثبات الاختلاف {...} . فليس ينبغي إذن أن يكون في المدد ↑: خ ة التي تستعمل شيء من هذه الأعراض ه: إن كنّا نقدّر فيها أنّها يكون بالحقيقة مشتملة على زمان عودة الاختلاف. بل إنمّا ينبغي أن نتخيّر منها ما كانت حاله ضدّ هذه الحال أعني المدد التي بها خاصّة يمكن أن يظهر الاختلاف إذا لم يكن يحيط بعودات تامّة من عودات الاختلاف أعني ألّا يقتصر ه – خ: يعرج على أن يكون مباديها من مسيرات مختلفة ه – خ: فقط بل من مسيرات عظيمة الاختلاف إمّا في المقدار وإمّا في القوّة. أمّا في المقدار فمثل أن يبتدئ في إحدى المدّتين من أقلّ السير ولا ينتهي إلى أعظم السير ويبتدئ في المدّة الأخرى من أعظم السير ولا ينتهي إلى أقلّ السير فإنّ بهذا الوجه ه – خ: بهذه الوجوه يكون فضل الزيادة في الطول غاية الفضل. وذلك أنّه إذا لم يكمّل الاختلاف أدواراً تامّة وخاصّة متى كان يلحق في اختلاف واحد ربع واحد أو ثلاثة أرباع كان الفضل الذي من قبل الاختلاف حينئذ فضلين بهما كانت المدّتان تكونان غير متساويتين. وأمّا في القوّة فمثل أن يبتدئ في كلّ واحدة من المدتّين من المسير الوسط إلّا أنّ الابتداء لا يكون من وسط واحد بعينه بل يكون في إحداهما من السير بحيث الزيادة ويكون في الأخرى من السير بحيث النقصان. فإنّ على هذا الوجه أيضاً خاصّة تكون فضلات الطول يخالف بعضها بعضاً غاية الاختلاف من غير أن يكون الاختلاف قد عاد إذ كان متى لحق في اختلاف واحد ربع واحد ↑واحد↑: خ دائرة أيضاً أو ثلاثة أرباع كان الفضل الذي من قبل الاختلاف فضلين ومتى كان الذي يلحقه نصف دائرة كان الفضل أربعة.
ومن أجل ذلك وجدنا أبرخس أيضاً قد يظنّ أنّه قد أحتاط بغاية ما يمكن من الاحتياط في اختبار المدّة ه – خ: المدد المستعملة في هذا الفحص فاستعمل الفضل في القمر على أنّ مبدأ إحدى المدّتين من أكثر السير وانتهاءها ليس عند أقلّ السير؛ ومبدأ المدّة الأخرى من أقلّ السير وانتهاءها ليس عند أكثر السير. وصحّح أيضاً الفضل الذي يكون من قبل اختلاف الشمس على أنّه يسير وذلك أنّ عودة الشمس أنّما ه – صح: أنما تنقص عن أدوار تامّة بقريب من ربع برج واحد، وإنّ كان ذلك ليس من برج واحد بعينه ولا من برج فضل الاختلاف فيه في كلّ واحدة من المدّتين سواء.
ولم نقل ما قلناه من ذلك ونحن نقصد الطعن على هذا الطريق الذي سلكوه ه – خ: سلكه في استخراج عودات الدورات، لكن لننبه على أنّ هذا الطريق متى استعمل فيه ما يجب من التثبيت ولزم فيه القياس المطرد، أمكن به إصابة ما قصد له ومتى أغفل (فيه) ↑ (فيه)↑: خ mark of omission with النظر في شيء من الأغراض التي وصفناها ولو اليسير منها حاد عن إدراك المطلوب فلم يوصل (به) ↑ (به)↑: خ mark of omission with إليه أصلاً؛ وإن يوافي جميع ما يجب أن يوجد على الحقيقة في مثل هذه الأرصاد، يعسر وجوده على المستقصى النظر المحتاطين في تخيّرها فضلاً عن غيرهم.
والدليل على ذلك أنّ عودة ↑: خ عودات الأدوار التي وصفناها في القياسات التي كانت من أبرخس أمّا عودة الشهور، كما قلنا، فإنّها قد استقصى حسابها على غاية ما كان يمكن من الصحّة حتّى أنّها ↑أنّها↑: خ به ليس توجد حائدة عن الحقّ بشيء محسوس أصلاً وأمّا عودة الاختلاف والعرض فإنّها يوجد فيها ↑فيها↑: فيهما خطاء له قدر ما يعتدّ به وقفنا نحن عليه بسهولة بالسبل التي هي أقرب وأسهل مأخذاً التي استعملناها في تمييز ما يجري هذا المجرى التي نحن من ذي قبل مبيّنوها مع مقدار اختلاف القمر بعد أن يتقدّم. فنصف ما يحتاج إليه فيما بعد الحركات الجزئيّة الوسطى التي تكون للطول وللاختلاف وللعرض على ما توافق أزمان العودات التي وضعت للحركات الدوريّة مضاف ه – خ: ونضف إليه ما يحصل ممّا نبيّنه من تقويمها.
〈IV.3〉 ج: في حركات القمر المستوية الجزئيّة
فإنّ نحن إذا ضاعفنا الحركة الوسطى التي نبيّن أنّها للشمس في اليوم الواحد بعينه وهي تسع وخمسون دقيقة وثمان ثواني وسبع عشرة ثالثة وثلاث عشرة رابعة واثنتا عشرة خامسة وإحدى وثلاثون سادسة بأيّام شهر واحد، وهي تسعة وعشرون يوماً وإحدى وثلاثون دقيقة (وثمان) وخمسون ثانية ↑ثانية↑: صح وعشرون ه – صح: وثمان ثوالث وتسع روابع وعشرون خامسة ثالثة Toomer, p. 179: 29;31,50,8,20d وزدنا على ما يكون من ذلك أجزاء دائرة واحدة وهي ثلاث مائة وستّون جزءاً حصل لنا الأجزاء التي يتحرّكها القمر وسطاً في الطول في الشهر الواحد ثلاث مائة وتسعة وثمانين جزءاً وستّ دقائق وستّاً ه – صح: وثلاثاً وعشرين ثانية وثالثة واحدة وأربعاً وعشرين رابعة وخامستين وثلاثين سادسة وتسعاً ه – خ – صح: وسبعاً وخمسين سابعة بالتقريب. فإذا قسّمنا هذه على أيّام الشهر التي وضعناها، خرجت لنا الحركة في اليوم الوسطى في الطول ثلاثة عشر جزءاً وعشر دقائق وأربعاً وثلاثين ثانية وثمانية وخمسين ثالثة وثلاثاً وثلاثين رابعة وثلاثين خامسة وثلاثين سادسة بالتقريب. Followed by a blank space.
وأيضاً إذا ضاعفنا المائتين والتسع والستّين الدورة التي للاختلاف بأجزاء دائرة واحدة، وهي ثلاث مائة وستّون جزءاً، وخرج لنا من العدد ستّة وتسعون ألفاً وثمان مائة وأربعون. فإذا قسّمنا هذه الأجزاء على أيّام المائتي الشهر والأحد والخمسين الشهر، وهي سبعة آلاف وأربع مائة واثنا عشر يوماً وعشر دقائق وأربع وأربعون ثانية وإحدى وخمسون ثالثة وأربعون رابعة، خرج لنا أيضاً حركة الاختلاف الوسطى في اليوم ثلاثة عشر جزءاً وثلاث دقائق وثلاث وخمسون ثانية وستّ وخمسون ثالثة وتسع وعشرون رابعة وثمان وثلاثون خامسة وثمان وثلاثون سادسة.
وكذلك إذا ضاعفنا الخمسة الآلاف والتسع مائة والثلث والعشرين العودة التي للعرض بأجزاء دورة واحدة، وهي ثلاث مائة وستّون جزءاً، خرج لنا من العدد ألفي ألف ومائة ألف واثنان وثلاثون ألفاً ومائتان وثمانون. فإذا قسّمنا هذه على أيّام الخمسة الآلاف والأربع مائة والثمانية والخمسين الشهر، وهي مائة ألف واحدة Toomer, p. 179: 161177;58,58,3,20d وأربعة وستّون ألفاً ومائة وسبعة وسبعون يوماً وثمان وخمسون دقيقة وثمان وخمسون ثانية وثلاث ثوالث ه – خ: (وخمسون ثالثة) وعشرون رابعة، حصل لنا أيضاً الحركة الوسطى في اليوم في العرض ثلاثة عشر جزءاً وثلاث عشرة دقيقة وخمس وأربعون ثانية وتسع وثلاثون ثالثة وأربعون رابعة وسبع عشرة خامسة وتسع عشرة سادسة.
وأيضاً إذا نحن نقصنا من حركة القمر الوسطى في اليوم في الطول حركة الشمس الوسطى في اليوم، حصل لنا حركة البعد بينهما الوسطى في اليوم اثنا عشر جزءاً وإحدى عشرة دقيقة وستّاً وعشرين ثانية وإحدى وأربعين ثالثة وعشرين رابعة وسبع عشرة خامسة وتسعاً وخمسين سادسة.
إلّا أنّا نحن بالسبل التي نحن مستعملوها كما فعلنا فيما بعد في هذا الفحص، قد نجد أمّا الحركة في الطول في اليوم فيكاد أن يكون غير مغادرة لمّا وصفناه من ذلك. ومن البيّن أنّ الأمر في البعد أيضاً كذلك. وأمّا حركة الاختلاف فإنّا نجدها أقلّ ممّا وضعناه من ذلك بإحدى عشرة رابعة وستّ وأربعين خامسة وتسع وثلاثين سادسة حتّى يكون مبلغه ه – خ: مبلغها ثلاثة عشر جزءاً وثلاث دقائق وثلاثاً وخمسين ثانية وستّاً وخمسين ثالثة وسبع عشرة رابعة وإحدى وخمسين خامسة وتسعاً وخمسين سادسة. وأمّا الحركة في العرض فأكثر ممّا وصفناه من ذلك فثمان روابع وتسع وثلاثين خامسة وثمان عشرة سادسة حتّى يكون مبلغها أيضاً ثلاثة عشر جزءاً وثلاث عشرة دقيقة وخمساً وأربعين ثانية وتسعاً ه – خ: (وسبعاً) وثلاثين ثالثة وثمانياً وأربعين رابعة وستّاً وخمسين خامسة وسبعاً وثلاثين سادسة.
فعلى هذا القياس إذا أخذنا من الحركات في اليوم من كلّ حركة جزءاً من أربعة وعشرين جزءاً منه حصلت لنا الحركة الوسطى في الساعة الواحدة أمّا للطول فاثنتان وثلاثون دقيقة وستّ وخمسون ثانية وسبع وعشرون ثالثة وستّ وعشرون رابعة وثلاث وعشرون خامسة وستّ وأربعون سادسة وخمس عشرة سابعة. وأمّا للاختلاف فاثنتان وثلاثون دقيقة وتسع وثلاثون ثانية وأربع وأربعون ثالثة وخمسون رابعة وأربع وأربعون خامسة وتسع وثلاثون سادسة وسبع وخمسون سابعة وثلاثون ثامنة. وأمّا للعرض فثلث وثلاثون دقيقة وأربع ثواني وأربع وعشرون ثالثة وتسع روابع واثنتان وثلاثون خامسة وإحدى وعشرون سادسة واثنتان وثلاثون سابعة وثلاثون ثامنة. وأمّا للبعد فثلاثون دقيقة وثمان وعشرون ثانية وستّ وثلاثون ثالثة وثلاث وأربعون رابعة وعشرون خامسة وخمس ه – خ: وأربع وأربعون سادسة وسبع وخمسون سابعة وثلاثون ثامنة.
وإذا نحن ضاعفنا الحركات في اليوم ثلاثين مرّة وأسقطنا منها الأدوار حصلت لنا الفضلة الوسطى للشهر الواحد. أمّا للطول فخمسة وثلاثون جزءاً وسبع عشرة دقيقة وتسع وعشرون ثانية وستّ عشرة ثالثة وخمس وأربعون رابعة وخمس عشرة خامسة. وأمّا للاختلاف واحد وثلاثون جزءاً وستّ وخمسون دقيقة وثمان وخمسون ثانية وثمان ثوالث وخمس وخمسون رابعة وتسع وخمسون خامسة وثلاثون سادسة. وأمّا للعرض فستّة وثلاثون جزءاً واثنتان وخمسون دقيقة وتسع وأربعون ثانية وأربع وخمسون ثالثة وثمان وعشرون رابعة وثمان عشرة خامسة وثلاثون سادسة. وأمّا للبعد فخمسة أجزاء وثلاث وأربعون دقيقة وعشرون ثانية وأربعون ثالثة وثمان روابع وتسع وخمسون خامسة وثلاثون سادسة.
وأيضاً إذا نحن ضاعفنا حركات اليوم الواحد بأيّام السنة المصريّة، وهي ثلاث مائة وخمسة وستّون يوماً، وأسقطنا ممّا يجتمع الأدوار التامّة، حصلت لنا الفضلة الوسطى للسنة. أمّا للطول فمائة وتسعة وعشرون جزءاً واثنتان وعشرون دقيقة وستّ وأربعون ثانية وثلاث عشرة ثالثة وخمسون رابعة واثنتان وثلاثون خامسة وثلاثون سادسة. وأمّا للاختلاف فثمانية وثمانون جزءاً وثلاث وأربعون دقيقة وسبع ثواني وثمان وعشرون ثالثة وإحدى وأربعون رابعة وثلاث عشرة خامسة وخمس وخمسون سادسة. وأمّا للعرض فمائة وثمانية وأربعون جزءاً واثنتان وأربعون دقيقة وسبع وأربعون ثانية واثنتا عشرة ثالثة وأربع وأربعون رابعة وخمس وعشرون خامسة وخمس سوادس. وأمّا للبعد فمائة وتسعة وعشرون جزءاً وسبع وثلاثون دقيقة وإحدى وعشرون ثانية وثمان وعشرون ثالثة وتسع وعشرون رابعة وثلاث وعشرون خامسة وخمس وخمسون سادسة.
فإذا ضاعفنا بعد ذلك أزمان الحركات للسنة بثمانية عشر لمّا في ذلك من سهولة المأخذ في رسم الجداول كما قلنا وأسقطنا الأدوار التامّة حصلت لنا الحصّة الوسطى لكلّ ثمان عشرة سنة. أمّا للطول فمائة وثمانية وستّون جزءاً وتسع وأربعون دقيقة واثنتان وخمسون ثانية وتسع ثوالث وتسع روابع وخمس وأربعون خامسة. وأمّا للاختلاف فمائة وستّة وخمسون جزءاً وستّ وخمسون دقيقة وأربع عشرة ثانية وستّ وثلاثون ثالثة واثنتان وعشرون رابعة وعشر خوامس وثلاثون سادسة. وأمّا للعرض فمائة وستّة وخمسون جزءاً وخمسون دقيقة وتسع ثواني وتسع وأربعون ثالثة وتسع عشرة رابعة وإحدى وثلاثون خامسة وثلاثون سادسة. وأمّا للبعد فمائة وثلاثة وسبعون جزءاً واثنتا عشرة دقيقة وستّ وعشرون ثانية واثنتان وثلاثون ثالثة وتسع وأربعون رابعة وعشر خوامس وثلاثون سادسة.
〈IV.4〉 د: في وضع جداول نقيّد بها مجازات القمر الوسطى In Toomer’s translation (p. 180; and Heiberg’s edition, p. 282) this title is placed just above the table.
فنحن راسمون كما رسمنا في الشمس ثلاثة جداول في خمسة وأربعين سطراً أيضاً، وفي كلّ جدول خمسة صفوف. ومثبتون في أوائل الصفوف عدد الأزمان، أمّا من الجدول الأوّل فالثمان عشرة الثمان عشرة السنة، وأمّا من الجدول الثاني فالسنين ثمّ تحتها أيضاً الساعات، وأمّا من الجدول الثالث فالشهور ثمّ تحتها أيضاً الأيّام. ومثبتون في الصفوف الأربعة الباقية من كلّ جدول حيال كلّ زمان ما يصيبه من الأجزاء. أمّا في الصفوف الثواني منها فالأجزاء التي للطول، وأمّا في الصفوف الثوالث فالتي للاختلاف، وأمّا في الصفوف الروابع فالتي للعرض، وأمّا في الصفوف الخوامس فالتي للبعد. وهكذا رسم الجداول.
حاصل ↑: من القمر في الطول في أوّل ملك بختنصر بحركته الوسطى يا جزء كب دقيقة من الثور وحاصله في الاختلاف رصح درجة مط دقيقة وحاصله في العرض أيّ بعده من النهاية الشماليّة ↑: في فلكه المائل. سنح جزءاً يه دقيقة. وبعده من الشمس ع جزءاً لز دقيقة. أصل وسط القمر لأوّل بختنصر ا يا كب بروج درج دقائق. أصل حصّة ح كح مط بروج درج دقائق. أصل حصّة العرض يا كد يه بروج درج دقائق.
الجدول الأوّل لحركات القمر الوسطى وهو خمسة صفوف | ||||||||||||||||||||||||||||||||
السنون المتزيّدة يح يح | حصّة الطول | حصّة الاختلاف | حصّة العرض | حصّة البعد |
||||||||||||||||||||||||||||
أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس |
|||||
يح | قسح | مط | نب | ط | ط | مه | | قنو | نو | يد | لو | كب | ي | ل | قنو | ن | ط | مط | يط | لا | ل | قعج | يب | كو | لب | مط | ي | ل |
||||
لو | شلز | لط | مد | يح | يط | ل | | شيج | نب | كط | يب | مد | كا | | شيج | م | يط | لح | لط | ج | | شمو | كد | نج | ه | لح | كا | |
||||
ند | قمو | كط | لو | كز | كط | يه | | قي | مح | مج | مط | و | لا | ل | قي | ل | كط | كز | نح | لد | ل | قنط | لز | يط | لح | كز | لا | ل |
||||
عب | شيه | يط | كح | لو | لط | | | رسز | مد | نح | كه | كح | مب | | رسز | ك | لط | يز | يح | و | | شلب | مط | مو | يا | يو | مب | |
||||
ص | قكد | ط | ك | مه | مح | مه | | سد | ما | يج | ا | ن | نب | ل | سد | ي | مط | و | لز | لز | ل | قمو | ب | يب | مد | ه | نب | ل |
||||
قح | رصب | نط | يب | ند | نح | ل | | ركا | لز | كز | لح | يج | ج | | ركا | | نح | نه | نز | ط | | شيط | يد | لط | يو | نه | ج | |
||||
قكو | قا | مط | ه | د | ح | يه | | لج | مب | يد | له | يج | ل | يز | نا | ح | مه | يو | م | ل | قلب | كز | ه | مط | مد | يج | ل |
|||||
قمد | رع | لح | نز | يج | يح | | | قعه | كط | نو | ن | نز | كد | | قعد | ما | يح | لد | لو | يب | | شه | لط | لب | كب | لج | كد | |
||||
قسب | عط | كح | مط | كب | كز | مه | | شلب | كو | يا | كز | يط | لد | ل | شلا | لا | كح | كج | نه | مج | ل | قيح | نا | نح | نه | كب | لد | ل |
||||
قف | رمح | يح | ما | لا | لز | ل | | قكط | كب | كو | ج | ما | مه | | قكح | كا | لح | يج | يه | يه | | رصب | د | كه | كح | يا | مه | |
||||
قصح | نز | ح | لج | م | مز | يه | | رفو | يح | م | م | ج | نه | ل | رفه | يا | مح | ب | لد | مو | ل | قه | يو | نب | ا | | نه | ل |
||||
ريو | ركه | نح | كه | مط | نز | | | فج | يد | نه | يو | كو | و | | فب | ا | نز | نا | ند | يح | | رعح | كط | يح | لج | ن | و | |
||||
رلد | لد | مح | يز | نط | و | مه | | رم | يا | ط | نب | مح | يو | ل | رلح | نب | ز | ما | يج | ل | صا | ما | مه | و | لط | يو | ل |
|||||
رنب | رج | لح | ي | ح | يو | ل | | لز | ز | كد | كط | ي | كز | | له | مب | يز | ل | لج | كا | | رسد | ند | يا | لط | كح | كز | |
||||
رع | يب | كح | ب | يز | كو | يه | | قصد | ج | لط | ه | لب | لز | ل | قصب | لب | كز | يط | نب | نب | ل | عح | و | لح | يب | يز | لز | ل |
||||
رفح | قفا | يز | ند | كو | لو | | | شن | نط | نج | ما | ند | مح | | شمط | كب | لز | ط | يب | كد | | رنا | يط | د | مه | و | مح | |
||||
شو | ز | مو | له | مه | مه | | قمز | نو | ح | يح | يو | نح | ل | قمو | يب | مو | نح | لا | نه | ل | سد | لا | لا | يز | نه | نح | ل |
|||||
شكد | قنح | نز | لح | مد | نه | ل | | شد | نب | كب | ند | لط | ط | | شج | ب | نو | مز | نا | كز | | رلز | مج | نز | ن | مه | ط | |
||||
شمب | شكز | مز | ل | ند | ه | يه | | قا | مح | لز | لا | ا | يط | ل | صط | نج | و | لز | ي | نح | ل | ن | نو | كد | كج | لد | يط | ل |
||||
شس | قلو | لز | كج | ج | يه | | | رنح | مد | نب | ز | كج | ل | | رنو | مج | يو | كو | ل | ل | | ركد | ح | ن | نو | كج | ل | |
||||
شعح | شه | كز | يه | يب | كد | مه | | نه | ما | و | مج | مه | م | ل | نج | لج | كو | يه | ن | ا | ل | لز | كا | يز | كط | يب | م | ل |
||||
شصو | قيد | يز | ز | كا | لد | ل | | ريب | لز | كا | ك | ز | نا | | ري | كج | لو | ه | ط | لج | | ري | لج | مد | ب | ا | نا | |
||||
تيد | رفج | و | نط | ل | مد | يه | | ط | لج | له | نو | ل | ا | ل | ز | يج | مه | ند | د | ل | كج | مو | ي | لد | نا | ا | ل |
|||||
تلب | صا | نو | نا | لط | ند | | | قسو | كط | ن | لب | نب | يب | | قسد | ج | نه | مج | مح | لو | | قصو | نح | لز | ز | م | يب | |
||||
تن | رس | مو | مج | مط | ج | مه | | شكج | كو | ه | ط | يد | كب | ل | شك | ند | ه | لج | ح | ز | ل | ي | ج | م | كط | كب | ل |
|||||
تسح | سط | لو | له | نح | يج | ل | | قك | كب | يط | مه | لو | لج | | قيز | مد | يه | كب | كز | لط | | قفج | كج | ل | يج | يح | لج | |
||||
تفو | رلح | كو | كح | ز | كج | يه | | رعز | يح | لد | كا | نح | مج | ل | رعد | لد | كه | يا | مز | ي | ل | شنو | له | نو | مو | ز | مج | ل |
||||
ثد | مز | يو | ك | يو | لج | | | عد | يد | مح | نح | ك | ند | | عا | كد | له | ا | و | مب | | قسط | مح | كج | يح | نو | ند | |
||||
ثكب | ريو | و | يب | كه | مب | مه | | رلا | يا | ج | لد | مج | د | ل | ركح | يد | مد | ن | كو | يج | ل | شمج | | مط | نا | مو | د | ل |
||||
ثم | كد | نو | د | لد | نب | ل | | كح | ز | يح | يا | ه | يه | | كه | د | ند | لط | مه | مه | | قنو | يج | يو | كد | له | يه | |
||||
ثنح | قصج | مه | نو | مد | ب | يه | | قفه | ج | لب | مز | كز | كه | ل | قفا | نه | د | كط | ه | يو | ل | شكط | كه | مب | نز | كد | كه | ل |
||||
ثعو | ب | له | مح | نج | يب | | | شما | نط | مز | كج | مط | لو | | شلح | مه | يح | كد | مح | | قمب | لح | ط | ل | يج | لو | |
|||||
ثصد | قعا | كه | ما | ب | كا | مه | | قلح | نو | ب | | يا | مو | ل | قله | له | كد | ز | مد | يط | ل | شيه | ن | لو | ج | ب | مو | ل |
||||
خيب | شم | يه | لج | يا | لا | ل | | رصه | نب | يو | لو | لج | نز | | رصب | كه | لج | نز | ج | نا | | قكط | ج | ب | له | نا | نز | |
||||
خل | قمط | ه | كه | ك | ما | يه | | صب | مح | لا | يب | نو | ز | ل | فط | يه | مج | مو | كج | كب | ل | شب | يه | كط | ح | ما | ز | ل |
||||
خمح | شيز | نه | يز | كط | نا | | | رمط | مد | مه | مط | يح | يح | | رمو | ه | نج | له | مب | ند | | قيه | كز | نه | ما | ل | يح | |
||||
خسو | قكو | مه | ط | لط | | مه | | مو | ما | | كه | م | كح | ل | مب | نو | ج | كه | ب | كه | ل | م | كب | يد | يط | كح | ل |
|||||
خفد | رصه | له | ا | مح | ي | ل | | رج | لز | يه | ب | ب | لط | | قصط | مو | يج | يد | كا | نز | | قا | نب | مح | مز | ح | لط | |
||||
ذب | قد | كد | نج | نز | ك | يه | | | لج | كط | لح | كد | مط | ل | شنو | لو | كج | ج | ما | كح | ل | رعه | ه | يه | يط | نز | مط | ل |
||||
ذك | رعج | يد | مو | و | ل | | | قنز | كط | مد | يد | مز | | | قنج | كو | لب | نج | ا | | | فح | يز | ما | نب | مز | | |
||||
ذلح | فب | د | لح | يه | لط | مه | | شيد | كه | نح | نا | ط | ي | ل | شي | يو | مب | مب | ك | لا | ل | رسا | ل | ح | كه | لو | ي | ل |
||||
ذنو | رن | ند | ل | كد | مط | ل | | قيا | كب | يج | كز | لا | كا | | قز | و | نب | لا | م | ج | | عد | مب | لد | نح | كه | كا | |
||||
ذعد | نط | مد | كب | لج | نط | يه | | رسح | يح | كح | ج | نج | لا | ل | رسج | نز | ب | ك | نط | لد | ل | رمز | نه | ا | لا | يد | لا | ل |
||||
ذصب | ركح | لد | يد | مج | ط | | | سه | يد | مب | م | يه | مب | | س | مز | يب | ي | يط | و | | سا | ز | كح | د | ج | مب | |
||||
ضي | لز | كد | و | نب | يح | مه | | ركب | ي | نز | يو | لز | نب | ل | ريز | لز | كا | نط | لح | لز | ل | رلد | يط | ند | لو | نب | نب | ل |
||||
عد | مح | يج | مد | لز | ل | ه | فد | كا | ند | نج | يه | مه | ه | عه | يد | مج | نط | يز | يه | ه | فح | لد | مط | يج | مد | مز | ||||||
الجدول الثاني لحركات القمر الوسطى وهو خمسة صفوف |
|||||||||||||||||||||||||||||||
السنون الثماني عشر | حصّة الطول | حصّة الاختلاف | حصّة العرض | حصّة البعد |
|||||||||||||||||||||||||||
أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس |
||||
ا | قكط | كب | مو | يج | ن | لب | ل | فح | مج | ز | كح | ما | يج | نه | قمح | مب | مز | يب | مد | كه | ه | قكط | لز | كا | كح | كط | كج | نه |
|||
ب | رنح | مه | لب | كز | ما | ه | | قعز | كو | يد | نز | كب | كز | ن | رصز | كه | لد | كه | كح | ن | ي | رنط | يد | مب | نو | نح | مز | ن |
|||
ج | كح | ح | يح | ما | لا | لز | ل | رسو | ط | كب | كو | ج | ما | مه | فو | ح | كا | لح | يج | يه | يه | كح | نب | د | كه | كح | يا | مه |
|||
د | قنز | لا | د | نه | كب | ي | | شند | نب | كط | ند | مد | نه | م | رلد | نا | ح | ن | نز | م | ك | قنح | كط | كه | نج | نز | له | م |
|||
ه | رفو | نج | نا | ط | يب | مب | ل | فج | له | لز | كج | كو | ط | له | كج | لج | نو | ج | مب | ه | كه | رفح | و | مز | كب | كو | نط | له |
|||
و | نو | يو | لز | كج | ج | يه | | قعب | يح | مد | نب | ز | كج | ل | قعب | يو | مج | يو | كو | ل | ل | نز | مد | ح | ن | نو | كج | ل |
|||
ز | قفه | لط | كج | لو | نج | مز | ل | رسا | ا | نب | ك | مح | لز | كه | شك | نط | ل | كط | ي | نه | له | قفز | كا | ل | يط | كه | مز | كه |
|||
ح | شيه | ب | ط | ن | مد | ك | | شمط | مد | نط | مط | كط | نا | ك | قط | مب | يز | ما | نه | ك | م | شيو | نح | نا | مز | نه | يا | ك |
|||
ط | فد | كد | نو | د | لد | نب | ل | عح | كح | ز | يح | يا | ه | يه | رنح | كه | د | ند | لط | مه | مه | فو | لو | يج | يو | كد | له | يه |
|||
ي | ريج | مز | مب | يح | كه | كه | | قسز | يا | يد | مو | نب | يط | ي | مز | ز | نب | ز | كد | ي | ن | ريو | يج | لد | مد | نج | نط | ي |
|||
يا | شمج | ي | كح | لب | يه | نز | ل | رنه | ند | كب | يه | لج | لج | ه | قصه | ن | لط | ك | ح | له | نه | شمه | ن | نو | يج | كج | كج | ه |
|||
يب | قيب | لج | يد | مو | و | ل | | شمد | لز | كط | مد | يد | مز | | شمد | لج | كو | لب | نج | ا | | قيه | كح | يز | ما | نب | مز | |
|||
يج | رما | نو | | نط | نز | ب | ل | عج | ك | لز | يب | نو | | نه | قلج | يو | يج | مه | لز | كو | ه | رمه | ه | لط | ي | كب | ي | نه |
|||
يد | يا | يح | مز | يج | مز | له | | قسب | ج | مد | ما | لز | يد | ن | رفا | نط | | نح | كا | نا | ي | يد | مج | | لح | نا | لد | ن |
|||
يه | قم | ما | لج | كز | لح | ز | ل | رن | مو | نب | ي | يح | كح | مه | ع | ما | مح | يا | و | يو | يه | قمد | ك | كب | ز | ك | نح | مه |
|||
يو | رع | د | يط | ما | كح | م | | شلط | كط | نط | لح | نط | مب | م | ريط | كد | له | كج | ن | ما | ك | رعج | نز | مج | له | ن | كب | م |
|||
يز | لط | كز | ه | نه | يط | يب | ل | سح | يج | ز | ز | م | نو | له | ح | ز | كب | لو | له | و | كه | مج | له | ه | د | يط | مو | له |
|||
يح | قسح | مط | نب | ط | ط | مه | | قنو | نو | يد | لو | كب | ي | ل | قنو | ن | ط | مط | يط | لا | ل | قعج | يب | كو | لب | مط | ي | ل |
|||
الساعات | حصّة الطول | حصّة الاختلاف | حصّة العرض | حصّة البعد |
|||||||||||||||||||||||||||
ا | | لب | نو | كز | كو | كج | مو | | لب | لط | مد | ن | مد | | لج | د | كد | ط | لب | | ل | كح | لو | مج | ك | مه |
|||||
ب | ا | ه | نب | ند | نب | مز | لب | ا | ه | يط | كط | ما | كط | ا | و | ح | مح | يط | د | مج | ا | | نز | يج | كو | ما | ل |
||||
ج | ا | لح | مط | كب | يط | يا | يح | ا | لز | نط | يد | لب | ا | لط | يج | يب | كح | لز | ه | ا | لا | كه | ن | ي | ب | يه |
|||||
د | ب | يا | مه | مط | مه | له | ه | ب | ي | لح | نط | كب | نح | ب | يب | يز | لو | لح | ط | كو | ب | ا | ند | كو | نج | كج | |
||||
ه | ب | مد | مب | يز | يا | نح | نا | ب | مج | يح | مد | يج | مج | ب | مه | كب | | مز | ما | مح | ب | لب | كج | ج | لو | مج | مه |
||||
و | ج | يز | لح | مد | لح | كب | لز | ج | يه | نح | كط | د | ج | يح | كو | كد | نز | يد | ط | ج | ب | نا | م | ك | د | ل |
|||||
ز | ج | ن | له | يب | د | مو | كج | ج | مح | لح | يج | نه | يب | ج | نا | ل | مط | و | مو | لا | ج | لج | ك | يز | ج | كه | يه |
||||
ح | د | كج | لا | لط | لا | ي | ي | د | كا | يز | نح | مه | نز | د | كد | له | يج | يو | يح | نب | د | ج | مح | نج | مو | مو | |
||||
ط | د | نو | كح | و | نز | لج | نو | د | نج | نز | مج | لو | د | نز | لط | لز | كه | نا | يد | د | لد | يز | ل | ل | و | مه |
|||||
ي | ه | كط | كد | لد | كج | نز | مب | ه | كو | لز | كح | كز | كو | ه | ل | مد | ا | له | كج | له | ه | د | مو | ز | يج | كز | ل |
||||
يا | و | ب | كا | ا | ن | كا | كح | ه | نط | يز | يج | يح | يا | و | ج | مح | كه | مد | نه | نز | ه | له | يد | مج | نو | مح | يه |
||||
يب | و | له | يز | كط | يو | مه | يه | و | لا | نح | ح | و | لو | نب | مط | ند | كح | و | ه | مج | ك | م | ط | |
|||||||
يج | ز | ح | يج | نو | مج | ط | ا | ز | د | لو | مب | نط | م | لط | ز | ط | نز | يد | د | | م | و | لو | يا | نز | كج | كط | مد |
|||
يد | ز | ما | ي | كد | ط | لب | مز | ز | لز | يو | كز | ن | كه | يط | ز | مج | ا | لح | يج | لج | ب | ز | و | م | لد | و | ن | كط |
|||
يه | ح | يد | و | نا | له | نو | لج | ح | ط | نو | يب | ما | ط | نط | ح | يو | و | ب | كج | ه | كج | ز | لز | ط | ي | ن | يا | يد |
|||
يو | ح | مز | ج | يط | ب | ك | ك | ح | مب | له | نز | لا | لط | ح | مط | ي | كو | لب | لز | مه | ح | ز | لز | مز | لج | لا | نط |
||||
يز | ط | يط | نط | مو | كح | مد | و | ط | يه | يه | مب | كب | لط | يط | ط | كب | يد | ن | مب | ي | و | ح | لح | و | كد | يو | نب | مد |
|||
يح | ط | نب | نو | يج | نه | ز | نب | ط | مز | نه | كز | يج | كج | نط | ط | نه | يط | يد | نا | مب | كح | ط | ح | له | ا | | يج | كط |
|||
يط | ي | كه | نب | ما | كا | لا | لح | ي | ك | له | يب | د | ح | لط | ي | كح | كج | لط | ا | يد | مط | ط | لط | ج | لز | مج | لد | يد |
|||
ك | ي | نح | مط | ح | مز | نه | كه | ي | نج | يد | نو | ند | نج | يط | يا | ا | كح | ج | ي | مز | يا | ي | ط | لب | يد | كو | ند | نط |
|||
كا | يا | لا | مه | لو | يد | يط | يا | يا | كه | ند | ما | مه | لز | نط | يا | لد | لب | كز | ك | يط | لب | ي | م | | نا | ي | يه | مد |
|||
كب | يب | مب | ج | م | مب | نز | يا | نح | لد | كو | لو | كب | لط | يب | ز | لو | نا | كط | نا | ند | يا | ي | كط | كز | نج | لو | كط |
||||
كج | يب | لز | لح | لا | ز | و | مج | يب | لا | يد | يا | كز | ز | يط | يب | م | ما | يه | لط | كد | يه | يا | م | نح | د | لو | نز | يد |
|||
كد | يج | ي | لد | نح | لج | ل | ل | يج | ج | نج | نو | يز | نا | نط | يج | يج | مه | لط | مح | نو | لز | يب | يا | كو | ما | ك | يز | نط |
|||
الجدول الثالث لحركات القمر الوسطى وهو خمسة صفوف | ||||||||||||||||||||||||||||||||
الشهور | حصّة الطول | حصّة الاختلاف | حصّة العرض | حصّة البعد |
||||||||||||||||||||||||||||
أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس |
|||||
ا | له | يز | كط | يو | مه | يه | | لا | نو | نح | ح | نه | نط | ل | لو | نب | مط | ند | كح | يح | ل | ه | مج | ك | م | ح | نط | ل |
||||
ب | ع | لد | نح | لج | ل | ل | | سج | نج | نو | يز | نا | نط | | عج | مه | لط | مح | نو | لز | | يا | كو | ما | ك | يز | نط | |
||||
ج | قه | نب | كز | ن | يه | مه | | صه | ن | ند | كو | مز | نح | ل | قي | لح | كط | مج | كد | نه | ل | يز | ي | ب | | كو | نح | ل |
||||
د | قما | ط | نز | ز | ا | | | قكز | مز | نب | له | مج | نح | | قمز | لا | يط | لز | نج | يد | | كب | نج | كب | م | له | نح | |
||||
ه | قعو | كز | كو | كج | مو | يه | | قنط | مد | ن | مد | لط | نز | ل | قفد | كد | ط | لب | كا | لب | ل | كح | لو | مج | ك | مد | نز | ل |
||||
و | ريا | مد | نه | م | لا | ل | | قصا | ما | مح | نج | له | نز | | ركا | يو | نط | كو | مط | نا | | لد | ك | د | | نج | نز | |
||||
ز | رمز | ب | كد | نز | يو | مه | | ركج | لح | مز | ب | لا | نو | ل | رنح | ط | مط | كا | يح | ط | ل | م | ج | كد | ما | ب | نو | ل |
||||
ح | رفب | يط | ند | يد | ب | | | رنه | له | مه | يا | كز | نو | | رصه | ب | لط | يه | مو | كح | | مه | مو | مه | كا | يا | نو | |
||||
ط | شيز | لز | كج | ل | مز | يه | | رفز | لب | مج | ك | كج | نه | ل | شلا | نه | كط | ي | يد | مو | ل | نا | ل | و | ا | ك | نه | ل |
||||
ي | شنب | ند | نب | مز | لب | ل | | شيط | كط | ما | كط | يط | نه | | ح | مح | يط | د | مج | ه | | نز | يج | كو | ما | كط | نه | |
||||
يا | كح | يب | كب | د | يز | مه | | شنا | كو | لط | لح | يه | ند | ل | مه | ما | ح | نط | يا | كج | ل | سب | نو | مز | كا | لح | ند | ل |
||||
يب | سج | كط | نا | كا | ج | | | كج | كج | لز | مز | يا | ند | | فب | لج | نح | نج | لط | مب | | سح | م | ح | ا | مز | ند | |
||||
الأيّام | حصّة الطول | حصّة الاختلاف | حصّة العرض | حصّة البعد |
||||||||||||||||||||||||||||
ا | يج | ي | لد | نح | لج | ل | ل | يج | ج | نج | نو | يز | نا | نط | يج | يج | مه | لط | مح | نو | لز | يب | يا | كو | ما | ك | يز | نط |
||||
ب | كو | كا | ط | نز | ز | ا | | كو | ز | مز | نب | له | مج | نح | كو | كز | لا | يط | لز | نج | يد | كد | كب | نج | كب | م | له | نح |
||||
ج | لط | لا | مد | نه | م | لا | ل | لط | يا | ما | مح | نج | له | نز | لط | ما | يو | نط | كو | مط | نا | لو | لد | ك | د | | نج | نز |
||||
د | نب | مب | يط | ند | يد | ب | | نب | يه | له | مه | يا | كز | نو | نب | نه | ب | لط | يه | مو | كح | مح | مه | مو | مه | كا | يا | نو |
||||
ه | سه | نب | ند | نب | مز | لب | ل | سه | يط | كط | ما | كط | يط | نه | سو | ح | مح | يط | د | مج | ه | س | نز | يج | كو | ما | كط | نه |
||||
و | عط | ج | كط | نا | كا | ج | | عح | كج | كج | لز | مز | يا | ند | عط | كب | لج | نح | نج | لط | مب | عج | ح | م | ح | ا | مز | ند |
||||
ز | صب | يد | د | مط | ند | لج | ل | صا | كز | يز | لد | ه | ج | نج | صب | لو | يط | لح | مب | لو | يط | فه | ك | و | مط | كب | ه | نج |
||||
ح | قه | كد | لط | مح | كح | د | | قد | لا | يا | ل | كب | نه | نب | قه | ن | ه | يح | لا | لب | نو | صز | لا | لج | ل | مب | كج | نب |
||||
ط | قيح | له | يد | مز | ا | لد | ل | قيز | له | ه | كو | م | مز | نا | قيط | ج | ن | نح | ك | كط | لج | قط | مج | | يب | ب | ما | نا |
||||
ي | قلا | مه | مط | مه | له | ه | | قل | لح | نط | كب | نح | لط | ن | قلب | يز | لو | لح | ط | كو | ي | قكا | ند | كو | نج | كب | نط | ن |
||||
يا | قمد | نو | كد | مد | ح | له | ل | قمج | مب | نج | يط | يو | لا | مط | قمه | لا | كب | يز | نح | كب | مز | قلد | ه | نج | لد | مج | يز | مط |
||||
يب | قنح | و | نط | مب | مب | و | | قنو | مو | مز | يه | لد | كج | مح | قنح | مه | ز | نز | مز | يط | كد | قمو | يز | ك | يو | ج | له | مح |
||||
يج | قعا | يز | لد | ما | يه | لو | ل | قسط | ن | ما | يا | نب | يه | مز | قعا | نح | نج | لز | لو | يو | ا | قنح | كح | مو | نز | كج | نج | مز |
||||
يد | قفد | كح | ط | لط | مط | ز | | قفب | ند | له | ح | ي | ز | مو | قفه | يب | لط | يز | كه | يب | لح | قع | م | يج | لح | مد | يا | مو |
||||
يه | قصز | لح | مد | لح | كب | لز | ل | قصه | نح | كط | د | كز | نط | مه | قصح | كو | كد | نز | يد | ط | يه | نا | م | ك | د | كط | مه |
|||||
يو | ري | مط | يط | لو | نو | ح | | رط | ب | كج | | مه | نا | مد | ريا | م | ي | لز | ج | ه | نب | قصه | ج | ا | كد | مز | مد |
|||||
يز | ركج | نط | ند | له | كط | لح | ل | ركب | و | يو | نز | ج | مج | مج | ركد | نج | نو | يو | نب | ب | كط | رز | يد | لج | مب | مه | ه | مج |
||||
يح | رلز | ي | كط | لد | ج | ط | | رله | ي | ي | نج | كا | له | مب | رلح | ز | ما | نو | م | نط | و | ريط | كو | | كد | ه | كج | مب |
||||
يط | رن | كا | د | لب | لو | لط | ل | رمح | يد | د | مط | لط | كز | ما | رنا | كا | كز | لو | كط | نه | مج | رلا | لز | كز | ه | كه | ما | ما |
||||
ك | رسج | لا | لط | لا | ي | ي | | رسا | يز | نح | مه | نز | يط | م | رسد | له | يج | يو | يح | نب | ك | رمج | مح | مو | مه | نط | م |
|||||
كا | رعو | مب | يد | كط | مج | م | ل | رعد | كا | نب | مب | يه | يا | لط | رعز | مح | نح | نو | ز | مح | نز | رنو | | ك | كح | و | يز | لط |
||||
كب | رفط | نب | مط | كح | يز | يا | | رفز | كه | مو | لح | لج | ج | رصا | ب | مد | له | نو | مه | لد | رسح | يا | مز | ط | كو | له | لح |
|||||
كج | شج | ج | كد | كو | ن | ما | ل | ش | كط | م | لد | ن | نه | لز | شد | يو | ل | يه | مه | مب | يا | رف | كج | يج | ن | مو | نج | لز |
||||
كد | شيو | يج | نط | كه | كد | يب | | شيج | لج | لد | لا | ح | مز | لو | شيز | ل | يه | نه | لد | لح | مح | رصب | لد | م | لب | ز | يا | لو |
||||
كه | شكط | كد | لد | كج | نز | مب | ل | شكو | لز | كح | كز | كو | لط | له | شل | مد | ا | له | كج | له | كه | شد | مو | ز | يج | كز | كط | له |
||||
كو | شمب | له | ط | كب | لا | يج | | شلط | ما | كب | كج | مد | لا | لد | شمج | نز | مز | يه | يب | لب | ب | شيو | نز | لج | ند | مز | مز | لد |
||||
كز | شنه | مه | مد | كا | د | مج | ل | شنب | مه | يو | ك | ب | كج | لج | شنز | يا | لب | نه | ا | كح | لط | شكط | ط | | لو | ح | ه | لج |
||||
كح | ح | نو | يط | يط | لح | يد | | ه | مط | ي | يو | ك | يه | لب | ي | كه | يح | لد | ن | كه | يو | شما | ك | كز | يز | كح | كج | لب |
||||
كط | كب | و | ند | يح | يا | مد | ل | يح | نج | د | يب | لح | لا | كج | لط | د | يد | لط | كا | نج | شنج | لا | نج | نح | مح | ما | لا |
|||||
ل | له | يز | كط | يو | مه | يه | | لا | نو | نح | ح | نه | نط | ل | لو | نب | مط | ند | كح | يح | ل | ه | مج | ك | م | ح | نط | ل |
||||
〈IV.5〉 ه: في أنّ الأصل البسيط أيضاً للقمر الأشياء ه – خ: (أشياء) التي تظهر واحدة بأعيانها من قبل الأصل التي ه: الذي يوضع فيه فلك خارج المركز ومن قبل الأصل الذي يوضع فيه فلك تدوير
ولمّا كان قد تتّبع هذه الأشياء نتبيّن الوجه الذي يكون به اختلاف القمر وكم مقدار اختلافه. فإنّا في هذا الموضع جاعلون الكلام في ذلك على أنّ هذا الاختلاف واحد. وهو الذي نجد جميع من كان قبلنا ما خلا الشاذّ عليه وحده وفقت أوهامهم وإيّاه قصدوا أعني الاختلاف الذي يتمّ في زمان العودة الذي ↑الذي↑: خ التي وضعناه. ↑: خ ها وأمّا فيما بعد فإنّا مبيّنون أنّ القمر يفعل اختلافاً آخر ثانياً بحسب أبعاده من الشمس، وأنّ أعظم ما يكون هذا الاختلاف في التربيعين ه – خ – ج: (اللذين على جنبي الامتلاء) جميعاً، وأنّه يعود مرّتين في زمان الشهر في الاجتماعات أنفسها والاستقبالات. ↑الاستقبالات↑: الامتلاءات وإنّما استعملنا هذا الترتيب في البرهان من أجل أنّ هذا الاختلاف لا يمكن أن يوجد أصلاً خلواً من اختلاف الأوّل إذ كان أبداً مقروناً به، وأمّا الأوّل فقد يمكن وجوده خلواً من الثاني وذلك أنّه أنّما يستخرج من قبل الكسوفات القمريّة وهذه الكسوفات ليس يقع فيها اختلاف محسوس ممّا يلزم من الذي بحسب الشمس ه – خ: (من قبل الشمس) .
ونحن لازمون في هذا البرهان المقدّم الطرق في هذا المعنى الذي نجد ه – ج: فأمّا في برهان الاختلاف المقدّم فنعمل بالأبواب التي رأينا أبرخس أيضاً قد استعملها. فإنّا أيضاً آخذون ثلاثة من الكسوفات القمريّة ومبيّنون كم يكون أكثر الفضل ه – خ: (من قبل الاختلاف) على الحركة الوسطى والمنزل ↑المنزل↑: الحاصل بالقياس إلى ذروة ه – خ: (نقطة) أبعد البعد وهذا الاختلاف، وإن كان يوجد على حياله، و شطب الكاتب حرف «و».يتمّ بالأصل الذي يوضع فيه فلك تدوير. وكانت الأشياء التي تظهر توجد بالأصل ه – خ: أيضاً الذي يوضع فيه فلك خارج المركز أشياء واحدة بأعيانها فإنّ الأولى أن ينسب إلى الأصل الثاني الاختلاف الذي يجتمع فيه الاختلافان جميعاً وهو الذي ه: الاختلاف الذي يلحق بحسب الشمس. وقد يمكنا أن نعلم أنّ في هذا الموضع أيضاً يكون ما يظهر أشياء ه – خ: (واحدة) بأعيانها بكلّ واحد من الأصلين الموضوعين، وإن لم يكن زمانا العودتين جميعاً متساويين كما بيّنّا في الشمس، أعني العودة التي بحسب الاختلاف والعودة التي توجد بالقياس إلى فلك البروج، بل كان الزمانان كما هما في القمر غير متساويين بعد أن يوضع النسب أيضاً فقط واحدة بأعيانها بما نحن واصفوه. وذلك بأن نجعل نظرنا في هذا الاختلاف البسيط نفسه المقصود له في القمر.
فنقول إنّه لمّا كانت عودة القمر بالقياس إلى فلك البروج أسرع من عودته بالقياس إلى هذا الاختلاف المقصود له، فمن البيّن أنّه في الأزمان المتساوية أمّا في الأصل الذي يوضع فيه فلك التدوير، فإنّ القوس التي يتحرّكها فلك التدوير على الفلك الموافق المركز لفلك البروج يكون أبداً أعظم في النسبة من القوس التي يجوزها القمر في فلك التدوير. وأمّا في الأصل الذي يوضع فيه الخروج عن المركز فإنّ القمر يتحرّك على الفلك الخارج المركز قوساً شبيهة بالقوس التي يتحرّكها على فلك التدوير، وأمّا ه – خ: (مركز) الفلك الخارج المركز فإنّه يتحرّك إلى الجهة التي إليها يتحرّك القمر حول مركز فلك البروج قوساً مقدارها المقدار الذي به المسير في الطول أكثر من المسير في الاختلاف، أعني زيادة القوس التي تقطع من الفلك الموافق المركز على القوس التي تقطع من فلك التدوير. فإنّ بهذا الوجه يبقى تشابه النسب محفوظاً ومع ذلك أيضاً تشابه أزمان كلّ واحدة من الحركتين في الأصلين جميعاً.
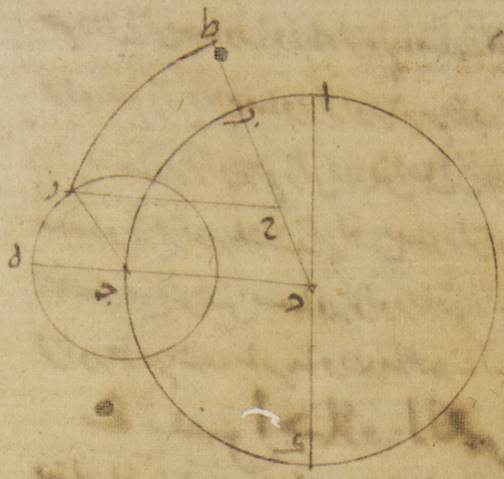
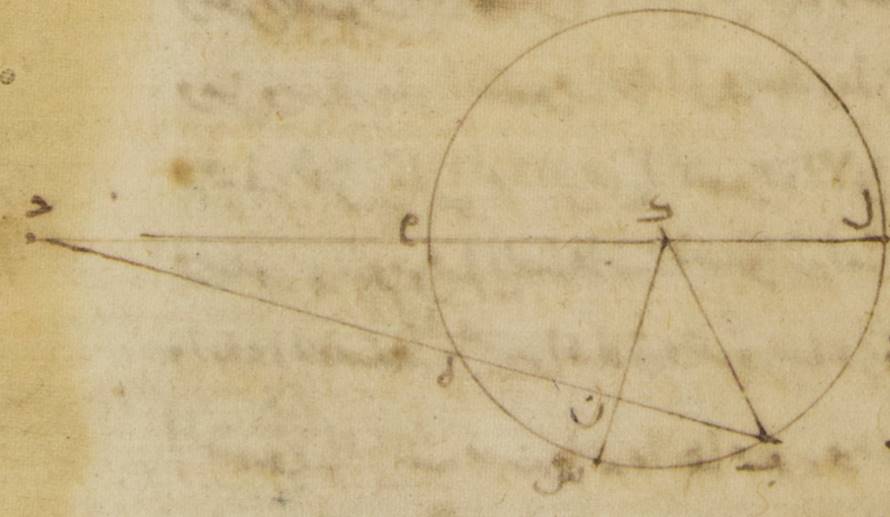
وإذ قد وطّأنا هذه الأشياء لما يلزم ضرورة من نفس ما قصد له آ: فليكن الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال وقطر ألف دال، ↑دال↑: كاف وفلك التدوير هاء زاي حول مركز جيم. ولننزّل أنّ فلك التدوير لمّا كان على نقطة ألف فإنّ القمر ه – خ: كان على نقطة هاء من فلك التدوير، وهي البعد الأبعد، وأنّ في زمان سواء سار فلك التدوير قوس ألف جيم وسار القمر قوس هاء زاي. ولنوصل خطّ هاء جيم دال وخطّ جيم زاي. فلأنّ قوس ألف جيم أعظم في النسبة من قوس هاء زاي. فلنفصل قوس باء جيم شبيهة بقوس هاء زاي، ولنوصل خطّ باء دال. فمن البيّن أنّ في زمان مساو لذلك الزمان تحرّك أيضاً الفلك الخارج المركز زاوية ألف دال باء وهي زاوية الفضل بين المسيرين جميعاً، وصار مركزه وبعده الأبعد على خطّ باء دال.
وإذا كان ذلك كذلك فلننزّل أنّ خطّ حاء دال مساو لخطّ جيم زاي. ولنرسم بمركز حاء وببعد حاء زاي الفلك الخارج المركز وهو زاي طاء. ولنوصل خطّ زاي حاء ونخرج خطّ دال باء على الاستقامة إلى نقطة طاء. This sentence is not included in Toomer’s translation.
أقول إنّ نسبة خطّ زاي حاء إلى خطّ حاء دال هي نسبة خطّ دال جيم إلى خطّ جيم زاي وإنّ بحسب هذا الأصل أيضاً يكون القمر على نقطة زاي، أعني أنّ قوس زاي طاء ه: أيضاً تكون شبيهة بقوس هاء زاي. فلأنّ زاوية باء دال جيم مساوية لزاوية زاي جيم هاء، فخطّ دال حاء مواز لخطّ جيم زاي. وهو أيضاً مساو له. فخطّ حاء زاي إذن مساو لخطّ جيم دال ومواز له. فتكون نسبة خطّ زاي جيم إلى خطّ جيم دال هي نسبة خطّ دال حاء إلى خطّ حاء زاي. Greek, p. 297: ΖΗ:ΗΔ=ΔΓ:ΓΖ; Toomer, p. 188: ZH:HD=DG:GZ. وأيضاً لأنّ خطّ جيم دال مواز لخطّ حاء زاي، فزاوية جيم دال باء مساوية لزاوية زاي حاء طاء؛ وقد كانت لنا زاوية جيم دال باء مساوية لزاوية هاء جيم زاي. فزاوية زاي حاء طاء إذن مساوية لزاوية هاء جيم زاي. This sentence is not included in Toomer’s translation. فيجب من ذلك أن تكون قوس زاي طاء شبيهة بقوس هاء زاي. ففي زمان سواء إذن صار القمر على نقطة زاي في كلّ واحد من الأصلين من قبل أنّ القمر تحرّك قوس هاء زاي من فلك التدوير وقوس طاء زاي من الفلك الخارج المركز اللتين قد تبيّن أنّهما متشابهتان ومركز فلك التدوير تحرّك قوس ألف جيم ومركز الفلك الخارج المركز تحرّك قوس ألف باء، وهي فضل قوس ألف جيم على قوس هاء زاي، وذلك ما كان ينبغي أن نبيّن.
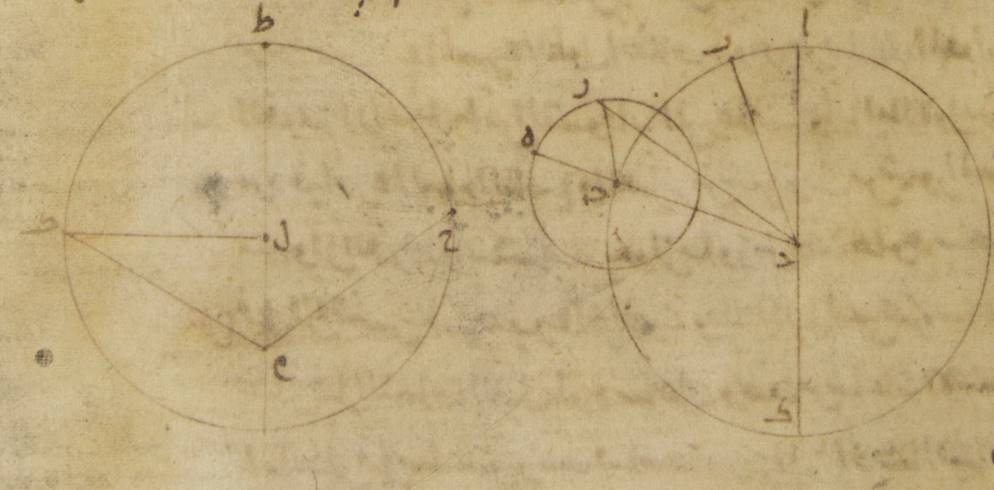
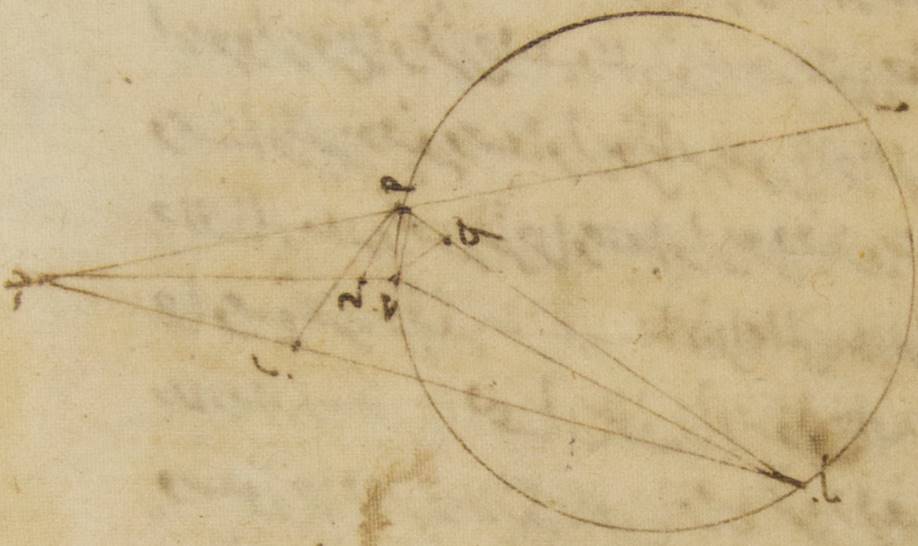
وقد تبيّن أيضاً أنّه لو كانت النسب متشابهة فقط ولم تكن متساوية، لا هي ولا الفلك الخارج المركز والفلك الموافق المركز ه – خ: (الذي مركزه مركز فلك البروج) ، فإنّ ذلك بعينه يلزم ممّا أنّا واصفه. فلنرسم كلّ واحد من الأصلين على حياله. ب: وليكن الفلك الذي مركزه مركز فلك البروج ألف باء جيم حول مركز دال وقطر ألف دال، ↑دال↑: كاف وفلك التدوير ه – خ: عليه هاء زاي حول مركز جيم. وأيضاً الفلك الخارج المركز ه – خ: عليه خطّ كاف حول مركز لام وقطر طاء لام، Toomer, p. 189: Let the eccenter be HΘK on center L and diameter ΘLM. It seems that HΘ in Greek was translated as حط which was then misinterpreted as خطّ (“line”), so now the Arabic text has “line K” which makes no sense. وليكن عليه مركز فلك البروج نقطة ميم. وليكن القمر على نقطة كاف ولنوصل أمّا هناك ه – خ: (في الصورة الأولى) فخطوط دال جيم هاء، جيم زاي، دال زاي وأمّا هاهنا فخطوط حاء ميم، كاف ميم، كاف لام.
ولننزّل أنّ نسبة خطّ دال جيم إلى خطّ جيم هاء هي نسبة خطّ طاء لام إلى خطّ لام ميم، وليتحرّك في زمان سواء أمّا فلك التدوير فزاوية ألف دال جيم، والقمر زاوية هاء جيم زاي، وأمّا الفلك الخارج المركز فزاوية حاء ميم طاء، والقمر أيضاً زاوية طاء لام كاف.
فمن قبل نسب الحركات التي وضعناها تكون زاوية هاء جيم زاي مساوية لزاوية طاء لام كاف وزاوية ألف دال جيم مساوية لزاويتي طاء لام كاف، حاء ميم طاء مجموعتين. وإذ كان ذلك كذلك، فأقول أيضاً إنّ على حسب كلّ واحد من الأصلين القمر يرى قد سار في زمان سواء قوساً سواء، أعني أنّ زاوية ألف دال زاي مساوية لزاوية حاء ميم كاف، فلأنّ في مبدأ المدّة لمّا كان القمر في البعدين الأبعدين كان يرى على خطّي دال ألف، ميم حاء وفي آخرها لمّا صار على نقطتي زاي، كاف صار يرى على خطّي دال زاي، ميم كاف. فلننزّل أنّ قوس جيم باء أيضاً شبيهة بكلّ واحدة من قوسي طاء كاف، هاء زاي ولنوصل خطّ باء دال. فلأنّ نسبة خطّ دال جيم إلى خطّ جيم زاي كنسبة خطّ كاف لام إلى خطّ لام ميم وهي تحيط بزاويتين متساويتين أعني اللتين عند نقطتي لام، جيم. فمثلّث جيم دال زاي مساوية زواياه لزاويا مثلّث لام كاف ميم، فالزوايا التي توتّرها الأضلاع المتناسبة متساوية. فزاوية جيم زاي دال مساوية لزاوية لام ميم كاف. لكن زاوية باء دال زاي مساوية لزاوية (لام ميم كاف لكن زاوية باء دال) (زاي مساوية لزاوية) جيم زاي دال من أجل أنّ خطّي جيم زاي، باء دال متوازيان لأنّ زاويتي زاي جيم هاء، باء دال جيم وضعنا متساويتين. فزاوية باء دال زاي إذن مساوية لزاوية لام ميم كاف. وقد كانت وضعت زاوية ألف دال باء وهي زاوية الفضل بين الحركتين مساوية لزاوية حاء ميم طاء وهي مسير الفلك الخارج المركز. فزاوية ألف دال زاي بأسرها إذن مساوية لزاوية حاء ميم كاف بأسرها، وذلك ما قصدنا لتبيينه.
〈IV.6〉 و: في تبيين اختلاف القمر الأوّل البسيط
فهذا مبلغ ما تقدّمه ممّا يحتاج إلى أن يتقدّم العلم به. ونحن جاعلون تبيين اختلاف القمر الذي إيّاه قصدنا في الأصل الذي يوضع فيه فلك التدوير للسبب الذي ذكرناه. ومستعملون أوّلاً من أقدم ما نقدر عليه من الكسوفات ثلاثة من أصحّ من نظنّه منها وأبلغها تحريراً فيما أثبت منه، ومستعملون بعد ذلك من الكسوفات التي كانت في زماننا ثلاثة أيضاً ممّا رصدناه نحن أنفسنا بغاية الاستقصاء. فإنّا إذا سلكنا هذه السبيل كنّا قد استعمالنا في هذا الفحص أطول ما قدرنا عليه من الزمان، وظهر أيضاً من ذلك أنّ الفضل الذي من قبل الاختلاف يحصل قريباً من واحد بعينه من قبل البرهانين ه: يعني الرصد القديم ورصده جميعاً، وأنّ فضلة الحركات الوسطى توجد موافقة لما تجتمع في الأزمان {...} الموصوفة بتقويمنا نحن. فليكن الأصل الذي يوضع فيه فلك التدوير كما قلنا لتبيين الاختلاف الأوّل الذي يوجد بنفسه على هذه الصفة. لنتوهّم في كرة ه – خ: فلك القمر فلك من كرة مركز فلك البروج وهو في سطحه وفلك آخر مائل عن هذا الفلك علي حسب مقدار مجاز القمر في العرض يتحرّك دوراً على استواء قدماً ه – خ: إلى خلاف توالي البروج حول مركز فلك البروج ومبلغ حركته بمقدار فضل الحركة في العرض على الحركة في الطول. ه: في بعض النسخ وذلك أنّ حركة الفلك المائل إذ كانت ضدّ حركة فلك التدوير فإنّها تنقص منها. فنضع الفلك الذي يقال له فلك التدوير يتحرّك على هذا الفلك المائل على استواء أيضاً تلقا حركة العالم ه – خ: وعلى توالي البروج لازماً في حركته للعودة في العرض. ومن البيّن أنّ هذه العودة إذا نظر فيها بالقياس إلى فلك البروج نفسه كانت الحركة التي تفعلها الحركة في الطول. ونضع القمر على فلك التدوير نفسه ينتقل في القوس التي عند البعد الأبعد قدماً لحركة العالم ه – خ: إلى خلاف توالي البروج لازماً لعودة الاختلاف، إلّا أنّ في هذا التبيين ه – خ: أنّ هذا في المسير الذي قصدنا له ليس يدخل ضرر من تركنا أن نضيف إلى ذلك التقدّم ↑: خ التقدير في العرض ولا ميل فلك القمر وذلك أنّه ليس يزيد فيحدث في المسير في الطول اختلاف ذو قدر من قبل هذا المقدار من الميل.
فالكسوفات الثلاثة القديمة ه: {رصد} الثلاثة كسوفات القديمة التي أخذناها من الكسوفات التي رصدت ببابل. أمّا الأوّل منها فإنّه كتب أنّه كان في السنة الأولى من سنيّ مردقياذ في اليوم التاسع والعشرين من شهر توت من شهور المصريّين منها في الليلة التي يليها اليوم الثلاثون منه وإنّ القمر ابتداء ينكسف بعد أن جاوز من وقت طلوعه ساعة واحدة بشيء صالح وأنّه انكسف كلّه. فمن قبل أنّ الشمس كانت حينئذ في آخر الحوت وكان الليل اثنتي عشرة ساعة ه – خ: استوائيّة بالتقريب، فمن البيّن أنّ مبدأ الكسوف كان قبل انتصاف الليل بأربع ساعات ونصف من ساعات الاستواء، وأنّ وسط زمانه إذ كان الكسوف تامّاً كان قبل ه – خ: نصف الليل ساعتين ونصف. فبإسكندريّة إذن إذ كنّا أنّما نعدّل مبلغ الساعات بالقياس إلى دائرة نصف النهار التي تمرّ بها وكانت دائرة نصف النهار التي تمرّ بها تتقدّم دائرة نصف النهار التي تمرّ ببابل بنصف وثلث ساعة بالتقريب من ساعات الاستواء كان وسط زمان هذا الكسوف قبل نصف الليل بثلاث ساعات وثلث من ساعات الاستواء، وفي تلك الساعة كان منزل ↑منزل↑: حاصل الشمس على الحقيقة بالحساب الذي وضعناه على أربعة وعشرين جزءاً ونصف بالتقريب من الحوت.
وأمّا الكسوف الثاني فكتب أنّه كان في السنة الثانية من سنيّ مردقباذ، هذا في اليوم الثامن عشر من شهر توت من شهور المصريّين منها في الليلة التي يليها اليوم التاسع عشر منه، وأنّه انكسف من ناحية الجنوب ثلاث أصابع في وقت انتصاف الليل نفسه. فلأنّا نجد وسط زمانه ببابل كان في وقت انتصاف الليل نفسه، فواجب أيضاً أن يكون كان بإسكندريّة قبل انتصاف الليل بنصف وثلث ساعة استوائيّة وفي تلك الساعة كان منزل ↑منزل↑: حاصل الشمس بالحقيقة على ثلاثة عشر جزءاً ونصف وربع بالتقريب من الحوت.
وأمّا الكسوف الثالث فكتب أنّه كان في هذه السنة الثانية لمردقباذ في اليوم الخامس عشر من شهر فامانوث من شهور المصريّين في الليلة التي يليها اليوم السادس عشر، وأنّ القمر ابتدأ ينكسف بعد طلوعه وانكسف منه من ناحية الشمال أكثر من نصفه، ولأنّ الشمس كانت في أوّل العذراء فإنّ مقدار الليل في ذلك الوقت ببابل إحدى عشرة ساعة بالتقريب من ساعات الاستواء، فيكون نصف الليل خمس ساعات ونصف. فكان إذن مبدأ الكسوف قبل انتصاف الليل بخمس ساعات *غايته* لأنّه ابتدأ بعد طلوعه وكان وسط زمانه قبل انتصاف الليل بثلاث ساعات ونصف من قبل أنّ زمان ما هذا مقداره من الأظلام يجب أن يكون كلّه ثلاث ساعات بالتقريب. فبإسكندريّة إذاً كان أيضاً وسط زمان هذا الكسوف قبل انتصاف الليل بأربع ساعات وثلث من ساعات الاستواء وفي تلك الساعة كان حاصل الشمس بالحقيقة على ثلاثة أجزاء وربع بالتقريب من العذراء.
فمن البيّن أنّ من وسط زمان الكسوف الأوّل إلى وسط زمان الكسوف الثاني قد تحرّكت الشمس، بل الشمس والقمر بعد الأدوار التامّة، ثلاث مائة وتسعة وأربعين جزءاً وخمس عشرة دقيقة، وتحرّكا من وسط زمان الكسوف الثاني إلى وسط زمان الكسوف الثالث مائة وتسعة وستّين جزءاً وثلاثين دقيقة. لكن المدّتين في هذين الزمانين اللذين في الوسط، أمّا المدّة منهما التّي بين الأوّل وبين الثاني فتحيط بثلاث مائة وأربعة وخمسين يوماً ومن الساعات الاستوائيّة أمّا إذا نظر في ذلك على الأمر المطلق فساعتين ونصف وأمّا إذا حسبت بحساب ه – خ: اختلاف الأيّام بلياليها المستوية فساعتين ونصف وجزء من خمسة عشر جزءاً من ساعة، وأمّا المدّة منهما التي بين الثاني وبين الثالث فتحيط بمائة وستّة وسبعين يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق أيضاً فعشرون ساعة ونصف وأمّا على الاستقصاء ↑الاستقصاء↑: الحقيقة فعشرون ساعة وخمس، والقمر يتحرّك على استواء. These words cannot be found in the English translation.
فإنّ هذا المقدار من الزمان لا يقع فيه اختلاف بشيء محسوس ولو كان أيضاً يقرب تقريباً ↑: تقر من دورانه الحقيقيّة أمّا في ثلاث مائة وأربعة وخمسين يوماً وساعتين ونصف وجزء من خمسة عشر جزءاً من ساعة استوائيّة، أمّا حركة الاختلاف بعد الأدوار التامّة فثلاث مائة وستّة أجزاء وخمس وعشرون دقيقة، وأمّا في الطول فثلاث مائة وخمسة وأربعون جزءاً وإحدى وخمسون دقيقة، وأمّا في مائة وستّة وسبعين يوماً وعشرين ساعة وخمس فيتحرّك أمّا حركة الاختلاف فمائة وخمسون جزءاً وستّ وعشرون دقيقة وأمّا في الطول فمائة وسبعون جزءاً وسبع دقائق بالتقريب.
فمن البيّن أنّ أجزاء المسافة الأولى من فلك التدوير وهي ثلاث مائة وستّة أجزاء وخمس وعشرون دقيقة زادت في حركة القمر الوسطى ثلاثة أجزاء وأربعاً وعشرين دقيقة، وأجزاء المسافة الثانية وهي مائة وخمسون جزءاً وستّ وعشرون دقيقة نقصت من حركته الوسطى سبعاً وثلاثين دقيقة.
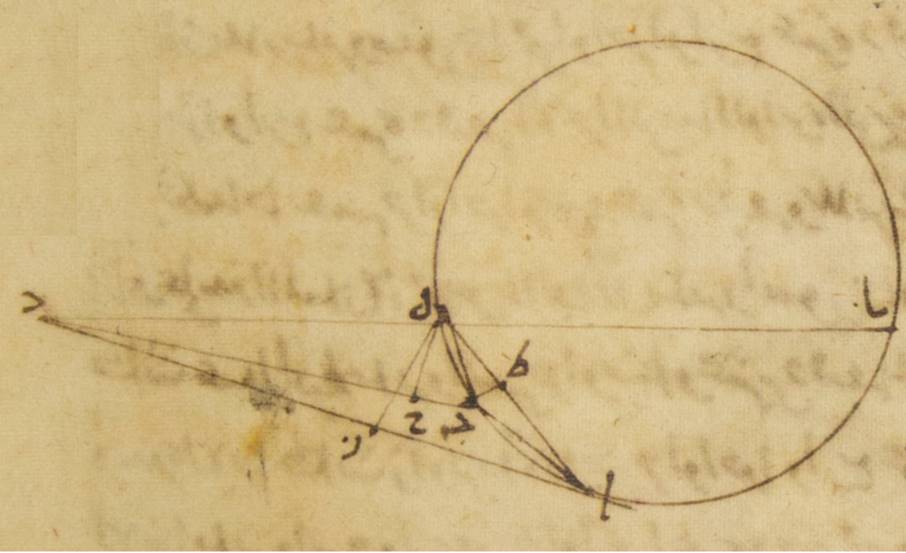
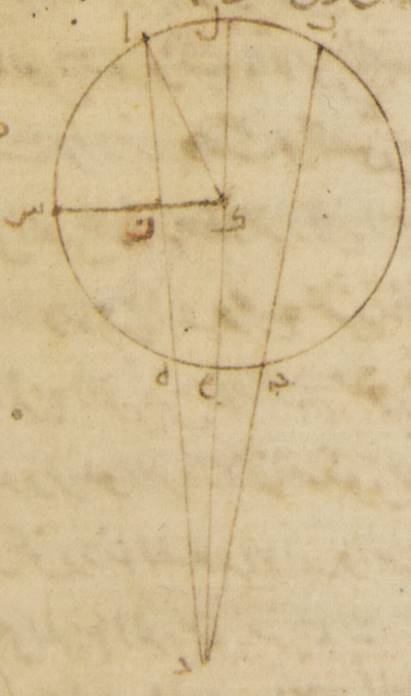
ج: فإذ قد وطّئت هذه الأشياء، فليكن فلك تدوير القمر ألف باء جيم ولننزّل أنّ نقطة ألف هي النقطة التي عليها كان القمر في وسط زمان الكسوف الأوّل، ونقطة باء النقطة التي عليها كان في وسط زمان الكسوف الثاني، ونقطة جيم النقطة التي عليها كان في وسط زمان الكسوف الثالث. ولنتوهّم نقلة القمر في فلك التدوير كأنّها يكون من نقطة باء إلى نقطة ألف ومن نقطة ألف إلى نقطة جيم حتّى تكون قوس ألف جيم باء، ه – خ: هي التي زاد فتحرّكها من الكسوف الأوّل إلى الكسوف الثاني، وهي ثلاث مائة وستّة أجزاء وخمس وعشرون دقيقة يزيد على حركته الوسطى ثلاثة أجزاء وأربعاء وعشرين دقيقة، وتكون قوس باء ألف جيم، ه – خ: هي التي تحرّكها من الكسوف الثاني إلى الكسوف الثالث وهي مائة وخمسون جزءاً وستّ وعشرون دقيقة، تنقص من حركته الوسطى سبعاً وثلاثين دقيقة. ومن قبل ذلك فإنّ المسير من نقطة باء إلى نقطة ألف إذ هو ثلاثة وخمسون جزءاً وخمس وثلاثون دقيقة، ينقص عن الحركة الوسطى هذه الأجزاء بأعيانها وهي ثلاثة أجزاء وأربع وعشرون دقيقة، والمسير من نقطة ألف إلى نقطة جيم إذ هو ستّة وتسعون جزءاً وإحدى وخمسون دقيقة فإنّه يزيد على الحركة الوسطى جزأين وسبعاً وأربعين دقيقة.
ومن البيّن أنّه ليس يمكن أن يكون أقرب البعد في فلك التدوير على قوس باء ألف جيم، إذ كانت هذه القوس هي قوس نقصان وكانت أقلّ من نصف دائرة وكنّا قد وضعنا أنّ أعظم الحركة أنّما يكون في البعد الأقرب. فإذ كان البعد الأقرب لا محالة على قوس جيم هاء باء فليؤخذ مركز فلك البروج والفلك المدير لمركز فلك التدوير ولتكن نقطة دال ولنوصل بينه وبين نقط الكسوفات الثلاثة بخطوط مستقيمة وهي دال ألف، دال هاء باء، دال جيم. وبالجملة كيما يكون نقلنا هذا المعنى إلى ما يشبهه من تبيين ما نحن بسبيله سهلاً متطابقاً كان تبييننا له بطريق الأصل الذي يوضع فيه فلك تدوير كمثل ما هو عليه الآن، أو كان بطريق الفلك الخارج المركز حتّى يكون مركزه ↑: خ الذي هو نقطة دال حينئذ أنّما يؤخذ داخلاً.
فلنخرج أحد هذه الثلاثة الخطوط التي توصل على الاستقامة وهو الذي من نقطة الكسوف الثاني إلى أن تلقى القوس التي بإزائها كما نجد عياناً هاهنا خطّ دال هاء باء قد أخرج إلى نقطة هاء من نقطة باء التي هي نقطة الكسوف الثاني ولنوصل بين النقطتين الباقيتين اللتين للكسوفين بخطّ مستقيم كما نوصل هاهنا خطّ ألف جيم. ولنوصل بين الفصل الذي حدث عن الخطّ الذي أخرج على الاستقامة كنقطة هاء وبين النقطتين الباقيتين بخطّين مستقيمين كما يوصل هاهنا خطّ هاء ألف وخطّ هاء جيم، وليخرج من ذلك الفصل عمودان على الخطّين ه: اللذين وصلا بين النقطتين الباقيتين وبين مركز فلك البروج كما نخرج هاهنا أمّا على خطّ ألف دال فعمود هاء زاي، وأمّا على خطّ جيم دال فعمود هاء حاء. ولنخرج أيضاً من إحدى النقطتين اللتين ذكرناهما كما نخرج هاهنا من نقطة جيم عمود على الخطّ الذي وصل بين النقطة الأخرى منهما كنقطة ألف وبين الفصل الزائد الذي حدث عن الخطّ المخرج على الاستقامة كنقطة هاء كما نخرج هاهنا على خطّ ألف هاء عمود جيم طاء. فإنّا من حيث ما أخذنا في استعمالنا هذا التدبير في الصورة وجدنا النسب التي تلزم فيها بالأعداد التي بها تبيّن واحدة بعينها. وإنّما يبقى اختيار المأخذ فقط بحسب ما يصلح ↑: يسهل في موضع موضع.
فلأنّ قوس باء ألف قد تبيّن أنّها توتّر من فلك البروج ثلاثة أجزاء وأربعاً وعشرين دقيقة ه – صح: تكون زاوية باء دال ألف أيضاً إذ هي عند مركزه أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فثلاثة أجزاء وأربع وعشرون دقيقة وأمّا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فستّة أجزاء وثمان وأربعون دقيقة. فيجب من ذلك أن تكون القوس أيضاً التي على خطّ هاء زاي ستّة أجزاء وثمانياً وأربعين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء زاي القائم الزاوية ثلاث مائة وستّون جزءاً. ويكون خطّ هاء زاي نفسه سبعة أجزاء وسبع دقائق بالأجزاء ه: التي بها دال هاء الموتّر مائة وعشرون جزءاً.
وعلى هذا المثال من قبل أنّ قوس باء ألف ثلاثة وخمسون جزءاً وخمس وثلاثون دقيقة تكون زاوية باء هاء ألف أيضاً إذ كانت عند المحيط ثلاثة وخمسين جزءاً وخمساً وثلاثين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً وبهذه الأجزاء كانت زاوية باء دال ألف ستّة أجزاء وثمانياً وأربعين دقيقة، فزاوية هاء ألف دال Greek, p. 308; Toomer, p. 195: EAZ إذن الباقية بهذه الأجزاء ستّ وأربعون جزءاً وسبع وأربعون دقيقة. فيجب من ذلك أن يكون أيضاً القوس التي على خطّ هاء زاي ستّة وأربعين جزءاً وسبعاً وأربعين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف هاء زاي القائم الزاوية ثلاث مائة وستّون جزءاً وخطّ هاء زاي نفسه سبعة وأربعون جزءاً وثمان وثلاثون دقيقة وثلاثون ثانية بالأجزاء التي بها هاء ألف الموتّر مائة وعشرون جزءاً. فالأجزاء إذن التي بها خطّ هاء زاي سبعة أجزاء وسبع دقائق وخطّ دال هاء على ما بيّنّا مائة وعشرون جزءاً يكون بها خطّ هاء ألف سبعة عشر جزءاً وخمساً وخمسين دقيقة واثنتين وثلاثين ثانية. وأيضاً لأنّ قوس باء ألف جيم توتّر من فلك البروج سبعاً وثلاثين دقيقة، تكون زاوية باء دال جيم أيضاً إذ هي عند مركزه أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فسبعاً وثلاثين دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فجزءاً واحداً وأربع عشرة دقيقة. فيجب من ذلك أن تكون القوس أيضاً التي على خطّ هاء حاء جزءاً واحداً وأربع عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء حاء القائم الزاوية ثلاث مائة وستّون جزءاً، وخطّ هاء حاء نفسه جزءاً واحداً وسبع عشرة دقيقة وثلاثين ثانية بالأجزاء التي بها خطّ دال هاء الموتّر مائة وعشرون جزءاً. وعلى هذا المثال لأنّ قوس باء ألف دال ↑دال↑: ج مائة وخمسون جزءاً وستّ وعشرون دقيقة تكون زاوية باء هاء جيم أيضاً إذ كانت عند المحيط مائة وخمسين جزءاً وستّاً وعشرين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، وبهذه الأجزاء كانت زاوية باء دال جيم جزءاً واحداً وأربع عشرة دقيقة فزاوية هاء جيم دال إذن الباقية بهذه الأجزاء مائة وتسعة وأربعون جزءاً واثنتا عشرة دقيقة. فيجب من ذلك أن يكون أيضاً القوس التي على خطّ هاء حاء مائة وتسعة وأربعين جزءاً واثنتي عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء حاء القائم الزاوية ثلاث مائة وستّون جزءاً، ويكون خطّ هاء حاء نفسه مائة وخمسة عشر جزءاً وإحدى وأربعين دقيقة وتسعاً وعشرين ثانية ه: في نقل حجّاج وأربعاً وعشرين ثانية Greek, p. 309: ριε μα κα; Toomer, p. 195: 115; 41, 21. بالأجزاء التي بها جيم هاء الموتّر مائة وعشرون جزءاً. فالأجزاء إذن التي بها خطّ هاء حاء جزءاً واحداً وسبع عشرة دقيقة وثلاثون ثانية وخطّ دال هاء على ما تبيّن مائة وعشرون جزءاً يكون بها خطّ جيم هاء جزءاً واحداً وعشرين دقيقة وثلاثاً وعشرين ثانية. وقد تبيّن أنّ خطّ هاء ألف بهذه الأجزاء سبعة عشر جزءاً وخمس وخمسون دقيقة واثنتان وثلاثون ثانية. وأيضاً من أجل أنّ قوس ألف جيم قد تبيّن أنّها ستّة وتسعون جزءاً وإحدى وخمسون دقيقة، تكون زاوية ألف هاء جيم أيضاً إذ هي عند المحيط ستّة وتسعين جزءاً وإحدى وخمسين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً. فيجب من ذلك أن تكون أيضاً القوس التي على خطّ جيم طاء ستّة وتسعين جزءاً وإحدى وخمسين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء القائم الزاوية ثلاث مائة وستّون جزءاً، والقوس التي على خطّ هاء طاء الأجزاء الباقية لنصف الدائرة وهي ثلاثة وثمانون جزءاً وتسع دقائق. فيكون إذن الخطّان اللذان يوتّرانهما أمّا خطّ جيم طاء منهما فتسعة وثمانون جزءاً وستّ وأربعون دقيقة وأربع عشرة ثانية بالأجزاء التي بها خطّ جيم هاء الموتّر مائة وعشرون جزءاً، وأمّا خطّ هاء طاء فبهذه الأجزاء تسعة وسبعون جزءاً وسبع وثلاثون دقيقة وخمس وخمسون ثانية فالأجزاء إذن التي بها خطّ جيم هاء جزء واحد وعشرون دقيقة وثلاث وعشرون ثانية. فيكون بها أمّا خطّ جيم طاء فجزء واحد وثمان ثواني، وأمّا خطّ هاء طاء فعلى هذا المثال ثلاث وخمسون دقيقة وإحدى وعشرون ثانية. وبهذه الأجزاء كان خطّ هاء ألف بأسره سبعة عشر جزءاً وخمس وخمسون دقيقة واثنتين وثلاثين ثانية. فخطّ طاء ألف إذن الباقي سبعة عشر جزءاً ودقيقتان وإحدى عشرة ثانية بالأجزاء التي تبيّن أنّ خطّ جيم طاء بها جزء واحد وثمان ثواني، والمربّع الذي يكون من خطّ ألف طاء مئتان وتسعون جزءاً وأربع عشرة دقيقة وتسع عشرة ثانية، والذي يكون من خطّ جيم طاء على ذلك المثال جزء واحد وسبع عشرة ثانية. فإذا جمعا كان منهما المربّع الذي يكون من خطّ ألف جيم مائتي جزء وأحد وتسعون جزءاً وأربع عشرة دقيقة وستّ وثلاثون ثانية. فخطّ ألف جيم إذن في الطول سبعة عشر جزءاً وثلاث دقائق وسبع وخمسون ثانية بالأجزاء التي بها خطّ دال هاء الموتّر مائة وعشرون جزءاً وخطّ جيم هاء جزء واحد وعشرون دقيقة وثلاث وعشرون ثانية. والأجزاء التي بها قطر فلك التدوير مائة وعشرون جزءاً، فإنّ خطّ ألف جيم بها تسعة وثمانون جزءاً وستّ وأربعون دقيقة وأربع عشرة ثانية وذلك أنّه يوتّر قوس ألف جيم وهي ستّة وتسعون جزءاً و إحدى وخمسون دقيقة. فالأجزاء إذاً التي بها خطّ ألف جيم تسعة وثمانون جزءاً وستّ وأربعون دقيقة وأربع عشرة ثانية وقطر فلك التدوير مائة وعشرون جزءاً يكون بها خطّ دال هاء ه: أيضاً ستّ مائة وأحداً وثلاثين جزءاً وثلاث عشرة دقيقة وثمانياً وأربعين ثانية ويكون خطّ جيم هاء بهذه الأجزاء سبعة أجزاء ودقيقتين وخمسين ه: في نقل الحجّاج وثمان ثواني ثانية. فيجب من ذلك أن تكون القوس أيضاً التي عليه وهي قوس جيم هاء ستّة أجزاء وأربعاً وثلاثين ه: وأربعين دقيقة وثلاثين ثانية Greek, p. 310: σ μδ α; Toomer p. 196: 6;44,1. بالأجزاء التي بها فلك التدوير ثلاث مائة وستّون جزءاً. وبهذه الأصول وضعت قوس باء ألف جيم مائة وخمسين جزءاً وستّاً وعشرين دقيقة. فقوس باء جيم هاء إذن بأسرها مائة وسبعة وخمسون جزءاً وإحدى عشرة دقيقة، Greek, p. 310: ρνζ ι α; Toomer p. 196: 157;10,1. ووترها وهو خطّ باء هاء مائة وسبعة عشر جزءاً وسبع وثلاثون دقيقة واثنتان وثلاثون ثانية بالأجزاء التي بها أمّا قطر فلك التدوير فمائة وعشرون جزءاً وأمّا خطّ هاء دال فستّ مائة وأحد وثلاثون جزءاً وثلاث عشرة دقيقة وثمان وأربعون ثانية.
فلو كان خطّ باء هاء قد وجد مساوياً لقطر فلك التدوير، فمن البيّن أنّ مركزه كان عليه واقعاً وكان يظهر من قبل ذلك النسبة بين القطرين. لكن لمّا كان أقصر منه وكانت قوس باء جيم هاء أصغر من نصف دائرة فمن البيّن أنّ مركز فلك التدوير سيقع خارج قطعة باء ألف جيم هاء.
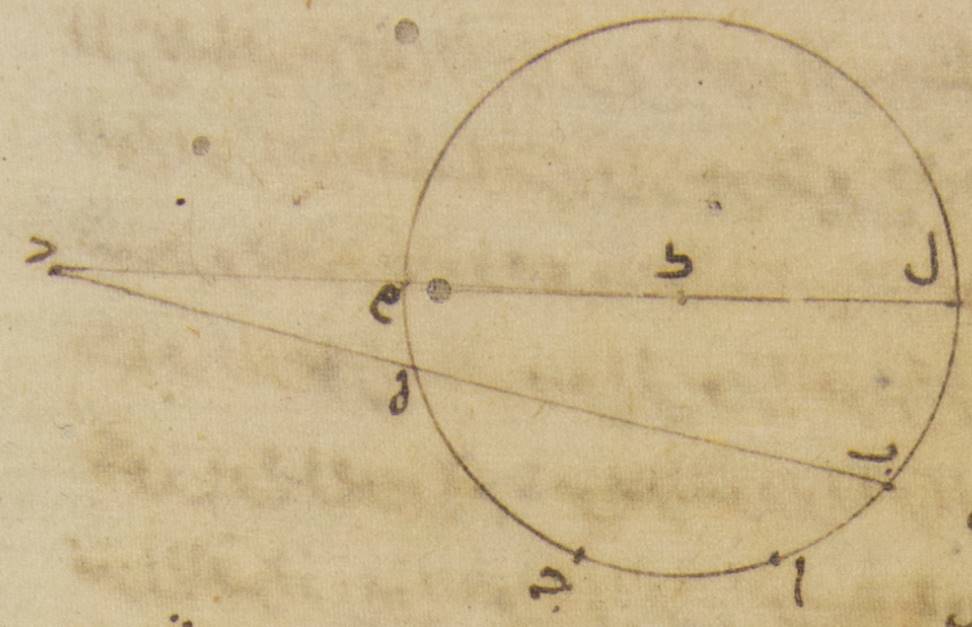
د: فلننزّل أنّه نقطة كاف ولنخرج من نقطة دال وهي مركز فلك البروج خطّ يمرّ بنقطة كاف وهو خطّ لام كاف ميم دال حتّى يكون لام أبعد البعد في فلك التدوير ونقطة ميم أقرب البعد. فمن قبل أنّ السطح القائم الزوايا الذي يحيط به خطّا باء دال، دال هاء مساو للسطح القائم الزوايا الذي يحيط به خطّ ألف دال، Toomer, p. 196: LD دال ميم، وقد بيّنّا أنّ الأجزاء التي بها قطر فلك التدوير أعني خطّ لام كاف ميم مائة وعشرون جزءاً، فإنّ خطّ باء هاء بها مائة وسبعة عشر جزءاً وسبع وثلاثون دقيقة واثنتان وثلاثون ثانية، وخطّ هاء دال بها ستّ مائة وأحد وثلاثون جزءاً وثلاث عشرة دقيقة وثمان وأربعون ثانية. ومن البيّن أنّ خطّ باء دال بأسره سبع مائة وثمانية وأربعون جزءاً وإحدى وخمسون دقيقة وعشرون ثانية، يكون إذن السطح القائم الزوايا الذي يحيط به خطّا باء دال، دال هاء أعني الذي يحيط به خطّا لام دال، دال ميم بهذه الأجزاء أربع مائة ألف واثنين وسبعين ألفاً وسبع مائة جزء وخمس دقائق واثنتين وثلاثين ثانية. وأيضاً لأنّ الخطّ الذي يحيط به خطّا لام دال، دال ميم مع المربّع الذي يكون من خطّ كاف ميم يكون منه المربّع الذي يكون من خطّ دال كاف، وخطّ كاف ميم إذ كان من مركز فلك التدوير فهو بهذه الأجزاء ستّون جزءاً، فإن نحن زدنا ثلاثة آلاف وستّ مائة جزء وهو مبلغ المربّع الذي يكون منه على الأجزاء التي ذكرناها وهي أربع مائة ألف واثنان وسبعون ألفاً وسبع مائة جزء وخمس دقائق واثنتان وثلاثون ثانية حصل لنا المربّع الذي يكون من خطّ دال كاف بهذه الأجزاء أربع مائة ألف وستّة وسبعين ألفاً وثلاث مائة جزء وخمس دقائق واثنتين وثلاثين ثانية. فيكون إذن خطّ دال كاف في الطول، وهو من مركز فلك ه – خ: الذي هو نصف قطر الفلك المدير لفلك التدوير الموافق مركزه لمركز فلك البروج، ستّ مائة وتسعين جزءاً وثمان دقائق واثنتين وأربعين ثانية بالأجزاء التي بها خطّ كاف ميم، وهو من مركز فلك التدوير، ه – صح: إلى محيطه ستّون جزءاً. فيجب من ذلك أن تكون ه – خ: إذا كانت الأجزاء التي بها الخطّ الذي من مركز الفلك المدير لفلك التدوير الموافق مركزه للناظر ه – صح: لمركز فلك البروج إلى محيطه ستّون جزءاً فإنّ ↑فإنّ↑: إن يكون الخطّ الذي من مركز فلك التدوير ↑: إلى محيطه بها خمسة أجزاء وثلاث عشرة دقيقة بالتقريب.
ه: فلنخرج في مثل هذه الصورة من مركز كاف عمود كاف نون سين على خطّ باء هاء ولنوصل خطّ باء كاف. فمن قبل أنّ الأجزاء التي بها خطّ دال كاف قد تبيّن أنّه ستّ مائة وتسعون جزءاً وثمان دقائق واثنتان وأربعون ثانية بها كان خطّ دال هاء ستّ مائة وأحداً وثلاثين جزءاً وثلاث عشرة دقيقة وثمانياً وأربعين ثانية (وخطّ نون هاء إذ هو نصف خطّ باء هاء بهذه الأجزاء ثمانية وخمسين جزءاً وثمانياً وأربعين) (دقيقة وستّاً وأربعين ثانية) وخطّ نون هاء إذ هو نصف خطّ باء هاء بهذه الأجزاء ثمانية وخمسين جزءاً وثمانياً وأربعين دقيقة وستّاً وأربعين ثانية حتّى يصير خطّ دال هاء نون بأسره بهذه الأجزاء ستّ مائة وتسعين جزءاً ودقيقتين وأربعاً وثلاثين ثانية. تكون إذاً الأجزاء التي بها خطّ دال كاف الموتّر مائة وعشرون جزءاً وإن ه: بها خطّ دال نون [*بها*] مائة وتسعة عشر جزءاً وثمان وخمسون دقيقة وسبع وخمسون ثانية والقوس التي عليه مائة وثمانية وسبعون جزءاً ودقيقتان بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال كاف نون القائم الزاوية ثلاث مائة وستّون جزءاً. فيجب من ذلك أن يكون أيضاً زاوية دال كاف نون أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فمائة وثمانية وسبعون جزءاً ودقيقتان، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فتسعة وثمانون جزءاً ودقيقة واحدة.
فقوس سين ميم إذن من فلك التدوير تسعة وثمانون جزءاً ودقيقة واحدة، وقوس لام باء سين الأجزاء الباقية لنصف الدائرة وهي تسعون جزءاً وتسع وخمسون دقيقة، وبهذه الأجزاء قوس باء سين إذ كان نصف قوس باء سين هاء ثمانية وسبعون جزءاً وخمس وثلاثون دقيقة ه – ج: وثلاثون ثانية وذلك أنّه قد بيّن أنّ قوس باء هاء مائة وسبعة وخمسون جزءاً وعشر دقائق ه: وإحدى عشر دقيقة بالتقريب. فقوس باء لام إذن الباقية من فلك التدوير وهي القوس التي هي كانت بعد القمر من أبعد البعد في وسط زمان الكسوف الثاني الذي ذكرناه اثنا عشر جزءاً وأربع وعشرون دقيقة.
وعلى هذا المثال لأنّ زاوية دال كاف نون قد تبيّن أنّها تسعة وثمانون جزءاً ودقيقة واحدة بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً تكون زاوية كاف دال نون الباقية وهي التي توتّر القوس التي تنقص من المسير الوسط في الطول بسبب الاختلاف الذي يكون من قبل قوس لام باء من فلك التدوير الأجزاء الباقية من قائمة واحدة وهي تسع وخمسون دقيقة. فكان منزل القمر إذن من الطول على الحركة الوسطى في وسط زمان الكسوف الثاني على أربعة عشر جزءاً وأربع وأربعين دقيقة من العذراء إذ كان حاصله على الصحّة ↑الصحّة↑: الحقيقة كان على ثلاثة عشر جزءاً وخمس وأربعين دقيقة منها وهي مبلغ الأجزاء التي كان أيضاً حاصل الشمس عليها من الحوت. ه – ط: وحده لثلثة كسوفات أخر
وأيضاً فإنّ الثلاثة الكسوفات التي أخذناها من الكسوفات التي رصدناها بغاية الاحتياط بإسكندريّة أمّا الأوّل منها فكان في السنة السابعة عشرة من سنيّ أذريانوس في الشهر المسمّى باوني عند المصريّين من تلك السنة في اليوم العشرين منه في الليلة التي يتلوها اليوم الحادي والعشرون منه. وحسبنا وسط زمان هذا الكسوف باستقصاء فوجدناه كان قبل انتصاف الليل بنصف وربع ساعة استوائيّة وانكسف كلّه وفي تلك الساعة كان حاصل الشمس بالحقيقة على ثلاثة عشر جزءاً وربع بالتقريب من الثور. وأمّا الكسوف الثاني منها فكان في السنة التاسعة عشرة من سنيّ أدريانوس في الشهر المسمّى خواق من شهور المصريّين منها في اليوم الثاني منه في الليلة التي يتلوها اليوم الثالث. وحسبنا وسط زمانه فوجدناه كان قبل انتصاف الليل ساعة استوائيّة وانكسف من ناحية الشمال نصف وثلث قطره وفي تلك الساعة كان حاصل الشمس بالحقيقة على خمس وعشرين جزءاً وسدس بالتقريب من الميزان. وأمّا الكسوف الثالث فإنّه كان في سنة عشرين من سنيّ أذريانوس في الشهر المسمّى عند المصريّين فرموثي منها في اليوم التاسع عشر منه في الليلة التي يتلوها اليوم العشرون. وحسبنا وسط زمانه فوجدناه كان بعد انتصاف الليل بأربع ساعات استوائيّة وانكسف نصف قطره من ناحية الشمال وكان حاصل الشمس في هذه الساعة أيضاً على أربعة عشرة جزءاً وخمس دقائق بالتقريب من الحوت.
فمن البيّن أنّ الأجزاء التي تحرّكها القمر هاهنا أيضاً بعد الدوائر التامّة من وسط زمان الكسوف الأوّل إلى وسط زمان الكسوف الثاني وهي الأجزاء التي تحرّكتها الشمس أيضاً مائة وأحد وستّون جزءاً وخمس وخمسون دقيقة، ومن وسط زمان الكسوف الثاني إلى وسط زمان الكسوف الثالث مائة وثمانية وثلاثون جزءاً وخمس وخمسون دقيقة. لكن زمان المدّة التي بين الكسوف الأوّل وبين الكسوف الثاني سنة واحدة مصريّة ومائة وستّة وستّون يوماً ومن قبل الساعات الاستوائيّة أمّا على الإطلاق فثلاثة وعشرون ساعة ونصف وربع ساعة وأمّا على الاستقصاء ↑الاستقصاء↑: الحقيقة فثلاث وعشرون ساعة ونصف وثمن ساعة. وزمان المدّة التي بين الكسوف الثاني وبين الكسوف الثالث سنة واحدة أيضاً مصريّة ومائة وسبعة وثلاثون يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق فخمس ساعات وأمّا على الاستقصاء ↑الاستقصاء↑: الحقيقة فخمس ساعات ونصف. وأيضاً فإنّ القمر يتحرّك على التوسّط بعد الأدوار التامّة أمّا في سنة واحدة ومائة وستّة وستّين يوماً وثلث وعشرين ساعة استوائيّة ونصف وثمن ساعة أمّا من حركة الاختلاف فمائة وعشرة أجزاء وإحدى وعشرون دقيقة، وأمّا من الحركة في الطول فمائة وتسعة وستّون جزءاً وسبع وثلاثون دقيقة بالتقريب، ويتحرّك في سنة واحدة ومائة وسبعة وثلاثين يوماً وخمس ساعات ونصف من ساعات الاستواء أمّا من حركة الاختلاف فأحد وثمانون جزءاً وثلاثون دقيقة Greek, p. 316: πα λς; Toomer, p. 199: 81;36. وأمّا من الحركة في الطول فمائة وسبعة وثلاثون جزءاً وأربع وثلاثون دقيقة بالتقريب.
فمن البيّن أنّ أجزاء المسافة الأولى من فلك التدوير وهي مائة وعشرة أجزاء وإحدى وعشرون دقيقة فقد نقصت من المسير الوسط في الطول سبعة أجزاء واثنتين وأربعين دقيقة وأجزاء المسافة الثانية وهي أحد وثمانون جزءاً وستّ وثلاثون دقيقة قد زادت في المسير الوسط في الطول جزءاً واحداً وإحدى وعشرين دقيقة.
وإذ قد وطّأنا هذه الأشياء فليكن أيضاً فلك التدوير للقمر ألف باء جيم، ولننزّل أنّ نقطة ألف هي النقطة التي عليها كان القمر في وسط زمان الكسوف الأوّل ونقطة، باء نقطة الكسوف الثاني، ونقطة جيم نقطة الكسوف الثالث. ولنتوهّم على ذلك المثال نقلة القمر تكون كأنّها من نقطة ألف إلى نقطة باء ثمّ إلى نقطة جيم حتّى تكون قوس ألف باء إذ هي مائة وعشرة أجزاء وإحدى وعشرون دقيقة تنقص كما قلنا من المسير الوسط في الطول سبعة أجزاء واثنتين وأربعين دقيقة، وتكون قوس باء جيم إذ هي أحد وثمانون جزءاً وستّ وثلاثون دقيقة يزيد في الطول جزءاً واحداً وإحدى وعشرين دقيقة؛ وتكون قوس جيم ألف الباقية إذ هي مائة وثمانية وستّون جزءاً وثلاث دقائق يزيد في الطول الأجزاء الباقية وهي ستّة أجزاء وإحدى وعشرون دقيقة.
فمن البيّن أنّه يجب أن يكون أبعد البعد على قوس ألف باء من قبل أنّه ليس يمكن ه: أن يكون لا على قوس باء جيم ولا على قوس جيم ألف إذ كانت كلّ واحدة منهما قوس زيادة وأقلّ من نصف دائرة. وليؤخذ على أنّ هذا يوضع It should be الوضع. هكذا مركز فلك البروج والفلك الذي عليه يتحرّك فلك التدوير، وليكن نقطة دال، ولنوصل بينه وبين نقط الكسوفات الثلاثة بخطوط دال هاء ألف، دال باء، دال جيم، ولنوصل خطّ باء جيم ولنخرج من نقطة هاء إلى نقطتي باء، جيم خطّا هاء باء، هاء جيم وعلى خطّي باء دال، جيم دال عمودا هاء زاي، هاء حاء ولنخرج أيضاً من نقطة جيم على خطّ باء هاء عمود جيم طاء.
فلأنّ قوس ألف باء توتّر من فلك البروج سبعة أجزاء واثنتين وأربعين دقيقة، تكون زاوية ألف دال باء أيضاً إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فسبعة أجزاء واثنتان وأربعون دقيقة، وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فخمسة عشر جزءاً وأربع وعشرون دقيقة. فيجب من ذلك أن تكون القوس التي على خطّ هاء زاي خمسة عشر جزاءً وأربعاً وعشرين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء زاي القائم الزاوية ثلاث مائة وستّون جزءاً وخطّ هاء زاي نفسه ستّة عشر جزءاً وأربع دقائق واثنتان وأربعون ثانية بالأجزاء التي بها دال هاء الموتّر مائة وعشرين جزءاً.
وعلى هذا المثال من أجل أنّ قوس ألف باء مائة وعشرة أجزاء وإحدى وعشرون دقيقة تكون زاوية ألف هاء باء إذ هي عند المحيط مائة وعشرة أجزاء وإحدى وعشرين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً وبهذه الأجزاء كانت زاوية ألف دال باء خمسة عشر جزءاً وأربعاً وعشرين دقيقة. فتكون إذاً زاوية هاء باء دال الباقية بهذه الأجزاء أربعة وتسعين جزءاً وسبعاً وخمسين دقيقة. فيجب أن تكون القوس التي على خطّ هاء زاي أيضاً أربعة وتسعين جزءاً وسبعاً وخمسين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء هاء زاي القائم الزاوية ثلاث مائة وستّون جزءاً، وخطّ هاء زاي نفسه ثمانية وثمانون جزءاً وستّ وعشرون دقيقة وسبع عشرة ثانية بالأجزاء التي بها خطّ باء هاء الموتّر مائة وعشرون جزءاً.
فالأجزاء إذن التي بها خطّ هاء زاي ستّة عشر جزءاً وأربع دقائق واثنتان وأربعون ثانية، وخطّ دال هاء على ما تبيّن مائة وعشرون جزءاً حتّى يكون بها خطّ باء هاء أيضاً أحداً وعشرين جزءاً وثمانياً وأربعين دقيقة وتسعاً وخمسين ثانية. وأيضاً لأنّ قوس جيم هاء ألف قد تبيّن أنّها توتّر من فلك البروج ستّة أجزاء وإحدى وعشرين دقيقة تكون زاوية ألف دال جيم أيضاً إذ هي عند مركز فلك البروج أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فستّة أجزاء وإحدى وعشرون دقيقة وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فاثنا عشر جزءاً واثنتان وأربعون دقيقة. فيجب أن تكون القوس التي على خطّ هاء حاء اثنا عشر جزءاً واثنتين وأربعين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال هاء حاء القائم الزاوية ثلاث مائة وستّون جزءاً وخطّ هاء حاء نفسه ثلاثة عشر جزءاً وستّ عشرة دقيقة وتسع عشرة ثانية بالأجزاء التي بها خطّ دال هاء الموتّر مائة وعشرون جزءاً.
وعلى هذا المثال لأنّ قوس ألف باء جيم جميعاً تكون مائة وأحد وتسعون جزءاً وسبع وخمسون دقيقة، فإنّ زاوية ألف هاء جيم أيضاً تكون إذ هي عند المحيط مائة وأحد وتسعين جزءاً وسبعاً وخمسين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً. وبهذه الأجزاء كانت زاوية ألف دال جيم اثنى عشر جزءاً واثنتين وأربعين دقيقة، فزاوية هاء دال جيم الباقية إذن هي بهذه الأجزاء مائة وتسعة وسبعون جزءاً وخمس عشرة دقيقة. فيجب أن تكون القوس التي على خطّ هاء حاء أيضاً مائة وتسعة وسبعين جزءاً وخمس عشرة دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء حاء القائم الزاوية ثلاث مائة وستّون جزءاً، ويكون خطّ هاء حاء نفسه مائة وتسعة عشر جزءاً وتسعاً وخمسين دقيقة وخمسين ثانية بالأجزاء التي بها خطّ جيم هاء الموتّر مائة وعشرين جزءاً.
فالأجزاء إذاً التي بها خطّ هاء حاء ثلاثة عشر جزءاً وستّ عشرة دقيقة وتسع عشر ثانية وخطّ دال هاء على ما تبيّن مائة وعشرون جزءاً، يكون بها خطّ جيم هاء ثلاثة عشر جزءاً وستّ عشرة دقيقة وعشرين ثانية. وبهذه الأجزاء تبيّن أنّ خطّ باء هاء أحد وعشرون جزءاً وثمان وأربعون دقيقة وتسع وخمسون ثانية. وأيضاً لأنّ قوس باء جيم أحد وثمانون جزءاً وستّ وثلاثون دقيقة تكون زاوية باء هاء جيم أيضاً إذ هي عند المحيط أحداً وثمانين جزءاً وستّاً وثلاثين دقيقة بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً. فيجب أن تكون القوس التي على خطّ جيم طاء أحداً وثمانين جزءاً وستّاً وثلاثين دقيقة بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم هاء طاء ثلاث مائة وستّون جزءاً والقوس التي على خطّ هاء طاء الأجزاء التي ينبغي من نصف دائرة وهي ثمانية وتسعون جزءاً وأربع وعشرون دقيقة. فالخطّان إذاً اللذان يوتّرانهما أمّا خطّ جيم طاء منهما فيكون ثمانية وسبعين جزءاً وأربعاً وعشرين دقيقة وسبعاً وثلاثين ثانية بالأجزاء التي بها خطّ هاء جيم الموتّر مائة وعشرون جزءاً وأمّا هاء طاء فيكون بهذه الأجزاء تسعين جزءاً وخمسين دقيقة واثنتين وعشرين ثانية. فالأجزاء إذن التي بها خطّ جيم هاء ثلاثة عشر جزءاً وستّ عشرة دقيقة وعشرون ثانية يكون بها خطّ جيم طاء ثمانية أجزاء وأربعين دقيقة وعشرين ثانية وخطّ هاء طاء على هذا المثال اثنا ه: ينبغي أن يكون خطّ هاء طاء عشرة أجزاء ودقيقتين وتسعاً وأربعين ثانية وهكذا هو في نقل الحجّاج. عشر جزءاً وتسع وأربعون دقيقة. Greek, p. 319: ΕΘ = ι β μθ; Toomer, p. 201: 10;2,49. وبهذه الأجزاء كان خطّ هاء باء بأسره أحداً وعشرين جزءاً وثمانياً وأربعين دقيقة وتسعاً وخمسين ثانية. فخطّ طاء باء الباقي إذن يكون أحد عشر جزءاً وستّاً وأربعين دقيقة وعشر ثواني بالأجزاء التي بها كان خطّ جيم طاء ثمانية أجزاء وأربعين دقيقة وعشرين ثانية. والمربّع الذي يكون من خطّ طاء باء مائة وثمانية وثلاثون جزءاً وإحدى وثلاثون دقيقة وإحدى عشرة ثانية، والمربّع الذي يكون من خطّ جيم طاء بهذه الأجزاء خمسة وسبعون جزءاً واثنتا عشرة دقيقة وسبع وعشرون ثانية، وهذان إذا جمعا كان منهما المربّع الذي يكون من خطّ باء جيم مائتين وثلاثة عشر جزءاً وثلاثاً وأربعين دقيقة وثمانياً وثلاثين ثانية. فخطّ باء جيم إذن في الطول أربعة عشر جزءاً وسبع وثلاثون دقيقة وعشر ثواني بالأجزاء التي بها خطّ دال هاء مائة وعشرون جزءاً وخطّ جيم هاء على هذا المثال ثلاثة عشر جزءاً وستّ عشر دقيقة وعشر ثواني. Toomer, p. 201: GE=13;16,20 لكن الأجزاء التي بها قطر فلك التدوير مائة وعشرون جزءاً بها خطّ باء جيم ثمانية وسبعون جزءاً وأربع وعشرون دقيقة وسبع وثلاثون ثانية وذلك أنّه يوتّر قوس باء جيم وهي أحد وثمانون جزءاً وستّ وثلاثون دقيقة. فالأجزاء إذن التي بها خطّ باء جيم ثمانية وسبعون جزءاً وأربع وعشرون دقيقة وسبع وثلاثون ثانية وقطر فلك التدوير مائة وعشرون جزءاً يكون بها خطّ دال هاء ستّ مائة وثلاثة وأربعين جزءاً وستّاً وثلاثين دقيقة وتسعاً وثلاثين ثانية ويكون بها خطّ جيم هاء أحداً وسبعين جزءاً وإحدى عشرة دقيقة وأربع ثواني. فيجب أن تكون القوس التي عليه وهي قوس جيم هاء اثنتي وسبعين جزءاً وستّاً وأربعين دقيقة وعشر ثواني بالأجزاء التي بها فلك التدوير ثلاث مائة وستّون جزءاً. وبهذه الأجزاء وضعت قوس جيم هاء ألف مائة وثمانية وستّين جزءاً وثلاث دقائق. فقوس هاء ألف إذاً الباقية خمسة وتسعون جزءاً وستّ عشرة دقيقة وخمسون ثانية ووترها وهو خطّ هاء ألف ثمانية وثمانون جزءاً وأربعون دقيقة وسبع عشرة ثانية بالأجزاء التي بها أمّا قطر فلك التدوير فمائة وعشرون جزءاً وأمّا خطّ هاء دال فستّ مائة وثلاثة وأربعون جزءاً وستّ وثلاثون دقيقة وتسع وثلاثون ثانية.
وأيضاً لأنّه قد تبيّن أنّ قوس هاء ألف أقلّ من نصف دائرة، فمن البيّن أنّ مركز فلك التدوير يقع خارج قطعة هاء ألف. فليوجد ولتكن نقطة كاف ولنوصل خطّ دال ميم كاف لام حتّى يكون أيضاً نقطة لام أبعد البعد ونقطة ميم أقرب القرب. فمن قبل أنّ السطح القائم الزوايا الذي يحيط به خطّا ألف دال، دال هاء متساو للذي يحيط به خطّا لام دال دال ميم وقد تبيّن أنّ الأجزاء التي بها قطر فلك التدوير وهو لام كاف ميم مائة وعشرون جزءاً بها خطّ هاء ألف Greek, p. 321; Toomer, p. 201: AE ثمانية وثمانون جزءاً وأربعون دقيقة وسبع عشر ثانية، وخطّ هاء دال بها ستّ مائة وثلاثة وأربعون جزءاً وستّ وثلاثون دقيقة وتسع وثلاثون ثانية، ومن البيّن أنّ خطّ ألف دال بأسره سبع مائة واثنان وثلاثون جزءاً وستّ عشرة دقيقة وستّ وخمسون ثانية يكون السطح القائم الزوايا الذي يحيط به خطّا ألف دال، دال هاء أعني الذي يحيط به خطّا لام دال، دال ميم بهذه الأجزاء أربع مائة ألف وأحد وسبعون ألفاً وثلاث مائة وأربعة أجزاء وستّاً وأربعين دقيقة وسبع عشر ثانية.
وأيضاً لأنّ السطح القائم الزوايا الذي يحيط به خطّا لام دال، دال ميم مع المربّع الذي من خطّ كاف ميم يكون منه المربّع الذي من خطّ دال كاف، وخطّ كاف ميم إذ هو من مركز فلك التدوير هو بهذه الأجزاء ستّون جزءاً، فإن نحن زدنا الثلاثة آلاف والستّ مائة التي هي المربّع الذي يكون منه على الأربع مائة ألف والأحد والسبعين الألف والثلاث مائة والأربعة الأجزاء والستّ والأربعين الدقيقة والسبع العشرة الثانية التي حصل لنا المربّع الذي من خطّ دال كاف بهذه الأجزاء أربع مائة ألف وأربعة وسبعين ألفاً وتسع مائة وأربعة أجزاء وستّاً وأربعين دقيقة وسبع عشرة ثانية. فيكون إذن خطّ دال كاف وفي الطول وهو الذي من مركز الفلك المدير لفلك التدوير الذي مركزه مركز فلك البروج ستّ مائة وتسعة وثمانين جزءاً وثمان دقائق بالأجزاء التي بها الخطّ الذي من مركز فلك التدوير ه: إلى محيطه ستّون جزءاً. فالأجزاء إذن التي بها الخطّ الذي بين مركز فلك البروج وبين مركز فلك التدوير ستّون جزءاً يكون بها الخطّ الذي من مركز فلك التدوير ه: إلى محيطه خمسة أجزاء وأربع عشرة دقيقة بالتقريب. وهذه النسبة قريبة من النسبة التي تبيّنت قبيل بالكسوفات التي كانت قبلنا.
ح: فلنخرج أيضاً في هذه الصورة بعينها من مركز كاف عمود على خطّ ألف هاء Greek, p. 322: ΔEA; Toomer, p. 202: DEA وليكن كاف زاي سين Here and in the following text (until the end of propositon 8, ح), the Arabic has Z (ز) where the Greek has N. ولنوصل خطّ ألف كاف. فمن قبل أنّ الأجزاء التي تبيّن أنّ خطّ دال كاف ه: بها ستّ مائة وتسعة وثمانون جزءاً وثمان دقائق بها كان خطّ دال هاء أيضاً ستّ مائة وثلاثة وأربعين جزءاً وستّاً وثلاثين دقيقة وتسعاً وثلاثين ثانية، وخطّ زاي هاء إذ هو نصف خطّ ألف هاء بهذه الأجزاء أربعة وأربعين جزءاً وعشرين دقيقة وثمان ثواني حتّى يكون خطّ دال هاء زاي بأسره بهذه الأجزاء ستّ مائة وسبعة وثمانين جزءاً وستّاً وخمسين دقيقة وسبعاً وأربعين ثانية. تكون الأجزاء التي بها خطّ دال كاف الموتّر مائة وعشرون جزءاً يكون بها خطّ دال زاي مائة وتسعة عشر جزءاً وسبعاً وأربعين دقيقة وستّاً وثلاثين ثانية، وتكون القوس التي عليه مائة وثلاثة وسبعين جزءاً وسبع عشرة دقيقة بالتقريب بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال كاف زاي القائم الزاوية ثلاث مائة وستّون جزءاً. فيجب أن تكون زاوية زاي كاف دال Greek, p. 322: ΔKN; Toomer, p. 202: DKN أيضاً أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً فمائة وثلاثة وسبعون جزءاً وسبع عشرة دقيقة، وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً فستّة وثمانون جزءاً وثمان وثلاثون دقيقة ونصفاً Greek, p. 322: πς λη Lʼ; Toomer, p. 202: 86;38,30° فقوس ميم هاء سين إذن من فلك التدوير ستّة وثمانون جزءاً وثمان وثلاثون دقيقة ونصف، فقوس لام ألف سين ما يبقى من نصف دائرة وهي ثلاثة وتسعون جزءاً وإحدى وعشرون دقيقة ونصف، وبهذه الأجزاء قوس ألف سين إذ هي نصف قوس ألف هاء سبعة وأربعون جزءاً وثمان وثلاثون دقيقة ونصف بالتقريب فقوس ألف لام الباقية إذن خمسة وأربعون جزءاً وثلاث وأربعون دقيقة. وقد كانت وضعت قوس ألف باء بأسرها بهذه الأجزاء مائة وعشرة أجزاء وإحدى وعشرين دقيقة، فيجب أن تكون قوس لام باء الباقية وهي قوس بعد القمر (كان) عن أبعد البعد في هذا الزمان الوسط من الكسوف الثاني أربعة وستّين جزءاً وثمانياً وثلاثين دقيقة.
وعلى هذا المثال من قبل أنّ زاوية دال كاف زاي Greek, p. 323: ΔKN; Toomer, p. 203: DKN قد تبيّن أنّها ستّة وثمانون جزءاً وثمان وثلاثون دقيقة بالتقريب بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً، يكون زاوية كاف دال زاي Greek, p. 323: KΔN; Toomer, p. 203: KDN الباقية من زاوية قائمة وهي ثلاثة أجزاء واثنتان وعشرون دقيقة، وقد كانت وضعت زاوية ألف دال باء بأسرها بهذه الأجزاء سبعة أجزاء واثنتين وأربعين دقيقة، فزاوية لام دال باء الباقية وهي التي توتّر القوس التي تنقص من المسير الوسط في الطول من فلك البروج بسبب الاختلاف الذي يكون من قبل قوس لام باء من فلك التدوير تكون أربعة أجزاء وعشرين دقيقة. فكان إذن حاصل القمر في الطول على الحركة الوسطى في وسط زمان الكسوف الثاني على تسعة وعشرين جزءاً وثلاثين دقيقة من الحمل إذ كان حاصله على الصحّة ↑الصحّة↑: الحقيقة كان على خمسة وعشرين جزءاً وعشر دقائق وهي مثل الأجزاء التي كان أيضاً حاصل الشمس عليها من الميزان.
〈IV.7〉 ز: في تصحيح حركات حركات: مجازات القمر الوسطى في الطول وفي الاختلاف
فمن قبل أنّا قد بيّنّا أنّ في الكسوف الثاني من الثلاثة الكسوفات القديمة كان حاصل القمر في وسط زمان ذلك الكسوف على الاستواء أمّا من الطول فعلى أربعة عشر وأربع وأربعين دقيقة من العذراء، وأمّا من الاختلاف فعلى اثني عشر جزءاً وأربع وعشرين دقيقة من البعد الأبعد من فلك التدوير؛ وفي الكسوف الثاني من الكسوفات التي كانت في زماننا تبيّن على ذلك المثال أنّ حاصل القمر على حركة الوسطى كان أمّا من الطول فعلى تسعة وعشرين جزءاً وثلاثين دقيقة من الحمل وأمّا من الاختلاف فعلى أربعة وستّين جزءاً وثمان وثلاثين دقيقة من البعد الأبعد. فظاهر أنّ في الزمان الذي بين هذين الكسوفين ه – ط: الزمان الذي من الكسوف الثاني القديم إلى الكسوف الثاني الحديث قد زاد فقطع ه: قَطْعُ القمر بحركته الوسطى بعد الدوائر ↑: ذات التامّة أمّا من الطول فمائتين وأربعة وعشرين جزءاً وستّاً وأربعين دقيقة وأمّا من الاختلاف فاثنين وخمسين جزءاً وأربع عشرة دقيقة.
لكن الزمان الذي بين الوقت الذي قبل انتصاف الليل بنصف وثلث ساعة استوائيّة من الليلة التي يتلوها اليوم التاسع عشر من اليوم الثامن عشر من الشهر المسمّى توت من السنة الثانية من سنيّ مردقباد وبين الوقت الذي قبل انتصاف الليل بساعة الاستوائيّة من الليلة التي يتلوها اليوم الثالث من اليوم الثاني من الشهر المسمّى خواق من السنة التاسعة عشرة من سنيّ أدريانوس مبلغه ثمان مائة سنة وأربع وخمسون سنة ه: سنة 854 مصريّة وثلاثة وسبعون يوماً ومن الساعات الاستوائيّة أمّا على الاطلاق أيضاً فثلاث وعشرون ساعة ونصف وثلث وأمّا على الحقيقة وبحسب الأيّام بلياليها المستوية فثلاث وعشرون ساعة وثلث. ومبلغ أيّام هذا الزمان كلّه ثلاث مائة ألف ه: يوم وأحد عشر ألفاً وسبع مائة وثلاثة وثمانون يوماً وثلاث وعشرون ساعة وثلث من ساعات الاستواء. ونجد ما تلحق هذه الأيّام من الزيادة ↑: خ ات بعد الدوائر ↑: ورات التامّة من قبل الحركات التي تقدّمنا فوضعناها الأيّام بحسب الأصول التي وضعت قبل هذا التصحيح أمّا من الطول فمائتين وأربعة وعشرون جزءاً ↑جزءاً↑: يوماً وستّ وأربعون دقيقة وأمّا من الاختلاف فاثنان وخمسون جزءاً وإحدى وثلاثون دقيقة. فتكون الحصّة من الطول قد وجدت كما قلنا غير مخالفة للتي حصّلناها بالأرصاد التي وضعت وأمّا حصّة الاختلاف فوجدت بفضل سبع عشرة (ساعة) دقيقة. فذلك ه: فلذلك لمّا قصدنا لتصحيح المسير في اليوم فإنّا قبل وضع الجداول قسمنا هذه السبع العشرة الدقيقة على هذه العدّة التي ذكرت للأيّام ونقصنا ما يصيب كلّ يوم وهو إحدى عشرة رابعة وستّ وأربعون خامسة وتسع وثلاثون سادسة من حركة الاختلاف الوسطى لليوم الذي أخذت قبل هذا التصحيح فوجدنا الحركة المصحّحة ثلاثة عشر جزءاً وثلاث دقائق وثلاثاً وخمسين ثانية وستّاً وخمسين ثالثة وسبع عشرة رابعة ه: ![]() وإحدى وخمسين خامسة وتسعاً وخمسين سادسة، ولزمنا ذلك في سائر ما يجتمع من التركيب في الجداول.
وإحدى وخمسين خامسة وتسعاً وخمسين سادسة، ولزمنا ذلك في سائر ما يجتمع من التركيب في الجداول.
〈IV.8〉 ح: في حاصل حركات القمر المستوية ↑المستوية↑: الوسطى في الطول وفي الاختلاف
وكيما نقيّد حاصلها في تلك السنة الأولى من سنيّ بختنصر في الشهر المسمّى عند المصريّين توت في اليوم الأوّل منه في انتصاف النهار، فإنّا أخذنا الزمان الذي بين ذلك الوقت وبين وسط زمان الكسوف الثاني من الكسوفات الثلاثة الأوّل التي هي أقرب إلى ذلك الوقت ه – ط: الزمان الذي من مرقياد إلى بخت نصر . وقد قلنا إنّ ذلك الزمان الوسط كان في السنة الثانية من سنيّ مردقياد في شهر توث من شهور المصريّين منها في اليوم الثامن عشر منه في الليلة التي يتلوها اليوم التاسع عشر منه قبل انتصاف الليل بنصف وثلث ساعة استوائيّة. وجملة هذا الزمان سبع وعشرون سنة من سنيّ المصريّين وسبعة عشر يوماً ومن الساعات على الإطلاق وعلى التحقيق نحو من إحدى عشرة ساعة وسدس. وما يصيب هذا المقدار من الزمان من الزيادة بعد الدوائر التامّة أمّا من الطول فمائة وثلاثة وعشرون جزءاً واثنتان وعشرون دقيقة، وأمّا من الاختلاف فمائة وثلاثة أجزاء وخمس وثلاثون دقيقة. فإن نحن نقصنا هذين من الحاصلين اللذين في وسط زمان الكسوف الثاني كلّ واحد منهما من نظيره وجدنا حاصل القمر كان في السنة الأولى من سنيّ بختنصر في شهر توث من شهور المصريّين منها في اليوم الأوّل منه في انتصاف النهار على الحركة الوسطى أمّا في الطول فأحد عشر جزءاً واثنتان وعشرون دقيقة من الثور وأمّا من الاختلاف فمائتان وثمانية وستّون جزءاً وتسع وأربعون دقيقة ه – ![]() ط: أصل القمر الأوّل [↑: الوسط] يوم من السنة الأولى من ملك بخت نصر الأوّل يا كب درج دقائق من الثور. فأمّا في الاختلاف رصح جزءاً مط دقيقة. من البعد الأبعد من فلك التدوير، ومن البيّن أنّه يكون من البعد على سبعين جزءاً وسبع وثلاثين دقيقة من قبل أنّ الشمس في ذلك الزمان بعينه قد تبيّن أنّه كان حاصلها خمس وأربعون دقيقة من الحوت.
ط: أصل القمر الأوّل [↑: الوسط] يوم من السنة الأولى من ملك بخت نصر الأوّل يا كب درج دقائق من الثور. فأمّا في الاختلاف رصح جزءاً مط دقيقة. من البعد الأبعد من فلك التدوير، ومن البيّن أنّه يكون من البعد على سبعين جزءاً وسبع وثلاثين دقيقة من قبل أنّ الشمس في ذلك الزمان بعينه قد تبيّن أنّه كان حاصلها خمس وأربعون دقيقة من الحوت.
〈IV.9〉 ط: في تصحيح مجازات القمر في العرض وحاصلها
فبهذه الأبواب قيّدنا الحركات الدوريّة في الطول وفي الاختلاف وحواصلها. وأمّا الحركات في العرض فقد كان أوّلاً يقع لنا نحن أنفسنا فيها خطاء فضلاً عن غيرنا بأنّا ه – خ: فإنّا نستعمل في ذلك رأي أبرخس في أنّ القمر يقدر فلكه الخاصّ له ستّ مائة وخمسين مرّة بالتقريب ويقدر دائرة الظلّ مرّتين ونصفاً في البعد الوسط ه – خ: الأوسط في الاتّصالات. فإنّ ذلك إذا وضع كذلك ووضع أيضاً مقدار ميل فلك القمر المائل كانت حدود كسوفاته الجزئيّة معطاة. فكنّا إذا أخذنا مدداً بين كسوفات وحسبنا من قبل مقدار الأظلام الذي في وسط زمان الكسوف المجازات الصحيحة في العرض في الفلك المائل من The scribe wrote an extra alif (ا) which he then crossed out. العقدتين كانت وحصّلنا بالطريق الذي بيّنّاه للفضل ه – خ: الفضل الذي بحسب الاختلاف من المجازات الصحيحة المجازات الدوريّة كنّا بهذا الطريق نستخرج حاصل العرض الدوريّ في أوساط أزمان الكسوفات، والفضلة التي تحصل بعد الدوائر التامّة في الزمان الذي بين تلك الكسوفات.
وأمّا الآن فإنّا استعملنا أبواباً أعظم غنا من تلك فليس ه: ولسنا نحتاج معها في إدراك ما نطلب من ذلك إلى شيء من تلك الأصول التي وضعت من قبل فوجدنا بها المجاز في العرض الذي حسب بتلك الأصول قد لحقه الخطاء. ولمّا أرينا ه – خ: رأينا بهذا الطريق الذي استخرجناه الآن من غير حاجة إلى تلك الأصول أنّ تلك الأصول أنفسها التي اعتقدت في المقادير وفي الأبعاد ليست على ما ظنّ بها {غذنا(؟)} فأصلحناها بها. ومثل ذلك فعلنا في الأصول التي وضعت لزحل ولعطارد فإنّا أزلنا ه: فأمّا أدركنا ↑أزلنا↑: غيّرنا ما شيءاً منها لم يكن فيما مضى أدركت على غاية الاستقصاء وذلك أنّه تهيّأ فيها فيما بعد أن رصدت ↑أن رصدت↑: خ لمن رصد أرصاد أشدّ تحصيلاً لا يلحقها الشكّ. فإنّه قد يجب على من شرع في هذا العلم شروع مؤثّر للحقّ على الصحّة وسلك طريق البحث والتحصيل ألّا يقتصر على استعمال الأبواب التي يتجدّد ه: خ{...تجد} له المؤدّية إلى الأمر الذي لا شكّ فيه تصحيح ه – خ: في تصحيح الأصول القديمة فقط، بل يستعملها أيضاً في تصحيح ما يعتقده هو من الأصول إن كانت سبيلها تلك السبيل، وألّا يستقبح في جنب ما يتضمّنه هذا العلم إذ كان أمراً جليلاً إلهيّاً إلّا يصل ه – خ: {...يل} بنفسه وحده إلى الأمر الصواب فيه على الحقيقة بل يستعين على ذلك ه – خ: بذلك على بغيره. ه – خ: غيره ونحن واصفون الوجه الذي به تبيّن كلّ واحد من هذه الأشياء في موضعه من كتابنا هذا فيما يستأنف وأمّا في هذا الوقت فإنّا لازمون نسق كلامنا ومقبلون على تبيين المجاز في العرض.
والباب في ذلك هو ه: نحو هذا أمّا أوّلاً فإنّا عند ما قصدنا ه – خ: له لتصحيح المجاز الوسط نفسه جعلنا نطلب كسوفين قمريّين من الكسوفات التي اثبتت على غاية التحرير بينهما من الزمان أكثر ما نقدر عليه، وكان مقدار الأظلام فيهما متساويين وكانا يليان عقدة واحدة وكانا جميعاً أمّا من ناحية الشمال وأمّا من ناحية الجنوب، وكان أيضاً القمر بعده ه – خ: {...} كلّ واحد منهما بعداً واحداً. فإنّ هذه الأشياء إذا كانت كذلك فواجب ضرورة أن يكون مركز القمر بعده سواء في كلّ واحد من الكسوفين من العقدة الواحدة بعينها في جهة واحدة، ومن أجل ذلك تكون مجازة الصحيح يشتمل في العرض على دوائر تامّة في الزمان الذي بين الكسوفين.
فأخذنا كسوفاً أوّلاً كان رصد على عهد دارا ه – خ: داريوس الأوّل ببابل في سنة إحدى وثلاثين من سنيّة في الشهر من شهور المصريّين المسمّى طوبي منها في اليوم الثالث منه في الليلة التي يتلوها اليوم الرابع منه في انتصاف الساعة السادسة منها. وقيل في هذا السكوف أنّ القمر انكسف من ناحية الجنوب إصبعين.
وأخذنا كسوفاً ثانياً رُصد بإسكندريّة في السنة التاسعة من سنيّ أذريانوس في الشهر من شهور المصريّين المسميّ ماحور منها في اليوم السابع عشر منه في الليلة التي يتلوها اليوم الثامن عشر منه قبل انتصافها بثلاث ساعات وثلث وخمس Toomer, p. 206: 3+3/5 من ساعات الاستواء، وانكسف من القمر على ذلك المثال سدس قطره من ناحية الجنوب.
وكان مجاز القمر في العرض في كلّ واحد من الكسوفين عند عقدة الذنب، فإنّ هذا قد يستدرك أيضاً من قبل تلك الأصول التي هي غير مجرّدة ه – خ: محرّرة؛ ه – خ: محدودة فضلاً عن غيرها، وكان بعده فيهما جميعاً قريباً من السواء وأدنى قليلاً من الوسط من البعد الأقرب. فإنّ ذلك أيضاً قد تبيّن الأشياء التي تقدّم بيانها في الاختلاف. فإذ كان القمر إذا انكسف من ناحية الجنوب كان مركزه أميل إلى ه – خ: أو أسفل من الوسط {بقليل} إلى البعد الأقرب وذلك يتسعين لنا ممّا تقدّم بيانه في الاختلاف فلأنّ إذا {قدر} انكساف القمر من ناحية الجنوب {يكون} مركزه إلى ناحية الشمال من فلك البروج. فظاهر أنّ في كلّ واحد من هذين الكسوفين كان مركز القمر متقدّماً لعقدة الذنب بالسواء. لكن أمّا في الكسوف الأوّل فكان بعد القمر من البعد الأبعد من فلك التدوير مائة جزء وتسع عشرة دقيقة. وذلك أنّ وسط زمانه كان ببابل قبل انتصاف الليل بنصف ساعة وكان بإسكندريّة قبل انتصاف الليل ساعة وثلث من ساعات الاستواء، والزمان الذي من وقت حاصل القمر كان على عهد بخت نصر إلى ذلك الوقت يجتمع منه مائتا سنة وستّ وخمسون سنة ومائة يوم واثنان وعشرون يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق فعشر ساعات وثلثان وأمّا بحسب الأيّام المستويّة فعشر ساعات وربع. ولذلك كان المجاز الصحيح أقلّ من المجاز الدوريّ بخمسة أجزاء. وأمّا في الكسوف الثاني فكان بعد القمر من البعد الأبعد من فلك التدوير مائتي جزء وأحداً وخمسين جزءاً وثلاثاً وخمسين دقيقة. فإنّ هاهنا أيضاً الزمان الذي من وقت حاصل القمر إلى ه – خ: على ذلك العهد إلى وسط زمان الكسوف ه – خ: الثاني يجتمع منه ثمان مائة سنة وإحدى وسبعون سنة ومائتا يوم وستّة وخمسون يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق فثمان ساعات وخمساً ساعة وأمّا على الحقيقة فثمان ساعات وجزء من اثني عشر جزءاً من ساعة. ومن قبل ذلك كان أيضاً المجاز الصحيح أكثر من المجاز الوسط بأربعة أجزاء وثلاث وخمسين دقيقة. ففي الزمان إذن الذي بين هذين الكسوفين، ومبلغه ستّ مائة سنة وخمس عشرة سنة من سنيّ المصريّين، ومائة وثلاثة وثلاثون يوماً وإحدى وعشرون ساعة ونصف وثلث من ساعات الاستواء كان مجاز القمر على الاستقصاء ↑الاستقصاء↑: الحقيقة في العرض يحيط بدوائر تامّة، ومجازه الدوريّ ينقص عن دوائر تامّة بالأجزاء التي يجتمع من الاختلافين جميعاً وهو ه – خ: وهي تسعة أجزاء وثلاث وخمسون ودقيقة إلّا أنّه ينقص عن المجازات الوسطى التي تقدّمنا، فوضعناها بحسب أصول أبرخس في هذا المقدار من الزمان عن عودات تامّة عشرة أجزاء وقريباً من دقيقتين. فقد زاد إذن المجاز الوسط في العرض على ما يوجبه تلك الأصول تسع دقائق.
فلمّا قسمنا هذه الدقائق على عدّة الأيّام المجتمعة من الزمان المقصود له وهي مائتا ألف يوم وأربعة وعشرون ألف يوم وستّ مائة وتسعة أيّام بالتقريب وأخذنا ما يحصل من ذلك وهو ثمان روابع وتسع وثلاثون خامسة وثمان عشرة سادسة فزدناه على الحركة الوسطى في اليوم الذي تقدّم بيانها على تلك الأصول وجدنا الحركة المصحّحة لليوم ثلاثة عشر جزءاً وثلاث عشر دقيقة وخمساً وأربعين ثانية وتسعاً وثلاثين ثالثة وثمانياً وأربعين رابعة وستّاً وخمسين خامسة وسبعاً وثلاثين سادسة ولزمنا ذلك أيضاً في سائر ما وضعناه في الجداول ممّا يجتمع من التركيب.
فلمّا تبيّنت وحصلت بهذا الوجه الحركة الدوريّة في العرض جعلنا نطلب أيضاً بعد ذلك لنقيّد حاصلها مدّة بين كسوفين لم تقع في أمرهما شبهة كان سائر ما فيهما موافقاً لما وجد في ذينك الكسوفين أعني أنّ بعدي القمر فيهما كانا قريبين من السواء وكان مقدار الأظلام متساويتين فيهما وكانا جميعاً أمّا من ناحية الشمال وأمّا من ناحية الجنوب ما خلا أنّ العقدة لم يكن فيهما واحدة لكن كانت في هذا ضدّها في الآخر.
فأوّل هذين الكسوفين الكسوف الذي كنّا استعملناه في تبيين الاختلاف أيضاً وهو الذي كان في السنة الثانية من سنيّ مردقياد في الشهر من شهور المصريّين المسمّى توث منها في اليوم الثامن عشر منه في الليلة التي يتلوها اليوم التاسع عشر منه أمّا ببابل ففي انتصافها، وأمّا بإسكندريّة فقبل انتصافها بنصف وثلث ساعة استوائيّة؛ وهذا الكسوف قيل فيه أنّ القمر انكسف من ناحية الجنوب ثلاث أصابع.
والكسوف الثاني منهما هو الكسوف الذي استعمله أيضاً أبرخس وكان في سنة عشرين من سنيّ دارا ه – خ: دارينوس الذي كان بعد فميس ه – خ: فليش في الشهر من شهور المصريّين المسمّى إبيفي منها في اليوم الثامن والعشرين منه في الليلة التي يتلوها اليوم التاسع والعشرون بعد أن مضى من الليل ستّ ساعات وثلث من ساعات الاستواء. وكان ما انكسف من القمر فيه على ذلك المثال ه: في ذلك الوقت من ناحية الجنوب ربع قطره وكان وسط زمانه أمّا ببابل فقبل انتصاف الليل بخمسي ساعة ه – خ: واحدة استوائيّة وذلك أنّ نصف الليل كان في ذلك الوقت ستّ ساعات ونصف وربع بالتقريب من ساعات الاستواء، وأمّا بإسكندريّة فقبل انتصاف الليل بساعة وربع من ساعات الاستواء.
وكلّ واحد من هذين الكسوفين كان والقمر في غاية بعده ه – خ: بعده الأبعد لكن الأوّل منهما كان عند عقدة الرأس والثاني كان عند عقدة الذنب حتّى أنّ هاهنا أيضاً كان مركز القمر أميل إلى الشمال عن فلك البروج في الكسوفين جميعاً سواء. ه – خ: بالسواء
ط: فليكن فلكه المائل ألف باء جيم حول قطر ألف جيم، ولننزّل أنّ نقطة ألف عقدة الرأس، ونقطة جيم عقدة الذنب ونقطة باء نهاية بعده في الشمال. ولنفصل قوسان متساويتان من لدن كلّ واحدة من عقدتي ألف، جيم ممّا يلي نقطة باء التي هي النهاية الشماليّة، ولتكونا قوسي ألف دال جيم هاء حتّى يكون مركز القمر أمّا في الكسوف الأوّل منهما فعلى نقطة دال وأمّا في الكسوف الثاني فعلى نقطة هاء.
لكن الزمان الذي بين وقت تحصيل القمر وبين الكسوف الأوّل سبع وعشرون سنة من سنيّ المصريّين وسبعة عشر يوماً ومن الساعات الاستوائيّة على الإطلاق وعلى الحقيقة إحدى عشرة ساعة وسدس. ولذلك كان بعد القمر من البعد الأبعد من فلك التدوير اثنا عشر جزءاً وأربعاً وعشرين دقيقة، وكان المجاز الدوريّ أكثر من المجاز الصحيح بتسع وخمسين دقيقة. والزمان الذي بين وقت تحصيل ه: {...} على عهد بختنصر القمر وبين الكسوف الثاني فعلى هذا المثال مائتان وخمس وأربعون سنة من سنيّ المصريّين وثلاث مائة يوم وسبعة وعشرين يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق [فعشر ساعات] ه – صح: ونصف وربع وأمّا على الحقيقة فعشر ساعات وربع. ومن قبل ذلك كان بعد القمر من البعد الأبعد من فلك التدوير جزأين وأربعاً وأربعين دقيقة وكان المجاز الدوريّ أكثر من المجاز الصحيح بثلاث عشرة دقيقة. والزمان الذي بين هذين الكسوفين *إذ* كان مبلغه مائتي سنة وثمان عشرة سنة من سنيّ المصريّين، وثلاث مائة يوم وتسعة أيّام وثلاثاً وعشرين ساعة وجزءاً من اثني عشر جزءاً من ساعة من ساعات الاستواء فإنّه يحصل منه على الحركة الوسطى التي تبيّنت للعرض فضله مبلغها مائة وستّون جزءاً وأربع دقائق.
فليكن إذا ه – خ - صح: لِما وضعناه المجاز للوسط لمركز Overlined by the scribe. القمر أمّا في الكسوف الأوّل من هذين الكسوفين فعلى نقطة زاي وأمّا في الكسوف الثاني فعلى نقطة حاء. فلأنّ قوس زاي حاء Greek, p. 334; Toomer, p. 209: ZBH مائة وستّون جزءاً وأربع دقائق وقوس دال زاي تسع وخمسون دقيقة وقوس هاء حاء ثلاث عشرة دقيقة، تجتمع ه – خ: فجميع قوس دال هاء مائة وستّون جزءاً وخمسون دقيقة فقوسا ألف دال هاء جيم إذن مجموعان هما ما يبقى من الأجزاء من نصف الدائرة وهي تسعة عشر جزءاً و عشر دقائق. وكلّ واحدة منهما إذا كانتا متساويتين هي بهذه الأجزاء تسعة أجزاء وخمس وثلاثون دقيقة. وهي الأجزاء التي بها كان المجاز الصحيح للقمر أمّا في الكسوف الأوّل فيقص ه – خ: فيقتصر عن عقدة الرأس وأمّا في الكسوف الثاني فيتقدّم الذنب قوس ألف زاي *إذن* بأسرها عشرة أجزاء وأربع وثلاثون دقيقة وقوس حاء جيم الباقية تسعة أجزاء واثنتان وعشرون دقيقة. فيجب أن يكون أيضاً المجاز الدوريّ للقمر أمّا في الكسوف الأوّل فكان مقصّراً عن عقدة الرأس بعشرة أجزاء وأربع وثلاثين دقيقة وكان بعده من نقطة باء، التي هي النهاية الشماليّة، ه –خ: بعينها مائتين وثمانين جزءاً وأربعاً وثلاثين دقيقة. وأمّا في الكسوف الثاني فكان متقدّماً لعقدة الذنب بتسعة أجزاء واثنتين وعشرين دقيقة وكان بعده من هذه النهاية الشماليّة بعينها ثمانين جزءاً وثمانياً وثلاثين دقيقة.
فإذ كان الآن الزمان *الأوّل* الذي بين وقت تحصيل القمر وبين وسط زمان الكسوف الأوّل من الكسوفين يحصل منه من الفضلة في العرض مائتا جزء وستّة وثمانون جزءاً وتسع عشرة دقيقة، فإنّا إن نحن نقصنا ذلك من أجزاء وقت تحصيل القمر في الكسوف الأوّل وهو مائتان وثمانون جزءاً وأربع وثلاثون دقيقة بعد أن يزيد عليها أجزاء دائرة واحدة، صار لنا حاصل العرض الدوريّ للقمر في السنة الأولى من سنيّ بختنصر في الشهر منها من شهور المصريّين المسمّى توث في اليوم الأوّل منه في انتصاف النهار على ثلاث مائة وأربعة وخمسين جزءاً وخمس عشر دقيقة من النهاية الشماليّة.
〈IV.10〉 ي: في حساب دور اختلاف القمر الأوّل البسيط وجداوله This chapter title is written in the margin of f. 66v with the siglum خ.
ونحن واضعون للتقويمات التي تستعمل في حساب الحركات في الاجتماعات والاستقبالات إذ كانت هذه المجازات ليس نحتاج فيها إلى شيء ممّا نحن على تبيينه من أمر اختلاف الثاني جدولاً للأقسام الجزئيّة بطريق الخطوط أيضاً كما عملنا في الشمس. ومستعملون في ذلك نسبة الستّين إلى الخمسة والربع وقاسمون على ذلك المثال الربعين اللذين يليان البعد الأبعد بستّة ستّة من الأجزاء والربعين اللذين يليان البعد الأقرب بثلاثة ثلاثة حتّى يكون أيضاً تخطيط هذا الجدول مثل تخطيط جدول الشمس، فتكون فيه خمسة وأربعون سطراً ويكون مقسوماً بثلاثة صفوف فالصفّان الأوّلان فيهما أعداد أجزاء الاختلاف والصفّ الثالث فيه ما يصيب قسم قسم *من زيادة قسم* من الزيادة أو النقصان موضوعاً حياله. فالنقصان يكون في حساب الحركات في الطول وفي العرض متى كان ه: العدد الذي يجتمع من الاختلاف من البعد الأبعد من فلك التدوير دون مائة وثمانين جزءاً، والزيادة تكون متى جاز ذلك العدد مائة وثمانين جزءاً. ه – خ – صح: فأمّا إذا كان مائة وثمانين سواء لم يكن في الحساب نقصان ولا زيادة. وهكذا رسم الجدول.
جدول اختلاف القمر الأوّل البسيط |
||||
الأعداد المشتركة | الزيادات | والنقصانات |
||
أجزاء | أجزاء | أجزاء | دقائق |
|
و | شند | 0 | كط |
|
يب | شمح | 0 | نز |
|
يح | شمب | ا | كه |
|
كد | شلو | ا | نج |
|
ل | شل | ب | يط |
|
لو | شكد | ب | مد |
|
مب | شيح | ج | ح |
|
مح | شيب | ج | ||
ند | شو | ج | ||
س | ش | د | ح |
|
سو | رصد | د | كد |
|
عب | رفح | د | لح |
|
عح | رفب | د | مط |
|
فد | رعو | د | نو |
|
ص | رع | د | نط |
|
صج | رسز | ه | 0 |
|
صو | رسد | ه | ا |
|
صط | رسا | ه | 0 |
|
قب | رنح | د | نط |
|
قه | رنه | د | ||
قح | رنب | د | نج |
|
قيا | رمط | د | مط |
|
قيد | رمو | د | مد |
|
قيز | رمج | د | لح |
|
قك | رم | د | لا |
|
قكج | رلز | د | كد |
|
قكو | رلد | د | يو |
|
قكط | رلا | د | ز |
|
قلب | ركح | ج | نز |
|
قله | ركه | ج | مو |
|
قلح | ركب | ج | له |
|
قما | ريط | ج | كج |
|
قمد | ريو | ج | ي |
|
قمز | ريج | ب | نز |
|
قن | ري | ب | مج |
|
قنج | رز | ب | كح |
|
قنو | رد | ب | يج |
|
قنط | را | ا | نز |
|
قسب | قصح | ا | ما |
|
قسه | قصه | ا | كه |
|
قسح | قصب | ا | ط |
|
قعا | قفط | 0 | نب |
|
قعد | قفو | 0 | له |
|
قعز | قفج | 0 | يح |
|
قف | قف | 0 | 0 |
|
〈IV.11〉 يا: في أنّ الخلاف الذي وقع لأبرخس في مقدار الاختلاف الذي يلحق القمر لم يقع من قبل الخلاف في الأصول التي عليها يعمل بل من قبل الحساب
وإذ قد بيّنت هذه الأشياء بما وصفنا، فبالواجب قد يبحث الإنسان عن السبب الذي له صارت النسبة التي حصلت لأبرخس من قبل كسوفات القمر التي استعملها ↑: خ لنا في الفحص عن هذا الاختلاف ليست النسبة التي بيّنّاها نحن ولا النسبة أيضاً الأولى التي بيّنّاها بالأصل الذي يعمل فيه على الخروج ه – خ: بالخروج عن المركز موافقة للثابتة The correct word should be للثانية as in the Greek text and Toomerʼs translation. التي استخرجها بالأصل الذي يعمل فيه على فلك التدوير. وذلك أنّه في التبيين الأوّل يحصل أنّ نسبة الخطّ الذي من مركز الفلك الخارج المركز إلى الخطّ الذي بين مركز هذا الفلك وبين مركز فلك البروج هي نسبة ثلاثة آلاف ومائة وأربعة وأربعين إلى ثلاث مائة وسبعة عشر وثلثين Toomer, p. 211: 327+2/3. بالتقريب وهذه النسبة هي نسبة ستّين إلى ستّة وربع. وفي التبيين الثاني يحصل أنّ نسبة الخظّ الذي بين مركز فلك البروج وبين مركز فلك التدوير إلى الخطّ الذي من مركز فلك التدوير وهي نسبة ثلاثة آلاف ومائة واثنين وعشرين ونصف إلى مائتين وسبعة وأربعين ونصف، وهذه هي نسبة ستّين جزءاً إلى أربعة أجزاء وستّ وأربعين دقيقة. ويكون أكثر فضل الاختلاف أمّا من قبل نسبة ستّين إلى ستّة وربع فخمسة أجزاء وتسعة وأربعون دقيقة، وأمّا من قبل نسبة ستّين جزءاً إلى أربعة أجزاء وستّ وأربعين دقيقة فأربعة أجزاء وأربع وثلاثون دقيقة، وأمّا عندنا فالنسبة ↑فالنسبة↑: خ فإنّ النسبة أنّما هي نسبة ستّين إلى خمسة وربع والفضل الموصوف الذي يقع منها يبلغ نحو من خمسة أجزاء.
فنقول في ذلك إنّا قد بيّنّا قبيل بالقول أنّ هذا الخطاء لم يقع من قبل الاختلاف في الأصول كما ظنّ قوم من قبل أنّ في كلّ واحد من ذينك الأصلين يوجد ما يظهر يلزم أشياء بأعيانها لا فرق بينها. ولو أثرنا ه – خ: أردنا أن نحسب ذلك بالأعداد لقد كنّا نجد النسبة التي تحدث من الأصلين جميعاً نسبة واحدة بعينها متى لزمنا الأمور ه – خ: منهما الأقدار الواحدة بأعيانها التي تظهر في كلّ واحد منهما لا أموراً ه – خ: لأمور مختلفة كما فعل أبرخس. فإنّه قد يمكن إذا جرى الأمر هذا المجرى إذ كانت الكسوفات التي تبنى عليها ليست تلك الكسوفات بأعيانها أن يلحق ه – خ: {يكون} الخطاء أمّا من قبل الأرصاد أنفسها وأمّا من قبل تحصيل حساب المدّتين اللتين بين الكسوفات. من ذلك أنّا نجد تلك الكسوفات أمّا ه – خ: على الاتّصالات فيها فقد رصدت على الصحّة وواقفت الأصول التي بيّنّاها نحن للحركة المستوية وللحركة المختلفة وأمّا حساب المدّة وهو الذي به تبيّن مقدار النسبة فلم يبالغ في العناية به غاية ما يمكن من المبالغة.
ونحن مبيّنون كلّ واحد من هذين الأمرين ومبتدون في ذلك بالكسوفات الأوّل الثلاثة. فنقول إنّ هذه الكسوفات الثلاثة ذكر أنّه أحضرها من كسوفات جملت ه – خ: جملة من بابل رصدت هناك وإنّ الأوّل منها كان في ولاية فانسطرانس بأثينيّة ه – خ: فاسطراطليس {والياً} على مدينة أثينا مدينة الحكماء في الشهر من شهورهم المسمّى بوسيداون ↑بوسيداون↑: خ سيدوسن وأنّه انكسف من القمر جزء يسير من دائرته من ناحية المشرق الصيفيّ وقد بقي من الليل نصف ساعة. قال وغاب وهو في بعد ينكسف. فهذا الزمان كان في سنة ثلاث مائة وستّة وستّين منذ ↑منذ↑: من عهد بختنصر في شهر توث من شهور المصريّين منها كما ذكر في اليوم السادس والعشرين منه في الليلة التي يتلوها اليوم السابع والعشرون منه بعد انتصاف الليل بخمس ساعات ونصف زمانيّة لأنّه قد كان بقي من الليل نصف ساعة. لكن لأنّ الشمس كانت في أواخر ه – خ: آخر الرامي فإنّ أزمان الساعة من ساعات الليل ببابل ثمانية عشر زماناً. وذلك أنّ الليل في ذلك الوقت هناك أربع عشرة ساعة وخمسان من ساعات الاستواء. فالخمس الساعات والنصف الزمانيّة يجتمع منها إذن ستّ ساعات وثلاثة أخماس ساعة من ساعات الاستواء. فمبدأ الكسوف إذن كان بعد انتصاف النهار من اليوم السادس والعشرين بثمان عشرة ساعة وثلاثة أخماس من ساعات الاستواء. ولأنّ ما استتر ه – خ: انكسف منه كان جزءاً يسيراً فواجب أن يكون زمان الكسوف كلّه ساعة ونصفاً بالتقريب، ومن البيّن أنّ وسط زمانه كان بعد تسع عشرة ساعة وثلث من ساعات الاستواء. فكان أيضاً وسط زمان هذا الكسوف بإسكندريّة بعد انتصاف نهار اليوم السادس والعشرين بثمان عشرة ساعة ونصف من ساعات الاستواء. والزمان الذي بين حاصل ه – خ: منزل القمر في ↑: خ أوّل السنة الأولى من سنيّ بختنصر وبين هذا الوقت الذي ذكرناه ثلاث مائة وخمسة وستّون سنة مصريّة وخمسة وعشرون يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق فثمان عشرة ساعة ونصف، وأمّا على الاستقصاء فثمان عشرة ساعة وربع.
وإذا حسبنا حاصل الشمس على حسب هذا الزمان بالأصول التي وضعناها وجدناه على الحقيقة على ثمانية وعشرين جزءاً وثمان عشرة دقيقة من الرامي ↑الرامي↑: صح ووجدنا حاصل ↑حاصل↑: خ منزل القمر أمّا بحركته الوسطى فعلى أربعة وعشرين جزءاً وعشرين دقيقة من التوأمين وأمّا بالحقيقة ه – خ: بحركة الحقيقة فعلى ثمانية وعشرين وسبع عشرة دقيقة من هذا البرج من قبل أنّ بعده في الاختلاف من البعد الأبعد من فلك التدوير مائتان وسبعة وعشرون جزءاً وثلاث وأربعون دقيقة.
وأيضاً فإنّه قال إنّ الكسوف الذي بعد هذا كان والوالي بأثينيّة فانسطراطن ه – خ: طيس في الشهر من شهورهم المسمّى *سعيروفورين وفي الشهر من شهور المصريّين المسمّى* فامانوث في اليوم الرابع والعشرين منه في الليلة التي يتلوها اليوم الخامس والعشرون منه *قال وانكسف من ناحية المشرق الصيفيّ بعد أن مضت الساعة الأولى منها. فيكون هذا الزمان أيضاً كان في سنة ثلاث مائة وستّ وستّين منذ عهد بختنصر في الشهر المسمّى فامانوث منها في اليوم الرابع والعشرين منه في الليلة التي يتلوها الخامس والعشرون منه Marked by the scirbe as
ˇقال وانكسف من ...الخامس والعشرون منهˇ. * قبل انتصاف الليل [*أكثره*] بخمس ساعات ونصف زمانيّة. لكن الشمس إذا ه – خ: إذ كانت في *أواخر* التوأمين فإنّ الساعة ه – خ: من الليل ببابل اثنا عشر زماناً فالخمس الساعات والنصف الزمانيّة، يحصل منها إذن من الساعات الاستوائيّة أربع ساعات وخمسا ↑وخمساً↑: صح ساعة. فمبدأ الكسوف إذن كان بعد انتصاف نهار اليوم الرابع والعشرين بسبع ساعات من ساعات الاستواء وثلاثة أخماس ساعة. لكن لمّا كان زمان الكسوف كلّه كتب أنّه كان ثلاث ساعات فمن البيّن أنّ وسطه كان بعد تسع ساعات وعشر ساعة من ساعات الاستواء. فواجب إذن أن يكون ه – خ: بإسكندريّة بعد انتصاف نهار اليوم الرابع والعشرين بثمان ساعات وربع بالتقريب من ساعات الاستواء. والزمان أيضاً الذي من وقت التحصيلات ثلاث مائة وخمس وستّون من سنيّ المصريّين ومائتا يوم وثلاثة أيّام ومن الساعات الاستوائيّة أمّا على الإطلاق فثمان ساعات وربع وأمّا على الاستقصاء فسبع ساعات ونصف وثلث. وبحسب هذا الزمان يجد حاصل ↑حاصل↑: خ منزل الشمس على الاستقصاء على أحد وعشرين جزءاً وستّ وأربعين دقيقة من التوأمين، ونجد حاصل ↑حاصل↑: خ منزل القمر بحركته الوسطى على ثلاثة وعشرين جزءاً وثمان وخمسين دقيقة من الرامي وأمّا على الحقيقة فعلى أحد وعشرين جزءاً وثمان وأربعين دقيقة وذلك أنّ بعده كان بالاختلاف من البعد الأبعد من فلك التدوير سبعة وعشرين جزءاً وسبعاً وثلاثين دقيقة. والمدّة التي من الكسوف الأوّل إلى الكسوف الثاني يجتمع منها أمّا من الأيّام فمائة يوم وسبعة وسبعون يوماً وثلاث عشرة ساعة وثلاثة أخماس ساعة من ساعات الاستواء، وأمّا من الأجزاء التي سارتها الشمس فمائة وثلاثة وسبعون جزءاً وثمان وعشرون دقيقة. فأمّا أبرخس فإنّه بيّن الأمر ه – خ: بنى الأمر فيه على ما بيّنه على أنّ هذه المدّة أمّا من الأيّام فمائة وسبعة وسبعون يوماً وثلاث عشرة ساعة ونصف وربع من ساعات الاستواء، وأمّا من الأجزاء فمائة وثلاثة وسبعون جزءاً إلّا ثمن جزء.
وأمّا الكسوف الثالث فذكر أنّه كان والوالي بأثينيّة إواندرس في الشهر من شهورهم المسمّى بوسيداون ↑بوسيداون↑: خ بوسدان وفي الشهر من شهور المصريّين المسمّى توث في اليوم السادس عشر منه في الليلة التي يتلوها اليوم السابع عشر، قال وانكسف كلّه من ناحية مشرق الصيف وقد مضى منها أربع ساعات وهذا الزمان يكون في سنة ثلاث مائة وسبع وستّين منذ عهد بختنصر في الشهر المسمّى توث منها في اليوم السادس عشر منه في الليلة التي يتلوها اليوم السابع عشر قبل انتصاف الليل [*أكثره*] ساعتين ونصف. ه – خ: زمانيّة لكن لأنّ الشمس كانت في الأجزاء الثواني ه – خ: في جزأين من الرامي، فإنّ الساعة من الليل كانت ببابل ثمانية عشر زماناً بالتقريب. فالساعتان إذن والنصف الزمانيّة يكون منها ثلاث ساعات من ساعات الاستواء. فيجب أن يكون أوّل الكسوف كان بعد انتصاف نهار اليوم السادس عشر بتسع ساعات استوائيّة لكن لمّا كان كلّه انكسف فإنّ زمان الكسوف كلّه كان أربع ساعات استوائيّة. ومن البيّن أنّ وسط زمانه كان بعد إحدى عشرة ساعة من انتصاف النهار. فبإسكندريّة إذن يجب أن يكون وسط الكسوف ه – خ: كلّه كان بعد انتصاف نهار اليوم السادس عشر بعشر ساعات وسدس ساعة استوائيّة. والزمان الذي من ه – خ: وقت التحصيلات إلى ذلك الوقت ثلاث مائة وستّ وستّون سنة مصريّة وخمس عشر يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق أيضاً فعشر ساعات وسدس وأمّا على الاستقصاء، فتسع ساعات ونصف وثلث. وبحسب هذا الزمان نجد حاصل الشمس باستقصاء على سبعة عشر جزءاً وثلاثين دقيقة من الرامي، وحاصل القمر أمّا بحركته الوسطى فعلى سبعة عشر جزءاً وعشرين دقيقة Greek, p. 343: ιζ κα; Toomer, p. 213: 17;21 Gemini. من التوأمين، وأمّا على الاستقصاء فعلى سبعة عشر جزءاً وثمان وعشرين دقيقة من قبل أنّ بعده بالاختلاف من البعد الأبعد من فلك التدوير مائة وأحد وثمانون جزءاً واثنتا عشرة دقيقة. والمدّة أيضاً من الكسوف الثاني إلى الكسوف الثالث يجتمع منها أمّا من الأيّام فمائة وسبعة وسبعون يوماً وساعتان من ساعات الاستواء، وأمّا من الأجزاء فمائة وخمسة وسبعون جزءاً وأربع وأربعون دقيقة. فأمّا أبرخس فإنّه أيضاً وضع هذه المدّة أمّا من الأيّام فمائة وسبعة وسبعون يوماً وساعة واحدة وثلثاً ↑وثلثاً↑: صح ساعة، وأمّا من الأجزاء فمائة وخمسة وسبعون جزءاً وثمن جزء. فهو ذا ه – خ: فهو إذاً نجده قد وقع له الخطاء في حساب المدّتين أمّا في الأيّام فبسدس ↑فبسدس↑: صح ثمّ بثلث ↑بثلث↑: صح ساعة استوائيّة، وأمّا في الأجزاء ففي كلّ واحدة من المدتّين بنحو من ثلاثة أخماس جزء واحد. وليس ما يدخل مقدار النسبة من قبل ذلك من الخلاف يسيراً.
ونحن منتقلون الآن بكلامنا إلى الكسوفات الثلاثة أيضاً التي أحضرها ه – خ: احتضرها؛ ه – خ: اختبرها ﯨاحره It might be بأجزة. (؟) التي قال فيها إنّها رصدت بإسكندريّة. فيقول إنّ الأوّل من هذه قال فيه إنّه كان في سنة أربع وخمسين من الدور الثاني من أدوار قلبش في الشهر من شهور المصريّين المسمّى ماسوري منها في اليوم السادس عشر ه: منه وابتداء القمر ينكسف في هذه الليلة قبل أن يطلع بنصف ساعة وتمّ آخر كسوفه في وسط الساعة الثالثة. ه: في نسخة أخرى زيادة وانكسف كلّه فكان إذن وسط زمانه في ابتداء الساعة الثانية وقبل انتصاف الليل بخمس ساعات زمانيّة وقبل انتصاف الليل أيضاً بمثل ذلك من ساعات الاستواء وذلك أنّ ه – خ – صح: ومعتدلة لأنّ الشمس كانت في أواخر العذراء. فيجب أن يكون وسط زمان هذا الكسوف كان بإسكندريّة بعد انتصاف نهار اليوم السادس عشر بسبع ساعات من ساعات الاستواء. والزمان الذي من ↑من↑: منذ وقت التحصيلات في السنة الأولى من سنيّ بختنصر ه – خ: إلى تلك السنة خمس مائة سنة وستّ وأربعون سنة وثلاث مائة وخمسة وأربعون يوماً ومن الساعات الاستوائيّة أمّا على الإطلاق فسبع ساعات وأمّا على الحقيقة فستّ ساعات ونصف. وفي هذا الزمان أيضاً نجد حاصل الشمس بالحقيقة على ستّة وعشرين جزءاً ونصف ه – خ – صح: في نقل الحجّاج وستّ دقائق
Greek, p. 345: κς ς; Toomer, p. 214: 26;6 Virgo. من العذراء ونجد حاصل القمر أمّا بحركته الوسطى فعلى اثنتي وعشرين جزءاً من الحوت وأمّا بالحقيقة فعلى ستّة وعشرين جزءاً وسبع دقائق من قبل أنّ بعده بالاختلاف من البعد الأبعد من فلك التدوير ثلاث مائة جزء وخمس عشرة دقيقة ه – صح: في نقل الحجّاج ثلاث عشرة دقيقة.
Toomer, p. 214: 300;13° .
وقال إنّ الكسوف الذي بعد هذا كان في سنة خمس وخمسين من هذا الدور نفسه ه – خ: بعينه في الشهر من شهور المصريّين المسمّى ماخير في اليوم التاسع منه وابتدأ وقد مضى من الليل خمس ساعات وثلث وانكسف كلّه. فكان إذا مبدأ الكسوف بعد إحدى عشرة ساعة وثلث ه – خ: استوائيّة من انتصاف نهار اليوم التاسع من قبل أنّ الشمس أيضاً كانت في أواخر الحوت، وكان وسطه بعد ثلاث عشرة ساعة وثلث من ساعات الاستواء من قبل أنّ القمر كلّه انكسف. والزمان الذي من وقت التحصيلات إلى ذلك الوقت خمس مائة سنة وسبع وأربعون سنة ومائة وثمانية وخمسون يوماً ومن ساعات الاستواء على الإطلاق وعلى الحقيقة نحو من ثلاث عشرة ساعة وثلث. وبحسب هذا الزمان نجد على ذلك المثال حاصل الشمس بالحقيقة على ستّة وعشرين جزءاً وسبع عشرة دقيقة من الحوت، وحاصل القمر أمّا بحركته الوسطى فعلى جزء وسبع دقائق من الميزان وأمّا على الحقيقة فعلى ستّة وعشرين جزءاً وستّ عشرة دقيقة من العذراء من قبل أنّ بحركة الاختلاف كان بعده من البعد الأبعد مائة وتسعة أجزاء وثمانياً وعشرين دقيقة. والمدّة التي من الكسوف الأوّل إلى الكسوف الثاني يحصل أمّا من الأيّام فمائة وثمانية وسبعون يوماً وستّ ساعات ونصف وثلث من ساعات الاستواء، وأمّا من الأجزاء فمائة وثمانون جزءاً وإحدى عشرة دقيقة. وأمّا أبرخس فبيّن ه – خ: فبنى الأمر فيما بينه على أنّ هذه المدّة أمّا من الأيّام فمائة وثمانية وسبعون يوماً وستّ ساعات من ساعات الاستواء وأمّا من الأجزاء فمائة وثمانون جزءاً وعشرون دقيقة.
وقال إنّ الكسوف الثالث كان في هذه السنة بعينها الخامسة والخمسين من الدور الثاني في الشهر من شهور المصريّين المسمّى ماسوري منها في اليوم الخامس منه، وابتدأ وقد مضى من الليل ستّ ساعات وثلثا ساعة وانكسف كلّه. وقال إنّ وسط زمان هذا الكسوف كان بعد أن مضى من الليل ثمان ساعات وثلث أكثره وذلك بعد انتصاف الليل بساعتين وثلث زمانيّة. لكن الشمس إذ كانت في وسط العذراء فإنّ بإسكندريّة كانت الساعة من الليل أربعة عشر زماناً وخمسي ↑وخمسي↑: صح زمان. فالساعتان إذن والثلث الزمانيّتان يكون منهما من ساعات الاستواء ساعتين وربع بالتقريب. فيجب أن يكون وسط زمانه كان بعد انتصاف نهار اليوم الخامس بأربع عشرة ساعة وربع من ساعات الاستواء. والزمان أيضاً الذي من وقت التحصيلات إلى ذلك الوقت خمس مائة وسبع وأربعون سنة مصريّة وثلاث مائة وأربعة وثلاثون يوماً ومن ساعات الاستواء أمّا على الإطلاق فأربع عشر ساعة وربع وأمّا على الحقيقة فثلاث عشرة ساعة ونصف وربع. وبحسب هذا الزمان نجد حاصل الشمس على الحقيقة على خمسة عشر جزءاً واثنتي عشرة دقيقة من العذراء، وحاصل القمر أمّا بحركته الوسطى فعلى عشرة أجزاء وأربع وعشرين دقيقة من الحوت، وأمّا على الحقيقة فعلى خمسة عشر جزءاً وثلاث عشرة دقيقة *منها* وذلك أنّه باختلاف كان بعده من البعد الأبعد في فلك التدوير مائتين وتسعة وأربعين جزءاً وتسع دقائق. والمدّة التي من الكسوف الثاني إلى الكسوف الثالث يحصل منها أمّا من الأيّام فمائة وستّة وسبعون ↑وسبعون↑: صح يوماً وخمسا ساعة استوائيّة وأمّا من الأجزاء فمائة وثمانية وستّون جزءاً وخمس وخمسون ↑وخمسون↑: صح دقيقة ↑: صح. وأمّا أبرخس فإنّه وضع أيضاً هذه المدّة أمّا من الأيّام فمائة وستّة وسبعون يوماً وساعة وثلث ساعة استوائيّة وأمّا من الأجزاء فمائة وثمانية وستّون جزءاً وثلاث وثلاثون دقيقة.
فقد نجده هاهنا أيضاً قد وقع له الخطاء أمّا في الأجزاء فبسدس جزءاً وخمس ↑وخمس↑: صح جزء بالتقريب وأمّا في الأيّام فبنصف وثلث ه – صح: وعشر ساعة استوائيّة ونصف وثلث وجزء من اثني عشر من ساعة استوائيّة بالتقريب ↑بالتقريب↑: صح وقد يدخل ذلك أيضاً في نسبة الأصل الموضوع من الخلاف ما له قدر يعتدّ به. Toomer, p. 215, note 75.
فقد وقفنا إذن على سبب ه – خ: وهذا الخطاء الذي ذكرنا قد يدخل أيضاً الاختلاف الكبيرالبيّن {...}. هذه المخالفة التي وقعت ووثقنا فضل ثقة باستعمال نسبة الاختلافات التي بيّنّاها على رأينا في اتّصالات القمر لا سيّما، وقد وجدنا هذه الكسوفات أنفسها فضلاً عن غيرها موافقة مطابقة للأصول التي وطّأناها ه – خ: وضعناها نحن.
تمّت المقالة الرابعة من كتاب بطلميوس المنسوب إلى التعاليم ↑: وهي يا قولاً والحمد لله كثيراً على عونه. ه: إسكندريّة ورودس تحت دائرة واحدة من دوائر نصف النهار غير أنّ عرض إسكندريّة ل نح.