〈IX〉 ابتداء المقالة التاسعة من كتاب بطلميوس المنسوب إلى التعاليم⊙
〈IX.1〉 آ: في مراتب أكر الشمس والقمر والكواكب الخمسة المتحيّرة
قال أمّا ما يتهيّأ أن نكتب على طريق الجمل من أمر الكواكب الثابتة أيضًا ليكون ما يظهر من أمرها إلى هذه الغاية موجودًا للسبيل إلى الازدياد في العلم بها فأحسبنا قد أتينا عليه⊙ وإذ قد بقي علينا من هذا العلم المعرفة بأمور الكواكب الخمسة المتحيّرة فنحن واصفون أمرها على طريق العموم فيما كان عامًّا فيها هربًا من تكرير القول ومتّبعون ذلك بالأمور الجزئيّة في باب باب من أبواب العلم بها وأوّل ذلك الكلام في مراتب أكرها هي أيضًا كيف الحال في مواضعها على أنّها تتحرّك على قطبي الدائرة المائلة التي تمرّ بأوساط البروج⊙ فأقول إنّا نجد القدماء من أصحاب التعاليم قد أجمعوا جميعًا فيما أحسب على أنّ هذه الأكر كلّها دون كرة الكواكب الثابتة وفوق كرة القمر وعلى أنّ الأكر الثلاث أعني كرة زحل وهي أعظمها وكرة المشتري وهي الثانية في العظم من الأكر التي دون كرة الكواكب الثابتة وكرة المرّيخ وهي دون هذه هي فوق أكر سائر الكواكب الباقية وفوق كرة الشمس⊙ فأمّا كرة الزهرة وكرة عطارد فإنّ من تقادم عهده منهم جعلها تحت كرة الشمس وقم ممّن أتى بعدهم جعلوهما أيضًا فوق كرة الشمس من قبل أنّهم لم يجدوهما أيضًا يستران الشمس في حال من الأحوال⊙ فأمّا نحن فإنّا نرى أنّ هذا القياس ليس ممّا يوثق به وذلك أنّه قد يمكن أن يكون كوكب من الكواكب دون الشمس ولا يكون لا محالة (في سطح من السطوح) ه - ص: في خطّ من الخطوط التي بالشمس وبأبصارنا بل يكون في سطح ه - ص: خطّ غيره فتكون لذلك لا يوجد لستر الشمس كما قد نجد ذلك في أكثر الاجتماعات التي تكون للقمر مع الشمس فإنّ القمر يكون حينئذ يسير تحت الشمس ولا يسترها عنّا φ وإذ كان ذلك كذلك وكنّا على وجه آخر لا نقدر على التوصّل إلى المعرفة بحقيقة الأمر إذ كان ليس يفعل ولا واحد من هذه الكواكب شيئًا محسوسًا من اختلاف المنظر ومن قبل ذلك وحده إذا ظهر نستخرج أبعاد الكواكب فإنّا نرى أنّ أقرب الترتيب إلى الإقناع وأولاه بالقبول ترتيب من تقادم عهده وذلك أنّه ترتيب يوجب الأمر الأشبه بالأمر الطبيعيّ من تصيير الشمس وسطًا بين الكواكب التي تبعد عنها البعد كلّه وبين الكواكب التي ليست كذلك بل هي أبدًا تسير حولها سيرًا لا تبعد معه عنها إلى أسفل بعدًا يمكن أن يفعل شيئًا من اختلاف المنظر له قدر يعتدّ به⊙
〈IX.2〉 ب: فيما يحتاج إلى أن يوطّأ للأصول التي يُعمل عليها في الكواكب المتحيّرة⊙
فهذا مبلغ ما نقوله في مراتب الأكر وإذ كان قصدنا أن نبيّن في الكواكب المتحيّرة الخمسة كما بيّنّا في الشمس والقمر الاختلافات كلّها التي ترى لها وأنّها تكون عن حركات جارية على استواء واستدارة لأنّ هذه الحركات مشاكلة لطبيعة الأجرام الإلاهيّة مباينةً للخروج عن النظام وعدم التشابه فقد ينبغي أن نعلم أنّ إصابة مثل هذا الأصل أمر عظيم القدر وتمام بالحقيقة للنظر التعاليميّ من الفلسفة غير أنّه صعب لأسباب كثيرة ولذلك لم يلحقه إلى هذه الغاية أحد ممّن تقدّمنا فإنّه لمّا كان ما قد يمكن أن يفوت البصر ه: {...}ظر للطافته في البحث عن حركات كلّ واحد من الكواكب الدوريّة بالأرصاد التي تعتبر بها فإنّ إحساسنا بما يقع فيه من الفصل فيما بعد وقوع الخطأ من الزمان إذا امتحنّاه كلّما كانت المدّة التي مضت منذ ذلك الوقت أقصر كان أسرع وكلّما كانت أطول كان أبطأ وكان الزمان الذي منه ابتدئت في الأصل: ابتدأت؛ ه - صح: ابتُدئت أرصاد الكواكب المتحيّرة التي نجدها مدوّنةً قصيرًا في جنب ما هذا مبلغ جلالته من العلم صار لذلك ما يتقدّم فيخبر به في الزمان الذي هو أضعاف مضاعفة لهذا الزمان غير موثوق به وقد يدخل أيضًا على الإنسان في البحث عن الاختلافات فيها شكّ ليس بصغير من قبل أنّه يرى في كلّ واحد منها اختلافان وهما غير متساويين في مقاديرهما وفي أزمان عوداتهما أحدهما يوجد بالقياس إلى الشمس والآخر بالقياس إلى أجزاء فلك البروج إلّا أنّما أبدًا يوجدان جميعًا مختلطين اختلاطًا يعسر معه تلخيص ما يخصّ واحدًا واحدًا منهما φ ومن قبل أنّ أكثر الأرصاد القديمة أثبتت على غير تحصيل ولا تدقيق وذلك أنّا أبدًا نجدها قد أدخل فيها وقوف ↑: مقام الكوكب وظهوره والعلم المأخوذ من كلّ واحد من هذين الأمرين خاصّةً ليس يقع وقوع ما لا شكّ فيه وذلك أنّ الوقوف ليس يفي بأن يدلّ على الزمان الصحيح لأنّ النقلة المكانيّة قد تكون في أيّام كثيرة غير محسوسة من قبل الوقوف ومن بعده φ والظهورات أيضًا تخفى قبل كلّ شيء أماكنُها أعني ظهورت الكواكب التي ترى أوّلًا أو آخرًا وليس بهذا فقط بل قد يمكن أن يقع في زمانه أيضًا ه - ص: خطأ من قبل اختلاف الهواء ومن قبل اختلاف أبصار من يرصده φ وبالجملة إنّ أرصاد هذه الكواكب التي تكون بالقياس إلى كوكب من الكواكب الثابتة متى تقادم عهدها إن لم يتأمّلها الإنسان فضل تأمّل ويستقصي أمرها من جميع الوجوه عسر عليه القياس على مبلغ ما بينها بالحساب وجرى ذلك مجرى الحزر والتخمين ليس لهذا الأمر فقط أعني لأنّ الخطوط التي فيما بين الكواكب التي ترصد {...}حدث ه: {...}حدث عند فلك البروج زوايا مختلفة لا قائمة لا محالة فلذلك بالحريّ يقع في تحصيل بعد الكوكب {...}طول ه: {...}طول وفي العرض خطأ كبير من قبل كثرة تصرّف ميل فلك البروج ولكن لأنّ البعد الواحد أيضًا بعينه الذي يكون بين الكوكب {...}لكوكب ه: {...}لكوكب إذا قرب من الأفق تبيّن للبصر أعظم وإذا قرب من توسّط السماء تبيّن أصغر فمن البيّن أنّ لذلك يمكن أن يحسب مرّةً على أنّه أعظم من البعد بالحقيقة ومرّةً على أنّه أصغر φ فأنا أرى أنّ ه: أنّ أبرخس إذ كان رجلًا يؤثر الحقّ غاية الإيثار من قبل هذه الأسباب كلّها ولا سيّما لأنّه لم يكن بعد تهيّأ له من قبل تقدّمه من الأرصاد المستقصاة ما يتوصّل به إلى ما يريده كما تهيّأ لنا نحن منها من قبله قصد إلى الأصول التي يعمل عليها في الشمس والقمر فبحث عنها وبيّن بغاية ما قدر عليه أنّها إنّما تكون لحركات مستوية وعلى استدارة فأمّا الأصول التي يعمل عليها في الكواكب الخمسة المتحيّرة فلم نجده في شيء ممّا وقع إلينا من كتبه شرع فيها أصلًا بل اقتصر على أن أثبت الأرصاد التي وقعت لها لما في ذلك من فضل الانتفاع به وبيّن بها أنّ ما يظهر غير موافق للأصول التي كان يعمل عليها أصحاب التعاليم في ذلك العصر فإنّه يشبه أن يكون كان يرى أنّه ليس ينبغي أن يقتصر على الحكم بأنّ كلّ واحد منهما له اختلافان ولا على أنّه قد يكون لكلّ واحد منهما رجوعات وأنها غير متساوية ومبلغها كذا على أنّ سائر أصحاب التعاليم إنّما بنوا الأمر في براهينهم الخطوطيّة على أنّ الاختلاف واحد بعينه وكذلك الرجوع ولا على أنّ هذين الاختلافين إنّما يكونان على دوائر خارجة المراكز أو على دوائر مركزها مركز فلك البروج إلّا أنّها تتحرّك بأفلاك تداوير أو على أمر يتمّ بالأمرين جميعًا والاختلاف الذي من قبل فلك البروج مبلغه كذا والاختلاف الذي بالقياس إلى الشمس مبلغه كذا فإنّ ذلك شيء قد نظر فيه جميع من رام أن يدلّ على الحركة المستوية في الاستدارة بالجدول الذي يسمّى الأبديّ إلّا أنّ ذلك قد اجتمع فيه أنّه بغير برهان وأنّه باطل وذلك أنّ بعضهم لم يلزم أصلًا ما يجب فيما قصد لتبيينه وبعضهم إنّما لزمه إلى موضع ما ثمّ فارقه بل كان أبرخس يرى أنّ من بلغ من جميع التعاليم هذا المبلغ من الاستقصاء وتحرّى الحقّ فليس يكتفي بالوقوف عند المعرفة بذلك كما ظنّ غيره من أنّ ذلك لا نقص عليهم فيه لكنّ الواجب على من قصد أن يقنع نفسه ومن يخاطبه أن يبيّن مقدار كلّ واحد من الاختلافين وأدوارهما بما يرى رؤية بيّنةً ويتّفق عليه وأن يخلط أيضًا الأمرين أعني وضع الدوائر التي يكون عليها هذان الاختلافان ومراتبها فيستخرج من ذلك العلم أيضًا بجهة حركتها ثمّ يطابق بأخرة ه: بأخرة جميع ما يوجد عيانًا إلّا الشاذّ منه بالجهة التي تخصّ الأصول التي وضعها فأنا أحسب أنّه قد كان تبيّن له نفسه فضلًا عن غيره أنّ هذا أمر عسير ولم أقل ما قلته من ذلك على جهة الافتخار به بل إنّما قلته كيما إن اضطرّنا هذا المعنى في نفسه في موضع من المواضع إلى أن نستعمل أشياء خارجة عن القياس مثال ذلك أن نقيم البراهين في الدوائر مجرّدةً التي ترسمها حركة هذه الكواكب في أكرها ونعمل على أنّها في سطح فلك البروج نفسه لأنّ ذلك أسهل في إقامة البراهين أو إلى أن يضع أشياء يجعلها أوائل من غير أن يكون بدء أمرها كان من أمر ظاهر لكنّها استخرجت بالمحنة المتّصلة فوجدت موافقةً مطابقةً لما وضع أوّلًا أو ألّا تجعل فيها كلّها الجهة في حركة الدوائر أو ميلها جهةً واحدةً لا تختلف لم ننكر ذلك وأجريناه مجرى ما يسلّم علمًا ما لأنّ استعمال شيء ممّا هذه سبيله ما لم يلزم من قبله فضل ذو قدر يعتدّ به أصلًا فليس يدخل ضررًا في الأمر المقصود له وأنّ ما وضع وضعًا من غير برهان فبعد أن يوجد موافقًا للأمور الظاهرة فليس يمكن أن يكون وجد من غير سلوك سبيل من سبل العلم وإن كانت الجهة التي بها أدرك يعسر وصفها لأنّ المبادئ الأول إمّا ألّا يكون لها بالطبع سبب أصلًا وإمّا أن يكون إن كان لها سبب فإنّ العبارة عنه يصعب مرامها وأنّه ليس ينبغي أن يستنكر الاختلاف الذي يقع في بعض المواضع في جهة الأصل الذي يعمل عليه في الدوائر ولا يظنّ أنّ ذلك خارج من القياس إذ كانت الأمور أيضًا التي ترى في الكواكب أنفسها توجد غير متشابهة ما كانت الحركة المسنونة في الاستدراة محفوظةً فيها كلّها على الإطلاق وكان مع ذلك كلّ واحد من الأمور الجزئيّة التي ترى إنّما تتبيّن بمعظم ما عليه الأصول التي عليها تعمل فيه وجملته. وما استعملناه من الأرصاد في تبيين كلّ واحد من هذه الأمور فإنّما قصدنا فيه إلى ما كان منها بعيدًا من أن يقع فيه الشكّ بغاية ما يمكن وهي الأرصاد التي وقعت عند مقارنة أو مقارنة شديدة لكوكب من الكواكب أو القمر وممّا أخذ من ذلك خاصّةً بآلات القياس بأنّ البصر كأنّه يمرّ على الاستقامة في الثقبين المتقاطرين اللذين في الحلقتين فترى الأبعاد المتساوية من كلّ موضع بقسيّ متشابهة ويتهيّأ أن يقف على مسيرات كلّ واحد من هذه الكواكب في الطول وفي العرض على الاستقصاء بالقياس إلى فلك البروج بإدارة الحلقة التي تقوم في الآلة مقام فلك البروج والثقب المتقابلة التي في الحلقتين اللتين تمرّان بقطبيه نحو ما يرصد⊙
〈IX.3〉 جـ: في عودات أدوار الكواكب الخمسة المتحيّرة
وإذ قد تقدّم العلم بهذه الأشياء على هذا النحو فنحن واصفون أوّلًا موافاة عودات أدوار كلّ واحد من الكواكب الخمسة المتحيّرة على التقريب التي هي أقلّ ما يكون منها على ما حسبها أبرخس وقد صحّحنا نحن هذه العودات بما ظهر من بعد تبيين أمر اختلافاتها من قبل المقايسة بين تحصيلاتها كيما سنبيّن إذا صرنا إلى ذلك الموضع إلّا أنّا تقدّمنا فوضعناها وضعًا كيما تكون الحركات الوسطى الجزئيّة للطول وللاختلاف في كلّ واحد من الكواكب موضوعةً ميسّرةً لحساب الاختلافات وذلك أنّ المسيرات الوسطى لا يقع فيها هاهنا وإن حسبت بالجليل من الحساب اختلاف يعتدّ به وقد ينبغي لك أن تفهم بالجملة من قولنا الحركة في الطول ه - ه: ظـ{ـاهر} أنّ الحركة في الطول هي حركة مركز فلك تدوير على الفلك الخارج المركز وحركة الاختلاف هي حركة {...} على فلك التدوير حركة مركز فلك التدوير على الفلك الخارج المركز وتفهم من قولنا حركة الاختلاف حركة الكوكب على فلك تدويره⊙ فنقول الآن إنّا نجد سبعًا وخمسين دورةً من دورات الاختلاف لكوكب زحل تستكمل في تسع وخمسين سنةً شمسيّة من السنين عندنا أعني التي تبتدئ من انقلاب أو استواء وتعود إلى ذلك الانقلاب أو الاستواء ويوم واحد أيضًا ونصف وربع يوم بالتقريب ومن البيّن أنّ ذلك يكون في دورتين من أدوار سير هذا الكوكب وجزء واحد وثلثي جزء وجزء من عشرين من جزء من قبل أنّ عدد أدوار سير الشمس في زمان العودة الذي لكلّ واحد من الكواكب الثلاثة التي الشمس أبدًا يلحقها بدورانها مساو أبدًا لعدد أدوار سير الكوكب منها في الطول وعدد عودات اختلافه إذا جمعا φ ونحن نجد خمسًا وستّين دورةً من أدوار الاختلاف (الذي) للمشتري تستكمل في إحدى وسبعين سنةً شمسيّةً مأخوذةً على ذلك المثال تنقص أربعة أيّام ونصف وثلث يوم وجزء من خمسة عشر جزءًا من يوم بالتقريب ومن أدوار سير هذا الكوكب في ستّة أدوار تبتدئ من أحد الانقلابين وتعود إليه بعينه ناقصةً أربعة أجزاء ونصف وثلث جزء φ ونجد سبعًا وثلاثين دورةً من أدوار الاختلاف للمرّيخ تستكمل في تسع وسبعين سنةً شمسيّةً من السنين عندنا وثلاثة أيّام وسدس وجزء من عشرين من يوم بالتقريب ومن أدوار سير الكوكب الذي يبتدئ من أحد الانقلابين ويعود إلى ذلك الانقلاب بعينه في اثنتين وأربعين دورةً وثلاثة أجزاء وستّ دقائق ه - ج - صح: وسدس جزء φ ونجد خمس دورات من دورات الاختلاف للزهرة تستكمل من السنين الشمسيّة عندنا في ثمان سنين إلّا يومين وربع وجزء من عشرين من يوم بالتقريب ومن أدوار السير في أدوار مساوية لأدوار الشمس وهي ثمان دورات تنقص جزأين وربع φ ونجد مائةً وخمسًا وأربعين دورةً من أدوار الاختلاف لعطارد تستكمل من هذه السنين في ستّ وأربعين سنةً ويوم واحد وجزء من ثلاثين من يوم بالتقريب ومن أدوار السير في أدوار مساوية أيضًا لأدوار الشمس وهي ستّ وأربعون دورةً وجزء واحد لكن إن نحن بسطنا زمان العودة في كلّ واحد من الكواكب فجعلناه أيّامًا على ما يوافق ما بيّنّاه من زمان السنة وبسطنا عدّة أدوار الاختلاف فيها فجعلناها آخرًا من الأجزاء التي قسمت بها الدائرة وهي ثلاث مائة وستّون جزءًا حصل لنا في كوكب زحل أمّا من الأيّام فأحد وعشرون ألف يوم وخمس مائة وأحد وخمسون يومًا وجزء من ثمانية عشر جزءًا من يوم ه - صح: في نقل الحجّاج وخمس وعشر يوم وأمّا من أجزاء الاختلاف فعشرون ألف جزء وخمس مائة وعشرون جزءًا φ وحصل في كوكب المشتري أمّا من الأيّام فخمسة وعشرون ألف يوم وتسع مائة وسبعة وعشرون يومًا وجزء من سبعة وثلاثين جزءًا من يوم ه - صح: في نقل الحجّاج وربع وخمس وسدس وأمّا من أجزاء الاختلاف فثلاثة وعشرون لف جزء وأربع مائة جزء φ وحصل في كوكب المرّيخ أمّا من الأيّام فثمانية وعشرون ألف يوم وثماني مائة وسبعة وخمسون يومًا وجزء من ثلاثة وخمسين جزءًا من يوم ه: في نقل الحجّاج ونصف وثلث ونصف عشر؛ ه - ص: الصحيح سبعة أعشار يوم وأمّا من أجزاء الاختلاف فثلاثة عشر ألف جزء وثلاث مائة وعشرون جزءًا⊙ وحصل في كوكب الزهرة أمّا من الأيّام فألفان وتسع مائة وتسعة عشر يومًا وجزء من اثنين وأربعين جزءًا من يوم ه: في نقل الحجّاج ونصف وخمس؛ ه - ص: والصحيح ثلثا يوم φ وأمّا من أجزاء الاختلاف فألف وثماني مائة جزءٍ⊙ وحصل في كوكب عطارد أمّا من الأيّام فستّة عشر ألفًا وثمان مائة يوم ويومان وجزء من أربعة وعشرين جزءًا من يوم ه: في نقل الحجّاج وخمسا يوم؛ ه - ص: والصحيح ثلث ونصف عشر يوم φ ⊙ وأمّا أجزاء الاختلاف فاثنان وخمسون ألف جزء ومائتا جزء⊙ فإذا قسمنا في كلّ واحد من هذه الكواكب عدّة أجزاء اختلافه الذي يخصّه على عدّة الأيّام حصل لنا حركة الاختلاف الوسطى في اليوم الواحد أمّا لزحل فسبعًا وخمسين دقيقةً وسبع ثواني وثلاث وأربعون ثالثةً وإحدى وأربعون رابعةً وثلاث وأربعون خامسةً وأربعون سادسةً بالتقريب⊙ وأمّا للمشتري فأربع وخمسون دقيقةً وتسع ثواني وثالثان وستّ وأربعون رابعةً وستّ وعشرون خامسةً⊙ وأمّا للمرّيخ فسبع وعشرون دقيقةً وإحدى وأربعون ثانيةً وأربعون ثالثةً وتسع عشرة رابعةً وعشرون خامسةً وثمان وخمسون سادسةً⊙ وأمّا للزهرة فستّ وثلاثون دقيقةً وتسع وخمسون ثانيةً وخمس وعشرون ثالثةً وثلاث وخمسون رابعةً وإحدى عشرة خامسةً وثمان وعشرون سادسةً⊙ وأمّا لعطارد فثلاثة أجزاء وستّ دقائق وأربع وعشرون ثانيةً وستّ ثوالث وتسع وخمسون رابعةً وخمس وثلاثون خامسةً وخمسون سادسةً⊙ فإن نحن أخذنا من كلّ واحد من هذه الأعداد جزءًا من أربعة وعشرين جزءًا منه حصلت لنا الحركة الوسطى للاختلاف في الساعة الواحدة⊙ أمّا لزحل فدقيقتان واثنتان وعشرون ثانيةً وتسع وأربعون ثالثةً وتسع عشرة رابعة وأربع عشرة خامسةً وتسع عشرة سادسةً⊙ وأمّا للمشتري فدقيقتان وخمس عشرة ثانيةً واثنتان وعشرون ثالثةً وستّ وثلاثون رابعةً وستّ وخمسون خامسةً وخمس سوادس⊙ وأمّا للمرّيخ فدقيقة واحدة وتسع ثواني وأربع عشرة ثالثةً وعشر روابع وثمان وأربعون خامسةً واثنتان وعشرون سادسةً وخمس وعشرون سابعةً⊙ وأمّا للزهرة فدقيقة واحدة واثنتان وثلاثون ثانيةً وثمان وعشرون ثالثةً وأربع وثلاثون رابعةً واثنتان وأربعون خامسةً وثمان وخمسون سادسةً وأربعون سابعةً⊙ وأمّا لعطارد فسبع دقائق وستّ وأربعون ثانيةً وسبع عشرة رابعةً وثمان وعشرون خامسةً وتسع وخمسون سادسةً وخمس وثلاثون سابعةً⊙ وإن نحن أيضًا ضاعفنا حركة كلّ واحد من هذه الكواكب في اليوم الواحد ثلاثين مرّةً حصلت لنا حركة الاختلاف الوسطى في الشهر⊙ أمّا لزحل فثمانية وعشرون جزءًا وثلاث وثلاثون دقيقةً وإحدى وخمسون ثانيةً وخمسون ثالثةً وإحدى وخمسون رابعةً وخمسون خامسةً⊙ وأمّا للمشتري فسبعة وعشرون جزءًا وأربع دقائق وإحدى وثلاثون ثانيةً وثلاث وعشرون ثالثةً وثلاث عشرة رابعةً⊙ وأمّا للمرّيخ فثلاثة عشر جزءًا وخمسون دقيقةً وخمسون ثانيةً وتسع ثوالث وأربعون رابعةً وتسع وعشرون خامسةً⊙ وأمّا للزهرة فثمانية عشر جزءًا وتسع وعشرون دقيقةً واثنتان وأربعون ثانيةً وستّ وخمسون ثالثةً وخمس وثلاثون رابعةً وأربع وأربعون خامسةً⊙ وأمّا لعطارد فثلاثة وتسعون جزءًا واثنتا عشرة دقيقةً وثلاث ثواني وتسع وعشرون ثالثةً وسبع وأربعون رابعةً وخمس وخمسون خامسةً⊙ وإن ضاعفنا على ذلك المثال الحركات في اليوم الواحد بأيّام سنة واحدة مصريّة وهي ثلاث مائة وخمسة وستّون يومًا حصلت لنا حركة الاختلاف الوسطى في السنة⊙ أمّا لزحل فثلاث مائة وسبعة وأربعون جزءًا واثنتان وثلاثون دقيقةً وثمان وأربعون ثالثةً وخمسون رابعةً وثمان وثلاثون خامسةً وعشرون سادسةً⊙ وأمّا للمشتري فثلاث مائة وتسعة وعشرون جزءًا وخمس وعشرون دقيقةً وثانية واحدة واثنتان وخمسون ثالثةً وثمان وعشرون رابعةً وعشر خوامس⊙ وأمّا للمرّيخ فمائة وثمانية وستّون جزءًا وثماني وعشرون دقيقةً وثلاثون ثانيةً وسبع عشرة ثالثةً واثنتان وأربعون رابعةً واثنتان وثلاثون خامسةً وخمسون سادسةً⊙ وأمّا للزهرة فمئتان وخمسة وعشرون جزءًا ودقيقة واحدة واثنتان وثلاثون ثانيةً وثماني وعشرون ثالثةً وأربع وثلاثون رابعةً وتسع وثلاثون خامسةً وخمس عشرة سادسةً⊙ وأمّا الفضلة لعطارد فثلاثة وخمسون جزءًا وستّ وخمسون دقيقةً واثنتان وأربعون ثانيةً واثنتان وثلاثون ثالثةً واثنتان وثلاثون رابعةً وتسع وخمسون خامسةً وعشر سوادس⊙ وكذلك أيضًا إذا ضاعفنا كلّ واحدة من السنين ثمان عشرة مرّةً كما فعلنا في جداول النيّرين حصلت لنا الفضلة الوسطى للاختلاف في كلّ ثمان عشرة سنةً مصريّةً أمّا لزحل فمائة وخمسة وثلاثون جزءًا وستّ وثلاثون دقيقةً وأربع عشرة ثانيةً وتسع وثلاثون ثالثةً وإحدى عشرة رابعةً وثلاثون خامسةً⊙ وأمّا للمشتري فمائة وتسعة وستّون جزءًا وثلاثون دقيقةً وثلاث وثلاثون ثانيةً وأربع وأربعون ثالثةً وسبع وعشرون رابعةً⊙ وأمّا للمرّيخ فمائة واثنان وخمسون جزءًا وثلاث وثلاثون دقيقةً وخمس ثواني وثماني عشرة ثالثةً وخمس وأربعون رابعةً وإحدى وخمسون خامسةً⊙ وأمّا للزهرة فتسعون جزءًا وسبع وعشرون دقيقةً وأربع وأربعون ثانيةً وأربع وثلاثون ثالثةً وثلاث وعشرون رابعةً وستّ وأربعون خامسةً وثلاثون سادسةً⊙ وأمّا لعطارد فمئتان وأحد وخمسون جزءًا وخمس وأربعون ثانيةً ه: وخمس وأربعون ثانيةً وخمس وأربعون ثالثةً وثلاث وخمسون رابعةً وخمس وأربعون خامسةً φ وقد حصل لنا ممّا يلزم من ذلك الحركات الوسطى في الطول أيضًا كيما لا يحتاج إلى بسط عدّة دورات السير أيضًا بأجزائها وإلى قسمتها على الزمان المفروض في كلّ واحد من الكواكب وذلك أنّ ملغ عدد الحركة الوسطى في الطول للزهرة ولعطارد من البيّن أنّها موافقة لمبلغ العدد الذي تقدّمنا فوصفناه في حركة الشمس وأمّا أعداد حركات الكواكب الثلاثة الباقية في الطول فإنّها الأعداد الباقية بعد عدد الاختلاف في كلّ واحد منها من عدد الشمس فتحصل لنا من قبل ذلك الحركة الوسطى في الطول في اليوم الواحد أمّا لزحل فدقيقتان وثلاث وثلاثون ثالثةً وإحدى وثلاثون رابعةً وثماني وعشرون خامسةً وإحدى وخمسون سادسةً⊙ وأمّا للمشتري فأربع دقائق وتسع وخمسون ثانيةً وأربع عشرة ثالثةً وستّ وعشرون رابعة وستّ وأربعون خامسةً وإحدى وثلاثون سادسةً⊙ وأمّا للمرّيخ فإحدى وثلاثون دقيقةً وستّ وعشرون ثانيةً وستّ وثلاثون ثالثةً وثلاث وخمسون رابعةً وإحدى وخمسون خامسةً وثلاث وثلاثون سادسةً⊙ وتحصل الحركة في الساعة الواحدة أمّا لزحل فخمس ثواني وثالثة واحدة وثلاث وعشرون رابعةً وثماني وأربعون خامسةً واثنتان وأربعون سادسةً وسبع ↑ - جـ: لا سوابع وثامنة واحدة φ وأمّا للمشتري فاثنتا عشرة ثانيةً وثمان وعشرون ثالثةً وستّ روابع وستّ خوامس وستّ وخمسون سادسةً وسبع عشرة سابعةً وثامنة ↑ - جـ: ک واحدة⊙ وأمّا للمرّيخ فدقيقة واحدة وثمان عشرة ثانيةً وستّ وثلاثون ثالثةً واثنتان وثلاثون رابعةً وأربع عشرة خامسةً وثماني وثلاثون سادسةً واثنتان وخمسون سابعةً وثلاثون ثامنةً φ وتحصل لنا الحركة في الشهر أمّا لزحل فجزء واحد وستّ عشرة ثانيةً وخمس وأربعون ثالثةً وأربع وأربعون رابعةً وخمس وعشرون خامسةً وثلاثون سادسةً⊙ وأمّا للمشتري فجزءان وتسع وعشرون دقيقةً وسبع وثلاثون ثانيةً وثلاث عشرة ثالثةً وثلاث وعشرون رابعةً وخمس عشرة خامسةً وثلاثون سادسةً⊙ وأمّا للمرّيخ فخمسة عشر جزءًا وثلاث وأربعون دقيقةً وثمان عشرة ثانيةً وستّ وعشرون ثالثةً وخمس وخمسون رابعةً وستّ وأربعون خامسةً وثلاثون سادسةً φ وتحصل الحركة في السنة أمّا لزحل فاثنا عشر جزءًا وثلاث عشرة دقيقةً وثلاث وعشرون ثانيةً وستّ وخمسون ثالثةً وثلاثون رابعةً وثلاثون خامسةً وخمس عشرة سادسةً⊙ وأمّا للمشتري فثلاثون جزءًا وعشرون دقيقةً واثنتان وعشرون ثانيةً واثنتان وخمسون ثالثةً واثنتان وخمسون رابعةً وثمان وخمسون خامسةً وخمس وثلاثون سادسةً⊙ وأمّا للمرّيخ فمائة وأحد وتسعون جزءًا وستّ عشرة دقيقةً وأربع وخمسون ثانيةً وسبع وعشرون ثالثةً وثمان وثلاثون رابعةً وخمس وثلاثون خامسةً وخمس وأربعون سادسةً φ وتحصل الحركة في كلّ ثمان عشرة سنةً أمّا الحركة الوسطى لزحل فمئتان وعشرون جزءًا ودقيقة واحدة وعشر ثواني وسبع وخمسون ثانيةً وتسع روابع وأربع خوامس وثلاثون سادسةً⊙ وأمّا فضلة المشتري فمائة وستّة وثمانون جزءًا وستّ دقائق وإحدى وخمسون ثانيةً وإحدى وخمسون ثالثةً وثلاث وخمسون رابعةً وأربع وثلاثون خامسةً وثلاثون سادسةً⊙ وأمّا فضلة المرّيخ فمئتان وثلاثة أجزاء وأربع دقائق وعشرين ثانيةً وسبع عشرة ثالثةً وأربع وثلاثون رابعةً وثلاث وأربعون خامسةً وثلاثون سادسةً⊙
〈IX.4〉 د: جداول حركات الكواكب الخمسة الوسطى للطول والاختلاف
فنحن مرتّبون أيضًا لسهولة الاستعمال لكلّ واحد من الكواكب على مراتبها جدولًا يجتمع من تركيب هذه الحركات الوسطى التي وضعناها ومؤلّفون هذه الجداول على مثال ما ألّفنا عليه سائر الجداول من خمسة وأربعين سطرًا وقاسمون كلّ جدول منها ثلاثة أقسام ومثبتون في القسم الأوّل من كلّ جدول ما يجتمع من العدد لثمان عشرة سنةً وفي القسم الثاني ما يجتمع من العدد لسنة سنة ولساعة ساعة وفي القسم الثالث ما يجتمع من العدد لشهر شهر وليوم يوم⊙ وهذه هي الجداول⊙
أصل وسط زحل لأوّل يوم من السنة الأولى من ملك بخت نصر الأوّل كو مج من الجدي وذلك ط كو مج بروج درج دقائق.
وأصله في الاختلاف على ا ز ب ه: صواب أصله في الاختلاف ا د ب. بروج درج دقائق من البعد الأبعد من فلك التدوير وهذا بقي الحصّة وأصله في الفلك الخارج ر يد ي ب درج دقائق من العقرب وهذا هو موضع أوجه في زمان بطلميوس.
أصل وسطا المشتري لأوّل يوم من السنة الأولى من ملك بخت نصر الأوّل د ما درج دقائق من الميزان و د ما بروج درج دقائق وحاصله في الاختلاف فعلى د {...} د بروج درج دقائق من البعد الأبعد من فلك التدوير قمو د وهذا بقي الحصّة وحاصله من البعد الأبعد من الفلك الخارج المركز ب ط خ: ه ب ط درج دقائق من السنبلة و{...} هو أوجه في زمان بطلميوس.
جدول حركات الكواكب الخمسة الوسطى للطول وللاختلاف |
|||||||||||||||
| عدد الشهور | جدول حركات المشتري في الشور والأيّام للطول وللاختلاف |
||||||||||||||
الطول |
الاختلاف |
||||||||||||||
| أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | أجزاء | دقائق | ثواني | ثوالث | روابع | خوامس | سوادس | ||
ا |
ب |
كط |
لز |
يج |
كج |
يه |
ل |
كز |
د |
لا |
كج |
يج |
|
|
|
ب |
د |
نط |
يد |
كو |
مو |
لا |
|
ند |
ط |
ب |
مو |
كو |
|
|
|
ج |
ز |
كح |
نا |
م |
ط |
مو |
ل |
فا |
يج |
لد |
ط |
لط |
|
|
|
د |
ط |
نح |
كح |
نج |
لج |
ب |
|
قح |
يح |
ه |
لب |
نب |
|
|
|
ه |
يب |
كح |
و |
و |
نو |
يز |
ل |
قله |
لو |
نو |
ه |
|
|
||
و |
يد |
نز |
مج |
ك |
يط |
لج |
|
قسب |
كز |
ح |
يط |
يح |
|
|
|
ز |
يز |
كز |
ك |
لج |
مب |
مح |
ل |
قفط |
لا |
لط |
مب |
لا |
|
|
|
ح |
يط |
نو |
نز |
مز |
و |
د |
|
ريو |
لو |
يا |
ه |
مد |
|
|
|
ط |
كب |
كو |
له |
|
كط |
يط |
ل |
رمج |
م |
مب |
كح |
نز |
|
|
|
ي |
كد |
نو |
يب |
يج |
نب |
له |
|
رع |
مه |
يج |
نب |
ي |
|
|
|
يا |
كز |
كه |
مط |
كز |
يه |
ن |
ل |
رصز |
مط |
مه |
يه |
كج |
|
|
|
يب |
كط |
نه |
كو |
م |
لط |
و |
|
شكد |
ند |
يو |
لح |
لو |
|
|
|
| الأيّام | الطول |
الاختلاف |
|||||||||||||
ا |
|
د |
نط |
يد |
كو |
مو |
لا |
|
ند |
ط |
ب |
مو |
كو |
|
|
ب |
|
ط |
نح |
كح |
نج |
لج |
ب |
ا |
مح |
يح |
ه |
لب |
نب |
|
|
ج |
|
يد |
نز |
مج |
ك |
يط |
لج |
ب |
مب |
كز |
ح |
يط |
يح |
|
|
د |
|
يط |
نو |
نز |
مز |
و |
د |
ج |
لو |
لو |
يا |
ه |
مد |
|
|
ه |
|
كد |
نو |
يب |
يج |
نب |
له |
د |
ل |
مه |
يج |
نب |
ي |
|
|
و |
|
كط |
نه |
كو |
م |
لط |
و |
ه |
كد |
ند |
يو |
لح |
لو |
|
|
ز |
|
لد |
ند |
ما |
ز |
كه |
لز |
و |
يط |
ج |
يط |
كه |
ب |
|
|
ح |
|
لط |
نج |
نه |
لد |
يب |
ح |
ز |
يج |
يب |
كب |
يا |
كح |
|
|
ط |
|
مد |
نج |
ي |
|
نح |
لط |
ح |
ز |
كا |
كد |
نز |
ند |
|
|
ي |
|
مط |
نب |
كد |
كز |
مه |
ي |
ط |
ا |
ل |
كز |
مد |
ك |
|
|
يا |
|
ند |
نا |
لح |
ند |
لا |
ما |
ط |
نه |
لط |
ل |
ل |
مو |
|
|
يب |
|
نط |
ن |
نج |
كا |
يح |
يب |
ي |
مط |
مح |
لج |
يز |
يب |
|
|
يج |
ا |
د |
ن |
ز |
مح |
د |
مج |
يا |
مج |
نز |
لو |
ج |
لح |
|
|
يد |
ا |
ط |
مط |
كب |
يد |
نا |
يد |
يب |
لح |
و |
لح |
ن |
د |
|
|
يه |
ا |
يد |
مح |
لو |
ما |
لز |
مه |
يج |
لب |
يه |
ما |
لو |
ل |
|
|
يو |
ا |
يط |
مز |
نا |
ح |
كد |
يو |
يد |
كو |
كد |
مد |
كب |
نو |
|
|
يز |
ا |
كد |
ه |
له |
ي |
مز |
يه |
ك |
لج |
مز |
ط |
كب |
|
||
يح |
ا |
كط |
مو |
ك |
ا |
نز |
يح |
يو |
يد |
مب |
مط |
نه |
مح |
|
|
يط |
ا |
لد |
مه |
لد |
كح |
مج |
مط |
يز |
ح |
نا |
نب |
مب |
يد |
|
|
ك |
ا |
لط |
مد |
مح |
نه |
ل |
ك |
يح |
ج |
|
نه |
كح |
م |
|
|
كا |
ا |
مد |
مد |
ج |
كب |
يو |
نا |
يح |
نز |
ط |
نح |
يه |
و |
|
|
كب |
ا |
مط |
مج |
يز |
مط |
ج |
كب |
يط |
نا |
يط |
ا |
ا |
لب |
|
|
كج |
ا |
ند |
مب |
لب |
يه |
مط |
نج |
ك |
مه |
كح |
ج |
مز |
نح |
|
|
كد |
ا |
نط |
ما |
مو |
مب |
لو |
كد |
كا |
لط |
لز |
و |
لد |
كد |
|
|
كه |
ب |
د |
ما |
ا |
ط |
كب |
نه |
كب |
لج |
مو |
ط |
ك |
ن |
|
|
كو |
ب |
ط |
م |
يه |
لو |
ط |
كو |
كج |
كز |
نه |
يب |
ز |
يو |
|
|
كز |
ب |
يد |
لط |
ل |
ب |
نه |
نز |
كد |
كب |
د |
يد |
نج |
مب |
|
|
كح |
ب |
يط |
لح |
مد |
كط |
مب |
كح |
كه |
يو |
يج |
يز |
م |
ح |
|
|
كط |
ب |
كد |
لز |
نح |
نو |
كح |
نط |
كو |
ي |
كب |
ك |
كو |
لد |
|
|
ل |
ب |
كط |
لز |
يج |
كج |
يه |
ل |
كز |
د |
لا |
كج |
يج |
|
|
|
أصل وسط المرّيخ لأوّل بخت نصر ج لب درج دقائق من الحمل وأصل الاختلاف وهو {مجرّد} من البعد الأبعد من فلك التدوير ي ك بج ه: صواب ي كز يج بروج درج دقائق وذلك سد يج أجزاء دقائق.
{...} الزهرة في الاختلاف وهي حصّتها لأوّل سنة من تأريخ بخت نصر عا ز درج دقائق من البعد الأبعد من فلك التدوير أصل وسطها هو أصل وسط الشمس ذاته وذلك يا 0 مه 0 بروج درج دقائق ثواني. أصلها من البعد الأبعد من الخارج ا يو ي 0 بروج درج دقائق ثواني وهذا هو أصل أوجها {فهذا} زدنا على موضع الأوج عا ز يكون موضع حاصل حصّة الزهرة لأوّل بخت نصر ج كز يز 0 بروج درج دقائق.
ط: أصل وسط عطارد لأوّل يوم من بخت نصر وهو أصل وسط الشمس بعينه وذلك هو يا 0 مه 0 بروج درج دقائق ثواني وأصله في الاختلاف وهي حصّة يا نه ه: صواب كا نه درج دقائق من البعد الأبعد من التدوير وأصله من بعده من البعد الأبعد من الفلك الخارج وهذا هو موضع أوجه ففي ا ي من الميزان فإذا زدنا عن موضع الأوج هذا يا نه درج دقائق يكون أصل حصّة عطارد لأوّل بخت نصر و يج ه بروج درج دقائق.
〈IX.5〉 ه: فيما يحتاج إلى تقديمه للأصول التي يعمل عليها في الكواكب الخمسة المتحيّرة⊙
ولمّا كان قد يتّصل بما وضعنا من ذلك الكلام في أمر الاختلافات التي تكون للكواكب الخمسة المتحيّرة في مسيرها في الطول فإنّا استخرجنا الأصول التي يعمل عليها فيها أمّا على الجليل من النظر فبهذه الأسباب وهي أنّ الحركات التي هي أبسط الحركات وفيها مع ذلك كفاية لما نقصد له من هذا المعنى لمّا كانت اثنتين كما قلنا وهما الحركة التي تكون تداوير خارجة مراكزها عن مركز فلك البروج والحركة التي تكون تداوير موافقة مراكزها لمركزه إلّا أنّ الكواكب تتحرّك عليها في أفلاك تداوير وكانت أيضًا الاختلافات التي ترى في واحد واحد من الكواكب على ذلك المثال صنفين أحدهما يوجد من قبل أجزاء فلك البروج والآخر يوجد من قبل أصناف تشكّل ه: يعني بالتشكّل القياس إلى الشمس في بعد الكوكب منها الكواكب عند الشمس.
فإنّا وجدنا في هذا الصنف الأخير من صنفي الاختلافات بالأرصاد المتّصلة التي وقعت لأصناف من التشكّل مختلفةً في أجزاء واحدة بأعيانها من فلك البروج في الكواكب الخمسة أيضًا ه - صح: (يعني بقوله أيضًا إنّ ما وجده من ذلك في الكواكب الخمسة إنّما وجده أيضًا بمثل ما وجده في الشمس) الزمان الذي من أعظم ما يكون من حركة الكوكب التي حركته الوسطى تكون أبدًا أعظم من الزمان الذي من حركته الوسطى إلى أقلّ ه: (يعني في هذا الموضع بأقلّ ما يكون من حركته أعظم φ) ما يكون من حركته وليس هذا المعنى ممّا يتهيّأ وقوعه في الأصل الذي يعمل فيه على فلك خارج المركز بل الأمر في ذلك الأصل يجري على ضدّ ذلك وذلك أنّ أعظم ما يكون من الحركة إنّما يكون فيه أبدًا في البعد الأقرب وفي الأصلين جميعًا الحركة من البعد الأقرب إلى نقطة المسير الوسط أقلّ من الحركة من المسير الوسط إلى البعد الأبعد وأمّا في الأصل الذي يعمل فيه على فلك التدوير فقد يتهيّأ وقوع ذلك المعنى إلّا أنّه إنّما يقع بأن يكون أعظم ما يكون من المسير في البعد الأبعد منه لا في البعد الأقرب كما كان في القمر أعني بأن يكون الكوكب إذا ابتدأ من البعد الأبعد لم تكن نقلته قدمًا لحركة العالم مثل نقلة القمر بل تلقاء حركته فلذلك جعلنا هذا الصنف أيضًا من الاختلاف إنّما يقع بأفلاك تداوير⊙ وأمّا الصنف الآخر من الاختلاف الذي يوجد بالقياس إلى أجزاء فلك البروج فإنّا وجدناه بضدّ هذه الحال بالقسيّ من فلك البروج ه - خ - صح: فإنّا وجدناه بضدّ هذه الحال بالقسيّ من فلك البروج التي وجدت قد لحقت زائدةً في ظهورات بأعيانها أو أصناف من التشكّل بأعيانها وذلك أنّا وجدنا الزمان الذي من أقلّ ما يكون من الحركة إلى الحركة الوسطى يكون أبدًا أعظم من الزمان الذي من الحركة الوسطى إلى أعظم ما يكون من الحركة وهذا المعنى قد يتهيّأ أيضًا وقوعه لكلّ واحد من الأصلين على ما بيّنّا من تشابههما في مبدأ كلامنا في الشمس إلّا أنّه أشبه وأليق وأخصّ بالأصل الذي يعمل فيه على فلك خارج المركز ففي هذا الفلك وضعنا أيضًا هذا الصن من الاختلاف من قبل أنّا وجدنا الصنف الآخر أيضًا كأنّه إنّما يخصّ الأصل الذي يعمل فيه على فلك تدوير فقط ه - ج: وأخبر كما أنّ الأخصّ والأوّل لا{...} جهة مركز الفلك الخارج و{...} أخذنا اختلافها والجهة {...} إنّما وجدناها جهة فلك التدو{ير} وأمّا بعد ما استخرجناه من ذلك على الجليل من النظر فإنّا بتأمّلنا بالرصد المتّصل المسيرات الجزئيّة في الأحوال التي يكون قوامها بالأصلين جميعًا إذا خالط كلّ واحد صاحبه واعتبار بعضها ببعض وجدنا الأمر ليس يمكن أن يكون يجري هذا المجرى مرسلًا في أنّ السطوح التي فيها ترسم الأفلاك الخارجة المراكز غير متحرّكة حتى تكون أبعاد ما بين الخطّ المستقيم الذي يمرّ بمراكزها ومركز فلك البروج وهو الذي عليه توجد أبعد أبعادها وأقرب أبعادها وبين نقطتي الانقلابين أو نقطتي الاستواءين أبعادًا واحدةً بأعيانها ولا في أنّ أفلاك التداوير تتحرّك مراكزها على الأفلاك الخارجة المراكز أعني على الأفلاك التي بحسبها تجوز أفلاك التداوير إذا تحرّكت على الاستواء تلقاء حركة الكلّ في الأزمان المتساوية زوايا متساوية بل وجدنا نقط البعد الأبعد من الأفلاك الخارجة المراكز تنتقل نقلةً يسيرةً على توالي البروج عمّا بينها وبين الانقلابين إلّا أنّها أيضًا نقلة مستوية حول مركز فلك البروج ومبلغها في كلّ واحد من الكواكب قريب ممّا خرج لنا من مبلغ النقلة التي تكون لكرة الكواكب الثابتة أيضًا أعني في كلّ مائة سنة جزءًا واحدًا على قدر ما وقفنا عليه إلى هذه الغاية φ ووجدنا أيضًا مراكز أفلاك التداوير إنّما تتحرّك على دوائر مساوية للأفلاك الخارجة المراكز التي يكون بها الاختلاف إلّا أنّ هذه الدوائر ليست على مراكز واحدة بأعيانها ه - ج: وليست مراكزها هي مراكزها لكنّها أمّا في سائر الكواكب الخمسة سوى كوكب عطارد فعلى مراكز ه - خ: فتدور أفلاك تداويرها على أفلاك خارجة المراكز ومراكزها تقسم الخطوط المستقيمة التي بين مراكز الأفلاك الخارجة المراكز ه - خ: التي يكون بها الاختلاف وبين مركز فلك البروج بنصفين وأمّا في كوكب عطارد فعلى مركز بعده من المركز المدبّر له بقدر بعد هذا المركز من المركز ه - صح: من المركز الذي تكون عليه حركة الاختلاف نحو البعد الأبعد وبعد هذا المركز أيضًا من المركز الذي عليه البصر موضوع فإنّ في هذا الكوكب أيضًا وحده نجد الفلك الخارج المركز كما وجدناه في القمر يتحرّك على المركز الذي تقدّم ذكره إلى ضدّ جهة حركة فلك التدوير فيدور ↑ - خ: فيه هو أيضًا في كلّ سنة قدمًا لحركة الكلّ دورةً واحدةً وذلك أنّا نجده هو أيضًا يصير في دورة واحدة من أدوار المسير في قربه الأقرب مرّتين كما يصير القمر في قربه الأقرب في كلّ شهر مرّتين⊙
〈IX.6〉 و: في الجهة التي جرى الأمر عليها في هذين الأصلين وما بينهما من الاختلاف⊙
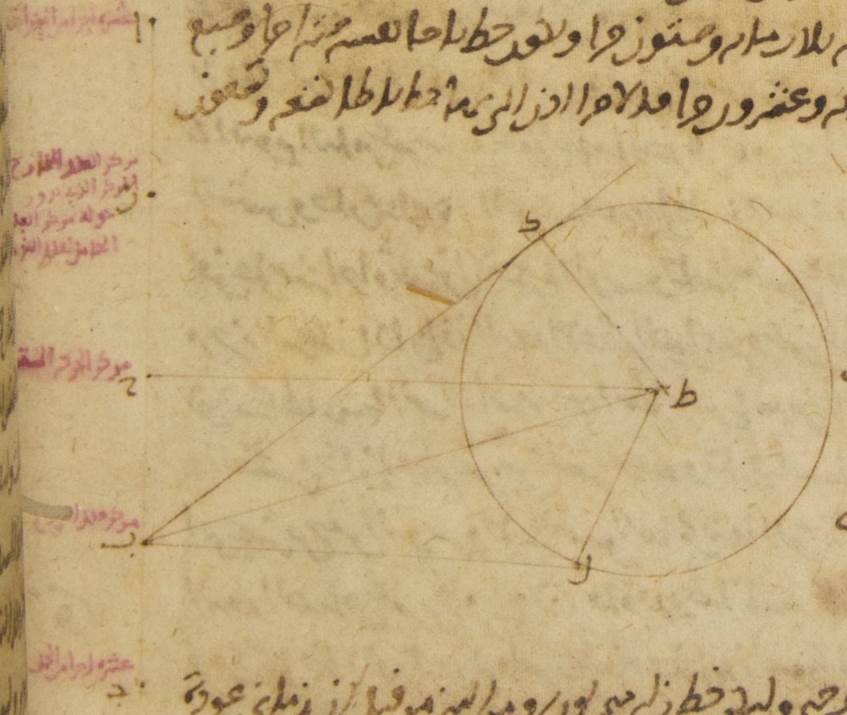
وقد يسهل ويقرب فهم الوجه الذي عليه جرى الأمر في حصول ما حصل من الأصول من قبل ما قدّمنا وضعه ممّا أنا واصفه آ: ليتوهّم أوّلًا في الأصل الذي يعمل عليه في سائر الكواكب ه: يعني عيـ{...} الخمسة فلك خارج المركز ألف باء جيم حول مركز دال وقطر يمرّ بنقطة دال وبمركز فلك البروج ألف دال جيم ولتكن غاية مركز فلك البروج أعني بصر الناظر نقطة هاء ولتكن عليه نقطة ألف أبعد البعد ونقطة جيم أقرب القرب ولنقسم خطّ دال هاء بنصفين على نقطة زاي ولنرسم على مركز زاي وببعد دال ألف دائرة ومن البيّن أنّها تكون مساويةً لدائرة ألف باء جيم ولتكن دائرة حاء طاء كاف ولنرسم على مركز طاء فلك تدوير لام ميم ولنوصل خطّ لام طاء ميم دال فنحن نضع أوّلًا أنّ سطح الأفلاك الخارجة المراكز مائل عن سطح فلك البروج وأنّ سطح فلك التدوير أيضًا مائل عن سطح الأفلاك الخارجة المراكز من أجل مسير الكواكب في العرض على ما سنبيّنه ه: هذان المعنيان بيّنهما في المقالة الثالثة عشرة من أمرها فما بعد ولكنّا في المسيرات في الطول طلبًا لسهولة العمل بتوهّمها كلّها في سطح واحد وهو سطح فلك البروج وذلك أنّه ليس يلحق في الطول فضل يعتدّ به من قبل (ميول) ↑: هذين الميلين إنّما مقدارهما ↑: صح المقدار الذي سيظهر أيضًا فيما بعد في واحد واحد من الكواكب φ ثمّ نقول إنّ هذا السطح
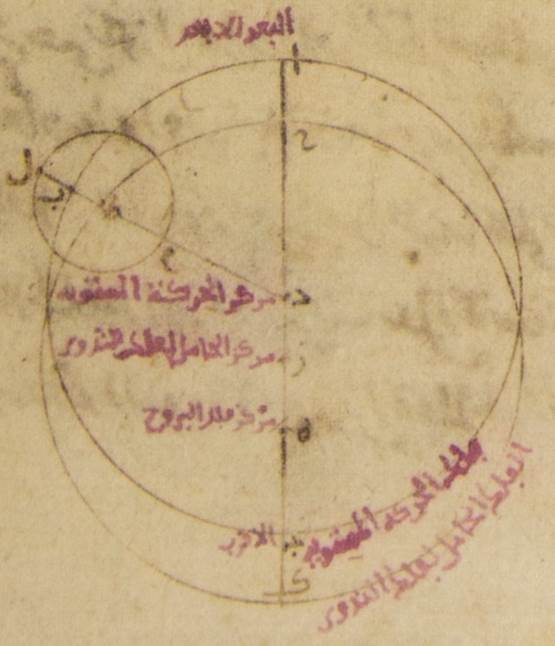 بأسره يدور على استواء على توالي البروج حول مركزها فينقل نقط البعد الأبعد والبعد الأقرب في كلّ مائة سنة جزءًا واحدًا وأنّ قطر فلك التدوير وهو خطّ لام طاء ميم تديره نقطة دال على استواء أيضًا على توالي البروج بقدر ما يلزم من عودة الكوكب في الطول وأنّه يدير بدورانه نقطتي لام ميم من فلك التدوير وأنّ نقطة طاء تتحرّك أبدًا على دائرة حاء طاء كاف الخارجة المركز وأنّ الكوكب نفسه يتحرّك على فلك تدوير لام ميم على استواء أيضًا وعلى حسب القطر المحاذي أبدًا لنقطة دال وأنّ عوداته يكون على قدر ما يلزم من الأدوار الوسطى ه: يعني ما تقدّم وصفه من الجداول التي للاختلاف الذي يكون بالقياس إلى الشمس وأنّ النقلة التي في البعد الأبعد إنّما تكون على توالي البروج φ وقد يتهيّأ أيضًا تصوّر ما يخصّ الأصل الذي يعمل عليه في حركة عطارد على هذا النحو ب: ليكن الفلك الخارج المركز الذي للاختلاف ألف باء جيم حول مركز دال والقطر الذي يمرّ بنقطة دال وبنقطة هاء التي هي مركز فلك البروج الذي يمرّ بالبعد الأبعد وهو نقطة ألف خطّ ألف دال هاء جيم وليوجد على خطّ ألف دال خطّ مساو لخطّ دال هاء نحو نقطة ألف وهي البعد الأبعد وليكن دال زاي ولنقرّ سائر الأشياء على حالها أعني أنّ السطح كلّه يدور حول نقطة هاء فننقل البعد الأبعد تلقاء حركة الكلّ بقدر نقلته في سائر الكواكب وأنّ فلك التدوير يدور حول نقطة دال على استواء ه: تلقاء حركة الكلّ بخطّ دال باء وأنّ الكوكب أيضًا يتحرّك على فلك تدويره على مثال سائر الكواكب ما خلا أنّا نضع هاهنا مركز الفلك الخارج المركز الآخر الذي عليه أبدًا مركز فلك التدوير ه - خ - صح: مركز فلك التدوير وهو أيضًا مساوٍ للفلك الأوّل الخارج المركز ص(يكون مركز فلك التدوير)ص يدور حول نقطة زاي إلى ضدّ الجهة التي إليها يتحرّك فلك التدوير أعني قدمًا لفلك البروج على استواء وعلى مساواة في السرعة له ويكون ه - خ - صح: يكون الذي يديره خطّ زاي حاء طاء حتّى يكون
بأسره يدور على استواء على توالي البروج حول مركزها فينقل نقط البعد الأبعد والبعد الأقرب في كلّ مائة سنة جزءًا واحدًا وأنّ قطر فلك التدوير وهو خطّ لام طاء ميم تديره نقطة دال على استواء أيضًا على توالي البروج بقدر ما يلزم من عودة الكوكب في الطول وأنّه يدير بدورانه نقطتي لام ميم من فلك التدوير وأنّ نقطة طاء تتحرّك أبدًا على دائرة حاء طاء كاف الخارجة المركز وأنّ الكوكب نفسه يتحرّك على فلك تدوير لام ميم على استواء أيضًا وعلى حسب القطر المحاذي أبدًا لنقطة دال وأنّ عوداته يكون على قدر ما يلزم من الأدوار الوسطى ه: يعني ما تقدّم وصفه من الجداول التي للاختلاف الذي يكون بالقياس إلى الشمس وأنّ النقلة التي في البعد الأبعد إنّما تكون على توالي البروج φ وقد يتهيّأ أيضًا تصوّر ما يخصّ الأصل الذي يعمل عليه في حركة عطارد على هذا النحو ب: ليكن الفلك الخارج المركز الذي للاختلاف ألف باء جيم حول مركز دال والقطر الذي يمرّ بنقطة دال وبنقطة هاء التي هي مركز فلك البروج الذي يمرّ بالبعد الأبعد وهو نقطة ألف خطّ ألف دال هاء جيم وليوجد على خطّ ألف دال خطّ مساو لخطّ دال هاء نحو نقطة ألف وهي البعد الأبعد وليكن دال زاي ولنقرّ سائر الأشياء على حالها أعني أنّ السطح كلّه يدور حول نقطة هاء فننقل البعد الأبعد تلقاء حركة الكلّ بقدر نقلته في سائر الكواكب وأنّ فلك التدوير يدور حول نقطة دال على استواء ه: تلقاء حركة الكلّ بخطّ دال باء وأنّ الكوكب أيضًا يتحرّك على فلك تدويره على مثال سائر الكواكب ما خلا أنّا نضع هاهنا مركز الفلك الخارج المركز الآخر الذي عليه أبدًا مركز فلك التدوير ه - خ - صح: مركز فلك التدوير وهو أيضًا مساوٍ للفلك الأوّل الخارج المركز ص(يكون مركز فلك التدوير)ص يدور حول نقطة زاي إلى ضدّ الجهة التي إليها يتحرّك فلك التدوير أعني قدمًا لفلك البروج على استواء وعلى مساواة في السرعة له ويكون ه - خ - صح: يكون الذي يديره خطّ زاي حاء طاء حتّى يكون
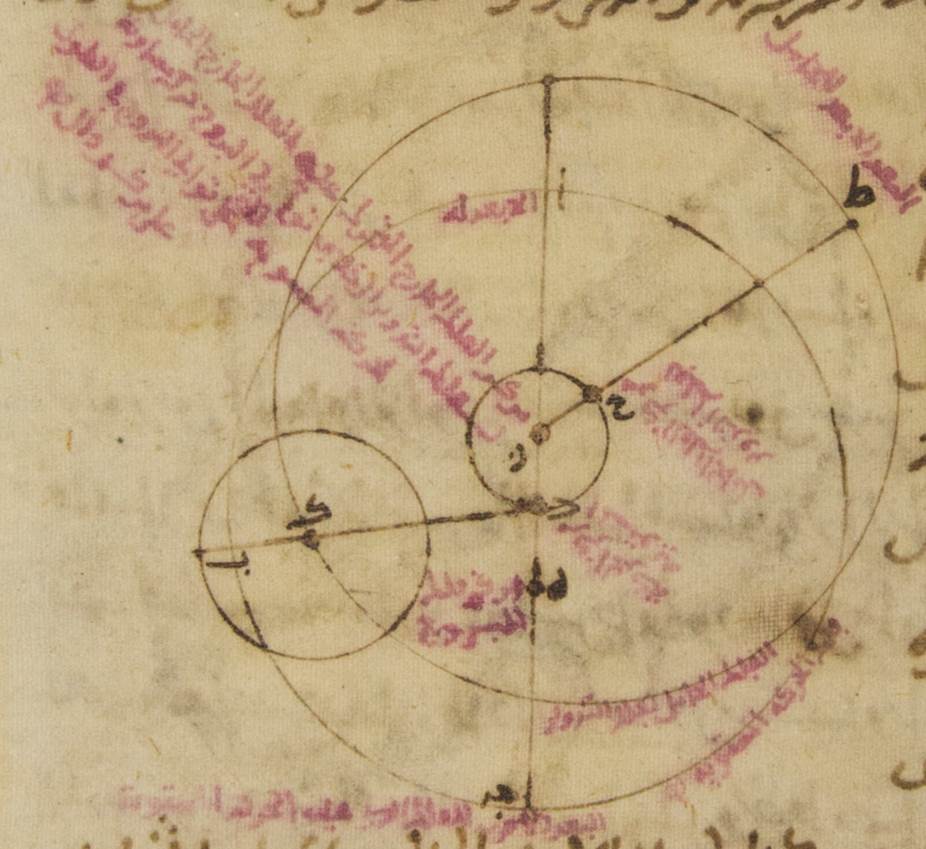 خطّا دال باء وزاي حاء طاء أمّا بالقياس إلى النقط من فلك البروج فإنّما يعود كلّ واحد منهما إلى الموضع الذي منه ابتداء في كلّ سنة مرّةً واحدةً وأمّا عودة أحدهما إلى الآخر فمن البيّن أنّها تكون في كلّ سنة مرّتين ويكون بعد هذا المركز أيضًا من نقطة زاي أبدًا مساويًا لكلّ واحد من خطّي هاء دال دال زاي كبعد زاي حاء حتّى تكون الدائرة الصغيرة التي ترسمها حركته قدمًا لحركة الكلّ على مركز زاي وببعد زاي حاء ينحاز ه - ص: نجتاز أبدًا بنقطة دال أيضًا التي هي مركز الفلك الأوّل الخارج المركز الثابت ويكون الفلك الخارج المركز المتحرّك يرسم في كلّ حال على مركز حاء وببعد حاء طاء المساوي لخطّ دال ألف كدائرة طاء كاف هاهنا ويكون فلك التدوير مركزه أبدًا عليه كما هو هاهنا على نقطة كاف φ وقد يزداد ويقوى فهم ما ↑ - خ: في ما وضعناه من ذلك بالأشياء التي تستبين في مقادير هذه الحركات في واحد واحد من الكواكب φ وستظهر فيما وضعناه من ذلك الأشياء التي كأنّها حركتنا ه - خ: (فإنّ ما حرّكها) (كما تحرّك) (الرسوم) (المثبتة) ه - خ - صح: لتنبيه على هذه الأصول التي وضعناها وتصحّ في مواضع كثيرة ه - ج: ويتبيّن مع ذلك ويوضح الـ{...} كثيرة الأسباب التي حركـ{...} هذه الجهات ⊙ وقد ينبغي أن نتقدّم فنعلم أنّ الأدوار في الطول إذ كانت لا تعود مع النقط من فلك البروج ولا مع نقط أبعد البعد أو أقرب القرب من الأفلاك الخارجة المراكز لما وضعناه من نقلتها فإنّ الحركات في الطول التي وضعناها على الجهة التي تقدّم وضعها ليس ه - خ: ليست التي تشتمل على العودات التي توجد بالقياس إلى نقط البعد الأبعد من الأفلاك الخارجة المراكز بل تكون بالقياس إلى الانقلابين والاستواءين على ما يلزم في زمان السنة عندنا φ فقد ه - خ - صح: وقد ينبغي أن نبيّن أوّلًا أنّ بحسب هذه الأصول أيضًا إذا كان المسير الوسط للكوكب في الطول بعده عن جنبي نقطة من نقط البعد الأبعد أو البعد الأقرب بالسواء فحينئذ يكون الفضل الذي من قبل الاختلاف المنسوب إلى فلك البروج في كلّ واحد من البعدين سواءً وأعظم ما يكون من البعد عن المسير الوسط في فلك التدوير في جهة ه: يعني جهة واحدة نحو البعد الأبعد واحدة بعينها حينئذ تكون أيضًا سواءً جـ: فليكن لفلك الخارج المركز الذي يتحرّك عليه مركز فلك التدوير ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم وليوضع عليه مركز فلك البروج نقطة زاي ومركز الفلك الخارج المركز الذي يفعل الاختلاف أعني المركز الذي نقول إنّ المسير الوسط لفلك التدوير على استواء عليه تكون نقطة حاء ولنجر خطّا باء حاء طاء دال حاء كاف وليكن بعدهما من نقطة ألف وهي البعد الأبعد سواءً حتّى تكون زاويتا ألف حاء باء ألف حاء دال متساويتين ولنرسم على نقطتي باء دال فلكا تدوير متساويان ولنوصل خطّا باء زاي دال زاي ولنخرج من نقطة زاي التي هي البصر خطّا زاي لام زاي ميم يماسّان فلكي التدوير في جهة واحدة أقول إنّ زاوية حاء باء زاي وهي زاوية الفضل الذي من قبل الاختلاف المنسوب إلى فلك البروج مساويةً لزاوية حاء دال زاي وأنّ زاوية باء زاي لام وهي زاوية أعظم ما ه: (يعني أعظم الأبعاد من الأوج من جهتيه لا في جهة واحدة) يكون من البعد في فلك التدوير مساويةً لزاوية دال زاي ميم التي هي نظيرتها فإنّ بذلك أيضًا تكون مقادير الأبعاد التي هي أعظم ه: يعني أعظم ما يكون البعد في فلك التدوير عن منزل مركزه الأبعاد من المسير الوسط الذي يكون عن اختلاط الاختلافين متساويةً⊙ فلنخرج أعمدةً أمّا من نقطتي باء دال فعمودا باء لام دال ميم على خطّي زاي لام زاي ميم وأمّا من نقطة هاء فعمودا هاء نون هاء سين
خطّا دال باء وزاي حاء طاء أمّا بالقياس إلى النقط من فلك البروج فإنّما يعود كلّ واحد منهما إلى الموضع الذي منه ابتداء في كلّ سنة مرّةً واحدةً وأمّا عودة أحدهما إلى الآخر فمن البيّن أنّها تكون في كلّ سنة مرّتين ويكون بعد هذا المركز أيضًا من نقطة زاي أبدًا مساويًا لكلّ واحد من خطّي هاء دال دال زاي كبعد زاي حاء حتّى تكون الدائرة الصغيرة التي ترسمها حركته قدمًا لحركة الكلّ على مركز زاي وببعد زاي حاء ينحاز ه - ص: نجتاز أبدًا بنقطة دال أيضًا التي هي مركز الفلك الأوّل الخارج المركز الثابت ويكون الفلك الخارج المركز المتحرّك يرسم في كلّ حال على مركز حاء وببعد حاء طاء المساوي لخطّ دال ألف كدائرة طاء كاف هاهنا ويكون فلك التدوير مركزه أبدًا عليه كما هو هاهنا على نقطة كاف φ وقد يزداد ويقوى فهم ما ↑ - خ: في ما وضعناه من ذلك بالأشياء التي تستبين في مقادير هذه الحركات في واحد واحد من الكواكب φ وستظهر فيما وضعناه من ذلك الأشياء التي كأنّها حركتنا ه - خ: (فإنّ ما حرّكها) (كما تحرّك) (الرسوم) (المثبتة) ه - خ - صح: لتنبيه على هذه الأصول التي وضعناها وتصحّ في مواضع كثيرة ه - ج: ويتبيّن مع ذلك ويوضح الـ{...} كثيرة الأسباب التي حركـ{...} هذه الجهات ⊙ وقد ينبغي أن نتقدّم فنعلم أنّ الأدوار في الطول إذ كانت لا تعود مع النقط من فلك البروج ولا مع نقط أبعد البعد أو أقرب القرب من الأفلاك الخارجة المراكز لما وضعناه من نقلتها فإنّ الحركات في الطول التي وضعناها على الجهة التي تقدّم وضعها ليس ه - خ: ليست التي تشتمل على العودات التي توجد بالقياس إلى نقط البعد الأبعد من الأفلاك الخارجة المراكز بل تكون بالقياس إلى الانقلابين والاستواءين على ما يلزم في زمان السنة عندنا φ فقد ه - خ - صح: وقد ينبغي أن نبيّن أوّلًا أنّ بحسب هذه الأصول أيضًا إذا كان المسير الوسط للكوكب في الطول بعده عن جنبي نقطة من نقط البعد الأبعد أو البعد الأقرب بالسواء فحينئذ يكون الفضل الذي من قبل الاختلاف المنسوب إلى فلك البروج في كلّ واحد من البعدين سواءً وأعظم ما يكون من البعد عن المسير الوسط في فلك التدوير في جهة ه: يعني جهة واحدة نحو البعد الأبعد واحدة بعينها حينئذ تكون أيضًا سواءً جـ: فليكن لفلك الخارج المركز الذي يتحرّك عليه مركز فلك التدوير ألف باء جيم دال حول مركز هاء وقطر ألف هاء جيم وليوضع عليه مركز فلك البروج نقطة زاي ومركز الفلك الخارج المركز الذي يفعل الاختلاف أعني المركز الذي نقول إنّ المسير الوسط لفلك التدوير على استواء عليه تكون نقطة حاء ولنجر خطّا باء حاء طاء دال حاء كاف وليكن بعدهما من نقطة ألف وهي البعد الأبعد سواءً حتّى تكون زاويتا ألف حاء باء ألف حاء دال متساويتين ولنرسم على نقطتي باء دال فلكا تدوير متساويان ولنوصل خطّا باء زاي دال زاي ولنخرج من نقطة زاي التي هي البصر خطّا زاي لام زاي ميم يماسّان فلكي التدوير في جهة واحدة أقول إنّ زاوية حاء باء زاي وهي زاوية الفضل الذي من قبل الاختلاف المنسوب إلى فلك البروج مساويةً لزاوية حاء دال زاي وأنّ زاوية باء زاي لام وهي زاوية أعظم ما ه: (يعني أعظم الأبعاد من الأوج من جهتيه لا في جهة واحدة) يكون من البعد في فلك التدوير مساويةً لزاوية دال زاي ميم التي هي نظيرتها فإنّ بذلك أيضًا تكون مقادير الأبعاد التي هي أعظم ه: يعني أعظم ما يكون البعد في فلك التدوير عن منزل مركزه الأبعاد من المسير الوسط الذي يكون عن اختلاط الاختلافين متساويةً⊙ فلنخرج أعمدةً أمّا من نقطتي باء دال فعمودا باء لام دال ميم على خطّي زاي لام زاي ميم وأمّا من نقطة هاء فعمودا هاء نون هاء سين
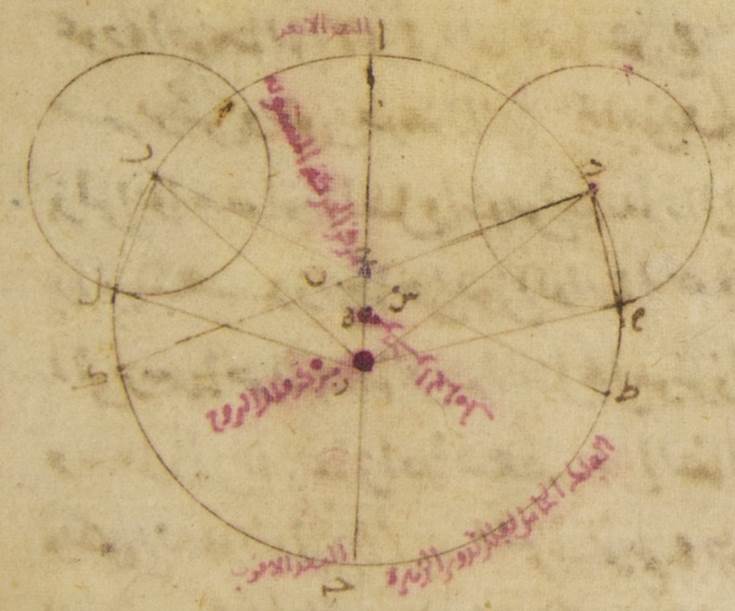 على خطّي باء طاء دال كاف فلأنّ زاوية سين حاء هاء مساوية لزاوية نون حاء هاء والزاويتين اللتين عند نقطتي نون سين قائمتان وخطّ هاء حاء مشترك للمثلّثين المتساويي الزوايا يكون خطّ نون حاء مساويًا لخطّ سين حاء وعمود هاء نون مساويًا لعمود هاء سين. فخطّا باء طاء دال كاف إذن متساويا البعد من مركز هاء فهما إذن متساويان ونصفاهما أيضًا متساويان فيكون خطّا باء حاء دال حاء الباقيان متساويين لكنّ خطّ حاء زاي مشترك والزاويتين اللتين تحيط بهما الأضلاع المتساوية وهما زاويتا باء حاء زاي دال حاء زاي متساويتان فقاعدة باء زاي إذن مساويةً لقاعدة دال زاي وزاوية حاء باء زاي مساوية لزاوية حاء دال زاي ولكنّ خطّ باء لام أيضًا الذي من مركز فلك التدوير مساوٍ لخطّ دال ميم والزاويتين اللتين عند نقطتي لام ميم قائمتان فزاوية باء زاي لام إذن مساوية أيضًا لزاوية دال زاي ميم وذلك ما كنّا قصدنا لتبيينه د: وليكن أيضًا بسبب الأصل الذي عليه عملنا في عطارد القطر الذي يمرّ بمراكز الدوائر وبالبعد الأبعد فيها ألف باء جيم ولننزل أنّ نقطة ألف مركز فلك البروج ونقطة باء مركز الفلك الخارج المركز الذي يفعل الاختلاف ونقطة جيم النقطة التي حولها يدور مركز الفلك الخارج المركز الحامل لفلك التدوير ولنخرج أيضًا خطّا باء دال باء هاء في الجهتين للحركة المستوية التي لفلك التدوير تلقاء حركة الكلّ وخطّا جيم زاي جيم حاء لدوران الفلك الخارج المركز قدمًا لحركة الكلّ على المساواة في السرعة حتّى تكون الزوايا التي عند نقطتي جيم باء متساوية وذلك بيّن فيكون خطّ باء دال موازيًا لخطّ جيم زاي وخطّ باء هاء موازيًا لخطّ جيم حاء ولنوجد على خطّي جيم زاي جيم حاء مركز الفلكين الخارجي المركز وليكونا نقطتي طاء كاف ولننزل أنّ الفلكين اللذين يرسمان عليهما اللذين عليهما يكون فلكا التدوير يمرّان بنقطتي لام ميم ه - ص - صح: هاء ودال ولنرسم أيضًا حول نقطتي دال هاء فلكا تدوير متساويان ولنوصل خطّا ألف دال ألف هاء ولنخرج خطّان يماسّان فلكي التدوير من جهة واحدة وليكونا خطّي ألف لام ألف ميم فينبغي أن نتبيّن أنّ على هذا الوجه أيضًا تكون زاوية ألف دال باء وهي زاوية الفضل الذي للاختلاف المنسوب إلى فلك البروج مساويةً لزاوية ألف هاء باء وأنّ زاوية دال ألف لام وهي زاوية أعظم ما يكون من البعد في فلك التدوير مساويةً لزاوية هاء ألف ميم فلنوصل خطوط باء طاء باء كاف طاء دال كاف هاء ولنخرج أعمدةً أمّا من نقطة جيم فعمودا جيم نون جيم سين على خطّي باء دال باء هاء وأمّا من نقطتي دال هاء فعمودا دال زاي هاء حاء على خطّي جيم زاي جيم حاء وعمودا دال لام هاء ميم على خطّي ألف لام ألف ميم فلأنّ زاوية جيم باء نون مساوية لزاوية جيم باء سين والزاويتين اللتين عند نقطتي نون سين قائمتان وخطّ جيم باء مشترك يكون خطّ جيم نون أيضًا مساويًا لخطّ جيم سين أعني أنّ خطّ دال زاي مساو لخطّ هاء حاء لكنّ خطّ دال طاء مساو لخطّ كاف هاء والزاويتين اللتين عند نقطتي زاي حاء قائمتان فتكون زاوية دال طاء زاي أيضًا مساوية لزاوية هاء كاف حاء وزاوية جيم طاء باء
على خطّي باء طاء دال كاف فلأنّ زاوية سين حاء هاء مساوية لزاوية نون حاء هاء والزاويتين اللتين عند نقطتي نون سين قائمتان وخطّ هاء حاء مشترك للمثلّثين المتساويي الزوايا يكون خطّ نون حاء مساويًا لخطّ سين حاء وعمود هاء نون مساويًا لعمود هاء سين. فخطّا باء طاء دال كاف إذن متساويا البعد من مركز هاء فهما إذن متساويان ونصفاهما أيضًا متساويان فيكون خطّا باء حاء دال حاء الباقيان متساويين لكنّ خطّ حاء زاي مشترك والزاويتين اللتين تحيط بهما الأضلاع المتساوية وهما زاويتا باء حاء زاي دال حاء زاي متساويتان فقاعدة باء زاي إذن مساويةً لقاعدة دال زاي وزاوية حاء باء زاي مساوية لزاوية حاء دال زاي ولكنّ خطّ باء لام أيضًا الذي من مركز فلك التدوير مساوٍ لخطّ دال ميم والزاويتين اللتين عند نقطتي لام ميم قائمتان فزاوية باء زاي لام إذن مساوية أيضًا لزاوية دال زاي ميم وذلك ما كنّا قصدنا لتبيينه د: وليكن أيضًا بسبب الأصل الذي عليه عملنا في عطارد القطر الذي يمرّ بمراكز الدوائر وبالبعد الأبعد فيها ألف باء جيم ولننزل أنّ نقطة ألف مركز فلك البروج ونقطة باء مركز الفلك الخارج المركز الذي يفعل الاختلاف ونقطة جيم النقطة التي حولها يدور مركز الفلك الخارج المركز الحامل لفلك التدوير ولنخرج أيضًا خطّا باء دال باء هاء في الجهتين للحركة المستوية التي لفلك التدوير تلقاء حركة الكلّ وخطّا جيم زاي جيم حاء لدوران الفلك الخارج المركز قدمًا لحركة الكلّ على المساواة في السرعة حتّى تكون الزوايا التي عند نقطتي جيم باء متساوية وذلك بيّن فيكون خطّ باء دال موازيًا لخطّ جيم زاي وخطّ باء هاء موازيًا لخطّ جيم حاء ولنوجد على خطّي جيم زاي جيم حاء مركز الفلكين الخارجي المركز وليكونا نقطتي طاء كاف ولننزل أنّ الفلكين اللذين يرسمان عليهما اللذين عليهما يكون فلكا التدوير يمرّان بنقطتي لام ميم ه - ص - صح: هاء ودال ولنرسم أيضًا حول نقطتي دال هاء فلكا تدوير متساويان ولنوصل خطّا ألف دال ألف هاء ولنخرج خطّان يماسّان فلكي التدوير من جهة واحدة وليكونا خطّي ألف لام ألف ميم فينبغي أن نتبيّن أنّ على هذا الوجه أيضًا تكون زاوية ألف دال باء وهي زاوية الفضل الذي للاختلاف المنسوب إلى فلك البروج مساويةً لزاوية ألف هاء باء وأنّ زاوية دال ألف لام وهي زاوية أعظم ما يكون من البعد في فلك التدوير مساويةً لزاوية هاء ألف ميم فلنوصل خطوط باء طاء باء كاف طاء دال كاف هاء ولنخرج أعمدةً أمّا من نقطة جيم فعمودا جيم نون جيم سين على خطّي باء دال باء هاء وأمّا من نقطتي دال هاء فعمودا دال زاي هاء حاء على خطّي جيم زاي جيم حاء وعمودا دال لام هاء ميم على خطّي ألف لام ألف ميم فلأنّ زاوية جيم باء نون مساوية لزاوية جيم باء سين والزاويتين اللتين عند نقطتي نون سين قائمتان وخطّ جيم باء مشترك يكون خطّ جيم نون أيضًا مساويًا لخطّ جيم سين أعني أنّ خطّ دال زاي مساو لخطّ هاء حاء لكنّ خطّ دال طاء مساو لخطّ كاف هاء والزاويتين اللتين عند نقطتي زاي حاء قائمتان فتكون زاوية دال طاء زاي أيضًا مساوية لزاوية هاء كاف حاء وزاوية جيم طاء باء
 مساوية لزاوية جيم كاف باء من قبل أنّ خطّ كاف جيم وضع مساويًا لخطّ جيم طاء وخطّ جيم باء مشترك وزاوية طاء جيم باء مساوية لزاوية كاف جيم باء فتكون زاوية باء طاء دال الباقية أيضًا مساوية لزاوية باء كاف هاء وتكون قاعدة باء دال مساوية لقاعدة باء هاء لكنّ خطّ باء ألف أيضًا مشترك وزاوية دال باء ألف مساوية لزاوية هاء باء ألف فتكون قاعدة ألف دال مساويةً لقاعدة ألف هاء وتكون زاوية ألف دال باء مساويةً لزاوية ألف هاء باء ولذلك بعينه من قبل أنّ خطّ دال لام أيضًا مساو لخطّ هاء ميم والزاويتين اللتين عند نقطتي لام ميم قائمتان تكون زاوية دال ألف لام مساوية لزاوية هاء ألف ميم وذلك ما كنّا قصدنا لتبيينه
مساوية لزاوية جيم كاف باء من قبل أنّ خطّ كاف جيم وضع مساويًا لخطّ جيم طاء وخطّ جيم باء مشترك وزاوية طاء جيم باء مساوية لزاوية كاف جيم باء فتكون زاوية باء طاء دال الباقية أيضًا مساوية لزاوية باء كاف هاء وتكون قاعدة باء دال مساوية لقاعدة باء هاء لكنّ خطّ باء ألف أيضًا مشترك وزاوية دال باء ألف مساوية لزاوية هاء باء ألف فتكون قاعدة ألف دال مساويةً لقاعدة ألف هاء وتكون زاوية ألف دال باء مساويةً لزاوية ألف هاء باء ولذلك بعينه من قبل أنّ خطّ دال لام أيضًا مساو لخطّ هاء ميم والزاويتين اللتين عند نقطتي لام ميم قائمتان تكون زاوية دال ألف لام مساوية لزاوية هاء ألف ميم وذلك ما كنّا قصدنا لتبيينه
〈IX.7〉 ز: في تبيين البعد الأبعد لكوكب عطارد وتنقّله
ولمّا علمنا ذلك استخرجنا أوّلًا الأجزاء من فلك البروج التي عليها يكون البعد الأبعد لكوكب عطارد أي ه - ج: ومن بعد علمنا بما تقدّم {...} {...} من أجزاء فلك أوساط {...} {...} الذي عليه البعد {...} لكوكب عطارد على هذه {...} الأجزاء التي هي بهذا الطريق وهو أنّا جعلنا نطلب أرصادًا لأعظم ما يكون من أبعاده كان فيها المسير الصباحيّ بعده من المسير الوسط للشمس ه - ج: {...} مسير الشمس الوسط مساوٍ لمسير عطارد الوسط أعني للكوكب مثل بعد المسير المسائي منه فإنّ ذلك إذا وجد فيما بيّنّاه يجب ضرورةً أن تكون النقطة من فلك البروج التي فيما بين المسيرين تحدّ البعد الأبعد في الفلك الخارج المركز فوجدنا في ذلك أرصادًا وإن كانت يسيرةً من قبل أنّ مثل هذا الازدواج قلّ ما يتّفق على الحقيقة إلّا أنّا نقدر بها على الوقوف على ما قصدنا له فأمّا القريبة العهد فهي هذه رصدنا نحن في السنة السادسة عشرة لأدريانوس في الشهر عند المصريّين المسمّى فامانوث منها في اليوم السادس عشر منه في العشيّة التي يتلوها اليوم السابع عشر كوكب عطارد بالآلة التي اتّخذناها للرصد وهو في غاية ما يكون من بعده من مسير الشمس الوسط وكان قياسنا له في ذلك الوقت بالكوكب المعروف بالدبران فرأينا حاصله في الطول على جزء واحد من الحوت لكنّ مسير الشمس الوسط كان حاصله في ذلك الوقت على تسعة أجزاء ونصف وربع جزء من الدلو فالبعد إذن الذي هو غاية البعد المسائيّ عن المسير الوسط كان أحدًا وعشرين جزءًا وربع جزء φ ورصدنا أيضًا في سنة ثمان عشرة لأدريانوس في الشهر عند المصريّين المسمّى إبيفي منها في اليوم الثامن عشر منه في الغلس من الليلة التي يتلوها اليوم التاسع عشر كوكب عطارد وهو في أبعد ما يكون من الشمس وكان يرى لطيفًا جدًّا خفيًّا وكان قياسنا له بالدبران أيضًا فرأينا حاصله على ثمانية عشر جزءًا ونصف وربع جزء من الثور لن كان حاصل الشمس في ذلك الوقت بمسيرها الوسط على عشرة أجزاء من التوأمين فهاهنا أيضًا كان أبعد البعد الصباحيّ من المسير الوسط مثل تلك الأجزاء وهي أحد وعشرون جزءًا وربع جزء فلمّا كان المسير الوسط للكوكب في أحد الرصدين كان حاصله على تسعة أجزاء ونصف وربع من الدلو وفي الرصد الآخر على عشرة أجزاء من التوأمين وكانت النقطة من فلك البروج التي فيما بين هذين الحاصلين يحصل على عشرة أجزاء من الحمل منقوصًا منها ثمّ جزء واحد فالقطر إذن الذي يمرّ بالبعد الأبعد كان موضعه في ذلك الوقت هذا الموضع⊙ ورصدنا نحن أيضًا بآلة القياس في السنة الأولى لأنطونيس في شهر إبيفي عند المصريّين منها في اليوم العشرين منه في العشيّة التي يتلوها اليوم الحادي والعشرون كوكب عطارد وهو في غاية بعده من مسير الشمس الوسط وكان قيامنا له في ذلك الوقت فالكوكب الذي على قلب الأسد فرأينا حاصله على سبعة أجزاء من السرطان لكنّ منزل الشمس بحركتها الوسطى كان في ذلك الوقت على عشرة أجزاء ونصف من التوأمين فكان إذن أبعد البعد المسائيّ من المسير الوسط ستّةً وعشرين جزءًا ونصف جزء φ وكذلك أيضًا رصدنا في السنة الرابعة من سني أنطونيس في شهر فامانوث عند المصريّين في اليوم الثامن عشر منه في الغلس من الليلة التي يتلوها اليوم التاسع عشر كوكب عطارد وكان أيضًا في أعظم ما يكون من بعده من الشمس وكان قياسنا له بالكوكب المعروف بقلب العقرب فرأينا حاصله على ثلاثة عشر جزءًا ونصف جزء من الجدي وكان حاصل الشمس بحركتها الوسطى على عشرة أجزاء من الدلو فهاهنا أيضًا كان أعظم البعد الصباحيّ من المسير الوسط مثل تلك الأجزاء وهي ستّة وعشرون جزءًا ونصف جزء φ فإذ كان المسير الوسط للكوكب في أحد الرصدين كان حاصله على عشرة أجزاء ونصف جزء من التوأمين وفي الآخر على عشرة أجزاء من الدلو وكانت النقطة من فلك البروج التي فيما بين هذين الحاصلين يحصل على عشرة أجزاء وربع جزء من الميزان فإنّ القطر الذي يمرّ بالبعد الأبعد كان موضعه في ذلك الوقت هذا الموضع فأمّا من هذه الأرصاد فإنّا وجدنا البعد الأبعد يقع على عشرة أجزاء بالتقريب من الحمل أو الميزان وأمّا بالأرصاد القديمة التي وقعت في أعظم أبعاد الكوكب من الشمس فإنّا نجده إنّما يقع على ستّة أجزاء من هذين البرجين على ما يخرجه الحساب ممّا نذكره منها⊙ فنقول إنّ في سنة ثلاث وعشرين من عهد ذيونوسيوس في الشهر المسمّى أدرن ه: هذا الاسم للشهر اشتقّ من اسم الدلو في لسان اليونانيّين منها في اليوم الحادي والعشرين منه كان عطارد بالغداة بعده من الكوكب الشديد الضياء الذي في ذنب الجدي إلى ناحية الشمال ثلاثة أمثال قطر ه - ص: قطر القمر وكان في ذلك الوقت حاصل هذا الكوكب الثابت على حسب مبادئنا نحن أعني المبادئ التي من نقطتي الانقلابين ونقطتي الاستواءين على اثنين وعشرين جزءًا وثلث من الجدي ومن البيّن أنّ ذلك كان حاصل كوكب عطارد أيضًا وكان حاصل الشمس بحركتها الوسطى على ثمانية عشر جزءًا وسدس جزء من الدلو فإنّ ذلك الوقت كان في سنة أربع مائة وستّ وثمانين من عهد بختنصّر في شهر جوان عند المصريّين في اليوم السابع عشر منه في الغلس من الليلة التي يتلوها اليوم الثامن عشر فكان إذًا أعظم البعد الصباحيّ من المسير الوسط خمسةً وعشرين جزءًا ونصفًا وثلث جزء فأمّا بعد مسائيّ أعظم ما يكون مساوٍ لهذا البعد على الحقيقة فإنّا لم نجد فيما وقع إلينا من الأرصاد لكنّا استخرجنا بالحساب ببعدين قريبين منه بعدًا مسائيًّا مساويًا له بهذا الوجه⊙ رصدنا عطارد في تلك السنة بعينها وهي سنة ثلاث وعشرين من عهد ذيونوسيوس في الشهر المسمّى طورن ه: اشتقّ من اسم الثور في اليوم الرابع منه بالعشيّ فوجد مقصّرًا عن الخطّ المستقيم الذي يمرّ بقرني الثور ثلاثة أمثال القمر وكان يرى كأنّه يساير الكوكب المعروف بالمشترك وبعده منه في الجنوب أكثر من ثلاثة أمثال القمر فكان حاصله أيضًا على حسب مبادئنا نحن على ثلاثة وعشرين جزءًا وثلثي جزء من الثور وكان ذلك الوقت في سنة أربع مائة وستّ وثمانين أيضًا من عهد بختنصّر في شهر فامانوث عند المصريّين في عشيّ اليوم الأوّل منه وكان حاصل الشمس في ذلك الوقت بحركتها الوسطى على تسعة وعشرين جزءًا ونصف من الحمل فكان إذن أعظم العد المسائيّ من المسير الوسط أربعةً وعشرين جزءًا وسدس جزء⊙ ورصدنا أيضًا كوكب عطارد في سنة ثمان وعشرين من عهد ذيونوسيوس في شهر ديدومن ه: {...}ـومن اسم {...}ـوأمين في اليوم السابع منه بالعشيّ فوجد على غاية الاستقامة مع رأسي التوأمين ووجد بعده في الجنوب من التوأم الجنوبيّ أقلّ من ضعف ما بين رأسيهما من البعد بثلث القمر فكان إذن حاصل كوكب عطارد في ذلك الوقت أيضًا على حسب مبادئنا نحن على تسعة وعشرين جزءًا وثلث من التوأمين وكان ذلك الوقت في سنة أربع مائة وإحدى وتسعين من عهد بختنصّر في شهر فرموثي عند المصريّين منها في اليوم الخامس منه في العشيّة التي يتلوها اليوم السادس وكان حاصل الشمس في ذلك الوقت بحركتها الوسطى على جزأين ونصف وثلث من التوأمين فكان إذن هذا البعد أيضًا ستّةً وعشرين جزءًا ونصف جزء فمن قبل أنّ مسير الشمس الوسط لمّا كان في تسعة وعشرين جزءًا ونصف من الحمل كان أعظم البعد منه أربعةً وعشرين جزءًا وسدس جزء ولمّا كان في جزأين ونصف وثلث من التوأمين كان أعظم البعد منه ستّةً وعشرين جزءًا ونصف جزء وكان البعد الصباحيّ الذي كنّا نطلب البعد ه: يعني المسائيّ الذي هو قرينه خمسةً وعشرين جزءًا ونصف وثلث جزء واستخرجنا الموضع الذي إذا كان فيه مسير الشمس الوسط كان البعد المسائيّ منه خمسةً وعشرين جزءًا ونصف وثلث جزء يفضل ما بين هذين الرصدين اللذين أثبتناهما وذلك أنّ الفضل بين المسيرين الوسطين في كلّ واحد من هذين الرصدين يحصل ثلاثةً وثلاثين جزءًا وثلث جزء والفضل فيما بين البعدين اللذين في الغاية عن المسير الوسط جزأين وثلث فيكون الذي يصيب الجزء والثلثي الجزء التي هي فضل الخمسة والعشرين الجزء والنصف والثلث على الأربعة والعشرين الجزء والسدس أربعةً وعشرين جزءًا بالتقريب فإذا نحن زدنا ذلك على الأجزاء من الحمل التسعة والعشرين الجزء والنصف خرج لنا المسير الوسط الذي فيه البعد المسائيّ الأعظم المساوي للبعد الصباحيّ وهو خمسة وعشرون جزءًا ونصف وثلث جزء على ثلاثة وعشرين جزءًا ونصف جزء من الثور والنقطة التي فيما بين الثمانية عشر الجزء والسدسين من الدلو وبين الثلاثة والعشرين الجزء والنصف من الثور يقع على خمسة أجزاء ونصف وثلث من الحمل φ وأيضًا فإنّ كوكب عطارد في سنة أربع وعشرين من سني ذيونوسيوس في الشهر المسمّى لاونطن في اليوم الثامن والعشرين منه بالعشيّ كان متقدّمًا للسماك الأعزل على ما قاس فحسب أبرخس أكثر من ثلاثة أجزاء قليلًا فكان حاصله إذن في ذلك الوقت على حسب مبادئنا على تسعة عشر جزءًا ونصف من العذراء وهذا الوقت كان في سنة أربع مائة وستّ وثمانين من عهد بختنصّر في الشهر عند المصريّين المسمّى فاوثفي في اليوم الثلاثين منه بالعشيّ وكان حاصل الشمس في ذلك الوقت بحركتها الوسطى على سبعة وعشرين جزءًا ونصف ه: ونصف وثلث من الأسد فكان إذن أعظم البعد المسائيّ من المسير الوسط أحدًا وعشرين جزءًا وثلثي جزء فحسبنا أيضًا البعد الصباحيّ القرين لهذا البعد برصدين ها أنا ذاكرهما رصد كوكب عطارد في سنة خمس وسبعين من عهد الكلدانيّين في الشهر المسمّى ذيوس في اليوم الرابع عشر منه بالغداة وكان فوق الكفّة الجنوبيّة من الميزان بذراع ونصف فكان إذًا حاصله في ذلك الوقت على حسب مبادئنا على أربعة عشر جزءًا وسدس جزء من الميزان وهذا الوقت كان في سنة خمس مائة واثنتي عشرة من عهد بختنصّر في شهر توث عند المصريّين في اليوم التاسع منه في غلس الليلة التي يتلوها اليوم العاشر وكان حاصل الشمس في ذلك الوقت بحركتها الوسطى ه - ص: بحركتها الوسطى على خمسة أجزاء وسدس من العقرب فكان إذا بعد البعد الصباحيّ أحدًا وعشرين جزءًا⊙ ورصد أيضًا كوكب عطارد في سنة سبع وستّين من عهد الكلدانيّين في الشهر المسمّى إيلاوس في اليوم الخامس منه بالغداة فكان فوق الجانب الشماليّ من جهة العقرب بذراع ونصف فكان إذًا حاصله في ذلك الوقت عندنا على جزأين وثلث جزء من العقرب وهذا الوقت كان في سنة خمس مائة وأربع وستّين من عهد بختنصّر في شهر توث عند المصريّين في اليوم السابع والعشرين سنة في غلس الليلة التي يتلوها اليوم الثامن والعشرون وكان فيه حاصل الشمس بحركتها الوسطى على أربعة وعشرين جزءًا ونصف وثلث جزء من العقرب وكان إذن هذا البعد اثنين وعشرين جزءًا ونصف فإذ كان أيضًا في هذين الرصدين الفضل بين المسيرين الوسطين يحصل تسعة عشر جزءًا وثلثي جزء والفضل من البعدين الأعظمين عن المسير الوسط جزءًا واحدًا ونصف جزء وكان من قبل ذلك الذي يصيب الثلثي الجزء اللذين هما فضل البعد المطلوب وهو أحد وعشرون جزءًا وثلثا جزء على البعد الأقلّ وهو أحد وعشرون جزءًا تسعة أجزاء بالتقريب فإذا زدنا هذه الأجزاء على الأجزاء من العقرب وهي خمسة أجزاء وسدس وحصل لنا البعد الوسط الذي يكون فيه أعظم البعد الصباحيّ مساويًا لأعظم البعد المسائيّ وهو أحد وعشرون جزءًا وثلثا جزء على أربعة عشر جزءًا وسدس جزء من العقرب والنقطة التي بين السبعة والعشرين الجزء والنصف والثلث من الأسد وبين الأربعة عشر الجزء والسدس من العقرب على ستّة أجزاء حاصله من الميزان⊙ فمن هذه الأرصاد ومن مطابقة ما يرى في سائر الكواكب من الأمور الجزئيّة لذلك وجدنا الأمر موافقًا لأنّ الأقطار التي تمرّ بالبعد الأبعد والبعد الأقرب في كلّ واحد من الكواكب الخمسة المتحيّرة يكون لها شيء من الانتقال إلى توالي البروج حول مركز فلك البروج وأنّ هذه النقلة مساوية في الزمان لنقلة كرة الكواكب الثابتة وذلك أنّا قد بيّنّا أن هذه الكرة تنتقل في كلّ مائة سنة نحوًا من جزء واحد ووجدنا هاهنا الزمان الذي منذ وقت الأرصاد القديمة الذي كان فيه البعد الأبعد لكوكب عطارد على ستّة أجزاء ومن زمان أرصادنا الذي تحرّك فيه قريبًا من أربعة أجزاء إذ كنّا وجدنا حاصله على عشرة أجزاء تحيط بنحو من أربع مائة سنة⊙
〈IX.8〉 ح: في أنّ كوكب عطارد أيضًا يصير في أقرب قربه في كلّ دورة مرّتين
ومن بعد وقوفنا على ذلك جعلنا نطلب مقادير أعظم الأبعاد من الشمس إذا كان مسير الشمس على أبعد البعد نفسه فإذا ↑: وَ كان أيضًا في البعد المجازيّ له على القطر فلم نجد العلم بذلك يتهيّأ بالأرصاد القديمة ووجدناه يتهيّأ بما رصدناه نحن بآلة القياس التي وضعناها فإنّه قد يوقف بذلك خاصّةً على أعظم العناء بهذه الآلة وذلك أنّه وإن لم ير بالقرب من الكواكب ه: يعني المتحيّرة التي ترصد شيء من الكواكب ه: يعني الثابتة التي تقدّم العلم بمواضعها وذلك شيء يقع في عطارد في أكثر الأمر من قبل أنّ كثيرًا من الكواكب الثابتة أقلّ ما يتهيّأ أن ترى من بعد من الشمس مساوٍ للبعد الذي يرى منه عطارد فقد يمكن أن يقاس الكوكب ه: يعني من المتحيّرة بهذه الآلة بكواكب ه: يعني الثابتة بعيدة عنها بعدًا كثيرًا فيوقف على موضع المطلوب منها في الطول وفي العرض فرصدنا كوكب عطارد في السنة التاسعة عشرة من سني أذريانوس في شهر أثور عند المصريّين في اليوم الرابع عشر منه في غداة الليلة التي يتلوها اليوم الخامس عشر وكان في أعظم بعده من الشمس وكان قياسنا له بالكوكب الذي على قلب الأسد فرأينا حاصله على عشرين جزءًا وخمس جزء من العذراء وكان حاصل الشمس بحركتها الوسطى على تسعة أجزاء وربع جزء من الميزان فكان إذن أعظم بعده من الشمس تسعة عشر جزءًا وجزء من عشرين من جزء⊙ ورصدناه أيضًا في تلك السنة بعينها في الشهر المسمّى باخور في اليوم التاسع عشر منه بالعشيّ وهو في أكثر بعده ه: {...}ـي من المسير الوسط وكان قياسنا له بالدبران فرأينا حاصله على أربعة أجزاء وثلث من الثور وكان حاصل الشمس بحركتها الوسطى على أحد عشر جزءًا وجزء من اثني عشر من جزء من الحمل فكان إذن هاهنا أيضًا أكثر بعده ثلاثةً وعشرين جزءًا وربع ومن البيّن من ذلك بيانًا واضحًا أنّ البعد الأبعد في الفلك الخارج المركز إنّما هو في الميزان لا في الحمل φ وإذ كان ذلك قد علم ه: فليكن القطر الذي يمرّ بالبعد الأبعد خطّ ألف باء جيم ولننزل أنّ مركز فلك البروج وهو الذي عليه البصر نقطة باء ونقطة ألف التي تحت ه: يعني بإزاء الجزء الجزء العاشر من الميزان ونقطة جيم النقطة التي تحت الجزء العاشر من الحمل ولنرسم فلكا تدوير متساويان حول نقطتي ألف جيم وليكونا الدائرة التي عليها دال والدائرة التي عليها هاء وليخرج من نقطة باء خطّان مستقيمان يماسّانها وليكونا خطّ باء دال وخطّ باء هاء ولنخرج من مركزيهما إلى موضعي التماس عمودا ألف دال جيم هاء فلأن البعد في الميزان الذي هو أعظم البعد الصباحيّ من المسير الوسط وجد بالرصد تسعة عشر جزءًا وجزءًا من عشرين من جزء تكون زاوية ألف باء دال أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فتسعة عشر جزءًا وثلاث دقائق وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فثمانية وثلاثون جزءًا وستّ دقائق فتكون القوس أيضًا التي على خطّ ألف دال ثمانيةً وثلاثين جزءًا وستّ دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث ألف باء دال القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ ألف دال تسعةً وثلاثين جزءًا وتسع دقائق بالتقريب بالأجزاء التي بها خطّ ألف باء الموتر مائة وعشرين جزءًا φ وأيضًا لأنّ البعد في الحمل الذي هو أعظم البعد المسائيّ من المسير الوسط وجد بالرصد ثلاثةً وعشرين جزءًا وربع تكون زاوية جيم باء هاء أيضًا أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فثلاثة وعشرون جزءًا وخمس عشرة دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فستّة وأربعون جزءًا وثلاثون دقيقةً فتكون لذلك القوس التي على خطّ جيم هاء ستّةً وأربعين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء جيم هاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ جيم هاء سبعة وأربعون جزءًا واثنتان وعشرون دقيقةً بالأجزاء التي بها خطّ باء جيم الموتر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ جيم هاء تسعة وثلاثون جزءًا وتسع دقائق وخطّ ألف باء مائة وعشرون جزءًا من قبل أنّ خطّ ألف دال مساوٍ لخطّ جيم هاء الذي من مركز فلك التدوير يكون بها خطّ باء جيم تسعةً وتسعين جزءًا وتسع دقائق وخطّ ألف باء جيم بأسره مائتين وتسعة عشر جزءًا وتسع دقائق فإذا قسم أيضًا هذا الخطّ بنصفين على نقطة زاي كان نصفه أيضًا وهو خطّ ألف زاي بهذه الأجزاء مائةً وتسعة أجزاء وأربعًا وثلاثين دقيقةً
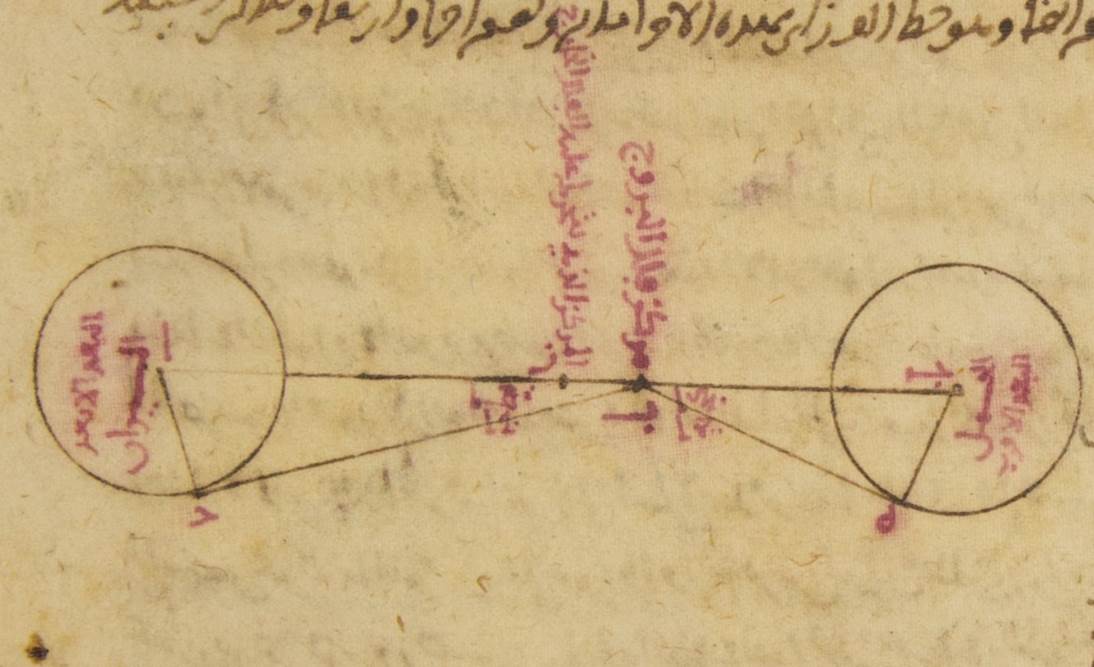 وكان الخطّ الذي فيما بين نقطتي باء زاي عشرة أجزاء وخمسًا وعشرين دقيقةً⊙ ومن البيّن أنّ نقطة زاي إمّا أن تكون مركز الفلك الخارج المركز الذي عليه تكون أبدًا مركز فلك التدوير وإمّا أن يكون حولها يدور أبدًا مركز هذا الفلك الذي ذكرناه فإنّ بهذا الوجه اذي ذكرناه (وإنّ بهذا الوجه) وحده يكون مركز فلك التدوير على ما تبيّن من نقطة زاي في كلّ واحد من الموضعين المتقاطرين اللذين وضعناه فيهما بعدًا سواءً لكن لمّا كانت نقطة زاي لو كانت هي نفسها مركز الفلك الخارج المركز الذي عليه يكون أبدًا مركز فلك التدوير لقد كان هذا الفلك الخارج المركز سيكون ثابتًا وكان البعد الأقرب في الحمل سيكون أقرب ما يكون من القرب من جميع الأوضاع من قبل أنّ خطّ باء جيم كان يكون أقصر جميع الخطوط التي توصل بين نقطة باء وبين الدائرة التي ترسم حول نقطة زاي ولكنّا نجد موضع البعد الأقرب في الحمل ليس هو أقرب مواضع البعد الأقرب في غيره بل البعد الأقرب في التوأمين وفي الدلو أقرب منه وهذان البعدان في هذين البرجين قريبان من السواء فمن البيّن أنّ نقطة زاي حولها يتحرّك مركز الفلك الخارج المركز الذي ذكرنا التي ضدّ الجهة التي إليها يدور فلك التدوير أعني قدمًا للبروج وحركته أيضًا في الدورة الواحدة مرّةً واحدةً فإنّ بهذا الوجه يكون مركز فلك التدوير يصير في أقرب قربه مرّتين في كلّ دورة φ فأمّا أنّ فلك التدوير يكون في التوأمين وفي الدلو في قرب أقرب من قربه الأقرب في الحمل فقد يمكنك أن تقف عليه من الأرصاد الذي ذكرناها آنفًا وذلك أنّا وجدنا في الأصل: وجد؛ ه: نا بالرصد الذي كان في سنة ستّ عشرة من سني أذريانوس في اليوم السادس عشر من شهر فامانوث أعظم البعد المسائيّ من المسير الوسط أحدًا وعشرين جزءًا وربع جزء وفي الرصد الذي كان في السنة الرابعة من سني أنطونيس في اليوم التاسع عشر من شهر فامانوث وجدنا أعظم البعد الصباحيّ من المسير الوسط ستّةً وعشرين جزءًا ونصف جزء وكانت الشمس في الرصدين جميعًا بحركتها الوسطى في عشرة أجزاء من الدلو φ وأيضًا في الرصد الذي كان في سنة ثمان عشرة من سني أذريانوس في اليوم التاسع عشر من شهر أبيقي وجدنا أعظم البعد الصباحيّ من المسير الوسط أحدًا وعشرين جزءًا وربع وفي الرصد الذي كان في السنة الأولى من سني أنطونيس في اليوم العشرين من شهر أبيفي وجدنا أعظم البعد المساوي من المسير الوسط ستّةً وعشرين جزءًا ونصف جزء وكانت الشمس في هذين الرصدين جميعًا بحركتها الوسطى في وسط من الجزء العاشر من التوأمين فيكون البعدان اللذان هما أعظم الأبعاد في الجهتين المتضادّتين اللذان في الدلو إذا جمعا والبعدان اللذان في التوأمين إذا جمعا كلّ واحد منهما سبعةً وأربعين جزءًا ونصف وربع جزء والبعدان جميعًا اللذان في الحمل إنّما هو ستّة وأربعون جزءًا ونصف لأنّ البعد المسائيّ فيه مساوٍ للبعد الصباحيّ ومبلغه على ما وجد بالرصد ثلاثة وعشرون جزءًا وربع جزء⊙
وكان الخطّ الذي فيما بين نقطتي باء زاي عشرة أجزاء وخمسًا وعشرين دقيقةً⊙ ومن البيّن أنّ نقطة زاي إمّا أن تكون مركز الفلك الخارج المركز الذي عليه تكون أبدًا مركز فلك التدوير وإمّا أن يكون حولها يدور أبدًا مركز هذا الفلك الذي ذكرناه فإنّ بهذا الوجه اذي ذكرناه (وإنّ بهذا الوجه) وحده يكون مركز فلك التدوير على ما تبيّن من نقطة زاي في كلّ واحد من الموضعين المتقاطرين اللذين وضعناه فيهما بعدًا سواءً لكن لمّا كانت نقطة زاي لو كانت هي نفسها مركز الفلك الخارج المركز الذي عليه يكون أبدًا مركز فلك التدوير لقد كان هذا الفلك الخارج المركز سيكون ثابتًا وكان البعد الأقرب في الحمل سيكون أقرب ما يكون من القرب من جميع الأوضاع من قبل أنّ خطّ باء جيم كان يكون أقصر جميع الخطوط التي توصل بين نقطة باء وبين الدائرة التي ترسم حول نقطة زاي ولكنّا نجد موضع البعد الأقرب في الحمل ليس هو أقرب مواضع البعد الأقرب في غيره بل البعد الأقرب في التوأمين وفي الدلو أقرب منه وهذان البعدان في هذين البرجين قريبان من السواء فمن البيّن أنّ نقطة زاي حولها يتحرّك مركز الفلك الخارج المركز الذي ذكرنا التي ضدّ الجهة التي إليها يدور فلك التدوير أعني قدمًا للبروج وحركته أيضًا في الدورة الواحدة مرّةً واحدةً فإنّ بهذا الوجه يكون مركز فلك التدوير يصير في أقرب قربه مرّتين في كلّ دورة φ فأمّا أنّ فلك التدوير يكون في التوأمين وفي الدلو في قرب أقرب من قربه الأقرب في الحمل فقد يمكنك أن تقف عليه من الأرصاد الذي ذكرناها آنفًا وذلك أنّا وجدنا في الأصل: وجد؛ ه: نا بالرصد الذي كان في سنة ستّ عشرة من سني أذريانوس في اليوم السادس عشر من شهر فامانوث أعظم البعد المسائيّ من المسير الوسط أحدًا وعشرين جزءًا وربع جزء وفي الرصد الذي كان في السنة الرابعة من سني أنطونيس في اليوم التاسع عشر من شهر فامانوث وجدنا أعظم البعد الصباحيّ من المسير الوسط ستّةً وعشرين جزءًا ونصف جزء وكانت الشمس في الرصدين جميعًا بحركتها الوسطى في عشرة أجزاء من الدلو φ وأيضًا في الرصد الذي كان في سنة ثمان عشرة من سني أذريانوس في اليوم التاسع عشر من شهر أبيقي وجدنا أعظم البعد الصباحيّ من المسير الوسط أحدًا وعشرين جزءًا وربع وفي الرصد الذي كان في السنة الأولى من سني أنطونيس في اليوم العشرين من شهر أبيفي وجدنا أعظم البعد المساوي من المسير الوسط ستّةً وعشرين جزءًا ونصف جزء وكانت الشمس في هذين الرصدين جميعًا بحركتها الوسطى في وسط من الجزء العاشر من التوأمين فيكون البعدان اللذان هما أعظم الأبعاد في الجهتين المتضادّتين اللذان في الدلو إذا جمعا والبعدان اللذان في التوأمين إذا جمعا كلّ واحد منهما سبعةً وأربعين جزءًا ونصف وربع جزء والبعدان جميعًا اللذان في الحمل إنّما هو ستّة وأربعون جزءًا ونصف لأنّ البعد المسائيّ فيه مساوٍ للبعد الصباحيّ ومبلغه على ما وجد بالرصد ثلاثة وعشرون جزءًا وربع جزء⊙
〈IX.9〉 ط: في النسبة والمقدار اللذين لاختلافي كوكب عطارد
وإذ قد تقدّم تبيين هذه الأشياء فقد بقي علينا الآن أن نبيّن على أيّ نقطة من خطّ ألف باء تكون عودة فلك التدوير في السنة بحركته على الاستواء على توالي البروج وكم بعد مركز الفلك الخارج المركز الذي تكون عودته بحركته قدمًا مساوٍ زمانها لزمان تلك العودة من نقطة زاي فنحن مستعملون في هذا الفحص أيضًا رصدين لبعدين من الأبعاد التي هي أعظم الأبعاد صباحيّ ومسائيّ يكون بعد المسير الوسط منهما جميعًا ربع دائرة في جهة واحدة بعينها من البعد الأبعد وفي هذا الموضع يكون أكثر ما يكون من الفضل الذي ه: الذي من قبل الاختلاف المنسوب إلى فلك البروج بالتقريب. فنقول إنّ في سنة أربع عشرة من سني أذريانوس في شهر ماسوري عند المصريّين في اليوم الثامن عشر منه بالعشيّ على ما أخذ عن ثاون من الأرصاد ووجد عطارد كما قال على أعظم بعده من الشمس وكان متخلّفًا عن الكوكب الذي على قلب الأسد بثلاثة أجزاء ونصف جزء فكان إذن حاصله على حسب مبادئنا نحن على ستّة أجزاء وثلث من الأسد بالتقريب وكانت الشمس في ذلك الوقت بحركتها الوسطى في عشرة أجزاء وجزء من اثني عشر من جزء من السرطان فكان إذن البعد الأعظم المسائيّ ستّةً وعشرين جزءًا وربع جزء⊙ ورصدنا نحن بآلة القياس كوكب عطارد في السنة الثانية من سني أنطونيس في شهر ماسوري عند المصريّين في اليوم الحادي والعشرين منه في الغلس وكان أعظم بعده من المسير الوسط وكان قياسنا له بالدبران فوجدنا حاصله على عشرين جزءًا وجزء من اثني عشر من جزء من التوأمين وكانت الشمس أيضًا بحركتها الوسطى في عشرة أجزاء وثلث من السرطان فكان إذن أعظم البعد الصباحيّ عشرين جزءًا وربع⊙ فإذ قد وطّأنا ذلك و: فليكن أيضًا القطر الذي يمرّ بالجزء العاشر من الميزان ومن الحمل خطّ ألف زاي باء جيم ولننزل كما فعلنا في الصورة التي قبل هذه أنّ نقطة ألف النقطة التي عليها يصير مركز فلك التدوير إذا كان تحت الجزء العاشر من الميزان ونقطة جيم النقطة التي عليها تصير إذا كان تحت الجزء العاشر من الحمل ونقطة باء مركز فلك البروج ونقطة زاي النقطة التي حولها يدور مركز الفلك الخارج المركز فينتقل قدمًا وليكن قصدنا أوّلًا أن نعلم كم بعد المركز الذي حوله نقول إنّ حركة فلك التدوير يكون على الاستواء وتلقاء حركة الكلّ ه - ج: عليه تكون الحركة السنويّة التي لفلك التدوير إلى {...} البروج من نقطة باء وليكن ذلك المركز نقطة حاء وليخرج من نقطة حاء خطّ على زوايا قائمة على خطّ ألف جيم ليكون بعده من البعد الأبعد ربع دائرة وليوجد عليه مركز فلك التدوير في هذين الرصدين اللذين وصفناهما ولتكن نقطة طاء من قبل أنّ هذين الرصدين كان بعد المسير الوسط فيهما أيضًا من البعد الأبعد ربع دائرة إذ كانت الشمس (كانت) في عشرة أجزاء من السرطان ولنرسم حول نقطة طاء فلك تدوير كاف لام ولنخرج من نقطة باء خطّان يماسّانه وليكونا باء لام باء كاف ولنوصل خط طاء كاف وخطّ طاء لام وخطّ باء طاء فلأنّ في هذا المسير الوسط الذي ذكرنا كان أعظم البعد الصباحيّ من المسير الوسط عشرين جزءًا وربع وأعظم البعد المسائيّ منه ستّةً وعشرين جزءًا وربع تكون زاوية كاف باء لام بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا ستّةً وأربعين جزءًا وثلاثين دقيقةً فنصفها إذن وهي زاوية كاف باء طاء ستّة وأربعون جزءًا وثلاثون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون لذلك القوس التي على خطّ طاء كاف ستّةً وأربعين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء طاء كاف القائم الزاوية ثلاث مائة وستّون جزءًا ويكون وترها وهو خطّ طاء كاف سبعةً وأربعين جزءًا واثنتين وعشرين دقيقةً بالأجزاء التي بها خطّ باء طاء الموتر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ طاء كاف الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق وخطّ باء زاي على ما تبيّن عشرة أجزاء وخمس وعشرون دقيقةً يكون بها خطّ باء طاء أيضًا تسعةً وتسعين جزءًا وتسع دقائق φ وأيضًا لأنّ الفضل بين هذين البعدين الأعظمين اللذين وضعناهما وهو ستّة أجزاء يشتمل على ضعف الفضل الذي من قبل الاختلاف المنسوب إلى فلك البروج وهذا الفضل تشتمل عليه زاوية باء طاء حاء فإنّ هذا شيء قد تقدّم بيانه تكون زاوية باء طاء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فثلاثة أجزاء وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فستّة أجزاء فتكون لذلك القوس التي على خطّ باء حاء أيضًا ستّة أجزاء بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء طاء حاء القائم الزاوية ثلاث مائة وستّون جزءًا ويكون خطّ باء حاء نفسه ستّة أجزاء وسبع عشرة دقيقةً بالأجزاء التي بها خطّ باء طاء الموتر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ باء طاء تسعة وتسعون
 جزءًا وتسع دقائق وخطّ باء زاي بها عشرة أجزاء وخمس وعشرون دقيقةً يكون بها خطّ باء حاء خمسة أجزاء واثنتي عشرة دقيقةً فخطّ باء حاء إذن قريب من نصف خطّ باء زاي وكلّ واحد من خطّي باء حاء حاء زاي خمسة أجزاء واثنتا عشرة دقيقةً بالتقريب بالأجزاء التي بها الخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق ز: ولنخرج أيضًا في مثل هذه الصورة بعينها من نقطة زاي في ضدّ الجهة التي فيها خطّ حاء طاء خطّ على زوايا قائمة على خطّ ألف جيم وليكن خطّ زاي ميم نون ومن البيّن من قبل أنّ زماني عودة خطّي حاء طاء زاي نون إذا تحرّكا في جهتين متضادّتين حتّى يتوافيا متساويان أنّ مركز الفلك الخارج المركز الذي عليه نقطة طاء وهي مركز فلك التدوير يكون حينئذ على هذا الخطّ ولننزل أنّ خطّ زاي نون مساوٍ لخطّ زاي ألف حتّى يكون خطّ زاي نون كما كان خطّ ألف زاي مركّبًا من الخطّ الذي من مركز الفلك الخارج المركز ومن الخطّ الذي بين المركزين أعني بين هذا المركز وبين نقطة زاي ولنوجد عليه مركز الفلك الخارج المركز ولتكن نقطة ميم ولنوصل خطّ زاي طاء فلأنّ زاوية ميم زاي حاء قائمة وزاوية طاء زاي حاء ليس بينها وبين القائمة كثير خلاف حتّى يكون خطّ باء زاي طاء أيضًا غير مخالف لخطّ مستقيم وقد كان تبيّن أنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق يكون بها خطّ باء زاي إذ كان مساويًا لخطّ ألف زاي مائةً وتسعة أجزاء وأربعًا وثلاثين دقيقةً وخطّ زاي طاء إذ كان مساويًا لخطّ باء طاء تسعةً وتسعين جزءًا وتسع دقائق بهذه الأجزاء فيكون خطّ نون ه: نون زاي طاء بأسره مائتي جزء وثمانية أجزاء وثلاثًا وأربعين دقيقةً ونصفه وهو خطّ نون ميم الذي من مركز الفلك الخارج المركز مائةً وأربعة أجزاء واثنتان وعشرون دقيقةً بالتقريب وخطّ زاي ميم الباقي وهو الذي بين المركزين خمسة أجزاء واثنتي عشرة دقيقةً وقد تبيّن أنّ كلّ واحد من خطّي باء حاء حاء زاي بهذه الأجزاء خمسة أجزاء واثنتا عشرة دقيقةً فقد حصلنا إذن أنّ ه: أنّ الأجزاء التي بها الخطّ الذي من مركز الفلك الخارج المركز مائة وأربعة أجزاء واثنتان وعشرون دقيقةً فيها كلّ واحد من الخطوط التي فيما بين كلّ مركزين من هذه المراكز خمسة أجزاء واثنتا عشرة دقيقةً والخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق فالأجزاء إذن التي بها الخطّ الذي من مركز الفلك الخارج المركز ستّون جزءًا يكون بها كلّ واحد من الخطوط التي فيما بين كلّ مركزين ثلاثة أجزاء ويكون الخطّ الذي من مركز فلك التدوير اثنين وعشرين جزءًا وثلاثين دقيقةً وهذه الأشياء هي التي قصدنا لتبيينها⊙ وقد نقدر أن نعلم أنّ هذه الأشياء إذا وضعت كذلك كانت الأبعاد العظمى التي في القرب الأقرب أيضًا موافقةً لما رصدنا منها أعني أنّه إذا كان المسير الوسط في الجزء العاشر من الدلو أو من التوأمين وكان بعده من البعد الأبعد ضلع المثلّث كانت الزاوية التي عند البصر الموترة لفلك التدوير سبعةً وأربعين جزءًا ونصف وربع جزء بالتقريب بما أنا واصفه ح: ليكن القطر الذي
جزءًا وتسع دقائق وخطّ باء زاي بها عشرة أجزاء وخمس وعشرون دقيقةً يكون بها خطّ باء حاء خمسة أجزاء واثنتي عشرة دقيقةً فخطّ باء حاء إذن قريب من نصف خطّ باء زاي وكلّ واحد من خطّي باء حاء حاء زاي خمسة أجزاء واثنتا عشرة دقيقةً بالتقريب بالأجزاء التي بها الخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق ز: ولنخرج أيضًا في مثل هذه الصورة بعينها من نقطة زاي في ضدّ الجهة التي فيها خطّ حاء طاء خطّ على زوايا قائمة على خطّ ألف جيم وليكن خطّ زاي ميم نون ومن البيّن من قبل أنّ زماني عودة خطّي حاء طاء زاي نون إذا تحرّكا في جهتين متضادّتين حتّى يتوافيا متساويان أنّ مركز الفلك الخارج المركز الذي عليه نقطة طاء وهي مركز فلك التدوير يكون حينئذ على هذا الخطّ ولننزل أنّ خطّ زاي نون مساوٍ لخطّ زاي ألف حتّى يكون خطّ زاي نون كما كان خطّ ألف زاي مركّبًا من الخطّ الذي من مركز الفلك الخارج المركز ومن الخطّ الذي بين المركزين أعني بين هذا المركز وبين نقطة زاي ولنوجد عليه مركز الفلك الخارج المركز ولتكن نقطة ميم ولنوصل خطّ زاي طاء فلأنّ زاوية ميم زاي حاء قائمة وزاوية طاء زاي حاء ليس بينها وبين القائمة كثير خلاف حتّى يكون خطّ باء زاي طاء أيضًا غير مخالف لخطّ مستقيم وقد كان تبيّن أنّ الأجزاء التي بها الخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق يكون بها خطّ باء زاي إذ كان مساويًا لخطّ ألف زاي مائةً وتسعة أجزاء وأربعًا وثلاثين دقيقةً وخطّ زاي طاء إذ كان مساويًا لخطّ باء طاء تسعةً وتسعين جزءًا وتسع دقائق بهذه الأجزاء فيكون خطّ نون ه: نون زاي طاء بأسره مائتي جزء وثمانية أجزاء وثلاثًا وأربعين دقيقةً ونصفه وهو خطّ نون ميم الذي من مركز الفلك الخارج المركز مائةً وأربعة أجزاء واثنتان وعشرون دقيقةً بالتقريب وخطّ زاي ميم الباقي وهو الذي بين المركزين خمسة أجزاء واثنتي عشرة دقيقةً وقد تبيّن أنّ كلّ واحد من خطّي باء حاء حاء زاي بهذه الأجزاء خمسة أجزاء واثنتا عشرة دقيقةً فقد حصلنا إذن أنّ ه: أنّ الأجزاء التي بها الخطّ الذي من مركز الفلك الخارج المركز مائة وأربعة أجزاء واثنتان وعشرون دقيقةً فيها كلّ واحد من الخطوط التي فيما بين كلّ مركزين من هذه المراكز خمسة أجزاء واثنتا عشرة دقيقةً والخطّ الذي من مركز فلك التدوير تسعة وثلاثون جزءًا وتسع دقائق فالأجزاء إذن التي بها الخطّ الذي من مركز الفلك الخارج المركز ستّون جزءًا يكون بها كلّ واحد من الخطوط التي فيما بين كلّ مركزين ثلاثة أجزاء ويكون الخطّ الذي من مركز فلك التدوير اثنين وعشرين جزءًا وثلاثين دقيقةً وهذه الأشياء هي التي قصدنا لتبيينها⊙ وقد نقدر أن نعلم أنّ هذه الأشياء إذا وضعت كذلك كانت الأبعاد العظمى التي في القرب الأقرب أيضًا موافقةً لما رصدنا منها أعني أنّه إذا كان المسير الوسط في الجزء العاشر من الدلو أو من التوأمين وكان بعده من البعد الأبعد ضلع المثلّث كانت الزاوية التي عند البصر الموترة لفلك التدوير سبعةً وأربعين جزءًا ونصف وربع جزء بالتقريب بما أنا واصفه ح: ليكن القطر الذي
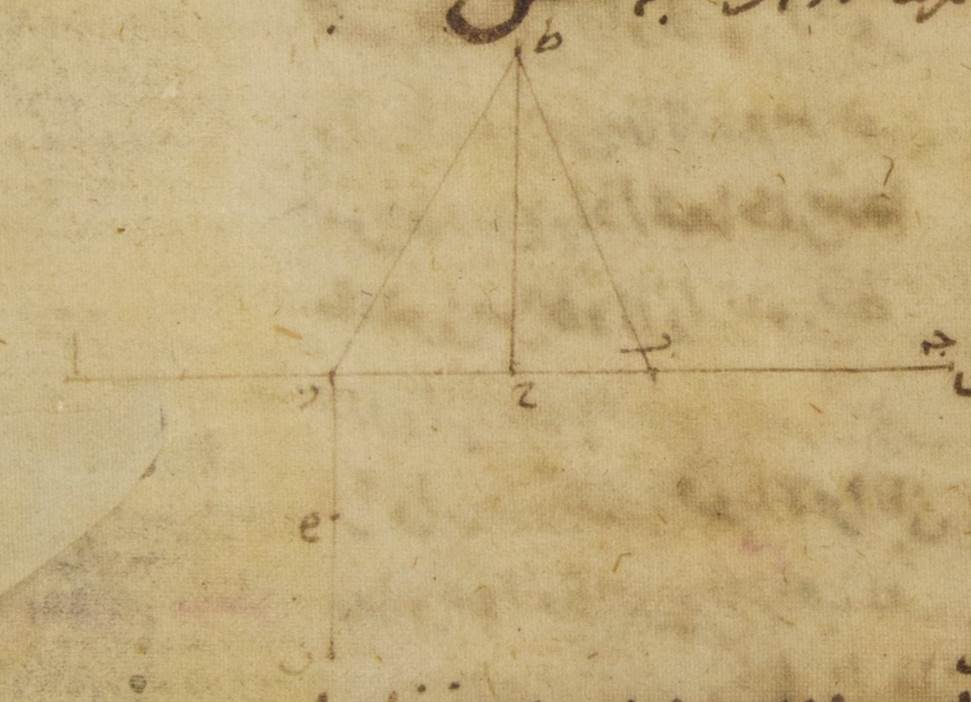 يمرّ بالبعد الأبعد خطّ ألف باء جيم دال هاء ولتكن عليه نقطة ألف البعد الأبعد ونقطة باء النقطة التي حولها ينتقل مركز الفلك الخارج المركز قدمًا ونقطة دال النقطة التي حولها ينتقل مركز فلك التدوير دبرًا ونقطة دال مركز فلك البروج ولنقرّر هاتان الحركتان جميعًا كلّ واحدة حول مركزها على تساوٍ في الزمان في في الجهتين المتضادّتين من نقطة ألف وهي البعد الأبعد ضلع المثلّث وليكن الخطّ المستقيم الذي يدير فلك التدوير خطّ جيم زاي والخطّ المستقيم الذي يدير مركز الفلك الخارج المركز خطّ باء حاء وليكن مركز الفلك الخارج المركز نقطة حاء ومركز فلك التدوير نقطة زاي ولنرسم حوله فلك تدوير ولنخرج خطّا دال طاء دال كاف يماسّان فلك التدوير ولنوصل خطّ جيم حاء وخطّ دال زاي وخطّ زاي طاء وخطّ زاي كاف ولنخرج من نقطة دال على خطّ جيم زاي عمود دال لام فينبغي أن نبيّن أنّ زاوية طاء دال كاف سبعة وأربعون جزءًا ونصف وربع جزء بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فلأنّ كلّ واحدة من زاويتي ألف باء حاء ألف حاء لام يوتر ضلع المثلّث وهي مائة وعشرون جزءًا بالأجزاء التي بها زاويتان قائمتان مائة وثمانون جزءًا فتكون كلّ واحدة من زاويتي جيم باء حاء دال جيم لام بهذه الأجزاء ستّين جزءًا لكنّ زاوية باء حاء جيم مساوية لزاوية باء جيم حاء من قبل أنّ خطّ باء جيم وضع مساويًا لخطّ باء حاء والزاويتين جميعًا هما ما يبقى من الأجزاء لتمام زاويتين قائمتين وهي مائة وعشرون جزءًا فكلّ واحدة منهما تكون ستّين جزءًا فمثلّث باء جيم حاء إذن متساوي الزوايا والأضلاع وزاوية دال جيم لام مساوية لزاوية باء جيم حاء فنقط حاء جيم لام زاي إذن على الاستقامة فيكون لذلك خطّ حاء زاي إذ كان من مركز الفلك الخارج المركز ستّين جزءًا بالأجزاء التي بها خطّ جيم حاء إذ كان مساويًا لخطّ جيم دال الذي بين المركزين ثلاثة أجزاء وخطّ جيم زاي الباقي بهذه الأجزاء سبعةً وخمسين جزءًا φ وأيضًا لأنّ زاوية دال جيم لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها ستّون جزءًا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها مائة وعشرون جزءًا تكون أيضًا القوس التي على خطّ دال لام مائة وعشرون جزءًا بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم دال لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم لام ما يبقى لتمام نصف دائرة وهو ستّون جزءًا فالخطّان إذن اللذان يوترانهما أمّا خطّ دال لام منهما فهو مائة وثلاثة أجزاء وخمس وخمسون دقيقةً بالأجزاء التي بها خطّ جيم دال الموتر مائة عشرون جزءًا وأمّا خطّ جيم لام فبهذه الأجزاء ستّون جزءًا فالأجزاء إذن التي بها خطّ جيم دال ثلاثة أجزاء وخطّ جيم زاي على ذلك المثال سبعة
يمرّ بالبعد الأبعد خطّ ألف باء جيم دال هاء ولتكن عليه نقطة ألف البعد الأبعد ونقطة باء النقطة التي حولها ينتقل مركز الفلك الخارج المركز قدمًا ونقطة دال النقطة التي حولها ينتقل مركز فلك التدوير دبرًا ونقطة دال مركز فلك البروج ولنقرّر هاتان الحركتان جميعًا كلّ واحدة حول مركزها على تساوٍ في الزمان في في الجهتين المتضادّتين من نقطة ألف وهي البعد الأبعد ضلع المثلّث وليكن الخطّ المستقيم الذي يدير فلك التدوير خطّ جيم زاي والخطّ المستقيم الذي يدير مركز الفلك الخارج المركز خطّ باء حاء وليكن مركز الفلك الخارج المركز نقطة حاء ومركز فلك التدوير نقطة زاي ولنرسم حوله فلك تدوير ولنخرج خطّا دال طاء دال كاف يماسّان فلك التدوير ولنوصل خطّ جيم حاء وخطّ دال زاي وخطّ زاي طاء وخطّ زاي كاف ولنخرج من نقطة دال على خطّ جيم زاي عمود دال لام فينبغي أن نبيّن أنّ زاوية طاء دال كاف سبعة وأربعون جزءًا ونصف وربع جزء بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فلأنّ كلّ واحدة من زاويتي ألف باء حاء ألف حاء لام يوتر ضلع المثلّث وهي مائة وعشرون جزءًا بالأجزاء التي بها زاويتان قائمتان مائة وثمانون جزءًا فتكون كلّ واحدة من زاويتي جيم باء حاء دال جيم لام بهذه الأجزاء ستّين جزءًا لكنّ زاوية باء حاء جيم مساوية لزاوية باء جيم حاء من قبل أنّ خطّ باء جيم وضع مساويًا لخطّ باء حاء والزاويتين جميعًا هما ما يبقى من الأجزاء لتمام زاويتين قائمتين وهي مائة وعشرون جزءًا فكلّ واحدة منهما تكون ستّين جزءًا فمثلّث باء جيم حاء إذن متساوي الزوايا والأضلاع وزاوية دال جيم لام مساوية لزاوية باء جيم حاء فنقط حاء جيم لام زاي إذن على الاستقامة فيكون لذلك خطّ حاء زاي إذ كان من مركز الفلك الخارج المركز ستّين جزءًا بالأجزاء التي بها خطّ جيم حاء إذ كان مساويًا لخطّ جيم دال الذي بين المركزين ثلاثة أجزاء وخطّ جيم زاي الباقي بهذه الأجزاء سبعةً وخمسين جزءًا φ وأيضًا لأنّ زاوية دال جيم لام أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فإنّها ستّون جزءًا وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فإنّها مائة وعشرون جزءًا تكون أيضًا القوس التي على خطّ دال لام مائة وعشرون جزءًا بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم دال لام القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم لام ما يبقى لتمام نصف دائرة وهو ستّون جزءًا فالخطّان إذن اللذان يوترانهما أمّا خطّ دال لام منهما فهو مائة وثلاثة أجزاء وخمس وخمسون دقيقةً بالأجزاء التي بها خطّ جيم دال الموتر مائة عشرون جزءًا وأمّا خطّ جيم لام فبهذه الأجزاء ستّون جزءًا فالأجزاء إذن التي بها خطّ جيم دال ثلاثة أجزاء وخطّ جيم زاي على ذلك المثال سبعة
 وخمسون جزءًا يكون بها خطّ دال لام جزأين وستًّا وثلاثين دقيقةً وخطّ جيم لام بها جزءًا واحدًا وثلاثين دقيقةً وخطّ لام زاي الأجزاء الباقية وهي خمسة وخمسون جزءًا وثلاثون دقيقةً ولأنّ ما يكون من هذا الخطّ وما يكون من خطّ دال لام إذا جمعا كان منهما ما يكون من خطّ دال زاي يكون خطّ دال زاي أيضًا في الطول خمسةً وخمسين جزءًا وأربعًا وثلاثين دقيقةً بالأجزاء التي بها وضع الخطّ الذي من مركز ه - ص: الفلك {...} {...} أعني خطّ زاي حاء {...} {...} والخطّ الذي من مركز فلك التدوير أعني كلّ واحد من خطّي زاي طاء زاي كاف اثنين وعشرين جزءًا وثلاثين دقيقةً فالأجزاء إذن التي بها خطّ دال زاي الموتر مائة وعشرون جزءًا يكون بها كلّ واحد من خطّي زاي طاء زاي كاف ثمانيةً وأربعين جزءًا وخمسًا وثلاثين دقيقةً وتكون كلّ واحدة من زاويتي زاي دال طاء زاي دال كاف سبعةً وأربعين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون زاوية طاء دال كاف بأسرها سبعةً وأربعين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وذلك ما كنّا قصدنا لتبيينه⊙
وخمسون جزءًا يكون بها خطّ دال لام جزأين وستًّا وثلاثين دقيقةً وخطّ جيم لام بها جزءًا واحدًا وثلاثين دقيقةً وخطّ لام زاي الأجزاء الباقية وهي خمسة وخمسون جزءًا وثلاثون دقيقةً ولأنّ ما يكون من هذا الخطّ وما يكون من خطّ دال لام إذا جمعا كان منهما ما يكون من خطّ دال زاي يكون خطّ دال زاي أيضًا في الطول خمسةً وخمسين جزءًا وأربعًا وثلاثين دقيقةً بالأجزاء التي بها وضع الخطّ الذي من مركز ه - ص: الفلك {...} {...} أعني خطّ زاي حاء {...} {...} والخطّ الذي من مركز فلك التدوير أعني كلّ واحد من خطّي زاي طاء زاي كاف اثنين وعشرين جزءًا وثلاثين دقيقةً فالأجزاء إذن التي بها خطّ دال زاي الموتر مائة وعشرون جزءًا يكون بها كلّ واحد من خطّي زاي طاء زاي كاف ثمانيةً وأربعين جزءًا وخمسًا وثلاثين دقيقةً وتكون كلّ واحدة من زاويتي زاي دال طاء زاي دال كاف سبعةً وأربعين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتكون زاوية طاء دال كاف بأسرها سبعةً وأربعين جزءًا وستًّا وأربعين دقيقةً بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا وذلك ما كنّا قصدنا لتبيينه⊙
〈IX.10〉 يے: في تصحيح أدوار حركات عطارد
ولمّا كان قد يتّصل بذلك وصف تقييد أدوار حركات كوكب عطارد وتحصيلاته فإنّا نجد حركاته في الطول أعني التي تحرّك فلك تدويره باستواء حول نقطة جيم معطاة من قرب من قبل أنّ حركات الشمس في الطول معطاة وأمّا حركات الاختلاف أعني التي تحرّك الكوكب في فلك تدويره حول مركزه فإنّا استخرجناها برصدين لا شكّ فيهما أحدهما من أرصادنا والآخر من الأرصاد القديمة فأمّا رصدنا نحن فإنّه على هذه الصفة⊙ رصدنا كوكب عطارد في السنة الثانية من سني أنطونيس وكانت هذه السنة سنة ثمان مائة وستّ وثمانين من عهد بختنصّر في شهر أنيقي عند المصريّين في اليوم الثاني منه في الليلة التي يتلوها اليوم الثالث بآلة القياس ولم يكن بعد صار في أعظم بعده المسائيّ وكان قياسنا له بالكوكب الذي على قلب الأسد فرأينا حاصله على سبعة عشر جزءًا ونصف من التوأمين ورأيناه في ذلك الوقت مختلفًا عن مركز القمر جزءًا واحدًا وسدس جزء وكان في ذلك الوقت بإسكندريّة قبل انتصاف الليلة التي يتلوها اليوم الثالث بأربع ساعات ونصف من ساعات الاستواء وذلك أنه كان المتوسّط للسماء في الآلة الجزء الثاني عشر من العذراء وكانت الشمس في ثلاثة وعشرين جزءًا من الثور لكن في تلك الساعة كان مسير الشمس الوسط بحسب الأصول التي بيّنّاها حاصلةً على اثنين وعشرين جزءًا وأربع وثلاثين دقيقةً من الثور وكان حاصل القمر على اثني عشر جزءًا وأربع عشرة دقيقةً من التوأمين وأمّا من الاختلاف فعلى مائتين وأحد وثمانين جزءًا وعشرين دقيقةً من البعد الأبعد من فلك التدوير فيحصل من ذلك أنّ مسير مركز القمر الحقيقيّ كان في سبعة عشر جزءًا وعشر دقائق من التوأمين ومسيره الذي يرى في ستّة عشر جزءًا وعشرين دقيقةً فكان إذن كوكب عطارد حاصله من هذا الوجه أيضًا لأنّه كان متخلّفًا عن مركز القمر بجزء واحد وسدس جزء على سبعة عشر جزءًا ونصف جزء فإذ قد وطّأنا ذلك ط: فليكن |17| القطر الذي يمرّ بالبعد الأبعد والبعد الأقرب ألف باء جيم دال هاء ↑: هاء ولننزل أنّ نقطة ألف منه النقطة التي عند البعد الأبعد ونقطة باء النقطة التي حولها ينتقل مركز الفلك الخارج المركز قدمًا ونقطة جيم النقطة التي حولها ينتقل مركز فلك التدوير دبرًا ونقطة دال مركز فلك البروج ولتحرّك خطّ جيم زاي نقطة زاي وهي مركز فلك التدوير حول نقطة جيم وزاوية ألف جيم زاي وتحرّك خطّ باء حاء نقطة حاء وهي مركز الفلك الخارج المركز حول نقطة باء زاوية ألف باء حاء ومن البيّن أنّها تكون أبدًا تساوي زماني الحركتين مساويةً لزاوية ألف جيم زاي ولنرسم حول نقطة زاي فلك تدوير طاء كاف لام ولننزل أنّ الكوكب على نقطة لام ولنوصل خطوط جيم حاء حاء زاي دال زاي كاف زاي لام ه: لام دال لام ولنخرج على خطّ جيم زاي طاء من نقطتي حاء دال عمودا حاء ميم دال زاي وعلى خطّ دال لام من نقطة زاي عمود لام سين وليكن قصدنا أن نعلم القوس من فلك التدوير التي هي بين البعد الأبعد وهو نقطة طاء وبين الكوكب الذي على نقطة لام فلأنّ الشمس بحركتها الوسطى كان منزلها في ذلك الوقت على اثنين وعشرين جزءًا وأربع وثلاثين دقيقةً من الثور والقرب الأقرب للكوكب على عشرة أجزاء بالتقريب من الحمل حتّى يكون مسيره الوسط في الطول بعده من القرب الأقرب اثنين وأربعين جزءًا وأربعًا وثلاثين دقيقةً تكون زاوية جيم باء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا مائتين وأربعين جزءًا وأربعًا وثلاثين دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة وثمانون جزءًا وثماني دقائق وكلّ واحدة من زاويتي باء حاء جيم باء جيم حاء من قبل أنّ خطّ باء جيم مساوٍ أبدًا لخطّ باء حاء بهذه الأجزاء مائةً وسبعةً وثلاثين جزءًا وستًّا وعشرين دقيقةً فتكون القوس من الدائرة التي ترسم حول مثلّث باء جيم حاء أمّا التي على خطّ حاء جيم فخمسة وثمانون جزءًا وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث باء حاء جيم ثلاث مائة وستّون جزءًا وأمّا التي على خطّ باء جيم فمائة وسبعة وثلاثون جزءًا وستّ وعشرون دقيقةً بتلك الأجزاء فالخطّان إذن اللذان يوترانهما أمّا خطّ جيم حاء منهما فأحد وثمانون جزءًا وعشر دقائق بالأجزاء التي بها قطر الدائرة مائة وعشرون جزءًا وأمّا خطّ باء جيم فبهذه الأجزاء مائة وأحد عشر جزءًا وتسع وأربعون دقيقةً فتكون الأجزاء التي بها خطّ باء جيم ثلاثة أجزاء فخطّ جيم حاء بها جزءان وإحدى عشرة دقيقةً وأيضًا لأنّ زاوية باء جيم حاء مائة وسبعة وثلاثون جزءًا وستّ وعشرون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية باء جيم ميم بهذه الأجزاء خمسة وثمانون جزءًا وثمان دقائق تكون زاوية حاء جيم ميم الأجزاء الباقية وهي اثنان وخمسون جزءًا وثمان عشرة دقيقةً فيجب من ذلك أن تكون أيضًا القوس التي على خطّ جيم ميم اثنين وخمسين جزءًا وثمان عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث حاء جيم ميم القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ جيم ميم ما يبقى لتمام نصف دائرة وهو مائة وسبعة وعشرون جزءًا واثنتان وأربعون دقيقةً فالخطّان إذن اللذان يوترانهما أمّا خطّ جيم ميم منهما فاثنان وخمسون جزءًا وثلاث وخمسون دقيقةً بالأجزاء التي بها خطّ جيم حاء الموتر مائة وعشرون جزءًا وأمّا خطّ جيم ميم فمائة وسبعة أجزاء وثلاث وأربعون دقيقةً بهذه الأجزاء فتكون إذن الأجزاء التي بها خطّ جيم حاء جزءان وإحدى عشرة دقيقةً وخطّ زاي حاء الذي من مركز الفلك الخارج المركز الحامل لفلك التدوير ستّون جزءًا فخطّ حاء ميم بها ثمان وخمسون دقيقةً وخطّ جيم ميم على ذلك المثال جزء وثمان وخمسون دقيقةً ولذلك يكون خطّ ميم زاي إذ كان إنّما هو أقلّ من خطّ زاي حاء الموتر بما لا قدر له بهذه الأجزاء ستّين جزءًا وخطّ جيم زاي الباقي ثمانيةً وخمسين جزءًا ودقيقتين وكذلك أيضًا من قبل أنّ زاوية دال جيم نون خمسة وثمانون جزءًا وثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا تكون القوس التي على خطّ دال نون خمسةً وثمانين جزءًا وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم دال زاي القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ جيم نون ما يبقى لتمام نصف دائرة وهو أربعة وتسعون جزءًا واثنتان وخمسون دقيقةً فالخطّان إذن اللذان يوترانهما أمّا خطّ دال نون منهما فيكون أحدًا وثمانين جزءًا وعشر دقائق بالأجزاء التي بها خطّ جيم دال الموتر مائة وعشرون جزءًا وأمّا خطّ جيم نون فبهذه الأجزاء ثمانية وثمانون جزءًا وثلاث وعشرون دقيقةً فالأجزاء إذن التي بها خطّ جيم دال ثلاثة أجزاء وخطّ جيم زاي على ما تبيّن ثمانية وخمسون جزءًا ودقيقتان يكون بها خطّ دال زاي جزأين ودقيقتين وخطّ جيم زاي على ذلك المثال جزأين وثلاث عشرة دقيقةً وخطّ نون زاي الأجزاء الباقية وهي خمسة وخمسون جزءًا وتسع وأربعون دقيقةً ولذلك يكون خطّ زاي دال الموتر خمسةً وخمسين جزءًا وإحدى وخمسين دقيقةً بالتقريب بالأجزاء التي بها أيضًا الخطّ الخارج من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً فالأجزاء إذن التي بها خطّ دال زاي الموتر مائة وعشرون جزءًا يكون بها خطّ دال نون أيضًا أربعة أجزاء واثنتين وعشرين دقيقةً والقوس التي عليه أربعة أجزاء وإحدى عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي نون القائم الزاوية ثلاث مائة وستّون جزءًا فتكون زاوية دال زاي نون أربعة أجزاء وإحدى عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية هاء دال زاي بأسرها تسعة وثمانون جزءًا وتسع عشرة دقيقةً لكنّ زاوية هاء دال لام بأسرها بهذه الأجزاء مائة وخمسة وثلاثون جزءًا من قبل أنّ الكوكب رئي في ذلك الوقت بعده من القرب الأقرب سبعةً وستّين جزءًا وثلاثين دقيقةً فزاوية زاي دال لام ما يبقى وهو خمسة وأربعون جزءًا وإحدى وأربعون دقيقةً فالقوس إذن التي على خطّ زاي شين خمسة وأربعون جزءًا وإحدى وأربعون دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث دال زاي سين القائم الزاوية ثلاث مائة وستّون جزءًا وخطّ زاي سين نفسه ستّة وأربعون جزءًا وخمس وثلاثون دقيقةً بالأجزاء التي بها خطّ دال نون الموتر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ دال زاي خمسة وخمسون جزءًا وإحدى وخمسون دقيقةً أعني التي بها خطّ زاي لام الذي من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً يكون بها خطّ راء سين أحدًا وعشرين جزءًا وإحدى وأربعين دقيقةً والأجزاء التي بها خطّ زاي لام الموتر مائةً وعشرين جزءًا يكون بها خطّ زاي سين أيضًا مائةً وخمسة عشر جزءًا وتسعًا وثلاثين دقيقةً فالقوس إذن التي على خطّ زاي سين مائة وتسعة وأربعون جزءًا ودقيقتان بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي لام سين القائم الزاوية ثلاث مائة وستّون جزءًا وزاوية زاي لام سين مائة وتسعة وأربعون جزءًا ودقيقتان بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وبهذه الأجزاء تبيّن أنّ زاوية دال لام خمسة وأربعون جزءًا وإحدى وأربعون دقيقةً وأنّ زاوية طاء زاي كاف على ذلك المثال أربعة أجزاء وإحدى عشرة دقيقةً فلذلك تكون زاوية طاء زاي لام بأسرها أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فمائة وثمانية وتسعون جزءًا وأربع وخمسون دقيقةً وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا
 فسبعة وتسعون جزءًا وسبع وعشرون دقيقةً فقوس طاء كاف لام من فلك التدوير التي هي كانت بعد كوكب عطارد في وقت الرصد من نقطة طاء التي هي البعد الأبعاد تسعة وتسعون جزءًا وسبع وعشرون دقيقةً وذلك ما قصدنا لتبيينه⊙ وأيضًا في سنة إحدى وعشرين من عهد ذيونوسيوس وكانت سنة أربع مائة وأربع وثمانين من عهد بختنصّر في الشهر المسمّى سفرسون ه: نسبة {...} في اليوم الثاني والعشرين منه وأمّا عند المصريّين ففي شهر توث في اليوم الثامن عشر منه في غداة الليلة التي يتلوها اليوم التاسع عشر كان بعد كوكب عطارد إلى توالي البروج من الخطّ المستقيم الذي يمرّ بالكوكب الشماليّ من جبهة العقرب وبالكوكب الذي في وسط الجبهة مقدار قطر القمر وكان بعده في الشمال من الكوكب الشماليّ من الجبهة مقدار قطري القمر لكنّ الكوكب الوسط من الكواكب التي في جبهة العقرب كان حاصله في ذلك الوقت على حسب مبادئنا على جزء واحد وثلثي جزء من العقرب وهو أميل إلى الجنوب عن فلك البروج بمثل ذلك φ والكوكب الشماليّ منها كان حاصله على جزأين وثلث جزء من العقرب وهو أميل إلى الشمال من فلك البروج بجزء واحد وثلث جزء فكان إذن حاصل كوكب عطارد أيضًا على ثلاثة أجزاء وثلث جزء من العقرب بالتقريب⊙ وقد نعلم أيضًا أنّه لم يكن بعد صار في أعظم ما يكون من بعده الصباحيّ من قبل أنّا وجدنا في هذا الرصد مثبتًا أنّه بعد أربعة أيّام في اليوم السادس والعشرين من الشهر المسمّى سغرينون صار بعده من ذلك الخطّ المستقيم بعينه إلى توالي البروج مقدار قطر القمر بأسره ونصف قطره وذلك أنّ البعد زاد بأنّ الشمس تحرّكت قريبًا من أربعة أجزاء وتحرّك الكوكب نصف قطر القمر وكان حاصل الشمس بحركتها الوسطى في اليوم التاسع عشر من الشهر المسمّى توث في الغلس على ما عندنا على عشرين جزءًا ونصف وثلث جزء من العقرب وكان البعد الأبعد للكوكب على ستّة أجزاء من الميزان من قبل أنّ السنين التي بين الرصدين إذا كانت أربع مائة سنة فإنّ انتقال البعد الأبعد يكون فيها نحوًا من أربع درج⊙ فإذ قد وطّأنا هذه الأشياء يے: فلنرسم أيضًا صورةً مثل الصورة التي تقدّمت غير أنّا نجعل في هذه الصورة الزاويتين اللتين في جهة نقطة ألف وهي البعد الأبعد لأنّ المسير في هذا الرصد مخالف للمسير في ذلك الرصد حادّتين ونجعل الخطّين اللذين نصفهما بالكوكب قدمًا من فلك التدوير ونجعل عمود زاي سين أعلى من خطّ زاي لام الذي من مركز فلك التدوير فلأنّ المسير الوسط للكوكب كان بعده من البعد الأبعد أربعةً وأربعين جزءًا وخمسين دقيقةً تكون زاوية ألف باء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة وأربعون جزءًا وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة وثمانون جزءًا وأربعون دقيقةً فتكون لذلك زاوية جيم باء حاء الباقية مائتين وسبعين جزءًا وعشرين دقيقةً وتكون كلّ واحدة من زاويتي باء جيم حاء باء حاء جيم بهذه الأجزاء أربعةً وأربعين جزءًا وخمسين دقيقةً فلذلك تكون الخطوط أيضًا التي توترها أمّا خطّ جيم حاء منها فأربعة وثمانون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها قطر الدائرة التي ترسم حول مثلّث باء جيم حاء مائة وعشرون جزءًا وأمّا كلّ واحد من خطّي باء جيم باء حاء بهذه الأجزاء فخمسة وأربعون جزءًا وستّ وأربعون دقيقةً فالأجزاء إذن التي بها كلّ واحد من خطّي باء جيم باء حاء ثلاثة أجزاء يكون بها خطّ جيم حاء خمسة أجزاء وثلاثًا وثلاثين دقيقةً⊙ وأيضًا لأنّ زاوية ألف جيم زاي قد وضعت تسعةً وثمانين جزءًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية باء جيم حاء على ذلك المثال أربعة وأربعون جزءًا وخمسون دقيقةً فتحصل زاوية زاي جيم بأسرها مائة وأربعة وثلاثون جزءًا وثلاثون دقيقةً تكون أيضًا القوس التي على خطّ حاء ميم مائةً وأربعةً وثلاثين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم حاء ميم القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم ما يبقى لتمام نصف دائرة وهو خمسة وأربعون جزءًا وثلاثون دقيقةً فالخطّان إذن اللذان يوترانهما أمّا خطّ ميم حاء منهما فيكون مائةً وعشرة أجزاء وأربعين دقيقةً بالأجزاء التي بها خطّ جيم حاء الموتّر مائة وعشرون جزءًا وأمّا خطّ جيم ميم بهذه الأجزاء فستّة وأربعون جزءًا وأربع وعشرون دقيقةً فتكون لذلك الأجزاء التي بها خطّ جيم حاء خمسة أجزاء وثلاث وثلاثون دقيقةً أعني الأجزاء التي بها خطّ زاي حاء الذي من مركز الفلك الخارج المركز ستّون جزءًا فخطّ حاء ميم بها خمسة أجزاء وسبع دقائق وخطّ حاء ميم على ذلك المثال جزأين وعشر دقائق فلذلك يحصل خطّ زاي ميم في الطول بهذه الأجزاء تسعةً وخمسين جزءًا وسبعًا وأربعين دقيقةً وخطّ زاي ميم جيم بأسره أحد وستّون جزءًا وسبع وخمسون دقيقةً وكذلك لأنّ زاوية دال جيم نون تسعة وثمانون جزءًا وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون أيضًا القوس التي على خطّ دال نون تسعةً وثمانين جزءًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم دال نون القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ جيم زاي ما يبقى لتمام نصف دائرة وهي تسعون جزءًا وعشرون دقيقةً فخطّ دال نون إذن ه: إذن من الخطّين اللذين يوترانهما أربعة وثمانون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها خطّ جيم دال الموتر مائة وعشرون جزءًا وخطّ جيم نون بهذه الأجزاء خمسة وثمانون جزءًا وستّ دقائق فالأجزاء إذن التي بها خطّ جيم دال ثلاثة أجزاء يكون بها خطّ دال نون جزأين وسبع دقائق وخطّ جيم نون على ذلك المثال جزأين وثمان دقائق وخطّ زاي حاء نون بأسره أربعة وستّون جزءًا وخمس دقائق ولذلك يكون أيضًا خطّ زاي دال الموتر بهذه الأجزاء أربعةً وستّين جزءًا وسبع دقائق فالأجزاء إذن التي بها خطّ زاي دال مائة وعشرون جزءًا يكون بها خطّ دال نون ثلاثة أجزاء وثمانيًا وخمسين دقيقةً والقوس التي عليه ثلاثة أجزاء وثمانيًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي نون القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون أيضًا زاوية دال زاي نون ثلاثة أجزاء وثمانيًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية زاي دال نون مائة وستّة وسبعون جزءًا واثنتا عشرة دقيقةً فتكون زاوية ألف دال نون الباقية بهذه الأجزاء خمسة وثمانون جزءًا واثنتان وخمسون دقيقةً لكنّ زاوية ألف دال لام قد وضعت بهذه الأجزاء أربعةً وخمسين جزءًا وأربعين دقيقةً من قبل أنّ الكوكب كان بعده في هذا الرصد من البعد الأبعد سبعةً وعشرين جزءًا
فسبعة وتسعون جزءًا وسبع وعشرون دقيقةً فقوس طاء كاف لام من فلك التدوير التي هي كانت بعد كوكب عطارد في وقت الرصد من نقطة طاء التي هي البعد الأبعاد تسعة وتسعون جزءًا وسبع وعشرون دقيقةً وذلك ما قصدنا لتبيينه⊙ وأيضًا في سنة إحدى وعشرين من عهد ذيونوسيوس وكانت سنة أربع مائة وأربع وثمانين من عهد بختنصّر في الشهر المسمّى سفرسون ه: نسبة {...} في اليوم الثاني والعشرين منه وأمّا عند المصريّين ففي شهر توث في اليوم الثامن عشر منه في غداة الليلة التي يتلوها اليوم التاسع عشر كان بعد كوكب عطارد إلى توالي البروج من الخطّ المستقيم الذي يمرّ بالكوكب الشماليّ من جبهة العقرب وبالكوكب الذي في وسط الجبهة مقدار قطر القمر وكان بعده في الشمال من الكوكب الشماليّ من الجبهة مقدار قطري القمر لكنّ الكوكب الوسط من الكواكب التي في جبهة العقرب كان حاصله في ذلك الوقت على حسب مبادئنا على جزء واحد وثلثي جزء من العقرب وهو أميل إلى الجنوب عن فلك البروج بمثل ذلك φ والكوكب الشماليّ منها كان حاصله على جزأين وثلث جزء من العقرب وهو أميل إلى الشمال من فلك البروج بجزء واحد وثلث جزء فكان إذن حاصل كوكب عطارد أيضًا على ثلاثة أجزاء وثلث جزء من العقرب بالتقريب⊙ وقد نعلم أيضًا أنّه لم يكن بعد صار في أعظم ما يكون من بعده الصباحيّ من قبل أنّا وجدنا في هذا الرصد مثبتًا أنّه بعد أربعة أيّام في اليوم السادس والعشرين من الشهر المسمّى سغرينون صار بعده من ذلك الخطّ المستقيم بعينه إلى توالي البروج مقدار قطر القمر بأسره ونصف قطره وذلك أنّ البعد زاد بأنّ الشمس تحرّكت قريبًا من أربعة أجزاء وتحرّك الكوكب نصف قطر القمر وكان حاصل الشمس بحركتها الوسطى في اليوم التاسع عشر من الشهر المسمّى توث في الغلس على ما عندنا على عشرين جزءًا ونصف وثلث جزء من العقرب وكان البعد الأبعد للكوكب على ستّة أجزاء من الميزان من قبل أنّ السنين التي بين الرصدين إذا كانت أربع مائة سنة فإنّ انتقال البعد الأبعد يكون فيها نحوًا من أربع درج⊙ فإذ قد وطّأنا هذه الأشياء يے: فلنرسم أيضًا صورةً مثل الصورة التي تقدّمت غير أنّا نجعل في هذه الصورة الزاويتين اللتين في جهة نقطة ألف وهي البعد الأبعد لأنّ المسير في هذا الرصد مخالف للمسير في ذلك الرصد حادّتين ونجعل الخطّين اللذين نصفهما بالكوكب قدمًا من فلك التدوير ونجعل عمود زاي سين أعلى من خطّ زاي لام الذي من مركز فلك التدوير فلأنّ المسير الوسط للكوكب كان بعده من البعد الأبعد أربعةً وأربعين جزءًا وخمسين دقيقةً تكون زاوية ألف باء حاء أمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فأربعة وأربعون جزءًا وخمسون دقيقةً وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فتسعة وثمانون جزءًا وأربعون دقيقةً فتكون لذلك زاوية جيم باء حاء الباقية مائتين وسبعين جزءًا وعشرين دقيقةً وتكون كلّ واحدة من زاويتي باء جيم حاء باء حاء جيم بهذه الأجزاء أربعةً وأربعين جزءًا وخمسين دقيقةً فلذلك تكون الخطوط أيضًا التي توترها أمّا خطّ جيم حاء منها فأربعة وثمانون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها قطر الدائرة التي ترسم حول مثلّث باء جيم حاء مائة وعشرون جزءًا وأمّا كلّ واحد من خطّي باء جيم باء حاء بهذه الأجزاء فخمسة وأربعون جزءًا وستّ وأربعون دقيقةً فالأجزاء إذن التي بها كلّ واحد من خطّي باء جيم باء حاء ثلاثة أجزاء يكون بها خطّ جيم حاء خمسة أجزاء وثلاثًا وثلاثين دقيقةً⊙ وأيضًا لأنّ زاوية ألف جيم زاي قد وضعت تسعةً وثمانين جزءًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية باء جيم حاء على ذلك المثال أربعة وأربعون جزءًا وخمسون دقيقةً فتحصل زاوية زاي جيم بأسرها مائة وأربعة وثلاثون جزءًا وثلاثون دقيقةً تكون أيضًا القوس التي على خطّ حاء ميم مائةً وأربعةً وثلاثين جزءًا وثلاثين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم حاء ميم القائم الزاوية ثلاث مائة وستّون جزءًا وتكون القوس التي على خطّ جيم ميم ما يبقى لتمام نصف دائرة وهو خمسة وأربعون جزءًا وثلاثون دقيقةً فالخطّان إذن اللذان يوترانهما أمّا خطّ ميم حاء منهما فيكون مائةً وعشرة أجزاء وأربعين دقيقةً بالأجزاء التي بها خطّ جيم حاء الموتّر مائة وعشرون جزءًا وأمّا خطّ جيم ميم بهذه الأجزاء فستّة وأربعون جزءًا وأربع وعشرون دقيقةً فتكون لذلك الأجزاء التي بها خطّ جيم حاء خمسة أجزاء وثلاث وثلاثون دقيقةً أعني الأجزاء التي بها خطّ زاي حاء الذي من مركز الفلك الخارج المركز ستّون جزءًا فخطّ حاء ميم بها خمسة أجزاء وسبع دقائق وخطّ حاء ميم على ذلك المثال جزأين وعشر دقائق فلذلك يحصل خطّ زاي ميم في الطول بهذه الأجزاء تسعةً وخمسين جزءًا وسبعًا وأربعين دقيقةً وخطّ زاي ميم جيم بأسره أحد وستّون جزءًا وسبع وخمسون دقيقةً وكذلك لأنّ زاوية دال جيم نون تسعة وثمانون جزءًا وأربعون دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وتكون أيضًا القوس التي على خطّ دال نون تسعةً وثمانين جزءًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث جيم دال نون القائم الزاوية ثلاث مائة وستّون جزءًا والقوس التي على خطّ جيم زاي ما يبقى لتمام نصف دائرة وهي تسعون جزءًا وعشرون دقيقةً فخطّ دال نون إذن ه: إذن من الخطّين اللذين يوترانهما أربعة وثمانون جزءًا وستّ وثلاثون دقيقةً بالأجزاء التي بها خطّ جيم دال الموتر مائة وعشرون جزءًا وخطّ جيم نون بهذه الأجزاء خمسة وثمانون جزءًا وستّ دقائق فالأجزاء إذن التي بها خطّ جيم دال ثلاثة أجزاء يكون بها خطّ دال نون جزأين وسبع دقائق وخطّ جيم نون على ذلك المثال جزأين وثمان دقائق وخطّ زاي حاء نون بأسره أربعة وستّون جزءًا وخمس دقائق ولذلك يكون أيضًا خطّ زاي دال الموتر بهذه الأجزاء أربعةً وستّين جزءًا وسبع دقائق فالأجزاء إذن التي بها خطّ زاي دال مائة وعشرون جزءًا يكون بها خطّ دال نون ثلاثة أجزاء وثمانيًا وخمسين دقيقةً والقوس التي عليه ثلاثة أجزاء وثمانيًا وأربعين دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي نون القائم الزاوية ثلاث مائة وستّون جزءًا فلذلك تكون أيضًا زاوية دال زاي نون ثلاثة أجزاء وثمانيًا وأربعين دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وزاوية زاي دال نون مائة وستّة وسبعون جزءًا واثنتا عشرة دقيقةً فتكون زاوية ألف دال نون الباقية بهذه الأجزاء خمسة وثمانون جزءًا واثنتان وخمسون دقيقةً لكنّ زاوية ألف دال لام قد وضعت بهذه الأجزاء أربعةً وخمسين جزءًا وأربعين دقيقةً من قبل أنّ الكوكب كان بعده في هذا الرصد من البعد الأبعد سبعةً وعشرين جزءًا
 وعشرين دقيقةً فتبقى زاوية زاي دال لام الباقية أحدًا وثلاثين جزءًا واثنتي عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فالقوس إذن التي على خطّ زاي سين أحد وثلاثون جزءًا واثنتا عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي دال سين القائم الزوية ثلاث مائة وستّون جزءًا وخطّ زاي سين نفسه اثنان وثلاثون جزءًا وستّ عشرة دقيقةً بالأجزاء التي بها خطّ دال نون الموتّر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ دال زاي أربعة وستّون جزءًا وسبع دقائق أعني الأجزاء التي بها خطّ زاي لام الذي من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً يكون بها خطّ زاي سين أيضًا سبعة عشر جزءًا وخمس عشرة دقيقةً فالأجزاء التي بها خطّ زاي لام الموتر مائة وعشرون جزءًا يكون بها على ذلك المثال خطّ زاي سين اثنين وتسعين جزءًا بالتقريب فتكون لذلك القوس التي على خطّ زاي سين مائة جزء وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي لام سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية زاي لام سين مائة جزء وثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كان تبيّن أنّ زاوية زاي دال لام بهذه الأجزاء أحد وثلاثون جزءًا واثنتا عشرة دقيقةً وزاوية طاء زاي كاف على ذلك المثال ثلاثة أجزاء وثمان وأربعون دقيقةً فتكون زاوية كاف زاي لام الباقية أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة وستّون جزءًا وثمان دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فاثنان وثلاثون جزءًا وأربع وثلاثون دقيقةً فكان إذن بعد هذا الكوكب في هذا الرصد من نقطة كاف التي هي البعد الأقرب من فلك التدوير اثنين وثلاثين جزءًا وأربعًا وثلاثين دقيقةً ومن البيّن أنّ بعده من البعد الأبعد كان مائتين واثني عشر جزءًا وأربعًا وثلاثين دقيقةً وقد تبيّن أنّ بعده كان أيضًا في وقت رصدنا نحن على ذلك المثال من البعد الأبعد من فلك التدوير تسعة وتسعون جزءًا وسبع وعشرون دقيقةً والزمان الذي بين الرصدين من السنين المصريّة أربع مائة سنة وسنتان ومائتا يوم وثلاثة وثمانون يومًا وثلاث عشرة ساعةً ونصف بالتقريب وهذا الزمان يشتمل من العودات التامّة لاختلاف الكوكب على ألف ومائتين وثمان وستّين عودةً وذلك أنّ كلّ عشرين سنةً مصريّةً يكون فيها من الأدوار ثلاثًا وستّين دورةً فيحصل في أربع مائة سنة من الأدوار ألف ومائتان وستّون دورةً وفي السنتين الباقيتين مع الأيّام الزائدة عليها ثمانية أدوار أخر تامّة فقد تبيّن لنا إذن ه: إذن أنّ في أربع مائة سنة وسنتين ومائتين وثلاثةً وثمانين يومًا وثلاث عشرة ساعةً ونصف قد فضل لكوكب عطارد بعد العودات التامّة لاختلافه وهي ألف ومائتان وثمان وستّون عودةً مائتان وستّة وأربعون جزءًا وثلاث وخمسون دقيقةً وهو مبلغ الأجزاء التي بها فضل الحاصل في زماننا على الحاصل في الزمان الذي قبله ونحو ذلك مبلغ الفضل الذي تحصّل أيضًا من الجداول التي تقدّمنا فوصفناها من قبل أنّ بهذه الأسباب صحّحنا حركات أدوار كوكب عطارد بأن بسطنا هذا الزمان الذي ذكرناه أيّامًا وبسطنا دورات الاختلاف مع الفضل أجزاءً فإنّ هذه الأجزاء إذا قسمت على عدّة الأيّام خرج لنا ما وضعناه آنفًا لكوكب عطارد من حركته الوسطى للاختلاف في اليوم الواحد⊙
وعشرين دقيقةً فتبقى زاوية زاي دال لام الباقية أحدًا وثلاثين جزءًا واثنتي عشرة دقيقةً بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فالقوس إذن التي على خطّ زاي سين أحد وثلاثون جزءًا واثنتا عشرة دقيقةً بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي دال سين القائم الزوية ثلاث مائة وستّون جزءًا وخطّ زاي سين نفسه اثنان وثلاثون جزءًا وستّ عشرة دقيقةً بالأجزاء التي بها خطّ دال نون الموتّر مائة وعشرون جزءًا فالأجزاء إذن التي بها خطّ دال زاي أربعة وستّون جزءًا وسبع دقائق أعني الأجزاء التي بها خطّ زاي لام الذي من مركز فلك التدوير اثنان وعشرون جزءًا وثلاثون دقيقةً يكون بها خطّ زاي سين أيضًا سبعة عشر جزءًا وخمس عشرة دقيقةً فالأجزاء التي بها خطّ زاي لام الموتر مائة وعشرون جزءًا يكون بها على ذلك المثال خطّ زاي سين اثنين وتسعين جزءًا بالتقريب فتكون لذلك القوس التي على خطّ زاي سين مائة جزء وثمان دقائق بالأجزاء التي بها الدائرة التي ترسم حول مثلّث زاي لام سين القائم الزاوية ثلاث مائة وستّون جزءًا فزاوية زاي لام سين مائة جزء وثمان دقائق بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا وقد كان تبيّن أنّ زاوية زاي دال لام بهذه الأجزاء أحد وثلاثون جزءًا واثنتا عشرة دقيقةً وزاوية طاء زاي كاف على ذلك المثال ثلاثة أجزاء وثمان وأربعون دقيقةً فتكون زاوية كاف زاي لام الباقية أمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءًا فخمسة وستّون جزءًا وثمان دقائق وأمّا بالأجزاء التي بها أربع زوايا قائمة ثلاث مائة وستّون جزءًا فاثنان وثلاثون جزءًا وأربع وثلاثون دقيقةً فكان إذن بعد هذا الكوكب في هذا الرصد من نقطة كاف التي هي البعد الأقرب من فلك التدوير اثنين وثلاثين جزءًا وأربعًا وثلاثين دقيقةً ومن البيّن أنّ بعده من البعد الأبعد كان مائتين واثني عشر جزءًا وأربعًا وثلاثين دقيقةً وقد تبيّن أنّ بعده كان أيضًا في وقت رصدنا نحن على ذلك المثال من البعد الأبعد من فلك التدوير تسعة وتسعون جزءًا وسبع وعشرون دقيقةً والزمان الذي بين الرصدين من السنين المصريّة أربع مائة سنة وسنتان ومائتا يوم وثلاثة وثمانون يومًا وثلاث عشرة ساعةً ونصف بالتقريب وهذا الزمان يشتمل من العودات التامّة لاختلاف الكوكب على ألف ومائتين وثمان وستّين عودةً وذلك أنّ كلّ عشرين سنةً مصريّةً يكون فيها من الأدوار ثلاثًا وستّين دورةً فيحصل في أربع مائة سنة من الأدوار ألف ومائتان وستّون دورةً وفي السنتين الباقيتين مع الأيّام الزائدة عليها ثمانية أدوار أخر تامّة فقد تبيّن لنا إذن ه: إذن أنّ في أربع مائة سنة وسنتين ومائتين وثلاثةً وثمانين يومًا وثلاث عشرة ساعةً ونصف قد فضل لكوكب عطارد بعد العودات التامّة لاختلافه وهي ألف ومائتان وثمان وستّون عودةً مائتان وستّة وأربعون جزءًا وثلاث وخمسون دقيقةً وهو مبلغ الأجزاء التي بها فضل الحاصل في زماننا على الحاصل في الزمان الذي قبله ونحو ذلك مبلغ الفضل الذي تحصّل أيضًا من الجداول التي تقدّمنا فوصفناها من قبل أنّ بهذه الأسباب صحّحنا حركات أدوار كوكب عطارد بأن بسطنا هذا الزمان الذي ذكرناه أيّامًا وبسطنا دورات الاختلاف مع الفضل أجزاءً فإنّ هذه الأجزاء إذا قسمت على عدّة الأيّام خرج لنا ما وضعناه آنفًا لكوكب عطارد من حركته الوسطى للاختلاف في اليوم الواحد⊙
〈IX.11〉 يا: في حاصل حركات أدوار كوكب عطارد
وكيما نقيّد تحصيلات الكواكب الخمسة كما قيّدنا حاصل الشمس وحاصل القمر في السنة الأولى من سني بختنصّر في شهر توث عند المصريّين في انتصاف نهار اليوم الأوّل منه أخذنا الزمان بين ذلك الوقت وبين أقدم الرصدين وأقربهما إليه. ومبلغه أربع مائة سنة وثلاث وثمانون سنةً وسبعة عشر يومًا وثمان عشرة ساعةً بالتقريب. وبإزاء هذا الزمان لفضلة الاختلاف للحركة الوسطى مائة وتسعون جزءًا وتسع وثلاثون دقيقةً. فإذا نقصنا هذه الأجزاء من أجزاء البعد في الرصد من البعد الأبعد وهي مائتان واثنا عشر جزءًا وأربع وثلاثون دقيقةً. صار لنا الحاصل في السنة الأولى من سني بختنصّر في شهر توث عند المصريّين في انتصاف نهار اليوم الأوّل منه أمّا للاختلاف من البعد الأبعد من فلك التدوير فعلى أحد وعشرين جزءًا وخمس وخمسين دقيقةً. وأمّا للطول وهو حاصل الشمس بعينه فعلى خمس وأربعين دقيقةً من الحوت. وأمّا البعد الأبعد من الفلك الخارج المركز فعلى جزء وسدس جزء من الميزان من قبل أنّ الجزء من مائة من هذه السنين التي ذكرناها يحصل أربعة أجزاء ونصف وثلث جزء بالتقريب.⊙ وذلك مبلغ فضل الستّة الأجزاء من الميزان التي وجدت بالرصد على الجزء والسدس⊙ تمّت المقالة التاسعة من كتاب بطلميوس المنسوب إلى التعاليم وهي يا قولًا والحمد لله على عونه كثيرًا كما هو أهله بسم الله الرحمن الرحيم عونك يا واحد جُمل ما في المقالة العاشرة من كتاب بطلميوس المنسوب إلى التعاليم⊙ الأولى في تبيين البعد الأبعد لكوكب الزهرة؛ الثانية في مقدار فلك تدوير هذا الكوكب⊙ الثالثة في أقدار خروج الفلك الخارج المركز الذي لهذا الكوكب عن المركز؛ الرابعة في تصحيح حركات هذا الكوكب الدوريّة؛ الخامسة في حاصل هذا الكوكب الدوريّة؛ السادسة فيما يحتاج أن يتقدّم فيعلم في تبيين أمر سائر الكواكب⊙ السابعة في تبيين الخروج عن المركز في كوكب المرّيخ وبعده الأبعد؛ الثامنة في تبيين مقدار فلك تدوير المرّيخ؛ التاسعة في تصحيح حركات المرّيخ الدوريّة⊙ العاشرة في حاصل حركات المرّيخ الدوريّة⊙