Ptolemaeus Arabus et Latinus

بسم الله الرحمن الرحيم

عونك يا واحد

جمل ما في المقالة الثانية من كتاب بطلميوس المنسوب إلى التعاليم

الأولى: في جملة موضع المسكون من الأرض؛ ه – صح: عندنا الثانية: كيف يعلم إذا فرض مقدار أطول ما يكون من النهار أنّ مقادير القسيّ التي تنفصل من الأفق بين دائرة معدّل النهار وبين الدائرة المائلة تكون مفروضة؛ الثالثة: كيف يعلم أنّ هذه الأشياء إذا كانت معلومة فإنّ ارتفاع القطب يكون مفروضاً وعكس ذلك؛ الرابعة: كيف ينبغي أن يحسب فيعلم من الذين تصير الشمس على سمت رؤوسهم في الأصل: روسهم ومتى وكم من مرّة؛ الخامسة: كيف يمكن أن يدرك ممّا وصفنا نسب المقاييس إلى أظلالها في الاستوائين في الأصل: الاستواأين والانقلابين في أنصاف النهار؛ السادسة: صفة خواصّ دائرة دائرة من الدوائر المتوازية؛ السابعة: فيما يطلع من دائرة معدّل النهار مع الدائرة التي تمرّ بأوساط البروج في الكرة المائلة؛ الثامنة: جداول للمطالع المتفاصلة بعشرة أجزاء عشرة أجزاء؛ التاسعة: في الأشياء الجزئيّة التي تعلم بعلم؛ ه- صح: المطالع العاشرة: في الزاويا التي تحدث بين دائرة البروج وبين دائرة نصف النهار؛ الحادية عشر: في الزوايا التي تحدث بين الدائرة المائلة وبين دائرة الأفق؛ الثانية عشر: في الزوايا التي تحدث بين دائرة البروج وبين الدائرة التي تمرّ بقطبي الأفق؛ الثالثة عشر: في صفة الزوايا والقسيّ التي ذكرت في دائرة دائرة من الدوائر المتوازية.

⟨II⟩ ابتداء المقالة الثانية من كتاب بطلميوس المنسوب إلى التعاليم

⟨II.1⟩  /T75/آ: في جملة موضع المسكون من الأرض عندنا

قال إنّا لمّا آتينا في المقالة الأولى من كتابنا هذا على ما يجب أن يتقدّم، فيعلم على الطريق المجمل من حال الكلّ بعضه عند بعض وعلى جميع ما ينتفع به في هذا العلم من أمر الكرة المنتصبة. فنحن نروم أن نتبع ذلك بأجلّ ما يلزم في الكرة المائلة أيضاً ونسلك فيه أسهل الطرق التي يمكن سلوكها وأيسرها.

/H88/ فنقول إنّ جملة ما ينبغي أن يتقدّم، فيعلم في هذا أيضاً هو أنّ الأرض لمّا كانت تنقسم بأربعة أرباع، تقع لها عن دائرة معدّل النهار وعن إحدى الدوائر المرسومة على قطبي هذه الدائرة فإنّ مقدار المسكون منها عندنا يحتوي عليه أحد الربعين الشماليّين على التقريب. وأبلغ ما يظهر به ذلك إمّا في العرض، وهو المسافة بين الجنوب والشمال، فإنّ ظلّ المقاييس في كلّ موضع عند استواء الليل والنهار يقع في أنصاف النهار إلى ناحية الشمال أبداً ولا يقع أصلاً إلى ناحية الجنوب. وأمّا في الطول، وهو المسافة بين المشرق والمغرب، فإنّا نجد الكسوفات بأعيانها التي كانت في زمان بعينه، وخاصّة كسوفات القمر، عند من كان في أقاصي المشرق من المسكونة عندنا وعند من كان في أقاصي المغرب، لا تتقدّم أو تتأخّر بأكثر من اثنتي في الأصل: اثني عشرة ساعة من الساعات الاستوائيّة؛ والربع نفسه في الطول أنّما مقدار مسافته اثنتا عشرة ساعة من قبل أنّه يفرزه أحد نصفي دائرة معدّل النهار.

وأمّا من الأشياء الجزئيّة فأوّل ما يجب أن نعلم ممّا يصلح لمّا قصدنا له أجل الخواصّ اللازمة في كلّ واحدة من الدوائر التي هي أميل إلى الشمال عن دائرة معدّل النهار الموازية لهذه الدائرة ممّا يقع في المساكن التي تحتها. /H89/ وهذه هي المعرفة ببعد قطبي الحركة الأولى عن الأفق أو بعد النقطة التي على سمت الرأس عن دائرة معدّل النهار في دائرة نصف النهار؛ /T76/ ومن الذين تصير الشمس على سمت رؤوسهم ومتى تصير كذلك وكم من مرّة بعرض ذلك؛ وأيّ نسب هي نسب الظلّ في الاستوائين في الأصل: الاستواأين والانقلابين في أنصاف النهار إلى المقاييس؛ وكم مقدار تفاضل الأيّام الطوال والأيّام القصار بالقياس إلى النهار المعتدل؛ وسائر ما يتّبع ذلك من في الأصل: مَن الزيادات والنقصانات الجزئيّة لكلّ يوم وليلة؛ ومعرفة ما يطلع من دائرة معدّل النهار مع الدائرة المائلة وما يغرب منها معها؛ وجميع ما نجده يلزم من أمر خواصّ الزوايا الحادثة عن أجل الدوائر العظام ومقاديرها.

⟨II.2⟩ ب: كيف نعلم إذا فرض مقدار أطول ما يكون من النهار ه – ج: يريد به معرفة سعة المشرق أنّ مقادير القسيّ التّي تنفصل من الأفق بين دائرة معدّل النهار وبين الدائرة المائلة تكون مفروضة

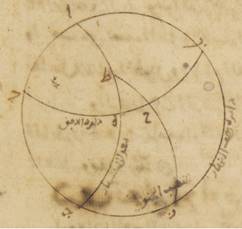
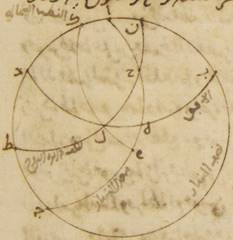
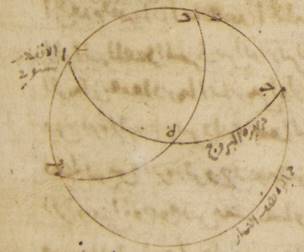
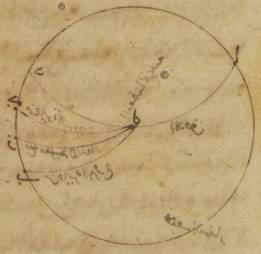
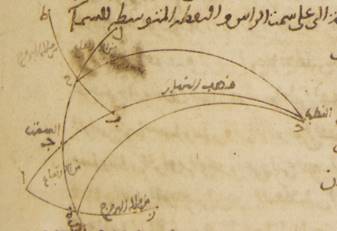
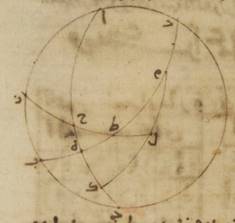
فلنضع بالجملة مثالاً لذلك الدائرة التي تمرّ على الجزيرة المسمّاة /H90/ رودش الموازية لدائرة معدّل النهار حيث ارتفاع القطب ستّة وثلاثون جزءاً وأطول ما يكون النهار أربع عشرة ساعة ونصف من الساعات الاستوائيّة. ه: آ ولتكن دائرة نصف النهار ألف باء جيم دال ونصف دائرة الأفق باء هاء دال وكذلك نصف دائرة معدّل النهار ألف هاء جيم وقطبها الجنوبيّ نقطة زاي. ولنضع نقطة الانقلاب الشتويّ من الدائرة التي تمرّ على أوساط البروج تطلع على نقطة حاء ولنرسم على نقطتي زاي حاء ربع شطب الكاتب حرف «من» دائرة من أعظم الدوائر ولتكن زاي حاء طاء. /T77/ ولنجعل أوّلاً مقدار أطول النهار مفروضاً وليكن القصد معرفة مقدار قوس حاء هاء من دائرة الأفق. فمن قبل أنّ دور الكرة أنمّا يكون على قطبي معدّل النهار، من البيّن أنّ نقطة حاء ونقطة طاء تصيران على دائرة نصف النهار وهي دائرة ألف باء في زمان واحد. وإذا ابتدأت نقطة حاء من المشرق ومرّت صاعدة على الأرض حتّى تنتهي إلى وسط السماء كان هذا الزمان هو الزمان الذي تحدّه قوس طاء ألف من دائرة معدّل النهار. وإذا ابتدأت من وسط السماء تحت الأرض وصارت إلى المشرق كان هذا الزمان هو الذي تحدّه قوس جيم طاء. /H91/ وقد يلزم من ذلك أيضاً أنّ زمان النهار، وهو  It should be هو to make the correct sense. ضعف الزمان الذي تحدّه قوس طاء ألف، وزمان الليل ضعف الزمان الذي تحدّه قوس جيم طاء. فإنّا قد نعلم على الإطلاق أنّ القطع التي فوق الأرض والتي تحت الأرض من الدوائر الموازية لدائرة معدّل النهار تقسمها كلّها بنصفين نصفين دائرة نصف النهار.

ولذلك فإنّ قوس هاء طاء إذا كانت نصف الاختلاف بين أقصر ما يكون من النهار أو أطوله وبين النهار المعتدل تكون ساعة وربع في هذه الدائرة الموازية التي جعلناها ه: ب؛ ا خ: فقوس ه ط إذن مثالاً. ومن البيّن أنّها تكون ثمانية عشر زماناً وخمساً وأربعين دقيقة؛ وقوس طاء ألف الباقية من الربع أحداً وسبعين زماناً وخمس عشرة دقيقة.

فعلى حسب ما تقدّم بيانه من قبل أنّه قد رسم فيما بين قوسين من أعظم الدوائر وهما قوسا ألف هاء، ألف زاي قوسا هاء باء، زاي طاء تتقاطعان على نقطة حاء؛ فنسبة وتر ضعف قوس طاء ألف إلى وتر ضعف قوس ألف هاء مؤلّفة من نسبة وتر ضعف قوس طاء زاي إلى وتر ضعف قوس زاي حاء، ونسبة وتر ضعف قوس حاء باء إلى وتر ضعف قوس باء هاء. لكن ضعف قوس طاء ألف مائة واثنان وأربعون جزءاً وثلاثون دقيقة ووتره مائة وثلاثة عشر جزءاً وسبع وثلاثون دقيقة وأربع وخمسون ثانية، وضعف قوس ألف هاء مائة وستّون ه – صح: وثمانون جزءاً، /H92/ ووتره مائة وعشرون جزءاً وضعف قوس زاي حاء مائة واثنان وثلاثون جزءاً وسبع عشرة دقيقة وعشرون ثانية ووتره مائة وتسعة أجزاء وأربع وأربعون دقيقة وثلاث وخمسون ثانية وضعف قوس زاي طاء مائة وثمانون جزءاً ووتره مائة وعشرون جزءاً.

فإن نقصنا من نسبة مائة وثلاثة عشر جزءاً وسبع وثلاثين دقيقة وأربع وخمسين ثانية إلى مائة وعشرين جزءاً نسبة مائة وعشرين جزءاً إلى مائة وتسعة أجزاء وأربع وأربعين دقيقة وثلاث وخمسين ثانية بقيت لنا نسبة وتر ضعف قوس حاء باء إلى وتر ضعف قوس باء هاء نسبة مائة وثلاثة أجزاء وخمس وخمسين دقيقة وستّ وعشرين ثانية إلى مائة وعشرين جزءاً. لكن وتر ضعف قوس باء هاء إذ كانت ربع دائرة مائة وعشرون جزءاً فوتر ضعف قوس حاء باء هو بهذه الأجزاء مائة وثلاثة أجزاء وخمس وخمسين دقيقة وستّ وعشرين ثانية. فيجب أن يكون ضعف قوس باء حاء مائة وعشرون جزءاً بالتقريب وقوس باء حاء نفسها بهذه الأجزاء ستّين جزءاً. فتبقى إذن قوس حاء هاء الباقية ثلاثون جزءاً. وذلك ما كان ينبغي أن نبيّنه.

⟨II.3⟩ ج: كيف يعلم أنّ هذه الأشياء إذا كانت معلومة

فإنّ ارتفاع القطب يكون مفروضاً وعكس ذلك

ولنضع أيضاً أنّ ذلك مفروض وليكن قصدنا معرفة ارتفاع القطب أعني قوس باء زاي من دائرة نصف النهار. فتكون في هذه الصورة بعينها نسبة وتر ضعف قوس هاء طاء إلى وتر ضعف قوس طاء ألف /H93/ مؤلّفة من نسبة وتر ضعف قوس هاء حاء إلى وتر ضعف قوس حاء باء ونسبة وتر ضعف قوس باء زاي إلى وتر ضعف ](قوس باء زاي إلى وتر ضعف)[ قوس زاي ألف. /T78/ لكن ضعف قوس هاء طاء سبعة وثلاثون جزءاً وثلاثون دقيقة، ووتره ثمانية وثلاثون جزءاً وأربع وثلاثون دقيقة واثنتان وعشرون ثانية، وضعف قوس طاء ألف مائة واثنان وأربعون جزءاً وثلاثون دقيقة، ووتره مائة وثلاثة عشر جزءاً وسبع وثلاثون دقيقة وأربع وخمسون ثانية. وأيضاً فإنّ ضعف قوس هاء حاء ستّون جزءاً، ووتره ستّون جزءاً، وضعف قوس حاء باء مائة وعشرون جزءاً، ووتره مائة وثلاثة أجزاء وخمس وخمسون دقيقة وثلاث وعشرون ثانية. فإن نقصنا من نسبة ثمانية وثلاثين جزءاً وأربع وثلاثين دقيقة واثنتين وعشرين ثانية إلى مائة وثلاثة عشر جزءاً وسبع وثلاثين دقيقة وأربع وخمسين ثانية نسبة ستّين جزءاً إلى مائة وثلاثة أجزاء وخمس وخمسين دقيقة وثلاث وعشرين ثانية، بقيت نسبة وتر ضعف قوس باء زاي إلى وتر ضعف قوس زاي ألف نسبة سبعين جزءاً وثلاث وثلاثين دقيقة بالتقريب إلى مائة وعشرين جزءاً. وأيضاً فإنّ وتر ضعف قوس زاي ألف مائة وعشرون جزءاً. فوتر ضعف قوس باء زاي إذاً بهذه الأجزاء سبعون جزءاً وثلاث وثلاثون دقيقة وضعف قوس باء زاي اثنان وسبعون جزءاً ودقيقة واحدة، وقوس باء زاي بهذه الأجزاء ستّة وثلاثون جزءاً بالتقريب. وأيضاً فلنجز الأمر وهذه الصورة على حالها على العكس حتّى تكون قوس باء زاي وهي /H94/ ارتفاع القطب مفروضة على ما رصدت ستّة وثلاثون جزءاً، وليكن قصدنا أن نعرف اختلاف أقصر ما يكون من النهار وأطول ما يكون منه بالقياس إلى النهار المعتدل وذلك هو ضعف قوس هاء طاء. فلذلك بعينه تكون نسبة وتر ضعف قوس زاي باء إلى وتر ضعف قوس باء ألف مؤلّفة من نسبة وتر ضعف قوس زاي حاء إلى وتر ضعف قوس حاء طاء ونسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء ألف. لكن ضعف قوس زاي باء اثنان وسبعون جزءاً ⟨ووتره سبعون جزءاً⟩ واثنتان وثلاثون دقيقة وثلاث ثواني، وضعف قوس باء ألف مائة وثمانية أجزاء، ووتره سبعة وتسعون جزءاً وأربع دقائق وستّ ه: وخمس وخمسون ثانية. وأيضاً فإنّ ضعف قوس زاي حاء مائة واثنان وثلاثون جزءاً وسبع عشرة دقيقة وعشرون ثانية ووتره مائة وتسعة أجزاء وأربع وأربعون دقيقة وثلاث وخمسون ثانية. وضعف قوس حاء طاء سبعة وأربعون جزءاً واثنتان وأربعون دقيقة وأربعون ثانية ووتره ثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة وخمس وخمسون ثانية. فإن نقصنا من نسبة سبعين جزءاً واثنتين وثلاثين دقيقة وثلاث ثواني إلى سبعة وتسعين جزءاً وأربع دقائق وستّ ه: وخمس وخمسين ثانية نسبة مائة وتسعة أجزاء وأربع وأربعين دقيقة وثلاث وخمسين ثانية إلى ثمانية وأربعين جزءاً وإحدى وثلاثين دقيقة وخمس وخمسين ثانية، بقيت نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء ألف نسبة واحد وثلاثين جزءاً وإحدى وعشرة دقيقة وثماني وعشرين ثانية إلى سبعة وتسعين جزءاً وأربع دقائق وستّ ه: وخمس وخمسين ثانية، فلأنّ هذه النسبة قريبة من نسبة ثمانية وثلاثين جزءاً وأربع وثلاثين دقيقة  إلى مائة وعشرين جزءاً، /H95/ ووتر ضعف قوس هاء ألف مائة وعشرون جزءاً يحصل وتر ضعف قوس هاء طاء بهذه الأجزاء ثمانية وثلاثين جزءاً وأربع وثلاثين دقيقة. فيكون ضعف قوس هاء طاء سبعة وثلاثين جزءاً وثلاثين دقيقة بالتقريب، ويكون من الساعات الاستوائيّة ساعتين ونصف، وذلك ما قصدنا لتبيينه.

وعلى هذا المثال تكون أيضاً قوس هاء حاء من دائرة الأفق مفروضة من قبل أنّ نسبة وتر ضعف قوس زاي ألف إلى وتر ضعف قوس ألف باء المفروضة مؤلّفة من نسبة وتر ضعف قوس زاي طاء إلى وتر ضعف قوس طاء حاء التي هي أيضاً مفروضة ومن نسبة وتر ضعف قوس حاء هاء إلى وتر ضعف قوس هاء باء. فإذ كانت قوس هاء باء مفروضة، فإنّ مقدار قوس هاء حاء أيضاً يحصل من ذلك. ومن البيّن أنّا وإن لم نضع نقطة حاء نقطة الانقلاب الشتويّ لكن جعلناها نقطة جزء غير ذلك من أجزاء الدائرة التي تمرّ على أوساط البروج أيّ جزء كان، كانت على هذا ه: ب المثال أيضاً كلّ واحدة من قوسي /T79/ هاء طاء، هاء حاء مفروضة إذ كنّا قد تقدّمنا فوضعنا في جدول الميل القسيّ من دائرة نصف النهار التي تنفرز بين جزء جزء من دائرة البروج وبين دائرة معدّل النهار وهي القسيّ النظائر لقوس حاء طاء.

/H96/ وقد يلزم عن ذلك أنّ الفصول من الدائرة التي تمرّ على أوساط البروج التي تحدث عن دوائر موازية بعينها، أعني الفصول التي بعدها من نقطة واحدة بعينها من نقطتي الانقلابين أيّهما كانت بعد سواء، تفصل من دائرة الأفق قطعاً واحدة بعينها في جهة واحدة من جهتي دائرة معدّل النهار. وتصير مقادير أيّامها ولياليها متساوية كلّ واحد منها مساوياً لنظيره.

وقد تبيّن أيضاً مع ذلك أنّ الفصول التي تحدث عن دوائر متوازية متساوية، أعني الفصول التي بعدها عن نقطة واحدة بعينها من نقطتي الاستوائين في الأصل: الاستواين أيّهما كانت بعد سواء تفصل من دائرة الأفق عن جنبي معدّل النهار قطعاً متساوية؛ وتصير مقادير الأيّام بلياليها النظائر متساوية على المبادلة.

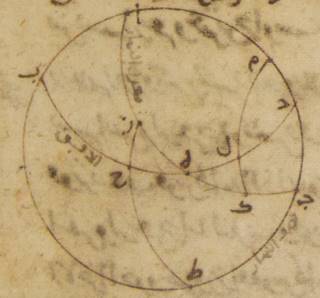
ب: وذلك أنّا إن جعلنا في هذه الصورة الموضوعة لنا نقطة كاف أيضاً النقطة التي عليها تفصل نصف دائرة الأفق (وهي ↑هي↑: ص بهده صح: بهد) الدائرة الموازية لمعدّل النهار المساوية للدائرة المرسومة على نقطة حاء؛ وتمّمنا قطعتي حاء لام، كاف ميم من الدوائر الموازية على المبادلة ومن البيّن أنّهما تكونان متساويتين. وأدرنا على نقطة كاف وعلى القطب الشماليّ وهو نقطة زاي ه – صح: نون ربع نون كاف سين. فإنّ قوس ألف طاء تكون مساوية لقوس سين جيم من قبل أنّ كلّ واحدة منهما شبيهة لكلّ واحدة من قوسي لام حاء ميم كاف؛ وتبقى قوس هاء طاء الباقية مساوية لقوس هاء سين. /H97/ فيكون ذو ثلاثة أضلاع هاء حاء طاء وذو ثلاثة أضلاع هاء كاف سين المتشابهان شطب الكاتب «ألف» و«نون»؛ ↑المتشابها↑: ص ضلعان من أحدهما مساويتان لضلعين من الآخر ضلع هاء طاء مساو لضلع هاء سين وضلع حاء طاء مساو لضلع كاف سين وكلّ واحدة من الزاويتين اللتين عند نقطتي طاء، سين قائمة فتكون قاعدة هاء حاء أيضاً مساوية لقاعدة كاف هاء.

⟨II.4⟩/T80/ د: كيف ينبغي أن يحسب فيعلم من الذين تصير الشمس على سمت رؤوسهم ومتى وكم من مرّة

وإذا علمت هذه الأشياء فقد يسهل أن يحسب فيعلم من ذلك من الذين تصير الشمس على سمت رؤوسهم ومتى وكم من مرّة تصير كذلك. فإنّه قد يظهر من قرب أنّ القوم الذين أبعاد الدوائر الموازية لمعدّل النهار التي هم تحتها أكثر من بعد نقطة الانقلاب الصيفيّ بأسره وهو ثلاثة وعشرون جزءاً وإحدى وخمسون دقيقة وعشرون ثانية بالتقريب، لا تصير الشمس أصلاً على سمت رؤوسهم. وأمّا القوم الذين هم تحت الدائرة الموازية التي بعدها من دائرة معدّل النهار هذا البعد الذي ذكرناه فقد تصير الشمس على سمت رؤوسهم مرّة واحدة عند الانقلاب الصيفيّ نفسه. ومن البيّن أنّ القوم الذين أبعاد الدوائر الموازية التي هم تحتها أقلّ من الأجزاء التي ذكرناها، فإنّها تصير على سمت رؤوسهم مرّتين. وأمّا الأوقات التّي تصير فيها على سمت رؤوسهم فقد تسهل معرفتها أيضاً من الجدول الذي وضعناه للميل، وذلك أنّك إذا نظرت كم بعد الدائرة الموازية التي تطلب معرفة ذلك فيها من دائرة معدّل النهار. ومن البيّن أنّ هذا البعد ممّا دون بعد الانقلاب الصيفيّ وطلبت ذلك المقدار بعينه في القسم الثاني من صفوف الجدول؛ ثمّ نظرت إلى ما حياله من الربع في القسم /H98/ الأوّل من صفوف الجداول وقعت على أنّ ذلك هو المقدار التي إذا أبعدت به الشمس عن كلّ واحدة من نقطتي الاستوائين في الأصل: الاستواين نحو الانقلاب الصيفيّ صارت على رؤوس الذين تحت تلك الدائرة الموازية.

⟨II.5⟩ ه: كيف يمكن أن يدرك ممّا وضعنا نسب المقاييس إلى أظلالها في الاستوائين في الأصل: الاستواين والانقلابين ه: انقلابين والمنقلبين المعنى فيهما واحد إلّا أنّ ثابت أختار الانقلابين في أنصاف النهار

وقد تبيّن أنّ هذه النسب التي قصدنا لها من نسب الأظلال إلى المقاييس قد يمكن أن تدرك بطريق أسهل إذا كانت قد علمت القوس التي بين الانقلابين والقوس التي بين الأفق وبين القطبين بهذا الوجه.

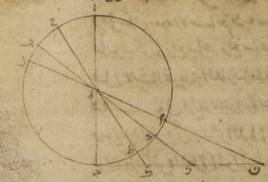
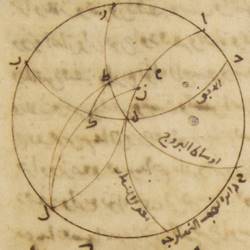
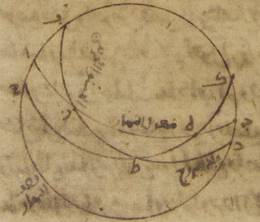
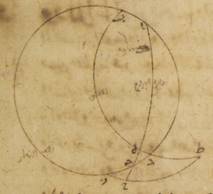
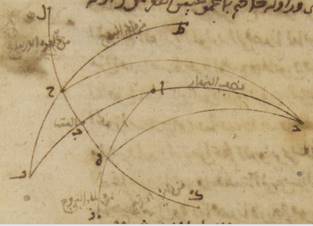
ج: لتكن دائرة نصف النهار ألف باء جيم دال حول مركز هاء، ولنضع النقطة التي على سمت الرؤوس نقطة ألف، ولنخرج منها قطر ألف هاء جيم، ولنخرج عليه في سطح دائرة نصف النهار خطّ جيم كاف زاي نون على زوايا قائمة. ومن البيّن أنّ هذا الخطّ يكون موازياً للفصل المشترك لدائرة الأفق ولدائرة نصف النهار. فلأنّ الأرض بأسرها قدرها عند كرة الشمس في الحسّ قدر النقطة والمركز، حتّى أنّه لا يكون بين مركز ه ه: صح وبين رأس المقياس فرق أو اختلاف. فلنتوهّم المقياس جىم هاء /H99/ وخطّ جيم كاف زاي نون الخطّ الذي عليه يقع في أنصاف النهار أطراف الأظلال. ولنجرّ على نقطة هاء شعاع ه – صح: نصف النهار الاستوائيّ في الأصل: الاستواي وشعاعا نصف النهار في الانقلابين؛ وليكن الشعاع الاستوائيّ في الأصل: الاستواي باء هاء دال زاي والشعاع الصيفيّ حاء هاء طاء كاف، والشعاع الشتويّ لام هاء ميم نون حتّى يكون خطّ جيم كاف الظلّ الصيفيّ، وخطّ جيم زاي الظل الاستوائيّ، في الأصل: الاستواي وخطّ جيم نون الظلّ الشتويّ.

فلأنّ قوس جيم دال، وهي مساوية لارتفاع القطب الشماليّ عن الأفق في الاقليم الذي وضعناه، هي ستّة وثلاثون جزءاً بالأجزاء التّي بها دائرة نصف النهار ثلاث مائة وستّون جزءاً /T81/ وكلّ واحدة من قوسي طاء دال، دال ميم بهذه الأجزاء ثلاثة وعشرون جزءاً وإحدى وخمسون دقيقة وعشرون ثانية. فمن البيّن أنّ قوس جيم طاء الباقية تكون اثني عشر جزءاً وثماني دقائق وأربعين ثانية؛ وتكون قوس جيم ميم بأسرها بهذه الأجزاء تسعة وخمسين جزءاً وإحدى وخمسين دقيقة وعشرين ثانية. فتكون الزوايا الراكبة عليها إمّا زاوية كاف هاء جيم منها فاثنا عشر جزءاً وثمان دقائق وأربعين ثانية بالأجزاء التّي بها أربع زوايا قائمة ثلاث مائة وستّون جزءاً؛ وأمّا زاوية زاي هاء جيم فتكون بهذه الأجزاء ستّة وثلاثين جزءاً؛ وأمّا زاوية نون هاء جيم فتكون على هذا المثال تسعة وخمسين جزءاً وإحدى وخمسين دقيقة وعشرين ثانية. وأمّا بالأجزاء التي بها زاويتان قائمتان ثلاث مائة وستّون جزءاً، فتكون بها زاوية كاف هاء جيم أربعة وعشرين جزءاً وسبع عشرة دقيقة وعشرين ثانية؛ وزاوية زاي هاء جيم بهذه الأجزاء اثنين وسبعين جزءاً؛ وزاوية نون هاء جيم على هذا المثال مائة وتسعة عشر جزءاً واثنتين وأربعين ه – صح: دقيقة وأربعين ثانية. /H100/ فالدوائر التي ترسم على مثلّثات كاف هاء جيم، زاي هاء جيم، نون هاء جيم القائمة الزوايا تكون القوس منها التي على خطّ جيم كاف أربعة وعشرين جزءاً وسبع عشرة دقيقة وعشرين ثانية؛ والقوس التي على خطّ جيم هاء وهي تمام نصف دائرة بهذه الأجزاء مائة وخمسة وخمسون جزءاً واثنتين وأربعين دقيقة وأربعين ثانية؛ والقوس التي على خطّ جيم زاي اثنين وسبعين جزءاً والقوس التي على خطّ جيم هاء على هذا المثال بهذه الأجزاء مائة وثمانية أجزاء؛ والقوس التي على خطّ جيم زاي ه – صح: نون مائة وتسعة عشر جزءاً واثنتين وأربعين دقيقة وأربعين ثانية؛ والقوس التي على خطّ جيم هاء الأجزاء الباقية أيضاً من نصف الدائرة وهي ستّون جزءاً وسبع عشرة دقيقة وعشرون ثانية؛ فيحصل خطّ جيم هاء من الخطوط التي توتّر القسيّ إمّا بالأجزاء التي بها خطّ جيم كاف خمسة وعشرون جزءاً وأربع عشرة دقيقة وثلاث وأربعون ثانية، فمائة وسبعة عشر جزءاً وثمان عشرة دقيقة وإحدى وخمسين ثانية، وإمّا بالأجزاء التي بها خطّ جيم زاي أيضاً سبعون جزءاً واثنتان وثلاثون دقيقة وأربع ثواني، فسبعة وتسعون جزءاً وأربع دقائق وستّاً وخمسين ثانية؛ وإمّا بالأجزاء التّي بها خطّ جيم نون على ذلك المثال مائة وثلاثة أجزاء وستّ وأربعون دقيقة وستّ عشرة ثانية فعلى هذا المثال ستّين جزءاً وخمس عشرة دقيقة واثنتين وأربعين ثانية. فالأجزاء إذاً التي بها مقياس جيم هاء ستّون جزءاً؛ فإنّ خطّ جيم كاف، وهو الظلّ الصيفيّ، يحصل بها اثني عشر جزءاً وخمساً وخمسين دقيقة؛ وخطّ جيم زاي، وهو ظلّ الاستواء، ثلاثة وأربعين جزءاً وستّاً وثلاثين دقيقة؛ وخطّ جيم نون، وهو الظلّ الشتويّ، مائة وثلاثة أجزاء وعشرون دقيقة بالتقريب.

/T82/ وقد يظهر من هذا المعنى عكس ذلك أيضاً، وهو أنّه إن فرض لنا نسبتان فقط أيّ النسبتين كانتا من الثلاث النسب التي وصفناها لمقياس جيم هاء إلى أظلاله كان ارتفاع القطب مفروضاً وكانت القوس التي بين الانقلابين مفروضة. وذلك من قبل أنّه إذا فرض أيضاً زاويتان من الزوايا التي هي عند نقطة هاء كانت الزاوية الباقية أيضاً مفروضة، لأنّ قوسي دال طاء، دال ميم متساويتان.  /H101/لكن ما يقع به الاستقصاء في الأرصاد أنفسها حتّي لا يشكّ فيه هو أن تؤخذ تلك ه: يعني يقوله تلك ارتفاع القطب والقوس التي بين الانقلابين على الوجه الذي أرشدنا إليه؛ فأمّا نسب الأظلال التي وصفناها إلى المقاييس فليست ه: يعني أنهّا ليس يجري ذلك المجرى من الصحة كذلك، من أجل أنّ زمان الأظلال في الاستوائين في الأصل: الاستواين غير محصّل بنفسه بوجه من الوجوه، وأطراف رؤوس الأظلال الشتويّة يعسّر تحريرها.

⟨II.6⟩و: صفة خواصّ دائرة دائرة من الدوائر المتوازية

وعلى مثال هذه الأشياء نذكر في سائر الدوائر المتوازية جليل خواصّها بأن نجعل تفاضل الميل بما يوجب تزيّد ربع ساعة ربع ساعة من ساعات الاستواء إذ كان في ذلك كفاية. فنصف جمل الأمر قبل الأشياء الجزئيّة اللازمة لها.

ونبتديء في ذلك من الدائرة الموازية التي تحت دائرة معدّل النهار، فنقول إنّ هذه الدائرة تكاد أن تكون هي الحدّ بين الربع بأسره المسكون من الأرض عندنا وبين الجزء الجنوبيّ. والأيّام والليالي فيها وحدها كلّها مساوية بعضها لبعض، إذ كانت كلّ واحدة من الدوائر التي في الكرة الموازية لمعدّل النهار عند ذلك ه: هكذا وجد في اليونانيّ وأنّما يعني يقوله عند ذلك في ذلك الموضع فقط يقسمها الأفق بنصفين حتّى تكون قطعها التي فوق الأرض متشابهة ومساوية في كلّ واحدة منها لقطعها التي تحت الأرض. وليس يكون ذلك ه: {بلغ الغرض بالآخر} والحمد لله على عونه في شيء من الميل أصلاً لكن معدّل النهار أيضاً وحده في /H102/ جميع المواضع يقسّمه الأفق بنصفين وتكون الأيّام فيه مساوية لليالي عند الحسّ إذ كان هو أيضاً من أعظم الدوائر. وأمّا سائر الدوائر الموازية فإنهّا تنقسم ه – ص: به بقسمين مختلفين. وتكون في مثل الناحية التي تسكنها ما كان من الدوائر أميل منه إلى الجنوب فإنّ قطعها التي فوق الأرض أصغر من قطعها التي تحت الأرض وأيّامها أقصر من لياليها؛ وما كان منها أميل منه إلى الشمال فبعكس ذلك، أعني أنّ قطعها التي فوق الأرض تكون أعظم وتكون أيّامها أطول زماناً.

والظلّ في هذه الدائرة الموازية يقع أيضاً إلى الجهتين، إذ كانت الشمس /T83/ تصير على سمت الرأس مرّتين عند الذين يسكنون تحتها، أعني في موضعي تقاطع دائرة معدّل النهار والدائرة المائلة حتّى تكون المقاييس عند ذلك فقط إذا كانت الشمس في وسط السماء لا ظلّ لها؛ والشمس إذا كانت تسير في نصف الدائرة الشماليّ وقعت أظلال المقاييس إلى ناحية الجنوب وإذا كانت تسير في نصف الدائرة الجنوبيّ وقعت الأظلال إلى ناحية الشمال. وفي هذا الموضع المقدار الذي به تكون المقاييس ستّين جزءاً يكون ه – ص: به في كلّ واحد من الظلّ الصيفيّ والظلّ الشتويّ ستّة وعشرين جزءاً ونصف جزء بالتقريب. وإذا قلنا بالجملة الأظلال فأنّما نعني الأظلال في انتصاف النهار، على أنّه ليس يقع فيها من قبل أنّ الاستوائين في الأصل: الاستواين والانقلابين لا يقع لا محالة في انتصاف النهار على الحقيقة اختلاف يعتدّ به. ه – خ: على الحقيقة اختلاف يعتدّ به من قبل أنّ الاستوائين والمنقلبين يمكن ألّا تقع في أنصاف النهار بالحقيقة.

ونقول أيضاً إنّ الذين سكناهم تحت معدّل النهار تسامت رؤوسهم من الكواكب، /H103/ الكواكب التي مدارها على معدّل النهار نفسه ويرون الكواكب كلّها طالعة وغاربة إذ كان قطبا الكرة على دائرة أفقهم بعينها، وكانا لا يرسمان دائرة أصلاً من الدوائر الموازية لا من الدوائر الدائمة الظهور ولا من الدائمة الخفاء ولا يبتران دوائر أنصاف النهار. ه – ج: تقطع قوساً من فلك نصف النهار وأمّا إنّ تحت دائرة معدّل النهار مساكن فيقولون إنّ ذلك قد يمكن أن يكون إذ كان هذا الموضع من الأرض في الغاية من اعتدال المزاج. وذلك أنّ الشمس لا يطول لبثها في النقط التي على سمت الرؤوس، لسرعة حركتها عند نقطتي الاعتدالين في العرض، حتّى يكون الصيف عندهم من قبل ذلك معتدل المزاج ولا تبعد في الانقلابين عن سمت الرؤوس بعداً كثيراً، فلا يشتدّ برد الشتاء عندهم. وأمّا أيّ المساكن هي هذه فلست أقدر أن أقول في ذلك ما أحيط بعلمه، لأنّه لم يصر إليها إلى هذه الغاية أحد ممّن عندنا وما يقال فيها فهو إلى أن يجرى مجرى الحدس أقرب منه إلى أن يجرى مجرى الخبر عن المشاهدة. فهذه هي خواصّ الدائرة الموازية التّي تحت معدّل النهار على جملة القول.

وأمّا سائر الدوائر الموازية التي من قبلها يرى بعض الناس أنّ المساكن تعرف، ه – خ: فيها؛ ه – خ: منها فنحن مقدّمون قبل ذكرها الأشياء التّي نعمّها كي ما لا نكرّر قولاً واحداً في كلّ واحدة منها. وهذه الأشياء هي أنّ كلّ واحدة من سائر الدوائر التي يتلو بعضها بعضاً فإنّما تصير /H104/ على سمت الرؤوس فيها من الكواكب، الكواكب التي بعدها من معدّل النهار في الدائرة المرسومة على قطبيه قوس مساوية للقوس التي هي بعد تلك الدائرة المقصود إليها نفسها من دائرة معدّل النهار. وإنّ الدائرة الدائمة الظهور يكون رسمها إذا جعل قطب معدّل النهار الشماليّ قطباً لها وجعل البعد ارتفاع القطب والكواكب التي تجوزها هذه الدائرة فيها دائمة الظهور. والدائرة الدائمة الخفاء يكون رسمها إذا جعل القطب الجنوبيّ قطباً لها وجعل البعد ذلك البعد نفسه والكواكب التي داخل هذه الدائرة دائمة الخفاء.

ونقول إنّ الدائرة ه – صح: الموازية الثانية تكون الدائرة التي يصير مبلغ أطول ما يكون من النهار فيها اثنتي عشرة ساعة وربع ه: ساعة من ساعات الاعتدال. وبعد هذه الدائرة من معدّل النهار أربعة أجزاء وربع جزء وترسم مارّة بالجزيرة المسمّاة طبروباني. وهذه الدائرة أيضاً من الدوائر التي يقع الظلّ فيها إلى الجهتين: إذ كانت الشمس تصير أيضاً عند من كان تحتها على سمت الرؤوس مرّتين ه – ج: في السنة والمقاييس فيها إذا كان بعد الشمس من الانقلاب الصيفيّ إلى كلّ واحدة من الجهتين تسعة وسبعين جزءاً ونصف جزء لا ظلّ لها في أوقات توسّط الشمس السماء؛ وإذا كانت الشمس تسير في هذه المائة والتسعة والخمسين الجزء، كان وقوع أظلال المقاييس إلى ناحية الجنوب عنها، وإذا /T84/ كان مسيرها في الأجزاء الباقية وهي مائتا جزء وجزء واحد كان وقوع الأظلال إلى ناحية الشمال عنها. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ في الاستوائين في  الأصل: استواين أربعة أجزاء وثلث جزء وواحد من اثني عشر من جزء، ويكون الظلّ الصيفيّ واحداً وعشرين جزءاً وثلث جزء، ويكون الظلّ الشتويّ اثنين وثلاثين جزءاً.

/H105/ والدائرة الموازية الثالثة هي الدائرة التي يصير مبلغ أطول ما يكون من النهار فيها اثنتي عشرة ساعة ونصف، وبعد هذه الدائرة من معدّل النهار ثمانية أجزاء وخمس وعشرون دقيقة وترسم مارّة بالخليج المسمّى أواليطس. وهذه الدائرة أيضاً من الدوائر التي يقع الظلّ فيها إلى الجهتين: إذ كانت الشمس تصير على سمت الرؤوس عند من يسكن تحتها مرّتين. والمقاييس فيها إذا كان بعد الشمس من الانقلاب الصيفيّ إلى كلّ واحدة من الجهتين تسعة وستّين جزءاً لا ظلّ لها في أوقات توسّط الشمس السماء. فالشمس إذا كانت تسير في هذه المائة والثمانية والثلاثين الجزء كان وقوع أظلال المقاييس إلى ناحية الجنوب عنها، وإذا كان مسيرها في الأجزاء الباقية وهي مائتا جزء واثنان وعشرون جزءاً كان وقوع الأظلال إلى ناحية الشمال عنها. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ في الاستوائين في الأصل: استواين ثمانية أجزاء ونصف وثلث جزء، والظلّ الصيفيّ ستّة عشر جزءاً ونصفاً وواحداً من اثني عشر، والظلّ الشتويّ سبعة وثلاثين جزءاً ونصفاً وثلثاً وواحداً من خمسة عشر من جزء.

والدائرة الموازية الرابعة هي التي يصير مبلغ أطول ما يكون من النهار فيها اثنتي عشرة ساعة ونصف وربع، وبعد هذه الدائرة من معدّل النهار اثنا عشر جزءاً ونصف جزء وترسم مارّة بالخليج المسمّى أواليطيقوس. وهذه الدائرة أيضاً من الدوائر التي تقع الظلّ فيها إلى الجهتين: إذ كانت الشمس تصير على سمت الرؤوس عند من يسكن تحتها أيضاً مرّتين والمقاييس فيها /H106/ إذا كان بعد الشمس من الانقلاب الصيفيّ إلى كلّ واحدة من الجهتين سبعة وخمسين جزءاً وثلثي جزء لا ظلّ لها في أوقات توسّط الشمس السماء. فالشمس ما دامت تسير في هذه المائة والخمسة العشر الجزء والثلث الجزء يكون وقوع أظلال المقاييس إلى ناحية الجنوب عنها، وإذا كان مسيرها في الأجزاء الباقية، وهي مائتا جزء وأربعة وأربعون جزءاً وثلثا جزء، كان وقوع الأظلال إلى ناحية الشمال عنها. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ في الاستوائين في الأصل: استواين ثلاثة عشر جزءاً وثلث جزء، والظلّ الصيفيّ اثني عشر جزءاً، والظلّ الشتويّ أربعة وأربعين جزءاً ونصف سدس جزء.

والدائرة الموازية الخامسة هي التي يصير مبلغ أطول ما يكون من النهار فيها ثلاث عشرة ساعة، وبعد هذه الدائرة من معدّل النهار ستّة عشر جزءاً وسبع وعشرون دقيقة وترسم مارّة بالجزيرة المسمّاة ماروي. وهذه الدائرة أيضاً من الدوائر التي يقع الظلّ فيها إلى الجهتين: إذ كانت الشمس تصير على سمت الرؤوس عند من يسكن تحتها مرّتين والمقاييس فيها إذا كان بعد الشمس من الانقلاب الصيفيّ إلى كلّ واحدة من جهتيه خمسة وأربعون جزءاً لا ظلّ لها في أوقات توسّط الشمس السماء. والشمس إذا كانت تسير في هذه التسعين الجزء كان وقوع أظلال المقاييس إلى ناحية الجنوب عنها، وإذا كان مسيرها في الأجزاء الباقية وهي مائتان وسبعون جزءاً كان وقوع الأظلال إلى ناحية الشمال عنها. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ في الاستوائين في الأصل: الاستواين سبعة عشر جزءاً ونصف وربع جزء، والظلّ الصيفيّ سبعة أجزاء ونصف وربع جزء والظلّ الشتويّ، خمسين جزءاً ه: {...} ونصف وثلث جزء. Toomer quotes the last passage from the Tinus manuscript, which he calls T (Toomer, p. 84, fn. 31).

والدائرة الموازية السادسة هي التي يصير مبلغ أطول ما يكون من النهار فيها ثلاث عشرة ساعة وربع من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار /T85/ عشرون جزءاً وأربع عشرة دقيقة وترسم مارّة باالمواضع المسمّاة أقابطو. وهذه الدائرة أيضاً من /H107/ الداوئر التي يقع الظلّ فيها إلى الجهتين: إذ كانت الشمس تصير فيها أيضاً على سمت الرؤوس مرّتين ه – صح: في السنة والمقاييس في انتصاف النهار، إذا كان بعد الشمس من الانقلاب الصيفيّ إلى كلّ واحدة من جهتيه أحد وثلاثون جزءاً لا ظلّ لها. والشمس إذا كان مسيرها في هذه الاثنين والستّين جزءاً كان وقوع أظلال المقاييس إلى ناحية الجنوب، وإذا كان سيرها في الأجزاء الباقية وهي مائتا جزء وثمانية وتسعون جزءاً كان وقوع الأظلال إلى ناحية الشمال. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ في الاستوائين اثنتي وعشرين جزءاً وسدس ه – خ: ا؛ خ: {...} جزء، والظلّ الصيفيّ ثلاثه أجزاء ونصف وربع جزء، والظلّ الشتويّ ثمانية وخمسين جزءاً وسدس جزء.

والدائرة الموازية السابعة هي التي يصير مبلغ أطول ما يكون من النهار فيها ثلاث عشرة ساعة ونصف من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار ثلاثة وعشرون جزءاً وإحدى وخمسون دقيقة وترسم مارّة بالجزيرة المسمّاة سوئني. وهذه الدائرة أوّل الدوائر التي تسمّى ذوات ظلّ واحد، وذلك أنّ أظلال المقاييس في انتصاف النهار لا يقع عند من سكن تحتها في وقت من الأوقات إلى ناحية الجنوب، لكن الشمس في الانقلاب الصيفيّ نفسه فقط تصير على سمت رؤوسهم ولا يرى للمقاييس حينئذ ظلّ. وذلك أنّ بعدهم عن معدّل النهار هو بعد الانقلاب الصيفيّ عنه. وأمّا سائر الزمان كلّه فإنّ أظلال المقاييس تقع فيه عندهم إلى ناحية الشمال. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ في الاستوائين /H108/ ستّة وعشرين جزءاً ونصف جزء، والظلّ الشتويّ خمسة وستّين جزءاً ونصف وثلث جزء، وأمّا الظلّ الصيفيّ فليس للمقاييس عندهم ظلّ على ما قلنا. وجميع الدوائر التي هي أميل إلى الشمال من هذه الدائرة حتّى تنتهي إلى الدائرة التي تحت ه – اخ: تحدّ المسكونة عندنا هي ذوات ظلّ واحد. وذلك أنّ المقاييس فيها في أنصاف النهار لا تصير في وقت من الأوقات لا ظلّ لها ولا تقع أظلالها من ناحية الجنوب، لكنّها تقع في الأزمان كلّها من ناحية الشمال، من قبل أنّ الشمس لا تصير على سمت رؤوسهم في وقت من أوقات.

والدائرة الموازية الثامنة هي التي يصير مبلغ أطول ما يكون من النهار فيها ثلاث عشرة ساعة ونصف وربع من ساعات الاستواء وبعد هذه الدائرة من معدّل النهار سبعة وعشرون جزءاً واثنتا عشرة دقيقة وترسم مارّة بالجزيرة المسمّاة بطولامايس التي في بلاد تيبايس وهي المعروفة بأرميس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ ثلاثة أجزاء ونصف، والظلّ في الاستوائين في الأصل: الاستواين ثلاثين جزءاً ونصف وثلث جزء، والظلّ الشتويّ أربعة وسبعين جزءاً وسدس جزء.

والدائرة الموازية التاسعة هي التي يصير مبلغ أطول ما يكون من النهار فيها أربع عشرة ساعة من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار ثلاثون جزءاً واثنتان وعشرون دقيقة وترسم مارّة بأسافل بلاد مصر. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ ستّة أجزاء ونصف وثلث، والظلّ في الاستوائين في الأصل: الاستواين خمسة وثلاثين جزءاً وواحداً من اثني عشر من جزء، والظلّ الشتويّ ثلاثة وثمانين جزءاً وواحداً من اثني عشر من جزء.

/T86/ والدائرة الموازية العاشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها أربع عشرة ساعة وربع من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار [من معدّل النهار] /H109/ ثلاثة وثلاثون جزءاً وثمان عشرة دقيقة، وترسم مارّة بوسط بلاد الشام. وفي هذا الموضع المقدار الذي يكون ه – صح: به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ عشرة أجزاء، والظلّ في الاستوائين في الأصل: الاستواين تسعة وثلاثين جزءاً ونصف، والظلّ الشتويّ ثلاثة وتسعين جزءاً وواحداً من اثني عشر من جزء.

والدائرة الموازية الحادية عشرة هي التيّ يصير مبلغ أطول ما يكون من النهار فيها أربع عشرة ساعة ونصف من ساعات الاستواء وبعد هذه الدائرة من معدّل النهار ستّة وثلاثون جزءاً وترسم مارّة بالجزيرة المسمّاة رودش. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ اثنا عشر جزءاً ونصف وثلث جزء وواحداً من اثني عشر من جزء، والظلّ في الاستوائين في الأصل: الاستواين ثلاثة وأربعين جزءاً ونصف وعشر جزءاً، والظلّ الشتويّ مائة جزء وثلاثة أجزاء وثلث جزء.

والدائرة الموازية الثانية عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها أربع عشرة ساعة ونصف وربع من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار ثمانية وثلاثون جزءاً وخمس وثلاثون دقيقة وترسم مارّة بالجزيرة المسمّاة سمرنا. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ خمسة عشر جزءاً ونصف وربع جزء، والظلّ في الاستوائين في الأصل: الاستواين سبعة وأربعين جزءاً ونصف وثلث، والظلّ الشتويّ مائة وأربعة عشر جزءاً ونصف وثلث وواحداً من اثني عشر من جزء.

والدائرة الموازية الثالثة عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها خمس عشرة ساعة من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار أربعون جزءاً وستّ وخمسون دقيقة وترسم مارّة بالبلاد المسمّاة السبنطس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ ثمانية عشر جزءاً ونصف، والظلّ في الاستوائين في الأصل: الاستواين اثنين وخمسين جزءاً وسدس، والظلّ الشتويّ مائة وسبعة وعشرون جزءاً ونصف وثلث جزء.

/H110/ والدائرة الموازية الرابعة عشرة هي التي يصير مبلغ ما يكون من النهار فيها خمس عشرة ساعة وربع من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار ثلاثة وأربعون جزءاً وربع جزء، وترسم مارّة بالجزيرة المسمّاة مساليا. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ عشرين جزءاً ونصف وثلث، والظلّ في الاستوائين خمسة وخمسين جزءاً ونصف وثلث جزء وواحداً من اثني عشر من جزء، والظلّ الشتويّ مائة وأربعون ه – اخ: وأربعة جزءاً وربع جزء.

والدائرة الموازية الخامسة عشر هي التي تصير مبلغ ما يكون من النهار فيها خمس عشرة ساعة ونصف من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار خمسة وأربعون جزءاً ودقيقة واحدة، وترسم مارّة بوسط بحر بنطس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ ثلاثة وعشرين جزءاً وربع جزء، والظلّ في الاستوائين في الأصل: الاستواين بهذه الأجزاء ستّين جزءاً، والظلّ الشتويّ مائة وخمسة وخمسون جزءاً وواحداً من اثني عشر من جزء.

/T87/ والدائرة الموازية السادسة عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها خمس عشرة ساعة ونصف وربع من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار ستّة وأربعون جزءاً وإحدى وخمسون دقيقة وترسم مارّة بعيون النهر المسمّى السطرس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ خمسة وعشرين جزءاً ونصف جزء، والظلّ في الاستوائين ثلاثة وستّين جزءاً ونصف وثلث جزء وجزء من اثني عشر من جزء، والظلّ الشتويّ مائة وأحد وسبعين جزءاً ونصف جزء.

والدائرة الموازية السابعة عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها ستّ عشرة ساعة من ساعات الاستواء، /H111/ وبعد هذه الدائرة من معدّل النهار ثمانية وأربعون جزءاً واثنتان وثلاثون دقيقة، وترسم مارّة بمغايض مخارج النهر المسمّى بورستانس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ سبعة وعشرين جزءاً ونصف جزء، والظلّ في الاستوائين في الأصل: الاستواين سبعة وستّين جزءاً ونصف وثلث جزء، والظلّ الشتويّ مائة وثمانية وثمانين جزءاً ونصف وثلث جزء. Toomer quotes this valus (188^5/6) from the Tunis manuscript (Toomer, p. 87, fn. 50).

والدائرة الموازية الثامنة عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها ستّ عشرة ساعة وربع من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار خمسون جزءاً وربع جزء، وترسم مارّة بوسط البحيرة المسمّاة مااوطس. وفي هذ الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ تسعة وعشرين جزءاً ونصف وواحداً من اثني عشر من جزء، والظلّ في الاستوائين في الأصل: الاستواين واحداً وسبعين جزءاً وثلثي جزء، والظلّ الشتويّ مائتين وعشرة أجزاء وثلث جزء.

والدائرة الموازية التاسعة عشرة هي التي يصير مبلغ أطول ما يكون من النهار فيها ستّ عشرة ساعة ونصف من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار أحد وخمسون جزءاً ونصف جزء، وترسم مارّة بأقاصي ناحية الجنوب من بلاد برطانيا. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ واحداً وثلاثين جزءاً وثلث جزء وواحد من اثني عشر من جزء، والظلّ في الاستوائين في الأصل: الاستواين خمسة وسبعين جزءاً وثلث وواحداً من اثني عشر من جزء، والظلّ الشتويّ مائتين وتسعة وعشرين جزءاً وثلثي جزء.

والدائرة الموازية العشرون هي التي يصير مبلغ أطول ما يكون فيها ستّة عشرة ساعة ونصف وربع من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار اثنان وخمسون جزءاً وخمسون دقيقة، وترسم مارّة بمغايض رينس. وفي هذا الموضع المقدار الذي به يكون المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ ثلاثة وثلاثين جزءاً وربع جزء، والظلّ في الاستوائين تسعة وسبعين جزءاً وواحداً من اثني عشر من جزء، والظلّ الشتويّ مائتين وثلاثة وخمسين جزءاً وسدس جزءاً.

/H112/ والدائرة الموازية الحادية والعشرون هي التي يصير مبلغ أطول ما يكون من النهار فيها سبع عشرة ساعة من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار أربعة وخمسون جزءاً ودقيقة واحدة وترسم مارّة بمغايض طانايس. وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ أربعة وثلاثين جزءاً ونصف وثلث وواحداً من اثني عشر من جزء والظلّ في الاستوائين اثنين وثمانين جزءاً ونصف وواحداً من اثني عشر من جزء والظلّ الشتويّ مائتين وثمانية وسبعين جزءاً ونصف وربع جزء.

/T88/ والدائرة الموازية الثانية والعشرون هي التي ⟨يصير⟩ مبلغ أطول ما يكون من النهار فيها سبع عشرة ساعة وربع من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار خمسة وخمسون جزءاً، وترسم مارّة بالموضع الذي يسمّى بريغانطيس من بلاد برطانيا الكبرى. وفي هذا الموضع المقدار الذي به يكون المقياس ستّين جزءاً يكون به الظلّ الصيفيّ ستّة وثلاثين جزءاً وربع جزء، والظلّ في الاستوائين خمسة وثمانين جزءاً وثلثي جزء، والظلّ الشتويّ ثلاث مائة جزء وأربعة أجزاء ونصف جزء.

والدائرة الموازية الثالثة والعشرون هي التي يصير مبلغ أطول ما يكون من النهار فيها سبع عشرة ساعة ونصف من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار ستّة وخمسون جزءاً وترسم مارّة بوسط بلاد برطانيا الكبرى. ه: هو أنّ برطانية الكبرى هي {...} عزموا {...} والتواريخ وفي هذا الموضع المقدار الذي به يكون المقياس ستّين جزءاً يكون به الظلّ الصيفيّ سبعة وثلاثين جزءاً وثلثي جزء والظلّ في الاستوائين ثمانية وثمانين جزءاً ونصف وثلث جزء والظلّ الشتوي ثلاث مائة وخمسة وثلاثين جزءاً وربع جزء.

/H113/ والدائرة الموازية الرابعة والعشرون هي التي يصير مبلغ أطول ما يكون من النهار فيها سبع عشرة ساعة ونصف وربع من ساعات الاستواء. وبعد هذه الدائرة من معدّل النهار سبعة وخمسون جزءاً وترسم مارّة بالموضع المسمّى قاطورقطونيس من بلاد برطانيا وفي هذا الموضع المقدار الذي يكون به المقياس ستّين جزءاً يكون به الظلّ الصيفيّ تسعة وثلاثين جزءاً وسدس، والظلّ في الاستوائين اثنين وتسعين جزءاً وثلث وواحداً من اثني عشر من جزء، والظلّ الشتويّ ثلاث مائة واثنين وسبعين جزءاً وثلثي جزء.

والدائرة الموازية الخامسة والعشرون هي التي يصير ⟨مبلغ⟩ أطول ما يكون من النهار فيها ثمان عشرة ساعة من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار ثمانية وخمسون جزءاً وترسم مارّة بنواحي الجنوب من بلاد برطانيا الصغرى. وفي هذا الموضع المقدار الذي به يكون المقياس ستّين جزءاً، يكون به الظلّ الصيفيّ أربعين جزءاً وثلثي جزء والظلّ في الاستوائين ستّة وتسعين جزءاً والظلّ الشتويّ أربع مائة وتسعة عشر جزءاً وواحداً من اثني عشر من جزء.

والدائرة الموازية السادسة والعشرون هي التي يصير مبلغ أطول ما يكون من النهار فيها ثمان عشرة ساعة ونصف من ساعات الاستواء، وبعد هذه الدائرة من معدّل النهار تسعة وخمسون جزءاً ونصف جزء، وترسم مارّة بالمواضع الوسطى من بلاد برطانيا الصغرى. وإنّما لم يستعمل في هذا الموضع التفاضل بربع ساعة من قبل أنّ الدوائر الموازية يصير حينئذ متّصلاً بعضها ببعض واختلاف الارتفاعات لا يجتمع منه عند ذلك ولا جزء واحد على التمام ومن قبل أنّه لا ينبغي لنا أن نستقصى أمر الدوائر التي هي أميل من الدوائر التي ذكرناها إلى الشمال على مثال ما استقصينا شرح أمر تلك الدوائر ولذلك رأينا أن وضعنا أيضاً نسب المقاييس إلى الأظلال فيها كما فعلنا في المواضع المحدودة من الفضل.

/H114/ فالموضع الذي يبلغ أطول ما يكون من النهار فيه تسع عشرة ساعة من ساعات الاستواء فإنّ بعد تلك الدائرة الموازية من دائرة معدّل النهار أحد وستّون جزءاً وترسم مارّة بأقاصي الشمال من بلاد برطانيا الصغرى. /T89/ والموضع الذي مبلغ أطول ما يكون من النهار فيه تسع عشر ساعة ونصف من ساعات الاستواء. فإنّ بعد تلك الدائرة الموازية من معدّل النهار اثنان وستّون جزءاً وترسم مارّة بالجزيرة المسماة أبوذو. والموضع الذي يبلغ أطول ما يكون من النهار فيه عشرون ساعة من ساعات الاستواء، فإنّ بعد تلك الدائرة الموازية من معدّل النهار ثلاثة وستّون جزءاً وترسم مارّة بالجزيرة المسماة تولي. والموضع الذي يبلغ أطول ما يكون من النهار فيه إحدى وعشرون ساعة من ساعات الاستواء، فإنّ بعد تلك الدائرة الموازية من معدّل النهار أربعة وستّون جزءاً ونصف جزو ترسم مارّة بأمم لا تعرفون من الصقالبة. والموضع الذي يبلغ أطول ما يكون من النهار فيه اثنتان وعشرون ساعة من ساعات الاستواء، فإنّ بعد تلك الدائرة الموازية من معدّل النهار خمسة وستّون جزءاً ونصف جزء. والموضع الذي يبلغ أطول ما يكون من النهار فيه ثلاث وعشرون ساعة من ساعات الاستواء، فإنّ بعد تلك الدائرة الموازية من معدّل النهار ستّة وستّون جزءاً. والموضع الذي يبلغ أطول ما يكون من النهار فيه أربع وعشرون ساعة من ساعات الاستواء، فإنّ بعد تلك الدائرة الموازية من معدّل النهار ستّة وستّون جزءاً ه – ج، صح: وسدس جزء ونصف جزء. وهذه أول الدائرة التي يقع الظلّ فيها دائراً. وذلك أنّ الشمس لمّا كانت لاتغيب هناك في الانقلاب الصيفيّ وحده /H115/ صارت أظلال المقاييس يقع إلى جميع جهات الأفق. وفي هذا الموضع دائرة الانقلاب الصيفيّ الموازية لمعدّل النهار دائمة الظهور، ودائرة الانقلاب الشتويّ دائمة الخفاء، من قبل أنّهما جميعاً يماسّان الأفق فيه على المبادلة. وتصير الدائرة المائلة أيضاً التي تمرّ بأوساط البروج هي الأفق إذا كان الطالع منها نقطة الاستواء الربيعيّ. ↑الربيعي↑: جيم

فإن أحبّ محبّ من قبل الازدياد في العلم أن يبحث بوجه آخر من أمر الدوائر أيضاً أحب محب من قبل الازدياد في العلم أن يبحث بوجه آخر من أمر الدوائر أيضاً: ه ‒ خ: فإن أحد أحبّ البحث من قبل الازدياد في العلم عن الدوائر التي. التي هي أميل إلى الشمال من الدوائر التي ذكرناها عن شيء من جلّ ما يلزم فيها عن شيء من جلّ ما يلزم فيها: ه – خ: ويجمل ما يعرض فيها وجد الموضع الذي ارتفاع القطب الشماليّ فيه سبعة وستّون جزءاً بالتقريب، لا يغيب هناك الخمسة العشر الجزء من الدائرة التي تمرّ بأوساط البروج عن كلّ واحدة من جنبتي الانقلاب الصيفيّ حتّى يكون مبلغ أطول ما يكون من النهار هناك ودور الأظلال إلى جميع جهات الأفق قريباً من شهر واحد. فإنّ هذه الأشياء أيضاً قد يسهل الوقوف عليها من قبل الجدول الذي وضعناه للميل. وذلك أنّ الأجزاء التي نجدها هي بعد الدائرة الموازية من معدّل النهار التي تجوز عن كلّ واحدة من جنبتي نقطة الانقلاب خمسة عشر جزءاً مثلاً. وتصير حينئذ مع القطعة التي محورها هي الدائرة التي تمرّ بأوساط البروج إمّا دائمة الظهور وإمّا دائمة الخفاء. فمن البيّن أنّ ارتفاع القطب الشماليّ ينقص عن أجزاء الربع وهي تسعون جزءاً بقدرها يعيّنها. بقدرها: ه – اخ: بقدر الأجزاء التي {...} عشر جزءاً إلى {...}

/H116/ وحيث يكون ارتفاع القطب تسعة وستّين جزءاً ونصف، فإنّك تجد هناك عن كلّ واحدة من جنبتي الانقلاب الصيفيّ ثلاثين جزءاً لا يغيب أصلاً حتّى يكون مبلغ أطول ما يكون من النهار /T90/ هناك ودور أظلال المقاييس قريباً من شهرين.

وحيث يكون ارتفاع القطب ثلاثة وسبعين جزءاً وثلث جزء، فأنّك تجد هناك عن كلّ واحدة من جنبتي الانقلاب الصيفيّ خمسة وأربعين جزءاً لا يغيب حتّى يكون مبلغ أطول ما يكون من النهار هناك ودور أظلال المقاييس تمتدّ إلى قريب من ثلاثة أشهر.

وحيث يكون ارتفاع القطب ثمانية وسبعين جزءاً وثلث جزء، فإنّك تجد هناك عن كلّ واحدة من جنبتي الانقلاب الصيفيّ ستّين جزءاً لا تغيب حتّى يكون مبلغ أطول ما يكون من النهار هناك ودور أظلال المقاييس قريباً من أربعة أشهر.

وحيث يكون ارتفاع القطب أربعة وثمانين جزءاً، فإنّك تجد هناك عن كلّ واحدة من جنبتي الانقلاب الصيفيّ خمسة وسبعين جزءاً لا يغيب حتّى يكون أيضاً مبلغ أطول ما يكون هناك من النهار قريباً من خمسة أشهر وتكون أظلال المقاييس تدور حولها قريباً من المدّة من الزمان.

وحيث يكون قطب الشماليّ مرتفعاً عن الأفق أجزاء الربع بأسره، وهو تسعون جزءاً، فهناك النصف بأسره من الدائرة التيّ تمرّ بأوساط البروج الذي هو أميل إلى الشمال عن دائرة معدّل النهار لا يصير في وقت من الأوقات تحت الأرض والنصف بأسره الذي هو أميل إلى الجنوب لا يصير في وقت من الأوقات فوق الأرض /H117/ حتّى يكون كلّ سنة يوماً واحداً وليلة واحدة كلّ واحد منهما قريباً من ستّة أشهر وتكون أظلال المقاييس في جميع الأوقات تدور حولها. ومن خواصّ هذه الميل أنّ قطب الشماليّ يكون على سمت الرؤوس وأنّ دائرة معدّل النهار تقوم هناك مقام الدائرة الأبديّة الظهور ومقام الدائرة الأبديّة الخفاء ومقام دائرة الأفق. إذ كانت تجعل النصف بأسره من الكرة الذي هو أميل منها إلى الشمال فوق الأرض في جميع الأوقات، والنصف هو أميل إلى الجنوب تحت الأرض. ه: بلغ العرض {؟} بحمد الله وعونه

⟨II.7⟩ز: فيما يطلع من دائرة معدّل النهار مع الدائرة التي تمرّ بأوساط البروج في الكرة المائلة.

فإذ قد وضعنا الأشياء الكلّية التي يعلم من أمر الميول فقد نتّبع ذلك أن نبيّن كيف لك أن نستخرج في ميل ميل ما يطلع أيضاً من الأزمان من دائرة معدّل النهار مع قسيّ الدائرة التي تمرّ بأوساط البروج. وبهذه الأشياء نجد السبيل إلى استخراج سائر الأمور الجزئيّة كلّها على حسب ما يلزم منها. ونحن مستعملون في ذلك ألقاب البروج على أقسام الدائرة المائلة الاثني عشر أيضاً أنفسها على أنّ مباديها تؤخذ من نقطتي الانقلابين ونقطتي الاستوائين. /H118/ فنسمّى القسم الأوّل من الاثني عشر الذي مبدأه من الاستواء الربيعيّ أخذاً نحو الجهة التي منها حركة الكلّ الحمل، والثاني الثور، وكذلك يجري الأمر في سائر الأقسام الاثني عشر على حسب ما أخذناه من ترتيب البروج الاثني عشر.

ونحن مبيّنون أوّلاً أنّ القسيّ من الدائرة التي تمرّ على أوساط البروج التي بعدها من نقطة واحدة بعينها من نقطتي الاستوائين بعد واحد تطلع دائماً مع قسيّ متساوية من دائرة معدّل النهار.

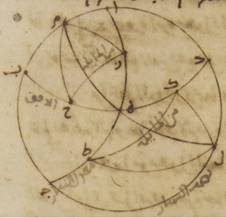
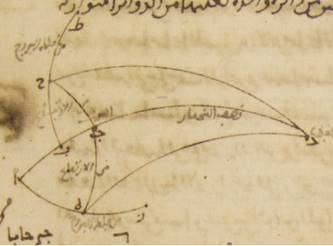
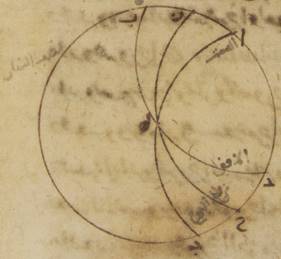
/T91/ ح: فلتكن دائرة نصف النهار ألف باء جيم دال، ونصف دائرة الأفق باء هاء دال، ونصف دائرة معدّل النهار ألف هاء جيم، وقطعتان من الدائرة المائلة قطعة زاي حاء وقطعة طاء كاف حتّى تضع كلّ واحدة من نقطتي زاي طاء النقطة التي على الاستواء الربيعيّ، والقوسين المفرزتين عن جنبتيها وهما قوسا زاي حاء، طاء كاف تطلعان ه: يعني أنّ ما يطلع منها يطلع على على نقطتي حاء، كاف. أقول إنّ القوسين من معدّل النهار اللتين تطلعان مع واحدة واحدة منهما، أعني قوس زاي هاء، طاء هاء، متساويتان.

/H119/ فليكن مكان قطبي معدّل النهار نقطتي لام، ميم ولنرسم بهما قطع من أعظم ما يكون من الدوائر وهي قطعة لام هاء ميم وأيضاً قطعة لام طاء وقطعة لام كاف وقطعة ميم زاي وقطعة ميم حاء. فلأنّ قوس زاي حاء مساوية لقوس طاء كاف، فإنّ الدائرتين المتوازيتين المرسومتين على نقطتي كاف حاء بعدهما عن جنبتي معدّل النهار بعد متساو. فتكون قوس لام كاف أيضاً مساوية ه – صح: لقوس ميم حاء وقوس هاء كاف مساوية لقوس هاء حاء فتصير أضلاع مثلّث لام كاف طاء مساوية لأضلاع مثلّث ميم هاء زاي وأضلاع مثلث لام هاء كاف مساوية لأضلاع مثلّث ميم هاء حاء. فزاوية كاف لام هاء مساوية لزاوية حاء ميم هاء وزاوية كاف لام طاء بأسرها مساوية لزاوية حاء ميم زاي فتصير زاوية هاء لام طاء الباقية مساوية لزاوية هاء ميم زاي الباقية فقاعدة هاء طاء مساوية لقاعدة هاء زاي. وذلك ما كان يجب أن نبيّنه.

ونحن أيضاً مبيّنون إن كلّ قوسين من معدّل النهار تطلعان مع قوسين من الدائرة التّي تمرّ على أوساط البروج متساويتين ومتساويتي البعد من نقطة انقلاب من الانقلابين بعينه، فمجموعهما مساو لمجموع /T92/ مطالعهما في الكرة المنتصبة.

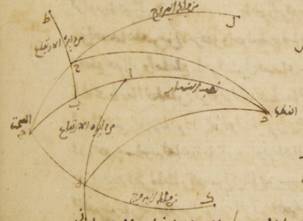
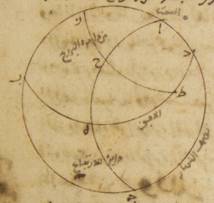
ه: فلنضع دائرة نصف النهار ألف باء جيم دال، ونضع من أنصاف الدوائر نصف دائرة معدّل النهار وهو ألف هاء جيم ونصف دائرة الأفق وهو باء هاء دال. /H120/ ونرسم قوسين من الدائرة المائلة متساويتين ومتساويتي البعد من النقطة الشتويّة وهما قوس زاي حاء على أن تضع نقطة زاي النقطة الخريفيّة وقوس طاء حاء على أنّ نقطة طاء النقطة الربيعيّة حتّى تكون نقطة حاء النقطة المشتركة لمطلعهما وللأفق من قبل أنّ قوسي زاي حاء، طاء حاء تفرزهما دائرة واحدة بعينها موازية لمعدّل النهار. ومن البيّن أنّه يطلع مع قوس طاء حاء قوس طاء هاء، ومع قوس زاي حاء قوس هاء زاي. فيظهر من ذلك من قرب أنّ قوس طاء هاء زاي بأسرها مساوية لمطالع قوسي زاي حاء، طاء حاء في الكرة المنتصبة.

فإنّا إن وضعنا قطب معدّل النهار الجنوبيّ نقطة كاف ورسمنا عليه وعلى نقطة حاء ربع دائرة من أعظم الدوائر وهو كاف حاء لام تقوم مقام الأفق في الكرة المنتصبة صارت أيضاً قوس طاء لام القوس التي تطلع مع قوس طاء حاء في الكرة المنتصبة وقوس زاي لام القوس التّي تطلع مع قوس حاء زاي على هذا المثال حتّى تكون قوسا طاء لام، لام زاي مجموعتين مساويتين لقوسي طاء هاء، هاء زاي مجموعتين وتشتمل على مجموع القوسين قوس واحدة بعينها وهي قوس طاء زاي وذلك ما كان ينبغي أن نبيّنه.

وقد استبان لنا بهذه الأشياء أنّا إن حسبنا في /H121/ ميل ميل المطالع الجزئيّة في ربع واحد فقط يبيّن لنا من ذلك وحصّل لنا مع مطالع ذلك الربع مطالع الثلاثة الأرباع الباقية.

و: وإذا كان ذلك كذلك، فلنضع أيضاً الدائرة الموازية التي تمرّ على الجزيرة المسمّاة رودس حيث يكون مبلغ أطول ما يكون من النهار أربع عشرة ساعة ونصف من الساعات الاستوائيّة، والقطب الشماليّ مرتفعاً عن الأفق ستّة وثلاثين جزءاً.

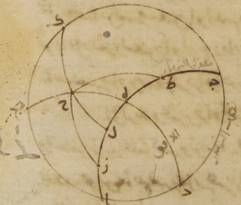
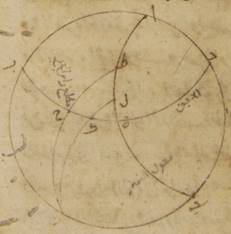
ولتكن دائرة نصف النهار ألف باء جيم دال، وعلى ذلك المثال نصف دائرة الأفق باء هاء دال، ونصف دائرة معدّل النهار ألف هاء جيم ونصف الدائرة التي تمرّ على أوساط البروج زاي حاء طاء، على أن يوضع التقاطع الذي يقع على حاء النقطة الربيعيّة. ونفرض قطب /T93/ معدّل النهار الشماليّ على نقطة كاف ونرسم ربع دائرة من أعظم الدوائر يمرّ بها وبتقاطع الدائرة التي تمرّ على أوساط البروج ودائرة الأفق الذي وقع على نقطة لام وهو كاف لام ميم.  This sentence is different from Tommerʼs translation.

ونجعل قوس حاء لام مفروضة وليكن قصدنا أن نستخرج مقدار القوس التي تطلع معها من معدّل النهار وهي قوس هاء حاء. ونجعل أوّلاً قوس حاء لام تحيط بالقسم من الاثني عشر الذي للحمل. فمن قبل أنّه قد رسم أيضاً فيما بين قوسين من أعظم الدوائر وهما قوسا هاء حاء، حاء لام ه – صح: هاء جيم جيم كاف قوسان من أعظم الدوائر وهما قوسا هاء دال، كاف ميم تتقاطعان على نقطة لام. فنسبة وتر ضعف قوس كاف دال إلى وتر ضعف قوس دال جيم /H122/ مؤلّفة من نسبة وتر ضعف قوس كاف لام إلى وتر ضعف قوس لام ميم ونسبة وتر ضعف قوس ميم هاء إلى وتر ضعف قوس هاء جيم. لكن ضعف قوس كاف دال اثنان وسبعون جزءاً ووتره سبعون جزءاً واثنتان وثلاثون دقيقة وأربع ثواني، وضعف قوس دال جيم مائة وثمانية أجزاء ووتره سبعة وتسعون جزءاً وأربع دقائق وستّ وخمسون ثانية.

وأيضاً فإنّ ضعف قوس كاف لام مائة وستّة وخمسون جزءاً وأربعون دقيقة وثانية واحدة، ووتره مائة وسبعة عشر جزءاً وإحدى وثلاثون دقيقة وخمس عشرة ثانية. وضعف قوس لام ميم ثلاثة وعشرون جزءاً وتسع عشرة دقيقة وتسع وخمسون ثانية، ووتره أربعة وعشرون جزءاً وخمس عشرة دقيقة وسبع وخمسون ثانية. فإن نقصنا من نسبة سبعين جزءاً واثنتين وثلاثين دقيقة وأربع ثواني إلى سبعة وتسعين جزءاً وأربع دقائق وستّ وخمسين ثانية نسبة مائة وسبعة عشر جزءاً وإحدى وثلاثين دقيقة وخمسين عشرة ثانية إلى أربعة وعشرين جزءاً وخمس عشرة دقيقة وسبعة وخمسين ثانية بقيت نسبة وتر ضعف قوس ميم هاء إلى وتر ضعف قوس هاء جيم نسبة ثمانية عشر جزءاً وخمس ثواني إلى مائة وعشرين جزءاً. ووتر ضعف قوس هاء جيم هو مائة وعشرون جزءاً، فوتر ضعف قوس ميم هاء إذن هو بهذه الأجزاء ثمانية عشر جزءاً وخمس ثواني. فيجب من ذلك أن يكون ضعف قوس ميم هاء سبعة عشر جزءاً وستّ عشرة دقيقة بالتقريب وقوس ميم هاء نفسها بهذه الأجزاء ثمانية وثمان وثلاثين دقيقة. لكن قوس حاء ميم بأسرها لمّا كانت تطلع في الكرة المنتصبة مع قوس حاء لام فيما قد تقدّم بيانه أنّها سبعة وعشرون جزءاً وخمسون دقيقة. فقوس هاء حاء الباقية إذن تسعة عشر جزءاً واثنتا عشرة دقيقة.

/H123/ وقد تبّين مع ذلك أنّ القسم من الاثني عشر الذي للحوت يطلع مع هذا المقدار بعينه من /T94/ الأزمان وهو تسعة عشر جزءاً واثنتا عشرة دقيقة، وكلّ واحد من القسمين من الاثني عشر الذين للسنبلة والميزان يطلع مع الأزمان الباقية من ضعف مطلعه في الكرة المنتصبة وهي ستّة وثلاثون زماناً وثمان وعشرون دقيقة.

وأيضاً فلتكن قوس حاء لام تحيط بأجزاء قسمين من الاثني عشر وهما الحمل والثور وذلك ستّون جزءاً. فلمّا وضعناه على أنّ سائر الأشياء باقية على حالها يصير ضعف قوس كاف لام مائة وثمانية وثلاثين جزءاً وتسعاً وخمسين دقيقة واثنتين وأربعين ثانية ووتره مائة واثنا عشر جزءاً وثلاث وعشرون دقيقة وستّ وخمسون ثانية. وضعف قوس لام ميم واحداً وأربعين جزءاً وثمان عشرة ثانية ووتره اثنان وأربعون جزءاً ودقيقة واحدة وثمان وأربعون ثانية. فإنّ نحن أيضاً نقصنا من نسبة سبعين جزءاً واثنتين وثلاثين دقيقة وأربع ثواني إلى سبعة وتسعين جزءاً وأربع دقائق وستّ وخمسين ثانية نسبة مائة واثني عشر جزءاً وثلاث وعشرين دقيقة وستّ وخمسين ثانية إلى اثنين وأربعين جزءاً ودقيقة واحدة وثمان وأربعين ثانية بقيت نسبة وتر ضعف قوس ميم هاء إلى وتر ضعف قوس هاء جيم نسبة اثنين وثلاثين جزءاً وستّ وثلاثين دقيقة وأربع ثواني إلى مائة وعشرين جزءاً. ووتر ضعف قوس هاء جيم مائة وعشرون جزءاً. فوتر ضعف قوس ميم هاء إذا بهذه الأجزاء اثنان وثلاثون جزءاً وستّ وثلاثون دقيقة وأربع ثواني. فيجب أن يكون ضعف قوس ميم هاء واحداً وثلاثون جزءاً واثنتين وثلاثين دقيقة بالتقريب، وقوس ميم هاء نفسها بهذه الأجزاء خمسة عشر جزءاً وستّ وأربعون دقيقة. لكن قوس ميم حاء بأسرها قد تبيّن أيضاً أنّها بهذه الأجزاء سبعة وخمسون جزءاً وأربع وأربعون دقيقة. فقوس هاء حاء الباقية أحد وأربعون جزءاً وثمان وخمسون دقيقة. فالحمل إذاً والثور يطلعان مجموعين في أحد وأربعين زماناً وثمان وخمسين دقيقة، /H124/ من ذلك الحمل قد تبيّن أنّه يطلع مع تسعة عشر زماناً واثني عشرة دقيقة. فالقسم إذن وحده من الاثني عشر الذي للثور يطلع مع اثنين وعشرين زماناً وستّ وأربعين دقيقة.

ولذلك بعينه أيضاً يكون القسم من الاثني عشر الذي للدلو يرتفع مع مثل هذه الأزمان وهي اثنان وعشرون زماناً وستّ وأربعون دقيقة وكلّ واحد من قسمي الأسد والعقرب مع ما تبقى من ضعف مطلعه في الكرة المنتصبة وهي سبعة وثلاثون زماناً ودقيقتان.

ولمّا كان أطول ما يكون من النهار أربع عشرة ساعة ونصف استوائيّة وأقصر ما يكون منه تسع ساعات ونصف، فمن البيّن أنّ نصف الدائرة الذي من السرطان إلى الرامي يرتفع مع مائتين وسبعة عشر زماناً وثلاثين دقيقة من معدّل النهار، ونصف الدائرة الذي من الجدي إلى التو⟨أ⟩م يرتفع مع مائة واثنين وأربعين زماناً وثلاثين دقيقة من معدّل النهار. فيكون كلّ واحد أيضاً من الربعين اللذين عن جنبتي النقطة ه – صح: الربيعيّة ترتفع مع أحد وسبعين زماناً وخمس عشرة دقيقة وكلّ واحد من الربعين الذين عن جنبتي النقطة الخريفيّة يرتفع مع مائة وثمانية أزمان وخمس وأربعين دقيقة. فيبقى إمّا كلّ واحد من القسم من الاثني عشر الذي للجوزاء والذي للجدي فيرتفع مع تسعة وعشرين زماناً وسبع عشرة دقيقة، وهي الأزمان الباقية من أزمان الربع التي هي أحد وسبعون زماناً وخمس عشرة دقيقة، وإمّا كلّ واحد من القسم من الاثني عشر الذي للسرطان والذي للقوس فيرتفع مع خمسة وثلاثين زماناً وخمس عشرة دقيقة، وهي ما يبقى أيضاً من هذا الربع من الأزمان التي هي مائة وثمانية أزمان وخمس وأربعون دقيقة.

/H125/ وظاهر أنّ لنا بهذا الوجه الذي جرينا عليه في هذه أن نستخرج المطالع التي مع الأجزاء التي هي أصغر من هذه الدائرة التي تمرّ بأوساط البروج. ولنا أيضاً أن نحسبها بأيسر من ذلك وأحكم على هذا الوجه.

ز: فلتكن أولاً دائرة نصف النهار ألف باء جيم دال، ونصف دائرة الأفق باء هاء دال، ونصف دائرة معدّل النهار ألف هاء جيم، ونصف الدائرة التّي تمرّ بأوساط البروج زاي هاء حاء على أن يوضع فصل هاء على النقطة الربيعيّة. ولنفصل ممّا يليها قوس هاء طاء كيف وقعت، ولنرسم قطعة من دائرة موازية لدائرة معدّل النهار تمرّ بنقطة طاء ولتكن طاء كاف. وليؤخذ قطب معدّل النهار وليكن لام ولنرسم ربعان من دائرتين من أعظم الداوئر تمرّان به وليكونا لام طاء ميم، لام كاف نون، وأيضاً ربع لام هاء.

/T95/ فمن البيّن من هذا العمل أنّ قطعة هاء طاء من الدائرة التي تمرّ على أوساط البروج إمّا في الكرة المنتصبة فتطلع مع قوس هاء ميم وإمّا في الكرة المائلة فمع القوس المساوية الزمان لقوس نون ميم، من قبل أنّ قوس طاء كاف من الدائرة الموازية التي تطلع معها قطعة هاء طاء، هي شبيهة بقوس نون ميم من دائرة معدّل النهار والقسيّ المتشابهة من الدوائر المتوازية تطلع في كلّ موضع في أزمان متساوية. /H126/ فمطلع قطعة هاء طاء إذا في الكرة المائلة أقلّ من مطلعها في الكرة المنتصبة بقوس هاء زاي ه – صح: نون. وقد تبيّن مع هذين الأمرين أنّه من الظاهر أنّ بالجملة إن رسمت قسيّ ما من أعظم الدوائر على ما رسمت قوس لام كاف زاي، ه – صح: نون فإنّ قطعة هاء زاي ه – صح: نون تجوز فصل ما بين مطالع القسيّ من الدائرة التي تمرّ بأوساط البروج التي تنفرز فيما بين نقطة هاء وبين الدائرة الموازية التي تمرّ بنقطة كاف في الكرة المنتصبة وبين مطالعها في الكرة المائلة.

ح: فإذ قد تقدّم ه: العلم بذلك، فلنجعل الرسم أيضاً فيه دائرة نصف النهار ه – صح: ونصفا دائرة الأفق ودائرة معدّل النهار فقط، ولنرسم من أعظم الدوائر تمرّان بنقطة زاي، وهي قطب معدّل النهار، الجنوبيّ وليكونا زاي حاء طاء، زاي كاف لام. ولننزّل أنّ نقطة حاء مشتركة للدائرة الموازية التي ترسم مارّة بنقطة الانقلاب الشتويّ ونقطة كاف مشتركة للدائرة التي ترسم مارّة مثلاً أوّلاً بأوّل /H127/ الحوت، أو بجزء آخر مفروض من أجزاء الربع أيّ جزء كان.

فقد خطّ أيضاً فيما بين قوسين من أعظم الدوائر وهما قوسا زاي طاء، هاء طاء قوسا زاي كاف لام، هاء كاف حاء. ه: يتقاطعان على نقطة كاف فنسبة وتر ضعف قوس طاء حاء إلى وتر ضعف قوس حاء زاي مؤلّفة من نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء لام ومن نسبة وتر ضعف قوس لام كاف إلى وتر ضعف قوس كاف زاي.

لكن في الميول كلّها ضعف قوس طاء حاء واحد بعينه مفروض وذلك أنّه قوس التّي بين الانقلابين. فمن أجل ذلك تكون القوس الباقية التيّ هي ضعف قوس حاء زاي أيضاً مفروضة. وعلى هذا المثال /T96/ في الأجزاء بأعيانها من الدائرة التي تمرّ بأوساط البروج ضعف قوس لام كاف في الميول كلّها واحد بعينه ↑بعينه↑: صح مفروض من قبل جدول الميل يبقى ذلك أيضاً ضعف قوس كاف زاي معلوماً. فيجب من ذلك أنّ نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء لام تبقى واحدة ↑واحدة↑: صح بعينها ↑بعينها↑: صح في الميول كلّها في الأجزاء بأعيانها من الدائرة التي تمرّ بأوساط البروج.

فإذا كان ذلك على ما وصفناه، فإنّا إن زيّدنا اختلاف قوس لام كاف، فأخذنا عشرة أجزاء عشرة أجزاء من الربع الذي من الاستواء الربيعيّ نحو نقطة الانقلاب الشتويّ. إذ كانت قسمة القسيّ التي هذا مبلغها فيها كفاية لمّا يحتاج إليه من العمل، صار لنا /H128/ ضعف قوس طاء حاء أبداً سبعة وأربعين جزءاً واثنتين وأربعين دقيقة وأربعين ثانية، ووتره ثمانية وأربعون جزءاً وإحدى وثلاثون دقيقة وخمساً وخمس ثانية. وضعف قوس حاء زاي مائة واثنان وثلاثون جزءاً وسبع عشرة دقيقة وعشرين ثانية، ووتره مائة وتسعة أجزاء وأربعاً وأربعين دقيقة وثلثاً وخمسين ثانية، وكذلك أيضاً.

أمّا في القوس التي بعدها من النقطة الربيعيّة عشرة أجزاء ممّا يلي الانقلاب الشتويّ فيكون ضعف قوس لام كاف ثمانية أجزاء وثلاث دقائق وستّ عشرة ثانية، ووتره ثمانية أجزاء وخمساً وعشرين دقيقة وتسعاً وثلاثين ثانية، وضعف قوس كاف زاي مائة وأحد وستّون جزءاً وستّاً وخمسين دقيقة وأربعاً وأربعين ثانية، ووتره مائة وتسعة عشر جزءاً واثنتين وأربعين دقيقة وأربع عشرة ثانية.

وأمّا في القوس التي بعدها على هذا المثال عشرون جزءاً فيكون ضعف قوس لام كاف خمسة عشر جزءاً وأربعاً وخمسين دقيقة وستّ ثواني، ووتره ستّة عشر جزءاً وخمساً وثلاثين دقيقة وستّاً وخمسين ثانية؛ ه – صح: وضعف قوس كاف زاي مائة وأربعة وستّون جزءاً وخمس دقائق وأربعاً وخمسين ثانية ووتره ووتره مائة وثمانية عشر جزءاً وخمسين دقيقة وسبعاً وأربعين ثانية.

وأمّا في القوس التي بعدها ثلاثون جزءاً فيكون ضعف قوس لام كاف ثلاثة وعشرين جزءاً وتسع عشرة دقيقة وثمانياً وخمسين ثانية، ووتره أربعة وعشرون جزءاً وخمس عشرة دقيقة وستّاً وخمسين ثانية؛ وضعف قوس كاف زاي مائة وستّة وخمسين جزءاً وأربعين دقيقة وثانيتين، ووتره مائة وسبعة عشر جزءاً وإحدى وثلاثين دقيقة وخمس عشرة ثانية.

وأمّا في القوس التي بعدها أربعون جزءاً /H129/ فيكون ضعف قوس لام كاف ثلاثين جرءاً وثمان دقائق وثمان ثواني ووتره واحد وثلاثون جزءاً وإحدى عشرة دقيقة وثلثاً وأربعين ثانية وضعف قوس كاف زاي مائة وتسعة وأربعون جزءاً وإحدى وخمسين دقيقة واثنتين وخمسين ثانية، ووتره مائة وخمسة عشر جزءاً واثنتين وخمسين دقيقة وتسعاً وعشرين ثانية.

وأمّا في القوس التي بعدها خمسون جزءاً فيكون ضعف قوس لام كاف ستّة وثلاثين جزءاً وخمس دقائق وستّاً وأربعين ثانية، ووتره سبعة وثلاثون جزءاً وعشر دقائق وتسعاً وثلاثين ثانية؛ وضعف قوس كاف زاي مائة وثلاثة وأربعون جزءاً وأربعاً وخمسين دقيقة وإحدى ه – صح: وأربع عشرة ثانية ووتره مائة وأربعة عشر جزءاً وخمس دقائق وأربعاً وأربعين ثانية.

وأمّا في القوس التي بعدها ستّون جزءاً /T97/ فيكون ضعف قوس لام كاف أحد وأربعون جزءاً وثمان عشرة ثانية، ووتره اثنين وأربعين جزءاً ودقيقة واحدة وثمان وأربعون ثانية؛ وضعف قوس كاف زاي مائة وثمانية وثلاثون جزءاً وتسعاً وخمسين دقيقة واثنتين وأربعين ثانية، ووتره مائة واثناعشر جزءاً وثلاثاً وعشرين دقيقة وسبعاً وخمسين ثانية.

وأماّ في القوس التي بعدها سبعون جزءاً فيكون ضعف قوس لام كاف أربعة وأربعين جزءاً وأربعة دقيقة واثنتين وعشرين ثانية، ووتره خمسة وأربعون جزءاً وستّاً وثلاثين دقيقة وثمان عشرة ثانية؛ وضعف قوس كاف زاي مائة وخمسة وثلاثين جزءاً وتسع عشرة دقيقة وثمانياً وثلاثين ثانية، ووتره مائة وعشرة أجزاء وتسعاً وخمسين دقيقة وسبعاً وأربعين ثانية.

وأمّا في القوس التي بعدها ثمانون جزءاً فيكون ضعف قوس لام كاف ستّة وأربعين جزءاً وستّاً وخمس دقيقة واثنتين وثلاثين ثانية، ووتره سبعة وأربعون جزءاً وسبعاً وأربعين دقيقة وأربعين ثانية؛ وضعف قوس كاف زاي مائة وثلاثة وثلاثون جزءاً وثلاث دقائق وثمانياً وعشرين ثانية، ووتره مائة وعشرة أجزاء وأربع دقائق وستّ عشرة ثانية.

ومن قبل ما وضعناه إن نقصنا من نسبة وتر ضعف قوس طاء حاء إلى وتر ضعف قوس حاء زاي، /H130/ أعني من نسبة ثمانية وأربعين جزءاً وإحدى وثلاثين دقيقة وخمس وخمسين ثانية إلى مائة وتسعة أجزاء وأربع وأربعين دقيقة وثلاث وخمسين ثانية واحدة واحدة من نسبة قوس لام كاف إلى قوس كاف زاي التي حصلت بزيادة عشرة أجزاء عشرة أجزاء، بقيت لنا (أيضاً) نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء لام في الميول كلّها نسبة ستّين جزءاً، أمّا في القوس التي بعدها كما قلنا عشرة أجزاء فإلى تسعة أجزاء وثلاث وثلاثين دقيقة. وأمّا في القوس التي بعدها عشرون جزءاً فإلى ثمانية عشر جزءاً وسبع وخمسين دقيقة. وأمّا في القوس التي بعدها ثلاثون جزءاً فإلى ثمانية وعشرين جزءاً ودقيقة واحدة. وأمّا في القوس التي بعدها أربعون جزءاً فإلى ستّة وثلاثين جزءاً وثلاث وثلاثين دقيقة. وأمّا في القوس التي بعدها خمسون جزءاً فإلى أربعة وأربعين جزءاً واثني عشرة دقيقة. وأمّا في القوس التي بعدها ستّون جزءاً فإلى خمسين جزءاً وأربع وأربعين دقيقة. وأمّا في القوس التي بعدها سبعون جزءاً فإلى خمسة وخمسين جزءاً وخمس وأربعين دقيقة. وأمّا في القوس التي بعدها ثمانون جزءاً فإلى ثمانية وخمسين جزءاً وخمس وخمسين دقيقة.

ومن هنالك قد يظهر لنا ه: أنّا في كلّ واحد من الميول أيضاً لمّا كان لنا ضعف قوس طاء هاء مفروضاً من قبل أنّ مبلغ أجزائه كمبلغ فضل أزمان نهار الاستواء على أقصر النهار، وكان وتره أيضاً مفروضاً وكانت نسبة وتر ضعفها إلى وتر ضعف قوس لام هاء مفروضة. فإنّ القوس نفسها تكون لنا مفروضة وضعف قوس هاء لام يكون مفروضاً. فإذا نقصنا نصف هذه القوس وهو قوس هاء لام نفسها، وهو مبلغ الفضل الذي تقدّم ذكره، من مطالع القوس المفروضة من دائرة البروج في الكرة المنتصبة، وجدنا مطالع تلك القوس بعينها في الميل الموضوع.

/H131/ فلنعد فنضع على طريق المثال ميل الدائرة الموازية التي تمرّ بالجزيرة المسمّاة رودس وهي الدائرة التي فيها ضعف قوس هاء طاء سبعة وثلاثون جزءاً وثلاثون دقيقة، ووتره ثمانية وثلاثون جزءاً وأربع وثلاثون دقيقة بالتقريب. فمن قبل أنّ نسبة ستّين جزءاً إلى ثمانية وثلاثين جزءاً وأربع وثلاثين دقيقة هي نسبة تسعة أجزاء وثلاث وثلاثين دقيقة إلى ستّة أجزاء وثمان دقائق، ونسبة ثمانية عشر جزءاً وسبع وخمسين دقيقة إلى اثني عشر جزءاً وإحدى عشرة دقيقة، ونسبة ثمانية وعشرين جزءاً ودقيقة واحدة إلى ثمانية عشر جزءاً وسبع دقائق، ونسبة ستّة وثلاثين جزءاً وثلاث وثلاثين دقيقة إلى ثلاثة وعشرين جزءاً وتسع وعشرين دقيقة، ونسبة أربعة وأربعين جزءاً واثنتي عشرة دقيقة إلى ثمانية وعشرين جزءاً وخمس وعشرين ثانية، ثانية: صح: دقيقة ونسبة خمسين جزءاً وأربع وأربعين دقيقة إلى اثنين وثلاثين جزءاً وسبع وثلاثين دقيقة، ونسبة خمسة وخمسين جزءاً وخمس وأربعين دقيقة إلى خمسة وثلاثين جزءاً واثنتين وخمسين دقيقة، ونسبة ثمانية وخمسين جزءاً وخمس وخمسين دقيقة إلى سبعة وثلاثين جزءاً واثنتين وخمسين دقيقة. /T98/ يصير أيضاً وتر ضعف قوس هاء لام في واحد واحد من التفاضل بعشرة أجزاء الأجزاء التي ذكرت بحسب ذلك ويصير نصف القوس التي على هذه أعني قوس هاء لام نفسها في العشرة الأولى جزأين وستّاً وخمسين دقيقة، وفي العشرة الثانية خمسة أجزاء وخمسين دقيقة، وفي العشرة الثالثة ثمانية أجزاء وثمانياً وثلاثين دقيقة، وفي العشرة الرابعة أحد عشر جزءاً وسبع عشرة دقيقة، وفي العشرة الخامسة ثلاثة عشر جزءاً واثنتين وأربعين دقيقة، وفي العشرة السادسة خمسة عشر جزءاً وستّاً وأربعين دقيقة، وفي العشرة السابعة سبعة عشرة جزءاً وأربعاً وعشرين دقيقة، وفي العشرة الثامنة ثمانية عشر جزءاً وأربعاً وعشرين دقيقة. ومن البيّن أنّها يكون في العشرة التاسعة بهذه الأجزاء ثمانية عشر ↑عشر↑: صح جزءاً وخمساً وأربعين ↑أربعين↑: صح دقيقة. فيجب من ذلك إذا كان في الكرة المنتصبة أيضاً أمّا القوس التي إلى العشرة الأولى فتطلع مع تسعة أزمان وعشر دقائق، وأمّا التي إلى العشرة الثانية فمع ثمانية عشر زماناً وخمس وعشرين دقيقة، وأمّا التي إلى الثالثة فمع سبعة وعشرين زماناً وخمسين دقيقة، /H132/ وأمّا التي إلى الرابعة فمع سبعة وثلاثين زماناً وثلاثين دقيقة، وأمّا إلى الخامسة فمع سبعة وأربعين زماناً ه: وثمان وثلاثين دقيقة، [وأمّا التي إلى الخامسة شطب الكاتب «فمع» وعشرين دقيقة] وأمّا التي إلى السادسة فمع سبعة وخمسين زماناً وأربع وأربعين دقيقة. وأمّا التي إلى السابعة فمع ثمانية وستّين زماناً وثمان عشرة دقيقة. وأمّا التي إلى الثامنة فمع تسعة وسبعين زماناً وخمس دقائق. وأمّا التي إلى التاسعة فمع أزمان الربع بأسره وهي تسعون زماناً.

فمن البيّن إنّا إن نقصنا من واحد واحد من المطالع الموضوعة في الكرة المنتصبة المقدار الموافق للتفاضل الذي يقع لقوس هاء لام، حصلت لنا أيضاً مطالع هذه القسيّ في الميل الموضوع. فتكون القوس التي إلى العشرة الأولى ترتفع مع الأزمان الباقية وهي ستّة أزمان وأربع عشرة دقيقة. والقوس التي إلى العشرة الثانية مع اثني عشر زماناً وخمس وثلاثين دقيقة. والقوس التي إلى العشرة الثالثة مع تسعة عشر زماناً واثنتي عشرة دقيقة. والتي إلى الرابعة مع ستّة وعشرين زماناً وثلاث عشرة دقيقة. والتي إلى الخامسة فمع ثلاثة وثلاثين زماناً وستّ وأربعين دقيقة. والتي إلى السادسة مع أحد وأربعين زماناً وثمان وخمسين دقيقة. والتي إلى السابعة مع خمسين زماناً وأربع وخمسين دقيقة. والتي إلى الثامنة مع ستّين زماناً وإحدى وأربعين دقيقة. والتي إلى التاسعة، وهي قوس الربع بأسره مع الأزمان التي تجتمع من نصف مقدار النهار، وهي أحد وسبعون زماناً وخمس عشرة دقيقة.

فالعشرات إذن أنفسها؛ أماّ الأولى منها فيرتفع منه مع ستّة أزمان وأربع عشرة دقيقة. وأمّا الثانية فمع ستّة أزمان وإحدى وعشرين دقيقة. وأمّا الثالثة فمع ستّة أزمان وسبع وثلاثين دقيقة. وأمّا الرابعة فمع سبعة أزمان ودقيقة واحدة. وأمّا الخامسة فمع سبعة أزمان وثلاث وثلاثين دقيقة. وأمّا السادسة فمع ثمانية أزمان واثني عشرة دقيقة. وأمّا السابعة فمع ثمانية أزمان وستّ وخمسين دقيقة. /T99/ وأمّا الثامنة فمع تسعة أزمان وسبع وأربعين دقيقة. وأمّا التاسعة فمع عشرة أزمان وأربع وثلاثين دقيقة.

/H133/ فإذ قد تبيّنت هذه القسيّ، فقد تبيّن معها أيضاً من ذلك من قبل ما تقدّم علمه مطالع سائر الأرباع على النسق. فنحسب أيضاً بهذا الوجه مطالع واحدة واحدة من العشرات في باقي الدوائر المتوازية ما منها ممكن أن يدرك به ما يحتاج إليه من الأمور الجزئيّة وبعضها ه – صح: ونضعها على طريق الجداول كيما يسهل بها السبيل في استخراج ما بعدها. ونبتديء في ذلك من الدائرة الموازية التي تحت معدّل النهار نفسه ونبلغ إلى الدائرة التي يجعل أطول النهار سبع عشرة ساعة، ونجعل التفاضل بينها بنصف ساعة نصف ساعة من قبل أنّ الفضل بين الدوائر التي تقع فيما بين النصف ساعة فضل ليس تجاوز التساوي بمقدار نعتدّ له. فأوّل ما نضع من الجداول عشرات الدائرة وهي ستّة وثلاثون عشرة. ثمّ نضع بإزاء كلّ واحدة منها على الولاء أزمان المطلع الموافق للميل وجملها على هذا الوجه. وهذه صورة الجدول:

⟨II.8⟩/H 134-41/ح: جداول للمطالع المتفاصلة بعشرة أجزاء عشرة أجزاء.

⟨II.9⟩/H142/ ط: في الأشياء الجزئيّة التي تعلم بعلم المطالع

وقد يظهرممّا نحن واصفوه من الأبواب أنّ أزمان المطالع إذ قد وضعناها على هذه الجهة التي وصفنا، فإنّ سائر ما ينتفع به في هذا الجزء من العلم يسهل تناوله كلّه من غير أن نحتاج في شيء منه إلى براهين خطوطيّة ولا رسم جدول زائد على ما رسمناه. The manuscript does not contain an Arabic version of the following sentence in Toomer’s translation of the Greek: This will become clear from the actual methods described below. (Toomer, p. 99)

فأوّل ذلك إنّا إذا أعطينا نهاراً أو ليلاً عرفنا مقداره بأن نحسب الأزمان من الاقليم الذي قصد قصده. أمّا أزمان النهار، فمن جزء الشمس إلى الجزء المقابل له على توالي البروج؛ وأمّا أزمان الليل، فمن الجزء المقابل لجزء الشمس إلى جزء الشمس نفسه. فإنّا إذا أخذنا ممّا يجتمع من الأزمان جزءاً من خمسة عشر جزءاً منه، حصلت لنا تلك المدّة المفروضة كم هي من الساعات الأستوائيّة. وإذا أخذنا جزءاً من اثني عشر جزءاً منه، حصلت لنا الساعة الزمانيّة لتلك المدّة بعينها كم من زمان هي.

وقد يستخرج أيضاً مقدار الساعة الزمانيّة بأسهل من هذا الوجه، وذلك بأن يؤخذ من هذا الجدول الذي وضعناه للمطالع تفاضل الجمل الموضوعة إمّا للنهار فبإزاء جزء الشمس وإمّا لليل فبإزاء الجزء المقابل له في الدائرة الموازية التي تحت معدّل النهار. وفي الدائرة الموازية التي للإقليم المفروض فإنّا إذا أخذنا سدس ما نجده من التفاضل ثمّ نظرنا فإن كان الجزء الذي نقصد لما حياله في نصف الدائرة الشماليّ زدناه على الأزمان الخمسة عشر التي لساعة واحدة استوائيّة، وإن كان في النصف الدائرة الجنوبيّ نقصناه من هذه الخمسة العشر الزمان حصل لنا من ذلك عدد أزمان الساعة الزمانيّة المقصود لها.

/T104/ ثمّ من بعد ذلك فإنّا نردّ الساعات الزمانيّة إذا فرضت لنا إلى ساعات استوائيّة. وذلك بأن نضاعف إمّا ساعات النهار فبأزمان ساعات ذلك النهار في الميل المقصود له، وإمّا ساعات الليل فبأزمان ساعات تلك الليلة. فإنّا إذا أخذنا من المجتمع جزءاً من خمسة عشر جزءاً منه حصل لنا عدد ساعات استوائيّة. وبعكس ذلك قد نردّ الساعات الاستوائيّة إذا فرضت لنا إلى ساعات زمانيّة بأن نضاعفها بخمسة عشر ونقسّمها على أزمان نظائرها من ساعات ذلك البعد المقصود له.

وأيضاً فأنّه إذا فرض لنا في وقت ساعة زمانيّة أيّ ساعة كانت، فإنّا وقت ساعة زمانيّة أيّ ساعة كانت فإنّا: ه – خ: زمان ساعات زمانيّة وعدتّها أيّ ساعات كانت فإنّا أوّلاً نستخرج الجزء من دائرة البروج ه: الطالع في ذلك الوقت بأن تضاعف عدد الساعات إمّا من النهار فالتي من طلوع الشمس وإمّا من الليل فالتي من مغيب الشمس بأزمان الساعات النظائر لها. /H144/ ويلقي ما اجتمع إمّا للنهار فإن نبتديء من جزء الشمس وإمّا لليل فمن الجزء المقابل له على توالي البروج نحسب مطالع الاقليم المقصود له فإلى أيّ جزء انتهى العدد قلنا أنّ ذلك الجزء هو الطالع في ذلك الوقت.

فإن أردنا استخراج الجزء الذي في وسط السماء فوق الأرض، فإنّا نضاعف أبداً الساعات الزمانيّة التي من نصف نهار اليوم الماضي إلى الساعة المفروضة بأزمان الساعات النظائر لها. فما بلغ من العدد ألقيناه بأن نبتديء من جزء الشمس على توالي البروج بحسب المطالع في الكرة المنتصبة وإلى أيّ جزء خرج العدد كان ذلك الجزء هو المتوسّط للسماء فوق الأرض في ذلك الوقت.

وعلى هذا المثال أيضاً نستخرج من قبل الجزء الطالع الجزء المتوسّط للسماء فوق الأرض بأن نعمد إلى جدول الاقليم المقصود له فنأخذ من الجماعة التي فيه العدد الموضوع حيال الجزء الطالع. فإنّا إذا نقصنا منه أبداً التسعين الزمان التي هي أزمان الربع وجدنا الجزء الذي حيال ذلك العدد من الجماعة التي في الكرة المنتصبة من الجدول متوسّطاً للسماء فوق الأرض في ذلك الوقت. وبعكس ذلك أيضاً قد نستخرج من قبل الجزء المتوسّط للسماء فوق الأرض الجزء الطالع. وذلك بأن نعمد إلى القسم من الجدول الذي للكرة /H145/ المنتصبة فنأخذ من الجماعة التي فيه العدد الذي هو حيال الجزء المتوسّط للسماء فإنّا إذا زدنا عليه أبداً الأزمان التسعين بأعيانها نظرنا من الجماعة التي للميل المقصود له أيّ جزء خرج حيال ذلك العدد فإنّا نجد ذلك الجزء هو الطالع في ذلك الوقت.

ومن البيّن أيضاً إنّ الذين يسكنون تحت دائرة واحدة بعينها من دوائر نصف النهار فإنّ الشمس تبعد عن نصف النهار أو عن نصف الليل عندهم من الساعات الاستوائيّة بالسواء؛ والذين ليس يسكنون تحت دائرة واحدة من دوائر نصف النهار، فإنّ مبلغ الأزمان الاستوائيّة التي تختلف بها بقدر فضل الأجزاء التي بها تخالف دائرة نصف النهار دائرة نصف النهار عند أهل واحد واحد من المسكنين.

⟨II.10⟩/T105/ ي: في الزوايا التي تحدث بين دائرة البروج وبين دائرة نصف النهار

وإذ قد بقي من هذا الباب من العلم الذي نحن بسبيله القول في الزوايا أعني التي تحدث عند ه – اخ: عن دائرة البروج. فقد ينبغي أن نقدّم فنوطّي أنّا نعني بقولنا زاوية قائمة يحيط بها دائرتان من أعظم الدوائر متى كانت الدائرة التي ترسم بالفصل المشترك للدائرتين على أنّه قطب لها وبأيّ بعد كان تكون القوس منها التي تجوزها القطعتان المحيطتان بالزاوية ربع الدائرة المرسومة؛ /H146/ وعلى الجملة أنّ نسبة تلك القوس المجوزة إلى الدائرة المرسومة عل الجهة التي وضعناها هي نسبة الزاوية التي يحيط بها ميل السطحين إلى الأربع الزوايا القائمة. فيجب من ذلك إذ كنّا قد وضعنا المحيط ثلاث مائة وستّين جزءاً أن يكون مبلغ أجزاء القوس المجوزة كمبلغ أجزاء الزاوية التي توتّرها بالأجزاء التي بها الزاوية القائمة تسعون جزءاً.

فالزوايا التي هي خاصّة نافعة في هذا الباب من العلم الذي نحن بسبيله من الزوايا التي تحدث عند الدائرة المائلة هي الزوايا التي يحيط بها التقاطع بينها وبين دائرة نصف النهار، والزوايا التي يحيط بها التقاطع بينها وبين الأفق في واحد واحد من الأوضاع، وكذلك أيضاً الزوايا التي يحيط بها التقاطع بينها وبين الدائرة العظمى التي ترسم مارّة بقطبي الأفق.

وقد يتبيّن مع بيان أمر هذه الزوايا القسيّ التي تنفرز من هذه الدائرة بين التقاطع وبين قطب الأفق أعني النقطة التي على سمت الرأس. فإن كلّ واحد من هذه الأشياء التي قصدنا لها إذا تبيّن كان له في هذا الباب نفسه من العلم غناء عظيم جدّاً وكان أيضاً من أنفع الأشياء وأكثرها جدوي فيما ينظر فيه من أمر اختلاف منظر القمر وذلك أنّه لن يمكن الوصول إلى معرفة ذلك دون الإحاطة بعلم هذه الأشياء.

/H147/ وإذا كانت الزوايا التي يحيط بها تقاطع الدائرتين أربعاً، أعني دائرة البروج وواحدة من الدوائر التي تقاطعها. وكان غرضنا أن نجعل كلامنا في زاوية واحدة المتشابهة الوضع فقد ينبغي أن نتقدّم فنخبر بأنّا أنّما نقصد بالجملة في كلامنا هذا من الزاويتين اللتين عن جنبتي القوس من فلك البروج التالية للفصل المشترك بين الدائرتين للزاوية التي ممّا يلي الشمال منهما حتّى يكون ما يلزم في الزوايا وما يقوم عليه البرهان في مقاديرها أنّما برهن أو لزم في الزوايا التي هذه حالها.

وإذا كان يتبيّن أمر الزوايا التي تحدث بين دائرة البروج وبين دائرة نصف النهار أسهل، فأنّا مبتدئون من هذه الزوايا ومبيّنون أوّلاً إن كلّ نقطتين من دائرة البروج بعدهما من نقطة واحدة بعينها من نقطتي الاستواء بعداً سواء فإنّها تجعل الزاويتين الموصوفتين متساويتين.

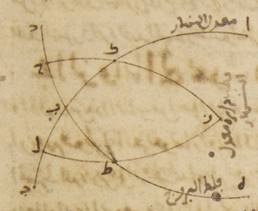
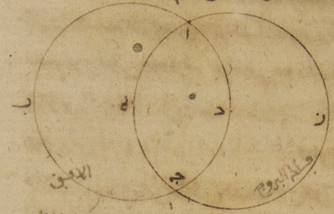
ط: فلتكن قوس معدّل النهار ألف باء جيم، ومن دائرة البروج قوس دال باء هاء، وقطب دائرة معدّل النهار نقطة زاي. ونفرز قوسان متساويتان عن جنبتي نقطة باء وهي نقطة من نقطتي الاستواء وليكونا باء حاء، باء طاء، ولنرسم قوسان من دوائر نصف النهار تمرّان بقطب زاي وبنقطتي حاء، طاء، /H148/ ولتكونا قوسي زاي كاف حاء، زاي طاء لام. أقول إنّ زاوية كاف حاء باء مساوية لزاوية زاي طاء هاء وهذا بيّن من قرب. وذلك أنّ مثلّث باء حاء كاف يصير متساوي /T106/ الزوايا لمثلّث باء طاء لام من قبل أنّ أضلاعه الثلاثة أيضاً متساوية لأضلاعه الثلاثة كلّ واحد لنظيره. أمّا ضلع حاء باء فمساو لضلع باء طاء، وأمّا ضلع حاء كاف فلضلع طاء لام، وأمّا ضلع باء كاف فلضلع باء لام. وذلك كلّه قد تبيّن فيما مضى؛ فزاوية كاف حاء باء إذا مساوية لزاوية باء طاء لام وذلك هو مساواتها لزاوية زاي طاء هاء.

وأيضاً فقد ينبغي أن نبيّن أنّ كلّ نقطتي من دائرة البروج بعدهما عن نقطة واحدة بعينها من نقطتي الانقلابين بعداً سواء. فإنّ الزاويتين اللتين تحدثان عندهما لدائرة البروج مع دائرة نصف النهار مجموعتين مساويتان لزاويتين قائمتين.

ي: فلتكن قوس من دائرة البروج ألف باء جيم وننزّل أنّ نقطة باء أحد الانقلابين ونفرز عن جنبتيه قوسان متساويتان ولتكونا باء دال، باء هاء. ولنرسم قوسان من دوائر نصف النهار تجوزان على نقطة دال ونقطة هاء وعلى نقطة زاي، /H149/ وهي قطب معدّل النهار، ولتكونا قوسي زاي دال، زاي هاء. أقول أنّ زاوية زاي دال باء وزاوية زاي هاء جيم مجموعتين مساويتان لزاويتين قائمتين. وهذا أيضاً بيّن من قرب من قبل أنّ نقطتي دال، هاء بعدهما من نقطة واحدة بعينها من نقطتي الانقلابين بعداً سواء. فقوس زاي دال أيضاً مساوية لقوس زاي هاء فزاوية زاي دال باء إذا مساوية لزاوية زاي هاء باء لكن زاويتي زاي هاء باء، زاي هاء جيم مساويتان لزاويتين قائمتين. فزاوية زاي دال باء إذن مع زاوية زاي هاء جيم مساويتان أيضاً لزاويتين قائمتين. وذلك ما كان ينبغي أن نبيّنه.

يا: فإذ قد تقدّم العلم بذلك فلتكن دائرة نصف النهار ألف باء جيم دال ونصف دائرة البروج ألف هاء جيم على أنّ نقطة ألف توضع الانقلاب الشتويّ ولنرسم بقطب ألف وببعد ضلع المربّع نصف دائرة باء هاء دال. فمن قبل أنّ دائرة نصف النهار ألف باء جيم دال قد مرّت بقطبي نصف دائرة ألف هاء جيم وبقطبي نصف دائرة باء هاء دال فإنّ قوس هاء دال ربع دائرة. /T107/ فزاوية دال ألف هاء إذن قائمة والزاوية أيضاً التي تحدث عن الانقلاب الصيفيّ لما تقدّم بيانه قائمة.

/H150/ يب: وأيضاً فلتكن دائرة نصف النهار ألف باء جيم دال، ونصف دائرة معدّل النهار ألف هاء جيم ولنرسم نصف دائرة البروج ألف زاي جيم على أنّ نقطة آ تكون نقطة الاستواء الخريفيّ. ولنرسم بقطب ألف وببعد ضلع المربّع ه: بلغ العرض بالأمّ والحمد لله على عونه. نصف دائرة باء زاي هاء دال.

/T108/ فلذلك بما كانت دائرة ألف باء جيم دال قد مرّت بقطبي نصف دائرة ألف هاء جيم وبقطبي نصف دائرة باء هاء دال. فإنّ كلّ واحدة من قوسي ألف زاي، هاء دال ربع دائرة. فتكون نقطة زاي الانقلاب الشتويّ وتكون قوس زاي هاء الأجزاء التي قد تبيّنت وهي ثلاثة وعشرون جزءاً وإحدى وخمسون دقيقة بالتقريب. فقوس زاي هاء دال إذاً بأسرها مائة وثلاثة عشر جزءاً وإحدى وخمسون دقيقة، وزاوية دال ألف زاي مائة وثلاثة عشر جزءاً وإحدى وخمسون دقيقة بالأجزاء التي بها زاوية ه: واحدة قائمة تسعون جزءاً. ولما تقدّم أيضاً بيانه تكون الزاوية التي تحدث عن نقطة الاستواء الربيعيّ الأجزاء الباقية بعد ذلك من زاويتين قائمتين وهي ستّة وستّون جزءاً وتسع دقائق.

يج: وأيضاً فلتكن دائرة نصف النهار ألف باء جيم دال، ونصف دائرة معدّل النهار ألف هاء جيم، ونصف دائرة البروج باء زاي دال حتّى توضع نقطة زاي /T109/ /H151/ الاستواء الخريفيّ، وقوس باء زاي أوّلاً واحداً من الأجزاء الاثني عشر الذي للعذراء، ونقطة باء مبدأ السنبلة وذلك بيّن. ولنرسم أيضاً بقطب باء وببعد ضلع المربّع نصف دائرة حاء طاء هاء كاف ولنقصد لاستخراج مقدار زاوية كاف باء طاء. فلأنّ دائرة نصف النهار ألف باء جيم دال تمرّ بقطبي نصف دائرة ألف هاء جيم وبقطبي دائرة حاء هاء كاف، فكّل واحدة إذاً من قسيّ باء حاء، باء طاء، هاء حاء تكون ربع دائرة. وللصورة نسبة وتر ضعف قوس باء ألف إلى وتر ضعف قوس ألف حاء مؤلّفة من نسبة وتر ضعف قوس باء زاي إلى وتر ضعف قوس زاي طاء ومن نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء حاء. لكن ضعف قوس باء ألف لما تقدّم بيانه ثلاثة وعشرون جزءاً وعشرون دقيقة، ووتره أربعة وعشرون جزءاً وستّ عشرة. وضعف قوس ألف حاء مائة وستّة وخمسون جزءاً وأربعون دقيقة ووتره مائة وسبعة عشر جزءاً وإحدى وثلاثون دقيقة. /H152/ وأيضاً ضعف قوس باء زاي ستّون جزءاً ووتره ستّون جزءاً. وضعف قوس زاي طاء مائة وعشرون جزءاً ووتره مائة وثلاثة أجزاء وخمس وخمسون دقيقة وثلاث وعشرون ثانية. فإنّ نحن إذن نقصنا من نسبة أربعة وعشرين جزءاً وستّ عشرة دقيقة إلى مائة وسبعة عشر جزءاً وإحدى وثلاثين دقيقة نسبة ستّين جزءاً إلى مائة وثلاثة أجزاء وخمس وخمسين دقيقة وثلاث وعشرين ثانية، بقيت نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء حاء نسبة اثنتي وأربعين جزءاً ه: وثمان وخمسين دقيق بالتقريب إلى مائة وعشرين جزءاً. لكن وتر ضعف قوس هاء حاء مائة وعشرون جزءاً فوتر ضعف قوس طاء هاء إذاً بهذه الأجزاء اثنان وأربعون جزءاً وثمان وخمسون دقيقة. فتكون ضعف قوس طاء هاء اثنتين وأربعين جزءاً بالتقريب وقوس طاء هاء نفسها بهذه الأجزاء أحد وعشرون جزءاً.

فقوس طاء هاء كاف إذن بأسرها وزاوية كاف باء طاء أيضاً مائة وأحد عشر جزءاً. ولما تقدّم بيانه يكون مقدار الزاوية أيضاً التي تحدث عن مبدأ العقرب هذه الأجزاء بأعيانها وهي مائة وأحد عشر جزءاً. ومقدار كلّ واحدة من الزاويتين اللتين تحدثان عن مبدأ الثور ومبدأ الحوت ما يبقى بعد ذلك من أجزاء زاويتين قائمتين وهي تسعة وستّون جزءاً.

وأيضاً في هذه الصورة بعينها ننزّل أنّ قوس زاي باء جزئان من الاثني عشر الجزء حتّى تكون نقطة باء مبدأ الأسد. ويكون على حسب ما وضعنا ضعف قوس باء ألف أحد وأربعون جزءاً، ووتره اثنان وأربعون جزءاً ودقيقتان؛ وضعف قوس ألف حاء مائة وتسعة وثلاثون جزءاً، ووتره مائة واثنا عشر جزءاً وأربع وعشرون دقيقة. /H153/ وأيضاً ضعف قوس باء زاي مائة وعشرون جزءاً، ووتره مائة وثلاثة أجزاء وخمس وخمسون دقيقة وثلاث وعشرون ثانية. وضعف قوس زاي طاء ستّون جزءاً ووتره ستّون جزءاً. فإنّ نحن إذا نقصنا أيضاً من نسبة اثنين وأربعين جزءاً ودقيقتين إلى مائة واثني عشر جزءاً وأربع وعشرين دقيقة نسبة مائة وثلاثة أجزاء وخمس وخمسين دقيقة وثلاث وعشرين ثانية إلى ستّين جزءاً، بقيت نسبة وتر ضعف قوس طاء هاء إلى وتر ضعف قوس هاء حاء نسبة خمسة وعشرين جزءاً وثلاث وخمسين دقيقة إلى مائة وعشرين جزءاً. فيصير إذن وتر ضعف قوس طاء هاء بهذه الأجزاء خمسة وعشرين جزءاً وثلاثاً وخمسين دقيقة. فيكون ضعف قوس طاء هاء بهذه الأجزاء خمسة وعشرين جزءاً بالتقريب، وقوس طاء هاء نفسها اثنا عشر جزءاً ونصف جزء. فقوس طاء هاء كاف إذن بأسرها وزاوية كاف باء طاء أيضاً مائة جزء وجزئان ونصف جزء. ومن قبل ذلك يكون مقدار الزاوية التي يحيط بها مبدأ الراميّ هذه الأجزاء بأعيانها مائة جزء وجزئان ونصف جزء، ومقدار كلّ واحدة من الزاويتين اللتين يحيط بها مبدأ التو⟨أ⟩م ومبدأ الدلو ما يبقى بعد ذلك من أجزاء زاويتين قائمتين وهي سبعة وسبعون جزءاً ونصف جزء.

فقد نبيّن ما قصدنا له وذلك أنّ لنا أن نسلك هذه السبيل بعينها فيما كان أيضاً من أجزاء الدائرة المائلة أصغر من هذه الأجزاء، لكن قد نكتفي فيما نحتاج أليه في هذا العلم بأن نجعل ما نفرضه جزءاً جزءاً من الاثني عشر الجزء.

⟨II.11⟩/T110/ /H154/ يا: في الزوايا التي تحدث بين الدائرة المائلة وبين دائرة الأفق

ومن بعد ذلك فإنّا مبيّنون كيف نعلم إذا فرض لنا ميل الزوايا أيضاً التي تحدث لدائرة البروج عند دائرة أفقه لأنّ طريق هذه الزوايا أيضاً أسهل من طريق ما يبقى بعدها. ومن البيّن أنّ الزوايا التي تحدث لدائرة البروج عند دائرة نصف النهار هي الزوايا التي تحدث له عند الأفق في الكرة المنتصبة. فكيما نعلم أيضاً الزوايا التي تحدث له في الكرة المائلة فقد ينبغي أن نبيّن أيضاً أوّلاً أنّ كلّ نقطتين في دائرة البروج بعدهما فيها من نقطة واحدة بعينها من نقطتي الاستواء بعد سواء تصير الزوايا الموصوفة التي تحدث عند أفق واحد بعينه متساوية.

يد: فلتكن دائرة نصف النهار ألف باء جيم دال، ونصف دائرة معدّل النهار ألف هاء جيم، ونصف دائرة الأفق باء هاء دال. ولنرسم من الدائرة المائلة قطعتا زاي حاء طاء، كاف لام ميم على أن يوضع كلّ واحد من نقطتي زاي، كاف الاستواء الخريفيّ، وعلى أنّ قوس زاي حاء مساوية لقوس كاف لام. /H155/ أقول إنّ زاوية هاء ⟨حاء⟩ طاء أيضاً ه – صح: مساوية لزاوية دال لام كاف و ذلك بيّن من قرب. وذلك أنّ مثلّث هاء زاي حاء أيضاً تصير مساوي الزوايا لمثلّث هاء كاف لام. وذلك أنّ الأضلاع الثلاثة مساوية للأضلاع الثلاثة من قبل ما تقدّم بيانه كلّ ضلع لنظيره؛ أمّا ضلع زاي حاء فلضلع كاف لام، وأمّا ضلع حاء هاء، الذي هو قطعة من الأفق، فلضلع هاء لام، وأماّ ضلع هاء زاي الذي هو المطلع فلضلع هاء كاف. فزاوية هاء حاء زاي إذن مساوية لزاوية هاء لام كاف، وزاوية هاء حاء طاء الباقية مساوية لزاوية دال لام كاف الباقية. /T111/ وأقول إنّ كلّ نقطتين متقابلتين منها فإنّ الزاوية الشرقيّة لإحداهما مع الزاوية الغربيّة للأخرى معادلتان لقائمتين.

يه: وذلك أنّا إن رسمنا دائرة الأفق ألف باء جيم دال، ودائرة البروج ألف هاء جيم زاي تتقاطعان على نقطتي ألف، جيم كانت زاويتا زاي ألف دال، دال ألف هاء مجموعتان معادلتين لزاويتين قائمتين، /H156/ لكن زاوية زاي ألف دال مساوية لزاوية زاي جيم دال. فتكون أيضاً زاويتا زاي جيم دال، دال ألف هاء تجتمع منهما قائمتان.

وقد يلزم إذ كانت هذه الأشياء على ما وصفنا وكنّا قد بيّنّا أيضاً أنّ الزوايا التي تحدث عند النقط التي بعدها من نقطة واحدة بعينها من نقطتي الاستواء بعد سواء بين دائرة البروج وبين أفق واحد بعينه متساوية أن يكون كلّ نقطتين أيضاً بعدهما من انقلاب واحد بعينه بعداً سواء. فإنّ الزاوية الشرقيّة لإحداهما مع الزاوية الغربيّة للأخرى مجموعتين مساويتان لزاويتين قائمتين.

فيجب من قبل ذلك ه: أيضاً أنّا متى علّمنا الزوايا الشرقيّة التي تحدث من الحمل إلى الميزان، تبيّن لنا معها الزوايا الشرقيّة التي للنصف الدائرة الآخر وتبيّن لنا أيضاً الزاوية الغربيّة التي لنصفي الدائرة. ونحن واصفون بإيجاز الوجه الذي له نتهيّأ تبيينها، ومستعملون أيضاً على طريق التمثيل تلك الدائرة الموازية بعينها أعني الدائرة التي ارتفاع القطب الشماليّ منها عن الأفق ستّة وثلاثون جزءاً.

فنقول أمّا ه – صح: أمّا الزوايا الزوايا التي تحدث عن نقطتي الاستواء الدائرة البروج عند الأفق فقد يمكن أدركها بسهولة. يو: وذلك أنّا إن رسمنا دائرة نصف النهار ألف باء جيم دال ونصف الدائرة الشرقي من الأفق المقصود له /H157/ ألف هاء دال، وربع دائرة معدّل النهار هاء زاي، /T112/ ومن دائرة البروج ربع هاء باء، ه: وربع هاء جيم على أن نتوهّم نقطة هاء عند ربع هاء باء النقطة الخريفيّة وعند ربع هاء جيم النقطة الربيعيّة. فتصير نقطة باء الانقلاب الشتويّ ونقطة دال ه – صح: جيم الانقلاب الصيفيّ. حصل من ذلك أنّه إذا كانت قوس دال زاي قد وضعت أربعة وخمسين جزءاً وكلّ واحدة من قوسي باء زاي، زاي دال ه – صح: جيم ثلاثة وعشرون جزءاً وإحدى وخمسين دقيقة بالتقريب، تصير قوس جيم دال ثلاثين جزءاً وتسع دقائق، وقوس باء دال بهذه الأجزاء سبعة وسبعون جزءاً وإحدى وخمسون دقيقة. /T113/ فيجب إذ كانت نقطة هاء قطب دائرة نصف النهار التي هي ألف باء جيم دال أن تكون أيضاً زاوية دال هاء جيم، وهي التي تحدث عن مبدأ الحمل، ثلاثين جزءاً وتسع دقائق بالأجزاء التي بها زاوية واحدة قائمة تسعون جزءاً؛ وتكون زاوية دال هاء باء وهي التي تحدث عن المبدأ الميزان بهذه الأجزاء سبعة وسبعين جزءاً وإحدى وخمسين دقيقة. لكن كيما نصحّ السبيل في سائر الزوايا أيضاً، فلنجعل قصدنا، على طريق التمثيل، أن نعلم الزاوية الشرقيّة التي تحدث عن مبدأ الثور والأفق.

يز: ولتكن دائرة نصف النهار ألف باء جيم دال، ونصف الدائرة الشرقيّ من الأفق المقصود له باء هاء دال. /H158/ ولنرسم نصف دائرة البروج ألف هاء جيم على أن تكون نقطة هاء مبدأ الثور. ولمّا كان هذا الأقليم، إذا طلع مبدأ الثور فيه، كان في وسط السماء تحت الأرض من السرطان سبعة عشر جزءاً وإحدى وأربعون دقيقة. فإنّا قد بيّنّا كيف يوقف على ذلك وما أشبهه بأهون سعي من قبل المطالع التي وضعناها. فإنّ قوس هاء جيم تكون أصغر من ربع دائرة. فلنرسم بقطب هاء وببعد ضلع المربّع قطعة من أعظم الدوائر ولتكن طاء حاء زاي، ولنتمّم ربع دائرة هاء جيم حاء وربع دائرة هاء دال طاء. فتصير أيضاً قوس دال جيم زاي وقوس زاي حاء طاء كلّ واحدة منهما ربع دائرة، و ↑و↑: اخمن أجل أنّ أفق باء هاء دال مخطوط على قطب دائرة نصف النهار وهي زاي حاء ه – صح: جيم دال وقطبي دائرة زاي حاء طاء وهي من أعظم الدوائر. وأيضاً لأنّ السبعة العشر الجزء والإحدى والأربعين الدقيقة من السرطان بعدها من معدّل النهار في الشمال على أعظم الدوائر المرسومة مارّاً بقطبيه اثنان وعشرون جزءاً وأربعون دقيقة، وذلك أنّ هذا أيضاً قد وصفناه وبعد معدّل النهار من نقطة زاي التي هي قطب الأفق على تلك القوس بعينها أعني قوس زاي هاء ↑هاء↑: ج؛ ه – صح: جيم دال ستّة وثلاثون جزءاً نحصل قوس زاي دال ه: أيضاً ثمانية وخمسين جزءاً وأربعين دقيقة. فإذ قد فرضت هذه فأنّه يصير حينئذ من أجل الصورة نسبة وتر ضعف قوس جيم دال إلى وتر ضعف قوس دال زاي /H159/ مؤلّفة من نسبة وتر ضعف قوس حاء ه – صح: جيم هاء إلى وتر ضعف قوس هاء حاء ومن نسبة وتر ضعف قوس حاء طاء إلى وتر ضعف قوس طاء زاي، لكن من أجل ما تقدّم وضعه أمّا ضعف قوس جيم دال فاثنان وستّون جزءاً وأربعون دقيقة، ووتره اثنان وستّون جزءاً وأربع وعشرون دقيقة؛ وأمّا ضعف قوس دال زاي فمائة وثمانون جزءاً ووتره مائة وعشرون. ه: جزءاً /T114/ و ه: أيضاًأمّا ضعف قوس جيم شطب الكاتب «دال» هاء فمائة وخمسة وخسون جزءاً واثنتان وعشرون دقيقة، ووتره مائة وسبعة عشر جزءاً وأربع عشرة دقيقة. وأمّا ضعف قوس هاء حاء فمائة وثمانون جزءاً، ووتره مائة وعشرون جزءاً. فإنّ نحن إذا نقصنا من نسبة اثنين وستّين جزءاً وأربع وعشرين دقيقة إلى مائة وعشرين جزءاً، نسبة مائة وسبعة عشر جزءاً وأربع عشر دقيقة إلى مائة وعشرين جزءاً بقيت لنا نسبة وتر ضعف قوس حاء طاء إلى وتر ضعف قوس طاء زاي نسبة ثلاثة وستّين جزءاً واثنتين وخمسين دقيقة إلى مائة وعشرين جزءاً. لكن وتر ضعف قوس طاء زاي مائة وعشرون جزءاً. فوتر ضعف قوس حاء طاء إذا بهذه الأجزاء ثلاثة وستّون جزءاً واثنتان وخمسون دقيقة. فيجب من ذلك أن يكون ضعف قوس حاء طاء أربعة وستّين جزءاً وعشرين دقيقة؛ وقوس حاء طاء نفسها وزاوية حاء هاء طاء بهذه الأجزاء اثنين وثلاثين جزءاً وعشر دقائق. وذلك ما كان ينبغي أن نبيّنه.

وينبغي أن نفهم مثل ذلك بعينه كيلا يطول الاقتصاص في كتابنا بتكريرنا معنى واحداً في واحد واحد ممّا قصدنا له في سائر الأجزاء الاثني عشر وسائر الأقاليم.

⟨II.12⟩/H160/ يب: في الزوايا التي تحدث بين هذه الدائرة وبين الدائرة التي تمرّ بقطبي الأفق.

وإذ قد بقي علينا الباب الذي ه – صح: به يتهيّأ أن نستخرج أيضاً الزوايا التي تحدث لدائرة البروج عند الدائرة التي تمرّ بقطبي الأفق في ميل ميل ووضع وضع. وكان يتبيّن مع بيانها أبداً كما قلنا مقدار القوس التي تنفرز The manuscript is here in disorder; the sheet following fol. 30 has been inserted as fol. 33. من الدائرة التي تمرّ بقطبي الأفق بين النقطة التي على سمت الرأس وبين الفصل بين هذه الدائرة وبين الدائرة المائلة. فنحن واصفون ما يحتاج أن يتقدّم فيعلم في هذا الفن ومبيّنون أوّلاً إن كلّ نقطتين من دائرة البروج يكون بعدهما عن انقلاب واحد بعينه بعداً سواء ويكون الزمانان اللذان يفرزانهما عن جنبتي دائرة نصف النهار، أحدهما ممّا يلي المشرق والآخر ممّا يلي المغرب متساويتين، فإنّ القوسين من الدائرتين العظيمتين اللتين بين النقطة التي على سمت الرأس وبينهما متساويتان وإنّ الزاويتين أيضاً اللتين تحدثان عندهما على الجهة التي لخّصناها مساويتان لزاويتين قائمتين.

يح: فلتكن من دائرة نصف النهار قطعة ألف باء جيم، ولنتعلّم عليها النقطة التي على سمت الرأس وليكن باء، وقطب معدّل النهار وليكن جيم. شطب الكاتب دال ولنرسم من دائرة البروج /H161/ قطعتا ألف دال هاء، ألف زاي حاء على أن يكون نقطتا دال، زاي بعدهما من انقلاب واحد بعينه بعداً سواء ويكونا يفرزان قوسين مساويتين من الدائرة الموازية التي تمرّ بهما عن جنبتي دائرة نصف النهار وهي ألف باء جيم. ولنرسم قسيّ من أعظم الدوائر تمرّ بنقطتي دال، زاي منها قوسان تمرّان بقطب معدّل النهار، وهو جيم، شطب الكاتب دال وليكونا قوسي جيم دال، جيم زاي ومنها قوسان تمرّان بنقطة باء، وهي التي على سمت الرأس، وليكونا قوسي باء دال، باء زاي. أقول إنّ قوس باء دال مساوية لقوس باء زاي، وإنّ زاوية باء دال هاء مع زاوية باء زاي ألف مساويتان لزاويتين قائمتين. فلأنّ نقطتي دال، زاي بعدهما في الدائرة الموازية التي تمرّ بهما عن جنبتي دائرة ألف باء جيم التي هي دائرة نصف النهار بقوسين متساويتين، فزاوية باء جيم دال مساوية لزاوية باء جيم زاي. /T115/ فمثلّثا باء جيم دال، باء جيم زاي قد ساوى ضلعان من أحدهما ضلعين من الآخر كلّ واحد لنظيره، أمّا ضلع جيم دال فلضلع جيم زاي، وأمّا ضلع باء جيم فمشترك بينهما، وساوت الزاوية التي يحيط بها الضلعان الزاوية التي يحيط بها الضلعان المساويان لهما أعني زاوية باء جيم دال لزاوية باء جيم زاي، فقاعدة باء دال إذاً تصير مساوية لقاعدة باء زاي /H162/ وزاوية باء دال جيم تساوي زاوية باء زاي دال. ه – صح: جيم

لكن لما كان قد تبيّن أنّ كلّ قوسين بعدهما من انقلاب واحد بعينه بعد سواء فإنّ الزاويتين اللتين تحدثان بينهما وبين الدائرة التي تمرّ بقطبي معدّل النهار مجموعتين مساويتان لزاويتين قائمتين، وجب أن يكون زاويتا جيم دال هاء، جيم زاي ألف معادلتين لقائمتين. وقد نبيّن أنّ زاوية باء دال جيم مساوية لزاوية باء زاي جيم فزاويتا باء دال هاء، باء زاي ألف إذن معادلتان لزاويتين قائمتين. وذلك ما كان ينبغي أن نبيّن.

وأيضاً قد ينبغي أن نبيّن أنّ كلّ نقطتين هما نقطة واحدة بعينها من دائرة البروج ويكون بعدها عن جنبتي دائرة نصف النهار بعداً سواء، فإنّ القوسين من أعظم الدوائر اللتين ترسمان من النقطة التي على سمت الرأس إليهما متساويتان وإنّ الزاويتين اللتين تحدثان عندهما مجموعتين أعني التي تلي المشرق والتي تلي المغرب مساويتان للزاوية التي تحدث عن دائرة نصف النهار عند تلك النقطة الواحدة بعينها مرّتين متى اتّفق في كلّ واحد من الموضعين أن يكون النقطتان المتوسّطتان للسماء إمّا جميعاً أميل إلى الشمال وإمّا جميعاً أميل إلى الجنوب عن النقطة التي على سمت الرأس.

ولننزّل أوّلاً أنّهما جميعاً أميل إلى الجنوب. يط: ولتكن من دائرة نصف النهار قطعة ألف باء جيم دال وعليها النقطة التي على سمت الرأس دال، ه – صح: جيم وقطب معدّل النهار دال. /H163/ ولنرسم القطعتان من دائرة البروج وليكونا ألف هاء زاي، باء حاء طاء على أن تكون نقطة هاء ونقطة حاء اللتين وضع أنّهما نقطة واحدة بعينها بعدهما من الجهتين من دائرة واحدة بعينها من الدوائر المتوازية من دائرة نصف النهار قوسين متساويتين. ولنرسم بهما أيضاً قطع من أعظم الدوائر إمّا من نقطة جيم ↑جيم↑: شطب الكاتب دال فقوسا جيم شطب الكاتب «دال» وحررّ «جيم صح» على فوقها. هاء، جيم حاء، وإمّا من نقطة دال فقوسا دال هاء، /T116/ دال حاء. فلتلك الأشياء بأعيانها التي ذكرنا فيما تقدّم إذ كانت نقطتا هاء، حاء إذا علّمنا دائرة واحدة بعينها موازية، فصّلنا منها عن جنبتي دائرة نصف النهار قوسين متساويتين. فإنّ مثلّثي جيم دال هاء، جيم دال حاء يصيران متساويتين الأضلاع والزوايا، فيصير ضلع جيم هاء مساويا لضلع جيم حاء. وأقول إنّ زاويتي جيم هاء زاي ه – صح: جيم هاء باء مجموعتين مساويتان لزاوية دال هاء زاي مرّتين.  Toomer, p. 116: GÊZ + GĤB = 2DÊZ = 2DĤB فلأنّ زاوية دال هاء زاي هي زاوية دال حاء باء وزاوية جيم هاء دال مساوية لزاوية دال حاء جيم، فزاويتا /H164/ جيم هاء دال، جيم حاء باء إذن مجموعتان مساويتان لزاوية دال هاء زاي. فيجب من ذلك أنّ زاوية جيم هاء زاي بأسرها وزاوية جيم حاء باء مجموعتين مساويتان لزاوية دال هاء زاي مرّتين.

ك: وأيضاً فلنرسم هذه القطع بأعيانها من الدوائر التي وضعناها لكن ننزّل أنّ نقطة ألف ونقطة باء أميل إلى الشمال من نقطة دال. ↑دال↑: جيم أقول إنّ ذلك بعينه يلزم في هذا الوضع أيضاً أعني أنّ زاويتي كاف هاء زاي، لام حاء باء مجموعتين مساويتان لزاوية دال هاء زاي مرّتين. فلأنّ زاوية دال هاء زاي هي زاوية دال حاء باء وزاوية دال هاء كاف مساوية لزاوية دال حاء لام تكون زاوية لام حاء باء بأسرها مساوية لزاويتي دال هاء زاي، دال هاء كاف مجموعتين. فيجب من ذلك أن يكون أيضاً زاويتا لام حاء باء، كاف هاء زاي مجموعتين مساويتين لزاوية دال هاء زاي مرّتين.

كا: وأيضاً فلنضع مثل هذه الصورة إلّا أنّا نجعل فيها النقطة المتوسّطة للسماء من القطعة الشرقيّة أعني نقطة ألف أميل إلى /H165/ الجنوب من نقطة جيم التي هي النقطة التي على سمت الرأس والنقطة المتوسّطة للسماء من القطعة التي تلي المغرب أعني نقطة باء أميل إلى الشمال من تلك النقطة بعينها. /T118/ أقول إنّ زاويتي جيم هاء زاي، لام حاء باء مجموعتين أعظم من زاوية دال هاء زاي مرّتين بزاويتين قائمتين. فمن قبل أنّ زاوية دال حاء جيم مساوية لزاوية دال هاء جيم لكن زاويتي دال حاء جيم، دال حاء لام مجموعتين مساويتان لقائمتين، يكون زاويتا دال هاء جيم، دال حاء لام مجموعتان مساويتين لزاويتين قائمتين. لكن زاوية دال هاء زاي هي زاوية دال حاء باء. فيكون زاويتا جيم شطب الكاتب «حاء» وحرّر «جيم صح» تحتها. هاء زاي، لام حاء باء. مجموعتان أعظم من زاويتي دال هاء زاي، دال حاء باء أعني من زاوية دال هاء زاي مرّتين بزاويتي دال هاء جيم، دال حاء لام اللتين هما معادلتان لقائمتين.

كب: فلنضع الآن في مثل هذه الصورة ممّا يبقى بعد ما وصفناه وهو أنّ النقطة المتوسّطة للسماء من القطعة التي تلي المشرق وهي نقطة ألف /H166/ أميل إلى الشمال من نقطة دال ه – صح: جيم والنقطة المتوسّطة للسماء من القطعة في الأصل: القطة التي تلي المغرب وهي نقطة باء أميل منها إلى الجنوب. أقول إنّ زاوية كاف هاء زاي وزاوية حاء ه – صح: جيم جيم ه – صح: حاء باء مجموعتين أصغر من زاوية دال هاء زاي مرّتين بزاويتين قائمتين. فمن قبل ما ذكرناه أيضاً تكون زاوية كاف هاء زاي وزاوية جيم حاء باء مجموعتان أصغر من زاوية دال هاء زاي وزاوية دال حاء باء مجموعتين؛ أعني زاوية دال هاء زاي مرّتين بزاويتي دال هاء كاف ه – صح: دال حاء جيم مجموعتين وهاتان الزاويتان معادلتان لقائمتين من قبل أنّ زاويتي دال هاء كاف، دال هاء جيم مجموعتين مساويتان لقائمتين وزاوية دال هاء جيم مساوية لزاوية دال حاء جيم. /T119/ وهذه هي الأشياء التي قصدنا لبيانها وقد يستبين أيضاً من قرب أنّه قد يمكن بأهون سعي معرفة الزاويا التي تحدث بالوجه الذي وضعناه عن الدائرة المائلة عند الدائرة العظمى التي تمرّ بالنقطة التي على سمت الرأس والقسيّ أيضاً الموصوفة من هذه الدائرة العظمى متى كانت هذه الزوايا والقسيّ على دائرة نصف النهار أو على دائرة الأفق على هذا النحو.

كج: وذلك أنّا إن رسمنا دائرة نصف النهار ألف باء جيم دال ونصف دائرة الأفق /H167/ باء هاء دال ونصف دائرة البروج زاي هاء حاء كيف ما كان وضعه. فإنّا إذا توهّمنا الدائرة العظمى التي ترسم مارّة بنقطة ألف، وهي النقطة التي على سمت الرأس، تمرّ بالنقطة منه المتوسّط للسماء وهي نقطة زاي، صارت هذه الدائرة ودائرة نصف النهار وهي ألف باء جيم دال ه: واحدة بعينها، وصارت لمّا نصف زاوية دال زاي هاء معلومة من قبل أنّ نقطة زاي مفروضة والزاوية التي تحدّها عند دائرة نصف النهار معلومة. وصارت قوس ألف زاي نفسها معلومة لأنّا قد علّمنا كم جزء من دائرة نصف النهار بعد نقطة زاي من دائرة معدّل النهار وبعد دائرة معدّل النهار من نقطة ألف التي على سمت الرأس. وإذ ه – صح: فإذا قد توهّمنا الدائرة العظمى التي ترسم مارّة بنقطة ألف، كأنّا قلنا دائرة ألف هاء جيم، تمرّ بالنقطة الطالعة منه، وهي نقطة هاء، فقد تصير أيضاً بهذا الوجه الذي بيّنّا لمّا نصف أنّ قوس ألف هاء تكون أبداً ربع دائرة لأنّ نقطة ألف قطب دائرة باء هاء دال الذي هو الأفق. وإذا ه – صح: وإذ كانت بهذا السبب بعينه زاوية ألف هاء دال قائمة وكانت الزاوية التي بين الدائرة المائلة وبين الأفق، أعني زاوية دال هاء حاء، معلومة، فإنّ زاوية ألف هاء حاء بأسرها تكون معلومة.

/H168/ فيكون ظاهراً إذا كانت هذه الأشياء على ما وصفنا أنّا متى حسبنا في ميل ميل الزوايا والقسيّ التي قبل دائرة نصف النهار فقط واقتصرنا منها أيضاً على زوايا وقسيّ البروج التي من مبدأ السرطان إلى مبدأ الجدي، وجمعنا ذلك حصل لنا معه أيضاً زوايا هذه البروج وقسيّها /T120/ التي بعد دائرة نصف النهار، وأيضاً زوايا وقسيّ سائر البروج التي قبل دائرة نصف النهار والتي بعدها. وكيما نبيّن الباب في هذه أيضاً في وضع وضع فنحن واصفون أيضاً على طريق المثال البرهان الكلّي الذي يستعمل في ذلك بشكل واحد نضعه بأن ننزّل في ذلك الميل بعينه، أعني الميل الذي ارتفاع القطب الجنوبيّ ه – صح: الشماليّ فيه عن أفقه ستّة وثلاثون جزءاً، أنّ رأس السرطان مثلاً بعده من دائرة نصف النهار نحو المشرق ساعة واحدة استوائيّة. وفي هذا الموضع ه – ج: الذي عليه الدائرة الموازية التي قصدنا لها يتوسّط السماء من التو⟨أ⟩مين ستّة عشر جزءاً واثنتا عشرة دقيقة ويطلع من العذراء سبعة عشر جزءاً وسبع وثلاثون دقيقة.

كد: فلتكن دائرة نصف النهار ألف باء جيم دال، ونصف دائرة الأفق باء هاء دال، ونصف دائرة البروج زاي حاء طاء على أنّ نقطة حاء مبدأ السرطان ونقطة زاي بعدها من مبدأ الجوزاء ستّة عشر جزءاً واثنتا عشرة دقيقة، ونقطة طاء بعدها من مبدأ العذراء سبعة عشر جزءاً وسبع وثلاثون دقيقة.

ولنرسم قطعة دائرة من أعظم الدوائر تمرّ بنقطة ألف وهي النقطة التي على سمت الرأس وبنقطة حاء التي /H169/ هي مبدأ السرطان، وليكن ألف حاء هاء جيم. ولننزّل أوّلاً أنّا قصدنا لأن نعلم قوس ألف حاء. فمن البيّن أنّ قوس طاء حاء زاي أحد وتسعون جزءاً وخمس وعشرون دقيقة، وقوس حاء طاء سبعة وسبعون جزءاً وسبع وثلاثون دقيقة. وعلى هذا المثال من قبل أنّ ستّة عشر جزءاً واثنتي عشرة دقيقة من الجوزاء تجوز من دائرة نصف النهار ممّا يلي الشمال عن دائرة معدّل النهار ثلاثة وعشرون جزءاً وسبع دقائق، ودائرة معدّل النهار بعدها من نقطة ألف، التي هي النقطة التي على سمت الرأس، ستّة وثلاثون جزءاً تكون قوس ألف زاي أيضاً اثني عشر جزءاً وثلثاً وخمسين دقيقة، وقوس باء زاي ما يبقى من الربع وهو سبعة وسبعون جزءاً وسبع دقائق. فإذ صارت هذه القسيّ معطاة، تكون أيضاً من قبل الصورة نسبة وتر ضعف قوس زاي باء إلى وتر ضعف قوس باء ألف مؤلّفة من نسبة وتر ضعف قوس زاي طاء إلى وتر ضعف قوس طاء حاء ومن نسبة وتر ضعف قوس حاء هاء إلى وتر ضعف قوس هاء ألف. لكن أمّا ضعف قوس زاي باء فمائة وأربعة وخمسون جزءاً وأربع عشرة دقيقة، ووتره مائة وستّة عشر جزءاً وتسع وخمسون دقيقة، /H170/ وأمّا ضعف قوس باء ألف فمائة وثمانون جزءاً، ووتره مائة وعشرون جزءاً. /T121/ وأيضاً فأمّا ضعف قوس زاي طاء فمائة واثنان وثمانون جزءاً وخمسون دقيقة ووتره مائة وتسعة عشر جزءاً وثمان وخمسون دقيقة. وأمّا ضعف قوس طاء حاء فمائة وخمسة وخمسون جزءاً وأربع عشرة دقيقة، ووتره مائة وسبعة عشر جزءاً واثنتا عشرة دقيقة. فإن نحن نقصنا من نسبة مائة وستّة عشر جزءاً وتسع وخمسين دقيقة إلى مائة وعشرين جزءاً نسبة مائة وتسعة عشر جزءاً وثمان وخمسين دقيقة إلى مائة وسبعة عشر جزءاً واثنتي عشرة دقيقة، بقيت لنا نسبة وتر ضعف قوس حاء هاء إلى وتر ضعف قوس هاء ألف نسبة مائة وأربعة عشر جزءاً وستّ عشرة دقيقة بالتقريب إلى مائة وعشرين جزءاً. لكن وتر ضعف قوس هاء ألف مائة وعشرون جزءاً. فوتر ضعف قوس هاء حاء إذن مائة وأربعة عشر جزءاً وستّ عشرة دقيقة. فيجب من ذلك أن يكون ضعف قوس حاء هاء مائة وأربعة وأربعين جزءاً وستّاً وعشرين دقيقة بالتقريب وقوس حاء هاء نفسها بهذه الأجزاء اثنان وسبعون جزءاً وثلاث عشرة دقيقة. فتبقى قوس ألف حاء الباقي من الربع وهو تسعة ه – خ: سبعة عشر جزءاً وسبعة وأربعون دقيقة. وذلك ما كان ينبغي أن نبيّنه.

كه: ثمّ من بعد ذلك قد نعلم زاوية ألف حاء طاء أيضاً على هذا النحو. لنضع هذه الصورة بعينها وندير بقطب حاء وببعد ضلع المربّع قطعة من أعظم الدوائر ولتكن كاف لام ميم. فيجب من ذلك من قبل أنّ الدائرة ألف حاء هاء قد رسمت مارّة بقطبي دائرة هاء طاء ميم وبقطبي دائرة كاف لام ميم أن يكون كلّ واحدة من قوسي /H171/ هاء ميم، كاف ميم ربع دائرة. وأيضاً من قبل الصورة

تكون نسبة وتر ضعف قوس حاء هاء إلى وتر ضعف قوس هاء كاف مؤلّفة من نسبة وتر ضعف قوس حاء طاء إلى وتر ضعف قوس طاء لام ومن نسبة وتر ضعف قوس لام ميم إلى وتر ضعف قوس ميم كاف. لكن أمّا ضعف قوس حاء هاء فمائة وأربعة وأربعون جزءاً وستّ وعشرون دقيقة ووتره مائة وأربعة عشر جزءاً وستّ عشرة دقيقة. وأمّا ضعف قوس هاء كاف فخمسة وثلاثون جزءاً وأربع وثلاثون دقيقة، ووتره ستّة وثلاثون جزءاً وثمان وثلاثون دقيقة. وأيضاً فأمّا قوس حاء طاء فمائة وخمسة وخمسون جزءاً وأربع عشرة دقيقة، ووتره مائة وسبعة عشر جزءاً وأثنتا عشرة دقيقة. وأمّا ضعف قوس طاء لام فأربعة وعشرون جزءاً وستّ وأربعون دقيقة، ووتره خمسة وعشرون جزءاً وأربع وأربعون دقيقة. فيجب من ذلك أن يكون إن نحن نقصنا من نسبة مائة وأربعة عشر جزءاً وستّ عشرة دقيقة إلى ستّة وثلاثين جزءاً وثمان وثلاثين دقيقة نسبة مائة وسبعة عشر جزءاً واثنتي عشرة دقيقة إلى خمسة وعشرين جزءاً وأربع وأربعين دقيقة، بقيت لنا نسبة وتر ضعف قوس لام ميم إلى وتر ضعف قوس ميم كاف نسبة اثنتي وثمانين جزءاً وإحدى عشرة دقيقة بالتقريب إلى مائة وعشرين جزءاً. لكن وتر ضعف قوس ميم كاف مائة وعشرون جزءاً. فوتر ضعف قوس لام ميم إذاً بهذه الأجزاء اثنان وثمانون جزءاً وإحدى عشرة دقيقة. /T122/ فيجب من ذلك أن يكون ضعف قوس لام ميم ستّة وثمانين جزءاً وثمانياً وعشرين دقيقة، وقوس لام ميم نفسها بهذه الأجزاء ثلاثة وأربعون جزءاً وأربع عشرة دقيقة، فتبقى قوس لام كاف وهي زاوية لام حاء كاف ستّة وأربعين جزءاً وستّاً وأربعين دقيقة. فتكون زاوية ألف حاء طاء ما يبقى بعد ذلك من زاويتين قائمتين وهو مأئة وثلاثة وثلاثون جزءاً وأربع عشرة دقيقة. وهذه هي الأشياء التي كان ينبغي أن نبيّنها.

⟨II.13⟩ يج: في صفة الزوايا والقسيّ التي ذكرت في دائرة دائرة من الدوائر المتوازية.

/H172/ أمّا الوجه في استخراج هذه الأشياء التي قصدنا لها فهو هذا الوجه بعينه في سائر ما بقي منها أيضاً لكن نحن كيما يكون لنا سائر الزوايا والقسيّ التي ربّما أحتجنا إليها فيما نبحث عنه من الأمور الجزئيّة معدّة ميسّرة. فإنّا حسبناها أيضاً بطريق الخطوط وابتدأنا من الدائرة الموازية التي تمرّ بالجزيرة المسمّاة ماروي وهي الدائرة التي مبلغ أطول ما يكون من النهار فيها ثلاث عشرة ساعة استوائيّة وبلغنا إلى الدائرة الموازية التي ترسم من وارء بحر بنطس مارّة بمغائض النهر المسمّى بروستانس حيث يكون مبلغ أطول النهار ستّ عشرة ساعة استوائيّة. واستعملنا التفاضل في شيء شيء أمّا في الأقاليم فبنصف ساعة نصف ساعة أيضاً كما عملنا في المطالع، وأمّا في أقسام دائرة البروج فبقسم قسم من أقسامه الاثني عشر، وأمّا في الأوضاع التي ممّا يلي الشرق أو الغرب من دائرة نصف النهار فبساعة ساعة من ساعات الاستوائيّة. ونحن جاعلون وصف هذه الأشياء على طريق الجداول في إقليم إقليم وبرج برج. ومثبتون في القسم الأوّل من جدول، جدول عدد الساعات الاستوائيّة التي للبُعد عن جنبتي دائرة نصف النهار من بَعد وضع مبدأ البرج على دائرة نصف النهار نفسها. وفي القسم الثاني مقادير القسيّ التي تكون كما قلنا فيما بين النقطة التي على سمت الرأس وبين مبدأ البرج المفروض. وفي القسم الثالث والرابع /H173/ مقادير الزوايا التي تحدث عن التقاطع الذي تقدّم وصفه على الوجه الذي لخّصناه من ذلك في القسم الثالث مقادير الزوايا الموضوعة ممّا يلي الشرق عن دائرة نصف النهار، وفي القسم الرابع مقادير ما يلي الغرب عنه منها. لكن قد ينبغي أن يكون ذاكراً لما ميّزناه منذ أول الأمر من أنّا أنّما أخذنا من الزاويتين اللتين تحدثان عن قطعة مائلة من دائرة البروج أبداً الزاوية التي تلي الشمال عن هذه القطعة ووضعنا المقدار في كلّ واحدة منها المقدار الذي به زاوية واحدة قائمة تسعون جزءاً. وهكذا عمل الجداول.